Extraordinary magnetic field effects on the LC phases of homochiral and racemic 4-cyanoresorcinol-based diamagnetic bent-core mesogens

Abstract

4-Cyanoresorcinol based bent-core compounds combining one branched chiral with one achiral linear end-chain have been synthesized in enatiomerically pure and one compound also in racemic form. All homochiral compounds form a chiral cybotactic nematic phase at relatively low temperature with a selective reflection ranging from the near IR to near UV. For the compound with the longest chains superparaelectric and antiferroelectric switching smectic phases were observed, whereas the corresponding racemate is non-polar. This is attributed to sterically induced polarization by the denser packing of uniform enantiomers due to chirality synchronization of the helical conformers. For the racemic mixture this chirality synchronization requires additional surface stabilization. There are unprecedented effects of an applied magnetic field (1 T) on the LC phases, leading to a layer shrinkage by 6–13% for the enantiomer and a layer expansion by 5–8% for the racemate. It is proposed that the magnetic field couples with the π-systems of the almost rod-like molecules. For the racemate this increases the core order, whereas for the enantiomer the reduction of the heliconical twist is considered to provide the major effect. These magnetic field effects could lead to new applications of chiral LC materials at the cross-over between rod-like and bent shapes.

---

1. Introduction

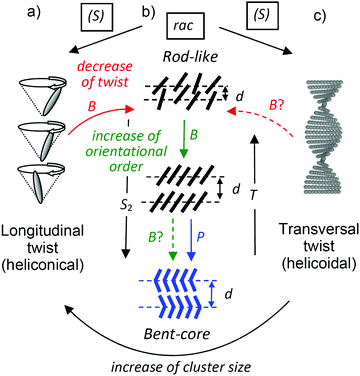
Functional soft matter systems, especially liquid crystals (LCs), are often composed of a rigid π-conjugated system combined with flexible chains.^1,2 Among them, molecules involving a bent π-conjugated polyaromatic unit, so-called bent-core molecules (Scheme 1), have attracted considerable attention, because they can form polar switchable (ferroelectric and antiferroelectric) LC phases.^3–8 Numerous systematic studies have been carried out on resorcinol derivatives substituted at the central 1,3-disubstituted benzene unit of the bent core,^9–16 for example, the cyano substitution in the 4-position (Scheme 1) leads to cybotactic nematic phases as well as to series of paraelectric and polar smectic phases depending on the structure of the rod-like wing groups and the length of the attached end chains.^16–24 Some achiral 4-cyanoresorcinol based bent-core compounds resulted in the emergence of short pitch heliconical smectic mesophases (Fig. 1a)^25–27 which received considerable attention due to mirror symmetry breaking by spontaneous helix formation and due to their potential applications in fast switching electro-optic (EO) display devices.^28–32 Related short pitch heliconical phases were also observed for LC phases of achiral bent mesogenic dimers in nematic (N_TB)³³ and smectic phases.³⁴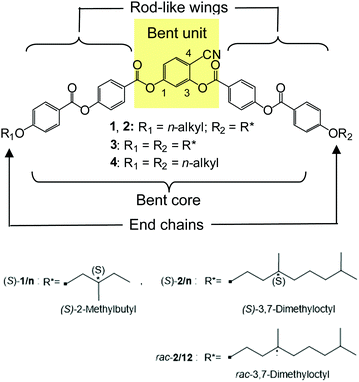

Scheme 1 Molecular structures of the 4-cyanoresorcinol based bent-core compounds 1/n and 2/n under discussion, and the related symmetric compounds 4¹⁸ with two linear alkyl chains and with two chiral chains (3²³); R* represents a branched chiral carbon chain, explained at the bottom; for space filling models of compounds 2, see Fig. S25 (ESI†) and for phase sequences and transition temperatures, see Table 1 and Table S4 (ESI†).

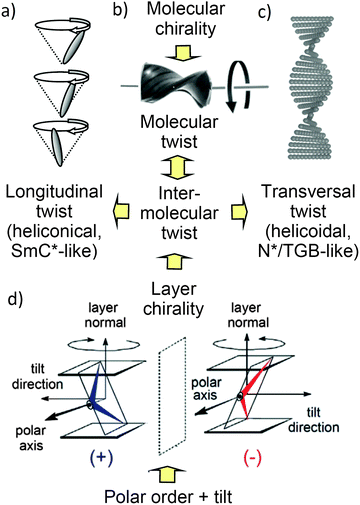Fig. 1 Distinct modes of chirality in LC phases. (a–c) Permanent molecular chirality leads to a bias of the helical twist of the conformers, shown in (b), which induces either (a) a longitudinal twist in an oblique helicoid (heliconical) structure or (c) a transversal twist in a right-angled helicoid (helocoidal) structure. (d) In the lamellar phases of achiral bent-core molecules the combination of polar order, tilt and layer normal define a right- or left-handed system, providing an additional source of chirality (see also Fig. S35, ESI†).

Heliconical phases with a much longer pitch of the longitudinal twist are known for tilted smectic phases (SmC*) of permanently chiral rod-like molecules,^35–38 whereas related chiral nematic phases (N*, cholesteric) have a helicoidal (transversal) twist (Fig. 1c).^39–42 Chirality and helicity have a major impact on the structure and the material properties of LCs and lead to numerous applications, for example in optics, electro-optics and photonics.^2,39,41,46 Moreover, geometric frustration arises by helicoidal twist developing in different spatial directions (blue phases^41,43–45) or by competition between helicoidal twist and long range lamellar order (e.g. twist grain boundary phases = TGB phases).^{8,39,41,46–49} Though chirality effects have been well studied for rod-like LCs and their dimeric,⁴⁹ oligomeric and polymeric analogs,^50,51 the investigation of chiral bent-core mesogens has much less been conducted and comparisons between enantiomerically pure compounds and their racemic mixtures are especially rare.^52–68 Molecular chirality can be incorporated into the bent-core molecules by the introduction of asymmetric carbon centers in the terminal chains.^52–59 In some cases the presence of a chiral moiety induces the emergence of the conventional chiral LC phases known from rod-like molecules such as cholesteric,⁶⁰ and blue phases (BPI-BPIII),^61,62 as well as chiral smectic²³ and TGB phases.^63,64 In other cases it has no influence on the mesophase type, as for example in the modulated smectic (B1) phase of biphenyl based bent-core molecules.^63,68 A series of several new helical superstructures were found for nematic phases of chiral bent dimesogens (N_TB*).⁴⁹ An important question concerns the transition from the right-angle helicoidal structure as known from the classical cholesteric N* phases of ordinary rod-like molecules, having transversal twist (see Fig. 1c), to the oblique helicoidal (=heliconical) nematic phases, having longitudinal twist (Fig. 1a), as known for the N_TB phases.⁶⁵ The latter are formed by bent molecules with small or negative twist elastic constant K₃₃. This transition from helicoidal to heliconical twist in a nematic phase was recently achieved by mixing a spontaneous mirror symmetry broken N_TB phase with an ordinary cholesteric phase.⁶⁵ The development of transversal twist is also likely to be distorted and the development of longitudinal twist is supported by the development of lamellar SmC_s*-clusters in the cybotactic nematic phases at the transition to the SmC_s* phases.

In previous work we have investigated several series of 4-cyanoresocinol based bent core mesogens showing a wide variety of LC phases at the transition from nematic to smectic¹⁶ and from non-polar to polar LC phases.⁶⁶ Moreover, they show a series of spontaneous mirror symmetry broken LC phases, involving superparaelectric SmC_sP_R^[*^] phases⁶⁷ and heliconical smectic phases (SmC_sP^hel_F).^{21,22,25–27} As a consequence, the question arose in how far the transient chirality of these spontaneously chiral phases can be affected by a permanent molecular chirality. In previous work we have introduced two stereogenic centers, which lead to highly chirality frustrated BPIII phases with high Kerr constants, replacing the nematic phase,^23,24 and diastereomerism between layer chirality and molecular chirality in the smectic phases.^23,59 Here we use only one stereogenic center, assuming to have smaller steric and chirality effects, to find new structures and effects by the interplay of these two sources of chirality, especially concerning the transition from transversal (helicoidal) to longitudinal (heliconical) twist (Fig. 1a–c).

In the lamellar phases of bent-core molecules the development of polar order leads to superstructural layer chirality (see Fig. 1d and Fig. S35, ESI†),³ providing an additional source of chirality. This layer chirality can assume diastereomeric relations with the permanent molecular chirality as well as with the spontaneously formed or chirality induced helicoidal and heliconical superstructures,^{8,17,22,23,59,63,68,69} leading to geometric frustration and the development of complexity in their self-assembly.^8,51,70

Whereas electric field effects on the LC phases of bent-core molecules are well studied and understood,^3–7 magnetic field effects are much less investigated, mainly for paramagnetic compounds.^71,72 Investigation of diamagnetic bent-core mesogens under the magnetic field was focused on the stabilization of nematic phases and attempts to induce phase biaxiality.^73–77 Magnetic fields up to 25 T were also found to suppress the onset of the BPIII phase of chiral bent-core mesogens by almost 1 K,⁷⁸ as well, the helical pitch in cholesteric phases was tuned.⁷⁹ Similarly, the heliconical and helicoidal superstructures in SmC* and TGBC* phases of chiral rod-like mesogens^80,81 were shown to be fully or partly removed under a sufficiently strong magnetic field. However, all these effects on diamagnetic LCs are very small or require high magnetic field strength.

Herein, we report a unique and unexpectedly strong effect of an applied magnetic field on the layer spacing of SmC and SmC* phases of chiral bent-core molecules. There is a huge effect of a relatively weak magnetic field of only 1 Tesla providing a change of the layer spacing by up to 13%, and surprisingly, the effect of the applied field is opposite for the racemate and the pure enantiomer. The newly designed, synthesized and investigated compound showing this phenomenon represents a member of a series of non-symmetric bent-core molecules derived from a 4-cyanoresorcinol central unit. In these compounds (S)-1/n, (S)-2/n and rac-2/12 (Schemes 1 and 2) a (S)-2-methylbutoxy or (S)/rac-3,7-dimethyloctyloxy substituted phenylbenzoate based rod-like wing is attached in ortho-position besides the CN group of the central 4-cyanoresorcinol derived core, and a linear n-alkoxy chain (R=C_nH_2n+1, n = 6–12) is positioned at the phenylbenzoate unit in para-position to CN at the opposite side (Scheme 2).

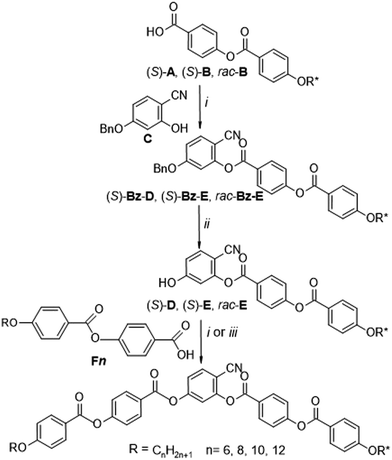Scheme 2 Synthesis of 4-cyanoresorcinol-based chiral bent-core molecules ((S)-1/n, (S)-2/n and rac-2/12). Reagents and conditions: (i) DCC, DMAP, dry CH₂Cl₂, 20 °C; (ii) Pd/C-10%, THF, 40 °C; (iii) (1) (COCl)₂, (2) dry pyridine, dry CH₂Cl₂ (for details, see ESI†).

2. Experimental

2.1 Synthesis

The synthesis of compounds (S)-1/n, (S)-2/n and rac-2/12 is described in Scheme 2. Firstly, (S)-4-[4-(2-methylbutoxy)benzoyloxy]benzoic acid (S)-A^23,82,83 and (S)-4-[4-(3,7-dimethyloctyloxy)benzoyloxy]benzoic acid (S)-B^23,84 were synthesized according to procedures reported in the literature.⁶⁴ Ethyl 4-hydroxybenzoate was alkylated with (S)-2-methylbutyl-1-tosylate (prepared from the commercially available (S)-(−)-2-methyl-1-butanol by tosylation⁸⁵) and (S)-3,7-dimethyloctyl-1-bromide (prepared from (S)-3,7-dimethyl-1-octanol by reaction with conc. aqu. HBr/conc. H₂SO₄⁸⁶) followed by hydrolysis of the ester group (10 N sodium hydroxide solution in ethanol). Esterification of the obtained (S)-4-(2-methylbutoxy)benzoic acid⁸⁷ and (S)-4-(3,7-dimethyloctyloxy)benzoic acid⁸⁴ with 4-hydroxybenzaldehyde using N,N′-dicyclohexylcarbodiimide (DCC) and 4-(dimethylamino)pyridine (DMAP),⁸⁸ followed by NaClO₂ oxidation⁸⁹ leads to the 4-benzoyloxybenzoic acids (S)-A and (S)-B.

The racemic compound rac-B was prepared in a similar way starting from racemic 3,7-dimethyl-1-octanol as described previously.²³ The 4-(4-n-alkyloxybenzoyloxy)benzoic acids^90,91Fn (n = 6, 8, 10, 12) were prepared starting with appropriate alkyl bromides by using the same procedures as described the above.⁹² 4-Benzyloxy-2-hydroxybenzonitrile C was prepared from commercially available 4-benzyloxy-2-hydroxybenzaldehyde by the formation of the oxime, followed by dehydration as previously reported.^16,64 The acylation of C first with the chiral or racemic benzoyloxybenzoic acids (S)-A, (S)-B or rac-B followed by hydrogenolytic debenzylation and acylation with the appropriate benzoic acid Fn leads to the target compounds (S)-1/n, (S)-2/n and rac-2/12 which were purified by column chromatography on silica gel using chloroform as eluent and recrystallized from ethanol. Detailed synthesis procedures and analytical data are given in the ESI.† Identical chemical structures of (S)-2/12 and its racemate rac-2/12 were confirmed by NMR investigation (Fig. S21–S24, ESI†), MS and thin-layer chromatography (for details, see ESI†).

2.2. Investigation

The liquid crystal properties of (S)-1/n, (S)-2/n and rac-2/12 were investigated by polarizing optical microscopy (POM) and differential scanning calorimetry (DSC). Transition temperatures were measured using a Mettler FP-82 HT hot stage and control unit in conjunction with a Leica DM2700P polarizing microscope. The associated enthalpies were obtained from DSC-thermograms which were recorded on a PerkinElmer DSC-7 (heating and cooling rate: 10 K min⁻¹) in a nitrogen atmosphere.

X-ray investigations were carried out at Cu-K_α line (λ = 1.54 Å) using a standard Coolidge tube source with a Ni-filter. Non-aligned samples were prepared on a glass slide while aligned samples were prepared in a glass capillary. All samples were slowly cooled (rate: 0.1 K min⁻¹) from the isotropic liquid phase to the mesophase. Alignment was achieved by cooling the sample under an applied magnetic field of ∼ 1 T (direction of the magnetic field is perpendicular to the X-ray beam) to the measuring temperature. The samples were held on a temperature-controlled heating stage and the diffraction patterns were recorded with a 2D detector (Vantec 500, Bruker); exposure time was 15–30 min. For the wide-angle X-ray scattering (WAXS) measurement the distance between the sample and the detector was defined to be 9.0 cm; for small-angle X-ray scattering (SAXS) measurement the distance is 26.9 cm. The obtained XRD patterns were transformed into 1D plots over the full Chi-range by using GADDS. For the calculation of the d-values and the line width (full width at half maximum = FWHM) of the magnetically aligned samples of rac-2/12 (B = 1 T) and of unaligned samples of (S)-2/12 (B = 0 and 1 T) and rac-2/12 (B = 0 T) different techniques were used to obtain comparable results. For the unaligned powder-like samples the integration of the signal was performed over the whole χ-range. For the aligned sample of rac-2/12, especially in the nematic phase, this integration technique cannot be used due to the dumbbell-like shape of the scattering (see Fig. 9a further below). In this case we performed an integration only over the χ-range for the scattering maxima. The mean average of all four scattering maxima was taken for the construction of the plots discussed in Section 3.5.

Electro-optical investigations were performed in a 10 μm polyimide (PI) non-coated ITO cell (EHC, Japan) with a measuring area of 1 cm². The cell was filled in the isotropic liquid phase. Switching experiments were carried out with the triangular-wave method using a combination of a function synthesizer (Agilent, model 33220A, load was set to 10 kΩ), an amplifier (Tabor electronics, model 9400), and the current response traces were recorded using an oscilloscope (Agilent, model DSO3202A) across a 5 kΩ resistance.

3. Results and discussion

3.1 The cholesteric phases of compounds (S)-1/n and (S)-2/n

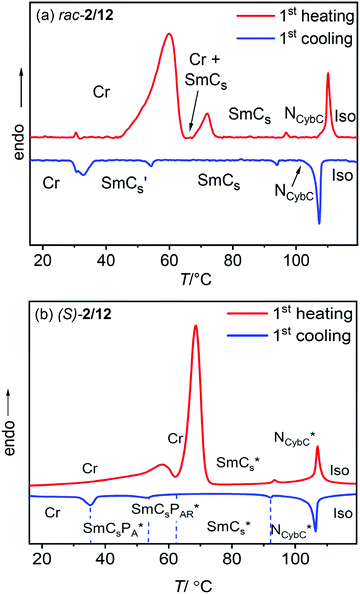
The mesophase type, transition temperatures (T/°C) and the corresponding enthalpies (ΔH/kJ mol⁻¹) are presented in Table 1. All synthesized compounds show an enantiotropic chiral nematic mesophase (cholesteric) (N*) which is identified by the characteristic colored oily-streak texture (see Fig. 3a–f and Fig. S30, ESI†). As shown further below, this chiral nematic phase is composed of skewed smectic clusters and therefore represents a cybotactic nematic phase (N_CybC*). Compounds (S)-1/n, (S)-2/6 and (S)-2/8 show a sequence of crystal (Cr) – cholesteric (N_CybC*) – isotropic liquid phase (Iso). On cooling from the isotropic liquid phase, compounds (S)-2/10 and (S)-2/12 with longer alkyl chains exhibit an enantiotropic N_CybC* mesophase as well as a transition to at least one additional smectic phase; the transition to this smectic phase is associated with a small peak in the DSC thermograms slightly above 50 °C (Fig. 2 and 5). Upon cooling the N_CybC* phases of all investigated compounds, the oily-streak texture changes the color from blue via green to red (see for example Fig. 3b–e and Fig. S30, ESI†), a behavior typical for N* phases which is due to the temperature dependence of the helicoidal pitch.^41,93,94 For (S)-2/10 and (S)-2/12 an optically uniaxial appearance with birefringent oily streaks is observed close to the isotropization temperature (Fig. 3a), because the short helix pitch provides a selective reflection with a wave length in the near UV range. For compound (S)-2/12 an optical isotropic cholesteric texture with oily streaks, in this case having the selective reflection in the near IR range, is also found at the low temperature end, just before the transition to the SmC_s* phase at 92 °C (Fig. 3f). This means that a selective reflection with a wide wave length range from the near UV to the near IR is covered in this case.

Table 1 Mesophases, transition temperatures and corresponding transition enthalpies of the compounds (S)-1/n, (S)-2/n and rac-2/12^a

Compd.	R*	R	T/°C [ΔH/kJ mol^−1]
a Peak temperatures and enthalpy values (in italics in brackets) taken from the 2nd heating and cooling scans at a rate of 10 K min^−1; abbreviations: Cr = crystalline phase (for compounds with multiple Cr-Cr transitions and stepwise melting, see for example Fig. 2, only the melting transition at highest temperature is given); Iso = isotropic liquid phase; NCybC* = chiral nematic (cholesteric) LC phase composed of SmCs layer fragments (skewed cybotactic chiral nematic phase); SmCs = tilted smectic phase with uniform tilt direction in adjacent layers (synclinic tilt); SmCs′ = SmCs phase with enhanced packing density; SmCs* = chiral SmCs phase; SmCsPAR* = paraelectric phase with antiferroelectric like response; SmCsPA* = antiferroelectric switching chiral SmCs phase; for DSC traces, see Fig. 2, 5 and Fig. S29; for textures, see Fig. 3, 6, 7 and Fig. S30–S33; a comparison with related achiral compounds and compounds with two chiral chain is given in Table S4 (ESI). b Partial crystallization. c It is unknown if this is a polar or nonpolar SmCs phase.
(S)-1/6	(S)-2-Methylbutyl	C6H13	H: Cr 85 [25.4] NCybC* 111 [0.7] Iso
			C: Iso 109 [−0.5] NCybC* 52 [−3.3] Cr^b
(S)-1/8	(S)-2-Methylbutyl	C8H17	H: Cr 82 [29.1] NCybC* 112 [0.5] Iso
			C: Iso 110 [−0.5] NCybC* 43 [−4.2] Cr^b
(S)-1/10	(S)-2-Methylbutyl	C10H21	H: Cr 85 [38.2] NCybC* 105 [0.3] Iso
			C: Iso 103 [−0.6] NCybC* 35 [−22.1] Cr
(S)-1/12	(S)-2-Methylbutyl	C12H25	H: Cr 81 [42.6] NCybC* 107 [0.8] Iso
			C: Iso 105 [−0.8] NCybC* 47 [−22.9] Cr
(S)-2/6	(S)-3,7-Dimethyloctyl	C6H13	H: Cr 69 [22.6] NCybC* 86 [0.4] Iso
			C: Iso 85 [−0.4] NCybC* 27 [−3.2] Cr^b
(S)-2/8	(S)-3,7-Dimethyloctyl	C8H17	H: Cr 86 [39.1] NCybC* 106 [0.7] Iso
			C: Iso 104 [−0.7] NCybC* 52 [−4.3] Cr^b
(S)-2/10	(S)-3,7-Dimethyloctyl	C10H21	H: Cr 72 [21.2] NCybC* 96 [0.7] Iso
			C: Iso 95 [−0.7] NCybC* 51 [−0.9] SmCs*^c < 10 Cr
(S)-2/12	(S)-3,7-Dimethyloctyl	C12H25	H: Cr 69 [16.1] SmCs* 93 [0.1] NCybC* 107 [1.6] Iso
			C: Iso 106 [−1.7] NCybC* 92 [−0.1] SmCs* 62 [—] SmCsPAR* 53 [0.2] SmCsPA* 35 [−0.8] Cr^b
rac-2/12	rac-3,7-Dimethyloctyl	C12H25	H: Cr1 60 [17.1] Cr2 72 [1.4] SmCs 97 [0.1] NCybC 110 [1.6] Iso
			C: Iso 108 [1.7] NCybC 94 [0.1] SmCs 54 [0.2] SmCs′ 33 [1.1] Cr^b

---

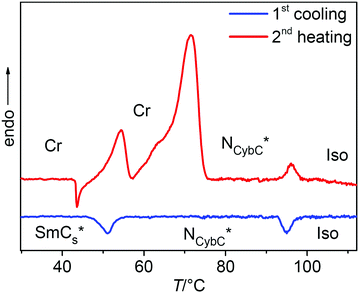Fig. 2 DSC thermograms of (S)-2/10 on 2nd heating and cooling (10 K min⁻¹); for the DSC traces of the other compounds (S)-1/n and (S)-2/n, see Fig. S29 (ESI†).

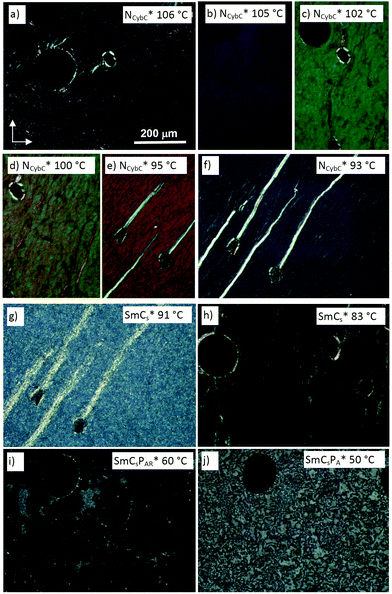Fig. 3 Textures of (S)-2/12 as observed between crossed polarizers on cooling from N_cybC* to SmC_sP_A* at the given temperatures in the indicated phases; (a)–(f) show the change of the selective reflection in the cholesteric phase range, being in the near UV range in (a) and in the near IR in (f); (h) was obtained after shearing the sample shown in (g); (i) was observed after spontaneous transition to the optically isotropic homeotropic texture (the small regions) with a bit higher birefringence are residues of the texture in (g); for more details of the transition g → j, see Fig. S33 (ESI†).

Despite of the significant cybotaxis, these chiral nematic phases behave like ordinary orthogonal helicoidal chiral nematics with transversal twist and the pitch developing perpendicular to the substrate surfaces (Fig. 3a–f). The transition to a heliconical structure appears to be associated with the N_CybC*–SmC_s* transition (Fig. 3f–h), meaning, that the effects of molecular bent and cluster formation are obviously not sufficient to induce a helicoidal → heliconical transition within the nematic phase range. Nevertheless, for the long chain compounds (S)-10 and (S)-12 with additional smectic phases, the helicoidal twist could be reduced upon approaching the SmC* range, which is likely to contribute to the strong increase of the selective reflection wave length (Fig. 3a–f). Moreover, there appear to be surface alignment effects, so that different textures can be observed for the chiral nematic phase of these long-chain compounds, one of them being surface induced with low birefringent (gray) fan texture of heliconical smectic surface layers (SmC_s*, see Fig. S30f, ESI†), coexisting with the selective reflecting helicoidal chiral nematic phase (N_CybC*) of the bulk material (Fig. S30f and g, ESI†).

3.2 Long chain compound (S)-2/10 with N_CybC*–SmC* transition

The LC phases of compound (S)-2/10 were investigated by XRD (see Fig. 4 and Table S1, ESI†). In the whole temperature range between 50 and 90 °C the WAXS is diffuse with a maximum around 0.45 nm (Fig. 4b), indicating the presence of exclusively LC phases in this temperature range. The SAXS is also diffuse between 60 and 90 °C, but significantly more intense than the wide-angle scattering, as typical for a cybotactic nematic phase (N_CybC*) of bent-core mesogens (Fig. 4a).^16,95,96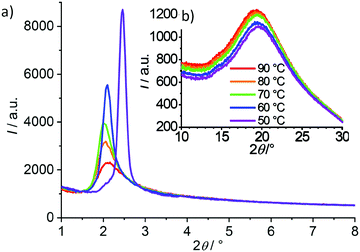

Fig. 4 (a) SAXS and (b) WAXS pattern of the N_CybC* phase (60–90 °C) and the SmC_s* phase (50 °C) of compound (S)-2/10, measured under a magnetic field of 1 T (no magnetic field effect on the d spacing is observed in this case, see Fig. S26; for additional data, see Table S1, ESI†).

The intensity of the SAXS increases almost continuously and the width decreases with lowering temperature, indicating a continuously growing size of the cybotactic clusters. At the phase transition around 52 °C the diffuse SAXS becomes a sharp peak, associated with a jump of the d-value from around 4.2 nm in the cholesteric phase to 3.6 nm in the smectic phase (Fig. 4, Fig. S26 and Table S1, ESI†). No additional diffraction peaks can be found besides the SAXS and therefore we attribute it to a layer reflection of a smectic phase.

A tilted organization of the molecules in the cybotactic clusters of the nematic phase (N_CybC*) and in the smectic phase (SmC_s*) can be deduced from the difference between molecular length (L_mol = 5.4 nm for 2/10) and the recorded d-spacings (d = 3.6–4.4 nm, see Table S1 and Fig. S26, ESI†). Additional confirmation is provided by investigation of aligned samples of the racemate of the next homologue (rac-2/12), as described further below. The smectic phase of compound (S)-2/10 was only observed on cooling as a monotropic LC phase and therefore could not be investigated in more detail due to crystallization and presently it cannot be decided if it is a polar or non-polar SmC_s* phase. The next even numbered homologue (S)-2/12 has an enantiotropic SmC_s* range, and therefore, the following detailed investigations were focused on (S)-2/12 and its racemic mixture rac-1/12.

3.3 DSC and optical investigation of the smectic phases of rac-2/12 and (S)-2/12

DSC-investigations. In Fig. 5, the DSC traces of the pure enantiomer (S)-2/12 are compared with its racemate rac-2/12; the LC-Iso transition temperatures of the racemate are about 3–4 K higher compared to the enantiomer, whereas the transitions between the LC phases and the associated transition enthalpy values are almost identical, (see also Table 1). In the cooling curves there are two additional phase transitions below the Iso–N_CybC transition, one around 92–94 °C for the N_CybC⁽*⁾–SmC_s⁽*⁾ transition and another one at 53–54 °C (Fig. 5). The third transition peak around 33–35 °C is attributed to a partial crystallization in both cases.

Fig. 5 DSC heating and cooling traces of (a) rac-2/12 and (b) (S)-2/12, recorded at 10 K min⁻¹.

Optical investigations. At the transition to the tilted smectic phase of (S)-2/12 (SmC_s*) the oily streaks texture of the N_CybC* phase changes to a non-specific birefringent sandy texture composed of small fans (see Fig. 3f–g). This texture slowly transforms into an optical isotropic homeotropic texture (layers become aligned parallel to the substrate surfaces, see Fig. S33, ESI†), which can also be obtained by shearing the sample between the glass plates (Fig. 3h). The unaxiality of this tilted smectic phase indicates a heliconical superstructure with a helical twist between the layers, the helix axis being perpendicular to the layer planes (Fig. 1a), and a pitch outside the visible optical wave length range. On further cooling, at 62 °C, a weak birefringence develops, which at 54 °C (Fig. 3i) suddenly increases in brightness and becomes a typical Schlieren texture as known for the B2 phases (SmCP_A phases) of bent-core mesogens (Fig. 3j). This means that the heliconical superstructure is distorted below 62 °C and completely removed at the phase transition at 53 °C.

The two phase transitions in the LC range are also visible by textural investigations of planar (Fig. 6a–d, left column) as well as homeotropic samples of the corresponding racemate rac-2/12 (Fig. 6e–g, right column). On cooling the planar aligned sample of the nematic phase (planes of the cybotactic clusters are perpendicular to the cell surfaces) the fan-like texture of a smectic phase develops at the transition around 94 °C, (Fig. 6a and b). This is immediately followed by the emergence of tilt domains, indicated by dark domains, at 58 °C having their maximum darkness if inclined by ∼30° with respect to the orientation of polarizer and analyzer (Fig. 6c). This is in line with a model where the tilt randomized SmC_s clusters in the N_CybC phase grow in coherence length, thus forming layers at the N_CybC to SmC_s transition. Immediately below this transition the phase appears almost SmA-like, i.e. without the typical tilt domains (see Fig. 6b and c) and on further cooling the tilt domains become clearly visible (Fig. 6c). It appears that close to the N_CybC to SmC_s transition the tilt correlation is weak or heliconical, and that it becomes uniformly synclinic with lowering temperature. The next transition at 54 °C is associated with another textural change (SmC_s → SmC_s′ transition, Fig. 6c and d) due to the further increasing packing density (see below).

Fig. 6 Textures of the (a–d) planar aligned (6 μm polyimide coated ITO cell, R is the rubbing direction) and (e–g) homeotropic samples (between non-treated microscopy glass plates) of the racemate rac-2/12 as observed on slow cooling (5 K min⁻¹) from the isotropic liquid phase into the distinct phases at the indicated temperatures; for additional textures at other temperatures, see Fig. S31 (ESI†).

The homeotropic aligned N_CybC phase of rac-2/12 (Fig. 6e) appears almost optically isotropic with only weak birefringence, the latter we attribute to thin surface layers with the tilted layers pinned to the surface. This is in line with a completely randomized tilt direction of the cybotactic SmC_s-like clusters in the N_CybC phase and an alignment of these clusters parallel to the substrate surfaces. At the N_CybC to SmC_s transition at 94 °C bright domain boundaries develop, though the texture remains almost isotropic (Fig. 6e and f). This means that despite of the tilt, the birefringence remains very small, which might be due to a persisting tilt randomization or a developing heliconical superstructure. Upon approaching the next phase transition at 54 °C the birefringence in the homeotropic texture increases considerably, indicating the transition to a significantly tilted smectic phase with uniform tilt-correlation (SmC_s′, Fig. 6f and g).

Mirror symmetry breaking in the SmC_s phase of rac-2/12. In order to uncover the origin of the low birefringence of the homeotropic SmC_s phase, rac-2/12 was investigated by polarizing microscopy between two polarizers. Rotating one polarizer by a small angle (1–5°) out of the 90° position visualizes a conglomerate of dark and bright areas. Inverting the direction of rotation inverts the brightness of the domains (Fig. 7a and c), whereas rotating the sample between the polarizers leads to no change (Fig. S32, ESI†). The combination of these observations is typical for a conglomerate of chiral domains. The presence of a surface supported heliconical organization with the helix axis perpendicular to the surfaces⁹⁷ is in line with the almost isotropic appearance of the homeotropic texture and its optical activity. Thus, for the racemic compound rac-2/12 a stochastically formed conglomerate with equal probability for either chirality sense is observed. Again, the slight birefringence is mainly attributed to surface layers.

Fig. 7 Chiral domains as observed in the SmC_s phase of rac-2/12 at T = 90 °C as (b) observed between crossed polarizers and (a and c) with the analyzer slightly rotated (a) in clockwise and (c) in counter clockwise direction. That the brightness of the domains does not change by rotating the sample between crossed polarizers is shown in Fig. S32 (ESI†).

Similar spontaneously formed chiral domains in SmC_s phases of achiral bent-core mesogens have previously been reported for the paraelectric SmC_sP_R^[*^] phases⁶⁷ and were also observed in some cybotactic nematic phases of bent-core mesogens (N_CybC^[*^]).^8,97,98 These spontaneous mirror symmetry broken LC phases of achiral bent-core molecules result from a combination of different effects, among them a small or negative twist elastic constant,⁹⁹ surface pinning effects⁹⁷ and a high degree of helicity of the molecular conformations.^6–8 However, the spontaneous formation of chiral domains in a SmC_s phase of a racemic mixture is according to our knowledge, reported here for the first time. It is a bit surprising, because uniform helical self-assembly in the domains leads to energetically different states for the permanently chiral (R)- and (S)-enantiomers. A spontaneous separation of the enantiomers would be diffusion controlled and therefore expected to be a slow process, whereas chirality synchronization of transiently chiral molecules in LC helical superstructures is known to be fast.^8,98 Nevertheless, the domain formation appears to be rapid and therefore it is assumed that the diastereomeric coupling between the permanent and transient molecular and supramolecular chirality is only weak⁸ and the synchronization of the transient chirality is dominating.

Upon approaching the next phase transition at 54 °C the birefringence in the homeotropic texture increases significantly, indicating the transition to a helix-free SmC_s′ phase (Fig. 6g). Thus, there are heliconical superstructures in the SmC_s ranges of the enantiomer as well as of the racemate of 2/12, in the first case being uniform and supported and biased by the permanent molecular chirality and in the second case as a conglomerate resulting from the spontaneous local chirality synchronization. In both cases the transition to the low temperature mesophase around 52–54 °C is associated with a loss of the helical self-assembly.

3.4 Electro-optical studies of rac-2/12 and (S)-2/12

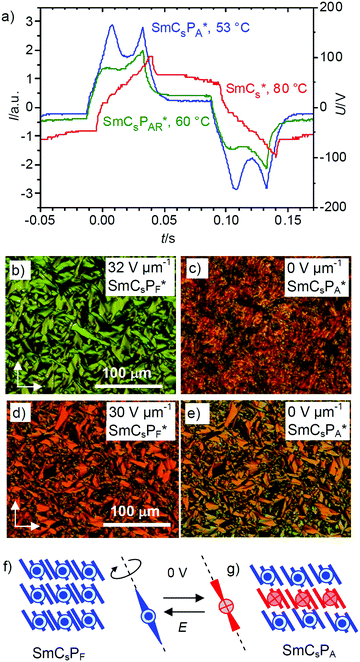
Compound (S)-2/12 and its racemate rac-2/12 were further investigated by electrical triangular wave field experiments. No current peaks could be observed in the N_CybC and N_CybC* phases of rac-2/12 and (S)-2/12, respectively, independent of the temperature and even under an applied voltage of up to 38 V_pp μm⁻¹; the same is found in the SmC and SmC′-ranges of rac-2/12. In contrast, already at the N_CybC*–SmC_s* transition of (S)-2/12 a single current peak emerges, which grows in intensity upon cooling and a second peak starts developing around 62 °C. The two polarization current peaks in each half period of an applied triangular wave field increase in size and have fully developed at the phase transition at 53 °C, indicating an antiferroelectric switching (Fig. 8a and Fig. S34, ESI†). The polarization value (P_s) reaches about 500 nC cm⁻² between 53 and 45 °C and upon further cooling it vanishes again due to partial crystallization. This polarization value is in the typical range as known for polar smectic (B2) phases of bent-core mesogens.

Fig. 8 (a) Switching current response curves of compound (S)-2/12 at 80 °C (SmC_s*), 60 °C (SmC_sP_AR*) and 53 °C (SmC_sP_A*), respectively, under a triangular wave field (380 V_pp, 50 Hz, 5 kΩ); (b and c) planar textures as observed between crossed polarizers at 65 °C, and (d and e) at 53 °C in a 10 μm non-coated ITO cell; (f and g) models showing the helix-free SmC_sP_F and SmC_sP_A structures and the switching between them by rotation around the molecular long axis.

It appears that in the SmC_s* range between 62 and 92 °C a paraelectric switching of polar domains takes place, whereas below 53 °C, i.e. in the SmC_s′ range of rac-2/12, a B2-like antiferroelectric switching SmC_sP_A* phase develops for (S)-2/12. Upon approaching the SmC_sP_A* phase the switching in the paraelectric SmC_s phase changes at 62 °C from a single peak type (SmC_sP_R*-like range) to a double peak type (SmC_sP_AR* range) with growing size of the polar clusters. This means that with lowering temperature the growing steric polarization of the bent molecules induces a transition from paraelectric via superparaelectric switching of polar domains to an antiferroelectric switching of the polar layers.⁶⁶ At a certain critical domain size, reached below 62 °C, the synpolar correlation of the domains changes to an antipolar. Thus, the observed sequence on cooling is N_CybC*–SmC_s*–SmC_sP_AR*–SmC_sP_A*.

Optical investigation under an applied DC field indicate no effect of the electric field on the optical textures of the SmC_s and SmC_s′ phases of the racemate rac-2/12. Investigation of the enantiomerically pure compound (S)-2/12 shows that under the applied E-field the extinctions in the planar samples are inclined with the directions of polarizer and analyzer, confirming a synclinic tilted SmC_sP_F-like state (Fig. 8b and d). Between 92 and 63 °C this field-induced state relaxes back to a nonspecific texture (Fig. 8c) due the distortion caused by the helix developing after switching off the applied electric field (helielectric switching³⁷). Below 62 °C the fan texture is retained after switching off the applied field (Fig. 8e). This means that the helix is permanently removed and only a change of the birefringence is observed, whereas the fan texture and the orientation of the extinctions in this texture do not change (Fig. 8d and e). It is concluded that the structure at 0 V is synclinic, too, but assumes an antiferroelectric polar correlation between the layers and hence it is SmC_sP_A in the ground state (Fig. 8g). This means that a SmC_sP_A ↔ SmC_sP_F switching takes place by rotation around the molecular long axis (Fig. 8f and g).

The tilted organization of the molecules in polar layers leads to a superstructural chirality of the layers, where polar direction, tilt direction and layer normal define either a right-handed or a left-handed Cartesian coordinate system (see Fig. 1d and Fig. S35, ESI†). Stacking layers with uniform chirality leads to the homochiral SmC_sP_F and SmC_aP_A structures, whereas stacking of layers with alternating chirality leads to racemic SmC_sP_A and SmC_aP_F structures (Fig. S35, ESI†).³ The observed formation of a polar smectic phase with racemic layer structure (SmC_sP_A), and the switching process taking place by rotation around the long axis, thus inverting the layer chirality (chirality flipping), indicate that the coupling between permanent molecular chirality and this superstructural layer chirality is only weak for (S)-2/12.^21,22 Nevertheless, the emerging antipolar correlation, leading to a local or long range racemic SmC_sP_A structure below 62 °C and 53 °C, respectively, disfavors the helix formation, so that below 62 °C the heliconical structure becomes unstable. Hence, the tendency to assume an antipolar organization with racemic structure is likely to be responsible for the loss of (chirality induced or spontaneous) heliconical self-assembly at the transition from SmC_s*/SmC_s to the low temperature smectic phases (SmC_sP_A*/SmCs′) of (S)-2/12 and rac-2/12, respectively.

Comparison of (S)-2/12 with the racemate rac-2/12 shows that uniform molecular chirality, allowing a denser packing of the molecules, is required for development of polar order in the smectic phases of this series of compounds. The polarization and the increasing contribution of the antipolar correlation between the synclinic tilted layers at reduced temperature are considered as resulting from a change of the molecular shape from being only weakly to more strongly bend. Thus, the polar switching is dominated by the steric induced polar order of the bent molecules, increasing with lowering temperature, and not directly caused by the reduced phase symmetry due to the permanent molecular chirality.⁵⁹ If polar order would be due to the reduction of the phase symmetry, as in the case of SmC_s* phases of rod-like molecules (C_2h → C₂), then ferroelectric switching by precession on a cone would be expected for these synclinic tilted smectic phases^39,41 instead of the actually observed switching by rotation around the long axis. The rotation around the long axis also indicates that the achieved packing density is even in the SmC_sP_A* phase of (S)-2/12 not sufficient to suppress this mode of switching. For the racemate rac-2/12, the sterically induced polar order in the SmC_s′ range is even insufficient to produce any polar switching because of the weaker chirality synchronization in the absence of the permanent chirality is incapable of providing the required packing density to achieve a significant polar domain size. Therefore, a transition from preferred synpolar to preferred antipolar domain correlation at the SmC_s–SmC_s′ transition of rac-2/12 is likely, but cannot be confirmed by electro-optical investigations.

3.5 X-ray scattering and magnetic field effects on the LC phases of rac-2/12 and (S)-2/12

Development of the tilt. The N*/N ranges of compound (S)-2/12 and its racemate rac-2/12 were investigated by XRD after slow cooling (0.1 K min⁻¹) from the isotropic liquid phase under a magnetic field with B ∼ 1 T (see Fig. 9a and b). The 2D diffraction pattern of rac-2/12 shows the typical dumbbell like shape with 4-maxima of the SAXS at d = 4.4 nm (Fig. 9a and c) indicating a skewed cybotactic nematic phase with a tilted organization of the molecules in the SmC-like clusters (N_CybC, see Fig. 9e), as typical for bent-core molecules.^16,95,96 The orientation of the two dumbbell-like streaks parallel to the equator indicates a preferred alignment of the molecules with their long axes parallel to the magnetic field direction (Fig. 9a and e) which is retained in the smectic phases (Fig. 9c).

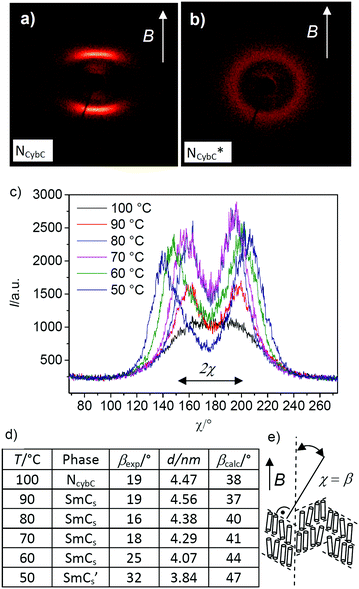Fig. 9 (a and b) 2D XRD patterns of (a) the N_CybC phase of compound rac-2/12 at T = 100 °C and (b) the N_cybC* phase of compound (S)-2/12 at T = 100 °C, both recorded under a magnetic field of ∼1 T; the arrows indicate the direction of the applied magnetic field; (c) χ-scans over the SAXS range (1–3°) of the diffraction patterns of the magnetically aligned rac-2/12 at the indicated temperatures with (d) numerical values of the tilt angles calculated from the χ-scans (β_exp) and from the layer spacing (β_calc) according to cos β_calc = d/L_mol (with L_mol = 5.7 nm); (e) shows the alignment of the molecules and the cybotactic SmC_s-clusters in the magnetic field; for more details, see Fig. S28 (ESI†).

The tilt angle in the cybotactic clusters of the N_CybC phase of rac-2/12, corresponding to the χ-angle between the scattering maxima and the meridian is β_exp = 19 ± 3° in the nematic phase at 100 °C and remains almost unchanged in the SmC_s-range down to 70 °C. The tilt increases upon approaching the transition to the SmC_s′ phase (25 ± 3° at 60 °C) and reaches 32 ± 3° in the SmC_s′ phase at 50 °C (see Fig. 9d and Fig. S28, ESI†). The measured d-value of the SAXS in the SmC_s phase at 90 °C is d = 4.56 nm, which according to cos β = d/L_mol (L_mol = 5.7 nm in a conformation shown in Fig. S25 (ESI†) with 120° bend of the aromatic core and stretched alkyl chains), would lead to an almost doubled tilt angle of β_cal = 37° (Fig. 9d) compared to β_exp = 19 ± 3°. This means that the effective molecular length (L_eff), as calculated from the measured tilt angle and the layer spacing is only 4.7 nm, which is much shorter than the measured value of L_mol = 5.7 nm (Fig. S25b, ESI†) due to conformational disorder or alkyl chain intercalation. Remarkably, the growing tilt starting at ∼60 °C does not lead to a reduction of the birefringence in the planar samples (Fig. 6b–d and Fig. S31, ESI†), meaning that the development of the tilt is accompanied by a simultaneously increasing orientational order parameter. Overall, the N_CybC–SmC_s transition is associated with an increase of the correlation length of the N_CybC clusters, while the tilt is retained; the transition SmC_s–SmC_s′ is associated with the restriction of the rotation around the molecular long axis, leading to an increase of the tilt due to the denser core packing.

For the enantiomer (S)-2/12 the SAXS forms a closed diffuse ring due to the distortion provided by the helicoidal organization of the homogeneously chiral molecules in the N_CybC* phase (Fig. 9b). This means, that due to the helicoidal superstructure, no sufficient alignment is achieved under the magnetic field and that the applied field cannot remove the helicoidal twist completely.

X-ray scattering in the smectic phases without magnetic field. In the following the effects of temperature and chirality on the XRD patterns is described in more detail. At first the discussion is focused on the investigations without applied magnetic field, shown by triangles in both diagrams 10a and 10b for rac-2/12 and (S)-2/12, respectively. In both cases the d(SAXS) value increases in the Iso⁽*⁾ and N⁽*⁾ phase ranges on cooling (black triangles). For the racemate from 3.6 nm in the Iso phase at 120 °C to 4.15 nm at 90 °C shortly below the N_CybC-SmC_s transition (Fig. 10a) and for the (S)-enantiomer from 3.35 to 4.55 nm (Fig. 10b). This is mainly attributed to the transition from a diffuse scattering in the isotropic liquid and the nematic phase, not obeying the Bragg law, to a Bragg-like peak in the smectic phases. Remarkably, this increase in Δd is for (S)-2/12 more than twice as large than for the racemate, thus indicating a strong effect of uniform chirality on lamellar self-assembly. However, what is even more surprising, is the development of the d-values in the smectic range on further cooling, which is very different for (S)-2/12 and rac-2/12. For the racemate rac-2/12 the layer spacing d increases a bit to d = 4.2 nm at 80 °C and then it decreases on further cooling to 3.65 nm at 50 °C (Fig. 10a, black triangles). In contrast, for (S)-2/12 the d-value is much larger right from the N_CybC*–SmC_s* transition and there is no significant change of the layer spacing on further cooling, it even slightly increases in this case and reaches d = 4.6 nm at 60 °C (Fig. 10b, black triangles). Thus, at 60 °C there is a huge difference of 0.8 nm, corresponding to almost 20%, between the layer spacings of the smectic phases of (S)-2/12 and its racemate rac-2/12.

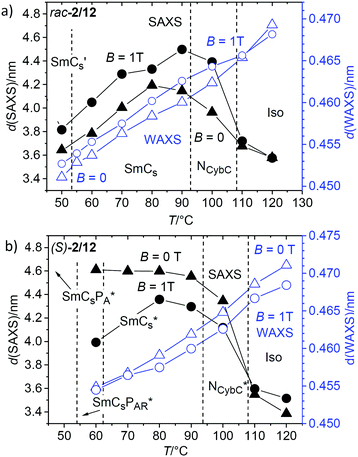Fig. 10 Temperature dependence of the d-values of the SAXS (black) and WAXS maxima (blue, see also Fig. S27, ESI†) of (a) rac-2/12 and (b) (S)-2/12 as measured on cooling either without applied magnetic field (triangles) or under the magnetic field of 1 T (dots). For (S)-2/12 the investigation could only be conducted down to 60 °C, due to crystallization, see also the comment in footnote;^100,101 for numerical data, see Tables S2 and S3 (ESI†).

It appears that for the racemate rac-2/12 there are two competing effects on the layer distance, one is the growing correlation length of the lamellar ordering (transition from diffuse to Bragg-like scattering), shifting the d-spacing to larger values and another one reducing the d-spacing. The latter could be due to a growing tilt, an increasing alkyl chain intercalation or an increasing conformational disorder of the alkyl chains upon lowering temperature. As the alkyl chain disorder is known to decrease with lowering temperature and the measured tilt does not change significantly down to ∼60 °C (see Fig. 9d) it is concluded that chain intercalation provides the major effect causing the decreasing d. For the pure enantiomer (S)-2/12 the chirality in the SmC_s* phase apparently inhibits this layer shrinkage, and hence, the alkyl chain intercalation at reduced temperature.

Though the development of the d-spacing of the SAXS is very different for rac-2/12 and (S)-2/12, there is almost no effect of chirality on the d-value of the diffuse WAXS maximum (blue triangles in Fig. 10a and b). In both cases there is a continuous decrease of the d-value with lowering temperature without recognizable effect of the phase transitions, in line with the almost continuously growing packing density. If there is any difference between the d = f(T) curves of (S)-2/12 and rac-2/12 or any effect of an applied magnetic field on these curves is difficult to say as the differences are very small (Δd < 0.003 nm) and thus within the range of instrumental error.¹⁰¹ It appears that at fixed temperature any decrease of the packing density is compensated by additional intercalation.

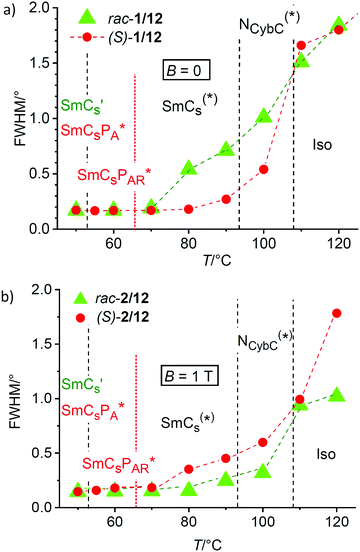
In Fig. 11a the development of the line width (FWHM) of the SAXS, which is inversely proportional to the correlation length (ξ) of the cybotactic clusters, is compared for (S)-2/12 (red dots) and rac-2/12 (green triangles). The scattering is diffuse in the isotropic liquid phase and the correlation lengths is almost the same for rac-2/12 and (S)-2/12. Slightly above the Iso⁽*⁾–N_CybC⁽*⁾ phase transition at 110 °C it is in both cases around ξ = 16 nm, corresponding to clusters of about three layers. The FWHM becomes smaller and the correlation length ξ increases at the transition to the nematic phase. On further cooling the development of the FWHM becomes different for (S)-2/12 and rac-2/12. For the racemic mixture there is an almost linear decrease of FWHM between 120 and 70 °C (Fig. 11a, green) with a relatively small step at the Iso–N_CybC* transition around 108 °C. For the (S)-enantiomer a significant jump to smaller values takes place already around the Iso-N_CybC* transition (Fig. 11a, red). This indicates an increased size of the cybotactic clusters in the N_CybC* phase of the homochiral compound (ξ ∼ 30 nm at 100 °C) compared to the N_CybC phase of the racemic mixture (ξ ∼ 20 nm at 100 °C). The jump in line width confirms the formation of almost infinite layers at the N_CybC*–SmC_s* transition of (S)-2/12, whereas the smooth change of d at the N_CybC–SmC_s transition of rac-2/12 suggests an almost continuous growth of the cybotactic clusters. Both T = f(FWHM) curves approach to each other around 60–70 °C where the line width becomes almost resolution limited in both cases (Fig. 11a). At this temperature infinite layers have developed and for (S)-2/12 the superparaelectric switching of polar clusters sets in a few degrees lower at 62 °C (see Table 1).

Fig. 11 Temperature dependence of the full width at half maximum (FWHM) of the SAXS of (S)-2/12 (red dots) and rac-2/12 (green triangles) in the distinct LC phases (a) without applied magnetic field and (b) under a magnetic field of 1 T.

The increase of the cluster size of (S)-2/12 compared to rac-2/12 is surprising, because one would expect that the chirality induced twist, especially the transversal twist, should have a destabilizing effect on lamellar self-assembly and cluster formation, but it seems that the opposite is the case. Thus, there appears to be a layer stabilizing effect of uniform chirality. This could arise from an improved packing of uniformly chiral molecules in the layers, which might be a result of the improved synchronization of the helix sense of helical molecular conformations under the biasing influence of the uniform permanent molecular chirality.^8,35 This intramolecular twist supports the development of an intermolecular helical twist, which for tilted arrangements of molecules is composed of two components. The transversal twist of the layers (helicoidal twist, see Fig. 1c and 12c) which distorts lamellar self-assembly and eventually leads to the TGB phases,⁴⁸ and the longitudinal twist along the layer normal, i.e. between the layers (Fig. 1a and 12a), leading to heliconical smectic phases (SmC*³⁷). Moreover, it is hypothesized that there is a conservation of the molecular helicity. This means that with growing cluster size the layer distorting transversal twist is not simply removed, but replaced by an increasing longitudinal twist, not distorting lamellar self-assembly (Fig. 12a and c). In the pure enantiomer (S)-2/12 the uniform molecular chirality favors a uniform sense of helicity, supporting a dense packing without intercalation, leading to larger d-values. In the racemate rac-2/12 the chirality synchronization is also present as expressed by spontaneous conglomerate formation (see Fig. 7). However, it is much weaker due to the absence of uniform (permanent) configurational chirality. Thus, the chirality synchronization becomes weaker, which allows more disorder, requiring the alkyl chain intercalation to retain a dense packing. The chirality synchronization obviously decreases with lowering temperature, either as the developing tendency of antipolar ordering supports a (SmC_sP_A-like) racemic phase structure, or due to the growing strength of the competing unfavorable diastereomeric relations between the synchronized molecular and supramolecular helicity and those molecules of the racemate, which have an opposite configuration. The reduced chirality synchronization distorts the packing and this requires deeper alkyl chain intercalation, then leading to the observed layer shrinkage upon approaching the SmC_s′ phase range.

Fig. 12 Schematic summary of the effects of chirality, temperature and magnetic field on the self-assembly of (S)-2/12 and its racemate rac-2/12; B = magnetic field, P = electric polarization, S₂ = the orientational order parameter; (a and c) show possible directions of the chirality induced twist, (a) shows the heliconical twist between the layers in SmC_s* phases and (c) the helicoidal twist as found in N* and TGB phases; (b) shows the development of the orientational order parameter, degree of intercalation and layer distance d in the smectic phases of rac-2/12 depending on T and B; there are also magnetic field effects on the chirality induced twist as indicated by curved arrows.

Effects of the magnetic field on X-ray scattering. As another surprising observation, the d spacing of the SAXS is strongly affected by a magnetic field with a strength of only 1 Tesla. In the LC phases of rac-2/12 (Fig. 10a) the d-spacing of the SAXS is increased by 0.2–0.35 nm under the magnetic field, and this increase becomes smaller with lowering temperature (Fig. 10a, black dots). Slightly below the N_CybC–SmC_s transition temperature at 90 °C the layer spacing under B = 1 T (Fig. 10a, d = 4.5 nm) becomes almost identical with the value measured for (S)-2/12 at the same temperature in the absence of a magnetic field (Fig. 10b, d = 4.55 nm). In contrast to the racemate, for (S)-2/12 the layer spacing is much larger at B = 0 and decreases significantly under the applied magnetic field, and this effect becomes stronger with lowering temperature (Fig. 10b, black dots). At 60 °C the layer spacing is reduced by amazing 0.6 nm under a magnetic field of only 1 T, corresponding to a reduction of d by 13%.

The effect on the racemate rac-2/12 can be attributed to an alignment of the weakly bent molecules with their average long axis parallel to the magnetic field direction (see Section 3.5). This leads to an increase of the orientational order parameter of the π-conjugated cores under the applied magnetic field, which also improves the chain order and thus reduces the space available for alkyl chain intercalation, and this leads to the observed increase of d under the magnetic field (Fig. 10a and 12b). This ordering effect of the magnetic field on the molecules also increases the correlation length of smectic order, which is in line with the observed reduction of the SAXS line width under the magnetic field (Fig. 13a, green vs. blue triangles). The effect of the magnetic field on the line width is especially strong in the Iso and N_CybC phase ranges. It continues in the upper temperature range of the SmC_s phase until the scattering becomes resolution limited below 70 °C upon approaching the transition to the SmC_s′ phase range at 53 °C.

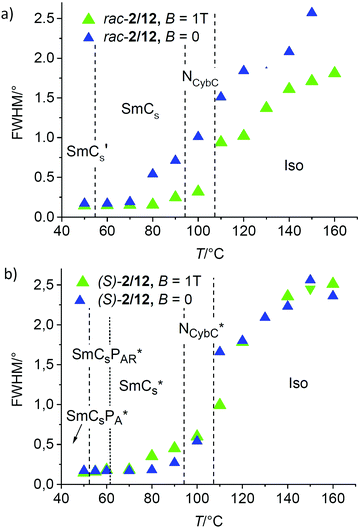Fig. 13 Effects of an applied magnetic field of B = 1 T on the line width (FWHM) of the SAXS in the distinct LC phases (a) of rac-2/12 and (b) the enantiomer compound (S)-2/12.

In contrast to the racemate, for the enantiomer (S)-2/12 there is a reduction of the d-spacing of the SAXS under the magnetic field which becomes stronger with lowering temperature (Fig. 10b). It was previously shown that a magnetic field can remove the chirality induced twist even under a comparatively low magnetic field, as reported for SmC* and TGBC* phases of uniformly chiral rod-like molecules.^80,81 The effect on the heliconical (longitudinal) twist of the SmC* and TGBC* phases is especially strong and therefore it is easily removed under low fields, whereas the transversal twist of the TGB structure itself requires much higher fields. Similar effect can also be assumed for the influence of the magnetic field on the chiral LC phases of (S)-2/12. It is suggested that the main effect of the magnetic field on (S)-2/12 is again an increase of the orientational order parameter, which in this case leads to a reduction of the longitudinal intermolecular (heliconical) twist between the layers. If the intramolecular (conformational) twist is conserved under the magnetic field, the removal of the heliconical twist has to be compensated by a simultaneously developing transversal twist in the layers, effectively reducing the orientational order parameter. Thus, the chain packing would become less dense and this is avoided by additional chain intercalation, which then reduces the d-value under the applied field (Fig. 10b and 12). Therefore, in the temperature range between 60 and 80 °C the d = f(T) curve of (S)-2/12 under the magnetic field (black dots in Fig. 10b) almost resembles that of rac-2/12 without magnetic field (black triangles in Fig. 10a) only shifted by about 0.2 nm to larger values than measured for rac-2/12. This shift of d is attributed to the general increase of the order parameter under the magnetic field. Accordingly, under a magnetic field rac-2/12 and (S)-2/12 have almost identical d-values in this temperature range (Fig. 10a and b). It means that under the field an almost identical order parameter and degree of alkyl chain intercalation is achieved for (S)-2/12 and rac-2/12. This is assumed to be due to the compensation of two opposing field effects, the reduction of the heliconical (longitudinal) twist, leading to increased transversal twist (reducing ξ) on the one hand, and the increase of the orientational order parameter, reducing the induced transversal twist (and increasing ξ) on the other hand. Due to this compensation there is also almost no effect of the applied magnetic field on the correlation length of smectic order (ξ) in the LC phases of (S)-2/12 below 80 °C (Fig. 13b) when the driving force for the heliconical twist is reduced by the emerging tendency of antipolar order (developing racemic SmC_sP_A structure). Only in the upper SmC* range, above ∼70 °C, there is some broadening of the line width, i.e. layer distortion, under the magnetic field (Fig. 13b). In this temperature range there is a stronger intrinsic twist, and therefore, the ordering magnetic field effect on (S)-2/12 appears to be sufficient for removing the heliconical (longitudinal) twist, but insufficient to fully remove the simultaneously developing transversal twist.

4. Conclusion

4-Cyanoresorcinol based non-symmetric bent-core compounds carrying one stereogenic center have been synthesized in enatiomerically pure and one compound in racemic form. All homochiral compounds form an enantiotropic chiral cybotactic nematic LC phase at relatively low temperature, close to ambient temperature, which is remarkably low for bent-core materials. In these N_CybC* phases the selective reflection band can be shifted by rising the temperature over a wide wave length range from the near IR via the visible range to the near UV.^79,102 The growth of the cluster size by lowering temperature reduces the transversal twist in the N_CybC* phase and this contributes to the extraordinary broad wave length range. Though short pitch helices can be obtained close to the transition to the isotropic liquid phase, no chirality frustrated blue phases, as found for the related 4-cyanoresorcinol based bent-core molecules with two chiral end-chains (BPIII), could be observed (compounds 3 in Scheme 1, see Table S4, ESI†).²³ Thus, it appears that in this class of compounds only two branched chiral chains can provide a sufficiently strong twist required for BPIII formation.

Compounds with long chains (n = 10, 12) form additional tilted smectic phases (SmCs⁽*⁾), but only for the compound combining a homochiral (S)-3,7-dimethyloctyloxy chiral unit with a n-dodecyloxy chain a polar switching smectic phases was observed, whereas the corresponding racemate is non-polar. This is attributed to a denser packing of uniform enantiomers due to chirality synchronization of their chirality biased helical conformers.⁸ For racemic mixtures this chirality synchronization is more difficult and requires additional surface stabilization.⁹⁷ Related achiral compounds with two linear n-alkyloxy chains (compounds 4 in Scheme 1) also form a polar SmCP_A phase besides the cybotactic nematic phase (Table S4, ESI†).^18,103 This indicates that chain branching distorts the core packing and removes polar order, and that this distortion by chain branching can be reduced or removed by chirality synchronization in the case of uniformly chiral compounds.

In the SmC_s* phases the switching takes place by rotation around the long axis (see Fig. 8f and g) which means that the polar switching is not the result of the reduced phase symmetry due to the permanent molecular chirality as known for rod-like molecules, but it is due to a sterically induced polarization, as known for bent-core molecules. A ferro-like helielectric switching occurs just after transition from the chiral nematic to the SmC_s* phase and below 62 °C a transition to antiferroelectric-like super-paraelectric (SmC_sP_AR*) and finally at 53 °C to an antiferroelectric polar switching (SmC_sP_A*) takes place as the polar correlation length in the layers grows with lowering temperature and the correlation between the layers simultaneously becomes antipolar with growing layer polarization.

Most interesting are the unprecedented huge effects of an applied magnetic field on the LC phases of the chiral compound (S)-2/12 as well as on its racemic mixture, leading to a layer shrinkage by up to 0.6 nm for the enantiomer and a layer expansion by 0.2–0.4 nm for the racemate under an applied field of only 1 T. It is proposed that the effect on the racemate is dominated by the coupling of the magnetic field with the almost rod-like π-conjugated molecules parallel to the field direction. In the case of the racemate the field induced increase of orientational order reduces the capability of alkyl chain intercalation, thus leading to a layer expansion. For the enantiomer the reduction of the longitudinal heliconical twist is likely to lead to an increased transversal twist within the layers, which then reduces the core order and allows chain intercalation, thus leading to the reverse effect, the field induced layer shrinkage.

Overall, this work shows that, though the coupling of the magnetic field with diamagnetic molecules is weak, it can lead to huge effects. The extraordinary strong effect of a magnetic field on the layer spacing could provide new applications of diamagnetic LC materials based on molecules at the cross-over between rod-like and bent shapes, by affecting their capability of chirality synchronization, and probably also by modulating the polar switching modes by magnetic fields. For the weakly bent compounds reported here the molecules couple with their long axis parallel to the magnetic field, whereas related molecules with a stronger bend are known to couple in an orthogonal way.^73–75 Thus, there are numerous possibilities for the coupling of magnetic and electric field effects in potential electro-magneto-optical devices which needs to be explored in future work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

H. O. is grateful to the Alexander von Humboldt Foundation for a research fellowship at Martin Luther University, Halle, Germany. B. B.-E. is grateful to the Alexander von Humboldt Foundation for financial support toward LC research. The work is also supported by the Deutsche Forschungsgemeinschaft (TS 39/24-2).

References

1. J. W. Goodby, E. J. Davis, R. J. Mandle and S. J. Cowling, Isr. J. Chem., 2012, 52, 863–880; C. Tschierske, Isr. J. Chem., 2012, 52, 935–959.
2. Q. Li, Nanoscience with Liquid Crystals, Springer Cham, 2014; T. Kato, J. Uchida, T. Ichikawa and T. Sakamoto, Angew. Chem., Int. Ed., 2018, 57, 4355.
3. D. R. Link, G. Natale, R. Shao, J. E. Maclennan, N. A. Clark, E. Korblova and D. M. Walba, Science, 1997, 278, 1924.
4. G. Pelzl, S. Diele and W. Weissflog, Adv. Mater., 1999, 11, 707.
5. R. A. Reddy and C. Tschierske, J. Mater. Chem., 2006, 16, 907.
6. K. V. Le, H. Takezoe and F. Araoka, Adv. Mater., 2017, 29, 1602737.
7. H. Takezoe and A. Eremin, Bent-shaped Liquid Crystals. Structures and Physical Properties, CRC Press, Boca Raton, 2017.
8. C. Tschierske, Liq. Cryst., 2018, 45, 2221; C. Tschierske and G. Ungar, ChemPhysChem, 2016, 17, 9.
9. W. Weissflog, H. Nadasi, U. Dunemann, G. Pelzl, S. Diele, A. Eremin and H. Kresse, J. Mater. Chem., 2001, 11, 2748.
10. U. Dunemann, M. W. Schröder, R. A. Reddy, G. Pelzl, S. Diele and W. Weissflog, J. Mater. Chem., 2005, 15, 4051.
11. V. Prasad, N. Nagendrappa Gowdru and M. Manjunath, Liq. Cryst., 2018, 45, 666.
12. C. V. Yelamaggad, M. Mathews, S. A. Nagamani, D. S. Shankar Rao, S. K. Prasad, S. Findeisen and W. Weissflog, J. Mater. Chem., 2007, 17, 284.
13. W. Weissflog, S. Sokolowski, H. Dehne, B. Das, S. Grande, M. W. Schröder, A. Eremin, S. Diele, G. Pelzl and H. Kresse, Liq. Cryst., 2004, 31, 923.
14. G. Pelzl and W. Weissflog, in Thermotropic Liquid Crystals: Recent Advances, ed. A. Ramamoorthy, Springer, Berlin, 2007, pp. 1–58.
15. C. Tschierske and D. J. Photinos, J. Mater. Chem., 2010, 20, 4263.
16. C. Keith, A. Lehmann, U. Baumeister, M. Prehm and C. Tschierske, Soft Matter, 2010, 6, 1704.
17. I. Wirth, S. Diele, A. Eremin, G. Pelzl, S. Grande, L. Kovalenko, N. Pancenko and W. Weissflog, J. Mater. Chem., 2001, 11, 1642.
18. L. Kovalenko, M. W. Schröder, R. A. Reddy, S. Diele, G. Pelzl and W. Weissflog, Liq. Cryst., 2005, 32, 857.
19. C. Keith, M. Prehm, Y. P. Panarin, J. K. Vij and C. Tschierske, Chem. Commun., 2010, 46, 3702.
20. G. Shanker, M. Prehm, M. Nagaraj, J. K. Vij and C. Tschierske, J. Mater. Chem., 2011, 21, 18711.
21. A. Lehmann, M. Alaasar, M. Poppe, S. Poppe, M. Prehm, M. Nagaraj, S. P. Sreenilayam, Y. P. Panarin, J. K. Vij and C. Tschierske, Chem. – Eur. J., 2020, 20, 4714.
22. M. Poppe, M. Alaasar, A. Lehmann, S. Poppe, M.-G. Tamba, M. Kurachkina, A. Eremin, M. Nagaraj, J. K. Vij, X. Cai, F. Liu and C. Tschierske, J. Mater. Chem. C, 2020, 8, 3316.
23. H. Ocak, B. Bilgin-Eran, M. Prehm, S. Schymura, J. P. F. Lagerwall and C. Tschierske, Soft Matter, 2011, 7, 8266.
24. K. V. Le, M. Hafuri, H. Ocak, B. Bilgin-Eran, C. Tschierske, T. Sasaki and F. Araoka, ChemPhysChem, 2016, 17, 1425.
25. Y. P. Panarin, M. Nagaraj, S. Sreenilayam, J. K. Vij, A. Lehmann and C. Tschierske, Phys. Rev. Lett., 2011, 107, 247801.
26. S. P. Sreenilayam, Y. P. Panarin, J. K. Vij, V. P. Panov, A. Lehmann, M. Poppe, M. Prehm and C. Tschierske, Nat. Commun., 2016, 7, 11369.
27. A. A. S. Green, M. R. Tuchband, R. Shao, Y. Shen, R. Visvanathan, A. E. Duncan, A. Lehmann, C. Tschierske, E. D. Carlson, E. Guzman, M. Kolber, D. M. Walba, C. S. Park, M. A. Glaser, J. E. Maclennan and N. A. Clark, Phys. Rev. Lett., 2019, 122, 107801.
28. Y. P. Panarin, M. Nagaraj, J. K. Vij, C. Keith and C. Tschierske, EPL, 2010, 92, 26002.
29. M. Nagaraj, Y. P. Panarin, J. K. Vij, C. Keith and C. Tschierske, Appl. Phys. Lett., 2010, 97, 213505.
30. Y. P. Panarin, S. P. Sreenilayam, J. K. Vij, A. Lehmann and C. Tschierske, J. Mater. Chem. C, 2017, 5, 12585.
31. S. P. Sreenilayam, Yu. P. Panarin, J. K. Vij, A. Lehmann, M. Poppe and C. Tschierske, Phys. Rev. Mater., 2017, 1, 035604.
32. J. K. Vij, Y. P. Panarin, S. P. Sreenilayam, M. Alaasar and C. Tschierske, Phys. Rev. Mater., 2019, 3, 045603.
33. (a) V. P. Panov, M. Nagaraj, J. K. Vij, Y. P. Panarin, A. Kohlmeier, M. G. Tamba, R. A. Lewis and G. H. Mehl, Phys. Rev. Lett., 2010, 105, 167801; (b) M. Cestari, S. Diez-Berart, D. A. Dunmur, A. Ferrarini, M. R. de la Fuente, D. J. B. Jackson, D. O. Lopez, G. R. Luckhurst, M. A. Perez-Jubindo, R. M. Richardson, J. Salud, B. A. Timimi and H. Zimmermann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 031704; (c) V. Borshch, Y. K. Kim, J. Xiang, M. Gao, A. Jakli, V. P. Panov, J. K. Vij, C. T. Imrie, M. G. Tamba, G. H. Mehl and O. D. Lavrentovich, Nat. Commun., 2013, 4, 2635; (d) C. H. Zhu, M. R. Tuchband, A. Young, M. Shuai, A. Scarbrough, D. M. Walba, J. E. Maclennan, C. Wang, A. Hexemer and N. A. Clark, Phys. Rev. Lett., 2016, 116, 147803.
34. M. Salamonczyk, N. Vaupotič, D. Pociecha, R. Walker, J. M. D. Storey, C. T. Imrie, C. Wang, C. Zhu and E. Gorecka, Nat. Commun., 2019, 10, 1922.
35. R. P. Lemieux, Acc. Chem. Res., 2001, 34, 845.
36. T. Matsumoto, A. Fukuda, M. Johno, Y. Motoyama, T. Yui, S.-S. Seomun and M. Yamashita, J. Mater. Chem., 1999, 9, 2051.
37. S. T. Lagerwall, Ferroelectric and Antiferroelectric Liquid Crystals, Wiley-VCH, Weinheim, 1999; S. T. Lagerwall, Ferroelectrics, 2004, 301, 15.
38. H. Takezoe, E. Gorecka and M. Cepic, Rev. Mod. Phys., 2020, 82, 897.
39. I. Dierking, Symmetry, 2014, 6, 444.
40. D. Coates, Liq. Cryst., 2015, 42, 653; F. Castles and S. M. Morris in Handbook of liquid crystals, ed. J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. F. Gleeson and P. Raynes, 2nd. Edn, Vol. 3, Weinheim (Germany), Wiley-VCH, 2014, pp. 493–518.
41. in Chirality in Liquid Crystals, ed. H. S. Kitzerow and C. Bahr, Springer, New York, 2001.
42. N. Katsonis, E. Lacaze and A. Ferrarini, J. Mater. Chem., 2012, 22, 7088.
43. D. C. Wright and N. D. Mermin, Rev. Mod. Phys., 1989, 61, 385.
44. (a) S. S. Gandhi and L.-C. Chien, Adv. Mater., 2017, 29, 1704296; (b) H. F. Gleeson, R. J. Miller, L. Tian, V. Görtz and J. W. Goodby, Liq. Cryst., 2015, 42, 760; (c) A. Yoshizawa, RSC Adv., 2013, 3, 25475; (d) H. K. Bisoyi and Q. Li, Acc. Chem. Res., 2014, 47, 3184.
45. J. Yamamoto, I. Nishiyama, M. Inoue and H. Yokoyama, Nature, 2004, 437, 525.
46. H. K. Bisoyi, T. J. Bunning and Q. Li, Adv. Mater., 2018, 30, 1706512.
47. M. Yoneya, Chem. Rec., 2011, 11, 66.
48. J. W. Goodby, Proc. R. Soc. A, 2012, 468, 1521.
49. (a) A. Zep, S. Aya, K. Aihara, K. Ema, D. Pociecha, K. Madrak, P. Bernatowicz, H. Takezoe and E. Gorecka, J. Mater. Chem. C, 2013, 1, 46; (b) R. Walker, D. Pociecha, J. M. D. Storey, E. Gorecka and C. T. Imrie, Chem. – Eur. J., 2019, 25, 13329.
50. G. Shanker, A. Bindushree, K. Chaithra, P. Pratap, R. Kumar Gupta, A. S. Achalkumar and C. V. Yelamaggad, J. Mol. Liq., 2019, 275, 849.
51. I. Nishiyama, Chem. Rec., 2009, 9, 340.
52. K. Kumazawa, M. Nakata, F. Araoka, Y. Takanishi, K. Ishikawa, J. Watanabe and H. Takezoe, J. Mater. Chem., 2004, 14, 157.
53. C. K. Lee, S. S. Kwon, T. S. Kim, E. J. Choi, S. T. Shin, W. C. Zin, D. C. Kim, J. H. Kim and L. C. Chien, Liq. Cryst., 2003, 30, 1401.
54. S. K. Lee, C. W. Park, J. G. Lee, K. T. Kang, K. Nishida, Y. Shimbo, Y. Takanishi and H. Takezoe, Liq. Cryst., 2005, 32, 1205.
55. S. K. Lee, S. Heo, J.-G. Lee, K.-T. Kang, K. Kumazawa, K. Nishida, Y. Shimbo, Y. Takanishi, J. Watanabe, T. Doi, T. Takahashi and H. Takezoe, J. Am. Chem. Soc., 2005, 127, 11085.
56. K. Nishida, M. Cepic, W. J. Kim, S. K. Lee, S. Heo, J. G. Lee, Y. Takanishi, K. Ishikawa, K.-T. Kang, J. Watanabe and H. Takezoe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021704.
57. J. Thisayukta, H. Niwano, H. Takezoe and J. Watanabe, J. Mater. Chem., 2001, 11, 2717.
58. S. Shadpour, A. Nemati, N. J. Boyd, L. Li, M. E. Prévôt, S. L. Wakerlin, J. P. Vanegas, M. Salamończyk, E. de Hegmann, C. Zhu, M. R. Wilson, A. I. Jákli and T. Hegmann, Mater. Horiz., 2019, 6, 959.
59. H. Ocak, M. Poppe, B. Bilgin-Eran, G. Karanlık, M. Prehm and C. Tschierske, Soft Matter, 2016, 12, 7405.
60. M. Mathews, R. S. Zola, D. Yang and Q. Li, J. Mater. Chem., 2011, 21, 2098–2103.
61. C. V. Yelamaggad, I. S. Shashikala, G. Liao, D. S. Shankar Rao, S. K. Prasad, Q. Li and A. Jakli, Chem. Mater., 2006, 18, 6100.
62. G. Liao, I. Shashikala, C. V. Yelamaggad, D. S. Shankar Rao, S. Krishna Prasad and A. Jákli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 051701.
63. (a) M. Nakata, D. R. Link, F. Araoka, J. Thisayukta, Y. Takanishi, K. Ishikawa, J. Watanabe and H. Takezoe, Liq. Cryst., 2001, 28, 1301; (b) G. Gesekus, I. Dierking, S. Gerber, M. Wulf and V. Vill, Liq. Cryst., 2004, 31, 145; (c) R. A. Reddy, B. K. Sadashiva and U. Baumeister, J. Mater. Chem., 2005, 15, 3303.
64. H. Ocak, B. Bilgin-Eran, D. Güzeller, M. Prehm and C. Tschierske, Chem. Commun., 2015, 51, 7512.
65. J. Xiang, Y. Li, Q. Li, D. A. Paterson, J. M. D. Storey, C. T. Imrie and O. D. Lavrentovich, Adv. Mater., 2015, 27, 3014.
66. (a) M. Alaasar, M. Prehm, S. Belau, N. Sebastian, M. Kurachkina, A. Eremin, C. Cheng, F. Liu and C. Tschierske, Chem. – Eur. J., 2019, 25, 6362; (b) M. Alaasar, M. Prehm, S. Poppe and C. Tschierske, Chem. – Eur. J., 2017, 23, 5541; (c) N. Sebastian, S. Belau, A. Eremin, M. Alaasar, M. Prehm and C. Tschierske, Phys. Chem. Chem. Phys., 2017, 19, 5895; (d) M. Alaasar, M. Prehm, M.-G. Tamba, N. Sebastian, A. Eremin and C. Tschierske, ChemPhysChem, 2016, 17, 278; (e) M. Alaasar, M. Prehm, M. Poppe, M. Nagaraj, J. K. Vij and C. Tschierske, Soft Matter, 2014, 10, 5003.
67. (a) M. Alaasar, M. Prehm, M. Nagaraj, J. K. Vij and C. Tschierske, Adv. Mater., 2013, 25, 2186; (b) M. Alaasar, M. Prehm, K. May, A. Eremin and C. Tschierske, Adv. Funct. Mater., 2014, 24, 1703.
68. H. Ocak, B. Bilgin-Eran, M. Prehm and C. Tschierske, Soft Matter, 2012, 8, 7773.
69. E. Gorecka, N. Vaupotic, A. Zep, D. Pociecha, J. Yoshioka, J. Yamamoto and H. Takezoe, Angew. Chem., Int. Ed., 2015, 54, 10155.
70. C. Tschierske, Angew. Chem., Int. Ed., 2013, 52, 8828.
71. (a) F. Hajjaj, T. Kajitani, H. Ohsumi, Y. Tanaka, K. Kato, M. Takata, H. Kitazawa, T. Arima, T. Aida and T. Fukushima, Nat. Commun., 2018, 9, 4431; (b) K. Suzuki, Y. Uchida, R. Tamura, S. Shimono and J. Yamauchi, J. Mater. Chem., 2012, 22, 6799; (c) Y. Uchida, K. Suzuki, R. Tamura, N. Ikuma, S. Shimono, Y. Noda and J. Yamauchi, J. Am. Chem. Soc., 2010, 132, 9746–9752.
72. (a) S. Kapuscinski, A. Gardias, D. Pociecha, M. Jasinski, J. Szczytko and P. Kaszynski, J. Mater. Chem. C, 2018, 6, 3079; (b) K. Bajzıkova, M. Kohout, J. Tarabek, J. Svoboda, V. Novotna, J. Vejpravova, D. Pociecha and E. Gorecka, J. Mater. Chem. C, 2016, 4, 11540.
73. V. Domenici, C. Alberto Veracini and B. Zalar, Soft Matter, 2005, 1, 408.
74. V. Domenici, C. Alberto Veracini, K. Fodor-Csorba, G. Prampolini, I. Cacelli, A. Lebar and B. Zalar, ChemPhysChem, 2007, 8, 2321.
75. M. A. Aliev, E. A. Ugolkova and N. Y. Kuzminyh, J. Mol. Liq., 2019, 292, 111395.
76. T. Ostapenko, D. B. Wiant, S. N. Sprunt, A. Jakli and J. T. Gleeson, Phys. Rev. Lett., 2008, 101, 247801.
77. O. Francescangeli, F. Vita, F. Fauth and E. T. Samulski, Phys. Rev. Lett., 2011, 107, 207801.
78. P. K. Challa, S. N. Sprunt, A. Jakli and J. T. Gleeson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 010501(R).
79. S. M. Salili, J. Xiang, H. Wang, Q. Li, D. A. Paterson, J. M. D. Storey, C. T. Imrie, O. D. Lavrentovich, S. N. Sprunt, J. T. Gleeson and A. Jakli, Phys. Rev. E, 2016, 94, 042705.
80. V. Domenici, A. Marini, C. Alberto Veracini, J. Zhang and R. Y. Dong, ChemPhysChem, 2007, 8, 2575.
81. V. Domenici, C. Alberto Veracini, V. Novotna and R. Y. Dong, ChemPhysChem, 2008, 9, 556.
82. M. Xie, J. Qin, Z. Hu and H. Zhao, Chin. Chem. Lett., 1992, 3, 775.
83. J. Qin, M. Xie, Z. Hu and H. Zhao, Synth. Commun., 1992, 22, 2253.
84. J. Barbera, L. Puig, P. Romero, J. L. Serrano and T. Sierra, J. Am. Chem. Soc., 2006, 128, 4487.
85. B. Otterholm, M. Nilsson, S. T. Lagerwall and K. Skarp, Liq. Cryst., 1987, 2, 757.
86. P. C. Jocelyn and N. Polgar, J. Chem. Soc., 1953, 132.
87. J.-S. Hu, B.-Y. Zhang, A.-J. Zhou, B.-G. Du and L.-Q. Yang, J. Appl. Polym. Sci., 2006, 100, 4234.
88. C. Tschierske and H. Zaschke, J. Prakt. Chem., 1989, 331, 365.
89. G. S. Lee, Y.-J. Lee, S. Y. Choi, Y. S. Park and K. B. Yoon, J. Am. Chem. Soc., 2000, 122, 12151.
90. (a) R. Achten, R. Cuypers, M. Giesbers, A. Koudijs, A. T. M. Marcelis and E. J. R. Sudhölter, Liq. Cryst., 2004, 31, 1167; (b) S. Balamurugan, P. Kannan, K. Yadupati and A. Roy, Liq. Cryst., 2011, 38, 1199.
91. D. Shen, A. Pegenau, S. Diele, I. Wirth and C. Tschierske, J. Am. Chem. Soc., 2000, 122, 1593.
92. K. Muhammad, S. Hameed, J. Tan and R. Liu, Liq. Cryst., 2011, 38, 333.
93. S.-W. Oh, S.-H. Kim and T.-H. Yoon, J. Mater. Chem. C, 2018, 6, 6520.
94. J. Watanabe and T. Nagase, Macromolecules, 1988, 21, 171.
95. A. Jakli, Liq. Cryst. Rev., 2013, 1, 65.
96. O. Francescangeli, F. Vita and E. T. Samulski, Soft Matter, 2014, 10, 7685.
97. P. S. Salter, P. W. Benzie, R. A. Reddy, C. Tschierske, S. J. Elston and E. P. Raynes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031701.
98. G. Pelzl, A. Eremin, S. Diele, H. Kresse and W. Weissflog, J. Mater. Chem., 2002, 12, 2591.
99. I. Dozov, Eur. Lett., 2001, 56, 247.
100. For details of the determination of the d-spacings in aligned and non-aligned samples, see Experimental.
101. Investigation under a magnetic field and without magnetic field were conducted in different instrumental set-ups so that small differences of the sample detector distance cannot be avoided. Therefore, the small differences of the d-values of the WAXS between (S)-2/12 and rac-2/12 cannot be interpreted with certainty (the WAXS curves represent averages of three measurements, see Tables S2 and S3). However, any change of the position of the reflection depending on temperature, i.e. the shape of the curves is fully reproducible in the three subsequente measurements .
102. C.-L. Yuan, W. Huang, Z.-G. Zheng, B. Liu, H. K. Bisoyi, Y. Li, D. Shen, Y. Lu and Q. Li, Sci. Adv., 2019, 5, eaax9501.
103. S. Chakraborty, M. K. Das, K. Keith and C. Tschierske, Mater. Adv., 2020, 1, 3545.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0tc05355d

---