Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optical absorption and shape transition in neutral SnN clusters with N ≤ 40: a photodissociation spectroscopy and electric beam deflection study†
Andreas
Lehr
 *,
Filip
Rivic
*,
Filip
Rivic
 ,
Marc
Jäger
,
Marc
Jäger
 ,
Martin
Gleditzsch
,
Martin
Gleditzsch
 and
Rolf
Schäfer
and
Rolf
Schäfer
Technical University of Darmstadt, Eduard-Zintl-Institut, Alarich-Weiss-Straße 8, 64287 Darmstadt, Germany. E-mail: andreas.lehr@tu-darmstadt.de
First published on 4th May 2022
Abstract
Neutral SnN clusters with N = 6–20, 25, 30, 40 are investigated in a joint experimental and quantum chemical study with the aim to reveal their optical absorption in conjunction with their structural evolution. Electric beam deflection and photodissociation spectroscopy are applied as molecular beam techniques at nozzle temperatures of 16 K, 32 K and 300 K. The dielectric response is probed following the approach in S. Schäfer et al., J. Phys. Chem A, 2008, 112, 12312–12319. It is improved on those findings and the cluster size range is extended in order to cover the prolate growth regime. The impact of the electric dipole moment, rotational temperature and vibrational excitation on the deflection profiles is discussed thoroughly. Photodissociation spectra of tin clusters are recorded for the first time, show similarities to spectra of silicon clusters and are demonstrated to be significantly complicated by the presence of multiphoton absorption in the low-energy region and large excess energies upon dissociation which is modelled by the RRKM theory. In both experiments two isomers for the clusters with N = 8, 11, 12, 19 need to be considered to explain the experimental results. Triple-capped trigonal prisms and double-capped square antiprisms are confirmed to be the driving building units for almost the entire size range. Three dominating fragmentation channels are observed, i.e. the loss of a tin atom for N < 12, a Sn7 fragment for N < 19 and a Sn10 fragment for N ≥ 19 with Sn15 subunits constituting recurring geometric motifs for N > 20. The prolate-to-quasispherical structural transition is found to occur at 30 < N ≤ 40 and is analyzed with respect to the observed optical behavior taking quantum chemical calculations and the Mie–Gans theory into account. Limitations of the experimental approach to study the geometric and electronic structure of the clusters at elevated temperatures due to vibrational excitation is also thoroughly discussed.
1 Introduction
Group 14 of the periodic table, comprising C, Si, Ge, Sn, Pb (and Fl), is arguably the most significant group of elements in all chemistry. The metals lead and tin are widely known for their use in the production of structural components and alloys, the semiconductors silicon and germanium constitute the foundation of modern technology and the nonmetal carbon, evidently, states the basis of organic life.1 It is in particular this nonmetal-to-semiconductor-to-metal transition along the group of these tetrel elements (referring to the most common valency of four) that intrigues engineers and researchers alike. With tin being on the very edge of this transition, it exhibits, as a consequence, two stable allotropes, the gray diamond cubic α-Sn and the white body-centered tetragonal β-Sn, resembling the zero-gap semiconductor2 (<286 K) and metal nature of this material, respectively. Albeit standing in the shadows of silicon (and also germanium) dominating the semiconductor industry, tin offers various desirable properties such as being non-toxic, inexpensive and a widespread element. Driven by the endeavor to further miniaturize electronic devices, silicon nanoparticles have already found their way into the microelectronic industry.3–6 Also tin nanoparticles are dealt in energy storage applications as promising anode material in next-generation batteries due to their high capacity.7–10 Since small clusters are well known for their physical properties being tremendously size, composition and charge state-dependent, thus being tunable, and with tin clusters showing similar structural growth patterns and optoelectronic properties as silicon clusters – as to be revealed by this study – a vast range of potential applications is expected to open up.After the first mass spectrometric detection of small tin clusters by simple vaporization in 1952,11 it took several years until their stabilities have been probed by means of determining atomization enthalpies.12–14 The time-resolved laser-induced fluorescence spectroscopy of the Sn2 dimer in 1982 provided accurate insights into the geometric and electronic structure15,16 and, besides early extended Hückel studies,17,18 opened up a playground for quantum chemists to study the low-lying excited states, equilibrium geometric constants and potential energy surfaces for small clusters up to Sn6 employing extensive multireference configuration interaction methods.19–27 While on the theoretical side density functional theory (DFT) has become today's routine for investigating the geometries and electronic structure of larger clusters,28–51 there have only been a few experimental studies validating the manifold of proposed geometries. Mass spectrometric investigations alone52,53 or involving photoionization and photofragmentation54–59 are usually not capable for obtaining structural information. Cationic tin cluster geometries have been successfully examined by ion mobility42,60–62 and low-energy surface collision measurements63,64 revealing a prolate growth pattern, similar to observations made for silicon and germanium clusters61 before quasispherical structures become favorable again for larger clusters. To study anionic clusters photoelectron spectroscopy has been proven one of the most powerful tools,65–71 but also ion mobility, trapped ion diffraction and collision induced dissociation experiments have been conducted.39,41,45 When talking about charged tin clusters, it is worth mentioning that for cationic species the abnormally high melting temperatures above the bulk value have been discovered for the first time.36,72–77 Also, the icosahedral stannaspherene cluster Sn122− which was found by photoelectron spectroscopy78–81 has acquired huge interest due to being the scaffold for paramagnetic superatoms82–84 as well as its relation to Zintl ions and (inter-)metalloid compounds.85–98 Neutral clusters, however, are more difficult to probe experimentally. There are only two kinds of studies addressing the geometry discrimination of neutral tin clusters, one which measures the formation energies of tin cluster distributions consisting of hundreds of atoms calorimetrically99,100 and one which focuses on the structure elucidation of SnN clusters with N = 6–20 based on measuring the Stark effect in combination with photoionization and quantum chemical calculations.37 The results presented here take up the findings of the latter study on the geometric evolution of small tin clusters, extend the size range and place special focus on the interplay between geometric structure and the optical absorption. Apart from a standalone study of a Sn14 cluster,51 the optoelectronic characteristics lack entirely both experimental and theoretical investigations making this the first such study employing a combined photodissociation spectroscopy and electric beam deflection approach supported by demanding quantum chemical calculations.
2 Experimental methods
An extensive presentation of the methodology and experimental details are described for both experimental approaches elsewhere.101–105 Therefore, only a brief overview is given here. In general, neutral and charged Sn clusters are generated by a pulsed (10 Hz) and He buffer gas perfused laser vaporization source which can be cooled down via a cryogenic nozzle (Tnozzle ≥ 16 K) prior to the expansion into high vacuum and the subsequent formation of the molecular beam.2.1 Electric beam deflection
In this experiment the molecular beam is formed by expansion into the high vacuum through a double-skimmer. Afterwards, it passes a mechanical shutter based on a hard drive disk106,107 which allows one to determine the velocity vx of the clusters in flight direction x.108 Two collimating slits shape the molecular beam to the rectangular profile of 0.4 mm width and 2.0 mm height. Here, the second collimating slit is located directly in front of the electric deflection unit which is based on the two-wire geometry to maintain a nearly constant gradient in the direction of deflection z.109 The deflection is probed by a scanning slit aperture such that the intensities of the mass signals are measured in dependence of the position along the inhomogeneous field. The clusters are ionized by an F2 excimer laser (7.89 eV) directly behind the scanning slit and detected in a time-of-flight mass spectrometer (TOF-MS). To avoid multiphotoionization and photofragmentation a plane-concave lense widens the profile of the F2 excimer laser along the direction of flight. To be able to interpret the beam deflection profiles, mass spectra with and without applied field are recorded alternatingly. Regarding the intensities of the beam deflection profiles shown in this work, these mass spectra pairs are recorded at every position in random order. In order to compare the beam deflection profiles from several experimental runs, the measured deflection dz has to be displayed independently of the cluster velocity vx which varies slightly in every run. Therefore, the measured deflection is converted into the mean projection of the dipole moment on the field direction![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) el,z of the SnN clusters. In eqn (1)mSn is the mass of the tin atom, dEz/dz the electric field gradient and l1 and l2 the lengths of the electric field and field free region, respectively.
el,z of the SnN clusters. In eqn (1)mSn is the mass of the tin atom, dEz/dz the electric field gradient and l1 and l2 the lengths of the electric field and field free region, respectively.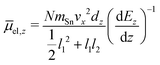 | (1) |
2.2 Photodissociation spectroscopy
After the expansion into high vacuum through a skimmer and thereby forming the molecular beam, an electric deflector is used to remove charged particles. The optical response is probed by longitudinal photodissociation spectroscopy employing an optical parametric oscillator combined with several harmonic generators, which covers the photon energy range of ħω = 1.9–5.4 eV. After the interaction with the dissociation laser, the neutral species are photoionized either by a Xe flash lamp (<10.3 eV) or an F2 excimer laser (7.89 eV) and are detected by a TOF-MS. The photon fluence is kept low to avoid multiphoton dissociation processes while recording photoionization mass spectra. Optical absorption spectra are measured by monitoring the mass signal depletion I/I0 as a function of the photon energy ħω and applying the Beer–Lambert law to calculate the dissociation cross section σ(ħω) assuming an one-photon absorption process. In eqn (2) a perfect overlap between the dissociation laser and the molecular beam has to be guaranteed and the photon fluence ϕ needs to be determined in a separate experiment.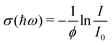 | (2) |
3 Computational methods
3.1 Genetic algorithm
Suitable structural candidates of the SnN clusters with N = 6–20, 25, 30, 40 are identified by means of an unbiased global optimization of the configurational space. This is accomplished with the help of the German Improved Genetic Algorithm (GIGA)112 at a plane-wave DFT level of theory using Quantum Espresso v6.4.1.113,114 In this process, the PBE exchange–correlation (xc) functional115,116 and the ultrasoft RRKJ pseudopotential117,118 (36 core electrons for tin) with a plane-wave kinetic energy cutoff of 400 eV were employed. The box size of the unit cell is determined dynamically such that no duplicate clusters are closer than 16 Å and self-interaction can be neglected. Spin polarization was implemented and a small Methfessel–Paxton smearing119 as well as non-linear core corrections120 were applied. The pool started with 15 up to 25 randomly generated structures for Sn6 up to Sn20. In order to render the search for symmetric structures more efficient, clusters containing triple-capped trigonal prism and double-capped square antiprism units have been used in the starting pool for Sn25, Sn30 and Sn40. The search routine was stopped when the most recent 1000 structures being generated did not appear below 1 eV relative to the pool global minimum (GM). For Sn40, i.e., a total of 5000 geometries were created. The results of the global optimization are analyzed with the help of our GA analysis software.1123.2 Geometry optimization and frequency analyses
All lowest-lying isomers are locally reoptimized using Gaussian16121 and NWChem v6.8.1.122,123 Orbital-based DFT with tight optimization criteria and a high-density numerical grid is applied employing the PBE0/cc-pVTZ-PP124–126 and LC-ω PBEh/def2-TZVPP125,127,128 xc functional/basis set combinations taking into account singlet and triplet spin configurations. Scalar relativistic corrections are effectively treated by the use of such pseudopotential-supported basis sets. The choice of the xc functional/basis set combination is justified by an extensive benchmark with experimental data of Sn6 and Sn751 as well as previous studies on doped tin clusters.129–132 CCSD(T)/cc-pVTZ-PP single-point energies on top of the PBE0/cc-pVTZ-PP optimized geometries have been computed using the domain-based local pair natural orbital (DLPNO) acceleration approach133–136 implemented in Orca v5.0.1.137–139 Furthermore, the CCSD(T) energies were computed using the TightPNO criteria and extrapolated to the complete basis set limit using the two-point extrapolation for the cc-pVTZ-PP and corresponding auxiliary basis sets.140 Only those clusters were considered for the analysis of the experiment with a relative energy of ΔE ≤ 0.20 eV with respect to the predicted GM on either of the three levels of theory. Some final structural isomers of larger clusters have only been found from reoptimizing corresponding cationic GA candidates. An overview of all reoptimized cationic SnN+ structures can be found in the ESI.† Harmonic frequency analyses are performed for all species in order to verify that the optimized geometries correspond to local minima on the potential energy surface. A summary of the vibrational frequencies of all structural isomers can be found in the ESI.†3.3 Dielectric and optical response
The moments of inertia and the dielectric properties comprising the electric dipole moment components and the isotropic electronic polarizability were taken from PBE0/cc-pVTZ-PP results due to their already demonstrated good accuracy-cost balance for tin-based clusters.51,129–132 With these properties, electric deflection profiles can be predicted by simulating the rotational dynamics of an ensemble of clusters in the electric field. Here, a classical approach is considered, since even for low rotational temperatures rotational states of high angular momentum quantum number J are still significantly populated.102 To give an example, already a rotational temperature of Trot = 1 K causes the rotational states of the smallest cluster under investigation, Sn6, to be significantly populated up to J = 30 considering a rotational constant of B = 0.44 m−1. A canonical ensemble of 5000 clusters is set up with an individually defined rotational state and Boltzmann-distributed with a defined rotational temperature. These clusters enter the electric field adiabatically such that the given rotational state does not change when entering the inhomogeneous field. Within the field, the Euler equations for a classical rotor are solved in a trajectory simulation for every time step.102,141 The resulting distribution of the electric dipole moments of the ensemble is then convoluted with the Gaussian function describing the experimental beam profile without applied electric field. This procedure yields the simulated electric deflection profiles which can be compared to the experiment. Note that this approach is only valid for rigid rotors. The shift of the simulated deflection profile is connected to the computed electronic polarizability of the cluster.37,102 Since the rotational temperature can only be estimated for a given nozzle temperature and the electric dipole moments resulting from quantum chemical calculations come with an uncertainty of up to 10–15%,142 it is necessary to investigate their influence on the simulated electric beam profiles of the tin clusters. For this, the electric deflection profile together with the classical trajectory simulations are shown exemplary for Sn10 with varied values of the electric dipole moments and rotational temperatures in the ESI.† This cluster is well suited for such a study because there is only one structural isomer present, which possesses only one non-zero component of the electric dipole moment. The results indicate that both reducing the electric dipole moment component and increasing the rotational temperature also yield a simulated deflection profile which describes the experimental data to a good approximation, so that one has to keep in mind that there is a certain freedom in choosing these two parameters. Because the experimental data for larger clusters with N > 18 could only be obtained with a higher nozzle temperature of 30 K, setting the rotational temperature to Trot = 20 K is considered appropriate.108,132 Furthermore, the calculation of an effective polarizability by using second-order perturbation theory (cf. ESI† for details) demonstrates that a rotational temperature of 20 K is the most reasonable choice for most cluster species. With these two things in mind, all trajectory simulations in this work have been carried out with the computed electric dipole moments and a rotational temperature of Trot = 20 K for reasons of consistency.Singlet excited states and corresponding transition dipole moments are calculated by means of time-dependent DFT (TDDFT) at the LC-ωPBEh/def2-TZVPP level of theory employing Gaussian16 and NWChem v6.8.1 to simulate the experimentally measured optical absorption spectra. Up to 1500 excited states for Sn40 had to be considered in order to cover the experimental accessible photon energy range. A natural transition orbital (NTO) analysis has been carried out aiming for a more intuitive picture of which (mixed) orbitals are involved in particle–hole excitations.143 The obtained oscillator strengths f are connected to the absorption cross sections σ by integration over the corresponding spectral bands given a certain full width at half maximum (FWHM), which is found to be 0.27 eV for photodissociation spectra recorded at 300 K and 0.20 eV at 32 K.
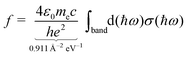 | (3) |
4 Preliminary considerations
4.1 Structural classification
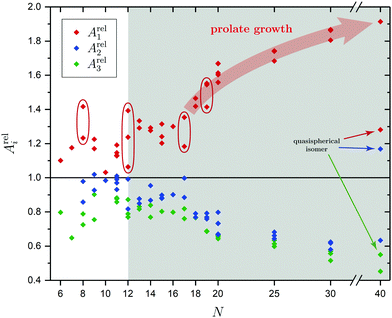
In order to tackle the prolate shape transition and to conceptionalize the cluster's prolateness, the cluster shapes are viewed as ellipsoids with their three semiaxes Ai (A1 ≥ A2 ≥ A3).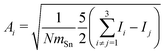 | (4) |
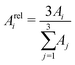 | (5) |
4.2 Fragmentation mechanisms
Before discussing the dielectric and optical behavior, it is worth looking first at the fragmentation mechanisms obtained for the investigated clusters. Since it is far less trivial to study this experimentally for neutral clusters compared to the charged species,42,63,64,111 the photodissociation experiment does not yield cluster-specific information on the photoinduced fragments. However, when varying the delay time of the spectroscopy laser, assuring that fragments will be ionized and detected by the TOF-MS, a considerable gain in the Sn7 and Sn10 mass signals is observed. This can be viewed as evidence for those fragmentation channels to be the most dominant ones. Moreover, dissociation energies for the energetically-lowest fragmentation paths have been calculated and compared with experimental values for the smallest clusters,14 as shown in Fig. 2 and further deepened in the ESI.† Although the correspondence of the calculated dissociation energies with the experimental ones is not quantitative, the trend with cluster size is covered reasonably well. Due to the particularly stable Sn7 and Sn10 units, three significant fragmentation channels can be observed. SnN clusters with N < 12 favor the loss of a tin atom. Clusters with N < 19 dissociate into a Sn7 unit whereas clusters with N ≥ 19 lead into a Sn10 fragment and another daughter cluster. It should be noted that the Sn15 unit is also comparatively stable which is in agreement with recent theoretical findings,44,47 but does not replace the Sn10 fragmentation channel for this size range. Interestingly, the computed dissociation energies resemble quite well the anti-magic abundance pattern of the clusters Sn13, Sn14, Sn17 and Sn20, which fragment more easily given the energy difference between the F2 excimer laser energy of 7.89 eV and their ionization potentials all being in the range 6.17–6.43 eV.59 The energetics of these dissociation mechanisms have a far-reaching impact on the evaluation of our photodissociation spectra when interpreted in terms of optical absorption, which is discussed in detail for Sn6, Sn7 and Sn10 in Sections 5.1 and 5.2 taking also multiphoton processes into account.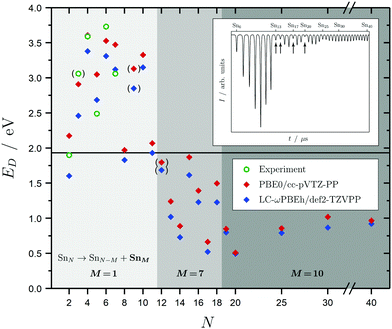 | ||
| Fig. 2 Dissociation energies ED in eV for the energetically most favorable fragmentation channels of the SnN clusters with N = 2–20, 25, 30, 40 averaged over all isomers in the given energy range. Experimental values for the incremental dissociation energies are estimated based on atomization enthalpies obtained from Knudsen cell mass spectrometry.14 The horizontal line at 1.9 eV gives the smallest accessible single-photon energy available in our photodissociation experiment. Over the size range studied, three regions can be distinguished: dissociation under the loss of an atom (light gray), a Sn7 (gray) and a Sn10 fragment (dark gray). Calculated dissociation energies in parantheses point to a differing fragmentation mechanism, i.e., loss of a Sn2 fragment for the Sn9 parent cluster and loss of Sn6 fragments for the Sn12 parent cluster. The Sn3 experimental dissociation energy in paranthesis has been evaluated assuming a linear geometry12 (in its lowest 1A1 and 3B2 state Sn3 is an isoscele triangle21) and has thus to be considered with care. The inset shows a typical time-of-flight mass spectrum after F2 excimer laser photoionization (7.89 eV) of the SnN clusters given as arbitrary intensity I in dependence of the flight time t; the naturally low-abundant clusters Sn13, Sn14, Sn17 and Sn20 are highlighted by arrows. | ||
4.3 Dissociation kinetics
To comprehend the fragmentation of the clusters on the experimental time scale, it is favorable to investigate the kinetics of the photodissociation process. Many small metal clusters have been found to fragment via statistical unimolecular dissociation110 such that the rate constant for dissociation k can be evaluated in terms of the Rice–Ramsperger–Kassel–Marcus (RRKM) theory.146–149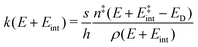 | (6) |
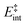 the internal energy comprising the “active” vibrational and rotational degrees of freedom at the initial and transition state,150ED the dissociation energy, s the reaction path degeneracy, n‡ the sum of ro-vibrational states at the transition state and ρ the density of ro-vibrational states. The latter two quantities are computed employing the Beyer–Swinehart direct count algorithm.151 The reaction path degeneracy s varies depending on the dissociation process as well as the cluster geometry and is chosen individually for all structural isomers. To give some expamples, s is set to the number of atoms for an atom-loss process of the Sn6 and Sn7 parent cluster, whereas it is lowered for larger clusters whenever there are peripheral tin atoms leaving behind a stable daughter subunit. The same holds for other fragmentation channels of larger clusters where a Sn7 or Sn10 cluster fragment is discernible in the parent cluster structure. The clusters are well known to have highly excited angular momentum already at very low rotational temperatures, which is why the angular momentum dependence in eqn (6) has been considered in the first place. However, in estimating approximate lifetimes of the clusters under experimental conditions, the angular momentum dependence is shown to cause only insignificant changes and could be reasonably dropped. Furthermore, it has been found to be of minor importance which vibrational mode is responsible for dissociation, especially as the cluster size increases. Therefore, anharmonic corrections to the vibrational frequencies have been neglected, although they can become important in certain situations due to the high degree of vibrational excitation common in unimolecular dissociation processes. The assumption is made that no activation barrier is related to the fragmentation process, thus drawing a direct relation between the transition state and dissociation energy for reactions of the type SnN → SnN−M + SnM. It should be noted that care has to be taken, since the activation barriers in general are not obtainable in a straightforward way and thus not regarded here. By calculating the rate of dissociation, lifetimes τ of the clusters can be estimated as a function of their excess energy E − ED as shown in Fig. 3 and listed fully in the ESI,† providing a useful insight into the dissociation behavior under the given experimental conditions. Due to the neglected activation barrier, the calculated lifetime and rate of dissociation have to be seen as lower and upper limit, respectively. Taking the Sn6 cluster as an example, the one-photon dissociation is expected to be detected at a photon energy of approximately 4.1 eV on the experimental time scale given the (calculated) dissociation energy of 3.53 eV.
the internal energy comprising the “active” vibrational and rotational degrees of freedom at the initial and transition state,150ED the dissociation energy, s the reaction path degeneracy, n‡ the sum of ro-vibrational states at the transition state and ρ the density of ro-vibrational states. The latter two quantities are computed employing the Beyer–Swinehart direct count algorithm.151 The reaction path degeneracy s varies depending on the dissociation process as well as the cluster geometry and is chosen individually for all structural isomers. To give some expamples, s is set to the number of atoms for an atom-loss process of the Sn6 and Sn7 parent cluster, whereas it is lowered for larger clusters whenever there are peripheral tin atoms leaving behind a stable daughter subunit. The same holds for other fragmentation channels of larger clusters where a Sn7 or Sn10 cluster fragment is discernible in the parent cluster structure. The clusters are well known to have highly excited angular momentum already at very low rotational temperatures, which is why the angular momentum dependence in eqn (6) has been considered in the first place. However, in estimating approximate lifetimes of the clusters under experimental conditions, the angular momentum dependence is shown to cause only insignificant changes and could be reasonably dropped. Furthermore, it has been found to be of minor importance which vibrational mode is responsible for dissociation, especially as the cluster size increases. Therefore, anharmonic corrections to the vibrational frequencies have been neglected, although they can become important in certain situations due to the high degree of vibrational excitation common in unimolecular dissociation processes. The assumption is made that no activation barrier is related to the fragmentation process, thus drawing a direct relation between the transition state and dissociation energy for reactions of the type SnN → SnN−M + SnM. It should be noted that care has to be taken, since the activation barriers in general are not obtainable in a straightforward way and thus not regarded here. By calculating the rate of dissociation, lifetimes τ of the clusters can be estimated as a function of their excess energy E − ED as shown in Fig. 3 and listed fully in the ESI,† providing a useful insight into the dissociation behavior under the given experimental conditions. Due to the neglected activation barrier, the calculated lifetime and rate of dissociation have to be seen as lower and upper limit, respectively. Taking the Sn6 cluster as an example, the one-photon dissociation is expected to be detected at a photon energy of approximately 4.1 eV on the experimental time scale given the (calculated) dissociation energy of 3.53 eV.
 | ||
| Fig. 3 RRKM lifetimes τ exemplary shown for the clusters Sn6, Sn8, Sn10, Sn16, Sn19, Sn30 and Sn40 for the lowest-energy isomers as a function of the excess energy E − ED. Dashed lines represent model results for the PBE0/cc-pVTZ-PP computed dissociation energies (also given in the top right box) and the solid line for Sn6 shows the result based on the experimentally estimated dissociation energy of 3.73 eV.14 The gray area can be understood as an approximate flight time window of the clusters between encountering the dissociation laser and the detection in the TOF-MS within the photodissociation experiment. | ||
5 Results
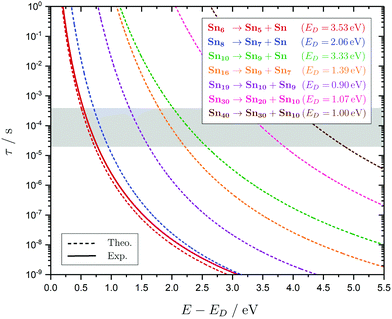
In the following subsections the geometries, the electric deflection profiles as well as the photodissociation spectra of the clusters, summarized in Fig. 4–9, will be discussed in detail. This joint experimental approach, often complementary in informational value, is demonstrated to be a powerful tool when combined with predictions from quantum chemistry to get a deeper understanding of the geometric and electronic structure of the clusters. It does not only shine light on the structural evolution of small tin clusters, but also yields details on the optical absorption and electronic structure of these particles.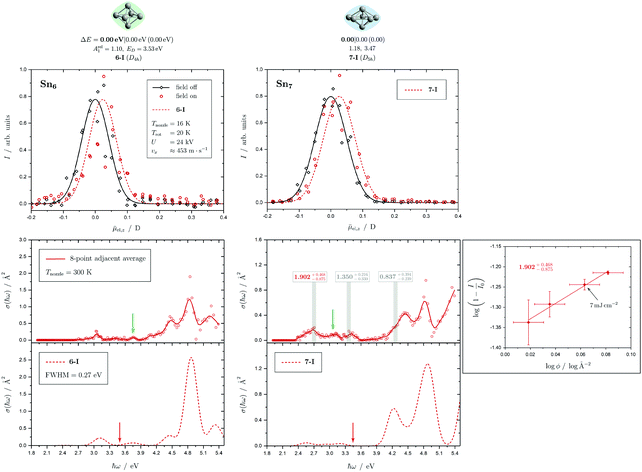 | ||
Fig. 4 Summary of all structural isomers (top), electric beam deflection measurements together with the corresponding classical trajectory simulations (center) and all photodissociation spectra together with the TDDFT simulations (bottom), here shown for the clusters Sn6 and Sn7. This caption serves as basis also for the following figures. Top: The geometries are shown together with their molecular point groups. The first line gives the energies ΔE relative to the GM in eV at the PBE0/cc-pVTZ-PP|CCSD(T)/cc-pVTZ-PP(LC-ωPBEh/def2-TZVPP) levels of theory. The second line gives the largest dimensionless semiaxis Arel1 for an ellipsoid as a measure of the cluster's prolateness, followed by the dissociation energy ED for the lowest fragmentation channel in eV at the PBE0/cc-pVTZ-PP level of theory. Recurring building units are highlighted in color: distorted octahedron (green), pentagonal bipyramid (blue), triple-capped trigonal prism (yellow), single- (violet) and double-capped square antiprism (red). All lowest-lying isomers have been found to be spin singlets. Center: The electric beam deflection profiles, given as arbitrary normalized intensity I as a function of the mean projection of the dipole moment on the field direction ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) el,z, are shown with (red circles) and without applied electric field (black diamonds). The latter one has been fitted by a Gaussian around the center of deflection (solid black line). The electric deflection profiles were recorded at lowest possible nozzle temperatures of 16 K and a deflection voltage of 24 kV for clusters N ≤ 19 as well as 30 K and 20 kV for N > 19 assuming uniform rotational temperatures of 20 K. The velocities were measured to be 453 ± 3 ms−1. Trajectory simulations have been performed employing moments of inertia, dipole moments and polarizabilities at the PBE0/cc-pVTZ-PP level of theory (dashed lines). Bottom: The photodissociation spectra, given as absorption cross section σ as a function of the photon energy ħω, are shown by discrete points (red circles) traced by an eight-point adjacent average (red solid line) to guide the eye. The photodissociation spectra were recorded at nozzle temperatures of 300 K (shown here) and 32 K (not shown here). For Sn7, at 2.70 eV (shown to the right), 3.35 eV and 4.25 eV, indicated by the gray vertical bars, the depletion 1 − I/I0 has been plotted against the photon fluence ϕ double-logarithmically, such that the number of absorbed photons can be extracted from the slope (given in gray boxes).110,152,153 The rather large uncertainties are due to the nature of the depletion experiment and are estimated from the deviation determined by the depletion and fluence error bars. Significantly lower energy densities than the indicated 7 mJ cm−2 in order to avoid such multiphoton absorption processes cannot be easily applied due to vanishingly small differences in mass signal ratios. TDDFT simulations were obtained at the LC-ωPBEh/def2-TZVPP level of theory by convoluting the discrete electronic transitions with Gaussians of an experimental FWHM of 0.27 eV at 300 K (dashed lines, shown here) and 0.20 eV at 32 K (dotted line, not shown here). Experimentally estimated dissociation energies are indicated by green arrows14 and computed dissociation energies at the PBE0/cc-pVTZ-PP level of theory for the energetically-lowest fragmentation channels averaged over all isomers are shown by red arrows when being above 1.8 eV. el,z, are shown with (red circles) and without applied electric field (black diamonds). The latter one has been fitted by a Gaussian around the center of deflection (solid black line). The electric deflection profiles were recorded at lowest possible nozzle temperatures of 16 K and a deflection voltage of 24 kV for clusters N ≤ 19 as well as 30 K and 20 kV for N > 19 assuming uniform rotational temperatures of 20 K. The velocities were measured to be 453 ± 3 ms−1. Trajectory simulations have been performed employing moments of inertia, dipole moments and polarizabilities at the PBE0/cc-pVTZ-PP level of theory (dashed lines). Bottom: The photodissociation spectra, given as absorption cross section σ as a function of the photon energy ħω, are shown by discrete points (red circles) traced by an eight-point adjacent average (red solid line) to guide the eye. The photodissociation spectra were recorded at nozzle temperatures of 300 K (shown here) and 32 K (not shown here). For Sn7, at 2.70 eV (shown to the right), 3.35 eV and 4.25 eV, indicated by the gray vertical bars, the depletion 1 − I/I0 has been plotted against the photon fluence ϕ double-logarithmically, such that the number of absorbed photons can be extracted from the slope (given in gray boxes).110,152,153 The rather large uncertainties are due to the nature of the depletion experiment and are estimated from the deviation determined by the depletion and fluence error bars. Significantly lower energy densities than the indicated 7 mJ cm−2 in order to avoid such multiphoton absorption processes cannot be easily applied due to vanishingly small differences in mass signal ratios. TDDFT simulations were obtained at the LC-ωPBEh/def2-TZVPP level of theory by convoluting the discrete electronic transitions with Gaussians of an experimental FWHM of 0.27 eV at 300 K (dashed lines, shown here) and 0.20 eV at 32 K (dotted line, not shown here). Experimentally estimated dissociation energies are indicated by green arrows14 and computed dissociation energies at the PBE0/cc-pVTZ-PP level of theory for the energetically-lowest fragmentation channels averaged over all isomers are shown by red arrows when being above 1.8 eV. | ||
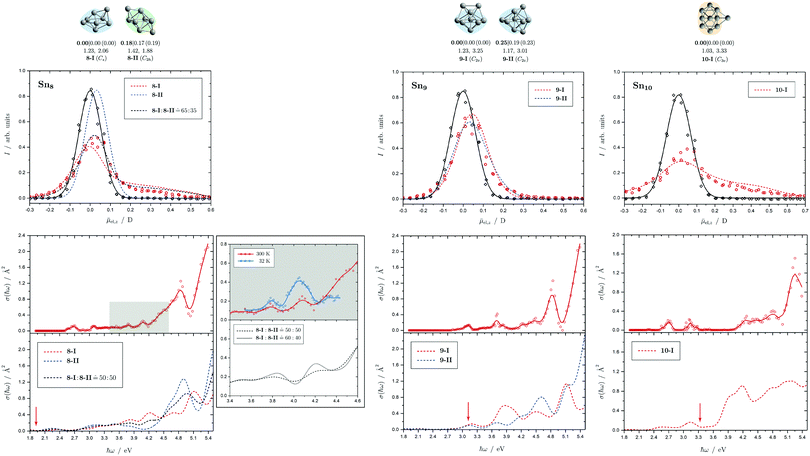 | ||
Fig. 5 Summary of all structural isomers (top), electric beam deflection measurements together with the corresponding trajectory simulations (center) and all photodissociation spectra together with the TDDFT simulations (bottom) for the clusters Sn8, Sn9 and Sn10. For details of this figure it is referred to the caption of Fig. 4. Bottom: For Sn8 at 300 K an isomer ratio 8-I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8-II 8-II ![[= with combining circumflex]](https://www.rsc.org/images/entities/char_003d_0302.gif) 50 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 is obtained which is shifted to 8-I 50 is obtained which is shifted to 8-I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8-II 8-II ![[= with combining circumflex]](https://www.rsc.org/images/entities/char_003d_0302.gif) 60 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 at 32 K. 40 at 32 K. | ||
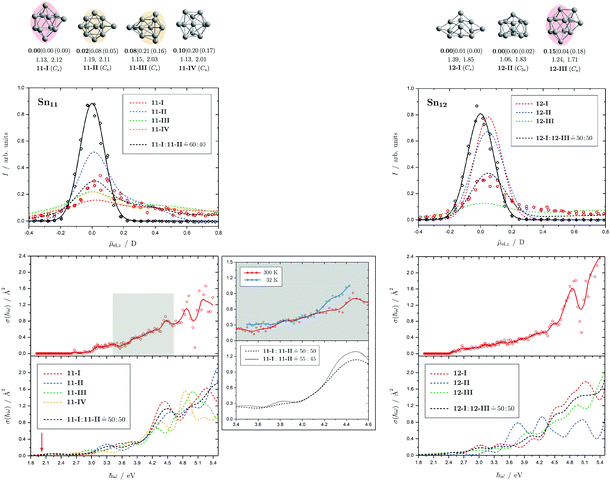 | ||
Fig. 6 Summary of all structural isomers (top), electric beam deflection measurements together with the corresponding trajectory simulations (center) and all photodissociation spectra together with the TDDFT simulations (bottom) for the clusters Sn11 and Sn12. For details of this figure it is referred to the caption of Fig. 4. Bottom: For Sn11 at 300 K an isomer ratio 11-I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11-II 11-II ![[= with combining circumflex]](https://www.rsc.org/images/entities/char_003d_0302.gif) 50 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 is obtained which is shifted to 11-I 50 is obtained which is shifted to 11-I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11-II 11-II ![[= with combining circumflex]](https://www.rsc.org/images/entities/char_003d_0302.gif) 55 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 at 32 K. For Sn12 both at 300 K and 32 K (not shown) a fitted isomer mixture of approximately 12-I 45 at 32 K. For Sn12 both at 300 K and 32 K (not shown) a fitted isomer mixture of approximately 12-I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12-III 12-III ![[= with combining circumflex]](https://www.rsc.org/images/entities/char_003d_0302.gif) 50 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 is found. 50 is found. | ||
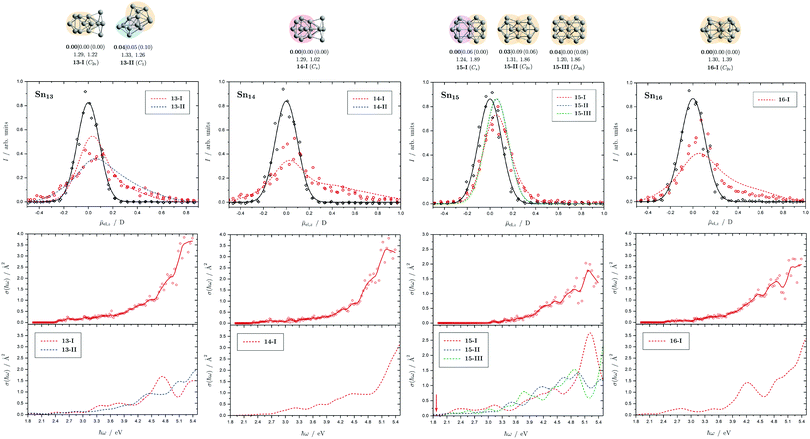 | ||
| Fig. 7 Summary of all structural isomers (top), electric beam deflection measurements together with the corresponding trajectory simulations (center) and all photodissociation spectra together with the TDDFT simulations (bottom) for the clusters Sn13, Sn14, Sn15 and Sn16. For details of this figure it is referred to the caption of Fig. 4. | ||
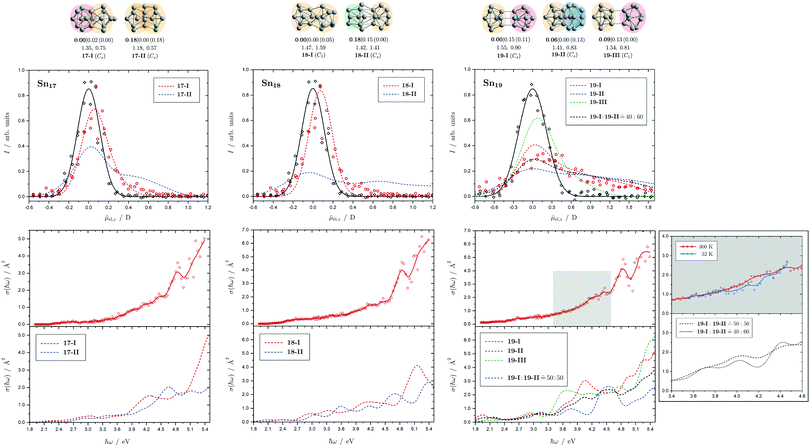 | ||
Fig. 8 Summary of all structural isomers (top), electric beam deflection measurements together with the corresponding trajectory simulations (center) and all photodissociation spectra together with the TDDFT simulations (bottom) for the clusters Sn17, Sn18 and Sn19. For details of this figure it is referred to the caption of Fig. 4. Bottom: For Sn19 at 300 K an isomer ratio 19-I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19-II 19-II ![[= with combining circumflex]](https://www.rsc.org/images/entities/char_003d_0302.gif) 50 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 is obtained which is shifted to 19-I 50 is obtained which is shifted to 19-I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19-II 19-II ![[= with combining circumflex]](https://www.rsc.org/images/entities/char_003d_0302.gif) 40 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 at 32 K. 60 at 32 K. | ||
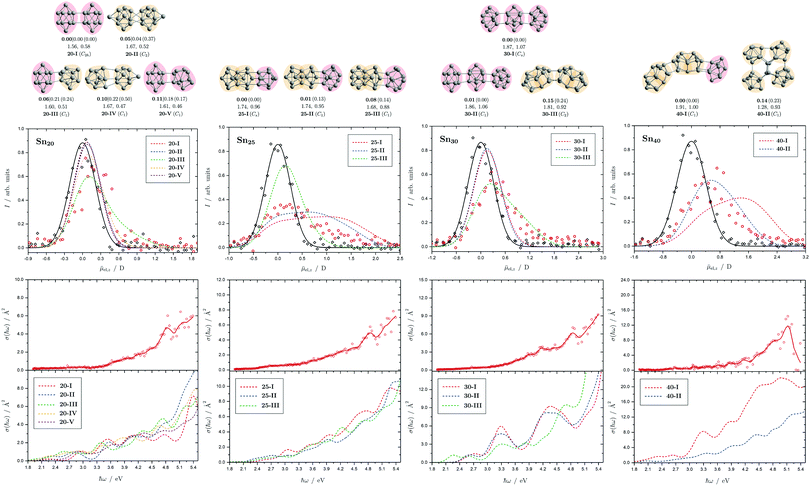 | ||
| Fig. 9 Summary of all structural isomers (top), electric beam deflection measurements together with the corresponding trajectory simulations (center) and all photodissociation spectra together with the TDDFT simulations (bottom) for the clusters Sn20, Sn25, Sn30 and Sn40. For details of this figure it is referred to the caption of Fig. 4. | ||
5.1 Sn6 and Sn7
The conjectured structure of the Sn6 hexamer is a distorted octahedron (D4h). This structure is consistent with electric deflection measurements and is also found to be the GM in global structure optimization. Characteristic of the optical spectrum is a longest wavelength light absorption at 3.0 eV and a very strong band with a trident signature at 4.7 eV. Both bands are well reproduced with respect to their appearance by the TDDFT calculation, but the measured intensity of the band at 4.7 eV is much lower than theoretically predicted. It should also be noted that the dissociation energy of Sn6 has been found to be 3.73 eV,14i.e., the longest wavelength light absorption is below the dissociation threshold and therefore requires the absorption of more than one photon for dissociation. This finding is on par with the low energy region of the Sn7 spectrum and is further investigated for this cluster. Fig. 3 shows the RRKM lifetime τ of the Sn6 cluster (and others) as a function of the excess energy E − ED and provides more insight into the dissociation characteristics. Given a realistic experimental time window of 100 μs, the cluster's fragmentation (depletion) should only be detectable at photon energies around 0.6 eV higher than the dissociation energy, further emphasizing the likelihood of multiphoton absorption processes. This picture is not significantly altered when using the DFT predicted dissociation energy of 3.53 eV.The corresponding structure of the heptamer Sn7 is a pentagonal bipyramid (D5h). This structure is also consistent with electric deflection measurements and global optimization. From 2.5–3.5 eV there is a weaker band with a trident shape and from 4.1–5.4 eV an intense band is observed, also consisting of three sub-bands. As for Sn6, the experimentally observed spectrum is reproduced almost quantitatively in terms of band shape by the TDDFT, although again the measured intensity of the band system at 4.1–5.4 eV is much lower than theoretically predicted. In contrast, the intensity of the bands between 2.5 and 3.5 eV is significantly increased compared to theory. To clarify the multiphoton nature of the light absorption, the dependence of the depletion on the laser fluence at three wavelengths was investigated, as shown in Fig. 4. It is found that a two-photon process is responsible for the observed band at 2.7 eV being below the experimental dissociation threshold of 3.06 eV.14 In contrast, the band at 4.3 eV results from a one-photon absorption. For the band at 3.4 eV, close above the dissociation threshold, both one- and two-photon absorption can lead to dissociation. Given the experimental dissociation energy of 3.06 eV14 and an excess energy of 0.8 eV, the clusters are not expected to fragment via a single photon at 3.4 eV. Since the clusters are assumed to be perfectly equilibrated in the nozzle, this discrepancy might be due to shortcomings in the RRKM model. Furthermore, the reported values for the absorption cross section were calculated from depletion via the Beer–Lambert law and thus do not capture the true character of the absorption process. This is the reason for the unusually large absorption cross sections at 2.5–3.5 eV compared to the band at 4.1–5.4 eV.
5.2 Sn8, Sn9 and Sn10
Two structural isomers have been identified for Sn8, on the one hand a polar single-capped pentagonal bipyramid (8-I) and on the other hand an unpolar double-capped octahedron with centrosymmetry (8-II). Both structural isomers appear to be present in the electric deflection experiment, with a clear predominance of the polar clusters at 16 K nozzle temperature. Both structural isomers contribute to the observed absorption spectrum at a nozzle temperature of 300 K. The bands at 3.7 and 4.1 eV result from the polar structure, the broad asymmetric band between 4.5–5.0 eV is mainly caused by the non-polar isomer. If the nozzle is cooled down to 32 K, the bands at 3.7 and 4.1 eV are enhanced, while the rising edge of the broad asymmetric band decreases. Hence, as the clusters are cooled, the fraction of the polar isomer increases significantly, just as observed in the electric deflection experiment at 16 K. Considering not only the intensity ratios directly obtained from electric deflection and spectral data, but also incorporating the impact of the temperature-dependent Boltzmann distribution (cf. ESI† for details), an upper bound for the energy difference ΔE of the two isomers can be determined. Neglecting differences in vibrational frequencies and rotational constants, an estimated value of ΔE < 0.01 eV is obtained, taking into account the different molecular point groups. Thus, the energy difference of almost 0.2 eV predicted theoretically is clearly too large. The fact that the CCSD(T) calculation only insignificantly improves on the relative energy of this isomer points towards the applied level of theory to be insufficient to accurately predict ΔE, possibility due to strongly contributing relativistic and static correlation effects. Due to the D2h symmetry of isomer 8-II, a maximum isomer mixture I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) II of 68
II of 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 should be observed at large temperatures. Since the absorption spectrum at 300 K demonstrates isomer 8-II to be present in slightly higher proportion, the D2h symmetry must be slightly broken which is also predicted at the LC-ωPBEh/def2-TZVPP level of theory (distortion towards Cs). Then a maximum isomer mixture of 50
32 should be observed at large temperatures. Since the absorption spectrum at 300 K demonstrates isomer 8-II to be present in slightly higher proportion, the D2h symmetry must be slightly broken which is also predicted at the LC-ωPBEh/def2-TZVPP level of theory (distortion towards Cs). Then a maximum isomer mixture of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 should be possible which is also approximately confirmed in the optical experiment.
50 should be possible which is also approximately confirmed in the optical experiment.
For Sn9, the previous quantum chemical calculations found a double-capped pentagonal bipyramid (9-II), which could explain the electric deflection behavior very well.37 Global optimization now indicates a different structure as GM, which is also a double-capped pentagonal bipyramid (9-I). The electric dipole moments of the two structural isomers differ only slightly, such that the electric deflection experiment can also be described very well with the structure now predicted as GM. The absorption spectra are also similar, although the agreement with respect to the band signature in the region between 3.0 and 5.0 eV fits better with the new GM in comparison with the experiment. Therefore, it can be assumed that this structural isomer is experimentally present.
A quadruple-capped trigonal prism (C3v) is found for Sn10 as the only low-energy structure in the global optimization. A distorted quadruple-capped trigonal prism with Cs symmetry, which has been identified as an energetically low-lying isomer in the cationic Sn10+ species, appears to be a transition state in the neutral system as discussed previously.37 With the neutral structural isomer the electric deflection experiment can be described sufficiently well. The corresponding absorption spectrum shows a good agreement with the experimental photodissociation spectrum. Both the two weak bands at 2.7 and 3.2 eV as well as the diffuse signature starting at 4.0 eV are correctly predicted theoretically, although the latter one is estimated to begin already at 3.7 eV by the TDDFT. With a comparatively large computed dissociation energy of 3.33 eV, this cluster is forecasted by the RRKM theory to fragment on the experimental time scale with one of the largest excess energies for its size range (cf.Fig. 3). This could be a reason why the shoulder of the absorption band at 3.7 eV in the theoretical absorption spectrum is suppressed in the photodissociation spectrum. Since the longest wavelength bands appear before and around this dissociation energy and, in comparison, have a high intensity, they are probably also due to multiphoton absorption processes.
5.3 Sn11 and Sn12
The electric deflection experiment indicates that already at nozzle temperatures above 50 K, the clusters with more than ten tin atoms are thermally excited to such an extent that the structures are no longer rigid but partially floppy. Accordingly, structure discrimination with the electric deflection experiment is only possible if the clusters are cooled down accordingly. In addition, the probability of finding several quasidegenerate structural isomers tends to increase. This is already the case for Sn11. Of the total of four predicted structural isomers, two are energetically nearly degenerate. On the one hand a triple-capped square antiprism (11-I) and on the other hand a quintuple-capped trigonal prism (11-II) is predicted. The isomers 11-III and 11-IV become even less plausible when considering the CCSD(T) relative energies. The electric deflection experiment indicates that isomers 11-I and 11-II are present in an approximately similar ratio in the experiment. The calculated absorption spectra of both isomers can reproduce the measured spectrum quite well, especially the increase in light absorption from 3.1 eV. However, the calculated spectra possess a stronger patterning in the region between 3.5 and 5.4 eV than is observed experimentally. This could indicate that both structural isomers are present in the experiment, thus washing out the theoretically predicted signatures. Cooling the cluster nozzle down leads to a slight increase in the triple-capped square antiprism fraction, so that this structural isomer probably represents the GM.For Sn12, the structural isomers are predicted to be two quadruple-capped square antiprisms of which one is substantially distorted (12-I) and one being very polar (12-III) as well as an icosahedron with a missing corner (12-II). The electric deflection experiment indicates the presence of the very polar isomer 12-III and the less polar isomer 12-I. CCSD(T) calculations support this finding by lowering the relative energy of 12-III compared to the DFT results. The time-averaged electric dipole moment is already partially quenched at nozzle temperatures of 50 K, so that structural discrimination requires low nozzle temperatures here as well. The observed absorption spectrum can also be interpreted as a superposition of the two antiprisms, such that a slowly increasing light absorption starting at 2.5 eV is observed without distinct absorption bands. Since the theoretically predicted absorption spectrum derived from the icosahedron has pronounced bands between 3.5 and 4.5 eV, this structural isomer can be excluded. It is interesting to note that the absorption spectrum of Sn12 is nearly independent of the nozzle temperature indicating quasidegenerate structural isomers.
5.4 Sn13, Sn14, Sn15 and Sn16
The two structural isomers of Sn13 are derived on the one hand from a triple-capped trigonal prism on which four more atoms are attached peripherally (13-I), and on the other hand from a pentagonal bipyramid, which is connected to a triple-capped trigonal prism via a triangular plane (13-II). This results in a slightly prolate shape in each case. An icosahedral isomer (Ih) predicted for cationic Sn13+, which has already been observed experimentally,42 is also found for the neutral species (ΔE = 1.42 eV) since the ag HOMO is not subject to Jahn-Teller (and pseudo Jahn-Teller) stabilization, but is not expected to be particularly stable due to a lowered HOMO–LUMO gap. The electric deflection measurements can best be explained by the presence of 13-II, although 13-I cannot be completely excluded. Isomer 13-II also explains the observed absorption spectrum very well. The overall result is a poorly structured broad light absorption that starts at 2.5 eV and then increases continuously to 5.4 eV. The pronounced absorption band of 13-I at 4.7 eV cannot be observed experimentally. However, a small amount of 13-I also cannot be excluded based on the absorption spectrum.One structural isomer has been identified for Sn14 in the given energy range, which is derived from a double-capped square antiprism to which additional four atoms are attached on one side. Another isomer much higher in energy has already been discussed and can be excluded.51 The electric deflection data are matched reasonably well. The observed absorption spectrum of Sn14 is rather featureless, with light absorption starting at 2.6 eV, then remaining approximately constant until 3.5 eV, increasing and then raising again more strongly from 4.7 eV onward. The calculated absorption spectrum shows a similar course.
Three isomers of Sn15 were found here, which all share a triple-capped trigonal prism building unit. In 15-I it is connected via a triangular face with a capped square antiprism, whereas in 15-II and 15-III two trigonal prisms, each triple-capped, are linked by a triangular face. The electric deflection data are very well described by 15-I. The light absorption increases steadily starting from 3.0 eV and shows a distinct band at 5.0 eV, which is also theoretically obtained for 15-I. However, the predicted absorption bands between 2.0 and 3.0 eV are not observed experimentally, which may be related to the fact that the single-photon absorption taking place is not sufficient for the photodissociation of the clusters. The comparatively large dissociation energy in the RRKM picture supports this observation.
The predicted structure of Sn16 consists of two triple-capped trigonal prisms connected by a square plane. A series of related structures were found for the cationic Sn16+, all corresponding to transition states of the neutral species. The neutral GM agrees moderately well with electric deflection measurements. The observed absorption spectrum can be well explained. On the one hand, this includes the onset of light absorption at 2.7 eV, which then remains approximately constant until 3.6 eV, followed by a stronger increase of the absorption cross sections until 5.4 eV. Only the theoretically predicted local maximum in the light absorption at 4.2 eV cannot be detected in such a pronounced way experimentally.
5.5 Sn17, Sn18 and Sn19
Two structural isomers are predicted for Sn17, a prolate quadruple-capped trigonal prism attached via two atoms to a double-capped square antiprism (17-I) and a more compact isomer constructed by superimposition of three triple-capped trigonal prims (17-II). The prolate structural isomer can describe the electric deflection data very well. The calculated absorption spectrum of isomer 17-I can also explain well the measured one, although the abrupt increase in light absorption at 4.0 eV is not particularly pronounced experimentally. The predicted rise at 4.5 eV to a plateau predicted for the more compact isomer is definitely not be observed in experiment.The structure of the predicted Sn18 GM (18-I) consists of two triple-capped trigonal prisms fused together. The second structural isomer (18-II) contains a triple-capped trigonal prism connected to nine further atoms containing a distorted octahedron. While 18-II is very polar, 18-I has a low electric dipole moment and the electric deflection measurements are thus well described by isomer 18-I. The agreement between measured and calculated absorption spectra for 18-I is satisfactory, and in particular the strong increase in light absorption starting at 4.6 eV is well reproduced.
Three isomers are obtained for Sn19, all of which are quite polar. The very prolate structures of 19-I and 19-III consist of two subunits linked together, each consisting of a triple-capped trigonal prism and a double-capped square antiprism. In contrast, 19-II is much more compact and also consists of a triple-capped trigonal prism connected to ten more atoms forming a superimposition of three pentagonal bipyramids. The electric deflection data indicate the presence of 19-I or 19-II, possibly both isomers are present together. All predicted optical spectra forecast a sudden increase in light absorption at 4.0 eV (19-I), 4.5 eV (19-II) and 3.5 eV (19-III). The fact that this is not observed experimentally points also to the presence of two structural isomers, presumably 19-I and 19-II, resulting in a rather uniform increase in light absorption. Lowering the nozzle temperature from 300 K to 32 K changes the course of the optical absorption slightly in favor of 19-II.
5.6 Sn20, Sn25, Sn30 and Sn40
The structural elucidation of Sn20 using electric deflection data is particularly challenging. In fact, a total of five structural isomers were found in an energy range of 0.11 eV relative to the GM and all of them have considerably low vibrational frequencies (cf. corresponding frequency plot in ESI†). They are all strongly prolate structures built from two interconnected subunits, namely different combinations of quadruple-capped trigonal prisms and double-capped square antiprisms. Isomers 20-I, 20-II, and 20-V have electric dipole moments that are clearly too small to explain the electric deflection data. In contrast, the dipole moment of 20-III appears to be slightly too large and that of 20-IV again too small; possibly both isomers are also present together, with the proportion of the more polar isomer 20-III clearly predominating. The strong increase in light absorption predicted for 20-I, 20-II and 20-IV starting at 5.0 eV cannot be confirmed experimentally. 20-III also seems best suited to describe the course of the absorption spectrum.For Sn25, a total of three isomers were found with the GA. All isomers are combinations of two triple-capped trigonal prisms fused together via a triangular plane (two of them resembling isomer 15-II), each interconnected with a double-capped square antiprism. The electric deflection data can best be described by the GM or isomer 25-II, although the simulated beam profiles are further broadened and suggest a larger electric dipole moment. This can be explained by taking into account the vibrational excitation. Since the larger clusters exhibit very soft vibrational modes, it is reasonable to assume a significant vibrational excitation and, hence, a partial quenching of the observed electric dipole moment even at a nozzle temperature of 30 K. This is more pronounced for clusters with a larger electric dipole moment, which is why this effect is not as prominent for the Sn20 cluster with even softer vibrational modes. The calculated absorption spectrum of isomer 25-I also fits very well to the rather structureless experimentally observed light absorption with a prominent peak at 4.8 eV, which, in contrast, is not predicted for 25-II and 25-III.
All structural isomers found for Sn30 resemble the prolate growth pattern either via interconnecting three double-capped square antiprisms (30-I and 30-II) or two 15-II units (30-III) indicating a similarity to the Sn25 cluster. The electric beam deflection profile is covered best by isomer 30-III (predicted as GM for the Sn30+ cluster), since 30-I and 30-II have dipole moment components being significantly too low. However, the additional presence of a very polar isomer being responsible for the large deflection is suggested. The absorption spectrum is again given by a monotonous increase with a characteristic signature between 3.9 and 5.1 eV. Since for the Sn30 cluster a significantly large excess energy is needed for photodissociation, the low-energy part of the spectrum is likely governed by multiphoton processes. Isomers 30-I and 30-II have strong peaks at 3.3 and 4.3 eV in common which are not observed experimentally and can thus be ruled out. Isomer 30-III yields a better correspondence although the features starting at 3.9 eV experimentally are predicted to appear approximately 0.8 eV below. Starting from Sn30, the experimental absorption cross sections are substantially lower than forecasted by the TDDFT implying that non-dissociative relaxation pathways might play a growing role in clusters of this size regime.
Interestingly, two structurally distinct isomers for Sn40 were found. Isomer 40-I continues the prolate and thread-like shape evolution by adding a double-capped square antiprism to a 30-III unit and isomer 40-II fuses four triple-capped trigonal prisms together peripherally via four central atoms forming an oblate geometry and opening up the appearance of quasispherical structures. The electric deflection data disagree with the more polar isomer 40-I due to its overestimated electric dipole moment. Isomer 40-II gives a much better fit with deviations in the simulated deflection profile within the expected error range. The onset of light absorption in the photodissociation spectrum starts around 2.4 eV, which, compared to the particularly large excess energy needed for photodissociation, hints again towards involved multiphoton phenomena. The measured data points exhibit more scattering being due to a lower abundance in the mass spectra. Therefore, the decline in absorption cross section >5.1 eV, where also the photon fluence is lowest and most fluctuating, has to be regarded with care. Whereas the strongly prolate isomer 40-I continues the trend of increasing light absorption with cluster size, the oblate isomer 40-II provides an absorption spectrum of significantly lower absorption cross section much better fitting the experimental course.
6 Discussion
6.1 Structural motifs and shape evolution
There are a few theoretical studies which deal with the structures of neutral SnN clusters up to N = 20,29–36,38,40,43,44,48–50 but only one joint computational and experimental investigation37 our results will be compared to. The structure elucidation is strongly improved by carrying out electric deflection measurements at 16 K together with additional photodissociation spectroscopy at 300 and 32 K as well as more sophisticated quantum chemical calculations. The pentagonal bipyramid found in the clusters with N = 6–9 is demonstrated not to be a dominant building unit for the assembly of larger clusters, but rather are the triple-capped trigonal prism and double-capped square antiprism which emerge at N = 10 and 11. New isomers could be confirmed to be (pro rata) present in the molecular beam for the clusters Sn9, Sn11, Sn12, Sn15, Sn17, Sn18, Sn19 and Sn20 which were either not found before by the GA or did not show enough differences in their electric deflection profiles alone for an unambiguous assignment. The experimental results of the clusters Sn8, Sn11, Sn12 and Sn19 suggest that more than one isomer, often differing in their polarities, are present in the molecular beam simultaneously, thus giving rise to a temperature-dependent study of their mixture and the energetics involved. While for the clusters Sn8, Sn11 and Sn19 a lowering of the nozzle temperature could adjust the isomer mixture in favor of a thermodynamically more stable structure, the cluster Sn12 shows a uniform distribution of the present isomers over the investigated temperature range.The prolate growth pattern and the gradual transition to more compact or quasispherical structures of the semiconductor clusters Si, Ge and Sn is well-known by now and was first probed experimentally by Jarrold et al. who performed ion mobility measurements on SnN+ clusters.60 Up to at least N = 65 elongated geometries were found with quasispherical isomers starting to appear from N = 35, thus indicating a delayed structural rearrangement compared to cationic Si and Ge clusters.61,62 For Pb clusters quasispherical structures were discovered for all size regimes. However, non-vanishing electric dipole moments and anomalies in the electronic polarizabilities support a covalent rather than metallic bonding up to at least N = 36.154 Cui et al. additionally found indirect evidence for the shape transition by recording photoelectron spectra of SnN− clusters which pointed towards a semiconductor-to-metal transition at N = 42.80 Many of the theoretically predicted structures were identified both in the neutral and cationic species, although often significantly distorted in the latter, but experimental evidence for the shape transition in neutral clusters is still sparse. Bachels and Schäfer estimated the crossover region from elongated to quasispherical geometries calorimetrically to occur at N = 45–85.99,100 From our selected studies on the clusters Sn25, Sn30 and Sn40 we can qualitatively confirm this observation. It is reasonable to believe that at least up to N = 30 prolate clusters are dominantly present in the molecular beam studies. The thread-like growth is characterized by connecting triple-capped trigonal prisms and double-capped square antiprisms as building blocks whose appearance already dates back to the smallest clusters under investigation. With Sn40 adopting an oblate plate-like motif, the gradual crossover in structure is limited to happen at 30 < N ≤ 40. This is also in agreement with DFT studies of Zang et al. who predict not only plate-like isomers for 40 ≤ N ≤ 44, but also the existence of Y-shaped isomers for 36 ≤ N ≤ 39 as emerging quasispherical structures.46 Li et al. further give indications for the presence of thread-like isomers as low-energy competitors up to N = 5044 and above.47
The evolution of elongated structures is also resembled by the cluster's binding energy, i.e. for an atomization or arbitrary dissociation process. As can be seen from Fig. 2, the dissociation energy for the lowest-energy fragmentation channel drops successively as the clusters start to grow in a prolate manner. Once a certain size is reached, it stays approximately constant due to the nearly invariable surface-to-volume ratio of the clusters, i.e. due to the approximately size-independent binding energy per atom.100
6.2 Microscopic impact of shape on optical absorption
The electronic transitions in the absorption spectra of the SnN clusters below 7 eV are given by a complicated manifold of 5p → 5p excitations with significant contributions of 5s orbitals both in the initial and final states. A d orbital polarization is present to a larger extent compared to Si and Ge clusters, but still pretty small. Already in the smallest clusters absorption bands correspond to many single-electron excitations with non-negligible oscillator strengths, which itself are most often described by more than two significantly contributing NTO pairs, impeding a clear and simple characterization of the nature of certain regions of the absorption spectra. It has been shown for Sn6 that several reference configurations are required in order to adequately treat the low-lying excited states.27 However, the oftentimes satisfactory up to quantitative agreement of the TDDFT spectra with the experimental course suggests that at least for the general features the disregard of multireference (and spin-orbit) effects is justified in several cases. Absorption spectra of the smallest clusters are dominated by distinct features which can be traced back to their molecular shape and symmetry as well as well separated (discrete) energy levels. From Sn12 onward, together with the approximate start of the prolate growth, the spectra become less inimitable, showing now a monotonous increase in light absorption. Interestingly, this observation is on par with findings from the absorption spectra of silicon clusters.155–160 This can partly be understood by the growing density of electronic states with cluster size, but does not explain fully the overall lack of features compared to the TDDFT absorption spectra. Although the vibrational finestructure has not been resolved in the photodissociation spectra, the large extent of vibrational excitation present at 300 K is causing a complicated hot band signature which is expected to, at least to some degree, alter the overall course of the measured spectrum. As already discussed in detail, the low-energy regime of the photodissociation spectra are frequently governed by multiphoton absorption as well as hidden absorption characteristics due to the cluster's excess energies needed for dissociation on the experimental time scale. Therefore, no reliable information can be extracted from the experimental absorption spectra and excited states computed by TDDFT have to be considered. In this regard no band gap closure has been observed for the size range studied and the optical band gap with an oscillator strength f ≥ 0.005 is still above 1.0 eV for the Sn30 and Sn40 cluster, inter alia, because of their relative stability (cf. band gap plot in ESI†) as predicted previously.44 In the high-energy regime of the absorption spectra of larger clusters charge-transfer excitations become quite frequent, although they never appear as distinct and individual features.Based on the analysis of the calculated electronic excitations, it would be of great interest to develop a microscopic picture which links the structural transition of the clusters to their optical absorption. This relation is well-documented for classical spheroids by the Mie–Gans theory utilizing dielectric functions of the corresponding bulk material.105,161,162 Whether this behavior also holds for the smallest clusters and if a plausible picture can be drawn quantum chemically is discussed in the following. Therefore, two cases have been examined in detail, the Sn19 cluster which exhibits a more and less prolate isomer as well as the Sn40 cluster which is shown to be strongly oblate, but has a very prolate isomer in theory too. The TDDFT spectra of the isomers 19-I and 19-II shown again in Fig. 10 are comparable in a sense that their low-energy region shares the same characteristics followed by an intense band at approximately 4.0 eV and 4.5 eV, respectively, before the absorption cross section continues to increase further. Interestingly, when the bonds connecting the two subunits in the more prolate isomer 19-I are compressed slightly, it is the intense band which is shifted towards higher photon energies by roughly 0.6 eV causing a subsequent increase of the absorption cross section now appearing at >5.0 eV. Due to the large amount of electronic transitions involved in this band, an unambiguous orbital picture could not be derived for this geometric alteration. However, it can be understood qualitatively in classical terms. The absorption spectrum of the undistorted isomer 19-I is quite well resembled by the Mie–Gans theory for a prolate spheroid with geometric dimensions taken from quantum chemistry. Upon distortion the predicted spectral course approaches the result of the Mie–Gans theory of a perfect sphere. The TDDFT spectrum of isomer 19-II being less prolate is already close to the result of a sphere. Regarding the prolate isomer 40-I and the experimentally suspected oblate isomer 40-II a similar agreement with the Mie–Gans theory is observed as depicted in Fig. 11.
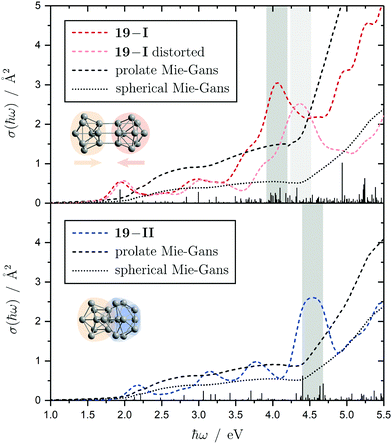 | ||
| Fig. 10 Calculated Sn19 absorption spectra for isomers 19-I (red) and 19-II (blue) at the LC-ω PBEh/def2-TZVPP level of theory. The discrete electronic transitions are convoluted by Gaussians with a FWHM of 0.27 eV. Characteristic absorption peaks are highlighted by gray bars. Additionally, an absorption spectrum is shown where the more prolate isomer 19-I is compressed about 0.15 Å along its Cs mirror plane (light red). The results of the Mie–Gans theory for a spherical and prolate particle (with an aspect ratio105 of A/B = 2.4 for isomer 19-I and A/B = 1.6 resembling isomer 19-II) are depicted for comparison. | ||
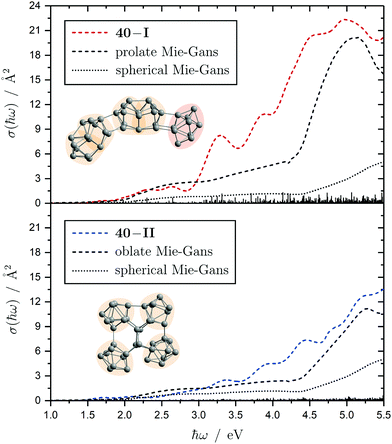 | ||
| Fig. 11 Calculated Sn40 absorption spectra for isomers 40-I (red) and 40-II (blue) at the LC-ω PBEh/def2-TZVPP level of theory. The discrete electronic transitions are convoluted by Gaussians with a FWHM of 0.27 eV. The results of the Mie–Gans theory for a spherical and prolate/oblate particle (with an aspect ratio105 of A/B = 3.7 for isomer 40-I and A/B = 0.4 resembling isomer 40-II) are depicted for comparison. | ||
One quantum chemical conspicuity is, however, worth noting. When comparing the distorted isomer 19-I to its undistorted structure (and also isomer 19-II to 19-I and isomer 40-II to 40-I) an increase in kinetic energy by about 1.5 eV is observed which can be traced back to those molecular orbitals involved in the transitions >3.5 eV. This situation is remotely reminiscent of the particle-in-a-cylinder model which has been applied to explain longitudinal plasmon resonances in the absorption spectra of metal nanorods.163 At first glance this problem does not seem to be transferable to prolate tin clusters with their intricate manifold of excitations leading to broad absorption bands, but given that band gaps of semiconductor nanowires were also shown to depend on the wire diameter,164,165 the applicability of this approach should be further tested.
6.3 Limitations of the experimental methodology
In this study it became clear that both the electric deflection and the photodissociation spectroscopy experiment, though oftentimes being interpreted successfully, suffer from certain limitations which will be summarized in the following. The key assumption to interpret the electric deflection profiles is based on the clusters being rigid rotors. Especially larger SnN clusters, as discussed for N ≥ 20, exhibit low vibrational modes and hence become floppy as a result of thermal excitation which partially quenches the electric dipole moment even at nozzle temperatures below 30 K. The electric dipole moments required for the classical trajectory simulations stem from DFT calculations and are often attributed with an error of up to 20%. Moreover, the rotational temperature, being responsible for populating the rotational states of the clusters in the trajectory simulation, is not known a priori and has to be estimated. For reasons of consistency the same rotational temperature of Trot = 20 K is applied for all clusters, although larger clusters with N ≥ 19 have been measured at higher nozzle temperatures of 30 K and thus likely have slightly higher rotational temperatures, too. In the ESI† electric dipole moments and polarizabilities have been deduced from the experimental deflection profiles by fitting a Gaussian function containing information about the broadening and deflection based on a first-order perturbation theory treatment. Calculated effective polarizabilities based on second-order perturbation theory102 as a function of the experimental electric dipole moments agree well with experimentally extracted polarizabilities giving confidence in the chosen rotational temperature of Trot = 20 K. This holds for many clusters even though they are treated as spherically-symmetric rotors, a clear contradiction to most of the clusters showing strongly prolate geometries. However, larger clusters exhibit effective polarizabilities which are too small compared to the experimentally extracted ones stressing again the thermal excitation of weak vibrational modes and the consequent quenching of the electric dipole moment. In some cases a Gaussian function is not an appropriate choice for the fit as is discussed for, i.e., Sn11 in the ESI.† Whenever two isomers seem to be present in the molecular beam, two Gaussian functions need to be fitted hampering this task further and adding a certain degree of freedom to those deduced parameters.The photodissociation spectrum corresponds to the true absorption spectrum only when there are no non-dissociative relaxation pathways present. The probability for this is expectedly altered over the studied size range of the clusters due to an increasing density of excited states with cluster size. In the spectra of the largest clusters the measured absorption cross sections are quite a bit lower than predicted by TDDFT which could owe to the mentioned phenomenon. Larger clusters with many vibrational modes and low dissociation energies are shown to exhibit great excess energies which impede a fragmentation on the experimental timescale rendering the light absorption invisible to this action spectroscopy. The excess energy takes values up to >4 eV (for the Sn40 cluster) scrutinizing a large region of the spectrum as to whether it can be simply compared to TDDFT results. The low-energy regime is further complicated due to the tin clusters being prone to multiphoton absorption processes as demonstrated for the Sn7 cluster and suspected to occur in several other species. Because of this no band gaps have been extracted here. Although the vibronic finestructure is not resolved, the significant excitation of virtually all vibrational modes at 300 K causes a complicated hot band structure which potentially alters the general course of the photodissociation spectrum slightly. Together with the electric deflection experiment, information on the energetics of the clusters have been obtained whenever more than one isomer were found to be present in the molecular beam simultaneously. This was possible due to the global assumption that the clusters are equilibrated within the nozzle. Although there is certain evidence for this assumption, it is still somewhat debatable whether the clusters are indeed perfectly equilibrated. It is also not fully clarified if a Boltzmann distribution of the thermally excited vibrational modes is the most appropriate assumption under the given conditions.
7 Conclusions
Electric beam deflection measurements and photodissociation spectroscopy together with quantum chemical calculations are applied to shine light on the geometric evolution as well as to unravel the optical absorption of neutral SnN clusters with N = 6–20, 25, 30, 40. In comparison to a previous study37 the size range of the clusters is extended and the dielectric response is probed at a lower nozzle temperature of 16 K. An improved GA routine and more sophisticated levels of theory, including the hybrid functionals PBE0 and LC-ωPBEh plus CCSD(T) calculations, are employed for the structural reoptimization as well as the calculation of properties such as the electric dipole moments and polarizabilities. In this regard, new energetically low-lying isomers for clusters with N = 9, 11, 12, 15, 17–20 are confirmed to be (partially) present in the molecular beam. Triple-capped trigonal prisms and double-capped square antiprisms are identified as dominant building blocks over almost the entire size range with the former one building Sn15 subunits which are particularly conspicuous for clusters with N > 20. The clusters are shown to adopt prolate shapes up to at most the oblate Sn40 cluster from where quasispherical structures are expected to gradually take over. Although this structural transition is well known from studies on charged tin clusters, it can be regarded the first size-specific experimental evidence of this transition for neutral tin clusters. Fragmentation likely occurs via the loss of a tin atom for clusters with N < 12, a Sn7 cluster for N < 19 and a Sn10 cluster for N ≥ 19 based on computation and evidence given by photodissociation. The impact of the rotational temperature, the electric dipole moment and thermal excitation of vibrational modes on simulating electric deflection profiles is discussed diligently. The latter manifests in the clusters becoming floppy and, hence, quenching the electric dipole moment to some extent. This was shown to be especially important for larger clusters with N ≥ 19.Photodissociation spectra of neutral tin clusters have been recorded for the first time illustrating similarities to absorption spectra of small silicon clusters. The spectra show distinct absorption features for the smallest clusters under study and become less structured with increasing cluster size starting approximately at N = 12 coinciding with the cluster's prolate growth. In many cases a comparison between the photodissociation spectra and absorption spectra predicted by TDDFT complement the results from the electric beam deflection leading to a more explicit structural elucidation. The electronic transitions are found to consist of a manifold of 5p → 5p excitations with significant contribution of 5s orbitals hampering an unambiguous classification of the observed absorption bands and their relation to structure. However, the general course of the absorption spectra can be understood in terms of the classical Mie–Gans theory for prolate/oblate spheroids and spheres. By varying the laser fluence multiphoton absorption is detected to be present in the low-energy regime of the spectra of many clusters. Furthermore, the dissociation kinetics on the experimental time scale between photoexcitation and detection play a tremendous role. RRKM theory is applied to estimate excess energies required for excitation energies being sufficient to cause dissociation. These can be as low as 0.6 eV for the smallest cluster, Sn6, and can raise up to >4.0 eV for Sn40 rendering large parts of the absorption spectrum invisible for photodissociation. Thermal excitation of vibrational modes and coupling of vibrational and electronic degrees of freedom is expected to also contribute to the spectra recorded at 300 K, further washing out the spectral signature possibly due to hot bands.
In both conducted experiments the simultaneous presence of two isomers for the clusters with N = 8, 11, 12 and 19 is observed. By comparing the isomer ratios in the electric deflection experiment at 16 K and photodissociation spectroscopy experiment at 32 K and 300 K, information about the energetics and dynamics of the structural rearrangement of the cluster isomers can be obtained. The findings scrutinize the isomer's relative energies which seem to be overestimated by quantum chemistry. Here, it would be valuable if more sophisticated results incorporating the multireference and relativistic nature become available, but also to tackle vibronic excitations. For the future it is highly desirable to merge dielectric deflection and absorption spectroscopy in a combined experiment in order to perform isomer-selective (photodissociation) spectroscopy on these species.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support for this project was provided by the Deutsche Forschungsgemeinschaft (Grant SCHA 885/15-2). A. L. thanks the Verband der Chemischen Industrie for a scholarship. Extensive calculations were conducted for this work on the Lichtenberg high-performance computer of the Technical University of Darmstadt. The authors thank the Hessian Competence Center for High Performance Computing funded by the Hessen State Ministry of Higher Education, Research, and the Arts for helpful advice.References
-
J.-X. Zhang, F. K. Sheong and Z. Lin, 50th Anniversary of Electron Counting Paradigms for Polyhedral Molecules. Structure and Bonding, Springer International Publishing, 2021, ch. 5, pp. 197–257 Search PubMed
.
- L. D. Anh, K. Takase, T. Chiba, Y. Kota, K. Takiguchi and M. Tanaka, Adv. Mater., 2021, 33, 2104645 CrossRef CAS PubMed
.
- C. C. Striemer, R. Krishnan and P. M. Fauchet, JOM, 2004, 56, 20–25 CrossRef CAS
.
- L. Pavesi, L. Dal Negro, C. Mazzoleni, G. Franzò and F. Priolo, J. Appl. Phys., 2004, 96, 3164–3171 CrossRef
.
-
L. Pavesi, Silicon Nanocrystals: Fundamentals, Synthesis and Applications, Wiley-VCH, Weinheim, 2010 Search PubMed
.
- X. Wen, P. Zhang, T. A. Smith, R. J. Anthony, U. R. Kortshagen, P. Yu, Y. Feng, S. Shrestha, G. Coniber and S. Huang, Sci. Rep., 2015, 5, 12469 CrossRef PubMed
.
- W. M. Zhang, J. S. Hu, Y. G. Guo, S. F. Zheng, L. S. Zhong, W. G. Song and L. J. Wan, Adv. Mater., 2008, 20, 1160–1165 CrossRef CAS
.
- K. Kravchyk, L. Protesescu, M. I. Bodnarchuk, F. Krumeich, M. Yarema, M. Walter, C. Guntlin and M. V. Kovalenko, J. Am. Chem. Soc., 2013, 135, 4199–4202 CrossRef CAS PubMed
.
- Z. Zhu, S. Wang, J. Du, Q. Jin, T. Zhang, F. Cheng and J. Chen, Nano Lett., 2014, 14, 153–157 CrossRef CAS PubMed
.
- L. R. Parent, Y. Cheng, P. V. Sushko, Y. Shao, J. Liu, C. M. Wang and N. D. Browning, Nano Lett., 2015, 15, 1177–1182 CrossRef CAS PubMed
.
- R. E. Honig, J. Chem. Phys., 1953, 21, 573–574 CrossRef CAS
.
- K. A. Gingerich, D. L. Cocke and U. V. Choudary, Inorg. Chim. Acta, 1975, 14, 10–12 CrossRef
.
- K. A. Gingerich, E. A. Ramakrishnan and J. E. Kingcade, High Temp. Sci., 1986, 21, 1–15 CAS
.
- G. Meloni, R. W. Schmude, J. E. Kingcade and K. A. Gingerich, J. Chem. Phys., 2000, 113, 1852–1856 CrossRef CAS
.
- V. E. Bondybey, M. Heaven and T. A. Miller, J. Chem. Phys., 1983, 78, 3593–3598 CrossRef CAS
.
- K. Pak, M. F. Cai, T. P. Dzugan and V. E. Bondybey, Faraday Discuss. Chem. Soc., 1988, 86, 153–162 RSC
.
- A. B. Anderson, J. Chem. Phys., 1975, 63, 4430–4456 CrossRef CAS
.
- L. L. Lohr, Inorg. Chem., 1981, 20, 4229–4235 CrossRef CAS
.
- K. Balasubramanian and K. S. Pitzer, J. Chem. Phys., 1983, 78, 321–327 CrossRef CAS
.
- G. Pacchioni, Mol. Phys., 1985, 55, 211–223 CrossRef CAS
.
- D. Dai and K. Balasubramanian, J. Chem. Phys., 1986, 85, 3401–3406 CrossRef
.
- D. Dai and K. Balasubramanian, J. Phys. Chem., 1992, 96, 9236–9243 CrossRef CAS
.
- D. Dai and K. Balasubramanian, J. Chem. Phys., 1992, 96, 8345–8353 CrossRef CAS
.
- W. Plass, H. Stoll, H. Preuss and A. Savin, J. Mol. Struct., 1995, 339, 67–81 CrossRef CAS
.
- D. Dai and K. Balasubramanian, J. Chem. Phys., 1996, 100, 19321–19325 CrossRef CAS
.
- D. Dai and K. Balasubramanian, J. Chem. Phys., 1998, 108, 4379–4385 CrossRef CAS
.
- C. Zhao and K. Balasubramanian, J. Chem. Phys., 2001, 115, 3121–3133 CrossRef CAS
.
- L. Si-Dian, R. Johnston and J. Murrell, Acta Phys.-Chim. Sin., 1993, 9, 642–649 Search PubMed
.
- P. Jackson, I. G. Dance, K. J. Fisher, G. D. Willett and G. E. Gadd, Int. J. Mass Spectrom. Ion Process., 1996, 157/158, 329–343 CrossRef CAS
.
- B. Wang, L. M. Molina, M. J. López, A. Rubio, J. A. Alonso and M. J. Stott, Ann. Phys., 1998, 7, 107–119 CrossRef
.
- Z. Y. Lu, C. Z. Wang and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 2329–2334 CrossRef CAS
.
- C. Jo and K. Lee, J. Chem. Phys., 2000, 113, 7268–7272 CrossRef CAS
.
- C. Majumder, V. Kumar, H. Mizuseki and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 233405 CrossRef
.
- R. Pushpa, S. Narasimhan and U. Waghmare, J. Chem. Phys., 2004, 121, 5211–5220 CrossRef CAS PubMed
.
- C. Majumder, V. Kumar, H. Mizuseki and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035401 CrossRef
.
- S. Krishnamurty, K. Joshi, D. G. Kanhere and S. A. Blundell, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045419 CrossRef
.
- S. Schäfer, B. Assadollahzadeh, M. Mehring, P. Schwerdtfeger and R. Schäfer, J. Phys. Chem. A, 2008, 112, 12312–12319 CrossRef PubMed
.
- C. C. Yang and S. Li, J. Phys. Chem. C, 2009, 113, 14207–14212 CrossRef CAS
.
- E. Oger, R. Kelting, P. Weis, A. Lechtken, D. Schooss, N. R. Crawford, R. Ahlrichs and M. M. Kappes, J. Chem. Phys., 2009, 130, 124305 CrossRef PubMed
.
- B. Assadollahzadeh, S. Schäfer and P. Schwerdtfeger, J. Comput. Chem., 2010, 31, 929–937 CAS
.
- A. Lechtken, N. Drebov, R. Ahlrichs, M. M. Kappes and D. Schooss, J. Chem. Phys., 2010, 132, 211102 CrossRef PubMed
.
- N. Drebov, E. Oger, T. Rapps, R. Kelting, D. Schooss, P. Weis, M. M. Kappes and R. Ahlrichs, J. Chem. Phys., 2010, 133, 224302 CrossRef PubMed
.
- N. Drebov and R. Ahlrichs, J. Chem. Phys., 2011, 134, 124308 CrossRef PubMed
.
- H. Li, H. Du, W. Chen, Q. Q. Shan, Q. Sun, Z. X. Guo and Y. Jia, J. Phys. Chem. C, 2012, 116, 231–236 CrossRef CAS
.
- A. Wiesel, N. Drebov, T. Rapps, R. Ahlrichs, U. Schwarz, R. Kelting, P. Weis, M. M. Kappes and D. Schooss, Phys. Chem. Chem. Phys., 2012, 14, 234–245 RSC
.
- Q. Zang, G. Chen and W. Lu, Chem. Phys. Lett., 2012, 552, 69–72 CrossRef CAS
.
- H. Li, W. Chen, F. Wang, Q. Sun, Z. X. Guo and Y. Jia, Phys. Chem. Chem. Phys., 2013, 15, 1831–1836 RSC
.
- Q. J. Zang, G. J. Chen, W. Qin, L. Z. Zhao and W. C. Lü, Chem. Res. Chin. Univ., 2013, 29, 579–583 CrossRef CAS
.
- P. G. A. Leyva, E. M. Sosa-Hernández, J. M. Montejano-Carrizales and F. Aguilera-Granja, Eur. Phys. J. D, 2015, 69, 1–7 CrossRef CAS
.
- D. Wu, Q. Du, X. Wu, R. Shi, L. Sai, X. Liang, X. Huang and J. Zhao, J. Chem. Phys., 2019, 150, 174304 CrossRef PubMed
.
- A. Lehr, M. Jäger, M. Gleditzsch, F. Rivic and R. Schäfer, J. Phys. Chem. Lett., 2020, 11, 7827–7831 CrossRef CAS PubMed
.
- J. Drowart and P. Goldfinger, Angew. Chem., 1967, 13, 589–628 CrossRef
.
- T. P. Martin and H. Schaber, J. Chem. Phys., 1985, 83, 855–858 CrossRef CAS
.
- J. R. Heath, Y. Liu, S. C. O'Brien, Q.-L. Zhang, R. F. Curl, F. K. Tittel and R. E. Smalley, J. Chem. Phys., 1985, 83, 5520–5526 CrossRef CAS
.
- J. C. Phillips, J. Chem. Phys., 1987, 87, 1712–1716 CrossRef CAS
.
- K. LaiHing, R. G. Wheeler, W. L. Wilson and M. A. Duncan, J. Chem. Phys., 1987, 87, 3401–3409 CrossRef CAS
.
- M. Watanabe, Y. Saito, S. Nishigaki and T. Noda, Jpn. J. Appl. Phys., 1988, 27, 344–347 CrossRef CAS
.
- D. S. Cornett, M. Peschke, K. LaiHing, P. Y. Cheng, K. F. Willey and M. A. Duncan, Rev. Sci. Instrum., 1992, 63, 2177–2186 CrossRef CAS
.
- S. Yoshida, K. Fuke and I. Introduction, Chem. Phys., 1999, 111, 3880–3890 CAS
.
- A. A. Shvartsburg and M. F. Jarrold, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 1235–1239 CrossRef CAS
.
- A. A. Shvartsburg and M. F. Jarrold, Chem. Phys. Lett., 2000, 317, 615–618 CrossRef CAS
.
- A. A. Shvartsburg, R. R. Hudgins, P. Dugourd and M. F. Jarrold, Chem. Soc. Rev., 2001, 30, 26–35 RSC
.
- Y. Tai, J. Murakami, C. Majumder, V. Kumar, H. Mizuseki and Y. Kawazoe, J. Chem. Phys., 2002, 117, 4317–4322 CrossRef CAS
.
- Y. Tai, J. Murakami, C. Majumder, V. Kumar, H. Alizuseki and Y. Kawazoe, Eur. Phys. J. D, 2003, 24, 295–298 CrossRef CAS
.
- G. Ganteför, M. Gausa, K. H. Meiwes-Broer and H. O. Lutz, Faraday Discuss., 1988, 86, 197–208 RSC
.
- G. Ganteför, M. Gausa, K. H. Meiwes-Broer and H. O. Lutz, Z. Phys. D, 1989, 12, 405–409 CrossRef
.
- J. Ho, M. L. Polak and W. C. Lineberger, J. Chem. Phys., 1992, 96, 144–154 CrossRef CAS
.
- J. Thøgersen, L. D. Steele, M. Scheer, C. A. Brodie and H. K. Haugen, J. Phys. B, 1996, 29, 1323–1330 CrossRef
.
- V. D. Moravec, S. A. Klopcic and C. C. Jarrold, J. Chem. Phys., 1999, 110, 5079–5088 CrossRef CAS
.
- Y. Negishi, H. Kawamata, A. Nakajima and K. Kaya, J. Electron Spectros. Relat. Phenomena, 2000, 106, 117–125 CrossRef CAS
.
- S. Osmekhin, M. Tchaplyguine, M. H. Mikkelä, M. Huttula, T. Andersson, O. Björneholm and S. Aksela, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 023203 CrossRef
.
- A. A. Shvartsburg and M. F. Jarrold, Phys. Rev. Lett., 2000, 85, 2530–2532 CrossRef CAS PubMed
.
- H. Haberland, Phys. World, 2000, 13, 27–28 CrossRef
.
- K. Joshi, D. G. Kanhere and S. A. Blundell, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155329 CrossRef
.
- K. Joshi, D. G. Kanhere and S. A. Blundell, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 235413 CrossRef
.
- F. C. Chuang, C. Z. Wang, S. Öğüt, J. R. Chelikowsky and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 165408 CrossRef
.
- G. A. Breaux, D. A. Hillman, C. M. Neal and M. F. Jarrold, J. Phys. Chem. A, 2005, 109, 8755–8759 CrossRef CAS PubMed
.
- L. F. Cui, X. Huang, L. M. Wang, D. Y. Zubarev, A. I. Boldyrev, J. Li and L. S. Wang, J. Am. Chem. Soc., 2006, 128, 8390–8391 CrossRef CAS PubMed
.
- S. Cantrill, Nat. Nanotechnol., 2006 DOI:10.1038/nnano.2006.11
.
- L. F. Cui, L. M. Wang and L. S. Wang, J. Chem. Phys., 2007, 126, 064505 CrossRef PubMed
.
- L.-F. Cui, X. Huang, L.-M. Wang, J. Li and L.-S. Wang, Angew. Chem., 2007, 119, 756–759 CrossRef
.
- V. Kumar and Y. Kawazoe, Appl. Phys. Lett., 2003, 83, 2677–2679 CrossRef CAS
.
- U. Rohrmann and R. Schäfer, Phys. Rev. Lett., 2013, 111, 133401 CrossRef PubMed
.
- T. M. Fuchs and R. Schäfer, Phys. Rev. A, 2018, 98, 063411 CrossRef CAS
.
- S. Bobev and S. C. Sevov, Inorg. Chem., 2001, 40, 5361–5364 CrossRef CAS PubMed
.
- B. Kesanli, J. Fettinger and B. Eichhorn, Chem. – Eur. J., 2001, 7, 5277–5285 CrossRef CAS
.
- M. Brynda, R. Herber, P. B. Hitchcock, M. F. Lappert, I. Nowik, P. P. Power, A. V. Protchenko, A. Růžička and J. Steiner, Angew. Chem., Int. Ed., 2006, 45, 4333–4337 CrossRef CAS PubMed
.
- S. J. Kim, S. D. Hoffman and T. F. Fässler, Angew. Chem., Int. Ed., 2007, 46, 3144–3148 CrossRef CAS PubMed
.
- G. Prabusankar, A. Kempter, C. Gemel, M. K. Schöter and R. A. Fischer, Angew. Chem., Int. Ed., 2008, 47, 7234–7237 CrossRef CAS PubMed
.
- C. Schrenk, I. Schellenberg, R. Pöttgen and A. Schnepf, Dalton Trans., 2010, 39, 1872–1876 RSC
.
- J. Q. Wang, S. Stegmaier, B. Wahl and T. F. Fässler, Chem. – Eur. J., 2010, 16, 1793–1798 CrossRef CAS PubMed
.
- S. Stegmaier and T. F. Fässler, J. Am. Chem. Soc., 2011, 133, 19758–19768 CrossRef CAS PubMed
.
- C. Schrenk, F. Winter, R. Pöttgen and A. Schnepf, Chem. – Eur. J., 2015, 21, 2992–2997 CrossRef CAS PubMed
.
- J. Wiederkehr, C. Wölper and S. Schulz, Chem. Commun., 2016, 52, 12282–12285 RSC
.
- A. P. Purdy, R. J. Butcher, J. P. Yesinowski, S. A. Fischer, D. Gunlycke and B. L. Chaloux, Inorg. Chem., 2018, 57, 4921 CrossRef CAS PubMed
.
- M. Binder, C. Schrenk and A. Schnepf, Chem. Commun., 2019, 55, 12148–12151 RSC
.
- L. Qiao, C. Zhang, C. C. Shu, H. W. Morgan, J. E. McGrady and Z. M. Sun, J. Am. Chem. Soc., 2020, 142, 13288–13293 CrossRef CAS PubMed
.
- J. E. McGrady, F. Weigend and S. Dehnen, Chem. Soc. Rev., 2022, 51, 628–649 RSC
.
- T. Bachels and R. Schäfer, Chem. Phys. Lett., 1999, 300, 177–182 CrossRef CAS
.
- T. Bachels, R. Schäfer and H. J. Güntherodt, Phys. Rev. Lett., 2000, 84, 4890–4893 CrossRef CAS PubMed
.
- S. Schäfer, M. Mehring, R. Schäfer and P. Schwerdtfeger, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 052515 CrossRef
.
-
S. Heiles and R. Schäfer, Dielectric Properties of Isolated Clusters: Beam Deflection Studies, Springer, Heidelberg, 2014 Search PubMed
.
- A. Shayeghi, R. L. Johnston and R. Schäfer, Phys. Chem. Chem. Phys., 2013, 15, 19715–19723 RSC
.
- M. Jäger, A. Shayeghi, V. Klippenstein, R. L. Johnston and R. Schäfer, J. Chem. Phys., 2018, 149, 244308 CrossRef PubMed
.
- A. Lehr, M. Jäger and R. Schäfer, J. Phys. Chem. C, 2020, 124, 1070–1076 CrossRef CAS
.
- L. P. Maguire, S. Szilagyi and R. E. Scholten, Rev. Sci. Instrum., 2004, 75, 3077–3079 CrossRef CAS
.
- L. P. Maguire, S. Szilagyi and R. E. Scholten, Rev. Sci. Instrum., 2007, 78, 019903 CrossRef
.
- T. M. Fuchs, F. Rivic and R. Schäfer, Phys. Rev. A, 2021, 104, 012820 CrossRef CAS
.
- J. M. Kellogg, I. I. Rabi, N. F. Ramsey and J. R. Zacharias, Phys. Rev., 1939, 56, 728–743 CrossRef CAS
.
- U. Ray, M. F. Jarrold, J. E. Bower and J. S. Kraus, J. Chem. Phys., 1989, 91, 2912–2921 CrossRef CAS
.
- M. F. Jarrold and E. C. Honea, J. Phys. Chem., 1991, 95, 9181–9185 CrossRef CAS
.
- M. Jäger, R. Schäfer and R. L. Johnston, Nanoscale, 2019, 11, 9042–9052 RSC
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. Distasio Jr., A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS
.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 8412–8415 CrossRef CAS PubMed
.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230 CrossRef PubMed
.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS
.
- S. Louie, S. Froyen and L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 1738–1742 CrossRef CAS
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, 2016 Search PubMed
.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. De Jong, Comp. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS
.
- E. Aprà, E. J. Bylaska, W. A. De Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. Van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin Del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-De-La-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, A. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed
.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS
.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569 CrossRef CAS
.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112 CrossRef CAS
.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Chem. Phys., 2009, 130, 054112 CrossRef PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- S. Heiles, R. L. Johnston and R. Schäfer, J. Phys. Chem. A, 2012, 116, 7756–7764 CrossRef CAS PubMed
.
- M. Gleditzsch, M. Jäger, L. F. Pašteka, A. Shayeghi and R. Schäfer, Phys. Chem. Chem. Phys., 2019, 21, 24478–24488 RSC
.
- M. Gleditzsch, T. M. Fuchs and R. Schäfer, J. Phys. Chem. A, 2019, 123, 1434–1444 CrossRef CAS PubMed
.
- M. Gleditzsch, L. F. Pašteka, D. A. Götz, A. Shayeghi, R. L. Johnston and R. Schäfer, Nanoscale, 2019, 11, 12878–12888 RSC
.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed
.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed
.
- D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 4054–4063 CrossRef CAS PubMed
.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 4–9 Search PubMed
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed
.
- D. G. Truhlar, Chem. Phys. Lett., 1998, 294, 45–48 CrossRef CAS
.
- P. Dugourd, R. Antoine, M. Abd El Rahim, D. Rayane, M. Broyer and F. Calvo, Chem. Phys. Lett., 2006, 423, 13–16 CrossRef CAS
.
- S. Heiles, S. Schäfer and R. Schäfer, J. Chem. Phys., 2011, 135, 034303 CrossRef CAS PubMed
.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS
.
- A. Heilmann, M. Quinten and J. Werner, Eur. Phys. J. B, 1998, 3, 455–461 CrossRef CAS
.
- V. G. Grigoryan, M. Springborg, H. Minassian and A. Melikyan, Comput. Theor. Chem., 2013, 1021, 197–205 CrossRef CAS
.
- O. K. Rice and H. C. Ramsperger, J. Am. Chem. Soc., 1927, 49, 1617–1629 CrossRef CAS
.
- O. K. Rice and H. C. Ramsperger, J. Am. Chem. Soc., 1928, 50, 617–620 CrossRef CAS
.
- R. A. Marcus and O. K. Rice, J. Phys. Colloid Chem., 1951, 55, 894–908 CrossRef CAS
.
- R. A. Marcus, J. Chem. Phys., 1952, 20, 359–364 CrossRef CAS
.
-
R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell Scientific Publications, Oxford, 1990 Search PubMed
.
- T. Beyer and D. F. Swinehart, Commun. ACM, 1973, 16, 379 CrossRef
.
- M. F. Jarrold and K. M. Creegan, Int. J. Mass Spectrom. Ion Process., 1990, 102, 161–181 CrossRef CAS
.
- Y. Shi, V. A. Spasov and K. M. Ervin, J. Chem. Phys., 1999, 111, 938–949 CrossRef CAS
.
- D. A. Götz, A. Shayeghi, R. L. Johnston, P. Schwerdtfeger and R. Schäfer, Nanoscale, 2016, 8, 11153–11160 RSC
.
- K. D. Rinnen and M. L. Mandich, Phys. Rev. Lett., 1992, 69, 1823–1826 CrossRef CAS PubMed
.
- K. D. Rinnen and M. L. Mandich, Z. Phys. D, 1993, 26, 147–149 CrossRef
.
- E. C. Honea, J. S. Kraus, J. E. Bower and M. F. Jarrold, Z. Phys. D, 1993, 26, 141–143 CrossRef CAS
.
- A. Rubio, J. Alonso, X. Blase, L. Balbás and S. Louie, Phys. Rev. Lett., 1996, 77, 247–250 CrossRef CAS PubMed
.
- Y. Z. Lan, Y. L. Feng, Y. H. Wen and B. T. Teng, J. Mol. Struct., 2008, 854, 63–69 CrossRef CAS
.
- L.-Z. Zhao, W.-C. Lu, W. Qin, Q.-J. Zang, K. M. Ho and C. Z. Wang, J. Phys. Chem. A, 2017, 121, 6388–6397 CrossRef CAS PubMed
.
- G. Mie, Ann. Phys., 1908, 330, 377–445 CrossRef
.
- R. Gans, Ann. Phys., 1912, 342, 881–900 CrossRef
.
- H. E. Johnson and C. M. Aikens, J. Phys. Chem. A, 2009, 113, 4445–4450 CrossRef CAS PubMed
.
- H. Yu, J. Li, R. A. Loomis, L. W. Wang and W. E. Buhro, Nat. Mater., 2003, 2, 517–520 CrossRef CAS PubMed
.
- H. Yu, J. Li, R. A. Loomis, P. C. Gibbons, L. W. Wang and W. E. Buhro, J. Am. Chem. Soc., 2003, 125, 16168–16169 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Geometries, symmetries and energetics of all SnN+ isomers; (relative) ellipsoid semiaxes of all SnN isomers; vibrational frequencies of all SnN isomers; dissociation and RRKM excess energies of all SnN isomers; Boltzmann correction for the fitted isomer mixtures in the electric beam deflection and photodissociation spectroscopy experiments of Sn8, Sn11, Sn12 and Sn19; impact of the rotational temperature and computed electric dipole moment on the electric beam deflection profile demonstrated for Sn10; computed moments of inertia, electric dipole moment components and polarizabilities as well as experimentally extracted electric dipole moments and polarizabilities of all SnN isomers; TDDFT fundamental and optical band gaps for all SnN clusters. See DOI: https://doi.org/10.1039/d2cp01171a |
| This journal is © the Owner Societies 2022 |