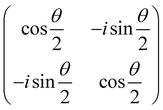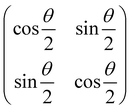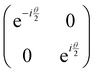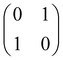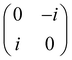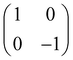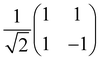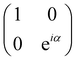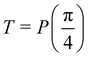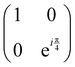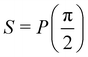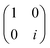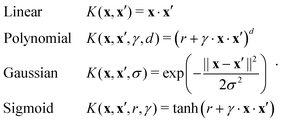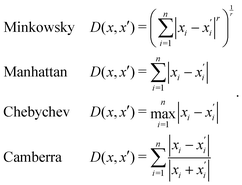Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum machine learning for chemistry and physics
Manas
Sajjan
 ab,
Junxu
Li†
ab,
Junxu
Li†
 bc,
Raja
Selvarajan†
bc,
Shree Hari
Sureshbabu‡
bc,
Raja
Selvarajan†
bc,
Shree Hari
Sureshbabu‡
 bd,
Sumit Suresh
Kale‡
bd,
Sumit Suresh
Kale‡
 ab,
Rishabh
Gupta‡
ab,
Vinit
Singh‡
ab and
Sabre
Kais
ab,
Rishabh
Gupta‡
ab,
Vinit
Singh‡
ab and
Sabre
Kais
 *abcd
*abcd
aDepartment of Chemistry, Purdue University, West Lafayette, IN-47907, USA. E-mail: kais@purdue.edu
bPurdue Quantum Science and Engineering Institute, Purdue University, West Lafayette, Indiana 47907, USA
cDepartment of Physics and Astronomy, Purdue University, West Lafayette, IN-47907, USA
dElmore Family School of Electrical and Computer Engineering, Purdue University, West Lafayette, IN-47907, USA
First published on 18th July 2022
Abstract
Machine learning (ML) has emerged as a formidable force for identifying hidden but pertinent patterns within a given data set with the objective of subsequent generation of automated predictive behavior. In recent years, it is safe to conclude that ML and its close cousin, deep learning (DL), have ushered in unprecedented developments in all areas of physical sciences, especially chemistry. Not only classical variants of ML, even those trainable on near-term quantum hardwares have been developed with promising outcomes. Such algorithms have revolutionized materials design and performance of photovoltaics, electronic structure calculations of ground and excited states of correlated matter, computation of force-fields and potential energy surfaces informing chemical reaction dynamics, reactivity inspired rational strategies of drug designing and even classification of phases of matter with accurate identification of emergent criticality. In this review we shall explicate a subset of such topics and delineate the contributions made by both classical and quantum computing enhanced machine learning algorithms over the past few years. We shall not only present a brief overview of the well-known techniques but also highlight their learning strategies using statistical physical insight. The objective of the review is not only to foster exposition of the aforesaid techniques but also to empower and promote cross-pollination among future research in all areas of chemistry which can benefit from ML and in turn can potentially accelerate the growth of such algorithms.
1 Introduction
The 21st century data revolution sparked by machine learning (ML) has yielded unprecedented applications in several domains of technology like natural language processing,1–3 translation,4,5 autonomous vehicles,6–8 robotics,9,10 image-recognition,11–13 recommender systems,14 web-searching15 and fraudulent email filtering16,17 and in medical sciences like bio-informatics,18,19 medical imaging,20 brain-computer interfacing21 and in social sciences22 and finance23 and even in problems like refugee integration.24 The primary reason for such prodigious advances is the uncanny ability of ML based protocols to detect and recognize unforeseen patterns in the data analyzed and integrate the acquired knowledge into decision-making, a process fancifully coined as ‘learning’. The fruitful use of this ability has been further accelerated by not only large-scale availability of shared databases and exponential growth of computing resources but also ingenuous algorithmic advances over the past few decades that precipitated in efficient dimensionality reduction25 and data-manipulation. Needless to say, this positively disruptive methodology has also fruitfully impacted several domains of physical sciences.26 Applications ranging from astronomy,27,28 particle-physics,29 atomic and molecular physics,30 optical manipulations of matter,31 forecasting of weather patterns and climate dynamics32,33 and even identification of evolutionary information from fossil records in paleontology34–36 have been recorded with an unforeseen success ratio. Chemical applications like understanding the electronic properties of matter,37,38 materials discovery with optimal properties,39,40 retrosynthetic design and control of chemical reactions,41–44 understanding reaction pathways45,46 on a potential energy surface, and cheminformatics47 have been analyzed using the newly acquired lens of ML and continue to register a meteoric rise. Simulations performed in a recent review48 bear testimony to this fact by highlighting that keywords based on ML have made steady appearances (≥102) across all divisions of chemistry over the last 20 years in technical journals of a particular publishing house. The number of such occurrences has specifically increased steadily for applications in physical chemistry/chemical physics. While ML based algorithms were enjoying this attention, much along the same time, the world was also witnessing the rapid emergence of another computing revolution which is fundamentally different from the familiar classical bit-based architecture. The new paradigm, called quantum computing,49 leverages the power of quantum parallelism and non-classical correlations like quantum entanglement to offer a platform that has shown algorithmic speed-up over the classical version in many instances.50–54 The natural question which has been posed in the community is whether quantum computing can also expand the horizon for predicting and identifying relevant features in a given data-set,55 lead to newer, more efficient algorithms for machine learning or even record algorithmic speed-up for some of the established toolkits that are now routinely employed by ML practitioners in physics and chemistry.56 In this review, we shall try to explore this exciting intersection.1.1 Scope of the review
The scope and philosophy of this review would thus be the following:1. Ref. 48 highlights that a survey has indicated that ML algorithms are increasingly becoming opaque to human comprehension. We feel that a part of the reason for this is the under-emphasis on the various methodologies that inform the basic building blocks of ML in recent reviews. Although such topics are usually covered elaborately in data-science textbooks57–59 yet the resources lack domain-specific examples/applications which a new researcher in the field may find beneficial. Thus a holistic yet detailed account which focuses on both the basic tools used by ML practitioners and how such tools are enabling various physico-chemical applications, consolidated in one place for researchers to use synergistically, is lacking. This review will try to address this gap.
2. We shall not only discuss the common tools that are used by traditional ML practitioners in theoretical and computational physics and chemistry but also delineate the analogues of these algorithms trainable on a quantum computer. This will be attained in two steps. First, we shall discuss the underlying theoretical framework of quantum versions of each of the vanilla ML algorithms in detail along with their classical counterparts. Second, the contributions made by both the classical and the quantum versions would be discussed separately while exploring each of the respective applications in subsequent parts of the review. To this end, it is important to clearly define certain terms which will set the tone for the review. All applications to be discussed in this review will entail deploying ML based algorithms on datasets involving features or representations of molecules/atoms and/or nanomaterials. Due to the specific nature of the data, we shall broadly call all such examples as instances of quantum machine learning (as is commonly done in this domain60,61) even if the analysis is performed on a classical computer. However, to distinguish examples wherein quantum computers have been used as a part of the training process for the ML algorithm we shall specifically call such applications as ‘quantum computing enhanced’. To the best of our knowledge, explicating such quantum computing enhanced variants in the physico-chemical domain has not been attempted in any of the recent reviews which distinctively sets this one apart from the rest in terms of coverage and focus.
3. We shall also discuss five different domains of physico-chemical applications which includes tomographic preparation of quantum states in the matter, classification of states and phases of matter, electronic structure of matter, force field parameterization for molecular dynamics and drug discovery pipeline. For each of these applications, we shall discuss ML algorithms (both the classical and quantum computing enhanced variants) that have been successfully used in recent literature focusing on as many different architectures as possible. The objective of treating such a diverse portfolio of applications is to ensure that the reader is aware of the many distinct domains in physical chemistry that have benefited immensely from ML over the past decade. Since the quantum-computing variants are still a nascent variety, bulk of the applications to be discussed will involve classical ML algorithms on quantum data even though the focus will certainly be on how the capabilities in each domain can be augmented with the former in the arsenal. To the best of our knowledge, such a diverse and comprehensive portfolio of applications consolidated in one place has not been presented in any single review most of which have been topical and focused on a single domain only. It must also be emphasized that the aforesaid list is by no means exhaustive. Indeed we shall enlist several other domains later which have not been discussed in this review. Topical reviews on such applications will be duly referenced which the interested reader may consult.
4. Lastly, another reason for the obscurity in the interpretation of machine learning algorithms especially those involving neural networks is the lack of clarity in the underlying learning process. Indeed, physicists and chemists are motivated to design computational tools which explicitly use physical laws and scientifically guided domain intuition to understand a given natural phenomenon. However, in most of machine learning algorithms, the models are initially agnostic to such physical principles. Instead they identify pertinent features and/or strategies directly from the data without the need for human intervention. While this process is intriguing, certain researchers may be reluctant to reap the full benefits of ML due to this fundamental difference in the operational paradigm. In this review we strive to address this issue by discussing several statistical physical tools which have been used in recent years to demystify the learning process. This is either completely absent or is less emphasized in recent reviews which we believe also fuels the increasing opacity as highlighted in ref. 48
1.2 Organization of the review
The organization of the review is as follows. In Section 2 we offer a glimpse of some basic notions in quantum computing to be used for understanding the subsequent portions of the review. In Section 3 we discuss in detail each of the commonly used architectures in ML and DL (both the classical and the quantum computing enhanced variants). The basic theoretical framework discussed in this section for each of the methods will be frequently referred to subsequently. In Section 4, we enlist and discuss in detail some of the recent reports wherein the power of quantum computers for machine learning tasks has been explicitly demonstrated or theoretically proven to be superior to that of classical models. In Section 5, we discuss the applications of ML in five different domains of physics and chemistry. In Section 6, we discuss several different models for explaining the learning mechanisms of deep learning algorithms using statistical physics. In Section 7, we conclude with a foray into emerging domains not discussed in this review.2 A short primer on quantum computing
In this section, we shall discuss some of the basic terminologies and conceptual foundations of quantum computing that will be used in the rest of the review. This is not only being done for completeness but with the motivation that since quantum computing as a paradigm is relatively new, it may be unfamiliar to traditional ML practitioners and/or new entrants into the field. To appreciate the quantum analogues of commonly used machine learning algorithms, a basic understanding of some of the operational concepts and terms used in this domain would be beneficial. This section would attempt to familiarize the reader with this knowledge. We shall visit the common operational paradigms of computing using quantum devices that are widely used. Just as in classical computers where one has binary bits encoded as {0,1} used for all logical operations, on a quantum computer the primary unit of information is commonly encoded within a qubit. To define a qubit, one would need two two-dimensional vectors commonly denoted as |0〉 and |1〉 and are referred to as computational basis states. Physically these two states can be the two hyperfine energy levels of an ion like in trapped-ion based quantum computing platforms62,63 or can be energy levels corresponding to different number of Cooper pairs in a superconducting island created between a Josephson junction and a capacitor plate64 or can be the highly excited electronic energy levels of a Rydberg atom based cold atomic-ensembles65,66 or polar molecules in pendular states67–71 to name a few. Mathematically the two states can be represented as |0〉 = (1 0)T and |1〉 = (0 1)T and collectively form a basis for the two-dimensional state space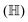 of the system.
of the system.
2.1 Single qubit state
The state of the qubit in the two-dimensional basis of (|0〉,|1〉) is defined by the unit trace positive semi-definite operator (denoted as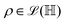 ) as follows:
) as follows: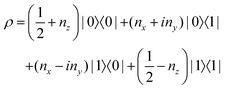 | (1) |
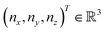 and
and 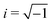 and the operators of the form |i〉〈j| ∀ (i,j) ∈ (0,1) correspond to familiar outer-product of two vectors.49 Positive semi-definiteness of the matrix in eqn (1) guarantees that nx2 + ny2 + nz2 ≤ 1, which allows the vector (nx,ny,nz)T to reside within a Bloch sphere.49 For pure states which are defined by the additional idempotency constraint of ρ2 = ρ, the inequality is saturated. One can then parameterize (nx,ny,nz)T = (cos
and the operators of the form |i〉〈j| ∀ (i,j) ∈ (0,1) correspond to familiar outer-product of two vectors.49 Positive semi-definiteness of the matrix in eqn (1) guarantees that nx2 + ny2 + nz2 ≤ 1, which allows the vector (nx,ny,nz)T to reside within a Bloch sphere.49 For pure states which are defined by the additional idempotency constraint of ρ2 = ρ, the inequality is saturated. One can then parameterize (nx,ny,nz)T = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,cos
ϕ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)T and establish a bijective correspondence with a vector (say
θ)T and establish a bijective correspondence with a vector (say 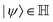 ) defined as
) defined as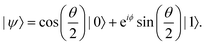 | (2) |
The parametric angles {θ ∈ [0,π], ϕ ∈ [0,2π]} are geometrically defined in the Bloch sphere in Fig. 1 Such states of the system defined by eqn (2) will be extensively used in this review and will be exclusively referred to for single-qubit states unless otherwise specified. For certain magnitudes of the parameter θ wherein both 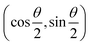 acquire non-zero values, the state of the system in eqn (2) is said to be in a superposition of the two basis states. Realization of such superpositions presents one of the fundamental differences between qubit paradigm of computing and the bit paradigm of computing as used in classical processors. The parametric angle ϕ controls the relative phase difference between the computational basis in such superposition states. However, a superposition even though is responsible for quantum parallelism would not survive a projective measurement protocol.49,72 Such measurements would collapse the state in eqn (2) in either the computational basis state |0〉 with probability
acquire non-zero values, the state of the system in eqn (2) is said to be in a superposition of the two basis states. Realization of such superpositions presents one of the fundamental differences between qubit paradigm of computing and the bit paradigm of computing as used in classical processors. The parametric angle ϕ controls the relative phase difference between the computational basis in such superposition states. However, a superposition even though is responsible for quantum parallelism would not survive a projective measurement protocol.49,72 Such measurements would collapse the state in eqn (2) in either the computational basis state |0〉 with probability 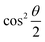 or in the computational basis state |1〉 with probability
or in the computational basis state |1〉 with probability 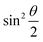 .
.
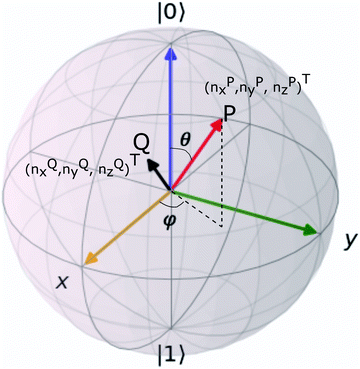 | ||
Fig. 1 The Bloch sphere (blue) and the parametric angles θ and ϕ as used in eqn (2). The point P marked in red lies on the surface of the Bloch sphere and has (nx,ny,nz)T = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,cos ϕ,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)T. Such states can be represented as in eqn (2). On the other hand, states like point Q (marked in black) lies inside the Bloch sphere nx2 + ny2 + nz2 ≤ 1 and cannot be represented as in eqn (2). The only way to denote such states would be using eqn (1). θ)T. Such states can be represented as in eqn (2). On the other hand, states like point Q (marked in black) lies inside the Bloch sphere nx2 + ny2 + nz2 ≤ 1 and cannot be represented as in eqn (2). The only way to denote such states would be using eqn (1). | ||
2.2 Multi-qubit state
For multiple qubits (say N), the corresponding state space is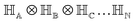 .49 One can thus define a computational basis using the Kronecker product such as |iA〉 ⊗ |iB〉,…,|iN〉, where the labels (A, B, C,…, N) are physically used to demarcate the state-space of each qubit. There are now 2N basis states generated from two choices (|0〉,|1〉) for each of ij, j ∈ {A, B,…, N}. Let us denote this set collectively as
.49 One can thus define a computational basis using the Kronecker product such as |iA〉 ⊗ |iB〉,…,|iN〉, where the labels (A, B, C,…, N) are physically used to demarcate the state-space of each qubit. There are now 2N basis states generated from two choices (|0〉,|1〉) for each of ij, j ∈ {A, B,…, N}. Let us denote this set collectively as 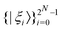 . For notational convenience such multi-qubit basis states will often be abbreviated in this review such as |iA, iB,…, iN〉 ≡ |iA〉, |iB〉,…, |iN〉 ≡ |iA〉 ⊗ |iB〉,…, |iN〉. A general state
. For notational convenience such multi-qubit basis states will often be abbreviated in this review such as |iA, iB,…, iN〉 ≡ |iA〉, |iB〉,…, |iN〉 ≡ |iA〉 ⊗ |iB〉,…, |iN〉. A general state 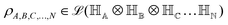 of the multi-qubit system would again correspond to a positive semi-definite operator with unit trace defined as
of the multi-qubit system would again correspond to a positive semi-definite operator with unit trace defined as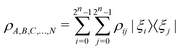 | (3) |
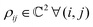 . One can also define a reduced state for each of the sub-system qubits (say for the K-th qubit) through partial tracing of the state ρA,B,C,…,N over computational basis states of the remaining qubits as follows:
. One can also define a reduced state for each of the sub-system qubits (say for the K-th qubit) through partial tracing of the state ρA,B,C,…,N over computational basis states of the remaining qubits as follows:| ρK = TrA,B,…,J,L,…,N (ρA,B,C,…,N) | (4) |
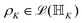 . Such operations are completely positive trace-preserving (CPTP) maps and hence generate valid states49,72 of the sub-system (often called the reduced density operator of the K-th qubit). Just like in the case of single qubits, if the general state in eqn (3) is pure (ρA,B,C,…,N2 = ρA,B,C,…,N) one can associate a vector (say
. Such operations are completely positive trace-preserving (CPTP) maps and hence generate valid states49,72 of the sub-system (often called the reduced density operator of the K-th qubit). Just like in the case of single qubits, if the general state in eqn (3) is pure (ρA,B,C,…,N2 = ρA,B,C,…,N) one can associate a vector (say 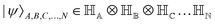 ) which in the multi-qubit computational basis is denoted as
) which in the multi-qubit computational basis is denoted as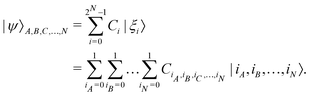 | (5) |
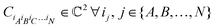 . For a normalized state as is usually considered in this review,
. For a normalized state as is usually considered in this review, 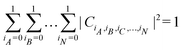 .
.
Other than the possibility of superposition over all basis states similar to the case of single-qubit as discussed in the previous section, it is also possible now to encounter a new phenomenon which has to do with non-classical correlation. The pure state in eqn (5) will be termed separable if ∃ scalars ζiA, γiB,…, ωiN for each sub-system such that CiA,iB,iC,…,iN = ζiA,γiB,…,ωiN ∀ (iA, iB,…, iN)T ∈ {0,1}N, i.e., if every coefficient is multiplicatively factorizable into scalars characterizing the 2D basis states of each sub-system qubit.49,72,73 For such a pure separable state it is possible to express eqn (5) as |ψ〉A,B,C,…,N = |ϕ1〉A⊗|ϕ2〉B…⊗|ϕN〉N wherein 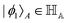 ,
, 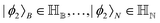 . If a state in eqn (5) is not separable then it is said to be entangled which is a non-classical correlation.
. If a state in eqn (5) is not separable then it is said to be entangled which is a non-classical correlation.
The presence of entanglement is another feature wherein computation using qubits can be different from that of the classical bit counterparts and is often leveraged in many different algorithms as a useful resource.50,51 Similar to that of the case of a single qubit, the probabilistic interpretation of a projective measurement on the state in eqn (5) is retained with the probability of collapsing onto a computational basis state |iA,iB,…,iN〉 is |CiA,iB,iC,…,iN|2. Unless otherwise stated by multi-qubit states in this review we shall almost always exclusively mean pure states of the kind given in eqn (5). Such states as we shall see can not only provide an efficient representation of the many-body states of any interacting quantum system in quantum simulations of stationary/time-independent processes but also for real and imaginary time evolution74,75 in quantum dynamics either through Lie–Trotter–Suzuki expansion76 or through variational frameworks.77
2.3 Quantum gates and quantum circuit based paradigm
Now that we know how to define quantum states of single and many qubits, it is important to learn how such states are transformed or manipulated. In the gate-model of quantum computing paradigm, transformations between states are achieved using unitary matrices which are represented as ‘quantum gates’. Since all quantum gates are unitary, the inverse of such gates necessarily exists and hence transformations using quantum gates alone are always reversible. The way to incorporate irreversibility into the paradigm is through making projective measurements as that disturbs the state vector irrevocably making it loose its present memory (interactions with the environment induces irreversibility too in the form of qubit decoherence.49 We shall return to this point later). Commonly used quantum gates and their matrix representation in the computational basis are given in Table 1. These gates act on either one, two or three qubits as has been indicated in the table. For visualization of the operations of single-qubit gates, in Fig. 2, we plot the corresponding operations for most commonly-used single qubit gates in the Bloch sphere. We see that for Rn(θ) the axis of rotation n can be either {x,y,z} and that decides the accessible state-space for a given initial state. For Hadamard transformation, the operation can be viewed as rotation about the axis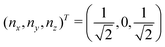 through an angle of π and hence creates the state
through an angle of π and hence creates the state 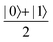 starting from |0〉. The S-gate
starting from |0〉. The S-gate 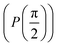 and T-gate
and T-gate 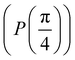 control the relative phases of |0〉 and |1〉 as shown in Fig. 2. Table 1 also discusses several commonly used multi-qubit gates. These operations are commonly used to entangle two or more qubits in a quantum circuit. For example one of the most celebrated two-qubit gate CNOT (see Table 1) can be interpreted as the following:
control the relative phases of |0〉 and |1〉 as shown in Fig. 2. Table 1 also discusses several commonly used multi-qubit gates. These operations are commonly used to entangle two or more qubits in a quantum circuit. For example one of the most celebrated two-qubit gate CNOT (see Table 1) can be interpreted as the following:| CNOT = |0〉〈0|c ⊗ It + |1〉〈1|c ⊗ Xt | (6) |
| CU0 = |0〉〈0|c ⊗ Ut + |1〉〈1|c ⊗ It. | (7) |
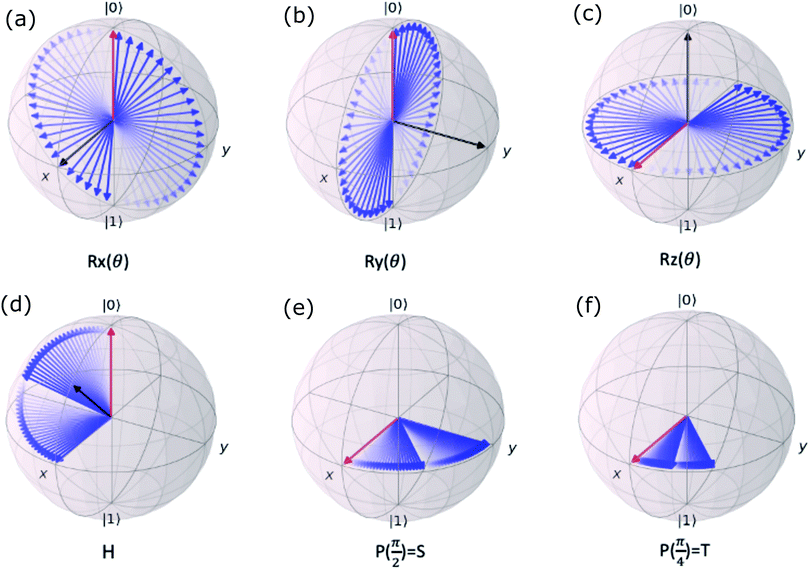 | ||
Fig. 2 (a) The operation Rx(θ) which involves rotation about the x-axis (marked in black) as shown in the Bloch sphere. The initial state is |0〉 (marked in red). (b) The operation Ry(θ) which involves rotation about the y-axis (marked in black) as shown in the Bloch sphere. The initial state is |0〉 (marked in red) (c) same as in (a), (b) but with Rz(θ) wherein the axis of rotation is z (marked in black). The initial state chosen here is (marked in red) 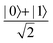 . (d) Hadamard transformation of the initial state |0〉 (marked in red) as visualized in the Bloch sphere. The operation can be viewed as rotation around the axis . (d) Hadamard transformation of the initial state |0〉 (marked in red) as visualized in the Bloch sphere. The operation can be viewed as rotation around the axis 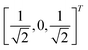 shown in black through an angle of π. Note that unlike the rotation gates in (a)–(c), Hadamard transformation does not have a variable user-defined angle of rotation and hence the final state starting from the said initial state is always fixed i.e. shown in black through an angle of π. Note that unlike the rotation gates in (a)–(c), Hadamard transformation does not have a variable user-defined angle of rotation and hence the final state starting from the said initial state is always fixed i.e.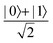 . (e) The transformation of the initial state . (e) The transformation of the initial state 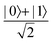 under phase-gate under phase-gate 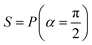 (see Table 1). The operation produces a final state (see Table 1). The operation produces a final state 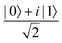 . (f) The transformation of the initial state . (f) The transformation of the initial state 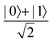 under T-gate where under T-gate where 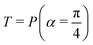 (see Table 1). The operation produces a final state (see Table 1). The operation produces a final state 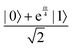 . The matrix representations of the operators in (a)–(f) are given in Table 1. . The matrix representations of the operators in (a)–(f) are given in Table 1. | ||
This interpretation extends to multi-qubit gates beyond two as well, except that the size of the control register now is more than one and many more possibilities of multiple controls are realizable (for example for a three qubit control unitary, the two controlling qubits can be in any of the four states |00〉c, |01〉c, |10〉c, and |11〉c, to initiate a non-trivial operation on the target). In the well-known Toffoli gate (see Table 1) the state of the target is flipped by an X operation conditioned on the joint state of two-qubits instead of one unlike in the CNOT gate. This means the operation is non-trivial only if this joint state is |11〉c. Intuitively, one-qubit gates are required to initiate superposition between the two-basis states of individual qubits as depicted within the Bloch sphere shown in Fig. 2 but multi-qubit gates are required to initiate correlation between the joint-states of several qubits. Both these operations are therefore necessary to create non-trivial many-body quantum states.
A certain subset of gates forms a universal set49 in the sense that any arbitrary n-qubit unitary operation can be approximately modelled as a finite sequence of gates from this set within a preset user-defined precision. The choice of this set is not unique and is largely determined by which gates are operationally convenient for implementation on a given platform used for constructing the quantum hardware. One popular choice is the ({Rx(θ), Ry(θ), Rz(θ), P(α), CNOT}) gate-set. Equivalent yet a minimalistic choice can be 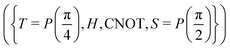 .49,73 One must emphasize that the use of universal gate-sets only guarantees reachability, i.e., the ability to approximately implement any desired unitary using a finite-sequence of gates from the set without placing any restriction on the number of gates inhabiting the sequence.73 Indeed it may so happen that implementation of certain n-qubit unitaries would require gate-sequences from the universal set with length scaling as O(cn), i.e., exponential. On the other hand, for certain other operations, the length of gate-sequences scaling as O(nk) (polynomial) is seen. Only the latter kind of unitaries can be hoped to be efficiently simulated on a quantum computer.
.49,73 One must emphasize that the use of universal gate-sets only guarantees reachability, i.e., the ability to approximately implement any desired unitary using a finite-sequence of gates from the set without placing any restriction on the number of gates inhabiting the sequence.73 Indeed it may so happen that implementation of certain n-qubit unitaries would require gate-sequences from the universal set with length scaling as O(cn), i.e., exponential. On the other hand, for certain other operations, the length of gate-sequences scaling as O(nk) (polynomial) is seen. Only the latter kind of unitaries can be hoped to be efficiently simulated on a quantum computer.
A quantum circuit is essentially an assembly of quantum gates which transforms the initial state of a multi-qubit system to the final desired state. The set of quantum gates operationally represents a user-defined unitary transformation. Such operations are frequently followed by measurement either on a computational basis or on the basis of an operator whose statistics in the prepared state are desired.49 The circuit representation of the commonly used gates is given in Fig. 3(a)–(d). A representative example of a quantum circuit built using some of the gates in Table 1 is given in Fig. 3(e). The circuit shows the preparation of a typical Bell state of the kind 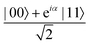 in a 2-qubit system with α being the relative phase difference between the two basis states (|00〉, |11〉). One practically useful way to interpret such a circuit is to probe the state of the system at various junctions. We have divided the circuit into four junctions. At the first junction labelled as (I), the joint state of the two qubits is the initial computational basis |00〉. At junction (II), the effect of Hadamard (H) on the first qubit yields a separable state wherein the first qubit is in an equal superposition of the single-qubit basis states and the second qubit is still in |0〉. The CNOT gate with the first qubit as the control and the second qubit as the target yields the state
in a 2-qubit system with α being the relative phase difference between the two basis states (|00〉, |11〉). One practically useful way to interpret such a circuit is to probe the state of the system at various junctions. We have divided the circuit into four junctions. At the first junction labelled as (I), the joint state of the two qubits is the initial computational basis |00〉. At junction (II), the effect of Hadamard (H) on the first qubit yields a separable state wherein the first qubit is in an equal superposition of the single-qubit basis states and the second qubit is still in |0〉. The CNOT gate with the first qubit as the control and the second qubit as the target yields the state 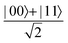 at junction (III). At junction (IV), the controlled-phase gate (CPHASE(α)) selectively creates a phase difference of α between the states |00〉 and |11〉 which results in the target state. Measurements on the target state on a computational basis would yield equal probability (½) of observing either the state |00〉 or |11〉 and zero probability of observing |01〉 or |10〉. Circuit representations of the quantum-enhanced machine learning algorithms shall appear throughout the review. Interpretations of each of them can be done analogously.
at junction (III). At junction (IV), the controlled-phase gate (CPHASE(α)) selectively creates a phase difference of α between the states |00〉 and |11〉 which results in the target state. Measurements on the target state on a computational basis would yield equal probability (½) of observing either the state |00〉 or |11〉 and zero probability of observing |01〉 or |10〉. Circuit representations of the quantum-enhanced machine learning algorithms shall appear throughout the review. Interpretations of each of them can be done analogously.
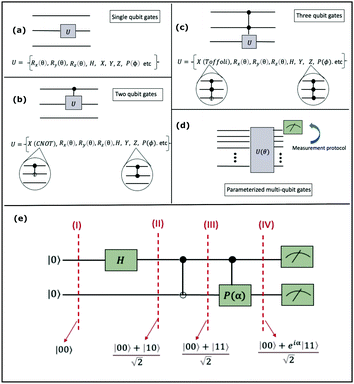 | ||
Fig. 3 Commonly used circuit representation of (a) 1-qubit gates and (b) 2-qubit gates. Special gates in this category like CNOT and CZ gates have slightly different representations than the rest as has been highlighted within the oval windows. One must note that the solid dot indicates the control qubit and the hollow dot with a plus, i.e., ⊕ indicates the target qubit. Its the target qubit whose state is actually altered conditioned on the state of the control qubit being |1〉 in this case. The operation need not always be controlled on state |1〉 for the control qubit. Indeed two-qubit gates where the non-trivial operations on the target initiated by the control is |0〉 are also routinely used (see text for more details). (c) 3-Qubit gates: special gates in this category like Toffoli gate and CCZ gate have slightly different representations than the rest as has been highlighted within the oval window. A similar interpretation as in (b) for the solid and hollow dots (⊕) must be followed in terms of the control and target qubits. (d) A generic n-qubit parameterized unitary. This is very often used to describe quantum circuits as we shall see later in this review. The explicit construction of gates in U(θ) is often omitted but is implied to be made up of elementary gates from (a) and (b) and occasionally even (c). The measurement protocol for any qubit will be denoted by boxes of the kind shown in green symbolically representing a monitoring device/meter. (e) A simple representative quantum circuit for the preparation of the Bell state 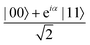 . To facilitate interpretation of the circuit, the state of both the two-qubits is illustrated at junctions (I), (II), (III), and (IV) after the operation of each elementary gate. To evaluate the states one can also use the matrix representation of the respective gates given in Table 1 and apply it to the initial state |00〉 with the unitaries on the left acting first. . To facilitate interpretation of the circuit, the state of both the two-qubits is illustrated at junctions (I), (II), (III), and (IV) after the operation of each elementary gate. To evaluate the states one can also use the matrix representation of the respective gates given in Table 1 and apply it to the initial state |00〉 with the unitaries on the left acting first. | ||
Development of quantum computing has been underway since the 1980s,78,79 but it gained unprecedented attention with the exponential speed-up reported in prime factorization by Peter Shor in the last decade of the 20th century.53 It was quickly realized, however, that uncontrolled interactions of the qubit register with the environmental bath lead to the loss of coherence of the initialized state. Moreover, for the experimental implementation of a digital quantum-computing platform, the gate-operations (unitary gates defined above) may be imperfect too.80 The collective effect of both of these would be to introduce noise or errors thereby hampering the performance of the algorithm. Quantum error-correction (QEC) schemes were proposed81 which can act to mitigate the effect of these noises. However scalable implementation of such protocols is challenging82,83 and is currently under development. In the current era, operational quantum devices are already a reality consisting of around 10–100 qubits but without any error-correction. This era of quantum computers is therefore termed noisy intermediate-scale quantum devices (NISQ).84 Due to the inherently erroneous gate operations, the algorithms developed for NISQ devices are designed to use shallow-circuit depth and usually variational and delegate a part of the computation to a classical processor.85 Such algorithms are meant to reap the maximum benefits from noisy hardwares and look for potential advantages. Such algorithms will be a key player in this review for understanding some of the near-term ML applications. These algorithms have proven to be advantageous for applications in chemistry/chemical physics,86–90 condensed-matter physics and materials science,91 atomic physics,92 high-energy physics,93,94 bio-chemistry,95 and finance.96 In contrast, there are algorithms like quantum phase estimation97,98 which have a provable exponential advantage but require high-circuit depth and hence are amenable to be implemented in fault-tolerant devices.
2.4 Quantum annealing based paradigm
This paradigm is particularly useful for solving optimization problems wherein the optimal solution can be encoded within the ground state of a given Hamiltonian of a system (say H2). The key working principle of the hardware operating under the annealing model is to prepare the ground state of a system which is efficiently prepared (say for a Hamiltonian H1), from which the ground state of the target Hamiltonian H2 is subsequently retrieved.| H(s) = A(s)H1 + B(s)H2 | (8) |
To be more specific, let the Hamiltonian of the system be H1, i.e., A(s) = 1, B(s) = 0, in eqn (8), whose ground state can be easily constructed. Thereafter the switching parameter s is varied until (A(s) = 0, B(s) = 1). If the variations are sufficiently ‘slow’ then the quantum adiabatic theorem99 guarantees that the evolution trajectory would be traversing the instantaneous ground states of Hamiltonian H(s) with high probability. Under such circumstances this implies that one would yield the ground state of the target Hamiltonian H2 at the end of the protocol with high fidelity (see eqn (8)). A popular quantum annealer D-wave uses ground states of Ising type Hamiltonians100 for encoding the solution to the problem being investigated. Optimization schemes like quadratic unconstrained binary optimization (QUBO), combinatoric problems etc. which can be mapped to such Hamiltonians can thus be efficiently solved using this paradigm.101–104 Except in a very small number of examples, this paradigm of quantum computing will not be explored much in this review. Interested readers may consult topical reviews like ref. 101,105.
3 A short primer on the commonly used toolkits in machine learning
3.1 Overview
Broadly problems tackled in machine learning can be categorized into 3 classes: supervised, unsupervised and reinforcement learning. We start off by discussing each of the categories independently and introduce commonly used terminologies within the machine learning community.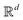 and yi belongs to
and yi belongs to 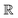 . The task is to identify the correct label for y* for a randomly chosen sample x* from that distribution. The dataset {(xi,yi)|i ∈ [N]} is referred to the training dataset. A loss function L(h(xi,w),yi) is defined based on the problem at hand that quantifies the error in the learning. Here h(x,w) refers to the hypothesis function that the learning procedure outputs and w refers to the parameters or weights over which the optimization is performed. An empirical risk minimization is carried over
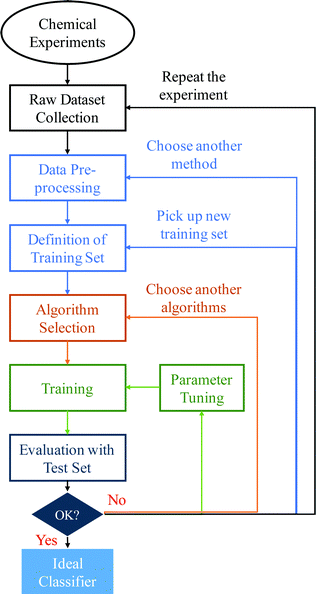
. The task is to identify the correct label for y* for a randomly chosen sample x* from that distribution. The dataset {(xi,yi)|i ∈ [N]} is referred to the training dataset. A loss function L(h(xi,w),yi) is defined based on the problem at hand that quantifies the error in the learning. Here h(x,w) refers to the hypothesis function that the learning procedure outputs and w refers to the parameters or weights over which the optimization is performed. An empirical risk minimization is carried over 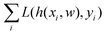 to output h(x,w*), where w* are the parameters output at the end of learning. A test data set is finally used to output the performance of h(x,w*) and used as a metric of comparison across several learning methods. The labelled dataset being used is manually subdivided into two subsets. One of the subset is used for training and the other for final validation and testing. The process of learning thus comprises 2 parts: trainability (empirical risk minimization over training data) and generalization (how well it performs on unseen data). Typically the optimization of parameters involves computing gradients of the loss function with respect to these parameters.
to output h(x,w*), where w* are the parameters output at the end of learning. A test data set is finally used to output the performance of h(x,w*) and used as a metric of comparison across several learning methods. The labelled dataset being used is manually subdivided into two subsets. One of the subset is used for training and the other for final validation and testing. The process of learning thus comprises 2 parts: trainability (empirical risk minimization over training data) and generalization (how well it performs on unseen data). Typically the optimization of parameters involves computing gradients of the loss function with respect to these parameters.
Apart from the parameters that are trained definitively through optimization schemes, other parameters referred to as hyperparameters become critically important for neural-network based supervised learning schemes (to be explored soon). Such parameters/variables are fixed manually by hand a priori. These may include, the learning technique employed, the number of parameters, the optimization procedure106 (standard gradient descent, stochastic gradient descent, and Adam optimizer), the parameter initialization scheme, the learning rate, the stopping conditions for training (the threshold for convergence or the number of parameter update iterations), batch sizes, choice of the loss function, etc.107
Examples of problems in a supervised learning procedure include classification, where the labels yi are discrete, and regression, where the labels yi are continuous and extrapolation to unknown cases is sought. Some of the techniques used exclusively for problems in this domain include, a support vector machine, kernel ridge regression wherein data are mapped to a higher-dimensional space for manipulation, Gaussian process regression, decision trees, and a Naive Bayes classifier. Other techniques not exclusive to this learning model include Neural networks whose applications have spanned every field of industry and research. We will discuss more about each of the above learning models in the subsequent section.
One is not restricted to using methods from either supervised or unsupervised learning exclusively for solving a problem. In practice we notice that a mix of methods are employed to solve a given problem. For instance, one might require dimensionality reduction or noise filtering or distribution learning using unsupervised methods prior to introducing labels and solving a classification problem with supervised methods. These methods are commonly referred to as semi-supervised learning109,110 or hybrid learning methods.
3.2 Classical and quantum variants of commonly used algorithms
In this section we shall elaborate on some of the commonly encountered machine and deep learning techniques that have been used extensively for physico-chemical studies. We shall discuss both the classical implementation of the algorithms and also the appropriate quantum versions.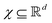 and
and 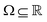 . m is the sample size of the training data-set D or the number of observations. It is often convenient to define a map ϕ such that
. m is the sample size of the training data-set D or the number of observations. It is often convenient to define a map ϕ such that 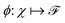 such that the new feature-space
such that the new feature-space 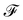 is usually a higher-dimensional space equipped with an inner product. For example if
is usually a higher-dimensional space equipped with an inner product. For example if 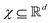 and
and  then p ≥ d. The Kernel
then p ≥ d. The Kernel 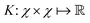 of the map ϕ(x) is then defined as follows:
of the map ϕ(x) is then defined as follows: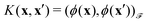 | (9) |
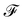 . For example, if
. For example, if  then the inner product can be familiar
then the inner product can be familiar 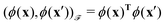 .
.
The importance of kernels lies in the fact that since the space 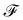 is high-dimensional, direct computation of the feature map ϕ(x) in that space might be intractable and/or expensive. However most algorithms using the kernel trick are designed such that the only quantity required would be the inner product K(x,x′) (see eqn (9)) without explicit construction or manipulation of ϕ(x) or ϕ(x′). Thus several popular kernel functions have been reported in the literature113,114 which can be computed directly from the entries x in the dataset D. Some of them are displayed below:
is high-dimensional, direct computation of the feature map ϕ(x) in that space might be intractable and/or expensive. However most algorithms using the kernel trick are designed such that the only quantity required would be the inner product K(x,x′) (see eqn (9)) without explicit construction or manipulation of ϕ(x) or ϕ(x′). Thus several popular kernel functions have been reported in the literature113,114 which can be computed directly from the entries x in the dataset D. Some of them are displayed below:
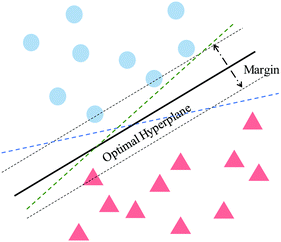
The success of the kernel trick has been extended to several important supervised machine learning algorithms like kernel-ridge regression, dimensionality reduction techniques like kernel-based principal component analysis, classification routines like k-nearest neighbor (see Section 3.2.4), support-vector machines (SVM) (see Section 3.2.7), etc. For classification tasks like in SVM the effect is more conventionally described as the inability of a hyperplane for linearly discriminating the data entries which can be ameliorated through the kernel trick of transporting the feature vectors x to a higher dimension ϕ(x) wherein such a separability is easily attainable. Both regression and classification algorithms will be discussed in detail in appropriate sections. In this section, we shall first discuss the kernel theory developed recently for quantum-computing enhanced machine learning techniques.
3.2.1.1 Quantum enhanced variants. The theory of quantum kernels has been formalized in ref. 116 and 117. For a given classical data set D = {(xi,yi)|xi ∈ χ, yi ∈ Ω ∀ i ∈ [m]} as defined above wherein xi ∈ χ, a data domain, ref. 116 defines a data-encoding feature map as a quantum state ρ(xi) = |ϕ(xi)〉〈ϕ(xi)| which is created from a data-encoding unitary
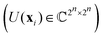 as |ϕ(xi)〉 = U(xi)|0〉n. This unitary U(xi) thus embeds each feature vector of the dataset within a quantum state ρ(xi). The state ρ(xi) is part of a Hilbert space
as |ϕ(xi)〉 = U(xi)|0〉n. This unitary U(xi) thus embeds each feature vector of the dataset within a quantum state ρ(xi). The state ρ(xi) is part of a Hilbert space 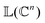 which is thereby equipped with an inner product defined as
which is thereby equipped with an inner product defined as 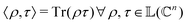 . The quantum variant of the kernel matrix entries from the dataset D is thus computed from this inner product as
. The quantum variant of the kernel matrix entries from the dataset D is thus computed from this inner product as| K(xi,xj) = Tr(ρ(x)iρ(xj)). | (10) |
The authors prove that such a definition of a quantum kernel indeed satisfies Mercer's conditions118 of positive-semi definiteness. The authors then define a reproducing kernel Hilbert space (RKHS) which is a span of basis functions  where the function f(x) = K(xi,x), i.e., each such basis function in the spanning set comprises quantum kernel matrix elements K(xi,x) as defined in eqn (10) with one input argument of the matrix element being made from a particular datum (say xi ∈ χ) of the dataset D. Any arbitrary function (say g(x)) that lives in the RKHS is thus a linear combination of such basis functions and is expressed as
where the function f(x) = K(xi,x), i.e., each such basis function in the spanning set comprises quantum kernel matrix elements K(xi,x) as defined in eqn (10) with one input argument of the matrix element being made from a particular datum (say xi ∈ χ) of the dataset D. Any arbitrary function (say g(x)) that lives in the RKHS is thus a linear combination of such basis functions and is expressed as
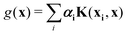 | (11) |
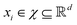 in dataset D defined in the above section. Using these vectors, one can define a design matrix often designated as X as follows:
in dataset D defined in the above section. Using these vectors, one can define a design matrix often designated as X as follows: | (12) |
 the objective is to fit a linear model of the kind X
the objective is to fit a linear model of the kind X![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) where
where 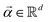 to the data and obtain the optimal fitting parameters. This can be done through the minimization of the following mean-squared error (MSE) loss
to the data and obtain the optimal fitting parameters. This can be done through the minimization of the following mean-squared error (MSE) loss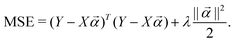 | (13) |
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) *) is the following:
*) is the following: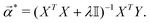 | (14) |
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) is necessary. This can be tackled by augmenting the design matrix as X → [
is necessary. This can be tackled by augmenting the design matrix as X → [![[1 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0031_20d1.gif) |X]T. Also extension to polynomial regression is straightforward as one can create a design matrix treating higher powers of xi as independent variables in each row of the design matrix as Xi → [xTi(x2i)T, (x3i)T,…, (xki)T] where xki denotes raising xi element-wise to the kth power.123,124
|X]T. Also extension to polynomial regression is straightforward as one can create a design matrix treating higher powers of xi as independent variables in each row of the design matrix as Xi → [xTi(x2i)T, (x3i)T,…, (xki)T] where xki denotes raising xi element-wise to the kth power.123,124
For the kernel variant of ridge-regression, if the prediction from the model is designated as ỹ(x,α), then the formalism represents the function ỹ(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,
,![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) ) as125,126
) as125,126
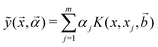 | (15) |
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) are trainable parameters and
are trainable parameters and ![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) are the hyper-parameters associated with the kernel K(x,xj,
are the hyper-parameters associated with the kernel K(x,xj,![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ). These hyperparameters are fixed at the beginning of the optimization and can be tuned for separate runs to modify accuracy. Using the labels yi of the training data set D defined before and eqn (15) one can now formulate a mean-squared error (MSE) loss (similar to eqn (13)) to learn the parameters
). These hyperparameters are fixed at the beginning of the optimization and can be tuned for separate runs to modify accuracy. Using the labels yi of the training data set D defined before and eqn (15) one can now formulate a mean-squared error (MSE) loss (similar to eqn (13)) to learn the parameters ![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) as below
as below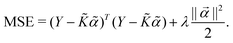 | (16) |
![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) is called the Gram matrix of the kernel125 with entries as follows:
is called the Gram matrix of the kernel125 with entries as follows:![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ij = K(xi,xj, ij = K(xi,xj,![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) ). ). | (17) |
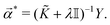 | (18) |
![[small alpha, Greek, vector]](https://www.rsc.org/images/entities/i_char_e118.gif) * is the dual formulation of the problem which involves minimizing the following Langrangian:127
* is the dual formulation of the problem which involves minimizing the following Langrangian:127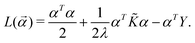 | (19) |
3.2.2.1 Quantum enhanced variants. Several quantum algorithms have been proposed in the last decade for solving linear systems which can be directly extended to the solution of the vanilla linear least-square fitting. The earliest was by Weibe et al.130 and is based on the Harrow, Hassidim, Lloyd (HHL) algorithm.131,132 The technique starts with a non-hermitian X matrix (say m × d as in the design matrix in our example above) which is required to be sparse. The algorithm assumes oracular access to a quantum state encoding its row space and also a state encoding the
![[y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0079_20d1.gif) . The key point of the routine is to expand the non-hermitian design matrix into a (m + d) × (m + d) dimensional matrix with which the quantum-phase estimation algorithm52 is performed. The ultimate product of this algorithm is a quantum state that encodes the fitted values. Even though extraction of the exact fitting parameters from the state might be exponentially hard yet prediction of a new y value for a given test-input can be made effortlessly through overlap with the register containing the fitted values. Variants of this algorithm for detecting statistic leverage score and matrix coherence have also been reported.133 Wang reported a quantum algorithm which can actually yield the fitted values as a vector just as in classical least squares.134 Both the method have query complexity which is O(log(m)). A subset of these algorithms has also been experimentally implemented on a variety of platforms like NMR,135 superconducting qubits,136 and photonic.137 Schuld et al.138 have also designed an algorithm which does not require the design matrix X to be sparse. The only requirement is that X†X should be well-represented by a low rank approximation, i.e., should be dominated by few eigenvalues only. The key point in the technique is to perform quantum-phase estimation with a density matrix ρ encoding X†X. The algorithm also returns the fitted values encoded within a quantum state with which efficient overlap of a new input can be initiated. An algorithm by Yigit et al.139 which solves for a linear system of equation through adiabatic Hamiltonian evolution has also been demonstrated recently. A variational algorithm amenable to the NISQ era for linear equation solver has also been reported.140 The algorithm takes as input a gate sequence U that prepares and encodes the state
. The key point of the routine is to expand the non-hermitian design matrix into a (m + d) × (m + d) dimensional matrix with which the quantum-phase estimation algorithm52 is performed. The ultimate product of this algorithm is a quantum state that encodes the fitted values. Even though extraction of the exact fitting parameters from the state might be exponentially hard yet prediction of a new y value for a given test-input can be made effortlessly through overlap with the register containing the fitted values. Variants of this algorithm for detecting statistic leverage score and matrix coherence have also been reported.133 Wang reported a quantum algorithm which can actually yield the fitted values as a vector just as in classical least squares.134 Both the method have query complexity which is O(log(m)). A subset of these algorithms has also been experimentally implemented on a variety of platforms like NMR,135 superconducting qubits,136 and photonic.137 Schuld et al.138 have also designed an algorithm which does not require the design matrix X to be sparse. The only requirement is that X†X should be well-represented by a low rank approximation, i.e., should be dominated by few eigenvalues only. The key point in the technique is to perform quantum-phase estimation with a density matrix ρ encoding X†X. The algorithm also returns the fitted values encoded within a quantum state with which efficient overlap of a new input can be initiated. An algorithm by Yigit et al.139 which solves for a linear system of equation through adiabatic Hamiltonian evolution has also been demonstrated recently. A variational algorithm amenable to the NISQ era for linear equation solver has also been reported.140 The algorithm takes as input a gate sequence U that prepares and encodes the state ![[y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0079_20d1.gif) and a design matrix X that is decomposable into implementable unitaries. The method implements a trainable unitary
and a design matrix X that is decomposable into implementable unitaries. The method implements a trainable unitary 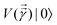 where
where 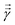 is a variational parameter. The aim of the unitary is to prepare a candidate state
is a variational parameter. The aim of the unitary is to prepare a candidate state 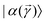 which encodes a prospective solution to the least-square problem. The prospective solution is tuned using a cost-function which measures the overlap of the state
which encodes a prospective solution to the least-square problem. The prospective solution is tuned using a cost-function which measures the overlap of the state 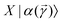 with the orthogonal subspace of the vector
with the orthogonal subspace of the vector ![[y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0079_20d1.gif) as follows:
as follows: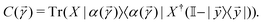 | (20) |
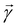 on a classical computer and the parameter vector is fed into the trainable unitary V for the next iteration until the desired convergence is met. The authors show that the above cost-function being a global one suffers from barren plateaus and is rendered untrainable for the size of design matrix X being close to 250 × 250. To evade the issue, they define local merit functions which remain faithful throughout. The ansatz used for encoding
on a classical computer and the parameter vector is fed into the trainable unitary V for the next iteration until the desired convergence is met. The authors show that the above cost-function being a global one suffers from barren plateaus and is rendered untrainable for the size of design matrix X being close to 250 × 250. To evade the issue, they define local merit functions which remain faithful throughout. The ansatz used for encoding 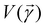 is the hardware-efficient ansatz and the algorithm showed logarithmic dependence on the error tolerance but near linear dependence on the condition number of the design matrix. The dependence on qubit requirements was found to be poly-logarithmic. The algorithm was implemented on an actual hardware for a design matrix of size 210 × 210. Recently, Yu et al. reported an algorithm for ridge-regression (linear variant)141 which like the one reported by Weibe requires oracular access to elements of the design matrix and
is the hardware-efficient ansatz and the algorithm showed logarithmic dependence on the error tolerance but near linear dependence on the condition number of the design matrix. The dependence on qubit requirements was found to be poly-logarithmic. The algorithm was implemented on an actual hardware for a design matrix of size 210 × 210. Recently, Yu et al. reported an algorithm for ridge-regression (linear variant)141 which like the one reported by Weibe requires oracular access to elements of the design matrix and ![[y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0079_20d1.gif) . The design matrix is expanded to make it hermitian and quantum-phase estimation is performed as before with respect to e−iXt as the unitary to encode the eigenvalues onto an extra register. The difference comes at this stage when an ancillary qubit is added and rotated to invert the eigenvalues. The rotation angles are dependant on the Ridge parameter λ. Like previous algorithm this also yields the final optimal parameters as a quantum state. The authors also propose another quantum algorithm (which can be used along with this) for the choice of the Ridge parameter which is similar in principle to the K-fold cross validation technique.142 To the best of our knowledge, no quantum algorithm has been proposed that directly attempts to implement the kernelized variant of Ridge-regression but any of the aforesaid ones can be trivially extended with the replacement of the design matrix with the Gram matrix of an appropriate kernel.
. The design matrix is expanded to make it hermitian and quantum-phase estimation is performed as before with respect to e−iXt as the unitary to encode the eigenvalues onto an extra register. The difference comes at this stage when an ancillary qubit is added and rotated to invert the eigenvalues. The rotation angles are dependant on the Ridge parameter λ. Like previous algorithm this also yields the final optimal parameters as a quantum state. The authors also propose another quantum algorithm (which can be used along with this) for the choice of the Ridge parameter which is similar in principle to the K-fold cross validation technique.142 To the best of our knowledge, no quantum algorithm has been proposed that directly attempts to implement the kernelized variant of Ridge-regression but any of the aforesaid ones can be trivially extended with the replacement of the design matrix with the Gram matrix of an appropriate kernel.
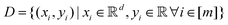 ). Here we define a design matrix (say
). Here we define a design matrix (say 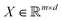 ) as in eqn (12) Formally the goal of PCA is to replace the matrix X with another matrix Z such that
) as in eqn (12) Formally the goal of PCA is to replace the matrix X with another matrix Z such that 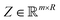 where R ≤ d.119,143,144 To do this for the usual linear variant of the PCA one defines a mean-centered data matrix (say B = X −
where R ≤ d.119,143,144 To do this for the usual linear variant of the PCA one defines a mean-centered data matrix (say B = X − ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) ) where
) where ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) is the stacked row-wise mean of the data matrix (mean of each feature over the samples). One then constructs the covariance matrix144 (Cov(B) = BTB,
is the stacked row-wise mean of the data matrix (mean of each feature over the samples). One then constructs the covariance matrix144 (Cov(B) = BTB, 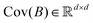 ) and diagonalizes it to get the d eigenvectors
) and diagonalizes it to get the d eigenvectors 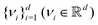 . From the set
. From the set 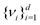 one picks up the R eigenvectors with the largest eigenvalues to form a new matrix (say
one picks up the R eigenvectors with the largest eigenvalues to form a new matrix (say 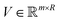 ) as
) as| V = (ν1, ν2, ν3,…, νR). | (21) |
| Z = XV. | (22) |
The kernel-based variant of PCA145 becomes important when the data need to be expressed in a high-dimensional subspace induced by the map ϕ as defined before, i.e., ∀ 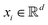 ,
, 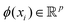 where p ≥ d. One can then construct the covariance matrix in this new feature space of the data as follows:
where p ≥ d. One can then construct the covariance matrix in this new feature space of the data as follows:
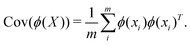 | (23) |
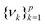 as follows:
as follows:| Cov(ϕ(X))νk = λkνk | (24) |
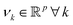 . However, since this space is high-dimensional, computation can be expensive. It is thus desirable to use the power of the kernel and design an algorithm wherein the explicit construction and/or manipulation of ϕ(X) is evaded. To do so, one can expand the eigenvectors νk as follows:
. However, since this space is high-dimensional, computation can be expensive. It is thus desirable to use the power of the kernel and design an algorithm wherein the explicit construction and/or manipulation of ϕ(X) is evaded. To do so, one can expand the eigenvectors νk as follows: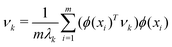 | (25) |
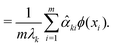 | (26) |
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) k ∀ k ∈ {1, 2,…, p} satisfies the eigenvalue equation for the Gram matrix (see eqn (17)) of the kernel as
k ∀ k ∈ {1, 2,…, p} satisfies the eigenvalue equation for the Gram matrix (see eqn (17)) of the kernel as![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif) ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) k = (λkm) k = (λkm)![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) k. k. | (27) |
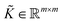 to get the coefficients of the eigenvectors of Cov(ϕ(X)) (see eqn (24)) without explicitly constructing ϕ(X) or even the covariance. Since valid kernels need to be positive-semi-definite as a condition imposed by Mercer's theorem,146,147 one can choose a subset (say R) from
to get the coefficients of the eigenvectors of Cov(ϕ(X)) (see eqn (24)) without explicitly constructing ϕ(X) or even the covariance. Since valid kernels need to be positive-semi-definite as a condition imposed by Mercer's theorem,146,147 one can choose a subset (say R) from 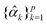 in the decreasing order of their eigenvalues λk and construct a matrix
in the decreasing order of their eigenvalues λk and construct a matrix 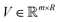 as
asV = (![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) 1, 1, ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) 2,…, 2,…, ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) R) R) | (28) |
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) k and the Kernel Gram matrix only as follows:148
k and the Kernel Gram matrix only as follows:148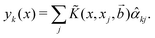 | (29) |
3.2.3.1 Quantum enhanced variants. The very first instance of performing principal component analysis on a quantum computer was put forward by Lloyd et al.149 The algorithm starts with a matrix say P which is positive-semi-definite. Even the usual linear variant of the PCA using the covariance matrices of the mean-centered data was discussed as an application for the method, yet the algorithm can be extended to any positive-semi-definite matrix including the Gram matrices of Kernels. Any such matrix P can be written as
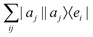 where |ei〉 is the computational basis and |aj〉 are column vectors of P normalized to 1149 and |aj| is the corresponding norm. The algorithm assumes that an oracular object exists that encodes the column space onto a quantum state as
where |ei〉 is the computational basis and |aj〉 are column vectors of P normalized to 1149 and |aj| is the corresponding norm. The algorithm assumes that an oracular object exists that encodes the column space onto a quantum state as 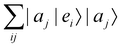 where |ei〉 is an orthonormal basis usually the standard computational basis. The corresponding reduced density matrix for the first register in this state is exactly the positive semi-definite matrix P. The crux of the method is to prepare the unitary e−iPt. This is done on a qubit register that encodes the reduced density matrix P as described above and also another density matrix (say σ). The repeated applications of e−iSδ on the joint state P ⊗ σ with n copies of P yield e−iPnδσe−iPnδ where S is the efficiently implementable SWAP operator. Once efficient preparation of the unitary e−iPnδ has been conducted one can thereafter use standard phase estimation algorithms52 to measure the first say R eigenvalues and eigenvectors of the desired matrix K and cast the data matrix X in the form of eqn (2). The algorithm produces the R eigenvectors with a time complexity of O(R
where |ei〉 is an orthonormal basis usually the standard computational basis. The corresponding reduced density matrix for the first register in this state is exactly the positive semi-definite matrix P. The crux of the method is to prepare the unitary e−iPt. This is done on a qubit register that encodes the reduced density matrix P as described above and also another density matrix (say σ). The repeated applications of e−iSδ on the joint state P ⊗ σ with n copies of P yield e−iPnδσe−iPnδ where S is the efficiently implementable SWAP operator. Once efficient preparation of the unitary e−iPnδ has been conducted one can thereafter use standard phase estimation algorithms52 to measure the first say R eigenvalues and eigenvectors of the desired matrix K and cast the data matrix X in the form of eqn (2). The algorithm produces the R eigenvectors with a time complexity of O(R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(m)) where m is the column dimension of the Gram matrix defined in (17). Since the above formulation relies on quantum-phase estimation to extract eigenvalues and eigenvectors of the Gram matrix, application of the procedure to near-term quantum devices is cost-prohibitive due to high-qubit and gate requirements. Recently Li et al.150 reported a new algorithm for the extraction of principal components of any positive-semi-definite matrix using a single ancillary qubit. The algorithm encodes a joint initial state of an ancillary qubit and the n-qubit positive semi-definite matrix (P in the notation and it could be a Gram matrix of the kernel as well as defined in eqn (17)) as |0〉〈0| ⊗ P. This state is evolved under the effect of the following Hamiltonian for a time δt (see circuit for implementing Trotterized evolution in Fig. 4)
log(m)) where m is the column dimension of the Gram matrix defined in (17). Since the above formulation relies on quantum-phase estimation to extract eigenvalues and eigenvectors of the Gram matrix, application of the procedure to near-term quantum devices is cost-prohibitive due to high-qubit and gate requirements. Recently Li et al.150 reported a new algorithm for the extraction of principal components of any positive-semi-definite matrix using a single ancillary qubit. The algorithm encodes a joint initial state of an ancillary qubit and the n-qubit positive semi-definite matrix (P in the notation and it could be a Gram matrix of the kernel as well as defined in eqn (17)) as |0〉〈0| ⊗ P. This state is evolved under the effect of the following Hamiltonian for a time δt (see circuit for implementing Trotterized evolution in Fig. 4)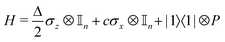 | (30) |
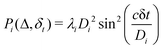 | (31) |
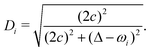 | (32) |
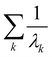 where λk are the eigenvalues of the Gram matrix) encodes columns of the target matrix V (see eqn (28)) onto the register scaled with
where λk are the eigenvalues of the Gram matrix) encodes columns of the target matrix V (see eqn (28)) onto the register scaled with 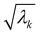 due to phase-kickback from the measurement. Note the final state thus prepared is not entirely the columns of eqn (28) but is scaled by the square root of the corresponding eigenvalues λk.
due to phase-kickback from the measurement. Note the final state thus prepared is not entirely the columns of eqn (28) but is scaled by the square root of the corresponding eigenvalues λk.
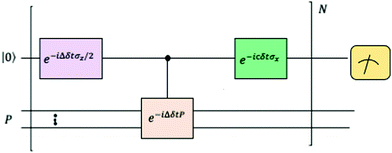 | ||
| Fig. 4 The schematic of the quantum circuit used for the Trotterized evolution as illustrated in ref. 150. The eigenvalues and eigenvectors of the positive-semi definite matrix P are desired. At the end of the evolution, the ancilla qubit is measured and the algorithm is considered successful if it collapses to state |1〉 (see text for more details). | ||
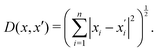 | (33) |
Generally, the relative distance is determined by using a distance metric instead of the absolute position of the instances. Apart from the Euclidean metric, some significant metrics are presented as follows:
3.2.4.1 Quantum enhanced variants. In 2013, Lloyd and coworkers proposed a quantum clustering algorithm for supervised or unsupervised QML,156 relying on the fact that estimating distances and inner products between post-processed vectors in N-dimensional vector spaces takes time O(log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) on a quantum computer whereas on a classical computer it would take O(N) time for sampling and estimating such distances and inner products, thereby apparently providing an exponential advantage.157 More discussion on this speedup on a quantum computer can be found in Section 5.2. The significant speedup of estimating distances provokes enormous enthusiasm for studying QML, particularly the quantum instance-based learning algorithms. Wiebe and coworkers developed the quantum nearest neighbor algorithm based on the Euclidean distance, and studied the performance on several real-world binary classification tasks.56 Moreover, assorted quantum kNN methods153,158,159 are proposed with heterogeneous distance metrics, assisting in solving a variety of pattern recognition problems.
N) on a quantum computer whereas on a classical computer it would take O(N) time for sampling and estimating such distances and inner products, thereby apparently providing an exponential advantage.157 More discussion on this speedup on a quantum computer can be found in Section 5.2. The significant speedup of estimating distances provokes enormous enthusiasm for studying QML, particularly the quantum instance-based learning algorithms. Wiebe and coworkers developed the quantum nearest neighbor algorithm based on the Euclidean distance, and studied the performance on several real-world binary classification tasks.56 Moreover, assorted quantum kNN methods153,158,159 are proposed with heterogeneous distance metrics, assisting in solving a variety of pattern recognition problems.
The structure of the quantum nearest-neighbor algorithm is shown in Fig. 6.56 The quantum nearest neighbor algorithm can be implemented briefly in three steps.56 First, for each training vector vj, prepare a state that encodes the distance between the test instance u and vj in an amplitude using the subroutine for an appropriate distance metric. Then, use coherent amplitude amplification to store the distance estimate as a qubit string without measuring the state. Finally, find the vj that minimizes the distance under certain distance metrics, and vj is the nearest instance. Label of the test instance u is thus predicted as the same label as vj.
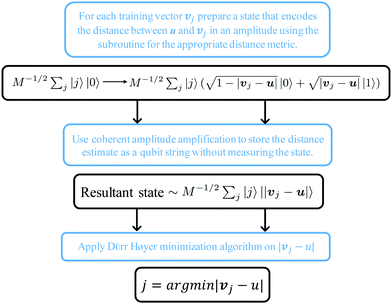 | ||
| Fig. 6 Scheme of the structure of the quantum nearest-neighbor algorithm.56 First for each training vector vj, prepare a state that encodes the distance between the test instance u and vj in the amplitudes using the subroutine for an appropriate distance metric. Then, use coherent amplitude amplification to store the distance estimate as a qubit string without measuring the state. Finally, find the vj that minimizes the distance under certain distance metrics, and vj is the nearest instance. Label of the test instance u is thus predicted as the same label as vj. | ||
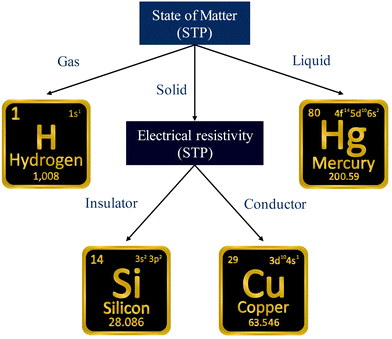
A simple example is shown in Fig. 7, where four chemical substances are classified using a decision tree model. Instances are classified starting from the first node, or the root node, where we study the state of matter at standard temperature and pressure (STP). If the instance is gas, then it will be assigned as hydrogen. If it is liquid, then it will be assigned as mercury. For the solid state, we further go to the next node, where we study its electrical resistivity (STP). The instance as conductor will be classified as copper, while that as an insulator is classified as silicon.
Constructing optimal binary decision trees is an NP-complete problem, making it possible to find efficient heuristics for constructing near-optimal decision trees.161 The feature that best divides the training data should be assigned as the root node of the tree. There are numerous methods for finding the feature that best divides the training data such as information gain162 and gini index.163 Comparison of individual methods may still be important when deciding which metric should be used for a particular dataset. We shall return to examples of decision trees in Sections 5.2 and 5.5.
3.2.5.1 Quantum enhanced variants. In 1998, Farhi and coworkers proposed a design of quantum decision trees, which can be experimentally implemented on a quantum computer that consists of enough spin-½ particles. They further studied a single time-independent Hamiltonian that evolves a quantum state through the nodes of a decision tree.164 It has been proven that if the classical strategy succeeds in reaching the n-th level of the decision tree in runtime polynomial in n, then the quantum algorithm also requires time polynomial of n to reach the same level. Moreover, they found examples where the interference allows a class of trees to be penetrated exponentially faster by quantum evolution than by a classical random walk. However, these examples could also be solved in polynomial time by different classical algorithms.
A quantum training dataset with n quantum data pairs can be described as
| D = {(|x1〉,|y1〉), (|x2〉,|y2〉),…, (|xn〉,|yn〉)} | (34) |
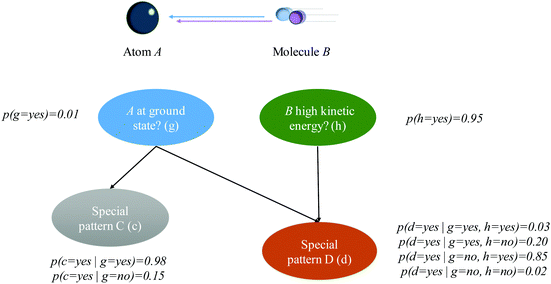
1. A set of variables and a set of directed edges between variables.
2. Each variable has a finite set of mutually exclusive states.
3. The variables together with the directed edges form a directed acyclic graph (DAG).
4. To each variable A with parents B1, B2,…, Bn, there is attached the conditional probability table (CPT) P(A|B1, B2,…, Bn).
The learning process of the BN methods generally contains two subtasks: the construction of the DAG network and the determination of parameters. The approach to design the structure is based on two observations.169 First, people can often readily assert causal relationships among variables. Second, causal relationships typically correspond to assertions of conditional dependence. In particular, to construct a Bayesian network for a given set of variables, we simply draw arcs from cause variables to their immediate effects. Sometimes the structure of the network is given; then the parameters in the CPT are usually learnt by estimating a locally exponential number of parameters from the data provided.168
Fig. 8 is an example of the BN assisted study of the scattering experiment between atom A and molecule beams B. Arcs should be drawn from cause to effect in the network. In chemical reactions we know that the initial states are causes, while the collected results are effects. The local probability distributions associated with a node are shown adjacent to the node. For simplicity, here we assume that all the features (nodes) are binary, such as the feature g will be set as ‘true’ or ‘yes’ as long as the kinetic energy of molecule beams B is equal or greater than some certain threshold. We shall return to applications of BN in Section 5.2.
3.2.6.1 Quantum enhanced variants. In 1995, Tucci proposed the first design of quantum BN, which could be constructed by replacing real probabilities in classical BN with quantum complex amplitudes.170 Leifer and Poulin proposed another model in 2008, constructing quantum BN based on probability distributions, quantum marginal probabilities and quantum conditional probabilities.171 However, neither of these models could provide any advantage compared with the classical models, because they cannot take into account the interference effects between random variables.172 A quantum-like BN based on quantum probability amplitudes was proposed by Moreira and Wichert in 2016,172 where a similarity heuristic method was required to determine the parameters.
On the other hand, in 2014, Low and coworkers discussed the principles of quantum circuit design to represent a Bayesian network with discrete nodes that have two states. Notably, it is reported that the graph structure of BN is able to efficiently construct a quantum state representing the intended classical distribution, and a square-root speedup time can be obtained per sample by implementing a quantum version of rejection sampling.173 Recently, Borujeni and coworkers further expanded the quantum representation of generic discrete BN with nodes that may have two or more states.174
There are mainly three steps to construct the quantum circuit representing a BN. First, map a BN node to one or more qubits depending on the number of states. The next step is to map the marginal or conditional probabilities of nodes to probability amplitudes associated with the qubits to be in the |0〉 and |1〉 states. The final step is to realize the required probability amplitudes using single-qubit and controlled rotation gates.
Fig. 9 is the quantum circuit representing the BN shown in Fig. 8. The quantum circuit shown in Fig. 9 is constructed based on the three steps discussed above. The first step is to assign qubits for each node shown in Fig. 8. Here for simplicity, we only assign one qubit for the corresponding node. There are in total four qubits, q1, q2, q3, and q4, corresponding to the four nodes, g, h, c, and d, all of which are initially set at the |0〉 state. Next, we need to map the conditional probabilities of nodes to probability amplitudes. In the BN shown in Fig. 8, there are only two possible results for each node, yes or no. Here, we use quantum state |0〉 to represent no, and state |1〉 to represent yes. Then we need to realize the required probability amplitudes using single-qubit and controlled rotation gates. Single-qubit rotation gates are applied to construct the independent probability for nodes g and h, as p(g = yes) and p(h = yes) have nothing to do with the states of other nodes. Node g is a root node. In other words, there are no arcs pointing to node g in Fig. 8, so that a single Ry(θ1) gate is applied on q1. The value of θ1 can be derived from the constraint,
| p(g = yes) = |〈1|q1|Ψ〉|2 | (35) |
| p(c = yes|g = yes) = |(〈1|q1 ⊗ 〈1|q3)|Ψ〉|2. | (36) |
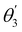 . To construct the condition probabilities with more than one condition, we need to include control rotation gates with more than one control qubit. For example, there are two arcs pointing to node d in Fig. 8, one of which comes from node g and the other comes from h. Thus, in the circuit there are four control–control–Ry gates where q1(g) and q2(h) are the control qubits and q4(d) is the target qubit corresponding to 4 different choices of configurations between g, h, i.e., when both are ‘yes’, both are ‘no’, and one of them is ‘yes’ and the other is ‘no’ and vice versa. The value of θ4 can be obtained from
. To construct the condition probabilities with more than one condition, we need to include control rotation gates with more than one control qubit. For example, there are two arcs pointing to node d in Fig. 8, one of which comes from node g and the other comes from h. Thus, in the circuit there are four control–control–Ry gates where q1(g) and q2(h) are the control qubits and q4(d) is the target qubit corresponding to 4 different choices of configurations between g, h, i.e., when both are ‘yes’, both are ‘no’, and one of them is ‘yes’ and the other is ‘no’ and vice versa. The value of θ4 can be obtained from| p(d = yes|g = yes, h = yes) = |(〈1|q1 ⊗ 〈1|q2 ⊗ 〈1|q4)|Ψ〉|2. | (37) |
 | ||
| Fig. 9 Quantum circuit for the BN shown in Fig. 8. For quantum versions of more complex BN structures refer to ref. 174. There are in total four qubits, q1, q2, q3, and q4, corresponding to the four nodes, g, h, c, and d, all of which are initially set at the |0〉 state. Ry gates are applied directly on root nodes to prepare the quantum states corresponding to the probability amplitudes. For example, node g is a root node (in other words, there are no arcs pointing to node g), so that a single Ry(θ1) gate is applied on q1. Control-Ry gates correspond to the arcs in the BN. For example, there is only a single arc pointing to node c, which comes from node g. Thus, in the circuit there are two control-Ry gates where q1 is the control qubit and q3 is the gate qubit. All the parameters can be derived from the DAG. | ||
 | (38) |
| yw,b(xt) = sgn(wTxt + b). | (39) |
 | (40) |
Fig. 10 is a scheme of the SVM classification with a hyperplane. Blue dots and red triangles represent the training instances with two labels. The black line represents the optimal hyperplane, which maximizes the margin between the blue and red instances. The red and blue dash lines are hyperlines that can separate the two groups apart, though the corresponding margin is less than the optimal one.
Sometimes due to the misclassified instances SVMs are not able to find any separating hyperplane that can perfectly separate two groups apart. Then the soft margin and penalty functions could be applied where some misclassifications of the training instances are accepted.175
Moreover, real-world problems often involve non-separable data, where there is no separating hyperplane initially even without misclassifications. Then the training data should be first mapped onto a higher dimensional space, where the separating hyperplane would be constructed. This higher-dimensional space is generally denoted as the transformed feature space, while the training instances occupy the input space. Instead of repeating the mapping process Φ(x) explicitly, the more popular approach is to calculate the Kernel functions defined in eqn (9) which allow inner products to be calculated directly in the feature space.175 After successfully constructing the hyperplane, new instances are mapped into the feature space by Kernel functions for classification.
SVM methods perform binary classification; thus, to solve multi-class problems we must reduce the problem into a set of multiple binary classification problems. A core advantage of SVM is that training the optimization problem of the SVM necessarily reaches a global minimum, instead of being trapped in a local minimum. We shall return to applications in Sections 5.2, 5.5 and 4.
3.2.7.1 Quantum enhanced variants. Enthused by the success of SVM assisted big data classification, Rebentrost and coworkers proposed the implementation of quantum SVM.177
Rewrite the weight vector w in eqn (38) and (39) as
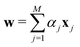 | (41) |
| F(b, α1, α2,…, αM)T = (0, y1, y2,…, yM)T | (42) |
| y(x′) = sgn[〈ψ|Ô|ψ〉] | (43) |
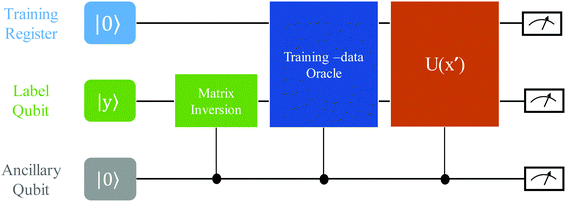 | ||
| Fig. 11 The schematic diagram of quantum SVM illustrated in ref. 176. The qubits can be assigned into three groups: training registers (blue) that represent the training instances, label qubit (green) that takes the label, and ancillary qubit (grey). The matrix inversion is employed to acquire hyperplane parameters. Then, the training-data oracle is applied to prepare the training-data state. Classification of new test instance x′ is introduced by operation U(x′). | ||
The circuit has three primary components in a nutshell as shown in Fig. 11: matrix inversion operation (green) is designed to acquire the hyperplane parameters; training-data oracle (blue) is included to prepare the training-data state; and U(x′) is to map the test instance x′ into quantum states. In a classical SVM, the hyperplane is obtained by minimizing the functional as shown in eqn (39), while in qSVM, the hyperplane is obtained via solving linear equations, which leads to an exponential speedup.
Let us now get into the details of the quantum version of the algorithm. The qubits can be assigned into three groups: training registers (blue) that represent the training instances, label qubit (green) that takes the label, and ancillary qubit (grey). The matrix inversion is employed to acquire hyperplane parameters. Then, the training-data oracle is applied to prepare the training-data state. Classification of a new test instance x′ is introduced by operation U(x′).
The training-data oracles are designed to return the quantum counterpart of the training data xi,
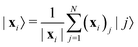 | (44) |
 into state |χ〉, where
into state |χ〉, where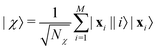 | (45) |
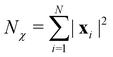 is the normalization factor.
is the normalization factor.
Optimization is implemented by the quantum algorithm solving linear equations, which provide exponential speedup compared to the classical version.178 Registers are initialized into state 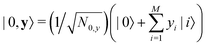 . After applying the matrix inversion operation, the quantum state is transformed to
. After applying the matrix inversion operation, the quantum state is transformed to
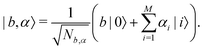 | (46) |
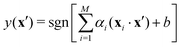 | (47) |
In spite of constructing quantum circuits to acquire the hyperplane, researchers further developed quantum kernel methods which harness the computational power of quantum devices. In 2019, researchers from Xanadu proposed to compute a classically intractable kernel by estimating the inner products of quantum states,179 while the kernel can then be fed into any classical kernel method such as the SVM. The crucial component of quantum kernel methods is quantum feature maps, which map a classical data point x as an n-qubit quantum state |ϕ(x)〉 nonlinearly, where the feature state |ϕ(x)〉 = U(x)|0〉 is obtained by a parameterized circuit family {U(x)}.180 In the learning process, quantum feature maps take the position of pattern recognition. More details about the quantum kernel methods can be found in Section 4 (Fig. 12 and 13).
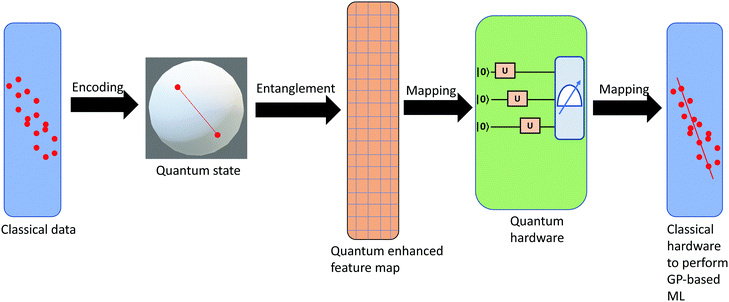 | ||
| Fig. 12 Schematic representing quantum-enhanced kernel for Gaussian process regression as described in ref. 181. | ||
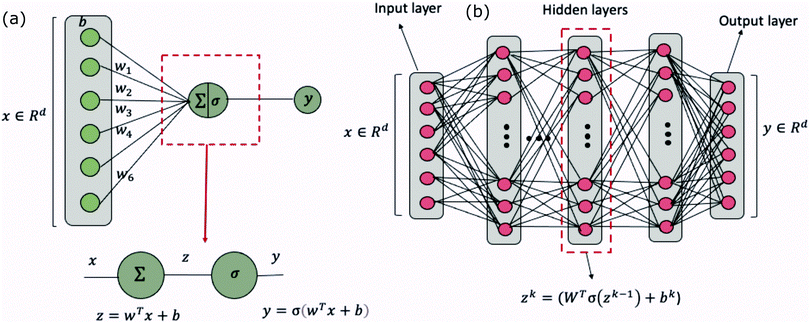 | ||
Fig. 13 (a) A schematic of a generalized perceptron. The input is a vector  and the output is and the output is 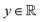 . The parameters of the model are . The parameters of the model are 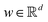 (often called weights) and b ∈ R (often called bias). The layer in between performs an affine transformation to yield a variable z and passes z as the argument of the non-linear activation function (often called weights) and b ∈ R (often called bias). The layer in between performs an affine transformation to yield a variable z and passes z as the argument of the non-linear activation function 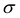 . Note that for Rosenblatt's perceptron187σ(z) = 1 if z ≥ 0 and 0 otherwise but any generalized activation function would be fine (see text for more details). (b) A feed-forward neural network obtained by stacking many neurons in several layers. The layers have an all to all connectivity pattern that may not necessarily be the case. The input is . Note that for Rosenblatt's perceptron187σ(z) = 1 if z ≥ 0 and 0 otherwise but any generalized activation function would be fine (see text for more details). (b) A feed-forward neural network obtained by stacking many neurons in several layers. The layers have an all to all connectivity pattern that may not necessarily be the case. The input is 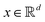 and the output, unlike in the case of a perceptron, is and the output, unlike in the case of a perceptron, is 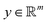 (in the figure m = d is shown but this may not be necessarily true). Each layer much like in the case of a perceptron performs an affine transform and then a non-linear activation. The case for the k-th layer is shown wherein the affine transformed variable is zk which is subsequently passed into an activation function (see text for details). (in the figure m = d is shown but this may not be necessarily true). Each layer much like in the case of a perceptron performs an affine transform and then a non-linear activation. The case for the k-th layer is shown wherein the affine transformed variable is zk which is subsequently passed into an activation function (see text for details). | ||
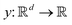 . The training set D is made up of n observations, D = {(xi,yi)|i = 1,…, n}. Performing regression to predict the form of y can be obtained in two ways:
. The training set D is made up of n observations, D = {(xi,yi)|i = 1,…, n}. Performing regression to predict the form of y can be obtained in two ways:
• Weight-space picture: having parameterized the function f, a prior is placed on the parameters of the model. Using the Bayes’ Rule, the probabilities are modified based on the observed data and the distribution is updated (called the posterior distribution). Then, the predictive posterior distribution on points xn is calculated by weighting all the possible predictions by their respective calculated posterior distributions. In order to improve the expressiveness of the model, the inputs are projected into a high dimensional space using a set of M basis functions to approximate y(x) by ỹ(x):
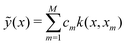 | (48) |
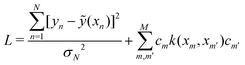 | (49) |
• Function-space picture: the prior in this case is specified in the function space. For every 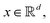 the distribution of f(x) along with the structure of covariance k(x,x′) = cov(f(x),f(x′)) is characterized. A Gaussian process (GP) is used to describe a distribution over functions. A GP is completely specified by its mean function m(x) and covariance function (k(x,x′)):
the distribution of f(x) along with the structure of covariance k(x,x′) = cov(f(x),f(x′)) is characterized. A Gaussian process (GP) is used to describe a distribution over functions. A GP is completely specified by its mean function m(x) and covariance function (k(x,x′)):
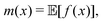 | (50) |
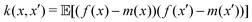 | (51) |
| f(x) ∼ GP(m(x),k(x,x′)) | (52) |
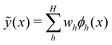 | (53) |
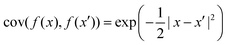 | (54) |
We shall return to applications of SVM in Sections 5.2 and 5.5.
3.2.8.1 Quantum enhanced variants. Matthew Otten et al.181 proposed a procedure to build quantum enhanced kernels while still capturing the relevant features of the classical kernels. As can be seen from the weight-space picture above, the quality of regression results is directly influenced by the choice of the kernel. Quantum computing enhanced kernels have the potential of being powerful in terms of performing higher dimensional regression tasks since quantum computers can represent functions that classical computers might not calculate efficiently. As coherent states approximate the squared exponential kernel, the classical feature maps corresponding to the squared exponential kernel can be first approximated using coherent states, which leads to a corresponding quantum kernel. A generic coherent state with parameter α can be written as follows:
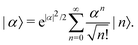 | (55) |
The input data are encoded as 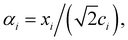 leading to the coherent state kernel:
leading to the coherent state kernel:
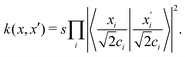 | (56) |
Since the coherent state can be written in terms of the displacement operator applied to the vacuum state, and truncating the Hilbert space at some maximum number of levels N, gives rise to the s finite-dimensional displacement operator 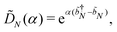 where
where ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) †N is the bosonic creation operator in the finite-dimensional Hibert space.
†N is the bosonic creation operator in the finite-dimensional Hibert space.
The finite-dimensional coherent state based kernels are first prepared on a qubit system by decomposing the N level displacement operator into log2(N) Pauli operators and then using Trotterization up to m steps on the qubit Hamiltonian. This defines the quantum feature map that approximates the feature map of the classical exponential squared kernel. Classically inspired quantum feature maps can then be applied to solve the requisite regression task.
In order to show a quantum advantage, an entanglement enhanced kernel can be prepared by using a multi-mode squeezing operator to entangle the different data dimensions for a multi-dimensional regression problem. Thereby, smaller quantum devices with only a few operations can perform higher-dimensional regression tasks. Following this, the GP-based ML task is performed on the classical hardware.
3.3 Artificial neural networks
In this section, we briefly review the various architectures of neural networks or deep learning algorithms that are commonly used for applications in physics and chemistry. As before, we not only focus on the training of each such architecture on a classical computer but also on the quantum algorithms proposed wherever applicable. Applications of NN are discussed in all sections from Sections 4 and 5.1–5.5. where
where  and
and  .184–186 The d-dimensional vector x is an input and the single number y is the output. The perceptron layer in between first makes an affine transformation on the input x using tunable parameters
.184–186 The d-dimensional vector x is an input and the single number y is the output. The perceptron layer in between first makes an affine transformation on the input x using tunable parameters 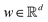 (often called weights) and
(often called weights) and 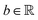 (often called bias). This transformation is as follows:
(often called bias). This transformation is as follows:| z = wTx + b. | (57) |
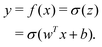 | (58) |
Logistic activation function. The original idea of a perceptron is to model a biological neuron in the central nervous system. The activation function serves the purpose of mimicking the biological neuron activation rate. Logistic functions are typical activation functions having a similar representation to a biological neuron activation rate.188 Sigmoid function is a traditional type of logistic functions. The sigmoid function is an increasing function with ‘S’ shape, assuming a continuous range of values from 0 to 1, as described in eqn (59).
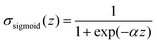 | (59) |
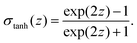 | (60) |
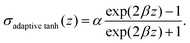 | (61) |
Rectified linear unit (ReLU). Rectified linear unit (ReLU) is defined as
| σReLU(z) = max(0,z). | (62) |
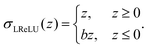 | (63) |
Exponential linear unit. Exponential linear unit (ELU) is defined as
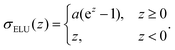 | (64) |
Multistate activation function (MSAF). Instead of combining numerous perceptrons with simple logistic activation functions, it is a simple way to achieve an N-state neuron by using an N-level activation function for real-valued neuronal states. Thus multistate activation functions (MSAF) are applied in ANN, which are generally multilevel step functions. As an example of MSAF, the N-level complex-signum activation function is defined as192
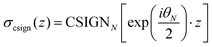 | (65) |
| CSIGNN(z) = exp(inθN), arg(z) ∈ [(n − 1)θN,nθN), n = 1, 2,…, N. | (66) |
A perceptron is trained by seeing if the output value y matches with the true or expected value. If such a matching did not happen based on some pre-defined metric then the parameters of the neuron (w,b) are optimized so that the output of the network matches up to the desired value. In Rosenblatt's perceptron,187 this optimization was done by simply adding the input vector x to the weights w if the perceptron underestimated the output value compared to the true label and subtracting the x if the perceptron over-estimated the output value compared to the true label. The bias b was updated by ±1 in the two cases, respectively, as well. Once the output of the perceptron agrees with the label, the neuron is said to have ‘learnt’ to perform the task.
Each such perceptron described is essentially equivalent to a biological neuron. A feed-forward neural network is obtained by stacking many such neurons, layer by layer such that the neurons in one layer are connected to those in the other layer. Operationally, the network models a non-linear function of the kind 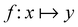 where
where 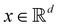 and
and 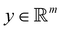 . The d-dimensional vector x is an input and the m dimensional vector y is the output. If the network has L layers of stacked neurons, this would mean that the first (input) and the last (output) layers will have d and m neurons, respectively. The layers in between are called hidden layers. Let us concentrate on the k-th and (k − 1)-th layers ((k,k − 1) ∈ {1, 2,…, L}) only. The affine transformation defined at the k-th layer will be parameterized by a weight matrix
. The d-dimensional vector x is an input and the m dimensional vector y is the output. If the network has L layers of stacked neurons, this would mean that the first (input) and the last (output) layers will have d and m neurons, respectively. The layers in between are called hidden layers. Let us concentrate on the k-th and (k − 1)-th layers ((k,k − 1) ∈ {1, 2,…, L}) only. The affine transformation defined at the k-th layer will be parameterized by a weight matrix 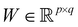 where q is the number of neurons in the k-th layer and p is the number of neurons in the (k − 1)-th layer and also by a bias vector
where q is the number of neurons in the k-th layer and p is the number of neurons in the (k − 1)-th layer and also by a bias vector  .58,184 The transformation acts on the activation response of the (k − 1)-th layer, i.e.,
.58,184 The transformation acts on the activation response of the (k − 1)-th layer, i.e., 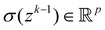 as follows:
as follows:
| zk = WTσ(zk−1) + bk. | (67) |
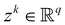 which is passed through an activation process using any of the activation functions defined before and fed into the next layer. This process is repeated until one reaches the last layer. At the last L-th layer the activation response is zL = y. This is compared with the true values/labels of the data (say y*). Many such metrics for the comparison can be defined, one simple example being the L2 norm of the difference vector ||y − y*||2 or even cross-entropy196 if both y and y* are probability distributions etc. Such metrics are often called merit-functions or cost functions. Once a cost-function is defined, the error in the metric is decided and this is used to evaluate the gradient of the cost-function with respect to the bias parameters of the L-th layer and the interconnecting weights between the L-th and (L − 1)-th layers. The process is then repeated for all the layers up until one reaches the first layer. In the end, one then has access to the gradient of the cost function with respect to the tunable parameters of all the layers. This method of acquiring the gradient is called back-propagation.197,198 Once all such gradients are obtained, one can update the parameters of the entire network using a simple gradient descent199 or sophisticated optimizers like ADAGRAD,200 RMSprop,199 ADAM,199,201 and NADAM.202 When the error metric has decreased below a certain preset threshold, the network is said to have been ‘trained’ to perform the task. At this point, predictions of the network are usually cross-validated using the data outside that of the labelled training examples. It must be noted that often the term multi-layer perceptron is used interchangeably for feed-forward neural networks even though historically as mentioned above the training algorithm of perceptrons is slightly different. For fairly large neural-networks with many neurons stacked within each layer, the risk of overfitting the data exists. This can be handled using appropriate regularization techniques203,204 or dropout.205
which is passed through an activation process using any of the activation functions defined before and fed into the next layer. This process is repeated until one reaches the last layer. At the last L-th layer the activation response is zL = y. This is compared with the true values/labels of the data (say y*). Many such metrics for the comparison can be defined, one simple example being the L2 norm of the difference vector ||y − y*||2 or even cross-entropy196 if both y and y* are probability distributions etc. Such metrics are often called merit-functions or cost functions. Once a cost-function is defined, the error in the metric is decided and this is used to evaluate the gradient of the cost-function with respect to the bias parameters of the L-th layer and the interconnecting weights between the L-th and (L − 1)-th layers. The process is then repeated for all the layers up until one reaches the first layer. In the end, one then has access to the gradient of the cost function with respect to the tunable parameters of all the layers. This method of acquiring the gradient is called back-propagation.197,198 Once all such gradients are obtained, one can update the parameters of the entire network using a simple gradient descent199 or sophisticated optimizers like ADAGRAD,200 RMSprop,199 ADAM,199,201 and NADAM.202 When the error metric has decreased below a certain preset threshold, the network is said to have been ‘trained’ to perform the task. At this point, predictions of the network are usually cross-validated using the data outside that of the labelled training examples. It must be noted that often the term multi-layer perceptron is used interchangeably for feed-forward neural networks even though historically as mentioned above the training algorithm of perceptrons is slightly different. For fairly large neural-networks with many neurons stacked within each layer, the risk of overfitting the data exists. This can be handled using appropriate regularization techniques203,204 or dropout.205
3.3.1.1 Quantum enhanced variants. Difficulties arise inevitably when attempting to include nonlinear activation functions into quantum circuits. The nonlinear activation functions do not immediately correspond to the mathematical framework of quantum theory, which describes system evolution with linear operations and probabilistic observation. Conventionally, it is thus extremely difficult to generate these nonlinearities with a simple quantum circuit. Researchers could build up quantum-classical hybrid neural networks, where the linear part corresponds to the quantum unitary operations in quantum layers, while the nonlinear part corresponds to the classical layers. In other words, the classical layer in the quantum-classical hybrid neural network is to serve as the activation function connecting different quantum layers. Fig. 14(a) is a scheme of the quantum-classical hybrid neural networks, where the linear part in the classical neural network is replaced by the quantum circuits. Fig. 15(b) shows an example construction of the hybrid quantum-classical neural network for 3 qubits, Fig. 14 (see ref. 206). The quantum-classical hybrid neural networks generally work as follows: firstly, the classical data are converted into the quantum state via a certain mapping process. Then, the quantum unitary operations will implement the linear calculation. Next, the qubits are all measured and the estimation value is sent out to the classical layer. The classical layer will implement the nonlinear calculation (serve as the activation function), and the output will be sent to the next quantum layer to repeat the steps above. Based on the hybrid quantum-classical neural networks, researchers could construct quantum deep neural networks to calculate ground state energies of molecules,206 to study the barren plateaus in the training process,207 and to recognize figures with transfer learning.208 More details of the hybrid quantum-classical neural networks for various tasks could be found in these applications.
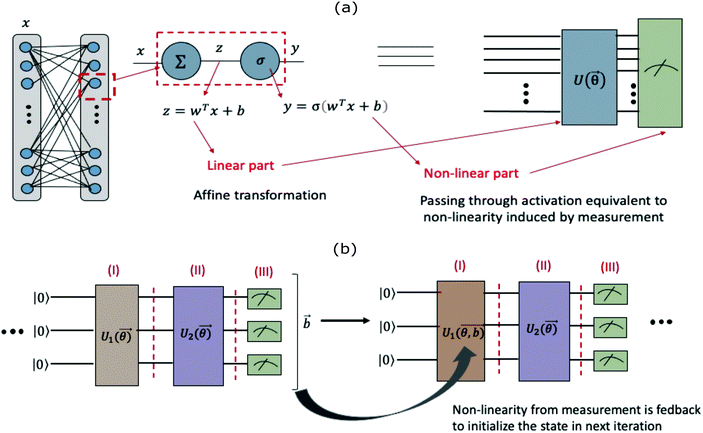 | ||
Fig. 14 (a) A scheme of the structure of a quantum-classical hybrid neural network for the realization of ANN. The linear part is accomplished with parameterized unitaries which defines the tunable weights and biases of the network whereas the non-linear activation is obtained from measurements in the quantum-classical hybrid neural network. (b) An example of the construction of the hybrid quantum-classical neural network for 3 qubits. Stage (I) refers to state-encoding with unitary U1, stage 2 is the actual variational circuit with parameterized unitary U2 and stage 3 is the measurement to reproduce the effect of non-linear activation. In the next iteration, the measurement results ![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) is used in the unitary U1 for state-encoding. This way the full feed-forward neural network proceeds. Training is done by variation of the parameters of U2 (see ref. 206 for details). is used in the unitary U1 for state-encoding. This way the full feed-forward neural network proceeds. Training is done by variation of the parameters of U2 (see ref. 206 for details). | ||
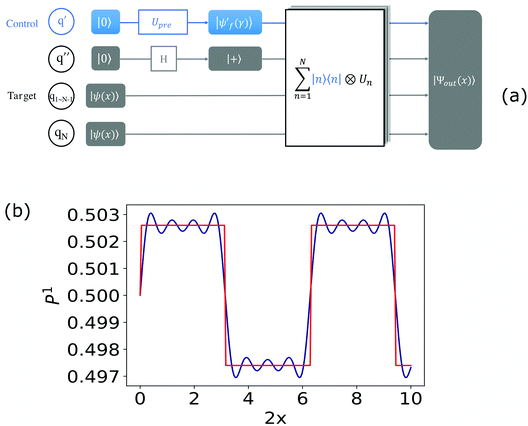 | ||
Fig. 15 (a) Shows the main structure of quantum circuits estimating arbitrary periodic functions. There are two main modules. The first one contains Upre acting on the auxiliary qubits q′, and Hadamard gates acting on q′′. The succeeding module is formed by N controlled unitary operations denoted as Un. q′ (blue color) are control qubits. q′ are converted to the state 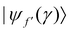 under the operation Upre, where γ is determined by FN. In (b), the blue curve represents the final output of the quantum circuit estimating square wave functions. Meanwhile, the red curve is the original shape of square wave functions. (a) and (b) are reproduced from ref. 209 under Creative Common CC BY license. under the operation Upre, where γ is determined by FN. In (b), the blue curve represents the final output of the quantum circuit estimating square wave functions. Meanwhile, the red curve is the original shape of square wave functions. (a) and (b) are reproduced from ref. 209 under Creative Common CC BY license. | ||
Though the unitary operations always correspond to linear calculation, the measurements could lead to nonlinearity. The repeat-until-success (RUS) circuit is a typical method implementing activation functions based on special measurements.210,211 In the RUS circuit, an ancillary qubit is connected with the input and the output qubit. After certain operations, the ancillary qubit is measured. If result |0〉 is obtained, then the desired output is generated. Otherwise, we need to correct the operation and apply it on the qubits, and then measure the ancillary qubit once again. The steps above should be repeated until we get the result |0〉. Thus the circuit is named repeat-until-success (RUS) circuit. In 2017, Cao and coworkers developed both the quantum feed forward neural network and quantum Hopfield network based on the RUS circuit.212 Sometimes in the hybrid quantum-classical neural networks, researchers also use special intermediate measurements to implement certain nonlinear functions.206
There are some other approaches to implement the activation functions in quantum neural networks. Activation functions can be implemented via the mapping process. In 2018, Daskin developed a simple quantum neural network with a periodic activation function,213 where the simple cos function is used as an activation function. There are also methods to implement activation function with the assistance of the phase estimation algorithm.214 Recently, our group also developed a quantum circuit to implement periodic nonlinear activation functions with multi copies of input.209Fig. 15(a) is a scheme of the circuit structure, and Fig. 15(b) shows the approximation of periodic square wave functions. The quantum circuit contains N-qubits to store the information on the different N-Fourier components and M + 2 auxiliary qubits with 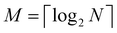 for control operations. The desired output will be measured in the last qubit qN with a time complexity of the computation of
for control operations. The desired output will be measured in the last qubit qN with a time complexity of the computation of 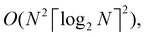 which leads to polynomial speedup under certain circumstances. In conclusion, it is an essential but still open question to find an optimal approach to implement nonlinear activation functions in quantum neural networks.
which leads to polynomial speedup under certain circumstances. In conclusion, it is an essential but still open question to find an optimal approach to implement nonlinear activation functions in quantum neural networks.
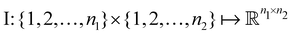 . For colored images, the only difference in the intensity distribution at the (i,j)th pixel (position in the intensity matrix) will be that instead of a scalar value, the intensity will be a vector of [R,G,B]T entries. If the total pixel count (n1n2) is too big, then converting the matrix into a 1D vector and using a feed-forward neural network as discussed before may be cumbersome and would require a large number of tunable parameters with the possibility of over-fitting. Besides, a 1D encoding loosens the spatial correlation in the intensity pattern among the neighboring pixels. CNN is designed to use as input the entire 2D matrix and hinges on understanding and identifying the spatial information (often called feature maps) and then condensing the information into feature vectors of reduced sizes which is then fed into a fully-connected feed-forward network for usual operations as described before.218–221 In other words, CNN is basically a simple neural network defined before in the final layer equipped with a robust feature-extractor before the final layer to remove redundancies and decrease parameter count.
. For colored images, the only difference in the intensity distribution at the (i,j)th pixel (position in the intensity matrix) will be that instead of a scalar value, the intensity will be a vector of [R,G,B]T entries. If the total pixel count (n1n2) is too big, then converting the matrix into a 1D vector and using a feed-forward neural network as discussed before may be cumbersome and would require a large number of tunable parameters with the possibility of over-fitting. Besides, a 1D encoding loosens the spatial correlation in the intensity pattern among the neighboring pixels. CNN is designed to use as input the entire 2D matrix and hinges on understanding and identifying the spatial information (often called feature maps) and then condensing the information into feature vectors of reduced sizes which is then fed into a fully-connected feed-forward network for usual operations as described before.218–221 In other words, CNN is basically a simple neural network defined before in the final layer equipped with a robust feature-extractor before the final layer to remove redundancies and decrease parameter count.
The key components which facilitate the CNN architecture are thus grouped into two parts: (a) feature extractor and (b) fully-connected neural network. The component (a) is further made up of the repeated use of the following categories of layers.
1. Convolutional layer:58 this is where the magic of CNN happens. For each feature the user wants to identify and extract from the image, this layer uses a spatial filter (kernel) denoted as K which is essentially a matrix that can slide over the output of the previous layer (or the intensity matrix of the input image if one is looking right after the first layer) and define a new feature map. In other words, the kernel acts on a chunk of the input matrix every time and the process is essentially a convolution. This feature map is obtained by a Frobenius inner product between the kernel and the chunk of the input it is acting on such that the resulting map has large entries only over the pixels (or (i,j) positions) wherein the kernel entries ‘are similar’ to the entries of the chunk i.e. the feature is present. This is done for every kernel (one corresponding to every feature that needs extraction) and for every feature map from the previous layer. Operationally let the input to the l-th layer from the (l − 1)-th layer comprise feature maps denoted as yl−1p each where p = 1, 2,…, αl−1 features. Each such map is of size βl−1 × γl−1. Then each of the output from the l-th layer denoted as ylp (p = 1, 2,…, αl−1) is a feature map of size βl × γl obtained by convolving against kernels as follows:
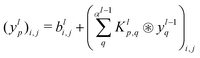 | (68) |
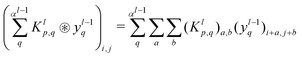 | (69) |
2. Activation layer: this layer is responsible for introducing non-linearity into the model using the input of the previous layer through the following expression
| (ylq)i,j = σ(yl−1q)i,j | (70) |
3. Pooling layer: this is where dimensional reduction or downsampling of the feature maps happens. This layer takes in the feature maps from the previous layer and uses windows of pre-defined sizes within each chunk of the feature map and preserves only one value within each such window to generate a new feature map with reduced dimension. The number of feature maps remains unchanged. The one value so selected can be the maximum value of all features within the window (max-pooling223–225) or may be the average value (average pooling224,225).
The architecture has repeated applications of these layers to ensure parameter sharing and efficient feature extraction. The output at the last layer of the feature-extractor is vectorized into a 1D format and fed into a completely connected deep-neural network at the end. This network then processes the input and generates the final output. For example, if the final desired output is a multi-label classification task, the connected neural network will have as many neurons as the number of labels with each neuron being a placeholder for a 1 or 0 denoting classification into the corresponding label or not. Fig. 16(a) illustrates pictorially all of these components.
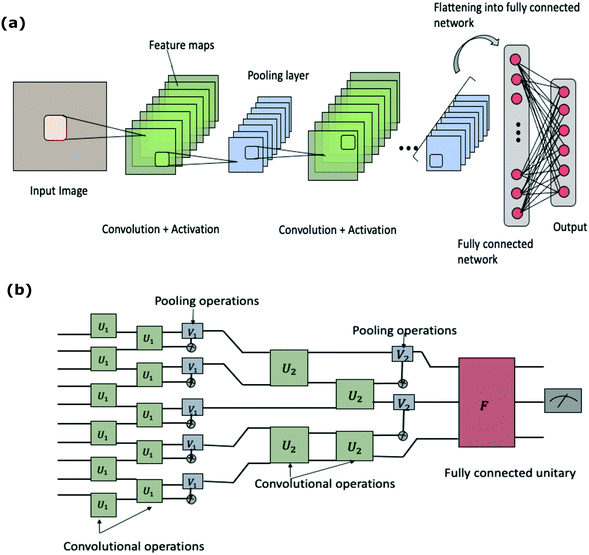 | ||
| Fig. 16 (a) The schematic of a typical convolutional neural network (CNN) is illustrated. The process starts with an input image from which feature maps are extracted through an element-wise product with a kernel and then activation through any of the activation functions discussed in the previous section. Such feature maps are depicted in green. The pooling operation (blue layer) thereafter reduces the size of the feature maps by preserving the values of a prescribed choice by the user within a certain window of each feature map. The two layers are repeated many times and then fed into a fully-connected neural network as discussed in the previous section. The output is read and back-propagation is used to train the parameters of the entire network. (b) The schematic of the quantum circuit as illustrated in ref. 215 for the realization of a CNN. The circuit receives an arbitrary input state say ρ0. The unitaries designated as Ui are responsible for convolutional operation whereas the unitaries designated as Vi are responsible for controlled operations in the pooling layer. The unitaries Vi are conditioned on the measurement results of neighboring unitaries. Such measurements reduce the qubit pool and are similar to dimensional reduction in conventional pooling layers. The operations are repeated several times until a fully-connected unitary (denoted as F) acts on. Certain qubits are measured subsequently to process the output. | ||
3.3.2.1 Quantum enhanced variants. In 2019, Cong et al.215 developed a quantum circuit based on CNN architecture which is used to classify an N-qubit quantum state with M-labels. In other words, given a training data set of M states {(|ψi〉,yi)} where yi are the binary classification labels associated with the states, the circuit can decide which of the training vectors the input unknown state resembles the most. This is useful in understanding whether a given state belongs to a particular phase with phase labels and shall be discussed later. The circuit architecture involves the following steps:
1. The initial inputs are mapped to a quantum state.
2. In the convolutional layer, the quantum state is transformed using a set of quasi-local unitaries labelled as Ui where i ∈ {1, 2,…}.
3. In the pooling layer, some of the qubits are measured and, conditioned on this measurement outcome, the unitaries for the remaining qubits are decided. This reduces the width of the circuit as certain qubits whose state has been readout are no longer a part of subsequent operations. Such controlled entangling unitaries are labelled as Vi where i ∈ {1, 2,…}.
4. The convolutional and the pooling layers are applied many times until the width of the circuit is reduced sufficiently.
5. Finally, a fully-connected layer of single and two-qubit gates (labelled as say F) is applied on the remaining qubits analogous to the fully-connected layer in classical CNN.
6. The final prediction from the algorithm is read by measuring certain qubits at the very end.
The circuit is described in Fig. 16(b) schematically.
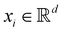 and a corresponding label
and a corresponding label 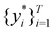 where
where 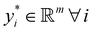 . The primary goal of the network is to produce a new sequence {yi}Ti=1 as the output such that each yi is close enough to
. The primary goal of the network is to produce a new sequence {yi}Ti=1 as the output such that each yi is close enough to 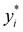 ∀ i as computed from a chosen metric and a preset threshold. In the vanilla RNN architecture,230 the primary functional unit which is used repeatedly for each input entry in the sequence consists of three layers of stacked neurons. The first layer is an input layer having d neurons (as the input entries xi are d-dimensional). The next layer is the hidden layer having say p neurons and is parameterized by weight matrices (Wz,Wx) and bias vector
∀ i as computed from a chosen metric and a preset threshold. In the vanilla RNN architecture,230 the primary functional unit which is used repeatedly for each input entry in the sequence consists of three layers of stacked neurons. The first layer is an input layer having d neurons (as the input entries xi are d-dimensional). The next layer is the hidden layer having say p neurons and is parameterized by weight matrices (Wz,Wx) and bias vector 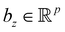 . The weight matrix
. The weight matrix 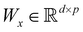 is responsible for the affine transformation on the input xi as discussed in the case of feed-forward neural networks. However, the primary difference from an usual feed-forward network is the presence of a second set of weight matrix
is responsible for the affine transformation on the input xi as discussed in the case of feed-forward neural networks. However, the primary difference from an usual feed-forward network is the presence of a second set of weight matrix 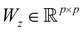 which performs an affine transform on the hidden layer activation response corresponding to the entry in the previous step i.e. for the last but one input entry xi−1. If the activation response from the hidden layer for xi is denoted as σ(zi) and the activation response for the previous entry xi−1 is denoted as σ(zi−1) then the two are related as
which performs an affine transform on the hidden layer activation response corresponding to the entry in the previous step i.e. for the last but one input entry xi−1. If the activation response from the hidden layer for xi is denoted as σ(zi) and the activation response for the previous entry xi−1 is denoted as σ(zi−1) then the two are related as| σ(zi) = σ(WTxxi + WTzσ(zi−1) + bz). | (71) |
Using this activation response (usually tanh) the last output layer now performs another affine transformation followed by the usual introduction of non-linearity through input to the activation process as follows:
| yi = σ(WTyσ(zi) + by) | (72) |
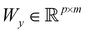 defines the inter-connections between the hidden layer and output layer and the bias vector
defines the inter-connections between the hidden layer and output layer and the bias vector  . The total number of tunable parameter vectors for this unit is 5 (Wz, Wx, Wy, bz, and by). For all subsequent input entries (i.e. xi+1, xi+2, etc.) the functional unit is repeatedly queried using the activation response (usually tanh) of the previous step as explained above. The total number of parameters (Wz, Wx, Wy, bz, and by) is kept the same for all such steps which leads to reduction in the number of variables through efficient sharing. Each such iteration generates a yi as explained. After the first pass through the entire data-set (a subset of the data-set can also be used depending on user preference), an ordered sequence {y}i is generated and a cost-function is defined to compare this sequence with the labelled sequence {y*}i. The error in this cost-function is minimized by updating the parameter set (Wz, Wx, Wy, bz, and by) using the gradient of the cost-function or any other optimizer as has been described in the case of feed-forward neural networks. The architecture is pictorially depicted in Fig. 17(a).
. The total number of tunable parameter vectors for this unit is 5 (Wz, Wx, Wy, bz, and by). For all subsequent input entries (i.e. xi+1, xi+2, etc.) the functional unit is repeatedly queried using the activation response (usually tanh) of the previous step as explained above. The total number of parameters (Wz, Wx, Wy, bz, and by) is kept the same for all such steps which leads to reduction in the number of variables through efficient sharing. Each such iteration generates a yi as explained. After the first pass through the entire data-set (a subset of the data-set can also be used depending on user preference), an ordered sequence {y}i is generated and a cost-function is defined to compare this sequence with the labelled sequence {y*}i. The error in this cost-function is minimized by updating the parameter set (Wz, Wx, Wy, bz, and by) using the gradient of the cost-function or any other optimizer as has been described in the case of feed-forward neural networks. The architecture is pictorially depicted in Fig. 17(a).
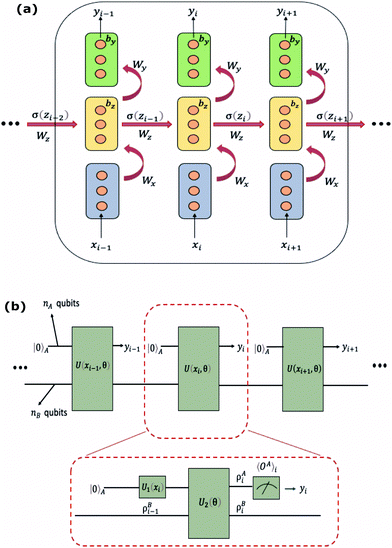 | ||
Fig. 17 (a) A schematic of recurrent neural network (RNN) architecture. The blue layer encodes the input sequence {x1, x2,…, xi−1, xi, xi+1,…}. The yellow layer is the hidden layer which processes the input and generates an activated response σ(xi) for the input xi. The key difference between RNN and other neural network architectures is that σ(xi) is fed onto the network when the next entry in the time-ordered sequence xi+1 is the input. This forms the core of the memory retention process in RNN. σ(xi) is also used by the final layer (green) to generate the output yi. The parameters of the network are the biases (by and bz) and the interconnecting weights (Wx, Wz, and Wy) between a pair of layers which are highlighted in the figure. (b) The schematic of the quantum circuit for processing time-ordered sequence using the RNN architecture as illustrated in ref. 231. Two qubit registers are invoked with nA and nB qubits and the input entry xi is encoded within the first register using U1(xi). The first and second registers are entangled using a parameterized unitary U2(θ) and thereafter an observable OA on the first register is measured to yield the output yi. The second register is left untouched and is responsible for carrying the memory for the next input xi+1. The circuit is adapted from ref. 231. The parameters of the entangling unitary gate  are optimized to make the output sequence {y1, y2, y3, …, yi−1, yi, yi+1,…} to the desired. are optimized to make the output sequence {y1, y2, y3, …, yi−1, yi, yi+1,…} to the desired. | ||
During back-propagation for long RNNs it is possible to encounter a situation wherein the gradient vector accrues a zero value (or grow unbounded in magnitude) with respect to parameters of nodes appearing at the beginning of the network. Such a situation is known as vanishing (exploding) gradient and if happens can render the model untrainable. Apart from changing the activation function from logistic ones like tanh to ReLU, one can adopt architectures of RNN like long-short term memory (LSTM) or gated recurrent unit (GRU)230,232–235 in such a case. LSTM networks introduced in ref. 236 also have successive repeating units/cells wherein the input to each cell is one entry of the ordered sequence xi (defined before) as well as the activation response (say hi−1) which was denoted as σ(zi−1) for vanilla RNN. The change in notation will be clarified soon. (The two quantities are conceptually similar though.) However the key difference with the vanilla version of RNN lies in the presence of a memory channel/carousel. The response of this memory channel from the previous cell (often denoted as ci−1) is also fed as input into the current cell. Inside the current cell there are three different networks/gates which work to erase, update the memory of the carousel entry and generate a new output yi as well (hi). The latter is fed back into the next cell as before in the case of vanilla RNN. The primary components inside each cell are the following:
(a) The forget gate: this takes in input (xi,hi−1)T and performs an affine transformation with weight matrices and bias (Wxf,Whf,bf)T wherein the subscript f stands for the forget gate. This is passed onto a sigmoid activation which outputs values between 0 and 1 only. The purpose of this gate is to read from the present input entries (xi,hi−1)T what features in the memory channel need to be erased (hence the name forget gate). If the output of the forget gate is denoted as fi the transformation is abbreviated as
| fi = σs (WTxfxi + WThfhi−1 + bf) | (73) |
(b) The next important gate is the input gate whose purpose is to decide what new information needs to be updated into the memory channel and at what places. Two operations are performed herein. The first involves creating an affine transformation of the input (xi,hi−1)T followed by sigmoid activation. The weights and biases in the process are (WxI,WhI,bI)T wherein I is for the input gate. This accomplishes the task of where to update the new information through the 0s and 1s of the sigmoid activation. The next operation is to create a candidate memory ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i for the memory channel using the input entries and parameters (WxIc,WhIc,bIc)T using a tanh activation to acquire values between ±1. The operations are as follows:
i for the memory channel using the input entries and parameters (WxIc,WhIc,bIc)T using a tanh activation to acquire values between ±1. The operations are as follows:
| Ii = σs(WTxIxi + WThIhi−1 + bI) | (74) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i = σtanh(WTxIcxi + WThIchi−1 + bIc) i = σtanh(WTxIcxi + WThIchi−1 + bIc) | (75) |
Ci = fi × Ci−1 + Ii × ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i i | (76) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i at the location specified by the Ii vector.
i at the location specified by the Ii vector.
(c) The third component is the output gate which is used to create an output hi to be fed into the next cell with data entry xi+1. The transformation is
| hi = (σs(WToxxi + WTohhi−1 + bo)) × σtanh(Ci). | (77) |
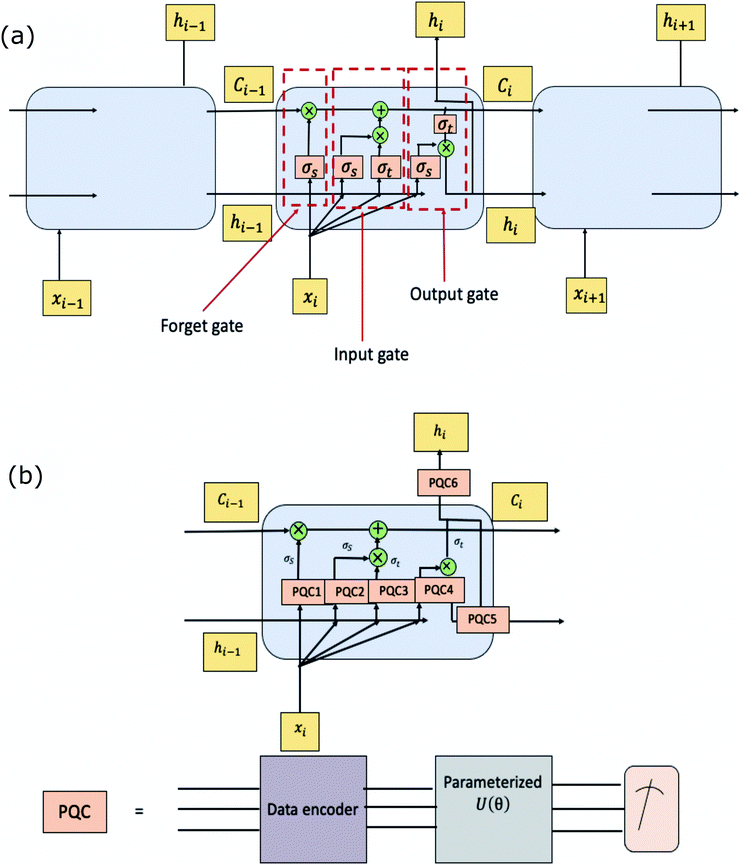 | ||
Fig. 18 (a) A schematic representation of a typical LSTM network as implemented in a classical processor. The three different processing gates – forget gate, input gate and output gate are illustrated (see text for details) along with the memory channel encoding Ci. ⊗ Indicates elementwise multiplication whereas ⊕ indicates elementwise addition. σt indicates tanh activation and σs indicates sigmoid activation. (b) The hybrid quantum-classical LSTM network implemented using parameterized quantum unitaries (PQC) in ref. 237. Each PQC has a data-encoding circuit and a variational circuit parameterized by angles (say  ). For say PQC1 to PQC4, the data encoder loads the concatenated vector (xi,hi−1)T. For PQC5 and PQC6, the output from PQC4 is processed and the memory channel is loaded (see text for more details). ). For say PQC1 to PQC4, the data encoder loads the concatenated vector (xi,hi−1)T. For PQC5 and PQC6, the output from PQC4 is processed and the memory channel is loaded (see text for more details). | ||
3.3.3.1 Quantum enhanced variants. Recently a quantum algorithm has been designed231 to implement the vanilla RNN architecture using a hybrid-variational framework. The algorithm uses a quantum circuit of two sets of qubits (say nA and nB). The input sequence of data is stored within the quantum states of one of the two registers through appropriate unitary operations. Both registers are then processed through unitaries with parameterized angles. The state of one of the register is measured subsequently to obtain the output whereas the other is untouched and passes onto the subsequent state to carry the memory of previous steps. The key ingredients of the protocol are:
1. Both the registers with nA and nB qubits are initialized to null kets.
2. The first input entry x0 is encoded onto the state of the register with nA qubits. Thereafter controlled unitaries are used to entangle the register with nA qubits and nB qubits. Such unitaries are parameterized by variational angles.
3. The expectation value of an operator OA is measured using the reduced density matrix of the first set of qubits (say ρ0A). This measurement yields y0. The second set of qubits (in the register with nB qubits) remains untouched. The first register is re-initialized to null kets.
4. For subsequent input entries (say x1, x2,…, xt, etc.), the second step above is repeated with the input xi encoded within the first register. This is followed by the third step. The state of the second register which is left pristine at each step retains the memory and information about previous input entries. This information is shared with the qubits in the first register through the parameterized entangling unitaries for each input.
5. The sequence of {y}i values so generated is fed into a cost function and the parameters of the entangling unitaries are updated for the next cycle from the knowledge of the errors.
The circuit is schematically illustrated in Fig. 17(b) A quantum version of the LSTM network has also been implemented recently using hybrid-variational circuits.237 The schema of the algorithm consists of 4 major components.
1. A data loader circuit: this component serves to map the concatenated form of the input vectors of the sequence xi and hi−1 (defined before in the classical variant) to quantum states. The circuit consists of Rz and Ry gates after a conversion to an equal superposition state using Hadamard transforms.
2. The next step involves parameterized unitaries with CNOT gates and single-qubit rotations. This block of parameterized unitary is used inside the input gate, the forget gate and the output gates (see Fig. 18(b)) for optimizing the response from each gate.
3. The measurement protocol on each such block of parameterized unitary in (2) using the input encoded within the state-preparation circuit in (1) yields the necessary affine transformation which is subsequently passed through an appropriate activation function for each gate as defined before in the classical variant (see Fig. 18(b)).
4. The parameters of the unitary in step (2) are updated through gradient estimates of a cost-function involving the error between the actual and the output from the network using a classical computer. The network was applied to many different problems including the dynamics of damped harmonic oscillators with good results.
The circuit is schematically illustrated in Fig. 18(b).
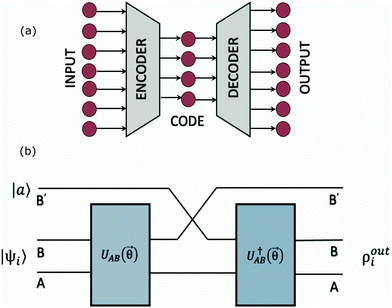 | ||
| Fig. 19 (a) Schematic representation of a classical autoencoder. The encoder takes classical input to create a compact space representation. The decoder acts on the code to output a representation from the input space. (b) Schematic representation of a circuit used in quantum autoencoder as illustrated in ref. 242. The encoder UAB acts on a circuit to create a code. The trash qubits are swapped out with a reference state and the decoder circuit works to reconstruct the input. | ||
Like any other feed forward neural networks it is trained through back-propagation to minimize the reconstruction error defined over it. For the simplest one layer encoder–decoder circuit, with weights, biases and element wise activation function W,b,σ and W′,b′,σ′, we can construct the L2 norm loss function as follows:
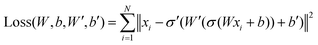 | (78) |
3.3.4.1 Quantum enhanced variants. To generalize a classical encoder to the quantum setting, we start with building a unitary circuit that allows information to be compressed into a smaller set of qubits with a garbage state in the remaining qubits that can be replaced with a reference state. We start with an ensemble of N pure states {|ψi〉AB}, where A is an n qubit system, and B is a k qubit system. Let U be the encoding unitary that takes as input a pure state from the ensemble. System B in the output is then swapped with a reference state and we try reconstructing the input state with a decoder given by the unitary U†. The objective function to maximize is given by
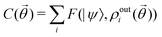 | (79) |
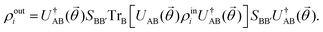 | (80) |
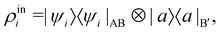 F denotes the fidelity between the states,
F denotes the fidelity between the states,  is a swap gate that swaps the corresponding qubits and
is a swap gate that swaps the corresponding qubits and  represents the parameters of the unitary circuit that needs to be trained. It can be observed that a perfect fidelity is obtained when the output state of the encoder circuit produces a product circuit, i.e., U|ψ〉AB = |
represents the parameters of the unitary circuit that needs to be trained. It can be observed that a perfect fidelity is obtained when the output state of the encoder circuit produces a product circuit, i.e., U|ψ〉AB = |![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) i〉A ⊗ |a〉B.242 Thus, we could alternatively define the maximizing objective function as the fidelity over the trash system B with respect to the reference state as
i〉A ⊗ |a〉B.242 Thus, we could alternatively define the maximizing objective function as the fidelity over the trash system B with respect to the reference state as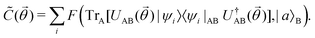 | (81) |
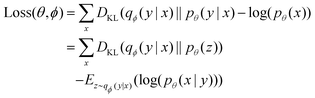 | (82) |
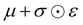 to allow for gradient back-propagation (the reparametrization trick), where ε ∼ N(0,I) and
to allow for gradient back-propagation (the reparametrization trick), where ε ∼ N(0,I) and  is an element-wise product.
is an element-wise product.
3.3.5.1 Quantum enhanced variants. Khoshaman et al.249 developed a quantum variational autoencoder that makes use of a quantum Boltzmann machine (QBM)250 to evaluate the gradient updates used in training. A QBM is an energy model defined as
| pθ(z) = Tr[Λze−Hθ] | (83) |
| Zθ = Tr[e−Hθ] | (84) |
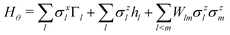 | (85) |
| H(pθ,qϕ) = −Ez∼qϕ[log(Tr[Λze−Hθ])] + log(Zθ) | (86) |
| ≥Ez∼qϕ[log(Tr[e−Hθ+lnΛz])] + log(Zθ) | (87) |
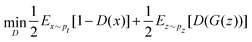 | (88) |
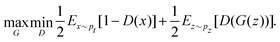 | (89) |
The parameters of the generator and discriminator are trained alternatively till the discriminator no longer is able to differentiate pf from pt. Thus the distributions are equal in the eyes of the discriminator and we have managed to create a generative model for the given training samples. The discriminator is discarded after the training. pz can be thought of as the distribution that represents the domain set of the problem and thus the generator works to extract features of the input vector. The trained generator can be further re-purposed for transfer learning on similar input data. A conditional extension referred to as cGAN (conditional GAN) allows for generating inputs from a specific class by imposing additional restrictions on the random input vector provided. This restriction can be envisioned as selecting from a specific class within the input domain. To train a cGAN the discriminator also needs to be provided with this additional label input to constrain classification within the chosen class.
3.3.6.1 Quantum enhanced variants. In the quantum generative adversarial network (QGAN),256 we have a source US that outputs true samples and a generator UG that outputs fake samples. Both US and UG take an input state |0〉⊗n, label |λ〉 and random noise |z〉 to output a density matrix in the system qubits. The noise vector supports to provide a distribution for the generator on the output qubit state corresponding to a given input label. With equal probability we choose between UG and US to create a density matrix that is fed into the discriminator. Alongside the sample output from US or UG provided, the discriminator takes as input the label |λ〉 used to generate the state, a bath |0〉⊗d that works as a scratchpad and an output qubit to measure the probability of the source of the sample. Fig. 20 provides a sketch for the working of the QGAN. The objective function can thus be given by,
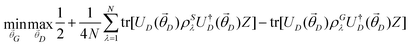 | (90) |
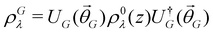 is the state output by the generator and Z represents the measurement made at the output qubit of the discriminator. The first and second terms in the trace come from the discriminators’ success in correctly predicting states from source and generator, respectively. The cost function has been derived using measurement probabilities to keep the expression linear, unlike the maximum likelihood optimization used for the classical case. Given the optimization function, gradients can be computed using a parameter shift trick or re-expressing it as a sum of simple unitary operations.257 For a complete discussion on the derivation of cost function, analyzing limiting cases and computing gradients corresponding to the parameters, refer ref. 248.
is the state output by the generator and Z represents the measurement made at the output qubit of the discriminator. The first and second terms in the trace come from the discriminators’ success in correctly predicting states from source and generator, respectively. The cost function has been derived using measurement probabilities to keep the expression linear, unlike the maximum likelihood optimization used for the classical case. Given the optimization function, gradients can be computed using a parameter shift trick or re-expressing it as a sum of simple unitary operations.257 For a complete discussion on the derivation of cost function, analyzing limiting cases and computing gradients corresponding to the parameters, refer ref. 248.
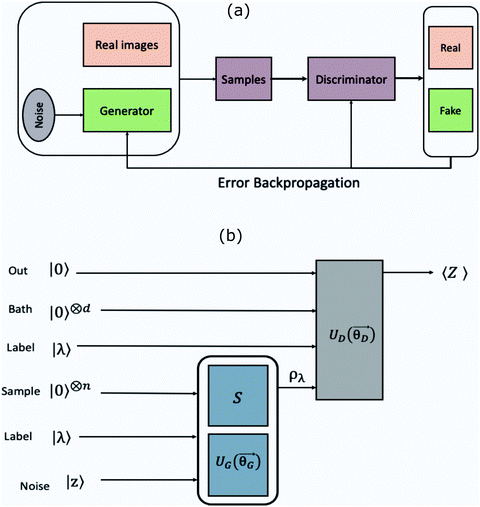 | ||
Fig. 20 (a) Schematic representation of classical GAN. The generator takes as input some noise to produce a sample. Samples from the real source and generator are fed to the discriminator. These work as labelled data for the discriminator to distinguish. The errors are used to backpropagate and train the generator and discriminator. (b) Schematic representation of the quantum circuit used in quantum GAN as illustrated in ref. 248. Samples are output from the real source S or the generator 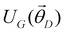 that takes as input some noise and label. This is then fed to the discriminator that takes as input some noise and label. This is then fed to the discriminator  along with the label qubits and scratch space(bath) to work on. The measured output qubit is used to backpropagate the errors through classical updates to give new circuit parameters. along with the label qubits and scratch space(bath) to work on. The measured output qubit is used to backpropagate the errors through classical updates to give new circuit parameters. | ||
3.4 Tensor networks
Tensor network states constitute an important set of variational quantum states for numerical studies of strongly correlated systems in physics and chemistry as they attempt to construct global quantum states from tensors associated with local degrees of freedom.258,259 Expressing a quantum many-body system defined on n qubits requires 2n complex coefficients. Storing and manipulating these numbers of coefficients on a classical computer pose a big challenge while simulating strongly correlated systems. Luckily physically relevant quantum states often possess a limited amount of entanglement wherein only a subset of these coefficients are necessary to describe these states efficiently. Tensor networks provide a natural language to model complex quantum systems (states and operators) on which the amount of entanglement (or correlations in the case of mixed-state dynamics) is conveniently restricted. The representation is such that the complexity of the structure grows linearly with qubit but exponentially with the amount of entanglement in the system. It thereby allows manipulation of quantum states residing in large Hilbert spaces with polynomial amount of resources. The classical simulation of low entangled systems (whose entanglement grows at most polynomially with system size n) becomes tractable using tensor network algorithms like Density Matrix Renormalization Group (DMRG) [discussed in detail in Section 3.4.5] and Time-Evolving Block Decimation (TEBD).260,261Tensor networks are the graphic representation of tensors in Einstein notation such that a rank-n tensor is represented by a box with n indices projecting out of it. The connections between tensors signify the set of indices of tensors which are contracted. Hence the final rank of a tensor network is determined by the number of free edges. A quantum state |ψ〉 in the n-dimensional Hilbert space is basically a rank-n tensor and can be written as,
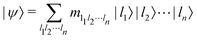 | (91) |
The idea of using tensor networks to represent quantum systems is motivated from the very famous Area Law262 which states that the ground state of the Hamiltonian resides in the low entangled space such that the entanglement entropy between any two partitions of the system grows as the area of the surface separating them. The entangled entropy is usually quantified in terms of the von Neumann entropy of a quantum many-body system which is defined as S(ρ) = −tr[ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ], where ρ is the density matrix of the state. It serves as a befitting measure of the degree of quantum correlation that exists between any of the two-partitions of the system under consideration. The area law has been proven only for gapped Hamiltonians in one-dimension by Hastings263 and has been studied intensively for higher dimensions [see section IV of review262 for a detailed discussion on the area law in higher dimensions]. The area law guarantees an efficient description of ground states by a matrix product state and justifies the density-matrix renormalization group algorithm. Each of these two methods will be discussed in detail in Sections 3.4.1 and 3.4.5, respectively.
ρ], where ρ is the density matrix of the state. It serves as a befitting measure of the degree of quantum correlation that exists between any of the two-partitions of the system under consideration. The area law has been proven only for gapped Hamiltonians in one-dimension by Hastings263 and has been studied intensively for higher dimensions [see section IV of review262 for a detailed discussion on the area law in higher dimensions]. The area law guarantees an efficient description of ground states by a matrix product state and justifies the density-matrix renormalization group algorithm. Each of these two methods will be discussed in detail in Sections 3.4.1 and 3.4.5, respectively.
Tensor networks can be broadly classified into two main groups: those based on the matrix product state (MPS), the tree tensor network state (TTN) and their higher dimension analogues (ex. PEPS); and those based on the multiscale entanglement renormalization ansatz (MERA). We shall discuss applications of TN in Section 5.2 and in Sections 4 and 5.3.
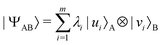 | (92) |
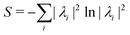 | (93) |
Sometimes entanglement entropy is measured in ebits where one ebit is the amount of entanglement possessed by a maximally entangled two-qubit Bell state. Now, if subsystems A and B are further partitioned into smaller subsystems, we are ultimately left with single-qubit subsystems. Let the states on these single-qubit subsystems be denoted by λ[i] and the diagonal matrices containing the Schmidt coefficients be denoted by λ[i]. Let these states be denoted by Λ[i] and the diagonal matrix containing the Schmidt coefficient be denoted by λ[i]. Then the quantum state reads as
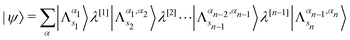 | (94) |
Matrix product states in theory can represent a maximally entangled state but the bond dimension at the middle cut would grow as O(2n).264 For an MPS with a fixed bond dimension χ, the quantum state residing in the n-qubit Hilbert space can now be represented using just O(nχ2) parameters. The area law limits the bond dimension of the ground state of local gapped Hamiltonians making them the best candidates for MPS representation. Evaluating inner products of two quantum states in MPS form takes O(nχ2) time.
The λ[i] matrices in the eqn (94) are usually absorbed into the nearby local tensor λ. The matrix product state is invariant of the contraction of λ[i] either to left or right. This gives MPS a gauge degree of freedom. Usually the gauge is fixed by choosing either of the two directions for multiplying λ[i] giving rise to the left and right canonical forms of MPS. The process is known as canonicalization.264,265 There is another kind of canonical form known as the mixed canonical form266 which is obtained by combining each (λ[i]) to the left (right) of a given special site to its left (right) neighbouring (Λ).
The structure of TTN is inspired from the spatial renormalization group.274 At every layer of TTN, coarse-graining is carried out between neighbouring sub-trees. Unlike MPS, the local tensors with access to physical indices in TTN are not connected directly to each other, the correlation between qubits is represented through the layers. The local correlation information is stored in the lower layers while the upper layers store long-range correlation information.
Each node in a TTN is a three-dimensional tensor (except the root/uppermost node) with at most one upper index α and two lower indices β1 and β2. The tensors can be written as  . The space required to store a TTN grows as O(ND3) (see theorem 4.1267), where N is the number of physical indices and D is the bond dimension of the local tensors. Each tensor in TTN is an isometry satisfying the following condition:
. The space required to store a TTN grows as O(ND3) (see theorem 4.1267), where N is the number of physical indices and D is the bond dimension of the local tensors. Each tensor in TTN is an isometry satisfying the following condition:
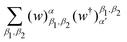 | (95) |
Choosing an isometric tensor as in eqn (95) is advantageous in numerous ways. It simplifies the optimization of TTN and calculation of the expectation values of local observables and it is also known to provide numerical stability to TTN algorithms.275 TTN can very well be generalized to higher dimensions by appropriately placing isometries across local physical indices and hierarchically merging sub-trees through more isometries. Tagliacozzo et al.275 in their studies demonstrate simulation of the transverse-field Ising model on the square lattice using a two-dimensional TTN. Their approach takes advantage of the area law which reduces their simulation cost to exp(N) instead of exp(N2).
Tree tensor networks form the basis of the multi-layer multi-configuration time-dependent Hartree (ML-MCTDH) methods which are used to perform quantum molecular dynamics simulations. In the report276 authors compute the vibrational eigenstates of acetonitrile using TTNs. ML-MCTDH methods are a generalization of the MCTDH methods which can be optimized using MPS as shown in the report.277 Authors make use of the DMRG algorithm to efficiently evaluate the mean-field operators represented in the MPS format. The runtime of the MCTDH methods scales exponentially with the system size, hence multi-layered MCTDH is used which makes use of Tucker decomposition to reduce the dimensionality of the problem and enables it to simulate larger systems.
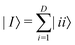 . Now the vertex can be defined by a k-rank tensor containing entangled states. Ultimately this tensor is projected onto the physical spin through a linear map,
. Now the vertex can be defined by a k-rank tensor containing entangled states. Ultimately this tensor is projected onto the physical spin through a linear map,  , where d is the local dimension of the physical state.
, where d is the local dimension of the physical state.
In one dimension (k = 2), an entangled pair of states is projected onto the physical index. While in a square lattice, each local tensor has at most four neighbours [see Fig. 21(d)]. Hence, the local tensor can be written as Λα,β,γ,δs, where s is the physical index and α, β, γ, and δ are bond indices. Hence storing a PEPS requires O(N2dD4) space, where N is the number of qubits along a side of the square, d is the dimension of the physical local state and D is the bond dimension. Performing computations on PEPSs is difficult;278 for instance, evaluating the inner products of PEPSs scales exponentially with D. This is because any partition which divides PEPSs into two equal parts always cuts the O(N) bonds; hence, while evaluating the inner product, one has to form a rank-O (N) tensor as an intermediate.
PEPSs can theoretically represent any state due to their generic structure given that their bond dimension can be arbitrarily large. Due to this universality, PEPSs serve as a variational ansatz in numerical simulation of a wide variety of quantum systems. It can easily prepare physically important states like GHZ and Cluster State279 using D = 2. With D = 3, PEPSs can prepare a resonance valence bond states.280 Kitaev's Toric code which finds its application in quantum error correction and demonstrates non-trivial topological properties can be prepared using PEPSs with D = 2.281 It is widely known that PEPSs can efficiently approximate ground states of gapped local Hamiltonian which satisfy the area law. In the report282 authors show that they can compute the expectation values of local observables in quasi-polynomial time. Jordan et al. proposed algorithms to compute the ground states and time evolution of two-dimensional Hamiltonians defined on infinite-size lattice using PEPSs.283 It is known that it is difficult to simulate systems with long-range correlations on PEPSs, but Gu et al. extensively studied these systems to demonstrate the power and versatility of PEPSs.284 They studied both systems which exhibit symmetry breaking phase transition (transverse field Ising model) and those that show topological phase transition (Z2 gauge model and double-semion model).
While PEPSs have been designed to study quantum systems on classical computers, there have been approaches to simulate them on a quantum computer for faster computations. Schwarz et al. in their report285 presented an algorithm to prepare a PEPS on a quantum computer which scales only polynomially with the spectral gap and the minimum condition number of the PEPS projectors. In the consecutive year they came up with another algorithm to prepare topologically projected entangled pair states on a quantum computer with a similar runtime.286 Specifically they simulated the resonance valence bond state which is hypothesized to contain the topological spin liquid phase.
There also exists an infinite version of MPS (PEPS) known as iMPS (iPEPS).283 They allow working directly in the thermodynamic limit without encountering the finite size or boundary effects. There have been accurate studies of continuous quantum phase transitions using iPEPS.287
The architecture of MERA is inspired from the Renormalization Group.265,290 Its structure is very similar to that of TTN with an additional type of tensors known as disentanglers (U) [shown in Fig. 21(c) using blue circles]. These are unitary tensors satisfying
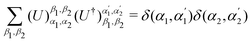 | (96) |
Entanglement in MERA builds up due to its layered structure. To dissect a sub-system of n-qubits from the system requires at least O(log(n)) bonds to be broken. Hence the maximum entanglement entropy generated by MERA goes as O(log(n)log(D)). That is why MERA allows logarithmic divergence from the area law.265,289
Storing a MERA on a classical computer requires space polynomial in number of qubits and the bond dimension. Performing computations using MERA is simplified due to its structure. It can perform efficient computation of local expectation values and correlators by only contracting over the shadow (causal cone) of the local operator, i.e., the tensor which are directly connected to the operator and those tensors on higher levels which are further connected to these tensors. The isometries and disentanglers which lie outside this shadow contract themselves with their conjugates to give unity.
Finding the ground state of a Hamiltonian is a challenging problem and yet is one of the core problem in physics, chemistry, and materials sciences. Even for one-dimensional k-local Hamiltonian it is known to be QMA-complete,292i.e., it's difficult to solve it in polynomial time even with access to a fully functional quantum computer.
The ground state of a gapped local Hamiltonian is known to reside in a low entanglement regime by the area law. DMRG algorithm makes use of this property to find the solution of the local Hamiltonian problem. The algorithm makes use of an ansatz which succinctly represents the state with bounded entanglement (matrix product state). The ground state of the Hamiltonian is attained by minimizing the energy of the system,
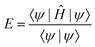 | (97) |
Before starting the algorithm the Hamiltonian has to be converted into a matrix product operator so that it is compatible with MPS. A k-local Hamiltonian can be written as 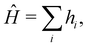 , where hi are local hermitian operators acting on at most k-qubits. Each hi can be converted into an MPO defined on k physical indices using recursive singular valued decomposition as explained in Section 3.4.1. Once local operators are converted into MPO, they can be added using the MPO addition operation, which is basically a direct sum operation over the bond indices (see Section 5.2 in ref. 266 for details).
, where hi are local hermitian operators acting on at most k-qubits. Each hi can be converted into an MPO defined on k physical indices using recursive singular valued decomposition as explained in Section 3.4.1. Once local operators are converted into MPO, they can be added using the MPO addition operation, which is basically a direct sum operation over the bond indices (see Section 5.2 in ref. 266 for details).
The initial MPS can be created using random tensors of desired dimension. At each step of DMRG a contiguous set of sites is chosen which is to be optimized and is designated as the system, while everything outside the system is called the environment which is kept fixed. By performing local optimization over the system states iteratively, the ground state of the given Hamiltonian is attained. Usually it requires several sweeps over the complete lattice to reach convergence which depend on the complexity of the Hamiltonian and also the choice of the initial state.
To perform local optimization over the system, the environment qubits are contracted to form a reduced Hamiltonian (HS) whose energy is then minimized.
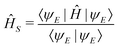 | (98) |
Energy minimization of ĤS can be analogously performed by solving the following eigenvalue problem: ĤS|ψS〉 = E|ψS〉.
The system state |ψS〉 so obtained updates the current system state. The system can be defined by any number of qubits. For single qubit systems the bond dimension remains fixed while working with two or more site systems can allow the bond dimensions to be changed dynamically. Basically, the local optimization procedure for a multi-site system returns the state defined on multiple qubits. This state has to be decomposed into an MPS using recursive singular value decomposition before replacing them at the current state. Since SVD gives us the complete set of singular values we can choose to trim the bond dimensions which are below the threshold of the accuracy required. Usually a larger system size means more accurate results and the trial state converges to the ground state in lesser number of sweeps. But it also increases the overall computational cost. The computational cost heavily depends on the local optimization procedure which can be improved by using iterative algorithms like Lanczos which only computes the smallest set of eigenvalues and eigenvector of a given operator. Since we are only interested in the ground state of reduced Hamiltonian, Lanczos algorithm can massively cut down the computation cost.
Since the dimensions of the associated tensor grow exponentially with the depth of the quantum circuit associated with it, it is possible to prepare certain tensor networks with a large bond dimension on a quantum computer that cannot be efficiently simulated on a classical computer. These states are of utmost importance because there is a definite quantum advantage associated with them. The authors in the report304 demonstrated the preparation of such a state called deep-MERA which can be represented by a local quantum circuit of depth D consisting of two-qubit gates. The expectation values of local observables of a DMERA can be computed in time 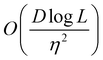 on a quantum computer while a classical computer would take O(eO(D)
on a quantum computer while a classical computer would take O(eO(D)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Llog(1/η)) time, where η is the desired precision and L is the number of qubits.
Llog(1/η)) time, where η is the desired precision and L is the number of qubits.
Schwarz et al.285 demonstrate a procedure to efficiently prepare PEPSs on a quantum computer that scales polynomially with the inverse of the spectral gap of Hamiltonian. Efforts have also been made to use the advantages of tensor networks and quantum circuit simultaneously by fusing them. In the report,305 authors introduced a hybrid tree tensor network architecture to perform quantum simulation of spin lattice Hamiltonian with short-range interactions. They simulated two-dimensional spin systems as large as 9 × 8 qubits which require operations acting on at most 9 qubits. Their method can be generalized to arbitrary trees to represent the N = O(gD−1) qubit system, where D and g are the maximal depth and degree of the tree. It would require O(Nk2) circuits for computation and the cost for measuring local expectation values would be O(Ngk4), where k is the bond dimension of the TTN. They provide an efficient representation of a quantum state whose elements can be evaluated on a near-term quantum device. When compared against standard DMRG on MPS and imaginary-TEBD on PEPSs, they produce results more accurate by up to two orders.
4 Case for quantum computing enhanced machine learning
4.1 Universal function approximation through supervised learning on a quantum computer
In this section, we shall specifically highlight some of the recent claims that propose a theoretical guarantee for supervised machine learning tasks on a quantum computer, with these claims being the successful mimicking of arbitrary unknown functional dependence with high accuracy. It is thus needless to say that the benefits of these claims if realized can enhance the learning capabilities of supervised models for both quantum and classical data even beyond the precincts of physical sciences.Several significant proposals have been reported recently that attempt to approximate a function (say f(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) )) using a quantum circuit where
)) using a quantum circuit where 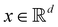 are classical data entries. Intuitively this can be framed as a supervised learning task where one has access to a dataset
are classical data entries. Intuitively this can be framed as a supervised learning task where one has access to a dataset 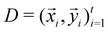 which is assumed to follow the functional inter-relationship f(
which is assumed to follow the functional inter-relationship f(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ). The crux of the problem is therefore to learn a hypothesis h(
). The crux of the problem is therefore to learn a hypothesis h(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) which closely mimics the actual function f(
) which closely mimics the actual function f(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) within a certain error tolerance. To perform such tasks on a quantum computer and learn the hypothesis h(
) within a certain error tolerance. To perform such tasks on a quantum computer and learn the hypothesis h(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) one needs to encode classical data onto a quantum state first. Mitarai et al.306 proposed a data-uploading scheme on a quantum circuit for such a scenario. The scheme maps
) one needs to encode classical data onto a quantum state first. Mitarai et al.306 proposed a data-uploading scheme on a quantum circuit for such a scenario. The scheme maps 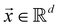 with −1 ≤ xi ≤ 1 ∀ i wherein one requires access to the nk-th power for each datum xi with k ∈ {1, 2, 3,…, d} into an
with −1 ≤ xi ≤ 1 ∀ i wherein one requires access to the nk-th power for each datum xi with k ∈ {1, 2, 3,…, d} into an 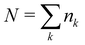 qubit state as
qubit state as 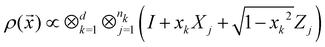 . The tensor product structure of the many-qubit state creates non-linear cross terms of the kind xmxn. Following this data-encoding, the state can be acted upon by any parameterized unitary (say
. The tensor product structure of the many-qubit state creates non-linear cross terms of the kind xmxn. Following this data-encoding, the state can be acted upon by any parameterized unitary (say  ). This will be followed by a measurement protocol using a pre-defined operator (say M) to learn the hypothesis function
). This will be followed by a measurement protocol using a pre-defined operator (say M) to learn the hypothesis function 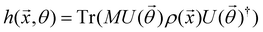 . The hypothesis function is optimized with respect to the parameters
. The hypothesis function is optimized with respect to the parameters 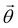 using an appropriate loss function L(h(
using an appropriate loss function L(h(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,θ),
,θ),![[y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0079_20d1.gif) ,
,![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) until the desired tolerance is reached, i.e., at
) until the desired tolerance is reached, i.e., at 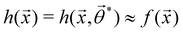 where
where 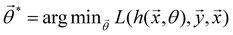 . The authors claim that the encoding above is capable of approximating a larger class of functions than what classical supervised learning tasks can achieve. To substantiate this claim, the authors argue that if classical processors could mimic every kind of function, which can be realized from such quantum data-encoding, then that would mean the classical device in principle learns the input–output relationship of complex computational models like quantum cellular automata307 which is known to not being achievable using polynomial resources (poly(N)) on a classical device. Numerical experiments for fitting the time evolution of the transverse Ising model and a binary classification task of a non-linearly separable data were performed with the above encoding with great success.
. The authors claim that the encoding above is capable of approximating a larger class of functions than what classical supervised learning tasks can achieve. To substantiate this claim, the authors argue that if classical processors could mimic every kind of function, which can be realized from such quantum data-encoding, then that would mean the classical device in principle learns the input–output relationship of complex computational models like quantum cellular automata307 which is known to not being achievable using polynomial resources (poly(N)) on a classical device. Numerical experiments for fitting the time evolution of the transverse Ising model and a binary classification task of a non-linearly separable data were performed with the above encoding with great success.
Perez-Salinas308 demonstrated how to construct single-qubit classfiers using efficient data-reuploading which is essentially sequential loading of classical data entries. Many powerful insights into the function learning ability of a quantum circuit through data-encoders have been recently elaborated in ref. 309. The work explicates if the data-encoding unitary is expressed as 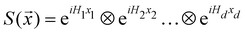 and r repetitions of such unitaries in the circuit are made along with parameterized unitaries (say
and r repetitions of such unitaries in the circuit are made along with parameterized unitaries (say 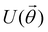 as above) for training the model then the frequency components of the hypothesis function h(
as above) for training the model then the frequency components of the hypothesis function h(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) when resolved in the Fourier basis are entirely controlled by the encoding Hamiltonian family {Hm}dm=1. However, the Fourier coefficients are influenced by the remaining part of the circuit i.e. the trainable unitaries
) when resolved in the Fourier basis are entirely controlled by the encoding Hamiltonian family {Hm}dm=1. However, the Fourier coefficients are influenced by the remaining part of the circuit i.e. the trainable unitaries 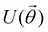 as well as the measurement operator M. The authors further show that repeating the encoding in parallel or in a sequence would lead to a similar frequency spectrum. Under the assumption that the trainable part of the circuit is general enough to realize any arbitrary unitary, then it is possible to choose encoding Hamiltonians {Hm}dm=1 that can generate any arbitrary frequency range asymptotically. Using this fact the authors prove that it is possible for the hypothesis function h(
as well as the measurement operator M. The authors further show that repeating the encoding in parallel or in a sequence would lead to a similar frequency spectrum. Under the assumption that the trainable part of the circuit is general enough to realize any arbitrary unitary, then it is possible to choose encoding Hamiltonians {Hm}dm=1 that can generate any arbitrary frequency range asymptotically. Using this fact the authors prove that it is possible for the hypothesis function h(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) learnt by such a quantum circuit to mimic any square integrable function within an arbitrarily preset tolerance. This thereby lends to universal –expressibility to such hypothesis functions. The importance of this result is many-fold as it allows one to not only realize that expressive power of the family of functions learnt from supervised learning task on a quantum circuit is extremely high but also allows one to design unitaries, set number of necessary repetitions, etc. to augment the learning process. Universality in discriminative learning wherein a hybrid quantum model to learn the parameters of an unknown unitary was used has also been illustrated recently.310 Other than these, expressive capacity of parameterized quantum circuits has been thoroughly investigated recently.311 Since most of the NISQ era quantum ML models are indeed variational, much of the insight from these studies is directly transferable.
) learnt by such a quantum circuit to mimic any square integrable function within an arbitrarily preset tolerance. This thereby lends to universal –expressibility to such hypothesis functions. The importance of this result is many-fold as it allows one to not only realize that expressive power of the family of functions learnt from supervised learning task on a quantum circuit is extremely high but also allows one to design unitaries, set number of necessary repetitions, etc. to augment the learning process. Universality in discriminative learning wherein a hybrid quantum model to learn the parameters of an unknown unitary was used has also been illustrated recently.310 Other than these, expressive capacity of parameterized quantum circuits has been thoroughly investigated recently.311 Since most of the NISQ era quantum ML models are indeed variational, much of the insight from these studies is directly transferable.
4.2 Power of kernel estimation and data-classification from quantum computers
In this section we shall highlight some of the key results that have been demonstrated in recent years regarding the superiority of constructing kernel matrix elements from the quantum computer as opposed to a classical processor. Such kernel estimates are necessary for a variety of supervised learning algorithms like kernel-ridge regression (see Section 3.2.2) or for classification tasks like in support-vector machine or SVM (see Section 3.2.7) to name a few. Kernel-ridge regression on a classical processor has been extensively used in chemistry for estimating density functionals,312 simulating non-adiabatic dynamics across potential energy surfaces,45 dissipative quantum dynamics128 and even procuring molecular and atomic properties like atomization energies.313,314 We shall return to a subset of these applications and explore them in detail in Section 5.3. Even for classification, kernelized variants of SVM on a classical processor have been useful for demarcating phases of matter, or for delineating malignant tumors from non-malignant ones315 which would be of use to biochemists and oncologists. We shall return to a subset of these applications in Section 5.2. Thus the learning capabilities of all the aforementioned algorithms can be augmented if quantum computing-enhanced kernel estimates are used. A kernelized SVM has also been used extensively for the drug-designing process, in drug-induced toxicity classification,316etc. We shall discuss some of these in Section 5.5. In fact a study has already demonstrated quantum advantage recently317 wherein a kernel SVM on an actual quantum device (ibmq_rochester) was used with classical processing to delineate active vs. inactive drug candidates for several diseases. The authors note a faster training time on a quantum processor than on the classical processor for larger dataset sizes. We shall discuss this specific example in detail in Section 5.5.4.It must be emphasized that for classification tasks, apart from the quantum Kernel methods, the quantum instance-based learning algorithms could also outperform classical learners. Estimating the distance between the test data and the training ones is always crucial in the instance-based learning algorithms. For instance, in the nearest neighbor algorithm, one of the most typical instance-based learning frameworks, the label of the test data is determined by the nearest training data. In 2013, Lloyd and coworkers proposed a quantum clustering algorithm for unsupervised QML,156 showing that estimating distances and inner products between post-processed vectors in N-dimensional vector spaces then takes time O(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) N) on a quantum computer. In contrast, sampling and estimating distances and inner products between post-processed vectors on a classical computer are exponentially hard.157 The significant speedup yields considerable power of the quantum instance-based learning algorithms as well. In fact a specific example of this class of algorithms which inherits the aforesaid advantage has also been recently designed by one of the authors318 and applied for phase classification of material VO2 which will be of importance to materials scientists. More details on such examples can be found in Section 5.2 and will not be elaborated herein. Here we shall specifically discuss the advantages of estimating the kernel on a quantum processor that has been noted recently for certain tasks which thereby promises exciting opportunities for kernelized quantum supervised learning with applications in physics and chemistry.
N) on a quantum computer. In contrast, sampling and estimating distances and inner products between post-processed vectors on a classical computer are exponentially hard.157 The significant speedup yields considerable power of the quantum instance-based learning algorithms as well. In fact a specific example of this class of algorithms which inherits the aforesaid advantage has also been recently designed by one of the authors318 and applied for phase classification of material VO2 which will be of importance to materials scientists. More details on such examples can be found in Section 5.2 and will not be elaborated herein. Here we shall specifically discuss the advantages of estimating the kernel on a quantum processor that has been noted recently for certain tasks which thereby promises exciting opportunities for kernelized quantum supervised learning with applications in physics and chemistry.
1. Quantum-enhanced feature maps and kernels are defined in Section 3.2.1. As mentioned therein, ref. 117 provides two strategies for efficiently performing kernel-based machine learning algorithms using a quantum computer. The first is an implicit approach wherein the kernel matrix is estimated through an inner product once a quantum circuit for state preparation with encoding classical data is in place. With access to the entries of the kernel-matrix from the quantum computer, the actual ML algorithm is then performed classically. The other approach is the explicit approach, where the full ML task is performed on the quantum computer itself. Ref. 117 adopts the first approach by encoding each entry xi of a given feature vector x ⊂ Rd in the phase information of a multi-mode squeezed state and shows that the corresponding kernel obtained through inner product of such states is expressive enough for classification tasks. To exemplify the second approach, it also used the two-mode squeezed state as a data-encoder and then applied a variational circuit (say W(θ)) followed by photon-number measurement and assigned the probability of a binary classification task to obtain two specific Fock states in the two-modes. Using the distribution obtained from the QC, the authors could linearly separate a dataset with 100% accuracy. However, the authors note that the primary data-encoding strategy adopted in the paper is through the preparation of squeezed states in continuous variable quantum computing which can be efficiently simulated classically.319,320 They further mention that inclusion of non-Gaussian elements like cubic-phase gates,97 non-linearity in photon-number measurements,321 classically intractable continuous-variable instantaneous quantum computing or CV-IQP circuits322 may lead to a non-trivial kernel estimation task wherein the power of quantum computers can be better used. Similar results as these are also reported in ref. 318 wherein classical data were not-only encoded within the phase information of a multi-mode squeezed state but also in the amplitude. Proper comparisons of such squeezed state encoded kernels with Gaussian kernels were also investigated using standard datasets from scikit learn.323
2. The first work to exemplify an advantage is ref. 324. The algorithm in ref. 324 performs a standard support-vector machine classification task (discussed in Section 3.2.7) with 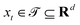 (training feature vectors for input) and
(training feature vectors for input) and 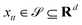 (testing feature vectors). The labels
(testing feature vectors). The labels 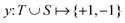 where the set y = {yt,ytt}. The algorithm only had access to the training labels (yt) and its job was to evaluate an approximation to the testing labels, i.e., obtain ỹtt ∀ xtt ∈ S which matches with ytt with high probability. Unlike in the previous reference, the data-encoding feature map used did not produce product states. The specific data-encoding unitary used is the following:
where the set y = {yt,ytt}. The algorithm only had access to the training labels (yt) and its job was to evaluate an approximation to the testing labels, i.e., obtain ỹtt ∀ xtt ∈ S which matches with ytt with high probability. Unlike in the previous reference, the data-encoding feature map used did not produce product states. The specific data-encoding unitary used is the following:
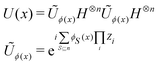 | (99) |
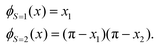 | (100) |
3. A recent report327 using the same feature-space encoding scheme as in ref. 324 above establishes that quantum enhanced kernels perform better for complex data classification tasks like geometric data patterns distributed according to Mersenne Twister distribution.328 Classical methods cannot achieve similar accuracy. However, if the data distribution is simple such that large differences exist between data that belong to the separating classes then classical kernels would perform as well. Also, the study claims that simpler data encoding circuits for computing entries of quantum kernels may be less effective for certain data-classification tasks. Another study329 has actually systematically studied the effect of noise and finite measurement samples and concluded that a high noise content may expectedly be detrimental to the estimation of kernel entries on the quantum computer. However, the report329 also proposes to mitigate the effect of the noise by classical pre-processing of the estimated noisy kernel like discarding the negative eigenvalues.
4. A clear and most decisive exhibition of the power of kernelized variant of a support-vector machine on a quantum computer for a classification task was highlighted in ref. 180. The motivation for the work was to demonstrate a specific example wherein estimation of the kernel Gram matrix on a classical processor would not only be not efficient, but the classification task itself would be provably disadvantageous. Also, the quantum advantage would be retained even in the presence of finite sampling errors. The classification task chosen was based on the famous discrete-logarithm problem. The problem entails finding  , where
, where  with p being a large prime number and g being the generator of the multiplicative cyclic group
with p being a large prime number and g being the generator of the multiplicative cyclic group 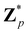 . By generator one means an element
. By generator one means an element 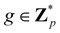 such that for every element
such that for every element 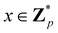 , one can write x = gm. In such a case, m is said to be the discrete-logarithm to base g of x in
, one can write x = gm. In such a case, m is said to be the discrete-logarithm to base g of x in 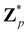 and is denoted by m = logg(x). It is believed that no classical algorithm can compute the discrete-logarithm in time which is polynomial in n = log2(p) even though quantum algorithms like Shor's algorithm is known to do it.53 The classifier function makes the following decision:
and is denoted by m = logg(x). It is believed that no classical algorithm can compute the discrete-logarithm in time which is polynomial in n = log2(p) even though quantum algorithms like Shor's algorithm is known to do it.53 The classifier function makes the following decision:
| fs(x) = +1 if logg(x) ∈ [s,s+(p − 3)/2] = −1 (otherwise). | (101) |
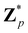 into two equal halves by mapping each of the halves to {+1, −1}. The authors prove that a classical learning algorithm for this task cannot achieve an accuracy more than 0.5 + 1/poly(n) indicating that the best classical algorithm can only do random guessing for unseen test data. For the kernelized quantum SVM, however, the authors propose the following quantum feature map/state:
into two equal halves by mapping each of the halves to {+1, −1}. The authors prove that a classical learning algorithm for this task cannot achieve an accuracy more than 0.5 + 1/poly(n) indicating that the best classical algorithm can only do random guessing for unseen test data. For the kernelized quantum SVM, however, the authors propose the following quantum feature map/state: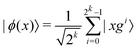 | (102) |
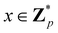 , k = n − t
, k = n − t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(n) for t being some constant.180 The state-preparation circuit which prepares the above state is shown to be efficient using Shor's algorithm.53 Using the above state-preparation strategy, the authors can estimate the kernel matrix for each entry in the training set as K(x,x′) = |〈ϕ(x)|ϕ(x′)〉|2. Using this kernel, the authors rely on the usual SVM algorithm on a classical processor to construct a separating hyperplane and optimize the parameters for it. Once the parameters for the hyperplane are determined, classification of new test data also requires kernel matrix elements when new kernel estimates from the QC are invoked again. The authors call this procedure support vector machine with quantum kernel estimation (SVM-QKE) indicating that the quantum computer is only involved in constructing the entries of the kernel. The authors prove that SVM-QKE yields a classifier that can segregate the data in testing and training set with an accuracy of 0.99 in polynomial time and with a probability of at least
log(n) for t being some constant.180 The state-preparation circuit which prepares the above state is shown to be efficient using Shor's algorithm.53 Using the above state-preparation strategy, the authors can estimate the kernel matrix for each entry in the training set as K(x,x′) = |〈ϕ(x)|ϕ(x′)〉|2. Using this kernel, the authors rely on the usual SVM algorithm on a classical processor to construct a separating hyperplane and optimize the parameters for it. Once the parameters for the hyperplane are determined, classification of new test data also requires kernel matrix elements when new kernel estimates from the QC are invoked again. The authors call this procedure support vector machine with quantum kernel estimation (SVM-QKE) indicating that the quantum computer is only involved in constructing the entries of the kernel. The authors prove that SVM-QKE yields a classifier that can segregate the data in testing and training set with an accuracy of 0.99 in polynomial time and with a probability of at least  over even random training samples. They further show that even when the QKE entries have a small additive perturbation due to finite sampling; the separating hyperplane so obtained is close to the exact one with high probability and so is the accuracy of the corresponding classifier. Since the kernel estimates from a classical processor cannot provably do better than random guessing, this classification task clearly explicates the superiority of quantum feature maps. Since then, several interesting demonstrations of kernel estimates on the quantum computer have emerged like using a linear combination of multiple quantum enhanced kernels with a variational circuit to enhance accuracy and expressivity over and beyond a single kernel for complex datasets,330 a fidelity based quantum kernel estimate between the members of the training dataset and the testing samples331 or even distinguishing the classical data entries directly after mapping to quantum states in the quantum feature space using metrics with a shallow circuit depth in a process which the authors call quantum metric learning.332 Like in the above cases, numerical experiments have also been reported on real devices like a 17-qubit classification task333 performed on Google's Sycamore to segregate data in a 67-dimensional space with appropriate noise-mitigation strategies.
over even random training samples. They further show that even when the QKE entries have a small additive perturbation due to finite sampling; the separating hyperplane so obtained is close to the exact one with high probability and so is the accuracy of the corresponding classifier. Since the kernel estimates from a classical processor cannot provably do better than random guessing, this classification task clearly explicates the superiority of quantum feature maps. Since then, several interesting demonstrations of kernel estimates on the quantum computer have emerged like using a linear combination of multiple quantum enhanced kernels with a variational circuit to enhance accuracy and expressivity over and beyond a single kernel for complex datasets,330 a fidelity based quantum kernel estimate between the members of the training dataset and the testing samples331 or even distinguishing the classical data entries directly after mapping to quantum states in the quantum feature space using metrics with a shallow circuit depth in a process which the authors call quantum metric learning.332 Like in the above cases, numerical experiments have also been reported on real devices like a 17-qubit classification task333 performed on Google's Sycamore to segregate data in a 67-dimensional space with appropriate noise-mitigation strategies.
4.3 Power of quantum-neural networks
In this section, we shall highlight some of the recent reports wherein the superiority of quantum computing enhanced neural network models has been demonstrated or theoretically proven in terms of its generalizability and expressive power, training capacity, resource and parameter requirements to mention a few. Neural networks in a classical processor have become the standard go-to method for many applications in chemistry and physics like in efficient state-preparation protocols using generative adversarial networks (see Section 3.3.6).334,335 Networks like CNN (see Section 3.3.2) have been used for the classification of phases of matter,336,337 in quantum state-tomography,338 and in structure and ligand based drug-designing protocols.339 Deep neural networks (see Section 3.3) have been also used for predicting molecular properties even with non-bonding interactions,340 in drug-induced toxicity detection,341 many-body structure of correlated quantum matter like molecules and materials,342,343 and even in molecular dynamics.344,345 Generative models like restricted Boltzmann machine based neural-network representation of many-body quantum states346 have been used for classification and understanding ground and excited state properties of quantum systems. We shall return to a subset of these applications in Sections 5.1–5.5. It is thus apparent that all the aforesaid algorithms stand to benefit from any quantum advantage seen in the development of neural network based models on a quantum processor. In fact, in certain cases, direct advantages have already been reported. For example, the authors have reported a quantum circuit-based implementation of a restricted Boltzmann machine based ansatz for any of the electronic states of molecules and materials347 which requires polynomial resources for its construction. Similarly for quantum version of CNN which has been used for the classification of phases in the Ising model,215 the authors claim a more parameter reduction. We shall return to these applications and their description in Sections 5.2 and 5.3. Herein we enlist some of the recent examples wherein quantum superiority has been seen or theoretically conjectured thereby promising many novel applications in chemistry and physics which can be realized in the future. More theoretical insight into the learning mechanisms and generalizability of quantum computing enhanced neural networks are discussed in detail in Section 6.4.1. Quantum-neural networks (QNN) have been discussed in Section 3.3. Each such network has three generic components – a data encoding circuit (often called feature map) which accepts classical data as the input and usually encodes them into the amplitudes of a quantum state (other encoding schemes are also possible; see ref. 116) followed by a layer of parameterized unitaries. Finally, measurement protocol is exercised whose outcome is post-processed on a classical computer to minimize a loss function and alter the parameters of the last layer of unitaries variationally until the desired convergence is reached. A recent report has suggested that such networks can be more expressive and faster trainable than the corresponding classical networks if the data encoding circuit possess non-trivial entangling gates which can identify hidden correlation among data entries.348 The work used an input data-set 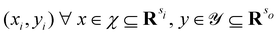 and a parameter vector θ ⊆ [−1,1]d. The input distribution p(x) is the prior distribution and p(y|x;θ) is the output distribution from the QNN given the input and specific parameter set. Using this they constructed the empirical Fisher information matrix (∈Rd×d)349 as follows:
and a parameter vector θ ⊆ [−1,1]d. The input distribution p(x) is the prior distribution and p(y|x;θ) is the output distribution from the QNN given the input and specific parameter set. Using this they constructed the empirical Fisher information matrix (∈Rd×d)349 as follows:
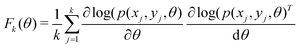 | (103) |
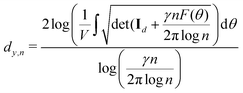 | (104) |
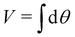 is the volume in parameter space and γ ∈ (0,1]. The physical motivation of defining an effective dimension is to quantify the expressibility of the model, i.e., estimate the size of the space all possible functions which the model class can successfully mimic with the Fisher information as the metric.351 Using the above definition of the effective dimension, the authors show that the full QNN has the highest effective dimension compared to the easy quantum model (without entangling gates in the circuit encoding the features) and even the classical neural network for (d = 40, si = 4, so = 2) and size of data n = 105–106 (see Fig. 3(a) in ref. 348). They also demonstrated that the full QNN trains faster and achieves lesser loss function values within smaller number of iterations compared to the other two (see Fig. 3(b) in ref. 348). The conclusion remains invariant to training even on the real hardware.
is the volume in parameter space and γ ∈ (0,1]. The physical motivation of defining an effective dimension is to quantify the expressibility of the model, i.e., estimate the size of the space all possible functions which the model class can successfully mimic with the Fisher information as the metric.351 Using the above definition of the effective dimension, the authors show that the full QNN has the highest effective dimension compared to the easy quantum model (without entangling gates in the circuit encoding the features) and even the classical neural network for (d = 40, si = 4, so = 2) and size of data n = 105–106 (see Fig. 3(a) in ref. 348). They also demonstrated that the full QNN trains faster and achieves lesser loss function values within smaller number of iterations compared to the other two (see Fig. 3(b) in ref. 348). The conclusion remains invariant to training even on the real hardware.
2. Recently, a new report has been published352 which extends the famous no-free lunch theorem353,354 to the learning process in a quantum neural network (QNN) wherein the training data-set may be intrinsically entangled with a third accessible register. The no-free lunch theorem (NFL) for classical learning task is deduced for an unknown map, say 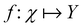 where the size of the set χ is dx and that of set Y is dy. One generates a training set S consisting of t points from this function defined as S = {(xi,yi)|xi ∈ χ, yi = f (xi) ∈ Y}ti=1. In general in the supervised learning setup, this set S is used to construct a merit-function
where the size of the set χ is dx and that of set Y is dy. One generates a training set S consisting of t points from this function defined as S = {(xi,yi)|xi ∈ χ, yi = f (xi) ∈ Y}ti=1. In general in the supervised learning setup, this set S is used to construct a merit-function 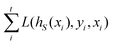 where hS (xi) is the hypothesis function that is expected to mimic the unknown function f. The merit-function is minimized to obtain the parameters defining the hypothesis function hS(x) which can then be used to make predictions for unseen x ∈ (χ ∩ Sc). To quantify how well the approximate function hS(x) resembles the actual one f one can define a risk function as follows:
where hS (xi) is the hypothesis function that is expected to mimic the unknown function f. The merit-function is minimized to obtain the parameters defining the hypothesis function hS(x) which can then be used to make predictions for unseen x ∈ (χ ∩ Sc). To quantify how well the approximate function hS(x) resembles the actual one f one can define a risk function as follows:
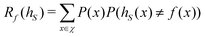 | (105) |
 | (106) |
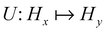 both of which are d-dimensional. The user herein has access to another auxillary quantum system (say R ∈ HR). The training set SQ contains t pairs of states which are entangled with R as follows:
both of which are d-dimensional. The user herein has access to another auxillary quantum system (say R ∈ HR). The training set SQ contains t pairs of states which are entangled with R as follows: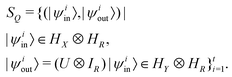 | (107) |
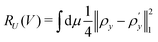 | (108) |
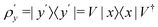 and |x〉 ∈ HX (not necessarily within SQ) and |y〉, |y′〉 ∈ HY and the measure dμ is over the Haar measure of states. The averaging of the above risk function over all training sets SQ and unitary maps U as before yields
and |x〉 ∈ HX (not necessarily within SQ) and |y〉, |y′〉 ∈ HY and the measure dμ is over the Haar measure of states. The averaging of the above risk function over all training sets SQ and unitary maps U as before yields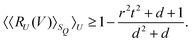 | (109) |
The bound actually holds for each SQ and hence averaging over SQ is unnecessary. It is derived under the assumption that over the training samples the outcomes of V and U match perfectly. Implication of the above bound is that for r = 1, the bound vanishes and the average risk can be minimized only if t = d = 2n where 2n is the dimension of HX. This indicates that if the input states are product states with the quantum system characterized by HR then exponentially many training samples might be required in n. This result was previously obtained in ref. 355. However for r ≠ 1 this is not the case. Specifically, in the limiting case of r = d, a single training example would suffice to saturate the lower bound on the average. For any r in between one can easily see that the number of training samples t can be set to be far fewer than d. The authors show numerical experiments on Rigetti's quantum processor for 2 × 2 unitaries and demonstrate that the average risk can be minimized well below the classically accessible limit by controlling r which alters entanglement with the third quantum system R. Similar results were obtained even in the simulator. The concrete proof of the theorem restores hope that the size of the training set can be small yet a quantum advantage can be retained as long as entanglement is used as a useful resource which is not possible classically. This result joins the group of other results wherein entanglement has served similar roles like in superdense coding356,357 or quantum teleportation.358,359
3. This example is different in spirit than the previous ones as it demonstrates how the quantum convolutional neural network (QCNN)215 which is discussed in detail in Section 3.3.2 can lead to efficient parameter reduction compared to other methods of quantum phase classification. The power of a quantum classifier over and beyond that of a classical classifier has already been demonstrated for certain tasks in some of the points above. The task for which the authors tested the QCNN was to segregate quantum states belonging to a particular phase given a training data-set S = {|ψ〉i,yi}Mi=1 where yi = {0,1} ∀ i are the corresponding labels. The specific example was the symmetry-protected topological phase of a 1D spin-chain. The algorithm requires only O(log(n)) parameters to classify such an n-qubit quantum state which the authors claim is a two-fold exponential reduction in parameter space compared to other quantum classifiers. This essentially means that the QCNN is more expressive compared to other classifiers as it solves a relatively low-dimensional optimization problem without sacrificing the accuracy of the task at hand. Similarly, they also show that the sample complexity of QCNN, which is defined as the number of copies of the input state that need to be accessed by the algorithm for correctly identifying the phase, is lesser than from other techniques like direct evaluation of expectation values of certain operators, which can also act as a marker of the phase. We shall return to this example in Section 5.2. Pesah et al.360 have demonstrated that in the conventional QCNN architecture there is an absence of barren plateaus as the gradient estimates vanish polynomially (and not exponentially) in the size of the system for random initialization. Recently, MacCormack et al. have extended the concept to introduce a variant of QCNN which is called the branching quantum convolutional network (bQCNN).361 In QCNN as discussed in Section 3.3.2, the primary idea is reduction of the number of qubits while preserving important features. The convolutional layers perform multi-qubit unitaries for generating entanglement among the qubits whereas in pooling layers certain number of qubits are discarded through measurements and controlled rotations on nearby qubits are performed conditioned on the measurement results of the discarded qubits. The new reduced set of qubits is then fed into the convolutional unitaries again and the process is repeated. For bQCNN, the authors make a deviation at the pooling layer. Instead of using certain measurement outcomes only of the discarded qubits, the authors use all possible outcomes or binary bit combinations to design several different channels/branches for subsequent convolutional operations each of which is realized for a given bit string. This enhances the parameter requirement drastically as noted in the report. However, the authors also demonstrate that the expressibility of the ansatz from bQCNN is higher than that of QCNN at a similar circuit depth.
4.4 Power of quantum computers for tensor-network based machine learning tasks
In this section, we highlight an advantage that has been recently reported for a classification task performed using a tensor network ansatz on a quantum computer. Such classification can be extended to the physico-chemical domain like in ligand selectivity for structure-based drug designing (see Section 5.5.1) with the quantum benefit reaped. An example of another tensor network based classification of phases of a spin-model can be found in Section 5.2. Besides, tensor networks on a classical processor have also been aggressively used for representing many-body states for a variety of applications like for spin-liquids,362 excitonic states in materials363 and molecules.364 Quantum advantages as have been noted for the example below can be extended to such applications. We shall discuss such prospects with concrete examples in Section 5.3.2.Recently, a report has illustrated the use of quantum architectures of tree and matrix product state tensor networks302 to demonstrate the working of a discriminative machine-learning model on MNIST dataset.365 The primary objective of the study was to perform classification and recognition of hand-written digits using a variational optimization procedure that can be efficiently carried out on a quantum hardware in the NISQ era. Classical data-entries (say 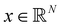 ) from the data-set are mapped to an N-qubit quantum state using the data-encoding protocol described below in eqn (110)
) from the data-set are mapped to an N-qubit quantum state using the data-encoding protocol described below in eqn (110)
 | (110) |
State |ϕ〉 is a product state which can easily be prepared by applying single qubit rotation gates on the |0〉⊗N state. After state preparation, each set of qubits (say 2V qubits where V is the number of virtual states) is acted upon by a parameterized unitary gate. The scheme is inspired from coarse-graining techniques. After each parameterized unitary operation, V qubits are discarded/reset and the other V qubits proceed to the next step where they are merged with V qubits coming from another set of 2V qubits. This process is continued until the last 2V qubits remain which are acted upon by a unitary gate to produce output qubits. One or more output qubits are measured to determine the probability distribution of the output labels. While the model is agnostic to the grouping of the qubit sets, it is usually wise to group qubits that represent local regions in the input data. This ansatz is motivated from a tree tensor network (see Fig. 22). The optimization problem which they solve involves classification of hand-written digits using a loss-function that penalizes the difference in the probability of attaining the true-label from the measurement protocol as opposed to the most-probable incorrect label. The algorithm used is adapted from Simultaneous Perturbation Stochastic Approximation (SPSA)366 with momentum being included inside the gradient estimates.199 The accuracy of the method as reported is extremely high, i.e., with the lowest percentage error being 87% and an average test accuracy of over 95%. The authors noted that for usual quantum algorithms, encoding such an N-qubit state and applying tunable unitaries would require N-physical qubits. However, the tree-structure in the ansatz with sequential measurements allows the authors to use ≈V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(N) physical qubits indicating that the scheme is qubit efficient. It must also be emphasized that merely using a tree-tensor network approach (TTN) on a classical processor would require a space complexity of O(N23V)367 where V is as defined before the number of virtual states. This result indicates that the TTN ansatz on the quantum computer is more expressive than a corresponding classical implementation as similar accuracies are afforded even with a reduced bond-dimension (bond-dimension is usually denoted by D where D = 2V and as seen here scales logarithmically for the quantum TTN version whereas would have a cubic scaling for a classical TTN). The authors also performed a systematic analysis of the effect of noise on the algorithm and concluded that the degradation of the performance was only 0.004 with a strongly enhanced (×10) noise parameters thereby indicating the resilience of the algorithm.
log(N) physical qubits indicating that the scheme is qubit efficient. It must also be emphasized that merely using a tree-tensor network approach (TTN) on a classical processor would require a space complexity of O(N23V)367 where V is as defined before the number of virtual states. This result indicates that the TTN ansatz on the quantum computer is more expressive than a corresponding classical implementation as similar accuracies are afforded even with a reduced bond-dimension (bond-dimension is usually denoted by D where D = 2V and as seen here scales logarithmically for the quantum TTN version whereas would have a cubic scaling for a classical TTN). The authors also performed a systematic analysis of the effect of noise on the algorithm and concluded that the degradation of the performance was only 0.004 with a strongly enhanced (×10) noise parameters thereby indicating the resilience of the algorithm.
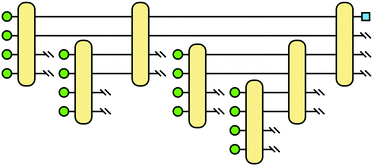 | ||
Fig. 22 The architecture for evaluating the discriminative tree tensor network model using a Qubit-efficient scheme with two virtual qubits (V) and 16 input states (N) as used in ref. 302. The architecture requires O(V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(N)) = 8 qubits for its operation. The qubits indicated with hash marks are measured and reset to accept input states in the next step. IOP Publishing. Reproduced with permission from W. Huggins, P. Patil, B. Mitchell, K. B. Whaley and E. M. Stoudenmire, Towards quantum machine learning with tensor networks, Quantum Sci. Technol., 2019, 4(2), https://doi.org/10.1088/2058-9565/aaea94. All rights reserved. log(N)) = 8 qubits for its operation. The qubits indicated with hash marks are measured and reset to accept input states in the next step. IOP Publishing. Reproduced with permission from W. Huggins, P. Patil, B. Mitchell, K. B. Whaley and E. M. Stoudenmire, Towards quantum machine learning with tensor networks, Quantum Sci. Technol., 2019, 4(2), https://doi.org/10.1088/2058-9565/aaea94. All rights reserved. | ||
5 Applications
5.1 State preparation protocols and quantum state tomography
With the rapid advancement of quantum technology in the past decade, there is an increased demand for efficient methods that can verify the generated quantum states according to specific needs. This is primarily important for the validation and benchmarking of the quantum devices. To address this, quantum state tomography (QST) aims to obtain the statistical inference of the unknown quantum state of the system based on the information of the expectation values of a complete set of observables.49,368–371 However, the traditional approach to QST has been pushed to its limits for the large quantum platforms available today.372 This is because the number of measurements required for full reconstruction of the quantum state scales exponentially with the system size which poses a critical challenge for performing QST even for moderately sized systems. Also, in order to obtain valuable insight on the physical observables of the system and to estimate them accurately, the measurement outcomes need to be stored and processed for which exponential amounts of classical memory and computing power are required which makes the technique infeasible for practical applications.Apart from the problem of exponential scaling for complex systems, another drawback for the accurate estimation of a quantum state is the inherent noise in the present day noisy intermediate-scale quantum (NISQ) devices.84 Because of this the measurements available are of limited fidelity and, in certain cases, some of the measurements are even not accessible. Several methods have been proposed as a means of an alternative approach to the traditional QST such as matrix product state tomography,371 neural network tomography,373–376 quantum overlapping tomography,377 and shadow tomography.378,379 Because of the noisy nature of the quantum systems since not all measurements are available at high fidelity, there have also been approaches that try to carry out QST based on incomplete measurements380–382 such as maximum likelihood estimation (MLE),383–388 Bayesian mean estimation (BME),389–392 and maximal entropy formalism based QST.393,394
Quantum detection and estimation theory has been a prominent field of research in quantum information theory since the 1970s395–397 and the rapid progress in quantum communication and computation in the past two decades motivated the use of big data for the classification of quantum systems through quantum learning and quantum matching machines.398 The notion of self-improvement of the performances of quantum machines via quantum learning was introduced by Ron Chrisley in 1995 in ref. 399 through the example of a barrier/slit/plate feed-forward back-propagation network. In a feed-forward network, parameterized non-linear functions map an input state to an output state space. The interactions with the environment help the networks to modify those parameters such that each network can better approximate the resulting function. The proposed quantum implementation of such a network involved setting up a barrier with several slits in front of a particle beam. Some of the slits are designated as input slits and the rest are the weight slits. Behind the barrier is a photo-sensitive plate on which the interference pattern is observed that serves as an output for each input slit configuration. Once an interference pattern of high resolution is obtained on the plate, the error, which is a function of the desired and actual output vectors, is calculated. The gradient descent method is applied by taking the partial derivative of the error function with respect to the control variables, the weights, and the slits are adjusted accordingly for the next reading so as to minimize the error function. After sufficient training, optimum values for the weight configuration are obtained that ensured minimal error on the training set. This feed-forward network established the correspondence between the neural networks and the quantum system and is one amongst the many diverse approaches for the practical implementation of quantum neural networks.400,401
One of the most valuable applications of quantum tomography is the validation and testing of near-term quantum devices called the NISQ devices. Leveraging the capabilities of the quantum hardware of the gate-based NISQ devices, Alejandro et al. in ref. 402 proposed a hybrid quantum-classical framework called the data-driven quantum circuit learning (DDQCL) algorithm for benchmarking and training shallow quantum circuits for generative modeling. Much like the various models encompassed within the Born machines,403–406 the authors captured the correlations in the data set using the 2N amplitudes of wave functions obtained from an N-qubit quantum circuit. However, the distinctive feature in their work is the use of quantum circuits as a model for the data set that naturally works as a Born machine, thereby avoiding the dependence on tensor networks for the same. They demonstrated their approach of training quantum circuits for the preparation of the GHZ state and coherent thermal states thereby illustrating the power of Born machines for approximating Boltzmann machines.
Finding an effective quantum circuit that can optimally carry out a desired transformation between the input and output quantum states also constitutes an important aspect of QST. In ref. 407 the authors proposed a machine learning based optimization algorithm for quantum state preparation and gate synthesis on photonic quantum computers. They used the continuous-variable quantum neural network architecture408 as an ansatz whose optimization was carried out on the Strawberry Fields software platform for photonic quantum computation.409 Using the proposed method, the authors were able to achieve high fidelities of over 99% using short-depth circuits given only the target state as an input.
Another quantum state preparation method was presented in ref. 410 based on reinforcement learning which is a machine learning training architecture framework that finds an optimal solution to a problem based on the principle of rewarding the desired actions and penalizing the negative actions. The authors made a comparative study of the performances of three reinforcement learning algorithms: tabular Q-learning (TQL), deep Q-learning (DQL), and policy gradient (PG), and two traditionally used non-machine-learning methods: stochastic gradient descent (SGD) and Krotov algorithms, demonstrating their efficiency with reference to quantum state preparations under certain control constraints. Their results illustrated the effectiveness of reinforcement learning algorithms in solving complex optimization problems as the algorithms, especially DQL and PG, performed better amongst the five algorithms considered for state preparation under different types of constraints.
Parameterized quantum circuits (PQC) are yet another machine learning model that utilizes the resources of both quantum and classical computation for application in a variety of data-driven tasks.411 Benedetti et al.411 presented a comprehensive review of various machine learning models involving PQC and also their application in diverse fields including quantum tomography. Another class of algorithms within the domain of quantum machine learning is hybrid quantum-classical Variational Quantum Algorithms (VQAs)412 that have been gaining popularity in recent years with numerous applications.413–419 VQAs try to reduce the quantum resource allocation by using shallow quantum circuits for carrying out computations on a quantum device. One such algorithm was proposed in ref. 420 by Wang et al. to prepare the quantum Gibbs state on near-term quantum hardware using parameterized quantum circuits. On such devices it is in general quite difficult to prepare the Gibbs state at arbitrary low temperatures just like finding the ground states of Hamiltonians.421 Preparation of the quantum Gibbs state of a given Hamiltonian has its application in a variety of fields like many-body physics, quantum simulations,422 and quantum optimization.423 In the method proposed by Wang et al. minimization of free energy serves as the loss function. However, within the calculation of free energy, estimation of entropy is the most challenging part.424 To tackle this problem they used truncation of the Taylor series of the von Neumann entropy at order K and, thus, the truncated free energy was set as the loss function whose minimum would correspond to the optimal parameters of the quantum circuit giving the Gibbs state. The estimation of the Taylor series expansion terms of entropy can be practically carried out using the well-known swap test,425,426 and therefore, their method can be physically realized on a near-term quantum hardware. To validate the approach they numerically showed the preparation of high-fidelity Gibbs state for Ising chain and XY spin-½ chain models and were able to achieve fidelity of at least 95% for a range of temperatures.
Another kind of quantum state preparation commonly termed as quantum state tomography relies on accessing experimentally measured observables. We shall discuss, here, how various techniques within the domain of machine learning/deep learning have been applied to perform QST.
As machine learning and neural networks became increasingly popular with their application in many diverse fields, the concoction of quantum mechanics and machine learning algorithms also started surfacing.156,177,427,428 The development of quantum annealing processors429 deemed a natural fit for testing the machine learning algorithms on a quantum hardware430,431 to check for any quantum advantage. In the initial stages quantum mechanics was only used to facilitate the training for solving classical problems which, in fact for certain problems, did result in obtaining polynomial speed-ups relative to the classical training methods.432 Although the training of the Boltzmann machines using quantum processors did result in accurate training at a lower cost, the success of machine learning algorithms based on classical Boltzmann distribution inspired the proposition of a quantum probabilistic model for machine learning called quantum Boltzmann machines (QBMs) based on Boltzmann distribution for quantum Hamiltonian.433 In QBMs, not only the training is performed utilizing the quantum nature of the processors but also the model in itself is inherently quantum. The data modeling and training of the Boltzmann machine are carried out using the equilibrium thermal states of the transverse Ising type Hamiltonian.
However, the training procedure used in ref. 433 suffered from two limitations: (a) brute force techniques are required to find out the transverse field terms as they cannot be learned through classical data making it very hard to find the full Hamiltonian, and (b) quantum Monte Carlo methods can be used to efficiently simulate the transverse Ising models, and therefore, using the training method with transverse Ising models in thermal equilibrium did not show a clear quantum advantage. In ref. 434, the authors proposed the quantum analog of the generative training model that included quantum data sets in the training set so that their QBM is capable of learning the quantum terms along with the classical ones. The training of the Boltzmann machine to incorporate quantum data was carried out through two methods: POVM-based Golden-Thompson training and state-based relative entropy training (quantum equivalence of KL divergence). The relative entropy training method allowed the QBM to clone the quantum states within a certain level of approximation and given a considerable number of copies of the density operator for the training of QBM, it could reproduce approximate copies of the input state. Thus, although different from the traditional quantum state tomography wherein an explicit representation of the state operator is available at the output, the generative training of the QBM resulted in a quantum process that can learn Hamiltonian models for complex quantum states which in itself is a form of partial tomography.
Machine learning techniques offer a big advantage of representing high dimensional data in the compressed form which can be really favourable for QST which in itself is a highly data-driven technique. In 2018, Torlai and colleagues373 utilized this property of the neural networks for obtaining the complete quantum mechanical description of highly entangled many-body quantum systems based on the availability of a limited set of experimental measurements. Their method involves the training of a restricted Boltzmann machine (RBM) using simulated measurement data for the true state. Their RBM architecture comprises a layer of visible neurons for encoding the measurement degrees of freedom and a hidden layer of binary neurons for encoding the tunable parameters. The training of the RBM is performed such that the generated probability distribution resembles closely the given data distribution and parameters are tuned depending on the desired degree of accuracy that is required for reconstruction. They demonstrated their approach by first benchmarking the neural network tomography of the N-qubit multipartite entangled W state. They also demonstrated QST for more complex systems consisting of quadratic spin Hamiltonians, namely the transverse-field Ising model and the XXZ spin-1/2 model.
According to the authors, their RBM model works really well for entangled many-body systems and quantum-optic states. However, when there is unstructured data as in the case of states generated from a random unitary operation, the performance of the RBM goes down. The paper also did not highlight some of the pertinent questions such as what should be the size of the training set, or the optimal number of hidden neurons, and the dominance of RBM over other contemporary machine-learning approaches. Also, in the demonstration of their approach, both in the case of the tomographic reconstruction of the W state or ground states of the quadratic-spin Hamiltonians, the wavefunctions considered are real which decreases the measurement degrees of freedom required for state reconstruction and thereby dramatically reduces the tomographic overhead.
Another neural network based quantum state estimation method empowered by machine learning techniques was presented in ref. 435 in 2018 for full quantum state tomography. Instead of reducing the number of mean measurements required for full state reconstruction, the work focuses on speeding up the data processing in full QST without the assumption of any prior knowledge of the quantum state. Their training model is based on standard supervised learning techniques and the state estimation is carried out using a regression process wherein a parameterized function is applied for the mapping of the measurement data onto the estimated states. For a single state reconstruction, the computational complexity of their model is  , where d is the dimension of the Hilbert space, and was the fastest amongst the full QST algorithms such as MLE, LRE, BME, etc. at that time.
, where d is the dimension of the Hilbert space, and was the fastest amongst the full QST algorithms such as MLE, LRE, BME, etc. at that time.
A further application of neural network in the field of state tomography was presented in ref. 376 where local measurements on reduced density matrices (RDMs)436–440 were used to characterize the quantum state. Using the recent approach of measuring RDMs and thereby reconstructing the full state is a convenient alternative to the traditional QST approaches as the whole system can be characterized in polynomial number of parameters as opposed to the exponential parameters required for full reconstruction in the traditional QST techniques. However, QST via local measurements on RDMs is a computationally hard problem.441 In this work, the authors addressed this problem using machine learning techniques by building a fully connected feedforward neural network, as shown in Fig. 23, to demonstrate the full reconstruction of the states for up to 7-qubit in simulation and also reconstructed 4-qubit nuclear magnetic resonance (NMR) states in experiments. Their approach also had comparable fidelities with the MLE method but with the additional advantage in terms of speed up and better noise tolerance.
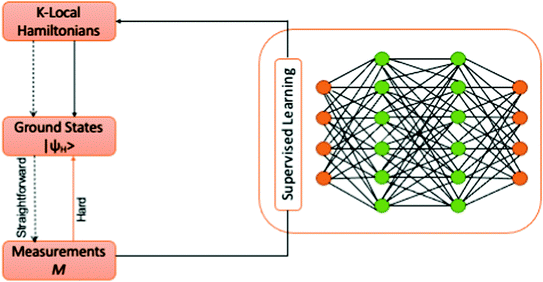 | ||
| Fig. 23 Local measurement based quantum state tomography via neural networks: the procedure starts with generating the training and test datasets, represented by dashed arrows, through random k-local Hamiltonians H to obtain the local measurement results M from the ground states ψH. The neural network is then trained using the training dataset which then produces the local measurements M, represented by black arrows. The measurements are used to find the Hamiltonian H followed by obtaining the ground states. The normal QST process follows the red arrow which is computationally hard. Figure is a schematic of the protocol illustrated in ref. 376. | ||
Another machine learning assisted quantum state estimation technique based on convolutional neural networks (CNN) (basic theoretical framework discussed in Section 3.3.2) was presented in ref. 338 in 2020 for reconstructing quantum states from a given set of coincidence measurements for both pure and mixed input states. Their approach involves feeding the noisy or incomplete set of simulated measurements to the CNN which then makes prediction of the τ-matrix based on the decomposition method discussed in ref. 442. The predicted matrix, which is the output, is then inverted to give the final density matrix. In order to compare the fidelity of the reconstructed states, the authors also implemented the Stokes reconstruction method442 and found a significant improvement in fidelity for not just noisy data sets but also when the projective measurements are incomplete and thereby demonstrating the advantage of CNN over typical reconstruction techniques.
As an alternative means of QST several methods have been proposed, such as MLE, BME, and least-squares (LS) inversion,443 for efficient reconstruction of the quantum state. Since measurements on many copies of the state are required for efficient reconstruction of the quantum state so in order to gain maximum information from the measurements on the next copy, the measurements are adjusted based on the already available information from the measurements made thus far. This method of reconstructing the quantum state through adaptive measurements is called adaptive quantum state tomography. One such approach was introduced in ref. 444 where self-learning algorithm was used in combination with different optimization strategies such as random selection, maximization of average information gain, and fidelity maximization for quantum state estimation. A generalization of self-learning algorithm was presented in ref. 390 in the form of adaptive Bayesian quantum tomography (ABQT) with the aim to optimally design quantum tomographic experiments based on full Bayesian inference and Shannon information. Through their adaptive tomography strategy the authors were able to achieve significant reduction in the number of measurements required for full state reconstruction in case of two qubits pure states in comparison to the Monte Carlo simulation of the qubit systems. The experimental realization of the ABQT method was also carried out in ref. 445 for two qubit quantum systems which did show a significant improvement in the accuracy of state estimation in comparison to the nonadaptive tomographic schemes. Recently, neural adaptive quantum state tomography (NAQT) was introduced in ref. 446 that utilizes the neural network framework to replace the standard method of Bayes’ update in the ABQT scheme and thereby obtained orders of magnitude faster processing in estimating the quantum state while retaining the accuracy of the standard model. Basically, in the adaptive Bayesian-type tomography, the quantum space is discretized into samples and with each sample there is an associated weight that gets updated with each new measurement according to the Bayes’ rule in order to update the prior distribution to the posterior distribution of the quantum state space. However, with the increase in the number of measurements the likelihood function becomes sharply peaked with a tiny subset of the sample states having the majority weights. This can lead to a numerical singularity which is then avoided by resampling of the weights onto the space states which is computationally a very expensive process. In ref. 446 the authors have used a machine learning algorithm to map the Bayesian update rule on a neural network to replace the traditional approach and thereby eliminate the problem of resampling of the weights saving the computational cost significantly without compromising on the accuracy of the reconstruction process. In comparison to the ABQT technique, the NAQT approach was able to speed up the reconstruction process by a factor of a million for approximately 107 measurements and is independent of the number of qubits involved and type of measurements used for estimating the quantum state.
In 2013, another useful method was proposed in ref. 441 wherein the linear regression estimation (LRE) model was used to identify optimal measurement sets to reconstruct the quantum state efficiently. The model was relatively straightforward where the authors converted the state estimation problem into a parameter estimation problem of a linear regression model and the LS method was employed to determine the unknown parameters. For a d-dimensional quantum state, the computational complexity of the method for state reconstruction is  and thereby saves up the cost of computation in comparison with the MLE or BME method. A natural extension to this work, in terms of both theory and experiment, was presented in ref. 448 in order to improve the tomography accuracy by better tomographic measurements via an adaptive tomography protocol that does not necessarily require non-local measurements from experiments. The method is called recursively adaptive quantum state tomography (RAQST) primarily because the parameters are updated using the recursive LRE proposed in ref. 441 and using the already collected data the measurement strategy is adaptively optimized for obtaining the state estimation. The authors also performed two-qubit state tomography experiments and showed the superiority of the RAQST method over the nonadaptive methods for quantum states with a high level of purity which is an important criterion for most forms of information processing methods.
and thereby saves up the cost of computation in comparison with the MLE or BME method. A natural extension to this work, in terms of both theory and experiment, was presented in ref. 448 in order to improve the tomography accuracy by better tomographic measurements via an adaptive tomography protocol that does not necessarily require non-local measurements from experiments. The method is called recursively adaptive quantum state tomography (RAQST) primarily because the parameters are updated using the recursive LRE proposed in ref. 441 and using the already collected data the measurement strategy is adaptively optimized for obtaining the state estimation. The authors also performed two-qubit state tomography experiments and showed the superiority of the RAQST method over the nonadaptive methods for quantum states with a high level of purity which is an important criterion for most forms of information processing methods.
Another significant machine learning approach is the generative adversarial network (GAN) (basic theoretical framework is discussed in Section 3.3.6) based QST334,335 that basically involves learning the map between the data and the quantum state unlike the RBM-based QST methods where the map yields a probability distribution. In the GAN method, two competing entities, generator G and discriminator D, engage with the objective to output a data distribution from some prior noisy distribution. Both G and D are parameterized non-linear functions consisting of multi-layered neural networks.251 With each step of optimization the generator becomes better at yielding outputs closer to the target data and the discriminator becomes better at detecting fake outputs. Inspired by the classical model, the quantum generative adversarial network (QGAN) was introduced in ref. 449 and 450 where quantum processors are used for running the neural nets of generator and discriminator as well as the data can be both quantum and classical. Thus, making the entire system quantum mechanical, at the end of the optimization process the generator can reproduce the true ensemble of quantum states without the discriminator being able to distinguish between the true and generated ensemble.
The first proof-of-principle experimental demonstration of the QGAN algorithm was presented in ref. 447 in a superconducting quantum circuit on datasets that are inherently quantum for both the input and the output. The QGAN algorithm employed was able to reproduce the statistics of the quantum data generated from a quantum channel simulator with a high level of fidelity (98.8% on average). Their experimental approach involves a superconducting quantum circuit for the generator G that outputs an ensemble of quantum states with a probability distribution to mimic the quantum true data whereas the discriminator D is used to carry out projective measurements on the true and the generated data in order to distinguish the two based on the measurement outcomes. The optimization process based on the gradient descent method consists of the adversarial learning by the discriminator and the generator in alternative steps that is terminated when the Nash equilibrium point is reached, i.e., G produces the statistics such that D can no longer differentiate between the fake and the true data. The experimental protocol of the implementation of the QGAN algorithm is shown in Fig. 24.
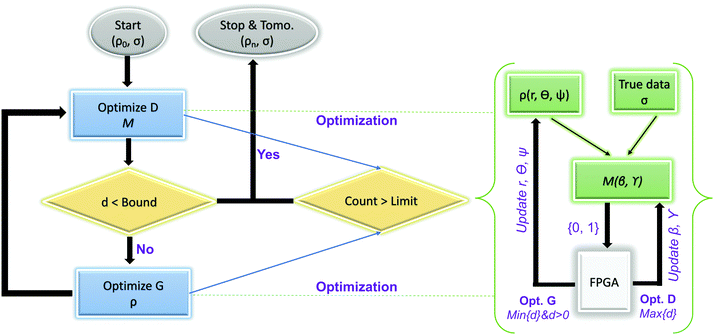 | ||
| Fig. 24 Flowchart demonstrating the experimental protocol of the QGAN algorithm in ref. 447 and the optimization scheme of the generator G and the discriminator D:G generates a random starting state ρ0(r0,θ0,ψ0) following which both D and G compete against each other by optimizing their strategies alternatively. The process is terminated when either D fails to discriminate the generated state ρ from the true state σ or the number of steps cstep reaches the limit. The optimization scheme, based on the gradient descent method, of D involves updating the parameters β and γ of the measurement operator M whereas r, θ, and ψ are updated to optimize G. The gradient estimation is carried out on a classical computer whereas field programmable gate arrays (FPGAs) are used for the measurement and control of the quantum system. | ||
In ref. 451 the authors introduced the conditional generative adversarial network (CGAN) based QST as in the standard GAN approach there is no control over the output as the generator input is random which can be addressed using CGAN. Because of the improved control over the output, CGAN led to many diverse applications in a variety of fields.452–456 With the CGAN based QST the authors were able to achieve higher fidelity of reconstruction, faster convergence and also reduced the number the measurements required for reconstructing a quantum state as compared to the standard model of state reconstruction using MLE. Also, with sufficient training on simulated data their model can even reconstruct the quantum states in a single shot. In their CGAN approach, the measurement operators ({Oi}) and the measurement statistics are the conditioning input to the generator which then outputs a density matrix ρG that is used to generate the measurement statistics by calculating tr(OiρG). These measurement statistics and the experimental measurement statistics serve as the input for the discriminator which then outputs a set of numbers to distinguish between the generated statistics and the true data. The standard gradient-based optimization techniques are then used to train the network which is completed when the discriminator is unable to differentiate between the generated statistics from the generator and the true data. With better control over the output the CGAN approach can further find its applications in efficiently eliminating noise from the experimental data by training it on noisy simulated data; in addition it can have potential advantages in adaptive tomography as well by improving the choice of adaptive measurements for better reconstruction of quantum states.
The huge success of the attention mechanism-based neural network generative model228,457,458 to learn long-range correlations in natural language processing (NLP)459 prompted for its application in QST owing to the entanglement among qubits that can also be learnt through the self-attention mechanism used in the former case. The self-attention mechanism computes a representation of a sequence by relating different positions of a single sequence and has been very successful in a variety of sub-fields under NLP.460,461 In ref. 459 the authors proposed the first purely self-attention based transduction model, the Transformer, for deriving global dependencies between input and output without the use of a recurrent neural network (RNN) or convolutions. Just like other transduction models, the Transformer also uses an architecture of fully connected layers for both the encoder and decoder228,462,463 using stacked self-attention that results in significantly faster training than architectures based on recurrent or convolutional layers. To the best of our knowledge the quantum-enhanced version of the Transformer has not been studied yet. However, the application of Transformer on quantum data has shown tremendous potential, as discussed below in the context of QST, for future research in this field.
The long-range correlations exhibited by entangled quantum systems can be modeled analogous to the sentences in natural language using informationally complete positive operator-valued measurements (IC-POVM). Therefore, with this motivation, recently, Cha et al. proposed the ‘attention-based quantum tomography’ (AQT)464 to reconstruct the mixed state density matrix of a noisy quantum system using the Transformer459 architecture for the neural network. In this work they first benchmark their approach against previous neural network based QST using RNN465 that demonstrated a high fidelity classical description of a noisy many-body quantum state. To compare the performance of AQT with other state-of-art tomographic techniques they considered the Greenberger–Horne–Zeilinger (GHZ) state as their target state for up to 90 qubits and a built-in simulated error resulting in a mixed state. They showed that the complexity of learning the GHZ state can be improved by an order of magnitude when compared with the RNN method. They also benchmark AQT against MLE for a 3-qubit system and found a superior quantum fidelity of reconstruction for the AQT with the additional advantage of being scalable to larger systems. Furthermore, they were also able to reconstruct the density matrix of a 6-qubit GHZ state using AQT, with a quantum fidelity of 0.977, which is currently beyond the tomographic capabilities of the IBM Qiskit.
QST becomes a formidable task as the size of the quantum system increases. In order to address this problem, in this section of the review, we present research based on several machine learning driven QST techniques such as RBM based QST for highly entangled many-body quantum systems, characterizing quantum systems using local measurements on RDMs, using CNN for state reconstruction, adaptive QST through self-learning and optimization based algorithms, VQAs for QST, generative models like GANs and attention based QST. Although the use of classical machine learning algorithms and deep neural networks has proven to be very effective in finding patterns in data, but for implementation on a quantum computer, loading classical data onto quantum devices can present a serious bottleneck for the implementation of these algorithms.466 Since a large number of independent parameters are required for reconstructing the quantum state that scales exponentially with the system size, and therefore, using quantum machine learning algorithms directly on the quantum states of the system can help in the learning and optimization of these parameters much more efficiently, owing to their ability in handling larger Hilbert space. As mentioned in the above sections, generative machine learning models such as quantum Boltzmann machine (QBM) and quantum generative adversarial network (QGAN) provide valuable insights into exploiting the full capabilities of the present day quantum computers in order to reproduce the desired quantum states. The improvement of quantum hardware with time also calls for their validation and benchmarking and QML can play a major role in the design of cost-effective quantum tomography techniques and protocols that can be easily implemented on the NISQ devices.
5.2 State classification protocols
Classification is always one of the most significant applications for classical machine learning (ML) or quantum machine learning (QML). Due to the fact that people are prone to make mistakes when establishing connections among various features, ML and QML are often able to improve the efficiency in dealing with classification problems. Each instance in the dataset used by machine learning algorithms should be represented with the same set of features, which could be continuous, categorical or binary.161 The learning process is then denoted as supervised machine learning if all instances are given with known labels. Generally, the classification problems can be divided as binary classification and multi-label classification. Binary classification is a classification with two possible outcomes. For example, classifying if an atom or molecule is excited or at ground state. Multi-label classification is a classification task with more than two possible outcomes. For example, classifying the electrical resistivity and conductivity of materials as a conductor, an insulator, a semiconductor or a superconductor. We shall focus extensively on the supervised QML assisted classification problems in chemical systems, specifically, where the output of instances admits only discrete un-ordered values and then discuss unsupervised learning strategies too.The process161,467 of applying supervised ML or QML to a typical classification problem with physico-chemical applications is demonstrated in Fig. 25. The first step is to collect the dataset from chemical experiments. Due to the very existence of errors in measurement and impurities in the reaction, in most cases the raw dataset contains noise and missing feature values, and therefore significant pre-processing is required.468 The second step is to select appropriate algorithms and initialize the classifier model. Then, split the dataset using cross-validation and feed the classifier model with the training data. Next, predict the label for a test dataset, and evaluate the error rate of the classifier model. Additionally, parameter tuning should be repeated until an acceptable evaluation with the test set is obtained.
Classifiers based on decision trees (see Section 3.2.5) play important roles in various chemical problems, such as toxicity prediction,469 mutagenesis analysis,470 and reaction prediction.471 However, quantum decision trees are hardly applied independently dealing with intricate chemical classification problems, since simplicity, one of the key advantages of decision tree, could be eclipsed during the complicated mapping and learning process in QML.
Decision trees are sometimes applied along with other algorithms to analyze and demonstrate the key features of the intricate classification process. Recently, Heinen and coworkers studied two competing reactive processes mainly with a reactant-to-barrier (R2B) machine learning model,472 where the decision tree generated by the R2B method systematically extracts the information hidden in the data and the model. Fig. 26 is a scheme of the tree generated from the R2B method. Blue dotted lines refer to an accepted change meaning that only compounds containing these substituents at the position are considered. Orange dotted lines refer to substitution declined, meaning that all compounds except the decision are kept. Vertical lines on the right of energy levels denote the minimum first (lower limit), and the third (upper limit) quartile of a box plot over the energy range. Numbers above the energy levels correspond to the number of compounds left after the decision. Lewis structures resemble the final decision.
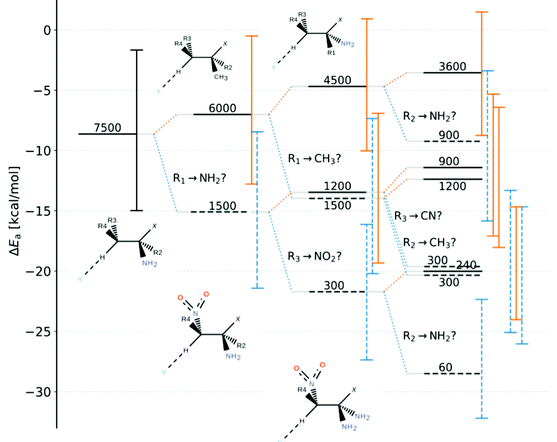 | ||
| Fig. 26 Decision tree using extracted rules and design guidelines. The decision tree is generated using the reactant-to-barrier (R2B) method estimated activation barriers to predict changes in barrier heights by starting at all reactions (first energy level on the left) and subsequently applying changes by substituting functional groups, leaving groups and nucleophiles with E2 (see ref. 472). Blue dotted lines refer to an accepted change meaning that only compounds containing these substituents at the position are considered. Orange dotted lines refer to substitution declined, meaning that all compounds except the decision are kept. Vertical lines on the right of energy levels denote the minimum first (lower limit), and the third (upper limit) quartile of a box plot over the energy range. Numbers above energy levels correspond to the number of compounds left after the decision. Lewis structures resemble the final decision. Reprinted from H. Stefan and V. Rudorff, G. Falk and V. Lilienfeld, O. Anatole, J. Chem. Phys., 2021, 155, 6, 064105 with the permission of AIP Publishing. | ||
In recent years there have been more than a few reports where Bayesian network (BN) (see Section 3.2.6) based methods are applied to solve various chemical classification problems. The BN approach shows fruitful capability for the prediction of chemical shifts in NMR crystallography,473 simulation of the entropy driven phase transitions,474 and particularly, the simulation of quantum molecular dynamics simulation.475
Quantum instance-based learning algorithms like k-NN (see Section 3.2.4) are also applied in chemical classification problems. Recently, researchers have studied the phase transition of VO2 based on a quantum instance-based learning algorithms.318 The training instances are first assigned into several sublabels via the quantum clustering algorithm, based on which a quantum circuit is constructed for classification. Fig. 27 is a scheme of the quantum circuit implementing the classification process of the quantum clustering algorithm. For training instances that are clustered into N sublabels, 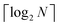 qubits are required representing the sublabels in the classifier circuit. Meanwhile,
qubits are required representing the sublabels in the classifier circuit. Meanwhile, 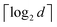 qubits are required to represent the test instance, where d is denoted as the dimension of the instance. For simplicity, here we assume that there are only 5 sublabels totally, and all instances are 2-d vectors. Thus, q1, q2, and q3 represent the possible sublabels and q4 represents the test instance, meanwhile Un is an operation corresponding to the centroid or mean value of the training instances under the same sublabel. Here Hadamard gates are applied on q1, q2, and q3, preparing a uniform distribution of the possible sublabels. To improve the accuracy, the weighting scheme can be included by assigning q1, q2, and q3 as some certain quantum states corresponding to the weights.
qubits are required to represent the test instance, where d is denoted as the dimension of the instance. For simplicity, here we assume that there are only 5 sublabels totally, and all instances are 2-d vectors. Thus, q1, q2, and q3 represent the possible sublabels and q4 represents the test instance, meanwhile Un is an operation corresponding to the centroid or mean value of the training instances under the same sublabel. Here Hadamard gates are applied on q1, q2, and q3, preparing a uniform distribution of the possible sublabels. To improve the accuracy, the weighting scheme can be included by assigning q1, q2, and q3 as some certain quantum states corresponding to the weights.
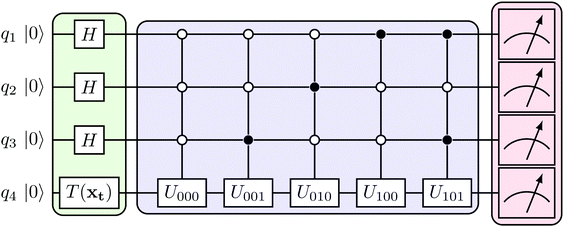 | ||
Fig. 27 Scheme of the structure of the quantum circuit implementing the classification process. For training instances that are clustered into N sublabels, 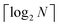 qubits are required representing the sublabels in the classifier circuit. Meanwhile, qubits are required representing the sublabels in the classifier circuit. Meanwhile, 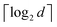 qubits are required to represent the test instance, where d is denoted as the dimension of the instance. For simplicity, here we assume that there are only 5 sublabels totally, and all instances are 2-d vectors. Thus, q1, q2, and q3 represent the possible sublabels and q4 represents the test instance, meanwhile Un is operation corresponding to the centroid or mean value of the training instances under the same sublabel. Figure is reproduced from ref. 318. (Under Creative Commons Attribution 4.0 International License.) qubits are required to represent the test instance, where d is denoted as the dimension of the instance. For simplicity, here we assume that there are only 5 sublabels totally, and all instances are 2-d vectors. Thus, q1, q2, and q3 represent the possible sublabels and q4 represents the test instance, meanwhile Un is operation corresponding to the centroid or mean value of the training instances under the same sublabel. Figure is reproduced from ref. 318. (Under Creative Commons Attribution 4.0 International License.) | ||
The process of classification of metallic and insulating states of VO2 is shown in Fig. 28. Fig. 28a demonstrates the original data used for classification. All training instances are 2-d vectors (pressure and temperature), while the label is denoted by color. Red dots represent the metallic state, and blue ones represent the insulating state. The phase transition line is indicated by the black solid curve. The sublabels left after quantum clustering algorithm is shown in Fig. 28b, where each sphere represents a sublabel, with center corresponding to the centroid or mean-value, and radius corresponding to the number of instances. Prediction of test instances is shown in Fig. 28c. Test instances in the blue part will be recognized with the label ‘insulating’, and the label of test instances in the yellow part will be predicted as ‘metallic’.
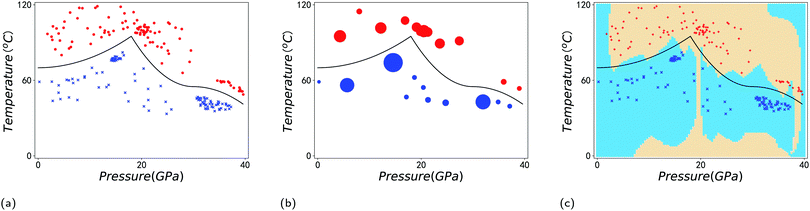 | ||
| Fig. 28 Classification of the metallic and insulating states of VO2 based on the quantum clustering algorithm. (a) Demonstrates the original data used for classification. All training instances are 2-d vectors (pressure and temperature), while the label is denoted by color. Red dots represent the metallic state, and blue ones represent the insulating state. Phase transition line is indicated by the black solid curve. The sublabels left after quantum clustering algorithm is shown in (b), where each sphere represents a sublabel, with center corresponding to the centroid or meanvalue, and radius corresponding to the number of instances. Prediction of test instances are shown in (c). Test instances in the blue part will be recognized with the label insulating, and the label of test instances in the yellow part will be predicted as metallic. Figure is reproduced from ref. 318 (under Creative Commons Attribution 4.0 International License). | ||
The quantum SVM (see Section 3.2.7) has also been applied to various classification problems, such as handwritten character recognition,176 solar irradiation prediction,476 and even the study of particle decays in high energy physics.477 Additionally, in experiments provable quantum advantage has been demonstrated by recent quantum classifiers based on a variational quantum classifier and a quantum kernel estimator—build on noisy intermediate-scale (NISQ) devices.324 Though there are only a few attempts to deal with specific chemical problems with quantum SVM methods, quantum SVMs demonstrate great capacity in classification problems, while the optimization process of quantum SVM leads to exponential speedup compared with the classical version. Therefore, there exists enormous potential for the quantum SVM methods to assist chemical classification and regression problems.
It is always one of the most crucial challenges in the study of many-body problems that the dimensionality of the Hilbert space grows exponentially with the system size, which leads to tremendous difficulty to solve the Shrödinger equations. Among the modern numerical techniques designed to study the complicated systems, neural networks (NNs) attract enormous attention due to their remarkable abilities to extract features and classify or characterize complex sets of data. Modern ANN architectures, especially the feed-forward neural networks (see Section 3.3.1) and convolutional neural networks (see Section 3.3.2) have been playing significant roles in the classification problems of various fields. It is reported that the neural network technologies can be used to discriminate phase transitions in correlated many-body systems,336 to probe the localization in many-body systems,478 and even to classify the entangled states from the separated ones.337
On the other hand, dramatic success of classical neural networks also provokes interest in developing the quantum version. More than 20 years ago, pioneers attempted to build up quantum neural networks (QNNs), particularly, the quantum version of feed-forward neural networks479 (see Section 3.3.1). There were also reports where the QNNs were applied into real classification problems, such as the vehicle classification.480 The rapid development of hardware further provided more possibilities for designing the QNN models.
Special-purpose quantum information processors such as quantum annealers and programmable photonic circuits are suitable fundamental implementation of deep quantum learning networks.55,481 Researchers also developed recurrent quantum neural networks (RQNNs) (see Section 3.3.3) that can characterize nonstationary stochastic signals.482,483 Additionally, there are some other QNN models aiming to supervised learning, such as the classifiers based on QNNs and measurements of entanglement.484 However, most of these models are actually hybrid models, as the activation functions are calculated classically, and the dataset are generally classical data.
In 2018 Farhi and Neven proposed a specific framework for building QNNs that can be used to do supervised learning both on classical and quantum data.485 For binary classification problems, the input instance can be represented by quantum state |z,1〉, where z is an n-bit binary string carrying information of the inputs, and an auxiliary qubit is set as |1〉 initially. Totally there are n + 1 qubits, n qubits representing the input instance, and 1 qubit representing the label. After the unitary operation U(θ), the auxiliary qubit is measured by a Pauli operator, denoted as Yn+1, and the measurement result 1 or −1 indicates the prediction of the label. With multiple copies, the average of the observed outcomes can be written as 〈z,1|U†(θ)Yn+1U(θ)|z,1〉. Furthermore, we can estimate the loss function
| loss(θ,z) = 1 − l(z)〈z,1|U†(θ)Yn+1U(θ)|z,1〉 | (111) |
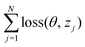 . However, in the numerical simulations, they did not find any case where the QNNs could show speedup over classical competitors for supervised learning.485
. However, in the numerical simulations, they did not find any case where the QNNs could show speedup over classical competitors for supervised learning.485
Meanwhile in 2018, researchers from Xanadu investigated the relationship between feature maps, kernel methods and quantum computing.179 There contains two main steps in the classification steps. They attempted to encode the inputs in a quantum state as a nonlinear feature map that maps data to the quantum Hilbert space. Inner products of quantum states in the quantum Hilbert space can be used to evaluate a kernel function. Then a variational quantum circuit is trained as an explicit classifier in feature space to learn a decision boundary. In the model, a vector (x1,x2)T from the input space X is mapped into the feature space F which is the infinite-dimensional space of the quantum system. The model circuit then implements a linear model in feature space and reduces the “infinite hidden layer” to two outputs. Though linear transformations are natural for quantum theory, nonlinearities are difficult to design in the quantum circuits. Therefore the feature map approach offers an elegant solution. Classical machine learning took many years from the original inception until the construction of a general framework for supervised learning. Therefore, towards the general implementation much efforts might be required as we are still at the exploratory stage in the design of quantum neural networks.
In 2019, Adhikary and coworkers proposed a quantum classifier using a quantum feature space,486 with both quantum variational algorithm and hybrid quantum-classical algorithm for training. The input are encoded into a multi-level system; therefore, the required number of training parameters is significantly lesser than those of the classical ones. Simulation based on four benchmark datasets (CANCER, SONAR, IRIS and IRIS2) shows that the quantum classifier could lead to a better performance with respect to some classical machine learning classifiers. In 2020, Wiebe's group proposed a circuit-centric quantum classifier,487 which is a class of variational circuits designed for supervised machine learning. The quantum classifier contains relatively few trainable parameters, and constructed by only a small number of one- and two-qubit quantum gates, as entanglement among the qubits plays a crucial role capturing patterns in the data. The optimal parameters are obtained via a hybrid gradient descent method. The circuit-centric quantum classifier shows significant model size reduction comparing the classical predictive models.487
The impressive success of these hybrid methods provide an alternative to study the chemistry classification problems. There are plenty of attempts to study the phase diagrams classification with classical machine learning methods.488,489 It would be of great interest to study these problems with quantum or hybrid classifiers.
Recently490 a report has proposed a variational quantum algorithm to classify phases of matter using a tensor network ansatz. The algorithm has been exemplified on the XXZ model and the transverse field Ising model. The classification circuit is composed of two parts: the first part prepares the approximate ground state of the system using a variational quantum eigensolver and feeds the state to the second part which is a quantum classifier which is used to label the phase of the state. Since the quantum state is fed directly into the classification circuit from the variational quantum eigensolver, it bypasses the data reading overhead which slows down many applications of quantum-enhanced machine learning. For both the parts, the quantum state 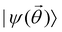 is represented using a shallow tensor network which makes the algorithms realizable on NISQ devices. The first part of the algorithm represents the Hamiltonian matrix H of the system in terms of Pauli strings and variationally minimizes the average energy
is represented using a shallow tensor network which makes the algorithms realizable on NISQ devices. The first part of the algorithm represents the Hamiltonian matrix H of the system in terms of Pauli strings and variationally minimizes the average energy 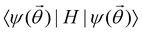 to prepare the ground state. A checkerboard tensor network scheme with a tunable number of layers L is used for the representation. For an n-qubit state, the ansatz requires O(nL) independent parameters, where L is the number of layers in the circuit. In this scheme, the maximally entangled state would require
to prepare the ground state. A checkerboard tensor network scheme with a tunable number of layers L is used for the representation. For an n-qubit state, the ansatz requires O(nL) independent parameters, where L is the number of layers in the circuit. In this scheme, the maximally entangled state would require 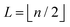 layers with periodic boundary conditions and for critical one-dimensional systems
layers with periodic boundary conditions and for critical one-dimensional systems 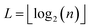 is enough. This can be contrasted with a UCCSD ansatz which requires typically O(n4) parameters491 thereby necessitating a higher dimensional optimization. As mentioned before, the second part of the circuit, i.e., the classifier receives the state from the VQE part and applies a unitary Uclass(ϕ). The unitary is again approximated using the Checkerboard tensor network ansatz. Then the output of the circuit is measured in Z-basis to determine the phase of the state using majority voting. For the transverse field Ising model the report demonstrated a 99% accuracy with a 4-layered classifier and for the XXZ model it was 94% accuracy with a 6-layered classifier (Fig. 29).
is enough. This can be contrasted with a UCCSD ansatz which requires typically O(n4) parameters491 thereby necessitating a higher dimensional optimization. As mentioned before, the second part of the circuit, i.e., the classifier receives the state from the VQE part and applies a unitary Uclass(ϕ). The unitary is again approximated using the Checkerboard tensor network ansatz. Then the output of the circuit is measured in Z-basis to determine the phase of the state using majority voting. For the transverse field Ising model the report demonstrated a 99% accuracy with a 4-layered classifier and for the XXZ model it was 94% accuracy with a 6-layered classifier (Fig. 29).
Picking up an appropriate algorithm is always crucial when dealing with the classification problems. The classifier evaluation is often based on prediction accuracy. Here we present three techniques to estimate classifier accuracy.161 One popular technique is to split the training instances into two groups, where two-thirds are regard as the training data and the other third is regard as the test data. Another technique is known as cross-validation. The training set is manually divided into exclusive and equal-sized subsets initially. Then for each subset the classifier is trained on all the other subsets. Thus, estimation of the error rate of the classifier is obtained by calculating the average of the error rate of each subset. The last one is denoted as leave-one-out validation, which is a special case of cross validation. In leave-one-out validation there is only a single instance in each subset. If the prediction accuracy cannot reach the demand, another supervised learning algorithm should be selected, as shown in Fig. 25.
Additionally, we will present some remarks about the techniques as follows. Even though the optimal solution always depends on the task at hand, these remarks can prevent the practitioners from selecting a wholly inappropriate algorithm. Logic-based systems often perform better when dealing with discrete features. Decision trees are in general resistant to noise because of their pruning strategies. In contrast, most decision tree algorithms cannot perform well when diagonal partitioning is required. Interference allows a class of quantum decision trees to be penetrated exponentially faster by quantum evolution than by a classical random walk. However, these examples could also be solved in polynomial time by different classical algorithms.164 BN methods are able to achieve their maximum prediction accuracy with a relatively small dataset. Besides, BN methods train very quickly since they require only a single pass on the data either to collect the frequencies or to compute the normal probability density functions. The graph structure of BNs can efficiently construct a quantum state representing the intended classical distribution, and a square-root speedup time can be obtained per sample by implementing a quantum version of rejection sampling.173 Lazy learning methods require zero training time as the training instance is initially stored. On the other hand, k-NN is quite sensitive to the irrelevant features, and is generally intolerant of noise. Quantum nearest neighbor algorithm and quantum nearest centroid algorithm both show significant speedup compared to the classical version. In certain cases, there are exponential or even super-exponential reductions over the classical analog.56 SVM methods generally perform better when dealing with classification problems with multi-dimensions and continuous features. Moreover, SVMs are still able to perform well when there exists a nonlinear relationship between the input and output features. However, a large sample size is required to achieve its maximum prediction accuracy. Optimization of quantum SVM is implemented by the quantum algorithm solving linear equations, leading to exponential speedup compared to the classical version.177
Let us now focus on unsupervised approaches to classification briefly. The learning process is denoted as unsupervised when the given training instances are not assigned with the desired labels. Due to the absence of supervision, the unsupervised learning can hardly be applied to distinguish various types of chemicals or detect some certain structures. Instead, unsupervised learning processes can find out the boundaries that divide the instances, so that they could be beneficial in the recognition of phase transitions. For instance, unsupervised machine learning methods can be applied to identify the phase transition to non-trivial many-body phases such as superfluids,492 or to detect the topological quantum phase transitions.493
One important approach in the unsupervised QML is clustering methods. The clustering methods can be assigned as instance-based learning algorithms. Consider the k-means problem of assigning given vectors to k clusters minimizing the average distance to the centroid of the cluster. The standard unsupervised learning method is Lloyds algorithm, which contains the following steps:494,495 (1) pick up the initial centroid randomly; (2) assign each vector to the cluster with the closest mean; (3) recalculate the centroids of the clusters; (4) repeat steps (1–2) until a stationary assignment is attained. Based on the classical version, in 2013, Lloyd and coworkers proposed the quantum unsupervised machine learning method,156 rephrasing the k-means problem as a quadratic programming problem which is amenable to solution by the quantum adiabatic algorithm. In 2018, Iordanis and coworkers proposed q-means, a new quantum algorithm for clustering problem, which provides substantial savings compared to the classical k-means algorithm. In 2017, researchers implemented a hybrid quantum algorithm for clustering on a 19-qubit quantum computer,496 which shows robustness to realistic noise.
Inspired by the success of neural network-based machine learning, Iris and coworkers proposed the quantum convolutional neural networks (QCNNs) in 2019215 (see Section 3.3.2). A paradigm is presented where the QCNN is applied to 1-D quantum phase recognition. There are less applications of unsupervised QML compared to supervised learning in chemical classification problems reported so far. However, recent advancements suggest the future that unsupervised QML could take a place in the study of complex many-body systems, especially in the recognition of phases.
5.3 Many-body structure and property prediction for molecules, materials, and lattice models and spin-systems
Kernel-ridge regression (see Section 3.2.2) has been extensively used in chemistry for a variety of other purposes too like predicting the energy of the highest occupied molecular orbital from three different molecular datasets506 using two different technique to encode structural information about the molecule or for the prediction of atomization energies313,507 through a Coulomb matrix representation of the molecule wherein the energy is expressed as a sum of weighted Gaussian functions. Recently, many new schemes to represent structural features have also been designed314,508 wherein information about the environment of each constituent atom is encoded within its M-body interaction elements each of which is a weighted sum of several Gaussian functions. The distance metric between each such interaction representation between element I and J is considered to be the usual Euclidean norm. Atomization energies, energies for even non-bonded interaction like in water clusters, predicted using such representations are extremely accurate.314 More such examples can be found in topical reviews like in ref. 509. Caetano et al.342 used Artificial Neural Networks (ANNs) (a theoretical framework discussed in Section 3.3) trained using the Genetic Algorithm (GA) to solve the Kohn–Sham equations for He and Li atoms. They used a network comprising of one neuron in the input layer, one hidden layer with eight neurons, and two neurons in the output layer. For the GA based optimization, the number of individuals N in the population was kept to 50. By generating the initial orbitals randomly and building the electron density, an effective Hamiltonian is constructed. The ANN is trained using GA to find the orbitals that minimize the energy functional and then the total energy is calculated, which is repeated until a convergence point. The results from the ANN were shown to be in good agreement with those of the other numerical procedures.
Performing higher order calculations like CCSD provides accurate results but has a very high computational cost. While, methods such as semi-empirical theory PM7, Hartree–Fock (HF), or DFT provide less accurate results but scale efficiently. The work by Ramakrishnan et al.510 corrects the lower-order methods to provide accurate calculations by training their Δ model to learn enthalpies, free energies, entropies, and electron correlation energies from a dataset consisting of organic molecules. The property of interest was corrected by expressing
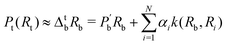 | (112) |
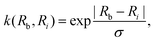 with σ being a hyperparameter that is tuned, |Rb − Ri| is the Manhattan norm511 measuring the similarity between the features of target molecule Rb and molecule in the data Ri.
with σ being a hyperparameter that is tuned, |Rb − Ri| is the Manhattan norm511 measuring the similarity between the features of target molecule Rb and molecule in the data Ri.
Burak Himmetoglu512 constructed a dataset incorporated from PubChem comprising of the electronic structures of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242 molecules composed of CHNOPS atoms. Having constructed the Coulomb matrices as in ref. 511 defined by
242 molecules composed of CHNOPS atoms. Having constructed the Coulomb matrices as in ref. 511 defined by
 | (113) |
Geometry optimization is a crucial task, which directly impacts the electronic structure calculations. The total energy calculations can prove to be quite expensive depending on the choice of the electronic structure method. Hence, the number of evaluations of the potential energy surface has to be reduced considerably. A novel gradient-based geometry optimizer was developed by Denzel and Kästner,513 that exploits Gaussian Process Regression or GPR (a theoretical framework discussed in Section 3.2.8) to find the minimum structures. By comparing Matérn kernel with the squared exponential kernel, the authors show that the performance is better when Matérn kernel is used. The performance of their optimizer was tested on a set of 25 test cases along with a higher dimensional molybdenum system, molybdenum amidato bisalkyl alkylidyne complex, and it was shown that the GPR based approach can handle the optimization quite well.
In the work by Carleo and Troyer,346 it was shown that by representing the many-body wavefunction in terms of ANNs, the quantum many-body problem can be solved. They used this idea to solve for the ground states and describe the time evolution of the quantum spin models, viz. transverse field Ising, and anti-ferromagnetic Heisenberg models. Expanding the quantum many-body state ψ in the basis |x〉:
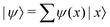 | (114) |
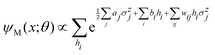 | (115) |
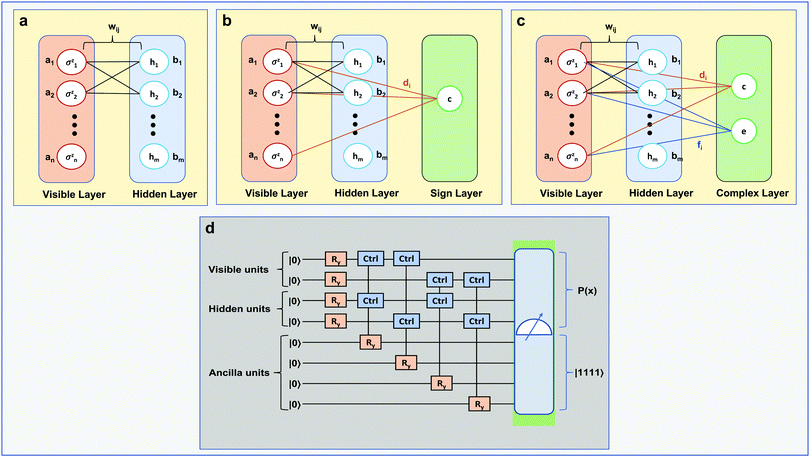 | ||
Fig. 30 The RBM architecture evolution. (a) The RBM architecture consisting of a visible layer and a hidden layer. The neurons in the visible layer represented encode a variable σzi∈ {1, −1} have biases denoted by ai and the neurons in the hidden layer encode a variable hj ∈ {1,−1} have biases denoted by bj. The weights associated with each connection between the visible node and the hidden node are denoted by wij (schematic of RBM as illustrated in ref. 346). (b) The three layered RBM architecture with the first two layers and their corresponding parameters the same as in (a). The third layer has one neuron which encodes a variable s(x) (see eqn (121) for the case with (e,fi) = (0,0) ∀i) and is known as the sign layer. The bias unit for the sign layer is represented by ci and the weights associated with each connection between the visible node and the sign node is denoted by di (schematic of RBM as illustrated in ref. 517). The sign layer does not share any connection with the hidden layer. (c) The three layered RBM architecture with the third layer consisting of two units. c and e denote the bias parameters of the unit representing the real part of the complex layer, and the unit representing the complex part of the complex layer, respectively; fi indicates the weights corresponding to the connections between σzi and the unit representing the complex part of the complex layer (schematic of RBM as illustrated in ref. 347, 518 and 519). (d) The quantum circuit to sample Gibbs distribution on quantum hardware. In general for n neurons in the visible layer and m neurons in the hidden layer, this quantum circuit would require m × n ancilla qubits as well. The circuit thus shown is for a special case of (n = m = 2). The circuit is responsible for simulating the amplitude field 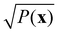 by sampling from the distribution P(x) as defined in eqn (120) (schematic of a quantum circuit as illustrated in ref. 347 and 519). by sampling from the distribution P(x) as defined in eqn (120) (schematic of a quantum circuit as illustrated in ref. 347 and 519). | ||
This NQS approach was then extended by Saito516 to compute the ground states of the Bose–Hubbard model. Here, the quantum state is expanded by the Fock states. One-dimensional optical lattice with 11 sites and 9 particles, and a two-dimensional lattice with 9 × 9 sites and 25 particles were studied. The optimization scheme is similar to that in ref. 346 and the ground states calculated for the 1D and 2D cases were shown to be in good agreement with those obtained from exact diagonalization and Gutzwiller approximation, respectively.
In the work by Coe,520 NNs were used to select important configurations in the configuration interaction (CI) method. By using just a single hidden layer, with binary occupations of the spin orbitals in the desired configurations, the transformed co-efficient of the configuration that fitted to the co-efficients in the training set is predicted. The important configurations of stretched CO and Co at its equilibrium geometry were shown to have accurate predictions. This work was extended in their follow-up paper,521 in which the potential energy curves for N2, H2O, and CO were computed with near-full CI accuracy.
Custódio et al.522 developed a feedforward neural network (a theoretical framework discussed in Section 3.3) to obtain a functional form for calculations pertaining to inhomogeneous systems within DFT and Local Spin Density Approximation (LSDA) framework. The network consists of an input layer with 3 neurons, a hidden layer with 20 neurons, and an output layer consisting of one neuron. The network was trained on 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891 numerically exact Lieb–Wu results for 1000 epochs. The authors test their network on non-magnetic and magnetic systems and through their results claim that the neural network functional is capable of capturing the qualitative behavior of energy and density profiles for all the inhomogeneous systems. In another closely related study,523 the authors attempt to construct the many-body wavefunction directly from 1D discretized electron density using a feed-forward neural network. The network was trained by a supervised learning scheme with the infidelity of the procured wave-function and the target wave-function within the training data. The model showed excellent performance for the Fermni–Hubbard Hamiltonian in both the metallic and the Mott-insulating phases. To bypass the need to construct the exponentially scaling many-body wavefunction, the authors also construct the density–density two-point auto-correlation function with remarkable accuracy. From such auto-correlation function, the power-law scaling parameters of different phases can be obtained.523
891 numerically exact Lieb–Wu results for 1000 epochs. The authors test their network on non-magnetic and magnetic systems and through their results claim that the neural network functional is capable of capturing the qualitative behavior of energy and density profiles for all the inhomogeneous systems. In another closely related study,523 the authors attempt to construct the many-body wavefunction directly from 1D discretized electron density using a feed-forward neural network. The network was trained by a supervised learning scheme with the infidelity of the procured wave-function and the target wave-function within the training data. The model showed excellent performance for the Fermni–Hubbard Hamiltonian in both the metallic and the Mott-insulating phases. To bypass the need to construct the exponentially scaling many-body wavefunction, the authors also construct the density–density two-point auto-correlation function with remarkable accuracy. From such auto-correlation function, the power-law scaling parameters of different phases can be obtained.523
A deep neural network titled SchNet was introduced524 and SchNOrd was introduced343, to predict the wavefunction on a local basis of atomic orbitals. By treating a molecule as a collection of atoms and having a descriptor for each atom, the output properties being predicted are a sum of all these atomic descriptions. The inputs to the network are the atom types and the position of these atoms in the Cartesian coordinates. The atom types are embedded in random initializations and are convoluted with continuous filters in order to encode the distances of these atoms. The interaction layers encode the interaction between different atoms, which essentially dictates the features of these atoms. These features are now input to a factorized tensor layer, which connects the features into pairwise combinations representing every pair of atomic orbitals. Multi-layer perceptrons (a theoretical framework discussed in Section 3.3) are then used to describe the pair-wise interactions within these pair of orbitals. This model was shown to predict with good accuracy the energies, Hamiltonians, and overlap matrices corresponding to water, ethanol, malondialdehyde, and uracil.
Hermann et al.525 extended the work by Schutt et al.524 by using SchNet for the representation of electrons in molecular environments. The representation of the wavefunction through their neural network titled PauliNet in association with the training done using variational Monte Carlo approaches very high accuracy for energies of Hydrogen molecules (H2), lithium hydride (LiH), beryllium (Be), boron (B), and a linear chain of hydrogen atoms (H10). The authors also investigated the scaling of PauliNet with the number of determinants and with system size on Li2, Be2, B2, and C2 and state the high accuracy in comparison to diffusion Monte Carlo (DMC) can be achieved quite fast. Having studied the energies for systems that have benchmark results, the authors move on to high accuracy prediction of the minimum and transition-state energies of cyclobutadiene.
Faber et al.526 introduced representations of atoms as a sum of multidimensional Gaussians in a given chemical compound for a Kernel-Ridge Regression (KRR) (a theoretical framework discussed in Section 3.2.8) based model to predict the electronic properties having learnt them from several datasets. By deriving analytical expressions for the distances between chemical compounds, the authors use these distances to make the KRR based model to learn the electronic ground state properties. In a follow-up paper from the same group,527 Christensen et al. provide a discretized representation as opposed to comparing atomic environments by solving the aforementioned analytical expression. In this work, the authors use KRR to learn the energy of chemical compounds and three other regressors, viz., operator quantum machine learning (OQML), GPR, and gradient-domain machine learning (GDML), are reviewed for the learning of forces and energies of chemical compounds.
In order to have an ML model that can generalize well in large datasets and have efficient tranferability, Huang and Lilienfeld528 introduced the atom-in-molecule (amon) approach where fragments of such amons with increasing size act as training data to predict molecular quantum properties. Considering only two and three-body interatomic potential based representations of amons, a subgraph matching procedure is adopted, which iterates over all the non-hydrogen atoms in the molecule, and identifies the relevant amons. The relevent amons are identified by converting the molecular geometry to a molecular graph with vertices specified by the nuclear charge of atoms and bond orders, then verifying if their hybridization state is preserved or not, and if such subgraphs are isomorphic to other identified subgraphs with some additional checks. Such amons are selected and sorted based on size.
Obtaining the right material that can be explored experimentally in a large database can prove to be a daunting task but provides very rewarding results. Multilayer Perceptrons (MLPs) were used by Pyzer-Knapp et al.529 in the High Throughput Virtual Screening (HTVS) of the Harvard Clean Energy Project, which was developed for the discovery of organic photovoltaic materials. The network consisting of linear input and output layers, three hidden layers with 128, 64, and 32 nodes, was trained on 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules and an additional 50
000 molecules and an additional 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules were considered to make up the validation set.
000 molecules were considered to make up the validation set.
Having performed an FT based high throughput screening, Choudhary et al.530 trained a Gradient Boosting Decision Tree (GBDT) (a theoretical framework discussed in Section 3.2.5) based supervised learning model on 1557 descriptors obtained from classical force-field inspired descriptors CFID. The model was used to classify the materials based on spectroscopic limited maximum efficiency (SLME) to be greater than 10% or not. The authors use this classification to prescreen over a million materials available through large crystallographic and DFT databases, with the goal of accelerating the prediction of novel high-efficiency solar cell materials.
By using a series of random forest models (a theoretical framework discussed in Section 3.2.5) trained at different threshold temperatures, Stanev et al.531 showed that the materials in the SuperCon database can be classified into two classes, above or below a critical temperature (Tc) of 10 K. The features required to be learnt by the model are obtained by using Materials Agnostic Platform for Informatics and Exploration (Magpie) based predictors from SuperCon along with a set of 26 predictors from AFLOW online Repositories. The authors also develop a regression model to predict the Tc of cuprate, iron-based and low-Tc materials.
Barett et al.532 showed the expressibility power of representing the wavefunction ansatz using an Autoregressive Neural Network (ARN). ARNs are a class of generative, sequential models that are feedforward, where observations from the previous time-steps are used to predict the value at the current time step. By developing an architecture with several sub-networks, each made up of a multi-level perceptron, to model the amplitudes and a separate sub-network to model the phase of the wavefunction, the authors go on to introduce a unique sampling procedure that scales with the number of unique configurations sampled and describe the efficiency of ARNs by computing the ground states of various molecules, achieving standard full configurational interaction results.
In order to discover non-centrosymmetric oxides, Prasanna V. Balachandran et al.533 developed a methodology combining group theroretic approach, ML, and DFT and applied it towards layered Ruddlesden–Popper oxides. Using group theory to establish a dataset consisting of 3253 total chemical compositions and performing PCA (a theoretical framework discussed in Section 3.2.3) and classification learning, the authors identify 242 relevant compositions that displayed potential for NCS ground state structures. Then, taking advantage of DFT, 19 compositions were predicted that were suggested for experimental synthesis. Autoencoders (a theoretical framework discussed in Section 3.3.4) are known for their ability to reduce the dimenisonality of the problem at hand and can be used to design molecules with specific desirable properties. This was used by Gómez-Bombarelli et al.534 by coupling an autoencoder with a neural network to generate molecular structures along with predicting the properties of molecules, which were represented by points in the latent space. Neural networks have also branched into the domain of generating complex crystalline nanomaterials, thanks to the work by Baekjun Kim et al.535 In this work, the authors base their approach with the use of Wasserstein GAN (WGAN) (a theoretical framework discussed in Section 3.3.6) with gradient penalty on the loss function on the critic (which is a renamed discriminator specific to the WGANs). By considering a training set consisting of 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 known zeolites, the network takes energy and materials dimensions (with the materials grid subdivided into silicon and oxygen atom grids) as the input, to produce 121 crystalline porous materials. Considering methane potential energy to be the energy dimension, and a user defined range from 18 kJ mol−1 to 22 kJ mol−1, the authors were able to successfully demonstrate inverse design of zeolites. Since the combinatorial space of multi-principal element alloys (MPEAs) is extensive, it becomes necessary to have a reliable method that accurately and rapidly predicts the intermetallics and their formation enthalpies. In accordance with this necessity, an ML model using GPR (a theoretical framework discussed in Section 3.2.8) with a sum kernel, which consists of the square exponential kernel and a white noise kernel, was developed.536 In this work, the ML model is trained on 1538 stable binary intermetallics from the Materials Project database and uses elemental properties as descriptors in order to learn the distribution that maps these descriptors to the formation enthalpies. By doing so, the authors show that stable intermetallics can be predicted using this method. They also perform transfer learning to predict ternary intermetallics in the aforementioned database, thereby informing about the generalizability of the model. With growing interest in superhard materials for various industrial applications, Efim Mazhni et al.537 developed a neural network on graphs model, with a linear embedding layer, followed by three convolutional layers, a pooling layer, and two linear transformations with softmax activation layers, to calculate hardness and fracture toughness. By training their network on the database of crystal structures by Materials Project, consisting of 8033 structures, the authors predict the bulk modulus and the shear modulus, from which Young's modulus and Poisson's ratio is obtained.
713 known zeolites, the network takes energy and materials dimensions (with the materials grid subdivided into silicon and oxygen atom grids) as the input, to produce 121 crystalline porous materials. Considering methane potential energy to be the energy dimension, and a user defined range from 18 kJ mol−1 to 22 kJ mol−1, the authors were able to successfully demonstrate inverse design of zeolites. Since the combinatorial space of multi-principal element alloys (MPEAs) is extensive, it becomes necessary to have a reliable method that accurately and rapidly predicts the intermetallics and their formation enthalpies. In accordance with this necessity, an ML model using GPR (a theoretical framework discussed in Section 3.2.8) with a sum kernel, which consists of the square exponential kernel and a white noise kernel, was developed.536 In this work, the ML model is trained on 1538 stable binary intermetallics from the Materials Project database and uses elemental properties as descriptors in order to learn the distribution that maps these descriptors to the formation enthalpies. By doing so, the authors show that stable intermetallics can be predicted using this method. They also perform transfer learning to predict ternary intermetallics in the aforementioned database, thereby informing about the generalizability of the model. With growing interest in superhard materials for various industrial applications, Efim Mazhni et al.537 developed a neural network on graphs model, with a linear embedding layer, followed by three convolutional layers, a pooling layer, and two linear transformations with softmax activation layers, to calculate hardness and fracture toughness. By training their network on the database of crystal structures by Materials Project, consisting of 8033 structures, the authors predict the bulk modulus and the shear modulus, from which Young's modulus and Poisson's ratio is obtained.
Tensor networks have been discussed in Section 3.4. Tensor networks have been applied to solve numerous problems in physics, chemistry and materials science (to review tensor network algorithms for simulating strongly correlated systems refer ref. 538). Recently Kshetrimayum et al.539 published a report developing tensor network models for strongly correlated systems in two spatial dimensions and extending them to more realistic examples. The specific material the authors chose is that of a quantum magnet Ca10Cr7O28 which is known to show properties of a quantum spin liquid in inelastic neutron scattering experiments.540 The material possesses a distorted breathing bilayer Kagome lattice crystal structure that is composed of Cr5+ ions with spin-1/2 moments. Despite having even number of spin-1/2 Cr5+ ions, the interactions lack the tendency to form a singlet state. The description of the lattice is shown in Fig. 31. The two Kagome layers are different from each other and each of them consists of two non-equivalent alternating triangles. The Hamiltonian of this compound consists of five distinct Heisenberg type interactions and is as follows:
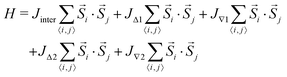 | (116) |
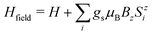 | (117) |
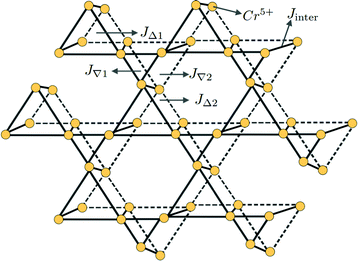 | ||
| Fig. 31 The crystal structure showing only the Cr5+ ions in Ca10Cr7O28. Five different interaction matrix elements as illustrated in eqn (116) are depicted. Reprinted from A. Kshetrimayum, C. Balz, B. Lake and J. Eisert, Tensor network investigation of the double layer Kagome compound Ca10Cr7O28, Ann. Phys., 2020, 421, 168292, Copyright (2022), with permission from Elsevier. | ||
The DMRG algorithm (see Section 3.4.5) has been extremely useful in finding the ground state of one-dimensional systems. Despite the success of DMRG, the method is not suitable for simulating a high-dimensional system. It requires projecting the multi-dimensional state into one dimension which causes the computation time to grow many-fold. Murg et al. in their report542 demonstrate a general approach to simulate ground states of systems in higher dimension using the tree tensor network ansatz (see Section 3.4.2). By exploiting the advantages of correlation scaling of TTN (correlations in TTN only deviates polynomially from the mean-field value compared to MPS which deviates exponentially)542 they efficiently simulate the two-dimensional Heisenberg model and interacting spinless fermions on a square lattice. They also demonstrate its working on the simulation of the ground state of Beryllium atom. Another study by Barthel et al.543 proposed an ansatz, Fermionic Operator Circuit (FOC), to simulate fermionic systems in higher dimension by mapping the fermionic operators onto known tensor network architectures, namely, MPS, PEPS, and MERA (see Sections 3.4.1, 3.4.3 and 3.4.4, respectively). FOC is composed of products of fermionic operators and are known to be parity symmetric. The biggest challenge in formulating a FOC is to manage the sign factors while reordering the fermionic operators. Authors propose an efficient scheme to contract an FOC which computationally scale similar to the contraction of standard TN architectures. The efficiency of the scheme emerges from the fact that while contracting Jordan–Wigner string within a causal cone (specifically referring to the MERA based FOC), the strings outside it are not accounted. The scheme provides a method to formulate fermionic problems in the tensor network notation so that they can be benefited from the existing tensor network algorithms. In another study,544 authors propose a PEPS based algorithm to classify quantum phases of matter in a fermionic system with a specific emphasis on topological phases. Authors introduce a Grassman number tensor network ansatz to study the exemplary Toric code model and fermionic twisted quantum double model which support topological phases. While working with fermionic problems in quantum chemistry, the choice of the most suitable orbital is very crucial. Author in the report545 propose a tool to optimize the orbitals using a tensor network.
Thermal state or Gibbs state provides efficient description of systems in equilibrium (see ref. 546 for a detailed review). Simulating these states at a finite temperature for higher dimensions is computationally challenging. Authors in the report547 propose an algorithm based on projected entangled pair states (see Section 3.4.3) to compute the thermal state of two-dimensional Ising model and Bose–Hubbard model on infinite square lattice. They use a method akin to annealing, i.e., cool down the state from a high temperature to attain the desired finite-temperature state. A thermal state can be described as, ρ = e−βH, where H is the Hamiltonian of the system and β is the inverse temperature. In the infinite temperature limit, the thermal state is described by just an identity matrix. The evolution of state can be performed by the operator e−ΔβH which can be approximated by Suzuki–Trotter expansion. The final state's description reads as
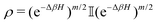 | (118) |
Moving a step further, there are states which do not thermalize due to many-body localization (MBL) and studying them is both interesting and difficult. In the report,548 authors propose an algorithm based on infinite PEPSs to simulate time evolution of disordered spin-1/2 XXZ Hamiltonian on a square lattice. They initialize the system in the Néel state |ψ0〉 and update it with the time evolution operator as
| |ψ(t)〉 = e−iHt|ψ0〉. |
Xia and Kais517 also developed a hybrid quantum machine learning algorithm, which involves a three-layered RBM approach as shown in Fig. 30(b). The first two layers encode the amplitude field similar to ref. 346, while the third layer consisting of one unit is to deal with the lack of sign (±1) in the electronic structure problems. Now the ansatz for state-vector |ψ〉 is given by:
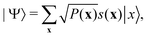 | (119) |
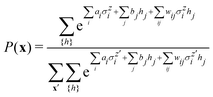 | (120) |
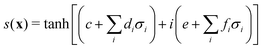 | (121) |
In order to simulate the distribution P(x), a quantum algorithm is proposed to sample from Gibb's distribution. The quantum circuit mainly consists of two types of operations:
• Single-qubit Ry gates that correspond to a rotational operation whose angle is determined by the bias parameters ai (visible) and bj (hidden) and is responsible for simulating the non-interaction of the distribution in eqn (120).
• A three-qubit gate C1–C2–Ry (efficiently representable by two-qubit and single-qubit operations) that is a controlled–controlled–rotation whose angle is determined by the connection parameter wij and is responsible for simulating the interaction between the visible and hidden layers of the distribution in eqn (120). The target qubit of each such controlled operations is an ancillary qubit which was re-initialized and re-used post-measurement.
A Boltzmann distribution for all configurations of the visible and hidden layers can be generated through the quantum circuit similar to as shown in Fig. 30(d). This algorithm is based on sequential applications of controlled-rotation operations, and tries to calculate the interacting part of the distribution P(x) with an ancillary qubit. The ancillary qubit was thereafter measured and conditioned on the measurement results sampling from P(x) is deemed successful. With P(x) computed through the quantum circuit and s(x) computed classically, |ψ〉 can now be minimized by using a gradient descent. Having described the method, the authors show the results corresponding to the ground states of H2, LiH, and H2O molecules (Fig. 32).
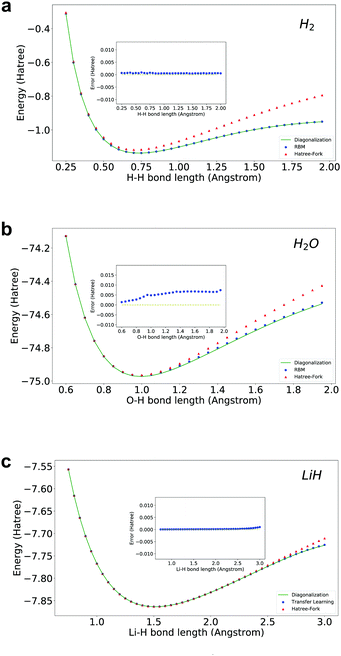 | ||
| Fig. 32 (a–c) Ground state energies of H2, LiH, and H2O, respectively. (d) Ground state energy of LiH having used a warm starting procedure. The inner panels indicate the error with respect to exact diagonalization values. The panel is reproduced from ref. 517 with permission under Creative Commons CC BY license. | ||
An extension to the work by Xia et al.517 was proposed in the study by Kanno,518 wherein an additional unit in the third layer of the RBM was introduced in order to tackle periodic systems and take into account the complex value of the wavefunction. So, the sign layer contains two units, one to encode the real part and the other to encode the complex part of the wavefunction as shown in Fig. 30(c). The authors construct the global electronic structure using DFT, then an effective model with just the target band. By using the maximally localized Wannier function for basis construction for the effective model, a Hubbard Hamiltonian for the target bands is built. The choice of the material is graphene with the target band being the valence band contributed by the 2pz orbitals of the two carbon atoms within an unit cell. Using the algorithm by Xia and Kais,517 this study shows the pristine valence band of graphene in the presence and absence of band splitting for a finite repulsion U parameter within the Hubbard Hamiltonian.518
In the above, ref. 517 and 518, the efficacy of the quantum circuit was tested by simulating it on a classical computer. To benchmark the performance on an actual quantum device, repeated use of a single ancilla qubit would not be operationally convenient. A slightly modified variant of the quantum circuit with (m × n) qubits in the ancilla register has been used thereafter to act as targets of the controlled operations347,519 as shown in Fig. 30(d). One must note that m denotes the number of neurons in the hidden layer and n denotes the number of neurons in the visible layer. Sureshbabu et al. in ref. 519 uses this circuit to benchmark implementation on two 27 qubit IBM-Q devices for the valence bands (within the tight-binding framework) of hexagonal boron nitride (h-BN) and monolayer graphene, respectively. A Hubbard Hamiltonian similar to ref. 518 was used to explore band-splitting as shown in Fig. 33(a and b). Excellent results were obtained even on an actual NISQ device through the use of measurement-error mitigation and repeated warm starting with well converged results for nearby k points in the energy trajectory.
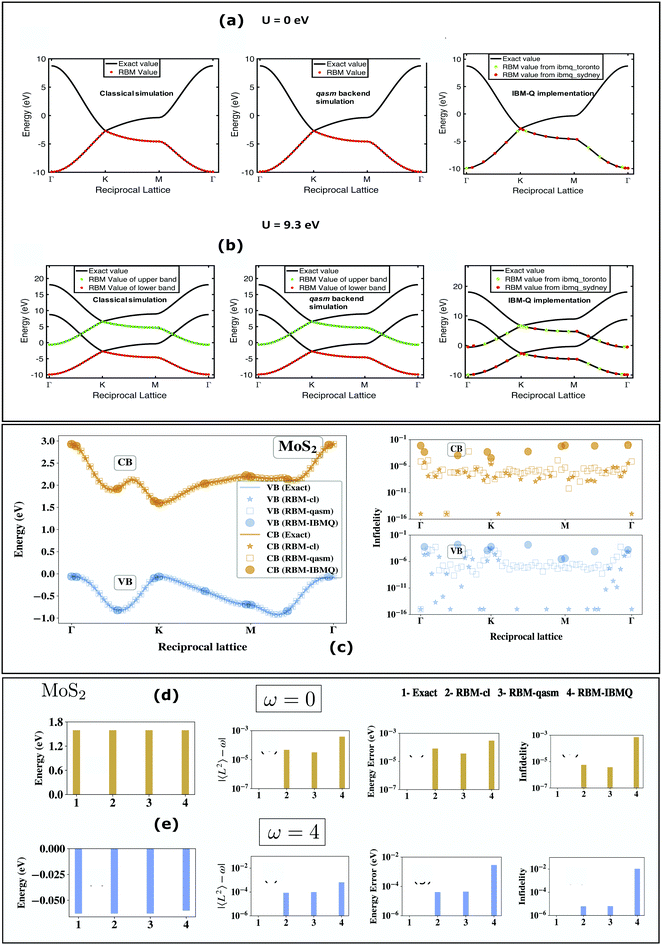 | ||
| Fig. 33 Band structures of 2D materials as computed from RBM implementation on classical computer, quantum simulator (qasm) and actual IBM-Q devices.519 (a) Valence band of graphene with the Hubbard U interaction = 0 eV. (b) Valence band of graphene with the Hubbard U interaction = 9.3 eV (Reprinted (adapted) with permission from S. H. Sureshbabu, M. Sajjan, S. Oh and S. Kais, J. Chem. Inf. Model., 2021, 61(6), 2667. Copyright 2021 American Chemical Society). (c) Valence (VB) and conduction bands (CB) of MoS2 obtained along with the infidelity of the target state learnt by the network in each flavor of RBM implementation. CB is obtained through the constrained minimization procedure.347 (d) The energy, constraint violation error, energy error and state infidelity comparison corresponding to symmetry filtering for MoS2 with the operator (L2) using the constrained minimization procedure.347 The eigenspace of this operator is labelled by ω = 0. (e) The energy, constraint violation error, energy error and state infidelity comparison corresponding to symmetry filtering for MoS2 with the operator (L2) and ω = 4 a.u. (Reprinted (adapted) with permission from M. Sajjan, S. H. Sureshbabu, and S. Kais, J. Am. Chem. Soc., 2021, DOI: 10.1021/jacs.1c06246. Copyright 2021 American Chemical Society.) | ||
The classical-quantum hybrid algorithms described above focus their attention on only computing the ground states of molecules and materials. In the work by Sajjan et al.,347 the authors use the idea of constrained optimization to obtain any arbitrary energy eigenstates of molecules and materials through a user-defined choice. The authors define a quadratic minimization problem with a penalty procedure to achieve the target state.347 The procedure is capable of producing a minimum energy state in the orthogonal complement sub-space of a given user-defined state. The latter state can be obtained from a prior run of the same algorithm. The authors also elucidate the protocol to systematically filter states using a symmetry operator (say S) of the Hamiltonian by sampling the symmetry eigenspace labelled by the eigenvalue (say ω). Apart from this in the same reference Sajjan et al.347 also deduce a generic lower bound for the successful sampling of the quantum circuit and thoroughly discuss special limiting cases. The lower bound can be surpassed with a tunable parameter which the user can set to ensure the ancilla register collapses into the favorable state enough number of times on repeated measurements of the quantum circuit as shown in Fig. 30(d). Only such measurements are important in constructing the distribution in eqn (120). The role of measurement error mitigation and warm-initialization on the algorithm, measurement statistics of the algorithm, transferability of the algorithm to related tasks, and the effect of hidden node density to name a few were thoroughly explored. Specific examples used were important categories of 2D-materials like transition metal di-chalcogenides (TMDCs) whose entire set of frontier bands (both valence and conduction), band-splitting due to spin–orbit coupling (SOC), etc., were accurately obtained even when implemented on 27-qubit IBMQ processors. Representative data for monolayer Molybdenum di-Sulfide (MoS2) for valence and conduction bands are shown in Fig. 33(c) and for symmetry filtering using squared-orbital angular momentum (L2) operator in Fig. 33(d and e). Molecular examples to study the effect of multi-reference correlation were explored both in the ground and excited states. In each case the performance of the algorithm was benchmarked with metric like energy errors, infidelity of the target state trained on the neural network, constraint violation, etc.
Tensor networks as described in Section 3.4 have been used as an ansatz to classically simulate numerous quantum systems with limited entanglement. One can map a quantum many-body state represented on a tensor network to quantum circuits so that it can harness the quantum advantage. The goal is to prepare variational states using quantum circuits which are more expressive than tensor networks or any other classical ansatz and also are difficult to simulate on classical computers. In a recent report, the authors549 use this idea to represent quantum states with variational parameters of quantum circuit defined on a few qubits instead of standard parameterized tensor used in DMRG (see Section 3.4.5). They show that sparsely parameterized quantum circuit tensor networks are capable of representing physical states more efficiently than the dense tensor networks. Authors refer to the standard tensor networks with all variable elements as Dense with a prefix ‘D’ while the quantum circuit tensor networks are referred with their names prefixed with ‘q’. In theory, the number of gates required to exactly recover a q-qubit unitary grows exponentially with q. The bond dimensions (D) between local tensors of tensor networks are encoded into quantum circuit using an unitary operator defined on q qubits where q = log2(D). Contrary to this, the authors claim that only a polynomial number of variational parameters of two qubit unitaries and isometries are sufficient to express the quantum state. Authors work with three types of local circuits to represent the unitary:
• Brick-wall circuit: it has a layered structure with successive layers fully connected via two-body unitary gates. In Fig. 34(a) a brick-wall circuit is shown with depth τ = 6. The effective correlation length is proportional to the depth; hence, the correlations in brick-wall circuit are known to spread slowly with increasing depth.
 | ||
| Fig. 34 A schematic diagram showing architectures of different local circuits. (a) A brick-wall circuit, (b) ladder circuit, and (c) MERA circuit. Each rank-4 tensor is represented by a circle denoting two-qubit unitary gates. The different colours represent different layers of the circuit. The arrows in the circuits show the direction of canonicalization. Depths of the circuits are six, four, and five, respectively. Reproduced from ref. 549 under Creative Commons Attribution 4.0 International license. | ||
• Ladder circuit: it also has a layered structure with denser connections. The first and the last qubits are entangled to each other in the first layer itself. This structure allows efficient propagation of correlations. Fig. 34(b) shows a ladder circuit with depth τ = 4.
• MERA circuit: its architecture is inspired from the MERA tensor networks (described in Section 3.4.4). It has isometric tensors and unitary disentanglers arranged in alternate layers. Fig. 34(c) shows a MERA circuit with depth τ = 5.
Two different paradigmatic Hamiltonians – Heisenberg and Fermi–Hubbard model have been used to test the efficacy of the technique using both local DMRG like optimization and global gradient based optimization. The minimization of the energy (E = 〈ψ|Ĥ|ψ〉) is performed using conjugate gradient550 and LBFGS-B.551
Empirically the relative error δE in the ground state energy was found to be inversely proportional to the polynomial of number of variational parameters n.
| δE(n) ∼ an−b | (122) |
| Ansatz | Heisenberg (a, b) | Hubbard (a, b) |
|---|---|---|
| qMPS-b | (20, 4) | (9, 1.9) |
| qMPS-l | (14, 3.1) | (10, 1.9) |
| qMERA-b | (15, 3.1) | (6.0, 1.4) |
| dMPS (DMRG) | (15, 2.9) | (8.0, 1.5) |
The parameter b gives the asymptotic behaviour of accuracy of the circuit depending on the number of parameters. A higher b indicates that for the same number of parameters, the model is approximating the ground state better. Hence, it is quite evident that ansatz based on quantum circuit tensor networks is more expressive compared to the standard classical variants studied in the report as the former yields comparable accuracy to the latter with a lower parameter cost. This clearly explicates the need for simulating tensor networks on a quantum-hardware to realize its optimum potential for understanding many-body quantum systems.
Being limited by the number of noiseless qubits available on any quantum hardware in the NISQ era, a recent report552 has illustrated how to decompose a 2N-qubit circuit into multiple N-qubit circuits. These N-qubit circuits can be run on NISQ devices while their results can be post-processed on a classical computer. In this formulation, the state |ψ〉 on 2N qubit system can be partitioned into smaller states defined on N qubits using Schmidt decomposition (similar to MPS defined in Section 3.4.1).
 | (123) |
 | (124) |
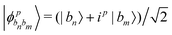 with
with 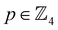 .
.
Authors use this approach to simulate the ground state of water molecule using VQE simulation. They use the frozen core approximation and to enforce spin symmetry set U = V. This yields ten spin orbitals of the water molecule in the STO-6G basis set which using the aforesaid scheme can be encoded into five qubits on the quantum processor. The formalism yields excellent values of energies for geometries which are distorted through stretching of the O–H bond in H2O molecules by using just 3 Schmidt coefficients even though the results degrade from the exact value for deformations of the H–O–H bond angle.
Another algorithm has been proposed based on tensor networks to solve for any eigenvector of a unitary matrix Q, given black-box access to the matrix. When working with a given Hamiltonian for a physical system, the black-box unitary can be prepared by applying the unitaries of the problem Hamiltonian and the mixing Hamiltonian alternatively for different times. In that case Q will be characterized by time-parameters. A parameterized unitary 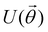 is used to define the state ansatz. The loss function for estimating the ground state of Q is simply maximizing the probability of projecting each qubit to |0〉. If k denotes a k-ebit matrix product state (MPS) then the value k value is iteratively increased until the desired accuracy is achieved. k ranges from 1 to
is used to define the state ansatz. The loss function for estimating the ground state of Q is simply maximizing the probability of projecting each qubit to |0〉. If k denotes a k-ebit matrix product state (MPS) then the value k value is iteratively increased until the desired accuracy is achieved. k ranges from 1 to  because the maximum entanglement produced by an n-qubit quantum circuit of depth m is
because the maximum entanglement produced by an n-qubit quantum circuit of depth m is  ebits. The implementation complexity of the algorithm (measured in terms of number of CNOT gates used) scales as O(l·n·r2) where n is the number of blocks and r is the rank of tensor network and l is the number of steps required to terminate the optimization routine. This algorithm has a significant advantage over other variational techniques in that it terminates when the state reaches the eigenstate of system.
ebits. The implementation complexity of the algorithm (measured in terms of number of CNOT gates used) scales as O(l·n·r2) where n is the number of blocks and r is the rank of tensor network and l is the number of steps required to terminate the optimization routine. This algorithm has a significant advantage over other variational techniques in that it terminates when the state reaches the eigenstate of system.
5.4 Estimation and parameterization of force fields in molecular dynamics
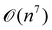 where n is the number of basis functions used.
where n is the number of basis functions used.
Thus ab initio calculations are known for their precision but they are computationally expensive restricting their application to smaller systems in the gas phase or solid-state periodic materials. To model larger systems we have to use a higher level of approximation and use empirical force field (FF) methods. Their computational efficiency allows the simulation of systems containing millions of atoms554,556 and exploration of much longer simulation time scales (100 ms).557 An FF is an analytical expression that denotes interatomic potential energy as a function of the coordinates of the system (for a particular configuration) and set of parameters. Depending on the intricacy of the underlying system different FFs are employed and today's scientific literature provides a myriad choices. But a standard expression for an FF resembles like
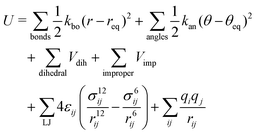 | (125) |
The first four terms are intramolecular contributions (the first term corresponds to bond stretching followed by bending, dihedral rotation, and improper torsion). The last two terms correspond to van der Waals (12-6 Lennard-Jones potential) and coulombic interactions. The parameters in FF (kbo, req, kan and θeq) are usually obtained via ab initio or semi-empirical calculations or by fitting to experimental data such as X-ray and electron diffraction, NMR, infrared, and Raman spectroscopy. A general review of the force fields for molecular dynamics can be found in ref. 558 and 559. The final aim of FF is to express all the quantum mechanical information in classical terms, splitting up the total electronic energy of the system into well-divided atom–atom contributions (coulombic, dispersion, etc.). However, it is an arduous task to split up the total electronic energy even after using precise quantum mechanical calculations. Thus while determining inter-molecular forces we need to consider crucial physical approximations which limit the accuracy. So depending on the system one chooses a certain level of approximation and uses the input data to optimize parameters which makes this approach empirical. Basic steps to form a new force field involve accessing the system to select a functional form for the system's energy. After this, we need to choose the data set which determines the parameters in the function defined earlier. Earlier people used to use experimental data from X-ray or neutron diffraction (for equilibrium bond lengths) and different spectroscopic techniques (for force constants). But in most of the cases, the experimental data used to be insufficient or inaccurate, thus nowadays ab initio data are preferred. Next, we optimize these parameters, in general; there exists colinearity between them i.e. these parameters are coupled (changing one would change another), so the optimization is done iteratively. The last step involves validation where we calculate different properties of the system which are not involved in the parametrization.
Thus the underlying assumptions behind an FF eventually limit the accuracy of the physical insights gained from them. Since conventional FFs do not explicitly model multi-body interactions, polarizations and bond breakings during a chemical reaction make their predictions highly inaccurate. Although there are specially developed FFs (AMOEBA, ReaxFF, RMDFF, ARMD)560–563 that include these effects at a certain computational cost, in most of these cases there exists ambiguity regarding the necessity of inclusion of these effects. Mixed Quantum Mechanics/Molecular Mechanics (QM/MM)564 becomes a handy tool while dealing with huge systems (bio-molecules). As the name suggests it employees quantum mechanical treatment for a subset of the problem (reactive region) and the rest of the problem (environment) is being treated classically. This way the QM/MM approach includes certain quantum correlations in bigger systems improving its accuracy (compared to FF). Although it may seem that the QM/MM approach is the most optimal way to simulate huge problems but one needs to consider huge “reactive region” to get converged results which eventually increases the computational cost.
Machine Learning Force Fields (ML FFs) combine the accuracy of ab initio methods with the efficiency of classical FFs and resolve the accuracy/efficiency dilemma. ML approaches evade solving equations and rely on recognizing the underlying pattern in the data and learning the functional correspondence between the input and the output data with unparalleled accuracy and efficiency.507,565 Unlike conventional FFs ML FFs do not require predetermined ideas about the bonding pattern assumptions. This distinctive feature makes ML approaches admirable in the chemical space and there are huge number of options ML models are available or MLFFs ranging from PhysNEt,566 sGDML,565 GAP,567 SchNet,568 HDNN569 and ANI.570 However, it is not trivial to extend the classical ML formalism to generate FFs. The reason being exacting standards are imposed on the ML FFs which offers an alternative to the already established benchmark FFs. Additionally, classical ML techniques (Natural Language Processing (NLP), Computer Vision, etc.) assume huge reference data sets while optimizing thousands of training parameters, whereas it is very difficult to get such extensive data sets in the case of natural sciences, since each data set is generated either from an expensive ab initio calculation or from rigorous experimental measurement. Thus data efficiency becomes a key factor while developing ML FFs, which is resolved by encoding the physical knowledge or laws directly into the architecture of the ML models.565,568 Ref. 571–573 discuss the construction of potential energy surfaces using different supervised machine learning techniques for complex chemical systems and electronically excited molecular states. A recent review by Unke et al.574 presents an in depth overview of ML FFs along with the step-by-step guideline for constructing and testing them. The rest of the section focuses on the application of ML to optimize the FF parameters in ReaxFF575 which eventually leads to more accurate physical insights. We will show specific example576 where ML is used for parameter optimization.
Refinement of parameters is essential while employing ReaxFF MD for chemical reactions. To get insights about static properties (energy, force or charge distribution) fitting of FF parameters is done by using specific quantum mechanical (QM) training data. Genetic algorithm577,578 and its multi-objective variant579 have been developed to ease out the parameter optimization using QM data. However, application of ReaxFF for dynamic non-equilibrium chemical reactions (chemical vapour deposition) is not straightforward, as it is unfeasible to gain QM training data set for fitting. In addition, the dynamical properties we would like to predict decide the computational cost and resources needed for parameter fitting. In such situations, ML-based approaches comes to our rescue. Hiroya and Shandan576 recognized the flexibility that ML-based models offer and used it to efficiently optimize the parameters in ReaxFF. Their approach uses the k nearest neighbor algorithm to get several local minima and then optimization is done using ML. The most distinctive feature in this approach is that it can combine efficiency from ML-based optimization with accuracy from other optimization techniques (Monte Carlo/genetic) making itself a powerful tool.
The first step in parameter optimization is creating a reference parameter data set (Pbe1, Pbe2,…, Dij, Rvdw,…, Pval2,…) for the given ReaxFF. The ReaxFF parameters encode the information about the system's potential energy's different terms (bonding, lone pairs, van der Waals etc.). This reference data set is then used for the random generation of N (≈100) different data sets. While generating random samples from the reference data two different strategies are implemented; in the first strategy, a random change is made in the ReaxFF parameter set which is followed by the second strategy where we exchange parameters between different ReaxFF data sets. During the random sampling process, it is important to find the sweet spot where the sampling process should not result in a huge deviation making the resultant random sample unphysical at the same time the resultant random sample should not be too close to the reference data (the model will be stuck at the local minima) (Fig. 35 and 36).
 | ||
| Fig. 35 A comparison of expressibility of quantum circuit tensor networks (qMPS, qMERA), standard tensor networks (dMPS and dMERA), and global quantum circuits (QC). The expressibility (or variational power) is measured by seeing the relation between relative energy error δE versus the number of variational parameters in the ansatz. Figures (a–c) are for Heisenberg model while (d–f) are for Fermi-Hubbard model of lattice size 32. The post-fixes ‘b’ and ‘l’ denote the brick-wall and ladder circuit. (a, b, d and e) The comparison between brick-wall and ladder qMPS acting on different number of qubits (q), QC and dMPS. (c and f) Comparison between qMERA-b with varying q, qMPS-b, and dMERA. Reproduced from ref. 549 under Creative Commons Attribution 4.0 International license. | ||
 | ||
| Fig. 36 Schematic representation of random sampling (a) initial parameter references (A, B, and C inside denote the initial parameter set to generate the reference ReaxFF parameter set); (b) definition of a parameter set and explanation about random modification scheme; and (c) entire image of the sampling space using the random modification scheme. The open dashed circles A, B, and C on the right side denote the sampling space in the vicinity of the initial ReaxFF parameter sets A, B, and C. The open dashed circle D denotes a new sampling space, which is different from A, B, and C. Figure adapted with permission from ref. 576. | ||
The next step involves score assessment where a score S(pi)ReaxFF is calculated for each training reference data set pi.
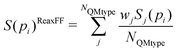 | (126) |
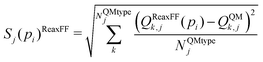 | (127) |
Here NQMtype is the number of geometry sets and NQMtypej corresponds to the number of different structures in the jth geometry set. These structures constitute a specific physical property (potential energy change as a function of volume change in α-Al2O3 crystal).
After evaluating the score of every training data ML is used for data analysis. There are three major steps: (1) use Random forest regression to extract important features, (2) update initial parameters by the k-nearest neighbor (k-NN) algorithm and (3) use grid search to get the optimal parameters. In the first step, random forest regression is employed, where the objective function for minimization can be written in the form of difference between the actual score calculated via ReaxFF and the estimated score via ML:
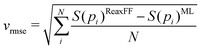 | (128) |
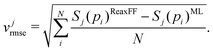 | (129) |
Here N is the number of random samples created and j denotes each structure group. The ML model is build by minimizing eqn (128) and (129). At the end of ML training important features are extracted which will be used further during grid search parameter optimization. The second step consists of applying the k-NN algorithm to divide the training data into k different groups on the basis of closest distance. For each group scores (eqn (127)) are calculated and the parameter set corresponding to the minimum score is selected eventually modifying the initial parameter set. The modified initial parameter set after the k-NN algorithm is not fully optimized, the reason being in a way it is being chosen from the initial data set. Thus grid search parameter optimization is used in the third step which is combined with the extracted parameters from the trained ML model.
Grid search parameter optimization (GSPO) is defined by three parameters n, l and m. Every geometry set (containing NQMtype various physical properties) has a corresponding ML model with different variations of important features. Depending on the importance of particular feature, groups are formed containing n elements. In Fig. 37 we take n = 4, the parameters corresponding to model A are sorted according to their importance (sensitivity). Since n = 4, first four important parameters are clubbed together forming group A; the next set of 4 will be named group B so on so forth. This process is repeated with all the ML models. Since each ML model has varying feature importance levels the groups will contain different parameters. GSPO is then carried out on individual groups by splitting it into m grid points. As each group contains n parameters the total number of grid points becomes mn. Getting scores eqn (126) for every grid point for comparison is a laborious task. ML alleviates this issue by selecting l test parameter sets from the haystack of mn different parameter sets. At every group, the scores of l test parameters are compared with the initial sets of parameters obtained from k-NN. If the score of a particular parameter set (in l) is less than the score of the initial sets of parameters the parameters are updated. However, it is still a time-consuming task to repeat the process for all the groups (A, B,…, Z). Since the score does not change much when the group is not sensitive enough. A new cutoff term nlayer is introduced which determines when to stop computing score for a particular group and move on to the next. For instance, if nlayer = 2 GSPO is carried out on group A (most important) and group B (next most important). After this GSPO moves on to ML model B.
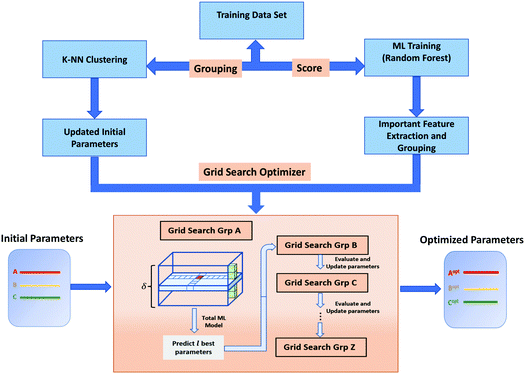 | ||
| Fig. 37 Illustration showing entire the machine learning scheme. Figure adapted from ref. 576. | ||
To summarize, while optimizing the parameters of ReaxFF broadly, there are three major steps involved: (1) use random forest regression to construct ML models and extract important features, (2) locate probable local minima using the k-nearest neighbour algorithm and (3) use grid search optimization to optimize the parameters using information from developed ML models. It is important to note that different optimized parameters sets will predict the potential energy decently (in agreement with QM), although their estimation for different physical properties will diverge. The reason is an unavoidable uncertainty is carried out corresponding to a particular physical property during the parameter estimation. Hiroya and Shandan576 used this approach on a pilot test in which the optimized parameters of ReaxFF were further used to simulate chemical vapour deposition (CVD) of an α-Al2O3 crystal. The optimized parameters decently predicted the crystal structure of α-Al2O3 even at high temperatures (2000 K). Stochastic behavior or the random forest algorithm used in different ML approaches results in hundreds of error evaluations during training for complex training jobs, where each error evaluation involves minimizing the energy for many molecules in the training data. Recently Mehmet et al.580 proposed a novel method that employs an automatic differentiation technique from the JAX library developed by Google to calculate the gradients of the loss function. It is impressive that the efficiency of the gradient-based local optimizer is independent of the initial approximation made for ReaxFF. Given reasonable computing resources, ML-assisted parameter optimization techniques are powerful tools that can be used to simulate wide spectra of reactive MD simulations.
In Non-Adiabatic (NA) Molecular Dynamics (MD) simulations Born–Oppenheimer (BO) approximation breaks down and the electronic and nuclear degrees of freedom cannot be treated independently. These simulations perform a pivotal role while understanding the dynamics of the excited states. Recently, supervised machine learning techniques have been employed which interpolate NA Hamiltonian along the classical path approximated NA-MD trajectories581–583 eventually speeding up NA MD simulations.45,584–586 NA MD simulations act as a robust resource especially while predicting macroscopic observables such as quantum yield without knowing the mechanism for the larger systems involving strong couplings in which it is difficult to choose a reaction coordinate.587–589 But they come with a cost of expensive ab initio calculations of geometry-dependent forces and energies or the different states. In such situations, ML techniques come to the rescue by predicting band gaps and NA coupling using a small fragment of ab initio training data.45,585,586,590,591 To predict the physical properties of materials, unsupervised ML techniques592–595 have been employed on the trajectories of NA MD simulations while explaining the dominant structural factors.596–598 Many times Mutual Information (MI) is used to identify unanticipated correlations between many important features. Results from MI are easier to interpret and it is supported by information-theoretic bound which makes it not sensitive to the size of the data set.598,599 These properties make it popular for its application in the chemical regime. For instance, a model of metal halide perovskites (MHPs) based on unsupervised MI unveiled the importance of geometric features as compared to the atomic velocities while predicting non-adiabatic Coupling (NAC).596
In a recent study by How et al.,600 supervised and unsupervised ML techniques have been used for feature selection, prediction of non-adiabatic couplings, and excitation energies of NA MD simulations of CsPbI3 metal halide perovskites (MHPs). MHPs have high optical absorption, low cost of manufacturing and long carrier diffusion601–603 which make them an ideal candidate for their use in optoelectronics and solar energy harvesting materials. In order to improve the design of MHPs it is important to develop a computationally efficient and a systematic NA MD which utilizes the theory as well as simulations to predict the physical properties of MHPs. How et al.600 fill this knowledge gap by employing MI on the NA MD trajectory data set of CsPbI3 perovskite and extracting the most important features that determine the NA Hamiltonian. The ML model is then validated by checking the performance of the extracted important features to predict the band gap and NAC. Their model showed surprising and counterintuitive results suggesting that the NA Hamiltonian can be predicted by using a single most important feature of the chemical environment information of any of the three elements in CsPbI3. This eventually leads to a drastic reduction in the dimensionality of the original 360-feature ML model developed from ML force fields to merely 12 featured ML models which can produce high-quality NA-MD simulation results which are further confirmed by the present theoretical knowledge about the electronic properties of CsPbI3. This dimensionality reduction technique helps alleviating the high computational cost of ab initio NA-MD and to extend NA-MD simulations to larger, more complex systems and longer time scales.
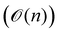 with the number of quantum oscillators compared to
with the number of quantum oscillators compared to 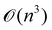 scaling when we consider an orbital based VQE Hamiltonian with n orbitals.608
scaling when we consider an orbital based VQE Hamiltonian with n orbitals.608
Anderson et al.606 showed the solubility of the proposed model by presenting a proof of principle example by calculating London dispersion energies for interacting I2 dimers on IBM quantum processor. While relaxing the harmonic approximation, classical methods heavily rely on path integral and Monte Carlo techniques for efficient sampling of two point correlators for Gaussian states created by harmonic Hamiltonians.609 Since sampling process for non-Gaussian ground states of anharmonic potentials is very expensive anharmonic electron-nuclear potentials remain unexplored using classical computational techniques. The VQA base approach shows a quantum advantage as it suffers negligible experimental overhead while performing relaxation of the harmonic approximation. Thus the VQA based approach provides a road-map that includes anharmonicity and higher order terms for simulation of realistic systems which are inaccessible for current classical methods. In conclusion quantum machine learning provides an efficient and accurate way to model realistic systems and may show a quantum advantage in the future.
A detailed theoretical description of the nonadiabatic (NA) process is limited by intricate coupling between nuclear and electronic degrees of freedom (DOF) eventually leading towards adverse scaling of classical computational resources as the system size grows. Although in principle Quantum Computers can simulate real-time quantum dynamics within polynomial time and memory resource complexity, quantum algorithms have not been extensively investigated for their application towards the simulation of NA processes. A recent study by Ollitrault et al.610 proposed a quantum algorithm for simulation of a rapid NA chemical process which scales linearly as the system size. Specifically, they propagated the nuclear wave packet across κ diabatic surfaces having nonlinear couplings (Marcus model). The algorithm requires three quantum registers. First quantization formalism is used for DOF, so the space and momentum are discretized and encoded in the position quantum register. The population transfer between κ diabatic potentials is encoded in ancilla registers and the nonlinear coupling in coupling register. The encoding scheme is efficient in terms of number of qubits required as it scales logarithmically with the precision. This majestic memory compression while storing the propagated wave function denotes an exponential quantum advantage as compared to its classical counterparts (Fig. 38).
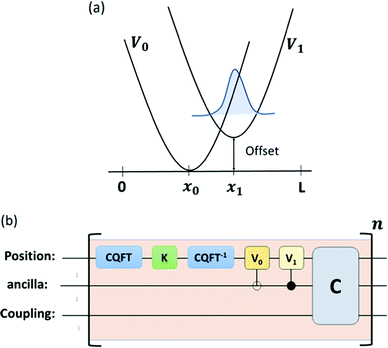 | ||
| Fig. 38 (a) Graphical description of the Marcus model; and (b) quantum circuit representation for the time evolution of the wave packet. The blocks represent the evolution operators shown in the form of quantum gates. CQFT, Vi, K and C correspond to centred quantum Fourier transform (used to switch from position to momentum space), ith potential, and Kinetic and coupling terms, respectively. Figure adapted from ref. 610. | ||
The algorithm was applied to simulate NA dynamics of a wave-packet on a simple two one-dimensional harmonic potential which is shifted in energy by a variable offset. In total 18 qubits were required to simulate this simple model. The characteristic feature of decline in the population transfer of the Marcus model in the inverted region was clearly observed in the simulation, showing an excellent agreement with the exact propagation. Although the simulation was not entirely implemented on the quantum processor the reason is the huge circuit depth of the quantum circuit corresponding to the dynamics parts which requires higher coherence time not attainable by the current generation of quantum processors. But the first part of the algorithm which prepares an initial Gaussian wave packet610 was implemented on an IBM Q device. The extension of this algorithm to higher dimensions is straightforward and a d dimensional polynomial potential energy surface (PES) can be encoded with 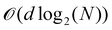 (N is the number of discrete grid points). Current classical algorithms611,612 are limited to simulations of molecular systems which are characterized by up to ten vibrational modes. Hence a quantum processor offering approximately 165 qubits with sufficient coherence time would alleviate this hurdle thus providing an immense quantum advantage while understanding fast chemical processes involving exciton formation, inter-system crossings, and charge separation.
(N is the number of discrete grid points). Current classical algorithms611,612 are limited to simulations of molecular systems which are characterized by up to ten vibrational modes. Hence a quantum processor offering approximately 165 qubits with sufficient coherence time would alleviate this hurdle thus providing an immense quantum advantage while understanding fast chemical processes involving exciton formation, inter-system crossings, and charge separation.
Although Quantum Machine Learning (QML) shows quantum advantage in electronic structure calculation, its application towards force field generation remains unexplored. A recent study by Kiss et al.613 learns a neural network potential energy surface and generates a molecular force field via systematic application of parametrized Quantum Neural Network (QNN) techniques on the data set generated from classical ab initio techniques. The proposed QNN model was applied on single molecules and the results show the competitive performance of the QNN model with respect to its classical counterparts. Additionally, the results suggest that a properly designed QNN model exhibits a larger effective dimension resulting in fast and stable training capabilities. This potentially hints towards a possible quantum advantage of QML's application in force field generation.
5.5 Drug-discovery pipeline and pharmaceutical applications
To deploy machine learning or deep learning algorithms in computer-aided drug discovery (CADD)615,616 it is important to access large molecular databases wherein such structural information about the target (receptor) and/or drug (ligand) candidates may be found. Such databases are screened to generate prospective hits based on either the binding affinity with the target above a threshold for structure based protocols or by looking at chemical similarities with previously known bio-active candidates for ligand-based protocols. For the second category, chemical databases like PubChem,617,618 ChEMBL,619 Drug-Bank,620 and DUD-E621 may be good choices. DUD-E contains many decoys (ligands/drug candidates which show similarity in properties but are not topologically similar in structure) which may be useful for the testing and validation of the trained models. For the first category wherein physical information about the target protein is necessary, databases like UnitProt,622 PDB,623–625 and PDBbind626 may be a useful resource. Combination databases, BindingDB,627 which contain experimental data for several ligands and targets together have also been employed extensively too. Most of these databases do encode the structural/physico-chemical attributes of the candidate molecule and/or the target into a computer-inputable format which are either numerically describable or string-based. These are called features or very simply molecular descriptors and often depending on the choice of the user other molecular descriptors can be generated using the accessed structural information with libraries like RDKit, etc. For the ligand/drug, generic features like number of atoms, molecular weight, number of isomers, etc. are often called 0D features as they do not describe the specific nature of the connectivity of atoms within the molecule and remain oblivious to conformational changes. 1D features like SMILES,628–630 SELFIES,631,632 and SMARTS633,634 which encode the connectivity pattern within the molecule using strings are quite commonly used. On the other hand, numeric features are based on fingerprints which usually represent the molecule as a binary vector with entry 1 (0) corresponding to the presence (absence) of certain prototypical substructures/functional groups. These are further divided into many categories like circular fingerprints like ECFP635 which are extremely popular as they are quickly generated, Morgan fingerprints,636 Molecular ACCess System (MACCS),637 Tree based fingerprints,638 and Atom pairs639,640 to name a few. Graph based 2D descriptors641,642 are also commonly used with the atoms in the molecule represented as vertices and the bonds between them as connectivity pattern. Adjacency matrix derived from such a graph can act as a molecular descriptor. Fig. 39(b) shows an example for representing a given molecule in the commonly used 1D and 2D formats. However, these 1D and 2D descriptors even though widely used are often less sensitive to stereochemistry within the molecule which may be important for evaluating binding proclivity with the target. 3D descriptors are useful for this purpose as detailed structural information like dihedral angles are important for this encoding.643,644 Higher dimensional encoding with information like specific conformational state, interaction with the solvent or the background residues of the target may also be used to enhance the predictive capacity of the model.643,644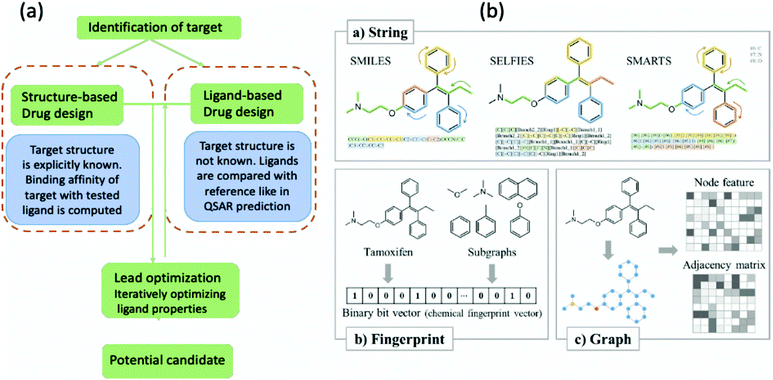 | ||
| Fig. 39 (a) The schematic overview of the key steps in computer-aided drug discovery (CADD). (b) Encoding the prospective drug/molecule into various representative formats614 for machine learning algorithms to act on. Reprinted from – a review on compound-protein interaction prediction methods: data, format, representation and model, 19, S. Lim, Y. Lu, C. Y. Cho, I. Sung, J. Kim, Y. Kim, S. Park and S. Kim, Comput. Struct. Biotechnol. J., 2021, 19, 1541–1556, Copyright (2021), with permission from Elsevier. | ||
In a similar study Yang-Bin Wang et al.649 developed a computational model with memory based on LSTM to construct a framework for drug–target interaction. Information about the drug–target pairs was obtained using Kegg,650 DrugBank651 and Super Target databases.652 Four classes of targets were considered, i.e., enzymes, ion-channels, GPCRs and nuclear receptors. From the dataset curated from the above bases, the drug–target interaction pairs with known affinities are set as positive examples while the remaining are treated as negative examples. The structural features of the protein was described using Position Specific Scoring Matrix (PSSM).649 For a protein consisting of N amino acids, PSSM is an N × 20 matrix with the (i,j)th element of the PSSM denoting the probability of mutating the ith amino acid in the sequence with the native amino acid from the list of 20. The PSSM was constructed using PSI BLAST.653 Legendre moments using the elements of PSSM was then constructed to remove redundancy in features. At the end 961 features were obtained for each protein sequence. The structural features of the drug were encoded molecular fingerprints. PubChem database was used for this purpose which defines 881 sub-structural features. As a result each drug/ligand was represented by an 881 dimensional Boolean vector denoting the presence or absence of these tagged molecular substructures. A total of 1842 dimensional vectors (881 + 961) for the molecule and the receptor target was reduced to 400 size feature vectors using sparse principal component analysis (SPCA). This combined feature vector was fed into the classifier. Multiple LSTM layers were stacked to get a deep LSTM setup, i.e., 4 hidden layers with 36 neurons were used. Overfitting was compensated by using dropout of randomly chosen neurons during the training process. Different performance metrics were used like ACC, true positive rate or even the standard AUC as defined before.654 Both hyperbolic tangent and logistic sigmoid were used as the activation function depending on the case (see Section 3.3.1). The output layer being a classifier uses a softmax. The method attained great accuracy across all performance metrics for all the 4 classes of drug–target chosen in comparison to traditional machine learning techniques or even multi-layer perceptrons. The multi-layer perceptron they trained had the same number of hidden units as the LSTM network being used for a fair comparison. The method performed reasonably well even with a small training sample size like 180 as was available for the nuclear-receptor family. In another recent study by Zheng et al.,655 a deep learning algorithm is developed with both CNN and LSTM. The target/receptor proteins are processed into a fixed length feature vector using a dynamic attentive CNN. 16–32 filters and 30 residual blocks were used in the construction of the dynamic attentive CNN.656 The drug candidate was represented as a 2D matrix similar to ref. 657. This is processed using a self-attentional LSTM network655 known as BiLSTM which extracts features. The number of hidden layers in the BiLSTM network was 64. Three kind of databases were used for numerical experiments. The first is DUD-E.658 This dataset has 102 target receptors across 8 protein families. Each receptor has 224 active drug molecules and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 inactive ones. The final dataset curated from this database had 22
000 inactive ones. The final dataset curated from this database had 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 active drug–protein interaction pair examples and 1
645 active drug–protein interaction pair examples and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407
407![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 145 negative ones. The second database used was Human659 containing 1998 unique proteins and 6675 interactions. The third database used is Binding DB660 which contains experimental results of binding affinities. The dataset curated from this had 39
145 negative ones. The second database used was Human659 containing 1998 unique proteins and 6675 interactions. The third database used is Binding DB660 which contains experimental results of binding affinities. The dataset curated from this had 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 747 positive examples and 31
747 positive examples and 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218 negative binding interaction pairs. The two feature vector of the target and the protein are combined and fed into a classifier which generated a probabilitty vector from it using sigmoid activation. This probability vector was then minimized against the data label of positive and negative interaction pairs using cross-entropy with regularization. The metric used to evaluate the final performance of the model is area under the ROC (Receiver-Operating Characteristic)661 curve. This metric is often abbreviated as AUC in the literature. Receiver-Operating Characteristic (ROC) curve enrichment metric (RE) is also used for the DUD-E dataset. For the Human dataset, the method achieved 98.7% for AUC, outperforming all traditional methods like Random Forests, Support-Vector Machines, etc. For DUD-E dataset, the method outperformed Vina647 and AtomNet662 to name a few. On BindingDB with seen and unseen drug–target pairs too, the model outperformed all traditional competitive algorithms. Visual demonstration of which amino acid residues of the target and what structural features/moieties in the drug are important for interaction was also provided.
218 negative binding interaction pairs. The two feature vector of the target and the protein are combined and fed into a classifier which generated a probabilitty vector from it using sigmoid activation. This probability vector was then minimized against the data label of positive and negative interaction pairs using cross-entropy with regularization. The metric used to evaluate the final performance of the model is area under the ROC (Receiver-Operating Characteristic)661 curve. This metric is often abbreviated as AUC in the literature. Receiver-Operating Characteristic (ROC) curve enrichment metric (RE) is also used for the DUD-E dataset. For the Human dataset, the method achieved 98.7% for AUC, outperforming all traditional methods like Random Forests, Support-Vector Machines, etc. For DUD-E dataset, the method outperformed Vina647 and AtomNet662 to name a few. On BindingDB with seen and unseen drug–target pairs too, the model outperformed all traditional competitive algorithms. Visual demonstration of which amino acid residues of the target and what structural features/moieties in the drug are important for interaction was also provided.
The first report for the use of deep-learning models in QSAR prediction after the publically accessible Merck challenge was due to Dahl et al.663 QSAR studies mainly focus on understanding what chemical composition and structural features of the prospective molecule of choice (ligand) might have the desired pharmacological activities against a chosen target (receptor). The study by Dahl et al. focused mainly on the effectiveness of multi-tasking while designing architectures for neural-networks (basic theoretical formalism discussed in Section 3.3). Multi-tasking refers to the ability of the network design wherein different outputs of interest are simultaneously retrievable. For instance, in the aforesaid study a single-task network would be training using molecular descriptors obtained from compounds within a single assay (data-set) as input features and using the activity of the said molecule as a performance label for comparing the output. However, this model of training requires huge data assemblies from single assays alone which may not always be available. To circumvent this issue, the authors of the aforesaid study combined data from multiple assays using an architecture in the final output layer wherein individual neurons are dedicated to each assay. The same molecule may have appeared in different assays with different activity labels. For any given such molecule, the input feature vector is the molecular descriptor. The output at each of the neurons in the final layer are the activity/inactivity classification values learnt by the network for each assay. This output is then compared against the recorded activity label obtained from the corresponding assay for back-propagation. The study used data from 19 such assays from PubChem database (see Table 1 in ref. 663) with each assay containing 104–105 compounds. The molecular descriptors used were generated using Dragon software664 as a feature vector of length 3764 for each compound. Although the model is a binary classification study, the performance metric used is AUC as defined before. The network was trained using Stochastic-Gradient Descent algorithm with momentum and the problem of over-fitting due to many tunable parameters was eschewed using drop-out.205 It was seen that the deep-learning network used outperformed traditional machine learning models in 14 out of the 19 assays. Among these 14, multi-task networks outperformed single-task models in 12 of the assays. These favorable results were retained by grouping similar molecules across different assays into a customized composite data-set. The depth of the neural network/addition of more hidden layers did not always produce improvement in the performance of the multi-task network which the authors attribute to the smallness of the data within each assay. All the deep-learning models used handled reasonably well correlated features in the input feature vector. In a related study Ramsundar et al.665 resolved certain questions about the efficacy of multi-task neural networks in virtual screening of candidate molecules against several targets using extremely large data-sets. 259 assays were used and divided into 4 groups – PCBA, DUD-E,658 MUV, and Tox21. Together all these databases had 1.6 M compounds. The validation scheme used is AUC as before and the feature vector of the studied compounds were ECPF4 fingerprints.635 All such collection of fingerprints for the molecule were hashed into a single bit vector. The trained network as before is a multi-task classifier with each neuron at the output layer having a softmax activation666 corresponding to each assay. The study found that such multi-task NN performed better than several ML models and the performance metric can be improved with increasing number of tasks and/or increasing the volume of data per task. Certain data-sets in the study showed better performance than others which was attributed to the shared set of compounds among such databases. However the biological class of the target receptor did not affect the performance metric too much. The study concluded by saying that extensive data-sharing among proprietary databases needs to happen to benchmark the performance of such models with bigger data-sets. Another study which thoroughly benchmarked the performance of deep neural networks against a commonly used machine learning model like Random Forest (RF) was due to Ma et al.667 The report used 15 Kaggle data-sets for training and another 15 for validation too. Each such data-set had around 104–105 candidates as molecular designs for drugs each labelled with response activity against designated target(s). The type of descriptors used for each of these molecules included combination of atom pairs and global donor–acceptor pairs668 as input feature vectors. The report used the squared Pearson correlation coefficient (R2)669 between observed and predicted activities in the testing set as the preferred metric of performance. The study showed that there was a mean improvement in R2 of 0.043 when using deep-neural network as opposed to RF against arbitrarily selected parameters. 4 of the data-set showed dramatic improvement in favor of deep-neural network whereas one favored RF. When refined parameter set was used instead of arbitrarily chosen ones, the trend is retained with an expectedly higher mean improvement of 0.051. Increasing the number of hidden layers and also number of neurons in each such hidden layer displayed a R2 in favor of deep neural network. Changing the activation function from sigmoid to ReLU666 also favored the deep network model for 8 data-sets. R2 was found to also favor networks when it is not pre-trained.
Deep learning models have also been deployed for the said purpose. In a recent one using artificial neural network, toxicity due to epoxide formation is thoroughly investigated.341 The study identified among a given set of drugs/ligands and targets which drug is susceptible to be epoxidized with natural oxidants in the biological medium by oxidants like cytochrome P450. Formation of such epoxidized metabolities can be harmful for the body as has been explicitly noted in the case of an anti-epileptic drug like carbamazepine677 which after epoxidation binds to nucleophillic sites within a protein forming a hapten adduct thereby triggering immune response.678 The product of such reactions need not always be an epoxide as the study suggests from previous reports679 for drugs like N-desmethyl triflubazam wherein a DNA adduct is formed post a transient epoxidation. The neural-network model used in the study not only decides if a given drug is epoxidizable but also focuses on identifying if the site of epoxidation (SOE) is a double bond or an aromatic ring. It further delineates such sites from site of hydroxylation (SOH) which shares some key structural features with SOEs and can also potentially lead to harmful oxidation products. The Accelrys Metabolite Database (AMD) was used from which a dataset of 389 molecules were curated having toxicity labels. These molecules had 411 aromatic SOEs, 168 double bond SOEs and 20 even single bond SOEs. Non-epoxidizable molecules were also included in the set thereafter to afford a proper distinction. To describe each bond within the specific molecule, 214 molecular descriptors/features were identified – 89 each for the left and right atom sharing the bond, 13 specific bond descriptor and 23 overall molecular descriptors. The neural network used had 1 input and 2 output layers. The top output layer was for the molecular epoxidation score whereas the last one for the specific bond epoxidation score. The training data involved using labelled binary vector within the molecule with the designated SOE marked as 1. Cross-entropy minimization was used as the cost function. The final metric of performance as before was AUC. The model outperformed logistic regression and other competitive algorithms in all departments like identification of SOEs, differentiation of SOEs and SOHs. The model could correctly identify SOE in carbamazepine which is absent in substitutes like oxcarbazepine with similar functionality, in the furan ring of furosemide680 and in severely hepatotoxic sudoxicam vs. its less problematic cousin like meloxicam.680 More such examples can be found in specialized topical reviews like ref.670.
However, recently, a study from Google's DeepMind (UK),686 has made enormous strides in predicting the 3D structure of a peptide from just a given sequence of amino acids solving this 50 year old grand challenge. Even though the algorithm uses a neural-network architecture trainable on a classical computer (and hence is not a quantum-computing enhanced algorithm), yet the performance of the method is so good that it deserves a special discussion. This novel algorithm has won the CASP14 challenge which involves a blind assessment of the efficacy of structure determination from amino acid sequence for proteins/peptides whose structure has been recently solved through explicit experimentation yet has not been publicly released in common databases. The neural network design is broken down into three components. The first component in the neural network architecture takes as input a 1D sequence of amino acid residues and searches multiple databases to generate multiple sequence alignments (MSAs) which are essentially sequence of previously identified amino acids closely resembling the target one and understanding the evolutionary history of the mutation of these MSAs. This is important to derive information about structural proximity between amino acid pairs which shows correlated mutation. This component then generates a template 3D structure also called pair representation as an initial hypothesis that is to be modified at later stages. The next functional unit is called the Evoformer and is the heart of the design. This takes as input both the pair representation and the MSA and subsequently refines the representation of each self-iteratively using the architecture of transformer.459 The third block takes the refined MSA and the pair representation and generates a 3D structure which is essentially cartesian co-ordinates of the individual atoms, i.e., the native 3D conformation of the protein/peptide. This process is repeated several times by feeding back the 3D structure into the Evoformer block until convergence. The final prediction seems to have surpassed all previously known methods with an accuracy of 0.95 Å root-mean square error from the target structure for 95% of the residues. This will definitely be a landmark study and for years to come one has to investigate the efficacy of the method for antibodies, synthetic peptide sequences for which evolutionary data to generate the initial MSA will be scarce. This method will positively impact understanding protein–protein interactions and also bring in new insight into diseases like Alzheimer's and Parkinson's. For structure based drug-discovery since at least one method exist now which can determine the 3D conformation efficiently thereby massively speeding up the product development pipeline, quantum computers can now help in understanding the drug–protein affinity and molecular docking mechanisms. The review by Cao et al.681 already identifies this possibility by noting that with algorithms like quantum phase estimation on fault-tolerant devices and variational eigensolvers for near term devices, we are capable of computing the potential energy surfaces of larger molecular systems efficiently and hence force-field calculations as is required for understanding molecular docking will also be greatly impacted.
For QSAR studies too, benchmarking the performance of quantum computer against classical processors has been documented recently in the work of Batra et al.317 The authors have used several molecular databases to identify prospective ligands for diseases like M. tubercolosis, Krabbe disease, SARS-CoV-2 in Vero cells, plague and hERG. With the curated data from the compound datasets feature vectors were constructed and used for binary classification of the compound in active or inactive using kernel-based SVM techniques (see Section 3.2.7 for basic theoretical formalism). The authors used several techniques to reduce the size of the feature vector such that the classification can be performed on a NISQ device (ibmq_rochester was used) using Qiskit. It was seen that for most datasets comparable accuracy on a quantum computer was attained too using the feature reduction techniques employed by the authors. A hybrid quantum-classical approach was also used for high-throughput virtual screening data screening with good accuracy and slightly faster run time for processing the data on a quantum computer than on a classical computer. Representative data from the study are displayed in Fig. 40.
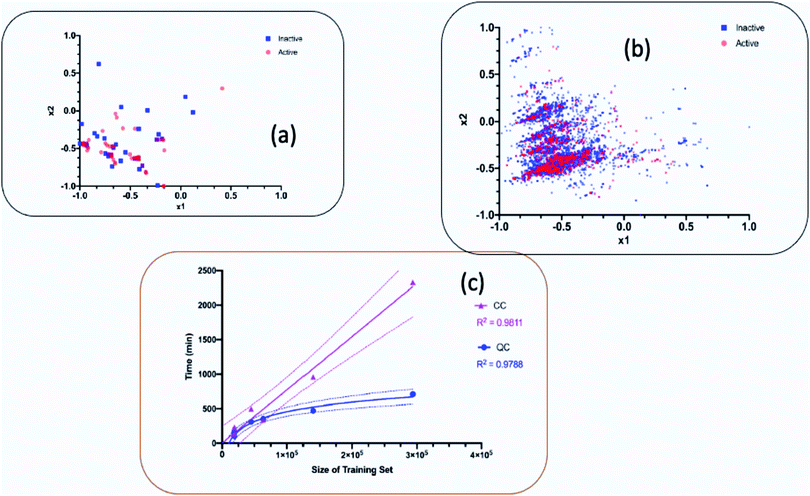 | ||
| Fig. 40 (a) Classification of ligands into active and inactive ones based on performance against SARS-CoV 2 in the space of the two most dominant features after application of two methods of feature extraction as in ref. 317; and (b) classification of ligands into active and inactive ones based on performance based on performance against M. tubercolosis in the space of the two most dominant features.317 (c) The run time required for screening training datasets of varying sizes on a quantum computer (QC) and a classical computer (CC). The training time shows sublinear scaling on QC displaying an advantage.317 Reprinted (adapted) with permission from K. Batra, K. M. Zorn, D. H. Foil, E. Minerali, V. O. Gawriljuk, T. R. Lane and S. Ekins, J. Chem. Inf. Model., 2021, 61, 6. Copyright 2021 American Chemical Society. | ||
Beyond the precincts of academic research, even the interest of industrial players on quantum-enabled technologies seems to be escalating rapidly. The report by Zinner et al.687 has identified that 17 out of 21 established pharmaceutical companies and 38 start-ups are directly working on enhancing and ameliorating the technical challenges in the drug discovery pipeline using quantum computers. 75% of such companies so far have been identified to be geographically in Europe and North America. The cumulative funding received by all the start-ups as per the report687 is €311 million with the top five funded start-ups being Cambridge Quantum Computing, Zapata, 1QBit, Quantum Biosystems and SeeQC. Most of the activity is directed towards virtual screening for ligand-based drug designing protocol and subsequent lead optimization.
The reports from Langione et al.688 and Evers et al. from McKinsey689 also systematically delineate what pharmaceutical industries should do to prepare themselves so as to attain a favorable position in order to leverage the quantum revolution. Both the reports agree that bio-pharmaceutical companies should start now to reap the benefits of early movers advantage. In fact ref. 688 mentions that it might be possible that tech-giants equipped with quantum computers with higher number of qubits and better noise-tolerance might enter the race of in silico drug discovery in the future relegating the task of post-design synthesis, clinical trials and commercialization to pharmaceutical companies. This can lead to a situation wherein companies may race to patent the best molecule that are responsive to a particular disease. However pharmaceutical companies are at an advantage here due to years of experience with computational drug-designing protocols. So strictly they do not have to change the inherent model or the business goal they already follow. They will likely be using a more capable device like a quantum computer to attain that goal. In order to avoid such undue competition, pharmaceutical companies should start now by assessing and answering a few key questions about the probable impact quantum computers are likely to have on the workflow and the specific product design the respective company is targeting. This can happen by understanding what are the key areas where development can be sought in the product design model the company is following and more importantly if those areas fall into the category of problems that can be solved efficiently on a quantum computer. The key directions to think would be would a quantum-computer enabled business provide an unprecedented value to their supply-chain or an undue advantage to their competitors. If the analysis is positive, one needs to then think of the time scale of such developmental changes and whether the resources the company has access to would be enough to sustain entry into the domain. Some of above resource overheads can be solved through appropriate memberships through consortium like QuPharm that categorically specializes in the designated area. QuPharm, as an organization, was developed by many member pharmaceutical companies for specifically understanding and optimizing the benefits the quantum revolution can have on the pharmaceutical industry. The consortium is known to have a collaboration with Quantum Economic Development Consortium (QED-C).687 Hardware needs can be sorted through collaborations with end-to-end technological providers like Google, IBM, Honeywell, Rigetti, Xanadu, etc. each of which have quantum computers of varying architecture and even on different platforms and have even promised to develop larger scale ones in the near future. For example Amgen, a pharmaceutical company has declared collaboration with both Amazon Braket and IBMQ.687 Boehringer, another pharmaceutical company has established collaboration with Google QuantumAI to develop algorithms for molecular dynamics simulation.687 New software solutions are necessary to interface with the quantum hardware for which commercially available varieties like Qiskit (IBM), OpenFermion (Google), and tKet (Cambridge Quantum Computing) can be leveraged. Companies can also initiate partnerships with firms like ProteinQure, GTN, Rahko, Qulab etc. which are developing softwares to specifically cater to advancing quantum-computing algorithms for drug discovery. Classical computing algorithms have also benefited from the ideas that were synthesized to initiate a rapid discovery of quantum algorithms over the last few years. Companies like Qubit Pharmaceuticals, Turbine etc. are developing such approaches and combining them with machine learning. Such collaborations with global and local companies with specialized expertise can result in engineering custom solutions to tackle specific problems during the drug discovery pipeline. Pharmaceutical companies can thus immensely benefit from such collaborative ventures.
Partnerships can be built with other pharmaceutical companies or start-ups too to share expertise and develop mutually beneficial quantum computing based drug-development protocols. The report by Zinner et al.687 has identified 17 pharmaceutical companies with publically disclosed collaborations with at least 12 start-ups. All the pharmaceutical companies are members of QuPharm, NEASQC etc. Among the big pharma corporations Merck (Germany) has invested €4 million on start-ups like SeeQC and has disclosed active collaboration with Rahko, HQC.690,691 Merck (USA) has made financial investment in Zapata.692 Non-equity partnerships like that by Amgen with QSimulate to develop advanced molecular simulation tools or like that by AstraZeneca with ProteinQure to design amino-acid sequences have also been seen.693 Some new collaborations are also announced which depicts not only the prospective promise associated with the technology but also the seriousness of the industry players. For example, Cambridge Quantum Computing has announced a collaboration with CrownBio and JSR LifeSciences about using quantum machine learning algorithms to identify multi-cancer genes biomarkers694 which can positively impact bioinformatics research. Apart from this, it would also be beneficial for pharmaceutical companies to collaborate with scientists in academia. Adopting a strategy that allows effective co-operation among all involved parties internal and/or external beyond the traditional organizational structure will accelerate growth and foster efficient and fast sharing of resources and knowledge which can otherwise be harder to access due to institutional barriers. The reports688,689 identify that recruitment of skilled technicians and professionals with training in developing algorithms on a quantum computer is necessary for pharmaceutical companies to enhance quantum-enabled research. The report by Zinner et al.687 conducted a thorough search across 21 pharmaceutical companies with a combined revenue of €800 billion in 2019 and reported that only about 50 employees were found designated to quantum-enabled technology. This is partly because quantum computing is an emerging technology and hence such a skillset may not be readily available among the usually hired talent pool of the pharmaceutical industries.688 Companies like IBM which hold outreach programs and workshops in quantum computing interfaces like Qiskit can be a useful resource. The other alternative might be looking into developing specialized programs internally to train scientists and engineers once hired.
6 Insight into learning mechanisms
Despite the enormous success of machine learning coming from network based models with large number of tunable parameters, little progress has been made towards understanding the generalization capabilities displayed by them.695 The choice of hyperparameters in these models have been based on trial and error with no analytical guidance, despite them showing enormous potential in analyzing data sets. Physics on the other hand has provided us with white box models of the universe around us that provide us with tools to predict and examine observed data. Intuition from statistical mechanics has helped provide understanding with respect to the learning limits of some network models. Seminal contributions in this regards include methods from spin glass theory, that have been used to extensively study associative memory of Hopfield networks696 and Valiants theory of learnable models that introduced statistical learning into the then existing logic based AI.697 Another major contribution comes from Gardner's usage of replica trick to calculate volume in the parameter space for feed forward neural networks in the case of both supervised and unsupervised models.698,699 The problem of learning was also shown to exhibit phase transitions in reference to generalization and training efficiency.700 A typical example of one such parameter is the ratio of input size to the number of model parameters. A diminishing value usually results in overfitting while a large one allows for successful generalization. The reader is encouraged to refer ref. 701–703 for some of the early studies that made use of statistical physics to understand multi layered network learning.We will see that some self averaging statistical properties in large random systems with microscopic heterogeneity give rise to macroscopic order that does not depend on the microscopic details. Learning these governing dynamics can play an important role in tuning the performance of machine learning techniques. One of the tools that provides an analytical handle in analyzing these details is the replica method.704 Replica methods have been used to explore the teacher–student model to provide information theoretic best estimates of the latent variables that teacher uses in generating the data matrix handed over to the student.705 This problem can be specialized to the case of providing a low rank matrix decomposition matrix of underlying input data. Interest on statistical methods has stayed dormant since 1990, due to the limited tractability of algorithms used in learning. It was sparked again with the contribution of Decelle706 to use spin glass theory to study stochastic block model that played a major role in understanding community detection in sparse networks. They observed second order phase transitions in the models that separated regions of efficient clustering when solved using belief propagation algorithms.707 For a comprehensive list of physics inspired research in the machine learning community, refer ref. 708.
Generative models are suitable for feature extraction apart from doing domain sampling. Within every layer of one such network, one could imagine some form of feature extraction being made to provide for a compact representation, which might later be used by generative models to learn the distribution of classifiers to do prediction. We point towards this feature extraction as the central idea for relating machine learning to renormalization group. We investigate to see if concepts like criticality and fixed points have something to reveal about the nature in which learning happens in the framework of deep learning and machine learning in general. Fig. 41 provides a schematic sketch of the methods that have been primarily explored in studying network models. In here we shall restrict our attention to cavity methods, Renormalization group and Replica methods. Refer ref. 709 for a thorough exploration of message passing algorithms.
 | ||
| Fig. 41 A schematic representation of the techniques borrowed from statistical physics that have been used to study model learning of networks in machine learning. | ||
A somewhat non rigorous argument for the remarkable working of these machine learning algorithm comes from noting the following two observations. Consider a vector of input size n taking v values and thus can span a space of vn possible configurations. Despite this being exponentially a large space for image datasets, we have managed to build relatively small networks that learn to identify the features of the image accurately. This is to be attributed to the realization that the class of relevant images comes from a relatively small subspace that is efficiently learnt by the neural network with relatively fewer nodes that scale as nv instead.710 This is much similar to how low energy states of interest of Hamiltonian mapping to small subspace of the Hilbert space. This simplification comes from the Hamiltonian having a low polynomial order, locality and symmetry built into it. Secondly, despite the vastness of all possible inputs that can be generated, most input data can be thought of coming from a Markovian process that identifies at each stage a select set of parameters. Thus the work of a deep learning machine would be to reverse some form of heirarchial markovian generative process using some minimal statistic function (A function f is minimal statistic if for some random variables y and x we have P(y|x) = P(y|T(x))) that retains the features of the probability distribution by preserving mutual Information.
The methods in the following subsection describe its working in the context of Ising model, so we start by describing one briefly. Ising is a model for representing classical spins or magnets arranged in a 2d lattice whose interaction with one another is quantified by the strength of the coupling. Each spin takes a binary configuration (+1, −1) of choosing to align up or down. At low temperatures spins prefer aligning in the same direction forming a magnet. At high temperatures the thermal fluctuations kill any order within the system causing them to arrange chaotically with no net observable magnetic field. A general Ising Hamiltonian is given by,
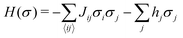 | (130) |
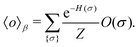 | (131) |
6.1 Replica method
Replica method is a way of computing self averaging expectation values of observables O(x) such that x is a minimizer of H(x,D) where D is the distribution of some input space. A typical example of H would be the cost function of a learning problem and D would be the dataset used for training in the problem. Fig. 42 provides a schematic representation of the use of replica method. Here we shall explore it in the context of Ising Hamiltonians. Consider the Ising model of N spins, given by the following Hamiltonian: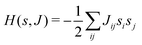 | (132) |
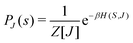 | (133) |
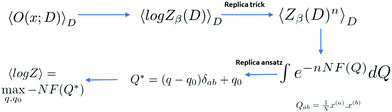 | ||
| Fig. 42 A schematic representation showing the use of replica replica trick and replica ansatz to compute the expectation value of self averaging observables. | ||
To study the patterns encoded within the Gibbs distribution, we start with computing the free energy average over all the realizations of J. This involves computing expectations of a logarithm which can be simplified using the following Replica trick:
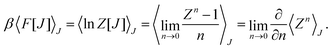 | (134) |
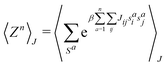 | (135) |
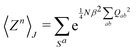 | (136) |
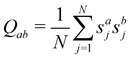 . Minimizing the free energy amounts to retaining patterns with maximal overlap. The non zero averaging can be interpreted as certain patterns being promoted within replicas and enforced across different realizations of J. The minimization of free energy gives a self consistent equation for Q,
. Minimizing the free energy amounts to retaining patterns with maximal overlap. The non zero averaging can be interpreted as certain patterns being promoted within replicas and enforced across different realizations of J. The minimization of free energy gives a self consistent equation for Q,| Qab = 〈sasb〉 | (137) |
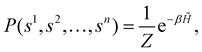 where
where 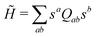 . The Hamiltonian
. The Hamiltonian ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) is symmetric with respect to permutation of indices and thus Qab = q for all a ≠ b. Minimizing the free energy with respect to the variable q gives a self consistent equation
is symmetric with respect to permutation of indices and thus Qab = q for all a ≠ b. Minimizing the free energy with respect to the variable q gives a self consistent equation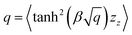 | (138) |
6.2 Cavity method
The cavity method712 provides for an alternative analysis to the results derived from Replica method. Consider the Ising Hamiltonian over N neurons reordered in the following fashion:| H(s,J) = −s1h1 + H−1 | (139) |
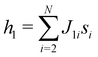 is the local field at site 1 and
is the local field at site 1 and 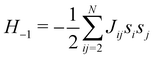 is the remaining Hamiltonian that defines the interaction over other spins. The distribution of h1 in the system of the remaining N − 1 neurons is given by
is the remaining Hamiltonian that defines the interaction over other spins. The distribution of h1 in the system of the remaining N − 1 neurons is given by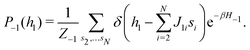 | (140) |
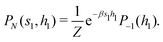 | (141) |
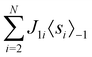 and variance
and variance 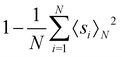 . The variance has inbuilt into it an approximation of vanishing correlations 〈sisj〉−1 that is equivalent to the single energy well approximation made in the Replica solution. Under this approximation we can write
. The variance has inbuilt into it an approximation of vanishing correlations 〈sisj〉−1 that is equivalent to the single energy well approximation made in the Replica solution. Under this approximation we can write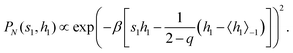 | (142) |
We expect 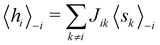 to be self averaging and have a Gaussian distribution (as Jik is uncorrelated with 〈sk〉−i) with a 0 mean and variance q over random realizations of Jik in the large N limit. Replacing the averaging over the neurons with an average over the Gaussian distribution we get
to be self averaging and have a Gaussian distribution (as Jik is uncorrelated with 〈sk〉−i) with a 0 mean and variance q over random realizations of Jik in the large N limit. Replacing the averaging over the neurons with an average over the Gaussian distribution we get
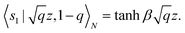 | (143) |
Since all the neurons are equivalent, neuron 1 replaced with any other neuron in eqn (142). The mean activity of neuron i is thus given by
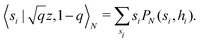 | (144) |
We can average over the above expression to write a self consistency condition on q. We thus get
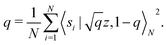 | (145) |
6.3 Renormalization group and RBM
Renormalization group (RG)713 is based on the idea that physics describing long range interactions can be obtained by coarse graining degrees of freedom at the short scale. Under this scheme small scale fluctuations get averaged out iteratively and certain relevant features becomes increasingly more prominent. This helps in building effective low energy physics, starting from microscopic description of the system. Despite its exactness and wide usage within the fields of quantum field theory and condensed matter, any form of exact RG computations in large systems is limited by computational power. RG was introduced within the context of Quantum Electrodynamics (QED)714 and played a crucial role in addressing the problem of infinities. A proper physical understanding was given by Kadanoff within condensed matter systems while proposing the idea of block spin renormalization group.715 This formed the ground for the later seminal work of Kenneth Wilson in producing the scaling laws of correlations near the critical point.716RG can be analytically studied for 1d Ising model, as decimation does not produce additional interaction terms, leaving the hierarchy of effective Hamiltonians tractable. Consider the following Ising spin Hamiltonian with N spins whose interaction is given by
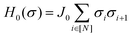 | (146) |
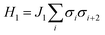 | (147) |
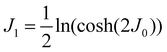 . This can be repeated recursively k times giving rise to Hk that depends on the remaining N/2k spins.
. This can be repeated recursively k times giving rise to Hk that depends on the remaining N/2k spins.
For the 2d Ising model doing renormalization using spin decimation is not feasible as this produces higher order interactions that are not tractable. Approximations of higher order interactions have been introduced to allow for analytical extensions.717 At the critical temperature the system exhibits conformal symmetry and this fixes the 2 point and higher point correlations along with the scaling dimensions. To verify that an observable A′ defined over the renormalized degrees of freedom remains invariant under renormalization, we will compute the expectation value over the initial probability distribution. Let p refer to the probability distribution generated by the initial Hamiltonian H over spins σ and p′ be the probability distribution generated by the renormalized Hamiltonian H′ over spins σ′. Thus,
 | (148) |
Note that this is only true for observables that are defined on the coarse grained degrees and does not work for those defined on the observables that are defined on the microscopic degrees as these correlations are washed out during renormalization. In the remainder of this section we shall talk about methods of generating RG flows using RBM on a uniform 2d Ising Hamiltonian. Any indication of RBM generating flows that approach criticality like RG should be indicated through correlators that follow the behavior of conformal fields.
RG flows can be well described in the space of parameters that weighs different operators that make up the Hamiltonian. As one coarse grains the Hamiltonian from UV (microscopic description) to an IR (macroscopic description) prescription, we observe that certain parameter weights flow to zero (monotonically decrease). These are termed as irrelevant operators as they play no role in the flow. Operators which regulate the flow with monotonically increasing weights are relevant operators. Within the space of all possible Hamiltonians lies a critical surface where the theory respects conformal symmetry with length scales that run to infinity. When the RG flow meets such a surface it results in a fixed point referred to as critical point. Critical points are usually associated with phase transitions. For example, the critical temperature of uniform 2d Ising with no external magnetic field is given by Tc = 2.269 and marks the demarcation between low temperature ferromagnetic and high temperature paramagnetic phases. We shall describe three different methods of generating RBM flows using: (a) learned weights (b) variational RG and (c) real space mututal information.
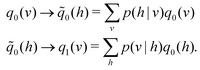 | (149) |
This produces a new distribution q1(v) that corresponds to a flow within the probability distribution and can be seen as the distribution generated by some Hamiltonian of the same statistical model with parameters λ1. This would correspond to a flow within the parameter space (λ0 → λ1). We would like to verify if such an transformation on the parameter space actually corresponds to an RG flow. We do that by implicitly computing correlation functions of certain operators and comparing against known results from RG.
The number of nodes in the successive layers is kept the same as the same RBM is used to produce the flow, unlike RG with reducing degrees of freedom as one flows. Its observed that the RBM flow generated in this method approaches the critical point, despite the RG flow moving away from unstable points. Despite these differences the authors still manage to provide accurate predictions of the cirtical exponents in ref. 15 and 16. At the critical temperature the Ising model enjoys conformal symmetry, giving rise to operators whose correlations scale by well known power laws. The authors of the paper have used sij = σij − ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) that has a weight of Δs = 1/8 and ε = sij(si+1,j + si−1,j + si,j+1 + si,j−1) −
that has a weight of Δs = 1/8 and ε = sij(si+1,j + si−1,j + si,j+1 + si,j−1) − ![[small epsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c6.gif) that has a weight of Δε = 1. The former operator sij acts as a estimator of reproducing long range correlations, as it dies off faster, while εij acts as a estimator for being able to reproduce short correlations when testing on the RBM.
that has a weight of Δε = 1. The former operator sij acts as a estimator of reproducing long range correlations, as it dies off faster, while εij acts as a estimator for being able to reproduce short correlations when testing on the RBM.
Monte Carlo is used to generate 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples of 10 × 10 square lattice Ising configurations according Boltzmann distribution at each temperature over 0 to 6 with increments of 0.1. A neural network is trained over these samples with supervised learning to predict the temperature. The RBM is then used to generate flows for temperatures close to the critical temperature. Samples collected from flow lengths of greater than 26 allows for predicting the proportionality constant A/Tc and scaling dimension Δm with a very high accuracy by fitting against
000 samples of 10 × 10 square lattice Ising configurations according Boltzmann distribution at each temperature over 0 to 6 with increments of 0.1. A neural network is trained over these samples with supervised learning to predict the temperature. The RBM is then used to generate flows for temperatures close to the critical temperature. Samples collected from flow lengths of greater than 26 allows for predicting the proportionality constant A/Tc and scaling dimension Δm with a very high accuracy by fitting against
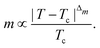 | (150) |
Fitting the average magnetization, m with temperature T from 2 different flows, eqn (150) helps compute the critical exponent Δm. We could rather compute the scaling dimension Δs and Δε from a single flow at different temperatures. This then allows us to interpolate and predict the dimension for the critical temperature. Δs is reproduced with a very high precision, indicating that the RBM flow preserves long range correlation, while high errors in predicting δε shows that short range correlations are usually lost.
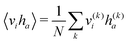 | (151) |
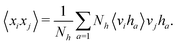 | (152) |
The above correlation is plotted with against |i − j| for renormalization over lattices of different sizes at the critical temperature for a RBM trained on data from a 2d Ising Hamiltonian with nearest neighbour interaction. A fall in correlation with the separation is noticed for large lattices and no pattern is obtained for small Ising lattice keeping the decimation ratio fixed. The RBM thus has managed to preserve the correlations with nearest neighbours showing some reminiscent behaviour of RG under some circumstance.
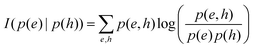 | (153) |
This procedure reproduces the Kadanoff renormalization when tested on a 2d lattice with 4 visible spins. Samples are generated from a square lattice of size 128 × 128. The effective temperature can be computed against a neural network trained with samples at different temperatures or as described in the earlier section or by plotting the temperature against the mutual information. The procedure reveals a clear separation in the phase transition while predicting the critical temperature with a very high accuracy.
6.4 Learnability of quantum neural networks
The examples discussed in previous sections demonstrate the power of neural networks with regards to generalization, for problems related to classification and generative modelling. We also seen how some of these classically inspired models can be understood from the standpoint of classical physics. Here we would like to address the question of learnability of quantum models with regards to expressibility, trainability and generalization for Quantum Neural Networks (QNN). The working of QNN involves 2 components:• Feature encoding layer: feature extraction is performed on raw classical data to extract relevant features for the model to train on. This might for example include denoising, data compression, privacy filtration. Unlike classical ML, for QNN we need to have an efficient method of encoding the feature output as part of quantum states. One might go for qubit encoding (phase encoding), basis encoding (initialize starting state in the computation basis state) or amplitude encoding (using QRAM).
• A function: in neural networks a generic non linear function this is implemented using layers of fully connected nodes, that seem to resemble multiple layers of RBM stacked over. In the case of QNN, a general unitary constructed from paramaterized quantum circuits is used. The ansatz that defines the unitary could be inspired by the problem at hand or could be a very general multilayered hardware efficient one.
Following this an optimizer is enrolled to compute gradients on the cost function of interest. The gradients of these operators may not directly correspond to another unitary operator, in which one needs to re-express them as a sum of terms with term corresponding to an efficient computation of expectation value of some observable for the corresponding unitary that is being the output. An example of this would be to use parameters shift rule to re-express gradients as differences.
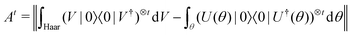 | (154) |
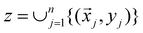 . Here
. Here ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) j represents the input vector and yj represents the label assigned to it. Thus the optimization procedure solves the following empirical minimization problem:
j represents the input vector and yj represents the label assigned to it. Thus the optimization procedure solves the following empirical minimization problem: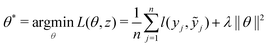 | (155) |
 | (156) |
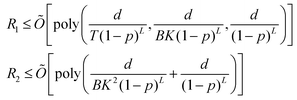 | (157) |
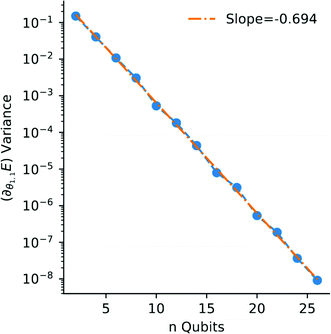 | ||
| Fig. 43 The plot shows sample variance of the gradient of a two-local Pauli term plotted as a function of the number of qubits on a semi-log plot. Reprinted from ref. 728 with permission under Creative Commons Attribution 4.0 International License. | ||
As polynomially deep (in terms of the number of qubits) ansatz built out of 2 qubit unitaries as form 2-design circuits,729 one is likely to encounter barren plateaus while training circuits with sufficiently large number of qubits. Barren plateaus can also arise from the use of global cost functions.730 Examples of this include computing ground state energies of highly non local Hamiltonians and preparing a given density matrix with high fidelity. Lorocca et al.731 shows that for controllable systems (roughly refers to ansatz with highly expressibility) the gradients decay by the dimension of the symmetry subspace to which the initial state prepared by the circuit belongs to (in the lack of any symmetry subspaces, it will be the dimension of the Hilbert space). However, one can tailor the ansatz to remain in the uncontrollable regime and sacrifice on expressibility to achieve approximately good results. Another unavoidable source of barren plateaus is the presence of gate noise in NISQ devices. Samson et al.732 show rigorously that for a noisy circuit the gradients vanish exponentially in the number of qubits with increasing depth.
7 Conclusions
In this review, we have explored some of the popular algorithms in machine learning that are used frequently for many physico-chemical applications. We discussed in detail not only the vanilla protocol implementable on a classical computer but also the quantum computing enhanced variants wherever applicable. Equipped with this underlying theoretical framework, we thereafter ventured to investigate five distinct domains of applications which includes tomographic state-reconstruction, state-classification methodologies, electronic structure and property prediction, paramaterizing force-fields for molecular dynamics and even drug discovery pipeline. Such an organizational paradigm places equal emphasis on the methodologies and the applications unlike in most other reviews, and is expected to be beneficial to new entrants in the field especially when supplemented with domain-specific examples as is the case in this review. Last but not the least, we offered an insight into the learning mechanisms, using tools from statistical physics and computer science, that have been used by researchers in recent years to understand the operational mechanism behind the training and feature-extracting ability of the deep-learning algorithms. In particular in the context of Ising Hamiltonians, the Replica and Cavity method provides for calculating observable expectation values that correspond to the least free energy (cost function). We followed this with a discussion on renormalization group searching for connections within deep learning and presented some methods that have been used in exploring the same. The kind of insight we believe reduces the obscurity of these models and the common reluctance associated with the fact that the learning dynamics of these protocols are unreliant on hard-coded physical principles or domain intuition.The applications explicated in this review cover a wide spectrum. As discussed even though the quantum-computing enhanced protocols are beginning to be duly recognized, we anticipate that we are still at a nascent stage scratching just the surface. For example, for modeling the electronic structure of molecules and materials there already exists a huge variety of methods ranging from learning the functional form of density functionals, approximating wavefunction, to learning the atomic environment descriptors to predict the atom types and properties which have shown great accuracy. Applying these ML methods with the help of quantum computers can further augment our capabilities especially when solving the electronic Schrodinger equation of large and strongly correlated systems are concerned. One can use the variational quantum generator (VQG) based hybrid quantum-classical architecture developed by Romero and Guzik733 in order to generate continuous classical probability distributions to perform chemical analysis, quantum state preparation, etc. The critical point and the critical exponents for a quantum phase transition can be determined using a QML approach through the finite-size scaling (FSS) analysis.734 Therefore, the development of QML approaches has a huge role to play in the coming years in the domain of electronic structure, materials, and property prediction methods. Similar statements can also be extended to computation of force-fields wherein classical ML techniques even though successful have only efficiently modelled small systems. For the drug discovery pipeline, as has been indicated in Section 5.5, key players in both industry and academia are recognizing the potential of quantum computers through investments and collaborative ventures. In the context of interpretability, analytically understanding how generalization of some of the models presented work while increasing the number of parameters with respect to the size of input space and the number of learning samples is still open. We would like to have a handle over the limit points of a given deep learning model and perturb to understand the neighborhood space much akin to having a conformal field theory that describes the critical surface and is used to explore the space of quantum field theories. Studies have been conducted in the context of 2d Ising model along the lines of analyzing information flow for RG and deep neural networks.735 Convergence towards critical points in these models is in stark contrast with it being an unstable point in the RG flow. It is important that further studies be conducted in models that have self organized criticality to probe if there exists a definitive relation and if the fixed points have anything to tell us about how choices are to be made in the models that we study, with respect to hyperparameters, cost function, optimizer choice and learning ability.
Since machine learning tasks are data-intensive efficient protocols for loading entries from a high-dimensional classical vector onto a quantum state without smarter preprocessing for feature extraction continues to be a significant challenge. The early domain of QML algorithms included HHL178 for PCA and clustering, required the assumption about the oracular presence of qRAM to enable efficient encoding of data. While the development of qRAMs is still an ongoing field of research, recent results claims that the exponential speedup in a subset of such algorithms is only due to the assumption that the encoding of data is efficient.736 Quantum inspired classical algorithms737 that manipulate l2 norm sampling distributions provide an exponential speedups in the case of recommendation systems imply the lack of provability concerning the quantum speedups of certain early QML algorithms. Another primary concern for the development of any quantum algorithms even beyond ML applications is the inherent presence of noise manifested from shorter coherence times of qubits and greater gate-infidelities especially of multi-qubit operations. The fundamental research related to the development of better qubits, improving gate fidelities in unitary operations, and improving the qubit connectivity is very much an active field of investigation among hardware engineers and physicists. New reports have been demonstrated with protected qubits resilient against certain kind of hardware noises.738 Fault-tolerant quantum computation wherein logical qubits are protected using more physical qubits like in stabilizer codes739 or qubit configurations based on topological properties of the underlying interactions81,740 have been proposed and is actively under development. First-ever such operation has been recently demonstrated on a trapped-ion platform.741 The process of such error correction can itself suffer from noise which can be mitigated by the quantum fault-tolerant threshold theorem742 provided noise levels are low. Partial suppression of bit and phase-flip errors have also been demonstrated.743 On the algorithmic side, algorithms that utilize the specific problem structure smartly have also been proposed.744 One also needs to thoroughly understand the noise resilience of some of the existing methods and investigate how much of hardware noise can be tolerated before the results are corrupted beyond a certain threshold and the proclaimed quantum advantages are lost. Proper certification schemes and figures of merit for benchmarking such algorithms are beginning to gain attention.745 With the increased activity on developing quantum ML algorithms underway, creating a provision for generalizability of these models is an important consideration and this aspect has been already discussed in Section 6.4.3. Some of the key open questions in this area would be a proper theoretical demonstration of asymptotic universality (as was discussed in Section 4) for the function class which quantum models can learn in the presence of trainable unitaries of finite circuit depth309 thereby relaxing the assumptions used thereof. Another interesting question would be proposing real-life applications tailored to take advantages of the universality in such function classes such that quantum benefits over classical learning can be seen. Resource dependence of such algorithms from the perspective of foundational aspects of quantum mechanics is also an interesting avenue for research. With regards to the trainability of ML models one of the major menaces to tackle is the presence of barren plateaus (see Section 6.4.4) in exploring high dimensional feature spaces to find optimal parameters that minimize the cost function. Much of the questions concerning how the possibility of such exponentially vanishing gradients needs to be handled and mitigated are essentially open to further investigation.
One must also note that there are other applications which have not been discussed in this review at all. Perhaps the most important one from the point of view of chemistry is modelling chemical reactions and computer aided rational design of molecules and synthetic strategies. In this technique one considers retro-synthetic pathways arising from a given product until a set of precursors which are commercially available or synthetically known in literature is obtained. Such pathways are scored on efficacy based on number of reactions involved, intermediates, reaction conditions, etc. Two different kinds of strategies are known in this regard. The first involves retrosynthetic disconnection based on domain knowledge or commonly used chemistry-inspired rules followed by subsequent ranking of the precursor steps. This can suffer for unknown or rare reactions where such intuition may not be available. The second category uses simple translation of the molecular descriptors of the reactants into products as is used in machine-induced linguistic translations. Promising results have been obtained for either category using ML/DL algorithms.746–750 For further information, the reader may consult already existing topical reviews like.41,751 To the best of our knowledge, the role of quantum computing in this area has not been explored. Another area which is very important is understanding non-unitary dynamical evolution of quantum systems and the role of coupling to the environment and the emergence of decoherence.752,753 Such open system dynamics have also begun to receive attention from the point of view of machine learning wherein the density matrix of the state is encoded as within an efficiently constructible ansatz. In a recent report128 Kernel-Ridge Regression (see Section 3.2.2) has been used to faithfully recover long-time dynamical averages of the spin-boson model when linearly coupled to a harmonic bath characterized by the Drude–Lorentz spectral density. Hierarchical equation of motion approach (HEOM) was used to train the model using short-time trajectories but the results when extrapolated beyond the training time intervals using Gaussian kernels leads to unprecedented accuracy. LSTM networks (see Section 3.3.3) have been used to model dynamical evolution of density operators for a coupled two-level system vibronically coupled to a harmonic bath.754 The population difference between the two levels and the real and imaginary part of the coherence was used as time series data for training at shorter times from the numerically exact multi-layer multi-configurational Time Dependent Hartree method (ML-MCTDH). Remarkable accuracy was seen being preserved even in the long-time limit. A similar result was also obtained with CNN755 (see Section 3.3.2) where input training data was the density matrix elements at various time steps and the prediction of the network through successive series of convolutions and max-pooling yielded accurate values of averages of the system operators (like the Pauli-z or σz(t)). For further elaboration on other such methods, the interested reader is referred to ref. 756–759.
Yet another promising area which is left untouched here is the use of physics-inspired machine learning algorithms which even though is beginning to gain attention in problems of physical or technological interest760–764 but has been sparsely adopted in chemistry.765 Reader may consult a recent review for further discussion.766 We thus see that the road ahead is ripe with possibilities that can be explored in future especially for the quantum-computing based ML variants. Hopefully with better error mitigating strategies767 and large scale devices with over 1000 qubits being promised in recent future by tech-giants,768 this burgeoning field will pick up momentum with enhanced capabilities to conduct many pioneering investigations.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge funding by the U.S. Department of Energy (Office of Basic Energy Sciences) under Award No. DE-SC0019215, the National Science Foundation under Award No. 1955907 and the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Quantum Science Center.Notes and references
- H. Li, Natl. Sci. Rev., 2017, 5(1), 24–26 CrossRef.
- A. Torfi, R. A. Shirvani, Y. Keneshloo, N. Tavaf and E. A. Fox, Natural Language Processing Advancements By Deep Learning: A Survey, 2021.
- T. P. Nagarhalli, V. Vaze and N. Rana, 2021 Third International Conference on Intelligent Communication Technologies and Virtual Mobile Networks (ICICV), 2021, pp. 1529–1534 Search PubMed.
- Y. Wu, M. Schuster, Z. Chen, Q. V. Le, M. Norouzi, W. Macherey, M. Krikun, Y. Cao, Q. Gao and K. Macherey, et al., 2016, arXiv preprint arXiv:1609.08144.
- A. Lopez, ACM Comput. Surv., 2008, 40, 1–49 CrossRef.
- C. E. Tuncali, G. Fainekos, H. Ito and J. Kapinski, 2018 IEEE Intelligent Vehicles Symposium (IV), 2018, pp. 1555–1562 Search PubMed.
- J. Janai, F. Güney, A. Behl and A. Geiger, et al. , Found. Trends Comput. Graph. Vis., 2020, 12, 1–308 CrossRef.
- M. Daily, S. Medasani, R. Behringer and M. Trivedi, Computer, 2017, 50, 18–23 Search PubMed.
- K. Siau and W. Wang, Cut. Bus. Technol. J., 2018, 31, 47–53 Search PubMed.
- H. A. Pierson and M. S. Gashler, Adv. Robotics, 2017, 31, 821–835 CrossRef.
- K. He, X. Zhang, S. Ren and J. Sun, Proceedings of the IEEE international conference on computer vision, 2015, pp. 1026–1034.
- K. He, X. Zhang, S. Ren and J. Sun, Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
- M. Wu and L. Chen, 2015 Chinese Automation Congress (CAC), 2015, pp. 542–546 Search PubMed.
- P. Covington, J. Adams and E. Sargin, Proceedings of the 10th ACM conference on recommender systems, 2016, pp. 191–198.
- M. Pazzani and D. Billsus, Mach. Learn., 1997, 27, 313–331 CrossRef.
- E. G. Dada, J. S. Bassi, H. Chiroma, A. O. Adetunmbi and O. E. Ajibuwa, et al. , Heliyon, 2019, 5, e01802 CrossRef PubMed.
- T. S. Guzella and W. M. Caminhas, Exp. Syst. Appl., 2009, 36, 10206–10222 CrossRef.
- T. Lengauer, O. Sander, S. Sierra, A. Thielen and R. Kaiser, Nat. Biotechnol., 2007, 25, 1407–1410 CrossRef CAS PubMed.
- P. Larranaga, B. Calvo, R. Santana, C. Bielza, J. Galdiano, I. Inza, J. A. Lozano, R. Armananzas, G. Santafé and A. Pérez, et al. , Briefings Bioinf., 2006, 7, 86–112 CrossRef CAS PubMed.
- B. J. Erickson, P. Korfiatis, Z. Akkus and T. L. Kline, Radiographics, 2017, 37, 505–515 CrossRef PubMed.
- S. Sakhavi, C. Guan and S. Yan, IEEE Trans. Neural Networks Learn. Syst., 2018, 29, 5619–5629 Search PubMed.
- J. Grimmer, M. E. Roberts and B. M. Stewart, Annu. Rev. Political Sci., 2021, 24, 395–419 CrossRef.
- J. B. Heaton, N. G. Polson and J. H. Witte, Appl. Stoch. Models Bus. Ind., 2017, 33, 3–12 CrossRef.
- K. Bansak, J. Ferwerda, J. Hainmueller, A. Dillon, D. Hangartner, D. Lawrence and J. Weinstein, Science, 2018, 359, 325–329 CrossRef CAS PubMed.
- L. Van Der Maaten, E. Postma and J. Van den Herik, et al. , J. Mach. Learn. Res., 2009, 10, 13 Search PubMed.
- G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto and L. Zdeborová, Rev. Modern Phys., 2019, 91, 045002 CrossRef CAS.
- N. M. Ball and R. J. Brunner, Int. J. Mod. Phys. D, 2010, 19, 1049–1106 CrossRef.
- Ž. Ivezić, A. J. Connolly, J. T. VanderPlas and A. Gray, Statistics, data mining, and machine learning in astronomy, Princeton University Press, 2014 Search PubMed.
- A. Radovic, M. Williams, D. Rousseau, M. Kagan, D. Bonacorsi, A. Himmel, A. Aurisano, K. Terao and T. Wongjirad, Nature, 2018, 560, 41–48 CrossRef CAS PubMed.
- P. B. Wigley, P. J. Everitt, A. van den Hengel, J. W. Bastian, M. A. Sooriyabandara, G. D. McDonald, K. S. Hardman, C. D. Quinlivan, P. Manju and C. C. Kuhn, et al. , Sci. Rep., 2016, 6, 1–6 CrossRef PubMed.
- J. Zhou, B. Huang, Z. Yan and J.-C. G. Bünzli, Light: Sci. Appl., 2019, 8, 1–7 CrossRef CAS PubMed.
- A. Chattopadhyay, E. Nabizadeh and P. Hassanzadeh, J. Adv. Modeling Earth Syst., 2020, 12, e2019MS001958 Search PubMed.
- X. Ren, X. Li, K. Ren, J. Song, Z. Xu, K. Deng and X. Wang, Big Data Res., 2021, 23, 100178 CrossRef.
- T. A. Monson, D. W. Armitage and L. J. Hlusko, PaleoBios, 2018, 35, 1–20 CrossRef.
- J. P. Spradley, B. J. Glazer and R. F. Kay, Palaeogeogr., Palaeoclimatol., Palaeoecol., 2019, 518, 155–171 CrossRef.
- I. C. Romero, S. Kong, C. C. Fowlkes, C. Jaramillo, M. A. Urban, F. Oboh-Ikuenobe, C. D’Apolito and S. W. Punyasena, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 28496–28505 CrossRef CAS PubMed.
- G. R. Schleder, A. C. Padilha, C. M. Acosta, M. Costa and A. Fazzio, J. Phys.: Mater., 2019, 2, 032001 CAS.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- O. A. von Lilienfeld and K. Burke, Nat. Commun., 2020, 11, 1–4 CrossRef PubMed.
- Y. Liu, C. Niu, Z. Wang, Y. Gan, Y. Zhu, S. Sun and T. Shen, J. Mater. Sci. Technol., 2020, 57, 113–122 CrossRef.
- F. Strieth-Kalthoff, F. Sandfort, M. H. Segler and F. Glorius, Chem. Soc. Rev., 2020, 49, 6154–6168 RSC.
- C. W. Coley, W. H. Green and K. F. Jensen, Acc. Chem. Res., 2018, 51, 1281–1289 CrossRef CAS PubMed.
- Z. Fu, X. Li, Z. Wang, Z. Li, X. Liu, X. Wu, J. Zhao, X. Ding, X. Wan and F. Zhong, et al. , Org. Chem. Front., 2020, 7, 2269–2277 RSC.
- D. Fooshee, A. Mood, E. Gutman, M. Tavakoli, G. Urban, F. Liu, N. Huynh, D. Van Vranken and P. Baldi, Mol. Syst. Des. Eng., 2018, 3, 442–452 RSC.
- D. Hu, Y. Xie, X. Li, L. Li and Z. Lan, J. Phys. Chem. Lett., 2018, 9, 2725–2732 CrossRef CAS PubMed.
- S. Amabilino, L. A. Bratholm, S. J. Bennie, A. C. Vaucher, M. Reiher and D. R. Glowacki, J. Phys. Chem. A, 2019, 123, 4486–4499 CrossRef CAS PubMed.
- A. Kumar, S. Loharch, S. Kumar, R. P. Ringe and R. Parkesh, Comput. Struct. Biotechnol. J., 2021, 19, 424–438 CrossRef CAS PubMed.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, 2021, arXiv preprint arXiv:2102.06321.
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press, USA, 10th edn, 2011 Search PubMed.
- C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres and W. K. Wootters, Phys. Rev. Lett., 1993, 70, 1895 CrossRef PubMed.
- A. Harrow, P. Hayden and D. Leung, Phys. Rev. Lett., 2004, 92, 187901 CrossRef PubMed.
- D. S. Abrams and S. Lloyd, Phys. Rev. Lett., 1999, 83, 5162–5165 CrossRef CAS.
- P. W. Shor, SIAM Rev., 1999, 41, 303–332 CrossRef.
- L. K. Grover, Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, 1996, pp. 212–219.
- J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe and S. Lloyd, Nature, 2017, 549, 195–202 CrossRef CAS PubMed.
- N. Wiebe, A. Kapoor and K. M. Svore, 2014, arXiv preprint arXiv:1412.3489.
- E. Alpaydin, Introduction to Machine Learning, The MIT Press, 2nd edn, 2010 Search PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, MIT Press, 2016 Search PubMed.
- M. Kubat, An Introduction to Machine Learning, 2017 Search PubMed.
- O. A. Von Lilienfeld, Angew. Chem., Int. Ed., 2018, 57, 4164–4169 CrossRef CAS PubMed.
- B. Huang, N. O. Symonds and O. A. V. Lilienfeld, Handbook of Materials Modeling, 2018, pp. 1–27 Search PubMed.
- H. Häffner, C. F. Roos and R. Blatt, Phys. Rep., 2008, 469, 155–203 CrossRef.
- C. D. Bruzewicz, J. Chiaverini, R. McConnell and J. M. Sage, Appl. Phys. Rev., 2019, 6, 021314 Search PubMed.
- M. Kjaergaard, M. E. Schwartz, J. Braumüller, P. Krantz, J. I.-J. Wang, S. Gustavsson and W. D. Oliver, Ann. Rev. Condens. Matter Phys., 2020, 11, 369–395 CrossRef.
- M. Saffman, T. G. Walker and K. Mølmer, Rev. Mod. Phys., 2010, 82, 2313 CrossRef CAS.
- M. Saffman, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 202001 CrossRef.
- Q. Wei, Y. Cao, S. Kais, B. Friedrich and D. R. Herschbach, ChemPhysChem, 2016, 17(22), 3714–3722 CrossRef PubMed.
- M. Karra, K. Sharma, B. Friedrich, S. Kais and D. R. Herschbach, J. Chem. Phys., 2016, 144(9), 094301 CrossRef PubMed.
- J. Zhu, S. Kais, Q. Wei, D. Herschbach and B. Friedrich, J. Chem. Phys., 2013, 138, 024104 CrossRef PubMed.
- Q. Wei, S. Kais, B. Friedrich and D. Herschbach, J. Chem. Phys., 2011, 134, 124107 CrossRef PubMed.
- Q. Wei, S. Kais, B. Friedrich and D. Herschbach, J. Chem. Phys., 2011, 135, 154102 CrossRef PubMed.
- J. Watrous, The theory of quantum information, Cambridge University Press, 2018 Search PubMed.
- J. Preskill, Lecture Notes for Ph219/CS219, http://theory.caltech.edu/~preskill/ph229/, Accessed: 2021-10-22.
- S.-H. Lin, R. Dilip, A. G. Green, A. Smith and F. Pollmann, PRX Quantum, 2021, 2, 010342 CrossRef.
- K. Yeter-Aydeniz, E. Moschandreou and G. Siopsis, Phys. Rev. A, 2022, 105, 012412 CrossRef CAS.
- C. Yi, Phys. Rev. A, 2021, 104, 052603 CrossRef CAS.
- S. Endo, J. Sun, Y. Li, S. C. Benjamin and X. Yuan, Phys. Rev. Lett., 2020, 125, 010501 CrossRef CAS PubMed.
- D. Deutsch, Proc. R. Soc. London, Ser. A, 1985, 400, 97–117 Search PubMed.
- P. Benioff, J. Stat. Phys., 1980, 22, 563–591 CrossRef.
- X. Hu and S. D. Sarma, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 012312 CrossRef.
- B. M. Terhal, Rev. Mod. Phys., 2015, 87, 307–346 CrossRef.
- A. Kitaev, Ann. Phys., 2003, 303, 2–30 CAS.
- E. Knill and R. Laflamme, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, 900 CrossRef CAS.
- J. Preskill, Quantum, 2018, 2, 79 CrossRef.
- K. Bharti, A. Cervera-Lierta, T. H. Kyaw, T. Haug, S. Alperin-Lea, A. Anand, M. Degroote, H. Heimonen, J. S. Kottmann and T. Menke, et al. , Rev. Mod. Phys., 2022, 94, 015004 CrossRef CAS.
- G. A. Quantum and Collaborators, F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, S. Boixo, M. Broughton and B. B. Buckley, et al. , Science, 2020, 369, 1084–1089 CrossRef PubMed.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre and N. P. Sawaya, et al. , Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS PubMed.
- K. Head-Marsden, J. Flick, C. J. Ciccarino and P. Narang, Chem. Rev., 2020, 121, 3061–3120 CrossRef PubMed.
- X. Yuan, S. Endo, Q. Zhao, Y. Li and S. C. Benjamin, Quantum, 2019, 3, 191 CrossRef.
- M. Cerezo, A. Arrasmith, R. Babbush, S. C. Benjamin, S. Endo, K. Fujii, J. R. McClean, K. Mitarai, X. Yuan and L. Cincio, et al. , Nat. Rev. Phys., 2021, 3, 625–644 CrossRef.
- B. Bauer, S. Bravyi, M. Motta and G. K.-L. Chan, Chem. Rev., 2020, 120, 12685–12717 CrossRef CAS PubMed.
- E. F. Dumitrescu, A. J. McCaskey, G. Hagen, G. R. Jansen, T. D. Morris, T. Papenbrock, R. C. Pooser, D. J. Dean and P. Lougovski, Phys. Rev. Lett., 2018, 120, 210501 CrossRef CAS PubMed.
- S. L. Wu, J. Chan, W. Guan, S. Sun, A. Wang, C. Zhou, M. Livny, F. Carminati, A. Di Meglio and A. C. Li, et al. , J. Phys. G: Nucl. Part. Phys., 2021, 48, 125003 CrossRef CAS.
- W. Guan, G. Perdue, A. Pesah, M. Schuld, K. Terashi, S. Vallecorsa and J.-R. Vlimant, Mach. Learn.: Sci. Technol., 2021, 2, 011003 Search PubMed.
- H.-P. Cheng, E. Deumens, J. K. Freericks, C. Li and B. A. Sanders, Front. Chem., 2020, 1066 Search PubMed.
- R. Orus, S. Mugel and E. Lizaso, Rev. Phys., 2019, 4, 100028 CrossRef.
- S. Lloyd and S. L. Braunstein, in Quantum Computation Over Continuous Variables, ed. S. L. Braunstein and A. K. Pati, Springer Netherlands, Dordrecht, 2003, pp. 9–17 Search PubMed.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- T. Albash and D. A. Lidar, Rev. Mod. Phys., 2018, 90, 015002 CrossRef.
- D-Wave System Documentation, https://docs.dwavesys.com/docs/latest/doc_getting_started.html, Accessed: 2021-10-22.
- P. Hauke, H. G. Katzgraber, W. Lechner, H. Nishimori and W. D. Oliver, Rep. Progress Phys., 2020, 83, 054401 CrossRef CAS PubMed.
- H. N. Djidjev, G. Chapuis, G. Hahn and G. Rizk, Efficient Combinatorial Optimization Using Quantum Annealing, 2018 Search PubMed.
- R. Y. Li, R. Di Felice, R. Rohs and D. A. Lidar, npj Quantum Inform., 2018, 4, 1–10 CrossRef.
- F. Neukart, G. Compostella, C. Seidel, D. Von Dollen, S. Yarkoni and B. Parney, Front. ICT, 2017, 4, 29 CrossRef.
- R. K. Nath, H. Thapliyal and T. S. Humble, 2021, arXiv preprint arXiv:2106.02964.
- S. Ruder, CoRR, 2016, https://arxiv.org/abs/1609.04747.
- T. M. Breuel, CoRR, 2015, https://arxiv.org/abs/1508.02788.
- Q. A. Wang, J. Phys. A: Math. Theor., 2008, 41, 065004 CrossRef.
- Y. Ouali, C. Hudelot and M. Tami, CoRR, 2020, https://arxiv.org/abs/2006.05278.
- V. K. Garg and A. Kalai, CoRR, 2017, https://arxiv.org/abs/1709.05262.
- W. B. Powell, CoRR, 2019, https://arxiv.org/abs/1912.03513.
- V. Francois-Lavet, P. Henderson, R. Islam, M. G. Bellemare and J. Pineau, Found. Trends Mach. Learn., 2018, 11, 219–354 CrossRef.
- B. Scholkopf and A. J. Smola, Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond, MIT Press, Cambridge, MA, USA, 2001 Search PubMed.
- M. G. Genton, J. Mach. Learn. Res., 2001, 2, 299–312 Search PubMed.
- T. Azim and S. Ahmed, Composing Fisher Kernels from Deep Neural Models, Springer, 2018, pp. 1–7 Search PubMed.
- M. Schuld and F. Petruccione, Supervised learning with quantum computers, Springer, 2018, vol. 17 Search PubMed.
- M. Schuld and N. Killoran, Phys. Rev. Lett., 2019, 122, 040504 CrossRef CAS PubMed.
- B. Ghojogh, A. Ghodsi, F. Karray and M. Crowley, 2021, arXiv preprint arXiv:2106.08443.
- S. L. Brunton and J. N. Kutz, Data-driven science and engineering: Machine learning, dynamical systems, and control, Cambridge University Press, 2019 Search PubMed.
- D. W. Marquardt and R. D. Snee, Amer. Statist., 1975, 29, 3–20 Search PubMed.
- G. C. McDonald, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2009, 1, 93–100 CrossRef.
- A. E. Hoerl, R. W. Kannard and K. F. Baldwin, Commun. Stat. Theory Methods, 1975, 4, 105–123 Search PubMed.
- E. Ostertagová, Proc. Eng., 2012, 48, 500–506 CrossRef.
- in Polynomial Regression, ed. J. O. Rawlings, S. G. Pantula and D. A. Dickey, Springer New York, New York, NY, 1998, pp. 235–268 Search PubMed.
- V. Vovk, Empirical inference, Springer, 2013, pp. 105–116 Search PubMed.
- K. Vu, J. C. Snyder, L. Li, M. Rupp, B. F. Chen, T. Khelif, K.-R. Müller and K. Burke, Int. J. Quantum Chem., 2015, 115, 1115–1128 CrossRef CAS.
- C. Saunders, A. Gammerman and V. Vovk, Ridge regression learning algorithm in dual variables, 1998.
- A. Ullah and P. O. Dral, New J. Phys., 2021, 23, 113019 CrossRef CAS.
- J. Westermayr, F. A. Faber, A. S. Christensen, O. A. von Lilienfeld and P. Marquetand, Mach. Learn.: Sci. Technol., 2020, 1, 025009 Search PubMed.
- N. Wiebe, D. Braun and S. Lloyd, Phys. Rev. Lett., 2012, 109, 050505 CrossRef PubMed.
- A. W. Harrow, A. Hassidim and S. Lloyd, Phys. Rev. Lett., 2009, 103, 150502 CrossRef PubMed.
- Y. Lee, J. Joo and S. Lee, Sci. Rep., 2019, 9, 1–12 CrossRef PubMed.
- Y. Liu and S. Zhang, Theor. Comput. Sci., 2017, 657, 38–47 CrossRef.
- G. Wang, Phys. Rev. A, 2017, 96, 012335 CrossRef.
- J. Pan, Y. Cao, X. Yao, Z. Li, C. Ju, H. Chen, X. Peng, S. Kais and J. Du, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 022313 CrossRef.
- Y. Zheng, C. Song, M.-C. Chen, B. Xia, W. Liu, Q. Guo, L. Zhang, D. Xu, H. Deng, K. Huang, Y. Wu, Z. Yan, D. Zheng, L. Lu, J.-W. Pan, H. Wang, C.-Y. Lu and X. Zhu, Phys. Rev. Lett., 2017, 118, 210504 CrossRef PubMed.
- S. Slussarenko and G. J. Pryde, Appl. Phys. Rev., 2019, 6, 041303 Search PubMed.
- M. Schuld, I. Sinayskiy and F. Petruccione, Phys. Rev. A, 2016, 94, 022342 CrossRef.
- Y. Subas, R. D. Somma and D. Orsucci, Phys. Rev. Lett., 2019, 122, 060504 CrossRef PubMed.
- C. Bravo-Prieto, R. LaRose, M. Cerezo, Y. Subasi, L. Cincio and P. J. Coles, 2019, arXiv preprint arXiv:1909.05820.
- C.-H. Yu, F. Gao and Q.-Y. Wen, IEEE Trans. Knowledge Data Eng., 2019, 33, 858–866 Search PubMed.
- D. Berrar, Encyclopedia of Bioinformatics and Computational Biology, Academic Press, Oxford, 2019, pp. 542–545 Search PubMed.
- I. T. Jolliffe and J. Cadima, Philos. Trans. R. Soc., A, 2016, 374, 20150202 CrossRef PubMed.
- I. T. Jolliffe, Principal component analysis for special types of data, Springer, 2002 Search PubMed.
- B. Schölkopf, A. Smola and K.-R. Müller, International conference on artificial neural networks, 1997, pp. 583–588.
- H. Q. Minh, P. Niyogi and Y. Yao, International Conference on Computational Learning Theory, 2006, pp. 154–168.
- C. Campbell, Neurocomputing, 2002, 48, 63–84 CrossRef.
- Q. Wang, 2012, arXiv preprint arXiv:1207.3538.
- S. Lloyd, M. Mohseni and P. Rebentrost, Nat. Phys., 2014, 10, 631–633 Search PubMed.
- Z. Li, Z. Chai, Y. Guo, W. Ji, M. Wang, F. Shi, Y. Wang, S. Lloyd and J. Du, Sci. Adv., 2021, 7, eabg2589 Search PubMed.
- Y. Li, R.-G. Zhou, R. Xu, W. Hu and P. Fan, Quantum Sci. Technol., 2020, 6, 014001 Search PubMed.
- T. Cover and P. Hart, IEEE Trans. Inform. Theory, 1967, 13, 21–27 Search PubMed.
- Y. Ruan, X. Xue, H. Liu, J. Tan and X. Li, Int. J. Theor. Phys., 2017, 56, 3496–3507 CrossRef.
- J. Gou, Z. Yi, L. Du and T. Xiong, Comput. J., 2012, 55, 1058–1071 CrossRef.
- Z. Geler, V. Kurbalija, M. Radovanović and M. Ivanović, Knowledge Inform. Syst., 2016, 48, 331–378 CrossRef.
- S. Lloyd, M. Mohseni and P. Rebentrost, 2013, arXiv preprint arXiv:1307.0411.
- S. Aaronson, Proceedings of the forty-second ACM symposium on Theory of computing, 2010, pp. 141–150 Search PubMed.
- J. Wiśniewska and M. Sawerwain, Vietnam J. Comput. Sci., 2018, 5, 197–204 CrossRef.
- Y. Wang, R. Wang, D. Li, D. Adu-Gyamfi, K. Tian and Y. Zhu, Int. J. Theor. Phys., 2019, 58, 2331–2340 CrossRef.
- S. K. Murthy, Data Min. Knowl. Discov., 1998, 2, 345–389 CrossRef.
- S. B. Kotsiantis, I. Zaharakis, P. Pintelas, et al., Emerging artificial intelligence applications in computer engineering, 2007, vol. 160, pp. 3–24 Search PubMed.
- E. B. Hunt, J. Marin and P. J. Stone, Experiments in induction, 1966 Search PubMed.
- L. Breiman, J. H. Friedman, R. A. Olshen and C. J. Stone, Classification and regression trees, Routledge, 2017 Search PubMed.
- E. Farhi and S. Gutmann, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 58, 915 CrossRef CAS.
- S. Lu and S. L. Braunstein, Quantum Inf. Process., 2014, 13, 757–770 CrossRef.
- K. Khadiev, I. Mannapov and L. Safina, 2019, arXiv preprint arXiv:1907.06840.
- X. Wu, V. Kumar, J. R. Quinlan, J. Ghosh, Q. Yang, H. Motoda, G. J. McLachlan, A. Ng, B. Liu and S. Y. Philip, et al. , Knowledge Inform. Syst., 2008, 14, 1–37 CrossRef.
- F. V. Jensen and T. D. Nielsen, Bayesian networks and decision graphs, Springer, 2007, vol. 2 Search PubMed.
- D. Heckerman, Innovations Bayesian Networks, 2008, pp. 33–82 Search PubMed.
- R. R. Tucci, Int. J. Mod. Phys. B, 1995, 9, 295–337 CrossRef.
- M. S. Leifer and D. Poulin, Ann. Phys., 2008, 323, 1899–1946 CAS.
- C. Moreira and A. Wichert, Front. Psychol., 2016, 7, 11 Search PubMed.
- G. H. Low, T. J. Yoder and I. L. Chuang, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 062315 CrossRef.
- S. E. Borujeni, S. Nannapaneni, N. H. Nguyen, E. C. Behrman and J. E. Steck, Exp. Syst. Appl., 2021, 176, 114768 CrossRef.
- V. Vapnik, The nature of statistical learning theory, Springer science & business media, 2013 Search PubMed.
- Z. Li, X. Liu, N. Xu and J. Du, Phys. Rev. Lett., 2015, 114, 140504 CrossRef.
- P. Rebentrost, M. Mohseni and S. Lloyd, Phys. Rev. Lett., 2014, 113, 130503 CrossRef.
- A. W. Harrow, A. Hassidim and S. Lloyd, Phys. Rev. Lett., 2009, 103, 150502 CrossRef PubMed.
- M. Schuld and N. Killoran, Phys. Rev. Lett., 2019, 122, 040504 CrossRef CAS.
- Y. Liu, S. Arunachalam and K. Temme, Nat. Phys., 2021, 17, 1013–1017 Search PubMed.
- M. Otten, I. R. Goumiri, B. W. Priest, G. F. Chapline and M. D. Schneider, 2020, arXiv preprint arXiv:2004.11280.
- C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning, MIT Press, Cambridge, MA, 2006, vol. 2 Search PubMed.
- V. L. Deringer, A. P. Bartók, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csányi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning (Information Science and Statistics), Springer-Verlag, Berlin, Heidelberg, 2006 Search PubMed.
- Y. Freund, R. Schapire and N. Abe, A short introduction to boosting, J. Jpn. Soc. Artif. Intell., 1999, 14(771–780), 1612 Search PubMed.
- A. J. Al-Mahasneh, S. G. Anavatti and M. A. Garratt, 2017 International Conference on Advanced Mechatronics, Intelligent Manufacture, and Industrial Automation (ICAMIMIA), 2017, pp. 1–6 Search PubMed.
- F. Rosenblatt, Psychological Rev., 1958, 65, 386 CAS.
- S. Haykin and N. Network, Neural Networks, 2004, 2, 41 Search PubMed.
- M. M. Lau and K. H. Lim, 2018 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES), 2018, pp. 686–690 Search PubMed.
- S. Sharma and S. Sharma, Towards Data Sci., 2017, 6, 310–316 Search PubMed.
- A. L. Maas, A. Y. Hannun, A. Y. Ng, et al., Proc. ICML, 2013, p. 3.
- S. Jankowski, A. Lozowski and J. M. Zurada, IEEE Trans. Neural Networks, 1996, 7, 1491–1496 CrossRef CAS.
- G. Tanaka and K. Aihara, IEEE Trans. Neural Networks, 2009, 20, 1463–1473 Search PubMed.
- B. Karlik and A. V. Olgac, Int. J. Artificial Intell. Exp. Syst., 2011, 1, 111–122 Search PubMed.
- F. Agostinelli, M. Hoffman, P. Sadowski and P. Baldi, 2014, arXiv preprint arXiv:1412.6830.
- P.-T. De Boer, D. P. Kroese, S. Mannor and R. Y. Rubinstein, Ann. Oper. Res., 2005, 134, 19–67 CrossRef.
- D. E. Rumelhart, G. E. Hinton and R. J. Williams, Nature, 1986, 323, 533–536 CrossRef.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS PubMed.
- S. Ruder, 2016, arXiv preprint arXiv:1609.04747.
- J. Duchi, E. Hazan and Y. Singer, J. Mach. Learn. Res., 2011, 12, 2121–2159 Search PubMed.
- D. P. Kingma and J. Ba, 2014, arXiv preprint arXiv:1412.6980.
- T. Dozat, Incorporating Nesterov Momentum into Adam, ICLR Workshop, 2016 Search PubMed.
- L. Wan, M. Zeiler, S. Zhang, Y. Le Cun and R. Fergus, International conference on machine learning, 2013, pp. 1058–1066 Search PubMed.
- F. Girosi, M. Jones and T. Poggio, Neural Comput., 1995, 7, 219–269 CrossRef.
- N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, J. Mach. Learn. Res., 2014, 15, 1929–1958 Search PubMed.
- R. Xia and S. Kais, Entropy, 2020, 22, 828 CrossRef CAS.
- J. R. McClean, S. Boixo, V. N. Smelyanskiy, R. Babbush and H. Neven, Nat. Commun., 2018, 9, 1–6 CrossRef CAS.
- A. Mari, T. R. Bromley, J. Izaac, M. Schuld and N. Killoran, Quantum, 2020, 4, 340 CrossRef.
- J. Li and S. Kais, New J. Phys., 2021, 23(10), 103022 CrossRef.
- N. Wiebe and V. Kliuchnikov, New J. Phys., 2013, 15, 093041 CrossRef.
- A. Paetznick and K. M. Svore, 2013, arXiv preprint arXiv:1311.1074.
- Y. Cao, G. G. Guerreschi and A. Aspuru-Guzik, 2017, arXiv preprint arXiv:1711.11240.
- A. Daskin, 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), 2018, pp. 2887–2891 Search PubMed.
- M. Schuld, I. Sinayskiy and F. Petruccione, Phys. Lett. A, 2015, 379, 660–663 CrossRef CAS.
- I. Cong, S. Choi and M. D. Lukin, Nat. Phys., 2019, 15, 1273–1278 Search PubMed.
- W. Rawat and Z. Wang, Neural Comput., 2017, 29, 2352–2449 CrossRef.
- A. Voulodimos, N. Doulamis, A. Doulamis and E. Protopapadakis, Comput. Intell. Neurosci., 2018, 2018, 13 Search PubMed.
- S. Albawi, T. A. Mohammed and S. Al-Zawi, 2017 International Conference on Engineering and Technology (ICET), 2017, pp. 1–6 Search PubMed.
- Y. LeCun, P. Haffner, L. Bottou and Y. Bengio, Shape, contour and grouping in computer vision, Springer, 1999, pp. 319–345 Search PubMed.
- A. Dhillon and G. K. Verma, Progress Artificial Intell., 2020, 9, 85–112 CrossRef.
- N. Aloysius and M. Geetha, 2017 International Conference on Communication and Signal Processing (ICCSP), 2017, pp. 0588–0592 Search PubMed.
- C. Kong and S. Lucey, 2017, arXiv preprint arXiv:1712.02502.
- L. Alzubaidi, J. Zhang, A. J. Humaidi, A. Al-Dujaili, Y. Duan, O. Al-Shamma, J. Santamara, M. A. Fadhel, M. Al-Amidie and L. Farhan, J. Big Data, 2021, 8, 1–74 CrossRef.
- D. Yu, H. Wang, P. Chen and Z. Wei, International conference on rough sets and knowledge technology, 2014, pp. 364–375 Search PubMed.
- Z. Li, S.-H. Wang, R.-R. Fan, G. Cao, Y.-D. Zhang and T. Guo, Int. J. Imaging Syst. Technol., 2019, 29, 577–583 CrossRef.
- W. Yin, K. Kann, M. Yu and H. Schütze, 2017, arXiv preprint arXiv:1702.01923.
- S. Selvin, R. Vinayakumar, E. Gopalakrishnan, V. K. Menon and K. Soman, 2017 international conference on advances in computing, communications and informatics (icacci), 2017, pp. 1643–1647.
- K. Cho, B. Van Merriënboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk and Y. Bengio, 2014, arXiv preprint arXiv:1406.1078.
- Y. Qin, D. Song, H. Chen, W. Cheng, G. Jiang and G. Cottrell, 2017, arXiv preprint arXiv:1704.02971.
- Y. Yu, X. Si, C. Hu and J. Zhang, Neural Comput., 2019, 31, 1235–1270 CrossRef.
- Y. Takaki, K. Mitarai, M. Negoro, K. Fujii and M. Kitagawa, Phys. Rev. A, 2021, 103, 052414 CrossRef CAS.
- A. Sherstinsky, Phys. D, 2020, 404, 132306 CrossRef.
- S. Yang, X. Yu and Y. Zhou, 2020 International workshop on electronic communication and artificial intelligence (IWECAI), 2020, pp. 98–101 Search PubMed.
- R. Dey and F. M. Salem, 2017 IEEE 60th international midwest symposium on circuits and systems (MWSCAS), 2017, pp. 1597–1600 Search PubMed.
- J. Chung, C. Gulcehre, K. Cho and Y. Bengio, 2014, arXiv preprint arXiv:1412.3555.
- S. Hochreiter and J. Schmidhuber, Neural Comput., 1997, 9, 1735–1780 CrossRef CAS PubMed.
- S. Y.-C. Chen, S. Yoo and Y.-L. L. Fang, 2020, arXiv preprint arXiv:2009.01783.
- A. Makhzani and B. Frey, K-sparse autoencoders, arXiv:1312.5663, 2013.
- P. Vincent, H. Larochelle, I. Lajoie, Y. Bengio and P.-A. Manzagol, J. Mach. Learn. Res., 2010, 11, 3371–3408 Search PubMed.
- R. Salakhutdinov and G. Hinton, Int. J. Approx. Reason., 2009, 50, 969–978 CrossRef.
- M. Ribeiro, A. E. Lazzaretti and H. S. Lopes, Pattern Recognition Lett., 2018, 105, 13–22 CrossRef.
- J. Romero, J. P. Olson and A. Aspuru-Guzik, Quantum Sci. Technol., 2017, 2, 045001 CrossRef.
- V. Shende, I. L. Markov and S. S. Bullock, Minimal universal two-qubit controlled-not-based circuits, Phys. Rev. A, 2004, 69(6), 062321 CrossRef.
- L. Lamata, U. Alvarez-Rodriguez, J. D. Martín-Guerrero, M. Sanz and E. Solano, Quantum Sci. Technol., 2018, 4, 014007 CrossRef.
- K. H. Wan, O. Dahlsten, H. Kristjánsson, R. Gardner and M. S. Kim, npj Quantum Inform., 2017, 3, 36 CrossRef.
- N. Dilokthanakul, P. A. M. Mediano, M. Garnelo, M. C. H. Lee, H. Salimbeni, K. Arulkumaran and M. Shanahan, 2016, arXiv preprint arXiv:1611.02648.
- W. Xu, H. Sun, C. Deng and Y. Tan, Proc. AAAI Conf. Artificial Intell., 2017, 31, 3358 Search PubMed.
- P.-L. Dallaire-Demers and N. Killoran, Phys. Rev. A, 2018, 98, 012324 CrossRef CAS.
- A. Khoshaman, W. Vinci, B. Denis, E. Andriyash, H. Sadeghi and M. H. Amin, Quantum Sci. Technol., 2018, 4, 014001 CrossRef.
- M. H. Amin, E. Andriyash, J. Rolfe, B. Kulchytskyy and R. Melko, Phys. Rev. X, 2018, 8, 021050 CAS.
- I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Generative Adversarial Nets, Advances in Neural Information Processing Systems 27, 2014 Search PubMed.
- J. Yu, Z. Lin, J. Yang, X. Shen, X. Lu and T. S. Huang, Generative image inpainting with contextual attention, Proceedings of the IEEE conference on computer vision and pattern recognition, 2018 Search PubMed , p. 5505.
- K. Schawinski, C. Zhang, H. Zhang, L. Fowler and G. K. Santhanam, Mon. Not. R. Astron. Soc.: Lett., 2017, slx008 CrossRef.
- X. Wang, K. Yu, S. Wu, J. Gu, Y. Liu, C. Dong, C. C. Loy, Y. Qiao and X. Tang, Esrgan: Enhanced super-resolution generative adversarial networks, 2018 Search PubMed , arXiv:1809.00219.
- B. Li, V. François-Lavet, T. Doan and J. Pineau, 2021, arXiv preprint arXiv:2102.07097.
- S. Lloyd and C. Weedbrook, Phys. Rev. Lett., 2018, 121, 040502 CrossRef CAS.
- M. Schuld, V. Bergholm, C. Gogolin, J. Izaac and N. Killoran, Phys. Rev. A, 2019, 99, 032331 CrossRef CAS.
- J. Biamonte and V. Bergholm, 2017, arXiv preprint arXiv:1708.00006.
- J. C. Bridgeman and C. T. Chubb, J. Phys. A: Math. Theor., 2017, 50(22), 223001 CrossRef.
- G. Vidal, Phys. Rev. Lett., 2004, 93, 040502 CrossRef.
- G. Vidal, Phys. Rev. Lett., 2003, 91, 147902 CrossRef PubMed.
- J. Eisert, M. Cramer and M. B. Plenio, Rev. Mod. Phys., 2010, 82, 277 CrossRef.
- M. B. Hastings, J. Stat. Mech.: Theory Exp., 2007, 2007, P08024 Search PubMed.
- R. Orús, Ann. Phys., 2014, 349, 117–158 Search PubMed.
- G. Vidal, 2009, arXiv preprint arXiv:0912.1651.
- U. Schollwöck, Ann. Phys., 2011, 326, 96–192 Search PubMed.
- V. Oseledets and E. E. Tyrtyshnikov, SIAM J. Sci. Comput., 2009, 31, 3744–3759 CrossRef.
- I. V. Oseledets, SIAM J. Sci. Comput., 2011, 33, 2295–2317 CrossRef.
- Y.-Y. Shi, L.-M. Duan and G. Vidal, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 022320 CrossRef.
- D. Nagaj, E. Farhi, J. Goldstone, P. Shor and I. Sylvester, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 214431 CrossRef.
- B. Friedman, J. Phys.: Condens. Matter, 1997, 9, 9021 CrossRef CAS.
- N. Nakatani and G. K.-L. Chan, J. Chem. Phys., 2013, 138, 134113 CrossRef.
- D. Castellana and D. Bacciu, Learning from Non-Binary Constituency Trees via Tensor Decomposition, 2020, https://arxiv.org/abs/2011.00860.
- M. E. Fisher, Rev. Mod. Phys., 1998, 70, 653 CrossRef.
- L. Tagliacozzo, G. Evenbly and G. Vidal, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235127 CrossRef.
- H. R. Larsson, J. Chem. Phys., 2019, 151, 204102 CrossRef.
- Y. Kurashige, J. Chem. Phys., 2018, 149, 194114 CrossRef.
- M. Kliesch, D. Gross and J. Eisert, Phys. Rev. Lett., 2014, 113, 160503 CrossRef CAS PubMed.
- R. Raussendorf and H. J. Briegel, Phys. Rev. Lett., 2001, 86, 5188 CrossRef CAS.
- F. Verstraete, M. M. Wolf, D. Perez-Garcia and J. I. Cirac, Phys. Rev. Lett., 2006, 96, 220601 CrossRef CAS.
- A. Y. Kitaev, Ann. Phys., 2003, 303, 2–30 CAS.
- M. Schwarz, O. Buerschaper and J. Eisert, Phys. Rev. A, 2017, 95, 060102 CrossRef.
- J. Jordan, R. Orús, G. Vidal, F. Verstraete and J. I. Cirac, Phys. Rev. Lett., 2008, 101(25), 250602 CrossRef CAS PubMed.
- Z.-C. Gu, M. Levin and X.-G. Wen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 205116 CrossRef.
- M. Schwarz, K. Temme and F. Verstraete, Phys. Rev. Lett., 2012, 108, 110502 CrossRef.
- M. Schwarz, K. Temme, F. Verstraete, D. Perez-Garcia and T. S. Cubitt, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 032321 CrossRef.
- P. Corboz, P. Czarnik, G. Kapteijns and L. Tagliacozzo, Phys. Rev. X, 2018, 8(3), 031031 Search PubMed.
- A. Milsted and G. Vidal, 2018, arXiv preprint arXiv:1812.00529.
- G. Vidal, Phys. Rev. Lett., 2008, 101, 110501 CrossRef CAS PubMed.
- G. Evenbly and G. Vidal, Phys. Rev. Lett., 2009, 102(18), 180406 CrossRef CAS PubMed.
- S. R. White, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10345 CrossRef CAS.
- J. Kempe, A. Kitaev and O. Regev, SIAM J. Comput., 2006, 35, 1070–1097 CrossRef.
- A. Kawaguchi, K. Shimizu, Y. Tokura and N. Imoto, 2004, arXiv preprint quant-ph/0411205.
- A. Dang, C. D. Hill and L. C. Hollenberg, Quantum, 2019, 3, 116 CrossRef.
- E. Dumitrescu, Phys. Rev. A, 2017, 96, 062322 CrossRef.
- C. Huang, F. Zhang, M. Newman, J. Cai, X. Gao, Z. Tian, J. Wu, H. Xu, H. Yu, B. Yuan, et al., 2020, arXiv preprint arXiv:2005.06787.
- F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. Brandao and D. A. Buell, et al. , Nature, 2019, 574, 505–510 CrossRef CAS PubMed.
- C. Huang, F. Zhang, M. Newman, X. Ni, D. Ding, J. Cai, X. Gao, T. Wang, F. Wu and G. Zhang, et al. , Nat. Comput. Sci., 2021, 1, 578–587 CrossRef.
- I. L. Markov and Y. Shi, SIAM J. Comput., 2008, 38, 963–981 CrossRef.
- J.-G. Liu, Y.-H. Zhang, Y. Wan and L. Wang, Phys. Rev. Res., 2019, 1, 023025 CrossRef CAS.
- S.-J. Ran, Phys. Rev. A, 2020, 101(3), 032310 CrossRef CAS.
- W. Huggins, P. Patil, B. Mitchell, K. B. Whaley and E. M. Stoudenmire, Quantum Sci. Technol., 2019, 4, 024001 CrossRef.
- A. Kardashin, A. Uvarov and J. Biamonte, Front. Phys., 2021, 644 Search PubMed.
- I. H. Kim and B. Swingle, 2017, arXiv preprint arXiv:1711.07500.
- X. Yuan, J. Sun, J. Liu, Q. Zhao and Y. Zhou, Phys. Rev. Lett., 2021, 127, 040501 CrossRef CAS PubMed.
- K. Mitarai, M. Negoro, M. Kitagawa and K. Fujii, Phys. Rev. A, 2018, 98, 032309 CrossRef CAS.
- P. Arrighi, Natural Comput., 2019, 18, 885–899 CrossRef CAS.
- A. Pérez-Salinas, A. Cervera-Lierta, E. Gil-Fuster and J. I. Latorre, Quantum, 2020, 4, 226 CrossRef.
- M. Schuld, R. Sweke and J. J. Meyer, Phys. Rev. A, 2021, 103, 032430 CrossRef CAS.
- H. Chen, L. Wossnig, S. Severini, H. Neven and M. Mohseni, Quantum Mach. Intell., 2021, 3, 1–11 CrossRef.
- S. Sim, P. D. Johnson and A. Aspuru-Guzik, Adv. Quantum Technol., 2019, 2, 1900070 CrossRef.
- J. C. Snyder, M. Rupp, K. Hansen, K.-R. Müller and K. Burke, Phys. Rev. Lett., 2012, 108, 253002 CrossRef PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- A. S. Christensen, L. A. Bratholm, F. A. Faber and O. Anatole von Lilienfeld, J. Chem. Phys., 2020, 152, 044107 CrossRef CAS PubMed.
- M.-W. Huang, C.-W. Chen, W.-C. Lin, S.-W. Ke and C.-F. Tsai, PLoS One, 2017, 12, e0161501 CrossRef.
- H. Sun, S. Shahane, M. Xia, C. P. Austin and R. Huang, J. Chem. Inf. Model., 2012, 52, 1798–1805 CrossRef CAS PubMed.
- K. Batra, K. M. Zorn, D. H. Foil, E. Minerali, V. O. Gawriljuk, T. R. Lane and S. Ekins, J. Chem. Inf. Model., 2021, 61(6), 2641–2647 CrossRef CAS PubMed.
- L. H. Li, D.-B. Zhang and Z. Wang, 2021, arXiv preprint arXiv:2108.11114.
- S. D. Bartlett, B. C. Sanders, S. L. Braunstein and K. Nemoto, in Efficient Classical Simulation of Continuous Variable Quantum Information Processes, ed. S. L. Braunstein and A. K. Pati, Springer Netherlands, Dordrecht, 2003, pp. 47–55 Search PubMed.
- S. L. Braunstein and P. van Loock, Rev. Mod. Phys., 2005, 77, 513–577 CrossRef.
- S. D. Bartlett and B. C. Sanders, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 042304 CrossRef.
- T. Douce, D. Markham, E. Kashefi, E. Diamanti, T. Coudreau, P. Milman, P. van Loock and G. Ferrini, Phys. Rev. Lett., 2017, 118, 070503 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- V. Havlček, A. D. Córcoles, K. Temme, A. W. Harrow, A. Kandala, J. M. Chow and J. M. Gambetta, Nature, 2019, 567, 209–212 CrossRef PubMed.
- T. Kusumoto, K. Mitarai, K. Fujii, M. Kitagawa and M. Negoro, npj Quantum Inform., 2021, 7, 1–7 CrossRef.
- K. Bartkiewicz, C. Gneiting, A. Černoch, K. Jiráková, K. Lemr and F. Nori, Sci. Rep., 2020, 10, 1–9 CrossRef PubMed.
- M. Guo and Y. Weng, Where can quantum kernel methods make a big difference?, 2022, https://openreview.net/forum?id=NoE4RfaOOa.
- M. Matsumoto and T. Nishimura, ACM Trans. Model. Comput. Simul., 1998, 8, 3–30 CrossRef.
- X. Wang, Y. Du, Y. Luo and D. Tao, Quantum, 2021, 5, 531 CrossRef.
- S. S. Vedaie, M. Noori, J. S. Oberoi, B. C. Sanders and E. Zahedinejad, 2020, arXiv preprint arXiv:2011.09694.
- C. Blank, D. K. Park, J.-K. K. Rhee and F. Petruccione, npj Quantum Inform., 2020, 6, 1–7 CrossRef.
- S. Lloyd, M. Schuld, A. Ijaz, J. Izaac and N. Killoran, 2020, arXiv preprint arXiv:2001.03622.
- E. Peters, J. Caldeira, A. Ho, S. Leichenauer, M. Mohseni, H. Neven, P. Spentzouris, D. Strain and G. N. Perdue, npj Quantum Inform., 2021, 7, 1–5 CrossRef.
- X. Yang, M. Kahnt, D. Brückner, A. Schropp, Y. Fam, J. Becher, J.-D. Grunwaldt, T. L. Sheppard and C. G. Schroer, J. Synchrotron Radiat., 2020, 27, 486–493 CrossRef.
- Z. Liu, T. Bicer, R. Kettimuthu, D. Gursoy, F. De Carlo and I. Foster, JOSA A, 2020, 37, 422–434 CrossRef.
- J. Carrasquilla and R. G. Melko, Nat. Phys., 2017, 13, 431–434 Search PubMed.
- J. Gao, L.-F. Qiao, Z.-Q. Jiao, Y.-C. Ma, C.-Q. Hu, R.-J. Ren, A.-L. Yang, H. Tang, M.-H. Yung and X.-M. Jin, Phys. Rev. Lett., 2018, 120, 240501 CrossRef CAS.
- S. Lohani, B. T. Kirby, M. Brodsky, O. Danaci and R. T. Glasser, Mach. Learn.: Sci. Technol., 2020, 1, 035007 Search PubMed.
- M. Ragoza, J. Hochuli, E. Idrobo, J. Sunseri and D. R. Koes, J. Chem. Inf. Model., 2017, 57, 942–957 CrossRef CAS PubMed.
- K. Yao, J. E. Herr, D. W. Toth, R. Mckintyre and J. Parkhill, Chem. Sci., 2018, 9, 2261–2269 RSC.
- T. B. Hughes, G. P. Miller and S. J. Swamidass, ACS Cent. Sci., 2015, 1, 168–180 CrossRef CAS.
- C. Caetano, J. Reis Jr, J. Amorim, M. R. Lemes and A. D. Pino Jr, Int. J. Quantum Chem., 2011, 111, 2732–2740 CrossRef CAS.
- K. T. Schütt, M. Gastegger, A. Tkatchenko, K.-R. Müller and R. J. Maurer, Nat. Commun., 2019, 10, 1–10 CrossRef PubMed.
- R. Galvelis and Y. Sugita, J. Chem. Theory Comput., 2017, 13, 2489–2500 CrossRef CAS PubMed.
- J. Zeng, L. Cao, M. Xu, T. Zhu and J. Z. Zhang, Nat. Commun., 2020, 11, 1–9 CrossRef PubMed.
- G. Carleo and M. Troyer, Science, 2017, 355, 602–606 CrossRef CAS PubMed.
- M. Sajjan, S. H. Sureshbabu and S. Kais, J. Am. Chem. Soc., 2021, 143(44), 18426–18445 CrossRef CAS PubMed.
- A. Abbas, D. Sutter, C. Zoufal, A. Lucchi, A. Figalli and S. Woerner, Nat. Comput. Sci., 2021, 1, 403–409 CrossRef.
- F. Kunstner, P. Hennig and L. Balles, Adv. Neural Inform. Process. Syst., 2019, 32, 1 Search PubMed.
- R. Karakida, S. Akaho and S.-I. Amari, The 22nd International Conference on Artificial Intelligence and Statistics, 2019, pp. 1032–1041.
- O. Berezniuk, A. Figalli, R. Ghigliazza and K. Musaelian, 2020, arXiv preprint arXiv:2001.10872.
- K. Sharma, M. Cerezo, Z. Holmes, L. Cincio, A. Sornborger and P. J. Coles, Phys. Rev. Lett., 2022, 128, 070501 CrossRef CAS PubMed.
- S. P. Adam, S.-A. N. Alexandropoulos, P. M. Pardalos and M. N. Vrahatis, in No Free Lunch Theorem: A Review, ed. I. C. Demetriou and P. M. Pardalos, Springer International Publishing, Cham, 2019, pp. 57–82 Search PubMed.
- M. M. Wolf, Mathematical Foundations of Supervised Learning, 2018, https://www-m5.ma.tum.de/Allgemeines/MA4801_2016S.
- K. Poland, K. Beer and T. J. Osborne, 2020, arXiv preprint arXiv:2003.14103.
- C. H. Bennett and S. J. Wiesner, Phys. Rev. Lett., 1992, 69, 2881–2884 CrossRef PubMed.
- A. Harrow, P. Hayden and D. Leung, Phys. Rev. Lett., 2004, 92, 187901 CrossRef PubMed.
- C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres and W. K. Wootters, Phys. Rev. Lett., 1993, 70, 1895–1899 CrossRef PubMed.
- Y.-H. Luo, H.-S. Zhong, M. Erhard, X.-L. Wang, L.-C. Peng, M. Krenn, X. Jiang, L. Li, N.-L. Liu, C.-Y. Lu, A. Zeilinger and J.-W. Pan, Phys. Rev. Lett., 2019, 123, 070505 CrossRef CAS PubMed.
- A. Pesah, M. Cerezo, S. Wang, T. Volkoff, A. T. Sornborger and P. J. Coles, Phys. Rev. X, 2021, 11, 041011 CAS.
- I. MacCormack, C. Delaney, A. Galda, N. Aggarwal and P. Narang, Phys. Rev. Res., 2022, 4, 013117 CrossRef CAS.
- H.-Y. Lee, N. Kawashima and Y. B. Kim, Phys. Rev. Res., 2020, 2, 033318 CrossRef CAS.
- S. C. Kuhn and M. Richter, Phys. Rev. B, 2020, 101, 075302 CrossRef CAS.
- K. Gunst, F. Verstraete, S. Wouters, O. Legeza and D. Van Neck, J. Chem. Theory Comput., 2018, 14, 2026–2033 CrossRef CAS PubMed.
- Y. LeCun, C. Cortes and C. Burges, MNIST handwritten digit database, 2010.
- J. C. Spall, Proceedings of the 31st conference on Winter simulation: Simulation-a bridge to the future-Volume 1, 1999, pp. 101–109.
- I. V. Oseledets and E. E. Tyrtyshnikov, SIAM J. Sci. Comput., 2009, 31, 3744–3759 CrossRef.
- S. Kais, Quantum Information and Computation for Chemistry, Wiley and Sons: Hoboken, NJ, 2014, vol. 154 Search PubMed.
- J. Altepeter, E. Jeffrey and P. Kwiat, Photonic State Tomography, Academic Press, 2005, vol. 52, pp. 105–159 Search PubMed.
- D. F. V. James, P. G. Kwiat, W. J. Munro and A. G. White, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 052312 CrossRef.
- K. Banaszek, M. Cramer and D. Gross, New J. Phys., 2013, 15, 125020 CrossRef.
- C. Song, K. Xu, W. Liu, C.-P. Yang, S.-B. Zheng, H. Deng, Q. Xie, K. Huang, Q. Guo, L. Zhang, P. Zhang, D. Xu, D. Zheng, X. Zhu, H. Wang, Y.-A. Chen, C.-Y. Lu, S. Han and J.-W. Pan, Phys. Rev. Lett., 2017, 119, 180511 CrossRef PubMed.
- G. Torlai, G. Mazzola, J. Carrasquilla, M. Troyer, R. Melko and G. Carleo, Nat. Phys., 2018, 14, 447–450 Search PubMed.
- J. Carrasquilla, G. Torlai, R. G. Melko and L. Aolita, Nat. Mach. Intell., 2019, 1, 155–161 Search PubMed.
- A. M. Palmieri, E. Kovlakov, F. Bianchi, D. Yudin, S. Straupe, J. D. Biamonte and S. Kulik, npj Quantum Inform., 2020, 6, 20 Search PubMed.
- T. Xin, S. Lu, N. Cao, G. Anikeeva, D. Lu, J. Li, G. Long and B. Zeng, npj Quantum Inform., 2019, 5, 1–8 Search PubMed.
- J. Cotler and F. Wilczek, Phys. Rev. Lett., 2020, 124, 100401 CrossRef CAS PubMed.
- S. Aaronson, Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, New York, NY, USA, 2018, pp. 325–338 Search PubMed.
- H.-Y. Huang, R. Kueng and J. Preskill, Nat. Phys., 2020, 16, 1050–1057 Search PubMed.
- E. T. Jaynes, Phys. Rev., 1957, 108, 171–190 CrossRef.
- E. H. Wichmann, J. Math. Phys., 1963, 4, 884–896 CrossRef CAS.
- A. Katz, Principles of Statistical Mechanics: The Information Theory Approach, W. H. Freeman, 1967 Search PubMed.
- Z. Hradil, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, R1561–R1564 CrossRef CAS.
- Y. S. Teo, H. Zhu, B.-G. Englert, J. Řeháček and Z. Hradil, Phys. Rev. Lett., 2011, 107, 020404 CrossRef PubMed.
- Y. S. Teo, B. Stoklasa, B.-G. Englert, J. Řeháček and Z. Hradil, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 042317 CrossRef.
- R. Blume-Kohout, Phys. Rev. Lett., 2010, 105, 200504 CrossRef PubMed.
- J. A. Smolin, J. M. Gambetta and G. Smith, Phys. Rev. Lett., 2012, 108, 070502 CrossRef PubMed.
- T. Baumgratz, A. Nüßeler, M. Cramer and M. B. Plenio, New J. Phys., 2013, 15, 125004 CrossRef.
- R. Blume-Kohout, New J. Phys., 2010, 12, 043034 CrossRef.
- F. Huszár and N. M. Houlsby, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 052120 CrossRef.
- J. M. Lukens, K. J. Law, A. Jasra and P. Lougovski, New J. Phys., 2020, 22, 063038 CrossRef.
- J. M. Lukens, K. J. Law and R. S. Bennink, 2020, arXiv preprint arXiv:2012.08997.
- R. Gupta, R. Xia, R. D. Levine and S. Kais, PRX Quantum, 2021, 2, 010318 CrossRef.
- R. Gupta, R. D. Levine and S. Kais, J. Phys. Chem. A, 2021, 7588–7594 CrossRef CAS PubMed.
- C. Helstrom, Mathematics in Science and Engineering, Academic Press, New York, 1976, vol. 123, pp. 1572–9613 Search PubMed.
- S. Gudder, et al. , Bull. (New Series) Am. Math. Soc., 1985, 13, 80–85 CrossRef.
- A. Peres, Quantum Theory: Concepts and Methods, Kluwer Academic Publishers, Boston, 1993 Search PubMed.
- M. Sasaki and A. Carlini, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 022303 CrossRef.
- R. Chrisley, New directions in cognitive science: Proceedings of the international symposium, Saariselka, 1995 Search PubMed.
- E. C. Behrman, J. Niemel, J. E. Steck and S. R. Skinner, Proceedings of the 4th Workshop on Physics of Computation, 1996, pp. 22–24.
- E. C. Behrman, J. E. Steck and S. R. Skinner, IJCNN'99. International Joint Conference on Neural Networks. Proceedings (Cat. No. 99CH36339), 1999, pp. 874–877.
- M. Benedetti, D. Garcia-Pintos, O. Perdomo, V. Leyton-Ortega, Y. Nam and A. Perdomo-Ortiz, npj Quantum Inform., 2019, 5, 1–9 CrossRef.
- S. Cheng, J. Chen and L. Wang, Entropy, 2018, 20, 583 CrossRef PubMed.
- E. M. Stoudenmire and D. J. Schwab, 2016, arXiv preprint arXiv:1605.05775.
- Z.-Y. Han, J. Wang, H. Fan, L. Wang and P. Zhang, Phys. Rev. X, 2018, 8, 031012 CAS.
- X. Gao, Z.-Y. Zhang and L.-M. Duan, Sci. Adv., 2018, 4, eaat9004 CrossRef CAS PubMed.
- J. M. Arrazola, T. R. Bromley, J. Izaac, C. R. Myers, K. Brádler and N. Killoran, Quantum Sci. Technol., 2019, 4, 024004 CrossRef.
- N. Killoran, T. R. Bromley, J. M. Arrazola, M. Schuld, N. Quesada and S. Lloyd, Phys. Rev. Res., 2019, 1, 033063 CrossRef CAS.
- N. Killoran, J. Izaac, N. Quesada, V. Bergholm, M. Amy and C. Weedbrook, Quantum, 2019, 3, 129 CrossRef.
- X.-M. Zhang, Z. Wei, R. Asad, X.-C. Yang and X. Wang, npj Quantum Inform., 2019, 5, 1–7 CrossRef.
- M. Benedetti, E. Lloyd, S. Sack and M. Fiorentini, Quantum Sci. Technol., 2019, 4, 043001 CrossRef.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, New J. Phys., 2016, 18, 023023 CrossRef.
- H.-Y. Huang, K. Bharti and P. Rebentrost, 2019, arXiv preprint arXiv:1909.07344.
- R. LaRose, A. Tikku, É. O’Neel-Judy, L. Cincio and P. J. Coles, npj Quantum Inform., 2019, 5, 1–10 CrossRef.
- M. Cerezo, K. Sharma, A. Arrasmith and P. J. Coles, 2020, arXiv preprint arXiv:2004.01372.
- X. Wang, Z. Song and Y. Wang, Quantum, 2021, 5, 483 CrossRef.
- Y. Wang, G. Li and X. Wang, 2021, arXiv preprint arXiv:2103.01061.
- G. Li, Z. Song and X. Wang, Proceedings of the AAAI Conference on Artificial Intelligence, 2021, pp. 8357–8365.
- R. Chen, Z. Song, X. Zhao and X. Wang, Quantum Sci. Technol., 2021, 7, 015019 CrossRef.
- Y. Wang, G. Li and X. Wang, Phys. Rev. Appl., 2021, 16, 054035 CrossRef CAS.
- D. Aharonov, I. Arad and T. Vidick, ACM Sigact News, 2013, 44, 47–79 CrossRef.
- A. M. Childs, D. Maslov, Y. Nam, N. J. Ross and Y. Su, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9456–9461 CrossRef CAS PubMed.
- R. D. Somma, S. Boixo, H. Barnum and E. Knill, Phys. Rev. Lett., 2008, 101, 130504 CrossRef CAS PubMed.
- A. Gheorghiu and M. J. Hoban, 2020, arXiv preprint arXiv:2002.12814.
- H. Buhrman, R. Cleve, J. Watrous and R. De Wolf, Phys. Rev. Lett., 2001, 87, 167902 CrossRef CAS PubMed.
- D. Gottesman and I. Chuang, 2001, arXiv preprint quant-ph/0105032.
- H. Neven, V. S. Denchev, G. Rose and W. G. Macready, 2008, arXiv preprint arXiv:0811.0416.
- K. L. Pudenz and D. A. Lidar, Quantum Inf. Process., 2013, 12, 2027–2070 CrossRef.
- M. W. Johnson, M. H. Amin, S. Gildert, T. Lanting, F. Hamze, N. Dickson, R. Harris, A. J. Berkley, J. Johansson and P. Bunyk, et al. , Nature, 2011, 473, 194–198 CrossRef CAS PubMed.
- S. H. Adachi and M. P. Henderson, 2015, arXiv preprint arXiv:1510.06356.
- M. Benedetti, J. Realpe-Gómez, R. Biswas and A. Perdomo-Ortiz, Phys. Rev. X, 2017, 7, 041052 Search PubMed.
- N. Wiebe, A. Kapoor, C. Granade and K. M. Svore, 2015, arXiv preprint arXiv:1507.02642.
- M. H. Amin, E. Andriyash, J. Rolfe, B. Kulchytskyy and R. Melko, Phys. Rev. X, 2018, 8, 021050 CAS.
- M. Kieferová and N. Wiebe, Phys. Rev. A, 2017, 96, 062327 CrossRef.
- Q. Xu and S. Xu, 2018, arXiv preprint arXiv:1811.06654.
- C. H. Baldwin, I. H. Deutsch and A. Kalev, Phys. Rev. A, 2016, 93, 052105 CrossRef.
- N. Linden, S. Popescu and W. Wootters, Phys. Rev. Lett., 2002, 89, 207901 CrossRef CAS PubMed.
- N. Linden and W. Wootters, Phys. Rev. Lett., 2002, 89, 277906 CrossRef CAS PubMed.
- J. Chen, Z. Ji, B. Zeng and D. Zhou, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 022339 CrossRef.
- J. Chen, H. Dawkins, Z. Ji, N. Johnston, D. Kribs, F. Shultz and B. Zeng, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 012109 CrossRef.
- B. Qi, Z. Hou, L. Li, D. Dong, G. Xiang and G. Guo, Sci. Rep., 2013, 3, 1–6 Search PubMed.
- D. F. James, P. G. Kwiat, W. J. Munro and A. G. White, Asymptotic Theory of Quantum Statistical Inference: Selected Papers, World Scientific, 2005, pp. 509–538 Search PubMed.
- T. Opatrny, D.-G. Welsch and W. Vogel, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 56, 1788 CrossRef CAS.
- D. G. Fischer, S. H. Kienle and M. Freyberger, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 61, 032306 CrossRef.
- G. I. Struchalin, I. A. Pogorelov, S. S. Straupe, K. S. Kravtsov, I. V. Radchenko and S. P. Kulik, Phys. Rev. A, 2016, 93, 012103 CrossRef.
- Y. Quek, S. Fort and H. K. Ng, npj Quantum Inform., 2021, 7, 1–7 CrossRef.
- L. Hu, S.-H. Wu, W. Cai, Y. Ma, X. Mu, Y. Xu, H. Wang, Y. Song, D.-L. Deng and C.-L. Zou, et al. , Sci. Adv., 2019, 5, eaav2761 CrossRef PubMed.
- B. Qi, Z. Hou, Y. Wang, D. Dong, H.-S. Zhong, L. Li, G.-Y. Xiang, H. M. Wiseman, C.-F. Li and G.-C. Guo, npj Quantum Inform., 2017, 3, 1–7 CrossRef.
- S. Lloyd and C. Weedbrook, Phys. Rev. Lett., 2018, 121, 040502 CrossRef CAS PubMed.
- P.-L. Dallaire-Demers and N. Killoran, Phys. Rev. A, 2018, 98, 012324 CrossRef CAS.
- S. Ahmed, C. S. Muñoz, F. Nori and A. F. Kockum, 2020, arXiv preprint arXiv:2008.03240.
- P. Isola, J.-Y. Zhu, T. Zhou and A. A. Efros, Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 1125–1134.
- T. Karras, S. Laine and T. Aila, 2018, arXiv preprint arXiv:1812.04948.
- T. Karras, S. Laine, M. Aittala, J. Hellsten, J. Lehtinen and T. Aila, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, pp. 8110–8119.
- Z. Yang, Z. Hu, C. Dyer, E. P. Xing and T. Berg-Kirkpatrick, Proceedings of the 32nd International Conference on Neural Information Processing Systems, 2018, pp. 7298–7309.
- S. Subramanian, S. Rajeswar, A. Sordoni, A. Trischler, A. Courville and C. Pal, Proceedings of the 32nd International Conference on Neural Information Processing Systems, 2018, pp. 7562–7574.
- J. Cheng, L. Dong and M. Lapata, 2016, arXiv preprint arXiv:1601.06733.
- A. P. Parikh, O. Täckström, D. Das and J. Uszkoreit, 2016, arXiv preprint arXiv:1606.01933.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Adv. Neural Information Process. Syst., 2017, 30, 1–11 Search PubMed.
- Z. Lin, M. Feng, C. N. D. Santos, M. Yu, B. Xiang, B. Zhou and Y. Bengio, 2017, arXiv preprint arXiv:1703.03130.
- R. Paulus, C. Xiong and R. Socher, 2017, arXiv preprint arXiv:1705.04304.
- D. Bahdanau, K. Cho and Y. Bengio, 2014, arXiv preprint arXiv:1409.0473.
- I. Sutskever, O. Vinyals and Q. V. Le, Adv. Neural Inform. Process. Syst., 2014, 27, 1 Search PubMed.
- P. Cha, P. Ginsparg, F. Wu, J. Carrasquilla, P. L. McMahon and E.-A. Kim, Mach. Learn.: Sci. Technol., 2021, 3, 01LT01 Search PubMed.
- J. Carrasquilla, G. Torlai, R. G. Melko and L. Aolita, Nat. Mach. Intell., 2019, 1, 155–161 CrossRef.
- S. Aaronson, Nat. Phys., 2015, 11, 291–293 Search PubMed.
- P. C. Sen, M. Hajra and M. Ghosh, Emerging technology in modelling and graphics, Springer, 2020, pp. 99–111 Search PubMed.
- S. Zhang, C. Zhang and Q. Yang, Appl. Artificial Intell., 2003, 17, 375–381 Search PubMed.
- A. Karim, A. Mishra, M. H. Newton and A. Sattar, ACS Omega, 2019, 4, 1874–1888 Search PubMed.
- Y. Chevaleyre and J.-D. Zucker, Conference of the Canadian Society for Computational Studies of Intelligence, 2001, pp. 204–214.
- G. Skoraczyński, P. Dittwald, B. Miasojedow, S. Szymkuć, E. Gajewska, B. A. Grzybowski and A. Gambin, Sci. Rep., 2017, 7, 1–9 Search PubMed.
- S. Heinen, G. F. von Rudorff and O. A. von Lilienfeld, J. Chem. Phys., 2021, 155, 064105 CrossRef CAS PubMed.
- E. A. Engel, A. Anelli, A. Hofstetter, F. Paruzzo, L. Emsley and M. Ceriotti, Phys. Chem. Chem. Phys., 2019, 21, 23385–23400 RSC.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- R. Krems, Phys. Chem. Chem. Phys., 2019, 21, 13392–13410 RSC.
- M. Senekane and B. M. Taele, et al. , Smart Grid Renewable Energy, 2016, 7, 293 CrossRef.
- J. Heredge, C. Hill, L. Hollenberg and M. Sevior, 2021, arXiv preprint arXiv:2103.12257.
- F. Schindler, N. Regnault and T. Neupert, Phys. Rev. B, 2017, 95, 245134 CrossRef.
- G. Purushothaman and N. B. Karayiannis, IEEE Trans. Neural Networks, 1997, 8, 679–693 CAS.
- J. Zhou, Third IEEE Symposium on Bioinformatics and Bioengineering, 2003. Proceedings, 2003, pp. 169–173 Search PubMed.
- V. Dumoulin, I. Goodfellow, A. Courville and Y. Bengio, Proceedings of the AAAI Conference on Artificial Intelligence, 2014.
- V. Gandhi, G. Prasad, D. Coyle, L. Behera and T. M. McGinnity, IEEE Trans. Neural Networks Learn. Syst., 2013, 25, 278–288 Search PubMed.
- Z. Gao, C. Ma, Y. Luo and Z. Liu, Eng. Appl. Artificial Intell., 2018, 76, 119–129 CrossRef.
- M. Zidan, A.-H. Abdel-Aty, M. El-shafei, M. Feraig, Y. Al-Sbou, H. Eleuch and M. Abdel-Aty, Appl. Sci., 2019, 9, 1277 CrossRef.
- E. Farhi and H. Neven, 2018, arXiv preprint arXiv:1802.06002.
- S. Adhikary, S. Dangwal and D. Bhowmik, Quantum Inf. Process., 2020, 19, 1–12 CrossRef.
- M. Schuld, A. Bocharov, K. M. Svore and N. Wiebe, Phys. Rev. A, 2020, 101, 032308 CrossRef CAS.
- D. Liu, G. Bai and C. Gao, J. Appl. Phys., 2020, 127, 154101 CrossRef CAS.
- G. Deffrennes, K. Terayama, T. Abe and R. Tamura, 2022, arXiv preprint arXiv:2201.01932.
- A. V. Uvarov, A. S. Kardashin and J. D. Biamonte, Phys. Rev. A, 2020, 102, 012415 CrossRef CAS.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- P. Broecker, F. F. Assaad and S. Trebst, 2017, arXiv preprint arXiv:1707.00663.
- Y. Che, C. Gneiting, T. Liu and F. Nori, Phys. Rev. B, 2020, 102, 134213 CrossRef CAS.
- S. Lloyd, IEEE Trans. Inform. Theory, 1982, 28, 129–137 CrossRef.
- D. J. MacKay and D. J. Mac Kay, Information theory, inference and learning algorithms, Cambridge University Press, 2003 Search PubMed.
- J. Otterbach, R. Manenti, N. Alidoust, A. Bestwick, M. Block, B. Bloom, S. Caldwell, N. Didier, E. S. Fried, S. Hong, et al., 2017, arXiv preprint arXiv:1712.05771.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- J. Schmidt, C. L. Benavides-Riveros and M. A. Marques, J. Phys. Chem. Lett., 2019, 10, 6425–6431 CrossRef CAS PubMed.
- M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Müller and K. Burke, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed.
- R. Nagai, R. Akashi and O. Sugino, npj Comput. Mater., 2020, 6, 1–8 CrossRef.
- L. Li, T. E. Baker, S. R. White and K. Burke, et al. , Phys. Rev. B, 2016, 94, 245129 CrossRef.
- P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. Marques and S. Botti, npj Comput. Mater., 2020, 6, 1–17 CrossRef.
- M. Fritz, M. Fernández-Serra and J. M. Soler, J. Chem. Phys., 2016, 144, 224101 CrossRef PubMed.
- Q. Liu, J. Wang, P. Du, L. Hu, X. Zheng and G. Chen, J. Phys. Chem. A, 2017, 121, 7273–7281 CrossRef CAS PubMed.
- K. Ryczko, D. A. Strubbe and I. Tamblyn, Phys. Rev. A, 2019, 100, 022512 CrossRef CAS.
- A. Stuke, M. Todorović, M. Rupp, C. Kunkel, K. Ghosh, L. Himanen and P. Rinke, J. Chem. Phys., 2019, 150, 204121 CrossRef PubMed.
- K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. Von Lilienfeld, A. Tkatchenko and K.-R. Muller, J. Chem. Theory Comput., 2013, 9, 3404–3419 CrossRef CAS PubMed.
- F. A. Faber, A. S. Christensen, B. Huang and O. A. von Lilienfeld, J. Chem. Phys., 2018, 148, 241717 CrossRef PubMed.
- P. O. Dral, Chemical Physics and Quantum Chemistry, Academic Press, 2020, vol. 81 of Advances in Quantum Chemistry, pp. 291–324 Search PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- B. Himmetoglu, J. Chem. Phys., 2016, 145, 134101 CrossRef PubMed.
- A. Denzel and J. Kästner, J. Chem. Phys., 2018, 148, 094114 CrossRef.
- K. Choo, A. Mezzacapo and G. Carleo, Nat. Commun., 2020, 11, 1–7 CrossRef PubMed.
- Y. Cao, J. Romero, J. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Chem. Rev., 2019, 119(19), 10856–10915 CrossRef CAS PubMed.
- H. Saito, J. Phys. Soc. Jpn., 2017, 86, 093001 CrossRef.
- R. Xia and S. Kais, Nat. Commun., 2018, 9, 1–6 CrossRef CAS PubMed.
- S. Kanno and T. Tada, Quantum Sci. Technol., 2021, 6, 025015 CrossRef.
- S. H. Sureshbabu, M. Sajjan, S. Oh and S. Kais, J. Chem. Inf. Model., 2021, 61(6), 2667–2674 CrossRef CAS PubMed.
- J. P. Coe, J. Chem. Theory Comput., 2018, 14, 5739–5749 CrossRef CAS PubMed.
- J. P. Coe, J. Chem. Theory Comput., 2019, 15, 6179–6189 CrossRef CAS PubMed.
- C. A. Custódio, É. R. Filletti and V. V. França, Sci. Rep., 2019, 9, 1–7 CrossRef PubMed.
- J. R. Moreno, G. Carleo and A. Georges, Phys. Rev. Lett., 2020, 125, 076402 CrossRef CAS PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- J. Hermann, Z. Schätzle and F. Noé, Nat. Chem., 2020, 12, 891–897 CrossRef CAS PubMed.
- F. A. Faber, A. S. Christensen, B. Huang and O. A. Von Lilienfeld, J. Chem. Phys., 2018, 148, 241717 CrossRef PubMed.
- A. S. Christensen, L. A. Bratholm, F. A. Faber and O. Anatole von Lilienfeld, J. Chem. Phys., 2020, 152, 044107 CrossRef CAS PubMed.
- B. Huang and O. A. von Lilienfeld, Nat. Chem., 2020, 12, 945–951 CrossRef CAS PubMed.
- E. O. Pyzer-Knapp, K. Li and A. Aspuru-Guzik, Adv. Funct. Mater., 2015, 25, 6495–6502 CrossRef CAS.
- K. Choudhary, M. Bercx, J. Jiang, R. Pachter, D. Lamoen and F. Tavazza, Chem. Mater., 2019, 31, 5900–5908 CrossRef CAS PubMed.
- V. Stanev, C. Oses, A. G. Kusne, E. Rodriguez, J. Paglione, S. Curtarolo and I. Takeuchi, npj Comput. Mater., 2018, 4, 1–14 CrossRef.
- T. D. Barrett, A. Malyshev and A. Lvovsky, 2021, arXiv preprint arXiv:2109.12606.
- P. V. Balachandran, J. Young, T. Lookman and J. M. Rondinelli, Nat. Commun., 2017, 8, 1–13 CrossRef PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- B. Kim, S. Lee and J. Kim, Sci. Adv., 2020, 6, eaax9324 CrossRef CAS PubMed.
- Z. Zhang, M. Li, K. Flores and R. Mishra, J. Appl. Phys., 2020, 128, 105103 CrossRef CAS.
- E. Mazhnik and A. R. Oganov, J. Appl. Phys., 2020, 128, 075102 CrossRef CAS.
- B. Bruognolo, PhD thesis, LMU, 2017.
- A. Kshetrimayum, C. Balz, B. Lake and J. Eisert, Ann. Phys., 2020, 421, 168292 CAS.
- C. Balz, B. Lake, J. Reuther, H. Luetkens, R. Schönemann, T. Herrmannsdörfer, Y. Singh, A. Nazmul Islam, E. M. Wheeler and J. A. Rodriguez-Rivera, et al. , Nat. Phys., 2016, 12, 942–949 Search PubMed.
- J. Biamonte, 2019, arXiv preprint arXiv:1912.10049.
- V. Murg, F. Verstraete, Ö. Legeza and R. M. Noack, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205105 CrossRef.
- T. Barthel, C. Pineda and J. Eisert, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 042333 CrossRef.
- C. Wille, O. Buerschaper and J. Eisert, Phys. Rev. B, 2017, 95, 245127 CrossRef.
- C. Krumnow, L. Veis, Ö. Legeza and J. Eisert, Phys. Rev. Lett., 2016, 117, 210402 CrossRef CAS PubMed.
- C. Gogolin and J. Eisert, Rep. Progress Phys., 2016, 79, 056001 CrossRef PubMed.
- A. Kshetrimayum, M. Rizzi, J. Eisert and R. Orús, Phys. Rev. Lett., 2019, 122, 070502 CrossRef CAS PubMed.
- A. Kshetrimayum, M. Goihl and J. Eisert, Phys. Rev. B, 2020, 102, 235132 CrossRef CAS.
- R. Haghshenas, J. Gray, A. C. Potter and G. K.-L. Chan, Phys. Rev. X, 2022, 12(1), 011047 CAS.
- J. R. Shewchuk et al. , An introduction to the conjugate gradient method without the agonizing pain, 1994 Search PubMed.
- N. N. Schraudolph, J. Yu and S. Günter, Artificial intelligence and statistics, 2007, pp. 436–443 Search PubMed.
- A. Eddins, M. Motta, T. P. Gujarati, S. Bravyi, A. Mezzacapo, C. Hadfield and S. Sheldon, PRX Quantum, 2022, 3, 010309 CrossRef.
- J. A. McCammon, B. R. Gelin and M. Karplus, Nature, 1977, 267, 585–590 CrossRef CAS PubMed.
- R. Schulz, B. Lindner, L. Petridis and J. C. Smith, J. Chem. Theory Comput., 2009, 5, 2798–2808 CrossRef CAS PubMed.
- D. E. Shaw, M. M. Deneroff, R. O. Dror, J. S. Kuskin, R. H. Larson, J. K. Salmon, C. Young, B. Batson, K. J. Bowers and J. C. Chao, et al. , Commun. ACM, 2008, 51, 91–97 CrossRef.
- A. D. MacKerell, Computational Methods for Protein Structure Prediction and Modeling, Springer, 2007, pp. 45–69 Search PubMed.
- M. I. Zimmerman and G. Bowman, Biophys. J., 2021, 120, 299a CrossRef CAS.
- M. Gonzalez, Ethématic school of the Societé Franccease of Neutronics, 2011, 12, 169–200 Search PubMed.
- A. D. MacKerell Jr, J. Comput. Chem., 2004, 25, 1584–1604 CrossRef PubMed.
- Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, J. Chem. Theory Comput., 2013, 9, 4046–4063 CrossRef CAS PubMed.
- A. Warshel, M. Kato and A. V. Pisliakov, J. Chem. Theory Comput., 2007, 3, 2034–2045 CrossRef CAS PubMed.
- O. T. Unke, M. Devereux and M. Meuwly, J. Chem. Phys., 2017, 147, 161712 CrossRef PubMed.
- T. Nagy, J. Yosa Reyes and M. Meuwly, J. Chem. Theory Comput., 2014, 10, 1366–1375 CrossRef CAS PubMed.
- H. M. Senn and W. Thiel, ANIE, 2009, 48, 1198–1229 CAS.
- S. Chmiela, H. E. Sauceda, I. Poltavsky, K.-R. Muller and A. Tkatchenko, Comput. Phys. Commun., 2019, 240, 38–45 CrossRef CAS.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed.
- A. P. Bartok, M. C. Payne, R. Kondor and G. Csanyi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- K. Schutt, P. Kessel, M. Gastegger, K. Nicoli, A. Tkatchenko and K.-R. Muller, J. Chem. Theory Comput., 2018, 15, 448–455 CrossRef PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- J. Westermayr and P. Marquetand, Chem. Rev., 2020, 121, 9873–9926 CrossRef PubMed.
- K. T. Schutt, F. Arbabzadah, S. Chmiela, K. R. Muller and A. Tkatchenko, Nat. Commun., 2017, 8, 1–8 CrossRef PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schutt, A. Tkatchenko and K.-R. Muller, Chem. Rev., 2021, 121(16), 10142–10186 CrossRef CAS PubMed.
- A. C. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- H. Nakata and S. Bai, J. Comput. Chem., 2019, 40, 2000–2012 CAS.
- L. Angibaud, L. Briquet, P. Philipp, T. Wirtz and J. Kieffer, Nucl. Instrum. Methods Phys. Res., Sect. B, 2011, 269, 1559–1563 CrossRef CAS.
- M. Dittner, J. Muller, H. M. Aktulga and B. Hartke, J. Comput. Chem., 2015, 36, 1550–1561 CrossRef CAS PubMed.
- A. Jaramillo-Botero, S. Naserifar and W. A. Goddard III, J. Chem. Theory Comput., 2014, 10, 1426–1439 CrossRef CAS PubMed.
- M. C. Kaymak, A. Rahnamoun, K. A. O'Hearn, A. C. van Duin, K. M. Merz Jr and H. M. Aktulga, ChemRxiv, Cambridge Open Engage, Cambridge, 2022 Search PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2013, 9, 4959–4972 CrossRef CAS PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2014, 10, 789–804 CrossRef CAS PubMed.
- P. Nijjar, J. Jankowska and O. V. Prezhdo, J. Chem. Phys., 2019, 150, 204124 CrossRef PubMed.
- P. O. Dral, M. Barbatti and W. Thiel, J. Phys. Chem. Lett., 2018, 9, 5660–5663 CrossRef CAS PubMed.
- B. Wang, W. Chu, A. Tkatchenko and O. V. Prezhdo, J. Phys. Chem. Lett., 2021, 12, 6070–6077 CrossRef CAS PubMed.
- Z. Zhang, Y. Zhang, J. Wang, J. Xu and R. Long, J. Phys. Chem. Lett., 2021, 12, 835–842 CrossRef CAS PubMed.
- W. Li, Y. She, A. S. Vasenko and O. V. Prezhdo, Nanoscale, 2021, 13, 10239–10265 RSC.
- L. Zhang, W. Chu, C. Zhao, Q. Zheng, O. V. Prezhdo and J. Zhao, J. Phys. Chem. Lett., 2021, 12, 2191–2198 CrossRef CAS PubMed.
- D. H. Olson, M. G. Sales, J. A. Tomko, T.-F. Lu, O. V. Prezhdo, S. J. McDonnell and P. E. Hopkins, Appl. Phys. Lett., 2021, 118, 163503 CrossRef CAS.
- J. Westermayr, M. Gastegger and P. Marquetand, J. Phys. Chem. Lett., 2020, 11, 3828–3834 CrossRef CAS PubMed.
- E. Posenitskiy, F. Spiegelman and D. Lemoine, Mach. Learn.: Sci. Technol., 2021, 2, 035039 Search PubMed.
- A. Glielmo, B. E. Husic, A. Rodriguez, C. Clementi, F. Noé and A. Laio, Chem. Rev., 2021, 121, 9722–9758 CrossRef CAS PubMed.
- A. M. Virshup, J. Chen and T. J. Martnez, J. Chem. Phys., 2012, 137, 22A519 CrossRef PubMed.
- X. Li, Y. Xie, D. Hu and Z. Lan, J. Chem. Theory Comput., 2017, 13, 4611–4623 CrossRef CAS PubMed.
- J. Peng, Y. Xie, D. Hu and Z. Lan, J. Chem. Phys., 2021, 154, 094122 CrossRef CAS PubMed.
- G. Zhou, W. Chu and O. V. Prezhdo, ACS Energy Lett., 2020, 5, 1930–1938 CrossRef CAS.
- P. Tavadze, G. Avendano Franco, P. Ren, X. Wen, Y. Li and J. P. Lewis, J. Am. Chem. Soc., 2018, 140, 285–290 CrossRef CAS PubMed.
- S. M. Mangan, G. Zhou, W. Chu and O. V. Prezhdo, J. Phys. Chem. Lett., 2021, 12, 8672–8678 CrossRef CAS PubMed.
- A. Kraskov, H. Stögbauer and P. Grassberger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 066138 CrossRef PubMed.
- W. B. How, B. Wang, W. Chu, A. Tkatchenko and O. V. Prezhdo, J. Phys. Chem. Lett., 2021, 12, 12026–12032 CrossRef CAS PubMed.
- W. Xiang, S. F. Liu and W. Tress, Energy Environ. Sci., 2021, 14, 2090–2113 RSC.
- M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. photonics, 2014, 8, 506–514 CrossRef CAS.
- N. Ahn, D.-Y. Son, I.-H. Jang, S. M. Kang, M. Choi and N.-G. Park, J. Am. Chem. Soc., 2015, 137, 8696–8699 CrossRef CAS PubMed.
- T. Bian, D. Murphy, R. Xia, A. Daskin and S. Kais, Mol. Phys., 2019, 117, 2069–2082 CrossRef CAS.
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Nature, 2017, 549, 242–246 CrossRef CAS PubMed.
- L. W. Anderson, M. Kiffner, P. K. Barkoutsos, I. Tavernelli, J. Crain and D. Jaksch, 2021, arXiv preprint arXiv:2110.00968.
- F. Cipcigan, J. Crain, V. Sokhan and G. Martyna, Rev. Mod. Phys., 2019, 91, 025003 CrossRef CAS.
- P. Gokhale, O. Angiuli, Y. Ding, K. Gui, T. Tomesh, M. Suchara, M. Martonosi and F. T. Chong, IEEE Trans. Quantum Eng., 2020, 1, 1–24 Search PubMed.
- M. J. Westbroek, P. R. King, D. D. Vvedensky and S. Dürr, Am. J. Phys., 2018, 86, 293–304 CrossRef.
- P. J. Ollitrault, G. Mazzola and I. Tavernelli, Phys. Rev. Lett., 2020, 125, 260511 CrossRef CAS PubMed.
- G. Capano, M. Chergui, U. Rothlisberger, I. Tavernelli and T. J. Penfold, J. Phys. Chem. A, 2014, 118, 9861–9869 CrossRef CAS PubMed.
- A. Zhugayevych and S. Tretiak, Ann. Rev. Phys. Chem., 2015, 66, 305–330 CrossRef CAS PubMed.
- O. Kiss, F. Tacchino, S. Vallecorsa and I. Tavernelli, 2022, arXiv:2203.04666 [physics, physics:quant-ph].
- S. Lim, Y. Lu, C. Y. Cho, I. Sung, J. Kim, Y. Kim, S. Park and S. Kim, Comput. Struct. Biotechnol. J., 2021, 19, 1541–1556 CrossRef CAS PubMed.
- G. Sliwoski, S. Kothiwale, J. Meiler and E. W. Lowe, Pharmacol. Rev., 2014, 66, 334–395 CrossRef PubMed.
- S. P. Leelananda and S. Lindert, Beilstein J. Org. Chem., 2016, 12, 2694–2718 CrossRef CAS PubMed.
- S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He and B. A. Shoemaker, et al. , Nucleic Acids Res., 2016, 44, D1202–D1213 CrossRef CAS PubMed.
- S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen and B. Yu, et al. , Nucleic Acids Res., 2019, 47, D1102–D1109 CrossRef PubMed.
- A. Gaulton, A. Hersey, M. Nowotka, A. P. Bento, J. Chambers, D. Mendez, P. Mutowo, F. Atkinson, L. J. Bellis and E. Cibrián-Uhalte, et al. , Nucleic Acids Res., 2017, 45, D945–D954 CrossRef CAS PubMed.
- D. S. Wishart, Y. D. Feunang, A. C. Guo, E. J. Lo, A. Marcu, J. R. Grant, T. Sajed, D. Johnson, C. Li and Z. Sayeeda, et al. , Nucleic Acids Res., 2018, 46, D1074–D1082 CrossRef CAS PubMed.
- M. M. Mysinger, M. Carchia, J. J. Irwin and B. K. Shoichet, J. Med. Chem., 2012, 55, 6582–6594 CrossRef CAS PubMed.
- R. Apweiler, A. Bairoch, C. H Wu, W. C. Barker, B. Boeckmann, S. Ferro, E. Gasteiger and H. Huang, et al. , Nucleic Acids Res., 2004, 32, D115–D119 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- H. Berman, K. Henrick, H. Nakamura and J. L. Markley, Nucleic Acids Res., 2007, 35, D301–D303 CrossRef CAS PubMed.
- S. K. Burley, H. M. Berman, G. J. Kleywegt, J. L. Markley, H. Nakamura and S. Velankar, Methods Mol. Biol., 2017, 1607, 627–641 CrossRef CAS PubMed.
- R. Wang, X. Fang, Y. Lu, C.-Y. Yang and S. Wang, J. Med. Chem., 2005, 48, 4111–4119 CrossRef CAS PubMed.
- M. K. Gilson, T. Liu, M. Baitaluk, G. Nicola, L. Hwang and J. Chong, Nucleic Acids Res., 2016, 44, D1045–D1053 CrossRef CAS PubMed.
- D. Weininger, J. Chem. Inform. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- D. Weininger, A. Weininger and J. L. Weininger, J. Chem. Inform. Comput. Sci., 1989, 29, 97–101 CrossRef CAS.
- N. M. O’Boyle, J. Cheminf., 2012, 4, 1–14 Search PubMed.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Mach. Learn.: Sci. Technol., 2020, 1, 045024 Search PubMed.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, 2019, arXiv preprint arXiv:1905.13741.
- A. Dalke, Chem. Cent. J., 2008, 2, 1 CrossRef PubMed.
- V. J. Sykora and D. E. Leahy, J. Chem. Inf. Model., 2008, 48, 1931–1942 CrossRef CAS PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- A. Cereto-Massagué, M. J. Ojeda, C. Valls, M. Mulero, S. Garcia-Vallvé and G. Pujadas, Methods, 2015, 71, 58–63 CrossRef PubMed.
- J. Duan, S. L. Dixon, J. F. Lowrie and W. Sherman, J. Mol. Graphics Modell., 2010, 29, 157–170 CrossRef CAS PubMed.
- J. Hert, P. Willett, D. J. Wilton, P. Acklin, K. Azzaoui, E. Jacoby and A. Schuffenhauer, J. Chem. Inform. Comput. Sci., 2004, 44, 1177–1185 CrossRef CAS PubMed.
- V. I. Pérez-Nueno, O. Rabal, J. I. Borrell and J. Teixidó, J. Chem. Inf. Model., 2009, 49, 1245–1260 CrossRef PubMed.
- M. Awale and J.-L. Reymond, J. Chem. Inf. Model., 2014, 54, 1892–1907 CrossRef CAS PubMed.
- N. De Cao and T. Kipf, 2018, arXiv preprint arXiv:1805.11973.
- D. Jiang, Z. Wu, C.-Y. Hsieh, G. Chen, B. Liao, Z. Wang, C. Shen, D. Cao, J. Wu and T. Hou, J. Cheminf., 2021, 13, 1–23 Search PubMed.
- P. Carracedo-Reboredo, J. Liñares-Blanco, N. Rodrguez-Fernández, F. Cedrón, F. J. Novoa, A. Carballal, V. Maojo, A. Pazos and C. Fernandez-Lozano, Comput. Struct. Biotechnol. J., 2021, 19, 4538 CrossRef CAS PubMed.
- X. Lin, X. Li and X. Lin, Molecules, 2020, 25, 1375 CrossRef CAS PubMed.
- J. B. Dunbar, R. D. Smith, C.-Y. Yang, P. M.-U. Ung, K. W. Lexa, N. A. Khazanov, J. A. Stuckey, S. Wang and H. A. Carlson, J. Chem. Inf. Model., 2011, 51, 2036–2046 CrossRef CAS PubMed.
- D. R. Koes, M. P. Baumgartner and C. J. Camacho, J. Chem. Inf. Model., 2013, 53(8), 1893–1904 CrossRef CAS PubMed.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461 CAS.
- Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, S. Guadarrama and T. Darrell, Proceedings of the 22nd ACM international conference on Multimedia, 2014, pp. 675–678 Search PubMed.
- Y.-B. Wang, Z.-H. You, S. Yang, H.-C. Yi, Z.-H. Chen and K. Zheng, BMC Med. Inf. Decis. Making, 2020, 20, 1–9 CrossRef CAS PubMed.
- M. Kanehisa, M. Araki, S. Goto, M. Hattori, M. Hirakawa, M. Itoh, T. Katayama, S. Kawashima, S. Okuda, T. Tokimatsu and Y. Yamanishi, Nucleic Acids Res., 2008, 36, D480–D484 CrossRef CAS PubMed.
- D. S. Wishart, C. Knox, A. Guo, S. Shrivastava, M. Hassanali, P. Stothard, Z. Chang and J. Woolsey, Nucleic Acids Res., 2006, 34, D668–D672 CrossRef CAS PubMed.
- S. Günther, M. Kuhn, M. Dunkel, M. Campillos, C. Senger, E. Petsalaki, J. Ahmed, E. G. Urdiales, A. Gewiess, L. J. Jensen, R. Schneider, R. Skoblo, R. B. Russell, P. E. Bourne, P. Bork and R. Preissner, Nucleic Acids Res., 2008, 36, D919–D922 CrossRef PubMed.
- Y. Wang, Z.-H. You, X. Li, X. Chen, T. Jiang and J. Zhang, Int. J. Mol. Sci., 2017, 18, 1–13 Search PubMed.
- J. A. Hanley and B. J. McNeil, Radiology, 1982, 143, 29–36 CrossRef CAS PubMed.
- H. Zhang, Z. Kang, H. Gong, X. Da and J. Wang, et al., The digestive system is a potential route of 2019-ncov infection: a bioinformatics analysis based on single-cell transcriptomes, bioRxiv, 2020 DOI:10.1101/2020.01.30.927806.
- K. He, X. Zhang, S. Ren and J. Sun, European conference on computer vision, 2016, pp. 630–645.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminf., 2017, 9, 1–14 Search PubMed.
- M. M. Mysinger, M. Carchia, J. J. Irwin and B. K. Shoichet, J. Med. Chem., 2012, 55, 6582–6594 CrossRef CAS PubMed.
- H. Liu, J. Sun, J. Guan, J. Zheng and S. Zhou, Bioinformatics, 2015, 31, i221–i229 CrossRef CAS PubMed.
- M. K. Gilson, T. Liu, M. Baitaluk, G. Nicola, L. Hwang and J. Chong, Nucleic Acids Res., 2016, 44, D1045–D1053 CrossRef CAS PubMed.
- K. H. Zou, A. J. O’Malley and L. Mauri, Circulation, 2007, 115, 654–657 CrossRef PubMed.
- I. Wallach, M. Dzamba and A. Heifets, CoRR, 2015, pp. 1–9, https://arxiv.org/abs/1510.02855.
- G. E. Dahl, N. Jaitly and R. Salakhutdinov, 2014, arXiv preprint arXiv:1406.1231.
- A. Mauri, V. Consonni, M. Pavan, R. Todeschini and M. Chemometrics, Commun. Math. Comput. Chem., 2006, 56, 237–248 CAS.
- B. Ramsundar, S. M. Kearnes, P. F. Riley, D. R. Webster, D. E. Konerding and V. S. Pande, 2015, pp. 1–9, https://arxiv.org/abs/1502.02072.
- C. Nwankpa, W. Ijomah, A. Gachagan and S. Marshall, 2018, arXiv preprint arXiv:1811.03378.
- J. Ma, R. P. Sheridan, A. Liaw, G. E. Dahl and V. Svetnik, J. Chem. Inf. Model., 2015, 55, 263–274 CrossRef CAS PubMed.
- R. E. Carhart, D. H. Smith and R. Venkataraghavan, J. Chem. Inf. Comput. Sci., 1985, 25, 64–73 CrossRef CAS.
- D. L. Alexander, A. Tropsha and D. A. Winkler, J. Chem. Inf. Model., 2015, 55, 1316–1322 CrossRef CAS PubMed.
- A. H. Vo, T. R. Van Vleet, R. R. Gupta, M. J. Liguori and M. S. Rao, Chem. Res. Toxicol., 2019, 33, 20–37 Search PubMed.
- A. D. Rodgers, H. Zhu, D. Fourches, I. Rusyn and A. Tropsha, Chem. Res. Toxicol., 2010, 23, 724–732 Search PubMed.
- G. L. Plaa and W. R. Hewitt, Toxicology of the Liver, CRC Press, 1998 Search PubMed.
- K. Z. Guyton, J. A. Thompson and T. W. Kensler, Chem. Res. Toxicol., 1993, 6, 731–738 Search PubMed.
- T. Nonoyama and R. Fukuda, J. Toxicol. Pathol., 2008, 21, 9–24 CrossRef CAS.
- R. Huang, N. Southall, Y. Wang, A. Yasgar, P. Shinn, A. Jadhav, D.-T. Nguyen and C. P. Austin, Sci. Trans. Med., 2011, 3, 80ps16 Search PubMed.
- N. Bhandari, D. J. Figueroa, J. W. Lawrence and D. L. Gerhold, Assay Drug Dev. Technol., 2008, 6, 407–419 CrossRef CAS PubMed.
- R. E. Pearce, J. Uetrecht and J. S. Leeder, Drug Metab. Dispos., 2005, 33, 1819–1826 CAS.
- V. L. M. Yip, J. L. Maggs, X. Meng, A. G. Marson, K. B. Park and M. Pirmohamed, The Lancet, 2014, 383, S114 CrossRef.
- K. B. Alton, R. M. Grimes, C. J. Shaw, J. E. Patrick and J. L. Mcguire, Drug Metab. Dispos., 1975, 3(5), 352–360 CAS.
- A. F. Stepan, D. P. Walker, J. N. Bauman, D. Price, T. A. Baillie, A. S. Kalgutkar and M. D. Aleo, Chem. Res. Toxicol., 2011, 24(9), 1345–1410 Search PubMed.
- Y. Cao, J. Romero and A. Aspuru-Guzik, IBM J. Res. Dev., 2018, 62(6), 1–6 Search PubMed.
- A. Perdomo-Ortiz, N. Dickson, M. Drew-Brook, G. Rose and A. Aspuru-Guzik, Sci. Rep., 2012, 2, 1–7 Search PubMed.
- L. Banchi, M. Fingerhuth, T. Babej, C. Ing and J. M. Arrazola, Sci. Adv., 2020, 6, eaax1950 CrossRef CAS PubMed.
- A. Robert, P. K. Barkoutsos, S. Woerner and I. Tavernelli, npj Quantum Inform., 2021, 7, 1–5 CrossRef.
- T. Babej, C. Ing and M. Fingerhuth, Coarse-grained lattice protein folding on a quantum annealer, arXiv preprint arXiv:1811.00713, 2018.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Ždek and A. Potapenko, et al. , Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- M. Zinner, F. Dahlhausen, P. Boehme, J. Ehlers, L. Bieske and L. Fehring, Drug Discovery Today, 2021, 26(7), 1680–1688 CrossRef CAS PubMed.
- M. Langione, F. Bobier, C. Meier, S. Hasenfuss and U. Schulze, Will Quantum Computing Transform Biopharma R&D? Accessed: 2021-10-12.
- M. Evers, A. Heid and E. Ostojic, Pharma's digital Rx: Quantum computing in drug research and development, Accessed: 2021-10-12.
- Merck KGaA, Darmstadt, Germany, and HQS Quantum Simulations Cooperate in Quantum Computing, Accessed: 2021-10-12.
- Rahko announces Merck collaboration, Accessed: 2021-10-12.
- C. Metinko, Zapata Computing Raises $ 38M As Quantum Computing Nears, Accessed: 2021-10-12.
- L. Siow, ProteinQure Collaborates with AstraZeneca to Design Novel Peptide Therapeutics, Accessed: 2021-10-12.
- M. Beyer, CrownBio and JSR Life Sciences Partner with Cambridge Quantum Computing to Leverage Quantum Machine Learning for Novel Cancer Treatment Biomarker Discovery, Accessed: 2021-10-12.
- C. Zhang, S. Bengio, M. Hardt, B. Recht and O. Vinyals, Commun. ACM, 2021, 64(3), 107–115 CrossRef.
- J. J. Hopfield, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 2554–2558 CrossRef CAS PubMed.
- L. G. Valiant, Commun. ACM, 1984, 27, 1134–1142 CrossRef.
- M. V. Tsodyks and M. K. Feigel’man, Europhys. Lett., 1988, 6(2), 101 CrossRef.
- E. Gardner, J. Phys. A: Math. Gen., 1988, 21(1), 257 CrossRef.
- G. Györgyi, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 7097–7100 CrossRef PubMed.
- E. Barkai, D. Hansel and I. Kanter, Phys. Rev. Lett., 1990, 65, 2312–2315 CrossRef PubMed.
- E. Barkai, D. Hansel and H. Sompolinsky, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 4146–4161 CrossRef PubMed.
- A. Engel, H. M. Köhler, F. Tschepke, H. Vollmayr and A. Zippelius, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 7590–7609 CrossRef PubMed.
- F. Morone, F. Caltagirone, E. Harrison and G. Parisi, Replica theory and spin glasses, arXiv preprint arXiv:1409.2722, 2014.
- L. Zdeborová and F. Krzakala, Adv. Phys., 2016, 65, 453–552 CrossRef.
- A. Decelle, F. Krzakala, C. Moore and L. Zdeborová, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 066106 CrossRef PubMed.
- J. S. Yedidia, W. T. Freeman and Y. Weiss, et al. , Exploring Artificial Intelligence in the New Millennium, 2003, 8, 0018–9448 Search PubMed.
- G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto and L. Zdeborová, Rev. Mod. Phys., 2019, 91, 045002 CrossRef CAS.
- O. Y. Feng, R. Venkataramanan, C. Rush and R. J. Samworth, A unifying tutorial on Approximate Message Passing, 2021 Search PubMed.
- H. W. Lin, M. Tegmark and D. Rolnick, J. Stat. Phys., 2017, 168, 1223–1247 CrossRef.
- J. R. L. de Almeida and D. J. Thouless, J. Phys. A: Math. Gen., 1978, 11(5), 983–990 CrossRef.
- M. Mézard, G. Parisi and M. A. Virasoro, Europhys. Lett., 1986, 1, 77–82 CrossRef.
- K. G. Wilson, Phys. Rev. B: Condens. Matter Mater. Phys., 1971, 4, 3174–3183 CrossRef.
- M. Gell-Mann and F. E. Low, Phys. Rev., 1954, 95, 1300–1312 CrossRef.
- L. P. Kadanoff, Phys. Phys. Fiz., 1966, 2, 263–272 Search PubMed.
- K. G. Wilson, Phys. Rev. B: Condens. Matter Mater. Phys., 1971, 4, 3174–3183 CrossRef.
- K. G. Wilson, Rev. Mod. Phys., 1975, 47, 773–840 CrossRef.
- P. Mehta and D. J. Schwab, An exact mapping between the variational renormalization group and deep learning, arXiv preprint arXiv:1410.3831, 2014.
- M. Koch-Janusz and Z. Ringel, Nat. Phys., 2018, 14, 578–582 Search PubMed.
- S. M. Apenko, Phys. A, 2012, 391(1–2), 62–77 CrossRef.
- S. Sim, P. D. Johnson and A. Aspuru-Guzik, Adv. Quantum Technol., 2019, 2, 1900070 CrossRef.
- B. Collins and P. Ŝniady, Commun. Math. Phys., 2006, 264, 773–795 CrossRef.
- A. Ambainis and J. Emerson, Quantum t-designs: t-wise independence in the quantum world, 2007.
- T. Hubregtsen, J. Pichlmeier, P. Stecher and K. Bertels, Quantum Mach. Intell., 2021, 3, 1–19 CrossRef.
- Y. Du, M.-H. Hsieh, T. Liu, S. You and D. Tao, PRX Quantum, 2021, 2, 040337 CrossRef.
- H.-C. Cheng, M.-H. Hsieh and P.-C. Yeh, 2015, arXiv preprint arXiv:1501.00559.
- L. Banchi, J. Pereira and S. Pirandola, PRX Quantum, 2021, 2, 040321 CrossRef.
- J. R. McClean, S. Boixo, V. N. Smelyanskiy, R. Babbush and H. Neven, Nat. Commun., 2018, 9(1), 1–6 CrossRef CAS PubMed.
- A. W. Harrow and R. A. Low, Commun. Math. Phys., 2009, 291, 257–302 CrossRef.
- M. Cerezo, A. Sone, T. Volkoff, L. Cincio and P. J. Coles, Nat. Commun., 2021, 12(1), 1–12 CrossRef PubMed.
- M. Larocca, P. Czarnik, K. Sharma, G. Muraleedharan, P. J. Coles and M. Cerezo, 2021, arXiv preprint arXiv:2105.14377.
- S. Wang, E. Fontana, M. Cerezo, K. Sharma, A. Sone, L. Cincio and P. J. Coles, Nat. Commun., 2021, 12(1), 1–11 CrossRef PubMed.
- J. Romero and A. Aspuru-Guzik, Adv. Quantum Technol., 2021, 4, 2000003 CrossRef.
- B. Khalid, S. H. Sureshbabu, A. Banerjee and S. Kais, 2022, arXiv preprint arXiv:2202.00112.
- J. Erdmenger, K. T. Grosvenor and R. Jefferson, Towards quantifying information flows: relative entropy in deep neural networks and the renormalization group, 2021 Search PubMed.
- E. Tang, Phys. Rev. Lett., 2021, 127, 060503 CrossRef CAS PubMed.
- E. Tang, Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, 2019, pp. 217–228 Search PubMed.
- B. Douçot and L. B. Ioffe, Rep. Progress Phys., 2012, 75, 072001 CrossRef PubMed.
- A. G. Fowler, M. Mariantoni, J. M. Martinis and A. N. Cleland, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 032324 CrossRef.
- X.-C. Yao, T.-X. Wang, H.-Z. Chen, W.-B. Gao, A. G. Fowler, R. Raussendorf, Z.-B. Chen, N.-L. Liu, C.-Y. Lu and Y.-J. Deng, et al. , Nature, 2012, 482, 489–494 CrossRef CAS PubMed.
- L. Egan, D. M. Debroy, C. Noel, A. Risinger, D. Zhu, D. Biswas, M. Newman, M. Li, K. R. Brown and M. Cetina, et al., 2020, arXiv preprint arXiv:2009.11482.
- D. Aharonov and M. Ben-Or, SIAM J. Comput., 2008, 38(4) DOI:10.1137/S0097539799359385.
- Z. Chen, K. J. Satzinger, J. Atalaya, A. N. Korotkov, A. Dunsworth, D. Sank, C. Quintana, M. McEwen, R. Barends and P. V. Klimov, et al. , Nature, 2021, 595, 383–387 CrossRef PubMed.
- A. Parra-Rodriguez, P. Lougovski, L. Lamata, E. Solano and M. Sanz, Phys. Rev. A, 2020, 101, 022305 CrossRef CAS.
- J. Eisert, D. Hangleiter, N. Walk, I. Roth, D. Markham, R. Parekh, U. Chabaud and E. Kashefi, Nat. Rev. Phys., 2020, 2, 382–390 CrossRef.
- J. S. Schreck, C. W. Coley and K. J. Bishop, ACS Cent. Sci., 2019, 5, 970–981 CrossRef CAS PubMed.
- J. L. Baylon, N. A. Cilfone, J. R. Gulcher and T. W. Chittenden, J. Chem. Inf. Model., 2019, 59, 673–688 CrossRef CAS PubMed.
- H. Dai, C. Li, C. W. Coley, B. Dai and L. Song, 2020, arXiv preprint arXiv:2001.01408.
- K. Lin, Y. Xu, J. Pei and L. Lai, 2019, arXiv preprint arXiv:1906.02308.
- B. Liu, B. Ramsundar, P. Kawthekar, J. Shi, J. Gomes, Q. Luu Nguyen, S. Ho, J. Sloane, P. Wender and V. Pande, ACS Cent. Sci., 2017, 3, 1103–1113 CrossRef CAS PubMed.
- S. Johansson, A. Thakkar, T. Kogej, E. Bjerrum, S. Genheden, T. Bastys, C. Kannas, A. Schliep, H. Chen and O. Engkvist, Drug Discov. Today Technol., 2019, 32–33, 65–72 CrossRef PubMed.
- H.-P. Breuer, F. Petruccione, et al., The theory of open quantum systems, Oxford University Press on Demand, 2002 Search PubMed.
- Z. Hu, R. Xia and S. Kais, Sci. Rep., 2020, 10(1), 1–9 CrossRef PubMed.
- K. Lin, J. Peng, F. L. Gu and Z. Lan, J. Phys. Chem. Lett., 2021, 12, 10225–10234 CrossRef CAS PubMed.
- L. E. Herrera Rodriguez and A. A. Kananenka, J. Phys. Chem. Lett., 2021, 12, 2476–2483 CrossRef CAS PubMed.
- P. P. Mazz, D. Zietlow, F. Carollo, S. Andergassen, G. Martius and I. Lesanovsky, Phys. Rev. Res., 2021, 3, 023084 CrossRef.
- I. Luchnikov, S. Vintskevich, D. Grigoriev and S. Filippov, Phys. Rev. Lett., 2020, 124, 140502 CrossRef CAS PubMed.
- F. Häse, C. Kreisbeck and A. Aspuru-Guzik, Chem. Sci., 2017, 8, 8419–8426 RSC.
- C. K. Lee, P. Patil, S. Zhang and C. Y. Hsieh, Phys. Rev. Res., 2021, 3, 023095 CrossRef CAS.
- A. Khan, E. Huerta and A. Das, Phys. Lett. B, 2020, 808, 135628 CrossRef CAS.
- T. Villmann, A. Engelsberger, J. Ravichandran, A. Villmann and M. Kaden, Neural Comput. Appl., 2020, 1–10 Search PubMed.
- C. Bellinger, R. Coles, M. Crowley and I. Tamblyn, Reinforcement Learning in a Physics-Inspired Semi-Markov Environment, Canadian Conference on Artificial Intelligence, 2020, pp. 55–56 Search PubMed.
- M. Trenti, L. Sestini, A. Gianelle, D. Zuliani, T. Felser, D. Lucchesi and S. Montangero, 2020, arXiv preprint arXiv:2004.13747.
- P. Tiwari and M. Melucci, IEEE Access, 2019, 7, 42354–42372 Search PubMed.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815 CrossRef CAS PubMed.
- G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang and L. Yang, Nat. Rev. Phys., 2021, 3, 422–440 CrossRef.
- Z. Chen, K. Satzinger, J. Atalaya, A. Korotkov, A. Dunsworth, D. Sank, C. Quintana, M. McEwen, R. Barends, P. Klimov, S. Hong, C. Jones, A. Petukhov, D. Kafri, S. Demura, B. Burkett, C. Gidney, A. Fowler, A. Paler and J. Kelly, Nature, 2021, 595, 383–387 CrossRef PubMed.
- IBM's roadmap for scaling quantum technology, https://research.ibm.com/blog/ibm-quantum-roadmap, Accessed: 2021-10-12.
Footnotes |
| † These authors contributed equally to this work. |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |