Open Access Article
Open Access ArticleOptical feedback control loop for the precise and robust acoustic focusing of cells, micro- and nanoparticles†
Cooper L.
Harshbarger
 *abc,
Michael S.
Gerlt
*abc,
Michael S.
Gerlt
 cd,
Jan A.
Ghadamian
c,
Davide C.
Bernardoni
cd,
Jan A.
Ghadamian
c,
Davide C.
Bernardoni
 ab,
Jess G.
Snedeker
ab,
Jess G.
Snedeker
 ab and
Jürg
Dual
ab and
Jürg
Dual
 c
c
aDepartment of Orthopedics, Balgrist University Hospital, University of Zurich, Zurich, Switzerland. E-mail: hcooper@ethz.ch
bInstitute for Biomechanics, Swiss Federal Institute of Technology Zurich, Zurich, Switzerland
cInstitute for Mechanical Systems, Swiss Federal Institute of Technology Zurich, Zurich, Switzerland
dInstitute for Chemical and Bioengineering, Swiss Federal Institute of Technology Zurich, Zurich, Switzerland
First published on 11th July 2022
Abstract
Despite a long history and the vast number of applications demonstrated, very few market products incorporate acoustophoresis. Because a human operator must run and control a device during an experiment, most devices are limited to proof of concepts. On top of a possible detuning due to temperature changes, the human operator introduces a bias which reduces the reproducibility, performance and reliability of devices. To mitigate some of these problems, we propose an optical feedback control loop that optimizes the excitation frequency. We investigate the improvements that can be expected when a human operator is replaced for acoustic micro- and nanometer particle focusing experiments. Three experiments previously conducted in our group were taken as a benchmark. In addition to being automatic, this resulted in the feedback control loop displaying a superior performance compared to an experienced scientist in 1) improving the particle focusing by at least a factor of two for 5 μm diameter PS particles, 2) increasing the range of flow rates in which 1 μm diameter PS particles could be focused and 3) was even capable of focusing 600 nm diameter PS particles at a frequency of 1.72075 MHz. Furthermore, the feedback control loop is capable of focusing biological cells in one and two pressure nodes. The requirements for the feedback control loop are: an optical setup, a run-of-the-mill computer and a computer controllable function generator. Thus resulting in a cost-effective, high-throughput and automated method to rapidly increase the efficiency of established systems. The code for the feedback control loop is openly accessible and the authors explicitly wish that the community uses and modifies the feedback control loop to their own needs.
Introduction
The Kundt's tube described in 1866 (ref. 1) is based on acoustophoresis, a contactless, label-free, and non-invasive method to actively control the position of particles over a wide range of sizes using acoustic pressure waves.2In 1938 Hillary W. St. Clair filed, to our knowledge, the first patent related to acoustophoresis “Sonic flocculator and method of flocculating smoke or the like”.3 Continued research on both the theoretical as well as the experimental aspect of acoustophoresis has led to a vast number of applications such as acoustic particle levitation,4 acoustic holograms5 and tweezers,6 aiding in 3D mechanical characterization7 and isolating cancer cells from blood8 to name only a few.
Despite a long history, a plethora of publications in the field and interesting applications demonstrated in research, only a small number of companies offer products based on acoustic particle manipulation.9 There are many reasons for this such as the currently imprecise manufacturing which could be tackled by improved cleanroom processes10 or by improving the predictability or reliability of devices using more complex production methods or designs.11–14 As for the enhanced understanding of the fundamental principles of acoustophoresis, aiding in device design, various computational models have been created.15–18 Aiding these computational models, deep learning can be used to find a device design that creates a desired acoustic potential.19
The beforehand mentioned approaches to improve the performance of acoustic devices place an emphasis on improving the theoretical device performance. When considering a prevalent application of acoustophoresis, focusing micro- and nanometer particles,20–26 additional methods have sought to further increase the experimental outcome. A successful outcome is achieved by reducing the influence of acoustic streaming vs. the acoustic radiation force. Due to the size dependent scaling, seen in eqn (2) and (6), this becomes increasingly difficult if the particles' size is decreased to below 1 micron. In addition, temperature changes must be taken into account, which result in a detuning of the device and therefore lower pressure amplitudes. An approach is to control the excitation frequency of the piezoelectric transducer which is enabling the focusing via a feedback control loop (FCL). This is accomplished by measuring the resonance response of the system and thus indirectly effects the outcome of the experiment. Two parameters are currently being used to measure the resonance, which are the impedance of the system27–29 or the electric current.30 The measured resonance behavior of the system is then used to tune the excitation frequency of the driving piezoelectric transducer. These state of the art methods of which parameters can be used to implement a FCL are summarized in Table 1.
It however has been noted that these approaches, which are based on measuring electric signals, might not be able to correctly identify the optimal excitation frequency of a coupled system consisting of the piezoelectric transducer and the microfluidic channel.31 To try and elevate this shortcoming, the system can be characterized a priori to an experiment to try and find the corresponding resonance frequencies32 or an FCL can be combined with a lookup table.29 However, all methods require additional electrical equipment and while increasing the performance of a system, they only indirectly influence the performance, especially for particles close to the critical radius as actuating the system at resonance does not guarantee an optimal streaming suppression. An optical FCL has been reported only in the context of particle positioning33 which uses a visual input to control the position of one particle in two dimensions. An optical FCL, which directly takes the desired outcome as the control signal, has not been presented before. Our goal was therefore to expand on the idea of an optical FCL, schematically represented in Fig. 1, which directly effects the performance of a system classified by the quality of the particle focusing. The shift from a resonance control to an optical control can also help in finding the optimal excitation frequency when acoustic streaming is present. Thus being able to focus particles that otherwise would be dominated by acoustic streaming. The FCL uses the particle linewidth (LW) as the parameter to optimize, where the LW is the spread of the particles in the microfluidic channel of a device, Fig. 2. The FCL can easily be integrated into any preexisting setup that allows for an optical readout during the experiment, increasing the sample throughput whilst not increasing the cost.
Optically automatizing the determination of an optimal excitation frequency leads to an increase of the acoustic force acting on the particles of interest. This lead to an improved performance of acoustophoretic devices when compared to three benchmark tests10 by 1) narrowing the focusing of the particles by at least a factor of two for 5 μm PS particles, 2) increasing the range of flow rates in which 1 μm diameter PS particles could be focused and 3) focusing particles with a diameter as small as 600 nm (Fig. 3). The manipulation of such small particles is a significant step, since in state of the art publications, a very complicated setup needs to be utilised to manipulate particles in this size range,34 or no fluid flow could be applied.35 Finally, we demonstrate the versatility of the setup by showing two different types of devices and modes of operation (Fig. 4) using biological cells. The above mentioned augmented performance, based on automatising the focusing, is needed for applications to be successful outside of laboratory settings. We therefore believe that our novel optical FCL can be used as a foundation to further the development and integration of acoustophoresis into market products.9,36 This is in line with the increasing need of simpler and more adaptable lab on a chip devices.37
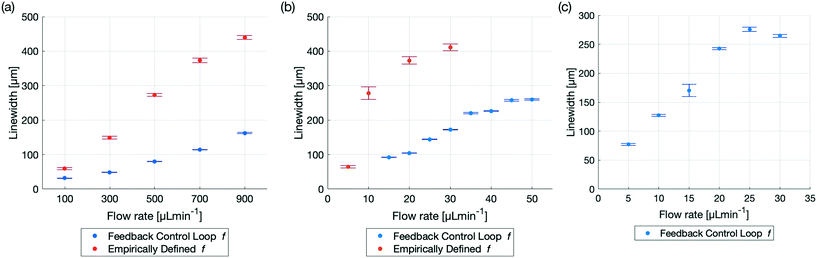 | ||
Fig. 3 Comparison of particle focusing in a glass capillary with a empirically defined excitation frequency43vs. an optimal excitation frequency found by the FCL for different particle sizes and flow rates. All results were generated with the same setup and capillary driving both piezoelectric transducers at V = 20 Vpp and the precise linewidth can be found in Table 2. (a) Comparison of 5 μm diameter PS particles for the flow rates: 100, 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, 700 and 900 μL min−1. The excitation frequency defined by the FCL is f = 1.7204 MHz. The improved linewidth is not only seen in the smaller linewidths at higher flow rates, but also in the smaller error bars, indicating a more precise and robust focusing. (b) The focusing of 1 μm diameter PS particles using an empirically defined frequency was possible for the flow rate of 5 μL min−1. At 10 μL min−1 the linewidth was already close to half of the diameter of the capillary and at higher flow rates, the focusing was nearly non existent. Employing the FCL, which found the frequency at f = 1.7204 MHz, focusing was possible even with flows up to 50 μL min−1. (c) 600 nm diameter PS particles could be focused by the FCL, when utilizing phase 1 and phase 2. The frequency defined by the FCL from phase 1 was 1.7202 MHz and phase 2 further iterated and found an improved excitation frequency at 1.72075 MHz. Even at high flow rates, e.g. 25 μL min−1 and 30 μL min−1 the linewidth was still smaller than half of the capillary diameter. 500, 700 and 900 μL min−1. The excitation frequency defined by the FCL is f = 1.7204 MHz. The improved linewidth is not only seen in the smaller linewidths at higher flow rates, but also in the smaller error bars, indicating a more precise and robust focusing. (b) The focusing of 1 μm diameter PS particles using an empirically defined frequency was possible for the flow rate of 5 μL min−1. At 10 μL min−1 the linewidth was already close to half of the diameter of the capillary and at higher flow rates, the focusing was nearly non existent. Employing the FCL, which found the frequency at f = 1.7204 MHz, focusing was possible even with flows up to 50 μL min−1. (c) 600 nm diameter PS particles could be focused by the FCL, when utilizing phase 1 and phase 2. The frequency defined by the FCL from phase 1 was 1.7202 MHz and phase 2 further iterated and found an improved excitation frequency at 1.72075 MHz. Even at high flow rates, e.g. 25 μL min−1 and 30 μL min−1 the linewidth was still smaller than half of the capillary diameter. | ||
Theoretical background
Acoustic radiation force (ARF)
The FCL demonstrated in this paper allows to precisely focus particles of interest. This focusing exploits the ARF which, given a spherical particle with a radius much smaller than the acoustic wavelength in an inviscid fluid, is commonly approximated as the negative Gradient of the Gor'kov potential38| Frad = −∇U, | (1) |
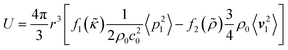 | (2) |
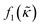 which is related to the relative compressibility and the dipole coefficient
which is related to the relative compressibility and the dipole coefficient 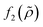 which is related to the relative density
which is related to the relative density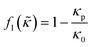 | (3) |
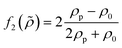 | (4) |
A standing wave is required for a large ARF magnitude. The resonance frequency for the nth ultrasonic resonance mode of a one-dimensional standing wave with hard wall boundary conditions is39
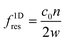 | (5) |
Stokes' drag force
In addition to the ARF, a second force, the Stokes' drag force produced by the acoustic streaming velocity vstr, acts on the particle in the fluid40,41| Fstr = 6πηr(vstr − vp), | (6) |
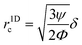 | (7) |
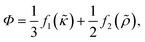 | (8) |
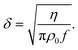 | (9) |
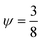 ,42 is r1Dc,a = 0.78
,42 is r1Dc,a = 0.78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μm. The numerical model for our specific geometry which describes the diminished influence of the acoustic streaming compared to the influence of the ARF described by Gerlt et al.,43 resulted in a numerical critical radius rc,n = 0.35 μm. This still does not match our experimental findings as will be seen in Table 2 and Fig. 4, hence providing further evidence that the critical radius for a given system is not known prior to an experiment.44
μm. The numerical model for our specific geometry which describes the diminished influence of the acoustic streaming compared to the influence of the ARF described by Gerlt et al.,43 resulted in a numerical critical radius rc,n = 0.35 μm. This still does not match our experimental findings as will be seen in Table 2 and Fig. 4, hence providing further evidence that the critical radius for a given system is not known prior to an experiment.44
| Flow rate [μL min−1] | LW for an empirical f [μm] | LW for FCL defined f [μm] |
|---|---|---|
| 5 μm diameter PS particles | ||
| 100 | 59.54 (±2.67) | 31.80 (±0.58) |
| 300 | 149.02 (±4.26) | 48.51 (±0.28) |
| 500 | 273.17 (±3.92) | 80.27 (±0.71) |
| 700 | 373.19 (±6.65) | 114.27 (±0.57) |
| 900 | 439.65 (±5.67) | 162.55 (±1.31) |
| 1 μm diameter PS particles | ||
| 5 | 65.02 (±3.92) | ** |
| 10 | 277.62 (±18.20) | ** |
| 15 | * | 92.21 (±0.72) |
| 20 | 372.93 (±10.42) | 104.61 (±0.26) |
| 25 | * | 144.14 (±0.63) |
| 30 | 411.29 (±9.94) | 172.41 (±0.89) |
| 35 | * | 216.66 (±1.91) |
| 40 | * | 225.83(±1.14) |
| 45 | * | 257.22 (±2.22) |
| 50 | * | 259.76 (±1.88) |
| 600 nm diameter PS particles | ||
| 5 | * | 77.23 (±1.50) |
| 10 | * | 127.42 (±1.57) |
| 15 | * | 170.37 (±10.48) |
| 20 | * | 242.52 (±1.80) |
| 25 | * | 275.95 (±3.74) |
| 30 | * | 264.81 (±2.61) |
Materials & methods
Setup
The setup employed is analogous to the one used in Gerlt et al.43 the fluid flow through a circular glass capillary (76 mm length, 1 mm outer diameter, 0.75 mm inner diameter) and a glass – silicon – glass device (device: 50 mm length, 12 mm width, 1.4 mm thickness; focusing channel: 15 mm length, 1 mm width, 0.2 mm height) was controlled by volumetric syringe pumps (Nemesys, Cetoni). A function generator, connected to the computer running the FCL, (AFG-2225, GW Instek) powered the piezoelectric transducers. The signal from the function generator was amplified (325LA Linear Power Amplifier, Electronics & Innovation) and monitored using an oscilloscope (UTD2025CL, UNI-T). For optical data acquisition a custom made setup from THORLABS consisting of specifically selected parts from the Cerna® series was used. The video feed generated with a 5× objective (M Plan Apo 5×/0.14, Mitutoyo) and a uEye camera (UI-3160CP Rev. 2.1, iDS, 1920 × 1200 pixels, 60 fps), as shown in Fig. 1 phase 0, was captured from one of the two computer screens and fed into the FCL running on PyCharm 2021.1.3 (Edu) with Python 3.8.Glass capillary
In order to compare the device performance as best as possible, the tests were performed with the same glass capillaries, piezoelectric transducers and production procedure that was used by Gerlt et al.43 the glass capillary (TW100-4, World Precision Instruments) has two piezoelectric transducers (10 mm length, 2 mm width, 1 mm thickness, Pz26, Meggitt Ferroperm) glued on using an electrically conductive Epoxy glue (H20E, Epoxy Technology). Copper cables (0.15 mm diameter) were attached to the piezoelectric transducers and the electrical connection was established with an electrically conductive silver paste.Glass–silicon–glass device
The glass–silicon–glass device, seen in in Fig. 4(c), was produced by bonding a 500 μm thick glass wafer to a 200 μm thick silicon wafer. Channels were patterned onto the exposed silicon wafer using photolithography (resist: S1828, Shipley, 4′000 rpm; developer: AZ351B, Microchemicals). The full thickness of the silicon wafer was etched away with an inductively coupled plasma (ICP) deep reactive ion etching (DRIE) machine (Estrellas, Oxford instruments). Following the etching, a 700 μm thick glass wafer was anodically bonded onto the exposed silicon wafer. The wafer was then diced into individual chips with a wafer saw (DAD3221, Disco corporation). Fused silica capillaries (164 ± 6 μm outer diameter, 100 ± 6 μm inner diameter, Molex) were inserted into the inlets and outlets of the chips and fixed with a two-component glue (5 Minute Epoxy, Devcon). The piezoelectric transducers, Epoxy glue, wiring and an electrically conductive silver pasted are the same ones used for the glass capillaries.Polystyrene particles
Green fluorescent polystyrene (PS) particles (microParticles GmbH, Germany) with diameters of 5.19 ± 0.14 μm, 1.08 ± 0.04 μm and 600 ± 20 nm were used for all experiments in Fig. 3 and all experiments were conducted with 0.5% v/v.Cell culture
The bone cancer cells used is the SaOs-2 cell line. The cell line was kept at the standard 37 °C and 5% CO2 and 95% air. The cell media used is DMEM – F12 Ham (D8437, Sigma) supplemented with 10% fetal bovine serum (10270106, Thermo) and 1% P/S. The cells were passaged when 60% confluency was reached. The diameter of the cells is 15.73 ± 0.42 μm (CellDrop BF, DeNovix).Feedback control loop (FCL)
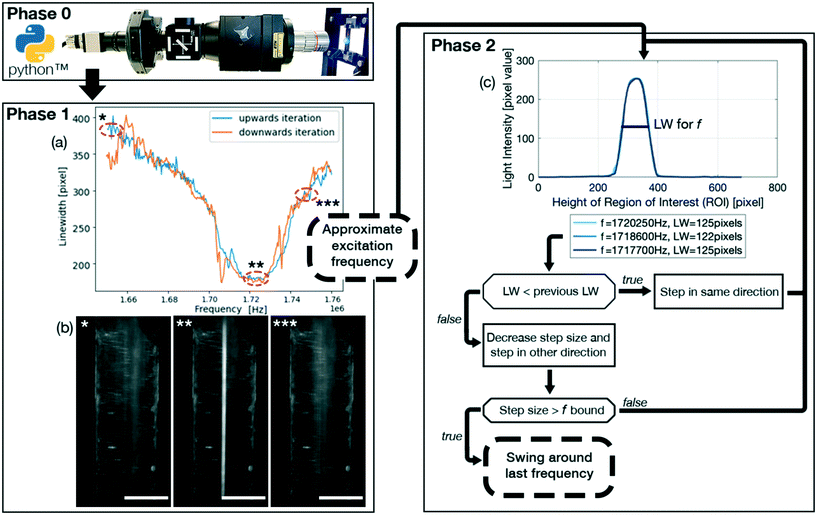
The FCL, shown schematically in Fig. 1 and available on Gitlab (https://gitlab.com/acoustofluidics/feedback-control-loop), is implemented in the widely used programming language Python and is split into 3 phases,• Phase 0: initialization of the system.
• Phase 1: approximate determination of an optimal excitation frequency.
• Phase 2: precise determination and stabilisation of the optimal excitation frequency.
A highlight of the code is the ImageGrab function. This allows the user to continuously capture the image directly from the computer screen of the computer controlling the imaging system in order to use the image for the FCL to determine the linewidth. This ensures that any preexisting optical setup can be utilized. Therefore, the imaging system does not need to be adapted to the FCL, thus being an augmentation without any additional costs. It is recommended to use two monitors, such that the plotting does not interfere with the screen capture.
In the following description, this typeset was used to highlight variables.
The set of parameters that need to be defined for phase 1 is comprised of: initial_time_delay_1 which is the initial time delay for system to settle, frequency_step_size_1 which is the frequency step size, time_delay_1 which is the time delay between frequency steps.
The set of parameters that need to be defined for phase 2 is comprised of: wait_time_transition_2 which is the time delay for the system to settle between phase 1 and phase 2. frequency_step_size_2 which is the frequency step size. time_delay_2 which is the time delay between the frequency steps. Threshold which is the threshold value for a change of direction, if the linewidth has not improved in the past ∣threshold∣ iterations. swing_value which is the value with which the step size is multiplied with after changing the direction of iteration. The swing_value is therefore ∈ (0, 1). freq_bound is the lower frequency boundary fora minimal step size. In our experience, a ∣freq_bound∣ = 20 [Hz] leads to optimal results.
It is recommended that for a first rough characterization of the system phase 1 is run at high flow rates, e.g. 100 μL min−1 and above, with particle diameters of at least a few micrometer diameter and in a large frequency range, e.g. ±10% of the expected resonance frequency. In a second round of characterisation, the frequency step sizes and frequency range can be decreased and shifted symmetrically around the approximately optimal excitation frequency and time_delays can be increased for an even more precise approximate excitation frequency. The thus found approximate excitation frequency can be constant over multiple days and experiments when using multi micrometer diameter particles. For particles around one micrometer in diameter or smaller it is recommended to use phase 2.
Linewidth calculation
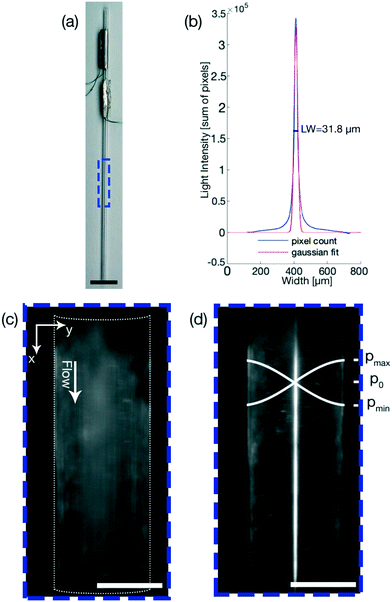
The linewidth was chosen as the parameter that the FCL optimizes, and in our case is defined as the spread of particles over the microfluidic channel, thus being a measure for the focusing of the particles. The linewidth is determined differently in phase 1 and phase 2.In phase 1 the linewidth is calculated by taking the sum of the pixel values of all the pixels in the direction of flow (indicated by the x-axis in Fig. 2(c)) and is plotted over the width of the channel (indicated by the y-axis in Fig. 2(c)). The linewidth is then calculated using a Gaussian fit as the region in which 2 standard deviations, or ∼70% of the total sum of the pixels, are located. This linewidth readout is then plotted over the frequency range as shown in Fig. 1(a).
In phase 2, as seen in Fig. 1(c), 4(e) and (g), the pixel distribution over the whole channel is displayed for a given frequency, where the pixel values range from 0 (pure black) to 255 (pure white). The resulting pixel value is the average pixel value of all the pixels in the direction of flow (indicated by the x-axis in Fig. 4(e) and (g)) and is plotted over the width of the channel (indicated by the y-axis in Fig. 4(e) and (g)). The linewidth is calculated the same way as for phase 1, but multiple frequencies are plotted, providing live output of how the particle distribution is evolving. The linewidth is given in the legend, with the corresponding frequency.
Results
The data presented provides a brief overview of some of the use cases where the FCL can be employed to increase device performance and throughput, whilst being independent of a human operator. Fig. 3 and Table 2 compare the relative performance between an excitation frequency determined empirically10 and the excitation frequency defined by the FCL. All experiments were conducted with 0.5% v/v.Improved focusing of 5 micrometer diameter PS particles
There is significant demand for narrow LWs at high flow rates to increase the throughput while minimizing clogging and it was recently demonstrated that flow rates of up to 1000 μL min−1 are relevant and achievable for cell separation.45 Flow rates of up to 900 μL min−1 were demonstrated, in ref. 43 albeit the focusing drastically decreased at high flow rates, Fig. 3. The FCL presented here is capable of focusing the PS particles down to a narrower LW, with an increased stability, where the stability increase is defined as the reduced size of the error of the measurements, as illustrated in Fig. 3 and Table 2. The FCL resulted in a LW which was half as narrow as the LW that resulted from determining the excitation frequency empirically for a flow rate of 100 μL min−1 (94 mms−1). For higher flow rates, the LW remained narrower by even larger margins and at a 900 μL min−1 (850 mms−1) flow rate the LW resulting from the FCL was about the same width as the LW for a flow rate of 300 μL min−1 for the empirically determined frequency. The frequency chosen for this comparison is f = 1.7204 MHz, found using only phase 1 of the FCL as in Fig. 1. Technically, phase 2 could have been run as well, but as the LW was already half of the LW when using the empirically determined excitation frequency (f = 1.74 MHz), phase 2 was omitted.Higher flow rate for 1 micrometer diameter PS particles
Decreasing the particle size increases the difficulty to focus the particles as the ARF decreases and therefore more precise excitation frequencies are required. Focusing of 1 μm diameter PS particles for instance is possible however, above 10 μL min−1 Gerlt et al.43 were not able to focus 1 μm PS particles, as the excitation frequency determined empirically has a limited precision. The FCL demonstrates that 1 μm particles can be focused beyond 10 μL min−1. Even at 5 times the flow rate (50 μL min−1 instead of 10 μL min−1) the particle LW was still narrower with the frequency chosen by the FCL, compared to the empirically chosen frequency in Fig. 3. The lack of focusing of the FCL of 5 and 10 μL min−1 flow rates can be attributed to PS particles being trapped in the device whereas the trapping can only be overcome at higher flow rates. As for the 5 μm PS particles, only phase 1 was used to generate this data.600 nanometer diameter PS particle focusing
Particle sizes greater than one micrometer in diameter are important, but with improving device designs and manufacturing precision, focusing of nanometer particles is a realistic aim. Building on the corpus of nanometer particle trapping46 and separation,47 the FCL demonstrated the capability to use bulk acoustic wave (BAW) devices to focus nanometer particles. When the particle radius is around the critical radius rc the acoustic streaming and thus the Stokes' drag force resulting from the acoustic streaming can dominate the movement of the particles in the fluid, therefore phase 1 and phase 2 of the FCL were run in order to find an excitation frequency at which the dominating force was still the ARF. eqn (7) indicates that the analytical and numerical critical radius where the AS dominates and no focusing is possible is r1Dc,a = 0.78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μm respectively rc,n = 0.35
μm respectively rc,n = 0.35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μm. The focusing of 600 nm diameter PS particles however show that both the analytical and the numerical solution both provide critical radii above which focusing was demonstrated in Fig. 3. While43 was not able to find any focusing of 600 nm diameter particles, the FCL presented here could identify excitation frequencies at which the 600 nm diameter particles could be focused. Even at higher flow rates, such as 30 μL min−1, the excitation frequency determined by the FCL proved to be good enough for focusing particles.
μm. The focusing of 600 nm diameter PS particles however show that both the analytical and the numerical solution both provide critical radii above which focusing was demonstrated in Fig. 3. While43 was not able to find any focusing of 600 nm diameter particles, the FCL presented here could identify excitation frequencies at which the 600 nm diameter particles could be focused. Even at higher flow rates, such as 30 μL min−1, the excitation frequency determined by the FCL proved to be good enough for focusing particles.
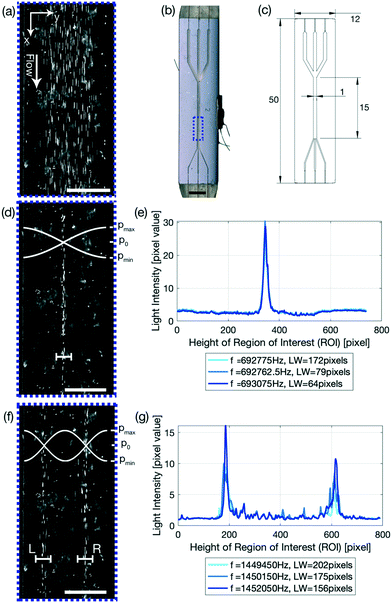
Glass–silicon–glass device and n = 1, 2 resonance mode
The glass capillary was used to demonstrate the focusing of PS particles using the FCL and to quantify the performance increase of the system. To further elucidate how powerful the FCL is, a glass–silicon–glass device was used. The glass–silicon–glass device demonstrates that the FCL is capable of not only finding an improved excitation frequency for other setups than glass capillaries and PS particles, but can furthermore focus biological cells in an n = 1 resonance mode as detailed in eqn (5). n > 1 resonance modes are however also important in many processes. By altering the frequency range, and only the frequency range, the FCL is able to define the optimal frequency for resonance modes n > 1, such as the n = 2 resonance mode shown in Fig. 1(f) and (g). This is made possible, as the FCL is searching for the narrowest LW, and only chooses to look at one line, thus enabling this feature of the FCL. Therefore it is not surprising that the LWs for the resonance modes n = 1 and n = 2 are approximately the same, Fig. 4(d) 31.28 ± 0.98 μm compared to (f) (L) 33.01 ± 5.27 μm and (R) 36.15 ± 1.00 μm, which also corresponds to the line width found for the 5 μm PS particles with a flow rate of 100 μL min−1 (31.80 ± 0.58 μm). Another interesting readout to point out from Fig. 4(e) and (g) is that, by keeping the total cell number constant, the pixel value of the light intensity drops by half if the mode is increased from n = 1 (e) to n = 2 (g) which is as expected as there are half as many cells per modal line, and indicates that the FCL could be used to read out sample concentration. Another value to note is that in Fig. 1(c) the pixel value is 255, indicating a pure white line, which is expected as the video shows a stream of white in the middle. The cells, which are too few in number to form a continuous line in the channel even when focused, and therefore leave black spots in between the individual cells, have a much smaller average pixel value. Thus indicating that using higher concentrations is beneficial as this suppresses background noise, while at the same time allows for a higher sample concentrations and thus results in a higher sample throughput.Conclusions
The FCL was compared against 3 experiments previously conducted in our lab43 and demonstrates a superior performance compared to experienced scientists in 1) reducing the linewidth by at least a factor of two for 5 μm PS particles, 2) increasing the range of flow rates in which 1 μm diameter PS particles could be focused and 3) identifying an excitation frequency for which 600 nm diameter PS particles could be focused. Furthermore, the FCL is capable of manipulating biological cells and resonance modes of n greater than 1.These results indicate that by replacing the human operator by an optical FCL, ceteris paribus, the performance of a device can be augmented by automating otherwise laborious tasks. This replacement increases the device reliability without increasing the production complexity, increases the throughput, overall yields narrower focusing and focusing of 600 nm diameter PS particles can be achieved. A limitation, was that for small particles and low flow rates, such as 1 μm diameter PS particles at 5 μL min−1 and 10 μL min−1, particles were trapped at the piezoelectric transducers. This could be prevented by adapting the code to search for an optimal excitation frequency and then placing a frequency offset on the found frequency as the ARF decreases with sub-optimal frequency selection. This idea could also be used to find an excitation frequency in which all particles are focused, and then placing a small offset in order to separate the particles by size. A further limitation was that particles below 600 nm diameter could not be focused. Provided an advanced imaging system with a higher resolution, we believe that even smaller particles could be focused. Research groups with devices already mounted on high resolution optical systems could for instance use the screen capture functionality function as an adapter for their optical system and test this hypothesis.
The FCL relies on an optical input to minimize the particle linewidth. The frequency thus chosen and continuously adapted by the FCL is therefore not necessarily the exact resonance frequency of the system, which sets the presented FCL apart from previously reported FCLs. As the FCL requires no additional equipment, provided that the setup has an optical readout and the function generator can be controlled by a computer, we thus present a cost-effective, high-throughput and automated method to rapidly increase the efficiency of established systems used for particle focusing. The source code for the FCL is openly accessible; ideas and augmentations from the community are welcomed.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from the Swiss Federal Institute of Technology (ETH Zurich), the University of Zurich and the Balgrist University Hospital.Notes and references
- A. Kundt, Ann. Phys., 1866, 203, 497–523 CrossRef
.
-
Microscale Acoustofluidics, ed. T. Laurell and A. Lenshof, The Royal Society of Chemistry, 2015, 10.1039/9781849737067
.
-
C. H. W. St, Sonic flocculator and method of flocculating smoke or the like, US Pat., 2215484, 1940 Search PubMed
.
- A. Marzo, S. A. Seah, B. W. Drinkwater, D. R. Sahoo, B. Long and S. Subramanian, Nat. Commun., 2015, 6, 8661 CrossRef CAS PubMed
.
- K. Melde, A. G. Mark, T. Qiu and P. Fischer, Nature, 2016, 537, 518–522 CrossRef CAS PubMed
.
- A. Ozcelik, J. Rufo, F. Guo, Y. Gu, P. Li, J. Lata and T. J. Huang, Nat. Methods, 2018, 15, 1021–1028 CrossRef CAS PubMed
.
- N. F. Läubli, J. T. Burri, J. Marquard, H. Vogler, G. Mosca, N. Vertti-Quintero, N. Shamsudhin, A. DeMello, U. Grossniklaus and D. Ahmed,
et al.
, Nat. Commun., 2021, 12, 1–11 CrossRef PubMed
.
- C. Magnusson, P. Augustsson, A. Lenshof, Y. Ceder, T. Laurell and H. Lilja, Anal. Chem., 2017, 89, 11954–11961 CrossRef CAS PubMed
.
- W. Connacher, N. Zhang, A. Huang, J. Mei, S. Zhang, T. Gopesh and J. Friend, Lab Chip, 2018, 18, 1952–1996 RSC
.
- M. S. Gerlt, N. F. Läubli, M. Manser, B. J. Nelson and J. Dual, Micromachines, 2021, 12, 542 CrossRef PubMed
.
- A. G. Steckel, H. Bruus, P. Muralt and R. Matloub, Phys. Rev. Appl., 2021, 16, 014014 CrossRef CAS
.
- P. Reichert, D. Deshmukh, L. Lebovitz and J. Dual, Lab Chip, 2018, 18, 3655–3667 RSC
.
- D. Carugo, T. Octon, W. Messaoudi, A. L. Fisher, M. Carboni, N. R. Harris, M. Hill and P. Glynne-Jones, Lab Chip, 2014, 14, 3830–3842 RSC
.
- M. S. Gerlt, P. Ruppen, M. Leuthner, S. Panke and J. Dual, Lab Chip, 2021, 21, 4487–4497 RSC
.
- F. Lickert, M. Ohlin, H. Bruus and P. Ohlsson, J. Acoust. Soc. Am., 2021, 149, 4281–4291 CrossRef CAS PubMed
.
- A. G. Steckel and H. Bruus, J. Acoust. Soc. Am., 2021, 150, 634–645 CrossRef CAS PubMed
.
- Y. Zhou, Eur. Phys. J. Plus, 2020, 135, 1–12 CrossRef
.
- N. Nama, R. Barnkob, Z. Mao, C. J. Kähler, F. Costanzo and T. J. Huang, Lab Chip, 2015, 15, 2700–2709 RSC
.
- S. J. Raymond, D. J. Collins, R. O'Rorke, M. Tayebi, Y. Ai and J. Williams, Sci. Rep., 2020, 10, 1–12 CrossRef PubMed
.
- P. Augustsson, J. T. Karlsen, H.-W. Su, H. Bruus and J. Voldman, Nat. Commun., 2016, 7, 1–9 Search PubMed
.
- M. E. Piyasena, P. P. Austin Suthanthiraraj, R. W. Applegate Jr, A. M. Goumas, T. A. Woods, G. P. López and S. W. Graves, Anal. Chem., 2012, 84, 1831–1839 CrossRef CAS PubMed
.
- A. Fornell, H. Pohlit, Q. Shi and M. Tenje, Sci. Rep., 2021, 11, 1–9 CrossRef PubMed
.
- G. P. Gautam, T. Burger, A. Wilcox, M. J. Cumbo, S. W. Graves and M. E. Piyasena, Anal. Bioanal. Chem., 2018, 410, 3385–3394 CrossRef CAS PubMed
.
- J. Shi, X. Mao, D. Ahmed, A. Colletti and T. J. Huang, Lab Chip, 2008, 8, 221–223 RSC
.
- R. J. Olson, A. Shalapyonok, D. J. Kalb, S. W. Graves and H. M. Sosik, Limnol. Oceanogr.: Methods, 2017, 15, 867–874 CrossRef
.
- I. Iranmanesh, H. Ramachandraiah, A. Russom and M. Wiklund, RSC Adv., 2015, 5, 74304–74311 RSC
.
- G. Goddard, J. C. Martin, S. W. Graves and G. Kaduchak, Cytometry, Part A, 2006, 69, 66–74 CrossRef PubMed
.
- P. P. A. Suthanthiraraj, M. E. Piyasena, T. A. Woods, M. A. Naivar, G. P. López and S. W. Graves, Methods, 2012, 57, 259–271 CrossRef PubMed
.
- D. M. Kalb, R. J. Olson, H. M. Sosik, T. A. Woods and S. W. Graves, PLoS One, 2018, 13, e0207532 CrossRef PubMed
.
- V. Farmehini, S. Kiendzior, J. P. Landers and N. S. Swami, ACS Sens., 2021, 6, 3765–3772 CrossRef CAS PubMed
.
- J. Dual, P. Hahn, I. Leibacher, D. Möller and T. Schwarz, Lab Chip, 2012, 12, 852–862 RSC
.
- V. Vitali, G. Core, F. Garofalo, T. Laurell and A. Lenshof, Sci. Rep., 2019, 9, 1–10 CrossRef PubMed
.
- M. T. M. Takeuchi, H. A. H. Abe and K. Y. K. Yamanouchi, Jpn. J. Appl. Phys., 1996, 35, 3244 CrossRef CAS
.
- P. Sehgal and B. J. Kirby, Anal. Chem., 2017, 89, 12192–12200 CrossRef CAS PubMed
.
- Z. Mao, P. Li, M. Wu, H. Bachman, N. Mesyngier, X. Guo, S. Liu, F. Costanzo and T. J. Huang, ACS Nano, 2017, 11, 603–612 CrossRef CAS PubMed
.
- J. Rufo, F. Cai, J. Friend, M. Wiklund and T. J. Huang, Nat. Rev. Methods Primers, 2022, 2, 2662–8449 Search PubMed
.
- S. Battat, D. A. Weitz and G. M. Whitesides, Lab Chip, 2022, 22, 530–536 RSC
.
- L. P. Gor'kov, Sov. Phys. Dokl., 1962, 773–775 Search PubMed
.
- H. Bruus, Lab Chip, 2012, 12, 20–28 RSC
.
-
W. L. M. Nyborg, Physical acoustics, Elsevier, 1965, vol. 2, pp. 265–331 Search PubMed
.
- J. Lighthill, J. Sound Vib., 1978, 61, 391–418 CrossRef
.
- P. B. Muller, R. Barnkob, M. J. H. Jensen and H. Bruus, Lab Chip, 2012, 12, 4617–4627 RSC
.
- M. S. Gerlt, A. Paeckel, A. Pavlic, P. Rohner, D. Poulikakos and J. Dual, Phys. Rev. Appl., 2022, 17, 014043 CrossRef CAS
.
- W. Qiu, H. Bruus and P. Augustsson, Phys. Rev. E, 2020, 102, 013108 CrossRef CAS PubMed
.
- E. Undvall, F. Garofalo, G. Procopio, W. Qiu, A. Lenshof, T. Laurell and T. Baasch, Phys. Rev. Appl., 2022, 17, 034014 CrossRef CAS
.
- B. Hammarström, T. Laurell and J. Nilsson, Lab Chip, 2012, 12, 4296–4304 RSC
.
- M. Wu, Z. Mao, K. Chen, H. Bachman, Y. Chen, J. Rufo, L. Ren, P. Li, L. Wang and T. J. Huang, Adv. Funct. Mater., 2017, 27, 1606039 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Python script for the feedback control loop; raw video data for all experiments; MATLAB codes to generate the figures from the raw video data. See DOI: https://doi.org/10.1039/d2lc00376g |
| This journal is © The Royal Society of Chemistry 2022 |