DOI:
10.1039/D2MA00185C
(Review Article)
Mater. Adv., 2022,
3, 5598-5644
Low-temperature water electrolysis: fundamentals, progress, and new strategies
Received
17th February 2022
, Accepted 15th May 2022
First published on 17th May 2022
Abstract
Water electrolysis is a promising technology for sustainable energy conversion and storage of intermittent and fluctuating renewable energy sources and production of high-purity hydrogen for fuel cells and various industrial applications. Low-temperature electrochemical water splitting technologies include alkaline, proton exchange membrane, and anion exchange membrane water electrolyses, which normally consist of two coupled half reactions: the hydrogen evolution reaction (HER) and the oxygen evolution reaction (OER). Despite the advances over decades, formidable challenges still exist and hinder the practical application of large-scale, energy-efficient, and economically viable water electrolysis, including large energy penalty, sluggish kinetics, high cost of precious metal based electrocatalysts, possible H2/O2 gas crossover, difficulty in storage, and distribution of H2. Herein, we first briefly introduce the fundamentals of water electrolysis, summarize the recommended standardized electrochemical characterization protocols, and demonstrate the metrics and key performance indicators that are used to evaluate the performances of HER and OER electrocatalysts and electrolyser cells. Then, we present six new strategies to mitigate the technical challenges in conventional water electrolysis. These emerging strategies for disruptive innovation of water electrolysis technology include overall water electrolysis based on bifunctional nonprecious electrocatalysts (or pre-catalysts), magnetic field-assisted water electrolysis, decoupled water electrolysis, hybrid water electrolysis, acid/alkaline asymmetric electrolyte electrolysis, and tandem water electrolysis. Finally, the remaining challenges, perspectives and future directions are discussed. This review will provide guidance and inspire more endeavours to deepen the mechanistic understanding and advance the development of water electrolysis.

Wei Li
| Dr Wei Li is a Research Assistant Professor in the Department of Mechanical and Aerospace Engineering at West Virginia University. He obtained his BS degree in Chemistry from the Ocean University of China in 2007 and PhD degree in Materials Science from the Institute of Chemistry, Chinese Academy of Sciences in 2012. He worked at Commonwealth Scientific and Industrial Research Organisation (CSIRO) in Australia as a postdoctoral fellow from 2012–2014. In 2015, he received his Marie-Curie COFUND fellowship and worked at International Iberian Nanotechnology Laboratory in Portugal. He worked at Utah State University in 2017–2018 and then moved to West Virginia University. He has been working on electrochemical energy storage and conversion, thermochemical looping, heterogeneous catalysis, water treatment and gas sensing. |

Hanchen Tian
| Hanchen Tian completed his PhD in the Department of Mechanical and Aerospace Engineering at West Virginia University in 2021. He is currently working as a Post-Doctoral Fellow at West Virginia University. His professional interests and expertise are novel materials for electrochemical energy conversion and computational fluid dynamics for electrochemical devices. |

Liang Ma
| Dr Liang Ma is currently an associate professor at the Hebei University of Engineering. He had been a visiting scholar at West Virginia University from September 2017 to March 2022. He has been working on solid oxide fuel cells, solid oxide electrolysis cells, high-temperature gas sensors and hot corrosion of high-temperature alloys. |

Yi Wang
| Yi Wang completed his PhD in the Department of Mechanical and Aerospace Engineering at West Virginia University in 2022. His professional interests and expertise are novel materials for electrochemical energy conversion and electrochemical high-temperature gas sensing devices. |

Xingbo Liu
| Xingbo Liu received his PhD in Materials Science from the University of Science and Technology Beijing in 1999, and subsequently joined West Virginia University (WVU) as a postdoc. Currently, he is the Statler Endowed Chair of Engineering in Benjamin M. Statler College of Engineering and Mineral Resources at WVU. His research focuses on electrochemical materials and processes for energy conversion and storage, including solid oxide fuel cells and electrolysis cells, batteries, and electrochemical corrosion. He has received numerous awards including R&D 100 Award, TMS Early Career Faculty Fellow, TMS Brimacombe Medal, etc. He is a Fellow of both American Ceramics Society and ASM International. |

Xuefei Gao
| Dr Xuefei Gao is currently a Scientist at Viatris in the USA. She obtained her PhD degree in Chemistry from the University of Science and Technology Beijing in 2014 and PhD degree in Materials Science & Engineering from West Virginia University (WVU) in 2020. She studied at North Dakota State University as a visiting scholar and worked at WVU and University of North Carolina at Chapel Hill as a postdoctoral fellow. Dr Gao has been working on the development of lateral flow strip biosensors for detecting heavy metal ions and nucleic acids, antibodies and biomarkers, surface-enhanced Raman spectroscopy materials, wettability engineering, oil/water separation techniques, electrochemical analysis and catalysis. |
1. Introduction
The strong reliance on fossil fuels has brought growing global concern in energy demand and environmental issues. Therefore, it is of vital importance to develop clean, renewable and sustainable energy source alternatives.1–3 However, many renewable energy sources such as solar and wind are intermittent and fluctuating, hence requiring efficient, economical and robust energy conversion and storage technologies.4–7 Among the various energy strategies,8–23 constructing an energy infrastructure that utilizes a sustainable and environmentally benign H2/water cycle can enable an ideal clean hydrogen economy energy future.24–31 Hydrogen (H2) has been considered as a clean and carbon-neutral energy carrier for use in grids and next-generation vehicles. Currently, over 90% of the H2 supply worldwide is from reforming fossil fuels, which is an energy intense process and results in greenhouse gas emissions.2,32–34 Electrochemical water electrolysis has emerged as a promising technique to convert electricity harvested from renewable energy sources into a high-purity hydrogen (H2) fuel. By driving the electrochemical water splitting reaction, the electricity arising from renewable energy sources is stored in high-purity H2.35–39 As an energy carrier, H2 can be stored, transported and consumed through the H2/O2 fuel cells that transform the chemical energy of H2 to electricity with water as the only by-product.40,41 Therefore, the electrochemical water electrolysis is considered as a core clean energy storage and conversion technology realizing the hydrogen economy, and includes two routes: low-temperature and high-temperature water electrolysis. The current low-temperature electrochemical water splitting technologies include alkaline (AWE), proton exchange membrane (PEMWE), and anion exchange membrane (AEMWE) water electrolyses. The present high-temperature water electrolysis technologies include the proton-conducting solid oxide electrolysis cell (H-SOEC, or the protonic ceramic electrolysis cell (PCEC)), the oxygen ion-conducting solid oxide electrolysis cell (O-SOFC) and the co-electrolysis of CO2 and steam. The high-temperature water electrolysis relies on proton or oxygen ion conducting ceramic oxide electrolytes at high operating temperatures (up to 1000 °C) which render enhanced reaction kinetics and thermodynamics and enable high output current densities and voltage efficiencies. However, the use of high temperatures and brittle ceramics leads to problems of improper sealing, cell cracking, and bulky system design making the SOFC not suitable for fluctuating and dynamic situations. In contrast, low-temperature water electrolysis, especially AWE and PEMWE, has the advantages of easy and compact designs, facile operation, and higher technology readiness levels (TRLs) towards commercialization and mature markets. Both routes demonstrate great potential to promote the hydrogen economy and their comparison has been previously reported (Table 1).42–60 This article focuses on the discussion of low-temperature water electrolysis.
Table 1 Comparison of low-temperature and high-temperature water electrolysis technologies
|
|
Low-temperature water electrolysis |
High-temperature water electrolysis |
| AWE |
PEMWE |
AEMWE |
SOEC |
| H-SOEC |
O-SOEC |
Co-electrolysis |
| AWE: alkaline water electrolysis, PEMWE: proton exchange membrane water electrolysis, AEMWE: anion exchange membrane water electrolysis, SOEC: solid oxide electrolysis cell, YSZ: yttria-stabilized zirconia, GDC: gadolinia-doped ceria, TRL: technology readiness level, n.a.: not available. |
| Charge carrier |
OH− |
H+ |
OH− |
H+ |
O2− |
O2− |
| Temperature |
20–80 °C |
20–200 °C |
20–60 °C |
300–650 °C |
500–1000 °C |
700–900 °C |
| Gas pressure |
2–10 bar |
15–30 bar |
<30 bar |
<30 bar |
<30 bar |
<30 bar |
| Current density |
0.2–0.5 A cm−2 |
0.6–3 A cm−2 |
0.2–2 A cm−2 |
0.1–3.9 A cm−2 |
0.3–2 A cm−2 |
Up to 2 A cm−2 |
| Cell voltage |
1.8–2.4 V |
1.8–2.2 V |
1.6–2.0 V |
1–1.4 V |
0.7–1.5 V |
0.9–1.5 V |
| Cell area |
≤4 m2 |
<0.13 m2 |
<0.03 m2 |
<0.0025 m2 |
<0.02 m2 |
<0.02 m2 |
| Electrolyte |
20–40 wt% KOH solution |
PEM |
AEM |
Proton conducing ceramic oxide |
Oxygen ion conducing ceramic oxide |
Oxygen ion conducing ceramic oxide |
| Anodes |
Transition metals and compounds |
IrO2, RuO2, and IrxRu1−xO2 |
Transition metals and compounds |
Perovskite or perovskite-like structured oxides |
Perovskite or perovskite-like structured oxides |
Perovskite or spinel-based oxide |
| Anodic reaction |
4OH− → O2 + 2H2O + 4e− |
2H2O → O2 + 4H+ + 4e− |
4OH− → O2 + 2H2O + 4e− |
2H2O → O2 + 4H+ + 4e− |
2O2− → O2 + 4e− |
2O2− → O2 + 4e− |
| Cathodes |
Transition metals, alloys, and compounds |
Pt and alloys |
Transition metals, alloys, and compounds |
Ni-Based cermet |
Perovskite or Ni-based cermet |
Ni-YSZ/GDC or perovskite oxides |
| Cathodic reaction |
4H2O + 4e− → 2H2 + 4OH− |
4H+ + 4e− → 2H2 |
4H2O + 4e− → 2H2 + 4OH− |
4H+ + 4e− → 2H2 |
2H2O + 4e− → 2H2 + 2O2− |
2H2O + 4e− → 2H2 + 2O2− |
| 2CO2 + 4e− → 2CO + 2O2− |
| Voltage efficiency |
60–80% |
65–82% |
52–67% |
60–100% |
81–100% |
50–85% |
| Specific stack energy consumption |
4.2–4.8 kW h Nm−3 |
4.4–5.0 kW h Nm−3 |
n.a. |
n.a. |
2.5–3.5 kW h Nm−3 |
n.a. |
| Lifetime stack |
<120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h 000 h |
<100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h 000 h |
5000 h |
n.a. |
<23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h 000 h |
n.a. |
| Specific system energy consumption |
5.0–5.9 kW h Nm−3 |
5.0–6.5 kW h Nm−3 |
n.a. |
n.a. |
3.7–3.9 kW h Nm−3 |
n.a. |
| Lifetime system |
20–30 years |
10–20 years |
n.a. |
n.a. |
n.a. |
n.a. |
| TRL |
9 |
6–8 |
4–5 |
4 |
5–6 |
4 |
| Applicability |
Mature |
Commercialization |
Lab-scale |
Lab-scale |
Demonstration |
Lab-scale |
| Advantages |
Low capital costs, no need of noble metals, relatively stable, large scale (MW stacks), and mature technology |
Compact design, fast response and start-up, dynamic operation, high purity of H2, high current densities, and high efficiency |
Combination of AWE and PEMWE merits |
Enhanced reaction kinetics and thermodynamics, low capital costs, high efficiency, intermediate temperature, and high purity of H2 |
Enhanced kinetics and thermodynamics, low capital costs, and high efficiency |
Enhanced kinetics and thermodynamics, low capital costs, high efficiency, and direct production of syngas |
| Disadvantages |
Corrosive electrolyte, gas crossover, low current densities, low efficiency, low operational pressure, and inferior dynamics |
High costs of PEMs and noble metals, acidic corrosion environment, limited durability, and small stack MW scale |
Low OH− conductivity and efficiency, limited durability, and small stack scale |
Mechanically unstable electrodes, cracking, safety concerns of improper sealing, high-temperature maintenance, bulky system design, and unsuitable for fluctuating and dynamic situations |
Water splitting consists of two half reactions: the hydrogen evolution reaction (HER) and the oxygen evolution reaction (OER), taking place at the cathode and the anode, respectively. Unfortunately, the sluggish kinetics and large energy barriers of both the HER and the OER make the water electrolysis require voltage inputs much larger than the theoretical thermodynamic voltage to reach appreciable H2 production rates, leading to relatively low energy efficiencies.61 Therefore, electrocatalysts are always needed to accelerate the kinetics and reduce the voltage inputs. At present, precious metal Pt and noble metal oxides (RuO2 and IrO2) are the state-of-the-art electrocatalysts for the HER and the OER, respectively.62 However, the scarcity, high cost and limited durability of these noble metal catalysts severely restrict their widespread application in large-scale production of H2 through water electrolysis on a global scale. As a result, great research efforts are devoted to developing nonprecious electrocatalyst alternatives for the electrocatalytic HER and OER, aiming to achieve low cost, high electrocatalytic activities and operational stability.63–70 Nevertheless, it still remains a challenge to unravel the mechanistic insights into the HER and the OER and optimize the compositions, structures, morphologies and properties of electrocatalysts. The community also lacks standardized protocols of electrochemical characterization to reliably and precisely evaluate the metrics and key performance indicators at the material and device levels. Additionally, a number of obstacles are present that hinder the scalable deployment of water electrolysers.71 (i) Due to the large energy barriers for the HER and the OER, expensive noble metal based electrocatalysts are usually required to reduce energy penalty and promote reaction kinetics, which should be replaced by cost-effective, active, and stable nonprecious electrocatalysts. It is of significance to address the incompatible integration of HER and OER electrocatalysts, as they are commonly developed under different pH conditions. (ii) The large amounts of bubbles attached on the electrodes can plague the mass transfer and ionic conductivity. (iii) The HER and OER in traditional water splitting are strictly coupled and hence H2 and O2 are produced simultaneously. This may result in potential explosive H2/O2 gas crossover and reactive oxygen species, which pose safety concerns and degrade the electrolyser membranes and electrodes. (iv) The OER is found to be the bottleneck reaction impairing the energy efficiency of overall water splitting; nevertheless, the product of the OER, O2, is not of high industrial value. (v) The potentials of the two half reactions of HER and OER are dependent on the pH value. Maintaining a stable pH gradient in two compartments in a proper manner may bring some appealing advantages; however, it is challenging to construct this asymmetric pH design. (vi) The cost-effective storage and transport of H2 still remain challenging. Thus, the on-site use and conversion of H2 produced from water electrolysis to value-added chemicals are of particular interest to local households in rural areas rendering low-cost distribution to complement the centralized H2 production. Although lots of review articles have reviewed the progress of electrocatalyst materials,2,62,68,69 there are few papers that comprehensively review the standardized electrochemical characterization practices, performance metrics of electrocatalysts and electrolysers and recent advances of new strategies to address the technical challenges of water electrolysis.
Herein, we first briefly introduce the fundamentals of water electrolysis from the perspective of thermodynamics. Next, we summarize the recommended standardized electrochemical characterization protocols, and demonstrate some common metrics and key performance indicators used to evaluate the performances of electrocatalysts and electrolyser cells. Then, we present several new strategies to mitigate the technical challenges in conventional water electrolysis. These emerging strategies for disruptive innovation of water electrolysis technology include (1) overall water electrolysis based on bifunctional nonprecious electrocatalysts (or pre-catalysts) for both the HER and OER, (2) magnetic field-assisted water electrolysis achieved by integrating magnetic electrocatalysts/electrodes with magnetic fields, (3) decoupled water electrolysis realized using redox mediators for temporally and/or spatially separating the HER from the OER, (4) hybrid water electrolysis by replacing the OER with alternative thermodynamically more favourable redox oxidation reactions to reduce energy penalty and upgrade valuable products beyond O2, (5) acid/alkaline asymmetric electrolyte electrolysis that enables the HER and the OER to occur at different pH values, and (6) tandem water electrolysis by integrating biocatalysts to convert in situ generated H2 to value-added products. Finally, the conclusions and remaining challenges are demonstrated. Most importantly, we provide perspectives on the future direction and endeavours to advance mechanistic understanding and deployment of viable water electrolysis for the hydrogen economy future.
2. Fundamentals of electrochemical water splitting
Generally, low-temperature water electrolysis is conducted at temperatures lower than 100 °C limited by the thermal stability of membranes. The overall electrochemical water splitting reaction is expressed as follows:| |
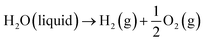 | (1) |
where the two half reactions are the HER taking place on a cathode and the OER occurring on an anode in a water electrolyser cell. Both reactions are pH-dependent (Fig. 1a), of which the equilibrium half-cell potentials (E0) at 1 atm and 298.15 K versus standard hydrogen electrode (SHE) are shown as follows, in acidic electrolytes (pH = 0):| |
| HER: 4H+ + 4e− → 2H2, E0c = 0.000 V | (2) |
| |
| OER: 2H2O → O2 + 4H+ + 4e−, E0a = 1.229 V | (3) |
in neutral electrolytes (pH = 7),| |
| HER: 4H2O + 4e− → 2H2 + 4OH−, E0c = −0.414 V | (4) |
| |
| OER: 2H2O → O2 + 4H+ + 4e−, E0a = 0.815 V | (5) |
in alkaline electrolytes (pH = 14),| |
| HER: 4H2O + 4e− → 2H2 + 4OH−, E0c = −0.828 V | (6) |
| |
| OER: 4OH− → O2 + 2H2O + 4e−, E0a = 0.401 V | (7) |
where E0c and E0a are the equilibrium half-cell potentials at the cathode and anode, respectively.73
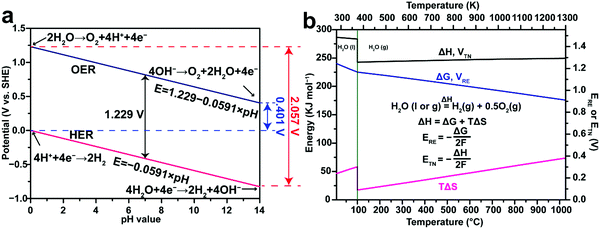 |
| | Fig. 1 (a) Thermodynamic potentials of the hydrogen evolution reaction (HER) and the oxygen evolution reaction (OER) in aqueous electrolytes with different pH values under standard conditions (298.15 K, 1 atm). (b) Thermodynamics of water splitting as a function of temperature at 0.1 MPa. ΔG is correlated with the thermodynamic reversible voltage (ERE), while ΔH is correlated with the thermal neutral voltage (ETN) in water electrolysis. ΔG and ERE share the same plot but refer to the left and right y axes, respectively. ΔH and ETN share the same plot but refer to the left and right y axes, respectively. Note that liquid water (H2O(l)) is the reactant at temperatures lower than 100 °C, while gaseous water vapor (H2O(g)) is the reactant at temperatures higher than 100 °C. The thermodynamic data in (b) are adapted from the NIST-JANAF Thermochemical Tables,72 and HSC Chemistry software. | |
The water splitting reaction is an endothermic reaction which is defined as follows:
where the change of the Gibbs free energy Δ
G0 is 237.1 kJ mol
−1, the enthalpy change Δ
H0 equals to 285.8 kJ mol
−1 and the thermal energy
TΔ
S0 is 48.7 kJ mol
−1 under standard conditions (298.15 K, 1 atm).
74 The total energy known as enthalpy is composed of both electrical and thermal energy. From the above thermodynamic perspectives, the water splitting reaction under standard conditions can be further expressed as follows:
| |
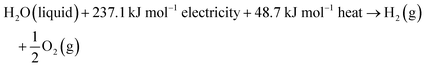 | (9) |
This suggests that splitting one mole of liquid water to produce 1 mol H
2 under standard conditions requires a theoretical total energy (Δ
H0) of 285.8 kJ including 237.1 kJ from electricity (Δ
G0) and 48.7 kJ from heat (
TΔ
S0). In low-temperature water electrolysis, heat can be supplied by the extra heat sources or Joule heating from electric and ionic currents flowing through the cell resistances. The thermodynamic reversible voltage (
ERE) corresponding to the change of the Gibbs free energy Δ
G0 is 1.23 V under standard conditions, calculated using the following equation:
| |
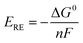 | (10) |
where
n = 2 is the number of transferred electrons for producing 1 mol H
2 and
F is Faraday's constant. The thermodynamic reversible voltage is the theoretical voltage to enable the initialization of water electrolysis.
Besides, the thermoneutral voltage (ETN) is calculated based on the enthalpy change ΔH0 as follows:
| |
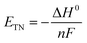 | (11) |
which is 1.48 V under standard conditions.
75 Apparently, this difference arises from the entropy change
TΔ
S0 in the overall process and must be balanced by either supplying or removing heat from the system. When the heat is completely supplied by the Joule heating from electric and ionic currents flowing through the internal resistances, this heat requirement is directly traceable back to the electricity supplied. In other words, 285.8 kJ of electricity instead of 237.1 kJ is the minimum required to split water. This translates into a thermoneutral voltage of 1.48 V. If an electrolyser works at 100% efficiency (
i.e. at 1.48 V under the standard conditions), the heat generated from the electrolyser equals to the heat needed for the electrolysis to proceed, and therefore, a thermoneutral situation is achieved. In other words, the electrolyser neither releases heat to the environment nor absorbs heat from the environment. If the voltage is below a cell voltage of 1.48 V (but above 1.23 V), the electrolysis cell acts as a refrigerator continuously absorbing heat from the surroundings. If the voltage is above 1.48 V, excess heat is generated and must be removed for an isothermal operation of the cells.
75 Note that all practical low-temperature water electrolysers operate above a cell voltage of 1.48 V owing to the various energy losses in the cells, and hence heat removal becomes a key engineering feature in designing water electrolysers. Moreover, the energy losses also include the activation, ohmic resistance and mass transport voltage losses, leading to a descriptor “overpotential” for both HER and OER which needs to be overcome by using efficient electrocatalysts and optimizing the electrolyte and mass transfer of reactants.
74 However, some recent studies focusing on overall water electrolysis by using transition metal compound electrodes for the electrocatalytic OER have demonstrated current densities of around 10 mA cm
−2 at voltages lower than the thermoneutral voltage of 1.48 V in their polarization curves recorded in two-electrode configuration at room temperature.
76–81 If the cathodic and anodic reactions are HER and OER in faradaic efficiencies of 100%, respectively, and no external heating is supplied as demonstrated in those reports, this electrochemical behaviour violates the thermodynamics principle. This issue may be caused by several reasons. On the one hand,
iR compensation may be erroneously conducted in the polarization curves.
82 On the other hand, the presented potentiodynamic polarization curves are not true steady-state polarization curves, and the cathodic and anodic reactions are not fully HER and OER in faradaic efficiencies of 100%. In particular, for the anodic reaction, the transition metal compound anodes may have not been fully conditioned to reach a steady state, and thus the real anodic oxidation of transition metal compounds occurs instead of OER when recording those polarization curves in the electrolytes. To avoid this issue and correctly report the electrochemical performance for overall water electrolysis at the prototype device level, both the cathode and the anode should be fully conditioned and steady-state polarization curves and the distance between two electrodes should be presented without
iR-correction. Meanwhile, the faradaic efficiencies for both anodic and cathodic reactions should be precisely measured.
Note that the above discussion applies to water electrolysis operating at 298.15 K, where the liquid H2O is the reactant. Fig. 1b demonstrates that ΔG and ΔH for the water splitting reaction change with temperature. Therefore, both ERE and ETN vary with temperature accordingly. When the reaction temperature is higher than 100 °C, the gaseous water vapor (H2O(g)) is the reactant, leading to a sudden drop of ΔH at 100 °C primarily caused by the latent heat of vaporization of water (40.8 kJ mol−1).83 At temperatures beyond the boiling point of water, steam electrolysis is performed using some modified high-temperature PEM water electrolysers (100–200 °C),84 or intermediate-temperature (400–600 °C) or high-temperature (700–900 °C) solid oxide electrolysis cells (SOEC).85–89 Generally, these high-temperature water electrolysers are more efficient due to the decreased internal resistance losses and improved HER and OER kinetics. Detailed discussion on high-temperature water electrolysis is beyond the scope of this review.
3. Electrochemical characterization and performance indicators
3.1 Summary of recommended practices for electrochemical characterization
It is of vital importance to rigorously perform electrochemical characterization, data analysis and assessment of electrochemical performances for electrocatalysts and electrodes at the material and device levels to avoid pitfalls and introduction of artefacts.82,90 However, the lack of reliable and standardized protocols makes it challenging to accurately evaluate and quantify the electrochemical performance indicators and metrics.91 As the high-temperature water electrolysis has significantly different practices and research paradigms in terms of electrode and cell fabrication as well as electrochemical characterization, this section primarily summarizes the proposed protocols and recommended practices reported in the literature in terms of setups, electrodes, electrochemical characterization, and data analysis for low-temperature water electrolysis.
A three-electrode cell setup is commonly used for characterizing the intrinsic electrochemical activities and stability for electrocatalysts on working electrodes. Plastic containers such as those made of polytetrafluoroethylene and polyoxymethylene are suggested to replace the glass beakers, in particular in alkaline electrolytes for mitigating contamination from glass corrosion.91–94 The cleaning procedures for glassware and plastic cells have been reported.91,95 To maintain the equilibrium potential at the thermodynamic standard values, the electrolytes must be fully purged and saturated by high-purity H2 and O2 rather than inert Ar or N2 throughout the electrochemical tests for HER and OER, respectively.91 An extra precaution should be taken for electrolytes to minimize the unintentional introduction of trace electrolyte impurities (e.g., Fe in KOH) into the working electrodes.92 The common working electrode substrates include planar glassy carbon, rotating ring-disk electrodes, indium tin oxide glasses, and porous metal or carbon meshes and foams. The geometric areas should be exactly defined. Normally, the electrocatalyst powder is deposited on the substrates by a common ink drop-casting method or in situ grown on the porous substrates. The recommended drop-casting protocols have been reported.91 Note that the use of porous substrates such as meshes and foams may bring about some issues in accurately evaluating the true intrinsic activities,82 although the electrocatalysts loaded on the porous substrates have been reported to deliver high apparent electrocatalytic activities.96,97 The porosity makes the electrochemically active surface area (ECSA) much larger than the geometric area. Depending on the fabrication method, the thickness, density, porosity, and purity of substrates as well as the surface coverage of active electrocatalyst components may vary. The foams are fixed using electrode holders with Pt or stainless-steel current collectors and thus their full immersion may lead to contamination from the metals in the holders. Even though partial immersion may minimize this issue, the capillary action of pores may result in underestimation of the geometric areas.96 It is suggested to exactly define the exposed geometric area by masking the excess areas with hot or epoxy glues.92 Counter electrodes should also be rationally selected. The projected area of a counter electrode needs to be larger than that of the working electrode to rapidly supply or sink electrons for the reactions at the working electrode.91 For the HER studies, high-purity graphite is recommended to replace noble metals such as Pt and Au, as the noble metals can be leached from the counter electrode and deposited on the working electrode under the cathodic reduction potential to enhance the electrocatalytic activity and electronic conductivity, leading to artefacts when evaluating the intrinsic activities of working electrodes.90–92,95,98–101 However, extra attention should be paid to the use of a carbon counter electrode for long-term tests, as the oxidative by-products and inherent impurities from carbon may diffuse into the electrolytes.91,102 For the OER studies, noble metals can be used as the counter electrode as their leaching is minimized under the cathodic potential.92 It is also suggested to separate the working and counter electrode compartments by using an ion-selective membrane or diaphragm to minimize the influence of gas bubbles produced by the counter electrode on the reactions at the working electrode.90 The common reference electrodes include Hg/HgO, saturated calomel electrode (SCE) of Hg/Hg2Cl2, Ag/AgCl, Ag/Ag2SO4, and Hg/Hg2SO4.91,103 The rational selection of a reference electrode is crucial to accurately and reliably assess the electrocatalyst potentials. In acidic electrolytes, a reference electrode of Hg/Hg2SO4 is generally used. In neutral electrolytes, a SCE (Hg/Hg2Cl2) reference is frequently adopted. In alkaline electrolytes, a reference electrode of Hg/HgO is recommended.92 Although the reference electrode Ag/AgCl has been widely used in previous electrocatalytic studies, it is not recommended as the leakage of silver and chloride ions from Ag/AgCl and diffusion of hydroxide into the filling chamber will potentially interfere with the measurement (Fig. 2a).104 The filling solution of a reference electrode should match with the cell electrolyte, minimizing the liquid junction potential. The use of Luggin–Haber capillaries is also suggested to reduce the distance between RE and WE and liquid junction potential. However, the Vycor glass frits are highly soluble in alkaline solutions and thus it is suggested to use alkaline-stable frits or thick Nafion films to replace Vycor glass frits.91 Prior to their use, the frits should be examined to avoid any blockage and bubble attachment.90 The reference electrode should be calibrated against RHE each time prior to the electrochemical tests according to a standard protocol.91,103 Many metrics and performance indicators are commonly used to evaluate the electrocatalytic performance of HER and OER electrocatalysts, including the reversible hydrogen electrode (RHE) potential, specific activity, mass activity, overpotential, Tafel slope, catalytic stability, turnover number and frequency, faradaic efficiency and energy efficiency.82,92,105–111 These metrics are crucial to design efficient electrocatalysts and compare their performance across different materials, which can provide insightful information with respect to the intrinsic activity and redox reaction kinetics. Generally, a three-electrode configuration is used to investigate a half reaction of either HER or OER, while the overall water splitting is evaluated in a two-electrode configuration. Therefore, the use of these metrics and performance indicators depends on the kind of configuration. The electrodes should be fully conditioned by repetitive cyclic voltammetry (CV) to reach a steady state.91 For collecting the electrochemical data, the steady-state polarization curves are highly recommended instead of linear scanning voltammetry (LSV).82,91,92,112 The steady-state polarization curves can be obtained by either chronopotentiometry (CP) or chronoamperometry (CA) with defined step sizes of current or potential response and time intervals. This is important to ensure the data reliability especially when the electrodes have large capacitive background currents arising from large ECSAs or the electrodes themselves are prone to reduction and oxidation under the cathodic and anodic potentials convoluting the true HER and OER currents, respectively. The extraction of meaningful kinetic currents requires background correction and iR-correction when evaluating the intrinsic activities of electrocatalysts in the working electrodes of three-electrode configuration.91,113 The background correction is to remove the contribution from capacitance current. Although it has been recommended to collect full CV curves at a low scan rate and make the background correction by averaging the cathodic and anodic branches, the use of steady-state polarization curves is more preferred, as the Tafel analyses derived from steady-state polarization curves are more accurate and reliable.112 For electrochemical reactions influenced by the mass transfer of reactants such as the hydrogen oxidation reaction (HOR) and the oxygen reduction reaction (ORR), an additional mass transfer correction is required.91 Although the HER was typically assumed to be free of diffusion limitation, it can be found in recent publications that it is also required to correct the hydrogen diffusion limitation in rotating disk electrode of Pt for accurate measurement of HER kinetics.114,115 The iR-correction is also required to correct the potential drop caused by the Ohmic losses arising from the ionic conduction in the electrolyte between the working and reference electrodes and any contact resistances.82,90–92,113,116 The Ohmic resistance is corrected according to
where
E is the
iR-corrected potential,
ERHE is the measured potential with respect to RHE,
i is the measured raw current value, and
Rs is the uncompensated series resistance that can be measured by either electrochemical impedance spectroscopy (EIS) or the current interrupt method. A typical EIS method is conducted by collecting the alternating circuit (AC) impedance spectra from 1 MHz to 0.1 Hz with a voltage perturbation of 10 mV
versus open circuit potential (OCP). The series resistance can be read as the magnitude of the impedance where the phase angle is close to zero in a Bode plot or the real part of the impedance where the imaginary part of the impedance is zero in a Nyquist plot (fitted to a suitable equivalent circuit model).
91,92 Theoretically, the full compensation of series resistance (100% correction) should be made to completely correct the Ohmic resistance; however, such 100%
iR-correction may lead to over
iR-correction and over-bent polarization curves especially when the Ohmic resistance is large.
82 This problem can be minimized when the reference electrode is close to the working electrode giving rise to a small series resistance. Many electrochemical workstations have the capability of automatic
iR-compensation to
in situ correct the Ohmic resistance during the dynamic measurement; nevertheless, this is not recommended due to the unreliable data and occurrence of voltage oscillation.
92,113 It is more preferred to collect the raw potential and current data, measure the
Rs and manually correct
iRs. This allows more flexibility with post-characterization data analysis and reduces the chance of errors. Note that the
Rs of a working electrode should be repeatedly measured at the initial, post-conditioning and post-electrochemical-characterization stages, as the active materials in the working electrodes may be subject to the phase change leading to variation in resistance. The working and counter electrode positions should not be changed in the cell in between the measurements, as these will influence the magnitude of
Rs. It is essential to report the detailed
iR-correction procedures and
Rs values, as these values have a considerable influence on the
iR-corrected overpotentials especially at relatively high current densities.
92 In contrast, conducting the
iR-correction is not recommended when evaluating the device-level performances of two-electrode alkaline, AEM and PEM electrolysers, as the real voltages without
iR-correction are more practically meaningful.
116 Many reports demonstrated the prototype two-electrode alkaline water electrolysis cells by placing two electrodes close each other in the electrolytes in the absence of separators, which does not provide reliable evaluation of electrolysers.
76–81 Once the raw electrochemical data are collected by using various techniques, and proper background and
iRs correction are performed, various electrochemical metrics and performance indicators can be obtained to assess the electrocatalysts and electrolysers.
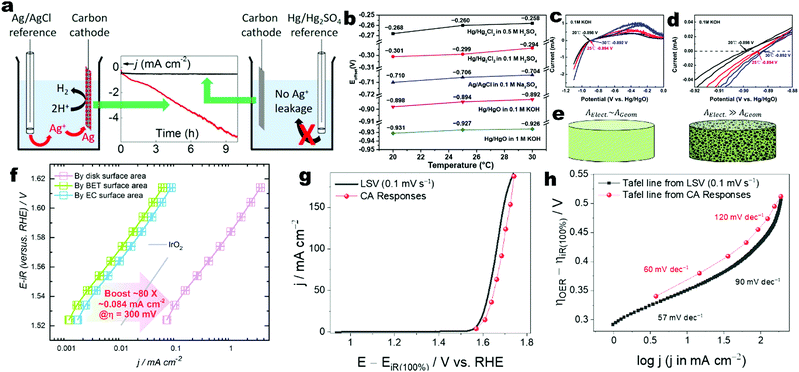 |
| | Fig. 2 (a) The influence of Ag+ leakage from the Ag/AgCl reference electrode in the measurement of the cathodic current on a carbon working cathode during the study of its electrocatalytic HER activity. Reprinted with permission from ref. 104. Copyright 2017 American Chemical Society. (b) Temperature-dependent Eoffset values of selected reference electrodes in different electrolytes and temperatures. (c) CV curves and (d) magnified view of the Hg/HgO reference electrode calibration to obtain the Eoffset values in 0.1 M KOH at different temperatures. (b–d) Adapted with permission from ref. 103. Copyright 2020 American Chemical Society. (e) Schematic of flat and porous electrodes with different geometric areas (AGeom) and ECSA (AElect.) comparison. Reprinted with permission from ref. 110. Copyright 2018 American Chemical Society. (f) Tafel plots of Co3O4 particles for OER in 1 M KOH where the OER current densities are normalized by the geometric disk area, BET surface area and ECSA and Tafel plot of benchmark IrO2 particles with current density normalized by their true surface area from real particle size calculation. Reprinted from ref. 120, Copyright 2018 with permission from Elsevier. (g) The potentiodynamic LSV curve of activated Co foil recorded at 0.1 mV s−1 and its steady-state polarization curve from CA responses for OER in 1 M KOH. Both curves are 100% iR-corrected. (h) The corresponding Tafel plots of activated Co foil derived from its LSV and steady-state polarization curves showing that the Tafel slope values are close in the lower overpotential region while show a significant difference in the higher overpotential region. (g and h) Reprinted with permission from ref. 112. Copyright 2021 American Chemical Society. | |
3.2 Key metrics and performance indicators
3.2.1. Reversible hydrogen electrode potential.
Although the SHE potential is widely used to evaluate many electrochemical redox reactions, the potentials versus SHE for both the HER and the OER are pH-dependent as shown in Fig. 1,117,118 rendering difficulties in evaluating and comparing the electrocatalytic performance of electrocatalysts under different pH conditions. Therefore, all potentials for HER and OER are recommended to be referenced to the RHE which is expressed as follows:| |
| ERHE = ESHE + pH × 2.303RT/F | (13) |
where ESHE is the measured potential of the designated reference electrode with respect to the SHE, pH is the real electrolyte pH value, R is the universal gas constant, T is the absolute temperature, F is the Faraday constant, and 2.303RT/F approximates to 0.059 V at 298 K. Because the RHE takes pH dependence into account, the equilibrium potentials of H2-redox and O2-redox are fixed at 0 and 1.23 V versus RHE at 298 K, respectively. Therefore, reporting the potential value with respect to RHE enables the ready comparison of electrocatalyst performances across electrolytes with varying pH values. As the SHE reference is not easy to handle, various reference electrodes are used depending on the electrolyte pH. Two methods have been widely used to convert the measured potentials of working electrodes referenced to the used reference electrode to the RHE potentials.91 The first method is to measure the real pH value of the electrolyte and calculate the RHE potential by using the following equation:103,119| |
| E (versus RHE) = Emeasured (versus reference electrode) + E0Ref (versus SHE) + 0.059 × pH | (14) |
where Emeasured (versus a reference electrode) is the measured potential of the working electrode with respect to the used reference electrode; E0Ref (versus SHE) is the standard thermodynamic potential of the used reference electrode, and pH is the real electrolyte pH value. Different reference electrodes have varied standard thermodynamic potentials (E0Ref (versus SHE)), which are given by the suppliers and determined by the reference electrode type and filling electrolytes.119 Although this method is frequently adopted by the community, this method is not recommended as it may lead to inaccurate potential values in an order of tens of mV.91 Possible reasons for the inaccuracy include (i) uncertainty in pH determination related to the limitation of the pH meter/probe capability, pH shift caused by the temperature change, and immeasurable single-ion activities. Two recent reports provide estimated pH values of NaOH/KOH (based on experimentally determined activity coefficients) and other common electrolytes.103,119 (ii) It is challenging to accurately determine the liquid junction potentials.91 (iii) The real E0Ref (versus SHE) may drift from the standard thermodynamic potential if the reference electrode is not properly maintained leading to variation of filling electrolytes and electrode material components.90 Therefore, the other method is recommended, which is the experimental calibration of the reference electrode against RHE in the real electrolyte under the H2 redox reaction.91,103 Two Pt electrodes are used as both the working and counter electrodes together with the reference electrode in the electrolytes same as those for electrocatalytic characterization. High-purity H2 is purged into the electrolyte for more than 30 min to saturate the electrolyte prior to calibration. The CV is performed at 1 mV s−1 in the reversible HER and HOR potential window (Fig. 2c and d) and the average value of two voltage intercepts for two branch curves at zero current is the experimentally determined conversion factor (Eoffset). Then, the measured potentials of the working electrode referenced to the used reference electrode can be converted to the RHE potential as follows:| |
| E (versus RHE) = Emeasured (versus reference electrode) − Eoffset | (15) |
where Emeasured (versus reference electrode) is the practically measured potential of the working electrode with respect to the specific reference electrode used in the test, and Eoffset is obtained in the calibration process. A recent publication reported the detailed procedures and summarized the calibration results of Hg/HgO, Hg/Hg2Cl2 and Ag/AgCl reference electrodes in different electrolytes (Fig. 2b).103 It is strongly recommended to convert the measured potential to RHE by calibrating the reference electrode experimentally, rather than calculating it through the measured pH.
3.2.2. Specific activity.
The specific activity of an electrocatalyst is defined as the current density (j) normalized by the electrocatalyst area at a given potential.82,121 Three kinds of areas are always used to calculate the current density including the geometrical electrode area, ECSA and specific surface area measured by the nitrogen adsorption–desorption characterization and calculated by the Brunauer–Emmett–Teller (BET) method.120,122 For an electrode with a smooth and flat surface, the current density can be normalized with the geometrical electrode surface.96,123 However, it is not appropriate to evaluate the activities of powder electrocatalysts and porous electrodes by normalizing their current densities with the geometrical electrode surfaces (Fig. 2e), as the roughness degree of the powders and porous electrodes will affect the fair comparison of intrinsic activities.96,110,120 The inappropriate use of the geometrical electrode surface will lead to an artificial effect to boost the activity and cannot reflect the intrinsic activity of an electrocatalyst. Therefore, for powder electrocatalysts and porous electrodes, it is recommended to evaluate the specific activity by normalizing the current density with the ECSA or BET surface area (Fig. 2f). The ECSA value can be measured by the double layer capacitance (Cdl) measurement in a non-faradaic potential window in either aqueous or more preferably aprotic electrolytes.124,125 Unfortunately, the specific capacitance used in this method to calculate ECSA depends on the surface active compositions and other complex factors and thus it is difficult to accurately obtain the true ECSA value, although a universal specific capacitance of 40 or 60 μF cm−2 regardless of materials has been widely used as an approximation.82,90–92,95,96,101,110,111,113 Alternatively, other methods can also be employed to measure the ECSAs of electrocatalysts including the hydrogen underpotential deposition, underpotential deposition of metal, CO stripping voltammetry, use of reversible redox probe molecules, and redox of surface metals.126–129 These methods are limited to some specific electrode compositions. Moreover, there are discrepancies in the ECSA values of the same material measured using different methods. Regardless of the adopted ECSA determination methods, it is challenging to determine the accurate true ECSA value. The BET measurement can be performed in the N2 adsorption–desorption experiments at 77 K, which is a standard procedure to assess the porosity of heterogeneous powder catalysts and adsorbents.130–146 The BET surface area may not reflect the true ECSA value especially for the materials with poor conductivities, since the sites where N2 molecules are adsorbed may not be electrochemically active.90 Furthermore, the BET surface areas of monolithic foam electrodes are difficult to precisely measure. In a word, the specific activity is a quantitative indicator to evaluate the intrinsic efficacy of target electrocatalysts which is a practical approximation of the activity per active site.106,122
3.2.3. Mass activity.
The catalytic performance of an electrocatalyst depends on the mass loading of the active catalyst. Therefore, the mass activity (reported as A mgcatalyst−1) is defined as the current density normalized by the mass of the active electrocatalyst at a given potential.82,121,147 High mass activity determined by particle size and morphology is important for the development of electrocatalysts for practical devices, which reduces the cost, size and weight.148 Most of the electrochemical metrics and indicators are mass-dependent and thus the mass loading should be reported. An ideal electrocatalyst should have both a high specific activity and mass activity. For practical electrolysis application, the optimal mass loading should maximize the coverage of the conductive substrate with the electrocatalyst and optimize the thickness of the electrocatalyst layer to facilitate the electron and mass transfer.
3.2.4. Overpotential.
Overpotential (η) refers to a potential difference between the real measured potential to achieve a given current density and the theoretical thermodynamic potential of either the HER or the OER under the same conditions. Normally, the electrocatalytic performance of electrocatalysts is studied under the standard conditions. The theoretical thermodynamic potentials of the HER and the OER are 0 and 1.23 V versus RHE under the standard conditions, respectively. Ideally, the overpotential is zero. However, an overpotential is always needed for the HER and the OER, primarily due to the presence of an activation barrier.82,90 The onset potential is critical to evaluate how much overpotential is required to enable the electrocatalytic current to take off. Unfortunately, the definition of onset potential is ambiguous.2 One way to determine the onset potential is to obtain the intersecting potential between the tangent in the non-faradaic region and the tangent in the faradaic region in the current–potential curves. The other way is to define the potential value at which the electrocatalyst reaches a given small current density (0.5–2 mA cm−2). In addition, comparing the overpotential (η10) required to reach a current density of ±10 mA cm−2 normalized to the electrode geometrical area is a popular method to rank the HER and OER electrocatalysts. However, this methodology originating from the studies of solar water splitting cells is not suitable for rationalizing the intrinsic chemistry difference in HER or OER electrocatalysts.122 The η10 value actually quantifies the electrochemical performance at the solar water splitting device level, which originates from another figure of metric, the solar-to-fuel (STF) conversion efficiency (the ratio between the total energy stored in hydrogen/oxygen and the total energy input from sunlight irradiation).149,150 The STF conversion efficiency for a one-step photoexcitation system must reach ca. 10% to render the hydrogen production cost competitive with that of the conventional methane steam reforming process.151 The current density expected in solar water splitting cells which shows an STF efficiency of 10% under 1 sun illumination is approximately 10 mA cm−2 per geometrical area of an electrode.152,153 Therefore, the η10 value cannot reflect the intrinsic activity of a particular electrocatalyst. With the purpose of investigating the intrinsic chemistry difference of an electrocatalyst, the activity analysis should refrain from metrics that are based on the current density per geometrical area of the working electrode, although many water electrolysis studies have adopted such metrics for screening the intrinsic activity of HER and OER electrocatalysts. However, the η10 metric still demonstrates its significance for benchmarking the device performance. To meet the practical requirements, the overpotentials at high current densities such as 1 A cm−2 are suggested to be reported.
3.2.5. Tafel slope.
The Tafel analysis is commonly used to understand the reaction kinetics and compare the catalytic kinetic properties of different electrocatalysts.154,155 The Tafel plot of an electrocatalytic process is generally obtained by replotting a polarization curve to a plot of log(j) versus η. The slope of the linear portion of the Tafel plot is defined as the dependence between the iR-compensated overpotential and the current density, which is expressed as follows:| |
d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(j)/dη = 2.303RT/αF log(j)/dη = 2.303RT/αF | (16) |
where j is the current density per geometrical electrode area, R is the ideal gas constant, T is the absolute temperature in Kelvin, F is the Faraday constant, and α is the symmetry factor variable.156 The Tafel slope helps to define the rate determining step by examining the sensitivity of the current response to the applied potential. The widely used method of extracting Tafel plots from potentiodynamic polarization curves such as LSV and CV can be misleading, as Tafel analysis should be done with steady-state response.112 The Tafel slope is highly dependent on the surface coverage that is influenced by the overpotential and rate-determining step (RDS). Shinagawa et al. reported the insight into Tafel slopes from microkinetic analysis of aqueous electrochemical reactions involving the HER and the OER.154 Both the surface coverage and Tafel slope are overpotential-dependent and must be in the steady state, which is not the case in LSV and CV. Moreover, the Tafel analysis must be done in the steady state and free of iR drop (i.e., 100% iR drop correction). Therefore, steady state polarization curves are recommended to be used for a precise Tafel analysis. Regardless of the scan rate, LSV and CV will remain potentiodynamic in nature, compromising the accuracy of Tafel slopes (Fig. 2g and h). Anantharaj et al. reported the detailed procedures to correctly perform the Tafel analysis by using the steady-state polarization curves.112 Note that it is not straightforward to draw a conclusive Tafel slope value for some electrocatalysts that do not show a linear fitting of the plot of log(j) versus η in a wide potential window.157–162 This will result in the overpotential-dependent Tafel slope.154,163 A smaller Tafel slope indicates the superior electrocatalytic kinetics of electrocatalysts.
3.2.6. Stability and durability.
The stability of an electrocatalyst is an important factor to evaluate its lifetime for practical applications, which is usually tested by subjecting it to repetitive CV at higher scan rates (accelerated degradation test), CP at a given current density and CA at a given potential/voltage. The current research on HER and OER electrocatalysts usually examines the stability for thousands of CV cycles. In the meantime, the stability of electrocatalysts and two-electrode electrolysers is studied using the CP or CA. For example, the durability tests have been reported at ±10 mA cm−2 per geometric area of an electrode for tens to thousands of hours.164,165 For industrially relevant hydrogen production, water electrolysers must be able to operate at much higher current densities (e.g., 0.5 to 2 A cm−2) to attain appreciable H2 production rates and meanwhile have extreme stability and long enough lifetime of at least thousands of hours to years.82 It is recommended to measure the concentrations of dissolved metal cations and some of non-oxygen counter ions (e.g. P and S) in the electrolytes and quantify the percentage of weight loss of active metal centres after the long-term stability tests.
3.2.7. Turnover number and turnover frequency.
The turnover number (TON) and turnover frequency (TOF) are two quantitative parameters to evaluate the intrinsic activity of an electrocatalyst.106,148,166 The TON is defined as the number of moles of electrons delivered per active surface metal atom or the rate of product molecules evolved (e.g., H2 and O2) per active surface metal atom, per total metal atoms including the subsurface metal, or per ECSA.167–169 The TOF refers to the turnover number per time unit (e.g., second) and is calculated as follows:| |
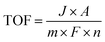 | (17) |
where J is the current density normalized with the geometrical electrode area at a given potential, A is the geometrical electrode area, m represents the number of electrons to produce 1 mol O2 (m = 4) or H2 (m = 2), F is the Faraday constant (96485.3 C mol−1) and n stands for the number of moles of surface or total metal atoms assuming that 100% charges passed are used to produce product molecules (faradaic efficiency = 100%). In principle, TOF is the best measure of the intrinsic catalytic activity. However, it is not straightforward to accurately determine TOF, because the true active sites of heterogeneous catalysts are very difficult to precisely identify. A more realistic method to calculate TOF is to take into account all relevant metal sites assuming all metal atoms as active sites. A TOF value determined in this way represents only a lower limit of the true TOFs;170,171 however, it allows for a fair and consistent comparison among catalysts prepared by different researchers. Given that TOF is typically a function of potential, the overpotential at which TOF is measured should be reported.
3.2.8. Faradaic efficiency.
In water electrolysis, faradaic efficiency is defined as the ratio of the measured amount of produced H2 or O2 to the theoretically calculated amount under the assumption that all the passed charge is utilized to form H2 or O2.172| |
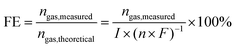 | (18) |
where FE is the faradaic efficiency, nH2,measured is the measured hydrogen or oxygen production rate (mol s−1), I is the current (A), n is the number of transferred electrons for producing 1 mol gas (n = 2 for H2 and n = 4 for O2) and F is Faraday's constant (96485.3 C mol−1). In the practical measurement, the amount of H2 or O2 is measured by gas chromatography (GC) analysis or the water–gas displacement method, while the passed charge during a given duration is monitored using an electrochemical workstation.82,92 For the GC analysis, the total volume of collected H2 and H2 calibration curve should be precisely measured. For the water–gas displacement method, the actual atmospheric pressure should be measured due to the possibly different deviation from the standard atmospheric pressure in the local area. An ideal electrocatalyst should possess 100% faradaic efficiency, while the faradaic efficiency losses are experienced in water electrolysers when electrons and ions participate in unwanted side reactions in the electrolytes and/or electrodes.
3.2.9. Energy efficiency.
Energy efficiency is widely used to evaluate the efficiency of the water electrolyser cells or systems. When only the electricity energy input for the electrolysis cell is taken into account and other energy inputs such as heat sources and other auxiliaries are neglected, the cell-level energy efficiency is calculated as follows:83| |
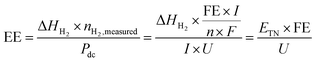 | (19) |
where EE is the cell-level energy efficiency, nH2,measured is the measured hydrogen production rate (mol s−1), Pdc is the power supplied by the external direct-current (dc) power supply (W), I is the current applied (A), U is the voltage applied (V), n is the number of transferred electrons for producing 1 mol H2 (n = 2), F is Faraday's constant, FE is the faradaic efficiency, ΔHH2 is the heating value of reaction enthalpy (i.e. heat of combustion) and ETN is the thermoneutral voltage resulting from ΔHH2 according to the eqn (11).
The energy efficiency is also called electrical efficiency or electricity-to-hydrogen energy conversion efficiency.83 It can also be regarded as the voltage efficiency, which is the ratio of the thermoneutral voltage to the real operating cell voltage.74,75 Note that there are two kinds of heating value of reaction enthalpy for H2 (ΔHH2) including the higher heating value (HHV) and lower heating value (LHV) when calculating the energy efficiency.83 The HHV (gross calorific value or gross energy) of H2 is defined as the amount of heat released by a specified quantity (e.g., 1 mol) initially at 25 °C once it is combusted and the product of water returns to 25 °C and is condensed to liquid H2O(l), which includes the latent heat of condensation of water in the combustion product. Under the standard conditions, the HHV of H2 (ΔHH2,HHV) is 285.8 kJ mol−1 corresponding to the thermoneutral voltage (ETN) of 1.48 V, while ΔGH2 is 237.1 kJ mol−1 corresponding to the thermodynamic reversible voltage (ERE) of 1.23 V. In contrast to the HHV, the LHV calculation assumes that the water product of a combustion process is in the vapor state at the end of combustion. Although its exact definition is not uniformly agreed upon, it is general to define the LHV (net calorific value) of H2 as the amount of heat released by combusting a specified quantity (e.g., 1 mol) initially at 25 °C and returning the temperature of the combustion products to 150 °C, which assumes the latent heat of condensation of water in the reaction products is not recovered. The limit of 150 °C is based on the acid gas dew point. Under these conditions, the LHV of H2 (ΔHH2,LHV) is 241.8 kJ mol−1 corresponding to the thermoneutral voltage (ETN) of 1.25 V, while ΔGH2 is 228.6 kJ mol−1 corresponding to the thermodynamic reversible voltage (ERE) of 1.18 V. For H2, the difference between HHV and LHV encompasses the sensible heat of water vapor between 150 °C and 100 °C, the latent heat of condensation at 100 °C, and the sensible heat of the condensed water between 100 °C and 25 °C.
For low-temperature water electrolysis, the calculations of energy efficiencies reported in the literature are not unified, adopting ΔHH2,HHV, ΔHH2,LHV or ΔGH2(H2O(l)) in different reports. It is noteworthy that the applied voltage U must be measured under the electrochemical steady state, suggesting both the OER and HER electrodes are well pre-conditioned without side reactions. Some articles have reported an applied voltage in a simple home-made two-electrode setup lower than the ETN (1.48 V), which is incorrect and caused by the over iR-correction and unsteady electrodes.76–81 For high-temperature water steam electrolysis, the energy efficiencies reported in the literature are generally calculated on the basis of ΔHH2,LHV. Note that some reports on high-temperature water electrolysis assume that the continuous supply from external waste heat sources is available which provides “free” thermal energy to drive the endothermic reactions when the practical SOEC operating voltage is below ETN but above ERE.85 This can result in an energy efficiency greater than 100%. In this case, the heat input should be included in the total energy input to obtain a meaningful energy efficiency value. Furthermore, the applied current should also be reported when reporting the energy efficiency, as it influences the applied voltage (U). Electrolyser manufacturers also use kilowatt hours per normal cubic meters (kW h Nm−3) or kilogram (kW h kg−1) of dry H2 as a measure of system efficiency, which sidesteps the LHV versus HHV controversy.83 Both HHV and LHV are easily converted to kW h kg−1. The U.S. Department of Energy (DOE) Fuel Cell Technologies Program Multi-Year Plan includes targets for distributed water electrolysis and for central wind water electrolysis using three measures of efficiency: HHV, LHV, and kW h kg−1.83 Therefore, it is recommended to specify the calculation details when reporting the energy efficiencies of developed water electrolysers for comparison.
4. New strategies for advanced water electrolysis
To overcome various technical challenges including incompatible integration of HER and OER electrocatalysts, large energy barrier, limited reactant mass transfer, possible H2/O2 crossover, sluggish kinetics of the bottleneck OER, incompatible pH-dependent overpotential and kinetics for the HER and the OER, storage and onsite use of H2,71 six emerging strategies are selected and summarized to address these challenges and advance the wide deployment of the water electrolysis technique (Fig. 3), including overall water electrolysis, magnetic field-assisted water electrolysis, decoupled water electrolysis, hybrid water electrolysis, acid/alkaline asymmetric electrolyte electrolysis, and tandem water electrolysis.
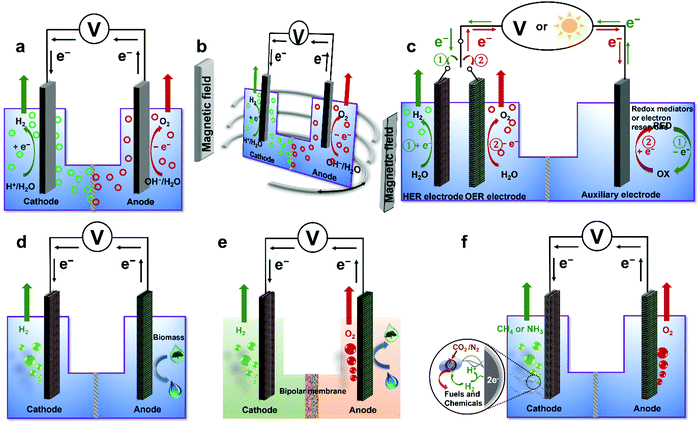 |
| | Fig. 3 Schematic illustrations of six emerging strategies for low-temperature water electrolysis. (a) Overall water electrolysis based on bifunctional nonprecious electrocatalysts (or pre-catalysts), (b) magnetic field-assisted water electrolysis, (c) decoupled water electrolysis, (d) hybrid water electrolysis, (e) acid/alkaline asymmetric electrolyte electrolysis, and (f) tandem water electrolysis. Adapted from ref. 173, Copyright 2018, with permission from Elsevier. | |
4.1 Overall water electrolysis
The standard thermodynamic potential for the HER and the OER depends on the pH value (Fig. 1). Based on the Nernst equation, acidic conditions (low pH) are favourable for HER rendering a low onset potential, while alkaline conditions (high pH) are beneficial for the OER delivering a low onset potential.117,118 Therefore, most developed HER electrocatalysts including Pt and nonprecious electrocatalysts demonstrate superior catalytic HER performance in acidic electrolytes. However, a few nonprecious OER electrocatalysts can survive in acidic electrolytes. Recent intensive research efforts have resulted in developing nonprecious OER catalysts or pre-catalysts superior to noble metal oxides such as RuO2 and IrO2 under alkaline conditions.174 In contrast, most of the nonprecious HER electrocatalysts still demonstrate inferior intrinsic electrocatalytic activities for HER compared to Pt, although some emerging nonprecious HER electrocatalysts such as NiMo alloys and Ni3N/Ni interfacial catalyst exhibit high apparent and specific activities comparable to Pt in alkaline electrolytes.124,175,176 The disparity of conditions that are favourable to HER and OER catalysts and the incompatibility of the components of HER and OER catalysts will likely cause complicated integration and mediocre performance in the overall electrochemical water splitting. In this respect, to accomplish overall water electrolysis, coupling of HER and OER electrolytes in the same pH electrolyte with bifunctional electrocatalysts is highly desirable. Due to the nature of the four successive proton-coupled electron transfer process, the overpotential of OER is typically higher than that of HER to deliver the same current density. The solution pH for favouring the OER is preferable, which is the alkaline electrolyte. Therefore, recent progress in overall water electrolysis focuses on developing active bifunctional Janus nonprecious electrocatalysts that serve as catalysts for HER and pre-catalysts for OER in the same alkaline media (Fig. 3a).66 The use of such Janus electrocatalysts with identical compositions would significantly simplify the design, integration of electrocatalysts and construction of water electrolysers, and potentially lower the production cost. Various kinds of bifunctional Earth-abundant electrocatalysts have been developed, including nanostructured transition metal phosphides, chalcogenides, carbides, borides, nitrides, oxides and (oxy)hydroxides.177–197
Cobo and co-workers developed a Janus cobalt-based catalytic material for both HER and OER in neutral electrolytes.199 A robust nanoparticulate electrocatalytic material, H2-CoCat, was prepared from cobalt salts in a phosphate buffer by electrodeposition, consisting of metallic cobalt coated with a cobalt-oxo/hydroxo-phosphate layer for electrocatalytic HER at modest overpotentials. Furthermore, it was converted on anodic equilibration into an amorphous cobalt oxide film (O2-CoCat or CoPi) which could catalyse the OER in a similar neutral solution.199 This Janus material inspired intensive research efforts in developing bifunctional catalyst/pre-catalysts for overall water splitting in alkaline and neutral electrolytes. Subsequently, Jiang et al. fabricated Co–P-derived films by electrodeposition, which showed catalytic performance for both HER and OER in 1.0 M KOH.200 They found that the major compositions of the as-prepared and post-HER films were metallic cobalt and low-crystallinity cobalt phosphide, which partially evolved to cobalt oxide during the OER. Later, Stern et al. developed Ni2P nanoparticles as the HER electrocatalyst and the pre-catalyst for OER in 1.0 M KOH.201 They clearly identified the formation of core–shell Ni2P/NiOx in the OER process and demonstrated that the two-electrode water electrolyser composed of both Ni2P electrodes could deliver 10 mA cm−2 at 1.63 V. Liu's and Shalom's groups independently developed crystalline Ni5P4 and NiP2 nanosheets by using the reaction between Ni and red P, and found that Ni5P4 could efficiently catalyse the HER in alkaline solutions and be in situ transformed to nickel (oxy)hydroxide on the surface to form core/shell NiPx/Ni(OH)2 under the anodic potential for catalysing the OER.202,203 Liu's group has demonstrated that the water electrolyser assembled using the Janus nickel phosphide electrodes could stably operate at 10 mA cm−2 at a small voltage lower than 1.65 V with a remarkable lifetime of 100 to 1000 hours and a high energy efficiency of over 90%.202,204 Li et al. employed the reaction between Co foam and red P to obtain the Janus CoP electrodes for catalysing both HER and OER in the alkaline solution and comprehensively elucidated the in situ oxidation and dephosphorization process during the conversion of CoP to cobalt (oxy)hydroxide upon the OER (Fig. 4a–f).198 The water electrolyser composed of Janus CoP electrodes exhibited better performance than the noble metal couples, 100% faradaic efficiency and remarkable stability for overall water electrolysis at relatively high current densities of 20 and 100 mA cm−2 for 1000 h (Fig. 4g–j). The same group also fabricated cobalt nickel phosphide nanowires on Ni foam (Ni@Co–Ni–P) as monolithic self-supported bifunctional electrodes for HER and OER in 1.0 M KOH.165 The ternary Co–Ni–P nanowires showed remarkable bifunctionality in catalysing the HER and serving as the pre-catalyst for OER. They constructed an alkaline water electrolyser by assembling two symmetrical Ni@Co–Ni–P electrodes as the cathode and anode, respectively, which exhibited outstanding catalytic performance for sustained water electrolysis at varying current densities from 10 to 240 mA cm−2. Even at a relatively high current density of 100 mA cm−2, the Ni@Co–Ni–P electrolyser was capable of operating for over 3000 h with little degradation and a high energy efficiency of 76%.165 Later, Li et al. developed monolithic Co3Se4 nanowires on Co foam (Co3Se4/CF), for the first time, via a facile one-pot hydrothermal process using selenourea.164 This electrode also showed Janus characteristics to serve as an active HER catalyst and a pre-catalyst for the OER in alkaline media. They revealed the complete transformation of Co3Se4 to CoOOH during the OER, which was the true active catalytic species. The Co3Se4/CF anode showed an exceptionally high catalytic current density of 397 mA cm−2 and a TOF of 6.44 × 10−2 s−1 at a low overpotential of 320 mV, a small Tafel slope of 44 mV dec−1, and outstanding electrocatalytic stability at various current densities for the OER. The water electrolyser constructed using two symmetrical Co3Se4/CF electrodes could deliver 10 and 100 mA cm−2 for over 3500 and 2000 h without noticeable degradation, respectively (Fig. 5).164 These alkaline electrolysers showed superior performance to those consisting of the Pt cathode and the RuO2 anode under similar conditions.
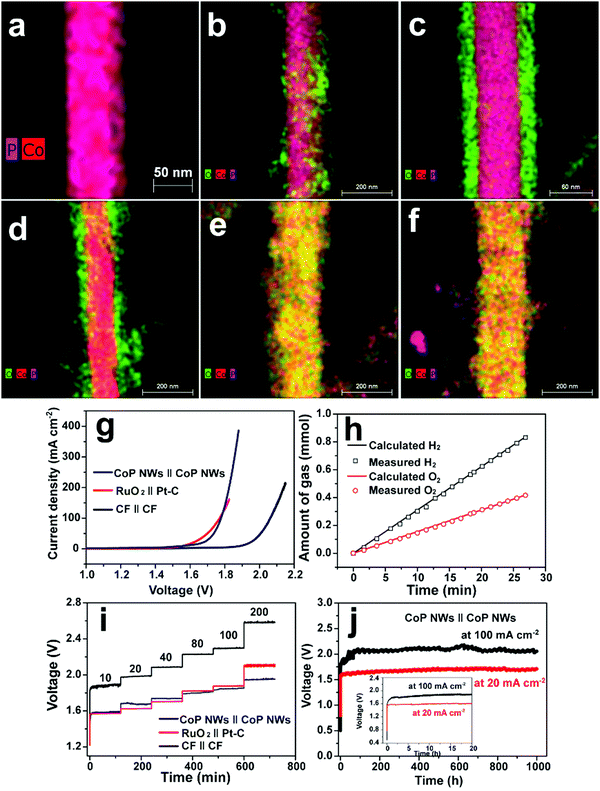 |
| | Fig. 4 Overlaps of high-angle annular dark-field scanning transmission electron microscopy and elemental mapping images of (a) pristine CoP nanowire, (b) CoP nanowire upon anodic oxidation for 20 s, (c) CoP nanowire upon anodic oxidation for 5 min, (d) CoP nanowire upon anodic oxidation for 30 min, (e) CoP nanowire upon anodic oxidation for 3 h and (f) CoP nanowire upon anodic oxidation for 6 h at 1.54 V vs. RHE in O2-saturated 1.0 M KOH. (g–j) Overall water splitting performance of the two-electrode CoP electrolysers. (g) Polarization curves of CoP nanowires (NWs), bare Co foam (CF) and RuO2(+)‖Pt–C(−) supported on CF. (h) Gas yield of H2 and O2 evolved over the CoP NW electrodes as a function of time at 100 mA cm−2. (i) Multi-step CP curves of the CoP NWs and bare CF electrolysers at varying current densities. (j) Long-term stability test of the CoP NW electrolyser at 20 and 100 mA cm−2. Inset: zoomed view of the curves in the first 20 h. All experiments were conducted in 1.0 M KOH at room temperature. Reproduced from ref. 198 with permission from the Royal Society of Chemistry under a CC BY-NC 3.0 licence. | |
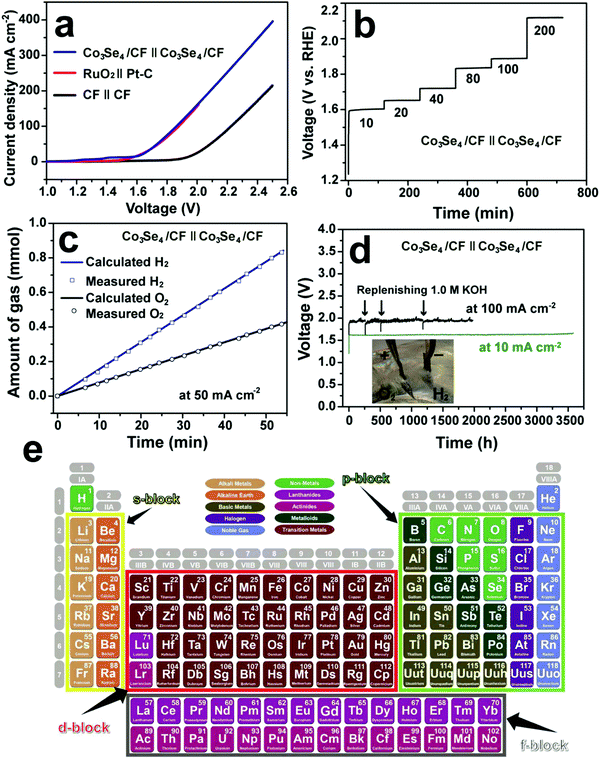 |
| | Fig. 5 Overall water splitting performance of the two-electrode electrolysers. (a) Polarization curves of Co3Se4/CF, CF and RuO2(+)‖Pt–C(−) supported on CF. (b) Multi-step CP curve of the Co3Se4/CF electrolyser at varying current densities. (c) Gas yield of H2 and O2 evolved over the Co3Se4/CF electrodes as a function of time at 50 mA cm−2. (d) Long-term stability CP test of the Co3Se4/CF electrolyser at 10 and 100 mA cm−2. Inset is a photograph showing the gas bubbling of H2 from the cathode and O2 from the anode at 100 mA cm−2. All experiments were conducted in 1.0 M KOH at room temperature. The polarization and CP curves are shown without iR correction. (a–d) Reproduced with permission from ref. 164. Copyright 2017, John Wiley and Sons, Inc. (e) The periodic table of s-, p-, d-, and f-block elements. Reproduced from ref. 205 with permission from John Wiley and Sons, Inc. under the Creative Commons CC BY license. | |
Recently, various strategies have been employed to develop efficient bifunctional electrodes for water electrolysis, including nano-architecture design, optimization of synergistic combination of metal elements and non-metallic elements (e.g. B, C, N, P, O, and chalcogens), in situ growth of active electrocatalysts on conductive substrates to produce self-supported monolithic electrodes and exploration of s-, p- and f-block metals (Fig. 5e) for discovery of advanced electrocatalysts containing multiple metal centres.205–207 As the nonprecious metal based electrocatalysts cannot sustain for a long time under the acidic OER conditions, the application of developed bifunctional Janus materials focuses on alkaline water electrolysis, which will potentially mitigate the incompatibility, simplify the device design, improve the longevity, and reduce the costs.
4.2 Magnetic field-assisted water electrolysis
The existing large energy barriers and limited reaction kinetics of the HER and the OER have motivated the research community to explore new electrocatalysts and engineer various inherent properties of electrocatalysts including morphologies, structures, compositions, interfaces, crystallinity, exposed crystal facets, phases, and defects to increase the intrinsic catalytic activities.208 Beyond this direction, novel external field-assisted electrocatalysis has emerged as a promising paradigm to promote the water electrolysis reactions.208–210 An external magnetic field has been employed to provide flexibility to engineer the water electrolysis process (Fig. 3b). For example, Berlinguette's group has recently investigated the relationship between the OER activity and magnetic field at the surface of the CoOx/F-doped tin oxide (FTO) conductive glass electrode by accurately controlling the distance between the magnet and OER electrode and quantified the enhancement of potentiostatic electrolysis OER current and Tafel slope as a function of magnetic flux density at the OER electrode.211 This new paradigm of magnetic field-assisted water electrolysis offers merits in terms of facile operation, dynamic regulation, and continuous, reversible, and universal control. Although the true mechanisms of magnetic field-assisted water electrolysis remain unclear, several effects of magnetic field on the reaction thermodynamics and kinetics of electrochemical processes have been reported including the magnetohydrodynamic (MHD) and micro-MHD effects, magnetothermal effect, electron spin selectivity effect, Maxwell stress effect and Kelvin force effect.212–214 This section reviews how these magnetic field-induced effects influence the electrochemical reactions for water electrolysis.
4.2.1 MHD and micro-MHD effects.
The HER and the OER usually suffer from the adhesion of gas bubbles on the surfaces of gas-evolving electrodes. The attached gas bubbles can decrease the ECSAs of electrodes, block the ion conduction pathways, and hamper the reactants from reaching the active sites. Thus, the large bubble coverage poses an additional potential barrier to charge transfer across the electrocatalyst–electrolyte interface, increasing the activation overpotential.208 Surface-attached bubbles not only increase ohmic resistance by preventing the ionic current flow from reaching a portion of the ECSA, but also induce a non-uniform distribution of current density in the area adjacent to the bubbles and affect the charge transfer in those regions. Furthermore, bubbles dispersed in the bulk electrolyte also increase the ohmic overpotential by reducing the number of available ion conduction pathways and thus lower the effective ionic conductivity of the electrolyte. The bubbles may also affect the mass transfer and lead to the formation of undesirable concentration gradients. An in-depth discussion on the influence of bubble evolution on the energy conversion efficiency in electrochemical reactions has been reviewed previously.215 These detrimental effects of bubbles can reduce the energy efficiency and electrode stability for water electrolysis. Although some passive methods have been developed to mitigate the bubble impacts including electrode morphology, structure and wettability engineering and addition of surfactants or additives to aqueous electrolytes,216 it is still challenging to minimize the bubble-induced effects. Therefore, various strategies that make use of external fields such as acoustic, centrifugal, and magnetic fields have been developed to promote bubble detachment.210 Among these external fields, the use of magnetic field is more facile to integrate with water electrolysers. The MHD and micro-MHD effects are the macroscopic and microscopic convection caused by the Lorentz force which the moving charged ions in the electrolyte under the electrolysis electric field are subjected to.212,217 The forms of magnetic convection on the electrode surface are illustrated in Fig. 6.
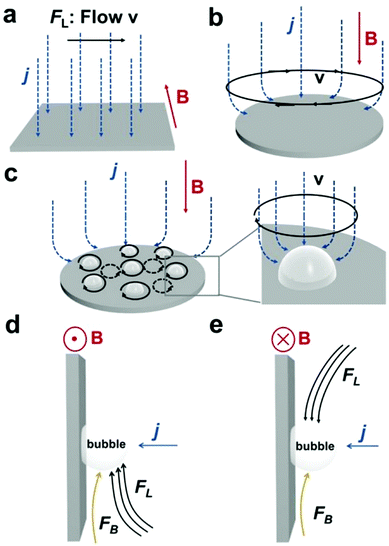 |
| | Fig. 6 MHD flow types under a static uniform magnetic field and the schematic illustrations of the MHD effect for electrodes. (a) The MHD flow is parallel to the electrode surface when the magnetic field direction B is perpendicular to the current density j (B⊥j). (b) MHD whirlpools around the electrode edge when B is parallel to j (B‖j). (c) Micro-MHD induced around the bubbles attached on the electrode surface when B‖j. Cases of the Lorentz force FL and the buoyancy force FB in the same direction (d) and opposite direction (e). Reprinted with permission from ref. 212. Copyright 2020, American Chemical Society. | |
The Lorentz force (FL) reaches maximum when the magnetic strength (B) is perpendicular to the current density j (B⊥j), making the magnetic convection parallel to the electrode surface (Fig. 6a). FL is zero when B is parallel to j (B‖j). Furthermore, the edge effect of a disk electrode and the bulge of insulating bubbles can distort the current lines, leading to the azimuthal FL (Fig. 6b and c). The MHD and micro-MHD effects influence the gas detachment on the gas-evolving electrodes. The bubble release size and dwell time depend on the net force (Fig. 6d and e). If the direction of FL and the buoyancy force (FB) is identical (e.g., upward), the upward pumping effect of MHD convection will decrease the average size of bubble detachment and dwell time and thus speed up the release of bubbles (Fig. 6d). Conversely, if FL has a downward direction opposite to the upward FB, the release of bubbles will be retarded. Therefore, the control of magnetic field is important to influence the bubble detachment. The micro-MHD effect on bubble detachment is controversial. Many studies reported the promoted release of bubbles due to the micro-MHD induced swirling as micro-stirrers,218–220 whereas some research studies have drawn the opposite conclusion.221 Whether the bubble detachment is promoted by the micro-MHD effect depends on the location of the low-pressure region in the bubble. It was proposed that the micro-MHD effect promotes the release of bubbles on the conventional electrode surface, while it enhances the pinning of bubbles on the microelectrode surface.222 The influence of MHD and micro-MHD on electrocatalytic reactions can reduce the ohmic polarization, activation overpotential and concentration polarization.212 The Bruggeman approximation describes the dependence of effective conductivity of an electrolyte filled with insulating gas bubbles as follows:
where k is the effective conductivity of the electrolyte with random suspension of gas bubbles, k0 is the conductivity of bubble-free electrolyte and f is the volume fraction of dispersed bubbles.212,223,224 The MHD can alleviate the supersaturated accumulation of bubbles, reduce the value of f and increase the conductivity, leading to decreased ohmic polarization. Furthermore, the MHD and micro-MHD effects can reduce the electrode masking and bubble coverage, ensuring the exposure of the effective electrochemically active area to reduce the activation overpotential.225,226 In addition, the forced flow induced by the MHD and micro-MHD effects can thin the diffusion layer and enhance the mass transfer. The concentration overpotential can be expressed as follows:| |
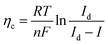 | (21) |
where ηc is the concentration overpotential, R is the ideal gas constant, T is the absolute temperature in Kelvin, F is the Faraday constant, n is the number of electrons involved in the electrode reaction, I is the current density and Id is the limiting current density.212 The limiting current density is related to the diffusion layer according to Fick's first law as follows:| |
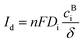 | (22) |
where Di is the ion diffusion coefficient, cBi is the concentration of ions in bulk solution, and δ is the diffusion layer thickness. When the MHD and micro-MHD effects reduce δ, the limiting current density will be increased, leading to a decrease of ηc.
The MHD effect has been found and fundamentally studied in some homogeneous electrochemical reactions, electrodeposition, and electropolymerization.227 For the electrodeposition of Ni,228 Fe,229 Co,230 and alloys under a magnetic field,231 some early studies found that the release of hydrogen bubbles produced by the competitive HER in the cathodes is promoted to facilitate the formation of smooth plated metal coating layers. In 2007, Fukunaka's group first reported promoted water electrolysis under a magnetic field.225 The voltage of water electrolysis with two Pt sheets as the cathode and anode decreased with the increased magnetic field strength in both acidic and alkaline electrolytes including 0.05 M H2SO4, 0.36 M KOH and 4.46 M KOH (Fig. 7a–c). The MHD convection can help to remove the bubble coverage and thus reduce the ohmic resistance. Meanwhile, the MHD convection enhanced the mass transfer rate of dissolved gas to reduce the degree of supersaturation and lowered the activation and concentration overpotentials for both HER and OER electrodes.232,233 Later, Matsushima et al. employed a high-speed digital camera to observe the nucleation, growth, and detachment of bubbles on transparent FTO conductive glass electrodes (Fig. 7d).226 The gas bubbles can stay at the nucleation sites in the absence of a magnetic field until natural convection is developed. In contrast, the bubbles can be swept away by the MHD convection as soon as they are nucleated in the presence of a magnetic field with a strength higher than 1 T and the nucleation number of bubbles decreases with the increase of magnetic strength. Lin et al. reported the direct visual observation of the effect of FL direction on the bubble motion on ferromagnetic Ni, paramagnetic Pt, and diamagnetic graphite electrodes.234Fig. 7e clearly demonstrates that the upward FL and FB together can facilitate the release of H2 and O2 bubbles, while the downward FL in an opposite direction to FB significantly slows the bubble detachment (Fig. 7f). The degree of MHD-induced enhancement in energy efficiency of water electrolysis on different electrodes follows the order of ferromagnetic Ni > paramagnetic Pt > diamagnetic graphite, where Ni showed the largest increase but there is insignificant boost for graphite under the magnetic field. They also systematically investigated the effects of inter-electrode distance and KOH electrolyte concentration on the electrolysis current density under different magnetic field intensities, revealing that a smaller electrode distance leads to larger enhancement and there is an optimal KOH concentration of 20 wt% to deliver the most significant boost in the current density under various magnetic field intensities ranging from 0.6 to 4.5 T. These results suggest that the integrated magnetic field is likely compatible with the current zero-gap configuration of alkaline electrolyser. Note that the influence of FL on the physical movement of OH− and H3O+ ions is negligible, because both ions in the aqueous solutions move by sequential proton hopping/transfer instead of physical motion, which is known as the Grotthuss mechanism.235
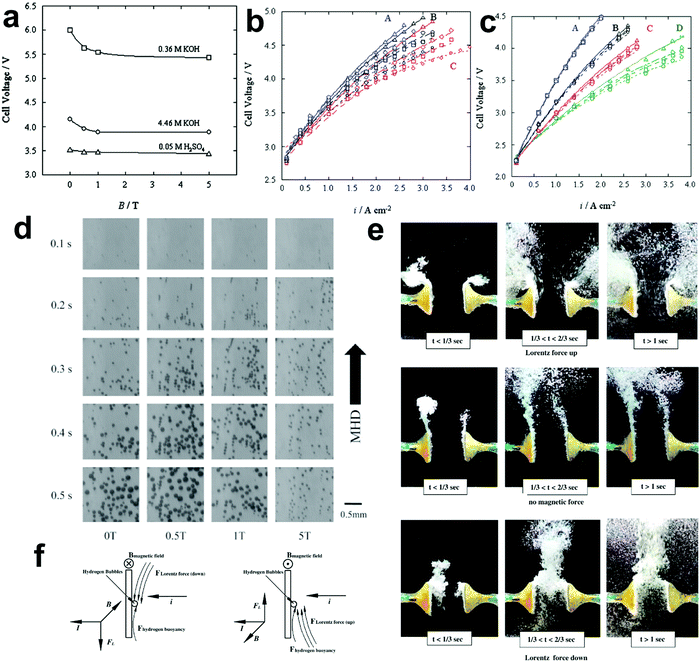 |
| | Fig. 7 (a) Cell voltage versus magnetic field intensity for water electrolysis by using Pt sheets as working and counter electrodes with a distance of 2 mm under a fixed current density of 1.8 A cm−2 in different aqueous electrolytes. (b) Polarization curves for water electrolysis in 4.46 M KOH electrolyte by using Pt sheets as working and counter electrodes with different electrode distances (A: 20 mm, B: 4 mm and C: 2 mm) and magnetic field intensities (triangle: 0 T, diamond: 0.5 T, square: 1 T and circle: 5 T). (c) Polarization curves for water electrolysis in 0.05 M H2SO4 electrolyte by using Pt sheets as working and counter electrodes with different electrode distances (A: 20 mm, B: 4 mm, C: 2 mm and D: 1 mm) and magnetic field intensities (triangle: 0 T, diamond: 0.5 T, square: 1 T and circle: 5 T). (a–c) Reproduced from ref. 225, Copyright 1948, with permission from IOP Publishing. (d) Images of tracking oxygen bubble evolution on a FTO electrode during the OER in 0.36 M KOH at a current density of 0.3 A cm−2 under different magnetic field intensities. Reprinted from ref. 226, Copyright 2013, with permission from Elsevier. (e) Photos of bubble convection under different magnetic-induced Lorentz force directions (water electrolysis voltage: 4 V, cathode and anode: Ni plates, electrolyte: 40 wt% KOH, electrode distance: 10 mm and magnetic field intensity: 4.5 T). (f) Schematic for the MHD effect in the vicinity of cathode under different Lorentz force directions. (e and f) Reprinted from ref. 234, Copyright 2012, with permission from Elsevier. | |
To date, the MHD and micro-MHD effects have been extensively reported for boosting the HER and/or the OER on Pt,233 Ni,236 Co3O4-loaded Ni foam,237 Ta,218 Cu,238 Ni–W alloy,239 and various steels.240 In addition to the experimental investigation, recent studies have employed theoretical modelling to gain insights into the MHD and micro-MHD effects (Fig. 8). Liu et al. reported the use of numerical simulation and modelling to systematically unravel the MHD and micro-MHD effects on various electrodes including porous metal foams,241,242 planar Pt sheets and microelectrodes under external magnetic fields,243,244 and magnetized Ni wires in the absence of an external magnetic field.236 The current lines are distorted within the porous electrode and thus the Lorentz force is induced even though the direction of magnetic field is parallel to that of apparent current lines. The velocity field distribution induced by the Lorentz force plays a key role in expelling bubbles off the pores. Surprisingly, the computational fluid dynamics (CFD) analysis illuminates that the micro-MHD generates a pair of low-pressure regions close to the low-half part of the bubble wall due to the rotating flow fluid around the bubble driven by the Lorentz force.222 The pressure difference around the bubble provides the growing bubble an external force which offers a stabilization impact to pin the bubble on the Cu microelectrode surface. However, for the macroelectrode, the lower part rotating flow is restrained by the electrode surface's no-slip conditions, and the upper part flow is more turbulent. Thus, a relative lower pressure region is formed above the top of bubble, which helps the bubble release from the macroelectrode surface. In addition to the reliance on an external magnetic source such as permanent magnet and electromagnet, the direct use of magnetized electrodes forming an internal magnetic field in the water electrolyser can simplify the system design. The in operando microscopic observation and simulation demonstrate that the residual magnetic field generated by magnetized electrodes gives rise to the Lorentz force and MHD convection and thus reduces the H2 bubble diameter and coverage.236 This new finding offers a new paradigm to develop energy-efficient water electrolysis using magnetized electrodes with high electrocatalytic activities.
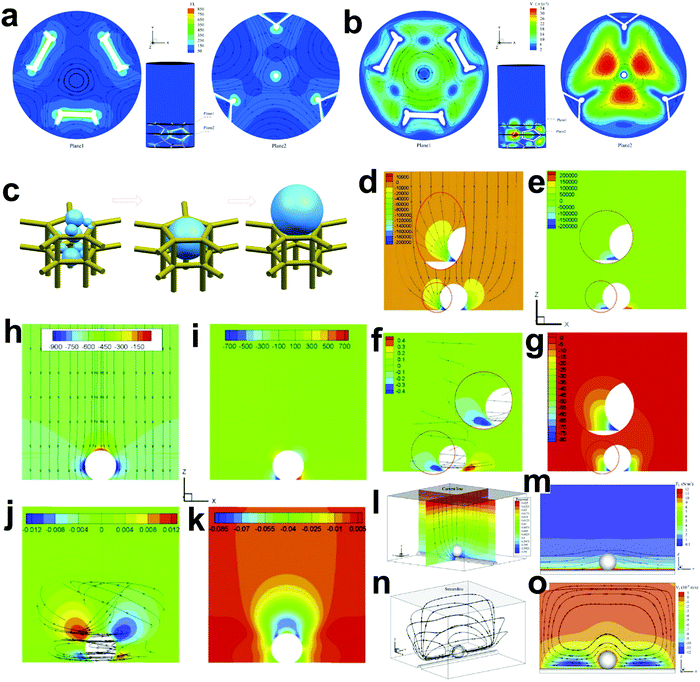 |
| | Fig. 8 (a) Lorentz force magnitude (contour) (Nm−3) and orientation (arrow lines) around the ligaments of a porous Ni electrode. (b) Velocity (m s−1) field distribution (contour) and streamlines (arrow lines) within the porous microstructure. (c) Schematic of nucleation of bubbles, the bubbles coalesce into a large one within the pore and large bubbles are expelled to release from the pore. Simulation results of the micro-MHD effect with a magnetic field on a microelectrode surface. (a–c) Reprinted from ref. 242, Copyright 2019, with permission from Elsevier. (d) Current distortion around the bubble wall (arrow lines) and the Z direction current density (contour, A m−2). (e) The Y direction Lorentz force per unit volume (Nm−3). (f) Velocity field distribution in the Y direction (m s−1) and the streamlines around the bubble. (g) Static pressure distribution around the bubble (Pa). Simulation results of the micro-MHD effect with an average current density of 60 mA cm−2 and a 0.9 T magnetic field on a macroelectrode surface. (h) Current distortion around the bubble wall (arrow lines) and the Z direction current density (contour, A m−2). (i) The Y direction Lorentz force per unit volume (Nm3). (j) Velocity field distribution in the Y direction (m s−1) and the streamlines around the bubble. (k) Static pressure distribution around the bubble (Pa). Simulation results of current distribution, the Lorentz force and velocity around the bubble for a magnetized nickel wire cathode. (d–k) Reprinted from ref. 222, Copyright 2015, with permission from Elsevier. (l) Current line distribution (arrow lines) and the electric potential (contour). (m) Lorentz force (FL) magnitude (Nm3) and direction (arrow lines). (n and o) Velocity component in the Y-axis direction (contour, Vy, m s−1) and streamlines (arrow lines) around the spherical bubble model. (l–o) Reprinted from ref. 236, Copyright 2019, with permission from Elsevier. | |
4.2.2 Magnetothermal effect.
The magnetothermal effect is derived from the magnetic hyperthermia in cancer therapy.245 It is generated by imposing an external high frequency alternating magnetic field (AMF) on magnetic nanoparticles to trigger localized heating.212 The HER and OER are electrochemical reactions governed by kinetic energy barriers and mass transfer. Increasing the electrochemical reaction temperature can reduce the overpotentials and promote the kinetics. Therefore, both PEM and alkaline water electrolysers commonly adopt global heating of the whole cell systems.208 However, this conventional global heating leads to some problems. It brings about high energy consumption and thereby increases the energy cost due to the inefficient heat exchange and requirement of heating bulk electrolytes and cell accessories. The continuous global heating also leads to intense corrosion of the whole electrolysers, which is detrimental to the lifetime of electrodes and reactors. Given that the electrocatalytic HER and OER take place at the electrocatalyst/electrolyte interfaces, localized heating in the vicinity of electrocatalysts is more energy-efficient and preferable. Inspired by the magnetic hyperthermia, Niether et al. employed a high frequency AMF to trigger the localized heating of the electrodes that are ingeniously designed on the basis of nickel-coated iron carbide (core–shell Fe2.2C@Ni) nanoparticles for enhanced alkaline water electrolysis.246Fig. 9 shows the alkaline water electrolyser under the high frequency AMF. The Fe2.2C served as the magnetic core demonstrating high heating-power properties under AMF, while the outer Ni shell acted as the electrocatalytically active species for both HER and OER in 1 M KOH electrolyte. The core–shell Fe2.2C@Ni delivered significantly decreased overpotentials for the HER and the OER with the increasing magnetic field intensity of AMF. Fig. 9b demonstrates the galvanostatic measurement of the Fe2.2C@Ni electrode for the OER, in which overpotential was instantaneously impacted when the AMF was switched on and off at different field intensities at an applied anodic current of 35 mA. This instantaneous response of the potential to AMF clearly reflects the pronounced localized heating of Fe2.2C@Ni. The full water electrolysis cell performance was also investigated in a zero-gap and flow-cell setup close to the commercial alkaline water electrolyser in the presence and absence of AMF, which substantiates that the water electrolysis voltage can be reduced by leveraging the magnetothermal effect upon the Fe2.2C@Ni electrodes induced by AMF-triggered localized heating. Note that the reduced voltage may be ascribed to the multiple synergy effects of improved mass transfer and kinetics and reduced energy barrier from localized heating and bubble coverage from MHD. As such, this work provides an interesting proof-of-concept for magnetothermal water electrolysis technology in a relatively non-destructive heating way which brings new vitality to alkaline water electrolysers. Nonetheless, further fundamental and engineering investigations are still required. First, the magnetothermal effect and other magnetic field induced effects are not explicitly deconvoluted to elucidate how they separately influence the activity enhancement. Second, unlike the use of a static permanent magnetic field, there is an additional energy input for high-frequency AMF. Therefore, the comparison between overall energy consumption by using AMF and conventional heating should be rigorously evaluated using technoeconomic analysis (TEA). Finally, more technical engineering improvements are needed in terms of screening other magnetic cores for better control over heating properties, optimizing surface HER and OER electrocatalysts and extending long-term stability of the magnetic core particles and surface electrocatalytically active species. In addition, the high-frequency induction heating generated by AMF has been employed for the rapid synthesis of Ni loaded MoO2 nanowires and NiFe layered double hydroxide as electrocatalysts of HER and OER in alkaline water electrolysis, respectively.247 This also opens up a new avenue for the synthesis of electrocatalysts by using magnetic fields.
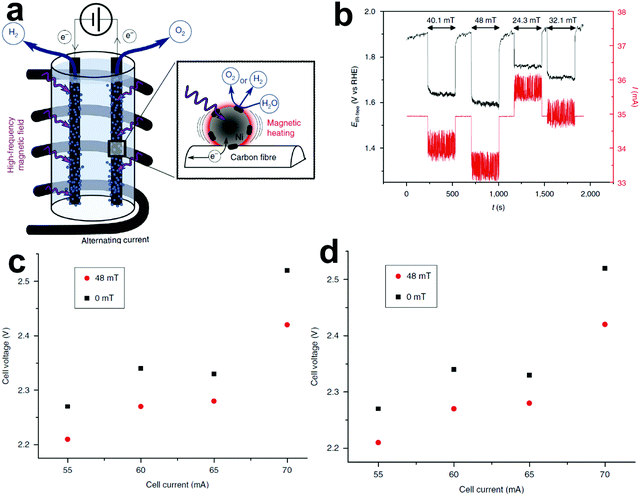 |
| | Fig. 9 (a) Schematic illustration of an alkaline water electrolysis cell operating inside the coil that produces an alternating magnetic field (AMF). Core–shell Fe2.2C@Ni nanoparticles loaded on the carbon nanofiber cloth serve as HER and OER electrocatalysts. (b) Chronopotentiometry measurement of Fe2.2C@Ni for the OER at a constant current of 35 mA under AMF of varying intensities. Alkaline water electrolyser cell voltage versus current with or without an AMF of 48 mT. (c) Measured voltage and (d) iR-corrected voltage. The voltage was measured in a two-electrode and zero-gap setup. Reprinted from ref. 246, Copyright 2018, with permission from Springer Nature. | |
4.2.3 Spin selectivity effect.
In low-temperature water electrolysis, the OER is a spin state transition process (Fig. 10a and b) which involves four-electron transfer and production of triplet-state paramagnetic O2 from singlet-state diamagnetic reactants such as H2O and OH−.248–250 Specifically, the ground spin state of H2O and OH− reactants is singlet with all paired electrons, while the ground state of molecular O2 product is triplet (3Σg) with the antibonding-molecular orbitals (frontier π* orbitals) occupied by two unpaired electrons with parallel alignment, leading to paramagnetic properties.251,252 There is also an excited state of singlet diamagnetic O2 (1Δg) with frontier π* orbitals occupied by two unpaired electrons with antiparallel alignment, which has an energy level of at least 1.0 eV higher than that of the ground triplet O2 (Fig. 10c and d).253–255 For nonmagnetic anodes, the high overpotential is associated with the notion that oxygen is initially produced in its diamagnetic excited state (singlet-state) and decays to the ground triplet state.254 The spin-conservation rule (i.e., angular momentum conservation) is a key selection rule for chemical reactions.254 From a quantum mechanics view, the kinetics of reactions where the total spin of the reactants differs from the total spin of the products with spin transition is theoretically low.256 Therefore, the OER requires an additional energy such as electrical potential, thermal disturbance, and magnetic field to proceed.248 Both electron transfer and orbital interactions between the catalyst and the reactant/intermediate show spin-dependent features, making the reaction kinetics and thermodynamics sensitive to the spin configurations. Thus, the magnetism (at least surface magnetism) of transition metal oxide (TMO) based electrocatalysts should play a role in the OER kinetics, as it is related to spin polarization (i.e., spin selectivity).249,251 Conversion from OH− (in alkaline electrolytes) or H2O (in acidic electrolytes) to O2 undergoes multistep processes of intermediate oxygen adsorbate species evolution. Generally, the oxygen valence electrons in the reactants of OH− or H2O (with 8 valence electrons per oxygen atom) at the electrocatalyst/electrolyte interfaces are extracted and pass through the interconnected particles and bulk of electrocatalyst and electronically conductive additives and eventually flow to the external circuits, releasing O2 with 6 valence electrons among which each frontier π* orbital of two antibonding-molecular orbitals is occupied by one unpaired electron with the same spin direction, respectively.248 The electron-deficient intermediate oxygen adsorbate species such as *OH, *O, *OOH, and *OO are bound with active sites at the electrocatalyst/electrolyte interfaces through chemisorption. The electron transfer from the oxygen adsorbates proceeds when the unoccupied energy levels in the conduction bands of active sites of electrocatalysts are lowered below the O 2p band centres of adsorbates by a positive potential applied on the anode where the OER occurs. For example, the energy gap between O 2p valence and unoccupied 3d conduction band of TM catalytic centres in TMO electrocatalysts has been elucidated to play a key role in the OER activity.257Fig. 10e–g present three widely reported mechanisms of diverse TMO based electrocatalysts for the OER in alkaline electrolytes, including the Eley–Rideal (ER) type adsorbate evolution mechanism (AEM), the Langmuir–Hinshelwood (LH) type AEM, and the lattice oxygen mechanism (LOM).248 The ER-type AEM takes place on single metal cation active sites involving evolution from the OH− reactant to *OH, *O, *OOH, and *OO intermediates to the O2 product eventually. The LH-type AEM occurs on two adjacent metal cation active sites. Similarly, the LOM also involves two active sites; however, one metal cation active site and the one lattice oxygen active site participate in this process. Both the LH-type AEM and LOM involve the evolution from the OH− reactant to *OH, *O, and *OO intermediates to the O2 final product bypassing the formation of *OOH. As mentioned above, the adsorption of reactants and intermediates on the electrocatalyst/electrolyte interface is owing to orbital overlaps, chemisorptive bond formation, and interfacial electron transfer. For 3d TMO electrocatalysts, the binding between intermediates and active sites has been proved to correlate with eg occupation.113,258 Since the descriptor eg electron number is intrinsically related to spin configuration, the electron spin of active sites is expected to influence the OER activity.259Fig. 10h and i demonstrate one example of the spin direction of four electrons (down–up–down–down) among all possible combinations for all three mechanisms.248 Apparently, three out of the four electrons transferring from the reactants/adsorbates must be in the same spin direction to generate the ground triplet-state O2 product regardless of the adopted pathways. If active sites are unable to efficiently extract three electrons with the same spin direction and one electron with the reverse spin direction, some electrons will undergo spin flipping during the transfer process to meet the spin selection requirement before producing O2. Extra activation energy (e.g., in the form of high overpotential) should be required to enable spin flipping if the corresponding electrocatalyst is unable to provide electrons that cater to the needs of spin selection. This will retard the reaction kinetics. Therefore, rational regulation of the electron spin configuration of electrocatalysts is expected to facilitate the OER.
 |
| | Fig. 10 (a and b) Molecular orbital diagrams of H2O, OH−, and O2 (triplet-state). Molecular orbital diagrams of (c) singlet-state and (d) triplet-state O2 molecules. (e–g) Proposed reaction routes for the OER in alkaline electrolytes on metal oxide-based electrocatalysts: (e) Eley–Rideal (ER) type adsorbate evolution mechanism (AEM), (f) Langmuir–Hinshelwood (LH) type adsorbate evolution mechanism, and (g) lattice oxygen mechanism (LOM). Possible outer electron behaviours during the OER for (h) single active site case (e.g., ER-type AEM) and (i) two adjacent active site scenarios (e.g., LH-type AEM and LOM). Red boxes present simplified hybrid orbitals of oxygen species. Black arrowed dashed lines and circles show the direction of electron transfer/hopping between adsorbates and active sites through chemisorptive bonding. Red arrowed dashed lines and circles denote electron depletion (transferring from surface to bulk). One example of the spin direction of four electrons which is down–up–down–down is illustrated here for clarity. Other combinations are also possible (not shown), if three out of the four electrons transferring from the reactants to the triplet-state O2 product are in the same spin direction. (a and e–i) Reprinted from ref. 248, Copyright 2020, with permission from Springer Nature. (b) Reprinted from ref. 249, Copyright 2020, with permission from John Wiley and Sons, Inc. (c and d) Reprinted with permission from ref. 253. Copyright 2018, American Chemical Society. | |
Gracia et al. have systematically investigated and found that the spin-polarized electrons in electrocatalysts can promote the formation of parallel spin aligned oxygen by quantum spin-exchange interactions (QSEIs) to enhance the OER kinetics.255,260,261 Various strategies have been developed to control spin selectivity and facilitate spin polarization of OER electrocatalysts, including functionalizing metal oxides with extrinsic chiral molecules as a spin polarizer with a chiral-induced spin selectivity (CISS) effect,253,262–264 engineering magnetic structures and domains of materials,265,266 and promoting electron spin polarization and ferromagnetic ordering with external magnetic fields.251,267,268 Recently, Garcés-Pineda et al. reported direct magnetic enhancement of the OER on magnetic oxides in 1 M KOH electrolyte using a moderate magnet (≤0.45 T) and suggested a hypothesis of magnetic field-induced spin selectivity effect accounting for the enhanced OER activity (Fig. 11).267 Various OER electrocatalysts with different magnetic properties have been investigated, including nonmagnetic IrO2, antiferromagnetic NiO and ZnFe2Ox, and highly magnetic NiZnFe4Ox and NiZnFeOx and others. From their polarization curves measured with and without a magnet, most of the TMO-based electrocatalysts demonstrated magnetocurrent (growth percentage relative to current measured without a magnetic field) enhancement except for IrO2. There is a roughly linear relationship between the magnetocurrent and magnetization of electrocatalysts (Fig. 11b). NiZnFe4Ox with the largest magnetization among all samples showed the maximum magnetocurrent regardless of exerting mechanical convection stirring. This seemed to rule out the MHD effect from the magnetic field. The magnetocurrent of NiZnFe4Ox is sensitive to the relative position of the magnet with respect to the electrode because of the varying magnetic field intensities in different positions (Fig. 11e). The polarization curves of NiZnFe4Ox display significant current enhancement in the presence of an external magnetic field. The magnetic enhancement effect is instantaneously shown under a magnetic field alternately switched on and off. The possible effects of counter and reference electrodes have been excluded. Furthermore, the magnetic enhancement effect is also not related to the electrocatalyst substrate and NiZnFe4Ox deposited on a diamagnetic fluorine-doped tin oxide glass substrate can also show magnetocurrent. This work preliminarily associated this effect with the spin alignment of oxygen atoms of intermediate species which is favoured by the magnetic field. A simplified mechanism of interaction of two oxygen atoms adsorbed on two surface metal centres (I2M mechanism) has been proposed (Fig. 11f), similar to the aforementioned LH-AEM (Fig. 10f).248 In the absence of a magnetic field, the two adsorbed oxygen atoms are in an antiparallel configuration leading to the evolution of the excited singlet diamagnetic O2, whereas the presence of a magnetic field enables ferromagnetic ordering and parallel electron spin polarization for the surface metal redox centres and thus promotes parallel electron spin polarization to produce ground triplet paramagnetic O2 due to the spin selectivity effect. The latter process has an energy level of at least 1.0 eV lower than the production of singlet O2. In other words, the magnetocurrent enhancement was assigned to the reduced energy needed to flip the local spin antiparallel orientation of two neighbouring sites to the spin parallel configuration, suggesting a more thermodynamically favoured OER pathway on the metal redox centres with parallel spin polarization. This pioneering work proposed an interesting method to tune the spin selectivity of magnetic oxide electrocatalysts by using an external magnet. However, future studies are also required for in-depth mechanistic understanding of how the magnetic field induced spin polarization influences the electrocatalytic OER process on various electrocatalysts in terms of theoretical calculations and the effects of magnetic properties of materials and magnetic fields on reaction energetics and kinetics.
 |
| | Fig. 11 (a) Comparison of the maximum magnetocurrent (growth percentage relative to the current measured without a magnetic field) for various OER electrocatalysts under an applied potential. (b) Correlation of the maximum magnetocurrent at 1.67 V vs. RHE with bulk magnetization. (c) Polarization curves of Ni foam electrodes magnetically decorated with NiZnFe4Ox particles in the presence (ON) or absence (OFF) of an external magnetic field. (d) Chronoamperometry results of NiZnFe4Ox decorated Ni foam electrodes at ∼1.67 V vs. RHE under a magnetic field alternately switched on and off. (e) Polarization curves of NiZnFe4Ox decorated Ni foils with and without an external magnetic field applied by approaching a permanent magnet with different orientations relative to the electrode position and schematic illustration of magnetic field force lines. (f) Simplified mechanism for the spin-dependent OER process with or without a magnetic field. Reprinted from ref. 267, Copyright 2019, with permission from Springer Nature. | |
Xu's group has systematically investigated the spin selectivity effect on a ferromagnetic CoFe2O4 based OER electrocatalyst that acted as a spin polarizer under a strong magnetic field (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe).251 When a magnetic field (higher than the coercivity) is applied to a ferromagnetic material, its magnetic moment will align along with the direction of magnetic field and thus the ferromagnetic ordering makes the material a spin polarizer and selective spin-filter for electron transfer during the catalytic reactions (Fig. 12a). Ferromagnetic CoFe2O4 (Fig. 12b) demonstrates a much higher electrocatalytic activity for the OER in 1 M KOH under a magnetic field. Furthermore, the enhanced activity of CoFe2O4 can remain even after the magnetic field is removed (Fig. 12c), as the magnetic moment can retain the aligned state in the magnetized CoFe2O4. When the magnetized CoFe2O4 is purposely demagnetized using an oscillating magnetic field, the OER performance of CoFe2O4 is reverted to the initial value without the application of a magnetic field. In contrast, both antiferromagnetic Co3O4 and paramagnetic IrO2 do not show a significant change in the OER performance with and without the application of a magnetic field. The Tafel slope of CoFe2O4 is changed from around 109 to 87.8 mV dec−1, indicating that the rate-determining step (RDS) of the first electron transfer from adsorbed OH− in the absence of a magnetic field is changed to a mixed RDS involving the first electron transfer step and second steps in the presence of a magnetic field (Fig. 12d). The magnetic enchantment effect on the OER performance of CoFe2O4 was observed at varying reaction temperatures. However, the positive influence of the magnetic field on the OER performance is decreased as the reaction temperature increases (Fig. 12e), because the arrangement of magnetic moments can be thermally disturbed. The ferromagnetic ordering in CoFe2O4 can be disturbed at elevated temperatures leading to a certain extent of demagnetization and hence reduced effect on the OER. Moreover, the OER current density of CoFe2O4 increases with the increase of the magnetic field intensity, as its magnetic moments become more orderly, while there is little change in the current density of Co3O4 and IrO2 with the increasing magnetic field strength. The possible effects of a magnetic field on MHD, improved mass transfer, and electrical conductivity were ruled out. No surface reconstruction (e.g., formation of cobalt oxyhydroxide) was found on CoFe2O4. The electron transfer at the catalytic interface depends on the transition probability related with the wavefunction integral between OH− and the active site. The extended X-ray absorption fine structure (EXAFS) reveals that only Co atoms in octahedral sites contribute to the effective ferromagnetic moment and are active sites. The orbitals of FM oxides create an intrinsically degenerate spin-polarized metallic state optimizing the wavefunction based on the inter-atomic reduction of the electron–electron repulsion (Fig. 12f). The theoretical computation demonstrates that there are stronger 3d–2p hybridization, FM ligand holes and higher spin density on the oxygen atoms for CoFe2O4 after the electron spin is aligned. These intrinsic properties can promote spin-selected charge transfer. Specifically, a dominant FM exchange between the ferromagnetic catalyst and adsorbed oxygen reactant species will take place with reduced electron–electron repulsion, inducing spin-dependent conductivity and decreasing the rate-limiting bonding energies, thus making the first electron transfer not the RDS. The spin selectivity effect can enhance the OER regardless of the single metal cation redox centre (i.e., ER-AEM) and lattice oxygen as active sites (Fig. 12g–h). The computed Pourbaix diagram implies that the surface of CoFe2O4 has an oxygen termination under the OER conditions. The reaction is initiated between a lattice oxygen on the surface and adsorbed oxygen species (OH−), and the first electron transfer step is regarded as O* + OH− → *OOH + e−. The CoFe2O4 with FM ligand hole can form oxygen termination with fixed spin direction and that first electron transfer step will induce the formation of triplet state intermediate OOH species that prefer to generate triplet O2 in a thermodynamically favoured pathway. In sharp contrast, for a reaction involving a non-magnetic reactant and product molecules such as methanol oxidation and ethylene glycol oxidation reactions, no magnetic effect was observed on CoFe2O4 as the reactants, intermediates, and products in these reactions are diamagnetic and there is no spin-selected electron transfer between the active metal site and adsorbed reaction species. Therefore, for the OER, the spin-polarized electron exchange between the ferromagnetic electrocatalyst and adsorbed oxygen species in the first electron transfer step takes place under the principle of spin angular momentum conservation, reducing the energy barrier for the generation of triplet O2 under the magnetic field.
000 Oe).251 When a magnetic field (higher than the coercivity) is applied to a ferromagnetic material, its magnetic moment will align along with the direction of magnetic field and thus the ferromagnetic ordering makes the material a spin polarizer and selective spin-filter for electron transfer during the catalytic reactions (Fig. 12a). Ferromagnetic CoFe2O4 (Fig. 12b) demonstrates a much higher electrocatalytic activity for the OER in 1 M KOH under a magnetic field. Furthermore, the enhanced activity of CoFe2O4 can remain even after the magnetic field is removed (Fig. 12c), as the magnetic moment can retain the aligned state in the magnetized CoFe2O4. When the magnetized CoFe2O4 is purposely demagnetized using an oscillating magnetic field, the OER performance of CoFe2O4 is reverted to the initial value without the application of a magnetic field. In contrast, both antiferromagnetic Co3O4 and paramagnetic IrO2 do not show a significant change in the OER performance with and without the application of a magnetic field. The Tafel slope of CoFe2O4 is changed from around 109 to 87.8 mV dec−1, indicating that the rate-determining step (RDS) of the first electron transfer from adsorbed OH− in the absence of a magnetic field is changed to a mixed RDS involving the first electron transfer step and second steps in the presence of a magnetic field (Fig. 12d). The magnetic enchantment effect on the OER performance of CoFe2O4 was observed at varying reaction temperatures. However, the positive influence of the magnetic field on the OER performance is decreased as the reaction temperature increases (Fig. 12e), because the arrangement of magnetic moments can be thermally disturbed. The ferromagnetic ordering in CoFe2O4 can be disturbed at elevated temperatures leading to a certain extent of demagnetization and hence reduced effect on the OER. Moreover, the OER current density of CoFe2O4 increases with the increase of the magnetic field intensity, as its magnetic moments become more orderly, while there is little change in the current density of Co3O4 and IrO2 with the increasing magnetic field strength. The possible effects of a magnetic field on MHD, improved mass transfer, and electrical conductivity were ruled out. No surface reconstruction (e.g., formation of cobalt oxyhydroxide) was found on CoFe2O4. The electron transfer at the catalytic interface depends on the transition probability related with the wavefunction integral between OH− and the active site. The extended X-ray absorption fine structure (EXAFS) reveals that only Co atoms in octahedral sites contribute to the effective ferromagnetic moment and are active sites. The orbitals of FM oxides create an intrinsically degenerate spin-polarized metallic state optimizing the wavefunction based on the inter-atomic reduction of the electron–electron repulsion (Fig. 12f). The theoretical computation demonstrates that there are stronger 3d–2p hybridization, FM ligand holes and higher spin density on the oxygen atoms for CoFe2O4 after the electron spin is aligned. These intrinsic properties can promote spin-selected charge transfer. Specifically, a dominant FM exchange between the ferromagnetic catalyst and adsorbed oxygen reactant species will take place with reduced electron–electron repulsion, inducing spin-dependent conductivity and decreasing the rate-limiting bonding energies, thus making the first electron transfer not the RDS. The spin selectivity effect can enhance the OER regardless of the single metal cation redox centre (i.e., ER-AEM) and lattice oxygen as active sites (Fig. 12g–h). The computed Pourbaix diagram implies that the surface of CoFe2O4 has an oxygen termination under the OER conditions. The reaction is initiated between a lattice oxygen on the surface and adsorbed oxygen species (OH−), and the first electron transfer step is regarded as O* + OH− → *OOH + e−. The CoFe2O4 with FM ligand hole can form oxygen termination with fixed spin direction and that first electron transfer step will induce the formation of triplet state intermediate OOH species that prefer to generate triplet O2 in a thermodynamically favoured pathway. In sharp contrast, for a reaction involving a non-magnetic reactant and product molecules such as methanol oxidation and ethylene glycol oxidation reactions, no magnetic effect was observed on CoFe2O4 as the reactants, intermediates, and products in these reactions are diamagnetic and there is no spin-selected electron transfer between the active metal site and adsorbed reaction species. Therefore, for the OER, the spin-polarized electron exchange between the ferromagnetic electrocatalyst and adsorbed oxygen species in the first electron transfer step takes place under the principle of spin angular momentum conservation, reducing the energy barrier for the generation of triplet O2 under the magnetic field.
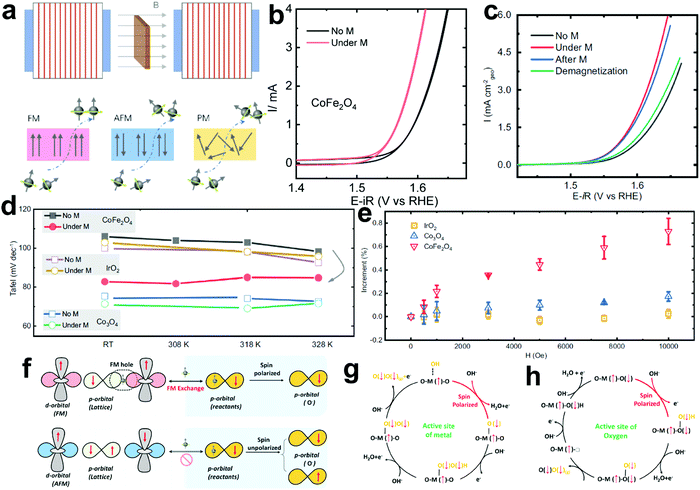 |
| | Fig. 12 (a) Schematic illustration of electron spin ordering for ferromagnetic (FM), antiferromagnetic (AFM) and paramagnetic (PM) materials under a constant magnetic field. (b) The CV curve of the CoFe2O4 electrocatalyst for OER in 1 M KOH with and without a magnetic field (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe). (c) LSV curves of the CoFe2O4 electrocatalyst for OER with and without a magnetic field (10 000 Oe). (c) LSV curves of the CoFe2O4 electrocatalyst for OER with and without a magnetic field (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe), after the removal of the magnetic field (after M), and after demagnetization. (d) Tafel slope values of CoFe2O4, Co3O4 and IrO2 with and without a magnetic field at various temperatures. (e) The increase percentage of the current density for CoFe2O4, Co3O4 and IrO2 under the applied magnetic field with different intensities. (f) Schematic diagram of spin electron transfer. FM holes exist in the M–O bonds and lattice oxygen where the FM exchange occurs and enhances the spin-selective charge transfer, providing less electronic repulsion and adsorbed oxygen species a fixed spin direction. The spin polarization pathways for two OER mechanisms with active sites of (g) a metal cation centre and (h) lattice oxygen. Reproduced from ref. 251 with permission from Springer Nature under a CC BY 4.0 licence. 000 Oe), after the removal of the magnetic field (after M), and after demagnetization. (d) Tafel slope values of CoFe2O4, Co3O4 and IrO2 with and without a magnetic field at various temperatures. (e) The increase percentage of the current density for CoFe2O4, Co3O4 and IrO2 under the applied magnetic field with different intensities. (f) Schematic diagram of spin electron transfer. FM holes exist in the M–O bonds and lattice oxygen where the FM exchange occurs and enhances the spin-selective charge transfer, providing less electronic repulsion and adsorbed oxygen species a fixed spin direction. The spin polarization pathways for two OER mechanisms with active sites of (g) a metal cation centre and (h) lattice oxygen. Reproduced from ref. 251 with permission from Springer Nature under a CC BY 4.0 licence. | |
Although the ferromagnetic ordering has proven effective to make the FM material a spin polarizer and selective spin-filter for electron transfer for the OER under an external magnetic field, most of the active OER electrocatalysts are not ferromagnetic such as metal oxyhydroxides coming from either direct synthesis or in situ conversion from metal oxide parents under the anodic potentials, which makes the spin manipulation difficult. To address this challenge, a new strategy of constructing ferromagnetic–antiferromagnetic (FM–AFM) or ferromagnetic–paramagnetic (FM–PM) core–shell composite particles has been developed to employ the interfacial spin coupling with the spin pinning effect to control the desired spin polarization state of the surface metal oxyhydroxide layer and adsorbed oxygen intermediate species.266 For example, composite particles consisting of FM Co3−xFexO4 cores and PM Co(Fe)OxHy shells have been developed for electrocatalytic OER in 1 M KOH. The FM Co3−xFexO4 core was first pre-magnetized to align the magnetic domains and establish long-range ordering. At the interface between the FM Co3−xFexO4 core and the PM Co(Fe)OxHy shell, the spin in the PM oxyhydroxide layer can be also aligned due to a strong interaction with FM magnetic domains with aligned spin, which is the spin pining effect and also results in spin selectivity to promote the OER. Additionally, FM–AFM Fe3O4@Ni(OH)2 core–shell particles have also been prepared as the OER electrocatalyst.265 The interfacial FM–AFM coupling facilitates the selective removal of electrons of AFM Ni(OH)2 with spin direction opposing the magnetic moment of the FM Fe3O4 core and thereby improves the OER kinetics. The thickness of the AFM shell plays a critical role in retaining the spin pinning. Meanwhile, the magnetic domain structure of the FM Fe3O4 core influences the electron transport process. For a multiple domain core, the applied magnetic field aligns the magnetic domains and optimizes the electron transport process for enhanced OER, whereas the single domain FM core with ordered magnetic dipoles promotes spin-selective electron transport with minimal scattering even without an external magnetic field, rendering no further enhancement of the OER under the magnetic field. In addition to the use of constant magnetic fields, a new magnetic stimulation method has been reported to tailor the spin electron state of the Co0.8Mn0.2 metal organic framework (MOF) for promoting the OER kinetics in 1 M KOH by using the high frequency alternating magnetic field induction.268 This designed MOF molecule has a feature of thermal-differentiated superlattice. The linked organic ligand molecules of 2,6-napthalenedicarboxylate acid have good thermal insulation and thus are used to construct heat-insulating layers. The coordinated magnetic ions (Co and Mn centres) are implanted into the interlayers to serve as the heat conduction region. When an alternating magnetic field is applied, the magnetic heating is strictly localized around magnetic ions and thus the magnetic exchange interaction can be enhanced to induce spin flip and reconfiguration. The localized magnetic heating in periodic spatial distribution can make the spin flip at particular active sites towards a thermodynamically favoured spin-dependent reaction pathway for the alkaline OER. The spin selectivity effect induced by the magnetic fields has attracted increasing attention. There are still many remaining challenges. More theoretical computations and in operando experimental characterization studies are still needed to fully elucidate the mechanisms. The specific requirement of magnetic properties to enable this effect may limit the pool of active electrocatalyst compositions. Furthermore, it is still challenging to maintain this effect for the long-term OER. All the studies only demonstrated the feasibility to enhance the OER in static and bulk 1 M KOH solution through this effect. It is unclear whether this effect can be really utilized to enhance the OER in the acidic PEM, alkaline and AEM based water electrolyses with zero-gap configuration and flowing water/electrolytes.
4.2.4 Maxwell stress effect.
The Maxwell stress effect is generated by the interaction of the magnetic field with the dipole moment in an element.212 The paramagnetic droplets can lead to positive and negative charges with demagnetization in two end sides when they are magnetized by an external uniform magnetic field. In this scenario, a stress of magnetic source exists to make the paramagnetic droplet deform transversely or longitudinally. The direction and intensity of the magnetic field determine the elongation direction and extent, influencing the interfacial tension, wettability, contact angle, and adhesion of the solid surface. As a result, the magnetic field influences the shape of the ionic cloud close to the electrode and the electrochemical electrolyte/electrode interface, the latter of which is crucial for the electrochemical reactions. The electrolyte/electrode interface consists of the Stern layer (0.5–10 nm) with a linear change of potential distribution and a diffusion layer (1–100 μm) with a nonlinear change of potential distribution. The Stern layer (i.e., double layer) is divided into the inner Helmholtz plane (IHP) and the outer Helmholtz plane (OHP), where the electron transfer, ion diffusion and hydrodynamics play a key role in the electrochemical reaction. The diffusion layer can be influenced by the convection, while the Stern layer is sensitive to surface tension and excess charge distribution. A magnetic field can demonstrate a micro-magneto-convection (MMC) effect on the diffusion layer decreasing its thickness. This effect has been found in the electrodeposition of transition metals accompanied by HER and commonly concurs with the MHD effect.269,270 Moreover, the magnetic field was found to influence the double layer, affecting the electrochemical capacitance and charge-transfer resistance and causing a shift of the outer Helmholtz plane through the Maxwell stress acting on the paramagnetic radical anion of one-electron nitrobenzene in acetonitrile solvent.271 The double layer capacitance is related to the surface tension at the electrolyte/electrode interface and a magnetostatic model based on Maxwell stress tensor accounts for the observed effects. This implies that the ECSA may be affected by the magnetic field. Although there is no report explicitly revealing the Maxwell stress effect on the electrocatalytic activity and ECSA of electrodes for water electrolysis, Sambalova et al. reported that a magnetic field acted on the electrochemical double layer, affecting the concentration gradient of hydroxide ions in the vicinity of the Pt electrode surface and promoting the HER in KOH electrolyte.272 Further fundamental understanding of this effect is required in the future.
4.2.5 Kelvin force effect.
The paramagnetic species can be subject to the Kelvin force in a non-uniform magnetic field.273 The paramagnetic species include cations, free radicals, and some molecular species with unpaired spin such as O2. Unlike the formally conservative Lorentz force inducing MHD convection, the Kelvin force is not conservative in the presence of a non-uniform distribution of paramagnetic species and thus can lead to convection in the vicinity of an electrode where a paramagnetic concentration gradient exists. For the electrochemical reactions, the Kelvin force can accelerate the mass transfer of paramagnetic species and hence enhance the reaction rate in the vicinity of the electrode. Additionally, when the gradient of the field is perpendicular to the gradient of concentration, the induced convection can thin the diffusion layer and increase the limiting current. The Kelvin force effect has been widely reported on the electrochemical pattern metallic electrodeposition and oxygen reduction reaction in the discharge process for alkaline Zn–air and PEM fuel cells in which metal cation and O2 reactants are paramagnetic species.212,273 To date, there are few reports on the in-depth investigation of this effect on water electrolysis. Very recently, Liu et al. briefly discussed the Kelvin effect on HER at a horizontal microelectrode when primarily studying the simulation of the micro-MHD effect.243 After donating an electron, the spin of the hydrogen ion makes it paramagnetic to some extent. There will be an upward Kelvin force exerted on a bubble and thus the release of bubble may be facilitated. Therefore, it is desirable to create a non-uniform magnetic field with a large local gradient or a large concentration gradient of paramagnetic particles with ferromagnetic electrodes to combine the Kelvin force effect with MHD convection to improve the water electrolysis efficiency.
4.2.6 Other effects.
Additionally, there are several other proposed magnetic field effects on the electrocatalytic water electrolysis. For example, Zhou et al. hypothesized that an external magnetic field with the magnetic direction perpendicular to the electrode surface may boost the electron transfer from the conductive substrate to the active electrocatalysts attached on the substrate.274 They transferred the ferromagnetic MoS2 flakes synthesized by the chemical vapor deposition to a glassy carbon substrate and used this MoS2 electrode for electrocatalytic HER in 0.5 M H2SO4. This ferromagnetic MoS2 electrode showed significant reduction of charge transfer resistance and HER overpotential in the presence of a vertical magnetic field, while the nonmagnetic MoS2 did not show any change under the same conditions. They hypothesized the effect of the magnetic field on the enhancement of electron transfer from the glassy carbon substrate to the MoS2 active sites; however, this study lacked further in-depth mechanistic investigation and did not exclude any contributions from other magnetic effects to improve the HER. Saha et al. reported that the ferro–paramagnetic coupling at the metal (Co3O4, Co and Ni–Co)/carbon nanotube interface decreased the magnetoresistance and hence charge transfer resistance.275 Furthermore, the dynamic swelling (volumetric expansion) of the interfacial catalyst was observed upon magnetization, leading to increased ECSA.
4.3 Decoupled water electrolysis
The overall water electrolysis always produces H2 and O2 simultaneously, and hence the rate of the HER is strictly linked to the rate of the OER. The concurrence of the HER and the OER will possibly lead to H2/O2 crossover, which is especially severe at low current densities (the rate of H2 and O2 production may be comparable to the rate of their crossover), low and variable power inputs and/or under high gas pressure, even if an ostensibly gas impermeable membrane is used (Fig. 13a).173 This will affect the purity of H2, requiring the downstream de-oxygenation purification. Moreover, the H2/O2 mixing may produce an explosive environment in the extreme case and at the less extreme end of the scale result in the formation of reactive oxygen species due to the coexistence of H2, O2 and electrocatalysts under electrocatalytic conditions, which pose safety concerns, degrade the electrolyser and shorten its operation lifespan.276–278 These issues call for alternative electrolyser designs, not only circumventing the crossover of H2/O2 gases but also enabling flexibility in controllable electrolysis products and device manufacture.
 |
| | Fig. 13 Schematic illustrations of electrolyser designs. (a) A conventional electrolyser for one-step overall water electrolysis. (b) An electrolyser design for decoupled water splitting with stepwise HER and OER in near-neutral electrolyte, wherein two working electrodes are alternately utilized in the working compartment, and a carbon electrode is used in the counter compartment containing an electron reservoir (ER) of either (ferrocenylmethyl)trimethylammonium chloride (FcNCl) or Na4[Fe(CN)6]. (c) An electrolyser design for stepwise HER and organic oxidation in alkaline electrolyte (1 M NaOH). Na4[Fe(CN)6] is introduced into the counter chamber with a carbon electrode. For (b) and (c), ER and ER+ denote the reduced (i.e., FcNCl or [Fe(CN)6]4−) and oxidized (i.e., FcNCl+ or [Fe(CN)6]3−) forms of the adopted electron reservoir, respectively. (d) The conversion between FcNCl/FcNCl+ electron reservoir redox couple. (e) The conversion between [Fe(CN)6]4−/[Fe(CN)6]3− electron reservoir redox couple. (a–c) Reprinted from ref. 173, Copyright 2018, with permission from Elsevier. | |
In this context, the concept of decoupled water electrolysis was proposed and explored for a broad range of applications.279–281 When the HER takes place on the cathode, the redox mediator is oxidized on the anode instead of the OER. Subsequently, the oxidized redox mediator is reduced back to its original state at the same electrode, coupling the OER on another working electrode. By cycling these two steps, the H2 and O2 can be produced in a stepwise way. In this way, the decoupled water electrolysis achieved by redox mediators can temporally and/or spatially separate the HER and the OER. Overall, the redox mediator functions as a reversible donor/acceptor for electrons and/or protons. When the redox mediator can accept or donate both the protons and electrons at the same time, it can buffer the pH during electrolysis and thereby is known as the electron-coupled-proton buffer (ECPB).282 The early practical realization of the decouple water electrolysis using such an ECPB was reported by Symes and Cronin in 2013.282 They used polyoxometalate phosphomolybdic acid (H3PMo12O40) to decouple the OER from the HER under acidic conditions. Later, they developed a series of organic ECPB redox mediators such as 1,4-hydroquinone derivative and anthraquinone-2,7-disulfonic acid.283,284 Such ECPB redox mediators should have a fast and reversible redox wave located in between the OER and HER onset potentials and should be stable when subjected to repeated redox cycling. Ideally, it should have a high solubility in water and low cost. Symes's and Cronin's groups also explored other inorganic polyoxometalate complexes including silicotungstic acid (STA) and phosphotungstic acid (PTA) as another kind of redox mediators which have more negative redox potentials than the HER onset potentials of the catalysts.33,285 Such redox mediators are different from the previous ECPB systems that have the redox potential situated in between the OER and HER onset potentials. The ECPB systems require that two steps are electrochemically driven. In contrast, the STA and PTA redox mediators are initially electrochemically reduced and accept protons, coupled with the OER. In the next non-electrochemical step, the reduced STA or PTA would spontaneously evolve hydrogen in contact with Pt, Ni5P4, Ni2P or Mo2C catalysts without any further energy input and this process regenerates the oxidized STA or PTA, as the HER onset potentials on those catalysts are more positive than the redox potentials of reduced STA and PTA.279,285 This approach also achieved the decoupled HER and OER. Girault's group has also used the combination of soluble V(III)/V(II) and Ce(IV)/Ce(III) redox mediators by using an adapted redox flow battery architecture for decoupled water electrolysis.286
However, these aforementioned redox mediators only function well in strongly acidic media, severely restricting the scope of optional electrocatalysts, particularly for the OER, as most of the nonprecious electrocatalysts are not stable in strongly acidic solutions. Therefore, two directions have been proposed to address this issue. On the one hand, the acidic redox mediator such as phosphomolybdic acid ECPB was separated from the alkaline electrolytes in both cathodic and anodic compartments using two bipolar membranes that can maintain the pH gradient between the acidic ECPB and alkaline electrolytes in the cathode and anode chambers.287 On the other hand, new redox mediators that are stable in neutral and alkaline electrolytes have been explored. Li et al. developed two kinds of novel proton-independent redox mediators that functioned in near neutral electrolytes, enabling the use of transition metal based electrocatalysts such as Co2P, Ni2P and metallic Ni for the HER and the OER.173 These two redox mediators are ferrocenylmethyl)trimethylammonium chloride (FcNCl) and Na4[Fe(CN)6], serving as a reversible donor/acceptor for electrons and thus are known as the electron reservoirs (Fig. 13d and e). These electron reservoir (ER) molecules should also have high solubility in water, fast and reversible redox feature positioned in between the HER and OER onset potentials, remarkable stability for repetitive redox cycling and low-cost composition and synthesis from abundant raw materials. The redox electrochemistry of such electron reservoirs does not involve protonation or deprotonation, eliminating the dependence on the use of strongly acidic electrolytes. Therefore, they can be used in a wide pH range from neutral to alkaline conditions. The principle for decoupled water splitting with the assistance of an electron reservoir is illustrated in Fig. 13b. A two-compartment H-cell is used with an ion exchange membrane. In the working compartment, both the HER (e.g., transition metal phosphide) and OER (e.g., Ni foam) electrodes are placed and a carbon counter electrode is put in the counter compartment containing the electron reservoir solution. In step 1, the HER electrode is connected to the carbon counter electrode and a negative voltage bias is applied. The HER occurs on such transition metal phosphide electrode, while the electron reservoir molecule is oxidized on the carbon electrode simultaneously. In this case, the voltage input is smaller than that required for overall water splitting, as the oxidation potential of the electron reservoir is less positive than the OER onset potential. As displayed in Fig. 14a, the redox potential of the FcNCl/FcNCl+ couple was positioned between the HER onset potential and OER onset potential. Fig. 14b shows the HER polarization curves of the Ni2P electrode with and without FcNCl, indicating that nearly 1 V voltage is saved in the presence of 50 mM FcNCl. After a certain amount of charge is passed (determined by the capacity of the electron reservoir), in step 2, the connection is switched from the HER electrode to the OER electrode. Then a sufficient positive voltage bias is applied to the OER electrode versus the carbon electrode, the OER takes place coupled with the reduction of the oxidized electron reservoir molecules back to the original state. Likewise, such positive voltage was smaller than that for overall water splitting because of the more positive reduction potential of the electron reservoir compared with the HER onset potential. Fig. 14c shows the OER polarization curves of the Ni foam with or without FcNCl+, suggesting that almost 1.8 V voltage is saved in the presence of FcNCl+. Gas chromatography (GC) characterization confirmed that only one gas product (either H2 or O2) was produced with 100% purity and faradaic efficiency in each step. The decoupled water electrolysis showed remarkable stability for 20 cycles in 50 h, indicating the robustness and little crossover of FcNCl upon repeated oxidation and reduction for long-term decoupled water electrolysis (Fig. 14d).173 Besides the soluble redox mediators, solid-state redox mediators have also been developed including NiOOH/Ni(OH)2 and MnO2/MnOOH,288–292 even though they are only stable in strong alkaline solutions and their redox capacities are limited by their electrode areas and mass loading. The decoupled water splitting concept is further extended to solar-driven decoupled water splitting.279 Cronin's group employed the ECPB of phosphomolybdic acid to achieve the solar-driven OER step.293 The step of OER coupled with ECPB reduction was conducted using a photoelectrochemical (PEC) cell, while the other step of HER and concomitant ECPB oxidation was still performed electrochemically. Li et al. and Landman et al. have achieved complete solar-driven decoupled water splitting by only using a photovoltaic (PV) cell to power both steps without an external voltage bias (Fig. 14e and f), demonstrating great promise for future solar-driven hydrogen economy.173,288
 |
| | Fig. 14 (a) Comparison of the cyclic voltammograms of 50 mM FcNCl (red), the HER on a glassy carbon (black) and Ni2P/Ni/Ni foam (green), and the OER on a glassy carbon (black) and Ni foam (blue) in a three-electrode configuration in 0.5 M Na2SO4. (b) Polarization curves of the HER on Ni2P/Ni/Ni foam and (c) the OER on Ni foam in a two-electrode configuration in 0.5 M Na2SO4 with and without 50 mM FcNCl/FcNCl+ electron reservoir in the counter chamber. (d) Charge evolution for repeated decoupled water electrolysis in 0.5 M Na2SO4 with 10 mM FcNCl in the counter compartment. Voltage bias between the working and counter electrodes was alternated at −1.6 V for HER on Ni2P/Ni/Ni foam and 1.8 V for OER on Ni foam. (e) Polarization curves of the HER on Ni2P/Ni/Ni foam in 0.5 M Na2SO4 with a carbon electrode in the counter chamber charged with 10 mM FcNCl and 0.5 M Na2SO4 with (red) and without (black) a 1.6 V photovoltaic (PV) cell under natural sunlight irradiation (iR-corrected). (f) HER current density on Ni2P/Ni/Ni foam with (red) and without (black) 10 mM FcNCl in the counter chamber driven by a PV cell under chopped sunlight irradiation and no iR correction was applied. Reprinted from ref. 173, Copyright 2018, with permission from Elsevier. | |
Finally, the decoupling strategy has been also extended beyond water electrolysis. MacDonald et al. used the redox mediator for selective hydrogenation of nitroarenes.294 They first conducted the reduction of STA coupled with concomitant OER.33 Then instead of discharging this reduced redox mediator to produce H2, they used it to drive the chemical reduction of nitroarenes to obtain aniline derivatives with excellent yields and recyclability. However, this method produced O2 in the first step, which is of low industrial value. Chen et al. demonstrated that the step of OER paired with the reduction of NiOOH could be replaced by the anodic oxidation of Zn to ZnO22− coupled with the reduction of NiOOH to Ni(OH)2 to form a NiOOH–Zn battery under alkaline conditions (Fig. 15).289 Li and co-workers also demonstrated the substitution of the OER step with electrochemical organic oxidation in alkaline solution (Fig. 13c).173 They first oxidized the electron reservoir of Na4[Fe(CN)6] to Na3[Fe(CN)6] with concomitant HER and then reduced Na3[Fe(CN)6] back to Na4[Fe(CN)6] paired with the electrochemical oxidation of a biomass-derived intermediate compound 5-hydroxymethylfurfural (HMF) to value-added 2,5-furandicarboxylic acid (FDCA) in 1 m NaOH.173 Hence, the decoupling strategies have tremendous potential for a broad range of applications such as water electrolysis, solar-driven water splitting, batteries,295–298 and electrochemical organic synthesis.
 |
| | Fig. 15 (a) Schematic of the operation mechanism of the electrolysis cell. Herein, the H2 production process (step 1; switching to K1) includes the cathodic reduction of H2O on the HER electrode and the anodic oxidization of the Ni(OH)2 electrode. Then, by switching to K2, the NiOOH electrode that was formed during Step 1 is coupled with a zinc anode to form a NiOOH–Zn battery, and its discharge (step 2′) depends on the cathodic reduction of the NiOOH electrode and the anodic oxidization of the zinc electrode. (b) The chronopotentiometry curve of the H2 production process (step 1, black line) and the discharge curve of the NiOOH–Zn battery (Step 2′, red line). The electrolysis for H2 production applied a current of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mA for 600 mA for 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s; then, the discharge profile of the NiOOH–Zn battery was also investigated with a current of 200 s; then, the discharge profile of the NiOOH–Zn battery was also investigated with a current of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mA. The inset of (b) is the cycle performance of the H2 production step (black line) and discharge step (red line) of the NiOOH–Zn battery with an applied current of 200 mA. The inset of (b) is the cycle performance of the H2 production step (black line) and discharge step (red line) of the NiOOH–Zn battery with an applied current of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mA. Step 1 requires a power input to produce H2 gas, whereas step 2′ can deliver energy to power other devices. Reproduced from ref. 289 with permission from Springer Nature under a CC BY 4.0 licence. mA. Step 1 requires a power input to produce H2 gas, whereas step 2′ can deliver energy to power other devices. Reproduced from ref. 289 with permission from Springer Nature under a CC BY 4.0 licence. | |
4.4 Hybrid water electrolysis
Regardless of the improvement of water electrolysis through the aforementioned approaches, the OER still takes place as the oxidation reaction requiring large overpotentials and is responsible for the major energy loss of water electrolysis, whereas its product O2 does not have high industrial value.71 To address the limitation of the OER, researchers have developed a new strategy of hybrid water electrolysis by replacing the OER with an alternative thermodynamically more favourable oxidation reaction, wherein various more readily oxidizable substrate molecules are screened.299–310 Du et al. have comprehensively reviewed the progress of hybrid water electrolysis and categorized this direction into three groups: (i) the reagent-sacrificing type that can produce H2 under small voltages while the sacrificial reactants (e.g. hydrazine and ammonia) are oxidized to valueless products; (ii) the pollutant-degradation type where the sacrificial reactants subject to oxidation are pollutants (e.g. urea, organic dyes, and H2S); and (iii) the value-added type that upgrades the organic reactants (e.g. biomass-derived chemicals, glucaric acid, tetrahydroisoquinolines) to valorised products.311 For example, the hybrid water electrolysis combined with the electrochemical organic oxidation has several merits.71 First, the onset potential of organic oxidation is less positive than that of the OER and as such a hybrid electrolyser can deliver higher current density with lower voltage input because of the more favourable oxidation thermodynamics of chosen organic substrate molecules, which contributes to the increased energy conversion efficiency. Second, the anode will generate value-added organic products, maximizing the payback of energy investment. Additionally, as the liquid organic compounds will be produced instead of the O2 gas, the H2/O2 mixing will be eliminated. Finally, a single compartment electrolysis cell without the use of any membranes or diaphragms can be possibly used if the organic substrates and oxidative products will not be easily reduced and not compete with the HER. This will help to reduce the cost from membranes. To realize all these merits, an ideal organic substrate should satisfy the following criteria: high solubility in water at room temperature, production of value-added nongaseous oxidative compounds, less positive oxidation potential at the anode compared to the onset of OER and little competition with HER at the cathode for organic reduction.
Chen et al. achieved such hybrid electrolysis to integrate the HER with oxidation of several alcohols such as ethanol, ethylene glycol, glycerol and 1,2-propandiol. They used Pt and strong alkaline solution (2 M NaOH) as the cathode for HER and electrolyte, respectively, similar to alkaline water electrolysis.299 The anode (Pd/TNTA-web) was three-dimensional nanostructured TiO2 nanotube arrays (TNTA-web) coated with Pd nanoparticles, which was fabricated through the anodization of a Ti fiber web followed by the chemical deposition and reduction method for the loading of Pd. All alcohols were more readily oxidized relative to the OER, leading to the smaller cell voltage (≤0.9 V) compared to the one for overall water splitting (1.76 V) at a current density of 1 A cm−2 and 80 °C. This hybrid electrolyser produced H2 and soluble organic acid salts, allowing for electrical energy saving up to 26.5 kW h per kg of H2 when the energy required for circulating the electrolyte through the anode was not taken into account.299 Sun's group has demonstrated a similar hybrid water electrolysis by using noble-metal-free electrodes and biomass-derived organic intermediates in the basic solution. 5-Hydroxymethylfurfural (HMF) represents a promising biomass-derived intermediate, because it can be transformed to various valuable products, including 2,5-furandicarboxylic acid (FDCA) via oxidation, which is regarded as a replacement of terephthalic acid for the production of polyamides, polyesters, and polyurethanes.300 The oxidation of HMF to FDCA has also been demonstrated by Li et al. in the decoupled water electrolyser as the second step.173 Here, one-step hybrid water electrolysis integrating HER with HMF oxidation was demonstrated in one step electrolysis in 1.0 M KOH solution.303 Two bifunctional Ni2P electrodes were used as an anode and cathode, respectively. The anodic current took off at a small potential less positive than that of the OER in the presence of 10 mM HMF, saving nearly 200 mV voltage input to reach the same current density of 100 mA cm−2. The nearly 100% yield of FDCA and unity faradaic efficiency were achieved and the addition of HMF did not influence the HER in the cathode. The two-electrode electrolyser displayed 200 mV voltage saving and nearly 100% faradaic efficiencies for production of both H2 and FDCA. This hybrid electrolysis can sustain for 3 cycles without obvious degradation.303 Later, Sun's group demonstrated the use of Ni3S2 or Ni electrodes for similar hybrid water electrolysis with selective organic substrate molecules including ethanol, benzyl alcohol, furfuryl alcohol and furfural (Fig. 16).300,301 The hybrid water electrolysis consisting of HER on the Ni3S2/Ni foam and HMF oxidation on the Ni3S2/Ni foam showed much smaller voltage than full water electrolysis on two identical electrodes and 100% faradaic efficiency for H2 production in 1.0 M KOH (Fig. 17). This hybrid water electrolysis demonstrates great potential for H2 production and electrochemical organic reforming.312–314 Normally, this hybrid water electrolysis technology produces H2 at the cathode and nongaseous oxidative products. Very recently, Wang et al. reported a novel hybrid water electrolyser that combines the cathodic HER and low-potential anodic oxidation of aldehyde with a low onset voltage of merely 0.1 V.315 Unlike conventional aldehyde electrooxidation at the anode, in which the hydrogen atom of the aldehyde group is oxidized into H2O at high potentials and nongaseous product molecules are generated, the low-potential aldehyde oxidation can produce H2 from the hydrogen atom of aldehyde at the anode. In other words, H2 can be produced at both the cathode and anode simultaneously. The demonstrated electrolyser requires an electricity input of only ∼0.35 kW h per m3 of H2, in contrast to the ∼5 kW h per m3 of H2 required for conventional water electrolysis. Therefore, the hybrid water electrolysis technology has great potential for future application.
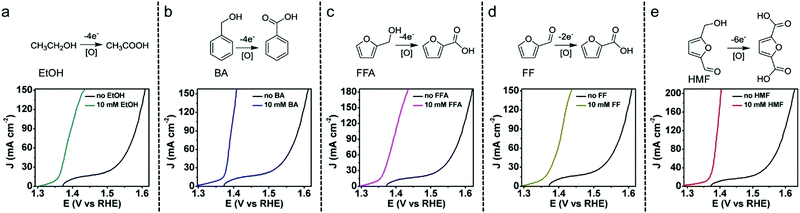 |
| | Fig. 16 Polarization curves of the Ni3S2/Ni foam in 1.0 M KOH for OER and in 1.0 M KOH containing different 10 mM organic substrates including (a) ethanol, (b) benzyl alcohol (BA), (c) furfuryl alcohol (FFA), (d) furfural (FF), and (e) 5-hydroxymethylfurfural (HMF). Reprinted with permission from ref. 300. Copyright 2016 American Chemical Society. | |
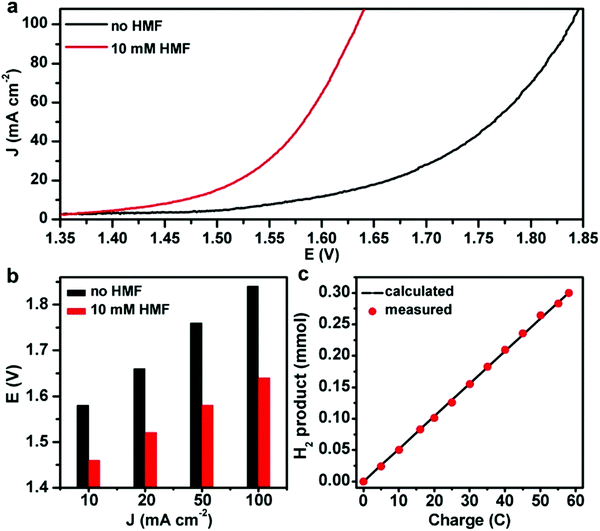 |
| | Fig. 17 (a) Two-electrode polarization curves and (b) comparison of the overpotentials to achieve benchmark current densities for the Ni3S2/NF couple in 1.0 M KOH with and without 10 mM HMF. (c) GC-measured H2 quantity compared with theoretically calculated H2 quantity assuming a 100% faradaic efficiency for the H2 production catalysed by the Ni3S2/NF working cathode in 1.0 M KOH solution with 10 mM HMF. Reprinted with permission from ref. 300. Copyright 2016 American Chemical Society. | |
4.5 Acid/alkaline asymmetric electrolyte water electrolysis
The potentials of two half reactions (HER and OER) are dependent on the pH value. Therefore, the entire water electrolysis voltage can be tuned by controlling the different pH values of electrolytes in the cathodic and anodic compartments. As shown in Fig. 1a, the potential gap between the HER and the OER can be theoretically reduced to 0.401 V by using an acidic electrolyte (pH = 0) in the cathodic compartment and an alkaline electrolyte (pH = 14) in the anodic compartment. On the contrary, the potential gap between the HER and the OER can be increased to 2.057 V by coupling an alkaline catholyte (pH = 14) for the HER with an acidic anolyte (pH = 0) for the OER. The water electrolysis voltage in the acid/alkaline asymmetric electrolytes is intrinsically related to the electrochemical neutralization energy (ENE) and dissociation energy.316 The ENE is related to the converted electrochemical voltage output when the spontaneous acid–base neutralization reaction takes place as follows:where the change of the Gibbs free energy ΔG0 = −79.9 kJ mol−1, the enthalpy change ΔH0 = −55.84 kJ mol−1 and the thermal energy TΔS0 = 24.06 kJ mol−1 under standard conditions (298.15 K, 1 atm). The neutralization energy can be harvested in the electrochemical form, which translates to a theoretical ENE voltage (EENE) of 0.828 V under the standard conditions (concentration of both H+ and OH− is 1 M) according to the Nernst equation. To effectively harvest the ENE, an asymmetric electrochemical cell should be obtained with the cathodic reaction consuming H+ in an acidic catholyte and anodic reaction consuming OH− in an alkaline anolyte. This asymmetric acid/alkaline electrochemical cell gives rise to a theoretical voltage of 0.0591 × ΔpH, which equals 0.828 V with ΔpH = 14. Therefore, the ENE may reduce the applied water electrolysis voltage through a rational design of electrolysers with asymmetric acid/alkaline electrolytes, as the harvested ENE from neutralization reaction can provide an additional internal voltage input.316 Normally, an appropriate ion-selective membrane separator is indispensable to maintain the ionic current flow and conductivity and avoid the direct neutralization. On the contrary, the theoretical energy required to dissociate one mole of water to H+ and OH− is 79.9 kJ mol−1 which is called the dissociation energy and translates to an additional external voltage input. The bipolar membrane (BPM) consisting of a cation-exchange membrane (CEM) and an anion exchange membrane (AEM) laminated together is a commonly used separator used in the asymmetric acid/alkaline electrochemical cells.317,318 Under a fixed external voltage direction, for the given OER and HER electrodes, the placement of two sides of a BPM and sequence of acid and alkaline electrolytes influence the operating process and voltage. Fig. 18 illustrates four configurations using acid/base asymmetric electrolytes in two compartments separated by a BPM for water electrolysis.316Fig. 18a shows the optimal configuration that can effectively use ENE to minimize the theoretical water electrolysis voltage. In this case, the HER and the OER take place in the acidic (pH = 0) and alkaline (pH = 14) electrolytes, respectively, and the BPM operates under the forward bias, during which the counter ions of acid (anions of X−) and base (cations of M+) can penetrate into the BPM providing ionic transport under the applied voltage. Therefore, the theoretical water electrolysis voltage in this case is only 0.401 V (Fig. 18e). However, the operation of a BPM under a forward bias may cause the accumulation of salt ions in the BPM and result in the contamination and delamination of the CEM and AEM layers. The configuration shown in Fig. 18b makes the HER and the OER occur in alkaline and acidic electrolytes, respectively, while the operation of the BPM remains under a forward bias, in which OH− and H+ move into the BPM and water is formed inside. This configuration cannot utilize the ENE and hence leads to a higher theoretical water electrolysis voltage of 2.057 V. The configuration shown in Fig. 18c enables the HER and the OER to occur in the acidic (pH = 0) and alkaline (pH = 14) electrolytes, respectively, like the one in Fig. 18a. Nevertheless, the BPM operates under the reverse bias and requires a theoretical voltage input of 0.828 to dissociate H2O into H+ and OH− which move towards the cathode and anode, respectively. Although the potential gap between the HER and the OER is 0.401 V, the addition of required water dissociation voltage input renders the theoretical overall water electrolysis voltage of 1.229 V. The fourth configuration shown in Fig. 18d renders the largest theoretical water electrolysis voltage of 2.885 V. Table 2 summarizes the electrode and membrane reactions and theoretical water electrolysis voltages for these four configurations.316 Although the configuration shown in Fig. 18a is the ideal one to minimize the voltage, intermittently replenishing acid and base is required and the issues of salt accumulation, fouling and delamination of BPM can impair the electrolyser lifetime. The configuration shown in Fig. 18c can harvest the ENE, whereas it is offset by the water dissociation energy in the BPM under reverse bias. Even though the theoretical water electrolysis voltage in this configuration is equal to that of water splitting in the symmetric electrolyte with the same pH, this configuration enables the HER and the OER to take place under their respective favourable pH conditions catalysed by nonprecious electrocatalysts with high activity and stability. In contrast to traditional alkaline water electrolysis, this configuration may further decrease the HER overpotential with the developed nonprecious HER electrocatalysts being stable in acids. In comparison to acidic PEM water electrolysis, this configuration allows the use of active and stable nonprecious electrocatalysts for the alkaline OER, eliminating the reliance on costly IrO2 and RuO2. Compared to the configuration shown in Fig. 18a, as the water dissociation enabled by the BPM can help to maintain the concentrations of OH− in the anode compartment and H+ in the cathode compartment, only water is replenished to sustain the water electrolysis instead of acid and base and the BPM may have a longer lifetime. The other two configurations cannot harvest the ENE, significantly increasing the voltage.
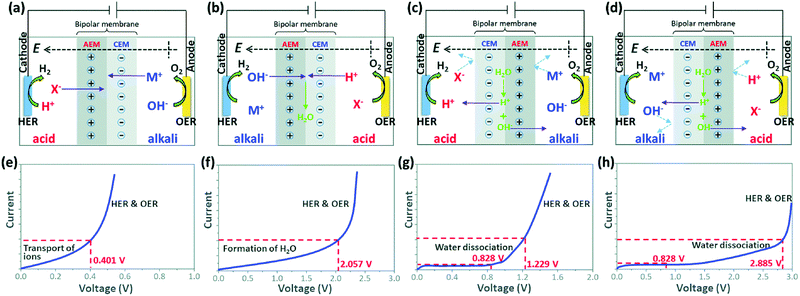 |
| | Fig. 18 (a–d) Schematic illustrations of four water electrolyser configurations using acid–base asymmetric electrolytes in two compartments separated by a BPM: (a) acidic cathode|AEM‖CEM|alkaline anode, (b) alkaline cathode|AEM‖CEM|acidic anode, (c) acidic cathode|CEM‖AEM|alkaline anode, and (d) alkaline cathode|CEM‖AEM|acidic anode. (e–h) Theoretical I–V curves of the four configurations corresponding to (a–d). Reproduced from ref. 316 with permission from the Royal Society of Chemistry. | |
Table 2 Summary of electrode redox reactions, processes in the membrane and voltages for four configurations shown in Fig. 18. Adapted from ref. 316 with permission from the Royal Society of Chemistry
| Configuration |
Cathodic reaction |
Anodic reaction |
Membrane |
Overall voltage |
ENE utilization |
|
Fig. 18a
|
4H+ + 4e− → 2H2, E0c = 0 V |
4OH− → O2 + 2H2O + 4e−, E0a = 0.401 V |
Counter ion transport |
−0.401 V |
Yes |
|
Fig. 18b
|
4H2O + 4e− → 2H2 + 4OH−, E0c = −0.828 V |
2H2O → O2 + 4H+ + 4e−, E0a = 1.229 V |
H+ and OH− transport and spontaneous neutralization releasing heat |
−2.057 V |
No |
|
Fig. 18c
|
4H+ + 4e− → 2H2, E0c = 0 V |
4OH− → O2 + 2H2O + 4e−, E0a = 0.401 V |
H2O → H+ + OH−, E0c = −0.828 V |
−1.229 V |
Yes (but offset by the required additional water dissociation energy) |
|
Fig. 18d
|
4H2O + 4e− → 2H2 + 4OH−, E0c = −0.828 V |
2H2O → O2 + 4H+ + 4e−, E0a = 1.229 V |
H2O → H+ + OH−, E0c = −0.828 V |
−2.885 V |
No |
Mallouk's group investigated the use of BPMs for water electrolysis in the symmetric neutral buffer electrolyte and acid/base asymmetric electrolyte.323 They studied the membrane potential of a BPM as a function of current density under forward and reverse bias conditions and found that the use of BPMs was not a viable solution for water electrolysis in the symmetric neutral buffer electrolyte but showed promising water splitting with a Pt cathode in 1 M H2SO4 and a NiFeOx anode in 1 M KOH under reverse bias in the configuration shown in Fig. 18c. Recently, Wen's group reported the water electrolysis using acidic catholyte and alkaline anolyte separated by a BPM under a forward bias, in which both the HER and OER were catalysed by bifunctional Ni2P nanorods (Fig. 19a).319 The effect of acid and base concentration (i.e., ΔpH) on the water electrolysis voltage was investigated (Fig. 19b and c). The lowest voltage of 1.12 V at 10 mA cm−2 was achieved with an onset voltage of 0.79 V using 0.5 M H2SO4 catholyte and 1 M KOH anolyte. The voltage was maintained for 20 h and then gradually increased due to the consumption of H+ in the catholyte and OH− in the anolyte, thus requiring replenishment of electrolytes. When the concentrations of H2SO4 and KOH increased to 3 and 6 M, respectively, the electrolysis voltage surprisingly increased, even though the increased ΔpH should have theoretically decreased the voltage. This is likely because the BPM suffers from poor chemical stability when exposed to strong acid and base with increased resistance. Later, the same group replaced Ni2P with bifunctional Ru–RuO2 nanoparticles loaded on carbon nanotubes in the similar electrolyser design, realizing a smaller onset potential of 0.65 V and lower voltage of 0.73 V at 10 mA cm−2 due to the higher electrocatalytic activities of Ru–RuO2 for acidic HER and alkaline OER.324 Liu's group used bifunctional cobalt nickel phosphide as the acidic HER and alkaline OER electrodes with an “irregular” BPM operating under a forward bias and the electrolyser could be driven to deliver 13 mA cm−2 using a photovoltaic cell of 0.908 V.325 Later, they used CoP–CoTe2 composite nanowires as the bifunctional HER and OER electrocatalysts with a similar water electrolyser configuration.326 They compared the BPM-assisted acid/alkaline asymmetric electrolyte water electrolysis under the forward and reverse bias conditions and found a voltage decrease by 720 mV at 10 mA cm−2 under the forward bias. Despite a smaller water electrolysis voltage enabled by the BPM under a forward bias, many studies focus on the reverse bias to achieve longer lifetime and reduce BPM delamination. In 2014, McDonald et al. reported the acid/alkaline asymmetric electrolyte water electrolysis using the Pt electrodes with a BPM under the reverse bias and proposed that the anion exchange layer (AEL)/cation exchange layer (CEL) interface can incorporate catalysts to facilitate water dissociation to reduce the overall voltage.327 Later, the BPM-assisted water splitting was demonstrated on a photoelectrochemical cell consisting of a Pt cathode and a BiVO4 photoanode and a tandem PV-water electrolyser composed of a CoP cathode and a NiFe LDH anode.328,329 The latter realized a solar-to-hydrogen (STH) efficiency of 12.7%. The ion transport mechanisms have been fundamentally investigated. Both ion crossover and local diffusion boundary layers play crucial roles in the voltage.330 The performance and lifetime of BPMs can be improved by using thin water dissociation catalysts, managing water transport, adjusting the thickness of individual AEL and CEL in the BPMs to minimize ion crossover, and increasing the ion-exchange capacity.331 Therefore, research interests have been attracted to constructing AEL/interfacial catalyst/CEL junctions towards advanced BPMs for water electrolysis. Mallouk's group prepared BPMs from a crosslinked AEL and a Nafion CEL, with a graphite oxide (GO) catalyst deposited at the junction using the layer-by-layer (LBL) assembly through hot pressing.332 The hot pressing of AEL and CEL commonly produces 2D BPM with a planar junction. BPMs with three-dimensional (3D) junction have been developed through electrospinning to facilitate the interfacial water dissociation. Deutsch's group compared the electrochemical performance between 2D BPM fabricated by hot pressing and 3D BPM prepared by LBL electrospinning of individual functional layer followed by hot pressing (Fig. 19d).320 GO was introduced into the junction as a water-dissociation catalyst for both. This 3D BPM exhibited lower resistance, better mechanical strength and higher efficiency for water dissociation and stability. Inorganic Al(OH)3 nanoparticles were also introduced into the junction of 3D BPM as a catalyst exhibiting superior water dissociation capability.333 Recently, decreasing the AEL thickness and the use of precious IrO2 as an interfacial water dissociation catalyst in the BPM have proven to show extraordinary electrochemical performance in a membrane electrode assembly (MEA) water electrolyser fed by pure water (Fig. 19e–g), delivering 9000 mA cm−2 at 2.2 V, two times higher than a PEM MEA water electrolyser under similar conditions.321 The correlation of water dissociation with interfacial catalyst composition and properties was unclear. Oener et al. first quantitatively measured the water dissociation kinetics and overpotential of noble metals and metal oxides based interfacial catalysts by using a BPM electrolyser and found that the water dissociation activity correlates with the alkaline HER activity for metal nanoparticles (Fig. 19h and i).322 The lowest water dissociation overpotential of the BPM was acquired by using the NiO or Ir coated with 10 layers of TiO2 by atomic layer deposition at the AEL surface and IrO2 at the CEL interface. This best BPM demonstrated a BPM MEA water electrolyser fed by pure water to show 500 mA cm−2 at 2.2 V (Fig. 19j).
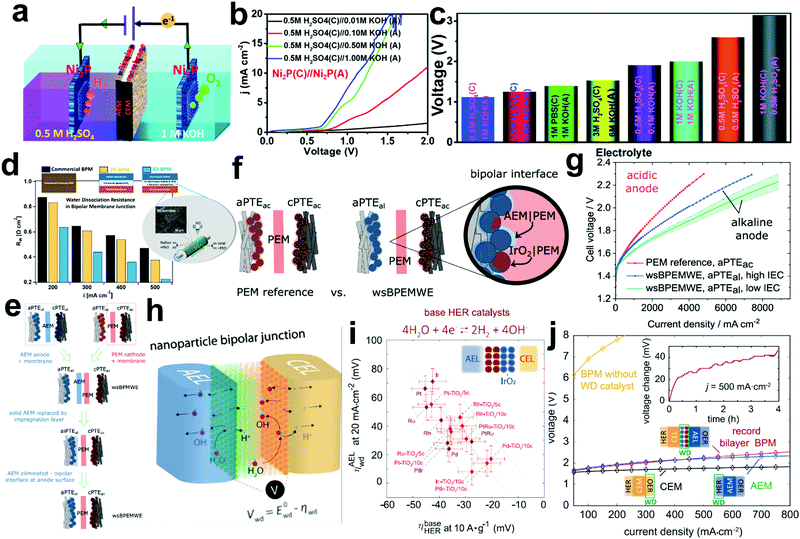 |
| | Fig. 19 (a) Schematic illustration of an acid/alkaline asymmetric electrolyte water electrolyser with Ni2P as the HER and OER electrodes and BPM under a forward bias. (b) The effect of anodic KOH concentration on the polarization curves in the presence of 0.5 M H2SO4. (c) The voltage at 10 mA cm−2 under different combinations of electrolytes in the cathodic (C) and anodic (A) compartments. (a–c) Reproduced from ref. 319 with permission from the Royal Society of Chemistry. (d) The comparison of resistance (Rw) of water dissociation in the interfacial junction for different BPMs at different current densities. Reprinted with permission from ref. 320. Copyright 2020 American Chemical Society. (e) The evolution from BPM water electrolysis MEA configuration (wsBPMWE) with a solid AEM to a new MEA configuration with an AEM impregnation layer in direct contact with the PEM indicating the decrease of AEM thickness. (f) The structure of wsBPEMWE MEAs comprising an anodic porous transport electrode with an alkaline ionomer (aPTEal), a PEM, and a cathodic porous transport electrode with an alkaline ionomer (cPTEal) with a variation of the ion-exchange capacity (IEC) of the Aemion binder in the aPTEal compared to a PEM reference consisting of aPTEac, PEM and cPTEac with an acidic ionomer binder of Nafion 212. (g) The polarization curves of different MEA configurations. The green area represents the confidence interval obtained from the standard deviation of three individual MEAs of the low IEC system. (e–g) Reprinted with permission from ref. 321. Copyright 2020 American Chemical Society under a license of CC-BY-NC-ND. (h) Different nanoparticles as water dissociation (WD) catalysts loaded on both the acidic CEL and basic AEL surfaces in the BPM interfaces. (i) The overpotentials for WD in a locally basic environment with IrO2 used as the stable WD catalyst on the acidic CEL surface correlate with the overpotentials measured for HER in 1 M KOH for selected nanoparticles coated on the basic AEL surfaces, consistent with the WD rate limiting the alkaline HER. (j) The polarization curves of PEM, AEM and BPM water electrolysers. The BPM interface contains either no WD catalysts or NiO encapsulated by 10 layers of TiO2 at the AEL surface and IrO2 at the CEL interface. (h–j) Reprinted with permission from ref. 322. Copyright 2020, AAAS. | |
For the BPM, the forward bias mode can exhibit a smaller theoretical voltage than the reverse bias one. Furthermore, the high cost, complex preparation process and limited lifetime of BPM restrict the wide application of BPM in the acid/alkaline asymmetric electrolyte water electrolysis. Therefore, several novel strategies have been developed to employ monopolar ion exchange membranes and even membraneless design for the acid/alkaline asymmetric electrolyte water electrolysis (Fig. 20).117,118,334,335,339 In order to fully exploit the merit of low voltage and mitigate the issues of salt accumulation at the junction, fouling and delamination of BPM under the forward bias, Nazemi et al. utilized two types of monopolar ion-exchange membranes (both CEM and AEM) and a middle chamber containing a near-neutral 0.6 M NaCl solution to achieve the concurrent HER catalysed by Pt in an acidic solution and the OER catalysed by Ir in a basic solution in one water electrolyser cell (Fig. 20a).334 This design is equivalent to the BPM under a forward bias but separates the AEL and CEL to form a middle reservoir to accommodate the salt accumulation. They compared this double monopolar membrane design with the BPM design under a reverse bias in terms of the whole electrolysis voltage and found that the energy required for the former design was 48% lower than that for the latter. Nevertheless, the introduction of NaCl into the electrolyte may bring about the risk of anode degradation and formation of Cl2 caused by chloride oxidation on the anode. Other groups only use a monopolar PEM for the acid/alkaline asymmetric electrolyte water electrolysis. For example, Weng et al. employed a PEM to separate 1 M NaOH and 0.5 M H2SO4 and the electrolyser delivered 5 mA cm−2 at 0.95 V but a limited stability was shown for merely 20 min.117 H2SO4-doped polybenzimidazole membranes were synthesized and used to separate 3 M H2SO4 catholyte and 6 M KOH anolyte for water electrolysis (Fig. 20b),335 showing a fair stability of 40 h at 1.4 V to deliver 100 mA cm−2 in contrast to the poor durability of the Nafion membrane under the same conditions. Apparently, the PEM permits the crossover of H+, leading to the direct neutralization of acid and base and gradual loss of the pH gradient across the PEM. To address this issue, a ceramic lithium superionic conductor film (Li1+x+yAlxTi2−xSiyP3−yO12, LATSP) was used as a separator (Fig. 20c).118 Li+ ions acted as the charge carrier and moved from the anolyte (1 M KOH and 0.5 M Li2SO4) to the catholyte (0.5 M H2SO4). Although the use of a ceramic LATSP separator can help to mitigate the H+ crossover and give a low onset potential of 0.78 V to initiate water electrolysis, its low Li-ion conductivity in aqueous electrolytes at room temperature resulted in large resistance and significantly restricted the current density. Beyond the use of membranes, a membraneless microfluidic electrolyser/fuel cell system with acid/alkaline asymmetric electrolytes has been developed (Fig. 20d), where the acid and alkaline electrolytes were injected through two adjacent microchannels.316,339 Because the diameter of microchannel was very small and the flow rates of electrolyte streams were high, the acidic and alkaline solutions did not mix during the short contact duration. Moreover, the density of OH− is higher than that of H+, and hence the H+ and OH− remained at the upper and lower layers, respectively, restricting the diffusion of two streams and crossover. However, the microfluidic structure limits its viability in the scale-up of water electrolysers. The acid/alkaline asymmetric electrolyte water electrolysis can be further adapted and integrated with the hybrid water electrolysis technology. As the alkaline OER suffers from sluggish kinetics and a large energy barrier, the electrochemical oxidation of other aqueous soluble molecules which is thermodynamically more favourable in alkaline electrolytes can replace the OER in the acid/alkaline asymmetric electrolyte water electrolysis (Fig. 20e–j). For example, the acidic HER coupled with the alkaline electrochemical oxidation of hydrazine, benzyl alcohol, glycerol, glucose, urea, and sulfion (S2−) has been reported.336–338,340–344 There are many merits in this direction. The electrolysis voltage input is smaller than that of common acid/alkaline asymmetric electrolyte water electrolysis with the alkaline OER and acidic HER. When the standard oxidation potential of a given molecule such as hydrazine and glycerol in the alkaline solution is significantly more negative than that of the acidic HER, the coupling of HER and alkaline oxidation of molecules can even generate hydrogen and electricity, simultaneously, suggesting that no electricity and voltage input are needed, and the device operates like a fuel cell with H2 production.336,340,341 The alkaline oxidation can also upgrade biomass-derived organic molecules to produce products more valuable than O2 for electrochemical valorisation. Diverse configurations including BPM under a forward bias, PEM, and the CEM + AEM + middle chamber design have been used in these studies. In the acid/alkaline asymmetric electrolyte water electrolysis, the optimization of the high-performance separator membrane plays a critical role and warrants further investigations.
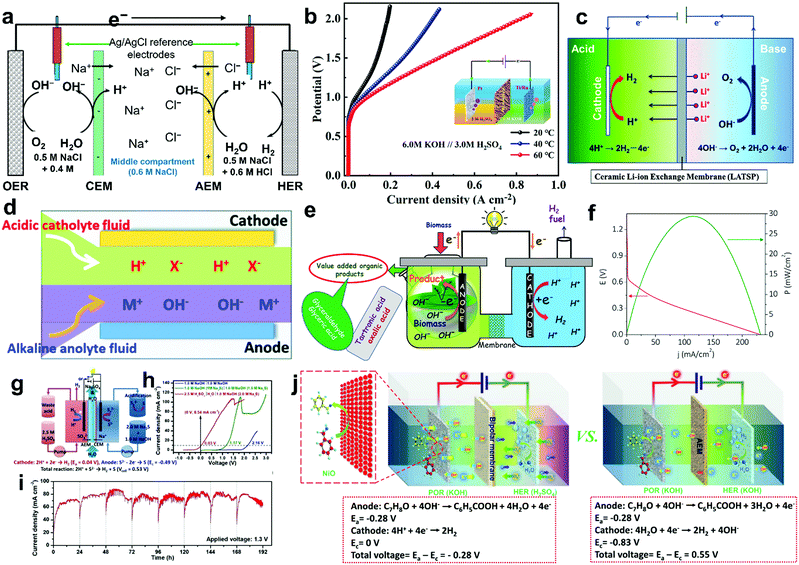 |
| | Fig. 20 New electrolyser designs for acid/alkaline asymmetric electrolyte water electrolysis. (a) Electrolyser setup with AEM, CEM and middle buffer chamber. Reprinted with permission from ref. 334. Copyright 2017, John Wiley and Sons, Inc. (b) Electrolyser with H2SO4-doped polybenzimidazole (PBI) based PEM separating 3 M H2SO4 catholyte and 6 M KOH anolyte and polarization curves at different temperatures. Reprinted from ref. 335, Copyright 2021, with permission from Elsevier. (c) Electrolyser with a ceramic Li-ion conductive membrane separating acidic catholyte and alkaline anolyte. Li-ions serve as the charge carriers for ionic current flow. Reproduced from ref. 118 with permission from the Royal Society of Chemistry. (d) Membraneless microfluidic electrolyser configuration. Reproduced from ref. 316 with permission from the Royal Society of Chemistry. (e) An electrochemical neutralization fuel cell for spontaneous coupling of biomass valorisation and hydrogen production with electricity output and (f) its polarization curve in the presence of 0.5 M glycerol in 2 M KOH anolyte and 2 M H2SO4 catholyte. (e and f) Reprinted with permission from ref. 336. Copyright 2020 American Chemical Society. (g) A flow electrolyser cell combining the acidic HER and alkaline sulfion oxidation (SOR). (h) Comparison of polarization curves for an alkali–alkali OER/HER cell, an alkali–alkali SOR/HER cell, and an alkali–acid SOR/HER cell. (i) Stability test of an alkali–acid SOR/HER cell at a voltage of 1.3 V. (g–i) Reprinted with permission from ref. 337. Copyright 2021, John Wiley and Sons, Inc. (j) Comparison of electrolysers integrating the alkaline phenylcarbinol oxidation reaction (POR) with acidic and alkaline HER. Reprinted from ref. 338, Copyright 2021, with permission from Elsevier. | |
4.6 Tandem water electrolysis
The cost-effective storage and transport of H2 still remain challenging.345 One potential approach to bypassing this challenge is the on-site use of H2 by directly consuming the produced H2 during water electrolysis to yield value-added chemical fuels (e.g., CH4 and NH3) using efficient heterogeneous biological catalysts. In this context, tandem water electrolysis has been developed. Fig. 3f illustrates the concept of tandem water electrolysis. An airtight two-compartment electrochemical cell is charged with Methanosarcina barkeri (M. barkeri) and CO2 in the cathodic chamber.346 Electricity or solar energy input can drive the water splitting, producing O2 on the anode and H2 on the cathode of inorganic electrocatalysts in the neutral electrolyte. The H2 is instantly consumed by M. barkeri in the presence of CO2 to produce value-added fuels. By using this setup, Chang's group reported that the methane production linearly increased with time under applied currents (1.0–7.5 mA) with an average faradaic efficiency above 74%. Because M. barkeri catalysed the transformation from H2 and CO2 to CH4 nearly at thermodynamic potential as a highly efficient biological catalyst, the only overpotential involved came from the HER and OER in a neutral solution. This hybrid bioinorganic system showed excellent durability for over 7 days. The carbon source for CH4 is the original CO2, as corroborated by an isotope labelling experiment.346 The tandem water electrolysis system has high flexibility. Various Earth-abundant and biocompatible electrocatalysts can be utilized. When integrated with photoelectrodes, solar-to-chemical conversion can be feasible. Recently, Nocera's group demonstrated a similar tandem water electrolysis system to covert the produced H2 to biomass or alcohol fuels with CO2, using Co–P as the HER electrocatalyst and Ralstonia eutropha as the biocatalyst.347 The CO2 reduction energy efficiency even exceeded that of natural photosynthetic systems. The same group also demonstrated a new tandem water electrolysis system that could produce NH3 from N2 and H2O with autotrophic bacterium Xanthobacter autotrophicus.348 It is noted that the biological catalysts or bacteria only operate well in neutral media.349–356 Therefore, the application of such tandem water electrolysis depends on the use of HER and OER electrocatalysts that can function efficiently in neutral solutions. This tandem water electrolysis is distinct from the electrochemical CO2 or N2 reduction where the proton required to produce CH4 and NH3 is from the electrolyte, while the present technology directly converts the produced H2 from HER into CH4 and NH3.
5. Summary, challenges and perspectives
In summary, this review demonstrates the fundamentals of water electrolysis from the perspective of thermodynamics, clarifies some recommended standardized electrochemical characterization protocols and experimental rigors, and maps out some common metrics and key performance indicators that evaluate the performances of electrocatalysts and electrolysers at the levels of both materials and devices. Furthermore, six typical innovative strategies are reviewed to circumvent a variety of technical challenges in conventional low-temperature water electrolysis, including overall water electrolysis, magnetic field-assisted water electrolysis, decoupled water electrolysis, hybrid water electrolysis, acid/alkaline asymmetric electrolyte electrolysis, and tandem water electrolysis.
In this burgeoning field of water electrolysis, there are still formidable challenges that hinder the development of high-performance water electrolysers to lower the cost of H2 production and enhance the energy efficiency towards practical application. This calls for more fundamental and engineering research. First, the lack of accurate, reliable, and standardized electrochemical test protocols makes it challenging to rigorously screen the electrocatalysts, and precisely assess the electrochemical metrics and performance indicators of electrocatalyst materials, MEA-based cells and stack systems for low-temperature water electrolysis. More efforts are needed to establish benchmarks and standard test protocols and develop a roadmap for fabrication, electrochemical data analysis and technoeconomic analysis. Electrochemical characterization must be rigorously conducted to report the performances and intrinsic activities for reliable comparison across a wide range of materials and testing conditions. Second, the six emerging strategies for advancing low-temperature water electrolysis still suffer from their respective inherent technical issues that are detrimental to the practical viability. For the overall water electrolysis, nonprecious bifunctional materials active for alkaline water electrolysis have been widely demonstrated. However, most reports only demonstrate alkaline water electrolyser prototypes by immersing Janus electrocatalysts in basic solutions without using any membranes or diaphragms to separate the cathode and anode. Such prototypes are impossible to directly operate in real applications because of the gas crossover in two close electrodes. The reported current densities of such prototype alkaline electrolysers are still incommensurate to those of commercially available alkaline water electrolysers. The dynamic oxidation of transition metal-based pre-catalysts under the OER conditions makes it difficult to identify the true active species, quantify the real number of active sites, evaluate the intrinsic activities, and rationalize the comparison of different electrocatalysts for screening. Advanced in operando characterization and computation techniques are required to track the changes of those materials under the dynamic oxidation, and precisely decipher the surface roughening, microstructure reconstruction, amorphization and mixed moieties. Few studies have reported the use of bifunctional electrocatalysts for AEM and PEM water electrolysis. Intensive efforts should be devoted to translating the developed alkaline stable bifunctional electrocatalysts to AEM water electrolysers and developing acid stable bifunctional electrocatalysts. For magnetic field-assisted water electrolysis, further fundamental research is still required to explicitly discern the dominant effect of a magnetic field on the water electrolysis due to the complex convolution of multiple effects of the magnetic field. The strategy of tuning spin selectivity on the material level has been successfully applied to the low-current alkaline water electrolysis. However, it is still unclear whether the electrocatalysts with optimal spin selectivity can be applied to high-current and long-term alkaline and AEM water electrolysis relevant to industrial applications. A recent investigation has emphasized that care must be taken to exactly control the position of the magnet and electrodes and observed the maximum enhancement (4.7%) for a CoOx anode, doubting the usefulness of this technique.211 Therefore, the systems integrating the static/alternating magnetic field and MAE-based water electrolysers with a zero gap configuration should be engineered and rigorous TEA should be performed to validate the viability of this technology. For decoupled water electrolysis, the cost of synthetic redox mediators should be reduced to become economically viable for large-scale application. Particularly, the solubility, stability, and fast redox kinetics of redox mediators or electron reservoirs are crucial factors to determine their viability for practical applications. The influences of redox mediators on membrane durability and corrosion of the porous transport layers (PTLs), bipolar plates (BPs), liquid transfer lines and other mechanical balance of plant (BOP) components for the water electrolysers warrant further investigation. The flow battery industry may offer helpful guidance and direction. The hybrid water electrolysis enables the integration of H2 production with electrochemical organic reforming and wastewater treatment. The selectivity for desirable value-added products from chosen organic oxidations is the primary goal and the separation and purification of products require optimization. The requirement of pumps that circulate the organic solutions is necessary like the current water electrolysers, as the continuously decreasing concentrations of organic substrates will reduce the current in static cells at pre-fixed voltages that avoid the OER. Nevertheless, most of reported studies investigated this technology without pumps. The influences of substrate molecules on the membrane stability and corrosion of the BOP components for the water electrolysers should be scrutinized. Furthermore, this strategy may restrict the candidate pool of organic substrates, as not all organic molecules have a sufficiently high solubility in water and many organic products are not stable and may spontaneously decompose in the electrochemical and aerobic environments. The organic electrosynthesis is witnessing a renaissance. More promising organic electrochemical reforming reactions may facilitate the success of the hybrid water electrolysis. For acid/alkaline asymmetric electrolyte water electrolysis, the high-performance BPMs with high chemical stability and AEL/CEL interface adhesion play a key role in practical viability. The forward bias operation mode is more promising to significantly lower the electrolysis voltage; however, salt accumulation and delamination remain a challenge to be solved. The reverse bias operation mode has great potential for practical application, as this technology can inherit the merits of PEM water electrolysis but significantly lower the cost by replacing the costly acid-stable IrO2 OER electrocatalysts with the developed transition metal based electrocatalysts. Nevertheless, the interfacial water dissociation capability and junction contact must be further optimized to minimize the entire electrolysis voltage and promote the ionic current flow at high current rates. Future efforts should focus on the fabrication of robust ion-exchange polymers and active interfacial water dissociation catalysts for high-performance BPMs. The use of monopolar ion-exchange membranes and even membraneless design demands further research efforts.358,359 It is promising to integrate the acid/alkaline asymmetric electrolyte water electrolysis with hybrid water electrolysis once the high-performance BPMs are successfully developed. For tandem water electrolysis, it is inspiring to see recent advances in this technology integrated with biological catalysts for on-site use of H2 from water to yield valuable chemicals and fuels from abundant staring molecules such as CO2 and N2. Nevertheless, the long-term durability, scalability and cost of these systems should be thoroughly analysed to determine the viability. Finding competent HER and OER electrocatalysts with high activities in near neutral electrolytes is challenging but will contribute to the development of such tandem electrolysis systems and possible seawater electrolysis. Third, a large gap exists between the fundamental research on electrocatalysts and industrial evaluation and application of water electrolysers. Despite great progress in improving apparent/intrinsic activities of electrocatalysts and understanding of electrocatalytic mechanisms, these obtained knowledge and achieved advances at the lab scale in terms of materials design, electrocatalyst performance and mechanistic insights into the electrocatalytic reactions have not translated to significant performance improvements, scaling-up and large-scale deployment of water electrolyser systems. The formidable challenges are related to the nature of the open electrochemical system for water electrolysers.357 For open water electrolyser systems, the gas and liquid management requires optimal engineering designs at both cell and stack levels. The properties of ion-exchange membranes and ionomers, mass loading of electrocatalysts, wettability and porosity of PTLs and flow channel design of BPs must be comprehensively engineered to optimize the electron and ion transport, avoid crossover of reactants and products, and precisely control liquid and gas flows for optimal mass transfer. At the system level, both the mechanical (e.g. pumps, heat exchangers, external circulation, gas processing and separation, temperature swing adsorption and deionizer systems) and electrical (e.g. AC to DC rectifier) BOP components are indispensable and play a key role in determining the system performance. The high performance (e.g., intrinsic activity and stability) of a single electrocatalyst component acquired in the flooded electrolytes with three-electrode and simple two-electrode configurations at the lab-scale may represent the maximum performance limit of a cell but cannot directly translate into better stack and system performance. The discrepancies of setup, hardware, operating conditions, and electrochemical evaluation conditions for lab-scale three-electrode (or two-electrode) cells and real-world MEA-based water electrolysers give rise to a large gap. For the three-electrode studies, a thin electrocatalyst layer
is deposited onto the conductive electrode substrate and immersed in the flooded liquid under possible rotating conditions, which fully optimizes the mixed electron and ion transfer and almost eliminates the factors of mass transfer and gas/liquid management for reactants and products. However, these engineering aspects play crucial roles in ensuring that the practical MEA-based water electrolysers operate well. In the fundamental research, the electrocatalysts are mostly studied at low current densities (<500 mA cm−2), in flooded static liquid electrolytes without separators and at room temperature for tens to hundreds of hours. These operating and electrochemical test conditions are distinct from those of MEA-based water electrolysers. These differences in setup and testing protocols result in large discrepancies in measured performances and challenges in direct transferability of lab results to practical systems, with lab-scale results obtained through three-electrode configurations commonly being more promising than those measured in MEA configurations. This calls for the standardized materials, setup and conditions reflecting realistic industrial operation and established methodology to bridge the gap between academia and industry in the field of water electrolysis. The new electrolyser designs by using various strategies are suggested to be tested by using the MEA configurations under realistic operation conditions such as accelerated stress tests, industrially relevant and fluctuating currents, elevated temperatures, flowing electrolytes, and frequent start-up and shut-down cycling. Last but not the least, the development of PTLs and BPs and the integration of water electrolysers with optimized BOPs call for more research efforts. Despite the core role of the MEA (composed of the membrane and electrocatalysts) in determining the electrolyser performance, a breakdown of the PEM water electrolyser system cost (Fig. 21) shows that the MEA cost only accounts for ∼14% of the system cost and ∼26% of the stack cost at the current system production rates. The PTLs and BPs made of titanium plates constitute a third of the stack cost, playing a key role in the gas/liquid management and determining the stack cost and performance. At the current low production and deployment rates, the MEA cost is not the limiting stack cost even with expensive Pt and IrO2 electrocatalysts, although the MEA design attracts the most efforts of materials and electrochemist communities. Rather, PTLs and BPs are the key influencing factors for the stack cost. Research efforts must be directed towards developing low-cost and corrosion-resistant porous conductive frameworks. This requires endeavours in advanced manufacturing and processing of metals and alloys. A water electrolyser system with a multitude of cells and stacks requires BOP equipment to ensure H2 processing, water/electrolyte circulation, heat management and power supply. The BOP cost accounts for almost half of the system cost, deserving much research focus. For new electrolyser technologies using soluble redox mediators and chemicals, their effects on the membrane conductivity and chemical stability and corrosion for hardware must be scrutinized. A major way to reduce the water electrolyser system cost is to scale up the system production rate. This underlines the need for further research on scaling-up of electrocatalysts, membranes, PTLs and BPs. It is noteworthy that high-purity water feeds produced by water desalination and purification systems are commonly required for water electrolysers. To reduce the cost of water purification for water electrolysis, recent research is motivated to revisit a technology of direct seawater electrolysis (DSE) despite its early research in 1980s,360–362 taking for granted that it has economic advantages. This has raised arguments. Although DSE may demonstrate fundamental research significance, recent reviews performed a quantitative analysis and found that DSE has substantial challenges and there are limited economic and environmental incentives of pursuing development efforts on this nascent technology.363,364 This is because the capital and operating costs of water purification are insignificant compared to those of electrolysis of pure water. In particular, the costly PEMs (e.g. Nafion) are vulnerable to foreign ions and cationic impurities, and are more than one order of magnitude more expensive than reverse osmosis membranes.365 On the contrary, the direct use of seawater feeds can lead to formidable challenges. The challenges of DSE include the variable composition of seawaters, potential oxidation of chloride to chlorine or ClO− as competing reactions to the OER, blocking and deactivation of expensive ion exchange membranes, corrosion and passivation of electrodes, biofouling (e.g. microbial contamination), low ionic conductivity of seawater, low energy efficiency of DSE, precipitation of alkali hydroxide, possibly dramatic pH fluctuations, formation of pH gradient and short lifetime.364 Moreover, the energy demand and cost of seawater purification are also insignificant compared to those of the electrolysis of pure water. The water purification step is projected to slightly increase the price of H2 by less than 1%, implying that the potential cost reduction of water electrolysis from the seawater feeds compared to pure water feeds is marginal even if all those challenges are overcome. Note that the DSE technology possesses some technical similarities with a well-established chlor-alkali process where high-concentration saline water feed rather than seawater is used due to the sensitivity of ion exchange membranes to impurities and H2 is also a by-product.366 However, the concept of using seawater for electrolysis may be economically meaningful in a process coupling seawater reverse osmosis and electrolysis of desalinated water363 or emerging technologies of high-temperature steam water electrolysis (e.g. high-temperature PEMWE at 100–200 °C, H-SOEC at 300–650 °C and O-SOEC at 500–1000 °C).85,86,361 In particular, the use of a low or medium grade heat source in the steam water electrolysis provides an opportunity to generate clean steam (free of salt contaminants) from seawater, low-grade or saline surface water without requiring complex water purification systems before it reaches the electrodes and electrolytes.367 Therefore, the steam water electrolysis is a promising technological complement to low-temperature water electrolysis. The new water electrolysers require benchmarking and comprehensive assessment in terms of performance metrics, scalability, economic factors, and deployment potential. All in all, concerted research efforts in both fundamental research and engineering should be integrated to accelerate the translation from lab-scale prototypes to industry-scale deployment of water electrolyser systems for realizing the future H2 economy.
 |
| | Fig. 21 Cost evaluation of a PEM water electrolyser system. (a–c) Breakdown of system and stack costs for PEM water electrolysers for the current situation (a), scaled system size (b) and scaled production rate (c). (d) System/pack cost as a function of the production rate for PEM water electrolysers, fuel cells and Li-ion batteries. Reprinted from ref. 357, Copyright 2020, with permission from Springer Nature. | |
Author contributions
Wei Li: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing – original draft, and writing – review & editing; Hanchen Tian: formal analysis, software, and writing – review & editing; Liang Ma: formal analysis, methodology, and writing – review & editing; Yi Wang: formal analysis, methodology, and writing – review & editing; Xingbo Liu: formal analysis, resources, and writing – review & editing; Xuefei Gao: conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing – original draft, and writing – review & editing.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
We thank Dr Fang Xia at Murdoch University and Dr Chuancheng Duan at Kansas State University for discussion of thermodynamics of water splitting as a function of temperature and HSC Chemistry software resource.
References
- J. Greeley and N. M. Markovic, Energy Environ. Sci., 2012, 5, 9246–9256 RSC.
- X. Zou and Y. Zhang, Chem. Soc. Rev., 2015, 44, 5148–5180 RSC.
- Y. Wang, L. Ma, W. Li, W. Li and X. Liu, J. Mater. Chem. A, 2020, 8, 20101–20110 RSC.
- S. M. Thalluri, J. Borme, D. Xiong, J. Xu, W. Li, I. Amorim, P. Alpuim, J. Gaspar, H. Fonseca, L. Qiao and L. Liu, Sustainable Energy Fuels, 2018, 2, 978–982 RSC.
- F. Barbir, Sol. Energy, 2005, 78, 661–669 CrossRef CAS.
- Y. Wang, L. Ma, W. Li, A. M. Deibel, W. Li, H. Tian and X. Liu, Adv. Compos. Hybrid Mater., 2022 DOI:10.1007/s42114-022-00480-9.
- Z. Zeng, W. Li, X. Chen and X. Liu, Adv. Funct. Mater., 2020, 30, 2004650 CrossRef CAS.
- T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC.
- O. Krishan and S. Suhag, Int. J. Energy Res., 2019, 43, 6171–6210 CrossRef.
- Z. Chen, Y. Yan, S. Xin, W. Li, J. Qu, Y.-G. Guo and W.-G. Song, J. Mater. Chem. A, 2013, 1, 11404–11409 RSC.
- W. Li, Y.-X. Yin, S. Xin, W.-G. Song and Y.-G. Guo, Energy Environ. Sci., 2012, 5, 8007–8013 RSC.
- X. Li, G. Wu, J. Chen, M. Li, W. Li, T. Wang, B. Jiang, Y. He and L. Mai, Appl. Surf. Sci., 2017, 392, 297–304 CrossRef CAS.
- D. M. Davies, M. G. Verde, O. Mnyshenko, Y. R. Chen, R. Rajeev, Y. S. Meng and G. Elliott, Nat. Energy, 2019, 4, 42–50 CrossRef.
- X. Li, W. Li, M. Li, P. Cui, D. Chen, T. Gengenbach, L. Chu, H. Liu and G. Song, J. Mater. Chem. A, 2015, 3, 2762–2769 RSC.
- X. Li, Y. Feng, M. Li, W. Li, H. Wei and D. Song, Adv. Funct. Mater., 2015, 25, 6858–6866 CrossRef CAS.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- M. A. Pellow, C. J. M. Emmott, C. J. Barnhart and S. M. Benson, Energy Environ. Sci., 2015, 8, 1938–1952 RSC.
- G. Li, Z. Chen and J. Lu, Chem, 2018, 4, 3–7 CAS.
- Z. Zeng and X. Liu, Adv. Mater. Interfaces, 2018, 5, 1701274 CrossRef.
- X. Li, W. Zhang, Y. Feng, W. Li, P. Peng, J. Yao, M. Li and C. Jiang, Electrochim. Acta, 2019, 294, 173–182 CrossRef CAS.
- X. Li, G. Wu, X. Liu, W. Li and M. Li, Nano Energy, 2017, 31, 1–8 CrossRef CAS.
- F. Song, W. Li, J. Yang, G. Han, T. Yan, X. Liu, Y. Rao, P. Liao, Z. Cao and Y. Sun, ACS Energy Lett., 2019, 4, 1594–1601 CrossRef CAS.
- Z. Zeng, W. Li, X. Chen, N. Zhang, H. Qi and X. Liu, ACS Sustainable Chem. Eng., 2020, 8, 3261–3272 CrossRef CAS.
- J. O. M. Bockris, Int. J. Hydrogen Energy, 1999, 24, 1–15 CrossRef CAS.
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS PubMed.
- J. O. M. Bockris, Int. J. Hydrogen Energy, 2013, 38, 2579–2588 CrossRef CAS.
- G. W. Crabtree, M. S. Dresselhaus and M. V. Buchanan, Phys. Today, 2004, 57, 39–44 CrossRef CAS.
- A. Saeedmanesh, M. A. Mac Kinnon and J. Brouwer, Curr. Opin. Electrochem., 2018, 12, 166–181 CrossRef CAS.
- I. Staffell, D. Scamman, A. Velazquez Abad, P. Balcombe, P. E. Dodds, P. Ekins, N. Shah and K. R. Ward, Energy Environ. Sci., 2019, 12, 463–491 RSC.
- X. Gao, L.-P. Xu, Z. Xue, L. Feng, J. Peng, Y. Wen, S. Wang and X. Zhang, Adv. Mater., 2014, 26, 1771–1775 CrossRef CAS PubMed.
- F. Song, W. Li, G. Han and Y. Sun, ACS Appl. Energy Mater., 2018, 1, 3–8 CrossRef CAS.
- N. Armaroli and V. Balzani, ChemSusChem, 2011, 4, 21–36 CrossRef CAS PubMed.
- B. Rausch, M. D. Symes, G. Chisholm and L. Cronin, Science, 2014, 345, 1326–1330 CrossRef CAS PubMed.
- J. D. Holladay, J. Hu, D. L. King and Y. Wang, Catal. Today, 2009, 139, 244–260 CrossRef CAS.
- V. R. Stamenkovic, D. Strmcnik, P. P. Lopes and N. M. Markovic, Nat. Mater., 2017, 16, 57–69 CrossRef CAS PubMed.
- A. Ursua, L. M. Gandia and P. Sanchis, Proc. IEEE, 2012, 100, 410–426 CAS.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- S. Sarwar, M.-C. Lin, M. R. Ahasan, Y. Wang, R. Wang and X. Zhang, Adv. Compos. Hybrid Mater., 2022 DOI:10.1007/s42114-022-00424-3.
- J. Zhao, K. Bao, M. Xie, D. Wei, K. Yang, X. Zhang, C. Zhang, Z. Wang and X. Yang, Adv. Compos. Hybrid Mater., 2022 DOI:10.1007/s42114-022-00455-w.
- Y. Cong, B. Yi and Y. Song, Nano Energy, 2018, 44, 288–303 CrossRef CAS.
- F. Song, W. Li and Y. Sun, Inorganics, 2017, 5, 40 CrossRef.
- D. Ferrero, A. Lanzini, M. Santarelli and P. Leone, Int. J. Hydrogen Energy, 2013, 38, 3523–3536 CrossRef CAS.
- M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934 CrossRef CAS.
- M. Ozturk and I. Dincer, Int. J. Hydrogen Energy, 2021, 46, 31511–31522 CrossRef CAS.
- J. Schefold, A. Brisse and H. Poepke, Int. J. Hydrogen Energy, 2017, 42, 13415–13426 CrossRef CAS.
- Y. Zheng, J. Wang, B. Yu, W. Zhang, J. Chen, J. Qiao and J. Zhang, Chem. Soc. Rev., 2017, 46, 1427–1463 RSC.
- M. David, C. Ocampo-Martínez and R. Sánchez-Peña, J. Energy Storage, 2019, 23, 392–403 CrossRef.
- F. P. Lohmann-Richters, S. Renz, W. Lehnert, M. Müller and M. Carmo, J. Electrochem. Soc., 2021, 168, 114501 CrossRef CAS.
- R. Pinsky, P. Sabharwall, J. Hartvigsen and J. O’Brien, Prog. Nucl. Energy, 2020, 123, 103317 CrossRef CAS.
- A. Buttler and H. Spliethoff, Renewable Sustainable Energy Rev., 2018, 82, 2440–2454 CrossRef CAS.
- S. A. Grigoriev, V. N. Fateev, D. G. Bessarabov and P. Millet, Int. J. Hydrogen Energy, 2020, 45, 26036–26058 CrossRef CAS.
- F. M. Sapountzi, J. M. Gracia, C. J. Weststrate, H. O. A. Fredriksson and J. W. Niemantsverdriet, Prog. Energy Combust. Sci., 2017, 58, 1–35 CrossRef.
- O. Schmidt, A. Gambhir, I. Staffell, A. Hawkes, J. Nelson and S. Few, Int. J. Hydrogen Energy, 2017, 42, 30470–30492 CrossRef CAS.
- Q. Fang, L. Blum and N. H. Menzler, J. Electrochem. Soc., 2015, 162, F907–F912 CrossRef CAS.
- L. Q. Le, C. H. Hernandez, M. H. Rodriguez, L. Zhu, C. Duan, H. Ding, R. P. O'Hayre and N. P. Sullivan, J. Power Sources, 2021, 482, 228868 CrossRef CAS.
- A. Hauch, R. Küngas, P. Blennow, A. B. Hansen, J. B. Hansen, B. V. Mathiesen and M. B. Mogensen, Science, 2020, 370, eaba6118 CrossRef CAS PubMed.
- M. Götz, J. Lefebvre, F. Mörs, A. McDaniel Koch, F. Graf, S. Bajohr, R. Reimert and T. Kolb, Renewable Energy, 2016, 85, 1371–1390 CrossRef.
- I. Dincer and C. Acar, Int. J. Hydrogen Energy, 2015, 40, 11094–11111 CrossRef CAS.
- W. Bian, W. Wu, B. Wang, W. Tang, M. Zhou, C. Jin, H. Ding, W. Fan, Y. Dong, J. Li and D. Ding, Nature, 2022, 604, 479–485 CrossRef CAS PubMed.
- S. Hu, H. Finklea, W. Li, W. Li, H. Qi, N. Zhang and X. Liu, ACS Appl. Mater. Interfaces, 2020, 12, 11126–11134 CrossRef CAS PubMed.
- M. Fang, G. Dong, R. Wei and J. C. Ho, Adv. Energy Mater., 2017, 7, 1700559 CrossRef.
- N.-T. Suen, S.-F. Hung, Q. Quan, N. Zhang, Y.-J. Xu and H. M. Chen, Chem. Soc. Rev., 2017, 46, 337–365 RSC.
- A. Eftekhari, Int. J. Hydrogen Energy, 2017, 42, 11053–11077 CrossRef CAS.
- B. Mondal and A. Dey, Chem. Commun., 2017, 53, 7707–7715 RSC.
- W.-F. Chen, J. T. Muckerman and E. Fujita, Chem. Commun., 2013, 49, 8896–8909 RSC.
- M.-I. Jamesh and X. Sun, J. Power Sources, 2018, 400, 31–68 CrossRef CAS.
- Y. Liu, C. Xiao, P. Huang, M. Cheng and Y. Xie, Chem, 2018, 4, 1263–1283 CAS.
- B. M. Hunter, H. B. Gray and A. M. Müller, Chem. Rev., 2016, 116, 14120–14136 CrossRef CAS PubMed.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086 RSC.
- M. Kartal, F. Xia, D. Ralph, W. D. A. Rickard, F. Renard and W. Li, Hydrometallurgy, 2020, 191, 105192 CrossRef CAS.
- B. You and Y. Sun, Acc. Chem. Res., 2018, 51, 1571–1580 CrossRef CAS PubMed.
- NIST-JANAF Thermochemical Tables, https://janaf.nist.gov/ DOI:10.18434/T42S31.
- Y. Cheng and S. P. Jiang, Prog. Nat. Sci., 2015, 25, 545–553 CrossRef CAS.
-
Z. Qi, Proton exchange membrane fuel cells, CRC Press, New York USA, 2013 Search PubMed.
-
J. Bockris, B. Conway, E. Yeager and R. White, Comprehensive treatise of electrochemistry: Electrochemical processing, Plenum Press, New York, USA, 1981 Search PubMed.
- Z. Zhang, C. Feng, C. Liu, M. Zuo, L. Qin, X. Yan, Y. Xing, H. Li, R. Si, S. Zhou and J. Zeng, Nat. Commun., 2020, 11, 1215 CrossRef CAS PubMed.
- Z. Zhuang, Y. Wang, C.-Q. Xu, S. Liu, C. Chen, Q. Peng, Z. Zhuang, H. Xiao, Y. Pan, S. Lu, R. Yu, W.-C. Cheong, X. Cao, K. Wu, K. Sun, Y. Wang, D. Wang, J. Li and Y. Li, Nat. Commun., 2019, 10, 4875 CrossRef PubMed.
- L.-G. He, P.-Y. Cheng, C.-C. Cheng, C.-L. Huang, C.-T. Hsieh and S.-Y. Lu, Appl. Catal., B, 2021, 290, 120049 CrossRef CAS.
- F. Jing, Q. Lv, J. Xiao, Q. Wang and S. Wang, J. Mater. Chem. A, 2018, 6, 14207–14214 RSC.
- Y. Jin, H. Wang, J. Li, X. Yue, Y. Han, P. K. Shen and Y. Cui, Adv. Mater., 2016, 28, 3785–3790 CrossRef CAS PubMed.
- Y. Yang, H. Yao, Z. Yu, S. M. Islam, H. He, M. Yuan, Y. Yue, K. Xu, W. Hao, G. Sun, H. Li, S. Ma, P. Zapol and M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 10417–10430 CrossRef CAS PubMed.
- S. Anantharaj, S. R. Ede, K. Karthick, S. Sam Sankar, K. Sangeetha, P. E. Karthik and S. Kundu, Energy Environ. Sci., 2018, 11, 744–771 RSC.
-
K. W. Harrison, R. Remick, A. Hoskin and G. D. Martin, Hydrogen Production: Fundamentals and Case Study Summaries, United States, 2010 Search PubMed.
- X. Sun, S. C. Simonsen, T. Norby and A. Chatzitakis, Membranes, 2019, 9, 83 CrossRef CAS PubMed.
- C. Duan, R. Kee, H. Zhu, N. Sullivan, L. Zhu, L. Bian, D. Jennings and R. O’Hayre, Nat. Energy, 2019, 4, 230–240 CrossRef CAS.
- Y. Wang, W. Li, L. Ma, W. Li and X. Liu, J. Mater. Sci. Technol., 2020, 55, 35–55 CrossRef.
- H. Qi, Y.-L. Lee, T. Yang, W. Li, W. Li, L. Ma, S. Hu, Y. Duan, G. A. Hackett and X. Liu, ACS Catal., 2020, 10, 5567–5578 CrossRef CAS.
- H. Qi, F. Xia, T. Yang, W. Li, W. Li, L. Ma, G. Collins, W. Shi, H. Tian, S. Hu, T. Thomas, E. M. Sabolsky, J. Zondlo, R. Hart, H. Finklea, G. A. Hackett and X. Liu, J. Electrochem. Soc., 2020, 167, 024510 CrossRef CAS.
- H. Qi, T. Thomas, W. Li, W. Li, F. Xia, N. Zhang, E. M. Sabolsky, J. Zondlo, R. Hart and X. Liu, ACS Appl. Energy Mater., 2019, 2, 4244–4254 CrossRef CAS.
- Y. Wang, H. Arandiyan, K. Dastafkan, Y. Li and C. Zhao, Chem. Res. Chin. Univ., 2020, 36, 360–365 CrossRef CAS.
- C. Wei, R. R. Rao, J. Peng, B. Huang, I. E. L. Stephens, M. Risch, Z. J. Xu and Y. Shao-Horn, Adv. Mater., 2019, 31, 1806296 CrossRef PubMed.
- M. B. Stevens, L. J. Enman, A. S. Batchellor, M. R. Cosby, A. E. Vise, C. D. M. Trang and S. W. Boettcher, Chem. Mater., 2017, 29, 120–140 CrossRef CAS.
- K. J. J. Mayrhofer, G. K. H. Wiberg and M. Arenz, J. Electrochem. Soc., 2008, 155, P1 CrossRef CAS.
- K. J. J. Mayrhofer, A. S. Crampton, G. K. H. Wiberg and M. Arenz, J. Electrochem. Soc., 2008, 155, P78 CrossRef CAS.
- K. Agrawal, A. A. Naik, S. Chaudhary, D. Parvatalu and V. Santhanam, Chem. – Asian J., 2021, 16, 3311–3325 CrossRef CAS PubMed.
- W. Zheng, M. Liu and L. Y. S. Lee, ACS Energy Lett., 2020, 5, 3260–3264 CrossRef CAS.
- A. Peugeot, C. E. Creissen, D. Karapinar, H. N. Tran, M. Schreiber and M. Fontecave, Joule, 2021, 5, 1281–1300 CrossRef CAS.
- J. Lee and J. H. Bang, ACS Energy Lett., 2020, 5, 2706–2710 CrossRef CAS.
- R. Wei, M. Fang, G. Dong and J. C. Ho, Sci. Bull., 2017, 62, 971–973 CrossRef CAS.
- R. Chen, C. Yang, W. Cai, H.-Y. Wang, J. Miao, L. Zhang, S. Chen and B. Liu, ACS Energy Lett., 2017, 2, 1070–1075 CrossRef CAS.
- J. G. Chen, C. W. Jones, S. Linic and V. R. Stamenkovic, ACS Catal., 2017, 7, 6392–6393 CrossRef CAS.
- W. Wang, J. Luo and S. Chen, Chem. Commun., 2017, 53, 11556–11559 RSC.
- S. Niu, S. Li, Y. Du, X. Han and P. Xu, ACS Energy Lett., 2020, 5, 1083–1087 CrossRef CAS.
- I. Roger and M. D. Symes, ACS Appl. Mater. Interfaces, 2017, 9, 472–478 CrossRef CAS PubMed.
- H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56, 9–35 CrossRef CAS.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed.
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. M. Chatman, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2015, 137, 4347–4357 CrossRef CAS PubMed.
- S. Jung, C. C. L. McCrory, I. M. Ferrer, J. C. Peters and T. F. Jaramillo, J. Mater. Chem. A, 2016, 4, 3068–3076 RSC.
- S. Anantharaj, S. R. Ede, K. Sakthikumar, K. Karthick, S. Mishra and S. Kundu, ACS Catal., 2016, 6, 8069–8097 CrossRef CAS.
- D. Voiry, M. Chhowalla, Y. Gogotsi, N. A. Kotov, Y. Li, R. M. Penner, R. E. Schaak and P. S. Weiss, ACS Nano, 2018, 12, 9635–9638 CrossRef CAS PubMed.
- S. Anantharaj and S. Kundu, ACS Energy Lett., 2019, 4, 1260–1264 CrossRef CAS.
- S. Anantharaj, S. Noda, M. Driess and P. W. Menezes, ACS Energy Lett., 2021, 6, 1607–1611 CrossRef CAS.
- W. T. Hong, M. Risch, K. A. Stoerzinger, A. Grimaud, J. Suntivich and Y. Shao-Horn, Energy Environ. Sci., 2015, 8, 1404–1427 RSC.
- J. Zheng, Y. Yan and B. Xu, J. Electrochem. Soc., 2015, 162, F1470–F1481 CrossRef CAS.
- W. Sheng, H. A. Gasteiger and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1529 CrossRef CAS.
- L. Yu and Z. Ren, Mater. Today Phys., 2020, 14, 100253 CrossRef.
- S. X. Weng and X. Chen, Nano Energy, 2016, 19, 138–144 CrossRef CAS.
- L. Chen, X. Dong, F. Wang, Y. Wang and Y. Xia, Chem. Commun., 2016, 52, 3147–3150 RSC.
- J. N. Hausmann, B. Traynor, R. J. Myers, M. Driess and P. W. Menezes, ACS Energy Lett., 2021, 6, 3567–3571 CrossRef CAS.
- S. Sun, H. Li and Z. J. Xu, Joule, 2018, 2, 1024–1027 CrossRef.
- K. A. Stoerzinger, M. Risch, B. Han and Y. Shao-Horn, ACS Catal., 2015, 5, 6021–6031 CrossRef CAS.
- C. Wei and Z. J. Xu, Small Methods, 2018, 2, 1800168 CrossRef.
- L. Trotochaud and S. W. Boettcher, Scr. Mater., 2014, 74, 25–32 CrossRef CAS.
- F. Song, W. Li, J. Yang, G. Han, P. Liao and Y. Sun, Nat. Commun., 2018, 9, 4531 CrossRef PubMed.
- Y. Yoon, B. Yan and Y. Surendranath, J. Am. Chem. Soc., 2018, 140, 2397–2400 CrossRef CAS PubMed.
- J. Mahmood, F. Li, S.-M. Jung, M. S. Okyay, I. Ahmad, S.-J. Kim, N. Park, H. Y. Jeong and J.-B. Baek, Nat. Nanotechnol., 2017, 12, 441 CrossRef CAS PubMed.
- M. Lukaszewski, M. Soszko and A. Czerwinski, Int. J. Electrochem. Sci., 2016, 11, 4442–4469 CrossRef CAS.
- S. Trasatti and O. A. Petrii, Pure Appl. Chem., 1991, 63, 711–734 CrossRef CAS.
- S. Trasatti and O. A. Petrii, J. Electroanal. Chem., 1992, 327, 353–376 CrossRef CAS.
- H. Li, W. Li, Y. Zhang, T. Wang, B. Wang, W. Xu, L. Jiang, W. Song, C. Shu and C. Wang, J. Mater. Chem., 2011, 21, 7878–7881 RSC.
- J. Y. Zheng, X. Wang, W. Li, Z. Cao, H. Wang, C. Zhang, W.-G. Song, Y. Ma and J. Yao, CrystEngComm, 2012, 14, 7616–7620 RSC.
- C.-Q. Chen, W. Li, C.-Y. Cao and W.-G. Song, J. Mater. Chem., 2010, 20, 6968–6974 RSC.
- W. Li, D. Chen, F. Xia, J. Z. Y. Tan, P.-P. Huang, W.-G. Song, N. M. Nursam and R. A. Caruso, Environ. Sci.: Nano, 2016, 3, 94–106 RSC.
- L. Cao, D. Chen, W. Li and R. A. Caruso, ACS Appl. Mater. Interfaces, 2014, 6, 13129–13137 CrossRef CAS PubMed.
- J. Z. Y. Tan, N. M. Nursam, F. Xia, M.-A. Sani, W. Li, X. Wang and R. A. Caruso, ACS Appl. Mater. Interfaces, 2017, 9, 4540–4547 CrossRef CAS PubMed.
- F. Niu, L.-S. Zhang, C.-Q. Chen, W. Li, L. Li, W.-G. Song and L. Jiang, Nanoscale, 2010, 2, 1480–1484 RSC.
- W. Li, L.-S. Zhang, Q. Wang, Y. Yu, Z. Chen, C.-Y. Cao and W.-G. Song, J. Mater. Chem., 2012, 22, 15342–15347 RSC.
- Y. Yu, C. Cao, W. Li, P. Li, J. Qu and W. Song, Nano Res., 2012, 5, 434–442 CrossRef CAS.
- C. Chen, Y. Yu, W. Li, C. Cao, P. Li, Z. Dou and W. Song, J. Mater. Chem., 2011, 21, 12836–12841 RSC.
- N. M. Nursam, J. Z. Y. Tan, X. Wang, W. Li, F. Xia and R. A. Caruso, ChemistrySelect, 2016, 1, 4868–4878 CrossRef CAS.
- J. Qu, W. Li, C.-Y. Cao, X.-J. Yin, L. Zhao, J. Bai, Z. Qin and W.-G. Song, J. Mater. Chem., 2012, 22, 17222–17226 RSC.
- Y. Lu, W. Li, J. Zhang, Y. Liu, P. Casey, S. Bateman, S. Z. Shen, J. Zhou, G. S. Zakharova and W. Chen, Ferroelectrics, 2015, 477, 93–102 CrossRef CAS.
- L.-S. Zhang, L.-Y. Jiang, C.-Q. Chen, W. Li, W.-G. Song and Y.-G. Guo, Chem. Mater., 2010, 22, 414–419 CrossRef CAS.
- W. Li, C.-Y. Cao, L.-Y. Wu, M.-F. Ge and W.-G. Song, J. Hazard. Mater., 2011, 198, 143–150 CrossRef CAS PubMed.
- L.-S. Zhang, W. Li, Z.-M. Cui and W.-G. Song, J. Phys. Chem. C, 2009, 113, 20594–20598 CrossRef CAS.
- W. Li, F. Xia, J. Qu, P. Li, D. Chen, Z. Chen, Y. Yu, Y. Lu, R. A. Caruso and W. Song, Nano Res., 2014, 7, 903–916 CrossRef CAS.
- L. Yu, S. Sun, H. Li and Z. J. Xu, Fundam. Res., 2021, 1, 448–452 CrossRef.
- F. Song, L. Bai, A. Moysiadou, S. Lee, C. Hu, L. Liardet and X. Hu, J. Am. Chem. Soc., 2018, 140, 7748–7759 CrossRef CAS PubMed.
- C. Jiang, S. J. A. Moniz, A. Wang, T. Zhang and J. Tang, Chem. Soc. Rev., 2017, 46, 4645–4660 RSC.
- T. Yao, X. An, H. Han, J. Q. Chen and C. Li, Adv. Energy Mater., 2018, 8, 1800210 CrossRef.
- S. Chen, T. Takata and K. Domen, Nat. Rev. Mater., 2017, 2, 17050 CrossRef CAS.
- I. Roger, M. A. Shipman and M. D. Symes, Nat. Rev. Chem., 2017, 1, 0003 CrossRef CAS.
- Y. Gorlin and T. F. Jaramillo, J. Am. Chem. Soc., 2010, 132, 13612–13614 CrossRef CAS PubMed.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801 CrossRef PubMed.
- Y.-H. Fang and Z.-P. Liu, ACS Catal., 2014, 4, 4364–4376 CrossRef CAS.
- W. Sheng, H. A. Gasteiger and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1529–B1536 CrossRef CAS.
- B. Cao, G. M. Veith, J. C. Neuefeind, R. R. Adzic and P. G. Khalifah, J. Am. Chem. Soc., 2013, 135, 19186–19192 CrossRef CAS PubMed.
- S. Schuldiner, J. Electrochem. Soc., 1952, 99, 488–494 CrossRef CAS.
- S. Schuldiner, J. Electrochem. Soc., 1954, 101, 426–432 CrossRef CAS.
- D. M. F. Santos, C. A. C. Sequeira, D. Macciò, A. Saccone and J. L. Figueiredo, Int. J. Hydrogen Energy, 2013, 38, 3137–3145 CrossRef CAS.
- M. F. Kibria, M. S. Mridha and A. H. Khan, Int. J. Hydrogen Energy, 1995, 20, 435–440 CrossRef CAS.
- Z. Liang, H. S. Ahn and A. J. Bard, J. Am. Chem. Soc., 2017, 139, 4854–4858 CrossRef CAS PubMed.
- B. E. Conway and L. Bai, J. Electroanal. Chem. Interfacial Electrochem., 1986, 198, 149–175 CrossRef CAS.
- W. Li, X. Gao, D. Xiong, F. Wei, W.-G. Song, J. Xu and L. Liu, Adv. Energy Mater., 2017, 7, 1602579 CrossRef.
- W. Li, X. Gao, X. Wang, D. Xiong, P.-P. Huang, W.-G. Song, X. Bao and L. Liu, J. Power Sources, 2016, 330, 156–166 CrossRef CAS.
- S. Anantharaj, P. E. Karthik and S. Noda, Angew. Chem., Int. Ed., 2021, 60, 23051–23067 CrossRef CAS PubMed.
- K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Energy Environ. Sci., 2012, 5, 7050–7059 RSC.
- J. R. McKone, B. F. Sadtler, C. A. Werlang, N. S. Lewis and H. B. Gray, ACS Catal., 2013, 3, 166–169 CrossRef CAS.
- F. Jiao and H. Frei, Energy Environ. Sci., 2010, 3, 1018–1027 RSC.
- Y. Liu, H. Cheng, M. Lyu, S. Fan, Q. Liu, W. Zhang, Y. Zhi, C. Wang, C. Xiao, S. Wei, B. Ye and Y. Xie, J. Am. Chem. Soc., 2014, 136, 15670–15675 CrossRef CAS PubMed.
- Y. Surendranath, M. W. Kanan and D. G. Nocera, J. Am. Chem. Soc., 2010, 132, 16501–16509 CrossRef CAS PubMed.
- J. Wang, F. Xu, H. Jin, Y. Chen and Y. Wang, Adv. Mater., 2017, 29, 1605838 CrossRef PubMed.
- W. Li, N. Jiang, B. Hu, X. Liu, F. Song, G. Han, T. J. Jordan, T. B. Hanson, T. L. Liu and Y. Sun, Chem, 2018, 4, 637–649 CAS.
- B. R. Wygant, K. Kawashima and C. B. Mullins, ACS Energy Lett., 2018, 3, 2956–2966 CrossRef CAS.
- J. Zhang, T. Wang, P. Liu, Z. Liao, S. Liu, X. Zhuang, M. Chen, E. Zschech and X. Feng, Nat. Commun., 2017, 8, 15437 CrossRef CAS PubMed.
- Y. Wang, G. Zhang, W. Xu, P. Wan, Z. Lu, Y. Li and X. Sun, ChemElectroChem, 2014, 1, 1138–1144 CrossRef CAS.
- B. Xiong, L. Chen and J. Shi, ACS Catal., 2018, 8, 3688–3707 CrossRef CAS.
- Y. Yan, B. Y. Xia, B. Zhao and X. Wang, J. Mater. Chem. A, 2016, 4, 17587–17603 RSC.
- W. Li, D. Xiong, X. Gao and L. Liu, Chem. Commun., 2019, 55, 8744–8763 RSC.
- X. Zhang, R. Lin, X. Meng, W. Li, F. Chen and J. Hou, Inorg. Chem., 2021, 60, 9987–9995 CrossRef CAS PubMed.
- F. Song, T. Zhang, Y. Qian, J. Shaw, S. Chen, G. Chen, Y. Sun and Y. Rao, Mater. Today Energy, 2021, 22, 100846 CrossRef CAS.
- J. Xu, T. Liu, J. Li, B. Li, Y. Liu, B. Zhang, D. Xiong, I. Amorim, W. Li and L. Liu, Energy Environ. Sci., 2018, 11, 1819–1827 RSC.
- W. Li, D. Xiong, X. Gao, W.-G. Song, F. Xia and L. Liu, Catal. Today, 2017, 287, 122–129 CrossRef CAS.
- D. Xiong, Q. Zhang, S. M. Thalluri, J. Xu, W. Li, X. Fu and L. Liu, Chem. – Eur. J., 2017, 23, 8749–8755 CrossRef CAS PubMed.
- D. Xiong, W. Li and L. Liu, Chem. – Asian J., 2017, 12, 543–551 CrossRef CAS PubMed.
- D. Xiong, Q. Zhang, W. Li, J. Li, X. Fu, M. F. Cerqueira, P. Alpuim and L. Liu, Nanoscale, 2017, 9, 2711–2717 RSC.
- D. Xiong, W. Li, X. Wang and L. Liu, Nanotechnology, 2016, 27, 375401 CrossRef PubMed.
- W. Li, X. Wang, D. Xiong and L. Liu, Int. J. Hydrogen Energy, 2016, 41, 9344–9354 CrossRef CAS.
- Z. Guo, L. Liu, J. Wang, Y. Cao, J. Tu, X. Zhang and L. Ding, Int. J. Hydrogen Energy, 2021, 46, 34194–34215 CrossRef CAS.
- S. Hu, W. Li, W. Li, N. Zhang, H. Qi, H. Finklea and X. Liu, J. Colloid Interface Sci., 2019, 555, 115–123 CrossRef CAS PubMed.
- S. Hu, W. Li, W. Li, N. Zhang, H. Qi, H. Finklea and X. Liu, Colloids Surf., A, 2019, 579, 123717 CrossRef CAS.
- Z. Zeng, W. Li, Q. Wang and X. Liu, Adv. Sci., 2019, 6, 1900711 CrossRef PubMed.
- J. Xu, J. Li, D. Xiong, B. Zhang, Y. Liu, K.-H. Wu, I. Amorim, W. Li and L. Liu, Chem. Sci., 2018, 9, 3470–3476 RSC.
- D. Xiong, X. Wang, W. Li and L. Liu, Chem. Commun., 2016, 52, 8711–8714 RSC.
- W. Li, D. Chen, F. Xia, J. Z. Y. Tan, J. Song, W.-G. Song and R. A. Caruso, Chem. Commun., 2016, 52, 4481–4484 RSC.
- J. Song, F. Xia, M. Zhao, Y. L. Zhong, W. Li, K. P. Loh, R. A. Caruso and Q. Bao, Chem. Mater., 2015, 27, 3471–3482 CrossRef CAS.
- W. Li, C.-Y. Cao, C.-Q. Chen, Y. Zhao, W.-G. Song and L. Jiang, Chem. Commun., 2011, 47, 3619–3621 RSC.
- W. Li, X. Gao, D. Xiong, F. Xia, J. Liu, W.-G. Song, J. Xu, S. M. Thalluri, M. F. Cerqueira, X. Fu and L. Liu, Chem. Sci., 2017, 8, 2952–2958 RSC.
- S. Cobo, J. Heidkamp, P.-A. Jacques, J. Fize, V. Fourmond, L. Guetaz, B. Jousselme, V. Ivanova, H. Dau, S. Palacin, M. Fontecave and V. Artero, Nat. Mater., 2012, 11, 802 CrossRef CAS PubMed.
- N. Jiang, B. You, M. Sheng and Y. Sun, Angew. Chem., Int. Ed., 2015, 54, 6251–6254 CrossRef CAS PubMed.
- L.-A. Stern, L. Feng, F. Song and X. Hu, Energy Environ. Sci., 2015, 8, 2347–2351 RSC.
- X. Wang, W. Li, D. Xiong, D. Y. Petrovykh and L. Liu, Adv. Funct. Mater., 2016, 26, 4067–4077 CrossRef CAS.
- M. Ledendecker, S. Krick Calderón, C. Papp, H.-P. Steinrück, M. Antonietti and M. Shalom, Angew. Chem., Int. Ed., 2015, 54, 12361–12365 CrossRef CAS PubMed.
- X. Wang, W. Li, D. Xiong and L. Liu, J. Mater. Chem. A, 2016, 4, 5639–5646 RSC.
- Z. Chen, H. Yang, Z. Kang, M. Driess and P. W. Menezes, Adv. Mater., 2022, 34, 2108432 CrossRef CAS PubMed.
- T. Wu, M.-Z. Sun and B.-L. Huang, Rare Met., 2022, 41, 2169–2183 CrossRef CAS.
- H. Yang, M. Driess and P. W. Menezes, Adv. Energy Mater., 2021, 11, 2102074 CrossRef CAS.
- J. Yao, W. Huang, W. Fang, M. Kuang, N. Jia, H. Ren, D. Liu, C. Lv, C. Liu, J. Xu and Q. Yan, Small Methods, 2020, 4, 2000494 CrossRef CAS.
- N. A. Burton, R. V. Padilla, A. Rose and H. Habibullah, Renewable Sustainable Energy Rev., 2021, 135, 110255 CrossRef CAS.
- M. Wang, Z. Wang, X. Gong and Z. Guo, Renewable Sustainable Energy Rev., 2014, 29, 573–588 CrossRef CAS.
- C. Hunt, Z. Zhang, K. Ocean, R. P. Jansonius, M. Abbas, D. J. Dvorak, A. Kurimoto, E. W. Lees, S. Ghosh, A. Turkiewicz, F. A. Garcés Pineda, D. K. Fork and C. P. Berlinguette, J. Am. Chem. Soc., 2022, 144, 733–739 CrossRef CAS PubMed.
- Y. Zhang, C. Liang, J. Wu, H. Liu, B. Zhang, Z. Jiang, S. Li and P. Xu, ACS Appl. Energy Mater., 2020, 3, 10303–10316 CrossRef CAS.
- V. Gatard, J. Deseure and M. Chatenet, Curr. Opin. Electrochem., 2020, 23, 96–105 CrossRef CAS.
- J. Linnemann, K. Kanokkanchana and K. Tschulik, ACS Catal., 2021, 11, 5318–5346 CrossRef CAS.
- A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. Fernández Rivas, Joule, 2020, 4, 555–579 CrossRef CAS.
- Z. Lu, W. Zhu, X. Yu, H. Zhang, Y. Li, X. Sun, X. Wang, H. Wang, J. Wang, J. Luo, X. Lei and L. Jiang, Adv. Mater., 2014, 26, 2683–2687 CrossRef CAS PubMed.
- L. M. A. Monzon and J. M. D. Coey, Electrochem. Commun., 2014, 42, 38–41 CrossRef CAS.
- J. A. Koza, S. Mühlenhoff, P. Żabiński, P. A. Nikrityuk, K. Eckert, M. Uhlemann, A. Gebert, T. Weier, L. Schultz and S. Odenbach, Electrochim. Acta, 2011, 56, 2665–2675 CrossRef CAS.
- J. A. Koza, M. Uhlemann, A. Gebert and L. Schultz, Electrochem. Commun., 2008, 10, 1330–1333 CrossRef CAS.
- J. A. Koza, S. Mühlenhoff, M. Uhlemann, K. Eckert, A. Gebert and L. Schultz, Electrochem. Commun., 2009, 11, 425–429 CrossRef CAS.
- D. Fernández, M. Martine, A. Meagher, M. E. Möbius and J. M. D. Coey, Electrochem. Commun., 2012, 18, 28–32 CrossRef.
- H. Liu, L.-m Pan, H. Huang, Q. Qin, P. Li and J. Wen, J. Electroanal. Chem., 2015, 754, 22–29 CrossRef CAS.
- R. E. D. L. Rue and C. W. Tobias, J. Electrochem.
Soc., 1959, 106, 827 CrossRef.
- H. Vogt, Electrochim. Acta, 1981, 26, 1311–1317 CrossRef CAS.
- T. Iida, H. Matsushima and Y. Fukunaka, J. Electrochem. Soc., 2007, 154, E112 CrossRef CAS.
- H. Matsushima, T. Iida and Y. Fukunaka, Electrochim. Acta, 2013, 100, 261–264 CrossRef CAS.
- I. Mogi, K. Watanabe and M. Motokawa, Mater. Trans., JIM, 2000, 41, 966–969 CrossRef CAS.
- O. Devos, A. Olivier, J. P. Chopart, O. Aaboubi and G. Maurin, J. Electrochem. Soc., 1998, 145, 401–405 CrossRef CAS.
- H. Matsushima, T. Nohira, I. Mogi and Y. Ito, Surf. Coat. Technol., 2004, 179, 245–251 CrossRef CAS.
- A. Krause, M. Uhlemann, A. Gebert and L. Schultz, Electrochim. Acta, 2004, 49, 4127–4134 CrossRef CAS.
- I. Ohno and M. Mukai, Electrodeposition Surf. Treat., 1975, 3, 213–218 CrossRef CAS.
- H. Matsushima, D. Kiuchi and Y. Fukunaka, Electrochim. Acta, 2009, 54, 5858–5862 CrossRef CAS.
- H. Matsushima, T. Iida and Y. Fukunaka, J. Solid State Electrochem., 2012, 16, 617–623 CrossRef CAS.
- M.-Y. Lin, L.-W. Hourng and C.-W. Kuo, Int. J. Hydrogen Energy, 2012, 37, 1311–1320 CrossRef CAS.
- C. Wei and Z. J. Xu, Chin. J. Catal., 2022, 43, 148–157 CrossRef CAS.
- H.-B. Liu, D. Zhong, J. Han, L.-M. Pan and Y. Liu, Int. J. Hydrogen Energy, 2019, 44, 31724–31730 CrossRef CAS.
- Y. Li, L. Zhang, J. Peng, W. Zhang and K. Peng, J. Power Sources, 2019, 433, 226704 CrossRef CAS.
- D. Fernández, Z. Diao, P. Dunne and J. M. D. Coey, Electrochim. Acta, 2010, 55, 8664–8672 CrossRef.
- L. Elias and A. Chitharanjan Hegde, Electrocatalysis, 2017, 8, 375–382 CrossRef CAS.
- M. F. Kaya, N. Demir, M. S. Albawabiji and M. Taş, Int. J. Hydrogen Energy, 2017, 42, 17583–17592 CrossRef CAS.
- Y. Liu, L.-M. Pan, H. Liu, T. Chen, S. Yin and M. Liu, Int. J. Hydrogen Energy, 2019, 44, 1352–1358 CrossRef CAS.
- H.-B. Liu, H. Xu, L.-M. Pan, D.-H. Zhong and Y. Liu, Int. J. Hydrogen Energy, 2019, 44, 22780–22786 CrossRef CAS.
- Y. Liu, L.-M. Pan and H.-B. Liu, Int. J. Hydrogen Energy, 2021, 46, 13923–13935 CrossRef CAS.
- H.-B. Liu, L.-M. Pan, Q.-J. Qin and P.-F. Li, J. Electroanal. Chem., 2019, 832, 293–302 CrossRef CAS.
- B. Seo and S. H. Joo, Nat. Energy, 2018, 3, 451–452 CrossRef.
- C. Niether, S. Faure, A. Bordet, J. Deseure, M. Chatenet, J. Carrey, B. Chaudret and A. Rouet, Nat. Energy, 2018, 3, 476–483 CrossRef CAS.
- G. Xiong, Y. Chen, Z. Zhou, F. Liu, X. Liu, L. Yang, Q. Liu, Y. Sang, H. Liu, X. Zhang, J. Jia and W. Zhou, Adv. Funct. Mater., 2021, 31, 2009580 CrossRef CAS.
- X. Li, Z. Cheng and X. Wang, Electrochem. Energy Rev., 2021, 4, 136–145 CrossRef CAS.
- Y. Sun, S. Sun, H. Yang, S. Xi, J. Gracia and Z. J. Xu, Adv. Mater., 2020, 32, 2003297 CrossRef CAS PubMed.
- J. Li, J. Ma, Z. Ma, E. Zhao, K. Du, J. Guo and T. Ling, Adv. Energy Sustainability Res., 2021, 2, 2100034 CrossRef.
- X. Ren, T. Wu, Y. Sun, Y. Li, G. Xian, X. Liu, C. Shen, J. Gracia, H.-J. Gao, H. Yang and Z. J. Xu, Nat. Commun., 2021, 12, 2608 CrossRef CAS PubMed.
- R. R. Nazmutdinov, E. Santos and W. Schmickler, Electrochem. Commun., 2013, 33, 14–17 CrossRef CAS.
- W. Zhang, K. Banerjee-Ghosh, F. Tassinari and R. Naaman, ACS Energy Lett., 2018, 3, 2308–2313 CrossRef CAS.
- E. Torun, C. M. Fang, G. A. de Wijs and R. A. de Groot, J. Phys. Chem. C, 2013, 117, 6353–6357 CrossRef CAS.
- J. Gracia, Phys. Chem. Chem. Phys., 2017, 19, 20451–20456 RSC.
- S. Chrétien and H. Metiu, J. Chem. Phys., 2008, 129, 074705 CrossRef PubMed.
- S. Hirai, S. Yagi, W.-T. Chen, F.-C. Chou, N. Okazaki, T. Ohno, H. Suzuki and T. Matsuda, Adv. Sci., 2017, 4, 1700176 CrossRef PubMed.
- C. Wei, Z. Feng, G. G. Scherer, J. Barber, Y. Shao-Horn and Z. J. Xu, Adv. Mater., 2017, 29, 1606800 CrossRef PubMed.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS PubMed.
- J. Gracia, J. Phys. Chem. C, 2019, 123, 9967–9972 CrossRef CAS.
- J. Gracia, R. Sharpe and J. Munarriz, J. Catal., 2018, 361, 331–338 CrossRef CAS.
- P. C. Mondal, N. Kantor-Uriel, S. P. Mathew, F. Tassinari, C. Fontanesi and R. Naaman, Adv. Mater., 2015, 27, 1924–1927 CrossRef CAS PubMed.
- P. C. Mondal, W. Mtangi and C. Fontanesi, Small Methods, 2018, 2, 1700313 CrossRef.
- W. Mtangi, F. Tassinari, K. Vankayala, A. Vargas Jentzsch, B. Adelizzi, A. R. A. Palmans, C. Fontanesi, E. W. Meijer and R. Naaman, J. Am. Chem. Soc., 2017, 139, 2794–2798 CrossRef CAS PubMed.
- J. Ge, R. R. Chen, X. Ren, J. Liu, S. J. H. Ong and Z. J. Xu, Adv. Mater., 2021, 33, 2101091 CrossRef CAS PubMed.
- T. Wu, X. Ren, Y. Sun, S. Sun, G. Xian, G. G. Scherer, A. C. Fisher, D. Mandler, J. W. Ager, A. Grimaud, J. Wang, C. Shen, H. Yang, J. Gracia, H.-J. Gao and Z. J. Xu, Nat. Commun., 2021, 12, 3634 CrossRef CAS PubMed.
- F. A. Garcés-Pineda, M. Blasco-Ahicart, D. Nieto-Castro, N. López and J. R. Galán-Mascarós, Nat. Energy, 2019, 4, 519–525 CrossRef.
- G. Zhou, P. Wang, H. Li, B. Hu, Y. Sun, R. Huang and L. Liu, Nat. Commun., 2021, 12, 4827 CrossRef CAS PubMed.
- A. Krause, J. Koza, A. Ispas, M. Uhlemann, A. Gebert and A. Bund, Electrochim. Acta, 2007, 52, 6338–6345 CrossRef CAS.
- H. Matsushima, A. Ispas, A. Bund and B. Bozzini, J. Electroanal. Chem., 2008, 615, 191–196 CrossRef CAS.
- P. Dunne and J. M. D. Coey, J. Phys. Chem. C, 2019, 123, 24181–24192 CrossRef CAS.
- O. Sambalova, E. Billeter, O. Yildirim, A. Sterzi, D. Bleiner and A. Borgschulte, Int. J. Hydrogen Energy, 2021, 46, 3346–3353 CrossRef CAS.
- L. M. A. Monzon and J. M. D. Coey, Electrochem. Commun., 2014, 42, 42–45 CrossRef CAS.
- W. Zhou, M. Chen, M. Guo, A. Hong, T. Yu, X. Luo, C. Yuan, W. Lei and S. Wang, Nano Lett., 2020, 20, 2923–2930 CrossRef CAS PubMed.
- J. Saha, R. Ball and C. Subramaniam, ACS Sustainable Chem. Eng., 2021, 9, 7792–7802 CrossRef CAS.
- L. Ghassemzadeh, K.-D. Kreuer, J. Maier and K. Müller, J. Phys. Chem. C, 2010, 114, 14635–14645 CrossRef CAS.
- V. Prabhakaran, C. G. Arges and V. Ramani, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1029–1034 CrossRef CAS PubMed.
- A. Berger, R. A. Segalman and J. Newman, Energy Environ. Sci., 2014, 7, 1468–1476 RSC.
- A. G. Wallace and M. D. Symes, Joule, 2018, 2, 1390–1395 CrossRef CAS.
- Z. P. Ifkovits, J. M. Evans, M. C. Meier, K. M. Papadantonakis and N. S. Lewis, Energy Environ. Sci., 2021, 14, 4740–4759 RSC.
- X. Liu, J. Chi, B. Dong and Y. Sun, ChemElectroChem, 2019, 6, 2157–2166 CrossRef CAS.
- M. D. Symes and L. Cronin, Nat. Chem., 2013, 5, 403–409 CrossRef CAS PubMed.
- B. Rausch, M. D. Symes and L. Cronin, J. Am. Chem. Soc., 2013, 135, 13656–13659 CrossRef CAS PubMed.
- N. Kirkaldy, G. Chisholm, J.-J. Chen and L. Cronin, Chem. Sci., 2018, 9, 1621–1626 RSC.
- L. MacDonald, J. C. McGlynn, N. Irvine, I. Alshibane, L. G. Bloor, B. Rausch, J. S. J. Hargreaves and L. Cronin, Sustainable Energy Fuels, 2017, 1, 1782–1787 RSC.
- V. Amstutz, K. E. Toghill, F. Powlesland, H. Vrubel, C. Comninellis, X. Hu and H. H. Girault, Energy Environ. Sci., 2014, 7, 2350–2358 RSC.
- W. Wu, X.-Y. Wu, S.-S. Wang and C.-Z. Lu, ACS Sustainable Chem. Eng., 2020, 8, 18528–18534 CrossRef CAS.
- A. Landman, H. Dotan, G. E. Shter, M. Wullenkord, A. Houaijia, A. Maljusch, G. S. Grader and A. Rothschild, Nat. Mater., 2017, 16, 646–651 CrossRef CAS PubMed.
- L. Chen, X. Dong, Y. Wang and Y. Xia, Nat. Commun., 2016, 7, 11741 CrossRef CAS PubMed.
- Y. Ma, X. Dong, R. Wang, D. Bin, Y. Wang and Y. Xia, Energy Storage Mater., 2018, 11, 260–266 CrossRef.
- B. Choi, D. Panthi, M. Nakoji, T. Kabutomori, K. Tsutsumi and A. Tsutsumi, Chem. Eng. Sci., 2017, 157, 200–208 CrossRef CAS.
- F. Song, T. Zhang, D. Zhou, P. Sun, Z. Lu, H. Bian, J. Dang, H. Gao, Y. Qian, W. Li, N. Jiang, H. Dummer, J. G. Shaw, S. Chen, G. Chen, Y. Sun and Y. Rao, ACS Mater. Lett., 2022, 4, 967–977 CrossRef CAS.
- J. Jia, L. C. Seitz, J. D. Benck, Y. Huo, Y. Chen, J. W. D. Ng, T. Bilir, J. S. Harris and T. F. Jaramillo, Nat. Commun., 2016, 7, 13237 CrossRef CAS PubMed.
- L. MacDonald, B. Rausch, M. D. Symes and L. Cronin, Chem. Commun., 2018, 54, 1093–1096 RSC.
- X. Chen, W. Li, S. Hu, N. G. Akhmedov, D. Reed, X. Li and X. Liu, Nano Energy, 2022, 98, 107269 CrossRef CAS.
- X. Chen, W. Li, Z. Zeng, D. Reed, X. Li and X. Liu, Chem. Eng. J., 2021, 405, 126969 CrossRef CAS.
- X. Chen, W. Li, Y. Xu, Z. Zeng, H. Tian, M. Velayutham, W. Shi, W. Li, C. Wang, D. Reed, V. V. Khramtsov, X. Li and X. Liu, Nano Energy, 2020, 75, 104869 CrossRef CAS.
- J. Zhang, C. Zhang, W. Li, Q. Guo, H. Gao, Y. You, Y. Li, Z. Cui, K.-C. Jiang, H. Long, D. Zhang and S. Xin, ACS Appl. Mater. Interfaces, 2018, 10, 5543–5550 CrossRef CAS PubMed.
- Y. X. Chen, A. Lavacchi, H. A. Miller, M. Bevilacqua, J. Filippi, M. Innocenti, A. Marchionni, W. Oberhauser, L. Wang and F. Vizza, Nat. Commun., 2014, 5, 4036 CrossRef CAS PubMed.
- B. You, X. Liu, N. Jiang and Y. Sun, J. Am. Chem. Soc., 2016, 138, 13639–13646 CrossRef CAS PubMed.
- B. You, X. Liu, X. Liu and Y. Sun, ACS Catal., 2017, 7, 4564–4570 CrossRef CAS.
- N. Jiang, B. You, R. Boonstra, I. M. Terrero Rodriguez and Y. Sun, ACS Energy Lett., 2016, 1, 386–390 CrossRef CAS.
- B. You, N. Jiang, X. Liu and Y. Sun, Angew. Chem., Int. Ed., 2016, 55, 9913–9917 CrossRef CAS PubMed.
- T. Take, K. Tsurutani and M. Umeda, J. Power Sources, 2007, 164, 9–16 CrossRef CAS.
- C. Lamy, T. Jaubert, S. Baranton and C. Coutanceau, J. Power Sources, 2014, 245, 927–936 CrossRef CAS.
- V. Bambagioni, M. Bevilacqua, C. Bianchini, J. Filippi, A. Lavacchi, A. Marchionni, F. Vizza and P. K. Shen, ChemSusChem, 2010, 3, 851–855 CrossRef CAS PubMed.
- A. T. Marshall and R. G. Haverkamp, Int. J. Hydrogen Energy, 2008, 33, 4649–4654 CrossRef CAS.
- A. Caravaca, A. de Lucas-Consuegra, A. B. Calcerrada, J. Lobato, J. L. Valverde and F. Dorado, Appl. Catal., B, 2013, 134–135, 302–309 CrossRef CAS.
- K. Li and Y. Sun, Chem. – Eur. J., 2018, 24, 18258–18270 CrossRef CAS PubMed.
- X. Liu, Y. Han, Y. Guo, X. Zhao, D. Pan, K. Li and Z. Wen, Adv. Energy Sustainability Res., 2022, 3, 2200005 CrossRef.
- L. Du, Y. Sun and B. You, Mater. Rep. Energy, 2021, 1, 100004 Search PubMed.
- S. Tang, Y. Liu and A. Lei, Chem, 2018, 4, 27–45 CAS.
- X. Liu, B. Li, G. Han, X. Liu, Z. Cao, D.-E. Jiang and Y. Sun, Nat. Commun., 2021, 12, 1868 CrossRef CAS PubMed.
- X. Liu, D. C. Y. Leong and Y. Sun, Green Chem., 2020, 22, 6531–6539 RSC.
- T. Wang, L. Tao, X. Zhu, C. Chen, W. Chen, S. Du, Y. Zhou, B. Zhou, D. Wang, C. Xie, P. Long, W. Li, Y. Wang, R. Chen, Y. Zou, X.-Z. Fu, Y. Li, X. Duan and S. Wang, Nat. Catal., 2022, 5, 66–73 CrossRef CAS.
- Y. Ding, P. Cai and Z. Wen, Chem. Soc. Rev., 2021, 50, 1495–1511 RSC.
- R. S. Reiter, W. White and S. Ardo, J. Electrochem. Soc., 2015, 163, H3132–H3134 CrossRef.
- X. Tongwen, Resour., Conserv. Recycl., 2002, 37, 1–22 CrossRef.
- Y. Li, J. Chen, P. Cai and Z. Wen, J. Mater. Chem. A, 2018, 6, 4948–4954 RSC.
- Y. Chen, J. A. Wrubel, W. E. Klein, S. Kabir, W. A. Smith, K. C. Neyerlin and T. G. Deutsch, ACS Appl. Polym. Mater., 2020, 2, 4559–4569 CrossRef CAS.
- B. Mayerhöfer, D. McLaughlin, T. Böhm, M. Hegelheimer, D. Seeberger and S. Thiele, ACS Appl. Energy Mater., 2020, 3, 9635–9644 CrossRef.
- S. Z. Oener, M. J. Foster and S. W. Boettcher, Science, 2020, 369, 1099–1103 CrossRef CAS PubMed.
- N. M. Vargas-Barbosa, G. M. Geise, M. A. Hickner and T. E. Mallouk, ChemSusChem, 2014, 7, 3017–3020 CrossRef CAS PubMed.
- M. Zhang, J. Chen, H. Li, P. Cai, Y. Li and Z. Wen, Nano Energy, 2019, 61, 576–583 CrossRef CAS.
- J. Xu, I. Amorim, Y. Li, J. Li, Z. Yu, B. Zhang, A. Araujo, N. Zhang and L. Liu, Carbon Energy, 2020, 2, 646–655 CrossRef CAS.
- I. Amorim, J. Xu, N. Zhang, Z. Yu, A. Araújo, F. Bento and L. Liu, Chem. Eng. J., 2021, 420, 130454 CrossRef CAS.
- M. B. McDonald, S. Ardo, N. S. Lewis and M. S. Freund, ChemSusChem, 2014, 7, 3021–3027 CrossRef CAS PubMed.
- D. A. Vermaas, M. Sassenburg and W. A. Smith, J. Mater. Chem. A, 2015, 3, 19556–19562 RSC.
- J. Luo, D. A. Vermaas, D. Bi, A. Hagfeldt, W. A. Smith and M. Grätzel, Adv. Energy Mater., 2016, 6, 1600100 CrossRef.
- D. A. Vermaas, S. Wiegman, T. Nagaki and W. A. Smith, Sustainable Energy Fuels, 2018, 2, 2006–2015 RSC.
- J. C. Bui, I. Digdaya, C. Xiang, A. T. Bell and A. Z. Weber, ACS Appl. Mater. Interfaces, 2020, 12, 52509–52526 CrossRef CAS PubMed.
- Z. Yan, L. Zhu, Y. C. Li, R. J. Wycisk, P. N. Pintauro, M. A. Hickner and T. E. Mallouk, Energy Environ. Sci., 2018, 11, 2235–2245 RSC.
- C. Shen, R. Wycisk and P. N. Pintauro, Energy Environ. Sci., 2017, 10, 1435–1442 RSC.
- M. Nazemi, J. Padgett and M. C. Hatzell, Energy Technol., 2017, 5, 1191–1194 CrossRef CAS.
- L. Wan, Z. Xu, P. Wang, Y. Lin and B. Wang, J. Membr. Sci., 2021, 618, 118642 CrossRef CAS.
- M. Itagi, Z. M. Bhat, R. Thimmappa, D. Pandit, M. C. Devendrachari, L. K. Sannegowda and M. O. Thotiyl, J. Phys. Chem. C, 2020, 124, 11284–11292 CrossRef CAS.
- L. Yi, Y. Ji, P. Shao, J. Chen, J. Li, H. Li, K. Chen, X. Peng and Z. Wen, Angew. Chem., Int. Ed., 2021, 60, 21550–21557 CrossRef CAS PubMed.
- C. Zhang, S. Ci, X. Peng, J. Huang, P. Cai, Y. Ding and Z. Wen, J. Energy Chem., 2021, 54, 30–35 CrossRef.
- H. Zou, J. Chen, Y. Fang, J. Ding, W. Peng and R. Liu, Nano Energy, 2016, 27, 619–626 CrossRef CAS.
- G. Wang, J. Chen, P. Cai, J. Jia and Z. Wen, J. Mater. Chem. A, 2018, 6, 17763–17770 RSC.
- S. Varhade, Z. M. Bhat, R. Thimmappa, M. C. Devendrachari, A. R. Kottaichamy, S. Khaire, S. P. Shafi and M. O. Thotiyl, Chem. Phys. Lett., 2018, 706, 553–557 CrossRef CAS.
- D. Zheng, J. Li, S. Ci, P. Cai, Y. Ding, M. Zhang and Z. Wen, Appl. Catal., B, 2020, 277, 119178 CrossRef CAS.
- G. Wang, J. Chen, Y. Li, J. Jia, P. Cai and Z. Wen, Chem. Commun., 2018, 54, 2603–2606 RSC.
- G. Wang and Z. Wen, Nanoscale, 2018, 10, 21087–21095 RSC.
- C.-Y. Cao, C.-Q. Chen, W. Li, W.-G. Song and W. Cai, ChemSusChem, 2010, 3, 1241–1244 CrossRef CAS PubMed.
- E. M. Nichols, J. J. Gallagher, C. Liu, Y. Su, J. Resasco, Y. Yu, Y. Sun, P. Yang, M. C. Y. Chang and C. J. Chang, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 11461–11466 CrossRef CAS PubMed.
- C. Liu, B. C. Colón, M. Ziesack, P. A. Silver and D. G. Nocera, Science, 2016, 352, 1210–1213 CrossRef CAS PubMed.
- C. Liu, K. K. Sakimoto, B. C. Colón, P. A. Silver and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6450–6455 CrossRef CAS PubMed.
- X. Gao, H. Xu, M. Baloda, A. S. Gurung, L.-P. Xu, T. Wang, X. Zhang and G. Liu, Biosens. Bioelectron., 2014, 54, 578–584 CrossRef CAS PubMed.
- X. Gao, L.-P. Xu, T. Wu, Y. Wen, X. Ma and X. Zhang, Talanta, 2016, 146, 648–654 CrossRef CAS PubMed.
- X. Gao and N. Wu, Electrochem. Soc. Interface, 2016, 25, 79–81 CrossRef CAS.
- X. Gao, P. Zheng, S. Kasani, S. Wu, F. Yang, S. Lewis, S. Nayeem, E. B. Engler-Chiurazzi, J. G. Wigginton, J. W. Simpkins and N. Wu, Anal. Chem., 2017, 89, 10104–10110 CrossRef CAS PubMed.
- X. Gao, L.-P. Xu, S.-F. Zhou, G. Liu and X. Zhang, Am. J. Biomed. Sci., 2014, 6, 41–57 CrossRef.
- X. Gao, J. Boryczka, P. Zheng, S. Kasani, F. Yang, E. B. Engler-Chiurazzi, J. W. Simpkins, J. G. Wigginton and N. Wu, Biosens. Bioelectron., 2021, 177, 112967 CrossRef CAS PubMed.
- X. Gao, J. Boryczka, S. Kasani and N. Wu, Anal. Chem., 2021, 93, 1326–1332 CrossRef CAS PubMed.
- P. Zheng, S. Kasani, W. Tan, J. Boryczka, X. Gao, F. Yang and N. Wu, Anal. Chim. Acta, 2022, 1203, 339721 CrossRef CAS PubMed.
- M. F. Lagadec and A. Grimaud, Nat. Mater., 2020, 19, 1140–1150 CrossRef CAS PubMed.
- J. Jin, K. Walczak, M. R. Singh, C. Karp, N. S. Lewis and C. Xiang, Energy Environ. Sci., 2014, 7, 3371–3380 RSC.
- D. V. Esposito, Joule, 2017, 1, 651–658 CrossRef CAS.
- S. Dresp, F. Dionigi, M. Klingenhof and P. Strasser, ACS Energy Lett., 2019, 4, 933–942 CrossRef CAS.
- W. Tong, M. Forster, F. Dionigi, S. Dresp, R. Sadeghi Erami, P. Strasser, A. J. Cowan and P. Farràs, Nat. Energy, 2020, 5, 367–377 CrossRef CAS.
- J. E. Bennett, Int. J. Hydrogen Energy, 1980, 5, 401–408 CrossRef CAS.
- M. A. Khan, T. Al-Attas, S. Roy, M. M. Rahman, N. Ghaffour, V. Thangadurai, S. Larter, J. Hu, P. M. Ajayan and M. G. Kibria, Energy Environ. Sci., 2021, 14, 4831–4839 RSC.
- J. N. Hausmann, R. Schlögl, P. W. Menezes and M. Driess, Energy Environ. Sci., 2021, 14, 3679–3685 RSC.
- L. Shi, R. Rossi, M. Son, D. M. Hall, M. A. Hickner, C. A. Gorski and B. E. Logan, Energy Environ. Sci., 2020, 13, 3138–3148 RSC.
-
T. F. O’Brien, T. V. Bommaraju and F. Hine, Handbook of Chlor-Alkali Technology, Springer, Boston, MA, USA, 2005 Search PubMed.
- C. K. Lim, Q. Liu, J. Zhou, Q. Sun and S. H. Chan, J. Power Sources, 2017, 342, 79–87 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Hanchen
Tian
*a,
Hanchen
Tian
 a,
Liang
Ma
ab,
Yi
Wang
a,
Xingbo
Liu
a,
Liang
Ma
ab,
Yi
Wang
a,
Xingbo
Liu
 a and
Xuefei
Gao
a and
Xuefei
Gao
 *c
*c
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h
000 h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h
000 h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h
000 h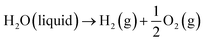

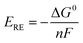
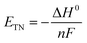

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(j)/dη = 2.303RT/αF
log(j)/dη = 2.303RT/αF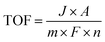
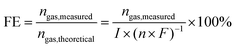
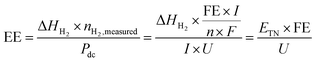




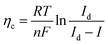
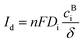





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe).251 When a magnetic field (higher than the coercivity) is applied to a ferromagnetic material, its magnetic moment will align along with the direction of magnetic field and thus the ferromagnetic ordering makes the material a spin polarizer and selective spin-filter for electron transfer during the catalytic reactions (Fig. 12a). Ferromagnetic CoFe2O4 (Fig. 12b) demonstrates a much higher electrocatalytic activity for the OER in 1 M KOH under a magnetic field. Furthermore, the enhanced activity of CoFe2O4 can remain even after the magnetic field is removed (Fig. 12c), as the magnetic moment can retain the aligned state in the magnetized CoFe2O4. When the magnetized CoFe2O4 is purposely demagnetized using an oscillating magnetic field, the OER performance of CoFe2O4 is reverted to the initial value without the application of a magnetic field. In contrast, both antiferromagnetic Co3O4 and paramagnetic IrO2 do not show a significant change in the OER performance with and without the application of a magnetic field. The Tafel slope of CoFe2O4 is changed from around 109 to 87.8 mV dec−1, indicating that the rate-determining step (RDS) of the first electron transfer from adsorbed OH− in the absence of a magnetic field is changed to a mixed RDS involving the first electron transfer step and second steps in the presence of a magnetic field (Fig. 12d). The magnetic enchantment effect on the OER performance of CoFe2O4 was observed at varying reaction temperatures. However, the positive influence of the magnetic field on the OER performance is decreased as the reaction temperature increases (Fig. 12e), because the arrangement of magnetic moments can be thermally disturbed. The ferromagnetic ordering in CoFe2O4 can be disturbed at elevated temperatures leading to a certain extent of demagnetization and hence reduced effect on the OER. Moreover, the OER current density of CoFe2O4 increases with the increase of the magnetic field intensity, as its magnetic moments become more orderly, while there is little change in the current density of Co3O4 and IrO2 with the increasing magnetic field strength. The possible effects of a magnetic field on MHD, improved mass transfer, and electrical conductivity were ruled out. No surface reconstruction (e.g., formation of cobalt oxyhydroxide) was found on CoFe2O4. The electron transfer at the catalytic interface depends on the transition probability related with the wavefunction integral between OH− and the active site. The extended X-ray absorption fine structure (EXAFS) reveals that only Co atoms in octahedral sites contribute to the effective ferromagnetic moment and are active sites. The orbitals of FM oxides create an intrinsically degenerate spin-polarized metallic state optimizing the wavefunction based on the inter-atomic reduction of the electron–electron repulsion (Fig. 12f). The theoretical computation demonstrates that there are stronger 3d–2p hybridization, FM ligand holes and higher spin density on the oxygen atoms for CoFe2O4 after the electron spin is aligned. These intrinsic properties can promote spin-selected charge transfer. Specifically, a dominant FM exchange between the ferromagnetic catalyst and adsorbed oxygen reactant species will take place with reduced electron–electron repulsion, inducing spin-dependent conductivity and decreasing the rate-limiting bonding energies, thus making the first electron transfer not the RDS. The spin selectivity effect can enhance the OER regardless of the single metal cation redox centre (i.e., ER-AEM) and lattice oxygen as active sites (Fig. 12g–h). The computed Pourbaix diagram implies that the surface of CoFe2O4 has an oxygen termination under the OER conditions. The reaction is initiated between a lattice oxygen on the surface and adsorbed oxygen species (OH−), and the first electron transfer step is regarded as O* + OH− → *OOH + e−. The CoFe2O4 with FM ligand hole can form oxygen termination with fixed spin direction and that first electron transfer step will induce the formation of triplet state intermediate OOH species that prefer to generate triplet O2 in a thermodynamically favoured pathway. In sharp contrast, for a reaction involving a non-magnetic reactant and product molecules such as methanol oxidation and ethylene glycol oxidation reactions, no magnetic effect was observed on CoFe2O4 as the reactants, intermediates, and products in these reactions are diamagnetic and there is no spin-selected electron transfer between the active metal site and adsorbed reaction species. Therefore, for the OER, the spin-polarized electron exchange between the ferromagnetic electrocatalyst and adsorbed oxygen species in the first electron transfer step takes place under the principle of spin angular momentum conservation, reducing the energy barrier for the generation of triplet O2 under the magnetic field.
000 Oe).251 When a magnetic field (higher than the coercivity) is applied to a ferromagnetic material, its magnetic moment will align along with the direction of magnetic field and thus the ferromagnetic ordering makes the material a spin polarizer and selective spin-filter for electron transfer during the catalytic reactions (Fig. 12a). Ferromagnetic CoFe2O4 (Fig. 12b) demonstrates a much higher electrocatalytic activity for the OER in 1 M KOH under a magnetic field. Furthermore, the enhanced activity of CoFe2O4 can remain even after the magnetic field is removed (Fig. 12c), as the magnetic moment can retain the aligned state in the magnetized CoFe2O4. When the magnetized CoFe2O4 is purposely demagnetized using an oscillating magnetic field, the OER performance of CoFe2O4 is reverted to the initial value without the application of a magnetic field. In contrast, both antiferromagnetic Co3O4 and paramagnetic IrO2 do not show a significant change in the OER performance with and without the application of a magnetic field. The Tafel slope of CoFe2O4 is changed from around 109 to 87.8 mV dec−1, indicating that the rate-determining step (RDS) of the first electron transfer from adsorbed OH− in the absence of a magnetic field is changed to a mixed RDS involving the first electron transfer step and second steps in the presence of a magnetic field (Fig. 12d). The magnetic enchantment effect on the OER performance of CoFe2O4 was observed at varying reaction temperatures. However, the positive influence of the magnetic field on the OER performance is decreased as the reaction temperature increases (Fig. 12e), because the arrangement of magnetic moments can be thermally disturbed. The ferromagnetic ordering in CoFe2O4 can be disturbed at elevated temperatures leading to a certain extent of demagnetization and hence reduced effect on the OER. Moreover, the OER current density of CoFe2O4 increases with the increase of the magnetic field intensity, as its magnetic moments become more orderly, while there is little change in the current density of Co3O4 and IrO2 with the increasing magnetic field strength. The possible effects of a magnetic field on MHD, improved mass transfer, and electrical conductivity were ruled out. No surface reconstruction (e.g., formation of cobalt oxyhydroxide) was found on CoFe2O4. The electron transfer at the catalytic interface depends on the transition probability related with the wavefunction integral between OH− and the active site. The extended X-ray absorption fine structure (EXAFS) reveals that only Co atoms in octahedral sites contribute to the effective ferromagnetic moment and are active sites. The orbitals of FM oxides create an intrinsically degenerate spin-polarized metallic state optimizing the wavefunction based on the inter-atomic reduction of the electron–electron repulsion (Fig. 12f). The theoretical computation demonstrates that there are stronger 3d–2p hybridization, FM ligand holes and higher spin density on the oxygen atoms for CoFe2O4 after the electron spin is aligned. These intrinsic properties can promote spin-selected charge transfer. Specifically, a dominant FM exchange between the ferromagnetic catalyst and adsorbed oxygen reactant species will take place with reduced electron–electron repulsion, inducing spin-dependent conductivity and decreasing the rate-limiting bonding energies, thus making the first electron transfer not the RDS. The spin selectivity effect can enhance the OER regardless of the single metal cation redox centre (i.e., ER-AEM) and lattice oxygen as active sites (Fig. 12g–h). The computed Pourbaix diagram implies that the surface of CoFe2O4 has an oxygen termination under the OER conditions. The reaction is initiated between a lattice oxygen on the surface and adsorbed oxygen species (OH−), and the first electron transfer step is regarded as O* + OH− → *OOH + e−. The CoFe2O4 with FM ligand hole can form oxygen termination with fixed spin direction and that first electron transfer step will induce the formation of triplet state intermediate OOH species that prefer to generate triplet O2 in a thermodynamically favoured pathway. In sharp contrast, for a reaction involving a non-magnetic reactant and product molecules such as methanol oxidation and ethylene glycol oxidation reactions, no magnetic effect was observed on CoFe2O4 as the reactants, intermediates, and products in these reactions are diamagnetic and there is no spin-selected electron transfer between the active metal site and adsorbed reaction species. Therefore, for the OER, the spin-polarized electron exchange between the ferromagnetic electrocatalyst and adsorbed oxygen species in the first electron transfer step takes place under the principle of spin angular momentum conservation, reducing the energy barrier for the generation of triplet O2 under the magnetic field.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe). (c) LSV curves of the CoFe2O4 electrocatalyst for OER with and without a magnetic field (10
000 Oe). (c) LSV curves of the CoFe2O4 electrocatalyst for OER with and without a magnetic field (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe), after the removal of the magnetic field (after M), and after demagnetization. (d) Tafel slope values of CoFe2O4, Co3O4 and IrO2 with and without a magnetic field at various temperatures. (e) The increase percentage of the current density for CoFe2O4, Co3O4 and IrO2 under the applied magnetic field with different intensities. (f) Schematic diagram of spin electron transfer. FM holes exist in the M–O bonds and lattice oxygen where the FM exchange occurs and enhances the spin-selective charge transfer, providing less electronic repulsion and adsorbed oxygen species a fixed spin direction. The spin polarization pathways for two OER mechanisms with active sites of (g) a metal cation centre and (h) lattice oxygen. Reproduced from ref. 251 with permission from Springer Nature under a CC BY 4.0 licence.
000 Oe), after the removal of the magnetic field (after M), and after demagnetization. (d) Tafel slope values of CoFe2O4, Co3O4 and IrO2 with and without a magnetic field at various temperatures. (e) The increase percentage of the current density for CoFe2O4, Co3O4 and IrO2 under the applied magnetic field with different intensities. (f) Schematic diagram of spin electron transfer. FM holes exist in the M–O bonds and lattice oxygen where the FM exchange occurs and enhances the spin-selective charge transfer, providing less electronic repulsion and adsorbed oxygen species a fixed spin direction. The spin polarization pathways for two OER mechanisms with active sites of (g) a metal cation centre and (h) lattice oxygen. Reproduced from ref. 251 with permission from Springer Nature under a CC BY 4.0 licence.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mA for 600
mA for 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s; then, the discharge profile of the NiOOH–Zn battery was also investigated with a current of 200
s; then, the discharge profile of the NiOOH–Zn battery was also investigated with a current of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mA. The inset of (b) is the cycle performance of the H2 production step (black line) and discharge step (red line) of the NiOOH–Zn battery with an applied current of 200
mA. The inset of (b) is the cycle performance of the H2 production step (black line) and discharge step (red line) of the NiOOH–Zn battery with an applied current of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mA. Step 1 requires a power input to produce H2 gas, whereas step 2′ can deliver energy to power other devices. Reproduced from ref. 289 with permission from Springer Nature under a CC BY 4.0 licence.
mA. Step 1 requires a power input to produce H2 gas, whereas step 2′ can deliver energy to power other devices. Reproduced from ref. 289 with permission from Springer Nature under a CC BY 4.0 licence.











