Open Access Article
Open Access ArticlePhoto-induced phase-transitions in complex solids
Sangeeta
Rajpurohit
 *,
Jacopo
Simoni
and
Liang Z.
Tan
*,
Jacopo
Simoni
and
Liang Z.
Tan

Molecular Foundry, Lawrence Berkeley National Laboratory, USA. E-mail: srajpurohit@lbl.gov
First published on 2nd November 2022
Abstract
Photo-induced phase-transitions (PIPTs) driven by highly cooperative interactions are of fundamental interest as they offer a way to tune and control material properties on ultrafast timescales. Due to strong correlations and interactions, complex quantum materials host several fascinating PIPTs such as light-induced charge density waves and ferroelectricity and have become a desirable setting for studying these PIPTs. A central issue in this field is the proper understanding of the underlying mechanisms driving the PIPTs. As these PIPTs are highly nonlinear processes and often involve multiple time and length scales, different theoretical approaches are often needed to understand the underlying mechanisms. In this review, we present a brief overview of PIPTs realized in complex materials, followed by a discussion of the available theoretical methods with selected examples of recent progress in understanding of the nonequilibrium pathways of PIPTs.
1. Introduction
Over the past few decades, advances in ultrafast science have resulted in promising routes to manipulate and control the properties of quantum materials on femtosecond timescales. Photo-induced phase-transitions (PIPTs) in complex solids have emerged as one of the most exciting fields in photonics and ultrafast science.1–4 These PIPTs on ultrafast timescales can be triggered by photo-induced nonthermal carrier populations or charge fluctuations, or also by direct optical excitation of phonon modes. Complex quantum materials such as transition-metal oxides and layered van der Waals systems belong to the class of materials with correlated electrons that interact with other degrees of freedom. Recent ultrafast studies of PIPTs in complex quantum materials have provided a new paradigm for controlling properties such as magnetism, metal–insulator transitions, ferroelectricity, etc.Here, we present a brief review of the recent progress in the field of ultrafast sciences, particularly PIPTs in complex systems. We present selected examples of experimental and theoretical studies of the photo-induced metal–insulator, magnetic, structural phase-transitions that illustrate the phenomenology of these PIPTs and how they can be understood in terms of their driving mechanisms and couplings between disparate degrees of freedom. For a broad review of progress in photoinduced phenomena in quantum materials, we refer to Torre et al.,4 and we refer to Koshihara et al. for a review experimental studies of PIPTs.5 An overview of PIPTs in charge-transfer organic salt is provided by Onda et al.6
2. Materials hosting PIPTs
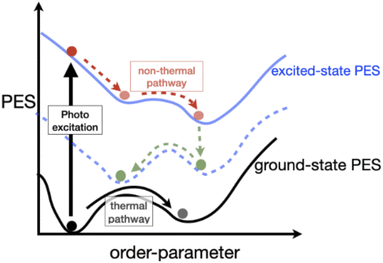
Complex quantum materials exhibit rich equilibrium phase diagrams as a result of the intimate coupling between electron, spin, and lattice degrees of freedom. The subtle balance among different interactions in these systems drives fascinating ordering phenomena such as magnetism, periodic lattice distortions, superconductivity, etc., resulting in several intriguing broken symmetry and exotic states. PIPTs can be broadly classified as those involving electronic, magnetic, or structural order parameters, or some combination thereof.Fig. 1 illustrates the physics of PIPTs. The light illumination excites electrons out of the ground state and drives the system into a new non-equilibrium state. This new state can be a transient state or a metastable state with a long lifetime. The excited system can also partially relax to a lower-energy configuration on the excited state potential energy surface. Unlike quasi-equilibrium phase-transitions driven by changes in temperature, pressure, and volume, PIPT are highly non-equilibrium in nature, and their study requires a different set of experimental and theoretical techniques. New phases emerge above threshold excitation fluences, at resonant excitation frequencies and at characteristic time scales. Compared to thermal phase-transitions, PIPTs occur at ultrafast timescales, and host out-of-equilibrium “hidden” phases, which remain unattainable under equilibrium conditions. Furthermore, the frequency- and polarization-sensitive coupling between the system and light opens possibilities for ultrafast manipulation and storage of information.
Recent ultrafast experimental studies have discovered phase-transition pathways between these symmetry-broken states.1–4 Moreover, selective modulation of electronic, lattice, and spin degrees with optical excitations disentangles their individual contribution to the formation of these states. Pump-probe spectroscopy with femtosecond lasers measures transient changes in the system induced by photoirradiation. Complementary experimental probes, such as time-resolved diffraction and angle resolved photoemission spectroscopy (ARPES) are available to monitor electronic, structural, and magnetic behavior during and after the PIPT.7–12
A prototypical example of an electronic PIPT is photo-induced charge density wave (CDW) melting or transformation. CDWs are characterized by simultaneous periodic modification of the electron density and lattice structure, driven by mechanisms such as Fermi-surface nesting, strong electron–phonon coupling, etc.13 The characteristic wavelengths of these CDW superlattices are 2–6 times the lattice constants with the coherent length scales of several nanometers.
Transition metal layered materials, such as 1T-TaS2 and RTe3, are typical hosts of PIPTs involving CDWs. The study of these materials in non-equilibrium states has led to a more detailed understanding of the mechanisms behind CDW formation,14–18 see Table 1. TbTe3 is a member of the RTe3 family known to host Fermi-surface nesting-driven CDW formation.19 The Fermi surface geometries in these systems includes large parallel sections that can be spanned by a single nesting vector q which induces an electronic instability towards band opening by adding new periodicity of charge density. The slight in-plane anisotropy in these systems makes the c-axis the preferred direction of the CDW order. Using time-resolved ARPES measurements, Schmitt et al.20 showed photo-induced closure of the band-gap at the Fermi level and hindered melting of CDW in TbTe3. The photoexcitation changes the electronic screening instantaneously which triggers ions dynamics towards a new potential minima in the presence of screening carriers. The longer timescales of the involved collective excited atomic vibrations explains the observed delay in the CDW melting and demonstrate the role of electron–phonon interaction in the origin of the CDW formation. A recent experimental pump-probe study on LaTe3 reported a PIPT in a symmetry-broken state where following the optical excitation, the CDW along the c-axis weakens and, subsequently, a different competing CDW along the a-axis appears.17 The nearly identical timescales of relaxation of this new CDW and re-establishment of the original CDW point to strong competition between the two orders due to the presence of topological defects, as suggested by a previous study,18 which suppresses the recovery of the original long-range CDW.
| Material (initial phase) | Electronic/magnetic PIPT | Structural PIPT | Hidden-phases |
|---|---|---|---|
| VO2 (monoclinic phase) | Insulator-to-metal at 800 nm; 2–9 mJ cm−2 (ref. 37) | Monoclinic-to-rutile at 800 nm; > 9 mJ cm−2 (ref. 37) | Monoclinic-metallic at 800 nm; between 2–9 mJ cm−2 (ref. 37) |
| 1T-TaS2 (SD-phase) | CDW-melting at 1.50 eV (50 fs pulse); 0.1 electrons/SD25 | PLD-melting at 790 nm (30 fs pulse); 0.5 mJ cm−2 (ref. 71) | Metallic-CDW at 800 nm (50 fs pulse); 1 mJ cm−2 (ref. 14) |
| RTe3 (R = Tb, La) (CDW along c-axis) | CDW-melting at 1.50 eV (50 fs pulse); 2 mJ cm−2 (ref. 20) | New CDW along a-axis at 800 nm (50 fs pulse); between 10–12 mJ cm−2 (ref. 17) | |
| RR′MnO3 (AFM & CO–OO) | AFM-to-FM at 1.55 eV (50 fs pulse); 5.8 mJ cm−2 (ref. 40) | Pbnm-to-P21m at 800 nm (55 fs pulse); > 4 mJ cm−2 (ref. 72) | Ferromagnetic-metallic at 800 nm/(30–50 shots); between 2–5 mJ cm−2 (ref. 32) |
| (EDO-TTF)2PF6 (organic salt) (0, +1, +1, 0) charge-distribution | Insulator-to-metal; (0, +1, +1, 0)-to-(0.5, 0.5, 0.5, 0.5) charge-distribution73 | New CO with (+1, 0, +1, 0) charge-distribution6,64 |
In other PIPTs, CDW formation is associated with insulator–metal transitions (IMT). 1T-TaS2 exhibits a metallic phase (T-state) with an undistorted crystal structure at high temperature and several commensurate and non-commensurate CDWs with decreasing temperature, including the well-known low-temperature Star-of-David (SD) type pattern; see Fig. 2-top. Previous theories suggesting that the low-temperature insulating CDW phase is Mott physics driven have been challenged by recent studies that emphasize the role of orbital ordering intertwined with CDW and their out-of-plane stacking.21–23 Ultrafast pump-probe studies reveal photo-induced IMT to a new metastable hidden CDW state (HCDW), which has a metallic character14–16 The IMT may be linked to the switching between these metastable states. A recent time-resolved XRD study identified the formation and breaking of interlayer dimer bonds between SD clusters24 as a driving mechanism of the phase-transition to the metallic hidden state. This is in agreement with earlier experimental work suggesting ultrafast electronic timescales, involving charge and orbital degrees of freedom, for phase-transitions.14,25–31
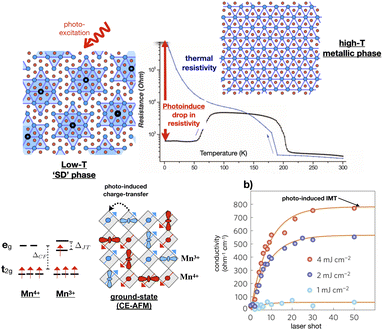 | ||
| Fig. 2 (Top) Optical resistive switching in 1T-TaS2. The graph in center shows change in resistivity with temperature is shown in blue. The photoexcitation in low-temperature ‘SD’ phase reduces the resistivity, indicated in red arrow, by orders of magnitude. This figure has been adapted/reproduced from ref. 14 with permission from AAAS, copyright 2014. (Bottom) The graph indicates step-like rise in conductivity in strain-engineered thin film of La2/3Ca1/3MnO3 on photoexcitation at 80 K corresponding to IMT. The CO, SO and OO pattern of La2/3Ca1/3MnO3 is shown in the left. Spin up and down Mn sites are indicated in blue and red. This figure has been adapted/reproduced from ref. 32 with permission from Springer, copyright 2016. | ||
Instead of being accompanied by CDWs, photo-induced IMTs can also be accompanied by structural phase-transitions. In VO2, the photo-induced IMT is a transition from the dimerized low-T monoclinic phase to the rutile phase of high-T.33–35 However, the connection between these two phase-transitions and the underlying mechanism remains unclear. Following early work showing photoexcitation as another route to initiate IMT in VO2,36 several ultrafast experimental attempts have been made to disentangle the lattice and electronic contributions in the transition. These experiments suggest a slow photo-induced IMT on picosecond time scales involving optical phonons, hinting at the lattice-assisted Peierls-type mechanism.33–35 Recently, it has been suggested37 that the change in crystal symmetry in the IMT above the threshold fluence occurs on the picosecond time scale, which is in agreement with earlier studies,33–35 this is due to a displacive transition in which all atoms collaboratively reshuffle themselves in the displacive mode. However, an analysis of X-ray scattering data, including the diffuse continuum,38 suggests that the transition is a result of an order-disorder transition, where the atoms move from the low- to the high-symmetry structure in a spatially incoherent manner.
The involvement of the spin degree of freedom further enriches the phenomenology of PIPTs. This is exemplified in strongly correlated transition-metal oxides, such as manganites and nickelates. While multiple-order parameters, linked to structural, electronic, and magnetic degrees of freedom, are already present during thermal phase-transitions, the selective perturbation of these order parameters through optical excitations leads to new types of transformations.32,39–44 In the Weyl semimetal system WTe2, shear strain is coupled to ultrafast switching of topological invariants.12 The form of the PIPTs depends sensitively on the details of the materials system. Ground state antiferromagnetic (AFM) insulating phase exhibiting long-range charge-order (CO) and orbital-order (OO) is transformed to a long-lived metastable hidden metallic phase by resonantly exciting intersite Mn3+ → Mn4+ transitions in a strain-engineered La2/3Ca1/3MnO3,32 see Fig. 2-bottom. The Mn3+ → Mn4+ excitations-driven relaxation of Jahn–Teller modes changes the lattice symmetry and affects the exchange-integral, which preserves the itinerancy of Mn-d electrons. In comparison, AFM order is transformed to ferromagnetic (FM) order above threshold excitation fluence in Pr0.7Ca0.3MnO3, attributed to fast non-equilibrium spin canting on shorter timescales than Jahn–Teller and breathing phonon periods.40
Even in laser-induced demagnetization processes which involve only the change of a single magnetic order parameter, the mechanism can potentially involve many other degrees of freedom. The processes of non-thermal laser-induced demagnetization can be distinguished between photomagnetic where the photons excite the electrons to states that have a direct influence on the magnetic properties; and optomagnetic where the magnetization change is induced by a Raman type mechanism.
Following the first experimental observation of laser-driven change of the magnetic state in ferromagnetic nickel,47 the ultrafast control of the magnetic state has been achieved not only in the case of ferromagnetic and ferrimagnetic metals, but also in the case of ferromagnetic semiconductors48 and dielectrics.49
Nonetheless, there is still uncertainty on the mechanism ultimately responsible for the laser-induced change of magnetic state on such a short time scale and several different driving forces have been proposed. These can be classified in at least three main categories, (a) out of equilibrium modification of the electronic and magnetic correlations;50,51 (b) relativistic effects and direct coupling between spins and laser;52 (c) coupling to lattice or magnon degrees of freedom.53,54 In general, many of these effects could be at play at the same time and the observed demagnetization is the result of their combined effect making the numerical modeling of the phenomenon extremely complex to carry out.
Many experiments have confirmed that laser-induced demagnetization in ferromagnetic transition metals takes place on a time scale of the order of approximately 500 fs or less.50,55 This has been demonstrated in the case of CoPt3,56 thin Fe and Ni films.57,58 In all these experiments the process was followed by radiation emission in the terahertz range.
Carrier induced ferromagnetism in semiconductors, that is caused by the magnetic exchange interaction between localized spins and the itinerant charge carriers (sp–d exchange interaction), provides an interesting alternative to the metallic ferromagnets for magnetization control.59 One of the first observations of photo-induced demagnetization in semiconductors was reported in the case of GaMnAs,60 but it occurred on a time scale of 1 ns. More recently demagnetization on a time scale of 1 ps was reported in the case of InMnAs by using combined terahertz and infrared excitations.61 In the case of ferrimagnetic garnet films, instead, optical control of the magnetization was shown to be possible on a time scale as short as few hundreds femtoseconds.49
Besides inorganic solids, several organic molecular complexes are also known to host PIPTs, for example, charge transfer (CT) molecular complexes.6,62–67 The CT complexes belong to the class of strongly-correlated organic crystals which consist of two types of π-conjugated molecules: an electron donor and an electron acceptor. Increased electronic interactions due to small overlap between π-orbitals of constituent donor and acceptor molecules make these strongly-correlated materials. The PIPT was first discovered in CT organic TTF-CA (tetrathiafulvalene-p-chloranil),6,68,69 which consists of chains of alternating electron-donor TTF and electron-acceptor CA molecules. The CT during photoexcitation in TTF-CA drives a PIPT which involves switching from a neutral to an ionic state.62 (EDO-TTF)2PF6 is another organic CT salt with strong el–el and el–ph coupling that exhibits a PIPT.70 In this system, EDO-TTF is a donor and PF6 is an acceptor. (EDO-TTF)2PF6 has a low-temperature insulating phase with a (0, +1, +1, 0) charge-distribution where ‘+1’ indicates a hole on the EDO-TTF molecule and ‘O’ means a neutral EDO-TTF molecule. At room temperature, the system is metallic where EDO-TTF carries an average charge of +0.5. This system exhibits a photoinduced hidden-phase with a (+1, 0, +1, 0) charge-distribution. This photoinduced hidden phase is driven by strong el–el interactions and cannot be achieved in thermal equilibrium.6,64 As another example, reflection-type femtosecond pump-probe spectroscopy was used to detect photoinduced melting of the spin-Peierls phase in the organic spin-Peierls alkali (M = K, Na)-tetracyanoquinodimethane (TCNQ) complexes.63
3. Theoretical descriptions of PIPTs
Technological applications of PIPTs require predictive descriptions based on clear understanding of the underlying pathways. These pathways involve a wide range of time scales (Fig. 3), from femtosecond light absorption electronic screening, to initial phonon dynamics on subpicosecond timescales, and to subsequent relaxation that sometimes last up to the order of nanoseconds. There is no single theoretical approach which can describe the evolution of the excitations covering all these time scales. In particular, in systems with strong correlations, predictive descriptions of PIPTs become more challenging. Here, we give a brief overview of the existing theoretical methods to study nonthermal dynamics, particularly PIPTs that are mainly driven by quantum effects. Fig. 3 illustrates the timescales of the physical processes involved in PIPTs and the appropriate theoretical methods used to study these processes. A wide range of explicit time-dependent theoretical methods, such as dynamical mean-field theory (DMFT), density-matrix renormalization group DMRG, and time-dependent density functional theory (TDDFT), are employed for out-of-equilibrium treatment of ultrafast processes.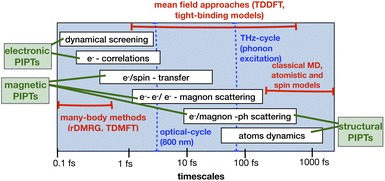 | ||
| Fig. 3 Timescales of elementary excitations and decay processes in complex quantum materials. The blue dashed lines indicate the time-period of single-cycle of optical pulse and THz electric field which excites electrons and phonons, respectively. This figure has been adapted/reproduced from ref. 45 and 46 with permissions from Elsevier and John Wiley and Sons, copyrights 1997 and 2012. | ||
The t-DMFT and t-DMRG approaches take into account many-particle effects and have been successful in describing PIPTs driven purely by strong electronic correlations and screening effects, such as the IMT in Mott insulators and excitonic insulators. The basic idea behind DMFT74 is to explicitly consider correlations within a local region while treating all non-local effects with dynamical mean-field to include quantum fluctuations.74 The remaining local problem then becomes a so-called quantum-impurity problem. The non-equilibrium extension of this approach, t-DMFT, has recently been applied to the study of PIPTs.75–77
t-DMFT has revealed a photoinduced hidden phase with a new orbital-order polarization in photoexcited KCuFe3 (Fig. 4-bottom). Within a 2-band Hubbard model, it as shown that the pathway to this hidden state relies on a non-thermal partial melting of the intertwined spin and orbital orders by photoinduced charge excitations in the presence of strong spin–orbital exchange interactions.79 Another non-equilibrium DMFT study with the Hubbard–Holstein model showed an ultrafast Mott-IM phase-transition induced by optical excitation of coherent phonon modes. The model revealed that nonlinear electron–phonon coupling is essential for this process.80 While this approach has been successful for few-level models, the solution of the non-equilibrium quantum impurity problem is expected to become increasingly challenging as more states are added to the problem.
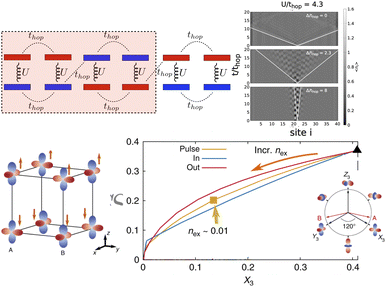 | ||
| Fig. 4 (Top) Long-lived local excitations in a dimerized chain induced by optical excitation, simulated with t-DMRG. (Top-left) Unit-cell with four-sites. (Top-right) Evolution of electron density after local excitation for different values of Δ/thop, where thop and Δ is hopping and onsite Hund's splitting between opposite spin–orbitals, in a chain with 40 lattice sites. The local excitations are long lived at small Δ/thop but spread with a “light-cone effect” at large Δ/thop. This figure has been adapted/reproduced from ref. 78 with permission from APS, copyright 2018. (Bottom) t-DMFT study showing photo-induced hidden-phase with new OO polarization in KCuF3. (Bottom-left) SO and OO in the equilibrium state. Linear combinations of eg-states |θ〉. (Bottom-right) Evolution of the total spin Sz component and OO, defined as the occupation difference X3 = 1/2(n2 − n1) between two eg-orbitals, in the long-time limit under three different non-equilibrium protocols, that is electric-field pulse (solid-pink), photo-doping electrons in (solid-yellow) and out (solid-blue). The inset shows the Z1–Z3 plane in the orbital pseudospin space. The X3, Y3, Z3 directions and their corresponding orbitals are marked. This figure has been adapted/reproduced from ref. 79 with permission from Springer, copyright 2018. | ||
The t-DMRG is a time-dependent extension of the original DMRG method to study non-equilibrium processes.81–84 Based on Schmidt decomposition, where the system is divided into two blocks A and B, the equilibrium DMRG method85–88 approximates the ground-state wave function as
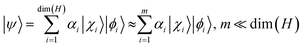 | (1) |
t-DMRG has been applied to PIPTs where electronic correlation plays a crucial role in the photoexcited state, such as photoexcitation of one-dimensional interacting fermions in periodic magnetic and ionic microstructures.89 With magnetic microstructures, the spin-selective photo-excitation weakens the original spin density pattern and a periodic charge modulation is induced. On the other hand, with ionic potentials the periodic charge density pattern starts melting, and a periodic modulation of the spin densities is induced. Similarly, long-lived bound excitations have been shown to emerge in the photoexcitated state of a one-dimensional dimerized chain with Coulomb interactions.78Fig. 4-top shows that the value of Δ/thop, where Δ is the Hund's splitting, controls the velocity of the spread of the excitation is seen to decrease, and hence their lifetime. The study suggests that the underlying AFM magnetic microstructure causes an increase in the relaxation times of excitations.
The application of t-DMRG to realistic systems with electron–phonon coupling has been broadly successful,90,91 with examples such as the study of carrier mobilities in organic semiconductors92 or large-scale excitonic dynamics in a system with electronic states coupled to hundreds of nuclear vibrations.93 Although the t-DMRG approach is flexible and can be applied to a wide variety of electronic models known for their quantum many-body effects, the approach is restricted mainly to one-dimensional systems. For higher dimensions, the presence of intrinsic quantum entanglement makes the truncation scheme unfavorable, restricting the accessible system size and accuracy.
In complex materials, not only are electronic correlations strong, but electron–phonon interactions can often play an important role as well. In the typical PIPT scenario involving electron–phonon coupling, photoexcitation first induces rapid changes in the electronic structure, followed by modification of the lattice structure to stabilize the new electronic order. As PIPTs in such systems involve large time and length scales of phonon modes, studying them with highly accurate many-body approaches discussed above is computationally unfeasible. Instead, their description involves different electronic, magnetic, and lattice pathways over long spatial and temporal scales. Several mean-field methods incorporating electron–phonon interactions have been developed for non-equilibrium phenomena in solids at reduced computational cost with good accuracy.
Real-time Time Dependent Density Functional Theory95,96 (rt-TDDFT) is the time dependent extension of Density Functional Theory (DFT).97,98 This is a mean field approach where electrons individually interact with the rest of the electronic system by means of an effective scalar potential, the Kohn–Sham (KS) potential vKS. The single particle electronic wave functions are evolved according to the following set of KS equations
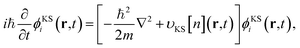 | (2) |
| υKS[n](r, t) = υH[n](r, t) + υxc[n](r, t) + υext(r, t). | (3) |
The exact TDDFT xc-potential υxc depends on the initial interacting and Kohn–Sham states (initial-state dependence) and the density at all previous times (memory).99 However, most TDDFT studies use the adiabatic approximation, where one assumes that the xc-potential reacts instantaneously and without memory to any temporal change in the charge density. This adiabatic approximation to the xc-potential fails to capture several photophysical and chemical processes.100–102 Several attempts that goes beyond the adiabatic approximation, including the time-dependent current density functional theory (TDCDFT),103,104 time-dependent deformation functional theory (TDDefFT)105,106etc., have been made to include memory effects in the xc-potential. Recently, the linear-response TDDFT nonadiabatic XC potential (XC kernel) was calculated with DMFT for spin-independent and spin-dependent cases.50,107 In these studies, the kernels were derived from the DMFT charge and spin susceptibilities, respectively.
The simplest rt-TDDFT approach ignores ion dynamics while evolving the electron wavefunctions according to the quantum mechanical equations of motion. Such an approach is suitable only for a time scale of the order of a hundred femtoseconds when the atomic displacements can be approximated to be small. For this reason rt-TDDFT simulations have been widely applied to study the ultrafast magnetization dynamics in transition metal ferromagnets,108–110 Heusler alloys111 and anti-ferromagnets.112 In order to reproduce these phenomena the basic rt-TDDFT eqn (2) and (3) are written in spinorial form to account for spin non-collinearity.113
Ab initio molecular dynamics (MD) can be divided in two main classes, namely the adiabatic and the non adiabatic approaches. Both classes of methods treat the electrons quantum mechanically, while the atoms obey the Newton's laws of motion.
The adiabatic methods are based on the so-called Born–Oppenheimer approximation.114 This approximation assumes that due to the difference in mass between the electrons and the ions the electronic dynamics occurs on a much faster time scale compared to the ionic one. At this level of approximation the electrons follow adiabatically the atom dynamics, however effects like atomic induced electronic excitation are neglected. For this reason the approach has limitations that become particularly relevant in the description of out of equilibrium processes typical of PIPTs. To this class belongs approaches like Born Oppenheimer quantum MD that have been employed to study non-thermal PIPTs in semiconducting systems like silicon and germanium115–119 and Car–Parrinello MD.120 The main limitation of the adiabatic approaches comes from the assumption that the potential field on which the atoms move can be approximated with the ground state electron energy surface. The introduction of non adiabatic effects in the atomic motion has been hotly debated for many decades.121 In general the atomic motion can induce transitions between adiabatic states, in turn, electronic excitation induces back-action on the atoms. These effects are particularly important in the case of PIPTs when the electronic subsystem is highly excited by the application of the laser field. The two most important non-adiabatic methods are (a) Ehrenfest quantum MD122,123 and (b) trajectory surface hopping method.124
Here we focus on Ehrenfest MD that is mostly used in the case of solids. This approach is based on the solution of two sets of coupled equations
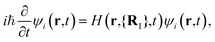 | (4) |
MI![[R with combining umlaut]](https://www.rsc.org/images/entities/b_char_0052_0308.gif) I = −∇IE[ρ(r, t)]. I = −∇IE[ρ(r, t)]. | (5) |
rt-TDDFT combined with Ehrenfest dynamics has been employed to study the ultrafast melting of silicon,125 photoexcitation induced charge density waves,94 PIPTs in transition-metal dichalcogenides126 and semiconductors.127 rt-TDDFT has been used126 to study the electronic and structural dynamics following photo-excitation in the low temperature IrTe2 phase which exhibits a periodic lattice distortion. Their study reveals that the microscopic force that initiates the photo-induced structural dynamics and phase-transition in IrTe2 originates from partial relaxation of the excited electrons of the anti-bonding states of the Ir–Ir dimer in the conduction band by lowering their energy levels.
A rt-TDDFT study of TaS2 revealed melting of the CDW and ‘SD’ pattern in photo-induced TaS2 on femtosecond time scales, see Fig. 5. The study further suggests that such photo-induced melting of the ‘SD’ pattern cannot be explained by the hot electron model, as it is driven by collective mode excitation due to intrinsic electron–nuclei coupled dynamics. A new photo-induced transient metallic state was found with spatially ordered atomic structures, different from ‘SD’ pattern.
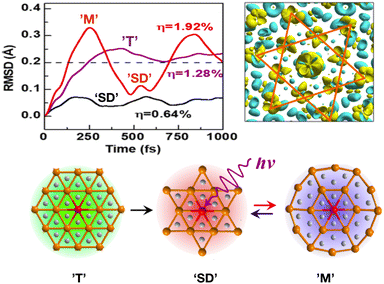 | ||
| Fig. 5 rt-TDDFT study of photo-induced melting of ‘Star-of-Davidson’ (SD) pattern in TaS2. (Top-left) Root mean square distance (RMSD) under three laser intensities, η = 0.64% (black), η = 1.28% (pink) and η = 1.92% (red). The system retains original SD structure at η = 0.64%, but exhibits photo-induced metallic state ‘T’ at η = 1.28%. At high intensity η = 1.92%, the periodic oscillations suggests a new photo-induced transient metallic state ‘M’ with a new spatially-ordered atomic distortions. (Top-right) Light-induced charge-density redistribution at t = 25 fs where yellow region shows increased density. (Bottom) Nature of ‘SD’, ‘T’ and ‘M’ states. This figure has been adapted/reproduced from ref. 94 with permission from ACS, copyright 2019. | ||
An important limitation of most non-adiabatic molecular dynamics methods is the classical treatment of atoms and the inadequate description of quantum coherence and decoherence effects.128 For example, theoretical studies of photoexcited state dynamics with full quantum-mechanical treatment of the electrons and atoms highlight the importance of nonadiabatic transitions between vibronic states in the photoinduced cooperative phenomena.129 Ehrenfest dynamics completely neglects quantum entanglement between the classical and quantum degrees of freedom, while the independent classical-trajectories in the original surface hopping method suffers from artificial overcoherence.124 To address these issues, several methods have been proposed to add decoherence in the original surface-hopping scheme.130,131
Besides the ab initio rt-TDDFT approach, the mean-field treatment of model Hamiltonians have also been successful in understanding the ultrafast response that take place during PIPTs. One approach is to build an effective tight-binding model with charge, spin, orbital and lattice degrees of freedom explicitly included, and with all relevant interactions such as Coulomb interactions, electron–phonon coupling, Hund's coupling etc.132,133 (Fig. 6). Such models are required for PIPTs which involve multiple order parameters. This study revealed melting of charge, orbital and lattice distortion in half-doped manganite Pr1/2Ca1/2MnO3 above a threshold fluence leading to a photoinduced metallic FM state. The emergence of FM order is attributed to optically induced spin-transfer (OISTR) between antiferromagnetically aligned ferromagnetic Mn chains. Such models aim to describe physics close to the Fermi level with good accuracy and scale well for calculations of large systems. In the field of ultrafast magnetization, model Hamiltonians with non-collinear magnetic moments, spin–orbit coupling, and electron–phonon coupling have been used to simulate photo-induced demagnetization.134
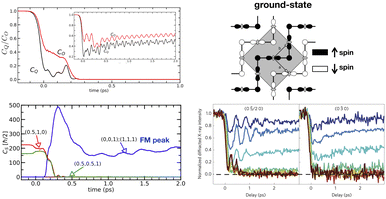 | ||
| Fig. 6 Tight-binding model study of photo-induced FM-metallic phase in CO and OO antiferromagnetic Pr1/2Ca1/2MnO3. (Right-top) CO, SO, and OO in equilibrium state. (Left-top) Evolution of CO and OO peak as at high and low (inset) fluence value. For higher fluences, CO and OO melt. (Left-bottom) Melting of the original SO (corresponding magnetic peaks are in green and red) and photo-induced FM order. (Right-bottom) Experimentally study showing melting of CO (left) and OO (right) at high fluences. This figure has been adapted/reproduced from ref. 72 and 132 with permissions from Springer and APS, copyrights 2014 and 2020. | ||
As an example of an application that accesses longer length scales, ultrafast generation of skyrmions was investigated within a 2-band electronic model with Rashba spin–orbit coupling to a Heisenberg spin model. It was shown that the spin–orbit coupling was the primary mechanism for the generation of these topological defects.135
In some PIPTs, the coupling between electrons and spins, or between electrons and phonons, only serves as an energy loss or decoherence mechanism instead of generating multiple order parameters. For such PIPTs, it suffices to include these couplings as an implicit dissipative effect. The femtosecond dynamics of magnetization in ferromagnetic semiconductors136 was studied using the Lindblad equation of motion.
| i∂t〈ρ〉 = 〈[ρ, H(t)]〉 + i∂t〈ρ〉|relax | (6) |
Purely atomistic models with only ionic degrees of freedom can be used to explain PIPTs that involve only structural order parameters. For example, using a time-dependent atomistic model that embodies all the relevant phonon modes in manganites, it was explained in ref. 72 that the melting of the original charge- and orbital-order together with Jahn–Teller distortions. In this study, the coupling between the experimentally determined time-dependent order parameter η(t), defined as the evolving electronic energy density, and the phonon modes is used in the atomistic model to induce structural dynamics. The optical pulse changes η(t) that induced coherent oscillations of atomic motions.
Finally, two (2TM) and three (3TM) temperature models are often employed to capture the non-equilibrium and relaxation dynamics after the PIPT for a few hundreds of picoseconds and beyond. The 2TM model137,138 is based on the assumption that the electrons and lattice subsystems have well defined temperatures after the first few hundreds femtoseconds of dynamics and that only one parameter is required to model their energy exchange (the electron–phonon relaxation rate). An alternative here is given by extensions to the TTM based on the Boltzmann equation with the inclusion of additional effects like the electron drifting.139 In the case of magnetic systems the Landau–Lifshitz–Gilbert (LLG) equation is usually employed to evolve the spin degrees of freedom. The 3TM is based on the same idea of the 2TM but extended to the case of magnetic systems.140 The energy is here allowed to flow between all three subsystems electron, lattice, and spin. A related approach involves the use of DFT with photoinduced carrier populations modeled by Fermi–Dirac distributions, to approximate excited state energy surfaces.141
4. Summary and future outlook
Ultrafast light-induced processes present a promising new frontier to create exotic quantum phases that are unattainable under equilibrium conditions. In this review, we provide a brief overview of recent experimental and theoretical advances in ultrafast science, especially in PIPTs. The examples discussed in the review illustrate the potential of PIPTs for tailoring material properties on ultrafast timescales. With the development of X-ray free electron lasers, future time-resolved inelastic resonant scattering (RIXS) techniques142 of optically excited quantum systems with strong correlations and interactions have the potential to probe several low-energy quasiparticles such as phonons,143 magnons,144,145 spinons,146 plasmons, excitons, charge excitations147etc., covering a wide range of momentum and energy transfers. Recent experimental studies with ultrafast electron diffraction (UED)148–151 have revealed transient electronic and lattice dynamics in materials at an atomic scale. These studies show that electron pulses have become a promising alternative to light and X-rays as an ultrafast probe152 to investigate ultrafast dynamics at unprecedented resolution. The recently developed time-resolved photoemission electron microscopy (TR-PEEM) is a powerful tool to visualize ultra-fast changes in materials with a temporal and spatial resolution of a few femtoseconds and nanometers.153,154 TR-PEEM has been applied to studying surface plasmon dynamics155 and photo-excited carrier dynamics in semiconductors.156,157Experimental evidence of Floquet–Bloch bands in topological insulators suggests Floquet engineering as a promising way to tailor properties.158,159 Recent observation of light-induced tuning of moiré patterns in layered van der Waals systems160,175 shows another example of tuning electronic and structural properties on ultrafast timescales. Another developing area of research in ultrafast sciences is photo-induced superconductivity motivated by the recent observation of transient superconductivity in light-induced materials that are non-superconducting in the equilibrium phase.1,161
On the theoretical side, while there has been substantial progress in recent years, new practical computational schemes for accessing large temporal and spatial scales are highly desirable. Although TDDFT is formally an exact theory, the adiabatic description of exchange and correlation has limitations, and better approximations for exchange-correlation functionals need to be developed.162 As we have seen, the rt-TDDFT approach with Ehrenfest dynamics is sufficient for describing some PIPTs. However, there are highly non-adiabatic photo-induced processes where the ground- and excited state PES are markedly different, such as non-radiative recombination and charge transfer. PIPTs which involve such behavior will likely require beyond-Ehrenfest methods.163–165 PIPTs which span multiple time scales may require proper treatment of ultrafast excitation as well as thermalization processes; the latter is another shortcoming of the Ehrenfest method.166 Surface hopping methods124,167,168 and their variants169–171 are a possible alternative for modeling PIPTs with greater precision. The balance of accuracy and computational efficacy is an important consideration in applying these algorithms to extended systems.
Approximations to TDDFT, such as time-dependent tight-binding,172,173 and other ab initio-based Hamiltonian models which include exchange and correlation effects, scale well for larger systems and are potential methods for studying correlated materials on longer time and length scales.132,133,135 A point of consideration is in the proper parameterization of such models from ab initio-based methods – if only data from ground state calculations are used in the parameterization, there is a possibility for errors to arise in the excited state PES. Likewise, basis set choices that are appropriate for the ground state could potentially be inadequate for the excited state if there is sufficient electronic delocalization during the excitation process. Unlike the use of maximally localized Wannier functions174 for ground state tight-binding, a canonical approach to parameterizing excited state tight-binding models, particularly for PIPTs, is not currently available.
While significant progress has been made in ultrafast science, there is still great scope for improvements in experimental techniques, development of theoretical methods, and exploration of new forms of PIPTs. This will deepen our understanding of non-equilibrium physics and will offer a comprehensive understanding of the nonthermal pathways of photo-induced phase-transitions in complex quantum materials.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
S. R. was supported by the Computational Materials Sciences Program funded by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. L. Z. T. and J. S. were supported by the Molecular Foundry, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.References
- D. Fausti, R. I. Tobey, N. Dean, S. Kaiser, A. Dienst, M. C. Hoffmann, S. Pyon, T. Takayama, H. Takagi and A. Cavalleri, Science, 2011, 331, 189, DOI:10.1126/science.1197294.
- C. Giannetti, M. Capone, D. Fausti, M. Fabrizio, F. Parmigiani and D. Mihailovic, Adv. Phys., 2016, 65, 58, arXiv:1601.07204 [cond-mat.supr-con] Search PubMed.
- B. Keimer and J. E. Moore, Nat. Phys., 2017, 13, 1045 Search PubMed.
- A. de la Torre, D. M. Kennes, M. Claassen, S. Gerber, J. W. McIver and M. A. Sentef, Rev. Mod. Phys., 2021, 93, 041002 CrossRef CAS.
- S. Koshihara, T. Ishikawa, Y. Okimoto, K. Onda, R. Fukaya, M. Hada, Y. Hayashi, S. Ishihara and T. Luty, Challenges for developing photo-induced phase transition (PIPT) systems: from classical (incoherent) to quantum (coherent) control of PIPT dynamics, Phys. Rep., 2022, 942, 1 CrossRef.
- K. Onda, H. Yamochi and S.-y. Koshihara, Acc. Chem. Res., 2014, 47, 3494 CrossRef CAS PubMed.
- C. W. Siders, A. Cavalleri, K. Sokolowski-Tinten, C. Tóth, T. Guo, M. Kammler, M. H. von Hoegen, K. R. Wilson, D. von der Linde and C. P. J. Barty, Science, 1999, 286, 1340, DOI:10.1126/science.286.5443.1340.
- A. Damascelli, Z. Hussain and Z.-X. Shen, Rev. Mod. Phys., 2003, 75, 473 CrossRef CAS.
- K. Sokolowski-Tinten, C. Blome, J. Blums, A. Cavalleri, C. Dietrich, A. Tarasevitch, I. Uschmann, E. Förster, M. Kammler, M. Horn-von-Hoegen and D. von der Linde, Nature, 2003, 422, 287 CrossRef CAS PubMed.
- D. M. Fritz, D. A. Reis, B. Adams, R. A. Akre, J. Arthur, C. Blome, P. H. Bucksbaum, A. L. Cavalieri, S. Engemann, S. Fahy, R. W. Falcone, P. H. Fuoss, K. J. Gaffney, M. J. George, J. Hajdu, M. P. Hertlein, P. B. Hillyard, M. H. von Hoegen, M. Kammler, J. Kaspar, R. Kienberger, P. Krejcik, S. H. Lee, A. M. Lindenberg, B. McFarland, D. Meyer, T. Montagne, E. D. Murray, A. J. Nelson, M. Nicoul, R. Pahl, J. Rudati, H. Schlarb, D. P. Siddons, K. Sokolowski-Tinten, T. Tschentscher, D. von der Linde and J. B. Hastings, Science, 2007, 315, 633, DOI:10.1126/science.1135009.
- N. Gedik, D.-S. Yang, G. Logvenov, I. Bozovic and A. H. Zewail, Science, 2007, 316, 425 CrossRef CAS PubMed.
- E. J. Sie, T. Rohwer, C. Lee and N. Gedik, Nat. Commun., 2019, 10, 3535 CrossRef PubMed.
- K. Rossnagel, J. Phys.: Condens. Matter, 2011, 23, 213001 CrossRef CAS PubMed.
- L. Stojchevska, I. Vaskivskyi, T. Mertelj, P. Kusar, D. Svetin, S. Brazovskii and D. Mihailovic, Science, 2014, 344, 177 CrossRef CAS PubMed.
- I. Vaskivskyi, J. Gospodaric, S. Brazovskii, D. Svetin, P. Sutar, E. Goreshnik, I. A. Mihailovic, T. Mertelj and D. Mihailovic, Sci. Adv., 2015, 1, e1500168, DOI:10.1126/sciadv.1500168.
- M. J. Hollander, Y. Liu, W.-J. Lu, L.-J. Li, Y.-P. Sun, J. A. Robinson and S. Datta, Nano Lett., 2015, 15, 1861 CrossRef CAS PubMed.
- A. Kogar, A. Zong, P. E. Dolgirev, X. Shen, J. Straquadine, Y.-Q. Bie, X. Wang, T. Rohwer, I. C. Tung, Y. Yang, R. Li, J. Yang, S. Weathersby, S. Park, M. E. Kozina, E. J. Sie, H. Wen, P. Jarillo-Herrero, I. R. Fisher, X. Wang and N. Gedik, Nat. Phys., 2020, 16, 159, arXiv:1904.07472 [cond-mat.mtrl-sci] Search PubMed.
- A. Zong, A. Kogar, Y.-Q. Bie, T. Rohwer, C. Lee, E. Baldini, E. Ergeçen, M. B. Yilmaz, B. Freelon, E. J. Sie, H. Zhou, J. Straquadine, P. Walmsley, P. E. Dolgirev, A. V. Rozhkov, I. R. Fisher, P. Jarillo-Herrero, B. V. Fine and N. Gedik, Nat. Phys., 2019, 15, 27, arXiv:1806.02766 [cond-mat.mtrl-sci] Search PubMed.
- J. Laverock, S. B. Dugdale, Z. Major, M. A. Alam, N. Ru, I. R. Fisher, G. Santi and E. Bruno, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 085114 CrossRef.
- F. Schmitt, P. S. Kirchmann, U. Bovensiepen, R. G. Moore, L. Rettig, M. Krenz, J.-H. Chu, N. Ru, L. Perfetti, D. H. Lu, M. Wolf, I. R. Fisher and Z.-X. Shen, Science, 2008, 321, 1649, DOI:10.1126/science.1160778.
- T. Ritschel, J. Trinckauf, K. Koepernik, B. Büchner, M. v. Zimmermann, H. Berger, Y. I. Joe, P. Abbamonte and J. Geck, Nat. Phys., 2015, 11, 328 Search PubMed.
- T. Ritschel, H. Berger and J. Geck, Phys. Rev. B, 2018, 98, 195134 CrossRef CAS.
- S.-H. Lee, J. S. Goh and D. Cho, Phys. Rev. Lett., 2019, 122, 106404 CrossRef CAS PubMed.
- Q. Stahl, M. Kusch, F. Heinsch, G. Garbarino, N. Kretzschmar, K. Hanff, K. Rossnagel, J. Geck and T. Ritschel, Nat. Commun., 2020, 11, 1247 CrossRef CAS PubMed.
- L. Perfetti, P. A. Loukakos, M. Lisowski, U. Bovensiepen, H. Berger, S. Biermann, P. S. Cornaglia, A. Georges and M. Wolf, Phys. Rev. Lett., 2006, 97, 067402 CrossRef CAS PubMed.
- S. Hellmann, M. Beye, C. Sohrt, T. Rohwer, F. Sorgenfrei, H. Redlin, M. Kalläne, M. Marczynski-Bühlow, F. Hennies, M. Bauer, A. Föhlisch, L. Kipp, W. Wurth and K. Rossnagel, Phys. Rev. Lett., 2010, 105, 187401 CrossRef CAS PubMed.
- M. Eichberger, H. Schäfer, M. Krumova, M. Beyer, J. Demsar, H. Berger, G. Moriena, G. Sciaini and R. J. D. Miller, Nature, 2010, 468, 799 CrossRef CAS PubMed.
- N. Dean, J. C. Petersen, D. Fausti, R. I. Tobey, S. Kaiser, L. V. Gasparov, H. Berger and A. Cavalleri, Phys. Rev. Lett., 2011, 106, 016401 CrossRef CAS PubMed.
- S. Hellmann, T. Rohwer, M. Kalläne, K. Hanff, C. Sohrt, A. Stange, A. Carr, M. M. Murnane, H. C. Kapteyn, L. Kipp, M. Bauer and K. Rossnagel, Nat. Commun., 2012, 3, 1069 CrossRef CAS PubMed.
- T.-R. T. Han, F. Zhou, C. D. Malliakas, P. M. Duxbury, S. D. Mahanti, M. G. Kanatzidis and C.-Y. Ruan, Sci. Adv., 2015, 1, e1400173, DOI:10.1126/sciadv.1400173.
- M. Ligges, I. Avigo, D. Golež, H. U. R. Strand, Y. Beyazit, K. Hanff, F. Diekmann, L. Stojchevska, M. Kalläne, P. Zhou, K. Rossnagel, M. Eckstein, P. Werner and U. Bovensiepen, Phys. Rev. Lett., 2018, 120, 166401 CrossRef CAS PubMed.
- J. Zhang, X. Tan, M. Liu, S. W. Teitelbaum, K. W. Post, F. Jin, K. A. Nelson, D. N. Basov, W. Wu and R. D. Averitt, Nat. Mater., 2016, 15, 956 CrossRef CAS PubMed.
- A. Cavalleri, C. Tóth, C. W. Siders, J. A. Squier, F. Ráksi, P. Forget and J. C. Kieffer, Phys. Rev. Lett., 2001, 87, 237401 CrossRef CAS PubMed.
- A. Cavalleri, T. Dekorsy, H. H. W. Chong, J. C. Kieffer and R. W. Schoenlein, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 161102 CrossRef.
- P. Baum, D.-S. Yang and A. H. Zewail, Science, 2007, 318, 788, DOI:10.1126/science.1147724.
- W. Roach and I. Balberg, Solid State Commun., 1971, 9, 551 CrossRef CAS.
- V. R. Morrison, R. P. Chatelain, K. L. Tiwari, A. Hendaoui, A. Bruhács, M. Chaker and B. J. Siwick, Science, 2014, 346, 445, DOI:10.1126/science.1253779.
- S. Wall, S. Yang, L. Vidas, M. Chollet, J. M. Glownia, M. Kozina, T. Katayama, T. Henighan, M. Jiang, T. A. Miller, D. A. Reis, L. A. Boatner, O. Delaire and M. Trigo, Science, 2018, 362, 572, DOI:10.1126/science.aau3873.
- M. Rini, R. Tobey, N. Dean, J. Itatani, Y. Tomioka, Y. Tokura, R. W. Schoenlein and A. Cavalleri, Nature, 2007, 449, 72 CrossRef CAS PubMed.
- T. Li, A. Patz, L. Mouchliadis, J. Yan, T. A. Lograsso, I. E. Perakis and J. Wang, Nature, 2013, 496, 69 CrossRef CAS PubMed.
- A. D. Caviglia, M. Först, R. Scherwitzl, V. Khanna, H. Bromberger, R. Mankowsky, R. Singla, Y.-D. Chuang, W. S. Lee, O. Krupin, W. F. Schlotter, J. J. Turner, G. L. Dakovski, M. P. Minitti, J. Robinson, V. Scagnoli, S. B. Wilkins, S. A. Cavill, M. Gibert, S. Gariglio, P. Zubko, J.-M. Triscone, J. P. Hill, S. S. Dhesi and A. Cavalleri, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 220401 CrossRef.
- V. Esposito, L. Rettig, E. M. Bothschafter, Y. Deng, C. Dornes, L. Huber, T. Huber, G. Ingold, Y. Inubushi, T. Katayama, T. Kawaguchi, H. Lemke, K. Ogawa, S. Owada, M. Radovic, M. Ramakrishnan, Z. Ristic, V. Scagnoli, Y. Tanaka, T. Togashi, K. Tono, I. Usov, Y. W. Windsor, M. Yabashi, S. L. Johnson, P. Beaud and U. Staub, Struct. Dyn., 2018, 5, 064501, DOI:10.1063/1.5063530.
- K. R. Beyerlein, A. S. Disa, M. Först, M. Henstridge, T. Gebert, T. Forrest, A. Fitzpatrick, C. Dominguez, J. Fowlie, M. Gibert, J.-M. Triscone, S. S. Dhesi and A. Cavalleri, Phys. Rev. B, 2020, 102, 014311 CrossRef CAS.
- V. Stoica, D. Puggioni, J. Zhang, R. Singla, G. L. Dakovski, G. Coslovich, M. H. Seaberg, M. Kareev, S. Middey, P. Kissin, R. D. Averitt, J. Chakhalian, H. Wen, J. M. Rondinelli and J. W. Freeland, arXiv, 2020, preprint, arXiv:2004.03694 [cond-mat.str-el], DOI:10.48550/arXiv.2004.03694.
- H. Petek and S. Ogawa, Prog. Surf. Sci., 1997, 56, 239 CrossRef CAS.
- U. Bovensiepen and P. Kirchmann, Laser Photonics Rev., 2012, 6, 589, DOI:10.1002/lpor.201000035.
- E. Beaurepaire, J.-C. Merle, A. Daunois and J.-Y. Bigot, Phys. Rev. Lett., 1996, 76, 4250 CrossRef CAS PubMed.
- J. Wang, C. Sun, Y. Hashimoto, J. Kono, G. A. Khodaparast, L. Cywiński, L. J. Sham, G. D. Sanders, C. J. Stanton and H. Munekata, J. Phys.: Condens. Matter, 2006, 18, R501 CrossRef CAS.
- A. Kirilyuk, A. Kimel, F. Hansteen, T. Rasing and R. V. Pisarev, Low Temp. Phys., 2006, 32, 748 CrossRef CAS.
- S. R. Acharya, V. Turkowski, G. P. Zhang and T. S. Rahman, Phys. Rev. Lett., 2020, 125, 017202 CrossRef CAS PubMed.
- B. Mueller, A. Baral, S. Vollmar, M. Cinchetti, M. Aeschlimann, H. Schneider and B. Rethfeld, Phys. Rev. Lett., 2013, 111, 167204 CrossRef CAS PubMed.
- Y. Hinschberger and P. Hervieux, Phys. Lett. A, 2012, 376, 813 CrossRef CAS.
- K. Carva, M. Battiato and P. M. Oppeneer, Phys. Rev. Lett., 2011, 107, 207201 CrossRef CAS PubMed.
- E. Carpene, E. Mancini, C. Dallera, M. Brenna, E. Puppin and S. De Silvestri, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174422 CrossRef.
- A. Kirilyuk, A. Kimel and T. Rasing, Rev. Mod. Phys., 2010, 82, 2731 CrossRef.
- L. Guidoni, E. Beaurepaire and J.-Y. Bigot, Phys. Rev. Lett., 2002, 89, 017401 CrossRef PubMed.
- E. Beaurepaire, G. Turner, S. Harrel, M. Beard, J.-Y. Bigot and C. Schmuttenmaer, Appl. Phys. Lett., 2004, 84, 3465 CrossRef CAS.
- D. Hilton, R. Averitt, C. Meserole, G. Fisher, D. Funk, J. Thompson and A. Taylor, Opt. Lett., 2004, 29, 1805 CrossRef CAS PubMed.
- H. Ohno, D. Chiba, F. Matsukura, T. Omiya, E. Abe, T. Dietl, Y. Ohno and K. Ohtani, Nature, 2000, 408, 944 CrossRef CAS PubMed.
- E. Kojima, R. Shimano, Y. Hashimoto, S. Katsumoto, Y. Iye and M. Kuwata-Gonokami, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 193203 CrossRef.
- E. Mashkovich, K. Grishunin, H. Munekata and A. Kimel, Appl. Phys. Lett., 2020, 117, 122406 CrossRef CAS.
- S. Iwai, S. Tanaka, K. Fujinuma, H. Kishida, H. Okamoto and Y. Tokura, Phys. Rev. Lett., 2002, 88, 057402 CrossRef CAS PubMed.
- K. Ikegami, K. Ono, J. Togo, T. Wakabayashi, Y. Ishige, H. Matsuzaki, H. Kishida and H. Okamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085106 CrossRef.
- K. Onda, S. Ogihara, K. Yonemitsu, N. Maeshima, T. Ishikawa, Y. Okimoto, X. Shao, Y. Nakano, H. Yamochi, G. Saito and S.-y. Koshihara, Phys. Rev. Lett., 2008, 101, 067403 CrossRef PubMed.
- T. Ishikawa, N. Fukazawa, Y. Matsubara, R. Nakajima, K. Onda, Y. Okimoto, S. Koshihara, M. Lorenc, E. Collet, M. Tamura and R. Kato, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115108 CrossRef.
- Y. Kawakami, S. Iwai, T. Fukatsu, M. Miura, N. Yoneyama, T. Sasaki and N. Kobayashi, Phys. Rev. Lett., 2009, 103, 066403 CrossRef CAS PubMed.
- H. Uemura and H. Okamoto, Phys. Rev. Lett., 2010, 105, 258302 CrossRef CAS PubMed.
- S. Koshihara, Y. Tokura, T. Mitani, G. Saito and T. Koda, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 6853 CrossRef CAS PubMed.
- K. Tanimura, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 144112 CrossRef.
- N. Fukazawa, M. Shimizu, T. Ishikawa, Y. Okimoto, S.-y. Koshihara, T. Hiramatsu, Y. Nakano, H. Yamochi, G. Saito and K. Onda, J. Phys. Chem. C, 2012, 116, 5892 CrossRef CAS.
- J. C. Petersen, S. Kaiser, N. Dean, A. Simoncig, H. Y. Liu, A. L. Cavalieri, C. Cacho, I. C. E. Turcu, E. Springate, F. Frassetto, L. Poletto, S. S. Dhesi, H. Berger and A. Cavalleri, Phys. Rev. Lett., 2011, 107, 177402 CrossRef CAS PubMed.
- P. Beaud, A. Caviezel, S. O. Mariager, L. Rettig, G. Ingold, C. Dornes, S.-W. Huang, J. A. Johnson, M. Radovic, T. Huber, T. Kubacka, A. Ferrer, H. T. Lemke, M. Chollet, D. Zhu, J. M. Glownia, M. Sikorski, A. Robert, H. Wadati, M. Nakamura, M. Kawasaki, Y. Tokura, S. L. Johnson and U. Staub, Nat. Mater., 2014, 13, 923 CrossRef CAS PubMed.
- M. Chollet, L. Guerin, N. Uchida, S. Fukaya, H. Shimoda, T. Ishikawa, K. Matsuda, T. Hasegawa, A. Ota, H. Yamochi, G. Saito, R. Tazaki, S. i. Adachi and S. y. Koshihara, Science, 2005, 307, 86, DOI:10.1126/science.1105067.
- A. Georges, G. Kotliar, W. Krauth and M. J. Rozenberg, Rev. Mod. Phys., 1996, 68, 13 CrossRef CAS.
- J. K. Freericks, V. M. Turkowski and V. Zlatić, Phys. Rev. Lett., 2006, 97, 266408 CrossRef CAS PubMed.
- M. Eckstein and P. Werner, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115115 CrossRef.
- M. Eckstein and P. Werner, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035122 CrossRef.
- T. Köhler, S. Rajpurohit, O. Schumann, S. Paeckel, F. R. A. Biebl, M. Sotoudeh, S. C. Kramer, P. E. Blöchl, S. Kehrein and S. R. Manmana, Phys. Rev. B, 2018, 97, 235120 CrossRef.
- J. Li, H. U. R. Strand, P. Werner and M. Eckstein, Nat. Commun., 2018, 9, 4581 CrossRef PubMed.
- F. Grandi, J. Li and M. Eckstein, Phys. Rev. B, 2021, 103, L041110 CrossRef CAS.
- G. Vidal, Phys. Rev. Lett., 2004, 93, 040502 CrossRef PubMed.
- S. R. White and A. E. Feiguin, Phys. Rev. Lett., 2004, 93, 076401 CrossRef PubMed.
- P. Schmitteckert, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 121302 CrossRef.
- A. J. Daley, C. Kollath, U. Schollwöck and G. Vidal, J. Stat. Mech.: Theory Exp., 2004, 2004, P04005 Search PubMed.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863 CrossRef PubMed.
- S. R. White, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10345 CrossRef CAS PubMed.
- U. Schollwöck, Rev. Mod. Phys., 2005, 77, 259 CrossRef.
- U. Schollwöck, Ann. Phys., 2011, 326, 96, arXiv:1008.3477 [cond-mat.str-el] Search PubMed.
- T. Köhler, S. Paeckel, C. Meyer and S. R. Manmana, Phys. Rev. B, 2020, 102, 235166 CrossRef.
- X. Xie, Y. Liu, Y. Yao, U. Schollwöck, C. Liu and H. Ma, J. Chem. Phys., 2019, 151, 224101, DOI:10.1063/1.5125945.
- A. Baiardi and M. Reiher, J. Chem. Theory Comput., 2019, 15, 3481 CrossRef CAS PubMed.
- W. Li, J. Ren and Z. Shuai, J. Phys. Chem. Lett., 2020, 11, 4930 CrossRef CAS PubMed.
- R. Borrelli and M. F. Gelin, Sci. Rep., 2017, 7, 9127 CrossRef PubMed.
- J. Zhang, C. Lian, M. Guan, W. Ma, H. Fu, H. Guo and S. Meng, Nano Lett., 2019, 19, 6027 CrossRef CAS PubMed.
- E. Runge and E. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- E. Gross and W. Kohn, Adv. Quantum Chem., 1990, 21, 255 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864 CrossRef.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, 1133 CrossRef.
- M. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287, DOI:10.1146/annurev-physchem-032511-143803 , PMID: 22242728..
- P. Elliott, J. I. Fuks, A. Rubio and N. T. Maitra, Phys. Rev. Lett., 2012, 109, 266404 CrossRef CAS PubMed.
- N. Helbig, J. Fuks, I. Tokatly, H. Appel, E. Gross and A. Rubio, Open problems and new solutions in time dependent density functional theory, Chem. Phys., 2011, 391, 1 CrossRef CAS.
- J. I. Fuks, N. Helbig, I. V. Tokatly and A. Rubio, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075107 CrossRef.
- G. Vignale and W. Kohn, Phys. Rev. Lett., 1996, 77, 2037 CrossRef CAS PubMed.
- G. Vignale, C. A. Ullrich and S. Conti, Phys. Rev. Lett., 1997, 79, 4878 CrossRef CAS.
- I. V. Tokatly and O. Pankratov, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 201103 CrossRef.
- C. A. Ullrich and I. V. Tokatly, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235102 CrossRef.
- V. Turkowski and T. S. Rahman, J. Phys.: Condens. Matter, 2017, 29, 455601 CrossRef PubMed.
- K. Krieger, J. Dewhurst, P. Elliott, S. Sharma and E. Gross, J. Chem. Theory Comput., 2015, 11, 4870 CrossRef CAS PubMed.
- K. Krieger, P. Elliott, T. Müller, N. Singh, J. Dewhurst, E. Gross and S. Sharma, J. Phys.: Condens. Matter, 2017, 29, 224001 CrossRef CAS PubMed.
- J. Dewhurst, S. Shallcross, P. Elliott, S. Eisebitt, C. v. Korff Schmising and S. Sharma, Phys. Rev. B, 2021, 104, 054438 CrossRef CAS.
- P. Elliott, T. Müller, J. Dewhurst, S. Sharma and E. Gross, Sci. Rep., 2016, 6, 38911 CrossRef CAS PubMed.
- J. Simoni, M. Stamenova and S. Sanvito, Phys. Rev. B, 2017, 96, 054411 CrossRef.
- Z. Qian and G. Vignale, Phys. Rev. Lett., 2002, 88, 056404 CrossRef PubMed.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457 CrossRef.
- P. Ji and Y. Zhang, J. Phys. D: Appl. Phys., 2013, 46, 495108 CrossRef.
- N. Medvedev, H. Jeschke and B. Ziaja, New J. Phys., 2013, 15, 015016 CrossRef CAS.
- E. Zijlstra, J. Walkenhorst and M. Garcia, Phys. Rev. Lett., 2008, 101, 135701 CrossRef PubMed.
- N. Medvedev, Z. Li and B. Ziaja, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 054113 CrossRef.
- P. Silvestrelli, A. Alavi, M. Parrinello and D. Frenkel, Phys. Rev. Lett., 1996, 77, 3149 CrossRef CAS PubMed.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471 CrossRef CAS PubMed.
- J. Tully, J. Chem. Phys., 2012, 137, 22A301 CrossRef PubMed.
- X. Li, J. Tully, H. Schlegel and M. Frisch, J. Chem. Phys., 2005, 123, 084106 CrossRef PubMed.
- P. Parandekar and J. Tully, J. Chem. Theory Comput., 2006, 2, 229 CrossRef CAS PubMed.
- J. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- C. Lian, S. Zhang and S. Meng, Phys. Rev. B, 2016, 94, 184310 CrossRef.
- W.-H. Liu, J.-W. Luo, S.-S. Li and L.-W. Wang, Phys. Rev. B, 2020, 102, 184308 CrossRef CAS.
- J. Bang, Y. Sun, X.-Q. Liu, F. Gao and S. Zhang, Phys. Rev. Lett., 2016, 117, 126402 CrossRef PubMed.
- B. F. E. Curchod, U. Rothlisberger and I. Tavernelli, ChemPhysChem, 2013, 14, 1314, DOI:10.1002/cphc.201200941.
- K. Ishida and K. Nasu, Phys. Rev. Lett., 2008, 100, 116403 CrossRef PubMed.
- M. D. Hack and D. G. Truhlar, J. Chem. Phys., 2001, 114, 9305, DOI:10.1063/1.1368388.
- F. J. Webster, J. Schnitker, M. S. Friedrichs, R. A. Friesner and P. J. Rossky, Phys. Rev. Lett., 1991, 66, 3172 CrossRef CAS PubMed.
- S. Rajpurohit, C. Jooss and P. E. Blöchl, Phys. Rev. B, 2020, 102, 014302 CrossRef CAS.
- S. Rajpurohit, L. Z. Tan, C. Jooss and P. E. Blöchl, Phys. Rev. B, 2020, 102, 174430 CrossRef CAS.
- Z. Chen and L.-W. Wang, Sci. Adv., 2019, 5, eaau8000, DOI:10.1126/sciadv.aau8000.
- E. Viñas Boström, A. Rubio and C. Verdozzi, npj Comput. Mater., 2022, 8, 62 CrossRef.
- J. Chovan and I. E. Perakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 085321 CrossRef.
- S. Anisimov, B. Kapeliovich and T. Perelman, J. Exp. Theor. Phys., 1974, 66, 375 Search PubMed.
- D. Zahn, F. Jakobs, Y. Windsor, H. Seiler, T. Vasileiadis, T. Butcher, Y. Qi, D. Engel, U. Atxitia, J. Vorberger and R. Ernstorfer, Phys. Rev. Res., 2021, 3, 023032 CrossRef CAS.
- J. Chen, D. Tzou and J. Beraun, Int. J. Heat Mass Transfer, 2006, 49, 307 CrossRef CAS.
- T. Roth, A. Schellekens, S. Alebrand, O. Schmitt, D. Steil, B. Koopmans, M. Cinchetti and M. Aeschlimann, Phys. Rev. X, 2012, 2, 021006 Search PubMed.
- C. Paillard, E. Torun, L. Wirtz, J. Íñiguez and L. Bellaiche, Phys. Rev. Lett., 2019, 123, 087601 CrossRef CAS PubMed.
- L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705 CrossRef CAS.
- M. Rossi, R. Arpaia, R. Fumagalli, M. Moretti Sala, D. Betto, K. Kummer, G. M. De Luca, J. van den Brink, M. Salluzzo, N. B. Brookes, L. Braicovich and G. Ghiringhelli, Phys. Rev. Lett., 2019, 123, 027001, arXiv:1902.09163 [cond-mat.supr-con] Search PubMed.
- W. S. Lee, J. J. Lee, E. A. Nowadnick, S. Gerber, W. Tabis, S. W. Huang, V. N. Strocov, E. M. Motoyama, G. Yu, B. Moritz, H. Y. Huang, R. P. Wang, Y. B. Huang, W. B. Wu, C. T. Chen, D. J. Huang, M. Greven, T. Schmitt, Z. X. Shen and T. P. Devereaux, Nat. Phys., 2014, 10, 883 Search PubMed.
- K.-J. Zhou, Y.-B. Huang, C. Monney, X. Dai, V. N. Strocov, N.-L. Wang, Z.-G. Chen, C. Zhang, P. Dai, L. Patthey, J. van den Brink, H. Ding and T. Schmitt, Nat. Commun., 2013, 4, 1470, arXiv:1301.1289 [cond-mat.supr-con] Search PubMed.
- J. Schlappa, K. Wohlfeld, K. J. Zhou, M. Mourigal, M. W. Haverkort, V. N. Strocov, L. Hozoi, C. Monney, S. Nishimoto, S. Singh, A. Revcolevschi, J. S. Caux, L. Patthey, H. M. Rønnow, J. van den Brink and T. Schmitt, Nature, 2012, 485, 82, arXiv:1205.1954 [cond-mat.str-el] Search PubMed.
- M. Hepting, L. Chaix, E. W. Huang, R. Fumagalli, Y. Y. Peng, B. Moritz, K. Kummer, N. B. Brookes, W. C. Lee, M. Hashimoto, T. Sarkar, J. F. He, C. R. Rotundu, Y. S. Lee, R. L. Greene, L. Braicovich, G. Ghiringhelli, Z. X. Shen, T. P. Devereaux and W. S. Lee, Nature, 2018, 563, 374, arXiv:1810.12332 [cond-mat.supr-con] Search PubMed.
- P. Zhu, Y. Zhu, Y. Hidaka, L. Wu, J. Cao, H. Berger, J. Geck, R. Kraus, S. Pjerov, Y. Shen, R. I. Tobey, J. P. Hill and X. J. Wang, New J. Phys., 2015, 17, 063004 CrossRef.
- T. Konstantinova, J. D. Rameau, A. H. Reid, O. Abdurazakov, L. Wu, R. Li, X. Shen, G. Gu, Y. Huang, L. Rettig, I. Avigo, M. Ligges, J. K. Freericks, A. F. Kemper, H. A. Dürr, U. Bovensiepen, P. D. Johnson, X. Wang and Y. Zhu, Sci. Adv., 2018, 4, eaap7427, DOI:10.1126/sciadv.aap7427.
- T. Konstantinova, L. Wu, W. G. Yin, J. Tao, G. D. Gu, X. J. Wang, J. Yang, I. A. Zaliznyak and Y. Zhu, npj Quantum Mater., 2020, 5, 80 CrossRef CAS.
- J. Li, L. Wu, S. Yang, X. Jin, W. Wang, J. Tao, L. Boatner, M. Babzien, M. Fedurin, M. Palmer, W. Yin, O. Delaire and Y. Zhu, Phys. Rev. X, 2022, 12, 021032 CAS.
- S. P. Weathersby, G. Brown, M. Centurion, T. F. Chase, R. Coffee, J. Corbett, J. P. Eichner, J. C. Frisch, A. R. Fry, M. Gühr, N. Hartmann, C. Hast, R. Hettel, R. K. Jobe, E. N. Jongewaard, J. R. Lewandowski, R. K. Li, A. M. Lindenberg, I. Makasyuk, J. E. May, D. McCormick, M. N. Nguyen, A. H. Reid, X. Shen, K. Sokolowski-Tinten, T. Vecchione, S. L. Vetter, J. Wu, J. Yang, H. A. Dürr and X. J. Wang, Rev. Sci. Instrum., 2015, 86, 073702, DOI:10.1063/1.4926994.
- A. Kubo, K. Onda, H. Petek, Z. Sun, Y. S. Jung and H. K. Kim, Nano Lett., 2005, 5, 1123 CrossRef CAS PubMed.
- K. Yu, D. Bayer, C. Wiemann, O. Gaier, M. Bauer and M. Aeschlimann, J. Nanomater., 2008, 2008, 249514 Search PubMed.
- A. Kubo, N. Pontius and H. Petek, Nano Lett., 2007, 7, 470 CrossRef CAS PubMed.
- K. Fukumoto, K. Onda, Y. Yamada, T. Matsuki, T. Mukuta, S.-i. Tanaka and S.-y. Koshihara, Rev. Sci. Instrum., 2014, 85, 083705, DOI:10.1063/1.4893484.
- K. Fukumoto, Y. Yamada, S. ya Koshihara and K. Onda, Appl. Phys. Express, 2015, 8, 101201 CrossRef.
- Y. H. Wang, H. Steinberg, P. Jarillo-Herrero and N. Gedik, Science, 2013, 342, 453, DOI:10.1126/science.1239834.
- J. W. McIver, B. Schulte, F. U. Stein, T. Matsuyama, G. Jotzu, G. Meier and A. Cavalleri, Nat. Phys., 2020, 16, 38 Search PubMed.
- M. Rodriguez-Vega, M. Vogl and G. A. Fiete, Ann. Phys., 2021, 435, 168434 CAS , special issue on Philip W. Anderson..
- M. Först, R. Mankowsky and A. Cavalleri, Acc. Chem. Res., 2015, 48, 380 CrossRef PubMed.
- S. Sharma, J. K. Dewhurst, A. Sanna and E. K. U. Gross, Phys. Rev. Lett., 2011, 107, 186401 CrossRef CAS PubMed.
- A. P. Horsfield, D. R. Bowler, A. J. Fisher, T. N. Todorov and C. G. Sánchez, J. Phys.: Condens. Matter, 2004, 16, 8251 CrossRef CAS.
- L. Kantorovich, Phys. Rev. B, 2018, 98, 014307 CrossRef CAS.
- P. Nijjar, J. Jankowska and O. V. Prezhdo, J. Chem. Phys., 2019, 150, 204124 CrossRef PubMed.
- V. Rizzi, T. N. Todorov, J. J. Kohanoff and A. A. Correa, Phys. Rev. B, 2016, 93, 024306 CrossRef.
- E. Tapavicza, G. D. Bellchambers, J. C. Vincent and F. Furche, Phys. Chem. Chem. Phys., 2013, 15, 18336 RSC.
- B. F. E. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305 CrossRef CAS PubMed.
- N. Shenvi, S. Roy and J. C. Tully, J. Chem. Phys., 2009, 130, 174107, DOI:10.1063/1.3125436.
- S. Roy, N. A. Shenvi and J. C. Tully, J. Chem. Phys., 2009, 130, 174716, DOI:10.1063/1.3122989.
- S. Roy, N. Shenvi and J. C. Tully, J. Phys. Chem. C, 2009, 113, 16311 CrossRef CAS.
- T. N. Todorov, J. Phys.: Condens. Matter, 2001, 13, 10125 CrossRef CAS.
- F. P. Bonafé, B. Aradi, B. Hourahine, C. R. Medrano, F. J. Hernández, T. Frauenheim and C. G. Sánchez, J. Chem. Theory Comput., 2020, 16, 4454 CrossRef PubMed.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419 CrossRef CAS.
- G. E. Topp, G. Jotzu, J.W. McIver, L. Xian, A. Rubio and M. A. Sentef, Phys. Rev. Res., 2019, 1, 023031 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |