Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of indirect transitions on valley polarization in WS2 and WSe2†
Rasmus H.
Godiksen
 a,
Shaojun
Wang
a,
Shaojun
Wang
 ab,
T. V.
Raziman
ab,
T. V.
Raziman
 a,
Jaime Gómez
Rivas
a,
Jaime Gómez
Rivas
 a and
Alberto G.
Curto
a and
Alberto G.
Curto
 *acd
*acd
aDep. Applied Physics and Institute for Photonic Integration, Eindhoven University of Technology, Eindhoven, The Netherlands. E-mail: A.G.Curto@TUe.nl
bMOE Key Lab. of Modern Optical Technologies and Jiangsu Key Lab. of Advanced Optical Manufacturing Technologies, School of Optoelectronic Science and Engineering, Soochow University, Suzhou 215006, China
cPhotonics Research Group, Ghent University-imec, Ghent, Belgium
dCenter for Nano- and Biophotonics, Ghent University, Ghent, Belgium
First published on 21st November 2022
Abstract
Controlling the momentum of carriers in semiconductors, known as valley polarization, is a new resource for optoelectronics and information technologies. Materials exhibiting high polarization are needed for valley-based devices. Few-layer WS2 shows a remarkable spin-valley polarization above 90%, even at room temperature. In stark contrast, polarization is absent for few-layer WSe2 despite the expected material similarities. Here, we explain the origin of valley polarization in both materials based on the interplay between two indirect optical transitions. We show that the relative energy minima at the Λ- and K-valleys in the conduction band determine the spin-valley polarization of the direct K–K transition. Polarization appears as the energy of the K-valley rises above the Λ-valley as a function of temperature and number of layers. Our results advance the understanding of the high spin-valley polarization in WS2. This insight will impact the design of both passive and tunable valleytronic devices operating at room temperature.
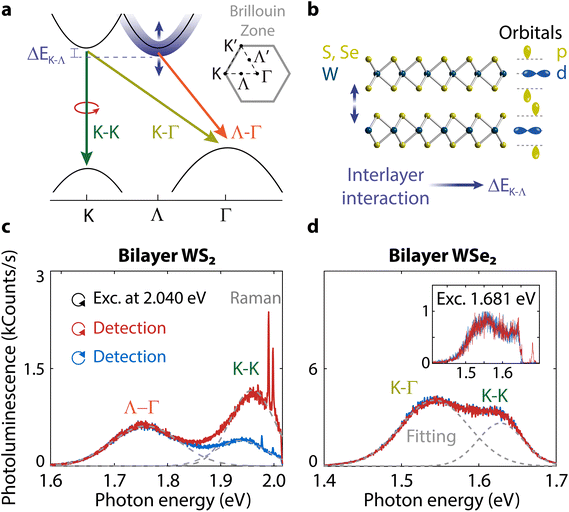
Transition metal dichalcogenides (TMDs) such as MoS2, WS2, or WSe2 are layered semiconductors with unique spin-valley physics. The coupling between spin and momentum for excited carriers opens a new path to access the valley degree of freedom.1 Valley polarization arises from a difference in exciton populations at the K- and K′-points of the hexagonal Brillouin zone (Fig. 1a),1–3 where local energy minima known as valleys lie. At these diametrically opposite points in reciprocal space, strong spin–orbit splitting occurs in the top valence bands. The different signs of the splitting in the K- and K′-valleys4 result in the coupling of spin and valley indexes and leads to spin-dependent optical and electronic properties. The K- and K′-valleys can be selectively excited using right- or left-handed circularly polarized light.5 TMDs constitute thus a fascinating platform for future valleytronic,6 optoelectronic,7–9 and nanophotonic10,11 devices exploiting the spin, valley, and layer indexes.
The layered nature of TMDs enables a high degree of control over valley polarization. A monolayer possesses a direct band gap, whereas in the few-layer regime the band gap becomes indirect.12–14 Light emission in few-layer TMDs is dominated by indirect transitions from the Λ- and K-points to the Γ-point in the band structure (Fig. 1a). These indirect transitions are typically unpolarized. At higher energy, polarized intravalley transitions with direct character can still occur in the K- or K′-valleys.15 The degree of circular polarization can be used as a proxy for valley polarization. It is defined as DOCP = (Iσ+ − Iσ−)/(Iσ+ + Iσ−), where Iσ+ and Iσ− are the photoluminescence intensities with right- and left-handed circular polarization, respectively. Valley polarization can reach values near unity at cryogenic temperatures for monolayer MoS2.16 With increasing temperature, however, the initial polarization quickly depolarizes due to intervalley scattering between the K- and K′-points,17 limiting applications at room temperature. At higher temperatures, a valley polarization enhancement for a monolayer has been realized through interaction with graphene,18,19 reaching up to 40% DOCP for graphene-encapsulated WS2.20 In contrast to the monolayer case, the DOCP reaches 65% for bilayer WS2 even at room temperature.21 Such a large spin-valley polarization in bilayer WS2 is not well understood yet.22,23
Despite sharing several properties with WS2 due to the common W atom, valley polarization is absent in WSe2 at room temperature. This discrepancy between bilayer WS2 and WSe2, illustrated in Fig. 1c and d, is inconsistent with theoretical predictions.15 Hence, it remains unresolved, as stated by Bussolotti et al.22 An understanding of the spin-valley properties that lead to high and low polarization in WS2 and WSe2 is, therefore, essential for practical applications at room temperature.24 Gaining insight into the spin-valley physics of bilayer TMDs would also be beneficial for spin-layer locking effects,25–28 layer-dependent spin relaxation,29 and the spin-valley Hall effect in few-layer systems.30,31
Here, we demonstrate the critical role of the Λ-valley on the spin-valley polarization in few-layer WS2 and WSe2 through a combined investigation of polarization- and temperature-resolved photoluminescence (PL). By varying both the number of layers and the temperature, we analyze the interplay between the momentum-allowed direct transition (K–K) and two momentum-forbidden indirect transitions (K–Γ and Λ–Γ). We find that a change in the dominant indirect transition channel with temperature determines the observation of spin-valley polarization. In bilayer WSe2, we reveal the existence of a crossover temperature at which the dominant indirect transition switches from K–Γ to Λ–Γ as the Λ-point energy shifts lower in energy than the K-point. Below this crossover temperature, the polarization of the direct K–K transition begins to increase even for highly off-resonant excitation. We demonstrate the dependence of the valley polarization of the direct K–K transition on the K–Λ energy difference in the conduction band. In contrast to WSe2, the Λ–Γ indirect transition dominates the emission in WS2 resulting in high polarization even at room temperature. Based on our results, we explain how both temperature and number of layers affect spin-valley polarization in WS2 and WSe2. Therefore, we identify a missing piece of the puzzle for understanding and achieving high spin-valley polarization in few-layer semiconductors.
Experimental methods
Sample fabrication
We deposit WS2 and WSe2 microcrystals onto SiO2/Si (285 nm thick SiO2) substrates by mechanical exfoliation from synthetic, bulk 2H crystals (HQ Graphene). We first determine the thickness of the flakes by optical contrast microscopy32 and by considering the energy of the indirect exciton emission in photoluminescence spectra.33 After optical measurements, we confirmed the thickness by atomic force microscopy.Optical measurements
We carry out photoluminescence measurements using a microscope in epi-fluorescence geometry (objective lens: Nikon CFI Plan Fluor ELWD 40×, NA = 0.6). We typically excite the microcrystals with a continuous-wave laser with photon energy 2.040 eV and a power of 12.2 μW before the objective lens, ensuring a power density in the linear response range for the TMDs. For WSe2, we also used a continuous-wave 1.796 eV laser with a power of 75.6 μW. For one measurement with bilayer WSe2, we used a supercontinuum laser (Fianium SC400, pulse duration ∼50 ps) with an acousto-optical filter tuned to 1.681 eV and 1.7 μW. To control the circular polarization in excitation, we employ a Babinet–Soleil compensator and a Stokes polarimeter (PolSNAP, Hinds Instruments) at the sample position to ensure circular polarization of the incident laser beam. In the detection path, we use a non-polarizing beamsplitter (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014 silver non-polarizing 50/50 bs, Chroma), and then either two 615 nm longpass filters (ET615LP Chroma), two 700 nm longpass filters (FELH0700, Thorlabs), or one 750 nm longpass filter (FELH0750, Thorlabs). For emission polarization analysis, we combine a quarter-wave plate (achromatic quarter-wave retarder, 600–1200 nm, Bernhard Halle) and a wire-grid polarizer (WP25M-UB, Thorlabs). After coupling into an optical fiber with core size 50 μm, we record PL spectra with an Andor Shamrock 303i spectrometer and an Andor Newton 970 EMCCD camera. For low-temperature measurements, we use a liquid helium flow cryostat (Oxford Instruments MicrostatHiRes) pumped to ultra-high vacuum.
014 silver non-polarizing 50/50 bs, Chroma), and then either two 615 nm longpass filters (ET615LP Chroma), two 700 nm longpass filters (FELH0700, Thorlabs), or one 750 nm longpass filter (FELH0750, Thorlabs). For emission polarization analysis, we combine a quarter-wave plate (achromatic quarter-wave retarder, 600–1200 nm, Bernhard Halle) and a wire-grid polarizer (WP25M-UB, Thorlabs). After coupling into an optical fiber with core size 50 μm, we record PL spectra with an Andor Shamrock 303i spectrometer and an Andor Newton 970 EMCCD camera. For low-temperature measurements, we use a liquid helium flow cryostat (Oxford Instruments MicrostatHiRes) pumped to ultra-high vacuum.
Results and discussion
Spin-valley polarization in few-layer WS2 and WSe2
First, we consider the typical band structure of a bilayer TMD (Fig. 1a). The bilayer band gap is indirect because the valence band maximum shifts from K to Γ from one to two layers. The nature of the indirect transition depends on the competition between the Λ and K conduction band energy minima (orange and light green arrows in Fig. 1a). To study the impact of these indirect transitions on polarization, we will exploit their dependence on temperature and number of layers to tune the band structure.The effect of interlayer interactions on the band structure is highly dependent on momentum, leading to a different layer and temperature dependence for the energy of the K–K, K–Γ, and Λ–Γ transitions (Table 1).17,34 At the K-point, d-orbitals from the transition metals determine the top-most band structure.5 Increasing the temperature expands the covalent bond length between the atoms reducing the energy gap at the K-point. The transition metal atoms are protected between the chalcogens, which results in insensitivity of the K-point to the surrounding medium and, therefore, to the number of layers. On the other hand, the chalcogen atoms lie close to both the surrounding medium and the adjacent layers. The chalcogen p-orbitals that dominate at the Λ-point extend outside the atomic plane, rendering it sensitive to interlayer interactions (Fig. 1b).34 With increasing temperature, the out-of-plane p-orbitals extend in length and come closer to each other, thereby increasing their interaction because the interlayer distance due to van der Waals forces between the layers is not temperature dependent. Consequently, the Λ-valley increases in energy with increasing temperature. Increasing the number of layers, on the contrary, results in a decrease of the Λ-valley energy because more out-of-plane p-orbitals interact with neighboring layers. As summarized in Table 1, we can utilize both temperature and the number of layers to alter the direct and indirect transitions of WS2 and WSe2.
| Energy | Increase in #L | Increase in T |
|---|---|---|
| E K–K | Near constant | Decreases |
| E Λ–Γ | Decreases | Increases |
| E K–Γ | Decreases | Decreases |
To compare the valley polarization of WS2 and WSe2, we excite our samples with circularly polarized light and measure the polarization of the emission with a circular polarization analyzer and a spectrometer (see Experimental methods). We observe a stark difference in circular polarization for bilayer WS2 and WSe2 (compare high and low values in Fig. 1c and d) for excitation with laser photon energy of 2.040 eV close to resonance with WS2. We confirmed that the low polarization for WSe2 is not due to off-resonant excitation by using two additional excitation energies of 1.796 eV and 1.681 eV (Fig. 1d, inset, and ESI Fig. S1†). We still observed no polarization at room temperature despite having nearly the same detuning with the K–K emission of 66 meV in WSe2 excited by 1.681 eV compared to WS2 excited by 2.040 eV. In this work, we will demonstrate the dependence of the polarization in WS2 and WSe2 on the indirect band gap character controlled by the energy difference ΔEK–Λ (Fig. 1a). To clarify the role played by ΔEK–Λ on the differences and similarities between the polarization of WS2 and WSe2, we measure next the changes in spectra and polarization as a function of the number of layers and temperature.
The role of the indirect optical transitions in polarization
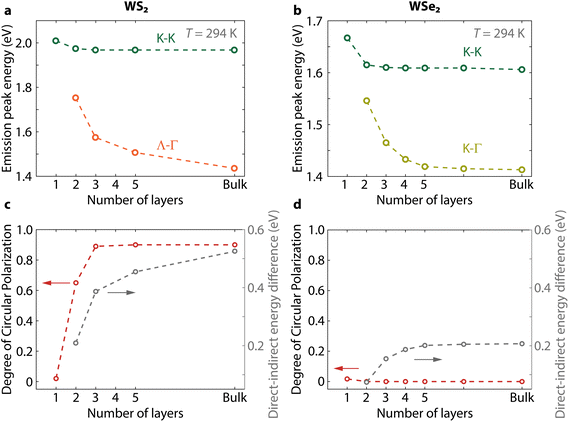
We prepare samples with varying numbers of layers of WS2 and WSe2. We measure their PL spectra and determine the position of the direct and indirect transition peaks (ESI Fig. S2†). The peak energies as a function of the number of layers show that the separation between the direct and indirect peaks increases faster with thickness for WS2 compared to WSe2 (Fig. 2a and b). This difference is a consequence of the origin of their indirect emission, which stems from Λ–Γ transitions in WS2 while it originates from K–Γ transitions in WSe2 at room temperature.34 The larger increase in energy shift with thickness for the Λ–Γ transition is due to the larger impact of interlayer interactions on the Λ-valley compared to the K-valley.Next, we measure the change of polarization for a varying number of layers (Fig. 2c and d, and ESI Fig. S3†). For WS2, the polarization of the K–K transition quickly increases from mono- to trilayer, reaching a DOCP = 0.89 and saturating for thicker samples. For WSe2, the polarization of the K–K transition remains absent for all thicknesses even when exciting closer to resonance (ESI Fig. S4†). As expected, the K–Γ and Λ–Γ transitions are unpolarized in all measurements (ESI Fig. S2 and S3†). We deconvolute the polarization contribution of each transition by fitting the spectra with Gaussian functions (see Experimental methods). Thanks to this fit, we remove any contribution from the unpolarized indirect PL emission in our polarization analysis to retrieve the DOCP for the PL maximum of the direct transition alone.
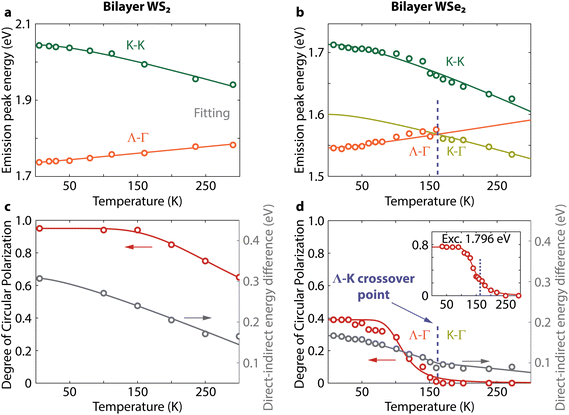
The insensitivity of the polarization to thickness in WSe2 is in clear contrast to the dependence in WS2. As the main change in band structure with increasing thickness is a decrease in energy of the Λ–Γ transition (EΛ–Γ), we can reasonably expect that an increasing difference between EK–K and EΛ–Γ could determine the increase in circular polarization in WS2. To validate this hypothesis, however, we need to determine the conditions required for increasing the DOCP in WSe2. Changing the temperature is a controllable way to perturb the band structure in both materials. Thus, we measure next the PL spectra and DOCP at lower temperatures and track the PL peak positions (Fig. 3 and ESI Fig. S4†). In bilayer WS2, the direct and indirect exciton peaks move to higher and lower energies with decreasing temperature, respectively (Fig. 3a). In WSe2, the situation is different. First, the K–Γ peak shifts to higher energy with decreasing temperature because the K-point is the conduction band minimum in this temperature range.34 Below 160 K, the indirect peak starts moving to lower energies with decreasing temperature (Fig. 3b), which is consistent with the indirect peak now arising from Λ–Γ transitions.
We describe the evolution of the peak energies with temperature (Fig. 3a and b) using the Varshni equation:35
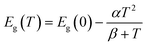 | (1) |
| Material/transition | E g (0) (eV) | α (meV K−1) | β (K) | |
|---|---|---|---|---|
| WS2 | K–K | 2.045 | 0.530 | 118.9 |
| Λ–Γ | 1.737 | −0.172 | 12.5 | |
| WSe2 | K–K | 1.713 | 0.530 | 139.3 |
| K–Γ | 1.600 | 0.316 | 96.6 | |
| Λ–Γ | 1.546 | −0.172 | 44.1 | |
The measured polarization rises with increasing number of layers in WS2 because it corresponds to a higher K–Λ energy separation of the conduction bands. Similarly, this energy separation also increases with decreasing temperature. Consequently, for bilayer WS2 the circular polarization increases with decreasing temperature as well (Fig. 3c). At temperatures from 300 to 160 K, valley polarization remains absent in WSe2 when excited off resonance at 2.040 eV. In this temperature range, the EK–K–EK–Γ separation does not vary substantially because both peaks shift to higher energy with decreasing temperature (gray points in Fig. 3d). Below T = 160 K, the indirect transition changes from K–Γ to Λ–Γ. Simultaneously, the polarization of the K–K transition starts to increase and saturates at low temperatures (Fig. 3d, including higher polarization under near resonant excitation). At these low temperatures, bilayer WSe2 behaves like bilayer WS2 because their indirect transitions have now both Λ–Γ character, as evidenced by their similar Varshni dependences.
Our polarization values at low temperature (T ∼ 10 K) are consistent with previous measurements using similar excitation energies for both materials.36,37 Reaching a DOCP of 0.39 at 35 K in bilayer WSe2, despite exciting 320 meV away from the K–K transition demonstrates the critical role of the Λ-valley in establishing the robust spin-valley polarization in few-layer WS2 and WSe2.
To compare the temperature dependence of polarization in few-layer WS2 and WSe2, we fit the DOCP as a function of temperature (Fig. 3c and d) using the expression
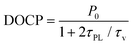 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔE/kBT),38 where c is a constant and ΔE is an activation energy needed to undergo K–K′ intervalley scattering (see ESI Table S1† for fitting parameters).
exp(−ΔE/kBT),38 where c is a constant and ΔE is an activation energy needed to undergo K–K′ intervalley scattering (see ESI Table S1† for fitting parameters).
Next, we explicitly demonstrate that the polarization of the direct K–K transition in WSe2 depends on the K–Λ energy difference in the conduction band, ΔEK–Λ. First, we retrieve ΔEK–Λ as a function of temperature from fitting Fig. 3b as ΔEK−Λ = EK−Γ − EΛ−Γ (Fig. 4a). The polarization of the K–K transition starts increasing when ΔEK–Λ becomes positive (Fig. 4b). Previously, the Γ-hill has been suggested to be involved in K–K′ intervalley scattering by slowing down the scattering of holes from K to K′ in bilayer WS2 compared to monolayer WS2.39 That hypothesis is not consistent, however, with the absence of valley polarization in WSe2 at higher temperatures, where the dominant indirect transition is K–Γ. Instead, the Λ-valley could play a similar role in the scattering of electrons. A comparison of ΔEK–Λ in the conduction band and ΔEΓ–K in the valence band (ΔEΓ−K = EK−K − EK−Γ) further supports the relevance of the Λ-valley on polarization (Fig. 4a). The energy difference in the valence band ΔEΓ–K is already far above the thermal energy at room temperature, so its weak increase at lower temperatures cannot influence polarization substantially. On the other hand, ΔEK–Λ is similar to the thermal energy near the Λ–K crossover. Thus, excitons will populate both Λ–Γ and K–Γ states, resulting in the weaker polarization increase before the Λ–K crossover (Fig. 3d). Our results thus highlight the important role of the Λ-valley in protecting spin-valley polarization in few-layer semiconductors.
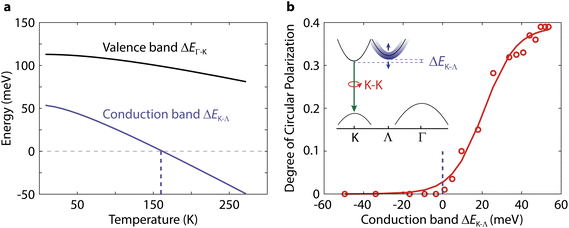 | ||
| Fig. 4 The polarization of the direct K–K transition in WSe2 depends on the energy difference between the conduction band points of the indirect transitions. (a) Temperature dependence of ΔEK–Λ in the conduction band and ΔEΓ–K in the valence band obtained from the three fits in Fig. 3b. (b) Polarization of the K–K photoluminescence excited with 2.040 eV as a function of the ΔEK–Λ conduction band difference. Inset: schematic of the band diagram responsible for the changes in K–K polarization determined by the value of ΔEK–Λ. | ||
Mechanisms for spin-valley polarization in few-layer semiconductors
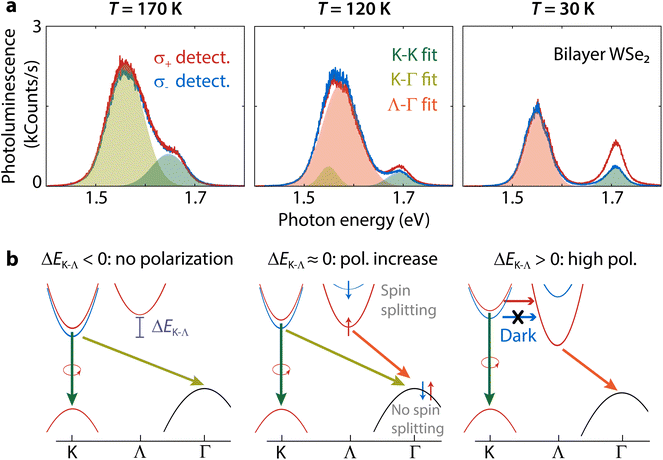
To better illustrate the appearance of polarization below the crossover temperature between indirect transitions, we depict how the band structure changes for three different temperatures (Fig. 5). When T > 160 K, the indirect transition is K–Γ and polarization is absent for the K–K transition (Fig. 5, left). As the temperature decreases, Λ moves to an energy similar to K. There is an intermediate temperature range where both K–Γ and Λ–Γ transitions contribute to the indirect emission and the K–K polarization starts to increase (Fig. 5, center). The overlap in emission from both indirect transitions is evident from the fitting of the indirect spectral band, where two Gaussians are necessary. Finally, as ΔEK–Λ increases, only the Λ-valley contributes to indirect emission resulting in a faster increase of polarization with decreasing temperature (Fig. 5, right).We discuss next how the Λ-valley could lead to a reduced intervalley scattering rate. We focus on two mechanisms for intervalley scattering and how they compare to our results:
(I) Intervalley scattering by phonons.40–42
(II) Intervalley scattering by the long-range exchange mechanism.17,43,44
The coupling between excitons and phonons can cause the spin to flip, but this process also requires phonons with the right momentum. A strong exciton–phonon coupling promotes spin-flipping.45 We extract the exciton–phonon coupling using the O'Donnell equation46 to fit the PL peaks in Fig. 3a and b. The results indicate that Λ–Γ excitons have a lower exciton–phonon coupling strength (ESI section S2.2†) and are thus the least likely to undergo intervalley scattering by phonons. Additionally, intervalley scattering by phonons can occur much faster for electrons due to the low spin splitting of the conduction band at the K-point enabling faster spin-flipping.40 Due to its lower energy and the very large spin splitting,47 the Λ-valley could introduce a very efficient ‘trap’ preventing electrons scattered by phonons from reaching the K′-valley. Thus, K–K′ intervalley scattering by phonons could be slowed down significantly when the Λ-valley is the conduction band minimum. Intervalley scattering by phonons is thus consistent with the polarization trends illustrated in Fig. 5.
Alternatively, the long-range exchange mechanism can cause a K–K exciton to undergo intervalley scattering by recombining and exciting an exciton at the K′-valley. Compared to phonons, it does not require any additional momentum. Since the process occurs more efficiently for excitons of higher kinetic energy, the Λ-valley slows down the K–K′ intervalley scattering rate by trapping K–K excitons of higher kinetic energy more efficiently. From the fitting of DOCP as a function of temperature with eqn (2), we note that the values of ΔE (ESI Table S1†) do not match with the phonon energy required for K–K′ intervalley scattering.48,49 ΔE could thus correspond better with the excess energy required by the long-range exchange mechanism. Nevertheless, such a simple fit likely does not take into account all of the temperature-dependent material parameters affecting the spin-valley polarization.18
Additionally, spin-forbidden dark excitons with lower energy than the bright excitons50 can increase polarization. Dark excitons have previously been attributed to the robust spin-valley polarization in monolayer tungsten systems with respect to both temperature and excitation energy.51 We demonstrate the presence of dark excitons in ESI section S2.3† and estimate a bright-dark splitting EBD = 37.9 meV, which is agreement with the value in monolayer WSe2.52 As there is no K–K′ intervalley exchange interaction for dark excitons,17 they can act as a reservoir for the bright exciton valley polarization.51 On the other hand, the K–Γ transition depopulates the dark exciton reservoir contributing to depolarization because there is no spin splitting at Γ.22 This situation is consistent with the low polarization at temperatures above the Λ–K crossover (Fig. 5, left). In the temperature range where EΛ < EK, the K–K dark exciton reservoir is restored due to the spin splitting at Λ,22,47 resulting in a high and robust polarization even for off-resonant excitation (Fig. 5, right).
Finally, we show for completeness that the dependence of polarization on the number of layers is also in agreement with the mechanism in Fig. 5 where polarization is controlled by ΔEK–Λ. For WS2, there is a significant difference in polarization between bilayers and trilayers at room temperature (DOCP ≈ 0.65 and 0.95 in Fig. 2c). The addition of one layer shifts the Λ-valley to lower energy, while the K-valley remains nearly constant (Fig. 2a), thus increasing ΔEK–Λ. To confirm this behavior in WSe2 as well, we perform temperature- and polarization measurements on WSe2 from one to four layers showing an increase of polarization with number of layers (ESI Fig. S7†). The results are consistent with the expectation of a smaller ΔEK–Λ energy separation at elevated temperatures with increasing thickness, resulting in the Λ–K crossover occurring at a higher temperature. The polarization at T = 35 K is much higher in bilayer WSe2 excited off resonance than in monolayer WSe2 excited near resonance (DOCP ≈ 0.79 compared to 0.23) despite the additional detuning. This polarization difference between bilayer and monolayer WSe2 is consistent with the Λ-valley offering additional protection for K–K′ intervalley scattering by phonons in bilayers.
Conclusion
In summary, we have demonstrated the impact of the Λ-valley on spin-valley polarization in WS2 and WSe2 through temperature- and polarization-resolved photoluminescence measurements. By varying the temperature and the number of layers, the position of the conduction band Λ-valley changes relative to the K-valley. We show that the conduction band Λ–K energy difference controls the K–K spin-valley polarization resulting in robust polarization. In bilayer WSe2, we correlate the appearance of polarization with the crossover between indirect transitions below T = 160 K, when the Λ-valley becomes the conduction band minimum. The polarization increases with the energy difference between the K- and Λ-valleys. This observation highlights the importance of the Λ-valley in blocking K–K′ intervalley scattering to stabilize polarization.Our results introduce the critical role of indirect optical transitions in spin-valley polarization in few-layer semiconductors, contributing in particular to the understanding of the exceptionally high spin-valley polarization in few-layer WS2. For WS2, the energy of the Λ-valley is already lower than the K-valley at room temperature. Polarization increases with the number of WS2 layers because of the higher K–Λ energy difference. The Λ-valley thus determines the contrast between the high polarization in few-layer WS2 and low polarization for monolayer WS2. It also causes the contrast between few-layer WS2 and WSe2 at room temperature. The protection of polarization by the emergence of an indirect transition is a striking manifestation of interlayer interactions at the sub-nanometer scale. The control of the band structure and its indirect transitions by changing the interlayer distance (e.g., using strain or pressure), tuning the band gap (e.g., via electrical gating), or through hetero- or homostructures opens a route to manipulate the entanglement of the spin, valley, and layer indexes for actively tunable valleytronics.
Author contributions
R.H.G., S.W., and A.G.C. designed the experiments. R.H.G. carried out the experiments assisted by S.W, while R.H.G. and T.V.R. analyzed the data. A.G.C. provided guidance during the experiments and analysis. All authors discussed the results. R.H.G. and A.G.C. wrote the manuscript with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Marcos H. D. Guimarães for useful discussions. This work was financially supported by the Netherlands Organisation for Scientific Research (NWO) through Gravitation grant “Research Centre for Integrated Nanophotonics” (024.002.033) and an NWO START-UP grant (740.018.009) and the Innovational Research Incentives Scheme (VICI Grant No. 680-47-628). Shaojun Wang was supported by the Starting Grant of Soochow University (Q415900120) and the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institutions.References
- K. F. Mak, K. He, J. Shan and T. F. Heinz, Control of valley polarization in monolayer MoS2 by optical helicity, Nat. Nanotechnol., 2012, 7, 494–498 CrossRef CAS PubMed
.
- H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Valley polarization in MoS2 monolayers by optical pumping, Nat. Nanotechnol., 2012, 7, 490–493 CrossRef CAS PubMed
.
- T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu and J. Feng, Valley-selective circular dichroism of monolayer molybdenum disulphide, Nat. Commun., 2012, 3, 887 CrossRef PubMed
.
- Z. Y. Zhu, Y. C. Cheng and U. Schwingenschlögl, Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 1–5 Search PubMed
.
- G. B. Liu, D. Xiao, Y. Yao, X. Xu and W. Yao, Electronic structures and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides, Chem. Soc. Rev., 2015, 44, 2643–2663 RSC
.
- C. Mai,
et al., Many-body effects in valleytronics: Direct measurement of valley lifetimes in single-layer MoS2, Nano Lett., 2014, 14, 202–206 CrossRef CAS PubMed
.
- W. Yao, D. Xiao and Q. Niu, Valley-dependent optoelectronics from inversion symmetry breaking, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1–7 Search PubMed
.
- K. M. Goodfellow, R. Beams, C. Chakraborty, L. Novotny and A. N. Vamivakas, Integrated nanophotonics based on nanowire plasmons and atomically thin material, Optica, 2014, 1, 149 CrossRef CAS
.
- K. F. Mak and J. Shan, Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides, Nat. Photonics, 2016, 10, 216–226 CrossRef CAS
.
- T. Chervy,
et al., Room Temperature Chiral Coupling of Valley Excitons with Spin-Momentum Locked Surface Plasmons, ACS Photonics, 2018, 5, 1281–1287 CrossRef CAS
.
- S.-H. Gong, F. Alpeggiani, B. Sciacca, E. C. Garnett and L. Kuipers, Nanoscale chiral valley-photon interface through optical spin-orbit coupling, Science, 2018, 359, 443–447 CrossRef CAS PubMed
.
- T. Cheiwchanchamnangij and W. R. L. Lambrecht, Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–4 CrossRef
.
- A. Splendiani,
et al., Emerging photoluminescence in monolayer MoS2, Nano Lett., 2010, 10, 1271–1275 CrossRef CAS PubMed
.
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Atomically thin MoS2: A new direct-gap semiconductor, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed
.
- Q. Liu, X. Zhang and A. Zunger, Intrinsic circular polarization in centrosymmetric stacks of transition-metal dichalcogenide compounds, Phys. Rev. Lett., 2015, 114, 1–5 Search PubMed
.
- K. F. Mak, K. He, J. Shan and T. F. Heinz, Control of valley polarization in monolayer MoS2 by optical helicity, Nat. Nanotechnol., 2012, 7, 494–498 CrossRef CAS PubMed
.
- T. Yu and M. W. Wu, Valley depolarization due to intervalley and intravalley electron-hole exchange interactions in monolayer MoS2, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 1–7 Search PubMed
.
- Y. Miyauchi,
et al., Evidence for line width and carrier screening effects on excitonic valley relaxation in 2D semiconductors, Nat. Commun., 2018, 9, 2598 CrossRef PubMed
.
- I. Paradisanos,
et al., Prominent room temperature valley polarization in WS2/graphene heterostructures grown by chemical vapor deposition, Appl. Phys. Lett., 2020, 116, 203102 CrossRef CAS
.
- E. Lorchat,
et al., Room-Temperature Valley Polarization and Coherence in Transition Metal Dichalcogenide-Graphene van der Waals Heterostructures, ACS Photonics, 2018, 5, 5047–5054 CrossRef CAS
.
- B. Zhu, H. Zeng, J. Dai, Z. Gong and X. Cui, Anomalously robust valley polarization and valley coherence in bilayer WS2, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11606–11611 CrossRef CAS PubMed
.
- F. Bussolotti,
et al., Roadmap on finding chiral valleys: screening 2D materials for valleytronics, Nano Futures, 2018, 2, 032001 CrossRef
.
- Y. Wang,
et al., Unveiling exceptionally robust valley contrast in AA-and AB-stacked bilayer WS2, Nanoscale Horiz., 2019, 4, 426–433 RSC
.
- C. Jiang,
et al., Microsecond dark-exciton valley polarization memory in two-dimensional heterostructures, Nat. Commun., 2018, 9, 1–8 CrossRef PubMed
.
- N. Zibouche, P. Philipsen, A. Kuc and T. Heine, Transition-metal dichalcogenide bilayers: Switching materials for spintronic and valleytronic applications, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 1–6 CrossRef
.
- A. M. Jones,
et al., Spin-layer locking effects in optical orientation of exciton spin in bilayer WSe2, Nat. Phys., 2014, 10, 130–134 Search PubMed
.
- C. Jiang,
et al., Zeeman splitting via spin-valley-layer coupling in bilayer MoTe2, Nat. Commun., 2017, 8, 1–6 Search PubMed
.
- M. Brotons-Gisbert,
et al., Spin-layer locking of interlayer valley excitons trapped in moiré potentials, Nat. Mater., 2020, 19, 630–636 CrossRef CAS PubMed
.
- M. H. D. Guimarães and B. Koopmans, Spin Accumulation and Dynamics in Inversion-Symmetric van der Waals Crystals, Phys. Rev. Lett., 2018, 120, 266801 CrossRef PubMed
.
- A. Kormányos, V. Zólyomi, V. I. Fal'ko and G. Burkard, Tunable Berry curvature and valley and spin Hall effect in bilayer MoS2, Phys. Rev. B, 2018, 98, 1–17 CrossRef
.
- M. Serlin,
et al., Intrinsic quantized anomalous Hall effect in a moiré heterostructure, Science, 2020, 367, 900–903 CrossRef CAS PubMed
.
- P. Blake,
et al., Making graphene visible, Appl. Phys. Lett., 2007, 91, 063124 CrossRef
.
- Y. Li, X. Li, T. Yu and G. Yang, Accurate identification of layer number for few-layer WS2 and WSe2 via spectroscopic study, Nanotechnology, 2018, 29, 124001 CrossRef PubMed
.
- W. Zhao,
et al., Origin of indirect optical transitions in few-layer MoS2, WS2, and WSe2, Nano Lett., 2013, 13, 5627–5634 CrossRef CAS PubMed
.
- Y. P. Varshni, Temperature dependence of the energy gap in semiconductors, Physica, 1967, 34, 149–154 CrossRef CAS
.
- B. Zhu, H. Zeng, J. Dai, Z. Gong and X. Cui, Anomalously robust valley polarization and valley coherence in bilayer WS2, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11606–11611 CrossRef CAS PubMed
.
- G. Wang,
et al., Exciton dynamics in WSe2 bilayers, Appl. Phys. Lett., 2014, 105, 182105 CrossRef
.
- B. Zhu, H. Zeng, J. Dai, Z. Gong and X. Cui, Anomalously robust valley polarization and valley coherence in bilayer WS2, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11606–11611 CrossRef CAS PubMed
.
- H. Su, A. Deng, Z. Zhen and J. F. Dai, Γ-valley assisted intervalley scattering in monolayer and bilayer WS2 revealed by time-resolved Kerr rotation spectroscopy, Phys. Rev. B, 2018, 97, 115426 CrossRef CAS
.
- A. Molina-Sánchez, D. Sangalli, L. Wirtz and A. Marini, Ab Initio Calculations of Ultrashort Carrier Dynamics in Two-Dimensional Materials: Valley Depolarization in Single-Layer WSe2, Nano Lett., 2017, 17, 4549–4555 CrossRef PubMed
.
- B. Miller,
et al., Tuning the Fröhlich exciton-phonon scattering in monolayer MoS2, Nat. Commun., 2019, 10, 807 CrossRef PubMed
.
- V. Chellappan, A. L. C. Pang, S. Sarkar, Z. E. Ooi and K. E. J. Goh, Effect of Phonons on Valley Depolarization in Monolayer WSe2, Electron. Mater. Lett., 2018, 14, 766–773 CrossRef CAS
.
- M. M. Glazov, E. L. Ivchenko, G. Wang, T. Amand, X. Marie, B. Urbaszek and B. L. Liu, Spin and valley dynamics of excitons in
transition metal dichalcogenide monolayers, Phys. Status Solidi B, 2015, 252, 2349–2362 CrossRef CAS
.
- F. Mahmood, Z. Alpichshev, Y. H. Lee, J. Kong and N. Gedik, Observation of Exciton-Exciton Interaction Mediated Valley Depolarization in Monolayer MoSe2, Nano Lett., 2018, 18, 223–228 CrossRef CAS PubMed
.
- Z. Wang,
et al., Intravalley Spin-Flip Relaxation Dynamics in Single-Layer WS2, Nano Lett., 2018, 18, 6882–6891 CrossRef CAS PubMed
.
- K. P. O'Donnell and X. Chen, Temperature dependence of semiconductor band gaps, Appl. Phys. Lett., 1991, 58, 2924 CrossRef
.
- A. Kormányos,
et al., k·p theory for two-dimensional transition metal dichalcogenide semiconductors, 2D Mater., 2015, 2, 022001 CrossRef
.
- E. Corro,
et al., Excited Excitonic States in 1L, 2L, 3L, and Bulk WSe2 Observed by Resonant Raman Spectroscopy, ACS Nano, 2014, 8, 9629–9635 CrossRef PubMed
.
- C. Sourisseau, F. Cruege, M. Fouassier and M. Alba, Second-order Raman effects, inelastic neutron scattering and lattice dynamics in 2H-WS2, Chem. Phys., 1991, 150, 281–293 CrossRef CAS
.
- X.-X. Zhang, Y. You, S. Yang, F. Zhao and T. F. Heinz, Experimental Evidence for Dark Excitons in Monolayer WSe2, Phys. Rev. Lett., 2015, 115, 257403 CrossRef PubMed
.
- M. Baranowski,
et al., Dark excitons and the elusive valley polarization in transition metal dichalcogenides, 2D Mater., 2017, 4, 025016 CrossRef
.
- G. Wang,
et al., In-Plane Propagation of Light in Transition Metal Dichalcogenide Monolayers: Optical Selection Rules, Phys. Rev. Lett., 2017, 119, 047401 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr04800k |
| This journal is © The Royal Society of Chemistry 2022 |