 Open Access Article
Open Access ArticlePerspectives on parity violation in chiral molecules: theory, spectroscopic experiment and biomolecular homochirality
Martin
Quack
 ,
Georg
Seyfang
and
Gunther
Wichmann
,
Georg
Seyfang
and
Gunther
Wichmann

Physical Chemistry, ETH Zürich, CH-8093 Zurich, Switzerland. E-mail: Martin@Quack.ch
First published on 2nd September 2022
Abstract
The reflection (or ‘mirror’) symmetry of space is among the fundamental symmetries of physics. It is connected to the conservation law for the quantum number parity and a fundamental ‘non-observable’ property of space (as defined by an absolute ‘left-handed’ or ‘right-handed’ coordinate system). The discovery of the violation of this symmetry – the non-conservation of parity or ‘parity violation’ – in 1956/1957 had an important influence on the further development of physics. In chemistry the mirror symmetry of space is connected to the existence of enantiomers as isomers of chiral (‘handed’) molecules. These isomers would relate to each other as idealized left or right hand or as image and mirror image and would be energetically exactly equivalent with perfect space inversion symmetry. Parity violation results in an extremely small ‘parity violating’ energy difference between the ground states of the enantiomers which can be theoretically calculated to be about 100 aeV to 1 feV (equivalent to 10−11 to 10−10 J mol−1), depending on the molecule, but which has not yet been detected experimentally. Its detection remains one of the great challenges of current physical–chemical stereochemistry, with implications also for fundamental problems in physics. In biochemistry and molecular biology one finds a related fundamental question unanswered for more than 100 years: the evolution of ‘homochirality’, which is the practically exclusive preference of one chiral, enantiomeric form as building blocks in the biopolymers of all known forms of life (the L-amino acids in proteins and D-sugars in DNA, not the reverse D-amino acids or L-sugars). In astrobiology the spectroscopic detection of homochirality could be used as strong evidence for the existence of extraterrestrial life, if any. After a brief conceptual and historical introduction we review the development, current status, and progress along these three lines of research: theory, spectroscopic experiment and the outlook towards an understanding of the evolution of biomolecular homochirality.
1. Introduction
Molecular chirality is of fundamental importance in stereochemistry and has, indeed, been crucial in the development of our understanding of the foundations of physical–chemical stereochemistry.1 Advances in the understanding and uses of chiral molecules are reflected by numerous Nobel prizes over more than a century beginning with the first to van't Hoff (1901, a founder of stereochemistry, while the prize citation emphasized other achievements) shortly thereafter to Emil Fischer (1902) and Alfred Werner (1913),2,3 and more recently V. Prelog (1975),4 W. S. Knowles, R. Noyori, and K. B. Sharpless in 2001 (ref. 5–7) or the most recent one in 2021 (ref. 8 and 9) as selected examples. Also molecular motors contain an important ‘chiral’ aspect.10–12 Chiral molecules are standard textbook13 and examination topics testing knowledge of chemical nomenclature.14 At the same time they are of crucial importance in chemical and pharmaceutical industry (see ref. 15 and 16 for example).The importance of molecular chirality in chemistry can also be exemplified by three special issues of Chimia over the first decades of the century. One, in 2001 describing the research of a large chemistry department after moving to new buildings at the start of the century,17 where a substantial fraction of the research groups worked on subjects with an essential ‘chirality’ component18–30 (and further research at least also partially on chirality aspects), one in 2008, devoted to the chemistry of chirality,31–40 and a last one in 2018 (ref. 41) where we might highlight the work on ultracold chiral molecules,42 new approaches to the determination of absolute configuration,43 and work on the CISS effect (chiral induced spin selectivity).44
At the same time chiral molecules have a deep connection to the foundations of physics through symmetries and conservation laws.45–47 Indeed, the discovery of the violation of space inversion symmetry, one of the fundamental symmetries of physics, or ‘parity violation’ in nuclear and elementary particle physics48–53 not only led to the development of the current ‘Standard Model of Particle Physics’ (SMPP),54–60 but also to an interesting interaction between high energy physics, molecular physics, chemistry, and also biochemistry and biology.61,62 This interaction results in the following at first perhaps surprising statements:63
(1) The fundamentally new physics arising from parity violation and the consequent electroweak theory in the SMPP leads to the prediction of fundamental new effects in the dynamics of chiral molecules and thus in the realm of chemistry.
(2) Parity violation in chiral molecules has possibly (but not necessarily) important consequences for the evolution of life.
(3) Possible experiments on molecular parity violation open a new window to looking at fundamental aspects of the standard model of high energy physics, and thus molecular physics might contribute to our understanding of the fundamental laws of physics.
Indeed, going beyond parity violation and the standard model, molecular chirality may provide a fresh look at time reversal symmetry and its violation and even the nature of time.46,64,65
The aim of the present article is to provide a perspective of the development and current status of theory and spectroscopic experiments in the field and also provide a brief account of the important open questions concerning the role of parity violation in the evolution of biomolecular homochirality. After a brief survey of the historical and conceptual background, we shall discuss the basic underlying quantum mechanical theory of the dynamics of chiral molecules and the role of parity violation as introduced by the SMPP and ‘electroweak quantum chemistry’. We shall then address the development of the experimental, spectroscopic approach to the study of parity violation in chiral molecules. Finally, we conclude with an outlook on the understanding of the possible role of parity violation in the evolution of biomolecular homochirality of life and also some further aspects of the role of symmetry violations and chirality in future developments of some fundamental physical problems. We shall concentrate on the conceptual aspects and the current status of the field and open questions and refer to some other reviews for more technical spectroscopic and theoretical details.46,66–68 We draw also from two recent lectures, one of which has appeared in print (in German).69,70 For the general spectroscopic and quantum dynamical background we refer to a recent book.71 As we cover different aspects of a broad range of interdisciplinary research, it is impossible to provide a complete literature survey and we apologize to those authors, whose work might be less than adequately cited. As molecular chirality and parity violation address some of the most fundamental aspects of understanding nature,64 we start here by a brief introduction of the historical background.72
2. The mirror symmetry of space and molecular chirality or dissymmetry as a geometrical and quasi-macroscopic concept
‘What could be more similar to my hand or to my ear and in all aspects more comparable than the image in the mirror? However, such a hand as seen in the mirror cannot replace the original hand in its location, because if this was a right hand then the one in the mirror appears as a left hand, and the mirror image of the right ear appears as a left ear, which never can take the place of the right one.” (Ref. 73, original in German, translated by us here).With this statement Immanuel Kant notes the remarkable observation that many objects in nature are ‘handed’ in the sense that their mirror image is similar and, indeed, symmetrically equivalent in most aspects, but not identical in the sense, that they are not structurally superimposable on the original.73 Today we call such ‘handed’ objects ‘chiral’ following a suggestion of Lord Kelvin74,75 from the ancient Greek word ‘χειϱ’ for hand. Kant, indeed, added an extensive discussion of this aspect of the world also in relation to the structure of space. Earlier, certainly Descartes (‘Cartesius’) had observed the handedness of his ‘Cartesian’ coordinate system,76 about which we learn at school with the ‘right hand rule’ or ‘right foot rule’ in mathematics courses77 and related notions are implicit in discussions of Newton and Leibniz on the structure of space.
One may wonder, when women or men discovered in history that a mirror image of a right hand is similar to a left hand. Mirrors have been used since antiquity and there are many reports in the ancient literature about mirror images also appearing on water surfaces, the story on Narcissus and Echo being famous, with the wonderful painting by Caravaggio. One can also find the understanding of the different structures of left and right hands in the old literature (in the book Jonah 4, 10–11 of the Bible, for instance, as cited with a brief hermeneutic discussion in ref. 66 and 69). But we have been strikingly unsuccessful in finding a discussion of the reversal of handedness by mirrors in the Greek philosophical literature, where one might suspect this to exist, or elsewhere in ancient literature, asking also specialists of the antiquity in this question. The images generated by different types of mirrors are discussed in Platon's dialogue ‘Timaios’ also in relation to the notion of left and right, but careful reading of the original text does not indicate an understanding of the effect on hands or the structural property of ‘handedness’.78
In more recent times, the ‘handedness’ of crystals was known from the early 19th century. Arago (1811)79 and Biot (1812–1818)80,81 showed that ‘handed’ quartz crystals rotated the plane of polarized light, an effect which was called ‘optical activity’. The rotation is opposite (‘dextro’ or ‘laevo’) for opposite forms of natural quartz (see Fig. 1, a ‘real’ example of such quartz crystals, which are the classic examples). Biot also reported the effect for liquids such as terpentine or solutions of camphor and related observations were made in this early period until 1830 by Eilhard Mitscherlich82 and Sir John Frederick William Herschel83 (see the historical discussion in ref. 84 and 85). Fresnel discussed observations with circularly polarized light.86 In this period also the technical term ‘dissymmetry’ was introduced for this property of handedness. Herschel already hypothesized that it might be a molecular property. The crucial experiment in this context was carried out by Pasteur (1848).87,88 He could separate crystals generated by a crystallisation from a solution of sodium–ammonium tartrate (the ‘para-tartrate’ form, which we would call a racemic mixture today, not optically active) into crystals of two opposite handed forms which appeared as a roughly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture (see Fig. 2). When he separately dissolved them, the solutions would be optically active and rotate the plane of polarized light in opposite directions. This was a most striking finding meeting with some scepticism, and Pasteur reported the story of the ‘refereeing’ of his manuscript:88 Biot had him repeat the experiment in his presence and after the successful completion he told Pasteur (then at age 26) ‘Mon cher enfant, j'ai tant aimé les sciences dans ma vie, que cela me fait battre le coeur’ (My dear child, I have loved science so much in my life that this makes my heart beat). One could hardly think of a more careful and critical and at the same time benevolent form of ‘refereeing’ (see also ref. 3).
1 mixture (see Fig. 2). When he separately dissolved them, the solutions would be optically active and rotate the plane of polarized light in opposite directions. This was a most striking finding meeting with some scepticism, and Pasteur reported the story of the ‘refereeing’ of his manuscript:88 Biot had him repeat the experiment in his presence and after the successful completion he told Pasteur (then at age 26) ‘Mon cher enfant, j'ai tant aimé les sciences dans ma vie, que cela me fait battre le coeur’ (My dear child, I have loved science so much in my life that this makes my heart beat). One could hardly think of a more careful and critical and at the same time benevolent form of ‘refereeing’ (see also ref. 3).
 | ||
| Fig. 1 Real D- and L-quartz, a gift from Dick Zare to M. Quack (after ref. 69). | ||
 | ||
| Fig. 2 Dissymmetric (chiral) crystal forms of sodium ammonium tartrate as redrawn here after the drawing of L. Pasteur (Fig. 1 and 4 in ref. 89). | ||
Shortly thereafter, optical activity was used in an investigation by Wilhelmy (1850),90 who studied quantitatively by optical activity measurements the kinetics of transformation of sugar in different acid solutions, which led him to a first formulation and integration of a (pseudo-)first order rate law as differential equation. This was another milestone both for kinetics and stereochemistry and appears also to be the first quantitative kinetic analysis of homogeneous catalysis,18,91 of relevance still today, as can be seen from ref. 5–9, 15 and 16.
While by 1850 the relation between chirality and optical activity had been discovered, the detailed understanding in terms of molecular structure came much later in the work of Le Bel and van't Hoff.1,92–95 Notably van't Hoff established the mirror image isomerism of chiral methane derivatives by a series of instructive investigations which we can schematically summarize in Fig. 3 and 4.
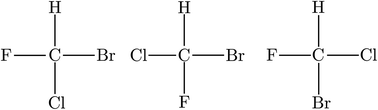 | ||
| Fig. 3 The wrong planar model structure with three different planar isomers of CHFClBr (after ref. 69 and 72). | ||
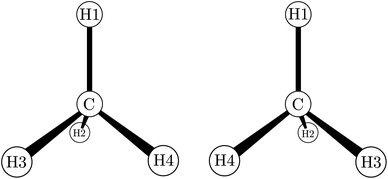 | ||
| Fig. 4 The two enantiomers of chiral methane derivatives (after ref. 66 and 69). With H1 = H, H2 = D, H3 = T and H4 = Mu (Muonium) one obtains a chiral methane isotopomer, and with H2 = NH2, H3 = COOH and H4 = R(variable) one obtains the amino acids of the D- and L-series. | ||
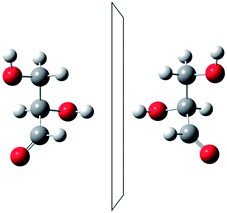
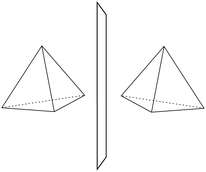
He noted, for example, that for the prototypical substituted methane derivative CHFClBr and related compounds the common notation of the formula in the plane (see Fig. 3) would suggest three different geometrical isomers, whereas only two were observed, and these two appeared to be nearly identical, except for optical activity (in those cases where this was known, but not known for this particular example at the time). This suggested the three-dimensional structures shown in Fig. 4 with just two isomers related to each other like image and mirror image or left and right hand. Fig. 5 and 6 show such structures with modern graphics for the amino acid alanine and the ‘simplest-sugar’ glyceraldehyde, which were shown to be optically active and obviously are chiral (or ‘dissymmetric’ in 19th century language). On the other hand, with four equal substituents arranged as a regular tetrahedron in CH4 the ‘mirror-image molecule’ can be superimposed on the original structure by a simple rotation (Fig. 7), and therefore there is only one form, the molecule is not chiral, or ‘achiral’ in modern language. These notions were quickly accepted and it was noted that in agreement with an early observation of Pasteur, in the chemistry of life one form was predominant, L-amino acids and D-sugars, whereas in the laboratory syntheses the other forms (D-amino acids and L-sugars) were equally likely. The predominance of one chiral form was recognized as a simple chemical signature of life, whereas Wöhler much earlier in the 19th century had shown by the synthesis of the ‘organic molecule’ urea from inorganic precursors, that ‘organic molecules’ are no unique signature of life processes. The D(dextro-) and L(laevo-) nomenclature for the isomers was introduced by Emil Fischer, who showed in 1894 that the enzymes as biochemical catalysts were acting in a ‘stereoselective’ fashion on only one form. He explained this by the geometrical fitting of enzyme and substrate as with a key and a lock writing in the conclusion of his article ‘On the influence of configuration on the action of enzymes’: ‘To use an image, I would say that enzyme and glycoside must fit like key and lock to have a chemical action upon each other. This representation has certainly gained in probability and value for stereochemical research, because evidence that the geometrical signature of molecules has such a large influence on chemical affinity even for mirror image forms had according to me to be obtained by actual observations’96 (original in German, translated by us here). One might add that an even better picture might be the fitting of right and left hands in gloves.97 This has many well known biological consequences, as we can distinguish by our sense of taste L-asparagine (slightly bitter) from D-asparagine (markedly sweet) as everybody can easily try out, or the different odor for different forms of many chiral molecules, and notably also the different activity of many chiral drugs, an important aspect in today's pharmaceutical industry15 with a world market for chiral chemicals estimated in 2019 at more than 50 billions (50 × 109) US Dollars. Following Kelvin, we call the two isomeric forms ‘enantiomers’ today, and more generally for general objects (also crystals) one may use ‘enantiomorphs’.74,75
 | ||
| Fig. 5 The two enantiomers of alanine (after ref. 69). | ||
 | ||
| Fig. 6 The two enantiomers of glyceraldehyde (after ref. 69). | ||
 | ||
| Fig. 7 Tetrahedron (achiral) with two identical, superimposable forms (after ref. 69). | ||
Fischer's D–L-nomenclature is still widely used in biochemistry today and he also introduced a convention to uniquely identify the geometry of the forms in relation to the geometry of macroscopic molecular models (as in Fig. 5 and 6). He did observe also, that, in principle, this convention was arbitrary and could not tell, which substance (say D or L) in the laboratory would actually correspond to the ‘absolute configuration’ of the one macroscopic model with its two possible forms, only the opposition of the two could be systematically classified. The determination of the ‘absolute configuration’ was first achieved by crystallography in 1951 by Bijvoet (see ref. 98 and 99). It turned out that the arbitrary conventional choice of Fischer was confirmed. Modern nomenclature follows another convention introduced by Cahn, Ingold and Prelog in 1966 (ref. 100) (see also ref. 14), the R and S nomenclature for the enantiomers, complemented by the P, M nomenclature for helical and axially chiral molecules. The conceptual foundations of the stereochemistry of chiral molecules in terms of classical structural models was essentially complete by the end of the 19th century and in practice is still in use in organic chemistry and biochemistry, including classical molecular dynamics for biomolecules used in modern times.4,8,9,13,101–103
We might mention here a beautiful book in which this ‘classical’ structure hypothesis, as effectively still used today by the practising chemist, is well represented and illustrated with many nice pictures.104,105 It is also perhaps amusing to note that Lewis Carroll in his famous Alice books in the 19th century has the young girl transgress the mirror and ask the cat: ‘Perhaps looking glass milk isn't good to drink?‘. There are rumours that Lewis Carroll (as Professor Dodgson in Oxford) had learned from a chemist colleague about the experiments of Wislicenus on the enantiomers of lactic acid106,107 (interestingly Wislicenus in this report from the chemistry club in Zurich speculates about isomers arising from the ‘arrangements of atoms in space’ in anticipation of the famous publications by van't Hoff93 and Le Bel92). This quick reception of scientific results in the general literature may remind one of Shakespeare's brief reference in the 17th century to the then just revived atomic theory in his play ‘as you like it’ (ca. 1601)72 or Michael Frayn's reference to the ‘Copenhagen interpretation’ of quantum mechanics in his play Copenhagen108 in the 20th century. Another entertaining example involving chirality is found in ‘The Documents in the Case’ by Dorothy Sayers and Robert Eustace (1930).109
We conclude this brief historical introduction by an important statement of van't Hoff94 who clearly expressed the consequences for the energetic and thermodynamic equivalence of the enantiomers arising from the symmetry. Considering the equilibrium in the reaction between R and S (a ‘stereomutation reaction’) he writes:
S(L) ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) R(D) R(D) | (1) |
| K = [R]/[S] = 1 | (2) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = − ΔRG°(T)/(RT) = 0, all T K = − ΔRG°(T)/(RT) = 0, all T | (3) |
| ΔRS°(T) = 0, all T | (4) |
| ΔRH°(T) = 0, all T | (5) |
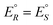 | (6) |
We have rewritten here van't Hoff's equations in modern notation. Because of the ‘exact symmetry’, as he writes, the ground state energies of the enantiomers 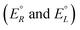 must be equal and all reaction energies ΔRH°, ΔRG° and entropies (ΔRS°) must be zero (see ref. 66 and 69 for further discussion and the exact quotation of the French text with its translation).
must be equal and all reaction energies ΔRH°, ΔRG° and entropies (ΔRS°) must be zero (see ref. 66 and 69 for further discussion and the exact quotation of the French text with its translation).
We anticipate here an important change which arose from developments in high energy physics of the second half of the 20th century. We know now that there is no such exact symmetry and in actual fact there is a slight ‘parity violating’ energy difference ΔpvE between the ground state of the enantiomers, say
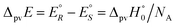 | (7) |
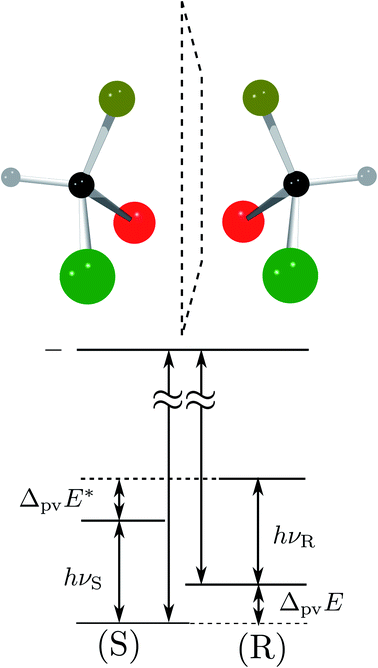 | ||
Fig. 8 Energy level scheme for the two enantiomers of CHFClBr including parity violation (see ref. 62 and 68). On the left the energy levels of the S-enantiomer are shown, on the right for the R-enantiomer. The top level is for an achiral state of well defined parity (here ‘−‘), common to both enantiomers. Following ref. 111 and 112S is calculated to be more stable than R by ΔpvE ≃ 200 aeV corresponding to about 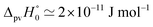 (see also Table 2 in Section 4.3). νS and νR are transition frequencies measured in the high-resolution spectra of the separated enantiomers (for instance in the infrared). Note that the difference between the transition energies hνS and hνR corresponds to the difference of the parity violating energy differences hνS − hνR = ΔpvE − ΔpvE* (see also Section 4.1). (see also Table 2 in Section 4.3). νS and νR are transition frequencies measured in the high-resolution spectra of the separated enantiomers (for instance in the infrared). Note that the difference between the transition energies hνS and hνR corresponds to the difference of the parity violating energy differences hνS − hνR = ΔpvE − ΔpvE* (see also Section 4.1). | ||
3. Molecular chirality in quantum mechanics: tunnel effect and parity violation as violation of mirror symmetry
3.1. Quantum mechanical tunneling in symmetrical and asymmetrical potentials
From 1925 onwards quantum mechanics provided a detailed theoretical understanding of how molecular structure and bonding arises113–120 and modern electronic structure theory as summarised in reviews and textbooks would claim that this understanding is essentially complete,121–125 particularly when relativistic effects are included as well.126,127 Indeed, Dirac already in 1929 made the statement:‘The underlying physical laws for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble. It therefore becomes desirable that approximate practical methods of applying quantum mechanics should be developed, which can lead to an explanation of complex atomic systems without too much computation.’119
This is one of the most frequently cited quotations in the quantum chemistry literature,128–130 even though often severely abbreviated.131 However, the statement was incorrect, as the weak nuclear force introducing parity violation was completely unknown by that time, but turns out to have important consequences in stereochemistry, as we shall see.
A first step in the quantum mechanical understanding of molecular chirality was taken by Friedrich Hund, who demonstrated, that the quantum mechanical behaviour of chiral molecules differed considerably from what one expects on the basis of the classical mechanical structural models.132,133 Let us consider in Fig. 9 as an example hydrogen-peroxide (HOOH) which in its equilibrium structure shows axial chirality with the two enantiomers shown (also considered as helical in analogy to the two snails shown in Fig. 9, we note that the two natural snails are not enantiomers at the microscopic level, both having proteins with the L-amino acids and DNA with D-sugars. According to Brunner, the relative abundance of the snails with the structure on the left compared to those with the structure on the right is 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is explained by the common D-sugar DNA leading to a preference of the structure on the left with respect to the right one134,135). It turns out that this description with quasi-rigid localized structures is quite inadequate for HOOH in quantum mechanics. By continuously changing the torsional angle indicated in Fig. 9, one can transform one enantiomer into the other: such a transformation from one enantiomer into the other is also possible in chiral molecules with a pyramidal, near tetrahedral structure as shown in Fig. 10 for the example of the ammonia isotopomer NHDT, where such a ‘stereomutation’ can be achieved by changing the angle with respect to a planar geometry of the four atoms.
1, which is explained by the common D-sugar DNA leading to a preference of the structure on the left with respect to the right one134,135). It turns out that this description with quasi-rigid localized structures is quite inadequate for HOOH in quantum mechanics. By continuously changing the torsional angle indicated in Fig. 9, one can transform one enantiomer into the other: such a transformation from one enantiomer into the other is also possible in chiral molecules with a pyramidal, near tetrahedral structure as shown in Fig. 10 for the example of the ammonia isotopomer NHDT, where such a ‘stereomutation’ can be achieved by changing the angle with respect to a planar geometry of the four atoms.
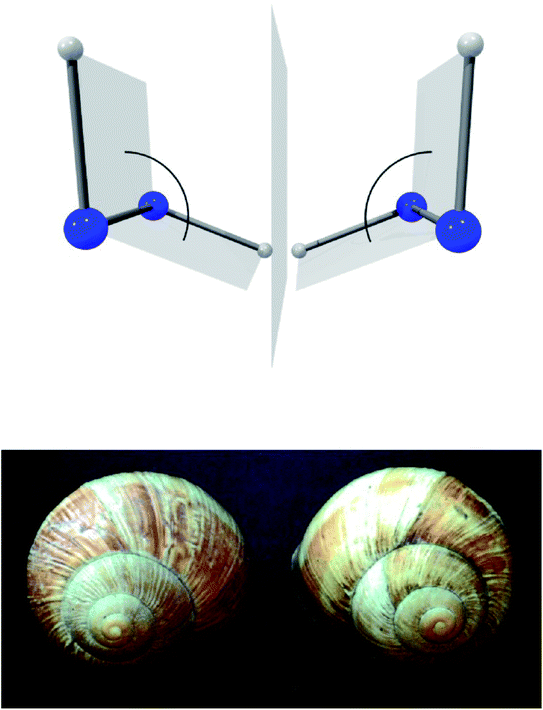 | ||
| Fig. 9 The classical chiral structures of hydrogen-peroxide H–O–O–H and of snails (as example of axial or helical chirality, after ref. 69). | ||
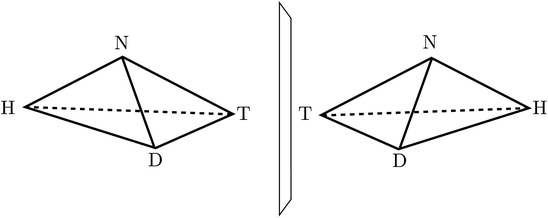 | ||
| Fig. 10 The classical structures of the chiral enantiomers of the ammonia isotopomer NHDT (after ref. 69). | ||
The transformation via planar transition structures in both examples is associated with a potential energy change shown schematically in Fig. 11.
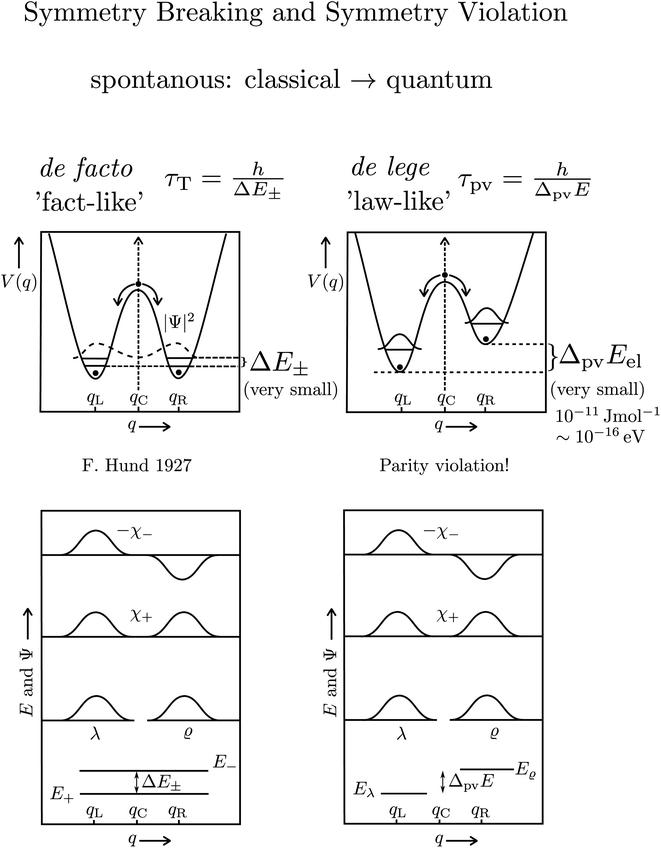 | ||
| Fig. 11 Illustration of the symmetric (parity conserving) potential on the left side following Hund 1927 for a chiral molecule with energy eigenstates of positive and negative parity separated by a tunneling splitting ΔE± and for an effective potential with parity violation on the right side leading to two localized ground states at the chiral structures separated by the parity violating energy difference ΔpvE (after ref. 67, see also ref. 136 and 137). ΔpvEel is the parity violating energy difference of the minima in the effective (electronic) potentials, whereas ΔpvE is the energy difference of the ground states of the two enantiomers (see Section 3.3), where we also use sometimes the ΔpvE0 in order to emphasize a ground state property. | ||
One may represent the stereomutation reaction from L to R (using the ‘physical’ notation left to right) by the motion of an effective mass in a potential energy V(q) as a function of the generalized coordinate q. In the time independent Schrödinger equation114–117 with a kinetic energy operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and a potential V(q) one obtains the eigenfunctions φk and energies Ek for the stationary states
and a potential V(q) one obtains the eigenfunctions φk and energies Ek for the stationary states
Ĥ = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) + V(q) + V(q) | (8) |
| Ĥφk(q) = Ekφk(q) | (9) |
| pk(q) = |φk(q)|2 | (10) |
It is seen that for the lowest energy levels (χ+ at E+ and χ− at E−) shown in the diagram this probability density has two equal maxima near the two enantiomeric structures, thus equal probability for finding each of the two enantiomers. In order to represent the experimental observation of localized enantiomers Hund considered the time dependent Schrödinger equation:114–117
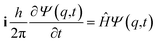 | (11) |
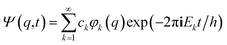 | (12) |
| P(q,t) = |Ψ(q,t)|2 | (13) |
If one retains just the two lowest terms in this sum (corresponding to χ+ = φ1 and −χ− = φ2 and energies E+ = E1 and E− = E2) one obtains a time dependent probability density (with ΔE1,2 = E2 − E1 = E− − E+)
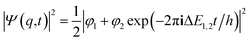 | (14) |
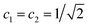 . This is an oscillatory function with a period
. This is an oscillatory function with a period| τ′ = h/ΔE± = h/(E2 − E1) | (15) |
Inspection of the graphical representation of the wave functions on the left hand side in Fig. 11 shows that this moves from a function λ located near the left minimum at t = 0
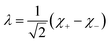 | (16) |
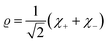 | (17) |
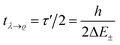 | (18) |
With these considerations Hund made two important observations: firstly the ‘reaction’ from one enantiomer to the other can occur, although neither of the energies E+ and E− is sufficient to overcome the ‘barrier maximum’ V(qc), a process which would be completely impossible in classical mechanics. This was the discovery of the quantum mechanical ‘tunnel effect’, with numerous later applications in chemistry and physics (see ref. 67 and 138 for the history and reviews). Secondly, when estimating parameters for the effective masses and potentials for the ‘inversion’ (from R to S) in the case of the chiral substituted methane derivatives, Hund found millions to billions of years for the stereomutation times, thus explaining the apparent stability of CHFClBr, amino acids or sugars for example (see ref. 139 for a critical discussion of the estimates, which does, however, not invalidate the conclusions). Indeed, F. Hund already discussed in some detail the dependence of tunneling splittings and tunneling times on the shape (both height and width) of the potential barrier and effective tunneling masses, and this dependence of tunneling times was also noted in later applications of the tunnel effect to explain radioactive α-decay (see ref. 138 for the history). A high and broad barrier and a large tunneling mass leads to long tunneling times.
The situation is quite different for the chiral molecules hydrogen-peroxide (HOOH) and the ammonia isotopomer, NHDT, which we have chosen here on purpose for illustration, as Hund's description is effectively correct for these examples. While the simple one-dimensional model for stereomutation used by Hund and discussed by us above for illustration of the concept has become textbook material, only recently full-dimensional ‘exact’ solutions of the time independent and time dependent Schrödinger equation have become possible, as this requires the solution in a space of 6 internal (vibrational) coordinates (q1, q2, …, q6) for the four atoms (nuclei) in these molecules and a potential hypersurface V(q1, q2, …, q6)140–146 (and further dimensions if external rotation is included142). This results in a 6-dimensional wave function Ψ(q1, q2, …, q6, t) and probability density (|Ψ|2). As a visualisation in a high dimensional space is not possible, one integrates over 5 coordinates (q1, …, q5) and represents the probability density as a function of one ‘reaction coordinate’ corresponding to the torsion angle τ in HOOH (still exact). Thereby one obtains a time dependent ‘wave packet’ as shown in Fig. 12 for HOOH which moves from one enantiomeric structure at the left to the other enantiomeric structure at the right in about 1.5 ps.140,141
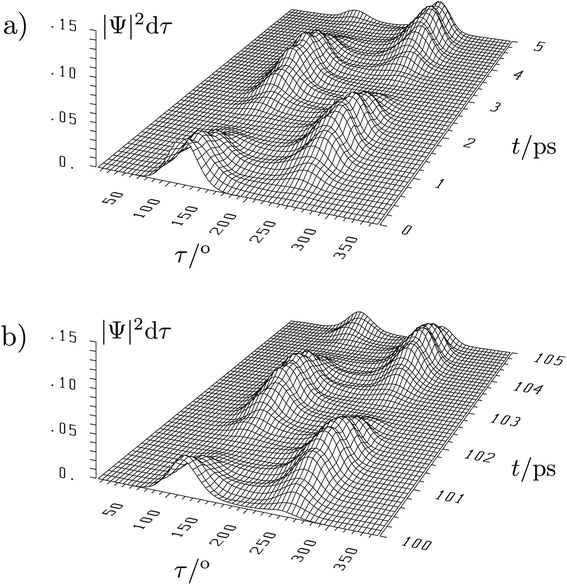 | ||
| Fig. 12 Six-dimensional wave packet evolution for H2O2 (HOOH) in its lowest quantum states. |Ψ|2dτ shows the time-dependent probability as a function of the torsional coordinate τ, where the probability density is integrated over all other coordinates. (a) shows the time interval from 0 to 5 ps and (b) the time interval from 100 to 105 ps with identical initial conditions at t = 0 as in (a).140,141 The migration of the wave packet from the left to the right corresponds to a change from one enantiomer of HOOH to the other in Fig. 9 with a transfer time according to eqn (18) of about 1.5 ps (after ref. 67). | ||
The corresponding result for the chiral ammonia isotopomer is shown in Fig. 13.142 Because of the short lifetime of the chiral, enantiomeric structures of HOOH or NHDT one may call such molecules ‘transiently chiral’. The time dependence could be easily followed by observing time dependent optical activity or circular dichroism (also by vibrational circular dichroism, VCD, or Raman optical activity, ROA), which will follow the wavepacket motion in a straightforward manner. We can note here the recent efforts on probing chirality on the femtosecond time scale.147,148 Also, on short time scales, vibrational excitation even of achiral molecules can show time dependent chirality, following the motion, say, of a quasiharmonic coherent oscillator state of an antisymmetric normal mode.61,149,150
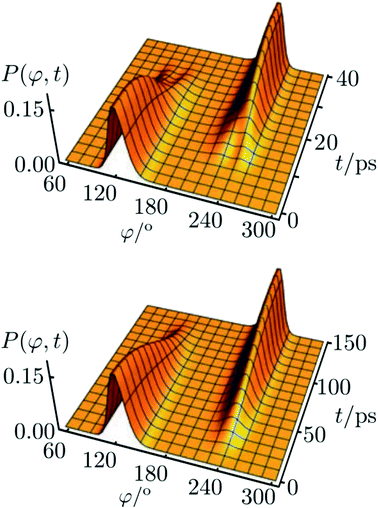 | ||
Fig. 13 Reduced probability density P(φ,t) as a function of the inversion coordinate φ and time t for NHDT. The two enantiomeric structures correspond to φ ≅ 120° and φ ≅ 240°, respectively, with φ = 180° corresponding to the planar geometry. The upper and lower panels show reduced probability densities (probability densities integrated over all other coordinates) for the tunnelling enhancement under coherent laser excitation (upper) and field-free (lower) dynamical schemes, respectively. The parameters of the laser pulse for tunneling enhancement are ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0 = 793.5 cm−1, Imax = 3.15 GW cm−2, and tp = 40 ps (after ref. 67 and 142). 0 = 793.5 cm−1, Imax = 3.15 GW cm−2, and tp = 40 ps (after ref. 67 and 142). | ||
The recent exact treatment for hydrogen-peroxide and ammonia isotopomers has also been extended to show various interesting effects such as mode selective tunneling stereomutation141 or tunneling enhancement and inhibition by coherent radiative excitation.142 We shall not pursue this in detail here but rather turn to the consequences of the asymmetry arising from parity violation, illustrated on the right hand side of Fig. 11. Here one can distinguish two dynamical limiting cases. If the asymmetry due to parity violation (ΔpvEel in the scheme of Fig. 11) is small compared to the tunneling splitting ΔE± in the symmetrical case
| ΔpvEel ≪ ΔE± | (19) |
| ΔpvEel ≫ ΔE± | (20) |
3.2. Symmetries, symmetry violations and approximate constants of the motion
The time evolution of a molecular (or any other ‘microscopic’) system according to the Schrödinger equation (eqn (11)) can also be written in a general abstract way by means of the time evolution operator Û(t,t0):71,151–153| Ψ(q,t) = Û(t,t0)Ψ(q,t0) | (21) |
This operator transforms the wavefunction Ψ(q,t0) at the initial time t0 to the wavefunction Ψ(q,t) at time t. Û satisfies a differential equation analogous to eqn (11) and for an isolated system with a time independent Ĥ it is given by an exponential function of Ĥ:
| Û(t,t0) = exp[−2πiĤ(t − t0)/h] | (22) |
For solutions with a more general time-dependent Ĥ see ref. 71 and 151–154. Another representation of time dependence in quantum dynamics makes use of the Heisenberg equations of motion155,156 for the operator ![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) (t) related to some observable Q, with the solution
(t) related to some observable Q, with the solution
![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) (t) = Û†(t,t0) (t) = Û†(t,t0)![[Q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0051_0302.gif) (t0)Û(t,t0) (t0)Û(t,t0) | (23) |
Instead of asking about the time dependence of observables, of which there are many, one might ask the opposite question, whether in a complex time evolving system there are observables which remain constant in time, the ‘constants of the motion’. These are all the observables Cj for which the corresponding operators Ĉj commute with the Hamiltonian Ĥ
| ĤĈj = ĈjĤ | (24) |
Making use of the solution of the Heisenberg equations of motion given by eqn (23) the time independence of Ĉj can be proven in one line, because Û being a function of Ĥ, eqn (22), it commutes with the Ĉj as well and it is also unitary Û†Û = 1, thus:
| Ĉj(t) = Û†(t,t0)Ĉj(t0)Û(t,t0) = Û†(t,t0)Û(t,t0)Ĉj(t0) = Ĉj(t0) | (25) |
The operators Ĉj form a group G, the symmetry group of the Hamiltonian.46,71,151,159 One can furthermore show that for a statistical ensemble described by the density operator ϱ also the expectation values 〈Ĉj(t)〉 = tr(ϱĈj) are time independent. Also, if Ψ(q,t) is an eigenfunction ζn(t) of Ĉj with eigenvalue Cjn one has
| 〈Ĉj(t)〉 = 〈ζn(t)|Ĉj(t0)|ζn(t)〉 = Cjn | (26) |
The eigenvalues Cjn are ‘good quantum numbers’ not changing in time. While this allows one to identify some simple structures, which do not change with time even in very complex time-dependent systems, one can proceed further by separating the Hamiltonian into contributions of different magnitude (Ĥ0 ≫ Ĥ1 ≫ Ĥ2etc.)
| Ĥ = Ĥ0 + Ĥ1 + Ĥ2 +… | (27) |
Then the energy levels of a molecule, say, would be described to a good approximation by Ĥ0, and when adding Ĥ1, this would change the energy only a little, being a small ‘perturbation’. The symmetry group G of the Hamiltonian may now depend on which terms are retained in eqn (27), with groups G0(Ĥ0), G1(Ĥ0 + Ĥ1), G2(Ĥ0 + Ĥ1 + Ĥ2), etc. Then one can have a symmetry or constant of the motion Ĉ0j belonging to G0(Ĥ0) which may not appear in G1(Ĥ0 + Ĥ1). Thus, if one observes a change in time for this observable corresponding to Ĉ0j, this cannot be due to Ĥ0, as Ĉ0j would be exactly time independent if only Ĥ0 is considered. The change of Ĉ0j in time must entirely arise from Ĥ1 (or Ĥ2, if any). At the same time, the different magnitudes of the contributions in Ĥ introduce a natural hierarchy of time scales, Ĥ0 leading to some possibly very fast changes for some observables but no change in Ĉ0j, the small Ĥ1 introducing a slow change of Ĉ0j, and so forth. This allows one to isolate very small contributions in the Hamiltonian arising from Ĥ1 independent of any large uncertainties, which may occur in the very large Ĥ0. To use a common picture: one can weigh the ‘captain’ directly without having to measure a difference in the weight of ‘ship + captain’ and ‘ship alone’, where the uncertainty in the latter measurement would be much larger than any possible weight of a captain. For the example of parity violation we shall have differences on the order of magnitude of typical electronic energies of molecules (say, on the order of 1 eV) compared to parity violating energies on the order of 100 aeV to 1 feV, more than 15 orders of magnitude smaller. One may compare this with the weight of a large ship (for example Queen Elisabeth 2) with about 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tons displacement and a captain with 50 to 100 kg, less than 6 orders of magnitude difference.
000 tons displacement and a captain with 50 to 100 kg, less than 6 orders of magnitude difference.
This concept can be made use of for theory, where the uncertainties in solutions of the Schrödinger equation may be due to theoretical or just numerical uncertainties, typically much larger than a fraction of 10−15: In quantum chemical calculations an uncertainty of 1 meV (in Ĥ0) would be considered quite acceptable, but is huge compared to 1 feV. The concept can also be made use of in the design of experiments, where a relative experimental uncertainty of less than 10−15 may be very difficult to achieve otherwise.
In a time dependent experiment one would follow the scheme of Fig. 14. One prepares a state of a given symmetry corresponding to a ‘good quantum number’ with respect to Ĥ0, and then follows the time dependence of this quantum number to observe an effect exclusively due to Ĥ1etc. This scheme can be used by means of various kinds of approximate symmetries such as nuclear spin symmetry158,159 or one can consider some specific symmetries from simplified molecular models for intramolecular vibrational energy flow in polyatomic molecules, for instance, and we have made extensive use of it in the past (see ref. 154 and 158–161 and our recent review,68 for example).
 | ||
| Fig. 14 Scheme for control of symmetries and time evolution in molecular dynamics (modified after ref. 157, see also ref. 68 and 97). | ||
However, the approach can also be used for testing fundamental symmetries of physics. These are given by the invariances of the Hamiltonian under:46
(1) Any translation in space
(2) Any translation in time
(3) Any rotation in space
(4) The reflection of all coordinates of all particles on the center of mass of the system (‘P’)
(5) ‘Time reversal’ (reversal of momenta and spins) (‘T’)
(6) Any permutation of identical particles (electrons or nuclei for the case of molecules)
(7) Charge conjugation – the replacement of all particles by the corresponding antiparticles (‘C’).
The symmetries are related to the corresponding conservation laws (for momentum, energy, angular momentum, parity, …) as has been discussed early on in quantum mechanics118,162 and in an interesting summary by Pauli163 for the three discrete symmetry operations C, P, T, which one may all consider as some kind of generalized ‘mirror symmetry’. Fig. 15 illustrates this for the case of the parity symmetry (‘P’, one uses also E* synonymously to denote the operation of space inversion symmetry in spectroscopy and molecular physics164). The inversion of the right handed coordinate system in the upper left part (as defined by the ‘right hand rule’ convention) by a mirror leads to the left handed coordinate system on the upper right side. The space inversion or parity operator on the right handed coordinate system changes (x → −x, y → −y, z → −z) into a left handed system as shown in the lower part. This can be transformed to the left handed ‘mirror’ image on the upper right by a rotation of 180° around the x axis, which corresponds to one of the symmetry operations under (3), the combination being obviously also a symmetry operation for the Hamiltonian, leading to a related constant of the motion, the space inversion P being the elementary operation. A further interesting aspect is the notion that each exact symmetry and conservation law leads to a fundamental ‘non-observable’ property of nature. This can be nicely understood with the statement by Einstein165 (original in German, as translated in ref. 46):
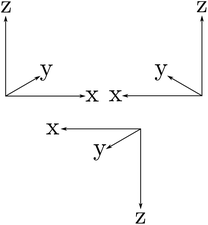 | ||
| Fig. 15 ‘Right handed’ Cartesian coordinate system (upper left), mirror image (upper right) and inverted (lower) coordinate systems being ‘left handed’. | ||
‘There are thus two types of Cartesian coordinate systems, which are called ‘right-handed’ and ‘left-handed’ systems. The difference between the two is familiar to every physicist and engineer. It is interesting that an absolute geometric definition of the right or left handedness is impossible, only the relationship of opposition between the two can be defined’.
For chiral molecules this implies that even if we can determine the ‘absolute’ configuration of a molecule in comparison to a macroscopic model in the laboratory, we cannot specify for either of the two whether they occur in a space with a left handed or right handed coordinate system. One way to illustrate this property of ‘non-observability’ is the so called ‘Ozma’ problem:65,166 if there were perfect space inversion symmetry, we would not be able to communicate to a distant civilization with a coded message (without sending a real chiral ‘model’), whether we are made of L-amino acids or of D-amino acids, for instance. This is another way of phrasing Einstein's statement. Van't Hoff and Einstein assumed space inversion symmetry to be universally valid and thus the ‘handedness’ of space would be ‘non-observable’. This was the common assumption until 1956/57, when parity violation was proposed and observed. Electroweak parity violation makes absolute handedness observable and removes a constant of motion and ‘good quantum number’ (parity). We have for the ‘electromagnetic Hamiltonian’ Ĥem
Ĥem![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) = = ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) Ĥem Ĥem | (28) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ψk = (+1)ψk ψk = (+1)ψk | (29) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ψj = (−1)ψj ψj = (−1)ψj | (30) |
The eigenfunctions of the Hamiltonian either are symmetric under space inversion (positive parity +1) or antisymmetric under inversion (negative parity −1). With electroweak parity violation due to the weak nuclear force we have Ĥem + Ĥweak
(Ĥem + Ĥweak)![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ≠ ≠ ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) (Ĥem + Ĥweak) (Ĥem + Ĥweak) | (31) |
One consequence is now that the ground state eigenfunctions of chiral molecules are localized and have no well defined parity as shown in the right hand part of Fig. 11 and the two states have different energies. Given this, the ‘handedness’ of space becomes ‘observable’ and we can communicate to a distant civilization of what type of amino acids we are made of predominantly (for instance the more stable ones, if that is established experimentally, see below). While the energy differences are truly minute, due to ‘weakness’ of Ĥweak, we can nevertheless compute them significantly and devise significant experiments, because of the different symmetries of Ĥem and Ĥweak, as discussed above. The different symmetry ‘isolates’ the effect of parity violation. We shall in the following subsection report on the development of the quantitative theory of parity violation and in Section 4 on the current development of experiments.
3.3. The quantitative theory of parity violation in chiral molecules
As mentioned, parity violation arises through the weak nuclear force introduced by Enrico Fermi in his early theory of radioactive β-decay.167 Initially, there was no suspicion of a violation of space inversion symmetry by this force, until the suggestion by Lee and Yang48 that assuming parity violation one could explain the so called Θ − τ puzzle of elementary particle physics, which led to the dramatically fast discovery of parity violation in high energy physics.49–53 This story is told in numerous places including historical articles and textbooks (see ref. 54, 163 and 168–170 for example). Fig. 16 shows a pictorial representation of the current view of fundamental forces in the standard model of particle physics (SMPP) as shown on the website of a large accelerator.171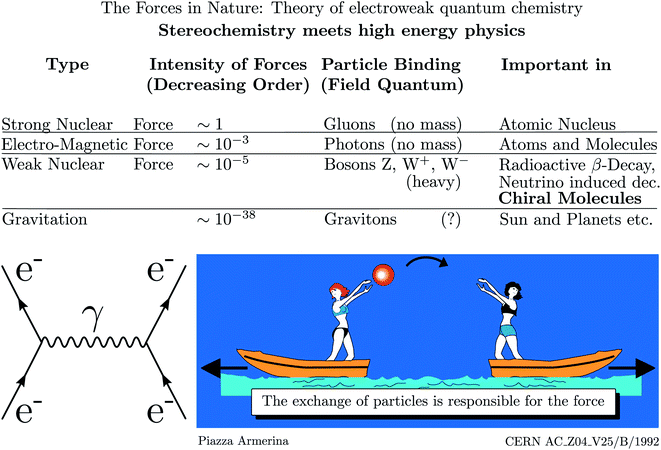 | ||
| Fig. 16 Forces in the standard model of particle physics (SMPP) and important effects. This is taken from the CERN website ref. 171, but the importance of the weak interaction for chiral molecules has been added here from our work (modified after ref. 63, in turn, adapted from ref. 171, Public Domain, we note that, while not referred to in ref. 171, the motif of the lightly dressed ladies throwing balls can be found in a mosaic at Piazza Armerina, Sicily, from the 4th century AD). We also added the Feynman diagram to the left representing the electromagnetic interaction between two electrons (e−) via the photon (γ) as field quantum (see also ref. 172). | ||
We have modified this picture by adding the importance of the weak nuclear force for the stereochemistry of chiral molecules. We have also added the Feynman diagram for the example of the electromagnetic interaction of two electrons to illustrate, how action at a distance is viewed in the SMPP172–174 (the diagrams are also sometimes called Stueckelberg diagrams, e.g. by Gell–Mann, or Feynman–Stueckelberg diagrams due to earlier contributions of Stueckelberg to the developments175–180). According to this view, the electromagnetic force, which is included in the ‘Schrödinger–Dirac’ like ordinary quantum chemistry, leads to the Coulomb repulsion, say, between two electrons by means of photons as field particles. In the picture the two electrons are compared to the ladies on two boats throwing a ball. If we do not see the exchange of the ball, we will only observe the accelerated motion of the boats resulting from the transfer of momentum in throwing the ball. We could interpret this motion as resulting from a repulsive ‘force’ between the two ladies on the boats. Similarly, we interpret the motion of the electrons resulting from ‘throwing photons as field particles’ as arising from the Coulomb law which forms the basis of the Hamiltonian in ordinary quantum chemistry. Different from the simple quasiclassical analogy, the Feynman diagram, which almost looks like representing such a picture, can be translated into quantitative mathematical equations, which then form the basis of a quantitative theoretical treatment of the interactions and dynamics.181 The Coulomb force with the 1/r potential energy law is of long range. The other fundamental forces arise similarly, but with other field particles. The strong force with very short range (0.1 to 1 fm) mediated by the gluons is important in nuclear physics but has only indirect influence in chemistry by providing the structures of the nuclei, which enter as parameters in chemistry, but there is otherwise normally no need to retain the strong force explicitly in chemistry. The weak force, on the other hand, is mediated by the W± and Z0 Bosons of very high mass (86.316 and 97.894 Dalton, of the order of the mass of a Rb to Mo nucleus) and short lifetime (0.26 yoctoseconds = 0.26 × 10−24 s for Z0 (ref. 68)). This force is weak and of short range (<0.1 fm) and one might think, that similar to the even weaker gravitational force (mediated by the still hypothetical graviton of spin 2), it should not contribute significantly to the forces between the particles in molecules (nuclei and electrons). Indeed, the weak force, because of its short range, becomes effective in atoms and molecules, when the electrons penetrate the nucleus and then it leads only to a very small perturbation on the molecular dynamics, which ordinarily might be neglected completely. However, in fact the weak force leads to a fundamental change as it has a different symmetry, violating space inversion symmetry, which is exactly valid for the strong and electromagnetic interactions (also gravitational interactions) according to present knowledge. When including the parity violating weak interaction, qualitative theory therefore tells us already that the ground state energies (and other properties) of enantiomers of chiral molecules will be different. The question remains then just how different the energies will be quantitatively. We shall not go into technical details here of the formulation of the quantitative theory of electroweak quantum chemistry (a term coined by us in ref. 182 and 183). However, some brief remarks may be in order concerning the development and current status of the theory of parity violation in chiral molecules, which has been reviewed in detail elsewhere46,63,136,184,185 (see also ref. 45, 182, 183, 186 and 187). The history of this theory can be broadly summarized in three phases.
In a first phase, after the discovery of parity violation in nuclear and high energy physics in 1957,48–53 qualitative suggestions were made concerning the role of parity violation in chiral molecules, with estimates which were often wrong by many orders of magnitude (in the period of about 1960–1980,188–190 see also the reviews in ref. 45, 46, 61 and 63 for many further references). In a second phase, attempts towards a quantitative theory started in about 1980, based on earlier work on the theory for atoms,191,192 extended approximately to molecules by Hegström, Rein and Sandars,193 Mason and Tranter194 and others195,196 (see also the further citations in ref. 46, 61, 63 and 186). It turned out, however, that these approaches were quite inadequate quantitatively.
A third phase started in 1993–1995 when in relation to our experimental project61,137 we also carefully reinvestigated the theory, rederiving it from its foundations in the standard model and critically analysing the steps towards ‘electroweak quantum chemistry’.182,183,197 Indeed, we found values for the parity violating energy differences ΔpvE in typical chiral ‘benchmark’ molecules often by one to two orders of magnitude larger as compared to previous results. In spite of some initial scepticism, which some audiences expressed towards the two-order of magnitude increase reported by us also in our lectures at the time (also in ref. 198, for example), our new, much larger values were subsequently confirmed by quite a few other theory groups199–202 (see ref. 46, 63, 136, 184 and 186 for further references). Today there seems to be general agreement on the new orders of magnitude from a number of quite different approaches (see for instance the recent summary in ref. 187), although the current results still scatter within about a factor of 2, which has various more technical reasons not to be discussed in detail here.
Fig. 17 illustrates the big quantitative jump discovered in our theoretical work in the mid 1990s and which stimulated much further theoretical work (and also experimental efforts). We summarize here the main steps in the theoretical development, which is described ‘from scratch’ up to practically useful equations in ref. 183 (see also the review in ref. 184, in particular, containing also some historical remarks).
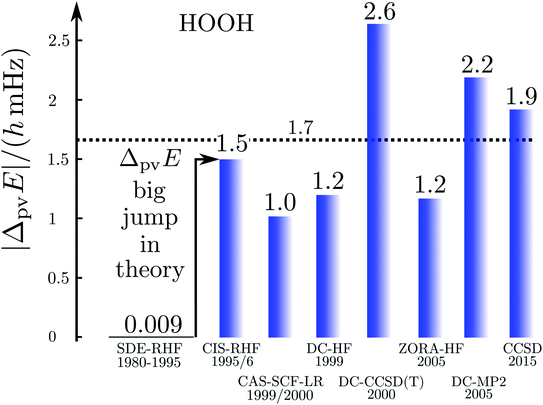 | ||
| Fig. 17 Graphical representation of the ‘big jump’ in theory occurring in 1995 (after ref. 186, values of the parity violating energy differences ΔpvE are shown for the benchmark molecule hydrogen-peroxide H2O2 (HOOH), note the extremely small unit for energy ΔpvE/h in millihertz). Table 1 provides a brief summary of numerical values with references. | ||
The starting point are the fully relativistic equations from the SMPP describing electron–neutron, electron–proton and electron–electron interactions in the order of their importance. In principle, one starts with electron–quark interactions at a more fundamental level (see184). One takes the low energy semirelativistic limit and then neglects also the electron–electron parity violating interactions which can be considered to be a smaller contribution only. For not too heavy nuclei of interest in simple inorganic and organic molecules (and also biomolecules) appropriate for fundamental studies one can use to a good approximation the Breit–Pauli form of the semirelativistic one- and two-electron spin–orbit interaction. For molecules involving heavy elements one can use as an alternative the Dirac Fock theory given by Laerdahl and Schwerdtfeger in 1999 (ref. 200) and related approaches,202,203 see also the reviews.136,184,185,204 Finally, one can represent the nucleus by a point like object with the electric charge −ZAe (ZA = number of protons) and an electroweak charge QA (neglecting also radiative corrections)
QA = [1 − 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(ΘW)]ZA − NA sin2(ΘW)]ZA − NA | (32) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(ΘW)] = 0.0724.71 We note that the value of the Weinberg parameter sin2
sin2(ΘW)] = 0.0724.71 We note that the value of the Weinberg parameter sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΘW (or weak mixing parameter) depends on the scheme used and the momentum transfer. At every step in these approximations one can, in principle, check these by the inclusion of the neglected effects, and none of the approximations is fundamental, although considerable computational effort may be necessary to improve upon them. The convergence of current theories as described by Fig. 17 and Table 1 would indicate that at least no ‘trivial’ effects have been overlooked, although tests by experiment seem advisable after past experience. We can add here that precision experiments on molecular parity violation can contribute in general ways to fundamental aspects of physics as well. If nuclear structure is well known, as is the case for the lighter nuclei up to argon at least, then precision experiments can contribute to a better understanding of the weak mixing angle according to eqn (32). On the other hand, for heavier nuclei, where the structure is less well known, precision experiments on parity violation could provide significant information on the neutron distribution in the nucleus, whereas many other experiments are most sensitive to the proton distribution. At this point it may also be of interest to refer to the extensive theoretical and experimental work available for atomic parity violation (see ref. 191, 192 and 215–221 for a small selection). While quite a number of successful spectroscopic observations of parity violation exist for atoms, these are restricted to very heavy atoms and this restriction remains probably valid for the foreseeable future. Because of uncertainties in both electronic and nuclear structure for heavy atoms, a quantitative theoretical analysis leads to relatively large uncertainties with respect to an analysis of fundamental parameters in the theory (such as sin2(ΘW)). A similar restriction is true also for recent efforts on studies of parity violation in diatomic molecules (so far unsuccessful, in contrast to atoms). We shall not discuss these further here and refer to the recent review by Berger and Stohner204 which has a focus on atoms and diatomic molecules.
ΘW (or weak mixing parameter) depends on the scheme used and the momentum transfer. At every step in these approximations one can, in principle, check these by the inclusion of the neglected effects, and none of the approximations is fundamental, although considerable computational effort may be necessary to improve upon them. The convergence of current theories as described by Fig. 17 and Table 1 would indicate that at least no ‘trivial’ effects have been overlooked, although tests by experiment seem advisable after past experience. We can add here that precision experiments on molecular parity violation can contribute in general ways to fundamental aspects of physics as well. If nuclear structure is well known, as is the case for the lighter nuclei up to argon at least, then precision experiments can contribute to a better understanding of the weak mixing angle according to eqn (32). On the other hand, for heavier nuclei, where the structure is less well known, precision experiments on parity violation could provide significant information on the neutron distribution in the nucleus, whereas many other experiments are most sensitive to the proton distribution. At this point it may also be of interest to refer to the extensive theoretical and experimental work available for atomic parity violation (see ref. 191, 192 and 215–221 for a small selection). While quite a number of successful spectroscopic observations of parity violation exist for atoms, these are restricted to very heavy atoms and this restriction remains probably valid for the foreseeable future. Because of uncertainties in both electronic and nuclear structure for heavy atoms, a quantitative theoretical analysis leads to relatively large uncertainties with respect to an analysis of fundamental parameters in the theory (such as sin2(ΘW)). A similar restriction is true also for recent efforts on studies of parity violation in diatomic molecules (so far unsuccessful, in contrast to atoms). We shall not discuss these further here and refer to the recent review by Berger and Stohner204 which has a focus on atoms and diatomic molecules.
| Methoda (and year) | ΔpvEel(HOOH) | ΔpvEel(HSSH) | |
|---|---|---|---|
| a Note the equivalence, in principle, of methods as given in the parentheses (CIS-RHF, CIS-LR, TDA) and (CPHF, RPA), differences arising only because of slight differences in numerical methods applied in the independent calculations by different authors. In ref. 187 −ΔpvEel = Epv(P) − Epv(M) was given for H2O2 (HOOH) in order to present positive values (see ref. 187 and 164 for an explanation of acronyms). For these axially chiral (‘helical’) molecules the P and M nomenclature is used by convention (e.g. see ref. 4 and 14). b Ref. 194. c Ref. 182 see also ref. 198. d Ref. 183. e Ref. 206. f Ref. 207. g Ref. 208. h In principle the TDA value of ref. 199 should be scaled by 75% to give a value of 120 × 10−14hc cm−1, see ref. 62 and 207. i Ref. 187. j Ref. 197. k Ref. 209. l Ref. 210. m Ref. 211. n Ref. 212. o Ref. 200. p Ref. 213. q Ref. 214. | |||
| Old | SDE-RHF (1984)b | −0.03 | 2.0 |
| CIS-RHF (1995/1996)c,d,e,f,g | −5 | 188.1 | |
| TDA (1997)h | −7 | 161.5 (120)h | |
| CPHF (2015)i | −2.9 | 242.0 | |
| MC-LR-RPA (2000)e,g,j,k,l | −2.8 | 185.0 | |
| CAS-SCF-LR (2000)j,k | −3.4 | — | |
| CCSD (2015)i | −6.4 | 238.3 | |
| ZORA-HF (2005)m | −3.9 | 294.5 | |
| ZORA-B3LYP (2005)n | −8.3 | 290.0 | |
| ZORA-BLYP (2005)n | −9.9 | 278.3 | |
| DC-HF (1999)o | −4.0 | 280.0 | |
| DC-MP2 (2005)p | −7.3 | 224.3 | |
| DC-CCSD(T) (2000)q | −8.8 | 215.1 | |
| New range (approx.) | −6 (±4) | 230 (±70) | |
In contrast, as we shall see below, certain spectroscopic studies on parity violation in chiral molecules have the promise to be successful in molecules involving only the lighter elements. They are thus of interest also in terms of fundamental physics. Furthermore, studies of parity violation in chiral molecules provide a direct link to effects that may be important for biochemistry and the evolution of biomolecular homochirality, which provides a further fundamental motivation for such studies. The scatter in the current results for ΔpvE of the benchmark molecule HOOH should not be taken as an indication that accurate calculations are not possible: indeed, the scatter is in part due to the fact that a somewhat hypothetical value of ΔpvEel is computed and to secondary effects. For molecules, where ΔpvE0 corresponds to a measurable quantity as a ground state energy difference, this can be accurately calculated, if also vibrational effects are taken into account (see discussion in ref. 46 and 112). We use here the index 0 in the symbol ΔpvE0 in order to emphasize a property of the ground state.
Without going into any detail of the theory for chiral molecules, we shall provide here a simplified summary of some of the main aspects and a few exemplary results. An instructive approximate form for the parity violating potential in chiral molecules is given by eqn (33) from perturbation theory
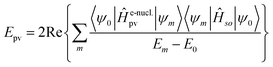 | (33) |
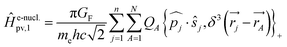 | (34) |
Here we use SI units with common symbols for the fundamental constants71 and in particular the Fermi constant
| GF = 1.4358510(8) × 10−62 J m3 | (35) |
One notes the small value for GF and the antisymmetry of 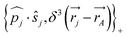 leading to the antisymmetry of the effective potential in eqn (40).197 The sums extend over all electrons (n) and all nuclei (N) in the molecule. {,}+ is the symbol for the anticommutator and
leading to the antisymmetry of the effective potential in eqn (40).197 The sums extend over all electrons (n) and all nuclei (N) in the molecule. {,}+ is the symbol for the anticommutator and ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) j is the momentum and ŝj the spin operator for the jth-electron. The Dirac-delta function
j is the momentum and ŝj the spin operator for the jth-electron. The Dirac-delta function 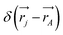 vanishes at all values except when
vanishes at all values except when 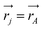 in the point nucleus approximation (see above). This part of the parity violating Hamiltonian is sufficient when discussing properties independent of nuclear spin. When nuclear spin IA is to be considered as for hyperfine structure or for NMR experiments one has to include a nuclear spin dependent term197
in the point nucleus approximation (see above). This part of the parity violating Hamiltonian is sufficient when discussing properties independent of nuclear spin. When nuclear spin IA is to be considered as for hyperfine structure or for NMR experiments one has to include a nuclear spin dependent term197
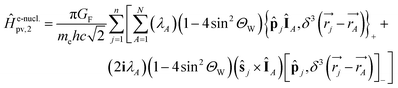 | (36) |
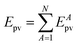 | (37) |
In ref. 183 one can find some illustrations for such individual contributions from atoms (generally dominated by the heavier atoms in the molecule). Furthermore as the neutron number is different for different isotopes, parity violation introduces a fundamentally new isotope effect arising from the weak nuclear charge QA: isotopic chirality is important for parity violation as pointed out in ref. 46 and 61 and calculated quantitatively in ref. 222. We should also mention, that eqn (33), which we gave here, because it leads to some instructive insight on the structure of the potential, in actual calculations this has slow convergence of the sum, when carried out numerically in this way.182,183 In practice one uses an expression from response theory eqn (38), which is known to be equivalent to eqn (33) as established through propagator methods and leads to numerical results with much faster convergence (see ref. 46, 63, 67 and 197 for discussions).
| Epv = 〈〈Ĥpv;Ĥso〉〉ω=0 = 〈〈Ĥso;Ĥpv〉〉ω=0 | (38) |
One can say that the parity violating potential Epv is the response of 〈Ψ0|Ĥpv|Ψ0〉 to the static (ω = 0) perturbation Ĥso or vice versa (see ref. 197 for details of the derivation). In contrast to atoms, the parity violating potential Epv in polyatomic (chiral) molecules depends on S = 3N − 6 internal coordinates describing the structure of the molecule. Similar to the ordinary electronic potential energy of the molecule it is a potential hypersurface in an S-dimensional space. As chiral molecules necessarily have at least 4 atoms, this is an at least 6-dimensional space (for the examples HOOH or NHDT the space would be just 6-dimensional). We can thus write with some general internal coordinates more explicitly
| Epv = Epv(q1,q2,q3,…,qs) | (39) |
This potential is antisymmetric with respect to the operation of space inversion ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) (or Ê* in the ‘spectroscopic’ nomenclature46), we can thus write with a symbolic notation for the inverted coordinates
(or Ê* in the ‘spectroscopic’ nomenclature46), we can thus write with a symbolic notation for the inverted coordinates ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) i:
i:
Ê*Epv R(q1,q2,q3,…,qs) = Epv S(![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 1, 1,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 2, 2,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 3,…, 3,…,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) s) = −Epv R(q1,q2,q3,…,qs) s) = −Epv R(q1,q2,q3,…,qs) | (40) |
We can define a parity violating energy difference
ΔpvE(q1,q2,q3,…,qs) = Epv R(q1,q2,q3,…,qs) − Epv S(![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 1, 1,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 2, 2,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 3,…, 3,…,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) s) s) | (41) |
The absolute values of these parity violating energy differences for given structures are very small, on the order of sub-feV typically for molecules composed of lighter atoms only. The sign of ΔpvE depends on the structure and we note that for some well defined convention (say R and S in the CIP convention or P and M for axially chiral molecules or D and L in another convention), ΔpvE may change sign even within a given domain (say all R). We denote by Epv R or Epv S that the potential refers to an R or S structure in the given convention. This is illustrated for the examples HOOH and HSSH in Fig. 18, where the potentials are shown as a function of just one coordinate, the torsional angle α indicated by the angle symbol in Fig. 9.
 | ||
| Fig. 18 Parity conserving (a) and parity-violating (b) potentials for H2O2 and H2S2 (after ref. 207). | ||
The parity violating potentials in the lower part of the figure are antisymmetric with respect to inversion at the point α = 0°, where they are zero by symmetry. On the other hand one sees a sign change also in the range of some chiral geometries with an ‘accidental’ value Epv = 0 at chiral geometries of about α = ±100°. Nevertheless it is true that two mirror image structures have exactly the same value but opposite sign for Epv (but possibly being zero), as the potential is strictly antisymmetric. On the other hand, the Born–Oppenheimer electronic potentials shown in the upper part of Fig. 18 are strictly symmetric with respect to inversion at α = 0°. This result is true also going beyond the Born–Oppenheimer approximation at higher levels of approximation and in fact the symmetry remains true for the exact electromagnetic Hamiltonian at all orders of precision: the difference of energies between mirror image (space inverted) structures is exactly zero by symmetry as long as only strong and electromagnetic interactions are included. We note that in ref. 208 higher dimensional parity violating potential hypersurfaces are discussed and some graphical representations for 2-dimensional surfaces are shown. As discussed in Section 3.1 with eqn (19) and (20) one must discuss the relative magnitude of the parity violating potentials in relation to tunneling processes connecting the two enantiomers. Only when parity violation dominates over tunneling, eqn (20), one will have localized wavefunctions and a measurable ground state energy difference ΔpvE0 between the enantiomers. We have systematically studied this for the series of hydrogen isotopomers XYYX, i.e. for the chalcogenic Y and X = H, D, T including also mixed compounds (i.e. with X,X′ different and Y,Y′ different) and further compounds ZYYZ with other elements Z and further compounds and this has been reviewed recently.67 A graphical summary can be found in Fig. 19, where the logarithm of the parity violating energy differences ΔpvE and tunneling splittings ΔE± (divided by h, i.e. in frequency units of Hz) is shown as a function of the logarithm of the ‘effective’ nuclear charge Zeff, taken to be the most highly charged nucleus in the molecule, for simplicity. It turns out that for HOOH and HSSH the tunneling splittings ΔE± for the symmetrical potentials are much larger than ΔpvE (they are off-scale in Fig. 19). Thus in HOOH and HSSH one does not find a measurable parity violating ground state difference ΔpvE, the ground state is delocalized and has almost pure parity, as also excited rovibrational-tunneling states. For the higher elements in the series the tunneling splittings become comparable to ΔpvE. TSeSeT being the first example where parity violation dominates, and for the tellurium and polonium compounds parity violation dominates already for the deuterated compounds, thus these molecules might, in principle, be useful for measurements of ΔpvE0 disregarding other problems arising from chemical properties and radioactivity.
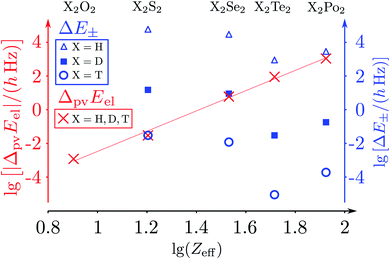 | ||
Fig. 19 Doubly logarithmic representation of the parity-violating energy differences ΔpvEel (as decadic logarithm, lg, electronic contribution from the parity-violating potential energy differences) as a function of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zeff in the series 1,2,3H − X − X −1,2,3H with X = O, S, Se, Te, Po and taking Zeff = ZX as the effective nuclear charge number (crosses ‘×’ for all isotopomers after ref. 186). ΔpvEel is essentially independent of the hydrogen isotope. This is compared with tunnelling splittings (ΔE±) where the dependence on the hydrogen isotope is essential (triangles for H, squares for D, circles for T). The results are from the summary in ref. 46, where the calculations for ΔpvEel were taken from ref. 197 for H2O2 and H2S2 (also from ref. 208). The results for ΔpvEel of H2Se2 and T2Se2 are from ref. 200, and the tunnelling splittings (ΔE± were taken from ref. 223–227). The slope of the straight-line fit is about 6.0(2), corresponding to about the Zeff5 law (see, however, the discussion in ref. 208). Zeff in the series 1,2,3H − X − X −1,2,3H with X = O, S, Se, Te, Po and taking Zeff = ZX as the effective nuclear charge number (crosses ‘×’ for all isotopomers after ref. 186). ΔpvEel is essentially independent of the hydrogen isotope. This is compared with tunnelling splittings (ΔE±) where the dependence on the hydrogen isotope is essential (triangles for H, squares for D, circles for T). The results are from the summary in ref. 46, where the calculations for ΔpvEel were taken from ref. 197 for H2O2 and H2S2 (also from ref. 208). The results for ΔpvEel of H2Se2 and T2Se2 are from ref. 200, and the tunnelling splittings (ΔE± were taken from ref. 223–227). The slope of the straight-line fit is about 6.0(2), corresponding to about the Zeff5 law (see, however, the discussion in ref. 208). | ||
The graphical representation in Fig. 19 is suggested by an equation originally given by Zel'dovich228,229 and complemented in ref. 46 by a geometry dependent factor fgeo (for Zel'dovich fgeo = 1)
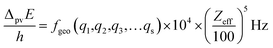 | (42) |
This would provide a simple estimate, if one takes some weighted average over the charge numbers of the nuclei in the molecule (in the simplest case a weighted average of the two heaviest nuclei46). The simple scaling with Z5 is suggested by the form of the operators, the effect of spin–orbit coupling and of the weak nuclear charges QA taking the simple approximation that the number of neutrons is roughly proportional to Z as well. One can also check for an empirical scaling Zeffn with an adjustable power n, which one could derive from a fit to the slope in the graph in Fig. 19. In this case one obtains n = 6.0(2) as an ‘empirical’ result (the straight line fit in Fig. 19). The problem in such scaling formulae arises from the complicated form of fgeo(q1,q2,q3,…qs) and a critical discussion can be found in ref. 208. An obvious way to find molecules with smaller tunneling splittings is to use compounds ZYYZ (or ZYYX etc.) with heavier Z-atoms and interesting examples are ClOOCl230–232 and ClSSCl.233,234Fig. 20 shows the torsional potential and the parity violating potential as a function of the torsional angle (with again scales on the ordinate axes being different by 15 orders of magnitude as shown). One can see very nicely the symmetry of the ‘electromagnetic’ (Born–Oppenheimer) potential in this case shown centered at the trans-structure (180°) and the antisymmetry of the parity violating potentials (for various calculations with slightly different quantum chemical methods). ClSSCl is an example where the tunneling splitting was shown to be at least 40 orders of magnitude smaller than the parity violating potentials233 as recently reconfirmed.227 Thus in this molecule, the ground states of each enantiomer are clearly localized at the chiral structures and one can significantly measure a ground state energy difference ΔpvE0 between the enantiomers of this molecule. This measurable energy difference for the ground state (or excited rovibrational states possibly including hyperfine substructures) can be calculated by the expectation values for the corresponding rovibronic (possibly nuclear spin hyperfine) state φ(k)evr:
ΔpvE(k) = 〈φ(k)evr|Epv R(q1,…,qs)|φ(k)evr〉 − 〈φ(k)evr|Epv S(![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) 1,…, 1,…,![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) s)|φ(k)evr〉 s)|φ(k)evr〉 | (43) |
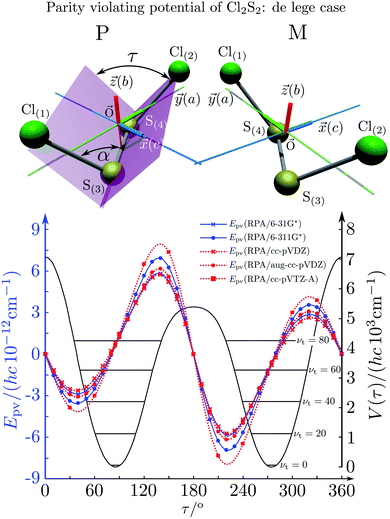 | ||
| Fig. 20 Calculated torsional potential (full line, right ordinate scale) and parity-violating potential (left ordinate scale, lines with various symbols for various approximations in the electroweak quantum chemistry233) for ClSSCl. The equilibrium structure and the definition of the torsional angle τ are shown in the upper part of the figure234 (after ref. 233). | ||
The ground state energy difference ΔpvE0 is a special case with k = 0. Sometimes the ΔpvE0 can be approximated by taking the values of the parity violating potentials at the equilibrium geometries ΔpvEel(qe). For ClSSCl, for example, one finds ΔpvE0 = hc × 1.35 × 10−12 cm−1 and ΔpvEel(qe) = hc × 1.29 × 10−12 cm−1,233 where the vibrational averaging was restricted to the torsional coordinate to obtain an estimate for the uncertainties introduced when neglecting vibrational averaging (see also ref. 112).
Fig. 21 illustrates another effect. The parity violating potential as a function of structure can change sign just when changing the conformation of some side chain without changing the configuration at the chiral center. This was discussed in detail for alanine183,235 as it is also of potential relevance for biological homochirality (see below). Changing the orientation for the carboxylato group has a great influence on the parity violating potential, being positive in about the range 50° to 140° and negative otherwise. However, the configuration at the ‘asymmetric carbon atom’ is, of course always the same, corresponding to L-alanine for all angles shown in Fig. 21.
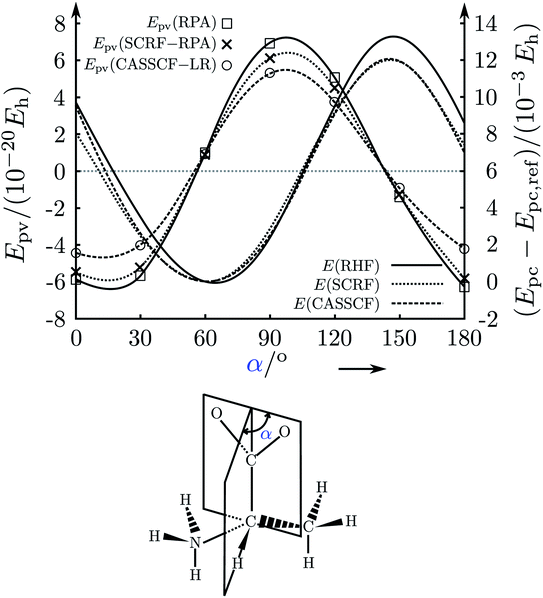 | ||
| Fig. 21 Calculated parity violating potential Epv (left ordinate scale) and parity conserving potential Epc (right ordinate scale) for alanine in the gas phase and in solution as a function of the orientation of the carboxylato group of the zwitterionic form of L-alanine (α in the upper part corresponding to the angle in the structure shown in the lower part). The dotted lines correspond to results in solution (labelled SCRF-RPA), the line labelled Epv(RPA), □, are for the gas phase. The dashed lines are from CASSCF-LR calculations, the highest level used. The ordinary lines without symbols represent the parity conserving potentials with a minimum near 60°. The differences between gas phase and solution are not very large and comparable changes are also found when changing the level of theory (after ref. 183 and 235). | ||
While in the present perspective article we do not review details of the implementation of the theory in the quantum chemical calculations a brief note on the practical aspects of these may be useful. In Zurich the earliest implementation used electronic wavefunctions (ψ0 and ψm in eqn (33), for example) from the standard Gaussian program package (see ref. 183 and supplementary material for details), later implementations used linear response theory, eqn (38) with the common Dalton package (see ref. 197 for a description). We also used an implementation with density functional theory (see ref. 184 not published in detail otherwise, but see also ref. 201 for example) and later with coupled cluster linear response theory in the open source PSI3 package.187 Several other implementations exist from the later work of other groups using various program packages and we refer to the reviews and the literature cited for further details.46,182,184–187 We might also note that in addition to the parity violating energy differences ΔpvE one can also calculate many other properties with some of these implementations, such as parity violating frequency shifts, average structures of the ground states, excited states, thermodynamic properties etc. (see e.g. ref. 110–112, 138 and 184), all of which are modified by parity violation.
4. Towards spectroscopic experiments
4.1. Developing experimental concepts and spectroscopic techniques for the study of parity violation in chiral molecules
As briefly mentioned in Section 3, successful spectroscopic experiments promise great progress in fundamental aspects of molecular and biomolecular stereochemistry and possibly also concerning precision experiments on parameters of the standard model of particle physics (SMPP). At the same time such experiments also present a major challenge because of the small magnitude of the predicted effects, and there are no ‘low hanging fruits’ to be harvested, even though the high hanging fruits may be of particularly good taste. As of today there seem to be only two reasonably advanced efforts worldwide, one in Zürich which started with first publications from 1986 (ref. 137) onwards and one in Paris, starting with first publications in 1999.236 The two projects have been reviewed for example in ref. 46, 62, 66, 67, 136, 237 and 238. Other groups have expressed interest in developing experimental projects (e.g. ref. 239), but there does not seem to be any concrete published record on progress in any of these. There have been proposals on a variety of experimental concepts on how to address parity violation in chiral molecules and we have summarized these before.46,62 None of these other schemes seem to be particularly promising or easier than the schemes used in current projects, but one should certainly also consider these and further possibilities. Here we shall discuss only the two different concepts for the currently ongoing projects. Fig. 22 shows a graphical survey of the historical development, from which one can get an overview over these really long term efforts. | ||
| Fig. 22 Graphical survey of the historical development of the two currently pursued experimental concepts (with (a) ref. 240, (b) ref. 241, (c) ref. 137, (d) ref. 242, (e) ref. 243, (f) ref. 244, (g) ref. 236, (h) ref. 245, (i) ref. 237, (j) ref. 238), (k) ref. 246, (l) ref. 247, (m) ref. 248). | ||
The different concepts can be understood with the energy level schemes shown in Fig. 8 and 23. In a scheme originally proposed by Letokhov in 1975 (ref. 240 and 249) one attempts to measure a difference in the high resolution spectra of the separate enantiomers S and R, which may for a particular transition have the frequency νS and νR in the different enantiomers. As one can see from the scheme in Fig. 8 this corresponds to a difference of parity violating energy differences ΔpvE in two corresponding molecular levels
| ΔpvE* − ΔpvE = h(νR − νS) | (44) |
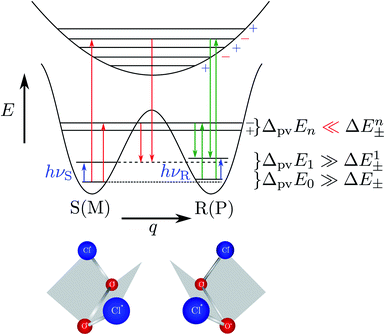 | ||
| Fig. 23 Enantiomers of chiral molecules of the general type X–Y–Y–X and scheme for the experiment to measure ΔpvE (red arrows for time-dependent experiment) and Δpvν = νs − νR (blue arrows). The combination of selected red and green arrows in the scheme leads to a measurement of ΔpvE in the frequency domain. The excited state of well defined parity (minus or plus signs) can be in an electronically excited state or in an excited vibrational-tunneling state as shown in ref. 231. The red arrow in absorption corresponds to a transition between an S and a negative parity level (energy hνS−). The green arrow in absorption corresponds to a transition between an R and a negative parity level (energy hνR−). The difference is hνS− − hνR− = ΔpvE0. The energy difference between the two blue absorption lines within R and S, hνS − hνR = ΔpvE0 − ΔpvE1, is the difference of parity violating energy differences (modified after ref. 69 and 136). | ||
The group of Letokhov has already tried to see a corresponding splitting of lines in infrared spectra of CHFClBr in a racemic mixture249 measuring at sub-Doppler resolution of about Δν/ν ≃ 10−8, which is almost ten orders of magnitude away from the effect as calculated later.111 Shortly thereafter Arimondo, Glorieux and Oka did sub-Doppler Lamb-dip spectroscopy on camphor with separated enantiomers, with about a similar precision.241 Again, the effect was calculated later to be much smaller250 for camphor as well. We have in Zurich followed Letokhov's scheme in parallel to our scheme, achieving high resolution analyses with hyperfine structure analysis of microwave and rovibrational infrared spectra of CHFClBr in supersonic jets.242,243 This work identified coincidences with CO2 laser lines and came to the conclusion, that with ultrahigh resolution sub-Doppler spectroscopy using these or related coincidences one might approach resolutions sufficient to identify parity violating effects.243 Such experiments were subsequently actually carried out in Paris achieving Δν/ν ≃ 2 × 10−13 (ref. 236) still several orders of magnitude away from the theoretically predicted effects.111 With subsequent improvements reviewed in ref. 237 and 238, the currently ongoing experiments appear to be promising for molecules involving very heavy elements, where the parity violating effects are relatively large. So far, no experiment along these lines has been successful, however.
In the other concept proposed by us in 1986,137 actually informally reported earlier on a few occasions between 1977 and 1986 already (see ref. 68 and references cited therein), one makes use of an ‘achiral’ excited molecular energy level of well defined parity which has radiative electric dipole transition moments connecting to both enantiomers (see Fig. 8 and 23). Using such a level, one can prepare a coherent superposition of well defined parity in the ground state and follow the time evolution of parity due to parity violation (see Section 4.2). From this, one obtains ΔpvE directly and separately (one could also measure some ΔpvE* separately, of course46). This scheme can also be carried out in frequency resolved experiments, when ΔpvE can then be isolated as a spectroscopic ‘combination difference’.61 We shall discuss now some aspects for the time dependent scheme in more detail.
4.2. Towards a measurement of ΔpvE and a test of sensitivity with an achiral molecule
Our approach in Zurich137 can be illustrated with the scheme outlined in Fig. 23. It uses the idea that either one may have a planar excited electronic state, where the rovibronic levels have essentially well defined parity or else one has a modest barrier for stereomutation in the electronic ground state, where one can thus reach by vibrational excitation with infrared lasers levels near to or above the barrier, where they can have large tunneling splittings and thus satisfy the condition in eqn (19), guaranteeing that they have essentially well defined parity, a typical tunneling switching situation.231 Then one can carry out an experiment following the schemes in Fig. 14 and 24. One first prepares with a sequence of two laser pulses a state of well defined parity at low energy, where the inequality eqn (20) applies. One can use rapid adiabatic passage (RAP) in a molecular beam experiment245 or chirped laser pulses232 or also stimulated Raman adiabatic passage (STIRAP).251 This prepared parity state is time dependent and evolves under parity violation according to eqn (11) and (12) which in the two state approximation becomes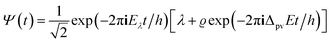 | (45) |
 | ||
| Fig. 24 Experimental molecular beam setup showing the three laser beams of the three steps (top part, scheme, middle part, modified after ref. 245 and below a photograph of the time-of-flight part of the actual setup). We note that the laser systems used in the experiment need actually much more space than this ‘core’ part of the experiment. In the back one can also see (just barely) a part of the setup for comb based high-resolution cavity-ring down spectroscopy of molecules in a supersonic jet expansion.252 | ||
Thus the populations of the positive and negative parity level become
| 1 − p+(t) = p−(t) = sin2(πΔpvEt/h) | (46) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x ≈ x2 for small values of the argument resulting in
x ≈ x2 for small values of the argument resulting in| 1 − p+(t) = p−(t) ≃ π2ΔpvE2t2/h2 | (47) |
This change in the populations can be observed spectroscopically because the rovibronic spectra of the parity isomers differ, as shown in Fig. 25. When one has a full assignment of the rovibronic spectrum of the R or S enantiomer (or a racemic mixture) one can label each line by a parity symbol ‘+’ or ‘−’, depending upon whether it connects to a positive or negative parity of the upper level in the transition, all lines being allowed in the spectrum for the ordinary chiral molecule (R or S or racemic mixture) of the upper part in Fig. 25. After preparation of a ‘negative parity isomer’ in the preparation steps only the blue lines marked with a + will appear due to electric dipole selection rules. As the character of the prepared state changes parity in time following eqn (46) and (47), this can be probed by detecting transitions at frequencies corresponding to the red lines marked ‘−‘, and the reverse would be true after initial preparation of a ‘positive parity isomer’. This detection can be carried out sensitively, say, by a UV laser multiphoton excitation–ionization technique. The sensitivity of this detection, i.e. how small a population in eqn (47) is detectable, determines in essence the size of ΔpvE which can be detected without the signal disappearing in the noise. We note that in a real experiment neither the parity selection will be perfect nor will the time evolution be completely free from external influences (collisions, fields, thermal radiation, etc.), these effects determining the ‘noise’ background limiting the measurement. On the other hand, the frequency resolution need only be sufficient to detect separate rovibrational levels, and for this a resolution of 1 MHz (often only 10 or 100 MHz, depending on the spectrum) will be sufficient and is readily available by current high resolution laser spectroscopic techniques for instance with the frequency comb based optical parametric oscillators (OPO's) used by us in ref. 245, but also with other laser techniques.
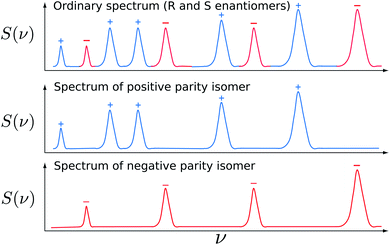 | ||
| Fig. 25 Schematic illustration of the spectral changes in the superposition experiment (modified after ref. 66 and 136). | ||
We have tested the method and its sensitivity with the setup shown in Fig. 24 and with an achiral molecule NH3, where the spectrum is extremely well known and assigned.245 The spectroscopic scheme of preparation and detection steps is shown in Fig. 26. These experiments, which also demonstrated new hyperfine structure resolution on excited vibrational states of NH3, show, of course, effective parity conservation in the time evolution, because NH3 is achiral with levels of well defined parity, which would also be the case for the chiral isotopomer NHDT having a large tunneling splitting in the ground state.142 However, the test experiment can be used for an estimate of the sensitivity of the current setup and therefore of the values ΔpvE, which would be detectable. It was concluded that values of ΔpvE ≃ 100 aeV should be measurable with the current experimental setup, and systematic improvements would allow the measurement of even smaller values of ΔpvE. Such values are predicted for chiral molecules involving only atoms not heavier than chlorine. Indeed, for the molecule ClOOCl parity violation is calculated to completely dominate over tunneling, making the molecule suitable, in principle, for a measurement of ΔpvE. In ref. 232 we have reported a complete simulation of the experiment with preparation and detection steps. The current progress in the experiment depends on obtaining adequate assignments of spectra for suitable chiral molecules identifying positive and negative parity levels as indicated schematically in Fig. 25. This turns out to be a non-trivial task with progress to be discussed in the next section. We shall, however, first discuss an interesting conceptual aspect. The prepared parity isomers in the experiment have the character of being at the same time R and S enantiomers corresponding to the wavefunctions χ+ and χ− indicated in Fig. 11, which carry equal weight for λ and ϱ which would be the chiral enantiomers. Such states are classically impossible and sometimes are called ‘Schrödinger's cat’ after the famous discussion of Schrödinger, which identified quantum mechanical states of a cat which is prepared in a thought experiment in a state where it is at the same time dead and alive (with some probability253), a situation which is classically absurd (see also a cartoon in ref. 66). We have noted occasionally that Schrödinger's ‘quantum cat’ analogy corresponds to a cruel experiment on an animal, which frequently comes out dead in the final step of the analysis (‘observation’). We therefore have proposed (for the analogous ‘parity isomer’) as a better analogy a quantum chameleon which stays alive and only changes color in the course of time, which would be a natural thing for a chameleon to do anyway (the change of a spectrum as in Fig. 25 is, of course, the analogue of a change of color68,254,255). Fig. 27 illustrates the quantum chameleon experiment. One starts out with a natural (chiral) chameleon (alive, say with S-alanine etc.) of some arbitrary color (shown colorless on top). In the preparation step one generates a well defined parity state for the chameleon with some color (say green for the positive parity). This implies that the chameleon is a superposition of the chameleon and its ‘mirror image’ enantiomer, which would be highly non-classical not only at the macroscopic level but also at the molecular level, all chiral molecules such as amino acids etc. would be prepared in a superposition of R and S enantiomers. This non-classical state would change color with time (staying a superposition) and in the end in any case the animal would stay alive, being subjected in the experiment only to some mild infrared radiation. In contrast to the Schrödinger cat the quantum chameleon is not in a superposition state of ‘dead and alive’ but in a superposition state of ‘left and right’ at the same time, which are both alive and stay alive in the final step. Whether at intermediate time the animal feels uncomfortable with such superpositions of R and S enantiomers we do not know, but we hope that all is comfortable and perfectly fine for the chameleon making it an allowed friendly experiment on an animal.
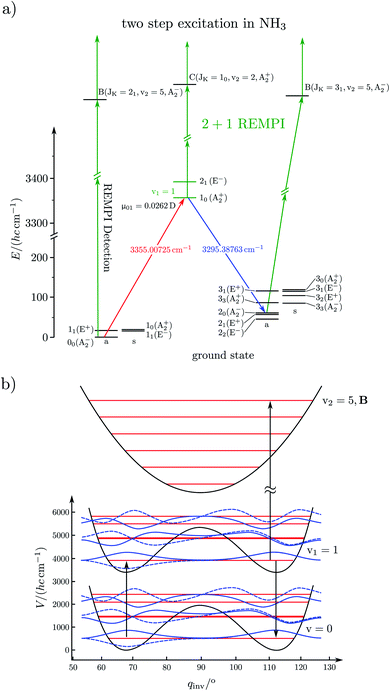 | ||
| Fig. 26 (a) Scheme of some of the rovibrational levels relevant for the one and two photon population transfer in NH3. The green line is for the REMPI detection. (b) Quasi-adiabatic channel potentials of NH3 for the lowest channel and the vibrationally excited channel with v1 = 1. The vibrational energies for the 3 lowest inversion levels are shown together with the corresponding wavefunctions as supported by the effective quasiadiabatic channel potentials (after ref. 245). | ||
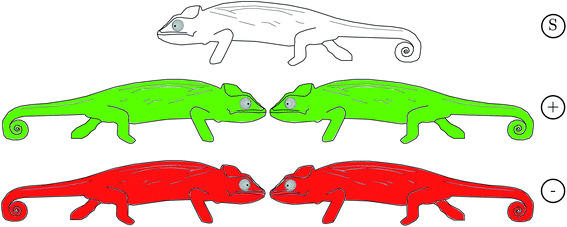 | ||
| Fig. 27 Time evolution of the ‘quantum chameleon’. It starts in some natural state of undefined color (top) being then prepared as a superposition state (two classical states at the same time left and right, green color corresponding to positive, ‘+’ parity), then changing color to red, corresponding to a negative parity state still with two classical structures at the same time but different phase (drawn with Inkscape256). | ||
4.3. Development of spectroscopic techniques and high resolution analyses for chiral molecules and the spectroscopic realization of a quantum chameleon
Identifying suitable molecules and their high resolution spectra as suitable for ‘ultra high’ resolution in view of a spectroscopic detection of parity violation in chiral molecules is important for all experimental concepts. Particularly for our approach as proposed in 1986,137 it is essential to have adequately resolved and analysed spectra in order to identify lines connecting to states of well defined parity in the excited state as discussed in Section 4.2.However, until 1986 there existed not a single example of a chiral molecule, where an analysis of an optical spectrum (IR, VIS, UV) had been achieved with full rovibrational resolution as needed for this approach. Such analyses seemed very difficult although not impossible at this time for molecules of the necessary minimum complexity related to chirality. In the meantime there has been much progress in developments of spectroscopic techniques which is reviewed elsewhere257–262 (see also many further articles contained in ref. 258). Specifically, progress has been made also on the analysis of high resolution spectra of chiral molecules and Table 2 provides a survey of chiral molecules for which parity violation has been studied theoretically and where preliminary high resolution analyses of optical spectra are available by now. The table retains only molecules, for which tunneling splittings in the ground state are negligible such that ΔpvE0 is an actually measurable ground state energy difference of the stable enantiomers according to the scheme on the right hand side of Fig. 11. These molecules are thus in principle suitable for studies of parity violation by one of the techniques discussed in Section 4.2, although not all are really very favourable for such studies, if |ΔpvE| is small. Here, we shall discuss one relatively favourable case: 1,2-dithiine (C4H4S2) shown in Fig. 28.284,285
| Molecule | |ΔpvE|/aeV | References |
|---|---|---|
a A preliminary value is small.
b Here theory calculated frequency shift values for the C–F stretching fundamental transition.
c Small preliminary value.
d Preliminary estimate is small.
e Strongly conformer dependent and in any case small.
f In most cases the ground state energy differences ΔpvE in aeV (attoelectronvolt, 10−18 eV) are approximated by the electronic energy differences at the equilibrium geometries, which is only a rough approximation. Dividing the values by 10.36 one obtains the reaction enthalpies 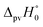 at 0 K in pico Joule mol−1 (1 pJ = 10−12 J). Dividing by 1.24 one obtains the corresponding reduced wavenumber (i.e. energy as hc × 10−14 cm−1). at 0 K in pico Joule mol−1 (1 pJ = 10−12 J). Dividing by 1.24 one obtains the corresponding reduced wavenumber (i.e. energy as hc × 10−14 cm−1).
|
||
| ClOOCl | 71.3 | 187, 231 and 232 |
| ClSSCl | 161.2 | 233 and 234 |
| PF35Cl37Cl | 3.5 | 222 and 262 |
| HSSSH | 198.4 | 263 and 264 |
| CHF35Cl37Cl | 260, 261 and 265–267 | |
| CHFClBr | 235.6 | 111, 112, 242 and 243 |
| CDFClBr | 235.6 | 112 and 268 |
| CHFClI | 269 and 270 | |
| CHFBrI | 269, 271 and 272 | |
| CHDTOH | 45.9 | 273 |
CHF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHF CHF |
17.4 | 187, 274 and 275 |
CHF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCl CHCl |
86.8 | 187 and 275 |
CHCl![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCl CHCl |
136.4 | 187 and 275 |
| D-Oxirane (CH2CHDO) | (0.025)c | 276 |
| D2 oxirane (trans CHDCHDO) | 277 | |
| F-Oxirane (cyclo-CH2CHFO) | 21.1 | 244, 278 and 279 |
| Cyclo-CH2CD2SO | 246 and 280 | |
| Cyclo-CH2CHDSO | 246 and 280 | |
| Cyano-oxirane CH2CHCNO | 12.4 | 281 and 282 |
| Cyano-aziridine CH2CHCNNH | 12.4 | 281 and 283 |
| 1,2-Dithiine C4H4S2 | 1364.0 | 284 and 285 |
| Alanine (CH3CHNH2COOH) | 6.2e | 182, 183 and 235 |
 | ||
| Fig. 28 The enantiomers of 1,2-dithiine are shown on the left together with the symmetric parity conserving (blue line, left ordinate scale) and antisymmetric parity violating potentials (red line, right ordinate scale) on the right (after ref. 284 and 285). | ||
For this molecule theory predicts ΔpvE/(hc) ≃ 1.1 × 10−11 cm−1 (corresponding to ΔpvE ≃ 1.36 feV) which is well in the range accessible to our current experimental technique. Also the tunneling splitting in the ground state has been estimated to be well below 10−20 cm−1, which guarantees that ΔpvE0 is, in principle, measurable.284 At the same time the barrier for stereomutation is calculated to be around 2500 cm−1, which makes large tunneling splittings at this and higher levels possible, in a range accessible to our comb-based high resolution laser (OPO) supersonic jet techniques245,252 (in addition to high resolution FTIR spectroscopy260,284,285). It is clear, however, that the analysis of rotation–vibration–tunneling spectra in a molecule of this complexity still presents a major challenge, particularly so at high energy in a very dense spectrum. Clearly progress on similar molecules, also newly designed ones, remains desirable in the future. Another relatively favourable candidate for experiments in Table 2 would be trisulfane (HSSSH) for experiments in the ground electronic state. For 1,3-dichloroallene one could use an excited electronic state as intermediate achiral state with levels of well defined parity. We note that one advantage of the experimental scheme following137 (as illustrated in Fig. 24) is, that there is no need to synthesize enantiopure samples. One can simply work with a racemate or an enantioenriched sample as it might be easily available.
At present we shall discuss an example of an achiral molecule of almost comparable complexity, where we have successfully achieved such an analysis of rotation-vibration-tunneling states in a tunneling switching situation.286–288 This has allowed us to demonstrate non-classical ‘quantum chameleon states’ involving ground state levels which are separated by energies corresponding to about hc × 0.8 cm−1. The example is m-D-phenol which exists in the two planar isomeric forms as syn- and anti-isomer, as shown in Fig. 29. While the electronic Born–Oppenheimer potential hypersurface has minima of identical energy for these isomers, small zero point energy effects lead to a small ground state energy difference of ΔE(syn–anti), which was predicted by theory to be much larger than the ground state tunneling splitting in the symmetric tunneling potential for ordinary phenol, which is about hc × 0.0019 cm−1.286
 | ||
| Fig. 29 The lowest adjusted adiabatic channel potential for meta-D-phenol including several torsional energy levels and wavefunctions. The two potential wells corresponding to the anti and syn structures are indicated by the two equilibrium structures (carbon atoms are shown in grey, hydrogen light grey, oxygen red and deuterium violet). The subscripts l and u refer to lower and upper levels, whose energies are referenced to the lowest quantum state as 0 and are given in terms of Ek/(hc cm−1). The superscripts + and − denote positive and negative parities. In the graphical representation the splittings can be seen only for the highest level but can be deduced from the energies given. The two minima of the adiabatic channel potentials are indicated by their negative values with respect to the energy zero. The eigenfunctions of the lower sublevels are shown in black, the ones for the upper sublevel in red color. One sees that for the two lowest torsional levels they are localised in one well (with effectively zero values in the other well, thus no visible line). In the higher torsional levels they are delocalized over both wells (after ref. 287 and 288). | ||
Thus in the lowest vibrational states of m-D-phenol, one has energy eigenstates separated by about 0.8 cm−1 with wavefunctions corresponding to localized syn- and anti-isomers as shown in Fig. 29. The situation is analogous to the asymmetric tunneling situation with parity violation in the right hand side of Fig. 11 with localized wavefunctions as well. However, the asymmetry in m-D-phenol has a different physical origin and is much larger (0.8 cm−1 corresponding to about 0.1 meV instead of 100 aeV for parity violation, 12 orders of magnitude smaller). Nevertheless also for the m-D-phenol we have a tunneling switching situation given the modest barrier for isomerization of only about 1000 cm−1. Thus for the torsional level vT = 2 at 600 cm−1, and higher, the eigenfunctions are delocalized and show an approximate symmetry similar to the symmetric case of ordinary phenol, a typical tunneling switching situation. Therefore one can by a sequence of laser pulses completely analogous to our discussion for chiral molecules in Section 4.2 generate an exotic ‘quantum chameleon’ state which is at the same time a syn- and anti-isomer, a classically impossible situation. Fig. 30 shows the result for a simulation of such an experiment. Because for the case of m-D-phenol these results are based on a successful analysis of the experimental high resolution spectra, the results of Fig. 30 can be considered equivalent to an experimental result, because the effective Hamiltonian used in the simulation fits the experimental high resolution spectroscopic results (see the discussions in ref. 18, 97 and 154 on this point). The population of syn- and anti-isomers at the end of the pulse sequence is constant in time. However, because it is a superposition of eigenstates of different energy, this is a time dependent state, and the time dependence can be observed by a change in the infrared spectrum for example as shown in Fig. 31 and 32. We have used here the results of ref. 288, but have chosen a width for the spectral ‘lines’ as it would correspond to a kinetic experiment with uncertainty limited simultaneous time and frequency resolution.289 These results can be considered as the analogue of our experimental scheme on parity violation. Because of the different orders of magnitude, the time scales are quite different. Also, here we use the scheme in the reverse way by analysing a frequency resolved spectrum to obtain the corresponding time resolved result. This is possible, because our frequency resolution is sufficient to do so. In the experiment on parity violation, we do not have the frequency resolution to measure the effect. However, by observing the time resolved result, we can obtain the desired energy resolved quantity ΔpvE.
 | ||
| Fig. 30 Preparation of the exotic non-classical superpositions of the syn- and anti-isomer structures in m-D-phenol by a sequence of laser pulses. One starts in the localized ground state (vT = 0) of the more stable anti-isomer, which is excited by a first (long) laser pulse to the lower tunneling sublevel of the excited torsional state (vT = 3). This is a delocalized ‘tunneling switching’ state. A second, short laser prepares the superposition of syn- and anti-states in the vT = 0 torsional level. The upper left shows the time dependent eigenstate populations (full lines) and laser pulses (dashed lines). The upper right part shows the wavepacket as probability |Ψ(φ,t)|2dφ as a function of the torsional angle. One recognizes the localized initial state, the delocalized intermediate state and the syn- and anti-superposition at the very end of the time range shown (after ref. 288). | ||
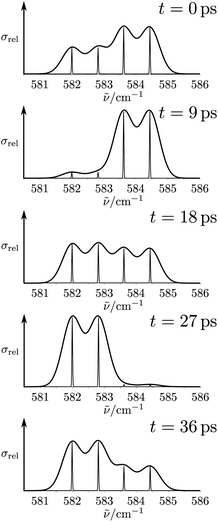 | ||
| Fig. 31 Time dependent infrared absorption spectrum (in the vT = 2 range) of the superposition state after the very end of the excitation shown in Fig. 30 (i.e. of the isolated molecule without further laser excitation), which defines t = 0 for the present figure. Neither the probability density nor the eigenstate populations change in the range of times (t = 0 to 36 ps) shown here. The time dependent change of the spectrum arises from a change of phases and corresponding approximate symmetries of the state in analogy to eqn (44)–(46). The width of the lines was chosen related to a time resolution of 9 ps (modified after ref. 288, where details are discussed). The spectra are calculated with effective spectroscopic Hamiltonian parameters derived from experiment.287,288 | ||
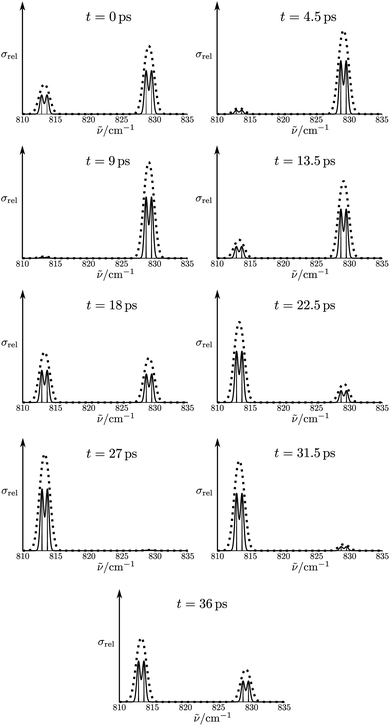 | ||
| Fig. 32 Time dependent infrared spectrum as observed by ‘kinetic spectroscopy’, with uncertainty limited time and frequency resolution (for the vT = 3 range). See also captions to Fig. 30 and 31. Here the width of the spectral lines was chosen to correspond to a time resolution of 4.5 ps (dashed lines) and about 10 ps (solid lines). One can nicely recognize the half-period of motion ∼20 ps corresponding to the energy difference of the two superposed eigenstates (in vT = 0: ΔE/(hc) ≈ 0.82 cm−1, after ref. 288, see also caption to Fig. 31). | ||
The structures of the molecular quantum chameleon states introduce also a completely new concept in the history of molecular structure as discussed in ref. 72. The parity isomers as also the superposition of syn- and anti-structures are a new kind of isomer, which may be called ‘bistructural’ isomers, implying that they represent two classical structures ‘at the same time’ (not a ‘mixture’ of two separate isomers). This is classically impossible, but perfectly possible in quantum mechanics. The properties of these bistructural isomers are different from mixtures of isomers. For instance, their spectra are quite different. Our approach to prepare such structures opens not only a window to obtain new results on parity violation, for example, but also paves a way towards a molecular quantum technology such as possibly quantum information and quantum computing,288 quantum switches or quantum machines, which will be very different from the ‘classical’ molecular switches and machines.10–12 We have noted before that various kinds of such superpositions of molecular isomers can be considered64 and the concept can be extended to tristructural and multistructural isomers. The time dependence observed for such nonclassical structures obviously depends on the energy difference between the ground states of the ordinary classical isomers. We have recently also presented results for the exotic superpositions of ortho- and para-nuclear spin isomers of ClSSCl, for which the time dependencies falls in the range between those of the syn- and anti-superpositions and the enantiomer superpositions.234 There will be a large field of research to be explored with many opportunities in the future. One fundamental test using this approach would be a test on the limits of validity of the superposition principle of quantum mechanics, that is the very foundations of quantum mechanics. Will it be possible to prepare such superpositions of enantiomers of molecules of arbitrary complexity, for example the ‘molecular knots’ as examples of topological enantiomers shown in Fig. 33.290 A surprising experiment testing for quantum mechanical superpositions was formulated in ref. 97 and the predicted outcome would be obvious from quantum mechanics, but it remains unknown, whether experiment will confirm it, if ever done. One may justly ask, whether there is a limit of size, mass or complexity, where quantum mechanics ceases to be valid. This may appear far-fetched, but hypotheses of such failures of quantum mechanics arising from weak effects of the gravitational interactions have been put forward.291 Another limitation of the superposition principle arising from Pfeifer's superselectionrule292,293 could be tested as well.
 | ||
| Fig. 33 The extreme example of knots as topological enantiomers as proposed by Sauvage and co-workers,11 which use classical mechanical structural concepts. The scheme of137 would prepare superpositions of such classical structures, for instance passing via excited electronic states where bonds are broken and the knots open. But are such quantum mechanical superpositions possible? (after ref. 290). | ||
5. Parity violation and biomolecular homochirality
In his Nobel prize lecture 1975 on ‘Chirality in chemistry’,4 V. Prelog concludes with a brief statement on the question of biomolecular homochirality:‘The time at my disposition also does not permit me to deal with the manifold biochemical and biological aspects of molecular chirality. Two of these must be mentioned, however, briefly. The first is the fact that although most compounds involved in fundamental life processes, such as sugars and amino acids, are chiral and although the energy of both enantiomers and the probability of their formation in an achiral environment are equal, only one enantiomer occurs in Nature; the enantiomers involved in life processes are the same in men, animals, plants and microorganisms, independent on their place and time on Earth. Many hypotheses have been conceived about this subject, which can be regarded as one of the first problems of molecular theology. One possible explanation is that the creation of living matter was an extremely improbable event, which occurred only once.’
Prelog refers here to the observation that in the biopolymers of life (with chiral amino acids in the proteins and chiral sugars in DNA) only the L-amino acids and only the D-sugars are used. Strictly speaking in other circumstances (not in the biopolymers) the other enantiomeric forms do occur also naturally in biological processes. Also the uniqueness of selection, say, of the whole series of natural L-amino acids depends upon the convention used. For instance with the R, S nomenclature there are not only S-amino acids selected. For example L-cystein is selected as D/L nomenclature identifies it as ‘L’ enantiomer by convention, but when using the CIP convention it will be R-cystein as this corresponds to L-cystein according to the rule in this case. But the basic fact remains true, as stated by Prelog, that for each particular amino acid and each sugar only one enantiomer occurs in the biopolymers.
Why this is so has been an enigma for more than a century, the phenomenon has been noted (with limited knowledge) already by Pasteur3,87–89 and by Fischer96 for instance, identifying this ‘homochirality’ as a simple chemical signature of life. While the statement of this long standing enigma by Prelog is thus essentially correct, we have noted in many friendly private discussions with him in Zurich in the early 1980's and in the publication dedicated to him at his 80th birthday meeting,137 that the premisses are incorrect: because of parity violation the energies of the enantiomers in an achiral environment are in fact not equal (that one might consider free space as chiral is a separate story, see ref. 69 and 72 for some of the history).
The question is then, how important this small asymmetry arising from parity violation will be for the origin of biomolecular homochirality.62 We anticipate here the short answer: we do not know, but at least one can say that the discovery in 1995 (ref. 182) of an increase by a factor of 10 to 100 of parity violating energy differences ΔpvE calculated from theory has made the possibility of an important effect of parity violation in the evolution of biomolecular homochirality more likely than it seemed before, but in any case the question remains open.62 There is an obvious relation to the other open question concerning the origin of life. How did life arise from ‘non-living matter’? This question, which refers to the frontier between the non-living and living refers to what is the very nature of life. The question ‘What is life?’ also has a long history with many debates in the scientific and the non scientific literature. Schrödinger asked the question from a physicist's perspective in his famous little book arising from lectures in 1943.294 Twenty years earlier, Thomas Mann has asked this question repeating it three times in a chapter ‘research’ (Forschungen) in his novel ‘Der Zauberberg’ (The Magic Mountain295), inspired by his stays in Arosa in the Swiss Alps as was Schrödinger in deriving ‘his equation’.114,296 Both books are frequently quoted in the context (see for example ref. 297). We shall take here the pragmatic point of view that we can distinguish the ‘living’ from the ‘non-living’ by inspection in a fairly straight-forward way.66 On these three open questions there exists, indeed, a huge literature, of which we shall mention here only a small selection.298–326 In ref. 62, 66 and 69 we have provided more extended discussion related to various questions on life in a ‘decision diagram’ or flow diagram reproduced here in Fig. 34. Without going into details we summarize here that at every step the related question is really open. However, there are for each step ‘opinions’ from what we have called communities of belief.61,65,66,69 For instance, whether life is rare in the universe, possibly singular, only existing on our planet, as surmised by Monod314 and perhaps Prelog,4 or else whether it is frequent, as seems to be the current majority opinion, according to some informal, non-representative ‘polls’ in lectures,66,69 is in reality completely open.65,69,327 This corresponds to the first step in the diagram of Fig. 34 (see also the reviews66,69).
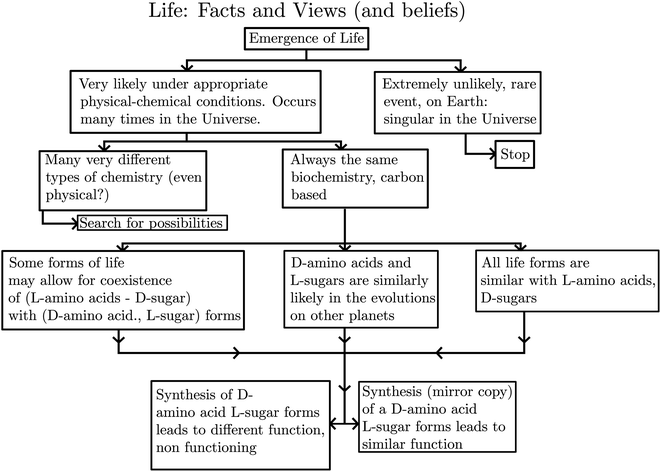 | ||
| Fig. 34 Summary as ‘flow diagram’ for opinions and beliefs on the emergence of life and of homochirality (modified after ref. 66 and 69). The ‘flow diagram’ can be read from the top to the bottom as a sequence of decisions between alternatives or options for hypotheses. For example at the first step one has the two alternative hypotheses of ‘frequent life’ in the universe or ‘rare life’ (singular, on Earth only) and similarly for the following steps. | ||
Here we shall focus on the question on homochirality addressed in the lower part of the diagram. One has essentially two large communities of belief. The first one assumes that homochirality arises simply by a chance selection in the early stages of the evolution, either pre-biological (non living matter) or a little later in early living species. This we have called the ‘de facto’ selection (by chance). The other community assumes that the ‘de lege’ asymmetry arising from parity violation has been important and the selection occurred by necessity, preferring one form over the other in analogy to the diagram in Fig. 11. The question could, in principle be answered by observation of possibly many different forms of life on exoplanets,328–330 which might be possible by a spectroscopic search for a systematic homochirality on these planets66,186 or perhaps within our solar system by space flight. The de facto hypotheses would predict a statistical distribution of ‘L’ or ‘D’ homochirality (if any). The de lege hypotheses would predict a preponderance of one form (perhaps even a unique selection of always the same form).
This question of life and biomolecular homochirality has been addressed as well in the non scientific literature already almost a century ago109 by D. Sayers and R. Eustace, well before Schrödinger. There one finds in the crucial section on solving a murder crime case by analytical spectroscopy in the form of a test for optical activity the following passage (shortened, with some omissions noted by ‘…’):
‘Life then, I suppose, is just one form of randomness…’ ‘What is life?’ I asked suddenly.‘Well Pontius if we could answer that question we should probably not need to ask the others.’ At present – chemically speaking – the nearest definition I can produce is some kind of bias… into a single asymmetric optically active substance. At the moment life appeared on this planet, something happened to the molecular structure of things. They got a twist…’
Indeed, we have called this ‘twist’ (giving preference to L-amino acids in the biopolymers of life) a quasi-fossil from the early phases of the evolution of life.66 Just as fossilized shells or bones of animals contain information on structural properties of ancient forms of life, the chemical preference of one kind of enantiomer may carry information on early phases of the ‘chemical evolution’ of life. Until today, we do not know, how to interpret this quasi-fossil, it remains a true enigma, to be solved by experiment or theory, or both together.
There exists a huge literature presenting all kinds of arguments on how life has originated from ‘chemistry’, often called ‘prebiotic chemistry’,331,332 and how homochirality arose in this process.333 It is quite impossible to discuss an even restricted ‘representative’ selection from these, but we shall mention some aspects here in an exemplary way, concentrating on essential concepts and some recent discussions. As we have often experienced the widespread ‘intuitive belief’ that energies in the sub-feV range cannot possibly have had any influence on the origin of biomolecular homochirality, we start here with an analogy referring to the role of the very small parity violating energies in our understanding of the dynamics and physical–chemical nature of chiral molecules, which has in fact been dramatically altered by parity violation, if we accept current theory for the moment without experimental test.
Consider again the diagram in Fig. 11. Without parity violation the quantum energy eigenstates are delocalized in the framework of quantum mechanics. One might then say, that given the small effects from parity violation this picture should remain true, with perhaps a minimal asymmetry in the delocalized ground state wavefunction. This argument is, indeed, correct for molecules such as HOOH or NHDT, where eqn (19) applies. However, when eqn (20) applies, which is in fact the case for all stable chiral molecules with lifetimes of a few days or weeks at least, then the extremely small parity violating energy difference ΔpvEel introduces an almost complete localization in either one or the other well in an asymmetric potential (an ‘all or nothing selection’).334 Some minor probability can be found also in the other well, but this is exponentially small and completely negligible. Thus parity violation, while very small, has a huge consequence for the structure of the eigenstates. This is true not only for the ground state but also for excited states at usual thermal energies for stable chiral molecules.
Of course, this analogy does not imply that parity violation must be similarly dominant in the evolution of biomolecular homochirality. Indeed, if this process were controlled by thermodynamics then one may consider a typical equilibrium constant for racemization, eqn (2), which would change because of parity violation from a value of K = 1 exactly to, say,
| K = 1 ± x × 10−14 | (48) |
(1) Kinetic mechanisms with a stochastic ‘all or nothing’ selection have been known for some time and have been repeatedly discussed.302,303,316–318,336–339 These could be supported by a random bias in crystallization or adsorption,340–343 or by some fluctuation in a liquid phase environment.344,345 With such an hypothesis a complete preference towards a homochiral system is expected, but it would lead to equal probability for ‘D’ or ‘L’ in repeated evolutions.
(2) If the transition from ‘non-living’ to ‘living’ matter is a singular event, which happens by chance in some chiral environment (say D- or L-quartz) favouring one enantiomer, then this ‘initial’ life would transmit the unique enantiomeric structure to further generations.320,346,347 One might consider also an initial enantiomeric (chiral) selectivity under the accidental influence of a local field.348,349 A currently popular hypothesis is the photochemical generation of an excess of one enantiomer by circularly polarized light in interstellar clouds from a nearby source for circularly polarized light as they were in fact predicted by models. The observation of non equilibrium distributions of enantiomers in meteorites has persuaded some to believe in such a mechanism, still under debate though.321,350–352
(3) One could have coexistence of two early life forms (or ‘almost life’) one ‘L’ one ‘D’ with equal chance for both, but one dying out because of an ‘accident’. This scenario follows Mark Green's parable of the two equal ‘runners’ (one ‘tripping’ stumbling and falling353).
(4) A low temperature phase transition due to parity violation might induce prebiotically, and even completely abiotically, also in inorganic matter, an enantiopure chemical environment in which life might then start.322,354,355
(5) High energy radiation (or particles) arising from a process involving parity violation might selectively destroy one enantiomer of prebiotic or biotic matter. This suggestion has been made quite early in the literature356 (see also ref. 338 and 357) and was complemented recently with further quite interesting suggestions.358
(6) One may have autocatalytic kinetic mechanisms which over geological time scales could select one enantiomer preferentially due to parity violation. Kondepudi and Nelson have proposed mechanisms which might be selective in this way in a lake with a plausible ‘chemical soup’ over time scales of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 100
000 to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 years, which is geologically short359,360 (see also ref. 62, 66 and 361). It should be made clear here, that the autocatalytic mechanism is of a formal mathematical nature and no attempt was made to simulate conditions as they may have prevailed on the early earth.362
000 years, which is geologically short359,360 (see also ref. 62, 66 and 361). It should be made clear here, that the autocatalytic mechanism is of a formal mathematical nature and no attempt was made to simulate conditions as they may have prevailed on the early earth.362
These 6 mechanisms, which by no means provide a complete list of existing proposals, can clearly be grouped into broad classes of ‘de facto’ selection (by chance, mechanisms (1)–(3)) and ‘de lege’ selection (by necessity, mechanisms (4)–(6)). We shall not enter into any further detailed discussion here, but we note that some of these have had firm believers with heated debates among the different communities of belief and sometimes false statements of evidence (see the discussions in ref. 62, 65 and 66 for further examples). The question arises, how to obtain conclusive evidence. One approach might be to repeat the total synthesis of life and evolution in the laboratory, clearly a difficult enterprise, so far without much success (see e.g. ref. 363 and 364). We note here, that so far not even the total synthesis of an enantiomeric copy of a simple existing bacterium has been successful, although already proposed in 1990.365
Another approach would be to investigate the conditions for certain mechanisms by systematic experiments complemented by theory and thereby approach an answer in a stepwise way. In this context there has been a most interesting series of experiments by Blackmond and coworkers366–372 in relation to the famous autocatalytic Soai mechanism373–378 (see also ref. 379). Using minor perturbations by substituting ‘heavy’ (non-hydrogen) isotopes such as 12C/13C or 14N/15N an estimate was made about the threshold energy differences (e.g. in terms of ΔG‡ in transition states) that can induce an amplification to homochirality in a Soai-type mechanism. This threshold was found to be about 10−5 J mol−1. While such small values are, indeed, interesting, they are obviously much larger than anything that might be expected to arise from parity violation, perhaps 10−10 J mol−1 or at most a little larger. Sometimes this gap on the order of 4 to 5 orders of magnitude has already been interpreted as excluding any important effect from parity violation in the evolution of biomolecular homochirality. However, such a conclusion is quite unjustified as it refers only to relatively simple mechanisms such as the Soai reaction. It is possible and even likely, that real-life mechanisms in early prebiotic or early biotic chemistry would be much more complex and more sensitive to small energy effects. In that sense the result, that energy differences on the order of 10−5 J mol−1 are estimated to suffice for a selection of homochirality on short time scales in simple autocatalytic mechanisms would lead to rather optimistic expectations to bridge the remaining gap of a few orders of magnitude with more sensitive and more complex mechanisms on longer time scales.
It has sometimes also been argued that a chemical evolution of homochirality is impossible on long time scales because chiral molecules in reactive environments would always racemize on long time scales. This argument is obviously invalid, as we have ‘living proof’ in the long lived existing homochirality of life, which, indeed, has used for millions of years chiral molecules in a permanently reactive chemical environment and has successfully avoided racemization by a ‘complex autocatalytic mechanism’, if one may say so.
Some might say that the de lege mechanism is intellectually more interesting, similar to a chess game being more interesting than a pure lottery. But passionate lottery players might reply that they do not care about intellectual interest, if only they win a large sum of money. We can add here that the de lege mechanisms correspond to the Darwinian concept of ‘survival of the fittest’, whereas the de facto mechanisms correspond to the trivial principle of ‘survival of the survivor’ (see also ref. 334).
Without entering into any further discussion of the many other suggestions and hypotheses, we conclude here with the statement that at present there is simply no proof or even compelling argument to exclude either a de lege mechanism (involving electroweak parity violation) or a de facto mechanism (by chance). Both are perfectly possible origins of today's biomolecular homochirality and it remains our task to find out, which of the two applies, possibly both under different circumstances.
6. Conclusion and outlook
Molecular chirality is intimately related to the history of stereochemistry and our understanding of molecular symmetry, structure, dynamics, and kinetics. The classical structural models have explained the stereoselectivity of enzymes in biology by means of Emil Fischer's key and lock principle and the empirical finding of the biomolecular homochirality of life. The initially assumed exact mirror symmetry between the enantiomers has led to the understanding of the role of parity in the quantum dynamics of chiral molecules and to the discovery of the tunnel effect by Friedrich Hund in 1927, in the early days of quantum mechanics. Parity violation – the violation of the ‘exact’ space inversion symmetry – discovered in high energy and nuclear physics much later in 1956/57 has introduced fundamentally new perspectives. It changes our basic concepts for the stereochemistry, structure and dynamics of chiral molecules. While tunneling according to Hund's treatment dominates over parity violation in transiently chiral molecules such as hydrogen-peroxide (HOOH), the chiral ammonia isotopomer (NHDT) or the aniline isotopomer (C6H5NHD), for example, we know now that for ordinary chiral molecules, which are stable for days or years, at least, such as CHFClBr, alanine or other amino acids, sugars etc., parity violation dominates completely over tunneling and is the decisive factor for a conceptually correct understanding of their structure and energetics.In contrast to the classical picture of van't Hoff with two symmetrically equivalent enantiomers with exactly equal energies, there is a small but physically significant and in principle measurable energy difference ΔpvE between their ground states, resulting in a non-zero reaction enthalpy and free energy for stereomutation (Section 3.1). The new and much larger orders of magnitude discovered for this energy difference in our theoretical work from 1995, has in the meantime been confirmed independently by theoretical work in other groups and can in this sense be considered to be well established (see Section 3.3). This has also improved the outlook for spectroscopic experiments, which are ongoing (see Section 4), although still without conclusive results, so far.
However, much of the spectroscopic ground work for such experiments has been completed by now and one can expect further most significant results for all of the possible outcomes of such experiments:
(1) If experiments confirm the theoretically predicted values for ΔpvE, then one can analyse the results of the precision experiments in terms of the standard model of particle physics (SMPP) in a range of quantum systems not yet tested in previous experiments, for example in molecules involving only ‘light’ nuclei up to, say, chlorine.
(2) If one finds, on the other hand, values of ΔpvE different from the theoretical predictions, this will lead to a fundamental revision of current theories for ΔpvE with even the potential for ‘new physics’. Unexpected surprises are possible.
(3) Finally, a profound experimental and theoretical understanding of ΔpvE in chiral molecules can be a first step towards a possible understanding of the implications of parity violation in the evolution of biomolecular homochirality.
While ΔpvE is still predicted to be very small, on the order of aeV to feV for molecules containing only elements from the first rows of the periodic system, it can be obtained significantly and separately from other effects by means of the concept of approximate symmetries and constants of the motion.
We have obtained also further results concerning fundamental concepts of physical–chemical stereochemistry. The possible preparation of ‘parity isomers’ of chiral molecules introduces the structural concept of ‘bistructural’ molecules (being ‘quantum chameleons’, at the same time R and S enantiomers but very different from a ‘racemic mixture’). The time evolution of the spectra of these bistructural molecules corresponds to the new intramolecular primary process of parity change with time arising from parity violation by the weak nuclear force. The concept of such bistructural ‘chameleon-like’ isomers can be extended to other types of isomers and has potential for quantum technology in the more distant future. Based on high resolution spectroscopic results, we have already demonstrated such exotic chameleon states for bistructural syn- and anti-m-D-phenol286–288 and also for different nuclear spin symmetry isomers (ortho- and para) in ClSSCl.234
We add here a brief discussion going beyond these now well established results. Charles Darwin is occasionally quoted with a statement ‘It is as absurd to think about the origin of life as it is absurd to think about the origin of matter’. However, if we do start this ‘absurd thinking’ we note three basic ‘asymmetries’ in our world (Fig. 35). We might consider these as ‘quasi-fossils’ carrying information about the evolution of matter and life.66 It turns out that the asymmetries C and CP between matter and antimatter, while experimentally and theoretically known in the SMPP,380 do not seem to be able so far to explain quantitatively the current preponderance of matter over antimatter in the universe.381 There remain open questions on this quasi-fossil from the origin of matter. Similarly, the observation of the current ‘homochirality of life’ (with L-amino acids in proteins and D-sugars in DNA) has contradictory explanations (de facto, by chance, or de lege – involving parity violation, see Section 5) and we do not know, which of the explanations is correct. The interpretation of this quasi-fossil from the origin of life66 remains completely open in spite of much work, which exists already.
 | ||
| Fig. 35 Three fundamental observations in our world, with so far unexplained relation to fundamental symmetries and their violation (after ref. 66). | ||
We can finally go beyond these two asymmetries by considering the general scheme for chiral molecules and their antimatter counter parts, in Fig. 36, which can be considered ‘antimatter stereochemistry’ (where we use the ‘physical nomenclature’ L and R for the stereoisomers and L* and R* for their antimatter counterparts).154 As we have discussed, CPT symmetry, which so far has never been found violated and is considered to be exact in the current SMPP requiring the pair of molecules L and R* to be exactly equivalent energetically (and similarly for R and L*), could be made the subject of a most sensitive spectroscopic test using chiral molecules.46,382 This test would be much more sensitive than other tests that have been made or proposed so far384–389 (see also ref. 68). The energy level scheme inserted in Fig. 36 illustrates this test schematically. When CPT symmetry holds, the energies of the pair (L, R*) on the one hand and of the pair (R, L*) on the other hand would be exactly equal by symmetry (dotted lines). By measuring ΔpvE for ordinary matter and ΔpvE* for antimatter stereoisomers using the scheme of ref. 137 and 382 as outlined in Section 4.2, one will test for the equality of ΔpvE and ΔpvE*, and observing a significant difference would prove CPT violation.382 A sensitivity on the order of Δm/m = 10−30 was estimated for such a test on chiral molecules whereas other proposals fall in the range Δm/m = 10−10 to 10−20. Obviously chiral antimatter molecules are currently not availably by any realistic approach, but the production of chiral hydrogen cluster (H2)n or Hm+ would be conceivable also for the antihydrogen counter parts,91 antihydrogen atoms having been produced at CERN.389 CPT symmetry can be related to a ‘non-observable’ which can be considered to concern the observation of a generalized direction of time when including antimatter with an absolute chiral molecular clock for example.65,186,327 Whether a violation of CPT symmetry will ever be found remains open, but even at the level of a direction of time in ordinary matter there remains an open question whether the second law of thermodynamics concerning the increase of entropy with time is due to a de lege or a de facto symmetry violation,46,65,186,327 and there are further interesting alternatives to be mentioned.390 We might refer in this context to various results and searches on the violation of time reversal symmetry and also its relation to the observation of the permanent electric dipole moment of the electron or neutron384,391–397 expected to be extremely small in the current SMPP (see also the review in ref. 46). Thus there remain numerous open questions related to the ‘stereochemistry of matter and antimatter’ as related to fundamental symmetries.
 | ||
| Fig. 36 Stereochemistry with antimatter (using the ‘physical’ notation L and R for enantiomers of ordinary matter and L* and R* for antimatter) as a possible test for CPT symmetry, which would require ΔpvE = ΔpvE* exactly (after ref. 46, 69, 154 and 382). The graphical background is from a painting by Ferdinand Hodler (Thuner See mit Spiegelung 1904, SIK-ISEA Archiv No. 9163), which we have used in lectures occasionally to illustrate CPT violation with matter–antimatter enantiomers.198,254,383 We were inspired to this use by the books,104,105 where the painting was used to illustrate approximate, ‘accidental’ symmetry but without reference to parity violation or CPT in chiral molecules. | ||
We conclude here with a brief discussion of the new perspectives parity violation introduces for stereochemical nomenclature of chiral molecules, without attempting to address the many ‘traditional’ misunderstandings, which exist in this area (see e.g.4, 13, 100, 107, 324 and 398 for such discussions), and which started already with the frequent mistranslation of Pasteur's terminology ‘dissymmetric’ into English and German texts as asymmetric (while properly it is ‘chiral’). It has been recently suggested that given the lack of exact mirror symmetry between the enantiomers of chiral molecules they should strictly not be called ‘enantiomers’ (see for instance399 but also elsewhere) but rather diastereomers. We think that such a change is quite unnecessary and even misleading. Considering the actual practice of the use of ‘enantiomers’ for the corresponding isomers of chiral molecules (such as D-alanine and L-alanine) it refers to the real substance synthesized, isolated and characterized in the laboratory. We use these names, when ordering such a compound from a supplier, and the language used is clearly defined in such a way that we get what we ordered, if the supplier is reliable. At this point and almost in every place where the term ‘enantiomer’ is used, no mention is made of ‘mirror symmetry’ anywhere. Thus it makes good sense to retain this well established usage and ‘practical definition’ of enantiomer as referring to the real molecule. We know now that these ‘enantiomers’ as a special kind of isomers show only an approximate mirror symmetry, because parity violation destroys the exact mirror symmetry. While it is true, that van't Hoff and most chemists assumed exact mirror symmetry, and this has entered frequent textbook definitions,400 there is no need to rely on that, and some statements by Pasteur can be interpreted in such a way, that he anticipated that the exact mirror symmetry may not be applicable, thus there is even historical precedent. Also the etymology of enantiomers of chiral molecules would be perfectly consistent with removing the ‘exact mirror symmetry’ from the definition. Indeed the ancient Greek εναντα or εναντιoς (enanta, enantios) has the meaning of ‘opposite to’ or standing opposite to each other (like two people looking at each other), μερoς (meros) standing for the ‘parts’ of which the molecules are made analogous to the use in isomers.46 Thus real enantiomers of chiral molecules would relate to each other like real left hand and real right hand, not implying mirror symmetry but implying arrangements of parts as in real left and right hands, which are not exactly mirror symmetric either. We might note here that already in Kant's statement he notes that the mirror image is ‘a left hand’ (and not ‘the left hand’) being obviously aware of the difference between the mirror image of the right hand, being ‘handed’ similar to left hands, but not identical to ‘the real left hand’.
In this sense we suggest to simply retain the ‘practical definition’ and usage of ‘enantiomer’, with which we can essentially retain the use in most of the existing literature except for some textbook definitions. Even these could be mildly adjusted by using ‘approximate mirror image’ (or ‘mirror image, except for effects arising from parity violation’).
One might wonder, whether one should have a terminology also describing the ‘exact’ mirror image, given that enantiomers are not exact mirror images of each other with the ‘practical definition’. We would suggest to logically use the word for mirror and mirror image in ancient Greek (τo ϰατoπτϱoν, katoptron). Thus the hypothetical mirror image isomer would become the ‘katoptromer’, which would certainly make sense from the point of view of etymology. Like the mirror image of our hand the ‘katoptromer’ is not a molecule in the real world, but only in the hypothetical mirror world, however.
For the real enantiomers made of antimatter, which are expected to exist, although so far none has been ever synthesized, one might simply use antimatter-enantiomers, or in shorthand AM-enantiomers or amenantiomers.
It has also been suggested (in ref. 399 and elsewhere) that the pairs (L, R*) and (L*, R) should be strictly called ‘enantiomers’, using actually a figure in ref. 399 similar to ours in ref. 382 (and earlier), or in Fig. 36. Considering Fig. 36 this would be to some extent justified, if CPT symmetry were guaranteed with absolute certainty (assumed in ref. 399). Again looking at past history, however, it may be wise to at least allow for a future empirical finding of CPT violation,382 as indicated by Fig. 36. In this figure we have made use of Hodler's well known painting indicating an approximate symmetry (in fact only roughly so) between the left and right part of the landscape. This would be the analog of the approximate symmetry of L and R (the exact symmetry being removed by parity violation). On the other hand the mirror symmetry between the image of the mountain L and the mirror image R* in the lake may be a much closer symmetry (and similarly for R and L*). However, the lake not being a perfect mirror, even that ‘mirror symmetry’ of CPT might not be perfect. Whether CPT symmetry violation will ever be found is quite unknown, and many think that there are good reasons to assume that it will never be found. What one can predict though, is that if it were found, this would be a discovery of greatest significance, overshadowing the discovery of parity violation by far, and measurements of parity violation in chiral molecules might play a role in such a discovery in the more distant future.
Author contributions
The author contributions can be seen from the list of references.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Our work has received financial support from an ERC Advanced Grant, from the Swiss National Science Foundation and ETH Zürich, in particular the Laboratory for Physical Chemistry. We acknowledge gratefully recent support and many fruitful discussions with Frédéric Merkt. Over the years numerous coworkers have contributed to our projects, too numerous to be mentioned in detail and we refer to the list of references and the lists given in ref. 91 and 401. We acknowledge early inspiration by gifts of books104,105 from Edgar Heilbronner and Jack Dunitz shortly after appearance of their books and from Alex von Zelewsky (ref. 109, after a lecture of MQ in 1997) and many discussions with them over many years. This article is dedicated to their memory.References
- J. H. van't Hoff, Vorlesungen über theoretische und physikalische Chemie: Die chemische Statik, Vieweg, Braunschweig, 1899, Heft 2 Search PubMed.
- A. Werner, Sur les composés métalliques à dissymétrie moléculaire, 1912, conférence faite devant la société chimique de France, 24 mai 1912, reprinted in ref. 3 Search PubMed.
- Louis Pasteur, J. H. van’t Hoff, A. Werner sur la dissymmétrie moléculaire, ed. C. Bourgois, Cox and Wyman Ltd, P.F.C. Dole, 1986, ISBN 2-267-00454-2 Search PubMed.
- V. Prelog, Chirality in Chemistry, in Les prix Nobel en 1975, Nobel lecture, The Nobel foundation Imprimerie Royale, P.A. Norstedt & Söhner, Stockholm, 1976 Search PubMed.
- W. S. Knowles, Asymmetric Hydrogenations (Nobel Lecture), Angew. Chem., Int. Ed., 2002, 41, 1998–2007 CrossRef CAS.
- R. Noyori, Asymmetric Catalysis: Science and Opportunities (Nobel Lecture), Angew. Chem., Int. Ed., 2002, 41, 2008–2022 CrossRef CAS PubMed.
- K. B. Sharpless, Searching for New Reactivity (Nobel Lecture), Angew. Chem., Int. Ed., 2002, 41, 2024–2032 CrossRef CAS PubMed.
- B. List, R. A. Lerner and C. F. Barbas, Proline-Catalyzed Direct Asymmetric Aldol Reactions, J. Am. Chem. Soc., 2000, 122, 2395–2396 CrossRef CAS , and The Nobel Prize in Chemistry 2021, https://www.nobelprize.org/prizes/chemistry/2021/press-release/.
- K. A. Ahrendt, C. J. Borths and D. W. C. MacMillan, New Strategies for Organic Catalysis: The First Highly Enantioselective Organocatalytic Diels-Alder Reaction, J. Am. Chem. Soc., 2000, 122, 4243–4244 CrossRef CAS , and The Nobel Prize in Chemistry 2021, https://www.nobelprize.org/prizes/chemistry/2021/press-release/.
- B. L. Feringa, The Art of Building Small: From Molecular Switches to Motors (Nobel Lecture), Angew. Chem., Int. Ed., 2017, 56, 11060–11078 CrossRef CAS PubMed.
- J. P. Sauvage, From Chemical Topology to Molecular Machines (Nobel Lecture), Angew. Chem., Int. Ed., 2017, 56, 11080–11093 CrossRef CAS PubMed.
- J. F. Stoddart, Mechanically Interlocked Molecules (MIMs)—Molecular Shuttles, Switches, and Machines (Nobel Lecture), Angew. Chem., Int. Ed., 2017, 56, 11094–11125 CrossRef CAS PubMed.
- K. Mislow, Introduction to Stereochemistry, Benjamin, New York, 1965 Search PubMed.
- V. Prelog and G. Helmchen, Basic Principles of the CIP-System and Proposals for a Revision, Angew. Chem., Int. Ed., 1982, 21, 567–583 CrossRef.
- Asymmetric catalysis on industrial scale: Challenges, approaches and solutions, ed. H. U. Blaser and H. J. Federsel, John Wiley & Sons, Ltd, Weinheim, 2nd edn, 2010 Search PubMed.
- Organometallics as catalysts in the fine chemical industry, ed. M. Beller and H. U. Blaser, Springer, Heidelberg, 2012 Search PubMed.
- A. Togni, The Department of Chemistry, ETH Zürich, in the new Hönggerberg bulidings, Chimia, 2001, 55, 752 CAS.
- M. Quack, Molecules in Motion, Chimia, 2001, 55, 753–758 CrossRef CAS.
- A. Baiker, Heterogeneous Catalysis - An Interdisciplinary Approach, Chimia, 2001, 55, 796–800 CrossRef CAS.
- A. Togni, A. Mezzetti, P. Barthazy, C. Becker, I. Devillers, R. Frantz, L. Hintermann, M. Perseghini and M. Sanna, Developing Catalytic Enantioselective Fluorination, Chimia, 2001, 55, 801–805 CrossRef CAS.
- P. S. Pregosin, Structural Organometallic Chemistry and its Relation to Homogeneous Catalysis, Chimia, 2001, 55, 806–808 CrossRef CAS.
- C. Böhler, T. Büttner, S. Deblon, G. Frasca, G. Frison, J. Geier, C. Laporte, F. Läng, S. Loss, P. Maire, N. Pè, H. Schönberg, M. Scherer, C. Widauer and H. Grützmacher, Bend the coin your way: Ligand design and main group element chemistry, Chimia, 2001, 55, 814–817 CrossRef.
- E. M. Carreira, Discovery and study of new reaction chemistry; applications in complex molecule assembly, Chimia, 2001, 55, 818–820 CrossRef CAS.
- F. Diederich, Design and synthesis of functional molecular architecture, Chimia, 2001, 55, 821–827 CrossRef CAS.
- D. Seebach, A. K. Beck, M. Brenner, C. Gaul and A. Heckel, From synthetic methods to γ-peptides - from chemistry to biology, Chimia, 2001, 55, 831–838 CrossRef CAS.
- A. Vasella, Facing Glycoscience, Chimia, 2001, 55, 839–843 CrossRef CAS.
- A. Detken, M. Ernst and B. H. Meier, Towards biomolecular structure determination by high-resolution solid-state NMR: Assignment of solid peptides, Chimia, 2001, 55, 844–851 CrossRef CAS.
- M. O. Ebert, D. Ackermann, S. Pitsch and B. Jaun, NMR study of the p-DNA duplex [(4′ → 2′)-3′-desoxyribopyranosyl-(m5CGDDTTm5CG)2] and comparison with its p-RNA analogue, Chimia, 2001, 55, 852–855 CrossRef CAS.
- D. Hilvert, Enzyme Engineering, Chimia, 2001, 55, 867–869 CrossRef CAS.
- F. Lode, M. Mazzotti and M. Morbidelli, A new reaction-separation unit: The simulated moving bed reactor, Chimia, 2001, 55, 883–886 CrossRef CAS.
- J. Lacour and E. Francotte, Chirality. Editorial, Chimia, 2008, 62, 460 CrossRef CAS.
- C. Gautier and T. Bürgi, Chiral Metal Surfaces and Nanoparticles, Chimia, 2008, 62, 465–470 CrossRef CAS.
- K. H. Ernst, Expression and Amplification of Chirality in Two-Dimensional Molecular Crystals, Chimia, 2008, 62, 471–475 CrossRef CAS.
- H. U. Blaser, G. Hoge, M. Lotz, U. Nettekoven, A. Schnyder and F. Spindler, Strategies for Accelerating the Development of Catalytic Enantioselective Reactions, Chimia, 2008, 62, 476–481 CrossRef CAS.
- J. Haesler and W. Hug, Raman Optical Activity: A Reliable Chiroptical Technique, Chimia, 2008, 62, 482–488 CrossRef CAS.
- A. Hennig, S. Bhosale, N. Sakai and S. Matile, CD Methods Development at the Bio-Nano Interface, Chimia, 2008, 62, 493–496 CrossRef CAS.
- M. G. Schrems, A. Wang and A. Pfaltz, Recent Progress in Iridium-Catalyzed Enantioselective Hydrogenation: Tetrasubstituted Olefins and Polyenes, Chimia, 2008, 62, 506–509 CrossRef CAS.
- P. Renaud, F. Beaufils, F. Dénès, L. Feray, C. Imboden and N. Kuznetsov, Stereoselective Radical Translocations, Chimia, 2008, 62, 510–513 CrossRef CAS.
- B. Therrien and G. Süss-Fink, Inducing Helical Chirality by Deforming Hexanuclear Metalloprismatic Structures, Chimia, 2008, 62, 514–518 CrossRef CAS.
- P. Vogel, Total Asymmetric Synthesis of Glycomimetics and Polypropionates of Biological Interest, Chimia, 2008, 62, 519–523 CrossRef CAS.
- M. Quack and J. Stohner, Chirality: Symmetries and Asymmetries. Editorial, Chimia, 2018, 72, 365 Search PubMed.
- T. A. Isaev and R. Berger, Towards ultracold chiral molecules, Chimia, 2018, 72, 375–378 CrossRef CAS PubMed.
- M. Pitzer, R. Berger, J. Stohner, R. Dörner and M. Schöffler, Investigating Absolute Stereochemical Configuration with Coulomb Explosion Imaging, Chimia, 2018, 72, 384–388 CrossRef CAS PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Chirality and Spin: A Different Perspective on Enantioselective Interactions, Chimia, 2018, 72, 394–398 CrossRef CAS PubMed.
- Symmetrie und Asymmetrie in Wissenschaft und Kunst, in Nova Acta Leopoldina NF 127, No. 412, ed. M. Quack and J. Hacker, Wissenschaftliche Verlagsgesellschaft, Stuttgart, 2016 (Book with contributions in English and German) Search PubMed.
- M. Quack, Fundamental Symmetries and Symmetry Violations from High Resolution Spectroscopy, in Handbook of High Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, New York, 2011, ch. 18, vol. 1, pp. 659–722 Search PubMed.
- H. Fritzsch, Symmetrien der Physik, in Symmetrie und Asymmetrie in Wissenschaft und Kunst, Nova Acta Leopoldina NF 127 Nr. 412, ed. M. Quack and J. Hacker, Wissenschaftliche Verlagsgesellschaft, Stuttgart, 2016, pp. 75–90 Search PubMed.
- T. D. Lee and C. N. Yang, Question of Parity Conservation in Weak Interactions, Phys. Rev., 1956, 104, 254–258 CrossRef CAS.
- C. S. Wu, E. Ambler, R. W. Hayward, D. D. Hoppes and R. P. Hudson, Experimental Test of Parity Conservation in Beta Decay, Phys. Rev., 1957, 105, 1413–1415 CrossRef CAS.
- H. Schopper, Circular polarization of gamma-rays - Further proof for parity failure in beta-decay, Phil. Mag., 1957, 2, 710–713 CrossRef CAS.
- H. Schopper, Die elastische Streuung von Gamma-Strahlen bei kleinen Streuwinkeln, Z. Phys., 1957, 147, 253–260 CrossRef.
- R. L. Garwin, L. M. Lederman and M. Weinrich, Observation of the failure of conservation of parity and charge conjugation in meson decays - the magnetic moment of the free muon, Phys. Rev., 1957, 105, 1415–1417 CrossRef CAS.
- J. I. Friedman and V. L. Telegdi, Nuclear emulsion evidence for parity nonconservation in the decay chain π+-μ+-ϵ+, Phys. Rev., 1957, 105, 1681–1682 CrossRef CAS.
- L. Hoddeson, L. Brown, M. Riordan and M. Dresden, The Rise of the Standard Model, Cambridge Uni. Press, Cambridge, 1999 Search PubMed.
- S. L. Glashow, Partial-symmetries of weak interactions, Nucl. Phys., 1961, 22, 579–588 CrossRef.
- S. Weinberg, A Model of Leptons, Phys. Rev. Lett., 1967, 19, 1264–1266 CrossRef.
- A. Salam, Weak and electromagnetic interactions, in Elementary Particle Theory: Relativistic Groups and Analyticity, Proc. of the 8th Nobel Symposium held May 19-25, (1968) at Aspenäs-gárden, Lerum, in the county of Älvsborg, Sweden, Almkvist & Wiksell, Stockholm, 1968, pp. 367–377 Search PubMed.
- M. J. G. Veltman, Nobel Lecture: From weak interactions to gravitation, Rev. Mod. Phys., 2000, 72, 341–349 CrossRef.
- G. 't Hooft, Nobel Lecture: A confrontation with infinity, Rev. Mod. Phys., 2000, 72, 333–339 CrossRef.
- P. Jenni, The Long Journey to the Higgs Boson and Beyond at the Large Hadron Collider (LHC), in Symmetrie und Asymmetrie in Wissenschaft und Kunst, Nova Acta Leopoldina NF 127 Nr. 412, ed. M. Quack and J. Hacker, Wissenschaftliche Verlagsgesellschaft, Stuttgart, 2016, pp. 99–117 Search PubMed.
- M. Quack, Structure and dynamics of chiral molecules, Angew. Chem., Int. Ed., 1989, 28, 571–586 ( Angew. Chem. , 1989 , 101 , 588–604 ) CrossRef.
- M. Quack, How important is parity violation for molecular and biomolecular chirality?, Angew. Chem., Int. Ed., 2002, 41, 4618–4630 ( Angew. Chem. , 2002 , 114 , 4812–4825 ) CrossRef CAS PubMed.
- M. Quack, Electroweak quantum chemistry and the dynamics of parity violation in chiral molecules, in Modelling Molecular Structure and Reactivity in Biological Systems, Proc. 7th WATOC Congress, Cape Town January 2005, ed. K. J. Naidoo, J. Brady, M. J. Field, J. Gao and M. Hann, Royal Soc. Chem., Cambridge, 2006, pp. 3–38 Search PubMed.
- M. Quack, The symmetries of time and space and their violation in chiral molecules and molecular processes, in Conceptual Tools for Understanding Nature. Proc. 2nd Int. Symp. of Science and Epistemology Seminar, Trieste April 1993, ed. G. Costa, G. Calucci and M. Giorgi, World Scientific Publ., Singapore, 1995, pp. 172–208 Search PubMed.
- M. Quack, Intramolekulare Dynamik: Irreversibilität, Zeitumkehrsymmetrie und eine absolute Moleküluhr, Nova Acta Leopold., 1999, 81, 137–173 CAS.
- M. Quack, On Biomolecular Homochirality as a Quasi-Fossil of the Evolution of Life, Adv. Chem. Phys., 2014, 157, 249–290 Search PubMed.
- M. Quack and G. Seyfang, Tunnelling and Parity Violation in Chiral and Achiral Molecules: Theory and High Resolution Spectroscopy, in Tunnelling in Molecules: Nuclear Quantum Effects from Bio to Physical Chemistry, ed. J. Kästner and S. Kozuch, Royal Society of Chemistry, Cambridge, England, 2020, pp. 192–244 Search PubMed.
- M. Quack, G. Seyfang and G. Wichmann, Fundamental and approximate symmetries, parity violation and tunneling in chiral and achiral molecules, Adv. Quantum Chem., 2020, 81, 51–104 CrossRef CAS.
- M. Quack, Die Spiegelsymmetrie des Raumes und die Chiralität in Chemie, Physik, und in der biologischen Evolution, in Symmetrie und Asymmetrie in Wissenschaft und Kunst, Nova Acta Leopoldina NF 127, Nr. 412, ed. M. Quack and J. Hacker, Wissenschaftliche Verlagsgesellschaft, Stuttgart, 2016, pp. 119–166 Search PubMed.
- M. Quack, Parity Violation in Chiral molecules: From Theory towards Spectroscopic Experiment and the Evolution of Biomolecular Homochirality, Lecture at Nobel Symposium 167 on Chiral Matter, Stockholm, island of Lindingö, 28 June to 1 July, 2021 Search PubMed.
- Molecular Spectroscopy and Quantum Dynamics, ed. R. Marquardt and M. Quack, Elsevier, Amsterdam, 1st edn, 2020, ISBN 978-012-817234-6 Search PubMed.
- M. Quack, The Concept of Law and Models in Chemistry, Eur. Rev., 2014, 22, S50–S86 CrossRef.
- I. Kant, Prolegomena zu einer jeden künftigen Metaphysik, die als Wissenschaft wird auftreten können, Riga, Hartknoch, 1783 Search PubMed.
- W. T. Kelvin, Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light. Founded on Mr. A. S. Hathaway's Stenographic Report of Twenty Lectures Delivered in Johns Hopkins University, Baltimore, in October (1884): Followed by Twelve Appendices on Allied Subjects, C. J. Clay, London, 1904 Search PubMed.
- W. T. Kelvin, The Molecular Tactics of a Crystal, Clarendon Press, Oxford, 1894 Search PubMed.
- R. Descartes, Oevres philosophiques (1618-1637), textes établis, présentés et annotés par Ferdinand Alquié, Garnier, Paris, 1963, vol. 3 Search PubMed.
- D. Laugwitz, Ingenieurmathematik., B. I.-Hochschultaschenbücher, Mannheim, 1964 Search PubMed.
- Platon, Sämtliche Werke Band 8, ed. K. H. Hülser, Insel Verlag, Frankfurt, 1991, pp. 282–285, Timaios, Kritias, numbers 46 a,b, Greek original with German translation Search PubMed.
- D. Arago, Mémoire sur une modification remarquable qu'éprouvent les rayons lumineux dans leur passage à travers certains corps diaphanes et sur quelques autres phénomènes d'optique. Mem. de l'Institut 12 (Part 1), 1811, pp. 93–134 Search PubMed.
- J. B. Biot, Mémoire sur un nouveau genre d'oscillation que les molécules de la lumière éprouvent en traversant certains cristaux, in Mémoires de la Classe des Sciences Mathématique et Physique de l'Académie Royale des Sciences de l'Institut de France, 1812, vol. 13, pp. 1–217, première partie (Lu à l'Institut le 30 novombre 1812, cinquième partie lu le 31 mai 1813, pp. 218–219) Search PubMed.
- J. B. Biot, Extrait d'un Mémoire sur les Rotations que certaines substances impriment aux axes de polarisation des rayons lumineux, Ann. Chim. Phys., 1818, 9, 372–389 Search PubMed.
- E. Mitscherlich, Ueber die Krystallisation der Salze, in denen das Metall der Basis mit zwei Proportionen Sauerstoff verbunden ist., Abhandl. Königl. Preuss. Akad. Wiss. Berlin (Phys. Klasse, 9. Dezember 1819), 1819, pp. 427–437, published by Georg Reimer, Berlin, 1820 Search PubMed.
- J. F. W. Herschel II, On certain remarkable Instances of deviation from Newton's Scale in the Tints developed by Crystals, with one Axis of Double Refraction, on exposure to Polarized Light and III. On the Rotation impressed by Plates of Rock Crystal on the Planes of Polarization of the Rays of Light, as connected with certain peculiarities in its Crystallization, Trans. Cambridge Philos. Soc., 1819, 1, 21–51 Search PubMed , published by Cambridge University Press, 1822..
- J. Gal, Louis Pasteur, language, and molecular chirality. I. Background and Dissymmetry, Chirality, 2011, 23, 1–16 CrossRef CAS PubMed.
- J. Gal, In defense of Louis Pasteur: Critique of Gerald Geison's deconstruction of Pasteur's discovery of molecular chirality, Chirality, 2019, 31, 261–282 CrossRef CAS PubMed.
- A. Fresnel, Considérations théoriques sur la polarisation de la lumière, Bull. Sci. Soc. Philomath., 1824, 147–158 Search PubMed.
- L. Pasteur, Sur les relations qui peuvent exister entre la forme cristalline, la composition chimique et le sens de la polarisation rotatoire, Ann. Chim. Phys., 1848, 24, 442–459 Search PubMed.
- L. Pasteur, Mémoire sur la relation qui peut exister entre la forme cristalline et la composition chimique, et sur la cause de la polarisation rotatoire, C. R. Hebd. Seances Acad. Sci., 1848, 26, 535–538 Search PubMed.
- L. Pasteur, Recherches sur les propriétés spécifiques des deux acides qui composent l'acide racémique, Ann. Chim. Phys., 1850, 28, 56–99 Search PubMed.
- L. Wilhelmy, Ueber das Gesetz, nach welchem die Einwirkung der Säuren auf den Rohrzucker stattfindet, Ann. Phys., 1850, 81, 413–428 CrossRef , 499–526, reprinted in Ostwalds Klassiker, also vol. 157, Ann. d. Physik..
- M. Quack, Molecular spectra, reaction dynamics, symmetries and life, Chimia, 2003, 57, 147–160 CrossRef CAS.
- J. A. Le Bel, Sur les relations qui existent entre les formules atomique des corps organiques et le pouvoir rotatoire de leurs dissolutions, Bull. Soc. Bot. Fr., 1874, 22, 337–347 Search PubMed.
- J. H. van't Hoff, Les formules de structure dans l'espace, Arch. Neerl. Sci. Exactes Nat., 1874, 9, 445–454 Search PubMed.
- J. H. van't Hoff, La chimie dans l'espace, Rotterdam, 1887, reprinted in Sur la dissymétrie moléculaire, Collection Epistème, Paris, 1986 (see ref. 3) Search PubMed.
- J. H. van't Hoff, Die Lagerung der Atome im Raum, Vieweg, Braunschweig, 3rd edn, 1908 Search PubMed.
- E. Fischer, Einfluss der Configuration auf die Wirkung der Enzyme, Ber. Dtsch. Chem. Ges., 1894, 27, 2985–2993 CrossRef CAS.
- M. Quack, Molecular femtosecond quantum dynamics between less than yoctoseconds and more than days: Experiment and theory, in Femtosecond Chemistry, Proc. Berlin Conf. Femtosecond Chemistry, Berlin (March 1993), ed. J. Manz and L. Wöste, Verlag Chemie, Weinheim, 1995, ch. 27, pp. 781–818 Search PubMed.
- J. M. Bijvoet, A. F. Peerdeman and A. J. van Bommel, Determination of the absolute configuration of optically active compounds by means of X-rays, Nature, 1951, 168, 271–272 CrossRef CAS , Proc. Koningkl. Ned. Akad. Wetenschap B54, 16, 1951..
- J. D. Dunitz, X-Ray Analysis and the Structure of Organic Molecules, Cornell University Press, Ithaca N. Y., 1979 Search PubMed.
- R. S. Cahn, C. Ingold and V. Prelog, Specification of molecular chirality, Angew. Chem., Int. Ed., 1966, 5, 385–415 ( Angew. Chem. , 1966 , 78 , 413–447 ) CrossRef CAS.
- M. Karplus, Development of Multiscale Models for Complex Chemical Systems: From H+H2 to Biomolecules (Nobel Lecture), Angew. Chem., Int. Ed., 2014, 53, 9992–10005 CrossRef CAS PubMed.
- W. F. van Gunsteren, D. Bakowies, R. Baron, I. Chandrasekhar, M. Christen, X. Daura, P. Gee, D. P. Geerke, A. Glättli, P. H. Hünenberger, M. A. Kastenholz, C. Oostenbrink, M. Schenk, D. Trzesniak, N. F. A. van der Vegt and H. B. Yu, Biomolecular Modeling: Goals, Problems, Perspectives, Angew. Chem., Int. Ed., 2006, 45, 4064–4092 CrossRef CAS PubMed.
- M. Parrinello, Breviarium de Motu Simulato Ad Atomos Pertinenti, Isr. J. Chem., 2022, e202100105 CAS.
- E. Heilbronner, Über die Symmetrie in der Chemie, Verlag Hans Erni Stiftung, Luzern, 1981, avec introduction par Maurice Cosanday Search PubMed.
- E. Heilbronner and J. Dunitz, Reflections on symmetry in chemistry and elsewhere, Verlag Helvetica Chimica Acta, Basel and VCH, Weinheim 1993, ISBN 3-527-28488-5 Search PubMed.
- O. Meister, Ber. Dtsch. Chem. Ges., 1869, 2, 619 CrossRef , reporting on Wislicenus, J. address to the Zürich chemical club (‘Chemische Harmonika’), 2 November 1869 (see also ref. 107)..
- J. D. Dunitz, Bad Language, Angew. Chem., Int. Ed., 2019, 58, 1248–1250 CrossRef CAS PubMed.
- M. Frayn, Copenhagen, Anchor Books, New York, 1998 Search PubMed.
- D. L. Sayers and R. Eustace, The Documents in the Case, Victor Gollancz Ltd., The Camelot Press, London, 1930 Search PubMed.
- M. Quack and J. Stohner, Molecular chirality and the fundamental symmetries of physics: Influence of parity violation on rovibrational frequencies and thermodynamic properties, Chirality, 2001, 13, 745–753 CrossRef CAS PubMed , Erratum: Chirality, 2003, 15, 375–376..
- M. Quack and J. Stohner, Influence of parity violating weak nuclear potentials on vibrational and rotational frequencies in chiral molecules, Phys. Rev. Lett., 2000, 84, 3807–3810 CrossRef CAS PubMed.
- M. Quack and J. Stohner, Combined multidimensional anharmonic and parity violating effects in CDBrClF, J. Chem. Phys., 2003, 119, 11228–11240 CrossRef CAS.
- W. Heisenberg, Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen, Z. Phys., 1925, 33, 879–893 CrossRef CAS.
- E. Schrödinger, Quantisierung als Eigenwertproblem I, Ann. Phys., 1926, 79, 361–376 CrossRef.
- E. Schrödinger, Quantisierung als Eigenwertproblem II, Ann. Phys., 1926, 79, 489–527 CrossRef.
- E. Schrödinger, Quantisierung als Eigenwertproblem III, Ann. Phys., 1926, 80, 437–490 CrossRef.
- E. Schrödinger, Quantisierung als Eigenwertproblem IV, Ann. Phys., 1926, 81, 109–139 CrossRef.
- M. Born, W. Heisenberg and P. Jordan, Zur Quantenmechanik. II, Z. Phys., 1926, 35, 557–615 CrossRef CAS.
- P. A. M. Dirac, Quantum mechanics of many-electron systems, Proc. Roy. Soc. London Series A, 1929, 123, 714–733 CAS.
- W. Heitler and F. London, Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik, Z. Phys., 1927, 44, 455–472 CrossRef CAS.
- K. Ruedenberg, The Physical Nature of the Chemical Bond, Rev. Mod. Phys., 1962, 34, 326–376 CrossRef CAS.
- T. Helgaker, P. Jorgensen and J. Olsen, Molecular Electronic-Structure Theory, Wiley, 2014 Search PubMed.
- H. F. Schaefer III, Quantum Chemistry, The development of ab initio methods in molecular electronic structure theory, Oxford Uni. Press, Oxford, 1984 Search PubMed.
- L. Pauling, The Nature of the Chemical Bond; An Introduction to Modern Structural Chemistry, Cornell University Press Ithaca, New York, 3rd edn, 1960 Search PubMed.
- G. Frenking and S. Shaik, The Chemical Bond: Fundamental Aspects of Chemical Bonding, Wiley-VCH, Weinheim, 2014 Search PubMed.
- M. Reiher and A. Wolf, Relativistic Quantum Chemistry, The Fundamental Theory of Molecular Science, Wiley VCH Weinheim, 1st edn, 2009 Search PubMed.
- P. Pyykkö, The Physics behind Chemistry and the Periodic Table, Chem. Rev., 2012, 112, 371–384 CrossRef PubMed.
- R. Hoffmann and J. P. Malrieu, Simulation vs. Understanding: A Tension, in Quantum Chemistry and Beyond. Part A. Stage Setting, Angew. Chem., Int. Ed., 2020, 59, 12590–12610 CrossRef CAS PubMed.
- R. Hoffmann and J. P. Malrieu, Simulation vs. Understanding: A Tension, in Quantum Chemistry and Beyond. Part B. The March of Simulation, for Better or Worse, Angew. Chem., Int. Ed., 2020, 59, 13156–13178 CrossRef CAS PubMed.
- R. Hoffmann and J. P. Malrieu, Simulation vs. Understanding: A Tension, in Quantum Chemistry and Beyond. Part C. Toward Consilience, Angew. Chem., Int. Ed., 2020, 59, 13694–13710 CrossRef PubMed.
- F. Neese, High-Level Spectroscopy, Quantum Chemistry, and Catalysis: Not just a Passing Fad, Angew. Chem., Int. Ed., 2017, 56, 11003–11010 CrossRef CAS PubMed.
- F. Hund, Zur Deutung der Molekelspektren II, Z. Phys., 1927, 42, 93–120 CrossRef CAS.
- F. Hund, Zur Deutung der Molekelspektren III. Bemerkungen über das Schwingungs- und Rotationsspektrum bei Molekeln mit mehr als zwei Kernen, Z. Phys., 1927, 43, 805–826 CrossRef CAS.
- H. Brunner, Rechts oder links in der Natur und anderswo, Wiley-VCH, Weinheim, 1999 Search PubMed.
- H. Brunner, Bild und Spiegelbild, GNT Verlag, Berlin, 2021 Search PubMed.
- M. Quack, J. Stohner and M. Willeke, High-resolution spectroscopic studies and theory of parity violation in chiral molecules, Annu. Rev. Phys. Chem., 2008, 59, 741–769 CrossRef CAS PubMed.
- M. Quack, On the measurement of the parity violating energy difference between enantiomers, Chem. Phys. Lett., 1986, 132, 147–153 CrossRef CAS.
- M. Quack and G. Seyfang, Atomic and Molecular Tunneling Processes in Chemistry, in Molecular Spectroscopy and Quantum Dynamics, ed. R. Marquardt and M. Quack, Elsevier, Amsterdam, 1st edn, 2020, ch. 7, pp. 231–282 Search PubMed.
- R. Janoschek, Theories on the origin of biomolecular homochirality, in: Chirality - From Weak Bosons to the α-Helix, ed. R. Janoschek, Springer, Berlin, 1991, ch. 2, pp. 18–33 Search PubMed.
- B. Fehrensen, D. Luckhaus and M. Quack, Mode selective stereomutation tunnelling in hydrogen peroxide isotopomers, Chem. Phys. Lett., 1999, 300, 312–320 CrossRef CAS.
- B. Fehrensen, D. Luckhaus and M. Quack, Stereomutation dynamics in hydrogen peroxide, Chem. Phys., 2007, 338, 90–105 CrossRef CAS.
- C. Fábri, R. Marquardt, A. Császár and M. Quack, Controlling tunneling in ammonia isotopomers, J. Chem. Phys., 2019, 150, 014102 CrossRef PubMed.
- R. Marquardt and M. Quack, Global Analytical Potential Energy Surfaces for High Resolution Molecular Spectroscopy and Reaction Dynamics, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, New York, 2011, vol. 1, ch. 12, pp. 511–549 Search PubMed.
- B. Kuhn, T. R. Rizzo, D. Luckhaus, M. Quack and M. A. Suhm, A new six-dimensional analytical potential up to chemically significant energies for the electronic ground state of hydrogen peroxide, J. Chem. Phys., 1999, 111, 2565–2587 CrossRef CAS , 135 pages of supplementary material published as AIP Document No PAPS JCPS A6-111-302905 by American Institute of Physics, Physics Auxiliary Publication Service, 500 Sunnyside, Blvd., Woodbury, N.Y. 1179-29999..
- R. Marquardt, K. Sagui, W. Klopper and M. Quack, Global analytical potential energy surface for large amplitude nuclear motions in ammonia, J. Phys. Chem. B, 2005, 109, 8439–8451 CrossRef CAS PubMed.
- R. Marquardt, K. Sagui, J. Zheng, W. Thiel, D. Luckhaus, S. Yurchenko, F. Mariotti and M. Quack, A Global Analytical Potential Energy Surface for the Electronic Ground State of NH3 from High Level Ab Initio Calculations, J. Phys. Chem. A, 2013, 117, 7502–7522 CrossRef CAS PubMed.
- D. Baykusheva, D. Zindel, V. Svoboda, E. Bommeli, M. Ochsner, A. Tehlar and H. J. Wörner, Real-time probing of chirality during a chemical reaction, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 23923–23929 CrossRef CAS PubMed.
- D. Baykusheva and H. J. Wörner, Attosecond Molecular Dynamics and Spectroscopy, in Molecular Spectroscopy and Quantum Dynamics, ed. R. Marquardt and M. Quack, Elsevier, Amsterdam, 1st edn, 2020, ch. 4, pp. 113–161 Search PubMed.
- R. Marquardt and M. Quack, Radiative excitation of the harmonic oscillator with applications to stereomutation in chiral molecules, Z. Phys. D: At., Mol. Clusters, 1996, 36, 229–237 CrossRef CAS.
- R. Marquardt, M. Quack and I. Thanopulos, Dynamical chirality and the quantum dynamics of bending vibrations of the CH chromophore in methane isotopomers, J. Phys. Chem. A, 2000, 104, 6129–6149 CrossRef CAS.
- F. Merkt and M. Quack, Molecular Quantum Mechanics and Molecular Spectra, Molecular Symmetry, and Interaction of Matter with Radiation, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, New York, 2011, vol. 1, ch. 1, pp. 1–55 Search PubMed.
- R. Marquardt and M. Quack, Chapter 1 - Foundations of Time Dependent Quantum Dynamics of Molecules Under Isolation and in Coherent Electromagnetic Fields, in Molecular Spectroscopy and Quantum Dynamics, ed. R. Marquardt and M. Quack, Elsevier, 2021, pp. 1–41 Search PubMed.
- M. Quack, in Reaction dynamics and statistical mechanics of the preparation of highly excited states by intense infrared radiation, ed. K. Lawley, I. Prigogine and S. A. Rice, John Wiley & Sons, Chichester and New York, Adv. Chem. Phys., 1982, vol. 50, pp. 395–473 Search PubMed.
- M. Quack, Molecular Quantum Dynamics from High-Resolution Spectroscopy and Laser Chemistry, J. Mol. Struct., 1993, 292, 171–195 CrossRef CAS.
- W. Heisenberg, Die physikalischen Prinzipien der Quantentheorie, Hirzel Verlag, Leipzig, 1980 Search PubMed.
- P. A. M. Dirac, The Principles of Quantum Mechanics, Clarendon Press, Oxford, 4th edn, 1958 Search PubMed.
- M. Quack, Comments on the role of symmetries in intramolecular quantum dynamics, Faraday Discuss., 1995, 102(90–93), 358–360 Search PubMed.
- M. Quack, Detailed symmetry selection-rules for reactive collisions, Mol. Phys., 1977, 34, 477–504 CrossRef CAS.
- M. Quack, Detailed symmetry selection rules for chemical reactions, in Symmetries and properties of non-rigid molecules: A comprehensive survey, ed. J. Maruani and J. Serre, Elsevier Publishing Co., Amsterdam, 1983, vol. 23, pp. 355–378 Search PubMed.
- A. Beil, D. Luckhaus, M. Quack and J. Stohner, Intramolecular vibrational redistribution and unimolecular reaction: Concepts and new results on the femtosecond dynamics and statistics in CHBrClF, Ber. Bunsen-Ges. Phys. Chem., 1997, 101, 311–328 CrossRef CAS.
- D. Luckhaus and M. Quack, The role of potential anisotropy in the dynamics of the CH-chromophore in CHX3 (C3v) symmetrical tops, Chem. Phys. Lett., 1993, 205, 277–284 CrossRef CAS.
- E. Wigner, Über die Erhaltungssätze in der Quantenmechanik, Nachr. Ges. Wiss. Goettingen, 1927, 375–381 Search PubMed.
- W. Pauli, Die Verletzung von Spiegelungs-Symmetrien in den Gesetzen der Atomphysik, Experientia, 1958, 14, 1–5 CrossRef.
- E. R. Cohen, T. Cvitas, J. G. Frey, B. Holmström, K. Kuchitsu, R. Marquardt, I. Mills, F. Pavese, M. Quack, J. Stohner, H. L. Strauss, M. Takami and A. J. Thor, Quantities, Units and Symbols in Physical Chemistry, IUPAC and Royal Society of Chemistry, RSC Publishing, Cambridge, 3rd edn, 2007 Search PubMed.
- A. Einstein, Grundzüge der Relativitätsteheorie, Vieweg, Wiesbaden, 1922 Search PubMed.
- M. Gardner and J. Mackey, The Ambidextrous Universe: Mirror Asymmetry and Time-Reversed Worlds, Basic Books, New York, 1964 Search PubMed.
- E. Fermi, Versuch einer Theorie der Beta-Strahlen, Z. Phys., 1934, 88, 161–177 CrossRef CAS.
- M. Quack, Error and Discovery: Why Repeating Can Be New, Angew. Chem., Int. Ed., 2013, 52, 9362–9370 CrossRef CAS PubMed , Irrtum und Erkenntnis: Wenn Wiederholen neu ist, Angew. Chem., 2013, 125, 9530–9538..
- T. D. Lee, Weak Interactions and Nonconservation of Parity, Science, 1958, 127, 569–573 CrossRef CAS PubMed.
- C. N. Yang, Law of Parity Conservation and Other Symmetry Laws, Science, 1958, 127, 565–569 CrossRef CAS PubMed.
- CERN, AC_Z04_V25/B/1992, https://cds.cern.ch/record/39722 Search PubMed.
- H. Fritzsch, The Fundamental Constants: A Mystery of Physics, World Scientific, 2005 Search PubMed.
- R. P. Feynman, The Theory of Positrons, Phys. Rev., 1949, 76, 749–759 CrossRef CAS.
- R. P. Feynman, Space-Time Approach to Quantum Electrodynamics, Phys. Rev., 1949, 76, 769–789 CrossRef.
- E. C. G. Stueckelberg, Relativistisch invariante Störungstheorie des Diracschen Elektrons I. Teil: Streustrahlung und Bremsstrahlung, Ann. Phys., 1934, 413, 367–389 CrossRef.
- E. Stueckelberg, Die Wechselwirkungskräfte in der Elektrodynamik und in der Feldtheorie der Kernkräfte. Teil II und III, Helv. Phys. Acta, 1938, 11, 51–80 Search PubMed.
- E. Stueckelberg, Un nouveau modèle de l'électron ponctuel en théorie classique, Helv. Phys. Acta, 1941, 14, 51–80 CAS.
- E. Stueckelberg, La signification du temps propre en mécanique ondulatoire, Helv. Phys. Acta, 1941, 14, 322–323 CAS.
- E. Stueckelberg, La mécanique du point matériel en théorie de relativité et en théorie des quanta, Helv. Phys. Acta, 1942, 15, 23–37 Search PubMed.
- E. Stueckelberg and A. Petermann, La normalisation des constantes dans la théorie des quanta, Helv. Phys. Acta, 1953, 26, 499–520 Search PubMed.
- M. Veltman, Diagrammatica: The Path to Feynman Rules, Cambridge University Press, Cambridge, 1994, reprinted 1995 Search PubMed.
- A. Bakasov, T. K. Ha and M. Quack, Ab initio calculation of molecular energies including parity violating interactions, in Chemical Evolution, Physics of the Origin and Evolution of Life, Proc. of the 4th Trieste Conference (1995), ed. J. Chela-Flores and F. Raulin, Kluwer Academic Publishers, Dordrecht, 1996, pp. 287–296 Search PubMed.
- A. Bakasov, T. K. Ha and M. Quack, Ab initio calculation of molecular energies including parity violating interactions, J. Chem. Phys., 1998, 109, 7263–7285 CrossRef CAS.
- M. Quack and J. Stohner, Parity violation in chiral molecules, Chimia, 2005, 59, 530–538 CrossRef CAS , Erratum for printer's errors: Chimia, 2005, 59, 712–712..
- R. Berger, Parity-violation effects in molecules, in Relativistic Electronic Structure Theory. Part 2 (Applications), ed. P. Schwerdtfeger, Elsevier, Amsterdam, 2004 Search PubMed.
- M. Quack, Frontiers in Spectroscopy (Concluding paper to Faraday Discussion 150), Faraday Discuss., 2011, 150, 533–565 RSC.
- L. Horný and M. Quack, Computation of molecular parity violation using the coupled-cluster linear response approach, Mol. Phys., 2015, 113, 1768–1779 CrossRef.
- Y. Yamagata, A hypothesis for the asymmetric appearance of biomolecules on earth, J. Theor. Biol., 1966, 11, 495–498 CrossRef CAS PubMed.
- A. S. Garay and P. Hraskó, Neutral currents in weak interactions and molecular asymmetry, J. Mol. Evol., 1975, 6, 77–89 CrossRef CAS PubMed.
- R. A. Harris and L. Stodolsky, Quantum beats in optical activity and weak interactions, Phys. Lett. B, 1978, 78, 313–317 CrossRef.
- M. A. Bouchiat and C. Bouchiat, Parity violation induced by weak neutral currents in atomic physics 1, J. Phys., 1974, 35, 899–927 CrossRef CAS.
- M. A. Bouchiat and C. Bouchiat, Parity violation induced by weak neutral currents in atomic physics 2, J. Phys., 1975, 36, 493–509 CrossRef CAS.
- R. Hegström, D. W. Rein and P. G. H. Sandars, Calculation of parity non-conserving energy difference between mirror-image molecules, J. Chem. Phys., 1980, 73, 2329–2341 CrossRef.
- S. F. Mason and G. E. Tranter, The parity-violating energy difference between enantiomeric molecules, Mol. Phys., 1984, 53, 1091–1111 CrossRef CAS.
- O. Kikuchi and H. Wang, Parity-violating energy shift of glycine, alanine, and serine in the zwitterionic forms, Bull. Chem. Soc. Jpn., 1990, 63, 2751–2754 CrossRef CAS.
- L. Wiesenfeld, Effect of atomic number on parity-violating energy differences between enantiomers, Mol. Phys., 1988, 64, 739–745 CrossRef CAS.
- R. Berger and M. Quack, Multiconfiguration linear response approach to the calculation of parity violating potentials in polyatomic molecules, J. Chem. Phys., 2000, 112, 3148–3158 CrossRef CAS.
- M. Quack, Fundamental Symmetry Principles in Relation to the Physical-Chemical Foundations of Molecular Chirality and Possible Biological Consequences, Lecture Notes in ‘Seventh College on Biophysics’ (Structure and Function of Biopolymers, Experimental and Theoretical Techniques) 4-29 March 1996, UNESCO and International Centre for Theoretical Physics, 1996, preprint H4.SMR/916-27, distributed and printed by ICTCP Trieste, Italy, March 1996 Search PubMed.
- P. Lazzeretti and R. Zanasi, On the calculation of parity-violating energies in hydrogen peroxide and hydrogen disulphide molecules within the random-phase approximation, Chem. Phys. Lett., 1997, 279, 349–354 CrossRef CAS.
- J. K. Laerdahl and P. Schwerdtfeger, Fully relativistic ab initio calculations of the energies of chiral molecules including parity-violating weak interactions, Phys. Rev. A, 1999, 60, 4439–4453 CrossRef CAS.
- A. C. Hennum, T. Helgaker and W. Klopper, Parity-violating interaction in H2O2 calculated from density-functional theory, Chem. Phys. Lett., 2002, 354, 274–282 CrossRef CAS.
- P. Schwerdtfeger, T. Saue, J. N. P. van Stralen and L. Visscher, Relativistic second-order many-body and density-functional theory for the parity-violation contribution to the C-F stretching mode in CHFClBr, Phys. Rev. A, 2005, 71, 012103 CrossRef.
- J. K. Laerdahl, P. Schwerdtfeger and H. M. Quiney, Theoretical Analysis of Parity-Violating Energy Differences between the Enantiomers of Chiral Molecules, Phys. Rev. Lett., 2000, 84, 3811–3814 CrossRef CAS PubMed.
- R. Berger and J. Stohner, Parity violation, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1396 Search PubMed.
- D. Andrae, M. Reiher and J. Hinze, A comparative study of finite nucleus models for low-lying states of few-electron high-Z atoms, Chem. Phys. Lett., 2000, 320, 457–468 CrossRef CAS.
- A. Bakasov, T. K. Ha and M. Quack, Studies of parity violation in chiral molecules: Molecular physics vs. accelerators and the Z3+d amplification law, Chimia, 1997, 51, 559 Search PubMed.
- A. Bakasov and M. Quack, Representation of parity violating potentials in molecular main chiral axes, Chem. Phys. Lett., 1999, 303, 547–557 CrossRef CAS.
- A. Bakasov, R. Berger, T. K. Ha and M. Quack, Ab initio calculation of parity-violating potential energy hypersurfaces of chiral molecules, Int. J. Quantum Chem., 2004, 99, 393–407 CrossRef CAS.
- R. Berger and M. Quack, Multiconfiguration linear response approach to the calculation of parity violating potentials in polyatomic molecules, Proc. 37 th IUPAC Congress, Berlin, 1999, vol. 2, p. 518 Search PubMed.
- R. Berger, Breit interaction contribution to parity violating potentials in chiral molecules containing light nuclei, J. Chem. Phys., 2008, 129, 154105 CrossRef PubMed.
- R. Berger, N. Langermann and C. van Wüllen, Zeroth-order regular approximation approach to molecular parity violation, Phys. Rev. A, 2005, 71, 042105 CrossRef.
- R. Berger and C. van Wüllen, Density functional calculations of molecular parity-violating effects within the zeroth-order regular approximation, J. Chem. Phys., 2005, 122, 134316 CrossRef PubMed.
- J. N. P. van Stralen, L. Visscher, C. V. Larsen and H. J. A. Jensen, First-order MP2 molecular properties in a relativistic framework, Chem. Phys., 2005, 311, 81–95 CrossRef CAS.
- J. Thyssen, J. K. Laerdahl and P. Schwerdtfeger, Fully Relativistic Coupled Cluster Treatment for Parity-Violating Energy Differences in Molecules, Phys. Rev. Lett., 2000, 85, 3105–3108 CrossRef CAS PubMed.
- R. Conti, P. Bucksbaum, S. Chu, E. Commins and L. Hunter, Preliminary Observation of Parity Nonconservation in Atomic Thallium, Phys. Rev. Lett., 1979, 42, 343–346 CrossRef CAS.
- S. C. Bennett and C. E. Wieman, Measurement of the 6S → 7S Transition Polarizability in Atomic Cesium and an Improved Test of the Standard Model, Phys. Rev. Lett., 1999, 82, 2484–2487 CrossRef CAS.
- V. M. Shabaev, K. Pachucki, I. I. Tupitsyn and V. A. Yerokhin, QED Corrections to the Parity-Nonconserving 6s-7s Amplitude in 133Cs, Phys. Rev. Lett., 2005, 94, 213002 CrossRef CAS PubMed.
- K. Tsigutkin, D. Dounas-Frazer, A. Family, J. E. Stalnaker, V. V. Yashchuk and D. Budker, Observation of a Large Atomic Parity Violation Effect in Ytterbium, Phys. Rev. Lett., 2009, 103, 071601 CrossRef CAS PubMed.
- M. Bouchiat, J. Guena, L. Pottier and L. Hunter, New observation of a parity violation in cesium, Phys. Lett. B, 1984, 134, 463–468 CrossRef.
- D. N. Stacey, Experiments on the Electro-Weak Interaction in Atoms, Phys. Scr., T, 1992, 40, 15–22 CrossRef.
- I. B. Khriplovich, Parity nonconservation in atomic phenomena, Gordon and Breach Science Publishers, Philadelphia, 1991, translated from the Russian by L. Ya. Yuzina Search PubMed.
- R. Berger, G. Laubender, M. Quack, A. Sieben, J. Stohner and M. Willeke, Isotopic chirality and molecular parity violation, Angew. Chem., Int. Ed., 2005, 44, 3623–3626 ( Angew. Chem. , 2005 , 117 , 3689–3693 ) CrossRef CAS PubMed.
- M. Gottselig, D. Luckhaus, M. Quack, J. Stohner and M. Willeke, Mode selective stereomutation and parity violation in disulfane isotopomers H2S2, D2S2, T2S2, Helv. Chim. Acta, 2001, 84, 1846–1861 CrossRef CAS.
- M. Gottselig, M. Quack, J. Stohner and M. Willeke, Mode-selective stereomutation tunneling and parity violation in HOClH+ and H2Te2 isotopomers, Int. J. Mass Spectrom., 2004, 233, 373–384 CrossRef CAS.
- M. Quack and M. Willeke, Theory of stereomutation dynamics and parity violation in hydrogen thioperoxide isotopomers 1,2,3HSO1,2,3H, Helv. Chim. Acta, 2003, 86, 1641–1652 CrossRef CAS.
- M. Gottselig, M. Quack and M. Willeke, Mode-selective stereomutation tunneling as compared to parity violation in hydrogen diselenide isotopomers 1,2,3H280Se2, Isr. J. Chem., 2003, 43, 353–362 CrossRef CAS.
- N. Sahu, J. O. Richardson and R. Berger, Instanton calculations of tunneling splittings in chiral molecules, J. Comput. Chem., 2021, 42, 210–221 CrossRef CAS PubMed.
- Y. B. Zel'dovich, Parity nonconservation in the first order in the weak-interaction constant in electron scattering and other effects, Soviet Physics - JETP, 1959, 9, 682–683 Search PubMed.
- Y. B. Zel'dovich, D. B. Saakyan and I. I. Sobel'man, Energy difference between right-hand and left-hand molecules, due to parity nonconservation in weak interactions of electrons with nuclei, Soviet physics, JETP Lett, 1977, 25, 94–97 Search PubMed , Pis'ma Zh. Eksp. Teor. Fiz. 25 No. 2 106-109, 1977..
- R. Prentner, M. Quack, J. Stohner and M. Willeke, On tunneling and parity violation in ClOOCl, Faraday Discuss. Chem. Soc., 2011, 150, 130–132 Search PubMed.
- M. Quack and M. Willeke, Stereomutation tunneling switching dynamics and parity violation in chlorineperoxide Cl-O-O-Cl, J. Phys. Chem. A, 2006, 110, 3338–3348 CrossRef CAS PubMed.
- R. Prentner, M. Quack, J. Stohner and M. Willeke, Wavepacket Dynamics of the Axially Chiral Molecule Cl-O-O-Cl under Coherent Radiative Excitation and Including Electroweak Parity Violation, J. Phys. Chem. A, 2015, 119, 12805–12822 CrossRef CAS PubMed.
- R. Berger, M. Gottselig, M. Quack and M. Willeke, Parity violation dominates the dynamics of chirality in dichlorodisulfane, Angew. Chem., Int. Ed., 2001, 40, 4195–4198 ( Angew. Chem. , 2001 , 113 , 4342–4345 ) CrossRef CAS PubMed.
- G. Wichmann, G. Seyfang and M. Quack, Time-dependent dynamics of nuclear spin symmetry and parity violation in dichlorodisulfane (ClSSCl) during and after coherent radiative excitation, Mol. Phys., 2021, 119, e1959073 CrossRef (29 pages), with supplementary material (44 pages)..
- R. Berger and M. Quack, Electroweak quantum chemistry of alanine: Parity violation in gas and condensed phases, ChemPhysChem, 2000, 1, 57–60 CrossRef CAS PubMed.
- C. Daussy, T. Marrel, A. Amy-Klein, C. T. Nguyen, C. J. Bordé and C. Chardonnet, Limit on the Parity Nonconserving Energy Difference between the Enantiomers of a Chiral Molecule by Laser Spectroscopy, Phys. Rev. Lett., 1999, 83, 1554–1557 CrossRef CAS.
- S. K. Tokunaga, C. Stoeffler, F. Auguste, A. Shelkovnikov, C. Daussy, A. Amy-Klein, C. Chardonnet and B. Darquié, Probing weak force-induced parity violation by high-resolution mid-infrared molecular spectroscopy, Mol. Phys., 2013, 111, 2363–2373 CrossRef CAS.
- A. Cournol, M. Manceau, M. Pierens, L. Lecordier, D. B. A. Tran, R. Santagata, B. Argence, A. Goncharov, O. Lopez, M. Abgrall, Y. Le Coq, R. Le Targat, H. Alvarez Martinez, W. K. Lee, D. Xu, P. E. Pottie, R. J. Hendricks, T. E. Wall, J. M. Bieniewska, B. E. Sauer, M. R. Tarbutt, A. Amy-Klein, S. K. Tokunaga and B. Darquié, A new experiment to test parity symmetry in cold chiral molecules using vibrational spectroscopy, Quantum Electron., 2019, 49, 288–292 CrossRef CAS.
- M. Schnell and J. Küpper, Tailored molecular samples for precision spectroscopy experiments, Faraday Discuss., 2011, 150, 33–49 RSC.
- V. S. Letokhov, On difference of energy levels of left and right molecules due to weak interactions, Phys. Lett. A, 1975, 53, 275–276 CrossRef.
- E. Arimondo, P. Glorieux and T. Oka, Observation of inverted infrared Lamb dips in separated optical isomers, Opt. Commun., 1977, 23, 369–372 CrossRef CAS.
- A. Beil, D. Luckhaus, R. Marquardt and M. Quack, Intramolecular energy-transfer and vibrational redistribution in chiral molecules - experiment and theory, Faraday Discuss., 1994, 99, 49–76 RSC.
- A. Bauder, A. Beil, D. Luckhaus, F. Müller and M. Quack, Combined high resolution infrared and microwave study of bromochlorofluoromethane, J. Chem. Phys., 1997, 106, 7558–7570 CrossRef CAS.
- H. Hollenstein, D. Luckhaus, J. Pochert, M. Quack and G. Seyfang, Synthesis, structure, high-resolution spectroscopy, and laser chemistry of fluorooxirane and 2H2-fluorooxirane, Angew. Chem., Int. Ed., 1997, 36, 140–143 ( Angew. Chem. , 1997 , 109 , 136–140 ) CrossRef CAS.
- P. Dietiker, E. Miloglyadov, M. Quack, A. Schneider and G. Seyfang, Infrared laser induced population transfer and parity selection in 14NH3: A proof of principle experiment towards detecting parity violation in chiral molecules, J. Chem. Phys., 2015, 143, 244305 CrossRef CAS PubMed.
- H. Gross, G. Grassi and M. Quack, The synthesis of [2-2H1] thiirane-1-oxide and [2,2-2H2] thiirane-1-oxide and the diastereoselective infrared laser chemistry of [2-2H1] thiirane-1-oxide, Chem.–Eur. J., 1998, 4, 441–448 CrossRef CAS.
- S. Albert, K. K. Albert and M. Quack, Very high resolution studies of chiral molecules with a Bruker IFS 120 HR: The rovibrational spectrum of CDBrClF in the range 600–2300 cm−1, in Proceedings Fourier Transform Spectroscopy, Trends in Optics and Photonics (TOPS), Optical Society of America, Washington DC, 2003, vol. 84, pp. 177–180 Search PubMed.
- S. Albert and M. Quack, High resolution rovibrational spectroscopy of chiral and aromatic compounds, ChemPhysChem, 2007, 8, 1271–1281 CrossRef CAS PubMed.
- O. N. Kompanets, A. R. Kukudzhanov, V. S. Letokhov and L. L. Gervits, Narrow resonances of saturated absorption of asymmetrical molecule CHFClBr and possibility of weak current detection in molecular physics, Opt. Commun., 1976, 19, 414–416 CrossRef CAS.
- J. Stohner and M. Quack, Recent results on parity violation in chiral molecules: Camphor and the influence of molecular parity violation, in Proceedings, 15th Symposium on Atomic and Surface Physics and Related Topics, Obergurgl, Österreich, 4. - 9.2.2006, ed. V. Grill and T. D. Märk, Innsbruck University Press, Innsbruck, 2006, pp. 196–199 Search PubMed.
- E. Miloglyadov, M. Quack, G. Seyfang and G. Wichmann, Precision experiments for parity violation in chiral molecules: the role of STIRAP, J. Phys. B: At. Mol. Opt. Phys., 2019, 52, 11–13 Search PubMed , ch. A2.3, 51–52, in ‘Roadmap on STIRAP applications’ by K. Bergmann, H. C. Nägerl, C. Panda, G. Gabrielse, E. Miloglyadov, M. Quack, G. Seyfang, G. Wichmann, S. Ospelkaus, A. Kuhn, S. Longhi, A. Szameit, P. Pirro, B. Hillebrands, X. F. Zhu, J. Zhu, M. Drewsen, W. K. Hensinger, S. Weidt, T. Halfmann, H. L. Wang, G. S. Paraoanu, N. V. Vitanov, J. Mompart, T. Busch, T. J. Barnum, D. D. Grimes, R. W. Field, M. G. Raizen, E. Narevicius, M. Auzinsh, D. Budker, A. Pálffy and C. H. Keitel, J. Phys. B: At. Mol. Opt. Phys., 2019, 52, 202001 CrossRef CAS.
- G. Wichmann, E. Miloglyadov, G. Seyfang and M. Quack, Nuclear spin symmetry conservation studied by cavity ring-down spectroscopy of ammonia in a seeded supersonic jet from a pulsed slit nozzle, Mol. Phys., 2020, 118, e1752946 CrossRef.
- E. Schrödinger, Die gegenwärtige Situation in der Quantenmechanik, Naturwissenschaften, 1935, 23, 807–812 CrossRef , 823–828 and 844–849..
- M. Quack, Telluride public lecture, 1995, unpublished, in part contained in ref. 327 Search PubMed.
- M. Quack, On the fundamental and approximate symmetries in molecular quantum dynamics and the preparation of exotic superposition isomers, Proc. Symp. MOLIM 2018 - Molecules in Motion Athens, ed. F. Merkt, M. Quack, I. Thanopulos and C. G. Vayenas, 2018, p. 36 Search PubMed.
- Inkscape Project, Inkscape, 0.91, https://inkscape.org Search PubMed.
- M. Quack, Spectra and dynamics of coupled vibrations in polyatomic molecules, Annu. Rev. Phys. Chem., 1990, 41, 839–874 CrossRef CAS.
- M. Quack and F. Merkt, Handbook of High Resolution Spectroscopy, Wiley, Chichester, New York, 2011, with preface of the editors and eight review articles from our group, as well as numerous articles by groups worldwide Search PubMed.
- S. Albert, K. Keppler Albert, H. Hollenstein, C. Manca Tanner and M. Quack, Fundamentals of Rotation-Vibration Spectra, in Handbook of High-Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, New York, 2011, vol. 1, ch. 3, pp. 117–173 Search PubMed.
- S. Albert, K. Keppler Albert and M. Quack, High Resolution Fourier Transform Infrared Spectroscopy, in Handbook of High Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, New York, 2011, vol. 2, ch. 26, pp. 965–1019 Search PubMed.
- M. Hippler, E. Miloglyadov, M. Quack and G. Seyfang, Mass and Isotope Selective Infrared Spectroscopy, in Handbook of High Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester; New York, 2011, vol. 2, ch. 28, pp. 1069–1118 Search PubMed.
- M. Snels, V. Horká-Zelenková, H. Hollenstein and M. Quack, High Resolution FTIR and Diode Laser Spectroscopy of Supersonic Jets, in Handbook of High Resolution Spectroscopy, ed. M. Quack and F. Merkt, Wiley, Chichester, New York, 2011, vol. 2, ch. 27, pp. 1021–1067 Search PubMed.
- S. Albert, I. Bolotova, Z. Chen, C. Fabri, M. Quack, G. Seyfang and D. Zindel, High-resolution FTIR spectroscopy of trisulfane HSSSH: a candidate for detecting parity violation in chiral molecules, Phys. Chem. Chem. Phys., 2017, 19, 11738–11743 RSC.
- C. Fábri, L. Horný and M. Quack, Tunneling and Parity Violation in Trisulfane (HSSSH): An Almost Ideal Molecule for Detecting Parity Violation in Chiral Molecules, ChemPhysChem, 2015, 16, 3584–3589 CrossRef PubMed.
- M. Snels and M. Quack, High-resolution Fourier-transform infrared-spectroscopy of CHCl2F in supersonic jets - Analysis of ν3, ν7, and ν8, J. Chem. Phys., 1991, 95, 6355–6361 CrossRef CAS.
- S. Albert, K. K. Albert and M. Quack, Rovibrational analysis of the ν4 and ν5 + ν9 bands of CHCl2F, J. Mol. Struct., 2004, 695, 385–394 Search PubMed.
- S. Albert, S. Bauerecker, M. Quack and A. Steinlin, Rovibrational analysis of the 2ν3, 3ν3 and ν1 bands of CHCl2F measured at 170 and 298 K by high-resolution FTIR spectroscopy, Mol. Phys., 2007, 105, 541–558 CrossRef CAS.
- S. Albert, K. Keppler, V. Boudon, P. Lerch and M. Quack, Combined Synchrotron-based high resolution FTIR and IR - diode laser supersonic jet spectroscopy of the chiral molecule CDBrClF, J. Mol. Spectrosc., 2017, 337, 105–123 CrossRef CAS.
- P. Schwerdtfeger, J. K. Laerdahl and C. Chardonnet, Calculation of parity-violation effects for the C-F stretching mode of chiral methyl fluorides, Phys. Rev. A, 2002, 65, 042508 CrossRef.
- P. Soulard, P. Asselin, A. Cuisset, J. R. Aviles Moreno, T. R. Huet, D. Petitprez, J. Demaison, T. B. Freedman, X. Cao, L. A. Nafie and J. Crassous, Chlorofluoroiodomethane as a potential candidate for parity violation measurements, Phys. Chem. Chem. Phys., 2006, 8, 79–92 RSC.
- S. Albert, K. K. Albert, S. Bauerecker and M. Quack, CHBrIF and molecular parity violation: First high resolution rovibrational analysis of the CF-stretching mode, in Proc. 16th SASP 2008, ed. R. D. Beck, M. Drabbels and T. R. Rizzo, Innsbruck University Press (IUP), Innsbruck, 2008, pp. 79–82 Search PubMed.
- S. Albert and M. Quack, Höchstauflösende FTIR-Spektroskopie. Trendbericht Physikalische Chemie 2013, Nachr. Chem., 2014, 62, 313–318 CrossRef.
- R. Berger, M. Quack, A. Sieben and M. Willeke, Parity-violating potentials for the torsional motion of methanol (CH3OH) and its isotopomers CD3OH, 13CH3OH, CH3OD, CH3OT, CHD2OH, and CHDTOH, Helv. Chim. Acta, 2003, 86, 4048–4060 CrossRef CAS.
- M. Gottselig and M. Quack, Steps towards molecular parity violation in axially chiral molecules. I.Theory for allene and 1,3-difluoroallene, J. Chem. Phys., 2005, 123, 84305 CrossRef PubMed.
- L. Horný and M. Quack, On coupled cluster calculations of parity violating potentials in chiral molecules (Discussion contribution), Faraday Discuss., 2011, 150, 152–154 Search PubMed.
- S. Albert, Z. Chen, K. Keppler, M. Quack, V. Schurig and O. Trapp, The Gigahertz and Terahertz spectrum of monodeuterooxirane (c-C2H3DO), Phys. Chem. Chem. Phys., 2019, 21, 3669–3675 RSC.
- Z. Chen, S. Albert, K. Keppler, P. Lerch, M. Quack, V. Schurig and O. Trapp, High resolution Gigahertz- and Terahertz Spectroscopy of the isotopically chiral molecule trans 2,3 di deutero oxirane C-CHDCHDO, Proc. International Symp. on Molecular Spectroscopy, Urbana, Ill. 21-25 June (2021) and Proc. MOLIM 2018 Molecules in Motion Int. Workshop on Molecular Quantum Dynamics and Kinetics, Athens, Greece 8–10 October, 2018 Search PubMed.
- F. Hobi, R. Berger and J. Stohner, Investigation of parity violation in nuclear spin-rotation interaction of fluorooxirane, Mol. Phys., 2013, 111, 2345–2362 CrossRef CAS.
- R. Berger, M. Quack and J. Stohner, Parity violation in fluorooxirane, Angew. Chem., Int. Ed., 2001, 40, 1667–1670 CrossRef CAS PubMed.
- H. Gross, Y. He, C. Jeitziner, M. Quack and G. Seyfang, Vibrational IR-multiphoton excitation of thiirane-1-oxide (C2H4SO) and d-thiirane-1-oxide (C2H3DSO), Ber. Bunsen-Ges. Phys. Chem., 1995, 99, 358–365 CrossRef CAS.
- R. Berger, M. Quack and G. S. Tschumper, Electroweak quantum chemistry for possible precursor molecules in the evolution of biomolecular homochirality, Helv. Chim. Acta, 2000, 83, 1919–1950 CrossRef CAS.
- S. Albert, P. Lerch, K. Keppler and M. Quack, THz Spectroscopy of cyano-oxirane (c-C2H3OCN) and methyl oxirane (c-C2H3OCH3) with synchrotron light, in Proc. SASP 2016, ed. J. Stohner and C. Yeretzian, Innsbruck University Press (IUP), Innsbruck, 2016, pp. 165–168 Search PubMed.
- K. Keppler, S. Albert, C. Manca Tanner, M. Quack and J. Stohner, Paper F04 in Proc. 27th Coll. High. Res. Mol. Spectr., Cologne, Germany, 29 August to 3 September, 2021 paper and Fall meeting of the Swiss Chemical Society September 2021, Chimia, 2021, 75(7/8), 670, (2022) Suppl. Paper PC-118 (ISSN 009-4293) Search PubMed.
- S. Albert, I. Bolotova, Z. Chen, C. Fábri, L. Horný, M. Quack, G. Seyfang and D. Zindel, High resolution GHz and THz (FTIR) spectroscopy and theory of parity violation and tunneling for 1,2-dithiine (C4H4S2) as a candidate for measuring the parity violating energy difference between enantiomers of chiral molecules, Phys. Chem. Chem. Phys., 2016, 18, 21976–21993 RSC.
- S. Albert, F. Arn, I. Bolotova, Z. Chen, C. Fábri, G. Grassi, P. Lerch, M. Quack, G. Seyfang, A. Wokaun and D. Zindel, Synchrotron-Based Highest Resolution Terahertz Spectroscopy of the ν24 Band System of 1,2-Dithiine (C4H4S2): A Candidate for Measuring the Parity Violating Energy Difference between Enantiomers of Chiral Molecules, J. Phys. Chem. Lett., 2016, 7, 3847–3853 CrossRef CAS PubMed.
- S. Albert, P. Lerch, R. Prentner and M. Quack, Tunneling and Tunneling Switching Dynamics in Phenol and Its Isotopomers from High-Resolution FTIR Spectroscopy with Synchrotron Radiation, Angew. Chem., Int. Ed., 2013, 52, 346–349 CrossRef CAS PubMed.
- S. Albert, Z. Chen, C. Fábri, P. Lerch, R. Prentner and M. Quack, A combined Gigahertz and Terahertz (FTIR) spectroscopic investigation of meta-D-phenol: observation of tunnelling switching, Mol. Phys., 2016, 114, 2751–2768 CrossRef CAS.
- C. Fábri, S. Albert, Z. Chen, R. Prentner and M. Quack, A Molecular Quantum Switch Based on Tunneling in Meta-D-phenol C6H4DOH, Phys. Chem. Chem. Phys., 2018, 20, 7387–7394 RSC.
- Y. B. He, J. Pochert, M. Quack, R. Ranz and G. Seyfang, Dynamics of unimolecular reactions induced by monochromatic IR radiation: Experiment and theory for CnFmHkI → CnFmHk + I probed with hyperfine-, Doppler- and uncertainty-limited time resolution of iodine-atom IR absorption, Faraday Discuss., 1995, 102, 275–300 RSC.
- M. Quack, Discussion contributions on molecular chirality and anharmonic vibrational dynamics of chiral molecules: On fundamental aspects of molecular chirality, Faraday Discuss., 1994, 99, 89–91 Search PubMed , 389–395 and 397–398..
- R. Penrose, From Quantum Foundations to Neuronal Microtubules: New Clues to the Basics of Conscious Mentality, Richard R. Ernst Lecture, ETH Zürich, 2012 Search PubMed.
- P. Pfeifer, Molecular Structure derived from first-principles quantum mechanics. Two examples, in Energy Storage and Redistribution in Molecules (Proc. 2 workshops, Bielefeld 1980), ed. J. Hinze, 1983, pp. 315–326 Search PubMed.
- H. Primas, Chemistry, Quantum Mechanics and Reductionism; Perspectives in Theoretical Chemistry, ed. G. Berthier, M. J. S. Dewar, H. Fischer, K. Fukui, G. G. Hall, H. Hartmann, H. H. Jaffé, J. Jortner, W. Kutzelnigg, K. Ruedenberg and E. Scrocco, Springer-Verlag, Berlin, Heidelberg, New York, 1981 Search PubMed.
- E. Schrödinger, What is life?: The physical aspect of the living cell, Univ. Press, Cambridge, 1951. Based on Lectures delivered under the auspices of the Institute at Trinity College, Dublin, in February 1943 Search PubMed.
- T. Mann, Der Zauberberg. Roman, S. Fischer, Berlin, 1924. The Magic Mountain Search PubMed.
- M. Quack, Myths, Challenges, Risks and Opportunities in Evaluating and Supporting Scientific Research, in Incentives and Performance: Governance of Research Organizations, ed. I. M. Welpe, J. Wollersheim, S. Ringelhan and M. Osterloh, Springer International Publishing, Cham, Heidelberg, New York, 2015, ch. 14, pp. 223–239 Search PubMed.
- M. Eigen, From strange simplicity to complex familiarity: a treatise on matter, information, life and thought, Oxford University Press, Oxford, 2013 Search PubMed.
- J. Jortner, Conditions for the emergence of life on the early Earth: Summary and reflections, Philos. Trans.: Biol. Sci., 2006, 361, 1877–1891 CrossRef CAS PubMed.
- Moleküle aus dem All?, ed. K. Al-Shamery, Wiley-VCH, Weinheim, 2011 Search PubMed.
- M. Eigen, Self-organization of matter and the evolution of biological macromolecules, Naturwissenschaften, 1971, 58, 465–523 CrossRef CAS PubMed.
- M. Eigen, J. McCaskill and P. Schuster, Molecular quasi-species, J. Phys. Chem., 1988, 92, 6881–6891 CrossRef CAS.
- M. Eigen, Steps Towards Life, Oxford Univ. Press, Oxford, 1996 Search PubMed.
- M. Eigen, Natürliche Auslese - eine physikalische Gesetzmässigkeit, in Moleküle aus dem All?, ed. K. Al-Shamery, Wiley-VCH, Weinheim, 2011 Search PubMed.
- A. Eschenmoser and E. Loewenthal, Chemistry of potentially prebiological natural products, Chem. Soc. Rev., 1992, 21, 1–16 RSC.
- A. Eschenmoser, Chemistry of Potentially Prebiological Natural-Products, Origins Life Evol. Biospheres, 1994, 24, 389–423 CrossRef CAS.
- J. M. Lehn, Toward Self-Organization and Complex Matter, Science, 2002, 295, 2400–2403 CrossRef CAS PubMed.
- J. M. Lehn, Toward complex matter: Supramolecular chemistry and self-organization, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4763–4768 CrossRef CAS PubMed.
- P. L. Luisi, The Emergence of life, Cambridge Univ. Press, Cambridge, 2006 Search PubMed.
- L. Miller and L. E. Orgel, The origins of life on the earth, Prentice-Hall, Englewood Cliffs, N.J., 1974 Search PubMed.
- L. E. Orgel, The origins of life: Molecules and natural selection, Chapman and Hall, London, 1973 Search PubMed.
- L. E. Orgel, The origin of life - a review of facts and speculations, Trends Biochem. Sci., 1998, 23, 491–495 CrossRef CAS PubMed.
- M. Quack, Molecular Parity Violation and Chirality: The Asymmetry of Life and the Symmetry Violations of Physics, in Quantum Systems in Chemistry and Physics: Progress in Methods and Applications, Proceedings of QSCP XVI, Kanazawa 11 to 17 September 2011, ed. K. Nishikawa, J. Maruani, E. Brändas, G. Delgado-Barrio and P. Piecuch, Progress in Theoretical Chemistry and Physics, Springer Science and Business Media, Dordrecht, 2012, ch. 3, pp. 47–76 Search PubMed.
- M. Quack, Die Asymmetrie des Lebens und die Symmetrieverletzungen der Physik: Molekulare Paritätsverletzung und Chiralität, in Moleküle aus dem All?, ed. K. Al-Shamery, Wiley-VCH, Weinheim, 2011, ch. 12, pp. 275–310 Search PubMed.
- J. Monod, Le Hasard et la Nécessité - Essai sur la philosophie naturelle de la biologie moderne, Editions du Seuil, Paris, 1970 Search PubMed.
- F. C. Frank, W. Bonner and R. N. Zare, On the one hand but not on the other: The challenge of the origin and survival of homochirality in prebiotic chemistry, in Chemistry for the 21st century, ed. E. Keinan and I. Schechter, Wiley-VCH, Weinheim, 2001, ch. 11, pp. 175–208 Search PubMed.
- F. C. Frank, On spontaneous asymmetric synthesis, Biochim. Biophys. Acta, 1953, 11, 459–463 CrossRef CAS.
- M. Eigen and R. Winkler, Das Spiel, Piper, München, 1975 Search PubMed.
- M. Bolli, R. Micura and A. Eschenmoser, Pyranosyl-RNA: chiroselective self-assembly of base sequences by ligative oligomerization of tetra nucleotide-2,3-cyclophosphates (with a commentary concerning the origin of biomolecular homochirality), Chem. Biol., 1997, 4, 309–320 CrossRef CAS PubMed.
- J. S. Siegel, Homochiral imperative of molecular evolution, Chirality, 1998, 10, 24–27 CrossRef CAS.
- H. Kuhn and J. Waser, Self organization of matter and the early evolution of life, in Biophysics, ed. W. Hoppe, W. Lohmann, H. Markl and H. Ziegler, Springer, Berlin, 1983 Search PubMed.
- U. Meierhenrich, Amino Acids and the Asymmetry of Life, Springer, Berlin, Heidelberg, 2008 Search PubMed.
- A. Salam, On biological macromolecules and the phase transitions they bring about, in Conceptual Tools for Understanding Nature, Proc. 2nd Intl. Symp. of Science and Epistemology Seminar, Trieste, 1993, ed. G. Costa, G. Calucci and M. Giorgi, World Scientific Publ., Singapore, 1995 Search PubMed.
- S. F. Mason, Chemical Evolution: Origins of the Elements, Molecules and Living Systems, Clarendon Press, Oxford, 1991 Search PubMed.
- K. Mislow, Absolute Asymmetric Synthesis: A Commentary, Collect. Czech. Chem. Commun., 2003, 68, 849–864 CrossRef CAS.
- H. Zepik, E. Shavit, M. Tang, T. R. Jensen, K. Kjaer, G. Bolbach, L. Leiserowitz, I. Weissbuch and M. Lahav, Chiral Amplification of Oligopeptides in Two-Dimensional Crystalline Self-Assemblies on Water, Science, 2002, 295, 1266–1269 CrossRef CAS PubMed.
- F. Capra and P. L. Luisi, The systems view of life: A unifying vision, Cambridge Univ. Press, Cambridge, 2014 Search PubMed.
- M. Quack, Time and Time Reversal Symmetry in Quantum Chemical Kinetics, in Fundamental World of Quantum Chemistry. A Tribute to the Memory of Per-Olov Löwdin, ed. E. J. Brändas and E. S. Kryachko, Kluwer Academic Publishers, Dordrecht, 2004, vol. 3, pp. 423–474 Search PubMed.
- X. Bonfils, X. Delfosse, S. Udry, T. Forveille, M. Mayor, C. Perrier, F. Bouchy, M. Gillon, C. Lovis, F. Pepe, D. Queloz, N. C. Santos, D. Ségransan and J. L. Bertaux, The HARPS search for southern extra-solar planets - XXXI. The M-dwarf sample, Astron. Astrophys., 2013, 549, A109 CrossRef.
- M. Mayor, Nobel Lecture: Plurality of worlds in the cosmos: A dream of antiquity, a modern reality of astrophysics, Rev. Mod. Phys., 2020, 92, 030502 CrossRef.
- D. Queloz, Nobel Lecture: 51 Pegasi b and the exoplanet revolution, Rev. Mod. Phys., 2020, 92, 030503 CrossRef.
- I. A. Chen and M. S. de Vries, From underwear to non-equilibrium thermodynamics: physical chemistry informs the origin of life, Phys. Chem. Chem. Phys., 2016, 18, 20005–20006 RSC.
- R. Krishnamurthy and N. V. Hud, Introduction: Chemical Evolution and the Origins of Life, Chem. Rev., 2020, 120, 4613–4615 CrossRef CAS PubMed.
- S. K. Kim, T. Ha and J. P. Schermann, Editorial of the PCCP themed issue, Phys. Chem. Chem. Phys., 2011, 13, 804–805 RSC , on biomolecular homochirality..
- M. Quack, Molecular infrared-spectra and molecular-motion, J. Mol. Struct., 1995, 347, 245–266 CrossRef CAS.
- W. A. Bonner, Parity violation and the evolution of biomolecular homochirality, Chirality, 2000, 12, 114–126 CrossRef CAS PubMed.
- G. Laurent, P. Gaspard and D. Lacoste, A robust transition to homochirality in complex chemical reaction networks, Proc. R. Soc. A, 2022, 478, 20210590 CrossRef.
- G. Laurent, D. Lacoste and P. Gaspard, Emergence of homochirality in large molecular systems, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2012741118 CrossRef CAS PubMed.
- V. Avetisov and V. Goldanskii, Mirror symmetry breaking at the molecular level, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 11435–11442 CrossRef CAS PubMed.
- F. Jafarpour, T. Biancalani and N. Goldenfeld, Noise-induced symmetry breaking far from equilibrium and the emergence of biological homochirality, Phys. Rev. E, 2017, 95, 032407 CrossRef PubMed.
- L. Addadi, J. Van Mil and M. Lahav, Photopolymerization in chiral crystals. 4. Engineering of chiral crystals for asymmetric (2π. + 2π) photopolymerization. Execution of an ’absolute’ asymmetric synthesis with quantitative enantiomeric yield, J. Am. Chem. Soc., 1982, 104, 3422–3429 CrossRef CAS.
- J. M. McBride and R. L. Carter, Spontaneous Resolution by Stirred Crystallization, Angew. Chem., Int. Ed., 1991, 30, 293–295 CrossRef.
- J. D. Dunitz and A. Gavezzotti, Proteogenic Amino Acids: Chiral and Racemic Crystal Packings and Stabilities, J. Phys. Chem. B, 2012, 116, 6740–6750 CrossRef CAS PubMed.
- A. J. Gellman and K. H. Ernst, Chiral Autocatalysis and Mirror Symmetry Breaking, Catal. Lett., 2018, 148, 1610–1621 CrossRef CAS.
- T. Sugimori, H. Hyuga and Y. Saito, Fluctuation Induced Homochirality, J. Phys. Soc. Jpn., 2008, 77, 064606 CrossRef.
- C. Tschierske and C. Dressel, Mirror Symmetry Breaking in Liquids and Their Impact on the Development of Homochirality in Abiogenesis: Emerging Proto-RNA as Source of Biochirality?, Symmetry, 2020, 12, 1098 CrossRef CAS.
- W. A. Bonner, Chirality and life, Origins Life Evol. Biospheres, 1995, 25, 175–190 CrossRef CAS PubMed.
- P. R. Kavasmaneck and W. A. Bonner, Adsorption of amino acid derivatives by d- and l-quartz, J. Am. Chem. Soc., 1977, 99, 44–50 CrossRef CAS PubMed.
- P. Kleindienst and G. H. Wagnière, Interferometric detection of magnetochiral birefringence, Chem. Phys. Lett., 1998, 288, 89–97 CrossRef CAS.
- S. Sitha, Breaking the chiral mirror of alanine with dipole moment and oriented electric field: Violations of parity degeneracy and a possible answer to nature's homochirality, Comput. Theor. Chem., 2021, 1205, 113446 CrossRef CAS.
- S. Pizzarello, The Chemistry of Life's Origin: A Carbonaceous Meteorite Perspective, Acc. Chem. Res., 2006, 39, 231–237 CrossRef CAS PubMed.
- S. Pizzarello and J. R. Cronin, Non-racemic amino acids in the Murray and Murchison meteorites, Geochim. Cosmochim. Acta, 2000, 64, 329–338 CrossRef CAS PubMed.
- D. P. Glavin, A. S. Burton, J. E. Elsila, J. C. Aponte and J. P. Dworkin, The Search for Chiral Asymmetry as a Potential Biosignature in our Solar System, Chem. Rev., 2020, 120, 4660–4689 CrossRef CAS PubMed.
- M. M. Green and V. Jain, Homochirality in Life: Two Equal Runners, One Tripped, Origins Life Evol. Biospheres, 2010, 40, 111–118 CrossRef PubMed.
- A. Salam, Chirality, phase transitions and their induction in amino acids, Phys. Lett. B, 1992, 288, 153–160 CrossRef CAS.
- J. Chela-Flores, Comments on a novel approach to the role of chirality in the origin of life, Chirality, 1991, 3, 389–392 CrossRef CAS.
- F. Vester, T. L. V. Ulbricht and H. Krauch, Optische Aktivität und die Paritätsverletzung im β-Zerfall, Naturwissenschaften, 1959, 46, 68 CrossRef CAS.
- T. L. V. Ulbricht, The origin of optical asymmetry on earth, Origins Life, 1975, 6, 303–315 CrossRef CAS PubMed.
- N. Globus and R. D. Blandford, The Chiral Puzzle of Life, Astrophys. J., Lett., 2020, 895, L11 CrossRef CAS.
- D. Kondepudi and G. W. Nelson, Chiral-symmetry-breaking states and their sensitivity in nonequilibrium chemical systems, Phys. A, 1984, 125, 465–496 CrossRef.
- D. K. Kondepudi and G. W. Nelson, Weak neutral currents and the origin of biomolecular chirality, Nature, 1985, 314, 438–441 CrossRef CAS.
- A. J. MacDermott and G. E. Tranter, Electroweak bioenantioselection, Croat. Chem. Acta, 1989, 62, 165–187 CAS.
- S. A. Benner, E. A. Bell, E. Biondi, R. Brasser, T. Carell, H. J. Kim, S. J. Mojzsis, A. Omran, M. A. Pasek and D. Trail, When Did Life Likely Emerge on Earth in an RNA-First Process?, ChemSystemsChem, 2020, 2, e1900035 CrossRef CAS.
- P. Schwille, Biologische Selbstorganisation im Reagenzglas - ein Weg zur künstlichen Zelle?, in Was ist Leben?, Nova Acta Leopoldina, ed. J. Hacker and M. Hecker, 2012, vol. 116, pp. 119–130 Search PubMed.
- P. Schwille, How Simple Could Life Be?, Angew. Chem., Int. Ed., 2017, 56, 10998–11002 CrossRef CAS PubMed.
- M. Quack, The Role of Quantum Intramolecular Dynamics in Unimolecular Reactions, Philosoph. Trans. Royal Soc.A, 1990, 332, 203–220 CAS.
- N. A. Hawbaker and D. G. Blackmond, Energy threshold for chiral symmetry breaking in molecular self-replication, Nat. Chem., 2019, 11, 957–962 CrossRef CAS PubMed.
- D. G. Blackmond, C. R. McMillan, S. Ramdeehul, A. Schorm and J. M. Brown, Origins of Asymmetric Amplification in Autocatalytic Alkylzinc Additions, J. Am. Chem. Soc., 2001, 123, 10103–10104 CrossRef CAS PubMed.
- J. Yu, A. X. Jones, L. Legnani and D. G. Blackmond, Prebiotic access to enantioenriched glyceraldehyde mediated by peptides, Chem. Sci., 2021, 12, 6350–6354 RSC.
- D. G. Blackmond, Asymmetric autocatalysis and its implications for the origin of homochirality, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5732–5736 CrossRef CAS PubMed.
- J. I. Murray, J. N. Sanders, P. F. Richardson, K. N. Houk and D. G. Blackmond, Isotopically Directed Symmetry Breaking and Enantioenrichment in Attrition-Enhanced Deracemization, J. Am. Chem. Soc., 2020, 142, 3873–3879 CrossRef CAS PubMed.
- D. G. Blackmond, Autocatalytic Models for the Origin of Biological Homochirality, Chem. Rev., 2020, 120, 4831–4847 CrossRef CAS PubMed.
- L. Legnani, A. Darù, A. X. Jones and D. G. Blackmond, Mechanistic Insight into the Origin of Stereoselectivity in the Ribose-Mediated Strecker Synthesis of Alanine, J. Am. Chem. Soc., 2021, 143, 7852–7858 CrossRef CAS PubMed.
- K. Soai, T. Shibata, H. Morioka and K. Choji, Asymmetric autocatalysis and amplification of enantiomeric excess of a chiral molecule, Nature, 1995, 378, 767–768 CrossRef CAS.
- T. Shibata, J. Yamamoto, N. Matsumoto, S. Yonekubo, S. Osanai and K. Soai, Amplification of a Slight Enantiomeric Imbalance in Molecules Based on Asymmetric Autocatalysis: The First Correlation between High Enantiomeric Enrichment in a Chiral Molecule and Circularly Polarized Light, J. Am. Chem. Soc., 1998, 120, 12157–12158 CrossRef CAS.
- K. Soai, S. Osanai, K. Kadowaki, S. Yonekubo, T. Shibata and I. Sato, d- and l-Quartz-Promoted Highly Enantioselective Synthesis of a Chiral Organic Compound, J. Am. Chem. Soc., 1999, 121, 11235–11236 CrossRef CAS.
- T. Kawasaki, Y. Matsumura, T. Tsutsumi, K. Suzuki, M. Ito and K. Soai, Asymmetric Autocatalysis Triggered by Carbon Isotope (13C12C) Chirality, Science, 2009, 324, 492–495 CrossRef CAS PubMed.
- I. Sato, H. Urabe, S. Ishiguro, T. Shibata and K. Soai, Amplification of Chirality from Extremely Low to Greater than 99.5% ee by Asymmetric Autocatalysis, Angew. Chem., Int. Ed., 2003, 42, 315–317 CrossRef CAS PubMed.
- Y. Kaimori, Y. Hiyoshi, T. Kawasaki, A. Matsumoto and K. Soai, Formation of enantioenriched alkanol with stochastic distribution of enantiomers in the absolute asymmetric synthesis under heterogeneous solid–vapor phase conditions, Chem. Commun., 2019, 55, 5223–5226 RSC.
- S. V. Athavale, A. Simon, K. N. Houk and S. E. Denmark, Demystifying the asymmetry-amplifying, autocatalytic behaviour of the Soai reaction through structural, mechanistic and computational studies, Nat. Chem., 2020, 12, 412–423 CrossRef CAS PubMed.
- M. Fidecaro and H. J. Gerber, The fundamental symmetries in the neutral kaon system—a pedagogical choice, Rep. Prog. Phys., 2006, 69, 1713–1770 CrossRef CAS.
- M. Dine and A. Kusenko, Origin of the matter-antimatter asymmetry, Rev. Mod. Phys., 2003, 76, 1–30 CrossRef.
- M. Quack, On the measurement of CP-violating energy differences in matter–antimatter enantiomers, Chem. Phys. Lett., 1994, 231, 4–6 CrossRef.
- M. Quack, Lecture including results of [382] among others, Verh. DPG IV, 1993, vol. 28, p. 244 Search PubMed.
- G. Gabrielse, Probing nature's fundamental symmetries. One slow particle at a time, in Symmetrie und Asymmetrie in Wissenschaft und Kunst, Nova Acta Leopoldina NF 127 Nr. 412, ed. M. Quack and J. Hacker, Wissenschaftliche Verlagsgesellschaft, Stuttgart, 2016, pp. 91–98 Search PubMed.
- C. Zimmermann and T. W. Hänsch, Antiwasserstoff: Die Schlüsseltechniken zur Erzeugung und Spektroskopie sind vorhanden, Phys. J., 1993, 49, 193–196 CrossRef CAS.
- T. W. Hänsch, Passion for precision, The Nobel Foundation, Stockholm, 2006 Search PubMed.
- B. Schwingenheuer, R. A. Briere, A. R. Barker, E. Cheu, L. K. Gibbons, D. A. Harris, G. Makoff, K. S. McFarland, A. Roodman, Y. W. Wah, B. Winstein, R. Winston, E. C. Swallow, G. J. Bock, R. Coleman, M. Crisler, J. Enagonio, R. Ford, Y. B. Hsiung, D. A. Jensen, E. Ramberg, R. Tschirhart, T. Yamanaka, E. M. Collins, G. D. Gollin, P. Gu, P. Haas, W. P. Hogan, S. K. Kim, J. N. Matthews, S. S. Myung, S. Schnetzer, S. V. Somalwar, G. B. Thomson and Y. Zou, CPT Tests in the Neutral Kaon System, Phys. Rev. Lett., 1995, 74, 4376–4379 CrossRef CAS PubMed.
- H. Dehmelt, R. Mittleman, R. S. Van Dyck and P. Schwinberg, Past Electron-Positron g − 2 Experiments Yielded Sharpest Bound on CPT Violation for Point Particles, Phys. Rev. Lett., 1999, 83, 4694–4696 CrossRef CAS.
- The ALPHA Collaboration and M. Ahmadi, et al., Investigation of the fine structure of antihydrogen, Nature, 2020, 578, 375–380 CrossRef PubMed.
- R. Riek, A Derivation of a Microscopic Entropy and Time Irreversibility From the Discreteness of Time, Entropy, 2014, 16, 3149–3172 CrossRef.
- J. J. Hudson, B. E. Sauer, M. R. Tarbutt and E. A. Hinds, Measurement of the Electron Electric Dipole Moment Using YbF Molecules, Phys. Rev. Lett., 2002, 89, 023003 CrossRef CAS PubMed.
- K. Z. Rushchanskii, S. Kamba, V. Goian, P. Vaněk, M. Savinov, J. Prokleška, D. Nuzhnyy, K. Knížek, F. Laufek, S. Eckel, S. K. Lamoreaux, A. O. Sushkov, M. Ležaić and N. A. Spaldin, A multiferroic material to search for the permanent electric dipole moment of the electron, Nat. Mater., 2010, 9, 649–654 CrossRef CAS PubMed.
- X. Wu, Z. Han, J. Chow, D. G. Ang, C. Meisenhelder, C. D. Panda, E. P. West, G. Gabrielse, J. M. Doyle and D. DeMille, The metastable Q3Δ2 state of ThO: a new resource for the ACME electron EDM search, New J. Phys., 2020, 22, 023013 CrossRef CAS.
- J. H. Smith, E. M. Purcell and N. F. Ramsey, Experimental Limit to the Electric Dipole Moment of the Neutron, Phys. Rev., 1957, 108, 120–122 CrossRef CAS.
- E. M. Purcell and N. F. Ramsey, On the Possibility of Electric Dipole Moments for Elementary Particles and Nuclei, Phys. Rev., 1950, 78, 807 CrossRef CAS.
- D. DeMille, J. M. Doyle and A. O. Sushkov, Probing the frontiers of particle physics with tabletop-scale experiments, Science, 2017, 357, 990–994 CrossRef CAS PubMed.
- V. Andreev, D. G. Ang, D. DeMille, J. M. Doyle, G. Gabrielse, J. Haefner, N. R. Hutzler, Z. Lasner, C. Meisenhelder, B. R. O'Leary, C. D. Panda, A. D. West, E. P. West and X. Wu, ACME Collaboration, Improved limit on the electric dipole moment of the electron, Nature, 2018, 562, 355–360 CrossRef CAS PubMed.
- K. Mislow and J. Siegel, Stereoisomerism and local chirality, J. Am. Chem. Soc., 1984, 106, 3319–3328 CrossRef CAS.
- L. D. Barron, Symmetry and Chirality: Where Physics Shakes Hands with Chemistry and Biology, Isr. J. Chem., 2021, 61, 517–529 CrossRef CAS.
- Compendium of chemical terminology: IUPAC recommendations, ed. V. Gold, K. L. Loening, A. D. McNaught and P. Sehmi, Blackwell Sci. Publ., Oxford, 1987 Search PubMed.
- R. R. Ernst, T. J. Carrington, G. Seyfang and F. Merkt, Editorial to the Special Issue of Molecular Physics, Mol. Phys., 2013, 111, 1939–1963 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |
