Open Access Article
Open Access ArticleOxidatively induced reactivity in Rh(III)-catalyzed 7-azaindole synthesis: insights into the role of the silver additive†
Ho
Ryu
 ab,
Bimal
Pudasaini
b,
Dasol
Cho
ab,
Bimal
Pudasaini
b,
Dasol
Cho
 ab,
Sungwoo
Hong
ab,
Sungwoo
Hong
 *ba and
Mu-Hyun
Baik
*ba and
Mu-Hyun
Baik
 *ba
*ba
aDepartment of Chemistry, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Republic of Korea. E-mail: mbaik2805@kaist.ac.kr; hongorg@kaist.ac.kr
bCenter for Catalytic Hydrocarbon Functionalizations, Institute for Basic Science (IBS), Daejeon 34141, Republic of Korea
First published on 31st August 2022
Abstract
A typical synthetic protocol for preparing 7-azaindoles involves the coupling of 2-aminopyridine and alkyne substrates using a Rh(III)-catalyst. The catalysis requires the assistance of an external Ag+ oxidant that is thought to regenerate the catalyst and increase the turnover efficiency. Density functional theory (DFT) simulations confirm that Ag+ can oxidize various neutral Rh(III) intermediates encountered at different stages of the catalysis. Among them, the catalytically relevant species is a cationic Rh(III)-pyridyl+ complex (2A), which undergoes C–H activation of pyridine and couples an internal alkyne substrate into the pyridyl ligand to form the desired 7-azaindole product. Computations reveal that the oxidation also accelerates the reaction steps, including C–H activation via concerted metalation deprotonation (CMD), 1,2-alkyne insertion, and reductive elimination, thus highlighting the role of Ag+ as a catalytic promoter for the oxidatively induced reactivity of the Rh-catalyst in 7-azaindole synthesis. DFT calculations show that the catalysis is inefficient without invoking an oxidatively induced reaction pathway.
Introduction
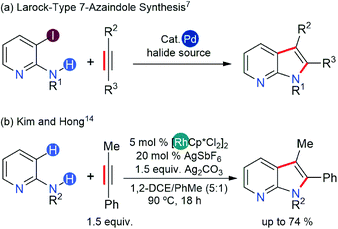
7-Azaindoles are an important class of fused hetero-carbocycles that are key scaffolds of cancer therapeutics and many other drugs for life-threatening conditions.1–6 The synthesis of 7-azaindoles can be achieved from either a five-membered pyrrole ring or a six-membered pyridine ring precursor subjected to appropriate cyclization mediated by transition metal catalysts (Scheme 1).7 The major caveat in these synthetic schemes is the ability of the pyrrole and pyridine precursors to strongly coordinate to transition metal catalysts and deactivate them.Recent trends demonstrate that performing a directed C–H or C–X (X = halogen) alkenylation of aminopyridines followed by annulation to afford 7-azaindoles offers a better strategy (Scheme 1).7 Ideally, a transition metal catalyst must be able to activate C–H or C–X bonds and undergo the final reductive elimination of C–N bonds to form a fused hetero-carbocycle. Late transition metals are the natural choice given their success in C–H or C–X bond activation6,8,9 and in C–N coupling reactions.10–12 The final ring closing step (annulation) via reductive elimination, however, necessitates the transition metal catalyst to possess the ability to undergo a two-electron oxidation during the catalytic cycle, which can be achieved either via oxidative addition of a low-valent transition metal into either the C–H or the C–X bond or via application of a stoichiometric amount of oxidants when the oxidative addition of the catalyst is not feasible.13
A few years ago, Hong14 developed an efficient protocol for 7-azaindole synthesis from 2-aminopyridine and internal alkynes using the Rh(III)-catalyst, thereby extending the substrate scope of indole synthesis, initially introduced by Fagnou.15,16 This synthetic protocol bypassed the low reactivity of the Rh(III) catalyst by modulating the coordination of 2-aminopyridine with a Lewis acid additive, Ag2CO3. The presumed role of this additive is three-fold: the putative Ag+ ion oxidizes the Rh-complex to counterbalance the two-electron reduction associated with reductive elimination; it counters the basicity of the aminopyridine substrate by binding to the pyridinic-N atom to form a Lewis acid–base adduct; the carbonate counter-anion participates in the proton-exchange steps of the catalysis, possibly assisting in the C–H activation step(s). Concurrently, Glorius and co-workers demonstrated the importance of Lewis acid additives in a related indole synthesis with an analogous d6-Co(III) catalyst.17 In this case, the Co(III) catalyst showed divergent reactivities based on whether the Lewis acid additive had the capability to oxidize the catalyst.17 Specifically, when the Lewis acid additive was also a strong oxidant, the catalysis followed a dehydrogenative annulation of a five-membered ring structure to furnish an indole product. In contrast, the catalysis yielded a six-membered ring structure to provide a quinoline product in the presence of a non-oxidizing Lewis acid. Computational studies revealed that the barrier for the final reductive elimination leading to an indole product is high, and there is a slight preference for the quinoline pathway even in the absence of a Lewis acid additive. Therein, the authors proposed a further reduction of barriers along the quinoline pathway due to Lewis acid additives, thus improving the catalytic activity and the chemoselectivity for the quinoline product, although no computational data for the proposed mechanism was provided.
The divergent reactivity in Glorius' report illustrates the importance of cooperativity between the catalyst and Lewis acid additives.17 In the synthesis of 7-azaindole,14 the cooperativity between the Rh(III) catalyst and Ag+ oxidant appears specific to the dehydrogenative annulation pathway as the quinoline products were not observed. Although the proposed roles of Ag+ ions in the 7-azaindole synthesis are well grounded,14 the absence of a quinoline product in Hong's experiments implies that the oxidizing ability of Ag+ ions solely would influence the regioselectivity. Furthermore, the mechanistic proposals in the current literature cannot explain the aforementioned observations if the function of the Ag+ oxidant is only to regenerate the catalyst after the product forming annulation step (Scheme 2a). Thus, it remains unclear how the Ag+ ions would direct the Rh-catalyst towards the dehydrative annulation pathway for 7-azaindole formation.
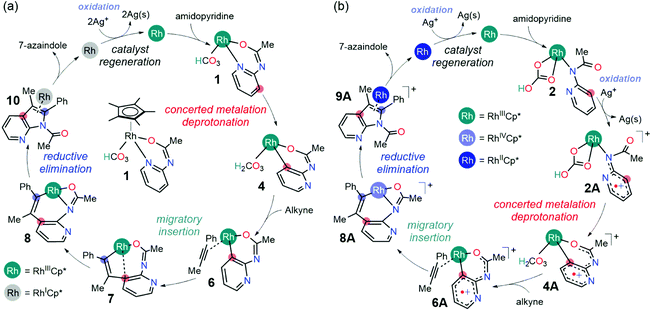 | ||
| Scheme 2 The mechanism for Rh(III)-catalyzed 7-azaindole synthesis: (a) mechanism adapted from indole synthesis,17 and (b) oxidatively induced catalytic mechanism (this work). | ||
Based on density functional theory (DFT) simulations, we propose that the oxidation of Rh(III) intermediates is possible at various stages of the catalysis. We arrive at this conclusion from a comparative analysis of the mechanistic pathways adapted from current literature (Scheme 2a) and an oxidatively induced reactivity in the formation of 7-azaindole (Scheme 2b). The results of this investigation also show that the oxidized Rh-complexes show superior reactivity to their neutral predecessors in converting 2-aminopyridine and internal alkynes into 7-azaindole.
Results and discussion
Considering that there were two types of Ag(I) additives employed in the 7-azaindole synthesis (Scheme 1b), it is easy to rationalize how the [Cp*RhCl2]2 precatalysts could transform into its active form 1. As the dehalogenation of [Cp*RhCl2]2 by the soluble Ag(I) additive has been demonstrated in related Rh-catalysis,18,19 we presume an identical fate of the pre-catalyst given the similarities in the experimental conditions. Thus, the reaction between [Cp*RhCl2]2 and four equivalents of AgSbF6 additive will form AgCl that will eventually precipitate out of the solution, leaving two equivalents of dicationic Cp*Rh(III) complex and four equivalents of [SbF6]– counter anions. Subsequently, the coordination of the 2-amidopyridine substrate onto the dicationic Cp*Rh(III) complex increases the acidity of the amide proton, making it susceptible for abstraction by the carbonate base originating from the Ag2CO3 additive.17 The deprotonation of the Rh-bound substrate by Ag2CO3 and the coordination of the resulting bicarbonate to the Rh center generates the proposed catalytic resting state, 1 (Scheme 2). From this catalytic resting state, various mechanistic scenarios are possible, which are discussed as follows.Mechanism without the oxidation of Rh(III)
The first consideration is the mechanistic scenario where the Ag(I) oxidant does not become functional until the azaindole product has been formed. This proposed mechanism, as illustrated in Fig. 1, closely resembles the currently accepted mechanism of indole synthesis,15,16 and recently this mechanism found relevance in the controlled synthesis of indole by a Co(III) catalyst.17 The catalysis is proposed to proceed from complex 1 with C–H activation at the meta position of the pyridine following a concerted metalation deprotonation (CMD) mechanism via complex 3 intermediacy. This C–H activation step necessitates the displacement of the Rh–pyridine bond in the formation of complex 3 such that the meta C–H bond lies in the vicinity of the Rh center. Furthermore, the Rh–arene interaction mediated through the meta-C center distorts the C–H bond out of the plane of the pyridine molecule and activates the C–H bond. In contrast to the C–H bond metathesis type mechanism that usually appears in the CMD mechanism, the proposed CMD mechanism involves a C–H activation step that is identical to the classical electrophilic aromatic substitution (SEAr),20 as the electrophilic attack on the arene by the transition metal enables a relatively weak base to deprotonate a C–H bond. Thus, the activated C–H bond can be deprotonated by the pendant carbonyl of the bicarbonate ligand resulting in the formation of rhodacycle intermediate 4 at 20.8 kcal mol−1 relative to 1. The overall barrier for the CMD step is 32.0 kcal mol−1, which can be considered a reasonable barrier for a reaction performed at 90 °C.14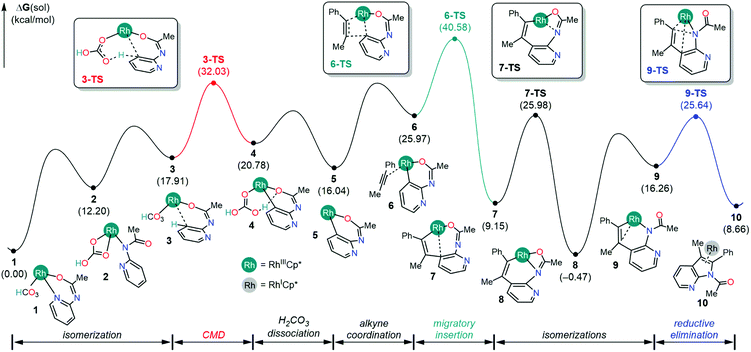 | ||
| Fig. 1 Reaction profile, in kcal mol−1, for the 7-azaindole formation without the oxidation by the Ag+ additive. | ||
Following the CMD step, the displacement of the carbonic acid from the rhodacycle intermediate 4 will ensue in a series of microsteps. First, the dissociation of carbonic acid from intermediate 4 liberates 4.7 kcal mol−1 free energy and forms intermediate 5 with a vacant coordination site. Then, the alkyne substrate coordinates to the Rh(III) center in an η2-fashion, resulting in the Rh(III) complex 6 at 26.0 kcal mol−1 in the free energy profile. Previously, Glorius and co-workers found that the alkyne substrate readily inserts into the cobalt–arene bond to form an eight-membered cobaltacycle with the step barriers of 8–9 kcal mol−1.17 In comparison, the step barrier to the alkyne insertion to form a similar eight-membered rhodacycle is 14.6 kcal mol−1, which is slightly higher presumably. Considering the catalytic resting state 1, the overall barrier for the alkyne insertion into the Rh–arene bond is 40.6 kcal mol−1, which is a significantly high barrier than the barrier reported by Glorius and co-workers in Co(III) mediated indole synthesis. Presumably, this difference in reactivity, in part, originates from a strong interaction between the pyridine ring and the Rh-center in the catalytic resting state 1.
Previously, it was hypothesized that the carbonic acid formed after the CMD step can decompose into H2O and CO2 to provide large thermodynamic stability to intermediate 5.17 To account for this possibility, the CMD product intermediate 4 was subjected to the simulation of an inner-sphere carbonic acid decomposition pathway featuring a series of proton transfer steps between iminoxy and carbonate ligands and liberating H2O and CO2, as illustrated in Fig. S1.† The overall barrier for the decomposition pathway is 35.3 kcal mol−1, which on the surface implies a more feasible reaction path than the dissociative path for the carbonic acid, as shown in Fig. 1. However, we need to take precautions before arriving at this conclusion. First of all, the carbonic acid dissociation gives a more thermodynamically stable intermediate 5 at 16.0 kcal mol−1, as shown in Fig. 1, than the proton transfer intermediate 5C at 29.3 kcal mol−1 (Fig. S1†). Assuming a low barrier for carbonate dissociation, one would expect the carbonic acid decomposition pathway to be more favorable than the inner-sphere carbonic acid decomposition. Thus, for the inner-sphere decomposition to occur, it would be imperative that the carbonic acid dissociates reversibly. Such a constrained mechanistic picture is unreasonable because carbonic acids are known for thermally decomposing into H2O and CO2 in the presence of other carbonates and bicarbonates.21,22 Therefore, once the carbonic acid liberates from the Rh-coordination, the reaction is unlikely to revert back to the intermediate 4 and undergo an inner-sphere carbonic acid decomposition.
Assuming that the reversibility of carbonic acid dissociation cannot be achieved under the reaction conditions, the reaction will simply halt after forming intermediate 5 until an alkyne substrate coordinates to the Rh-center. Upon the coordination, the alkyne insertion becomes kinetically and thermodynamically feasible in furnishing the product intermediate 7 because the barrier for migratory insertion is only 24.5 kcal mol−1 as the reactant intermediate 5 is not in reversible equilibrium with the initial state (1). The resulting intermediate from migratory insertion is an eight-membered bicyclic intermediate 7 that is 6.9 kcal mol−1 more stable than 5. A notable feature of 7 is the Rh–arene interaction which can be displaced by a stronger Rh–amide chelate, giving rise to intermediate 8 that is 15.6 kcal mol−1 more stable than 5. Finally, the 7-azaindole product can form as a result of the reductive elimination of Rh–C and Rh–N bonds to a new C–N bond and the Cp*Rh(I) complex. The barrier for reductive elimination is 26.1 kcal mol−1, and the Rh(I) product intermediate 10 is 9.1 kcal mol−1 uphill from 8. It is generally believed that the Cp*Rh(I) complexes may be oxidized by two electrons to regenerate Cp*Rh(III) complex 1 and participate in the subsequent catalytic cycle.17 Thus, two equivalents of Ag(I) reagents, relative to the 2-amidopyridine substrate, are typically employed with the anticipation that the solution phase Ag+ will facilitate the regeneration of 1.
Effect of the Ag+ oxidant
Considering the possibility of redox-activity of the Rh complexes in the presence of the Ag(I) oxidant, we examined whether the stationary states that appear in the Gibbs energy profile in Fig. 1 can be oxidized in the presence of Ag+. Here, it is important to note that the thermodynamic driving force for the reduction of silver cations is the formation of elemental silver in the solid-state, and standard DFT tools are severely limited for handling solid-state redox properties. While the standard reduction potential of silver cations in aqueous media is +0.80 V,23 the redox events of our interest would occur in the solvation media of 1,2-dichloroethane (DCE). To circumvent the difficulty in modeling the standard reduction potential of silver, we utilize the state function properties of Gibbs energy in a hypothetical thermodynamic cycle. The proposed thermodynamic model, as illustrated in Scheme 3, applies corrections to the standard reduction potentials in different solvation environments as the partitioning Gibbs energy of the redox-active solutes between the solvents. Thus, ΔGox (DCE) = −nF[Eo + Eox(aq.)] + [ΔG2(solv.) − ΔG1(solv.)] as illustrated in Scheme 3. | ||
| Scheme 3 Thermodynamic cycle to evaluate electron transfer between the silver oxidant and Rh(III) complexes. | ||
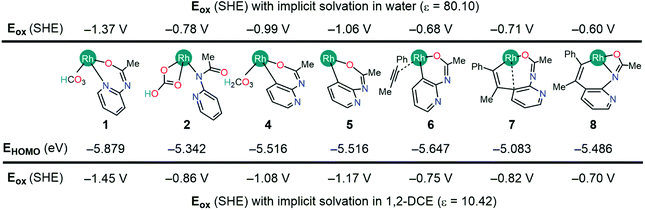
Fig. 2 tabulates the potentials for the generation of cationic Rh(III) species in both 1,2-dichloroethane (DCE) and aqueous solvents in reference to the standard hydrogen electrode (SHE). The calculated potentials differ roughly by about 0.1 V, with slightly lower potentials in aqueous solutions owing to the better stability of the oxidized species.24 Specifically, the Nernstian equilibrium between the aforementioned species and their cationic partners occurs at about −0.78, −0.68, −0.71, and −0.60 V respectively against a reference SHE. As the reduction of silver cations offers an energy of +0.8 V, an aqueous Rh(III) complex 2 will oxidize if it encounters a hydrated Ag+ oxidant. Using the thermodynamic cycle of Scheme 3, we predict that the oxidation of 2 in DCE will liberate a Gibbs free energy of ∼8.0 kcal mol−1. Thus, the catalytic mechanism as illustrated in Fig. 1 will be intercepted by the oxidation of 2, and the mechanistic exploration must consider the cationic Rh-intermediates in order to attain a comprehensive understanding of the catalysis.
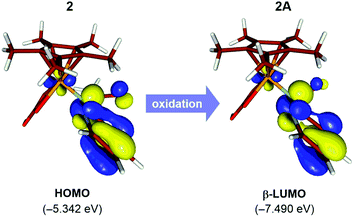
The natural population analysis of the oxidation mechanism for intermediate 2 reveals ligand-centered oxidation as opposed to the anticipated Rh-centered oxidation (Fig. 3). Specifically, the calculated charges on the formally anionic pyridyl ligand increase from the overall NPA charge of −0.61e in intermediate 2 to +0.17e upon oxidation to 2A, accounting for an electron density loss of 0.79e from the pyridyl ligand (Table S2†). The frontier orbitals also exhibit the ligand-based oxidation of 2. The redox-active molecular orbital in the intermediate 2 is the HOMO that primarily consists of orbitals with π-symmetry on the pyridine moiety, as illustrated in Fig. 3. During oxidation, the HOMO orbital of 2 loses an electron leaving the radical delocalized on the pyridyl ligand and while the Rh center maintains its +3 oxidation state.
Oxidatively induced reactivity
As discussed previously, the feasibility of oxidation of intermediate 2, which appears in the early stages of the catalytic cycle, suggests an active role of cationic Rh-intermediates (Fig. 4). This mechanistic scenario deviates from our current understanding of the Rh(III) catalyzed annulation reactions,17 where the catalysis has been proposed to occur through neutral Rh-species. The deviation from the neutral pathway introduces subtle differences in the mechanism that are highlighted in the remainder of this article.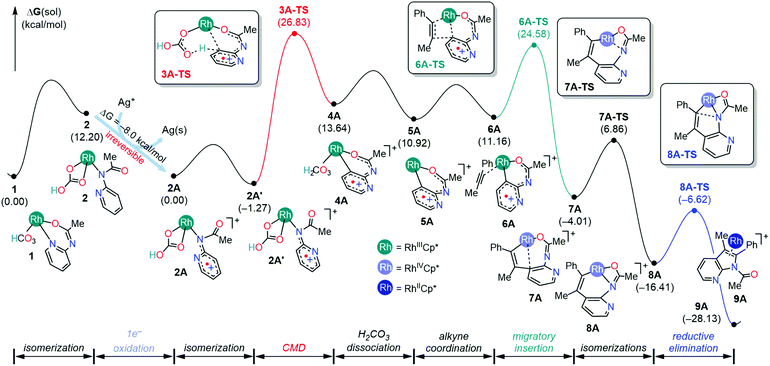 | ||
| Fig. 4 Reaction mechanism of Rh(III/IV)-catalyzed synthesis of 7-azaindole in the presence of the Ag+ oxidant. Gibbs energies, in parenthesis, are in kcal mol−1. | ||
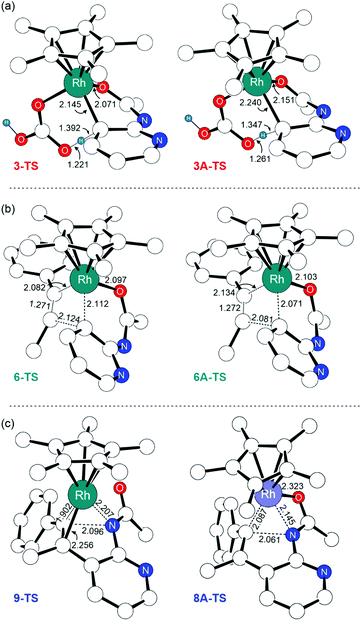
The first noticeable difference was observed in the CMD step (Fig. 5a). In the neutral pathway, the C–H bond at the meta-position of the pyridine undergoes a pre-activation due to Rh–arene interaction mediated through the meta-C center in intermediate 3. This Rh–arene interaction distorts the C–H bond out of the plane of the pyridine molecule and presumably makes the proton more acidic. But in the cationic pathway, the Rh–arene interaction prior to the CMD is not observed due to the oxidation of the pyridyl ligand. Instead, the CMD will proceed as a direct proton transfer to the bicarbonate ligand while simultaneously forming a Rh–C bond (Fig. 4). Furthermore, the displacement of 3A-TS geometry along with the imaginary frequency towards 3A to examine whether such pre-activation of the C–H bond also exists in the cationic pathway led to optimized geometry of 2A′. Thus, the pre-activation of the meta(C–H) bond by Rh in the CMD step does not occur as the existence of intermediate 3A could not be confirmed as a stationary point of the reaction profile. The overall barrier for the CMD in the cationic pathway, 3A-TS, is 28.1 kcal mol−1, which is 3.9 kcal mol−1 lower than that of the CMD pathway involving the neutral 3-TS. Thus, the oxidation of 2 by the silver cation creates a relatively more facile CMD route by forming 2A as a new catalytic resting state.
Analogous to the transformations in the neutral pathway as illustrated in Fig. 1, the CMD product intermediate 4A can undergo a series of processes to ultimately furnish the 7-azaindole product. The displacement of carbonic acid from the intermediate 4A by the phenylacetylene substrate is ∼2.5 kcal mol−1 downhill, which results in the formation of intermediate 6A. Then, the intermediate 6A proceeds with an unusual 1,2-alkyne insertion process, in which the substrate inserts into the Rh–C bond; meanwhile the Rh center is oxidized by one electron to reach a +4 oxidation state, and the pyridyl radical cation is reduced by one electron. Mulliken spin density analysis revealed that the unpaired electron in 6A and 6A-TS delocalized over the 2-amidopyridyl ligand backbone, whereas the unpaired spin in 7A is largely populated at the Rh center (Table S4†). These observations imply that the transformation involves an oxidatively induced migratory insertion of a methyl phenylacetylene substrate where the Rh center is oxidized by one electron only after passing through the transition state, 6A-TS.
The frontier orbitals of 6A, 6A-TS, and 7A confirm the proposed electronic reorganization mechanism associated with alkyne insertion (Fig. S2†). Both 6A and 6A-TS geometries feature α-HOMOs delocalized over the pyridyl ligand indicative of the presence of Rh(III) and pyridyl radical cations in 6A-TS. The alkyne insertion product 7A features the Rh centered α-HOMO indicative of a radical center on Rh because one electron transfer to the pyridyl ligand has reduced upon alkyne insertion. We hypothesize that the alkyne insertion creates structural distortions that lead to the destruction of the π-conjugation between the pyridyl–amide fragment, and the formation of a new π-conjugation interaction between Rh–alkenyl and the pyridyl ligand. This effect can also be realized by inspecting the frontier orbitals, where the π-conjugation between the pyridyl–amide fragment present in the SOMOs of 6A and 6A-TS vanishes from the SOMO upon the formation of 7A (Fig. S2†), and a new π-interaction between Rh and alkenyl fragment is observed.
Following the alkyne insertion, the eight-membered metallacycle 7A isomerizes to a more stable six-membered metallacycle 8A. The isomerization replaces the Rh–O bond with the Rh–N bond and stabilizes the Rh-complex by 12.4 kcal mol−1. We presume that the stabilization arises from the stronger bonding preference of the Rh center for the amido ligand than for the oxide ligand. Finally, the ensuing reductive elimination of alkenyl and amido ligands leads to the cyclization and the formation of the desired 7-azaindole product. Unlike the neutral pathway, the reductive elimination has a low barrier (8A-TS, ΔG‡ = 9.8 kcal mol−1) and is thermodynamically downhill (ΔG = −11.7 kcal mol−1), indicating that the reductive elimination is more feasible from the high valent Rh(IV) complex. Finally, the cationic Rh(II)Cp* complex will then reenter the catalytic cycle when the 2-amidopyridine substrate and carbonate ion displace the bound 7-azaindole, and the silver oxidant transforms Rh(II) into Rh(III), thus regenerating complex 1.
Conclusion
DFT calculations of the mechanism in the formation of 7-azaindole in the presence of a Cp*Rh(III) complex and silver additives revealed the following: the reduction of Ag+ and the generation of cationic Rh-intermediates in 7-azaindole improve the reactivity of the Rh catalyst as the barriers of the elementary steps decrease significantly. One plausible explanation for the higher reactivity is the access of higher oxidation states which makes the Rh-catalyst more electrophilic. We presume that the increase in the electrophilicity enables kinetically feasible C–H activation via CMD, 1,2-alkyne insertion, and reductive elimination steps. In addition to the oxidizing role, the silver carbonate additive supplies carbonates and bicarbonates that facilitate C–H activation via the CMD mechanism.The enhanced catalytic activity is possible because the thermal equilibrium between species 1 and 2 is perturbed by the oxidation of Rh-bicarbonate species (2) in the presence of silver cations. After the redox event, the resulting metallic silver will undergo a phase separation from the organic solvent. Therefore, the oxidative transformation of 2 into 2A is considered an irreversible process that leads to a separate free energy surface. Under the Nernstian equilibrium conditions, however, the oxidation of 2 is considered a reversible process, and the catalytic activity could diminish significantly as the oxidized species 2A could also revert back to intermediate 1. Because the oxidation of 2 only releases a Gibbs free energy of about −8.0 kcal mol−1, the thermodynamic driving force is insufficient to make 2A the new catalytic resting state. Consequently, the barriers for CMD and alkyne insertion are 31.0 kcal mol−1 (3A-TS) and 28.8 kcal mol−1 (6A-TS) respectively. These barriers are higher than the barriers of 28.1 kcal mol−1 (3A-TS) and 25.9 kcal mol−1 (6A-TS) considered under the irreversible redox events, but are lower than the barriers in the neutral pathway, 32.0 and 40.6 kcal mol−1 respectively. The calculated barriers suggest that some kinetic advantage is received even when the redox process is reversible. Here, we emphasize that the redox reversibility of Ag is not observed under the experimental conditions, and two equivalents of Ag oxidant are consumed for every 2-aryl-7-azaindole produced.14 Thus, computational results presented here not only showcase the mechanistic detail highlighting the precise role of the Ag+ oxidant, but also open future avenues for DFT simulations to predict catalyst and oxidant combinations in 7-azaindole synthesis.
Computational method
All calculations use density functional theory (DFT) implemented in the Jaguar 9.1 suite of programs25 at the B3LYP26,27 approximation of electron density, including the D3 dispersion correction of Grimme28 (B3LYP-D3). Geometry optimization was performed with the 6-31G** basis set for main group elements, whereas rhodium was described with the Los Alamos LANL2DZ basis set corresponding to the relativistic effective core potentials (ECPs).29–31 The energies of optimized structures were reevaluated with a higher quality triple-ζ basis set cc-pVTZ(-f),32 in combination with the LACV3P basis set for rhodium.33 Zero-point and entropic contributions to Gibbs energy are derived from harmonic vibrational frequencies calculated with small basis sets (B3LYP-D3/6-31G**/LANL2DZ). Solvation energies were obtained from the gas phase geometries under a self-consistent reaction field (SCRF)34–36 formalism that uses linearized Poisson–Boltzmann equations to solve the solvation effects from solvents with a dielectric constant ε = 10.42 for 1,2-dichloroethane. The procedure to obtain the solution phase Gibbs energies is described in a tutorial article.37Data availability
Further details of computational data involving the atomic charge of natural population analysis (NPA), Mulliken spin densities, cartesian coordinates and vibrational frequencies of DFT-optimized structures are available in the ESI†.Author contributions
M.-H. B. and H. R. conceived the project; H. R. and D. C. carried out the computational studies in consultation with M.-H. B. and S. H.; H. R. and B. P. analyzed the computational result and prepared the draft of the manuscript; M.-H. B. and S. H. contributed with an advisory role in the project and manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported financially by the Institute for Basic Science (IBS-R10-A1 and IBS-R10-A2).Notes and references
- J.-Y. Mérour, F. Buron, K. Plé, P. Bonnet and S. Routier, Molecules, 2014, 19, 19935–19979 CrossRef PubMed.
- B. Daydé-Cazals, B. Fauvel, M. Singer, C. Feneyrolles, B. Bestgen, F. Gassiot, A. Spenlinhauer, P. Warnault, N. Van Hijfte, N. Borjini, G. Chevé and A. Yasri, J. Med. Chem., 2016, 59, 3886–3905 CrossRef PubMed.
- S. Hong, J. Kim, J. H. Seo, K. H. Jung, S.-S. Hong and S. Hong, J. Med. Chem., 2012, 55, 5337–5349 CrossRef CAS PubMed.
- N. Sharma and Anurag, Mini-Rev. Med. Chem., 2019, 19, 727–736 CrossRef CAS PubMed.
- U. K. Bandarage, M. P. Clark, E. Perola, H. Gao, M. D. Jacobs, A. Tsai, J. Gillespie, J. M. Kennedy, F. Maltais, M. W. Ledeboer, I. Davies, W. Gu, R. A. Byrn, K. Nti Addae, H. Bennett, J. R. Leeman, S. M. Jones, C. O'Brien, C. Memmott, Y. Bennani and P. S. Charifson, ACS Med. Chem. Lett., 2017, 8, 261–265 CrossRef CAS PubMed.
- P. Kannaboina, K. Mondal, J. K. Laha and P. Das, Chem. Commun., 2020, 56, 11749–11762 RSC.
- D. R. Motati, R. Amaradhi and T. Ganesh, Org. Chem. Front., 2021, 8, 466–513 RSC.
- C. B. Lavery, R. McDonald and M. Stradiotto, Chem. Commun., 2012, 48, 7277–7279 RSC.
- (a) R. Santhoshkumar and C.-H. Cheng, Chem.–Eur. J., 2019, 25, 9366–9384 CrossRef CAS PubMed; (b) Z. Liu and R. C. Larock, Angew. Chem., Int. Ed., 2007, 46, 2535–2538 CrossRef CAS PubMed.
- N. N. Pham, T. T. Dang, N. T. Ngo, A. Villinger, P. Ehlers and P. Langer, Org. Biomol. Chem., 2015, 13, 6047–6058 RSC.
- P. Ruiz-Castillo and S. L. Buchwald, Chem. Rev., 2016, 116, 12564–12649 CrossRef CAS PubMed.
- D. R. White, E. C. Bornowski and J. P. Wolfe, Isr. J. Chem., 2020, 60, 259–267 CrossRef CAS PubMed.
- K. Ghosh, Y. Nishii and M. Miura, ACS Catal., 2019, 9, 11455–11460 CrossRef CAS.
- Y. Kim and S. Hong, Chem. Commun., 2015, 51, 11202–11205 RSC.
- D. R. Stuart, M. Bertrand-Laperle, K. M. N. Burgess and K. Fagnou, J. Am. Chem. Soc., 2008, 130, 16474–16475 CrossRef CAS PubMed.
- D. R. Stuart, P. Alsabeh, M. Kuhn and K. Fagnou, J. Am. Chem. Soc., 2010, 132, 18326–18339 CrossRef CAS PubMed.
- Q. Lu, S. Vásquez-Céspedes, T. Gensch and F. Glorius, ACS Catal., 2016, 6, 2352–2356 CrossRef CAS.
- J. Kim, K. Shin, S. Jin, D. Kim and S. Chang, J. Am. Chem. Soc., 2019, 141, 4137–4146 CrossRef CAS PubMed.
- S. Jin, J. Kim, D. Kim, J.-W. Park and S. Chang, ACS Catal., 2021, 11, 6590–6595 CrossRef CAS.
- J. F. Bunnett and R. E. Zahler, Chem. Rev., 1951, 49, 273–412 CrossRef CAS.
- M. Kumar, D. H. Busch, B. Subramaniam and W. H. Thompson, J. Phys. Chem. A, 2014, 118, 5020–5028 CrossRef CAS PubMed.
- M. Kumar, D. H. Busch, B. Subramaniam and W. H. Thompson, J. Phys. Chem. A, 2014, 118, 10155–10156 CrossRef CAS.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, 93rd Edition, CRC Press, 2012 Search PubMed.
- H. Svith, H. Jensen, J. Almstedt, P. Andersson, T. Lundbäck, K. Daasbjerg and M. Jonsson, J. Phys. Chem. A, 2004, 108, 4805–4811 CrossRef CAS.
- A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- P. J. Hay, P. Jeffrey Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- LACV3P, a triple-zeta contraction of the LACVP basis set developed by Schrodinger Inc..
- B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788 CrossRef CAS.
- S. R. Edinger, C. Cortis, P. S. Shenkin and R. A. Friesner, J. Phys. Chem. B, 1997, 101, 1190–1197 CrossRef CAS.
- M. Friedrichs, R. Zhou, S. R. Edinger and R. A. Friesner, J. Phys. Chem. B, 1999, 103, 3057–3061 CrossRef CAS.
- H. Ryu, J. Park, H. K. Kim, J. Y. Park, S.-T. Kim and M.-H. Baik, Organometallics, 2018, 37, 3228–3239 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: computational data including cartesian coordinates and vibrational frequencies of DFT-optimized structures. See https://doi.org/10.1039/d2sc01650h |
| This journal is © The Royal Society of Chemistry 2022 |