From a Möbius-aromatic interlocked Mn₂B₁₀H₁₀ wheel to the metal-doped boranaphthalenes M₂@B₁₀H₈ and M₂B₅ 2D-sheets (M = Mn and Fe): a molecules to materials continuum using DFT studies

Abstract

The inherent tendency of BR fragments to undergo coupling is utilized to predict M₂B₁₀H₁₀ and M₂@B₁₀H₈ complexes (where M = Mn and Fe). Electronic structure analysis of Mn₂B₁₀H₁₀ (7) shows that the metal d-orbitals stabilize the interlocked boron wheel structure, forming an unprecedented geometrical pattern with Möbius aromaticity. The two additional electrons in Fe₂@B₁₀H₁₀ (8) stabilize a twisted [10]boraannulene structure. The removal of 2H from 7 and 8 leads to the planar structures Mn₂@B₁₀H₈ (11) and Fe₂@B₁₀H₈ (10), respectively. The stability of the planar arrangements is due to multicentered (σ + π) bonding, where π-donation occurs from the M₂ (M = Fe and Mn) unit to the borocyclic unit. The presence of 10π electrons in M₂@B₁₀H₈ relates it to naphthalene, having Hückel π-aromaticity. The condensation of naphthalene to graphene in two dimensions suggests the ability to build the different metal boride monolayers FeB₅ and Fe₂B₅, considering Fe₂@B₁₀ as the building block, bringing this molecular boron chemistry into the solid state. One of the predicted monolayers, β-Fe₂B₅, is found to be the global minimum in the planar arrangement based on a USPEX crystal structure search algorithm. Electronic structure analysis further shows that the stabilization mechanism in the molecular building block remains unaltered in the solid state.

---

Introduction

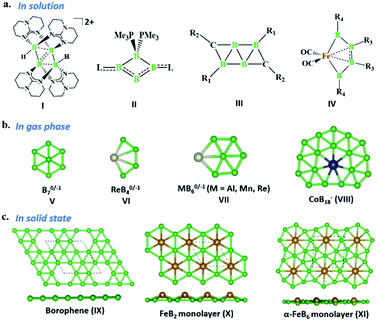
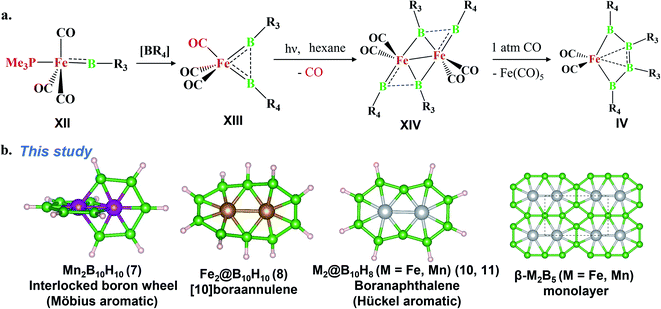
The last two decades has witnessed explosive growth in three apparently parallel fields in the area of boron chemistry.^1–7 The first part of this growth involved several successful attempts to stabilize boron complexes with an increasing number of boron atoms in the solution phase,^8–18e.g., B₄ (I, II),^19,20 carboranes (C₂B₄R₄; III),²¹ and metallaborocycles ((CO)₂FeB₄R₄; IV).²² Here, the electron deficiency of boron was fulfilled using Lewis donor ligands and transition-metal templates, and this led to many unusual structural and bonding variations.^{2–4,23–26} A parallel development in the gas phase involved the generation of size-selected boron clusters (B_n) and metal–boron clusters (M_xB_n) with different types of multicentered bonding (e.g., V–VIII).^{5–7,27–32} Although the absence of ligands in VI distinguishes its chemical bonding from IV, the unique π-bonding is important in both.^33,34 The structural variations of B_n and M_xB_n clusters largely depend on the size of the atoms. For example, MB₆^0/−1 clusters (VII) favour a C_2v structural type, due to the large size of M (where M = Al, Mn, and Re), in comparison with B₇^0/−1 clusters (V), which favour a C_6v structure (a nearly flat hexagonal pyramid).^29,35,36 The preference for adopting a seven-member ring in the case of a 3d transition metal, e.g., Co in CoB₁₈⁻ (VIII), was shown recently by Wang and co-workers.³⁷ The study of several planar and quasi-planar boron clusters led to the discovery of borophene, analogous with the hexagonal C₆ motif of graphene,³⁸ on metal surfaces.^39–43 The inevitability of holes in borophenes and consequent polymorphism give the unique opportunity to fine tune the electronic and mechanical properties of these 2D systems via limiting the number of holes and by incorporating metal atoms.^44–52 Different metal boride monolayers, e.g., FeB₂ (X) and FeB₆ (XI), were proposed to expand the application of 2D materials, and the design was inspired by M@B_n clusters.^53–61 The rapid growth in these different areas of boron chemistry practiced under very different experimental conditions invites us to bridge these apparently unrelated fields by finding common threads.

B–B coupling to build the larger boron unit B₄ (I) was achieved by Himmel and co-workers via coupling two boron analogues of ethyl cation units.¹⁹ The close similarity between the B₄ unit in I and the Si chain in β-SiB₃ led the hypothesis that boron chain polymers with such rhomboidal units could be obtained.^19,62 The ligand architecture of I restricts it from undergoing further coupling. However, the synthesis of the tetra-atomic boron(0) complex II, starting from a B₂ complex stabilized by Lewis donor ligands, paved the way to achieving the rule-breaking planar C₂B₄R₄ complex III, as reported by Kinjo and co-workers recently.^20,21 The presence of labile PMe₃ ligands in II gives space to increase the ring size. Due to the lack of labile ligands in complex III, increasing the ring size further is not easy and necessitates an alternative path. Although standalone borylene is not stable in solution, a transition metal can be used as an effective template to hold and arrange it for coupling. One such reaction, carried out by Braunschweig and co-workers, uses an Fe center to form the contiguous B₄ chain IV, starting from the Fe–(borylene) complex XII and proceeding through Fe–bis(borylene) XIII and the bimetallic intermediate XIV.²² The formation of XIII from XII, an 18e complex with approximate trigonal bipyramidal (tbp) geometry, involves the transfer of a borylene fragment from Mo(CO)₅[BN(SiMe₃)₂] (Scheme 2a).²² The replacement of a Lewis donor ligand with a BR fragment was possible due to their isolobal relationship. Although XIII exists without direct B–B σ-bonds, Fe(CO)₃B₂H₂ has a B–B coupled structure (1, Scheme 3a), as the global minimum shows the inherent tendency of the BR fragment to undergo coupling (Scheme 3a).³³ The electron-donating substituent N(SiMe₃)₂ weakens the σ-skeleton of the coupled product and hinders the B–B coupling process in XIII,³³ while the ancillary ligand CO forces B–B coupling reactions to give IV.²² The two N(SiMe₃)₂ ligands attached to B centers in IV do not allow further B–B coupling beyond the B₄ unit. In addition, had further B–B coupling taken place, the resultant Fe@B₆R₆ structure would have been highly strained due to the small cavity size. This suggests design strategies with larger ring and ligand attachments are needed for further catenation and possible extension to the solid state.

Scheme 1 (a) Structurally characterized complexes with B₄, C₂B₄, and metallaborocycle FeB₄ units in the solution phase. (b) Different planar and quasi-planar B_n and MB_n clusters in the gas phase. (c) Borophene (hole density = 1/9) and metal boride monolayers in extended systems. L = 1-[2,6-di-isopropylphenyl]-2-methoxy-3,3-bis(trimethylsilyl)-1,2-azaborolidine, R₁ = 1-[2,6-diisopropylphenyl]-2-methoxy-3,3-bis(trimethylsilyl)-2,3-dihydro-1H-1,2-azaborol-5-yl, R₂ = NH(dip), dip = 2,6-di-isopropylphenyl.

Scheme 2 (a) A transition-metal-assisted B–B homocatenation reaction in the solution phase. The source of [BR₄] is a Mo(CO)₅BR₄ complex. [R₃ = 2,3,5,6-tetramethylphenyl, R₄ = N(SiMe₃)₂]. (b) The prediction of an interlocked boron wheel [Mn₂B₁₀H₁₀ (7)], [10]boraannulene [Fe₂@B₁₀H₁₀ (8)], boranaphthalene [M₂@B₁₀H₈ (M = Fe and Mn; 10 and 11)], and its possible extension to give β-Fe₂B₅ monolayers.

Scheme 3 The optimized structures of (a) Fe(CO)₃B₂H₂ (1, C_2v), (b) Cr@B₆H₆ (2, C_6v), (c) Fe@B₆H₆ (3, D_6h), (d) MnB₆⁻ (C_2v in a quintet state), (e) Mn₂(CO)₁₀ (4, D_4d), (f) Fe(BH)₅ (5, C_s), (g) Mn₂(BH)₁₀ (6, D_4d), and (h) Mn₂B₁₀H₁₀ (7, D_2d) at the BP86 level of theory with the def2-tzvp basis set. Complexes 1, 2, and 5 are obtained via the isolobal replacement of CO with BH from the corresponding 18e metal carbonyl complexes. Complex 6 is not a minimum on the PES. (i) The HOMO−3 of 6 (the examples shown in (a)–(e) are known in the literature and are considered here for comparison purposes).

Here, we report the design of (1) an interlocked boron wheel, Mn₂B₁₀H₁₀ (7), having an unprecedented geometrical pattern with Möbius aromaticity, (2) [10]boraannulene Fe₂@B₁₀H₁₀ (8), (3) a boron analog of naphthalene, M₂@B₁₀H₈ (M = Mn and Fe), having Hückel aromaticity (11, 10), and (4) the metal boride monolayers FeB₅ and Fe₂B₅, taking Fe₂@B₁₀ as the building block and bringing this molecular boron chemistry into the solid state (Scheme 2b). The global minimum search algorithm USPEX⁶³ further shows that one of the Fe₂B₅ monolayers, β-Fe₂B₅, designed in this study is a global minimum on the planar PES. The thermal and kinetic stabilities of these designed monolayers with metallic properties are also presented here. This study illustrates the relationships between the chemistry of boron in solution, gas, and solid states.

Computational details

All the molecular calculations are carried out using the Gaussian 09 program package (version D).⁶⁴ Geometry optimization is performed using the dispersion-corrected BP86 functional with Becke–Johnson damping (BP86-D3(BJ)) and the def2-tzvp basis set for all atoms.^65,66 The nature of stationary points is examined via vibrational frequency calculations at the same level of theory. Natural bond orbital (NBO) analysis is performed to obtain natural population analysis (NPA) charges and Wiberg bond orders with the NBO6 method at the same level of theory.⁶⁷ Nucleus-independent chemical shift (NICS)⁶⁸ calculations are performed to check the extent of cyclic delocalization at the BP86/6-31G(d,p) level of theory. Chemical bonding analysis using the adaptive natural density partitioning (AdNDP) method⁶⁹ is carried out using the MultiWfn program.⁷⁰ Quantum theory of atoms in molecules (QTAIM) analysis is carried out using the AIMALL package⁷¹ with the wavefunction files generated using the BP86 functional with the LANL2DZ basis set for Mn and the 6-31G(d,p) basis set for all other elements (B, C, H, and O).

All solid-state calculations are performed using the Vienna ab initio simulation package (VASP).^72–74 The generalized gradient approximation (GGA) approach with the Perdew–Burke–Ernzerhof (PBE) functional⁷⁵ is used to incorporate the exchange–correlation functional to treat the interactions between electrons, with PAW⁷⁶ pseudopotentials used to treat the electron–ion interactions. The energy cutoff for the plane wave basis set is 500 eV and the equivalent set of a k point grid with spacing of 2π × 0.02 Å⁻¹ is taken for Brillouin zone integration. The electronic energy convergence threshold is set to 10⁻⁶ eV for energy and 10⁻³ eV Å⁻¹ for force. Phonon dispersion analysis is performed using Phonopy code with the finite displacement method, interfaced with the density functional perturbation theory implemented in VASP.⁷⁷ The ab initio molecular dynamics simulations are performed for 6 ps with a canonical (NVT) ensemble at temperatures of 500 K, 1000 K, and 1500 K with a time step of 1.0 fs. The initial structures are built up from the corresponding optimized structures. Chemical bonding analysis to generate the projected crystal orbital Hamiltonian (PCOHP)⁷⁸ population curve is carried out using the Local Orbital Basis Suite Towards Electronic-Structure Reconstruction (LOBSTER) program (version 3.1.0) with the plane-wave/PAW wavefunction generated using VASP based on the corresponding optimized structures.⁷⁹ A comprehensive crystal structure search for the two-dimensional Fe₂B₅ monolayer is performed using the evolutionary algorithm USPEX code (with local minimization schemes within unit cells of 7 and 14 atoms).⁶³ The population size was set to 60 and the maximum number of generations was maintained at 60, with 60% of the lowest-enthalpy structures allowed to produce the next generation through heredity (60%), lattice mutation (30%), and atomic permutation (10%). The thickness parameter was set to 0.1 to search for planar or near-planar configurations.

Results and discussion

We begin with the design principle of the interlocked boron wheel Mn₂B₁₀H₁₀ (7) and compare it with B₁₄, an interlocked boron cluster.⁸⁰ Then we discuss the stability of 7 and compare it with M@B₆H₆ (M = Cr and Fe) to measure the ring strain involved in the system. An electronic structure description of 7 follows next, with an emphasis on the role of metal d-orbitals and cyclic electron delocalization in governing the stability. Then we discuss the interlocked to planar transition via adding electrons, either through changing the metal center or removing exohedral H atoms, to give [10]boraannulene (Fe₂@B₁₀H₁₀, 8) and boranaphthalene (M₂@B₁₀H₈, M = Mn and Fe; 11, 10), respectively, providing detailed electronic structure descriptions. Next, we show the potential to obtain different metal boride monolayers, FeB₅ and Fe₂B₅, considering Fe₂@B₁₀ as a building block, and we compare those monolayers with other possible monolayers obtained using the USPEX global minimum search algorithm. The kinetic and thermal stabilities of the proposed monolayers are also studied. Then, we present electronic structure analysis of the β-Fe₂B₅ monolayer, the global minimum in the planar form, and a comparison with 10. Finally, we extend the study to a Mn₂B₅ monolayer.

Design principle of the interlocked boron wheel Mn₂B₁₀H₁₀ (7)

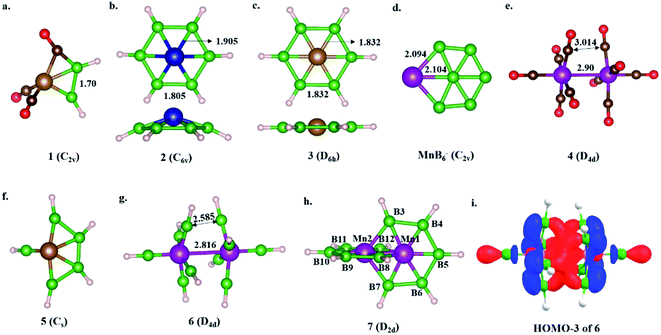
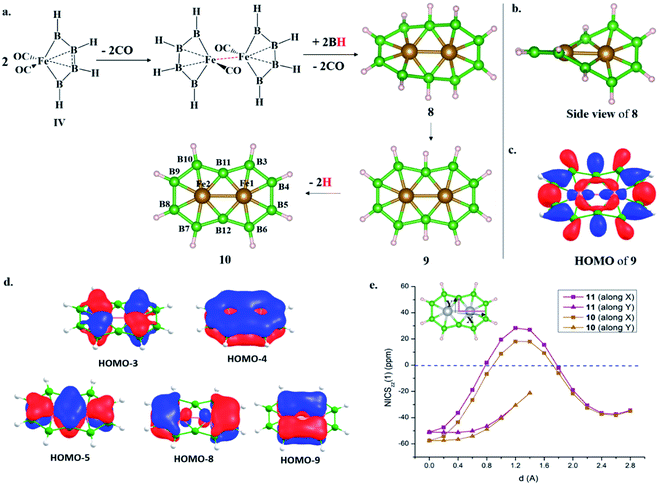
The isolobal relationship between BR and CO and the presence of a B–B bond in 1 (Scheme 3a) led us to check what happens when all the CO ligands in 1 are replaced with isolobal BH fragments. Optimization leads to structure 5, where four of the BH units are coupled (Scheme 3f). Geometrical constraint restrict the fifth BH unit from undergoing coupling, while the replacement of the six CO ligands of an 18e Cr(CO)₆ complex with six BH units results in six-member-ring formation (2),⁸¹ implying the inherent tendency of BH fragments to undergo coupling (Scheme 3b). The out-of-plane movement of the Cr atom from the ring center (0.61 Å) indicates that the six-member ring is too small to accommodate a transition metal. However, Fe@B₆H₆ (3) is planar with elongated B–B bonds (1.832 Å) (Scheme 3c). The additional 2e sit in the non-bonding d_z² orbital of Fe.⁸² Although the unique bonding features of 3 (ref. 82) and its 2D analog, the γ-FeB₆ monolayer,⁵⁴ allowed Fe to sit in the plane of the ring, the inevitability of the strain associated with the six-member ring was clear from the out-of-plane movement of Fe atoms from the hexagonal ring in the case of the FeB₂ monolayer (Scheme 1c, X).⁵³ We considered if it were possible to increase the ring radius. Obvious choices include replacing one of the B centers with a larger-sized atom, preferably a transition metal, and increasing the ring size. Here, we start with an 18e bimetallic complex, Mn₂(CO)₁₀ (4, Scheme 3e), where one of the octahedral Mn sites involves a direct Mn–Mn single bond. The optimized structure of Mn₂(BH)₁₀ with D_4d symmetry (6) is not a minimum on the potential energy surface (Scheme 3g). The Mn–B distances (1.763 Å and 1.828 Å) are close to that of a Mn–B double bond due to strong π-back bonding from Mn to the B centers. Noticeably, the Mn–Mn distance decreases upon going from 4 to 6: from 2.90 Å to 2.816 Å. The equatorial BH units are bent towards each other with a short B–B distance of 2.585 Å, which is in contrast to the equatorial CO ligands in 4, which have a long C–C distance of 3.0 Å. An orbital correlation diagram shows that the only HOMO of 4 has undergone stabilizing interactions in 6 and become HOMO−3 due to additional interactions between equatorial BH units (Scheme 3g and Fig. S1a‡). QTAIM locates bond critical points (BCP) between equatorial BH groups of 6, implying electron density accumulation (Fig. S1c‡). The presence of B–B BCPs hints towards B–B coupling. Following up on the imaginary frequencies led to the interlocked structure 7, where each Mn is coordinated to five boron centers and one Mn center, resulting in a six-member ring (Scheme 3h). The replacement of the Mn centers in 7 with boron ended up in cluster formation, a typical behavior of boron. This further proves that metal centers play a crucial role in determining the stability of structural type 7. QTAIM analysis does not locate any BCPs between orthogonal boron centers at the interlocked positions (B3–B8/12 and B7–B8/12) (Fig. S2a‡), distinguishing 7 from the previously reported interlocked cluster B₁₄.⁸⁰ In the case of B₁₄, two interlocked B₇ units undergo multicentered cluster bonding, and this was named “all-boron fullerene”.⁸⁰ Therefore, it is safe to conclude that the two intervening rings, orthogonal to each other, undergo no out-of-plane interactions and can be considered as interlocked wheels. Although there are reports of metal-centered boron wheels,²⁷ this is the first report of an interlocked metal wheel with a direct metal–metal bond. Complex 7 fulfills all criteria for a molecule to be kinetically stable and viable,⁸³ which are: (a) a high lowest vibrational frequency value (120 cm⁻¹), (b) a high HOMO–LUMO gap (1.87 eV), much higher than M@B_n wheels,⁸⁴ and (c) resistance towards fragmentation and isomerization at room temperature. The thermal stability of 7 is verified via performing AIMD simulations at 300 K. A snapshot taken at the end of a 20 ps simulation (Fig. S2b‡) with a time step of 1 fs shows that the interlocked geometry is well preserved. Each six-member ring of 7 has one Mn at the periphery and one Mn at the ring center. The outer Mn–B distances are closer to the Mn–B distances observed in MnB₆⁻ clusters (Scheme 3d). The two types of B–B bonds in 7 (1.806 Å and 1.821 Å) are intermediate between 2 and 3, indicating the release of ring strain upon going from 3 to 7 (Scheme 3). However, the B–B distances are significantly longer due to the presence of Mn at the ring center.

Electronic structure description of 7 – Möbius aromaticity

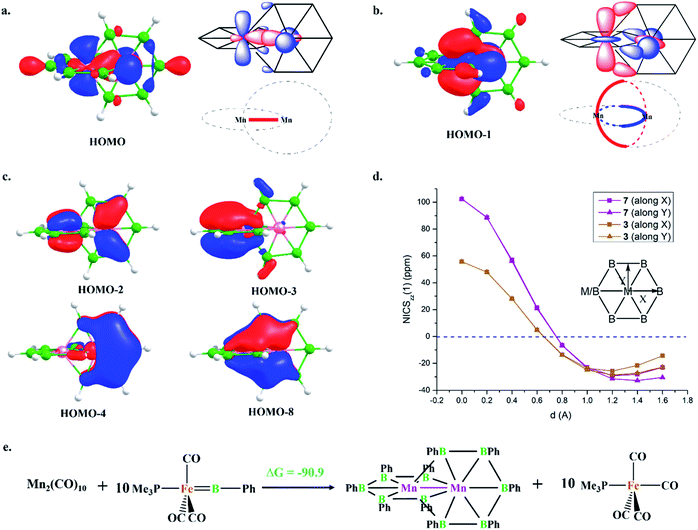
HOMO and HOMO−1 are responsible for the interlocked geometrical pattern, where HOMO is an Mn–Mn σ-boding orbital and HOMO−1 is a B–Mn–B bonding orbital (Fig. 1a and b). Therefore, 7 is an example of a new class of interlocked boron wheel where the d-orbitals of the metal provide the stability. In addition, there are other delocalized MOs reflecting typical multicentered (σ + π) bonding (Fig. S2c‡). The decomposition of the WBIs of B–B bonds into sigma and π components also indicates significant π contributions (Table 1). The multicentered bonding is further confirmed based on AdNDP analysis (Fig. S3‡). The presence of four π-MOs makes the system Möbius aromatic (Fig. 1c). In order to probe the cyclic π-delocalization, NICS_zz(1) values are calculated at different positions above the planar six-member ring (Fig. 1d). A paramagnetic ring current was observed on top of the metal center, dropping sharply while moving towards the periphery, and a diamagnetic ring current is observed after 0.8 Å. The strong diamagnetic ring current at the ring periphery suggests effective cyclic π-delocalization. A comparison between 7 and 3, a 6π Hückel aromatic complex, shows that the diamagnetic ring current values are comparable. The kinetic and thermal stability of 7 prompted us to formulate an equation (Fig. 1e) to compare the stability of Mn₂B₁₀Ph₁₀ with respect to known metal complexes. The high exothermicity of the reaction (−90.9 kcal mol⁻¹) suggests that Mn₂B₁₀Ph₁₀ is a promising target for synthetic efforts. 7 can be considered an intermediate between cluster and planar forms.

Fig. 1 The important molecular orbitals of 7: (a) HOMO and (b) HOMO−1 with schematic representations and (c) all π-MOs. (d) NICS_zz(1) scan curves of 7 and 3 with the distance (d) increasing from the top of the metal center towards the periphery along X and Y. (e) Energetics for the formation of Mn₂B₁₀Ph₁₀ at the BP86 level of theory using the LANL2DZ basis set for Mn and Fe and the 6-31G(d,p) basis set for all other atoms.

Table 1 Important bond lengths and corresponding Wiberg bond indices of 3, 7, and 10 obtained at the BP86 level of theory with the def2-tzvp basis set for all atoms

Molecule		Bond length (Å)	WBI [σ, π]
Fe@B6H6 (3)	Fe–B1	1.832	0.545
	B–B	1.832	0.749 [0.601 (81%), 0.148 (19%)]
Mn2@B10H10 (7)	Mn1–Mn2	2.113	0.502
	Mn1–B3	1.924	0.438
	Mn1–B4	1.874	0.604
	Mn1–B5	1.888	0.575
	Mn1–B8	2.184	0.330
	B3–B4	1.821	0.681 [0.605 (88%), 0.076 (12%)]
	B4–B5	1.806	0.707 [0.599 (88%), 0.108 (12%)]
Fe2@B10H8 (10)	Fe1–Fe2	2.488	0.329
	Fe1–B3	1.950	0.473
	Fe1–B4	1.919	0.525
	Fe1–B11	1.930	0.444
	B3–B4	1.710	0.831 [0.737 (88%), 0.094 (12%)]
	B4–B5	1.734	0.797 [0.791 (88%), 0.096 (12%)]
	B3–B11	1.664	0.928 [0.815 (88%), 0.113 (12%)]

---

An interlocked to planar transition – [10]boraannulene (Fe₂@B₁₀H₁₀; 8) and boranaphthalene (M₂@B₁₀H₈; M = Fe and Mn)

The addition of electrons has the tendency to encourage structural transition towards a planar form.⁸⁵ The optimization of the complex Fe₂@B₁₀H₁₀ (8) closes the ring and gives twisted [10]boraannulene as a minimum, where each Fe atom is coordinated to 6 boron centers and one Fe center, forming a seven-member ring (Fig. 2a). Another way of reaching 8 is via mimicking the dimerization step of the B–B catenation reaction, the second step of the reaction in Scheme 2a, followed by the isolobal replacement of CO with BH, starting from IV (R = H) (Fig. 2a). This further proves the inherent tendency of BH fragments to undergo coupling and the preference of a 3d transition metal to sit in the seven-member ring. The planar structure of 9 is not a minimum on the PES. An orbital correlation diagram between 8 and 9 shows that the HOMO−2 of 8 destabilizes along the path and becomes the HOMO of 9 (Fig. S4‡). The HOMO of 9 involves anti-bonding interactions between hydrogen atoms sitting at the junction positions and nearby hydrogens, resulting in strong torsional strain (Fig. 2c). The imaginary frequencies of complex 9 correspond to the in-plane and out-of-plane motion of H atoms at junction positions. Therefore, the removal of these leads to the stable complex Fe₂@B₁₀H₈ (10). The orbital evolution upon going from 8 to 10 is shown in Fig. S4.‡ Cyclic π-delocalization increases when going from 8, with its out-of-plane arrangement, to 10, with a planar arrangement (Fig. S5‡).

Fig. 2 (a) The design principle of Fe₂@B₁₀H₁₀ (8) and Fe₂@B₁₀H₈ (10), starting from a B–B homocatenated complex (IV, R = H); planar Fe₂@B₁₀H₁₀ (9) is not a minimum. (b) A side view of Fe₂@B₁₀H₁₀ (8). (c) The HOMO of 9. (d) The five π-MOs of 10. (e) NICS_zz(1) scan curves of 10 and 11 with the distance (d) increasing from the top of the ring center towards the periphery along X and Y directions.

The orientation of the Fe₂ unit in 10 is unique. Although there are reports of M₂@B_n complexes, the orientation of M₂ in the plane of the ring with M–M bonding has never been considered. The Fe–Fe bond length (2.513 Å) is in the single-bond distance range. The Fe–B bond distances are shorter than Fe–B single bonds and comparable to Fe–B distances in Fe–borylene complexes, implying sigma and pi bonding (Table 1). The B–B bond distances (1.67–1.73 Å) in 10 are significantly shorter than the B–B distances in 3 and 7, resulting in the relief of strain in 10, where Fe is in the center of the seven-membered rings (Table 1). The preference of a seven-member hole for the 3d transition metal Co was also observed in Co@B₁₈⁻. The Wiberg bond index (WBI) values for the B–B bonds and their sigma and pi decomposition also support a strong B–B sigma skeleton in 10 compared to 3 and 7. The planar structure is stabilized by delocalized multicentered (σ + π) bonding (Fig. S6‡). 10 has five multi-centered π-bonding orbitals (Fig. 2d). The presence of ten π-electrons in 10 (Fig. 2d) fulfills Hückel π-aromaticity criteria and associates it with naphthalene (Fig. S7‡). NICS_zz(1) above the ring center is −57.5 ppm, confirming the aromatic nature. The NICS_zz(1) scan curves with distance (d) increasing from the top of the ring center towards the periphery along the X and Y directions show a strong diamagnetic ring current in all positions, except for positions nearby metal centers (Fig. 2e). Therefore, 10 can be considered as boranaphthalene. The major difference between C₁₀H₈ and 10 is their σ bonding frameworks. The eleven C–C σ-bonding orbitals in C₁₀H₈ now become ten 3c–2e Fe–B–B, one 6c–2e Fe₂–B₄, and one 8c–2e Fe₂–B₆ delocalized σ-bonding orbital, according to AdNDP analysis (Fig. S8‡). The B11–B12 interaction is via the delocalized 6c–2e orbital, mainly concentrated on Fe1–Fe2–B11–B12 centers, and 8c–2e bonding orbital.

Möbius aromaticity to Hückel aromaticity

We have shown that the removal of exohedral H can add electrons to cluster bonding.⁸⁵ The removal of 2H from the B3 and B8 centers of 7 leads to the planar Mn₂B₁₀H₈ structure 11. 11 and 10 are similar except for the fact that 11 has a triplet ground state. The singlet state with a δ²(δ*)⁰ electronic configuration localized on the Mn centers is 15.0 kcal mol⁻¹ higher in energy. Due to the long Mn–Mn distance, δ–δ* splitting is low. Therefore, the promotion of one electron from a δ to a δ* orbital stabilizes the triplet state due to large exchange stabilization. In the case of 10, both the δ and δ* orbitals are doubly occupied and the singlet state is the most stable one. Since δ and δ* are localized on metal centers with very weak bonding interactions, the nature of chemical bonding in Fe₂@B₁₀H₈ and Mn₂B₁₀H₈ is similar. The presence of 8π electrons in 7 and 10π electrons in 11 makes the transformation from 7 to 11 an interesting example of a Möbius to Hückel aromatic transition.

The realization of III (Scheme 1a) with two bare B-centers suggests the possibility of obtaining boranaphthalene (10 and 11) in solution.²¹

It should be noted that icosahedral arrangements of M₂B₁₀H₁₀ (M = Mn and Fe), similar to icosahedral M₂B₁₀ (M = Rh and Ir),⁸⁶ are more stable than 7 and 8 (Fig. S9 and Table S1‡). However, the relative energy differences are lower in the case of icosahedral M₂B₁₀H₈ (M = Mn and Fe) and 11 and 10 (Fig. S8 and Table S1‡). The relative energy order reverses when the monoanionic system of icosahedral M₂B₁₀H₈ (M = Mn and Fe) and 11 and 10 are considered (Fig. S8 and Table S2‡).

A roadmap to solids – the design principle of FeB₅ and Fe₂B₅ monolayers

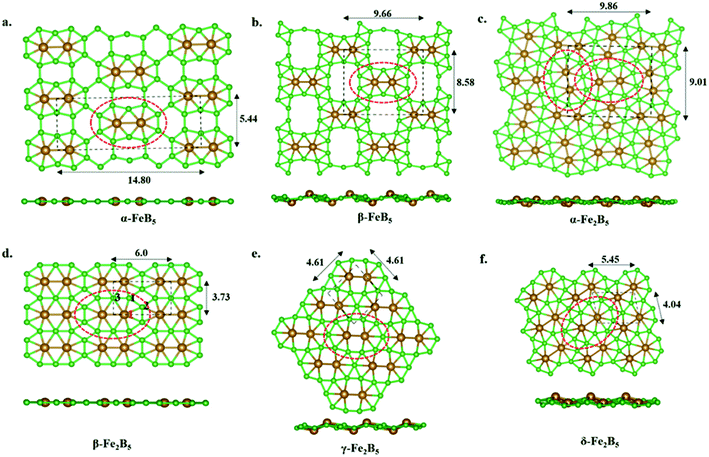
Our continuous efforts to make connections between different parts of chemistry motivated us to extend molecular boron chemistry to solid-state chemistry via considering 10 as a basic building block. Different modes of condensation of units of 10 can lead to different metal borides (Fe_xB_y). The simplest possible condensation, through B–B single bond connection, leads to an α-FeB₅ monolayer, where each Fe₂@B₁₀ unit is surrounded by eight hexagonal holes (Fig. 3a). The special stability of triangular boron units allows us to consider an edge-connected B–B condensation mode to give a β-FeB₅ monolayer with four ten-member holes surrounding the parent Fe₂@B₁₀ unit (Fig. 3b). In the parent monomer, 10, the Fe₂ unit sits in the 10-member ring of B₁₀H₈. Therefore, the addition of an Fe₂ unit into the 10-member holes of the β-FeB₅ monolayer can lead to a stable α-Fe₂B₅ monolayer (Fig. 3c). One can also visualize an α-Fe₂B₅ monolayer as a result of the edge-sharing of parent Fe₂@B₁₀, where two nearby Fe₂ units are nearly perpendicular in orientation. Similarly, another mode of edge-sharing of Fe₂@B₁₀ units leads to β-Fe₂B₅, where Fe₂ units are parallel to each other (Fig. 3d).

Fig. 3 Different optimized 2D monolayers derived from 10: (a) α-FeB₅, (b) β-FeB₅, (c) α-Fe₂B₅, (d) β-Fe₂B₅ (the numbering of three unique boron atoms is given in black, and Fe is denoted using red), (e) γ-Fe₂B₅, and (f) δ-Fe₂B₅. Two different views of each monolayer are shown. Unit cells are indicated by the black dotted lines and lattice parameters are given in Å. Parent building blocks are highlighted using red dotted circles.

Unlike the molecular analog, all the 2D monolayers have a magnetic ground state, as observed recently for the FeB₃ monolayer.⁸⁷ A comparison between non-magnetic and magnetic states shows that the magnetic states lie 56 meV, 236 meV, 1319 meV, and 204 meV lower in energy than the nonmagnetic sates for α-FeB₅, β-FeB₅, α-Fe₂B₅, and β-Fe₂B₅ in their respective unit cells. COHP analysis of the nonmagnetic states shows an appreciable antibonding population at the Fermi level (Fig. S9‡). Adding spin polarization removes these antibonding interactions from the Fermi level due to exchange stabilization and provides stability.

The thermodynamic stabilities of these monolayers are obtained via calculating their cohesive energies using the formula: E_coh = (xE_Fe + yE_B − E_FexBy)/(x + y), where E_Fe, E_B, and E_FexBy are the total energies of a single Fe atom, a single B atom, and one unit cell of the Fe_xB_y monolayer, respectively. The computed cohesive energies for α-FeB₅, β-FeB₅, α-Fe₂B₅, and β-Fe₂B₅ are 5.64 eV per atom, 5.66 eV per atom, 5.68 eV per atom, and 5.74 eV per atom, respectively. The relatively high cohesive energies in comparison with previously reported 2D monolayers of FeB₂ (5.62 eV per atom) and FeB₆ (5.61–5.85 eV per atom) at the same level of theory suggest the high stability of these 2D sheets. Due to the presence of several holes surrounding the Fe₂@B₁₀ units in FeB₅ monolayers and the lower cohesive energies, we focused on the Fe₂B₅ monolayers in the following discussion.

Global minimum search with Fe₂B₅ monolayers

A comprehensive global minimum search using the molecular formula Fe₂B₅ followed by the full relaxation of random structures in conjunction with VASP code, as implemented in the USPEX program package, shows that β-Fe₂B₅ is found to be the global minimum in the planar arrangement. It gives two more structures, γ-Fe₂B₅ and δ-Fe₂B₅, with cohesive energies of 5.61 eV per atom and 5.63 eV per atom, respectively (Fig. 3e and f). The Fe₂@B₁₀ unit in the γ-Fe₂B₅ monolayer is significantly different to the molecular unit 10. In γ-Fe₂B₅, the loss of Fe–B bonding interactions at the junction positions of the repeating Fe₂@B₁₀ units makes it an unstable monolayer with one imaginary frequency (80 cm⁻¹). The repeating unit of δ-Fe₂B₅ is Fe₂B₁₁, where two iron atoms are in 8-member and 7-member holes, respectively. The low cohesive energy of δ-Fe₂B₅ compared to β-Fe₂B₅ further proves that a 7–7 hole combination for the two iron centers is better than an 8–7 combination, validating the unique stability of Fe₂@B₁₀ in β-Fe₂B₅ and its corresponding molecular analog 10. Therefore, we continue our discussion, considering β-Fe₂B₅ as a representative example. The unit cell of β-Fe₂B₅ consists of 2 Fe atoms and 5 B atoms, with the optimized lattice parameters being a = 5.997 Å and b = 3.724 Å, respectively. There are three unique Fe–B bonds in the β-Fe₂B₅ monolayer, similar to 10. The Fe1–B1, Fe1–B2, and Fe1–B3 distances are 1.929 Å, 2.040 Å, and 2.188 Å, respectively, and the B–B bond lengths are in the range of 1.645–1.711 Å. A comparison of these distances between 10 and the β-Fe₂B₅ monolayer shows close similarity, except for the Fe1–B3 distance, which changes from 1.930 Å to 2.188 Å. This large change is to maintain the symmetry of the repeating unit in the extended system.

Kinetic and thermal stability of the β-Fe₂B₅ monolayer

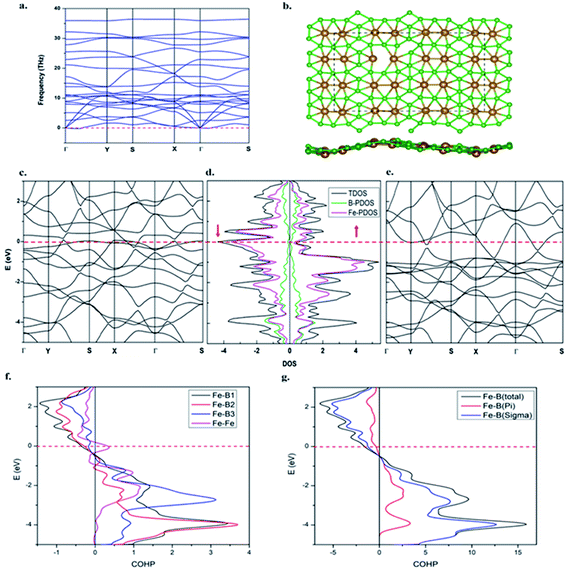
The dynamic stability of the β-Fe₂B₅ monolayer is confirmed via computing the phonon dispersion along the high-symmetry lines in the first Brillouin zone, with no appreciable imaginary frequency (Fig. 4a). The highest frequency of the β-Fe₂B₅ monolayer is 35.7 THz (≈1191 cm⁻¹), higher than the highest frequencies of MoS₂ sheets (473 cm⁻¹)⁸⁸ and FeB₂ (873 cm⁻¹),⁵³ and comparable to a FeB₆ monolayer (≈1000–1300 cm⁻¹), indicating strong Fe–B and B–B chemical bonding. The thermal stability of the β-Fe₂B₅ monolayer is also verified via performing AIMD simulations at 1000 K using a 3 × 3 supercell. A snapshot taken at the end of a 6 ps simulation (Fig. 4b) with a time step of 1 fs shows that the framework of the planar sheet is well preserved. Therefore, the β-Fe₂B₅ monolayer is shown to be energetically, dynamically, and thermally stable.

Fig. 4 (a) Phonon spectra. (b) A snapshot of the equilibrium structure of the β-Fe₂B₅ monolayer at 1000 K after 6 ps of AIMD simulation. (c) The spin polarized band structure for the spin-down channel. (d) The total and projected DOS. (e) The spin polarized band structure for the spin-up channel. (f) The projected COHP plots for different Fe–B bonds and Fe–Fe bonds in the unit cell. (g) The projected COHP plot for Fe–B (total) and its decomposition into sigma and pi components. All the plots are for the β-Fe₂B₅ monolayer.

The electronic structure of the β-Fe₂B₅ monolayer

Projected crystal orbital Hamiltonian (PCOHP) analysis of the different Fe–B bonds of the β-Fe₂B₅ monolayer shows robust bonding between the metal and boron framework (Fig. 4f). Decomposition of the PCOHP curve of the Fe–B bond into σ and π components separately and further shows that both σ and π bonding interactions are responsible for the stability of the β-Fe₂B₅ monolayer (Fig. 4g), reflecting the close similarity of chemical bonding in the β-Fe₂B₅ sheet with the parent complex 10. The spin-resolved density of states (DOS) and corresponding electronic band structures show the metallic nature of β-Fe₂B₅, and the high peaks of the DOS around the Fermi level are mainly composed of Fe-d states (Fig. 4c–e).

The Mn₂B₅ monolayer

The geometric and electronic structure similarities between 10 and 11 prompted us to extend the study to the Mn₂B₅ monolayer, considering the β-Fe₂B₅ skeleton (Fig. S10a‡), which also has excellent kinetic and thermal stability (Fig. S10b and c‡) with robust Mn–B (σ + π) bonding (Fig. S10g and h‡). The spin-resolved density of states (DOS) and the corresponding electronic band structures show the metallic nature of β-Mn₂B₅, and the high peaks of the DOS around the Fermi level are mainly composed of Mn-d states (Fig. S10d–f‡).

Conclusions

The 18e rule, an isolobal analogy, and the inherent tendency of BR fragments to undergo coupling are utilized to predict an interlocked boron wheel (7) with an unprecedented geometrical pattern. Although Mn at the center of the six-member ring adds strain into the system, the presence of the other Mn atom at the ring periphery releases strain compared to 3, and the metal d-orbitals provide stability by making this an 8π Möbius aromatic system. The addition of two electrons via changing the metal from Mn to Fe gives twisted [10]boraannulene (8). The removal of 2H from 8 and 7 leads to the planar structures Fe₂@B₁₀H₈ (10), by releasing torsional strain, and Mn₂@B₁₀H₈ (11), by reducing the ring strain with an increase in the ring size from six to seven, respectively. Effective π-donation from the M₂ (M = Fe and Mn) units of 10 and 11 to the borocycle B₁₀H₈ fulfills the Hückel 10π-aromatic criteria and associates these with naphthalene. However, the presence of characteristic multicentered σ and π bonding distinguishes 10 and 11 from typical naphthalene bonding. Considering the central Fe₂@B₁₀ unit of 10 as a potential building block, we proposed different extended 2D metal borides, FeB₅ and Fe₂B₅ monolayers, bringing this molecular chemistry into the solid state. A study of alternative structures that are not as easily related to iron naphthalide (Fe₂@B₁₀) using the USPEX global minimum search algorithm further shows that β-Fe₂B₅, designed in this study, is a global minimum in the planar arrangement. Chemical bonding analysis of β-Fe₂B₅ further shows that the molecular bonding mechanism is preserved in the solid state. The proposed monolayer, β-Fe₂B₅, has excellent kinetic and thermal stability with metallic character. The strategy adopted in this study will inspire many related studies to obtain a continuum in this area of boron chemistry.

Data availability

All the xyz coordinates are given in the ESI file.‡ The data that support the findings of this study are available upon reasonable request from the authors.

Author contributions

Sagar Ghorai (SG) and Eluvathingal D. Jemmis (EDJ) conceived the project. All calculations and analysis are done by SG who also wrote the first draft of the manuscript. EDJ and SG iterated the manuscript many times to get to the final stage.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Supercomputer Education and Research Centre, IISc for computational facilities. SG thanks IISc for a research fellowship. EDJ thanks SERB-DST for funding through the Year of Science Chair Professorship.

References

1. E. D. Jemmis and E. G. Jayasree, Acc. Chem. Res., 2003, 36, 816–824.
2. H. Braunschweig, R. D. Dewhurst and A. Schneider, Chem. Rev., 2010, 110, 3924–3957.
3. H. Braunschweig and R. D. Dewhurst, Angew. Chem., Int. Ed., 2013, 52, 3574–3583.
4. J. T. Goettel and H. Braunschweig, Coord. Chem. Rev., 2019, 380, 184–200.
5. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W.-L. Li, C. Romanescu, L.-S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358.
6. W.-L. Li, X. Chen, T. Jian, T.-T. Chen, J. Li and L.-S. Wang, Nat. Rev. Chem., 2017, 1, 0071.
7. L.-S. Wang, Int. Rev. Phys. Chem., 2016, 35, 69–142.
8. R. Kinjo, B. Donnadieu, M. A. Celik, G. Frenking and G. Bertrand, Science, 2011, 333, 610–613.
9. L. Kong, Y. Li, R. Ganguly, D. Vidovic and R. Kinjo, Angew. Chem., Int. Ed., 2014, 53, 9280–9283.
10. D. A. Ruiz, G. Ung, M. Melaimi and G. Bertrand, Angew. Chem., Int. Ed., 2013, 52, 7590–7592.
11. R. Bertermann, H. Braunschweig, R. D. Dewhurst, C. Hörl, T. Kramer and I. Krummenacher, Angew. Chem., Int. Ed., 2014, 53, 5473.
12. W. Lu, H. Hu, Y. Li, R. Ganguly and R. Kinjo, J. Am. Chem. Soc., 2016, 138, 6650–6661.
13. D. Wu, R. Ganguly, Y. Li, S. N. Hoo, H. Hirao and R. Kinjo, Chem. Sci., 2015, 6, 7150–7155.
14. D. Wu, L. Kong, Y. Li, R. Ganguly and R. Kinjo, Nat. Commun., 2015, 6, 7340.
15. H. Braunschweig, R. D. Dewhurst, F. Hupp, M. Nutz, K. Radacki, C. W. Tate, A. Vargas and Q. Ye, Nature, 2015, 522, 327–330.
16. M.-A. Légaré, M. Rang, G. Bélanger-Chabot, J. I. Schweizer, I. Krummenacher, R. Bertermann, M. Arrowsmith, M. C. Holthausen and H. Braunschweig, Science, 2019, 363, 1329–1332.
17. S. S. Rohman, B. Sarmah, B. Borthakur, G. S. Remya, C. H. Suresh and A. K. Phukan, Organometallics, 2019, 38, 2770–2781.
18. M. Asay, C. Jones and M. Driess, Chem. Rev., 2011, 111, 354–396.
19. S. Litters, E. Kaifer, M. Enders and H.-J. Himmel, Nat. Chem., 2013, 5, 1029–1034.
20. W. Lu, Y. Li and R. Kinjo, J. Am. Chem. Soc., 2019, 141, 5164–5168.
21. W. Lu, D. C. H. Do and R. Kinjo, Nat. Commun., 2020, 11, 3370.
22. H. Braunschweig, Q. Ye, A. Vargas, R. D. Dewhurst, K. Radacki and A. Damme, Nat. Chem., 2012, 4, 563–567.
23. M.-A. Légaré, C. Pranckevicius and H. Braunschweig, Chem. Rev., 2019, 119, 8231–8261.
24. H. Braunschweig, R. D. Dewhurst and V. H. Gessner, Chem. Soc. Rev., 2013, 42, 3197–3208.
25. L. Zhao, M. Hermann, N. Holzmann and G. Frenking, Coord. Chem. Rev., 2017, 344, 163–204.
26. R. Borthakur, K. Saha, S. Kar and S. Ghosh, Coord. Chem. Rev., 2019, 399, 213021.
27. C. Romanescu, T. R. Galeev, W.-L. Li, A. I. Boldyrev and L.-S. Wang, Acc. Chem. Res., 2012, 46, 350–358.
28. I. Boustani, Phys. Rev. B, 1997, 55, 16426–16438.
29. L. F. Cheung, J. Czekner, G. S. Kocheril and L.-S. Wang, J. Am. Chem. Soc., 2019, 141, 17854–17860.
30. T. Jian, X. Chen, S.-D. Li, A. I. Boldyrev, J. Li and L.-S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591.
31. S. Pan, J. Barroso, S. Jalife, T. Heine, K. R. Asmis and G. Merino, Acc. Chem. Res., 2019, 52, 2732–2744.
32. J. Barroso, S. Pan and G. Merino, Chem. Soc. Rev., 2022, 51, 1098–1123.
33. S. Ghorai and E. D. Jemmis, Chem.–Eur. J., 2018, 24, 17844–17851.
34. L. F. Cheung, G. S. Kocheril, J. Czekner and L.-S. Wang, J. Am. Chem. Soc., 2020, 142, 3356–3360.
35. L. F. Cheung, G. S. Kocheril, J. Czekner and L.-S. Wang, J. Phys. Chem. A, 2020, 124, 2820–2825.
36. A. N. Alexandrova, A. I. Boldyrev, H.-J. Zhai and L.-S. Wang, J. Phys. Chem. A, 2004, 108, 3509–3517.
37. W.-L. Li, T. Jian, X. Chen, T.-T. Chen, G. V. Lopez, J. Li and L.-S. Wang, Angew. Chem., Int. Ed., 2016, 55, 7358–7363.
38. Z. A. Piazza, H.-S. Hu, W.-L. Li, Y.-F. Zhao, J. Li and L.-S. Wang, Nat. Commun., 2014, 5, 3113.
39. H. Liu, J. Gao and J. Zhao, Sci. Rep., 2013, 3, 3238.
40. G. P. Campbell, A. J. Mannix, J. D. Emery, T.-L. Lee, N. P. Guisinger, M. C. Hersam and M. J. Bedzyk, Nano Lett., 2018, 18, 2816–2821.
41. A. J. Mannix, X.-F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516.
42. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563.
43. Z. Zhang, Y. Yang, G. Gao and B. I. Yakobson, Angew. Chem., Int. Ed., 2015, 54, 13022–13026.
44. X. Wu, J. Dai, Y. Zhao, Z. Zhuo, J. Yang and X. C. Zeng, ACS Nano, 2012, 6, 7443–7453.
45. E. S. Penev, S. Bhowmick, A. Sadrzadeh and B. I. Yakobson, Nano Lett., 2012, 12, 2441–2445.
46. L. Shi, C. Ling, Y. Ouyang and J. Wang, Nanoscale, 2017, 9, 533–537.
47. C. Ling, L. Shi, Y. Ouyang, X. C. Zeng and J. Wang, Nano Lett., 2017, 17, 5133–5139.
48. X. Tang, W. Sun, Y. Gu, C. Lu, L. Kou and C. Chen, Phys. Rev. B, 2019, 99, 045445.
49. N. Karmodak and E. D. Jemmis, Angew. Chem., Int. Ed., 2017, 56, 10093–10097.
50. N. Karmodak and E. D. Jemmis, J. Phys. Chem. C, 2018, 122, 2268–2274.
51. N. Karmodak, E. D. Jemmis and B. I. Yakobson, in 2D Boron: Boraphene, Borophene, Boronene, ed. I. Matsuda and K. Wu, Springer International Publishing, Cham, 2021, pp. 27–49,  DOI:10.1007/978-3-030-49999-0_2.
52. P. Ranjan, J. M. Lee, P. Kumar and A. Vinu, Adv. Mater., 2020, 32, 2000531.
53. H. Zhang, Y. Li, J. Hou, A. Du and Z. Chen, Nano Lett., 2016, 16, 6124–6129.
54. H. Zhang, Y. Li, J. Hou, K. Tu and Z. Chen, J. Am. Chem. Soc., 2016, 138, 5644–5651.
55. L. Z. Zhang, Z. F. Wang, S. X. Du, H. J. Gao and F. Liu, Phys. Rev. B, 2014, 90, 161402.
56. J. Wang, M. Khazaei, M. Arai, N. Umezawa, T. Tada and H. Hosono, Chem. Mater., 2017, 29, 5922–5930.
57. X. Qu, J. Yang, Y. Wang, J. Lv, Z. Chen and Y. Ma, Nanoscale, 2017, 9, 17983–17990.
58. B. Song, Y. Zhou, H.-M. Yang, J.-H. Liao, L.-M. Yang, X.-B. Yang and E. Ganz, J. Am. Chem. Soc., 2019, 141, 3630–3640.
59. J. Li, X. Fan, Y. Wei, J. Liu, J. Guo, X. Li, V. Wang, Y. Liang and G. Chen, J. Mater. Chem. C, 2016, 4, 10866–10875.
60. J. Li, Y. Wei, X. Fan, H. Wang, Y. Song, G. Chen, Y. Liang, V. Wang and Y. Kawazoe, J. Mater. Chem. C, 2016, 4, 9613–9621.
61. Y. Jiao, F. Ma, X. Zhang and T. Heine, Chem. Sci., 2022, 13, 1016–1022.
62. M. M. Balakrishnarajan and R. Hoffmann, J. Am. Chem. Soc., 2004, 126, 13119–13131.
63. C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720.
64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Version D, 2009.
65. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824.
66. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
67. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
68. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
69. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
70. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
71. T. A. Keith, AIMAll (Version 19.10.12), TK Gristmill Software, Overland Park KS, USA, 2019.
72. G. Kresse and J. Hafner, Phys. Rev. B, 1993, 48, 13115–13118.
73. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
74. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186.
75. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
76. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775.
77. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
78. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
79. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
80. L. Cheng, J. Chem. Phys., 2012, 136, 104301.
81. L. Li, C. Xu, B. Jin and L. Cheng, J. Chem. Phys., 2013, 139, 174310.
82. J. Hou, Q. Duan, J. Qin, X. Shen, J. Zhao, Q. Liang, D. Jiang and S. Gao, Phys. Chem. Chem. Phys., 2015, 17, 9644–9650.
83. R. Hoffmann, P. v. R. Schleyer and H. F. Schaefer III, Angew. Chem., Int. Ed., 2008, 47, 7164–7167.
84. K. Ito, Z. Pu, Q.-S. Li and P. v. R. Schleyer, Inorg. Chem., 2008, 47, 10906–10910.
85. N. Karmodak, R. Chaliha and E. D. Jemmis, Inorg. Chem., 2019, 58, 3627–3634.
86. W.-y. Liang, J. Barroso, S. Jalife, M. Orozco-Ic, X. Zarate, X. Dong, Z.-H. Cui and G. Merino, Chem. Commun., 2019, 55, 7490–7493.
87. C. Tang, K. K. Ostrikov, S. Sanvito and A. Du, Nanoscale Horiz., 2021, 6, 43–48.
88. A. Molina-Sánchez and L. Wirtz, Phys. Rev. B, 2011, 84, 155413.

---

Footnotes

† This article is dedicated to Professor Peter Gill for his achievements in chemistry and services to chemists.

‡ Electronic supplementary information (ESI) available: Correlation diagrams of 4–6 and 8–9–10; QTAIM analysis of 4, 6 and 7; important molecular orbitals of 7 and 10; AdNDP analysis of 7 and 10; a comparison of the π molecular orbitals of 10 and naphthalene; projected COHP plots for different metal boride monolayers; geometric and electronic structure analysis of the β-Mn₂B₅ monolayer; Cartesian coordinates of the studied complexes. See https://doi.org/10.1039/d2sc02244c

---