Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metal–organic frameworks as O2-selective adsorbents for air separations†
David E.
Jaramillo
 a,
Adam
Jaffe‡
a,
Adam
Jaffe‡
 a,
Benjamin E. R.
Snyder
a,
Alex
Smith
a,
Benjamin E. R.
Snyder
a,
Alex
Smith
 b,
Eric
Taw
cd,
Rachel C.
Rohde
b,
Eric
Taw
cd,
Rachel C.
Rohde
 a,
Matthew N.
Dods
a,
William
DeSnoo§
b,
Katie R.
Meihaus
a,
T. David
Harris
a,
Matthew N.
Dods
a,
William
DeSnoo§
b,
Katie R.
Meihaus
a,
T. David
Harris
 a,
Jeffrey B.
Neaton
bef and
Jeffrey R.
Long
a,
Jeffrey B.
Neaton
bef and
Jeffrey R.
Long
 *acd
*acd
aDepartment of Chemistry, University of California Berkeley, Berkeley, California 94720, USA. E-mail: jrlong@berkeley.edu
bDepartment of Physics, University of California Berkeley, Berkeley, California 94720, USA
cDepartment of Chemical and Biomolecular Engineering, University of California Berkeley, Berkeley, California 94720, USA
dMaterials Science Division, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
eMolecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, California 94720, USA
fKavli Nanosciences Institute at Berkeley, Berkeley, California 94720, USA
First published on 11th August 2022
Abstract
Oxygen is a critical gas in numerous industries and is produced globally on a gigatonne scale, primarily through energy-intensive cryogenic distillation of air. The realization of large-scale adsorption-based air separations could enable a significant reduction in associated worldwide energy consumption and would constitute an important component of broader efforts to combat climate change. Certain small-scale air separations are carried out using N2-selective adsorbents, although the low capacities, poor selectivities, and high regeneration energies associated with these materials limit the extent of their usage. In contrast, the realization of O2-selective adsorbents may facilitate more widespread adoption of adsorptive air separations, which could enable the decentralization of O2 production and utilization and advance new uses for O2. Here, we present a detailed evaluation of the potential of metal–organic frameworks (MOFs) to serve as O2-selective adsorbents for air separations. Drawing insights from biological and molecular systems that selectively bind O2, we survey the field of O2-selective MOFs, highlighting progress and identifying promising areas for future exploration. As a guide for further research, the importance of moving beyond the traditional evaluation of O2 adsorption enthalpy, ΔH, is emphasized, and the free energy of O2 adsorption, ΔG, is discussed as the key metric for understanding and predicting MOF performance under practical conditions. Based on a proof-of-concept assessment of O2 binding carried out for eight different MOFs using experimentally derived capacities and thermodynamic parameters, we identify two existing materials and one proposed framework with nearly optimal ΔG values for operation under user-defined conditions. While enhancements are still needed in other material properties, the insights from the assessments herein serve as a guide for future materials design and evaluation. Computational approaches based on density functional theory with periodic boundary conditions are also discussed as complementary to experimental efforts, and new predictions enable identification of additional promising MOF systems for investigation.
1. Introduction
1.1 Current air separation technologies and their limitations
Oxygen is one of the foundational gases of the industrial sector.1 Today, fossil fuel combustion alone consumes O2 directly from air on a massive scale of ∼25 gigatonnes per year, about 8 gigatonnes more than the annual natural production of O2.2 Moreover, enriched (>21%) or high-purity oxygen (>95%) is essential for numerous applications, including within the medical and aerospace industries,1,3 as well as in a variety of chemical processes, such as the production of phthalic anhydride, acetaldehyde synthesis via the Wacker Process, and ethylene oxide production.1,4 The COVID-19 pandemic has also highlighted the importance of medical-grade oxygen and its existing supply chain issues.5 These and many other processes depend on the separation of oxygen from air. As a result, this process is performed on a scale of hundreds of millions of tonnes per year.6Importantly, high-purity O2 is also critical for next-generation carbon capture processes poised to play a critical role in reducing emissions from large-scale combustion plants. For example, oxy-fuel power plants, which are currently in the pilot stage, use O2 (∼95%) instead of air to produce a concentrated CO2 flue gas stream.7–9 This process renders post-combustion CO2 capture more viable by reducing the energy needed for regeneration while also decreasing NOx emissions. Likewise, high-purity O2 is necessary for carrying out pre-combustion CO2 capture in fossil fuel gasification plants.10,11
Approximately 70% of O2 generated in industry is obtained via cryogenic distillation of air,12 which is predominantly a centralized process that takes place in large air separation plants. First pioneered by Linde in the late 19th century, this process exploits the small difference in the boiling points of O2 and N2 (Table 1).1,13 In brief, low-temperature air is fed into large distillation columns that feature pressure and temperature gradients and numerous trays where liquid and vapor phases equilibrate. Within these columns, nitrogen vapor rises and increases in purity, while liquid oxygen descends the columns and increases in purity. Cryogenic distillation plants can generate O2 with 95% purity or higher at 1000 to 5000 tonnes per day. This method is a remarkable feat of engineering, considering the small difference in vapor pressure between the two gases. Nevertheless, cryogenic separation units are very capital-intensive projects that require operation at relatively high capacities.14 As a result, the energy required to separate one tonne of O2 from air is approximately 245 kW h (Table 2),6,14 more than four times greater than the minimum separation work of 58 kW h per tonne at 25 °C (see ESI Section S1†).14 Further, owing primarily to the similar vapor pressures of argon and O2,13 achieving O2 purities greater than 95% requires additional expensive refrigeration that increases the overall energy demand per tonne of O2.6
| N2 | O2 | Ar | |
|---|---|---|---|
| Molar fraction | 0.78 | 0.21 | 00.93 |
| Normal boiling point (K) | 77.3 | 90.2 | 87.3 |
| Kinetic diameter (Å) | 3.64 | 3.47 | 3.54 |
| Polarizability × 1025 (cm3) | 17.703 | 15.812 | 16.411 |
| Quadrupole moment × 1026 (esu cm2) | 1.52 | 0.39 | 0 |
| Electron affinity (eV) | <0 | 0.450 | <0 |
| Cryogenic distillationa | Adsorptive separationsb | Membrane separationsc | |
|---|---|---|---|
| a Values obtained from ref. 6, 14, and 19. b Values obtained from ref. 6, 14, and 19. c Values obtained from ref. 6 and 20. The largest reported capacity per day is an estimate from ref. 6. | |||
| Operating pressures | 1–6 bar | 0.2–6 bar | 1–6 bar |
| Operating temperatures | 77–298 K | 298–318 K | 298–318 K |
| O2 purity achieved | >95% | <95% | <50% |
| O2 production scale per day | 1000 tonnes | 100 tonnes | 10 tonnes |
| Largest reported capacity per day | 5000 tonnes (Air Liquide) | 340 tonnes (Linde) | 25 tonnes |
| Energy demand per tonne | 220–270 kW h at 95% purity | 500 kW h at 95% purity | 300 kW h at 40% purity |
Adsorptive air separation represents the second most common process for oxygen production, accounting for ∼20% of O2 produced in industry.14 This approach currently exploits differences in the polarizability and quadrupole moment of O2 and N2 (Table 1). Briefly, pressurized air is fed through beds containing an adsorbent that selectively binds N2. The most commonly used adsorbent is a low-silica zeolite exchanged with lithium ions, known as Li-LSX,12,15 which features exposed Li+ sites that preferentially interact with N2. Once the adsorbent is saturated with the gas, the bed is depressurized to near ambient pressure, resulting in elution of an O2-enriched stream, followed by N2. A process operating under such conditions is referred to as pressure swing adsorption (PSA). Air can also be fed into the adsorbent bed at near ambient pressure, and in this case vacuum or heat can then be applied to regenerate the adsorbent, in so-called vacuum swing adsorption (VSA) or temperature swing adsorption (TSA) processes.12,14,16,17 Further, the above separation methods can be combined to engender pressure-temperature or vacuum-temperature swing adsorption processes. Importantly, adsorptive air separations can serve a complementary role to cryogenic distillation, as they can operate under a more variable load (for instance, by changing the number of adsorbent beds in use), are substantially less capital-intensive for small-scale applications, and entail minimal startup time. Adsorptive air separation plants typically consume 500 kW h per tonne of O2 produced at 90–95% purity,14,18 although a much lower value of 270 kW h per tonne of O2 has been reported (Table 2).12 This energy demand is nearly double that of cryogenic distillation, and the resulting oxygen purity is generally lower. This higher energy cost arises due to the need to regenerate the adsorbent, as discussed above. Additionally, zeolites typically exhibit low N2 uptake, and therefore substantial quantities of adsorbent material are required—roughly 1 tonne of zeolite is needed for producing 1 tonne of O2 per day. In all, these shortcomings preclude the more wide-spread application of Li-LSX adsorbents for air separations.
Polymeric membrane-based air separations are the youngest commercial technology for extracting O2 from air, and operate by passing an air stream through a series of membrane units.18–20 These processes function under a solution-diffusion mechanism and discriminate oxygen and nitrogen based on their permeabilities. Industrially relevant membranes are permselective with respect to oxygen, and so the resulting permeate is O2-enriched air. As a result of their mechanism of operation, membrane separations can be carried out continuously under ambient conditions, without the need for regeneration. As such, polymer membranes have the potential to offer considerable reductions in capital costs and operating expenses relative to adsorption and cryogenic distillation. However, for the majority of membranes studied to date, permeate O2 concentrations are limited by the minor solubilization difference between O2 and N2.21 This shortcoming, combined with similarities in the kinetic diameters of N2 and O2, manifests as a permeability-selectivity tradeoff that limits permeate purities to below 40–50% O2.18,21 Note that ceramic membranes, which function through a different mechanism, may find use in industrial applications. However, these membranes typically require very high temperatures to operate, in the range of 800−900 °C.19,22
1.2 The potential impact of O2-selective adsorbents in air separations
In general, established air separation technologies operate by distinguishing O2 and N2 based on relatively small differences in their boiling points, polarizabilities, and quadrupole moments. However, the property that most distinguishes O2 from N2 (and Ar) is its electron affinity (Table 1). Oxygen can readily accept one or two electrons from a single metal center, whereas nitrogen is generally redox-inactive.23 Biological systems exploit this difference to selectively and reversibly bind O2 using iron(II)- and copper(I)-containing proteins. In particular, hemoglobin and myoglobin,24,25 hemerythrin,26 and hemocyanin27 are representative examples of proteins containing metal sites that bind O2via electron transfer.The realization of adsorbents that are capable of similar strong yet reversible chemisorption of O2 could transform the air separation industry. Indeed, because the partial pressure of O2 in air is approximately four times less than that of N2, the amount of O2-selective adsorbent needed to process a given quantity of air will be one quarter of the quantity needed for an analogous N2-selective adsorbent. As a result, even in a scenario where the enthalpy of O2 binding in an O2-selective adsorbent is comparable to the N2 binding enthalpy in Li-LSX, the overall regeneration energy needed for the O2-selective material would be substantially lower, perhaps even 50% lower, assuming the material exhibits a high selectivity for O2 (ESI Section S2†).28 In principle, energy-efficient O2-selective adsorbents could be implemented in all air separation applications that currently utilize N2-selective adsorbents. Additionally, O2-selective adsorbents could promote the adoption of new separation processes based on adsorption, including small-scale, variable-load oxygen production, mixed-matrix membrane air separations, and hybrid processes with cryogenic distillation. Overall, a commercially viable O2-selective adsorbent could support the decentralization of oxygen production and utilization. Furthermore, O2-selective adsorbents with high volumetric capacities might be less costly than cryogenic distillation for mid- and even large-scale air separations, enabling the use of smaller contactors and thereby incurring lower capital expenses.29
1.3 Metal–organic frameworks as O2-selective adsorbents
Research focused on the development of O2-selective adsorbents has been ongoing since the 1970s,30–34 although few materials have been discovered that show thermodynamic selectivity for oxygen over nitrogen, and no O2-selective adsorbent is commercially viable at present. Extensive early work focused on the development of molecular compounds that bind O2 in solution and in the solid-state, most notably featuring cobalt(II).30–34 However, many of these complexes exhibit poor stabilities, low capacities, and/or irreversible O2 binding, making them unsuitable for implementation in practical air separation processes. Immobilization of cobalt complexes on porous solid substrates, such as silicates and polymers,35–37 has been shown to improve cycling performance, but these materials typically exhibit low O2 capacities. Considering these shortcomings, an ideal adsorbent would incorporate a high density of redox-active open metal sites immobilized in a robust, rigid porous framework.Metal–organic frameworks (MOFs) can satisfy both criteria. These crystalline, porous materials are assembled from metal nodes and multitopic organic linkers, and they have emerged as promising candidates to replace traditional adsorbents in numerous industrial applications.38,39 Structure types of MOFs span a vast library, and in some cases, the as-synthesized material features metal ions with coordination spheres that are completed with solvent molecules introduced during synthesis. Removal of this solvent with heating under reduced pressure (desolvation) generates coordinatively-unsaturated (or “open”) metal centers that can directly interact with adsorbate molecules. The appropriate choice of metal and linker can give rise to a material featuring open metal sites that preferentially bind certain guests based on specific selectivity handles, including gas polarizability,40 π-acidity,41 and electron affinity.42
In 2010, the metal–organic framework Cr3(btc)2 (btc3− = 1,3,5-benzenetricarboxylate) was reported to strongly bind O2via electron transfer to form a CrIII–O2− adduct.42 The pristine material features a high-density of exposed chromium(II) sites and accordingly displays a high O2 uptake of 11 wt% at 298 K and an O2/N2 selectivity of ∼22 based on single-component adsorption data, notably five times higher than that achieved with cobalt(II) molecules immobilized on silica.36 This discovery represented a significant advance in the design of O2-selective adsorbents and validated the strategy of using redox-active open metal sites in MOFs to target guests based on differences in electron affinity. However, because of the highly exothermic O2 binding in Cr3(btc)2, the material capacity decreases with repeated cycling, likely owing to incomplete regeneration of the open metal sites and/or sample degradation. This result therefore also underscores the importance of designing a material exhibiting selective and reversible O2 binding. Since this seminal work, several studies have focused on the design of MOFs featuring open metal sites that are capable of selective oxygen capture via electron transfer chemistry.43–45 This effort has focused on the chemical space containing monovalent, divalent, and trivalent redox-active metal sites in diverse coordination environments, ranging from anionic oxygen donors in a square pyramidal geometry to nitrogen heterocycles in a trigonal pyramidal geometry.42–48 Although no MOF has been discovered to date that can be considered a commercially viable O2-selective adsorbent, a number of promising systems and materials design strategies have emerged in recent years.
In this Perspective, we provide a comprehensive survey of the field of O2-selective MOFs with the goal of motivating continued progress and new directions in this emerging area of research. A summary of key molecular and biological systems that reversibly bind O2 is presented in Section 2 to introduce the various species known to form upon binding and reduction of O2 at open metal sites, as well as relevant design considerations for tuning O2 binding in MOFs. In Section 3, these concepts are applied in a survey of key framework materials studied to date, which highlights progress and promising areas for future exploration. A critical contribution in the latter section is an in-depth examination of the relevant thermodynamic parameters and working conditions for adsorptive air separation processes. Traditionally, only O2 binding enthalpies have been presented in the literature along with O2/N2 selectivities at a range of temperatures, precluding meaningful comparisons across materials. We discuss the free energy of O2 binding as the most important metric to consider when evaluating and designing new MOFs for practical air separations and calculate ΔG values for preliminary comparison and benchmarking of existing materials. In Section 4, density functional theory (DFT) approaches for materials evaluation are discussed that can support experimental efforts, and promising MOF targets based on the aforementioned thermodynamic considerations are identified. A brief summary and conclusions are presented in Section 5.
2. Design inspiration from molecular and biological examples of reversible O2 binding
2.1 Fundamental considerations
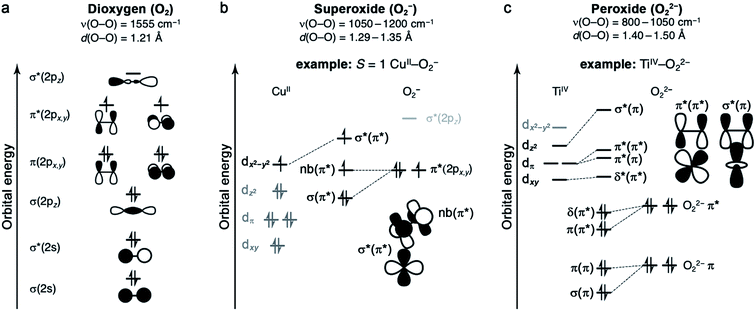
Oxygen binding at a redox-active metal center is an exothermic reaction, facilitated by a strong charge-transfer component. The resulting enthalpic driving force is offset to varying degrees by an entropic penalty.49,50 The entropy of O2 binding is made up of translational, rotational, vibrational, and electronic components (ESI Section S3†), and ultimately cannot exceed the entropy of free O2.51 Typically, the greater the degree of charge transfer, the stronger the metal–oxygen bonding, and the fewer degrees of freedom for the bound O2. As such, enthalpy and entropy tend to correlate broadly.49 Nevertheless, as discussed below, it is important to quantify ΔS in addition to ΔH, because small entropic changes can meaningfully impact ΔG under practical conditions for O2 separations.The properties of O2 as a ligand are determined by its frontier molecular orbitals (Fig. 1a).49,52 As a result of its filled and stable π and σ bonding orbitals, oxygen features a strong O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond and is a poor π donor. Each π* orbital contains an unpaired electron, giving rise to the S = 1 ground state of dioxygen. Finally, O2 features a high-energy vacant σ*(2pz) orbital. One- or two-electron reduction results in partial or complete filling of the π* orbitals and the formation of superoxide (O2−) or peroxide (O22−) ligands, respectively. Successive reductions weaken and break the O–O π bond, simultaneously stabilizing the σ*(2pz) orbital such that it can participate in back-bonding interactions.53 While it is generally useful to classify oxygen as a ligand according to the level of reduction, from neutral dioxygen to peroxide, transition metal–O2 complexes can be highly covalent, which can complicate the assignment of formal oxidation states.
O double bond and is a poor π donor. Each π* orbital contains an unpaired electron, giving rise to the S = 1 ground state of dioxygen. Finally, O2 features a high-energy vacant σ*(2pz) orbital. One- or two-electron reduction results in partial or complete filling of the π* orbitals and the formation of superoxide (O2−) or peroxide (O22−) ligands, respectively. Successive reductions weaken and break the O–O π bond, simultaneously stabilizing the σ*(2pz) orbital such that it can participate in back-bonding interactions.53 While it is generally useful to classify oxygen as a ligand according to the level of reduction, from neutral dioxygen to peroxide, transition metal–O2 complexes can be highly covalent, which can complicate the assignment of formal oxidation states.
2.2 Dioxygen complexes
Stable metal–O2 molecular complexes are rare because neutral O2 is generally a poor ligand. Nonetheless, there are cases where O2 binding induces a perturbation of the metal electronic structure that imparts stability in the absence of appreciable net electron transfer. For example, the Pauling and Coryell model of hemoglobin involves O2 binding to an initially high-spin (S = 2) heme iron(II) center, resulting in singlet O2 bound to a low-spin (S = 0) iron(II).54 This model is qualitatively correct for the picket fence iron porphyrin, FeII(TpivPP)(1-MeIm) (TpivPP = meso-tetra(α,α,α,α-o-pivalamidophenyl)porphyrin; 1-MeIm = 1-methylimidazole),51,55,56 a hemoglobin model complex, but is not fully descriptive of hemoglobin (see Section 2.6).57 While there is no discrete electron transfer from iron to O2 in this complex, the binding is nonetheless very exothermic in the solid state (ΔH = −65.3 kJ mol−1, Table 3), and importantly reversible.51 Indeed, no degradation of the complex was observed over the course of more than 200 O2 binding/vacuum cycles. This strong yet reversible binding stems in part from strong backbonding from the metal into the O2 π* orbital, enabled by the high degree of porphyrin-iron covalency.56 Additionally there is σ-donation from O2 to the dz2 orbital of iron. These interactions collectively weaken the O–O bond, resulting in a redshifted O–O stretch of 1159 cm−1, which is within the diagnostic range for superoxide.58 This example illustrates the limitations of formal assignments in highly covalent metal–O2 interactions and demonstrates that the O–O stretching frequency is not always sufficient to assign the degree of O2 reduction definitively.59 Furthermore, this result suggests targeting iron-based frameworks with highly covalent bonding between metal and linker as a strategy to achieve strong, reversible O2 binding.| Compound | −ΔH (kJ mol−1) | −ΔS (J mol−1 K−1) | ΔG298 (kJ mol−1) | M–O2 assignment | Ref. |
|---|---|---|---|---|---|
| a Collected in the solid state. 1-MeIm = N-methylimidazole. b Binding of the O2 to the first site in human hemoglobin in a buffer solution with pH = 7.6. c Binding of O2 to the fourth site human hemoglobin in a buffer solution with pH = 7.6. d N4 = N1N1N4N4-Tetrakis(2-(pyridin-4-yl)ethyl)butane-1,4-diamine. e Binding of O2 to P interruptus hemocyanin in buffer solution with pH = 9.6. | |||||
| Fe(TpivPP)(1-MeIm)O2a | 65.3 | 183.0 | −10.8 | FeII–O2 | 55 |
| Co(TpivPP)(1-MeIm)O2a | 55.6 ± 3.8 | 192.5 ± 12 | 1.70 | CoIII–O2− | 62 |
| (Hemoglobin)O2b | 43.1 ± 4.6 | 74.1 ± 15.5 | −21.0 | FeII–O2/FeIII–O2− | 91 |
| (Hemoglobin)(O2)4c | 85.0 ± 18.0 | 190.6 ± 60.2 | −28.1 | FeII–O2/FeIII–O2− | 91 |
| [Cu2(N4PY2)(O2)]2+d | 58 ± 2 | 165 ± 8 | −9.0 | Cu2O22− | 64 |
| (Hemocyanin)O2e | 46 | 67 | −26 | Cu2O22− | 50 |
2.3 Superoxide (O2−) complexes
Metal–O2− complexes form upon transfer of a single electron from a reducing metal center (e.g., CrII, MnI, FeII, NiI, and CuI) into the half-filled π* orbital of O2.52 Population of this antibonding orbital weakens the π bond of O2, resulting in a modest elongation of the O–O distance from 1.21 to 1.29–1.35 Å, as well as a redshift of the O–O stretching mode from 1555 cm−1 to 1050–1200 cm−1 (Fig. 1b).23,60 Superoxide may bind in either a side-on or an end-on mode. The end-on binding mode involves localization of negative charge on the proximal oxygen and a bent M–O–O angle. Side-on binding, while potentially more sterically demanding, can improve metal–superoxide orbital overlap. For both binding modes, the unpaired electron on superoxide resides in a π* orbital, and magnetic coupling between the superoxide and metal center is determined by overlap of this orbital with half-filled metal d orbitals. For example, in an end-on d9 copper(II) superoxide complex (Fig. 1b), the singly occupied dx2−y2 orbital is orthogonal to the superoxide π* non-bonding orbital, affording an S = 1 ground state that arises from ferromagnetic coupling between the metal and O2−.61The formation of end-on superoxide upon O2 binding is also well-documented for five-coordinate cobalt(II) Schiff base complexes. Oxygen binding in solution results in the formation of a superoxide ion bound to cobalt(III), with enthalpies ranging from −33 to −77 kJ mol−1, and a corresponding high entropic penalty of >150 J mol−1 K−1.24 The oxygenation of cobalt(II) Schiff base complexes in solution is often reversible, although it is very dependent on solvent and temperature. Particularly at high temperature and in non-polar solvents, the formation of a CoIII2(μ2-O22−) species can occur, which is usually an irreversible process.24 Another well-known CoIII–O2− complex is Co(TpivPP)(1-MeIm)(O2), a model for cobalt-substituted hemoglobin that reversibly binds O2 (Table 3).58,62,63
2.4 Peroxide (O22−) complexes
In general, peroxide complexes form upon transfer of two electrons from one or more metal centers to fill the formerly half-occupied π* orbitals of O2. In compounds featuring a metal prone to two-electron chemistry, such as titanium(II), manganese(II), or a second- or third-row transition metal, both electrons may derive from the same metal center.52 Reduction of O2 to peroxide is associated with significant lengthening of the O–O bond, from 1.21 to 1.40–1.50 Å, as well as a pronounced redshift in the O–O stretching mode to approximately 800–1050 cm−1 (Fig. 1c).60 In mononuclear complexes, peroxide tends to bind in a side-on fashion, as there is no efficient mechanism for polarizing the O22− charge on a single oxygen atom (Fig. 1c). One notable peroxide complex is oxy-hemocyanin, which features a binuclear copper(II) core with a side-on bridging O22−.27 This oxygen-binding protein has inspired the development of a diverse class of molecular mimics,50 including [Cu2(N4PY2)(O2)]2+ (N4 = N1,N1,N4,N4-tetrakis(2-(pyridin-4-yl)ethyl)butane-1,4-diamine), which binds O2 reversibly in solution.64 Interestingly, increasing temperature and decreasing O2 pressure in the headspace of the reaction vessel enables repeated cycling between oxygenated and deoxygenated forms. This molecule binds O2via single-electron transfer from each copper(I), and this event is associated with an enthalpy of −58 kJ mol−1 and an entropy of −165 J mol−1 K−1, such that the reaction is exergonic at 298 K (Table 3).2.5 Metal and ligand selection and secondary-sphere effects
As discussed above, reversible O2 binding at open metal sites can generate a spectrum of O2 species and binding modes. Further fine-tuning of O2 binding affinity can be accomplished by changing the metal identity in an isostructural series of compounds, perturbing the electronic structure of the metal via ligand modifications,61–63 or by altering the steric and noncovalent interactions in the secondary coordination sphere (Fig. 2).33,49,65 The first effect is well-illustrated by the series of complexes (TPP)M(O2)(py) (TPP = tetraphenylporphyrin; M = CrII, FeII, or CoII; py = pyridine), wherein the equilibrium constant for oxygenation increases from Co to Cr (Fig. 2a).66–69 Indeed, O2 binding in Cr(TPP)(py) is irreversible, even at low temperatures.68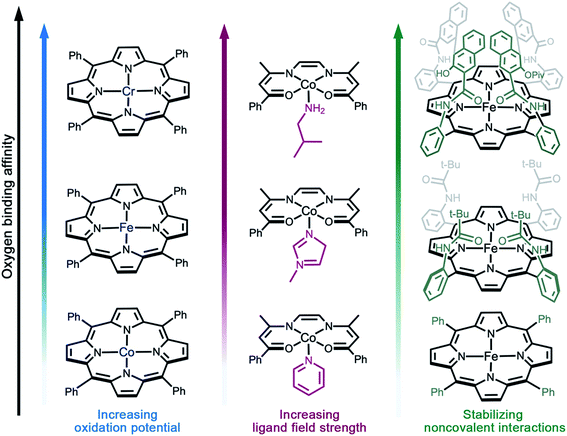 | ||
| Fig. 2 Illustration of design strategies from molecular chemistry to enhance O2 binding affinity. (a) Utilizing early- to mid-transition metals,67–69 (b) increasing the ligand field strength,71 and (c) using bulky side groups that engage in stabilizing non-covalent interactions with the reduced O2 species.55,67,82 Axial solvent ligands are omitted for clarity; in the single coronet iron porphyrin (top right), the distal two naphthalene molecules have been modified for simplicity. | ||
Examples of electronic structure perturbation by ligand modification abound for divalent first-row metal complexes.49,65,69–71 In numerous cobalt(II) five-coordinate Schiff base and five-coordinate porphyrin complexes, cobalt adopts a low-spin, d7 configuration (S = 1/2), with the unpaired electron residing in the dz2 orbital.72–75 Oxygen binds end-on to the metal site, mediated by a dz2–π* orbital interaction that enables electron transfer.76 It is possible to destabilize the dz2 energy by changing the axial ligand, which lowers the potential for metal-centered oxidation, thereby increasing O2 affinity (Fig. 2b).49,65,76,77 In addition, derivatization of the axial ligand can modify the σ and π bonding contributions to oxygen binding. Analogously, subtle modifications to the linker in cobalt(II) frameworks have been shown to give rise to substantial differences in O2 binding enthalpies (see Section 3.5).
Noncovalent interactions can also stabilize bound O2 or promote reversible O2 binding, as exemplified in several biomimetic systems,55,78–85 and hydrogen bonding is known to stabilize the reduced O2 species bound in myoglobin and hemoglobin.70,86 Additionally, incorporating steric bulk around the metal–O2 adduct can stabilize reactive O2 intermediates. For example, iron(II)–porphyrin compounds undergo irreversible oxidation to form oxo-bridged dinuclear species in solution.87 In contrast, the picket fence iron(II) porphyrin FeII(TpivPP)(1-MeIm)2 features substantial steric bulk around the metal center, which prevents bridge formation and enables reversible O2 binding at 25 °C (Fig. 2c).55 More recent strategies combining steric protection with favorable non-covalent interactions have also proven fruitful. For example, single-coronet and twin-coronet iron(II) porphyrins featuring hydroxyl-functionalized dinaphthalene moieties have been designed to replicate the hydrophobic environment of the active sites in hemoglobin and myoglobin and to promote biomimetic hydrogen bonding interactions with bound O2.82,83 Despite their ubiquity in biology and small molecule chemistry, secondary sphere interactions remain underutilized in MOF chemistry and represent a worthwhile target for future research in the design of O2-selective materials.88
2.6 Lessons from biology: cooperative O2 binding
Hemoglobin is the prototypical iron-containing O2 transport protein and features four subunits, with each containing a heme active site.89,90 The heme iron(II) center is a five-coordinate species with the fifth site occupied by an axial histidine ligand, resulting in a high spin (S = 2) ground state. Dioxygen binds the first heme site with an enthalpy of −43.1 kJ mol−1, yielding a diamagnetic species with an end-on bound O2.91 A recent study of oxyhemoglobin using X-ray spectroscopy and a valence bond configuration interaction multiplet model revealed mixed low spin FeII/FeIII character with at least 50% iron(III), reflecting a highly covalent Fe–O2 interaction.57 The change in the iron(II) spin state upon O2 binding is associated with the depopulation of iron-based orbitals with σ* character, resulting in a contraction of the iron–nitrogen bonds. This local structural change is propagated to the global protein structure via the axial histidine, effecting a transition from the so-called ‘tense’ state (low O2 affinity) to the ‘relaxed’ state (high O2 affinity).89 This change facilitates subsequent O2 binding events at the other heme sites. For example, O2 binding to the fourth heme is associated with an enthalpy of −85.0 kJ mol−1 (Table 3).91 This cooperativity is key to the function of hemoglobin, enabling the capture and release of relatively large quantities of O2 in response to a small change in oxygen partial pressure, and is associated with a sigmoidal O2 binding curve. An unrealized goal in the design of O2-selective MOFs is to harness cooperativity to enhance material working capacities for O2 separations, an approach that has proven to be effective for other gaseous adsorbents, including CO2 and CO.92,93 As discussed below (see Section 3.4), a triazolate-based framework featuring high-spin iron(II) has been shown to react with O2 to form low-spin iron(III) bound to superoxide, reminiscent of the mechanism of O2 binding in hemoglobin.45 As such, further exploration of the reduction of O2 to superoxide by iron-containing MOFs of different topologies may be a fruitful direction in pursuit of cooperative O2 binding in MOFs.3. Oxygen-selective metal–organic frameworks
3.1 Enthalpy and entropy considerations for O2 adsorbents
The enthalpy of O2 binding at an open metal site is a critical parameter for evaluating the adsorption performance of a material. Indeed, the energy consumption of an adsorption process depends heavily on the enthalpy of adsorption, and in some cases, the enthalpy can represent half of the total energy required for adsorbent regeneration.94 As such, the O2 binding enthalpy is a critical metric to optimize in the design of a commercially relevant O2-selective MOF, and one that can be judiciously tuned using synthetic chemistry. Perhaps unsurprisingly, there has been a historical focus on this particular parameter. In general, the lower the O2 binding enthalpy of a material, the lower the corresponding energy demand for adsorbent regeneration. However, if the enthalpy of O2 binding is too low, the material may not exhibit sufficient selectivity for O2 over N2.The enthalpy of N2 binding at open metal sites has been experimentally determined for a number of frameworks44,45,95,96 with corresponding values typically ranging from −10 to −25 kJ mol−1 (vs. ΔH = −22.5 kJ mol−1 for Li-LSX97). Accordingly, candidate MOFs for O2-selective air separations should ideally exhibit O2 binding enthalpies well above this range. However, materials that exhibit O2 binding enthalpies that surpass −80 kJ mol−1 may not afford any energy savings over the current industrial benchmark, N2-selective Li-LSX, due to the energy required to regenerate the O2 adsorbent (see ESI Section S2†). Thus, to provide a baseline for analysis, we propose −45 kJ mol−1 as a reasonable target O2 binding enthalpy, which would correspond to a material regeneration energy that is ∼50% less than that required for Li-LSX.28,97 While an even higher enthalpy of adsorption is likely to be associated with greater O2/N2 selectivity, it would come at the cost of greater energy demand for regeneration.
While the enthalpy of O2 binding is a key factor that will impact the overall energy of adsorbent-based air separations, this parameter must be considered together with the entropy of adsorption. Indeed, it is ΔG, and not ΔH alone, that determines the adsorption properties of a material. In particular, ΔG for the primary O2 binding site will determine the working capacity under a given set of conditions.98 This information is necessary to establish the potential performance of the material in an adsorptive process (see Section 3.5). As such, a binding enthalpy of −45 kJ mol−1 is desirable as long as the corresponding entropy of binding results in an appropriate ΔG for the adsorption process. Relative to binding enthalpy, it is much more difficult to tune the entropy of O2 binding via metal and/or linker modifications. Entropies of adsorption are not typically reported in the literature, and currently there is no consistent method for reporting both ΔH and ΔS for O2-selective adsorbents.99 As such, to enable a more rigorous comparison of materials in this Perspective, we calculated enthalpy and entropy values for several key O2-selective frameworks using published Langmuir–Freundlich fits or O2 adsorption data (see ESI Sections S4 and S5 for details and Tables S1–S9†).44–47,88 More generally, we suggest that routine determination of binding enthalpies and entropies is a critical facet of materials characterization, requiring minimal additional work, that will enable more rigorous development and benchmarking of MOFs for practical application.
3.2 Key framework structure types
Despite the effectively limitless structural variability possible for metal–organic frameworks, a relatively limited number of frameworks have been studied for selective O2 adsorption. Here, we briefly describe six key framework structure types that have been studied for selective O2 capture (Fig. 3).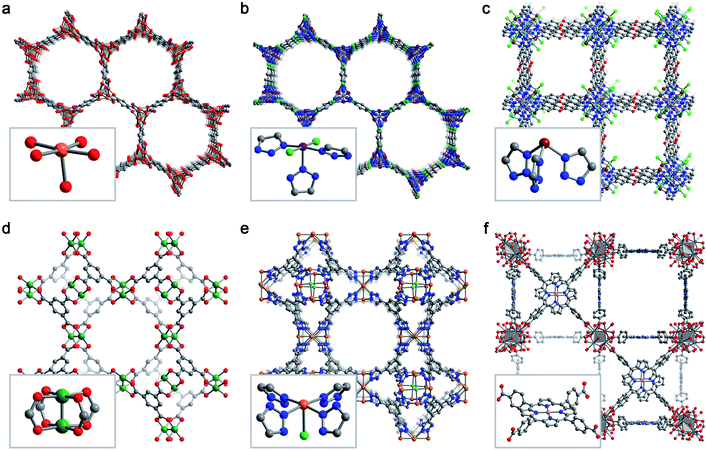 | ||
| Fig. 3 Representative structures obtained from powder X-ray diffraction (a, b, e), powder neutron diffraction (c, d), or single-crystal X-ray diffraction (f) depicting the six MOF structure types discussed in Section 3.2. Insets show the first coordination sphere of each open metal site. (a) Fe2(dobdc),43 (b) Co2Cl2(bbta),88 (c) CuI-MFU-4l,110 (d) Cu3(btc)2,115 (e) Fe-BTTri,124 and (f) Mn-PCN-224.47 Orange, purple, green, pink, grey, red, and blue spheres represent Fe, Co, Cu, Mn, C, O, and N atoms, respectively; H atoms are omitted for clarity. | ||
| MOF | Theoretical O2 capacitya | Experimental uptake at 1 barb | IAST/T (K) | −ΔHO2 (kJ mol−1) | O–Oc (cm−1) | Ref. | |||
|---|---|---|---|---|---|---|---|---|---|
| mmol g−1 | wt (%) | mmol g−1 | wt% | T (K) | |||||
| a Calculated based on gravimetric density of open metal sites. b For Cr-BTT, Cr3(btc)2, and Fe2(dobdc), reported uptakes in wt% were converted to mmol g−1; all other framework capacities were reported in mmol g−1 and converted to wt%. c Stretching frequencies reported at temperatures associated with reversible O2 binding. | |||||||||
| Cr-BTT | 3.94 | 11.2 | 2.57 | 7.59 | 298 | 2570/298 | 65 | 1193 | 123 |
| Cr3(btc)2 | 6.43 | 17.1 | 3.9 | 11 | 298 | 1129 | 42 | ||
| CuI-MFU-4l | 1.69 | 5.13 | 2.33 | 6.94 | 233 | 53 | 46 | ||
| Fe-BTTri | 3.91 | 11.1 | 5.90 | 15.9 | 195 | 27/195 | 51 | 1199 | 45 |
| Mn-PCN-224 | 0.73 | 2.3 | 0.86 | 2.7 | 298 | 49.6(8) | 984 | 47 | |
| Co2(OH)2(bbta) | 6.45 | 17.1 | 7.57 | 19.5 | 195 | 42/195 | 49(2) | 1151 | 88 |
| Co-BDTriP | 3.87 | 11.0 | 4.8 | 13 | 195 | 105/195 | 47(1) | 44 | |
| Fe2(dobdc) | 6.54 | 17.3 | 8.16 | 20.7 | 211 | 8/214 | 41 | 1129 | 43 |
| Co-BTTri | 3.86 | 11.0 | 4.8 | 13 | 195 | 41/195 | 34(1) | 44 | |
| Fe-PCN-224 | 0.73 | 2.3 | 0.26 | 0.83 | 298 | 34(4) | 129 | ||
| Co-PCN-224 | 0.73 | 2.3 | 2.00 | 6.02 | 195 | 15.2(6) | 130 | ||
3.3 Tuning O2 binding through ligand modification
Typically, MOFs that feature open metal sites are constructed using weak-field linkers, such as 2,5-dioxido-1,4-benzenedicarboxylate.100,133 As such, the metal nodes are best described as Lewis acidic134 and generally interact weakly with oxygen.95 A telling example is Co2(dobdc), which remains high-spin when bound to CO, and exhibits an O2 binding enthalpy of just −18.56(3) kJ mol−1.96 As discussed in Section 2, strong oxygen binding in molecular cobalt complexes is well documented,49 but it was only in 2016 that a cobalt(II)-based framework with a stronger ligand field than Co2(dobdc) was reported. The material Co-BTTri exhibits a modest O2 adsorption enthalpy of −34(1) kJ mol−1 (Table 4) for loadings up to ∼2 mmol g−1 (6 wt%).44 Vibrational modes corresponding to the O2 adduct could not be observed at room temperature, but calculations suggest there is only partial electron transfer from cobalt(II) to O2 (0.31 electron equivalents). The theoretical uptake of the material, assuming one bound O2 at each low-spin cobalt(II) site, is 3.86 mmol g−1 (11.0 wt%); however, the experimental uptake at the cobalt sites was approximately 2.8 mmol g−1 (8.2 wt%), as determined from the inflection point in the plot of the isosteric heat of adsorption as a function of loading. This lower than expected capacity is common in frameworks with open metal sites and may be due to the presence of residual coordinated synthesis solvent or blocked pore access135 or potentially even metal site vacancies.136,137 Interestingly, the N2 enthalpy of adsorption in Co-BTTri is only −12(1) kJ mol−1,44 and this relatively weak affinity for N2 suggests that the low-spin cobalt(II) sites are neither strongly Lewis acidic or π-basic.Replacement of the triangular BTTri3− linker with the more basic BDTriP3−, which features one pyrazolate and two triazolate donors, yields the framework Co-BDTriP.44 Characterization of this material via single-crystal X-ray diffraction supports the presence of a statistical distribution of five unique cobalt centers coordinated by a combination of triazolates and pyrazolates. Notably, at very low loadings, the isosteric heat of O2 adsorption in Co-BDTriP is −47(1) kJ mol−1, corresponding to O2 bound at approximately 12% of the cobalt(II) sites in the material. This enthalpy is much larger than the highest binding enthalpy characterized for Co-BTTri (and within the range observed for cobalt(II) Schiff complexes, see Section 2.3), and was ascribed to O2 binding at cobalt sites ligated by three or more pyrazolates. Relative to the enthalpy of O2 binding in Co-BTTri at low-loading, this larger value can be rationalized as arising from a greater degree of charge transfer from cobalt(II) to O2, resulting from the more basic (electron-donating) pyrazolate groups. With increasing gas loading, the enthalpy of O2 binding in Co-BDTriP decreases, and at a loading of approximately 1 mmol g−1, Co-BDTriP and Co-BTTri exhibit similar binding enthalpies. Interestingly, increasing the linker basicity from Co-BTTri to Co-BDTriP has little effect on the enthalpy of N2 adsorption. The more basic linker environment in Co-BDTriP may destabilize the dz2 orbital of cobalt(II) relative to that in Co-BTTri, yielding a less Lewis-acidic metal center and thereby diminishing the σ interaction between the HOMO of N2 and cobalt, compensating for any enhanced π-backbonding. Considering the enhancement in O2 binding enthalpy at low loadings upon moving from Co-BTTri to Co-BDTriP, a promising target may be the material Co3[(Co4X)3(BTP)8]2 (hereafter, Co-BTP, H3BTP = 1,3,5-tri(1H-pyrazol-4-yl)benzene), featuring all pyrazolate donors. Such a material isostructural to Co-BTTri and Co-BDTriP has not yet been isolated, although the framework Co3(BTP)2 has previously been synthesized,138 suggesting that appropriate synthetic conditions may yield Co-BTP. In general, the results for Co-BTTri and Co-BDTriP indicate that further investigation of suitable frameworks featuring basic azolate-based linkers and cobalt(II) centers is a worthwhile pursuit.
The open metal sites in Co2Cl2(bbta) exhibit a square pyramidal metal coordination geometry, similar to that in Co-BTTri and Co-BDTriP. However, the metal sites are ligated by two trans basal chloride ions and three triazolates (Fig. 3b).105 The O2 binding enthalpy of −15 kJ mol−1 in Co2Cl2(bbta)88 is significantly lower than in Co-BTTri and Co-BDTriP, and perhaps surprisingly, even lower than in Co2(dobdc). Here, the replacement of a strong σ-donating nitrogen ligand with a weakly σ-donating chloride likely attenuates metal-to-oxygen charge transfer, and thus the cobalt(II) sites in Co2Cl2(bbta) are both insufficiently reducing and poor Lewis acids.
Replacing the bridging chlorides in Co2Cl2(bbta) with more basic hydroxides yields the material Co2(OH)2(bbta).106 This framework exhibits an O2 binding enthalpy of −49(2) kJ mol−1 at low loadings, the highest value reported to date for a cobalt framework.88In situ variable-temperature diffuse reflectance Fourier transform spectroscopy (DRIFTS) was used to characterize the O2 binding and revealed an O–O stretch at 1151 cm−1, consistent with a superoxide moiety bound end-on to cobalt(III). DRIFTS data also indicate that the superoxide is stabilized by hydrogen bonding interactions with the bridging hydroxo groups of the framework, reminiscent of the stabilization of superoxide in oxygen binding proteins. Calculations suggest that this secondary coordination lowers the binding energy of O2 by 20 kJ mol−1, highlighting the significant impact of subtle coordination sphere changes in isostructural MOFs. This additional interaction also contributes to a very large entropy of adsorption of −186(7) J mol−1 K−1.
Interestingly, the calculated saturation capacity of the strong O2 binding site in Co2(OH)2(bbta)—determined from fits using a dual-site Langmuir model—was found to be 2.46 mmol g−1, only 38% of the theoretical capacity based on open metal site density. However, data from powder X-ray diffraction analysis revealed that the actual occupancy is much higher (approximately 75%), indicating that the chosen adsorption model was not adequate for describing the O2 uptake in this material. Together with in situ DRIFTS data obtained at different O2 loadings, these results revealed that O2 binding weakens as a function of loading, a rare example of example of negatively cooperative gas binding in a metal–organic framework.139 Notably, the same extended lattice interactions that promote initial strong O2 binding contribute to this unusual effect. Indeed, with increasing O2 loading, the proportion of cobalt(III)–O2− moieties also increases, rendering neighboring cobalt(II) sites less electron-donating and therefore less likely to bind O2via electron transfer. This unexpected result highlights that the nature of electronic communication between metal sites in MOFs must be tuned carefully to achieve desired O2 binding properties. Here, the appropriate choice of a secondary metal could potentially give rise to an ordered mixed-metal framework of the type CoM(OH)2(bbta) that exhibits a high enthalpy of O2 binding in the absence of negative cooperativity. In this case, it may be possible to achieve an O2 uptake as high as 3 mmol g−1. However, due to the presence of hydrogen bonding interactions, even in this case, O2 binding is still likely to be associated with a high entropic penalty. As an alternative, replacing the hydroxide moieties with bridging methoxide or methylthiolate anions would remove such interactions and potentially still provide sufficient reducing power at the metal center to ensure a high binding enthalpy.
3.4 Tuning O2 binding through metal selection
One of the most well-studied isostructural framework series is M2(dobdc) (M = MnII, FeII, CoII, NiII, CuII, ZnII).133 Excluding the iron variant, the open metal sites in this family behave like Lewis acids, and generally, they preferentially bind N2 over O2,43,95,96 given the greater polarizability and quadrupole moment of N2 (Table 1).97 Characterization of O2 binding in the Mn, Co, Ni, and Cu variants revealed that the metal–O2 interactions are also predominately electrostatic in nature.95,96The case of O2 binding in Fe2(dobdc) is unique and can be partly rationalized by the fact that iron(II) exhibits a lower ionization energy than MnII, CoII, NiII, and CuII. Uptake of O2 in Fe2(dobdc) results in very steep adsorption isotherm and occurs via superoxide or peroxide formation, depending on the temperature.43 At 211 K, ∼90% of the iron sites reversibly bind O2, with a total uptake for the material of 6.54 mmol g−1 (17.3 wt%) at 1 bar. Notably, the material is stable to repeated cycling and exhibits no loss in capacity at 211 K over the course of at least 13 adsorption/desorption cycles. The enthalpy of O2 adsorption in this material was calculated to be −41 kJ mol−1. Although this value is lower than the binding enthalpy determined for Co2(OH)2(bbta), the associated O2 moiety in Fe2(dobdc) is more reduced than that bound in Co2(OH)2(bbta), as judged from their respective O–O stretches of 1129 and 1151 cm−1 (Table 4). The enhanced stabilization of bound O2 in Co2(OH)2(bbta) relative to Fe2(dobdc) can again be ascribed to the substantial enthalpic contribution from hydrogen bonding (as discussed above). At room temperature, O2 binding in Fe2(dobdc) results in irreversible formation of iron(III)–peroxide species at half of the iron sites, with the second reducing equivalent provided by the remaining iron sites. As expected, the O–O bond of the reduced moiety is substantially weakened, and a very low O–O stretch of 790 cm−1 was characterized via IR spectroscopy. The ordered substitution of 50% or more of the iron(II) sites in Fe2(dobdc) with another divalent metal could potentially suppress the electron transfer between metal sites that leads to irreversible peroxide formation and enable access to a material exhibiting high, reversible O2 uptake. Of note, while metal⋯metal communication in Fe2(dobdc) has a deleterious effect on O2 uptake, it is interesting to consider how the participation of two adjacent metal sites in one reduction and binding event, as observed here, could be manipulated via linker and secondary-sphere interactions to achieve positive cooperativity in O2 binding.
The framework Fe-BTTri was recently reported, enabling preliminary evaluation of the influence of metal identity on O2 binding in M-BTTri. Interestingly, the local iron coordination environment in this material bears some resemblance to the heme site of hemoglobin.45 At 195 K, 64% of the exposed high-spin iron(II) framework sites bind O2via superoxide formation with an enthalpy of −51 kJ mol−1, which is 1.5 times that of the binding enthalpy in Co-BTTri. The material reversibly adsorbs 3.3 mmol g−1 (9.6 wt%) of O2 at 195 K and 210 mbar over the course of 5 cycles. In situ DRIFTS data obtained at 195 K revealed an O–O stretch at 1199 cm−1, which, together with Mössbauer data, confirms the presence of superoxide bound to low-spin iron(III), reminiscent of the mechanism of O2 binding in hemoglobin (Section 2.6). This complete electron transfer from iron(II) to O2 contrasts with the partial electron transfer upon O2 binding in Co-BTTri. Above 258 K, O2 binding is irreversible.
The M-PCN-224 (M = MnII, FeII, CoII) framework class is another instructive example to evaluate the importance of metal identity for O2 binding in MOFs.47,129,130 In contrast to what is observed for M2(dobdc), the enthalpy of O2 binding in M-PCN-224 increases from cobalt to iron to manganese, consistent with the general trend observed for metalloporphyrin complexes (Section 2). Note, however, that O2 binding to Mn-PCN-224 (ref. 47) is a two-electron process, whereas one-electron reduction occurs upon O2 uptake in the other two frameworks. In Mn-PCN-224, 85% of the manganese(II) sites bind O2 with an enthalpy of −49.6(8) kJ mol−1. The resulting adduct is an η2-peroxomanganese(IV), and the reaction is reversible upon purging with argon.
The framework Fe-PCN-224 (ref. 129) provides a rare example of a base-free heme model. In this material, the high-spin ferrous centers bind O2 at 195 K to form low-spin iron(III)–superoxo moieties, as characterized using single-crystal X-ray diffraction and Mössbauer spectroscopy data collected at 100 K. Oxygen binding is only appreciable at 195 K and below, and from low-temperature (141, 156, and 195 K) isotherm data the O2 binding enthalpy was determined to be −34(4) kJ mol−1, consistent with the formation of a superoxo moiety. Notably, this value is substantially lower than that associated with O2 binding in hemoglobin as well as in biomimetic compounds that feature a bound axial imidazole.51,91 Using reported isotherm data obtained at higher temperatures (226, 273, and 298 K), we calculated an even lower binding enthalpy of −19(2) kJ mol−1. The large difference in the enthalpy values for the given temperature regimes suggests that binding of O2 at and near room temperature is associated with the formation of an iron–O2 adduct distinct from that observed at lower temperatures. In all, these data suggest that electron transfer from iron to O2 in this system is temperature-dependent, and further studies are warranted to investigate this possibility.
Dioxygen binding in Co-PCN-224 (ref. 130) results in the formation of a low-spin CoIII–superoxide complex, as characterized via single-crystal X-ray diffraction and EPR spectroscopy performed at 85 K. Oxygen adsorption data collected at higher temperatures (113, 141, 156, and 195 K) were used to calculate an enthalpy of O2 binding of −15.2(6) kJ mol−1, which is much lower than that associated with superoxide formation in Co(TpivPP)(1-MeIm) (Table 3). It is possible that at the higher temperatures associated with isotherm data collection, O2 binding results in a CoII–O2 species. Indeed, an enthalpy of −15.2(6) kJ mol−1 is more consistent with reported enthalpies of −15 and −18.56(3) kJ mol−1 associated with the formation of CoII–O2 adducts in Co2Cl2(bbta)88 and Co2(dobdc),96 respectively. In all, the above results suggest that the detailed investigation of O2 binding modes in Fe-PCN-224 and Co-PCN-224 as a function of temperature, including the determination of enthalpies and entropies, represents a worthwhile fundamental study.
3.5 Evaluating optimal ΔG for O2-selective adsorptive processes
As discussed above, values of ΔH are traditionally reported for O2-selective adsorbents, but the ΔG of O2 binding is a more meaningful metric for evaluating the performance of a material under practical working conditions. In particular, the ΔG of O2 binding is a key parameter for determining the useable surface coverage, Δθ, defined as the difference between the surface coverage under adsorption (θads) and desorption (θdes) conditions (see ESI Section S6†).98 The maximal value of Δθ under a given set of working conditions is 1, corresponding to complete coverage of the primary O2 binding sites upon adsorption (θads = 1) and zero coverage upon desorption (θdes = 0). Thus, for a given set of target conditions, it is possible to calculate an optimal ΔG value that will maximize theoretical useable capacity. Note that this analysis is intended as a useful starting point, and a comprehensive evaluation of a candidate material will necessarily consider other factors such as O2/N2 selectivity (see Section 3.6) and adsorption kinetics.The specific working conditions for an adsorptive air separation process depend on a multitude of factors, including capital and operating costs, production scale, location, and load variability.12,18,94,140,141 For the purposes of the present assessment, we considered a VSA process under two sets of working conditions, namely adsorption of air at 1 bar and 298 K and desorption at 10 or 1 mbar, which are common minimum pressures for dry reciprocating pumps. Based on progress achieved thus far in the development of O2-selective MOFs and the inherent tunability of these materials, we propose that these conditions represent reasonable targets and additionally would afford considerable costs and energy savings relative to current technologies.
Optimal surface coverage under these two sets of conditions is achieved for ΔG298 values of −10.49 and −7.64 kJ mol−1, for desorption at 1 and 10 mbar, respectively. These values are shown as blue and purple lines, respectively, in the plot of ΔS vs. ΔH given in Fig. 4a. The points plotted in Fig. 4a represent the calculated values of ΔG at 298 K associated with O2 binding at the open metal sites in eight reported frameworks and the hypothetical material Co-BTP, based on calculated ΔS and ΔH values (see the ESI Section S5 for details and Table S11†). An implicit assumption in comparing these data is that the ΔH and ΔS values for each framework are temperature-independent, given the range of temperatures (typically well below 298 K) used to collect adsorption data. While this assumption is not always valid, as discussed previously for Fe- and Co-PCN-224, these results are intended to serve as a proof-of-concept demonstration of using ΔG as a key parameter for more comprehensive benchmarking than has been accessible based on ΔH alone. Overall, the data in Fig. 4a highlight that O2 binding in most of the MOFs analyzed is not sufficiently exergonic for achieving optimal useable surface coverage under the considered conditions. The one outlier is CuI-MFU-4l, for which the ΔG of O2 binding at the open copper(I) sites is calculated to be −6(1) kJ mol−1. The hypothetical material Co-BTP is also predicted to have a near-optimal ΔG of −11 kJ mol−1. Interestingly, recall the ΔG298 of O2 binding in the molecule Fe(TpivPP)(1-MeIm)2 is −10.8 kJ mol−1 (Table 3), which suggests that the pursuit of new framework types featuring analogous iron–porphyrin units may be a promising design strategy. Ultimately, using these values as a guideline for evaluating materials must be done with caution, considering that an optimal ΔG298 value must be associated with a sufficiently high enthalpy of adsorption to ensure selectivity over N2 while minimizing regeneration energy.
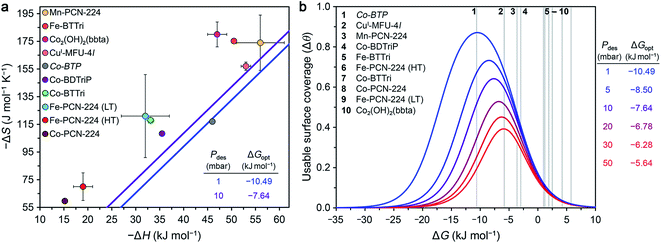 | ||
| Fig. 4 (a) Calculated enthalpy and entropy values of O2 binding in nine selected frameworks as discussed in the text (colored circles). The optimal Gibbs free energies (ΔGopt) that maximize O2 useable surface coverage (Δθ) at 298 K for a VSA process with adsorption at 0.21 bar and desorption 1 and 10 mbar are plotted as blue and purple lines, respectively (see Section S6 of the ESI†). (b) O2 useable surface coverage at 298 K plotted as a function of ΔG for a range of desorption pressures, following adsorption at 0.21 bar. The optimal Gibbs free energy (ΔGopt) associated with the maximum useable capacity at each pressure is also given. The Gibbs free energies of O2 binding for the same frameworks in (a) are shown in the plot as grey bars. As a result of the non-linear relationship between Δθ and ΔG, minor deviations from ΔGopt have a significant impact on the value of Δθ. See Tables S13 and S14† for the calculated working capacity of each framework under the considered VSA process conditions. | ||
We also determined Δθ as a function of ΔG for several desorption pressures ranging from 1 to 50 mbar, as shown in Fig. 4b, where the same frameworks from Fig. 4a are indicated as numbered grey lines. As a result of the non-linear dependence of Δθ on ΔG and the desorption pressure (see ESI Section S6†), minor deviations in ΔG and Pdes can dramatically impact Δθ. For example, the lowest desorption pressures are associated with the largest gains in surface coverage. Only CuI-MFU-4l and Co-BTP exhibit ΔG values that give rise to optimal useable surface coverage. Targeting materials that exhibit similar open metal sites and associated enthalpy and entropy values is a worthwhile pursuit.
The combined use of high temperature and vacuum to regenerate an adsorbent, in a so-called vacuum temperature swing adsorption (VTSA) process, can give rise to higher useable surface coverages than accessible with the use of VSA or TSA alone.14 Additionally, incorporating a temperature swing for desorption enables the recovery of waste heat, albeit generally at the expense of slower cycle times. We assessed the performance of the same MOFs considered above in a VTSA process involving adsorption of air at 298 K and 1 bar (0.21 mbar O2) and desorption at 338 K and 10 mbar (Table 5). Under these conditions, Co-BTP and CuI-MFU-4l again exhibit the highest useable surface coverages of all the frameworks, with Δθ = 0.86 and 0.71, respectively. These values are comparable to that achieved using a VSA process and desorption at 1 mbar and 298 K. In other words, the Δ40 K temperature swing compensates for the 10-fold weaker vacuum in this process. Finally, we emphasize that the foregoing analysis is helpful only to compare the ΔG of adsorption across different frameworks and relative to a defined process condition, and this parameter alone is not sufficient to qualify benchmark adsorbents. It is also critical to consider other factors, such as the density of binding sites in an adsorbent, as well as its O2/N2 selectivity (as discussed below).
| MOF | Surface coverage, Δθ | Working capacity (mmol g−1) | Working capacity (g L−1) |
|---|---|---|---|
| a The inflection point was approximated from the second derivative of the enthalpy versus loading, estimated using the finite difference method. | |||
| Co-BTP | 0.86 | 2.4 | 78.0 |
| CuI-MFU-4l | 0.71 | 1.1 | 20.3 |
| Co-BDTriP | 0.43 | 0.90 | 29.2 |
| Mn-PCN-224 | 0.52 | 0.29 | 4.3 |
| Co-BTTri | 0.083 | 0.23 | 6.8 |
| Fe-BTTri | 0.095 | 0.22 | 6.2 |
| Fe-PCN-224 HT | 0.088 | 0.048 | 0.77 |
| Co-PCN-224 | 0.068 | 0.048 | 0.75 |
| Co2(OH)2(bbta) | 0.014 | 0.035 | 1.2 |
| Fe-PCN-224 LT | 0.039 | 0.021 | 0.34 |
3.6 O2 working capacities and selectivities
To estimate the working capacities of the nine investigated frameworks under the aforementioned VTSA process conditions—O2 adsorption at 298 K and 0.21 bar/desorption at 10 mbar and 338 K—we first determined an estimated gravimetric O2 capacity in each case (in units of mmol g−1), based on the inflection point in the plot of enthalpy of adsorption as a function of loading (see the ESI Section S5 for details and Table S12†). The gravimetric working capacity in each case was then calculated as the product of this estimated capacity and the process-specific Δθ value for each MOF. Separately, volumetric working capacities (in units of g L−1) were calculated as the analogous product of Δθ and the estimated volumetric capacity in each case. Each estimated volumetric capacity was obtained as the product of the theoretical volumetric capacity (calculated from the single-crystal density) and the multiplicative factor [estimated capacity (mmol g−1)]/[theoretical capacity (mmol g−1)] (see Table S12† for details; note that the volumetric density of a pellet might differ substantially from the single-crystal value). Table 5 summarizes the resulting gravimetric and volumetric working capacities for each framework in the VTSA process. The materials CuI-MFU-4l and Co-BDTriP exhibit the highest working capacities of the eight reported frameworks considered, although these capacities are relatively low (∼1 mmol g−1). Interestingly, the gravimetric working capacity of Co-BTP is predicted to be 2.4 mmol g−1. Under the VSA process conditions described earlier, CuI-MFU-4l and Co-BDTriP again exhibit the highest volumetric and gravimetric working capacities of the reported materials (see Fig. S2 and Tables S13, S14†). It is noteworthy that the useable surface coverage and gravimetric and volumetric working capacities of those two frameworks are largest even though their associated enthalpies of O2 binding are not the highest of the materials considered. Ultimately, these data emphasize the importance of considering both ΔH and ΔS when evaluating potential material targets.
We selected CuI-MFU-4l, Co-BDTriP, and Co-BTP to further investigate the effects of desorption temperature on volumetric working capacities and useable surface coverages in a VTSA process involving adsorption of air at 298 K and 1 bar (0.21 bar O2) and desorption at 0.2 bar (see Fig. S3 and S4,† respectively). The working capacities of CuI-MFU-4l and Co-BDTriP increase with increasing desorption temperature until they begin to plateau above 370 K, reaching values of ∼21 and 29 g L−1, respectively, at 418 K. In the case of Co-BTP, the working capacity is projected to increase with temperature up to at least 418 K, the highest temperature considered. As might be expected, the useable surface coverage of each material also generally increases with increasing desorption temperature (Fig. S4†). Interestingly, at the lowest desorption temperatures, CuI-MFU-4l and Co-BDTriP exhibit slightly higher working capacities and useable surface coverages than Co-BTP, whereas Co-BTP outperforms both frameworks at the highest desorption temperatures.
Table 4 includes the reported O2/N2 IAST selectivities for several frameworks for a 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79 O2/N2 mixture at 1 bar. Because these values are reported at different temperatures, it is difficult to draw precise comparisons. Nonetheless, we note some key takeaways. For instance, the selectivity of Co-BDTriP is more than double that of Co-BTTri at 195 K, highlighting the power of ligand modifications to tune adsorption properties. However, the most practical materials will be those that are highly selective for O2 at ambient temperature or above.14,152 Cr-BTT displays the highest 298 K IAST selectivity of all the materials examined, although it is not entirely stable to repeated cycling.123 Calculated 298 K IAST values for CuI-MFU-4l and Co-BDTriP, which exhibit the highest calculated capacities at 298 K, are 6.5 and 14, respectively, for a 21
79 O2/N2 mixture at 1 bar. Because these values are reported at different temperatures, it is difficult to draw precise comparisons. Nonetheless, we note some key takeaways. For instance, the selectivity of Co-BDTriP is more than double that of Co-BTTri at 195 K, highlighting the power of ligand modifications to tune adsorption properties. However, the most practical materials will be those that are highly selective for O2 at ambient temperature or above.14,152 Cr-BTT displays the highest 298 K IAST selectivity of all the materials examined, although it is not entirely stable to repeated cycling.123 Calculated 298 K IAST values for CuI-MFU-4l and Co-BDTriP, which exhibit the highest calculated capacities at 298 K, are 6.5 and 14, respectively, for a 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79 O2/N2 mixture at 1 bar (Fig. S5 and S6†). Note that these values are based on isotherm data collected at lower temperatures (203 to 233 K), and it will be important to validate these estimates experimentally. Even still, based on all the metrics evaluated above, these two MOFs clearly stand apart from the rest as the most promising O2-selective adsorbents, and it may be worthwhile to pursue synthetic variants that exhibit further optimized O2 adsorption properties suitable for practical applications.
79 O2/N2 mixture at 1 bar (Fig. S5 and S6†). Note that these values are based on isotherm data collected at lower temperatures (203 to 233 K), and it will be important to validate these estimates experimentally. Even still, based on all the metrics evaluated above, these two MOFs clearly stand apart from the rest as the most promising O2-selective adsorbents, and it may be worthwhile to pursue synthetic variants that exhibit further optimized O2 adsorption properties suitable for practical applications.
3.7 O2 adsorption without metal coordination
We conclude Section 3 with a brief overview of some additional frameworks that have been shown to selectively bind O2via mechanisms that do not involve redox-active open metal sites. As only a small fraction of frameworks studied to date feature such sites, it is of interest to explore alternative strategies for achieving selective O2 uptake in metal–organic frameworks.4. Density functional theory calculations of O2 binding in MOFs
4.1 DFT-based methods for predicting O2 binding energies in MOFs
Density functional theory-based computational studies of O2 binding in MOFs can play an important role in supporting experimental design and characterization efforts, and in advancing understanding of binding mechanisms. In general, it can be a challenge to predict the nature of small molecule binding at coordinatively-unsaturated, open-shell transition metals in MOFs using contemporary DFT methods, given that unit cells may contain hundreds of atoms, and because standard functionals can fail to adequately treat exchange and correlation effects associated with van der Waals dispersion and states having open-shell spin and localized d orbital character. Previous studies that have predicted energies associated with O2 binding to open metal sites in MOFs have used DFT calculations that either treat the full crystalline system with periodic boundary conditions160–162 or focus on the local O2 binding environment using cluster models.44,163,164MOFs are highly ordered, crystalline materials that can be modeled using periodic boundary conditions, and periodic DFT calculations, typically carried out using an entire unit cell, can enable a realistic description of the framework structure. Important onsite correlation effects—associated with redox-active transition metal centers with open d shells—can be addressed with periodic DFT calculations using hybrid functions or semi-empirical Hubbard U corrections (so-called “DFT + U calculations”),161 which act on the d-states localized on the metal centers. Although empirical in nature and approximate, Hubbard U corrections can lead to improved treatments of electron–electron interactions and are less computationally expensive than using hybrid functionals on a MOF with a large unit cell. It should be noted that prior calculations of energies associated with O2 (ref. 160 and 161) and CO2 (ref. 40 and 165) binding in MOFs using DFT + U have shown that the energies can increase or decrease monotonically with increasing U, depending on the nature of binding. While it is possible to obtain Hubbard U values with a first-principles approach, such values do not always improve agreement with experiment.158,162
Cluster calculations, where only a small number of atoms near the binding site are treated explicitly, can reduce computational complexity while allowing for a more accurate treatment of open-shell systems, through more efficient use of hybrid functionals or more rigorous treatment of local interactions, for example through the use of so-called higher-rung density functionals or even beyond-DFT wave-function based quantum chemistry approaches. However, care must be taken when choosing this approach, as cluster calculations do not consider long-range interactions, which may be important in influencing experimental O2 binding properties. Relatedly, cluster calculations typically “lock in” the positions of certain atoms, fixing them to their periodic bulk positions, to prevent atomic displacements that would be unfeasible or unrealistic in the extended MOF system. If the initial constrained bond lengths are unfeasibly large (or small) based on the experimentally known spin state for an O2-bound metal site, it can be difficult to converge the calculation to the correct spin state. Knowledge of the metal–ligand bond lengths alone leaves some ambiguity for how one ought to fix the atomic positions in the cluster. This ambiguity is less of an issue when performing calculations with periodic boundary conditions, where the atomic positions and lattice parameters can relax with greater freedom. For scenarios where calculations on truncated MOF clusters are desirable due to the aforementioned advantages, a periodic DFT calculation at a lower level of theory can first be performed to establish reasonable bounds for variations in bond lengths.44
4.2 DFT calculations of O2 binding in M–benzenetrisazolates
In this section, we describe the results of DFT calculations performed using clusters and periodic boundary conditions to determine predicted O2 binding energies in the M-BTT, M-BTTri, and hypothetical M-BTP frameworks (M = CrII, MnII, FeII, CoII). The M–benzenetrisazolates were chosen for this purpose as they represent the largest and most thoroughly investigated family of materials studied to date for O2 capture and exhibit promising capacities, adsorption enthalpies, and metal site densities.For DFT cluster calculations, we used the four-metal cluster [M4Cl(azolate)8]− to represent the local binding site and the TPSSh hybrid functional (see Fig. S7 and ESI Section S7.2† for details). As shown in Fig. 5a, our DFT calculations predict an increase in the O2 binding strength with increasing basicity of the azolate linker for all four metals considered, consistent with available experimental data. The calculated O2 binding energies for the model clusters for Fe-BTTri, and Co-BTTri are larger than the experimentally determined enthalpies for the frameworks, but we note that the degree of over- or under-estimation is heavily influenced by the choice of exchange-correlation functional (see Table S18†). Overall, our calculations suggest that Mn-BTP, Fe-BTT,125 and Co-BTP may be promising materials for O2 separations, given that their predicted binding energies are near the proposed optimal binding enthalpy of −45 kJ mol−1 (refer to Section 3.1). We note that while the synthesis of Co-BTT has been reported,127 its O2 adsorption properties have not been investigated. Based on these calculations and the experimental enthalpies of O2 adsorption in the congeners with more basic ligands (Co-BTTri and Co-BTTriP), Co-BTT is not likely of interest for further study related to air separations.
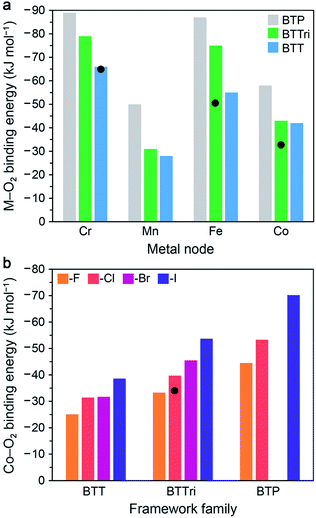 | ||
| Fig. 5 (a) Results of DFT cluster calculations for O2 binding energies in a series of model four-metal clusters [M4Cl(azolate)8]− (M = CrII, MnII, FeII, and CoII; azolate = pyrazolate, triazolate, or tetrazolate to represent BTP3−, BTTri3−, or BTT3− linkers). The TPSSh functional was used for M = MnII, FeII, and CoII, and M06 was used for CrII (see Section S7.2 of the ESI† for details). Experimental enthalpy values are shown as black circles for Cr-BTT, Fe-BTTri, and Co-BTTri. As can be seen, TPSSh tends to overestimate experimental binding energies. Binding energies trend with the basicity of the azolate across all metals. (b) DFT calculations with periodic boundary conditions (PBE-D3 + U, U = 3.3 eV) for O2 binding energies for the series of [(Co4X)3(benzenetrisazolate)8] (X = F−, Cl−, Br−, and I−; benezentrisazolate = BTT3−, BTTri3−, and BTP3−). The experimental O2 binding enthalpy for Co-BTTri is shown as a black circle. Notably, binding energies trend with the electropositivity of the halide. | ||
Our calculations of O2 binding to open metal sites in the M–benzenetrisazolate frameworks were carried out using periodic boundary conditions with an eye toward identifying other isostructural materials that may display O2 binding enthalpies near the proposed optimal value of −45 kJ mol−1. We started with the experimentally determined structure for Co-BTTri and replaced the linker or halide to obtain the various structures considered. Calculations were performed on unit cells of the type [(Co4X)3(benzenetrisazolate)8] (X = F−, Cl−, Br−, and I−; benezentrisazolate = BTT3−, BTTri3−, and BTP3−) without charge balancing cations. As such, to represent the anionic framework accurately with an overall neutral unit cell, we added three extra electrons and a positive neutralizing background charge (see ESI Section S7.1† for details). All of the atoms and the lattice vectors were then relaxed. We performed all DFT calculations with PBE + U, and we also employed a pairwise correction term, Grimme D3, to capture van der Waals dispersion corrections. These periodic DFT + D3 + U calculations ultimately enabled us to perform full geometry optimizations without constraining the positions of the atoms, as is necessary in the cluster calculations.
As shown in Fig. 5b, these calculations predict that the O2 binding energy increases upon moving from X = F− to I−. This result may be explained by considering that the electron density around the cobalt sites will increase with the electropositivity of the μ4-halide, and therefore charge transfer to O2 would be increasingly favored. The results further suggest that Co3[(Co4Br)3(BTTri)8]2, Co3[(Co4I)3(BTTri)8]2, Co3[(Co4F)3(BTP)8]2, and Co3[(Co4Cl)3(BTP)8]2 may be promising target materials. While the absolute binding energies will be dependent upon the choice of exchange–correlation functional, including the choice of the method used to treat dispersion interactions and the Hubbard U value chosen, it is expected that trends found with a given functional should hold for other choices of functional. Thus, since Co3[(Co4Cl)3(BTTri)8]2 has an experimental binding energy below the target value of −45 kJ mol−1, based on our calculated trends, we would expect that Co3[(Co4X)3(BTTri)8]2 with X = Br or I would have binding enthalpies close to −45 kJ mol−1. Since no members of the Co3[(Co4X)3(BTP)8]2 series have yet been synthesized, whether any of its variants would have a binding enthalpy near −45 kJ mol−1 is unclear, although we would expect from our trends that Co3[(Co4Cl)3(BTP)8]2 would bind O2 more strongly than Co3[(Co4Cl)3(BTTri)8]2 and that substituting chloride with larger halides would increase the binding enthalpy.
4.3 Benchmarking entropic contributions to O2 binding in MOFs
While the calculation of O2 binding enthalpies is important for evaluating candidate adsorbents, the free energy of adsorption enables a more holistic evaluation of material performance, as discussed in detail above. Obtaining vibrational properties from calculations allows one to additionally calculate ΔS and estimate the ΔG of adsorption. With the calculated free energy in hand, one can also estimate the adsorption isotherm from an ab initio calculation. In addition, vibrational calculations provide the O–O stretching frequency, an important observable for determining the degree of charge transfer to dioxygen.Given the predominant focus in the experimental literature on the enthalpy of O2 binding in candidate MOFs, computational efforts have also often focused on this thermodynamic variable. To support future computational and experimental efforts in this area, we investigated how accurately cluster calculations can estimate the ΔS of O2 binding for the systems of interest here. We chose the M-PCN-224 (M = MnII, FeII, CoII) family as a model system because (i) their experimental O2 binding entropies span a wide range of values (see Fig. 4a) and (ii) the cubic pore shape, face-centered location of the porphyrins (see Fig. 3f), and pore size (approximately 19 Å) are such that one may less ambiguously select the relevant cluster—in this case the metal–porphyrin molecule—when compared to the M-BTTri series.
We first examined various functionals for their accuracy in predicting binding energy. In the case of Mn-porphyrin, many commonly used functionals, even ones benchmarked to transition metal datasets (e.g., MN15, ωB97X-D, M06, PBE0),166–169 failed to predict the peroxide species bound to Mn(II) (see ESI Section S7.3 for details and Table S20†). Both TPSSh and B97M-rV yielded good estimates of binding energies, but B97M-rV requires far more expensive frequency calculations. Ultimately, TPSSh correctly identified the peroxide and superoxide species that form upon O2 binding in Mn- and Fe-porphyrin, respectively. The calculated entropy of O2 binding in Mn-porphyrin is very close to the value calculated for Mn-PCN-224 using the Clausius–Clapeyron relationship (−179 vs. −174 ± 20 J mol−1 K−1, respectively, see Tables S20 and S11†). Similarly, the calculated entropy of O-2 binding in Fe-porphyrin is −143 J mol−1 K−1, consistent with the value of −121 ± 30 J mol−1 K−1 determined for Fe-PCN-224 at low temperature (Tables S21 and S11†). In contrast, TPSSh did not identify the superoxide species bound in Co-porphyrin, and the calculated O2 binding entropy is much larger than that determined for Co-PCN-224 (−139 vs. −59.6 ± 0.7 J mol−1 K−1, respectively).
5. Conclusions and outlook
As a result of their high surface areas and atom-level tunability, metal–organic frameworks have emerged as promising candidates for O2-selective adsorptive air separations. In particular, a number of MOFs featuring coordinatively-unsaturated redox-active metal sites have been discovered to date that are capable of selectively binding O2 over N2. Additional strategies for selective O2 adsorption have also begun to emerge, such as outer-sphere electron transfer from redox-active frameworks and non-redox-mediated chemisorption of O2. Overall, the continued investigation of new MOFs and O2 adsorption mechanisms is a key fundamental driver of this important, nascent area of research.With an eye toward practical applications, frameworks with open metal sites are the most promising materials studied to date. Design strategies have focused on tuning the linker and local coordination environment to generate open metal sites that are sufficiently reducing for selective O2 binding and can be regenerated using relatively mild swings in temperature or pressure. However, significant improvements are still needed to render MOFs competitive with the incumbent adsorptive air separation technology based on nitrogen-selective zeolites.
Drawing on inspiration from molecular and biological systems that strongly and reversibly bind O2, we have identified design considerations for further enhancing selective, reversible O2 uptake in MOFs (Section 2), surveyed key frameworks studied to date for selective O2 uptake (Sections 3.2–3.4), and evaluated relevant performance metrics (Sections 3.5 and 3.6). While the enthalpy of O2 binding has traditionally been used to judge material performance, it is the free energy of adsorption, ΔG, that is most important in evaluating suitability for a practical separation process. Thus, going forward, it will be critical for researchers to adopt a more holistic approach, considering both the enthalpy and entropy of O2 binding in the evaluation of any new MOF for air separations. Other important parameters to consider are gravimetric and volumetric O2 capacities, based on exposed metal site density, which can readily be estimated from experimental data.
For new frameworks, it will be critical to characterize these properties under working conditions relevant for practical separations, and ambient temperature data should be reported when possible. More rigorous characterization will in turn enable a greater fundamental understanding of O2 binding at open metal sites. Never has it been so facile to determine thermodynamic parameters for O2 binding across isostructural series, as exemplified in the case of the M-PCN-224 (M = MnII, FeII, CoII) frameworks. Importantly, this understanding will also carry over to other fields working on O2 activation and reactivity.170
The free energy of O2 binding can ultimately be used to determine optimal working conditions for a given adsorbent, or alternatively, to identify an optimal adsorbent for a given set of working conditions. Using available experimental data, we put the latter concept into practice and evaluated the performance of nine MOFs in representative vacuum swing and vacuum/temperature swing adsorption processes. Two known MOFs, CuI-MFU-4l and Co-BDTriP, and the hypothetical material Co-BTP, stood out from this analysis as top performers. Beyond this practical insight, these results also suggest that design iterations based on the former two frameworks (and pursuit of Co-BTP) are promising research directions.
Finally, it is important to note that the guidelines established here encompass only material-level factors that can be tuned to accelerate the development of O2-selective MOFs. Beyond initial design, characterization, and identification of promising candidates, numerous system level factors will also be key to consider in prioritizing materials, such as pellet density, thermal conductivity, cost of synthesis, and impurity resilience. In all, there is a wealth of chemistry yet to be explored in the development of MOFs for selective O2 capture.
Author contributions
D. E. J, T. D. H., and J. R. L. conceived the manuscript. D. E. J., A. J., B. E. R. S., A. S., E. T., R. R., M. N. D., W. D., J. B. N., T. D. H., and J. R. L. prepared and contributed to portions of the manuscript. K. R. M. provided a critical review and contributed to revisions.Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Department of Energy Office of Science, Office of Basic Energy Sciences, under Award DESC0019992. Work by T. D. H. was supported by the U.S. Army Research Office (W911NF-14-1-0168/P00005). A. J. gratefully acknowledges the National Institute of General Medical Sciences of the National Institutes of Health for support through a postdoctoral fellowship under award number F32GM131587. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. B. E. R. S is grateful for support through an Arnold O. Beckman Postdoctoral Fellowship in Chemical Sciences.References
- M. J. Kirschner, A. Alekseev, S. Dowy, M. Grahl, L. Jansson, P. Keil, G. Lauermann, M. Meilinger, W. Schmehl, H. Weckler and C. Windmeier, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2017, pp. 1–32 Search PubMed.
- J. Huang, J. Huang, X. Liu, C. Li, L. Ding and H. Yu, Sci. Bull., 2018, 63, 1180–1186 CrossRef CAS.
- D. Cecere, E. Giacomazzi and A. Ingenito, Int. J. Hydrogen Energy, 2014, 39, 10731–10747 CrossRef CAS.
- C. Baukal, Oxygen-Enhanced Combustion, CRC Press, 2nd edn, 2013 Search PubMed.
- M. Behnam, J. Bernstein, T. Gambell and S. Karunakaran, McKinsey Article, COVID-19 exposes a critical shortage of oxygen in developing countries, 2020 Search PubMed.
- S. S. Hashim, A. R. Mohamed and S. Bhatia, Renew. Sustain. Energy Rev., 2011, 15, 1284–1293 CrossRef CAS.
- I. Saanum and M. Ditaranto, Energy Fuel., 2017, 31, 4445–4451 CrossRef CAS.
- M. B. Toftegaard, J. Brix, P. A. Jensen, P. Glarborg and A. D. Jensen, Prog. Energy Combust. Sci., 2010, 36, 581–625 CrossRef CAS.
- R. J. Allam, Energy Proc., 2009, 1, 461–470 CrossRef CAS.
- D. Jansen, M. Gazzani, G. Manzolini, E. Van Dijk and M. Carbo, Int. J. Greenh. Gas Control, 2015, 40, 167–187 CrossRef CAS.
- N. Perrin, C. Paufique and M. Leclerc, Energy Proc., 2014, 63, 524–531 CrossRef CAS.
- R. T. Yang, in Adsorbents: Fundamentals and Applications, John Wiley & Sons, Inc., 2003, pp. 280–381 Search PubMed.
- F. G. Kerry, Industrial gas handbook: Gas separation and purification, Taylor and Franciss Group, LLC, Boca Raton, Florida, 2007 Search PubMed.
- T. Banaszkiewicz, M. Chorowski and W. Gizicki, AIP Conf. Proc., 2014, 1573, 1373–1378 CrossRef CAS.
- C.C. Chaod, US Pat., 4859217, 1989 Search PubMed.
- R. Kumar, Sep. Sci. Technol., 1996, 31, 877–893 CrossRef CAS.
- S. Basu and A. K. Debnath, Advanced Ultrasupercritical Thermal Power Plant and Associated Auxiliaries, 2019 Search PubMed.
- A. R. Smith and J. Klosek, Fuel Process. Technol., 2001, 70, 115–134 CrossRef CAS.
- B. Belaissaoui, Y. Le Moullec, H. Hagi and E. Favre, Sep. Purif. Technol., 2014, 125, 142–150 CrossRef CAS.
- K. C. Chong, S. O. Lai, H. S. Thiam, H. C. Teoh and S. L. Heng, J. Eng. Sci. Technol., 2016, 11, 1016–1030 Search PubMed.
- L. M. Robeson, J. Membr. Sci., 1991, 62, 165–185 CrossRef CAS.
- S. M. Hashim, A. R. Mohamed and S. Bhatia, Adv. Colloid Interface Sci., 2010, 160, 88–100 CrossRef CAS PubMed.
- P. L. Holland, Dalton Trans., 2010, 39, 5415–5425 RSC.
- F. Basolo, B. M. Hoffman and J. A. Ibers, Acc. Chem. Res., 1975, 8, 384–392 CrossRef CAS.
- J. P. Collman, Acc. Chem. Res., 1977, 10, 265–272 CrossRef CAS.
- R. E. Stenkamp, Chem. Rev., 1994, 94, 715–726 CrossRef CAS.
- E. I. Solomon, P. Chen, M. Metz, S. K. Lee and A. E. Palmer, Angew. Chem., Int. Ed., 2001, 40, 4570–4590 CrossRef CAS PubMed.
- A. Jayaraman and R. T. Yang, Chem. Eng. Sci., 2005, 60, 625–634 CrossRef CAS.
- M. Xu, H. C. Wu, Y. S. Lin and S. Deng, Chem. Eng. J., 2018, 354, 62–74 CrossRef CAS.
- M. Calvin and R. H. Bailes, J. Am. Chem. Soc., 1947, 69, 1886–1893 CrossRef PubMed.
- D. Chen, A. E. Martell and Y. Sun, Inorg. Chem., 1989, 28, 2647–2652 CrossRef CAS.
- D. Chen and A. E. Martell, Inorg. Chem., 1987, 26, 1026–1030 CrossRef CAS.
- G. Q. Li and R. Govind, Ind. Eng. Chem. Res., 1994, 33, 755–783 CrossRef CAS.
- D. Ramprasad, G. P. Pez, B. H. Toby, T. J. Markley and R. M. Pearlstein, J. Am. Chem. Soc., 1995, 117, 10694–10701 CrossRef CAS.
- R. J. P. Corriu, E. Lancelle-Beltran, A. Mehdi, C. Reyé, S. Brandès and R. Guilard, J. Mater. Chem., 2002, 12, 1355–1362 RSC.
- G. Dubois, R. Tripier, S. Brandès, F. Denat and R. Guilard, J. Mater. Chem., 2002, 12, 2255–2261 RSC.
- N. D. Hutson and R. T. Yang, Ind. Eng. Chem. Res., 2000, 39, 2252–2259 CrossRef CAS.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- J. R. Li, R. J. Kuppler and H. C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- K. Lee, J. D. Howe, L. C. Lin, B. Smit and J. B. Neaton, Chem. Mater., 2015, 27, 668–678 CrossRef CAS.
- D. E. Jaramillo, D. A. Reed, H. Z. H. Jiang, J. Oktawiec, M. W. Mara, A. C. Forse, D. J. Lussier, R. A. Murphy, M. Cunningham, V. Colombo, D. K. Shuh, J. A. Reimer and J. R. Long, Nat. Mater., 2020, 19, 517–521 CrossRef CAS PubMed.
- L. J. Murray, M. Dinca, J. Yano, S. Chavan, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7856–7857 CrossRef CAS PubMed.
- E. D. Bloch, L. J. Murray, W. L. Queen, S. Chavan, S. N. Maximoff, J. P. Bigi, R. Krishna, V. K. Peterson, F. Grandjean, G. J. Long, B. Smit, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14814–14822 CrossRef CAS PubMed.
- D. J. Xiao, M. I. Gonzalez, L. E. Darago, K. D. Vogiatzis, E. Haldoupis, L. Gagliardi and J. R. Long, J. Am. Chem. Soc., 2016, 138, 7161–7170 CrossRef CAS PubMed.
- D. A. Reed, D. J. Xiao, H. Z. H. Jiang, K. Chakarawet, J. Oktawiec and J. R. Long, Chem. Sci., 2020, 11, 1698–1702 RSC.
- D. Denysenko, M. Grzywa, J. Jelic, K. Reuter and D. Volkmer, Angew. Chem., Int. Ed., 2014, 53, 5832–5836 CrossRef CAS PubMed.
- A. T. Gallagher, J. Y. Lee, V. Kathiresan, J. S. Anderson, B. M. Hoffman and T. D. Harris, Chem. Sci., 2018, 9, 1596–1603 RSC.
- J. A. Mason, L. E. Darago, W. W. Lukens and J. R. Long, Inorg. Chem., 2015, 54, 10096–10104 CrossRef CAS PubMed.
- E. C. Niederhoffer, J. H. Timmons and A. E. Martell, Chem. Rev., 1984, 84, 137–203 CrossRef CAS.
- K. D. Karlin, S. Kaderli and A. D. Zuberbühler, Acc. Chem. Res., 1997, 30, 139–147 CrossRef CAS.
- J. P. Collman, J. I. Brauman and K. S. Suslick, J. Am. Chem. Soc., 1975, 97, 7185–7186 CrossRef CAS PubMed.
- M. H. Gubelmann and A. F. Williams, in Transition Metal Complexes Structures and Spectra, Springer, 1983, pp. 1–65 Search PubMed.
- M. J. Baldwin, D. E. Roo, J. E. Pate, K. Fujisawa, N. Kitajima and E. I. Solomon, J. Am. Chem. Soc., 1992, 114, 10421–10431 CrossRef CAS.
- L. Pauling and C. Coryell, Proc. Natl. Acad. Sci. USA, 1936, 210–216 CrossRef CAS PubMed.
- J. P. Collman, R. R. Gagne, C. Reed, T. R. Halbert, G. Lang and W. T. Robinson, J. Am. Chem. Soc., 1975, 97, 1427–1439 CrossRef CAS PubMed.
- S. A. Wilson, T. Kroll, R. A. Decreau, R. K. Hocking, M. Lundberg, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 2013, 135, 1124–1136 CrossRef CAS PubMed.
- J. J. Yan, T. Kroll, M. L. Baker, S. A. Wilson, R. Decréau, M. Lundberg, D. Sokaras, P. Glatzel, B. Hedman and K. O. Hodgson, Proc. Natl. Acad. Sci. USA, 2019, 116, 2854–2859 CrossRef CAS PubMed.
- J. P. Collman, J. I. Brauman, T. R. Halbert and K. S. Suslick, Proc. Natl. Acad. Sci. USA, 1976, 73, 3333–3337 CrossRef CAS PubMed.
- J. M. Praetorius, D. P. Allen, R. Wang, J. D. Webb, F. Grein, P. Kennepohl and C. M. Crudden, J. Am. Chem. Soc., 2008, 130, 3724–3725 CrossRef CAS PubMed.
- C. J. Cramer, W. B. Tolman, K. H. Theopold and A. L. Rheingold, Proc. Natl. Acad. Sci. USA, 2003, 100, 3635–3640 CrossRef CAS PubMed.
- J. W. Ginsbach, R. L. Peterson, R. E. Cowley, K. D. Karlin and E. I. Solomon, Inorg. Chem., 2013, 52, 12872–12874 CrossRef CAS PubMed.
- J. P. Collman, R. R. Gagne, J. Kouba and H. Ljusberg-Wahren, J. Am. Chem. Soc., 1974, 96, 6800–6802 CrossRef CAS PubMed.
- J. P. Collman, J. I. Brauman, K. M. Doxsee, T. R. Halbert, S. E. Hayes and K. S. Suslick, J. Am. Chem. Soc., 1978, 100, 2761–2766 CrossRef CAS.
- K. D. Karlin, M. S. Haka, R. W. Cruse and Y. Gultneh, J. Am. Chem. Soc., 1985, 107, 5828–5829 CrossRef CAS.
- R. D. Jones, D. A. Summerville and F. Basolo, Chem. Rev., 1979, 79, 139–179 CrossRef CAS.
- F. A. Walker, D. Beroiz and K. M. Kadish, J. Am. Chem. Soc., 1976, 98, 3484–3489 CrossRef CAS PubMed.
- C. J. Weschler, D. L. Anderson and F. Basolo, J. Am. Chem. Soc., 1975, 97, 6707–6713 CrossRef CAS PubMed.
- C. A. Cheung, S. K. Grimes, C. J. Wong and J. Reed, J. Am. Chem. Soc., 1976, 98, 5028–5030 CrossRef.
- F. A. Walker, J. Am. Chem. Soc., 1972, 95, 1154–1159 CrossRef PubMed.
- L. S. Chen, M. E. Koehler, B. C. Pestel and S. C. Cummings, J. Am. Chem. Soc., 1978, 100, 7243–7248 CrossRef CAS.
- M. J. Carter, D. P. Rillema and F. Basolo, J. Am. Chem. Soc., 1974, 96, 392–400 CrossRef CAS.
- B. M. Hoffman, D. L. Diemente and F. Basolo, J. Am. Chem. Soc., 1970, 92, 61–65 CrossRef CAS.
- B. M. Hoffman, F. Basolo and D. L. Diemente, J. Am. Chem. Soc., 1973, 95, 6497–6498 CrossRef CAS.
- B. B. Wayland, J. V Minkiewicz and M. E. Abd-Elmageed, J. Am. Chem. Soc., 1974, 96, 2795–2801 CrossRef CAS.
- L. M. Engelhardt and M. Green, J. Chem. Soc., Dalton Trans., 1972, 6, 724–728 RSC.
- A. Dedieu, M. M. Rohmer and A. Veilard, J. Am. Chem. Soc., 1976, 98, 5789–5800 CrossRef CAS.
- A. E. Martell, Acc. Chem. Res., 1982, 15, 155–162 CrossRef CAS.
- T. Nishiura, Y. Chiba, J. Nakazawa and S. Hikichi, Inorg. Chem., 2018, 57, 14218–14229 CrossRef CAS PubMed.
- G. D. Armstrong and A. G. Sykes, Inorg. Chem., 1986, 25, 3135–3139 CrossRef.
- P. E. Ellis, J. E. Linard, T. Szymanski, R. D. Joanes, J. R. Budge and F. Basolo, J. Am. Chem. Soc., 1980, 102, 1889–1896 CrossRef CAS.
- J. P. Collman, J. I. Brauman, K. M. Doxsee, T. R. Halbert, E. Bunnenberg, R. E. Linder, G. N. LaMar, J. Del Gaudio, G. Lang and K. Spartalian, J. Am. Chem. Soc., 1980, 102, 4182–4192 CrossRef CAS.
- A. Kossanyi, F. Tani, N. Nakamura and Y. Naruta, Chem.–Eur. J., 2001, 7, 2862–2872 CrossRef CAS.
- F. Tani, M. Matsura, K. Ariyama, T. Setoyama, T. Shimada, S. Kobayashi, T. Hayashi, T. Matsuo, Y. Hisaeda and Y. Naruta, Chem.–Eur. J., 2003, 9, 862–870 CrossRef CAS PubMed.
- J. P. Collman, J. I. Brauman, K. M. Doxsee, T. R. Halbert and K. S. Suslick, Proc. Natl. Acad. Sci. USA, 1978, 75, 564–568 CrossRef CAS PubMed.
- B. Ward, C.-B. Wang and C. K. Chang, J. Am. Chem. Soc., 1981, 103, 5236–5238 CrossRef CAS.
- S. E. V. Phillips and B. P. Schoenborn, Nature, 1981, 292, 81–82 CrossRef CAS PubMed.
- D. H. Chin, G. N. La Mar and A. L. Balch, J. Am. Chem. Soc., 1980, 102, 4344–4350 CrossRef CAS.
- J. Oktawiec, H. Z. H. Jiang, J. G. Vitillo, D. A. Reed, L. E. Darago, B. A. Trump, V. Bernales, H. Li, K. A. Colwell, H. Furukawa, C. M. Brown, L. Gagliardi and J. R. Long, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed.
- W. A. Eaton, E. R. Henry, J. Hofrichter and A. Mozzarelli, Nat. Struct. Biol., 1999, 6, 351–358 CrossRef CAS PubMed.
- K. L. Bren, R. Eisenberg and H. B. Gray, Proc. Natl. Acad. Sci. USA, 2015, 112, 13123–13127 CrossRef CAS PubMed.
- C. R. Johnson, D. W. Ownby, S. J. Gill and K. S. Peters, Biochemistry, 1992, 31, 10074–10082 CrossRef CAS PubMed.
- T. M. McDonald, J. A. Mason, X. Kong, E. D. Bloch, D. Gygi, A. Dani, V. Crocella, F. Giordanino, S. O. Odoh and W. S. Drisdell, Nature, 2015, 519, 303–308 CrossRef CAS PubMed.
- D. A. Reed, B. K. Keitz, J. Oktawiec, J. A. Mason, T. Runčevski, D. J. Xiao, L. E. Darago, V. Crocellà, S. Bordiga and J. R. Long, Nature, 2017, 550, 96–100 CrossRef CAS PubMed.
- B. A. Mersmann, B. Fill, R. Hartmann and S. Maurer, Chem. Eng. Technol., 2000, 23, 937–944 CrossRef.
- M. H. Rosnes, D. Sheptyakov, A. Franz, M. Frontzek, P. D. C. Dietzel and P. A. Georgiev, Phys. Chem. Chem. Phys., 2017, 19, 26346–26357 RSC.
- M. I. Gonzalez, J. A. Mason, E. D. Bloch, S. J. Teat, K. J. Gagnon, G. Y. Morrison, W. L. Queen and J. R. Long, Chem. Sci., 2017, 8, 4387–4398 RSC.
- D. Y. Koh, B. R. Pimentel, V. P. Babu, N. Stephenson, S. W. Chai, A. Rosinski and R. P. Lively, Microporous Mesoporous Mateer., 2018, 256, 140–146 CrossRef CAS.
- H. Swenson and N. P. Stadie, Langmuir, 2019, 35, 5409–5426 CrossRef CAS PubMed.
- A. Nuhnen and C. Janiak, Dalton Trans., 2020, 49, 10295–10307 RSC.
- N. L. Rosi, J. Kim, M. Eddaoudi, B. Chen, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 1504–1518 CrossRef CAS PubMed.
- P. D. C. Dietzel, Y. Morita, R. Blom and H. Fjellvåg, Angew. Chem., Int. Ed., 2005, 44, 6354–6358 CrossRef CAS PubMed.
- P. D. C. Dietzel, B. Panella, M. Hirscher, R. Blom and H. Fjellvåg, Chem. Commun., 2006, 1, 959–961 RSC.
- S. R. Caskey, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2008, 130, 10870–10871 CrossRef CAS PubMed.
- P. Q. Liao, X. Y. Li, J. Bai, C. T. He, D. D. Zhou, W. X. Zhang, J. P. Zhang and X. M. Chen, Chem.–Eur. J., 2014, 20, 11303–11307 CrossRef CAS PubMed.
- A. J. Rieth, Y. Tulchinsky and M. Dincã, J. Am. Chem. Soc., 2016, 138, 9401–9404 CrossRef CAS PubMed.
- X. F. Lu, P. Q. Liao, J. W. Wang, J. X. Wu, X. W. Chen, C. T. He, J. P. Zhang, G. R. Li and X. M. Chen, J. Am. Chem. Soc., 2016, 138, 8336–8339 CrossRef CAS PubMed.
- A. J. Rieth, A. M. Wright, G. Skorupskii, J. L. Mancuso, C. H. Hendon and M. Dinca, J. Am. Chem. Soc., 2019, 141, 13858–13866 CrossRef CAS PubMed.
- S. S. Park, Y. Tulchinsky and M. Dinca, J. Am. Chem. Soc., 2017, 139, 13260–13263 CrossRef CAS PubMed.
- D. Denysenko, M. Grzywa, M. Tonigold, B. Streppel, I. Krkljus, M. Hirscher, E. Mugnaioli, U. Kolb, J. Hanss and D. Volkmer, Chem.–Eur. J., 2011, 17, 1837–1848 CrossRef CAS PubMed.
- D. Denysenko, J. Jelic, K. Reuter and D. Volkmer, Chem.–Eur. J., 2015, 21, 8188–8199 CrossRef CAS PubMed.
- G. M. Su, H. Wang, B. R. Barnett, J. R. Long, D. Prendergast and W. S. Drisdell, Chem. Sci., 2021, 12, 2156–2164 RSC.
- R. Röβ-Ohlenroth, B. Bredenkötter and D. Volkmer, Organometallics, 2019, 38, 3444–3452 CrossRef.
- P. Schmieder, M. Grzywa, D. Denysenko, M. Hambach and D. Volkmer, Dalton Trans., 2015, 44, 13060–13070 RSC.
- S. Biswas, M. Grzywa, H. P. Nayek, S. Dehnen, I. Senkovska, S. Kaskelc and D. Volkmer, Dalton Trans., 2009, 33, 6487–6495 RSC.
- S. S. Y. Chui, S. M. F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS PubMed.
- L. Xie, S. Liu, C. Gao, R. Cao, J. Cao, C. Sun and Z. Su, Inorg. Chem., 2007, 46, 7782–7788 CrossRef CAS PubMed.
- J. I. Feldblyum, M. Liu, D. W. Gidley and A. J. Matzger, J. Am. Chem. Soc., 2011, 133, 18257–18263 CrossRef CAS PubMed.
- P. Maniam and N. Stock, Inorg. Chem., 2011, 50, 5085–5097 CrossRef CAS PubMed.
- M. Kramer, U. Schwarz and S. Kaskel, J. Mater. Chem., 2006, 16, 2245–2248 RSC.
- O. Kozachuk, K. Yusenko, H. Noei, Y. Wang, S. Walleck, T. Glaser and R. A. Fischer, Chem. Commun., 2011, 47, 8509–8511 RSC.
- C. R. Wade and M. Dinca, Dalton Trans., 2012, 41, 7931–7938 RSC.
- Y. Yue, H. Arman, Z. J. Tonzetich and B. Chen, Z. Anorg. Allg. Chem., 2019, 645, 797–800 CrossRef CAS.
- E. D. Bloch, W. L. Queen, M. R. Hudson, J. A. Mason, D. J. Xiao, L. J. Murray, R. Flacau, C. M. Brown and J. R. Long, Angew. Chem., Int. Ed., 2016, 55, 8605–8609 CrossRef CAS PubMed.
- D. A. Reed, D. J. Xiao, M. I. Gonzalez, L. E. Darago, Z. R. Herm, F. Grandjean and J. R. Long, J. Am. Chem. Soc., 2016, 138, 5594–5602 CrossRef CAS PubMed.
- K. Sumida, S. Horike, S. S. Kaye, Z. R. Herm, W. L. Queen, C. M. Brown, F. Grandjean, G. J. Long, A. Dailly and J. R. Long, Chem. Sci., 2010, 1, 184–191 RSC.
- M. Dinča, A. Dailly, Y. Liu, C. M. Brown, D. A. Neumann and J. R. Long, J. Am. Chem. Soc., 2006, 128, 16876–16883 CrossRef PubMed.
- S. Biswas, M. Maes, A. Dhakshinamoorthy, M. Feyand, D. E. De Vos, H. Garcia and N. Stock, J. Mater. Chem., 2012, 22, 10200–10209 RSC.
- D. Feng, W. C. Chung, Z. Wei, Z. Y. Gu, H. L. Jiang, Y. P. Chen, D. J. Darensbourg and H. C. Zhou, J. Am. Chem. Soc., 2013, 135, 17105–17110 CrossRef CAS PubMed.
- J. S. Anderson, A. T. Gallagher, J. A. Mason and T. D. Harris, J. Am. Chem. Soc., 2014, 136, 16489–16492 CrossRef CAS PubMed.
- A. T. Gallagher, M. L. Kelty, J. G. Park, J. S. Anderson, J. A. Mason, J. P. S. Walsh, S. L. Collins and T. D. Harris, Inorg. Chem. Front., 2016, 3, 536–540 RSC.
- C. J. Yu, M. D. Krzyaniak, M. S. Fataftah, M. R. Wasielewski and D. E. Freedman, Chem. Sci., 2019, 10, 1702–1708 RSC.
- D. Z. Zee and T. D. Harris, Chem. Sci., 2020, 11, 5447–5452 RSC.
- E. D. Bloch, M. R. Hudson, J. A. Mason, S. Chavan, V. Crocellà, J. D. Howe, K. Lee, A. L. Dzubak, W. L. Queen, J. M. Zadrozny, S. J. Geier, L. C. Lin, L. Gagliardi, B. Smit, J. B. Neaton, S. Bordiga, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2014, 136, 10752–10761 CrossRef CAS PubMed.
- R. Poloni, K. Lee, R. F. Berger, B. Smit and J. B. Neaton, J. Phys. Chem. Lett., 2014, 5, 861–865 CrossRef CAS PubMed.
- W. L. Queen, M. R. Hudson, E. D. Bloch, J. A. Mason, M. I. Gonzalez, J. S. Lee, D. Gygi, J. D. Howe, K. Lee, T. A. Darwish, M. James, V. K. Peterson, S. J. Teat, B. Smit, J. B. Neaton, J. R. Long and C. M. Brown, Chem. Sci., 2014, 5, 4569–4581 RSC.
- M. Asgari, S. Jawahery, E. D. Bloch, M. R. Hudson, R. Flacau, B. Vlaisavljevich, J. R. Long, C. M. Brown and W. L. Queen, Chem. Sci., 2018, 9, 4579–4588 RSC.
- S. J. Geier, J. A. Mason, E. D. Bloch, W. L. Queen, M. R. Hudson, C. M. Brown and J. R. Long, Chem. Sci., 2013, 4, 2054–2061 RSC.
- V. Colombo, S. Galli, H. J. Choi, G. D. Han, A. Maspero, G. Palmisano, N. Masciocchi and J. R. Long, Chem. Sci., 2011, 2, 1311–1319 RSC.
- A. M. Wright, Z. Wu, G. Zhang, J. L. Manusco, R. J Comito, R. W. Day, C. H. Hendon, J. T. Miller and M. Dincă, Chem, 2018, 4, 2894–2901 CAS.
- D. M. Ruthven and S. Farooq, Gas Sep. Purif., 1990, 4, 141–148 CrossRef CAS.
- T. R. Gaffney, Curr. Opin. Solid State Mater. Sci., 1996, 1, 69–75 CrossRef CAS.
- K. S. Walton and D. S. Sholl, AIChE J., 2015, 61, 2757–2762 CrossRef CAS.
- R. Krishna and J. M. Van Baten, Phys. Chem. Chem. Phys., 2011, 13, 10593–10616 RSC.
- P. Billemont, N. Heymans, P. Normand and G. De Weireld, Adsorption, 2017, 23, 225–237 CrossRef CAS.
- R. Krishna and J. M. Van Baten, ACS Omega, 2020, 5, 20535–20542 CrossRef CAS PubMed.
- E. D. Akten, R. Siriwardane and D. S. Sholl, Energy Fuel., 2003, 17, 977–983 CrossRef CAS.
- J. Liu, S. Keskin, D. S. Sholl and J. K. Johnson, J. Phys. Chem. C, 2011, 115, 12560–12566 CrossRef CAS.
- L. Ohlin and M. Grahn, J. Phys. Chem. C, 2014, 118, 6207–6213 CrossRef CAS.
- M. Sin, N. Kavoosi, M. Rauche, J. Pallmann, S. Paasch, I. Senkovska, S. Kaskel and E. Brunner, Langmuir, 2019, 35, 3162–3170 CrossRef CAS PubMed.
- J. A. Mason, T. M. McDonald, T. H. Bae, J. E. Bachman, K. Sumida, J. J. Dutton, S. S. Kaye and J. R. Long, J. Am. Chem. Soc., 2015, 137, 4787–4803 CrossRef CAS PubMed.
- M. K. Taylor, T. Runčevski, J. Oktawiec, J. E. Bachman, R. L. Siegelman, H. Jiang, J. A. Mason, J. D. Tarver and J. R. Long, J. Am. Chem. Soc., 2018, 140, 10324–10331 CrossRef CAS PubMed.
- A. Jaffe, M. E. Ziebel, D. M. Halat, N. Biggins, R. A. Murphy, K. Chakarawet, J. A. Reimer and J. R. Long, J. Am. Chem. Soc., 2020, 142, 14627–14637 CrossRef CAS PubMed.
- M. L. Aubrey, B. M. Wiers, S. C. Andrews, T. Sakurai, S. E. Reyes-Lillo, S. M. Hamed, C. J. Yu, L. E. Darago, J. A. Mason, J. O. Baeg, F. Grandjean, G. J. Long, S. Seki, J. B. Neaton, P. Yang and J. R. Long, Nat. Mater., 2018, 17, 625–632 CrossRef CAS PubMed.
- I. Gallardo and G. Guirado, Phys. Chem. Chem. Phys., 2008, 10, 4456–4462 RSC.
- J. M. Aubry, C. Pierlot, J. Rigaudy and R. Schmidt, Acc. Chem. Res., 2003, 36, 668–675 CrossRef CAS PubMed.
- S. Shimomura, M. Higuchi, R. Matsuda, K. Yoneda, Y. Hijikata, Y. Kubota, Y. Mita, J. Kim, M. Takata and S. Kitagawa, Nat. Chem., 2010, 2, 633–637 CrossRef CAS PubMed.
- D. F. Sava Gallis, K. W. Chapman, M. A. Rodriguez, J. A. Greathouse, M. V. Parkes and T. M. Nenoff, Chem. Mater., 2016, 28, 3327–3336 CrossRef CAS.
- H. Kim, D. G. Samsonenko, M. Yoon, J. W. Yoon, Y. K. Hwang, J. S. Chang and K. Kim, Chem. Commun., 2008, 4697–4699 RSC.
- B. Tu, Q. Pang, H. Xu, X. Li, Y. Wang, Z. Ma, L. Weng and Q. Li, J. Am. Chem. Soc., 2017, 139, 7998–8007 CrossRef CAS PubMed.
- A. S. Rosen, M. R. Mian, T. Islamoglu, H. Chen, O. K. Farha, J. M. Notestein and R. Q. Snurr, J. Am. Chem. Soc., 2020, 142, 4317–4328 CrossRef CAS PubMed.
- A. S. Rosen, J. M. Notestein and R. Q. Snurr, J. Chem. Phys., 2020, 152, 224101 CrossRef CAS PubMed.
- S. N. Maximoff and B. Smit, Nat. Commun., 2014, 5, 1–9 Search PubMed.
- Y. Wang, J. Yang, Z. Li, Z. Zhang, J. Li, Q. Yang and C. Zhong, RSC Adv., 2015, 5, 33432–33437 RSC.
- B. Supronowicz, A. Mavrandonakis and T. Heine, J. Phys. Chem. C, 2013, 117, 14570–14578 CrossRef CAS.
- G. W. Mann, K. Lee, M. Cococcioni, B. Smit and J. B. Neaton, J. Chem. Phys., 2016, 144, 174104 CrossRef PubMed.
- S. P. de Visser and M. J. Stillman, Int. J. Mol. Sci., 2016, 17, 1–25 Search PubMed.
- P. Rydberg and L. Olsen, J. Phys. Chem. A, 2009, 113, 11949–11953 CrossRef CAS PubMed.
- N. S. Venkataramanan, A. Suvitha, H. Nejo, H. Mizuseki and Y. Kawazoe, Int. J. Quantum Chem., 2011, 110, 2340–2351 CrossRef.
- T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092–3103 CrossRef CAS PubMed.
- X. Huang and J. T. Groves, Chem. Rev., 2018, 118, 2491–2553 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc03577d |
| ‡ Current address: Department of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, Indiana 46556, USA. |
| § Current address: Department of Chemistry, University of California Davis, Davis, California 95616, USA. |
| This journal is © The Royal Society of Chemistry 2022 |