Doping strategy and mechanism for oxide and sulfide solid electrolytes with high ionic conductivity†
Yue
Wang
 abcde,
Yujing
Wu
abcd,
Zhixuan
Wang
abcd,
Liquan
Chen
abcde,
Yujing
Wu
abcd,
Zhixuan
Wang
abcd,
Liquan
Chen
 abcd,
Hong
Li
*abcde and
Fan
Wu
*abcde
abcd,
Hong
Li
*abcde and
Fan
Wu
*abcde
aTianmu Lake Institute of Advanced Energy Storage Technologies, Liyang 213300, Jiangsu, China. E-mail: hli@iphy.ac.cn; fwu@iphy.ac.cn
bYangtze River Delta Physics Research Center, Liyang 213300, Jiangsu, China
cKey Laboratory for Renewable Energy, Beijing Key Laboratory for New Energy Materials and Devices, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing, 100190, China
dUniversity of Chinese Academy of Sciences, Beijing, 100049, China
eNano Science and Technology Institute, University of Science and Technology of China, Suzhou 215123, China
First published on 3rd February 2022
Abstract
Ionic conductivity is a critical parameter required for superionic conductors to be successfully applied as solid electrolytes in all-solid-state batteries. Various methods have been developed to improve the ionic conductivity of solid electrolytes by researchers worldwide. Herein, the research progress achieved by Kilner's group in improving the ionic conductivity of garnet-type solid electrolytes is summarized, focusing on the effects and the underlying mechanism of the doping strategies. Moreover, the characterization methodologies for ion diffusion are discussed in detail, where a 6Li:7Li isotope couple is employed for inter-diffusion and the corresponding isotopic profiles are tested, followed by tracer experiments to directly measure the diffusion coefficient. Inspired by this work, we extend similar strategies to argyrodite sulfide SE (Li6PS5I) to greatly improve its ionic conductivity. This work can therefore serve as a handy tool for improving ionic conductivity in both oxide and sulfide solid electrolytes, providing an in-depth understanding of the underlying lithium diffusion mechanism and improving the methodology.
1 Introduction
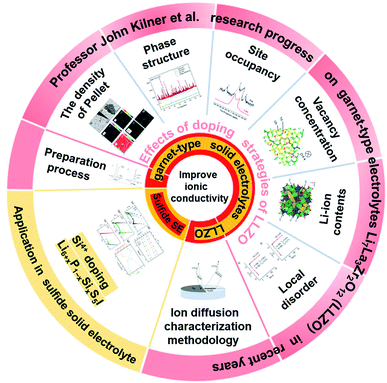
Lithium-ion batteries (LIBs) have become the dominant energy storage technology due to their high energy density, long cycle life and stable battery chemistry.1–3 However, the use of organic liquid electrolytes (LEs) in conventional LIBs leads to safety issues such as flammability, explosion and leakage, which raise serious safety concerns in electric vehicles.4,5 Therefore, the development of all-solid-state batteries (ASSBs) is the first choice to ultimately solve the safety problems associated with LIBs. An all-solid-state lithium-ion battery consists of a cathode electrode, an anode electrode and a solid electrolyte. Solid electrolytes (SEs) are composed of non-flammable and volatile components, which can transmit lithium ions and prevent electronic transmission simultaneously, eliminating safety risks such as battery smoke and fire.6–9 Thus, they are an ideal chemical power source for electric vehicles and large-scale energy storage.10–14 To find solid electrolytes with excellent ionic conductivity compared with liquid electrolytes, significant research efforts have been made and great success has been achieved, especially in the case of sulfide- and oxide-based solid electrolytes.15–24 Among the different types of oxide SEs, the garnet-type electrolyte Li7La3Zr2O12 (LLZO) has been widely studied due to its wide electrochemical window, high temperature stability, ambient-environment processibility and good thermal safety. However, many issues and challenges still exist in the application of LLZO in all-solid-state lithium ion batteries (ASSLIBs). Firstly, LLZO-based SEs are unstable in air due to the following two-step reaction mechanism in ambient air: (1) the formation of LiOH·H2O intermediates by Li+/H+ exchange; (2) the formation of Li2CO3 on the surface of LLZO due to the reaction of LiOH·H2O with CO2. The Li2CO3 passivation layer subsequently degrades ionic conductivity and increase interfacial resistance. Furthermore, the ionic conductivities of cubic and tetragonal LLZO are 10−4 S cm−1 and 10−6 S cm−1, respectively,25,26 which are too low to be used as the key SE component in ASSLIBs. Moreover, cubic-structured LLZO is only stable at high temperatures and tends to transform into the tetragonal phase at room temperature (RT) by the Li sublattice disorder, resulting in low ionic conductivity at RT. Thus, to solve the above-mentioned problems, various scholars have devoted much effort and great progress has been made, where among them, John A. Kilner has provided unique insights into the development of LLZO, including processing techniques, effects of humidity on its function and stability, double-ion doping strategy to achieve enhanced ionic conductivity, and new characterization methodology of ion migration (Fig. 1).Herein, the research progress achieved by their group on Li-conducting oxide SEs in recent years is first summarized (as shown in Fig. 2). The effects of the sintering atmosphere and processing conditions and single-ion substitution (Ga3+/Ge4+) and dual-ion substitution (Ga3+ and Sc3+) techniques on LLZO discovered by them are discussed in detail. Based on this, the six different effects of doping strategies on LLZO are extracted from microstructure/macrostructure perspectives, including pellet density, phase structure, ion occupancy behaviors, Li-ion content, vacancy concentration and local disorder. Moreover, the characterization methodology of lithium diffusion coefficients proposed by them is elaborated, where an 6Li:7Li isotope couple is employed for inter-diffusion and the corresponding isotopic profiles are tested by secondary ion mass spectrometry (SIMS), followed by tracer experiments to directly measure the diffusion coefficient. This method pioneers the development of characterization methodologies for the direct measurement of the ionic transport by charge carriers in solid superionic conductors.
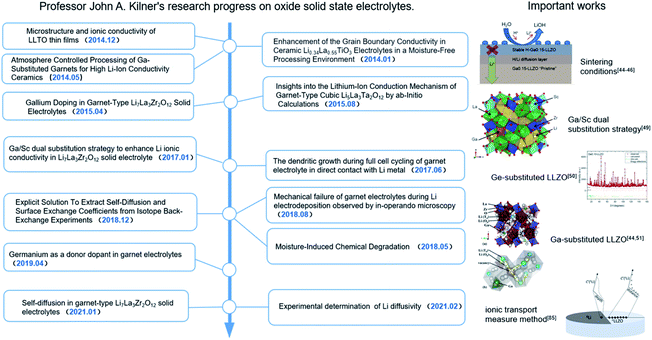 | ||
| Fig. 2 John A. Kilner's research progress on Li conducting oxide solid-state electrolytes and important works on the garnet-type electrolyte Li7La3Zr2O12 (LLZO). | ||
It is worth noting that oxides and sulfides share the same ionic diffusion and defect transport mechanisms as inorganic SEs, and thus studies on Li+ ion conduction in sulfide SEs can refer to their oxide counterparts. Argyrodite-type Li6PS5X (LPSX, X = Cl, Br, and I) is a promising family of sulfide SEs due to the low cost of its raw materials and high ionic conductivity,27–31 where Li6PS5Cl and Li6PS5Br have high ionic conductivities (>1 × 10−3 S cm−1) and have been widely studied. However, the poor interface between Li6PS5Cl/Li6PS5Br and the electrode material (especially Li metal anode) deteriorates the battery performance due to the strong reducing capability of metallic lithium and serious reaction at the interface.32–38 Alternatively, although Li6PS5I (LPSI) has a relatively low ionic conductivity of 10−6 S cm−1 (ref. 29) due to its low I−/S2−exchange disorder, the high iodine concentration in LPSI can greatly improve its interfacial stability with Li metal. Thus, if its ionic conductivity can be improved, LPSI can become a promising candidate for use in ASSLBs. Therefore in this work, inspired by John A. Kilner's work in the field of oxide SEs, similar strategies are applied to the argyrodite LPSI sulfide SE to enhance its ionic conductivity and lower the activation energy for Li migration, which corroborates the versatility and underlying mechanisms of their work.
2 Synthesis and processing conditions of oxide solid-state electrolytes
Most works on Li-conducting LLZO have reported air-processing steps because of their low cost and simple fabrication. However, the low density and high grain-boundary resistance of LLZO seem to be caused by its reactivity with atmospheric moisture. The recent study by Larraz et al.39 showed the structural changes in LLZO upon exposure to different levels of atmospheric moisture, leading to a large decrease in Li-ion conductivity. The authors claimed that these changes were probably due to the high reactivity of Li+ with H+ from water or the introduction of water molecules into the structure, leading to proton exchange. Bernuy-Lopez et al.40 and Aguesse et al.41 further studied the effects of moisture-induced chemical degradation and proton–lithium exchange on Li conduction and Li-ion dynamics in the bulk, where MAS NMR was used to characterize the effect of protonation caused by atmospheric moisture during sintering. Dense ceramic materials free of degradation and Li+/H+ exchange were obtained by controlling the sintering conditions under a dry O2 atmosphere. Electrochemical impedance spectroscopy (EIS) data showed that by controlling the contact with moisture during the preparation process, high-Li+-conductivity materials were produced.
Fig. 3a shows an overlay of the 1H solid-state NMR spectra of Ga-substituted garnet-type SE Li7La3Zr2O12 (LZLGO)40 synthesized under O2 at 1085 °C. The spectrum of the sample exposed to air for three days (H-LZLGO) was also recorded. It can clearly be observed that the intensity of the two signals (at −1.5 and 4.8 ppm) for H-LZLGO is significantly larger than that for LZLGO. The 1H signal at 4.8 ppm coincides with the 1H chemical shift value of the protons in Li7−xHxLa3Sn2O12, corroborating the presence of protons inside the material.42 The second signal with the characteristic shift of −1.5 ppm is in agreement with the chemical shift value reported previously for LiOH.43 The relative intensities of the two signals at −1.5 and 4.8 ppm are very close to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. Accordingly, the following protonation mechanism was proposed:40 water molecules dissociate into H+ and OH− ions after being adsorbed on the surface of LLZO, where H+ ions are incorporated in the garnet and Li+ are excluded from it to maintain the charge balance. The Li+ ions react with the remaining OH− to form LiOH. To reveal the impact of moisture-induced chemical degradation and proton–lithium exchange on the Li-ion dynamics in the bulk, low-energy ion scattering (LEIS) and focused ion beam-secondary ion mass spectrometry (FIB-SIMS) in combination with EIS were further performed. Fig. 3b reveals that H+/Li+ exchange occurs at the surface, resulting in the formation of LiOH corrosion layer products, which are readily washed away in the water bath. An H-Ga0.15-LLZO region is formed below the surface layer, under which a chemical diffusion profile of H+ exists until the bulk non-protonated “pristine” Ga0.15-LLZO is reached. In addition, this moisture-sensitive behavior has also been observed in perovskite-structured materials. The 1H NMR MAS spectra of Li3xLa 2/3−xTiO3 (LLTO) samples measured at RT under air (LLTO-A), synthetic air (LLTO-SA) and oxygen atmosphere (LLTO-O) are presented in Fig. 3c. Two clear peaks can be observed in the spectrum of LLTO-A, whereas no significant magnetization can be observed in the corresponding 1H spectra of the LLTO-SA and LLTO-O samples. The 1H spectrum of LLTO-A is fitted by two Lorentzian lines centered at 5.6 and 3.5 ppm. The relative intensities of both lines are 54% and 46%, respectively. Similar signals were observed previously by Bohnké and co-workers in LLTO samples exposed to water,44 which were assigned to distinct proton populations inside the LLTO lattice. The absence of proton magnetization in the 1H NMR MAS spectra of the LLTO-SA and LLTO-O samples indicates that the Li+/H+ exchange process can be effectively suppressed by minimizing humidity during the synthetic process. Fig. 3d shows the Nyquist plots of LLTO sintered in air, synthetic air and oxygen atmosphere, respectively. It can be seen from the comparison that the conductivity of the samples obtained in air is significantly lower. These findings highlight the importance of the sintering and processing conditions, particularly the sintering atmosphere, in increasing the grain-boundary conductivity. Notably, all the doping strategies reported in John A. Kilner's work were accomplished using a dry O2 preparation process.
1 ratio. Accordingly, the following protonation mechanism was proposed:40 water molecules dissociate into H+ and OH− ions after being adsorbed on the surface of LLZO, where H+ ions are incorporated in the garnet and Li+ are excluded from it to maintain the charge balance. The Li+ ions react with the remaining OH− to form LiOH. To reveal the impact of moisture-induced chemical degradation and proton–lithium exchange on the Li-ion dynamics in the bulk, low-energy ion scattering (LEIS) and focused ion beam-secondary ion mass spectrometry (FIB-SIMS) in combination with EIS were further performed. Fig. 3b reveals that H+/Li+ exchange occurs at the surface, resulting in the formation of LiOH corrosion layer products, which are readily washed away in the water bath. An H-Ga0.15-LLZO region is formed below the surface layer, under which a chemical diffusion profile of H+ exists until the bulk non-protonated “pristine” Ga0.15-LLZO is reached. In addition, this moisture-sensitive behavior has also been observed in perovskite-structured materials. The 1H NMR MAS spectra of Li3xLa 2/3−xTiO3 (LLTO) samples measured at RT under air (LLTO-A), synthetic air (LLTO-SA) and oxygen atmosphere (LLTO-O) are presented in Fig. 3c. Two clear peaks can be observed in the spectrum of LLTO-A, whereas no significant magnetization can be observed in the corresponding 1H spectra of the LLTO-SA and LLTO-O samples. The 1H spectrum of LLTO-A is fitted by two Lorentzian lines centered at 5.6 and 3.5 ppm. The relative intensities of both lines are 54% and 46%, respectively. Similar signals were observed previously by Bohnké and co-workers in LLTO samples exposed to water,44 which were assigned to distinct proton populations inside the LLTO lattice. The absence of proton magnetization in the 1H NMR MAS spectra of the LLTO-SA and LLTO-O samples indicates that the Li+/H+ exchange process can be effectively suppressed by minimizing humidity during the synthetic process. Fig. 3d shows the Nyquist plots of LLTO sintered in air, synthetic air and oxygen atmosphere, respectively. It can be seen from the comparison that the conductivity of the samples obtained in air is significantly lower. These findings highlight the importance of the sintering and processing conditions, particularly the sintering atmosphere, in increasing the grain-boundary conductivity. Notably, all the doping strategies reported in John A. Kilner's work were accomplished using a dry O2 preparation process.
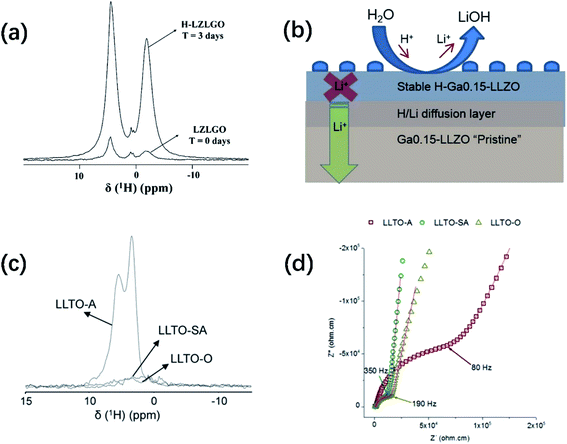 | ||
| Fig. 3 (a) Relative 1H NMR intensities recorded for a garnet sample without air contact (LZLGO) and after 3 days of contact with air (H-LZLGO). Reproduced with permission from ref. 40. Copyright, 2014, the American Chemical Society. (b) Schematic illustration of the surface composition of the garnet grain and evolution with depth. Reproduced with permission from ref. 45. Copyright, 2018, the American Chemical Society. (c) 1H MAS NMR (50 kHz) spectra recorded for different LLTO samples. The intensities are mass-normalized. (d) Room-temperature Nyquist plots of the LLTO samples sintered in different atmospheres: LLTO-A (squares), LLTO-SA (circles) and LLTO-O (triangles) in the frequency range of 10 MHz to 7 Hz. Reproduced with permission from ref. 41. Copyright, 2014, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
3 Effects of doping strategy in garnet-type LLZO electrolytes
It is well known that ion doping is an effective method to improve the ionic conductivity of materials.46–50 Therefore, a deep understanding of the effects of various ion doping mechanisms on conductivity is vital for the optimization of SEs.LLZO is considered a promising SE owing to its negligible electronic transport, wide electrochemical window, and good chemical stability. Although cubic-phase LLZO has higher ionic conductivity than tetragonal-phase LLZO, it is still far below the performance of traditional liquid electrolytes. Therefore various types of elemental doping have been attempted to improve the ionic conductivity of LLZO. John A. Kilner and group conducted a series of in-depth studies on the ion-transport mechanism of Ge-, Ga- and Sc-doped LLZO, and the doping strategies are summarized in Fig. 4. This section reviews the mechanisms that may affect conductivity in terms of macroscopic property (the density of pellets) and microscopic structures (phase structure, site occupancy, vacancy concentration, Li content and local disorder).
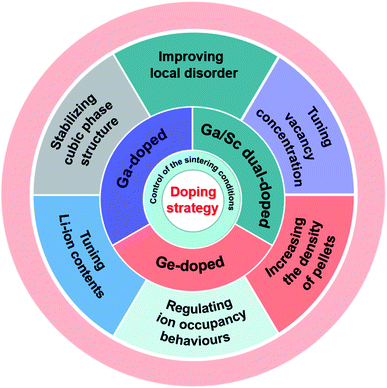 | ||
| Fig. 4 Sintering conditions, doping elements and doping strategies adopted by John A. Kilner's group to improve the ionic conductivity of garnet-type Li7La3Zr2O12 SE. | ||
3.1 Improving the density of pellets
The presence of pores during the sintering of LLZO electrolytes leads to higher grain boundary resistance and greatly reduces the mechanical strength of the material. At high temperatures, lithium volatilization and internal air bubbles cannot be eliminated, resulting in a low density of LLZO solid electrolyte and low ionic conductivity. Therefore, it is necessary to increase the sintering density and reduce the grain boundary resistance to improve the total conductivity of this material.Extensive attempts have been made to further increase the density of LLZO through multiple routes. Most researchers prefer high-pressure technology such as cold isostatic pressing (CIP, LLZO powder is pressed before sintering process) or isostatic pressing (HIP, LLZO powder is pressed during the sintering process) to gain SE pellets with high density. In addition to high-pressure technology, the spark plasma sintering (SPS) technique has also been used.51 Unfortunately, most of these strategies enhance the density of the LLZO pellets at a high production cost, which makes their mass production unrealistic. Another densification strategy is to apply sintering aid. The addition of sintering aids can reduce the sintering duration at high temperatures and facilitate ion migration during sintering, which can also improve the sintering density of LLZO. For example, El Shinawi et al.52 reported a method using Ga as a sintering aid and obtained a pellet density close to 92%.
Different from the above-mentioned strategies, controlling the sintering conditions by using a dry O2 atmosphere and minimizing contact with atmospheric moisture can also contribute to better densification. Bernuy-Lopez et al.40 achieved a theoretical density of up to 94% for LZLGO, while the samples sintered in air rarely surpassed 70%. This strategy avoids the degradation process due to the exchange between Li+ and H+ from atmospheric moisture. Therefore, atmosphere control is another effective method to produce high-density ceramic pellets.
In addition to atmosphere control, their experimental results showed that the density of garnet can also be improved by Ga/Sc/Ge doping. In the case of Ga3+-doped LLZO, a portion of Ga3+ reacts with excess Li+ ions to form LiGaO2, which then resides on the grain boundaries as a secondary phase to facilitate pellet densification. For Sc-substituted LGLZ (Li7−3x+yGaxLa3Zr2−yScyO12), the Sc and Zr cations interact in the second phase, as shown in Fig. 5a and b, which probably act as the reaction intermediate and sintering aid during thermal treatment to obtain a high density of pellets. The results of geometric density measurement of sintered pellets indicates a high density of 94% for LGLZ-Sc. For Ge doping, chemical analysis using TOF-SIMS mapping (Fig. 5c–g) showed a homogeneous Ge distribution in the grains and some enrichment at the grain boundaries, which is possibly due to the presence of a GeO2–Li2O eutectic during high-temperature sintering. This phase is similar to the well-known Li2O–Al2O3 alumina eutectic in Al-doped LLZO and is beneficial to grain growth and densification. The geometrically calculated relative density of the Ge0.1-LLZO (Li7−4xGexLa3Zr2O12) material was calculated to be 98% (using lattice parameters from Rietveld refinement of neutron diffraction data).53
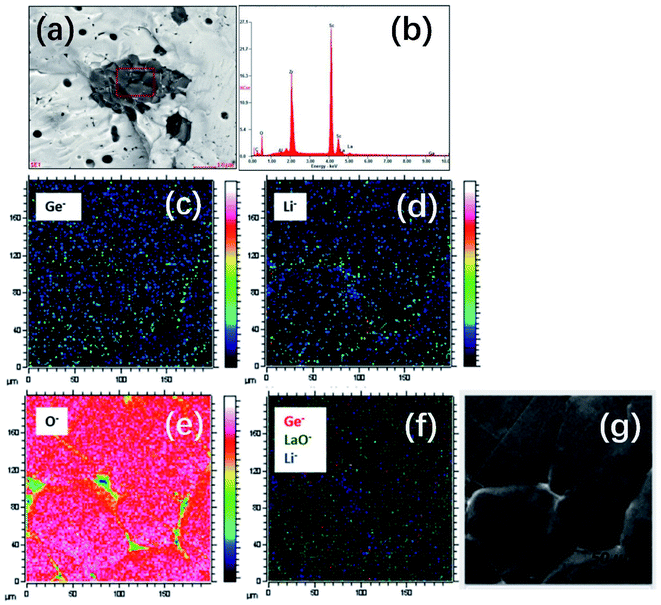 | ||
| Fig. 5 (a and b) SEM-EDS analysis of the secondary phase observed in LGLZ-Sc. Reproduced with permission from ref. 54. Copyright, 2017, the American Chemical Society. (c–g) TOF-SIMS maps of the Ge0.10-LLZO (x = 0.10) pellet surface (optical image shown on the far right), showing 74Ge−, 7Li− and 16O− secondary ion maps of counts of selected species over total ion counts and an overlay of 74Ge−, 155(LaO)− and 7Li− species (in red, green and blue, respectively). Maps were captured with a Bi+ primary ion beam (25 kV, 0.2 pA) and a Cs+ sputter gun (1 kV, 64 nA) operated in the non-interlaced burst alignment mode (using a 1s:1s:1s sputter:wait:analyse cycle) (for interpretation of the references to color in the figure legend, readers are referred to the web version of this article). Reproduced with permission from ref. 53. Copyright, Clearance Center. | ||
3.2 Stabilizing cubic phase structure
LLZO has two different crystal structures, i.e., tetragonal phase (space group I41/acd) and cubic phase (space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d).55 The difference in LLZO crystal structures results in a two-orders of magnitude higher ion conductivity for cubic LLZO than that of tetragonal LLZO. However, the cubic phase is unstable at RT and can be easily converted into the tetragonal phase, reducing the ionic conductivity. Therefore, stabilizing the cubic phase to improve its RT ionic conductivity is one of the key issues associated with the use of LLZO as an SE in lithium-ion batteries. Current studies have shown that the doping strategy is one of the most effective methods to inhibit a change in crystal structure and stabilize the cubic phase.56,57
d).55 The difference in LLZO crystal structures results in a two-orders of magnitude higher ion conductivity for cubic LLZO than that of tetragonal LLZO. However, the cubic phase is unstable at RT and can be easily converted into the tetragonal phase, reducing the ionic conductivity. Therefore, stabilizing the cubic phase to improve its RT ionic conductivity is one of the key issues associated with the use of LLZO as an SE in lithium-ion batteries. Current studies have shown that the doping strategy is one of the most effective methods to inhibit a change in crystal structure and stabilize the cubic phase.56,57
Jalem et al.58 first studied the effect of Ga3+ doping on the stabilization of cubic-phase LLZO. According to the electronuclear equilibrium mechanism (eqn (1), in Kröger–Vink notation), doping Ga3+ ions in all the Li sites introduces two Li vacancies 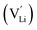 . It has been reported that the Li-ion sublattice is always ordered (all Li sites are either full or empty) in tetragonal-LLZO, while disordered (all Li symmetry sites are partially occupied) in cubic-LLZO. Therefore, the presence of more Li vacancies in the crystal lattice leads to an increase in the disordering of the Li sublattice to stabilize the cubic phase, as follows:
. It has been reported that the Li-ion sublattice is always ordered (all Li sites are either full or empty) in tetragonal-LLZO, while disordered (all Li symmetry sites are partially occupied) in cubic-LLZO. Therefore, the presence of more Li vacancies in the crystal lattice leads to an increase in the disordering of the Li sublattice to stabilize the cubic phase, as follows:
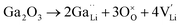 | (1) |
The cubic-phase stability of Ga-doped LLZO by forcefield-based simulations and thermal expansion/contraction monitoring of undoped and doped LLZO models was investigated. Fig. 6a shows the Li–Li radial distribution function g(r) profiles of undoped (x = 0) and Ga-doped (x = 0.30) 3 × 3 × 3 supercell models for LLZO, which demonstrate a tendency of Li ordering in the undoped LLZO model at 300 K for both the heating and cooling directions. The broader peaks, absence of a valley region at around r ≈ 3.0 Å, and shallower valleys at 4.5 Å < r < 5.0 Å and r > 6.0 Å indicate the lack of ordering tendency in the Ga-doped model at 300 K. At 800 K, Li disordering is depicted in Fig. 6a, embodied by smoother peaks. Meanwhile, at 300 K, Li+ becomes localized at specific sites, shown as peak narrowing (Fig. 3c) and peak splitting (Fig. 3e) compared to the 800 K g(r) plots. The g(r) plots show that the lack of Li ordering tendency and Ga3+ led to the stabilization of cubic-phase LLZO. As shown in Fig. 6d, for the undoped cell, a bend in the thermal expansion plot can be observed in both the heating (red) and cooling (blue) directions, with an onset temperature of ∼600 K. The authors assigned this bend as the phase transition point. However, the bend in the thermal data in Fig. 6d disappeared in both the heating and cooling directions in Fig. 6e and f (1 and 2 Ga atoms added, respectively), which signifies the suppression of the tetragonal phase.
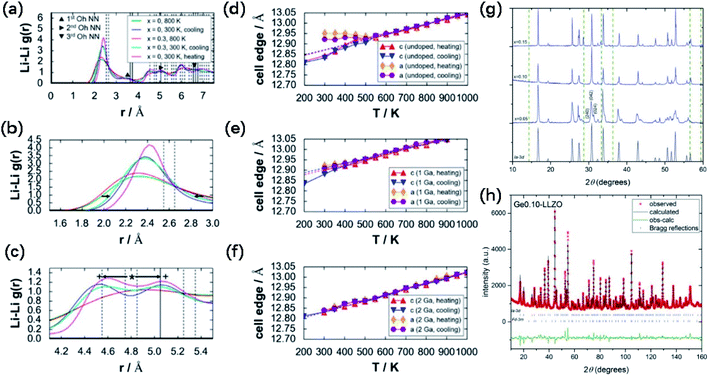 | ||
Fig. 6 (a) Calculated Li–Li radial distribution function g(r) profiles for undoped (x = 0; 300 and 800 K in the heating direction and 300 K in the cooling direction) and doped (x = 0.30; 800 K in the heating direction and 300 K in the cooling direction) 3 × 3 × 3 LLZO cell models, (b) enlarged view of the g(r) plot in (a), highlighting the narrowing of the peak from 800 to 300 K in the range of 1.5 Å ≤ r ≤ 3.0 Å (see arrows), and (c) enlarged view of the g(r) plot in (a), highlighting the peak splitting from 800 K (*) to 300 K (+) in the range of 4.1 Å ≤ r ≤ 5.5 Å (see arrows). Vertical lines (dashed and solid) indicate discrete peak locations for the tetragonal phase (8a-16f-32g). Thermal expansion plots with respect to the monitored reaction coordinates (lattice constants c and a) for (d) undoped, (e) 1 Ga atom, and (f) 2 Ga atom 1 × 1 × 1 (I cell) models (Ga3+ added at the 24d site). Dashed lines show linear fitting for 600 K ≤ T ≤ 1000 K, in both heating (red) and cooling (blue) directions. Reproduced with permission from ref. 58. Copyright, 2015, the American Chemical Society. (g) Comparison of the XRD patterns of Li7−4xGexLa3Zr2O12 pellets with x = 0.05, 0.10 and 0.15. (h) NPD pattern with Rietveld refinement, showing observed, calculated and difference (obs-calc.) patterns fitting to Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d space group and pyrochlore La2Zr2O7 impurity (space group Fd d space group and pyrochlore La2Zr2O7 impurity (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), occupying 5.79 wt% of the total (with the Bragg reflections shown as short vertical lines). Reproduced with permission from ref. 53. Copyright, Clearance Center. m), occupying 5.79 wt% of the total (with the Bragg reflections shown as short vertical lines). Reproduced with permission from ref. 53. Copyright, Clearance Center. | ||
Germanium is another effective dopant in stabilizing the cubic phase in garnet LLZO SEs. The effect of a series of Li7−4xGexLa3Zr2O12 compounds with nominal Ge concentrations (x) of 0.05, 0.10 and 0.15 a.p.f.u (atoms per formula unit) on the stability of the cubic phase was also investigated. The XRD patterns (Fig. 6g) show the sharpest peaks of cubic-phase crystallization at x = 0.10. At lower concentrations of Ge (x = 0.05), cubic lattice stabilization is not as effective, resulting in a splitting and broadening of the diffraction peaks, indicative of tetragonal character. The pattern for x = 0.15 is cubic but with undesirable La2Zr2O7 impurity peaks, which is possibly due to a low initial amount of stoichiometric Li for this composition to stabilize Ge4+-substituted Li sites, preventing the formation of a stable garnet crystal structure. Neutron powder diffraction (Fig. 6h) showed that Ge4+ substitutes Li+ at the 24d tetrahedral site, giving a best fit for this site when the concentration was fixed at 0.10 Ge a.p.f.u. Specifically, 0.10 Ge4+ is sufficient to stabilize the cubic phase to give the critical Li content of 6.6 Li a.p.f.u.
According to the investigation of Ge/Ga doping, the use of a higher-valent dopant enables stabilization of the cubic phase with a lower dopant content than cations with lower oxidation states.
3.3 Regulating ion occupancy behaviours
The first step to analyze the transport mechanism of lithium ions in the lattice is to obtain the lithium ion sites. The difference in the site occupancy behaviors of Li and the effects on Li ion diffusivity/conductivity after substituting lithium with Ge/Ga dopants in LLZO were studied.40,41In c-LLZO, the Li ions occupy three different sites, namely, the tetrahedral (24d), octahedral (48g), and off-centered octahedral (96h) sites. The 3D network structure in c-LLZO is formed by face-sharing tetrahedron and octahedron. To date, the Ga distribution in the LLZO framework is still difficult to fully characterize. 71Ga NMR spectroscopy conducted by Howard et al.59 for Li5.5Ga0.5La3Zr2O12 (1 × 10−4 S cm−1) revealed a single broad peak with a chemical shift of ∼221 ppm, which is attributed to Ga3+ at the tetrahedral sites. Rettenwander et al.60 suggested that Ga3+ mainly occupies the Li96h octahedral site based on the relatively large NMR asymmetry parameter (ηQ = 0.46(3)), which is also supported by Allen et al.61 However, Bernuy-Lopez40 found that Ga3+ ions tend to substitute Li+ at the 24d tetrahedral site and keep Li+ at the 48g/96h site with good continuity. The 71Ga solid-state MAS NMR spectrum of highly conductive microcrystalline LZLGO is shown in Fig. 7a and b, together with the spectrum simulated using the values listed in Table S1.† The chemical shift value obtained from the fit is ∂iso = 207 ± 10 ppm, indicating that the Ga3+ ions in LZLGO are in tetrahedral coordination. DFT calculations were also used to investigate LZLGO, indicating that the Ga ions in the tetrahedral Li24d sites are more stable than that in the Li48g+96h sites. Therefore, the high mobility of Li+ in LZLGO can be ascribed to the preferential occupancy of Ga3+ in tetrahedral Li24d sites, inducing Li vacancies, thus increasing the ratio of Li48g+96h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li24d. In contrast, if the Ga ions occupy the tetrahedral sites, high Ga contents may be detrimental for the free movement of Li along the tetrahedral–octahedral site channels, thus decreasing the conductivity. Moreover, Buannic54 investigated the occupation of Ga and Li upon Ga/Sc dual substitution using NMR and DFT methods (Fig. 7c). Ga3+ preferentially occupies the Li24d sites with a low Sc concentration, whereas for a higher Sc concentration, Ga3+ moves from the tetrahedral 24d to octahedral 96h sites, hindering the Li percolation network. As shown in Fig. 7d and Table S2,† Rietveld refinement of the NPD pattern suggests the existence of super-valent dopant Ge4+ at the 24d tetrahedral site. The Ge atoms were refined at both the Li24d and Li96h sites, but preferential occupancy of only the Li24d site was observed.
Li24d. In contrast, if the Ga ions occupy the tetrahedral sites, high Ga contents may be detrimental for the free movement of Li along the tetrahedral–octahedral site channels, thus decreasing the conductivity. Moreover, Buannic54 investigated the occupation of Ga and Li upon Ga/Sc dual substitution using NMR and DFT methods (Fig. 7c). Ga3+ preferentially occupies the Li24d sites with a low Sc concentration, whereas for a higher Sc concentration, Ga3+ moves from the tetrahedral 24d to octahedral 96h sites, hindering the Li percolation network. As shown in Fig. 7d and Table S2,† Rietveld refinement of the NPD pattern suggests the existence of super-valent dopant Ge4+ at the 24d tetrahedral site. The Ge atoms were refined at both the Li24d and Li96h sites, but preferential occupancy of only the Li24d site was observed.
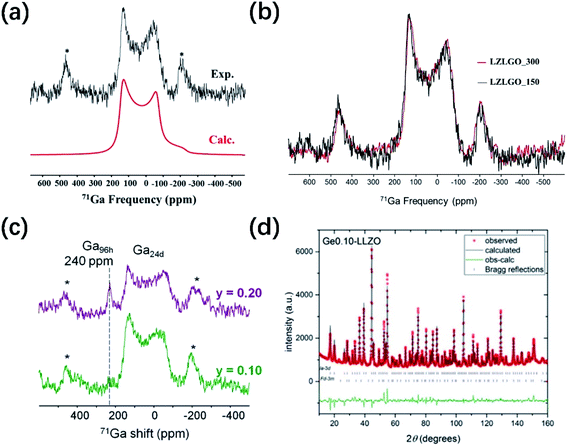 | ||
Fig. 7 (a) 71Ga solid-state NMR spectrum recorded for the LZLGO sample (black) and the corresponding spectrum calculated using the parameters listed in table 3 (red). Asterisks (*) denote the location of spinning sidebands. Reproduced with permission from ref. 40. Copyright, 2014, the American Chemical Society. (b) 71Ga spectra of LZLGO-150 and LZLGO-300. Reproduced with permission from ref. 40. Copyright, 2014, the American Chemical Society. (c) 71Ga solid-state NMR spectra of Li6.55+yGa0.15La3Zr2−yScyO12. The asterisks denote the spinning sidebands of the broad quadrupolar resonance. Reproduced with permission from ref. 54. Copyright, 2017, the American Chemical Society. (d) NPD pattern with Rietveld refinement, showing observed, calculated and difference (obs-calc.) patterns fitted to the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d space group and pyrochlore La2Zr2O7 impurity (space group Fd d space group and pyrochlore La2Zr2O7 impurity (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), occupying 5.79 wt% of the total (with the Bragg reflections shown as short vertical lines). Reproduced with permission from ref. 53. Copyright, Clearance Center. m), occupying 5.79 wt% of the total (with the Bragg reflections shown as short vertical lines). Reproduced with permission from ref. 53. Copyright, Clearance Center. | ||
The above analyses support the view that by adjusting the content of aliovalent dopants, the preferential occupancy of doped ions (Al3+, Ga3+ and Ge4+) at the tetrahedral Li24d sites can induce Li vacancies and increase the ratio of Li48g+96h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li24d, thus enhancing the lithium ion conductivity of LLZO.
Li24d, thus enhancing the lithium ion conductivity of LLZO.
3.4 Tuning vacancy concentrations
Ionic diffusion in solids is mediated by the hopping of atoms in their crystal lattice. A high concentration of mobile-ion carriers, often in the form of vacancies and interstitials, is crucial to achieve high ionic conductivity.62 However, besides the stabilizing effect on the cubic phase, it is not clear how vacancy defects influence the path topology and Li+ ion migration mechanism in doped LLZO. Jalem et al.58 and Kuganathan et al.63 revealed the potential Li+ ion migration mechanism induced by different vacancy concentrations on conductivity behavior by combining five theoretical methods, including percolation theory, van Hove space time correlation, radial distribution function, trajectory density and vacancy mechanism.Interestingly, the relationship between Ga concentration, x, and bulk Li+ conductivity for cubic-phase Li7−3xGaxLa3Zr2O12 (0 ≤ x ≤ 0.3) follows two different trends, a decreasing trend for 0 ≤ x ≤ 0.10 and a relatively flat trend for 0.10 < x ≤ 0.30 (Fig. 8a). The former can be explained primarily by the increasing number of inaccessible Li vacancies (due to the formation of Ga3+–Li vacancy clusters) for use in initiating Li+ migration and concerting Li+ motion. The latter is likely governed by the subsequent increase in the number of accessible Li vacancies (at higher x) and the more directed motion of Li+ in the retained percolated pathways due to the increasing average Ga3+–Li+ repulsion. As mentioned above, doping with Ga3+ at the Li sublattice can introduce Li vacancies 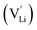 . However, given that Li vacancies are expected to be strongly coupled with the substitutional Ga3+, these vacancies become inaccessible to a migrating Li+ ion according to the following association reactions:
. However, given that Li vacancies are expected to be strongly coupled with the substitutional Ga3+, these vacancies become inaccessible to a migrating Li+ ion according to the following association reactions:
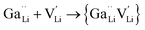 | (2) |
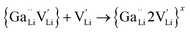 | (3) |
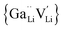 is a defect cluster formed by one Ga3+ and one Li vacancy and
is a defect cluster formed by one Ga3+ and one Li vacancy and 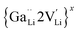 is a neutral cluster formed by one Ga3+ and two Li vacancies. For 0.05 ≤ x ≤ 0.10, higher-order clusters may be involved as the Ga content is further increased, lowering the number of accessible vacancies
is a neutral cluster formed by one Ga3+ and two Li vacancies. For 0.05 ≤ x ≤ 0.10, higher-order clusters may be involved as the Ga content is further increased, lowering the number of accessible vacancies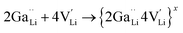 | (4) |
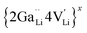 is a higher-order neutral cluster formed by 2Ga3+ and 4 Li vacancies. Hence, as shown in Fig. 8b, the degree of hopping by Li(j) into a vacant Li(i) site decreases with an increase in the number of guest Ga3+ cations, which trap the Li vacancies. Therefore, the linear decrease in conductivity can be explained. At higher x (for 0.10 ≤ x ≤ 0.30), the number of accessible or free Li vacancies (not strongly coupled with Ga3+) increases. As shown in Fig. 8c, some segments of the network illustrated by the trajectory densities disappear, which is the result of the Li+ ion transport pathways being blocked by Ga3+. However, percolated pathways still remain, making long-range Li+ transport possible.
is a higher-order neutral cluster formed by 2Ga3+ and 4 Li vacancies. Hence, as shown in Fig. 8b, the degree of hopping by Li(j) into a vacant Li(i) site decreases with an increase in the number of guest Ga3+ cations, which trap the Li vacancies. Therefore, the linear decrease in conductivity can be explained. At higher x (for 0.10 ≤ x ≤ 0.30), the number of accessible or free Li vacancies (not strongly coupled with Ga3+) increases. As shown in Fig. 8c, some segments of the network illustrated by the trajectory densities disappear, which is the result of the Li+ ion transport pathways being blocked by Ga3+. However, percolated pathways still remain, making long-range Li+ transport possible.
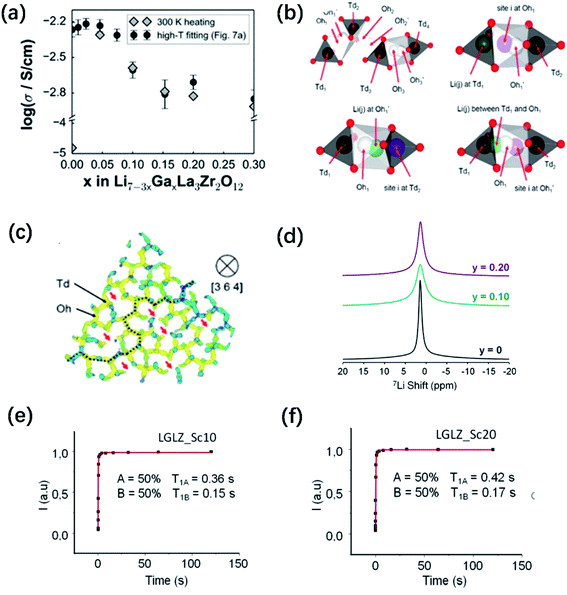 | ||
Fig. 8 (a) Comparison of Li+ conductivities for different Ga-doped LLZO samples. Predicted variation in bulk conductivity vs. Ga content at room temperature as extrapolated from high-temperature MD simulation data and as extracted from the 300 K MD run in the heating direction. (b) Illustration of the Li site linkage within the garnet LLZO framework. Td1, Td2, Td3, and Td4 are 24d sites inside distinct Td cages (black), whereas Oh1-Oh1′, Oh2-Oh2′, and Oh3-Oh3′ are 96h site pairs inside distinct Oh cages (white). A typical site-to-site connection can be described as Td1–Oh1-Oh1′–Td2–Oh2-Oh2′–Td3–Oh3-Oh3′–Td4. (b) Idealized representations of site separations for Li(i) Li(j) within 1 Å ≤ r ≤ 2 Å of the distinct part of the van Hove Gd(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) plot: Td1(i)–Oh1(j), Oh1′(i)–Td2(j), and a case with an intermediate position for Li(j), respectively. (c) 〈111〉-view of Li trajectory density (4 × 10−5 Å−3 isosurface level, 25% max saturation), projected on the [3 6 4] direction and highlighting the path connectivity formed by the Td and Oh sites. Cutting planes are shown in blue. Red arrows and the dashed line indicate lost Li paths and percolated Li pathway (retained), respectively, after Ga3+ doping. The sampling interval for data collection is set to 100 fs. Reproduced with permission from ref. 58. Copyright, 2015, the American Chemical Society. (d) 7Li solid-state NMR spectra of Li6.55+yGa0.15La3Zr2−yScyO12. 7Li T1 relaxation curves for (e) LGLZ-Sc10 and (f) LGLZ-Sc20. Reproduced with permission from ref. 75. Copyright, 2017, the American Chemical Society. ,t) plot: Td1(i)–Oh1(j), Oh1′(i)–Td2(j), and a case with an intermediate position for Li(j), respectively. (c) 〈111〉-view of Li trajectory density (4 × 10−5 Å−3 isosurface level, 25% max saturation), projected on the [3 6 4] direction and highlighting the path connectivity formed by the Td and Oh sites. Cutting planes are shown in blue. Red arrows and the dashed line indicate lost Li paths and percolated Li pathway (retained), respectively, after Ga3+ doping. The sampling interval for data collection is set to 100 fs. Reproduced with permission from ref. 58. Copyright, 2015, the American Chemical Society. (d) 7Li solid-state NMR spectra of Li6.55+yGa0.15La3Zr2−yScyO12. 7Li T1 relaxation curves for (e) LGLZ-Sc10 and (f) LGLZ-Sc20. Reproduced with permission from ref. 75. Copyright, 2017, the American Chemical Society. | ||
3.5 Tuning Li-ion contents
Generally, the highest RT ionic conductivity of LLZO has been achieved by doping Ga3+, and more recently Fe3+ in the Li sublattice.64–67 However, a higher doping content at the Li site in the LLZO structure would also reduce the Li+ content.Subsequently, an innovative dual-substitution strategy was developed Buannic et al.54 to increase the Li content in doping technology. In the dual-substitution strategy, the first dopant cation Ga3+ was introduced in the Li sites to stabilize the fast-conducting cubic phase, and the second doping ion Sc3+ was used to partially populate the Zr sites to increase the Li ion concentration by charge compensation. The dual-substitution strategy can be described by the following crystal chemistry (defect) reactions, using Kröger–Vink notations:
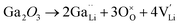 | (5) |
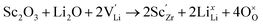 | (6) |
With an overall resulting reaction of:
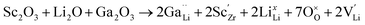 | (7) |
In Li7−3x+yGaxLa3Zr2−yScyO12, the substitution of x moles of Ga3+ in the Li+ sites decreases the number of moles of Li by 3x. Simultaneously, substitution of y moles of Zr4+ by Sc3+ allows fine tuning of the number of Li+ charge carriers by the incorporation of y moles of Li+. This aliovalent dual-substitution strategy allows finer control over the Li content in cubic Li7La3Zr2O12 according to the resulting stoichiometry (Li7−3x+yGaxLa3Zr2−yScyO12). Accordingly, the lithium ion conductivity of dual-ion substituted Li7−3x+yGaxLa3Zr2−yScyO12 can reach up to 1.8 × 10−3 S cm−1 at RT.
3.6 Improving local disorder
Many ionic conductors undergo an order-disorder superionic transition with sharply increased ionic conductivity at high temperature. For example, cubic-structure lithium garnet (high-temperature phase) shows much higher ionic conductivity at room temperature compared with tetragonal-structure lithium garnet (low-temperature phase). This is attributed to the disordering of lithium in the tetrahedral and octahedral sites in the cubic structure, which is ordered in the tetragonal phase.68–70 Order-disorder phase transitions resulting in increased ionic conductivity have also been observed in several sodium-ion and proton conductors.71–74 Based on this, Buannic et al.54 proposed dual-ion substitution of Li7La3Zr2O12, which offers new opportunities for fine tuning the local Li structure in garnet electrolytes. This unique local Li structure has a beneficial effect on the transport properties of the garnet.Regarding 7Li NMR (Fig. 8d), the spectra of both LGLZ-Sc show similar chemical shifts but variations in line width, especially compared to the single-ion-substituted garnet Li6.55Ga0.15La3Zr2O12. This broadening highlights a larger distribution of chemical environments in LGLZ-Sc with more local disorder surrounding the Li cations, in sharp contrast with the narrow peak of single-ion substituted garnets. The observed differences in the local Li structure are expected to influence the transport properties of dual-ion-substituted garnets. To evaluate the Li-ion dynamics at the localized scale, saturation recovery experiments were performed. As shown in Fig. 8e and f and Table S3,† the multi-exponential behavior in the Li spin-lattice relaxation times (T1) for the dual-ion-substituted samples further reveals the presence of a heterogeneous distribution of Li environments. While all the samples host a Li population with a relaxation time in the range of 0.38(2) s, the dual-ion-substituted samples accommodate a second population of Li+ with a shorter relaxation time of 0.16(1) s, indicating the presence of Li+ with faster local motion.
Overall, the ionic conductivity can be effectively improved by increasing the local disorder surrounding the charge carrier, therefore increasing its local mobility.
4 Ion diffusion characterization methodology
Measuring the diffusion coefficient of lithium in fast ionic conductors, such as LLZO, can provide critical information on the ionic transport mechanism. However, this type of measurement requires high spatial-resolution and time-resolution detection techniques. Nuclear magnetic resonance (NMR) spectroscopy, muon spin-relaxation (μSR) and quasi-elastic neutron scattering (QENS) are the main microscopic techniques used to investigate ion diffusion in fast ionic conductors. These techniques usually offer long-range diffusion behaviors by indirectly measuring atomic-scale lithium jumps in powder samples.Solid-state NMR spectroscopy has been proven to be a versatile tool to study ion dynamics. Mobile ions (e.g., Li+) can be directly probed by NMR,28,76,77 and then the jump frequency, jump distance, diffusion coefficient, diffusion path topology, activation energy, and correlation effects during ion transport can be evaluated. Then, ion transport events falling within the time scales of NMR spectroscopy can be characterized.78 Li NMR techniques can be used to provide direct insights into the Li dynamics and precisely quantify the ion diffusivity in solids over a large dynamic range.79–81 Pulsed gradient NMR has been used for macroscopic analysis on powder and membrane samples but requires high-temperature measurements and complex interpretation. To convert jump frequencies (probed at very short length scales) into diffusivities, model assumptions must be applied. Additionally, the observed lithium mobility may depend on the particle size of the sample. The ions are ‘reflected’ on the surface of the particles, resulting in a decrease in the apparent diffusivity for smaller particles, which is denoted as the ‘diffracted’ diffusion.82 Muon spin relaxation (μ+SR) is a characterization technique that analyzes the effects of implanted spin-polarized muons on a material. Also, μ+SR study enables the examination of the local dynamics of lithium ions without extrinsic interferences. This technique provides a local probe to examine the dynamic behavior in powered samples without the need for contacts or pellets. μSR spectroscopy is an established technique for investigating the lithium-ion diffusion in solid-state materials.83–86 Quasi-elastic neutron scattering (QENS) probes ion diffusion and rotation processes at the atomic scale, although a large amount of sample (typically ∼10 g) is often required.87 QENS is sensitive to motion processes at the time scale of 10−8 to 10−12 s. According to QENS, parameters related to the ion dynamics at the atomic scale, such as the ion jump distance, jump frequency, and random diffusion coefficient, can be obtained.88 This method is often used to detect H-containing compounds. However, in the case of lithium diffusion detection, the preparation of 7Li-enriched materials or more accurate measurement is required due to the small incoherent cross-section of lithium. Electrochemical impedance spectroscopy (EIS) is a common macroscopic technique used to characterize lithium transport. Impedance data from EIS measurements can be used to extract the conductivity, where Dσ can be deduced from Nernst–Einstein relation. With careful measurements and data analysis, EIS can be used to distinguish the contribution between ions and electrons and determine the ionic transport process within the grain and across grain boundaries.89,90 Neutron radiography (NR) has been used to measure macroscopic lithium tracer diffusion coefficients in some materials,91–93 which provides the lithium isotope concentration via the neutron transmitted image by virtue of the large difference in neutron absorption coefficients between two stable lithium isotopes. The obtained diffusion data can be estimated from the ionic conductivity through the Nernst–Einstein relation with a correlation parameter, the difference of which does not exceed one order. However, the limited spatial resolution of neutron detectors requires long diffusion path lengths to characterize the diffusion process. This highlights the importance of multiple techniques for studying Li diffusion processes in solid-state electrolytes, and this an alternative methodology for determining the lithium diffusion coefficients was proposed by Brugge et al.94 This method involves stable tracer experiments, whereby an 6Li:7Li isotope couple (consisting of Li metal and a dense LLZO pellet) is left to inter-diffuse and the resulting isotopic profiles are measured using secondary ion mass spectrometry (SIMS). By using tracer experiments, direct measurement of the diffusion coefficient is possible. This allows the measurement of true long-range diffusion on a macroscopic and easily visualizable scale.
The specific experiments are as follows: Li and LiF are deposited using an organic molecular beam deposition system successively to prepare the samples. A metallic source of lithium tracer ions (6Li metal, 95.4% enriched, Sigma Aldrich) is placed in contact with an LLZO pellet of natural lithium isotopic abundance (denoted as Cbg and equal to 7.59% (ref. 95)). The 6Li metal is placed onto half of one surface (in a semicircular patch) of a cylindrical LLZO pellet and pressed down, with a sharp edge made by a scalpel. This method was selected to simulate the setup of an all-solid-state lithium metal battery, enabling the study of the interface behavior of lithium metal with LLZO. Following the contact of 6Li metal with the LLZO pellet, the diffusion of 6Li from the enriched metal source through LLZO is followed as a function of exchange time (and distance). Using FIB-SIMS depth-profiling, both through the interface of metal/LLZO (‘direct depth-profiling’ method) and at varying distances from the lithium metal edge (‘sampling’ method) can be studied. Fig. 9 shows a schematic illustration of both methods. FIB-SIMS depth-profiling was chosen as the analysis method due to the ease of sample preparation. It avoids the need for the post-exchange cutting and polishing required for TOF-SIMS lines before they can be analyzed.47 Furthermore, it enables relatively deep depth profiles (several micrometres) to be obtained, which is typically not possible in the TOF-SIMS depth-profiling mode. Finally, an FEI FIB200-SIMS ion microscope was used to collect surface mass spectra and to obtain chemical information as a function of depth, including changes in the concentration of the two stable lithium isotopes. This work reported RT lithium diffusivities of 2–8 × 10−13 m2 s−1 for doped LLZO, using an estimation of the lithium diffusion length. This result is in good agreement with that obtained by electrochemical impedance spectroscopy.
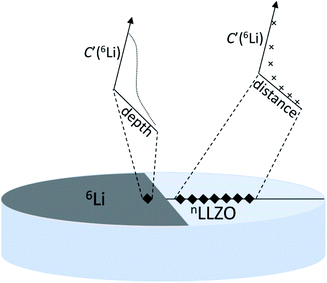 | ||
| Fig. 9 Schematic illustration of two methods to detect lithium diffusion coefficients in solid-state lithium. The ‘direct depth-profiling’ method measured through the Li metal/LLZO interface and the ‘sampling’ method conducted by consecutive depth-profiling at increasing distances from 6Li metal. Reproduced with permission from ref. 94. Copyright, 2021, The Author(s). Published by IOP Publishing Ltd. | ||
In addition to the lithium-ion diffusion coefficient of the electrolyte itself, it is very important to understand the ion transport mechanism from the lithium metal electrode to the electrolyte for the development of solid-state batteries. For established non-tracer methods such as impedance spectroscopy and NMR spectroscopy, probing the diffusion and conductivity on different time- and length-scales requires more tracer-based experiments to obtain reliable comparative data. However, in this work,94 an estimation of the diffusion coefficient was obtained directly by measuring the diffusion length of lithium over a fixed time. Accordingly, this method can be extended to any Li–metal-stable SE or any reactive SE with a stable protective interlayer. Furthermore, this work laid the groundwork for further quantitative diffusion analysis of Li-conducting solid ceramic electrolytes and their interfaces with electrodes.
5 Underlying mechanism of doping strategy in LLZO garnet-type electrolytes
A series of studies (in Section 3) allowed us to gain valuable insights into the relationship between microstructure and ion-transport property in garnet LLZO electrolytes. Four important features of doping strategies for increasing the ionic conductivity of LLZO are suggested as follows.(a) Adjusting the ion occupancy ratio of Li ions using different dopants and doping concentration can lead to faster ionic conduction. For instance, by adjusting the content of aliovalent dopants, the preferential occupancy of doped ions (Al3+, Ga3+ and Ge4+) on the tetrahedral Li24d sites can induce Li vacancies and increase the ratio of Li48g+96h![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li24d, thus enhancing the lithium conductivity in LLZO.
Li24d, thus enhancing the lithium conductivity in LLZO.
(b) The migration mechanism of lithium ions can be changed by regulating the concentration of lithium vacancies through aliovalent doping. In LLZO, Li+ migration occurs via Li vacancies. Thus, doping minor ions in the Li sublattice can introduce a low concentration of Li vacancies, which initiates Li+ ion migration and concerts Li+ motion. However, as the number of Li vacancies increases, more doping ions will block the Li+ ion transport pathways and impair the ionic conductivity.
(c) By charge compensation based on aliovalent-ion doping, the Li+ concentration increases to increase the Li+ transference number in the electrolyte. For example, a strategy to partially substitute Zr4+ with Sc3+ has been previously investigated to increase the Li content in Li7La3Zr2O12 to obtain a new stoichiometry (Li7−3x+yGaxLa3Zr2−yScyO12). The increase in mobile Li+ ions significantly enhances the Li+ conductivity in the Li7La3Zr2O12 SE.
(d) Structural disorder caused by aliovalent doping enhances the ionic conductivity of Li conducting materials. In garnet SEs, the disordered Li–O octahedron allows Li+ to disassociate more easily. Both single- and dual-substitution can promote the disordering of the Li sublattice to stabilize the cubic phase and enhance the ionic conductivity. In particular, the addition of Sc in the dual-substitution strategy of LLZO increases the disorder of the Li network at the local scale (i.e., broader distribution of chemical environments), which enhances the local mobility of a part of the Li population.
The above-mentioned doping strategies were mainly developed based on ion diffusion via defect transport mechanism, and thus should not be limited to LLZO. Thus, to verify their universal applicability to other inorganic fast-ion-conductors, similar strategies and mechanisms are also applied to sulfide SEs, halide SEs and hydride SEs in the following section.
6 Application in inorganic SEs
Ion doping is more commonly used to optimize the conductivity of LLZO. At present, multiple doping elements have been adopted, including Ta5+, Nb5+, Te6+, W6+, Ti4+, Al3+, and Ga3+. John A. Kilner's study on LLZO has laid a good experimental and theoretical foundation for other scholars. In particular, the proposed dual ion doping system (i.e., Ga3+–Sc3+ system) presents a high ionic conductivity of 1.8 × 10−3 S cm−1 at 27 °C by stabilizing the cubic phase and increasing the concentration of lithium ions. Moreover, the calculated activation energy of LLZO-Ga and interpretation of the EIS mechanism allowed data verification and theoretical analysis in the studies by Rettenwander et al.96 and Gulin et al.976.1 Application in sulfide SEs
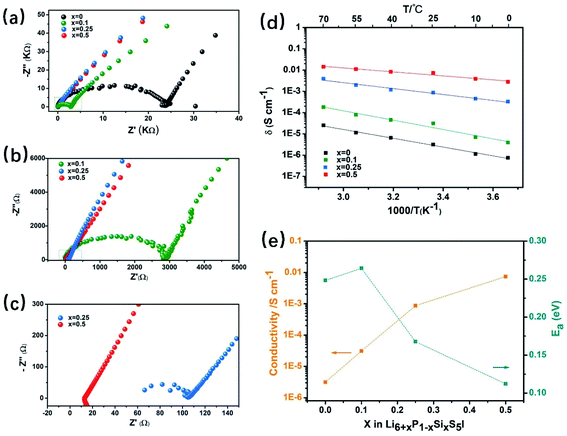
Recently, the class of argyrodites, Li6PS5X (X = Cl, Br, and I), has attracted considerable interest due to its low cost, dynamic interfacial stability with electrode materials, decent mechanical properties and solution-processible synthesis. However, unlike Li6PS5X (X = Cl and Br) with high RT ionic conductivity (σ = 10−2 to 10−3 S cm−1), the I-analogue, Li6PS5I, is known for its three-orders of magnitude lower Li-ion conductivity (σ ∼ 10−6 S cm−1) than the former. It has been reported29,98,99 that its lower ionic conductivity is due to the highly-ordered arrangement of I−/S2− in the I-containing structure, whereas in its Cl− and Br− analogues, a significant amount of site-disorder between X− and free S2− exists. Therefore, inspired by the aliovalent doping strategies53,54,58 in LLZO, the ionic conductivity of Li6PS5I is expected to be improved by the four doping mechanisms mentioned above.Herein, the aliovalent substitution of lithium superionic argyrodites Li6+xP1−xSixS5I is explored. Fig. 10a–c show the Nyquist plots of Li6+xP1−xSixS5I (0 ≤ x ≤ 0.5) at room temperature. The results show that Li6PS5I without any Si substitution has a very low ionic conductivity of 3.13 × 10−6 S cm−1, which is in agreement with the previously reported literature.29,100 The impedance of the samples gradually decreases as the Si content increases to x = 0.5, where the highest RT ionic conductivity of 7.34 × 10−3 S cm−1 with a 2345-times increase is achieved. Fig. 10d shows a comparison of the Arrhenius plots of the Li6PS5I and Li6+xP1−xSixS5I (0 ≤ x ≤ 0.5) SEs derived from a series of temperatures ranging from 0 to 70 °C (an interval of 15 °C for each point). The ionic conductivity of the Li6+xP1−xSixS5I (0 ≤ x ≤ 0.5) SE at any given temperature is about three-orders of magnitude higher than that of Li6PS5I SE without Si substitution. Furthermore, the activation energy of Li+ ion transport in the Li6.5P0.5S0.5S5I structure (Fig. 10e) calculated from the slope of the Arrhenius plot is 0.11 eV, which is much lower than that of Li6PS5I (0.25 eV). Thus, it can be concluded that aliovalent Si4+ doping can significantly improve the ionic conductivity and reduced the Li+ ion motional activation energy simultaneously.
This modification can be explained by the same mechanism of the above-mentioned doping strategy. On the one hand, according to mechanism (a), adjusting the ion occupancy ratio of Li ions using different dopants and doping concentrations can lead to faster ionic conduction. In this work, the Li+ content increased by aliovalent Si4+ doping in Li6+xP1−xSixS5I (0 ≤ x ≤ 0.5) to facilitate diffusion in the Li+ substructure. On the other hand, the Si4+ in the P5+ sites increases the I−/S2− site-disorder and changes the lithium substructure, which can greatly influence the ionic conductivity. The site-disorder and substructure facilitate inter-cage jump and promote Li+ migration, resulting in an increase in ionic conductivity and a sharp reduction in the activation energy. This viewpoint has also been corroborated by works reported by other groups. For example, Ohno et al.100 found that substitution with Si contents of >20 at% led to an increase in I−/S2− site disorder by Neutron powder diffraction and Rietveld analysis. Zhang et al.98 confirmed the occurrence of I−/S2− site disorder by Si4+ doping through XRD Rietveld refinement. Overall, we experimentally verified the universality of the LLZO doping strategy (in Section 5) in sulfide SEs.
6.2 Application in other SEs
Halide SEs and hydride SEs have attracted interest from researchers in recent years due to their unique advantages. Halide SEs have high air stability and electrochemical stability (oxidation resistance), but their relatively low ionic conductivity compared to other types of SEs (10−2 S cm−1 for sulfide SEs at 25 °C) has made them relatively less attractive in the past few years. A significant breakthrough was achieved in 2018 by Tetsuya et al.101 in the synthesis of Li3YCl6 and Li3YBr6 halide SEs with a high ionic conductivity of 0.03–1.7 × 10−3 S cm−1. Subsequently, halide electrolytes have attracted significant attention, and thus the same insights into improving the ion conductivity in Section 5 were also used for halide SEs. Zeier and coworkers102 conducted pair distribution function (PDF) analyses and found that M2/M3 (M = Y or Er) site disordering caused by the mechanochemical synthesis process was responsible for the large difference in Li+ conductivity. Kwak et al.103 reported a new type of halide SE (Fe3+-substituted Li2ZrCl6, Li2+xZr1−xFexCl6), which showed a maximum conductivity of 0.98 mS cm−1. Fitting attempts to replace the Zr2(M2) and Zr3(M3) atoms with Fe also resulted in very good agreement factors in EXAFS spectra, revealing that the Fe3+ ions randomly substituted in the Zr sites in the Li2ZrCl6 structure with mixed M2/M3 site disordering. Therefore, the metal site disordering in Li2+xZr1−xFexCl6 contributes to the enhanced Li+ migration. Meanwhile, according to mechanism (c), aliovalent substitution can increase the concentration of effective charge carriers, which also improves the ion conductivity. Moreover, for a solid solution of Li4SiO4 and Li2.5Al0.5SiO4, the highest Li+ conductivity is achieved at an optimal concentration of fully occupied Li+ sites and vacancies.104 According to Wang et al.,105 for Li3YCl6 and Li3YBr6 SEs, both the Y3+ and Li+ cations locate at the octahedral sites with the halogen anions (Cl− or Br−). It should be noted that due to the 3+ valence state of Y3+ compared to 1+ of Li+ and Cl−/Br−, the presence of Y3+ would introduce two intrinsic vacancies. This means that the octahedral sites are actually occupied by Li+, Y3+, and vacancies with a molar ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The intrinsic vacancies in Li3YCl6 and Li3YBr6 are believed to be essential for their high ionic conductivities.
2. The intrinsic vacancies in Li3YCl6 and Li3YBr6 are believed to be essential for their high ionic conductivities.
Hydrides have been widely studied as SEs for next-generation LIBs since 2007. Lithium-borohydride (LiBH4)-based SEs, as typical complex hydrides, exhibit a wide electrochemical window of up to 5 V (vs. Li/Li+). Meanwhile, LiBH4 SEs are also compatible with lithium metal anodes and sulfur cathodes. However, LiBH4 SE has an orthorhombic unit cell (space group Pnma), showing low Li-ion conductivity (10−8 S cm−1) at RT. Only at ∼110 °C, it shows a polymorphic/orthorhombic to hexagonal (e.g., P63mc) transition, increasing the ionic conductivity by several orders of magnitude (∼10−3 S cm−1 at 120 °C).106,107 To improve the RT Li+ ionic conductivity, partial anion substitution has been implemented. Orimo et al. reported108 that high-temperature phase LiBH4 can be stabilized at low temperature by partial doping with Li halides (LiX, where X represents Cl, Br, and I). Among the LiBH4–LiX composites, 3LiBH4–LiI showed a relatively high ionic conductivity of 2 × 10−5 S cm−1 at 27 °C. More recently, sulfide (P2S5) was introduced in a hydride system and a high lithium ionic conductivity was reported by Hauback et al.109 The structural analysis and characterization suggest that the BH4 and PS4 groups may belong to the same molecular structure, where [BH4]− can be partially replaced by [PS4]3−. Zhang et al.110 reported dual-ion-substituted (100-x)(3LiBH4–LiI)-xP2S5 (LLPx, 0 ≤ x ≤ 50), which helped successfully stabilize the high-temperature phase at room temperature. A high lithium ionic conductivity of 2.3 × 10−4 S cm−1 was realized at 30 °C. These studies suggest that partial substitution of [BH4]− by I− and [PS4]3− can further stabilize the high temperature phase, thereby obtaining high Li+ conductors, which is consistent with the universal strategies for improving ionic conductivity reported above.
7 Conclusion
In summary, the progress achieved in investigating the crystal structure, conductivity and preparation methods of LLZO garnet-type SEs by John A. Kilner and his group was systematically reviewed and discussed in depth herein. Specifically, the strategies for improving the ionic conductivity of LLZO garnet-type SEs and their underlying mechanism were extracted and revealed. In addition, the ion-diffusion characterization methodology and alternative methodology for determining the lithium diffusion coefficients proposed by John A. Kilner et al. were summarized, which pioneer the development of methods to directly measure the ionic transport of species in solids. Meanwhile, the same doping strategies were extended in this work to sulfide SE(Li6PS5I) to realize a great improvement in its ionic conductivity and corroborate their applicability in various types of SEs. This review provides some theoretical guidance for the subsequent design and development of all SEs. In summary, rational element doping designs, such as increasing local disorder, regulating the migration mechanism of lithium ions and adjusting the ion occupancy ratio of Li ions, are potential directions to achieve ionic conductivity close to or even higher than that of organic LEs in solid electrolytes.Author contributions
Y. W. and F. W. conceived the framework of the article and determined the theme of the article. Y. W. investigated the relevant literature and performed experiments. Y. W., Y. J. W., and Z. W. wrote the manuscript. F. W., H. L., and L. C. revised the manuscript. F. W. supervised the project. All authors participated in the discussion and commented on the manuscript.Conflicts of interest
The authors declare no conflicting financial interests.Acknowledgements
This work is supported by Key Program-Automobile Joint Fund of National Natural Science Foundation of China (Grant No. U1964205), Key R&D Project funded by Department of Science and Technology of Jiangsu Province (Grant No. BE2020003), General Program of National Natural Science Foundation of China (Grant No. 51972334), General Program of National Natural Science Foundation of Beijing (Grant No. 2202058), Cultivation Project of Leading Innovative Experts in Changzhou City (CQ20210003), National Overseas High-level Expert Recruitment Program (Grant No. E1JF021E11), Talent Program of Chinese Academy of Sciences, “Scientist Studio Program Funding” from Yangtze River Delta Physics Research Center and Tianmu Lake Institute of Advanced Energy Storage Technologies (Grant No. TIES-SS0001), Joint research program supported by Science and Technology Research Institute of China Three Gorges Corporation (Grant 202103402).References
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed
.
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed
.
- Y. Liu, Y. Wang, F. Wang, Z. Lei, W. Zhang, K. Pan, J. Liu, M. Chen, G. Wang, F. Ren and S. Wei, Nanomaterials, 2019, 9(12), 1689 CrossRef CAS PubMed
.
- T. H. Wu, Y. Zhang, Z. D. Althouse and N. Liu, Mater. Today Nano, 2019, 6, 100032 CrossRef
.
- Q. Wang, L. Jiang, Y. Yu and J. Sun, Nano Energy, 2019, 55, 93–114 CrossRef CAS
.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1(4) DOI:10.1038/nenergy.2016.30
.
- W. Greatbatch, J. H. Lee, W. Mathias, M. Eldridge, J. R. Moser and A. A. Schneider, IEEE Trans. Biomed. Eng., 1971, 18(5), 317–323 CAS
.
- B. B. Owens, J. Power Sources, 2000, 90, 2–8 CrossRef CAS
.
- B. B. Owens, Solid State Ionics, 1992, 1, 665–672 CrossRef
.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS
.
- J. Janek and W. G. Zeier, Nat. Energy, 2016, 1(9) DOI:10.1038/nenergy.2016.141
.
- S. Kim, H. Oguchi, N. Toyama, T. Sato, S. Takagi, T. Otomo, D. Arunkumar, N. Kuwata, J. Kawamura and S. I. Orimo, Nat. Commun., 2019, 10, 1081 CrossRef PubMed
.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed
.
- F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, J. Power Sources, 2018, 389, 198–213 CrossRef CAS
.
- K. H. Park, Q. Bai, D. H. Kim, D. Y. Oh, Y. Zhu, Y. Mo and Y. S. Jung, Adv. Energy Mater., 2018, 8(18), 1800035 CrossRef
.
- C. Yu, F. Zhao, J. Luo, L. Zhang and X. Sun, Nano Energy, 2021, 83, 105858 CrossRef CAS
.
- S. Chen, D. Xie, G. Liu, J. P. Mwizerwa, Q. Zhang, Y. Zhao, X. Xu and X. Yao, Energy Storage Materials, 2018, 14, 58–74 CrossRef
.
- W. Fitzhugh, F. Wu, L. Ye, H. Su and X. Li, Small, 2019, 15, e1901470 CrossRef PubMed
.
- V. Patil, A. Patil, S. J. Yoon and J. W. Choi, J. Nanosci. Nanotechnol., 2013, 13, 3665–3668 CrossRef CAS PubMed
.
- W. L. Huang, N. Zhao, Z. J. Bi, C. Shi, X. X. Guo, L. Z. Fan and C. W. Nan, Mater. Today Nano, 2020, 10, 100075 CrossRef
.
- H. Huo, J. Liang, N. Zhao, X. Li, X. Lin, Y. Zhao, K. Adair, R. Li, X. Guo and X. Sun, ACS Energy Lett., 2020, 5, 2156–2164 CrossRef CAS
.
- N. Zhao, W. Khokhar, Z. Bi, C. Shi, X. Guo, L.-Z. Fan and C.-W. Nan, Joule, 2019, 3, 1190–1199 CrossRef CAS
.
- H. Huo, X. Li, Y. Sun, X. Lin, K. Doyle-Davis, J. Liang, X. Gao, R. Li, H. Huang, X. Guo and X. Sun, Nano Energy, 2020, 73, 104836 CrossRef CAS
.
- K. Chen, M. Huang, Y. Shen, Y. Lin and C. W. Nan, Solid State Ionics, 2013, 235, 8–13 CrossRef CAS
.
- S. Teng, J. Tan and A. Tiwari, Curr. Opin. Solid State Mater. Sci., 2014, 18(1), 29–38 CrossRef CAS
.
- Y. Jin and P. J. McGinn, J. Power Sources, 2011, 196, 8683–8687 CrossRef CAS
.
- H. Deiseroth, S. Kong, H. Eckert, J. Vannahme, C. Reiner, T. Zaiß and M. Schlosser, Angew. Chem., 2008, 120, 767–770 CrossRef
.
- C. Yu, S. Ganapathy, J. Hageman, L. van Eijck, E. R. H. van Eck, L. Zhang, T. Schwietert, S. Basak, E. M. Kelder and M. Wagemaker, ACS Appl. Mater. Interfaces, 2018, 10, 33296–33306 CrossRef CAS PubMed
.
- M. A. Kraft, S. P. Culver, M. Calderon, F. Bocher, T. Krauskopf, A. Senyshyn, C. Dietrich, A. Zevalkink, J. Janek and W. G. Zeier, J. Am. Chem. Soc., 2017, 139, 10909–10918 CrossRef CAS PubMed
.
- W. Fitzhugh, F. Wu, L. Ye, W. Deng, P. Qi and X. Li, Adv. Energy Mater., 2019, 9(21), 1900807 CrossRef
.
- L. Liu, J. Xu, S. Wang, F. Wu, H. Li and L. Chen, eTransportation, 2019, 1, 100010 CrossRef
.
- P. Albertus, S. Babinec, S. Litzelman and A. Newman, Nat. Energy, 2017, 3, 16–21 CrossRef
.
- L. Fan, S. Wei, S. Li, Q. Li and Y. Lu, Adv. Energy Mater., 2018, 8, 1702657 CrossRef
.
- Y. Zhu, X. He and Y. Mo, ACS Appl. Mater. Interfaces, 2015, 7, 23685–23693 CrossRef CAS PubMed
.
- S. Wenzel, S. J. Sedlmaier, C. Dietrich, W. G. Zeier and J. Janek, Solid State Ionics, 2018, 318, 102–112 CrossRef CAS
.
- Y. Wang, Y. Lv, Y. Su, L. Chen, H. Li and F. Wu, Nano Energy, 2021, 106589 CrossRef CAS
.
- J. Xu, L. Liu, N. Yao, F. Wu, H. Li and L. Chen, Mater. Today Nano, 2019, 8, 100048 CrossRef
.
- J. Peng, D. Wu, F. Song, S. Wang, Q. Niu, J. Xu, P. Lu, H. Li, L. Chen and F. Wu, Adv. Funct. Mater., 2021, 2105776 Search PubMed
.
- G. Larraz, A. Orera and M. L. Sanjuán, J. Mater. Chem. A, 2013, 1, 11419 RSC
.
- C. Bernuy-Lopez, W. Manalastas, J. M. Lopez del Amo, A. Aguadero, F. Aguesse and J. A. Kilner, Chem. Mater., 2014, 26, 3610–3617 CrossRef CAS
.
- F. Aguesse, J. M. López del Amo, V. Roddatis, A. Aguadero and J. A. Kilner, Adv. Mater. Interfaces, 2014, 1, 1300143 CrossRef
.
- C. Galven, J. Dittmer, E. Suard, F. Le Berre and M.-P. Crosnier-Lopez, Chem. Mater., 2012, 24, 3335–3345 CrossRef CAS
.
- Y. Y. Hu, Z. Liu, K. W. Nam, O. J. Borkiewicz, J. Cheng, X. Hua, M. T. Dunstan, X. Yu, K. M. Wiaderek, L. S. Du, K. W. Chapman, P. J. Chupas, X. Q. Yang and C. P. Grey, Nat. Mater., 2013, 12, 1130–1136 CrossRef CAS PubMed
.
- A. Boulant, J. F. Bardeau, A. Jouanneaux, J. Emery, J. Y. Buzaré and O. Bohnke, Dalton Trans., 2010, 39, 3968–3975 RSC
.
- R. H. Brugge, A. K. O. Hekselman, A. Cavallaro, F. M. Pesci, R. J. Chater, J. A. Kilner and A. Aguadero, Chem. Mater., 2018, 30, 3704–3713 CrossRef CAS
.
- P. Lu, L. Liu, S. Wang, J. Xu, J. Peng, W. Yan, Q. Wang, H. Li, L. Chen and F. Wu, Adv. Mater., 2021, e2100921 CrossRef PubMed
.
- F. Wu, W. Fitzhugh, L. Ye, J. Ning and X. Li, Nat. Commun., 2018, 9, 4037 CrossRef PubMed
.
- R.-J. Chen, M. Huang, W.-Z. Huang, Y. Shen, Y.-H. Lin and C.-W. Nan, Solid State Ionics, 2014, 265, 7–12 CrossRef CAS
.
- M. Huang, A. Dumon and C.-W. Nan, Electrochem. Commun., 2012, 21, 62–64 CrossRef CAS
.
- Y. Ren, Y. Shen, Y. Lin and C. W. Nan, ACS Appl. Mater. Interfaces, 2019, 11, 5928–5937 CrossRef CAS PubMed
.
- S.-W. Baek, J.-M. Lee, T. Y. Kim, M.-S. Song and Y. Park, J. Power Sources, 2014, 249, 197–206 CrossRef CAS
.
- H. El Shinawi and J. Janek, J. Power Sources, 2013, 225, 13–19 CrossRef CAS
.
- R. H. Brugge, J. A. Kilner and A. Aguadero, Solid State Ionics, 2019, 337, 154–160 CrossRef CAS
.
- L. Buannic, B. Orayech, J.-M. López Del Amo, J. Carrasco, N. A. Katcho, F. Aguesse, W. Manalastas, W. Zhang, J. Kilner and A. Llordés, Chem. Mater., 2017, 29, 1769–1778 CrossRef CAS
.
- Y. Shimonishi, A. Toda, T. Zhang, A. Hirano, N. Imanishi, O. Yamamoto and Y. Takeda, Solid State Ionics, 2011, 183, 48–53 CrossRef CAS
.
- Q. Liu, Z. Geng, C. Han, Y. Fu, S. Li, Y.-b. He, F. Kang and B. Li, J. Power Sources, 2018, 389, 120–134 CrossRef CAS
.
- S. Guo, Y. Sun and A. Cao, Chem. Res. Chin. Univ., 2020, 36, 329–342 CrossRef CAS
.
- R. Jalem, M. J. D. Rushton, W. Manalastas, M. Nakayama, T. Kasuga, J. A. Kilner and R. W. Grimes, Chem. Mater., 2015, 27, 2821–2831 CrossRef CAS
.
- M. A. Howard, O. Clemens, E. Kendrick, K. S. Knight, D. C. Apperley, P. A. Anderson and P. R. Slater, Dalton Trans., 2012, 41, 12048–12053 RSC
.
- D. Rettenwander, C. A. Geiger, M. Tribus, P. Tropper and G. Amthauer, Inorg. Chem., 2014, 53, 6264–6269 CrossRef CAS PubMed
.
- J. Allen, J. Wolfenstine and E. Rangasamy, J. Power Sources, 2012, 206, 315–319 CrossRef CAS
.
- J. C. Bachman, S. Muy, A. Grimaud, H. H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed
.
- N. Kuganathan, M. J. D. Rushton, R. W. Grimes, J. A. Kilner, E. I. Gkanas and A. Chroneos, Sci. Rep., 2021, 11, 451 CrossRef CAS PubMed
.
- D. Rettenwander, G. Redhammer, F. Preishuber-Pflugl, L. Cheng, L. Miara, R. Wagner, A. Welzl, E. Suard, M. M. Doeff, M. Wilkening, J. Fleig and G. Amthauer, Chem. Mater., 2016, 28, 2384–2392 CrossRef CAS PubMed
.
- H. Salimkhani, A. Yurum and S. A. Gursel, Ionics, 2021, 27(9), 3673–3698 CrossRef CAS
.
- D. Rettenwander, C. A. Geiger, M. Tribus, P. Tropper, R. Wagner, G. Tippelt, W. Lottermoser and G. Amthauer, J. Solid State Chem., 2015, 230, 266–271 CrossRef CAS PubMed
.
- D. Rettenwander, C. A. Geiger and G. Amthauer, Inorg. Chem., 2013, 52, 8005–8009 CrossRef CAS PubMed
.
- H. El-Shinawi, E. J. Cussen and S. A. Corr, Dalton Trans., 2017, 46, 9415–9419 RSC
.
- N. Bernstein, M. D. Johannes and K. Hoang, Phys. Rev. Lett., 2012, 109(20), 205702 CrossRef CAS PubMed
.
- E. J. Cussen, J. Mater. Chem., 2010, 20, 5167 RSC
.
- E. Ortiz, R. A. Vargas and B. E. Mellander, J. Phys.: Condens. Matter, 2006, 18, 9561–9573 CrossRef CAS
.
- H. Fjeld, K. Toyoura, R. Haugsrud and T. Norby, Phys. Chem. Chem. Phys., 2010, 12, 10313–10319 RSC
.
- T. J. Udovic, M. Matsuo, W. S. Tang, H. Wu, V. Stavila, A. V. Soloninin, R. V. Skoryunov, O. A. Babanova, A. V. Skripov, J. J. Rush, A. Unemoto, H. Takamura and S. Orimo, Adv. Mater., 2014, 26, 7622–7626 CrossRef CAS PubMed
.
- N. Verdal, T. J. Udovic, V. Stavila, W. S. Tang, J. J. Rush and A. V. Skripov, J. Phys. Chem. C, 2014, 118, 17483–17489 CrossRef CAS
.
- L. Buannic, B. Orayech, J.-M. López Del Amo, J. Carrasco, N. A. Katcho, F. Aguesse, W. Manalastas, W. Zhang, J. Kilner and A. Llordés, Chem. Mater., 2017, 29, 1769–1778 CrossRef CAS
.
- C. Yu, S. Ganapathy, E. R. H. van Eck, L. van Eijck, S. Basak, Y. Liu, L. Zhang, H. W. Zandbergen and M. Wagemaker, J. Mater. Chem. A, 2017, 5, 21178–21188 RSC
.
- H. Wang, C. Yu, S. Ganapathy, E. R. H. van Eck, L. van Eijck and M. Wagemaker, J. Power Sources, 2019, 412, 29–36 CrossRef CAS
.
- Y. Gao, A. M. Nolan, P. Du, Y. Wu, C. Yang, Q. Chen, Y. Mo and S. H. Bo, Chem. Rev., 2020, 120, 5954–6008 CrossRef CAS PubMed
.
- M. Wilkening, W. Kuchler and P. Heitjans, Phys. Rev. Lett., 2006, 97, 065901 CrossRef CAS PubMed
.
- M. Wilkening, A. Kuhn and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(5) DOI:10.1103/physrevb.78.054303
.
- M. Wilkening and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(2) DOI:10.1103/physrevb.77.024311
.
- K. Hayamizu, S. Seki and T. Haishi, J. Chem. Phys., 2017, 146, 024701 CrossRef PubMed
.
- M. Månsson and J. Sugiyama, Phys. Scr., 2013, 88, 068509 CrossRef
.
- J. Sugiyama, J. Phys. Soc. Jpn., 2013, 82, SA023 CrossRef
.
- M. Amores, T. E. Ashton, P. J. Baker, E. J. Cussen and S. A. Corr, J. Mater. Chem. A, 2016, 4, 1729–1736 RSC
.
- H. Nozaki, M. Harada, S. Ohta, I. Watanabe, Y. Miyake, Y. Ikedo, N. H. Jalarvo, E. Mamontov and J. Sugiyama, Solid State Ionics, 2014, 262, 585–588 CrossRef CAS
.
- M. Karlsson, Phys. Chem. Chem. Phys., 2015, 17, 26–38 RSC
.
- H. Jobic and D. N. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS
.
- I. Riess, Solid State Ionics, 2003, 157, 1–17 CrossRef CAS
.
- W. Lai and S. M. Haile, J. Am. Ceram. Soc., 2005, 88, 2979–2997 CrossRef CAS
.
- S. Takai, K. Yoshioka, H. Iikura, M. Matsubayashi, T. Yao and T. Esaka, Solid State Ionics, 2014, 256, 93–96 CrossRef CAS
.
- S. Takai, Solid State Ionics, 2004, 171, 107–112 CrossRef CAS
.
- S. Takai, M. Kamata, S. Fujine, K. Yoneda, K. Kanda and T. Esaka, Solid State Ionics, 1999, 123, 165–172 CrossRef CAS
.
- R. H. Brugge, R. J. Chater, J. A. Kilner and A. Aguadero, J. Phys.: Energy, 2021, 3, 034001 CAS
.
- K. Rosman and P. Taylor, J. Phys. Chem. Ref. Data, 1998, 10, 1275 CrossRef
.
- D. Rettenwander, G. Redhammer, F. Preishuber-Pflugl, L. Cheng, L. Miara, R. Wagner, A. Welzl, E. Suard, M. M. Doeff, M. Wilkening, J. Fleig and G. Amthauer, Chem. Mater., 2016, 28, 2384–2392 CrossRef CAS PubMed
.
- V. Gulin, W. J. Bowman, Q. Lu, J. Wang, R. J. Chater, A. Ainara, S. Rachel, T. Jeff, H. Adrian and W. Iradwikanari, Chem. Mater., 2018, 8b01713 Search PubMed
.
- J. Zhang, L. Li, C. Zheng, Y. Xia, Y. Gan, H. Huang, C. Liang, X. He, X. Tao and W. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 41538–41545 CrossRef PubMed
.
- F. Zhao, J. Liang, C. Yu, Q. Sun, X. Li, K. Adair, C. Wang, Y. Zhao, S. Zhang, W. Li, S. Deng, R. Li, Y. Huang, H. Huang, L. Zhang, S. Zhao, S. Lu and X. Sun, Adv. Energy Mater., 2020, 10(9), 1903422 CrossRef CAS
.
- S. Ohno, B. Helm, T. Fuchs, G. Dewald, M. A. Kraft, S. P. Culver, A. Senyshyn and W. G. Zeier, Chem. Mater., 2019, 31, 4936–4944 CrossRef CAS
.
- T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Adv. Mater., 2018, 30, 1–7 CrossRef PubMed
.
- R. Schlem, S. Muy, N. Prinz, A. Banik, S. Yang, M. Zobel and W. G. Zeier, Adv. Energy Mater., 2020, 10(6), 1–10 Search PubMed
.
- H. Kwak, D. Han, J. Lyoo, J. Park, S. H. Jung, Y. Han, G. Kwon, H. Kim, S. T. Hong, K. W. Nam and Y. S. Jung, Adv. Energy Mater., 2021, 11, 2003190 CrossRef CAS
.
-
A. R. West, Solid State Chemistry and its Applications, John Wiley & Sons, New York, 2014 Search PubMed
.
- S. Wang, Q. Bai, A. M. Nolan, Y. Liu, S. Gong, Q. Sun and Y. Mo, Angew. Chem., Int. Ed. Engl., 2019, 58, 8039–8043 CrossRef CAS PubMed
.
- A. E. I. Kharbachi, E. Pinatel, I. Nuta and M. Baricco, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2012, 39, 90 CrossRef
.
- M. Matsuo, Y. Nakamori, S. I. Orimo, H. Maekawa and H. Takamura, Appl. Phys. Lett., 2007, 91(22), 112104 CrossRef
.
- M. Matsuo and S. I. Orimo, Adv. Energy Mater., 2011, 1(2), 161–172 CrossRef CAS
.
- A. E. Kharbachi, J. Wind, A. Ruud, A. B. Høgset and B. C. Hauback, Phys. Chem. Chem. Phys., 2020, 22(25), 13872–13879 RSC
.
- T. Zhang, Y. Shao, X. Zhang, Y. Huang, S. Wang, W. Zhou, P. Li, G. Xia and X. Yu, Small Methods, 2021, 5, e2100609 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta10966a |
| This journal is © The Royal Society of Chemistry 2022 |