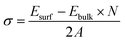Vacancy assisted growth of copper tantalum sulfide nanocrystals†
Anamul
Haque
 ab,
Soheil
Ershadrad
ab,
Soheil
Ershadrad
 c,
Trupthi Devaiah
Chonamada
c,
Trupthi Devaiah
Chonamada
 ab,
Dipankar
Saha
ab,
Dipankar
Saha
 de,
Biplab
Sanyal
de,
Biplab
Sanyal
 *c and
Pralay K.
Santra
*c and
Pralay K.
Santra
 *a
*a
aCentre for Nano and Soft Matter Sciences (CeNS), Bengaluru, 562162, India. E-mail: psantra@cens.res.in
bManipal Academy of Higher Education (MAHE), Manipal, 576104, India
cDepartment of Physics and Astronomy, Materials Theory, Uppsala University, Box 516, SE-751 20, Uppsala, Sweden. E-mail: biplab.sanyal@physics.uu.se
dSchool of Chemical and Process Engineering, University of Leeds & CMAC, Leeds, LS29JT, UK
eResearch Complex at Harwell (RCaH), Rutherford Appleton Laboratory, Harwell, Didcot, Oxon, OX11 0FA, UK
First published on 6th June 2022
Abstract
Cu-based ternary chalcogenides have received significant interest as an alternative to conventional photovoltaic materials. CuInS2 and CuInSe2 are the most studied copper-based ternary chalcogenides for photovoltaics. Recently, copper tantalum sulfide (CuTaS3) has been proposed as a potential light absorber for photovoltaics. The synthesis conditions and growth mechanism of ternary systems control the final composition and crystal structure. However, such studies have not been explored for copper tantalum sulfides. Here, we studied the formation and growth mechanism of Cu3TaS4 nanocrystals (NCs) primarily using X-ray diffraction, transmission electron microscopy, and density functional theory (DFT) calculations. The reactions proceed via the formation of cubic Cu2−xS NCs due to soft Lewis acid – soft Lewis base interaction. The Cu2−xS have Cu vacancies, which can be controlled by the relative concentration of the Cu precursor. Ta incorporation occurs in the Cu2−xS NCs at Cu vacancy sites, followed by the diffusion of Ta by replacing Cu into the lattice. Low packing of atoms in Cu3TaS4 provides suitable diffusion channels for Ta and Cu atoms. The diffusion barriers of Ta atoms outweigh that of Cu atoms, implying a reaction rate controlled by Ta diffusion. Thus by varying the relative Cu precursor concentration, the concentration of Cu-vacancies in Cu2−xS can be tuned, which controls the growth rate of Cu3TaS4. Understanding of the growth mechanism obtained in this paper will significantly contribute to the rational synthesis of various Cu-based ternary chalcogenides that is not possible by direct synthesis and hence will have an impact on potential applications in photovoltaics and photocatalysis.
Introduction
Cadmium and lead-based chalcogenide nanocrystals (NCs) have gained interest in the photovoltaics (PV) community as emerging candidates for large-area, low-cost, and high-efficiency PV devices.1–5 However, the usage of heavy metal ions limits the practical applicability of these materials.6 Binary and ternary copper chalcogenide NCs have emerged as an alternative for heavy metal chalcogenides since these NCs can be directly synthesized with controlled sizes, shapes, crystal structures, and stoichiometries. As a result, they provide good control over the optoelectronic properties and serve as a template for ternary chalcogenides.7–13 Additionally, relatively low cost and low toxicity of Cu2−xS and Cu-based ternary chalcogenides make them attractive candidates for PV as well as in photocatalysis.Among the Cu-based ternary chalcogenides, CuInS2 and CuInSe2 are most studied as light absorbers in thin-film solar cells for over three decades.14–17 Compared to the bulk, the NCs of these ternary chalcogenides have the added advantages of tuning electronic properties by controlling the size and can be deposited on various substrates by low-cost solution-based deposition.18 These ternary chalcogenides NCs are synthesized in a one-pot synthesis – however, the reactivity of the two cationic precursors has to be balanced which is achieved by tuning the appropriate precursor, passivating ligand, and reaction temperature.9,19–23 In a one-pot synthesis, both the cationic and anionic precursors are added together. Cu+ is a soft Lewis acid (η = 6.28 eV) and the other cationic species e.g., In3+, Ga3+, having a higher oxidation state, are generally hard Lewis acid.20,24 A variety of sulfur precursors have been used in these reactions, which vary from soft Lewis base (e.g., alkanethiols,19 1-dodecanethiol25) to hard Lewis base (e.g., thiourea26–28).
In many cases, the binary nanocrystals are first synthesized followed by subsequent cation exchange to form desired ternary or heterostructured NCs. Owing to the low charge and high mobility of Cu+, the post-synthetic cation exchange is feasible in Cu2−xS to produce multiple heterostructures – Cu2−xS–MnS,29 Cu2−xS–ZnS,30–35 Cu2−xS–CdS,36 Cu2−xS–PbS,37 Cu2−xS–In2S3.38,39 The final heterostructure depends on various parameters such as cationic radius, the initial crystal structure, and the reactivity of the facets of the crystal through which the cation exchange occurs, etc. Chen et al., have reported the different crystal structures of CdS when the cation exchange is performed on djurleite Cu1.94S (wurtzite CdS) and covellite CuS (hollow cubic CdS).40 Manna et al. have observed that the InP nucleate at the corners of hexagonal Cu2−xP before propagating inward towards the center for a complete conversion of Cu2−xS to InP NCs.41 In both homovalent and aliovalent cation exchange processes, the nanoscale Kirkendall effect caused hollow ternary chalcogenides.26,42–45 Sapra et al., have developed MoSe2–Cu2S nanoheterostructures, where the Cu2S islands grow vertically on top of the defect site present on the MoSe2 surface.46 Donega et al., have indeed reported the CuInS2 NCs and Cu2−xS-CuInS2 heterostructured NCs by partial indium cation exchange into Cu2−xS NCs.47,48 Steimle et al., have demonstrated a multi-step sequential cation exchange of Cu1.8S nanorod to form multicomponent axially segmented heteronanorods having eight segments, six different elements, and 11 interfaces.49
In 2017, Heo et al. theoretically identified CuTaS3 as a strong light absorber that exhibits metal d and sulfur p character near the band edges.50 As this material has intermetal d0–d10 transitions, it can exhibit a strong onset coupled with high absorption. Based on spectroscopic limited maximum efficiency for PV calculations, they predicted the theoretical power conversion efficiency to be 28% for a 300 nm thick absorber of CuTaS3, which is higher than the CuInSe2 of the same thickness. The Cu-based ternary chalcogenides often exhibit multiple phases, and it is important to study the growth of these nanocrystals. The synthesis of Cu–Ta–S ternary chalcogenides NCs was not attempted earlier. Due to its potential applications, it is important to synthesize the Cu–Ta–S ternary chalcogenide, particularly in NCs that helps in solution processed device fabrication. Overall, the understanding of the growth mechanism of such NCs systems is also required for rational synthesis of Cu-based ternary chalcogenides.
Here we report the hot injection synthesis of copper tantalum sulfide NCs. We carried out the reactions under three different reaction conditions – Cu rich, Ta rich, and equimolar concentration of Cu and Ta. Experimentally, we probed the formation and growth mechanism by X-ray diffraction and transmission electron microscopy (TEM). Under all three reaction conditions, cubic Cu3TaS4 NCs were formed. Rietveld analysis and UV-Vis absorption studies show the formation of Cu2−xS NCs at the beginning of the reaction followed by Ta incorporation into Cu2−xS NCs, converting them to Cu3TaS4 NCs. These results were further substantiated with high-resolution transmission electron microscopic (HRTEM) images. We used density functional theory (DFT) to calculate the energetics and predict the diffusion model for Ta incorporation into Cu2−xS NCs to form Cu3TaS4 NCs.
Experimental section
Chemicals
Copper(I) chloride (CuCl, 99.995%, Sigma-Aldrich), tantalum(V) chloride (TaCl5, 99.999%, Sigma-Aldrich), carbon disulfide (CS2, 99.5%, Central Drug House (P) Ltd) oleylamine (OLA, 70%, Sigma-Aldrich), and n-hexane (95%, Spectrochem), methanol (>98%, Spectrochem) were used as received.Synthesis of Cu–Ta–S nanocrystals
In a 50 mL three-neck round bottom flask, CuCl and TaCl5 were taken in 14.76 mL (44.8 mmol) of OLA. The reaction mixture were heated at 120 °C for 1 hour under vacuum. The total cation precursor (Cu + Ta) was kept constant at 5.84 mmol, whereas the relative concentrations of Cu and Ta precursors were varied. The individual quantities are mentioned in Table S1 in the ESI.† The reaction temperature was increased to 290 °C under a nitrogen atmosphere to completely dissolve the precursor salts and held the reaction mixture was kept for 1 hour to ensure the complete dissolution of the precursors. Before the sulfur precursor injection, the reaction temperature was raised to 300 °C. 1.35 mL of CS2 was swiftly injected into the reaction flask. Periodically aliquots were collected from the reaction mixture to probe the growth mechanism of the NCs. The schematic diagram of the synthesis procedure is shown in Fig. S1.†The collected aliquots were cooled to room temperature before diluting with hexane. The diluted reaction mixture was centrifuged at 3000 rpm for 3 minutes to get the precipitate of the nanoparticles, which were washed two times by dispersing in 2 mL hexane and reprecipitating with 6 mL of methanol. The washed precipitate was finally dispersed in hexane for further characterization.
Characterization
A PerkinElmer, Lambda-45 UV-vis spectrometer was used to record the UV-visible absorption spectra. Powder X-ray diffraction (PXRD) of the NCs were carried out on drop cast thin-films on glass substrates using a Rigaku Smart Lab diffractometer equipped with parallel beam optics and Cu Kα radiation (40 kV, 30 mA) with a grazing angle of 2°. Transmission electron microscopy studies were carried out using the TALOS F200S G2 microscope at 200 kV.Rietveld refinement
Rietveld refinements51 were carried out using FullProf Suite.52 Refined instrumental parameters were zero point displacement and background parameters. Refined structural parameters for all phases were scale factor, unit cell parameters and peak profile using Thompson–Cox–Hastings pseudo-Voigt (TCHpV) profile parameters.52 Instrumental resolution was taken into account by refining TCHpV profile parameters for the Si standard and included them in an instrumental resolution file (*.irf) implemented in the refinements.Computational methods
First-principles calculations based on density functional theory (DFT) were performed using the Vienna Ab initio Simulation Package (VASP).53,54 For these calculations, projector-augmented wave potentials55 and a plane-wave basis set with an energy cut-off of 500 eV was employed. The exchange-correlation potential was approximated by the generalized gradient approximation (GGA) with Perdew, Burke, and Ernzerhof (PBE) functional.56 For Brillouin zone integration of Cu2S and Cu3TaS4, a 9 × 9 × 9 k-point grid in the Monkhorst–Pack scheme57 was used. To simulate the vacancies, a supercell of 2 × 2 × 2 was built and the vacancies were created in this structure at random positions. The equilibrium configuration of atoms and lattice constants was determined by minimizing the total energy of the system using the conjugate gradient method until force components on each atom were reached below 0.01 eV Å−1. Saddle points and minimum energy diffusion paths between two stable states were found through climbing image Nudged Elastic Band (NEB) calculations, using VTST tool,58 where five intermediate images along the diffusion path were considered and a spring force of −5 eV Å−2 was set between them. Vacancy formation energies were calculated using the following expression,| Ef = ECu2−xS − ECu2S + EFcc−Cu |
Surface calculations were performed on a 2 × 2 supercell of a thin film with three unit cell thickness (expanded parallel to surface), where a vacuum of 20 Å was added along the c-axis to avoid interaction between periodic images. Since rearrangement of atoms only occurs near the surface, the position of atoms in the lowermost layers in the unit cell along the c-axis was fixed during geometry optimization to maintain the bulk properties. The surface energy of different crystalline facets was calculated based on the following expression,
Results and discussion
Cu–Ta–S is known to exist in two different crystal structures – the orthorhombic phase having a composition of CuTaS3 and the cubic phase of Cu3TaS4.50,59 The synthesis of the Cu–Ta–S NCs was carried out by the standard hot injection method with an excess amount of the sulfur precursor (molar ratio ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8). The details of the synthesis procedure are mentioned in the experimental section. The powder X-ray diffraction (PXRD) pattern of the washed NCs synthesized with a 1
8). The details of the synthesis procedure are mentioned in the experimental section. The powder X-ray diffraction (PXRD) pattern of the washed NCs synthesized with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Cu
1 ratio of Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta is shown in Fig. 1a along with the two standard diffraction patterns: orthorhombic CuTaS3 (space group: Pnma) and cubic Cu3TaS4 (space group: P
Ta is shown in Fig. 1a along with the two standard diffraction patterns: orthorhombic CuTaS3 (space group: Pnma) and cubic Cu3TaS4 (space group: P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m). The nanocrystals formed in the cubic phase, instead of the intended orthorhombic phase which has the cation (Cu
3m). The nanocrystals formed in the cubic phase, instead of the intended orthorhombic phase which has the cation (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta) ratio of 1
Ta) ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Separate syntheses having Cu-rich (Cu
1. Separate syntheses having Cu-rich (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 3
Ta = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and Ta-rich (Cu
1) and Ta-rich (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1
Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) precursor concentrations were also carried out, however, both the conditions yielded NCs in the cubic Cu3TaS4 phase only (Fig. S2 in the ESI†). In agreement with experimental results, ab initio calculations also indicate that the formation of Cu3TaS4 instead of CuTaS3 NCs is more favoured from an energetic point of view. In fact, calculation of the formation energy per formula unit (f.u) of the cubic Cu3TaS4 and orthorhombic CuTaS3 phases (shown in Table S2†) revealed that the cubic phase has a formation energy of −4.99 eV f.u−1 (−0.62 eV per atom) which is quite lower than the orthorhombic phase (−2.49 eV f.u−1 equivalent to −0.50 eV per atom). We believe that this energetic privilege of Cu3TaS4, added to its better structural compatibility with Cu2−xS, drive the system to form Cu3TaS4 crystals, instead of CuTaS3.
3) precursor concentrations were also carried out, however, both the conditions yielded NCs in the cubic Cu3TaS4 phase only (Fig. S2 in the ESI†). In agreement with experimental results, ab initio calculations also indicate that the formation of Cu3TaS4 instead of CuTaS3 NCs is more favoured from an energetic point of view. In fact, calculation of the formation energy per formula unit (f.u) of the cubic Cu3TaS4 and orthorhombic CuTaS3 phases (shown in Table S2†) revealed that the cubic phase has a formation energy of −4.99 eV f.u−1 (−0.62 eV per atom) which is quite lower than the orthorhombic phase (−2.49 eV f.u−1 equivalent to −0.50 eV per atom). We believe that this energetic privilege of Cu3TaS4, added to its better structural compatibility with Cu2−xS, drive the system to form Cu3TaS4 crystals, instead of CuTaS3.
From a structural point of view, the transformation of Cu2−xS into Cu3TaS4 can be modelled via a diffusion-mediated mechanism. For this purpose, the structural configuration of cubic Cu2S crystal is shown in Fig. 1b, where Cu atoms occupy tetrahedral sites, each of which is bonded to four S atoms, creating symmetrically equivalent Cu sites. By optimizing the given structure, the lattice parameter and the symmetry group were found to be a = 5.58 Å and Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, respectively. In Fig. 1c, the formation of vacancies in tetrahedral sites is schematically shown. We calculated the formation energy of vacancies for a Cu1.8S, with a vacancy concentration of 9.37% to be −1.18 eV per vacancy, verifying the spontaneous formation of vacancies in Cu2S. As the concentration of vacancies increases, around x = 0.4, another cubic phase of Cu2−xS becomes stable with a symmetry of F
m, respectively. In Fig. 1c, the formation of vacancies in tetrahedral sites is schematically shown. We calculated the formation energy of vacancies for a Cu1.8S, with a vacancy concentration of 9.37% to be −1.18 eV per vacancy, verifying the spontaneous formation of vacancies in Cu2S. As the concentration of vacancies increases, around x = 0.4, another cubic phase of Cu2−xS becomes stable with a symmetry of F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m. To predict which of these phases is dominant in the process, we calculated the vacancy formation energy in Cu1.6S to be −0.5 eV per vacancy. In addition, we found that the formation energy of Cu1.8S is 20 meV per atom lower than that of Cu1.6S crystals, calculated with respect to bulk sulfur and FCC copper. Therefore, it can be inferred that in presence of sufficient Cu atoms, the formation of Cu1.8S crystal is energetically more favorable compared to Cu1.6S. Considering Cu1.8S as the initial phase of the reaction, the formation of Cu3TaS4 crystals can be justified based on the structural similarities between the two crystals. For ease of comparison, the crystal structure of Cu3TaS4 and CuTaS3 are shown in Fig. 1d and e, respectively. The lattice parameter and symmetry group of Cu3TaS4 were calculated to be a = 5.56 Å and P
3m. To predict which of these phases is dominant in the process, we calculated the vacancy formation energy in Cu1.6S to be −0.5 eV per vacancy. In addition, we found that the formation energy of Cu1.8S is 20 meV per atom lower than that of Cu1.6S crystals, calculated with respect to bulk sulfur and FCC copper. Therefore, it can be inferred that in presence of sufficient Cu atoms, the formation of Cu1.8S crystal is energetically more favorable compared to Cu1.6S. Considering Cu1.8S as the initial phase of the reaction, the formation of Cu3TaS4 crystals can be justified based on the structural similarities between the two crystals. For ease of comparison, the crystal structure of Cu3TaS4 and CuTaS3 are shown in Fig. 1d and e, respectively. The lattice parameter and symmetry group of Cu3TaS4 were calculated to be a = 5.56 Å and P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m. One can note that, in contrast to CuTaS3, the crystal structure of Cu2S, Cu2−xS, and Cu3TaS4 basically share the same skeleton except for a number of substitutions that take place between Cu, vacancy, and Ta atoms. Compatibility of the lattice parameters in Cu2S (5.58 Å) and Cu3TaS4 (5.56 Å), combined with their overall similarity, suggest that after the spontaneous formation of vacancies in Cu2S, Ta atoms diffuse into the Cu2−xS structure to create Cu3TaS4 crystals.
3m. One can note that, in contrast to CuTaS3, the crystal structure of Cu2S, Cu2−xS, and Cu3TaS4 basically share the same skeleton except for a number of substitutions that take place between Cu, vacancy, and Ta atoms. Compatibility of the lattice parameters in Cu2S (5.58 Å) and Cu3TaS4 (5.56 Å), combined with their overall similarity, suggest that after the spontaneous formation of vacancies in Cu2S, Ta atoms diffuse into the Cu2−xS structure to create Cu3TaS4 crystals.
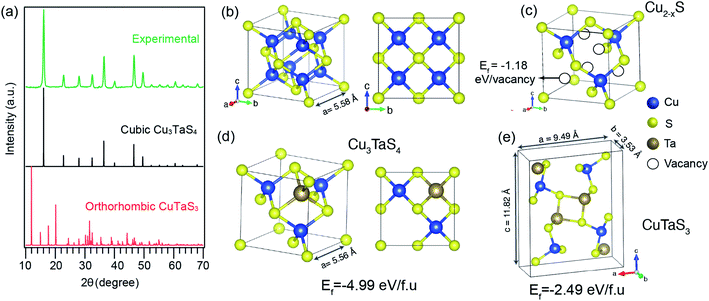
We further probed the growth mechanism of the ternary chalcogenide NCs by collecting the reaction aliquots at different times. The PXRD patterns of the precipitates of the reaction mixture for the Cu-rich (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 3
Ta = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) reaction at different times are shown in Fig. 2a. The diffraction peaks of the precipitate collected at the early stage of the reaction match with the cubic Cu2−xS (x = 0.2). After five minutes of the reaction, new peaks appeared and those are identified to Cu3TaS4. The diffraction peaks of Cu2−xS overlaps with Cu3TaS4. With the progress of the reaction, the intensity of the Cu2−xS (220) peak decreases while Cu3TaS4 (100) peak intensity increases, implying that Cu2−xS NCs are converting to Cu3TaS4. Beyond 30 minutes of the reaction, the diffraction peak positions and the intensities do not vary and the pattern matches well with Cu3TaS4 suggesting the end product of the reaction is the cubic phase Cu3TaS4. For an equal amount of Cu and Ta (Cu
1) reaction at different times are shown in Fig. 2a. The diffraction peaks of the precipitate collected at the early stage of the reaction match with the cubic Cu2−xS (x = 0.2). After five minutes of the reaction, new peaks appeared and those are identified to Cu3TaS4. The diffraction peaks of Cu2−xS overlaps with Cu3TaS4. With the progress of the reaction, the intensity of the Cu2−xS (220) peak decreases while Cu3TaS4 (100) peak intensity increases, implying that Cu2−xS NCs are converting to Cu3TaS4. Beyond 30 minutes of the reaction, the diffraction peak positions and the intensities do not vary and the pattern matches well with Cu3TaS4 suggesting the end product of the reaction is the cubic phase Cu3TaS4. For an equal amount of Cu and Ta (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1
Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), Cu3TaS4 was already present at the early stage of the reaction, with probably some amount of Cu2−xS (Fig. 2b). Due to the overlapping peaks, the presence of both the phases could not be confirmed from these qualitative observations. However, at the end of the reaction, i.e., 30 minutes, only the cubic Cu3TaS4 was observed. In the Ta-rich synthesis (Cu
1), Cu3TaS4 was already present at the early stage of the reaction, with probably some amount of Cu2−xS (Fig. 2b). Due to the overlapping peaks, the presence of both the phases could not be confirmed from these qualitative observations. However, at the end of the reaction, i.e., 30 minutes, only the cubic Cu3TaS4 was observed. In the Ta-rich synthesis (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1
Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), we observed a mixture of TaS2 and Cu3TaS4 at the beginning of the reaction as shown in Fig. 2c. The PXRD pattern of TaS2 (space group: P
3), we observed a mixture of TaS2 and Cu3TaS4 at the beginning of the reaction as shown in Fig. 2c. The PXRD pattern of TaS2 (space group: P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1) is clearly distinct from the Cu3TaS4 or Cu2−xS. In this case, the TaS2 peaks disappear with time and only Cu3TaS4 NCs are present at the end of the reaction, suggesting that all TaS2 are converted to Cu3TaS4 NCs. From these PXRD results, we conclude that the variation of precursor amount in the reaction plays a role during the growth of the NCs, but the final composition remains the same. In a Cu-rich reaction, cubic Cu2−xS forms at an early stage, which then converts to Cu3TaS4; whereas in a Ta-rich reaction, TaS2 forms first and then converts to Cu3TaS4. The formation rate of Cu3TaS4 varies with the relative concentration of the Cu and Ta precursors.
m1) is clearly distinct from the Cu3TaS4 or Cu2−xS. In this case, the TaS2 peaks disappear with time and only Cu3TaS4 NCs are present at the end of the reaction, suggesting that all TaS2 are converted to Cu3TaS4 NCs. From these PXRD results, we conclude that the variation of precursor amount in the reaction plays a role during the growth of the NCs, but the final composition remains the same. In a Cu-rich reaction, cubic Cu2−xS forms at an early stage, which then converts to Cu3TaS4; whereas in a Ta-rich reaction, TaS2 forms first and then converts to Cu3TaS4. The formation rate of Cu3TaS4 varies with the relative concentration of the Cu and Ta precursors.
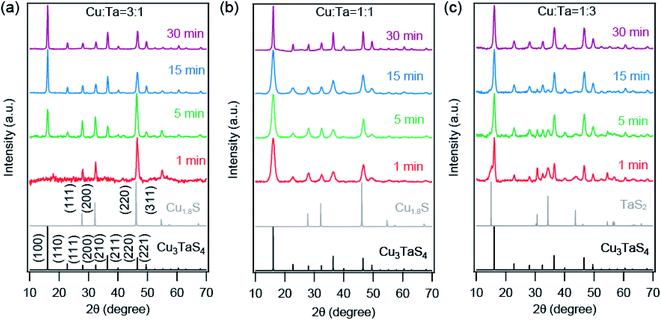
We employed Rietveld refinement to quantify (a) the relative phase fraction, (b) lattice parameter, and (c) particles sizes of Cu2−xS and Cu3TaS4 in the reaction. The PXRD patterns along with the Rietveld refinement profiles for three different precursor concentrations are shown in Fig. S3.† The resulting phase fractions of Cu2−xS (dashed traces with open circles) and Cu3TaS4 (solid traces with filled circles) for reaction 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (black traces) and 1
1 (black traces) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (red trace) are shown in Fig. 3a. For the Cu-rich reaction, the phase fraction of Cu2−xS is 100% at the beginning of the reaction, however, the relative phase fraction of Cu2−xS decreases rapidly, and consequently the amount of Cu3TaS4 increases (see Table 1). At the end of 30 minutes of the reaction, the phase fraction of Cu3TaS4 is found to be 100%. Unlike the Cu-rich reaction, the Cu
1 (red trace) are shown in Fig. 3a. For the Cu-rich reaction, the phase fraction of Cu2−xS is 100% at the beginning of the reaction, however, the relative phase fraction of Cu2−xS decreases rapidly, and consequently the amount of Cu3TaS4 increases (see Table 1). At the end of 30 minutes of the reaction, the phase fraction of Cu3TaS4 is found to be 100%. Unlike the Cu-rich reaction, the Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1
Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 has 65% as Cu3TaS4 and 35% of Cu2−xS, clearly indicating the formation of Cu3TaS4 is faster in a Cu-deficient system. By the end of 15 minutes, the major product is Cu3TaS4 NCs with a relative phase fraction of 89%.
1 has 65% as Cu3TaS4 and 35% of Cu2−xS, clearly indicating the formation of Cu3TaS4 is faster in a Cu-deficient system. By the end of 15 minutes, the major product is Cu3TaS4 NCs with a relative phase fraction of 89%.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 3
Ta = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reaction
1 reaction
Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 3 Ta = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1 Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
||||
|---|---|---|---|---|---|
| Reaction time (min) | Phase fraction | Reaction time (min) | Phase fraction | ||
| Cu2−xS | Cu3TaS4 | Cu2−xS | Cu3TaS4 | ||
| 1 | 100 | 0 | 1 | 34.6 ± 3.8 | 65.4 ± 2.4 |
| 5 | 78.0 ± 1.84 | 22.0 ± 0.6 | 5 | 33.4 ± 3.1 | 66.6 ± 3.0 |
| 15 | 44.0 ± 1.69 | 56.0 ± 1.2 | 15 | 10.7 ± 1.7 | 89.3 ± 2.0 |
| 30 | 0 | 100 | 30 | 0 | 100 |
The lattice parameters of Cu2−xS and Cu3TaS4 as a function of the reaction time are shown in Fig. 3b (lattice parameters are mentioned in Table S3† and Rietveld refinement factors are mentioned in Table S4†). For comparison, the lattice parameter of standard Cu1.8S (ICSD file number: 41142) and cubic Cu3TaS4 (ICSD file number: 185524) are shown by the solid horizontal blue and cyan line. Lattice parameter of Cu2−xS (shown by the dashed line) increases as a function of time for both reactions. Earlier reports suggest that Cu2−xS with higher vacancies have relatively smaller lattice parameters.60 The lattice parameter of standard Cu2−xS for x = 0.4 (ICSD file number: 628786) is shown by the horizontal purple line. Although both the Cu1.6S and Cu1.8S have cubic crystal structures, the lattice parameter of Cu1.6S is much smaller than Cu1.8S. Indirectly, the increase in the lattice parameter indirectly suggests the Cu vacancies in Cu2−xS decrease with reaction time. Also, the lattice parameter of Cu2−xS at a given reaction time is higher for the Cu-rich reaction compared to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reaction indicating fewer Cu vacancies in Cu2−xS for the Cu-rich reaction. At the same time, there was no significant change in Cu3TaS4.
1 reaction indicating fewer Cu vacancies in Cu2−xS for the Cu-rich reaction. At the same time, there was no significant change in Cu3TaS4.
In literature, it is well known that the Cu vacancies in Cu2−xS NCs exhibit a localized surface plasmon resonance (LSPR) peak in the NIR region.61 We collected the absorption spectra for different reactions to understand how the LSPR, thus Cu-vacancies vary with reaction time. The absorption spectra of the NCs for three different precursor concentrations at different reaction times are shown in Fig. S4 in the ESI.† At the early stage of the reactions, a broad absorption peak appears at ∼1100 nm, which is due to the LSPR of Cu2−xS, which was noticed for the Cu-rich and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 precursor ratio. The LSPR peak for the Cu-rich reaction was low in intensity and decreases with reaction time. The same LSPR peak for the 1
1 precursor ratio. The LSPR peak for the Cu-rich reaction was low in intensity and decreases with reaction time. The same LSPR peak for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reaction has a much higher intensity at the beginning of the reaction and it red-shifts as well as the intensity of the peak decreases with the reaction time. We did not observe the typical LSPR peak for the Cu
1 reaction has a much higher intensity at the beginning of the reaction and it red-shifts as well as the intensity of the peak decreases with the reaction time. We did not observe the typical LSPR peak for the Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1
Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 reaction. These results suggest that the Cu-rich reaction forms Cu2−xS with a fewer number of Cu-vacancies, whereas the vacancy increases significantly with a decrease in the Cu precursor in the reaction mixture. The increase of Cu vacancy in Cu2−xS for the lower Cu reaction supports the Rietveld refinement results. It is worthful to note that the reaction proceeds faster with increasing Cu vacancy in Cu2−xS system.
3 reaction. These results suggest that the Cu-rich reaction forms Cu2−xS with a fewer number of Cu-vacancies, whereas the vacancy increases significantly with a decrease in the Cu precursor in the reaction mixture. The increase of Cu vacancy in Cu2−xS for the lower Cu reaction supports the Rietveld refinement results. It is worthful to note that the reaction proceeds faster with increasing Cu vacancy in Cu2−xS system.
We also investigated the growth of these NCs through transmission electron microscopy (TEM). Representative TEM images are shown in Fig. 4 for all three precursor ratios. Primarily the big particles (∼90 nm) of Cu2−xS were present at the very beginning (∼1 minute) for the Cu-rich reaction. With reaction time, these bigger particles transformed into smaller particles (∼10 nm) having a square shape, and these can be identified as Cu3TaS4 NCs. The average particle size of Cu3TaS4 NCs increases from ∼10 nm to ∼20 nm with the reaction time, as shown in Fig. 4m. For Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1
Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the square-shaped Cu3TaS4 NCs particles were present at the beginning of the reaction and there were no changes in the overall shape of the particles. For Ta-rich samples, we have the square-shaped particles, which become slightly irregular in shape with the progress of the reaction time. Both the average size and size distribution increase with the reaction. We compared the average size as measured from TEM with the crystallite sizes calculated from the Rietveld analysis of the diffraction pattern and both the sizes match well with each other, suggesting all the particles are highly crystalline – that could be due to the high-temperature synthesis.
1, the square-shaped Cu3TaS4 NCs particles were present at the beginning of the reaction and there were no changes in the overall shape of the particles. For Ta-rich samples, we have the square-shaped particles, which become slightly irregular in shape with the progress of the reaction time. Both the average size and size distribution increase with the reaction. We compared the average size as measured from TEM with the crystallite sizes calculated from the Rietveld analysis of the diffraction pattern and both the sizes match well with each other, suggesting all the particles are highly crystalline – that could be due to the high-temperature synthesis.
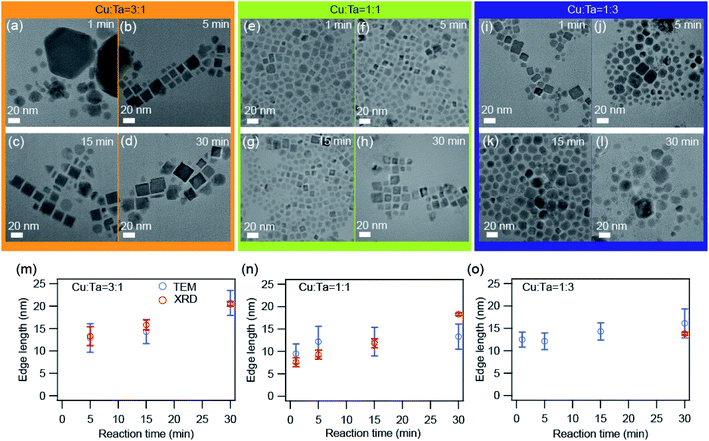 | ||
Fig. 4 TEM images of the synthesized NCs. (a–d) Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 3 Ta = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (e–h) Cu 1, (e–h) Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1 Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and (i–l) Cu 1, and (i–l) Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1 Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for different reaction times: 1 min, 5 min, 15 min, and 30 min. The scale bar is 20 nm. The average edge length as a function of reaction time for (m) Cu 3 for different reaction times: 1 min, 5 min, 15 min, and 30 min. The scale bar is 20 nm. The average edge length as a function of reaction time for (m) Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 3 Ta = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (n) Cu 1, (n) Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1 Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and (o) Cu 1, and (o) Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1 Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. The error bars indicate the size distribution. The average size calculated from TEM images are shown by blue solid circles and the size calculated from the XRD peaks after Rietveld refinement is shown by open black circles. The size distribution histograms are shown in Fig. S5.† 3. The error bars indicate the size distribution. The average size calculated from TEM images are shown by blue solid circles and the size calculated from the XRD peaks after Rietveld refinement is shown by open black circles. The size distribution histograms are shown in Fig. S5.† | ||
The high-resolution transmission electron microscopic (HRTEM) images show some interesting information about the growth of these NCs. The representative images for Cu-rich and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Cu and Ta are shown in Fig. 5. We found that a core–shell heterostructure has formed at an early stage of the reaction. We highlighted the core with brown color and the shell with cyan color. The interplanar distances (0.28 nm and 0.19 nm) of the core region either matched with the (200) or (220) planes of Cu1.8S. The interplanar distances (0.51 nm) of the shell region are larger than the core region and match with the (100) plane of Cu3TaS4. We observed this heterostructure only for the Cu-rich and Cu
1 ratio of Cu and Ta are shown in Fig. 5. We found that a core–shell heterostructure has formed at an early stage of the reaction. We highlighted the core with brown color and the shell with cyan color. The interplanar distances (0.28 nm and 0.19 nm) of the core region either matched with the (200) or (220) planes of Cu1.8S. The interplanar distances (0.51 nm) of the shell region are larger than the core region and match with the (100) plane of Cu3TaS4. We observed this heterostructure only for the Cu-rich and Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1
Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reaction. With reaction time, both the number of such heterostructured NCs goes down as well as the average size of the core Cu2−xS decreases. For the Ta-rich reaction, TaS2 and Cu3TaS4 particles were separately present at the beginning of the reaction as shown in Fig. S6† and TaS2 NCs were not observed at the later stage of the reaction.
1 reaction. With reaction time, both the number of such heterostructured NCs goes down as well as the average size of the core Cu2−xS decreases. For the Ta-rich reaction, TaS2 and Cu3TaS4 particles were separately present at the beginning of the reaction as shown in Fig. S6† and TaS2 NCs were not observed at the later stage of the reaction.
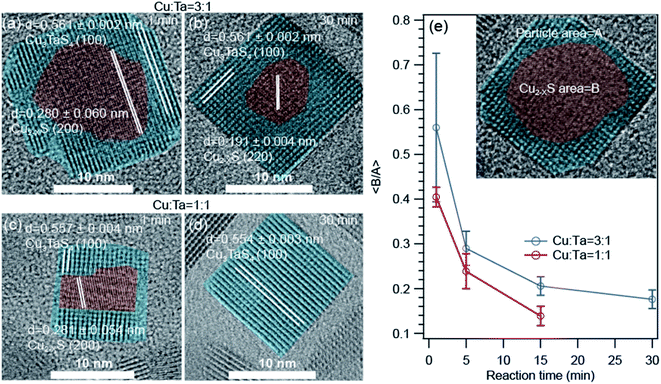 | ||
Fig. 5 High resolution transmission electron microscopy (HRTEM) images of the core–shell type Cu2−xS – Cu3TaS4 NCs. (a and b) NCs of 1 min, and 30 min reaction for Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 3 Ta = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. (c and d) NCs of 1 min, and 30 min reaction for Cu 1. (c and d) NCs of 1 min, and 30 min reaction for Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1 Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The HRTEM images for Cu; Ta = 1 1. The HRTEM images for Cu; Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 reactions are shown in Fig. S6.† (e) The average of core to particle area ratio as a function of reaction time for Cu 3 reactions are shown in Fig. S6.† (e) The average of core to particle area ratio as a function of reaction time for Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 3 Ta = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and Cu 1 and Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ta = 1 Ta = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Inset figure is schematic presentation of the core–shell type Cu1.8S – Cu3TaS4 NCs. 1. Inset figure is schematic presentation of the core–shell type Cu1.8S – Cu3TaS4 NCs. | ||
As the area of the core and shell region in the TEM images represent the volume of the respective materials, we quantified the respective ratios of the core to shell region as a function of reaction time for Cu-rich and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Cu and Ta (Fig. 5e) to understand how the core–shell structure vanish with time. The core is indicated with an area of ‘A’ and the overall particle with an area of ‘B’ as shown in the inset. We find that the average core to shell area ratio decreases systematically with increasing reaction time. The rate of this change is higher for the 1
1 ratio of Cu and Ta (Fig. 5e) to understand how the core–shell structure vanish with time. The core is indicated with an area of ‘A’ and the overall particle with an area of ‘B’ as shown in the inset. We find that the average core to shell area ratio decreases systematically with increasing reaction time. The rate of this change is higher for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Cu and Ta compared to the Cu-rich reaction.
1 ratio of Cu and Ta compared to the Cu-rich reaction.
To bring better insight into the mechanism of Ta incorporation in Cu2−xS crystals, we computationally studied the formation energies and diffusion barriers of the low-index surfaces. We found that the probability of finding Ta atoms as interstitial (2.31 eV per defect) or substitution (3.73 eV per defect) defects is marginal, due to unfavourable formation energies. In contrast, it was found that vacancy sites are suitable settlements for Ta atoms. Accordingly, the formation energy of the first Ta atom, to occupy one out of six vacancies in a 2 × 2 × 2 supercell of Cu1.8S, is −1.60 eV per Ta. Adding another Ta to this system changes the formation energy to Ef = −0.24 eV per Ta. After the number of Ta atoms passes a threshold (three in this case), the formation energy changes sign (with Ef = 0.06, 0.96 and 1.28 eV per Ta for third, fourth and fifth Ta atoms, respectively), a signal that the crystal has reached its capacity and cannot accept more Ta atoms. An interpretation can be that in addition to the inward diffusion of Ta, extra Cu atoms need to diffuse out from the region where Cu3TaS4 is going to be formed.
Based on these assumptions, we predict that the formation of experimentally observed core–shell structure is governed by a diffusion mediated mechanism, where the concentration gradient pushes Ta atoms to diffuse from the solution into the Cu2−xS structure, and extra Cu atoms need to move out to create a Cu depleted zone, required for the formation of Cu3TaS4. As a side effect of this collective movement, the vacancy sites in the path of the migrant Cu atoms get occupied, dwindling the vacancy concentration of the core Cu2−xS region, and increasing its lattice parameter (see Fig. 3b, and its discussion). Since the primary nucleation of Cu3TaS4 appears on facets, we studied energetics by calculating the surface energies of the low index planes in Cu2S as shown in Fig. 6a. It can be seen that the most stable planes are the {110} family with a surface energy of 30 meV Å−2. The {100} planes come in second place with 52 meV Å−2, and {111} planes are the least energetically favourable ones with 100 meV Å−2. Although these results suggest that Cu2S NCs only expose their {110} surfaces, we believe that due to the deformation caused by vacancies at the high reaction temperature (T = 300 °C), the preferred surface of Cu2−xS can be a combination of these facets, as evident in Fig. 5. We further calculated the diffusion barrier of one Ta atom to get incorporated into each of these surfaces. To do this, the initial stage of Ta diffusion was considered to be 3 Å above the surface, and the final stage was Ta located in a vacant site. We found that along all paths, the diffusion barriers are relatively low, zero in the case of diffusion into {100} surface, 6 and 67 meV for {110} and {111} surfaces, respectively. The size of these energy barriers is small enough to be overcome by the thermal fluctuation of atoms at T = 300 °C. Thus, we predict that the nucleation and growth of Cu3TaS4 should start uniformly from all facets, leading to a semi-spherical core of Cu2−xS, similar to what can be seen in Fig. 5. We also calculated the surface formation energy of Cu3TaS4 for low index cubic planes (see Fig. 6b). It was found that energetically, Cu3TaS4 crystals should prefer to expose their {100} surfaces more than the other ones as σ100 (47 meV Å−2) < σ110 (64 meV Å−2) < σ111 (231 meV Å−2). Thus, as a rule of thumb, the clean cubic surfaces found in Fig. 5, can be attributed to the formation of {100} facets in Cu3TaS4 NCs. We further estimated the diffusion barrier of Ta inside the bulk of Cu2−xS. In this tightly packed structure, Ta needs to overcome a large energy barrier of 5.63 eV to diffuse between two neighbouring vacant Cu sites. The magnitude of this energy barrier shows that the diffusion of Ta into the depth of Cu2−xS is a rare event, and Cu2−xS to Cu3TaS4 transformation takes place at the boundary of two phases, leading to the formation of a core–shell structure. After the initial formation of Cu3TaS4 on facets, Ta atoms need to diffuse through the bulk structure of Cu3TaS4 to reach Ta depleted inner zones. Meanwhile, to satisfy stoichiometric constraints, a portion of Cu atoms needs to diffuse out of the Cu2−xS core and along their way, they have to pass through Cu3TaS4 shell. Thus, we further studied the energy costs of Ta and Cu diffusion into bulk Cu3TaS4, where the results are shown in Fig. 6c. The low packing concentration of atoms in Cu3TaS4 provides suitable diffusion channels (parallel to 〈100〉 crystal edges) for Ta and Cu atoms as evident from Fig. 6c. We calculated the energy landscape along these diffusion paths, finding that Ta atoms have to overcome two periodic diffusion barriers of 1.58 and 1.78 eV, with a periodicity equivalent to that of Cu3TaS4 unit cell (5.56 Å). In a similar scenario, Cu atoms can escape the core region by overcoming two periodic diffusion barriers of 0.18 eV and 0.45 eV, while passing the Cu3TaS4 diffusion channels.
Combining all these pieces to create a collective picture, the formation of the core–shell structure can be explained. Firstly, Ta atoms diffuse into Cu vacancy sites readily available on the surface of Cu2−xS to form primary nucleation sites for growth of Cu3TaS4. The lower formation energy of Cu3TaS4 compared to Cu2−xS propels this structural transformation further, by causing an outward flow of Cu atoms through diffusion channels that naturally exist in Cu3TaS4 structure. Simultaneously, the Ta concentration gradient creates a flow of Ta atoms in a direction opposite to that of Cu atoms, through the same diffusion channels. Since the diffusion barrier for Ta atoms are more than three times higher than that of Cu atoms (bigger size of Ta atoms is one contributing factor to this), the rate of reaction is controlled by Ta diffusion. As the core of NCs is not easily reachable for Ta atoms, NCs form a core–shell structure, where the size of inner core region shrinks by the passage of reaction time. The size of Cu2−xS parent crystals is one of the factors that determines the core to shell ratio during the reaction. In other words, bigger Cu2−xS crystals are more prone to keep the remnant core region even at the end of the reaction. Another contributing factor is the vacancy concentration in Cu2−xS crystals, to host the Ta atoms. A higher vacancy concentration will make Ta incorporation faster and also create a finer distribution of Cu3TaS4 nucleation sites. Since vacancy concentration depends on the relative precursor concentrations, we can tune this to control the reaction rate.
Conclusion
In this work, we synthesized cubic Cu3TaS4 NCs by hot injection synthesis. Due to the soft Lewis acid nature of Cu+, it reacts with CS2, a soft Lewis base to form cubic Cu2−xS. Further, Ta gets incorporated into the Cu2−xS NCs at the Cu vacancy site followed by the diffusion through the lattice. A Cu-rich reaction produces a lesser amount of Cu vacancies and slower incorporation of Ta, whereas a Cu deficit or low concentration condition produces a larger concentration of Cu vacancies that helps in faster incorporation of Ta, thus the faster formation of Cu3TaS4 NCs. DFT calculations suggest that Ta prefers to occupy the Cu vacancies in Cu2−xS, followed by Ta diffusion into the lattice. Simultaneously, an outward flow of Cu atoms maintains the stoichiometric constraints imposed by Cu3TaS4. The strength of the energy barrier for Ta diffusion is similar for {100}, {110} and {111} surfaces, which allows the nucleation growth of Cu3TaS4 uniformly through all facets as observed in HRTEM images. Higher energy barriers found along the Ta diffusion path compared to Cu atoms imply that the reaction is controlled by the sluggish Ta diffusion, which is the origin of the core–shell structure found in NCs. The insights provided here will help in developing the synthesis of other ternary chalcogenides – which are otherwise not possible by direct synthesis.Author contributions
P. K. S. conceived the idea and supervised the experimental work and B. S. led the theoretical work. A. H. carried out the synthesis and characterization. T. D. C. assisted in TEM measurements and analysis. D. S. analyzed the powder XRD data (with A. H.). S. E. performed the DFT calculations (with B. S.). All authors discussed the results and contributed to writing the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the Central Research Facilities, Centre for Nano and Soft Matter Sciences, Bengaluru. TEM Facility, funded by a TPF Nanomission, GoI project at the Centre is gratefully acknowledged. The authors also acknowledge the Department of Science and Technology, India, and SERB (CRG/2018/001698) for the financial support. A. H. acknowledges the student fellowship from the Centre. T. D. C acknowledges the Inspire Fellowship from the Department of Science and Technology (DST), India. The computations were enabled in project SNIC 2021/3-38 by resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC, PDC and HPC2N partially funded by the Swedish Research Council through grant agreement no. 2018-05973. B. S. also acknowledges allocation of supercomputing hours in PRACE DECI-17 project Q2Dtopomat. B. S. acknowledges financial support from the Swedish Research Links programme Grant (2017-05447) provided by Swedish Research Council.References
- H. Fu, J. Mater. Chem. C, 2018, 6, 414–445 RSC.
- J. Patel, F. Mighri, A. Ajji and T. K. Chaudhuri, Nano Energy, 2014, 5, 36–51 CrossRef CAS.
- Y. Min, G. D. Moon, C. E. Kim, J.-H. Lee, H. Yang, A. Soon and U. Jeong, J. Mater. Chem. C, 2014, 2, 6222–6248 RSC.
- M. V. Kovalenko, Nat. Nanotechnol., 2015, 10, 994–997 CrossRef CAS PubMed.
- D. Wang, F. Yin, Z. Du, D. Han and J. Tang, J. Mater. Chem. A, 2019, 7, 26205–26226 RSC.
- H. Ron, Environ. Health Perspect., 2006, 114, 165–172 CrossRef.
- A. C. Berends, M. J. J. Mangnus, C. Xia, F. T. Rabouw and C. de Mello Donega, J. Phys. Chem. Lett., 2019, 10, 1600–1616 CrossRef CAS PubMed.
- K. E. Knowles, K. H. Hartstein, T. B. Kilburn, A. Marchioro, H. D. Nelson, P. J. Whitham and D. R. Gamelin, Chem. Rev., 2016, 116, 10820–10851 CrossRef CAS PubMed.
- A. D. P. Leach and J. E. Macdonald, J. Phys. Chem. Lett., 2016, 7, 572–583 CrossRef CAS PubMed.
- W. van der Stam, A. C. Berends and C. de Mello Donega, ChemPhysChem, 2016, 17, 559–581 CrossRef CAS PubMed.
- D. Moodelly, P. Kowalik, P. Bujak, A. Pron and P. Reiss, J. Mater. Chem. C, 2019, 7, 11665–11709 RSC.
- D. Aldakov, A. Lefrançois and P. Reiss, J. Mater. Chem. C, 2013, 1, 3756–3776 RSC.
- L. De Trizio and L. Manna, Chem. Rev., 2016, 116, 10852–10887 CrossRef CAS PubMed.
- S. Ishizuka, J. Nishinaga, K. Beppu, T. Maeda, F. Aoyagi, T. Wada, A. Yamada, J. Chantana, T. Nishimura, T. Minemoto, M. M. Islam, T. Sakurai and N. Terada, Phys. Chem. Chem. Phys., 2022, 24, 1262–1285 RSC.
- A. Ennaoui, M. Bär, J. Klaer, T. Kropp, R. Sáez-Araoz and M. C. Lux-Steiner, Prog. Photovoltaics, 2006, 14, 499–511 CAS.
- R. Klenk, J. Klaer, R. Scheer, M. C. Lux-Steiner, I. Luck, N. Meyer and U. Rühle, Thin Solid Films, 2005, 480–481, 509–514 CrossRef CAS.
- R. Scheer, R. Klenk, J. Klaer and I. Luck, Sol. Energy, 2004, 77, 777–784 CrossRef CAS.
- C. Coughlan, M. Ibáñez, O. Dobrozhan, A. Singh, A. Cabot and K. M. Ryan, Chem. Rev., 2017, 117, 5865–6109 CrossRef CAS.
- R. Xie, M. Rutherford and X. Peng, J. Am. Chem. Soc., 2009, 131, 5691–5697 CrossRef CAS PubMed.
- J. Kolny-Olesiak and H. Weller, ACS Appl. Mater. Interfaces, 2013, 5, 12221–12237 CrossRef CAS.
- H. Zhong, S. S. Lo, T. Mirkovic, Y. Li, Y. Ding, Y. Li and G. D. Scholes, ACS Nano, 2010, 4, 5253–5262 CrossRef CAS PubMed.
- H. Zhong, Y. Zhou, M. Ye, Y. He, J. Ye, C. He, C. Yang and Y. Li, Chem. Mater., 2008, 20, 6434–6443 CrossRef CAS.
- J. J. Nairn, P. J. Shapiro, B. Twamley, T. Pounds, R. von Wandruszka, T. R. Fletcher, M. Williams, C. Wang and M. G. Norton, Nano Lett., 2006, 6, 1218–1223 CrossRef CAS PubMed.
- S. O. M. Hinterding, A. C. Berends, M. Kurttepeli, M.-E. Moret, J. D. Meeldijk, S. Bals, W. van der Stam and C. de Mello Donega, ACS Nano, 2019, 13, 12880–12893 CrossRef CAS PubMed.
- L. Li, A. Pandey, D. J. Werder, B. P. Khanal, J. M. Pietryga and V. I. Klimov, J. Am. Chem. Soc., 2011, 133, 1176–1179 CrossRef CAS PubMed.
- H.-J. Yang, C.-Y. Chen, F.-W. Yuan and H.-Y. Tuan, J. Phys. Chem. C, 2013, 117, 21955–21964 CrossRef CAS.
- C. Yu, J. C. Yu, H. Wen and C. Zhang, Mater. Lett., 2009, 63, 1984–1986 CrossRef CAS.
- Y. Vahidshad, M. N. Tahir, A. I. zad, S. M. Mirkazemi, R. Ghazemzadeh and W. Tremel, J. Mater. Chem. C, 2015, 3, 889–898 RSC.
- J. Zhou, F. Huang, J. Xu and Y. Wang, CrystEngComm, 2013, 15, 4217–4220 RSC.
- L. Yi, A. Tang, M. Niu, W. Han, Y. Hou and M. Gao, CrystEngComm, 2010, 12, 4124–4130 RSC.
- S.-K. Han, M. Gong, H.-B. Yao, Z.-M. Wang and S.-H. Yu, Angew. Chem., Int. Ed., 2012, 51, 6365–6368 CrossRef CAS PubMed.
- F. Huang, X. Wang, J. Xu, D. Chen and Y. Wang, J. Mater. Chem., 2012, 22, 22614–22618 RSC.
- H. Ye, A. Tang, L. Huang, Y. Wang, C. Yang, Y. Hou, H. Peng, F. Zhang and F. Teng, Langmuir, 2013, 29, 8728–8735 CrossRef CAS.
- D.-H. Ha, A. H. Caldwell, M. J. Ward, S. Honrao, K. Mathew, R. Hovden, M. K. A. Koker, D. A. Muller, R. G. Hennig and R. D. Robinson, Nano Lett., 2014, 14, 7090–7099 CrossRef CAS PubMed.
- C. Xia, A. Pedrazo-Tardajos, D. Wang, J. D. Meeldijk, H. C. Gerritsen, S. Bals and C. de Mello Donega, Chem. Mater., 2021, 33, 102–116 CrossRef CAS PubMed.
- M. D. Regulacio, C. Ye, S. H. Lim, M. Bosman, L. Polavarapu, W. L. Koh, J. Zhang, Q.-H. Xu and M. Y. Han, J. Am. Chem. Soc., 2011, 133, 2052–2055 CrossRef CAS PubMed.
- T. T. Zhuang, F. J. Fan, M. Gong and S.-H. Yu, Chem. Commun., 2012, 48, 9762–9764 RSC.
- S. H. Choi, E. G. Kim and T. Hyeon, J. Am. Chem. Soc., 2006, 128, 2520–2521 CrossRef CAS PubMed.
- W. Han, L. Yi, N. Zhao, A. Tang, M. Gao and Z. Tang, J. Am. Chem. Soc., 2008, 130, 13152–13161 CrossRef CAS PubMed.
- L. Chen, Z. Kong, H. Tao, H. Hu, J. Gao and G. Li, Nanoscale, 2022, 14, 3907–3916 RSC.
- L. De Trizio, R. Gaspari, G. Bertoni, I. Kriegel, L. Moretti, F. Scotognella, L. Maserati, Y. Zhang, G. C. Messina, M. Prato, S. Marras, A. Cavalli and L. Manna, Chem. Mater., 2015, 27, 1120–1128 CrossRef CAS PubMed.
- G. Xiao, Y. Zeng, Y. Jiang, J. Ning, W. Zheng, B. Liu, X. Chen, G. Zou and B. Zou, Small, 2013, 9, 793–799 CrossRef CAS PubMed.
- H. Cao, X. Qian, C. Wang, X. Ma, J. Yin and Z. Zhu, J. Am. Chem. Soc., 2005, 127, 16024–16025 CrossRef CAS PubMed.
- G. Chen, M. Niu, L. Cui, F. Bao, L. Zhou and Y. Wang, J. Phys. Chem. C, 2009, 113, 7522–7525 CrossRef CAS.
- L. Mu, F. Wang, B. Sadtler, R. A. Loomis and W. E. Buhro, ACS Nano, 2015, 9, 7419–7428 CrossRef CAS PubMed.
- M. S. Hassan, S. Bera, D. Gupta, S. K. Ray and S. Sapra, ACS Appl. Mater. Interfaces, 2019, 11, 4074–4083 CrossRef CAS.
- C. Xia, C. H. M. van Oversteeg, V. C. L. Bogaards, T. H. M. Spanjersberg, N. L. Visser, A. C. Berends, J. D. Meeldijk, P. E. de Jongh and C. de Mello Donega, ACS Nano, 2021, 15, 9987–9999 CrossRef PubMed.
- W. van der Stam, A. C. Berends, F. T. Rabouw, T. Willhammar, X. Ke, J. D. Meeldijk, S. Bals and C. de Mello Donega, Chem. Mater., 2015, 27, 621–628 CrossRef CAS.
- B. C. Steimle, J. L. Fenton and R. E. Schaak, Science, 2020, 367, 418–424 CrossRef CAS PubMed.
- J. Heo, L. Yu, E. Altschul, B. E. Waters, J. F. Wager, A. Zunger and D. A. Keszler, Chem. Mater., 2017, 29, 2594–2598 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245–8257 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. B. Kehoe, D. O. Scanlon and G. W. Watson, J. Mater. Chem. C, 2015, 3, 12236–12244 RSC.
- A. A. Ivanov, I. V Tarasova, V. T. Bublik, R. K. Akchurin, I. V Shchetinin, N. Y. Tabachkova, D. A. Pshenay-Severin and V. B. Osvenskii, Phys. Solid State, 2018, 60, 2295–2299 CrossRef CAS.
- Y. Xie, A. Riedinger, M. Prato, A. Casu, A. Genovese, P. Guardia, S. Sottini, C. Sangregorio, K. Miszta, S. Ghosh, T. Pellegrino and L. Manna, J. Am. Chem. Soc., 2013, 135, 17630–17637 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta02714c |
| This journal is © The Royal Society of Chemistry 2022 |