Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Materials design principles of amorphous cathode coatings for lithium-ion battery applications†
Jianli
Cheng
 ab,
Kara D.
Fong
ab,
Kara D.
Fong
 bc and
Kristin A.
Persson
bc and
Kristin A.
Persson
 *ab
*ab
aDepartment of Materials Science and Engineering, University of California, Berkeley, CA 94720-1760, USA. E-mail: kapersson@lbl.gov
bEnergy Storage and Distributed Resources Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
cDepartment of Chemical and Biomolecular Engineering, University of California, Berkeley, CA 94720-1760, USA
First published on 7th October 2022
Abstract
Cathode surface coatings present one of the most popular and effective solutions to suppress cathode degradation and improve cycling performance of lithium-ion batteries (LIBs). In this work, we carry out an extensive high-throughput computational study to develop materials design principles governing amorphous cathode coating selections for LIBs. Our high-throughput screening includes descriptors to evaluate the thermodynamic stability, electrochemical stability, chemical reactivity with electrolytes and cathodes, and ionic diffusion of the cathode coatings. In the ionic diffusion analysis, we mainly focus on Li-containing compounds. From the 20 selected materials, we highlight the formidable challenge of mitigating oxygen diffusion when selecting an ideal cathode coating, and suggest 7 promising coating candidates: Li3B11O18, LiZr2(PO4)3, LiB3O5, LiPO3, LiSb3O8, LiAlSiO4 and LiTaSiO5. Combining the screening results and detailed ionic diffusion analysis of the selected cathode coatings, we summarize the general selection guidelines of amorphous cathode coatings for LIBs.
Introduction
Lithium-ion batteries (LIBs) are ubiquitous in portable electronic devices and have enabled the development of cleaner energy storage and electric vehicles (EVs). For the past decade, LIB-powered EVs have gradually penetrated the automotive market. With an increasing demand of reducing greenhouse gas emissions, the global fleet of EVs will continue to rise for the coming decade.1 Future improvements in LIBs include high energy density cathode materials to enable longer driving range; however these materials frequently operate at high potential and experience surface degradation with associated performance degradation under extended cycling. The current commercialized cathode materials of LIBs are classified as layered (LiNiaCobMncO2, NMC), spinel (LiMn2O4) and olivine (LiFePO4). Regardless of their crystal structure, these cathode materials all exhibit surface degradation and detrimental surface phase transformations, which compromise the cycle life and thermal stability of LIBs. For example, upon a higher voltage operation (>4.3 V), surface oxygen evolution triggers an irreversible transformation in NMC cathodes from layered phase into a mixture of spinel and rock salt phases that deteriorates capacity retention.2 Similarly, in LiMn2O4, surface oxygen loss causes considerable compressive lattice strain, which densifies the cathode surface and blocks the Li-migration pathways.3 The LiFePO4 cathode exhibits an excellent capacity retention, however, its eventual failure is associated with the surface amorphization and oxygen loss after the prolonged cycling.4 In addition, side reactions between the electrolyte and cathode lead to transition metals dissolution and surface impedance build-up, which further accelerate the capacity/voltage fade.5 Therefore, it is of high interest to engineer the cathode surface to achieve high energy density LIBs with a stable, safe, and long-term cycling performance.56A common strategy to stabilize the cathode surface is to apply a multifunctional protective layer to mitigate surface degradation and simultaneously maintain facile Li+ transport.6 Such cathode coatings typically exhibit an amorphous character, with a thickness between 1 to 10 nm.7,8 A variety of coating materials have been explored and shown varying degrees of effectiveness in enhancing the cyclability of LIBs, such as metal oxides (e.g., Al2O3 (ref. 9)), nonmetal oxides (e.g., B2O3 (ref. 10)), polyanionic oxides (e.g., Li3B11O18 (ref. 11)), and fluorides (e.g., AlF3 (ref. 12)), etc. However, several reported cathode coatings have been found to exhibit chemical and/or electrochemical instability and large overpotential during cycling. For example, Al2O3 and ZnO effectively mitigate the side reactions of the cathode surface with the electrolyte,9,13 however, the metal oxide coating layer forms a metal oxyfluoride or a metal fluoride layer by scavenging F− from HF in the electrolyte.13,14 Furthermore, because of its inherent low Li+ ion diffusivity, Al2O3 coatings can lead to large overpotentials and reduced capacity, even at a thickness as low as 2 nm.15,16 On the other hand, Li-containing compounds have been found to exhibit better capacity retention than their non-lithiated counterparts, due to their improved ability to transport Li+.17 However, a recent study found that an NMC cathode surface still transforms from a layered structure into an oxygen loss-induced rock-salt structure after cycling, even when conformally coated with a Li3B11O18 layer.11 Similar surface reconstruction phenomenon has been observed in Al2O3- and AlF3-coated cathodes,12,18 regardless of liquid-electrolyte or solid-electrolyte battery implementations. As different coating materials may enhance one aspect of performance while hindering or falling short of another, ultimately, the question is what are the optimal coating design choices given the battery application, and can we provide a systematic guidance to identify them?
Given the complex reactions between the cathode, coating and electrolyte and the difficulty in deconvoluting experimentally measured solid state ionic diffusion, first-principles modeling provides robust guidelines for new cathode coatings. Aykol et al. reported a high-throughput screening of crystalline oxides materials that can stabilize the cathodes in a liquid-electrolyte battery system.19 However, ionic diffusivity in the coatings was not considered. Liu et al. screened Li-containing crystalline fluoride materials and identified 10 promising coating materials along with their calculated Li+ migration barriers.20 Xiao et al. screened crystalline Li-containing cathode coatings for solid-state batteries and proposed three polyanionic compounds as the most appealing candidates.21 We note that the ionic diffusion analyses in all previous computational screening work have addressed exclusively the crystalline coating materials, whereas cathode coatings are often amorphous or polycrystalline. In addition, due to their isotropic non-periodic structures, amorphous films tend to be more conformal than polycrystalline films, with reduced grain boundaries, dislocations, or other defect regions.22 Therefore, amorphous coatings provide a better cathode surface protection against surface oxygen loss and side reactions with electrolytes than polycrystalline coatings. Their unique processability also enables high degrees of interfacial contact with electrodes.22 Moreover, many amorphous solids, such as Li3PO4 and Al2O3, have been found to exhibit higher Li+ conductivity than their crystalline phases.23,24 However, to our best knowledge, no study has considered O2− diffusion in amorphous films, which is directly related to the oxygen-loss-induced cathode surface densification. In addition, Li+ and O2− diffusion corresponds to the kinetics of the coatings but has never been applied broadly or systematically enough to derive design rules. In this work, we carry out an extensive high-throughput computational study to develop materials design principles governing amorphous cathode coating selections for LIBs. We evaluate the thermodynamic stability, electrochemical stability, chemical reactivity with electrolytes and cathodes, as well as the Li+ and O2− diffusion in amorphous cathode coatings. Based on the trends in the screening results and ionic transport, we summarize general guidelines for selecting amorphous cathode coatings.
Computational details
First-principles calculation
All density functional theory (DFT) calculations are performed using the Vienna Ab initio Simulation Package (VASP),25,26 with Projector Augmented Wave (PAW) potentials.27 The generalized gradient approximation (GGA) as parameterized by the Perdew–Burke–Ernzerhof (PBE)28 is used for the exchange-correlation functional. For AIMD simulations, we employ Γ-point only Brillouin zone integration at a plane-wave cutoff energy of 400 eV and a time step of 2 fs.We utilize a “liquid-quench” process to generate the amorphous structures, in which heating, equilibration, and quenching are performed through an AIMD workflow, which can be found as part of the open-source mpmorph package at https://github.com/materialsproject/mpmorph. We use the Packmol package29 to generate all initial amorphous structures. To generate the “liquid” phase of the amorphous structures, we equilibrate the structures at 3000 K using a sequence of 4 ps AIMD simulations in the NVT ensemble until the external pressure and energy are converged. Next, the structures are simulated for an additional 10 ps, from which three independent configurations are selected and quenched to 0 K to obtain the ground-state amorphous structures. To perform ion diffusion analysis, we equilibrate the ground-state structure at T = 1800, 2000, 2200, 2400, 2600, and 2800 K, and then simulate an 80 ps diffusion trajectory at each corresponding temperature. The equilibration procedure follows the same steps used to equilibrate the “liquid” amorphous structure. In the end, there are three independent diffusion trajectories at each temperature. Further details about the entire AIMD and DFT workflows can be found in ref. 30.
Self-diffusion coefficients and overpotentials
From the obtained diffusion trajectories, we calculate the self-diffusion coefficients (D) of Li+ and O2− ions in amorphous structures using the Einstein relation: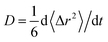 , where t is the time, r is the ion position and 〈Δr2〉 is the mean square displacement (MSD). Within the temperature window 1800–2800 K, there are three D values calculated from three independent diffusion trajectories at each temperature. The D values at room temperature are extrapolated from those at high temperatures using the Arrhenius relation of D as a function of T: D = D0
, where t is the time, r is the ion position and 〈Δr2〉 is the mean square displacement (MSD). Within the temperature window 1800–2800 K, there are three D values calculated from three independent diffusion trajectories at each temperature. The D values at room temperature are extrapolated from those at high temperatures using the Arrhenius relation of D as a function of T: D = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT), where kB is the Boltzmann constant, D0 is the pre-exponential factor and Ea is the activation energy of ion diffusion. In addition, the trajectories at lower temperatures (e.g. 1800 K) frequently exhibit fewer ionic hops, which incurs higher statistical uncertainties of fitted D values than those at higher temperatures (e.g. 2800 K). Therefore, we consider the uncertainty of the D values at each temperature when linearly fitting log
exp(−Ea/kBT), where kB is the Boltzmann constant, D0 is the pre-exponential factor and Ea is the activation energy of ion diffusion. In addition, the trajectories at lower temperatures (e.g. 1800 K) frequently exhibit fewer ionic hops, which incurs higher statistical uncertainties of fitted D values than those at higher temperatures (e.g. 2800 K). Therefore, we consider the uncertainty of the D values at each temperature when linearly fitting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D vs. 1/T by assigning the standard deviation of log
D vs. 1/T by assigning the standard deviation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D as the uncertainty for each averaged D.
D as the uncertainty for each averaged D.
From the calculated room temperature Li+ diffusivity DLirt, we estimate the overpotential, ΔV, across a cathode coating layer using a theoretical model which assumes a constant potential gradient, a uniform Li+ concentration and the Einstein relation to relate Li+ mobility and diffusion coefficient in the coating.31,32 The model calculates ΔV as a function of current density, coating thickness, Li+ concentration, Li+ diffusivity and temperature, providing a qualitative evaluation on coating's ability to transport Li+ ions. The relation between ΔV and DLirt follows the methodology used in the earlier work,24,33 namely:
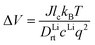 | (1) |
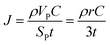 | (2) |
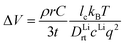 | (3) |
In the ESI† we provide the full derivation and assumptions for eqn (1). According to eqn (2), the current density J is normalized by the cathode surface area, while experimentally, J is more commonly normalized by geometric area of the cathode disk. In addition, we assume that the entire spherical cathode particle surface area is available for Li+ intercalation.
Oxygen flux and transport time
We use the Onsager transport equations to estimate the O2− flux JO under the driving force of the oxygen chemical potential gradient ∇μO across the coating layer, which can expressed as:| JO = −LOO∇μO | (4) |
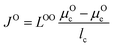 | (5) |
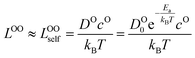 | (6) |
Materials database and descriptors
The entire database used in this study contains 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 crystalline compounds, which are queried from the Materials Project (v2021.11.10).38 The materials properties include DFT calculated total energies, formation energies, energies above convex hull (Ehull), band gaps (Eg), etc. It should be noted that at zero temperature, the Gibbs free energy of a crystalline polymorph is always lower than that of its amorphous state.39 However, there is no universal description for the energetics of the amorphous materials, therefore we use the energies of the crystalline phases to approximate the stability of the amorphous phases. Indeed, the distribution of synthesizable crystalline polymorph energies tends to follow the trend of the amorphous energies.39
323 crystalline compounds, which are queried from the Materials Project (v2021.11.10).38 The materials properties include DFT calculated total energies, formation energies, energies above convex hull (Ehull), band gaps (Eg), etc. It should be noted that at zero temperature, the Gibbs free energy of a crystalline polymorph is always lower than that of its amorphous state.39 However, there is no universal description for the energetics of the amorphous materials, therefore we use the energies of the crystalline phases to approximate the stability of the amorphous phases. Indeed, the distribution of synthesizable crystalline polymorph energies tends to follow the trend of the amorphous energies.39
| ΔG0 = Gproducts − Greactants | (7) |
At room temperature, we assume the entropy contributions of solid phases are negligible while the entropy contributions of gaseous species (O2, F2, Cl2, H2 and N2) are much higher than that of solid phases. For the gaseous species, their entropy values S at room temperature are taken from the JANAF tables.40 Thus, ΔG0 can be approximated as:
| ΔG0 ≈ Hproducts − Hreactants − T(Sgaseous products − Sgaseous reactants) | (8) |
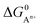 , to ΔG0 in eqn (8).
, to ΔG0 in eqn (8). 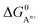 can be calculated as:
can be calculated as: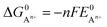 | (9) |
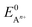 is the standard oxidation potential of the An+ ion taken from the IUPAC publication.42 Next, the free energy of a given reaction can be obtained as:
is the standard oxidation potential of the An+ ion taken from the IUPAC publication.42 Next, the free energy of a given reaction can be obtained as: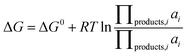 | (10) |
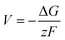 | (11) |
Results and discussion
Screening process
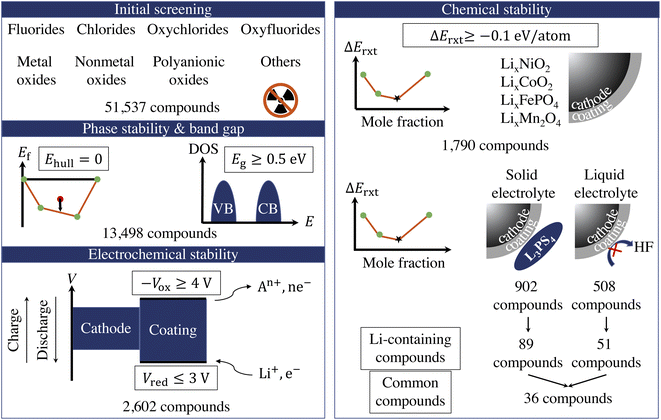
Fig. 1 illustrates the sequential high-throughput screening procedure for cathode coating materials with descriptors including radioactivity, energy above convex hull (Ehull), band gap (Eg), reduction limit (Vred), oxidation limit (−Vox), and reaction energy (ΔErxt) with cathodes and electrolytes.We exclude compounds containing radioactive elements and categorize the remaining compounds in 8 groups based on their anion chemistry: fluorides, chlorides, oxyfluorides, oxychlorides, metal oxides, nonmetal oxides, polyanionic oxides and others. We use Ehull values given in the Materials Project database38 to screen for the thermodynamically stable compounds and select only the compounds that are on the convex-hull, i.e., Ehull = 0. Furthermore, we are interested in electronically insulating coating materials that can block the electron transfer between the cathode and electrolyte and the subsequent electrolyte oxidation at high voltage.12 Therefore, we exclude all metallic compounds and compounds that exhibit a bandgap, Eg, less than 0.5 eV. However, it should be noted that there is a positive effect of a conductive surface coating on the performance of the cathode, as it provides an electron-conducting media that facilitates the charge transfer at the electrode surface.44 For example, carbon-coating on LiFePO4 has proven to deliver a higher active material loading and energy density in a full-size battery.45 The use of Ehull and Eg descriptors returns 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 compounds for further consideration.
498 compounds for further consideration.
In addition, a coating material that participates in the redox reaction during extensive cycling may cause degradation of the surface film, thus a loss of the surface protection.15 Therefore, we retain only electrochemically stable compounds that can sustain the desirable voltage window. The electrochemical stability window of a cathode coating represents the voltage range (versus Li metal) in which the material is thermodynamically stable upon Li (de)intercalation. It consists of two components: the reduction limit (Vred) during discharge and oxidation limit (−Vox) during charge. The reduction (cathodic) limit of a cathode coating with composition AaBbCc… is defined as the voltage limit at which the material lithiates to AaBbCc…Liδ. The discharge reaction can be expressed as:
| AaBbCc… + δLi+ + δe− → [aA,bB,cC,…,δLi]min | (12) |
| AaBbCc… → δAn+ + nδe− + [(a − δ)A,bB,cC,…]min | (13) |
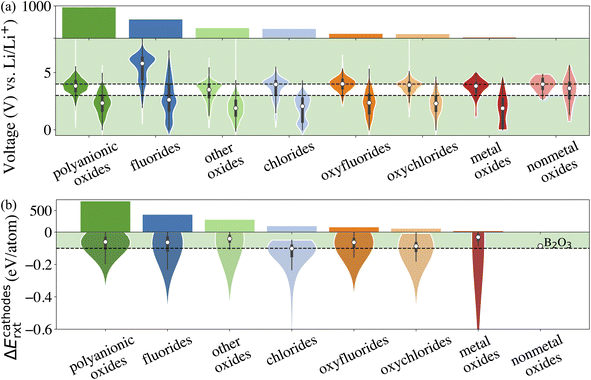
The fourth attribute we consider is the chemical stability of the cathode coatings. It has been shown that a coating material can react with cathodes and electrolytes to form new phases at cathode/coating and coating/electrolyte interfaces, respectively.7,16 Therefore, we screen for cathode coatings that are inert to chemical reactions with both cathodes and electrolytes. The reaction energy ΔErxt is calculated using DFT-computed energies of the reactants and products, and a more negative ΔErxt indicates a more reactive chemical reaction. We set the criterion for chemically stable cathode coatings as: ΔErxt ≥ −0.1 eV per atom.21 We calculate ΔErxt between cathodes and coating materials using the commonly used cathodes, layered LiNiO2 and LiCoO2, spinel LiMn2O4, and olivine LiFeOP4. Both lithiated and half-lithiated cathodes are considered corresponding to the discharge and charge cycles, respectively. We select the most negative ΔErxt, i.e., the most favorable chemical reaction, as the ΔEcathodesrxt for each compound, and we plot ΔEcathodesrxt for each category that pass the electrochemical stability descriptor in Fig. 2b. In Fig. S2,† we also plot ΔErxt of each selected cathode material. We find that compared with other cathodes, LiNiO2 tends to exhibit a more negative ΔErxt, therefore reacts more favorably with the coating materials. In addition, oxides coatings are less prone to react with cathodes than fluorides and chlorides. Specifically, all the electrochemically stable metal oxides exhibit low reactivity with common cathodes and pass the chemical stability descriptor. This round of screening returns 1790 compounds for further consideration with polyanionic oxides having the largest number of candidates (714).
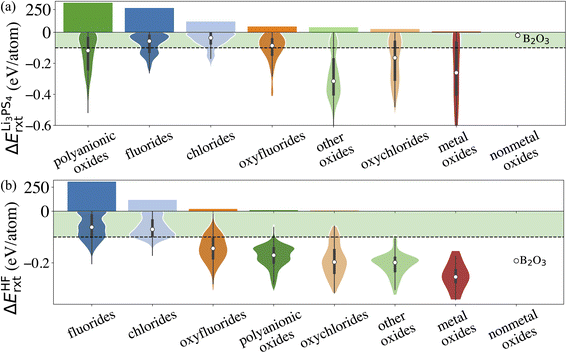
Similarly, we calculate ΔErxt between coating materials and representative electrolyte components. In this study, we consider the commonly used Li3PS4 solid electrolyte and LiPF6-based non-aqueous liquid electrolytes, respectively, and categorize the coating materials based on their reactivity. In the case of LiPF6-based electrolytes, we calculate ΔErxt between coating materials and HF, which is known to react strongly with both cathodes and coating materials. Fig. 3 illustrates the distribution of ΔErxt with Li3PS4 and HF for the compounds that are chemically stable with the cathodes. We find that most fluorides and chlorides have lower chemical reactivity with both Li3PS4 and HF than oxides compounds, thus are chemically compatible with both the cathodes and electrolytes. On the other hand, most oxides compounds are not chemically inert in LiPF6-based liquid electrolytes due to a high reactivity with HF. It should be noted that these chemical reactions may only happen at the coating/electrolyte interface and render a partially fluorinated oxides coating layer, which could be beneficial for the cycling performance.46 Therefore, even though we categorize the coatings based their chemical compatibility with liquid and solid electrolyte, the materials may be effective in both conditions. It should be noted that in LiPF6-based liquid electrolyte systems, besides fluorination of the coating layer from an HF attack, other organic species and Li2CO3 can also be found on the surface of the coated cathodes. We only consider the HF attack to broadly capture the chemical compatibility between coatings and LiPF6-based liquid electrolytes in a high-throughput fashion. This round of screening returns 902 and 508 coating candidates that are chemically compatible with Li3PS4 and LiPF6 based electrolytes, respectively.
In this study, we are mainly interested in the Li-containing compounds, as lithiated compounds tend to exhibit a higher ionic conductivity.30 Adding the Li-containing criterion, the entire screening procedure returns 89 and 51 Li-containing compounds that pass the proposed criteria for stability with respect to Li3PS4 solid state electrolyte and HF, respectively, with 36 compounds that are chemically compatible with both Li3PS4 and HF. In Fig. S2,† we summarize the numbers of Li-containing compounds for each category that pass the phase stability, electrochemical stability, and chemical stability descriptors. We find that oxides coatings, especially polyanionic oxides, account for the largest number of coatings for Li3PS4-based LIB, followed by fluorides and chlorides. On the other hand, the majority of coatings for LiPF6-based LIB are fluorides and chlorides. The common coatings only consist of the fluorides and chlorides. In Table S3,† we list the calculated voltage windows, reduction and oxidation reactions, and reaction energies for the 104 Li-containing compounds that pass the screening criteria. In ESI,† we list the calculated material attributes of coating candidates.
Ion diffusion analysis
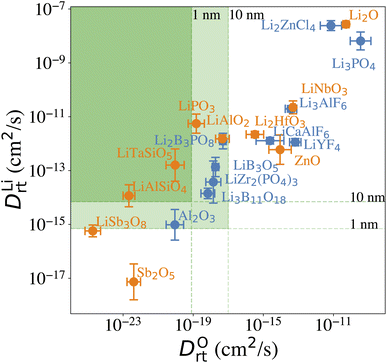
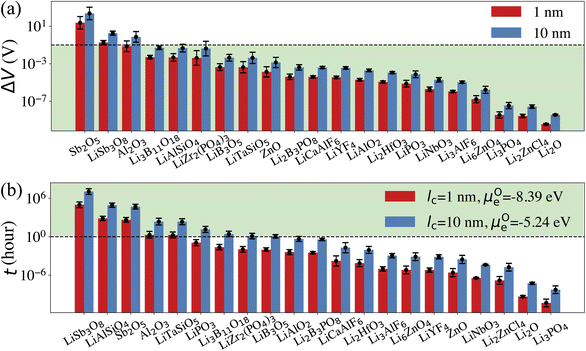
Our computational screening procedure has narrowed down the coatings of interest to 104 Li-containing compounds. Besides providing facile Li+ diffusion pathways, an optimal cathode coating should block O2− diffusion such that the oxygen-loss-induced cathode surface reconstruction can be mitigated. Therefore, to evaluate Li+ and O2− transport in the screened amorphous coatings, we calculate ionic diffusivity, flux, and transport time through the coating materials using ab initio molecular dynamics (AIMD) simulations and Onsager transport models, as described in Computational details. Due to the high computational cost of investigating the ionic diffusivity of all promising coating candidates, we select 9 representative compounds, consisting of polyanionc oxides Li3B11O18, LiZr2(PO4)3, Li3PO4, Li2B3PO8 and LiB3O5, fluorides Li3AlF6, LiCaAlF6, LiYF4 and chloride Li2ZnCl4, and analyze their ion diffusion. Fig. 4 illustrates the distribution of DLirt and DOrt in the selected compounds, along with 7 Li-containing compounds that are filtered out by electrochemical or chemical stability criterion: LiNbO3, Li2HfO3, LiAlO2, LiTaSiO5, LiPO3, LiAlSiO4, and LiSb3O8, and 4 binary oxides: Li2O, ZnO, Al2O3, Sb2O5. Our calculations show that in general, Li+ and O2− diffusion is correlated, i.e., a compound with a higher DLirt also has a higher DOrt. For example, the DLirt and DOrt in Li3PO4 are 10−9 and 10−10 cm2 s−1, respectively, both of which are higher than those in LiAlSiO4 (DLirt = 10−14 cm2 s−1, DOrt = 10−23 cm2 s−1). The correlation between Li+ and O2− diffusion can be explained by ionic conduction mechanism in amorphous structures. Our previous study30 showed that Li+ and O2− diffusion consists of discrete vibrational and translational motions. During vibrational motions, Li+ is bonded to more O2− ions than during translational motions, and its translation to another vibration site is activated by the Li–O bond breaking/formation process, which effectively explains the correlated transport between Li+ and O2−. In addition, we find that for compounds consisting of the same species, a compound with a higher Li+ concentration also has a higher Li+ and O2− diffusion. For example, comparing Li3B11O18 and LiB3O5, we find that LiB3O5, which has a higher Li+ concentration, exhibits a higher DLirt and DOrt. Similar behavior is found in LiPO3 and Li3PO4, relating to their DLirt and DOrt. Our results are consistent with Xu et al.'s work in which they found that a higher Li+ solubility will enhance the Li+ transport across the coating.24 In our work, we further demonstrate that, unfortunately, a higher Li+ concentration also correlates with increased, detrimental O2− transport.From the calculated DLirt and DOrt, we evaluate the coating suitability of the selected compounds in terms of their ability to facilitate Li+ transport while blocking O2− transport. Low Li+ diffusivity within the cathode coating layer can increase resistance and capacity loss at higher C-rates due to the resulting large overpotential at higher currents.47 Thus, for the selected coating compounds, we estimate the overpotential, ΔV, at the cathode surface. We set the criterion for overpotential imposed by the coating as ΔV ≤ 0.1 V, above which the Li+ transport across the coating will be significantly compromised. In this study, we choose LiNiO2 as the relevant cathode material, with density ρ = 4.78 g cm−3 and a theoretical capacity C = 274 mA h g−1. Eqn (3) shows that a smaller ΔV can be realized by reducing the cathode particle size and coating thickness, and selecting a coating with high Li+ diffusivity DLirt and concentration cLi. By assuming a radius r = 1 μm LiNiO2 primary particle and a 1C rate current density through the coating, the current density J is estimated to be 0.044 mA cm−2. Finally, using DLirt and the Li+ concentration of the compounds, we calculate the ΔV values across a 1 and 10 nm conformal coating, respectively. Fig. 5a shows that for 1 nm surface coatings, all the selected compounds, except Sb2O5 (23 V) and LiSb3O8 (0.18 V), result in overpotentials below 0.1 V, which indicates a sufficient Li+ transport in these compounds. The overpotential of the Al2O3 coating is found to be 0.07 V. When the coating thickness is increased to 10 nm, the overpotentials of Sb2O5, LiSb3O8 and Al2O3 coatings increase to 230 V, 1.8 V and 0.7 V, respectively, while the overpotentials of other compounds are still below 0.1 V. Using an r = 1 μm LiNiO2 primary particle in a 1C rate current density, we estimate the minimum Li+ diffusivity DLirt to meet the overpotential criterion of ΔV ≤ 0.1 V. By assuming a Li+ concentration cLi = 1022 cm−3, we find that DLirt = 7 × 10−16 cm2 s−1 and 7 × 10−15 cm2 s−1 for a 1 and 10 nm cathode coating, respectively, which are represented by the horizontal dashed lines in Fig. 4.
To evaluate the effectiveness of these coatings in blocking O2− transport, we estimate the O2− flux JO and the time t required for O2− to diffuse through the coating. We assume the oxygen-loss-induced surface rocksalt layer mainly consists of NiO, which is densified from the layered NiO2. As NiO2 → NiO + 1/2O2, we estimate t for surface NiO2 layer to lose half of its oxygen and transform into an NiO layer. Let cOmax denote the O2− concentration in NiO2 and Vs represent the shell volume of the surface NiO layer. 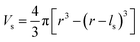 , where ls is the thickness of the surface NiO layer. Thus, the upper bound value of the number of O2− ions removed from the cathode surface is N = 0.5VscOmax and the O2− diffusion time t can be expressed as:
, where ls is the thickness of the surface NiO layer. Thus, the upper bound value of the number of O2− ions removed from the cathode surface is N = 0.5VscOmax and the O2− diffusion time t can be expressed as:
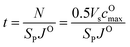 | (14) |
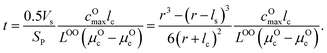 | (15) |
μ Oc can be estimated from the cathode densification reaction consistent with the phase diagram. At a high charge state, layered NiO2 would densify to rocksalt NiO and spinel Ni3O4 with oxygen being released at μOc = −4.95 eV, which is equal to the DFT-calculated total energy of an O2 atom. μOe can be estimated from two different conditions: (1) using the condition where the electrolyte reacts with O2− and forms a new compound (Li3PS4 reacts with O2− and forms Li3PO4 at μOe = −8.39 eV) and (2) using the condition where O2− loses electrons to the carbon network and forms O2 (at room temperature and PO2 = 0.21 atm, μOe = −5.24 eV). Thus, we estimate −8.39 ≤ μOe ≤ −5.24 eV. Eqn (15) indicates that for a given cathode coating and a given size of LiNiO2 primary particle, a longer O2− diffusion time t can be realized by a smaller oxygen chemical potential gradient, i.e., higher lc and μOe. By assuming an r = 1 μm LiNiO2 primary particle and an ls = 2 nm surface NiO layer, we estimate the time t for O2− ions to diffuse through the selected coatings (see Fig. 5b). We consider a range of conditions by varying lc and μOe, with lc = 10 nm, μOe = −5.24 eV corresponding to the slowest O2− diffusion and lc = 1 nm, μOe = −8.39 eV corresponding to the fastest O2− diffusion. Fig. 5b shows the calculated O2− diffusion time t in the selected compounds. We select the compounds with an estimated O2− diffusion time longer than 1 h such that not all O2− ions that are evolved from surface NiO2 layer have diffused through the coating under 1C rate. We find that LiSb3O8, LiAlSiO4, Sb2O5, Al2O3, LiTaSiO5, LiPO3, Li3B11O18, LiZr2(PO4)3 and LiB3O5 exhibit an estimated O2− diffusion time longer than 1 h. Next, we estimate the upper limit of O2− diffusivity to have t ≥ 1 h. As mentioned earlier, we approximate LOOrt ≈ LOOrt,self. Using eqn (6), we can directly calculate LOOrt from self-diffusion coefficient DOrt:
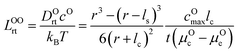 | (16) |
Next, we use the same cathode particle configuration and assume an O2− concentration cO = 1022 cm−3 in a coating layer. We find that DOrt = 8 × 10−20 cm2 s−1 for lc = 1 nm, μOe = −8.39 eV and DOrt = 1 × 10−17 cm2 s−1 for lc = 10 nm, μOe = −5.24 eV, which are represented by the vertical dashed lines in Fig. 4. Therefore, the green region in Fig. 4 represents the favorable Li+ and O2− diffusivity window, and a compound falling on the top left area is more desirable in terms of facilitating Li+ transport while blocking O2− transport. It should be noted that the effect of different cathode materials on ΔV and t is marginal (see Fig. S4†). Therefore, the calculated ΔV, t, and Li+ and O2− diffusivity window are applicable for other cathodes, such as Ni-based NMC and LiCoO2.
Five observations can be made from the high-throughput screening results and the estimated overpotential ΔV and O2− diffusion time t:
(1) Among the nine Li-containing compounds that pass the computational screening, only Li3B11O18, LiZr2(PO4)3 and LiB3O5 have been found to exhibit both ΔV ≤ 0.1 V and t ≥ 1 h. However, the thickness of the considered coatings should be large enough (e.g. 10 nm) to improve their oxygen-retaining ability. Experimentally, Zhang et al. demonstrated that an amorphous Li3B11O18 coating layer with a few nanometers thickness exhibits excellent chemical/electrochemical stability and can significantly improve the capacity retention of NMC cathodes.11 However, the surface structure of NMC particles still evolved from a layered phase to a rocksalt phase after cycling. Our recent calculations showed facile O2− transport in the amorphous Li3B11O18 material, which leads to an oxygen-loss induced surface phase transition. In this work, we predict that a thicker Li3B11O18 coating layer (e.g. 10 nm) is beneficial to mitigate the oxygen-loss induced surface densification and further improve the cycling performance of NMC cathodes. In addition, Wang et al. reported that amorphous LiZr2(PO4)3 coated LiCoO2 exhibits better capacity retention and rate performance than bare LiCoO2.48 The enhanced cycling performance was attributed to an enhanced Li-ion diffusion and a significantly mitigated chemical reactions between LiCoO2 and sulfide-based solid electrolytes by the protective LiZr2(PO4)3 coating layer, which agrees well with our ion diffusion and chemical stability analysis. However, based on our O2− diffusion in amorphous LiZr2(PO4)3 analysis, we expect that the 2 nm LiZr2(PO4)3 coating used in their study is not thick enough to mitigate oxygen loss from LiCoO2 surface and it's likely that the LiCoO2 cathodes still suffer from oxygen-loss induced surface reconstruction at prolonged cycling and high charge.49 Therefore, we predict that a thicker LiZr2(PO4)3 coating (e.g. 10 nm) could further improve the cycling performance of LiCoO2.
(2) Among the nine Li-containing compounds that do not pass the computational screening, LiPO3, LiSb3O8, LiAlSiO4 and LiTaSiO5 can also be considered as promising cathode coatings mainly because of their exceptional oxygen retaining ability. LiPO3 exhibits a high oxidation limit (4.9 V) and a reaction energy ΔErxt = −0.11 eV per atom with LiNiO2 to form LiNiPO4 and Li3PO4, therefore is screened out by our chemical stability criterion: ΔErxt ≥ −0.1 eV per atom. However, both LiNiPO4 and Li3PO4 coatings have been reported to enhance the rate capability and cycle performance of cathode materials50,51 and the chemical reaction may only happen at the interface of LiPO3 and LiNiO2 considering the sluggishness of solid state reactions. Experimentally, Chong et al.8 coated LiNi0.5Mn1.5O4 (LNM) particles with a 1 nm thickness of amorphous LiPO3 and found that the LiPO3 coating can significantly reduce the cell impedance and facilitate Li+ ion transport, which is in good agreement with our calculations. LiSb3O8 also exhibits a high oxidation limit (5.0 V), but its predicted reduction limit (3.2 V) is higher than our reduction limit criterion: Vred ≤ 3 V. However, its lithiated compound LiSbO3 is expected to exhibit a higher Li+ diffusion, which may offset its relatively high overpotential. In addition, LiSb3O8 reacts favorably with both HF and LiS3PS4, i.e. ΔErxt ≤ 0.1 eV per atom. We note that these chemical reactions may only happen at the coating/electrolyte interface and the reaction products could form a passivation layer to prevent further reactions. LiAlSiO4 exhibits excellent oxygen retention, but its oxidation limit (|Vox| = 3.9 V) is lower than our oxidation limit criterion: |Vox| ≥ 4 V. However, LiAlSiO4 decomposition involves the O2 evolution reaction, which is likely to have sluggish kinetics.52,53 Therefore, the overpotential of the LiAlSiO4 decomposition reaction may increase its oxidation limit, i.e., |Vox| ≥ 4 V. Experimentally, Deng et al.54 cycled an amorphous LiAlSiO4-coated LNM cathode with an electrochemical window from 3.5 to 4.9 V for 150 cycles and found improved capacity retention, lower Mn-dissolution and faster Li+ transport in LiAlSiO4-coated LNM, compared to uncoated LNM. Our calculated Li+ diffusivity in LiAlSiO4, 1.16 × 10−14 cm2 s−1, is also in good agreement with their reported value, 7.96 × 10−15 cm2 s−1. Therefore, despite its limitations, we include LiAlSiO4 in the list of promising cathode coatings. Similarly, LiTaSiO5 is another potentially effective cathode coating, despite its low oxidation limit (|Vox| = 3.9 V).
(3) Fluoride and chloride materials exhibit exceptional electrochemical and chemical stability as well as low overpotentials due to their fast Li+ transport. However, our calculations also show that the fluoride and chloride coatings are O2− transparent, which means that halide-coated cathode surfaces will be prone to oxygen loss and are likely to transform over time into a densified rocksalt phase.
(4) Although non-Li containing, Al2O3 can be considered as a promising cathode coating. We estimate that the diffusion time of oxygen in an Al2O3 coating varies between 2 to 227 h, depending on lc and ∇μO (see Fig. 4). Thus, we predict that an NMC cathode coated with a thin Al2O3 coating layer, such as 1 nm, is still prone to surface oxygen loss, especially when cycled at low C-rate. This result could explain why a 3 nm Al2O3 surface coating is not sufficient to stabilize NMC cathode surface when cycled at C/7.18 On the other hand, a thicker Al2O3 coating layer can effectively mitigate O2− transport, which results in a better cathode surface protection; David et al. showed that an Al2O3 ALD coating can effectively prevent surface reconstruction of NMC cathodes even after 760 cycles,55 which indicates that a thick and conformal Al2O3 coating was applied on the NMC cathodes in their study.
(5) An optimal amorphous cathode coating should not only exhibit sufficient thermodynamic stability, electrochemical stability and chemical stability, but also a low O2− diffusivity and a high Li+ diffusivity to achieve oxygen-retaining and surface-protective functions while avoiding significant losses in rate capability. However, the correlation between Li+ and O2− diffusion in amorphous coatings highlights the inherent contradiction in identifying cathode coating materials with optimal Li+ transport as well as O2− blocking ability. In general, Li+ diffusion in Li-containing compounds is fast enough to avoid a large overpotential. As a higher Li+ diffusion may compromise a coating's ability to block O2− diffusion, for compounds with same chemistry, a compound with a lower Li+ concentration is thus preferred. For example, the Li+ concentrations in LiPO3 and Li3PO4 are 20% and 37.5%, respectively. Fig. 4 shows that both LiPO3 and Li3PO4 exhibit a facile Li+ diffusion, but LiPO3 exhibits an improved oxygen retention as compared to Li3PO4. In addition, the oxidation limit of LiPO3 (4.9 V) is higher than that of Li3PO4 (4.0 V).
Conclusions
In summary, we have carried out an extensive high-throughput computational study to develop materials design principles governing amorphous cathode coating selections for Li-ion battery applications. Our high-throughput screening includes descriptors to evaluate the thermodynamic stability, electrochemical stability, chemical reactivity with electrolytes and cathodes, and ionic diffusion in the cathode coatings. We consider reactivity with the commonly used Li3PS4 solid state electrolyte and with HF as a particularly detrimental representative of liquid electrolyte degradation. We find that polyanionic oxides account for the largest number of cathode coatings for Li3PS4-based LIB, followed by fluorides and chlorides. On the other hand, the majority of cathode coatings that are inert to chemical reactions with HF are fluorides and chlorides. Combing the screening results and ionic diffusion analysis of 20 selected compounds, we summarize the promising cathode coatings and general materials design principles:(1) Li+ and O2− diffusion are highly correlated, therefore, a higher Li+ transport promotes higher O2− transport. In Li-containing compounds, the Li+ diffusion rate is generally fast enough to avoid a large overpotential. When selecting a cathode coating with same chemistry, a compound with a lower Li concentration is preferred, as it exhibits an improved oxygen retention as well as a higher oxidation limit.
(2) Mitigating O2− diffusion is a formidable challenge when selecting an ideal cathode coating as most thin conformal coatings will transport oxygen under prolonged cycling and high voltage. Our results show that in addition to the four experimentally confirmed cathode coatings: Li3B11O18, LiZr2(PO4)3, LiPO3 and LiAlSiO4, we also identify three new promising cathode coatings: LiB3O5, LiSb3O8 and LiTaSiO5.
(3) Based on our ionic diffusion analysis, we find that BOxy−, SiOxy−, POxy− and SbOxy− anion groups tend to exhibit an improved oxygen retention. Therefore, we expect that compounds such as LiBa(B3O5)3, LiAl(Si2O5)2, LiTi2(PO4)3, LiScP2O7, LiK(PO3)2, and LiCs(PO3)2 could also be potentially effective cathode coatings. On the other hand, F− and Cl− anion groups tend to exhibit faster Li+ and O2− diffusion as compared to the oxides. Thus, they are not ideal for high-voltage cathode coatings where the driving force for oxygen loss is high. However, their inherent fast Li+ diffusivity may render them promising candidates as the solid-state electrolytes or lithium metal coatings.
(4) A non-Li-containing compound generally exhibits slower Li+ diffusion but better oxygen retention ability as compared to its lithiated counterpart. We mainly consider Li-containing compounds in this study, however, we expect that effective cathode coatings can also be found in non-lithiated compounds, such as Al2O3. Based on our identified anion groups above, we expect that compounds, such as ScBO3, HfSiO4, ZrP2O7 and AlPO4, could be potentially effective cathode coatings. A follow-up study on non-Li-containing coatings will be presented in a later report.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr. Gerbrand Ceder and Dr. Muratahan Aykol for useful discussions. This work was intellectually led by the Battery Materials Research (BMR) program under the Assistant Secretary for Energy Efficiency and Renewable Energy, Office of Vehicle Technologies of the U.S. Department of Energy, Contract DEAC02-05CH11231. This research used resources of the National Energy Research Scientific Computing Center (NERSC).References
- W. Li, E. M. Erickson and A. Manthiram, Nat. Energy, 2020, 5, 26–34 CrossRef CAS
.
- S.-K. Jung, H. Gwon, J. Hong, K.-Y. Park, D.-H. Seo, H. Kim, J. Hyun, W. Yang and K. Kang, Adv. Energy Mater., 2014, 4, 1300787 CrossRef
.
- X. Gao, Y. H. Ikuhara, C. A. J. Fisher, R. Huang, A. Kuwabara, H. Moriwake, K. Kohama and Y. Ikuhara, J. Mater. Chem. A, 2019, 7, 8845–8854 RSC
.
- M. Gu, W. Shi, J. Zheng, P. Yan, J.-g. Zhang and C. Wang, Appl. Phys. Lett., 2015, 106, 203902 CrossRef
.
- D. H. Jang and S. M. Oh, J. Electrochem. Soc., 1997, 144, 3342–3348 CrossRef CAS
.
- S. Kalluri, M. Yoon, M. Jo, H. K. Liu, S. X. Dou, J. Cho and Z. Guo, Adv. Mater., 2017, 29, 1605807 CrossRef PubMed
.
- S.-T. Myung, K. Izumi, S. Komaba, H. Yashiro, H. J. Bang, Y.-K. Sun and N. Kumagai, J. Phys. Chem. C, 2007, 111, 4061–4067 CrossRef CAS
.
- J. Chong, J. Zhang, H. Xie, X. Song, G. Liu, V. Battaglia, S. Xun and R. Wang, RSC Adv., 2016, 6, 19245–19251 RSC
.
- A. M. Wise, C. Ban, J. N. Weker, S. Misra, A. S. Cavanagh, Z. Wu, Z. Li, M. S. Whittingham, K. Xu, S. M. George and M. F. Toney, Chem. Mater., 2015, 27, 6146–6154 CrossRef CAS
.
- A. Zhou, W. Wang, Q. Liu, Y. Wang, X. Yao, F. Qing, E. Li, T. Yang, L. Zhang and J. Li, J. Power Sources, 2017, 362, 131–139 CrossRef CAS
.
- Y. Zhang, Y. Tian, Y. Xiao, L. J. Miara, Y. Aihara, T. Tsujimura, T. Shi, M. C. Scott and G. Ceder, Adv. Energy Mater., 2020, 1903778 CrossRef CAS
.
- J. Zheng, M. Gu, J. Xiao, B. J. Polzin, P. Yan, X. Chen, C. Wang and J.-G. Zhang, Chem. Mater., 2014, 26, 6320–6327 CrossRef CAS
.
- J.-Z. Kong, H.-F. Zhai, X. Qian, M. Wang, Q.-Z. Wang, A.-D. Li, H. Li and F. Zhou, J. Alloys Compd., 2017, 694, 848–856 CrossRef CAS
.
- M. Bettge, Y. Li, B. Sankaran, N. D. Rago, T. Spila, R. T. Haasch, I. Petrov and D. P. Abraham, J. Power Sources, 2013, 233, 346–357 CrossRef CAS
.
- X. Zhang, I. Belharouak, L. Li, Y. Lei, J. W. Elam, A. Nie, X. Chen, R. S. Yassar and R. L. Axelbaum, Adv. Energy Mater., 2013, 3, 1299–1307 CrossRef CAS
.
- Y. S. Jung, A. S. Cavanagh, A. C. Dillon, M. D. Groner, S. M. George and S.-H. Lee, J. Electrochem. Soc., 2010, 157, A75–A81 CrossRef CAS
.
- J. S. Park, X. Meng, J. W. Elam, S. Hao, C. Wolverton, C. Kim and J. Cabana, Chem. Mater., 2014, 26, 3128–3134 CrossRef CAS
.
- J. R. Croy, D. C. O'Hanlon, S. Sharifi-Asl, M. Murphy, A. Mane, C. W. Lee, S. E. Trask, R. Shahbazian-Yassar and M. Balasubramanian, Chem. Mater., 2019, 31, 3891–3899 CrossRef CAS
.
- M. Aykol, S. Kim, V. I. Hegde, D. Snydacker, Z. Lu, S. Hao, S. Kirklin, D. Morgan and C. Wolverton, Nat. Commun., 2016, 7, 13779 CrossRef CAS PubMed
.
- B. Liu, D. Wang, M. Avdeev, S. Shi, J. Yang and W. Zhang, ACS Sustainable Chem. Eng., 2020, 8, 948–957 CrossRef CAS
.
- Y. Xiao, L. J. Miara, Y. Wang and G. Ceder, Joule, 2019, 3, 1252–1275 CrossRef CAS
.
- Z. A. Grady, C. J. Wilkinson, C. A. Randall and J. C. Mauro, Front. Energy Res., 2020, 8, 218 CrossRef
.
- V. Lacivita, N. Artrith and G. Ceder, Chem. Mater., 2018, 30, 7077–7090 CrossRef CAS
.
- S. Xu, R. M. Jacobs, H. M. Nguyen, S. Hao, M. Mahanthappa, C. Wolverton and D. Morgan, J. Mater. Chem. A, 2015, 3, 17248–17272 RSC
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed
.
- J. Cheng, E. Sivonxay and K. A. Persson, ACS Appl. Mater. Interfaces, 2020, 12, 35748–35756 CrossRef CAS PubMed
.
- I. Enculescu and B. Iliescu, Cryst. Res. Technol., 1997, 32, 879–891 CrossRef CAS
.
- J. Verhoogen, Am. Mineral., 1952, 37, 637–655 CAS
.
- M. R. Laskar, D. H. K. Jackson, S. Xu, R. J. Hamers, D. Morgan and T. F. Kuech, ACS Appl. Mater. Interfaces, 2017, 9, 11231–11239 CrossRef CAS PubMed
.
- K. D. Fong, J. Self, B. D. McCloskey and K. A. Persson, Macromolecules, 2020, 53, 9503–9512 CrossRef CAS
.
- R. Jung, M. Metzger, F. Maglia, C. Stinner and H. A. Gasteiger, J. Electrochem. Soc., 2017, 164, A1361–A1377 CrossRef CAS
.
- T. Hatsukade, A. Schiele, P. Hartmann, T. Brezesinski and J. Janek, ACS Appl. Mater. Interfaces, 2018, 10, 38892–38899 CrossRef CAS PubMed
.
- S. S. Zhang, Energy Storage Materials, 2020, 24, 247–254 CrossRef
.
-
A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, 2013 Search PubMed
.
- M. Aykol, S. S. Dwaraknath, W. Sun and K. A. Persson, Sci. Adv., 2018, 4, eaaq0148 CrossRef PubMed
.
- M. W. Chase, J. L. Curnutt, J. R. Downey, R. A. Mcdonald, A. N. Syverud and E. A. Valenzuela, J. Phys. Chem. Ref. Data, 1982, 11, 695–940 CrossRef CAS
.
- A. Wang, R. Kingsbury, M. McDermott, M. Horton, A. Jain, S. P. Ong, S. Dwaraknath and K. A. Persson, Sci. Rep., 2021, 11, 1–10 CrossRef PubMed
.
-
A. J. Bard, R. Parsons and J. Jordan, Standard Potentials in Aqueous Solution, 2017 Search PubMed
.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2016, 28, 266–273 CrossRef CAS
.
- Z. Chen, Y. Qin, K. Amine and Y. K. Sun, J. Mater. Chem., 2010, 20, 7606–7612 RSC
.
- I. Belharouak, C. Johnson and K. Amine, Electrochem. Commun., 2005, 7, 983–988 CrossRef CAS
.
- J. W. Kim, D. H. Kim, D. Y. Oh, H. Lee, J. H. Kim, J. H. Lee and Y. S. Jung, J. Power Sources, 2015, 274, 1254–1262 CrossRef CAS
.
- X. Li, J. Liu, X. Meng, Y. Tang, M. N. Banis, J. Yang, Y. Hu, R. Li, M. Cai and X. Sun, J. Power Sources, 2014, 247, 57–69 CrossRef CAS
.
- L. Wang, X. Sun, J. Ma, B. Chen, C. Li, J. Li, L. Chang, X. Yu, T. S. Chan, Z. Hu, M. Noked and G. Cui, Adv. Energy Mater., 2021, 11, 2100881 CrossRef CAS
.
- J. Geder, H. E. Hoster, A. Jossen, J. Garche and D. Y. Yu, J. Power Sources, 2014, 257, 286–292 CrossRef CAS
.
- S. W. Cho, G. O. Kim and K. S. Ryu, Solid State Ionics, 2012, 206, 84–90 CrossRef CAS
.
- Q. Gan, N. Qin, Z. Wang, Z. Li, Y. Zhu, Y. Li, S. Gu, H. Yuan, W. Luo, L. Lu, Z. Xu and Z. Lu, ACS Appl. Energy Mater., 2020, 3, 7445–7455 CrossRef CAS
.
- Y. Zhu, X. He and Y. Mo, ACS Appl. Mater. Interfaces, 2015, 7, 23685–23693 CrossRef CAS PubMed
.
- B. D. McCloskey, R. Scheffler, A. Speidel, G. Girishkumar and A. C. Luntz, J. Phys. Chem. C, 2012, 116, 23897–23905 CrossRef CAS
.
- J. C. Deng, Y. L. Xu, L. Li, T. Y. Feng and L. Li, J. Mater. Chem. A, 2016, 4, 6561–6568 RSC
.
- L. David, K. Dahlberg, D. Mohanty, R. E. Ruther, A. Huq, M. Chi, S. J. An, C. Mao, D. M. King, L. Stevenson and D. L. Wood, ACS Appl. Energy Mater., 2019, 2, 1308–1313 CrossRef CAS
.
- J. Cheng, L. Mu, C. Wang, Z. Yang, H. Xin, F. Lin and K. Persson, J. Mater. Chem. A, 2020, 8, 23293–23303 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ta06051e |
| This journal is © The Royal Society of Chemistry 2022 |