Recovering sensitivity lost through convection in pure shift NMR

Abstract

Practical pure shift NMR experiments, especially on instruments equipped with cryoprobes, can sometimes give very disappointing results. Here we show for the first time that this is a consequence of signal loss due to sample convection, and demonstrate a simple adjustment to common pure shift NMR experiments that restores the lost signal.

---

Pure shift NMR methods,^1–4 which greatly improve resolution and simplify spectra by suppressing the effects of homonuclear scalar couplings, are proving increasingly popular. While for the most part very robust, pure shift methods can occasionally yield unexpectedly poor results, even – indeed, especially – on the best NMR equipment. Pure shift NMR experiments typically include delays of tens of ms, and routinely use field gradient pulses to suppress unwanted signals. Consequently, they are susceptible to any sample motion, such as that caused by thermal convection. Cryogenic probes have become commonplace, as they provide the highest NMR sensitivity, but they also generate large temperature gradients. Because the solvents commonly used for organic chemistry NMR samples, including chloroform, methylene chloride, and acetone, have a high propensity to convect, this can result in near-total loss of signal in pure shift spectra. Here we illustrate the problem with a representative sample on a typical instrument, demonstrate the origin of the signal loss, and describe a simple solution. Modifying the field gradient pulse amplitudes used in pure shift NMR experiments refocuses the effect of convection and thus restores all the lost signal.

When studying complex samples, NMR spectroscopists often seek to simplify ¹H spectra by avoiding the signal overlap caused by ¹H–¹H scalar couplings. This can be achieved with pure shift methods, which typically divide the ¹H spin population into active spins (those observed) and passive spins (those manipulated to suppress the effects of couplings). The net result is that only the signals from active spins are seen, and these signals appear in the spectrum as singlets.

Pure shift ¹H NMR spectra are most commonly obtained by using active spin refocusing (ASR) pulse sequence elements, such as the band-selective (BS),^5,6 Zangger-Sterk (ZS),⁷ PSYCHE,^8,9 and BIRD^10,11 elements, to reverse the effects of scalar couplings. Band-selective pure shift experiments offer nearly 100% sensitivity, but can only measure part of a pure shift ¹H spectrum at a time, typically making multiple experiments necessary.⁵ On the other hand, broadband pure shift experiments that capture the full ¹H chemical shift range incur a sensitivity penalty, which varies based on how the active/passive spin selection is performed. Of the original signal, only about 1% is retained with ¹³C-BIRD (since only ¹³C-bonded protons are observed^10,11). This increases to ∼5% for Zangger-Sterk methods, where active spins are spatially selected in different horizontal “slices” of the active volume,⁷ and up to 20% for PSYCHE, which uses low flip angle frequency-swept pulses to make a statistical selection of the active spins.⁸

Because of the relatively high sensitivity cost of pure shift methods, researchers are often inclined to use equipment such as cryogenic probes. Unfortunately, as will be seen, this can sometimes lead to disappointing results. The left panel of Fig. 1 shows that under typical conditions (top), both the sensitivity and the spectral purity of a Zangger-Sterk pure shift ¹H NMR spectrum of strychnine in CDCl₃ measured using a cryoprobe are greatly reduced. A high-quality spectrum can only be obtained by substantially increasing the flow rate of the nitrogen gas used for temperature regulation (bottom) – but still with a 50% loss in sensitivity.

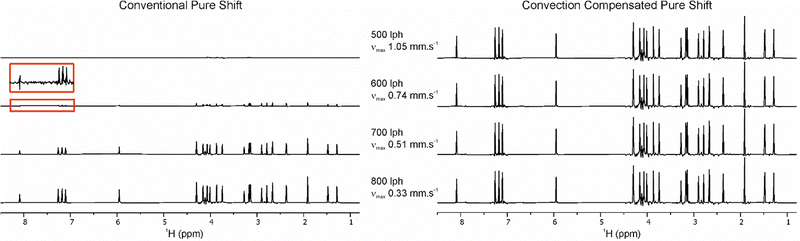Fig. 1 500 MHz ¹H Zangger-Sterk pure shift NMR spectra for strychnine in CDCl₃ at 288 K with different gas flow rates on a TCI cryoprobe, measured using the pulse sequence of Fig. 2 with an rSNOB selective pulse of 74 ms duration combined with a 1.5% spatial encoding gradient G₀. ν_max values are maximum convection velocities, measured experimentally (see ESI,† Section 2). (Left) Typical coherence transfer pathway (CTP) gradient strengths G₁ and G₂ (+47% and +31%, respectively); (right) calculated optimum values (+47% and −41.2%, respectively) for compensating convection.

The experimental parameters used for the left panel of Fig. 1 are typical of those in common use hitherto, which are designed for optimum spectral purity. When these parameters were used to set up automated pure shift experiments on two different 500 MHz NMR spectrometers, it was noticed that using mobile solvents such as chloroform-d on a cryoprobe led to very disappointing results compared to the same experiment run on a room-temperature probe, or on a sample in e.g. DMSO-d₆. The offending pure shift ¹H NMR spectra showed low signal-to-noise ratio, and sometimes also phase distortions. As seen in the left panel of Fig. 1, ¹H Zangger-Sterk pure shift NMR spectra with conventional parameter settings were relatively satisfactory, albeit with disappointing signal-to-noise ratio, when a strong gas flow was used for temperature regulation (bottom), but degraded progressively as the gas flow was lowered to normal levels (top). Unfortunately, such strong gas flows can lead to mechanical instability of the probe and sample, with vibration degrading experimental results.

These symptoms are characteristic of the problems caused by sample convection in experiments that use pulsed field gradients. Convection is present to varying degrees in almost all liquid state NMR samples. The rate of convection depends inter alia on the solvent used and the nominal sample temperature, but importantly also on the sample tube diameter and material, and on the probehead design.^12–16 The most familiar form of convection, Rayleigh–Bénard, occurs when a volume of fluid is colder above and warmer below and vertical movement is induced, causing the warmer, less dense fluid to rise whilst the colder, denser fluid sinks. Rayleigh–Bénard convection is a critical phenomenon: it only occurs if the vertical temperature gradient crosses a critical threshold determined by the sample geometry and fluid properties.

NMR probes typically use an upward airflow past the sample tube for sample temperature regulation. It might be hoped, therefore, that convection would only be observed if the target temperature were significantly above the quiescent sample temperature. Unfortunately, this is not the case. This is because of a second mechanism, Hadley convection, that is driven by horizontal, rather than vertical, temperature gradients, but still causes upward and downward vertical flow. Hadley convection is not a critical phenomenon; convection is therefore present to some degree in all practical liquid state NMR experiments.^12,13

Most modern multiple pulse NMR experiments use pulsed field gradients to suppress the effects of experimental imperfections. Such experiments require the sample to remain stationary, as any net movement between gradient pulses can cause a phase shift in the signal. In a convecting sample, a distribution of flow velocities is observed, with equal amounts of sample flowing upwards and downwards. The net signal is consequently attenuated, to a degree that depends on the rate of convection. Increasing the variable temperature (VT) gas flow rate improves heat exchange between the gas and all parts of the sample, reducing temperature gradients. This in turn reduces the rate of convection, decreasing the unwelcome signal attenuation. Fig. 1 lists the maximum flow velocity magnitudes v_max that were determined experimentally (see ESI,† Section 2) for the different VT gas flow rates.

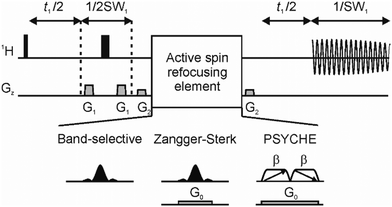
The impact of bulk motion, such as convection, is particularly severe in experiments designed to measure the tiny displacements caused by molecular diffusion. Various NMR pulse sequences have therefore already been developed to correct for sample convection in diffusion experiments, by refocusing the velocity-induced signal phase shifts.^17–19 It is straightforward to apply the same principles to pulse sequences for pure shift NMR, examples of which are shown in Fig. 2.

Fig. 2 Pulse sequences for pure shift NMR measurements using interferogram (pseudo-2D) acquisition. Narrow and wide rectangles represent hard 90° and 180° radiofrequency pulses, respectively. Various active spin refocusing (ASR) elements may be used, for example a selective 180° refocussing pulse with a simultaneous weak spatial encoding gradient G₀ (Zangger-Sterk) or without (band-selective), or a pair of low flip angle frequency swept pulses with a weak gradient (PSYCHE). Gradient pulses G₁ and G₂ enforce the required coherence transfer pathway (CTP). The incremented delays t₁/2 provide the evolution time required for interferogram acquisition.

Assuming that the effect of the Zangger-Sterk selective 180° pulse can be approximated as an instantaneous inversion at its midpoint, the gradient pulse parameters necessary to compensate for convection can be calculated from first principles (see Mathematica notebooks provided at https://doi.org/10.48420/23864202). If the gradient pulses G₁ and G₂ in Fig. 2 are rectangular and of duration δ, the duration of the Zangger-Sterk selective pulse is pw, and the times between the midpoints of the pulses G₁ and between the midpoints of the pulses G₂ are Δ₁ and Δ₂ respectively, then the optimal amplitude of G₂ to cancel the effects of convection on signal phase and amplitude is

G^opt₂ = (4G₁Δ₁δ − G₀pw²)/(4Δ₂δ). (1)

For half-sine shaped gradient pulses G₁ and G₂, the expression becomes

G^opt₂ = (8G₁Δ₁δ − πG₀pw²)/(8Δ₂δ). (2)

Fig. 1 (right panel) shows that if the optimum value of G₂ is used, clean spectra with full signal amplitude are seen over the full range of VT gas flow rates studied. G₂ is chosen for adjustment since the amplitude G₀ is determined by the range of chemical shifts required, and the influence of G₁ is small because Δ₁ ≪ Δ₂ in practical experiments. Changing the gradient amplitude G₂ in this way very slightly reduces the efficiency of coherence transfer pathway enforcement, but this is a negligible price to pay for the large sensitivity improvement that can be obtained.

Further confirmation of the origin of the signal losses shown in Fig. 1 (left panel) is given by Fig. 3. Here, the experimental signal amplitudes as a function of the gradient amplitude G₂ are compared with the result of fitting the experimental results to the theoretical signal dependence for Hadley convection, with the maximum velocity v_max as the only variable parameter. A strong correlation is seen between theory (solid lines) and experiment (points), with an overall shape which is a distorted and displaced “sinc” (sin x/x) function. The horizontal displacement is attributable to the slight reduction in the effect of G₀ caused by the finite time taken for the selective pulse to achieve signal inversion. The maximum velocity values obtained by fitting the results of pure shift experiments agree very well with those measured independently for different temperature regulation conditions, in a variety of cooled and room-temperature probes (see ESI,† Section 4).

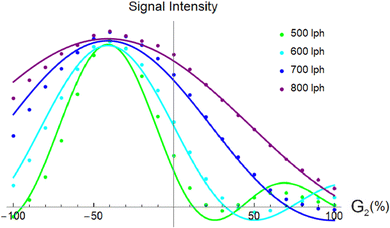Fig. 3 Intensity in arbitrary units of the pure shift H15a signal of strychnine as a function of the percentage gradient strength G₂. Pure shift spectra were measured at 288 K with different gas flow rates using the Zangger-Sterk sequence of Fig. 2, with a 74 ms duration rSNOB selective pulse and a spatial encoding gradient G₀ of +1.5%. Experimental data are plotted as points, and the solid lines were obtained by fitting the experimental data to the attenuation calculated for this pulse sequence for Hadley convection in an infinite cylinder, with v_max as the only adjustable parameter.

Of the four commonly-used pure shift methods – Zangger-Sterk, band-selective, PSYCHE and BIRD – BIRD uses a short ASR and is therefore the least vulnerable to convective signal losses. In experiments using the same sample and experimental parameters as Fig. 1 and with 600 lph VT gas flow, the signal intensity variations seen for the Zangger-Sterk, band-selective and PSYCHE methods show four trends in common. (i) Signal intensity varies approximately as a sinc function of G₂. (ii) Signal amplitudes with typical gradient amplitudes are substantially reduced, with about 25% signal loss for the BS experiment, 70% for ZS, and 85% for PSYCHE. (iii) The duration of the ASR element is the most important parameter, a longer element making the sequence more vulnerable to convection. (iv) Close to full signal can be restored by using the value of G₂ calculated from the remaining experimental parameters, using eqn (1) or (2) as appropriate. A small change in sequence timing is required to accommodate such a correction for the BS sequence (see ESI†), and the spatiotemporal averaging used in the PSYCHE ASR prevents full convection compensation, leaving a small residual signal loss that varies with chemical shift.^8,20

Investigation of the unexpectedly poor results often seen for pure shift NMR experiments on cryoprobes has uncovered the role played by convection. A minor, if counterintuitive, modification to experimental parameters, adjusting the amplitudes of two field gradient pulses, almost completely restores the lost signal, and enables excellent results to be obtained where conventional experiments fail almost completely. Convection can of course be reduced by using NMR tubes with smaller internal diameters, but since this sacrifices sensitivity by reducing the amount of sample in the active volume it offers at best a Pyrrhic victory. On the other hand, cryoprobes designed for small-diameter NMR tubes (e.g. 3 mm OD as opposed to 5 mm) should be intrinsically much less susceptible to sample convection. While the importance of convection compensation is well-established in NMR experiments for measuring diffusion, it has been largely overlooked in other contexts, with just two other applications (to 1D NOESY¹⁴ and gradient shimming²¹) reported to our knowledge. The results obtained suggest both that the parameters in current use for most pure shift NMR experiments should be adjusted, and that similar changes may substantially improve the performance both of a wide range of other pulsed field gradient-enhanced experiments on cryoprobes, and of experiments such as online reaction monitoring that use flowing samples.

EC: conceptualisation, funding acquisition, investigation, visualisation, writing – original draft; HMF: investigation; RWA, LC, GAM, MN: supervision; GAM: conceptualisation, formal analysis, funding acquisition, project administration, software, visualisation; all authors: methodology, writing – review and editing.

This work was supported by the Engineering and Physical Sciences Research Council (grant numbers EP/K039547/1, EP/R018790/1, EP/V007580/1 and studentship EP/T517823/1-2480860 to HMF) the University of Manchester (Dame Kathleen Ollerenshaw Fellowship to LC) and by the Consejería de Educación, Ciencia y Universidades of the Comunidad de Madrid (grant number 2022-T1/BMD-24030 to LC). Part of this work was performed using the PRISM core facility (Biogenouest, Univ Rennes, Univ Angers, INRAE, CNRS, FRANCE). For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any author accepted manuscript version arising. All experimental data, Mathematica notebooks used for fitting, Bruker pulse sequences and macros are freely available at https://doi.org/10.48420/23864202.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. R. W. Adams, EMagRes, 2014, 3, 1–15,  DOI:10.1002/9780470034590.emrstm1362.
2. L. Castañar and T. Parella, Magn. Reson. Chem., 2015, 53, 399–426.
3. K. Zangger, Prog. Nucl. Magn. Reson. Spectrosc., 2015, 86–87, 1–20.
4. L. Castañar, Magn. Reson. Chem., 2017, 55, 47–53.
5. L. Castañar, P. Nolis, A. Virgili and T. Parella, Chem. – Eur. J., 2013, 19, 17283–17286.
6. J. Ying, J. Roche and A. Bax, J. Magn. Reson., 2014, 241, 97–102.
7. K. Zangger and H. Sterk, J. Magn. Reson., 1997, 124, 486–489.
8. M. Foroozandeh, R. W. Adams, N. J. Meharry, D. Jeannerat, M. Nilsson and G. A. Morris, Angew. Chem., Int. Ed., 2014, 53, 6990–6992.
9. M. Foroozandeh, G. A. Morris and M. Nilsson, Chem. – Eur. J., 2018, 24, 13988–14000.
10. A. Lupulescu, G. L. Olsen and L. Frydman, J. Magn. Reson., 2012, 218, 141–146.
11. J. R. Garbow, D. P. Weitekamp and A. Pines, Chem. Phys. Lett., 1982, 93, 504–509.
12. I. Swan, M. Reid, P. W. A. Howe, M. A. Connell, M. Nilsson, M. A. Moore and G. A. Morris, J. Magn. Reson., 2015, 252, 120–129.
13. T. M. Barbosa, R. Rittner, C. F. Tormena, G. A. Morris and M. Nilsson, RSC Adv., 2016, 6, 95173–95176.
14. A. Jerschow and N. Müller, J. Magn. Reson., 1998, 132, 13–18.
15. N. M. Loening and J. Keeler, J. Magn. Reson., 1999, 139, 334–341.
16. A. Jerschow, J. Magn. Reson., 2000, 145, 125–131.
17. A. Jerschow and N. Müller, J. Magn. Reson., 1997, 125, 372–375.
18. M. J. Stchedroff, A. M. Kenwright, G. A. Morris, M. Nilsson and R. K. Harris, Phys. Chem. Chem. Phys., 2004, 6, 3221–3227.
19. M. Nilsson and G. A. Morris, J. Magn. Reson., 2005, 177, 203–211.
20. J.-N. Dumez, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 109, 101–134.
21. C.-L. Evans, G. A. Morris and A. L. Davis, J. Magn. Reson., 2002, 154, 325–328.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and sample details, convection measurements, further results and pulse sequence code. See DOI: https://doi.org/10.1039/d3cc04112c

---