A review of recent advances and applications of machine learning in tribology†
Abhishek T.
Sose
 ,
Soumil Y.
Joshi
,
Soumil Y.
Joshi
 ,
Lakshmi Kumar
Kunche
,
Lakshmi Kumar
Kunche
 ,
Fangxi
Wang
,
Fangxi
Wang
 and
Sanket A.
Deshmukh
and
Sanket A.
Deshmukh
 *
*
Department of Chemical Engineering, Virginia Tech, Blacksburg, VA 24061, USA. E-mail: sanketad@vt.edu
First published on 26th January 2023
Abstract
In tribology, a considerable number of computational and experimental approaches to understand the interfacial characteristics of material surfaces in motion and tribological behaviors of materials have been considered to date. Despite being useful in providing important insights on the tribological properties of a system, at different length scales, a vast amount of data generated from these state-of-the-art techniques remains underutilized due to lack of analysis methods or limitations of existing analysis techniques. In principle, this data can be used to address intractable tribological problems including structure–property relationships in tribological systems and efficient lubricant design in a cost and time effective manner with the aid of machine learning. Specifically, data-driven machine learning methods have shown potential in unraveling complicated processes through the development of structure–property/functionality relationships based on the collected data. For example, neural networks are incredibly effective in modeling non-linear correlations and identifying primary hidden patterns associated with these phenomena. Here we present several exemplary studies that have demonstrated the proficiency of machine learning in understanding these critical factors. A successful implementation of neural networks, supervised, and stochastic learning approaches in identifying structure–property relationships have shed light on how machine learning may be used in certain tribological applications. Moreover, ranging from the design of lubricants, composites, and experimental processes to studying fretting wear and frictional mechanism, machine learning has been embraced either independently or integrated with optimization algorithms by scientists to study tribology. Accordingly, this review aims at providing a perspective on the recent advances in the applications of machine learning in tribology. The review on referenced simulation approaches and subsequent applications of machine learning in experimental and computational tribology shall motivate researchers to introduce the revolutionary approach of machine learning in efficiently studying tribology.
1. Introduction
Tribology – the fundamental science of interacting surfaces in relative motion – has fascinated researchers due to its applications in different fields including energy,1,2 biomedicine,3 biology,4 food,5 automobiles,6 and aerospace.7,8 Thus, it is no surprise that key elements in tribology, such as motion dynamics and interfacial mechanism as well as attributes of surfaces in motion, such as friction, wear, adhesion, indentation, lubrication, and so on, have been extensively studied.9–12 For example, high energy consumption, failure of industrial processes, mechanical equipment, and increased transportation cost caused by unavoidable friction and wear have motivated researchers to understand the tribological phenomenon at different time and length scales.13–16 In recent years, a majority of these studies have developed and employed state-of-the-art experimental methods with the intention of reducing friction and wear, which account for one-fifth of all annual energy consumption.17 Specifically, advanced experimental techniques such as nanoindentation, atomic force microscopy and imaging,18 digital image correlation,19 and in situ spectroscopy, have been developed with the aim of studying tribological systems. Significant progress has been made in studying tribology at nano- and micro-scales through quantum ab initio simulations, as well as empirical, and mathematical approaches such as continuum mechanics,20,21 multi-scale,22 atomistic,23 and coarse-grained molecular dynamics (CG MD) simulations,24 non-equilibrium molecular dynamics (NEMD) simulations,25 reactive molecular dynamics (RMD) simulations,26 probabilistic and stochastic modeling,27–29 finite element method,30 and fractal methodology.31,32One of the effective ways to overcome and control friction and wear is through lubrication.33 In recent decades, numerous studies have been conducted to enhance lubrication in moving components of machinery by developing novel lubricants. These include novel varieties of solid-based lubricants including ball-bearings, diamond-like carbon (DLC), etc. or liquid-based lubricants like composites of gels, mineral or vegetable oils, among others. Moreover, the reinforcement of solid-state materials like short carbon fibers (SCFs), graphite, titanium oxide (TiO2) particles, boron carbide (B4C), titanium carbide (TiC), silicon carbide (SiC), and/or fly ash in oil/polymer-based liquids have enhanced lubrication.34–36 However, due to limited knowledge on the individual contributions of functionalities of each component and uncertainty associated with it, the development of new hybrid materials remains challenging. Moreover, the traditional methods to create these hybrid materials mainly rely on a highly inefficient, trial and error approach. Modern-day data-driven techniques of ML have emerged as new approaches for understanding and advancing complex processes in tribological studies. This is because, with the aid of ML, higher-dimensional problems and datasets can be modeled with ease and at a minimal cost, with better adaptive abilities to changing conditions.37 Several studies have combined the design of experiments (DOE) and modeling techniques with ML to accelerate the design of tribological materials with the desired characteristics/properties.38,39 This, in turn, has enabled researchers to analyze, predict, optimize, and accelerate the discovery of tribological materials by successfully establishing structure–property or structure–functionality relations in the existing available data.40,41 Thus, it is no surprise that there has been a surge in the use of ML for tribological applications recently (2010-today) as compared to that until 2010.
The field of tribology has been explored in recent years by reviewing applications of artificial neural networks (ANNs), as well as other machine learning (ML) techniques.37,42,43 Most of these reviews are focused on models developed using experimental data, with relatively low emphasis on computationally modeled tribological studies.38,44 This is because, in spite of the enormous amounts of data generated using computational approaches, the use of ML to solve tribological problems has been scarce. To the best of our knowledge, this is the first comprehensive review article with a focus on applications of ML with experimental and molecular simulations studies in tribology. Specifically, we provide details of different ML methods used to perform tribological studies as well as their applications in predicting and/or studying properties and performance of tribological systems and designing novel lubricants. Thus, making this review more appealing to all the relevant scientific communities. We highlight a detailed procedure used for data-generation, including description on design of experiments (DOE), as well as the pre-processing of the experimental and/or computational data for ML methods.38 Consequently, the importance of having the appropriate data for pre-processing tools and methods is demonstrated in improving the predictive accuracy of models based on the available data. There is a particular emphasis on integrating machine learning with optimization algorithms to resolve an important task of tuning hyperparameters during model training and the use of ML models as surrogates or objective functions during optimization. Thus, the goal of this comprehensive review is to provide insights into tribology obtained from the molecular modeling techniques and discuss recent trends of ML in the field of tribology.
We have divided this review article into six sections as presented in Fig. 1 as the contents and Table S1 of ESI.† According to different ML algorithms applied, Section 3 is divided into the 9 subsections in the subsequent order of the material formulation of (i) lubricants and (ii) composites material formulation, including (a) polymer matrix composites (PMCs), (b) metal matrix composites (MMCs), and (c) ceramic matrix composites (CMCs). Following the section on emerging, new and unexplored tribological materials, the challenges and our perspective on the applications of ML are also presented.
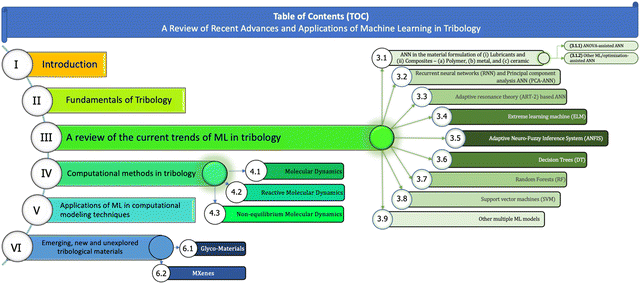 | ||
| Fig. 1 The visual representation of the table of contents (overall flow) of the review is presented. | ||
2. Fundamentals of tribology
2.1 Experimental studies of tribology
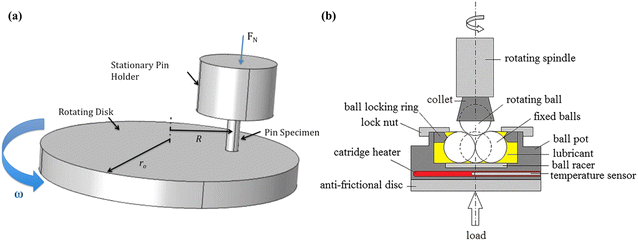
Experimentally, tribological materials, either pure or composite, are generally assessed through a number of test rigs including pin-on-disk (POD), four-ball tester, rub shoe, etc. to determine physical bulk or chemical tribological properties including interfacial friction, wear, and surface energy. Here, two of the widely used test rigs to generate training data for ML models are discussed:In general, the evaluation metric for a given tribological material is through their wear characteristics like the CoF, SWR, WSD, and/or mechanical properties like compressive and tensile moduli, and strength. Typically, these properties are used to train the ML models and the following subsection describes these properties:
(i) Coefficient of friction (CoF). The CoF can be quantified as the amount of friction occurring between two surfaces. The expression for CoF can be given by eqn (1):
 | (1) |
In the case of a low CoF, the force required for a sliding action to occur is substantially less than in the case of a high CoF.
(ii) Specific wear rate. Wear is defined as the irreversible material loss resulting from sliding of the interacting surfaces. The SWR (Ws) is calculated by the following eqn (2):
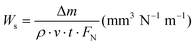 | (2) |
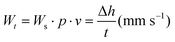 | (3) |
2.2 Introduction to machine learning algorithms and their applications
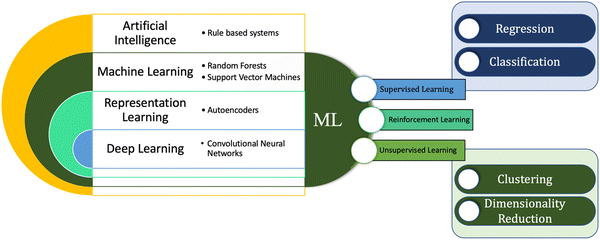
ML has been demonstrated in numerous studies to develop a thorough understanding of structure–property relationships in complex higher dimensional tribological problems.47–50 In addition to quantifying frictional and wear behavior, ML has proven to be effective in the design of new lubricant materials for desired tribological applications such as ball-bearing, shaft seals, piston rings, spacecrafts, etc.12,37,38,43,51 In light of the fact that the impact of multiple complex factors on a system remains uncertain in tribology, the potential of ML also goes beyond purely academic perspectives into actual industrial applications.52,53 In general, the formulation of ML models is driven either by the deterministic approach of logic and algorithmic theory or the stochastic way of probability theory. Data preprocessing followed by an appropriate choice of the algorithm and hyperparameter tuning, constitutes the training phase of ML models. The constructed and trained ML system can thereby be used to model, analyze, and predict solutions to that problem. Given a myriad of formulated algorithms, they can be broadly classified as either ‘supervised’, ‘unsupervised’ and ‘reinforcement’ learning techniques as shown in Fig. 3.54 The supervised learning approach is designed to learn through a feature-property relationship, such that the model learns over time by evaluating and improving the labeled output for a given input vector. A supervised learning model can be successfully constructed by identifying and defining a vector of unique features that are anticipated to significantly affect the outcome. Examples of supervised learning techniques include SVM, DT, RF, the Naive-Bayes model, and so on.55 An unsupervised learning approach, on the other hand, uses an unlabeled dataset for analyzing and clustering data based on its common characteristics.56K-means clustering algorithm, hierarchical clustering, density-based spatial clustering of applications with noise (DBSCAN), etc. constitute the examples for unsupervised learning method. Another important category of ML models is ‘reinforcement learning’, which may be classified as supervised learning, employing an approach of a reward-punishment mechanism.57 These ML models can be multi-layered feedforward NN, convolutional NN (CNN), RNN, modular NN (MNN), radial basis function NN (RBFNN), etc.58In the field of tribology, the tribological performance of materials are not only related to their material composition or physical/chemical properties, but also on the experimental testing conditions such as external temperature, pressure, humidity, etc. Thus, it is crucial to understand how the performance of a material is influenced by different experimental parameters. A systematic approach of determining the important factors affecting friction and wear in complex problems can be challenging as it may require running plenty of experiments. The design of experiments (DOE) including full and fractional DOE, as well as Taguchi method can be effective as they allow a systematic study of the effect of input parameters on outcome in addition to a simple, robust, efficient, and systematic way of designing experiments.59 The orthogonality of this DOE allows the effects of each variable to be separated from one another. Taguchi's method of DOE, in addition to the reduced number of experiments, is one of the most robust, efficient, and systematic methods to provide a parameters design for the experiments. Taguchi's method is particularly useful when operating on a set of 3 to 50 variables in which only a few variables have significant contributions and interactions are relatively minor.60 Several studies have successfully demonstrated the use of orthogonal arrays generated by the Taguchi methodology to reduce the number of experiments.61,62 Data obtained from these experiments are employed to model, analyze, and predict/answer the required questions, through ML/AI models. This is reviewed and discussed in-depth in the following sections, which are divided into subsections according to the aforementioned ML algorithms implemented in their studies.
3. Applications of ML algorithms in tribological experiments
3.1 Artificial neural networks (ANN)
ANNs, due to their adaptive learning, generalization, model independence, and analytical capabilities have proven vital in studying, designing, and predicting material formulations with enhanced properties in various fields of research.63–69 Particularly, ANNs have been broadly used for optimizing minimum wear rate, high lubrication, and/or the minimum CoF. Initial successful research on the implementation of ANN includes fretting wear damage prediction,70 tool wear,71 faulty rolling bearings diagnosis,72 composites’ tribological properties prediction, surface roughness, and disk brake performance. In general, the application of ANNs to lubricant design has not only led to the discovery of novel lubricants with different additives, but has also provided physical insights into the formulation and correlation between inputs of new lubricants and resulting outputs. The recent articles on the applications of ML in the design and development of triboinformatics,38 lubricants,37 MMCs,73 and structural materials74 further shed light on the current advances in the field of tribology using ML methods. The following sections provide a review of the formulation of lubricants and composites through the utilization of ANNs.Jones et al. were the first to endeavor to model an ANN on finite available data from POD, four-ball, and rub shoe rig experiments on perfluoropolyether (PFPE) lubricant.80 They showed that the ANN model accurately predicted the wear rate while also emphasizing on the influence of 6 input variables and specifications of material systems like sliding speed, distance, viscosity, applied load, CoF, and temperature on their tribological properties. They reported that the input layer dampened with a feedback loop (RNN architecture) was most suitable to predict the wear behavior. Because RNNs recirculate previous outputs along with new inputs from the input layer, they are able to learn better from past instances.80 Bhaumik and Kamaraj studied for the first time, a blend of 60% glycerol and 40% castor oil (NCO), which produced a 37% reduced CoF compared to NCO and cashew nut shell liquid (CNSL) and 50% less CoF to commercial mineral oil (CMO). A total of 60 data points collected from experiments from four-ball tester rigs on the lubricant developed by varying volumetric levels of mentioned three oils were used to train an ANN model. Ignoring the testing conditions, only the significance of the content of oil (in vol%) was studied on CoF and WSD.81 Humelnicu et al. used ANN to predict the low CoF composite of the diesel oil combined with two vegetable oils, namely, sunflower oil and rapeseed oil. The resulting mixture comprising 4% sunflower oil and 0% rapeseed oil indicated lower CoF compared to 0% sunflower oil and 20% rapeseed oil. In addition, ANN successfully predicted reduced CoF for 6.5% sunflower oil and 0% rapeseed oil compared to pure diesel oil, which was in good agreement with the experimental observation.82
Durak et al. successfully illustrated the use of feed-forward back-propagation neural network (BPNN) to explore the frictional behavior of the polytetrafluoroethylene (PTFE)-based additives in mineral oil under different loads and rotating speeds of the journal bearings.83 A 3-5-3-1 BPNN architecture was implemented with load, velocity, and additive concentration as input to predict CoF as output with 98% accuracy. Their study reported the successful experimental validation of ANN predicted PTFE loadings for different forces in the optimal hydrodynamic lubrication regime. Particularly, in experiments, 10–15% of PTFE at 153 N load, and 3–5% of PTFE at 253 N yielded maximum reduction CoF, while the same was observed in ANN for 15% of PTFE at 153 N, and 10–15% of PTFE at 253 N. These four articles, as summarized in Table S2 (ESI†), successfully operated on determining a perfect blend of different oils including mineral, vegetable, and commercial oils using ANN.
(a) Polymer matrix composites (PMC). Polymers, when combined with additives/fillers like carbon (CF) or glass fibers (GF) form PMC, which generally have improved thermal conductivity, mechanical, and tribological properties compared to the pure polymer.84,85 PMCs exhibit interesting tribological properties, including their chemical stability, extreme temperature, and wear resistance.11,84,86,87 Owing to these properties, PMCs are applied as lubricants in spacecrafts, automobile engines and under high vacuum conditions.88–92 For example, poly (ether ether ketone) (PEEK) composites have been examined largely for their low CoFs and high wear resistance.93–97 It has also been reported that the wear resistance of higher molecular weight PEEK was more than that of lower molecular weight PEEK.93
PTFE, a material possessing a high wear rate but with a low CoF,98 when blended with PEEK forms a PMC displaying a blend of both, low CoF and low wear rates.93 Lu and Friedrich, in their study, reported the value of the lowest CoF for a PEEK blend with 15% PTFE, as it formed a lubricating transfer film on the steel interface.93 Furthermore, a reinforcement of CF with PEEK polymer decreased the wear CoF at high temperatures (>493 K).94 At higher temperatures (>493 K), local surface heating of the contact area was observed, which led to a decrease in the specific shear stress and thus, also the CoF.94 PEEK matrix reinforced with CF matrix exhibited a low CoF compared to aramid fiber matrix.96 A higher enhancement in the reduction of abrasive wear was observed when PEEK was reinforced with CF compared to glass fiber.97 SEM images of CF reinforced PEEK (CF-PEEK) have shown that the surface of CF-PEEK was smoother as compared to aramid fiber matrix.95 The time required to remove a fiber from the surface was shorter in the case of aramid fiber matrix than CF-PEEK as the fiber had to be broken into many pieces before final removal could take place in CF-PEEK.96 Additionally, a higher degree of crystallinity of PEEK reduced the abrasive and sliding wear of the matrix.99 Owing to these advantages, it becomes imperative to determine a precise blend of PMCs in order to achieve enhanced tribological performance. However, in light of the large design space for exploration, the design of an optimal PMC for the desired applications continues to be a challenge. Therefore, in recent years, researchers have circumvented this issue through various data-driven techniques like ANN.100 We list these papers used to predict the properties of PMCs in Table S3 (ESI†) and discuss them here.
Friedrich and coworkers were pioneers in successfully implementing the ANN technique for predicting the mechanical and wear properties of PMCs.67,101–107 The early work of Jones et al. was followed by the work of Velten et al. as they modeled ANN for wear volume prediction in short fiber reinforced polymeric bearing when in contact with a steel ball. In Velten et al.'s ANN model, 10 input variables were utilized and pre-processing through PCA was applied for dimensionality reduction, and to identify the correlations between input variables.108 Subsequently, Zhang, Friedrich, and Velten predicted the SWR and CoF using multi-layer feed-forward ANN on composites of polyamide reinforced by short fibers. Particularly, they reported the influence of learning rules including bayesian regularization, Powell–Beale conjugate gradient algorithm (CGB), BFGS quasi-Newton method, Adaptive learning rate (GDX), and Levenberg–Marquardt algorithm (LM) on the coefficient of determination (B). In addition, the influence of altering ANN architectures i.e., 9-25-1, 9-50-1, 9-20-10-1, 9-15-10-5-1, and 9-12-8-5-5-1 and varying number of training data sets on B, which is formulated as shown in eqn (4), was also investigated.109
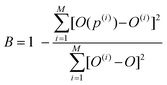 | (4) |
A survey by Frangu and Ripa110 revealed the applications of neural networks (NN) for modeling and predictions in continuous nonlinear approximation and classification data.110 Later, Zhang et al., who focused on the erosive wear of three polymers, i.e., polyethylene (PE), polyurethane (PUR), and epoxy modified by hydrothermally decomposed polyurethane (EP-PUR), introduced the compelling potential of ANNs to study polymer composites.67,101 Jiang et al. followed up this work by investigating the wear properties like SWR, CoF, and mechanical properties such as compressive strength and modulus, tensile strength (Ts) and flexural strength (Fs) in polyamide 4.6 (PA 4.6: synthesized with diaminobutane (C4 diamine) and adipic acid (C6 diacid)), and 6.6 (PA 6.6: synthesized with hexamethylene-diamine (C6 diamine) and adipic acid (C6 diacid)) composites. They varied material compositions, including PA 4.6 matrix content with GF, PTFE filler and graphite filler, at different surrounding conditions like temperature, normal force, and sliding speed to train their ANN model.102,104 In another study, Jiang et al. shifted their focus to polyphenylene sulfide (PPS) composites reinforced with SCFs and TiO2 particles. An excellent agreement of their ANN model with their experimental validation confirmed that introducing fillers to PPS improved the wear resistance (4.0 × 10−7 mm3 N−1 m−1) for a specific composition (PPS with 15 vol% SCF and 5 vol% TiO2). ANN-based models are also efficient at modeling nonlinear relationships between material compositions and testing conditions with wear characteristics, so estimating optimal compositions is simplified.103 This study by Jiang et al. was further accelerated by Gyurova by incorporating the graphite and PTFE in PPS composites blended with SCF and TiO2 fillers. A set of 90 data obtained from a POD experiment by varying loads and sliding velocities was used to train the ANN model. The inputs also included material composition and thermo-mechanical properties like tensile and compressive properties of materials to predict the SWR and CoF as outputs. To minimize the mean relative error and predict the CoF, ANNs were trained separately on gradient descent back-propagation algorithm with momentum and adaptive learning rate. Uniquely, the efficiency and performance of the ANNs were improved by removing irrelevant network nodes through a network optimization technique called the optimal brain surgeon (OBS) algorithm.111–113 The predictions on pruned data showed a good agreement with experimental data while portraying better accuracy than the ANN model trained on unpruned data.105 Further, in their second study, they suggested that the tribological characteristics predicted by ANNs were primarily altered by the material type, applied pressure, and sliding speed in the POD experiment. The composite data, predicted using their ANN models and experimental data were in fair agreement, resulting in the best wear resistance (i.e., lowest SWR) for the composition of PPS with 15 vol% SCF and 8 vol% submicron TiO2.106 Effectively enough, the model was able to predict the SWR and CoF with reduced mean relative errors (0.55 for SWR and 0.1 for CoF) compared to their previous study.104,105 Busse and Schlarb further improved this wear rate prediction efficiency (six times higher than their previous studies) by using the LM training algorithm with mean squared error regularization as a performance function.114 The aforementioned study by Gyurova106 also evaluated the effect of the size of the data set (of composites of PPS with TiO2 and SCF) used to train the ANN model.114
Zhu et al. showed that an increase in the number of training data points can further improve the accuracy of ANN prediction. The tribological properties of the composites of PTFE reinforced by the CF and TiO2 particle were predicted by an ANN model. 12 compositions of PTFE reinforced with CF (ranging 5–25 wt%), and TiO2 particles (ranging from 3–15 wt%) were utilized. The varying sliding velocities, applied normal loads, and the material composition along with corresponding mechanical properties, were used as input to predict the wear volume loss and CoF. Interestingly, the least mean squared errors were shown in a multi-layered model (with an architecture of 7-[15-10-5]3-1) by the scaled conjugate gradient (SCG) algorithm with tan-sigmoid transfer functions between input and hidden layers and linear transfer functions between hidden and output layers. For the case of moderate-level testing conditions, they concluded that the exhibited best wear resistance for PTFE (79 vol%) was due to a synergistic effect of CF (15 vol%) and TiO2 (6 vol%), while the lowest CoF for PTFE/CF/TiO2 content at 69/25/6%.115
A study on the CoF and weight loss of the composites of PEEK reinforced by using 30 wt% CF (PEEK-CF30) was performed by LiuJie et al.116 Using a non-linear ANN model through BPNN; they determined that pv factor (a mechanical factor i.e. product of applied pressure and sliding speed) significantly influenced CoF whereas contact temperature affected the weight loss. Kranthi and Satapathy investigated epoxy resin (Araldite LY 556) composites reinforced with pine wood dust (PWD) using POD experiments.117 Employing ANN on the data obtained from full-factorial DOE experiments (L9(34) orthogonal array), they constructed a 3-10-1 topology with sliding velocity, PWD content, and applied load as inputs. The experimental validation of ANN predictions was in good accordance with SWR errors <8%. They also rank PWD content, sliding velocity, and normal load in the order of most influential parameters for SWR.117 Following up, Rout and Satapathy investigated the epoxy composites blended with (5–20 wt%) rice husk (RH) for their SWR calculation using POD setup. They utilized an L16 orthogonal array determined from Taguchi DOE to obtain the experimental parameters. ANN model with 3-6-1 architecture, including RH content (wt%), sliding velocity and applied load as inputs for SWR as output was developed. In the 16 data points that were used, ANN predictions were in reasonable agreement with experiments since the errors were ≤9.64%.118 Additionally, the work by Padhi and Satapathy illustrated the use of a BPNN on the experimental data obtained from Taguchi's experimental design on epoxy composites with SGF and blast furnaces slag (BFS). A data set of 16 parameters were run experimentally using a POD setup, and a SWR was determined. An ANN-trained model was used to estimate the SWR for composites with BFS (errors between 0.9% and 5.1%) and without BFS (errors between 2.5% and 6.9%).119 Dai et al. designed novel antiwear additives by applying the BPNN-assisted quantitative structure tribo-ability relationship (QSTR) model.120 This study investigated 90 structural descriptors, including octanol-water partition coefficient, 3D Jurs descriptors, and topological and quantum indices for 36 additives, to determine their WSD area under three loads.
Umar Nirmal investigated the frictional performance of polyester (T-BFRP) composite reinforced by treated betelnut fiber.121 They trained an ANN model on 492 experimental sets of a block-on-disk experiment with normal load, sliding distance, and fiber orientation as inputs, used to predict the CoF. ANN trained with LM training function, and Logsig transfer function yielded the lowest errors compared to other training algorithms.121 The work by Nasir et al. also highlighted the good accuracy of the LM training function in training ANN to predict the frictional performance of a polymeric composite of polyester resin reinforced by multi-layered GF. Here, a large dataset of 7389 parameters of experimental disk-on-flat tribometer setup was utilized with different fiber orientations, applied normal load, sliding speed, and test duration as the input. Interestingly, higher accuracy was shown by a single-layered model with a large number of neurons (90% in prediction) as compared to a multi-layered model with fewer neurons.122 Parikh and Gohil investigated polyester composites reinforced with cotton fibers and fly ash to study composites’ wear responses. Experiments were conducted on the POD setup to evaluate a devised composite. A Box Behnken DOE was utilized to determine the experimental operating parameters with sliding velocity, applied load, and sliding distance as three inputs. An ANN model was trained with a total of 7 inputs including above three operating parameters and four composites specifications (polyester, cotton fiber polyester composite, 3 wt% fly ash filled CFPC, and 5 wt% fly ash filled CFPC). An ANN architecture of 7-10-1 was generated to achieve excellent agreement of predictions with experiments with R2 value of 0.90916.123 Another prime example of determining an optimum composition with reduced SWR using ANN on the polyester (epoxy thermoset) composites generated by utilizing waste marble dust as the fillers was demonstrated by Nayak and Satapathy.124 In their study, wear trials using POD tests were performed on 25 test parameters generated by varying sliding velocity, sliding distance, normal load, and marble dust content with the assistance of the Taguchi L25 orthogonal array.
Zakaulla et al. formulated and designed polycarbonate composites blended with graphene (GR) and B4C particles through an injection molding process. They demonstrated the proficient use of ANN on the database collected through POD experiments. Employing material compositions (volume content of polycarbonate, GR, and B4C) and operating conditions (applied load and sliding speed) as inputs, and SWR and CoF as outputs. The effect of the number of hidden layers and the number of neurons in hidden layers on the training ANN model was shown. A topology of 5-10-5-2 yielded the best results with CoD for SWR and CoF were 0.9375 and 0.9853 respectively. A polycarbonate composite with 10 vol% GR and 5 vol% B4C produced the lowest CoF (0.13) and SWR (35 μm). They attribute their decrease in wear with increasing GR content to the interlocking with polycarbonate which aids in enhanced load transfer.125 Yet another study exemplifies the successful use of ANN on polypropylene composite reinforced by blast furnace glass by Padhi and coworkers.126 Both above studies used the Taguchi method to perform experiments on distinct arrays of parameters to generate input for the ANN model. Particularly, this study emphasizes the significant influence of sliding velocity and BFS filler content on the minimization of SWR.126
Kurt and Oduncuoglu magnificently illustrated that sliding speed and normal load significantly affected the wear volume losses. Their study comprised an ANN model trained on 125 datasets extracted from established literature on ultrahigh molecular weight polyethylene (UHMWPE) composites reinforced with zinc oxide (ZnO), zeolites, carbon nanotubes (CNT), CF, graphene oxide (GO), and wollastonite. A total of 11 inputs as shown in Fig. 4(a), including the weight% of each component, in addition to ZnO and zeolite sizes as well as sliding speeds and applied load, were used to train conventional feed-forward BPNN (with LM training function and logistic sigmoid transfer function) to predict the wear volume loss. A sensitivity analysis shown in Fig. 4(b) indicates that wear volume loss is significantly affected by the sliding speed, followed by the applied load, ZnO wt%, UHMWPE wt% and zeolite wt%. This study also involved volume loss calculation through a theoretical formulation, of which the volume loss is plotted against ANN predicted losses and experimental testing results as shown in Fig. 4(c) and (d) respectively.127 Zhang et al. studied PEEK-based composite with SiC filler materials using ANN.128 The model was successfully trained using applied load and sliding velocity as input variables to predict CoF and wear accurately. They observed that both outputs were significantly influenced by sliding conditions when the applied load was larger than 9N. On the other hand, for applied load <9N, they reported that the relationship between CoF and sliding velocity was parabolic.128 Overall, Zhang et al. conclude their work by attributing the effect of testing conditions that affected the contact temperature in the experiments.
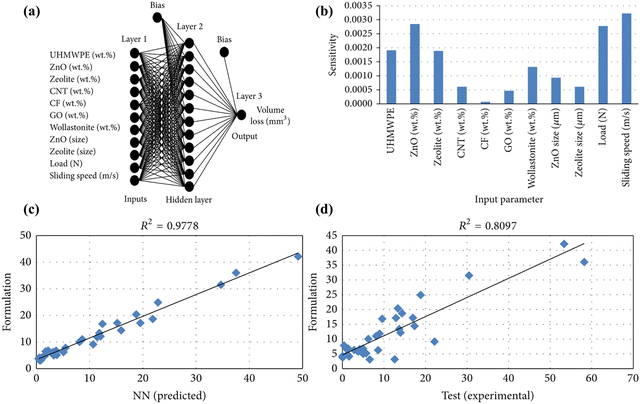 | ||
| Fig. 4 (a) A schematic diagram representing ANN structure with an architecture of 11-12-1 is shown. (b) Sensitivity analysis of wear volume loss w.r.t. the 11 input parameters. A plot of formulated value of wear loss plotted against (c) ANN predicted volume loss values and (d) experimental results. Reproduced from ref. 127 with permission from Hindawi, copyright 2015. | ||
(b) Metal matrix composites. Metals, primarily aluminum, magnesium, and titanium, reinforced with other materials such as ceramic, other alloys, and organic compounds can be classified as MMCs.129 MMCs are characterized by high specific strength, low density, controlled thermal expansion, high fatigue resistance, good corrosion resistance, thermal stability, enhanced electrical performance, and remarkable tribological behavior.130 Therefore, they have been utilized in aerospace, automobile, electronics, petrochemical, and biomedical sectors.131–134 The tribological performance of MMCs was successfully enhanced by the variation of the composition of fillers and reinforcement with materials such as alumina, SiC, and B4C.134–137 Moreover, an increase in their tribological performances was shown by reinforcement of these MMCs with CNT.138–140 For example, a study by Zhou et al. showed a maximum decrease in the CoF at 20 wt% of CNT, which was attributed to increased surface fraction of CNTs, resulting in the reduced contact area between Al matrix and steel pin.138 On the other hand, several studies show that excessive addition of nanoparticles led to their agglomeration on the surface of MMCs, which adversely affected the tribological properties of MMC.139,140 Thus, the ability to a priori design MMCs with desired tribological performance under different conditions remains an open challenge. In principle, ANN models, which are capable of modeling and handling nonlinear, complex relationships can be used to address this challenge.141 Indeed, several studies have exemplified the utilization of ANN for designing MMCs to minimize the tribological properties such as SWR, CoF, wear loss, etc.142–149 Table S4 (ESI†) and text below summarizes the studies on MMCs that apply ANN approach.
A study by Saravanan et al. splendidly demonstrated the use of ANN on the prediction of wear behavior and CoF of composites of aluminum alloys reinforced with rice husk ash (RHA).150 The POD experiments were performed on the parameters generated by an orthogonal array (L27) based on the Taguchi technique. Specifically, the input parameters, applied load, sliding speed, RHA particle size, the weighted content of RHA and wear rate, and CoF as outputs were used to train a four-layered feed-forward BPNN. The LM training function yielded the best prediction results (∼95% for both CoF and SWR). The morphological study showed that aluminum reinforced with RHA particles exhibited a lower wear rate due to their slightly plastic deformation.150 Satyanarayana et al. successfully demonstrated the use of ANN to model the wear behavior of aluminum MMCs blended with red mud nanoparticles. In this study, POD experiments were performed on the devised composite of different compositions and deformation by varying applied load, and sliding velocity. A regression model and an ANN model were trained on these experimental results with a goal to predict the volumetric rate. Their results indicate that the composite with 10% red mud fraction and 30% deformation yielded minimum volumetric wear. Further, their ANN model (MAPE: 7.3% and R2: 0.989) with 4-7-6-1 topology exhibited superior modeling performance compared to their regression model (MAPE: 12.96% and R2: 0.9775) assumably due to its excellent ability to model non-linear relationship.151
In addition, a study by Genel et al. showed that the wear resistance of zinc–aluminum alloy could be significantly improved by alumina fiber reinforcement. An ANN model trained on sliding speed, applied loads, alumina fiber fraction, and orientation as input parameters were used to predict the wear performance of the composites. ANN model with the prediction of 94.2% and 99.4% for SWR and CoF, respectively, with a mean relative error (MRE) between experimental and predicted values of 2.4% and 0.43%, respectively, were reported.152 Furthermore, Kumar et al. predicted the wear rate and CoF of aluminum-fly ash composites with 95% accuracy using an ANN model.153 Particularly, a 4-6-2 architecture, with load, sliding speed, fly ash particle size, and their wt% as inputs were utilized with 98 training and 10 testing data sets. These studies further showed that the time and cost of the experimental process of designing an optimal material composition could be averted through the ANN models.153
Hayajneh et al. investigated the wear mass loss for composites of aluminum–copper alloy reinforced with SiC using ANN. Specifically, the weight content of copper and SiC in addition to the time of the POD test was used as an input for ANN to predict mass loss. A Neuralware's rule of thumb was used to determine the optimal number of neurons in the hidden layer as shown in eqn (5) to form the ANN architecture of 3-6-6-1 with the normalized squared error of 8.5 × 10−5.
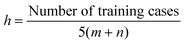 | (5) |
A356, another aluminum silicon alloy was investigated by Özyürek et al. to fabricate MMCs with SiC reinforcements by thixomoulding method to study their wear behavior.155 A 64 experimental (POD) data sets with manufacturing temperature, applied load, sliding distance, and weight content of SiC as inputs and resulting weight loss, as an output, were used to train the ANN model. A topology of 4-5-3-2-1 was used along with the Fermi transfer function to achieve excellent agreement between experiments and predictions with R2 value of 0.9985.155 Another study by Shabani and Mazahery illustrated the use of a combination of ANN and finite element method (FEM) to model the wear properties of A356 alloy MMCs blended with B4C. FEM was utilized to determine the temperature gradient and cooling rate as two input parameters for the ANN model in addition to the sliding distance of POD experiments, and boron nitride's particle size and volume content. The ANN model with 5-4-2 architecture and sigmoid activation function for their neurons was utilized to determine SWR and variation of porosity. An ANN model with MSE values of approximately 0.2 suggested that predictions were in excellent agreement with experimental results.156 Rashed and Mahmoud were successful in modeling the wear behavior of A356 MMCs with SiC using ANN. Applied load, weight content and particle size of SiC, and the testing temperature were used as inputs, with 7 neurons in hidden layers to determine SWR as one output neuron was established to form 4-7-1 topology. The predictions of ANN were in good agreement with experimental observations with R-value of ∼0.99, and MRE ∼6%.157
Pramod et al. employed ANN to model the prediction behavior of aluminum alloy (Al7075) MMCs reinforced with aluminum oxide (Al2O3) particulates. The weight content of Al2O3, applied load, sliding distance, and density were used as inputs to predict SWR. The L27 orthogonal array obtained from Taguchi DOE to determine the experimental parameters. A topology of 4-5-7-1 was exercised to model this non-linear relationship with an average value of regression R2 = ∼0.99 and errors within 5%.158 Veeresh Kumar et al. exemplified the superior tribological performance of aluminum 6061 alloy when it was reinforced with Al2O3. Their study demonstrated the use of BPNN to model these composites on the data obtained from POD experiments. The process/experimental design parameters were determined from the L27 orthogonal array of Taguchi DOE. Similar to the aforementioned paper, ANN model with 4-5-7-1 was constructed to determine wear tallness loss (output) with sliding distance, applied load, weight content of Al2O3, and density as inputs. A prediction error within 5% and correlation R2 value of 0.999 suggested a good agreement of ANN predictions with experiments.158
Mehra et al. investigated the fabrication process of RZ-5 magnesium alloy MMCs blended with TiC to reduce their wear properties. The experiments showed that the introduction of TiC improved the hardness of the RZ5 alloy. Moreover, the ANN model with Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm was trained on the experimental data with sliding distance and applied load as inputs to predict CoF. A topology of 2-2-1-1 was utilized to achieve the errors that were within 3.5% compared to their experimental results, which suggested the high-quality proficiency of NNs in the least possible time.159
Younesi et al. exercised application of ANN in designing nickel-free stainless-steel composites (NFSS) reinforced with hydroxyapatite (HA). The composites were characterized through POD experiments to estimate appropriate HA content in NFSS, applied load, and sliding distance for reduced wear loss. BPNN was employed with LM training algorithm, and with 3-5-5-1 topology and R2-value of 0.999, while the prediction errors <12% for the volume loss. Owing to the higher accuracy of their ML model, they employed it as a surrogate for determining the volume loss of different composite for varying applied loads and sliding distances (0–1000 m).160
(c) Ceramic matrix composites. CMCs are ceramic fiber-reinforced materials that are formed by embedding ceramic fibers in a ceramic matrix and they possess high oxidation and corrosion resistance and are stable at elevated temperatures.161 C/SiC matrix composites are widely used in vehicle braking systems.162 Compared to C/C, composites of C/SiC have higher oxidation and wear resistance.162 But the problem with CMCs is that they are brittle and possess low fracture resistance.163 Hence research on CMCs is primarily focused on the enhancement of their toughness and ductility. CMCs are mostly applied while sliding against metal counterparts.164 Reduction in the wear and increase in the tribological compatibility with the iron surface by reducing the adhesion of Si3N4 composites has been observed by the addition of SiC whiskers.165,166 The maximum reduction of wear in Si3N4 composites has been observed at a composition of 30 wt% SiC whisker.164 The addition of TiC particles to Al2O3 composite ceramic has been shown to enhance the tribological performance of Al2O3 composite when sliding on an iron surface.166 Reinforcement of alumina matrix composite with GR also leads to a significant reduction in the CoF, with the lowest values observed at 0.3 wt% GR in Gr/Al composite.167,168 The CoF for Gr/Al increases with an increase in the applied load and decreases with the sliding speed.168
In the context of this review article, the application of ANN in designing CMCs remains limited.169,170 Malazdrewicz and Sadowski were the first to venture in predictions of wear for CMCs through ANN.169 Specifically their study included curation of data for cementitious composites blended with high-calcium fly ash. Their ANN model constituted 9 input parameters including content of cement, fly ash, water, fine aggregate, coarse aggregate, superplasticizer, air entraining agent, age of concrete, and time of testing to predict the depth of wear as an output using a model with topology 9-18-1. This study successfully demonstrated the use of ANN in CMCs design by predicting wear with linear coefficient R2 value or 0.998 and 0.997 for training and testing w.r.t. experimental results.169 Another successful work has been reported by Bucholz et al. for design of CMCs.170 Since their work includes the integration of other ML methods (DT and principal component analysis) with ANN, it is discussed in Section 3.7.
(a) PMC. Siddhartha and Singh exercised ANN and ANOVA to formulate and fabricate polyester composites and their functionally graded materials (FGMs) reinforced with SGF. Taguchi DOE was employed to design the POD process parameters like applied load, sliding velocities, sliding distances, and the fiber content in composite. ANOVA results suggested that applied normal load (p = 34.54%) significantly affected both SWR and CoF, followed by the SCF content, and others. ANN model with 4-10-1 topology showed errors <14% for SWR and <10% for CoF. They concluded their study of PMC design with a finding of 6% SCF reinforced polyester exhibited lowest SWR. Moreover, SCFs show incisive effect on Ts and Fs on FGMs than their homogenous counterparts.172
Egala et al. attempted the work of the composites of epoxy resins blended with castor oil fibers (Ricinus communis).173 Additionally, they also employed an ANOVA model to investigate the effect of these individual parameters on the output. ANOVA predicted that the applied load followed by fiber length and sliding distance were highly influential on gravimetric wear, CoF, and interfacial temperature. In this study, a regression model, single hidden layer ANN model and multiple hidden layer ANN models were developed and compared. These models were trained with input parameters viz. fiber length, normal applied load, and sliding distance of the POD experiments designed through a full-factorial approach to predict outputs. They reported that multiple hidden layer ANN performed best followed by single hidden layer ANN and regression analysis. Uniquely, this study utilized 73 different ANN models with varying algorithms, including cascade forward BPNN, feed-forward BPNN, and layer recurrent algorithm. Additionally, they conducted a study on varying hidden layers and number of neurons, and different transfer functions like Logsig and Purelin with constant LM training function.174–176 Here, the predictions by cascades forward BPNN and feed-forward BPNN (errors ±5% and ±4.5%) were efficient and reliable compared to linear regression models (errors ±8%). They predicted epoxy reinforcement with 40% unidirectional short five mm-fiber length castor oil fiber improved wear by 65% to 70%, CoF by 31% to 40%, and interfacial temperature by 19% to 24%.173
(b) MMC. The study by Vettivel et al. exhibited the numerical modeling approach of ANOVA to predict the SWR and CoF with a 99% confidence level for the copper–tungsten (Cu–W) powder composites.177 In their follow up study, Vettivel et al. employed ANN to predict the hardness, CoF, and SWR for Cu–W composite powder. A total of 4 inputs i.e. sliding distance, applied load, sintering temperature, and weight content of tungsten was employed to train the model. In particular, 10 different ANN architectures with LM training algorithms were designed. Specifically, an architecture 4-7-4-3 yielded best train-test-validation performance with a total MSE values <0.05, and R2 values of 1, 0.99624, and 0.99046 for hardness, CoF, and SWR, respectively.178 Furthermore, Leema et al. investigated the copper–tungsten composites using a radial basis function neural network (RBFNN) to predict hardness, CoF and SWR. An architecture of 4-140-3 was employed such that tungsten weight content, applied load, sliding distance, and sintering temperature (while preparing samples) were used as inputs. The accuracy in terms of R-value of ∼0.97 (SWR) and ∼0.99 (CoF) for training, while ∼0.976 and ∼0.965 in testing was achieved. This validated a good agreement of experiments with RBFNN predictions.179 Moreover, Arif et al. exercised the powerful approach of feed-forward BPNN integrated with statistics (ANOVA) to investigate the tribological performance of aluminum hybrid composites reinforced with SiC and zirconia. It was determined that the most influential parameters were sliding speed, zirconia content, and applied load based on the full factorial analysis. However, the effect of each parameter in the exact amount of percentage i.e. sliding distance (79.47%), zirconia wt% (10.35%), and applied load (6.7%) on the wear loss performance of each composite was reported through ANOVA. The ANN model with the aforementioned three variables in addition to sliding speed was developed with a topology of 4-10-1, to accurately predict the wear loss as compared to experiments.180
Thankachan et al. demonstrated the use of ANOVA combined with BPNN to predict the tribological behavior of copper surface strengthened by a mixture of aluminum nitride and boron nitride particles. The experimental set of parameters was designed by L27 Taguchi's orthogonal array with varying volumetric fractions of particles, sliding speed, applied load, and sliding distances as the input parameters.181 Stojanovic et al. investigated the aluminum hybrid composites mixed with A356 alloy, which was further reinforced with SiC and graphite. In this study, the L27 orthogonal array of experimental parameters was generated using the Taguchi method to design experiments. ANOVA technique was performed to determine that GR composites with 3 wt% exhibited the lowest wear and friction. Additionally, an ANN model was trained with 3-20-30-2 architecture trained on LM function and logarithmic sigmoid and linear transfer functions. The comparison of predictions by ANN with ANOVA illustrated that ML algorithms perform precisely better than statistical methods. An ANN model with one hidden layer of 7 neurons and LM training function successfully predicted the optimized SWR with higher accuracy compared to the referenced regression model.182
Agarwal et al. investigated the effect of powder-chip reinforcement for LM6 aluminum alloy to reduce SWRs using BPNN. While maintaining the sliding speed at 300 rpm at an applied load of 15 N, only sliding distances (varied from 125 m to 750 m) and reinforcement content (10 to 25%) were used as input for training the ANN model. With an architecture of 2-5-1, the total mean squared error (MSE) of 1.11% was reported. In addition, ANOVA was used to determine the interaction effects between the input parameters. Particularly, reinforcement incorporation (adjusted sum of squares (Adj SS) = 11.225) showed a dominant effect on the wear rate compared to sliding distance (Adj SS = 8.475).183 Ritapure and Kharde developed an ANN model to examine and predict the SWR for Al–25Zn alloy based MMCs blended with SiC. Taguchi's L16 orthogonal array was determined and accordingly experiments were performed on POD setup. With sliding speed, temperature, applied load and filler (SiC) content as input, ANOVA, regression and ANN models were developed to calculate SWR. Through ANOVA, the dominance of testing temperature was evident followed by applied load, SiC content and sliding velocity. An ANN model with R2 = ∼0.99 outperformed the regression model with R2 = ∼0.98 by a fine margin, while both models showed reasonable agreement with experimental validation. Their results suggested that highest wear resistance and hardness was observed for 15 wt% SiC reinforcement with an increase in its Ts.184
Prakash et al. investigated the copper MMCs reinforced with MWCNTs with POD experiments. The obtained results were analyzed through statistical (ANOVA) and ML (ANN) algorithms to determine the wear loss. Taguchi's DOE was used to obtain an L16 orthogonal array to optimize the experimental parameters such as volume fraction of MWCNTs, applied load and sliding distance. In the ANOVA, MWCNT content (76.48%) was found to be the most influential factor, followed by the applied load (12.18%) and the sliding distance (9.91%). The ANN model was constructed with these 3 inputs and 1 hidden layer with 7 neurons and 1 output i.e. wear loss. This model with R2 value of 99.5% was in excellent agreement with experiments and exhibited superior predictability than ANOVA predictions.185
Kavimani and Prakash employed ANN and ANOVA to study and analyze the magnesium (AZ31 alloy) MMCs with varying reinforcements of reduced graphene oxide (r-GO). Four input parameters, namely, applied load, r-GO weight content, sliding distance, and sliding velocity were determined to be influential in training of the ANN model. Using the Taguchi method of DOE, an L27 orthogonal array with three levels of variation of input parameters was determined. The mean-effective plot describing the signal-to-noise ratio of each individual parameter is shown Fig. 5(a). Their ANN model development involved studying the variation of the number of neurons in the hidden layer. The corresponding MAE results are shown in Fig. 5(b). An architecture of 4-7-1 yielded 98.4% accuracy (R2 = 0.984) for the prediction of SWR as shown in Fig. 5(c). ANOVA results suggested that applied load (38.85%) is the most influential parameter determining MMC's SWR, while sliding distance was the least (12.33%).186 In their follow-up study, Kavimani et al. investigated the wear and friction behavior of Mg MMC reinforced with r-GO now doped with SiC. Similar to their previous study, the L27 orthogonal array for varying the applied load, sliding distance, sliding speed, and the weight contents of r-GO and SiC were determined through the Taguchi DOE method. The ANN model with an R2-value of 0.998 was shown for an architecture 5-8-1, while ANOVA predicted that the weight content of r-GO and applied load were the most influential parameters determining the SWR.187
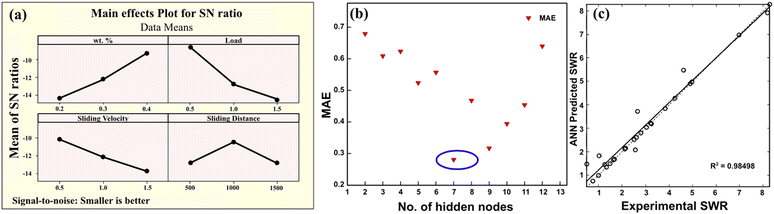 | ||
| Fig. 5 (a) The mean-effective plots show the signal-to-noise ratio of each individual parameter. (b) The variation of MAE with the changing number of neurons in the hidden layer. Highlighted point with 7 neurons shows the lowest MAE error. (c) The results for the predictions of ANN validated against experiments for wear rate. Reproduced from ref. 186 with permission from Elsevier, copyright 2017. | ||
(i) Monte-Carlo-based ANN. In Monte Carlo simulations, stochastic processes are modeled and their outcomes are estimated using probabilistic numerical techniques.194 In regards to any mathematical problem, repeated sampling of the parameter space can enable equilibrium to be reached faster than analytical deterministic methods, depending on the complexity of the problem. Monte-Carlo's theory has exhibited proficiency in modeling a variety of real-world probabilistic processes.194 Compared to this traditional deterministic method, a probabilistic approach of the Monte-Carlo (MC) method, which can generate random scenarios (variables), may help in developing/modeling ANN faster with efficient computational usage.
A few studies have demonstrated the successful use of MC in sensitivity analysis, uncertainty quantification, and so on.195,196 An appropriate choice of hyperparameters and as such determining the weights of neurons remains challenging. Therefore, MC-ANN, introduced by Li et al. exercises the MC approach to estimate the weights of each neuron in a probabilistic manner.188 A faster and more accurate MC-ANN aids in better non-linear mapping ability and improved fitting effect of samples. The comparison of the workflow of MC-ANN that is featured in the work of Li et al. is shown in Fig. 6(a) and (b). They trained and compared MC-based ANN (MC-ANN) and BPNN, exhibiting a better accuracy of MC-ANN (RMSE 0.97 and 0.007) compared to BPNN (RMSE 2.08 and 0.019) for SWR and CoF, respectively as shown in Fig. 6(c) and (d). This study investigated the tribological behavior of PTFE resin composites reinforced with aramid pulp, mica, copper (Cu), nano-SiO2, and potassium titanate whisker (PTW). 18 different compositions were formulated using orthogonal table L18 (37), and the experimental data conducted in triplicate on a quasi-static test rig were used to train the ANN model. The gray relational analysis (GRA) was employed to optimize formulation design and determine weight factors and non-linear dependency of the ingredients. In the context of variation and volatility of the data, MC-ANN performs better than conventional ANN because it uses repeated random sampling and a variety of transfer functions like sigmoid, polynomial, tanh, and Gauss functions.188
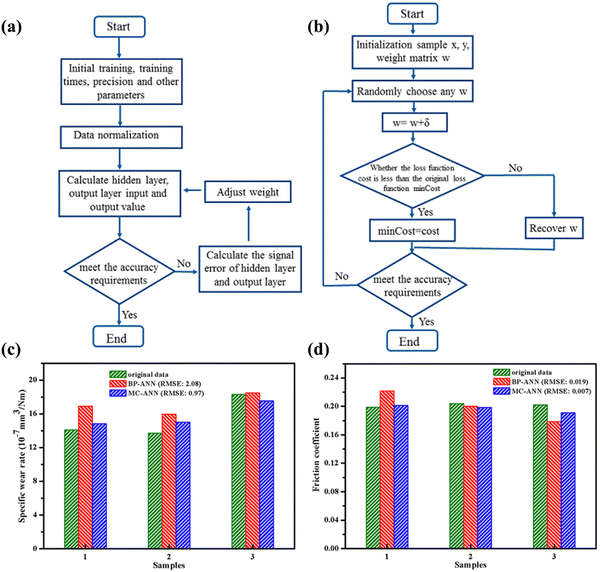 | ||
| Fig. 6 The schematic representation of the workflow of (a) BPNN and (b) MC-ANN. The results for (c) SWR and (d) CoF are also shown in bar graphs. Reproduced from ref. 188 with permission from Wiley Online Library, copyright 2019. | ||
(ii) Improved bat algorithm (IBA). A meta-heuristic global optimization algorithm, improved bat algorithm (IBA) is based on the echolocation characteristics of the bat.197,198 With the improved exploration and local search capability, IBA exhibits superior performance compared to the original bat algorithm (BA). In search of prey, bats (explorers) fly randomly with certain velocity and emitting (adjustable) frequency, depending on the distance from the target.
A novel work by Gangwar and Pathak integrating an IBA optimization with ANN that overwhelms the challenges of the training process of complex and non-linear ANN models.189 This work exemplifies the efficient and effective training of ANN models to evaluate and predict the wear characteristics of ZA-27 alloy reinforced with marble dust particles (MDp). Taguchi design of the experiment was utilized to generate an L25 orthogonal array for unique parameters (applied normal load, sliding distance, velocity, marble dust composition, etc.) for POD setup. Compared to other training algorithms like backpropagation, genetic algorithms, particle swarm optimization, and so on, the flexibility and stability in the tuning of IBA allow us to attain convergence faster by introducing a new velocity, position search equation, and Sugeno inertia weights.199,200 As a result, the local optima stagnation was overcome, and prediction accuracy for SWR of 97% with a mean squared error of 0.26 was obtained for this study. Employing optimization-assisted ANN, one can save the tedious task of brute-force training a complex NN model, and accelerate the process of optimization and prediction.189
(iii) Non-dominated sorting genetic algorithm (NSGA-II). One of the most popular multi-objective optimization evolutionary algorithms, NSGA-II, exhibits three main features: (i) a fast nondominated sorting process, (ii) a fast crowded distance estimation procedure, and (iii) a simple crowded comparison procedure.201,202 As a part of multi-objective optimization (MoGA), NSGA-II has shown its reliability in optimizing machining process parameters. Compared to the Pareto-archived evolution strategy (PAES) and the Strength Pareto EA (SPEA), NSGA-II is able to maintain a better spread of solutions and convergence on the Pareto-optimal front.
A recent work by Vinoth and Datta also exemplifies the usage of ANN to predict the mechanical properties of UHMWPE composites reinforced with CNT and GR.190 ANN model was trained on previously reported 153 experimental data with varying composition within composites, particle size, and mechanical properties as input (7 no.). Here, two ANN models were trained to determine Young's modulus (Y) and Ts, with 3 and 5 hidden layers, respectively. A feed-forward ANN with scaled conjugate gradient backpropagation with hyperbolic tangent transfer function assisted in achieving correlation coefficients of 0.93 and 0.97 for Y and Ts, respectively. A multi-objective function to attain optimum values of Y and Ts were executed by employing a non-dominated sorting genetic algorithm (NSGA) based on Pareto-optimality theory.201,203 The optimized composites were further experimentally subjected to tribological and mechanical characterization. This process successfully demonstrated the use of ML integrated with optimization to improve the properties, specifically the excellent wear rate of the predicted composites compared to the literature available 153 datasets.190
(iv) Genetic algorithm (GA). In the theory of Darwin's natural selection, GAs are iterative processes that evaluate the fit between data over multiple generations in an iterative manner.204 There have been successful applications of GAs for material development in recent years, including metal–organic frameworks, metals, and their oxides, and composites, to optimize large and complex design spaces to develop materials that are tailored for specific applications.205 They are developed by following a set of rational design principles that produce material structures that can be synthesized for various applications.206–208
Given the large design space spanning through varying content of different vegetable oils and nano friction modifiers (FMs), Bhaumik et al. successfully employed GA assisted by ANN.191 They successfully trained an ANN model with 80 and 120 data available on four-ball tester and POD experiments, respectively. Their study aimed to design an optimal blend of different vegetable oils (viz. coconut oil, castor oil, and palm oil) with nano FMs, including MWCNT and GR. Two three-layered ANN models were trained, each for POD and four-ball tester experiments, with CoF as the output parameter. Particularly, the data on the amounts of three vegetable oils, dimensions, and amounts of nano FMs, in addition to their respective experimental setup parameters, were used. Further, these two ANN models integrated with a GA were operated to optimize the output constraint CoF and design two lubricants: Lube A: 40% castor oil, 40% palm oil, and 20% coconut oil with 0.7% MWCNT and 0% GR and Lube B: 33.3% castor oil, 33.3% palm oil and 33.3% coconut oil with 1% MWCNT and 1% GR for four-ball tester and POD setup, respectively. Contrary to the work by Li et al. where an MC optimization algorithm was used to tune the weights of neurons, here, the ANN surrogate model is used as an objective function to optimize input variables.188 This study showed a fair agreement of ANN predictions with their experimental results. This study was further extended in developing a quintessential combination of multiple FMs including GR, graphite, MWCNT, and ZnO nanoparticles blended with castor oil.192 The data generated from POD experiments performed on lubricants designed by varying above components were used to train the ANN model. The GA optimization with ANN models as an objective function was employed to successfully predict a novel lubricant that comprised 0.66 wt% each of graphite, MWCNTs, and ZnO in castor oil. This lubricant yielded a reduction of 50% and 87% in the CoF and WSD, respectively. Their study highlights the contributions of different FMs on CoF, as illustrated in Fig. 7(a), particularly the surface plots (Fig. 7(b)) for the CoF shed the light on varying concentrations of FMs. Moreover, the lubrication mechanism emphasizes the use of FMs in reducing friction as shown in Fig. 7(c).192
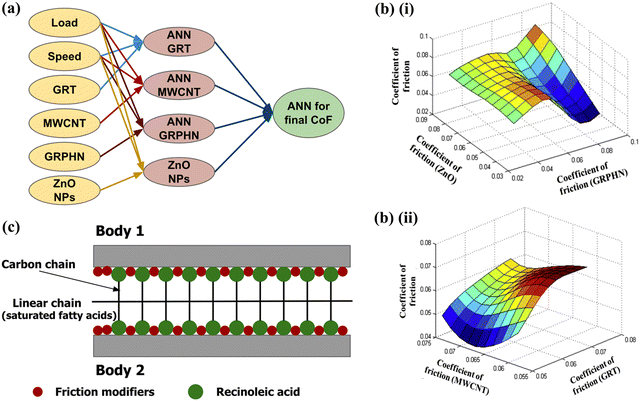 | ||
| Fig. 7 (a) The schematic representation of ANN used in this study. (b) The surface plots for the variation of CoF with varying (i) ZnO and GR, (ii) MWCNT and graphite content. (c) Representation of the nano-fillers aiding the lubrication regime. Reproduced from ref. 192 with permission from Elsevier, copyright 2019. | ||
Mahapatra et al. developed polyester composites reinforced with e-glass fiber and ceramic particulates including cement by-pass dust (CBPD), Al2O3, and SiC. An L27 orthogonal array from Taguchi DOE was utilized to determine the initial input parameters, namely, impact velocity, filler content, stand-off distance, impingement angle and erodent size in an air jet type erosion test rig. An architecture of 5-12-1 yielded errors less than 14% for the ANN predictions compared to experimental results. In addition, an ANOVA indicated that CBPD exhibited superior filler properties compared to alumina and SiC fillers. Subsequently, GA was employed to determine and report the optimal test factors for all three fillers.193
Table S7 (ESI†) tabulates applications of other ML algorithms to investigate the process variables or tribological behavior. These other ML algorithms include RNN, PCA, ART-2 ANN, ELM, ANFIS, DT, RF, SVM, regression, KNN, GBM, and so on. Detailed information on these models, including their development and advantages, follows the table.
3.2 Recurrent NN (RNN) and principal component analysis (PCA) based ANN
PCA is a dimensionality reduction technique, transforming such a large set of variables into a total lower number of dimensions, representing the information from a larger set.209,210 A study by Kolodziejczyk delineated the dynamical frictional behavior using the model on wear resulting from dry fretting.70 Specifically they trained two ANN models i.e. static ANN and dynamic RNN for solving static and dynamic problems, respectively. (i) Static ANN: Firstly, their study utilized the PCA to exhibit the dimensional reductionality employed in high dimensional and complex models, which could further be used in training an ANN model. Taking 6 input factors, PCA successfully identified only four parameters, viz. number of cycles (NoC), the amplitude of displacement, pressure, and roughness, had the least correlation factor to be utilized for ANN model training. Therefore, a static ANN model with 4-3-1 architecture was trained on tansig transfer functions for input and hidden layers. In contrast, the purelin transfer function was applied for the output layer to achieve a 1.8% mean relative error. Comparing the results of the ANN model with their multiple regression analyses (MRA), they concluded that ANN successfully mapped the non-linear region of the data – particularly, the physical interpretation of input mechanical properties and their response in their ANN model. (ii) Dynamic RNN: The preprocessing of this real-time data involved normalization and bisection, and therefore, one extra input i.e. CoF was added to train the model. An algorithm similar to static ANN was used to train RNN with an architecture of 5-12-1. Despite 95.9% accuracy, the authors concluded this work by reporting more data was required for better modeling.703.3 Adaptive resonance theory (ART-2) based neural network and BPNN
An adaptive resonance model is an unsupervised learning approach that mimics the brain's ability to recognize patterns in environments that are constantly changing.211 This algorithm relies on a recurrence (feedback) approach in order to regulate learning ability, so that the neurons' weights converge faster. ART-2 model not only solves the problem of pattern and situation recognition but also can be used to study and predict the structure and values of time series.212 An ART-2 model was employed by Subrahmanyam and Sujatha, which was further compared with conventional multilayered feed-forward ANN with error backpropagation (EBP).213 These ML models were trained for the diagnosis/detection of localized defects in ball bearings. The experimental data of vibration acceleration signals for normal bearing and two different defective bearings was used to train models. Compared to BPNN, the learning of the ART-2 algorithm was found to be about 100 times faster, with a 100% reliability in detection of faulty bearing in comparison to the normal bearing. However, ART-2 was inefficient in distinguishing localized defects in different ball bearing states. Moreover, BPNN was capable of diagnosing localized defects with 95% success rate. However, while BPNN showed 100% success in identifying defective ball bearings, it exhibited a slower learning rate.2133.4 Extreme learning machine (ELM)
ELM is an ML model with a single hidden feedforward NN.214 However, unlike gradient-based back propagation, it uses Moore–Penrose generalized inverse method to estimate the output weights. Consequently, they converge faster than conventional methods and produce promising results.215 Mujtaba et al. recently utilized ELM as well as integrated the Cuckoo search optimization process with response surface methodology (RSM) (Box–Behnken DOE).216 The tribological behavior of biodiesel produced from optimizing process variables of ultrasound-assisted transesterification of palm-sesame oil was examined. The process variables such as time, catalyst amount, methanol to oil ratio, and duty cycle were optimized to improve the cold flow characteristics and average CoF of produced biodiesel. This study also highlighted that CoF prediction using ELM model is computationally less intensive and more accurate as compared to DOE model. The predicted average CoF for P50S50 biodiesel was lower than palm biodiesel and B10 commercial diesel by 2.29% and 12.37%, respectively.3.5 Adaptive neuro fuzzy inference system (ANFIS)
A hybrid predictive model that uses both NNs and Takagi-Sugeno fuzzy inference system217 logic to provide mapping relationships between input and output is called ANFIS. This approach allows us to train the non-linear models with rapid learning and adaptive capability.218 Babajanzade Roshan et al. exercised ANFIS modeling and optimization approach to maximize mechanical properties of friction stir welding (FSW).219 ANFIS model with generalized bell type of membership function was developed to map relationships between inputs (welding speed, pin profile and rotary speed of tool) and outputs (Ts, yield strength, and hardness of welded joints). By the virtue of both single response and multi-response problems, the highest mechanical properties were observed at a welding speed of 1.75 mm s−1, and square pin tool with the rotary speed of 1400 rotations per minute (RPM), axial force of 7.5 kN, which were further validated in their experiments. They mentioned that the axial force plays a critical role in determining CoF due to the frictional heat generation between the tool shoulder and plate surface. A subsequent increase in axial force from 5 kN to 7.5 kN saw a rise in hardness due to improved joint efficiency and increased tensile properties, which saw defects and tunnels if the force was further increased. Moreover, the effects of rotary speed and welding speed emphasize their significant role due to heat generation, cooling rates, and/or welding efficiency.219Dewan et al. investigated the effects of process variables including, spindle speed, plunge force, and welding speed for the FSW process through ANFIS and ANN.218 A small data set of 73 welds were used to train models to predict the ultimate tensile strength (UTS) of FSW joints. Overall, 1200 ANFIS models were generated by varying the number and types of membership functions (MFs), a combination of above mentioned three input variables and empirical force index (EFI) derived from three process parameters. A schematic of the ANFIS structure with 5 layers is shown in Fig. 8(a), where the number of nodes in the input layer is determined by the number of inputs and membership functions, while hidden layers are given by the number of fuzzy rules.218 The prediction based on the ANFIS model developed on three input variables (V, Fz, and EFI) compared to experimental UTS is plotted in Fig. 8(b). In addition, the surface plot for predicted UTS values from the ANFIS model with two input variables V and EFI is presented in Fig. 8(c). In general, their study highlighted that ANFIS models performed better than ANN due to their lower prediction errors. Their analysis indicated a strong relationship between EFI and UTS, as well as a non-linear correlation of EFI with the other three inputs N, V, and Fz. Their ANFIS model is proficient to estimate appropriate weld process parameters to achieve desired joint strength.220
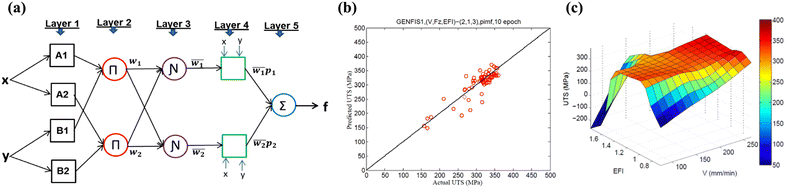 | ||
| Fig. 8 (a) The schematic representation of ANFIS used in this study. (b) Comparison of ANFIS predictions of UTS w.r.t. experimental values. (c) The surface plots for the variation of UTS with varying (i) EFI, and (ii) welding speed. Reproduced from ref. 220 with permission from Elsevier, copyright 2016. | ||
3.6 Decision trees (DT)
DT is a supervised learning algorithm used for classification or regression, based on the simple decision control rules (decision nodes) and predicted actions (branches).221 In addition to the simplicity in understanding and interpretability, DTs require minimal preprocessing irrespective of hard or soft data. Bucholz et al. have illustrated the use of DTs in designing ceramic pairings by using data from dry sliding POD experiments.170 A total of 24 ceramic samples spanning through 15 variables were generated using POD tribometer experiments. However, a multivariate problem necessitates a dimensionality reduction step, which would result in efficient recursive partitioning through DT. Initial exploration through PCA suggested that the first two principal components (PCs) captured ∼65.8% variation, which could be sufficient for higher information gain. Fig. 9(a) shows an evident grouping among oxides, chalcogenides, halides, and pnictides, and Fig. 9(b) illustrates the corresponding property relation. PCA suggested that the key material properties such as cation electronegativity, melting temperature, and Madelung constant were critical in determining the data-driven friction model. A regressive DT was developed with these attributes as well as Rij distance, cation radius, and charge, as the decision nodes as shown in Fig. 9(c). The trained DT model with R2 accuracy of ∼0.89 in the prediction of CoF, was in excellent agreement with the experimental validation.170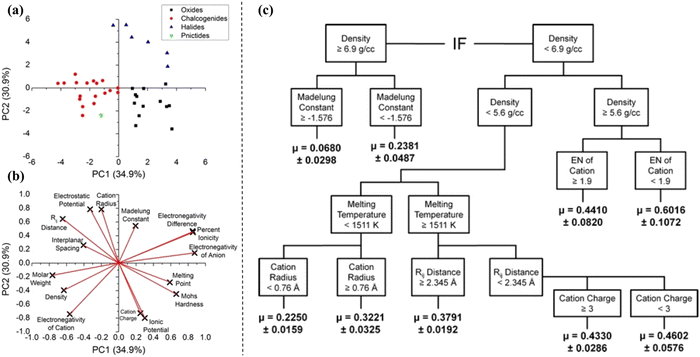 | ||
| Fig. 9 (a and b) Representation of PCA analysis for grouping oxides, chalcogenides, halides, and pnictides and their respective property relationships. (c) The schematic representation of the DT constructed on the basis of PCA results. Reproduced from ref. 170 with permission from Springer Nature, copyright 2012. | ||
3.7 Random forests (RF)
A RF is an ensemble learned technique constructed from many independent DT.221 Specifically, the RF model is trained via bagging and bootstrap aggregating techniques to overcome DT's missing data and overfitting problems. Prost et al. utilized the RF classifier to predict the states of operation for tribological sliding experiments in oscillating and translatory motion.53 The tedious and time-consuming task of labeling states of operating conditions was overcome by a semi-automated process based on dimensionality reduction, PCA, and clustering algorithms, k-means. This study emphasized on the flexibility of the labeling approach since it is a critical step and may require the expert knowledge of tribologists. Particularly, with four operating states (steady-1, steady-2, precritical, and critical), their RF model with a training accuracy of ∼0.94 on the high-resolution force signals, was validated against the labeled dataset of another experiment.533.8 Support vector machines (SVM)
Support vector machines are based on statistical learning.222 One of the most robust prediction methods, SVM is efficient for non-linear classification specifically for high-dimensional feature space. Yin et al. investigated the acoustic emissions (AE) from the experiments conducted under varying operating conditions of the gas face seal test rig.223 SVM regression model was trained and validated through leave-one-out (LOO) cross-validation on the data obtained from experiments to predict the eccentric load on the stator of the seal. This study primarily highlights the use of vectorization and SVR to estimate the load in gas face seal test rig experiments.223The work conducted by Das et al. sheds light on the internal defect identification in the FSW process using real-time torque signals.224 Discrete wavelet transforms and statistical features including dispersion, asymmetry, and excess were computed to analyze these experimentally obtained signals. Moreover, general regression models, ANN, and support vector regression (SVR) models were trained on these signals to predict the UTS. Particularly, the SVR model's prediction performance with the error of 0.5% was better than even ANN with 3-5-1 architecture with the error of 3.1% and regression models with 13.6%.224
3.9 Multiple ML models
Despite the extensive efforts, the relevance of different ML for appropriate applications has not been fully explored. In some cases, black-box ML algorithms have proven useful in identifying correlations in data and developing characterization models with a minimal cost and effort. In such manner, Perĉic et al. employed various ML and AI techniques to model and predict the dependencies of synthesizing process parameters on nanoscale friction of Al2O3, TiO2, molybdenum disulphide (MoS2), and aluminum (Al) thin films.225 The lateral force microscopy (LFM) within a centroidal Voronoi tessellation (CVT) process included normal forces, sliding velocities, and temperature as input parameters. This study employed ML algorithms like MLP ANN, random DT and RF, SVR, age-layered population structure, grammatical evolution, and symbolic regression multi-gene programming (SRMG). The numerical evaluation of prediction performances of these models through RMSE, MAE, and R2-value suggested that SRGM model exhibited highest accuracy (R2-value: 0.72–0.91). By using this approach, simple functional descriptions influencing nanoscale friction for variable parameters in study were derived.225Moreover, tribological operators like a brake or clutch which are an essential safety component of any automobile regardless of the conditions, modeling the wear phenomena and CoF remains a time-consuming and challenging task. Data driven approaches to model brake linens can be exercised through a number of ML approaches. To that extent, Timur and Aydin evaluated the CoF of brakes through the application of 7 different ML regression models.226 This includes linear, SVM, Gaussian process, pace, simple linear, least median square, and isotonic on 1050 experimental data points, with a 10-fold-cross validation. The models were trained on data that was generated by varying the speed, pressure, and heat, which had a significant impact on the CoF. Out of 7 different models, isotonic regression showed lowest RMSE of 0.0014 and highest correlation coefficient (0.99). An isotonic regression model, which is suitable in multidimensional scaling problems, can be described as a flexible linear model that can be fitted in order to predict data in series, which resulted in the best performance by this model. Moreover, in general, the models showed the RMSE values <0.01 and correlation coefficient with test experiments of >0.99.226
A recent study by Hasan et al. successfully incorporated and compared different ML algorithms in the tribological behavior of aluminum-based alloys and aluminum–graphite MMCs, including ANN, RF, SVM, k-nearest neighbors (KNN), and gradient boosting machines (GBM).227,228 The experimental data obtained from the literature, including seven material variables (hardness, Ts, yield strength, ductility, heat treatment, processing procedure, and SiC content) and three tribological test variables (sliding distance, sliding velocity, and applied load from POD experiments) was used to train these supervised ML models to predict the CoF and SWR. They found that the RF model performed better compared to other models in predicting wear behavior, which can be traced to its bagging mechanism. The RF algorithm can handle high levels of variability and fluctuations in the dataset. GBM and KNN, however, showed excellent prediction performance for aluminum base alloys and Al/Gr MMCs, respectively.227,228
In their critical review, Marian et al. highlighted that numerical design and optimization of surface micro-texturing in EHL lubricated contacts to control friction and wear.229 In their subsequent study, Marian et al. investigated EHL contacts’ fluid film parameters by employing ML and AI approaches, specifically, SVM, GPR, and ANN. Their work demonstrated better flexibility and higher accuracy in the predicting film's thickness compared to analytical counterparts of EHL simulations. The data available from finite-element method (FEM) simulations and Latin hypercube sampling, comprising 12 input parameters including sliding surfaces mechanical and elastic properties, applied load, sliding velocities, and lubricant properties, with minimum and central lubricant gap as output were used to train the ML model. An ANN architecture of 12-12-12-2 was implemented to achieve an accuracy of 1.0. In addition, the study of effect of variation of number of neurons, hidden layers, different activation functions, and varying number of input data was also conducted. Similar to ANN, SVM (R2 = 0.997) and GPR (R2 = 1.0) showed excellent prediction accuracy. Moreover, the comparison of computational time for ANN prediction was ∼26 times faster than FEM-based simulation.230
4. Molecular simulations in tribology
To complement the aforementioned experimental methods that provide macroscopic information, molecular simulations providing insights on tribological processes at the nanoscale, have emerged as a powerful tool. This study of tribological systems, termed as nanotribology, is associated with the study of micro- to nano-scale friction and wear phenomena such as adhesion, scratch, friction, and wear rate properties at the atomic level, as well as the interfacial properties between two surfaces.23,231,232 While the experimental exploration of nanotribology necessitates the use of costly specialized equipment and is subject to high probabilities of error, computer simulations like MD simulations not only lower the expense of experimentation but also allow for more experiments with little risk to the environment.233,234 Additionally, MD simulations provide insight into molecular-level interactions and the interfacial structural characteristics that are challenging to examine through experiments.235,236 Besides, MD simulations also aid in the determination of a material's chemical, mechanical, and structural properties, as well as the validation of experimental data at the molecular-level.233 Because quantum mechanical ab initio calculations are confined to systems of hundreds of atoms, atomistic tribology MD simulations have historically been approached using empirical classical models of atomic interactions. These models are, however, developed to fit both experimental data and ab initio calculation results.237 Below we have highlighted a number of studies that have used different types of MD simulations to gain fundamental insights on different tribological systems.4.1 Molecular dynamics (MD)
MD simulations have been applied to tribological studies involving crystal growth, drying, and wetting at solid–liquid interfaces,238,239 structural-property examinations to understand the layering of molecules,240,241 nanotribological properties of hard materials due to sliding, rolling, vibrations, etc.13,242 Researchers have also utilized MD approaches to visualize the material removal rate during rolling machining and the influence of the indenter on the workpiece in the previous decade.243 Besides studying the surface of materials, MD simulations have also been utilized to study friction between two sliding surfaces and the structure of these interfaces at the atomic-level. The introduction of nanoparticles for improving tribological characteristics has sparked interest in interfacial layer studies.244–246 The fluid molecule layer on the solid–liquid contact is known as the interfacial layer. When compared to a bulk fluid, it has a thickness of 1–3 nm and a more organized molecular structure.246Researchers are increasingly interested in exploring the interfacial layer of nanoparticles in various tribological systems using computational approaches. The interaction between water and the talc mineral surface, as well as the adsorption of the cationic surfactant DTAB (dodecyl trimethyl ammonium bromide) was studied using an MD simulation approach by Du and Miller.247 Talc, a significant magnesium silicate mineral, is made up of three layers held together only by van der Waals forces, which can slide over one another – making it an interesting lubricant.248 The goal of the research was to look at the interfacial structure of water as well as the configuration of adsorbed molecules at the talc basal plane and edge surfaces. The study revealed that the distribution of water normal to certain surfaces was significantly influenced by the substrate's crystal structure. The lack of hydrogen binding sites at the surface resulted in weak binding between water and the talc surface leading to the formation of voids around the substrate as shown in Fig. 10(a)(i) and (ii). It was also found that exposed oxygen and silicon groups at the edges helped strengthen the interactions between talc and water. Similarly, stronger interactions were observed between the hydrophobic basal plane of talc and the tails of surfactant DTAB. All these factors can have a significant effect on the performance of talc as a lubricant in different conditions.247 MD simulations have also been used to identify the lubrication mechanism of carbon nano-onions. This study by Bucholz et al. identified and simulated two mechanisms of rolling and sliding responsible for reducing the CoF between two diamond like carbon (DLC) substrates.249 The ability of the nano-onions to roll between the substrates was found to be inhibited by higher pressures and by the presence of a diamond core within the nano-onion, resulting in interfacial bonds. It was also reported that as the nano-onions transitioned from rolling to sliding, the CoF significantly increased.249
 | ||
| Fig. 10 (a) Snapshots of equilibrated DTAB/water/talc basal plane surface for different simulation times. The color representations are as follows: red-oxygen, white-hydrogen, yellow-silicon, green-magnesium, light blue-carbon, dark blue-nitrogen, and purple-bromide. Reproduced from ref. 247 with permission from Elsevier, copyright 2007. (b) (i) Top view of metal surface (green) with adsorbed lubricant (red COOH group) molecules as well as a schematic illustrating their spatial arrangement, (ii) Shear stress as a function of the compressive normal stress under shear flow for a fixed Fe–COOH interaction strength. The schematics (insets) indicate behaviors of the molecular flow in two characteristic regimes: uniform shear flow (left) and stick–slip motion (right). Reproduced from ref. 255 with permission from Springer Nature, copyright 2020. | ||
Another form of classical MD involves the use of coarser beads to represent groups of atoms in atomistic simulations.250 Known as coarse-graining, this approach has been instrumental in studying larger systems that require longer time scales and computational efficiency.251,252 Traditionally, CG MD simulations have been used to study much larger tribological systems like polymer architectures, self-assembled particles, etc.252–254 A study by Albina et al. investigated the properties of lubricants enclosed between nanostructured metal (Fe) surfaces by obtaining a relationship between normal stress and the shear stress exerted on the lubricant molecules using CG MD simulations. The slope of shear stress vs. normal stress was used to calculate the CoF at different conditions. It was observed that the lubricant molecules preferentially adsorbed to Fe atoms due to strong Fe-COOH interactions as shown in Fig. 10(b)(i). It also was reported that while the strength of the interactions between Fe and the lubricant molecules had little effect on the CoF below the crucial normal stress, as the stress value exceeded, delamination of oil from the metal surfaces occurred resulting in a rapid lateral motion as shown in Fig. 10(b)(ii).255 Similarly, in a recent study by Kobayashi et al., the authors developed CG bead-spring models for polar PFPE to generate nanometer-thick films sheared between solid surfaces.256 These systems were simulated to investigate the lubricant dynamic behavior when two types of substrate surface roughnesses were used. More information pertaining to the use of classical MD in tribological systems can be found in a recent review by Srivastava et al.233 as well as several other review articles.232,257,258
4.2 Reactive molecular dynamics (RMD)
Following the classical MD simulations, reactive molecular dynamics (RMD) simulations have also been utilized to study tribological applications as they can capture the ‘making’ and ‘breaking’ of chemical bonds in order to mimic tribochemical reactions.259–261 Specifically, their ability to model chemical bonding/debonding has enabled their widespread use in studies aimed at understanding the relevant tribochemical processes that determine friction and wear in sliding contacts. Surface characterization and observation, an essential tool for understanding tribochemical processes and correlating tribofilm composition with friction and wear behavior, still remains a major experimental problem. Experimental research has thus been supplemented with RMD that helps us “see” into a tribological interface, somewhat tackling this difficulty.26 The accuracy of these RMD simulations is a direct result of their underlying force fields. These force fields are based on Abell's notion of bond order, in which the strength of a bond is determined by the nearby chemical environment.262 Abell, Tersoff, and Brenner's bond order concept began as an estimated chemical pseudopotential theory, in which the intricate core electron movements are smoothed using an effective potential.262–264 Bond angles and a symmetry notion account for radical production and investigating the relationship between contacts and local atomic coordination numbers. This resulted in the first- and second-generation reactive empirical bond order (REBO) potentials, which were optimized for carbon-based materials, as well as the adaptive intermolecular REBO (AIREBO) potential, which more realistically treats graphite interlayer repulsion by introducing non-bonded interactions and torsional parameters.265,266 This family of potentials has been found to be extremely successful in describing carbon-based compounds essential to tribology such as hydrocarbons, diamond, and GR.267–269 To circumvent the restrictions of fixed-charge bond order formalisms, recent reactive potentials adopt a variable charge method. The charge-optimized many-body (COMB) potential and reactive force field (ReaxFF) are two of the most well-known instances of this in tribochemistry.270–272RMD simulations have been employed for studying chemical reactions that take place between solid substances and their interfaces, within the lubricating substances, or between the lubricant and solid surfaces. The REBO potential was used by Harrison and Brenner and was utilized to investigate the tribochemistry and wear between diamond surfaces ending with hydrogen and ethyl groups.273 Hydrogen atoms sheared off ethyl groups were found to either recombine with radical sites or abstract another H to form H2 molecules at the interface. The formation and breaking of bonds between radical sites on opposing surfaces was discovered as the process of molecular wear debris formation.273 A further study by Harrison and co-workers focused on tribochemical explanations for the friction performance of H-terminated diamond and H-free amorphous carbon tribopairs using REBO potential.274 Due to increased adhesion via tribochemical processes, films with a larger fraction of surface sp2-hybridized carbon were found to display higher levels of friction (relative to sp3).275 In another path-breaking study by Berman et al., using AIREBO potentials, assisted in discovering the mechanism of macroscale superlubricity that was achieved using GR in combination with crystalline diamond nanoparticles and amorphous DLC. Simulations, alongside experimental observations, revealed that sliding GR patches over nanodiamond particles resulted in nanoscrolls with a smaller contact area that slid smoothly against the amorphous diamond-like carbon surface.13 Studies on hydrogenated DLC coatings using a screening potential based on REBO showed that the passivation caused by the migration of methylene groups from one surface to another led to a reduction in friction.276–278 These studies have also revealed the formation of an amorphous adsorbed layer due to the mechanical dissociation of bonds when polished diamond experiences an sp3 to sp2 order–disorder transition, the catastrophic interface failure between self-mated diamond and the amorphous C surfaces due to the formation of hybridized carbon chains, the formation of soft sp2 + sp amorphous C with interspersed nanodiamond grits upon repeated collisions between diamond asphericities, etc.279
RMD simulations have also been used for studying the dry friction between tungsten and silica-based surfaces.278,280 Studying the sliding behavior of rough tungsten upon tungsten carbide, grain refinement was observed at the surface of the tungsten substrate using a modified Tersoff potential.281 However, the carbide surface displayed a mixed amorphous layer owing to discrete atomic events at the tungsten-carbide sliding surface. When the carbide counter-body was replaced with DLC, hydrogen diffusion into the tungsten surface was observed into the distorted tungsten surface. Similarly, tungsten transfer was also observed in case of non-hydrogenated DLC counter bodies. However, significantly lower transfer was observed when the system was lubricated as shown in Fig. 11(a).278,280 Similar studies on silica-based surfaces, employing the Tersoff potential, showed that shear created denser amorphous surfaces in diamond-cubic silicon and silicon.282 Studies have also explored the shear-driven chemical reactions between lubricants and solids such as water and silica.283 Yue et al. showed that submonolayer water aided wear in silicon oxide by supplying oxygen for the formation of Si–O–Si bonds across the sliding contact, thus increasing the interfacial mixing rates. However, when the amount of water was sufficient to form a full monolayer, the degree of atom transfer, and thus wear, reduced dramatically since the silicon atoms could no longer make Si–O–Si bonds as shown in Fig. 11(b).284 Similarly, another study by Wen et al. showed that aqueous H2O2 oxidized the Si substrate faster than H2O, resulting in faster Si atom loss.284–286 A few studies have investigated solid–liquid reactions between hexadecane with sliding surfaces of W, WC, or DLC with a screened REBO potential.287 Similarly, a considerable amount of work has been carried out by Martini and collaborators using reactive FFs to study interactions between solid and liquid lubricants, nanoscale contact and sliding, etc.288–291 Comprehensive details regarding the use of RMD simulations in tribological applications can also be further accessed in a detailed review article by Martini et al.26
 | ||
| Fig. 11 (a) Atomistic state of ta-C/W sliding couples at 300 K for both dry and lubricated conditions after the two bodies have been pulled apart. The color representations are as follows: green-tungsten, purple-DLC, yellow-hexadecane lubricant. For the dry sliding conditions, significant transfer from the tungsten surface onto the DLC is observed, while in the lubricated case almost no transfer occurs. Reproduced from ref. 278 with permission from Elsevier, copyright 2014. (b) Snapshot views of the vertical separation at a 20 m s−1 speed for 100 ps after sliding two amorphous SiO2 slabs for 1 ns in the presence of 100 water molecules at 500 K. The separation time is shown in each frame. Water molecules are enough to create a full monolayer and thus prevent wear in the sliding surfaces. The color representations are as follows: green-hydrogen, purple-Si of lower slab, yellow-Si of upper slab, blue-O of lower slab, red-O of upper slab, gray-O of water. Reproduced from ref. 284 with permission from American Chemical Society, copyright 2016. | ||
4.3 Non-equilibrium molecular dynamics (NEMD)
Non-equilibrium molecular dynamics (NEMD) simulations are used to model the flow of atoms or a group of atoms. The perturbation of equilibrium may be necessitated by external environmental factors like force, temperature or pressure gradient, etc.292 In the context of tribology, NEMD simulations, which involve applying a shear force to the simulated system, have also led to a better understanding of both dry friction, where the sliding surfaces are in close contact, and wet friction, where the surfaces are separated by a liquid lubricant.293–295 A number of factors must be considered in order to perform NEMD simulations, including the inherent limitations of the time and length scales that can be modeled, as well as the accuracy of the representation of intramolecular and intermolecular interactions, similar to classical MD. The fundamental consequence of the short accessible timescales in NEMD simulations is that relatively high shear rates are required to ensure that the parameters of interest (most typically the viscosity) achieve a stable state.296 Simulating lower shear rates has long been a goal of NEMD simulations in order to permit direct overlap with experiments and real-world components. With this goal, over the last three decades, numerous improvements to the original NEMD techniques have been suggested to increase their signal-to-noise ratio, simplify their implementation, and extend them to different experimental circumstances.25,297,298NEMD simulations have been carried out to study free and confined liquid lubricants. For several linear (C16, C22, and C28) and branched (5,12-dipropyl hexadecane) alkanes, Khare et al. were able to replicate lower shear rates and thereby reproduce the Newtonian plateau.299 The NEMD simulations of n-Newtonian decane's viscosity were in good accord with experiments. Using a united atom (UA) force field which included repulsive and attractive interactions through a Lennard Jones (LJ) potential, they were able to predict the viscosity and thus, the rheological behavior of these lubricant-sized alkanes.299 The shear-thinning behavior of lubricant-sized molecules has also been studied using NEMD simulations. From 1996 to 2022, several studies have investigated the different shear-thinning behaviors of a number of small molecules using the ever-evolving techniques of NEMD simulations.293,300–305 Dini and collaborators have used NEMD simulations to study nanotribology,306–312 including, to investigate the mechanochemistry of phosphate esters confined within sliding iron surfaces,313 and to derive the transient-time correlation function (TTCF) expression for the computation of shear stress and slip velocity.314 More details regarding the use of NEMD simulations in tribological applications can be found in several articles available in the literature.25,310
5. Applications of ML integrated with computational modeling techniques
The theoretical modeling techniques have demonstrated the ability to simulate the experiments at nano- and macro scale. However, despite the fact that computational researchers have provided many remarkable insights through MD, CG MD, NEMD, RMD, and so on, the immense data generated through MD approach from every time step still remains underexplored. To that extent only few studies have shown the potential to explore this data wisely and efficiently in the field of tribology.315–318 Table S8 (ESI†) tabulates these four articles describing their tribological investigations on different materials using ML algorithms in MD and DFT.Quach et al.315 applied a Python-based Molecular Simulation and Design Framework (MOSDeF)319 with a signac data and workflow management framework320,321 to perform high-throughput screening of CoF and adhesion force for about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 monolayer films.321 These two properties are then used as the expected labels for the ML model using the RF algorithm. The 32–42 input physical and chemical features were taken from the RDKit cheminformatics library.321 The high-throughput screening NEMD simulation results first suggested 22 monolayer designs with target tribological properties which are low CoF and low adhesion force. According to the MD results, the shape and size of the terminal groups play a significant role in determining the CoF of the monolayer. The charge distribution polarity and hydrogen bonding had a strong effect on increasing the adhesion force. The RF models’ performance indicates a positive correlation with the size of the datasets, and a training dataset of 1000 points is sufficient. Besides, the RF models trained on a limited dataset could still give meaningful predictions for monolayer designs outside the training set, which suggested a good transferability.315
000 monolayer films.321 These two properties are then used as the expected labels for the ML model using the RF algorithm. The 32–42 input physical and chemical features were taken from the RDKit cheminformatics library.321 The high-throughput screening NEMD simulation results first suggested 22 monolayer designs with target tribological properties which are low CoF and low adhesion force. According to the MD results, the shape and size of the terminal groups play a significant role in determining the CoF of the monolayer. The charge distribution polarity and hydrogen bonding had a strong effect on increasing the adhesion force. The RF models’ performance indicates a positive correlation with the size of the datasets, and a training dataset of 1000 points is sufficient. Besides, the RF models trained on a limited dataset could still give meaningful predictions for monolayer designs outside the training set, which suggested a good transferability.315
Kadupitiya et al. conducted NEMD simulations and applied PCA on the data obtained from these simulations.316 Specifically, a study was conducted to investigate the rheological properties of squalane under elastohydrodynamic lubrication (EHL) conditions, the lubricant under large pressure of more than 500 MPa and strain rate greater than 105 s−1, which is difficult to achieve in an experiment at the same time.316 Orientation tensors for all-atom pairs were collected from the NEMD simulation trajectories to examine the relationship between rheological properties and the molecular order change of squalane, which in total resulted in 6 × 435 dimensions data. Then, PCA was applied to reduce the 6 dimensions to 2 for visualization and analysis. It has been demonstrated that the dimension reduction methods successfully group the atom pairs for small rates and pressures systems which show a significant change in the flow behavior. Besides, it also indicated the ability to describe the shear flow of small-molecular liquids.
The statistical model of Bayesian analysis estimates the uncertainty of an event using the probabilistic interpretation. Using the Bayes theorem, probabilities are calculated and updated based on the prior data.322,323 A posterior distribution is determined by combining knowledge from existing data in terms of prior distributions and the observations in the form of likelihood function.324 A complex data sets can be modeled with extreme flexibility and certainty through monte carlo sampling techniques.325,326 Baboukani et al. exercised the Bayesian learning approach and transfer learning technique integrated with DFT and MD simulations approach.317 Particularly, the data generated from DFT and MD simulations included descriptors like structural, electronic, thermal, electron–phonon coupling, mechanical and chemical results, which were used as input for ML models. Using the ML model and the above inputs, a potential energy surface of maximum energy barrier (MEB) was estimated. In their study, they explored various 2D materials including GR and transition metal dichalcogenides (TMDCs) families as lubrication additives, as they are known to reduce the friction and wear. Based on the fact that Bayesian models are excellent models in the case of missing data, sparse data or noisy data, the prediction of potential energy surface (PES) through ML models was simplified. The most accurate model for a single-layer 2D material against a similar layer in an inert environment, with the MSE < 0.25 was developed and validated against MD simulations in this study. This combinatorial approach of statistical learning and molecular simulations aided in developing, predicting, and validating the robustness of the MEB–PES successfully.317
The Bayesian approach can be also extended through integration with the NN algorithm. Zaidan et al. applied a Bayesian neural network (BNN) to model the fluid-friction relation of lubricant.318 To solve the difficulty of statistical imbalance of data for lubrication performance, the Gaussian mixture model was introduced, and the data was grouped into four clusters for analysis. The data for frictional behavior was obtained from MD simulations using a toy model. The inputs for the BNN was a 25-dimensional array describing the structure information for a system, which is sufficient to capture the fluid characteristics in MD, the output is the shear response. The BNN model was good to deal with uncertainty and prevent overfitting; it could successfully predict the shear with the error around its mean prediction, which can clearly figure out the poorly sampled regions in the dataset.
5.1 ML in MD: our perspective
It should be noted that although the use of ML has been extensively examined in experimental tribological studies, only four papers,315–318 to the best of our knowledge, have implemented ML in computational modeling studies. The combinatorial approach of ML with MD simulations demonstrated the efficient exploration of MD-obtained data. Through data-driven approaches in MD, it is possible to develop models around the simulation trajectories including positions, velocities, forces as well as the energetics of the system. In addition, the human brain may not be able to extract definitive conclusions from various descriptive modeling analyses. Therefore, to identify the structure–property relationships in complex multi-dimensional problems, ML can be effective in extracting and analyzing hidden features. A ML algorithm learned from these input-output relationships can serve as a surrogate model for the tribological simulations or experiments. This surrogate model as an objective function in the optimization techniques like PSO, GA, etc. remain a much efficient approach to design novel materials.A deep-learning approach called convolutional neural networks (CNN) has proven highly effective in image classification, segmentation and object detection, due to its ability to extract high-level features.327–329 Few studies have reviewed the advancements of CNN and summarized their exemplary applications through various architectures.330 Moreover, classical CNN models like LeNet, GoogleNet, RestNet, U-Net, and so on, eliminate the need to tune hyperparameters. A recent study in our group demonstrated a proof-of-concept study of CNN to map 3-dimensional structure of bottlebrush polymers and analyze shapes of complex structures.331 CNNs, either in 1D, 2D, or 3D, which have shown significant potential to extract structural/imaging features to build their relationship with output in various research fields may prove valuable to assist these MD applications in tribology.332–336
Researchers may find it challenging to train ML models at present since they may be unable to identify a combination of features that are appropriate for their learning objectives. Therefore, other deep learning (DL) methods like restricted self-organizing maps (SOMs), restricted Boltzmann machine (RBM), and autoencoders (both stacked and denoising) may assist researchers for feature map generation. In addition, the lack of data in experiments may also contribute to the challenges encountered when using ML. Consequently, deep generative models such as generative adversarial networks (GAN), variational autoencoders (VAE), and deep belief networks (DBN) have been useful in developing models in the absence of large quantities of data.337–340 A VAE that encodes or decodes sequences of inputs to and from a continuous latent space, with a much lower computational budget, is called syntax-directed VAE (SDVAE) was integrated with Gaussian process regression (GPR) to design novel polymer with high glass transition temperature (Tg) and bandgap by Batra et al.62 The approach can be applied to the development of new polymer lubricants as a classification model could be trained using the data with the known polymers and their tribological properties such as CoF, wear resistance etc. Although a couple of studies have shown applications of deep learning models like RNN and radial basis function neural networks (RBFNN), the promising prospects of these algorithms are still underexplored. Specifically, these models may allow one to identify new lubricants with enhanced performances (i.e., reducing CoF and improving wear resistances). Therefore, in general, through the use of these deep learning methods, traditional challenges associated with handling big data, lack of flexibility and multi-task learning in simpler machine learning methods, as well as high computational costs can be overcome. Moreover, surrogate ML or DL models for experiments and simulations both offer an efficient and accelerated method to explore a large design space in material discovery.
6. Emerging materials
Even though our review focuses on the application of different ML algorithms in tribology, the materials used in this study remain largely unrecognized. Only a handful of materials including soft polymers, oils, alloys, etc. have been explored. Here, we shed light on other unexplored or less explored classes of materials such as glycomaterials and MXenes.341–345 Following sections discuss recent advances of these materials in tribological investigations. Although ML has shown the ability to explore composites and lubricants, we believe these new classes of materials are capable of advancing tribological performances through integration with ML.6.1 Glyco-materials
Matrix composites cater to the needs of automobiles and several other types of industries including mining, construction and manufacturing. Despite these diverse applications, their heavy usage can lead to damage of the environment as they are extracted from conventional sources of energy and are toxic in nature.346 These composites, unfortunately, are not environment friendly and researchers have been venturing to identify greener alternatives to petroleum-based lubricants.347 In light of this issue, bio-lubricants are viewed as a potential replacement for petroleum-based and matrix composite lubricants.76,346,348–350 Bio-lubricants, are generally extracted from renewable sources of energy and their greatest advantage is that they are environmentally friendly.349,350 Bio-lubricants possess desirable characteristics including high lubricity, good temperature-viscosity relationship, biodegradability and low volatility and lower costs.346,348 However, bio-lubricants suffer from a drawback, which is low oxidation stability.351 This drawback can be circumvented by several chemical processes including esterification,352 acetylation353 and epoxidation.354,355 Thermal stability and antioxidant properties of castor oil, which is a bio-lubricant were found to be enhanced by the addition of lignin-based compounds.356 Bio-lubricants derived by epoxidation of waste cooking oil similarly showed improved low temperature performance and oxidation stability compared to waste cooking oil.357 The enhancement of thermal and oxidation stability of vegetable oils was made possible by genetically modifying the organisms from which they are extracted.346,358,359 Most commonly used genetically modified oils are sunflower, canola and soybean oils. Gene modification of the organisms is done by DNA transcription in a way that increases the oleic acid content and decreases the linoleic acid content of the vegetable oils.360 The pour point of vegetable oils can also be improved by increasing the unsaturated long chain or saturated short chain fatty acid content of the oil.360 Non-conventional hydrocarbons derived by electrochemical decarboxylation, hydro-deoxygenation and ketonic decarboxylation of fatty acids are also available as bio-lubricants.361 These hydrocarbon-based bio-lubricants can potentially be the replacement for synthetic lubricants. Glycomaterials, are carbohydrate based materials that comprise of complex chains of sugars, called glycans. They have the potential to be developed as a new generation bio-compatible lubricants as they are available from renewable energy resources, in addition to being environmentally friendly. For instance, starch when suspended in water has the capability to act as a lubricant.362 However, the dissolution of starch in water is challenging because of the formation of intermolecular hydrogen bonds between the hydroxyl groups of starch. Solubility of starch in water can be improved by reacting starch with a cyclic dicarboxylic acid anhydrate or by heating it at high temperature and pressure.362–364 This reaction leads to breakage of strong hydrogen bonded intermolecular structure which reduces the crystalline nature of starch and thereby enhances its solubility in water. Loss of crystalline structure of starch leads to the formation of free hydroxyl groups of glucose which interact with ester groups of triglycerides present in fatty acids forming starch-oil composites which are used as lubricants.362,365 Starch-oil lubricants are completely derived from renewable sources of energy and are also environmentally friendly. Chemically modified starch contains free hydroxyl groups which increases the polarity of the surface and thereby its CoF.366 Addition of canola oil to chemically modified starch interacts with the free hydroxyl groups of starch and thereby decreases the CoF.366,367 Overall applications of glycomaterials are yet to be fully explored and glycomaterials, in general, show a lot of promise of becoming the lubricants of the next generation due to their abundant availability and bio-degradability. Thus, it is necessary to focus in this direction as heavy use of environmentally hazardous materials is a threat to nature.6.2 MXenes
MXenes are emerging two dimensional (2D) materials, which are synthesized by chemical delamination of ternary or quaternary layered carbides or nitrides of metals.343,368,369 These materials have wide range of applications including electrochemical storage, lubrication, light emitting diodes (LED), thermal heaters, sensors and optoelectronics.368,369 Ti3C2 coated on copper disk was able to reduce the CoF and wear rate by 4 times and 10 times, respectively, as compared to uncoated copper disks.370 Enhanced lubricative properties of Ti3C2 arise from the creation of a carbon-rich lubricating transferred film by the friction induced graphitization.370 TiO2/Ti3C2Tx nanocomposites when mixed with base oil lubricant were able to reduce the CoF between the steel surfaces by 2.5 times.371 This reduction in the CoF value was due to the formation of uniform tribofilm on the steel surface which thereby reduces the scratching of the steel surface.371 The tribological performance of PAO8 base oil was enhanced by the addition of Ti3C2Tx nanosheets.372 The maximum decrease in the CoF and wear volume were observed when the Ti3C2Tx concentration was 0.8 wt% and this improved tribological performance is attributed to the adherence of Ti3C2Tx nanosheets to the surfaces and thereby preventing the direct contact between them.372 Addition of Mo2CTx to lithium hexafluorophosphate-based ionic liquid leads to reduction in the value of CoF between Si3N4–sapphire interfaces at pressures (1.42 GPa) exceeding the superlubricity regime.373 Enhanced lubricity and anti-wear performance of the IL was improved due to the tribochemical reaction between the IL and Mo2CTx.373 Ti3C2Tx-nanoparticles when used as a solid lubricant were able to reduce the CoF by 300% as compared to the value of CoF between bare steel surfaces.374 A theoretical DFT study on MXenes has provided a detailed perspective on the effect of surface terminations on tribological properties of MXenes. –F and –O terminated MXenes exhibit low adhesion which leads to enhancement in their tribological performance as compared to –OH terminated MXenes. The presence of higher amounts of –F and –O groups on MXenes demonstrates weaker adhesion to ferrous substrates which helps in lubricant deportation under sliding conditions.3757. Overall challenges and conclusion
Overall, researchers have magnificently exemplified the powerful approach of ML and AI, primarily using experimental data. Specifically, numerous studies have incorporated the use of ANN in studying non-linear relationships between input variables (operating conditions and material composition) and output (wear and friction). However, only few studies have demonstrated the applicability of other ML models, which may be attributed primarily to their inability of mapping existing non-linear data. Moreover, the proficiency exhibited by ANN on a smaller data set is unparalleled compared to other ML models. Unfortunately, the lack of data, guidance regarding how to use data, and uncertainty regarding learning objectives have resulted in a limited number of publications pertaining to the use of machine learning across a wide range of fields. This task has been assisted in part by deep learning models such as CNN, SOMs, RBM, and autoencoders as they can construct a feature map. It is possible to use these models as surrogates where the user lacks knowledge about the use of input features. Moreover, these models can be implemented for classification as well as regression analysis. Beginners in the field should consider the classic inbuilt models (such as LeNet, GoogleNet, U-Net, etc.) as a resource.The interpretability of big data through ANN, given they are often encountered, remains challenging. For example, in the development of BPNN, the challenges include a large number of samples, slow simulation speed, choice of appropriate hyperparameters like number of hidden layers and neurons comprising it, a choice of training functions and transfer functions and so on. According to the available data, a choice of a desired number of neurons and number of hidden layers can be estimated. Moreover, statistical analysis like ANOVA has proven helpful in interpreting data and associated important input parameters. In order to develop ML models efficiently, it is necessary not only to select the most appropriate algorithms for the desired applications, but also to possess a thorough understanding of their workings. Moreover, ML combined with optimization algorithms like Monte Carlo methods, and improved bat algorithms have indicated that hyperparameter tuning can be performed with a high degree of efficiency. Another aspect of using ML as an objective function by evolutionary-based optimization algorithms has also been discussed.
It has been demonstrated that computational modeling techniques are capable of simulating tribological experiments at microscopic level. To that intent, remarkable insights through MD (including MD, RMD, and NEMD), exemplary properties using DFT are exhibited. These computational approaches generate enormous amounts of data at every time step, however, only a few researchers have exploited molecular simulations data with ML methods. This can be attributed to the lack of tools to processing tools as well as clear paths to integrate this data with ML models. We believe that in the coming years, with more widespread applicability of ML methods and innovations, they will be integrated more frequently with molecular simulations to perform analysis on simulations trajectories. This, in turn, will enable us to discover hidden patterns, structures, and mechanisms at the nanoscale that may not be captured with traditional analysis methods, thus assisting the discovery of new lubricants for various tribological applications.
We also review current trends of ML in tribological applications and encourage the exploration of other classes of materials like glycomaterials and MXenes. Overall, with these emerging materials efforts to develop and implement ML models that can potentially assist experiments and simulations are needed.
Abbreviation list
| AE | Acoustic emissions |
| AIREBO | Adaptive intermolecular reactive empirical bond order |
| GDX | Adaptive learning rate |
| ANFIS | Adaptive neuro-fuzzy inference system |
| ART-2 | Adaptive resonance theory |
| Adj SS | Adjusted sum of squares |
| ASTM | American society for testing and materials |
| ANOVA | Analysis of variance |
| ANN | Artificial neural network |
| BPNN | Back propagation neural network |
| BA | Bat algorithm |
| BNN | Bayesian neural network |
| BFS | Blast furnace slag |
| BFGS | Broyden–Fletcher–Goldfarb–Shanno |
| CF | Carbon fiber |
| CNT | Carbon nanotube |
| CNSL | Cashew nut shell liquid |
| CBPD | Cement by-pass dust |
| CVT | Centroidal Voronoi tessellation |
| CMC | Ceramic matrix composite |
| CG MD | Coarse grained molecular dynamics |
| CoF | Coefficient of friction |
| CMO | Commercial mineral oil |
| CNN | Convolutional neural network |
| CC | Correlation coefficient |
| CFPC | Cotton fiber polyester composite |
| DT | Decision trees |
| DFT | Density functional theory |
| DBSCAN | Density-based spatial clustering of applications with noise |
| DOE | Design of experiments |
| DLC | Diamondlike carbon |
| DTAB | Dodecyl trimethyl ammonium bromide |
| EHL | Elastohydrodynamic lubrication |
| EFI | Empirical force index |
| EBP | Error back propagation |
| ELM | Extreme learning machine |
| FEM | Finite element method |
| FF | Force field |
| FM | Friction modifier |
| FSW | Friction stir welding |
| FGM | Functionally graded materials |
| GA | Genetic algorithm |
| T g | Glass transition temperature |
| GBM | Gradient boosting machine |
| GR | Graphene |
| GO | Graphene oxide |
| GRA | Gray relational analysis |
| HA | Hydroxyapatite |
| IBA | Improved bat algorithm |
| KNN | K nearest neighnours |
| LFM | Lateral force microscopy |
| LOO | Leave one out |
| LJ | Lennard Jones |
| LM | Levenberg–Marquardt |
| LED | Light emitting diodes |
| ML | Machine Learning |
| MDp | Marble dust particles |
| MEB | Maximum energy barrier |
| MAE | Mean absolute error |
| MRE | Mean relative error |
| MSE | Mean squared error |
| MF | Membership function |
| MMC | Metal matrix composite |
| MNN | Modular neural network |
| MD | Molecular dynamics |
| MOSDeF | Molecular simulation and design framework |
| MC | Monte carlo |
| MWCNT | Multi walled carbon nanotube |
| MoGA | Multi-objectives genetic algorithm |
| MRA | Multiple regression analyses |
| NCO | Neutralized castor oil |
| NFSS | Nickel-free stainless steel composites |
| NN | Neural network |
| NEMD | Non-equilibrium molecular dynamics |
| NSGA | Non-sorting genetic algorithm |
| PAES | Pareto-archived evolution strategy |
| PFPE | Perfluoropolyether |
| POD | Pin-on-disk |
| PWD | Pine wood dust |
| PEEK | Poly ether ether ketone |
| PA | Polyamide |
| PEK | Polyetherketone |
| PE | Polyethylene |
| PMC | Polymer matrix composite |
| PPS | Polyphenylene sulfide |
| PTFE | Polytetrafluoroethylene |
| EP-PUR | Polyurethane |
| PTW | Potassium titanate whisker |
| PES | Potential energy surface |
| CGB | Powell–Beale conjugate gradient algorithm |
| PC | Principal component |
| PCA | Principal component analysis |
| QSTR | Quantitative structure tribo-ability relationship |
| RBFNN | Radial basis function neural network |
| RF | Random forests |
| REBO | Reactive empirical bond order |
| ReaxFF | Reactive force field |
| RMD | Reactive molecular dynamics |
| RNN | Recurrent neural networks |
| r-GO | Reduced graphene oxide |
| RSM | Response surface methodology |
| RH | Rice husk |
| RHA | Rice husk ash |
| RMSE | Root mean squared error |
| RPM | Rotations per minute |
| SCG | Scaled conjugate gradient |
| SCF | Short carbon fiber |
| SGF | Short glass fiber |
| SWR | Specific wear rate |
| SPEA | Strength pareto evolutionary algorithm |
| SVM | Support vector machine |
| SVR | Support vector regression |
| SRGM | Symbolic regression multi-gene programming |
| T s | Tensile strength |
| TTCF | Transient-time correlation function |
| TMDC | Transition metal dichalcogenide |
| T-BFRP | Treated betelnut fiber polyster |
| UTS | Ultimate tensile strength |
| UHMWPE | Ultra high molecular weight polyethylene |
| UA | United atom |
| WMD | Waste marble dust |
| WSD | Wear scar diameter |
| Y | Young's modulus |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by GlycoMIP, a National Science Foundation Materials Innovation Platform funded through Cooperative Agreement DMR-1933525. S. A. D. acknowledges the Institute for Critical Technology and Applied Science (ICTAS) Junior Faculty Award.References
- B. Bhushan, Introduction to Tribology, John Wiley & Sons, 2013 Search PubMed.
- W. K. Shafi, A. Raina, M. I. Ul Haq and A. Khajuria, Interdisciplinary aspects of tribology, Int. Res. J. Eng. Technol., 2018, 5, 5–8 Search PubMed.
- D. Dowson, Bio-tribology, Faraday Discuss., 2012, 156, 9–30 RSC.
- R. Hauert and U. Müller, An overview on tailored tribological and biological behavior of diamond-like carbon, Diamond Relat. Mater., 2003, 12, 171–177 CrossRef CAS.
- S. Prakash, D. D. Y. Tan and J. Chen, Applications of tribology in studying food oral processing and texture perception, Food Res. Int., 2013, 54, 1627–1635 CrossRef.
- M. Priest and C. M. Taylor, Automobile engine tribology—approaching the surface, Wear, 2000, 241, 193–203 CrossRef CAS.
- W. R. Jones and M. J. Jansen, Tribology for space applications, Proc. Inst. Mech. Eng., Part J, 2008, 222, 997–1004 CrossRef CAS.
- A. A. Voevodin, J. P. O’Neill and J. S. Zabinski, Nanocomposite tribological coatings for aerospace applications, Surf. Coat. Technol., 1999, 116–119, 36–45 CrossRef.
- H. Tang, J. Sun, J. He and P. Wu, Research Progress of Interface Conditions and Tribological Reactions: A Review, J. Ind. Eng. Chem., 2021, 94, 105–121 CrossRef CAS.
- H. Czichos, Tribology and Its Many Facets: From Macroscopic to Microscopic and Nano-scale Phenomena, Meccanica, 2001, 36, 605–615 CrossRef.
- Y. Ren, L. Zhang, G. Xie, Z. Li, H. Chen, H. Gong, W. Xu, D. Guo and J. Luo, A review on tribology of polymer composite coatings, Friction, 2021, 9, 429–470 CrossRef CAS.
- L. Liu, M. Zhou, L. Jin, L. Li, Y. Mo, G. Su, X. Li, H. Zhu and Y. Tian, Recent advances in friction and lubrication of graphene and other 2D materials: Mechanisms and applications, Friction, 2019, 7, 199–216 CrossRef.
- D. Berman, S. A. Deshmukh, S. K. R. S. Sankaranarayanan, A. Erdemir and A. V. Sumant, Friction. Macroscale superlubricity enabled by graphene nanoscroll formation, Science, 2015, 348, 1118–1122 CrossRef CAS PubMed.
- D. Berman, S. A. Deshmukh, S. K. R. S. Sankaranarayanan, A. Erdemir and A. V. Sumant, Extraordinary macroscale wear resistance of one atom thick graphene layer, Adv. Funct. Mater., 2014, 24, 6640–6646 CrossRef CAS.
- A. Kurdi, N. Alhazmi, H. Alhazmi and T. Tabbakh, Practice of Simulation and Life Cycle Assessment in Tribology-A Review, Materials, 2020, 13, 3489 CrossRef CAS PubMed.
- Z. Ye, Tribological phenomena at the atomic scale interface: 2D materials and beyond, University of California, Merced, 2016 Search PubMed.
- K. Holmberg and A. Erdemir, Influence of tribology on global energy consumption, costs and emissions, Friction, 2017, 5, 263–284 CrossRef CAS.
- Z. Li and F. Mangolini, Recent Advances in Nanotribology of Ionic Liquids, Exp. Mech., 2021, 61, 1093–1107 CrossRef CAS.
- A. J. McGhee, E. O. McGhee, J. E. Famiglietti and K. D. Schulze, Dynamic Subsurface Deformation and Strain of Soft Hydrogel Interfaces Using an Embedded Speckle Pattern With 2D Digital Image Correlation, Exp. Mech., 2021, 61, 1017–1027 CrossRef.
- K. L. Johnson and K. L. Johnson, Contact Mechanics, Cambridge University Press, 1987 Search PubMed.
- D. A. Hills and D. Nowell, Solid Mechanics and Its Applications, 1994 Search PubMed.
- J. Li, J. Zhang, W. Ge and X. Liu, Multi-scale methodology for complex systems, Chem. Eng. Sci., 2004, 59, 1687–1700 CrossRef CAS.
- B. Bhushan, J. N. Israelachvili and U. Landman, Nanotribology: friction, wear and lubrication at the atomic scale, Nature, 1995, 374, 607–616 CrossRef CAS.
- D. Pan, C. Liu, X. Qi, Y. Yang and X. Hao, A tribological application of the coarse-grained molecular dynamics simulation and its experimental verification, Tribol. Int., 2019, 133, 32–39 CrossRef CAS.
- J. P. Ewen, D. M. Heyes and D. Dini, Advances in nonequilibrium molecular dynamics simulations of lubricants and additives, Friction, 2018, 6, 349–386 CrossRef CAS.
- A. Martini, S. J. Eder and N. Dörr, Tribochemistry: A Review of Reactive Molecular Dynamics Simulations, Lubricants, 2020, 8, 44 CrossRef.
- V. A. Zhuravlev, On the question of theoretical justification of the Amontons-Coulomb law for friction of unlubricated surfaces, Proc. Inst. Mech. Eng., Part J, 2007, 221, 893–898 CrossRef.
- J. A. Greenwood, J. B. P. Williamson and F. P. Bowden, Contact of nominally flat surfaces, Proc. R. Soc. London, Ser. A, 1966, 295, 300–319 CAS.
- P. R. Nayak, Random Process Model of Rough Surfaces, J. Lubr. Technol., 1971, 93, 398–407 CrossRef.
- A. A. Yevtushenko and P. Grzes, The FEM-Modeling of the Frictional Heating Phenomenon in the Pad/Disc Tribosystem (A Review), Numer. Heat Transfer, Part A, 2010, 58, 207–226 CrossRef.
- D. J. Whitehouse, Fractal or fiction, Wear, 2001, 249, 345–353 CrossRef CAS.
- F. M. Borodich, in Encyclopedia of Tribology, ed. Q. J. Wang and Y.-W. Chung, Springer US, Boston, MA, 2013, pp. 1249–1258 Search PubMed.
- B. J. Hamrock, Fundamentals of Fluid Film Lubrication, McGraw-Hill Science, Engineering & Mathematics, 1994 Search PubMed.
- P. L. Menezes, C. J. Reeves, P. K. Rohatgi and M. R. Lovell, in Tribology for Scientists and Engineers: From Basics to Advanced Concepts, ed. P. L. Menezes, M. Nosonovsky, S. P. Ingole, S. V. Kailas and M. R. Lovell, Springer New York, New York, NY, 2013, pp. 341–389 Search PubMed.
- Y.-Y. Zhang, Q. Chen, X.-L. Mo, P. Huang, Y.-Q. Li, C.-C. Zhu, N. Hu and S.-Y. Fu, Tribological behavior of short carbon fiber reinforced polyetherimide composite under water lubrication conditions, Compos. Sci. Technol., 2021, 216, 109044 CrossRef CAS.
- C. Birleanu, M. Pustan, M. Cioaza, A. Molea, F. Popa and G. Contiu, Effect of TiO2 nanoparticles on the tribological properties of lubricating oil: an experimental investigation, Sci. Rep., 2022, 12, 5201 CrossRef CAS PubMed.
- A. Rosenkranz, M. Marian, F. J. Profito, N. Aragon and R. Shah, The Use of Artificial Intelligence in Tribology—A Perspective, Lubricants, 2020, 9, 2 CrossRef.
- M. Marian and S. Tremmel, Current Trends and Applications of Machine Learning in Tribology—A Review, Lubricants, 2021, 9, 86 CrossRef CAS.
- U. M. R. Paturi, S. Cheruku and N. S. Reddy, The Role of Artificial Neural Networks in Prediction of Mechanical and Tribological Properties of Composites—A Comprehensive Review, Arch. Comput. Methods Eng., 2022, 1–41 Search PubMed.
- E. Ciulli, Tribology and industry: From the origins to 4.0, Front. Mech. Eng. Chin., 2019, 5, 55 CrossRef.
- Z. Zhang, N. Yin, S. Chen and C. Liu, Tribo-informatics: Concept, architecture, and case study, Friction, 2021, 9, 642–655 CrossRef.
- S. Tremmel and M. Marian, Machine Learning in Tribology—More than Buzzwords?, Lubricants, 2022, 10, 68 CrossRef.
- I. Argatov, Artificial neural networks (ANNs) as a novel modeling technique in tribology, Front. Mech. Eng. Chin., 2019, 5, 30 CrossRef.
- U. M. R. Paturi, S. T. Palakurthy and N. S. Reddy, The Role of Machine Learning in Tribology: A Systematic Review, Arch. Comput. Methods Eng., 2022, 1–53 Search PubMed.
- F. E. Kennedy, Y. Lu and I. Baker, Contact temperatures and their influence on wear during pin-on-disk tribotesting, Tribol. Int., 2015, 82, 534–542 CrossRef CAS.
- M. Mubashshir and A. Shaukat, The Role of Grease Composition and Rheology in Elastohydrodynamic Lubrication, Tribol. Lett., 2019, 67, 104 CrossRef.
- Y. Yin, J. Bao and L. Yang, Wear performance and its online monitoring of the semimetal brake lining for automobiles, Ind. Lubr. Tribol., 2014, 66, 100–105 CrossRef.
- G. Xiao and Z. Zhu, Friction materials development by using DOE/RSM and artificial neural network, Tribol. Int., 2010, 43, 218–227 CrossRef CAS.
- Y. Ao, Q. J. Wang and P. Chen, Simulating the worn surface in a wear process, Wear, 2002, 252, 37–47 CrossRef CAS.
- L. Haviez, R. Toscano, M. El Youssef, S. Fouvry, G. Yantio and G. Moreau, Semi-physical neural network model for fretting wear estimation, J. Intell. Fuzzy Syst., 2015, 28, 1745–1753 Search PubMed.
- M. R. Hilton and P. D. Fleischauer, Applications of solid lubricant films in spacecraft, Surf. Coat. Technol., 1992, 54–55, 435–441 CrossRef.
- A. Bustillo, D. Y. Pimenov, M. Matuszewski and T. Mikolajczyk, Using artificial intelligence models for the prediction of surface wear based on surface isotropy levels, Robot. Comput. Integr. Manuf., 2018, 53, 215–227 CrossRef.
- J. Prost, U. Cihak-Bayr, I. A. Neacşu, R. Grundtner, F. Pirker and G. Vorlaufer, Semi-Supervised Classification of the State of Operation in Self-Lubricating Journal Bearings Using a Random Forest Classifier, Lubricants, 2021, 9, 50 CrossRef.
- T. Wuest, D. Weimer, C. Irgens and K.-D. Thoben, Machine learning in manufacturing: advantages, challenges, and applications, Prod. Manuf. Res., 2016, 4, 23–45 Search PubMed.
- V. Nasteski, An overview of the supervised machine learning methods, HORIZONS.B, 2017, 4, 51–62 CrossRef.
- A. Olaode, G. Naghdy and C. Todd, Unsupervised classification of images: a review, Int. J. Image Data Fusion, 2014, 8, 325–342 Search PubMed.
- R. S. Sutton and A. G. Barto, Reinforcement Learning, second edition: An Introduction, MIT Press, 2018 Search PubMed.
- H. Dong, Z. Ding and S. Zhang, Deep Reinforcement Learning, Springer Nature Singapore, 2020 Search PubMed.
- G. Taguchi, System of experimental design; engineering methods to optimize quality and minimize costs, 1987 Search PubMed.
- M. N. Islam and A. Pramanik, Comparison of Design of Experiments via Traditional and Taguchi Method, J. Adv. Manuf. Syst., 2016, 15, 151–160 CrossRef.
- S. J. Kim, K. S. Kim and H. Jang, Optimization of manufacturing parameters for a brake lining using Taguchi method, J. Mater. Process. Technol., 2003, 136, 202–208 CrossRef.
- L. Tong, C. Su and C. Wang, The optimization of multi-response problems in the Taguchi method, Int. J. Qual. Reliab. Manage., 1997, 14, 367–380 CrossRef.
- C. S. Vui, G. K. Soon, C. K. On, R. Alfred and P. Anthony, 2013 IEEE International Conference on Control System, Computing and Engineering, 2013, pp. 477–482.
- G. K. Purushothama, A. U. Narendranath, D. Thukaram and K. Parthasarathy, ANN applications in fault locators, Int. J. Electr. Power Energy Syst., 2001, 23, 491–506 CrossRef.
- J. A. Freeman and D. M. Skapura, Neural Networks: Algorithms, Applications, and Programming Techniques, Addison-Wesley, 1991 Search PubMed.
- O. I. Abiodun, A. Jantan, A. E. Omolara, K. V. Dada, N. A. Mohamed and H. Arshad, State-of-the-art in artificial neural network applications: A survey, Heliyon, 2018, 4, e00938 CrossRef PubMed.
- Z. Zhang and K. Friedrich, Artificial neural networks applied to polymer composites: a review, Compos. Sci. Technol., 2003, 63, 2029–2044 CrossRef CAS.
- G. B. Goh, N. O. Hodas and A. Vishnu, Deep learning for computational chemistry, J. Comput. Chem., 2017, 38, 1291–1307 CrossRef CAS PubMed.
- S. Al-Zubaidi, J. A. Ghani and C. H. Che Haron, Application of ANN in Milling Process: A Review, Modell. Simul. Mater. Sci. Eng., 2011 DOI:10.1155/2011/696275.
- T. Kolodziejczyk, R. Toscano, S. Fouvry and G. Morales-Espejel, Artificial intelligence as efficient technique for ball bearing fretting wear damage prediction, Wear, 2010, 268, 309–315 CrossRef CAS.
- R. Quiza, L. Figueira and J. Paulo Davim, Comparing statistical models and artificial neural networks on predicting the tool wear in hard machining D2 AISI steel, Int. J. Adv. Manuf. Technol., 2008, 37, 641–648 CrossRef.
- R. A. Kanai, R. G. Desavale and S. P. Chavan, Experimental-Based Fault Diagnosis of Rolling Bearings Using Artificial Neural Network, J. Tribol., 2016, 138, 031103 CrossRef.
- A. Kordijazi, T. Zhao, J. Zhang, K. Alrfou and P. Rohatgi, A Review of Application of Machine Learning in Design, Synthesis, and Characterization of Metal Matrix Composites: Current Status and Emerging Applications, JOM, 2021, 73, 2060–2074 CrossRef CAS.
- T. D. Sparks, S. K. Kauwe, M. E. Parry, A. M. Tehrani and J. Brgoch, Machine Learning for Structural Materials, Annu. Rev. Mater. Res., 2020, 50, 27–48 CrossRef CAS.
- S. A. S. Amiril, E. A. Rahim and S. Syahrullail, A review on ionic liquids as sustainable lubricants in manufacturing and engineering: Recent research, performance, and applications, J. Cleaner Prod., 2017, 168, 1571–1589 CrossRef CAS.
- A. Z. Syahir, N. W. M. Zulkifli, H. H. Masjuki, M. A. Kalam, A. Alabdulkarem, M. Gulzar, L. S. Khuong and M. H. Harith, J. Cleaner Prod., 2017, 168, 997–1016 CrossRef CAS.
- C. L. Mahoney, E. R. Barnum, W. W. Kerlin, K. J. Sax and W. S. Saari, Effect of Radiation on the Stability of Synthetic Lubricants, 5th World Petroleum Congress, 1959.
- E. E. Klaus, E. J. Tewksbury and M. R. Fenske, Preparation, Properties, and Some Applications of Super-Refined Mineral Oils, ASLE Trans., 1962, 5, 115–125 CrossRef CAS.
- A. D. Abbott, A. Doyle Abbott and L. O. Bowman, The Determination of Alkalinity in Diesel Engine Lubricating Oils and Additives, J. Jpn. Pet. Inst., 1966, 9, 184–193 CrossRef.
- S. P. Jones, R. Jansen and R. L. Fusaro, Preliminary Investigation of Neural Network Techniques to Predict Tribological Properties, Tribol. Trans., 1997, 40, 312–320 CrossRef CAS.
- S. Bhaumik and M. Kamaraj, Artificial neural network and multi-criterion decision making approach of designing a blend of biodegradable lubricants and investigating its tribological properties, Proc. Inst. Mech. Eng., Part J, 2021, 235, 1575–1589 CrossRef CAS.
- C. Humelnicu, S. Ciortan and V. Amortila, Artificial Neural Network-Based Analysis of the Tribological Behavior of Vegetable Oil–Diesel Fuel Mixtures, Lubricants, 2019, 7, 32 CrossRef.
- E. Durak, Ö. Salman and C. Kurbanoğlu, Analysis of effects of oil additive into friction coefficient variations on journal bearing using artificial neural network, Ind. Lubr. Tribol., 2008, 60, 309–316 CrossRef.
- P. L. Menezes, P. K. Rohatgi and E. Omrani, Self-Lubricating Composites, Springer Berlin Heidelberg, 2018 Search PubMed.
- K. Friedrich, Z. Lu and A. M. Hager, Recent advances in polymer composites’ tribology, Wear, 1995, 190, 139–144 CrossRef CAS.
- P. Sutor, Solid Lubricants: Overview and Recent Developments, MRS Bull., 1991, 16, 24–30 CrossRef CAS.
- R. L. Fusaro, Self-lubricating polymer composites and polymer transfer film lubrication for space applications, Tribol. Int., 1990, 23, 105–122 CrossRef CAS.
- I. M. Allam, Solid lubricants for applications at elevated temperatures, J. Mater. Sci., 1991, 26, 3977–3984 CrossRef CAS.
- K. Friedrich and P. Reinicke, Friction and wear of polymer-based composites, Mech. Compos. Mater., 1998, 34, 503–514 CrossRef CAS.
- M. N. Gardos, Self-lubricating composites for extreme environment applications, Tribol. Int., 1982, 15, 273–283 CrossRef CAS.
- R. L. Fusaro, Evaluation of Several Polymer Materials for Use as Solid Lubricants in Space, Tribol. Trans., 1988, 31, 174–181 CrossRef CAS.
- E. R. Booser, Tribology data handbook: an excellent friction, lubrication, and wear resource, CRC press, 1997 Search PubMed.
- Z. P. Lu and K. Friedrich, On sliding friction and wear of PEEK and its composites, Wear, 1995, 181–183, 624–631 CrossRef CAS.
- K. Friedrich, J. Karger-Kocsis and Z. Lu, Effects of steel counterface roughness and temperature on the friction and wear of PE(E)K composites under dry sliding conditions, Wear, 1991, 148, 235–247 CrossRef CAS.
- M. Cirino, K. Friedrich and R. B. Pipes, Evaluation of polymer composites for sliding and abrasive wear applications, Composites, 1988, 19, 383–392 CrossRef CAS.
- M. Cirino, R. B. Pipes and K. Friedrich, The abrasive wear behaviour of continuous fibre polymer composites, J. Mater. Sci., 1987, 22, 2481–2492 CrossRef CAS.
- P. B. Mody, T.-W. Chou and K. Friedrich, Effect of testing conditions and microstructure on the sliding wear of graphite fibre/PEEK matrix composites, J. Mater. Sci., 1988, 23, 4319–4330 CrossRef CAS.
- S. K. Biswas and K. Vijayan, Friction and wear of PTFE—a review, Wear, 1992, 158, 193–211 CrossRef CAS.
- H. Voss and K. Friedrich, On the wear behaviour of short-fibre-reinforced peek composites, Wear, 1987, 116, 1–18 CrossRef CAS.
- A. Suresh, A. P. Harsha and M. K. Ghosh, Erosion Studies of Short Glass Fiber-reinforced Thermoplastic Composites and Prediction of Erosion Rate Using ANNs, J. Reinf. Plast. Compos., 2010, 29, 1641–1652 CrossRef CAS.
- Z. Zhang, N.-M. Barkoula, J. Karger-Kocsis and K. Friedrich, Artificial neural network predictions on erosive wear of polymers, Wear, 2003, 255, 708–713 CrossRef CAS.
- Z. Jiang, Z. Zhang and K. Friedrich, Prediction on wear properties of polymer composites with artificial neural networks, Compos. Sci. Technol., 2007, 67, 168–176 CrossRef CAS.
- Z. Jiang, L. A. Gyurova, A. K. Schlarb, K. Friedrich and Z. Zhang, Study on friction and wear behavior of polyphenylene sulfide composites reinforced by short carbon fibers and sub-micro TiO2 particles, Compos. Sci. Technol., 2008, 68, 734–742 CrossRef CAS.
- Z. Jiang, L. Gyurova, Z. Zhang, K. Friedrich and A. K. Schlarb, Neural network based prediction on mechanical and wear properties of short fibers reinforced polyamide composites, Mater. Des., 2008, 29, 628–637 CrossRef CAS.
- L. A. Gyurova, P. Miniño-Justel and A. K. Schlarb, Modeling the sliding wear and friction properties of polyphenylene sulfide composites using artificial neural networks, Wear, 2010, 268, 708–714 CrossRef CAS.
- L. A. Gyurova and K. Friedrich, Artificial neural networks for predicting sliding friction and wear properties of polyphenylene sulfide composites, Tribol. Int., 2011, 44, 603–609 CrossRef CAS.
- L. A. Gyurova, Z. Jiang, A. K. Schlarb, K. Friedrich and Z. Zhang, Friction, Wear and Wear Protection, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011, pp. 417–422 Search PubMed.
- K. Velten, R. Reinicke and K. Friedrich, Wear volume prediction with artificial neural networks, Tribol. Int., 2000, 33, 731–736 CrossRef.
- Z. Zhang, K. Friedrich and K. Velten, Prediction on tribological properties of short fibre composites using artificial neural networks, Wear, 2002, 252, 668–675 CrossRef CAS.
- L. Frangu and M. Ripa, Artificial neural networks applications in tribology--a survey, 2001 NATO Advanced Study Institute on Neural Networks for Instrumentation, Measurement, and Related Industrial Applications: Study Cases, 2001, pp. 35–42 Search PubMed.
- B. Hassibi and D. Stork, Second order derivatives for network pruning: Optimal brain surgeon, Adv. Neural Inf. Process. Syst., 1992, 5, 164–171 Search PubMed.
- B. Hassibi, D. G. Stork and G. J. Wolff, IEEE International Conference on Neural Networks, 1993, vol. 1, pp. 293–299.
- B. Hassibi, D. G. Stork and G. Wolff, Optimal brain surgeon: Extensions and performance comparisons, Adv. Neural Inf. Process. Syst, 1993, 6, 263–270 Search PubMed.
- M. Busse and A. K. Schlarb, in Tribology of Polymeric Nanocomposites, ed. K. Friedrich and A. K. Schlarb, Butterworth-Heinemann, Oxford, 2nd edn, 2013, pp. 779–793 Search PubMed.
- J. Zhu, Y. Shi, X. Feng, H. Wang and X. Lu, Prediction on tribological properties of carbon fiber and TiO2 synergistic reinforced polytetrafluoroethylene composites with artificial neural networks, Mater. Des., 2009, 30, 1042–1049 CrossRef CAS.
- X. LiuJie, J. P. Davim and R. Cardoso, Prediction on tribological behaviour of composite PEEK-CF30 using artificial neural networks, J. Mater. Process. Technol., 2007, 189, 374–378 CrossRef.
- G. Kranthi and A. Satapathy, Evaluation and prediction of wear response of pine wood dust filled epoxy composites using neural computation, Comput. Mater. Sci., 2010, 49, 609–614 CrossRef CAS.
- A. Rout and A. Satapathy, Analysis of Dry Sliding Wear Behaviour of Rice Husk Filled Epoxy Composites Using Design of Experiment and ANN, Proc. Eng., 2012, 38, 1218–1232 CrossRef CAS.
- P. K. Padhi and A. Satapathy, Analysis of Sliding Wear Characteristics of BFS Filled Composites Using an Experimental Design Approach Integrated with ANN, Tribol. Trans., 2013, 56, 789–796 CrossRef CAS.
- K. Dai and X. Gao, Estimating antiwear properties of lubricant additives using a quantitative structure tribo-ability relationship model with back propagation neural network, Wear, 2013, 306, 242–247 CrossRef CAS.
- U. Nirmal, Prediction of friction coefficient of treated betelnut fibre reinforced polyester (T-BFRP) composite using artificial neural networks, Tribol. Int., 2010, 43, 1417–1429 CrossRef CAS.
- T. Nasir, B. F. Yousif, S. McWilliam, N. D. Salih and L. T. Hui, Proc. Inst. Mech. Eng., Part C, 2010, 224, 419–429 CrossRef.
- H. H. Parikh and P. P. Gohil, in Durability and Life Prediction in Biocomposites, Fibre-Reinforced Composites and Hybrid Composites, ed. M. Jawaid, M. Thariq and N. Saba, Woodhead Publishing, 2019, pp. 301–320 Search PubMed.
- S. K. Nayak and A. Satapathy, Wear analysis of waste marble dust-filled polymer composites with an integrated approach based on design of experiments and neural computation, Proc. Inst. Mech. Eng., Part J, 2020, 234, 1846–1856 CrossRef CAS.
- M. Zakaulla, F. Parveen, Amreen, Harish and N. Ahmad, Artificial neural network based prediction on tribological properties of polycarbonate composites reinforced with graphene and boron carbide particle, Mater. Today: Proc., 2020, 26, 296–304 CAS.
- P. K. Padhi, A. Satapathy and A. M. Nakka, Processing, characterization, and wear analysis of short glass fiber-reinforced polypropylene composites filled with blast furnace slag, J. Thermoplast. Compos. Mater., 2015, 28, 656–671 CrossRef CAS.
- H. I. Kurt and M. Oduncuoglu, Application of a Neural Network Model for Prediction of Wear Properties of Ultrahigh Molecular Weight Polyethylene Composites, Int. J. Polym. Sci., 2015 DOI:10.1155/2015/315710.
- G. Zhang, S. Guessasma, H. Liao, C. Coddet and J.-M. Bordes, Investigation of friction and wear behaviour of SiC-filled PEEK coating using artificial neural network, Surf. Coat. Technol., 2006, 200, 2610–2617 CrossRef CAS.
- K. K. Chawla, in Composite Materials: Science and Engineering, ed. K. K. Chawla, Springer New York, New York, NY, 2012, pp. 197–248 Search PubMed.
- D. K. Sharma, D. Mahant and G. Upadhyay, Manufacturing of metal matrix composites: A state of review, Mater. Today: Proc., 2020, 26, 506–519 CAS.
- A. D. Moghadam, B. F. Schultz, J. B. Ferguson, E. Omrani, P. K. Rohatgi and N. Gupta, Functional Metal Matrix Composites: Self-lubricating, Self-healing, and Nanocomposites-An Outlook, JOM, 2014, 66, 872–881 CrossRef.
- E. Omrani, A. D. Moghadam, P. L. Menezes and P. K. Rohatgi, New Emerging Self-lubricating Metal Matrix Composites for Tribological Applications, Mater. Form., Mach. Tribol., 2016, 63–103 Search PubMed.
- S. V. Prasad and R. Asthana, Aluminum Metal–Matrix Composites for Automotive Applications: Tribological Considerations, Tribol. Lett., 2004, 17, 445–453 CrossRef CAS.
- A. Macke, B. F. Schultz, P. K. Rohatgi and N. Gupta, Metal Matrix Composites for Automotive Applications, Adv. Compos. Mater. Automot. Appl., 2013, 311–344 Search PubMed.
- N. Natarajan, S. Vijayarangan and I. Rajendran, Wear behaviour of A356/25SiCp aluminium matrix composites sliding against automobile friction material, Wear, 2006, 261, 812–822 CrossRef CAS.
- A. Shafiei-Zarghani, S. F. Kashani-Bozorg and A. Zarei-Hanzaki, Microstructures and mechanical properties of Al/Al2O3 surface nano-composite layer produced by friction stir processing, Mater. Sci. Eng., A, 2009, 500, 84–91 CrossRef.
- G. H. Kumar, B. R. R. Bapu, R. Sagar and H. Mohit, The abrasive wear behaviour of Al-SiCp composites for automotive parts, Frontiers in Automobile and Mechanical Engineering-2010, 2010, pp. 54–59 DOI:10.1109/FAME.2010.5714798.
- S.-M. Zhou, X.-B. Zhang, Z.-P. Ding, C.-Y. Min, G.-L. Xu and W.-M. Zhu, Fabrication and tribological properties of carbon nanotubes reinforced Al composites prepared by pressureless infiltration technique, Composites, Part A, 2007, 38, 301–306 CrossRef.
- S. R. Dong, J. P. Tu and X. B. Zhang, An investigation of the sliding wear behavior of Cu-matrix composite reinforced by carbon nanotubes, Mater. Sci. Eng., A, 2001, 313, 83–87 CrossRef.
- L. Y. Wang, J. P. Tu, W. X. Chen, Y. C. Wang, X. K. Liu, C. Olk, D. H. Cheng and X. B. Zhang, Friction and wear behavior of electroless Ni-based CNT composite coatings, Wear, 2003, 254, 1289–1293 CrossRef CAS.
- T. S. Mahmoud, Artificial neural network prediction of the wear rate of powder metallurgy Al/Al2O3 metal matrix composites, Proc. Inst. Mech. Eng., Part J, 2012, 226, 3–15 CAS.
- A. Canakci, S. Ozsahin and T. Varol, Prediction of Effect of Reinforcement Size and Volume Fraction on the Abrasive Wear Behavior of AA2014/B4Cp MMCs Using Artificial Neural Network, Arabian J. Sci. Eng., 2014, 39, 6351–6361 CrossRef CAS.
- A. Aherwar, A. Singh and A. Patnaik, Prediction of effect of tungsten filled Co-30Cr-4Mo-1Ni metal matrix biomedical composite alloy on sliding wear peculiarity using Taguchi methodology and ANN, Adv. Mater. Process. Technol., 2017, 3, 665–688 Search PubMed.
- A. Nagaraj and S. Gopalakrishnan, A Study on Mechanical and Tribological Properties of Aluminium 1100 Alloys 6% of RHAp, BAp, CSAp, ZnOp and Egg Shellp Composites by ANN, Silicon Chem., 2021, 13, 3367–3376 CrossRef CAS.
- T. Mutuk, M. Gürbüz and H. Mutuk, Prediction of wear properties of graphene-Si3N4 reinforced titanium hybrid composites by artificial neural network, Mater. Res. Express, 2020, 7, 086511 CrossRef CAS.
- K. K. Ekka and S. R. Chauhan, and Varun, Study on the sliding wear behaviour of hybrid aluminium matrix composites using Taguchi design and neural network, Proc. Inst. Mech. Eng., Part J, 2016, 230, 537–549 CAS.
- I. Dinaharan, R. Palanivel, N. Murugan and L. R. Frans, Predicting the wear rate of AA6082 aluminum surface composites produced by friction stir processing via artificial neural network, Multidiscip. Model. Mater. Struct., 2019, 16, 409–423 CrossRef.
- V. Sivananth, P. Karuppusamy and K. Lingadurai, Wear and corrosion behaviour of titanium carbide reinforced metal matrix composites for automobile brake disc application, Int. J. Mater. Eng. Innovation, 2019, 10, 246–267 CrossRef CAS.
- V. S. Sreebalaji and K. R. Kumar, Artificial neural networks and multi response optimisation on EDM of aluminium (A380)/fly ash composites, Int. J. Comput. Mater. Sci. Surf. Eng., 2016, 6, 244–262 Search PubMed.
- S. D. Saravanan and M. Senthilkumar, Prediction of tribological behaviour of rice husk ash reinforced aluminum alloy matrix composites using artificial neural network, Russ. J. Non-Ferrous Met., 2015, 56, 97–106 CrossRef.
- G. Satyanarayana, G. Swami Naidu and N. H. Babu, Artificial neural network and regression modelling to study the effect of reinforcement and deformation on volumetric wear of red mud nano particle reinforced aluminium matrix composites synthesized by stir casting, Bol. Soc. Esp. Ceram. Vidrio, 2018, 57, 91–100 CrossRef CAS.
- K. Genel, S. C. Kurnaz and M. Durman, Modeling of tribological properties of alumina fiber reinforced zinc–aluminum composites using artificial neural network, Mater. Sci. Eng., A, 2003, 363, 203–210 CrossRef.
- K. R. Kumar, K. M. Mohanasundaram, G. Arumaikkannu and R. Subramanian, Artificial neural networks based prediction of wear and frictional behaviour of aluminium (A380)–fly ash composites, Tribol. Mater. Surf. Interfaces, 2012, 6, 15–19 CrossRef CAS.
- M. Hayajneh, A. M. Hassan, A. Alrashdan and A. T. Mayyas, Prediction of tribological behavior of aluminum–copper based composite using artificial neural network, J. Alloys Compd., 2009, 470, 584–588 CrossRef CAS.
- D. Özyürek, A. Kalyon, M. Yıldırım, T. Tuncay and İ. Çiftçi, Experimental investigation and prediction of wear properties of Al/SiC metal matrix composites produced by thixomoulding method using Artificial Neural Networks, Mater. Des., 2014, 63, 270–277 CrossRef.
- M. O. Shabani and A. Mazahery, Prediction of wear properties in A356 matrix composite reinforced with B4C particulates, Synth. Met., 2011, 161, 1226–1231 CrossRef CAS.
- F. S. Rashed and T. S. Mahmoud, Prediction of wear behaviour of A356/SiCp MMCs using neural networks, Tribol. Int., 2009, 42, 642–648 CrossRef CAS.
- R. Pramod, G. B. Veeresh Kumar, P. S. S. Gouda and A. T. Mathew, A Study on the Al2O3 reinforced Al7075 Metal Matrix Composites Wear behavior using Artificial Neural Networks, Mater. Today: Proc., 2018, 5, 11376–11385 CAS.
- D. Mehra, S. V. Sujith, M. M. Mahapatra and S. P. Harsha, Modeling of wear process parameters of in-situ RZ5–10wt%TiC Composite using artificial neural network, Mater. Today: Proc., 2018, 5, 24124–24132 CAS.
- M. Younesi, M. E. Bahrololoom and M. Ahmadzadeh, Prediction of wear behaviors of nickel free stainless steel–hydroxyapatite bio-composites using artificial neural network, Comput. Mater. Sci., 2010, 47, 645–654 CrossRef CAS.
- C. Zhang, Understanding the wear and tribological properties of ceramic matrix composites, in Advances in Ceramic Matrix Composites, ed. I. M. Low, Woodhead Publishing, 2014, pp. 312–339 Search PubMed.
- W. Krenkel and N. Langhof, Ceramic Matrix Composites for High Performance Friction Applications, Proceedings of the IV Advanced Ceramics and Applications Conference, 2017, pp. 13–28.
- I. W. Donald and P. W. McMillan, Ceramic-matrix composites, J. Mater. Sci., 1976, 11, 949–972 CrossRef CAS.
- K. Friedrich, Advances in Composite Tribology, Elsevier, 2012 Search PubMed.
- S. T. Buljan and V. K. Sarin, Silicon nitride-based composites, Composites, 1987, 18, 99–106 CrossRef CAS.
- P. F. Becher and G. C. Wei, Toughening behavior in SiC-whisker-reinforced alumina, J. Am. Ceram. Soc., 1984, 67, C–267 CrossRef.
- C. Sun, Y. Huang, Q. Shen, W. Wang, W. Pan, P. Zong, L. Yang, Y. Xing and C. Wan, Embedding two-dimensional graphene array in ceramic matrix, Sci. Adv., 2020, 6, eabb1338 CrossRef CAS PubMed.
- X. Gao, H. Yue, E. Guo, S. Zhang, B. Wang, E. Guan, S. Song and H. Zhang, Preparation and tribological properties of homogeneously dispersed graphene-reinforced aluminium matrix composites, Mater. Sci. Technol., 2018, 34, 1316–1322 CrossRef CAS.
- S. Malazdrewicz and Ł. Sadowski, An intelligent model for the prediction of the depth of the wear of cementitious composite modified with high-calcium fly ash, Compos. Struct., 2021, 259, 113234 CrossRef CAS.
- E. W. Bucholz, C. S. Kong, K. R. Marchman, W. G. Sawyer, S. R. Phillpot, S. B. Sinnott and K. Rajan, Data-Driven Model for Estimation of Friction Coefficient Via Informatics Methods, Tribol. Lett., 2012, 47, 211–221 CrossRef CAS.
- S. R. A. Fisher, The correlation between relatives on the supposition of Mendelian inheritance, Royal Society of Edinburgh, 1918 Search PubMed.
- Siddhartha and A. K. Singh, Mechanical and dry sliding wear characterization of short glass fiber reinforced polyester-based homogeneous and their functionally graded composite materials, Proc. Inst. Mech. Eng., Part J, 2015, 229, 274–298 CAS.
- R. Egala, G. V. Jagadeesh and S. G. Setti, Experimental investigation and prediction of tribological behavior of unidirectional short castor oil fiber reinforced epoxy composites, Friction, 2021, 9, 250–272 CrossRef CAS.
- J. Schmidhuber, Deep learning in neural networks: an overview, Neural Network, 2015, 61, 85–117 CrossRef PubMed.
- K. Levenberg, A method for the solution of certain non-linear problems in least squares, Quart. Appl. Math., 1944, 2, 164–168 CrossRef.
- D. W. Marquardt, An Algorithm for Least-Squares Estimation of Nonlinear Parameters, J. Soc. Ind. Appl. Math., 1963, 11, 431–441 CrossRef.
- S. C. Vettivel, N. Selvakumar, R. Narayanasamy and N. Leema, Numerical modelling, prediction of Cu–W nano powder composite in dry sliding wear condition using response surface methodology, Mater. Des., 2013, 50, 977–996 CrossRef CAS.
- S. C. Vettivel, N. Selvakumar and N. Leema, Experimental and prediction of sintered Cu–W composite by using artificial neural networks, Mater. Des., 2013, 45, 323–335 CrossRef CAS.
- N. Leema, P. Radha, S. C. Vettivel and H. Khanna Nehemiah, Characterization, pore size measurement and wear model of a sintered Cu–W nano composite using radial basis functional neural network, Mater. Des., 2015, 68, 195–206 CrossRef CAS.
- S. Arif, M. T. Alam, A. H. Ansari, M. B. N. Shaikh and M. Arif Siddiqui, Analysis of tribological behaviour of zirconia reinforced Al-SiC hybrid composites using statistical and artificial neural network technique, Mater. Res. Express, 2018, 5, 056506 CrossRef.
- T. Thankachan, K. Soorya Prakash and M. Kamarthin, Optimizing the Tribological Behavior of Hybrid Copper Surface Composites Using Statistical and Machine Learning Techniques, J. Tribol., 2018, 140 DOI:10.1115/1.4038688.
- B. Stojanović, A. Vencl, I. Bobić, S. Miladinović and J. Skerlić, Experimental optimisation of the tribological behaviour of Al/SiC/Gr hybrid composites based on Taguchi’s method and artificial neural network, J. Brazil. Soc. Mech. Sci. Eng., 2018, 40 DOI:10.1007/s40430-018-1237-y.
- M. Agarwal, M. Kumar Singh, R. Srivastava and R. K. Gautam, Microstructural measurement and artificial neural network analysis for adhesion of tribolayer during sliding wear of powder-chip reinforcement based composites, Measurement, 2021, 168, 108417 CrossRef.
- P. P. Ritapure and Y. R. Kharde, SiC contents and pin temperature effect on tribological properties of Al25Zn/SiC composites, Int. J. Refract. Met. Hard Mater., 2019, 82, 234–244 CrossRef CAS.
- K. S. Prakash, T. Thankachan and R. Radhakrishnan, Parametric optimization of dry sliding wear loss of copper–MWCNT composites, Trans. Nonferrous Met. Soc. China, 2017, 27, 627–637 CrossRef CAS.
- V. Kavimani and K. S. Prakash, Tribological behaviour predictions of r-GO reinforced Mg composite using ANN coupled Taguchi approach, J. Phys. Chem. Solids, 2017, 110, 409–419 CrossRef CAS.
- V. Kavimani, K. S. Prakash and T. Thankachan, Experimental investigations on wear and friction behaviour of SiC@r-GO reinforced Mg matrix composites produced through solvent-based powder metallurgy, Composites, Part B, 2019, 162, 508–521 CrossRef CAS.
- S. Li, M. Shao, C. Duan, Y. Yan, Q. Wang, T. Wang and X. Zhang, J. Appl. Polym. Sci., 2019, 136, 47157 CrossRef.
- S. Gangwar and V. K. Pathak, Dry sliding wear characteristics evaluation and prediction of vacuum casted marble dust (MD) reinforced ZA-27 alloy composites using hybrid improved bat algorithm and ANN, Mater. Today Commun., 2020, 25, 101615 CrossRef CAS.
- A. Vinoth and S. Datta, Design of the ultrahigh molecular weight polyethylene composites with multiple nanoparticles: An artificial intelligence approach, J. Compos. Mater., 2020, 54, 179–192 CrossRef CAS.
- S. Bhaumik, B. R. Mathew and S. Datta, Computational intelligence-based design of lubricant with vegetable oil blend and various nano friction modifiers, Fuel, 2019, 241, 733–743 CrossRef CAS.
- S. Bhaumik, S. D. Pathak, S. Dey and S. Datta, Artificial intelligence based design of multiple friction modifiers dispersed castor oil and evaluating its tribological properties, Tribol. Int., 2019, 140, 105813 CrossRef.
- S. S. Mahapatra and A. Patnaik, Study on mechanical and erosion wear behavior of hybrid composites using Taguchi experimental design, Mater. Des., 2009, 30, 2791–2801 CrossRef CAS.
- A. T. Sose, H. D. Cornell, B. J. Gibbons, A. A. Burris, A. J. Morris and S. A. Deshmukh, Modelling drug adsorption in metal–organic frameworks: the role of solvent, RSC Adv., 2021, 11, 17064–17071 RSC.
- P. Doubilet, C. B. Begg, M. C. Weinstein, P. Braun and B. J. McNeil, Probabilistic sensitivity analysis using Monte Carlo simulation. A practical approach, Med. Decis. Making, 1985, 5, 157–177 CrossRef CAS PubMed.
- G. Wübbeler, M. Krystek and C. Elster, Evaluation of measurement uncertainty and its numerical calculation by a Monte Carlo method, Meas. Sci. Technol., 2008, 19, 084009 CrossRef.
- X.-S. Yang, in Nature Inspired Cooperative Strategies for Optimization (NICSO 2010), ed. J. R. González, D. A. Pelta, C. Cruz, G. Terrazas and N. Krasnogor, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 65–74 Search PubMed.
- S. Yilmaz and E. U. Kucuksille, Improved bat algorithm (IBA) on continuous optimization problems, Lect. Notes Softw. Eng., 2013, 279–283 CrossRef.
- V. K. Pathak and A. K. Srivastava, A novel upgraded bat algorithm based on cuckoo search and Sugeno inertia weight for large scale and constrained engineering design optimization problems, Eng. Comput., 2022, 38, 1731–1758 CrossRef.
- H. T. Rauf, S. Malik, U. Shoaib, M. N. Irfan and M. I. Lali, Adaptive inertia weight Bat algorithm with Sugeno-Function fuzzy search, Appl. Soft Comput., 2020, 90, 106159 CrossRef.
- K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Trans. Evol. Comput., 2002, 6, 182–197 CrossRef.
- N. Srinivas and K. Deb, Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms, Evol. Comput., 1994, 2, 221–248 CrossRef.
- K. Deb, Multi-Objective Optimization using Evolutionary Algorithms, John Wiley & Sons, 2001 Search PubMed.
- S. Forrest, Genetic algorithms: principles of natural selection applied to computation, Science, 1993, 261, 872–878 CrossRef CAS PubMed.
- S. P. Collins, T. D. Daff, S. S. Piotrkowski and T. K. Woo, Materials design by evolutionary optimization of functional groups in metal–organic frameworks, Sci. Adv., 2016, 2, e1600954 CrossRef PubMed.
- T. K. Patra, V. Meenakshisundaram, J.-H. Hung and D. S. Simmons, Neural-Network-Biased Genetic Algorithms for Materials Design: Evolutionary Algorithms That Learn, ACS Comb. Sci., 2017, 19, 96–107 CrossRef CAS PubMed.
- S. P. Collins, T. D. Daff, S. S. Piotrkowski and T. K. Woo, Materials design by evolutionary optimization of functional groups in metal–organic frameworks, Sci. Adv., 2016, 2, e1600954 CrossRef PubMed.
- Y. G. Chung, D. A. Gómez-Gualdrón, P. Li, K. T. Leperi, P. Deria, H. Zhang, N. A. Vermeulen, J. Fraser Stoddart, F. You, J. T. Hupp, O. K. Farha and R. Q. Snurr, Sci. Adv., 2016, 2, e1600909 CrossRef PubMed.
- H. Abdi and L. J. Williams, Principal component analysis, Wiley Interdiscip. Rev. Comput. Stat., 2010, 2, 433–459 CrossRef.
- M. Ringnér, What is principal component analysis?, Nat. Biotechnol., 2008, 26, 303–304 CrossRef PubMed.
- S. Grossberg, Adaptive Resonance Theory: how a brain learns to consciously attend, learn, and recognize a changing world, Neural Network, 2013, 37, 1–47 CrossRef PubMed.
- A. V. Gavrilov and O. K. Alsova, Time series prediction using the adaptive resonance theory algorithm ART-2, J. Phys.: Conf. Ser., 2019, 1333, 032004 CrossRef.
- M. Subrahmanyam and C. Sujatha, Using neural networks for the diagnosis of localized defects in ball bearings, Tribol. Int., 1997, 30, 739–752 CrossRef.
- G.-B. Huang, Q.-Y. Zhu and C.-K. Siew, Extreme learning machine: Theory and applications, Neurocomputing, 2006, 70, 489–501 CrossRef.
- J. Wang, S. Lu, S.-H. Wang and Y.-D. Zhang, A review on extreme learning machine, Multimed. Tools Appl., 2022, 81, 41611–41660 CrossRef.
- M. A. Mujtaba, H. H. Masjuki, M. A. Kalam, H. C. Ong, M. Gul, M. Farooq, M. E. M. Soudagar, W. Ahmed, M. H. Harith and M. Yusoff, Ultrasound-assisted process optimization and tribological characteristics of biodiesel from palm-sesame oil via response surface methodology and extreme learning machine-Cuckoo search, Renewable Energy, 2020, 158, 202–214 CrossRef CAS.
- T. Takagi and M. Sugeno, Fuzzy identification of systems and its applications to modeling and control, IEEE Trans. Syst. Man Cybern., 1985, SMC-15, 116–132 Search PubMed.
- J.-S. R. Jang, ANFIS: adaptive-network-based fuzzy inference system, IEEE Trans. Syst. Man Cybern., 1993, 23, 665–685 CrossRef.
- S. Babajanzade Roshan, M. Behboodi Jooibari, R. Teimouri, G. Asgharzadeh-Ahmadi, M. Falahati-Naghibi and H. Sohrabpoor, Optimization of friction stir welding process of AA7075 aluminum alloy to achieve desirable mechanical properties using ANFIS models and simulated annealing algorithm, Int. J. Adv. Manuf. Technol., 2013, 69, 1803–1818 CrossRef.
- M. W. Dewan, D. J. Huggett, T. Warren Liao, M. A. Wahab and A. M. Okeil, Prediction of tensile strength of friction stir weld joints with adaptive neuro-fuzzy inference system (ANFIS) and neural network, Mater. Des., 2016, 92, 288–299 CrossRef CAS.
- S. K. Singh, K. K. Bejagam, Y. An and S. A. Deshmukh, Machine-Learning Based Stacked Ensemble Model for Accurate Analysis of Molecular Dynamics Simulations, J. Phys. Chem. A, 2019, 123, 5190–5198 CrossRef CAS PubMed.
- V. N. Vapnik, An overview of statistical learning theory, IEEE Trans. Neural Network, 1999, 10, 988–999 CrossRef CAS PubMed.
- Y. Yin, X. Liu, W. Huang, Y. Liu and S. Hu, Gas face seal status estimation based on acoustic emission monitoring and support vector machine regression, Adv. Mech. Eng., 2020, 12, 1687814020921323 Search PubMed.
- B. Das, S. Pal and S. Bag, Torque based defect detection and weld quality modelling in friction stir welding process, J. Manuf. Process., 2017, 27, 8–17 CrossRef.
- M. Perčić, S. Zelenika and I. Mezić, Artificial intelligence-based predictive model of nanoscale friction using experimental data, Friction, 2021, 9, 1726–1748 CrossRef.
- M. T
![[i with combining dot above]](https://www.rsc.org/images/entities/char_0069_0307.gif) mur and F. Aydin, Anticipating the friction coefficient of friction materials used in automobiles by means of machine learning without using a test instrument, Turk. J. Electr. Eng. Comput. Sci., 2013, 21, 1440–1454 CrossRef.
mur and F. Aydin, Anticipating the friction coefficient of friction materials used in automobiles by means of machine learning without using a test instrument, Turk. J. Electr. Eng. Comput. Sci., 2013, 21, 1440–1454 CrossRef. - M. S. Hasan, A. Kordijazi, P. K. Rohatgi and M. Nosonovsky, Triboinformatic modeling of dry friction and wear of aluminum base alloys using machine learning algorithms, Tribol. Int., 2021, 161, 107065 CrossRef CAS.
- M. S. Hasan, A. Kordijazi, P. K. Rohatgi and M. Nosonovsky, Triboinformatics Approach for Friction and Wear Prediction of Al-Graphite Composites Using Machine Learning Methods, J. Tribol., 2022, 144 DOI:10.1115/1.4050525.
- M. Marian, A. Almqvist, A. Rosenkranz and M. Fillon, Numerical micro-texture optimization for lubricated contacts—A critical discussion, Friction, 2022, 10, 1772–1809 CrossRef.
- M. Marian, J. Mursak, M. Bartz, F. J. Profito, A. Rosenkranz and S. Wartzack, Predicting EHL film thickness parameters by machine learning approaches, Friction, 2022, 1–22 Search PubMed.
- O. M. Braun and A. G. Naumovets, Nanotribology: Microscopic mechanisms of friction, Surf. Sci. Rep., 2006, 60, 79–158 CrossRef CAS.
- S. D. Kenny, D. Mulliah, C. F. Sanz-Navarro and R. Smith, Molecular dynamics simulations of nanoindentation and nanotribology, Philos. Trans. R. Soc., A, 2005, 363, 1949–1959 CrossRef CAS PubMed.
- I. Srivastava, A. Kotia, S. K. Ghosh and M. K. A. Ali, Recent advances of molecular dynamics simulations in nanotribology, J. Mol. Liq., 2021, 335, 116154 CrossRef CAS.
- J. D. Schall and D. W. Brenner, Molecular dynamics simulations of carbon nanotube rolling and sliding on graphite, Mol. Simul., 2000, 25, 73–79 CrossRef CAS.
- A. T. Sose, E. Mohammadi, P. F. Achari and S. A. Deshmukh, Determination of accurate interaction parameters between the molybdenum disulfide and water to investigate their Interfacial properties, J. Phys. Chem. C, 2022, 126, 2013–2022 CrossRef CAS.
- A. T. Sose, E. Mohammadi, F. Wang and S. A. Deshmukh, Investigation of structure and dynamics of water confined between hybrid layered materials of graphene, boron nitride, and molybdenum disulfide, J. Mater. Sci., 2022, 57, 10517–10534 CrossRef CAS.
- J. D. Schall, P. T. Mikulski, G. M. Chateauneuf, G. Gao and J. A. Harrison, Molecular dynamics simulations of tribology, Superlubricity, 2007, 79–102 Search PubMed.
- M. Kitabata, K. Fujimoto, N. Yoshii and S. Okazaki, A molecular dynamics study of local pressures and interfacial tensions of SDS micelles and dodecane droplets in water, J. Chem. Phys., 2016, 144, 224701 CrossRef PubMed.
- P. Geysermans, Molecular dynamics of the asymmetric solid–liquid interface, Mol. Phys., 2005, 103, 2717–2724 CrossRef CAS.
- A. Montazeri and A. Mobarghei, Nanotribological behavior analysis of graphene/metal nanocomposites via MD simulations: New concepts and underlying mechanisms, J. Phys. Chem. Solids, 2018, 115, 49–58 CrossRef CAS.
- P. Faucon, J. M. Delaye, J. Virlet, J. F. Jacquinot and F. Adenot, Study of the structural properties of the C□S□H(I) BY molecular dynamics simulation, Cem. Concr. Res., 1997, 27, 1581–1590 CrossRef CAS.
- Z. Fan, W. Chen, V. Vierimaa and A. Harju, Efficient molecular dynamics simulations with many-body potentials on graphics processing units, Comput. Phys. Commun., 2017, 218, 10–16 CrossRef CAS.
- V.-T. Nguyen and T.-H. Fang, Material removal and interactions between an abrasive and a SiC substrate: A molecular dynamics simulation study, Ceram. Int., 2020, 46, 5623–5633 CrossRef CAS.
- P. Naeiji, F. Varaminian and M. Rahmati, Comparison of the thermodynamic, structural and dynamical properties of methane/water and methane/water/hydrate systems using molecular dynamic simulations, J. Nat. Gas Sci. Eng., 2017, 44, 122–130 CrossRef CAS.
- H. Guo and N. Zhao, Interfacial layer simulation and effect on Cu-Ar nanofluids thermal conductivity using molecular dynamics method, J. Mol. Liq., 2018, 259, 40–47 CrossRef CAS.
- W. Yu and S. U. S. Choi, The Role of Interfacial Layers in the Enhanced Thermal Conductivity of Nanofluids: A Renovated Maxwell Model, J. Nanopart. Res., 2003, 5, 167–171 CrossRef CAS.
- H. Du and J. D. Miller, A molecular dynamics simulation study of water structure and adsorption states at talc surfaces, Int. J. Miner. Process., 2007, 84, 172–184 CrossRef CAS.
- P. Huang, Interfacial Phenomena of Talc Flotation and Depression, University of California, Berkeley, 1994 Search PubMed.
- E. W. Bucholz, S. R. Phillpot and S. B. Sinnott, Molecular dynamics investigation of the lubrication mechanism of carbon nano-onions, Comput. Mater. Sci., 2012, 54, 91–96 CrossRef CAS.
- S. Y. Joshi and S. A. Deshmukh, A review of advancements in coarse-grained molecular dynamics simulations, Mol. Simul., 2021, 47, 786–803 CrossRef CAS.
- S. Y. Joshi, S. Singh, K. K. Bejagam and S. A. Deshmukh, Dehydration of polymer chains initiates graphene folding in water, Carbon, 2021, 180, 244–253 CrossRef CAS.
- S. Y. Joshi, S. Singh and S. A. Deshmukh, Coarse-grained molecular dynamics integrated with convolutional neural network for comparing shapes of temperature sensitive bottlebrushes, npj Comput. Mater., 2022, 8, 45 CrossRef.
- E. Mohammadi, S. Y. Joshi and S. A. Deshmukh, A review of computational studies of bottlebrush polymers, Comput. Mater. Sci., 2021, 199, 110720 CrossRef CAS.
- P. Tian, Molecular dynamics simulations of nanoparticles, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2008, 104, 142–164 RSC.
- J.-M. Albina, A. Kubo, Y. Shiihara and Y. Umeno, Coarse-Grained Molecular Dynamics Simulations of Boundary Lubrication on Nanostructured Metal Surfaces, Tribol. Lett., 2020, 68, 1–9 CrossRef.
- Coarse-Grained Molecular Dynamic Simulations of Nanometer-Thick Polar Lubricant Films Sheared Between Solid Surfaces With Random Roughness, https://ieeexplore.ieee.org/abstract/document/7110364, (accessed 5 July 2022).
- L. C. Zhang and K. Mylvaganam, Nano-Tribological Analysis by Molecular Dynamics Simulation—A Review, J. Comput. Theor. Nanosci., 2006, 167–188 CrossRef CAS.
- R. Komanduri and L. M. Raff, A review on the molecular dynamics simulation of machining at the atomic scale, Proc. Inst. Mech. Eng., Part B, 2001, 215, 1639–1672 CrossRef.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, The ReaxFF reactive force-field: development, applications and future directions, npj Comput. Mater., 2016, 2, 1–14 CrossRef.
- S. B. Sinnott and D. W. Brenner, Three decades of many-body potentials in materials research, MRS Bull., 2012, 37, 469–473 CrossRef.
- J. A. Harrison, J. David Schall, S. Maskey, P. T. Mikulski, M. Todd Knippenberg and B. H. Morrow, Review of force fields and intermolecular potentials used in atomistic computational materials research, Appl. Phys. Rev., 2018, 5, 031104 Search PubMed.
- G. C. Abell, Empirical chemical pseudopotential theory of molecular and metallic bonding, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6184–6196 CrossRef CAS PubMed.
- J. Tersoff, New empirical approach for the structure and energy of covalent systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6991–7000 CrossRef PubMed.
- D. W. Brenner, Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9458–9471 CrossRef CAS PubMed.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons, J. Phys.: Condens. Matter, 2002, 14, 783–802 CrossRef CAS.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, A reactive potential for hydrocarbons with intermolecular interactions, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- N. Orekhov, G. Ostroumova and V. Stegailov, High temperature pure carbon nanoparticle formation: Validation of AIREBO and ReaxFF reactive molecular dynamics, Carbon, 2020, 170, 606–620 CrossRef CAS.
- M. Białoskórski and J. Rybicki, Mechanical Properties of Single-walled Carbon Nanotubes Simulated with AIREBO Force-Field, Comput. Methods Sci. Technol., 2012, 18, 67–77 CrossRef.
- M. Zarshenas, K. Moshkunov, B. Czerwinski, T. Leyssens and A. Delcorte, Molecular Dynamics Simulations of Hydrocarbon Film Growth from Acetylene Monomers and Radicals: Effect of Substrate Temperature, J. Phys. Chem. C, 2018, 122, 15252–15263 CrossRef CAS.
- J. Yu, S. B. Sinnott and S. R. Phillpot, Charge optimized many-body potential for the Si/SiO2 system, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 085311 CrossRef.
- T.-R. Shan, B. D. Devine, J. M. Hawkins, A. Asthagiri, S. R. Phillpot and S. B. Sinnott, Second-generation charge-optimized many-body potential for Si/SiO2 and amorphous silica, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 235302 CrossRef.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- J. A. Harrison and D. W. Brenner, J. Am. Chem. Soc., 1994, 116, 10399–10402 CrossRef CAS.
- G. T. Gao, P. T. Mikulski and J. A. Harrison, J. Am. Chem. Soc., 2002, 124, 7202–7209 CrossRef CAS PubMed.
- J. D. Schall, J. David Schall, G. Gao and J. A. Harrison, J. Phys. Chem. C, 2010, 114, 5321–5330 CrossRef CAS.
- L. Pastewka, S. Moser and M. Moseler, Tribol. Lett., 2010, 39, 49–61 CrossRef CAS.
- P. Stoyanov, P. Stemmer, T. T. Järvi, R. Merz, P. A. Romero, M. Scherge, M. Kopnarski, M. Moseler, A. Fischer and M. Dienwiebel, ACS Appl. Mater. Interfaces, 2013, 5, 6123–6135 CrossRef CAS PubMed.
- P. Stoyanov, P. A. Romero, R. Merz, M. Kopnarski, M. Stricker, P. Stemmer, M. Dienwiebel and M. Moseler, Acta Mater., 2014, 67, 395–408 CrossRef CAS.
- L. Pastewka, S. Moser, P. Gumbsch and M. Moseler, Anisotropic mechanical amorphization drives wear in diamond, Nat. Mater., 2011, 10, 34–38 CrossRef CAS PubMed.
- P. Stoyanov, P. A. Romero, T. T. Järvi, L. Pastewka, M. Scherge, P. Stemmer, A. Fischer, M. Dienwiebel and M. Moseler, Tribol. Lett., 2013, 50, 67–80 CrossRef CAS.
- N. Juslin, P. Erhart, P. Träskelin, J. Nord, K. O. E. Henriksson, K. Nordlund, E. Salonen and K. Albe, Analytical interatomic potential for modeling nonequilibrium processes in the W–C–H system, J. Appl. Phys., 2005, 98, 123520 CrossRef.
- G. Moras, A. Klemenz, T. Reichenbach, A. Gola, H. Uetsuka, M. Moseler and L. Pastewka, Shear melting of silicon and diamond and the disappearance of the polyamorphic transition under shear, Phys. Rev. Mater., 2018, 2, 083601 CrossRef CAS.
- J. Wen, T. Ma, W. Zhang, A. C. T. van Duin, D. M. van Duin, Y. Hu and X. Lu, J. Phys. Chem. C, 2019, 123, 26467–26474 CrossRef CAS.
- J. Yeon, A. C. T. van Duin and S. H. Kim, Langmuir, 2016, 32, 1018–1026 CrossRef CAS PubMed.
- D.-C. Yue, T.-B. Ma, Y.-Z. Hu, J. Yeon, A. C. T. van Duin, H. Wang and J. Luo, Langmuir, 2015, 31, 1429–1436 CrossRef CAS PubMed.
- J. Wen, T. Ma, W. Zhang, A. C. T. van Duin and X. Lu, Comput. Mater. Sci., 2017, 131, 230–238 CrossRef CAS.
- P. A. Romero, L. Mayrhofer, P. Stoyanov, R. Merz, M. Kopnarski, M. Dienwiebel and M. Moseler, Atomistic Insights Into Lubricated Tungsten/Diamond Sliding Contacts, Front. Mech. Eng., 2019, 5, 6 CrossRef.
- A. Rosenkranz, H. L. Costa, M. Z. Baykara and A. Martini, Tribol. Int., 2021, 155, 106792 CrossRef CAS.
- K. R. Hasz, M. R. Vazirisereshk, A. Martini and R. W. Carpick, Bifurcation of nanoscale thermolubric friction behavior for sliding on MoS2, Phys. Rev. Mater., 2021, 5, 083607 CrossRef CAS.
- Z. Chen, A. Khajeh, A. Martini and S. H. Kim, Origin of High Friction at Graphene Step Edges on Graphite, ACS Appl. Mater. Interfaces, 2021, 13, 1895–1902 CrossRef CAS PubMed.
- R. Chen, A. Jusufi, A. Schilowitz and A. Martini, J. Vac. Sci. Technol., A, 2020, 38, 022201 CrossRef CAS.
- F. Wang, A. T. Sose, S. K. Singh and S. A. Deshmukh, Dual-Force Zone Nonequilibrium Molecular Dynamics Simulations on Nanoporous Metal–Organic Framework Membranes for Separation of H2/CH4 Mixtures, ACS Appl. Nano Mater., 2022, 5, 4048–4061 CrossRef CAS.
- V. Jadhao and M. O. Robbins, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7952–7957 CrossRef CAS PubMed.
- T. Kuwahara, P. A. Romero, S. Makowski, V. Weihnacht, G. Moras and M. Moseler, Mechano-chemical decomposition of organic friction modifiers with multiple reactive centres induces superlubricity of ta-C, Nat. Commun., 2019, 10, 151 CrossRef PubMed.
- S. Loehlé and M. Righi, Lubricants, 2018, 6, 31 CrossRef.
- E. J. Maginn and J. R. Elliott, Ind. Eng. Chem. Res., 2010, 49, 3059–3078 CrossRef CAS.
- G. P. Morriss and D. J. Evans, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 792–797 CrossRef PubMed.
- D. J. Evans and G. P. Morriss, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 4142–4148 CrossRef CAS PubMed.
- R. Khare, J. de Pablo and A. Yethiraj, J. Chem. Phys., 1997, 107, 6956–6964 CrossRef CAS.
- S. T. Cui, P. T. Cummings and H. D. Cochran, J. Chem. Phys., 1996, 104, 255–262 CrossRef CAS.
- H. J. Choi, Q. Guo, P. S. Chung and M. S. Jhon, IEEE Trans. Magn., 2007, 43, 903–905 CAS.
- G. Arya, E. J. Maginn and H.-C. Chang, Efficient viscosity estimation from molecular dynamics simulation via momentum impulse relaxation, J. Chem. Phys., 2000, 113, 2079–2087 CrossRef CAS.
- S. Bair, C. McCabe and P. T. Cummings, Comparison of nonequilibrium molecular dynamics with experimental measurements in the nonlinear shear-thinning regime, Phys. Rev. Lett., 2002, 88, 058302 CrossRef PubMed.
- B. V. Raghavan and M. Ostoja-Starzewski, Shear-thinning of molecular fluids in Couette flow, Phys. Fluids, 2017, 29, 023103 CrossRef.
- P. Liu, J. Lu, H. Yu, N. Ren, F. E. Lockwood and Q. J. Wang, Lubricant shear thinning behavior correlated with variation of radius of gyration via molecular dynamics simulations, J. Chem. Phys., 2017, 147, 084904 CrossRef PubMed.
- J. P. Ewen, C. Gattinoni, F. M. Thakkar, N. Morgan, H. A. Spikes and D. Dini, A Comparison of Classical Force-Fields for Molecular Dynamics Simulations of Lubricants, Materials, 2016, 9, 651 CrossRef PubMed.
- J. S. Bhamra, J. P. Ewen, C. A. Latorre, J. A. R. Bomidi, M. W. Bird, N. Dasgupta, A. C. T. van Duin and D. Dini, Interfacial Bonding Controls Friction in Diamond–Rock Contacts, J. Phys. Chem. C, 2021, 125, 18395–18408 CrossRef CAS.
- J. P. Ewen, C. Gattinoni, N. Morgan, H. A. Spikes and D. Dini, Nonequilibrium Molecular Dynamics Simulations of Organic Friction Modifiers Adsorbed on Iron Oxide Surfaces, Langmuir, 2016, 32, 4450–4463 CrossRef CAS PubMed.
- J. P. Ewen, S. Echeverri Restrepo, N. Morgan and D. Dini, Nonequilibrium molecular dynamics simulations of stearic acid adsorbed on iron surfaces with nanoscale roughness, Tribol. Int., 2017, 107, 264–273 CrossRef CAS.
- J. P. Ewen, E. R. Fernández, E. R. Smith and D. Dini, Model. Simul. Tribol. Problems Technol., 2020, 95–130 CAS.
- D. M. Heyes, D. Dini and E. R. Smith, Incremental viscosity by non-equilibrium molecular dynamics and the Eyring model, J. Chem. Phys., 2018, 148, 194506 CrossRef CAS PubMed.
- H. Gao, J. P. Ewen, R. Hartkamp, M. H. Müser and D. Dini, Scale-Dependent Friction–Coverage Relations and Nonlocal Dissipation in Surfactant Monolayers, Langmuir, 2021, 37, 2406–2418 CrossRef CAS PubMed.
- C. Ayestarán Latorre, J. E. Remias, J. D. Moore, H. A. Spikes, D. Dini and J. P. Ewen, Mechanochemistry of phosphate esters confined between sliding iron surfaces, Commun. Chem., 2021, 4, 1–11 CrossRef PubMed.
- L. Maffioli, E. R. Smith, J. P. Ewen, P. J. Daivis, D. Dini and B. D. Todd, Slip and stress from low shear rate nonequilibrium molecular dynamics: The transient-time correlation function technique, J. Chem. Phys., 2022, 156, 184111 CrossRef CAS PubMed.
- C. D. Quach, J. B. Gilmer, D. Pert, A. Mason-Hogans, C. R. Iacovella, P. T. Cummings and C. McCabe, High-throughput screening of tribological properties of monolayer films using molecular dynamics and machine learning, J. Chem. Phys., 2022, 156, 154902 CrossRef CAS PubMed.
- J. C. S. Kadupitiya and V. Jadhao, Probing the Rheological Properties of Liquids Under Conditions of Elastohydrodynamic Lubrication Using Simulations and Machine Learning, Tribol. Lett., 2021, 69, 82 CrossRef CAS.
- B. Sattari Baboukani, Z. Ye, K. G. Reyes and P. C. Nalam, Prediction of Nanoscale Friction for Two-Dimensional Materials Using a Machine Learning Approach, Tribol. Lett., 2020, 68, 57 CrossRef CAS.
- M. A. Zaidan, F. F. Canova, L. Laurson and A. S. Foster, Mixture of Clustered Bayesian Neural Networks for Modeling Friction Processes at the Nanoscale, J. Chem. Theory Comput., 2017, 13, 3–8 CrossRef CAS PubMed.
- A. Z. Summers, J. B. Gilmer, C. R. Iacovella, P. T. Cummings and C. McCabe, MoSDeF, a Python Framework Enabling Large-Scale Computational Screening of Soft Matter: Application to Chemistry-Property Relationships in Lubricating Monolayer Films, J. Chem. Theory Comput., 2020, 16, 1779–1793 CrossRef CAS PubMed.
- C. S. Adorf, P. M. Dodd, V. Ramasubramani and S. C. Glotzer, Simple data and workflow management with the signac framework, Comput. Mater. Sci., 2018, 146, 220–229 CrossRef.
- G. Landrum, et al., RDKit: Open-source cheminformatics.
- J. M. Bernardo and A. F. M. Smith, Bayesian Theory, John Wiley & Sons, 2009 Search PubMed.
- W. M. Bolstad and J. M. Curran, Introduction to Bayesian Statistics, John Wiley & Sons, 2016 Search PubMed.
- R. van de Schoot, S. Depaoli, R. King, B. Kramer, K. Märtens, M. G. Tadesse, M. Vannucci, A. Gelman, D. Veen, J. Willemsen and C. Yau, Bayesian statistics and modelling, Nat. Rev. Methods Primers, 2021, 1, 1–26 CrossRef CAS.
- A. Savara and E. A. Walker, CheKiPEUQ intro 1: Bayesian parameter estimation considering uncertainty or error from both experiments and theory, ChemCatChem, 2020, 12, 5385–5400 CrossRef CAS.
- E. A. Walker, K. Ravisankar and A. Savara, CheKiPEUQ intro 2: Harnessing uncertainties from data sets, Bayesian design of experiments in chemical kinetics, ChemCatChem, 2020, 12, 5401–5410 CrossRef CAS.
- S. Xie, T. Yang, X. Wang and Y. Lin, 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015.
- M. W. Floyd, J. T. Turner and D. W. Aha, 2017 AAAI Spring Symposium Series, 2017.
- C. Tang, Y. Feng, X. Yang, C. Zheng and Y. Zhou, 2017 4th International Conference on Information Science and Control Engineering (ICISCE), 2017, pp. 723–728.
- Z. Li, F. Liu, W. Yang, S. Peng and J. Zhou, A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects, IEEE Trans. Neural Netw. Learn. Syst., 2021 DOI:10.1109/TNNLS.2021.3084827.
- S. Y. Joshi, S. Singh and S. A. Deshmukh, Coarse-grained molecular dynamics integrated with convolutional neural network for comparing shapes of temperature sensitive bottlebrushes, npj Comput. Mater., 2022, 8, 1–12 CrossRef.
- V. Pandiyan, J. Prost, G. Vorlaufer, M. Varga and K. Wasmer, Identification of abnormal tribological regimes using a microphone and semi-supervised machine-learning algorithm, Friction, 2022, 10, 583–596 CrossRef.
- M. Wang, L. Yang, Z. Zhao and Y. Guo, Intelligent prediction of wear location and mechanism using image identification based on improved Faster R-CNN model, Tribol. Int., 2022, 169, 107466 CrossRef.
- Y. Peng, J. Cai, T. Wu, G. Cao, N. Kwok, S. Zhou and Z. Peng, A hybrid convolutional neural network for intelligent wear particle classification, Tribol. Int., 2019, 138, 166–173 CrossRef.
- X. Liu, L. Cheng, G. Chen, X. Wang and J. Wang, Recognition of fatigue and severe sliding wear particles using a CNN model with multi-scale feature extractor, Ind. Lubr. Tribol., 2022, 74, 884–891 CrossRef.
- P. S. Desai, V. Granja and C. F. Higgs, Lifetime Prediction Using a Tribology-Aware, Deep Learning-Based Digital Twin of Ball Bearing-Like Tribosystems in Oil and Gas, Processes, 2021, 9, 922 CrossRef CAS.
- K. Wang, C. Gou, Y. Duan, Y. Lin, X. Zheng and F.-Y. Wang, Generative adversarial networks: introduction and outlook, IEEE/CAA J. Autom. Sin., 2017, 4, 588–598 Search PubMed.
- A. Creswell, T. White, V. Dumoulin, K. Arulkumaran, B. Sengupta and A. A. Bharath, Generative Adversarial Networks: An Overview, IEEE Signal Process. Mag., 2018, 35, 53–65 Search PubMed.
- J. Gui, Z. Sun, Y. Wen, D. Tao and J. Ye, A Review on Generative Adversarial Networks: Algorithms, Theory, and Applications, IEEE Trans. Knowl. Data Eng., 2021, 1 Search PubMed.
- D. P. Kingma and M. Welling, Auto-encoding variational bayes, arXiv, 2013 DOI:10.48550/arXiv.1312.6114.
- C. R. Shurer, Y. Wang, E. Feeney, S. E. Head, V. X. Zhang, J. Su, Z. Cheng, M. A. Stark, L. J. Bonassar, H. L. Reesink and M. J. Paszek, Stable recombinant production of codon-scrambled lubricin and mucin in human cells, Biotechnol. Bioeng., 2019, 116, 1292–1303 CrossRef CAS PubMed.
- W. Kightlinger, K. F. Warfel, M. P. DeLisa and M. C. Jewett, Synthetic Glycobiology: Parts, Systems, and Applications, ACS Synth. Biol., 2020, 9, 1534–1562 CrossRef CAS PubMed.
- R. M. Ronchi, J. T. Arantes and S. F. Santos, Ceram. Int., 2019, 45, 18167–18188 CrossRef CAS.
- M. Malaki and R. S. Varma, Mechanotribological Aspects of MXene-Reinforced Nanocomposites, Adv. Mater., 2020, 32, e2003154 CrossRef PubMed.
- M. Marian, K. Feile, B. Rothammer, M. Bartz, S. Wartzack, A. Seynstahl, S. Tremmel, S. Krauß, B. Merle, T. Böhm, B. Wang, B. C. Wyatt, B. Anasori and A. Rosenkranz, Ti3C2Tx solid lubricant coatings in rolling bearings with remarkable performance beyond state-of-the-art materials, Appl. Mater. Today, 2021, 25, 101202 CrossRef.
- N. J. Fox and G. W. Stachowiak, Tribol. Int., 2007, 40, 1035–1046 CrossRef CAS.
- S. Boyde, Green lubricants. Environmental benefits and impacts of lubrication, Green Chem., 2002, 4, 293–307 RSC.
- S. Soni and M. Agarwal, Green Chem. Lett. Rev., 2014, 7, 359–382 CrossRef.
- J. Salimon, N. Salih and E. Yousif, Eur. J. Lipid Sci. Technol., 2010, 112, 519–530 CrossRef CAS.
- D. Kania, R. Yunus, R. Omar, S. A. Rashid and B. M. Jan, J. Pet. Sci. Eng., 2015, 135, 177–184 CrossRef CAS.
- J. Salimon, B. M. Abdullah, R. M. Yusop and N. Salih, Synthesis, reactivity and application studies for different biolubricants, Chem. Cent. J., 2014, 8, 16 CrossRef PubMed.
- G. Appiah, S. K. Tulashie, E. E. A. Akpari, E. R. Rene and D. Dodoo, Int. J. Energy Res., 2022, 46, 3860–3890 CrossRef CAS.
- N. Salih, J. Salimon and E. Yousif, Ind. Crops Prod., 2011, 34, 1089–1096 CrossRef CAS.
- K. D. Carlson, R. Kleiman and M. O. Bagby, J. Am. Oil Chem. Soc., 1994, 71, 175–182 CrossRef CAS.
- V. V. Goud, A. V. Patwardhan and N. C. Pradhan, Studies on the epoxidation of mahua oil (Madhumica indica) by hydrogen peroxide, Bioresour. Technol., 2006, 97, 1365–1371 CrossRef CAS PubMed.
- M. A. Jedrzejczyk, S. Van den Bosch, J. Van Aelst, K. Van Aelst, P. D. Kouris, M. Moalin, G. R. M. Haenen, M. D. Boot, E. J. M. Hensen, B. Lagrain, B. F. Sels and K. V. Bernaerts, ACS Sustainable Chem. Eng., 2021, 9, 12548–12559 CrossRef CAS.
- W. Li and X. Wang, J. Oleo Sci., 2015, 64, 367–374 CrossRef CAS PubMed.
- S. Marmesat, A. Morales, J. Velasco and M. Carmen Dobarganes, Food Chem., 2012, 135, 2333–2339 CrossRef CAS PubMed.
- N. H. Jayadas and K. Prabhakaran Nair, Tribol. Int., 2006, 39, 873–878 CrossRef CAS.
- C. J. Reeves, A. Siddaiah and P. L. Menezes, Coconut oil as base oil for industrial lubricants—evaluation and modification of thermal, oxidative and low temperature properties, J. Bio- Tribo-Corrosion, 2017, 3, 873–878 Search PubMed.
- C. K. Ho, K. B. McAuley and B. A. Peppley, Renewable Sustainable Energy Rev., 2019, 113, 109261 CrossRef CAS.
- G. Biresaw, J. Synth. Lubr., 2004, 21, 43–57 CrossRef CAS.
- A. Viswanathan, Effect of Degree of Substitution of Octenyl Succinate Starch on the Emulsification Activity on Different Oil Phases, J. Environ. Polym. Degrad., 1999, 7, 191–196 CrossRef CAS.
- G. F. Fanta and K. Eskins, Carbohydr. Polym., 1995, 28, 171–175 CrossRef CAS.
- G. Biresaw and S. M. Erhan, J. Am. Oil Chem. Soc., 2002, 79, 291–296 CrossRef CAS.
- G. Biresaw and R. Shogren, J. Synth. Lubr., 2008, 25, 17–30 CrossRef CAS.
- G. Biresaw, J. A. Kenar, T. L. Kurth, F. C. Felker and S. M. Erhan, Lubr. Sci., 2007, 19, 41–55 CrossRef CAS.
- A. Iqbal, J. Hong, T. Y. Ko and C. M. Koo, Improving oxidation stability of 2D MXenes: synthesis, storage media, and conditions, Nano Convergence, 2021, 8, 9 CrossRef CAS PubMed.
- M. Khazaei, A. Ranjbar, M. Arai, T. Sasaki and S. Yunoki, J. Mater. Chem. C, 2017, 5, 2488–2503 RSC.
- W. Lian, Y. Mai, C. Liu, L. Zhang, S. Li and X. Jie, Ceram. Int., 2018, 44, 20154–20162 CrossRef CAS.
- M. Xue, Z. Wang, F. Yuan, X. Zhang, W. Wei, H. Tang and C. Li, RSC Adv., 2017, 7, 4312–4319 RSC.
- Y. Liu, X. Zhang, S. Dong, Z. Ye and Y. Wei, J. Mater. Sci., 2017, 52, 2200–2209 CrossRef CAS.
- S. Yi, Y. Guo, J. Li, Y. Zhang, A. Zhou and J. Luo, Synthesis and tribological property of Ti3C2TX nanosheets, Friction, 2022, 52, 2200–2209 Search PubMed.
- A. Rosenkranz, P. G. Grützmacher, R. Espinoza, V. M. Fuenzalida, E. Blanco, N. Escalona, F. J. Gracia, R. Villarroel, L. Guo, R. Kang, F. Mücklich, S. Suarez and Z. Zhang, Appl. Surf. Sci., 2019, 494, 13–21 CrossRef CAS.
- E. Marquis, M. Cutini, B. Anasori, A. Rosenkranz and M. C. Righi, Nanoscale MXene Interlayer and Substrate Adhesion for Lubrication: A Density Functional Theory Study, ACS Appl. Nano Mater., 2022, 5, 10516–10527 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03692d |
| This journal is © the Owner Societies 2023 |