Open Access Article
Open Access ArticleTowards de novo design of transmembrane α-helical assemblies using structural modelling and molecular dynamics simulation
Ai
Niitsu
 *a and
Yuji
Sugita
*a and
Yuji
Sugita
 *abc
*abc
aTheoretical Molecular Science Laboratory, RIKEN Cluster for Pioneering Research, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan. E-mail: ai.niitsu@riken.jp; sugita@riken.jp
bComputational Biophysics Research Team, RIKEN Center for Computational Science, 7-1-26 Minatojima-minamimachi, Chuo-ku, Kobe, Hyogo 650-0047, Japan
cLaboratory for Biomolecular Function Simulation, RIKEN Center for Biosystems Dynamics Research, 6-7-1 Minatojima-minamimachi, Chuo-ku, Kobe, Hyogo 650-0047, Japan
First published on 17th January 2023
Abstract
Computational de novo protein design involves iterative processes consisting of amino acid sequence design, structural modelling and scoring, and design validation by synthesis and experimental characterisation. Recent advances in protein structure prediction and modelling methods have enabled the highly efficient and accurate design of water-soluble proteins. However, the design of membrane proteins remains a major challenge. To advance membrane protein design, considering the higher complexity of membrane protein folding, stability, and dynamic interactions between water, ions, lipids, and proteins is an important task. For introducing explicit solvents and membranes to these design methods, all-atom molecular dynamics (MD) simulations of designed proteins provide useful information that cannot be obtained experimentally. In this review, we first describe two major approaches to designing transmembrane α-helical assemblies, consensus and de novo design. We further illustrate recent MD studies of membrane protein folding related to protein design, as well as advanced treatments in molecular models and conformational sampling techniques in the simulations. Finally, we discuss the possibility to introduce MD simulations after the existing static modelling and screening of design decoys as an additional step for refinement of the design, which considers membrane protein folding dynamics and interactions with explicit membranes.
1. Introduction
Rational protein design is a bottom-up approach for understanding protein folding by exploring relationships between amino acid sequences and tertiary/quaternary structure. In addition, the ability to create artificial proteins with desired structures and functions provides novel protein materials for applications in therapeutics and molecular devices.1 Remarkable progress has been made in protein design research in the last decade. Originally started with simplified sequence patterning, the rational design of artificial proteins with highly complex structures and functions is now attainable, assisted by recent advances in computational structure prediction and design methods2 as well as the increasing number of high-resolution experimental structures. High-resolution structures provide the sequence-to-structure relationships that can guide protein design. The total number of unique protein sequences in the structure database (Protein Data Bank (PDB; https://www.rcsb.org/)3) is approximately 76000, of which the majority are water-soluble proteins. In contrast, the number of unique sequences in the Membrane Proteins of Known Structure database (mpstruc; https://blanco.biomol.uci.edu/mpstruc/)4 is approximately 1400. This ratio between water-soluble and membrane proteins in structure databases is reflected in the number of reported structures of rationally designed proteins,2 highlighting that membrane protein design is still in its infancy.Approaches to designing a new artificial protein can be roughly classified into two types: using a scaffold of natural proteins or creating one from scratch. Consensus design is representative of the former design approach. It utilises the multiple sequence alignment (MSA) of a target protein family,5 as it relies on scaffold structures optimised through evolution. This makes the design process relatively straightforward, whereas lower degrees of freedom are left in the protein structures to be designed. The latter de novo protein design explores a wider structural space, including protein folds that do not exist (or are not yet observed) in nature. This is more challenging than consensus design, as it requires a deeper understanding of protein folding. Fig. 1 shows a few representative designed proteins available on the PDB. This highlights that de novo designed proteins tend to have simpler and more symmetric structures than those obtained through consensus design because of their design rationales.
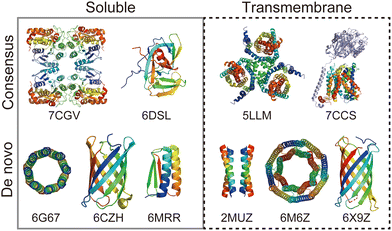 | ||
| Fig. 1 Representative structures of rationally designed soluble (left) and transmembrane (right) proteins deposited to PDB. (top) Consensus designs: full consensus L-threonine 3-dehydrogenase (7CGV);9 engineered intein with atypical split-site (6DSL);10 thermostabilized EAAT1 (5LLM);11 consensus-mutated xCT-CD98hc complex (7CCS).12 (bottom) De novo designs: parallel eight-helix coiled–coil CC-Type2-II (6G67);13 mini-fluorescence-activating proteins mFAP0 (6CZH);14 Foldit1 designed by citizen scientists (6MRR);15 Zn2+ transporter ROCKER (2MUZ);16 transmembrane nanopore TMH4C4 (6M6Z);17 transmembrane beta-barrel (6X9Z).18 | ||
Based on statistics in the structural database and previous design studies, the most challenging combination of targets and methods is the de novo design of membrane proteins. To achieve highly accurate de novo designs, further understandings of membrane protein folding are necessary, as well as deeper knowledge of biological membrane environments. Molecular dynamics (MD) simulations can be a promising approach for investigating structural dynamics, folding processes, and molecular interactions at atomistic resolutions. All-atom MD simulations of a relatively small membrane protein in a lipid bilayer are feasible using conventional PC clusters or GPU computers. Transmembrane α-helices and their assemblies are fundamental structures in all membrane proteins and are suitable targets in MD simulations not yet fully explored in the design field.6 In this perspective article, by focusing on membrane α-helical assemblies, we introduce recent designs and the remaining challenges. Furthermore, we illustrate recent molecular models and conformational sampling algorithms in MD simulations, which could be applicable to the de novo design of transmembrane α-helical assemblies as the final additional step for increasing the success rate. Because this perspective article is not intended to cover the full history of rational protein design, see other reviews for more comprehensive methods and developments.2,7,8
2. Methods for the rational design of membrane proteins
In this section, we review current approaches for designing membrane proteins and their outcomes. Fig. 2 shows two major methods: consensus design and computational de novo design.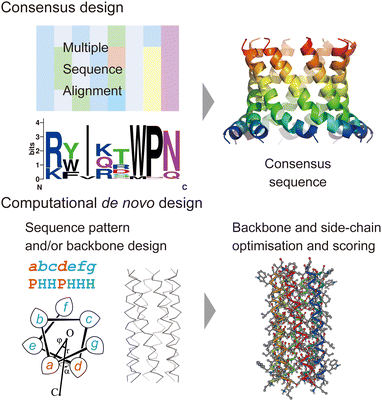 | ||
| Fig. 2 Consensus design (top) and de novo design (bottom). The consensus design involves multiple sequence alignments (MSAs), which yield consensus residues in amino acid sequences. Computational de novo design consists of sequence pattern design and backbone design followed by iterative optimisation of backbone and sidechain structure models. The 3D model was created using CC Builder 2.0.19 | ||
2.1 Consensus design
Consensus design uses MSAs for a target protein and its homologues. By selecting the most conserved amino acid at each position, successful designs can provide greater structural stability while preserving or even enhancing their functions (Fig. 2).5 Multiple sequence alignments among a protein family can be obtained using sequence alignment databases, such as Pfam,20 SMART,21 and InterPro.22 Alternatively, homologous sequences can be globally searched in various protein sequence databases using protein BLAST searches23 (https://blast.ncbi.nlm.nih.gov/Blast.cgi). To identify consensus sequences, web servers, such as EMBOS Cons24 (https://www.ebi.ac.uk/Tools/msa/emboss_cons/) and WebLogo25 (https://weblogo.berkeley.edu/logo.cgi), are available. There are also web tools that provide automated prediction of stabilising consensus substitutions to a target protein: consensus finder (https://kazlab.umn.edu/), which performs MSA and consensus sequence analysis, and FireProt (https://loschmidt.chemi.muni.cz/fireprotweb/), which combines MSA and structural modelling. Notably, approximately 50% of single mutations with conserved residues contribute to improved stability, and the rest are neutral or destabilizing.5 Nonetheless, multiple mutations in the design of a full consensus sequence are known to result in high stability. One reason for this is that the residues in a folded protein could co-vary to maintain the structure through evolution.26–28 Related to this idea, evolutionary coupling algorithms have been developed, in which contacting residues are identified through covariation analysis of MSA data.29 Evolutionary information can also guide the design and modelling of proteins.30 The combination of MSA and structural modelling was further extended through machine learning to accurately predict 3D protein structures using AlphaFold231 and RosettaFold.32In terms of the consensus design for membrane proteins, MSA data of a target membrane protein usually have the inherent ability to make it highly stable in membrane environments. This eliminates the need to consider the effect of membranes on designed sequences and is likely to increase the success rate. Consensus design has been applied to increase the thermal stability of membrane proteins that are difficult to treat experimentally.5,11,12 New artificial membrane proteins were also designed using MSA data. One example is a four-transmembrane protein, REAMP, which was designed based on a sequence pattern obtained from MSA of a small multidrug resistance protein family using only four types of amino acids.33
Another example is the cWza peptide, whose sequence was optimised through MSA of the membrane domain of the bacterial polysaccharide exporter, Wza34 (Fig. 3a). The Wza protein exists in the outer membrane of Gram-negative bacteria and forms octameric pores. Based on its crystal structure,35 it consists of four domains: domains 1–3 are periplasmic and domain 4 has a transmembrane barrel structure with eight parallel helices arranged in rotational symmetry (Fig. 3b). To form a stable peptide pore based on domain 4 of Wza, three peptides with the wild-type sequence, a consensus sequence (cWza), and a cWza sequence with Cys substitution to Tyr373 (Y373C) were designed (Fig. 3a). Molecular dynamics simulations of the barrel models of cWza and Y373C predicted that Y373C can form a more stable barrel than cWza (Fig. 3c). In octameric barrel models and MD simulations, the Cys substitution stabilises Knobs-into-Hole packing between helices, which contributes the pore stability (Fig. 3d). Indeed, single-channel electrical recordings where real-time pore formation can be observed36 showed that Y373C formed the most stable pore among these three peptides, almost equivalent to the pores formed by natural proteins (Fig. 3e). The cWza and the wild-type peptides showed two-state pores and no pore formation, respectively. Further characterisation of the Y373C pore indicated that it consists of at least eight parallel helices, consistent with the protein crystal structure. These results highlight that the combination of MSA and rational design guided by structure modelling and MD simulations can be a powerful approach for obtaining novel, stable membrane proteins.
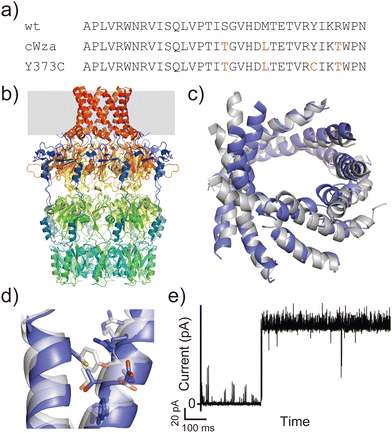 | ||
| Fig. 3 Consensus design of cWza peptide. (a) Amino acid sequences of wild-type, cWza, and cWza-Y373C peptides. Mutated consensus residues are shown in red. (b) Crystal structure of Wza protein (PDB ID: 2J58).35 The outer membrane region is shown with a grey background. (c) Snapshots of cWza (grey) and cWza-Y373C (blue) barrel structures after 200 ns all-atom MD simulations with a DPhPC bilayer in 1 M KCl. (d) Overlayed structures of cWza (grey) and cWza-Y373C (blue) barrel models at the helix–helix interface around the Y/C373 residue. Residues involved in the Knobs-Into-Hole packing are shown with sticks. (e) Electrical recording of the cWza-Y373C peptide representing its pore formation. | ||
2.2 De novo design
Historically, the de novo design of membrane proteins was initiated with the simple sequence patterning of α-helical peptides using structural motifs found in natural helical bundles, such as [GAS]xxx[GAS], ([GAS]-x6)n, and coiled coils.7 Building on these pioneering designs, recent advances in computational protein design have enabled us to conduct sequence and structural designs involving iterations of backbone-structure optimisation, side-chain search to satisfy the backbone structure, and further structural optimisation of the all-atom model (Fig. 2). The keys to successful designs lie in finding physically plausible (i.e. designable) backbone structures which realise target folds8,37,38 and reliable structural modelling and assessment with appropriate force fields upon side-chain addition.2,7,8 These processes often involve generating hundreds to thousands of sequences/structures followed by rapid scoring. Therefore, these are aided by computational design suites such as Rosetta,39 ISAMBARD,40 OSPREY,41 Damietta,42 and dTERMen.43 In the de novo design of membrane proteins, the implementation of the effect of a lipid bilayer into an amino acid sequence is one more important key for successful designs. There are two methods to introduce the membrane environment to the computational design of transmembrane α-helical assemblies: (1) optimising a protein structure starting from a water-soluble one, followed by replacing membrane-exposed positions in a designed sequence with amino acid residues that specify its membrane topology, and (2) using scoring functions that include information about the interaction between amino acid residues and a lipid bilayer.In the former approach, a tight helix–helix packing is optimised, and the exterior of helical bundles is designed towards a transmembrane topology by introducing hydrophobic and aromatic/Lys residues to match the alkyl-chain and interface regions, respectively. For example, Baker et al. reported assemblies of subunits with multi-pass transmembrane helices stabilised by hydrogen-bond networks found in the de novo design of soluble helical bundles.44 Transmembrane pores consisting of four transmembrane subunits were converted from the design of water-soluble barrels17 using the Rosetta design suite.39 Another example is a peptide-based ion channel constructed by converting and optimising a water-soluble coiled–coil peptide barrel into a transmembrane topology.45 In this design, a water-soluble coiled–coil barrel with five heptad repeats (alphabetical register: abcdefg) designed previously46 was used as the scaffold. Polar residues Thr and Ser were incorporated in two of five heptad repeats at a and d positions, respectively, which gave a crystal structure of a hexameric barrel exhibiting a hydrogen-bond network within polar residues and water molecules. Residues at the barrel exterior (b, c, and f positions) were further optimised to create the transmembrane peptide using the ISAMBARD modelling package.40 The peptide with four repeats of the best-scored heptad (TVISAfA) formed a stable ion-conducting channel, as confirmed by single-channel electrical recordings. Interestingly, the heptad with a lower packing score (TLLSAfA) showed bursting currents, which are often observed in natural amphipathic peptides. This result indicated that both optimal coiled–coil packing and hydrogen-bond networks are required to obtain a stable peptide channel.
The latter scoring function includes a membrane environment through implicit membrane models. The design framework Rosetta MP47 utilises a biologically realistic implicit membrane model48 that is useful for modelling and engineering natural membrane proteins. A successful example of de novo design through modelling in a membrane environment is ROCKER,49 a Zn2+ ion transporter comprising four antiparallel α-helices. The four-helix bundle was designed using the Lazaridis implicit membrane model (IMM150) and CHARMM force field.51,52 The design process also includes two-state structure models depending on ion binding, which facilitates ion transport across the membrane. Including structural dynamics in the design of membrane proteins such as ROCKER is still very challenging but necessary for creating novel functional proteins. Towards de novo designs of a variety of membrane protein structures and functions, a deeper understanding of the physical and chemical features of interactions between solvent, lipids, and proteins is required.
3. MD simulations in the rational design of membrane α-helical peptides and proteins
MD simulations can provide two important dynamics regarding the interaction of transmembrane α-helices with solvents and membranes. The first is to understand the structural dynamics of transmembrane α-helices and their interactions with lipid molecules in the membrane. The other is membrane folding dynamics, which includes conformational changes between random-coil structures in bulk solution, formation of α-helical structures on the membrane surface or in the transmembrane, and assemblies of multiple α-helices in the membrane. In this section, we describe how these two types of simulations can be used to design membrane α-helical peptides and proteins.3.1 MD simulations in membrane protein design
Molecular dynamics simulations can be used to sample the structural dynamics of natural proteins embedded in a lipid bilayer, which provides information about “where to design”. This approach is common in nanopore engineering.53,54 As an example of α-helical proteins, Barth et al. identified the amino acid residues that contribute to conformational changes in GPCRs in MD simulations, and then, modified the residues to create artificial GPCRs with a perturbed response.55 In terms of the de novo design, DeGrado et al. found a stable packing motif in MD simulations of pentameric α-helical barrel phospholamban and designed a new artificial transmembrane parallel pentamer using the sequence pattern.56 This study indicated that the van der Waals interaction contributes to the packing of apolar residues between α-helices, and that the geometry of helices in such packing is strictly determined.These studies show that MD simulations are useful for evaluating the stability of membrane-embedded protein structures. It will be able to evaluate structural models of de novo designed proteins using explicit solvents and lipids. However, sampling only the transmembrane state of the designed target structure may not specify the native structure of the designed protein. There can be sub-stable structures likely to exist during the folding processes. Thus, folding simulations will be also beneficial for investigating the relative stability of the target and alternative structures.
3.2 Folding simulations of amphipathic peptides and their applications to design
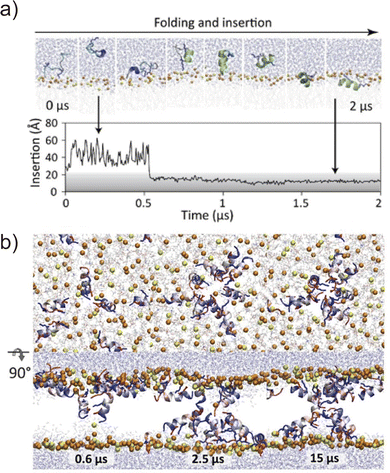
Folding simulations of transmembrane α-helical assemblies can identify key interactions between the solvent, lipid, and α-helices, which ultimately lead peptides into the most stable conformation. Because of the long timescale (from ms to hours), conventional MD simulations of membrane protein folding usually require a very long computational time. Unlike natural membrane proteins supported by chaperones, natural amphipathic peptides spontaneously form transmembrane assemblies; therefore, they are major targets for membrane protein folding simulations.57–59 Many of these are anti-microbial agents. This has been another motivation for investigating folding mechanisms. Ulmschneider et al. demonstrated that folding events, including membrane binding, insertion, association, and dissociation of multiple anti-microbial peptides, can be sampled through all-atom conventional MD simulations. To accelerate these slow dynamical processes, they simulated at high temperatures.60 They employed high-temperature MD simulation for the de novo design of a 14-residue pore-forming peptide with sequence patterning61 (Fig. 4). Through a comparison of several peptide sequences in simulations, the best pore-forming peptide was selected and synthesised, which was confirmed to be a membrane-active anti-microbial peptide. This approach is powerful but only applicable to α-helices that are stable in lipid bilayers at high temperatures. In addition, the simulation typically takes weeks to months. As an alternative approach, splitting folding events will help to understand the folding mechanisms.62The first process of membrane peptide assembly is the binding of peptides from the aqueous phase to the membrane surface. In recent studies, the binding mechanisms of amphipathic peptides, such as a membrane fusion peptide from the SARS-CoV2 spike protein,63 amphipathic lipid packing sensor peptide,64 and influenza haemagglutinin fusion peptide,65 have been analysed using the highly mobile membrane mimetic (HMMM) model.66 The HMMM model significantly boosts lipid diffusion while maintaining the atomic details of the membrane surface (see Section 4.1). The formation of an α-helix is thought to occur upon interfacial binding67,68 or accompanying peptide insertion.69 They are shown in the free-energy landscapes obtained using enhanced sampling methods.70
The next step involves peptide insertion and assembly in the lipid bilayers. A common approach to insertion simulation is to apply an external force to peptides along the bilayer normal (z-axis). Taking pore formation of honeybee toxin melittin peptides as an example, umbrella sampling indicated that multiple peptides co-ordinately insert and form a toroidal pore when lipid head groups are flipped by an applied force.71 Another study using umbrella sampling showed that six melittins best stabilise a membrane pore in a collective pore formation, which is consistent with the experimental results.72 These folding simulations combined with biophysical experiments of natural amphipathic α-helices have demonstrated that their assembling mechanism follows more complex pathways than the traditional two-state model.59 Moreover, peptide assemblies tend to have multiple conformations or oligomer states of which stability is low. Related to the rational peptide design focusing on folding processes, Tsuda et al. screened AI-generated membrane-permeable peptides through free-energy calculation of peptide translocation across a membrane.73 This example suggests that it is becoming realistic to compare designed sequences using MD simulations if the number of candidates can be narrowed down to a few before the simulations. The assembling simulation is not yet a common approach to investigate designed α-helical peptide bundles with tight helix–helix packing. Comparing the folding of stable assemblies of designed peptides with the promiscuous association of amphipathic peptide assemblies would be interesting to understand how these peptides assemble through different molecular mechanisms in membranes.
4. Advanced simulation techniques of membrane transmembrane α-helices
Considering the slow dynamics of membrane protein folding from the bulk aqueous phase to the membrane environment, performing long-time MD simulations may not be sufficient. In this section, we introduce current molecular models of proteins and lipids as well as enhanced conformational sampling algorithms to tackle challenging MD simulations of folding and other slow conformational dynamics.4.1 Membrane models at different resolutions
All-atom MD simulations provide detailed atomistic information on the conformational dynamics of membrane proteins as well as their interactions with biological membranes. Molecular dynamics simulations of a relatively small membrane protein formed with only a few transmembrane α-helices in a lipid bilayer are now feasible using conventional PC clusters or GPU computers, if reliable starting structures are available. To introduce membrane environments into the simulations, several methods with different resolutions were proposed, as shown in Fig. 5.74All-atom force fields, such as AMBER,75 CHARMM,76 GROMOS,77 and OPLS,78 include bonded and non-bonded interaction parameters of many lipid molecules. The initial structure of a membrane–protein complex can be readily constructed using modelling tools such as VMD79 and CHARMM-GUI.80,81 Two different lipid models are available: all-atom and united-atom models. In the simulations of membrane α-helices, the former is recommended because the latter has been suggested to cause the undesired unfolding of α-helical peptides.82 The increasing accuracy of all-atom force fields for membrane–protein systems has been supported by continuous efforts, particularly regarding the treatment of non-bond interactions. The particle mesh Ewald (PME) method83 is usually employed to calculate long-range electrostatic interactions; recently, the PME has been proposed for use in Lennard-Jones interactions (LJ-PME) as well. In conventional MD simulations of proteins, LJ interactions are treated as short-range interactions, considering those at a certain cut-off distance. Recent studies suggested that the use of PME for both electrostatic and LJ interactions in MD simulations can have a critical impact on membrane properties.84 To adopt LJ-PME in MD simulations of membranes or membrane proteins, re-parameterisations of non-bonded interactions are required. CHARMM36/LJ-PME85,86 and FUJI87 were re-parameterised for the use of LJ-PME. For soluble disordered protein structures, strong intramolecular interactions caused very compact conformations in the MD simulations, which disagreed with the experimental observations. To overcome this problem, Best et al. introduced a scaling parameter for protein–water LJ interactions to emphasise a water–protein interaction of approximately 10% from the original force field.88 For transmembrane α-helix dimers in membranes, MD simulations using the original force fields underestimated the stability of dimer structures compared to those in experiments.89 Best et al. also proposed weakening protein–lipid interactions by approximately 10% from the original strength and obtained more reasonable results in their simulations. This suggests that a proper balance of non-bonded interactions between proteins, membranes, and water molecules is essential for predicting protein structures in MD simulations.
Predicting the kinetics of proteins requires accurate force fields and sufficient conformational sampling for MD simulations. The simulation lengths of all-atom MD simulations of membranes are still not sufficient to examine slow diffusive motions of lipid molecules in membranes, motivating the development of approximated molecular models of lipid molecules.74 The HMMM model66 (Fig. 5c) is a combination of an organic solvent layer sandwiched by lipid molecules with shorter hydrocarbon chains. The HMMM model is particularly useful for sampling binding events of peripheral membrane proteins near the lipid-bilayer surface because of the acceleration of lipid lateral diffusion by a factor of 10 compared to the conventional lipid models. Coarse-grained (CG) lipid models (Fig. 5b) can significantly reduce the computational cost by mapping from several atoms to one CG particle. In MARTINI90 and SPICA91 CG models, proteins are modelled as an elastic network model with predefined restraints to maintain protein structures. They are useful for examining the assembly of transmembrane α-helices in various membrane environments92 and for predicting interactions between transmembrane α-helices and lipid molecules, including cholesterol.91 An alternative is the PACE model,93,94 which consists of all-atom protein and CG MARTINI lipid models. It can be used to investigate large-scale conformational transitions of membrane proteins, which are not available with elastic network models in MARTINI and SPICA.
To apply further approximations and reduce the computational costs, implicit membrane models (e.g. IMM1,50 generalised born with simple switching (GBSWmemb),95 and GB using molecular volume (GBMV)96 have been developed. They assume different dielectric constants for the aqueous and membrane layers to maintain the structural and dynamical properties of membrane proteins (Fig. 5d). Implicit membranes are often used to simulate membrane protein folding and aggregation because of their faster relaxation processes and lower computational costs than explicit solvent/membrane simulations.68,95 In these simulations, enhanced conformational sampling algorithms such as replica-exchange molecular dynamics (REMD)97 are often employed. The near-atomic CG protein model PRIMO also includes an implicit membrane model.98 Recently, an implicit micelle model for membrane protein simulations has been developed (Fig. 5e).99 This model can be used to model structures derived from NMR and X-ray crystallography where detergents and nano-discs are often selected to solubilise membrane proteins, and to compare the effects of micellar and membrane environment to membrane protein structures.
Selecting the most suitable membrane model for the system of interest while maintaining a good balance between accuracy and the required computational resources is important. When the low efficiency of conformational sampling is a bottleneck for a selected membrane model, a common approach is multiscale simulations at different resolutions.70,74 Alternatively, the enhanced sampling method described below can be combined with each membrane model to address this issue.
4.2 Enhanced conformational sampling methods for transmembrane α-helices
The slow conformational dynamics of transmembrane proteins, such as alternative-access motions of membrane transporters, are difficult to simulate using brute-force MD simulations. Recently, various enhanced sampling algorithms have been applied to slow motions of membrane peptides or proteins in explicit lipid bilayers.70 One of the most popular approaches is to apply restraint potentials along the structural dynamics of interest (known as collective variables (CV)). Metadynamics (MTD),100 adaptive bias MD (ABMD),101 and umbrella sampling102 are categorised as this type, providing free energy changes or the potential of mean forces along the predefined CV. If necessary, the multistate Bennett acceptance ratio (MBAR)103 is applied to the simulation trajectories to avoid the effect of restraint potentials or biases. The global free-energy minimum states along the CV can be regarded as the most stable protein structure.When reasonable CVs describing the dynamics of membrane proteins are not easily found, other enhanced sampling methods are necessary. Accelerated MD (aMD)104 including an improved version, Gaussian accelerated MD (GaMD),105 lowers the energy barriers between different conformational states, enhancing conformational transitions between them. Another option is the replica-exchange molecular dynamics (REMD) method,97 in which parallel MD simulations with different temperatures or parameters are simulated. The exchange of temperatures and/or parameters between replicas enables random walks of trajectories in temperature/parameter spaces to avoid trapping at one of the local energy minima. As a result, the simulations explore a wider conformational space of a transmembrane protein in a lipid bilayer, which corresponds to a longer MD simulation. Many variants of REMD have been proposed to date, such as replica-exchange with solute tempering (REST106/REST2107–109/gREST110), replica-exchange umbrella sampling (REUS)111 (or Hamiltonian REMD112), and surface-tension replica-exchange MD (γ-REMD).113 Importantly, combined methods, such as multi-dimensional REMD,111 gREST/REUS,114 and GaREUS (Gaussian accelerated replica-exchange umbrella sampling115), are extremely powerful algorithms because they can enhance not only global motions but also local motions with high energy barriers.
Applications of REMD and other enhanced sampling methods for transmembrane proteins in implicit membranes have been summarised previously.70 Here, we discuss a gREST simulation of wild-type and G380R mutant fibroblast growth factor receptor3 (FGFR3) in an explicit solvent and membrane.116 The transmembrane domain of FGFR3 consists of two α-helices as homodimers. The dimer interface is largely changed upon ligand binding to the extracellular domain and then transfers the signal towards the intracellular kinase domains.117,118 For wild-type FGFR3, the homodimeric structures were analysed by solution NMR with micelles119 and solid NMR with lipid bilayers,120 wherein the interface of α-helices was completely different (Fig. 6a). To solve this problem, the gREST method is an effective conformational sampling algorithm, where the simulation system is divided into the solute region and the rest of the solvent region, and only the solute temperatures are varied in replicas, keeping the solvent temperature at physiological temperature. In the FGFR3 simulations, the solute region was defined for the FGFR3 dimer and lipid bilayer to accelerate transmembrane α-helices in the membrane (Fig. 6b). In the gREST simulations, 12 replicas which cover solute temperatures from 310.15 to 350.94 K were simulated using the CHARMM36m force field with a reduced protein–lipid LJ interaction (NBFIX = 0.9).89 In the gREST simulation, the predicted structure of the transmembrane α-helix dimer had the same dimer interface as that predicted by solid-state NMR. Another key result of the simulation was the structural differences between wild-type FGFR3 and the G380R mutant, which shows constitutive activation. As shown in Fig. 6c, the G380R mutant shows tight contacts between G375 and the extracellular interface, whereas the wild type has loose conformations. The conformational difference between wild-type and G380R might mimic that between the inactive and active states in FGFR3 signal transduction. The G375C mutation also causes constitutive activation, which was predicted at the dimer interface of the G380 α-helix dimer in the gREST simulation. This application suggests that powerful enhanced sampling algorithms and balanced force fields are both necessary to reliably predict the structures of transmembrane α-helices in membranes.
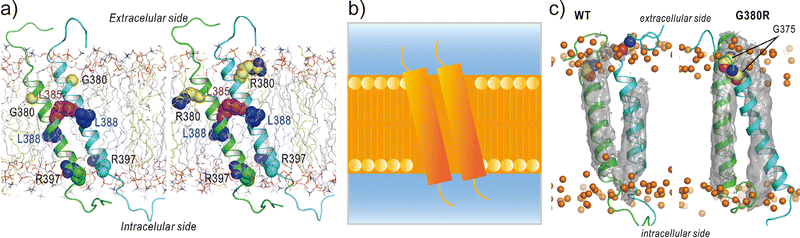 | ||
| Fig. 6 gREST simulations of FGFR3 homodimer structures. (a) Initial structures of wild type and G380R mutant of FGFR3 predicted with PREDDIMER.121 Key amino-acid residues (G/R380, L385, L388, R397) are highlighted as spherical models. (b) Setup of gREST simulations. LJ, Coulomb, dihedral, and CMAP energy terms in both FGFR3 and membrane are treated as the solute region, whereas all the water molecules are treated as solvent. (c) Stable structures of wild type and G380R mutant of FGFR3 predicted with gREST simulations. In G380R mutant, G375 is located at the contact interface near the extracellular side. Adapted with permission from Matsuoka et al., J. Comp. Chem., 2020, 41, 561–572. Copyright 2019, Wiley Periodicals, Inc. | ||
5. Future challenges in de novo designs of membrane α-helical assemblies
As discussed in Section 2, the current strategy in designing membrane α-helix assemblies involves optimising helix–helix packing of the fixed backbone structure in the same manner as for water-soluble proteins. For incorporating the membrane environment in designs, hydrophobic or membrane interfacial amino acid residues are placed on the exterior of the designed helical bundles, or the static model structures are scored in implicit membranes. These approaches have yielded a few successful designs for stable membrane α-helical assemblies.However, there are remaining challenges. Firstly, behind previous successful designs, the current design methods often yield peptides exhibiting unexpected promiscuous associations in lipid bilayers, which are only found in experiments,45 leading to the low success rate. Secondly, such low success rate for membrane peptide/protein design could be due to the sequence optimisation with fixed backbone structures since alternative folding free energy minima are not inspected. This has been also suggested in the water-soluble protein design.122 The fixed-backbone strategy also makes it very challenging to design dynamic conformational changes, although it is important for functional membrane proteins.
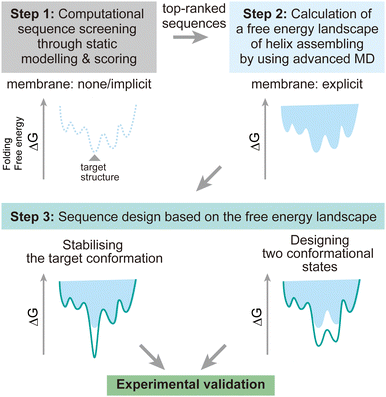
To address these challenges, here we discuss possibilities to introduce additional steps using MD simulations after the screening of design decoys by the existing fast scoring methods (Fig. 7). There are two points which can be achieved by using MD simulations:
(1) The designed structures can be modelled in explicit lipid bilayers. As we introduced, MD simulations provide a variety of methods to explicitly introduce a lipid bilayer at different resolutions. These enables us to consider dynamic interactions between the solvent, lipids, and proteins, which are more complex than in an aqueous solution environment. In particular, the continuous improvement in all-atom force fields has supported highly accurate modelling of membrane peptides and proteins.
(2) Dynamic conformational sampling and folding simulations through advanced MD simulations provide the free energy landscapes for the structures of designed peptide assemblies. In terms of the combination of MD simulations and computational protein design, it has been demonstrated that MD simulations can aid to refine top-ranked structure models and assess their stability after initial screening of decoys.123,124 In recent designs of membrane α-helical assemblies, static structural modelling followed by only conventional MD has been a common approach. The free energy landscapes of the designed assemblies obtained from advanced MD simulations will guide further sequence optimisation in two directions. One is towards the lower free energy minimum of the designed structure as a native fold, followed by experimental structure/function analyses. Through this optimisation process, the success rate of membrane protein design could be significantly increased. The cost of computation time may even compensate that of many experimental trials, considering the general difficulty in structural analyses of membrane α-helical assemblies. Another possibility is towards designing two conformations for implementing functions such as receptors and ion channels, which will produce novel artificial protein materials.
Advanced MD simulations are of course not applicable to hundreds of design decoys due to the significant increase of computational cost. Nonetheless, through selecting appropriate resolutions and sampling method, it is now possible to conduct advanced MD simulations for several sequences of membrane α-helical assemblies, as described in section 4, before proceeding to experimental analysis. Multiscale simulations can be useful for achieving a good balance between accuracy and available computing resources. These can be combined with enhanced sampling methods to efficiently investigate the conformational dynamics. More challenging folding simulations would require careful selection of lipid models and enhanced sampling methods suitable for each folding process (membrane partitioning, insertion, and assembling) of α-helices to overcome the slow dynamics.
When successful, the folding simulations of the designed membrane α-helical assemblies will provide valuable information that can be extended to a general understanding of membrane protein folding. After decades of experimental and simulation studies, generalising association mechanisms of natural membrane-active peptides is considered difficult owing to promiscuous interactions of the amphipathic helices.59 It would be interesting to test whether the folding simulations differently predict a membrane peptide assembly designed with tight helix–helix packing compared to natural peptides. To extract key interactions from the complex folding processes, recent advances in machine learning may help to analyse simulation data. Using all-atom and CG folding simulation trajectories of multiple membrane α-helical assemblies as learning datasets, the relationships between key interactions and amino acid sequence patterns could be extracted. The proposed design approach may open a new door to understanding general membrane protein folding and designing membrane peptide/protein complexes with new functions.
Data availability
The data in this perspective article are available from the corresponding author upon reasonable request.Author contributions
Y. S. and A. N.: conceptualisation, writing – original draft, writing – review & editing, and visualisation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported, in part, by MEXT/JSPS KAKENHI Grant Numbers 19H05645 and 21H05249 (to Y. S.), 21H00412, 21J40162, and 22H05438 (to A. N.), JST, PRESTO Grant Number JPMJPR22A9 (to A. N.), RIKEN pioneering projects in “Biology of Intracellular Environments”, “Glycolipidlogue initiative” (to Y. S.), and MEXT “Program for Promoting Research on the Supercomputer Fugaku (Biomolecular dynamics in a living cell/MD-driven Precision Medicine)”.Notes and references
- B. Kuhlman and P. Bradley, Nat. Rev. Mol. Cell Biol., 2019, 20, 681–697 CrossRef.
- D. N. Woolfson, J. Mol. Biol., 2021, 433, 167160 CrossRef.
- H. M. Berman, Nucleic Acids Res., 2000, 28, 235–242 CrossRef PubMed.
- S. H. White, Nature, 2009, 459, 344–346 CrossRef PubMed.
- B. T. Porebski and A. M. Buckle, Protein Eng., Des. Sel., 2016, 29, 245–251 CrossRef PubMed.
- A. Niitsu, J. W. Heal, K. Fauland, A. R. Thomson and D. N. Woolfson, Phil. Trans. R. Soc. B, 2017, 372, 8–13 CrossRef PubMed.
- I. V. Korendovych and W. F. DeGrado, Q. Rev. Biophys., 2020, 53, e3 CrossRef CAS PubMed.
- X. Pan and T. Kortemme, J. Biol. Chem., 2021, 296, 100558 CrossRef CAS PubMed.
- T. Motoyama, N. Hiramatsu, Y. Asano, S. Nakano and S. Ito, Biochemistry, 2020, 59, 3823–3833 CrossRef CAS PubMed.
- A. J. Stevens, G. Sekar, J. A. Gramespacher, D. Cowburn and T. W. Muir, J. Am. Chem. Soc., 2018, 140, 11791–11799 CrossRef CAS.
- J. C. Canul-Tec, R. Assal, E. Cirri, P. Legrand, S. Brier, J. Chamot-Rooke and N. Reyes, Nature, 2017, 544, 446–451 CrossRef CAS.
- K. Oda, Y. Lee, P. Wiriyasermkul, Y. Tanaka, M. Takemoto, K. Yamashita, S. Nagamori, T. Nishizawa and O. Nureki, Protein Sci., 2020, 29, 2398–2407 CrossRef CAS PubMed.
- G. G. Rhys, C. W. Wood, E. J. M. Lang, A. J. Mulholland, R. L. Brady, A. R. Thomson and D. N. Woolfson, Nat. Commun., 2018, 9, 4132 CrossRef PubMed.
- J. Dou, A. A. Vorobieva, W. Sheffler, L. A. Doyle, H. Park, M. J. Bick, B. Mao, G. W. Foight, M. Y. Lee, L. A. Gagnon, L. Carter, B. Sankaran, S. Ovchinnikov, E. Marcos, P.-S. Huang, J. C. Vaughan, B. L. Stoddard and D. Baker, Nature, 2018, 561, 485–491 CrossRef CAS PubMed.
- B. Koepnick, J. Flatten, T. Husain, A. Ford, D.-A. Silva, M. J. Bick, A. Bauer, G. Liu, Y. Ishida, A. Boykov, R. D. Estep, S. Kleinfelter, T. Nørgård-Solano, L. Wei, F. Players, G. T. Montelione, F. Dimaio, Z. Popović, F. Khatib, S. Cooper and D. Baker, Nature, 2019, 570, 390–394 CrossRef CAS PubMed.
- N. H. Joh, T. Wang, M. P. Bhate, R. Acharya, Y. Wu, M. Grabe, M. Hong, G. Grigoryan and W. F. DeGrado, Science, 2014, 346, 1520–1524 CrossRef CAS PubMed.
- C. Xu, P. Lu, T. M. Gamal El-Din, X. Y. Pei, M. C. Johnson, A. Uyeda, M. J. Bick, Q. Xu, D. Jiang, H. Bai, G. Reggiano, Y. Hsia, T. J. Brunette, J. Dou, D. Ma, E. M. Lynch, S. E. Boyken, P. S. Huang, L. Stewart, F. DiMaio, J. M. Kollman, B. F. Luisi, T. Matsuura, W. A. Catterall and D. Baker, Nature, 2020, 585, 129–134 CrossRef CAS PubMed.
- A. A. Vorobieva, P. White, B. Liang, J. E. Horne, A. K. Bera, C. M. Chow, S. Gerben, S. Marx, A. Kang, A. Q. Stiving, S. R. Harvey, D. C. Marx, G. N. Khan, K. G. Fleming, V. H. Wysocki, D. J. Brockwell, L. K. Tamm, S. E. Radford and D. Baker, Science, 2021, 371, eabc8182 CrossRef.
- C. W. Wood and D. N. Woolfson, Protein Sci., 2018, 27, 103–111 CrossRef CAS.
- J. Mistry, S. Chuguransky, L. Williams, M. Qureshi, A. Salazar Gustavo, E. L. L. Sonnhammer, S. C. E. Tosatto, L. Paladin, S. Raj, L. J. Richardson, R. D. Finn and A. Bateman, Nucleic Acids Res., 2021, 49, D412–D419 CrossRef CAS.
- I. Letunic, S. Khedkar and P. Bork, Nucleic Acids Res., 2021, 49, D458–D460 CrossRef CAS PubMed.
- M. Blum, H.-Y. Chang, S. Chuguransky, T. Grego, S. Kandasaamy, A. Mitchell, G. Nuka, T. Paysan-Lafosse, M. Qureshi, S. Raj, L. Richardson, G. A. Salazar, L. Williams, P. Bork, A. Bridge, J. Gough, D. H. Haft, I. Letunic, A. Marchler-Bauer, H. Mi, D. A. Natale, M. Necci, C. A. Orengo, A. P. Pandurangan, C. Rivoire, C. J. A. Sigrist, I. Sillitoe, N. Thanki, P. D. Thomas, S. C. E. Tosatto, C. H. Wu, A. Bateman and R. D. Finn, Nucleic Acids Res., 2021, 49, D344–D354 CrossRef.
- S. F. Altschul, T. L. Madden, A. A. Schaffer, J. Zhang, Z. Zhang, W. Miller and D. J. Lipman, Nucleic Acids Res., 1997, 25, 3389–3402 Search PubMed.
- F. Madeira, M. Pearce, A. R. N. Tivey, P. Basutkar, J. Lee, O. Edbali, N. Madhusoodanan, A. Kolesnikov and R. Lopez, Nucleic Acids Res., 2022, 50(W1), W276–W279 CrossRef PubMed.
- G. E. Crooks, G. Hon, J.-M. Chandonia and S. E. Brenner, Genome Res., 2004, 14, 1188–1190 CrossRef PubMed.
- U. Gobel, C. Sander, R. Schneider and A. Valencia, Proteins, 1994, 18, 309–317 CrossRef PubMed.
- I. N. Shindyalov, N. A. Kolchanov and C. Sander, Protein Eng., 1994, 7, 349–358 CrossRef PubMed.
- D. Altschuh, T. Vernet, P. Berti, D. Moras and K. Nagai, Protein Eng., 1988, 2, 193–199 CrossRef CAS.
- D. S. Marks, L. J. Colwell, R. Sheridan, T. A. Hopf, A. Pagnani, R. Zecchina and C. Sander, PLoS One, 2011, 6, e28766 CrossRef CAS.
- V. Frappier and A. E. Keating, Curr. Opin. Struct. Biol., 2021, 69, 63–69 CrossRef CAS.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Zidek, A. Potapenko, A. Bridgland, C. Meyer, S. A. A. Kohl, A. J. Ballard, A. Cowie, B. Romera-Paredes, S. Nikolov, R. Jain, J. Adler, T. Back, S. Petersen, D. Reiman, E. Clancy, M. Zielinski, M. Steinegger, M. Pacholska, T. Berghammer, S. Bodenstein, D. Silver, O. Vinyals, A. W. Senior, K. Kavukcuoglu, P. Kohli and D. Hassabis, Nature, 2021, 596, 583–589 CrossRef CAS.
- M. Baek, F. DiMaio, I. Anishchenko, J. Dauparas, S. Ovchinnikov, G. R. Lee, J. Wang, Q. Cong, L. N. Kinch, R. D. Schaeffer, C. Millan, H. Park, C. Adams, C. R. Glassman, A. DeGiovanni, J. H. Pereira, A. V. Rodrigues, A. A. van Dijk, A. C. Ebrecht, D. J. Opperman, T. Sagmeister, C. Buhlheller, T. Pavkov-Keller, M. K. Rathinaswamy, U. Dalwadi, C. K. Yip, J. E. Burke, K. C. Garcia, N. V. Grishin, P. D. Adams, R. J. Read and D. Baker, Science, 2021, 373, 871–876 CrossRef CAS.
- C. J. Lalaurie, V. Dufour, A. Meletiou, S. Ratcliffe, A. Harland, O. Wilson, C. Vamasiri, D. K. Shoemark, C. Williams, C. J. Arthur, R. B. Sessions, M. P. Crump, J. L. R. Anderson and P. Curnow, Sci. Rep., 2018, 8, 14564 CrossRef PubMed.
- K. R. Mahendran, A. Niitsu, L. Kong, A. R. Thomson, R. B. Sessions, D. N. Woolfson and H. Bayley, Nat. Chem., 2017, 9, 411–419 CrossRef CAS PubMed.
- C. Dong, K. Beis, J. Nesper, A. L. Brunkan-Lamontagne, B. R. Clarke, C. Whitfield and J. H. Naismith, Nature, 2006, 444, 226–229 CrossRef CAS.
- B. Sakmann and E. Neher, Single-channel recording, Plenum Press, New York, 2nd edn, 1995 Search PubMed.
- R. Helling, H. Li, R. Melin, J. Miller, N. Wingreen, C. Zeng and C. Tang, J. Mol. Graph. Model., 2001, 19, 157–167 CrossRef CAS PubMed.
- R. B. Hill, D. P. Raleigh, A. Lombardi and W. F. Degrado, Acc. Chem. Res., 2000, 33, 745–754 CrossRef CAS PubMed.
- J. K. Leman, B. D. Weitzner, S. M. Lewis, J. Adolf-Bryfogle, N. Alam, R. F. Alford, M. Aprahamian, D. Baker, K. A. Barlow, P. Barth, B. Basanta, B. J. Bender, K. Blacklock, J. Bonet, S. E. Boyken, P. Bradley, C. Bystroff, P. Conway, S. Cooper, B. E. Correia, B. Coventry, R. Das, R. M. De Jong, F. Dimaio, L. Dsilva, R. Dunbrack, A. S. Ford, B. Frenz, D. Y. Fu, C. Geniesse, L. Goldschmidt, R. Gowthaman, J. J. Gray, D. Gront, S. Guffy, S. Horowitz, P.-S. Huang, T. Huber, T. M. Jacobs, J. R. Jeliazkov, D. K. Johnson, K. Kappel, J. Karanicolas, H. Khakzad, K. R. Khar, S. D. Khare, F. Khatib, A. Khramushin, I. C. King, R. Kleffner, B. Koepnick, T. Kortemme, G. Kuenze, B. Kuhlman, D. Kuroda, J. W. Labonte, J. K. Lai, G. Lapidoth, A. Leaver-Fay, S. Lindert, T. Linsky, N. London, J. H. Lubin, S. Lyskov, J. Maguire, L. Malmström, E. Marcos, O. Marcu, N. A. Marze, J. Meiler, R. Moretti, V. K. Mulligan, S. Nerli, C. Norn, S. Ó’Conchúir, N. Ollikainen, S. Ovchinnikov, M. S. Pacella, X. Pan, H. Park, R. E. Pavlovicz, M. Pethe, B. G. Pierce, K. B. Pilla, B. Raveh, P. D. Renfrew, S. S. R. Burman, A. Rubenstein, M. F. Sauer, A. Scheck, W. Schief, O. Schueler-Furman, Y. Sedan, A. M. Sevy, N. G. Sgourakis, L. Shi, J. B. Siegel, D.-A. Silva, S. Smith, Y. Song, A. Stein, M. Szegedy, F. D. Teets, S. B. Thyme, R. Y.-R. Wang, A. Watkins, L. Zimmerman and R. Bonneau, Nat. Methods, 2020, 17, 665–680 CrossRef CAS PubMed.
- C. W. Wood, J. W. Heal, A. R. Thomson, G. J. Bartlett, A. Ibarra, R. L. Brady, R. B. Sessions and D. N. Woolfson, Bioinformatics, 2017, 33, 3043–3050 CrossRef CAS.
- P. Gainza, K. E. Roberts, I. Georgiev, R. H. Lilien, D. A. Keedy, C. Y. Chen, F. Reza, A. C. Anderson, D. C. Richardson, J. S. Richardson and B. R. Donald, Methods Enzymol., 2013, 523, 87–107 CAS.
- J. Skokowa, B. Hernandez Alvarez, M. Coles, M. Ritter, M. Nasri, J. Haaf, N. Aghaallaei, Y. Xu, P. Mir, A.-C. Krahl, K. W. Rogers, K. Maksymenko, B. Bajoghli, K. Welte, A. N. Lupas, P. Müller and M. ElGamacy, Nat. Commun., 2022, 13, 2948 CrossRef CAS PubMed.
- J. Zhou, A. E. Panaitiu and G. Grigoryan, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 1059–1068 CrossRef CAS.
- P. Lu, D. Min, F. DiMaio, K. Y. Wei, M. D. Vahey, S. E. Boyken, Z. Chen, J. A. Fallas, G. Ueda, W. Sheffler, V. K. Mulligan, W. Xu, J. U. Bowie and D. Baker, Science, 2018, 359, 1042–1046 CrossRef CAS PubMed.
- A. J. Scott, A. Niitsu, H. T. Kratochvil, E. J. M. Lang, J. T. Sengel, W. M. Dawson, K. R. Mahendran, M. Mravic, A. R. Thomson, R. L. Brady, L. Liu, A. J. Mulholland, H. Bayley, W. F. DeGrado, M. I. Wallace and D. N. Woolfson, Nat. Chem., 2021, 13, 643–650 CrossRef CAS.
- A. R. Thomson, C. W. Wood, A. J. Burton, G. J. Bartlett, R. B. Sessions, R. L. Brady and D. N. Woolfson, Science, 2014, 346, 485–488 CrossRef.
- R. F. Alford, J. Koehler Leman, B. D. Weitzner, A. M. Duran, D. C. Tilley, A. Elazar and J. J. Gray, PLoS Comput. Biol., 2015, 11, e1004398 CrossRef PubMed.
- R. F. Alford, P. J. Fleming, K. G. Fleming and J. J. Gray, Biophys. J., 2020, 118, 2042–2055 CrossRef PubMed.
- N. H. Joh, T. Wang, M. P. M. Bhate, R. Acharya, Y. Wu, M. Grabe, M. Hong, G. Grigoryan and W. F. DeGrado, Science, 2014, 346, 1520–1524 CrossRef.
- T. Lazaridis, Proteins, 2003, 52, 176–192 CrossRef PubMed.
- J. Huang and A. D. MacKerell, Jr., J. Comput. Chem., 2013, 34, 2135–2145 CrossRef PubMed.
- R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and A. D. Mackerell, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed.
- D. Anand, G. V. Dhoke, J. Gehrmann, T. M. Garakani, M. D. Davari, M. Bocola, L. Zhu and U. Schwaneberg, Chem. Commun., 2019, 55, 5431–5434 RSC.
- C. Cao, N. Cirauqui, M. J. Marcaida, E. Buglakova, A. Duperrex, A. Radenovic and M. Dal Peraro, Nat. Commun., 2019, 10, 4918 CrossRef.
- K. Y. M. Chen, D. Keri and P. Barth, Nat. Chem. Biol., 2020, 16, 77–86 CrossRef CAS PubMed.
- M. Mravic, J. L. Thomaston, M. Tucker, P. E. Solomon, L. Liu and W. F. DeGrado, Science, 2019, 363, 1418–1423 CrossRef CAS.
- D. P. Tieleman and M. S. P. Sansom, Int. J. Quantum Chem., 2001, 83, 166–179 CrossRef CAS.
- J. P. Ulmschneider and M. B. Ulmschneider, Acc. Chem. Res., 2018, 51, 1106–1116 CrossRef CAS PubMed.
- S. Guha, J. Ghimire, E. Wu and W. C. Wimley, Chem. Rev., 2019, 119, 6040–6085 CrossRef CAS.
- C. H. Chen, M. C. R. Melo, N. Berglund, A. Khan, C. de la Fuente-Nunez, J. P. Ulmschneider and M. B. Ulmschneider, Curr. Opin. Struct. Biol., 2020, 61, 160–166 CrossRef CAS PubMed.
- C. H. Chen, C. G. Starr, E. Troendle, G. Wiedman, W. C. Wimley, J. P. Ulmschneider and M. B. Ulmschneider, J. Am. Chem. Soc., 2019, 141, 4839–4848 CrossRef CAS PubMed.
- N. Frazee, V. Burns, C. Gupta and B. Mertz, Methods Mol. Biol., 2021, 2315, 161–182 CrossRef.
- D. Gorgun, M. Lihan, K. Kapoor and E. Tajkhorshid, Biophys. J., 2021, 120, 2914–2926 CrossRef CAS PubMed.
- K. D. Wildermuth, V. Monje-Galvan, L. M. Warburton and J. B. Klauda, J. Chem. Theory Comput., 2019, 15, 1418–1429 CrossRef.
- J. L. Baylon and E. Tajkhorshid, J. Phys. Chem. B, 2015, 119, 7882–7893 CAS.
- Y. Z. Ohkubo, T. V. Pogorelov, M. J. Arcario, G. A. Christensen and E. Tajkhorshid, Biophys. J., 2012, 102, 2130–2139 CrossRef CAS PubMed.
- M. J. McKay, F. Afrose, R. E. Koeppe, 2nd and D. V. Greathouse, Biochim. Biophys. Acta, Biomembr., 2018, 1860, 2108–2117 CrossRef CAS.
- W. Im and C. L. Brooks, 3rd, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6771–6776 CrossRef PubMed.
- H. Nymeyer, T. B. Woolf and A. E. Garcia, Proteins, 2005, 59, 783–790 CrossRef.
- T. Mori, N. Miyashita, W. Im, M. Feig and Y. Sugita, Biochim. Biophys. Acta Biomembr., 2016, 1858, 1635–1651 CrossRef PubMed.
- D. Sun, J. Forsman and C. E. Woodward, Langmuir, 2015, 31, 9388–9401 CrossRef PubMed.
- Y. Miyazaki, S. Okazaki and W. Shinoda, Biochim. Biophys. Acta, Biomembr., 2019, 1861, 1409–1419 CrossRef.
- D. P. Tran, S. Tada, A. Yumoto, A. Kitao, Y. Ito, T. Uzawa and K. Tsuda, Sci. Rep., 2021, 11, 10630 CrossRef.
- S. J. Marrink, V. Corradi, P. C. T. Souza, H. I. Ingólfsson, D. P. Tieleman and M. S. P. Sansom, Chem. Rev., 2019, 119, 6184–6226 CrossRef CAS PubMed.
- C. J. Dickson, B. D. Madej, Å. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879 CrossRef PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell, Jr. and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef PubMed.
- I. Marzuoli, C. Margreitter and F. Fraternali, J. Chem. Theory Comput., 2019, 15, 5175–5193 CrossRef PubMed.
- A. Maciejewski, M. Pasenkiewicz-Gierula, O. Cramariuc, I. Vattulainen and T. Rog, J. Phys. Chem. B, 2014, 118, 4571–4581 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14(33–38), 27–38 Search PubMed.
- E. L. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Davila-Contreras, Y. Qi, J. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, J. Comput. Chem., 2014, 35, 1997–2004 CrossRef PubMed.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- Y. Wang, T. Zhao, D. Wei, E. Strandberg, A. S. Ulrich and J. P. Ulmschneider, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2280–2288 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- C. L. Wennberg, T. Murtola, B. Hess and E. Lindahl, J. Chem. Theory Comput., 2013, 9, 3527–3537 CrossRef CAS.
- Y. Yu, A. Krämer, R. M. Venable, B. R. Brooks, J. B. Klauda and R. W. Pastor, J. Chem. Theory Comput., 2021, 17, 1581–1595 CrossRef CAS.
- Y. Yu, A. Krämer, R. M. Venable, A. C. Simmonett, A. D. Mackerell, J. B. Klauda, R. W. Pastor and B. R. Brooks, J. Chem. Theory Comput., 2021, 17, 1562–1580 CrossRef CAS PubMed.
- N. Kamiya, M. Kayanuma, H. Fujitani and K. Shinoda, J. Chem. Theory Comput., 2020, 16, 3664–3676 CrossRef CAS.
- R. B. Best, W. Zheng and J. Mittal, J. Chem. Theory Comput., 2014, 10, 5113–5124 CrossRef CAS.
- J. Domański, M. S. P. Sansom, P. J. Stansfeld and R. B. Best, J. Chem. Theory Comput., 2018, 14, 1706–1715 CrossRef PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- S. Seo and W. Shinoda, J. Chem. Theory Comput., 2019, 15, 762–774 CrossRef CAS PubMed.
- C. D. Li, M. Junaid, H. Chen, A. Ali and D. Q. Wei, J. Chem. Inf. Model., 2019, 59, 339–350 CrossRef CAS PubMed.
- M. D. Ward, S. Nangia and E. R. May, J. Comput. Chem., 2017, 38, 1462–1471 CrossRef CAS PubMed.
- C. K. Wan, W. Han and Y. D. Wu, J. Chem. Theory Comput., 2012, 8, 300–313 CrossRef CAS PubMed.
- W. Im, M. Feig and C. L. Brooks, Biophys. J., 2003, 85, 2900–2918 CrossRef CAS PubMed.
- M. S. Lee, M. Feig, F. R. Salsbury and C. L. Brooks, J. Comput. Chem., 2003, 24, 1348–1356 CrossRef CAS PubMed.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- P. Kar, S. M. Gopal, Y.-M. Cheng, A. Panahi and M. Feig, J. Chem. Theory Comput., 2014, 10, 3459–3472 CrossRef CAS.
- T. Mori and Y. Sugita, J. Chem. Theory Comput., 2020, 16, 711–724 CrossRef.
- A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566 CrossRef CAS.
- V. Babin, C. Roland and C. Sagui, J. Chem. Phys., 2008, 128, 134101 CrossRef.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- M. R. Shirts and J. D. Chodera, J. Chem. Phys., 2008, 129, 124105 CrossRef.
- D. Hamelberg, J. Mongan and J. A. Mccammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS PubMed.
- Y. Miao, V. A. Feher and J. A. McCammon, J. Chem. Theory Comput., 2015, 11, 3584–3595 CrossRef CAS.
- P. Liu, B. Kim, R. A. Friesner and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13749–13754 CrossRef CAS.
- L. Wang, R. A. Friesner and B. J. Berne, J. Phys. Chem. B, 2011, 115, 9431–9438 CrossRef CAS.
- T. Terakawa, T. Kameda and S. Takada, J. Comput. Chem., 2011, 32, 1228–1234 CrossRef CAS PubMed.
- S. L. C. Moors, S. Michielssens and A. Ceulemans, J. Chem. Theory Comput., 2011, 7, 231–237 CrossRef CAS.
- M. Kamiya and Y. Sugita, J. Chem. Phys., 2018, 149, 072304 CrossRef PubMed.
- Y. Sugita, A. Kitao and Y. Okamoto, J. Chem. Phys., 2000, 113, 6042–6051 CrossRef CAS.
- H. Fukunishi, O. Watanabe and S. Takada, J. Chem. Phys., 2002, 116, 9058–9067 CrossRef CAS.
- T. Mori, J. Jung and Y. Sugita, J. Chem. Theory Comput., 2013, 9, 5629–5640 CrossRef CAS.
- S. Re, H. Oshima, K. Kasahara, M. Kamiya and Y. Sugita, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 18404–18409 CrossRef CAS.
- H. Oshima, S. Re and Y. Sugita, J. Chem. Theory Comput., 2019, 15, 5199–5208 CrossRef CAS PubMed.
- D. Matsuoka, M. Kamiya, T. Sato and Y. Sugita, J. Comput. Chem., 2020, 41, 561–572 CrossRef CAS PubMed.
- A. Arkhipov, Y. Shan, R. Das, N. F. Endres, M. P. Eastwood, D. E. Wemmer, J. Kuriyan and D. E. Shaw, Cell, 2013, 152, 557–569 CrossRef CAS.
- N. F. Endres, R. Das, A. W. Smith, A. Arkhipov, E. Kovacs, Y. Huang, J. G. Pelton, Y. Shan, D. E. Shaw, D. E. Wemmer, J. T. Groves and J. Kuriyan, Cell, 2013, 152, 543–556 CrossRef CAS.
- E. V. Bocharov, D. M. Lesovoy, S. A. Goncharuk, M. V. Goncharuk, K. Hristova and A. S. Arseniev, Structure, 2013, 21, 2087–2093 CrossRef CAS PubMed.
- H. Tamagaki, Y. Furukawa, R. Yamaguchi, H. Hojo, S. Aimoto, S. O. Smith and T. Sato, Biochemistry, 2014, 53, 5000–5007 CrossRef CAS PubMed.
- A. A. Polyansky, A. O. Chugunov, P. E. Volynsky, N. A. Krylov, D. E. Nolde and R. G. Efremov, Bioinformatics, 2014, 30, 889–890 CrossRef CAS PubMed.
- C. Norn, B. I. M. Wicky, D. Juergens, S. Liu, D. Kim, D. Tischer, B. Koepnick, I. Anishchenko, P. Foldit, D. Baker and S. Ovchinnikov, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2017228118 CrossRef CAS.
- F. Radom, A. Plückthun and E. Paci, PLoS Comput. Biol., 2018, 14, e1006182 CrossRef.
- J. Ludwiczak, A. Jarmula and S. Dunin-Horkawicz, J. Struct. Biol., 2018, 203, 54–61 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2023 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: