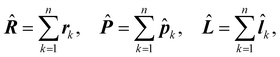Open Access Article
Open Access ArticleElectronic current densities and origin-independent property densities induced by optical fields
Francesco F.
Summa†
 ,
Guglielmo
Monaco†
,
Guglielmo
Monaco†
 ,
Paolo
Lazzeretti†
and
Riccardo
Zanasi†
,
Paolo
Lazzeretti†
and
Riccardo
Zanasi†
 *
*
Dipartimento di Chimica e Biologia “A. Zambelli”, Università degli Studi di Salerno, via Giovanni Paolo II 132, Fisciano 84084, SA, Italy. E-mail: rzanasi@unisa.it
First published on 26th August 2023
Abstract
The interaction of a molecule with optical fields is customarily interpreted by means of induced time-dependent electric polarizabilities, magnetizabilities and mixed electric-magnetic polarizabilities. In general, these properties can be rationalized by integrals of density functions formulated in terms of induced charge and current densities. In this perspective, we focus on what has been done so far at the theoretical level, and on what can be expected to be unveiled from the topological study of suitable density functions, endowed with the fundamental requirement of origin invariance. Densities characterized by such a property can be integrated all over the configuration space to obtain electric dipole polarizability and optical rotatory power. Corresponding maps visualize domains mainly involved in the molecular response. The diagonal components of origin-independent density tensor functions that, on integration, yield corresponding electric dipole polarizability tensor of benzene, naphthalene, phenanthrene and ovalene, have been computed, confirming the ubiquitous presence of counter-polarization regions in the proximity of the atomic nuclei. They are associated with toroidal electron currents, induced by time derivative of the electric field of impinging radiation. Electron (de)localization in these systems is readily observed and estimated. The optical rotation density of the carbonyl chromophore is studied in detail. Its essential feature is the separation in quadrants of alternating sign of density about the CO bond. The presence of an extrachromophoric perturbation determines asymmetry in the extension of the quadrant distribution, thus causing optical rotation.
1 Introduction
One can reasonably ask if certain regions of the electronic cloud of a molecule in the presence of electromagnetic perturbation are more involved in its reaction. In fact, the existence of moieties inducing and exalting, or diminishing, the effect of external fields and/or intramolecular electric and magnetic dipoles at the nuclei, may significantly influence the phenomenology and determine observable outcomes in response properties, e.g., electric polarizabilities, magnetizabilities and optical rotatory power.Chemists have long studied the possibility of visualizing the influence of some substituents bestowing a particular quality, e.g., acting in a way analogous to that of a chromophore on imparting a specific color to a given compound. For instance, molecular charge density maps have customarily been employed in the physical rationalization of bonding, reactivities, and molecular properties.1–5
Polarizability densities within simple one-electron atomic systems have been investigated by Theimer and Paul,6 and by Orttung and Vosooghi.7 An application to inert gases was considered by Oxtoby and Gelbart.8 Nonetheless, Sipe and Van Kranendonk analyzed some restrictions of the polarizability density idea applied to atoms and molecules in an arbitrary, nonuniform electric field.9
The concept of nonlocal polarizability density, first proposed by Maaskant and Oosterhoff in their theoretical study of optical rotatory power,10 has been widely adopted by Hunt et al. in several papers, dealing with van der Waals interaction,11,12 short-range interactions on molecular dipoles, quadrupoles, and polarizabilities,13 infrared and Raman intensities,14 forces on nuclei in interacting molecules,15 and vibrational circular dichroism, in relation to electric-field shielding tensors.16
More particularly, the general idea of densities, functions of position r, suitable to compute molecular response properties by integration in d3r all over the molecular domain, has been analyzed in two seminal papers17,18 by Jameson and Buckingham, who also pointed out the origin independence of some electric and magnetic property densities as a fundamental requirement for their physical usefulness.
The nuclear magnetic shielding density defined via the Biot–Savart law of classical electrodynamics19 was examined as a topical example of function,17 depending on the difference between the position of electrons and a reference nucleus, and consequently invariant of the origin of the coordinate system. Upon integration, such a function leads to the magnetic shielding of a given nucleus.
On the other hand, the density functions of electric dipole polarizability and magnetizability were shown to depend on the origin of coordinates,18 which limits their reliability and physical usefulness. Nevertheless, some authors adopted definitions relying on the concept of polarization density induced by a static electric field to calculate electric dipole polarizabilities20,21 and hyperpolarizabilities.22–24
More recently, it has been suggested that origin-invariant densities of electric polarizability, generated by static and dynamic electric fields, e.g., that associated with a monochromatic plane wave, can be defined via the current density vector induced by time-derivative of the electric field,25,26 oscillating with frequency ω, carried by the wave. In fact, the polarizability density is identical to the current density tensor (CDT)27 and yields a practical recipe for computations, as recently shown.28
Much in the same way, a translationally invariant density of optical rotatory power is obtained by the trace of the CDT associated with the current density vector induced by the magnetic field carried by the plane wave.26,29 A few compounds, presenting interesting features from the chemical point of view, have been studied here.
This paper is organized as follows: the state of the art is reviewed in Section 2 by recalling the essential theoretical tools previously developed to define current density vectors and tensors needed for a computational approach to origin-invariant densities of electric dipole polarizability (EDP) and natural optical rotation, the latter related to the trace of the mixed electric dipole–magnetic dipole polarizability (MEMDP) tensor; applications are described in two separate parts of section 3, the first dedicated to EDP density, the second to MEMDP density; some final remarks concerning outlook and future work are given in section 4.
2 State of the art
Recent progress in the computation of origin invariant current densities, induced by optical fields associated with a monochromatic wave, is recalled in the following. After a brief preliminary excursus, see section 2.1, outlining the notation adopted, we focus in particular on the connection between induced electronic currents and two response properties, namely static and dynamic electric dipole polarizability, section 2.2, and optical rotatory power of chiral molecules, section 2.3.Two 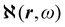 density functions of static, i.e, ω = 0, and dynamic polarizability tensor α(ω) are examined in section 2.2. The former is usually taken into account20,21,24 and depends on the origin of the reference system; accordingly it is discarded as computationally unpractical, in favor of an alternative, translationally invariant density
density functions of static, i.e, ω = 0, and dynamic polarizability tensor α(ω) are examined in section 2.2. The former is usually taken into account20,21,24 and depends on the origin of the reference system; accordingly it is discarded as computationally unpractical, in favor of an alternative, translationally invariant density 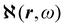 , based on the definition of current density tensor linked up with time derivative of the optical electric field carried by monochromatic radiation.
, based on the definition of current density tensor linked up with time derivative of the optical electric field carried by monochromatic radiation.
In the following section 2.3, it is shown that the MEMDP tensor κ′(ω), introduced to interpret the optical activity of chiral molecules, can be expressed in terms of a series of density functions26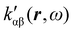 , which can be integrated all over the three-dimensional space to evaluate components and trace of κ′(ω). Computational approaches to the density
, which can be integrated all over the three-dimensional space to evaluate components and trace of κ′(ω). Computational approaches to the density 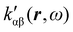 , based on frequency-dependent electronic current densities induced by monochromatic light shone on a probe molecule, has been developed26,29 and implemented at the time-dependent density functional theory (TD-DFT) level for the calculation of the optical rotation of chiral molecules.30–33
, based on frequency-dependent electronic current densities induced by monochromatic light shone on a probe molecule, has been developed26,29 and implemented at the time-dependent density functional theory (TD-DFT) level for the calculation of the optical rotation of chiral molecules.30–33
The dependence of 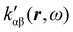 on the origin of the coordinate system has been investigated in connection with the corresponding change of
on the origin of the coordinate system has been investigated in connection with the corresponding change of 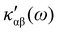 . It is shown that only the trace of the density function defined via dynamic current density evaluated using continuous translation of the origin of the coordinate system, for static34–37 and optical magnetic field,25 is invariant of origin. Accordingly, this function is recommended as a tool quite useful to determine the molecular domains which determine optical activity to a major extent.
. It is shown that only the trace of the density function defined via dynamic current density evaluated using continuous translation of the origin of the coordinate system, for static34–37 and optical magnetic field,25 is invariant of origin. Accordingly, this function is recommended as a tool quite useful to determine the molecular domains which determine optical activity to a major extent.
2.1 Theoretical framework
Adopting the same notation as in previous papers,28,29,38,39 for a molecule with n electrons and N clamped nuclei, i.e., within the Born–Oppenheimer (BO) approximation,40 charge, mass, position, canonical and angular momentum of the k-th electron are indicated, in the configuration space, by −e, me, rk,![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) k = −iħ∇k,
k = −iħ∇k, ![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) k = rk ×
k = rk × ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) k, k = 1, 2…n. Hereafter, the SI units are used and standard tensor formalism is employed, e.g., the Einstein convention of implicit summation over two repeated Greek indices is in force. Capitals denote n-electron operators, e.g., for position, canonical and angular momentum,
k, k = 1, 2…n. Hereafter, the SI units are used and standard tensor formalism is employed, e.g., the Einstein convention of implicit summation over two repeated Greek indices is in force. Capitals denote n-electron operators, e.g., for position, canonical and angular momentum,then, electric and magnetic dipole operators become
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) = −e = −e![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) , , | (1) |
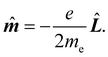 | (2) |
Time-dependent quantum mechanical perturbation theory41 is used to obtain expressions for the polarization charge density and current density induced in the electrons of a molecule by optical fields, assuming that the eigenvalue problem for the time-independent BO electronic Hamiltonian Ĥ(0)Ψ(0)j = E(0)jΨ(0)j has been solved, determining a set of eigenfunctions Ψ(0)j and corresponding energy eigenvalues E(0)j. The reference (ground) state is indicated by Ψ(0)a and the natural transition frequencies are ωja = (E(0)j − E(0)a)/ħ.
Within the McWeeny normalization,42 the n-electron density matrix
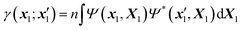 | (3) |
| X1 ≡ {x2,…,xn}, X = {x1,X1}, dX1 ≡ {dx2,…,dxn}. | (4) |
Inserting the reference (ground) state Ψ(0)a of the molecule in eqn (3) and integrating over ds1, one gets
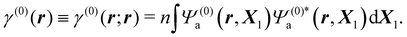 | (5) |
Thus, ρ(0)(r) = −eγ(0)(r) is the electronic charge density in the absence of perturbation.
The probability current density42 is defined as
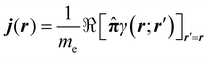 | (6) |
![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e1de.gif) = = ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) + eA. + eA. | (7) |
The Bloch gauge43 is adopted for the vector potential A. The electron current density corresponding to (6) is obtained by multiplying by −e, i.e., J = −ej. The interaction Hamiltonian considered in the present work does not contain terms depending on electron spin, therefore the probability current density (6) includes only orbital contributions.
2.2 Electric dipole polarizability density
The time-dependent electric field E of a monochromatic plane wave with frequency ω generates a first-order polarization density25 of the electron cloud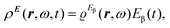 | (8) |
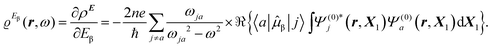 | (9) |
To first-order in E, the electric dipole moment induced in the electron distribution is defined by the integral
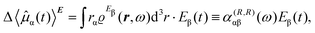 | (10) |
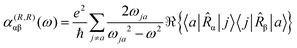 | (11) |
The product of vector components within the integral of eqn (10), a dyadic, can be interpreted as a polarizability density tensor function
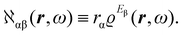 | (12) |
The electronic polarization density (8) is independent of origin, since 〈a|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) β|j〉 is origin-independent, but
β|j〉 is origin-independent, but 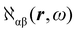 depends on the origin of rα. Therefore eqn (10) and (12) are unsuitable for calculations, since they do not meet the fundamental requirement pointed out by Jameson and Buckingham.18
depends on the origin of rα. Therefore eqn (10) and (12) are unsuitable for calculations, since they do not meet the fundamental requirement pointed out by Jameson and Buckingham.18
A more practical computational recipe is arrived at by an alternative procedure.26,29 To first-order, the time-derivative Ė induces an electronic current density
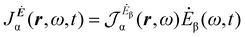 | (13) |
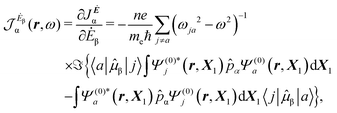 | (14) |
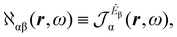 | (15) |
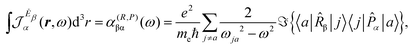 | (16) |
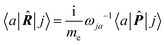 | (17) |
The previous considerations apply in the case of dynamic polarizability; in the static case one simply puts ω = 0 in eqn (14).
Multiplying the origin-independent electric dipole polarizability density tensor by E(ω,t), we obtain
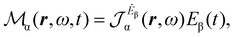 | (18) |
2.3 Electric dipole–magnetic dipole polarizability density
The first-order perturbed polarization density induced by time-derivative of the dynamic magnetic field is written as25,26,29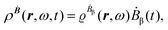 | (19) |
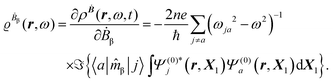 | (20) |
The first-order electric dipole moment, induced in the electron distribution by time derivative of the time-dependent magnetic field Ḃ of a monochromatic plane wave with frequency ω, is given by25,26,29
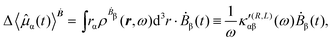 | (21) |
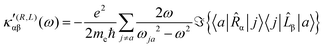 | (22) |
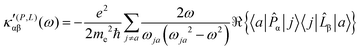 | (23) |
The trace of the MEMDP tensor, either (22) or (23), is related to the angle of natural optical rotation through the Rosenfeld equation.44,45 In SI units,
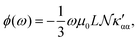 | (24) |
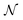 is the number density of optically active molecules.46 Most commonly used is the specific rotation power47,48
is the number density of optically active molecules.46 Most commonly used is the specific rotation power47,48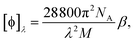 | (25) |
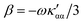 . Eqn (25) provides the specific rotation in the usual deg [dm g cm−3]−1 units, when the radiation wavelength λ is in cm, the molecular mass M is in g mol−1 and β is in cm4. Optical rotations calculated in the dipole-length gauge, i.e., using the trace of MEMDP (22), are origin dependent for approximate calculation methods, whereas in the velocity gauge (23) they are not, even using truncated basis sets. It is usually assumed that the closer optical rotation estimates in length and velocity gauges, the higher the quality of the computation.
. Eqn (25) provides the specific rotation in the usual deg [dm g cm−3]−1 units, when the radiation wavelength λ is in cm, the molecular mass M is in g mol−1 and β is in cm4. Optical rotations calculated in the dipole-length gauge, i.e., using the trace of MEMDP (22), are origin dependent for approximate calculation methods, whereas in the velocity gauge (23) they are not, even using truncated basis sets. It is usually assumed that the closer optical rotation estimates in length and velocity gauges, the higher the quality of the computation.
A MEMDP density can be defined for the (R,L) formalism via the integrand function in (21)
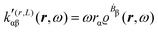 | (26) |
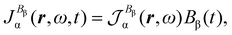 | (27) |
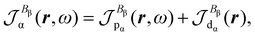 | (28) |
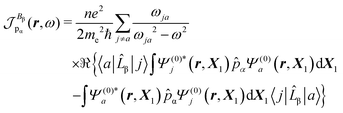 | (29) |
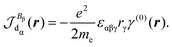 | (30) |
Indeed, allowing equality
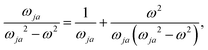 | (31) |
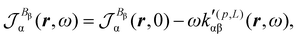 | (32) |
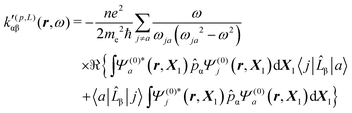 | (33) |
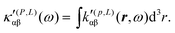 | (34) |
MEMDP density (26) depends on the origin of rα and both densities (26) and (33) depend on the origin of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) β. Therefore, their use is impractical for computational purposes. In particular, in view of an optical rotation density, the trace of both densities is also origin dependent and of no practical interest, see ref. 29 for further details.
β. Therefore, their use is impractical for computational purposes. In particular, in view of an optical rotation density, the trace of both densities is also origin dependent and of no practical interest, see ref. 29 for further details.
An origin-invariant definition is arrived at by considering the CDT associated with the frequency-dependent and origin-invariant current density obtained via the CTOCD-DZ computational scheme for static34–37 and optical magnetic field25
| JBDZ(r,ω,t) ≡ IB(r,ω,t) = JBp(r,ω,t) + JBΔ(r,ω,t). | (35) |
The corresponding CDT is defined as
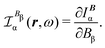 | (36) |
In eqn (35) a new term JBΔ(r,ω,t) replaces the conventional diamagnetic contribution. The corresponding CDT is given by
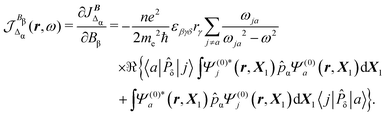 | (37) |
Substituting (31) in (37), after some manipulation we obtain the trace
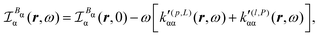 | (38) |
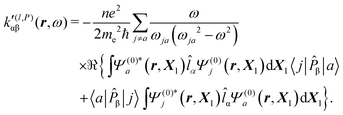 | (39) |
It is worth noting that spatial integration of eqn (39) leads to the MEMDP tensor κ′(L,P) that is simply transposed with respect to κ′(P,L) given in eqn (23).
Now, eqn (38) suggests that a suitable definition of origin-independent MEMDP density is
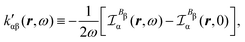 | (40) |
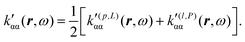 | (41) |
In the static limit, i.e., ω → 0, eqn (40) is indeterminate. However, in this limit, the trace (41) vanishes, as can be inferred viaeqn (33) and (39). At any rate, eqn (40) defines an origin-independent MEMDP tensor density for any r all over the molecular domain, regardless of the approximation used for the calculation, which is an essential requisite postulated by Jameson and Buckingham17,18 for computational purposes. We remark that definition (40) is slightly different from that introduced in ref. 29, since 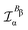 for ω = 0 has been removed. This improved definition finds his analogue for the integrated property in the modified velocity gauge (MVG) formulation of Pedersen et al.49 over the origin-independent velocity gauge of Grimme et al.50 At any rate, the integral in d3r of the trace of the second (static) term on the r.h.s. of eqn (40) vanishes for a complete basis set. Thus, the trace (41) can be used to obtain an origin-independent specific rotation power density, by means of an equation similar to (25), i.e.,
for ω = 0 has been removed. This improved definition finds his analogue for the integrated property in the modified velocity gauge (MVG) formulation of Pedersen et al.49 over the origin-independent velocity gauge of Grimme et al.50 At any rate, the integral in d3r of the trace of the second (static) term on the r.h.s. of eqn (40) vanishes for a complete basis set. Thus, the trace (41) can be used to obtain an origin-independent specific rotation power density, by means of an equation similar to (25), i.e.,
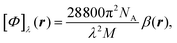 | (42) |
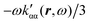 . Spatial integration of the specific rotation power density (42) provides exactly the same optical rotation obtained adopting the velocity gauge.
. Spatial integration of the specific rotation power density (42) provides exactly the same optical rotation obtained adopting the velocity gauge.
3 Applications
Densities of the electric dipole polarizability (EDPD) and specific rotation power (SRPD) were implemented at the time-dependent Hartree–Fock (TD-HF) and density functional theory (TD-DFT) level within the SYSMOIC program package.51,52 Full implementation details can be found in ref. 28, 29 and 38, along with a number of preliminary examples, which were presented for a few molecules for both EDPD and SRPD. One of the main features of the implementation consists of transforming transition amplitudes from the time-dependent calculation into perturbed molecular orbitals, which permits orbital decomposition of the results, which are origin-independent for both densities. We believe that this last feature is particularly interesting because it represents a practical analysis tool to deepen the study of the structure–property relationship, especially in the case of the optical rotation, a topic recently addressed for the length gauge.53In the following, we review the main results obtained so far and present new cases of study, which illustrate the usefulness of EDPD and SRPD in sections 3.1 and 3.2 respectively.
3.1 Electric dipole polarizability density (EDPD)
As discussed in Section 2.2, only the electric dipole polarizability density (15) is quite practical for computational purposes.So far, we have studied a series of atoms and simple molecules in terms of static and dynamic electric dipole polarizability density28 and in terms of electric dipole polarization current density.38 What emerged can be summarized as follows: (i) despite an always positive polarizability in the transparent region far from absorption, the dipole moment density (18) is found counter-oriented with respect to the induced electric field in regions close to the nuclei of a molecule, with the exception of He and H atoms, as for example, in H2, LiH, and BeH2; (ii) in terms of current induced by time derivative of the electric field, these regions of counter-polarization correspond to the inner portion of toroidal currents, which are found ubiquitous in the proximity of all the nuclei in a molecule, except hydrogen, for any orientation of the inducing field; and (iii) quite obviously, the higher the electron density, the higher is the polarizability density.
As a further application, we considered the possibility of describing electron (de)localization in terms of EDPD, focusing in particular on aromatic molecules. As shown previously,54ab initio calculations of π current density maps and dipole polarizability contributions confirm the expected correlation for monocycles, but show the limitations of polarizability as a measure of aromaticity – indeed, this is not our aim. On the other hand, it is reasonable to think about a connection between electron density and EDPD and this is what we preferred to look at carefully.
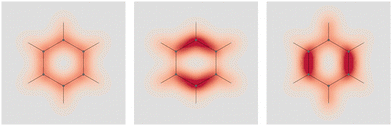
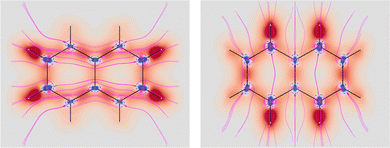
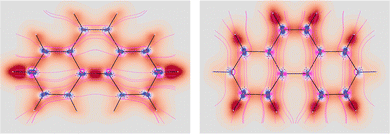
Four molecules have been taken into account: benzene, naphthalene, phenanthrene, and ovalene. Their geometries were optimized at the HF/6-31G(d) level, assuming standard Cartesian axis orientations. Origin independent EDPDs (15) were calculated using the TD-HF method55 and the 6-31G(d) basis set.56,57 For all molecules a radiation wavelength of 633 nm was used, which is sufficiently far away from any absorption. Superimposed streamlines on EDPD plots represent trajectories of the current density induced by Ė, see eqn (13), at t = 0. Terms in-plane and out-of-plane will be used to indicate the diagonal tensor components whose indices correspond to directions parallel and perpendicular to the molecular plane, respectively.
No regions of negative polarization density can be seen in Fig. 1. On moving to the molecular plane, see Fig. 2, a region of counter-polarization appears around each carbon atom, irrespective of the direction of the inducing electric field. For the two in-plane components, the extension of the negative regions follows the opposing arrangement. Of course, on the molecular plane the π-electron density vanishes, therefore the electric polarization of the σ-electrons can be observed. It is mainly localized around C–H bonds, four of them in one direction and the other two in the other direction, in accordance with the opposing arrangement. In terms of the current density tensor, multiplying 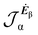 by the time derivative of the electric field, see eqn (13), the current density vector induced by an oriented radiation can be obtained. In the benzene molecule, the corresponding vector fields induced by a unitary Ė are superimposed upon the in-plane components in the central and right plots of Fig. 2.
by the time derivative of the electric field, see eqn (13), the current density vector induced by an oriented radiation can be obtained. In the benzene molecule, the corresponding vector fields induced by a unitary Ė are superimposed upon the in-plane components in the central and right plots of Fig. 2.
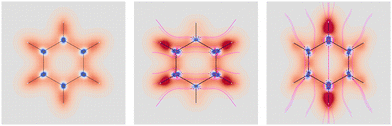 | ||
Fig. 2 EDPD of benzene over the molecular plane. Left  ; center and right in-plane components. Trajectories (in magenta) of the current density (13) induced by the time derivative of the electric field are superimposed to the in-plane components. See caption to Fig. 1 for other details. ; center and right in-plane components. Trajectories (in magenta) of the current density (13) induced by the time derivative of the electric field are superimposed to the in-plane components. See caption to Fig. 1 for other details. | ||
It is worth noting that the section of toroidal flow in each counter-polarization region. In many cases, for the benzene and the other molecules, they have the shape of a topological circumference formed by a pair of heteroclinic streamlines that connect two conjugated saddle-nodes.38 From the saddle nodes, other trajectories emerge, delimiting the vector field. In other cases, the topological circumferences open up and the toroidal flow runs over more than one nucleus. Counter-polarization regions and toroidal currents are strictly related.38
 , one observes that the density is not uniformly distributed, in particular it is higher about Cα–Cβ bonds. On the molecular plane, see Fig. 4, C–H bonds show the larger polarization in the opposing arrangement fashion. The same occurs in counter-polarization regions close to carbon nuclei. As can be clearly noticed, sections of toroidal flow, represented by topological circumferences of streamlines connecting conjugated saddle-nodes, incorporate perfectly the regions of negative polarization.
, one observes that the density is not uniformly distributed, in particular it is higher about Cα–Cβ bonds. On the molecular plane, see Fig. 4, C–H bonds show the larger polarization in the opposing arrangement fashion. The same occurs in counter-polarization regions close to carbon nuclei. As can be clearly noticed, sections of toroidal flow, represented by topological circumferences of streamlines connecting conjugated saddle-nodes, incorporate perfectly the regions of negative polarization.
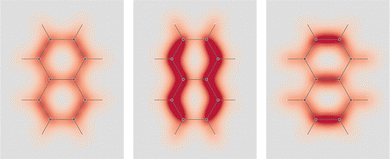 | ||
Fig. 3 EDPD of naphthalene over a plane located at 1 a.u. below the molecular plane. Left  ; center and right in-plane components. See caption to Fig. 1 for other details. ; center and right in-plane components. See caption to Fig. 1 for other details. | ||
 | ||
| Fig. 4 EDPD in-plane components of naphthalene over the molecular plane. See captions to Fig. 1 and 2 for other details. | ||
 shown in the left plot of Fig. 5. The double bond is clearly visible as a site of major polarization density. However, the density distribution over the two external rings is not perfectly uniform as in benzene. In particular, the density in correspondence of C2–C3 (C6–C7) is a bit lower with respect to the other bonds. Also in this case, the in-plane components show an opposite arrangement, with the one showing the alternating bonds more intense than the other. Moving on the molecular plane, see. Fig. 6, the opposite arrangement of polarizability density located about C–H bonds is observed. Also the bridge C–C bond linking the two external rings is characterized by strong density. The counter-polarization regions go in parallel, together with the sections of ubiquitous toroidal patterns.38
shown in the left plot of Fig. 5. The double bond is clearly visible as a site of major polarization density. However, the density distribution over the two external rings is not perfectly uniform as in benzene. In particular, the density in correspondence of C2–C3 (C6–C7) is a bit lower with respect to the other bonds. Also in this case, the in-plane components show an opposite arrangement, with the one showing the alternating bonds more intense than the other. Moving on the molecular plane, see. Fig. 6, the opposite arrangement of polarizability density located about C–H bonds is observed. Also the bridge C–C bond linking the two external rings is characterized by strong density. The counter-polarization regions go in parallel, together with the sections of ubiquitous toroidal patterns.38
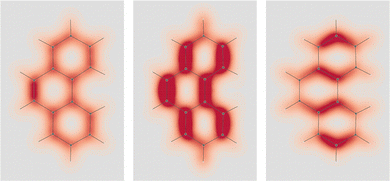 | ||
Fig. 5 EDPD of phenanthrene over a plane located at 1 a.u. below the molecular plane. Left  ; center and right in-plane components. See caption to Fig. 1 for other details. ; center and right in-plane components. See caption to Fig. 1 for other details. | ||
 | ||
| Fig. 6 EDPD in-plane components of phenanthrene over the molecular plane. See captions to Fig. 1 and 2 for further details. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds, i.e., ovalene, in which a maximum of four Clar's sextets and as many C
C double bonds, i.e., ovalene, in which a maximum of four Clar's sextets and as many C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds can be allocated. Computed EDPD of ovalene is shown in Fig. 7. Within the plot of
C double bonds can be allocated. Computed EDPD of ovalene is shown in Fig. 7. Within the plot of  , on the left of the figure, one can clearly discern the four C
, on the left of the figure, one can clearly discern the four C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds located at the top-right, top-left, bottom-right, and bottom-left corners. Clar's sextets are hidden a little by the non uniform density distribution, see rings at the top, bottom, center-right, and center-left. They are visible with greater clarity in the right plot of Fig. 7 relative to one of the two in-plane components, which are characterized by a slightly more complex, though not less intriguing, opposing arrangement.
C double bonds located at the top-right, top-left, bottom-right, and bottom-left corners. Clar's sextets are hidden a little by the non uniform density distribution, see rings at the top, bottom, center-right, and center-left. They are visible with greater clarity in the right plot of Fig. 7 relative to one of the two in-plane components, which are characterized by a slightly more complex, though not less intriguing, opposing arrangement.
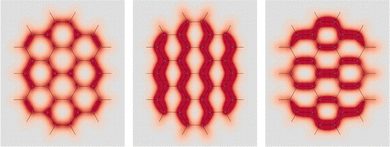 | ||
Fig. 7 EDPD of ovalene over a plane located at 1 a.u. below the molecular plane. Left 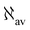 ; center and right in-plane components. See caption to Fig. 1 for further details. ; center and right in-plane components. See caption to Fig. 1 for further details. | ||
Over the molecular plane, ovalene displays the EDPD in-plane components shown in Fig. 8. The opposing arrangement of the polarizability density mainly located around C–H bonds is clearly observable. Some C–C bonds also contribute. The omnipresence of counter-polarization regions, embedded within domains of toroidal currents, is further verified also in ovalene, particularly in the vicinity of the innermost carbon atoms.
 | ||
| Fig. 8 EDPD in-plane components of ovalene over the molecular plane. See captions to Fig. 1 and 2 for further details. | ||
3.2 Specific rotation power density (SRPD)
As discussed above in Section 2.3, only the specific rotation power density (42), connected with the trace (41) of the MEMDP density tensor, and defined by the dynamic origin-invariant current density (35), is suitable for computational purposes.In order to emphasize the main features of SRPD, we have recently presented some results for the hydrogen peroxide molecule,29 reporting SRPD maps which visualize 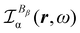 , at λ = 355 nm for a number of chiral conformations, varying the HO–OH torsional angle θ between 0° and 180°. We observed that SRPD is mainly located in the vicinity of oxygen atoms, with a conspicuous alternation of sign. For the two achiral conformations at θ = 0° and θ = 180°, the symmetry of density is consistent with the obviously vanishing optical rotation. In particular, SRPD changes sign by reflection through a symmetry plane, over which it vanishes at all points. For the intermediate chiral conformations, the absence of symmetry planes gives rise to positive and negative regions which do not cancel one another.
, at λ = 355 nm for a number of chiral conformations, varying the HO–OH torsional angle θ between 0° and 180°. We observed that SRPD is mainly located in the vicinity of oxygen atoms, with a conspicuous alternation of sign. For the two achiral conformations at θ = 0° and θ = 180°, the symmetry of density is consistent with the obviously vanishing optical rotation. In particular, SRPD changes sign by reflection through a symmetry plane, over which it vanishes at all points. For the intermediate chiral conformations, the absence of symmetry planes gives rise to positive and negative regions which do not cancel one another.
In summary, for this simple example, the SRPD provided by the CDT evaluated via the CTOCD-DZ approach is a function characterized by high intensity peaks of opposite sign in the proximity of atoms, whose symmetry is clearly connected with the integrated property. It provides more precise understanding of how the absence of symmetry planes gives rise to optical rotation.
As a next step, we first focus on the optical activity generated by the presence of a light absorbing unit, such as an inherently achiral carbonyl chromophore, which cannot exhibit any optical rotatory power by itself without the intervention of an extrachromophoric perturbation. The analysis that we can carry out, considering the SRPD, is quite interesting. Passing from the highly symmetrical system constituted by the carbon monoxide molecule to increasingly less symmetrical systems like formaldehyde and acetaldehyde, the latter in two conformations, one achiral and the other chiral, we can study in detail how SRPD changes.
In carbon monoxide, each spatial point of the molecular space belongs to a σv symmetry plane of the C∞v symmetry point group, therefore [Φ]λ(r) is zero at every r.
In formaldehyde, two σv planes of symmetry of the C2v symmetry point group, divide the SRPD scalar field in four regions of alternating sign. This can be observed on the top panel of Fig. 9 where SRPD changes sign on passing from one side to another of each plane, for a pair of iso-surface values (±100 deg[dm g cm−3]−1a0−3), computed by the TD-DFT method.58,59 The calculation was carried out adopting the B3LYP functional60,61 and the aug-cc-pVTZ,62,63 for the radiation wavelength of 589.3 nm (sodium D-line). Obviously, the optical activity vanishes also in this case, i.e., 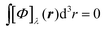 , the four regions equivalent and opposed in sign by symmetry. However, it is interesting to observe that each of the four regions integrates, at this level of theory, to 6895 deg[dm g cm−3]−1 in absolute value, that is, a very large estimate, compared with usual specific optical rotations.
, the four regions equivalent and opposed in sign by symmetry. However, it is interesting to observe that each of the four regions integrates, at this level of theory, to 6895 deg[dm g cm−3]−1 in absolute value, that is, a very large estimate, compared with usual specific optical rotations.
The achiral conformation of acetaldehyde is characterized by one plane of symmetry. Despite that, as in the case of formaldehyde, the SRPD field around the carbonyl group is partitioned into four regions of alternating sign, which are in absolute value equivalent by symmetry only by reflection through the unique symmetry plane, see plot in the middle of Fig. 9. Consequently, there is no optical activity, since the positive contribution to the specific optical rotation (+8516 deg [dm g cm−3]−1) cancels out exactly the negative one (−8516 deg [dm g cm−3]−1).
A chiral conformation of acetaldehyde was set by rotating the methyl group until one of the protons is at right angles to the carbonyl plane. The plot of calculated SRPD is displayed in the bottom panel of Fig. 9. Remarkably, the loss of symmetry does not change what appears to be an essential feature of the carbonyl group represented by the separation of the SRPD in quadrants, which are no longer equivalent in absolute value by symmetry.
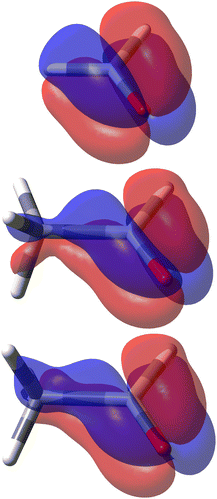
The decomposition into origin-independent orbital contributions provides an explanation of this separation, which recalls some aspects of the famous octant rule.64 Indeed, according to the results of the TD-DFT calculation, the first excited state is a virtual transition from the HOMO to the LUMO (n → π*). Moreover, the orbital decomposition analysis shows that the HOMO provides the dominant contribution to SRPD, since plots calculated using only the HOMO contribution are indistinguishable from that calculated ones using the full set of MOs. Now, the HOMO shape is shown in Fig. 10 and, as can be observed, it presents a nodal surface which bisects the H3 C–C–H angle and is perpendicular to the plane of the carbonyl group. Such a nodal surface provides, together with the nodal surface of the π* LUMO, the observed separation in quadrants of SRPD. A similar discussion based on transition densities has also been reported in ref. 32.
Looking at the two signed surfaces in the bottom panel of Fig. 9, it is not easy to notice a predominance of one over the other. However, spatial integration of the SRPD leads to a non vanishing negative specific rotatory power, [ϕ]589.3 = −69.2 deg [dm g cm−3]−1, resulting from a negative contribution which is only a little bigger than the positive contribution, i.e., −8314.7 and +8245.5 deg [dm g cm−3]−1 respectively.
The remarkable ratio of approximately two orders of magnitude between individual contributions and total specific rotatory power is commonly found also in other systems. Therefore, it may well account for the known difficulties to obtain accurate theoretical optical rotations,30,65 as even small effects, for example, interaction with the solvent66,67 or molecular vibration,68–70 can produce considerable variations of the final result, which also may easily change sign.
However, to check the quality of the results exposed above, we report in Table 1 the specific rotatory power of the chiral conformation of acetaldehyde, calculated for three commonly used wavelengths, using basis sets of increasing quality at the B3LYP level of theory; GIAO predictions, along with optical rotations determined within modified-velocity and length gauges, are listed. Considering the GIAO results obtained adopting the aug-cc-pV5Z basis set as the best of the series, it is interesting to observe the good performance of the modified-velocity and length gauges already using the TZ basis set.
| λ (nm) | Basis set | GIAO | Modified-velocity | Length |
|---|---|---|---|---|
| 633 | DZ | −52.7 | −49.7 | −54.8 |
| TZ | −53.6 | −57.4 | −56.3 | |
| QZ | −55.2 | −56.4 | −56.3 | |
| 5Z | −56.1 | — | — | |
| 589.3 | DZ | −63.7 | −59.7 | −66.1 |
| TZ | −64.8 | −69.2 | −68.0 | |
| QZ | −66.6 | −68.1 | −68.0 | |
| 5Z | −67.7 | — | — | |
| 355 | DZ | −414.7 | −349.1 | −417.5 |
| TZ | −412.0 | −439.1 | −433.8 | |
| QZ | −428.4 | −439.1 | −439.8 | |
| 5Z | −436.8 | — | — | |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O chromophore determines its optical rotation. Among many possible choices, we have considered (1S,4S)-norbornenone as a suitable candidate for its large optical rotation and for a number of other interesting facts briefly summarized as follows. Owing to substantially similar solution phase optical rotations measured at the sodium D-line for different solvents,71–73 it was assumed for a long time that the optical rotation of this molecule is very little affected by solvent effects. The presumed lack of solvent effect was somehow hidden also by the apparently good agreement found with the B3LYP/aug-cc-pVDZ estimate of the OR obtained for the free molecule.30 However, as reported successively,74 this was found to be not true. Notably, the experimental rotatory power exhibited by isolated (vapor-phase) molecules is much lower in magnitude and in good accord with coupled cluster predictions computed using both the origin-independent dipole-velocity and origin-dependent dipole length representations.74,75 Last but not least, the constructive interaction of the two chromophores (C
O chromophore determines its optical rotation. Among many possible choices, we have considered (1S,4S)-norbornenone as a suitable candidate for its large optical rotation and for a number of other interesting facts briefly summarized as follows. Owing to substantially similar solution phase optical rotations measured at the sodium D-line for different solvents,71–73 it was assumed for a long time that the optical rotation of this molecule is very little affected by solvent effects. The presumed lack of solvent effect was somehow hidden also by the apparently good agreement found with the B3LYP/aug-cc-pVDZ estimate of the OR obtained for the free molecule.30 However, as reported successively,74 this was found to be not true. Notably, the experimental rotatory power exhibited by isolated (vapor-phase) molecules is much lower in magnitude and in good accord with coupled cluster predictions computed using both the origin-independent dipole-velocity and origin-dependent dipole length representations.74,75 Last but not least, the constructive interaction of the two chromophores (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) has been invoked to explain the otherwise unusually large specific rotation of (1S,4S)-norbornenone.76
C) has been invoked to explain the otherwise unusually large specific rotation of (1S,4S)-norbornenone.76
In the light of what has been discussed above for the simple acetaldehyde case, we have now the possibility to analyze where the large specific rotation of (1S,4S)-norbornenone originates in terms of SRPD and, in particular, where major contributions are located and how many they are.
For the calculation of the MEMDP we have used the B3LYP/aug-cc-pVDZ combination of functional and basis set as adopted by Stephens et al. in ref. 30. The result is shown in Fig. 11. As can be observed, there is an amazing partition of the SRPD in quadrants, quite similar to that studied before for much simpler systems. This makes us think that we are really observing the essential features of MEMDP of the carbonyl chromophore. Moreover, as can be readily noted in Fig. 11, the predominance of blue sectors over the red ones well agrees with the negative value of [ϕ]D, estimated via spatial integration as large as −1195 deg [dm g cm−3]−1, in accord with previous DFT calculations.30,74,75 Once again, we observe very large positive and negative contributions, which are calculated to be 4704 and −5899 deg [dm g cm−3]−1. This explains why even small variations of big contributions lead to large optical rotations, which turn out to be very sensitive to the environment, i.e. free molecule vs. solution phase, and the calculation method. Norbornenone contains a second chromophore, i.e., a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond, which, seemingly, does not play a substantial role in determining the total optical rotation density at the sodium D-line, apart from the possibility of providing an influence as an extrachromophoric perturbing agent.76
C double bond, which, seemingly, does not play a substantial role in determining the total optical rotation density at the sodium D-line, apart from the possibility of providing an influence as an extrachromophoric perturbing agent.76
4 Conclusions
Two origin-independent polarizability density tensor functions have been defined and evaluated for a number of molecules. They are as follows: (i) the time-dependent electric dipole polarizability density (EDPD) and (ii) the average time-dependent mixed electric dipole–magnetic dipole polarizability density (MEMDPD). They have been employed to rationalize origin-independent properties induced by optical fields, thus paving the way for topological studies aimed at discovering domains of molecular space and functional groups which influence electromagnetic response to a higher extent.The origin-independence of these densities constitutes an essential requisite of their physical meaning, quite recommendable for computational purposes.
EDPD coincides with a current density tensor fully characterizing the electron flow induced by time derivative of the oscillating electric field of the radiation. Its integral equals the dynamic electric dipole polarizability, therefore EDPD is effectively an electric dipole polarizability density. In the limit of zero frequency, it defines the static polarizability density.
EDPD is shown here to be useful for detecting regions of electron distribution in which polarization density is larger and where counter-polarization densities appear, in connection with a peculiar shape of induced currents, referred to as toroidal flow. Despite the always positive value of total static electric dipole polarizability far from absorption, counter-polarization in regions close to the atomic nuclei of a molecule, except protons, is ubiquitous and always deeply connected with toroidal electron currents.
Application to aromatic hydrocarbons confirms the ability of EDPD to indicate where electron delocalization occurs and to distinguish aromatic rings and localized double bonds.
Much remains to be done. In perspective, we would like to put in a to-do list: (i) the need for more clearly differentiating various kinds of aromatic rings, which was partially achieved in the molecules examined, but still deserves to be investigated at the quantitative level and (ii) extending the topological study of polarizability density to different kinds of functional groups and verifying if their features are transferable from one molecule to another.
Also MEMDPD is itself a current density tensor connected with the electronic currents induced by the oscillating magnetic field of the radiation. It vanishes in the limit of zero frequency. Its trace is related to the optical rotation density, or, more conveniently, to the specific rotation power density (SRPD).
As far as SRPD is concerned, we remark that it can be dissected in origin-independent orbital contributions and that it integrates to obtain MVG optical rotations. It can be used in conjunction with a variety of quantum mechanical methods, coupled cluster in particular,49 to analyze the optical rotation of chiral molecules without recourse to London orbitals. The perspective is to extend the study to other achiral chromophores, e.g., double and triple C–C bonds, cyano groups, aromatic rings, etc., to cite quite a few. Moreover, a very interesting case worth studying would be that of chromophores that are themselves chiral, as, for instance, helicenes and compounds containing non-planar diene moieties. Last but not least, a very important goal to achieve would be that of predicting in which way a chiral perturbation acts on the SRPD topology.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from MUR (Ministero dell'Università e della Ricerca), FARB 2020 and FARB 2021, is gratefully acknowledged.References
- R. F. W. Bader, in Int. Rev. Sci. – Theoretical chemistry, ed. A. D. Buckingham and C. A. Coulson, Butterworths, London, Boston, 1975, p. 43 Search PubMed.
- R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press, Oxford University Press, Oxford [England], New York, 1994 Search PubMed.
- P. Popelier, P. Smith and A. Hinchliffe, Quantum topological Atoms, Royal Society of Chemistry, United Kingdom, 2002, vol. 8, pp. 391–448 Search PubMed.
- A. Morgenstern, T. R. Wilson and M. E. Eberhart, J. Phys. Chem. A, 2017, 121, 4341–4351 CrossRef CAS PubMed.
- A. D. Buckingham, Advances in Chemical Physics, John Wiley & Sons, Inc., 2007, pp. 107–142 Search PubMed.
- O. Theimer and R. Paul, J. Chem. Phys., 1965, 42, 2508–2517 CrossRef CAS.
- W. H. Orttung and D. Vosooghi, J. Phys. Chem., 1983, 87, 1432–1437 CrossRef CAS.
- D. W. Oxtoby and W. M. Gelbart, Mol. Phys., 1975, 30, 535–547 CrossRef CAS.
- J. Sipe and J. Van Kranendonk, Mol. Phys., 1978, 35, 1579–1584 CrossRef CAS.
- W. Maaskant and L. Oosterhoff, Mol. Phys., 1964, 8, 319–344 CrossRef.
- K. L. C. Hunt, J. Chem. Phys., 1983, 78, 6149–6155 CrossRef CAS.
- K. L. C. Hunt and J. E. Bohr, J. Chem. Phys., 1986, 84, 6141–6150 CrossRef CAS.
- K. L. C. Hunt, J. Chem. Phys., 1984, 80, 393–407 CrossRef CAS.
- K. L. C. Hunt, J. Chem. Phys., 1989, 90, 4909–4915 CrossRef CAS.
- K. L. C. Hunt and Y. Q. Liang, J. Chem. Phys., 1991, 95, 2549–2559 CrossRef CAS.
- K. L. C. Hunt and R. A. Harris, J. Chem. Phys., 1991, 94, 6995–7002 CrossRef CAS.
- C. J. Jameson and A. D. Buckingham, J. Phys. Chem., 1979, 83, 3366–3371 CrossRef CAS.
- C. J. Jameson and A. D. Buckingham, J. Chem. Phys., 1980, 73, 5684 CrossRef CAS.
- J. D. Jackson, Classical electrodynamics, Wiley, New York, 3rd edn, 1999 Search PubMed.
- A. Alparone, Sci. World J., 2013, 2013, 1–9 Search PubMed.
- N. Otero, C. Van Alsenoy, C. Pouchan and P. Karamanis, J. Comput. Chem., 2015, 36, 1831–1843 CrossRef CAS PubMed.
- M. Nakano, I. Shigemoto, S. Yamada and K. Yamaguchi, J. Chem. Phys., 1995, 103, 4175–4191 CrossRef CAS.
- S. Yamada, M. Nakano, I. Shigemoto, S. Kiribayashi and K. Yamaguchi, Chem. Phys. Lett., 1997, 267, 445–451 CrossRef CAS.
- M. Nakano, H. Fukui, T. Minami, K. Yoneda, Y. Shigeta, R. Kishi, B. Champagne, E. Botek, T. Kubo, K. Ohta and K. Kamada, Theor. Chem. Acc., 2011, 130, 711–724 Search PubMed.
- P. Lazzeretti, J. Chem. Phys., 2018, 149, 154106 CrossRef PubMed.
- P. Lazzeretti, J. Chem. Phys., 2019, 150, 184117 CrossRef PubMed.
- P. Lazzeretti, J. Chem. Phys., 2018, 148, 134109 CrossRef PubMed.
- F. F. Summa, G. Monaco, P. Lazzeretti and R. Zanasi, J. Phys. Chem. Lett., 2021, 12, 8855–8864 CrossRef CAS PubMed.
- F. F. Summa, G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, Molecules, 2021, 26, 4195 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, J. R. Cheeseman and M. J. Frisch, J. Phys. Chem. A, 2001, 105, 5356–5371 CrossRef CAS.
- J. Autschbach, S. Patchkovskii, T. Ziegler, S. J. A. van Gisbergen and E. J. Baerends, J. Chem. Phys., 2002, 117, 581–592 CrossRef CAS.
- J. Autschbach, Chirality, 2009, 21, E116–E152 CrossRef CAS PubMed.
- J. Autschbach, L. Nitsch-Velasquez and M. Rudolph, in Time-Dependent Density Functional Response Theory for Electronic Chiroptical Properties of Chiral Molecules, ed. R. Naaman, D. N. Beratan and D. Waldeck, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, pp. 1–98 Search PubMed.
- P. Lazzeretti, M. Malagoli and R. Zanasi, Chem. Phys. Lett., 1994, 220, 299–304 CrossRef CAS.
- P. Lazzeretti, Theor. Chem. Acc., 2012, 131, 1222 Search PubMed.
- R. Zanasi, P. Lazzeretti, M. Malagoli and F. Piccinini, J. Chem. Phys., 1995, 102, 7150 CrossRef CAS.
- R. Zanasi, J. Chem. Phys., 1996, 105, 1460 CrossRef CAS.
- F. F. Summa, G. Monaco, R. Zanasi and P. Lazzeretti, J. Chem. Phys., 2022, 156, 054106 CrossRef CAS PubMed.
- F. F. Summa, G. Monaco, R. Zanasi and P. Lazzeretti, J. Chem. Phys., 2022, 156, 154105 CrossRef CAS PubMed.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484 CrossRef.
- P. W. Langhoff, S. T. Epstein and M. Karplus, Rev. Mod. Phys., 1972, 44, 602–644 CrossRef CAS.
- R. McWeeny, Methods of molecular quantum mechanics, Academic Press, London, 2nd edn, 1992 Search PubMed.
- F. Bloch, in W. Heisenberg und die Physik Unserer Zeit, ed. F. Bopp, Friedr. Wieveg & Son, Braunschweig, 1961, pp. 93–102 Search PubMed.
- L. Rosenfeld, Z. Phys., 1929, 52, 161–174 CrossRef.
- L. Rosenfeld, Theory of Electrons, North-Holland Publishing Company, 1951 Search PubMed.
- L. D. Barron and A. D. Buckingham, Annu. Rev. Phys. Chem., 1975, 26, 381–396 CrossRef CAS.
- E. U. Condon, Rev. Mod. Phys., 1937, 9, 432–457 CrossRef CAS.
- P. Stephens, F. Devlin, J. Cheeseman and M. Frisch, Chirality, 2002, 14, 288–296 CrossRef CAS PubMed.
- T. B. Pedersen, H. Koch, L. Boman and A. M. S. de Merás, Chem. Phys. Lett., 2004, 393, 319–326 CrossRef CAS.
- S. Grimme, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 361, 321–328 CrossRef CAS.
- G. Monaco, F. F. Summa and R. Zanasi, J. Chem. Inf. Model., 2020, 61, 270–283 CrossRef PubMed.
- G. Monaco, F. F. Summa and R. Zanasi, SYSMOIC Version 3.3, 2022, https://SYSMOIC.chem.unisa.it/MANUAL/ Search PubMed.
- T. Balduf and M. Caricato, Theor. Chem. Acc., 2023, 142, 11 Search PubMed.
- P. Fowler and A. Soncini, Chem. Phys. Lett., 2004, 383, 507–511 CrossRef CAS.
- P. Jørgensen and J. Linderberg, Int. J. Quantum Chem., 1970, 4, 587–602 CrossRef.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. E. Casida, Recent Advances in Computational Chemistry, WORLD SCIENTIFIC, 1995, vol. 1, pp. 155–192 Search PubMed.
- M. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- W. Moffitt, R. B. Woodward, A. Moscowitz, W. Klyne and C. Djerassi, J. Am. Chem. Soc., 1961, 83, 4013–4018 CrossRef CAS.
- P. Stephens, D. McCann, J. Cheeseman and M. Frisch, Chirality, 2005, 17, S52–S64 CrossRef CAS PubMed.
- Y. Kumata, J. Furukawa and T. Fueno, Bull. Chem. Soc. Jpn., 1970, 43, 3920–3921 CrossRef CAS.
- B. Mennucci, J. Tomasi, R. Cammi, J. R. Cheeseman, M. J. Frisch, F. J. Devlin, S. Gabriel and P. J. Stephens, J. Phys. Chem. A, 2002, 106, 6102–6113 CrossRef CAS.
- J. Kongsted, T. B. Pedersen, M. Strange, A. Osted, A. E. Hansen, K. V. Mikkelsen, F. Pawlowski, P. Jørgensen and C. Hättig, Chem. Phys. Lett., 2005, 401, 385–392 CrossRef CAS.
- K. Ruud and R. Zanasi, Angew. Chem., Int. Ed., 2005, 44, 3594–3596 CrossRef CAS PubMed.
- J. Kongsted, T. B. Pedersen, L. Jensen, A. E. Hansen and K. V. Mikkelsen, J. Am. Chem. Soc., 2005, 128, 976–982 CrossRef PubMed.
- K. Mislow and J. G. Berger, J. Am. Chem. Soc., 1962, 84, 1956–1961 CrossRef CAS.
- J. M. Janusz, L. J. Gardiner and J. A. Berson, J. Am. Chem. Soc., 1977, 99, 8509–8510 CrossRef CAS.
- D. A. Lightner, J. K. Gawronski and T. D. Bouman, J. Am. Chem. Soc., 1980, 102, 5749–5754 CrossRef CAS.
- P. Lahiri, K. B. Wiberg, P. H. Vaccaro, M. Caricato and T. D. Crawford, Angew. Chem., Int. Ed., 2013, 53, 1386–1389 CrossRef PubMed.
- T. D. Crawford and P. J. Stephens, J. Phys. Chem. A, 2008, 112, 1339–1345 CrossRef CAS PubMed.
- M. Caricato, P. H. Vaccaro, T. D. Crawford, K. B. Wiberg and P. Lahiri, J. Phys. Chem. A, 2014, 118, 4863–4871 CrossRef CAS PubMed.
Footnote |
| † All authors contributed equally to this work. |
| This journal is © the Owner Societies 2023 |