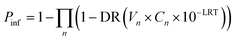Open Access Article
Open Access ArticleScience-based pathogen treatment requirements for direct potable reuse†
Brian M.
Pecson‡
 *a,
Anya
Kaufmann‡
*a,
Anya
Kaufmann‡
 *a,
Daniel
Gerrity
b,
Charles N.
Haas
*a,
Daniel
Gerrity
b,
Charles N.
Haas
 c,
Edmund
Seto
d,
Nicholas J.
Ashbolt
e,
Theresa
Slifko
f,
Emily
Darby
c,
Edmund
Seto
d,
Nicholas J.
Ashbolt
e,
Theresa
Slifko
f,
Emily
Darby
 a and
Adam
Olivieri
g
a and
Adam
Olivieri
g
aTrussell Technologies, Oakland, California, USA. E-mail: brianp@trusselltech.com; anyak@trusselltech.com
bApplied Research and Development Center, Southern Nevada Water Authority, Las Vegas, Nevada, USA
cDrexel University, Philadelphia, Pennsylvania, USA
dUniversity of Washington, Seattle, Washington, USA
eUniversity of South Australia, Adelaide, Australia
fMetropolitan Water District of Southern California, Los Angeles, California, USA
gEOA, 1410 Jackson Street, Oakland, California, USA
First published on 20th October 2023
Abstract
Specifying appropriate pathogen treatment requirements is critical to ensure that direct potable reuse (DPR) systems provide consistent and reliable protection of public health. This study leverages several research efforts conducted on behalf of the California State Water Resources Control Board to provide guidance on selecting science-based pathogen treatment requirements for DPR. Advancements in pathogen detection methods have produced new robust, high-quality datasets that can be used to characterize the distribution of pathogen concentrations present in raw wastewater. Such probabilistic distributions should replace the deterministic point estimate approach previously used in regulatory development. Specifically, to calculate pathogen treatment requirements, pathogen distributions should be used in probabilistic quantitative microbial risk assessments that account for variability in concentrations. This approach was applied using the latest high-quality datasets to determine the log reduction targets necessary to achieve an annual risk goal of 1 in 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 infections per person as well as a more stringent daily risk goal of 2.7 × 10−7 infections per person. The probabilistic approach resulted in pathogen log reduction targets of 13-log10 for enteric viruses, 10-log10 for Giardia, and 10-log10 for Cryptosporidium. An additional 4-log10 level of redundancy provides protection against undetected failures while maintaining high degrees of compliance with the daily (99%) and annual risk goals (>99%). The limitations of the use of molecular pathogen data are also discussed. While the recommendations and findings are targeted for California, they are broadly applicable to the development of DPR regulations outside California and the U.S.
000 infections per person as well as a more stringent daily risk goal of 2.7 × 10−7 infections per person. The probabilistic approach resulted in pathogen log reduction targets of 13-log10 for enteric viruses, 10-log10 for Giardia, and 10-log10 for Cryptosporidium. An additional 4-log10 level of redundancy provides protection against undetected failures while maintaining high degrees of compliance with the daily (99%) and annual risk goals (>99%). The limitations of the use of molecular pathogen data are also discussed. While the recommendations and findings are targeted for California, they are broadly applicable to the development of DPR regulations outside California and the U.S.
Water impactPathogen log-reduction requirements for direct potable reuse (DPR) must ensure reliable protection of public health, but should be appropriately selected to avoid the economic, societal, and environmental costs of over-treatment. This study recommends both a framework and specific requirements for pathogen control in DPR using the highest-quality pathogen monitoring data in probabilistic microbial risk assessments. |
1 Introduction
By eliminating the passage of water through the environment, direct potable reuse (DPR) creates the closest connection between the treatment and consumption of recycled waters. Compared to indirect potable reuse (IPR), this proximity greatly reduces the time that is available to detect and respond to treatment-related issues. This presents new challenges for the control of wastewater contaminants, particularly enteric pathogens, which can cause acute public health effects after even a single exposure.1 Specifying pathogen treatment requirements is therefore a critical step in the development of DPR regulations, whose primary goal is to ensure consistent and reliable public health protection. These requirements should protect both healthy and sensitive populations.1,2California has already developed regulations for two forms of IPR (groundwater recharge and surface water augmentation), and the California State Water Resources Control Board (State Water Board) is under legislative mandate to develop DPR regulations by the end of 2023. In its 2016 DPR feasibility assessment, the State Water Board concluded that it needed to modernize the process of developing pathogen log reduction targets (LRTs) for DPR by 1) developing a new high-quality dataset to better characterize pathogen concentrations in raw wastewater, and 2) implementing an updated probabilistic approach for determining LRTs.3,4 The probabilistic approach prioritizes the use of high-quality monitoring methods to develop robust datasets that are used to describe statistical functions (probability distributions) that characterize the likely range in pathogen concentrations. The distributions are used to estimate microbial risk as well as the likelihoods that those values occur within a given range. The probabilistic approach allows for the risk manager to consider the entire distribution of risk and eliminates the need to assume extreme estimates for pathogen concentrations that could erroneously overestimate risk.
To meet this goal, the State Water Board undertook three research projects related to enteric pathogen control: two related to the characterization of pathogen concentrations in wastewater and the third in the application of these new data to develop treatment requirements. In the first, a 14-month pathogen monitoring campaign was conducted to better characterize the concentrations of representative enteric pathogens in raw wastewater.5,6 This study was deemed critical because these concentrations define the starting point for calculating LRTs: higher raw wastewater concentrations require greater levels of treatment to reduce pathogen concentrations down to acceptable drinking water levels (and vice versa). The second research effort evaluated how these concentrations would be impacted during periods of higher disease occurrence, such as during outbreaks.7 Because the State Water Board acknowledged the need for improved methods to “provide more complete information on [pathogen] concentrations and their variability”,3 the pathogen monitoring effort developed new standard operating protocols (SOPs) adhering to strict QA/QC regimes to ensure the new data were of the highest quality.
The third research effort focused on how to use the data to determine the level of treatment needed to meet the State's risk goal of 2.7 × 10−7 infections per person per day.8 The main product of this effort is a publicly-accessible, web-based tool called DPRisk (https://cawaterdatadive.shinyapps.io/DPRisk/) that uses quantitative microbial risk assessment (QMRA) to 1) evaluate risk-based treatment requirements and 2) assess the performance of candidate DPR trains in meeting these goals.9 The DPRisk tool meets the State Water Board's goal of implementing a probabilistic QMRA method to confirm the necessary removal values for human-infectious viruses, Giardia, and Cryptosporidium.3 The research effort also provided the State Water Board's Division of Drinking Water (DDW) with quantitative insight regarding how key inputs in the QMRA impact pathogen risk and DPR treatment requirements.
This paper synthesizes the findings from the three pathogen research efforts to identify new scientifically supported pathogen LRTs using the highest-quality data sources and probabilistic risk assessment methods. It also provides recommendations for identifying and using high-quality data sources, describes challenges with the use of molecular pathogen data, and shows how redundancy can mitigate the impacts of treatment failures. While the effort was focused on developing recommendations for California, the approach and information are also transferable to other developed regions. Both the DPRisk tool and the new dataset provide flexibility to be adapted for site-specific conditions in other locations. If a more localized dataset is desired, the approach could be adopted for the monitoring campaign, integrated into the new dataset distributions,10 and evaluated using site-specific conditions within DPRisk.
2 Methods
2.1 QMRA model and LRT calculation
The standard QMRA model from ref. 1 was used in this analysis to assess both daily and annual risk of infection:where
P inf = probability of infection
n = number of exposure periods
DR = dose–response function for the reference pathogen
V n = volume of water ingested
C n = pathogen concentration in the source water
LRT = log removal target
DDW has stated that they will use an infection-based risk target based on the 1 in 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 risk of infection per person per year.11 It will be adapted, however, as a more stringent daily risk goal of 2.7 × 10−7 infections per person per day by dividing the annual risk evenly across each day of the year (10−4 infections per person per year/365 days). To evaluate the LRT required to meet the daily risk goal, LRT values were input into the equation above in increments of 0.1 starting at 0 up to 22. A Monte Carlo analysis was used to capture inherent variability in pathogen concentrations at a 15-minute interval. Risk for a given 15-minute period was then calculated from the pathogen concentration, exposure volume, and LRT occurring. The 15-minute interval was selected for several reasons: 1) many potable reuse regulations require that treatment process performance be measured “continuously”, which is defined as at least once every 15 minutes, 2) the State Board wanted the modeling to capture the variability in process performance at the same frequency as the monitoring, 3) the minimum duration of a process failure would be no less than 15 minutes based on this frequency, and 4) the use of higher frequency data allowed each day to be characterized by distributions (rather than point estimates) of both influent raw wastewater pathogen concentrations and unit process performance. Daily risk was then calculated for the given LRT. The LRT value resulting in the smallest difference between the calculated daily probability of infection and the daily risk goal was stored as the LRT for a single day. This process was simulated 10
000 risk of infection per person per year.11 It will be adapted, however, as a more stringent daily risk goal of 2.7 × 10−7 infections per person per day by dividing the annual risk evenly across each day of the year (10−4 infections per person per year/365 days). To evaluate the LRT required to meet the daily risk goal, LRT values were input into the equation above in increments of 0.1 starting at 0 up to 22. A Monte Carlo analysis was used to capture inherent variability in pathogen concentrations at a 15-minute interval. Risk for a given 15-minute period was then calculated from the pathogen concentration, exposure volume, and LRT occurring. The 15-minute interval was selected for several reasons: 1) many potable reuse regulations require that treatment process performance be measured “continuously”, which is defined as at least once every 15 minutes, 2) the State Board wanted the modeling to capture the variability in process performance at the same frequency as the monitoring, 3) the minimum duration of a process failure would be no less than 15 minutes based on this frequency, and 4) the use of higher frequency data allowed each day to be characterized by distributions (rather than point estimates) of both influent raw wastewater pathogen concentrations and unit process performance. Daily risk was then calculated for the given LRT. The LRT value resulting in the smallest difference between the calculated daily probability of infection and the daily risk goal was stored as the LRT for a single day. This process was simulated 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times to develop a distribution of LRTs that met the daily risk goal.
000 times to develop a distribution of LRTs that met the daily risk goal.
To evaluate daily risk for a given LRT or distribution of LRTs, a Monte Carlo analysis was used to capture the variability in pathogen concentrations at 15-minute intervals and a distribution of daily risk was developed by simulating the process 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times. To evaluate annual risk, a Monte Carlo process was used to sample from the daily risk distribution. This process was repeated to produce 100 simulations of annual risk.
000 times. To evaluate annual risk, a Monte Carlo process was used to sample from the daily risk distribution. This process was repeated to produce 100 simulations of annual risk.
In this study, the model was used to evaluate the impact of differing assumptions about wastewater pathogen concentrations and dose–response models on the LRT required to meet the daily risk threshold for each reference enteric pathogen. The model was also used to evaluate the impact of failures in treatment on the ability to meet daily and annual risk goals and evaluate the level of redundancy that would adequately protect against failures. To model failures, the LRTs in the model are adjusted to account for changes in the level of treatment. Information about the duration, magnitude, and frequency of failure assumed in this study is provided in section 3.3.
2.2 Reference pathogens and concentrations
The reference pathogens that were selected for this analysis are the same reference pathogens that have been used to develop LRTs for IPR in California: enteric virus, Giardia, and Cryptosporidium.12 Historically, enteroviruses have been used as the reference pathogen for establishing virus concentrations in source waters.2,13,14 For DPR, however, the State Board included a greater diversity of human-infectious viruses in their monitoring campaign including enteroviruses, noroviruses, and adenoviruses. This suite of viruses was selected based on their public health burden, their ability to be quantified with both culture- and molecular-based methods (i.e., enterovirus and adenovirus), and their inclusion in previous water reuse-related QMRAs. Ultimately, adenovirus was determined to require lower LRTs than the other viruses and so was not included in the present analysis, though details on adenovirus distributions are available.5,10 Concentrations of these pathogens in raw wastewater were recently evaluated as a part of the State Board's pathogen monitoring campaign,5 henceforth referred to as DPR-2. The State Board developed LRTs for DPR using different data for raw wastewater concentrations. Table 1 shows the distributions of pathogen concentration in raw wastewater that were utilized for this analysis and that were utilized by the State Board to develop their LRTs. Discussion on the rationale for selection of these data for the analysis is included in section 3.1. Separate criteria for bacteria were not included based on the assumption that specifying requirements for virus and protozoa would provide a high degree of control over bacterial pathogens as well.2,15,16| Reference pathogen | Distribution of concentration in raw wastewatera | Units | Data source |
|---|---|---|---|
| a Values are log10 transformed. Normal distribution parameters listed as (mean, standard deviation). GC – genome copies. MPN – most probable number. b Norovirus GII was selected based on it being present at higher concentrations than both GIA and GIB. c To develop recommended LRTs, the authors recommend an additional layer of conservatism that includes an assumption that only 10% of the total viruses present were culturable which effectively shifts the mean of this distribution to 4.2. d Giardia cysts and Cryptosporidium oocysts determined microscopically. Infective cysts and oocysts were conservatively assumed to be equivalent to the total number determined microscopically. US EPA has previously provided rationale for this assumption based presumption that overestimation of infectivity would be offset by underestimation of recovery.22 | |||
| Norovirus GIIb | Normal (4.0, 1.2) | GC L−1 | 5 |
| Point (9.0) | GC L−1 | 17, 18 | |
| Enterovirus spp. | Normal (3.2, 1.0)c | MPN L−1 | 5 |
| Giardia spp.d | Normal (4.0, 0.4) | Cysts per L | 5 |
| Point (5.0) | Cysts per L | 19, 18 | |
| Cryptosporidium spp.d | Normal (1.9, 0.6) | Oocysts per L | 10 |
| Point (4.0) | Oocysts per L | 20, 21, 18 | |
To evaluate the impact of the different assumptions about raw wastewater pathogen concentrations (i.e., distribution vs. point estimate) on the required LRT to meet the daily risk goal, the QMRA model was run holding all other variables constant (i.e., dose–response and consumption).
2.3 Pathogen dose–response
A summary of the pathogen dose–response models used in this study is provided in Table 2. The dose–response models are used to calculate the probability of infection for healthy adults based on the exposure dose. For consistency with the State Board's approach to developing DPR LRTs, the exponential dose–response model for Giardia lamblia23 and the beta-Poisson dose–response model for Cryptosporidium spp.24 were used. For norovirus, two dose–response models were utilized to evaluate risk of infection. The hypergeometric dose–response25 was used for consistency with the State Board's approach and to represent the upper bound risk of infection and the fractional-Poisson dose–response26 was used to represent the lower bound risk of infection, in line with recommendations from Van Abel et al.27 As with pathogen methods, the dose–response models continue to evolve—the DPRisk tool allows for existing and future models to be incorporated into the analyses. Finally, to evaluate risk of infection from enterovirus, an approach that is in line with the methods used for developing virus reduction requirements for the U.S. EPA Surface Water Treatment Rule was used. This approach utilizes the approximate beta-Poisson dose–response model for Rotavirus assuming that the entire population is susceptible to infection.28| Reference pathogen | Model | Parameters | Parameter values | Units | Ref. |
|---|---|---|---|---|---|
| a For this analysis, the approximate beta-Poisson dose–response model was used instead of the hypergeometric dose–response model due to the significant differences in computing time between the two and the relatively small differences in resulting infection rate at low doses. b Rotavirus dose–response function used in conjunction with enterovirus occurrence data for consistency with the virus reduction requirements of the Surface Water Treatment Rule. FFU: fluorescence focus units. | |||||
| Norovirus (GI) | Hypergeometrica | Alpha | 0.04 | GC | 25 |
| Beta | 0.055 | ||||
| Norovirus (GI and GII.4) | Fractional Poisson | P | 0.72 | GC | 26 |
| U | 1106 | ||||
| Beta | 2.80 | ||||
| Giardia lamblia | Exponential | r | 0.0199 | Cysts | 23 |
| Cryptosporidium spp. | Beta-Poisson | Alpha | 0.116 | Oocysts | 24 |
| Beta | 0.121 | ||||
| Rotavirus | Approximate beta-Poisson | Alpha | 0.253 | FFU | 28 |
| Beta | 0.426 | ||||
2.4 Exposure
Exposure to enteric pathogens in DPR is assumed to occur via ingestion of treated water. There are a number of different approaches for modeling the amount of tap water a person consumes. Several risk assessments have used the base e lognormal distribution (based on mL per day) with mean and standard deviation of 7.492 and 0.407, respectively, developed by Roseberry and Burmaster29 to model tap water consumption.30–32 However, for consistency with the State Board's approach for developing LRTs for DPR, this study utilized a static assumption of 2 L per day of consumption modeled as 96 consumption events of 20.8 mL to represent equal consumption during each 15-minute period in a day. The State Board selected this approach because it ensured that every 15-minute failure period would be captured in the modeling. At the opposite extreme, consumption could be modeled as a single 2-L event per day, which would decrease the frequency of consuming off-spec water, but would increase the magnitude.9 DPRisk provides the flexibility to model the full range of exposure assumptions.2.5 Analysis of viral genome copy-to-infectious unit ratios
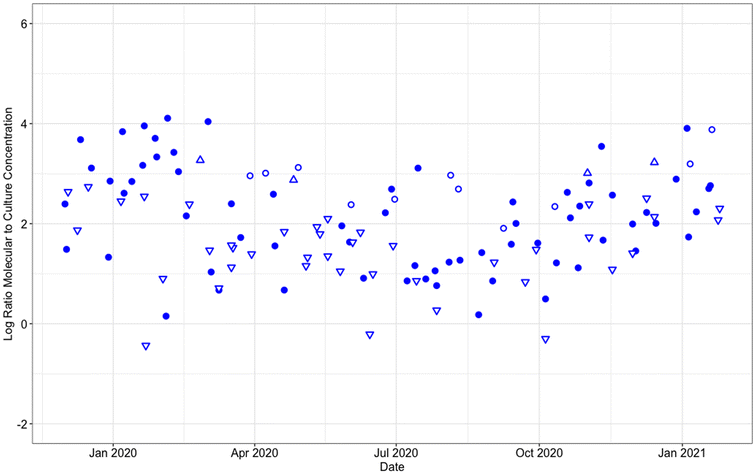
In the DPR-2 pathogen monitoring study, the concentrations of enteroviruses and mammalian adenoviruses (Mastadenovirus spp.) were measured in 122 raw wastewater samples using both culture and molecular methods.5 The ratio of genome copies (GC) to infectious units (IU) was calculated for each virus sample by dividing the recovery-corrected concentration measured using the molecular method by the recovery-corrected concentration measured using the culture method. Based on these samples, a distribution of ratios was developed for both enteroviruses and adenoviruses. The ratios were log10 transformed before proceeding with the statistical analysis.The log10-transformed GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratio data were fitted to a normal distribution using the function “fitdistcens” from the R package “fitdistRplus,” which estimates the mean and standard deviation for censored datasets using maximum likelihood estimation.33 Samples with virus concentrations below the limit of quantification (LOQ) for the molecular methods resulted in left-censored GC
IU ratio data were fitted to a normal distribution using the function “fitdistcens” from the R package “fitdistRplus,” which estimates the mean and standard deviation for censored datasets using maximum likelihood estimation.33 Samples with virus concentrations below the limit of quantification (LOQ) for the molecular methods resulted in left-censored GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios since the numerator in the ratio (GC) was below the LOQ; the right bound for these data points was based on the molecular method LOQ. Samples with virus concentrations below the LOQ for the culture methods resulted in right-censored GC
IU ratios since the numerator in the ratio (GC) was below the LOQ; the right bound for these data points was based on the molecular method LOQ. Samples with virus concentrations below the LOQ for the culture methods resulted in right-censored GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios since the denominator in the ratio (IU) was below the LOQ; the left bound for these data points was based on the culture method LOQ. Data points where the culture and molecular concentrations were both below the LOQ were excluded from the distribution. Approximately 9% of the samples (11/122 samples) had enterovirus concentrations below the LOQ with both the culture and molecular methods, and 19% of the samples (23/122 samples) had adenovirus concentrations below the LOQ with both the culture and molecular methods.
IU ratios since the denominator in the ratio (IU) was below the LOQ; the left bound for these data points was based on the culture method LOQ. Data points where the culture and molecular concentrations were both below the LOQ were excluded from the distribution. Approximately 9% of the samples (11/122 samples) had enterovirus concentrations below the LOQ with both the culture and molecular methods, and 19% of the samples (23/122 samples) had adenovirus concentrations below the LOQ with both the culture and molecular methods.
3 Results and discussion
3.1 Selection and modeling of raw wastewater pathogen data
The selection of appropriate pathogen datasets and the models used to describe them are critical topics for regulatory development. The most important criterion for data selection is quality. Advancements in pathogen detection methods have allowed for the collection of higher quality data over time, providing an opportunity to replace lower-quality data with new higher-quality data. For example, one study used by the State Water Board to develop the 10-log Cryptosporidium LRT requirement for the IPR regulations collected 34 samples in Norwegian wastewater.20 The 50 μl sample volumes that were used resulted in low method sensitivity given that the identification of a single oocyst resulted in a detection limit of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 oocysts per L. The maximum value reported in the study—24
000 oocysts per L. The maximum value reported in the study—24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 oocysts per L—was just above the method's detection limit. Because the majority of the values were below the detection limit, the study could only describe the upper half of the distribution (i.e., from the 60th percentile onward). The inability to describe the lower end of the pathogen distribution is an important limitation because it can lead to higher estimated risk values that require higher LRTs at the lower end of the distributions. This uncertainty may also lead regulators to select point estimates at the extreme of the distribution for fear of incorrectly describing the full distribution.
000 oocysts per L—was just above the method's detection limit. Because the majority of the values were below the detection limit, the study could only describe the upper half of the distribution (i.e., from the 60th percentile onward). The inability to describe the lower end of the pathogen distribution is an important limitation because it can lead to higher estimated risk values that require higher LRTs at the lower end of the distributions. This uncertainty may also lead regulators to select point estimates at the extreme of the distribution for fear of incorrectly describing the full distribution.
In light of these limitations, the DPR-2 study identified several characteristics of “optimal” high-quality datasets and then adapted methods to meet these criteria.5 The optimized methods improved sensitivity and allowed the distributions to be characterized from the lowest through the highest concentrations. For example, the DPR-2 Cryptosporidium method analyzed 1-L samples that provided increased sensitivity than the aforementioned 50-μl method, with the detection rate increasing from 40% to 98%. Additionally, matrix spikes were added to each sample to correct the concentrations for recovery efficiency. Several recent studies evaluating the accuracy of environmental monitoring have highlighted the importance of this and other QA/QC steps, since failing to correct for recovery efficiency can introduce errors of several orders of magnitude.34 Methods were adapted to meet a set of optimal criteria, and the subsequent campaign yielded the most robust raw wastewater pathogen dataset collected to date, encompassing multiple targets and detection methods (i.e., microscopy, culture and molecular) (Table 3).
| Optimal criteria | Compliance of DPR-2 dataset |
|---|---|
| Large sample size | 120 samples evaluated using nine different assays |
| Two protozoa (Giardia and Cryptosporidium) enumerated via immunofluorescent microscopic methods | |
| Five viruses (enterovirus, adenovirus, norovirus GI and GII, SARS-CoV-2) enumerated with culture and/or molecular methods | |
| High method sensitivity | >90% detection rate for culture- and microscopy-based methods |
| Compatible with QMRA | Culture and microscopy can be used directly in QMRA without conversions to estimate concentrations of infectious pathogens based on molecular data (i.e., genome copies) |
| QA/QC | Full suite of QA/QC controls for all samples including matrix spikes for each protozoa sample and every other virus sample |
| Geographic/scale distribution | Sampling at five wastewater treatment plants varying in size from 17 to 292 MGD representing one-quarter of the California population |
| Temporal distribution | 24 samples at each sampling location over 14 month period |
To expand the dataset to include other geographic locations and time periods, Darby et al. identified other historical datasets meeting a minimum set of criteria and developed an approach to combine these highest-quality data into single pathogen distributions.10 All data points from each of the selected studies were pooled together and log-transformed to produce a normally distributed dataset. The parameters of the resulting log-normal distribution were defined and values from the distribution were sampled for the estimation of LRT requirements. The authors acknowledge that this pooling approach may obscure site-specific variations at the tails of the distributions, but believe it is still advantageous to incorporate the variation across multiple locations into a single distribution. Site-specific monitoring could be used to confirm the appropriateness of the DPR-2 dataset when applied in other locations.
The analysis showed that the new DPR-2 data are aligned with the historical distributions, with the exception of a Cryptosporidium dataset collected in Australia that led to a small but relevant shift in the distribution.21 The recovery-corrected distributions characterize concentrations from the low through the high concentrations providing confidence in the data across the full extent of the distribution. The authors recommend that the aggregated distributions comprising the DPR-2 and high-quality historical datasets be used as the basis for regulatory development in California. This approach was also endorsed by the expert panel helping the state water board evaluate the public health protectiveness of the DPR criteria.35
The use of distributions in probabilistic assessments would represent an important shift from the point estimate approach the State Water Board used to develop their IPR regulations. Previously, the State Water Board used the single highest value reported in the literature to characterize wastewater concentrations of enteric virus, Giardia, and Cryptosporidium12 and they are using the same approach for DPR.18 The point estimate approach includes significant conservatism in that it assumes every raw influent wastewater contains the highest pathogen concentrations ever reported in the literature at all times. The use of conservative point estimates may be justified if there is significant uncertainty associated with the values or when the data only provide confidence in the highest values in the distribution, such as was the case previously for Cryptosporidium.20 However, when high-quality data meeting the optimal criteria are available, the full distribution of pathogens should replace point estimates and be incorporated in probabilistic assessments of risk. The authors recommend that regulators use the new recovery-corrected distributions to replace earlier point estimates.
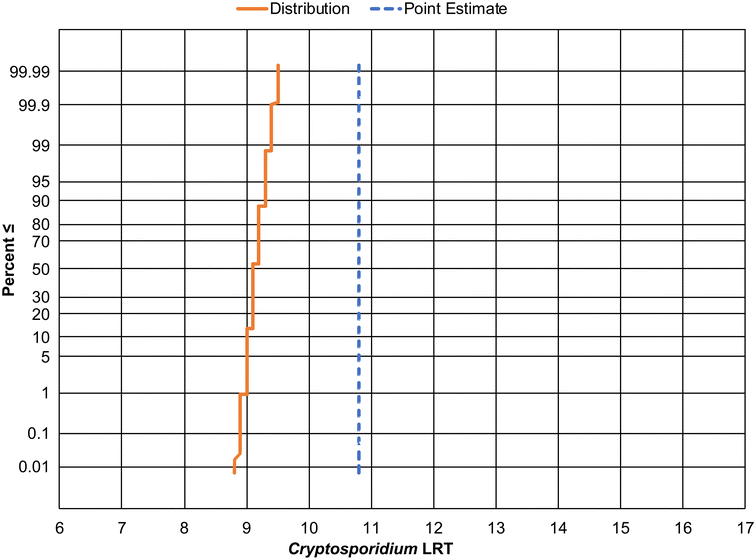
This decision is relevant for regulatory development because it can impact the LRT required to protect public health. The following example shows how the Cryptosporidium LRT would be impacted by the use of 1) a conservative point20 or 2) the aggregated, DPR-2 distribution10 by keeping all other QMRA inputs equal (see Methods). The point estimate leads to a single LRT value of approximately 11 logs to achieve the daily risk goal of 2.7 × 10−7 infections per person per day (Fig. 1). The aggregated DPR-2 distribution, however, results in a distribution of LRTs spanning from 8.8 to 9.5 logs over the 0.01st to the 99.99th percentile. As a result, the new, higher quality data provide a scientific justification for a treatment goal that is 1.5-logs lower than the LRT developed using the point estimate. A reduction in the LRT should not be misconstrued as a reduction in public health protection. While the public health goal remains the same—to provide treatment that reduces risk to acceptably low levels—our understanding of what it takes to achieve these goals has advanced. This advancement shows that layers of conservatism that were once justified can now be removed without compromising public health. In a time when the effects of climate change are impacting access to water sources across the globe, potable reuse will be increasingly relied upon as a necessary mitigation strategy. Selecting appropriate treatment requirements—neither too low nor too high—will increase the sustainability of potable reuse, reducing costs and expanding implementation in resource-scarce areas. Unnecessarily high treatment requirements may only increase the burden on municipalities without resulting in a real increase in public health protection.
 | ||
| Fig. 1 Cryptosporidium log reduction target (LRT) required to meet a risk goal of 2.7 × 10−7 infections per person per day based on the use of a point estimate of wastewater concentration using data from Robertson et al.20 (blue dashed line) or a distribution of concentrations from Darby et al.10 (orange solid line). Y-Axis denotes the probability that a given LRT would either meet or be below the daily risk goal. | ||
3.2 Limitations of molecular pathogen data
The use of molecular data is another relevant topic because certain public health pathogens—including noroviruses—can only be quantified with molecular methods like polymerase chain reaction (PCR). The State Water Board used the highest recorded point estimate for noroviruses in raw wastewater—a value of approximately 9.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 genome copies (GC) per L—to establish a virus LRT requirement of 16 logs.36 The State assumed that every GC detected in the wastewater is associated with an infectious norovirus virion, i.e., a GC
log10 genome copies (GC) per L—to establish a virus LRT requirement of 16 logs.36 The State assumed that every GC detected in the wastewater is associated with an infectious norovirus virion, i.e., a GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratio of 1
IU ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This approach is in line with earlier recommendations to assume all GCs are infectious “unless proven otherwise”.37
1. This approach is in line with earlier recommendations to assume all GCs are infectious “unless proven otherwise”.37
Several new lines of evidence provide a rationale for modifying the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 GC
1 GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU assumption. For years, researchers have shown that genomic material remains detectable for viruses that have been inactivated,38,39 demonstrating that GCs alone are not reliable indicators of infectivity. SARS-CoV-2 provides the most recent evidence of a virus whose GCs are present in wastewater without being infective.40 DPR-2 provides new quantitative data that further supports that GC
IU assumption. For years, researchers have shown that genomic material remains detectable for viruses that have been inactivated,38,39 demonstrating that GCs alone are not reliable indicators of infectivity. SARS-CoV-2 provides the most recent evidence of a virus whose GCs are present in wastewater without being infective.40 DPR-2 provides new quantitative data that further supports that GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios in raw wastewater are not static but fluctuate over a wide range. Enteroviruses were quantified by culture and molecular methods and showed GC
IU ratios in raw wastewater are not static but fluctuate over a wide range. Enteroviruses were quantified by culture and molecular methods and showed GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios that ranged from as low as 1
IU ratios that ranged from as low as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to as high as 10
1 to as high as 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 2). GC
1 (Fig. 2). GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios for adenovirus ranged from approximately 1
IU ratios for adenovirus ranged from approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 100
1 to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (data not shown). Recent work with an emerging norovirus culture system has shown that this phenomenon also applies to norovirus.41 The norovirus molecular signal persists longer than viable norovirus in the environment, showing that GC
1 (data not shown). Recent work with an emerging norovirus culture system has shown that this phenomenon also applies to norovirus.41 The norovirus molecular signal persists longer than viable norovirus in the environment, showing that GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios vary and are not statically 1
IU ratios vary and are not statically 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
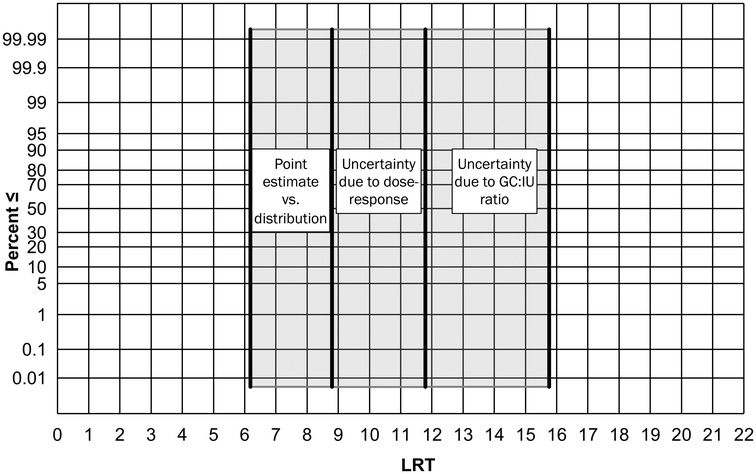
Using the new DPR-2 data to bookend potential GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratios introduces 4 logs of variability in the resulting LRT. If applied to the State Water Board's norovirus LRT derivation, the LRT would extend from a single 16-log point estimate to a range spanning from as low as 12- to as high as 16-logs (Fig. 3). The uncertainty in the infectivity of GCs also impacts estimates of norovirus risk. The authors support recommendations to use a range of dose–response functions in QMRA.27 Using both high-end and low-end dose–response models (represented by the hypergeometric and fractional Poisson models) results in an approximate 3-log range for norovirus LRTs (Fig. 3). Using the DPR-2 distribution of norovirus concentrations rather than the point estimate introduces another 3-logs of variability (Fig. 3). Coupling together these three factors—1) the 4-log variability associated with the GC
IU ratios introduces 4 logs of variability in the resulting LRT. If applied to the State Water Board's norovirus LRT derivation, the LRT would extend from a single 16-log point estimate to a range spanning from as low as 12- to as high as 16-logs (Fig. 3). The uncertainty in the infectivity of GCs also impacts estimates of norovirus risk. The authors support recommendations to use a range of dose–response functions in QMRA.27 Using both high-end and low-end dose–response models (represented by the hypergeometric and fractional Poisson models) results in an approximate 3-log range for norovirus LRTs (Fig. 3). Using the DPR-2 distribution of norovirus concentrations rather than the point estimate introduces another 3-logs of variability (Fig. 3). Coupling together these three factors—1) the 4-log variability associated with the GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU ratio, 2) the 3-log variability associated with dose–response functions, and 3) the 3–4
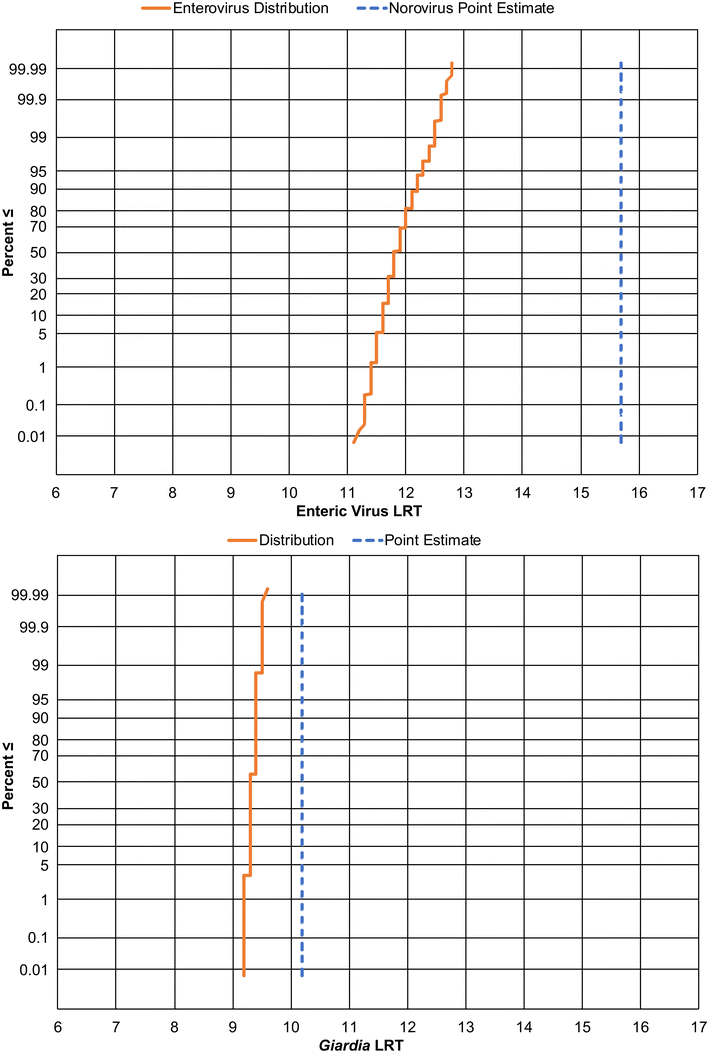
IU ratio, 2) the 3-log variability associated with dose–response functions, and 3) the 3–4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log variability associated with the distribution vs. point estimate—leads to a >10 order of magnitude level of uncertainty for norovirus. The range of potential LRTs therefore extends from 6 to 16 logs (Fig. 3). While the authors acknowledge the public health importance of norovirus, current knowledge gaps lead to excessive degrees of uncertainty in estimating LRTs. Rather than arbitrarily selecting a single LRT from within this range, such as the 16-log extremity proposed by the State Water Board, the authors recommend the use of alternate reference pathogens to establish virus LRTs.
log variability associated with the distribution vs. point estimate—leads to a >10 order of magnitude level of uncertainty for norovirus. The range of potential LRTs therefore extends from 6 to 16 logs (Fig. 3). While the authors acknowledge the public health importance of norovirus, current knowledge gaps lead to excessive degrees of uncertainty in estimating LRTs. Rather than arbitrarily selecting a single LRT from within this range, such as the 16-log extremity proposed by the State Water Board, the authors recommend the use of alternate reference pathogens to establish virus LRTs.
An alternative is the approach used by US EPA in the development of virus requirements for the 1989 Surface Water Treatment Rule.2,42 EPA acknowledged there was a wide diversity of relevant viruses, and one way to address this diversity was to assume worst-case characteristics along two lines: occurrence and infectivity. Specifically, EPA coupled the occurrence data of enteroviruses (a group of culturable human viruses present in high concentrations in wastewater) with the dose–response function for rotavirus (a highly infective human pathogen). This combination was intended to provide conservatism in viral treatment requirements. The approach benefits from regulatory precedent established with both the federal Surface Water Treatment Rule and all of California's IPR regulations.13 The authors recommend the use of this EPA approach for determining enteric virus treatment requirements based on its high degree of conservatism, consistency with previous regulatory frameworks, and independence from the limitations of molecular data.
3.3 Failure and redundancy
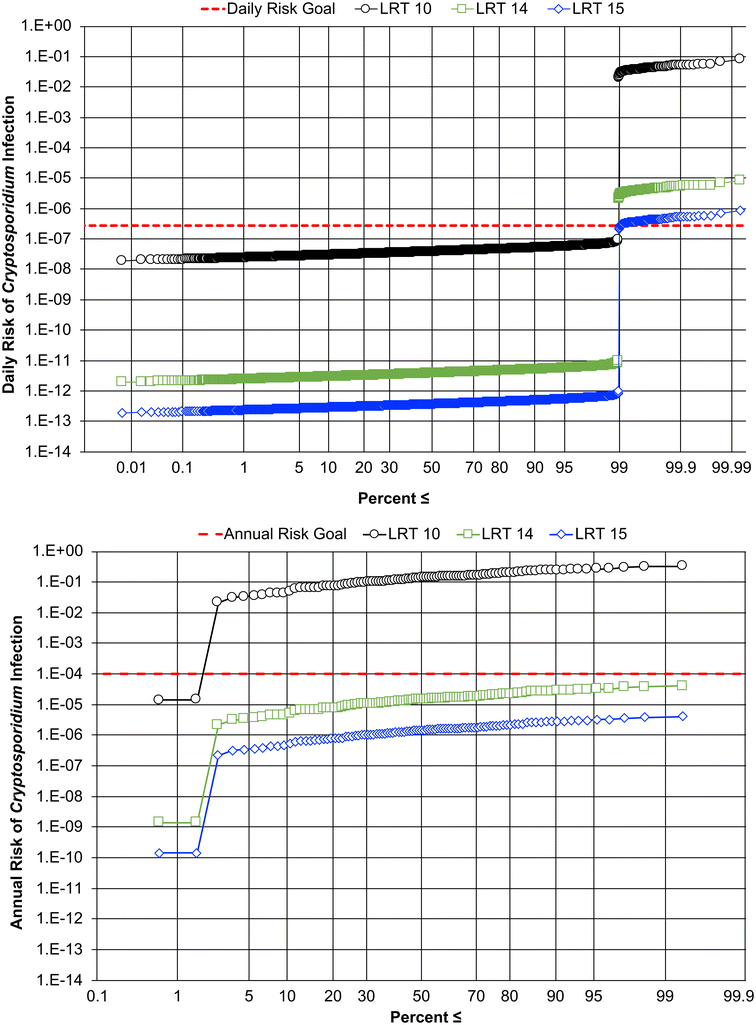
In many cases, DPR projects will have no environmental buffer to dampen out the water quality impacts of treatment failures. DPR systems may need additional protections to compensate for this loss. To size these protections appropriately, it is important to quantify the impact that undetected treatment failures would have on risk. The increase in risk is linked to three characteristics of the failure itself: duration, magnitude, and frequency. Many regulations will require “continuous” monitoring of pathogen control barriers, where continuous can be practically defined as no less than once every 15 minutes. Given this practical constraint, it is important to characterize the risk implications of an undetected failure occurring within this 15-minute window. In terms of magnitude, the largest impact on risk will result from the loss of the highest credited unit process. The simultaneous failure of multiple unit processes could also result in high magnitude impacts; however, previous studies have shown that 1) unit process failures that impact pathogen control are rare and 2) unit process performance is independent of the performance of upstream processes, meaning that the failure of an upstream process does not necessarily result in a cascade of downstream failures.31,43,44 For California's potable reuse regulations, the maximum allowable credit for a unit process is 6-logs (e.g., the 6-log credit awarded to the UV advanced oxidation process (AOP) for virus, Giardia, and Cryptosporidium). Over the course of 24 hours, a 6-log failure for 15 minutes would result in a 4-log increase in daily risk, as the other 95 daily time intervals with nominal operation would ‘buffer’ the 15-min failure. In other words, one 15-min failure out of 96 total 15-min time intervals results in an approximate 2-log buffer. Longer duration failures would lead to additional increases in risk up until the maximum duration that can occur over a single day: 24 hours. This upper end failure scenario would result in a 6-log increase in risk during that day. Overall, the impact of a large magnitude (6-log) failure would be to increase the daily risk within a 4- to 6-log window.One strategy to protect against undetected failures is to require sufficient treatment redundancy to offset the 4- to 6-log increase in risk. To evaluate these benefits, 4 and 5 logs of redundancy were added to the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log Cryptosporidium LRT described previously. The impact of a 6-log, 24-hour failure occurring 1% of the year (i.e., 3.65 days per year) on the daily and annual risk profiles is shown in Fig. 4. Even with a high (1%) rate of failure, a DPR system providing at least 4 logs of redundancy would protect against large, undetected failures and achieve the 2.7 × 10−7 daily risk goal 99% of the time (>361 days per year) and the 10−4 annual risk goal >99% of the time. Based on these findings, 4-logs of redundancy would be sufficient to protect DPR systems against even frequent, large magnitude failures. Identical redundancy requirements apply for virus and Giardia (see ESI†). While redundancy provisions are ultimately a risk management decision, this analysis provides a scientific basis to justify a 4-log redundancy requirement.
log Cryptosporidium LRT described previously. The impact of a 6-log, 24-hour failure occurring 1% of the year (i.e., 3.65 days per year) on the daily and annual risk profiles is shown in Fig. 4. Even with a high (1%) rate of failure, a DPR system providing at least 4 logs of redundancy would protect against large, undetected failures and achieve the 2.7 × 10−7 daily risk goal 99% of the time (>361 days per year) and the 10−4 annual risk goal >99% of the time. Based on these findings, 4-logs of redundancy would be sufficient to protect DPR systems against even frequent, large magnitude failures. Identical redundancy requirements apply for virus and Giardia (see ESI†). While redundancy provisions are ultimately a risk management decision, this analysis provides a scientific basis to justify a 4-log redundancy requirement.
3.4 Recommended criteria for pathogen log reduction targets
Based on the analysis and assumptions presented above, the authors recommend the following pathogen LRTs for DPR.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log) up to the nearest integer results in an enteric virus LRT of 13 logs (Fig. 5, top, solid orange line) compared to the LRT of 16 determined by the State Board's approach using a point estimate of norovirus concentrations (Fig. 5, top, dashed blue line). The authors also recommend including a redundancy requirement of 4-logs when aiming to provide protection against undetected failures. This ensures a high degree of compliance with the daily risk goal of 2.7 × 10−7 infections per person and the annual risk goal of 1 × 10−4 infections per person. Note that rounding the LRT up to the nearest integer should help offset any potential underestimation of the tail of the aggregated distribution.
log) up to the nearest integer results in an enteric virus LRT of 13 logs (Fig. 5, top, solid orange line) compared to the LRT of 16 determined by the State Board's approach using a point estimate of norovirus concentrations (Fig. 5, top, dashed blue line). The authors also recommend including a redundancy requirement of 4-logs when aiming to provide protection against undetected failures. This ensures a high degree of compliance with the daily risk goal of 2.7 × 10−7 infections per person and the annual risk goal of 1 × 10−4 infections per person. Note that rounding the LRT up to the nearest integer should help offset any potential underestimation of the tail of the aggregated distribution.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log) up to the nearest integer results in a Giardia LRT of 10 logs (Fig. 5, bottom, solid orange line), compared to the State Board's approach that utilized a point estimate for Giardia concentrations that ultimately results in a similar LRT of 10 logs (Fig. 5, bottom, dashed blue line). The authors recommend including a redundancy requirement of 4-logs when aiming to provide protection against undetected failures and to ensure a high degree of compliance with the daily risk goal of 2.7 × 10−7 infections per person and the annual risk goal of 1 × 10−4 infections per person. Note that rounding the LRT up to the nearest integer should help offset any potential underestimation of the tail of the aggregated distribution.
log) up to the nearest integer results in a Giardia LRT of 10 logs (Fig. 5, bottom, solid orange line), compared to the State Board's approach that utilized a point estimate for Giardia concentrations that ultimately results in a similar LRT of 10 logs (Fig. 5, bottom, dashed blue line). The authors recommend including a redundancy requirement of 4-logs when aiming to provide protection against undetected failures and to ensure a high degree of compliance with the daily risk goal of 2.7 × 10−7 infections per person and the annual risk goal of 1 × 10−4 infections per person. Note that rounding the LRT up to the nearest integer should help offset any potential underestimation of the tail of the aggregated distribution.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log) up to the nearest integer results in an LRT of 10 logs (Fig. 1, solid orange line), compared to the LRT of 11 determined by the State Board's approach that utilized a point estimate for Cryptosporidium concentrations (Fig. 1, dashed blue line). The authors recommend including a redundancy requirement of 4-logs to provide protection against undetected failures and to ensure a high degree of compliance with the daily risk goal of 2.7 × 10−7 infections per person and the annual risk goal of 1 × 10−4 infections per person. Note that rounding the LRT up to the nearest integer should help offset any potential underestimation of the tail of the aggregated distribution.
log) up to the nearest integer results in an LRT of 10 logs (Fig. 1, solid orange line), compared to the LRT of 11 determined by the State Board's approach that utilized a point estimate for Cryptosporidium concentrations (Fig. 1, dashed blue line). The authors recommend including a redundancy requirement of 4-logs to provide protection against undetected failures and to ensure a high degree of compliance with the daily risk goal of 2.7 × 10−7 infections per person and the annual risk goal of 1 × 10−4 infections per person. Note that rounding the LRT up to the nearest integer should help offset any potential underestimation of the tail of the aggregated distribution.
A summary of the recommendations is presented in Table 4.
| Virus | Giardia | Cryptosporidium | |
|---|---|---|---|
| a See Table 1 for statistical distribution parameters. b See Table 2 for dose response model parameters.LRT – log10 reduction target for pathogen control; N/A – not applicable. | |||
| Raw wastewater dataset | Aggregated DPR-2 enterovirus culture distribution10a | Aggregated DPR-2 Giardia distribution10a | Aggregated DPR-2 Cryptosporidium distribution10a |
| Modifications | Assume 10% of total viruses quantified through culture | N/A | N/A |
| Dose response | Rotavirus beta-Poissonb | Exponentialb | Beta-Poissonb |
| Minimum LRTs for public health protection | 13-log | 10-log | 10-log |
| Redundancy against undetected failures | 4-log | 4-log | 4-log |
| Overall LRT requirements | 17-log | 14-log | 14-log |
4 Conclusions
The preceding analysis stems from the development and review of draft DPR regulations in California, and for this reason, the authors make the following recommendations to the California State Water Board's Division of Drinking Water. However, these recommendations are also broadly applicable to the development of DPR regulations outside California and even outside the U.S.• Distributions of pathogen concentrations, rather than point estimates, should be used for regulatory development, particularly when high-quality datasets are available.
• The aggregated, recovery-corrected DPR-2 dataset includes robust, high-quality data that should be used as the basis for raw wastewater inputs for QMRA. Modifications of the dataset (e.g., adjustments to account for incomplete virus enumeration through culture methods) should be considered for additional conservatism.
• Given the unavailability of high-quality pathogen data, the authors recommend the use of the aggregated DPR-2 dataset as a starting place for QMRA in locations within and outside the U.S. Site-specific monitoring could be used to confirm the appropriateness of the DPR-2 dataset in that location. When appropriate, the new data could be integrated using the approach of Darby et al. to create a more robust dataset.10
• Quantitative microbial risk assessments should be conducted using probabilistic approaches incorporating pathogen concentration distributions rather than deterministic methods relying exclusively on point estimates. Publicly-available, online tools such as DPRisk can be used for such analyses.
• Culture- and microscopy-based data reduce the uncertainty associated with the interpretation of molecular data. If molecular data are used, uncertainties should be understood by bookending the GC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IU and dose response assumptions with both upper- and lower-end estimates.
IU and dose response assumptions with both upper- and lower-end estimates.
• The conclusions from a quantitative microbial risk assessment are a product of the underlying assumptions. Thus, risk assessments must be transparent and reproducible. To ensure reproducibility, publicly-available platforms like DPRisk can be used to catalog all decisions.
• The quantitative benefits of both treatment (i.e., engineered unit processes) and non-treatment barriers (e.g., small environmental buffers) should be assessed and incorporated into DPR criteria. Even small environmental buffers can provide redundancy and protection against failures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the California State Water Resources Control Board with funding from Proposition 1 Water Recycling Research (Water Bond 2014) via Grant Agreement No. D1705002, and by the Metropolitan Water District of Southern California with funding from the Future Supply Actions Funding Program via Agreement No. 180315. The authors would like to thank Robert Brownwood and Claire Waggoner (State Water Resources Control Board) and Julie Minton (The Water Research Foundation) for managing and overseeing the research effort.References
-
C. N. Haas, J. B. Rose and C. P. Gerba, Quantitative microbial risk assessment, Wiley, New York, 1999 Search PubMed
.
- S. Regli, J. B. Rose, C. N. Haas and C. P. Gerba, Modeling the risk from Giardia and viruses in drinking water, J. - Am. Water Works Assoc., 1991, 83, 76–84 CrossRef CAS
.
- State Water Resources Control Board, Investigation on the feasibility of developing uniform water recycling criteria for direct potable reuse: Report to the legislature September 2016 - Public Review Draft, State Water Resources Control Board, Sacramento, CA, 2016 Search PubMed.
- A. W. Olivieri, J. Crook, M. A. Anderson, R. J. Bull, J. E. Drewes, C. N. Haas, W. Jakubowski, P. L. McCarty, K. L. Nelson, J. B. Rose, D. L. Sedlak and T. J. Wade, Evaluation of the Feasibility of Developing Uniform Water Recycling Criteria for Direct Potable Reuse, California State Water Resources Control Board, Fountain Valley, CA, 2016 Search PubMed.
- B. M. Pecson, E. Darby, R. Danielson, Y. Dearborn, G. D. Giovanni, W. Jakubowski, M. Leddy, G. Lukasik, B. Mull, K. L. Nelson, A. Olivieri, C. Rock and T. Slifko, Distributions of waterborne pathogens in raw wastewater based on a 14-month, multi-site monitoring campaign, Water Res., 2022, 213, 118170 CrossRef CAS PubMed
.
- B. Pecson, E. Darby, G. Di Giovanni, M. Leddy, K. L. Nelson, C. Rock, T. Slifko, W. Jakubowski and A. Olivieri, DPR-2: Pathogen Monitoring in Untreated Wastewater, The Water Research Foundation, Alexandria, VA, 2021 Search PubMed.
- K. Wigginton, R. Lahr, A. Bardha and N. Rockey, DPR-3: Feasibility of collecting pathogens in wastewater during outbreaks, Water Research Foundation, Alexandria, VA, 2021 Search PubMed.
- B. Pecson, N. Ashbolt, C. Haas, T. Slifko, A. Kaufmann, D. Gerrity, E. Seto and A. Olivieri, DPR-1: Tools to Evaluate Quantitative Microbial Risk and Plant Performance/Reliability, The Water Research Foundation, Alexandria, VA, 2021 Search PubMed.
- E. Seto and D. Gerrity, Guidance Document for DPRisk, The Water Research Foundation, Alexandria, VA, 2021 Search PubMed.
- E. Darby, A. Olivieri, C. Haas, G. Di Giovanni, W. Jakubowski, M. Leddy, K. L. Nelson, C. Rock, T. Slifko and B. M. Pecson, Identifying and aggregating high-quality pathogen data: a new approach for potable reuse regulatory development, Environ. Sci.: Water Res. Technol., 2023, 9, 1646–1653 RSC
.
- State Water Resources Control Board, A Proposed Framework for Regulating Direct Potable Reuse in California, State Water Resources Control Board, Sacramento, CA, 2nd edn, 2019 Search PubMed.
- B. Hultquist, Basis for California's 12-10-10 log removal requirements presented in part at the 20th Annual WateReuse Research Conference, Denver, CO, May 22-24, 2016 Search PubMed.
- DDW, Regulations Related to Recycled Water, California Code of Regulations, Titles 22 and 17, 2018 Search PubMed.
- B. A. Macler and S. Regli, Use of microbial risk assessment in setting US drinking water standards, Int. J. Food Microbiol., 1993, 18, 245–256 CrossRef CAS PubMed
.
- EPA, Guidance Manual for Compliance with the Filtration and Disinfection Requirements for Public Water Systems Using Surface Water Sources, 1991 Search PubMed.
- E. Amoueyan, S. Ahmad, J. N. S. Eisenberg and D. Gerrity, Equivalency of indirect and direct potable reuse paradigms based on a quantitative microbial risk assessment framework, Microb. Risk Anal., 2019, 12, 60–75 CrossRef
.
- S. E. Eftim, T. Hong, J. Soller, A. Boehm, I. Warren, A. Ichida and S. P. Nappier, Occurrence of norovirus in raw sewage – A systematic literature review and meta-analysis, Water Res., 2017, 111, 366–374 CrossRef CAS PubMed
.
- Division of Drinking Water, Derivation of log removal values for the Addendum to A Framework for Regulating Direct Potable Reuse, https://www.waterboards.ca.gov/drinking_water/certlic/drinkingwater/direct_potable_reuse.html.
-
T. Asano, F. L. Burton, H. L. Leverenz, R. Tsuchihashi and G. Tchobanoglous, Water reuse: issues, technologies, and applications, McGraw-Hill, New York, 2007 Search PubMed
.
- L. J. Robertson, L. Hermansen and B. K. Gjerde, Occurrence of Cryptosporidium oocysts and Giardia cysts in sewage in Norway, Appl. Environ. Microbiol., 2006, 72, 5297–5303 CrossRef CAS PubMed
.
- Tetra Tech, Observed and Predicted Oocyst Concentration Distributions as the Starting Point for Quantitative Microbial Risk Analysis of Tertiary Treatment, 2011 Search PubMed.
- EPA, Long Term 2 Enhanced Surface Water Treatment Rule (Final Rule), 40 CFR Part 9, 141, and 142, 2006 Search PubMed.
- J. B. Rose, C. N. Haas and S. Regli, Risk assessment and control of waterborne giardiasis, Am. J. Public Health, 1991, 81, 709–713 CrossRef CAS PubMed
.
- M. J. Messner and P. Berger, Cryptosporidium infection risk: results of new dose-response modeling, Risk Anal., 2016, 36, 1969–1982 CrossRef PubMed
.
- P. F. M. Teunis, C. L. Moe, P. Liu, S. E. Miller, L. Lindesmith, R. S. Baric, J. Le Pendu and R. L. Calderon, Norwalk virus: How infectious is it?, J. Med. Virol., 2008, 80, 1468–1476 CrossRef PubMed
.
- M. J. Messner, P. Berger and S. P. Nappier, Fractional Poisson-A Simple Dose-Response Model for Human Norovirus, Risk Anal., 2014, 34, 1820–1829 CrossRef PubMed
.
- N. Van Abel, M. E. Schoen, J. C. Kissel and J. S. Meschke, Comparison of risk predicted by multiple norovirus dose–response models and implications for quantitative microbial risk assessment, Risk Anal., 2017, 37, 245–264 CrossRef PubMed
.
- R. L. Ward, D. I. Bernstein, E. C. Young, J. R. Sherwood, D. R. Knowlton and G. M. Schiff, Human rotavirus studies in volunteers: determination of infectious dose and serological response to infection, J. Infect. Dis., 1986, 154, 871–880 CrossRef CAS PubMed
.
- A. M. Roseberry and D. E. Burmaster, Lognormal distributions for water intake by children and adults, Risk Anal., 1992, 12, 99–104 CrossRef CAS PubMed
.
-
C. Haas and J. N. S. Eisenberg, in Water Quality: Guidelines, Standards & Health, ed. L. Fewtrell and J. Bartram, IWA Publishing, London, UK, 2001 Search PubMed
.
- B. M. Pecson, S. C. Triolo, S. Olivieri, E. C. Chen, A. N. Pisarenko, C. C. Yang, A. Olivieri, C. N. Haas, R. S. Trussell and R. R. Trussell, Reliability of pathogen control in direct potable reuse: Performance evaluation and QMRA of a full-scale 1 MGD advanced treatment train, Water Res., 2017, 122, 258–268 CrossRef CAS PubMed
.
- T. Westrell, O. Bergstedt, T. A. Stenström and N. J. Ashbolt, A theoretical approach to assess microbial risks due to failures in drinking water systems, Int. J. Environ. Health Res., 2003, 13, 181–197 CrossRef CAS PubMed
.
- M. L. Delignette-Muller and C. Dutang, fitdistrplus: An R Package for Fitting Distributions, J. Stat. Softw., 2015, 64, 1–34 Search PubMed
.
- S. Petterson, R. Grøndahl-Rosado, V. Nilsen, M. Myrmel and L. J. Robertson, Variability in the recovery of a virus concentration procedure in water: Implications for QMRA, Water Res., 2015, 87, 79–86 CrossRef CAS PubMed
.
- A. Olivieri, J. Crook, R. Bull, J. Drewes, C. Gerba, C. Haas, A. Pruden, J. B. Rose, S. Snyder, J. E. Taylor, G. Tchobanoglous and M. P. Wehner, Memorandum of Findings: Expert Panel Preliminary Findings and Recommendations on Draft DPR Criteria, NWRI, Fountain Valley, CA, 2022 Search PubMed.
- Division of Drinking Water, Response to Expert Panel preliminary findings, recommendations, and comments on the draft DPR criteria, Sacramento, CA, 2022 Search PubMed.
- C. P. Gerba, W. Q. Betancourt and M. Kitajima, How Much Reduction of Virus is Needed for Recycled Water: A Continuous Changing Need for Assessment?, Water Res., 2017, 108, 25–31 CrossRef PubMed
.
- K. R. Wigginton, B. M. Pecson, T. Sigstam, F. Bosshard and T. Kohn, Virus Inactivation Mechanisms: Impact of Disinfectants on Virus Function and Structural Integrity, Environ. Sci. Technol., 2012, 46, 12069–12078 CrossRef CAS PubMed
.
- C. N. Haas, Quantitative Microbial Risk Assessment and Molecular Biology: Paths to Integration, Environ. Sci. Technol., 2020, 54, 8539–8546 CrossRef CAS PubMed
.
- M. D. Sobsey, Absence of virological and epidemiological evidence that SARS-CoV-2 poses COVID-19 risks from environmental fecal waste, wastewater and water exposures, J. Water Health, 2021, 20, 126–138 CrossRef PubMed
.
- M. Shaffer, K. Huynh, V. Costantini, K. Bibby and J. Vinjé, Viable Norovirus Persistence in Water Microcosms, Environ. Sci. Technol. Lett., 2022, 9, 851–855 CrossRef CAS PubMed
.
- EPA, Surface Water Treatment Rule, 40 CFR 141.70-141.75, 1989 Search PubMed.
- A. Olivieri, D. Eisenberg, J. Soller, J. Eisenberg, R. Cooper, G. Tchobanoglous, R. Trussell and P. Gagliardo, Estimation of pathogen removal in an advanced water treatment facility using Monto Carlo simulation, Water Sci. Technol., 1999, 40, 223–233 CrossRef CAS
.
- K. H. Tng, J. Currie, C. Roberts, S. H. Koh, M. Audley and G. L. Leslie, Resilience of Advanced Water Treatment Plants for Potable Reuse, Australian Water Recycling Centre of Excellence, Brisbane, Australia, 2015 Search PubMed.
- D. Donia, E. Bonanni, L. Diaco and M. Divizia, Statistical correlation between enterovirus genome copy numbers and infectious viral particles in wastewater samples, Lett. Appl. Microbiol., 2010, 50, 237–240 CrossRef CAS PubMed
.
- C. P. Gerba and W. Q. Betancourt, Assessing the Occurrence of Waterborne Viruses in Reuse Systems: Analytical Limits and Needs, Pathogens, 2019, 8(3), 107 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ew00362k |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |