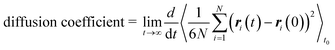Effects of MOF linker rotation and functionalization on methane uptake and diffusion†
Shuwen
Yue
 a,
Changhwan
Oh
a,
Changhwan
Oh
 ab,
Aditya
Nandy
ab,
Aditya
Nandy
 ac,
Gianmarco G.
Terrones
ac,
Gianmarco G.
Terrones
 a and
Heather J.
Kulik
a and
Heather J.
Kulik
 *ac
*ac
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: hjkulik@mit.edu
bDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
cDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 2nd January 2023
Abstract
The flexible degrees of freedom in metal–organic frameworks (MOFs) can have significant effects on guest molecule behavior. However, in the majority of studies applying molecular simulations to MOFs, the framework is assumed to be rigid in order to minimize computational cost. Here we assess the significance of this assumption on a representative example of methane uptake and diffusion in UiO-66. We introduce an open-source code to modify MOFs through functionalization and linker rotation and we perform Grand Canonical Monte Carlo and molecular dynamics simulations of methane in each of the functionalized and linker-rotated derivatives of UiO-66. We find that linker rotation moderately influences methane uptake and significantly influences methane diffusion. Our assessment provides ranges of property values that serve as measures of uncertainty of these two properties associated with linker rotation. We further determine that void volume fraction and minimum pore size are the features that govern methane uptake and diffusion, respectively. These findings illustrate the impact of linker rotation on MOFs and provide design principles to guide future investigations.
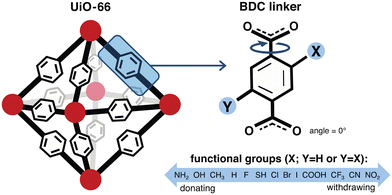
Design, System, ApplicationMetal–organic frameworks (MOFs) have great potential as materials for gas storage and separations. A common design approach is to tune functional groups in the MOF structures to optimize for relevant properties such as gas uptake and diffusion. These properties can be predicted from molecular simulations, where many studies assume a rigid framework. In this work, we describe an ‘uncertainty’ associated with this rigid framework assumption by quantifying the influence of linker rotation. We show that rotating linkers can impact methane diffusion more than tuning functional groups. Linker rotation affects methane uptake to a lesser extent. Our study also uncovers the key geometric features of void volume fraction and minimum pore diameter as the ‘knobs’ controlling methane uptake and diffusion, respectively. These findings serve as promising avenues for the design of MOF structures to optimize for gas storage and separations. |
1. Introduction
Metal–organic frameworks (MOFs) are attractive materials with applications in gas storage,1–9 catalysis,10,11 and separations.12–15 There exist large and diverse databases of these materials, both experimentally synthesized16 and hypothetical,17–19 which can be screened to identify MOFs with ideal properties, typically with molecular simulation (e.g., to predict gas adsorption or diffusivity). In the vast majority of prior studies using molecular simulation, the MOF framework is assumed to be rigid to reduce computational cost and to avoid defining force fields with greater complexity. However, there are many modes of framework motion possible in MOFs – breathing, swelling, and linker rotation, among others.33 The dynamics of linker rotation have been probed experimentally, both in empty MOFs and in the presence of guest molecules.21–25 Framework motion can influence guest molecule behavior, and the adsorbed guest molecules can also affect framework motion and pore size,23,26,27 including through ‘gate-opening’ mechanisms where linkers experience steric effects that lead to larger pores and framework changes. MOF linker functionalization can alternately enhance or suppress linker dynamics, depending on the functional group.28 All of these forms of motion can be altered further by temperature, pressure, light, and mechanical forces.21,22,26,29–33 In order to make accurate and reliable computational predictions of properties such as gas adsorption and diffusivity in MOFs, it is important to understand the influence of framework motion.While MOF gas adsorption properties are most typically studied by holding the MOF framework completely rigid, framework motion in MOFs has been studied using force fields with terms that allow for framework movement. These flexible force field parameters allow framework atoms to structurally adjust on-the-fly in response to changing gas pressure.19,25,27,34–48 Flexible force field parameters are available in the general universal force field (UFF)49 and Dreiding50 force fields, but they were developed without specificity to MOF environments.44,51,52 Consequently, properties such as the diffusion coefficient obtained from these different flexible force fields vary by an order of magnitude.45,53 MOF-specific flexible parameters have been derived and are more accurate, but to date only a few force fields using these parameters have been constructed.54–56 Another method of handling flexibility is to collect an ensemble of empty framework snapshots from highly accurate but computationally expensive simulations using ab initio approaches,45 followed by less expensive but longer-time simulations for each snapshot where the framework is held rigid. This approach allows for a less computationally demanding means of accessing the variation in channel environment, but it relies on the assumption that the presence of guest molecules has a negligible impact on the dynamic configurations of the MOF, which does not hold true for all MOFs.26,27
These computational approaches to incorporate flexibility have shown that framework motion can have strong effects on guest molecule properties,19,34–38 such as adsorption39–41 and diffusivity,25,27,42–48,57 in accordance with experiment.20,47,58–65 Yang et al.47 studied the diffusion of methane in UiO-66 using flexible force fields and observed a significant improvement in prediction over rigid force fields, although predictions were still lacking in quantitative and qualitative agreement with experiment. Yang and Sholl27 recently studied the impact of flexibility for combinations of a diverse set of MOFs and guest molecules. They determined that the necessity of flexible framework treatment is case dependent, and the rigid assumption can be valid for cases where guest molecules are much smaller than channel pore sizes.24,43,44 Similarly, for gas adsorption, flexibility has been shown to be important in some cases (CO2 in MIL-53 (ref. 66)) and less significant in others (H2 in IRMOF-1 (ref. 67)). Meza-Morales et al. identified the greater importance of one form of flexibility, linker rotation, over cell deformation for CO2 adsorption in rigid coordinated polymers by performing simulations in structures with manually adjusted linker angles and framework volumes.68
Given the complexity of how framework motion impacts guest molecule properties such as uptake and diffusivity, it is useful to provide a quantitative assessment of the importance of each of the modes of framework motion to guide future computational studies. In this work, we investigate the consequence of the rigid framework assumption for linker rotation while all other modes are held constant to systematically probe its influence on gas uptake and diffusion. We apply our study to the representative case of methane in UiO-66 and its functionalized derivatives. We first develop an open-source MOF functionalization and modification tool to computationally functionalize and twist MOF linkers, and we apply this tool to construct structures covering the full angular range of linker rotation in UiO-66 and its functionalized derivatives. Over this variation of chemistry and orientation, we show that linker rotation moderately influences methane uptake and significantly influences methane diffusivity. Our assessment provides a range of uncertainty on methane diffusion/uptake properties in functionalized derivatives of UiO-66 caused by linker rotation, in comparison to previous MOF studies that report properties for only a single rotamer. We also assess the relative importance of geometric and chemical features in predicting gas adsorption and diffusivity with the goal of uncovering the governing mechanisms of each of these properties.
2. Methods
MOF modification tool
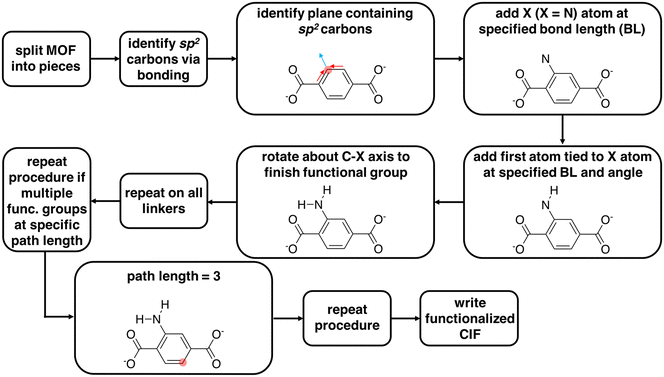
We used molSimplify69 and developed further code extensions for MOFs70,71 to modify existing CIF files by adding functional groups to linkers and rotating linkers. This code is freely available in a public Github repository at https://github.com/hjkgrp/molSimplify. The functionalization module is capable of mono- or di-functionalizing all linkers in a MOF unit cell (e.g., six benzene-1,4-dicarboxylate, BDC, linkers for UiO-66) uniformly with functional groups of the same identity. The functionalization can only presently be carried out at C–H bonds of sp2 carbon atoms because functionalization of sp3 carbon atoms introduces ambiguities due to chirality. The functional group is selected from a pre-defined set of functional groups for which we have carried out gas-phase geometry optimizations that we use to determine and store angles and bond distances in a lookup table (ESI† Table S1).We now summarize the procedure for adding functional groups to existing structures and generating new CIF files (Fig. 1). First, we separate a MOF into its constituent inorganic secondary building units (SBUs) and linkers.70,71 Upon identifying all linkers, the code identifies sp2 carbon atoms to functionalize. For a chosen sp2 carbon atom, the code determines the plane of the functionalization from the carbon atom and the two adjacent bonded atoms. The first atom of the functional group, X (e.g., N in NH2), is then added to this plane with a C–X bond vector composed of the sum of the two remaining sp2 carbon bond vectors (Fig. 1 and ESI† Table S1). For each functional group, angles and bond distances from the lookup table are used to define the placement of additional atoms (ESI† Table S1). If the user wishes to add more than one functional group, they must provide a bond path length (i.e., on the molecular graph) between the first functionalized carbon atom and subsequent functionalizable carbon atoms. The code identifies compatible carbon atoms satisfying the bond path length and carries out the functionalization until the total number of functionalizations requested by the user is achieved. The linker functionalization procedure described above is uniformly repeated across all linkers in the MOF cell. With this code, a user can functionalize a MOF an arbitrary number of times without knowing the atom indices of the functionalizable atoms a priori. The functional groups are then added to the cell in fractional coordinates, and a CIF file is written for the functionalized version of the MOF.
For functional groups not supported in the lookup table, the code supports user-provided functional groups. In order to functionalize with an unsupported functional group, the user must add to the molSimplify code an XYZ file of geometry optimized BDC with the desired functional group. The user also must specify in a Python file the functional group atom indices in the XYZ file. The molSimplify code aligns the provided coordinates to the CIF file to be functionalized in order to functionalize select carbon atoms and write a new functionalized CIF file.
The linker rotation module rotates linkers that contain carboxylate end groups with a well-defined rotation axis (i.e., rotatable C–C bonds in the linker lie on a straight line). The code uses molSimplify69 to interpret the periodic molecular graph using the atomic coordinates of the CIF file for each of the functionalized MOFs. From the connectivity information, the code identifies the carboxyl group that is connected to the metal atom (i.e., Zr for UiO-66). Then, the rotation axis is defined as the vector between two carbon atoms in two carboxyl groups of the linker (ESI† Fig. S2). Excluding the terminal carboxylate groups, the remaining atoms of the linker that are not on the rotation axis are then rotated about this rotation axis. With this rotation tool, a user can rotate all linkers of the MOF unit cell uniformly with any desired angles. For the application in this work, the original structure of UiO-66 was obtained from the Cambridge Structural Database (deposition number 889529 (ref. 72)) and optimized using CRYSTAL-14 (ref. 73) with the B3LYP74–76 global-hybrid functional and POB-TZVP77,78 basis set for all atoms. We anticipate the influence on the final structure from approximations made for the optimization of the initial structure are small relative to the subsequent linker rotation and functionalization procedure. All generated structures are deposited in the ESI.†
Geometric features
We obtained geometric features of all functionalized derivatives of UiO-66 using Zeo++.79,80 Three different pore sizes, as defined by Zeo++, were calculated: the largest free sphere (Df), the largest included sphere (Di), and the largest included sphere along the free sphere path (Dif). Df is the diameter of the largest sphere that can pass through the MOF pore channel, which represents the minimum pore diameter. Di is the diameter of the largest sphere that can fit inside the channel. Dif is similar to Di but its definition requires it to lie along the free sphere path, or a continuous path from one side of the unit cell to the other. Di and Dif are representative of the size of the largest pore inside the whole MOF and along the free sphere path, respectively. We also obtained the void volume fraction (defined in Zeo++ as “volumetric pore volume”). Lastly, we calculated the buried volume (% Vbur)81,82 of each functional group studied, which approximates the space occupied by a given functional group.Gas uptake simulations
We computed the uptake of methane in all generated framework structures from Grand Canonical Monte Carlo (GCMC) simulations using the RASPA simulation package.83 We measured the pure component uptake of methane at a high pressure of 65 bar, the standard methane storage pressure,84 and a low pressure of 5.8 bar. For all simulations, we maintained a temperature of 298 K and assumed a rigid framework. Gas–gas and framework–gas interactions were represented by UFF49 for framework atoms and the TraPPE85 force field for guest molecules. Lennard–Jones interactions were cut and shifted at 12.8 Å. Cross interactions were obtained using Lorentz–Berthelot combining rules.86,87 In order to avoid artifacts due to periodic boundary effects, simulations were conducted on a supercell made up of a 3 × 3 × 3 replication of a single unit cell to ensure that the cell lengths exceeded twice the interaction cutoffs. All GCMC simulations consisted of 4000 initialization cycles and then 6000 equilibrium cycles. Uncertainties in uptake values were estimated from the standard deviation from 5 block averages with a 95% confidence interval.Gas diffusion simulations
We performed molecular dynamics (MD) simulations in the canonical (NVT) ensemble using the LAMMPS software package88 to obtain self-diffusion coefficients of methane in all generated frameworks. We used the LAMMPS interface53 to convert framework structures from CIF format to LAMMPS input format. All force field parameters were the same as those of the GCMC simulations, and all framework atoms in the supercell were fixed. The temperature of the gas was maintained at 298 K using a Nosé–Hoover thermostat89,90 with a relaxation time of 0.1 ps. The simulations ran for 0.5 ns of equilibration time and 29.5 ns of production time, using a timestep of 1 fs.The self-diffusion coefficient was then calculated from the mean-squared displacement (MSD) following the Einstein relation,
Due to the long 30 ns sampling necessary for each of the seven rotamers for every functionalization, we limited the diffusion coefficient simulations to only five functional groups: H (unfunctionalized BDC), OH, Cl, Br, and COOH. We studied the mono-functionalized structures for each of these functional groups, along with the di-functionalized structure for the OH functional group. For each functionalized derivative and rotamer, the number of methane molecules loaded into the framework corresponded to the equilibrium uptake at the standard methane storage pressure of 65 bar at 298 K obtained from the previously described GCMC simulations.
3. Results and discussion
3a. Effects of rotation and functionalization on pore geometry
We constructed a set of structures of UiO-66 functionalized derivatives and rotamers to study how these variations in structure impact methane uptake and diffusion. In total, we studied up to 13 functional groups for gas uptake, including H (i.e., the unfunctionalized case), Cl, Br, I, F, CH3, CF3, NH2, NO2, OH, COOH, CN, and SH (Fig. 2). This set was chosen to explore a range of functional group sizes (i.e., to vary MOF pore size) and chemical characteristics. We constructed UiO-66 structures with BDC linkers both mono-functionalized and di-functionalized (para) with each functional group to further modulate pore size. For each functionalized UiO-66 derivative as well as the unfunctionalized case, we generated structures for seven linker rotamers (0°, 30°, 60°, 90°, 120°, 150°, 180°) so that we could systematically assess the role of linker rotation (Fig. 2).While our study probes a full 180° range of BDC rotation, the probability of each rotamer is unknown, and asymmetric rotations (i.e., where linkers are rotated asynchronously) are also not considered. The UiO-66 structure from the experimental crystal structure where the benzene is approximately in the same plane as the carboxyl groups, referred to as the unrotated (angle = 0°) rotamer in our study, is assumed to be the state with the highest probability density. As there are no reports of the energetics of each of the rotamers in the presence of methane loading, it would be useful to estimate these energetics in future work to account for the relative probability of such states when computing uptake and diffusion. Because we do not have a statistical distribution of each rotamer, our analysis on the geometric features, uptake, and diffusion is only informative of the sensitivity of each property of interest when the full range of symmetric linker rotation is explored. To avoid a combinatorial explosion, asynchronous linker rotations were not considered, but including them could lead to even larger predicted sensitivities if those rotations change the pore geometry even more. Inclusion of asynchronous linker rotations that could allow for more realistic linker configurations will be considered in future work. Our study thus provides a range of uncertainty on properties of the unrotated rotamer rather than a standard deviation or other more commonly employed confidence metric.
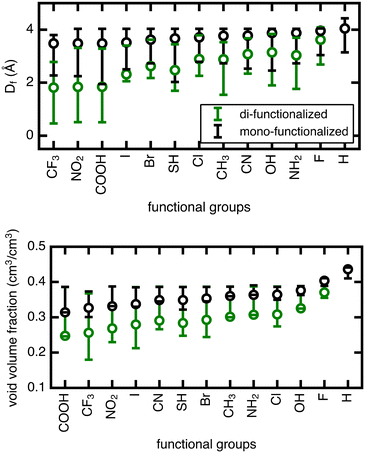
For each of the UiO-66 functional derivatives and rotamers generated, we also obtained a set of geometric and chemical features to correlate to methane uptake and diffusion (ESI† Fig. S10). We would expect features that describe the pore geometry, such as Df and void volume fraction, to explain how changes in functional group and orientation of the linkers alter methane uptake and diffusion. Both features were obtained for the full set of functionalized derivatives in this study (Fig. 3).
The range in Df due to linker rotation is 1–2 Å for the mono-functionalized derivatives and up to 3 Å for di-functionalized derivatives, which is quite significant given that the channel width of the unfunctionalized structure is around 4 Å. Smaller pore sizes in the di-functionalized derivatives are expected due to the more crowded channel environments caused by the added functional groups. This results in a larger overall range of pore sizes when the linker is rotated in the di-functionalized case. The void volume fraction is also smaller for the more crowded di-functionalized derivatives, but it varies strongly for larger functional groups (∼20% for di-functionalized CF3) and minimally for smaller functional groups (<5% for mono- or di-functionalized F).
The unrotated (angle = 0°) rotamer is the configuration that has been most commonly studied for gas properties in UiO-66 in previous work. For the mono-functionalized derivatives, the unrotated linker leads to a pore near the upper limit of possible pore sizes, and most rotations only make the pore smaller. For di-functionalized derivatives, the unrotated linker generally leads to a pore in the middle of the possible pore size range, hence linker rotation can result in either increases or decreases in pore size. As for void volume fraction, the unrotated rotamer is often on the low end of the range for several of the mono- and di-functionalized derivatives, but in other cases it resides in the middle. Therefore, void volume fraction can similarly increase or decrease upon rotation away from an angle of 0°, although to a lesser degree.
3b. Effects of number of functional groups on methane uptake and diffusion
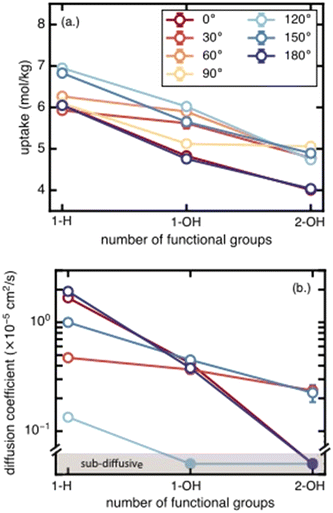
We next assess the impact of the number of functional groups on BDC linkers for each functional group species on methane uptake and diffusion. Moving from unfunctionalized to the mono-functionalized and di-functionalized OH-derivatives of UiO-66 decreases the uptake by ∼2 mol kg−1 due to decreased void volume (Fig. 4). The uptake decreases by a similar amount across all rotamers. A similar trend is observed for methane diffusion: additional functional groups lead to more crowded pore channels, which create steric barriers that impede methane molecules and reduce molecular transport. The number of rotamers showing Fickian diffusion (i.e., an MSD that varies linearly in time) drops from five (of seven total rotamers) for the unfunctionalized structure to two for the di-functionalized derivatives (Fig. 4 and S4–S6†). The only two cases where Fickian diffusion persists also have the two largest Df values. While methane uptake varies by only a moderate amount (∼2 mol kg−1) over the range of all rotamers, methane diffusivity spans from the Fickian diffusive regime (largest diffusion coefficient ∼2 × 10−5 cm2 s−1) to sub-diffusive over the same range of linker rotation angles. This large span of diffusion coefficients persists for the unfunctionalized, mono-functionalized, and even di-functionalized derivatives. This observation suggests that there exists some uncertainty in the methane diffusion coefficient due to the unknown degree of linker rotation in the presence of the diffusing gas; this uncertainty is not considered in previous work that used a rigid framework assumption.3c. Effects of functional group identity on methane uptake and diffusion
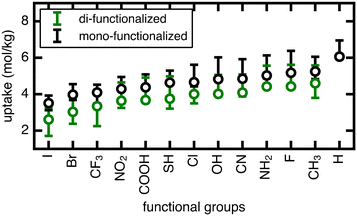
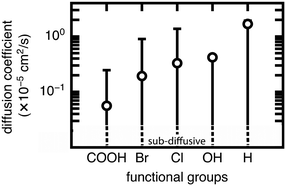
We now extend our investigation of the roles of linker rotation in methane uptake and diffusion to additional functional groups: 13 functional groups for uptake, and five functional groups for diffusion coefficient (see Methods). These simulations were performed for each UiO-66 functionalized derivative for all seven rotamers, each with three independent simulations to obtain statistical uncertainties.We quantify the span of methane uptake and diffusion over all linker rotation angles for each set of functionalized UiO-66 derivatives and compare to our observations for the OH case. For methane uptake, the span of <2 mol kg−1 shown for OH-functionalized UiO-66 is consistent with the unfunctionalized case and all additional 11 functional groups studied in both the mono- and di-functionalized derivatives (Fig. 5). The di-functionalized structures generally correspond to methane uptakes ∼1 mol kg−1 lower than those of the mono-functionalized structures due to decreased available void space in the presence of an additional functional group. For methane diffusion, the rotamers span the range from the Fickian regime to sub-diffusive for all three additional functional groups studied, consistent with observations in the OH-functionalized case (Fig. 6 and S5–S9†). Nevertheless, the upper limit of diffusion coefficients changes for each functional group, where the unfunctionalized structure (i.e., H) accesses the largest methane diffusivities and the largest functional group, COOH, is limited to lower diffusivities (ESI† Fig. S4 and S7).
The rank order of functional groups with methane uptake is largely unchanged when taking into account properties obtained with the same, consistent linker rotation across functional groups. Nevertheless, the variation due to rotation within a single functional group is comparable to the variation arising from changing functional group identity. Thus, the span of uptakes for many of the functional groups overlap strongly, suggesting that if we take into account the possibility that different functional groups could alter linker orientation preferences, then the influence of functional group on methane uptake is uncertain. Even more significant differences with linker rotation are observed for methane diffusion, where the order of functional groups based on corresponding methane diffusion coefficients can vary significantly when considering small, consistent changes caused by linker rotation. For example, if a rigid framework assumption were made using the unrotated linker rotamer, the OH-functionalized derivative would exhibit the largest methane diffusivity of the four functionalized derivatives studied. However, this could be far exceeded by the diffusion coefficient of methane in Br- and Cl-functionalized derivatives at modest degrees of linker rotation.
3d. Correlating descriptors to methane uptake and diffusion
To identify important features which govern methane uptake and diffusion, we obtained Pearson's correlation coefficients between each of these properties and a set of geometric and chemical features computed for the UiO-66 derivatives (Table 1, ESI† Fig. S10 and S11). The geometric features include the void volume fraction, the minimum pore diameter Df, the maximum pore diameter Di, the maximum pore diameter which lies along a connected path through the structure Dif, and the buried volume (% Vbur). The chemical features include the difference in electronegativity between the two most distant atoms from the BDC ring (Δχ) and the Lennard–Jones parameter (ε) of the functional group atom with the highest bond path from the terminal BDC carbon. The ε value defines the well depth of the Lennard–Jones potential which is characteristic of the strength of interaction between the functional group and methane molecules. However, one limitation of this descriptor is that all elements of the same type are equivalent regardless of local bonding environment, and so it does not distinguish polar and non-polar hydrogen atoms. Therefore, we note that the chemical features used in this work can only provide a coarse view of the influence of functional group chemistry on methane uptake and diffusion. Future studies will incorporate density functional theory-based chemical descriptors to represent the functional groups in order to provide more insight into the role of chemical features.| Void volume fraction | D f | D if | D i | ε | Δχ | % Vbur | |
|---|---|---|---|---|---|---|---|
| a The correlation analysis for methane uptake is performed on all 13 functionalized derivatives (mono- and di-functionalized) with 7 rotamers each. b The analysis for methane diffusion is performed on 5 mono-functionalized derivatives with 7 rotamers each. | |||||||
| Methane uptakea | 0.81 | 0.29 | 0.45 | 0.45 | 0.54 | 0.17 | 0.59 |
| Methane diffusionb | 0.48 | 0.63 | 0.30 | 0.31 | 0.11 | 0.31 | 0.45 |
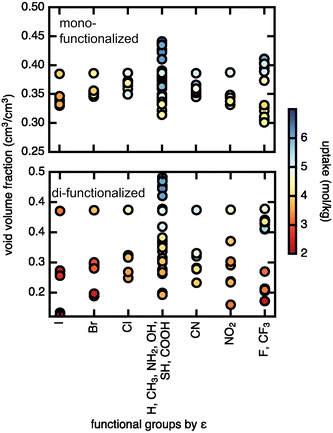
The geometric feature with the largest correlation with methane uptake was found to be the void volume fraction where larger void volumes allow for more methane molecules to occupy the pores. This trend is observed at both high (65 bar) and low (5.8 bar) pressure, although the correlation is weaker at low pressure (ESI† Fig. S11). For methane diffusion, the most correlated geometric feature was the minimum pore size, Df, which is representative of the narrow gates between octahedral and tetrahedral cages and modulates whether or not molecules freely move from cage to cage. Consistent with our observation of the sometimes limited role of functional group identity, chemical features did not show particularly strong correlation with methane uptake or diffusion. Nevertheless, of the two properties considered, the most relevant feature was the Lennard–Jones parameter ε. Future work on a larger set of MOFs and functional groups could compute (i.e., from first-principles with density functional theory) or tabulate additional chemical descriptors in search of quantities that correlate more strongly with uptake or diffusion characteristics. For the purpose of this work, we proceeded with our evaluation using Df and void volume fraction as the geometric features and ε as the chemical feature.
We assessed the relationship between void volume fraction and methane uptake (Fig. 7). The trend of higher uptake with larger void volume fraction is particularly pronounced in the case of the di-functionalized derivatives, where uptakes above 5 mol kg−1 are only observed for large void volume fractions (∼0.4), and uptakes below 3 mol kg−1 are observed for smaller (∼0.2) void volume fractions, indicating that very small void volume fractions will lead to low uptake. The Lennard–Jones parameter, ε, on the other hand shows no significant correlation with methane uptake. A similar but weaker trend is observed at low pressures, where for di-functionalized derivatives neither void volume fraction nor ε shows clear correlation with methane uptake (ESI† Fig. S12). We conclude that the pore void volume fraction is the primary feature in governing methane uptake.
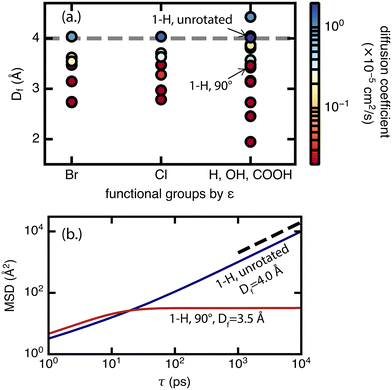
For diffusion, the minimum pore size Df, which varies mostly due to linker rotation, is the dominant feature in comparison to chemical interaction represented by the ε value (Fig. 8). This result is expected because methane has very weak interactions with the framework. This is also consistent with the recent experimental work of Kurihara et al.,24 where a similar conclusion was reached for CO2 in CID-Me and it was determined that the rate of diffusion has more to do with the molecular diameter of adsorbate relative to pore size rather than host–guest interaction strength. As for the significance of the minimum pore size Df, steric effects and “crowdedness” of pore channels play a strong role in the ability of methane molecules to travel between UiO-66 pore cages. Furthermore, methane diffusion undergoes a sharp transition from the sub-diffusive regime to the Fickian diffusive regime at Df ∼ 4 Å (i.e., the only points with diffusion coefficients above 1 × 10−5 cm2 s−1 have Df of 4.0 Å or larger in Fig. 8, see also ESI† Fig. S5–S9). This “critical pore size” is close to the size of the methane molecule (here taken to be 3.73 Å, the Lennard–Jones parameter σ of methane as defined by the TraPPE force field). Generalizing this result to other MOF and molecule pairs, we conclude that to achieve diffusion in the Fickian regime, the size of the MOF pore should be at minimum the size of the guest molecule. This observation is also consistent with several other studies that suggest the incorporation of framework flexibility in simulations is only necessary for systems where the guest molecule is similar or larger in size compared to the pore size.24,43,44
4. Conclusions
Molecular simulation represents an efficient approach to screen large databases of MOFs for properties relevant for gas transport and storage. In most prior simulation studies, MOF frameworks have been assumed to be rigid to minimize computational cost, neglecting the multiple modes of framework motion such as linker rotation, breathing, and swelling. These modes of motion are highly coupled with guest molecule uptake and functionalization of MOF linkers, among many other variables. It is therefore useful to isolate each mode separately to study its influence on relevant properties of gas uptake and diffusion.We systematically assessed the influence of linker rotation in a representative case of methane uptake and diffusion in functionalized derivatives of UiO-66. We first developed an open-source code to add functional groups to BDC linkers in UiO-66 as well as to modify linker rotation angles. Using this code, we constructed a set of UiO-66 derivatives spanning 13 different functional groups and 7 different rotation angles covering the full 180° possible range. We found that linker rotation significantly influences the void volume and pore size in the MOF channel, which in turn impact methane uptake and diffusion, respectively. The most influential feature affecting uptake is the void volume fraction, which corresponds to the amount of void space available for methane guest molecules to occupy. For methane diffusion, the most informative feature was determined to be the minimum pore size, which is representative of “gates” between tetrahedral and octahedral cages in UiO-66 and controls whether guest molecules can traverse between the cages. In our study, we observed gate-opening/closing by rotating linkers to uncover a “critical pore size” of ∼4 Å where diffusion switches from the Fickian regime to sub-diffusive. Chemical features of functional groups studied in this work, on the other hand, had limited apparent correlation with either methane uptake or diffusion. It should be noted that these observations for methane, a gas that interacts weakly with the surrounding framework, may not hold for molecules capable of stronger chemical interactions with the framework. Future studies with more complex molecules such as CO2 and H2O will provide a broader perspective on influence of geometric and chemical features in uptake and diffusion in MOFs. Furthermore, the incorporation of flexibility, whether through flexible force fields or quantum chemical methods, to better represent linker motion and kinetics would be of interest in future investigations. Our present study characterizes ranges for the degree of possible influence of linker rotation on methane uptake and diffusion in UiO-66. Whereas previous MOF studies report these properties at a single rotamer, we show that there can be significant variation when assessing the full degree of possible linker orientations.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
S. Y. was supported by the Center for Enhanced Nanofluidic Transport, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award DE-SC0019112. C. O. was supported by an MIT Portugal Seed Fund. A. N. was partially supported by the National Science Foundation Graduate Research Fellowship Program (Grant Number #1122374). G. G. T. was partially supported by an Alfred P. Sloan Foundation Scholarship (Grant Number G-2020-14067). The authors acknowledge Adam H. Steeves for providing a critical reading of the manuscript.References
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- H. C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674 CrossRef CAS PubMed.
- S. Han, Y. Huang, T. Watanabe, S. Nair, K. S. Walton, D. S. Sholl and J. Carson Meredith, Microporous Mesoporous Mater., 2013, 173, 86–91 CrossRef CAS.
- X. Lin, I. Telepeni, A. J. Blake, A. Dailly, C. M. Brown, J. M. Simmons, M. Zoppi, G. S. Walker, K. M. Thomas, T. J. Mays, P. Hubberstey, N. R. Champness and M. Schröder, J. Am. Chem. Soc., 2009, 131, 2159–2171 CrossRef CAS PubMed.
- L. J. Murray, M. Dinča and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314 RSC.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472 CrossRef CAS PubMed.
- Y. He, W. Zhou, G. Qian and B. Chen, Chem. Soc. Rev., 2014, 43, 5657–5678 RSC.
- Y. Peng, V. Krungleviciute, I. Eryazici, J. T. Hupp, O. K. Farha and T. Yildirim, J. Am. Chem. Soc., 2013, 135, 11887–11894 CrossRef CAS PubMed.
- B. Li, H.-M. Wen, W. Zhou, J. Q. Xu and B. Chen, Chem, 2016, 1, 557–580 CAS.
- D. Yang and B. C. Gates, ACS Catal., 2019, 9, 1779–1798 CrossRef CAS.
- A. Bavykina, N. Kolobov, I. S. Khan, J. A. Bau, A. Ramirez and J. Gascon, Chem. Rev., 2020, 120, 8468–8535 CrossRef CAS PubMed.
- M. Z. Ahmad, T. A. Peters, N. M. Konnertz, T. Visser, C. Téllez, J. Coronas, V. Fila, W. M. de Vos and N. E. Benes, Sep. Purif. Technol., 2020, 230, 115858 CrossRef CAS.
- T.-H. Bae, J. S. Lee, W. Qiu, W. J. Koros, C. W. Jones and S. Nair, Angew. Chem., 2010, 122, 10059–10062 CrossRef.
- M. H. Mohamed, Y. Yang, L. Li, S. Zhang, J. P. Ruffley, A. G. Jarvi, S. Saxena, G. Veser, J. K. Johnson and N. L. Rosi, J. Am. Chem. Soc., 2019, 141, 13003–13007 CrossRef CAS PubMed.
- Z. Xie, T. Li, N. L. Rosi and M. A. Carreon, J. Mater. Chem. A, 2014, 2, 1239–1241 RSC.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2011, 4, 83–89 CrossRef PubMed.
- Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Cryst. Growth Des., 2017, 17, 5801–5810 CrossRef.
- P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. M. Moosavi, M. M. Maroto-Valer, J. A. Reimer, J. A. R. Navarro, T. K. Woo, S. Garcia, K. C. Stylianou and B. Smit, Nature, 2019, 576, 253–256 CrossRef CAS PubMed.
- Y. Wang, C. Tan, Z. Sun, Z. Xue, Q. Zhu, C. Shen, Y. Wen, S. Hu, Y. Wang, T. Sheng and X. Wu, Eur. J. Chem., 2014, 20, 1341–1348 CrossRef CAS PubMed.
- A. Gonzalez-Nelson, F. X. Coudert and M. A. van der Veen, Nanomaterials, 2019, 9, 330 CrossRef CAS PubMed.
- D. I. Kolokolov, A. G. Stepanov, V. Guillerm, C. Serre, B. Frick and H. Jobic, J. Phys. Chem. C, 2012, 116, 12131–12136 CrossRef CAS.
- A. E. Khudozhitkov, H. Jobic, D. I. Kolokolov, D. Freude, J. Haase and A. G. Stepanov, J. Phys. Chem. C, 2017, 121, 11593–11600 CrossRef CAS.
- T. Kurihara, M. Inukai and M. Mizuno, J. Phys. Chem. Lett., 2022, 13, 7023–7028 CrossRef CAS PubMed.
- H. Jin and Y. Li, Curr. Opin. Chem. Eng., 2018, 20, 107–113 CrossRef.
- P. B. Shukla and J. K. Johnson, J. Phys. Chem. C, 2022, 126, 17699–17711 CrossRef CAS.
- Y. Yang and D. S. Sholl, J. Mater. Chem. A, 2022, 10, 4242–4253 RSC.
- S. Devautour-Vinot, S. Diaby, D. da Cunha, C. Serre, P. Horcajada and G. Maurin, J. Phys. Chem. C, 2014, 118, 1983–1989 CrossRef CAS.
- G. Férey and C. Serre, Chem. Soc. Rev., 2009, 38, 1380–1399 RSC.
- C. Serre, F. Millange, C. Thouvenot, M. Noguès, G. Marsolier, D. Louër and G. Férey, J. Am. Chem. Soc., 2002, 124, 13519–13526 CrossRef CAS PubMed.
- M. Agrawal and D. S. Sholl, ACS Appl. Mater. Interfaces, 2019, 11, 31060–31068 CrossRef CAS PubMed.
- M. Agrawal, S. Bhattacharyya, Y. Huang, K. C. Jayachandrababu, C. R. Murdock, J. A. Bentley, A. Rivas-Cardona, M. M. Mertens, K. S. Walton, D. S. Sholl and S. Nair, J. Phys. Chem. C, 2017, 122, 386–397 CrossRef.
- A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096 RSC.
- S. Horike, S. Shimomura and S. Kitagawa, Nat. Chem., 2009, 1, 695–704 CrossRef CAS PubMed.
- F.-X. Coudert, Chem. Mater., 2015, 27, 1905–1916 CrossRef CAS.
- M. Witman, S. Ling, S. Jawahery, P. G. Boyd, M. Haranczyk, B. Slater and B. Smit, J. Am. Chem. Soc., 2017, 139, 5547–5557 CrossRef CAS PubMed.
- S. Jawahery, C. M. Simon, E. Braun, M. Witman, D. Tiana, B. Vlaisavljevich and B. Smit, Nat. Commun., 2017, 8, 1–9 CrossRef PubMed.
- J. J. Wardzala, J. P. Ruffley, I. Goodenough, A. M. Schmidt, P. B. Shukla, X. Wei, A. Bagusetty, M. De Souza, P. Das, D. J. Thompson, C. J. Karwacki, C. E. Wilmer, E. Borguet, N. L. Rosi and J. K. Johnson, J. Phys. Chem. C, 2020, 124, 28469–28478 CrossRef CAS.
- R. Anderson, J. Rodgers, E. Argueta, A. Biong and D. A. Gómez-Gualdrón, Chem. Mater., 2018, 30, 6325–6337 CrossRef CAS.
- C. Gu, Y. Liu, W. Wang, J. Liu and J. Hu, Front. Chem. Sci. Eng., 2020, 15, 437–449 CrossRef.
- H. Demir and S. Keskin, J. Phys. Chem. C, 2022, 126, 9875–9888 CrossRef CAS PubMed.
- A. García-Sánchez, D. Dubbeldam and S. Calero, J. Phys. Chem. C, 2010, 114, 15068–15074 CrossRef.
- C. Han, Y. Yang and D. S. Sholl, J. Phys. Chem. C, 2020, 124, 20203–20212 CrossRef CAS.
- M. V. Parkes, H. Demir, S. L. Teich-McGoldrick, D. S. Sholl, J. A. Greathouse and M. D. Allendorf, Microporous Mesoporous Mater., 2014, 194, 190–199 CrossRef CAS.
- E. Haldoupis, T. Watanabe, S. Nair and D. S. Sholl, ChemPhysChem, 2012, 13, 3449–3452 CrossRef CAS PubMed.
- B. C. Bukowski and R. Q. Snurr, ACS Appl. Mater. Interfaces, 2020, 12, 56049–56059 CrossRef CAS PubMed.
- Q. Yang, H. Jobic, F. Salles, D. Kolokolov, V. Guillerm, C. Serre and G. Maurin, Eur. J. Chem., 2011, 17, 8882–8889 CrossRef CAS PubMed.
- B. C. Bukowski, F. J. Keil, P. I. Ravikovitch, G. Sastre, R. Q. Snurr and M.-O. Coppens, Adsorption, 2021, 27, 683–760 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 2002, 114, 10024–10035 CrossRef.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 2002, 94, 8897–8909 CrossRef.
- J. A. Greathouse and M. D. Allendorf, J. Phys. Chem. C, 2008, 112, 5795–5802 CrossRef CAS.
- L. Hertäg, H. Bux, J. Caro, C. Chmelik, T. Remsungnen, M. Knauth and S. Fritzsche, J. Membr. Sci., 2011, 377, 36–41 CrossRef.
- P. G. Boyd, S. M. Moosavi, M. Witman and B. Smit, J. Phys. Chem. Lett., 2017, 8, 357–363 CrossRef CAS PubMed.
- L. Zhao, Q. Yang, Q. Ma, C. Zhong, J. Mi and D. Liu, J. Mol. Model., 2011, 17, 227–234 CrossRef CAS PubMed.
- B. Zheng, M. Sant, P. Demontis and G. B. Suffritti, J. Phys. Chem. C, 2012, 116, 933–938 CrossRef CAS.
- S. K. Achar, J. J. Wardzala, L. Bernasconi, L. Zhang and J. K. Johnson, J. Chem. Theory Comput., 2022, 18, 3593–3606 CrossRef CAS PubMed.
- C. H. Sharp, B. C. Bukowski, H. Li, E. M. Johnson, S. Ilic, A. J. Morris, D. Gersappe, R. Q. Snurr and J. R. Morris, Chem. Soc. Rev., 2021, 50, 11530–11558 RSC.
- G. E. Cmarik, M. Kim, S. M. Cohen and K. S. Walton, Langmuir, 2012, 28, 15606–15613 CrossRef CAS PubMed.
- J. A. Mason, J. Oktawiec, M. K. Taylor, M. R. Hudson, J. Rodriguez, J. E. Bachman, M. I. Gonzalez, A. Cervellino, A. Guagliardi, C. M. Brown, P. L. Llewellyn, N. Masciocchi and J. R. Long, Nature, 2015, 527, 357–361 CrossRef CAS PubMed.
- M. K. Taylor, T. Runčevski, J. Oktawiec, M. I. Gonzalez, R. L. Siegelman, J. A. Mason, J. Ye, C. M. Brown and J. R. Long, J. Am. Chem. Soc., 2016, 138, 15019–15026 CrossRef CAS PubMed.
- L. Wu, W. Wang, R. Liu, G. Wu and H. Chen, R. Soc. Open Sci., 2018, 5, 181378 CrossRef CAS PubMed.
- T. M. Osborn Popp, A. Z. Plantz, O. M. Yaghi and J. A. Reimer, ChemPhysChem, 2020, 21, 32–35 CrossRef CAS PubMed.
- F. Walenszus, V. Bon, J. D. Evans, S. Kaskel and M. Dvoyashkin, J. Phys. Chem. Lett., 2020, 11, 9696–9701 CrossRef CAS PubMed.
- N. A. Ramsahye, J. Gao, H. Jobic, P. L. Llewellyn, Q. Yang, A. D. Wiersum, M. M. Koza, V. Guillerm, C. Serre, C. L. Zhong and G. Maurin, J. Phys. Chem. C, 2014, 118, 27470–27482 CrossRef CAS.
- M. K. Taylor, T. Runčevski, J. Oktawiec, J. E. Bachman, R. L. Siegelman, H. Jiang, J. A. Mason, J. D. Tarver and J. R. Long, J. Am. Chem. Soc., 2018, 140, 10324–10331 CrossRef CAS PubMed.
- F. Salles, A. Ghoufi, G. Maurin, R. G. Bell, C. Mellot-Draznieks and G. Férey, Angew. Chem., Int. Ed., 2008, 47, 8487–8491 CrossRef CAS PubMed.
- J. A. Greathouse, T. L. Kinnibrugh and M. D. Allendorf, Ind. Eng. Chem. Res., 2009, 48, 3425–3431 CrossRef CAS.
- P. J. Meza-Morales, D. A. Gómez-Gualdrón, R. R. Arrieta-Perez, A. J. Hernández-Maldonado, R. Q. Snurr and M. C. Curet-Arana, Dalton Trans., 2016, 45, 17168–17178 RSC.
- E. I. Ioannidis, T. Z. Gani and H. J. Kulik, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS PubMed.
- S. M. Moosavi, A. Nandy, K. M. Jablonka, D. Ongari, J. P. Janet, P. G. Boyd, Y. Lee, B. Smit and H. J. Kulik, Nat. Commun., 2020, 11, 4068 CrossRef CAS PubMed.
- A. Nandy, C. Duan and H. J. Kulik, J. Am. Chem. Soc., 2021, 143, 17535–17547 CrossRef CAS PubMed.
- Q. Yang, V. Guillerm, F. Ragon, A. D. Wiersum, P. L. Llewellyn, C. Zhong, T. Devic, C. Serre and G. Maurin, Chem. Commun., 2012, 48, 9831–9833 RSC.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 2002, 98, 11623–11627 CrossRef.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459 CrossRef CAS PubMed.
- J. Laun, D. Vilela Oliveira and T. Bredow, J. Comput. Chem., 2018, 39, 1285–1290 CrossRef CAS PubMed.
- R. L. Martin, B. Smit and M. Haranczyk, J. Chem. Inf. Model., 2012, 52, 308–318 CrossRef CAS PubMed.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- L. Falivene, R. Credendino, A. Poater, A. Petta, L. Serra, R. Oliva, V. Scarano and L. Cavallo, Organometallics, 2016, 35, 2286–2293 CrossRef CAS.
- MORFEUs: Buried Volume, https://kjelljorner.github.io/morfeus/buried_volume.html, (accessed October 21, 2022) Search PubMed.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
- C. M. Simon, J. Kim, D. A. Gómez-Gualdrón, J. S. Camp, Y. G. Chung, R. L. Martin, R. Mercado, M. W. Deem, D. Gunter, M. Haranczyk, D. S. Sholl, R. Q. Snurr and B. Smit, Energy Environ. Sci., 2015, 8, 1190–1199 RSC.
- M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1998, 102, 2569–2577 CrossRef CAS.
- D. Berthelot, C. R. Hebd. Seances Acad. Sci., 1898, 126, 1703 Search PubMed.
- H. A. Lorentz, Ann. Phys., 1881, 248, 127–136 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Angle and distance lookup table used by MOF functionalization code for atom placements; rotation axis on terephthalic acid used for MOF linker rotation code; convergence of diffusion coefficient over simulation time; MSD of 1-H, 1-OH, 2-OH, 1-Br, and 1-COOH functionalized UiO-66; Pearson's correlation coefficients for chemical features and geometric features to methane uptake and diffusion (PDF). Structures and simulation input files for all MOFs studied in this work (ZIP). See DOI: https://doi.org/10.1039/d2me00237j |
| This journal is © The Royal Society of Chemistry 2023 |