Modeling size and edge functionalization of MXene-based quantum dots and their effect on electronic and magnetic properties

Abstract

In the last six years, the synthesis of MXene-based quantum dots (MXQDs) has gained widespread attention. Due to the quantum confinement effect, it is possible to significantly improve their properties compared to 2D counterparts, such as higher chemical stability and better electronic and optical properties. However, despite the growing interest in their properties, much remains unexplored. One of the biggest challenges is to study in more detail the structure of quantum dots, in particular, their edge functionalization and its effect on their properties. In this paper, the structural stability and electronic and magnetic properties of Ti₂CO₂ QDs based on different lateral dimensions and edge functionalization (–O, –F, and –OH) are investigated using density functional theory. The study shows that the energy gap of Ti₂CO₂–O QDs decreases with increasing lateral size for both nonmagnetic (spin-unpolarized, close shell) and magnetic (spin-polarized, open shell) cases. Furthermore, the magnetic behavior of quantum dots was revealed by shrinking from 2D Ti₂CO₂ to 0D Ti₂CO₂ QDs with lateral dimensions below 1.4 nm. The binding energy confirms the stability of all three types of edge functionalization, while the most stable structure was observed under fully saturated edge oxygenation. Moreover, it was also found that the spin density distribution and the energy gap of Ti₂CO₂–X QDs (X = O, F, and OH) are both dependent on the type of atom saturation. Size and edge confinement modeling has been demonstrated to be an effective tool for tuning the electronic and magnetic properties of MXQDs. Moreover, the observed enhanced spin polarization together with tunable magnetic properties makes the ultrafine Ti₂CO₂–X QDs promising candidates for spintronic applications.

---

1 Introduction

In 2011, a new class of 2D materials named MXenes was discovered with the general chemical formula M_n+1X_nT_x, where M is a transition metal atom (e.g., Ti, V, Sc, Mo, Ta, or Nb), X can be carbon or nitrogen atoms and T represents surface terminating groups like –O, –OH, –F and/or –Cl and n = 1–4.¹ They have a typical planar morphology with excellent structural stability, good electrical conductivity, a tunable surface, and other unique chemical properties, thus having a wide range of applications in various fields (e.g., biosensors, batteries, adsorption, catalysis, energy storage, and environmental research).^2–4 Despite the appearance of some interesting phases (semiconductors,⁵ excitonic insulators,⁶ or antiferromagnets⁷), unfortunately, most of the MXenes have exhibited metallic conductivity without an intrinsic band gap, which limits their applications in several fields (e.g., applications in laser diodes, light emitting diodes, and field-effect transistors).⁸ Furthermore, MXenes exhibit a low photoluminescence (PL) response in aqueous solution and their use in biological and optical applications is significantly limited.⁹ Recently, theoretical and experimental studies have shown that shrinking 2D materials to a 0D structure (a quantum dot, QD, which is less than 10 nanometers in size) can bring about additional unexpected and fascinating properties due to a combination of edge effects, surface area, and quantum confinement. At the same time, the inherent advantages of 2D counterparts are preserved.¹⁰ There are several types of QDs, such as graphene,¹¹ black phosphorus¹² and/or boron nitride,¹³ that have benefited from the quantum confinement and edge effect. For instance, when a 2D graphene sheet is reduced to 0D, it begins to fluoresce.¹⁴ In addition, hBN-derived QDs have shown improvements in photoluminescence, band gap tunability, and functionality compared to their 2D counterparts.¹³

Motivated by these unique characteristics of QDs, interest in MXene-derived QDs (MXQDs) has also begun to grow in the last six years. Several studies suggest that MXQDs can be synthesized and exhibit quite different photoluminescence and absorption properties than 2D MXenes. The first described MXQDs were Ti₃C₂ monolayers synthesized by the hydrothermal method.⁹ Xue et al. found that the average size, shape, and properties of MXQDs can be tailored by choosing the reaction temperature, pressure, and pH of the solution. The authors prepared water-soluble Ti₃C₂ MXQDs at 100 °C, 120 °C, and 150 °C with average lateral particle sizes of 2.9, 3.7, and 6.2 nm, respectively.⁹ Later, MXQDs with one or two heteroatoms (S, N, P, etc.) were also synthesized by mixing the corresponding elemental precursors. For example, Xu et al.¹⁵ prepared S, N co-doped Ti₃C₂T_x QDs ranging in size from 2.6 to 4.7 nm, which exhibited multi-color blue, yellow, and orange luminescence. In addition, Guan et al.¹⁶ reported N, P co-doped Ti₃C₂T_x QDs with an average lateral size of 2.7 nm. Similarly, this type of QD realized green fluorescence for the first time at a wavelength of approximately 560 nm. The second widely used method is the solvothermal method, in which the precursor solution is usually a non-aqueous organic solvent instead of water. This method is more efficient than the hydrothermal method, because it allows precise control of the size or shape of the products. For example, Xu and co-workers¹⁷ synthesized three different Ti₃C₂T_x MXQDs by a solvothermal method using ethanol (e-Ti₃C₂T_x), DMF (f-Ti₃C₂T_x), and DMSO (s-Ti₃C₂T_x QDs). The average particle size depends on the solvent, i.e., 2.5, 3.3, and 1.8 nm for e-Ti₃C₂T_x, f-Ti₃C₂T_x and s-Ti₃C₂T_x QDs, respectively. Furthermore, the optical properties can also be tailored by using different solvents with white PL emission achieved in DMSO and blue in DMF and ethanol.

Although many successful syntheses have been achieved and many studies indicate interesting optical and electronic properties of MXQDs, much is to be explored. The least information is known about the structure of MXQDs, in particular on the functionalization of the edges/surfaces and their influence on the properties. Although several studies on the influence of functional groups on the electronic, optical, or magnetic properties of other types of QDs have been reported,^18–21 information on the functionalization of MXQDs is lacking, except for the study by Ding and co-authors,⁸ in which they revealed that with increasing lateral size, the energy gaps of Ti₃C₂ QDs with H passivation range from 2.76 to 1.14 eV. To the best of our knowledge, no studies have been published on the different sizes and types of edge functionalization of Ti₂CO₂ QDs. In this work, we constructed four Ti₂CO₂ QDs with different lateral sizes and we model the edge termination using three functional atoms/groups such as –O, –F, and –OH. Moreover, we investigated the effect of these models on their electronic and magnetic properties too. In the case of the size effect, the energy gap of fully oxygenated Ti₂CO₂ QDs decreases gradually with increasing lateral size for both the nonmagnetic (spin-unpolarized, closed-shell) and magnetic (spin-polarized, open-shell) quintet states from 4.89 to 3.34 eV and from 7.29^α to 5.84^α eV, respectively (the α index means major α spin). Furthermore, our study reveals that Ti₂CO₂ QDs with a high edge-to-area ratio (lateral size less than 1.4 nm) have spin-polarized edge states, which theoretically can generate magnetic properties. In all three edge-functionalization cases (–O, –F, and –OH), the stability was confirmed by the edge binding and Gibbs energies with the most stable structure observed for fully saturated edge oxygenation. The lowest ground state energy for all edge functionalizations of Ti₂CO₂–X QDs was found to be a spin-polarized state (open shell). Moreover, the study demonstrates the possibility of tuning the energy gap and spin density distribution by using different kinds of edge functionalization (O, F, and OH) of Ti₂CO₂–X QDs. In this study, we also focused on the appropriate computational method and basis set to describe both electronic and magnetic properties, where hybrid functionals were found to be the most suitable.

2 Computational methods

A 2D Ti₂CO₂ nanosheet⁵ was used as a model system to prepare different lateral sizes of Ti₂CO₂ quantum dots (QDs) composed of 67 to 145 atoms. All calculations were performed using the Gaussian16 program package²² and GaussView²³ was used to visualize the optimized structures and spin density. In vacuo geometry optimization of all studied Ti₂CO₂ QDs was performed in various spin states at the ωB97XD²⁴ level of theory employing the 6-31G**²⁵ basis set and in the case of open-shell systems, unrestricted DFT formalism was used. For comparison, additional geometry optimization of the QD1 (Ti₂₄C₇O₃₆) model was performed at several levels of theory (CAM-B3LYP,²⁶ B3LYP,^27–29 HSE06,³⁰ PBE,³¹ BLYP,^28,32 RevTPSS³³ and M06L³⁴) using different basis sets: 6-311G**,^35,36 cc-pVTZ³⁷ and Def2TZVP.³⁸ The RMS strength criterion was set to 3.0 × 10⁻⁴ in atomic units in the geometry optimization case. Due to the problematic convergence of the studied molecules, the quadratically convergent (XQC) SCF³⁹ procedure was used. We carefully inspected the magnetic behavior of our system, i.e., we performed calculations for various values of the spin S. The values of spin S are represented by the multiplicity M = 2S + 1 as well as the magnetic moment m = 2S. Subsequently, the stability of the unrestricted wave function for systems with higher spin contamination was tested (by using the Stable = Opt calculation). Spin contamination occurs when higher spin states are mixed with the desired spin state in a wave function, potentially causing a slight decrease/increase in the calculated total energy due to increased variations freedom. However, this variation is an artifact of an incorrect wave function. If there is no spin contamination, the expected value of the total spin, 〈S²〉, should be equal to S(S + 1), where S can take the values 0 (singlet), 1/2 (doublet), 1 (triplet), 3/2 (quartet), and so forth.⁴⁰ Common consensus is that if [〈S²〉 − S(S + 1)]/[S(S + 1)] < 10%, sufficiently accurate energies are obtained.⁴¹ The frequency calculations have also been carried out using the same level of theory as that of geometry optimization to ensure that they correspond to true minima in the potential energy surface. To verify the correctness of the ground state, a more detailed analysis of the ferromagnetic/antiferromagnetic spin density distribution was performed using the definition region (by using Guess = fragment).

The relative energy ΔE [eV] is defined as the difference between the total energy of the lower and higher spin states and the energy gap Δ_g [eV] is defined as:

Δ_g = ε_LUMO − ε_HOMO, (1)

where ε_LUMO and ε_HOMO denote the lowest unoccupied molecular orbital (LUMO) eigenvalue and the highest occupied molecular orbital (HOMO) eigenvalue, respectively. In order to evaluate the thermodynamic stability of the investigated Ti₂CO₂–X QDs, the edge binding energy E_eb, zero point energy-corrected edge binding energy E₀, and Gibbs free energy G were generally defined according to equations:

E_eb/0 = ((E_MXQD) − (E_B + nE_E))/n (2)

G_eb = ((G_MXQD) − (G_B + nG_E))/n (3)

where subscript MXQD denotes the ground states of Ti₂CO₂–X, subscript B the corresponding ground state of bare Ti₂CO₂ QDs without edge functionalization, subscript E denotes the isolated edge atoms and/or group (O, F and/or OH) and n is the number of isolated edge atoms/groups. Some additional DFT and GW calculations were performed using the plane-wave VASP program package (see the ESI†).

3 Results and discussion

3.1 Basis sets and density functional effects

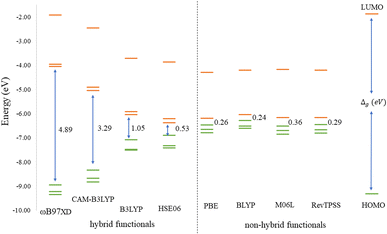
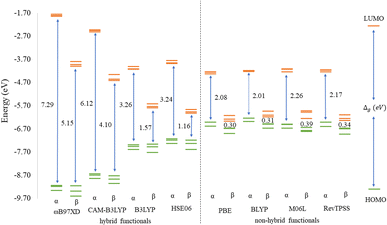
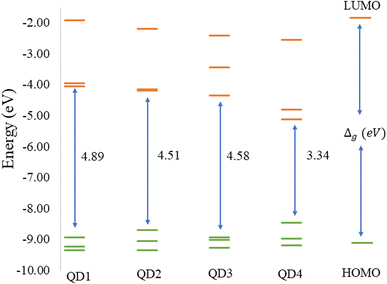
Before discussing the modeling of QDs (size and edge functionalization) and their electronic and magnetic properties, the first results on the influence of basis sets and the level of theory are presented. For this comparison, a fully edge-saturated Ti₂₄C₇O₃₆ QD (denoted as QD1) was chosen as the most stable model (for more information on the choice, see ESI, Fig. S1 and Table S1†). In the subsequent step, we have chosen closed-shell (denoted as CS) singlet and open-shell (denoted as OPS) quintet states (S = 2 and M = 5) with magnetic moment m = 4 μ_B as the reference states (inspired by the ground state in the case of the PBE and the ωB97XD functional, respectively, see Table S2†). We fully optimized all considered structures and evaluated singlet-quintet energy differences ΔE. In addition, the HOMO and LUMO energies are essential parameters that determine the electronic and optical behavior of molecules. Therefore, ΔE and Δ_g were chosen as the comparison parameters.

3.1.1 Basis sets. For the choice of basis sets, we considered correlation-consistent Dunning basis sets (polarized valence triple-zeta cc-pVTZ), Pople distributed valence basis sets (triple- 6-311G** and double-zeta 6-31G**), and the Karlsruhe triple-zeta Def2TZVP basis set, as shown in Table S3.† Both 6-311G** and 6-31G** basis sets provide reasonable values compared to the cc-pVTZ basis set, which can be considered as the closest limits to the entire basis set and thus more accurate compared to the Pople basis set. Comparisons of results obtained from the Pople style basis sets with the cc-pVTZ basis set do not show any quantitative differences with the obtained ΔE and Δ_g, where the quintet state is preferred as the ground state (based on the positive value of ΔE) with an energy gap of around 7.20^α/5.10^β eV (see Table S3†). The performance of the relatively small and computationally “cheap” computing base set 6-31G** is surprising because it provides an energy gap comparable to that obtained using much larger and computationally “expensive” basis sets and also often fails in transition metal complexes.⁴² In the case of the def2-TZVP basis set, we observe a decrease in the relative energy of almost half (0.37 eV) that of the cc-pVTZ basis set; however, the value of the relative energy remains positive, indicating that the ground state is a quintet. Similarly, the energy gap is qualitatively consistent, with only a slight underestimate of approximately 0.10 eV. Therefore, the results indicate that the choice of the basis set does not have a significant impact on the description of the electrical and magnetic properties of Ti₂CO₂ QDs. For the following reasons, the computationally “cheap” Pople style double-zeta 6-31G** basis set is chosen for further research. To verify the obtained results, the PAW (projector augmented wave) approach used within plane-wave basis sets was also tested using the PBE and HSE06 density functionals described in more detail in the following Section 3.1.2. The expected values of the total spin, 〈S²〉 presented in Table S3† correspond to the theoretical value of S(S − 1) = 6.00 (no spin contamination) for the quintet with the four unpaired electrons (m = 4 μ_B).

3.1.2 DFT functionals. The effect of the level of theory was investigated using hybrid and non-hybrid functionals to compare their relative accuracy and to select the most promising method to properly describe the electronic and magnetic properties of Ti₂CO₂–O QDs. The selected hybrid functionals were the long-range correction functionals (ωB97XD and CAM-B3LYP), the Becke 3-parameter (exchangeable) Lee–Yang–Parr functional (B3LYP), and a functional using correlation decoupled from the PBE range (HSE06). Pure generalized gradient approximation (GGA) functionals (PBE and BLYP) and meta-GGA functionals (RevTPSS and M06L) were selected as non-hybrid functionals (see Table S4†). The largest ΔE value of about 0.66 eV is observed for long-range corrected hybrid functionals (ωB97XD and CAM-B3LYP). In the case of hybrid B3LYP and HSE06 functionals, the relative energy is reduced by approximately 0.30 eV and 0.20 eV, respectively, compared to ωB97XD. However, positive relative energy values are observed in all the hybrid functionals used, indicating that the quintet state (magnetic state) is energetically more favorable than the singlet state (non-magnetic state; see also Table S4†). In contrast, the non-hybrid GGA (PBE and BLYP) functionals yield ΔE a negative value of around −0.30 eV, as well as the meta-GGA (RevTPSS and M06L) functionals. The negative value of ΔE indicates a closed shell (singlet state) as the preferred one. Thus, in the case of non-hybrid functionals, we have found a non-magnetic state as the ground state (see also Table S4†). To confirm the effect of magnetism, PBE and HSE06 calculations were also carried out using the PAW approach implemented in the plane-wave VASP program package (Table S2†). The results are consistent with previous findings, i.e., for the non-hybrid PBE functional, a singlet (nonmagnetic) state was found to be more stable, while for the hybrid functional HSE06, the quintet state with magnetic moment m = 4 μ_B is preferred.

Method differences were also found in the case of the energy gaps which are depicted in Fig. 1 and 2. It is found that the highest value of the energy gap is observed for the ωB97XD hybrid functional, i.e., 4.89 eV for the singlet and 7.29^α/5.15^β eV for the quintet state (m = 4 μ_B). The most significant energy gap reduction can be observed for non-hybrid functionals, i.e., for all four used functionals, the energy gap value for the singlet is approximately 0.30 eV and about 2.00^α/0.30^β eV for the quintet (with magnetic moment 4 μ_B). In addition, Fig. 1 shows that in the case of non-hybrid functionals in the singlet state, LUMO/LUMO−1 energies are degenerate, while no degeneracy is observed in the case of hybrid functionals. Similarly, in the quintet state case (Fig. 2), degeneracy for both HOMO/HOMO+1 and LUMO/LUMO−1 pairs is found in the case of non-hybrid functionals, while in the case of hybrid functionals, degeneracy is observed in the case of LUMO/LUMO−1. Our results, in line with the conclusion we made for Ti₂CO₂ MXene,⁷ suggest that the GGA and meta-GGA density functionals underestimate the energy gap and incorrectly describe the magnetism in MXQD.

Fig. 1 Energy diagram of the three highest occupied (green lines) and three lowest unoccupied (orange lines) molecular orbitals of the singlet QD1 model using different model density functionals. The Δ_g (in eV) values indicate the difference between the LUMO and HOMO.

Fig. 2 Energy diagram of the three highest occupied (green lines) and three lowest unoccupied (orange lines) molecular orbitals of the quintet QD1 model using different model density functionals. The Δ_g (in eV) values indicate the difference between the LUMO and HOMO.

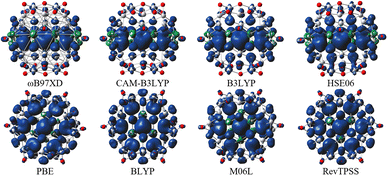
For all hybrid functionals, the spin density distribution (Fig. 4) is localized on three carbon atoms, and the ferromagnetic configuration is located in the center of the molecule. Meanwhile for non-hybrid functions the largest spin density is observed localized on the central carbon and the rest of the spin density is symmetrically distributed on all other carbon atoms (for the values of the magnetic moment see Table S5 in Fig. S3†).

In general, it is essential to note that hybrid functionals prefer higher spin states, whereas pure GGA functionals prefer lower spin states. Thus, to reliably determine the ground state, further study is required, especially at the experimental level. Nevertheless, hybrid functionals provide typically more accurate results compared to GGA functionals.⁴³ Moreover, Radoń⁴⁴ in his study observed that in some of the transition metal complexes investigated, the effect of the exact exchange admixture on the spin-state energetics (i.e., strong stabilization of the high-spin state versus the low-spin state) was often not observed. He has found that metal-centered exchange interactions are not particularly sensitive to the admixture of exact exchange and the sensitivity to the exchange functional comes from the metal–ligand bond.

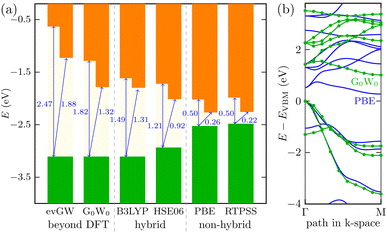
It is most likely that the hybrid functional will be the best choice for the QD description; however, the Ti₂₄C₇O₃₆ cluster is quite an unknown system. We, therefore, decided to perform additional calculations on the Ti₂CO₂ monolayer (using the periodic plane-wave VASP program). We reoptimized the geometrical structure from our previous studies^5,7 and tested the energy spectrum of the monolayer system. Besides GGA (PBE), meta-GGA (RevTPSS), and hybrid density functionals (HSE06 and B3LYP), we also used the many-body perturbation GW method. This method is far beyond DFT and is regarded as quite an established reference method in condensed matter physics. We also recently proved good accuracy of the GW approach in the Sc-based monolayer MXene case.⁴⁵ We can see in Fig. 3 that the trend of opening the gap when moving from GGA to hybrid density functionals is preserved as in the QD case. In periodic calculations, we could not use long-range hybrid functionals and, instead, focused on the GW method providing a quasiparticle band structure. Direct comparison of the quasiparticle band structure from the so-called single-shot (PBE orbital-based) variant G₀W₀ and GGA PBE structure is depicted in Fig. 3b for the most important Γ − M path of the 2D Ti₂CO₂ hexagonal Brillouin zone. As shown in Fig. 3a, the G₀W₀ quasiparticle gap is slightly larger than the hybrid B3LYP gap. On the other hand, when one iterates GW eigenvalues (evGW variant of the GW method), both direct and indirect gaps are significantly opened (cf.Fig. 3a for final values, and Fig. S4† for the gap evolution with GW iterations): Δ^dir_g = 1.82 eV → 2.47 eV and Δ^indir_g = 1.32 eV → 1.82 eV, respectively. We note that our GW calculations with a “standard” setting⁴⁶ were renormalized to the well-converged precise values of G₀W₀ of Ding et al.⁴⁷ In summary, to recover the behavior of the accurate GW method, density functionals providing larger gaps than standard hybrid density functionals HSE06 or B3LYP (as long-range hybrid ones) should be used for modeling Ti-based quantum dot systems, where GW cannot be used.

For all the aforementioned reasons and following many-body GW results on 2D Ti₂CO₂, we decided to use the long-range corrected ωB97XD hybrid functional to further study the MXene quantum dots (MXDQs). Moreover, with respect to possible later calculations of MXQD absorption spectra by the TD-DFT method, long-range hybrid density functionals (as ωB97XD) seem prospective. We note that such density functionals with the Pople-style double-zeta 6-31G** basis set were useful also in studies of the structural and optical properties of carbon dots.⁴⁸

Fig. 3 Energy diagram for the 2D Ti₂CO₂ MXene: (a) comparison of the band gaps (direct and indirect) using a scheme with the valence band maximum (VBM, green area = occupied bands) and conduction band minimum (CBM, orange area = unoccupied bands) using different density functionals and the many-body GW method; (b) the band structure for the Γ − M path in the Brillouin zone from the GGA PBE density functional (blue line) and many-body GW method (green dotted lines are eye-guides).

Fig. 4 Spin density of quintet state (m = 4 μ_B) QD1 using different model density functionals. Titanium, carbon, and oxygen atoms are shown in light grey, dark grey, and red, respectively. The isosurface values are 0.002 e/bohr³ (blue color represents positive and green color represents negative spin density).

3.2 Modeling of size

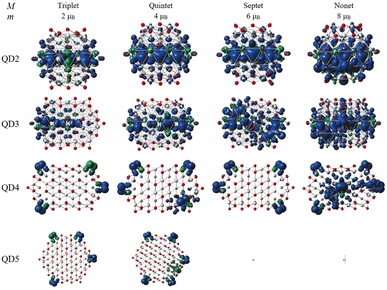
The second part of the study examined the effect of lateral size on the electronic and magnetic properties of oxygen-edged Ti₂CO₂ QDs, referred to as Ti₂CO₂–O. We constructed four Ti₂CO₂–O QDs denoted as QDn (n = 1–4): Ti₂₄C₇O₃₆ (QD1), Ti₃₂C₁₀O₄₆ (QD2), Ti₄₀C₁₃O₅₆ (QD3), and Ti₅₄C₁₉O₇₂ (QD4); see Fig. 5. The corresponding lateral sizes were between 1.1 and 1.75 nm. In general, the 2D Ti₂CO₂ monolayers form hexagonal cells,^5,7 and only a slight elongation of the Ti–O bond on the lateral side occurs after shrinkage to QDs (see the ESI† for details). A crucial aspect to consider is the spin multiplicity M and/or magnetic moment μ_B of the studied QDs. For the larger models (QD3 and QD4 with lateral sizes greater than 1.5 nm), the nonmagnetic spin-nonpolarized, singlet state is energetically preferred as shown in Table 1. In contrast, in the case of QD1 and QD2 (with lateral sizes smaller than 1.4 nm), the magnetic spin-polarized state with higher multiplicity (quintet state, m = 4 μ_B) is energetically preferred. For the QD1 model, the singlet open shell (antiferromagnetic) state is energetically very close with an absolute energy difference of 0.03 eV, as shown in Table 1. However, the expected values of the total spin, 〈S²〉 = 1.97, is highly biased for the antiferromagnetic case (the open shell singlet theoretical value should be S(S − 1) = 0 with zero unpaired electrons), which leads to an increase in the total energy due to the admixture of the higher-energy state. In contrast, the expected values of the total spin 〈S²〉 = 6.05 for the quintet state corresponds to the theoretical value of S(S − 1) = 6 for three unpaired electrons, i.e., no spin contamination occurs. Therefore, it can be assumed that the true ground state is the quintet state with a magnetic moment of 4 μ_B.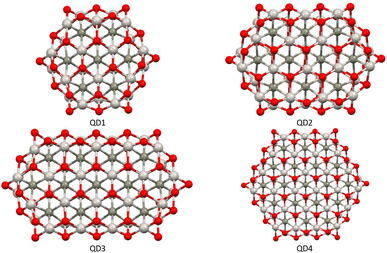

Fig. 5 Top views of optimized Ti₂CO₂–O QDs with different sizes. Titanium, carbon, and oxygen atoms are shown in light grey, dark grey, and red, respectively.

Table 1 ωB97XD/6-31G** relative energies ΔE [eV] with respect to the electronic ground state (in bold) and 〈S²〉 expectation values for different sizes of Ti₂CO₂–O QDs in various spin states S represented by multiplicity M and magnetic moment m [μ_B/QD]

S	M	m	QD1		QD2		QD3		QD4
			ΔE	〈S^2〉	ΔE	〈S^2〉	ΔE	〈S^2〉	ΔE	〈S^2〉
a The open shell singlet was converted to the closed shell. b Spin states were not calculated.
0	Singlet CS	0	0.65	0.00	0.59	0.00	0.00	0.00	0.00	0.00
0	Singlet OPS	0	0.03	1.97	0.40	1.03	2.93	2.04	—^a	—
1	Triplet	2	0.21	2.95	0.37	2.04	2.92	3.04	3.17	3.03
2	Quintet	4	0.00	6.05	0.00	6.06	2.17	6.04	6.29	6.06
3	Septet	6	2.10	12.05	2.54	12.08	4.34	12.08	–^b	—
4	Nonet	8	4.77	20.07	4.95	20.08	6.92	20.09	–^b	—

---

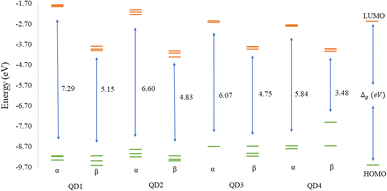
The values of the gap Δ_g are shown in Fig. 6 and 7 for quintet (m = 4 μ_B) and singlet (m = 0 μ_B) states, respectively. It is evident that Δ_g is strongly affected by the size of the Ti₂CO₂–O QD, because the gap energy decreases due to the quantum confinement effect: the Δ_g decreases from 7.29^α/5.15^β eV in QD1 to 5.84^α/3.48^β eV in QD4 (see Fig. 6) in the case of the quintet state (with magnetic moment 4 μ_B). This trend is also confirmed for the nonmagnetic (singlet) state, which is preferred for QD3 and QD4, where the value of Δ_g decreases from 4.89 eV in QD1 to 3.34 eV in QD4 (see Fig. 7). Thus, the value of the gap can be expected to be close to the value of 2D materials if the QD size is large enough, consistent with the theoretical study of Ding.⁸ In addition, Δ_g is an important stability index that may be used to characterize the chemical reactivity and stability of molecules via the principle of maximum hardness.⁴⁹ In this sense, a molecule with a larger energy gap is termed a hard molecule, meaning higher chemical stability. Thus, from the reduction of Δ_g with the increase of the system, it is evident that the largest chemical hardness coincides with the smallest size, which is the most stable structure. This characteristic behavior gives rise to the possibility of tuning the properties (mainly electronic, magnetic and/or optical) of quantum dots depending on their size.

Fig. 6 ωB97XD/6-31G** energy diagram of the three highest occupied (green lines) and three lowest unoccupied (orange lines) molecular orbital of the quintet state (m = 4 μ_B) Ti₂CO₂–O QDs with the different sizes. The Δ_g values (in eV) indicate the difference between the LUMO and HOMO energies.

Fig. 7 ωB97XD/6-31G** energy diagram of the three highest occupied (green lines) and three lowest unoccupied (orange lines) molecular orbitals of the singlet state (m = 0 μ_B) Ti₂CO₂–O with different sizes. The Δ_g values (in eV) indicate the difference between the LUMO and HOMO energies.

The spin density distribution of Ti₂CO₂–O QDs with different sizes obtained at the ωB97XD/6-31G** level of theory is shown in Fig. 8. At the small quantum dot sizes (QD1–QD2, lateral size up to 1.4 nm), positive spin densities (blue color) are found to be more localized in the center of the molecule on carbon atoms with ferromagnetic configuration. However, the aforementioned high spin contamination can have significant effects on the geometry and population analysis and can significantly affect the spin density. Therefore, alternative spin distribution possibilities were explored in particular antiferromagnetic ordering and/or spin distribution on titanium and oxygen atoms (edge functionalization). Nevertheless, ferromagnetic spin ordering as well as localization on carbon atoms proved to be more advantageous. Conversely, in the case of quantum dots with lateral sizes larger than 1.5 nm (QD3 and QD4), the spin density localizes to oxygen atoms at the edge of the molecule due to edge functionalization. This spin distribution implies that the magnetism is the result of edge functionalization groups and an edge-to-area ratio that vanishes with increasing size. The edge-to-area ratio of a quantum dot is defined as the ratio of the number of atoms located on the surface (edge) to the total number of atoms (area) and is crucial in determining the electronic and magnetic properties of quantum dots. In smaller QDs with a high edge-to-area ratio, the edge may contain a larger number of unpaired electrons, which can interact to create a magnetic field, leading to magnetism involving inner atoms. While in larger QDs with a smaller edge-to-area, the edge effect is negligible and the 2D material properties dominate. This effect is evident in Fig. 8, where for QDs with lateral sizes above 1.5 nm (QD3 and QD4), only a weak polarization at the edge of the QD is observed, which is induced by the oxygen atoms at the edge. The edge effect of the oxygen atoms is not spread inside the quantum dot, and the non-magnetic behavior rather mimics the 2D material (2D Ti₂CO₂ is non-magnetic^5,7). In contrast, for QDs with lower lateral dimensions up to 1.4 nm (QD1 and QD2), the edge-to-area ratio is higher and the edge-atom effect dominates, producing more spin-polarized segments that interact and can generate magnetic behavior inside the quantum dot. Based on the obtained results, it can be assumed that, when the quantum dot size is sufficiently shrunk (lateral size smaller than 1.4 nm), the edge functionalization can affect its magnetic properties, and the finite size model converges to a magnetic solution. Similar behavior has been observed in the case of graphene quantum dots (GQDs) with zigzag edges where the magnetic properties of GQDs have been theoretically predicted and subsequently experimentally demonstrated.^50–52 In addition, hydroxyl passivation of the zigzag edge has been investigated as a promising method to obtain magnetic properties.⁵³ For this reason, we also decided to investigate the possibility of tuning the properties of QDs by modeling their edges (see the next section).

Fig. 8 Spin density for different sizes and spin multiplicities of Ti₂CO₂–O QDs. The isosurface values are 0.002 e/bohr³ (blue color represents positive and green color represents negative spin density). Titanium, carbon and oxygen atoms are shown in light grey, dark grey and red, respectively. Septet and nonet for QD5 are not calculated.

3.3 Edge termination

3.3.1 Thermodynamic stability. Last but not least we focused on the possibility of the terminating Ti₂CO₂ QD edge. Since the surface of 2D MXenes has a high tendency to end with O, F and/or OH groups,⁵⁴ we decided to choose edge-oxygenation, edge-fluorination, and edge-hydroxylation. To further distinguish and characterize the studied MXQDs, the following notation is used: Ti₂CO₂–X (X = O, F, OH) denotes the functionalization of the edges of MXQDs. Due to the computational complexity, the QD1 model (containing 24 Ti, 7 C, 24 O, and 12 X atoms) was chosen as the size for the study of edge functionalization (see Fig. 9).

Fig. 9 Optimized structures of the studied Ti₂CO₂–X QDs with different edge functionalization (X = O, F, OH). Titanium, carbon, oxygen, fluorine, and hydrogen atoms are shown in light grey, dark grey, red, light blue, and white, respectively.

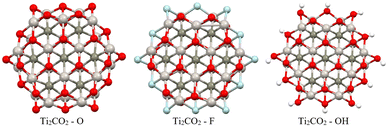
Firstly, full optimization of Ti₂CO₂–X structures was done including subsequent frequency analysis (to ensure that all eigenvalues of the Hessian are positive). In order to evaluate the thermodynamic stability of the investigated Ti₂CO₂–X, the edge binding energy E_eb, zero point energy-corrected edge binding energy E₀, and Gibbs free energy G were defined according to eqn (2) and (3) presented in Section 2. Based on these definitions, negative values of E_eb and G represent a spontaneous reaction that leads to higher stability of the product as a reactant. And a more negative value indicates a more energetically favorable (spontaneous) reaction. From the negative values of E_eb and G (see Table 2), we conclude that all structures/edges of Ti₂CO₂–X QDs under investigation are thermodynamically stable. The negative value of Gibbs energy also indicates that the formation of Ti₂CO₂–X QDs is an exothermic (spontaneous) reaction. From the relevant values of E_eb and G, it is clear that oxygen saturation is the preferred edge-termination since the order decreases with the terminal group and the sequence is in the order Ti₂CO₂–O < Ti₂CO₂–F < Ti₂CO₂–OH (see Table 2). The lowest values of E_eb and G for the Ti₂CO₂–O QDs may be due to the stronger interaction between the O and Ti atoms resulting from the shorter bond length of Ti–O, which ranges from 1.77 to 2.05 Å, than those of Ti–F from 1.98 to 2.22 Å and Ti–OH from 2.03 to 2.44 Å. It can also be clearly seen from Fig. 9 that the overall QD structure is not affected by the change of atoms at the edge, where we observe only a slight shortening of the bonds between Ti–C in the case of –F and –OH saturation (see also Table S8†).

Table 2 ωB97XD/6-31G** relative energies ΔE [eV] with respect to the electronic ground state (in bold), 〈S²〉 expectation values, energy gap Δ_g, edge binding energies E_eb [eV] (Gibbs free energy change [eV] in parentheses) of the QD2 with the different edge functionalization. Calculations were performed in various spin states S represented by multiplicity M and magnetic moment m [μ_B/QD]. The superscripts α and β stand for alpha and beta LUMO–HOMO gaps, respectively

S	M	m	O			F			OH
			ΔE	〈S^2〉	Δ g	ΔE	〈S^2〉	Δ g	ΔE	〈S^2〉	Δ g
a Values of zero point corrected relative energy E0 in eV.
0	Singlet CS	0	0.65	0.00	4.89	0.94	0.00	4.36	0.65	0.00	4.29
0	Singlet OPS	0	0.03	1.97	5.14^α/5.11^β	0.36	3.94	5.11^α/4.82^β	0.01	3.64	5.03^α/5.22^β
1	Triplet	2	0.21	2.95	4.73^α/5.03^β	0.35	4.78	4.94^α/5.39^β	0.00	4.70	5.31^α/5.11^β
2	Quintet	4	0.00	6.05	7.29^α/5.15^β	0.00	7.42	5.38^α/5.02^β	0.05	7.60	5.31^α/5.14^β
3	Septet	6	2.10	12.05	5.92^α/5.42^β	0.32	12.77	5.29^α/5.11^β	0.46	13.04	5.22^α/5.12^β
4	Nonet	8	4.77	20.07	6.00^α/5.22^β	0.69	20.05	5.29^α/6.89^β	0.48	20.08	5.23^α/6.85^β
E eb			−7.04, −6.94^a (−6.52)			−6.62, −6.23^a (−6.23)			−5.78, −5.56^a (−5.10)

---

3.3.2 Magnetic and electronic properties. After studying the structural stability of the edge termination, we now turn to a discussion of the impact of chemical edge modifications on the spin density, magnetic ordering, and energy gap. As mentioned previously in Section 3.2, the ground state of Ti₂CO₂–O with the notation QD1 is a spin-polarized quintet state (m = 4 μ_B). Similarly, we find that spin-polarized states are preferred in the case of Ti₂CO₂–F and Ti₂CO₂–OH, with the quintet state being favored in the case of edge-fluorination, while in the case of edge-hydroxylation, the three states are close together (singlet OPS (m = 0 μ_B), triplet (m = 2 μ_B) and quintet (m = 4 μ_B), see Table 2). However, it should be noted that strong spin contamination is observed in both Ti₂CO₂–OH and Ti₂CO₂–F, which indicates the mixing of energy states that can lead to misassignment of the ground state. Therefore, additional calculations were performed to confirm the stability of the wave function, resulting in a stable wave function for all edge terminations. Thus, in the case of edge fluorination and/or hydroxylation, the determination of the ground state is challenging, and future studies of MXQDs with such types of edge terminations should be approached with considerable caution. Nonetheless, if the ground state is considered as a nonet (m = 8 μ_B) with the expected value of the total spin, 〈S²〉 corresponding to the theoretical value (S(S + 1) = 20.0), the spin-polarized state is still the more favorable with a positive value of ΔE (0.27 and 0.31 eV for Ti₂CO₂–F and Ti₂CO₂–OH, respectively). Thus, these results suggest that Ti₂CO₂–X with lateral dimensions up to 1.4 nm exhibit magnetism independent of the edge termination group, and the magnetic behavior is caused by the effect of the edge-to-surface ratio (as explained in Section 3.2).

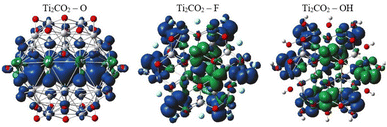
In order to provide an additional study on the effect of edge functionalization on the magnetic properties, we plot spin density distribution for the studied Ti₂CO₂–X QDs in Fig. 10 (see also Fig. S2†). The spin densities are observed at the center of the molecule, around the carbon atoms in the Ti₂CO₂–O QD, which indicates that the origin of the ferromagnetism in these flakes is the active unpaired electrons from C atoms and the neighboring transition Ti metals. And the spin-up density is dominant, as shown by the blue cubes in Fig. 10.

Fig. 10 Spin density distribution for ground states of QD1s Ti₂CO₂–X with different edge functionalization (X = O, F, OH). Titanium, carbon and oxygen atoms are shown in light grey, dark grey and red, respectively. The isosurface values are 0.002 e/bohr³ (blue color represents positive and green color represents negative spin density).

In contrast, for bare Ti₂CO₂, Ti₂CO₂–F and Ti₂CO₂–OH QDs, the spin densities are localized around the transition Ti atoms predominantly at the edge of the molecule, where both the spin-up and spin-down densities are comparable (see Fig. 10 and S2†). Thus, the observed ferrimagnetism in these flakes is activated by unpaired electrons from transition metals. These differences arise from the charge transfer between Ti and edge atoms, where the two unpaired electrons in the oxygen atoms affect the magnetic ordering at the edge more strongly and significantly weaken the ferrimagnetic ordering (which is observed in the bare structure) compared to the –F/OH groups. The comparable spin up/down densities will decrease the spin polarization in these QDs with respect to Ti₂CO₂–O QDs. Thus, the enhancement of spin polarization and the tunable magnetic properties make ultra-small Ti₂CO₂–O QDs interesting for spintronic devices. Previous studies have demonstrated that quantum confinement and finite-size effects cause a sensitive electronic structure to chemical edge modifications.^18–21 Our results are consistent with these studies, where an increase in Δ_g is observed for QDs with saturated edges compared to the bare structure. The energy gap of bare QDs is increased by approximately 50% upon edge oxidation (see Table S1†). In the case of the quintet state (m = 4 μ_B), changing the edge termination leads to a decrease in Δ_gα from 7.3 eV for edge oxygenation to about 5 eV for edge fluorination and hydroxylation, as shown in Table 2. This result demonstrates that the energy gap can be tuned significantly by chemical modification of the Ti₂CO₂–X QD edge with different atomic and molecular groups. Moreover, in the context of the maximum hardness principle, where the molecule with the highest value of Δ_g can be considered the most stable, these results confirm previous findings, i.e., edge-oxygenation can be considered the most likely edge termination.

4 Conclusions

The structural stability and electronic, and magnetic properties of hexagonal Ti₂CO₂ QDs with edge termination have been investigated under the effect of different lateral sizes and edge functionalization. The calculated negative binding and Gibbs free energies indicate that all selected Ti₂CO₂–X QDs (X = O, F, OH) are stable and the edge termination reaction is exothermic, with the highest stability observed for fully saturated Ti₂CO₂–O QDs. The electronic and magnetic properties are highly dependent on the size of the Ti₂CO₂–O QDs, and in parallel, the study demonstrated that the energy gaps, as well as the spin density, can be tuned by changing the functionalization of the edges. We subsequently revealed that the reduction of 2D Ti₂CO₂ MXenes to sufficiently small Ti₂CO₂–X QDs (less than 1.4 nm in size) can produce magnetic behavior due to an edge-to-area ratio that vanishes with increasing size. Meanwhile the change of the edge group does not affect the overall magnetic behavior observed for all types of terminations. However, the change in the type of confinement has a significant influence on the type of magnetization and distribution of spin density.

In the case of Ti₂CO₂–O QDs, we found that the distribution of spin density is strongly localized in the carbon atoms in the center of the MXQD as a ferromagnetic one. In Ti₂CO₂–F and Ti₂CO₂–OH QDs, the up and down spin densities are distributed as more ferrimagnetic ones located mainly near the edge with a total spin of 4 originated from the unpaired electrons of the titanium metal and neighbor C atoms. The spin polarization is then higher in the Ti₂CO₂–O QD due to the higher spin-up density. Furthermore, the study showed that the size and functionalization of the edges affect the energy gaps. In the case of Ti₂CO₂–O QDs, the energy gap decreases significantly with increasing lateral size for both the magnetic (the open shell) case (from 7.29^α/5.15^β to 5.84^α/3.48^β eV) and the nonmagnetic (closed shell) case (from 4.89 to 3.34 eV). In the case of edge-functionalization change, we observe an increased energy gap compared to bare Ti₂CO₂ QDs, with the highest value of the energy gap observed for Ti₂CO₂–O QDs (the energy gap of the ground state (quintet, m = 4 μ_B) for the bare Ti₂CO₂ and Ti₂CO₂–X QDs with –O, –F and –OH is 4.21/4.31, 7.29/5.15, 5.38/5.02, and 5.31/5.11 eV, respectively).

Finally, we proved that standard GGA density functional theory fails in the right description of the ground magnetic properties of MXene-based QDs by comparison to hybrid DFT calculations and showed that our approach is necessary for correct predictions and design. It is expected that this study will provide valuable information to understand the design of new lateral sizes as well as edge modeling of MXQDs to further study the tuning of electronic, magnetic, and optical behavior for desired applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This article has been produced with the financial support of the Czech Science Foundation (number 21-28709S) and the European Union under the LERCO project (number CZ.10.03.01/00/22_003/0000003) via the Operational Programme Just Transition. The computations were performed at the IT4Innovations National Supercomputing Center through e-INFRA CZ (ID:90140).

Notes and references

1. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253.
2. M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005.
3. J. Zhu, E. Ha, G. Zhao, Y. Zhou, D. Huang, G. Yue, L. Hu, N. Sun, Y. Wang, L. Y. S. Lee, C. Xu, K.-Y. Wong, D. Astruc and P. Zhao, Coord. Chem. Rev., 2017, 352, 306–327.
4. D. Xiong, X. Li, Z. Bai and S. Lu, Small, 2018, 14, 1703419.
5. T. Ketolainen and F. Karlický, J. Mater. Chem. C, 2022, 10, 3919–3928.
6. N. Kumar and F. Karlický, Appl. Phys. Lett., 2023, 122, 183102.
7. T. Sakhraoui and F. Karlický, ACS Omega, 2022, 7, 42221–42232.
8. Y. Ding, X. Nie, H. Dong, N. Rujisamphan and Y. Li, Phys. E, 2020, 124, 114328.
9. Q. Xue, H. Zhang, M. Zhu, Z. Pei, H. Li, Z. Wang, Y. Huang, Y. Huang, Q. Deng, J. Zhou, S. Du, Q. Huang and C. Zhi, Adv. Mater., 2017, 29, 1604847.
10. X. Wang, G. Sun, N. Li and P. Chen, Chem. Soc. Rev., 2016, 45, 2239–2262.
11. D. Pan, J. Zhang, Z. Li and M. Wu, Adv. Mater., 2010, 22, 734–738.
12. P. Chen, N. Li, X. Chen, W.-J. Ong and X. Zhao, 2D Materials, 2017, 5, 014002.
13. B. Huo, B. Liu, T. Chen, L. Cui, G. Xu, M. Liu and J. Liu, Langmuir, 2017, 33, 10673–10678.
14. Z. Zhang, J. Zhang, N. Chen and L. Qu, Energy Environ. Sci., 2012, 5, 8869–8890.
15. X. Quan, Y. Wenjing, W. Yangyang, L. Shengkun, L. Zheng, O. Wee-Jun and L. Neng, Appl. Mater. Today, 2019, 16, 90–101.
16. Q. Guan, J. Ma, W. Yang, R. Zhang, X. Zhang, X. Dong, Y. Fan, L. Cai, Y. Cao, Y. Zhang, N. Li and Q. Xu, Nanoscale, 2019, 11, 14123–14133.
17. G. Xu, Y. Niu, X. Yang, Z. Jin, Y. Wang, Y. Xu and H. Niu, Adv. Opt. Mater., 2018, 6, 1800951.
18. J. Feng, Q. Guo, H. Liu, D. Chen, Z. Tian, F. Xia, S. Ma, L. Yu and L. Dong, Carbon, 2019, 155, 491–498.
19. H. Abdelsalam, H. Elhaes and M. A. Ibrahim, Chem. Phys. Lett., 2018, 695, 138–148.
20. Y. Li, H. Shu, X. Niu and J. Wang, J. Phys. Chem. C, 2015, 119, 24950–24957.
21. H. Abdelsalam, V. A. Saroka, M. Ali, N. H. Teleb, H. Elhaes and M. A. Ibrahim, Phys. E, 2019, 108, 339–346.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci and D. J. Hratch, Gaussian 16, Revision B.01, 2016.
23. R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6, Semichem Inc., Shawnee Mission, KS, 2019.
24. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
25. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984.
26. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
28. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
29. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
30. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
32. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
33. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2011, 106, 179902.
34. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
35. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
36. K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065.
37. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
38. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
39. G. B. Bacskay, Chem. Phys., 1981, 61, 385–404.
40. A. Szabo and N. S. Ostlund, Modern Quantum Chemistry, Dover Publications, Mineola, New York, 1996.
41. F. Karlický and M. Otyepka, Int. J. Quantum Chem., 2014, 114, 987–992.
42. F. Karlický and M. Otyepka, J. Chem. Theory Comput., 2011, 7, 2876–2885.
43. M. Reiher, O. Salomon and B. Artur Hess, Theor. Chem. Acc., 2001, 107, 48–55.
44. M. Radoń, Phys. Chem. Chem. Phys., 2014, 16, 14479–14488.
45. M. Dubecký, S. Minárik and F. Karlický, J. Chem. Phys., 2023, 158, 054703.
46. GW calculations by the VASP code using N_B = 384 bands (24 of them updated in GW), plane-wave energy cut-off E_cut = 500 eV, GW cut-off E^GW_cut = 200 eV, Δz = 20 Å distance to perpendicular image, and 18 × 18 × 1 k-point grid.
47. Y. Ding, X. Nie, H. Dong, N. Rujisamphan and Y. Li, Nanoscale Adv., 2020, 2, 2471–2477.
48. M. Sudolská, M. Dubecký, S. Sarkar, C. J. Reckmeier, R. Zbořil, A. L. Rogach and M. Otyepka, J. Phys. Chem. C, 2015, 119, 13369–13373.
49. R. G. Pearson, Acc. Chem. Res., 1993, 26, 250–255.
50. W. L. Wang, S. Meng and E. Kaxiras, Nano Lett., 2008, 8, 241–245.
51. J. Fernández-Rossier and J. J. Palacios, Phys. Rev. Lett., 2007, 99, 177204.
52. G. Z. Magda, X. Jin, I. Hagymási, P. Vancsó, Z. Osváth, P. Nemes-Incze, C. Hwang, L. P. Biró and L. Tapasztó, Nature, 2014, 514, 608–611.
53. Y. Sun, Y. Zheng, H. Pan, J. Chen, W. Zhang, L. Fu, K. Zhang, N. Tang and Y. Du, npj Quantum Mater., 2017, 5, 2397–4648.
54. R. Ibragimova, M. J. Puska and H.-P. Komsa, ACS Nano, 2019, 13, 9171–9181.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00474k

---