Strategies and applications of generating spin polarization in organic semiconductors
Ke
Meng
ab,
Lidan
Guo
*a and
Xiangnan
Sun
 *abc
*abc
aKey Laboratory of Nanosystem and Hierarchical Fabrication, National Center for Nanoscience and Technology, Beijing 100190, P. R. China. E-mail: guold@nanoctr.cn; sunxn@nanoctr.cn
bCenter of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, P. R. China
cSchool of Material Science and Engineering, Zhengzhou University, Zhengzhou 450001, P. R. China
First published on 12th June 2023
Abstract
The advent of spintronics has undoubtedly revolutionized data storage, processing, and sensing applications. Organic semiconductors (OSCs), characterized by long spin relaxation times (>μs) and abundant spin-dependent properties, have emerged as promising materials for advanced spintronic applications. To successfully implement spin-related functions in organic spintronic devices, the four fundamental processes of spin generation, transport, manipulation, and detection form the main building blocks and are commonly in demand. Thereinto, the effective generation of spin polarization in OSCs is a precondition, but in practice, this has not been an easy task. In this context, considerable efforts have been made on this topic, covering novel materials systems, spin-dependent theories, and device fabrication technologies. In this review, we underline recent advances in external spin injection and organic property-induced spin polarization, according to the distinction between the sources of spin polarization. We focused mainly on summarizing and discussing both the physical mechanism and representative research on spin generation in OSCs, especially for various spin injection methods, organic magnetic materials, the chiral-induced spin selectivity effect, and the spinterface effect. Finally, the challenges and prospects that allow this topic to continue to be dynamic were outlined.
1. Introduction
Since the discovery of the giant magnetoresistance effect (GMR) in Fe/Cr multilayer films by Fert1 and Grunberg,2 the use of electron spin as an information carrier for storage, transport, and processing has become one of the major driving forces for modern scientific and technological progress. Currently, spintronics is an interdisciplinary field that focuses on studying spin-related phenomena and developing advanced spintronic devices according to novel physical mechanisms.3,4 In spintronics, the spin relaxation time and the spin diffusion length, which describe the time and spatial scale of spin information reservation, are crucial microscopic physical quantities. Materials with high spin lifetimes and long-range coherent spin transport are considered favorable for sophisticated spin manipulation and advanced spintronic applications, including devices, circuits, and quantum technology.5,6 Organic semiconductors (OSCs) possess ultra-long spin lifetimes (even beyond seconds) in theory due to their extremely weak spin–orbit coupling (SOC) and hyperfine interactions (HFIs), which are much higher than the typical value for inorganic semiconductors.6–8 Incidentally, such a high spin lifetime does not lead to long spin diffusion lengths for OSCs because the carrier transfer in OSCs is characterized by hopping between localized states, resulting in a relatively low carrier mobility.9 For example, most OSCs have spin diffusion lengths of less than 100 nm, whereas inorganic semiconductors with a Bloch band structure typically have spin diffusion lengths in excess of μm (e.g., Si, Ge, and GaAs).10–13 In addition, unlike their inorganic counterparts, OSCs typically exhibit special localized electronic states due to their strong and complex electron–phonon coupling. The unique charge–spin relationship exhibited in these localized electronic states is expected to yield novel and rich spin-related phenomena within the π-conjugated OSC systems.6,14 In terms of spintronic devices that take advantage of the excellent spin transport properties of OSCs, many novel multifunctional devices, including spin-organic light emitting diodes (spin-OLEDs),15,16 spin-organic photovoltaic (spin-OPV) devices17,18 and novel spin memory devices,19,20 have been demonstrated. Some original physical insights into the spin-related phenomenon in OSCs have also been presented, such as the magnetic field effect,21,22 the spinterface effect,14,23 the chiral-induced spin selectivity (CISS) effect,24,25 spin transport principles,26,27 and the spin crossover effect.28,29 Notably, all of these successful investigations cannot be separated from the generation process of spin information in OSCs.The transfer of spin in spintronic devices is the main research content in organic spintronics, which determines the fundamental properties of devices.5 In a spintronic device, the spin carriers will first experience spin generation, followed by spin transport, manipulation, and detection.3,4,30 Therefore, generating spin-polarized carriers is a prerequisite for either spin transport/manipulation or functionality research, which is also one of the most central factors for determining the performance of spintronic devices and studying spin-related phenomena.31 Spin-polarized generation refers to the unbalanced numbers of spin-up and spin-down electrons that occur in OSCs, which can be quantified by spin polarization (P) and defined as P = (N↑ − N↓)/(N↑ + N↓), where N↑ and N↓ denote the majority spin and minority spin electrons in OSCs, respectively.
Unlike magnetic materials, common OSCs are non-magnetic with symmetric spin-up and spin-down density of states, leading to the fact that spin polarized generation in these non-magnetic OSCs occurs through external spin injection from ferromagnetic (FM) electrodes or other methods. However, effectively injecting spin signals into OSCs is not a simple task, due to the presence of a strong spin-flip scattering process at the FM electrode/semiconductor interface.5,32,33 To solve this issue, several spin injection methods have been utilized in recent decades to achieve efficient spin injection. These methods include direct electrical spin injection, tunnel spin injection, photon photoemission spin injection, hot electron spin injection, and ferromagnetic resonance spin pumping, which have greatly promoted the early development of organic spintronics and also laid an important foundation for future development. However, dispensed with spin injection, spin polarization can spontaneously occur in some organic molecules with special chemical structures. For example, magnetism may be observed in certain unique molecular-chemical structures and molecular assemblies with open-shell electronic structures, exhibiting spontaneous spin polarization due to magnetism.6 Moreover, the spinterface effect and the CISS effect can exhibit spin filtering, leading to spin polarization in organic materials.23,25 The above spin-polarized generation strategies not only promote the early development of organic spintronics but also offer great potential for further development.
In this review, we provide a systematic discussion on spin-polarized generation strategies in OSCs. According to the origination of spin-polarized information, external spin injection through the FM electrode/OSC junction and active spin polarization induced by the properties of the OSCs are discussed. First, we introduce several spin injection methods based on the FM electrode/OSC junctions in terms of the basic physical principles and device designs, as well as some representative developments. Second, focusing on the behavior of spontaneous spin polarization in organic systems, we discussed the organic magnets, spin filter effect via the spinterface and CISS effect, and their research advances. Finally, to guide readers, we outline the conclusion and outlook of spin generation in OSCs.
2. Spin polarization generated by spin injection
Spin injection using FM electrodes is commonly used to create spin polarization in OSCs. Unlike conventional OSCs with non-magnetic properties, the spin arrangement of electrons in ferromagnets will possess preferential orientations, representing the macroscopic magnetization direction of the material, due to the intrinsic difference between the number of spin-up and spin-down electrons.4 This makes the charge current passing through the FM metal process of high value for spin polarization. The FM metal–OSC junction, formed by the FM metal in contact with the OSC, is the most elementary spin-injection configuration. It is expected that when the current driven by an external bias flows from the FM metal into the OSC, the electrons will maintain the preferential orientation of the spins from the FM metal, thereby generating spin-polarized information in the OSC. However, strong spin-flip scattering at the FM metal/OSC interface will result in a quick loss of spin information at the OSC side, making it difficult to achieve efficient spin injection in practice, even though electrical spin injection with the help of the FM metal is conceptually simple.31 In this context, to obtain highly spin-polarized signals in OSCs, numerous efforts, both technical and theoretical, have been undertaken by the organic spintronics community. In the following sections, we focus on describing the physical mechanisms and experiments of representative spin injection techniques, which include direct electrical spin injection, tunnel spin injection, optical emission spin injection, hot electron spin injection, and ferromagnetic resonance spin pumping.2.1. Direct electric spin injection
At equilibrium, the carriers in OSCs with non-magnetic properties carry no net spin and are therefore non-spin-polarized. If a FM material comes into contact with an OSC, the FM–OSC interface will be formed. When an external voltage bias is applied to the FM electrode/OSC structure, the spin-polarized carriers (electrons and holes) from the FM electrode will be across the interface and further injected into the OSC. This process can alter the original spin distribution and generate spin polarization. This method of generating spin polarization is one of the most straightforward injection approaches and is also known as direct electrical spin injection.31 In order to demonstrate the success of spin injection, spin valves are the most common and popular prototype devices, which are also a medium for investigating the spin transport/manipulation process.4 Organic spin valves possess a typical sandwich structure with an organic layer located in between two electrodes with varying coercivity. In operation, as shown in Fig. 1a, the spin-polarized electrons from one FM electrode were injected into the OSC layer, driven by an applied bias voltage, and the spin-polarized current was detected in the FM electrode on the other side. The output signal of the device, the resistance or the current, depended on the relative direction of magnetization of the two FM electrodes. In particular, if the magnetization direction of both electrodes was antiparallel, the device would exhibit a high-resistance state, while in parallel, the device would display a low-resistance state (Fig. 1b). This phenomenon is known as the spin valve effect, which can be described by parametric magnetoresistance (MR), and defined as MR = (RAP − RP)/RP × 100%, where RAP and RP represent the device resistance of the two FM electrodes in the antiparallel and parallel states of the magnetization direction, respectively. If relatively thick organic thin films are used as spin-transport media, the detection of the spin valve effect could be regarded as evidence that spin polarization is generated and maintained in OSCs.34,35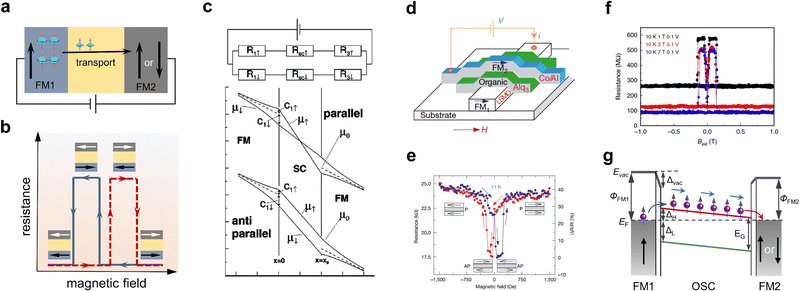 | ||
| Fig. 1 (a) Schematic of the organic spin valve. (b) The schematic of magnetoresistance response in a spin valve. (c) Schematic of the equivalent two-current circuit and electrochemical potentials in a device with a structure of FM electrode/semiconductor/FM electrode. In the top panel, the current is split into spin-up and spin-down components. The bottom panel contains the case of parallel and antiparallel magnetization of two FM electrodes. Reproduced with permission from ref. 33. Copyright 2010 by the American Physical Society. (d) The first vertical organic spin valve with an LSMO/Alq3/Co structure. (e) MR response in the first vertical spin valve. (d, e) Reproduced with permission from ref. 34. Copyright 2004, Nature Publishing Group. (f) The MR response in an LPGMO/Aiq3/Co device measured at 10 K. Reproduced with permission from ref. 44. Copyright 2019, Nature Publishing Group. (g) Energy level alignment and spin-reserved transport pathway of the typical spin valve with an FM1/OSC/FM2 structure. Evac is the vacuum level, ΦM is the work function, EF is the Fermi level, ΔL and ΔH are the energy of LUMO and HOMO with respect to EF of the metal, ΔEvac is the shift of vacuum level caused by interface dipolar, and EG is the energy gap of the OSC. | ||
It is naturally expected that when a voltage is applied to the FM electrode/non-magnetic material junction with an ohmic contact, the highly spin-polarized carriers from the FM could easily be injected into the non-magnetic material by ohmic transport. Indeed, the efficient electrical spin injection has been previously realized in FM metal/non-magnetic metal systems with an ohmic contact.36,37 However, in some experiments, spin injection efficiency was observed to be rather low, even at very low temperatures, when this method was used to study spin injection in an FM metal/inorganic semiconductor junction with an ohmic contact.38 To shed light on this phenomenon, based on the diffusion equation, Schmidt et al. first theoretically showed that spin injection efficiency was dependent on the physical parameters of the ferromagnet and semiconductors.33Fig. 1c shows the scheme of the spin-up and spin-down equivalent circuit and electrochemical potentials for an FM electrode/semiconductor/FM electrode structure. Based on their model, in the diffusion injection region, the spin polarization of injected current in the semiconductor can be given by
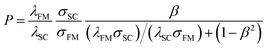 | (1) |
According to eqn (1), the use of a suitable spin injection source, preferably with 100% spin polarization, offers a promising approach to enhance spin injection. La0.67Sr0.33MnO3 (LSMO) is a half-metallic FM material with nearly 100% spin polarization at low temperatures, which is a promising material to be used as the spin injection electrode. By using LSMO as the spin injection electrode, two pioneering studies by Dediu et al. and Xiong et al. have provided successful demonstrations of spin injection into OSCs.34,35Fig. 1d shows the first vertical spin valve with a structure of LSMO/Alq3 (8-hydroxy-quinoline aluminium)/Co employed by Xiong et al., where an MR value as high as −40% was obtained at 11 K (Fig. 1e). Starting from two pioneering studies, the generation of spin polarization in OSCs was demonstrated in more organic spin valves, which consisted of LSMO electrodes and a wider variety of small molecules and polymers, such as N,N′-bis-(1-naphtalenyl)-N,N′-bis-(phenyl) benzidiane (α-NPD), 4,4′-bis99-(ethyl-3-carbazovinylene)-1,1′-biphenyl (CVB), N2200, and poly(3-hexylthiophene) (P3HT).41–43 To date, other than LSMO electrodes, various half-metallic ferromagnets with nearly 100% spin polarization, including (La2/3Pr1/3)5/8Ca3/8MnO3 (LPCMO),44 Fe3O4,45 and Co2MnSi,46 have been employed in organic spintronic devices. The application of high-spin polarization ferromagnets plays an important role in the research of organic spin devices, and many high-performance organic spintronic devices have been fabricated using these materials. For example, Yang et al. reported on the largest MR, reaching 440% at 10 K (Fig. 1f), in an Alq3-based spin valve in which an electronically phase-separated manganate LPCMO ferromagnet was used.44 In addition, applications based on these electrodes have facilitated the exploration of some novel spin-dependent phenomena, such as the spinterface effect in spin valves with an LSMO/Alq3/Co structure.23 Despite these advances, the majority of the reported devices based on half-metallic electrodes cannot operate at room temperature because their high spin polarization only occurs at low temperatures. To efficiently achieve room-temperature spin injection, it is therefore of significant value to study organic spintronic devices using high Curie temperature ferromagnets (e.g., Fe3O4, Fe, Co, Ni, and permalloys) as spin polarization sources.
Of note, no direct conclusions should be made that spin-polarized carriers cannot be efficiently injected into OSCs with a conductivity mismatch between the FM electrode and OSCs. This is due to certain limitations of the model proposed by Schmidt. The model is based on the diffusion equation, completely ignoring the presence of spin-dependent resistance at the ferromagnet–semiconductor interface. In fact, spin-dependent interface resistance has shown a significant effect on spin injection and can improve the efficiency of spin injection, which is described in detail in Section 2.2.47,48 In addition, this model assumes an ohmic contact, but in practice, a Schottky contact usually forms at the interface when an FM electrode and an OSC come into contact. Fig. 1e shows the energy-level alignment at the metal/OSC interface. In this case, the injection barriers at the interface will build up between the Fermi level of the metallic contact and the charge-transporting level (mainly referring to the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO)) of the OSCs. Numerous studies in organic electronics over the past decades have shown that these barriers will dramatically influence the charge injection and charge extraction, thus determining the performance of the devices.49,50 In organic spintronics, the Schottky barrier at the FM metal/OSC interface could significantly increase the interface resistance, which has shown a detrimental effect on the spin injection process.40,51 For example, in several experiments, it was found that lowering the interfacial barrier at the FM/OSC interface can favor spin injection.52 Incidentally, when the interfacial resistance of the FM electrode/OSC contact is spin-dependent, the spin polarization of the current injected into the OSC will be enhanced, similar to tunnel spin injection.11
2.2. Tunnel spin injection
When an insulating and sufficiently thin tunnel barrier is introduced between the FM electrode and the OSC, the mechanism for current to flow through the interface turns into quantum tunneling.47,48 This approach is known as tunnel spin injection, in which the spin polarization state of the carriers injected into the OSC is conserved. The two-current resistor model for this situation is shown in Fig. 2a, and the corresponding theoretical description was proposed by Rashba.47 Taking the presence of the tunneling barrier into account, the injection coefficient, γ, in a semiconductor can be written as follows: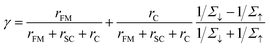 | (2) |
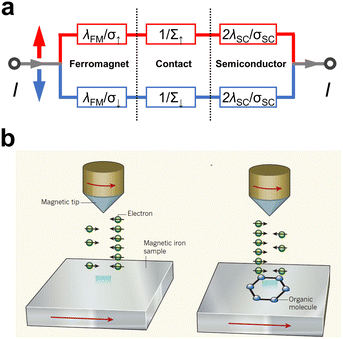 | ||
| Fig. 2 (a) Two current resistor models for a ferromagnet/contact/semiconductor junction. If rc ≫ rFM, rSC, the applied voltage mainly across the contact and the spin-polarized current can be injected into the semiconductor. (b) Schematic diagrams of the spin transport measurement of FM/OSC utilizing an SP-STM technique. Reproduced with permission from ref. 63. Copyright 2010, Nature Publishing Group. | ||
In organic spintronics, some efforts have focused on the insertion of different insulating layers, such as aluminum oxide (AlOx),53–57 LiF,15,58,59 MgO,60 and MoOx,16 between the FM electrode and the OSC to study their effects on spin transport properties. Several reports have demonstrated that the introduction of an ultra-thin insulating layer will play a positive role in improving the injection efficiency of spin-polarized carriers and device performance. The combination of interfacial resistance and conventional room-temperature ferromagnets can achieve a large and reliable spin-polarized current in the organic layers, enabling room-temperature organic spin devices. For example, by using an AlOx interface layer, Sun et al. achieved an air-stable OSV device with a Co/AlOx/BCP (bathocuproine)/NiFe structure that could operate at room temperature.61 Furthermore, it should be noted that the spacer layer could avoid complex interactions between the FM metal and the OSC, contributing to improving the repeatability of the device. As a result, some multifunctional spintronic devices will inevitably require interfacial layers. For example, the use of LiF in spin-OLED devices will enhance the spin injection and operating voltage, whereas the presence of AlOx in the spin-OPV devices will increase the repeatability of the device.15,17
The spin-polarized scanning tunneling microscope (SP-STM) technique, which uses vacuum as a barrier, is an important application of tunnel spin injection.62 The technique is a modified form of STM, with a magnetic tip and magnetic substrate, in which the tunneling current intensity in the working condition is sensitive to the imbalance between the two spin orientations of the electrons from the sample to the tip, i.e., the tunneling magnetoresistance (TMR) effect, as shown in Fig. 2b.63 This allows for the analysis of spin-dependent phenomena in organic molecules at the atomic level, due to its spin sensitivity and atomic-scale resolution. Using this advantage, researchers have investigated some molecules, and the properties of hybridized molecules have been unveiled. An SP-STM study of the spin transport of Fe in contact with a single organic molecule, phthalocyanine (H2Pc) and Co-phthalocyanine (CoPc), was carried out by Atodiresei et al. and Brede et al., who directly observed some intriguing spin-dependent phenomena.64,65 First, the researchers observed that the spin polarization of the tunneling injection current was reversed in the absorbed molecule, which provided direct evidence that the hybrid OSC could act as a spin filter in addition to acting as a spin transport medium. Second, local spin polarization was different at different regions in the molecule, such as for organic ligands and metal ions. The reason for both discoveries was attributed to the formation of hybrid molecular orbitals due to the strong coupling of the dz2 orbitals of Fe with the molecule's pz orbitals. In another work, the same technique was employed for exploring the Cr(001)/C60 system, where high TMR values of 100% were obtained from the differential conductance spectrum vs. voltage spectra, which was also caused by specific hybridized molecular levels.66 In this manner, this technique can provide important experimental support for elucidating the spin injection process at hybrid FM/OSC interfaces from a microscopic point of view.
2.3. Hot electron spin injection
Hot electron spin injection, which utilizes spin-polarized hot electrons to directly inject the transporting levels of a semiconductor across the metal/semiconductor interface barrier without suffering from conductivity mismatch problems, is another robust and efficient method for electrical injection into OSCs.67 Hot electrons possess much higher energy levels than the Fermi energy of a material (much greater than kBT), serving as essentially non-equilibrium carriers. The scattering probability of hot electrons will follow Fermi's golden rule, which is significantly different from the electrons at the Fermi level described by the Fermi–Dirac distribution.68 Typically, in the case of hot electron transport in metals, inelastic electron–electron scattering is the dominant mechanism. Once this scattering event occurs, hot electrons will relax to the Fermi level and lose a portion of their energy. In contrast, if no scattering process occurs, these electrons will ideally undergo ballistic transport without any loss of energy.69To describe hot electron spin injection, we can consider a typical vertical multilayer configuration, as shown in Fig. 3a and b. In this configuration, a tunnel junction composed of a non-magnetic metal emitter (E)/an insulating layer/a FM metal base (B) will act as a hot electron generator, and the semiconductor will act as a hot electron collector (C). When a voltage bias, VEB, is applied between the emitter and the base, electrons from the emitter can tunnel through the insulating layer into the base, generating an emitter current. These injected electrons in the base are hot electrons and are initially non-spin-polarized. During transport through the base, since the majority spin and minority spin electrons will have different mean free paths in FM metals, hot electrons will exhibit a ballistic spin filter effect. In this effect, the spin polarization can be expressed as
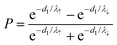 | (3) |
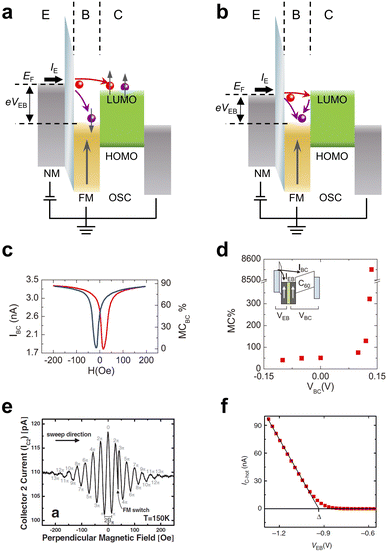 | ||
| Fig. 3 (a) and (b) Schematic layout and energy band diagram of a hot electron spin device. The red solid circles represent electrons that are regarded as “hot”, while the blue one corresponds to Fermi electrons. (c) Magnetic response in a C60-based magnetic tunnel transistor. (c and d) Manipulation of the MC response by changing the base-collector voltage. Reproduced with permission from ref. 78. Copyright 2012 by AIP Publishing. (e) Hanle effect measured in a hot electron spin transistor with 350 μm Si. Reproduced with permission from ref. 72. Copyright 2007 by the American Physical Society. (f) Hot electron current IC-hot as a function of the applied emitter-base voltage VEB in a C60-based hot electron transistor. Reproduced with permission from ref. 69. Copyright 2014, Nature Publishing Group. | ||
Except for using an FM metal base as a spin polarizer, a combination of an FM metal emitter with a non-magnetic metal base can also be used as an alternative configuration of hot electron spin injection.72,73 In this configuration, the spin polarization of the injected hot electrons will be determined by the asymmetric density of states of the FM emitter rather than the ballistic spin filtering process. Therefore, compared to a device structure with an FM base, a device based on an FM emitter will produce a smaller spin polarization. However, because the non-magnetic base has a larger free path than the FM base, the spin current and spin density injected into the semiconductor should be greater, which will be advantageous for spin transport measurements.
Considering the advantage of the ballistic spin filter effect, a series of studies have been reported, initially using inorganic semiconductors and then gradually applying it to OSC systems. A particularly successful prototype device based on hot-electron spin injection was the spin-valve transistor proposed by Monsma et al., which was the first working hybrid FM metal/semiconductor spintronic device.67,70,74 In such a device, a huge magnetocurrent (MC), defined as MC = (IP − IAP)/IAP × 100%, where IP and IAP are the collector currents for the parallel and antiparallel orientations of the magnetization in the device, respectively, could be expected and obtained at room temperature. Later, other derivative devices based on hot electron spin injection were proposed and demonstrated, such as a magnetic tunnel transistor and a hot electron spin transistor.71,75,76 With respect to hot electron spin injection in OSCs, a hot electron spin injection efficiency as high as 85% was detected using photoelectron spectroscopy, when spin-polarized hot electrons were injected from Co into CuPc.77 In a solid-state device study, Gobbi et al. reported on a C60-based magnetic tunnel transistor with an Al/Al2O3/Co/Cu/NiFe/C60/Al structure, where the metallic spin valve Co/Cu/NiFe acted as the base and C60 was employed to collect the spin-filtered hot electrons.78 As displayed in Fig. 3c and d, an MC ratio of up to 89% at room-temperature was detected by only applying an emitter bias, and it was also demonstrated that the MC ratios could be arbitrarily tuned by the collector bias.
It has been well demonstrated that efficient hot electron spin injection is highly superior for the study of spin transport and spin manipulation. In a complex and sophisticated hot electron spin transistor, Appelbaum et al. achieved ultra-long coherent spin transport of up to 350 microns in Si.72 More intriguingly, the researchers achieved spin manipulation based on the Hanle effect, describing the spin precession and dephasing phenomena, with a precession angle of 13π (Fig. 3e) which was an unprecedented resolution. Unfortunately, to the best of our knowledge, no such study has been reported in OSC systems, because hot electron spin injection into OSCs is still in the preliminary stage.
Except for the above applications, the basic concept of hot electron spin injection offers the possibility of determining the location of the charge-transporting level of OSCs by spectroscopic studies. Jiang et al. and Gobbi et al. constructed an organic hot electron transistor with an FM metal as the base.69,79 In this device, other than realizing hot electron spin injection into the LUMO levels of OSCs, the researchers extracted energy level alignment at the metal/OSC interface by monitoring the hot electron current versus the emitter bias (Fig. 3f), also known as hot-electron spectroscopy. This spectroscopy application, as a solid-state variant of ballistic-electron-emission spectroscopy,80,81 offers outstanding value for characterizing energetics problems at metal/organic interfaces, as measured under the device operating conditions and without any material parameter requirements. As research has progressed, it has been demonstrated that hot electron spectroscopy is not only suitable for a wide range of organic materials (small molecules, polymers) but also allows for the position determination of different energy levels (HOMO, LUMO, and LUMO+1).82–84
In summary, all of the above devices and the application of hot electron spin injection imply a promising future for injecting spin-polarized hot electrons into OSCs, which may further promote the development of organic spintronics. However, until now, spin polarization information after hot-electron spin injection has remained unknown, as devices are not equipped with a spin detector. This is partly due to the complexity of hot electron spintronic devices and the inherently fragile nature of OSCs, which limits reliable device fabrication. Therefore, to fully exploit the advantages of this spin injection method, in terms of spin transport and spin manipulation, the implementation of spin detection in OSCs should be a top priority.
2.4. Photon photoemission spin injection
Optical spin injection is also a reliable and valuable spin injection method. Spin-based spectroscopy obtained from the optical spin injection approach can reveal the details of spin injection at the ferromagnet–semiconductor interface, such as spin injection efficiency. Therefore, the optical spin injection and detection technique is considered an excellent complement to the macroscopic spintronic device study.85,86 The basic principle of conventional optical spin injection is as follows: when circularly polarized light is applied to a semiconductor, electrons in the valence band with a certain total angular momentum are excited to the conduction band with a specific spin orientation by selective interband transition, eventually producing the spin-polarized carriers.87 Therefore, such a method can be applied primarily to direct bandgap semiconductor systems such as Ge and GaAs.88,89 To date, conventional optical spin injection and detection techniques have not been well demonstrated in organic systems, due to the extremely weak SOC strength and their so-called π-conjugated structures. Fortunately, the development of the photon photoemission spin injection technique enables us to overcome this challenge, allowing for the direct monitoring of electron injection from ferromagnets into OSCs in real-time through ultra-short femtosecond laser pulses.77,86,90 The main experimental methods are spin-resolved two-photon photoelectron spectroscopy (SR-2PPE) and time-resolved spin-resolved two-photon photoelectron spectroscopy (STR-2PPE). These two methods are similar in principle, with the only difference being that the STR-2PPE method includes the time-resolved function. Herein, we introduce the working principle of the 2 PPE technique based on the more advanced STR-2PPE method. As shown in Fig. 4a, an ultrashort laser pulse that acts on the FM metal/OSC junction will excite the electrons in the FM metal from the initial Fermi surface to a higher energy level, generating hot electrons.90 A fraction of these spin-polarized hot electrons can be ballistically injected into the unoccupied orbitals of the OSC near the FM metal/OSC interface. Subsequently, by applying a second laser pulse, time-delayed with respect to the first laser, the electrons remaining in the OSC can be excited into the vacuum. Finally, the momentum, energy, and spin-related properties of the photoemitted electrons entering the vacuum will be determined in the equipped spin-dependent detectors, providing the corresponding spin injection information.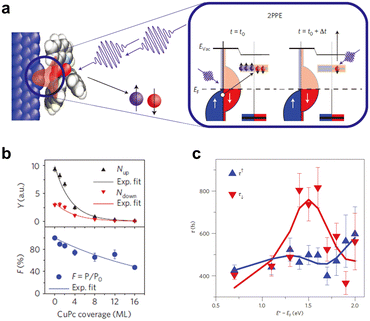 | ||
| Fig. 4 (a) Schematic illustration of spin injection via the STR-2PPE technique. In this experiment, the electron was excited only after the absorption of two-photon energies. Δt is the delay time between two laser pulses, and Evac is the vacuum level. (b) Normalized spin injection efficiency (F) and the number of majority/minority electrons (Y) versus CuPc coverage measured by the SR-2PPE experiment. Reproduced with permission from ref. 77. Copyright 2008, Nature Publishing Group. (c) The spin lifetimes of unoccupied hybrid interface states in the Alq3 molecule measured by the STR-2PPE technique. E* − EF is the energy with respect to the Fermi level of Co. (a and c) Reproduced with permission from ref. 90. Copyright 2013, Nature Publishing Group. | ||
In this advanced technique, the detected spin polarization, P, can be written as
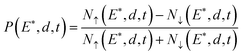 | (4) |
Besides the cases mentioned above where light can influence spins, the light emission of OSCs is also strongly affected by spins.15,93,94 It is therefore worth introducing the magnetic field effect in OLED devices. As is well known, 75 percent of the triplet state excitons and 25 percent of the singlet state excitons will be formed simultaneously in the electroluminescence process of OLED devices.15,95 Thereinto, only 25% of the singlet state contributes to the luminescence, because the transition from the triplet state to the ground state is spin forbidden, which strongly limits the luminescence efficiency in OLED devices. In this context, one effective strategy to increase the electroluminescence efficiency is to use spin-polarized currents to increase the density of singlet excitons in the organic active layer. Unlike common OLED devices with non-magnetic electrodes, a representative prototype device of this strategy is spin-OLED, which consists of two FM electrodes sandwiched by an organic active layer. In this device, the electrons and holes injected from either side of the electrode are spin-polarized, and the direction of spin-polarization of both is controlled by the magnitude of the magnetic field. At this point, the injection of controlled spin-polarized carriers will alter the spin ratios of the carrier recombination within the organic layer, thereby manipulating the singlet/triplet ratios and producing spin-dependent electroluminescence emission. Although early literature discusses the prototype design for spin-OLEDs, this goal is not easily attainable, in part due to the low efficiency of bipolarized spin injection under operating conditions.96 A giant leap for spin-OLEDs was made in 2012 by Nguyen et al., who demonstrated a reliable magneto-electroluminescence response of more than 1% in a typical device configuration of LSMO/D-DOO-PPV/LiF/Co, where LiF is used to enhance spin-polarized electron injection while the OSC layer chooses the D-DOO-PPV with excellent spin transport property.15 In addition, the magnetic field effect, which describes the phenomenon that the magnetic field has the ability to modify the steady-state electroluminescence of a non-magnetic OSC, is another strategy to enhance electroluminescence efficiency. Such an effect arises from magnetic field-induced spin interactions between microscopic particles within the OSCs, which can directly alter the spin mixing between the singlet and triplet excitons and thus the singlet/triplet ratios. Currently, many physical models have been proposed to explain these interesting spin-dependent results in OLED devices, including the HFI mechanism,97,98 SOC mechanism,99,100 triplet-charge annihilation mechanism,98,101 Δg mechanism,102 trap mechanism,103 singlet fission mechanism,104 and triplet fusion mechanism.105 Overall, with continued in-depth research, these spin-related mechanisms have become a powerful tool for understanding and optimizing OLED devices.
2.5. Spin pumping injection
Pure spin current, describing the flow of an electron's spin angular momentum and without a net charge current, is another important form of spin polarization in addition to spin-polarized charge currents. Spintronic devices based on pure spin currents have the characteristic of low power consumption due to the absence of Joule heat generated by charge flow, which is of great significance for information transmission and storage. Generally, the well-established method of ferromagnetic resonance-induced spin pumping has been employed to inject spin current from FM electrodes into non-magnetic materials.106–109 The basic idea behind spin pumping for the bilayer structure of an FM material/OSC is shown in Fig. 5a, which involves two main processes. First, under the conditions of both an external magnetic field and microwaves, the precession of magnetization gives rise to an excess of spin angular momentum in the FM material. Therefore, excited ferromagnetic resonance can occur when the precession frequency of magnetization coincides with the frequency of the external microwave field. This magnetization dynamic behavior of an FM material can be modeled using the Landau–Lifshitz–Gilbert equation.110 Subsequently, pure spin currents can be pumped into the OSC through exchange interactions at the FM material–OSC interface, with the precession of the FM layer additionally damped. The theoretical description of spin pumping was first proposed by Tserkovnyak et al., in which the spin pump current, IpumpS, is given by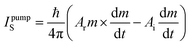 | (5) |
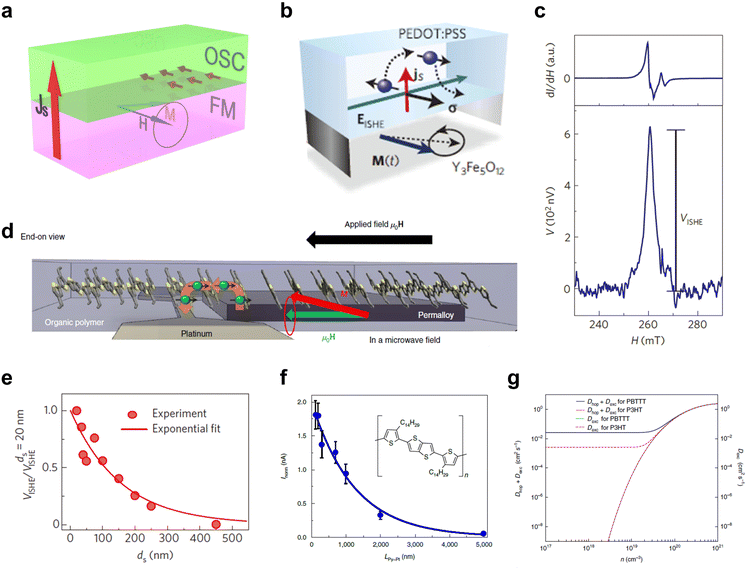 | ||
| Fig. 5 (a) Schematic illustration of spin pumping, showing a spin current injected from the FM into the OSC at ferromagnetic resonance. (b) Operating principle based on spin pumping and ISHE in the bilayer device with a structure of Y3Fe5O12/PEDOT:PSS. (c) Microwave absorption (ferromagnetic resonance signal dI/dH versus field H) and the voltage spectra measured at 20 mV microwave excitation. (b and c) Reproduced with permission from ref. 112. Copyright 2013, Nature Publishing Group. (d) Illustrations of spin-current injection, transport, and detection in the spin pumping device with a trilayer architecture. (e) Thickness dependence of the normalized ISHE voltage for a vertical Ni80Fe20/PBTTT/Pt device. Reproduced with permission from ref. 109. Copyright 2014, Nature Publishing Group. (f) The thickness dependence of ISHE-induced current for a lateral device with a structure of Ni80Fe20/F4TCNQ-doped PBTTT/Pt. (g) Theoretical modeling of the diffusion coefficient as a function of the carrier density for PBDBTT and P3HT. (d, f and g) Reproduced with permission from ref. 117. Copyright 2019, Nature Publishing Group. | ||
Unlike spin-polarized current detection via magnetoresistance or magnetoconductivity, the pure spin current should be detected via the spin-charge conversion process. Saitoh et al. proposed the electrical detection of pure spin current using the inverse spin Hall effect (ISHE) to convert pure spin current into charge current by deflecting the spin-up and spin-down in opposite directions.113 Based on this effect, the generating charge current Jc perpendicular to both the spin current Js and spin polarization σ can be expressed by Jc = (2e/ħ)θSHEJ × σ, where θSHE denotes the spin Hall angle that reflects the spin-to-charge conversion efficiency of the material. Accordingly, detected materials with strong SOC are expected to produce a large Jc, since it has been demonstrated that strong SOC generally corresponds to a large θSHE. As a result, it is challenging to detect ISHE signals in organic materials where the SOC is very weak. Nevertheless, Ando et al. made a breakthrough on this issue in a bilayer architecture composed of Y3Fe5O12/poly(3,4-ethylenedioxythiophene):poly(4-styrenesulphonate) (PEDOT:PSS) as shown in Fig. 5b, where the magnetic insulator Y3Fe5O12 and PEDOT:PSS performed spin injection and spin detection, respectively.112 Experimental results demonstrated pure spin current injection and the ISHE in conducting polymers (Fig. 5c), despite the inherently weak SOC of PEDOT:PSS. However, attributing the observed voltage entirely to the ISHE has remained controversial, as the presence of a temperature gradient can also give rise to a voltage signal, experimentally.114 Regarding this controversy, Qaid et al. recently demonstrated that the ISHE did appear in PEDOT:PSS, by designing experiments to eliminate potential spurious signals, although the inverse spin Hall voltage (VISHE) was much smaller.115 Of note, in the three pure spin current experiments described above, low-energy continuous-wave microwaves were used as the excitation source to induce ferromagnetic resonance. Technically, this led to the production of small ISHE signals in the organic solids. To acquire strong detection signal strength, an improved pure spin current injection technology was reported by Sun et al. in 2016, in which the high-energy pulsed microwaves acted as the excitation source.116 By systematically measuring the ISHE responses of several organic materials, this technique was found to be well generalized, both for molecules with strong SOC (Pt-containing polymers) and weak SOC (such as PEDOT:PSS, DOO-PPV, and C60).
Apart from the above-mentioned detection of the ISHE response in weak-SOC OSCs, a trilayer architecture formed by an FM material/a OSC/a heavy metal has been more frequently used to study pure spin current injection in OSCs. In this device structure, as shown in Fig. 5d, the pure spin current injected by ferromagnetic resonance spin pumping must transport through the OSC before flowing into the heavy metal, where the spin-charge conversion will be performed by the ISHE.117 Therefore, this device architecture enables more straightforward detection of the pure spin current, making it possible to gain spin transport information in OSCs. Building on this idea, Watanabe et al. fabricated the first OSC-based vertical pure spin current device structured by Ni80Fe20/PBTTT/Pt, where PBTTT was poly(2,5-bis(3-alkylthiophen-2-yl)thieno[3,2-b]thiophene.109 A long spin diffusion length of up to 200 nm and a long spin relaxation time over a millisecond were obtained in PBTTT. In this device, the spin diffusion length (λs) of the organic spacer was derived from the thickness dependence (d) of VISHE (Fig. 5e), according to the relation VISHE ∝ e−d/λs. In addition, once the values of the spin diffusion length and mobility (μ) were obtained, following the relationship, τs = eλs2/kBTμ, we could calculate the magnitude of the spin relaxation time (τs). Recently, based on F4TCNQ-doped PBTTT, Wang et al. prepared a lateral pure spin current device with a Ni80Fe20/OSC/Pt structure.117 Remarkably, the researchers observed a very long spin-diffusion length of more than 1 μm (Fig. 5f), which was the maximum value reported to date and far exceeding that of other materials. The ultra-long spin diffusion length was attributed to the exchange coupling spin transport mode in doped-PBTTT. Because doping led to the carrier concentration in doped-PBTTT exceeding 1018 cm−3, exchanging coupling spin transport proposed by Yu27,118,119 could be stimulated, as shown in Fig. 5g. The above investigations revealed the outstanding advantages of ferromagnetic resonance-induced spin pumping and the ISHE in studying spin dynamics in OSCs, which could be one of the most important platforms for the study of organic spintronics. Other than PBTTT, the spin transport properties of many other molecules have been investigated using this approach, including Alq3, DNTT (dinaphtho[2,3-b:2,3-f]thieno[3,2-b]thiophene), and its derivatives, SY-PPV (super yellow poly-phenylene-vinylene), fullerene, pentacene, PEDOT:PSS, and PBDTTT-C-T.111,120–125 In future development, we believe that spin pumping injection and pure spin current devices should expand to other research directions, such as multifunctionalities, beyond the current spin injection/transport research.
3. Spin polarization generated by organic systems
Typical FM metals intrinsically possess different spin-up and spin-down densities of states because of exchange interactions. This unbalance in the spin populations will lead to spontaneous spin polarization of FM metals, thus resulting in the macroscopic magnetization phenomenon. Organics are generally considered difficult to achieve spontaneous spin polarization, due to their closed-shell electronic structure and weak spin interactions. Therefore, in the early stages of organic spintronics, the generating spin polarization in OSCs mainly stems from the spin injection process using FM electrode/OSC junctions, as mentioned in Section 2, rather than spin polarization induced by OSCs. However, the appearance of some novel spin-dependent effects and the emergence of organic magnetic materials with special structures have transformed our understanding of the spin polarization phenomenon in organic systems. The combination of conducting electricity and active spin polarization in organic matters offers the possibility of designing novel functional devices and exploring novel spin-based physical phenomena, which have attracted extensive attention. In this section, we systematically describe and discuss the phenomenon and progress of spin polarization induced by organic ferromagnets, organic charge-transfer complexes, the spinterface effect, and the CISS effect.3.1. Spontaneous spin polarization in organic magnetic materials
The materials widely used in spintronics consist of FM materials capable of exhibiting spontaneous spin polarization phenomena and are indispensable elements in both fundamental scientific research and technological applications in organic spintronics. Organic materials with ferromagnetism properties are of equal importance for organic spintronics. Due to their magnetic nature, organic magnets with the spin filtering effect can be used as alternatives to FM metal electrodes, which can improve conductivity mismatch caused by excessively large FM metal conductivity. Also, when used as a channel material for spin transport, the addition of the spin degree of magnetism can open the door to versatility and new physical phenomena. Organic magnets offer a promising material system for quantum technology research due to the presence of long quantum coherence times and significant quantum effects.126As early as 1963, McConnell proposed the idea of ferromagnetic coupling in organic systems from a theoretical point of view, which guided the design and synthesis of organic ferromagnets.127 At present, numerous experiments have demonstrated that through a rational structural design, the introduction of defects, hydrogenation, or oxidation, organic materials can exhibit ferromagnetism similar to their inorganic counterparts.
First, the unique molecular structure design allows for access to organic materials with an open-shell structure, thereby exhibiting ferromagnetism. In 1987, a pure π-conjugated organic ferromagnet, poly-BIPO, was first discovered by polymerizing BIPO (1,4-bis-(2,2,6,6-tetramethyl-4-oxy-4-piperidyl-l-oxyl)-butadiin), where the side group suspended on the zigzag carbon backbone encompassed an unpaired electron, forming an open-shell structure.128 Within poly-BIPO, the main chain featured antiferromagnetic interactions between the π-electrons, while all of the side chain radicals gave rise to a highly ordered spin arrangement that eventually yielded pronounced ferromagnetism. Of note, the Curie temperature of poly-BIPO reached 400 K. Except for molecules with quasi-one-dimensional structures, polymers designed with ring-like structures could also appear magnetically ordered. Fig. 6a illustrates a cyclic polymer with a large magnetic moment and high magnetic ordering, composed of macrocyclic with a spin quantum number (S) of two combined cross-linked S = 1/2 modules.129 In this material, the ferromagnetic and antiferromagnetic coupling between the modules enabled the material to behave magnetically. The ferromagnetic behavior of the material, however, existed only below 10 K, and the magnetic properties were susceptible to external magnetic fields. These important early findings stimulated enthusiasm for research on organic ferromagnets, and many magnetic materials with different molecular structures have been successfully designed and synthesized. Recently, two room-temperature organic ferromagnets, poly-tetracyanoquinodimethane (p-TCNQ) and perylenediimide (PDI) radical crystals, were experimentally synthesized to improve the performance of organic ferromagnetism.130,131 For p-TCNQ, the magnetic properties were derived from the stable radicals around the triazine moieties (Fig. 6b), which ultimately exhibited a saturation magnetization intensity of 10−3 emu g−1, as well as a high Curie temperature (TC = 495 K) and superior stability under laboratory conditions.130 In comparison, the PDI radical (Fig. 6c) crystal was characterized by a higher saturation magnetization intensity of 1.2 emu/g.131 In this crystal, the close π–π stacking distance and high concentration of radical anions led to strong spin–exchange interactions. Furthermore, this material possessed excellent semiconductor properties, with a Hall electron mobility of 0.5 cm2 V−1 s−1. Of note, spontaneous spin polarization will occur not only in ferromagnetic systems but also in ferrimagnetic systems. Experiments have revealed that organic ferrimagnets can be produced by building suitable molecular structures, for example, typical PNNBNO (2-[3′,5′-bis(N-tert-butylaminoxyl)phenyl]-4,4,5,5-tetramethyl-4,5-dihydro-1H-imidazol-1-oxyl-3-oxide) materials.132
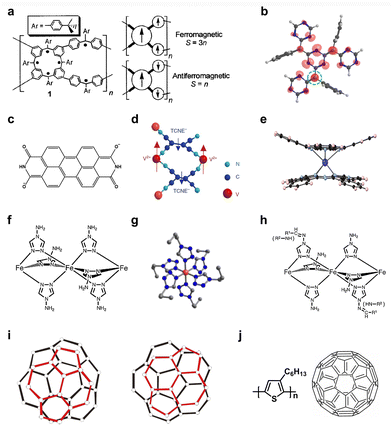 | ||
| Fig. 6 The molecular structures of ring-like polymer 1 (a), a twisted TCNQ unit (b), a PDI radical (c), V(TCNE)x (d), and TbPc2 (e), [Fe(Rtrz)3](ClO4)2 (f), [Fe(ptz)6](BF4)2 (g), and [Fe(Rtrz)3](ClO4)2-PCA (or RhB). (i) Configuration of the paramagnetic phase (left panel) and ferromagnetic phase (right panel) in the TDAE-C60 crystal. (j) The molecular structure of P3HT and C60 in the P3HT-nw-C60 system. (a) Reproduced with permission from ref. 129. Copyright 2001, American Association for the Advancement of Science. (b) Reproduced with permission from ref. 130. Copyright 2018, Cell Press. (d) Reproduced with permission from ref. 135. Copyright 2018, Nature Publishing Group. (e) Reproduced with permission from ref. 126. Copyright 2020, Nature Publishing Group. (f and h) Reproduced with permission from ref. 147. Copyright 2015, Wiley. (g) Reproduced with permission from ref. 148. Copyright 2013, American Chemical Society. (i) Reproduced with permission from ref. 170. Copyright 2000, Nature Publishing Group. | ||
Alternatively, molecular magnets, composed of metal ions and organic components, are also crucial types of ferromagnetic materials that can display both magnetic and quantum effect properties at a single molecular scale.126 In this type of material system, highly anisotropic transition metal ions or lanthanide ions will produce a large ground-state spin amplitude, making the system magnetic. As shown in Fig. 6d, utilizing transition metal vanadium(V) with tetracyanoethylene (TCNE) ligands, Manriquez et al. synthesized a room-temperature molecular magnet V(TCNE)x·γ(CH2Cl2) (x ≈ 2, γ ≈ 1/2) featuring a magnetically ordered temperature of about 400 K.133 Within this molecule, antiferromagnetic coupling between the V2+ ion (with spin S = 3/2) and the two [TCNE]− anions (with spin S = 1/2) was responsible for the magnetically ordered behavior. Interestingly, it had a fully spin-polarized semiconducting electronic structure, meaning it could serve as a prospective candidate for replacing ferromagnetic metals as electrodes to build spintronics devices. Using the V[TCNE]2 material as the electrode and rubrene as the transport media, Li et al. prepared an all-organic spin device with a V[TCNE]2/Rubrene/V[TCNE]2 structure, in which a negative MR was detected due to spin-dependent tunneling effects.134 In addition, the generation, transport, and detection of magnon in V[TCNE]2 were given attention.135 Other than transition metal-based molecular magnets, molecular magnets can be built using rare earth ions as spin carriers due to their strong anisotropy and strong spin–orbit coupling. In this regard, as shown in Fig. 6e, bis(phthalocyaninato)terbium(III) (TbPc2) is an important rare-earth-based single-molecule magnet, composed of two π-conjugated planar ligands phthalocyaninato (Pc) sandwiched by a Terbium (Tb), with their magnetic property provided by the Tb3+ metal ion.136,137 This material has been investigated in organic spintronics devices due to its unique spin properties. A lateral spintronic device with a palladium/π-conjugated supramolecules/palladium structure was fabricated by Urdampilleta et al., where the active layer consisted of a supramolecule formed by TbPc2 with carbon nanotubes through supramolecular π–π interactions.138 During operation, the local magnetic moment of TbPc2 would lead to a significant magnetic field dependence of conductance, and eventually, up to 300% magnetoresistance was observed below 1 K. In another work, a single-molecule spin transistor inserted with TbPc2 allowed for the ability to detect the quantum dynamics of a single nuclear spin.139 In summary, molecular magnets synthesized using transition metals (including Fe, Co, Ni, V, and Mn) or rare earth elements (such as Tb, Dy, Ho, Er, Tm, and Yb) have been widely reported and implemented so far.
In parallel, another class of material system that has received a lot of attention from researchers is functional molecular magnetic materials with bistability. Such materials, which possess two thermodynamically stable phases, allow for the reversible manipulation of spin states, making them valuable in fields such as quantum computing, molecular switching, and high-density information storage.140–143 The single-molecule magnets with a nanoscale mentioned above are typical bistable molecular materials because of their ability to respond to external magnetic fields. In particular, a pronounced magnetic memory behavior is shown under DC fields, while a slow relaxation of the magnetization is observed under AC fields.144 Beyond that, the spin crossover (SCO) complex, which contains transition metal ions with a d4–d7 electronic configuration, is another representative bistable molecular magnetic system. The generation of this SCO phenomenon, which describes the phenomenon of transition metal ions switching between high-spin (HS) and low-spin (LS) states, is related to two important physical quantities, the crystal-field splitting energy (Δo) and the spin-pairing energy (Pe), since their relative magnitudes determine the HS state and the LS state of the compound. For this reason, under moderately strong coordination fields (Δo ≈ Pe), where the energy difference between HS and LS states is less, SCO materials are likely to occur. To date, it has been shown that SCO material has been discovered for many different systems, and their transition between HS and LS can be induced by the variation of various external stimuli, such as light irradiation, temperature, guest absorption/desorption, or pressure. For the case of temperature-induced SCO complexes, the most commonly reported system is the one-dimensional polymer system [Fe(Rtrz)3]An–mH2O (n = 1, 2; m = 0–5).145–147 In this system, an SCO behavior with a thermal hysteresis loop has been observed. Meanwhile, many experiments have shown that the SCO properties of such materials can be modulated by varying solvent molecules, crystalline states, and R-groups, such as [Fe(Rtrz)3](ClO4)2 (see Fig. 6f). It is worth noting that, in general, SCO complexes tend to exhibit the HS state at high temperatures and the LS state at low temperatures, but in some cases, a transition from the HS state to the LS state can also be observed as the temperature rises. For light-induced spin transitions, an interesting case is the octahedral iron(II) complexes [Fe(ptz)6](BF4)2 (see Fig. 6g), in which modulation of the spin state by light and tristability in this SCO material was demonstrated.148 In addition, to obtain some new multifunctional magnetic materials, researchers have experimented with introducing luminescence- and chirality-related groups into SCO systems.147,149 For example, Wang et al. prepared hybrid SCO materials with synergy between the luminescence and SCO properties by grafting the luminescence groups PCA (1-pyrenecarboxaldehyde) and RhB (rhodamine B) into the [Fe(Rtrz)3](ClO4)2 system, see shown in Fig. 6h.147 On the whole, as research continues, the study of SCO complexes has now yielded many impressive fruits, not only in the design and preparation of a wide variety of materials but also in the discovery of novel physical phenomena, including light-induced excited spin-state trapping (LIESST) effect,150–152 reverse LIESST effect,153 multi-step SCO,154,155 and coupling effect,156,157etc.
In addition to the above molecules with intrinsic magnetic properties, ferromagnetism can be induced by the introduction of defects, doping, oxidation, or hydrogenation in non-magnetic materials. By treating C60 films on a SiO2 substrate with proton irradiation, Mathew et al. discovered that the local defects produced by irradiation resulted in local magnetic moments, so ferromagnetism would be exhibited.158 Proton irradiation obtained similar results for other materials, including graphite, carbon nanotubes, and graphene. In addition, excellent ferromagnetic properties have been observed in fullerenes treated with hydrogenation or oxidation. For example, it was experimentally found that the saturation magnetization intensity of oxidized C60 could reach 10−3μB (Bohr magneton)/C60, and the location of spin density distribution was influenced by oxygen pressure, i.e., the distribution was mainly at oxygen ions at low pressure, while it was mainly on fullerenes at high pressure.159 In terms of doping, weak ferromagnetism was observed in ClO4− doped PMTH and P3MT, which originated from interactions between the dopant ions and the polaritons in the polymer.160
Following introducing various organic magnetic materials, we want to further discuss the effects of magnetic properties on spin injection and spin transport in organic spintronic devices. To investigate spin injection, molecular spin valves were fabricated by a self-assembled monolayer (SAM) with or without magnetic properties as an interface modification layer.161,162 However, there is not yet sufficient evidence that the magnetic properties of the molecules have a significant effect on spin injection, according to a few results of the current study. In contrast, the hybrid interface (spinterface effect) formed by the reaction between the magnetic molecules and the FM electrode on contact has been shown to modulate the spin injection.163,164 In this respect, one of the straightforward experimental results is that the NiFe/NaDyClq/AlOx/Co and NiFe/AlOx/NaDyClq/Co spin valves display opposite magnetoresistance signs.164 More details of the impact of spinterface effects on spin-injection properties will be introduced in Section 3.3. As for spin transport, one preliminary study has been made by Bedoya-Pinto et al. In this case, trinuclear lanthanoid quinoline molecules, Ln3q9·nH2O (where Ln = Tb3+, or Y3+ ions, q = 8-hydroxyquinoline), with distinct magnetic properties (from paramagnetic to diamagnetic) are chosen as spin transport channels.165 By characterizing a molecular spin valve with a Co/AlOx/Ln3q9/NiFe structure, no significant difference in magnetoresistance was observed for both molecules, directly demonstrating that the magnetic properties of Ln3q9 molecules have a negligible effect on coherent spin transport across the Ln3q9 layer. The reason can be explained: the charge transfer can occur through the π-conjugated 8-hydroxyquinoline, while the Ln ions have less contribution. In fact, the application of magnetic molecules with magnetic centers capable of influencing charge transporters to spin transport research is highly desirable, because it may provide new degrees of freedom to modulate spin transport and develop new spin-based applications. Unfortunately, however, this has not yet been reported. In summary, research on integrating magnetic molecules into spintronic device architectures is still in the early stages, and the corresponding advances are slow.
Undoubtedly, it is expected that organic magnetic materials will exhibit interesting spin manipulation behavior in devices due to their rich set of spin functional properties, such as the slow relaxation of the magnetization and spin switching. However, to date, little research has been conducted and no obvious breakthroughs have been made. Overcoming such challenges and advancing this research is a multidisciplinary task and require a concerted effort by chemists, physicists, and engineers. From a device perspective, it is necessary to ensure that the magnetic molecular films retain robust intrinsic magnetic properties, while simultaneously requiring the films to exhibit a smooth and flat surface. With this purpose, various film preparation techniques, such as vacuum sublimation, spin-coating, dip coating, or Langmuir–Blodgett deposition, can be employed. From a material point of view, the majority of ferromagnetic materials have shown difficulty combining the dual properties of excellent magnetic properties and electrical conductivity. For this reason, the continuation of room temperature operation of organic magnets with a high saturation magnetization strength and high mobility has remained a challenge that must be addressed. From a physical point of view, a well-developed physical model of the organic magnetic systems would undoubtedly provide a guide for the targeted design of molecules and the interpretation of experimental results.
3.2. Spontaneous spin polarization in organic charge transfer systems
The organic charge transfer complex, generally assembled by two or more types of donor and acceptor molecules, is a material with the ability to both lose and gain electrons and normally exhibits much more abundant electrical, magnetic, and optical properties compared to homogeneous OSC. Structurally, it can be divided into bilayer heterojunctions, bulk heterojunctions, and molecular heterojunctions. The success of organic charge transfer complexes has been achieved in the field of organic optoelectronics, where the highest photovoltaic conversion efficiency of organic photovoltaic devices based on bulk heterojunctions has now exceeded 19%.166 Beyond the field of optoelectronics, this system has also drawn the attention of organic spintronics. One appealing aspect is that non-magnetic organic materials assembled into organic charge-transfer complexes may exhibit ferromagnetism. In this system, ferromagnetism results from the charge transfer process between the components, breaking the closed-shell structure into an open-shell structure, unlike the mechanism of the single-component organic ferromagnets presented in Section 3.1. Furthermore, in some organic charge-transfer complexes, the charge, spin, orbitals, and phonons of the carriers will be strongly coupled to each other, leading to interesting multiferroic properties.167 In this context, this system offers great potential for studying functional devices due to their rich physical properties.Allemand et al. first experimentally observed the macroscopic magnetization of the charge transfer system TDAE-C60 (tetrakis(dimethylamino)ethylene-fullerene), in which the Curie temperature was 16.1 K, indicating that the charge transfer complex could be used as an effective spontaneous spin polarization platform.168 Follow-up studies revealed that spin polarization of the TDAE-C60 system mainly occurred within the C60 molecule and was highly associated with the orientation of C60.169–171 From the perspective of molecular configuration, TDAE-C60 crystals exhibited two different magnetic behaviors at low temperatures, namely, the paramagnetic phase and the ferromagnetic phase, corresponding to situations where the 6–6 double bond was directed toward the centers of the hexagons (see the left panel in Fig. 6i) and pentagons (see the right panel in Fig. 6i) of the adjacent C60 molecules.170 This revealed that in addition to charge transfer, the crystal structure and molecular structure configuration were important conditions for creating ferromagnetism in organic charge transfer complexes. Building on this representative achievement, more charge transfer systems with ferromagnetic properties have emerged, including P3HT-nw-C60, P3HT-nw-PCBM, SWCNT-C60, and coronene-TCNQ.172–175 Meanwhile, theoretical studies have found that different electron–phonon coupling coefficients of the constituent elements (donors and acceptors) will contribute to ferromagnetism. Taking the P3HT-nw-C60 system (Fig. 6j) as an example, P3HT and C60 will have different electron–phonon coupling, with different magnetic moments after charge transfer, −0.92μB for P3HT and 1μB for C60, making the system process a net spin polarization.176
Alongside ferromagnetism, several charge-transfer complex systems can be characterized by multiferroic properties. Multiferroic materials generally refer to materials containing two or more elementary iron sequences with coupling between the interactions, including ferromagnetic, ferroelectric, ferroelastic, magnetoelectric coupling, and magnetoelastic coupling. Regarding ferromagnetic (P3HT-nw)0.75-(C60)0.25, Ren et al. noted that the applied electric field increased the magnetization intensity of the sample, resulting in a typical magnetoelectric coupling effect.172 Recently, Wei et al. prepared a charge-transfer complex coronene-TCNQ with three room-temperature ferromagnetisms, which had similar crystal structures but significant differences in the lattice constants and unit cell volumes.175 The results showed that the variations in cell volume in coronene-TCNQ could significantly affect the saturation magnetization intensity, leading to magnetoelastic coupling. Currently, multiple charge-transfer complex systems, such as P3HT:PCBM, SWCNT-C60, C60:SWCNT:PVDF, and P3HT-nW:CH3NH3PbBr3 have been observed to exhibit multiferroic properties.173,174,177 In fact, remarkable progress has been made in organic charge-transfer complexes with ferromagnetic and multiferroic properties. However, compared to single components, this system will have more complex spin interactions, and there are still many unanswered questions regarding the source of spontaneous spin polarization and the coupling mechanism.
3.3. Spin polarization generated by the chiral-induced spin selectivity (CISS) effect
Chiral molecules with unique structures, especially helical molecules, can allow for the generation and modulation of spin polarization in current, and this phenomenon originates from the CISS effect. As shown in Fig. 7a, when a non-spin polarized current flows through the chiral molecules, one of the spin-oriented electrons matching the chirality of the molecules will preferentially be transported.25 Conversely, electrons with anther spin orientation will be inhibited, thus generating a spin-polarized current. This effect was discovered in an experiment by Ray et al., who found that spin-up and spin-down electrons had different transmission probabilities in thin films composed of chiral stearoyl lysine.178 Following an in-depth study of the CISS effect, the spin polarization phenomenon in various types of chiral materials was demonstrated experimentally, such as DNA, protein, chiral supramolecules, chiral polymers, chiral organic–inorganic hybrid perovskites, and two-dimensional materials, indicating a generic phenomenon.179–188 From a technological point of view, unlike traditional methods, the CISS effect represents an alternative approach that can actively generate spin polarization in non-magnetic and weak-SOC material systems under zero magnetic field conditions at room temperature. The other fascinating property is their high spin polarization rate at room-temperature after the CISS effect, even up to 80%, exceeding the intrinsic value reported for common inorganic ferromagnets, where spin polarization rates of Fe, Co, and Ni are in the range of 20–40%.187,189 Spin polarization in chiral materials can typically be characterized using conductive-probe atomic force microscopy. The spin polarization rate P can be calculated by the following formula: P = 100% × (I+ − I−)/(I+ + I−), where I+ and I− denote the measured current at a given voltage when the applied magnetic field is in opposition (see Fig. 7b).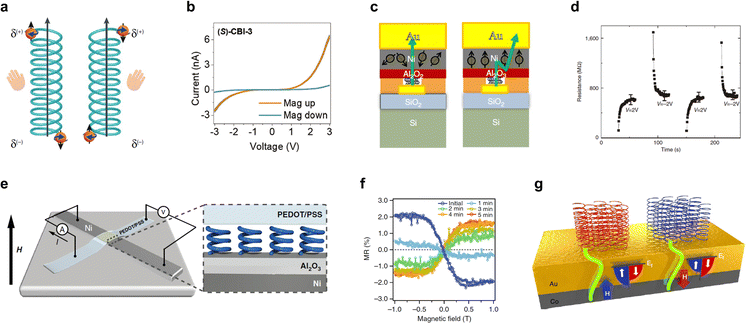 | ||
| Fig. 7 (a) A schematic description of CISS in chiral molecules. Reproduced with permission from ref. 25. Copyright 2019, Nature Publishing Group. (b) Current–voltage curves of a chiral molecule measured using a conductive-probe atomic force microscope at room temperature. Reproduced with permission from ref. 189. Copyright 2020, Wiley. (c) Schematic illustration of a chiral AHPA-L-based magnetic random access memory. The left and right panels correspond to schematic diagrams of the device with low and high output resistance, respectively. (d) The memory function of a chiral molecule-based magnetic random access memory. (c and d) Reproduced with permission from ref. 197. Copyright 2013, Nature Publishing Group. (e) Schematic drawing of a chiral overcrowded alkene-based tunnel junction device with a Ni/Al2O3/overcrowded alkene/PEDOT:PSS structure. (f) Magnetoresistance responses of the left-handed molecule under different exposure times to visible light. (e and f) Reproduced with permission from ref. 194. Copyright 2019, Nature Publishing Group. (g) Schematic of magnetization by the transfer of specific spins due to the adsorption of chiral molecules. Reproduced with permission from ref. 195. Copyright 2017, Nature Publishing Group. | ||
To explain the high spin selectivity behavior in chiral molecules, some theoretical mechanisms behind the CISS effect have been put forward. For helical structures, the chiral-induced SOC mechanism190,191 has been commonly used, as shown in Fig. 7a. According to this model, chiral-induced inversion symmetry breaking will give rise to a built-in helical electric field, Ehelix, in chiral systems that are determined by the helix angle and twist angle. If electrons with a momentum p move along a helical electric field, the SOC of this system can be described by Hso ∝ (Ehelix × p)σ. In this case, the electron spin states will be subjected to an equivalent magnetic field B related to the direction of the electron motion and its chiral structure. Field B can be depicted as
| B = (v/c2) × Ehelix | (6) |
Chiral molecules with the CISS effect are of great significance for organic spintronics. Due to its unique spin generation mechanism, many new spintronic applications without magnetic fields have emerged. Devices that can operate without magnetic fields offer great value for industrial applications. Fig. 7c shows a chiral magnetic memory device, composed of Au, chiral a-helix L-polyalanine (AHPA-L), and Ni.19 In this device, combining the CISS effect and the spin-transfer torque effect, the magnetic random access memory can be realized using chiral AHPA-L molecules without the presence of a ferromagnetic fixed layer (Fig. 7d). In another study, a chiral molecule-based spin-LED was reported, with a complex ITO/m-PEDOT:PSS/(S-/R-MBA)2PbI4/CsPbI3/TPBI/LiF/Al structure, in which the chiral molecule (S-/R-MBA)2PbI4 acted as a spin filter to generate spin-polarized holes via the CISS effect.186 Under in operando conditions, the spin-polarized holes recombined with the non-spin-polarized electrons at the CsPbI3 layer, thus emitting circularly polarized light without magnetic electrodes and magnetic fields. Eventually, a circularly polarized luminescence of 2.6% at room temperature was successfully achieved by Kim et al. Additionally, chiral materials can serve as an important platform for studying spin manipulation phenomena. Recent experiments demonstrated that right-handed and left-handed chiral conformations could be inverted by external stimuli such as light irradiation and thermal activation, thus manipulating the spin polarization arising from the CISS effect. As proof of principle, Suda et al. prepared a chiral overcrowded alkene-based tunnel junction device, as shown in Fig. 7e.194 The researchers successfully demonstrated the four switching states of spin polarization directions in the device (Fig. 7f). Also, manipulating magnetism in chiral systems by chirality-induced orbital angular momentum has attracted attention. For example, Dor et al. showed that ferromagnets could be magnetized using a novel strategy, through the adsorption of chiral molecules, which did not require an external magnetic field or spin-polarized currents, as shown in Fig. 7g.195
Beyond current progress, we believe that the unique spin-charge relationships of chiral molecules will open up new and innovative opportunities for quantum computing, light harvesting and other innovative spintronic and optoelectronic devices in the future. For chiral molecules, first, more interesting and exciting spin-based electronic and optoelectronic devices, with no classical counterpart, are expected to emerge in combination with the CISS effect and its other wealth of unique physical properties, including chiral-phonon-activated spin Seebeck effect,196 optical spin controllability,197 valley pseudospin,198 chiral spinterface effect, magneto-optical Kerr effect,199 and optoelectronic properties. Of course, achieving this goal will require additional effort in both chiral molecule assembly and device preparation. Second, the chiral structure imparts chiral optical effects to the molecular material, including circular dichroism and circularly polarized luminescence properties,200 which will broaden the application of organic materials in optical display imaging, light field modulation and detection, and photocatalyzed asymmetric synthesis. However, insufficient variety of material systems, complex structures, and unclear structure–activity relationships continue to be major obstacles. Third, the origin of molecular chirality is associated with parity-breaking interactions, while chiral molecules have rather long spin-coherent lifetimes. Quantum computing with chiral spin states is therefore likely to be of great importance for scientific research and practical application in the future. In superconducting circuits, for example, a three-qubit chiral gate has been demonstrated experimentally.201
3.4. Spin polarization induced by the spinterface effect
Spin polarization can be generated not only by the bulk properties of ferromagnets and organics but also by the spin-dependent FM metal/OSC interface properties. With the development of organic spintronic devices, a unique phenomenon has been gradually realized, namely, a device with the same device structure that can output MR signals with widely varying amplitudes and signs. For example, Xiong et al. detected a negative MR (>40%) for a spin valve with an LSMO/Alq3/Co structure, while a positive MR (>300%) was obtained by Barraud et al.23,34 In accordance with the modified Jullière's model, MR is expressed as MR = 2P1P2e−d/λs/(1 + P1P2e−d/λs), where P1 and P2 denote the spin polarization at injection and detection, and d is the effective distance between the injection and detection electrodes.34 Therefore, these results indicated that compared to the former research, the spin polarization in the latter research had to undergo enhancement and reversal that depended on the detail of the metal/OSC interface. This interesting phenomenon belonged to the spinterface effect, which could be exploited to create and control the spin polarization in OSCs.14,202One phenomenological model describing the spinterface effect was proposed by Barraud et al.23 When molecules make direct contact with an FM metal, coupling will occur between the molecular orbitals and the spin-split electronic structure of the FM metal, resulting in the hybrid FM metal/OSC interface. According to this model, the molecular density of state, Dσ, at the interface can be given by
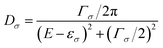 | (7) |
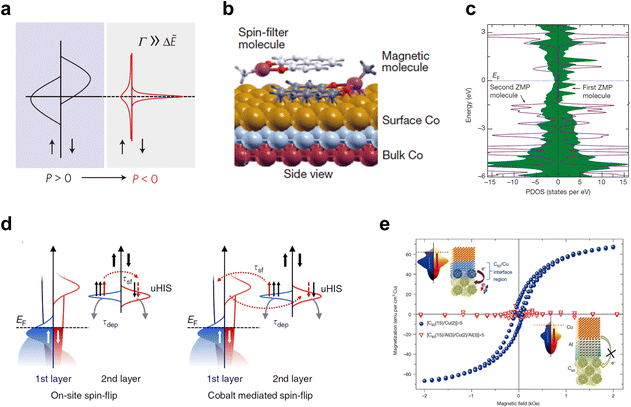 | ||
| Fig. 8 (a) Schematic illustration of the broadening and shifting molecular energy levels at the hybrid metal/organic interface. Reproduced with permission from ref. 23. Copyright 2010, Nature Publishing Group. (b and c) The spin-filter effect at the hybrid Co/ZMP interface. (b) The side view at the ZMP-Co interface. (c) The spin-resolved PDOS for the first and second ZMP molecules absorbed on the Co surface. (b,c) Reproduced with permission from ref. 204. Copyright 2013, Nature Publishing Group. (d) Schematic representations of the model of the dynamic spin filtering effect. Reproduced with permission from ref. 92. Copyright 2016, Nature Publishing Group. (e) Room-temperature ferromagnetism induces via the spinterface effect in Cu/C60 multilayers. Reproduced with permission from ref. 205. Copyright 2013, Nature Publishing Group. | ||
To gain more insight into spin polarization induced by the spinterface effect, several efforts have focused on revealing the details of the spin filtering effect on the OSC side. Utilizing an advance SP-STM, Brede et al. and Atodiresei et al. carried out investigations on the process of spin-polarized electron transport through molecules (H2Pc and CoPc) adsorbed on Fe at the single-molecule scale.65,91 Their experimental results provided direct evidence that the hybrid interface states in the first molecular layer could generate spin polarization with a completely opposite sign for the substrate. Three years later, a study of the Co/zinc methyl phenalenyl (ZMP) junction provided further insight into the spin filtering effect at the FM metal/OSC interface.204 The results demonstrated that strong coupling at the interface mainly influenced two molecular layers, as schematically shown in Fig. 8b. The first ZMP layer with incipient non-magnetic properties became ferromagnetic due to strong chemisorption, with a net magnetic moment approaching 0.11 μB. For the second ZMP layer, although it did not exhibit a net magnetic moment, the π–π interactions with the first layer led to a spin-split LUMO level of about 0.14 eV (Fig. 8c). As a result, from the spin-dependent electronic structure perspective, the interfacial molecular layers acted as spin filters, capable of large spin polarization when the current was injected across this interface. In both cases, according to the different electronic properties of the hybrid molecular layers, the filtering mechanism could be divided into the metallic spin filter (in the case of the first ZMP layer with metallic properties) and resistive spin filter (in the case of the second ZMP layer), respectively. Furthermore, another significant mechanism consists of the dynamic spin filtering effect, as already mentioned in Section 2.4, which was first discovered in the Co/Alq3 system by using the 2 PPE technique.92 For the first molecular layer, the spin-dependent electronic structure in Co/Alq3 was found to be similar to the hybrid Co/ZMP system. However, for the second Alq3 layer physisorbed on the Co, as shown in Fig. 8d, the spin-split level was not observed, but unoccupied hybrid interface states with spin-dependent lifetimes were observed. This phenomenon was due to the emergence of quasi-elastic spin-flip scattering within the second layer of Alq3 molecules, leading to dynamic spin relaxation. In this context, the three spin-filtering mechanisms provide a detailed picture of the spinterface effect, which can significantly influence the creation of spin polarization in OSCs.
In parallel, the spinterface effect has shown a significant influence on the magnetic characteristics at the metal side. The changes in magnetic characteristics can alter the spin injection process at the FM metal/OSC interface, and subsequently, spin polarization in OSCs. Al Ma’Mari et al. showed that the non-magnetic transition metals, Mn and Cu, could be converted to ferromagnetic characteristics after contact with C60.205Fig. 8e shows the result of room-temperature magnetization for the Cu/C60 multilayer system. This meaningful feature arises because the DOS of metal will undergo spin-split by coupling between the 3d electrons of Cu and the π-bonded p electrons of C60. In addition to the local magnetic moment, the changes in other magnetic properties, such as magnetic anisotropy and ferromagnetic exchange coupling, have also been demonstrated experimentally.206–208
The above studies provided clearer awareness of the fact that the spinterface effect depends on the coupling degrees. In this context, suitable interface engineering may offer an opportunity for manipulating the spin-polarized states injected into OSCs, which may be beneficial to tailoring organic spintronics devices with specific functions. To date, different approaches have been demonstrated to tune the spin interface effect, including doping,91,209 molecular isomers,210 molecular symmetry,211,212 and the element substitution of molecules; however,213,214 more applications at the device level need to be explored.
4. Challenges and outlook
In this review, we discussed the generation of spin polarization in OSCs, as well as the related investigation of theories and devices, mainly in terms of spin injection and spin polarization induced by organic materials or the spinterface effect. Based on the existing achievements together with the continued interdisciplinary collaboration and innovative exploration by researchers, we can expect to see more exciting advances in the field of organic spintronics and make further progress toward the ultimate goal of creating high-performance and low-cost spintronic applications. In the process of making efforts towards this goal, some challenges still need to be addressed and are summarized as follows.Regarding spin injection, the successful demonstration of several mechanisms has encouraged the development of organic spintronics; however, how to obtain and maintain a high spin polarization in OSCs at room temperature is still challenging. First, undertaking more exploration into the optimization of the preparation process is a key step. Due to their soft nature, OSCs are highly susceptible to damage by FM metal atoms during the preparation of FM metals on OSCs, resulting in the formation of a so-called dead layer. The presence of a dead layer with irregular shape can reduce spin injection efficiency across the FM metal/OSC interface.32,215 So far, various preparation methods have been developed to overcome this problem (e.g., buffer layer assisted growth,216 low-temperature rate-control deposition,61 lamination,217 and indentation23) with some success, but this problem is still not fully resolved. Furthermore, after spin injection into OSCs, spin polarization will decay exponentially away from the interface due to the spin relaxation process within organics. To maintain high spin polarization in OSCs, it is necessary to develop materials that can maintain spin for longer periods of time (spin relaxation time) and over longer distances (spin diffusion length). Organic materials have longer spin lifetimes compared to conventional inorganic semiconductors, but the spin diffusion lengths are generally very short. The spin diffusion length can be given by Einstein's relation, 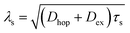 , where Dhop is the spin transport diffusion coefficient in the hopping transport mode, depending on material mobility, and Dex is the spin diffusion coefficient in the exchange coupling transport mode, related to the carrier concentration.27 Given this relation, to improve the spin diffusion length of OSCs, a promising strategy involves developing materials with high mobility or increasing the carrier concentration through appropriate doping.218,219 Thus, organic single crystals, which have both high mobility and minimal defect density, can serve as candidate materials for optimizing spin transport properties, mainly Dhop.10,220,221 At present, however, the preparation process is a major limitation for reliable single-crystal spintronic devices. In addition, it has been experimentally demonstrated that increasing the carrier concentration using semiconductor doping technology provides an effective approach for improving Dex and spin diffusion length of OSCs in pure spin current devices,117 but this has not yet been experimentally studied in charge transport-type spintronic devices.
, where Dhop is the spin transport diffusion coefficient in the hopping transport mode, depending on material mobility, and Dex is the spin diffusion coefficient in the exchange coupling transport mode, related to the carrier concentration.27 Given this relation, to improve the spin diffusion length of OSCs, a promising strategy involves developing materials with high mobility or increasing the carrier concentration through appropriate doping.218,219 Thus, organic single crystals, which have both high mobility and minimal defect density, can serve as candidate materials for optimizing spin transport properties, mainly Dhop.10,220,221 At present, however, the preparation process is a major limitation for reliable single-crystal spintronic devices. In addition, it has been experimentally demonstrated that increasing the carrier concentration using semiconductor doping technology provides an effective approach for improving Dex and spin diffusion length of OSCs in pure spin current devices,117 but this has not yet been experimentally studied in charge transport-type spintronic devices.
For spin polarization induced in organics, there is still considerable room for improvement in terms of materials and mechanisms. Significant evidence has now shown that organic ferromagnets and chiral materials with CISS effects have substantial potential as spin-generating sources for the construction of advanced spin devices. However, their research in organic spintronic applications is still in its infancy. From a materials perspective, organic magnetic materials with strong saturable magnetism operating at room temperature and chiral organic materials with excellent semiconducting properties are in development. Furthermore, for organic magnetic materials, exploring the sources of magnetism and building a sound theory of organic magnetism is important for guiding materials design. However, due to the complexity of these systems, organic magnetic materials, unlike conventional inorganic ferromagnets, still lack a comprehensive understanding of the microphysical origin of spontaneous spin polarization in many systems. Therefore, developing the theory of organic ferromagnetism is highly desirable and a matter for further effort. For the spinterface effect, actively controlling the spin-dependent electronic structure at the hybrid FM metal/OSC interface offers the possibility of manipulating spin polarization in OSCs, but this remains a challenge.
The Hanle effect describes the spin precession and dephasing phenomena, which is not only the most convincing piece of evidence for spin generation/transport processes but also serves as an important physical basis for achieving spin manipulation. This effect has been well demonstrated in some typical inorganic semiconductor materials (e.g., silicon, and GaAs) and non-magnetic metals.11,71,222 However, the experimental demonstration of the Hanle effect in OSCs remains a dark cloud over the field of organic spintronics and should not be ignored, as the effect has not yet been universally demonstrated in organics. Yu theoretically proposed an exchange-coupling spin transport mechanism, the presence of which suppressed the spin precession in OSCs, making it difficult to detect the Hanle effect.27 The precondition for stimulating this transporting mode was that organic materials contain high concentrations of charge carriers, such as doped organics. However, for the more common case of low carrier concentrations, the hopping transport mode is thought to take place, a situation in which the Hanle effect would be observed, but it has remained elusive in current experiments. Therefore, the debate on whether the Hanle effect can be detected widely in OSC systems will continue, requiring further research, both experimental and theoretical. In experimental investigations, other types of device geometries that have been successful in inorganic counterparts, such as non-local spintronic devices223 and hot electron spin transistor devices,71 may provide some insights into this topic.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work is supported financially by the National Natural Science Foundation of China (Grant No. 52250008, 52050171, 51973043, 22175047, 52103203, 52103338 and 91963126), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB36020000), the Ministry of Science and Technology of the People's Republic of China (2017YFA0206600), the CAS Instrument Development Project (Grant No. YJKYYQ20170037), the Beijing Natural Science Foundation (Grant No. 4222087, 2222086) and Shandong Province (Grant No. ZR2020ME070), the China Postdoctoral Science Foundation (Grant No. 2021M690802), the Beijing National Laboratory for Molecular Sciences (Grant No. BNLMS201907), and the CAS Pioneer Hundred Talents Program.References
- M. N. Baibich, J. M. Broto, A. Fert, F. N. Vandau, F. Petroff, P. Eitenne, G. Creuzet, A. Friederich and J. Chazelas, Phys. Rev. Lett., 1988, 61, 2472–2475 CrossRef CAS PubMed.
- G. Binasch, P. Grunberg, F. Saurenbach and W. Zinn, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 4828–4830 CrossRef CAS PubMed.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnar, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488–1495 CrossRef CAS PubMed.
- I. Zutic, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323–410 CrossRef CAS.
- V. A. Dediu, L. E. Hueso, I. Bergenti and C. Taliani, Nat. Mater., 2009, 8, 707–716 CrossRef CAS PubMed.
- S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355 RSC.
- C. Boehme and J. M. Lupton, Nat. Nanotechnol., 2013, 8, 612–615 CrossRef CAS PubMed.
- S. Sanvito, Nat. Mater., 2007, 6, 803–804 CrossRef CAS PubMed.
- G. Szulczewski, S. Sanvito and M. Coey, Nat. Mater., 2009, 8, 693–695 CrossRef CAS PubMed.
- X. L. Yang, A. K. Guo, L. D. Guo, Y. Q. Liu, X. N. Sun and Y. L. Guo, ACS Mater. Lett., 2022, 4, 805–814 CrossRef CAS.
- X. H. Lou, C. Adelmann, S. A. Crooker, E. S. Garlid, J. Zhang, K. S. M. Reddy, S. D. Flexner, C. J. Palmstrom and P. A. Crowell, Nat. Phys., 2007, 3, 197–202 Search PubMed.
- T. Sasaki, T. Oikawa, T. Suzuki, M. Shiraishi, Y. Suzuki and K. Noguchi, Appl. Phys. Lett., 2010, 96, 122101 CrossRef.
- A. Jain, J. C. Rojas-Sanchez, M. Cubukcu, J. Peiro, J. C. Le Breton, E. Prestat, C. Vergnaud, L. Louahadj, C. Portemont, C. Ducruet, V. Baltz, A. Barski, P. Bayle-Guillemaud, L. Vila, J. P. Attane, E. Augendre, G. Desfonds, S. Gambarelli, H. Jaffres, J. M. George and M. Jamet, Phys. Rev. Lett., 2012, 109, 106603 CrossRef CAS PubMed.
- M. Cinchetti, V. A. Dediu and L. E. Hueso, Nat. Mater., 2017, 16, 507–515 CrossRef CAS PubMed.
- T. D. Nguyen, E. Ehrenfreund and Z. V. Vardeny, Science, 2012, 337, 204–209 CrossRef CAS PubMed.
- J. P. Prieto-Ruiz, S. G. Miralles, H. Prima-Garcia, A. Lopez-Munoz, A. Riminucci, P. Graziosi, M. Aeschlimann, M. Cinchetti, V. A. Dediu and E. Coronado, Adv. Mater., 2019, 31, 1806817 CrossRef PubMed.
- X. N. Sun, S. Velez, A. Atxabal, A. Bedoya-Pinto, S. Parui, X. W. Zhu, R. Llopis, F. Casanova and L. E. Hueso, Science, 2017, 357, 677–680 CrossRef CAS PubMed.
- K. Bairagi, D. G. Romero, F. Calavalle, S. Catalano, E. Zuccatti, R. Llopis, F. Casanova and L. E. Hueso, Adv. Mater., 2020, 32, 1906908 CrossRef CAS PubMed.
- O. Ben Dor, S. Yochelis, S. P. Mathew, R. Naaman and Y. Paltiel, Nat. Commun., 2013, 4, 2256 CrossRef PubMed.
- L. E. Hueso, I. Bergenti, A. Riminucci, Y. Q. Zhan and V. Dediu, Adv. Mater., 2007, 19, 2639–2642 CrossRef CAS.
- J. Kalinowski, M. Cocchi, D. Virgili, P. Di Marco and V. Fattori, Chem. Phys. Lett., 2003, 380, 710–715 CrossRef CAS.
- T. L. Francis, O. Mermer, G. Veeraraghavan and M. Wohlgenannt, New J. Phys., 2004, 6, 185 CrossRef.
- C. Barraud, P. Seneor, R. Mattana, S. Fusil, K. Bouzehouane, C. Deranlot, P. Graziosi, L. Hueso, I. Bergenti, V. Dediu, F. Petroff and A. Fert, Nat. Phys., 2010, 6, 615–620 Search PubMed.
- K. Ray, S. P. Ananthavel, D. H. Waldeck and R. Naaman, Science, 1999, 283, 814–816 CrossRef CAS PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Nat. Rev. Chem., 2019, 3, 250–260 CrossRef CAS.
- Z. G. Yu, Phys. Rev. Lett., 2011, 106, 106602 CrossRef CAS PubMed.
- Z. G. Yu, Phys. Rev. Lett., 2013, 111, 016601 CrossRef CAS PubMed.
- P. Gutlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427 RSC.
- T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari, L. Joly, F. Scheurer, G. Rogez, T. K. Yamada, P. Ohresser, E. Beaurepaire and W. Wulfhekel, Nat. Commun., 2012, 3, 938 CrossRef PubMed.
- C. Chappert, A. Fert and F. N. Van Dau, Nat. Mater., 2007, 6, 813–823 CrossRef CAS PubMed.
- G. Schmidt, J. Phys. D: Appl. Phys., 2005, 38, R107–R122 CrossRef CAS.
- D. L. Sun, E. Ehrenfreund and Z. V. Vardeny, Chem. Commun., 2014, 50, 1781–1793 RSC.
- G. Schmidt, D. Ferrand, L. W. Molenkamp, A. T. Filip and B. J. van Wees, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R4790–R4793 CrossRef CAS.
- Z. H. Xiong, D. Wu, Z. V. Vardeny and J. Shi, Nature, 2004, 427, 821–824 CrossRef CAS PubMed.
- V. Dediu, M. Murgia, F. C. Matacotta, C. Taliani and S. Barbanera, Solid State Commun., 2002, 122, 181–184 CrossRef CAS.
- M. Johnson and R. H. Silsbee, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 5326–5335 CrossRef PubMed.
- M. Johnson, Phys. Rev. Lett., 1993, 70, 2142–2145 CrossRef CAS PubMed.
- P. R. Hammar, B. R. Bennett, M. J. Yang and M. Johnson, Phys. Rev. Lett., 1999, 83, 203–206 CrossRef CAS.
- F. J. Yue, Y. J. Shi, B. B. Chen, H. F. Ding, F. M. Zhang and D. Wu, Appl. Phys. Lett., 2012, 101, 022416 CrossRef.
- H. J. Jang and C. A. Richter, Adv. Mater., 2017, 29, 1602739 CrossRef PubMed.
- F. J. Wang, C. G. Yang, Z. V. Vardeny and X. G. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245324 CrossRef.
- F. Li, T. Li, F. Chen and F. P. Zhang, Sci. Rep., 2015, 5, 9355 CrossRef PubMed.
- R. G. Geng, R. C. Subedi, H. M. Luong, M. T. Pham, W. C. Huang, X. G. Li, K. L. Hong, M. Shao, K. Xiao, L. A. Hornak and T. D. Nguyen, Phys. Rev. Lett., 2018, 120, 086602 CrossRef CAS PubMed.
- W. T. Yang, Q. Shi, T. Miao, Q. Li, P. Cai, H. Liu, H. X. Lin, Y. Bai, Y. Y. Zhu, Y. Yu, L. Deng, W. B. Wang, L. F. Yin, D. L. Sun, X. G. Zhang and J. Shen, Nat. Commun., 2019, 10, 3877 CrossRef PubMed.
- X. M. Zhang, S. Mizukami, T. Kubota, Q. L. Ma, M. Oogane, H. Naganuma, Y. Ando and T. Miyazaki, Nat. Commun., 2013, 4, 1392 CrossRef PubMed.
- Y. Kawasugi, T. Ujino and H. Tada, Org. Electron., 2013, 14, 3186–3189 CrossRef CAS.
- E. I. Rashba, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R16267–R16270 CrossRef CAS.
- A. Fert and H. Jaffres, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 184420 CrossRef.
- J. Hwang, A. Wan and A. Kahn, Mater. Sci. Eng., R, 2009, 64, 1–31 CrossRef.
- S. Braun, W. R. Salaneck and M. Fahlman, Adv. Mater., 2009, 21, 1450–1472 CrossRef CAS.
- L. D. Guo, Y. Qin, X. R. Gu, X. W. Zhu, Q. Zhou and X. N. Sun, Front. Chem., 2019, 7, 428 CrossRef CAS PubMed.
- H. J. Jang, K. P. Pernstich, D. J. Gundlach, O. D. Jurchescu and C. A. Richter, Appl. Phys. Lett., 2012, 101, 102412 CrossRef.
- J. H. Shim, K. V. Raman, Y. J. Park, T. S. Santos, G. X. Miao, B. Satpati and J. S. Moodera, Phys. Rev. Lett., 2008, 100, 226603 CrossRef CAS PubMed.
- J. Schoonus, P. G. E. Lumens, W. Wagemans, J. T. Kohlhepp, P. A. Bobbert, H. J. M. Swagten and B. Koopmans, Phys. Rev. Lett., 2009, 103, 146601 CrossRef CAS PubMed.
- X. N. Sun, A. Bedoya-Pinto, Z. P. Mao, M. Gobbi, W. J. Yan, Y. L. Guo, A. Atxabal, R. Llopis, G. Yu, Y. Q. Liu, A. Chuvilin, F. Casanova and L. E. Hueso, Adv. Mater., 2016, 28, 2609–2615 CrossRef CAS PubMed.
- V. Dediu, L. E. Hueso, I. Bergenti, A. Riminucci, F. Borgatti, P. Graziosi, C. Newby, F. Casoli, M. P. De Jong, C. Taliani and Y. Zhan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 115203 CrossRef.
- M. Gobbi, F. Golmar, R. Llopis, F. Casanova and L. E. Hueso, Adv. Mater., 2011, 23, 1609–1613 CrossRef CAS PubMed.
- L. Schulz, L. Nuccio, M. Willis, P. Desai, P. Shakya, T. Kreouzis, V. K. Malik, C. Bernhard, F. L. Pratt, N. A. Morley, A. Suter, G. J. Nieuwenhuys, T. Prokscha, E. Morenzoni, W. P. Gillin and A. J. Drew, Nat. Mater., 2011, 10, 39–44 CrossRef CAS PubMed.
- D. Ciudad, M. Gobbi, C. J. Kinane, M. Eich, J. S. Moodera and L. E. Hueso, Adv. Mater., 2014, 26, 7561–7567 CrossRef CAS PubMed.
- G. Szulczewski, H. Tokuc, K. Oguz and J. M. D. Coey, Appl. Phys. Lett., 2009, 95, 202506 CrossRef.
- X. N. Sun, M. Gobbi, A. Bedoya-Pinto, O. Txoperena, F. Golmar, R. Llopis, A. Chuvilin, F. Casanova and L. E. Hueso, Nat. Commun., 2013, 4, 2794 CrossRef.
- R. Wiesendanger, Rev. Mod. Phys., 2009, 81, 1495–1550 CrossRef CAS.
- S. Sanvito, Nature, 2010, 467, 664–665 CrossRef CAS PubMed.
- N. Atodiresei, J. Brede, P. Lazic, V. Caciuc, G. Hoffmann, R. Wiesendanger and S. Blugel, Phys. Rev. Lett., 2010, 105, 066601 CrossRef PubMed.
- J. Brede, N. Atodiresei, S. Kuck, P. Lazic, V. Caciuc, Y. Morikawa, G. Hoffmann, S. Blugel and R. Wiesendanger, Phys. Rev. Lett., 2010, 105, 047204 CrossRef PubMed.
- S. L. Kawahara, J. Lagoute, V. Repain, C. Chacon, Y. Girard, S. Rousset, A. Smogunov and C. Barreteau, Nano Lett., 2012, 12, 4558–4563 CrossRef CAS PubMed.
- R. Jansen, J. Phys. D: Appl. Phys., 2003, 36, R289–R308 CrossRef CAS.
- T. Arnold, A. Atxabal, S. Parui, L. E. Hueso and F. Ortmann, Adv. Funct. Mater., 2018, 28, 1706105 CrossRef.
- M. Gobbi, L. Pietrobon, A. Atxabal, A. Bedoya-Pinto, X. Sun, F. Golmar, R. Llopis, F. Casanova and L. E. Hueso, Nat. Commun., 2014, 5, 4161 CrossRef CAS PubMed.
- D. J. Monsma, R. Vlutters and J. C. Lodder, Science, 1998, 281, 407–409 CrossRef CAS PubMed.
- I. Appelbaum, B. Q. Huang and D. J. Monsma, Nature, 2007, 447, 295–298 CrossRef CAS PubMed.
- B. Huang, D. J. Monsma and I. Appelbaum, Phys. Rev. Lett., 2007, 99, 177209 CrossRef PubMed.
- I. Appelbaum, Philos. Trans. R. Soc., A, 2011, 369, 3554–3574 CrossRef CAS PubMed.
- D. J. Monsma, J. C. Lodder, T. J. A. Popma and B. Dieny, Phys. Rev. Lett., 1995, 74, 5260–5263 CrossRef CAS PubMed.
- S. van Dijken, X. Jiang and S. S. P. Parkin, Appl. Phys. Lett., 2002, 80, 3364–3366 CrossRef CAS.
- K. Mizushima, T. Kinno, T. Yamauchi and K. Tanaka, IEEE Trans. Magn., 1997, 33, 3500–3504 CrossRef CAS.
- M. Cinchetti, K. Heimer, J. P. Wustenberg, O. Andreyev, M. Bauer, S. Lach, C. Ziegler, Y. L. Gao and M. Aeschlimann, Nat. Mater., 2009, 8, 115–119 CrossRef CAS PubMed.
- M. Gobbi, A. Bedoya-Pinto, F. Golmar, R. Llopis, F. Casanova and L. E. Hueso, Appl. Phys. Lett., 2012, 101, 102404 CrossRef.
- J. S. Jiang, J. E. Pearson and S. D. Bader, Phys. Rev. Lett., 2011, 106, 156807 CrossRef CAS PubMed.
- L. D. Bell and W. J. Kaiser, Phys. Rev. Lett., 1988, 61, 2368–2371 CrossRef CAS PubMed.
- W. J. Kaiser and L. D. Bell, Phys. Rev. Lett., 1988, 60, 1406–1409 CrossRef CAS PubMed.
- A. Atxabal, T. Arnold, S. Parui, S. Hutsch, E. Zuccatti, R. Llopis, M. Cinchetti, F. Casanova, F. Ortmann and L. E. Hueso, Nat. Commun., 2019, 10, 2089 CrossRef CAS PubMed.
- A. Atxabal, T. Arnold, S. Parui, E. Zuccatti, M. Cinchetti, F. Casanova, F. Ortmann and L. E. Hueso, Mater. Horiz., 2019, 6, 1663–1668 RSC.
- A. Atxabal, S. Braun, T. Arnold, X. N. Sun, S. Parui, X. J. Liu, C. Gozalvez, R. Llopis, A. Mateo-Alonso, F. Casanova, F. Ortmann, M. Fahlman and L. E. Hueso, Adv. Mater., 2017, 29, 1606901 CrossRef PubMed.
- Y. Ohno, D. K. Young, B. Beschoten, F. Matsukura, H. Ohno and D. D. Awschalom, Nature, 1999, 402, 790–792 CrossRef CAS.
- Z. V. Vardeny, Nat. Mater., 2009, 8, 91–93 CrossRef PubMed.
- G. Lampel, Phys. Rev. Lett., 1968, 20, 491–493 CrossRef CAS.
- D. T. Pierce and F. Meier, Phys. Rev. B: Solid State, 1976, 13, 5484–5500 CrossRef CAS.
- J. M. Kikkawa and D. D. Awschalom, Nature, 1999, 397, 139–141 CrossRef CAS.
- S. Steil, N. Grossmann, M. Laux, A. Ruffing, D. Steil, M. Wiesenmayer, S. Mathias, O. L. A. Monti, M. Cinchetti and M. Aeschlimann, Nat. Phys., 2013, 9, 242–247 Search PubMed.
- M. Cinchetti, S. Neuschwander, A. Fischer, A. Ruffing, S. Mathias, J. P. Wustenberg and M. Aeschlimann, Phys. Rev. Lett., 2010, 104, 217602 CrossRef PubMed.
- A. Droghetti, P. Thielen, I. Rungger, N. Haag, N. Grossmann, J. Stockl, B. Stadtmuller, M. Aeschlimann, S. Sanvito and M. Cinchetti, Nat. Commun., 2016, 7, 12668 CrossRef CAS PubMed.
- D. R. McCamey, H. A. Seipel, S. Y. Paik, M. J. Walter, N. J. Borys, J. M. Lupton and C. Boehme, Nat. Mater., 2008, 7, 723–728 CrossRef CAS PubMed.
- J. M. Lupton, D. R. McCamey and C. Boehme, Chem. Phys. Lett., 2010, 11, 3040–3058 CAS.
- R. H. Friend, R. W. Gymer, A. B. Holmes, J. H. Burroughes, R. N. Marks, C. Taliani, D. D. C. Bradley, D. A. Dos Santos, J. L. Bredas, M. Logdlund and W. R. Salaneck, Nature, 1999, 397, 121–128 CrossRef CAS.
- G. Salis, S. F. Alvarado, M. Tschudy, T. Brunschwiler and R. Allenspach, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 085203 CrossRef.
- S. P. Kersten, A. J. Schellekens, B. Koopmans and P. A. Bobbert, Phys. Rev. Lett., 2011, 106, 197402 CrossRef CAS PubMed.
- P. Desai, P. Shakya, T. Kreouzis and W. P. Gillin, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 235202 CrossRef.
- J. Rybicki and M. Wohlgenannt, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 153202 CrossRef.
- J. Rybicki, T. D. Nguyen, Y. Sheng and M. Wohlgenannt, Synth. Met., 2010, 160, 280–284 CrossRef CAS.
- V. Ern and R. E. Merrifield, Phys. Rev. Lett., 1968, 21, 609–611 CrossRef CAS.
- F. J. Wang, H. Bassler and Z. V. Vardeny, Phys. Rev. Lett., 2008, 101, 236805 CrossRef CAS PubMed.
- M. S. Meruvia, J. A. Freire, I. A. Hummelgen, J. Gruber and C. F. O. Graeff, Org. Electron., 2007, 8, 695–701 CrossRef CAS.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- R. C. Johnson and R. E. Merrifie, Phys. Rev. B: Solid State, 1970, 1, 896–902 CrossRef.
- Y. Tserkovnyak, A. Brataas and G. E. W. Bauer, Phys. Rev. Lett., 2002, 88, 117601 CrossRef PubMed.
- Y. Tserkovnyak, A. Brataas and G. E. W. Bauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 224403 CrossRef.
- K. Ando, S. Watanabe, S. Mooser, E. Saitoh and H. Sirringhaus, Nat. Mater., 2013, 12, 622–627 CrossRef CAS PubMed.
- S. Watanabe, K. Ando, K. Kang, S. Mooser, Y. Vaynzof, H. Kurebayashi, E. Saitoh and H. Sirringhaus, Nat. Phys., 2014, 10, 308–313 Search PubMed.
- T. L. Gilbert, IEEE Trans. Magn., 2004, 40, 3443–3449 CrossRef CAS.
- A. Wittmann, G. Schweicher, K. Broch, J. Novak, V. Lami, D. Cornil, E. R. McNellis, O. Zadvorna, D. Venkateshvaran, K. Takimiya, Y. H. Geerts, J. Cornil, Y. Vaynzof, J. Sinova, S. Watanabe and H. Sirringhaus, Phys. Rev. Lett., 2020, 124, 027204 CrossRef CAS PubMed.
- K. Ando, S. Takahashi, J. Ieda, H. Kurebayashi, T. Trypiniotis, C. H. W. Barnes, S. Maekawa and E. Saitoh, Nat. Mater., 2011, 10, 655–659 CrossRef CAS PubMed.
- E. Saitoh, M. Ueda, H. Miyajima and G. Tatara, Appl. Phys. Lett., 2006, 88, 182509 CrossRef.
- P. Wang, L. F. Zhou, S. W. Jiang, Z. Z. Luan, D. J. Shu, H. F. Ding and D. Wu, Phys. Rev. Lett., 2018, 120, 047201 CrossRef CAS PubMed.
- M. M. Qaid, M. R. Mahani, J. Sinova and G. Schmidt, Phys. Rev. Res., 2020, 2, 013207 CrossRef CAS.
- D. L. Sun, K. J. van Schooten, M. Kavand, H. Malissa, C. Zhang, M. Groesbeck, C. Boehme and Z. V. Vardeny, Nat. Mater., 2016, 15, 863–869 CrossRef CAS PubMed.
- S. J. Wang, D. Venkateshvaran, M. R. Mahani, U. Chopra, E. R. McNellis, R. Di Pietro, S. Schott, A. Wittmann, G. Schweicher, M. Cubukcu, K. Kang, R. Carey, T. J. Wagner, J. N. M. Siebrecht, D. Wong, I. E. Jacobs, R. O. Aboljadayel, A. Ionescus, S. A. Egorov, S. Mueller, O. Zadvorna, P. Skalski, C. Jellett, M. Little, A. Marks, I. McCulloch, J. Wunderlich, J. Sinova and H. Sirringhaus, Nat. Electron., 2019, 2, 98–107 CrossRef CAS.
- Z. G. Yu, Nat. Commun., 2014, 5, 4842 CrossRef CAS PubMed.
- Z. G. Yu, Nanoelectron. Spintron., 2015, 1, 1–18 Search PubMed.
- Y. Tani, Y. Teki and E. Shikoh, Appl. Phys. Lett., 2015, 107, 242406 CrossRef.
- M. Kimata, D. Nozaki, Y. Niimi, H. Tajima and Y. Otani, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 224422 CrossRef.
- S. W. Jiang, S. Liu, P. Wang, Z. Z. Luan, X. D. Tao, H. F. Ding and D. Wu, Phys. Rev. Lett., 2015, 115, 086601 CrossRef CAS PubMed.
- H. L. Liu, J. Y. Wang, A. Chanana and Z. V. Vardenya, J. Appl. Phys., 2019, 125, 142908 CrossRef.
- M. Groesbeck, H. L. Liu, M. Kavand, E. Lafalce, J. Y. Wang, X. Pan, T. H. Tennahewa, H. Popli, H. Malissa, C. Boehme and Z. V. Vardeny, Phys. Rev. Lett., 2020, 124, 067702 CrossRef CAS PubMed.
- T. Li, L. Q. Xu, X. H. Xiao, F. Chen, L. Cao, W. B. Wu, W. Tong and F. P. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 2708–2716 CrossRef CAS PubMed.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- H. M. McConnell, J. Chem. Phys., 1963, 39, 1910 CrossRef CAS.
- Y. V. Korshak, T. V. Medvedeva, A. A. Ovchinnikov and V. N. Spector, Nature, 1987, 326, 370–372 CrossRef CAS.
- A. Rajca, J. Wongsriratanakul and S. Rajca, Science, 2001, 294, 1503–1505 CrossRef CAS PubMed.
- J. Mahmood, J. Park, D. Shin, H. J. Choi, J. M. Seo, J. W. Yoo and J. B. Baek, Chem, 2018, 4, 2357–2369 CAS.
- Q. L. Jiang, J. Zhang, Z. Q. Mao, Y. Yao, D. K. Zhao, Y. H. Jia, D. H. Hu and Y. G. Ma, Adv. Mater., 2022, 34, 2108103 CrossRef CAS PubMed.
- Y. Hosokoshi, K. Katoh and K. Inoue, Synth. Met., 2003, 133, 527–530 CrossRef.
- J. M. Manriquez, G. T. Yee, R. S. McLean, A. J. Epstein and J. S. Miller, Science, 1991, 252, 1415–1417 CrossRef CAS PubMed.
- B. Li, C. Y. Kao, J. W. Yoo, V. N. Prigodin and A. J. Epstein, Adv. Mater., 2011, 23, 3382–3386 CrossRef CAS PubMed.
- H. L. Liu, C. Zhang, H. Malissa, M. Groesbeck, M. Kavand, R. McLaughlin, S. Jamali, J. J. Hao, D. L. Sun, R. A. Davidson, L. Wojcik, J. S. Miller, C. Boehme and Z. V. Vardeny, Nat. Mater., 2018, 17, 308–312 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Okubo, N. Tanaka, T. Lino and Y. Kaizu, Inorg. Chem., 2003, 42, 2440–2446 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, N. Tanaka, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, Inorg. Chem., 2004, 43, 5498–5500 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klyatskaya, J. P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502–506 CrossRef CAS PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360 CrossRef CAS PubMed.
- T. Matsumoto, G. N. Newton, T. Shiga, S. Hayami, Y. Matsui, H. Okamoto, R. Kumai, Y. Murakami and H. Oshio, Nat. Commun., 2014, 5, 3865 CrossRef CAS PubMed.
- T. Liu, H. Zheng, S. Kang, Y. Shiota, S. Hayami, M. Mito, O. Sato, K. Yoshizawa, S. Kanegawa and C. Y. Duan, Nat. Commun., 2013, 4, 2826 CrossRef.
- K. Bairagi, O. Iasco, A. Bellec, A. Kartsev, D. Z. Li, J. Lagoute, C. Chacon, Y. Girard, S. Rousset, F. Miserque, Y. J. Dappe, A. Smogunov, C. Barreteau, M. L. Boillot, T. Mallah and V. Repain, Nat. Commun., 2016, 7, 12212 CrossRef CAS PubMed.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
- J. Krober, E. Codjovi, O. Kahn, F. Groliere and C. Jay, J. Am. Chem. Soc., 1993, 115, 9810–9811 CrossRef CAS.
- T. Q. Hung, F. Terki, S. Kamara, M. Dehbaoui, S. Charar, B. Sinha, C. Kim, P. Gandit, I. A. Gural'skiy, G. Molnar, L. Salmon, H. J. Shepherd and A. Bousseksou, Angew. Chem., Int. Ed., 2013, 52, 1185–1188 CrossRef CAS PubMed.
- C. F. Wang, R. F. Li, X. Y. Chen, R. J. Wei, L. S. Zheng and J. Tao, Angew. Chem., Int. Ed., 2015, 54, 1574–1577 CrossRef CAS PubMed.
- X. W. Feng, C. Mathoniere, I. R. Jeon, M. Rouzieres, A. Ozarowski, M. L. Aubrey, M. I. Gonzalez, R. Clerac and J. R. Long, J. Am. Chem. Soc., 2013, 135, 15880–15884 CrossRef CAS PubMed.
- M. Oppermann, F. Zinna, J. Lacour and M. Chergui, Nat. Chem., 2022, 14, 739–745 CrossRef CAS PubMed.
- S. Decurtins, P. Gutlich, C. P. Kohler, H. Spiering and A. Hauser, Chem. Phys. Lett., 1984, 105, 1–4 CrossRef CAS.
- M. A. Halcrow, Chem. Soc. Rev., 2008, 37, 278–289 RSC.
- S. Ohkoshi, K. Imoto, Y. Tsunobuchi, S. Takano and H. Tokoro, Nat. Chem., 2011, 3, 564–569 CrossRef CAS PubMed.
- A. Hauser, Chem. Phys. Lett., 1986, 124, 543–548 CrossRef CAS.
- E. Trzop, D. P. Zhang, L. Pineiro-Lopez, F. J. Valverde-Munoz, M. C. Munoz, L. Palatinus, L. Guerin, H. Cailleau, J. A. Real and E. Collet, Angew. Chem., Int. Ed., 2016, 55, 8675–8679 CrossRef CAS PubMed.
- W. Liu, Y. Y. Peng, S. G. Wu, Y. C. Chen, M. N. Hoque, Z. P. Ni, X. M. Chen and M. L. Tong, Angew. Chem., Int. Ed., 2017, 56, 14982–14986 CrossRef CAS PubMed.
- F. Prins, M. Monrabal-Capilla, E. A. Osorio, E. Coronado and H. S. J. van der Zant, Adv. Mater., 2011, 23, 1545–1549 CrossRef CAS PubMed.
- K. S. Kumar and M. Ruben, Coord. Chem. Rev., 2017, 346, 176–205 CrossRef.
- S. Mathew, B. Satpati, B. Joseph, B. N. Dev, R. Nirmala, S. K. Malik and R. Kesavamoorthy, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 075426 CrossRef.
- Y. Murakami and H. Suematsu, Pure Appl. Chem., 1996, 68, 1463–1467 CrossRef CAS.
- A. A. Correa, L. Walmsley, L. O. S. Bulhoes, W. A. Ortiz, A. J. A. de Oliveira and E. C. Pereira, Synth. Met., 2001, 121, 1836–1837 CrossRef CAS.
- G. Cucinotta, L. Poggini, A. Pedrini, F. Bertani, N. Cristiani, M. Torelli, P. Graziosi, I. Cimatti, B. Cortigiani, E. Otero, P. Ohresser, P. Sainctavit, A. Dediu, E. Dalcanale, R. Sessoli and M. Mannini, Adv. Funct. Mater., 2017, 27, 1703600 CrossRef.
- L. Poggini, G. Cucinotta, A. M. Pradipto, M. Scarrozza, P. Barone, A. Caneschi, P. Graziosi, M. Calbucci, R. Cecchini, V. A. Dediu, S. Picozzi, M. Mannini and R. Sessoli, Adv. Mater. Interfaces, 2016, 3, 1500855 CrossRef.
- S. G. Miralles, A. Bedoya-Pinto, J. J. Baldovi, W. Canon-Mancisidor, Y. Prado, H. Prima-Garcia, A. Gaita-Arino, G. M. Espallargas, L. E. Hueso and E. Coronado, Chem. Sci., 2018, 9, 199–208 RSC.
- A. Bedoya-Pinto, S. G. Miralles, S. Velez, A. Atxabal, P. Gargiani, M. Valvidares, F. Casanova, E. Coronado and L. E. Hueso, Adv. Funct. Mater., 2018, 28, 1702099 CrossRef.
- A. Bedoya-Pinto, H. Prima-Garcia, F. Casanova, E. Coronado and L. E. Hueso, Adv. Electron. Mater., 2015, 1, 1500065 CrossRef.
- L. Zhu, M. Zhang, J. Q. Xu, C. Li, J. Yan, G. Q. Zhou, W. K. Zhong, T. Y. Hao, J. L. Song, X. N. Xue, Z. C. Zhou, R. Zeng, H. M. Zhu, C. C. Chen, R. C. I. MacKenzie, Y. C. Zou, J. Nelson, Y. M. Zhang, Y. M. Sun and F. Liu, Nat. Mater., 2022, 21, 656–663 CrossRef CAS PubMed.
- W. Qin, B. B. Xu and S. Q. Ren, Nanoscale, 2015, 7, 9122–9132 RSC.
- P. M. Allemand, K. C. Khemani, A. Koch, F. Wudl, K. Holczer, S. Donovan, G. Gruner and J. D. Thompson, Science, 1991, 253, 301–303 CrossRef CAS PubMed.
- D. Mihailovic, D. Arcon, P. Venturini, R. Blinc, A. Omerzu and P. Cevc, Science, 1995, 268, 400–402 CrossRef CAS PubMed.
- B. Narymbetov, A. Omerzu, V. V. Kabanov, M. Tokumoto, H. Kobayashi and D. Mihailovic, Nature, 2000, 407, 883–885 CrossRef CAS PubMed.
- K. Tanaka, K. Yoshizawa, T. Sato, T. Yamabe, K. Okahara and A. A. Zakhidov, Solid State Commun., 1993, 87, 1055–1059 CrossRef CAS.
- S. Q. Ren and M. Wuttig, Adv. Mater., 2012, 24, 724–727 CrossRef CAS PubMed.
- W. Qin, D. Jasion, X. M. Chen, M. Wuttig and S. Q. Ren, ACS Nano, 2014, 8, 3671–3677 CrossRef CAS PubMed.
- W. Qin, M. G. Gong, X. M. Chen, T. A. Shastry, R. Sakidja, G. L. Yuan, M. C. Hersam, M. Wuttig and S. Q. Ren, Adv. Mater., 2015, 27, 734–739 CrossRef CAS PubMed.
- M. M. Wei, K. P. Song, Y. Y. Yang, Q. K. Huang, Y. F. Tian, X. T. Hao and W. Qin, Adv. Mater., 2020, 32, 2003293 CrossRef CAS PubMed.
- L. Yang, S. X. Han, X. L. Ma, W. Qin and S. J. Xie, Sci. Rep., 2017, 7, 8384 CrossRef PubMed.
- M. M. Wei, M. S. Niu, P. Q. Bi, X. T. Hao, S. Q. Ren, S. J. Xie and W. Qin, Adv. Opt. Mater., 2017, 5, 1700644 CrossRef.
- S. G. Ray, S. S. Daube, G. Leitus, Z. Vager and R. Naaman, Phys. Rev. Lett., 2006, 96, 036101 CrossRef CAS PubMed.
- Z. T. Xie, T. Z. Markus, S. R. Cohen, Z. Vager, R. Gutierrez and R. Naaman, Nano Lett., 2011, 11, 4652–4655 CrossRef CAS PubMed.
- B. Gohler, V. Hamelbeck, T. Z. Markus, M. Kettner, G. F. Hanne, Z. Vager, R. Naaman and H. Zacharias, Science, 2011, 331, 894–897 CrossRef CAS PubMed.
- N. Peer, I. Dujovne, S. Yochelis and Y. Paltiel, ACS Photonics, 2015, 2, 1476–1481 CrossRef CAS.
- P. Roy, N. Kantor-Uriel, D. Mishra, S. Dutta, N. Friedman, M. Sheves and R. Naaman, ACS Nano, 2016, 10, 4525–4531 CrossRef CAS PubMed.
- V. Kiran, S. P. Mathew, S. R. Cohen, I. H. Delgado, J. Lacour and R. Naaman, Adv. Mater., 2016, 28, 1957–1962 CrossRef CAS PubMed.
- Q. Qian, H. Y. Ren, J. Y. Zhou, Z. Wan, J. X. Zhou, X. X. Yan, J. Cai, P. Q. Wang, B. L. Li, Z. Sofer, B. Li, X. D. Duan, X. Q. Pan, Y. Huang and X. F. Duan, Nature, 2022, 606, 902–908 CrossRef CAS PubMed.
- H. P. Lu, J. Y. Wang, C. X. Xiao, X. Pan, X. H. Chen, R. Brunecky, J. J. Berry, K. Zhu, M. C. Beard and Z. V. Vardeny, Sci. Adv., 2019, 5, 902–908 Search PubMed.
- Y. H. Kim, Y. X. Zhai, H. P. Lu, X. Pan, C. X. Xiao, E. A. Gaulding, S. P. Harvey, J. J. Berry, Z. V. Vardeny, J. M. Luther and M. C. Beard, Science, 2021, 371, 1129–1133 CrossRef CAS PubMed.
- L. Jia, C. C. Wang, Y. C. Zhang, L. Yang and Y. Yan, ACS Nano, 2020, 14, 6607–6615 CrossRef CAS PubMed.
- P. C. Mondal, N. Kantor-Uriel, S. P. Mathew, F. Tassinari, C. Fontanesi and R. Naaman, Adv. Mater., 2015, 27, 1924–1927 CrossRef CAS PubMed.
- C. Kulkarni, A. K. Mondal, T. K. Das, G. Grinbom, F. Tassinari, M. F. J. Mabesoone, E. W. Meijer and R. Naaman, Adv. Mater., 2020, 32, 1904965 CrossRef CAS PubMed.
- A. M. Guo and Q. F. Sun, Phys. Rev. Lett., 2012, 108, 218102 CrossRef PubMed.
- R. Gutierrez, E. Diaz, R. Naaman and G. Cuniberti, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 081404 CrossRef.
- F. Evers, A. Aharony, N. Bar-Gill, O. Entin-Wohlman, P. Hedegard, O. Hod, P. Jelinek, G. Kamieniarz, M. Lemeshko, K. Michaeli, V. Mujica, R. Naaman, Y. Paltiel, S. Refaely-Abramson, O. Tal, J. Thijssen, M. Thoss, J. M. van Ruitenbeek, L. Venkataraman, D. H. Waldeck, B. H. Yan and L. Kronik, Adv. Mater., 2022, 34, 2106629 CrossRef CAS PubMed.
- J. R. Brandt, F. Salerno and M. J. Fuchter, Nat. Rev. Chem., 2017, 1, 0045 CrossRef CAS.
- M. Suda, Y. Thathong, V. Promarak, H. Kojima, M. Nakamura, T. Shiraogawa, M. Ehara and H. M. Yamamoto, Nat. Commun., 2019, 10, 2455 CrossRef PubMed.
- O. Ben Dor, S. Yochelis, A. Radko, K. Vankayala, E. Capua, A. Capua, S. H. Yang, L. T. Baczewski, S. S. P. Parkin, R. Naaman and Y. Paltiel, Nat. Commun., 2017, 8, 14567 CrossRef CAS PubMed.
- K. Kim, E. Vetter, L. Yan, C. Yang, Z. Q. Wang, R. Sun, Y. Yang, A. H. Comstock, X. Li, J. Zhou, L. F. Zhang, W. You, D. L. Sun and J. Liu, Nat. Mater., 2023, 22, 322–328 CrossRef CAS PubMed.
- G. K. Long, C. Y. Jiang, R. Sabatini, Z. Y. Yang, M. Y. Wei, L. N. Quan, Q. M. Liang, A. Rasmita, M. Askerka, G. Walters, X. W. Gong, J. Xing, X. L. Wen, R. Quintero-Bermudez, H. F. Yuan, G. C. Xing, X. R. Wang, D. T. Song, O. Voznyy, M. T. Zhang, S. Hoogland, W. B. Gao, Q. H. Xiong and E. H. Sargent, Nat. Photonics, 2018, 12, 528–533 CrossRef CAS.
- Y. Y. Chen, J. Q. Ma, Z. Y. Liu, J. Z. Li, X. F. Duan and D. H. Li, ACS Nano, 2020, 14, 15154–15160 CrossRef CAS PubMed.
- Z. J. Huang, B. P. Bloom, X. J. Ni, Z. N. Georgieva, M. Marciesky, E. Vetter, F. Liu, D. H. Waldeck and D. L. Sun, ACS Nano, 2020, 14, 10370–10375 CrossRef CAS PubMed.
- N. Berova, L. Di Bari and G. Pescitelli, Chem. Soc. Rev., 2007, 36, 914–931 RSC.
- D. W. Wang, C. Song, W. Feng, H. Cai, D. Xu, H. Deng, H. K. Li, D. N. Zheng, X. B. Zhu, H. Wang, S. Y. Zhu and M. O. Scully, Nat. Phys., 2019, 15, 382–386 Search PubMed.
- M. F. Sun and W. B. Mi, J. Mater. Chem. C, 2018, 6, 6619–6636 RSC.
- H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605–625 CrossRef CAS.
- K. V. Raman, A. M. Kamerbeek, A. Mukherjee, N. Atodiresei, T. K. Sen, P. Lazic, V. Caciuc, R. Michel, D. Stalke, S. K. Mandal, S. Blugel, M. Munzenberg and J. S. Moodera, Nature, 2013, 493, 509–513 CrossRef CAS PubMed.
- F. Al Ma'Mari, T. Moorsom, G. Teobaldi, W. Deacon, T. Prokscha, H. Luetkens, S. Lee, G. E. Sterbinsky, D. A. Arena, D. A. MacLaren, M. Flokstra, M. Ali, M. C. Wheeler, G. Burnell, B. J. Hickey and O. Cespedes, Nature, 2015, 524, 69–74 CrossRef PubMed.
- Y. J. Hsu, Y. L. Lai, C. H. Chen, Y. C. Lin, H. Y. Chien, J. H. Wang, T. N. Lam, Y. L. Chan, D. H. Wei, H. J. Lin and C. T. Chen, J. Phys. Chem. Lett., 2013, 4, 310–316 CrossRef CAS PubMed.
- K. Bairagi, A. Bellec, V. Repain, C. Chacon, Y. Girard, Y. Garreau, J. Lagoute, S. Rousset, R. Breitwieser, Y. C. Hu, Y. C. Chao, W. W. Pai, D. Li, A. Smogunov and C. Barreteau, Phys. Rev. Lett., 2015, 114, 247203 CrossRef CAS PubMed.
- R. Friedrich, V. Caciuc, N. S. Kiselev, N. Atodiresei and S. Blugel, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 115432 CrossRef.
- S. Steil, K. Goedel, A. Ruffing, I. Sarkar, M. Cinchetti and M. Aeschlimann, Synth. Met., 2011, 161, 570–574 CrossRef CAS.
- Y. Wang, J. G. Che, J. N. Fry and H. P. Cheng, J. Phys. Chem. Lett., 2013, 4, 3508–3512 CrossRef CAS.
- X. H. Wang, Z. Y. Zhu, A. Manchon and U. Schwingenschlogl, Appl. Phys. Lett., 2013, 102, 111604 CrossRef.
- S. Goumri-Said, M. B. Kanoun, A. Manchon and U. Schwingenschlogl, J. Appl. Phys., 2013, 113, 013905 CrossRef.
- N. Atodiresei, V. Caciuc, P. Lazic and S. Blugel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 172402 CrossRef.
- J. Y. Wang, A. Deloach, W. Jiang, C. M. Papa, M. Myahkostupov, F. N. Castellano, F. Liu and D. B. Dougherty, Phys. Rev. B, 2017, 95, 241410 CrossRef.
- W. C. Sun, L. D. Guo, S. H. Hu, X. W. Zhu, X. T. Zhang, W. P. Hu and X. N. Sun, Org. Electron., 2021, 99, 106311 CrossRef CAS.
- D. L. Sun, L. F. Yin, C. J. Sun, H. W. Guo, Z. Gai, X. G. Zhang, T. Z. Ward, Z. H. Cheng and J. A. Shen, Phys. Rev. Lett., 2010, 104, 236602 CrossRef PubMed.
- S. S. Ding, Y. Tian, H. L. Wang, Z. Zhou, W. B. Mi, Z. J. Ni, Y. Zou, H. L. Dong, H. J. Gao, D. B. Zhu and W. P. Hu, ACS Nano, 2018, 12, 12657–12664 CrossRef CAS PubMed.
- B. Maennig, M. Pfeiffer, A. Nollau, X. Zhou, K. Leo and P. Simon, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195208 CrossRef.
- C. Gaul, S. Hutsch, M. Schwarze, K. S. Schellhammer, F. Bussolotti, S. Kera, G. Cuniberti, K. Leo and F. Ortmann, Nat. Mater., 2018, 17, 439–444 CrossRef CAS PubMed.
- C. L. Wang, H. L. Dong, L. Jiang and W. P. Hu, Chem. Soc. Rev., 2018, 47, 422–500 RSC.
- J. Tsurumi, H. Matsui, T. Kubo, R. Hausermann, C. Mitsui, T. Okamoto, S. Watanabe and J. Takeya, Nat. Phys., 2017, 13, 994–998 Search PubMed.
- M. Johnson and R. H. Silsbee, Phys. Rev. Lett., 1985, 55, 1790–1793 CrossRef CAS PubMed.
- N. Tombros, C. Jozsa, M. Popinciuc, H. T. Jonkman and B. J. van Wees, Nature, 2007, 448, 571–574 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |
