DOI:
10.1039/D2NR07073A
(Paper)
Nanoscale, 2023,
15, 9710-9717
High-speed nanoscale optical trapping with plasmonic double nanohole aperture†
Received
17th December 2022
, Accepted 26th April 2023
First published on 27th April 2023
Abstract
Optical trapping with plasmonic double nanohole (DNH) apertures has proven to be an efficient method for trapping sub-50 nm particles due to their suppressed plasmonic heating effect and very high electric field enhancement in the gap region of the aperture. However, plasmonic tweezers are generally diffusion-limited, requiring particles to diffuse down to a few tens of nanometres from the high field enhancement regions before they can be trapped. The loading of target particles to the plasmonic hotspots can take several minutes for diluted samples. In this work, rapid particle transport and trapping of a 25 nm polystyrene sphere is demonstrated, leveraging an electrothermoplasmonic flow induced upon application of an AC field in the presence of a laser-induced temperature gradient. Using this approach, we demonstrate the rapid transport of a 25 nm polystyrene particle across a distance of 63 μm and trapping at the DNH under 16 s. This platform shows great potential for applications involving simultaneous trapping and plasmon-enhanced spectroscopies, such as Raman enhancement via the intense electric field enhancement in the DNH gap.
 Justus C. Ndukaife | Justus Ndukaife received a Ph.D. in Electrical Engineering from Purdue University, USA in 2017, and MSc degree from Purdue Northwest and a BSc degree with First Class Honors from the University of Lagos. Ndukaife's interdisciplinary research is focused on optical nanotweezers enabled by nanophotonics including plasmonics and resonant dielectric metasurfaces for single extracellular vesicle analysis, as well as for the enhancement of on-chip quantum light sources. He has made major contributions in the field optical nanotweezers and his research works have been published in the top peer-reviewed journals including Nature Nanotechnology, Science, ACS Nano, and Nano Letters. He is an inventor of seven US patents relating to optical nanotweezers. In recognition of his scientific contributions, Ndukaife received a global Rising Stars of Light award for the year 2020. His global iCANX talk on Optical Nanotweezeers research attracted more than 260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 viewers world-wide. His other honors include NSF CAREER award, Chancellor's award for excellence in research, the Year 2017 Prize in Physics by the Dimitris N. Chorafas Foundation, the Purdue College of Engineering Outstanding Research Award, NSBE Golden Torch Award, Best Paper Award at the ASME conference, and a Carnegie African Diaspora Fellowship Award. 000 viewers world-wide. His other honors include NSF CAREER award, Chancellor's award for excellence in research, the Year 2017 Prize in Physics by the Dimitris N. Chorafas Foundation, the Purdue College of Engineering Outstanding Research Award, NSBE Golden Torch Award, Best Paper Award at the ASME conference, and a Carnegie African Diaspora Fellowship Award. |
Introduction
Since the pioneering works on optical trapping by Arthur Ashkin,1 the dynamic manipulation of micron and sub-micron particles down to the sub-wavelength scale enabled by optical tweezers has inspired numerous studies in various fields, including biological2–6 and environmental7,8 sciences. In a typical optical tweezer setup, a laser beam focused to a diffraction-limited spot induces an optical force that stems from gradients in the highly nonuniform focused field. This gives rise to an attractive or repulsive force on a particle in the vicinity of the focused field, towards or away from the focal point, depending on the polarizability of the particle relative to the surrounding medium. The optical force on particles much larger than the wavelength of the trapping laser can be described using a ray optics model. In this model, the optical force is described by directly considering the momentum exchange between the impinging light rays and the particle, stemming from the reflection and refraction of the incident rays.9 To describe the optical gradient force on particles much less than the trapping wavelength in the Rayleigh limit (a ≪ λ), the dipole approximation is considered and is given by the expression,| | 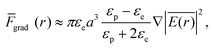 | (1) |
where ![[F with combining overline]](https://www.rsc.org/images/entities/i_char_0046_0305.gif) grad is the optical gradient force, a is the particle radius,
grad is the optical gradient force, a is the particle radius, 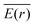 is the position-dependent electric field of the trapping laser, εp, and εm are the complex permittivities of the particle and medium, respectively. Despite the widespread applications of optical tweezers, they suffer some fundamental limitations. Firstly, the optical gradient force is proportional to the third power of the particle radius as described by the dipole approximation. This implies that as the particle size gets smaller, the optical force decreases by orders of magnitude, resulting in higher intensity gradients being required to trap smaller particles. Secondly, optical tweezers are diffraction-limited, which implies that the high laser intensity required to trap sub-100 nm particles can only be achieved by increasing the laser power. The trapping of various particles including biological species and nano plastics down to the 100 nm range can be achieved with laser powers between a few tens to a few hundred mW.7,10–12 However, stable trapping of nanoscopic particles in the sub-50 nm range requires several hundred mW7, which results in degradation and damage of the particles over short time spans.1In situ analysis of nanoscopic particles is of great interest in biological and environmental sciences. In biological sciences, the trapping of small extracellular vesicles in the sub-100 nm range is desirable to investigate the heterogeneity of these species for diagnostic and drug delivery purposes.2,4,6 The investigation of nano plastic pollution in oceans resulting from the degradation of industrially produced plastic debris has become of great importance recently, as this poses a public health threat.13In situ optical trapping and Raman-enabled chemical characterization of nano plastics down to the 50 nm range was recently demonstrated using laser powers exceeding 100 mW,7 enabling unambiguous discrimination between nano plastics and organic matter. Previous approaches to characterize nano plastics, such as TEM/SEM, fluorescent microscopy, and nanoparticle tracking analysis7 provide no information about the chemical composition of these nano plastics. Thus, it is imperative to devise methods for non-destructive low-power trapping of nanoscopic polymer particles in the sub-50 nm range.
is the position-dependent electric field of the trapping laser, εp, and εm are the complex permittivities of the particle and medium, respectively. Despite the widespread applications of optical tweezers, they suffer some fundamental limitations. Firstly, the optical gradient force is proportional to the third power of the particle radius as described by the dipole approximation. This implies that as the particle size gets smaller, the optical force decreases by orders of magnitude, resulting in higher intensity gradients being required to trap smaller particles. Secondly, optical tweezers are diffraction-limited, which implies that the high laser intensity required to trap sub-100 nm particles can only be achieved by increasing the laser power. The trapping of various particles including biological species and nano plastics down to the 100 nm range can be achieved with laser powers between a few tens to a few hundred mW.7,10–12 However, stable trapping of nanoscopic particles in the sub-50 nm range requires several hundred mW7, which results in degradation and damage of the particles over short time spans.1In situ analysis of nanoscopic particles is of great interest in biological and environmental sciences. In biological sciences, the trapping of small extracellular vesicles in the sub-100 nm range is desirable to investigate the heterogeneity of these species for diagnostic and drug delivery purposes.2,4,6 The investigation of nano plastic pollution in oceans resulting from the degradation of industrially produced plastic debris has become of great importance recently, as this poses a public health threat.13In situ optical trapping and Raman-enabled chemical characterization of nano plastics down to the 50 nm range was recently demonstrated using laser powers exceeding 100 mW,7 enabling unambiguous discrimination between nano plastics and organic matter. Previous approaches to characterize nano plastics, such as TEM/SEM, fluorescent microscopy, and nanoparticle tracking analysis7 provide no information about the chemical composition of these nano plastics. Thus, it is imperative to devise methods for non-destructive low-power trapping of nanoscopic polymer particles in the sub-50 nm range.
To overcome these fundamental challenges with conventional optical tweezers, plasmonic nanotweezers have emerged as promising alternatives, enabling the low power trapping of nanoscopic particles down to the 20 nm scale,14,15 due to the extreme confinement of light beyond the diffraction limit.16 Plasmonic cavities can confine light down to scales on the order of a few tens of nanometres via the excitation of localized surface plasmon resonance (LSPR), which arises from the collective oscillations of surface plasmons in metallic nanostructures. Plasmonic traps have been widely demonstrated in literature14,15,17 but still suffer from two fundamental limitations. Firstly, metals are known to be lossy due to the non-zero imaginary component of the permittivity, which results in plasmonic heating effects in the presence of high electric fields at optical frequencies.18 This often gives rise to positive thermophoretic effects whereby trapped particles are repelled from the plasmonic hotspot towards colder regions, decreasing the trapping stability.19,20 Jones et al.21 showed that illuminating resonant bowtie plasmonic antennas could result in thermophoretic depletion of 100 nm polystyrene spheres from the vicinity of the plasmonic antenna. To mitigate heating effects in plasmonic traps, plasmonic apertures in continuous metallic films have been investigated14,22 because they efficiently dissipate heat through the continuous metallic film resulting in suppressed photo-thermal heat generation. Particularly, plasmonic double nanohole (DNH) apertures14,15,23,24 have sparked considerable interest owing to their capability to efficiently trap 20 nm particles and smaller. Trapping of 12 nm polystyrene beads has been demonstrated with plasmonic DNH apertures.15 They have also been used for the trapping and analysis of various conformational states of single proteins.14 Despite the promising performance of plasmonic DNH traps, they remain inherently diffusion-limited, requiring particles to diffuse to a few tens of nanometres from the plasmonic hotspots before trapping can occur. This may take several minutes for trapping events to occur, depending on the concentration of the particle solution. To overcome the diffusion limitation in plasmonic tweezers, Ndukaife et al.25 showed that by illuminating a single antenna and applying an ac field, a long-range electrothermoplasmonic flow (ETP flow) can be induced by the photo-thermal heating of a single antenna, enabling rapid delivery and subsequent trapping of 300 nm polystyrene beads to the plasmonic hotspot with radial velocity magnitudes exceeding 10 μm s−1. However, efficient delivery and trapping of sub-50 nm particles using this approach remain challenging due to the increased diffusion coefficient of smaller particles and decreased optical force. In this work, we demonstrate on-demand rapid particle transport and efficient trapping of single 25 nm polystyrene spheres suspended in deionized water using single plasmonic double nanohole apertures milled in a 100 nm thick gold film deposited on a glass substrate. Our approach of using a plasmonic aperture mitigates heating effects by efficiently dissipating heat in the continuous gold film. Despite the suppressed plasmonic heating, we show that a sufficient thermal gradient is generated at the plasmonic hotspot, generating ETP velocities exceeding 50 μm s−1.
ETP simulation model for plasmonic double nanohole aperture
Photo-thermal effects in plasmonic systems give rise to temperature gradients, which result in gradients in the electrical permittivity and conductivity of the given medium. An AC field applied in the presence of gradients in the electrical properties of a dielectric liquid medium induces an electrical body force25–27 given by:| | | fETP = ρfE1 − 1/2 |El|2∇εm, | (2) |
where El is the local electric field, ρf is the volume charge density of the induced free charges, and εm is the permittivity of the medium. The first term in eqn (2) results from a columbic force acting on free charges in suspension throughout the medium while the second term arises due to microscopic polarization in the dielectric medium.27 ETP flow modelling of the system is done using a finite-element-method software, COMSOL Multiphysics. ETP flow is modelled using a similar approach previously described in literature.25 Firstly, the electric field E in the gap of the DNH and the surrounding media is solved using the wave equation,| | | ∇ × ∇ × E − k02ε(r)E = 0, | (3) |
where k0 is the wave number given by 2π/λ and ε(r) is the complex permittivity of the medium. Next, the temperature field is computed by solving the heat source density q(r) generated by E, given by q(r) = 1/Re(J·E). Where J is the current density induced in the vicinity of the plasmonic aperture. The temperature field T(r) is then computed by solving the steady-state heat equation,| | | ∇[κ∇T(r) + ρcpT(r)u(r)] = q(r), | (4) |
where κ, ρ, and cp are the thermal conductivity, density, and heat capacity of the medium, while u(r) is the induced velocity field. For natural thermoplasmonic convection, the Boussinesq approximation for buoyancy-driven convection is applied to obtain the body force term given by,25| | | Fb = gρβ(T)[T(r) − T0], | (5) |
where g, ρ, and β(T) are the gravitational constant, density, and thermal expansivity of the medium respectively. The ETP body force given in eqn (2) can be expanded using a perturbative approach28 and decomposed into radial and axial components25 given by,| | 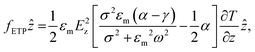 | (6) |
| |  | (7) |
where σ and ω are the electrical conductivity and AC frequency respectively. 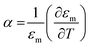 and
and 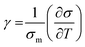 , with values −0.004 K−1 and −0.02 K−1, respectively.25 The total body force F in the system is given by the sum of buoyancy convection and ETP body forces. The fluid velocity field is then computed by solving the incompressible Navier Stokes equation given by,
, with values −0.004 K−1 and −0.02 K−1, respectively.25 The total body force F in the system is given by the sum of buoyancy convection and ETP body forces. The fluid velocity field is then computed by solving the incompressible Navier Stokes equation given by,| | | ρ(u(r)·∇)u(r) + ∇p(r) − η∇2u(r) = F | (8) |
where η is the viscosity of the medium and ∇p(r) is the pressure gradient in the medium. FEM simulations for the velocity field are shown in Fig. 2(d), 3(a) and (c).
Results and discussion
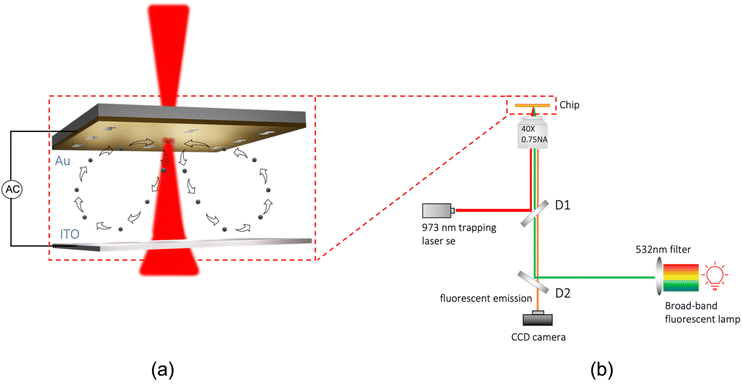
The schematic design of the double nanohole aperture is shown in Fig. 2(c) and S2b (ESI Fig. 2b†), with S2a showing the top view SEM micrograph of the DNH. The plasmonic aperture is milled in a 100 nm thick Au film deposited on a silica substrate with a 10 nm Cr adhesion layer. Two 100 nm diameter holes are made side by side with their centers 140 nm apart, and a rectangle connecting them is milled in the Au film forming a 30 nm gap depicted in the right panel of S2b. Previous works on DNH apertures in Au films15,29 made by focused ion beam milling have shown that this fabrication method often results in the widening of the top gap of the DNH, as shown in the left panel of S2b. To account for this effect in FDTD and FEM simulations, the top gap is taken to be 60 nm wide while the bottom gap is taken to be 30 nm wide. The DNH sample was first treated with Poly (sodium 4-styrenesulfonate) (PSS) for 10 minutes and rinsed with potassium chloride (KCl) for 5 minutes to prevent the negatively charged polystyrene particles from sticking to the Au surface, after which the sample was then blow-dried. Subsequently, the DNH sample was made into a microfluidic chip using 120 μm thick dielectric spacers, sandwiching the Au film with an ITO-coated coverslip above the Au film. The DHN is illuminated under a 40× objective with a 973 nm trapping laser focused to a spot size of 1.33 μm with its polarization aligned perpendicular to the center-to-center axis of the 100 nm diameter holes. During fabrication, a marker is made on the chip to indicate the center-to-center axis of the DNH aperture. Trapping experiments in this work are done with fluorescently labelled 25 nm polystyrene beads with a 532 nm excitation wavelength. A fluorescence lamp coupled with a 532 nm filter is used for the excitation. Fluorescence emission from trapped particles is collected with a CCD camera as shown in Fig. 1(b). FDTD and FEM electromagnetic simulations are run with Lumerical and COMSOL Multiphysics, respectively, with the refractive indices of water and silica taken to be 1.33 and 1.45, respectively. Fig. 2(a) shows an FDTD simulation of the normalized intensity enhancement of the DNH in the XY plane at Z = −20 nm, showing over 60 times enhancement in the local light intensity in the gap region for an incident laser with a polarization perpendicular to the center-to-center axis of the DNH.
 |
| | Fig. 1 Schematic diagram and experimental setup. (a) Schematic diagram showing rapid electrothermoplasmoinc (ETP) enabled transport of 25 nm polystyrene spheres towards the plasmonic hotspot. The illuminated double nanohole generates temperature gradients which induce an ETP flow upon the application of an AC field. (b) Experimental setup. D1 and D2 represent dichroic mirrors. | |
 |
| | Fig. 2 Optical and thermal simulations. (a) FEM simulation showing the intensity enhancement in the XY plane at Z = −20 nm. This shows intense enhancement in the gap of the DNH. The inset shows an SEM micrograph of the DNH aperture. (b) Optical power dissipation density in the XY plane at Z = −50 nm, showing that the optical power dissipated in the Au film by the plasmonic aperture is very tightly confined to the vicinity of the DNH. (c) Schematic design of the DNH aperture showing how the axes are defined. (d) ZX cross section at Y = 0 showing the distribution of the temperature rise and the velocity vector plot, with the vector arrows proportional to the magnitude of the velocity vector resulting from a Gaussian beam with an intensity of 11.4 mW μm−2 and beam diameter 1.33 μm. This shows a maximum temperature rise of 15 K and velocity magnitudes exceeding 70 μm s−1 for a 10 V AC at 20 kHz. | |
In Fig. 2(b), we plot the optical power dissipation density in the vicinity of the DNH for an illumination intensity of 11.4 mW μm−2, showing the highly non-uniform dissipation of optical power around the DNH. This shows that the heat generated by the plasmonic aperture can be fully accounted for within a 500 × 500 × 100 nm3 bounding volume cantered around the DNH. To model the temperature rise in the system, first an FEM simulation is run to determine the total optical power dissipation density in a 500 × 500 × 100 nm3 bounding volume centered around the DNH to fully capture the optical power dissipation resulting from the plasmonic enhancement. The optical power dissipation density in the rest of the Au film was defined using the following equation as shown in previous works,25,26
| | 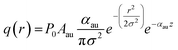 | (9) |
where
P0 is the incident power,
Aau is the absorption of the Au film without the DNH, and
αau is the absorption coefficient of the Au film at the illumination wavelength. The first exponential term in
eqn (9) accounts for the effect of the Gaussian beam where
σ is the waist radius of the focused laser, while the second exponential term accounts for Beer's law.
Fig. 2(d) shows the highly localized temperature field generated with a maximum temperature of 15 K along with the ETP velocity vector plot. Typically, plasmonic antennas often result in significant temperature rise exceeding 20 K
25 due to inefficient dissipation of heat by the surrounding dielectric media in the vicinity of the plasmonic antenna. With the double nanohole aperture, the region of the plasmonic enhancement is surrounded by a continuous metallic film which results in efficient dissipation of heat away from the hot spot, owing to the high thermal conductivity of the Au film (317 W mK
−1) relative to water (0.59 W mK
−1). Despite the suppressed temperature rise in this system, we show that significant ETP flow is still generated, as shown by the velocity vector arrows in
Fig. 2(d). In-plane ETP simulations in
Fig. 3(a and c) show radial flow velocity magnitudes up to 20 μm s
−1 for an illumination intensity of 11.4 mW μm
−2 and a 10 V AC bias applied at 20 kHz.
Fig. 3(b) shows the experimental radial velocity magnitudes in the
XY plane generated through particle image velocimetry (PIV) analysis using 300 nm polystyrene tracer particles (ESI Movie 1
†), while
Fig. 3(c) shows the corresponding simulation in the
XY plane at
Z = −2.3 μm.
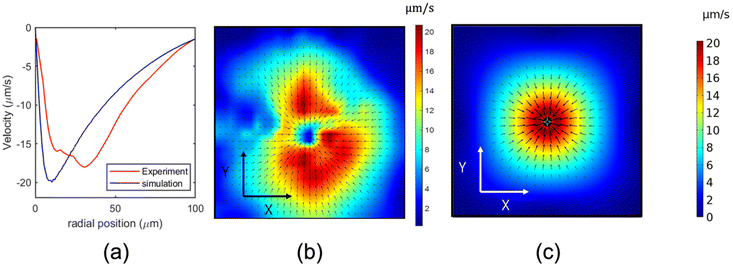 |
| | Fig. 3 ETP results for an illumination intensity of 11.4 mW μm−2 (a) Radial velocity magnitudes for (b) and (c). (b) Experimental ETP velocity plot in the XY plane generated using particle image velocimetry (PIV) analysis showing radial velocities exceeding 20 μm s−1 for a 10 V, 20 kHz applied AC. (c) FEM simulation for the ETP flow in the XY plane at Z = −2.3 μm for a 10 V, 20 kHz applied AC. | |
The radial velocity magnitudes in Fig. 3(b and c) are plotted against the radial distance from DNH in Fig. 3(a). The experimental and simulated plots are in agreement. Next, we applied Maxwell's stress tensor technique to calculate the Z component of the optical force and potential along the Z axis for a 25 nm polystyrene particle localized at X = 0, Y = 0, as shown in Fig. 4(a). To realize an efficient ETP-enabled transport and trapping of 25 nm polystyrene beads, we must consider the particle–surface interaction force FPS which arises due to the interaction between the surface charges on the particle and their image charge in the metallic film resulting from the applied voltage. At higher frequencies, the fluid drag force is dominant over FPS due to AC frequency being greater than the charge relaxation time of the fluid. This results in particles getting pulled away from the hotspot in the Z direction after they approach the hotspot, as shown in ESI Movie 1.† At lower frequencies, however, FPS begins to dominate, and this results in the aggregation of particles at the hotspot due to the radial component of the ETP force, shown in frame 1 of S3 and ESI Movie 2,† as the particles remain close to the surface due to the prevalence of FPS over the ETP induced drag force, making it possible for optical gradient force Fz to pull particles into the trap. To experimentally demonstrate ETP-enabled transport and trapping of 25 nm polystyrene spheres, we used a 10 V AC voltage applied at 3 kHz. This ensures that FPS dominates over the ETP-induced drag force, localizing the particle near the Au surface. As the particle approaches the hotspot, Fz pulls the particle into the trap and the AC voltage is immediately turned off. To fully understand the trapping mechanism of this system despite having an optical potential of about −0.9KBT shown in Fig. 4(a) we must consider the synergy between the optical and thermophoretic potentials of this system. Polystyrene beads of about 25 nm and below are known to experience negative thermophoresis in contrast to larger sized beads due to the size dependence of the Soret coefficient.30–33 Using the value for the Soret coefficient presented in ref. 33, we show the thermophoretic force contributions in Fig. 4(c) using the equation Ftherm = KBT(r)ST∇T(r), where KB is the Boltzmann constant, T(r) is the position-dependent temperature, and ST is the Soret coefficient. Fig. 4(b) shows the attractive nature of the thermophoretic force for which a thermophoretic potential up to −3KBT was computed. The thermophoretic potential was obtained by integrating Ftherm along the line Z (X = 0, Y = 0). Considering both contributions from optical and thermophoretic forces, we achieved a total potential up to −3.9KBT as shown in Fig. 4(d), which is sufficient to trap the particle.
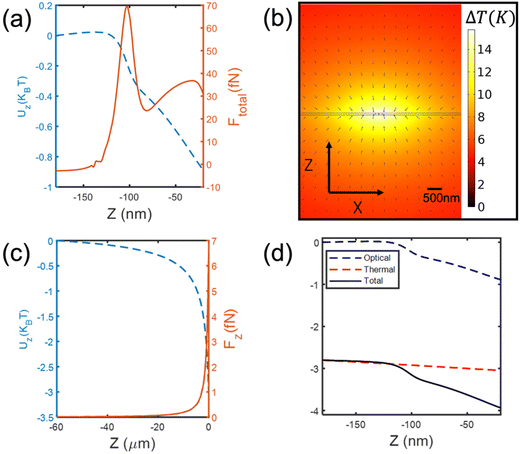 |
| | Fig. 4 Optical and thermophoretic force calculations at X = 0, Y = 0. (a) Maxwell stress tensor calculation for the Z component of the optical force and the corresponding optical potential along the Z direction for a 25 nm polystyrene bead. (b) FEM temperature rise simulation showing the direction of the thermophoretic force (black arrows). This shows that the thermophoretic force contributes to the trapping. (c) Finite element method (FEM) calculations for the Z component thermophoretic force and its potential along the Z axis for a 25 nm polystyrene bead. (d) Total potential along the Z (X = 0, Y = 0) direction due to contributions from the Z components of the optical and thermophoretic forces. This is obtained by summing the optical (blue) and thermal (red) potentials. | |
The experimental results presented in Fig. 5(a) shows how a 25 nm polystyrene bead is transported over a 63 μm distance under 16 s. This is captured in ESI Movie 5.† Once the particle is localized by the optical force, the AC field is turned off, as shown in frame 3 of Fig. 5(a). Despite aggregation of particles at the hotspot prior to trapping, only a single particle gets trapped at the hotspot, demonstrating the self-limiting nature of the double nanohole trap, shown in frame 2 of S3. Fig. 5(b) shows the particle position plot for a trapped 25 nm polystyrene sphere at the plasmonic hotspot for two different intensities corresponding to ESI Movies 3 and 4,† which were obtained using a CMOS camera operating at 10 frames per second. The data presented in Fig. 5(b) was obtained by applying a custom particle tracking Python code to ESI Movies 3 and 4.† Furthermore, to accurately obtain the trapping stiffness, we applied a motion blur correction function34 to the particle position data in Fig. 5(b) using the same approach used in ref. 34. We obtained trapping stiffnesses kx = 0.104 fN nm−1 and ky = 0.108 fN nm−1 for an intensity of 11.4 mW μm−2, using the equipartition theorem ½KBT = ½kii2, where KB is the Boltzmann constant, T is the temperature taken to be 308 K, ki is the trap stiffness, and i2 is the particle position variance for i2 = x2, y2. It is important to note that it was not possible to trap 25 nm polystyrene beads away from the DNH apertures using the laser powers described here, showing that we observed near-field trapping. The realization of high-speed transport and efficient trapping of 25 nm polymer beads is crucial for applications such as SERS coupled Raman tweezers spectroscopy of nano plastics, making it possible to obtain single particle Raman spectrum rapidly in dilute samples.
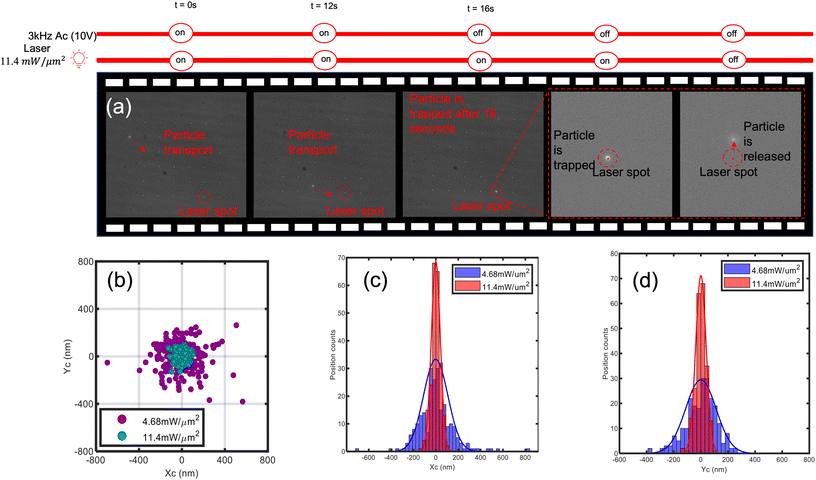 |
| | Fig. 5 ETP transport and trapping of a 25 nm polystyrene particle. (a) ETP transport of a 25 nm polystyrene bead from a distance 63 μm away within 16 seconds under an AC voltage of 10 V and 3 kHz frequency. The particle remains trapped at the hotspot after the AC voltage is turned off and gets released after the trapping laser is turned off. (b) Particle position plot for a 25 nm polystyrene bead trapped at the plasmonic hotspot for two different laser intensities. This shows increased particle localization at higher laser intensities, where Xc and Yc represent the centre of the particle. (c) Particle position histograms for the position of the particle in (b) along the X axis for two different laser intensities. (d) Particle position histograms for the position of the particle in (b) along the Y axis for two different laser intensities. | |
Conclusion
Plasmonic apertures in metallic films have emerged as promising alternatives to plasmonic antennas for trapping nanoscopic particles down to the single protein level, with the continuous metallic films enabling more efficient dissipation of the heat generated by the plasmonic hotspot compared to plasmonic antennas. The diffusion limitation in plasmonic nanotweezers arises from the requirement for particles to diffuse down to a few tens to nanometres in the vicinity of the hotspot, which could take several minutes in dilute samples. In this work, we have shown that by inducing an electrothermoplasmonic flow in the presence of a temperature gradient and an applied AC field, high-speed transport and trapping of 25 nm polystyrene particles can be achieved. Using a 20 kHz–10 V AC bias and an intensity of 11.4 mW μm−2, we showed that velocity magnitudes up to70 μm s−1 could be achieved (S4). Using this approach, we demonstrated efficient trapping and transport of 25 nm polystyrene beads. Single particle analysis is of great importance for studies on nano plastic pollution in seas and oceans, however, existing methods to analyse these nanoscopic polymers such as TEM/SEM, fluorescent microscopy, and nanoparticle tracking analysis provide no information on the chemical composition of these particles. To overcome this challenge, the use of Raman tweezers microspectroscopy technique for single nano plastics analysis has shown promising results but however requires powers exceeding 100 mW for stable trapping of sub-50 nm nano plastics, which is detrimental to target particles, and results in low SNR. Our platform shows great potential to solve this problem by enabling low-power trapping of sub-50 nm materials and enhanced electric field enhancement, which could provide SERS enhancement simultaneously for trapped particles. To extend this work for Raman analysis, the aperture can be tuned to be resonant near the Raman excitation wavelength, enabling simultaneous single particle trapping and SERS amplification.
Conflicts of interest
There are no conflicts to declare.
References
-
A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm and S. Chu, Observation of a single-beam gradient force optical trap for dielectric particles, 1986, vol. 11 Search PubMed.
- M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Biophys. J., 1997, 72, 1335–1346 CrossRef CAS PubMed.
- Y. Tan, C. Wing Kong, S. Chen, S. H. Cheng, R. A. Li and D. Sun, J. Biomech., 2012, 45, 123–128 CrossRef PubMed.
- P. Jing, Y. Liu, E. G. Keeler, N. M. Cruz, B. S. Freedman and L. Y. Lin, Biomed. Opt. Express, 2018, 9, 771 CrossRef CAS PubMed.
- H. M. Nussenzveig, Eur. Biophys. J., 2018, 47, 499–514 CrossRef CAS PubMed.
- F. M. Fazal, D. J. Koslover, B. F. Luisi and S. M. Block, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 15101–15106 CrossRef CAS PubMed.
- R. Gillibert, G. Balakrishnan, Q. Deshoules, M. Tardivel, A. Magazzù, M. G. Donato, O. M. Maragò, M. Lamy De La Chapelle, F. Colas, F. Lagarde and P. G. Gucciardi, Environ. Sci. Technol., 2019, 53, 9003–9013 CrossRef CAS PubMed.
- C. Schwaferts, V. Sogne, R. Welz, F. Meier, T. Klein, R. Niessner, M. Elsner and N. P. Ivleva, Anal. Chem., 2020, 92, 5813–5820 CrossRef CAS PubMed.
- A. Ashkin, Biophys. J., 1992, 61, 569–582 CrossRef CAS PubMed.
- S. G. Kruglik, F. Royo, J. M. Guigner, L. Palomo, O. Seksek, P. Y. Turpin, I. Tatischeff and J. M. Falcón-Pérez, Nanoscale, 2019, 11, 1661–1679 RSC.
- J. Penders, I. J. Pence, C. C. Horgan, M. S. Bergholt, C. S. Wood, A. Najer, U. Kauscher, A. Nagelkerke and M. M. Stevens, Nat. Commun., 2018, 9, 4256 CrossRef PubMed.
- J. Penders, A. Nagelkerke, E. M. Cunnane, S. v. Pedersen, I. J. Pence, R. C. Coombes and M. M. Stevens, ACS Nano, 2021, 15, 18192–18205 CrossRef CAS PubMed.
- V. K. Sharma, X. Ma, B. Guo and K. Zhang, Chemosphere, 2021, 271 Search PubMed.
- Y. Pang and R. Gordon, Nano Lett., 2012, 12, 402–406 CrossRef CAS PubMed.
- Y. Pang and R. Gordon, Nano Lett., 2011, 11, 3763–3767 CrossRef CAS PubMed.
- G. Volpe, O. M. Maragò, H. Rubinsztein-Dunlop, G. Pesce, A. B Stilgoe, G. Volpe, G. Tkachenko, V. G. Truong, S. N. Chormaic, F. Kalantarifard, P. Elahi, M. Käll, A. Callegari, M. I. Marqués, A. A. R. Neves, W. L. Moreira, A. Fontes, C. L. Cesar, R. Saija, A. Saidi, P. Beck, J. S. Eismann, P. Banzer, T. F. D. Fernandes, F. Pedaci, W. P. Bowen, R. Vaippully, M. Lokesh, B. Roy, G. Thalhammer-Thurner, M. Ritsch-Marte, L. P. García, A. V. Arzola, I P. Castillo, A. Argun, T. M. Muenker, B. E. Vos, T. Betz, I. Cristiani, P. Minzioni, P. J. Reece, F. Wang, D. McGloin, J. C. Ndukaife, R. Quidant, R. P. Roberts, C. Laplane, T. Volz, R. Gordon, D. Hanstorp, J. T. Marmolejo, G. D. Bruce, K. Dholakia, T. Li, O. Brzobohatý, S. H. Simpson, P. Zemánek, F. Ritort, Y. Roichman, V. Bobkova, R. Wittkowski, C. Denz, G. V. P. Kumar, A. Foti, M. G. Donato, P. G. Gucciardi, L. Gardini, G. Bianchi, A. V. Kashchuk, M. Capitanio, L. Paterson, P. H. Jones, K. Berg-Sørensen, Y. F. Barooji, L. B. Oddershede, P. Pouladian, D. Preece, C. B. Adiels, A. C. De Luca, A. Magazzù, D. B. Ciriza, M. A. Iatì and G. A. Swartzlander, J. Phys.: Photonics, 2023, 5, 022501 Search PubMed.
- K. Wang, E. Schonbrun, P. Steinvurzel and K. B. Crozier, Nat. Commun., 2011, 469 CrossRef PubMed.
- E. H. Hill, J. Li, L. Lin, Y. Liu and Y. Zheng, Langmuir, 2018, 34, 13252–13262 CrossRef CAS PubMed.
- Y. Zhang, C. Min, X. Dou, X. Wang, H. P. Urbach, M. G. Somekh and X. Yuan, Light: Sci. Appl., 2021, 10 Search PubMed.
- C. Hong, S. Yang, I. I. Kravchenko and J. C. Ndukaife, Nano Lett., 2021, 21, 4921–4927 CrossRef CAS PubMed.
- S. Jones, D. Andrén, P. Karpinski and M. Käll, ACS Photonics, 2018, 5, 2878–2887 CrossRef CAS.
- M. L. Juan, R. Gordon, Y. Pang, F. Eftekhari and R. Quidant, Nat. Phys., 2009, 5, 915–919 Search PubMed.
- A. A. Al Balushi and R. Gordon, ACS Photonics, 2014, 1, 389–393 Search PubMed.
- Z. Xu, W. Song and K. B. Crozier, ACS Photonics, 2018, 5, 2850–2859 Search PubMed.
- J. C. Ndukaife, A. V. Kildishev, A. G. A. Nnanna, V. M. Shalaev, S. T. Wereley and A. Boltasseva, Nat. Nanotechnol., 2016, 11, 53–59 CrossRef CAS PubMed.
- C. Hong, S. Yang and J. C. Ndukaife, Nat. Nanotechnol., 2020, 15, 908–913 CrossRef CAS PubMed.
-
J. R. Melcher, Electric Fields and oving Media, 1974, vol. 17 Search PubMed.
-
A. Ramos, H. Morgan, N. G. Green and A. Castellanos, J. Phys. D: Appl. Phys., 1998, 31182338 Search PubMed.
- M. Ghorbanzadeh, S. Jones, M. K. Moravvej-Farshi and R. Gordon, ACS Photonics, 2017, 4, 1108–1113 CrossRef CAS.
- M. Braibanti, D. Vigolo and R. Piazza, Phys. Rev. Lett., 2008, 100(10), 108303 CrossRef PubMed.
- O. Syshchyk, D. Afanasenkau, Z. Wang, H. Kriegs, J. Buitenhuis and S. Wiegand, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 129 CrossRef PubMed.
- Y. Lamhot, A. Barak, O. Peleg and M. Segev, Phys. Rev. Lett., 2010, 105(16), 163906 CrossRef PubMed.
- S. A. Putnam, D. G. Cahill and G. C. L. Wong, Langmuir, 2007, 23, 9221–9228 CrossRef CAS PubMed.
- W. P. Wong and K. Halvorsen, Opt. Express, 2006, 14, 12517–12531 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Chuchuan
Hong
a,
Chuchuan
Hong
 a and
Justus C.
Ndukaife
a and
Justus C.
Ndukaife
 *abc
*abc
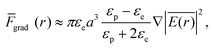
![[F with combining overline]](https://www.rsc.org/images/entities/i_char_0046_0305.gif) grad is the optical gradient force, a is the particle radius,
grad is the optical gradient force, a is the particle radius, 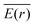 is the position-dependent electric field of the trapping laser, εp, and εm are the complex permittivities of the particle and medium, respectively. Despite the widespread applications of optical tweezers, they suffer some fundamental limitations. Firstly, the optical gradient force is proportional to the third power of the particle radius as described by the dipole approximation. This implies that as the particle size gets smaller, the optical force decreases by orders of magnitude, resulting in higher intensity gradients being required to trap smaller particles. Secondly, optical tweezers are diffraction-limited, which implies that the high laser intensity required to trap sub-100 nm particles can only be achieved by increasing the laser power. The trapping of various particles including biological species and nano plastics down to the 100 nm range can be achieved with laser powers between a few tens to a few hundred mW.7,10–12 However, stable trapping of nanoscopic particles in the sub-50 nm range requires several hundred mW7, which results in degradation and damage of the particles over short time spans.1In situ analysis of nanoscopic particles is of great interest in biological and environmental sciences. In biological sciences, the trapping of small extracellular vesicles in the sub-100 nm range is desirable to investigate the heterogeneity of these species for diagnostic and drug delivery purposes.2,4,6 The investigation of nano plastic pollution in oceans resulting from the degradation of industrially produced plastic debris has become of great importance recently, as this poses a public health threat.13In situ optical trapping and Raman-enabled chemical characterization of nano plastics down to the 50 nm range was recently demonstrated using laser powers exceeding 100 mW,7 enabling unambiguous discrimination between nano plastics and organic matter. Previous approaches to characterize nano plastics, such as TEM/SEM, fluorescent microscopy, and nanoparticle tracking analysis7 provide no information about the chemical composition of these nano plastics. Thus, it is imperative to devise methods for non-destructive low-power trapping of nanoscopic polymer particles in the sub-50 nm range.
is the position-dependent electric field of the trapping laser, εp, and εm are the complex permittivities of the particle and medium, respectively. Despite the widespread applications of optical tweezers, they suffer some fundamental limitations. Firstly, the optical gradient force is proportional to the third power of the particle radius as described by the dipole approximation. This implies that as the particle size gets smaller, the optical force decreases by orders of magnitude, resulting in higher intensity gradients being required to trap smaller particles. Secondly, optical tweezers are diffraction-limited, which implies that the high laser intensity required to trap sub-100 nm particles can only be achieved by increasing the laser power. The trapping of various particles including biological species and nano plastics down to the 100 nm range can be achieved with laser powers between a few tens to a few hundred mW.7,10–12 However, stable trapping of nanoscopic particles in the sub-50 nm range requires several hundred mW7, which results in degradation and damage of the particles over short time spans.1In situ analysis of nanoscopic particles is of great interest in biological and environmental sciences. In biological sciences, the trapping of small extracellular vesicles in the sub-100 nm range is desirable to investigate the heterogeneity of these species for diagnostic and drug delivery purposes.2,4,6 The investigation of nano plastic pollution in oceans resulting from the degradation of industrially produced plastic debris has become of great importance recently, as this poses a public health threat.13In situ optical trapping and Raman-enabled chemical characterization of nano plastics down to the 50 nm range was recently demonstrated using laser powers exceeding 100 mW,7 enabling unambiguous discrimination between nano plastics and organic matter. Previous approaches to characterize nano plastics, such as TEM/SEM, fluorescent microscopy, and nanoparticle tracking analysis7 provide no information about the chemical composition of these nano plastics. Thus, it is imperative to devise methods for non-destructive low-power trapping of nanoscopic polymer particles in the sub-50 nm range.
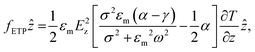

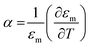 and
and 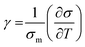 , with values −0.004 K−1 and −0.02 K−1, respectively.25 The total body force F in the system is given by the sum of buoyancy convection and ETP body forces. The fluid velocity field is then computed by solving the incompressible Navier Stokes equation given by,
, with values −0.004 K−1 and −0.02 K−1, respectively.25 The total body force F in the system is given by the sum of buoyancy convection and ETP body forces. The fluid velocity field is then computed by solving the incompressible Navier Stokes equation given by,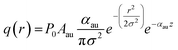


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 viewers world-wide. His other honors include NSF CAREER award, Chancellor's award for excellence in research, the Year 2017 Prize in Physics by the Dimitris N. Chorafas Foundation, the Purdue College of Engineering Outstanding Research Award, NSBE Golden Torch Award, Best Paper Award at the ASME conference, and a Carnegie African Diaspora Fellowship Award.
000 viewers world-wide. His other honors include NSF CAREER award, Chancellor's award for excellence in research, the Year 2017 Prize in Physics by the Dimitris N. Chorafas Foundation, the Purdue College of Engineering Outstanding Research Award, NSBE Golden Torch Award, Best Paper Award at the ASME conference, and a Carnegie African Diaspora Fellowship Award.



