Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Control of the structure and morphology of polypeptide/surfactant spread films by exploiting specific interactions†
Javier
Carrascosa-Tejedor
 *ab,
Laura M.
Miñarro
a,
Marina
Efstratiou
b,
Imre
Varga
*ab,
Laura M.
Miñarro
a,
Marina
Efstratiou
b,
Imre
Varga
 c,
Maximilian W. A.
Skoda
c,
Maximilian W. A.
Skoda
 d,
Philipp
Gutfreund
d,
Philipp
Gutfreund
 a,
Armando
Maestro
a,
Armando
Maestro
 ef,
M. Jayne
Lawrence
ef,
M. Jayne
Lawrence
 *b and
Richard A.
Campbell
*b and
Richard A.
Campbell
 *b
*b
aInstitut Laue-Langevin, 71 Avenue des Martyrs, CS20156, 38042 Grenoble, France. E-mail: carrascosa-tejedor@ill.fr
bDivision of Pharmacy and Optometry, Faculty of Biology, Medicine and Health, University of Manchester, Oxford Road, Manchester M13 9PT, UK. E-mail: jayne.lawrence@manchester.ac.uk; richard.campbell@manchester.ac.uk
cInstitute of Chemistry, Eötvös Loránd University, 112, Budapest H-1518, Hungary
dISIS Neutron and Muon Source, Rutherford Appleton Laboratory, Harwell Campus, Didcot OX11 0QX, UK
eIKERBASQUE—Basque Foundation for Science, Plaza Euskadi 5, Bilbao, 48009, Spain
fCentro de Física de Materiales (CSIC, UPV/EHU) - Materials Physics Center MPC, Paseo Manuel de Lardizabal 5, E-20018 San Sebastián, Spain
First published on 12th June 2023
Abstract
We demonstrate control of the structure and morphology of polypeptide/surfactant films at the air/water interface as a function of the maximum compression ratio of the surface area, exploiting a recently developed film formation mechanism that requires minimal quantities of materials involving the dissociation of aggregates. The systems studied are poly(L-lysine) (PLL) or poly(L-arginine) (PLA) with sodium dodecyl sulfate (SDS), chosen because the surfactant (i) interacts more strongly with the latter polypeptide due to the formation of hydrogen bonds between the guanidinium group and its oxygen atoms, and (ii) induces bulk β-sheet and α-helix conformations of the respective polypeptides. The working hypothesis is that such different interactions may be used to tune the film properties when compressed to form extended structures (ESs). Neutron reflectometry reveals that application of a high compression ratio (4.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) results in the nanoscale self-assembly of ESs containing up to two PLL-wrapped SDS bilayers. Brewster angle microscopy provides images of the PLL/SDS ESs as discrete regions on the micrometre scale while additional linear regions of PLA/SDS ESs mark macroscopic film folding. Ellipsometry demonstrates high stability of the different ESs formed. The collapse of PLL/SDS films upon compression to a very high ratio (10
1) results in the nanoscale self-assembly of ESs containing up to two PLL-wrapped SDS bilayers. Brewster angle microscopy provides images of the PLL/SDS ESs as discrete regions on the micrometre scale while additional linear regions of PLA/SDS ESs mark macroscopic film folding. Ellipsometry demonstrates high stability of the different ESs formed. The collapse of PLL/SDS films upon compression to a very high ratio (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is irreversible due to the formation of solid domains that remain embedded in the film upon expansion while that of PLA/SDS films is reversible. These findings demonstrate that differences in the side group of a polypeptide can have a major influence on controlling the film properties, marking a key step in the development of this new film formation mechanism for the design of biocompatible and/or biodegradable films with tailored properties for applications in tissue engineering, biosensors and antimicrobial coatings.
1) is irreversible due to the formation of solid domains that remain embedded in the film upon expansion while that of PLA/SDS films is reversible. These findings demonstrate that differences in the side group of a polypeptide can have a major influence on controlling the film properties, marking a key step in the development of this new film formation mechanism for the design of biocompatible and/or biodegradable films with tailored properties for applications in tissue engineering, biosensors and antimicrobial coatings.
Introduction
Polypeptides are biocompatible and biodegradable polymers composed of a repeating sequence of amino acids linked by peptide bonds. They have attracted attention as promising biomaterials in numerous studies since they exhibit unique properties such as designability, biocompatibility, susceptibility to proteolysis, tuned hydrophilicity/hydrophobicity, inherent chirality and the ability to self-assemble in secondary structures (α-helices or β-sheets).1 The latter property influences their size, rigidity, and function and facilitates the formation of well-defined supramolecular assemblies.2,3 Indeed, the secondary structure of polypeptides can determine their antibacterial activity,4 the stiffness of a gel,5 or the morphology of self-assembled vesicles.6 This is a unique property of polypeptides that many widely studied synthetic polymers such as poly(sodium styrene sulfonate) (NaPSS),7,8 poly(ethyleneimine) (PEI)9,10 or poly(diallyl dimethyl ammonium chloride) (Pdadmac)11,12 do not present. There are 20 different natural amino acids and a wide variety of non-natural ones that offer the possibility to build polypeptides with a rich chemical diversity using the facile ring-opening polymerization method.13 The possibility to modify polypeptides including functional groups such as sugar moieties, reactive handles, charged species or surface active groups allows one to design a large number of different biomaterials.14 In addition, they are versatile as they can be designed to respond to various stimuli (temperature, pH, ionic strength, light, enzymatic/biological or magnetic), allowing control of their properties and structure.13Polypeptides have been widely used for the creation of multilayers in applications such as tissue engineering15 or drug delivery,16 both consisting exclusively of polypeptides17 and in conjunction with other polyelectrolytes.18 They have also been used to tune interactions with non-ionic surfactants,19 form polyplexes with nucleic acids in gene delivery,20 and polypeptide/surfactant (PP/S) complexes.21 However, despite significant advances made during the last decades in the field of oppositely charged polyelectrolyte/surfactant (P/S) mixtures at the air/water interface, examples of work to tune and develop PP/S film properties are scarce.22,23 Furthermore, the properties of P/S films cannot be directly extrapolated to PP/S films since, in addition to the electrostatic interactions, polypeptides can adopt secondary structures and form multiple hydrogen bonds. Previously, the equilibrium24 and dynamic25 properties of poly-L-lysine (PLL)/sodium dodecyl sulfate (SDS) mixtures were studied at the air/water interface. It was suggested that PLL adopts a β-sheet conformation at the interface, although this was inferred only from surface tension measurements. The application of neutron reflectometry (NR) later allowed direct quantification of the amounts of PLL and SDS at different pH values.26 Differences between the results obtained by surface tensiometry and NR were rationalised in terms of different polypeptide conformations that affected only the surface tension values.
Recently, we have demonstrated precise control over the formation of extended structures (ESs) in PLL/SDS films at the air/water interface using a Langmuir trough with respect to compression or expansion of the surface area.27 The structures of these films consist of a surfactant monolayer, a layer of polypeptide bound to the surfactant headgroups (together, hereon in, referred to as the ‘surface monolayer’) as well as discrete patches either of surfactant bilayer wrapped by polypeptide or bound surfactant hemimicelles; the two possibilities were not distinguished from the experimental data. Reversible control of the quantity of a single additional layer of ESs using the Langmuir trough barriers was demonstrated up to a coverage of 18.8 ± 0.7%. In this work, PLL/SDS films were created using a film formation methodology,28 which was recently developed using P/S mixtures by exploiting the dissociation and interfacial spreading of material from aggregates that had self-assembled in solution due to lack of colloidal stability of formed complexes.29 The spreading of these aggregates at the air/water interface results in their dissociation, and the film remains kinetically trapped due to the entropy of counterion release, which means that films can be formed using minimal quantities of materials, offering potential economic or environmental advantages over gel films formed in mixed P/S systems.30 Possibilities to trigger the formation of ESs through changing the charge and/or structure of the aggregates, and tune the resulting interfacial morphology through successive spreading of aggregates or compression of the surface area, were also demonstrated.31 It has also been shown in recent work that the rigidity of the polyelectrolyte plays an important role in the formation of ESs in adsorbed layers from mixed systems.32 To the best of the authors’ knowledge, these are the only examples of investigations in the literature on adsorbed layers or trapped films of oppositely charged PP/S mixtures at the air/water interface. Thus, this work provides a basis for the future development of PP/S films spread using the recently developed aggregate dissociation mechanism at the air/water interface, which has not been broadly exploited to date.
Given the multiple applications and all the above-mentioned characteristics that make polypeptides unique from other polyelectrolytes, the study of PP/S films at the air/water interface is of great interest, especially for applications where biocompatibility and biodegradability are essential. The present work involves a comparison of films involving different PP/S systems: PLL/SDS and poly-(L-arginine) (PLA)/SDS. The molecular structures of PLL, PLA and SDS are shown in Fig. 1. While PLL has a pKa value of 9,33 PLA has a pKa value of 13.8.34 As a result, both polypeptides are essentially fully charged in the experiments conducted in this work. Consequently, they exhibit strong electrostatic interactions with oppositely charged molecules or surfaces. Lysine side chains terminate in an ammonium group in which the charge is localized, while arginine side chains terminate in a guanidinium group where the charge is delocalized within three ammonium groups. Although they present a similar chemical structure, the interaction of the ammonium group of PLL with SDS is purely electrostatic, yet the guanidinium group can form additional hydrogen bonds that make the PLA/SDS interaction stronger.35 Thus, specific PP/S headgroup interactions influence the resulting properties of the mixtures. Indeed, it has been shown that SDS induces the β-sheet conformation of PLL24,26,36–39 and the α-helix conformation of PLA38–41 in solution. Furthermore, it was shown that the secondary structure of polypeptides when forming complexes in solution is maintained when deposited as multilayers on solids,42 which suggests that these differences may mean that PP/S films containing ESs may exhibit distinct physicochemical properties.
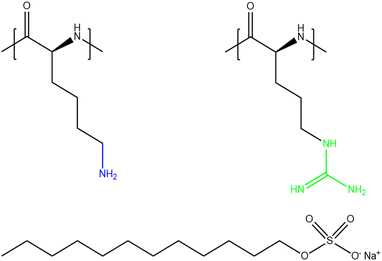 | ||
| Fig. 1 Chemical structures of PLL (left), PLA (right) and SDS (bottom). The ammonium group of PLL and the guanidinium group of PLA are highlighted in blue and green, respectively. | ||
The aim of the present work is to resolve differences in the structure and morphology of PLL/SDS and PLA/SDS films spread at the air/water interface using the recently developed aggregate dissociation mechanism with respect to changing maximum coverage of ESs. In this respect, the coverage of ESs is tuned by changing the minimum value of the surface area, A, upon film compression to reach different maximum compression ratios, defined as A0/A, where A0 is the initial surface area when the film is spread. Through the use of biocompatible materials, the scope is to understand how specific PP/S interactions may be tuned in the future development of new films for biomedical applications. An approach is used to manipulate films to different maximum compression ratios to determine if a higher coverage of ESs than previously observed can be obtained, and if any increase in coverage affects the film properties. The underlying hypothesis is that as these two PP/S systems adopt distinct secondary structures in the bulk, there may be distinct physicochemical properties of their spread films when compressed to produce ESs. It is hoped that this work will help us to understand better the influence on spread film properties of the polyelectrolyte rigidity,32 where the hierarchy is β-sheet > α-helix > random coil. The application of a powerful combination of reflectometry techniques – neutron reflectometry (NR), ellipsometry and Brewster angle microscopy (BAM) – allows us to resolve key processes that determine the dynamic behaviour of these PP/S films with respect to different lengths on the micrometre- and nanoscale.
Materials and methods
Materials
15–30 kDa (∼176 amino acids per molecule) (poly-(L-lysine) hydrobromide and 5–15 kDa (∼64 amino acids per molecule) poly-L-arginine hydrochloride powders, sodium dodecyl sulfate, sodium dodecyl-d25 sulfate (d-SDS), ethanol (≥99.8%) and D2O were purchased from Sigma Aldrich. PLL, PLA, d-SDS and D2O were used as received. Polydisperse polypeptide samples were used to mimic those used in commercial applications. SDS was recrystallized twice in ethanol followed by drying under vacuum. Ultra-pure water was generated by passing deionized water through a Milli-Q unit (total organic content ≤4 ppb, resistivity = 18 MΩ cm).Sample preparation
PLL and PLA stock solutions at 1000 ppm were prepared by dissolving 5 mg of each respective powder in 5 mL of H2O, then rotating the vial for a few hours, before 200 ppm solutions were prepared by diluting 1 mL of each stock solution to 5 mL. A stock solution of SDS 10 mM was prepared in H2O and diluted to the required concentration for each experiment. Note that the polypeptide concentrations are expressed in ppm w/v.Fresh mixtures of PP/S aggregates were always prepared immediately before use to limit the growth of large aggregates prior to the experiment. First, an aliquot of 200 ppm PLL or PLA solution was poured into a clean vial containing a magnetic stirrer. Then, an aliquot of the same volume of SDS was rapidly added to the vial with stirring maintained for 3–5 s. Thus, the concentrations of polypeptide and surfactant in the final solution were half of those in the aliquots.
ζ-Potential
ζ-Potential measurements of PP/S mixed solutions were carried out using a Zetasizer Nano ZS90 and the M3-PLAS technique (Malvern Instruments Ltd, U.K.) to estimate the charge of the aggregates. The charge of the aggregates was determined at a constant polypeptide concentration of 100 ppm as a function of the bulk SDS concentration in the ranges 0.4–1.0 mM and 0.2–1.0 mM for PLL and PLA, respectively.Langmuir technique
Use of a Langmuir trough allows the study of the dynamic behaviour of the spread PP/S films during changes of A. The troughs used have two barriers that move symmetrically to record surface pressure (Π)–A isotherms during consecutive compression/expansion cycles and stability measurements of the films over time at a constant area. Troughs of different sizes were used according to the requirements of the different setups of the applied techniques (NR, ellipsometry or BAM). The isotherms are presented as a function of A/A0 (the inverse of the compression ratio) in order to compare the data obtained using different troughs. The Wilhelmy plate method has been used to record the variation of Π defined as the difference between the surface tension of pure water and that of the film, using a filter paper plate.The different troughs used in the present work are Kibron G1 and G2 (Finland) and Nima 721BAM (UK). A volume of 1130 μl of 100 ppm PLL with 0.80 mM SDS or 1500 μl of 100 ppm PLA with 0.62 mM SDS was used to create the initial films in the experiments done with the G1 trough. The amount spread was chosen to obtain a surface monolayer at Π = 5–10 mN m−1, which allows to study the surface monolayer/ESs transitions during successive cycles. The volume spread and the speed of the barriers were scaled to be consistent between the areas of the different troughs used. The trough and barriers were carefully cleaned with Decon 90 detergent, ethanol and water before filling them with Milli-Q water.
Neutron reflectometry
NR is a widely used technique in the study of interfaces that allows the composition and structure perpendicular to the interface on the nanoscale to be determined accurately.43–45 In an NR experiment, a neutron beam is incident onto the interface under study at grazing incident angles. Specular reflectometry occurs when the angle of incidence, θ, and the angle of reflection are equal. The reflectivity, R, is defined as the ratio between the reflected and the incident intensity and is recorded as a function of the momentum transfer normal to the interface, Qz, defined as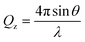 | (1) |
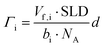 | (2) |
Specular NR measurements were performed on the time-of-flight reflectometer INTER at the ISIS Pulsed Neutron and Muon Source (Didcot, UK) to resolve the structure of PLL/SDS films at a high compression ratio. Two different grazing incident angles of 0.8° and 2.3° and a wavelength range of λ = 1.5–16 Å were used. The absolute reflectivity was calibrated using a pure D2O subphase. Three different isotopic contrasts were recorded: (1) d-SDS/ACMW (air contrast matched water, a mixture of 8.1% v/v D2O in H2O, SLD = 0 Å−2), in which the scattering is dominated by the surfactant and is essential for determining the coverage of the surfactant monolayer and the ESs; (2) d-SDS/D2O, which allows determination of the amount of PLL in the film as the SLDs of d-SDS (6.69 × 10−6 Å−2) and D2O (6.36 × 10−6 Å−2) are close in value; and (3) h-SDS/D2O, in which the scattering is dominated by the subphase and therefore it is very sensitive to the penetration of h-SDS to the ESs. The values of b, SLD and Vm of each of the components, information about the model applied to fit the data, and details of the fitting procedure can be found in section 1 of the ESI.† The data were analysed using the Motofit package and the different contrasts were co-refined.46 The general procedure of fitting the data with different isotopic contrasts using a structural model with the minimum number of layers required has been followed.
Ellipsometry
Ellipsometry is an optical technique based on the polarization changes that light undergoes when it is reflected at an interface. These changes are defined by the ratio of the overall Fresnel reflectivity coefficients of the parallel (rP) and the perpendicular (rS) components of the electric field, whose relative amplitude and phase change by different amounts. In experimental measurements of ellipsometry, the ellipsometric angles Δ, defined as the phase shift between the two components, and Ψ, where tan Ψ is the amplitude ratio, can be directly obtained.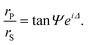 | (3) |
In contrast to studies at solid/liquid interfaces that can be tuned to provide sensitivity of Ψ and Δ to the density and thickness of interfacial material,47 the application of ellipsometry in the study of thin transparent films at the air/water interface offers poor sensitivity of Ψ to the film properties and often only values of Δ are interpreted.28,48,49 The values of dΔ = ΔPP/S (for the PP/S film) − Δwater (for pure water which approximately accounts for the contribution of surface roughness) are reported as an approximate measure of the total surface amount of the PP/S films. The relatively small probed area (∼1 mm2) and the fast acquisition time (∼5 s) make ellipsometry an ideal technique to do time/spatial resolved experiments as temporal fluctuations in the signal can reveal the presence of inhomogeneities in the interface on the micrometer scale.28,48,50
The ellipsometry data were recorded using two different ellipsometers coupled to a Langmuir trough. A Beaglehole Picometer Light ellipsometer (New Zealand) equipped with a He–Ne laser with a wavelength of λ = 632.8 nm was used to record the variation of dΔ during compression/expansion cycles at an angle of incidence of 51° and a data acquisition rate of 0.2 Hz. An Accurion EP4 ellipsometer (Germany) equipped with a blue diode laser with a wavelength of λ = 489.2 nm was used to record the stability measurements presented in section 2 of the ESI† at an angle of incidence of 50° and a data acquisition rate of 0.1 Hz.
Brewster angle microscopy
BAM is a direct and non-invasive imaging technique used to characterize the in-plane organization of fluid films at the air/water interface and the presence of lateral inhomogeneities.51 When p-polarized light is directed at the Brewster angle (∼53.1°) onto the air/water interface, the reflectivity is almost zero. The presence of a thin film at the air/water interface whose refractive index is different from that of water causes the reflection of the incident light allowing visualization and imaging of the film under study. Any additional material that thickens the film will contribute to the reflected light. Thus, a dark image is observed when light is directed onto the air/water interface or a homogenous layer, yet the presence of inhomogeneous patches of ESs will be observed as brighter regions. An Accurion Nanofilm EP3 Brewster angle microscope (Germany) equipped with a Nd:YAG laser (λ = 532 nm), a 10× objective and a CCD detector was used at an angle of incidence θ = 53.1°. Background was not subtracted.Results and discussion
A characterization of the charge of PP/S aggregates in mixed solutions was carried out first with a fixed polypeptide concentration of 100 ppm as a function of the bulk SDS concentration. Fig. 2 shows the results obtained for the PLL/SDS and the PLA/SDS systems. The variation of the ζ-potential as function of the bulk SDS concentration follows a similar trend as that of other P/S systems.28,29,52 The increase of the concentration of SDS results in a transition from positive to negative surface charge density. The concentration of surfactant needed to produce neutral PLL/SDS or PLA/SDS aggregates is 0.63 and 0.57 mM, respectively. The experimental values are close to the equivalent monomer concentration of 100 ppm of the polypeptides of 0.48 and 0.52 mM, respectively, evidencing strong binding between the components at the point of charge neutrality. Nevertheless, the lower excess of SDS required to neutralize PLA/SDS aggregates (0.05 mM) compared to PLL/SDS aggregates (0.15 mM) suggests that the interaction of SDS with PLA is even stronger than with PLL. The PP/S interaction strength depends on the electrostatic interactions between the charged groups and the hydrophobic interactions between surfactant chains. Since the same surfactant is used, the differences observed might arise from different specific PP/S interactions. The stronger affinity of SDS to PLA found in this work is in agreement with isothermal titration calorimetry results where it was observed that the enthalpy upon SDS binding to PLA and PLL was −15.4 ± 1 and −6.9 ± 1 kJ mol−1, respectively.53 In addition, it has also been demonstrated that the electrophoretic mobility of arginine in sodium sulfate solutions was lower than that of lysine.35 These results are also in agreement with the molecular dynamics simulations, where a greater affinity of sulfate to the guanidinium group was predicted and was attributed to the planar geometry of the group allowing hydrogen bonding with the two sulfate oxygen atoms. It may be noted that the strong binding at the point of charge neutrality observed in both systems is similar in behaviour to other systems previously reported, such as Pdadmac/SDS52 or PEI/SDS,54 but it contrasts sharply with that of NaPSS/dodecyltrimethylammonium bromide (DTAB),28 where for a bulk polyelectrolyte concentration of 100 ppm, the excess of surfactant needed to neutralize the aggregates is 5.5 mM. These differences may be related to the ability of the polyelectrolyte to wrap surfactant aggregates, which would be significantly influenced by its stiffness,55–57 and it has also been found that more rigid polyelectrolytes form denser films.7 Thus, the experimental charge neutrality may be an important parameter when assessing the stability of formed ESs in P/S or PP/S films, given that they were shown to be stable over time for PLL/SDS films with strong bulk binding27 and unstable for NaPSS/DTAB films with weaker bulk binding.31 Furthermore, it has been recently demonstrated that the rigidity of the polymer plays an important role in the stabilization of ESs in adsorbed layers in mixed P/S systems.32 Although the compensation of interfacial charges was identified as the main driving force for the formation of ESs, the possibility to control the 2D to 3D nature of the film by increasing the polyelectrolyte rigidity was demonstrated. The low binding efficiency of DTAB to NaPSS at the point of charge neutrality could be related also with its low persistence length (∼1 nm), which may explain the difficulty to form stable ESs when this system is used.31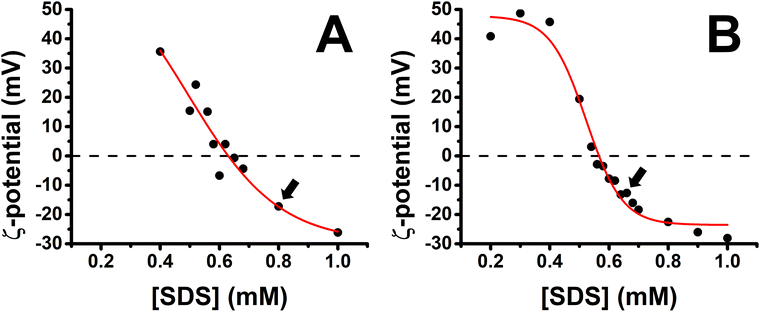 | ||
| Fig. 2 Variation of the ζ-potential of (A) PLL/SDS (reproduced from ref. 27) and (B) PLA/SDS aggregates as a function of the concentration of SDS. The black circles represent the experimental data points and the red line a sigmoidal fit. The black dashed lines indicate neutral charge. The standard error in the ζ-potential values was found to be around 10%, smaller than the symbol size. Black arrows indicate the concentrations used to create the films. | ||
Bulk SDS concentrations of 0.80 and 0.62 mM were chosen to create the spread PLL/SDS and PLA/SDS films, respectively, because aggregates overcharged with an excess of surfactant have been shown to be efficient in forming ESs in previous studies.27,31 It is worth noting that the release of counterions to the bulk results in a very dilute electrolyte concentration (∼30 μM) that is not expected to influence the spread film properties significantly. Indeed, spread films of the NaPSS/DTAB system exhibit persistent loss of material over time at elevated ionic strength of 100 mM,31 for which there is no evidence from the ellipsometry data of either PP/S system in Fig. 3.
We reported previously the structure of PLL/SDS films at a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio using NR and a coverage of 19% of ESs was shown.27 Nevertheless, it was not clear whether there was an additional PLL layer underneath the ESs as the inclusion of a low coverage of it in the model resulted in equivalent model fits to the experimental data. The structure of PLL/SDS films at a 4.5
1 compression ratio using NR and a coverage of 19% of ESs was shown.27 Nevertheless, it was not clear whether there was an additional PLL layer underneath the ESs as the inclusion of a low coverage of it in the model resulted in equivalent model fits to the experimental data. The structure of PLL/SDS films at a 4.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio is studied here using NR in the hope that increased coverage of any PLL layer that may be present in the ESs would allow it to be clearly resolved. If we assume that all of the surfactant expelled from the surface monolayer is incorporated in the surfactant bilayer structure, resolved for PLL/SDS films in our recent work,27 coverage of the ESs should in principle reach 100% at a 4
1 compression ratio is studied here using NR in the hope that increased coverage of any PLL layer that may be present in the ESs would allow it to be clearly resolved. If we assume that all of the surfactant expelled from the surface monolayer is incorporated in the surfactant bilayer structure, resolved for PLL/SDS films in our recent work,27 coverage of the ESs should in principle reach 100% at a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio. Therefore, this approach tests the hypothesis that if all the material remains bound to the film upon further compression, a second layer of ESs would form beyond this compression ratio.
1 compression ratio. Therefore, this approach tests the hypothesis that if all the material remains bound to the film upon further compression, a second layer of ESs would form beyond this compression ratio.
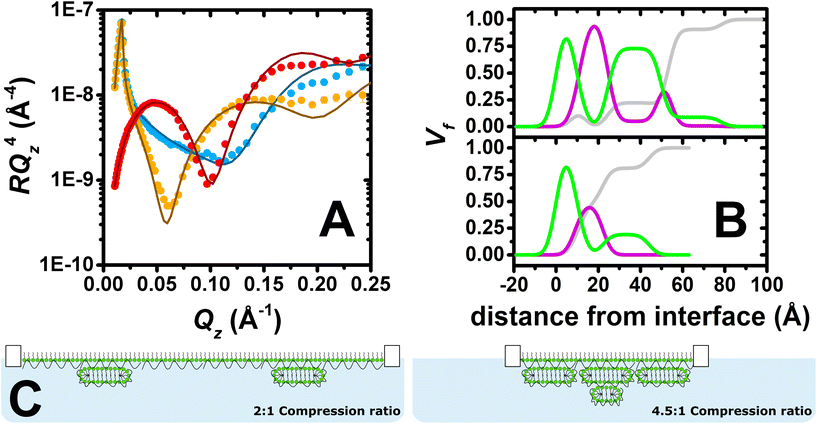
Fig. 3A shows the neutron reflectivity profiles measured and the model fits obtained from the analysis. The sharp and clear Kiessig fringes in the reflectivity profiles indicate the presence of a multilayered structure. Further evidence for the lateral domains of ESs on the micrometre scale includes a slight indication of off-specular neutron scattering and attenuation of the total reflection of D2O by 4%. From the position of the minimum in the d-SDS/ACMW contrast (Qz = 0.1 Å−1), the presence of ESs with a length scale around 60 Å can be deduced. An optimised model of 6 stratified layers was found to be necessary to fit the data: (1) SDS tails, (2) SDS headgroups with PLL and solvent, (3) PLL, (4) PLL/SDS ESs with solvent, (5) PLL and (6) PLL/SDS ESs with solvent. Given the complexity of the structure and the large number of parameters to be determined, in the NR fit, the roughness was set to a value of 3.5 consistent with the presence of capillary waves and surface tension. Nevertheless, it is important to observe that when this parameter was unconstrained during the fitting process, the other parameters fitted to the same values within the error, and the roughness value increased to 5 Å, resulting in a 23% reduction in χ2. We will return to this point later. More details about the model, together with a table of optimised fitting parameters, can be found in section 1 of the ESI.† The analysis confirms our hypothesis that the compression of the film beyond a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 leads to the formation of a second layer of ESs. Furthermore, compatible with a physical picture where polyelectrolyte screens the oppositely charged headgroups in adjacent surfactant bilayers, a PLL layer was required between the two layers of ESs, as described in section 2 of the ESI.† An additional layer of PLL beneath the second layer of ESs did not, however, improve the quality of the fit, most likely due to its low coverage.
1 leads to the formation of a second layer of ESs. Furthermore, compatible with a physical picture where polyelectrolyte screens the oppositely charged headgroups in adjacent surfactant bilayers, a PLL layer was required between the two layers of ESs, as described in section 2 of the ESI.† An additional layer of PLL beneath the second layer of ESs did not, however, improve the quality of the fit, most likely due to its low coverage.
Fig. 3B shows the volume fraction profiles corresponding to the analysis for both the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (bottom) and 4.5
1 (bottom) and 4.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (top) compression ratios. The high volume-fraction of PLL and SDS in the surface monolayer as well as in the first layer of ESs (i.e. second peak of surfactant in green) in both cases evidences the presence of a very compact film at the interface. In the case of the 4.5
1 (top) compression ratios. The high volume-fraction of PLL and SDS in the surface monolayer as well as in the first layer of ESs (i.e. second peak of surfactant in green) in both cases evidences the presence of a very compact film at the interface. In the case of the 4.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio, however, there is an additional ‘tail’ of surfactant that is attributed to additional layer of ESs. It should be further noted that absence of a Bragg diffraction peak in any of the reflectivity profiles shows that P/S aggregates with an internal liquid crystalline structure were not resolved to have remained trapped in the spread film.58 Thus, it can be concluded that high compression of the PLL/SDS spread film results in a highly compact arrangement of the surface monolayer as well as the formation of an additional layer of ESs below the first layer of ESs once it reaches maximum coverage. Fig. 3C shows a two-dimensional schematic illustration of the structures of PLL/SDS films at 2
1 compression ratio, however, there is an additional ‘tail’ of surfactant that is attributed to additional layer of ESs. It should be further noted that absence of a Bragg diffraction peak in any of the reflectivity profiles shows that P/S aggregates with an internal liquid crystalline structure were not resolved to have remained trapped in the spread film.58 Thus, it can be concluded that high compression of the PLL/SDS spread film results in a highly compact arrangement of the surface monolayer as well as the formation of an additional layer of ESs below the first layer of ESs once it reaches maximum coverage. Fig. 3C shows a two-dimensional schematic illustration of the structures of PLL/SDS films at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 4.5
1 and 4.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratios; illustrations are merely representative and are not to scale.
1 compression ratios; illustrations are merely representative and are not to scale.
Having demonstrated for the first time the ability to increase the coverage and the number of layers of ESs by increasing the compression ratio of a spread PP/S film, we turn in the following sub-sections to the dynamic behaviour of PLL/SDS and PLA/SDS films during compression/expansion cycles as a function of the maximum compression ratio. First, the results of PLL/SDS films using a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio already published27 are compared with ones obtained on PLA/SDS films. Subsequently, data from samples involving two higher maximum compression ratios of 5
1 compression ratio already published27 are compared with ones obtained on PLA/SDS films. Subsequently, data from samples involving two higher maximum compression ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 10
1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are described. Thus, both the influence of (i) specific polypeptide/headgroups interactions and (ii) the maximum compression ratio on the properties of the films will be considered.
1 are described. Thus, both the influence of (i) specific polypeptide/headgroups interactions and (ii) the maximum compression ratio on the properties of the films will be considered.
Maximum compression ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1
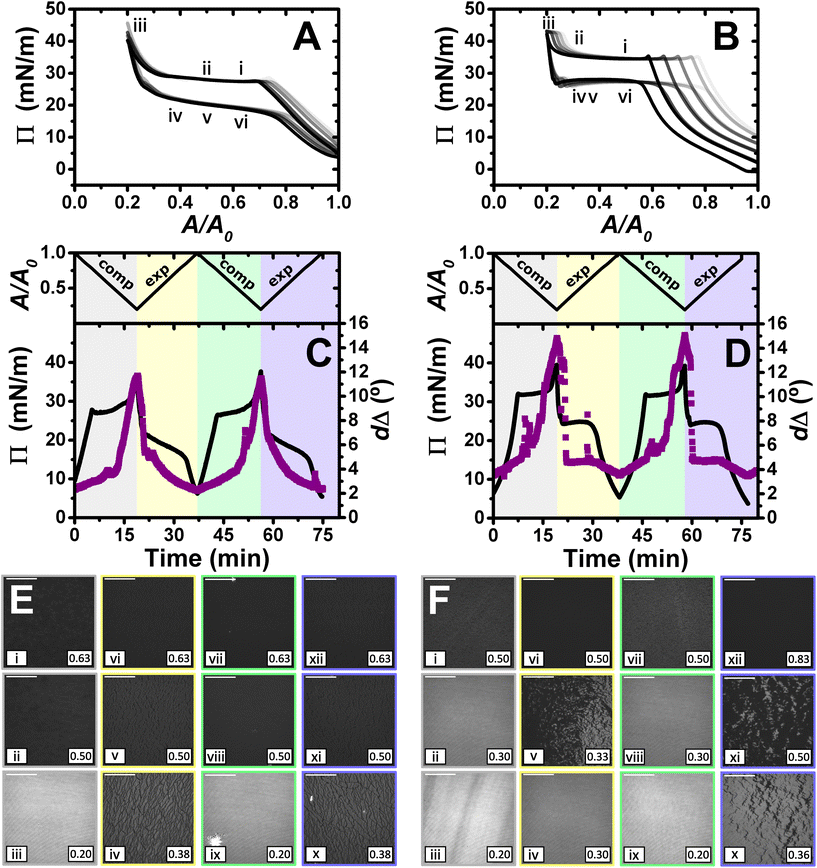
Fig. 4 shows the results obtained in the study of the dynamic behaviour of PLL/SDS and PLA/SDS films during consecutive compression/expansion cycles using the Langmuir trough, ellipsometry and BAM up to a maximum compression ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It is worth noting that considering the volume and concentration of SDS in the spreading aliquot and the volume of water in the Langmuir trough, the final SDS concentration in both PP/S systems is less than 7 μM, where SDS alone still presents negligible surface activity,59 hence, the interfacial properties measured are determined by the spread film. Through application of multiple experimental techniques previously,27 the Π–A isotherms of PLL/SDS films can be described as follows. The data are characterized by three different regions (Fig. 4A). First, compression of the film leads to an increase in the number of surfactant molecules per unit area in the surface monolayer, which results in a continuous increase in Π (from state i through state ii to state iii). Second, further compression of the film leads to its collapse as shown by the constant collapse pressure, Πc, at ∼28 mN m−1: this is attributed to retention of the most compact state of the surface monolayer and ejection of surplus material to ESs upon further compression of the film (beyond state iii through state iv to state v).27,31 Third, expansion of the film is characterized by a large hysteresis in Π, the presence of a pseudo–plateau and the merging of the isotherm on expansion into the isotherm on compression at large A/A0, consistent with the reincorporation of material back into the surface monolayer yet with a kinetic barrier (through state vi). The macroscopic properties of the film are reproducible over successive cycles. Consistent with the above description, the values of dΔ from ellipsometry continue to increase beyond the surface pressure collapse (Fig. 4C), and it was data from NR that allowed us to confirm not only that ΓSDS exceeds that in an SDS monolayer at ×2 its critical micelle concentration (cmc),60 but that the coverage of the surface monolayer remains constant and the excess material is ejected into the ESs. BAM images (Fig. 4E) also support this physical picture as the morphologies shown contain discrete regions on the μm-scale that grow in number with increasing compression only at higher compression ratios than the surface pressure collapse (states iv and v).
1. It is worth noting that considering the volume and concentration of SDS in the spreading aliquot and the volume of water in the Langmuir trough, the final SDS concentration in both PP/S systems is less than 7 μM, where SDS alone still presents negligible surface activity,59 hence, the interfacial properties measured are determined by the spread film. Through application of multiple experimental techniques previously,27 the Π–A isotherms of PLL/SDS films can be described as follows. The data are characterized by three different regions (Fig. 4A). First, compression of the film leads to an increase in the number of surfactant molecules per unit area in the surface monolayer, which results in a continuous increase in Π (from state i through state ii to state iii). Second, further compression of the film leads to its collapse as shown by the constant collapse pressure, Πc, at ∼28 mN m−1: this is attributed to retention of the most compact state of the surface monolayer and ejection of surplus material to ESs upon further compression of the film (beyond state iii through state iv to state v).27,31 Third, expansion of the film is characterized by a large hysteresis in Π, the presence of a pseudo–plateau and the merging of the isotherm on expansion into the isotherm on compression at large A/A0, consistent with the reincorporation of material back into the surface monolayer yet with a kinetic barrier (through state vi). The macroscopic properties of the film are reproducible over successive cycles. Consistent with the above description, the values of dΔ from ellipsometry continue to increase beyond the surface pressure collapse (Fig. 4C), and it was data from NR that allowed us to confirm not only that ΓSDS exceeds that in an SDS monolayer at ×2 its critical micelle concentration (cmc),60 but that the coverage of the surface monolayer remains constant and the excess material is ejected into the ESs. BAM images (Fig. 4E) also support this physical picture as the morphologies shown contain discrete regions on the μm-scale that grow in number with increasing compression only at higher compression ratios than the surface pressure collapse (states iv and v).
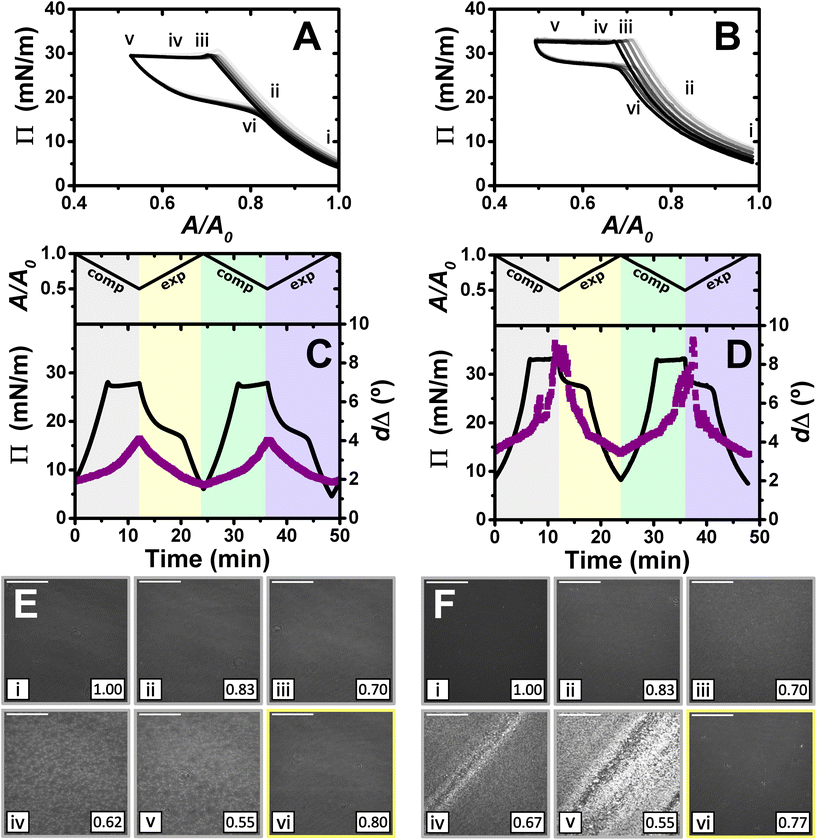 | ||
Fig. 4
Π–A isotherms of (A) PLL/SDS and (B) PLA/SDS films to a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio during 5 consecutive compression expansion cycles. The shade of the data indicates the number of the cycle, with cycle 1 being the lightest and cycle 5 the darkest; indices i–vi indicate different compression states. Variation of Π (black line) and dΔ (purple squares) as a function of time during two consecutive compression expansion cycles of (C) PLL/SDS and (D) PLA/SDS films. The variations of A versus time is also included at the top of the panels. The different shadowed areas indicate the compression/expansion of the film. BAM images of (E) PLL/SDS (reproduced from ref. 27) and (F) PLA/SDS films corresponding to states i–vi as indicated in panels A and B and using the colour code of panels C and D. Scale bars are 100 μm. 1 compression ratio during 5 consecutive compression expansion cycles. The shade of the data indicates the number of the cycle, with cycle 1 being the lightest and cycle 5 the darkest; indices i–vi indicate different compression states. Variation of Π (black line) and dΔ (purple squares) as a function of time during two consecutive compression expansion cycles of (C) PLL/SDS and (D) PLA/SDS films. The variations of A versus time is also included at the top of the panels. The different shadowed areas indicate the compression/expansion of the film. BAM images of (E) PLL/SDS (reproduced from ref. 27) and (F) PLA/SDS films corresponding to states i–vi as indicated in panels A and B and using the colour code of panels C and D. Scale bars are 100 μm. | ||
The Π–A response of PLA/SDS films (Fig. 4B) is qualitatively similar to that of PLL/SDS films, exhibiting the three characteristic regions mentioned above. Therefore, we could expect that the dynamic behaviour of these films may be explained with a similar physical picture. The ellipsometry data (Fig. 4D) show that the amount of material at the interface increases continuously with the compression beyond the surface pressure collapse and there is no evidence of loss of material from one cycle to the other. Thus, formation of ESs in PLA/SDS films is strongly inferred. In addition, the presence of fluctuations in dΔ is probably related to the presence of film inhomogeneities with a higher density of material.48,50 Lastly, the BAM images (Fig. 4F) clearly show the formation of discrete micro-domains after the collapse and the presence of areas with high intensity that are consistent with the dΔ fluctuations (states iv and v), even though they appear to have a distinct morphology from the ESs observed for PLL/SDS. Therefore, we can conclude that the PLA/SDS system exhibits the formation of ESs and that we can control their formation with the compression/expansion of the film, as has been previously reported for the PLL/SDS system.27 Furthermore, it is shown that the properties of the films and the morphology of the ESs can be tuned by using polypeptides with different side chains that interact differently with the surfactant.
Although the surface pressure responses of both systems to the compression/expansion cycles are similar, there are significant differences worth noting. The first one is the ΠC, ∼28 mN m−1 and ∼34 mN m−1 for the PLL and PLA/SDS films, respectively, while Π of an SDS monolayer at its cmc is 31 mN m−1.59 It has been shown that the interaction of SDS with different other polyelectrolytes gives rise to very different interfacial properties, varying significantly the minimum surface tension, i.e., the higher Π reached.26,48 Hence, the polyelectrolyte properties influence significantly the maximum compression state of the SDS molecules that can be reached before the film collapses.60 This is also supported by the ellipsometry data, as the amount of interfacial material is significantly higher for PLA. One could expect that the differences in ΠC may be related to the ability of the polypeptide to interact with surfactant headgroups with a contribution in the plane of the headgroups layer (see Fig. 4). However, the molecular volumes of lysine and arginine amino acids are 177 and 181 Å3,61 respectively, which are very similar. While the interaction between lysine monomers and the sulfate headgroup is purely electrostatic, the guanidinium group presents additional interactions due to the formation of hydrogen bonds with the oxygen atoms from the sulfate.35 This difference gives rise to lateral interactions between the different chemical groups that may explain the formation of a layer with a higher coverage of surfactant in the surface monolayer. This interpretation is also in agreement with the discussion of the zeta-potential results presented above, where a smaller excess bulk surfactant concentration was required to neutralize PLA than PLL aggregates. Another significant difference is the slope of the pseudo-plateau during the expansion, which is significantly lower for the PLA/SDS system. This could be related to the rate at which the material from the ESs is reincorporated into the surface monolayer upon film expansion. This would imply that PLA/SDS material recovery occurs much faster with a slope close to zero during a plateau on film expansion, while the higher slope in the case of PLL suggests that the reincorporation of the material from the ESs into the surface monolayer is slower than their formation, as has been demonstrated using NR.27 Nevertheless, NR of PLA/SDS films (beyond the scope of the present work) would be necessary to confirm this inference, since ellipsometry cannot distinguish between material present in the surface monolayer and the ESs. The collapse mechanism of both systems when compressed to a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is reversible, reflecting the high efficiency of respreading from the ESs back to the surface monolayer over the full expansion of the film.
1 is reversible, reflecting the high efficiency of respreading from the ESs back to the surface monolayer over the full expansion of the film.
Having demonstrated the formation of ESs for both PP/S systems during dynamic compression/expansion cycles, Π and dΔ were recorded at a constant compression ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to study the stability of the films. The results, presented in section 3 of the ESI,† show that both films are stable for more than 1 h, making them robust and amenable for possible transfer applications.
1 to study the stability of the films. The results, presented in section 3 of the ESI,† show that both films are stable for more than 1 h, making them robust and amenable for possible transfer applications.
Maximum compression ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1
Higher compression ratios have also been applied to resolve if the film response and resulting morphologies can be tuned with respect to PP/S interactions in the films that contain a second layer of ESs. For this purpose, a maximum compression ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 5) and the same spread volume and speed of the barriers were used as in the experiments described above. Compression of the films beyond a ratio of 2
1 (Fig. 5) and the same spread volume and speed of the barriers were used as in the experiments described above. Compression of the films beyond a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 results in the appearance of a new region during the compression where the Π starts to increase again (Fig. 5A and B). This result is surprising since the maximum Π of the system is broadly related to the most compact state of the surfactant in the surface monolayer. This new region would imply that the surface coverage of the surface monolayer is further increased, giving rise to an increase in the number of SDS molecules per unit area and a decrease in the amount of solvent in the headgroups layer. Although this is possible, in principle, considering that there is 23% of water in the headgroups layer when the film is compressed by a ratio of 2
1 results in the appearance of a new region during the compression where the Π starts to increase again (Fig. 5A and B). This result is surprising since the maximum Π of the system is broadly related to the most compact state of the surfactant in the surface monolayer. This new region would imply that the surface coverage of the surface monolayer is further increased, giving rise to an increase in the number of SDS molecules per unit area and a decrease in the amount of solvent in the headgroups layer. Although this is possible, in principle, considering that there is 23% of water in the headgroups layer when the film is compressed by a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,27 it was observed that the Wilhelmy plate is pulled sideways in the high-Π region, suggesting the formation of a solid film that exerts an additional force on the sensor, consistent with very low water content in PLL/SDS films resolved using NR above. An experiment reported in section 4 of the ESI† demonstrates that indeed the measured values of Π are affected below A/A0 = 0.33, hence hereon in we will refer to values of Π that exceed Πc as values of an ‘apparent Π’. Another significant difference with respect to the data above on films compressed to a ratio of 2
1,27 it was observed that the Wilhelmy plate is pulled sideways in the high-Π region, suggesting the formation of a solid film that exerts an additional force on the sensor, consistent with very low water content in PLL/SDS films resolved using NR above. An experiment reported in section 4 of the ESI† demonstrates that indeed the measured values of Π are affected below A/A0 = 0.33, hence hereon in we will refer to values of Π that exceed Πc as values of an ‘apparent Π’. Another significant difference with respect to the data above on films compressed to a ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is the appearance of a second collapse in the PLA/SDS system, which could be related to a change in the film structure after full coverage of the first layer of ESs is reached.
1 is the appearance of a second collapse in the PLA/SDS system, which could be related to a change in the film structure after full coverage of the first layer of ESs is reached.
The ellipsometry data (Fig. 5C and D) show that the approximate amount of material at the interface increased further beyond film compression of a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. The dΔ values increase by factors of 2.9 and 1.7 with respect to the 2
1 ratio. The dΔ values increase by factors of 2.9 and 1.7 with respect to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio for PLL and PLA, respectively. It is worth noting that in going from a compression ratio of 2
1 compression ratio for PLL and PLA, respectively. It is worth noting that in going from a compression ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 5
1 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, assuming that no material is lost from the interface, the amount of material should increase by a factor of 2.5, so the higher value obtained here for PLL/SDS films, in combination with the steeper slope in the ellipsometry data upon increasing compression ratio, suggest that there is could be a contributions to dΔ from anisotropy of the ESs and/or increasing roughness as noted above in relation to the NR fits.
1, assuming that no material is lost from the interface, the amount of material should increase by a factor of 2.5, so the higher value obtained here for PLL/SDS films, in combination with the steeper slope in the ellipsometry data upon increasing compression ratio, suggest that there is could be a contributions to dΔ from anisotropy of the ESs and/or increasing roughness as noted above in relation to the NR fits.
BAM images of PLL/SDS and PLA/SDS films (Fig. 5E and F) show a continuous increase in the number of ESs until a homogeneous, high-intensity image is observed, suggesting a very high coverage of ESs. The PLA/SDS system presents additional linear regions with higher intensity that could be related to folding of the film when the ESs layer reaches maximum coverage, which is consistent with the second plateau observed in the Π–A isotherm. During expansion, fracture and reincorporation of the material can be observed gradually in the PLL/SDS system, whereas for the PLA system the solid film disappears abruptly shortly after the start of its expansion. The dΔ values during expansion are in good agreement with the morphologies observed using BAM. The gradual disappearance of the solid film in the PLL/SDS system is translated into a continuous decrease of dΔ during expansion. However, the PLA system shows a dramatic drop in the values during expansion followed by a plateau, attributed to whether or not the solid domains are in the region of the interface illuminated by the laser. Then, the value of dΔ in the plateau coincides with the value at the collapse during compression. These observations confirm that the material is reincorporated by efficiently filling the surface area created upon expansion at a very similar rate to the barriers movement during expansion, i.e., with minimal kinetic barrier. The stability of the films compressed to a maximum ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was also studied by Π and ellipsometry, as reported in section 3 of the ESI,† showing stable dΔ values for more than 1 h, albeit with more relaxtion in Π for PLA/SDS than PLL/SDS films.
1 was also studied by Π and ellipsometry, as reported in section 3 of the ESI,† showing stable dΔ values for more than 1 h, albeit with more relaxtion in Π for PLA/SDS than PLL/SDS films.
Maximum compression ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1
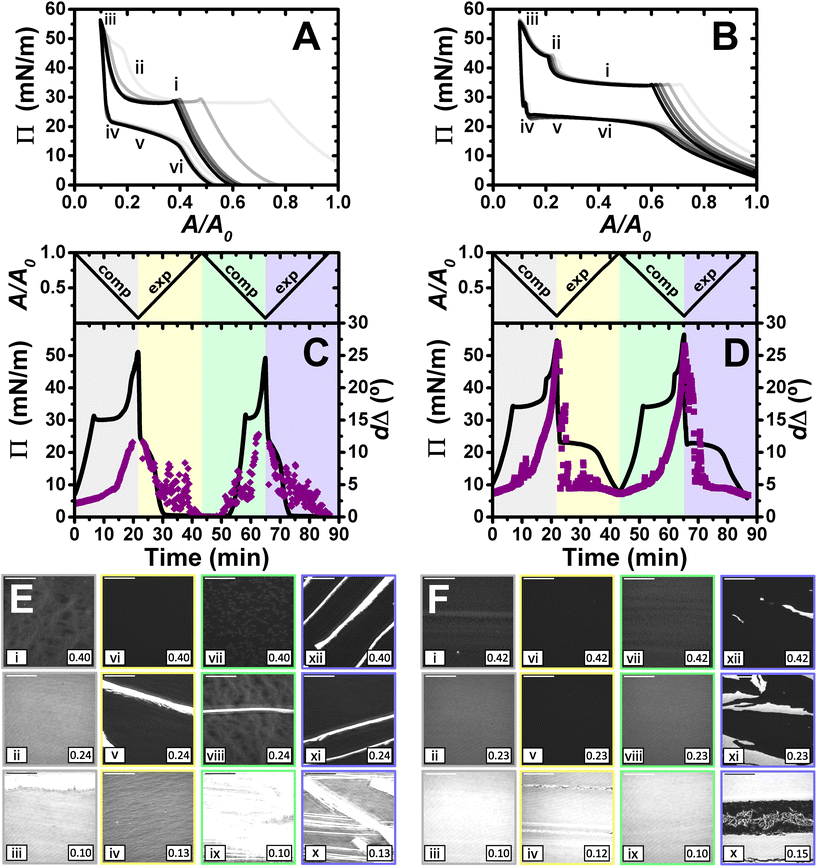
Lastly, films were compressed to a maximum ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the results obtained are shown in Fig. 6. The isotherms show qualitatively similar behaviour to that described above for the maximum compression ratio of 5
1, and the results obtained are shown in Fig. 6. The isotherms show qualitatively similar behaviour to that described above for the maximum compression ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. However, there are a number of differences that give us additional information about the systems, especially in the case of PLL/SDS. A second kink in the apparent Π of the PLL/SDS film and large shifts of the isotherms from the first to the second and third cycles are observed (Fig. 6A). These features may suggest that loss of material to the bulk occurs during the second kink. However, the apparent Π values reached in the minimum area are constant during the successive cycles, which precludes irreversible loss.
1. However, there are a number of differences that give us additional information about the systems, especially in the case of PLL/SDS. A second kink in the apparent Π of the PLL/SDS film and large shifts of the isotherms from the first to the second and third cycles are observed (Fig. 6A). These features may suggest that loss of material to the bulk occurs during the second kink. However, the apparent Π values reached in the minimum area are constant during the successive cycles, which precludes irreversible loss.
Similarly to the data on films with a maximum compression ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the ellipsometry data show a continuous increase in dΔ during compression. However, the expansion is characterized by an initial region with a continuous decrease in dΔ followed by large temporal fluctuations that are present also in the subsequent full compression/expansion cycle. In addition, although the dΔ values at the beginning of the second cycle are lower, the ones at the maximum compression ratio are similar, suggesting that there is no irreversible loss of material from the spread film.
1, the ellipsometry data show a continuous increase in dΔ during compression. However, the expansion is characterized by an initial region with a continuous decrease in dΔ followed by large temporal fluctuations that are present also in the subsequent full compression/expansion cycle. In addition, although the dΔ values at the beginning of the second cycle are lower, the ones at the maximum compression ratio are similar, suggesting that there is no irreversible loss of material from the spread film.
We consider now the morphology of the spread films from the two systems in turn. BAM images presented in Fig. 6E show the fracture of the solid PLL/SDS film during the first compression (state iii) and the presence of solid domains throughout the rest of the experiment (states v, viii, ix, x, xi, and xii). The characteristic behaviour of PLL/SDS films compressed to a maximum ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 can be explained by combining the information obtained from the different techniques. The application of high compression ratios results in the formation of a solid film that is fractured when a 10
1 can be explained by combining the information obtained from the different techniques. The application of high compression ratios results in the formation of a solid film that is fractured when a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio is reached. The expansion of the film is characterized by the presence of solid domains observed in the BAM images that contain a much larger amount of material and explain the large dΔ fluctuations. A similar behaviour has been reported for other polymers at the air/water interface.50,62 Thus, we can conclude that film compression to a maximum ratio of 10
1 compression ratio is reached. The expansion of the film is characterized by the presence of solid domains observed in the BAM images that contain a much larger amount of material and explain the large dΔ fluctuations. A similar behaviour has been reported for other polymers at the air/water interface.50,62 Thus, we can conclude that film compression to a maximum ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 gives rise to the irreversible formation of solid domains whose excess of material is not respread and remain trapped at the interface coexisting with the surface monolayer. Finally, the apparent Π–A isotherms can now be explained by the fact that after the formation of these solid domains, the excess of material trapped in them does not contribute to the apparent Π until the solid film forms again. Thus, the surface monolayer region is displaced considerably but the same apparent Π and dΔ values are always reached at maximum film compression.
1 gives rise to the irreversible formation of solid domains whose excess of material is not respread and remain trapped at the interface coexisting with the surface monolayer. Finally, the apparent Π–A isotherms can now be explained by the fact that after the formation of these solid domains, the excess of material trapped in them does not contribute to the apparent Π until the solid film forms again. Thus, the surface monolayer region is displaced considerably but the same apparent Π and dΔ values are always reached at maximum film compression.
The behaviour of PLA/SDS films compressed to a maximum ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 shown in Fig. 6F is very similar to that presented above for a maximum compression ratio of 5
1 shown in Fig. 6F is very similar to that presented above for a maximum compression ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, but interestingly in this case, the second kink in the apparent Π results in a small shift of the isotherm in the successive cycles. The ellipsometry data show a very high amount of material in the film (approximately double dΔ), and a very similar trend when a 10
1, but interestingly in this case, the second kink in the apparent Π results in a small shift of the isotherm in the successive cycles. The ellipsometry data show a very high amount of material in the film (approximately double dΔ), and a very similar trend when a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 compression ratio is reached. Temporary fluctuations can be observed related to the presence of film folding and the characteristic plateau during expansion. The values of dΔ at the minimum and maximum areas are reproducible from the first to the second cycle, showing once again the great capacity of these systems to stabilise the formation of ESs and to respread their material back to the surface monolayer during film expansion. BAM images show the formation of the solid film during the first cycle without fracturing the film (state iii). Instead, the images at high compression ratios suggest that the PLA/SDS film folds during the second collapse (states ii and iv). Thus, while the PLL/SDS film exhibits an irreversible collapse mechanism at high Π leading to the formation of solid domains that are trapped at the interface, the PLA/SDS system exhibits a reversible collapse mechanism in which the film folds and excess material is respread in the surface monolayer during expansion.
1 compression ratio is reached. Temporary fluctuations can be observed related to the presence of film folding and the characteristic plateau during expansion. The values of dΔ at the minimum and maximum areas are reproducible from the first to the second cycle, showing once again the great capacity of these systems to stabilise the formation of ESs and to respread their material back to the surface monolayer during film expansion. BAM images show the formation of the solid film during the first cycle without fracturing the film (state iii). Instead, the images at high compression ratios suggest that the PLA/SDS film folds during the second collapse (states ii and iv). Thus, while the PLL/SDS film exhibits an irreversible collapse mechanism at high Π leading to the formation of solid domains that are trapped at the interface, the PLA/SDS system exhibits a reversible collapse mechanism in which the film folds and excess material is respread in the surface monolayer during expansion.
These results suggest that PLL/SDS films can form solid aggregates that redisperse with greater difficulty than PLA/SDS aggregates. The significant differences observed in the behaviour of these systems may be related to the interaction between the polypeptide molecules. Although we do not have direct evidence about the secondary structure of the polypeptides at the interface, previous studies suggest that the secondary structure is maintained when the polypeptides are deposited on solid surfaces.42 While the α-helices formed by PLA side chains face outward and thus decrease interactions between them, it is understood that β-sheets present edges free to form hydrogen bonds with other β-sheet edges of other molecules.63,64 This could give rise to the formation of an extensive hydrogen bond network throughout the film that would confer a more rigid structure and stability to the aggregates formed by PLL/SDS. These observations are in agreement with the formation of solid precipitates due to inter-chain hydrogen bonding between β-sheets and the formation of coacervates when random-coiled or α-helical polypeptides interact between them.2 Indeed, amyloid fibrils are used in numerous biomedical applications because they are made up of β-sheets which give them a rigid and cohesive nature and excellent mechanical properties such as large persistence length.2 Lastly, it is worth noting that the properties of individual polypeptide chains have a great influence on the properties of the aggregates they form. Thus, the results obtained here also agree with the greater rigidity of β-sheets with respect to the α-helices. The behaviour using a maximum compression ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 represents additional evidence of the above explanation. The β-sheet conformation that PLL adopts when interacting with SDS in bulk is characterised by an extensive network of hydrogen bonds and is stiffer than the α-helical structure adopted by PLA.38,65 Additional hydrogen bonding between PLL chains at high compression ratios and edge-to-edge interactions between different β-sheets could give rise to aggregation and formation of the solid domains observed that remain trapped at the air/water interface. Although the results are consistent with a β-sheet conformation for PLL and an α-helix conformation for PLA, the application of circular dichroism and Fourier transform infrared spectroscopy in the future will be essential to understand better the role of the secondary structure if conserved in ESs spread PP/S films.
1 represents additional evidence of the above explanation. The β-sheet conformation that PLL adopts when interacting with SDS in bulk is characterised by an extensive network of hydrogen bonds and is stiffer than the α-helical structure adopted by PLA.38,65 Additional hydrogen bonding between PLL chains at high compression ratios and edge-to-edge interactions between different β-sheets could give rise to aggregation and formation of the solid domains observed that remain trapped at the air/water interface. Although the results are consistent with a β-sheet conformation for PLL and an α-helix conformation for PLA, the application of circular dichroism and Fourier transform infrared spectroscopy in the future will be essential to understand better the role of the secondary structure if conserved in ESs spread PP/S films.
Conclusions
We have demonstrated in the present work that specific PP/S interactions can be exploited to tune the resulting structures and morphologies of spread films prepared using a recently developed aggregate dissociation mechanism during their compression to different maximum ratios of the surface area. PLL/SDS films show the presence of discrete ESs after the collapse until a solid film is formed. In contrast, PLA/SDS films show linear regions as well with a higher amount of material related to film folding. In addition, application to the highest compression ratios studied (up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) shows that PLL/SDS films form more stable solid aggregates that redisperse with greater difficulty upon expansion and even become trapped at the interface. Different morphologies of the ESs are evident depending on the maximum compression ratio applied. PLA/SDS films show reversible collapse regardless of the compression ratio used, whereas PLL/SDS films show irreversible collapse at the highest compression ratio applied. Previous studies have shown that NaPSS/DTAB and PLL/SDS spread films exhibit 1
1) shows that PLL/SDS films form more stable solid aggregates that redisperse with greater difficulty upon expansion and even become trapped at the interface. Different morphologies of the ESs are evident depending on the maximum compression ratio applied. PLA/SDS films show reversible collapse regardless of the compression ratio used, whereas PLL/SDS films show irreversible collapse at the highest compression ratio applied. Previous studies have shown that NaPSS/DTAB and PLL/SDS spread films exhibit 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry.27,31 This leads to the screening of the electrostatic repulsions along the polyelectrolyte chains which increase their flexibility. This may play an important role in the ability of the films to reincorporate during the expansion the material expelled to ESs during compression.
1 stoichiometry.27,31 This leads to the screening of the electrostatic repulsions along the polyelectrolyte chains which increase their flexibility. This may play an important role in the ability of the films to reincorporate during the expansion the material expelled to ESs during compression.
NR data recorded over the full Qz-range results showed the ability of PLL/SDS films to nucleate a high coverage of ESs when a sufficiently high compression ratio is applied. The low amount of water in these films and the presence of two distinct layers of ESs present a consistent physical picture with the solid films observed using BAM. Future application of the low-QZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 and mid-QZ
28 and mid-QZ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 approaches of NR will be essential to deeply understand the dynamic behaviour of such highly compressed films.
27 approaches of NR will be essential to deeply understand the dynamic behaviour of such highly compressed films.
Although there is no direct evidence of retention of the secondary structure of PLL and PLA in the ESs of the spread films, the work was based on the hypothesis that different secondary structures formed in bulk complexes of the two systems may result in distinct film properties where ESs are present, and this turned out to be correct. The results indicate that the films obtained in this work are more rigid than the ones obtained before using a flexible random-coil polyelectrolyte,31 which is consistent with the higher stiffness of the β-sheet and α-helix conformations with respect to the random coil and with previous studies showing the important role that polyelectrolyte stiffness plays in ESs formation.32 Therefore, we may approach the possibility of designing with high precision PP/S films that form ESs. Nevertheless, a systematic study with polyelectrolytes presenting different stiffness will help to understand the influence of the stiffness on the formation of ESs and the macroscopic properties of the spread films, e.g. their reversibility.
In summary, high potential of using polypeptides in combination with oppositely charged surfactants in spread films at the air/water interface has been demonstrated. The richness of these molecules in terms of chemical diversity, biodegradability, biocompatibility, biomimicry, and the possibility of controlling their primary and secondary structure and, therefore, their function, in film applications opens up a wide field of research. While we have described in the present work how properties of two types of PP/S films are distinct and can be controlled, the study also provides a platform for the development of spread films from a broad range of PP/S systems in the future. Thus, the continuation of this research on films involving different polypeptides and surfactants holds potential to deliver an important contribution to the development of new biomaterials with applications in tissue engineering,66 biosensors67 or antimicrobial coatings.68
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank ISIS Neutron and Muon Source for allocations of neutron beam time (https://doi.org/10.5286/ISIS.E.RB2210138), the Partnership for Soft Condensed Matter (PSCM) for lab support, Benoit Laurent for technical assistance with the ellipsometer, and Robert Jacobs for helpful discussions. IV acknowledges the financial support from the Hungarian National Research, Development and Innovation Office (NKFIH K116629). AM acknowledges the financial support from MICINN under grant PID2021-129054NA-I00 and the IKUR Strategy of the Basque Government (IKUR Neutronics). ME and RC acknowledge the Engineering and Physical Research Council (UK) for support with grant EP/V029495/1.References
- Z. Song, Z. Han, S. Lv, C. Chen, L. Chen, L. Yin and J. Cheng, Chem. Soc. Rev., 2017, 46, 6570–6599 RSC.
- Z. Song, H. Fu, R. Wang, L. A. Pacheco, X. Wang, Y. Lin and J. Cheng, Chem. Soc. Rev., 2018, 47, 7401–7425 RSC.
- C. Bonduelle, Polym. Chem., 2018, 9, 1517–1529 RSC.
- M. Xiong, M. W. Lee, R. A. Mansbach, Z. Song, Y. Bao, R. M. Peek, C. Yao, L. F. Chen, A. L. Ferguson, G. C. L. Wong and J. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13155–13160 CrossRef CAS PubMed.
- A. M. Oelker, S. M. Morey, L. G. Griffith and P. T. Hammond, Soft Matter, 2012, 8, 10887–10895 RSC.
- K. E. Gebhardt, S. Ahn, G. Venkatachalam and D. A. Savin, J. Colloid Interface Sci., 2008, 317, 70–76 CrossRef CAS PubMed.
- C. Stubenrauch, P. A. Albouy, R. V. Klitzing and D. Langevin, Langmuir, 2000, 16, 3206–3213 CrossRef CAS.
- F. Schulze-Zachau and B. Braunschweig, Phys. Chem. Chem. Phys., 2019, 21, 7847–7856 RSC.
- E. Tran, A. N. Mapile and G. L. Richmond, J. Colloid Interface Sci., 2021, 599, 706–716 CrossRef CAS PubMed.
- K. Ciunel, M. Armélin, G. H. Findenegg and R. von Klitzing, Langmuir, 2005, 21, 4790–4793 CrossRef CAS PubMed.
- E. Guzmán, H. Ritacco, J. E. F. Rubio, R. G. Rubio and F. Ortega, Soft Matter, 2009, 5, 2130–2142 RSC.
- A. Akanno, E. Guzmán, L. Fernández-Peña, S. Llamas, F. Ortega and R. G. Rubio, Langmuir, 2018, 34, 7455–7464 CrossRef CAS PubMed.
- Y. Shen, X. Fu, W. Fu and Z. Li, Chem. Soc. Rev., 2015, 44, 612–622 RSC.
- T. J. Deming, Chem. Rev., 2016, 116, 786–808 CrossRef CAS PubMed.
- Z. Tang, Y. Wang, P. Podsiadlo and N. A. Kotov, Adv. Mater., 2006, 18, 3203–3224 CrossRef CAS.
- D. Alkekhia, P. T. Hammond and A. Shukla, Annu. Rev. Biomed. Eng., 2020, 22, 1–24 CrossRef CAS PubMed.
- D. T. Haynie, L. Zhang, J. S. Rudra, W. Zhao, Y. Zhong and N. Palath, Biomacromolecules, 2005, 6, 2895–2913 CrossRef CAS PubMed.
- J. J. Richardson, J. Cui, M. Björnmalm, J. A. Braunger, H. Ejima and F. Caruso, Chem. Rev., 2016, 116, 14828–14867 CrossRef CAS PubMed.
- H. Sjögren, C. A. Ericsson, J. Evenäs and S. Ulvenlund, Biophys. J., 2005, 89, 4219–4233 CrossRef PubMed.
- D. W. Pack, A. S. Hoffman, S. Pun and P. S. Stayton, Nat. Rev. Drug Discovery, 2005, 4, 581–593 CrossRef CAS PubMed.
- E. A. Ponomarenko, A. J. Waddon, K. N. Bakeev, D. A. Tirrell and W. J. MacKnight, Macromolecules, 1996, 29, 4340–4345 CrossRef CAS.
- E. Guzmán, S. Llamas, A. Maestro, L. Fernández-Peña, A. Akanno, R. Miller, F. Ortega and R. G. Rubio, Adv. Colloid Interface Sci., 2016, 233, 38–64 CrossRef PubMed.
- E. Guzmán, L. Fernández-Peña, F. Ortega and R. G. Rubio, Curr. Opin. Colloid Interface Sci., 2020, 48, 91–108 CrossRef.
- J. H. Buckingham, J. Lucassen and F. Hollway, J. Colloid Interface Sci., 1978, 67, 423–431 CrossRef CAS.
- J. Lucassen, F. Hollway and J. H. Buckingham, J. Colloid Interface Sci., 1978, 67, 432–440 CrossRef CAS.
- J. Penfold, I. Tucker, R. K. Thomas, D. J. F. Taylor and X. L. Zhang, Langmuir, 2006, 22, 7617–7621 CrossRef CAS PubMed.
- J. Carrascosa-Tejedor, A. Santamaria, A. Tummino, I. Varga, M. Efstratiou, M. J. Lawrence, A. Maestro and R. A. Campbell, Chem. Commun., 2022, 58, 10687–10690 RSC.
- R. A. Campbell, A. Tummino, B. A. Noskov and I. Varga, Soft Matter, 2016, 12, 5304–5312 RSC.
- R. Mészáros, L. Thompson, M. Bos, I. Varga and T. Gilányi, Langmuir, 2003, 19, 609–615 CrossRef.
- C. Monteux, C. E. Williams, J. Meunier, O. Anthony and V. Bergeron, Langmuir, 2004, 20, 57–63 CrossRef CAS PubMed.
- A. Tummino, J. Toscano, F. Sebastiani, B. A. Noskov, I. Varga and R. A. Campbell, Langmuir, 2018, 34, 2312–2323 CrossRef CAS PubMed.
- L. Braun, M. Uhlig, O. Löhmann, R. A. Campbell, E. Schneck and R. von Klitzing, ACS Appl. Mater. Interfaces, 2022, 14, 27347–27359 CrossRef CAS PubMed.
- M. Zheng, M. Pan, W. Zhang, H. Lin, S. Wu, C. Lu, S. Tang, D. Liu and J. Cai, Bioact. Mater., 2021, 6, 1878–1909 CrossRef CAS PubMed.
- C. A. Fitch, G. Platzer, M. Okon, B. E. Garcia-Moreno and L. P. McIntosh, Protein Sci., 2015, 24, 752–761 CrossRef CAS PubMed.
- E. Wernersson, J. Heyda, A. Kubíčková, T. Křížek, P. Coufal and P. Jungwirth, J. Phys. Chem. B, 2010, 114, 11934–11941 CrossRef CAS PubMed.
- I. Satake and J. T. Yang, Biopolymers, 1976, 15, 2263–2275 CrossRef CAS PubMed.
- K. Takeda, A. Iba and K. Shirahama, Bull. Chem. Soc. Jpn., 1982, 55, 985–989 CrossRef CAS.
- P. Novotná and M. Urbanová, Anal. Biochem., 2012, 427, 211–218 CrossRef PubMed.
- P. Novotná and M. Urbanová, Chirality, 2015, 27, 965–972 CrossRef PubMed.
- R. W. McCord, E. W. Blakeney and W. L. Mattice, Biopolymers, 1977, 16, 1319–1329 CrossRef CAS PubMed.
- S. Ichimura, K. Mita and M. Zama, Biopolymers, 1978, 17, 2769–2782 CrossRef CAS.
- F. Boulmedais, M. Bozonnet, P. Schwinté, J. C. Voegel and P. Schaaf, Langmuir, 2003, 19, 9873–9882 CrossRef CAS.
- R. A. Campbell, Curr. Opin. Colloid Interface Sci., 2018, 37, 49–60 CrossRef CAS.
- M. W. A. Skoda, Curr. Opin. Colloid Interface Sci., 2019, 42, 41–54 CrossRef CAS.
- A. Maestro and P. Gutfreund, Adv. Colloid Interface Sci., 2021, 293, 102434 CrossRef CAS PubMed.
- A. Nelson, J. Appl. Crystallogr., 2006, 39, 273–276 CrossRef CAS.
- M. L. Ainalem, R. A. Campbell and T. Nylander, Langmuir, 2010, 26, 8625–8635 CrossRef CAS PubMed.
- K. Tonigold, I. Varga, T. Nylander and R. A. Campbell, Langmuir, 2009, 25, 4036–4046 CrossRef CAS PubMed.
- O. Y. Milyaeva, G. Gochev, G. Loglio, R. Miller and B. A. Noskov, Colloids Surf., A, 2017, 532, 108–115 CrossRef CAS.
- H. Motschmann, R. Reiter, R. Lawall, G. Duda, M. Stamm, G. Wegner and W. Knoll, Langmuir, 1991, 7, 2743–2747 CrossRef CAS.
- W. Daear, M. Mahadeo and E. J. Prenner, Biochim. Biophys. Acta, 2017, 1859, 1749–1766 CrossRef CAS PubMed.
- I. Varga and R. A. Campbell, Langmuir, 2017, 33, 5915–5924 CrossRef CAS PubMed.
- G. Skvarnavičius, D. Dvareckas, D. Matulis and V. Petrauskas, ACS Omega, 2019, 4, 17527–17535 CrossRef PubMed.
- A. Mezei and R. Mészáros, Langmuir, 2006, 22, 7148–7151 CrossRef CAS PubMed.
- T. Wallin and P. Linse, Langmuir, 1996, 12, 305–314 CrossRef CAS.
- P. Hansson, Langmuir, 2001, 17, 4167–4180 CrossRef CAS.
- A. Akinchina and P. Linse, J. Phys. Chem. B, 2003, 107, 8011–8021 CrossRef CAS.
- R. A. Campbell, M. Yanez Arteta, A. Angus-Smyth, T. Nylander and I. Varga, J. Phys. Chem. B, 2012, 116, 7981–7990 CrossRef CAS PubMed.
- J. R. Lu, A. Marrocco, T. J. Su, R. K. Thomas and J. Penfold, J. Colloid Interface Sci., 1993, 158, 303–316 CrossRef CAS.
- R. A. Campbell, Y. Saaka, Y. Shao, Y. Gerelli, R. Cubitt, E. Nazaruk, D. Matyszewska and M. J. Lawrence, J. Colloid Interface Sci., 2018, 531, 98–108 CrossRef CAS PubMed.
- B. Jacrot, Rep. Prog. Phys., 1976, 39, 953 CrossRef.
- T. Reda, H. Hermel and H.-D. Höltje, Langmuir, 1996, 12, 6452–6458 CrossRef CAS.
- J. S. Richardson and D. C. Richardson, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 2754–2759 CrossRef CAS PubMed.
- P.-N. Cheng, J. D. Pham and J. S. Nowick, J. Am. Chem. Soc., 2013, 135, 5477–5492 CrossRef CAS PubMed.
- S. Perticaroli, J. D. Nickels, G. Ehlers, H. O'Neill, Q. Zhang and A. P. Sokolov, Soft Matter, 2013, 9, 9548–9556 RSC.
- D. L. Nettles, A. Chilkoti and L. A. Setton, Adv. Drug Delivery Rev., 2010, 62, 1479–1485 CrossRef CAS PubMed.
- M. Puiu and C. Bala, Bioelectrochemistry, 2018, 120, 66–75 CrossRef CAS PubMed.
- M. Salwiczek, Y. Qu, J. Gardiner, R. A. Strugnell, T. Lithgow, K. M. McLean and H. Thissen, Trends Biotechnol., 2014, 32, 82–90 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Neutron reflectivity fitting procedure, (2) NR fitting demonstration of PLL between the ESs, (3) surface pressure and ellipsometry stability measurements, and (4) verification of surface pressure values at high compression ratios. See DOI: https://doi.org/10.1039/d2nr07164a |
| This journal is © The Royal Society of Chemistry 2023 |