Energy level alignments between organic and inorganic layers in 2D layered perovskites: conjugation vs. substituent
Eti
Mahal
 ,
Shyama Charan
Mandal
,
Shyama Charan
Mandal
 ,
Diptendu
Roy
,
Diptendu
Roy
 and
Biswarup
Pathak
and
Biswarup
Pathak
 *
*
Department of Chemistry, Indian Institute of Technology Indore, Indore 453552, India. E-mail: biswarup@iiti.ac.in
First published on 3rd April 2023
Abstract
2D layered hybrid perovskites have attracted huge attention due to their interesting optoelectronic properties and chemical flexibility. Depending upon their electronic structures and properties, these materials can be utilised in various optoelectronic devices like photovoltaics, LEDs and so on. In this context, study of the excited energy levels of the organic spacers can help us to align the excited energy levels of the organic unit with the excitonic level of the inorganic unit according to the requirement of a particular optoelectronic device. We have explored the role of 3-phenyl-2-propenammonium on the electronic structure of a perovskite containing this cation as a spacer. Our results clearly demonstrate the active participation of conjugated ammonium spacers in the electronic structure of a perovskite. Also, we have considered a variety of amines to identify the best alignment with common inorganic units and studied the role of substituents and conjugation on the energy level alignment. Placing the triplet excited level of an organic spacer below the lowest excitonic level of the inorganic unit can induce energy transfer from the inorganic to organic unit, finally resulting in phosphorescence emission. We have shown that the triplet energy level of 3-anthracene-2-propeneamine/3-pyrene-2-propeneamine can be tuned in such a way that there can be an excitonic energy transfer from the Pb2I7/PbI4 inorganic unit-based perovskites. Therefore, perovskite material with such combinations of organic spacer cations will be very useful for light emission applications.
Introduction
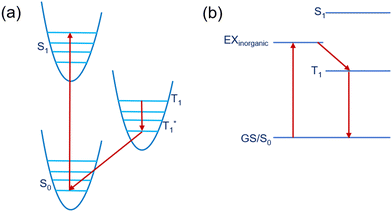
Recently, reduced dimensional perovskites have gained huge interest in optoelectronic material research due to their impressive stability in operational conditions.1–3 These materials are an example of natural multiple quantum wells (MQW), where inorganic layers act as wells and organic cation layers act as barriers.4,5 Among various reduced dimensional perovskites, Ruddlesden Popper (RP) phase systems are at the forefront of study, which have the chemical formula A2A′n−1MnX3n+1 where A and A′ are the spacer cation and cage cation, respectively, M is the metal, X is the halide, and n is the thickness of the MQW which determines the extent of the quantum and dielectric confinement along with the optical property of the material. RP perovskite systems have versatile optoelectronic properties through their chemical and quantum mechanical degrees of freedom. Moreover, these materials are used to develop colourful LEDs, efficient solar cells, and spintronic devices.6–11 However, for perfect utilization of these 2D layered perovskite materials in a particular optoelectronic device, they need to have specific electronic and optical properties based on the requirements of that device.Efficient optoelectronic material can be realized through organic spacer modulation by targeting specific properties from a molecular perspective.12 By using the wide range of organic cations available and utilising their orbital energies to tune the energy levels of the perovskite material, we can achieve particular properties based on our need. Hence, finding out the best material requires a high throughput understanding of the electronic structure and properties at the molecular level. One of the important requirements to make an efficient optoelectronic device is the alignment of the energy levels between the organic and inorganic moieties of the hybrid halide perovskite material.13–15 The results of the work of Stupp and co-workers16 suggested the great potential for functional improvement by using polynuclear rings containing ammonium cations, which showcased improved optoelectronic properties as an outcome of the better match between the organic and inorganic energy levels. Yang and co-workers17 have also reported the presence of conjugated cationic states on the near edge states of the perovskite material. Therefore, the electronic energy levels of the inorganic metal halide and organic moieties can be selectively aligned by applying several criteria on the organic cation such as the extent of conjugation and effect of substitution. On the basis of the variation principle of the inorganic metal halide and organic cation electronic structures, 2D hybrid perovskite research community can find a suitable direction. In this context, transfer of the excitonic energy from the inorganic metal halide unit to the lowest triplet states of the organic spacer has been one of the main focuses over the past few years. In particular, the strong spin orbit coupling in inorganic perovskite results weakly bound Wannier–Mott excitons. Kandada and co-workers18 have described the excitons in 2D halide perovskite quantum-well-like structures by a Wannier model. In contrast, the organic cations have strongly bound Frenkel excitons. Kunugita and co-workers19 have observed efficient energy transfer from Wannier excitons to the triplet state of naphthalene molecules in 2D halide perovskites. If the triplet state of the organic part of the optoelectronic material lies below the exciton level of the inorganic perovskite (metal halide unit), it can induce an energy transfer from the inorganic to the organic triplet state (T1) and finally phosphorescence emission from T1* to S0.20 A schematic diagram of the excited states of an organic molecule is shown in Fig. 1.
In a recent work, Wu and co-workers21 demonstrated a highly efficient solar cell based on their designed spacer cation 3-phenyl-2-propenammonium (PPA) which possesses multifunctional properties. Along with the extra double bond induced extended conjugation, there are several more hydrogen atoms that cause notable H-contact with the inorganic layers. This feature resulted in an impressive performance of the solar cell devices composed of PPA spacer cations and Pb2I7 as the inorganic unit. However, the particular contribution of the PPA molecule on the electronic structure and properties of PPA based layered hybrid halide perovskites still remains unexplored. In addition, such conjugated spacer molecules have a high potential to be utilised for the preferred alignment of excited energy levels in the inorganic and organic layers. Hence, proper understanding of the alignment of the energy levels between the inorganic and organic units of the material is highly desired for the typical application in optoelectronic devices. Neukirch and co-workers22 have shown in their work that the energy level alignment between the perovskite layer and spacer cations can be modulated through extended conjugation. However, they have not considered the conjugation extended to the close vicinity of the primary ammonium group. To distinguish the influence of the conjugated unit attached to the primary ammonium group, we have taken PPA cation as our prime unit and played with the functional groups. Finally, we have analysed the functional group influence on the energy level alignment of the PPA spacer cation-based perovskites.
Here, we have used density functional theory (DFT) to obtain the excitation energy levels of a set of organic cations. At first, we studied the electronic properties of the two 2D layered hybrid halide perovskite materials containing PPA cation as the spacer with molecular formula, (PPA)2PbI4 with n = 1 and (PPA)2(MA)0.5(FA)0.5Pb2I7 with n = 2. Here, PPA is the spacer cation labelled as A while MA and FA are cage cations labelled as A′ in the general formula A2A′n−1MnX3n+1. Where, MA and FA are abbreviated forms of the methylammonium and formamidinium cations, respectively. Then we tried to explore the importance of conjugation in the spacer cation of the layered hybrid halide perovskite and how the conjugation can control the alignment of the excited state energy levels between the inorganic and organic layers. We started with PPA and then checked the contribution of a set of functional groups ranging from electron withdrawing to electron donating. Also, we took into consideration the functional groups with extended conjugation. To identify the perfect match between the inorganic metal halide unit and organic spacer we calculated the lowest triplet excitation energies of the organic spacers. Moreover, the nature of the excitations in dynamic conditions were investigated using the ab initio molecular dynamics (AIMD) simulation. Singlet and triplet excitation energies calculated in gas phase geometries give similar results to those obtained under dynamic conditions. Finally, we tried to match the considered organic cations with known perovskite exciton levels to predict the different type of energy level alignments.
Methods
For the geometry optimization and electronic structure calculation of the layered hybrid perovskite materials we used the Quantum Espresso (QE)23 program package. Here we adapted the GGA-PBE24 exchange correlation functional for the geometry relaxation and considered scalar relativistic ultrasoft pseudopotentials25 including electrons from the 2s, 2p orbital for O, N, and C; 1s orbital for H; 5s, 5p orbital for I; and 6s, 6p, 5d orbital for Pb explicitly. A plane wave basis set cutoff of 50 and 400 Ry for the wave functions and augmented density were used, respectively. The perovskite systems ions as well as the cell parameters were allowed to relax for all the calculations. Also, the Monkhorst pack26k-point sampling of 4 × 4 × 1 was implemented with the DFT-D3 dispersion correction as formulated by Grimme27 for the relaxation of all the systems. For a more accurate prediction of the electronic structure of the material we used the HSE06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 hybrid functional with 43%
28 hybrid functional with 43%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29 Hartree–Fock exchange using the GGA-PBE optimized geometry. In addition, spin orbit coupling (SOC) was also considered for the electronic structure calculations using HSE06 considering the sensitivity of higher elements towards relativistic effects. A plane wave basis set cutoff of 40 Ry for the smooth part of the wave functions and a Fock energy cutoff of 80 Ry was set during HSE06 + SOC calculations along with a Monkhorst pack k-point sampling of 2 × 2 × 1. Also, we took norm-conserving pseudopotentials with electrons from I 5s, 5p; O, N, C 2s, 2p; H 1s; Pb 5s, 5p, 6s, 6p, 5d shells explicitly for the HSE06 + SOC calculations. These methodologies are reported to give good results for such systems.30
29 Hartree–Fock exchange using the GGA-PBE optimized geometry. In addition, spin orbit coupling (SOC) was also considered for the electronic structure calculations using HSE06 considering the sensitivity of higher elements towards relativistic effects. A plane wave basis set cutoff of 40 Ry for the smooth part of the wave functions and a Fock energy cutoff of 80 Ry was set during HSE06 + SOC calculations along with a Monkhorst pack k-point sampling of 2 × 2 × 1. Also, we took norm-conserving pseudopotentials with electrons from I 5s, 5p; O, N, C 2s, 2p; H 1s; Pb 5s, 5p, 6s, 6p, 5d shells explicitly for the HSE06 + SOC calculations. These methodologies are reported to give good results for such systems.30
Ab initio molecular dynamics simulations were done within the DFT framework as implemented in the Vienna ab initio simulation package (VASP).31–36 The projector augmented-wave (PAW) method was used to describe the electron–core interaction within a plane-wave basis set of kinetic energy cutoff 500 eV and GGA-PBE functional.24 A Γ-centered k-point grid of 4 × 4 × 1 was used to sample the Brillouin zone. The MD simulations were carried out using a canonical ensemble at 300 K temperature controlled by a Nosé–Hoover thermostat in a 10 ps trajectory with 1 fs timesteps.37
For the excitation energy levels calculations of the organic molecules, the Gaussian 09 D.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 suite of programme was employed. The Pople basis set 6-311++G**
38 suite of programme was employed. The Pople basis set 6-311++G**![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39–41 and Becke 3-parameter Lee–Yang–Parr (B3LYP)42–46 hybrid functional was applied for the calculations. We used the ΔSCF approach to calculate triplet excitations owing to its good predictive power for the S0 geometry triplet and T1* geometry triplet energies.47 Whereas, lowest energy singlet excitations are calculated using TDDFT48 due to its reliability to predict singlet excitation energies in organic molecules for charge transfer and optical excitations.
39–41 and Becke 3-parameter Lee–Yang–Parr (B3LYP)42–46 hybrid functional was applied for the calculations. We used the ΔSCF approach to calculate triplet excitations owing to its good predictive power for the S0 geometry triplet and T1* geometry triplet energies.47 Whereas, lowest energy singlet excitations are calculated using TDDFT48 due to its reliability to predict singlet excitation energies in organic molecules for charge transfer and optical excitations.
Results and discussion
At first, we discussed the geometries and properties of the PPA spacer cation based 2D lead halide perovskites (n = 1–2). In the beginning we studied (PPA)2(MA)0.5(FA)0.5Pb2I7 which is a n = 2 category 2D perovskite system. We performed the geometry relaxation of this material starting from the experimentally reported crystal structure by Wu and co-workers.21 Subsequently we designed (PPA)2PbI4 computationally and performed first principles calculations. Fig. 2 displays the optimized structures of the two considered perovskites.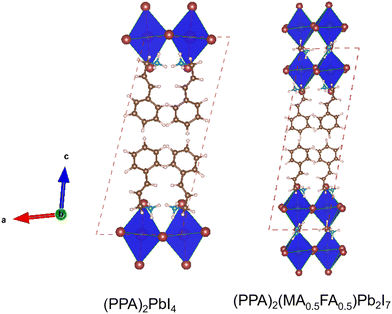 | ||
| Fig. 2 Optimised geometries of the considered 2D metal halide perovskites. Colours: hydrogen (white), carbon (brown), nitrogen (blue), iodine (wine) and lead (grey). | ||
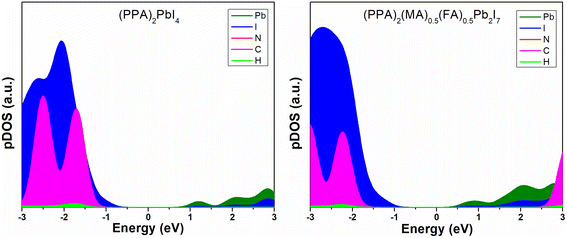
After performing the geometry optimization at the GGA-PBE level of theory, we performed single point calculations using the HSE06 + SOC method to obtain more accurate band gap values. The HSE06 + SOC calculated band gaps of (PPA)2PbI4 and (PPA)2(MA)0.5(FA)0.5Pb2I7 are 2.26 and 1.99 eV, respectively. (PPA)2PbI4 is a pure 2D perovskite whereas (PPA)2(MA)0.5(FA)0.5Pb2I7 is a quasi 2D perovskite possessing two metal halide layers in between the organic spacer layers. This imposes 3D contribution onto the quasi 2D perovskite system. As a result of this 3D contribution, the n = 2 system possesses a much lower band gap compared to the n = 1 one. Despite having a larger spacer cation that ensures a larger inorganic layer distance, the band gap in (PPA)2PbI4 is smaller compared to other similar 2D halide-based perovskites such as (PEA)2PbI4, (BA)2PbI4 (∼2.4 eV) calculated at the same level of theory.49 From this observation, we can infer the importance of conjugation in the spacer cation on the band gap of a 2D hybrid perovskite. Additionally, (PPA)2PbI4 has the potential for application in optoelectronic devices. We further continued our study extracting the density of states of the materials to obtain the specific contributions from the elements to the electronic states of the material (Fig. 3).
There is a noticeable contribution of the carbon components close to the edge of the valence band in (PPA)2PbI4 compared to that in the (PPA)2(MA)0.5(FA)0.5Pb2I7. In the case of (PPA)2(MA)0.5(FA)0.5Pb2I7, the small cage cations MA and FA are also present. Along with PPA, MA and FA show contributions to the organic components in the pDOS plot of (PPA)2(MA)0.5(FA)0.5Pb2I7 perovskite. However, it is worth mentioning that in the (PPA)2PbI4 perovskite, there are no cage cations present, unlike in the (PPA)2(MA)0.5(FA)0.5Pb2I7 perovskite. As a result, the contribution from the PPA spacer cation alone in the valence band edge of the (PPA)2(MA)0.5(FA)0.5Pb2I7 is a little less than that in (PPA)2PbI4. For this reason, the carbon components in (PPA)2PbI4 are closer to the band edges in comparison to that in (PPA)2(MA)0.5(FA)0.5Pb2I7. Apart from this, the carbon components in (PPA)2PbI4 contribute more significantly to the valence band edge with respect to (PEA)2PbI4.49 Although the PPA spacer cation is slightly larger in size than PEA, it has one extra conjugated π-bond that places it closer to the valence band edge of the material. Hence, the position of the cationic states on the perovskite material electronic structure gives a clear idea of the influence of conjugation on the electronic structure, which can be utilised for different application purposes. Although it is difficult to find out the best choice of material for an optoelectronic device by studying different large perovskite systems, we can get an idea of their electronic properties just through exploring the excited state energy levels of the organic spacer molecules.
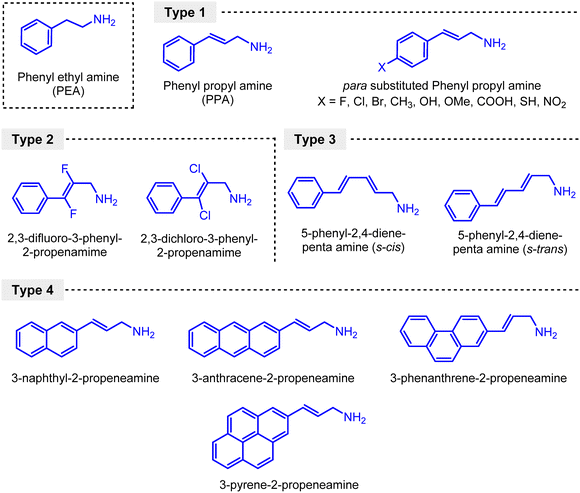
Through analysing the density of states plots of the PPA based perovskites, we were encouraged to further study the properties of the organic cation. We first studied the excitation energy levels of the PPA molecule and checked the alignment of these excited states with the perovskite exciton levels. Following this, we studied the excited states of various molecules with functionalising the PPA molecule in different aspects. Motivated by various experimental reports where people have used differently functionalised organic molecules as spacer cations in 2D perovskites, we considered a set of amines for our work. Substituent groups were added in the para position of the phenyl ring in the PPA molecule ranging from electron donating to electron withdrawing nature along with an increase in extended conjugation. In Fig. 4 we illustrated the structures of the considered spacer molecules to obtain the excitation energy levels of a set of organic cations.
There are several reports of 2D perovskites with para substituted spacer cations.50,51 We classified our considered cations into four types. In the first type (type I), we varied the substituent group on the para position of the phenyl ring in the PPA cation from electron withdrawing to electron donating in nature. Several electron donating/withdrawing groups like halogens (−I, +R), CH3 (+I), SH (+R), OH, OMe (−I, +R), COOH and NO2 (−R) were substituted at the para position. There are easy synthetic methodologies to synthesise such para-substituted phenyl propyl amines.52 In the case of type-II, we checked the effects of the electron withdrawing functionality through F/Cl substitutions on the C–C π bond of the propyl amine tail. In the next class (type-III), we considered extended conjugation though one extra C–C π bond to the propyl amine tail in the cis and trans configuration. Particularly, we considered s-cis and s-trans isomer of 5-phenyl-2,4-diene-pentaamine. These amines can be synthesized using methodologies reported by Taylor and co-workers.53 There were some reports of polynuclear ring ammonium-based 2D halide perovskites (n = 1) where they identified a significant contribution from the organic spacers to the band edges of the perovskite material.16 So, in the fourth type the phenyl ring was replaced by polynuclear rings.
For theoretical support of our calculated findings, we compared the results reported by Neukirch and co-workers22 for phenyl ethyl amine (PEA) and observed good agreement with their report. For phenyl ethyl amine (PEA), we found a T1 value of 4.38 eV (Table 1), whereas it was previously reported as 4.43 eV. Similarly, T1* for phenyl ethyl amine was 3.73 eV and 3.77 eV for our calculated and their reported values, respectively. The triplet and singlet energy levels of PPA are quite interesting. Both the triplet and singlet energies decrease significantly in comparison to the PEA. The T1 energy decreases from 4.38 eV in PEA to 3.28 eV in PPA (Table 1). Also, the T1* and S1 energies decrease in PPA in comparison to PEA. In contrast, varying the substituent groups at the para position of PPA did not deliver any considerable change to the excitation energies. Rather, we observed that irrespective of the electron donating or withdrawing effect, the main controlling factor is conjugation in the first type of cations as the increase in conjugation decreases triplet and singlet energies (Table 1). Among the substituted cases, the para nitro substitution gives the lowest T1 energy (2.88 eV). Being curious, we added a nitro group substitution on three positions (two ortho and one para). However, that increases the triplet energy to 3.03 eV (Table 1) with respect to one nitro substituted case (2.88 eV). This could be due to hampering of the extended conjugation in the presence of three nitro groups. However, the relaxed triplet energy (T1*) decreases noticeably. In the next type (type II) the addition of the F atom on the trans configuration of the propyl double bond did not change the excited energy levels significantly but the addition of Cl in a similar manner increases the T1 and decreases the T1* (Table 1). This could be due to the cancellation of the −I effect from the two F atoms at the trans position in 2,3-difluoro-3-phenyl-2-propenamime. Whereas, in the case of the Cl substituent, the large size of Cl and +R effect could be responsible for the increase in the energy of the triplet state. We observed that these substitutions couldn't help to improve the conjugation and lower the triplet energies. Hence, in the third type rather than further substitution we tried to increase conjugation through increasing the number of π bonds. Interestingly both the s-cis and s-trans conformations of 5-phenyl-2,4-diene-pentaamine significantly decrease the triplet energies (Table 1). This happened due to the extension in the conjugation that stabilises the molecular orbitals. In our last class of cations (fourth) we considered polynuclear rings (Table 1). We observed that in the case of 3-naphthyl-2-propeneamine, the excited energy levels decrease in comparison to PPA, whereas the triplet and singlet energies decrease noticeably for anthracene and phenanthrene based cations in 3-anthracene-2-propeneamine and 3-phenanthrene-2-propeneamine, respectively. However, in 3-phenanthrene-2-propeneamine, the T1 energy is larger even in comparison to 3-naphthyl-2-propeneamine. This is due to the antiaromaticity (NICS value 40.18) in the triplet state of 3-phenanthrene-2-propeneamine compared to the 3-naphthyl-2-propeneamine (NICS value 8.37). Much smaller triplet and singlet energies also observed in 3-pyrene-2-propeneamine. The lowest triplet energy value was observed in 3-anthracene-2-propeneamine.
| Amines | T1 | T1* | S0 → S1 |
|---|---|---|---|
| Phenyl ethyl amine (PEA) | 4.38 (4.43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21) 21) |
3.73 (3.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21) 21) |
5.27 (5.43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21) 21) |
| 3-Phenyl-2-propenamime (PPA) | 3.28 | 2.68 | 4.68 |
| 4F-PPA | 3.28 | 2.68 | 4.57 |
| 4Cl-PPA | 3.20 | 2.63 | 4.51 |
| 4Br-PPA | 3.19 | 2.62 | 4.47 |
| 4OH-PPA | 3.20 | 2.64 | 4.41 |
| 4SH-PPA | 3.06 | 2.54 | 4.23 |
| 4CH3-PPA | 3.24 | 2.32 | 4.60 |
| 4OCH3-PPA | 3.10 | 2.33 | 4.29 |
| 4COOH-PPA | 3.02 | 2.52 | 4.30 |
| 4NO2-PPA | 2.88 | 2.42 | 3.73 |
| 2,4,6-NO2-PPA | 3.03 | 0.99 | 2.96 |
| 2,3-Difluoro-3-phenyl-2-propenamime | 3.23 | 2.12 | 4.67 |
| 2,3-Dichloro-3-phenyl-2-propenamime | 3.74 | 1.82 | 4.63 |
| 5-Phenyl-2,4-diene-pentaamine (s-cis) | 2.55 | 1.83 | 3.93 |
| 5-Phenyl-2,4-pentadieneamine (s-trans) | 2.58 | 2.02 | 4.08 |
| 3-Naphthyl-2-propeneamine | 2.93 | 2.52 | 4.00 |
| 3-Anthracene-2-propeneamine | 2.10 | 1.80 | 3.13 |
| 3-Phenanthrene-2-propeneamine | 3.05 | 2.53 | 3.70 |
| 3-Pyrene-2-propeneamine | 2.26 | 1.89 | 3.38 |
To verify the excitation energies in dynamic conditions, we performed AIMD simulations. We took two phases i.e., n = 1 and n = 2 of PPA based perovskites for the molecular dynamics simulation. After performing the simulation, we calculated the T1 energies of the cations. Our calculated T1 energies demonstrated broadening of the excitation energies of the cations in the presence of the perovskite environment (Fig. 5).
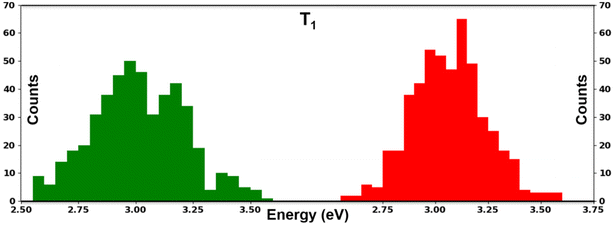 | ||
| Fig. 5 Histograms of T1 energies obtained from post MD molecular geometries (n = 1 green and n = 2 red). | ||
The broadening of the excitation energies of the organic molecules is due to the occurrence of thermal fluctuations in the perovskite environment. The bond angles as well as C–C, C–N and C–H bond lengths of the PPA molecule fluctuate randomly in the post equilibrium geometries due to the continuous heating and cooling processes during the simulation. In (Fig. 5) we presented histograms of the T1 excitation energies of organic molecular geometries obtained throughout the molecular dynamics simulations. We extracted the geometries of the cations from the perovskite structures of the simulation cell and calculated the T1 excitation energies. Notably, the PPA cation experienced very similar broadening for both the n = 1 and n = 2 phases of the perovskites. The average values (3.0–3.2 eV) of the excitation energies of the molecular geometries obtained across the simulation cell are smaller than that of the isolated molecule (3.28 eV). This is a clear consequence of the fluctuations in the bond angle and bond lengths experienced in the post equilibrium geometries. Although the broadening of excitation energies gives evidence for the importance of finite temperature dynamics, the average value of the T1 energy (3.1 eV) is close to the T1 energy (3.28 eV) obtained from the relaxed geometries. So, we have used the excitation energies obtained from the relaxed geometries of the molecules to align the energy levels of organic cations with the perovskites.
In the inorganic layer of the perovskite the excitons are weakly bound Wannier–Mott excitons. Due to the strong spin orbit coupling and highly dielectric nature of the metal halide layer, the singlet and triplet excitonic levels are difficult to differentiate. Here we have considered the lowest excitonic energy from ref. 54 and 55 as the perovskite exciton level. However, low dielectric organic cations result in strongly bound Frenkel excitons. Proper alignment of the perovskite exciton level with the triplet energy level of the organic cation can induce an energy transfer from the perovskite to the organic triplet and this energy can further radiatively transfer, relaxing the molecule to the singlet state. This radiative energy transfer from the triplet to the singlet state of the organic cation can be utilised in different devices. By aligning the perovskite exciton level and calculated T1 energy we predicted some preferred combinations of the perovskite and organic spacer cation. In Table 2, we have listed the spacer cations connecting to the particular perovskite by which they are expected to form a material with the property of resonance energy transfer.
| Perovskite system | Lowest exciton energy level (Ex) (from reference) | Expected preferred combination |
|---|---|---|
| Pb2I7 | 2.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 54 |
3-Anthracene-2-propeneamine (2.10) |
| PbI4 | 2.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 54 |
3-Pyrene-2-propenamime (2.26) |
| PbBr4 | 3.20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55 |
4Cl-PPA (3.20) |
| 4OH-PPA (3.20) | ||
| 4Br-PPA (3.19) | ||
| 4OCH3-PPA (3.10) | ||
| 4SH-PPA (3.06) | ||
| 3-Phenanthrene-2-propeneamine (3.05) | ||
| 2,4,6-NO2-PPA (3.03) | ||
| 4COOH-PPA (3.02) | ||
| 3-Naphthyl-2-propeneamine (2.93) | ||
| 4NO2-PPA (2.88) | ||
| PbCl4 | 3.70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55 |
— |
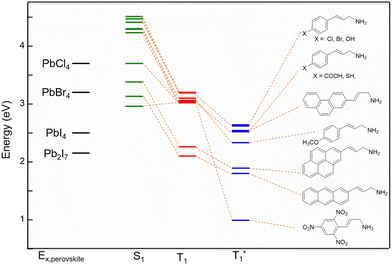
We started with the n = 2 Pb2I7 perovskite layer, which has the lowest exciton energy level at 2.15 eV.54 Among our considered ammonium cations, only one spacer molecule is found to be appropriate for the preferred combination with this inorganic layer. For the energy transfer from this inorganic layer, the best choice from our set of cations is the 3-anthracene-2-propeneamine which has a T1 excitation level at 2.10 eV. This molecule has a low energy triplet state at 1.80 eV where the molecule can relax after the energy transfer from the perovskite inorganic layer to T1 and then further radiate emitting red light. The next inorganic layer we listed in table is the n = 1, I based PbI4. In this case also we have got one spacer among our considered set of cations. The 3-pyrene-2-propenamime with a T1 energy level at 2.26 eV could be a good combination with the PbI4 inorganic layer with an exciton energy level at 2.50 eV.54 The excitonic energy can be transferred to the T1 (2.26 eV) state and then before the radiative process the molecule can relax to the T1* level of 1.89 eV. From the perovskite material of this combination, we can obtain red light.
The next inorganic perovskite candidate is Br based PbBr4 with a perovskite excitonic level at 3.20 eV.55 A total of ten spacer molecules were screened to determine the possibility of energy transfer from the perovskite exciton level to the high energy triplet level of the organic molecule. Among the ten spacers, the Cl, Br, and OH substitution at the para position can emit in the blue region. SH, COOH substitution at the para position and NO2 substitution at the 2,4,6 position of the PPA molecule and 3-naphthyl-2-propeneamine are eligible for blue/cyan light emission. In contrast, OCH3 and NO2 substitution at the para position of the PPA molecule are potential candidates for green light emission. Another candidate to explore with PbBr4 is 3-phenanthrene-2-propeneamine, which has a T1 at 3.05 and T1* at 0.99 eV, making it a promising candidate for emission in the IR region. However, we did not find any preferred match from our selected spacer candidates for another halide Cl based PbCl4 inorganic layer.
Although some of our selected spacers did not fit the criteria for proper energy level alignment with the four considered inorganic perovskite layers, they have potential for emission in various regions (Fig. 6). The PPA cation and its p-F and p-CH3 substitutions comes with a high energy triplet state slightly above the exciton level of the PbBr4 perovskite and much lower than PbCl4. So, they are not capable of inducing the excitonic energy transfer from the perovskite. In addition, the s-cis and s-trans isomers of 5-phenyl-2,4-diene-pentaamine have T1 energy (2.55 and 2.58 eV) slightly larger than the PbI4 inorganic layer. However, they have T1* at 1.83 and 2.02 eV, showing potential for emission of red and orange light, respectively.
In some of the spacers we observed noticeably reduced S1 energy levels and they even sit below the exciton level of the metal halide layer. For these cases, we can expect an excitonic energy transfer to the S1 level. 3-Anthracene-2-propeneamine and 2,4,6-NO2-PPA have S1 energy of 3.13 and 2.96 eV, respectively. The S1 level of these two cations is situated below the excitonic energy level of the PbBr4 inorganic layer. Thus, we can have an excitonic energy transfer to the S1 of these two cations when these are combined with the PbBr4 unit. Also, the 3-pyrene-2-propeneamine has an S1 energy level at 3.38 eV, which is below the excitonic energy of the PbCl4 layer. So, this cation can induce an excitonic transition from the PbCl4 inorganic layer to its excited singlet state.
Conclusions
In conclusion, we have presented a detailed study about the predictability of the energy level alignment between the inorganic and organic units of layered hybrid perovskites by analysing the excitation levels of the organic spacers. Our results reveal that an extension in conjugation rather than substituent group variation has a significant contribution to the organic inorganic energy level alignment. We have calculated and investigated the excitation energy levels of a series of organic cations to find out the best combinations where induction of excitonic energy transfer from inorganic to organic units would be possible and after this energy transfer of inorganic exciton to organic triplet excited state, radiative emission could happen. This study has turned out to be successful in finding some preferred combinations that are able to emit different colours and can be used for different light emitting devices. By performing molecular dynamics simulations, we have also verified the feasibility of our results at finite temperature conditions. Noticeably, our predicted combinations have high potentials for light emitting devices. Our study gives a clear direction for optimizing the hybrid perovskite properties through conjugated organic spacers and designing materials for optoelectronic devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank IIT Indore for the lab and computing facilities. This work is supported by DST-SERB [project number: CRG/2018/001131 and CRG/2022/000836] and CSIR [project number: 01(3046)/21/EMR-II]. E. M., S. C. M. and D. R. thanks Ministry of Education for the research fellowship.References
- I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, Angew. Chem., Int. Ed., 2014, 53, 11232–11235 CrossRef CAS PubMed.
- C. C. Stoumpos, D. H. Cao, D. J. Clark, J. Young, J. M. Rondinelli, J. I. Jang, J. T. Hupp and M. G. Kanatzidis, Chem. Mater., 2016, 28, 2852–2867 CrossRef CAS.
- L. N. Quan, M. Yuan, R. Comin, O. Voznyy, E. M. Beauregard, S. Hoogland, A. Buin, A. R. Kirmani, K. Zhao, A. Amassian, D. H. Kim and E. H. Sargent, J. Am. Chem. Soc., 2016, 138, 2649–2655 CrossRef CAS PubMed.
- C. Katan, N. Mercier and J. Even, Chem. Rev., 2019, 119, 3140–3192 CrossRef CAS PubMed.
- D. Sapori, M. Kepenekian, L. Pedesseau, C. Katan and J. Even, Nanoscale, 2016, 8, 6369–6378 RSC.
- K. T. Cho, G. Grancini, Y. Lee, E. Oveisi, J. Ryu, O. Almora, M. Tschumi, P. A. Schouwink, G. Seo and S. Heo, Energy Environ. Sci., 2018, 11, 952–959 RSC.
- E. R. Dohner, A. Jaffe, L. R. Bradshaw and H. I. Karunadasa, J. Am. Chem. Soc., 2014, 136, 13154–13157 CrossRef CAS PubMed.
- M. D. Smith and H. I. Karunadasa, Acc. Chem. Res., 2018, 51, 619–627 CrossRef CAS PubMed.
- L. Mao, W. Ke, L. Pedesseau, Y. Wu, C. Katan, J. Even, M. R. Wasielewski, C. C. Stoumpos and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 3775–3783 CrossRef CAS PubMed.
- H. Tsai, W. Nie, J. C. Blancon, C. C. Stoumpos, C. M. M. Soe, J. Yoo, J. Crochet, S. Tretiak, J. Even, A. Sadhanala, G. Azzellino, R. Brenes, P. M. Ajayan, V. Bulović, S. D. Stranks, R. H. Friend and M. G. Kanatzidis, Stable Light-Emitting Diodes Using Phase-Pure Ruddlesden–Popper Layered Perovskites, Adv. Mater., 2018, 30, 1704217 CrossRef PubMed.
- J. Wang, C. Zhang, H. Liu, R. McLaughlin, Y. Zhai, S. R. Vardeny, X. Liu, S. McGill, D. Semenov, H. Guo, R. Tsuchikawa, V. V. Deshpande, D. Sun and Z. V. Vardeny, Nat. Commun., 2019, 10, 129 CrossRef PubMed.
- E. Mahal, S. C. Mandal and B. Pathak, J. Phys. Chem. C, 2022, 126, 9937–9947 CrossRef CAS.
- M. D. Smith, B. A. Connor and H. I. Karunadasa, Chem. Rev., 2019, 119, 3104–3139 CrossRef CAS PubMed.
- D. B. Mitzi, K. Chondroudis and C. R. Kagan, Inorg. Chem., 1999, 38, 6246–6256 CrossRef CAS PubMed.
- B. Traore, L. Pedesseau, L. Assam, X. Che, J.-C. Blancon, H. Tsai, W. Nie, C. C. Stoumpos, M. G. Kanatzidis, S. Tretiak, A. D. Mohite, J. Even, M. Kepenekian and C. Katan, ACS Nano, 2018, 12, 3321–3332 CrossRef CAS PubMed.
- J. V. Passarelli, D. J. Fairfield, N. A. Sather, M. P. Hendricks, H. Sai, C. L. Stern and S. I. Stupp, J. Am. Chem. Soc., 2018, 140, 7313–7323 CrossRef CAS PubMed.
- J. Xue, R. Wang, X. Chen, C. Yao, X. Jin, K.-L. Wang, W. Huang, T. Huang, Y. Zhao, Y. Zhai, D. Meng, S. Tan, R. Liu, Z.-K. Wang, C. Zhu, K. Zhu, M. C. Beard, Y. Yan and Y. Yang, Science, 2021, 371, 636–640 CrossRef CAS PubMed.
- S. Neutzner, F. Thouin, D. Cortecchia, A. Petrozza, C. Silva and A. R. S. Kandada, Phys. Rev. Mater., 2018, 2, 064605 CrossRef CAS.
- K. Ema, M. Inomata, Y. Kato, H. Kunugita and M. Era, Phys. Rev. Lett., 2008, 100, 257401 CrossRef CAS PubMed.
- M. M. Elshanawany, A. G. Ricciardulli, M. Saliba, J. Wachtveitl and M. Braun, Nanoscale, 2021, 13, 15668–15676 RSC.
- J. Xi, I. Spanopoulos, K. Bang, J. Xu, H. Dong, Y. Yang, C. D. Malliakas, J. M. Hoffman, M. G. Kanatzidis and Z. Wu, J. Am. Chem. Soc., 2020, 142, 19705–19714 CrossRef CAS PubMed.
- J. Leveillee, C. Katan, J. Even, D. Ghosh, W. Nie, A. D. Mohite, S. Tretiak, A. Schleife and A. J. Neukirch, Nano Lett., 2019, 19, 8732–8740 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- M.-H. Du, J. Phys. Chem. Lett., 2015, 6, 1461–1466 CrossRef CAS PubMed.
- A. Mahata, E. Mosconi, D. Meggiolaro and F. De Angelis, Chem. Mater., 2020, 32, 105–113 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- M. J. Frisch, et al., Gaussian Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- W. J. Hehre, K. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- J. Gavnholt, T. Olsen, M. Engelund and J. Schiøtz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075441 CrossRef.
- C. A. Guido, S. Knecht, J. Kongsted and B. Mennucci, J. Chem. Theory Comput., 2013, 9, 2209–2220 CrossRef CAS PubMed.
- E. Mahal, S. C. Mandal and B. Pathak, Mater. Adv., 2022, 3, 2464–2474 RSC.
- J. Hu, I. W. H. Oswald, S. J. Stuard, M. M. Nahid, N. Zhou, O. F. Williams, Z. Guo, L. Yan, H. Hu, Z. Chen, X. Xiao, Y. Lin, Z. Yang, J. Huang, A. M. Moran, H. Ade, J. R. Neilson and W. You, Nat. Commun., 2019, 10, 1276 CrossRef PubMed.
- M.-H. Tremblay, J. Bacsa, B. Zhao, F. Pulvirenti, S. Barlow and S. R. Marder, Chem. Mater., 2019, 31, 6145–6153 CrossRef CAS.
- K. Wang, P. Jiang, M. Yang, P. Ma, J. Qin, X. Huang, L. Ma and R. Li, Green Chem., 2019, 21, 2448–2461 RSC.
- R. Bastin, M. Liron and R. J. K. Taylor, Synlett, 2008, 14, 2183–2187 Search PubMed.
- J.-C. Blancon, H. Tsai, W. Nie, C. C. Stoumpos, L. Pedesseau, C. Katan, M. Kepenekian, C. M. M. Soe, K. Appavoo, M. Y. Sfeir, S. Tretiak, P. M. Ajayan, M. G. Kanatzidis, J. Even, J. J. Crochet and A. D. Mohite, Science, 2017, 355, 1288–1292 CrossRef CAS PubMed.
- K.-Z. Du, Q. Tu, X. Zhang, Q. Han, J. Liu, S. Zauscher and D. B. Mitzi, Inorg. Chem., 2017, 56, 9291–9302 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |