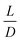Buoyant magnetic milliswimmers reveal design rules for optimizing microswimmer performance†
Emma
Benjaminson‡
 a,
Taryn
Imamura‡
a,
Aria
Lorenz
a,
Sarah
Bergbreiter
abc,
Matthew
Travers
c and
Rebecca E.
Taylor
a,
Taryn
Imamura‡
a,
Aria
Lorenz
a,
Sarah
Bergbreiter
abc,
Matthew
Travers
c and
Rebecca E.
Taylor
 *abd
*abd
aDepartment of Mechanical Engineering, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, USA. E-mail: bex@andrew.cmu.edu; Fax: +1-412-268-3348; Tel: +1-412-268-2500
bElectrical and Computer Engineering, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, USA
cThe Robotics Institute, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, USA
dDepartment of Biomedical Engineering, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, USA
First published on 14th August 2023
Abstract
Magnetically-actuated swimming microrobots are an emerging tool for navigating and manipulating materials in confined spaces. Recent work has demonstrated that it is possible to build such systems at the micro and nanoscales using polymer microspheres, magnetic particles and DNA nanotechnology. However, while these materials enable an unprecedented ability to build at small scales, such systems often demonstrate significant polydispersity resulting from both the material variations and the assembly process itself. This variability makes it difficult to predict, let alone optimize, the direction or magnitude of microswimmer velocity from design parameters such as link shape or aspect ratio. To isolate questions of a swimmer's design from variations in its physical dimensions, we present a novel experimental platform using two-photon polymerization to build a two-link, buoyant milliswimmer with a fully customizable shape and integrated flexible linker (the swimmer is underactuated, enabling asymmetric cyclic motion and net translation). Our approach enables us to control both swimming direction and repeatability of swimmer performance. These studies provide ground truth data revealing that neither the first order nor second order models currently capture the key features of milliswimmer performance. We therefore use our experimental platform to develop design guidelines for tuning the swimming speeds, and we identify the following three approaches for increasing speed: (1) tuning the actuation frequency for a fixed aspect ratio, (2) adjusting the aspect ratio given a desired range of operating frequencies, and (3) using the weaker value of linker stiffness from among the values that we tested, while still maintaining a robust connection between the links. We also find experimentally that spherical two-link swimmers with dissimilar link diameters achieve net velocities comparable to swimmers with cylindrical links, but that two-link spherical swimmers of equal diameter do not.
1 Introduction
Microswimmers are an essential technology for navigating microscale environments and serving as manipulators in microscale manufacturing.1–4 The field of swimming robots has generated a wide variety of swimmer designs,1–4 as well as actuation and control strategies,5–10 that successfully address the challenge of overcoming the Scallop Theorem.11 For example, Xing et al. constructed a multilink swimmer (3–5 links) with revolute joints using two-photon polymerization, and demonstrated net translation through a fluid using a sinusoidally oscillating magnetic field as a control input.12 Dreyfus et al., as well as recent work from our lab by Harmatz et al., demonstrated that microspheres could be chained together with various DNA nanostructures,8,13 and both Maier et al. and Pauer et al. used microspheres coated in DNA nanostructures to achieve net translation by leveraging the DNA's flexibility to serve as a “flagella”, reminiscent of the motion of eukaryotic cells.14,15However, the relative polydispersity of common microscale building materials – such as magnets and polymer microspheres13 – increases as we move to smaller scales. For example, Harmatz et al. reported an interquartile range of 0.32 μm for a population of commercial microspheres that were nominally 6.2 μm in diameter, and demonstrated that pocketing-based self-assembly techniques can reduce the variability present in common building materials.13 Recent work by Pauer et al. has reported polydispersity in both microswimmer speed and direction,15 indicating that a lack of population-level uniformity is a key limitation for experimentally realized microscale swimming robots.
This polydispersity in performance directly limits our ability to develop and validate models of microscale swimming. In this work we address this gap by introducing a mesoscale approach for systematically adjusting various swimmer design parameters (such as link shape or aspect ratio) in order to directly observe the effects that these changes have on swimmer net velocity. Our findings will impact not only the microswimmer field but also the emerging field of nanoscale swimming robots that can use DNA nanotechnology in conjunction with other nanoscale materials such as spherical particles.16,17 We note that fabrication and optimization of DNA-based nanoswimmers could open a new realm of possibilities for interacting with nanoscale environments.
Looking to the future of nanorobots, we hypothesize that one of the simplest nanoswimmer designs capable of achieving net locomotion is a two-link system, where both links are spherical nanoparticles, joined via DNA nanotechnology components such as nanotubes.13,18 These two-link systems have one link that is controlled by an externally applied magnetic field and is connected to a second link by a flexible joint. This flexible actuator design enables asymmetric cyclic motion that leads to net translation and overcomes the Scallop Theorem.11 However, like Pauer et al., we observe polydispersity in both swimming speed and direction that limits our ability to optimize performance. Further, two-link swimmer systems have previously been modeled, for example by Grover et al. and Gutman et al.,19–21 but these models use first order systems and represent each link as a cylinder, which is not consistent with many previous microswimmer designs. Therefore, there remains an open question of whether or not the insights provided by these prior works will apply to designing micro- and nanoswimmers with spherical links.3
In order to investigate how to design fast microswimmers without the confounding variables of shape polydispersity and linker polydispersity, we can leverage two-photon polymerization to build precise milliswimmers. Two-photon polymerization (TPP) provides the sub-micron resolution required for manufacturing milliswimmers with arbitrary link shapes, as well as an integrated flexible connector analogous to nanoscale connectors such as DNA nanotubes.4,22,23 There are many instances of microrobots constructed with TPP, including examples of helices, rollers and tumblers, flexible flagella,4 and even multi-link swimmers.12 However, none of these swimmers provide buoyancy control, which is important to prevent the possibility of the swimmers crawling on the surface – nanoswimmers are small enough to be buoyant in their fluid environments, and any representative model must replicate this behavior. To address this gap in our ability to build and model microscale and nanoscale two-link systems, we built a buoyant experimental platform on the milliscale that we can use to experiment with the design and control of various two-link systems to find parameters that can be applied to smaller scale systems to increase their net velocities.
In addition to our novel demonstration of a two-link, buoyant swimmer built with TPP, we attempt to model the system with both first and second order approaches. We find that neither approach shows close agreement with our experimental results, nor are they capable of representing inter-swimmer variation. This finding identifies a need within the field for more investigation into how closely our dynamics models match experimental realizations.
The goal of building fast swimmers is an important one because in commercial or medical settings, it will be important for the swimmers to operate quickly, both for cost considerations as well as to minimize time spent inside a patient during a procedure for safety. From our experimental data, we found that (1) there is typically a peak velocity that occurs at a particular actuation frequency for a given aspect ratio of the swimmer; (2) the aspect ratio of each link can be tuned to shift the frequency at which the maximum velocity occurs and (3) when selecting between the tested values of {6.3 × 10−8, 1.2 × 10−7} N m rad−1 (corresponding to flexible joints of length {80, 40} μm), the smaller stiffness value leads to faster swimmers.
We then extended our model and experimental realization to studying two-link swimmers with spherical links, since many micro- and nanoscale swimmers are built with spherical components, in order to understand the effect that the link shape will have on the swimmer's velocity. When comparing our model predictions to our experimental results, we found that our model predicted that both spherical swimmer designs would not achieve net translation, while we found experimentally that swimmers with dissimilar link diameters did indeed achieve net velocities comparable to swimmers built with cylindrical links. This finding highlights an opportunity for the field to apply more detailed fluid dynamics modeling to better understand why two-link spherical swimmers can achieve net translation.
2 Results
2.1 Milliswimmer design, manufacturing and control
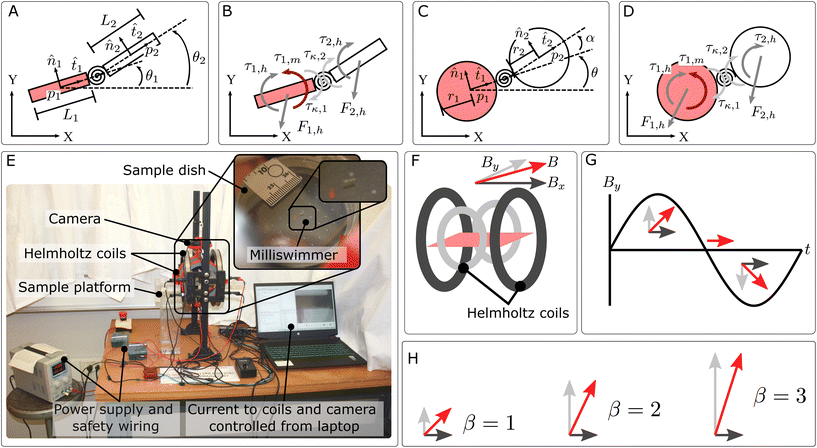
We have developed a novel millimeter-scale, buoyant swimming robot that can be manufactured using two-photon polymerization and magnetized by adding a small ferromagnetic cube in a specially designed pocket, as shown in Fig. 1. The swimmer is made buoyant by forming hollow chambers in the middle of each link that trap a small amount of air. Drainage ports are added to each chamber to allow excess photoresist trapped during printing to be removed in a post-processing step. We present details of the design in the ESI,† demonstrating how we used bubble formation theory to size the drainage ports to minimize the probability of air escaping from the swimmer's internal chambers.24 We discuss the different swimmer designs we tested before selecting a positively buoyant design in Section 2.3. Ultimately, we chose to size the chambers to ensure that the swimmer will float, even in cases where the inserted magnet is heavier than its predicted average mass.To assess the accuracy and precision of the printed milliswimmer dimensions, we measured the three TPP-fabricated cylindrical swimmers of nominal link length 1015 μm. As shown in Table 1, we find actual dimensions in good agreement with the nominal dimensions. Using FIJI25 to analyze light microscopy images with measurement uncertainty of 1 μm, we found that, per swimmer, none of the measurement variations exceeded 2.8%. Further, the means of the swimmer dimensions varied by between 0.58% and 1.6%, indicating a multifold improvement in monodispersity of printed structures as compared with commercially available polymer microspheres.13 Additional details are provided in the ESI.†
| Value | Link 1 length [μm] | Link 1 diameter [μm] | Link 2 length [μm] | Link 2 diameter [μm] |
|---|---|---|---|---|
| Swimmer 1 mean ± std. dev. (% var.) | 1021 ± 7 (0.69%) | 495 ± 7 (1.3%) | 984 ± 9 (0.87%) | 499 ± 6 (1.2%) |
| Swimmer 2 mean ± std. dev. (% var.) | 998 ± 6 (0.62%) | 497 ± 3 (0.60%) | 995 ± 7 (0.69%) | 497 ± 5 (1.1%) |
| Swimmer 3 mean ± std. dev. (% var.) | 1017 ± 9 (0.87%) | 510 ± 6 (1.3%) | 994 ± 28 (2.8%) | 510 ± 7 (1.4%) |
| Nominal | 1015 | 508 | 1015 | 508 |
|---|---|---|---|---|
| Mean ± std. dev. of the means | 1012 ± 12 | 500 ± 8 | 991 ± 6 | 502 ± 7 |
| % variation (std. dev./mean) | 1.2% | 1.6% | 0.58% | 1.4% |
Potentially the greatest benefit of this approach is the standardization of the connector geometry itself. In our microscale swimmers, the DNA-based linkages are self-assembled and resulting swimmers are coated with linking molecules. TPP-based milliswimmers do not experience similar uncontrolled decoration of their outer surface.
However, despite improvements in control of the geometry of these structures, the addition of glue for fixing the ferromagnet, as well as the addition of opaque nail polish, which is needed to increase visibility and seal the drainage ports, contributes additional geometric variability to the swimmer design. This assembly process is shown in Fig. 1C, and additional details are provided in Section 3.1. The addition of nail polish and glue, while essential to the swimmer construction and experimental procedure, nonetheless create an interruption along the swimmer's outer profile that may cause variation in performance from swimmer to swimmer, as we discuss further below. Moreover, swimmer performance may differ from model predictions due to surface roughness generated from the TPP printing process. As shown in Fig. 1A, slicing and hatching parameters can lead to the formation of layers and texture on the printed structures’ surface. While the print recipe – and by extension the surface roughness – is consistent among milliswimmers of the same type, these features are not captured in the model, leading to possible inconsistencies.
The milliswimmers are actuated by applying an external magnetic field with an orientation that is sinusoidally oscillating. The magnetic field is created by two orthogonal pairs of Helmholtz coils as shown in Fig. 2E. Each pair of coils creates a field, and the field lines are oriented along the axis connecting the two coils, as shown in Fig. 2F. That is, for the coils oriented along the horizontal axis, shown in dark gray, they produce a field in the x direction, Bx. The coils along the vertical axis, in light gray, produce a field oriented along the y axis, By. As demonstrated in Fig. 2G, the magnitude of the By component is varied in time according to a sinusoidal function, and this causes the net direction of the external field, B (shown as the red arrow), to sweep about the x axis. We can vary the frequency at which By oscillates, and we can also vary the magnitude of By relative to Bx – we call this the magnetic field amplitude ratio, 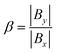 – as shown in Fig. 2H. The magnetic field amplitude ratio controls the size of the angle that the swimmer sweeps through in one oscillation.
– as shown in Fig. 2H. The magnetic field amplitude ratio controls the size of the angle that the swimmer sweeps through in one oscillation.
2.2 Design optimization
Here, we formally define the design optimization problem that we solve in this work. Our goal is to investigate how the shape of the swimmer will affect its swimming velocity. In previous work done by several researchers studying continuously flexible filaments,10,26,27 a common set of design parameters was defined, which we will adapt for our discretized two-link system. These design parameters are:(1) Frequency of the sinusoidally varying externally applied magnetic field, f
(2) Aspect ratio for cylindrical links, 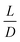 , where L is the link length and D is the link diameter
, where L is the link length and D is the link diameter
(3) Torsion spring constant, κ, i.e. the joint stiffness
(4) Link shape, which can be either cylindrical or spherical
Our primary metric will be the net velocity of the milliswimmer, νnet. The net velocity is computed by considering only the start and end points of the swimmer; we chose this metric because real-world applications will likely require swimmers that can reach a target location quickly. We define νnet as:
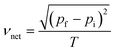 | (1) |
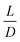 and κ), as well as the control scheme parameter (f), we can experimentally sample the design space and plot the results against the model predictions to find design rules for maximizing our performance metric, νnet.
and κ), as well as the control scheme parameter (f), we can experimentally sample the design space and plot the results against the model predictions to find design rules for maximizing our performance metric, νnet.
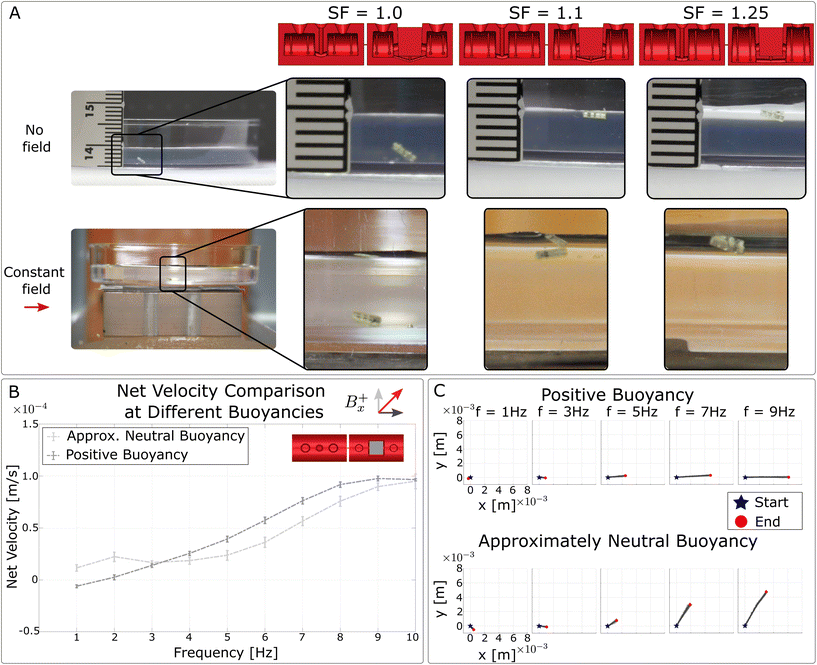
2.3 Milliswimmers are positively buoyant
In this section, we first show that our milliswimmer is positively buoyant and floats at the top surface of the fluid, which minimizes any confounding effects of interactions with the container walls on our observations of the milliswimmer's motion. We also experimentally compare the observed motion of the swimmer while positively buoyant (at the top of the fluid) to its motion while approximately neutrally buoyant (in the middle of the fluid). Additional details and calculations are shown in the ESI.†We begin by noting that it is difficult to find an accurate estimate of the density of cured IP-S photoresist, and this led us to make conservative design choices when constructing our buoyant milliswimmers. During early prototyping, we found that a solid milliswimmer sank to the bottom of a dish containing water. Therefore, we conservatively estimated that the cured IP-S photoresist would be more dense than water and set its density to 1200 kg m−3 for our calculations.
We designed the swimmer to have hollow interior chambers sized to trap sufficient air to ensure buoyancy, even with uncertain knowledge of the density of the photoresist. In our design process, we assumed that the magnet mass would be 3.5 × 10−8 kg (see the ESI† for details on the derivation of this value). This is a conservative mass estimate, which we calculated after speaking with the magnet manufacturer, who reported that the magnets can be damaged during manufacturing by the tooling, leading to variations in the final magnet size.
Each link also had a system of drainage ports to allow uncured photoresist to be removed during post-processing. We calculated that the diameter of the orifices in the milliswimmer design was small enough to prevent air from escaping while the milliswimmer was submerged (see ESI† for details), and we also sealed off the ports using nail polish, which helped visualize the swimmer during experiments.
We built several versions of our nominal cylindrical swimmer design, and each version had a different amount of air trapped in its interior. We sized the milliswimmer air chambers to produce a buoyant force that was equivalent to the swimmer's weight, adjusted by some safety factor. We defined the safety factor, SF, as a multiplier of the upward buoyant force applied to each swimmer link:
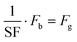 | (2) |
We first tested the behavior of these swimmers by placing them in a Petri dish filled with Percoll, without an externally applied magnetic field. As shown in Fig. 3A, we found that the true neutral buoyant point is between a safety factor of 1.0 and 1.1, because the swimmer with a safety factor of 1.0 sank, while the swimmer with a slightly larger volume of air (safety factor 1.1) floated at the top surface of the fluid.
After imaging the swimmers at their steady-state resting places in Percoll, we placed the same swimmers in the same fluid in a uniform magnetic field. The magnetic field had a component along the horizontal plane, but no component in the vertical plane. We imaged the swimmers in this field and found that, as expected, the magnetic field in the plane did not affect the swimmers’ vertical positions within the Petri dish. (This is shown in the second row of images in Fig. 3A.)
Note that each swimmer shown in Fig. 3A was built with a different magnet, so some variation in the magnet's mass and amount of glue and nail polish used will have affected the behavior of the corresponding swimmer. This could explain why the swimmer constructed with a safety factor of 1.0 was not truly neutrally buoyant: we may have underestimated the mass of the magnet, glue, and nail polish, and so when the swimmer was constructed, the excess mass caused the swimmer to sink.
Given that we were aware that some variation in the mass of the magnets existed, we conducted a second test where we varied the density of the Percoll, rather than the mass of the swimmer, to artificially adjust the swimmer's buoyancy to be nearly neutral. Specifically, we added water to Percoll to reduce the fluid's density. The purpose of this test was to achieve a nearly neutrally buoyant state so that we could compare the milliswimmer's velocity in the middle of the Petri dish (away from either the top or bottom surface) against the observed velocity at the top of the fluid. Note that, although this approach of mixing Percoll with water gave us the ability to finely tune the swimmer's observed buoyancy, it nonetheless affected the dynamic viscosity of the fluid, thereby adding a confounding variable to this experiment.
We found that by adding 1.2 mL of distilled water to 6.0 mL of Percoll, it would take more than 1 minute for the swimmer to rise from the bottom of the dish to the top. We determined that this was close to neutral buoyancy for the purposes of our swim tests, which have a duration of 1 minute. We then placed the swimmer in this mixture of Percoll and water in our test setup and ran a frequency sweep over the range [1, 10] Hz for this swimmer (n = 5 tests). We plotted these data in comparison to the same frequency sweep for the same swimmer in pure Percoll, as shown in Fig. 3B.
We can see that the net velocities in both cases are similar in magnitude, although there is variation in the observed swimming direction. In particular, we saw that the swimmer in the lower density fluid swam at a more pronounced angle away from the horizontal. This may be caused by the reduced fluid viscosity and density, which could affect the hydrodynamic drag experienced by the swimmer. The swimmer in the low-density fluid mixture also slowly moved through the fluid along the z-axis, which may also have affected its swimming direction.
Ultimately, the variation in swimming direction indicates that there is some difference in the swimmer's behavior between the two test cases, but there are two confounding variables: the varied fluid properties (density, viscosity) as well as the fact that the swimmer was slowly moving along the vertical axis through the lower-density fluid. Despite these confounding variables affecting the results, the magnitude of the swimmer velocities are similar over the frequency range we tested, suggesting that our swimmer's behavior while positively buoyant at the top of the fluid can be used as an informative example for how to optimize the swimmer design to maximize its net velocity.
Based on these results, we chose to build all subsequent swimmers using a buoyancy force safety factor of 1.25. We chose this value with the intention of maximizing the likelihood that all swimmers would be positively buoyant and float along the top surface of the fluid, despite observed variations in the magnet mass.
2.4 First and second order models show limited agreement
In this section we explore the extent to which first and second order dynamics models for our two-link swimmers are capable of capturing the behavior we observe experimentally. We begin with a first order model because this approach is commonly used in the literature for two-link microswimmmer systems, as demonstrated by Grover et al. and Gutman and Or.20,21 We then show that, based on the observed velocities and associated Reynolds numbers of the system, we chose to recast the model as a second order system. We conclude with our findings and recommendations for future development for more accurate models of real-world two-link swimming robots.We represent our swimmer as two cylindrical links connected with a torsion spring, similar to the models presented by Grover et al. and Gutman and Or.20,21 As shown in Fig. 2A, we can use the center of mass of the first link, point p1 = [x1, y1], and the angle of each link written with respect to the inertial frame, to completely describe the swimmer's configuration, that is: [x1, y1, θ1, θ2] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) . To derive the equations of motion for this system, we can balance the forces and torques that act on this swimmer, as shown in Fig. 2B. The corresponding equations of motion are:
. To derive the equations of motion for this system, we can balance the forces and torques that act on this swimmer, as shown in Fig. 2B. The corresponding equations of motion are:
| −F1,h − F2,h = 0 | (3) |
| −τp1,h1 − τp2,h1 + τ1,m = 0 | (4) |
| −τp2,h2 − τκ,2 = 0. | (5) |
Eqn (3) is a sum of the forces acting on the entire system, and eqn (4) is the sum of the torques acting on the entire system. In order to solve for the final state variable, we also write eqn (5), which is the sum of the torques acting on link 2, specifically. Forces Fi,h are the hydrodynamic drag forces that act on the i-th link with respect to the x and y axes of the inertial frame. The torques due to hydrodynamic drag are written as τpi,hj, where the torque is acting on link i and written with respect to point pj. The torque due to magnetic misalignment acting on link 1 is τ1,m (this misalignment between the externally applied magnetic field and the swimmer's ferromagnetic cube creates a torque that causes the swimmer to reorient to follow the externally applied field). Note that we assume that only link 1 is magnetized in this work, and our experimental realization matches this. The torque produced by the torsion spring acting on link 2 is τκ,2. Notice that, in the first order model, the sum of the forces and torques in each direction are equal to zero because we assume that our swimmer is in a low Reynolds number regime and therefore the dynamics are quasistatic. The details of the model derivation, as well as all parameters used, are presented in the ESI† (we use values taken from experimental data, averaged over the three swimmers, with the exception of the physical dimensions, where we use nominal values). Together, these equations define the dynamics of the swimmer system. We solve eqn (3)–(5) for 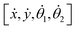 and use the result to simulate the dynamics using an ODE solver in MATLAB.
and use the result to simulate the dynamics using an ODE solver in MATLAB.
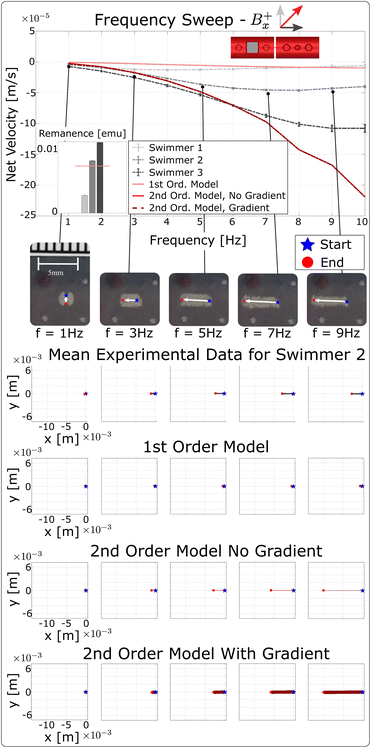
We conducted a frequency sweep to establish a baseline set of experimental data using a nominal cylindrical milliswimmer design, and then we compared the observed behavior to our first order model predictions. We assembled three two-link milliswimmers with cylindrical links and performed a frequency sweep test by increasing the frequency from 1 to 10 Hz, holding β = 1. We denote the positive direction of the magnetic field along the x-axis as Bx+. The results are presented in Fig. 4. We note that in all the analyses we conduct, we omit the first and last 3 seconds of data from our calculation of the net velocity. This allows us to exclude any transient behavior and report a net velocity that represents the steady-state behavior of the system.
For test conditions Bx+, corresponding to Fig. 4, our first order model (light red solid line) predicts that the magnitude of the net velocities will increase with increasing actuation frequency to a maximum of approximately −9.6 × 10−6 m s−1 at 10 Hz. However, our experimental results do not agree well with the first order model, as they show velocities that are generally larger in magnitude than the model predictions. For example, Swimmers 2 and 3 exhibit maximum velocities of approximately (−4.6 ± 0.1) × 10−5 m s−1 at 8 Hz and (−11 ± 0.6) × 10−5 m s−1 at 10 Hz, respectively. (The uncertainty in the reported mean velocity is the standard deviation over 5 trials.) Swimmer 1 demonstrates a slower maximum velocity of (−1.3 ± 0.1) × 10−5 m s−1 at 4 Hz.
Note that the data shown in Fig. 4 also demonstrate that the experimentally observed velocities follow our expectations for swimming direction based on the literature, which is that the direction of the swimmer's net displacement is opposite the direction of the traveling wave along the swimmer's longitudinal axis. (Notice that the three nominal swimmers tested here swam in the opposite direction to the swimmer tested in Section 2.3. This is because the swimmer in Section 2.3 was constructed with the magnet oriented 180° compared to the magnet orientation used to build all other swimmers tested in this work.) The experimental results also show good repeatability per swimmer. The standard deviations are generally an order of magnitude smaller than the mean velocities. We can also see in Fig. 4 a set of plots for the mean experimental data for Swimmer 2 – the dark gray line represents the mean trajectory averaged over 5 trials, and the light gray shading shows the standard deviation.
In addition to considering the magnitude and direction of the swimmers’ velocities in the experiments and the model, we can also compare the trends in net velocity as the actuation frequency increases from 1 to 10 Hz. Our first order model predicts that as the actuation frequency increases, the magnitude of the swimmer's net velocity will monotonically increase. However, our experimental data suggest that the swimmer's velocity can plateau as the frequency continues to increase. For example, in Fig. 4, Swimmer 1 and 2's velocities increased until some peak value was reached (at 4 Hz and 8 Hz, respectively), and after this value the velocities decreased. And while Swimmer 3's maximum velocity occurred at 10 Hz, we can see that the increases in the velocity in the [7, 9] Hz region were not as large as the increases we saw at frequencies below 7 Hz.
In order to understand why our model was underestimating the milliswimmer's net velocity relative to the experimental data, we calculated the Reynolds number of the milliswimmer using both its net velocity as well as its instantaneous velocity. The instantaneous velocity is larger because the swimmer is sweeping back and forth about the x-axis following the control input, leading to a larger total displacement each cycle compared to the net displacement per cycle. We found that the Reynolds number for the nominal, cylindrical milliswimmer calculated with net velocity is 7.7 × 10−4. If, however, we use the instantaneous velocity, then the Reynolds number for a swimmer actuated at 1 Hz is 0.12 and at 10 Hz it is 1.2 (see the ESI† for the complete calculation). These values are large enough that we cannot consider them as “low” anymore, and so we need to account for inertial forces in our dynamics model.
Given this result, we revised our first order model to include inertia, as follows. We can rewrite the equations of motion as a sum of all the forces acting on both links in the x and y directions, and then sum the torques acting on each link individually. Each equation will include the corresponding inertial terms. Thus we can write the equations of motion for our cylindrical milliswimmer as:
m1![[p with combining umlaut]](https://www.rsc.org/images/entities/b_i_char_0070_0308.gif) 1 = −F1,h 1 = −F1,h | (6) |
m2![[p with combining umlaut]](https://www.rsc.org/images/entities/b_i_char_0070_0308.gif) 2 = −F2,h 2 = −F2,h | (7) |
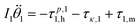 | (8) |
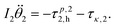 | (9) |
The equivalent system of equations for spherical links is available in the ESI.† Here, inertia is captured by the mi![[p with combining umlaut]](https://www.rsc.org/images/entities/b_i_char_0070_0308.gif) i and
i and 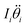 terms for the ith link. As we were building our second order model, the model tended to significantly overestimate the milliswimmer's net velocity as compared to the experimental data. We hypothesized that the inclusion of inertia in the model shifted its behavior closer to what we would expect to see for a swimming robot with larger Reynolds numbers. Specifically, at higher Reynolds numbers, other assumptions in the model – including the assumption that the hydrodynamic drag force Fh can be formulated as Stokes’ drag – may be slightly less accurate for our milliswimmers than for smaller-scale systems. To account for this, we experimented with fitting the drag coefficient, kt, to our experimental data instead of using a calculated value. We note that the analytical expression for kt assumes an ideal cylinder in a fluid, but SEM images (such as those shown in Fig. 1) reveal that the surface of the swimmers is actually textured by print lines produced while the layers of photoresist were cured. The print lines are on the same length scale as the silica beads of the Percoll that the milliswimmers are submerged in, and so there may be additional interactions between the milliswimmer surface and the Percoll components that we need to account for in our model. There are also surface imperfections due to the addition of nail polish and the presence of the magnet pocket, which could also affect the surface interactions with the Percoll.
terms for the ith link. As we were building our second order model, the model tended to significantly overestimate the milliswimmer's net velocity as compared to the experimental data. We hypothesized that the inclusion of inertia in the model shifted its behavior closer to what we would expect to see for a swimming robot with larger Reynolds numbers. Specifically, at higher Reynolds numbers, other assumptions in the model – including the assumption that the hydrodynamic drag force Fh can be formulated as Stokes’ drag – may be slightly less accurate for our milliswimmers than for smaller-scale systems. To account for this, we experimented with fitting the drag coefficient, kt, to our experimental data instead of using a calculated value. We note that the analytical expression for kt assumes an ideal cylinder in a fluid, but SEM images (such as those shown in Fig. 1) reveal that the surface of the swimmers is actually textured by print lines produced while the layers of photoresist were cured. The print lines are on the same length scale as the silica beads of the Percoll that the milliswimmers are submerged in, and so there may be additional interactions between the milliswimmer surface and the Percoll components that we need to account for in our model. There are also surface imperfections due to the addition of nail polish and the presence of the magnet pocket, which could also affect the surface interactions with the Percoll.
We used gradient descent to fit the values of kt to the mean experimental data for the three nominal cylindrical milliswimmers. The details are provided in the ESI,† and we report the final values that we used in our second order model in Table 2, alongside the analytical values of kt that are computed per the literature.21,28,29 We can see that the fitted values of kt are 1–2 orders of magnitude larger, indicating that there is significantly more hydrodynamic drag at play than the analytical expression would predict. Secondly, we can see that the fitted values of kt increased as the surface area of the links increased (i.e. the fitted values for the large aspect ratio swimmer are greater than for the nominal design), suggesting that the hydrodynamic drag is affected by the interactions between the surface of the swimmer and the silica beads in the fluid medium. This contrasts with the trend in the analytical expression for kt, where the value decreased for the swimmer with a larger aspect ratio.
We plotted our second order model's predicted trajectories as shown in Fig. 4 – the second order model with no magnetic field gradient (we include this in a subsequent iteration of the model, see below) is plotted as the medium red solid line. We can see that the second order model now predicts net velocities that are on the same order of magnitude as the experimental data over the range of frequencies that we tested. However, our second order model, like our first order model, predicts that the net velocities will continue to increase in magnitude as the actuation frequency increases, and does not show a roll-off occurring within the tested frequency range. We also found that when we used the model to predict the motion of the swimmer in the Bx− case – where the swimmer initial conditions start with the magnetic link's magnetic moment oriented 180° away from the direction of the Bx component of the magnetic field – that it took many cycles for the simulated swimmer to re-orient itself in the direction of the magnetic field, which disagreed with experimental results that showed the swimmer was able to re-orient itself within the first few cycles. This suggests that our second order model, with a fitted kt value, does not capture transient behavior well.
We also observed slight deviations in trajectory for our nominal swimmers (i.e. swimming at a slight angle to the horizontal) which we hypothesized could be due to the effect of nonzero magnetic field gradients present in the workspace. Even an ideal pair of Helmholtz coils produces a small nonzero magnetic field gradient within the workspace that could affect our swimmers’ motion. We can write the force exerted by the magnetic field gradient as the dot product of the milliswimmer's magnetization and the gradient of the externally applied magnetic field, F∇B = VM·∇B (where V is the volume of the magnet, M is its magnetization and ∇B is the magnetic field gradient). We introduced the model for a single Helmholtz coil in a previous work30 and extended it to apply to two pairs of Helmholtz coils here.31 The full derivation is presented in the ESI.†
Given that we had evidence of the possible presence of a magnetic field gradient in the workspace, we used our second order model with the magnetic field gradient included to investigate how these parameters might affect our swimmers’ motion. The magnetic field gradient appears to have no substantial effect on the magnitude of the net velocities – the medium red and dark red lines overlap on the plot at the top of Fig. 4. However, we can see that the magnetic field gradient does seem to affect the distance that the swimmer travels during an oscillation – in the bottom row of plots in Fig. 4, the predicted trajectory from the second order model with the gradient included shows a wider sweep in the y direction for every actuation cycle, compared to the second order model that does not include the gradient. This suggests that the magnetic field gradient has a more substantial effect in the y direction, and tends to pull the swimmer up or down depending on the exact field configuration.
In this section, we showed that, by incorporating inertia into our model, we were able to achieve closer agreement with our experimental observations, indicating that our milliswimmer is operating at a mesoscale between high and low Reynolds number environments. However, none of our modeling approaches were ultimately able to capture other features of the swimmer behavior that we observed experimentally, such as the roll-off in net velocity with increasing frequency. We suggest that new models are needed for capturing the behavior of mesoscale swimmers and that ground truth experimental data generated using milliswimmer studies can be used to develop and validate them.
2.5 Effect of various design parameters on swimming performance
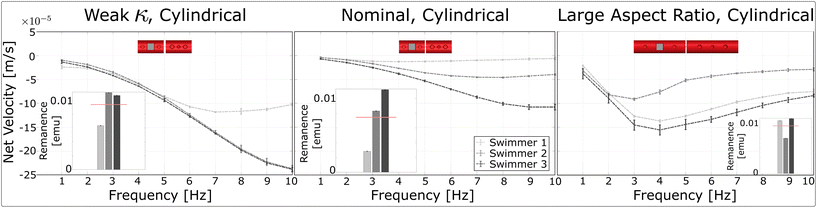
We tested the effect of varying several design parameters on milliswimmer performance in search of opportunities to maximize net velocity. We found that varying the aspect ratio of the links allows us to tune the frequency at which the maximum velocity occurs, and that reducing the stiffness of the flexible linker (modeled as a torsion spring with spring constant κ) from 1.2 × 10−7 N m rad−1 to 6.3 × 10−8 N m rad−1 led to increased net velocities.In Fig. 5 we tested the aspect ratio of individual links, defined as the ratio of the length of the cylinder to the diameter of the cylinder. We found that increasing the aspect ratio to 4 (i.e. building a longer cylinder) led to a differently shaped net velocity curve, one that peaked at lower frequencies than for swimmers with smaller aspect ratios. We found this by experimentally testing ratios of 2 (the nominal design) and 4 over a range of frequencies f = [1, 10] Hz, with β = 1. Our experimental data show that the higher aspect ratio leads to an earlier peak in the net velocity. The experimental data showed peaks around 3–4 Hz for the 3 swimmers that we tested with 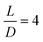 , compared to the nominal swimmer data which peaked near the top of the frequency range. These results show that the aspect ratio of the swimmer shifts the location of the maximum net velocity along the frequency range.
, compared to the nominal swimmer data which peaked near the top of the frequency range. These results show that the aspect ratio of the swimmer shifts the location of the maximum net velocity along the frequency range.
Next, we experimented with decreasing the torsion spring constant to investigate how it affected the milliswimmers’ net velocity. We used the nominal cylindrical design with a reduced torsion spring constant as our experimental verification. We found empirically that it is prohibitively difficult to manipulate swimmers constructed with beams longer than 80 μm, which led us to test a minimum torsion spring stiffness of 6.3 × 10−8 N m rad−1. We tested three copies of the weak κ swimmer design over a range of frequencies f = [1, 10] Hz, holding β = 1. In Fig. 5, we can see that the velocity curves for the weaker torsion spring are larger than those for the nominal swimmer design with a stronger torsion spring.
The data in Fig. 5 also shows that there is some correlation between the measured remanence of each swimmer and its net velocity. That is, the faster swimmers had larger remanences for a given link design. However, if we directly compare swimmers with similar remanences across designs, we can still see substantial differences in their frequency sweeps that can be attributed to the differences in their link designs. For example, Swimmer 3 of the nominal design and Swimmers 1 and 3 of the large aspect ratio design have similar remanences, but the large aspect ratio swimmers display substantially different trends in their net velocity. And if we compare Swimmer 3 of the nominal design with Swimmers 2 and 3 of the weak torsion spring design, we also see that the swimmers with the weaker torsion spring had substantially larger net velocities over the frequency sweep compared to the nominal design.
2.6 Recommendations for two-link cylindrical swimmer design
Given our findings in the previous sections, we can now identify some guidelines for maximizing two-link cylindrical swimmer velocity:(1) Actuation frequencies can be adjusted to attain faster velocities, as long as the hardware has a sufficiently high sampling rate to effectively generate those frequencies (we recommend using a function generator as in the work by Pauer et al.15 or data acquisition hardware). For higher aspect ratios, the peak net velocity is observed at lower frequencies in the experimental data.
(2) Larger aspect ratios shift the frequency at which the peak velocity occurs, assuming all other parameters remain constant. Doubling the aspect ratio from 2 to 4 shifted the peak velocity from near 10 Hz to near 4 Hz, as shown in the experimental data.
(3) The stiffness of the joint between the links should be reduced to increase the swimming velocity, when comparing the torsion spring values of 1.2 × 10−7 N m rad−1 and 6.3 × 10−8 N m rad−1, as shown in the experimental data.
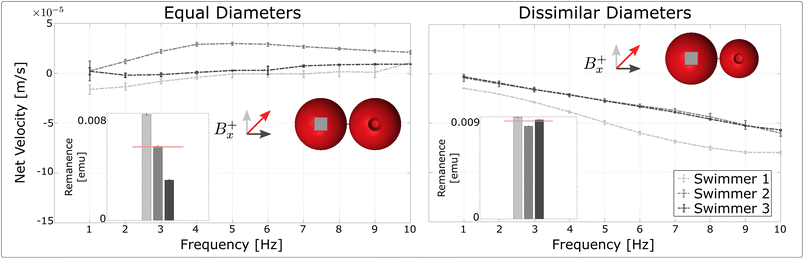
2.7 Spherical milliswimmers
In addition to investigating design principles for cylindrical systems, we also extended our approach to studying two-link milliswimmers with spherical links, since spherical components are popular for building micro- and nanoscale systems. As shown in the CAD insets in Fig. 6, we constructed two types of spherical milliswimmers: a design with links of equal diameter, and a second configuration where the second link (the one without the magnet) has a diameter that is 75% of the diameter of the first link. We collected experimental data for 3 swimmers of each design over 5 trials and compared the results to our model predictions.In Fig. 6, the experimental results show that the swimmer built with equally sized links achieved negligible net translation for any frequency. In contrast, the swimmers built with dissimilar sized links did exhibit net velocities that were comparable to the net velocities of the nominal cylindrical design. This finding agrees with the results presented in Harmatz et al. which also showed that swimmers built with two differently sized spherical particles were able to achieve net translation through the fluid.13
We also wrote first and second order dynamics models for our spherical swimmers, using the same approach presented in Section 2.4. We found that our models always predicted that the spherical swimmers, regardless of their design, would not achieve net translation (the full derivation is presented in the ESI†).
We hypothesize that the spherical model does not predict any net displacement because it assumes a perfectly isotropic distribution of hydrodynamic drag about each link. It may be that anisotropic drag must be applied to each link individually in order to break the Scallop Theorem and achieve net displacement. It is possible that, experimentally, anisotropic drag forces are applied to each link individually, either because the outer profiles of the links are not perfectly spherical (as demonstrated by the SEM image of the spherical link in Fig. 1), or perhaps because the motion of the fluid about the two links creates an asymmetric condition that we do not represent in our model. Overall, these results indicate that relatively simple models of two-link spherical milliswimmers fail to adequately predict the experimentally observed behavior for all designs. It highlights an opportunity for the field to investigate – possibly using computational fluid dynamics – why two-link spherical milliswimmers with dissimilar link diameters show significant velocities, but equally sized swimmers do not.
3 Methods
3.1 Milliswimmer assembly process
The milliswimmers are constructed using two-photon polymerization (Nanoscribe Photonic Professional GT2 platform). Glass coverslips coated with indium tin oxide (ITO) on one side are used as the printing substrate (part number DiLL 0000381). The conductive side is spin-coated in a layer of Dextran at 2000 rpm for 5 minutes to ensure the print can be easily removed from the coverslip after printing. A dip-in laser lithography (DiLL) printing process is used with IP-S resin and a 25× objective. The standard IP-S 25× ITO Solid (3D MF) settings are used as a starting point in the DeScribe application. The most significant changes that were made to the slicing settings were to adjust the cross-hatching to alternate orthogonal directions on every layer and to ensure that individual blocks are supported by blocks in the previous layer. (A more complete description of the printing parameters is provided in the ESI.†) After printing is complete, the result is developed in propylene glycol monomethyl ether acetate (PGMEA) for 45 minutes and then washed in 99% isopropyl alcohol for 3 minutes.Based on our discussion of the possible effect of surface roughness on hydrodynamic drag, we researched methods for smoothing the printing process, although we did not implement them in this work because they are more time-intensive. Surface roughness due to TPP printing can be decreased by optimizing slicing and hatching distance parameters. Advanced Nanoscribe printing parameters such as adaptive slicing and slope evaluation allow for the printing of smooth surfaces such as microoptics. These parameters operate by evaluating the structure's slope and decreasing slicing distance when the structure's slope is shallower, increasing the print time and allowing for the creation of smooth structures such as lenses.32 In future studies, these parameters could be incorporated into the milliswimmer fabrication process and optimized to create structures more closely matched to our model assumptions.
As shown in Fig. 1C, after each swimmer is printed, we first add opaque nail polish to each link to ensure that we can visualize the swimmer with our camera during testing. Nail polish is also used to seal the drainage ports as a second method to ensure that air trapped in the hollow chambers does not escape. Next, the ferromagnet (SuperMagnetMan C0005-10) is placed by hand in the appropriate pocket in the design using forceps. A small droplet of glue (Loctite Super Glue ULTRA Liquid Control) is added with the forceps to ensure that the magnet is fixed in place. The assembly is allowed to dry overnight prior to testing.
3.2 Control environment
We actuate the milliswimmer using two pairs of Helmholtz coils (3B Scientific Physics, Pasco) arranged orthogonally about a central point, as shown in Fig. 2E. The milliswimmer itself is submerged in a Petri dish filled with Percoll (Sigma-Aldrich) and the lid is sealed with laboratory tape to prevent evaporation. A rigid plastic stand supports the Petri dish, which is held on the arm of the stand using double-sided tape and several points of contact to repeatably fix the dish in place. The surface underneath the Petri dish is covered in black paper with white grid marks as a high-contrast backdrop for collecting video data. We mark the northwest corner of the region on the grid where we conduct our testing with red ink. A ruler is also fixed to the surface of the lid so that we can set the scale of the videos during data analysis.The Helmholtz coils are controlled via a motor controller (Basic Micro Roboclaw 2x7A motor controller) that modulates the current from a power supply (Tekpower) to generate magnetic fields of a specific magnitude. The motor controller receives commands from a custom Python script running on a laptop that is also collecting video from a webcam (Logitech). We measure the externally applied magnetic fields using a three-axis magnetometer (Infineon). All the experiments performed in this work are run on this setup. We track the swimmers in the video data using a custom macro in FIJI25 and analyze the trajectories with custom MATLAB scripts. Details on how the experiments are conducted and analyzed are presented in the ESI.†
Note that we chose to run our tests in Percoll, not in water (as in Harmatz et al.13) or in glycerin (as in Grover et al.20). We tested actuating the swimmer in all three fluids, and found that Percoll was the best choice for two reasons: it appeared to create a low Reynolds number environment, and we found that the swimmer velocities were sufficiently large to be detectable in a reasonable amount of time. In water, the swimmer still appeared to have some momentum, indicating that it was not a low Reynolds number environment. In glycerin, the swimmer was certainly in a low Reynolds number environment, but it moved so slowly that it would have been prohibitively time consuming to run frequency sweeps.
3.3 Data analysis
We extract the swimmer trajectory data from the videos collected during the swim tests of each swimmer. Videos are converted to down-sampled .avi files and imported into FIJI.25 We use a custom macro written for FIJI that prompts the user to crop the video, then the region of interest is thresholded to a black-and-white representation. The white pixels corresponding to the swimmer are dilated as required to connect all the pixels together so that they accurately represent the swimmer's shape. The macro then extracts the centroid data for the swimmer in every frame and exports it to a .csv file. We also extract measurements from the videos to determine the correct scale factor from pixels to meters. We use custom MATLAB scripts to read in the data, compute the net velocity, and plot the data against our model predictions.The magnetometer data characterizing the external magnetic fields applied by the experimental setup are processed using a custom MATLAB script. We compute the offset in the sensor readings for the ambient magnetic field with the coils switched off. We also compute the magnitude of the magnetic fields for every value of β and for Bx oriented in both the positive and negative directions; these magnitude values are adjusted by the offset calculated above. We also apply a fast Fourier transform to extract the frequency of oscillation of the fields to verify that they match the desired values in the range [1, 10] Hz.
3.4 Vibrating sample magnetometer procedure
We used a vibrating sample magnetometer (Lakeshore) to characterize the magnetic moment of each milliswimmer that we constructed. Milliswimmers were individually fixed on a plastic sequin using sugar dissolved in deionized water as an “adhesive”. The plastic sequin was then attached to the vibrating sample magnetometer's (VSM) sample probe using double-sided tape. The VSM was calibrated and the applied field was set to 0 G so that we could measure the remanence of each ferromagnetic cube. (Although the test environment applies a nonzero external field to the milliswimmers, the response of a ferromagnet to an external field is a linear increase to its magnetic moment in a zero field – i.e. its remanence – so the remanence is correlated to the strength of the ferromagnet's response to all nonzero fields.) We use a custom MATLAB script to compute the average magnetic moment for each sample from at least 30 measurements collected over 5 minutes.4 Conclusions
In this work, we developed design rules for maximizing the velocity of a two-link milliswimmer using experimental data obtained from a buoyant, flexible milliswimmer design. From our experimental data, we found that tuning the actuation frequencies as well as the aspect ratios allows the designer to select the frequency at which the peak velocity will occur. In addition, weaker torsion spring joints (when considering values of 1.2 × 10−7 N m rad−1 and 6.3 × 10−8 N m rad−1) were also shown to lead to higher net velocities. It was noted that neither a first order model nor a second order model (incorporating the magnetic field gradient and a custom drag parameter) were able to accurately predict the magnitude and direction of the swimmers’ velocities when compared to experimental data gathered for multiple swimmer designs.We also demonstrated that two-link spherical milliswimmers with dissimilar link diameters are able to achieve net propulsion, while spherical swimmers with equally sized diameters do not swim effectively. As current models fail to capture the motion of two-link spherical milliswimmers with dissimilar link sizes, this identifies the need for future investigations into dynamic link drag as a potential driver for locomotion in spherical systems.
In this work we have reduced variations in the physical dimensions of a novel milliswimmer platform and demonstrated its use in identifying design guidelines for small-scale swimming robots. This approach can be extended to predict the swimming behavior of other novel milliswimmer designs with increasing complexity. Findings obtained from this platform could also inform predictions of the swimming behavior of micro- and nanoscale swimmers and be used to optimize their performance. Our platform's improved geometric monodispersity has revealed new research directions and will ultimately support new dynamics model development.
Author contributions
Conceptualization, E. B., T. I., A. L., S. B., M. T., and R. E. T.; data curation, E. B., and T. I.; formal analysis, E. B.; funding acquisition, E. B., T. I., M. T., and R. E. T.; investigation, E. B., T. I., and A. L.; methodology, E. B.; project administration, S. B., M. T., and R. E. T.; resources, E. B., T. I., and A. L.; software, E. B.; supervision, S. B., M. T., and R. E. T.; validation, E. B.; visualization, E. B., and T. I.; writing – original draft, E. B., and T. I.; writing – review & editing, E. B., T. I., A. L., S. B., M. T., and R. E. T.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Department of Mechanical Engineering (S. B., R. E. T.) and the Robotics Institute (M. T.) at Carnegie Mellon University, the National Science Foundation Graduate Research Fellowship Program DGE1745016 and DGE2140739 (E. B. and T. I.), the National Science Foundation Cyber Physical Systems 1739308 (M. T., R. E. T.) and the National Science Foundation National Robotics Institute 2132886 (M. T., R. E. T.). The authors acknowledge the Data Storage Systems Center (DSSC) and its sponsoring companies, for support and the use of facilities. Thank you to Andrew Gamble for support in using the DSSC resources. Thanks also to Sukjun Kim for his expertise in two-photon polymerization.Notes and references
- C. Hu, S. Pané and B. J. Nelson, Annu. Rev. Control Robot. Auton. Syst., 2018, 1, 53–75 CrossRef.
- W. Zhang, Z. Zhang, S. Fu, Q. Ma, Y. Liu and N. Zhang, ChemPhysMater, 2023, 2, 114–125 CrossRef.
- Y. Hou, H. Wang, R. Fu, X. Wang, J. Yu, S. Zhang, Q. Huang, Y. Sun and T. Fukuda, Lab Chip, 2023, 23, 848–868 RSC.
- F. Rajabasadi, L. Schwarz, M. Medina-Sánchez and O. G. Schmidt, Prog. Mater. Sci., 2021, 120, 100808 CrossRef CAS.
- P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagués, J. Phys. Chem. B, 2008, 112, 16525–16528 CrossRef CAS PubMed.
- S. Jeon, S. Kim, S. Ha, S. Lee, E. Kim, S. Y. Kim, S. H. Park, J. H. Jeon, S. W. Kim, C. Moon, B. J. Nelson, J.-y. Kim, S.-W. Yu and H. Choi, Sci. Rob., 2019, 4, eaav4317 CrossRef PubMed.
- U. Kei Cheang, H. Kim, D. Milutinović, J. Choi and M. J. Kim, J. Bionic Eng., 2017, 14, 245–259 CrossRef.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 2–5 CrossRef PubMed.
- E. Diller, J. Zhuang, Z. Lum, M. R. Edwards and M. Sitti, Appl. Phys. Lett., 2014, 104, 174101 CrossRef.
- Y. Harduf, D. Jin, Y. Or and L. Zhang, Soft Rob., 2018, 5, 389–398 CrossRef PubMed.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- L. Xing, P. Liao, H. Mo, D. Li and D. Sun, IEEE Access, 2021, 9, 29279–29292 Search PubMed.
- I. M. Harmatz, M. J. Travers and R. E. Taylor, J. Microelectromech. Syst., 2020, 29, 990–995 CAS.
- A. M. Maier, C. Weig, P. Oswald, E. Frey, P. Fischer and T. Liedl, Nano Lett., 2016, 16, 906–910 CrossRef CAS PubMed.
- C. Pauer, A. Venczel, M. Dass, T. Liedl and J. Tavacoli, Adv. Mater. Technol., 2022, 7, 2200450 CrossRef.
- S. V. Pogu, D. Dehariya, D. N. Yadav and A. K. Rengan, Mol. Syst. Des. Eng., 2023, 8, 416–430 RSC.
- J. S. Kahn and O. Gang, Angew. Chem., Int. Ed., 2022, 61, e202105678 CrossRef CAS PubMed.
- T. Imamura, U. M. Sonmez, M. Travers, S. Bergbreiter and R. E. Taylor, 22nd Intl. Conf. Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), 2023 Search PubMed.
- J. S. Grover, MSc thesis, Carnegie Mellon University, 2018 Search PubMed.
- J. S. Grover, D. Vedova, N. Jain, M. Travers and H. Choset, Proc. RSS, Freiburg im Breisgau, Germany, 2019.
- E. Gutman and Y. Or, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 013012 CrossRef PubMed.
- X. Zhou, Y. Hou and J. Lin, AIP Adv., 2015, 5, 030701 CrossRef.
- A.-I. Bunea, N. del Castillo Iniesta, A. Droumpali, A. E. Wetzel, E. Engay and R. Taboryski, Micro, 2021, 1, 164–180 CrossRef.
- T. K. Sherwood, Mass transfer, McGraw-Hill, New York, 1975 Search PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- M. Roper, R. Dreyfus, J. Baudry, M. Fermigier, J. Bibette and H. A. Stone, Proc. R. Soc. A, 2008, 464, 877–904 CrossRef.
- E. Gauger and H. Stark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021907 CrossRef PubMed.
- J. Gray and G. J. Hancock, J. Exp. Biol., 1955, 32, 802–814 CrossRef.
- R. G. Cox, J. Fluid Mech., 1970, 44, 791–810 CrossRef.
- E. Benjaminson, M. Travers and R. Taylor, IEEE IROS, 2020, pp. 6332–6338.
- W. R. Smythe, Static and dynamic electricity, McGraw-Hill, New York, 3rd edn, 1967 Search PubMed.
- K. Vanmol, A. Kandeel, G. Y. Belay, H. Thienpont, H. Ottevaere and J. Van Erps, 26th MOC, 2021.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr02846a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |


![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif)
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif)