Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Development of prediction model for cloud point of thermo-responsive polymers by experiment-oriented materials informatics†
Mai
Hayakawa
a,
Kosuke
Sakano
a,
Rei
Kumada
a,
Haruka
Tobita
a,
Yasuhiko
Igarashi
b,
Daniel
Citterio
 a,
Yuya
Oaki
a,
Yuya
Oaki
 a and
Yuki
Hiruta
a and
Yuki
Hiruta
 *a
*a
aDepartment of Applied Chemistry, Faculty of Science and Technology, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama 223-8522, Japan. E-mail: hiruta@applc.keio.ac.jp
bFaculty of Engineering, Information and Systems, University of Tsukuba, 1-1-1 Tennodai, Tsukuba 305-8573, Japan
First published on 26th April 2023
Abstract
Thermo-responsive polymers having a lower critical solution temperature (LCST) have attracted attention for biological applications such as drug delivery, diagnosis, and coating materials. In recent years, research on predicting LCST by utilizing machine learning has been conducted. However, since these methods targeted only copolymers combining specific monomer structures, they are not versatile, and multiple trials are still required to obtain new thermo-responsive polymers with the desired LCST. In this study, a prediction model for cloud point temperature (TCP) was built by a combination of materials informatics and chemical insight, named sparse modeling for small data (SpM-S) using a small dataset of polymers collected from the literature as training data. This approach created a model that is interpretable, easy to calculate, and versatile. The prediction accuracy was validated using data from different literature sources and experimental test data. The model was able to predict the TCP of polymers containing monomers not included in the dataset as well as polymers containing monomers included in the dataset. The predictive model has the potential to guide the design of new thermo-responsive polymers, and to contribute to efficient development of thermo-responsive polymers.
Introduction
Stimuli-responsive polymers, which change their properties in response to specific external stimuli, such as temperature,1 light,2 pH,3 and ions,4 are used in a wide range of fields, such as drug delivery systems, diagnostics, and coating materials.5–8Among them, thermo-responsive polymers, which exhibit a temperature-dependent phase transition, are one of the most widely studied stimuli-responsive polymers. Thermo-responsive polymers have a lower critical solution temperature (LCST) or upper critical solution temperature (UCST) in aqueous solution.9 Compared to UCST-type polymers, many studies have been reported on LCST-type polymers applied to the biomedical field, because they undergo a phase transition at physiological temperature and conditions,10 which are less sensitive to pH and ionic strength.11–13 Thanks to these advantages, LCST-type polymers have been actively studied.12,14 Experimental characterization of such LCST phenomena has been studied using various measurement methods, including cloud point measurements,15 dynamic light scattering,16 and differential scanning calorimetry.17 Among them, simple assays of clouding behaviour are still the most common to study this type of phase separation process, which is important in various applications of thermo-responsive polymers.18
In designing thermo-responsive polymers, the control of LCST is an important issue for applications. The LCSTs of thermo-responsive polymers can be controlled by changing monomer ratio,19–22 molecular weight,23,24 and the structure of end groups.25,26 Furthermore, phase transition properties of thermo-responsive polymers are affected by the concentrations of ionic species,27,28 and the content of organic solvents.29,30 In addition to these experimental methods, some studies have predicted cloud point temperature (TCP) by creating regression equations based on molecular weight, degree of polymerization, or monomer ratio.31–33 To develop new thermo-responsive polymers, it is necessary to appropriately select type and composition ratio of monomers from an unlimited number of possible combinations. Therefore, controlling LCST of thermo-responsive polymers remains a challenge for researchers.
Recently, machine learning has been applied to predict and control the physical properties of materials and explore new ones.34–37 Although applying machine learning to polymers is generally difficult due to the complex structure–function relationships,38 it is beginning to be used in the field of thermo-responsive polymers.39,40 Kumar and co-workers showed the prediction and control of the TCP of poly(2-oxazoline) via machine learning.39 The method of gradient boosting with decision trees enabled highly accurate TCP control in a design space consisting of four repeating units and various molecular weights. Although the model was limited to the prediction of these structures because of the descriptors such as molecular weight and degree of polymerization of the copolymers in the four poly(2-oxazoline) repeating units, they provide motivation to extend the study of TCP control using machine learning. In addition, other groups have reported the prediction of TCP of polymers consisting of N-isopropylacrylamide (NIPAAm) and methoxy triethyleneglycol acrylate (MTGA) in aqueous salt solutions, utilizing a technique called support vector regression.40 Although the application of this model is limited to poly(NIPAAm-MTGA), it shows that machine learning can be used to understand the phase-transition behaviour of LCST-type thermo-responsive polymers. However, these prediction models were applicable only to copolymers of specific monomer combinations. They cannot be applied to the prediction of thermo-responsive polymers with monomers or copolymer compositions not used in the models. In addition, these studies have fixed explanatory variables and have not reached the point of searching for variables that contribute significantly to TCP among many chemical parameters. There is still room for improvement in TCP prediction model development. Therefore, we have attempted to establish guidelines for the TCP of thermo-responsive polymers using a new approach based on a machine learning method for small data.
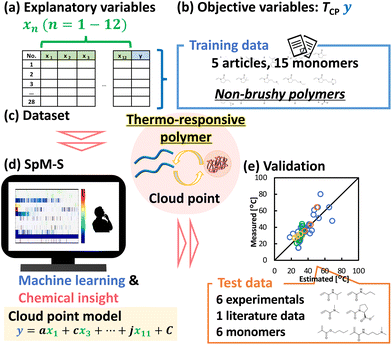
In general, the success of prediction or exploration for materials depends on the amount of data.36 However, sufficient data is not always available for the target materials. Our group has focused on sparse modeling for small data (SpM-S). Sparse modeling is an approach to represent the whole of high-dimensional data using a limited number of descriptors extracted by machine learning.41 This approach has been applied to a variety of fields, such as image data and image compressions.42 It is applicable to small data because of extraction of a limited number of significant descriptors from high-dimensional data.43 SpM-S, which combines sparse modeling and chemical insights, has been successfully used to predict nanosheet size and yield in an example of process optimization and to explore new organic anode and cathode materials for lithium ion batteries in materials exploration.43–45 Here, we applied SpM-S to develop an TCP prediction model for thermo-responsive polymers based on a small dataset collected from the literature. Furthermore, the model was validated with the TCP prediction of thermo-responsive polymers with monomers and copolymer compositions that were not incorporated in the training dataset (Fig. 1).
Experimental
Data collection of objective variables y from the literature
Objective variables for training data, TCPs of the polymers (the temperature at 50% of the optical transmittance of the polymer solution), were collected from 6 references.46–51Data collection and calculation for explanatory variables
x 1–3 were collected from 6 references.46–51 The molecular weights, and poly dispersity index (PDI) of the polymers (x1–2) were collected from gel permeation chromatography (GPC) analysis. Concentrations of polymers (x3) were collected from experimental values of optical transmittance measurements. Hansen-solubility parameters (x4–6) were calculated by the HSP software (HSPiP 5th edition ver. 5.3.06). Chemical properties of monomers (x7–12) were calculated by ChemDraw (ver. 21.0.0).The dataset containing 28 y and xn (n = 1–12) was prepared (Table S1 in the ESI†). Exhaustive search with linear regression (ES-LiR) was performed by Python. The results were summarized in the weight diagram to extract the descriptors by combination with our chemical insights. The linear prediction model was prepared by the selected descriptors after five-fold cross validation.
Chemicals
N-Isopropylacrylamide (NIPAAm), kindly provided by KJ Chemicals Co., Ltd (Tokyo, Japan), was purified by recrystallization from n-hexane, and then dried under vacuum. 2,2′-Azobisisobutyronitrile (AIBN), 2-(dodecylthiocarbonothioylthio)-2-methylpropionic acid (DDMAT), N,N-dimethylacrylamide (DMAAm) and 1,3,5-trioxane were purchased from Tokyo Chemical Industries (Tokyo, Japan). DMAAm was purified by passing through a short column of activated basic alumina to remove the inhibitor. n-Propylamine was purchased from Nakalai Tesque (Kyoto, Japan). Acryloyl chloride was purchased from Sigma-Aldrich (St Louis, MO, USA). N-n-Propylacrylamide (NNPAAm) was synthesized with n-propylamine and acryloyl chloride as previously reported.52 Ultrapure water (18.2 MΩ cm) was obtained from a PURELAB flex water purification system (ELGA, Veolia Water, Marlow, U.K.).General procedure for the synthesis of thermo-responsive polymers
Thermo-responsive polymers were synthesized by reversible addition–fragmentation chain transfer (RAFT) polymerization. The corresponding monomers, DDMAT as RAFT chain transfer agent (CTA), AIBN as radical initiator, and the internal standard of 1,3,5-trioxane (10 eq. to DDMAT) were dissolved in 1,4-dioxane. The reaction mixture was degassed by bubbling with N2 for 30 min, and heated at 70 °C for 17 h. The reaction mixtures were purified by reprecipitation in diethyl ether, followed by drying to a white powder.Characterization of thermo-responsive polymers
1H NMR spectra were recorded on a JNM ECA-500 spectrometer (JEOL, Japan). All chemical shifts are relative to an internal standard of non-deuterated solvent residual peaks (CDCl3: δ = 7.26 ppm or CD3OD δ = 3.31 ppm). The molecular weights of polymers (Mn,NMR) are calculated using starting monomers to RAFT CTA ratios and the monomer conversion of each reaction monitored by 1H NMR. The molecular weights (Mn,GPC) and PDIs of the polymers were determined by a GPC system (Prominence, CMB-20A system controller, DGU-20A3R degasser, LC-20AR pump, SIL-20ACHT autosampler, RID-20A refractive index detector, and CTO-20AC column oven; Shimadzu, Kyoto, Japan), and using columns: TSKgel guardcolumnα, two TSKgelα-M (TOSOH, Tosoh, Japan) connected in series; mobile phase: DMF containing 10 mM LiBr used as eluent at a flow rate of 0.7 mL min−1 at 40 °C. Calibrations were done with polyethylene oxide standards. The TCPs of the polymers were determined by measuring their optical transmittance in aqueous solution (0.5 w/v%). The optical transmittance was measured at various temperatures at 600 nm using a UV-Vis spectrophotometer (V-730BIO, JASCO, Tokyo, Japan). The temperature was controlled using an ETCS-761 Peltier system (JASCO) and a CTU-100 circulating thermostat unit (JASCO) at a heating rate of 0.1 °C min−1. The TCPs were determined as the temperature at 50% of the optical transmittance of the polymer solution.Results and discussion
Selection of literature references and explanatory variables for the dataset
Since LCST is defined by several measurement methods, such as optical transmittance, dynamic light scattering, and differential scanning calorimetry, LCSTs, which represent the objective variable in this work, were collected only from references in which it is defined as the temperature at 50% of optical transmittance.First, TCP was set as the objective variable, and factors that could be related to it were collected as explanatory variables. The explanatory variables (xn: n = 1–12) were selected and prepared based on our insights and experience (Fig. 1a, Table 1 and Table S1†). They included both parameters related to polymers (xn: n = 1–3) and those related to monomers (xn: n = 4–12). Molecular weight and PDI as typically measured when polymers are synthesized were selected as explanatory variables for the polymers. As an experimental value when measuring TCP, the polymer concentration is also selected as explanatory variable. Physicochemical parameters that can be easily calculated by HSPiP and ChemDraw were selected as explanatory variables for the monomers used in polymers. This allows us to build an interpretable and simple predictive model for TCP without experiments and complex simulation and calculation. In the case of copolymers, the parameters of each monomer were averaged by composition ratio and then used as explanatory variables. It is not necessary to separate the case for homopolymers and copolymers. In addition, it allows us to apply to copolymers constructed of more than 3 monomers. In this study, the influence of terminal substituent characteristics on TCP was considered to be low, and it was decided not to include it as an explanatory variable.
| Polymers | Monomers | ||
|---|---|---|---|
| x n | Parameters | x n | Parameters |
| a Literature data. b Calculated data by HSPiP. c Calculated data by ChemDraw. | |||
| 1 | Molecular weighta | 4 | HSP dispersityb |
| 2 | Poly dispersity (PDI)a | 5 | HSP polarityb |
| 3 | Concentrationa | 6 | HSP hydrogen bondingb |
| 7 | Molecular weight | ||
| 8 | Boiling pointc | ||
| 9 | Molar refractive indexc | ||
| 10 | Topological polar surface areac | ||
| 11 | C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pc Pc |
||
| 12 | CMRc | ||
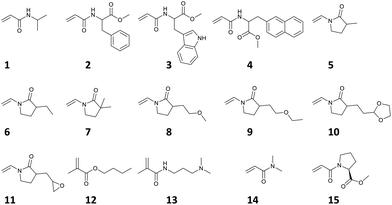
Previously, it has been reported that the dominant parameter determining TCP is different between copolymers containing monomers of a brushy nature such as oligo(ethylene glycol) methacrylate (OEGMA) and those containing only non-brushy monomers. As for brush copolymers, graft density had great influence on the TCP, whereas for non-brush copolymers, surface area-normalized hydrophobicity of copolymers has strong influence on the TCP. Considering this knowledge, our predictive model, which uses the average value from the composition ratio of each monomer as explanatory variables, is appropriate for limited application to TCP prediction for non-brushy copolymers. In the present work, reported TCP data of non-brushy polymers, which consisted of monomers 1 to 15, were manually collected from literature references (Fig. 1b, Scheme 1, Fig. S1 and Tables S1, S2†).46–50 This dataset covers a variety of homopolymers and random copolymers, not limited to any particular structure. Finally, a small training dataset containing 28 objective variables (y) and 12 explanatory variables (x) was prepared (Fig. 1c and Table S1†).
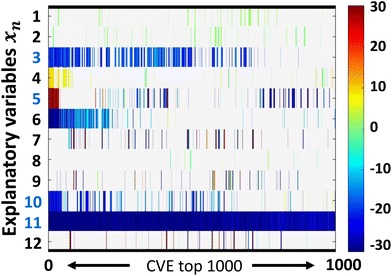
Construction of the prediction model
ES-LiR was used to extract the descriptors. In ES-LiR, linear regression models are prepared by all possible combinations of xn, 2n − 1 combinations. In this case, a total of 212 − 1(4094) regression models were prepared, and the results were sorted in ascending order of the cross-validation error (CVE).The weight diagram shows the top 1000 prediction models with the lowest CVE values (Fig. 1d and2). In the weight diagram, the coefficients of the models were indicated by a cold color for negative correlations and a warm color for positive correlations. Interpretation of the weight diagram and construction of the final model were performed from a chemical perspective. In the present results, x3 (concentration of polymer), x5 (HSP-polarity of monomer), x10 (tPSA of monomer), and x11 (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of monomer) were densely blue colored in the weight diagram. From these variables, we selected the final descriptors, x3 (concentration of polymer), x5 (HSP-polarity of monomer), x11 (C
P of monomer) were densely blue colored in the weight diagram. From these variables, we selected the final descriptors, x3 (concentration of polymer), x5 (HSP-polarity of monomer), x11 (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of monomer) based on chemical insights. First, it is known that polymer chains tend to aggregate in aqueous solution at higher polymer concentrations. Therefore, it was reasonable that the explanatory variable x3 (concentration of polymer) was extracted as negatively correlated descriptor. Next, x5 (HSP-polarity of monomer) was extracted because it is one of the parameters related to solubility. In addition, x11 (C
P of monomer) based on chemical insights. First, it is known that polymer chains tend to aggregate in aqueous solution at higher polymer concentrations. Therefore, it was reasonable that the explanatory variable x3 (concentration of polymer) was extracted as negatively correlated descriptor. Next, x5 (HSP-polarity of monomer) was extracted because it is one of the parameters related to solubility. In addition, x11 (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of monomer) was extracted. C
P of monomer) was extracted. C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is the calculated value of the distribution equilibrium between octanol and water, which is the hydrophobicity index. The smaller the value, the more hydrophilic the compound. With increasing hydrophilicity, TCP also increases. Therefore, it is considered as a negatively correlated parameter. In contrast, x10 (tPSA of monomer) was not included in the final predictive model even though it was extracted as a negatively correlated descriptor. From the chemical perspective, an increase in polar surface area is expected not to decrease, but to increase the TCP due to overall increase of polarity. Therefore, tPSA was removed from the final model based on chemical insights. Surprisingly, x1 (molecular weight of polymer) positively correlated to cloud-point, while it should correlate negatively.53 This is probably because the molecular weights of polymers are determined by GPC, and thus no correlation in absolute molecular weight could be obtained among the literature references due to the differences in the GPC columns used and types of standard polymer samples. Based on the above considerations, the prediction model was described using x3 (Concentration of polymer), x5 (HSP-polarity of monomer) and x11 (C
P is the calculated value of the distribution equilibrium between octanol and water, which is the hydrophobicity index. The smaller the value, the more hydrophilic the compound. With increasing hydrophilicity, TCP also increases. Therefore, it is considered as a negatively correlated parameter. In contrast, x10 (tPSA of monomer) was not included in the final predictive model even though it was extracted as a negatively correlated descriptor. From the chemical perspective, an increase in polar surface area is expected not to decrease, but to increase the TCP due to overall increase of polarity. Therefore, tPSA was removed from the final model based on chemical insights. Surprisingly, x1 (molecular weight of polymer) positively correlated to cloud-point, while it should correlate negatively.53 This is probably because the molecular weights of polymers are determined by GPC, and thus no correlation in absolute molecular weight could be obtained among the literature references due to the differences in the GPC columns used and types of standard polymer samples. Based on the above considerations, the prediction model was described using x3 (Concentration of polymer), x5 (HSP-polarity of monomer) and x11 (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of monomer) (Fig. 1d and eqn (1)) with a root mean squared error (RMSE) of 7.13 °C, where xn are normalized by the frequency distribution such that the mean is 0 and the standard deviation is 1.
P of monomer) (Fig. 1d and eqn (1)) with a root mean squared error (RMSE) of 7.13 °C, where xn are normalized by the frequency distribution such that the mean is 0 and the standard deviation is 1.
| y = −0.520x3 − 25.8x5 − 21.4x11 + 35.3 | (1) |
Synthesis of thermo-responsive copolymers for validation
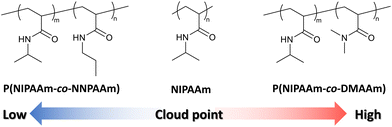
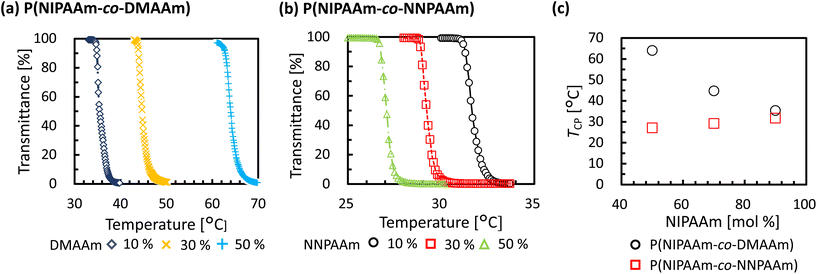
To evaluate the validity of the constructed prediction model, thermo-responsive copolymers with non-brushy monomers were synthesized. One of the monomers used to synthesize copolymers was N-isopropylacrylamide (NIPAAm), and its homopolymer, poly(N-isopropylacrylamide) (PNIPAAm) is the most well-known thermo-responsive polymer. NIPAAm was copolymerized with N,N-dimethylacrylamide (DMAAm) or N-propylacrylamide (NNPAAm), which were selected to have higher or lower TCP than PNIPAAm (Fig. 3). Six types of copolymers with different NIPAAm/DMAAm or NIPAAm/NNPAAm ratios were synthesized by RAFT polymerization. The composition ratio of NIPAAm was set to be identical in each polymer, ranging from 50% to 90%.Molecular weight was measured using GPC (Fig. S2†), and narrow PDI of synthesized copolymers was confirmed. Optical transmittance measurements were then performed using a UV-vis spectrophotometer to obtain cloud-point test data. The temperature-dependent optical transmittances of synthesized thermo-responsive polymers in water are shown in Fig. 4. All polymers exhibited a sharp phase-transition at different temperatures according to the monomer composition ratio. The TCP of copolymers depended on the composition ratio (Table 2). In the case of P(NIPAAm-co-DMAAm), a lower content of NIPAAm resulted in an increase in TCP, while the opposite trend was observed for P(NIPAAm-co-NNPAAm). In summary, test data for the prediction model was obtained over a wide temperature range by synthesizing NIPAAm-based thermo-responsive copolymers.
| Polymer | Composition ratios of NIPAAm in feed [mol%] | Actual composition ratios of NIPAAm [mol%] | M n,NMR | M n,GPC | PDI | T CP[°C] |
|---|---|---|---|---|---|---|
| P(NIPAAm90-co-DMAAm10) | 90 | 90 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1.20 | 35.4 |
| P(NIPAAm70-co-DMAAm30) | 70 | 70 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1.16 | 44.7 |
| P(NIPAAm50-co-DMAAm50) | 50 | 50 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1.27 | 64.0 |
| P(NIPAAm90-co-NNPAAm10) | 90 | 90 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1.18 | 31.7 |
| P(NIPAAm70-co-NNPAAm30) | 70 | 70 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1.23 | 29.2 |
| P(NIPAAm50-co-NNPAAm50) | 50 | 50 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.27 | 27.1 |
Validation of prediction model with literature data and synthesized polymers
The constructed prediction model was validated using the test data from references that have not been included in the model building dataset,49,54 and synthesized polymers, as described above (Fig. 1e and Tables S3–S5†). Test data from a literature reference and the experiment was substituted into the prediction model (eqn (1)). The higher the TCP, the greater the deviation between the measured and the estimated data, predicting a lower TCP than the measured data (Fig. 5a). To improve prediction accuracy of the TCP in the higher temperature range, the coefficients of the prediction model (eqn (1)) were corrected using a literature reference providing data for higher TCP51 (Fig. S3 and Tables S6, S7†). The final prediction model was constructed following equation (eqn (2)) with an RMSE of 8.88 °C.| y = −1.00x3 − 33.0x5 − 34.3x11 + 37.4 | (2) |
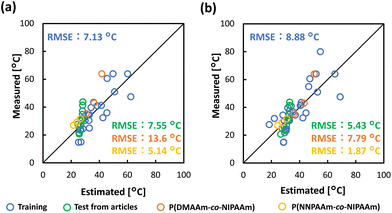 | ||
| Fig. 5 The relationship between estimated TCPs from prediction model and measured values: (a) Compared by prediction model of eqn (1). (b) Compared by prediction model of eqn (2) with corrected coefficients. | ||
The RMSE was 5.43 °C for the test data from literature references (Fig. 5b, green plots). This value was comparable to the training data, indicating high prediction accuracy. Prediction accuracy was also confirmed with the synthesized copolymers, P(NIPAAm-co-DMAAm) whose monomer species were used in the dataset. The test data of P(NIPAAm-co-DMAAm), whose TCP exhibits a higher value than that of PNIPAAm, had an RMSE of 7.79 °C (Fig. 5b, orange plots). This RMSE value was also comparable to the training data, indicating high prediction accuracy. NIPAAm and DMAAm are the monomer species included in the dataset, respectively, but not their copolymers. This result indicates that this model can be applied to TCP prediction of polymers whose monomer combination is not included in the dataset. The applicability of this model was also investigated for copolymers containing a monomer not included in the dataset. P(NIPAAm-co-NNPAAm), which exhibits a lower TCP than PNIPAAm, had an RMSE of 1.87 °C, showing high prediction accuracy (Fig. 5b, yellow plot). As for monomers used to construct the polymer, NIPAAm has been included in the dataset, while NNPAAm was not. Considering this result, this prediction model was also able to predict TCP for polymers composed of monomers not in the dataset.
Conclusions
The TCP prediction of thermo-responsive polymers was achieved with the assistance of materials informatics with SpM-S. The descriptors, concentration of polymer, HSP-polarity of monomer, and C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P of monomer, were extracted by the combination of ES-LiR and chemical insights. Finally, the regression equation for TCP prediction was obtained from 33 datasets. To validate the constructed prediction model, six types of copolymers with different NIPAAm/DMAAm or NIPAAm/NNPAAm ratios were synthesized. The constructed model showed good correlation with the experimentally measured the TCPs of P(NIPAAm-co-DMAAm) and P(NIPAAm-co-NNPAAm) and the TCPs extracted from literature references over a wide temperature range from 20 °C to 65 °C. To the best of our knowledge, this prediction model for TCP is the first example applied to predict polymers with monomers and combinations not included in the dataset. In addition, the model has the advantage of being interpretable, simple to calculate, and versatile, and the potential to provide a rough guideline to TCP for thermo-responsive polymers. This study is expected to lead to the efficient development of LCST-type polymers.
P of monomer, were extracted by the combination of ES-LiR and chemical insights. Finally, the regression equation for TCP prediction was obtained from 33 datasets. To validate the constructed prediction model, six types of copolymers with different NIPAAm/DMAAm or NIPAAm/NNPAAm ratios were synthesized. The constructed model showed good correlation with the experimentally measured the TCPs of P(NIPAAm-co-DMAAm) and P(NIPAAm-co-NNPAAm) and the TCPs extracted from literature references over a wide temperature range from 20 °C to 65 °C. To the best of our knowledge, this prediction model for TCP is the first example applied to predict polymers with monomers and combinations not included in the dataset. In addition, the model has the advantage of being interpretable, simple to calculate, and versatile, and the potential to provide a rough guideline to TCP for thermo-responsive polymers. This study is expected to lead to the efficient development of LCST-type polymers.
Author contributions
Mai Hayakawa: methodology, investigation, writing – original draft. Kosuke Sakano: formal analysis. Rei Kumada: writing – review & editing. Haruka Tobita: formal analysis. Yasuhiko Igarashi: software, supervision. Daniel Citterio: writing – review & editing, supervision. Yuya Oaki: conceptualization, writing – review & editing, supervision. Yuki Hiruta: conceptualization, methodology, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was partly supported by Grant-in Aid for Scientific Research (C) (Grant No. 21K06495) to Y. H. from the Japan Society for the Promotion of Science (JSPS), and by the Program for the Advancement of Next Generation Research Projects (Type C) at Keio to Y. H.References
- K. Suwa, K. Morishita, A. Kishida and M. Akashi, J. Polym. Sci., Part A: Polym. Chem., 1997, 35, 3087–3094 CrossRef CAS.
- F. D. Jochum and P. Theato, Chem. Soc. Rev., 2013, 42, 7468–7483 RSC.
- S. Dai, P. Ravi and K. C. Tam, Soft Matter, 2008, 4, 435 RSC.
- X.-J. Ju, L. Liu, R. Xie, C. H. Niu and L.-Y. Chu, Polymer, 2009, 50, 922–929 CrossRef CAS.
- A. S. Hoffman, Adv. Drug Delivery Rev., 2013, 65, 10–16 CrossRef CAS PubMed.
- H. Sun, C. P. Kabb, M. B. Sims and B. S. Sumerlin, Prog. Polym. Sci., 2019, 89, 61–75 CrossRef CAS.
- P. Yang, F. Zhu, Z. Zhang, Y. Cheng, Z. Wang and Y. Li, Chem. Soc. Rev., 2021, 50, 8319–8343 RSC.
- Y. Hiruta, Polym. J., 2022, 54, 1419–1430 CrossRef CAS.
- D. Roy, W. L. A. Brooks and B. S. Sumerlin, Chem. Soc. Rev., 2013, 42, 7214 RSC.
- F. Doberenz, K. Zeng, C. Willems, K. Zhang and T. Groth, J. Mater. Chem. B, 2020, 8, 607–628 RSC.
- Q. Zhang and R. Hoogenboom, Prog. Polym. Sci., 2015, 48, 122–142 CrossRef CAS.
- M. Sponchioni, U. C. Palmiero and D. Moscatelli, Mater. Sci. Eng., C, 2019, 102, 589–605 CrossRef CAS PubMed.
- L. Sixdenier, A. Augé, Y. Zhao, E. Marie and C. Tribet, ACS Macro Lett., 2022, 11, 651–656 CrossRef CAS PubMed.
- A. Bordat, T. Boissenot, J. Nicolas and N. Tsapis, Adv. Drug Delivery Rev., 2019, 138, 167–192 CrossRef CAS PubMed.
- H. G. Schild and D. A. Tirrell, J. Phys. Chem., 1990, 94, 4352–4356 CrossRef CAS.
- J.-F. Lutz, K. Weichenhan, Ö. Akdemir and A. Hoth, Macromolecules, 2007, 40, 2503–2508 CrossRef CAS.
- Y. Hiruta, Y. Nagumo, A. Miki, T. Okano and H. Kanazawa, RSC Adv., 2015, 5, 73217–73224 RSC.
- D. E. Bergbreiter and H. Fu, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 186–193 CrossRef CAS.
- C. Porsch, S. Hansson, N. Nordgren and E. Malmström, Polym. Chem., 2011, 2, 1114–1123 RSC.
- J.-F. Lutz, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 3459–3470 CrossRef CAS.
- S. Nishimura, K. Nishida, T. Ueda, S. Shiomoto and M. Tanaka, Polym. Chem., 2022, 13, 2519–2530 RSC.
- A. A. A. Smith, C. L. Maikawa, H. L. Hernandez and E. A. Appel, Polym. Chem., 2021, 12, 1918–1923 RSC.
- D. G. Lessard, M. Ousalem and X. X. Zhu, Can. J. Chem., 2001, 79, 1870–1874 CrossRef CAS.
- N. S. Ieong, M. Hasan, D. J. Phillips, Y. Saaka, R. K. O'Reilly and M. I. Gibson, Polym. Chem., 2012, 3, 794 RSC.
- P. J. Roth, F. D. Jochum, F. R. Forst, R. Zentel and P. Theato, Macromolecules, 2010, 43, 4638–4645 CrossRef CAS.
- A. Podevyn, K. Arys, V. R. de la Rosa, M. Glassner and R. Hoogenboom, Eur. Polym. J., 2019, 120, 109273 CrossRef.
- Y. Hiruta, Y. Nagumo, Y. Suzuki, T. Funatsu, Y. Ishikawa and H. Kanazawa, Colloids Surf., B, 2015, 132, 299–304 CrossRef CAS.
- Y. Zhang, S. Furyk, D. E. Bergbreiter and P. S. Cremer, J. Am. Chem. Soc., 2005, 127, 14505–14510 CrossRef CAS PubMed.
- R. Hoogenboom, H. M. L. Thijs, D. Wouters, S. Hoeppener and U. S. Schubert, Soft Matter, 2008, 4, 103–107 RSC.
- F. M. Winnik, H. Ringsdorf and J. Venzmer, Macromolecules, 1990, 23, 2415–2416 CrossRef CAS.
- R. Hoogenboom, H. M. L. Thijs, M. J. H. C. Jochems, B. M. van Lankvelt, M. W. M. Fijten and U. S. Schubert, Chem. Commun., 2008, 5758 RSC.
- I. Akar, R. Keogh, L. D. Blackman, J. C. Foster, R. T. Mathers and R. K. O'Reilly, ACS Macro Lett., 2020, 9, 1149–1154 CrossRef CAS.
- I. Akar, J. C. Foster, X. Leng, A. K. Pearce, R. T. Mathers and R. K. O'Reilly, ACS Macro Lett., 2022, 11, 498–503 CrossRef CAS PubMed.
- G. H. Gu, J. Noh, I. Kim and Y. Jung, J. Mater. Chem. A, 2019, 7, 17096–17117 RSC.
- K. Rajan, Annu. Rev. Mater. Res., 2015, 45, 153–169 CrossRef CAS.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 54 CrossRef.
- Y. Oaki and Y. Igarashi, Bull. Chem. Soc. Jpn., 2021, 94, 2410–2422 CrossRef CAS.
- N. E. Jackson, M. A. Webb and J. J. de Pablo, Curr. Opin. Chem. Eng., 2019, 23, 106–114 CrossRef.
- J. N. Kumar, Q. Li, K. Y. T. Tang, T. Buonassisi, A. L. Gonzalez-Oyarce and J. Ye, npj Comput. Mater., 2019, 5, 73 CrossRef.
- H. Tokuyama, H. Mori, R. Hamaguchi and G. Kato, Chem. Eng. Sci., 2021, 231, 116325 CrossRef CAS.
- R. Tibshirani, M. Wainwright and T. Hastie, Statistical Learning with Sparsity: The Lasso and Generalizations, Chapman and Hall/CRC, Philadelphia, PA, 2015 Search PubMed.
- E. Candès and J. Romberg, Inverse Probl., 2007, 23, 969–985 CrossRef.
- R. Mizuguchi, Y. Igarashi, H. Imai and Y. Oaki, Nanoscale, 2021, 13, 3853–3859 RSC.
- H. Numazawa, Y. Igarashi, K. Sato, H. Imai and Y. Oaki, Adv. Theory Simul., 2019, 2, 1900130 CrossRef CAS.
- K. Sakano, Y. Igarashi, H. Imai, S. Miyakawa, T. Saito, Y. Takayanagi, K. Nishiyama and Y. Oaki, ACS Appl. Energy Mater., 2022, 5, 2074–2082 CrossRef CAS.
- Y. Hiruta, R. Kanazashi, E. Ayano, T. Okano and H. Kanazawa, Analyst, 2016, 141, 910–917 RSC.
- T. Nishio, R. Kanazashi, A. Nojima, H. Kanazawa and T. Okano, J. Chromatogr. A, 2012, 1228, 148–154 CrossRef CAS PubMed.
- G.-T. Chen, C.-H. Wang, J.-G. Zhang, Y. Wang, R. Zhang, F.-S. Du, N. Yan, Y. Kou and Z.-C. Li, Macromolecules, 2010, 43, 9972–9981 CrossRef CAS.
- Y. Hiruta, M. Shimamura, M. Matsuura, Y. Maekawa, T. Funatsu, Y. Suzuki, E. Ayano, T. Okano and H. Kanazawa, ACS Macro Lett., 2014, 3, 281–285 CrossRef CAS PubMed.
- H. Mori, H. Iwaya, A. Nagai and T. Endo, Chem. Commun., 2005, 4872 RSC.
- T. Maeda, K. Yamamoto and T. Aoyagi, J. Colloid Interface Sci., 2006, 302, 467–474 CrossRef CAS PubMed.
- Y. Kametani, F. Tournilhac, M. Sawamoto and M. Ouchi, Angew. Chem., Int. Ed., 2020, 59, 5193–5201 CrossRef CAS.
- J.-F. Lutz, Ö. Akdemir and A. Hoth, J. Am. Chem. Soc., 2006, 128, 13046–13047 CrossRef CAS PubMed.
- H. Kanazawa, E. Ayano, C. Sakamoto, R. Yoda, A. Kikuchi and T. Okano, J. Chromatogr. A, 2006, 1106, 152–158 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3py00314k |
| This journal is © The Royal Society of Chemistry 2023 |