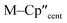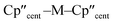Electronic structure comparisons of isostructural early d- and f-block metal(III) bis(cyclopentadienyl) silanide complexes

Abstract

We report the synthesis of the U(III) bis(cyclopentadienyl) hypersilanide complex [U(Cp′′)₂{Si(SiMe₃)₃}] (Cp′′ = {C₅H₃(SiMe₃)₂-1,3}), together with isostructural lanthanide and group 4 M(III) homologues, in order to meaningfully compare metal-silicon bonding between early d- and f-block metals. All complexes were characterised by a combination of NMR, EPR, UV-vis-NIR and ATR-IR spectroscopies, single crystal X-ray diffraction, SQUID magnetometry, elemental analysis and ab initio calculations. We find that for the [M(Cp′′)₂{Si(SiMe₃)₃}] (M = Ti, Zr, La, Ce, Nd, U) series the unique anisotropy axis is conserved tangential to ; this is governed by the hypersilanide ligand for the d-block complexes to give easy plane anisotropy, whereas the easy axis is fixed by the two Cp′′ ligands in f-block congeners. This divergence is attributed to hypersilanide acting as a strong σ-donor and weak π-acceptor with the d-block metals, whilst f-block metals show predominantly electrostatic bonding with weaker π-components. We make qualitative comparisons on the strength of covalency to derive the ordering Zr > Ti ≫ U > Nd ≈ Ce ≈ La in these complexes, using a combination of analytical techniques. The greater covalency of 5f³ U(III) vs. 4f³ Nd(III) is found by comparison of their EPR and electronic absorption spectra and magnetic measurements, with calculations indicating that uranium 5f orbitals have weak π-bonding interactions with both the silanide and Cp′′ ligands, in addition to weak δ-antibonding with Cp′′.

---

Introduction

Transition metal (TM) silicon chemistry is well-established, with technological applications being actively developed¹ for solid-state silicide materials used in microelectronics, ceramics and catalysis,² and molecular silanide complexes that effect (hydro)silylation of unsaturated substrates.^3–5 In comparison, f-block silicon chemistry is less well developed but shows promise,⁶ with lanthanide (Ln) silicides used to fortify low-alloy steels,⁷ Ln silanide catalysts employed in unsaturated hydrocarbon polymerisations,^8,9 and actinide (An) silicides showing potential for use as high-density nuclear fuels.^10–13 Given that the physicochemical properties of the f-elements have been exploited in numerous technologies,^14,15 it follows that a deeper understanding of f-block silicon chemistry could lead to new applications that complement d-block silicon analogues.

f-Block silicon chemistry has continued to slowly develop and now includes multiple examples of cyclopentadienyl (Cp)-supported M–Si bonds.⁶ Schumann reported the first Ln(III) examples, [Li(DME)₃][Ln(Cp)₂(SiMe₃)₂] (Ln = Dy, Ho, Er, Tm, Lu), in the late 1980s;^16–18 since then, other Ln(III) Cp-supported silanide complexes have included [Ln(C₅Me₄R)₂{SiH(SiMe₃)₂}] (R = Me; Ln = Sc, Y, Nd, Sm, R = Et; Ln = Nd, Sm) by Tilley and Rheingold,^19,20 [Lu(Cp*)₂{SiH₂(o-MeOC₆H₄)}] (Cp* = {C₅Me₅}) by Castillo and Tilley,⁸ [K(2.2.2-crypt)][Y(C₅H₄Me)₃(SiH₂Ph)] by Evans,²¹ and a series of [Ln(Cp)₃(SiR₃)]⁻ anions (Ln = La, Ce; SiR₃ = Si(H)Mes₂, Si(H)Ph₂, Si(Me)Ph₂, SiPh₃; Mes = C₆H₂Me₃-2,4,6) by Fang;²² Baumgartner and Marschner have reported a wide variety of this class of complex, including [K₂(18-crown-6)₂Cp][Ln(Cp)₂{[Si(SiMe₃)₂SiMe₂]₂}] (Ln = Tm, Ho, Tb, Gd),²³ [K(18-crown-6)][Ln(Cp)₃{Si(SiMe₃)₃}] (Ln = Ho, Tm) and [{K(18-crown-6)}₂Cp][Ln(Cp)₃{Si(SiMe₃)₃}] (Ln = Ce, Sm, Gd, Tm),²⁴ and the Y(III) complexes [K(DME)₄][Y(Cp)₂(L)] (L = {[Si(SiMe₃)₂SiMe₂]₂O}²⁵ or {[Si(SiMe₃)₂SiMe₂]₂}).²⁶ Reports of complexes that contain structurally authenticated Cp-supported An–Si bonds are currently limited to the U(III) silylenes [U(Cp′)₃{Si(NMe₂)[PhC(N^tBu)₂]}] (Cp′ = {C₅H₄SiMe₃}) and [U(Cp′)₃{Si[PhC(NⁱPr)₂]₂}] by Arnold,²⁷ and the An(IV) silanides [An(Cp′)₃{Si(SiMe₃)₃}] (An = Th, U) by some of us;²⁸ Porchia,²⁹ Tilley,³⁰ and Marks³¹ have all reported examples of An silanide complexes that were not characterised in the solid state.

It has recently been demonstrated that the extent of covalency in f-block M–Si bonds can be established by a combination of ²⁹Si NMR spectroscopy and density functional theory (DFT) calculations.³² However, this approach is currently limited to diamagnetic complexes and the vast majority of f-block complexes are paramagnetic; conversely, pulsed EPR spectroscopy has been applied to quantify An–C bond covalency in 5f³ U(III) and 6d¹ Th(III) substituted Cp complexes.³³ Although no U(III) silanide complex has been structurally authenticated to date, we posited that a substituted Cp-supported system could provide the necessary kinetic stabilisation. Ti(III) bis-Cp silanide complexes have been extensively studied by fluid solution continuous wave (CW) EPR spectroscopy, including mononuclear complexes with bidentate silanides,^34,35 and monodentate silanides supported by a tethered donor atom or neutral co-ligand,^34,36–38 as well as dinuclear Ti(III) complexes;³⁹ however, powder and frozen solution spectra are rare.³⁹ The only EPR spectra of nd¹ Zr(III) and Hf(III) bis-Cp silanides reported to date are of [K(18-crown-6)][M(Cp)₂{[Si(SiMe₃)₂SiMe₂]₂}].³⁵

We reasoned that a series of early d- and f-block M(III) complexes containing M–Si bonds could be achieved by using two substituted Cp ligands and one bulky silanide. We decided to adapt our previous strategy where we prepared An(IV) silanide complexes with three Cp′ and one hypersilanide ligand, {Si(SiMe₃)₃};²⁸ we were encouraged to continue using hypersilanide as this has provided the largest number of f-block silanide complexes to date,⁶ and to increase the size of the Cp′ ring to Cp′′ ({C₅H₃(SiMe₃)₂-1,3}) in an effort to maintain kinetic stabilization of the M–Si bonds when the number of coordinated ligands is reduced. The approach of using multiple silyl groups increases the number of signals to assign in ²⁹Si NMR spectra, but this was preferred to the use of related alkyl-substituted silanide ligands that we have only previously found applicable to Ln(II) systems.³² Here we report the synthesis of an isostructural family of M(III) complexes, [M(Cp′′)₂{Si(SiMe₃)₃}] (M = Ti, Zr, La, Ce, Nd, U), providing an opportunity to directly compare the electronic structures of early d- and f-block silanide bonds. This is predominantly achieved using a combination of CW EPR spectroscopy and complete active space self-consistent field-spin orbit (CASSCF-SO) calculations, complemented by supporting characterisation data including single crystal X-ray diffraction, elemental analysis, SQUID magnetometry, and NMR, UV-vis-NIR and ATR-IR spectroscopies. By comparing the electronic structures of 5f³ U(III) with 4f³ Nd(III), and nd¹ Ti(III) and Zr(III) with 4f¹ Ce(III), we rationalise differences in magnetic anisotropy, d-orbital splitting, orbital mixing, and covalency in the complexes reported herein, and observe clear differences between early d-block, Ln and An metal-silicon bonding regimes.

Results

Synthesis

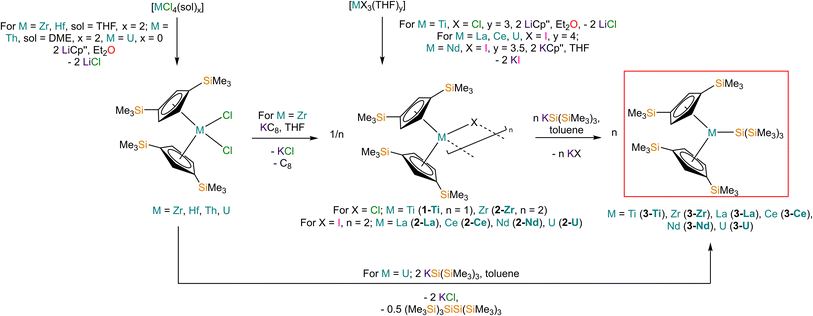
Salt elimination reactions between [Ti(Cp′′)₂Cl] (1-Ti) or [{M(Cp′′)₂(μ-X)}₂] (X = Cl, M = Zr (2-Zr); X = I, M = La (2-La), Ce (2-Ce), Nd (2-Nd), U (2-U)) with one or two equivalents of [K{Si(SiMe₃)₃}],⁴⁰ respectively, in toluene gave the heteroleptic M(III) silanide complexes [M(Cp′′)₂{Si(SiMe₃)₃}] (3-M; M = Ti, Zr, La, Ce, Nd, U) in 34–77% yields following work-up and recrystallisation from pentane (Scheme 1). The Ti(III) starting material 1-Ti was prepared directly from the reaction of two equivalents of LiCp′′^41,42 with [TiCl₃(THF)₃],⁴³ whilst 2-Zr was synthesised by reduction of [Zr(Cp′′)₂Cl₂]⁴⁴ using KC₈.⁴⁵ The f-block precursors 2-M were generated,^45–47 by the reaction of two equivalents of KCp′′⁴⁸ with [MI₃(THF)_y] (y = 4, M = La,⁴⁹ Ce,⁴⁹ U,^50,51y = 3.5, M = Nd;⁴⁹ see ESI for full Experimental details‡). Physical characterisation data of 1-3-M support the proposed formulations.

Scheme 1 Synthetic routes to complexes 3-M.

We found that 3-U could also be prepared by the reaction of [U(Cp′′)₂Cl₂]⁵² with two equivalents of [K{Si(SiMe₃)₃}] in 77% yield following work-up and recrystallisation from pentane. The reaction of [U(Cp′′)₂Cl₂] with one equivalent of [K{Si(SiMe₃)₃}] exclusively resulted in reduction of the red U(IV) starting material to the dark green U(III) complex [{U(Cp′′)₂(μ-Cl)}₂], with oxidative coupling of the silanide to give colourless crystals of (Me₃Si)₃SiSi(SiMe₃)₃; addition of a second equivalent of [K{Si(SiMe₃)₃}] to the reaction mixture gave 3-U. The facile reduction of [U(Cp′′)₂Cl₂] by [K{Si(SiMe₃)₃}] was expected, given the accessible U(IV) → U(III) reduction potential (E⁰ = −0.63 V).⁵³ We could not prepare Hf(III) and Th(III) homologues of 3-M using these procedures; although the M(IV) precursors [M(Cp′′)₂Cl₂] (M = Hf, Th,⁵² see ESI‡ for full Experimental details) can be prepared in appreciable yields. Lappert previously reported that the reduction of [Th(Cp′′)₂Cl₂] with Na/K alloy in THF gave [Th(Cp′′)₃] by ligand scrambling;⁵⁴ we found that some decomposition occurred when [M(Cp′′)₂Cl₂] (M = Hf, Th) were treated with KC₈ in THF, and though no products could be identified from the Hf reaction, we identified crystals of [Th(Cp′′)₃] by single crystal XRD.⁵⁴

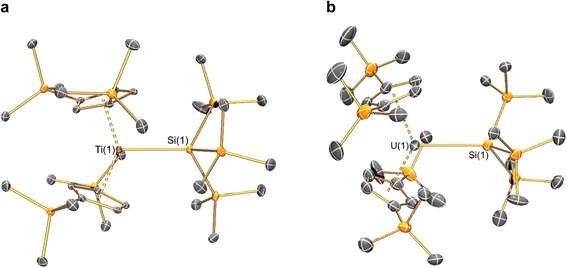
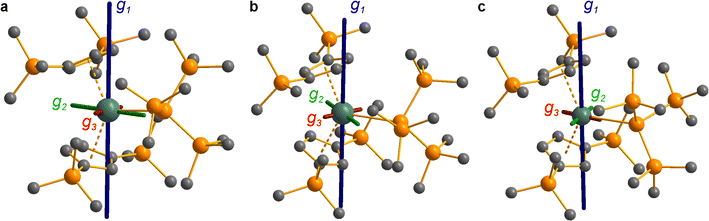
Structural characterisation

The solid-state molecular structures of [Hf(Cp′′)₂Cl₂], 2-Nd, 2-U and 3-M were verified by single crystal XRD, and only 3-M are discussed here for brevity; datasets for [Zr(Cp′′)₂Cl₂],⁴⁴ [Th(Cp′′)₂Cl₂],⁵² [U(Cp′′)₂Cl₂],⁵²1-Ti,⁴⁶2-Zr,⁴⁵2-La⁴⁷ and 2-Ce⁴⁷ have previously been reported. As 3-M are isostructural only 3-Ti and 3-U are shown in Fig. 1 and key metrical parameters for all 3-M are compiled in Table 1 (see ESI Fig. S80–S86‡ for depictions of the solid-state structures of other complexes). Treating the Cp′′ centroids as coordination points, 3-M can be described as exhibiting distorted pseudo-trigonal planar geometries. The M–Si distances are consistently ∼0.20–0.40 Å longer than the sums of the respective M–Si single-bond covalent radii reported by Pyykkö⁵⁵ of 2.52 (3-Ti), 2.70 (3-Zr), 2.96 (3-La), 2.79 (3-Ce), 2.90 (3-Nd) and 2.86 Å (3-U). We attribute this to the combination of sterically encumbered Cp′′ and hypersilanide ligands, together with the SiMe₃ groups in the latter withdrawing a substantial amount of charge density from the silanide centre by negative hyperconjugation.^56,57

Fig. 1 Molecular structures of: (a) 3-Ti determined at 100 K and (b) 3-U determined at 150 K, with selective atom labelling. Displacement ellipsoids set at 30% probability level and hydrogen atoms removed for clarity.

Table 1 M–Si and M–Cl bond lengths (Å), mean distances (Å) and angles (°) for 1-M and 3-M

Parameter	1-Ti ^46	1-Zr	3-Ti	3-Zr	3-La	3-Ce	3-Nd	3-U
a DFT-optimised structure.
M–Si or M–Cl	2.347(3)	2.4534	2.7720(2)	2.902(2)	3.178(2)	3.153(2)	3.112(2)	3.116(2)
	2.037(4)	2.1801	2.0508(2)	2.1841(4)	2.5215(2)	2.5005(2)	2.4489(9)	2.4726(2)
	138.45(14)	134.58	141.04(3)	133.830(2)	132.54(5)	133.11(3)	132.37(2)	131.02(4)

---

Complex 3-U (Fig. 1b) exhibits a relatively short U–Si distance of 3.116(2) Å compared to [U(Cp′)₃{Si(NMe₂)[PhC(N^tBu)₂]}] (3.1637(7) Å) and [U(Cp′)₃{Si[PhC(NⁱPr)₂]₂}] (3.1750(6) Å),²⁷ which contain dative silylene U(III)–Si bonds, in accord with the increased electrostatic attraction between the negatively charged hypersilanide and the U(III) centre in 3-U. Additionally, the U–Si bond length of 3-U is ca. 0.05 Å longer than the previously reported complex [U(Cp′)₃{Si(SiMe₃)₃}] (3.0688(8) Å),²⁸ consistent with the increased ionic radii of U(III) vs. U(IV) (six-coordinate U(III) = 1.025 Å, whilst U(IV) = 0.89 Å).⁵⁸ There are essentially negligible changes to the 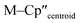distances and 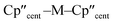angles when comparing 3-M to 1-Ti and 2-M for the same metal. The orientation of the Cp′′ ligands with respect to each other are typically invariant within each series, with the ring trimethylsilyl substituents arranged to minimise inter-ligand steric repulsions;⁴⁷1-Ti and 3-Ti are outliers due to the high steric demands about the smaller Ti(III) centre (six-coordinate Ti(III) = 0.67 Å).⁵⁸

Previously reported neutral Ti(III) bis-Cp silanide complexes contain shorter Ti–Si bonds than that found for 3-Ti (Fig. 1a), though these all contain less sterically demanding Cp ligands and a PMe₃ ancillary ligand: [Ti(Cp)₂(SiH₃)(PMe₃)] (2.594(2) Å),³⁴ [Ti(Cp)₂(SiH₂Ph)(PMe₃)] (2.635(7) Å),⁵⁹ and [Ti(Cp)₂(SiHPh₂)(PMe₃)] (2.652(2) Å).³⁶ However, the mean Ti–Si bond length of the anionic Ti(III) complex [K(18-crown-6)][Ti(Cp)₂{[Si(SiMe₃)₂SiMe₂]₂}] (2.770(3) Å),⁶⁰ which features a bidentate silanide ligand, is statistically equivalent to that of 3-Ti; similarly, the Zr–Si bond length of 3-Zr is comparable to those present in [K(18-crown-6)][Zr(Cp)₂{[Si(SiMe₃)₂SiMe₂]₂}] (Zr–Si: 2.8503(11), 2.8950(10) Å)³⁵ and the Ce–Si distance of 3-Ce is invariant to that of [{K(18-crown-6)}₂Cp][Ce(Cp)₃{Si(SiMe₃)₃}] (Ce–Si: 3.155(5) Å).²⁴ Conversely, the La–Si distance in 3-La is intermediate to those seen in [La{μ-η:⁵κ¹-SiC₄(SiMe₃)₂-1,4-Ph₂-2,3}(μ-η⁸:η⁸-C₈H₈)K(THF)₃]₂ for the η⁵ – (3.0888(5) Å) and κ¹ – (3.2908(6) Å) bound silole.⁶¹ Complex 3-Nd contains the first structurally authenticated Nd–Si bond, precluding a literature comparison; however, the Ln–Si distances for the 3-Ln series vary in accord with the expected periodic trend for Ln(III) ionic radii.⁵⁸

NMR spectroscopy

Multinuclear NMR spectroscopy was performed on 1-Ti, 2-M and 3-M (see ESI Fig. S1–S42‡ for annotated NMR spectra); we focus here on the spectra of 3-M. With the exception of diamagnetic 3-La, the collection of reliable NMR spectra for 3-M was challenging due to paramagnetism. C₆D₆ solutions of 3-Ti and 3-Zr also showed decomposition at ambient temperatures (t_½ca. 2 h); δ_Si resonances at −116.11 and −11.97 ppm grew in intensity during data collection (see ESI Fig. S25 and S27‡) that were assigned to the organosilane HSi(SiMe₃)₃ by comparison with an authentic sample.⁶² An additional resonance observed in the ²⁹Si NMR spectrum of 3-Ti at −21.83 ppm was attributed to silicone grease, whilst in 3-Zr a signal at δ_Si = −9.83 ppm could not be confidently assigned. Previous reports of complexes containing Ti(III)–Si and Zr(III)–Si bonds showed that solution decomposition processes are commonly observed by NMR spectroscopy.^24,35,60 The rest of the 3-M series were stable in C₆D₆ solution at ambient temperature for a sufficient duration for multinuclear NMR spectra to be acquired (ca. 1 h; experiments had to be performed at relatively fast acquisition times to obtain data that are representative of freshly prepared solutions, e.g. 1D ²⁹Si INEPT 128 scans).

For diamagnetic 3-La the ¹H NMR spectrum showed the four expected resonances: two inequivalent Cp-H signals for the 4,5- and 2-Cp-H positions at 7.17 and 7.46 ppm, respectively, and two resonances in a ratio of 4 : 3 for the chemically inequivalent trimethylsilyl environments, δ_H: 0.25 (Cp-SiCH₃) and 0.55 ppm (Si(SiCH₃)₃); these correlated with five resonances in the ¹³C NMR spectrum. The ²⁹Si NMR spectra of 3-La revealed three resonances; those at −6.57 and −10.32 ppm were respectively assigned as Si(SiCH₃)₃ and Cp-SiCH₃via a ¹H-²⁹Si HMBC experiment, whilst a weak signal at −130.25 ppm correlated with the ¹H resonances of the hypersilanide ligand; the latter signal can only be tentatively assigned as the quaternary metal-bound silicon atom due to quadrupolar broadening from coupling to 99.9% abundant I = 7/2 ¹³⁹La nuclei.

The ¹H NMR spectra of paramagnetic 3-M all exhibited signals for the two chemically inequivalent trimethylsilyl environments; resonances for the two Cp′′ ring proton environments were not observed due to paramagnetic line-broadening. As with 3-La, Cp-SiCH₃ resonances in all cases are upfield of those assigned to Si(SiCH₃)₃, albeit paramagnetically shifted (Cp-SiCH₃δ_H/ppm: 0.14 (3-Ti), 0.88 (3-Zr), −8.33 (3-Ce), −11.64 (3-Nd), −14.79 (3-U); Si(SiCH₃)₃δ_H/ppm: 1.60 (3-Ti), 2.97 (3-Zr), −1.11 (3-Ce), −2.02 (3-Nd), −5.90 (3-U)). Both of the trimethylsilyl environments were present in the ¹³C NMR spectrum of 3-U (δ_C/ppm: −28.48, Cp-SiMe₃; 17.11, Si(SiMe₃)), whilst only the hypersilanide resonances were seen for 3-Ce (8.39 ppm) and 3-Nd (19.79 ppm) and no signals could be assigned for 3-Ti and 3-Zr; in all cases assignments were confirmed by ¹H-¹³C HSQC correlation experiments. Finally, only one signal was observed in the ²⁹Si NMR spectrum of 3-Nd (22.18 ppm), whilst no ²⁹Si NMR signals could be seen for 3-Ti, 3-Zr, 3-Ce or 3-U. The experimental parameters of the ¹H-²⁹Si HMBC experiment prohibited correlation with ¹H NMR resonances, therefore we cannot confidently assign the ²⁹Si NMR resonance observed for 3-Nd; however, this is unlikely to be due to the metal-bound silicon atom, as this resonance is not observed in the 1D²⁹Si NMR spectra of diamagnetic 3-La. To the best of our knowledge there have not been any previous reports of ²⁹Si NMR chemical shifts for paramagnetic M(III)–Si complexes in the literature for the metals studied here.⁶³

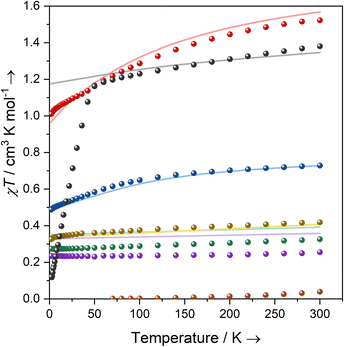
Magnetism

Solutions of 1-Ti, 2-Zr and 3-M (M = Ti, Zr, Ce, Nd, U) in C₆D₆ were prepared at 0 °C and the effective magnetic moments (μ_eff) and molar magnetic susceptibilities (χ_M) were measured by the Evans method immediately upon warming to 300 K (Table 2, ESI Fig. S43–S52‡).⁶⁴ Solution magnetic susceptibilities for 1-Ti and 3-M are in good agreement with the corresponding data obtained from powdered samples examined by variable-temperature SQUID magnetometry, and CASSCF calculations (Table 2, Fig. 2 and ESI Fig. S94a–S99a‡). Magnetic susceptibility and field-dependent magnetisation data (ESI Table S5 and Fig. S94–S96‡) for 1-Ti, 3-Ti and 3-Zr indicate isolated S = 1/2 systems, as expected for mononuclear nd¹ complexes. Previous studies of 2-Zr have reported that this complex is essentially diamagnetic based on NMR chemical shifts,⁶⁵ but also that it exhibits an EPR spectrum in solution.⁴⁵ We find near-zero magnetic susceptibility for a powder sample of 2-Zr, implying that the two S = 1/2 centres are strongly antiferromagnetically coupled in the solid state (Fig. 2). A solution of 2-Zr in C₆D₆ at 300 K was found to be paramagnetic by the Evans method, but less than expected for two uncoupled S = 1/2 (0.26 compared to 0.75 cm³ K mol⁻¹), indicating weaker antiferromagnetic coupling than in the solid state, some minor sample decomposition, and/or the presence of some monomeric [Zr(Cp′′)₂Cl] (1-Zr) in solution as proposed by Antiñolo et al.⁶⁵ SQUID magnetometry and EPR spectra of 2-Ce, 2-Nd and 2-U showed extensive exchange interactions between the metal ions; these data are challenging to model,⁶⁶ and will be communicated in a separate publication as they are outside the main focus of this study.

Table 2 Magnetic moment, μ_eff (μ_B), and product of the molar susceptibility and temperature, χ_MT (cm³ K mol⁻¹), of 1-Ti and 3-M at 300 K. Determined by Evans method on solutions in C₆D₆, SQUID magnetometry on powder samples, CASSCF calculations and free ion values for monomeric ions

Complex	Solution		Powder		CASSCF calculations		Free ion^14
	μ eff	χ M T	μ eff	χ M T	μ eff	χ M T	μ eff	χ M T
a CAS(3,7) active space averaging over all 5f^3 configurations.
1-Ti	1.63	0.33	1.61	0.33	1.77	0.39	1.73	0.38
2-Zr	1.43	0.26	0.56	0.04	—	—	—	—
3-Ti	1.93	0.47	1.83	0.42	1.81	0.41	1.73	0.38
3-Zr	1.71	0.37	1.43	0.26	1.69	0.36	1.73	0.38
3-Ce	2.34	0.69	2.41	0.73	2.41	0.73	2.54	0.81
3-Nd	3.54	1.56	3.49	1.52	3.54	1.57	3.62	1.64
3-U	3.16	1.25	3.33	1.38	3.28^a	1.35^a	3.62	1.64

---

Fig. 2 Temperature dependence of the product of magnetic susceptibility and temperature (χT) for powder samples of 1-Ti (green), 2-Zr (orange), and 3-M: M = Ti (yellow), Zr (purple), Ce (blue), Nd (red), U (black) with CASSCF-calculated curves of mononuclear complexes in corresponding colours (solid lines). CASSCF of 3-U uses an active space of 7 × 5f orbitals averaging over 35 spin quartets and 112 spin doublets.

Complexes 3-Ce and 3-Nd are more strongly magnetic than 3-Ti and 3-Zr due to the presence of orbital angular momentum; the smooth decrease in χ_MT with reducing temperature arises from crystal field splitting of the lowest total angular momentum multiplet. Assuming well-isolated ground Kramers doublets for 3-Ce and 3-Nd, the 2 K magnetisation data suggest |±5/2〉 and |±9/2〉 ground states, respectively (ESI Table S5, Fig. S97b and S98b;‡ in an axial crystal field, M_sat = ½g_Jm_J, where g_J is the Landé g-factor⁶⁷). For 3-U the μ_eff (χ_MT) of 3.32 μ_B (1.38 cm³ K mol⁻¹) at 300 K is characteristic of a ⁴I_9/2 U(III) ion;²⁷ this value smoothly decreases to 3.05 μ_B (1.16 cm³ K mol⁻¹) at 50 K, then rapidly decreases to 0.98 μ_B (0.12 cm³ K mol⁻¹) at 1.8 K. The sharp decrease below 50 K occurs due to slow thermalisation of the sample on cooling (see ESI for details‡). The M_sat value at 2 K and 7 T is diagnostic of a |±9/2〉 ground state (ESI Fig. S99b‡). Alternating current susceptibility measurements on 3-U show out-of-phase signals owing to slow relaxation of magnetisation below 5 K (ESI Fig. S102–S105‡), which modelling suggests arises due to Raman and quantum tunnelling of magnetisation (QTM) processes (ESI Fig. S106 and Tables S6, S7‡). Slow relaxation is common for U(III) complexes,^68–75 however, as there is no effective barrier observed for the reversal of magnetisation and closed hysteresis loops around zero field (ESI Fig. S101‡), we do not refer to 3-U as a single-molecule magnet, following several literature definitions.^76,77

UV-vis-NIR spectroscopy

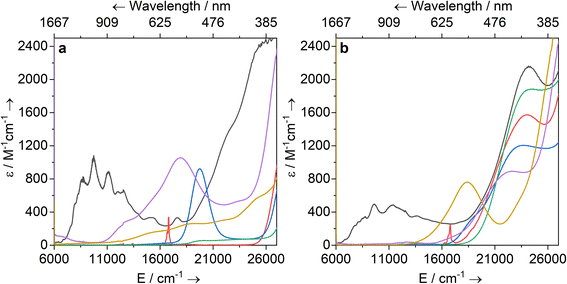
Solutions of 1-Ti, 2-M and 3-M were prepared at 0 °C in toluene (2 mM concentration for all complexes) and warmed to room temperature to immediately record UV-vis-NIR spectra (Fig. 3; see ESI Fig. S65–S79‡ for individual spectra). Some spectra, most notably 2-Nd and 2-U, contain several jagged features; this is attributed to a combination of the most intense absorption maxima being close to the detector limit at the concentrations used, and the spectral resolution of 1 nm. Intense charge transfer (CT) absorptions tailing in from the UV region are found for 3-Zr ([small upsilon, Greek, macron]_max = 22 400 cm⁻¹; ε = 890 M⁻¹ cm⁻¹), 3-La ([small upsilon, Greek, macron]_max = 22 200 cm⁻¹; ε = 1880 M⁻¹ cm⁻¹), 3-Ce ([small upsilon, Greek, macron]_max = 23 500 cm⁻¹; ε = 1200 M⁻¹ cm⁻¹), 3-Nd ([small upsilon, Greek, macron]_max = 24 000 cm⁻¹; ε = 1570 M⁻¹ cm⁻¹) and 3-U ([small upsilon, Greek, macron]_max = 24 200 cm⁻¹; ε = 2160 M⁻¹ cm⁻¹) (Fig. 3b). These transitions were not observed for 1-Ti or 2-M (Fig. 3a), and therefore can be assigned to changes in CT upon replacing a halide with hypersilanide. Apart from this CT band, the spectra of 2-La, 3-Zr and 3-La are otherwise essentially featureless.

Fig. 3 UV-vis-NIR spectra of (a) 1-Ti and 2-M (M = Zr, La, Ce, Nd, U) and (b) 3-M (M = Ti, Zr, La, Ce, Nd, U) in toluene (2 mM) between 6000 and 27 000 cm⁻¹ (1667–370 nm). Legend: M = Ti (yellow), Zr (purple), La (green), Ce (blue), Nd (red), U (black).

Complex 3-Nd has an additional absorption in the visible region ([small upsilon, Greek, macron]_max = 16 800 cm⁻¹; ε = 260 M⁻¹ cm⁻¹), as does 2-Nd ([small upsilon, Greek, macron]_max = 16 800 cm⁻¹; ε = 330 M⁻¹ cm⁻¹; ESI Fig. S71 and S78‡), thus we propose these bands are Nd(III) f–f transitions of the ⁴I_9/2 → ⁴G_5/2 states.^78,79 Complex 3-Ce is red and has a shoulder on the CT band at 18 700 cm⁻¹, while 2-Ce is bright pink and has an intense, broad absorption at [small upsilon, Greek, macron]_max = 19 700 (ε = 920 M⁻¹ cm⁻¹); these are assigned to 4f¹ → 5d¹ transitions, as observed for other Ce(III) complexes with Cp ligands.^80–84 The NIR region of 3-U studied here ([small upsilon, Greek, macron]_max > 6000 cm⁻¹) is populated with a broad set of absorptions (ε = 200–500 M⁻¹ cm⁻¹) corresponding to normally Laporte-forbidden f–f transitions of significant intensity (Fig. 3a). The increased intensity is attributed to mixing of 5f orbitals with 6d and ligand orbitals allowing for intensity-stealing;^53,85,86 similar transitions are observed in 2-U (Fig. 3b) and previously reported U(III) complexes.^27,74,87

The UV-vis-NIR spectrum of 3-Ti features an intense CT band that tails into the visible region up to ca. 22 000 cm⁻¹ and a second broad absorption band at [small upsilon, Greek, macron]_max = 18 300 cm⁻¹ (ε = 760 M⁻¹ cm⁻¹) that is assigned to overlapping d–d transitions with substantial charge-transfer character, accounting for their higher than expected intensities.⁸⁸ The spectrum for 1-Ti also exhibits multiple overlapping d–d transitions >14 000 cm⁻¹. Finally, the spectrum for 2-Zr shows a broad absorption at 17 900 cm⁻¹ (ε = 1060 M⁻¹ cm⁻¹) with a weaker shoulder at 13 100 cm⁻¹ (ε = 300 M⁻¹ cm⁻¹), and a broad low intensity NIR feature at ca. 6300 cm⁻¹ (ε = 110 M⁻¹ cm⁻¹). We assign the former two absorptions as d–d transitions based on CASSCF calculations (see below), which also suggests the latter is not a 2-Zr d–d transition; this low-energy feature could arise from a fraction of 1-Zr in toluene solution, as suggested by the Evans method magnetic moment (see above).

EPR spectroscopy

EPR spectra have been recorded at two frequencies where possible and simulations have modelled both spectra simultaneously in EasySpin;⁸⁹ full details of simulations are included in the ESI (Tables S8–S12 and Fig. S107–S121‡). EPR spectra of 2-Ce, 2-Nd and 2-U show significant exchange interactions between the metal ions, and these will be studied in a separate publication.

Titanium and zirconium, nd¹. A fluid solution spectrum of 1-Ti gives g_iso = 1.9620 (ESI Fig. S107‡), in agreement with the literature value in toluene (g_iso = 1.961)⁹⁰ and confirming that 1-Ti is stable in solution (g_ave from frozen solution is 1.9624, see below). In contrast, 3-Ti and 3-Zr decompose over several hours at room temperature in fluid aromatic solutions, consistent with nd¹ complexes being kinetically labile, particularly when coordinatively unsaturated.⁹¹ Reproducible frozen solution spectra for 2-Zr, 3-Ti and 3-Zr could be obtained for these complexes by dissolving powders in a solvent mixture (9 : 1 toluene : hexane) that was pre-cooled to ca. 250 K, then frozen at 77 K and measured immediately. The g-values obtained for monomeric nd¹ complexes (1-Ti, 3-Ti and 3-Zr) with this method are generally in excellent agreement with the powder spectra (Table 4).

The powder EPR spectrum of 2-Zr is isotropic with g = 1.9825 and a half-field transition, indicating that these transitions arise from a triplet state, reflecting the dimeric structure in the solid state (ESI Fig. S112–S114‡). There is one previous report of an EPR spectrum of 2-Zr with g_iso = 1.9506 and A_iso = 60 MHz in fluid toluene solution at 300 K.⁴⁵ Measurement of a frozen solution sample of 2-Zr (see Section 12 of the ESI‡) gives clearly anisotropic spectra (g₁ = 1.9961, g₂ = 1.9834, g₃ = 1.8618; the g₃ resonance is at 360 and 1307 mT at X- and Q-band frequencies, respectively, far outside the spectral range of the powder spectrum of 2-Zr, ESI Fig. S115 cf. S112‡) and the half-field transition is absent (ESI Fig. S114‡). These data suggest that the dimer breaks apart in solution to form monomeric 1-Zr (S = 1/2), in accord with solution magnetic susceptibility and UV-vis-NIR data (see above); there may be some 2-Zr still present in the frozen solution; however, at 50 K the signal (arising from Boltzmann population of the triplet state) is dwarfed by the S = 1/2 spectrum. Thus, we henceforth discuss these frozen solution results as representing 1-Zr.

Ti(III) and Zr(III) are S = 1/2 and are expected to have anisotropic g-values (g1, g2, g3) close to the free electron value (ge ≈ 2.0023), with deviations from ge (Δgi = gi − ge) reflecting second order spin–orbit coupling with low energy crystal field states.92 X-band EPR spectra of frozen solutions of 1/3-Ti clearly show three g-features (47Ti/49Ti hyperfine coupling not resolved), while spectra of 1/3-Zr show a similar rhombic pattern superimposed with hyperfine coupling to the 91Zr nuclear spin (11% abundant I = 5/2; Table 4, Fig. 4, ESI Fig. S115 and S117‡). Superhyperfine coupling to α-29Si and β-29Si have been observed before,35 but are not resolved here. Complexes 1/3-Ti/Zr have a consistent axial pattern of g-values reflecting their similar structures; Δg1 is −0.003 to −0.017, Δg2 is −0.02 to −0.03, and Δg3 is −0.09 to −0.28 (Fig. 4, Table 3 and ESI Table S11‡). The g3 value is most sensitive to the different complexes, with larger Δg3 for 3-Ti/Zrvs.1-Ti/Zr, and also larger Δg3 for Zr(III) vs. Ti(III) in isostructural complexes. Complexes 3-Ti/Zr are significantly more anisotropic than previous reports of Ti(III) and Zr(III) bis-Cp silanide complexes, which are pseudo-tetrahedral: Δgave values (gave = (g1 + g2 + g3)/3) of 3-Ti/Zr are −0.076 to −0.109 compared to Δgiso = −0.004 to −0.021.34–39 The EPR spectra of 1/3-Ti/Zr are more comparable to pseudo-trigonal planar bent metallocenes [M(CpR)2X].88 The pattern of 91Zr hyperfine constants (Table 4; one large and two small) are typical for 4dz21 ground states with z aligned along g1,92 which also suggests an electronic structure tending to pseudo-trigonal planar environments.

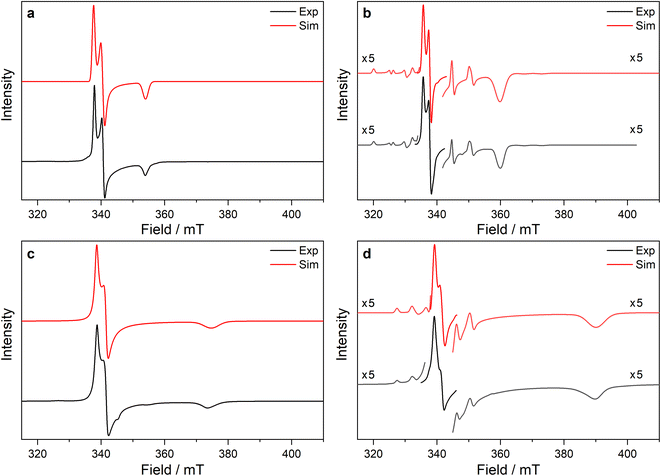Fig. 4 Frozen solution CW X-band EPR spectra of (a) 1-Ti at 130 K and 5 mM, (b) 1-Zr at 50 K and 5 mM, (c) 3-Ti at 130 K and 1 mM, (d) 3-Zr at 130 K and 5 mM in 9 : 1 toluene : hexane. Simulations using parameters from ESI Tables S9 and S10‡ are shown in red.

Table 3 CW EPR g-values of studied complexes as solid powders or in toluene : hexane (9 : 1) frozen solutions (FS). Band frequency: X = 9.37–9.47 GHz, K = 24 GHz, Q = 34 GHz

Complex	State/temperature	Band(s)	g 1	g 2	g 3
a Anisotropy in g-values not resolved. b Two species observed in solution, relative abundance given in brackets.
1-Ti	FS/130 K	X, Q	1.9990	1.9818	1.9065
	Powder/50 K	X, K	1.9957	1.9800	1.8964
	CASSCF	—	1.9994	1.9655	1.8370
3-Ti	FS/130, 50 K	X, Q	1.9955	1.9781	1.8030
	Powder/55, 50 K	X, Q	1.9946	1.9778	1.7914
	CASSCF	—	1.9950	1.9595	1.7173
1-Zr	FS/50 K	X, Q	1.9961	1.9834	1.8618
	CASSCF	—	1.9973	1.9524	1.8214
2-Zr	Powder/50 K	X, Q	1.9825^a	1.9825^a	1.9825^a
	CASSCF	—	1.9944	1.9224	1.8262
3-Zr	FS/130 K	X, Q	1.9874	1.9728	1.7280
	Powder/130 K	X, Q	1.9853	1.9758	1.7176
	CASSCF	—	1.9897	1.9438	1.6719
3-Ce	FS/7 K	X	3.907	<0.4	<0.4
	Powder/8, 5 K	X, Q	3.884	0.888	0.493
	CASSCF	—	3.775	1.016	0.562
3-Nd	FS/7 K	X	5.225	0.360	<0.4
	Powder/7, 5 K	X, Q	5.490	<0.4	<0.4
	CASSCF	—	5.526	0.296	0.146
3-U	FS/5 K	X	5.949 (44%), 5.536 (56%)^b	<0.4	<0.4
	Powder/7, 5 K	X, Q	6.055	<0.4	<0.4
	CASSCF	—	6.130	0.076	0.007

---

Table 4 CW EPR hyperfine coupling constants (MHz) of 1-Zr and 3-Zr as toluene : hexane (9 : 1) frozen solutions (FS). Band frequency: X = 9.37–9.47 GHz, Q = 34 GHz

Complex	State/temperature	Band	A 1	A 2	A 3
a Upper limit of A3: hyperfine not resolved within linewidth.
1-Zr	FS/50 K	X, Q	173.5	137	138
3-Zr	FS/130 K	X, Q	131	91	80^a

---

Powder spectra of ground samples of 1-Ti, 3-Ti, 2-Zr and 3-Zr are considerably broadened relative to frozen solution spectra (likely owing to unresolved intermolecular dipolar interactions), resulting in overlap of the g₁ and g₂ features (see ESI Fig. S108, S110, S112 and S116‡).

Cerium 4f¹, neodymium 4f³ and uranium 5f³. The powder EPR spectra of 3-Ce at 7 K are characteristic of a rhombic S_eff = 1/2 with three g-features characterised at X-band and one at Q-band (Fig. 5a, ESI Fig. S118a and b‡). Simultaneous modelling of the spectra give g₁, g₂ and g₃ of 3.884, 0.888 and 0.493, respectively. The large g₁ suggests majority |±5/2〉 component of the ground state, consistent with the M_sat value. The frozen solution X-band EPR spectrum of 3-Ce in toluene : hexane (9 : 1) has g₁ of 3.907 and transverse g-values less than 0.4 (ESI Fig. S118c‡), indicating a geometry change in solution to form a more axial ground state.

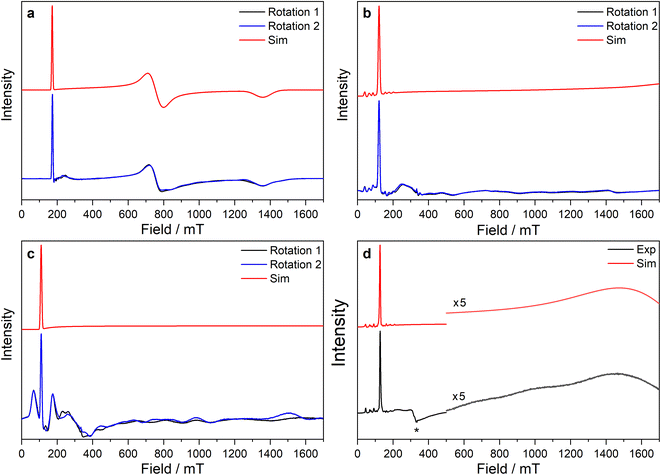Fig. 5 CW X-band EPR spectra of (a) 3-Ce powder at 8 K, (b) 3-Nd powder at 7 K, (c) 3-U powder at 7 K, (d) 15 mM frozen solution of 3-Nd in 9 : 1 toluene : hexane at 7 K. Two perpendicular orientations of powder spectra are shown in black and blue. Simulations using parameters from ESI Table S12‡ are shown in red. Asterisk (*) denotes feature intrinsic to cavity.

The X-band powder EPR spectrum of 3-Nd at 7 K revealed only a single g₁ feature of the ground Kramers doublet with resolved ¹⁴³Nd and ¹⁴⁵Nd hyperfine coupling within the accessible field range (Fig. 5b and ESI Fig. S119a–c‡). The g₁ value of 5.490 is less than the value of 6.55 expected for a pure |±9/2〉, but is larger than the maximum g value for a pure |±7/2〉 state, implying a mixed |±9/2〉 ground doublet, consistent with the M_sat value. Whilst g₂ and g₃ were not visible in the powder spectrum, a frozen solution X-band spectrum showed part of a g₂ feature at the highest fields, estimated as g₂ = 0.360 (Fig. 5d).

The powder X-band EPR spectrum of 3-U at 7 K exhibits a sharp feature at g = 6.055 (Fig. 5c), assigned as the g₁ feature of an axial S_eff = 1/2 ground state with g₂, g₃ < 0.4. This indicates a majority |±9/2〉 ground state, consistent with the M_sat value. Two broader peaks were observed at 67 and 175 mT (g = 9.94 and 3.82), however, the Q-band EPR spectrum was too weak to establish whether these peaks behaved as true g-features. The extra features cannot be explained by dipolar interactions (ESI Fig. S121‡), and we have not been able to assign them. Solution X-band spectra of 3-U at 5 K showed two sharp g₁ features at 5.949 and 5.536, indicating two very similar axial species present in solution (ESI Fig. S120c and d‡).

CASSCF calculations

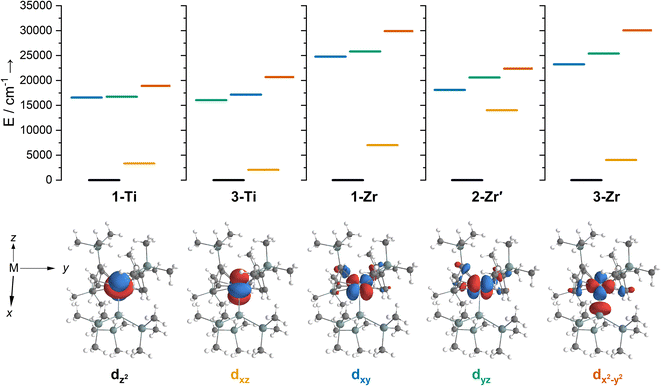
We have investigated the electronic structures of 1-Ti/Zr, 2-Zr and 3-M by CASSCF-SO calculations (performed in OpenMolcas,^93,94 see ESI for details‡). For discussion of the data we adopt the coordinate system of Petersen and Dahl, with x along the M–Si/Cl axis, y tangential to Cp′′–M–Cp′′ and z perpendicular to the plane defined by the Cp′′ centroids and coordinating Si/Cl atom.^95,96

Titanium and zirconium, nd¹. For 1-Ti, 3-Ti and 3-Zr we used the single crystal XRD structures, while for 1-Zr we used a DFT-optimised geometry (ESI Table S13‡). State-averaged (SA) CAS(7,8)SCF calculations were performed averaging over five doublets, with an active space of the five 3d or 4d orbitals and three almost doubly occupied M–L bonding orbitals with considerable (17–25%) d_xy, d_yz, and d_x²−y² character (ESI Fig. S122–S125‡). Calculations for 2-Zr used the crystal structure with one Zr(III) centre replaced with diamagnetic Y(III) (2-Zr′), averaging over 5 doublets in an active space of five 4d orbitals, three 4p orbitals and four almost doubly occupied M–L bonding orbitals with 15–19% d character (ESI Fig. S126‡). The active space differs for 2-Zr′ because the symmetry match of the Zr 4d_xz orbital and chloride σ-orbitals results in stronger bonding and anti-bonding interactions compared to 1/3-Ti/Zr, requiring a pair of orbitals to be included in the active space. Furthermore, 4p orbitals were included as they displaced the M–L bonding orbitals in orbital optimisation if not included initially.

Complexes 1/3-Ti/Zr showed similar results, with the nd1 electrons located in their respective ndz2 orbitals. A dz21 ground state is standard for bent metallocenes [M(CpR)2X] and is consistent with our analysis of the 91Zr hyperfine coupling (see above).88 The excited states place d–d transitions for 1-Ti and 3-Ti between 16 000 and 21 000 cm−1 (Fig. 6, ESI Tables S14 and S15‡), in reasonable agreement with experiment (Fig. 3). For 3-Zr, the d–d transitions are calculated at higher energies (23 224, 25 402 and 30 058 cm−1, ESI Table S18‡) and are thus obscured by the CT band in agreement with experiment (Fig. 3).

Fig. 6 Top – state energies for (left to right) 1-Ti, 3-Ti, 1-Zr, 2-Zr′ and 3-Zr, coloured according to majority d-orbital contribution to singly occupied state-specific natural orbital: d_z² (black), d_xz (yellow), d_xy (blue), d_yz (green) and d_x²−y² (orange). Near-degenerate 3d_xy and 3d_yz orbitals are significantly mixed for 1-Ti. Bottom – corresponding singly occupied state-specific natural orbitals for 3-Ti with an isosurface of 0.04 e Å⁻³, labels indicate the majority d-orbital contribution to the orbital.

The dimeric structure of 2-Zr results in the lowest energy d–d transition calculated for 2-Zr′ shifting from below 5000 cm⁻¹ for 1-Ti, 3-Ti and 3-Zr to 14 031 cm⁻¹, with the other d–d transitions at 18 101, 20 609 and 22 362 cm⁻¹ (Fig. 6 and ESI Table S17‡); the former band corresponds well with the low energy shoulder at 13 100 cm⁻¹ (ε = 300 M⁻¹ cm⁻¹; Fig. 3), while the latter three agree well with the broad absorption at 17 900 cm⁻¹ (ε = 1060 M⁻¹ cm⁻¹; Fig. 3). There are no predicted d–d transitions in this region for 1-Zr, which has a low-energy band predicted at 7010 cm⁻¹ and all other d–d transitions would be hidden beneath the CT band tailing from the UV region (ESI Table S16‡). These calculations agree with experimental data (see above) that both 1-Zr and 2-Zr are present in solution.

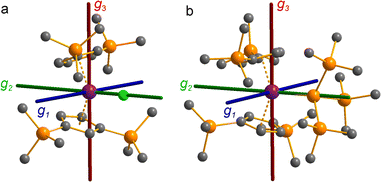
The pattern of calculated g-values for 1/3-Ti/Zr well-reproduces the experimental data (Table 3, ESI Tables S14–S16 and S18‡), while the absolute shifts in g₂ and g₃ are overestimated (ESI Table S11‡). The CASSCF calculations also give insight into the orientations of the g-values: for all 1/3-Ti/Zr, the largest value g₁ is along the z direction (pseudo-three-fold), the intermediate value g₂ is along x (M–Cl/Si bond), and the smallest value g₃ is along y (tangential to Cp′′–M–Cp′′; Fig. 7 and ESI Fig. S134‡). While orbital energies do not strictly exist in a SA-CASSCF calculation, in this case the five states are each dominated by a single configuration with the unpaired electron located in one of the five d-orbitals, so approximate d-orbital energies can be determined by assigning the state energies to the energy of the singly occupied natural orbital for that state (Fig. 6, ESI Fig. S127, S128, S130–S132 and ESI Tables S14–S18‡).

Fig. 7 CASSCF-calculated magnetic axes (blue: g₁, most magnetic; green: g₂, intermediate; red: g₃, least magnetic) for (a) 1-Ti and (b) 3-Ti. Transition metal, silicon, chlorine and carbon shown as purple, orange, green and grey respectively. Hydrogen atoms are excluded for clarity.

We find that the d_z² orbital remains lowest in energy in all cases, followed by the d_xz orbital, which varies significantly in energy between complexes. The d_xy and d_yz orbitals lie far higher in energy (16 000–26 000 cm⁻¹) and are relatively close in energy to each other, whilst the d_x²−y² orbital is highest in energy as chloride and hypersilanide are both strong σ-donor ligands. This is consistent with the Lauher-Hoffmann bonding model of a naked bent metallocene,^88,97 with an additional monodentate ligand. With these orbital energies we can rationalise the observed g-values. Spin–orbit coupling along z cannot mix in any excited state into a ground state with the electron in the d_z² orbital,⁹² and so Δg_z is approximately zero which agrees well with experiment (ESI Table S11‡; small deviations away from g_e are ascribed to mixing of d_x²−y² into the ground state⁹⁵). Spin–orbit coupling along x (y) can mix in a state with an unpaired electron in d_yz (d_xz) into the ground state to shift g_x (g_y), where Δg_x (Δg_y) is inversely proportional to the energy of the excited orbital (ESI eqn (S4) and (S5)‡). As d_xz is much lower in energy than d_yz, Δg_y is larger than Δg_x, and as the d shell is less than half-filled all Δg are negative; hence g₃ is along y and g₂ is along x; this explains the obtained ab initio orientations (Fig. 7 and ESI Fig. S134‡).

The value of Δg₃ reflects the energy of the d_xz orbital and therefore the π-bonding character of the X ligand; this has been used previously to construct a π-donor spectrochemical series for [Ti(Cp*)₂X].⁸⁸ Between 1-Ti/Zr and 3-Ti/Zr Δg₃ doubles, reflecting the d_xz orbital being 40% lower in energy for 3-Ti/Zr; this is because chloride is a π-donor and d_xz is formally π-antibonding in 1-Ti/Zr (the nominal d_xz orbitals have 1.9% and 3.1% Cl 2p_z character for 1-Ti and 1-Zr, respectively; ESI Fig. S127 and S130‡). In contrast, hypersilanide is a weak π-acceptor, and such interactions can be seen with a very low isosurface value (ESI Fig. S129 and S133‡). Upon moving from Ti to Zr there is more effective overlap of the 4d and ligand orbitals, leading to a larger crystal field splitting (Fig. 6), and a decrease in the metal contribution to the singly occupied natural orbitals (ESI Tables S14–S16 and S18‡). Spin–orbit coupling also increases moving from Ti to Zr, which acts to increase |Δg|, whilst increased d-orbital splitting and ligand–metal mixing oppose this; as all Δg become more negative upon going from 1/3-Ti to 1/3-Zr, spin–orbit coupling is the dominant effect.

Cerium 4f¹. For 3-Ce, a CAS(1,7)SCF calculation averaged over seven spin doublets was performed for an active space containing seven 4f orbitals. The resulting spin-free states were mixed with spin–orbit calculation to obtain the states of the ²F_5/2 ground term (ESI Table S19‡). The ground state for 3-Ce is predicted to be 90% |±5/2〉 and 8% |±1/2〉, consistent with the slightly reduced M_sat and g₁ values from those expected for a pure |±5/2〉 ground doublet; the calculated g-values are in good agreement with experiment (Table 3). Differing from 1/3-Ti/Zr, the easy axis (g₁) is oriented tangential to the Cp′′–M–Cp′′ direction (y), with the intermediate axis (g₂) along the Ce–Si bond (x) and the hard axis (g₃) along z (Fig. 8a). The magnetic anisotropy of 4f ions is often dictated by pure electrostatic considerations,^98,99 and so the dominance of a |±5/2〉 ground state (which has an oblate spheroidal 4f electron density) with its easy axis along y indicates the pair of sandwich-like Cp′′ ligands are stronger influences than the hypersilanide. This is similar to the situation in [CeCp^ttt₂Cl] (Cp^ttt = {C₅H₂tBu₃-1,2,4}), which has a ground state of 97% |±5/2〉 and 3% |∓1/2〉, compared to [CeCp^ttt₂{(C₆F₅-κ¹-F)B(C₆F₅)₃}], which has a 100% |±5/2〉 ground state.⁷⁸ The larger extent of |±1/2〉 mixing in the ground state of 3-Ce compared to [CeCp^ttt₂Cl] (reflected also in the experimental g₁-values of these two complexes: 3.884 vs. 4.19,⁷⁸ respectively) argues for a stronger crystal field of hypersilanide over chloride; note that is the opposite of the discussion above for 1-Ti/Zrvs.3-Ti/Zr as the bonding interactions with 4f orbitals are irrelevant and the more diffuse chloride ligand provides a weaker electrostatic field.

Fig. 8 CASSCF-calculated magnetic axes (blue: g₁, easy; green: g₂, intermediate; red: g₃, hard) for complexes 3-Ce (a), 3-Nd (b) and 3-U (c). Length of the magnetic axes reflects the size of the g-values. Metal, silicon and carbon shown as metallic green, orange and grey respectively. Hydrogen atoms are omitted for clarity.

Neodymium and uranium, nf³. The electronic structures of 3-Nd and 3-U were investigated by CAS(3,7)SCF calculations using an active space consisting of the seven nf orbitals and averaging over 35 spin quartets and 112 spin doublets (entire 5f³ configuration), and then mixing with spin–orbit coupling (Fig. 8b, c, ESI Tables S20 and S21‡). The crystal field splitting of the ⁴I_9/2 ground term for 3-Nd gives a mixed ground doublet with 76% |±9/2〉 + 15% |±5/2〉 + 5% |±1/2〉, whose g-values match reasonably well with experiment (Table 3): the mixed ground state composition explains the lower g₁ and M_sat values than predicted for a pure |±9/2〉 state. Despite the large mixing, the pattern of g-values appears more axial with smaller and similar g₂ and g₃ values. Like for 3-Ce, the easy axis (g₁) is aligned tangentially to the Cp′′–M–Cp′′ direction (y), with g₂ and g₃ in the perpendicular xz plane (Fig. 8b). Also likewise to 3-Ce, the dominant |±9/2〉 ground state and the easy axis orientation are indicative of the Cp′′ ligands dominating the electrostatic potential as |±9/2〉 also has an oblate spheroidal 4f electron density.^98,99

CASSCF calculations on 3-U averaging over all 5f³ states reproduce well the experimental susceptibility and g₁ value, and suggest a 95% |±9/2〉 ground state. Like 3-Ce and 3-Nd, the oblate spheroidal electron density of |±9/2〉 in 3-U is orientated with g₁ tangential to Cp′′–M–Cp′′ (Fig. 8c).^98,99 However, this CASSCF calculation overestimates M_sat; averaging instead over only the ⁴I_9/2 ground term (13 spin quartets) gives a more accurate reproduction of M_sat but underestimates g₁ and the magnetic susceptibility (ESI Fig. S99 and ESI Table S22‡), suggesting a slightly more mixed ground state of 89% |±9/2〉 + 6% |±5/2〉. The true ground state composition of 3-U is likely between these values, but it is certainly less mixed than that of 3-Nd.

The CAS(3,7)SCF averaged orbitals for 3-U (35 quartets and 112 doublets) showed small 6d orbital contributions (∼5%), so we extended the active space to also include two low-lying 6d orbitals (6d_z² and 6d_xz, ESI Fig. S136,‡ in accordance with 3-Ti and 3-Zr, see above). Averaging over all f³ and f²d¹ configurations in this active space, the f²d¹ states lie at ∼7000 cm⁻¹ (ESI Fig. S138‡), suggesting that spin- and Laporte-allowed f → d transitions contribute to the broad band from 6000 to 17 000 cm⁻¹ in the UV-vis-NIR spectrum (Fig. 3). Examining the averaged molecular orbitals with a low isosurface value showed that the 5f orbitals participate in weak δ-antibonding and π-bonding with Cp′′, and weak π-bonding with low lying vacant orbitals on Si (ESI Fig. S137‡).

Discussion

From the single crystal X-ray diffraction and DFT-optimised structural data it can be seen that the M–Si bonds are 0.26–0.30 Å longer than the corresponding M–Cl bonds in 1/3-Ti/Zr after correcting for the difference in single-bond covalent radii (Table 1).⁵⁵ The steric bulk of the hypersilanide ligand imposes the longer M–Si bonds, which leads to weaker M–Si bonding interactions through reduced orbital overlap. The bonding in the {M(Cp′′)₂}⁺ fragments are expected to be similar in 1-Mvs.3-M. Whilst the orientation of Cp′′ rings changes, the key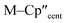 distances and 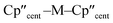angles for Zr(III) are virtually unchanged, and for Ti(III) there are only modest respective increases of these metrics of 0.014 Å and 2.6°.

The 3d1 and 4d1 systems 3-Ti and 3-Zr exhibit ndz21 ground state occupancies, with spin density perpendicular to the 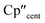, , 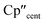Si plane. The ndz21 ground state is non-bonding and is favoured by strong anti-bonding interactions of the remaining nd-orbitals with the two Cp′′ ligands as well as with the hypersilanide ligand, which acts as a σ-donor. The hypersilanide ligand also acts as a weak π-acceptor, giving rise to a low energy ndxz1 excited state in both cases (<10 000 cm−1). The stabilisation of ndz2 and ndxz orbitals is echoed in 3-U, where low energy f3 → f2d1 transitions are seen above 6000 cm−1. However, for 3-Ce and 3-Nd the fn → fn−1d1 transitions are not proximate to the ground states, as expected.

Due to the orbitally non-degenerate ground state, the anisotropy of the g-tensors in 3-Ti and 3-Zr are dominated by second-order spin–orbit coupling with the nd_xz¹ excited state. This results in a large shift of g_y away from g_e, where y is tangential to Cp′′–M–Cp′′. In f-block complexes with near-complete f-orbital degeneracy, anisotropy in the ground state is dictated by electrostatics, and we find that the bis-Cp′′ crystal field dominates over the hypersilanide contribution. This favours oblate f-electron density in the ground state, giving ground states dominated by |±5/2〉, |±9/2〉 and |±9/2〉, for 3-Ce, 3-Nd and 3-U, respectively, with the magnetic easy axis tangential to Cp′′–M–Cp′′. These data indicate that the M–Si bonds in 3-Ti and 3-Zr are both more covalent than the M–Si bonds in 3-Ln and 3-U, whilst the greater covalency of the M–Si bonds in 3-Zrvs.3-Ti is also evident from the respective magnitudes of 4d vs. 3d crystal field splitting.

The presence of slow magnetic relaxation for 3-U and the lack of such behaviour for 3-Nd is an outlier compared to literature examples, where analogous f³ compounds tend to show more similar behaviour.^75,100 It is likely that faster magnetic relaxation occurs for 3-Nd due to the lower purity of the ground state, which itself is likely to arise due to mixing with low energy spin–orbit states at 65 and 176 cm⁻¹: the more-pure ground state in 3-U on the other hand, is well-separated from the lowest excited states at 330 and 524 cm⁻¹, which likely arises from a larger crystal field effect due to 5f vs. 4f orbitals. This is in accord with the UV-vis-NIR spectrum of 3-U, where the f → d transitions are low energy for U(III),⁵³ and are a hallmark of polarised covalent metal–ligand bonding.¹⁵ The greater involvement of 5f vs. 4f orbitals in M–Si bonds was also seen in ab initio calculations. It follows that the M–Si bond in 3-U has greater covalency than that of 3-Nd, with the M–Si bonds of 3-La, 3-Ce and 3-Nd assumed to show similar predominantly electrostatic character due to their valence 4f orbitals.

Conclusions

We have reported the synthesis and characterisation of a series of isostructural early d- and f-block M(III) bis(cyclopentadienyl) hypersilanide complexes, providing the first structurally authenticated examples of U(III) and Nd(III) silanides. By using a combination of CW EPR spectroscopy and CASSCF calculations we have shown that the d-block complexes herein have 3/4dz21 ground states aligned perpendicular to the coordination plane, with the hypersilanide ligand acting as a strong σ-donor and weak π-acceptor to impart axial anisotropy through π-bonding with low-lying ndxz orbitals; as expected, the orbital splitting is greater for 4dz21 Zr(III) vs. 3dz21 Ti(III). In contrast, the early f-block Ln/U(III) silanide 4/5fn complexes exhibit predominantly ionic bonding, with the dominant crystal field imparted by the Cp′′ ligands favouring oblate spheroidal f-electron densities and magnetic easy axes tangential to Cp′′–M–Cp′′.

The uranium silanide complex was found to exhibit increased covalency over Ln congeners, with calculations showing weak π-bonding between the 5f orbitals and both the silanide and Cp′′ ligands, and weak δ-antibonding between 5f orbitals and Cp′′. The greater crystal field imposed for 5f³ U(III) vs. 4f³ Nd(III) gave a purer ground state due to the energies of low-lying excited states being raised to the extent that they can no longer mix, switching on slow magnetic relaxation in the former complex below 5 K. The U(III) congener additionally displayed low energy 5f³ → 5f²6d¹ electronic transitions from 6000 to 17 000 cm⁻¹, signifying that the nd_z² and nd_xz orbitals have been stabilised in a similar manner to Ti(III) and Zr(III) homologues. Together, the combination of data acquired herein show the qualitative ordering of the extent of covalency to be Zr > Ti ≫ U > Nd ≈ Ce ≈ La, and reveal clear differences between the compositions of early d-block, Ln and An M–Si bonds.

Data availability

Research data files supporting this publication are available from FigShare at: https://doi.org/10.6084/m9.figshare.20459439.

Author contributions

B. L. L. R., S. T. L. and D. P. M. provided the original concept. B. L. L. R. synthesised and characterised the compounds and solved and refined the crystal structures. G. K. G. collected and interpreted EPR and magnetic data and performed calculations. A. J. W. further refined the crystallographic data and finalised CIFs. J. E.-K. carried out supporting synthetic and characterisation work. N. F. C. supervised the EPR, magnetism and calculations components. D. P. M. and S. T. L. supervised the synthetic component and directed the research. B. L. L. R., G. K. G., D. P. M., S. T. L. and N. F. C. wrote the manuscript, with contributions from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the University of Manchester for a PhD studentship for B. L. L. R. (Nuclear Endowment) and access to the Computational Shared Facility, and the European Research Council (StG-851504, CoG-816268 and CoG-612724) and the UK EPSRC (EP/M027015/1, EP/P001386/1, and EP/S033181/1) for funding. We thank Ivana Borilovic for collecting preliminary EPR data, and Adam Brookfield for supporting EPR measurements. We acknowledge the EPSRC UK National Electron Paramagnetic Resonance Service for access to the EPR facility and the SQUID magnetometer. S. T. L. thanks the Alexander von Humboldt Foundation for a Friedrich Wilhelm Bessel Research Award and N. F. C. thanks the Royal Society for a University Research Fellowship (URF191320).

References

1. R. Waterman, P. G. Hayes and T. D. Tilley, Acc. Chem. Res., 2007, 40, 712–719.
2. X. Chen and C. Liang, Catal. Sci. Technol., 2019, 9, 4785–4820.
3. W. Gao, X. Zhang, X. Xie and S. Ding, Chem. Commun., 2020, 56, 2012–2015.
4. A. Walczak, H. Stachowiak, G. Kurpik, J. Kaźmierczak, G. Hreczycho and A. R. Stefankiewicz, J. Catal., 2019, 373, 139–146.
5. V. Srinivas, Y. Nakajima, K. Sato and S. Shimada, Org. Lett., 2018, 20, 12–15.
6. B. L. L. Reánt, S. T. Liddle and D. P. Mills, Chem. Sci., 2020, 11, 10871–10886.
7. F. Pan, J. Zhang, H.-L. Chen, Y.-H. Su, C.-L. Kuo, Y.-H. Su, S.-H. Chen, K.-J. Lin, P.-H. Hsieh and W.-S. Hwang, Materials, 2016, 9, 417.
8. I. Castillo and T. D. Tilley, Organometallics, 2001, 20, 5598–5605.
9. A. D. Sadow and T. D. Tilley, J. Am. Chem. Soc., 2005, 127, 643–656.
10. J. T. White, A. T. Nelson, J. T. Dunwoody, D. D. Byler, D. J. Safarik and K. J. McClellan, J. Nucl. Mater., 2015, 464, 275–280.
11. T. L. Wilson, E. E. Moore, D. Adorno Lopes, V. Kocevski, E. Sooby Wood, J. T. White, A. T. Nelson, J. W. McMurray, S. C. Middleburg, P. Xu and T. M. Besmann, Adv. Appl. Ceram., 2018, 117, S76–S81.
12. U. E. Humphrey and M. U. Khandaker, Renewable Sustainable Energy Rev., 2018, 97, 259–275.
13. S. He and J. Cai, Ann. Nucl. Energy, 2020, 140, 107303.
14. D. A. Atwood, The Rare Earth Elements: Fundamentals and Applications, John Wiley & Sons, Ltd, Chichester, UK, 2012.
15. I. Grenthe, J. Drożdżynński, T. Fujino, E. C. Buck, T. E. Albrecht-Schmitt and S. F. Wolf, in The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein and J. Fuger, Springer, Dordrecht, 3rd edn, 2006, pp. 253–698.
16. H. Schumann, S. Nickel, E. Hahn and M. J. Heeg, Organometallics, 1985, 4, 800–801.
17. H. Schumann, S. Nickel, J. Loebel and J. Pickardt, Organometallics, 1988, 7, 2004–2009.
18. H. Schumann, J. A. Meese-Marktscheffel and F. E. Hahn, J. Organomet. Chem., 1990, 390, 301–308.
19. N. S. Radu, T. D. Tilley and A. L. Rheingold, J. Organomet. Chem., 1996, 516, 41–49.
20. N. S. Radu, T. D. Tilley and A. L. Rheingold, J. Am. Chem. Soc., 1992, 114, 8293–8295.
21. D. H. Woen, D. N. Huh, J. W. Ziller and W. J. Evans, Organometallics, 2018, 37, 3055–3063.
22. X. Pan, C. Wu, H. Fang and C. Yan, Inorg. Chem., 2022, 61, 14288–14296.
23. R. Zitz, H. Arp, J. Hlina, M. Walewska, C. Marschner, T. Szilvási, B. Blom and J. Baumgartner, Inorg. Chem., 2015, 54, 3306–3315.
24. R. Zitz, J. Hlina, H. Arp, D. Kinschel, C. Marschner and J. Baumgartner, Inorg. Chem., 2019, 58, 7107–7117.
25. A. Pöcheim, C. Marschner and J. Baumgartner, Inorg. Chem., 2021, 60, 8218–8226.
26. A. Pöcheim, R. Zitz, J. Hönigsberger, C. Marschner and J. Baumgartner, Inorg. Chem., 2022, 61, 17527–17536.
27. I. J. Brackbill, I. Douair, D. J. Lussier, M. A. Boreen, L. Maron and J. Arnold, Chem.–Eur. J., 2020, 26, 2360–2364.
28. B. L. L. Reánt, V. E. J. Berryman, J. A. Seed, A. R. Basford, A. Formanuik, A. J. Wooles, N. Kaltsoyannis, S. T. Liddle and D. P. Mills, Chem. Commun., 2020, 56, 12620–12623.
29. M. Porchia, N. Brianese, U. Casellato, F. Ossola, G. Rossetto, P. Zanella and R. Graziani, J. Chem. Soc. Dalton Trans., 1989, 677–681.
30. N. S. Radu, M. P. Engeler, C. P. Gerlach, T. D. Tilley and A. L. Rheingold, J. Am. Chem. Soc., 1995, 117, 3621–3622.
31. W. A. King and T. J. Marks, Inorg. Chim. Acta, 1995, 229, 343–354.
32. B. L. L. Réant, V. E. J. Berryman, A. R. Basford, L. E. Nodaraki, A. J. Wooles, F. Tuna, N. Kaltsoyannis, D. P. Mills and S. T. Liddle, J. Am. Chem. Soc., 2021, 143, 9813–9824.
33. A. Formanuik, A.-M. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. L. McInnes and D. P. Mills, Nat. Chem., 2016, 9, 578–583.
34. L. Hao, A.-M. Lebuis and J. F. Harrod, Chem. Commun., 1998, 35, 1089–1090.
35. H. Arp, M. Zirngast, C. Marschner, J. Baumgartner, K. Rasmussen, P. Zark and T. Müller, Organometallics, 2012, 31, 4309–4319.
36. E. Samuel, Y. Mu, J. F. Harrod, Y. Dromzee and Y. Jeannin, J. Am. Chem. Soc., 1990, 112, 3435–3439.
37. L. Hao, A.-M. Lebuis, J. F. Harrod, H.-G. Woo and E. Samuel, Chem. Commun., 1998, 229, 2013–2014.
38. A. Sauermoser, T. Lainer, G. Glotz, F. Czerny, B. Schweda, R. C. Fischer and M. Haas, Inorg. Chem., 2022, 61, 14742–14751.
39. C. T. Aitken, J. F. Harrod and E. Samuel, J. Am. Chem. Soc., 1986, 108, 4059–4066.
40. C. Marschner, Eur. J. Inorg. Chem., 1998, 221–226.
41. P. Jutzi and R. Sauer, J. Organomet. Chem., 1973, 50, C29–C30.
42. Y. A. Ustynyuk, Y. N. Luzikov, V. I. Mstislavsky, A. A. Azizov and I. M. Pribytkova, J. Organomet. Chem., 1975, 96, 335–353.
43. N. A. Jones, S. T. Liddle, C. Wilson and P. L. Arnold, Organometallics, 2007, 26, 755–757.
44. A. Antiñolo, M. F. Lappert, A. Singh, D. J. W. Winterborn, L. M. Engelhardt, C. L. Raston, A. H. White, A. J. Carty and N. J. Taylor, J. Chem. Soc. Dalton Trans., 1987, 1463–1472.
45. P. B. Hitchcock, M. F. Lappert, G. A. Lawless, H. Olivier and E. J. Ryan, J. Chem. Soc. Chem. Commun., 1992, 474–476.
46. M. F. Lappert, W. P. Leung, R. A. Bartlett and P. P. Power, Polyhedron, 1989, 8, 1883.
47. F. Ortu, J. M. Fowler, M. Burton, A. Formanuik and D. P. Mills, New J. Chem., 2015, 39, 7633–7639.
48. M. J. Harvey, T. P. Hanusa and M. Pink, J. Chem. Soc., Dalton Trans., 2001, 1128–1130.
49. K. Izod, S. T. Liddle and W. Clegg, Inorg. Chem., 2004, 43, 214–218.
50. L. R. Avens, S. G. Bott, D. L. Clark, A. P. Sattelberger, J. G. Watkin and B. D. Zwick, Inorg. Chem., 1994, 33, 2248–2256.
51. A. J. Gaunt, A. E. Enriquez, S. D. Reilly, B. L. Scott and M. P. Neu, Inorg. Chem., 2008, 47, 26–28.
52. P. C. Blake, M. F. Lappert, R. G. Taylor, J. L. Atwood, W. E. Hunter and H. Zhang, J. Chem. Soc., Dalton Trans., 1995, 3335–3341.
53. S. T. Liddle, Angew. Chem., Int. Ed., 2015, 54, 8604–8641.
54. P. C. Blake, M. F. Lappert, J. L. Atwood and H. Zhang, J. Chem. Soc., Chem. Commun., 1986, 1148–1149.
55. P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197.
56. A. Bande and J. Michl, Chem.–Eur. J., 2009, 15, 8504–8517.
57. C. Marschner, in Functional Molecular Silicon Compounds I, Structure and Bonding, ed. D. Scheschkewitz, Springer, Cham, 2014, vol. 155, pp. 163–228.
58. R. D. Shannon, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32, 751–767.
59. J. Britten, Y. Mu, J. F. Harrod, J. Polowin, M. C. Baird and E. Samuel, Organometallics, 1993, 12, 2672–2676.
60. M. Zirngast, U. Flörke, J. Baumgartner and C. Marschner, Chem. Commun., 2009, 5538–5540.
61. X. Sun, L. Münzfeld, D. Jin, A. Hauser and P. W. Roesky, Chem. Commun., 2022, 58, 7976–7979.
62. S. Kyushin, H. Sakurai and H. Matsumoto, Chem. Lett., 1998, 107–108.
63. C. J. Windorff and W. J. Evans, Organometallics, 2014, 33, 3786–3791.
64. S. K. Sur, J. Magn. Reson., 1989, 82, 169–173.
65. A. Antiñolo, M. F. Lappert, G. A. Lawless and H. Olivier, Polyhedron, 1989, 8, 1882.
66. J. Mayans, L. Tesi, M. Briganti, M.-E. Boulon, M. Font-Bardia, A. Escuer and L. Sorace, Inorg. Chem., 2021, 60, 8692–8703.
67. J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453.
68. F. Moro, D. P. Mills, S. T. Liddle and J. van Slageren, Angew. Chem., Int. Ed., 2013, 52, 3430–3433.
69. S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669.
70. J. D. Rinehart and J. R. Long, J. Am. Chem. Soc., 2009, 131, 12558–12559.
71. J. D. Rinehart, K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7572–7573.
72. K. R. Meihaus, J. D. Rinehart and J. R. Long, Inorg. Chem., 2011, 50, 8484–8489.
73. M. A. Antunes, L. C. J. Pereira, I. C. Santos, M. Mazzanti, J. Marçalo and M. Almeida, Inorg. Chem., 2011, 50, 9915–9917.
74. D. P. Mills, F. Moro, J. McMaster, J. van Slageren, W. Lewis, A. J. Blake and S. T. Liddle, Nat. Chem., 2011, 3, 454–460.
75. J. D. Rinehart and J. R. Long, Dalton Trans., 2012, 41, 13572–13574.
76. M. J. Giansiracusa, G. K. Gransbury, N. F. Chilton and D. P. Mills, in Encyclopedia of Inorganic and Bioinorganic Chemistry, ed. R. A. Scott, John Wiley, Chichester, 2021,  DOI:10.1002/9781119951438.eibc2784.
77. N. F. Chilton, Annu. Rev. Mater. Res., 2022, 52, 79–101.
78. J. Liu, D. Reta, J. A. Cleghorn, Y. X. Yeoh, F. Ortu, C. A. P. Goodwin, N. F. Chilton and D. P. Mills, Chem.–Eur. J., 2019, 25, 7749–7758.
79. V. A. Volkovich, A. B. Ivanov, S. M. Yakimov, D. V. Tsarevskii, O. A. Golovanova, V. V. Sukhikh and T. R. Griffiths, AIP Conf. Proc., 2016, 1767, 020023.
80. R. J. Lang, Can. J. Res. A, 1936, 14, 127–130.
81. P. N. Hazin, C. Lakshminarayan, L. S. Brinen, J. L. Knee, J. W. Bruno, W. E. Streib and K. Folting, Inorg. Chem., 1988, 27, 1393–1400.
82. W. K. Kot, PhD thesis, University of California, Berkeley, 1991.
83. G. Blasse and A. Bril, J. Chem. Phys., 2004, 47, 5139–5145.
84. M. Suta, N. Harmgarth, M. Kühling, P. Liebing, F. T. Edelmann and C. Wickleder, Chem.–Asian J., 2018, 13, 1038–1044.
85. D. E. Morris, R. E. Da Re, K. C. Jantunen, I. Castro-Rodriguez and J. L. Kiplinger, Organometallics, 2004, 23, 5142–5153.
86. C. R. Graves, P. Yang, S. A. Kozimor, A. E. Vaughn, D. L. Clark, S. D. Conradson, E. J. Schelter, B. L. Scott, J. D. Thompson, P. J. Hay, D. E. Morris and J. L. Kiplinger, J. Am. Chem. Soc., 2008, 130, 5272–5285.
87. A. J. Wooles, D. P. Mills, F. Tuna, E. J. L. McInnes, G. T. W. Law, A. J. Fuller, F. Kremer, M. Ridgway, W. Lewis, L. Gagliardi, B. Vlaisavljevich and S. T. Liddle, Nat. Commun., 2018, 9, 2097.
88. W. W. Lukens, M. R. Smith and R. A. Andersen, J. Am. Chem. Soc., 1996, 118, 1719–1728.
89. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
90. M. Křižan, J. Honzíček, J. Vinklárek, Z. Růžičková and M. Erben, New J. Chem., 2015, 39, 576–588.
91. C. E. Housecroft and A. G. Sharpe, Inorganic Chemistry, 5th edn, Pearson, Harlow, 2018.
92. F. E. Mabbs and D. Collison, Electron Paramagnetic Resonance of d Transition Metal Compounds, Elsevier Science, Amsterdam, 1992.
93. I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. L. Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P. O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964.
94. F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D. C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117.
95. J. L. Petersen and L. F. Dahl, J. Am. Chem. Soc., 1975, 97, 6416–6422.
96. J. L. Petersen and L. F. Dahl, J. Am. Chem. Soc., 1975, 97, 6422–6433.
97. J. W. Lauher and R. Hoffmann, J. Am. Chem. Soc., 1976, 98, 1729–1742.
98. J. Sievers, Z. Phys. B: Condens. Matter, 1982, 45, 289–296.
99. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
100. J. J. Le Roy, S. I. Gorelsky, I. Korobkov and M. Murugesu, Organometallics, 2015, 34, 1415–1418.

---

Footnotes

† Dedicated to Professor Peter Junk on the occasion of his 60th birthday.

‡ Electronic supplementary information (ESI) available. CCDC 2195632–2195640. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc04526e

§ Contributed equally as co-first authors.

---