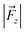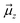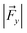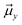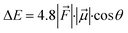Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A porphyrin-based molecular cage guided by designed local-electric field is highly selective and efficient†
Shakir Ali
Siddiqui
 a,
Sason
Shaik
a,
Sason
Shaik
 *b,
Surajit
Kalita
*b,
Surajit
Kalita
 a and
Kshatresh Dutta
Dubey
a and
Kshatresh Dutta
Dubey
 *a
*a
aDepartment of Chemistry, School of Natural Sciences, Shiv Nadar Institution of Eminence Delhi-NCR, India. E-mail: kshatresh.dubey@snu.edu.in
bInstitute of Chemistry, The Hebrew University of Jerusalem Israel, Jerusalem, Israel. E-mail: sason@yfaat.ch.huji.ac.il
First published on 4th September 2023
Abstract
The present work outlines a general methodology for designing efficient catalytic machineries that can easily be tweaked to meet the demands of the target reactions. This work utilizes a principle of the designed local electric field (LEF) as the driver for an efficient catalyst. It is demonstrated that by tweaking the LEF, we can catalyze the desired hydroxylation products with enantioselectivity that can be changed at will. Using computation tools, we caged a synthetic analog of heme porphyrin (HM1) and investigated the pharmaceutically relevant conversion of tetralin to tetralol, inside the modified supramolecular cage. The QM/MM calculations demonstrate a resulting catalytic efficiency with virtually absolute R-selectivity for the tetralin hydroxylation. Our calculations show that the LEF of the supramolecular cage and HM1 exert a strong electric field along the Fe–O reaction axis, which is the main driving force for enhanced reactivity. At the same time, the supramolecular cage applies a lateral LEF that regulates the enantioselectivity. We further demonstrate that swapping the charged/polar substitution in the supramolecular cage switches the lateral LEF which changes the enantioselectivity of hydroxylation from R to S.
1. Introduction
We outline here a general methodology for designing efficient catalysts that can easily be tweaked to meet the demands of the target reactions. The work utilizes computational design principles1–5 towards this goal. The principles are then applied to design a supramolecular cage that possesses an efficient scaffold, which can be easily modified to catalyze the formation of desired hydroxylation products with enantioselectivity at will.Still though, there are two major caveats in such catalyst design; (a) the choice of scaffold for designing, and (b) the codification of the descriptor that affects the catalysis.6–8 For the initial scaffold, enzymes could be an alternative; however, the low thermal stabilities9,10 and low tolerance towards the organic solvents11,12 remain a major challenge for an enzymatic scaffold. In addition, the enzymes are giant macromolecular systems that are very selective for their native reactions. As such, evolving an enzyme for a new activity requires a large random mutation in the protein matrix.13–15 However, supramolecular complexes such as organic cages could be a better alternative as they possess a relatively smaller size and an active site architecture analogous to the enzymes.16–19 Herein, we show a supramolecular cage could be used as an efficient scaffold that can easily be tweaked for the desired product.
The electrostatic field of the supramolecular cage is an ideal choice for a catalytic effector19 and could resolve (b) i.e., the codification of the descriptor. It is established that the preorganization of the electrostatic field is responsible for catalysis and has been well established for the enzyme catalysis.20 Indeed, recent studies by several groups have shown that the local electric fields (LEFs) of enzymes and/or solvents constitute the main catalytic elements for several reactions.21–27 This fact is also supported by several recent studies where the application of oriented external electric field (OEEF)28–30 along the “reaction axis” significantly enhances the rate of reactions and controls their product selectivity.31–38 As such, the LEF along the reaction axis can be used as an effector of the catalytic activity26 in our target cages. Herein we demonstrate that a methodological design of LEF in a supramolecular cage brings about the desired reactivity and selectivity of C–H hydroxylation reactions.
1.1 The model system
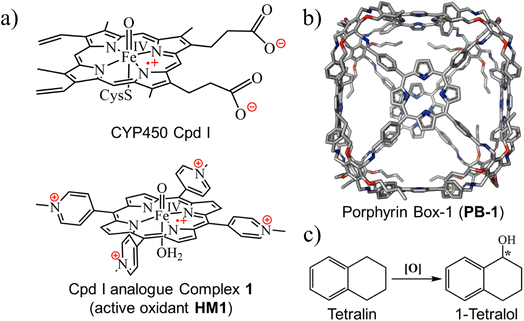
Our choice of initial catalyst is a synthetic porphyrin derivative, HM1 in Fig. 1a, which was developed by Groves et al.39 and demonstrated to enhance hydrogen abstraction reactions in aqueous solutions. The rate-enhancement capability of HM1 was later shown to originate in the LEF of the charged peripheral substituents.21For the supramolecular scaffold, we selected the porous organic cage (Fig. 1b), which was synthesized by Kim et al., and named porphyrin box, PB-1.16 As was shown by Kim et al., PB-1 possesses exceptional chemical stability and applicability; including selective gas sorption, encapsulation of guest molecules, etc. Importantly, such porous organic cages were reported to preserve their stability even after post-synthetic modification (PSM)40–42 of some functional groups of such cages. Therefore, we deem this supramolecular scaffold to be an ideal starting platform that can be selectively modified (see ESI, Fig. S1 and S2†) for tailoring the LEF along the reaction axis of HM1, as well as for encapsulating target substrates for oxidation.
As a substrate that can be used to explore reactivity and selectivity, we chose the conversion of tetralin to tetralol (Fig. 1c), which involves both C–H hydroxylation and enantioselectivity of the product. Thus, (R)-1-tetralol is extensively used to treat several disorders such as obsessive-compulsive disorder, post-traumatic stress, premenstrual dysphoric disorder, and social anxiety.43–45 Can the chosen cage produce (R)-1-tetralol? Can it produce, on demands, also (S)-1-tetralol?
As shown in the foregoing sections, we can tailor the magnitude of the LEF as well as its specific orientation and produce a supramolecular cage that enhances reactivity and enantioselectivity.
2. Computational details
In the present study, we used MD simulations for the entrapment, conformational and binding stabilities of TLN & HM1 inside the cage, QM/MM calculations for the mechanism and electronic structure investigations, quantification of the local electric field and QM-only DFT calculations to study the effect of the oriented external electric field (OEEF) onto the reaction axis. The details of each method are described below.2.1 System preparation
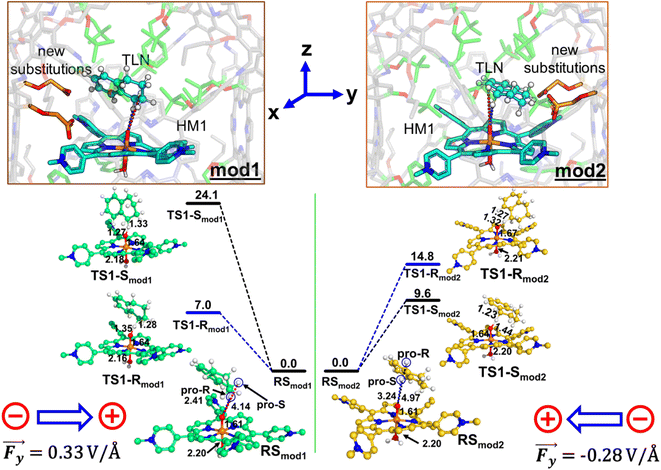
We chose the porous organic cage, created by Kim et al.16 and known as porphyrin box PB-1, for the initial supramolecular scaffold, and modelled it for entrapment of substrate and stability of HM1 using the flowchart in Fig. 2. The detailed description of the modelling procedure is discussed in Text S1 of the ESI.† The PB-1 was optimized with AM1 semi-empirical theory.46 The parameters for PB-1 cage were generated using the antechamber module of Amber20 for GAFF2 parameters47 for a QM-optimized geometry at the AM1 level of theory. The parameters for oxidant HM1 were prepared by the MCPB.py program, a python-based metal parameter builder used to generate a forcefield for the metal center of the protein, employing the bonded model approach.48 Again, the partial atomic charges and missing parameters for tetralin (TLN) substrate were obtained from the RESP charge fitting method for the QM-optimized geometry at the HF/6-31G* level of theory.49,50 After docking the HM1 & TLN inside the so-created cages, all the complexes were solvated in a rectangular box of CHCl3 solvent molecules with a 10 Å cutoff from the supramolecular cage boundary using the CHCl3BOX using leap module. A suitable quantity of Cl− ions were supplied to balance out the system's overall charge in each case.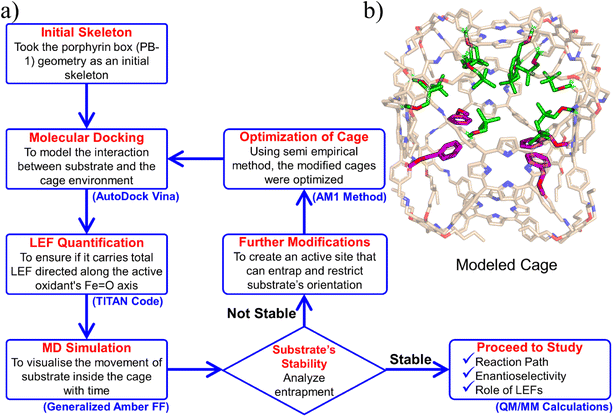 | ||
| Fig. 2 (a) A flowchart of the protocol to engineer the porphyrin box for the substrate and active oxidant HM1. (b) Modeled cage, here modifications are highlighted in green. | ||
2.2. MD simulations
The various systems were minimized in two phases after the complexes were initially built up to get rid of the poor connections. In step 1, only solvent molecules were minimized using the conjugate gradient minimizer after 5000 steps of the steepest descent. Using the same minimizer, as in step 1, all of the complexes were minimized in step 2 without any constraints.All the systems were then gently equilibrated from 10 to 300 K under the NVT ensemble for 50 ps with a weak restraint of 5 kcal mol−1 Å−2. Subsequently, a density equilibrium was performed using the NPT ensemble at a targeted temperature of 300 K and pressure of 1 atm for 1 ns using the Langevin thermostat52 and the Berendsen barostat,53 with a weak restraint of 1 kcal mol−1 Å−2. Following the removal of all restraints, the systems were further equilibrated for 3 ns, and then 100 ns of production simulations for each system were run and the convergence of the simulation is checked. Furthermore, these procedures were replicated three more times. The covalent bonds that contain hydrogens were constrained using the SHAKE algorithm,51 and a particle mesh Ewald (PME) method52 was utilized to treat long-range electrostatic interactions during all the MD simulations. The entire simulation was run with an integration step of 2 fs. The Amber20 package's GPU version was used to run all of the MD simulations.53
2.3. QM/MM calculations
The reaction mechanism and the electronic structure were investigated using QM/MM calculations for the snapshot from the MD trajectory. The QM regions included the oxidant HM1 and the substrate tetralin (TLN), for which the coordinates for the QM region for QM/MM optimized geometry can be found in this ESI.† The entire supramolecular modeled cage and solvent molecules within 8 Å of HM1 were included in the ‘active region’ of the QM/MM calculations. The atoms in the ‘active region’ interact with the QM atoms through electrostatic and van der Waals interactions and the corresponding polarization effects were considered in the subsequent QM/MM calculations. All the QM/MM calculations were performed using ChemShell,54,55 by combining Turbomole56,57 for the QM part and DL_POLY58 for the MM part. The MM region was described using the Amber force field generated for the cage, and the electronic embedding scheme was used to account for the polarizing effect of the enzyme environment on the QM region.During QM/MM geometry optimizations, the QM region was computed using the hybrid UB3LYP functional59 with the def2-SVP basis set. All of the QM/MM transition states (TSs) were located by relaxed potential energy surface (PES) scans followed by full TS optimizations using the P-RFO optimizer60 implemented in the HDLC code. The results were further validated with single-point calculations at a higher basis set, def2-TZVP. All calculations were performed for the doublet and sextet states since recent studies showed that the pristine oxidant HM1 displays two-state reactivity (doublet and sextet spins) in gas phase.21,61
2.4. Quantification of the local electric fields (LEFs) and electrostatic stabilization energy
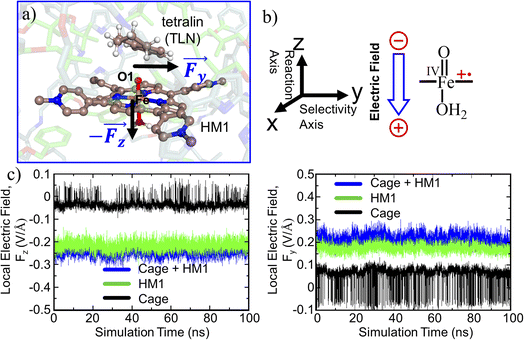
The TITAN and TUPÃ codes were used to quantify the local electric fields (LEFs) present in the systems.22,62,63 Using the TUPÃ code, we quantified the evolution of LEFs for solvated cage, oxidant HM1 & entire system from whole MD simulation trajectory at 10 ps time intervals, along the reaction axis, (z-axis, Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) as well as the selectivity axis (y-axis). The solvent molecules present in the 3 Å vicinity of HM1 were included. The electric fields along the MD trajectory were measured using the point charge distribution included in the parameter topology file.
O) as well as the selectivity axis (y-axis). The solvent molecules present in the 3 Å vicinity of HM1 were included. The electric fields along the MD trajectory were measured using the point charge distribution included in the parameter topology file.
For the QM/MM optimized RS and TS geometries, the LEF along both the axes were quantified using in-house TITAN code. The quantification included the charges of methyl pyridinium cationic periphery of HM1, entire cage and the solvent molecule near 3 Å of HM1. Dipole moments were calculated for H2O–Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, porphyrin and TLN substrate. Then interaction/stabilization energy were calculated using the following relationship:30
O, porphyrin and TLN substrate. Then interaction/stabilization energy were calculated using the following relationship:30
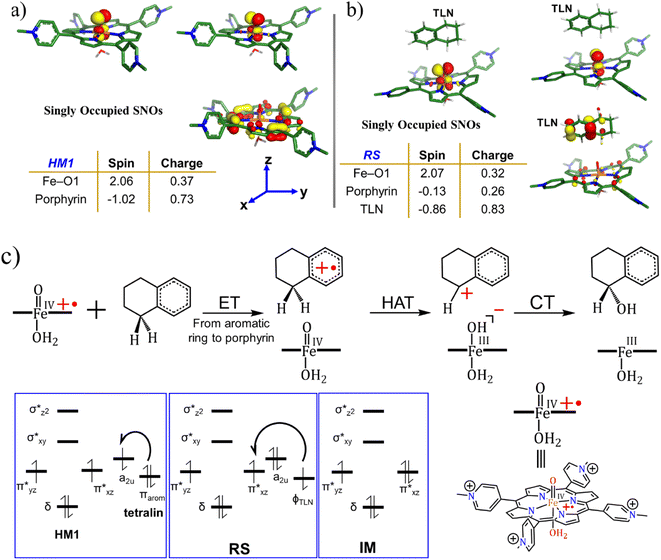
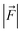 is the LEF intensity in V Å−1, the
is the LEF intensity in V Å−1, the 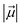 is the magnitude of dipole moment in Debye and θ is the angle between LEF and dipole moment vectors. For electric field and dipole moments, GAUSSIAN convention is used.30,64
is the magnitude of dipole moment in Debye and θ is the angle between LEF and dipole moment vectors. For electric field and dipole moments, GAUSSIAN convention is used.30,64
Furthermore, QM-only single point calculations were performed with and without oriented external electric fields (OEEFs) for the stripped RS and TS geometries. For frequency calculations, we used the hybrid UB3LYP/def2-SVP level of theory59 and single-point calculations at a higher basis set, def2-TZVP. These effects were studied using Gaussian09 program.65
2.5. Adaptive steered molecular dynamics (ASMD) simulations
For efficient catalysis the entry and exit of the substrate/product is crucial, and therefore, we determined the route and feasibility of substrate entry and product escape in the designed cage, using adaptive steered molecular dynamics (ASMD) simulations.53 In so doing, we applied an external force in a predetermined direction and performed 20 iterative simulations of ASMD by using the end-to-end distance between the iron center of Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and the ‘C’ of the substrate/product as our reaction coordinate. The adaptive steering was continued along the reaction coordinate from 3 to 23 Å in 10 stages until the substrate/product was entirely outside of the cage. We assigned a spring constant of 10 kcal mol−1 Å−2, and used a velocity of 0.5 Å ns−1 for simulations of a total duration of 800 ns. Finally, we calculated the potential of mean force (PMF), from entire 800 ns of simulation which characterizes the free energy change along a reaction coordinate during different intermediate stages of a product exit using the Jarzynski's equality66 -
O and the ‘C’ of the substrate/product as our reaction coordinate. The adaptive steering was continued along the reaction coordinate from 3 to 23 Å in 10 stages until the substrate/product was entirely outside of the cage. We assigned a spring constant of 10 kcal mol−1 Å−2, and used a velocity of 0.5 Å ns−1 for simulations of a total duration of 800 ns. Finally, we calculated the potential of mean force (PMF), from entire 800 ns of simulation which characterizes the free energy change along a reaction coordinate during different intermediate stages of a product exit using the Jarzynski's equality66 -| 〈exp(−βW)〉 = exp(−βΔG) | (1) |
3. Results & discussion
3.1 Encapsulation of the active oxidant and the substrate inside the modeled cage
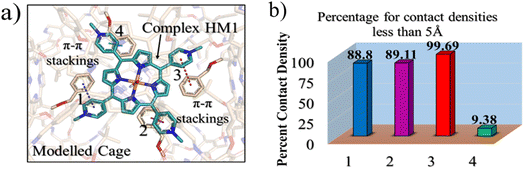
Initially, we tailored PB-1 to better fit HM1 using a protocol shown in Fig. 2a. Since, the active oxidant HM1 contains four peripheral pyridinium groups, we anticipated that it could be stabilized in the cage with the aid of π–π stacking interactions, and therefore, we introduced phenyl rings inside the walls of PB-1. The initial substitution for entrapment of only HM1 can be found in the ESI (Fig. S1).† The simulation of the modified cage and its resident HM1 substantiates our reasoning that the stability of the complex was mainly driven by π–π stacking interactions. Subsequently, we docked the tetralin substrate in the so modified cage. After a few rounds of subsequent modifications that preserve the stability of HM1 and the binding of the substrate during simulations (see ESI, Fig. S2 and S5–S7†), we eventually achieved our final ‘modeled cage’ is shown in Fig. 2b. Here, the violet color shows modifications to stabilize HM1, while green represents the requisite modifications that stabilize the substrate binding.3.2 Testing the role of the LEF on reactivity and selectivity
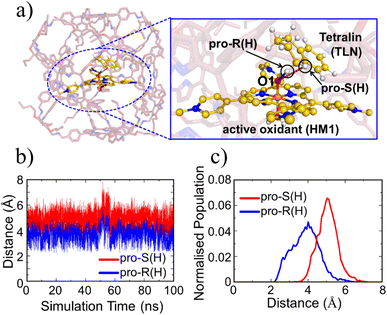
This section demonstrates that the unusual impact of the cage on reactivity and enantioselectivity originates in the combined LEF of HM1 and the container PB1. This is done by initially evaluating the combined LEF effects on the RS and TS species along the reaction coordinate. Subsequently, we investigate the role of the LEF in determining the special electronic structures of these species. This was complemented by determining the LEF role on the enantioselectivity of the reaction. And finally, by showing that we can get enantioselectivity at will, by simply flipping the direction of the lateral LEF.While oxidant HM1 is known to be intrinsically reactive in H-atom-transfer (HAT) reactions,21,39,61 the enantioselectivity has not been explored. As can be seen from Fig. 5a which represents a snapshot from 100 ns MD simulation, the substrate occupies a very a close position to the oxidant, and both pro-R and pro-S hydrogen atoms are also in the proximity of the oxo-iron moiety of HM1. The proximities of these hydrogen atoms are also persistent throughout the simulations which can be verified by the distance vs. time plot (Fig. 5b) and the plot of distance vs. population (Fig. 5c). At the same time, it is apparent that the pro-R hydrogen is closer than the pro-S one. As mentioned earlier, hydroxylation of tetralin at pro-R position has medicinal importance.43 It is noteworthy that our modeled system gives a clear preference for pro-R selectivity, and is thus of industrial relevance.
 | ||
| Fig. 6 (a) The key geometric data as well as QM/MM optimized geometries of 2RS, 2IM(R) and 2PC(R). The optimized geometries of 2TS1(R), 2TS2(R) and for the corresponding sextet state species can be found in ESI, Fig. S9 & S10.† (b) The complete ZPE corrected QM/MM/UB3LYP/def2-TZVP reaction profile diagram for the R-enantioselective C–H hydroxylation of tetralin into (R)-1-tetralol by active oxidant HM1 entrapped inside the modelled cage. All the calculations have been performed for both doublet and sextet states. Distances are in Å, and energies are reported in kcal mol−1 relative to RS. Note that RS, TS and PS, here, stand for reactant state, transition state and product state. | ||
Furthermore, it is seen that the H-transfer energy barrier is merely 4.8 kcal mol−1, and the process is preferred for the pro-R H-abstraction. Notably, the reaction is mediated by IM1, which involves a tetralinyl cation and Fe(III)–OH− heme species. Subsequently, the substrate cation attacks the Fe–OH bond and generates the R-tetralol product. By comparison, the pro-S H-abstraction barrier is 7.81 kcal mol−1 (see ESI, Fig. S11 & S12†). Based on the energy barrier difference, the R/S ratio at 298.15 K, corresponds to 159![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for R/S-enantioselectivity of the Tetralol (see ESI, Fig. S11†). Clearly the cage modifies both the reactivity and enantioselectivity of HM1. To further substantiate the role of cage, we performed separate calculations by stripping the cage and details for the same are shown in Fig. S13 of the ESI.†
1 for R/S-enantioselectivity of the Tetralol (see ESI, Fig. S11†). Clearly the cage modifies both the reactivity and enantioselectivity of HM1. To further substantiate the role of cage, we performed separate calculations by stripping the cage and details for the same are shown in Fig. S13 of the ESI.†
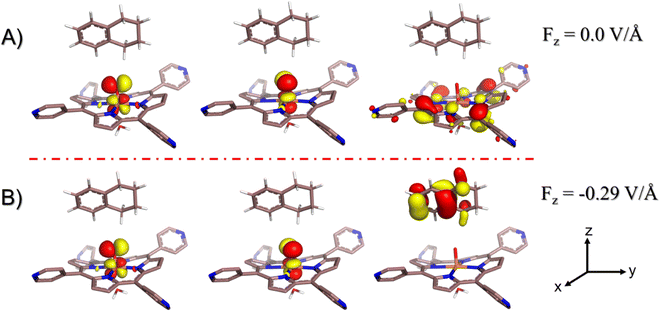
In contrast to the previous study with HM1,21 here there is no spin crossover during the H-transfer step, since the reaction prefers to occur almost exclusively on the doublet state surface. Thus, the cage environment perturbs the electronic states and creates a preference for the doublet state. At the same time, the final R-alcohol product is most stable in the sextet state, as happens in many reactions of P450.67
 | ||
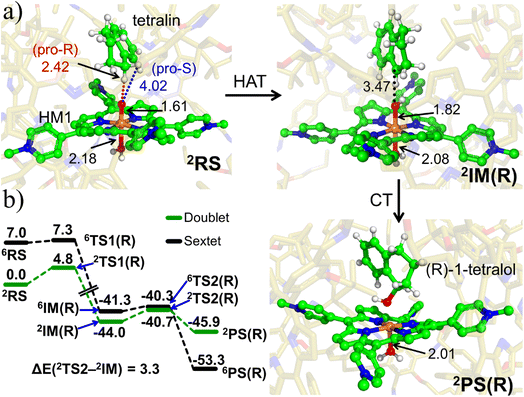
| Fig. 7 The spin natural orbitals (SNOs), mulliken spin density and charges for (a) lone active oxidant HM1 and (b) reactant state, RS. TLN refers to the substrate tetralin. All the electronic structure calculations were carried out for the doublet ground state of the complex. (c) A complete reaction mechanism along with the orbital occupation during reaction. See ESI† for Mulliken spin density and charges, Table S1.† | ||
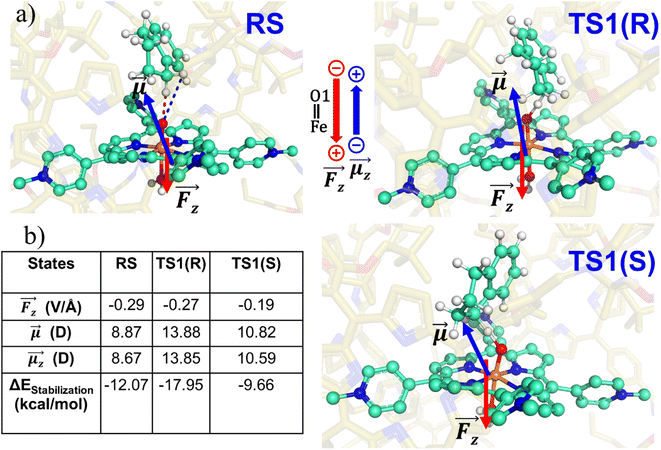
To substantiate the role of the LEF, we quantify in Fig. 8 the LEF exerted by the cage along the reaction axis using the TITAN program. As we can see, the LEF significantly stabilizes the TS state for the R-enantioselectivity compared with the TS for the S-enantioselectivity. Herein, the LEF calculation and analysis are more focused on the RS and TS1 state, being the rate-determining step. It plays a crucial role in the overall reaction kinetics because it is the step that significantly impacts the overall reaction rate.
Let us then proceed with the calculation of stabilization energy of the two chiral isomers of the TS in the presence of the 2D-LEF. For this purpose, we employ the following relationship:
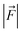 is the LEF intensity in V Å−1, the
is the LEF intensity in V Å−1, the 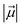 is the magnitude of dipole moment in Debye and θ is the angle between LEF and dipole moment vectors. The results are collected in Table 1.
is the magnitude of dipole moment in Debye and θ is the angle between LEF and dipole moment vectors. The results are collected in Table 1.
Table 1 reveals that the TS1(R) is better aligned than TS1(S) in the direction of the LEF, and it possesses relatively higher dipole moments along the y- and z-axes. As such, this dipole moment of TS1(R) will interact more strongly with the LEF than TS1(S), which possesses a lower z-LEF and higher y-EEF which is misoriented and destabilizes this TS. As such, the pro-S TS is less stabilized compared with the pro-R TS. The interaction energy calculations predict that the two directional electric fields complement each other for the reactivity and the selectivity. Clearly therefore, the LEF of the system is the decisive factor for the exclusive R-selective pathway and for its enhanced reactivity. This was further supported by a separate calculation, in which we stripped the cage and charged substitution, and found no enantioselectivity (see ESI, Fig. S13†).
3.3 Can the LEF of the supramolecular cage be tweaked to get enantioselectivity at will?
Since a y-directional electric field in our cage causes R-enantioselective reaction, we set out to reverse the LEF of the cage (see ESI, Fig. S14†) and produce S-enantioselectivity. When modifications were done along the y-axis for both the cases, this removed the pre-existing y-LEF in both directions. Fig. 10 shows that when we place a charged substituent in the negative y-direction (mod1), we achieve an absolute R enantioselectivity. The explicitly introduced groups are the carboxylate terminals which have −1 electronic charge for both the groups (total −2), which overpowers the overall LEF, leading to a dominant electrostatic effect along the y-axis in both the positive and negative directions. In contrast, when we place the same charged substitution on the positive y-direction (mod2), the reaction becomes S-enantioselective. Therefore, simply flipping the direction of the designed LEF in the supramolecular cages creates absolute enantioselectivity at will!4. Conclusions
In the present work, we demonstrate that a methodological design of LEF in a supramolecular cage brings about the desired reactivity and selectivity of C–H hydroxylation reactions. Using rational designing principles, the supramolecular cage can be strategically modified to entrap the desired product. Furthermore, the designed local electric field lateral to the reaction axis provides absolute enantioselectivity of the product, and it can be tailored to produce the desired enantioselectivity. Finally, the LEF along the reaction axis can readily facilitate the electron transfer process, which in turn, enhances the reactivity several fold.As such, the present work demonstrates a new state-of-art catalyst design which is sustainable and recyclable for different product formations.
Data availability
All data needed to reproduce the work, are available in ESI material associated with this article.†Author contributions
SAS and SK perfomed the calculations and data analysis. KDD supervised and conceptualized the project. KDD and SS wrote the manuscript.Conflicts of interest
There is no conflict to declare.Acknowledgements
KDD acknowledges the Department of Biotechnology, Ministry of Science and Technology, Govt. of India for the Ramalingaswami re-entry grant (BT/RLF/Re-entry/10/2017). SS is supported by the Israel Science Foundation (grant 520/18). We gratefully acknowledge Dr Ajoy Kapat and Mr Raktim Deka, Shiv Nadar Institution of Eminence for the valuable discussions.References
- R. L. Greenaway, V. Santolini, M. J. Bennison, B. M. Alston, C. J. Pugh, M. A. Little, M. Miklitz, E. G. B. Eden-Rump, R. Clowes, A. Shakil, H. J. Cuthbertson, H. Armstrong, M. E. Briggs, K. E. Jelfs and A. I. Cooper, Nat. Commun., 2018, 9, 1–11 CrossRef CAS PubMed.
- E. Berardo, R. L. Greenaway, L. Turcani, B. M. Alston, M. J. Bennison, M. Miklitz, R. Clowes, M. E. Briggs, A. I. Cooper and K. E. Jelfs, Nanoscale, 2018, 10, 22381–22388 RSC.
- T. K. Piskorz, V. Martí-Centelles, T. A. Young, P. J. Lusby and F. Duarte, ACS Catal., 2022, 5806–5826 CrossRef CAS PubMed.
- G. Montà-González, F. Sancenón, R. Martínez-Máñez and V. Martí-Centelles, Chem. Rev., 2022, 122, 13636–13708 CrossRef PubMed.
- A. G. Slater, P. S. Reiss, A. Pulido, M. A. Little, D. L. Holden, L. Chen, S. Y. Chong, B. M. Alston, R. Clowes, M. Haranczyk, M. E. Briggs, T. Hasell, G. M. Day and A. I. Cooper, ACS Cent. Sci., 2017, 3, 734–742 CrossRef CAS PubMed.
- D. J. Durand and N. Fey, Chem. Rev., 2019, 119, 6561–6594 CrossRef CAS PubMed.
- X. Wang, G. Zhang, L. Yang, E. Sharman and J. Jiang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1369 Search PubMed.
- M. J. Hülsey, C. W. Lim and N. Yan, Chem. Sci., 2020, 11, 1456–1468 RSC.
- M. Roca, H. Liu, B. Messer and A. Warshel, Biochemistry, 2007, 46, 15076–15088 CrossRef CAS PubMed.
- G. Feller, J. Phys.: Condens.Matter, 2010, 22, 323101 CrossRef PubMed.
- Q. Ji, S. Xiao, B. He and X. Liu, J. Mol. Catal. B: Enzym., 2010, 66, 264–269 CrossRef CAS.
- S. Sharma and S. S. Kanwar, Sci. World J., 2014, 1–15 Search PubMed.
- M. Marin-Argany, J. Güell-Bosch, L. M. Blancas-Mejía, S. Villegas and M. Ramirez-Alvarado, Protein Sci., 2015, 24, 1829–1840 CrossRef CAS PubMed.
- H. H. Guo, J. Choe and L. A. Loeb, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9205–9210 CrossRef CAS PubMed.
- D. M. Taverna and R. A. Goldstein, Proteins: Struct., Funct., Bioinf., 2002, 46, 105–109 CrossRef CAS PubMed.
- S. Hong, M. R. Rohman, J. Jia, Y. Kim, D. Moon, Y. Kim, Y. H. Ko, E. Lee and K. Kim, Angew. Chem., Int. Ed., 2015, 54, 13241–13244 CrossRef CAS PubMed.
- T. Hasell and A. I. Cooper, Nat. Rev. Mater., 2016, 1, 1–14 Search PubMed.
- J. H. Zhang, S. M. Xie, M. Zi and L. M. Yuan, J. Sep. Sci., 2020, 43, 134–149 CrossRef CAS PubMed.
- V. Vaissier Welborn and T. Head-Gordon, J. Phys. Chem. Lett., 2018, 9, 3814–3818 CrossRef CAS PubMed.
- A. Warshel, P. K. Sharma, M. Kato and W. W. Parson, Biochim. Biophys. Acta, Proteins Proteomics, 2006, 1764, 1647–1676 CrossRef CAS PubMed.
- T. Stuyver, R. Ramanan, D. Mallick and S. Shaik, Angew. Chem., 2020, 132, 7989–7994 CrossRef.
- K. D. Dubey, T. Stuyver and S. Shaik, J. Phys. Chem. B, 2022, 126(49), 10285–10294 CrossRef CAS PubMed.
- S. D. Fried and S. G. Boxer, Annu. Rev. Biochem., 2017, 86, 387 CrossRef CAS PubMed.
- D. Bím and A. N. Alexandrova, ACS Catal., 2021, 11, 6534–6546 CrossRef PubMed.
- F. Sebastiani, T. A. Bender, S. Pezzotti, W.-L. Li, G. Schwaab, R. G. Bergman, K. N. Raymond, F. D. Toste, T. Head-Gordon and M. Havenith, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 32954–32961 CrossRef CAS PubMed.
- S. A. Siddiqui and K. D. Dubey, Phys. Chem. Chem. Phys., 2022, 24, 1974–1981 RSC.
- S. Yadav, S. Shaik, S. A. Siddiqui, S. Kalita and K. D. Dubey, J. Chem. Inf. Model., 2022, 62, 1025–1035 CrossRef CAS PubMed.
- N. J. English, in Effects of Electric Fields on Structure and Reactivity, 2021, pp. 263–316 Search PubMed.
- M. T. Blyth and M. L. Coote, Eff. Electr. Fields Struct. React., 2021, pp. 119–146 Search PubMed.
- S. Shaik, D. Danovich, K. D. Dubey and T. Stuyver, in Effects of Electric Fields on Structure and Reactivity, 2021, pp. 12–70 Search PubMed.
- H. Li, T. A. Su, V. Zhang, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, J. Am. Chem. Soc., 2015, 137, 5028–5033 CrossRef CAS PubMed.
- S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1091–1098 CrossRef CAS PubMed.
- Z. Wang, D. Danovich, R. Ramanan and S. Shaik, J. Am. Chem. Soc., 2018, 140, 13350–13359 CrossRef CAS PubMed.
- K. Dutta Dubey, T. Stuyver, S. Kalita and S. Shaik, J. Am. Chem. Soc., 2020, 142, 9955–9965 CrossRef CAS PubMed.
- S. Shaik, D. Danovich, J. Joy, Z. Wang and T. Stuyver, J. Am. Chem. Soc., 2020, 142, 12551–12562 CrossRef CAS PubMed.
- A. C. Aragones, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531, 88–91 CrossRef CAS PubMed.
- S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145 RSC.
- C. Foroutan-Nejad and R. Marek, Phys. Chem. Chem. Phys., 2014, 16, 2508–2514 RSC.
- S. R. Bell and J. T. Groves, J. Am. Chem. Soc., 2009, 131, 9640–9641 CrossRef CAS PubMed.
- P. T. Smith, B. P. Benke, L. An, Y. Kim, K. Kim and C. J. Chang, ChemElectroChem, 2021, 8, 1653–1657 CrossRef CAS.
- Y. Yusran, Q. Fang and S. Qiu, Isr. J. Chem., 2018, 58, 971–984 CrossRef CAS.
- H. Wang, Y. Jin, N. Sun, W. Zhang and J. Jiang, Chem. Soc. Rev., 2021, 50, 8874–8886 RSC.
- E. Kalay and E. Şahin, Chirality, 2021, 33, 447–453 CrossRef CAS PubMed.
- M. P. Mayhew, A. E. Roitberg, Y. Tewari, M. J. Holden, D. J. Vanderah and V. L. Vilker, New J. Chem., 2002, 26, 35–42 RSC.
- Y. Yang and A. L. Boehman, Combust. Flame, 2010, 157, 495–505 CrossRef CAS.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- D. Vassetti, M. Pagliai and P. Procacci, J. Chem. Theory Comput., 2019, 15, 1983–1995 CrossRef CAS PubMed.
- P. Li and K. M. Jr, J. Chem. Inf. Model. , 2016, 56(4), 599–604 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly and P. A. Kollman, J. Am. Chem. Soc., 2002, 115, 9620–9631 CrossRef.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- R. Salomon-Ferrer, A. W. Gotz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed.
- P. Sherwood, A. H. De Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28 CrossRef CAS.
- S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 101–110 CAS.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. Van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1996, 104, 1040–1046 CrossRef CAS.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- G. Ricciardi, E. J. Baerends and A. Rosa, ACS Catal., 2016, 6, 568–579 CrossRef CAS.
- T. Stuyver, J. Huang, D. Mallick, D. Danovich and S. Shaik, J. Comput. Chem., 2020, 41, 74–82 CrossRef CAS PubMed.
- M. D. Polêto and J. A. Lemkul, J. Comput. Chem., 2022, 43, 1113–1119 CrossRef PubMed.
- S. Sowlati-Hashjin, M. Karttunen and C. F. Matta, in Effects of Electric Fields on Structure and Reactivity, 2021, pp. 225–262 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, See also URL http://http//www.gaussian.com.
- C. Jarzynski, Phys. Rev. Lett., 1997, 78, 2690 CrossRef CAS.
- S. Shaik, S. Cohen, Y. Wang, H. Chen, D. Kumar and W. Thiel, Chem. Rev., 2010, 110, 949–1017 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The supplementary information provided contains the results of the replica simulations, effect of OEEF, supplementary texts, modification details, Mulliken spin and charges, QM/MM optimized structures, reactions profiles, QM/MM energy values and QM region coordinates (XYZ) of the molecular geometries from the QM/MM calculations. XYZ coordinated are also supplied in ZIP format. See DOI: https://doi.org/10.1039/d3sc01720f |
| ‡ A choice which is statistically more relevant relative to stochastically chosen snapshots. |
| This journal is © The Royal Society of Chemistry 2023 |