Open Access Article
Open Access ArticleGaining control on optical force by the stimulated-emission resonance effect†
Tetsuhiro
Kudo
*a,
Boris
Louis
bc,
Hikaru
Sotome
 d,
Jui-Kai
Chen
b,
Syoji
Ito
d,
Jui-Kai
Chen
b,
Syoji
Ito
 *de,
Hiroshi
Miyasaka
*de,
Hiroshi
Miyasaka
 d,
Hiroshi
Masuhara
d,
Hiroshi
Masuhara
 *fg,
Johan
Hofkens
*fg,
Johan
Hofkens
 *bh and
Roger
Bresolí-Obach
*bh and
Roger
Bresolí-Obach
 *bi
*bi
aLaser Science Laboratory, Toyota Technological Institute, Hisakata, Tempaku-ku, Nagoya 468-8511, Japan. E-mail: kudo@toyota-ti.ac.jp
bLaboratory for Photochemistry and Spectroscopy, Division for Molecular Imaging and Photonics, Department of Chemistry, Katholieke Universiteit Leuven, Belgium. E-mail: johan.hofkens@kuleuven.be
cDivision of Chemical Physics and NanoLund, Lund University, P.O. Box 124, Lund, Sweden
dDivision of Frontier Materials Science and Center for Promotion of Advanced Interdisciplinary Research, Osaka University, Toyonaka, Osaka 560-8531, Japan. E-mail: sito@chem.es.osaka-u.ac.jp
eResearch Institute for Light-induced Acceleration System (RILACS), Osaka Metropolitan University, 1-2, Gakuen-cho, Naka-ku, Sakai, Osaka 599-8570, Japan
fDepartment of Applied Chemistry, College of Science, National Yang Ming Chiao Tung University, Hsinchu, Taiwan. E-mail: masuhara@masuhara.jp
gCenter for Emergent Functional Matter Science, National Yang Ming Chiao Tung University, Hsinchu, Taiwan
hMax Planck Institute for Polymer Research, Mainz 55128, Germany
iAppLightChem, Institut Químic de Sarrià, Universitat Ramon Llull, Barcelona, Catalunya, Spain. E-mail: roger.bresoli@iqs.edu
First published on 22nd August 2023
Abstract
The resonance between an electronic transition of a micro/nanoscale object and an incident photon flux can modify the radiation force exerted on that object, especially at an interface. It has been theoretically proposed that a non-linear stimulated emission process can also induce an optical force, however its direction will be opposite to conventional photon scattering/absorption processes. In this work, we experimentally and theoretically demonstrate that a stimulated emission process can induce a repulsive pulling optical force on a single trapped dye-doped particle. Moreover, we successfully integrate both attractive pushing (excited state absorption) and repulsive pulling (stimulated emission) resonance forces to control the overall exerted optical force on an object, validating the proposed non-linear optical resonance theory. Indeed, the results presented here will enable the optical manipulation of the exerted optical force with exquisite control and ultimately enable single particle manipulation.
Introduction
Since the pioneering work of Ashkin and co-workers about exerting optical forces onto a single particle by a tightly focused laser beam,1 optical trapping/tweezers have been extensively expanded and applied to various research fields to manipulate micro- and nanoscale objects.2–6 Optical trapping is based on the fact that photon momentum can be transferred to objects, resulting in a so-called radiation force. The three most common optical forces are the gradient, scattering and absorption forces.1 In a solution, a particle can only be stably trapped when the gradient force is larger than the sum of scattering and absorption force.7 For this reason, efforts have been executed to modify the overall balance of those optical forces such as modifying the optical properties of the trapped material or the optical potential fields.8–10Among them, the optical resonance effect (ORE) is a promising strategy that takes advantage of an electronic transition of the material to drastically modify the induced optical force on the trapped particle(s).11 Under this condition, the trapping laser is resonant with the said electronic transition, modifying the polarizability of the system. The ORE theory was initially developed considering only the optical linear region.12 Thus, the optical force should linearly increase with the resonant laser power. Experimental studies showed that the Brownian motion of dye molecules, dye-labeled antibodies, and dye-doped polystyrene particles was altered upon resonant excitation.13–17 However, the observed motion cannot be quantitatively rationalized by only considering linear ORE theory. Therefore, the ORE theory needed to be further refined by considering non-linear optical processes such as excited state absorption.18–20 Indeed, the proposed non-linear ORE theory was demonstrated by subsequent resonant optical trapping experiments.21
Given the opportunities provided by the non-linear ORE theory, we have recently reported that the resonance force is strongly enhanced at a solution interface using a two-laser excitation system. For example, we observed a 4-fold (400%) trapping stiffness enhancement compared to a 10–35% reported in other works in bulk solution.22 This large difference has two main origins: on one hand, the optical force balance is different at the interface as it acts as a physical barrier for upwardly moving particles and therefore all the optical forces positively contribute to the trapping of the particle.23–26 On the other hand, we used a two-laser system: a widefield laser for exciting the dye to the first singlet excited state (S0 → S1), while the trapping laser was resonant with an upper excited state transition (S1 → Sn).15,27 Under this condition, the number of optical resonant cycles (S1–Sn–S1) is widely increased compared with the single laser system (S0–S1–S0) due to the shorter Sn lifetime compared to S1. The non-linearly increased ORE not only includes the commonly considered polarizability enhancement, but also the absorption and gradient forces, which guides the particle toward the interface. The latter force also immobilizes the particle leading to an increase in optical stiffness.22 We have further refined this strategy to achieve chemical control over the optical trapping force by taking advantage that triplet excited states can be quenched by some specific molecules (e.g., O2) and therefore the ORE force can be tuned by the concentration of the chemical quencher.28
Inspired by the potential of non-linear electronic absorption processes on ORE, we speculate that stimulated emission (SE) can also be used to control the induced optical force, but with an opposite effect as the phase of the induced polarization is flipped (π-shifted) by a population inversion. SE is a non-linear transition, where S1 relaxation to S0 occurs via emission of a photon triggered by S1 interaction with an incident resonant photon.29–31 For instance, SE has gained relevance as SE promoted by a very intense donut shape depletion laser (STED) is one of the main strategies used in super-resolution microscopy to break the diffraction limit.32–34 In this work, we use a two-laser system to control the exerted radiation force on a single dye-doped polystyrene microparticle (PS MP) trapped at the glass/solution interface. Similar to previous works,22,28 a widefield laser (561 nm) is used to excite the dye embedded inside the particle (S0 → S1), while a tightly focused depletion laser (640 nm) is used to trap and simultaneously promote the SE (S1 → S0) non-linear process. As the SE photon has the same direction as the depletion laser,29,30 the MP receives the optical force in the opposite manner from the conventional situation, yielding a repulsive gradient force and an optical pulling force due to the recoil of stimulated emission, respectively, instead of conventional attractive gradient force and absorption/scattering forces along the light propagation. In overall, a pulling (repulsive) instead of a pushing (attractive) ORE force is exerted on the MP. We support the proposed ORE model with comprehensive experimental evidence from both spectroscopic and MP's trapping stiffness viewpoints as well as with theoretical calculations of radiation force that is exerted during the SE phenomenon. Finally, as a proof of concept that multiple ORE forces can be exerted on the same object, we introduced a three laser system: (i) a 561 nm widefield laser to excite the dye molecules from S0 to S1; (ii) a tightly 1064 nm focused laser to trap the particle and to simultaneously induce Sn–S1–Sn ORE cycles (pushing ORE); and (iii) a 640 nm widefield laser with SE purposes (depopulation of S1 and pulling ORE). Under this condition, the overall optical force is modulated as a function of the extension of the pushing and pulling ORE, respectively. The demonstration of the conceptually expanded ORE is expected to ultimately enable single resonant particle/molecule manipulation in solution at room temperature.
Results and discussion
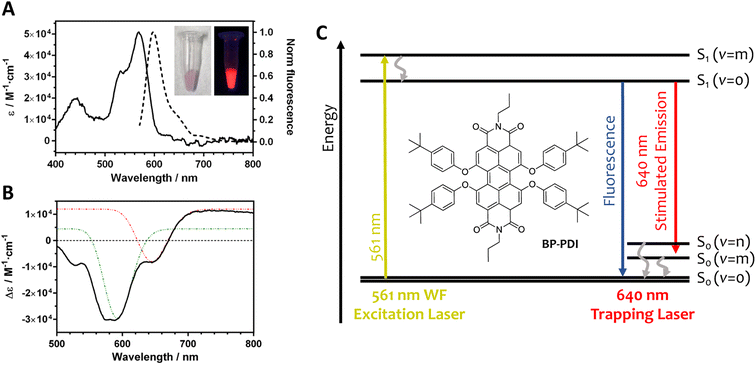
In this work, we have chosen a tetra t-phenoxy perylenediimide derivative (BP-PDI; Fig. 1) as the resonant dye for the following reasons: (i) PDI derivatives are good dyes for STED microscopy; (ii) PDIs are photostables in non-aqueous environment; (iii) PDIs have a large fluorescence quantum yield; and (iv) PDIs have a small S1 to Sn absorption cross section at the SE wavelength range.35 Moreover, the additional four t-phenoxy moieties hamper the aggregation of the dye molecules by steric hindrance. The BP-PDI dopped PS MPs were obtained via diffusion and entrapment of the BP-PDI dye molecules through solvent-induced swelling of 1 μm PS MPs.36 As the dyeing process was not very efficient (Table S1†), we repeated the dyeing protocol for 5 cycles, achieving a final BP-PDI dye loading of approximately 1.3 millions of dye molecules for each PS MP, estimated by absorption spectroscopy. Fluorescence imaging of the MPs reveals that the BP-PDI dye molecules are distributed inside the MPs without the formation of local cluster aggregates (Fig. S1†). The morphology and the size of the obtained BP-PDI MPs was studied by scanning electron microscopy (SEM), revealing that their size (890 ± 20 nm) and morphology (spherical) did not significantly change during the swelling procedure (Fig. S2†). Moreover, the volume of each BP-PDI molecule is estimated as 1.3 nm3 (calculated at AM1 level of theory;37 Fig. S3†), which corresponds to only 0.33% of the MP volume considering all the dye molecules. Thus, the combination of a low BP-PDI dye density and the presence of bulky t-phenoxy moieties should effectively prevent the formation of BP-PDI aggregates within the MPs.In toluene, BP-PDI molecules absorb photons up to 600 nm, with an absorption maximum at 567 nm (ε = 5 × 104 M−1 cm−1; Fig. 1A). In its monomeric form, BP-PDI is a highly emissive dye with its fluorescence band centered at 600 nm. Of note, we have studied the BP-PDI photophysical properties in toluene, because the polarity and the aromaticity properties of toluene mimic the PS microenvironment. The SE process of BP-PDI has been studied by femtosecond transient spectroscopy (Fig. 1B). The transient absorption spectrum of BP-PDI is characterized by negative and positive bands in the shorter and longer wavelength region than 670 nm, respectively. The negative band is due to the superposition between the depletion of the S0 state (<580 nm) and the SE from the S1 state (580–670 nm), while the positive band is ascribable to the absorption of the S1 state. Fig. 1C shows a Jablonski diagram with all the BP-PDI electronic transitions, which can play a role in the non-linear ORE phenomena.
The optical setup used here is in principle similar to that of our previous work (Fig. S4†).22,38,39 However, considering the spectroscopic properties of BP-PDI, we have chosen a 640 nm laser as the optical trapping source and simultaneously inducing SE when the BP-PDI S1 state is populated. An additional 561 nm widefield laser was used to photoexcite the BP-PDI molecules to S1. At low MP concentration, a single BP-PDI dye-dopped MP is trapped at the interface upon switching on the 640 nm trapping laser. The motion of this MP is confined (see representative examples of the motion of the trapped MP at selected experimental conditions in Fig. S5†). Under this condition, the optical force exerted on the trapped MP can be represented in terms of optical trapping stiffness, which is the restoring force constant of the system calculated by fitting Hooke's restoring force law to the spatial distribution of a single trapped MP (see a detailed description of the methodology for determine the optical trapping stiffness in ESI; Fig. S6†).
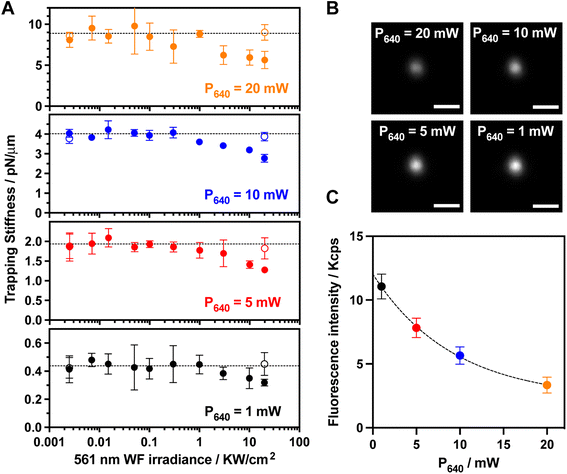
As expected in absence of photoexcitation, the trapping stiffness of a single trapped BP-PDI MP linearly increases with the trapping laser power (Fig. 2A and S7†). We observed that the trapping stiffness does not significantly change when the 561 nm widefield excitation laser irradiation is up to 1000 W cm−2, while a significant decrease of the trapping stiffness is observed at larger irradiance values. As a first control experiment, we photobleached the BP-PDI molecules embedded inside the trapped MP, and the initial trapping stiffness was recovered (open symbols in Fig. 2A). A second control on bare PS MP did also not show the trapping stiffness decrease when trapped in the aforementioned conditions (Fig. S8†). One may speculate, that the decrease of the trapping stiffness is simply due to a local temperature elevation, leading to an enhanced Brownian motion. However, we ruled out this hypothesis because we theoretically calculated an upper limit for the temperature elevation range from 0.5 to 5 °C for the different tested conditions (see ESI and Fig. S9† for further details).40 Therefore, the observed trapping stiffness decrease can be directly related to the ORE. Although the relative value of the trapping stiffness decrease is similar for all the tested trapping laser powers, the absolute decrease changes with the trapping laser power.
To verify the origin of the non-linear optical process, we recorded the fluorescence images (λobs = 580–620 nm) of the trapped BP-PDI MP using the highest 561 nm excitation irradiance power (20 kW cm−2) for each trapping laser power (Fig. 2B). The fluorescence intensity from 580 to 620 nm (far away from 640 nm SE laser wavelength) decreases with a non-linear exponential trend upon increasing the 640 nm trapping (depleting) laser power (Fig. 2C) as previously reported for a SE process.41 In view of both experimental results (trapping stiffness and fluorescence dependence on the 561 nm WF irradiance), we hypothesize that the observed trapping stiffness decrease is induced by an ORE pulling force that arises from the non-linear SE process.
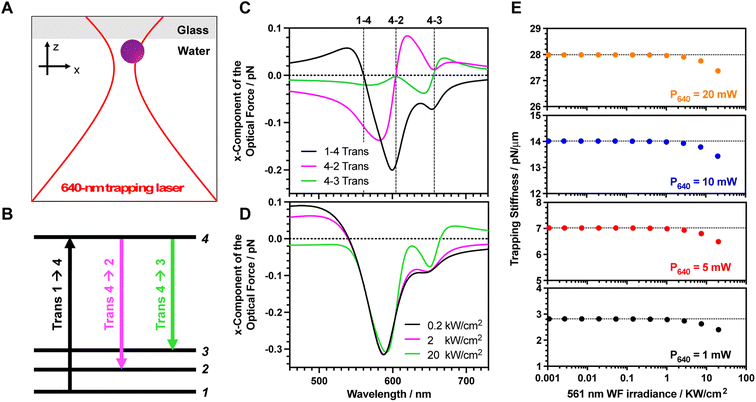
To confirm the proposed hypothesis, we calculate the optical force exerted on the dye molecules under the intense focused laser beam. A four-level energy scheme, including vibrational states, is assumed as the theoretical model (Fig. 3A).19 The parameters have been mostly chosen based on the spectroscopic measurements. The electronic transition energies between the different states are calculated by fitting both ground and excited state spectra with Gaussian functions (2.21, 2.05 and 1.89 eV for the 1 → 4, 2 → 4, and 3 → 4 electronic transitions, respectively). As the fluorescence spectrum is a mirror image of the absorption spectrum (Fig. 1A), we assign the fluorescence peak at 604 nm (2.05 eV) and the shoulder at 656 nm (1.89 eV) to the vibrational progression (S1(v = 0) to S0(v = 0) and S1(v = 0) to S0(v = 1), respectively). Indeed, the normal mode calculation revealed that these vibrational energy levels originate from C–C stretching modes of the BP-PDI backbone around 1300 cm−1 (Fig. S10†). The transition dipole moments for each transition are estimated by integrating the molar extinction coefficients along wavelengths (5.70, 5.44 and 3.38 Debye for the 1 → 4, 2 → 4, and 3 → 4 electronic transitions, respectively; Table S2†). The dephasing constant was set at 20 meV (around 33 fs) which is a realistic parameter42 for a dye entrapped inside a polymeric matrix. Note that its order of magnitude is similar to the room temperature energy (kBT). The S1 lifetime is 6.4 ns obtained by time-resolved fluorescence (Fig. S11†). The vibrational relaxation times of organic molecules from 3 → 2 and 2 → 1 states are in the few picosecond range.43 Thus, both lifetimes are assumed as 1.5 ps. In a previous work,22 we demonstrated that the amount of ORE cycles is mainly determined by the S1 lifetime. To confirm this claim, we calculated the optical force spectra for 3 different vibrational relaxation lifetimes (0.15, 1.5 and 15 ps; Fig. S12†) and no significant differences are observed. Finally, the number of entrapped dyes molecules per PS MP is 1.3 × 106 as we have estimated above.
Considering the above-mentioned parameters, we calculated the optical force as a function of the trapping laser wavelength (Fig. 3B). The optical force calculation was performed when the dye molecule is located nearby the laser focus (x,z = 120,0 nm), where the gradient force becomes larger as detailed in Fig. S13.† Under this condition, the exerted optical force can be decomposed into three independent contributions, which are attributed to those transitions involving the absorption (1 → 4 transition) and emission (4 → 2 and 4 → 3 transitions) of a photon. The overall ORE force exerted on the dyes is determined by a linear combination of these three transitions and the force sign depends on which transition becomes dominant.
Of note, an attractive gradient force towards the focus will push the MP towards the interface, while a repulsive gradient force will induce a pulling effect outward the laser focus. Indeed, these attractive (pushing) and repulsive (pulling) forces increase (positive ORE) and decrease (negative ORE) the trapping stiffness. Additionally, these forces contribute to increase/decrease the friction with the solution/glass interface, respectively, which also indirectly affects the trapping stiffness. Then, the overall optical stiffness is determined by adding these pushing and pulling forces to the enhanced polarization of the MP due to population of the S1. Next, we will describe the optical force arising from each transition to further understand their role:
1 → 4 transition (black line Fig. 3B): an attractive pushing force toward the focus is transferred to the dye when the trapping laser wavelength is red-detuned with respect to the ground state absorption peak (around 560 nm). The phase of the trapping laser and the induced polarization become the same at the red-detuned region, as is widely described in the laser cooling field.44–46 Instead, a blue-detuned laser (with respect to the ground absorption peak) results in a repulsive pulling force since the phase is opposite (see a detailed description at the ESI†).
4 → 2 transition (magenta line Fig. 3B): the phase relation between the laser and the polarization is inverted when the transition starts from an upper excited state to a lower energy state as occurs in the non-linear SE transition. For instance, the blue-detuned laser for 4 → 2 transition results in an attractive pushing force. At the blue-detuned region, the phase of the laser and induced polarization are in phase, thereby the gradient force becomes attractive.
4 → 3 transition (green line Fig. 3B): similarly, the blue-detuned laser for the 4 → 3 transition also results in the attractive pushing force as shown in around 450–660 nm wavelength region. However, the amplitude of the force is smaller compared to that of the 4 → 2 transition because the transition dipole moment of the 4 → 3 transition is smaller than that of the 4 → 2 transition.
The individual contribution of each transition depends on the excitation laser irradiance as the population of S1 affects both 4 → 2 and 4 → 3 SE transitions in a non-linear fashion. Fig. 3C shows the overall ORE optical force spectrum for different 561 nm excitation laser irradiances. Depending on the trapping laser wavelength, the force amplitude and sign are drastically modulated. If we focus on what occurs using a 640 nm trapping laser, we observed that the optical force exerted on the dye becomes weaker upon increasing the 561 nm excitation laser irradiance (Fig. 3C). Under this condition, the repulsive pulling force of the 4 → 2 transition due to the red-detuned laser becomes dominant over the other two transitions. If we extrapolate the exerted optical force on a single BP-PDI molecule to the overall dye-doped MP, we observe a decrease in the trapping stiffness upon increasing the 561 nm excitation laser irradiance (Fig. 3D). Indeed, the calculated decrease in the trapping stiffness has a similar trend to the obtained experimental results (Fig. 2A). Thus, the theoretical calculation reveals that the observed repulsive pulling ORE effect is due to the 4 → 2 SE transition. In detail, the 640 nm trapping laser (which is a red-detuned laser for 4 → 2 transition) provides the repulsive gradient force during the SE processes. Besides, the MP receives the pulling force from the 640 nm laser, which is opposite to the direction of the light propagation as shown in Fig. S13B.† This pulling force is originated from a recoil of stimulated emission, which contribute to decrease the friction between particle and glass coverslip, which indirectly also decreases the trapping stiffness.
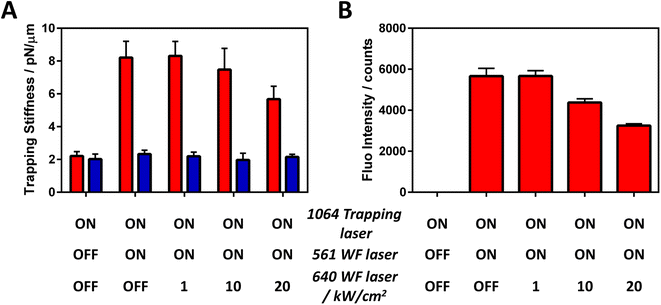
Once the individual contribution of SE has been understood, we integrate it on the recently developed non-linear ORE theory (Fig. S14†). On one hand, the positive pushing ORE was previously observed by excited state absorption (S1–Sn–S1 cycle) with another dye-doped particle using a similar two-laser system: a 488 nm WF laser (resonant with S0 → S1 transition) and a 1064 nm trapping laser (resonant with S1 → Sn transition).22 On the other hand, the negative pulling ORE has been reported above. The combination of both non-linear transitions could potentially expand the trapping stiffness range of a trapped object. To test this idea, we designed a new experiment using a three-laser system: a 561 nm WF laser (resonant with S0 → S1 transition), a 640 nm WF laser (resonant with S1 SE) and a 1064 nm trapping laser (resonant with S1 → Sn transition).
As expected, the trapping stiffness increases when the 561 nm widefield excitation laser is switched on as this enables the upper excited state (S1–Sn–S1) resonance cycle (Fig. 4A). To our delight, we observed a trapping stiffness decrease when the third 640 nm WF laser was simultaneously switched on with high irradiance. Of note, if the same irradiance is used for both 561 and 640 nm WF lasers, no significant trapping stiffness reduction is observed as the SE cross-section is typically smaller than the S1 excited state absorption cross section,47 limiting the SE-based negative ORE to only high photon pressure. Moreover, the trapping stiffness decrease is related to the BP-PDI fluorescence decrease (Fig. 4B), confirming that the observed trapping stiffness decrease is due to a SE process. As a control, we photobleached the BP-PDI molecules and no enhancement nor decrease of the trapping stiffness is observed (blue bars Fig. 4A). Based on our understanding, the decrease in the trapping stiffness is ascribed to two different factors, both directly related with SE. The first one is due to SE-induced S1 depopulation. A smaller photostationary S1 concentration as well as a faster S1 decay reduces the amount of S1–Sn–S1 resonant cycles, yielding a smaller positive pushing ORE force. The second is caused by an indirect effect; the reduction of the friction with the interface by the negative pulling ORE force, leading to a decrease in the optical trapping stiffness.
Thus far, including our previous work on the excited state cyclic transition,22 we have shown that the optical force is meticulously controlled, reflecting the transient molecular excited states. Thus, we have only demonstrated this effect using continuous wave (CW) lasers. However, we believe that the optical force can be further finely and temporarily controlled by coherent manipulation of the molecular states with a pump-probe ultrashort pulsed laser technique.21 Recently, Oyamada et al. have reported the optical trapping of single small molecules at the gap of a single metal nanodimer by plasmonic effect at room temperature,48 we propose that the conceptually-expanded ORE described at the interface paves the way to ultimately enable single resonant particle/molecule selective trapping and manipulation in solution at room temperature using optical forces. This ORE-based methodology could have the potential to become an alternative to other (non-light involved) trapping techniques such as Anti-Brownian ELectrokinetic (ABEL) or dielectrophoretic traps.49,50 Even more, the role of ORE forces has been recently expanded from a single particle system to the ensemble particle level,51 where the ORE force triggers the gathering and assembling of dye-doped particles at an interface as well as modifying the assembly morphology.
Conclusion
Like other non-linear optical processes, stimulated emitted photons can exert a resonant optical force on an object. However, the sign of this force is opposite to the conventional optical resonance effect initiated from the ground state of electronic transition of dye molecules. This leads to a decrease (instead of an increase) in the trapping stiffness, when the object is trapped at an interface. This finding is experimentally described for the first time, and it is fully supported by non-linear resonant radiation force theory. Moreover, the combination of attractive/pushing (excited state transition) and repulsive/pulling (stimulated emission transition) optical resonance forces offers a unique possibility to achieve an unprecedented control of the overall optical force balance in a wide range of research fields from optics over biochemistry, to analytical chemistry, physical chemistry, and soft matter, among others.Data availability
Details on materials and methods, the estimation of the temperature elevation of a single BP-PDI doped polystyrene microparticle trapped by a tightly focused 640 nm laser beam, description of red- and blue-detuned laser on optical trapping, SEM images, 3D optimized chemical structure of BP-PDI, optical scheme of the microscope used, trapping stiffness analysis, spectroscopic and optical force simulation details are included in the ESI.† Other data are available from the corresponding author upon reasonable request.Author contributions
R. B.-O. and T. K. designed the study, performed the experiments, and analyzed the data. S. I., H. M., J. H. contributed to the design of the study and data analysis. B. L. contributed to the development of data analysis methodology. H. S. and H. M. performed the transient absorption spectroscopy experiments. J.-K. C. performed the SEM experiments. T. K., R. B.-O. and H. M. wrote the first version of the manuscript. T. K., S. I., H. M., J. H. and R. B.-O. supervised the project. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science and Technology (NSTC) of Taiwan (NSTC 110-2113-M-A49-016-), by the Flemish Government through long-term structural funding Methusalem (CASAS2, Meth/15/04), by the Fonds voor Wetenschappelijk Onderzoek-Vlaanderen (FWO, W002221N), by a bilateral agreement between FWO and MOST (VS00721N), by the internal funds of KU Leuven (C14/22/085), by JSPS KAKENHI (JP21KK0092, JP21H01889, JP22K19007, JP21H04964, JP 21K14555, JP21K18943, and JP21H04640) and by JST-Mirai (Number JPMJMI21G1). J. H gratefully acknowledges support from the MPI as MPI fellow. T. K. thanks Inoue Foundation for Science (Inoue Science Research Award), and Toyota Physical and Chemical Research Institute (Toyota Riken Scholar). R. B. O. and B. L. thank the FWO for a postdoctoral grant (12Z8120N) and a PhD grant (11B1121N), respectively. R. B.-O. also thanks the Agencia Estatal de Investigación of Spain for a Ramon y Cajal contract (RYC2021-032773-I). H. M. also acknowledges the Center for Emergent Functional Matters Science of NYCU from the Featured Area Research Center Program within the framework of the Higher Education Project by the Ministry of Education (MOE) in Taiwan.References
- A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm and S. Chu, Observation of a single-beam gradient force optical trap for dielectric particles, Opt. Lett., 1986, 11, 288–290 CrossRef CAS PubMed.
- A. Ashkin and J. M. Dziedzic, Optical trapping and manipulation of viruses and bacteria, Science, 1987, 235, 1517–1520 CrossRef CAS PubMed.
- A. H. J. Yang, et al., Optical manipulation of nanoparticles and biomolecules in sub-wavelength slot waveguides, Nature, 2009, 457, 71–75 CrossRef CAS PubMed.
- M. R. Pollard, et al., Optically trapped probes with nanometer scale tips for femto-Newton force measurement, New J. Phys., 2010, 12, 113056 CrossRef.
- G. Brügger, L. S. Froufe-Pérez, F. Scheffold and J. J. Sáenz, Controlling dispersion forces between small particles with artificially created random light fields, Nat. Commun., 2015, 6, 7460 CrossRef.
- K. A. Forbes, D. S. Bradshaw and D. L. Andrews, Optical binding of nanoparticles, Nanophotonics, 2019, 9, 1–17 CrossRef.
- H. B. Xin, Y. C. Li, Y.-C. Liu, Y. Zhang, Y.-F. Xiao and B. J. Li, Optical Forces: From Fundamental to Biological Applications, Adv. Mater., 2020, 32, 2001994 CrossRef CAS PubMed.
- M. L. Juan, M. Righini and R. Quidant, Plasmon nano-optical tweezers, Nat. Photonics, 2011, 5, 349–356 CrossRef CAS.
- Y. Jiang, T. Narushima and H. Okamoto, Nonlinear optical effects in trapping nanoparticles with femtosecond pulses, Nat. Phys., 2010, 6, 1005–1009 Search PubMed.
- T. Sugiyama, K. Yuyama and H. Masuhara, Laser trapping chemistry: from polymer assembly to amino acid crystallization, Acc. Chem. Res., 2012, 45, 1946–1954 CrossRef CAS PubMed.
- J. P. Gordon and A. Ashkin, Motion of atoms in a radiation trap, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 21, 1606 CrossRef CAS.
- T. Iida and H. Ishihara, Theoretical study of the optical manipulation of semiconductor nanoparticles under an excitonic resonance condition, Phys. Rev. Lett., 2003, 90, 057403 CrossRef PubMed.
- M. A. Osborne, S. Balasubramanian, W. S. Furey and D. Klenerman, Optically biased diffusion of single molecules studied by confocal fluorescence microscopy, J. Phys. Chem. B, 1998, 102, 3160–3167 CrossRef CAS.
- H. Li, D. Zhou, H. Browne and D. Klenerman, Evidence for resonance optical trapping of individual fluorophore-labeled antibodies using single molecule fluorescence spectroscopy, J. Am. Chem. Soc., 2006, 128, 5711–5717 CrossRef CAS PubMed.
- C. Hosokawa, H. Yoshikawa and H. Masuhara, Enhancement of biased diffusion of dye-doped nanoparticles by simultaneous irradiation with resonance and non-resonance laser beams, Jpn. J. Appl. Phys., 2006, 45, L453–L456 CrossRef CAS.
- M. L. Juan, et al., Cooperatively enhanced dipole forces from artificial atoms in trapped nanodiamonds, Nat. Phys., 2017, 13, 241–245 Search PubMed.
- H. Fujiwara, K. Yamauchi, T. Wada, H. Ishihara and K. Sasaki, Optical selection and sorting of nanoparticles according to quantum mechanical properties, Sci. Adv., 2021, 7, eabd9551 Search PubMed.
- T. Kudo and H. Ishihara, Proposed nonlinear resonance laser technique for manipulating nanoparticles, Phys. Rev. Lett., 2012, 109, 087402 CrossRef PubMed.
- T. Kudo and H. Ishihara, Resonance optical manipulation of nanoobjects based on nonlinear optical response, Phys. Chem. Chem. Phys., 2013, 15, 14595–14610 RSC.
- H. Ishihara, Optical manipulation of nanoscale materials by linear and nonlinear resonant optical responses, Adv. Phys.: X, 2021, 6, 1 Search PubMed.
- T. Kudo, H. Ishihara and H. Masuhara, Resonance optical trapping of individual dye-doped polystyrene particles with blue- and red-detuned lasers, Opt. Express, 2017, 25, 4655–4664 CrossRef CAS PubMed.
- R. Bresolí-Obach, T. Kudo, B. Louis, Y.-C. Chang, I. G. Scheblykin, H. Masuhara and J. Hofkens, Resonantly enhanced optical trapping of single dye-doped particles at an interface, ACS Photonics, 2021, 8, 1832–1839 CrossRef.
- T. Kudo, S.-J. Yang and H. Masuhara, A single large assembly with dynamically fluctuating swarms of gold nanoparticles formed by trapping laser, Nano Lett., 2018, 18, 5846–5853 CrossRef CAS.
- C.-H. Huang, et al., Surface plasmon resonance effect on laser trapping and swarming of gold nanoparticles at an interface, Opt. Express, 2020, 28, 27727–27735 CrossRef CAS PubMed.
- A. Caciagli, R. Singh, D. Joshi, R. Adhikari and E. Eiser, Controlled optofluidic crystallization of colloids tethered at interfaces, Phys. Rev. Lett., 2020, 125, 068001 CrossRef CAS PubMed.
- H. Masuhara and K. Yuyama, Optical Force-Induced Chemistry at Solution Surfaces, Annu. Rev. Phys. Chem., 2021, 72, 25 CrossRef PubMed.
- H. Fukumura and H. Masuhara, The mechanism of dopant induced laser ablation. Possibility of cyclic multiphotonic absorption in excited states, Chem. Phys. Lett., 1994, 221, 373–378 CrossRef CAS.
- R. Bresolí-Obach, S. Nonell, H. Masuhara and J. Hofkens, Chemical Control Over Optical Trapping Force at an Interface, Adv. Opt. Mater., 2022, 10, 2200940 CrossRef.
- H. Kogelnik and C. V. Shank, Stimulated emission in a periodic structure, Appl. Phys. Lett., 1971, 18, 152 CrossRef CAS.
- B. Fain and P. W. Milonni, Classical stimulated emission, J. Opt. Soc. Am. B, 1987, 4, 78–85 CrossRef CAS.
- Y. Z. Xu, R. H. Xu, Z. Wang, Y. Zhou, Q. F. Shen, W. C. Ji, D. F. Dang, L. J. Meng and B. Z. Tang, Recent advances in luminescent materials for super-resolution imaging via stimulated emission depletion nanoscopy, Chem. Soc. Rev., 2021, 50, 667–690 RSC.
- S. W. Hell and J. Wichmann, Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy, Opt. Lett., 1994, 19, 780–782 CrossRef CAS PubMed.
- H. Blom and J. Widengren, Stimulated Emission Depletion Microscopy, Chem. Rev., 2017, 117, 7377–7427 CrossRef CAS PubMed.
- G. Vicidomini, P. Bianchini and A. Diaspro, STED super-resolved microscopy, Nat. Methods, 2018, 15, 173–182 CrossRef CAS PubMed.
- J. Hotta, E. Fron, P. Dedecker, K. P. F. Janssen, C. Li, K. Müllen, B. Harke, J. Bückers, S. W. Hell and J. Hofkens, Spectroscopic rationale for efficient stimulated-emission depletion microscopy fluorophores, J. Am. Chem. Soc., 2010, 132, 5021–5023 CrossRef CAS PubMed.
- T. Behnke, C. Würth, K. Hoffmann, M. Hübner, U. Panne and U. Resch-Genger, Encapsulation of hydrophobic dyes in polystyrene micro- and nanoparticles via swelling procedures, J. Fluoresc., 2011, 21, 937–944 CrossRef CAS PubMed.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, Development and use of quantum mechanical molecular models. 76. AM1: a new general purpose quantum mechanical molecular model, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- B. Louis, et al., Fast-tracking of single emitters in large volumes with nanometer precision, Opt. Express, 2020, 28, 28656–28671 CrossRef PubMed.
- B. Louis, et al., Unravelling 3D dynamics and hydrodynamics during incorporation of dielectric particles to an optical trapping site, ACS Nano, 2023, 17, 3797–3808 CrossRef CAS PubMed.
- D. Lu, F. Gámez and P. Haro-González, Temperature Effects on Optical Trapping Stability, Micromachines, 2021, 12, 954 CrossRef PubMed.
- S. W. Hell, K. I. Willig, M. Dyba, S. Jakobs, L. Kastrup, and W. Westphal, Nanoscale resolution with focused light: STED and other RESOLFT microscopy concepts, in Handbook of Biological Confocal Microscopy, 2006, ch. 31, pp. 571–579 Search PubMed.
- E. M. H. P. Van Dijk, J. Hernando, J. J. García-López, M. Crego-Calama, D. N. Reinhoudt, L. Kuipers, M. F. García-Parajo and N. F. van Hulst, Single-molecule pump-probe detection resolves ultrafast pathways in individual and coupled quantum systems, Phys. Rev. Lett., 2005, 94, 0780302 CrossRef PubMed.
- M. E. Paige and C. B. Harris, Ultrafast studies of chemical reactions in liquids: Validity of gas phase vibrational relaxation models and density dependence of bound electronic state lifetimes, Chem. Phys., 1990, 149, 37–62 CrossRef CAS.
- C. S. Adams and E. Riis, Laser cooling and trapping of neutral atoms, Prog. Quantum Electron., 1997, 21, 1–79 CrossRef CAS.
- C. Cohen-Tannoudji, J. Dupont-Roc and G. Grynberg, Atom-Photon Interactions, John Wiley & Sons, 1998, p. 377 Search PubMed.
- T. Kudo and H. Ishihara, Theory of radiation force exerted on dye-doped molecules irradiated by resonant laser, Phys. Status Solidi C, 2011, 8, 66–69 CrossRef CAS.
- M. Bouzin, G. Chirico, L. D'Alfonso, L. Sironi, G. Soavi, G. Cerullo, B. Campanini and M. Collini, Stimulated emission properties of fluorophores by CW-STED single molecule spectroscopy, J. Phys. Chem. B, 2013, 117, 16405–16415 CrossRef CAS PubMed.
- N. Oyamada, H. Minamimoto and K. Murakoshi, Room-temperature molecular manipulation via plasmonic trapping at electrified interfaces, J. Am. Chem. Soc., 2022, 144, 2755–2764 CrossRef CAS PubMed.
- A. E. Cohen and W. E. Moerner, Method for trapping and manipulating nanoscale objects in solution, Appl. Phys. Lett., 2005, 86, 093109 CrossRef.
- A. E. Cohen and W. E. Moerner, Suppressing Brownian motion of individual biomolecules in solution, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 4362 CrossRef CAS PubMed.
- Y.-C. Chang, R. Bresolí-Obach, T. Kudo, J. Hofkens, S. Toyouchi and H. Masuhara, The optical absorption force allows controlling colloidal assembly morphology at an interface, Adv. Opt. Mater., 2022, 10, 2200231 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc01927f |
| This journal is © The Royal Society of Chemistry 2023 |