Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Δ2 machine learning for reaction property prediction†
Qiyuan
Zhao
 a,
Dylan M.
Anstine
a,
Dylan M.
Anstine
 b,
Olexandr
Isayev
b,
Olexandr
Isayev
 *b and
Brett M.
Savoie
*b and
Brett M.
Savoie
 *a
*a
aDavidson School of Chemical Engineering, Purdue University, West Lafayette, IN 47906, USA. E-mail: bsavoie@purdue.edu
bDepartment of Chemistry, Carnegie Mellon University, Pittsburgh, PA 15213, USA. E-mail: olexandr@olexandrisayev.com
First published on 19th July 2023
Abstract
The emergence of Δ-learning models, whereby machine learning (ML) is used to predict a correction to a low-level energy calculation, provides a versatile route to accelerate high-level energy evaluations at a given geometry. However, Δ-learning models are inapplicable to reaction properties like heats of reaction and activation energies that require both a high-level geometry and energy evaluation. Here, a Δ2-learning model is introduced that can predict high-level activation energies based on low-level critical-point geometries. The Δ2 model uses an atom-wise featurization typical of contemporary ML interatomic potentials (MLIPs) and is trained on a dataset of ∼167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reactions, using the GFN2-xTB energy and critical-point geometry as a low-level input and the B3LYP-D3/TZVP energy calculated at the B3LYP-D3/TZVP critical point as a high-level target. The excellent performance of the Δ2 model on unseen reactions demonstrates the surprising ease with which the model implicitly learns the geometric deviations between the low-level and high-level geometries that condition the activation energy prediction. The transferability of the Δ2 model is validated on several external testing sets where it shows near chemical accuracy, illustrating the benefits of combining ML models with readily available physical-based information from semi-empirical quantum chemistry calculations. Fine-tuning of the Δ2 model on a small number of Gaussian-4 calculations produced a 35% accuracy improvement over DFT activation energy predictions while retaining xTB-level cost. The Δ2 model approach proves to be an efficient strategy for accelerating chemical reaction characterization with minimal sacrifice in prediction accuracy.
000 reactions, using the GFN2-xTB energy and critical-point geometry as a low-level input and the B3LYP-D3/TZVP energy calculated at the B3LYP-D3/TZVP critical point as a high-level target. The excellent performance of the Δ2 model on unseen reactions demonstrates the surprising ease with which the model implicitly learns the geometric deviations between the low-level and high-level geometries that condition the activation energy prediction. The transferability of the Δ2 model is validated on several external testing sets where it shows near chemical accuracy, illustrating the benefits of combining ML models with readily available physical-based information from semi-empirical quantum chemistry calculations. Fine-tuning of the Δ2 model on a small number of Gaussian-4 calculations produced a 35% accuracy improvement over DFT activation energy predictions while retaining xTB-level cost. The Δ2 model approach proves to be an efficient strategy for accelerating chemical reaction characterization with minimal sacrifice in prediction accuracy.
1 Introduction
Automated reaction network prediction can elucidate key reaction mechanisms, predict reaction outcomes, and guide catalyst design toward improving the yield of valuable products.1–3 Unlike traditional network exploration algorithms that are based on encoded reaction types, automated reaction prediction methods can discover unexpected reaction mechanisms and new reaction types with limited use of heuristic rules.4,5 The use of automated reaction prediction is widespread and has been successfully applied in research areas such as biomass conversion,6 combustion chemistry,7–9 and heterogeneous catalysis.10–13 However, the main bottleneck of large-scale automated reaction prediction methods is the cost of locating transition states (TSs) on the atomic potential energy surface (PES). Even though various algorithms have been developed to accelerate TS searches, including single-ended searches (e.g., AFIR14 and SSWM15) and double-ended searches (e.g., NEB16 and string methods17–19), energy and force evaluations must be performed at high levels of theory to obtain accurate activation energies and reaction energies.To overcome large computing requirements, machine learning (ML) approaches have been adopted in recent years to accelerate reaction-rate predictions by reducing the dependency on DFT calculations. The methods can be classified into three directions. The first approach is to use ML interatomic potentials (MLIPs) rather than high-level quantum chemistry to explore the PES. A variety of neural network (NN) based force-fields have been developed to simulate equilibrium structures, including ANI,20 AIMNet,21 PaiNN,22 and Allegro,23 among others. More recently, reactive MLIPs have been developed to locate the TS and explore the minimum energy pathway (MEP).6,24–28 However, there is a scarcity of large generalized reaction databases, and as a result, reactive MLIPs are currently limited to specific chemistries and configurations. The second approach is to predict the TS geometries based on the geometries of reactant(s) and product(s), thereby circumventing the PES exploration for a TS. For example, Pattanaik et al. trained a graph neural network to predict TSs of isomerization reactions, which shows a 71% accuracy in reproducing the DFT-level optimized TS.29 Makoś et al. trained a generative adversarial network on the same dataset, but did not further validate that the resulting TS matched to the input reaction.30 However, DFT-level refinements of the predicted TSs are still required to obtain accurate activation energies with the current limitations of these models. The third approach is to directly predict the activation energy based on the reactant and product.31 Heinen et al. and Stuyver et al. trained a kernel ridge regression model32 and a graph neural network33 on a dataset of ∼4000 SN2 and E2 reactions, respectively, achieving a mean absolute error (MAE) of 2.5 and 2.6 kcal mol−1. A series of models based on chemprop,34 a directed message passing neural network (D-MPNN), were trained on a more diverse reaction database generated by Grambow et al.35 When tested on an independent test set, the best MAE reached ∼3.0 kcal mol−1.36–38 Ismail et al. trained an artificial neural network (ANN) on the same dataset and reached a modestly lower MAE of ∼2.8 kcal mol−1 on a withheld testing set.39 One concern for models that only use 2D information is that they are incapable of predicting more than one transition state for a given reactant/product pair, which potentially makes them more sensitive to conformational biases present in their training data. Presently, ML models based on this strategy have yet to achieve both chemical accuracy (<1 kcal mol−1) and transferability beyond narrow types of chemical species.
There are two factors that limit the predictive accuracy of ML models applied to reaction properties. One is the limited amount and/or accuracy of the available training data. The datasets used for training the aforementioned ML models contain only up to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reactions and did not use conformational sampling to identify the lowest energy TSs for each reaction. The second limitation is the amount of chemical information that can be derived from the input representation. Common molecular fingerprints (e.g., Morgan fingerprints40) fail to capture information about atomic sequences, while representations based on two-dimensional molecular graphs do not distinguish between conformations. The emergence of reaction databases with larger chemical coverage and conformational sampling, such as the Reaction Graph Depth 1 (RGD1) database,41 mitigates the first limitation. Adopting a 3D molecular representation would eliminate the second.
000 reactions and did not use conformational sampling to identify the lowest energy TSs for each reaction. The second limitation is the amount of chemical information that can be derived from the input representation. Common molecular fingerprints (e.g., Morgan fingerprints40) fail to capture information about atomic sequences, while representations based on two-dimensional molecular graphs do not distinguish between conformations. The emergence of reaction databases with larger chemical coverage and conformational sampling, such as the Reaction Graph Depth 1 (RGD1) database,41 mitigates the first limitation. Adopting a 3D molecular representation would eliminate the second.
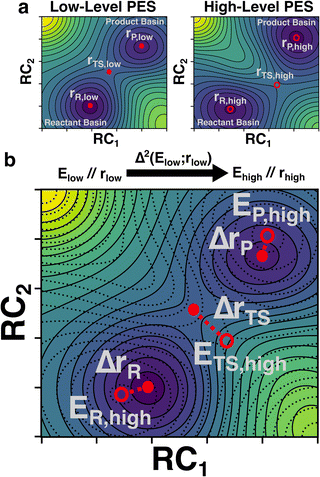
In this study, we develop a ML model that uses optimized geometries and energies calculated at a low-level of theory (e.g., semi-empirical quantum chemistry) to predict the energies of structures optimized at an analogous critical point at a high-level of theory (e.g. density functional theory) (Fig. 1). The critical point on the potential energy surface (PES) is either an equilibrium structure (ES) or a TS and may show large geometric deviations between the low and high levels of theory (Fig. 1a). Despite these deviations, the model is tasked with predicting the high-level energy at the high-level critical-point based only on the low-level inputs (Fig. 1b). We refer to our trained predictor as a Δ2 model, where the Δ in geometry is learned implicitly and the Δ in property (i.e., energy in this case) is learned explicitly. In contrast, Δ models typically only learn a difference in property (e.g., an energy difference at a given geometry) without simultaneously learning a difference in geometry.42,43 Our findings show that the Δ2 model, trained on ∼167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 reactions, achieves accurate predictions of the activation energy in both internal and external test sets. Fine-tuning the model on 2000 reactions computed at the Gaussian-4 (G4) level of theory further reduced the prediction errors by ∼1.5 kcal mol−1 compared with direct DFT calculations. In addition, the benefits of the Δ2 model in distinguishing different reaction conformations and accurately predicting the lowest activation energy are illustrated by a subset of test reactions.
000 reactions, achieves accurate predictions of the activation energy in both internal and external test sets. Fine-tuning the model on 2000 reactions computed at the Gaussian-4 (G4) level of theory further reduced the prediction errors by ∼1.5 kcal mol−1 compared with direct DFT calculations. In addition, the benefits of the Δ2 model in distinguishing different reaction conformations and accurately predicting the lowest activation energy are illustrated by a subset of test reactions.
2 Methodology
2.1 Database
The Δ2 model was trained using the RGD1 dataset, which contains ∼210![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 distinct reactions with up to ten heavy (carbon, nitrogen, and oxygen) atoms.41 The RGD1 database covers a diverse reaction space because it is generated by a graph-based exploration without the use of encoded reaction types. For a detailed description of the RGD1 database, we direct readers to our previous publication.41 Here, we briefly recapitulate the central steps of database generation that are relevant to the data processing in this work. RGD1 generation started with a graphical enumeration of 700
000 distinct reactions with up to ten heavy (carbon, nitrogen, and oxygen) atoms.41 The RGD1 database covers a diverse reaction space because it is generated by a graph-based exploration without the use of encoded reaction types. For a detailed description of the RGD1 database, we direct readers to our previous publication.41 Here, we briefly recapitulate the central steps of database generation that are relevant to the data processing in this work. RGD1 generation started with a graphical enumeration of 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 “breaking two bonds, forming two bonds (b2f2)” model reactions from reactants sampled from PubChem. A reaction conformational sampling strategy44 was applied to generate up to three conformations for each enumerated reaction, followed by a doubled-ended TS search, Berny optimization, and intrinsic reaction coordinate (IRC) validation at the GFN2-xTB45 level of theory. The GFN2-xTB optimized TSs were further refined using Gaussian16 quantum chemistry engine46 at the B3LYP-D3/TZVP47–50 level of theory. After DFT-level optimization, there is a chance that the TS may no longer correspond to the same reaction as the xTB-level TS (i.e., the TS corresponds to an “unintended” reaction, because it does not connect the same reactant and product identified by the GFN2-xTB level IRC calculation). The DFT-level TSs were classified as intended or unintended using an XGBoost model that exhibits a testing set accuracy of ∼95%.
000 “breaking two bonds, forming two bonds (b2f2)” model reactions from reactants sampled from PubChem. A reaction conformational sampling strategy44 was applied to generate up to three conformations for each enumerated reaction, followed by a doubled-ended TS search, Berny optimization, and intrinsic reaction coordinate (IRC) validation at the GFN2-xTB45 level of theory. The GFN2-xTB optimized TSs were further refined using Gaussian16 quantum chemistry engine46 at the B3LYP-D3/TZVP47–50 level of theory. After DFT-level optimization, there is a chance that the TS may no longer correspond to the same reaction as the xTB-level TS (i.e., the TS corresponds to an “unintended” reaction, because it does not connect the same reactant and product identified by the GFN2-xTB level IRC calculation). The DFT-level TSs were classified as intended or unintended using an XGBoost model that exhibits a testing set accuracy of ∼95%.
Several data processing steps were applied to prepare the RGD1 data for training the Δ2 model. First, TS data points were only considered duplicates if both the xTB-level and DFT-level TSs were identical (as opposed to only if the DFT-level TS was identical). This was done because the Δ2 model uses the GFN2-xTB geometry as an input and so retaining distinct xTB-level TSs that converge to same DFT level TS is useful for learning the implicit deviations between these geometries. Second, only intended TSs that correspond to the same reaction at both the DFT-level and xTB-level were used to train the Δ2 model. Unintended TSs cannot be used for training a Δ2 model, because the xTB-level TS does not correspond to the same reaction as the DFT-level TS in such cases and so a reference ground truth label is unavailable. Third, an additional effort was made to remove unintended TSs from the training data that might have been misclassified as intended by the XGBoost model. A 5-fold cross-validation (CV) was performed on all TSs to identify outliers. After training and testing the Δ2 model (vide infra) on each fold, each TS appeared once as a test data point and the corresponding deviation between the predicted energy and the reference value was defined as the deviation for each TS. IRC calculations were performed on 7242 TSs with a deviation greater than 10 kcal mol−1 (an empirically determined criterion). The IRC calculations identified 4057 of these TSs to be “unintended” and they were excluded from the dataset. In total 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893 distinct reactions (only forward reactions are counted in this number, forward and reverse would be 2×) passed these filters and were used to train and test the Δ2 model. The entire dataset is provided as ESI.†
893 distinct reactions (only forward reactions are counted in this number, forward and reverse would be 2×) passed these filters and were used to train and test the Δ2 model. The entire dataset is provided as ESI.†
Among the 185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893 reactions, 122
893 reactions, 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 964 are compositionally unique (i.e., they have a unique combination of reactant(s) and product(s)), while the other 62
964 are compositionally unique (i.e., they have a unique combination of reactant(s) and product(s)), while the other 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 929 represent different TS conformations for reactions contained within the 122
929 represent different TS conformations for reactions contained within the 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 964. A 90-10 training and testing split was applied to the 122
964. A 90-10 training and testing split was applied to the 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 964 unique reactions. When creating these splits, reactions with different conformations were partitioned to the training or testing set as a group to ensure that the testing set was composed of unseen reaction compositions and reaction conformations.
964 unique reactions. When creating these splits, reactions with different conformations were partitioned to the training or testing set as a group to ensure that the testing set was composed of unseen reaction compositions and reaction conformations.
The Δ2 model is trained on the geometries and energies associated with critical points, not on the reactions or activation energies directly. Thus each reaction in the testing and training set is associated with multiple geometries: the TS and the ESs of the individual reactants and products. To ensure that each chemical structure was exclusively assigned to either the training or testing set, only ESs exclusively appearing in the training reactions were included in the training set, while all other ESs, including those shared between the training and testing reactions, were assigned to the testing set. The shared ESs are a result of certain reactants or products being involved in multiple reactions, which also accounts for the similar number of unique ESs (122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 856) and unique reactions (122
856) and unique reactions (122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 964). The resulting testing set thus exclusively contains unseen ESs and TSs corresponding to unseen reactant–product pairs. In total 273
964). The resulting testing set thus exclusively contains unseen ESs and TSs corresponding to unseen reactant–product pairs. In total 273![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 687 chemical structures (167
687 chemical structures (167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 TSs and 106
269 TSs and 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 ESs) and 35
418 ESs) and 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062 chemical structures (18
062 chemical structures (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624 TSs and 16
624 TSs and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 438 ESs) were included in the training and testing sets, respectively.
438 ESs) were included in the training and testing sets, respectively.
All model performance results reported in the figures are for testing set predictions. For the activation energy predictions, the testing set contains activation energies of both forward and reverse directions. For enthalpy of reaction predictions, only enthalpies of reaction of the forward reactions are reported (the reverse are redundant).
2.2 Structural similarity
The Δ2 model is designed to predict properties computed at geometries optimized at a high-level model chemistry based on analogous properties and geometries optimized with a low-level model chemistry. A potentially important factor that affects the prediction accuracy is the magnitude of geometric deviation between the low and high levels of theory. To quantify the differences in molecular geometries, mass-weighted root-mean-squared-displacements (RMSDs) between the aligned geometries at each level of theory were computed (Fig. S1a†). RMSD is a first-level analysis that is sensitive to the entire conformation of each structure, however, for chemical reactions, structural changes in the reactive portions of each TS are oftentimes the defining features. To better describe the structural similarity between the TSs calculated at each level of theory, the maximum reactive bond length change (MBLC) between the low-level and high-level TSs was also calculated. For the example reaction shown in Fig. S4,† two bonds between atoms A and B and atoms C and D break and two bonds between atoms A and C and atoms B and D form; the MBLC is 0.58 Å in this case and corresponds to the CD-bond, which shows the largest deviation between the two levels of theory. To avoid including data points with large geometric inconsistencies that suggest different reaction chemistry being described by GFN2-xTB and DFT, a threshold of ≤1 Å was applied for both RMSD and MBLC (i.e., violating either criteria led to exclusion), resulting in the exclusion of 1.1% (3351 out of 308![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 749) of the datapoints in the RGD1 database. A similar threshold was also applied in a previous study.51 The distributions of RMSD and MBLC are provided in Fig. S1.† After RMSD and MBLC threshold screening, 270
749) of the datapoints in the RGD1 database. A similar threshold was also applied in a previous study.51 The distributions of RMSD and MBLC are provided in Fig. S1.† After RMSD and MBLC threshold screening, 270![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 723 (164
723 (164![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 TSs and 106
323 TSs and 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 ESs) and 34
400 ESs) and 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 (18
675 (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 TSs and 16
238 TSs and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437 ESs) data points were retained to form the final training and testing sets, respectively.
437 ESs) data points were retained to form the final training and testing sets, respectively.
2.3 Model architecture
The Δ2 model applied in this work is a neural network (NN) potential constructed using a variant of the AIMNet2-NSE architecture.52 The salient features and differences relevant for the current work are described below. AIMNet2-NSE was developed using a message passing approach,52 where the model learns an abstract and flexible chemical representation that is iteratively updated based on the representations of neighboring atoms. Briefly, our AIMNet Δ2 model first converts the local atom-centered geometries into atomic environment vectors (AEVs). These AEVs take the form of atom-centered symmetry functions that describe the local chemical environment of an atom using a number of gaussian probes with a set of width and peak position parameters. Details of the AEV functional forms can be found in previous works.20,21 The AEVs calculated in this work are truncated at 7.0 Å and consist of 24 atom-centered symmetry functions. Atomic numbers are embedded into a 16-dimensional learnable space that serves as the abstract hidden state representation for message passing, which we will refer to as the atomic feature vector (AFV). AFVs are updated over two message-passing iterations prior to energy predictions. This number of message-passing steps was selected based on preliminary tests that showed sufficient prediction accuracy and revealed that additional iterations did not yield noticeable gains in performance. As a high-level overview, a single message-passing step consists of constructing so-called embedded AEVs that are then passed through a through a multilayer perceptron (MLP) to obtain an updated AFV. Specifically, the Δ2 model combines geometric (symmetry functions) and nuclear (atomic embeddings) information into embedded AEVs through a summation of outer products between the AEV components and AFVs of neighboring atoms. A set of embedded radial and vector AEVs are concatenated, flattened, and passed through a MLP to predict AFV updates.As a modification to the original AIMNet-NSE implementation, atom-centered point charges are initially predicted with a separate message-passing neural network that also uses embedded AEVs as the input. This design decision was informed by our model testing, where it was found that a separate message-passing neural network could be quickly trained for robust initial charge estimates. These atom-centered point charges are concatenated alongside embedded AEVs during the Δ2 model forward pass, and they are updated via neural charge equilibration52 during every message-passing iteration. Each message-passing iteration has a dedicated MLP to encourage model flexibility. The MLP used in the final message pass creates a single vector, of size 256, for each atom that is passed through an additional MLP for predicting the atomic contributions to the total energy.
The Δ2 model was trained using the L2 loss of the total energy of the target species calculated at the low-level critical point (i.e., either an ES or TS), where the ground truth values are the high-level of theory energies calculated at the high-level critical point (Fig. 2). Despite being common MLIP training practice, atomic force components were not used in the Δ2 objective function because the aim of the model is to infer the energy differences at PES critical points. Model training was carried out with a batch size of 100, the rectified Adam optimizer,53 and a cosine annealing scheduler54 that smoothly reduced the learning rate from 10−4 to 10−6 over 2000 epochs. To improve the quality of predictions, an ensemble of eight independent Δ2 models were trained with the same training dataset but different parameter initializations, and the inferred energies are reported as the average over the ensemble.
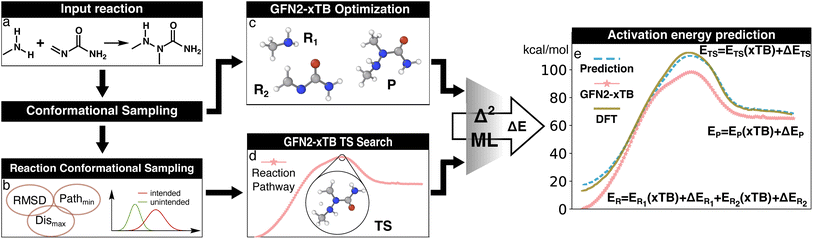 | ||
| Fig. 2 Illustration of the Δ2 Machine learning model architecture. For an input reaction (a), two workflows are applied to search for transition states (TS) and equilibrium structures (ES). To obtain the ESs, the separated reactant(s) and product(s) are subjected to conformational sampling and geometric optimization at the low level of theory (i.e., GFN2-xTB in this study, c). The TSs are located by a reaction conformational sampling step that jointly optimizes reactant and product conformers for success in a double-ended search (b, see ref. 44 for more details), followed by double-ended TS localization at the low level of theory (d). The resulting geometries and energies are fed into the Δ2 model, which is built on an atom-wise featurized message-passing architecture. The output thermochemistry properties, like energies and enthalpies, are used to calculate the high-level activation energy and the enthalpy of reaction corresponding to the high-level geometries (e). | ||
2.4 External test sets
Two external test sets were introduced to evaluate model transferability.55 The first contains three unimolecular decomposition networks of γ-ketohydroperoxide (KHP), propylene carbonate (PC), and methyl butanoate (MB). In total, 324 reactions containing up to seven heavy atoms (carbon, nitrogen, and oxygen) were collected from these networks after excluding reactions appearing in the RGD1 database. This external test consists of reactants of size and chemistry (CHON) similar to RGD1. The second external set contains 118 reactions possible in the first step of L-glucose pyrolysis. L-glucose (C6H12O6) contains 12 heavy atoms, which is beyond the molecular size of any species in the RGD1 database. In addition, the high reactivity introduced by multiple hydroxyl groups poses a unique challenge for predicting activation energies because such features are modestly represented in the training data.2.5 Transfer learning for predicting G4 energies
The RGD1 database was constructed at the B3LYP-D3/TZVP level of theory. To explore the feasibility of using transfer learning to achieve higher accuracy for the Δ2 model, 2000 reactions were randomly selected to perform Gaussian-4 (G4) calculations (without geometric optimization) on the reactant, product, and TS geometries.56 In total 2000 TSs and 3142 corresponding unique reactants and products (ESs) were computed by the G4 method. Although G4 is one of the most accurate single reference methods, G4 calculations have a dissuadingly large computational cost. Thus, ∼1% of the training dataset was selected to perform these calculations and fine-tune the pre-trained xTB-DFT Δ2 model to a higher level of accuracy with transfer learning.3 Results and discussion
The activation energy (ΔE†) deviations between GFN2-xTB and B3LYP-D3/TZVP were computed for the whole RGD1 database, which serves as a baseline comparison of the Δ2 model (Fig. 3a). GFN2-xTB typically underestimates the activation energies of lower barrier reactions (ΔE† < 120 kcal mol−1) and overestimates the activation energies of higher barrier reactions (ΔE† > 120 kcal mol−1). This inconsistency leads to an overall MAE of 11.9 kcal mol−1 and the difficulty of estimating the deviation through a straightforward linear regression. The Δ2 model improves the ΔE† prediction accuracy by a factor of ∼7−9 (Fig. 3b), where the root-mean-square error (RMSE) and mean absolute error (MAE) were reduced from 15.3 and 11.9 kcal mol−1 to 2.26 and 1.32 kcal mol−1, respectively. Moreover, the Δ2 model implicitly learns to correct the range specific over/underestimations of the direct GFN2-xTB prediction, which can be seen in the increase of the R2 score from 0.74 to 0.99. Considering the wide span of the reaction space and the large range of target ΔE† values (0–188 kcal mol−1), the MAE of 1.3 kcal mol−1 is an encouraging result, indicating that the Δ2 model can outperform alternative models using only information from reactants and products.32,36,39 Out of 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 test reactions (including both forward and backward pathways), only 249 reactions had an absolute error over 10 kcal mol−1, in other words, 99.3% of predicted ΔE† were within a 10 kcal mol−1 deviation range (96.2% and 81.0% are within 5 and 2 kcal mol−1, respectively). A detailed analysis of 28 reactions (14 TSs) with absolute errors exceeding 20 kcal mol−1 is provided in Fig. S3.† In addition to the activation energy prediction, the Δ2 model was also applied to predict the enthalpy of reaction resulting in an even better MAE of 0.58 kcal mol−1 (Fig. S2†).
358 test reactions (including both forward and backward pathways), only 249 reactions had an absolute error over 10 kcal mol−1, in other words, 99.3% of predicted ΔE† were within a 10 kcal mol−1 deviation range (96.2% and 81.0% are within 5 and 2 kcal mol−1, respectively). A detailed analysis of 28 reactions (14 TSs) with absolute errors exceeding 20 kcal mol−1 is provided in Fig. S3.† In addition to the activation energy prediction, the Δ2 model was also applied to predict the enthalpy of reaction resulting in an even better MAE of 0.58 kcal mol−1 (Fig. S2†).
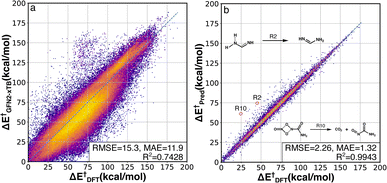 | ||
| Fig. 3 DFT-baseline and Δ2 model performance on the RGD1 testing set. Correlation between activation energies computed using GFN2-xTB (a) and the Δ2 model (b) with the ground-truth DFT values (x axes). The datapoints are colored based on bivariate kernel density estimations (yellow: high, purple: low). For each plot, units for both axes, RMSE, and mean absolute error (MAE) values are in kcal mol−1. 2 out of 14 outliers with prediction error larger than 20 kcal mol−1 are shown in the inset, while other outliers are provided in Fig. S3.† | ||
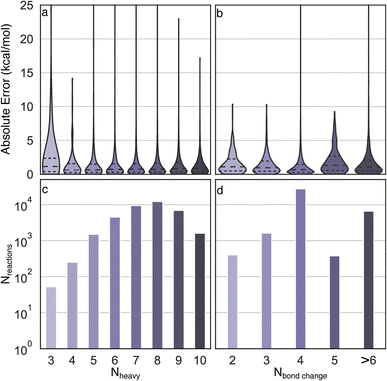
Uniform error distributions were observed across different sizes and types of reactions (Fig. 4), which is a common challenge for recently reported models.36 The reactions with three heavy atoms have a relatively large MAE of 3.2 kcal mol−1, which is mainly due to the lack of training data and one outlier in the test set (R2 in Fig. S3†). However, it is worth highlighting that the lack of accuracy of these systems is moot because directly performing DFT calculations of small species is a trivial task with modern computational resources. Consistently low MAEs (<1.4 kcal mol−1) can be obtained for reactions with four to ten heavy atoms, indicating the Δ2 model is insensitive to size across the diversity of reactions examined. For reactions with different numbers of bond changes, the MAEs of all types of reactions are below 2 kcal mol−1, indicating the Δ2 model exhibits transferability to numerous reaction mechanisms, despite training data scarcity for certain types. For example, the reactions with five bond changes and greater than six bond changes have MAEs of 1.94 kcal mol−1 and 1.66 kcal mol−1, respectively, which demonstrates that the Δ2 model can be applied to a wide reaction space.
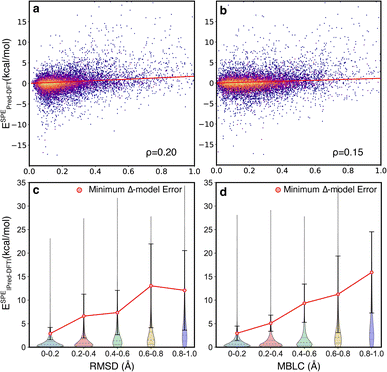
The motivating hypothesis behind the development of the Δ2 model is that the geometric deviations between the low-level and high-level models can be learned implicitly while the energy deviations can be learned explicitly. This would be falsified by the observation of model errors that were strongly correlated with large geometric deviations between the low-level and high-level geometries, because this would indicate that the model is acting as a Δ model with predictions that are conditioned on high congruence between the geometries. To examine the effect of geometric deviations on the prediction errors, two measures (RMSD and MBLC) of geometric deviations between GFN2-xTB optimized and B3LYP-D3 optimized geometries are compared jointly with the signed error of the energy predicted by the Δ2 model at ESs and TSs (Fig. 5). For both measures, the majority of the data points are around the center line, i.e., the mean signed error of zero, and thus, there is no clear trend between prediction accuracy and structural differences. The Spearman's rank correlation coefficients (ρ) between the two measures of geometric deviations and the absolute error are similarly low, with ρ = 0.2 for RMSD and ρ = 0.15 for MBLC, and a least-squares linear fit shows a very weak linear trend.
To provide a quantitative measure of the size of the correlation between structural deviation and accuracy, the errors from the Δ2 model were compared with the errors associated with using the B3LYP-D3/TZVP//GFN2-xTB energies to estimate the B3LYP-D3/TZVP//B3LYP-D3/TZVP energies (Fig. 5c and d). This latter measure is the lower limit of the errors for a Δ model trained to predict energies at a given geometry rather than at different fixed-points. The comparison was calculated for two hundred TSs that were sampled to span the structural deviations shown in the figure (See ESI Section 5† for additional details). The differences in this comparison are qualitative, with the Δ2 model showing errors 3 − 5x lower that the theoretically perfect Δ model across the various distributions. These observations are consistent with the hypothesis that the size of the geometric deviation should not be a strong indicator of prediction error for the Δ2 model because the geometry differences between the low-level and high-level are implicitly learned during training.
Two unique features of the RGD1 database are the inclusion of reactions that have chemically equivalent reactants and products but that still undergo bond rearrangements (denoted as ΔHr = 0 reactions), and the inclusion of reactions with multiple transition state conformations connecting the same reactant and product. These two subsets of reactions challenge models based on molecular fingerprinting and general two-dimensional (i.e., graph) molecular representations. The former cannot retain atomic mapping and will therefore return a “null” reaction, while the latter cannot describe conformational effects and is restricted to providing a single value prediction (i.e., the reactant and product graphs have a one-to-many non-functional relationship to the different TS conformers). The Δ2 model can naturally handle these two types of reactions because its predictions are based on the 3D structure. Benchmark accuracy on these corresponding reactions of the test set are shown in Fig. 6a and b. The MAE and RMSE of 603 ΔHr = 0 reactions are 1.09 and 2.17 kcal mol−1, respectively, while the target activation energy ranged from 15 to 170 kcal mol−1 (Fig. 6a).
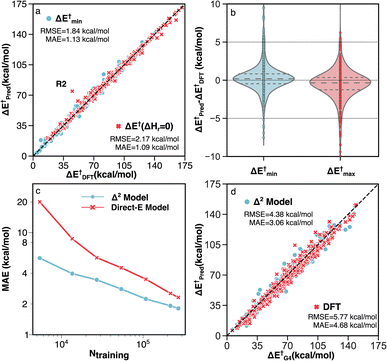 | ||
| Fig. 6 Performance of the Δ2 model on different subsets of testing data. (a) Parity plot of model predictions vs. DFT (B3LYP-D3/TZVP) data for reactions with identical reactants and products (red) and reactions with multiple TS conformations (blue). The outlier R2 is discussed in detail in Section S3.† (b) Error distributions for predicting the minimum (blue) and maximum (red) activation energies across multiple TS conformations. (c) MAE vs. the number of training data points for the direct-E model (red) and Δ2 model (blue). (d) Parity plot of activation energies calculated by G4 vs. DFT (red) and the Δ2 model trained with transfer learning (blue). | ||
For the 660 reactions with multiple TS conformations and a range of activation energies greater than 5 kcal mol−1, the Δ2 model accurately predicts both the lowest (ΔE†min) and highest (ΔE†max) activation energies (Fig. 6b) among the TS conformers. The MAE and RMSE of ΔE†min, which plays the most important role in modeling the kinetics of a reactive system with transition state theory (TST), are 1.13 and 1.84 kcal mol−1, respectively (Fig. 6a). The ΔE†max is also accurately predicted with MAE and RMSE of 1.40 and 2.30 kcal mol−1, respectively. As a result, the Δ2 model is able to reproduce the range of activation energies (max–min) among different reaction conformations, which represents the effect of conformational sampling, with an MAE and RMSE of 1.83 and 2.79 kcal mol−1, respectively.
To assess the impact of the training dataset size on the model performance, the MAEs of the Δ2 model were calculated for training a single model from scratch using different amounts of training data and fixed hyperparameters (Fig. 6c). For comparison, a model was trained to directly predict the DFT-level fixed-point energy using the low-level fixed-point geometry, rather than the difference between low and high-level fixed points energies (“Direct-E model”, Fig. 6c). The difference in slopes is caused by the difference in complexity between learning the DFT energy directly (red) and learning the difference in fixed-point energy (blue). This creates the largest accuracy difference in the data-scarce regime, whereas with sufficient data, both models should asymptotically approach the same accuracy (i.e., the accuracy limited only by the irreducible error of the dataset). Neither model shows evidence of accuracy saturation, suggesting further opportunities for dataset curation.
Since the accuracy of a ML model is bound by the accuracy of the training data, i.e., the accuracy of B3LYP-D3/TZVP in our case, including higher accuracy reference data is one strategy to improve the inference of the Δ2 model. A transfer learning approach was applied with G4 calculations on 2000 TSs and 3142 equilibrium structures, which corresponds to ∼1% of the entire DFT dataset. A comparison between the G4 ground-truth data, B3LYP-D3/TZVP DFT, and the transfer learning Δ2 predictions are shown in Fig. 6d. We observe that including a small amount of G4 data (5142 data points) enables the ensemble of five Δ2 models to achieve a MAE that is 1.62 kcal mol−1 lower than DFT predictions on the G4 test data (3.06 compared 4.68 kcal mol−1, respectively, Fig. 6d). It is important to highlight that the transfer learning Δ2 model operates on GFN2-xTB geometries, meaning that the accuracy improvement of 35% compared to the DFT calculation only requires xTB-level cost (as shown in section S4, the runtime of the Δ2 model is negligible compared with xTB). The data efficiency of the transfer learning approach illustrates the high flexibility of the Δ2 model in that only a small amount of data is required to alter the target level of theory.
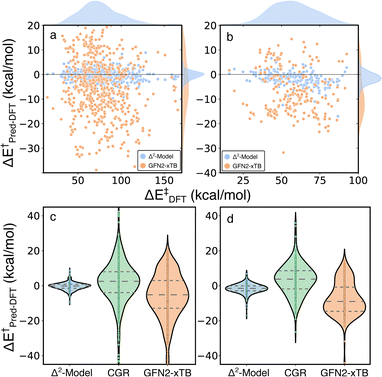
The Δ2 model was also applied to two external test sets, unimolecular decomposition networks (EXT1) and glucose pyrolysis reactions (EXT2), to evaluate model transferability (Fig. 7 and S4†). The mean signed error (MSE) of activation energies computed by GFN2-xTB with respect to those computed by B3LYP-D3/TZVP are −5.69, −7.57 and −5.71 kcal mol−1, in EXT1, EXT2, and the RGD1 database, respectively (the systematic bias can be clearly observed in Fig. 3a). The Δ2 model reduces the systematic MSE bias to −0.02 kcal mol−1 for EXT1 and reduces the MSE to −1.32 kcal mol−1 for EXT2, which is consistent with the corresponding deviation from the baseline theory (i.e. MSEs of −5.69, −7.57 kcal mol−1 in EXT1 and EXT2, respectively). The MAE of 1.52 kcal mol−1 in EXT1 indicates the transferability of the Δ2 model across the reaction space within ten heavy atoms (C, H, N, O), and the feasibility of using the model as a drop-in replacement for DFT in many reaction characterization tasks. A larger MAE of 2.33 kcal mol−1 is observed for EXT2, which we attribute to the systematic bias in EXT2 (i.e., MSE of −1.32 kcal mol−1) and suggests that the transferability of the Δ2 model is limited by the baseline theory. A recently developed activation energy prediction model based on a representation of condensed graph of reaction (denoted as CGR, composed of an ensemble of five models) was applied to these two test sets.37 The CGR model combines a popular cheminformatics reaction representation, namely condensed graph of reaction, with a graph convolutional neural network architecture and reaches an activation energy prediction accuracy of ∼4 kcal mol−1 on a withheld testing set. The reaction dataset used to train the CGR model contains no more than seven heavy atoms,35 which is the same as EXT1 and is much smaller than EXT2. Although comparing models trained at different levels of theory is not ideal, the magnitude of the MAEs and uncertainties (9.38/2.94 and 7.51/2.32 kcal mol−1 for EXT1 and EXT2, respectively) are larger than can be explained by functional choice alone and indicates a lower transferability of the CGR model, which was solely trained on the 2D representations of reactants and products.
4 Conclusions and outlook
The maturation of machine learning methods in predicting reaction properties has created new opportunities in automated reaction prediction. Nevertheless, the relatively low accuracy and the lack of generality and transferability of existing models remain prohibitive for most applications. In this study, we have shown how these limitations can be side-stepped using the Δ2 model, which comes at the cost of GFN2-xTB but is able to provide beyond-DFT level accuracy. The performance of this model was investigated in four scenarios. First, the Δ2 model achieves a MAE of 1.3 kcal mol−1 on the withheld testing set, which is the most accurate prediction of activation energy by an ML model for general organic (C, H, O, N) chemical reactions to date. Second, the Δ2 model accurately predicts the activation energies of “null” reactions and reactions with multiple TS conformations. In particular, the ability to distinguish the activation energies of different reaction conformations and accurately predict the lowest activation energy is essential in reaction prediction tasks. Third, the generality of the Δ2 model was tested on two external test sets, one containing three unimolecular decomposition networks and the other involving the first step pyrolysis reactions of L-glucose. For reactions distributed in the same reaction space as the training dataset, the Δ2 model achieves similar performance, while for reactions outside the training data, the prediction error is slightly increased but still reliable. Finally, the transferability of the Δ2 model was demonstrated by altering the high-level target theory from DFT to G4. By fine-tuning the model with G4 values corresponding to only 1% of the training data, the model outperforms the prediction accuracy of DFT calculations on the same reactions.There are still several avenues for improving the current approach. First, activation energy predictions that approach the chemical accuracy are only available for reactions containing up to ten C, N, and O atoms. To extend the accurate performance to a more diverse reaction space, either a larger, more complex reaction database or an ad-hoc transfer learning approach on additional specific datasets are needed. Second, the current model is only trained on neutral closed-shell species. There are no fundamental obstacles to extending the approach to ionic and open-shell molecules, but data curation and benchmarking need to be performed, which are currently underway. With these and other foreseeable improvements, the ML models are likely to facilitate the adoption of black-box automated reaction prediction methods to serve as a general tool for the chemical community.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its ESI files.† The code for this study is available through GitHub under the MIT License [https://github.com/zhaoqy1996/Delta2ML].Author contributions
Q. Z.: conceptualization, investigation, methodology, software, formal analysis, data curation, visualization, writing – original draft. D. M. A.: investigation, methodology, software, writing – original draft. O. I.: conceptualization, funding acquisition, resources, supervision. B. M. S: conceptualization, funding acquisition, resources, writing – review & editing, supervision.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The work performed by Q. Z., D. M. A., O. I., and B. M. S was made possible by the Office of Naval Research (ONR) through support provided by the Energetic Materials Program (MURI grant number: N00014-21-1-2476, Program Manager: Dr Chad Stoltz). B. M. S also acknowledges partial support for this work from the Dreyfus Program for Machine Learning in the Chemical Sciences and Engineering. Computational resources for this work were provided by the Frontera computing project at the Texas Advanced Computing Center. Frontera is made possible by the National Science Foundation award OAC-1818253.References
- J. P. Unsleber and M. Reiher, Annu. Rev. Phys. Chem., 2020, 71, 121–142 CrossRef CAS.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Angew. Chem., Int. Ed., 2020, 59, 22858–22893 CrossRef CAS.
- I. Ismail, R. Chantreau Majerus and S. Habershon, J. Phys. Chem. A, 2022, 126, 7051–7069 CrossRef CAS PubMed.
- Y. V. Suleimanov and W. H. Green, J. Chem. Theory Comput., 2015, 11, 4248–4259 CrossRef CAS.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- P.-L. Kang, C. Shang and Z.-P. Liu, J. Am. Chem. Soc., 2019, 141, 20525–20536 CrossRef CAS PubMed.
- H. J. Curran, P. Gaffuri, W. J. Pitz and C. K. Westbrook, Combust. Flame, 1998, 114, 149–177 CrossRef CAS.
- C. K. Westbrook, Y. Mizobuchi, T. J. Poinsot, P. J. Smith and J. Warnatz, Proc. Combust. Inst., 2005, 30, 125–157 CrossRef.
- S. M. Sarathy, C. K. Westbrook, M. Mehl, W. J. Pitz, C. Togbe, P. Dagaut, H. Wang, M. A. Oehlschlaeger, U. Niemann, K. Seshadri and P. S. Veloo, Combust. Flame, 2011, 158, 2338–2357 CrossRef CAS.
- X.-J. Zhang, C. Shang and Z.-P. Liu, J. Chem. Phys., 2017, 147, 152706 CrossRef.
- C. F. Goldsmith and R. H. West, J. Phys. Chem. C, 2017, 121, 9970–9981 CrossRef CAS.
- T. Iwasa, T. Sato, M. Takagi, M. Gao, A. Lyalin, M. Kobayashi, K.-i. Shimizu, S. Maeda and T. Taketsugu, J. Phys. Chem. A, 2018, 123, 210–217 CrossRef PubMed.
- Q. Zhao, Y. Xu, J. Greeley and B. M. Savoie, Nat. Commun., 2022, 13, 4860 CrossRef CAS PubMed.
- S. Maeda, T. Taketsugu and K. Morokuma, J. Comput. Chem., 2014, 35, 166–173 CrossRef CAS PubMed.
- C. Shang and Z. P. Liu, J. Chem. Theory Comput., 2013, 9, 1838–1845 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- B. Peters, A. Heyden, A. T. Bell and A. Chakraborty, J. Chem. Phys., 2004, 120, 7877–7886 CrossRef CAS PubMed.
- A. Behn, P. M. Zimmerman, A. T. Bell and M. Head-Gordon, J. Chem. Phys., 2011, 135, 224108 CrossRef PubMed.
- P. M. Zimmerman, J. Chem. Phys., 2013, 138, 184102 CrossRef PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- R. Zubatyuk, J. S. Smith, J. Leszczynski and O. Isayev, Sci. Adv., 2019, 5, eaav6490 CrossRef CAS PubMed.
- K. Schütt, O. Unke and M. Gastegger, International Conference on Machine Learning, 2021, pp. 9377–9388 Search PubMed.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Nat. Commun., 2023, 14, 579 CrossRef CAS PubMed.
- K. Yao, J. E. Herr, D. W. Toth, R. Mckintyre and J. Parkhill, Chem. Sci., 2018, 9, 2261–2269 RSC.
- S.-D. Huang, C. Shang, P.-L. Kang, X.-J. Zhang and Z.-P. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1415 CAS.
- T. A. Young, T. Johnston-Wood, V. L. Deringer and F. Duarte, Chem. Sci., 2021, 12, 10944–10955 RSC.
- S. J. Ang, W. Wang, D. Schwalbe-Koda, S. Axelrod and R. Gómez-Bombarelli, Chem, 2021, 7, 738–751 CAS.
- S. Zhang, M. Makoś, R. Jadrich, E. Kraka, K. Barros, B. Nebgen, S. Tretiak, O. Isayev, N. Lubbers, R. Messerly, et al., Exploring the frontiers of chemistry with a general reactive machine learning potential, 2022 Search PubMed.
- L. Pattanaik, J. B. Ingraham, C. A. Grambow and W. H. Green, Phys. Chem. Chem. Phys., 2020, 22, 23618–23626 RSC.
- M. Z. Makoś, N. Verma, E. C. Larson, M. Freindorf and E. Kraka, J. Chem. Phys., 2021, 155, 024116 CrossRef PubMed.
- T. Lewis-Atwell, P. A. Townsend and M. N. Grayson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1593 CAS.
- S. Heinen, G. F. von Rudorff and O. A. von Lilienfeld, J. Chem. Phys., 2021, 155, 064105 CrossRef CAS PubMed.
- T. Stuyver and C. W. Coley, J. Chem. Phys., 2022, 156, 084104 CrossRef CAS PubMed.
- K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley and M. Mathea, et al. , J. Chem. Inf. Model., 2019, 59, 3370–3388 CrossRef CAS.
- C. A. Grambow, L. Pattanaik and W. H. Green, Sci. Data, 2020, 7, 1–8 CrossRef.
- C. A. Grambow, L. Pattanaik and W. H. Green, J. Phys. Chem. Lett., 2020, 11, 2992–2997 CrossRef CAS PubMed.
- E. Heid and W. H. Green, J. Chem. Inf. Model., 2022, 62, 2101–2110 CrossRef CAS.
- K. A. Spiekermann, L. Pattanaik and W. H. Green, J. Phys. Chem. A, 2022, 126, 3976–3986 CrossRef CAS PubMed.
- I. Ismail, C. Robertson and S. Habershon, J. Chem. Phys., 2022, 157, 014109 CrossRef CAS PubMed.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- Q. Zhao, S. M. Vaddadi, M. Woulfe, L. A. Ogunfowora, S. S. Garimella, O. Isayev and B. M. Savoie, Sci. Data, 2023, 10, 145 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- Q. Zhao, N. C. Iovanac and B. M. Savoie, J. Chem. Inf. Model., 2021, 61, 2798–2805 CrossRef CAS PubMed.
- Q. Zhao, H.-H. Hsu and B. M. Savoie, J. Chem. Theory Comput., 2022, 18, 3006–3016 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016, Gaussian Inc., Wallingford CT Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- J. Lu, C. Wang and Y. Zhang, J. Chem. Theory Comput., 2019, 15, 4113–4121 CrossRef CAS.
- R. Zubatyuk, J. S. Smith, B. T. Nebgen, S. Tretiak and O. Isayev, Nat. Commun., 2021, 12, 4870 CrossRef CAS PubMed.
- L. Liu, H. Jiang, P. He, W. Chen, X. Liu, J. Gao and J. Han, On the Variance of the Adaptive Learning Rate and Beyond, 2019, https://arxiv.org/abs/1908.03265 Search PubMed.
- I. Loshchilov and F. Hutter, SGDR: Stochastic Gradient Descent with Warm Restarts, 2016, https://arxiv.org/abs/1608.03983 Search PubMed.
- Q. Zhao, B. M. Savoie, Angew. Chem. Int. Ed., 2022, 61, 46 Search PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A detailed analysis of outliers, the performance of applying machine learning force field as the low-cost method, extension to the enthalpy of reaction prediction, some figures and tables referenced in the main text. See DOI: https://doi.org/10.1039/d3sc02408c |
| This journal is © The Royal Society of Chemistry 2023 |