Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Improving the molecular spin qubit performance in zirconium MOF composites by mechanochemical dilution and fullerene encapsulation†
Lucija
Vujević
a,
Bahar
Karadeniz
 *a,
Nikola
Cindro
*a,
Nikola
Cindro
 b,
Andraž
Krajnc
c,
Gregor
Mali
b,
Andraž
Krajnc
c,
Gregor
Mali
 c,
Matjaž
Mazaj
c,
Matjaž
Mazaj
 c,
Stanislav M.
Avdoshenko
d,
Alexey A.
Popov
c,
Stanislav M.
Avdoshenko
d,
Alexey A.
Popov
 d,
Dijana
Žilić
d,
Dijana
Žilić
 *a,
Krunoslav
Užarević
*a,
Krunoslav
Užarević
 *a and
Marina
Kveder
*a
*a and
Marina
Kveder
*a
aRuđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia. E-mail: bahar.karadeniz@irb.hr; dijana.zilic@irb.hr; krunoslav.uzarevic@irb.hr; kveder@irb.hr
bDepartment of Chemistry, University of Zagreb, 10000 Zagreb, Croatia
cNational Institute of Chemistry, Hajdrihova 19, SI-1001 Ljubljana, Slovenia
dLeibniz IFW Dresden, Helmholtzstrasse 20, D-01069 Dresden, Germany
First published on 16th August 2023
Abstract
Enlarging the quantum coherence times and gaining control over quantum effects in real systems are fundamental for developing quantum technologies. Molecular electron spin qubits are particularly promising candidates for realizing quantum information processing due to their modularity and tunability. Still, there is a constant search for tools to increase their quantum coherence times. Here we present how the mechanochemical introduction of active spin qubits in the form of 10% diluted copper(II)-porphyrins in the diamagnetic PCN-223 and MOF-525 zirconium-MOF polymorph pair can be achieved. Furthermore, the encapsulation of fullerene during the MOF synthesis directs the process exclusively toward the rare PCN-223 framework with a controllable amount of fullerene in the framework channels. In addition to the templating role, the incorporation of fullerene increases the electron spin–lattice and phase-memory relaxation times, T1 and Tm. Besides decreasing the amount of nuclear spin-bearing solvent guests in the non-activated qubit frameworks, the observed improved relaxation times can be rationalized by modulating the phonon density of states upon fullerene encapsulation.
1 Introduction
A fundamental step towards developing of quantum technologies is building a qubit, a quantum bit that can exist in a coherent superposition state, unlike the classical bit that can possess only two states, 0 and 1.1 Among different ways of qubit realization, electron spin in molecular magnetic compounds, where the spin originates from the organic radical, transition metal ion or lanthanide, is particularly promising technology due to the facile manipulation of the electron quantum states by an electromagnetic irradiation.2,3 The main prerequisite for building a quantum device is the entanglement of qubits to achieve a state that is not the simple product of individual qubits. The inclusion of molecular spin qubits into the specifically tailored environment enables the study of the effect of spatial separation and interactions within the framework on the qubit performance, unraveling the role of phonon environment and spin–spin interactions on the operating speed of the qubit (spin–lattice relaxation time rate, 1/T1) and on the time limit in which the computation must be performed (phase-memory time, Tm).4 Much effort is put into suppressing various origins of spin decoherence, such as due to the framework noise and interaction with nearby nuclei.5 To fully realize the potential of molecular spins for quantum information processing, it is necessary to build structurally well-defined arrays of spatially resolved molecular spins, hence combining improved spin coherence properties with optical or electrical access to their quantum states.5–7Metal–organic frameworks (MOFs)8,9 assert as an ideal platform for controllable spatial resolution of qubit sites.4,10 These coordination polymers combine the coordination preferences of the metal cation nodes with different geometry of organic linkers to form a plethora of diverse topologies characterized by permanent porosity, different nature of the interior walls, and approachable metal nodes, not only on the surface but also in the interior of MOF particles. The modularity and tunability of MOFs, particularly MOFs of the fourth generation, made them one of the most investigated material classes today, with many potential application areas.11,12 In terms of quantum technologies, the variable topologies, periodicity, chemical diversity, and high internal ordering of MOFs provide an ideal and tunable platform for spatial resolution and manipulation of molecular spins, leading towards an emerging class of 3D-qubit array materials.4 Building such a MOF platform with long coherence time is a demanding task as the spin carriers need to be sufficiently separated from each other, while it is still not possible to maintain spatial precision at a molecular level in MOFs with highly diluted spin carriers. Also, MOFs inherently carry the magnetic noise of the ligands and guest molecules in the matrix, which may lead to the decoherence of qubits and usually shorter qubit lifetimes than required for quantum information processing (QIP) or quantum sensing.13,14 Most of these issues are, however, amendable, and it has been reported that including the copper(II)-porphyrin building blocks in highly porous and activated MOFs results in spin coherence detectable up to liquid-nitrogen temperatures, making these materials attractive from the perspective of quantum information science.4 Therefore, understanding quantum system interactions with its respective environment plays a key step in controlling decoherence processes expressed in terms of T1 and Tm (an approximation of spin–spin relaxation time T2) relaxation times.15
A promising class of MOFs for quantum computing are porphyrinic zirconium carboxylate MOFs built from tetratopic porphyrinic ligand, tetrakis(4-carboxyphenyl)porphyrin (H2TCPP), and hexanuclear or octanuclear oxozirconium(IV) clusters.16,17 Zirconium carboxylate MOFs18 are widely researched due to their resistance to water and corrosive atmospheres,19,20 and framework-stability upon linker removal, leading to increased porosity of the material and larger distancing between the spin carriers.21,22 Despite zirconium(IV) clusters and resulting MOFs being diamagnetic, the spin active atom or group can be coordinated in the porphyrin center and efficiently separated by the coordination of the metalloporphyrin with binding carboxylate groups in the MOF structure.23 Porphyrin MOFs are rare zirconium MOFs displaying more than one topology.24 For some of the six known topologies, a polymorphic transition is also possible, for example, in the case of MOF-525 and PCN-223 polymorph pair (Fig. 1).25 Freedman's group, in their recent proof-of-concept work, exploited cobalt(II) porphyrin molecular magnets diluted in a highly porous hexa-coordinated (on the zirconium cluster) PCN-224 MOF17 matrix for accomplishing a porous array of clocklike qubits, to tackle the issue with magnetic noise of the nuclear-spins rich MOF carrier.26 The same group showed how the incorporation of spin-active copper(II) porphyrins into the PCN-224 results in porous molecular spin-based qubits with detectable coherence among the highly-concentrated spins in the framework up to 80 K (Fig. 1).4,27 In this context, copper(II) porphyrins, where the copper bears S = 1/2 electronic spin, became attractive and extensively studied model systems for quantum information processing applications. The coherence parameters in terms of T1 and Tm were investigated using pulse ESR spectroscopy in addition to continuous wave (CW)-ESR.10,23,28 Not only the molecular spin-based qubits with high porosity and missing linkers, such as PCN-224, are suitable molecular spin qubit candidates. In our recent work, we showed how mechanochemistry29 provides a controllable pathway to synthesizing phase-pure twelve-coordinated PCN-223 and MOF-525 polymorphs.25 By introducing paramagnetic centers (Cu(II), Fe(III), and Mn(II)) in the porphyrin linker, a superhyperfine splitting was observed in CW-ESR spectra of the more porous MOF-525 polymorph. In contrast, the same feature was less pronounced in PCN-223 where the nearest distance between the paramagnetic centers is 1.07 nm.25 The observed phenomenon denoted these materials as potential candidates for applications in quantum information processing.
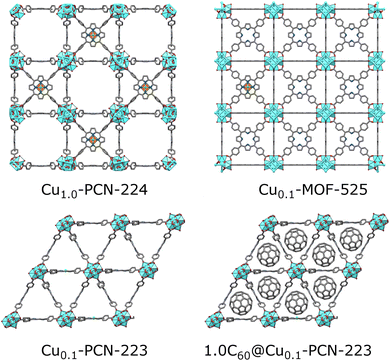 | ||
| Fig. 1 Porphyrinic Zr-MOFs considered for quantum information processing application; six-coordinated PCN-224 with a low population of linkers allowed for dense Cu(II) spin-arrays (orange-green polyhedra in the center of porphyrin moiety).4 MOF-525 and PCN-223 involved in this study are twelve-coordinated, with a dense population of mixed TCPP linkers involving 10 percent of Cu(II)-TCPP, which may lead to better stability of materials. The introduction of fullerene steers the formation exclusively towards the PCN-223 framework, with the fullerene populating the voids of the MOF. | ||
An interesting strategy for manipulating the coherence among the spin carriers in framework materials is an introduction of guests that influence the framework properties and affect the height of the energy barrier, which may positively influence the T1-relaxation time.30,31 Our recent work showed that the introduction of C60 fullerene to sodalite ZIF-8 framework resulted in the stiffening of the framework and increased resistance to electromagnetic radiation, which depended on the ratio of the encapsulated fullerene.32 Here, we choose fullerene as an almost nuclear spin-free to reduce spin pollution, possibly increase the rigidity of the framework, and influence Tm. The fullerene as a solid guest was also chosen to avoid a need for frozen CS2 suspensions as reported by Freedman's group13 or challenges related to the activation and removal of spin-pollutants in MOFs.33
Here, the presented study focuses on the modulation of copper(II)-porphyrin qubit properties in the MOF-525 and PCN-223 polymorphic pair by diluting the spin carriers in the MOF structure and encapsulating the fullerene in the cavities of these spin-active frameworks. Whereas the proper distancing of the spin centers in MOFs is a well-known prerequisite for establishing coherence among the molecular spin carriers, where the MOF-525 showed to be advantageous, we are particularly interested to see how the controllable incorporation32 of a nanosized functional guest such as C60 fullerene within the channels of formed molecular spin-based qubit will be reflected on the coherence of the spin arrays in the robust and non-activated MOF samples.34
While previously MOF-525 was the predominant product of solution and mechanochemical syntheses,25 the introduction of fullerene inverts the selectivity of framework formation towards rarer PCN-223 polymorph, with the fullerene serving as a template and residing in triangular channels along the crystallographic c axis (Fig. S2†). For this study, we also prepared two fulleretic molecular spin-based qubits PCN-223 frameworks with different amounts of encapsulated C60 fullerene. The CW-ESR spectra analyses unravel magneto-structural characteristics of the copper-porphyrin qubit environment, including the local symmetry of the copper center in terms of g and hyperfine A tensors for both diluted molecular spin-based qubits. Besides direct measuring of spin-relaxation times, other pulsed ESR experiments were performed, such as HYSCORE and Rabi oscillations, to gain relevant information about the interactions with the environment's nuclei. The experimental and theoretical results point towards the multifunctional role of the fullerene for the prolongation of coherence times among the spin carriers, involving the reduction of spin noise and altering the spin–phonon interactions.
2 Results and discussion
Synthesis, DFT, IR, solid-state NMR, and CW/pulse ESR studies of 12-connected porpyhrinic zirconium MOF polymorphs, Cu-MOF-525 (cubic, ftw), Cu-PCN-223 (hexagonal, shp) and their composites, are presented. The copper(II) ratio in the porphyrin centers of the synthesized MOFs was diluted to 10% copper(II) as the copper(II)–copper(II) interactions cause line broadening in CW-ESR and destroy electron spin coherence in pulse ESR.2.1 Synthesis
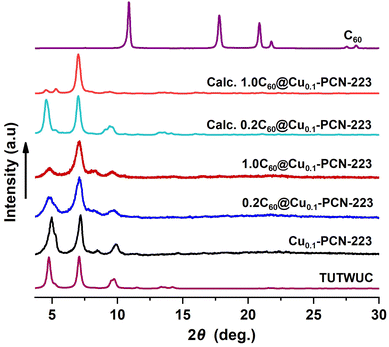
Our group recently reported the synthesis and controlled topology transformation of metallated and metal-free MOF-525 and PCN-223 by mechanochemistry.25 The here investigated multivariate Cu0.1-MOF-525 and Cu0.1-PCN-223 frameworks were synthesized in the same manner, with the difference that the CuTCPP and H2TCPP ligands were milled together in the desired ratio before the introduction of the zirconium source and the MOF formation, to ensure the homogeneous distribution of the diluted CuTCPP in the framework. The mechanochemical formation reactions are almost quantitative, yielding the insoluble MOF product without other H2TCPP byproducts observable in the PXRD of the crude product. The washing of the product is colorless, which further points towards the high efficiency of these reactions (the H2TCPP gives highly colored solutions even in low concentrations). A controlled amount of fullerene C60 (20 and 100 mol%) was successfully encapsulated into Cu0.1-PCN-223 using the one-pot liquid-assisted grinding (LAG) MOF formation.32 Noteworthy, in our previous work, the MOF-525 was predominant product, and PCN-223 polymorph could be obtained only in specific reaction conditions.25Interestingly, the presence of C60 in the reaction mixture drives the formation exclusively towards hexagonal shp-C60@Cu0.1-PCN-223 polymorph, even with the reaction conditions that would in all cases afford the cubic ftw-Cu0.1-MOF-525 phase.25 C60 thus acted as a template providing the C60@Cu0.1-PCN-223 composite, and no traces of MOF-525 have been detected in any product. Tentatively, the arrangement of the linkers and channel size of PCN-223 polymorph is more suitable for encapsulating C60. While the similar templating effect of C60 has been reported previously on tuning the cavity size of multi-porphyrin macrocycles,35 no similar effect has been, to the best of our knowledge, reported for any zirconium carboxylate framework. The washing of the crude milling product was almost colorless, indicating, together with the FTIR and PXRD analyses, that the C60 guest was included in the pores of the frameworks in its entirety. After the C60 capture, DMF is still present in the pores of the products, but in a lower amount than in the non-fulleretic analogs (Fig. S3†). The PCN-223 structure has voids along the crystallographic a-axis that are too narrow for the accommodation of C60, but suitable for smaller DMF molecules (Fig. S2†).
Synthesized MOFs and MOF composites are phase-pure and highly crystalline, and no free fullerene is visible in products after washing (Fig. 2). The disappearance of C60 peaks in the PXRD patterns confirms the absence of C60 crystals on the surface of MOF composites. PXRD data also provide a qualitative measure of the encapsulation of C60 within the PCN-223 framework. The intensity of the low angle peak, 2θ = 4.80, decreases due to the modified electron density in the MOF cage as a result of loading C60 in the channels of PCN-223 framework,32,36 which is also corroborated here by DFT. Calculated PXRD data closely matched the experimentally observed PXRD data, supporting the reduction of the low-angle peak intensity (Fig. 2), which is the effect of guest inclusion into the cage, similar to the previously observed behavior in fulleretic ZIF-8 hybrids.32 The weak Bragg reflection occurring in the fulleretic MOFs derived from the DFT study (please see Section 2.2) and not clearly visible in experimental data is likely due to the fullerene being fixed in one position, while the spectroscopic and computational studies suggest it to be heavily rotationally disordered.
Due to hard-to-control defects in the MOF structures and the dynamic nature of the MOF pore content that can exchange with the atmosphere, the analysis of MOFs composition is a demanding task, which is, for example, best visible in the problems related to the determination of one of the most researched and essential features of MOFs, their porosity.37 Zirconia porphyrin MOFs are not an exemption, showing up to 40% of missing linker defects without the collapse of the MOF structure.38 For the samples prepared in this work, the elemental analysis showed missing linkers defects in all products, an increase in carbon content, and a decrease in the hydrogen and nitrogen content after the encapsulation of fullerene. Here however, we primarily aimed to determine the ratio of copper to zirconium to establish whether the targeted implementation of the 10% of copper(II) spin carriers to the framework was successful since the variation in copper(II) content can affect the Tm. To quantify the Cu/Zr ratio in the studied multivariate MOFs and establish the C60 content in their pores, we performed inductively coupled plasma mass spectrometry (ICP-MS) and energy dispersive X-ray spectroscopy on a Cs-probe corrected transmission electron microscope (EDAX-TEM) analyses (Fig. S1†).
ICP-MS data found the molar ratio of Zr(IV)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu(II) to be 18
Cu(II) to be 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for C60@Cu0.1-PCN-223 (20
1 for C60@Cu0.1-PCN-223 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 estimated), 1.92
1 estimated), 1.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for C60@Cu1.0-PCN-223 (2
1 for C60@Cu1.0-PCN-223 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 estimated), and 20
1 estimated), and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for fullerene-free Cu0.1-MOF-525 (20
1 for fullerene-free Cu0.1-MOF-525 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 estimated). The analysis showed ca. 10-fold lower quantity of Cu(II) spin carriers in the framework with diluted Cu(II) spin carriers, C60@Cu0.1-PCN-223. Also, the absolute values of Zr(IV) and Cu(II) in the fulleretic frameworks confirmed the high loading of C60 in the framework, as can be seen by the differences in the Zr(IV) and Cu(II) content established for C60 encapsulated and C60-free MOF frameworks (ESI, Materials and methods†). The deviations from the idealized formulae may be due to the defects in structure and variable content of guests in the framework that we could not remove from the framework by standard activation procedures. EDAX-TEM showed homogeneous distribution of copper(II) spin carriers in both fulleretic phases, the C60@Cu0.1-PCN-223 and C60@Cu1.0-PCN-223 (ESI, Fig. S1†). The relative molar ratio of the Zr/Cu in these samples corresponds well to the ICP-MS analysis, being approximately ten times higher for C60@Cu0.1-PCN-223 than the Zr/Cu for C60@Cu1.0-PCN-223. The absolute values and the carbon content in the frameworks were not possible to estimate by this method due to the samples being collected at the carbon foil influencing the measurement.
1 estimated). The analysis showed ca. 10-fold lower quantity of Cu(II) spin carriers in the framework with diluted Cu(II) spin carriers, C60@Cu0.1-PCN-223. Also, the absolute values of Zr(IV) and Cu(II) in the fulleretic frameworks confirmed the high loading of C60 in the framework, as can be seen by the differences in the Zr(IV) and Cu(II) content established for C60 encapsulated and C60-free MOF frameworks (ESI, Materials and methods†). The deviations from the idealized formulae may be due to the defects in structure and variable content of guests in the framework that we could not remove from the framework by standard activation procedures. EDAX-TEM showed homogeneous distribution of copper(II) spin carriers in both fulleretic phases, the C60@Cu0.1-PCN-223 and C60@Cu1.0-PCN-223 (ESI, Fig. S1†). The relative molar ratio of the Zr/Cu in these samples corresponds well to the ICP-MS analysis, being approximately ten times higher for C60@Cu0.1-PCN-223 than the Zr/Cu for C60@Cu1.0-PCN-223. The absolute values and the carbon content in the frameworks were not possible to estimate by this method due to the samples being collected at the carbon foil influencing the measurement.
We can conclude from these analyses that the mechanochemical formation provided MOFs with the desired ratio of Cu-spin carriers in the framework and the homogeneous distribution at the TEM resolution. It must be noted that we could not completely control the distribution of the CuTCPP in the framework at a molecular level. As in other materials with diluted active spin carriers (for example, defects in nano-diamonds), the controllable implementation of diluted active species to MOFs is still a complex and hard-to-achieve issue. It is possible in some specific cases, for example, when the ligands have different binding functionalities, as in the case of bimetallic MOF-74 formation.29,39 Here, however, Cu-TCPP and H2TCPP have the same binding functionalities and affinity towards zirconium-MOF formation, so their implementation to the framework is largely stochastic. Regardless, the ESR analyses showed efficient separation of copper centers in the formed multivariate MOFs (please see section CW-ESR spectroscopy below).
2.2 DFT study
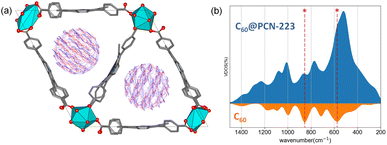
The system size allows a comprehensive DFT study (DFT/PAW/PBE-D, see ESI† for computational details) of the stability and dynamics of the PCN-223 framework with C60 molecules inside. The PCN-223 framework is relatively spacious, and after full optimization, no significant change in the C–C bond parameters of the C60 fullerene itself could be observed. The calculations also reveal a lack of significant affinity of the fullerene molecules toward the MOF framework, and the C60 molecules tend to stay in the middle of the voids.Within the channel, molecules appear to be well isolated from other parallel channels, although the distance between the closest molecules from the adjacent channels is roughly 6 Å (Fig. S2†). At the same time, the distance between the C60 molecules within a single channel is 8 Å, which undermines the possibility of significant electronic interaction between them. High-density fillings would be required to provide significant intermolecular interaction among the fullerenes within the channel. Further investigation of the system using the DFTB/MD method reveals that molecules can freely rotate on-site (Fig. 3a). Fig. 3a shows the time-averaged trajectory of the carbon cage atoms along the 100 picosecond trajectory while the vibrational densities of states are shown in Fig. 3b. The time-averaging smooths out continuous molecular motion along with the principal components of rotations. Within the channel, such a rotation would undoubtedly lead to a sizeable disorder. The aforementioned dense packing might partially prevent intense rotations.
2.3 FTIR-ATR spectroscopy
FTIR-ATR data of Cu0.1-MOF-525, Cu0.1-PCN-223, and (20% and 100%), C60@Cu0.1-PCN-223 are consistent with their counterparts in the literature.25 The appearance of a new vibrational peak at 526 cm−1 with a slight shift in the spectrum of (20% and 100%) C60@Cu0.1-PCN-223 is clearly assigned to the most dominant vibration signal of pristine C60, at 523 cm−1, proving the incorporation of C60 into the framework while the other vibration peaks of pristine C60 overlap with the framework features (Fig. S3†). The FTIR data reveals the presence of formamide solvent in the framework.2.4 NMR spectroscopy
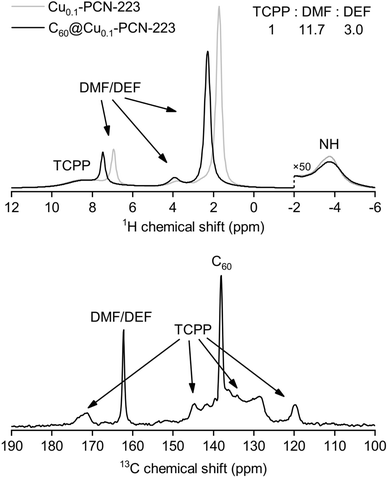
The results of solid-state NMR spectroscopy are presented in Fig. 4. Peak assignment was performed from the analysis of CPMAS and HETCOR spectra (Fig. S4 and S5†). The signal of 13C nuclei of C60 in the C60@Cu0.1-PCN-223, appearing at ca. 138 ppm, is narrow, suggesting that fullerene is free-standing and rotating inside the MOF channels. Any stronger anisotropic interaction with proximal paramagnetic copper centers is thus motionally averaged out. In the sodalite zeolitic-imidazolate-framework-8, fullerene was completely immobilized in the discrete voids of the framework, and its inclusion led to the stiffening of the framework.32 Here, the 13C MAS NMR spectra of C60@Cu0.1-PCN-223 in the region between 125 ppm and 135 ppm, and at about 145 ppm show that the incorporation of C60 to the PCN-223 framework leads to small shifts in the TCPP signal position, but it is hard to determine the precise effect of the C60 inclusion on the framework properties. 1H and 13C MAS recorded for 1.0C60@Cu1.0-PCN-223 corroborate that the DMF and DEF used for washing and aging are still present within the pores of the network. Moreover, the downfield shifts of the 1H signals suggest that the formamide molecules are either brought closer to the porphyrin rings upon C60 encapsulation or experience a reduced chemical shift averaging effect due to their motion being impeded by the encapsulated fullerenes.402.5 CW-ESR spectroscopy
CW-ESR spectra of various MOFs recorded at 40 K showing axial symmetry are presented in Fig. 5. It can be noticed that both Cu0.1-MOF-525 and Cu0.1-PCN-223 exhibit typical CW-ESR spectra of the diluted copper porphyrin monomers (Fig. 5a).28,41 The strong hyperfine coupling of the unpaired electron spin with the copper nuclear magnetic moment (I = 3/2) results in four lines, three of which are resolved in the low-field part of the spectrum. In comparison with the previously reported ESR spectra, which did not reflect the interaction with four nitrogen atoms from the porphyrin macrocycle in the first derivation of the absorption ESR spectra due to the high copper concentration (100% Cu, Cu1.0-PCN-223),25 here presented data exhibit strong modulation of the high-field part of the spectrum (Fig. 5a). This superhyperfine interaction in the ESR spectra of a sample with a lower concentration of copper ions (10% Cu) provides evidence of the capability of mechanochemical procedures to dilute metal ions in the molecular framework in a largely controllable manner.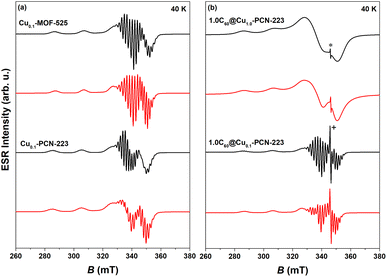 | ||
| Fig. 5 Experimental (black) and simulated CW-ESR spectra (red) of various MOFs recorded at 40 K: (a) Cu0.1-MOF-525 and Cu0.1-PCN-223, (b) 1.0C60@Cu1.0-PCN-223 and 1.0C60@Cu0.1-PCN-223. Asterisk in the figure indicates the fullerene-radical (FR) signal at g ≈ 2.003 while “+” denotes truncation of the peak. Parameters of the simulated spectra are reported in Table S1.† | ||
The experimental spectra were simulated using EasySpin software42 assuming axial symmetry of g tensor and A hyperfine tensor while all four nitrogen atoms in the porphyrin ring were assumed to be equivalent.43 In specific, the tensor components g‖ and A‖ correspond to the orientation perpendicular to the porphyrin plane while g⊥ and A⊥ represent planar, plane orientation.4 In the interaction of the copper electron spin (S = 1/2) with the copper nucleus spin (ICu = 3/2) the same hyperfine coupling for natural-abundance mixture of copper isotopes (63Cu and 65Cu) was assumed.41 Therefore, the following spin-Hamiltonian for copper electron spin was used:
| HCu = μBBgS + SACuICu + SANIN | (1) |
The simulation parameters42 and the corresponding spectra are given in Table S1† and Fig. 5b. The obtained data are in accordance with the NMR and DFT studies and the literature stating that encapsulated fullerene is free-standing inside the cage.32
2.6 Pulse ESR spectroscopy
Two-pulse echo detected field-swept ESR spectra of various MOFs were recorded at 80 K in order to assign the spectral positions for relaxation time measurements in pulsed ESR experiments (Fig. 6a). Two Cu(II) magnetic field resonances were chosen, which correspond to two principles g-tensor values g‖ = 2.2 and g⊥ = 2.06.4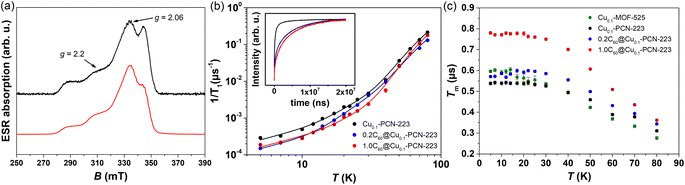 | ||
| Fig. 6 (a) Experimental (black) and simulated (red) two-pulse echo detected field-swept ESR spectrum of Cu0.1-PCN-223 recorded at T = 80 K. The tensor values g‖ = 2.2 and g⊥ = 2.06 labeled by arrows indicate the magnetic field spectral positions at which spin dynamics was undertaken. (b) Temperature dependence of the electron spin–lattice relaxation rate, 1/T1, of Cu0.1-PCN-223 (black), 0.2C60@Cu0.1-PCN-223 (blue) and 1.0C60@Cu0.1-PCN-223 (red) measured at g‖ spectral position. Full lines denote best-fits of the experimental data according to the eqn (2) with the parameters given in Table 1. In the inset to the figure, magnetization recovery curves are given in the inversion recovery experiment detected at 5 K. (c) Temperature dependence of the electron-spin phase-memory relaxation time, Tm, in various MOFs at g‖ spectral position. | ||
The fullerene encapsulation alters the phonon density of states of the material, affecting thus relaxation times. To understand the experimental data, various mechanisms transferring the spin excitation energy to the crystal lattice were considered. Since no thermally accessible electronic excited states are expected for copper(II) complexes, the Orbach-Aminov mechanism was neglected.48,49 Finally, three main processes of the spin–lattice relaxation rate, 1/T1, were assigned to adequately reproduce the experimental data: direct one-phonon, two-phonon Raman, and local mode-mediated processes.48 In this context, assuming the Debye type of phonon spectrum, experimental 1/T1 values were fitted according to equation48,50
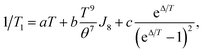 | (2) |
| Compound | g position | a, 1/(Kμs) | b, 1/(K2μs) | θ, K | c, 1/μs | Δ, K | R 2 |
|---|---|---|---|---|---|---|---|
| Cu0.1-MOF-525 | g ‖ | (3.2 ± 0.3)10−5 | (4 ± 2)10−5 | 77 ± 22 | 7 ± 4 | 285 ± 35 | 0.999683 |
| Cu0.1-MOF-525 | g ⊥ | (6.±1)10−5 | (4 ± 2)10−5 | 66 ± 35 | 9 ± 4 | 292 ± 31 | 0.999429 |
| Cu0.1-PCN-223 | g ‖ | (5.1 ± 0.3)10−5 | (3 ± 1)10−5 | 74 ± 18 | 5 ± 2 | 273 ± 26 | 0.99984 |
| Cu0.1-PCN-223 | g ⊥ | (8.6 ± 0.7)10−5 | (4.0 ± 0.9)10−5 | 67 ± 19 | 7 ± 2 | 290 ± 20 | 0.99979 |
| 0.2C60@Cu0.1-PCN-223 | g ‖ | (2.9 ± 0.2)10−5 | (3.3 ± 0.7)10−5 | 82 ± 12 | 4 ± 2 | 281 ± 36 | 0.999908 |
| 0.2C60@Cu0.1-PCN-223 | g ⊥ | (6.1 ± 0.9)10−5 | (3 ± 1)10−5 | 77 ± 36 | 5 ± 2 | 280 ± 33 | 0.999775 |
| 1.0C60@Cu0.1-PCN-223 | g ‖ | (3.2 ± 0.2)10−5 | (2 ± 1)10−5 | 94 ± 40 | 6 ± 2 | 289 ± 30 | 0.999683 |
| 1.0C60@Cu0.1-PCN-223 | g ⊥ | (6.1 ± 0.5)10−5 | (2 ± 2)10−5 | 94 ± 44 | 8 ± 3 | 306 ± 28 | 0.999718 |
The results of the fitting presented in Table 1 clearly show that the anisotropy of T1 regarding the spectral positions of g‖ and g⊥ is present in all the samples studied. The analogous anisotropy of T1 data was reported for similar copper porphyrin structures in PCN-224.4,27 Along with the seminal work presented by Eaton's group,52 the very recent work by Kazmierczak and Hadt53 has investigated both experimentally and theoretically a library of Cu(II) and V(IV) complexes exhibiting comparable T1 anisotropy. A theory based on the spin–orbit coupling wave functions and different ligand field contributions at two g-positions successfully reproduced inversion recovery measurements performed at 100 K. It is interesting to note that here observed anisotropy of T1 (Table 1) is most visible in the region of lowest temperatures studied where the direct process is governing the electron spin relaxation.
Additionally, Table 1 shows two main differences between MOF samples with and without fullerene. First, the samples containing fullerene exhibit a smaller value of parameter a than those without fullerene, implying a slowing down of the direct process. Second, related to the Raman process, a considerable trend in Debye temperature towards higher values in the presence of fullerene can be noticed despite large uncertainties of the fitted values. The larger Debye temperature might be related to the combined effect of the increased number of oscillators and the speed of sound upon fullerene incorporation in MOF matrix.54 The values for Debye temperatures obtained here have the same order of magnitude as the value of 102 K found for MOF-5.55 Regarding the local-mode mediated process, energy values of Δ ≈ 280 K (200 cm−1) were obtained (Table 1). This value is too high for the acoustic phonons to be involved, while it is too low to account for the lowest fullerene vibration (270 cm−1). Therefore, we can assume that these modes probably belong to MOF since a similar Δ was found for all the samples irrespective of the incorporation of fullerene. Therefore, we can propose that fullerene encapsulation prolongates T1 relaxation time of copper porphyrin MOFs by slowing down direct and Raman processes.
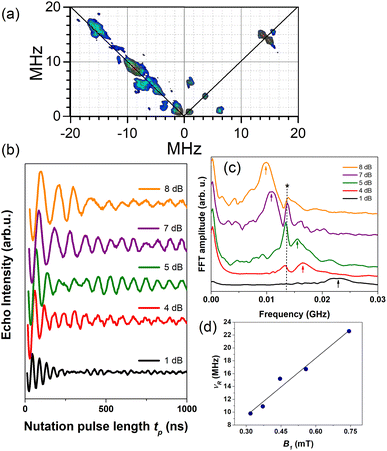 | ||
| Fig. 7 (a) HYSCORE performed at 5 K and g‖ spectral position for 1.0C60@Cu0.1-PCN-223 plotted after data processing. (b) Rabi oscillations recorded for 1.0C60@Cu0.1-PCN-223 at 20 K and g‖ spectral position applying various microwave power attenuation. (c) Fast Fourier transform (FFT) of the Rabi oscillations with an asterisk denoting Larmor frequency of proton spins ≈13.5 MHz while arrows denote Rabi frequencies. (d) Linear dependence of the Rabi frequency, νR, as a function of the oscillating microwave field, B1, calculated according to ref. 63 and 64. | ||
3 Conclusion
In summary, this study shows how the mechanochemical processing accomplished through a robust one-pot ball-milling procedure allowed for control over the ratio of active spin copper(II) carriers and the amount of fullerene C60 guest embedded into the channels of moderately porous porphyrinic zirconium MOFs with twelve-coordinated oxocluster nodes. The use of C60 leads to topological selectivity by governing the formation towards the hard-to-obtain PCN-223 phase, even from reactions that exclusively yield phase-pure cubic MOF-525 polymorph in the absence of fullerene. Here presented experimental evidence points to the possibility of fine-tuning the electron spin relaxation times via fullerene content in the MOF cavity, where an increase in T1 and Tm, detected in MOF fulleretic hybrids, can be directly related to the ratio of the fullerene guest. It should be emphasized that the increase in the electron spin coherence was observed in the presence of solvent guests without the necessity for MOF activation which usually leads to the collapse of the structure. We propose that fullerene encapsulation prolongates both relaxation times of copper porphyrin MOFs, first through the partial exchange of the nuclear spin-bearing solvents with rigid almost nuclear spin-free fullerenes affecting Tm, but also through slowing down direct and Raman processes affecting thus T1. The nutation experiments presenting linear dependence of the Rabi oscillation on the intensity of the oscillating field indicate the possibility of creating an arbitrary superposition of states, proving that coherent manipulation between the electron spin states in the studied fulleretic MOF hybrids can be achieved. In this way, even the non-activated and densely coordinated zirconium-porphyrin frameworks become viable molecular spin qubit matrices, where the inferior and least porous Cu0.1-PCN-223 candidate becomes the best qubit performer after the fullerene inclusion. Using similar solid-state strategies, we aim to test how altering the spin carrier species and including fullerene and endometallofullerene derivatives in more porous zirconium-porphyrinic MOFs, such as MOF-525 and well-established six-coordinated framework PCN-224, will affect their spin coherence properties.Data availability
All the supporting calculation and experimental data is a part of ESI.†Author contributions
The project was conceived and supervised by KU, BK, DŽ, and MK. BK prepared MOF materials and their diluted and composite phases. NC was involved in the synthesis and characterization of ligands. LV, DŽ, and MK performed CW and pulse ESR measurements and analyses. AK and GM conducted, analyzed, and prepared solid-state NMR spectroscopy. MM carried out and analysed energy dispersive X-ray spectroscopy (EDAX) measurements. SMA and AAP conducted DFT (density functional theory) calculations and molecular dynamics (MD) simulations and wrote part of the DFT study. The initial draft of the manuscript was written by DŽ, BK, MK, and KU. BK and LV prepared the figures and graphical abstract. All authors discussed the results and contributed to the final preparation of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported in part by the Croatian Science Foundation through grant IP-2018-01-3168, by the “Research Cooperability” Program of the Croatian Science Foundation funded by the European Union from the European Social Fund under the Operational Programme Efficient Human Resources 2014–2020, through grant PZS-2019-02-4129, and by the DAAD-MZO bilateral project “New generation of magnetic MOF composites based on controllable confinement of selected endofullerenes”. A. K., G. M. and M. M. acknowledge the financial support from the Slovenian Research Agency (research core funding no. P1-0021). A. A. P. thanks Deutsche Forschungsgemeinschaft for financial support (grants PO 1602/6-1 and 1602/11-1). Goran Dražić is acknowledged for the TEM/EDAX mapping measurements.Notes and references
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- C.-J. Yu, M. D. Krzyaniak, M. S. Fataftah, M. R. Wasielewski and D. E. Freedman, Chem. Sci., 2019, 10, 1702–1708 RSC.
- M. J. Graham, J. M. Zadrozny, M. S. Fataftah and D. E. Freedman, Chem. Mater., 2017, 29, 1885–1897 CrossRef CAS.
- T. Andlauer and P. Vogl, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 045307–045314 CrossRef.
- S. L. Bayliss, P. Deb, D. W. Laorenza, M. Onizhuk, G. Galli, D. Freedman and D. D. Awschalom, Phys. Rev. X, 2022, 12, 031028–031036 CAS.
- H.-C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673–674 CrossRef CAS PubMed.
- S. Kitagawa, R. Kitaura and S.-I. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375 CrossRef CAS PubMed.
- T. Yamabayashi, M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M. E. Boulon, E. Morra, S. Benci, R. Torre, M. Chiesa, L. Sorace, R. Sessoli and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 12090–12101 CrossRef CAS PubMed.
- S. Kitagawa, Acc. Chem. Res., 2017, 50, 514–515 CrossRef CAS PubMed.
- J. D. Evans, V. Bon, I. Senkovska, H. C. Lee and S. Kaskel, Nat. Commun., 2020, 11, 2690–2701 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. F. Freedman, ACS Cent. Sci., 2015, 1, 488–492 CrossRef CAS PubMed.
- S. Takahashi, I. S. Tupitsyn, J. van Tol, C. C. Beedle, D. N. Hendrickson and P. C. E. Stamp, Nature, 2011, 476, 76–79 CrossRef CAS PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E-Freedman, R. H. Goldsmith, T. G. III, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem, 2020, 4, 490–504 CrossRef CAS PubMed.
- W. Morris, B. Volosskiy, S. Demir, F. Gándara, P. L. McGrier, H. Furukawa, D. Cascio, J. F. Stoddart and O. M. Yaghi, Inorg. Chem., 2012, 51, 6443–6445 CrossRef CAS PubMed.
- D. Feng, W.-C. Chung, Z. Wei, Z.-Y. Gu, H.-L. Jiang, Y.-P. Chen, D. J. Darensbourg and H.-C. Zhou, J. Am. Chem. Soc., 2013, 135, 17105–17110 CrossRef CAS PubMed.
- J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850–13851 CrossRef PubMed.
- J. E. Mondloch, M. J. Katz, N. Planas, D. Semrouni, L. Gagliardi, J. T. Hupp and O. K. Farha, Chem. Commun., 2014, 50, 8944–8946 RSC.
- X. Liu, N. K. Demir, Z. Wu and K. Li, J. Am. Chem. Soc., 2015, 137, 6999–7002 CrossRef CAS PubMed.
- H. Wu, Y. S. Chua, V. Krungleviciute, M. Tyagi, P. Chen, T. Yildirim and W. Zhou, J. Am. Chem. Soc., 2013, 135, 10525–10532 CrossRef CAS PubMed.
- M. J. Katz, Z. J. Brown, Y. J. Colón, P. W. Siu, K. A. Scheidt, R. Q. Snurr, J. T. Hupp and O. K. Farha, Chem. Commun., 2013, 49, 9449–9451 RSC.
- A. Urtizberea, E. Natividad, P. J. Alonso, M. A. Andrés, I. Gascón, M. Goldmann and O. Roubeau, Adv. Funct. Mater., 2018, 28, 1801695–1801710 CrossRef.
- Z. Chen, S. L. Hanna, L. R. Redfern, D. Alezi, T. Islamoglu and O. K. Farha, Coord. Chem. Rev., 2019, 386, 32–49 CrossRef CAS.
- B. Karadeniz, D. Žilić, I. Huskić, L. S. Germann, A. M. Fidelli, S. Muratović, I. Lončarić, M. Etter, R. E. Dinnebier, D. Barišić, N. Cindro, T. Islamoglu, O. K. Farha, T. Friščić and K. Užarević, J. Am. Chem. Soc., 2019, 141, 19214–19220 CrossRef CAS PubMed.
- J. M. Zadrozny, A. T. Gallagher, T. D. Harris and D. F. Freedman, J. Am. Chem. Soc., 2017, 139, 7089–7094 CrossRef CAS PubMed.
- C.-J. Yu, S. von Kugelgen, M. D. Krzyaniak, W. Ji, W. R. Dichtel, M. R. Wasielewski and D. E. Freedman, Chem. Mater., 2020, 32, 10200–10206 CrossRef CAS.
- S. Richert, J. Cremers, H. L. Anderson and C. R. Timmel, Chem. Sci., 2016, 7, 6952–6960 RSC.
- T. Stolar and K. Užarević, CrystEngComm, 2020, 22, 4511–4525 RSC.
- X. Zhang, V. Vieru, X. Feng, J.-L. Liu, Z. Zhang, B. Na, W. Shi, B.-W. Wang, A. K. Powell, L. F. Chibotaru, S. Gao, P. Cheng and J. R. Long, Angew. Chem., Int. Ed., 2015, 54, 9861–9865 CrossRef CAS PubMed.
- J. Vallejo, F. R. Fortea-Pérez, E. Pardo, S. Benmansour, I. Castro, J. Krzystek, D. Armentano and J. Cano, Chem. Sci., 2016, 7, 2286–2293 RSC.
- V. Martinez, B. Karadeniz, N. Biliškov, I. Lončarić, S. Muratović, D. Žilić, S. A. Avdoshenko, M. Roslova, A. A. Popov and K. Užarević, Chem. Mater., 2020, 32, 10628–10640 CrossRef CAS.
- J. L. Woodliffe, R. S. Ferrari, I. Ahmed and A. Laybourn, Coord. Chem. Rev., 2021, 428, 213578 CrossRef CAS.
- L. Sun, L. Yang, J.-H. Dou, J. Li, G. Skorupskii, M. Mardini, K. O. Tan, T. Chen, C. Sun, J. J. Oppenheim, R. G. Griffin, M. Dincă and T. Rajh, J. Am. Chem. Soc., 2022, 144, 19008–19016 CrossRef CAS PubMed.
- A. R. Mulholland, C. P. Woodward and S. J. Langford, Chem. Commun., 2011, 47, 1494–1496 RSC.
- D.-Y. Zheng, E.-X. Chen, C.-R. Yeab and X.-C. Huang, J. Mater. Chem. A, 2019, 7, 22084–22091 RSC.
- J. W. M. Osterrieth, J. Rampersad, D. Madden, N. Rampal, L. Skoric, B. Connolly, M. D. Allendorf, V. Stavila, J. L. Snider, R. Ameloot, J. a. Marreiros, C. Ania, D. Azevedo, E. Vilarrasa-Garcia, B. F. Santos, X.-H. Bu, Z. Chang, H. Bunzen, N. R. Champness, S. L. Griffin, B. Chen, R.-B. Lin, B. Coasne, S. Cohen, J. C. Moreton, Y. J. Colón, L. Chen, R. Clowes, F.-X. Coudert, Y. Cui, B. Hou, D. M. D'Alessandro, P. W. Doheny, M. Dinca, C. Sun, C. Doonan, M. T. Huxley, J. D. Evans, P. Falcaro, R. Ricco, O. Farha, K. B. Idrees, T. Islamoglu, P. Feng, H. Yang, R. S. Forgan, D. Bara, S. Furukawa, E. Sanchez, J. Gascon, S. Telalović, S. K. Ghosh, S. Mukherjee, M. R. Hill, M. M. Sadiq, P. Horcajada, P. Salcedo-Abraira, K. Kaneko, R. Kukobat, J. Kenvin, S. Keskin, S. Kitagawa, K.-i. Otake, R. P. Lively, S. J. A. DeWitt, P. Llewellyn, B. V. Lotsch, S. T. Emmerling, A. M. Pütz, C. Martí-Gastaldo, N. M. Padial, J. García-Martínez, N. Linares, D. Maspoch and J. A. Suárez, Adv. Mater., 2022, 34, 2201502–2201524 CrossRef CAS PubMed.
- S. M. Shaikh, P. M. Usov, J. Zhu, M. Cai, J. Alatis and A. J. Morris, Inorg. Chem., 2019, 58, 5145–5153 CrossRef CAS PubMed.
- G. Ayoub, B. Karadeniz, A. J. Howarth, O. K. Farha, I. Đilović, L. S. Germann, R. E. Dinnebier, K. Užarević and T. Friščić, Chem. Mater., 2019, 31, 5494–5501 CrossRef CAS.
- M. Yamashina, Y. Tanaka, R. Lavendomme, T. K. Ronson, M. Pittelkow and J. R. Nitschke, Nature, 2019, 574, 511 CrossRef CAS PubMed.
- C. Finazzo, C. Calle, S. Stoll, S. Doorslaer and A. Schweiger, Phys. Chem. Chem. Phys., 2006, 8, 1942–1953 RSC.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- P. Basu, J. Chem. Educ., 2001, 78, 666–669 CrossRef CAS.
- K. L. Cunningham, K. M. McNett, R. A. Pierce, K. A. Davis, H. H. Harris, D. M. Falck and D. R. McMillin, Inorg. Chem., 1977, 36, 608–613 CrossRef.
- V. Gómez-Vidales, A. Borja-Miranda, S. Cortez-Maya, O. Amelines-Sarria, M. Rivera and M. Martínez-García, Open Chem. J., 2016, 3, 25–34 CrossRef.
- D. Dubois, G. Moninot, W. Kutner, M. T. Jones and K. M. Kadish, J. Phys. Chem., 1992, 96, 7137–7145 CrossRef CAS.
- K. M. Kadish and M. M. Morrison, Bioinorg. Chem., 1977, 7, 107–115 CrossRef CAS PubMed.
- Y. Zhou, B. E. Bowler, G. R. Eaton and S. S. Eaton, J. Magn. Reson., 1999, 139, 165–174 CrossRef CAS PubMed.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275 RSC.
- M. Kveder, D. Merunka, M. Jokić, J. Makarević and B. Rakvin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 052201–052205 CrossRef.
- N. P. Kazmierczak, R. Mirzoyan and R. G. Hadt, J. Am. Chem. Soc., 2021, 143, 17305–17315 CrossRef CAS PubMed.
- J.-L. Du, G. R. Eaton and S. S. Eaton, J. Magn. Reson., Ser. A, 1995, 117, 67–72 CrossRef CAS.
- N. P. Kazmierczak and R. G. Hadt, J. Am. Chem. Soc., 2022, 144, 20804–20814 CrossRef CAS PubMed.
- C. Kittel, Introduction to Solid State Physics, John Wiley, New York, Chichester, Brisbane, Toronto, Singapore, 7th edn, 1996 Search PubMed.
- B. Huang, Z. Ni, A. Millward, A. McGaughey, C. Uher, M. Kaviany and O. Yaghi, Int. J. Heat Mass Transfer, 2007, 50, 405–411 CrossRef CAS.
- R. Mirzoyan, N. P. KazmierczakRyan and R. G. Hadt, Chem.–Eur. J., 2021, 27, 9482 CrossRef CAS PubMed.
- C. Finazzo, C. Calle, S. Stoll, S. Van Doorslaer and A. Schweiger, Phys. Chem. Chem. Phys., 2006, 8, 1942–1953 RSC.
- D. Gourier, O. Delpou, A. Bonduelle, L. Binet, I. Ciofini and H. Vezin, J. Phys. Chem. B, 2010, 114, 3714–3725 CrossRef CAS PubMed.
- C. S. Burns, E. Aronoff-Spencer, C. M. Dunham, P. Lario, N. I. Avdievich, W. E. Antholine, M. M. Olmstead, A. Vrielink, G. J. Gerfen, J. Peisach, W. G. Scott and G. L. Millhauser, Biochemistry, 2002, 41, 3991–4001 CrossRef CAS PubMed.
- S. Van Doorslaer and E. Vinck, Phys. Chem. Chem. Phys., 2007, 9, 4620–4638 RSC.
- Y. Deligiannakis, M. Louloudi and N. Hadjiliadis, Coord. Chem. Rev., 2000, 204, 1–112 CrossRef CAS.
- K. I. Silva, B. C. Michael, S. J. Geib and S. Saxena, J. Phys. Chem. B, 2014, 118, 8935–8944 CrossRef CAS PubMed.
- G. R. Eaton, S. S. Eaton, R. W. Quine, D. Mitchell, V. Kathirvelu and R. T. Weber, J. Magn. Reson., 2010, 205, 109–113 CrossRef CAS PubMed.
- G. Jeschke, in Instrumentation and Experimental Setup, Springer US, Boston, MA, 2007, pp. 17–47 Search PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. F. Freedman, J. Am. Chem. Soc., 2014, 136, 15841–15844 CrossRef CAS PubMed.
- L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016, 7, 2074–2083 RSC.
- Y.-H. Fang, Z. Liu, Y.-X. Wang, S. Zhou, S.-D. Jiang and S. Gao, Inorg. Chem. Front., 2020, 7, 3875–3881 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and additional characterization. See DOI: https://doi.org/10.1039/d3sc03089j |
| This journal is © The Royal Society of Chemistry 2023 |