Mesomerism induced temperature-dependent multicomponent phosphorescence emissions in ClBDBT

Abstract

Quantum mechanics/molecular mechanics (QM/MM) and molecular dynamics (MD) methods were applied to systematically investigate the temperature-dependent phosphorescence emission of dibenzo[b,d]thiophen-2-yl(4-chlorophenyl)methanone (ClBDBT) and its derivatives. The calculated temperature-dependent spectra on the lowest triplet state (T₁) are in good agreement with the experimental observations, which means that the two-component white light emission should stem from the T₁ state. The further MD simulations demonstrate the existence of two mesomerism structures at room temperature which can emit two lights simultaneously. The multi-component light emissions induced by mesomerism structures have advantages in balancing the distribution of excitons which could be beneficial to obtain pure white light along with stable Commission Internationale de l'Éclairage (CIE) coordinates. We hope this mesomerism concept can be further used to design new white light emitters based on room-temperature phosphorescence.

---

1 Introduction

Single molecule white light emitters (SMWLEs),^1,2 which can be used to replace multiple emitters, have drawn extensive attention due to their superior properties of no phase segregation, no color aging, and good reproducibility.^3–7 Recently, purely organic SMWLEs by using room temperature phosphorescence (RTP) and aggregation-induced emission (AIE) are becoming a hot topic due to their longer emission lifetime and unique material characteristics.^8–10 However, it is still a great challenge to achieve efficient purely organic RTP SMWLEs.¹ Broadly speaking, when designing RTP white light materials, one needs to address the following three issues, the first relies on the large spin–orbit coupling (SOC) to afford efficient intersystem crossing (ISC) to generate the RTP phosphorescence;^9,11,12 the second is to simultaneously emit multi-component light, such as three primary colours (red, green and blue) or two complementary colours (e.g. blue and orange);^3,13 the last one is that the distribution of excitons to generate the multi-component light should be balanced, which can result in pure white light along with stable Commission Internationale de l'Éclairage (CIE) coordinates.¹ Current studies on RTP white light molecules focus on the first issue, while the last two issues are hard to manipulate for both theoretical and experimental chemists.¹ As far as we know, up to now, only a few molecules, including dibenzo[b,d]thiophen-2-yl(4-chlorophenyl)methanone (ClBDBT),³ (4-bromophenyl)(4-chlorophenyl)methanone (BCBP),³ 5-bromo-2-(4-(trifluoromethyl)phenyl)isoindoline-1,3-dione (ImBr),¹⁴ dibenzo[a,c]phenazine (DPPZ),¹³ and 1,2,3,4-tetraphenyloxazolium bromide (Top-Br),¹⁵ have been reported as RTP white light materials. However, in many cases, successful identification of white light emission should be attributed to accidental observations rather than deliberate molecular design.⁸

In these purely organic RTP white light molecules, the first proposed ClBDBT-based AIE-active luminophores can be denoted as the prototype for RTP white light materials.³ In ClBDBT, the theoretical study assigned the two emission bands, which could be mixed to generate white light, to the two low-lying triplet excited states, T₁ and T₂, respectively.³ More importantly, they also found a temperature dependence of spectral shape in ClBDBT. At room temperature, ClBDBT showed two emission bands around 467 and 551 nm. When the temperature dropped below 250 K, a new sharp peak emerged around 503 nm in addition to the original two peaks.³ Similarly, the temperature-dependent emission was also found in triphenylamine (TPA) based AIE-active RTP luminophores in which a new peak emerged as the temperature was decreased to 77 K.¹⁶ However, the further theoretical investigations indicated that the multicomponent emission bands at 77 K were attributed to different local minima in the lowest triplet state (T₁). In this discussion, the origin of temperature-dependent multi-component emissions is still unclear and more theoretical investigations are needed to bring out the essentials of RTP multi-component emitters.

In this work, the temperature-dependent RTP of ClBDBT will be illustrated from a mesomerism point of view by the combination of electronic structure calculations and molecular dynamics (MD) simulations. Based on our theoretical investigations, we have proposed a general strategy to obtain multi-component emissions with a balanced distribution of excitons, which can be further used to guide the design of new RTP SMWLEs.

2 Results and discussion

2.1. Low-lying electronic states

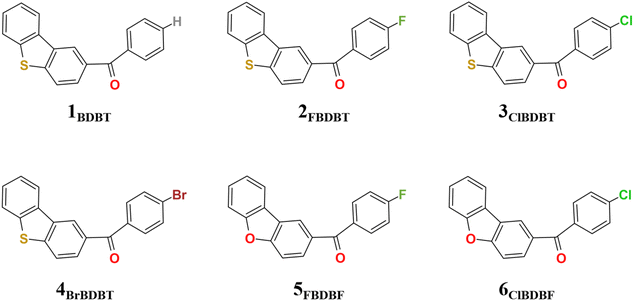
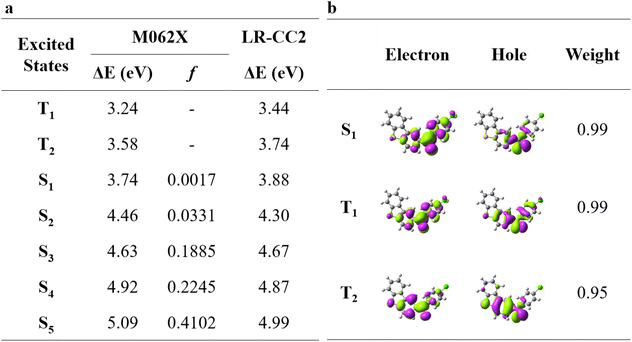
In this work, besides ClBDBT, five additional systems of dibenzo[b,d]thiophen-2-yl(phenyl)methanone (BDBT), dibenzo[b,d]thiophen-2-yl(4-fluorophenyl)methanone (FBDBT), dibenzo[b,d]thiophen-2-yl(4-bromophenyl))methanone (BrBDBT), dibenzo[b,d]furan-2-yl(4-fluorophenyl)methanone (FBDBF) and dibenzo[b,d]furan-2-yl(4-chlorophenyl)methanone (ClBDBF) were also investigated (see Fig. 1). The computed vertical excitation energies of 3_ClBDBT based on the ground state equilibrium geometries for the low-lying excited states can be depicted in Fig. 2, and the results of the other systems are collected in Tables S1–S5.† Through analysis, the experimental absorption spectra (ca. 250–300 nm) of 3_ClBDBT should be assigned to highly singlet excited states (S₂–S₅) according to their large oscillator strengths (f = 0.0331–0.4102), and the calculated vertical excitation energies are 4.46–5.09 eV (244–278 nm) at the M062X17/6-311G** level and 4.30–4.99 eV (248–288 nm) at the CC2 (ref. ¹⁸ and ¹⁹)/cc-pVDZ level, respectively. Meanwhile, the vertical excitation energies from the M062X functional are in good agreement with the ones from the CC2 method, which indicates that the M062X functional is suitable to describe the low-lying electronic states of BDBTs. As shown in Fig. 2b, the lowest singlet excited state (S₁) with a negligible oscillator strength (f = 0.0017) can be denoted as a dark state which can be characterized as the n → π* excitation (1nπ*) by the natural transition orbital (NTO) analysis. Below the S1 state, two low-lying triplet excited states, T₁ and T₂, are found. The NTO analysis suggests that both T₁ and T₂ can be denoted as the mix of n → π* (3nπ*) and π → π* (3ππ*) excitations. The results for the others systems (1_BDBT, 2_FBDBT, 4_BrBDBT, 5_FBDBF, and 6_ClBDBF) show similar trends to 3_ClBDBT (see Fig. S1–S5†).

Fig. 1 Geometrical structures for 1_BDBT, 2_FBDBT, 3_ClBDBT, 4_BrBDBT, 5_FBDBF, and 6_ClBDBF.

Fig. 2 Franck–Condon excitation and the characteristics of low-lying excited states of 3_ClBDBT. (a) The vertical excitation energies (ΔE in eV) and oscillator strengths (f) for the low-lying singlet and triplet excited states computed at the M062X/6-311G** and CC2/cc-pVDZ levels, respectively. (b) Leading NTOs with isovalue = 0.02 involved in S₁, T₁, and T₂ at their respective optimized structures.

2.2. Energy relaxation after Franck–Condon excitation

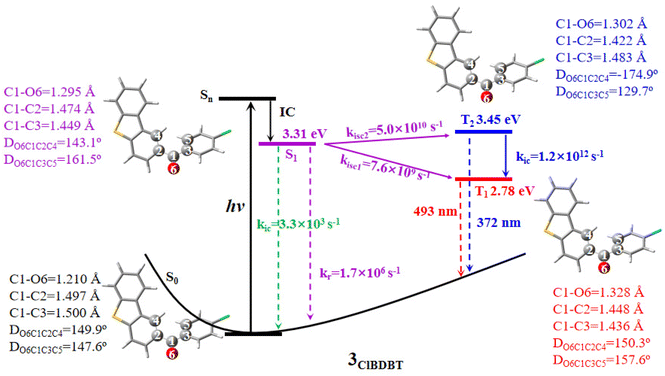
Here we use 3_ClBDBT as an example to illustrate the energy transfer pathway after Franck–Condon (FC) excitation. As shown in Fig. 3, the FC excitation of 3_ClBDBT (the results of other systems can be found in Fig. S6–S10,† respectively) should be assigned to the S_n (n > 1) state (see discussion 2.1.). After the FC excitation, the system can quickly decay to the S₁ state via internal conversion (IC). Below the S₁ state, one can find three low-lying electronic states, T₂, T₁, and S₀. Since both T₁ and T₂ states contain the π → π* components, according to the EI-Sayed rule,²⁰ the ISC channels should not be neglected. And thus, starting from S₁, three possible relaxation processes including S₁ → T₂, S₁ → T₁, and S₁ → S₀ could take place. In order to determine the optimal path, the radiative and nonradiative rates from the S₁ state are computed by MOMAP.^21–23 As shown in Fig. 3, the radiative and nonradiative or internal conversion rates (k_r = 1.7 × 10⁶ s⁻¹ and k_ic = 3.3 × 10³ s⁻¹) for S₁ → S₀ are much smaller than the intersystem crossing rates (k_isc2 = 5.0 × 10¹⁰ s⁻¹ for S₁ → T₂ and k_isc1 = 7.6 × 10⁹ s⁻¹ for S₁ → T₁). This is due to the fact that low frequency vibrational modes, which can induce fast vibrational relaxation, could be restricted in 3_ClBDBT crystals. Consequently, compared to the radiative path, the ISC processes (S₁ → T₂ and S₁ → T₁) are main relaxation channels, and these two ISC pathways have larger SOCs, 32.9 cm⁻¹ for S₁/T₂ and 15.1 cm⁻¹ for S₁/T₁, respectively. More importantly, the T₁ emission band was computed to be around 493 nm by CC2 which falls within the scope of the experimentally observed phosphorescence band (ca. 450–650 nm). However, the T₂ emission band calculated by CC2 is about 372 nm, which is beyond the range of experimentally observed phosphorescent bands.³ Similar results can also be found in 1_BDBT, 2_FBDBT, 4_BrBDBT, 5_FBDBF, and 6_ClBDBF (see Table S6†). In general, if the T₂ state can emit the phosphorescence according to Anti-Kasha’s rule,²⁴ a large energy difference between T₂ and T₁ is required to suppress the quick internal conversion from T₂ to T₁.²⁵ In addition, the IC rate (k_ic) (T₂ → T₁) for 3_ClBDBT is calculated as high as 6.2 × 10¹² s⁻¹, indicating that the T₂ state is not stable and can undergo an ultra-fast IC to reach T₁. In this discussion, the experimentally observed phosphorescence emission bands should be from the T₁ state.

Fig. 3 The adiabatic energy levels, radiative (k_r) and nonradiative (k_ic and k_isc) rates, as well as T₁ and T₂ emission wavelengths for 3_ClBDBT. The ground state energy (−1660.75414666 a.u.) of 3_ClBDBT is set as the reference at the CC2/cc-pVDZ level. The geometrical parameters for some important bonds and dihedral angles are also shown.

2.3. Two RTP emissions

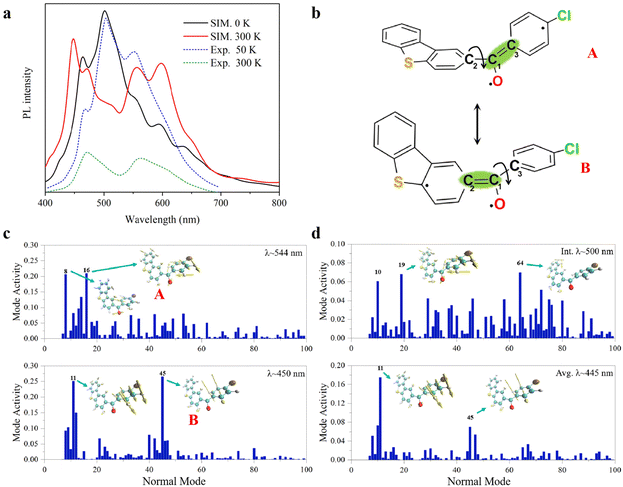
In the T₁ state, the phosphorescence emission spectra of 3_ClBDBT are simulated and shown in Fig. 4a. Considering both computational cost and accuracy, here the phosphorescence spectra are predicted by 50 sampling points with Wigner distribution^26,27 based on the optimized T₁ structure in the crystalline state at low temperature (0 K) and high temperature (300 K), respectively. As shown in Fig. 4a, the simulated spectra at 0 K show a sharp peak at about 500 nm, corresponding to the experimental peak around 503 nm at low temperature (50 K). The structure with the 500 peak has a stable conjugation framework, which is close to the structure of the T₁ minimum of 3_ClBDBT, with a small RMSD value (0.13) (see Fig. S11†). Beside this main peak, two shoulder peaks are also found at about 450 and 544 nm, which are in good agreement with the experimental peaks at about 467 and 551 nm, respectively. As the temperature is increased to 300 K, the intensity of the initial 500 peak is greatly decreased, and meanwhile the intensities of the peaks of 450 and 544 are significantly increased. Finally, two distinguishable bands are generated with ca. 400–500 and ca. 530–650 nm, which is consistent with the two experimental RTP bands at 450–500 nm and ca. 530–650 nm, respectively.³ Besides, the simulated phosphorescence spectra of 1_BDBT, 2_FBDBT, 4_BrBDBT, 5_FBDBF, and 6_ClBDBF were also computed based on Wigner distribution (see Fig. S12†). 1_BDBT, 2_FBDBT, and 4_BrBDBT show a similar trend to 3_ClBDBT, and two emission bands could be observed at room temperature. This is also consistent with experimental observations. However, for 5_FBDBF and 6_ClBDBF, only one band can be observed at room temperature. Thus, the base compounds with dibenzothiophene (BDBTs) should be important for the generation of two emission bands. Here the importance of the dibenzothiophene group can also be understood by two important mesomerism structures (see Fig. 4b). In dibenzothiophene, the sulfur atom could stabilize the radical electron leading two mesomeric structures more stable than the others, and as a result, two emission bands dominated by these two stable mesomeric structures can be observed. Furthermore, in 3_ClBDBT, both the chlorine and sulfur atoms have similar electronegativity, and thus two mesomeric structures are more likely to be coherent and produce white light. In order to reveal the origin of the two RTP bands, take 3_ClBDBT for example, two typical structures A and B with emission wavelengths of 554 and 450 nm (see Fig. 4c), respectively, are selected in Wigner distribution to perform the vibration mode analysis. In addition, an energetic small barrier of ca. 4.0 kcal mol⁻¹ between the two structures can be found by the rotation of the dihedral of C₄C₂C₁O₆ or C₅C₃C₁O₆ (as shown in Fig. S13†). Thus, with such a small barrier, it might be easier to regulate the structures by means of temperature. As shown in Fig. 4b and c, for the A structure, the emission band at 544 nm is mainly produced by the contributions of vibration modes 8 and 16 which can be characterized as the mixture of stretching and torsional motions along the C₁–C₂ bond (see Fig. 4b). While for the B structure, the emission band at 450 nm is mainly generated by the contributions of vibration modes 11 and 45 which can be characterized as the torsion of the C₁–C₃ bond (see Fig. 4b). Consequently, two emission bands at 300 K could be attributed to the two mesomerism structures of ˙O6–C1=C3 (A) and ˙O6–C1=C2 (B), respectively (see Fig. 3b), and the sharp peak at 0 K arises from the stable conjugated structures which are close to the T₁ minimum. In order to clarify the experimental phenomenon that the 500 peak vanishes at 300 K, the combined quantum mechanics and molecular mechanics (QM/MM)²⁸ molecular dynamics (MD) simulations are carried out to illustrate the temperature effect on the peak shape around 500 nm. In the MD simulation of 3_ClBDBT, the initial stable conjugated structure with an emission wavelength of 500 nm is generated from Wigner distribution at the temperature of 0 K and then subjected to the simulation at a high temperature of 300 K with the aim of exploring the time evolution of the conformation. The analysis of the MD trajectory in Fig. S14† shows that the distance between C1 and O6 is gradually increased from 1.17 to 1.33 Å in the first two picoseconds, and then it basically fluctuates around 1.33 Å after two picoseconds, indicating that the C=O double bond has been broken and changed into the C–O single bond when the dynamics is in equilibrium. The other species have similar performance with slight differences in numerical values, as shown in Fig. S15–S19.† More importantly, it is found that the variations of dihedral angles of O₆C₁C₂C₄ and O₆C₁C₃C₅ (see Fig. S20†) show a significant negative correlation, which can also be observed in the other systems (see Fig. S21–S25†). In other words, when one dihedral angle of O₆C₁C₂C₄ is close to 180°, the other dihedral angle of O₆C₁C₃C₅ is slightly deviated from 180°, and vice versa, indicating the existence of the mesomerism structures between ˙O6–C1=C3 (A) and ˙O6–C1=C2 (B), as shown in Fig. 4b. When the dynamic equilibrium is reached, the representative structure is selected from the MD simulation trajectory according to the clustering analysis (see Fig. S26†), and its emission wavelength is calculated to be 445 nm (see Fig. 4d), which is very close to one (450 nm) of the two phosphorescence emission bands. And the subsequent vibration mode analysis for this structure indicates that the emission band at 445 nm has the same coherent activity of the vibrational modes (11 and 45) as the emission band at 450 nm. This indicates that with the increase of temperature, the initial structure with the emission wavelength of 500 nm at 0 K will spontaneously transform into the structure with the emission wavelength of 445 nm. These findings can well illustrate the experimental observations, and two RTP emission bands should be naturally arising from two mesomerism structures A and B in the T₁ state.

Fig. 4 Simulated spectra and vibration analysis, (a) the simulated phosphorescence spectra of 3_ClBDBT with the temperature of 0 K (solid black line) and 300 K (solid red line) in comparison with experimental spectra of 50 K (dot blue line) and 300 K (dot green line); (b) two mesomerism structures of A and B; coherent activity of the vibrational normal modes for (c) structures with PL bands (λ) at ca. 544 and 450 nm, respectively, from Wigner sampling at 300 K. and (d) structures from QM/MM MD simulations at 300 K of initial structure (λ = 500 nm) and the averaged structure (λ = 445 nm). The most active modes are represented as an inset. The simulated spectra are shifted by −0.14 eV in order to be consistent with experimental observations.

3 Conclusion

In summary, the temperature-dependent phosphorescence emissions of 1_BDBT, 2_FBDBT, 3_ClBDBT, 4_BrBDBT, 5_FBDBF, and 6_ClBDBF have been systematically investigated with the QM/MM method and MD simulations. The phosphorescence emission spectra with different temperatures are simulated with Wigner distribution on the T₁ state, and the results for 1_BDBT, 2_FBDBT, 3_ClBDBT, and 4_BrBDBT are in good agreement with the experimental observations in which the middle sharp peak around 500 nm vanishes as the temperature rises from 0 to 300 K, and thus the other two RTP bands, which can be mixed to emit white light, should stem from the T₁ state. The further MD simulations reveal that as the temperature rises from 0 to 300 K, the stable conjugated structure with the emission around 500 nm is broken and changed into the twisted structure. As a result, the three peaks at low temperature turn into two emission bands at room temperature. Furthermore, the simulation trajectory demonstrates the existence of two mesomerism structures at room temperature with emissions around 450 and 544 nm, respectively. These two mesomerism structures are characterized as the bond length alteration (BLA) along the two linked double bonds between the two aromatic rings in 3_ClBDBT. At room temperature, the twist of the two aromatic rings could stabilize the two mesomerism structures, respectively, and the system emits two phosphorescence simultaneously corresponding to the two stable mesomerism diabatic states. More importantly, these two mesomerism structures consist of the same electronic state which could balance the distribution of excitons for the multi-component light emissions, and have the advantage of obtaining the pure white light along with the stable CIE coordinate. We hope this mesomerism concept could be further applied to design other multi-component light emission materials.

4 Computational details

A total of six systems were studied in this work, 1_BDBT, 2_FBDBT, 3_ClBDBT, 4_BrBDBT, 5_FBDBF, and 6_ClBDBF, respectively. Therein, 1_BDBT, 3_ClBDBT, and 4_BrBDBT have crystal structures from experiment, while the others were constructed by substituting O or F atoms in the crystal structure of 3_ClBDBT. Density functional theory (DFT) was used to optimize the structures of the singlet ground state (S₀) and lowest triplet excited state (T₁), while time-dependent functional theory (TDDFT) was used to optimize the structures of singlet (S₁) and triplet (T₂) excited states. The M062X¹⁷ functional with the basis set of 6-311G** was used for the above optimizations, and the same functional and basis set were used for frequency calculations to ensure truly minima with the Gaussian 16 package. Besides M062X/6-311G**, CC2/cc-pVDZ was also used to accurately describe excitation energies with the Molpro2012 package.²⁹ Moreover, the radiative (kr, s-1), nonradiative (knr, s-1), intersystem crossing rates (kisc, s-1) were computed with the MOMAP package,^21,30,31 and the spin–orbit couplings were obtained with the ORCA package.³²

In QM/MM MD simulations, systems with 216 molecules for 1_BDBT, and 108 molecules for 2_FBDBT, 3_ClBDBT, 4_BrBDBT, 5_FBDBF and 6_ClBDBF were manually constructed by simply extending the original crystal cell. And then the system was subjected to the combined quantum mechanics and molecular mechanics molecular dynamics (QM/MM MD) simulation implemented in the Amber package.³³ The missing Amber force field parameters for these four molecules were generated using the Antechamber tool³⁴ on the basis of the GAFF force field.³⁵ Partial charges of all the atoms were computed as Mulliken charges using the Gaussian16 package.³⁶ One molecule at the center of the system was chosen as the QM region and the rest of the system was set to the MM region (see Fig. S27†). During the MD simulation, the molecules in the MM region were fixed and the molecule in the QM region was allowed to move freely. The cutoff value for the calculation of the non-bonded interaction is 999.0 Å to fully consider all the interactions in the current aperiodic model. The temperature of the system was scaled to 300 K by the Langevin thermostat.³⁷ The time step for the MD integration was 1 fs. The total time length of the simulation was 10 ps. The molecule in the QM region was optimized at the M062X/6-311++G** level.¹⁷ The spin multiplicity and charge of the molecule were 3 and 0, respectively.

For the spectra simulation, the structures were generated by the Wigner distribution by using the NEWTON-X 2.2 package.^38,39 For Wigner distribution, the amplitude Q_n and momentum P_n for each normal mode are randomly given from a harmonic oscillator distribution, and then the velocities and Cartesian coordinates for all atoms are generated by the inverse transformation. For the vibration analysis, we project the velocity into each normal mod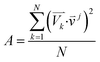e, where [small nu, Greek, vector]^j is the jth normal mode 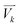is the normalized velocity for the kth structure, and N is the total number of sampling structures.

Data availability

All supporting data are provided in the ESI.†

Author contributions

Z. X. Q. initiated this project. Z. J. Z. contributed to all electronic structure calculations. J. L. Z. contributed to molecular dynamic simulations. Y. J. G. contributed to MOMAP calculations. Z. J. Z. and Z. X. Q. validated all data. Z. J. Z. wrote the original draft, and Z. X. Q. and J. L. Z. reviewed and edited the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported in part by the 2020-JCJQ project (GFJQ2126-007) and the National Natural Science Foundation of China (no. 21873036). We gratefully acknowledge HZWTECH for providing computational facilities.

References

1. Z. Chen, C. L. Ho, L. Wang and W. Y. Wong, Adv. Mater., 2020, 32, e1903269.
2. Y. Wen, H. Liu, S. Zhang, J. Cao, J. De and B. Yang, Adv. Opt. Mater., 2020, 8, 1901995.
3. Z. He, W. Zhao, J. W. Y. Lam, Q. Peng, H. Ma, G. Liang, Z. Shuai and B. Z. Tang, Nat. Commun., 2017, 8, 416.
4. C. Li, J. Liang, B. Liang, Z. Li, Z. Cheng, G. Yang and Y. Wang, Adv. Opt. Mater., 2019, 7, 1801667.
5. T. Ishi-i, H. Tanaka, I. S. Park, T. Yasuda, S.-i. Kato, M. Ito, H. Hiyoshi and T. Matsumoto, Chem. Commun., 2020, 56, 4051–4054.
6. Y. Liu, M. Nishiura, Y. Wang and Z. Hou, J. Am. Chem. Soc., 2006, 128, 5592–5593.
7. S. H. Kim, S. Park, J. E. Kwon and S. Y. Park, Adv. Funct. Mater., 2011, 21, 644–651.
8. N. A. Kukhta and M. R. Bryce, Mater. Horiz., 2021, 8, 33–55.
9. J. Guo, C. Yang and Y. Zhao, Acc. Chem. Res., 2022, 55, 1160–1170.
10. S. Hirata, Adv. Opt. Mater., 2017, 5, 1700116.
11. H. Liu, W. Liu, N. Ando, S. Yamaguchi and H. Zhang, J. Mater. Chem. C, 2021, 9, 2738–2743.
12. W. Zhao, Z. He, J. W. Y. Lam, Q. Peng, H. Ma, Z. Shuai, G. Bai, J. Hao and B. Z. Tang, Chem, 2016, 1, 592–602.
13. C. Zhou, S. Zhang, Y. Gao, H. Liu, T. Shan, X. Liang, B. Yang and Y. Ma, Adv. Funct. Mater., 2018, 28, 1802407.
14. J.-A. Li, J. Zhou, Z. Mao, Z. Xie, Z. Yang, B. Xu, C. Liu, X. Chen, D. Ren, H. Pan, G. Shi, Y. Zhang and Z. Chi, Angew. Chem., Int. Ed., 2018, 57, 6449–6453.
15. J. Wang, X. Gu, H. Ma, Q. Peng, X. Huang, X. Zheng, S. H. P. Sung, G. Shan, J. W. Y. Lam, Z. Shuai and B. Z. Tang, Nat. Commun., 2018, 9, 2963.
16. T. Wang, Z. Hu, X. Nie, L. Huang, M. Hui, X. Sun and G. Zhang, Nat. Commun., 2021, 12, 1364.
17. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
18. D. Kats, T. Korona and M. Schutz, J. Chem. Phys., 2007, 127, 064107.
19. D. Kats, T. Korona and M. Schutz, J. Chem. Phys., 2006, 125, 104106.
20. M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16.
21. Z. Shuai, Chin. J. Chem., 2020, 38, 1223–1232.
22. Z. Shui and Q. Peng, Phys. Rep., 2014, 537, 123–156.
23. Z. Shui and Q. Peng, Natl. Sci. Rev., 2017, 4, 224–239.
24. J. C. del Valle and J. Catalán, Phys. Chem. Chem. Phys., 2019, 21, 10061–10069.
25. P. She, J. Duan, J. Lu, Y. Qin, F. Li, C. Liu, S. Liu, Y. Ma and Q. Zhao, Adv. Opt. Mater., 2022, 10, 2102706.
26. R. Schinke, Photodissociation Dynamics: Spectroscopy and Fragmentation of Small Polyatomic Molecules, Cambridge University Press, Cambridge, 1995.
27. J. P. Dahl and M. Springborg, J. Chem. Phys., 1988, 88, 4535–4557.
28. H. M. Senn and W. Thiel, Atomistic Approaches in Modern Biology: From Quantum Chemistry to Molecular Simulations, 2007, vol. 268, pp. 173–290.
29. H. J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, 3rd, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
30. Z. Shuai and Q. Peng, Natl. Sci. Rev., 2017, 4, 224–239.
31. Z. Shuai and Q. Peng, Phys. Rep., 2014, 537, 123–156.
32. M. A. L. Marques, M. J. T. Oliveira and T. Burnus, Comput. Phys. Commun., 2012, 183, 2272–2281.
33. D. A. Case, T. E. Cheatham III, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr., A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688.
34. J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260.
35. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
37. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
38. M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26–33.
39. M. Barbatti, G. Granucci, M. Ruckenbauer, F. Plasser, R. Crespo-Otero, J. Pittner, M. Persico and H. Lischka, NEWTON-X: A package for Newtonian Dynamics Close to the Crossing Seam (v. 2.2), 2018, available via the internet at: http://www.newtonx.org.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc03963c

---