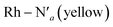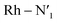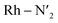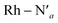Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ligand-centered to metal-centered activation of a Rh(III) photosensitizer revealed by ab initio molecular dynamics simulations†
Iria Bolaño
Losada
and
Petter
Persson
 *
*
Division of Computational Chemistry, Department of Chemistry, Lund University, Box 124, SE-22100 Lund, Sweden. E-mail: petter.persson@teokem.lu.se
First published on 2nd November 2023
Abstract
Excited state evolution of the rhodium(III) complex [Rh(III)(phen)2(NH3)2]2+ (phen = 1,10-phenanthroline) has been investigated theoretically to gain a better understanding of light-driven activation of high-energy metal centered states. Ab initio molecular dynamics (AIMD) simulations show the significance of asymmetric motion on a multidimensional potential energy landscape around the metal center for activated crossover from triplet ligand centered (3LC) to triplet metal centered (3MC) states on picosecond timescales. Significant entropic differences arising from the structural distributions of the 3LC and 3MC states revealed by the simulations are found to favor the forward crossover process. Simulations at different temperatures provide further insight into the interplay between structural and electronic factors governing the 3LC → 3MC dynamics as a concerted two-electron energy transfer process, and the broader implications for photoinduced generation of high-energy 3MC states of interest for emerging photocatalytic applications are outlined.
1 Introduction
Transition metal complexes that combine efficient light-harvesting with long-lived, high-energy excited states are widely used in molecular photocatalysis and related photochemical applications.1–3 Many such photochemical applications have relied on metal-to-ligand charge-transfer (MLCT) excited state schemes, for example with the well-known Ru(II) polypyridyl type of octahedral d6 complexes.4 In contrast, involvement of metal centered (MC) excited states has largely been avoided through various ligand design strategies as their population often leads to undesirable excited state energy losses.3 Utilization of MC excited states for photochemical applications is, however, emerging as an interesting line of research, with the potential to access a unique set of excited state properties.5 This makes it interesting to explore the fundamental photophysical and photochemical properties of suitable prototype complexes in greater detail.5–8 Recent progress utilizing transition metal complexes with photoactivated MC states includes several Cr(III) d3 complexes,9 some Fe(II) d6 complexes,10 as well as a few recent examples of Co(III) d6 complexes.11–14 One concern for the photochemical utilization of 3MC states is the weak absorption of Laport-forbidden direct dd-excitations. One strategy to overcome this limitation is to activate high-energy 3MC states indirectly through energy transfer from another chromophoric unit with better light-harvesting capabilities.8 This can be achieved as an intramolecular activation from an initially excited CT or ligand centered (LC) state. Another challenge with the involvement of MC states in d6 complexes is the population of anti-bonding eg orbitals that frequently causes substantial excited state energy losses, associated with weakened metal–ligand (M–L) bonds.15,16 Activated crossover into high-energy 3MC states following initial LC excitation is, however, known from studies of prototype Rh(III) complexes, as evidenced by experimental observations of dual photoluminescence (PL) from both the 3LC and 3MC states, as well as photochemical quenching experiments involving the 3MC state.17–26 The effect on the relative energy between the 3LC and 3MC and its impact on the state-to-state crossover efficiency was studied experimentally for a series of tris-phenanthroline derivatives, with the general formula [Rh(III)(phen)2XY]n+ (phen = 1,10-phenanthroline), by tuning the ligand field strength.19Quantum chemical simulations offer significant opportunities to gain detailed insight into several different aspects of the excited state evolution of transition metal complexes. A variety of many-state quantum dynamical simulation methods have provided important insights into the ultrafast dynamics associated with initial relaxation processes within a dense manifold of excited states.27–35 Some simulations have also covered the explicit interplay between excited state deactivation processes and solvent relaxation and reorganization processes.36
In this work, we investigate the 3LC → 3MC state crossover activation in the prototype Rh(III) phenanthroline complex, [Rh(phen)2(NH3)2]3+, using ab initio molecular dynamics (AIMD) simulations conducted at the density functional theory (DFT) level. The [Rh(phen)2(NH3)2]3+ complex provides a good prototype system to investigate such 3LC → 3MC crossover dynamics computationally as experimental observations of dual emission in the 170–200 K temperature range point to a favorable 3LC–3MC balance, similar to what has also been reported for the [Rh(III)(phen)3]3+ complex.19,24,37,38 We focus on intramolecular aspects of activated 3LC → 3MC crossover dynamics on picosecond timescales, i.e. excited state dynamics taking place on the lowest excited triplet potential energy surface following any initial ultrafast ISC and IC processes as well as initial local relaxation of the initially populated 3LC state. This provides a largely complementary set of computational challenges compared to many recent studies focused on the earliest ultrafast multi-state relaxation processes, and places a greater focus on accounting for large-scale structural distortions on a complex multidimensional molecular energy landscape on timescales that can extend to tens of picoseconds and longer.
2 Computational details
Full geometry optimizations of structurally distinct relaxed 3LC and 3MC states in the [Rh(phen)2(NH3)2]3+ complex were performed at the unrestricted DFT (uDFT) level of theory using the B3LYP* hybrid functional with reduced 15% Hartree–Fock exchange (HFex) and the 6-311G(d,f) basis set with the Stuttgart–Dresden SDD effective core potential for the central Rh atom.39–42 An implicit Polarizable Continuum Model (PCM) was applied to account for a water solvent environment.43 The nature of the various states was confirmed by frequency analysis. All calculations were conducted using the Gaussian09 software.44Optimized structures at the B3LYP*(15% HFex)/6-311G(d,f)/(water) in the 3MC and 3LC excited states were chosen as starting geometries for subsequent AIMD calculations using the atom centered density matrix propagation (ADMP) model.45 The size of the basis set was reduced to 3-21G in order to reduce the computational costs, and motivated by test calculations indicating only minor differences for the calculated energy differences between the relaxed 3LC and 3MC states according to a comparison with the larger 6-311G(d,f) basis set. Explicit solvent structure and dynamics were neglected in this study focusing mainly on intramolecular rearrangement aspects, and an overall solvent response was approximated with the PCM model. The temperature dependence of the dynamics was investigated at constant selected temperatures (170 K, 200 K, 298 K, and 330 K) imposed by a standard thermostat. A minimum energy path was calculated as a complementary way to track the 3MLCT → 3MC conversion (details in ESI†).
3 Results and discussion
3.1 Triplet potential energy surface
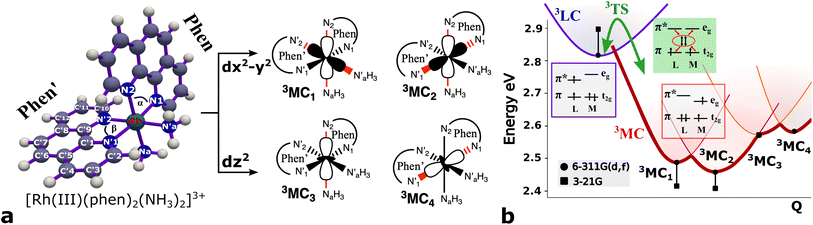
Several local triplet state minima were identified for the [Rh(III)(phen)2(NH3)2]3+ complex from a first exploration of the triplet PES by means of unconstrained geometry optimizations and single point quantum chemical calculations. A single 3LC state minimum, identified as a local excitation on one of the phenanthroline ligands (designated as phen′), as well as a set of four non-degenerate local minima of 3MC nature were identified by geometry optimizations. Different orientations of the eg orbitals relative to the M–L bonds allow for up to six different 3MC states associated with Jahn–Teller distortions along different M–L axes. The C2 rotation axis, characteristic of the C2 point group to which [Rh(III)(phen)2(NH3)2]3+ complex belongs more specifically, reduces the number of unique 3MC states to four. A graphical representation of the eg orbital orientations along different M–L bonds, together with the names for the corresponding states adopted in this report (3MC1, 3MC2, 3MC3 and 3MC4), are described in Fig. 1. Additionally, it can be noted that the more distorted octahedral coordination in the heteroleptic complex breaks the orbital degeneracy in the eg orbital set more strongly compared to the homoleptic parent complex [Rh(III)(phen)3]3+. This potentially increases the energy offset between the distinct 3MC states. Indeed, different emission band broadening characteristics for the two Rh complexes of ∼40 cm−1 in acetonitrile at 297 K for [Rh(III)(phen)3]3+ and ∼60 cm−1 in a water/ethylene mixture at 170 K for [Rh(III)(phen)2(NH3)2]3+ provides a likely experimental indication of such differences in the MC state PES landscapes.19,38The M–L bonds of the relaxed 3MC state geometries show bond elongations and contractions with respect to the 3LC, similar to what has been reported for several ruthenium polypyridine complexes.16,46–48 The Jahn–Teller distorted 3MC states can thus be identified to involve a single axis for eg-dz2 type orbitals, or an equatorial mode involving two orthogonal axes for eg-dx2−y2 type orbitals. The 3MC1, 3MC2, 3MC3 and 3MC4 states were identified at the B3LYP*/6-311G(d,f) computational level, while only the first three 3MC states were found at the lower level of theory B3LYP*/3-21G (energies shown in Fig. 1b). Reasonable reliability of the calculations employing the 3-21G basis set was, however, validated against the results for the larger 6-311G(d,f) basis set in terms of the relative state energy trends agreeing to within 0.05 eV, and average M–L bond lengths agreeing to within 0.004 Å (details in Fig. SI.1, Tables SI.2 and SI.3†). Furthermore, the relative energy ordering among the 3MC and 3LC states is conserved with the smaller basis set. The calculations predict 3MC2 to be the lowest energy 3MC state, and thus the most likely populated states in the triplet energy surface according to Kasha's rule (2.46 eV and 2.41 eV above the singlet ground state (1GS) for the B3LYP*/6-311G(d,f) and B3LYP*/3-21G levels of theory, respectively). Additionally, an almost isoenergetic second equatorial distorted 3MC1 state was found to be higher in energy by only 0.03 eV at the B3LYP*/6-311G(d,f) and 0.01 eV at the B3LYP*/3-21G levels of theory, respectively. Both axial distorted states, 3MC3 and 3MC4, were calculated to be ∼0.1 eV higher compared to the equatorial distorted states. Gibbs free energies also support the equatorial distortion as the most favorable compared to the axial distortion (Table SI.3†). From the first principles calculations, population of either the 3MC2 or the 3MC1 state can thus be expected as a result of excited state relaxation, although no information can be immediately extracted regarding the depopulation mechanism of the initially populated 3LC state. AIMD simulations were therefore initiated for the [Rh(III)(phen)2(NH3)2]3+ complex, with the aim to reveal the crossover dynamics as well as further properties associated with the population dynamics of thermally accessible states.
3.2 3LC dynamics
To better understand the triplet state dynamics in [Rh(III)(phen)2(NH3)2]3+ after initial optical excitation and intersystem crossing into a 3LC excited state, we initially performed AIMD calculations at 170 K, 200 K, and 298 K.A detailed analysis of the spin density distributions on the different molecular fragments from 7.5 ps simulations conducted at 170 K, 200 K, and 298 K only shows significant spin density values for one of the two phenanthroline ligands (labelled phen′ in Fig. 1a) with average spin density values of 1.99 (full spin density progression in Fig. SI.5†). The large spin density on the phen′ ligand indicates that the lowest energy 3LC states is characterized by a localized electron excitation on that particular ligand. Any ligand-to-ligand excitation transfer is discarded within the studied temperatures and time range since the spin density values remain essentially negligible on all the other ligands. The spin density localised on the Rh metal of barely ∼0.01 also contradicts conversion to, or strong M–L mixing with, any 3MC state in the simulation.19,38 This spin density distribution on the phen′ fragment was further analyzed over the simulation (details in ESI†). The spin density is mainly delocalised over the inner part of the phenanthroline frame. In particular the 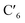 and
and 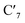 carbons, as numbered in Fig. 1a, accumulates larger spin density (∼2.0) during the 7.5 ps simulation. The electronic structure in the 3LC state also correlates with stiff M–L bonds with all six M–L bond distances ∼ 2.1 Å, and with fluctuations of merely 0.05 Å at 298 K, 0.04 Å at 200 K and 0.03 Å at 170 K (details in Fig. SI.3†). Both structural and electronic properties are thus consistent with triplet dynamics constrained to a localized 3LC excited state that only displays small motion in close vicinity of the 3LC structural minimum.
carbons, as numbered in Fig. 1a, accumulates larger spin density (∼2.0) during the 7.5 ps simulation. The electronic structure in the 3LC state also correlates with stiff M–L bonds with all six M–L bond distances ∼ 2.1 Å, and with fluctuations of merely 0.05 Å at 298 K, 0.04 Å at 200 K and 0.03 Å at 170 K (details in Fig. SI.3†). Both structural and electronic properties are thus consistent with triplet dynamics constrained to a localized 3LC excited state that only displays small motion in close vicinity of the 3LC structural minimum.
3.3 3MC dynamics
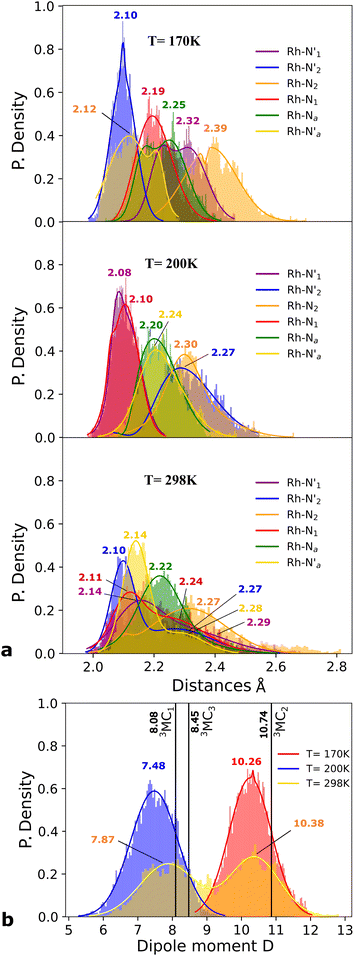
Static uDFT calculations predicted the presence of four distinct 3MC states (3M1, 3MC2, 3MC3 and 3MC4), but the dynamic distribution and conversions between these states are unknown. Therefore, AIMD simulations were also considered on the MC triplet PES at 170 K, 200 K, and 298 K with the aim to investigate transitions between the different local 3MC states, as well as the multi-dimensionality of the global 3MC PES.M–L bond distance distribution plots are analysed in Fig. 2a for the selected temperatures. The M–L bond distance distributions for the 200 K simulation show sharp peaks for all of the six bonds that are significantly displaced to longer bond distances compared with the 3LC state bond distributions. Three sets of bond distributions with similar mean distances and peak broadening that reveal similar bond characteristics can be identified (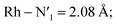 Rh – N1 = 2.10 Å;
Rh – N1 = 2.10 Å; 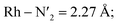 Rh – N2 = 2.30 Å). Such structural asymmetry is consistent with general expectations for Jahn–Teller distortions due to an eg metal d-orbital population. Similar bond distortions of up to ∼0.2 Å in a 3MLCT → 3MC transition with equatorial distortion in [Ru(II)(bqp)3]2+ complex has, for example, also been reported at the uDFT level.48 All the bond elongations and contractions at 200 K suggest the population of a single dx2−y2 d-type-orbital, and the M–L bond values also correlate well with the calculated distances in the fully relaxed 3MC1 excited state.
Rh – N2 = 2.30 Å). Such structural asymmetry is consistent with general expectations for Jahn–Teller distortions due to an eg metal d-orbital population. Similar bond distortions of up to ∼0.2 Å in a 3MLCT → 3MC transition with equatorial distortion in [Ru(II)(bqp)3]2+ complex has, for example, also been reported at the uDFT level.48 All the bond elongations and contractions at 200 K suggest the population of a single dx2−y2 d-type-orbital, and the M–L bond values also correlate well with the calculated distances in the fully relaxed 3MC1 excited state.
A clearly different set of M–L bond distance distribution profiles (top Fig. 2a) at the temperature of 170 K compared to what was seen for 200 K provides a first indication that another distinctive 3MC excited state is populated in this simulation. Two bond distributions with average distances of ∼2.1 Å (blue and orange peaks) are shorter than the remaining four coordination sites in agreement with an eg-dx2−y2 orbital assignment characteristic of the 3MC2 state (Fig. 1a). Other prominent structural changes due to the reorientation of the d-orbital lobes towards both chelation sites in the phen ligand is the reduction of the bite angle α by 8 degrees, if compared with the 3LC geometry (Fig. SI.7†). The geometry distortion in the lowest energy 3MC2 state also affects the electronic properties significantly, as evidenced from the clear fluctuation in the calculated total dipole moment of the molecule for the simulations conduced at different temperatures according to Fig. 2a. This shows an increase of the dipole moment from 7.48 Debye (D) (blue peak) in the 3MC1 state (200 K simulation) to 10.26 D (red peak) corresponding to the 3MC2 state (170 K simulation). Both 3MC1 and 3MC2 calculated dipole moments by uDFT minimization calculations (8.08 D and 10.74 D) reinforce the general state assignments, and the electronic identity of each 3MC state. Larger peak broadening additionally suggest that the 3MC1 is able to move over a larger accessible volume in the multidimensional PES compared to the 3MC2 state.
Finally, we consider a simulation of the 3MC dynamics at 298 K. At this higher temperature, the M–L bond distributions access a wide range of distances during the simulation, and with more than one distribution peak. Furthermore, the dipole moment histogram at 298 K shows a bimodal distribution characteristic of alternating population of two relatively distinct local electronic states (yellow distribution in Fig. 2b).
The AIMD structural data for the 298 K simulation also indicates population of at least two 3MC states with populated dx2−y2 orbital, but different orbital orientation. For further understanding of the dynamics between different local 3MC states, the trajectories of the six bonds were classified according to the relative bond distance ordering in Fig. 3. A remarkable transition between bond distances occurs after 2500 fs during a total transition time of ∼400 fs (grey frame). Finally, the 2900–3500 fs time interval (blue frame) shows bond distances that fully correlate with the 3MC1 excited state. Repetitive transition pattern between 3MC1 and 3MC2 states observed in the continuation time sampling within the 7500 fs, alludes to the established equilibrium between 3MC1 and 3MC2 states. The state transition, which also coincides with a discontinuity in the metal spin density, displays simultaneous symmetrical Rh – N1 and 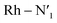 and asymmetrical Na and
and asymmetrical Na and 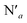 bond stretching. Electronic and structural attributes of the identified intermediate state coincides with the uDFT relaxed structure referred to as 3MC4, and distinguished by the characteristic axial elongation associated with electron population of one dz2 orbital. Therefore the dynamical equilibrium between the two equatorial states and lower lying 3MC states was revealed to implicate transient population of at least one higher energy 3MC states. Based on the observed transitions, the rate constant kIC for the 3MC1 → 3MC2 IC can be estimated to be 2.5 × 1012 s−1 at room temperature.
bond stretching. Electronic and structural attributes of the identified intermediate state coincides with the uDFT relaxed structure referred to as 3MC4, and distinguished by the characteristic axial elongation associated with electron population of one dz2 orbital. Therefore the dynamical equilibrium between the two equatorial states and lower lying 3MC states was revealed to implicate transient population of at least one higher energy 3MC states. Based on the observed transitions, the rate constant kIC for the 3MC1 → 3MC2 IC can be estimated to be 2.5 × 1012 s−1 at room temperature.
3.4 3LC → 3MC crossover dynamics
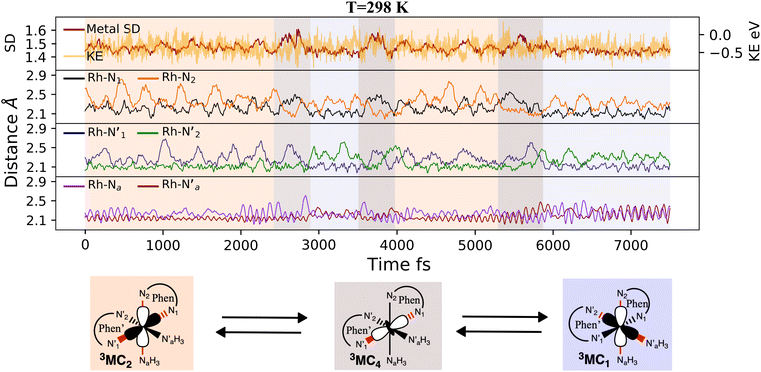
Here, we consider longer MD simulations starting from the 3LC state and performed with the aim to investigate the crossover dynamics from 3LC to the 3MC state manifold. The uncertainty of the crossover timescale, together with the large computational requirements for long AIMD simulations encouraged us to sample moderately higher temperatures of 298 K and 330 K.First, an AIMD simulation at 330 K shown in the top panel of Fig. 4a showed an abrupt increase in the metal spin density after ∼2300 fs. During the transition, the metal spin density increases from 0.1 to 1.4, indicating that the 3MC is populated within a couple of picoseconds. Further insight into the electronic structure rearrangement taking place during the crossover can be extracted from consideration of the singly occupied and unoccupied frontier molecular orbitals participating in the electronic transition. The αSOMO orbital represented as 1a in Fig. 4a shows the predominant π ligand orbital characteristic of the 3LC, but with metal-d contributions to the orbital escalating as the system approaches the transition state. Just before the electronic structure redistribution, only small-scale structural changes in the M–L bond distances (with constant ∼ 2.1 Å distances) are registered, mainly in the Rh – N1 bond reaching a distance of 2.23 Å right before the transition occurs. αSOMO orbital (3a in Fig. 4a) at the discussed simulation time already suggests some atomic contribution from a metal d-orbital. The Rh – N1 bond stretching is, however, only emphasized after ∼200 fs, indicating that there is a sub-picosecond geometry equilibration period after the electronic crossover to the 3MC state. The Rh – NH3 and Rh – N2 bond distances are barely distorted during this equilibration interval of 200 fs, which is indicative of an axial Jahn–Teller distortion of the 3MC4 state. The first deactivation step of the 3LC excited state to a higher energy 3MC state is also confirmed by the nature of the αSOMO orbital 4a with a characteristic dz2 orbital lobe orientation along the 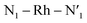 axis. A second IC process from the higher energy 3MC4 state towards the lower energy 3MC2 state subsequently occurs in less than 500 fs (tIa mark), after temporarily reaching a maximum Rh – N bond stretching of 2.92 Å. This particular initial distortion could potentially represent a sweet spot for initiating photochemical reactions.
axis. A second IC process from the higher energy 3MC4 state towards the lower energy 3MC2 state subsequently occurs in less than 500 fs (tIa mark), after temporarily reaching a maximum Rh – N bond stretching of 2.92 Å. This particular initial distortion could potentially represent a sweet spot for initiating photochemical reactions.
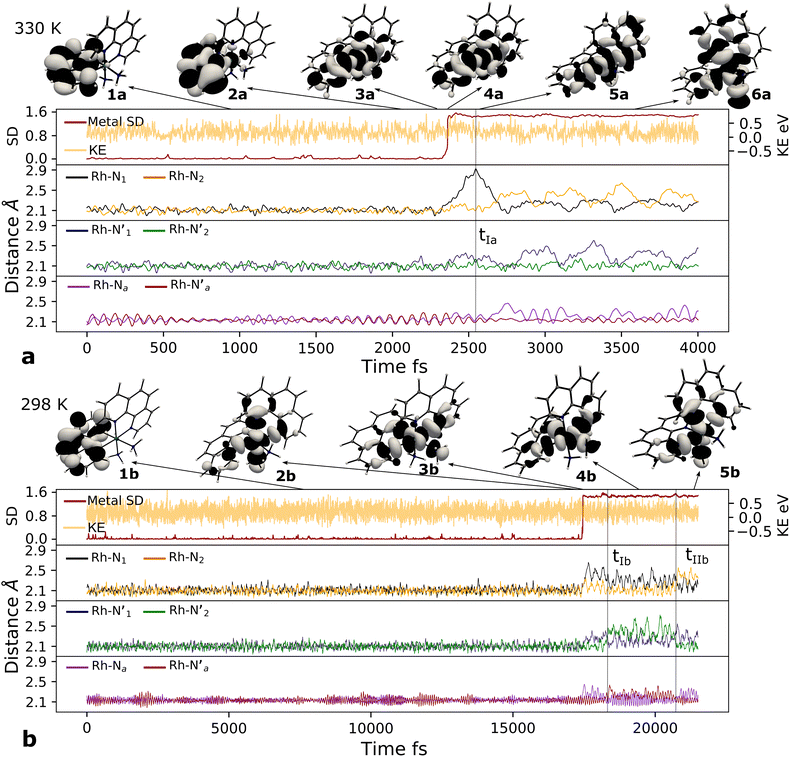
Triplet crossover dynamics was also simulated at a lower temperature of 298 K as shown in Fig. 4b. This simulation was conducted to check for the presence of alternative deactivation channels, and to further assess the crossover dynamics as a temperature-dependent process. In the 298 K simulation, the 3LC lifetime was extended significantly to ∼17 ps in order to successfully capture a crossover event.
While the limited simulation data precludes a reliable Arrhenius analysis that can be correlated quantitatively with the experimentally observed temperature-dependence, it is already notable that the simulations over a range of moderate temperatures shows a clear temperature-dependence of the crossover rate. Furthermore, the transition times in the 1–20 ps time range are consistent with the crossover being an activated process with a small effective transition barrier in basic agreement with a relaxed minimum energy path (details in ESI†). Similar to the 330 K simulation, however, it can be noted that the actual crossover transition remains fast as observed in the rapid accumulation of spin density on the metal center at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 fs. Subsequent geometry relaxation is once again observed after the transition, confirmed by the Rh – N1 bond stretching to 2.6 Å. Although the αSOMO orbital 2b shows population of the 3MC3 state rather than the 3MC4 observed in the previous simulated temperature, the 3LC excited state is still deactivated through a higher energy MC state. This initial population of the 3MC3 state is rapidly converted into the 3MC4 excited state in ∼900 fs (as supported by 3bαSOMO orbital). An observed second populated 3MC4 state achieves even longer lifetimes up to ∼2300 fs (tIb mark), before finally deactivating to the calculated lower energy 3MC2 excited state (tIIb mark).
440 fs. Subsequent geometry relaxation is once again observed after the transition, confirmed by the Rh – N1 bond stretching to 2.6 Å. Although the αSOMO orbital 2b shows population of the 3MC3 state rather than the 3MC4 observed in the previous simulated temperature, the 3LC excited state is still deactivated through a higher energy MC state. This initial population of the 3MC3 state is rapidly converted into the 3MC4 excited state in ∼900 fs (as supported by 3bαSOMO orbital). An observed second populated 3MC4 state achieves even longer lifetimes up to ∼2300 fs (tIb mark), before finally deactivating to the calculated lower energy 3MC2 excited state (tIIb mark).
Next, we consider the electronic rearrangement taking place during the crossover 3LC → 3MC in greater detail. This transition is clearly shown by the simulations to proceed as a two-electron process involving the two semi-populated frontier orbitals, similar to what can be expected from a basic intramolecular excitation energy transfer perspective. In particular, the transition involves one electron hopping from the higher energy π* on the initially excited phen ligand to one of the metal centered eg orbitals, together with a hole hopping from the lower-lying occupied π level on the same phen ligand to one of the t2g orbitals on the metal (π → d). The metal center activation can in principle be achieved in a concerted or step-wise fashion via electron hopping followed by hole hopping or the equivalent reverse path as illustrated in Fig. 5a. In order to resolve the 3LC → 3MC mechanism in detail from the simulations, the weights of the molecular orbital coefficients from the metal d-atomic-orbitals in the αSOMO and beta semi-unoccupied molecular orbital (βSUMO) were tracked for a series of snapshots with an interval of 4 fs during a 400 fs time window around the transition region (shown in Fig. 5b for 330 K and 298 K and a movie representation for the 298 K simulation in the ESI†). Minor metal orbital contributions to both αSOMO and βSUMO for the initial part of the simulation agrees with a 3LC nature during the early part of the reaction window, but quickly ascends up to ∼0.4 for the αSOMO and to ∼0.7 in the βSUMO as the transition progresses. An appreciable increase in atomic d-orbital contributions in the relevant frontier molecular orbitals is observed simultaneously for the αSOMO and βSUMO, and also matches closely with the reported increase of spin density on the metal. These findings support that the two-electron transition indeed proceeds in a concerted fashion without any significant involvement of transiently populated one-electron charge-transfer states. While the two-electron transfer is in good accordance with the net resulting experimental observation of the crossover activation of the 3MC state, it is notable that the structural distortions coupled with intramolecular coulombic and exchange interactions promotes the simultaneous transition of both the electron and the hole all the way down to ultrafast timescales, rather than the crossover being driven by one or the other electronic transitions.
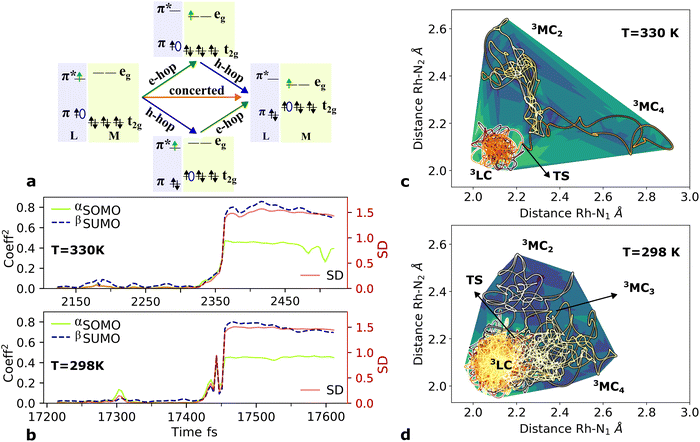
Finally, the AIMD simulations also highlight the importance of statistical factors influencing the crossover dynamics beyond what can be extracted from static calculations of transition barriers and scans of reaction paths. In particular, the simulations indicate a clear significance of entropy factors related to the accessible PES volume for the different states. This effective area, as an intrinsic characteristic of the distinct excited states dynamics for both sampled temperatures, are already revealed in the trajectories within the phen M–L bonds during the simulation time as represented in Fig. 5c and d. The population area of the 3LC state at 330 K is significantly more narrowly localized (in terms of phen M–L bond distortions) than at 298 K so that the transition state (TS) is essentially reached without any initial geometry stretching. In contrast, a TS at 298 K is only reached by bond stretching after significantly longer state sampling. The two highest energy 3MC excited states behave as important intermediate states, reflecting the complexity of multi-step deactivation paths towards the ultimate population of the lowest 3MC2 state.
The larger accessible volume in the 3MC product state corresponds an increase of the reaction entropy. Since the 3LC → 3MC transition is mainly ruled by M–L Jahn–Teller distortions, we assess the change in accessible coordinate space in the simulations by the six M–L bond distributions. In this approximation, the accessible volume of each state can be expressed as the product of the standard deviations of each M–L bond (δli) by
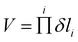 | (1) |
The entropy change of the crossover reaction (ΔSr) then relates with the Boltzmann constant kB and the partition function in terms of volume changes between the 3MC state (VMC) and the 3LC state (VLC) as
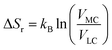 | (2) |
The standard deviations for the six M–L bonds for the studied system [Rh(III)(phen)2(NH3)2]3+ complex together with the final active volume V (calculated using eqn (1)) in the three sampled temperatures (298 K, 200 K and 170 K) are tabulated in Table SI.4.† For the 298 K simulations, where equilibration between different local 3MC minima takes place, the reaction entropy for a 3LC → 3MC process, ΔSr, is estimated to be 41.86 J K−1 mol−1. The ΔSr calculated from AIMD trajectories agrees well with the corresponding energies calculated from static quantum chemical calculations ∼40 J K−1 mol−1 (Table SI.5†), validating the employed protocol and emphasizing that the entropy change is mainly driven by the M–L bond distortions. This provides a considerable entropy contribution to the reaction free energy for the finely balanced 3LC–3MC dynamics. This also highlights that entropy factors should be considered to properly assess the driving force and reversibility for these activated crossover processes beyond what has traditionally been done to assess the temperature-dependent activation behaviour in these complexes.19
4 Conclusions
AIMD simulations were used to investigate 3LC → 3MC crossover dynamics in the rhodium complex [Rh(III)(phen)2(NH3)2]3+ on picosecond timescales. Initial results from quantum chemical calculations revealed a clear difference in the triplet potential energy landscape between well-defined 3LC states on the phen ligands on one hand, and a more complex 3MC potential energy landscape comprising several local minima with distinct structural and electronic characteristics on the other hand.The AIMD simulations provide further insight into the multidimensional dynamics taking place on the complex triplet PES. First, 3LC internal state dynamics reveal a narrow and well-defined range of accessible geometries closely constrained near the ground state geometry. In contrast, 3MC dynamics is revealed to involve significant structural mobility on a flat 3MC PES that includes facile transitions between several Jahn–Teller distorted minima. The MC dynamics notably includes fast transitions through higher-energy MC states connecting different low-energy parts of the full 3MC PES. Notably, the large difference in thermally accessible coordinate space between the LC and MC parts of the triplet PES indicates that entropic effects will have a significant influence on the free energy balance and effective driving force governing the 3LC → 3MC crossover dynamics.
Simulations of the 3LC → 3MC process at different temperatures showed a significant influence of the temperature on the crossover rate, consistent with an activated process characterized by a small energy barrier. The simulations also reveal further details of the triplet dynamics proceeding via a complex cascade involving several local 3MC states following the initial crossover from the 3LC state. Analysis of the AIMD simulations also enabled an in-depth assessment of the electric rearrangements taking place during the 3LC → 3MC crossover. In particular, the 3LC → 3MC transition is seen to involve a rapid redistribution of both the excited electron and the accompanying hole from one of the phen ligands to the metal center that takes place in a fully concerted fashion on a sub-picosecond timescale. This corresponds to a spin-allowed intramolecular two-electron excitation energy transfer process that takes place dynamically as a structure-driven weakening of the ligand field splitting of the metal center. It is interesting to consider as a topic for further investigation that the two-electron nature of this process appears to provide a fundamentally different set of opportunities and limitations for tuning of the excited state landscape compared to the corresponding one-electron case encountered in more widely studied 3MLCT → 3MC deactivation processes.
Finally, the in-depth understanding of this 3LC → 3MC transition provides useful insights for further developments of transition metal complexes that aim to utilize 3MC states for photochemical applications more broadly. In particular, 3LC → 3MC crossover is confirmed to provide a promising approach to overcome problems associated with weak absorption and ultrafast initial energy losses from direct excitations into 3MC states more generally, as long as the full complexity of the triplet potential energy landscape and associated dynamics revealed by simulations is taken into consideration.
Data availability
DFT energies and geometry details, trajectories and electron structure analysis of the MD simulations, NEB calculation analysis, and cartesian coordinates of the optimized structures are available in the ESI.† A αSOMO 3LC → 3MC transition dynamics MP4 movie at 298 K is also available in the ESI.†Author contributions
PP supervised the project and IBL performed the calculations. PP and IBL contributed to the manuscript preparation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Martin Trulsson for valuable discussions. The Swedish Research Council (VR 2021-05303) as well as eSSENCE and NanoLund are gratefully acknowledged for support. We also acknowledge computational resources provided at the LUNARC and NSC supercomputing centres through generous SNIC/NAISS allocations.Notes and references
- N. Sinha and O. S. Wenger, J. Am. Chem. Soc., 2023, 145, 4903–4920 CrossRef CAS PubMed.
- C. Förster and K. Heinze, Chem. Soc. Rev., 2020, 49, 1057–1070 RSC.
- D. Zigmantas, T. Polívka, P. Persson and V. Sundström, Chem. Phys. Rev., 2022, 3, 041303 CrossRef CAS.
- C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed.
- P. S. Wagenknecht and P. C. Ford, Coord. Chem. Rev., 2011, 255, 591–616 CrossRef CAS.
- S. I. Ting, S. Garakyaraghi, C. M. Taliaferro, B. J. Shields, G. D. Scholes, F. N. Castellano and A. G. Doyle, J. Am. Chem. Soc., 2020, 142, 5800–5810 CrossRef CAS PubMed.
- C. Förster and K. Heinze, Chem. Phys. Rev., 2022, 3, 041302 CrossRef.
- E. R. Welin, C. Le, D. M. Arias-Rotondo, J. K. McCusker and D. W. C. MacMillan, Science, 2017, 355, 380–385 CrossRef CAS PubMed.
- S. Otto, M. Grabolle, C. Förster, C. Kreitner, U. Resch-Genger and K. Heinze, Angew. Chem., Int. Ed., 2015, 54, 11572–11576 CrossRef CAS PubMed.
- M. D. Woodhouse and J. K. McCusker, J. Am. Chem. Soc., 2020, 142, 16229–16233 CrossRef CAS PubMed.
- S. Kaufhold, N. W. Rosemann, P. Chábera, L. Lindh, I. Bolaño Losada, J. Uhlig, T. Pascher, D. Strand, K. Wärnmark, A. Yartsev and P. Persson, J. Am. Chem. Soc., 2021, 143, 1307–1312 CrossRef CAS PubMed.
- N. Sinha, B. Pfund, C. Wegeberg, A. Prescimone and O. S. Wenger, J. Am. Chem. Soc., 2022, 144, 9859–9873 CrossRef CAS PubMed.
- A. Y. Chan, A. Ghosh, J. T. Yarranton, J. Twilton, J. Jin, D. M. Arias-Rotondo, H. A. Sakai, J. K. McCusker and D. W. C. MacMillan, Science, 2023, 382, 191–197 CrossRef CAS PubMed.
- M. M. Alowakennu, A. Ghosh and J. K. McCusker, J. Am. Chem. Soc., 2023, 145, 20786–20791 CrossRef CAS PubMed.
- K. Eastham, P. A. Scattergood, D. Chu, R. Z. Boota, A. Soupart, F. Alary, I. M. Dixon, C. R. Rice, S. J. O. Hardman and P. I. P. Elliott, Inorg. Chem., 2022, 61, 19907–19924 CrossRef CAS PubMed.
- A. Soupart, F. Alary, J. L. Heully, P. I. Elliott and I. M. Dixon, Coord. Chem. Rev., 2020, 408, 213184 CrossRef CAS.
- T. Thomas and G. Crosby, J. Mol. Spectrosc., 1971, 38, 118–129 CrossRef CAS.
- J. D. Petersen, R. J. Watts and P. C. Ford, J. Am. Chem. Soc., 1976, 98, 3188–3194 CrossRef CAS.
- M. T. Indelli and F. Scandola, Inorg. Chem., 1990, 29, 3056–3058 CrossRef CAS.
- T. Thomas, R. Watts and G. Crosby, J. Chem. Phys., 1973, 59, 2123–2131 CrossRef CAS.
- J. Brozik and G. Crosby, Chem. Phys. Lett., 1996, 255, 445–450 CrossRef CAS.
- D. Carstens and G. Crosby, J. Mol. Spectrosc., 1970, 34, 113–135 CrossRef CAS.
- H. Miki, M. Shimada, T. Azumi, J. Brozik and G. Crosby, J. Phys. Chem., 1993, 97, 11175–11179 CrossRef CAS.
- M. T. Indelli, A. Carioli and F. Scandola, J. Phys. Chem., 1984, 88, 2685–2686 CrossRef CAS.
- M. T. Indelli, C. Chiorboli and F. Scandola, Photochemistry and Photophysics of Coordination Compounds I, 2007, pp. 215–255 Search PubMed.
- F. Barigelletti, D. Sandrini, M. Maestri, V. Balzani, A. Von Zelewsky, L. Chassot, P. Jolliet and U. Maeder, Inorg. Chem., 1988, 27, 3644–3647 CrossRef CAS.
- C. Sousa, M. Llunell, A. Domingo and C. de Graaf, Phys. Chem. Chem. Phys., 2018, 20, 2351–2355 RSC.
- S. Iuchi and N. Koga, Phys. Chem. Chem. Phys., 2016, 18, 4789–4799 RSC.
- M. Pápai, Inorg. Chem., 2021, 60, 13950–13954 CrossRef PubMed.
- L. M. L. Daku, Phys. Chem. Chem. Phys., 2019, 21, 650–661 RSC.
- D. B. Zederkof, K. B. Møller, M. M. Nielsen, K. Haldrup, L. González and S. Mai, J. Am. Chem. Soc., 2022, 144, 12861–12873 CrossRef CAS PubMed.
- S. Mai and L. González, Chem. Sci., 2019, 10, 10405–10411 RSC.
- A. Šrut, S. Mai, I. V. Sazanovich, J. Heyda, A. Vlček, L. González and S. Záliš, Phys. Chem. Chem. Phys., 2022, 24, 25864–25877 RSC.
- M. Heindl, J. Hongyan, S. A. Hua, M. Oelschlegel, F. Meyer, D. Schwarzer and L. González, Inorg. Chem., 2021, 60, 1672–1682 CrossRef CAS PubMed.
- L. Freitag and L. Gonzalez, Inorg. Chem., 2014, 53, 6415–6426 CrossRef CAS PubMed.
- D. J. Hsu, D. Leshchev, I. Kosheleva, K. L. Kohlstedt and L. X. Chen, J. Chem. Phys., 2020, 152, 204115 CrossRef CAS PubMed.
- F. Bolletta, A. Rossi, F. Barigelletti, S. Dellonte and V. Balzani, Gazz. Chim. Ital., 1981, 111, 155–158 CAS.
- M. Nishizawa, T. Suzuki, S. Sprouse, R. Watts and P. Ford, Inorg. Chem., 1984, 23, 1837–1841 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. K., J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.02, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704 CrossRef CAS.
- C. N. Tsai, S. Mazumder, X. Z. Zhang, H. B. Schlegel, Y. J. Chen and J. F. Endicott, Inorg. Chem., 2015, 54, 8495–8508 CrossRef CAS PubMed.
- I. M. Dixon, J. L. Heully, F. Alary and P. I. Elliott, Phys. Chem. Chem. Phys., 2017, 19, 27765–27778 RSC.
- O. A. Borg, S. S. M. C. Godinho, M. J. Lundqvist, S. Lunell and P. Persson, J. Phys. Chem. A, 2008, 112, 4470–4476 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc04381a |
| This journal is © The Royal Society of Chemistry 2023 |