Net-clipping as a top-down approach for the prediction of topologies of MOFs built from reduced-symmetry linkers

Abstract

Reticular materials constructed from regular molecular building blocks (MBBs) have been widely explored in the past three decades. Recently, there has been increasing interest in the assembly of novel, intricate materials using less-symmetric ligands; however, current methods for predicting structure are not amenable to this increased complexity. To address this gap, we propose herein a generalised version of the net-clipping approach for anticipating the topology of metal–organic frameworks (MOFs) assembled from organic linkers and different polygonal and polyhedral MBBs. It relies on the generation of less-symmetric nets with less-connected linkers, via the rational deconstruction of more-symmetric and more-connected linkers in edge-transitive nets. We applied our top-down strategy to edge-transitive nets containing 4-c tetrahedral, 6-c hexagonal, 8-c cubic or 12-c hexagonal prism linkers, envisaging the formation of 102 derived and 46 clipped nets. Among these, we report 33 new derived nets (icn7–icn39) and 6 new clipped nets (icn1–icn6). Importantly, the feasibility of using net-clipping to anticipate clipped nets is supported by literature examples and new experimental additions. Finally, we suggest and illustrate that net-clipping can be extended to less-regular, non-edge transitive nets as well as to covalent–organic frameworks (COFs), thus opening new avenues for the rational design of new reticular materials exhibiting unprecedented topologies.

---

Introduction

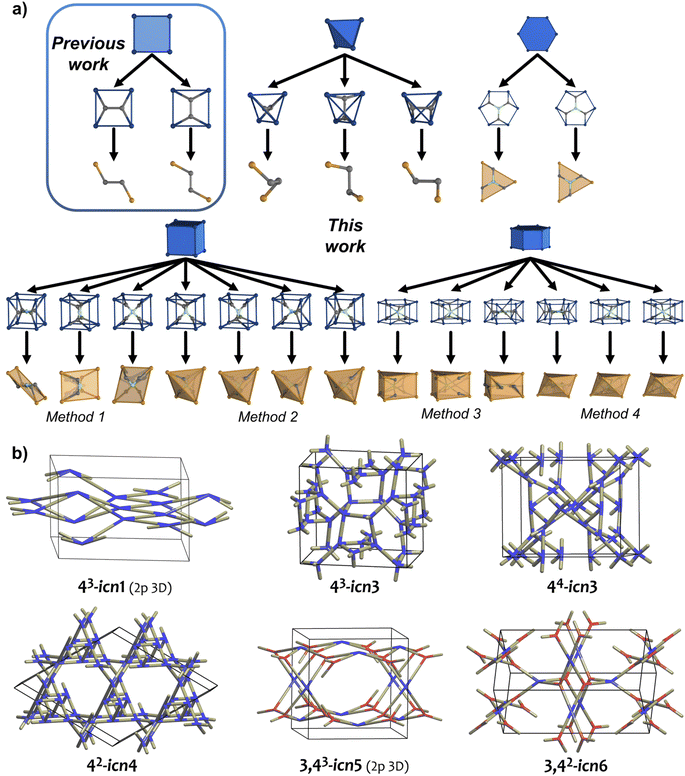
Reticular materials are crystalline, periodic networks assembled by strong bonds, which have been increasingly studied as a promising class of porous solids due to their high level of control, tunability and outstanding performance in many applications pertaining to energy, environment, biomedicine, etc.^1–3 The high scope of their properties relies on a wide catalogue of readily available molecular building blocks (MBBs), either organic or inorganic, that can contribute to the framework's features.^4,5 The simplification of each MBB into their basic geometry, connectivity and directionality features has allowed the rational classification of metal–organic frameworks (MOFs) and covalent–organic frameworks (COFs) into underlying nets with various topologies, and probably more importantly, the prediction of their structural features, offering various design opportunities for distinct programmed pores or channels.^6–9

The growing interest in reticular chemistry demands new approaches for the rational design of materials with ever-greater complexity. Examples of these approaches include supermolecular building blocks (SBBs)^10,11 and layers (SBLs),^12–14 which relate nets with polyhedra (MOPs) or layers (2D MOFs), respectively; or the merged-nets approach, which relates different nets of compatible symmetry for the rational design of mixed-linker MOFs.¹⁵ Indeed, over the past few years, structural complexity has been introduced by the desymmetrisation of simple organic linkers, by changing the direction of the binding carboxylic groups through geometric design in bent,¹⁶ twisted¹⁷ or zigzag fashion,^18,19 or through combinations thereof,²⁰ yielding structures that differ from the default or expected nets. However, current methods for structural prediction in reticular chemistry are insufficient for desymmetrised MBBs: presently, there are no general approaches for non-standard parameters such as angles, torsions, width, etc.^21–24 Recently, our group reported net-clipping, the first top-down structural-prediction approach, which we used for the de-reticulation of edge-transitive nets assembled from 4-c square-like MBBs to deduce the topology of MOFs based on less-symmetric zigzag linkers.¹⁹ This strategy, whose fundamentals are reversed from the design of the obtained merged nets, permits the prediction of MOF structures that break the basic principles of reticulation, thereby elucidating mismatch topologies and their construction.

Herein we propose to extend the net-clipping strategy to MOFs made of MBBs of higher symmetry and/or connectivity than 4-c square-like MBBs, as a method that rationalise and anticipate MOFs that could be built up with linkers that are less-symmetric than the original MBBs. Accordingly, we have adapted the net-clipping strategy to nets assembled from 4-connected (4-c) tetrahedral, 6-c hexagonal, 8-c cubic and 12-c hexagonal prismatic organic MBBs. Through our analysis we have generated 102 derived and 46 clipped nets, of which 33 derived nets (named icn7–icn39) and 6 clipped nets (named icn1–icn6) have never, to the best of our knowledge, previously been reported. The coordinates of all 39 nets are given in the ESI† as cif file (with the connectivity according to the latest Topocif dictionary)²⁵ and have been deposited in the personal.ttd database included in the TopCryst system.²⁶ Moreover, we experimentally validated our strategy by synthesising three of these less-symmetric linkers, which enabled us to assemble three new MOFs whose topologies match those predicted via net-clipping.

Results and discussion

Theoretical deduction: design strategy for net-clipping

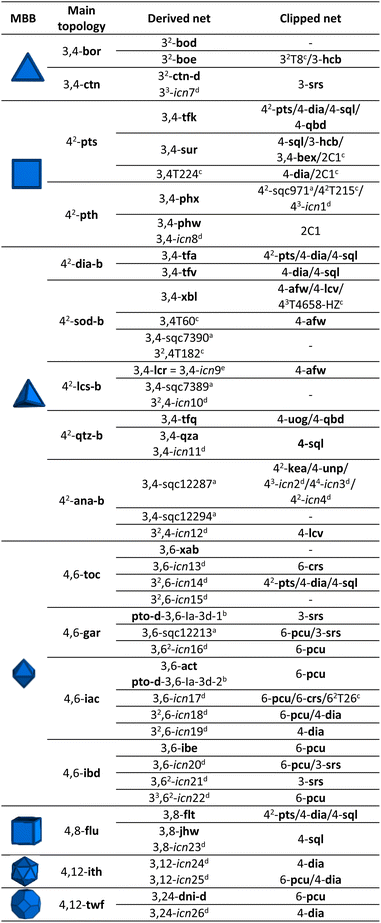
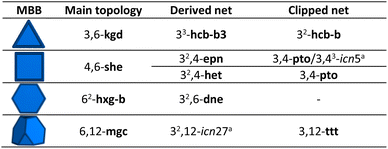
Among the most extensively used organic MBBs to reticulate materials, we selected those which could be clipped symmetrically. Ideally, the clipping of a chosen node should produce a new node with half of the original connectivity, which could be rebuilt to the original node upon application of a C₂ operation. We found that linkers with tetrahedral, hexagonal, cubic, or hexagonal prismatic shapes matched this condition (Fig. 1a). Note that highly connected nodes with cubic or hexagonal prismatic directionality can be clipped into two different modes. In contrast, nodes with octahedral, trigonal prismatic, cuboctahedra, or icosahedral directionality cannot be clipped this way, given the absence of a C₂-symmetry axis. Interestingly, we found that these latter nodes present two triangular faces in the same direction, which frustrate the node-clipping and the absence of the C₂ operation (Fig. S1†).

Fig. 1 (a) Schematic of the deconstruction of (from left to right): a 4-c square MBB into a zigzag MBB; a 4-c tetrahedral MBB into a turned-twisted MBB; a 6-c hexagonal MBB into a 3-c twisted triangular MBB; an 8-c cubic MBB into a 4-c square-like or a 4-c tetrahedral MBB; and a 12-c hexagonal prismatic MBB into a 6-c octahedral or a 6-c trigonal prismatic MBB. This approach comprises two steps: firstly, the splitting of each node into a set of less-symmetric nodes and edges; and secondly, the symmetric clipping of half of the original node's connectivity. (b) Representation of the 6 new clipped nets accessible for MOFs constructed with turned-twisted MBBs (icn1, icn2, icn3, and icn4), 3-c twisted triangular MBBs (icn5) and 4-c square-like MBBs (icn6). For clarity, here and in the tables, we report the coordination of the independent nodes before the icn symbol. The two nets icn1 and icn5 are 2-periodic 3D (thick layers).

In the present work, we analysed the 54 edge-transitive nets (with D-symbol size ≤ 32, and excluding those with collisions)²⁷ and selected those comprising nodes with connectivity 4, 6, 8, or 12 matching vertex figures of tetrahedra, hexagons, cubes or hexagonal prisms, respectively.²⁸ We then derived these nets by splitting their nodes to reduce the symmetry of the MBB (Fig. 1a; for the detailed procedure, see ESI†).²⁹ The symmetrical clipping of half of the connecting groups resulted in less-symmetric MBBs, transforming the new 3-c node into a new edge. This process led to the formation of 2-c turned-twisted linkers from 4-c tetrahedral MBB; 3-c twisted triangular linkers from 6-c hexagonal MBBs; 4-c square-like or tetrahedral linkers from 8-c cubic MBB; and 6-c triangular prismatic or octahedral linkers from 12-c hexagonal prismatic MBBs. This work enabled the discovery of 39 new topologies, providing a facile approach to study and understand the derived nets.³⁰

Net-clipping of 4-c tetrahedra

We began by selecting the 17 edge-transitive nets assembled by the combination of 4-c tetrahedral MBBs with other polygonal and polyhedral MBBs. Among the six uninodal nets, five (dia, sod, lcs, qtz, ana) were considered to be in their binary form (net-b), to allow for selective splitting (Table 1). The sixth tetrahedral net, lcv, was excluded, due to the impossibility of generating a binodal net according to its connection circuits (Fig. S2†). The binary form of a net is a bipartite graphs, and bipartite graphs contain only even cycles, so nets with odd cycles (lcv, hxl) cannot be transformed in a binary form. We then derived these nets by splitting the 4-c nodes into two 3-c nodes with a 90° connection between them.²⁹ Note that, when embedded in a net, this split can be performed in three distinct orientations (Fig. 1a). When transposed into a MOF, this symmetry reduction process, followed by erasing of two opposite connecting groups, generated a new linker shape, which we named turned-twisted, where the connecting groups are twisted in one axis and turned 90° in another axis (Fig. S3†).

Table 1 Net-clipping of all the derived nets from 4-c tetrahedral nodes in the 16 selected edge-transitive nets^a

a For the derived nets, letters indicate the following: ^aSystre nets in the Epinet database; ^bToposPro binodal nets;^31cToposPro symbol for 3-periodic nets; and ^dnew nets found using net-clipping approach. ^eicn9 is the same as lcr, a recent addition to RCSR not recognized by Systre.

---

Applying net-clipping to the various derived nets generated from the selected edge-transitive nets revealed the exhaustive list of possible combinations of this new set of nodes in different topologies, which can further be translated to organic linkers in reticular chemistry. Table 1 summarises the 49 resultant derived nets, of which we describe here, for the first time ever, 20 (named icn7–icn26).³² Additionally, we identified 24 possible clipped nets that can be built with a turned-twisted linker, from which 4 are new nets (named as icn1–icn4) (Fig. 1b).³² From this study, we found that clipping nets made of tetrahedral MBBs can produce 3D nets, 2D layers or 1D chains from the same parent net, due to the different splitting modes/orientation of the tetrahedra. For example, in the case of the pts net, the possible clipped nets are the 3D pts and dia topologies, the 2D sql, hcb and bex topologies, and the 1D qbd and the double-bridged linear topologies.

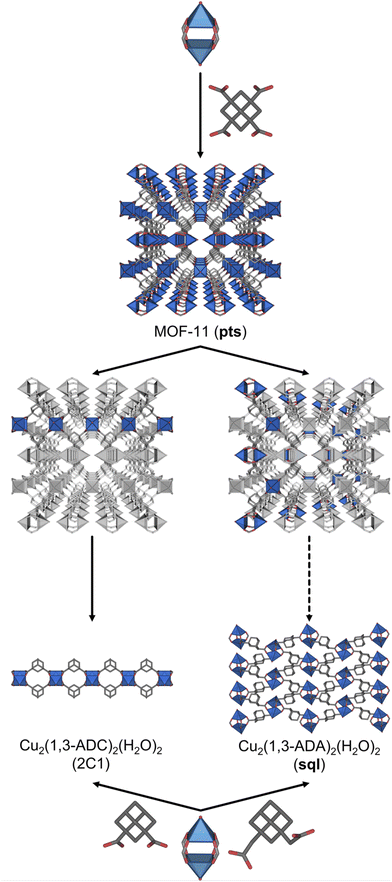
To corroborate our net-clipping approach, we identified a pts MOF, MOF-11, made by linking 4-c square-like Cu-based paddlewheels by tetrahedral 1,3,5,7-adamantane-tetracarboxylate (1,3,5,7-ATC) linkers (Fig. 2).³³ Remarkably, two of these seven anticipated nets have already been found experimentally. When clipped, the tetrahedral 1,3,5,7-ATC linker is converted into the turned-twisted 1,3-adamantane-dicarboxylate (1,3-ADC), which had already been combined with 4-c square-like Cu(II) paddlewheels by Zheng et al. to obtain the anticipated one-dimensional chain (here as double bridged). In a second example, the same authors similarly combined a closely related linker, 1,3-adamantane-diacetate (1,3-ADA), which incorporates a methylene group in each of the two carboxylic acid arms of 1,3-ADC.³⁴ Significantly, with this linker, they observed the formation of a sql-MOF, also corresponding to a net that we predicted by net-clipping a MOF made of 4-c square-like and tetrahedral MBBs.

Fig. 2 Schematic of the net-clipping approach applied to the formation of metal–organic materials from tetrahedral 1,3,5,7-ATC linker to turned-twisted 1,3-ADC (left) or 1,3-ADA (right) linkers combined with 4-c paddlewheel Cu(II) MBBs.

Net-clipping of 6-c hexagons

There are five edge-transitive nets constructed with hexagons: the 2D kgd and hxl topologies; and the 3D she, hxg-b and mgc nets. Among these, we excluded the hxl topology, due to the unfeasibility to generate a binodal net due to the presence of odd cycles, as for the aforementioned tetrahedral lcs net (Fig. S4†). In the remaining four nets (kgd, she, hxg-b, and mgc), we derived the hexagon into a central triangle bound to three triangles (Table 2). Then, we erased half of their connections to generate a triangular polygon (Fig. 1a). Table 2 shows the 5 derived and 4 clipped nets resulting from applying the net-clipping approach to these nets made of 6-c hexagonal MBBs. Note that, for these types of nets, there is only a dimensional reduction from the predicted 3D derived epn net to the 2D (more precisely a 2-periodic 3D thick layer) clipped icn5 net. Among these derived/clipped nets, we also identified a new derived net from the parent mgc net, the icn27 net,³² as well as a new clipped net from the parent she net, the aforementioned icn5 net (Fig. 1b).³² Interestingly, the hxg-b net cannot be clipped into another net without affecting the connectivity of the two 6-c nodes simultaneously.

Table 2 Net-clipping of all the derived nets from 6-c hexagonal nodes in the 4 selected edge-transitive nets^a

a For the derived nets, letters indicate the following: ^anew nets found using the net-clipping approach.

---

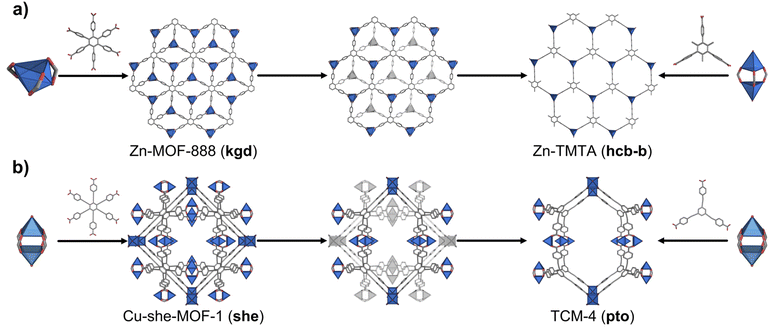
Application of our net-clipping approach to hexagonal MBBs is strongly corroborated by the literature. For example, kgd Zn-MOF-888 (ref. 35) is made by connecting a 3-c Zn(II) metal through the hexagonal 1,2,3,4,5,6-hexakis(4-carboxyphenyl)benzene (CPB). This CPB linker is clipped into the corresponding trigonal 4,4′,4′′-(2,4,6-trimethylbenzene-1,3,5-triyl)tribenzoate (TMTA) linker, which, when assembled with the 3-c Zn(II) cluster forms the hcb-b layer,³⁶ as predicted by our net-clipping approach (Fig. 3a). A second example is she-MOF-1,³⁷ which comprises 4-c Cu(II) paddlewheels joined by the extended hexagonal linker 1,2,3,4,5,6-benzene-hexaethynylbenzoate (BHEB) (Fig. 3b). According to net-clipping, combination of the 4-c Cu(II) paddlewheels with the corresponding clipped 1,3,5-benzene-trisethynylbenzoate (BTEB) should lead to the formation of a 3D pto MOF (Table 2). Remarkably, this prediction was verified upon the formation of pto TCM-4.³⁸ Moreover, this correlation was also observed for she-MOF-2,³⁷ made of the hexagonal hexatopic 1,2,3,4,5,6-hexakis(4-carboxybiphenyl)benzene (CBPB), and for MOF-388, containing the triazine functionalized 4,4′,4′′-(triazine-2,4,6-triyl-tris(benzene-4,1-diyl))tribenzoate (TAPB), which exhibits the anticipated underlying pto topology (Fig. S5†).³⁹

Fig. 3 Schematic of the net-clipping approach applied to formation of reticular materials from (a) hexagonal CPB linker to a trigonal TMTA linker combined with 3-c Zn(II) MBBs; and (b) from a hexagonal BHEB linker to a trigonal BTEB combined with 4-c paddlewheel Cu(II) MBBs.

Net-clipping of 8-c cubes

To expand our net-clipping approach to more highly-connected MBBs (connectivity ≥ 8), we began by analysing the 7 binodal edge-transitive nets made of 8-c cubic MBBs. We noticed that the cube presents two accessible clipping modes: one into a square, and one into a tetrahedron (Fig. 1a). According to Chen et al.,⁴⁰ a cubic node can be split into a tetrahedron surrounded by 4 triangles (Method 1), or into a square connected to 4 triangles (Method 2). As shown in Table 3, our use of these methods afforded 34 derived nets, 12 of which were unprecedented (icn28–icn39),³² and 16 clipped nets. Among these latter nets, we discovered a new net topology, which we named icn6 (Fig. 1b).³²

Table 3 Net-clipping of all the derived nets from 8-c cubic nodes in the 7 selected edge-transitive nets^a

a For the derived nets, letters indicate the following: ^aSystre nets in the Epinet database; ^bToposPro symbol for 3-periodic nets; ^cnew nets found using the net-clipping approach; M1: Method 1; and M2: Method 2.

---

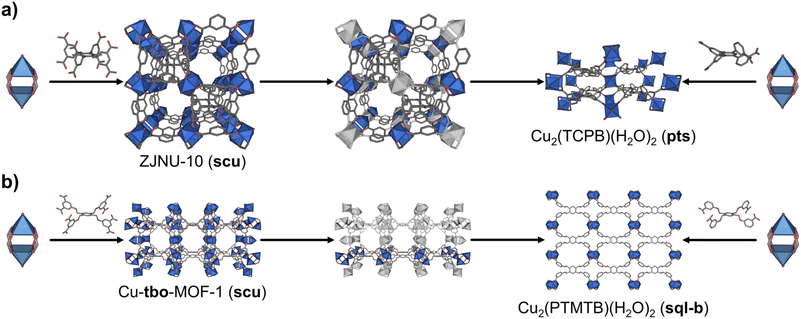
In comparison to MOFs built up from organic MBBs of lower connectivity, there are not many examples of MOFs that contain 8-c cubic organic MBBs in the literature. Gao et al. synthesised an scu MOF, ZJNU-10, that is constructed by connecting 4-c Cu(II) paddlewheels through the 8-c cubic 3,6-dimethyl-1,2,4,5-tetra(5′-isophthalate)benzene (DMTIB) linker (Fig. 4a).⁴¹ The net-clipping of scu yields a 2D sql-b net, a 3D ssb net, or a 3D lvt-b net when the cube is clipped into a square; or a 3D pts net when the cube is clipped into a tetrahedron. Significantly, the same group reported a pts MOF by connecting 4-c Cu(II) paddlewheels with the 4-c 1,2,4,5-tetrakis(3-carboxyphenyl)-benzene (TCPB) linker. Interestingly, this latter 4-c linker can be seen as the clipped tetrahedron version of the 8-c linker (Fig. 4a and S6†).⁴² Thus, the topology of the synthesised pts MOF cited matches perfectly with that predicted by our net-clipping approach.

Fig. 4 Schematic of the net-clipping approach applied to formation of metal–organic materials from (a) a cubic DMTIB linker to a tetrahedral TCPB linker, combined with 4-c paddlewheel Cu(II) MBBs; and (b) from a cubic PTMTI linker to a square PTMTB linker, combined with 4-c paddlewheel Cu(II) MBBs.

Next, motivated by the paucity of literature examples of MOFs that supported our net-clipping of MOFs made of 8-c cubic MBBs, we synthesised a new 4-c linker, representing the clipped square-like version of an 8-c cubic linker used to make the Cu-tbo-MOF-1.¹² Cu-tbo-MOF-1 is made by linking 4-c Cu(II) paddlewheels to 8-c 5,5′,5′′,5′′′-[1,2,4,5-phenyltetramethoxy]tetraisophthalate (PTMTI) linkers. It exhibits the aforementioned scu underlying topology when this 8-c linker is considered as a single node, and the tbo-b (tbo-b3) underlying topology when the linker is simplified into more regular 3-c and 4-c nodes. Importantly, the MOF created with the corresponding clipped 4-c square-like linker generated one of the two expected nets: the sql 2D net (Table 3). This topology contrasts sharply to the 3D pts net that we had expected to see from having used the clipped tetrahedral linker. The desymmetrisation of these 8-c PTMTI linkers into a 4-c linker generated 3,3′,3′′,3′′′-[1,2,4,5-phenyltetramethoxy]tetrabenzoate (PTMTB). Once this linker had been prepared, it was reacted with copper(II) nitrate salt in the presence of DMF and HBF₄ under solvothermal conditions, to yield blue square-shaped crystals. SCXRD analysis of the crystal structure confirmed the formation of a MOF layer with the expected sql-b topology (Fig. 4b, right).³²

Net-clipping of 12-c hexagonal prisms

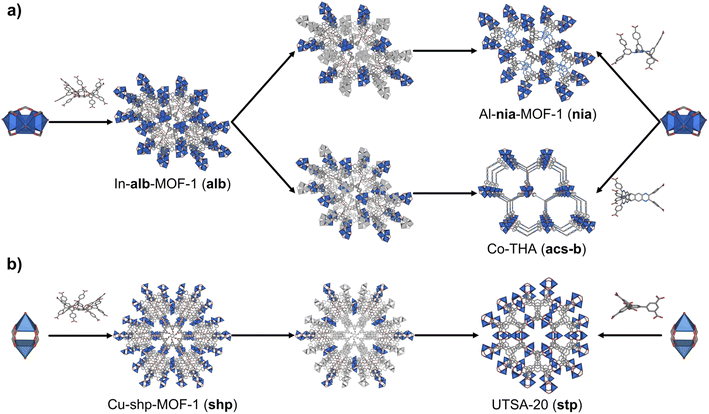
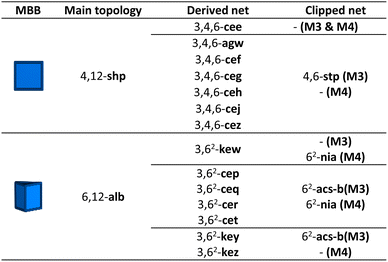
Finally, we considered the highest connectivity from the selected polyhedra, the hexagonal prism, which is only found in two edge-transitive nets, the shp and alb topologies. As in the previous case, hexagonal prismatic MBBs also allow for two clipping modes: one into a 6-c trigonal prism (Method 3); and one into a 6-c octahedron (Method 4) (Fig. 1a). Following both methods, net-clipping of MOFs made of 12-c hexagonal prismatic MBBs generated 14 derived nets and 3 clipped nets (Table 4). Thus, in the alb net, clipping the 12-c hexagonal prism to a 6-c trigonal prism (Method 3) affords the binodal acs-b topology, whereas clipping it into an octahedron (Method 4) yields a nia net. On the other hand, the 12-c hexagonal prism of the shp net can only be clipped into a trigonal prism, which affords the stp net. Our prediction of these nets via net-clipping is reinforced by several MOFs reported in the literature. In-alb-MOF-1 is a 3D structure built up from the connection of 6-c In-trimer clusters through 12-c 1,2,3,4,5,6-hexakis[3,5-bis(4-carboxyl-phenyl)phenoxymethyl]benzene (BCPB) linkers (Fig. 5a).⁴³ As we had anticipated, net-clipping of alb topology induced the formation of two possible nets exhibiting the acs-b (Method 3) or nia (Method 4) topologies. Despite the lack of a reported MOF built by combining these clusters and the clipped version of H₁₂BCPB, we did find a closely related MOF, Al-nia-MOF-1, made of analogous 6-c Al-trimer clusters and the 6-c 5′,5′′′′,5′′′′′′′-((1,3,5-triazine-2,4,6-triyl)tris(azanediyl))tris-(([1,1′:3,1′′-terphenyl]-4,4′′ dicarboxylate)) (TTATTDC) linker. This TTATTDC linker shows an octahedral shape similar to that which the clipped 6-c linker from H₁₂BCPB (Method 4) would exhibit. Importantly, Al-nia-MOF-1 showed the anticipated underlying nia topology (Fig. 5a, top).⁴⁴ Additionally, we found Co-THA, which is formed by linking analogous Co-trimer clusters with the 6-c triptycene-hexaacetate (THA) linker, which could be seen as the clipped trigonal prismatic version of a 12-c hexagonal prismatic MBB. In this case, the anticipated acs-b net had also been formed (Fig. 5a, bottom).⁴⁵ Regarding shp nets, Cu-shp-MOF-1 is a reported framework constructed by the connection of 4-c Cu(II) paddlewheels through 12-c BCPB linkers (Fig. 5b).⁴³ Despite the lack of reports on this MOF, made by combining Cu(II) paddlewheels with the clipped version of H₁₂BCPB, we again found an analogous one in the literature: in this case, UTSA-20,⁴⁶ in which 4-c Cu(II) paddlewheels are connected by 6-c 3,3′,3′′,5,5′,5′′-benzene-1,3,5-triyl-hexabenzoate (BHB) linkers, which is a clipped trigonal prismatic version of a 12-c hexagonal prismatic MBB. This MOF exhibits an underlying stp topology, thus matching with the anticipated topology of the clipped net from the main shp topology.

Table 4 Net-clipping of all the derived nets (methods 3 and 4) from 12-c hexagonal prism nodes in the 7 selected edge-transitive nets^a

a M1: Method 1; and M2: Method 2.

---

Fig. 5 Schematic of the net-clipping approach applied to formation of metal–organic materials from (a) a hexagonal prism BCPB linker clipped to an octahedral TTATTDC, and trigonal prism THA linkers combined with a 6-c trimer M(III) MBBs; and (b) a hexagonal prism BCPB linker clipped to a distorted trigonal prism BHB linker, combined with 4-c paddlewheel Cu(II) MBBs.

Net-clipping out of edge-transitive nets: the first proof of concept

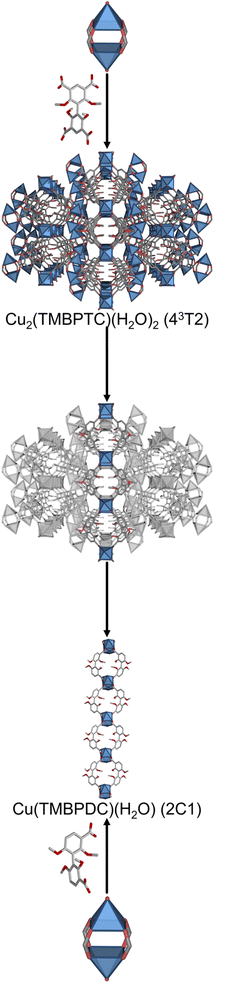
In our attempts to assemble a MOF made of a 4-c tetrahedral MBB exhibiting an edge-transitive net, we created a 4³T2 MOF with a formula of Cu₂(TMBPTC)(H₂O)₂ that is built up from connecting 4-c Cu(II) paddlewheels through 4-c tetrahedral 2,2′,6,6′-tetramethoxy-[1,1′-biphenyl]-3,3′,5,5′-tetracarboxylate (TMBPTC) linkers. This 4³T2 topology,³² which does not belong to an edge transitive net, is based on two squared nodes joined by a tetrahedral node in a [34] transitivity. In it, the tetrahedral nodes are distributed in a primitive cubic conformation that exhibits a slight shift between two pairs of cubic units (Fig. S17 and S18†). This shift results in a desymmetrisation of the square MBBs in two different positions produced by the desymmetrisation of the elongated tetrahedral MBB,^21,47–50 altering the circuits of connection and frustrating the formation of two 4-cycles seen in both pts and pth nets. Instead, a 4-cycle and a diamond-like 6-cycle are formed.

Inspired by the formation of the aforementioned 4³T2 MOF, we decided to use this net to challenge our net-clipping approach to ascertain whether MOFs made of less-symmetric linkers could be anticipated from less regular nets. To this end, we applied the net-clipping strategy to the 4³T2 net resulting in the prediction of two different clipped nets: the 2D sql and the 1D 2C1 topologies.

Next, we designed and synthesised the rigid 2,2′,6,6′-tetramethoxy-[1,1′-biphenyl]-3,3′-dicarboxylate (TMBPDC) linker, which is the clipped, turned-twisted version of the 4-c tetrahedral TMBPTC linker. In TMBPDC, the steric hindrance induced by the methoxy groups locks the linker conformation into a turned-twisted shape⁴⁸ that is twisted 90° relative to its reported homologous zigzag linker (Fig. S24†).¹⁹ As we predicted, replacing the tetratopic TMBPTC ligand with the ditopic H₂TMBPDC let to the formation of the predicted metal–organic 1D 2C1 chain. Thus, reaction of copper(II) nitrate salt and H₂TMBPDC in the presence of DMF and H₂O under solvothermal conditions yielded green polyhedral crystals. SCXRD revealed the formation of a coordination polymer with formula Cu(TMBPDC)(H₂O), which crystallises in the P2₁/c space group (Fig. 6). In this structure, two pairs of linkers connect to the same 4-c Cu paddlewheel by double bridging.⁵¹

Fig. 6 Schematic of the net-clipping approach applied to formation of metal–organic materials from a tetrahedral TMBPTC linker to a turned-twisted TMBPDC (left) combined with 4-c paddlewheel Cu(II) MBBs.

Conclusions

In summary, we have generalised the use of net-clipping as a top-down approach to unveil the different topologies that should be accessible for MOFs assembled from organic linkers and different polyhedral MBBs. In our approach, these organic linkers are low-symmetry/connected linkers derived from clipping of higher symmetry/connection linkers in edge-transitive nets. We applied net-clipping to edge-transitive nets made of 4-c tetrahedral, 6-c hexagonal, 8-c cubic, and 12-c hexagonal prismatic linkers, anticipating the formation of 102 derived and 46 clipped nets. Among them, 33 new derived nets (icn7–icn39) and 6 new clipped nets (icn1–icn6) were not previously described. The discovery of all these nets underscores the potential of net-clipping for the discovery and rational design of MOFs exhibiting new underlying topologies. Moreover, we first demonstrated that the use of net-clipping can also be extended to less regular, non-edge transitive nets, a fact that will surely increase the discovery of available topologies in a near future. However, this process will require the study of thousands of complex topologies, representing an exciting challenge for simulation tools. Finally, we postulated that net-clipping could also be applied to covalent–organic frameworks (COFs), which we corroborated through a brief literature survey. The 2D kgd COF-360 is an imine-linked COF created by linking the 6-c hexagonal hexaformylphenyl benzene (HFPB) linker and the 3-c 1,3,5-tris(p-aminophenyl)benzene (TAPB) linker.⁵² From our study, we expected the clipped net to exhibit an hcb-b topology, which is precisely what had been observed for TFPB-TAPB-COF,⁵³ a COF synthesised by imine-based linkage of TAPB and the 3-c 1,3,5-tris(4-formylphenyl)benzene (TFPB), the latter linker being the clipped version of HFPB (Fig. S25†). Thus, we are confident that net-clipping will continue to inform the design of future porous materials such as MOFs and COFs, by enabling the assembly of new, otherwise inaccessible topologies.

Data availability

Data available on request.

Author contributions

B. O.-R., I. I. and D. M. conceived the idea of the project. B. O.-R., J. R.-B. and C. V. designed, synthesized, and characterized the organic linkers. B. O.-R. designed, synthesized, and characterized the metal–organic materials, and performed the theoretical deduction. B. O.-R. and D. M. P. validated the topological analysis of the new nets. I. I. and J. J. performed the SCXRD analysis and solved the structures. B. O.-R., V. G., I. I. and D. M. wrote the manuscript. All authors contributed to the revision of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No. 101019003, Grants Ref. PID2021-124804NB-I00 and PID2021-123287OB-I00 funded by MCIN/AEI/10.13039/501100011033/and by “ERDF A way of making Europe”, and the Catalan AGAUR (project 2021 SGR 00458). It was also funded by the CERCA program/Generalitat de Catalunya. ICN2 is supported by the Severo Ochoa Centres of Excellence programme, Grant CEX2021-001214-S, funded by MCIN/AEI/10.13039.501100011033. J. R.-B. thanks the Ministerio de Ciencia, Innovación y Universidades for a FPU predoctoral contract (FPU17/00688). C.V. thanks the RyC contract (RYC-2016-20187) funded by MCIN/AEI/10.13039/501100011033 and by “European Union NextGenerationEU/PRTR”. D. M. P. thanks the MUR for the grant PRIN2020 “Nature Inspired Crystal Engineering (NICE)” and Prof. Vladislav A. Blatov at the Samara Center for Theoretical Materials Science for providing the free ToposPro software (https://topospro.com).³²

Notes and references

1. M. J. Kalmutzki, N. Hanikel and O. M. Yaghi, Sci. Adv., 2018, 4, eaat9180.
2. N. W. Ockwig, O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176–182.
3. O. M. Yaghi, Mol. Front. J., 2019, 3, 66–83.
4. A. Stein, S. W. Keller and T. E. Mallouk, Science, 1993, 259, 1158–1164.
5. M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319–330.
6. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789.
7. M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2012, 112, 675–702.
8. O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Phys. Chem. Chem. Phys., 2007, 9, 1035–1043.
9. F. A. Wells, Three dimensional nets and polyhedra, Wiley, New York, 1977.
10. F. Nouar, J. F. Eubank, T. Bousquet, L. Wojtas, M. J. Zaworotko and M. Eddaoudi, J. Am. Chem. Soc., 2008, 130, 1833–1835.
11. J. J. Perry IV, J. A. Perman and M. J. Zaworotko, Chem. Soc. Rev., 2008, 38, 1400–1417.
12. J. F. Eubank, H. Mouttaki, A. J. Cairns, Y. Belmabkhout, L. Wojtas, R. Luebke, M. Alkordi and M. Eddaoudi, J. Am. Chem. Soc., 2011, 133, 14204–14207.
13. J. F. Eubank, L. Wojtas, M. R. Hight, T. Bousquet, V. C. Kravtsov and M. Eddaoudi, J. Am. Chem. Soc., 2011, 133, 17532–17535.
14. B. Q. Ma, K. L. Mulfort and J. T. Hupp, Inorg. Chem., 2005, 44, 4912–4914.
15. H. Jiang, J. Jia, A. Shkurenko, Z. Chen, K. Adil, Y. Belmabkhout, L. J. Weselinski, A. H. Assen, D. X. Xue, M. O'Keeffe and M. Eddaoudi, J. Am. Chem. Soc., 2018, 140, 8858–8867.
16. M. Eddaoudi, J. Kim, D. Vodak, A. Sudik, J. Wachter, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4900–4904.
17. M. Eddaoudi, J. Kim, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2002, 124, 376–377.
18. V. Guillerm, T. Grancha, I. Imaz, J. Juanhuix and D. Maspoch, J. Am. Chem. Soc., 2018, 140, 10153–10157.
19. B. Ortín-Rubio, H. Ghasempour, V. Guillerm, A. Morsali, J. Juanhuix, I. Imaz and D. Maspoch, J. Am. Chem. Soc., 2020, 142, 9135–9140.
20. N. Alsadun, G. Mouchaham, V. Guillerm, J. Czaban-Jóźwiak, A. Shkurenko, H. Jiang, P. M. Bhatt, P. Parvatkar and M. Eddaoudi, J. Am. Chem. Soc., 2020, 142, 20547–20553.
21. J. K. Schnobrich, O. Lebel, K. A. Cychosz, A. Dailly, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2010, 132, 13941–13948.
22. V. Guillerm and D. Maspoch, J. Am. Chem. Soc., 2019, 141, 16517–16538.
23. F. Haase, G. A. Craig, M. Bonneau, K. Sugimoto and S. Furukawa, J. Am. Chem. Soc., 2020, 142, 13839–13845.
24. H. Wang, X. Dong, J. Lin, S. J. Teat, S. Jensen, J. Cure, E. V. Alexandrov, Q. Xia, K. Tan, Q. Wang, D. H. Olson, D. M. Proserpio, Y. J. Chabal, T. Thonhauser, J. Sun, Y. Han and J. Li, Nat. Commun., 2018, 9, 1745.
25. http://www.iucr.org/resources/cif/dictionaries/cif_topology .
26. A. P. Shevchenko, A. A. Shabalin, I. Y. Karpukhin and V. A. Blatov, Sci. Technol. Adv. Mater.: Methods, 2022, 2, 250–265 . https://topcryst.com/.
27. M. Li, M. O'Keeffe, D. M. Proserpio and H. F. Zhang, Cryst. Growth Des., 2020, 20, 4062–4068.
28. O. Delgado-Friedrichs and M. O'Keeffe, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, 63, 344–347.
29. J. F. Eubank, R. D. Walsh, P. Poddar, H. Srikanth, R. W. Larsen and M. Eddaoudi, Cryst. Growth Des., 2006, 6, 1453–1457.
30. M. Li, D. Li, M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2014, 114, 1343–1370.
31. V. A. Blatov and D. M. Proserpio, Acta Crystallogr., Sect. A: Found. Crystallogr., 2009, 65, 202–212.
32. V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586.
33. B. Chen, M. Eddaoudi, T. M. Reineke, J. W. Kampf, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2000, 122, 11559–11560.
34. Y. Z. Zheng, Z. Zheng, M. L. Tong and X. M. Chen, Polyhedron, 2013, 52, 1159–1168.
35. F. M. Amombo Noa, E. Svensson Grape, S. M. Brülls, O. Cheung, P. Malmberg, A. K. Inge, C. J. Mckenzie, J. Mårtensson and L. Öhrström, J. Am. Chem. Soc., 2020, 142, 9471–9481.
36. X. Zhao, H. He, F. Dai, D. Sun and Y. Ke, Inorg. Chem., 2010, 49, 8650–8652.
37. D. A. Gómez-Gualdrón, Y. J. Colón, X. Zhang, T. C. Wang, Y. S. Chen, J. T. Hupp, T. Yildirim, O. K. Farha, J. Zhang and R. Q. Snurr, Energy Environ. Sci., 2016, 9, 3279–3289.
38. N. Zhu, M. J. Lennox, G. Tobin, L. Goodman, T. Düren and W. Schmitt, Chem. – Eur. J., 2014, 20, 3595–3599.
39. H. Furukawa, Y. B. Go, N. Ko, Y. K. Park, F. J. Uribe-Romo, J. Kim, M. O'Keeffe and O. M. Yaghi, Inorg. Chem., 2011, 50, 9147–9152.
40. Z. Chen, H. Jiang, M. Li, M. O'Keeffe and M. Eddaoudi, Chem. Rev., 2020, 120, 8039–8065.
41. X. Gao, T. Xu, Z. Jiang, H. Yu, Y. Wang and Y. He, Dalton Trans., 2019, 48, 16793–16799.
42. D. Yan, B. Chen and Q. Duan, Inorg. Chem. Commun., 2014, 49, 34–36.
43. Z. Chen, Ł. J. Weseliński, K. Adil, Y. Belmabkhout, A. Shkurenko, H. Jiang, P. M. Bhatt, V. Guillerm, E. Dauzon, D. X. Xue, M. O'Keeffe and M. Eddaoudi, J. Am. Chem. Soc., 2017, 139, 3265–3274.
44. D. Alezi, J. Jia, P. M. Bhatt, A. Shkurenko, V. Solovyeva, Z. Chen, Y. Belmabkhout and M. Eddaoudi, Inorg. Chem., 2022, 61, 10661–10666.
45. P. Chandrasekhar, G. Savitha and J. N. Moorthy, Chem. – Eur. J., 2017, 23, 7297–7305.
46. Z. Guo, H. Wu, G. Srinivas, Y. Zhou, S. Xiang, Z. Chen, Y. Yang, W. Zhou, M. O'Keeffe and B. Chen, Angew. Chem., Int. Ed., 2011, 123, 3236–3239.
47. A. G. Wong-Foy, O. Lebel and A. J. Matzger, J. Am. Chem. Soc., 2007, 129, 15740–15741.
48. J. Pang, S. Yuan, J. Qin, C. Liu, C. Lollar, M. Wu, D. Yuan, H. C. Zhou and M. Hong, J. Am. Chem. Soc., 2017, 139, 16939–16945.
49. X. L. Lv, L. Feng, L. H. Xie, T. He, W. Wu, K. Y. Wang, G. Si, B. Wang, J. R. Li and H. C. Zhou, J. Am. Chem. Soc., 2021, 143, 2784–2791.
50. J. Ma, L. D. Tran and A. J. Matzger, Cryst. Growth Des., 2016, 16, 4148–4153.
51. H. Furukawa, J. Kim, N. W. Ockwig, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2008, 130, 11650–11661.
52. B. Zhang, H. Mao, R. Matheu, J. A. Reimer, S. A. Alshmimri, S. Alshihri and O. M. Yaghi, J. Am. Chem. Soc., 2019, 141, 11420–11424.
53. L. Zhai, N. Huang, H. Xu, Q. Chen and D. Jiang, Chem. Commun., 2017, 53, 4242–4245.

---

Footnote

† Electronic supplementary information (ESI) available: The 39 new nets are deposited in the Topcryst database²⁶ as icnx (where ICN stands for “Institut Català de Nanociència i Nanotecnologia, and x the number of the net). CCDC 2270218–2270220. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc04406h

---