Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamic shapes of floppy vesicles enclosing active Brownian particles with membrane adhesion†
Priyanka
Iyer
 ,
Gerhard
Gompper
,
Gerhard
Gompper
 and
Dmitry A.
Fedosov
and
Dmitry A.
Fedosov
 *
*
Theoretical Physics of Living Matter, Institute of Biological Information Processing and Institute for Advanced Simulation, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: p.iyer@fz-juelich.de; g.gompper@fz-juelich.de; d.fedosov@fz-juelich.de
First published on 25th April 2023
Abstract
Recent advances in micro- and nano-technologies allow the construction of complex active systems from biological and synthetic materials. An interesting example is active vesicles, which consist of a membrane enclosing self-propelled particles, and exhibit several features resembling biological cells. We investigate numerically the behavior of active vesicles, where the enclosed self-propelled particles can adhere to the membrane. A vesicle is represented by a dynamically triangulated membrane, while the adhesive active particles are modelled as active Brownian particles (ABPs) that interact with the membrane via the Lennard-Jones potential. Phase diagrams of dynamic vesicle shapes as a function of ABP activity and particle volume fraction inside the vesicle are constructed for different strengths of adhesive interactions. At low ABP activity, adhesive interactions dominate over the propulsion forces, such that the vesicle attains near static configurations, with protrusions of membrane-wrapped ABPs having ring-like and sheet-like structures. At moderate particle densities and strong enough activities, active vesicles show dynamic highly-branched tethers filled with string-like arrangements of ABPs, which do not occur in the absence of particle adhesion to the membrane. At large volume fractions of ABPs, vesicles fluctuate for moderate particle activities, and elongate and finally split into two vesicles for large ABP propulsion strengths. We also analyze membrane tension, active fluctuations, and ABP characteristics (e.g., mobility, clustering), and compare them to the case of active vesicles with non-adhesive ABPs. The adhesion of ABPs to the membrane significantly alters the behavior of active vesicles, and provides an additional parameter for controlling their behavior.
1. Introduction
In recent years, there has been a growing interest in a variety of active matter systems which operate far from equilibrium and show rich dynamical behaviors and functions.1–4 Examples include biological systems ranging from cells to tissues,5,6 collections of micro-swimmers,7,8 and active engineered systems.9,10 The growing research interest has been nurtured by rapid developments in microscale and nanoscale technologies which already allow for a well-controlled construction of complex multicomponent active systems and materials.9,11,12 A prominent example is cell-mimicking systems, which are generally constructed from cell-based biological constituents, and include active nematics made of driven biofilaments,13,14 and growing and dividing droplet-based or vesicle-based compartments.15,16 In many other examples, biological materials are combined with active synthetic constituents with a hope to mimic various biological systems or even go beyond their functionality.17,18 Here, an interesting example is a closed membrane enclosing biological micro-swimmers such as bacteria19–21 or synthetic self-propelled particles.18,22–25 Active components inside the soft confinement exert forces on the surface, leading to highly dynamic non-equilibrium shape changes which resemble certain processes in living cells such as the formation of filopodia and lamellipodia,5,26,27 and active shape fluctuations of the membrane.28–30The main features that differentiate active vesicles from various membrane structures in equilibrium31,32 are active force generation due to the enclosed active components and dynamic shape changes of the membrane. For instance, swimming bacteria or motile synthetic particles within a vesicle induce the formation of tethers and protrusions which dynamically elongate and retract.18–20 In equilibrium, string-of-pearls-like and tubular protrusions can be formed by amphipathic peptides or BAR domain proteins,32,33 but these structures are static and correspond to a minimum of total energy. Therefore, different physical mechanisms govern the formation of various membrane structures in equilibrium and in non-equilibrium active vesicles. In particular, the curvature-induced clustering of active particles34–36 at the membrane leads to the concentration of active forces at spots with a high curvature. Moreover, there exists a positive feedback mechanism between the induction of strong curvature by active particles and their clustering in places with large curvature, so that the shape of active vesicles is altered dynamically and collectively.18,23 Furthermore, active components within a vesicle give rise to a significant increase in membrane tension due to the swim pressure exerted by the particles.37
Apart from active forces, the deformation of a membrane can also occur as a consequence of adhesive interactions between the membrane and enclosed particles.38–42 In particular, adhesive interactions result in partial or full wrapping of the particles by the membrane, which can significantly reduce the force required for tether formation. Furthermore, the adhesion of multiple particles to the membrane often induces membrane-mediated interactions between the particles, leading to a cooperative wrapping of particles by the membrane41 and the formation of various particle structures at the membrane surface.43–47 These interactions can enhance or reduce the clustering of active particles, potentially altering the behavior of active vesicles. In addition, it is plausible to expect that the adhesive interactions between the particles and the membrane can facilitate the existence of active forces away from the membrane (i.e., pulling forces), which is not possible for non-adhesive active particles which exert pushing forces toward the membrane. Finally, adhesive interactions of particles and pathogens with a cell membrane are essential for a variety of biological processes such as membrane translocation, viral budding, and phagocytosis.48–51
In our study, we investigate numerically the combined effect of particle activity and adhesive interactions on the behavior of active vesicles. Fluid membrane vesicles are modeled as dynamically triangulated surfaces52,53 enclosing a number of active Brownian particles (ABPs). Adhesive interactions between the ABPs and the membrane are incorporated through the Lenard-Jones potential, whose strength is varied to induce various degrees of ABP wrapping by the membrane. A phase diagram of dynamic vesicle shapes is constructed as a function of the ABP propulsion strength and the volume fraction of particles within the vesicle. The presence of ABP adhesion to the membrane leads to qualitative changes in the phase diagram in comparison to that for non-adhesive ABPs.18 For a weak particle activity, the adhesion interactions dominate, yielding nearly static vesicle shapes, which are similar to those in equilibrium with only adhesive interactions present. For moderate particle activities and volume fractions, complex tether structures filled with string-like arrangements of ABPs are formed, and characterized by a number of branching points. In contrast, for non-adhesive ABPs, the formed tethers show no significant branching, and the ABPs generally cluster at the end of membrane tethers.18,23 Finally, for a strong particle propulsion, active forces from the ABPs dominate over the adhesion interaction, and the resulting behavior of active vesicles is similar to those with non-adhesive ABPs. Also, membrane properties of the active vesicles and the characteristics of ABP clustering and mobility are analysed and compared to those of non-adhesive ABPs.
The article is organized as follows. Section 2 provides all necessary details about the employed methods and models, including the parameters used in simulations. Section 3.1 presents dynamic shape diagrams for two strengths of the ABP adhesion to the membrane. Membrane tension and the importance of ABP adhesion are discussed in Section 3.2. Vesicle shape fluctuations are analysed in Section 3.3, and ABP characteristics are presented in Section 3.4. Finally, we conclude in Section 4.
2. Methods and models
An active vesicle is represented by a closed fluid membrane of spherical topology with radius R, enclosing Np active Brownian particles (ABPs). The activity of the particles is described by the dimensionless Peclet number Pe = σvp/Dt, where σ is the particle diameter, vp is the propulsion velocity, and Dt is the translational diffusion coefficient. Note that Pe is a measure of the propulsion force fp of ABPs, with vp = fp/γp and Dt = kBT/γp, where γp is the translational friction coefficient, so that Pe = fpσ/kBT. Particle volume fraction within the vesicle is given by ϕ = Np(σ/2R)3. Table 1 presents all simulation parameters.2.1 Model of adhesive active Brownian particles
ABPs are modeled as active spherical particles without hydrodynamic interactions. Each ABP experiences a propulsion force fp that acts along an orientation vector ei. The force results in a propulsion velocity vp = fp/γp. The orientation vector ei is subject to orientational diffusion ėi = ζi × ei, where ζi is a Gaussian random process with 〈ζi(t)〉 = 0 and 〈ζi(t)·ζj(t′)〉 = 6Drδijδ(t − t′) with a rotational diffusional coefficient Dr. Dr is related to the ABP diameter σ and translational diffusion coefficient Dt as Dt = Drσ2/3.Interactions between different ABPs and membrane particles are implemented through the 12-6 Lennard-Jones (LJ) potential
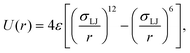 | (1) |
2.2 Membrane model
The vesicle is modeled by a dynamically triangulated membrane of spherical topology consisting of Nv linked vertices.52,53 The interaction between linked vertices is controlled via a tethering potential52,54 that is a combination of attractive and repulsive parts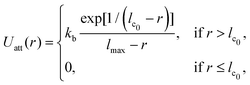 | (2) |
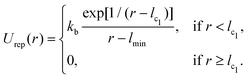 | (3) |
The membrane bending elasticity is modeled by the Helfrich curvature energy,55
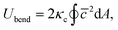 | (4) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) = (c1 + c2)/2 is the mean local curvature at the membrane surface element dA. In the discretized form, it becomes56,57
= (c1 + c2)/2 is the mean local curvature at the membrane surface element dA. In the discretized form, it becomes56,57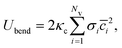 | (5) |
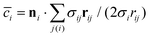 is the discretized mean curvature at vertex i, ni is the unit normal at the membrane vertex i,
is the discretized mean curvature at vertex i, ni is the unit normal at the membrane vertex i, 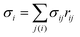 is the area corresponding to vertex i (the area of the dual cell), j(i) corresponds to all vertices linked to vertex i, and σij = rij(cot
is the area corresponding to vertex i (the area of the dual cell), j(i) corresponds to all vertices linked to vertex i, and σij = rij(cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 + cot
θ1 + cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2)/2 is the length of the bond in the dual lattice, where θ1 and θ2 are the angles at the two vertices opposite to the edge ij in the dihedral. In practice, since the dihedral terms corresponding to σij are additive, the local curvature at each vertex can be calculated by summing over contributions from all triangles containing that vertex.
θ2)/2 is the length of the bond in the dual lattice, where θ1 and θ2 are the angles at the two vertices opposite to the edge ij in the dihedral. In practice, since the dihedral terms corresponding to σij are additive, the local curvature at each vertex can be calculated by summing over contributions from all triangles containing that vertex.
The area conservation is imposed locally to each triangle by the potential
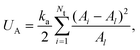 | (6) |
Membrane fluidity is modelled by a stochastic flipping of bonds following a Monte–Carlo scheme. The bond shared by each pair of adjacent triangles can be flipped to connect the two previously unconnected vertices.52,57 The flipping is performed with a frequency ν and probability pf. An energetically favorable bond flip is accepted with a probability of p = 1. For an energetically unfavorable flip, the resulting change in energy due to an attempted bond flip ΔU = ΔUatt + ΔUrep + ΔUA determines the probability of the flipping as p = exp[−ΔU/kBT]. The resulting membrane fluidity can be characterized by a 2D membrane viscosity for the selected frequency ν and flipping probability pf.54,58 Note that the two bond-flipping parameters ν and pf can conceptually be combined into a single flipping probability or frequency. However, the use of two parameters is computationally advantageous, as the flipping procedure is computationally expensive. With two parameters, the flipping can be performed not every time step, which is controlled by ν, while an implementation with a single parameter would require checks for bond flipping at every time step.
2.3 Equation of motion
The system evolves in time according to the Langevin equation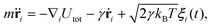 | (7) |
![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) i and ṙi represent the second and first time derivatives of particle positions, ∇i is the spatial derivative at particle i, and Utot is the sum of all interaction potentials described above. The effect of a viscous fluid is mimicked by the friction co-efficient γ, whose value can be different for membrane particles and ABPs, see Table 1. Thermal fluctuations are modelled as a Gaussian random process ξi with 〈ξi(t)〉 = 0 and 〈ξi(t)⋅ξj(t′)〉 = 6δijδ(t − t′). Inertial effects are minimized by performing the simulations in the over-damped limit with m and γ such that τt = m/γ < 1 ≪ τr = Dr−1 ≈ 0.1τ. The positions and velocities of all particles are integrated using the velocity-Verlet algorithm.59
i and ṙi represent the second and first time derivatives of particle positions, ∇i is the spatial derivative at particle i, and Utot is the sum of all interaction potentials described above. The effect of a viscous fluid is mimicked by the friction co-efficient γ, whose value can be different for membrane particles and ABPs, see Table 1. Thermal fluctuations are modelled as a Gaussian random process ξi with 〈ξi(t)〉 = 0 and 〈ξi(t)⋅ξj(t′)〉 = 6δijδ(t − t′). Inertial effects are minimized by performing the simulations in the over-damped limit with m and γ such that τt = m/γ < 1 ≪ τr = Dr−1 ≈ 0.1τ. The positions and velocities of all particles are integrated using the velocity-Verlet algorithm.59
2.4 ABP adhesion and membrane wrapping
Adhesion interactions between the ABPs and the membrane are mediated by the LJ potential whose strength is characterized by the potential depth ε. Adhesion strength determines the degree of particle wrapping by the membrane, with energetic costs due to membrane bending and tension. The ratio of the membrane bending modulus κ and the lateral tension λ defines a length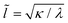 , below which membrane deformations are mainly controlled by the bending energy, while deformations on length scales larger than
, below which membrane deformations are mainly controlled by the bending energy, while deformations on length scales larger than ![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) are dominated by tension.39 If tension is neglected and the membrane covers area Awrap ≤ πσ2 of the particle (e.g., partial wrapping), the adhesion (Ead) and bending (Ebend) energies are given by
are dominated by tension.39 If tension is neglected and the membrane covers area Awrap ≤ πσ2 of the particle (e.g., partial wrapping), the adhesion (Ead) and bending (Ebend) energies are given by| Ead = −ωAwrap, Ebend = 8κAwrap/σ2, | (8) |
To relate the adhesion strength ω per unit area and the strength ε of the LJ potential in simulations, we consider the attraction of a single membrane vertex to an ABP, such that ε = 2ωAl with 2Al being the area of the vertex. For the parameters in Table 1, the transition from the unwrapped to a wrapped state is expected at ωmin = 8κ/σ2 which implies εc ≃ 4kBT. In our simulations, adhesive interactions between ABPs and the membrane are exerted up to a distance of σ from the membrane surface, and are therefore long ranged. Theoretical predictions of particle wrapping for long-ranged adhesive interactions indicate that the transition to the fully wrapped state is gradual,41 which is consistent with the area Awrap of particle wrapping as a function of ε shown in Fig. 1(a). Awrap in simulations is calculated as the number of membrane vertices within a cutoff distance radh from the ABP center, multiplied by the vertex area Av = A0/Nv. Thus, the fully wrapped state requires adhesion interactions with ε > εc. For further simulations, we have selected two adhesion strengths of ε = 2.5kBT and ε = 3.5kBT, which correspond to a moderate degree of wrapping illustrated in Fig. 1(b and c).
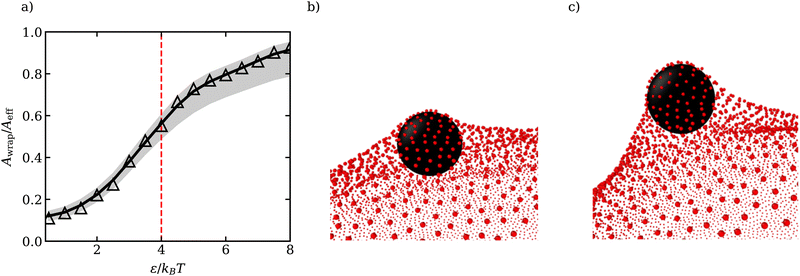 | ||
| Fig. 1 (a) Fraction of wrapped area Awrap of the ABP as a function of ε. Awrap represents the area of membrane vertices around the cutoff distance radh = 1.16σ/2 from the ABP (see Appendix A for the estimation of radh). The grey region corresponds to Awrap estimates based on the cutoffs radh + μ (lower bound) and radh + 3μ (upper bound), where μ is the variance of the ABP-membrane distance distribution in the fully wrapped state (see Appendix A). The dashed red line marks theoretical predictions of the critical εc for the transition from unwrapped to fully wrapped state38 and Aeff = 4πradh2 is the effective particle area. Due to the long range of interactions between the particle and the membrane, the transition is gradual and the particle is only partially wrapped at εc.41 (b and c) Partially wrapped states of a particle (black) by the membrane (red) for (b) ε = 2.5kBT and (c) ε = 3.5kBT. | ||
3. Results
3.1 Dynamic phase diagram
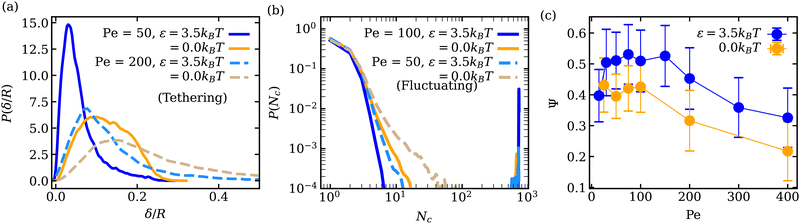
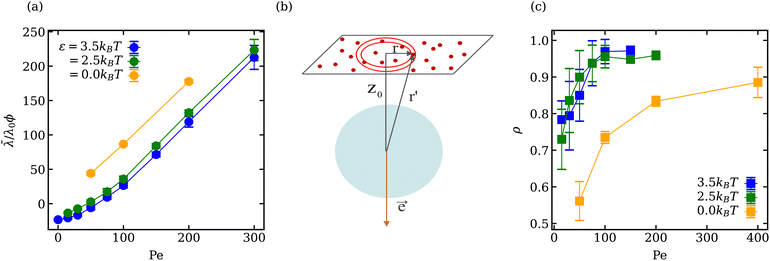
Fig. 2 presents phase diagrams of dynamic shape changes of active vesicles as a function of Pe and ϕ for two different adhesion strengths ε (see also Movies S1–S4, ESI†). At small Pe ≲ 50, the formation of buds for low particle densities, ring-like aggregates of ABPs for intermediate ϕ values, and ABP aggregates with a hexagonal closed-packed (HCP) structure for large ϕ are observed and illustrated in Fig. 3 for Pe = 15. Some of these structures have previously been observed in studies of passive particles adhering to a membrane.43–46 Furthermore, for Pe ≲ 50, ABPs adhered to the membrane show little dynamics, suggesting that adhesive forces dominate over particle activity. As a result, active vesicles for Pe ≲ 50 are close to an equilibrium state, with ABP aggregate structures similar to those of equilibrium systems at Pe = 0.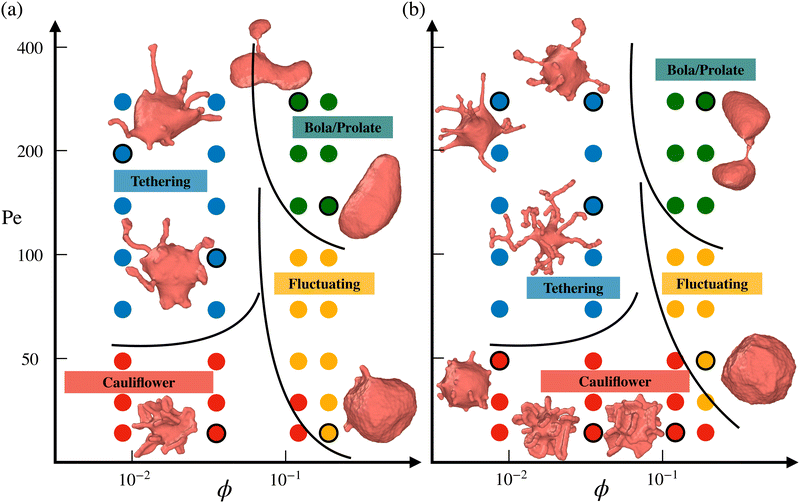 | ||
| Fig. 2 Phase diagrams of vesicle-shape changes as a function of Pe and ϕ for two different adhesion strengths (a) ε = 2.5kBT and (b) ε = 3.5kBT. Four regions are observed, including the tethering (blue symbols), bola/prolate (green symbols), fluctuating (yellow symbols), and cauliflower (red symbols) regimes. The points corresponding to the displayed snapshots have black outlines. The black lines provide an approximate demarcation of the different regimes, serving as a guide to the eye. For a visual illustration of dynamic shape changes of active vesicles, see also Movies S1–S4 (ESI†). | ||
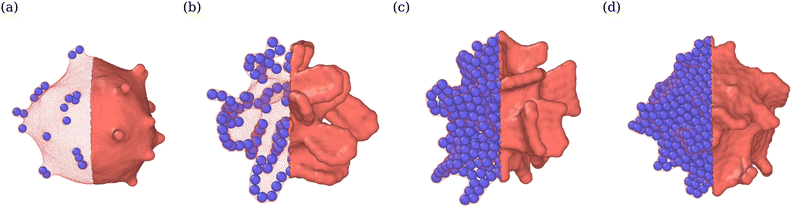 | ||
| Fig. 3 Vesicle shapes in the near-equilibrium “cauliflower” regime at Pe = 15 and ε = 3.5kBT for (a) ϕ = 0.009, (b) ϕ = 0.04 (see Movie S4, ESI†), (c) ϕ = 0.12, and (d) ϕ = 0.18. Different nearly-frozen structures of the ABPs are observed, including ring-like and sheet-like arrangements. The left half of the membrane is made transparent so that the arrangement of ABPs is visible. | ||
In the near-equilibrium “cauliflower” regime at low ABP densities, both individually wrapped particles and short strings of several ABPs within membrane tubes (see Fig. 3(a)) are observed due to the competition between repulsive curvature-mediated interactions47 and the in-plane motion from ABP propulsion. As the ABP volume fraction is increased, strong cooperative wrapping of ABPs is observed, as shown in Fig. 3(b and c). Here, it is likely that the gain in energy due to the cooperative wrapping overcomes the curvature-mediated repulsion. Cooperative wrapping of several particles is also enhanced by the interaction range of an adhesion potential.41 Furthermore, the vesicle is free to change its volume in our simulations, and therefore, the area fraction of adhered membrane can be large. As a result, extreme deformations of the vesicle with protruding ring-like and sheet-like structures are observed and illustrated in Fig. 3(b and c). For the largest volume fraction of ABPs (ϕ = 0.18), membrane deformations are reduced (see Fig. 3(d)) in comparison to the cases of ϕ = 0.04 and ϕ = 0.12, because the gain in adhered membrane area is restricted at some point by the volume of the ABP content. Therefore, if the vesicle volume were constrained to near-spherical values, membrane deformations are expected to be reduced, since the gain in adhered membrane would be restricted by an increase in membrane tension due to the constrained vesicle volume. Note that for the lower adhesion strength of ε = 2.5kBT, membrane deformations are less pronounced than in the case of ε = 3.5kBT (see Fig. 2 for Pe ≲ 50) due to the competition between adhesion and bending energies.
As Pe is increased, ABP propulsion starts to dominate over the adhesive forces, and the non-equilibrium nature of active vesicles becomes apparent. At low particle densities (ϕ ≲ 0.07), ABP activity leads to the formation of dynamic tether-like structures, which are filled by string-like arrangements of ABPs. This behavior is qualitatively different from the tether formation by ABPs in the absence of adhesive interactions, where particle clustering takes place at the end of a tether.18,23 Note that the string-like arrangement of particles in membrane tubes is favored by long-ranged adhesive interactions.41,60 Another qualitative difference of the formed tethered structures by adhesive ABPs in comparison to those by non-adhesive active particles18,23 is that the tethered structures in Fig. 2 are often highly branched. Since ABPs spend a considerable time in string-like configurations within membrane tethers, ABPs can change their orientation due to rotational diffusion and initiate branch formation from the existing tether. In the absence of adhesive interactions, ABPs quickly travel between the base of a tether and its end (or vise versa), and thus cannot easily initiate branched tethers.18,23 Therefore, adhesive interactions promote the formation of branched tether structures and stabilize them. At the lower adhesion strength of ε = 2.5kBT, ABPs cluster more at tether ends than for the case of ε = 3.5kBT, and result in less branched structures, as shown in Fig. 2. A similar effect is observed with increasing particle activity (or Pe), suggesting that branched tether structures and string-like arrangements of ABPs are indeed a consequence of particle adhesion to the membrane, which is lost when ABPs have a sufficient force to detach from the membrane. Note that the tethering regime for adhesive ABPs occurs at significantly lower Pe numbers when compared to the non-adhesive ABP case18,23 because particle adhesion facilitates wrapping, reducing the energy barrier required for the formation of tethers.
At large particle densities (ϕ ≳ 0.07) and for Pe values beyond the cauliflower regime, a fluctuating phase first develops, where shape changes of the vesicle are moderate and resemble membrane fluctuations. In Section 3.3, we will show that vesicle shape fluctuations for adhesive ABPs are different from those for the non-adhesive ABP case.18 As Pe is further increased for ϕ ≳ 0.07, the ABPs form large clusters which can push in opposing directions and result in vesicle elongation or even splitting into two vesicles, similar to the non-adhesive ABP case.18 Thus, the effect of adhesive interactions is prevalent only for low to intermediate Pe values, where the adhesive forces are larger than or comparable to ABP propulsion forces.
The diagrams in Fig. 2 are primarily constructed through visual inspection of vesicle shapes and their dynamic changes. This is sufficient because the vesicle conformations in Fig. 2 display significant qualitative differences between the various phases: long thin tethers emerging from the mother vesicle in the tethering phase, nearly spherical shapes with strong fluctuations in the fluctuating phase, large asphericity and whole shape deformation in the bola/prolate phase, and nearly static vesicle shapes with several particle-filled protrusions in the cauliflower phase. Classification of vesicle shapes can also be based on a quantitative analysis of their characteristics,23 such as the squared distance from the center of mass which is large in the tethering phase, and vesicle asphericity for the fluctuating and bola/prolate phases. However, for the performed simulations, a more quantitative characterization seems to be of little benefit. Possibly, the quantitative characterization might become useful for a much higher sampling density of simulated parameter space.
3.2 Membrane tension
The mean vesicle tension![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) computed from local membrane stresses (see Appendix B) for different adhesion energies is shown in Fig. 4(a). Tension is calculated every Δt = 0.01τr (τr ≈ 0.1τ) within the time range 0.4τr < t < 5τr and averaged over all time frames. For small Pe ≲ 50 in the case of adhesive ABPs, the mean tension of the vesicle is slightly negative, which indicates local compression of the membrane vertices. The local contraction of the membrane is facilitated by adhesive interactions, which are relatively long ranged, and favor the adhesion of more membrane vertices to the ABPs, leading to local compression of the membrane within the adhesion area. Furthermore, at small Pe, active particles generate a relatively low swim pressure at the membrane, so that the membrane tension remains slightly negative.
computed from local membrane stresses (see Appendix B) for different adhesion energies is shown in Fig. 4(a). Tension is calculated every Δt = 0.01τr (τr ≈ 0.1τ) within the time range 0.4τr < t < 5τr and averaged over all time frames. For small Pe ≲ 50 in the case of adhesive ABPs, the mean tension of the vesicle is slightly negative, which indicates local compression of the membrane vertices. The local contraction of the membrane is facilitated by adhesive interactions, which are relatively long ranged, and favor the adhesion of more membrane vertices to the ABPs, leading to local compression of the membrane within the adhesion area. Furthermore, at small Pe, active particles generate a relatively low swim pressure at the membrane, so that the membrane tension remains slightly negative.
Membrane tension ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) for ε > 0 in Fig. 4(a) exhibits two different regimes. For Pe < 100, the dependence of
for ε > 0 in Fig. 4(a) exhibits two different regimes. For Pe < 100, the dependence of ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) is non-linear, while for Pe > 100,
is non-linear, while for Pe > 100, ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) increases linearly with increasing Pe, similar to the case of ε = 0. For active vesicles with non-adhesive ABPs, the linear growth in
increases linearly with increasing Pe, similar to the case of ε = 0. For active vesicles with non-adhesive ABPs, the linear growth in ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) is determined by the swim pressure37 of ABPs on the membrane, such that
is determined by the swim pressure37 of ABPs on the membrane, such that ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) /λ0 = χPeϕ, where λ0 = R2kBT/(πσ4) is a normalization factor and χ is the active tension weight related to the alignment of propulsion direction with the membrane normal.23 Therefore, the linear regime of
/λ0 = χPeϕ, where λ0 = R2kBT/(πσ4) is a normalization factor and χ is the active tension weight related to the alignment of propulsion direction with the membrane normal.23 Therefore, the linear regime of ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) for active vesicles with adhesive ABPs is also due to the swim pressure of ABPs on the membrane, because for large Pe, the ABP propulsion force dominates over adhesion interactions. However, the non-linear dependence of
for active vesicles with adhesive ABPs is also due to the swim pressure of ABPs on the membrane, because for large Pe, the ABP propulsion force dominates over adhesion interactions. However, the non-linear dependence of ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) for Pe < 100 and ε > 0 is due to the interplay of swim pressure and particle adhesion to the membrane. Interestingly, the proportionality
for Pe < 100 and ε > 0 is due to the interplay of swim pressure and particle adhesion to the membrane. Interestingly, the proportionality ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) ∼ Peϕλ0 suggests that the active tension should increase as R2 with increasing vesicle size for a fixed ABP volume fraction. This would favor prolate and bola states over tethering for large vesicles.
∼ Peϕλ0 suggests that the active tension should increase as R2 with increasing vesicle size for a fixed ABP volume fraction. This would favor prolate and bola states over tethering for large vesicles.
The location of the transition from the non-linear to the linear increase in ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) with increasing Pe can be estimated using a simple model, where an adhesive particle placed at a distance z0 from a flat membrane attempts to escape the surface, see Fig. 4(b). The attractive force exerted on the particle due to the membrane patch at a distance
with increasing Pe can be estimated using a simple model, where an adhesive particle placed at a distance z0 from a flat membrane attempts to escape the surface, see Fig. 4(b). The attractive force exerted on the particle due to the membrane patch at a distance 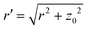 with an area 2πrdr is given by
with an area 2πrdr is given by
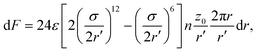 | (9) |
![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) of the particle points away from the membrane along the normal, force balance implies
of the particle points away from the membrane along the normal, force balance implies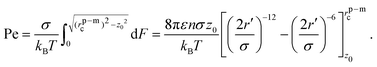 | (10) |
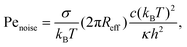 | (11) |
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) σ of a flat tensionless membrane on a length scale of the particle size σ, where
σ of a flat tensionless membrane on a length scale of the particle size σ, where 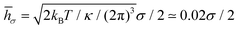 . The range of c ∈ (0.01,0.23) corresponds to a broad range of Penoise ∈ (20,500). Recent experiments of particle wrapping by a lipid membrane64 suggest a much narrower range of c ∈ (0.03,0.06), corresponding to Penoise ∈ (65,130). Taking the median value of Penoise ≃ 100 for c= 0.045, Pe required for the ABP detachment becomes Pedetach = Pemax − Penoise ≃ 290. From simulations of a single ABP adhered to a fluctuating membrane with ε = 3.0kBT, the detachment force corresponds to Pe ≃ 200. This Pe value is in a reasonable agreement with the theoretical estimate of Pedetach, taking into account that Penoise is very sensitive to the choice of h and c. The transition from the non-linear to linear increase in
. The range of c ∈ (0.01,0.23) corresponds to a broad range of Penoise ∈ (20,500). Recent experiments of particle wrapping by a lipid membrane64 suggest a much narrower range of c ∈ (0.03,0.06), corresponding to Penoise ∈ (65,130). Taking the median value of Penoise ≃ 100 for c= 0.045, Pe required for the ABP detachment becomes Pedetach = Pemax − Penoise ≃ 290. From simulations of a single ABP adhered to a fluctuating membrane with ε = 3.0kBT, the detachment force corresponds to Pe ≃ 200. This Pe value is in a reasonable agreement with the theoretical estimate of Pedetach, taking into account that Penoise is very sensitive to the choice of h and c. The transition from the non-linear to linear increase in ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) in Fig. 4(a) corresponds to Pe ≈ 100. This value is lower than the theoretical estimate, which is likely due to the presence of frequent inter-ABP collisions at ϕ = 0.18, and enhanced membrane fluctuations facilitated by active particles (see Section 3.3). Interestingly, a shift between the
in Fig. 4(a) corresponds to Pe ≈ 100. This value is lower than the theoretical estimate, which is likely due to the presence of frequent inter-ABP collisions at ϕ = 0.18, and enhanced membrane fluctuations facilitated by active particles (see Section 3.3). Interestingly, a shift between the ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) curves for ε = 0 and ε > 0 in Fig. 4(a) also corresponds to about Pe ≃ 100.
curves for ε = 0 and ε > 0 in Fig. 4(a) also corresponds to about Pe ≃ 100.
Since membrane tension is affected by the ABP adhesion, we also compute the fraction ρ of particles which are in a direct contact with the membrane, i.e. within a distance of 0.625σ from the membrane accounting for only one layer of ABPs. ρ is measured every Δt = 0.1τr within the time range 0.4τr < t < 5τr, and averaged over all time frames. Fig. 4(c) shows that ρ for adhesive ABPs is nearly twice larger than for non-adhesive particles at low Pe. As Pe is increased, ρ rapidly approaches unity for the cases with ε > 0 and levels off for Pe > 100, while in the absence of adhesion, ρ reaches a value of 0.88 only at Pe = 400. Therefore, adhesive interactions make a difference even at large Pe. Although the fraction ρ of near-membrane ABPs seem to follow the same trend for ε = 0 and ε > 0, the physical mechanisms are different. For ε = 0, an increase in Pe leads to an increase in the number of ABPs at the membrane due to activity-induced accumulation of ABPs at surfaces.34,67 ABPs spend on average more time at the surface with increasing Pe, since the escape times decrease with decreasing rotational diffusion, leading to an increase in ρ. Furthermore, there exists a feedback mechanism between particle accumulation and membrane curvature,18,23 as the propulsion force exerted on the membrane induces a larger local curvature and ABPs accumulate in regions of the large curvature.35,36 For the cases with ε > 0, this mechanism is also partially relevant, however, already at low Pe, most of the particles are located at the membrane due to adhesive interactions. The fraction ρ at low Pe for adhesive ABPs in Fig. 4(c) does not reach unity because of the strong wrapping of particles by the membrane, whose area is insufficient for all ABPs at ϕ = 0.18. As Pe is increased and ABPs have a sufficient force to detach from the membrane, near-equilibrium frozen “cauliflower” structures with strong particle wrapping dissolve and the activity-induced accumulation of ABPs results in ρ to approach unity. Note that even though the fraction of ABPs at the membrane for ε > 0 is larger than that for ε = 0, it does not contribute in the same way to membrane tension. For ε = 0, the larger is the fraction ρ, the larger is the mean membrane tension ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) due to an increasing swim pressure. For ε > 0, even though an increase in Pe leads to an increase in
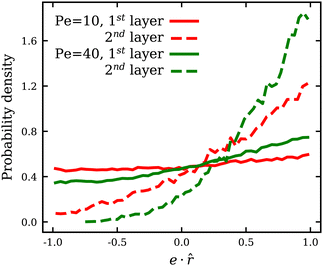
due to an increasing swim pressure. For ε > 0, even though an increase in Pe leads to an increase in ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) for the same reason, ABP adhesion reduces mean membrane tension because of long-ranged adhesive interactions discussed above. Moreover, at low Pe, a number of adhered ABPs may temporarily be oriented away from the membrane without detaching from it, which results in a reduction of the total swim pressure. Fig. 5 shows the distribution of the projection e·
for the same reason, ABP adhesion reduces mean membrane tension because of long-ranged adhesive interactions discussed above. Moreover, at low Pe, a number of adhered ABPs may temporarily be oriented away from the membrane without detaching from it, which results in a reduction of the total swim pressure. Fig. 5 shows the distribution of the projection e·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) of the orientation vector e of ABPs onto their normalized radial position vector
of the orientation vector e of ABPs onto their normalized radial position vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) measured from the center of mass of the vesicle. Positive/negative values of e·
measured from the center of mass of the vesicle. Positive/negative values of e·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) correspond to ABP orientations toward/away from the membrane (i.e. extensile/contractile stresses). Note that at low Pe, there is a considerable fraction of ABPs in the first layer with e·
correspond to ABP orientations toward/away from the membrane (i.e. extensile/contractile stresses). Note that at low Pe, there is a considerable fraction of ABPs in the first layer with e·![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) < 0, i.e. pointing away from the membrane, whereas in the second layer, the vast majority of APBs points toward the membrane. When ABPs arrive at the membrane from the bulk, they must point toward the membrane and exert extensile active stresses. At low Pe, and sufficiently strong adhesion, such that the residence time at the membrane exceeds the rotational diffusion time τr, ABPs in the first layer can re-orient and exert forces away from the membrane, even though they do not seem to destabilize the static shapes. At larger Pe, before the re-orientation due to rotational diffusion can take place, ABPs slide along the membrane and continue to exert extensile stresses on the membrane, which is similar to the case of ε = 0.36 Furthermore, only ABPs that are in direct contact with the membrane can exert contractile stresses due to adhesion. In contrast, extensile stresses can come from all ABPs, independently of their contact with the membrane. As a result, the generated active tension is generally positive and increasing with Pe, as shown in Fig. 4(a).
< 0, i.e. pointing away from the membrane, whereas in the second layer, the vast majority of APBs points toward the membrane. When ABPs arrive at the membrane from the bulk, they must point toward the membrane and exert extensile active stresses. At low Pe, and sufficiently strong adhesion, such that the residence time at the membrane exceeds the rotational diffusion time τr, ABPs in the first layer can re-orient and exert forces away from the membrane, even though they do not seem to destabilize the static shapes. At larger Pe, before the re-orientation due to rotational diffusion can take place, ABPs slide along the membrane and continue to exert extensile stresses on the membrane, which is similar to the case of ε = 0.36 Furthermore, only ABPs that are in direct contact with the membrane can exert contractile stresses due to adhesion. In contrast, extensile stresses can come from all ABPs, independently of their contact with the membrane. As a result, the generated active tension is generally positive and increasing with Pe, as shown in Fig. 4(a).
3.3 Vesicle shape fluctuations
In the fluctuating regime, we analyse vesicle shape changes by computing the fluctuation spectrum of a membrane cross-section, as outlined in Appendix C. Fluctuation spectra of active vesicles at ϕ = 0.18 are presented in Fig. 6 for various ε and Pe values. The fluctuation spectra can be divided into the three regimes with respect to the mode number l: (i) low l ≲ 10 where the ABP activity or adhesion dominate, (ii) intermediate 10 ≲ l ≲ lσ where the competition between the ABP propulsion and adhesion is important, with lσ = 2πR/σ ≃ 50 being a wavelength of the ABP size, and (iii) large l ≳ lσ where passive bending rigidity of the membrane dominates. At low mode numbers l ≲ 10 and small Pe ≲ 50 values, a plateau-like region is observed, which is more pronounced for large adhesion strengths. This indicates that large-wavelength fluctuations are suppressed in the presence of adhesion at low Pe due to nearly non-dynamic ABP clusters adhered to the membrane. The suppression of large wavelength fluctuations has also been observed in cells due to the presence of an underlying cytoskeleton.68,69 Thus, the adhesion of particles to the membrane leads to a membrane confinement effect, significantly reducing fluctuations at low l modes. As Pe is increased, the ABPs attain sufficient propulsion force to detach from the membrane, accompanied by the disappearance of the plateau region at low l. Furthermore, the exponent β of fluctuation modes at low l ∈ [2,8] becomes β < − 1 (see the inset in Fig. 6(a)), which is a clear signature of active membrane fluctuations.18,19β decreases as a function of Pe, demonstrating the enhancement of low-mode fluctuations due to ABP activity.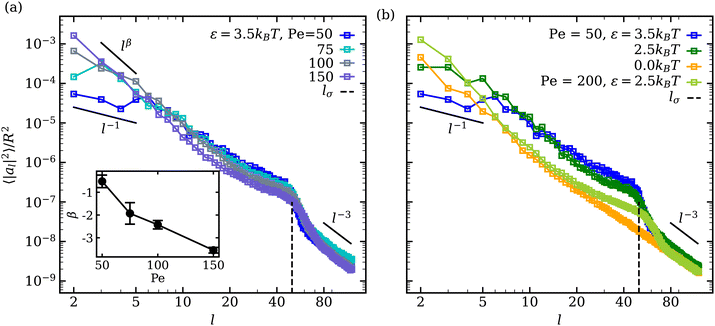 | ||
| Fig. 6 Mode spectra of vesicle-shape fluctuations for ϕ = 0.18 at (a) ε = 3.5kBT for different Pe values and at (b) Pe = 50 for different ε values. Large wavelength (low mode) fluctuations are suppressed at low Pe for a strong ABP adhesion, resulting in a plateau-like region at l ≲ 10. The inset in (a) shows the exponent β of low-mode fluctuations with increasing Pe. The error bars are estimated from the covariance matrix of the fitted model.61 The dashed lines indicate the mode number lσ = 2πR/σ ≃ 50, representing a wavelength of the ABP size. | ||
A shift in the fluctuation-spectrum curves for different adhesion strengths and intermediate l values at Pe = 50 in Fig. 6(b) is likely due to the fact that a number of adhered ABPs can enhance membrane fluctuations by exerting temporary forces in the direction away from the membrane without detaching from it. Note that a reduction in tension for ε > 0 cannot significantly contribute to this shift in fluctuation spectrum, because the effect of membrane tension is expected to be present for l ≲ 10–15,18 while the observed shift extends significantly beyond those l values. Furthermore, for Pe = 200 and ε = 2.5kBT in Fig. 6(b), the shift in fluctuation spectrum nearly disappears despite the fact that the mean membrane tension is significantly larger than in the case of Pe = 50 and ε = 0 (see Fig. 4(a)). This suggests that the combination of ABP activity (i.e., applied forces in the direction away from the membrane) and adhesion is responsible for the shift in fluctuation spectrum for Pe ≲ 100.
Another interesting feature in the fluctuation spectra in Fig. 6 for adhesive ABPs with ε > 0 is the enhancement of amplitudes al2 at l ≃ 40–60 corresponding to the ABP size, since lσ = 2πR/σ ≃ 50. This local enhancement in al2 represents the wrapping of adhesive ABPs by the membrane, as it is consistently reduced at Pe = 200 in comparison to Pe = 50. Finally, at large l, the squared fluctuation amplitudes decay as l−3 irrespective of ABP adhesion or Pe, corresponding to the bending-dominated regime of membrane fluctuations.
3.4 ABP clustering and mobility
Adhesion of ABPs to the membrane must decrease their overall mobility. Fig. 7(a) presents distributions of fixed-time displacements δ of single ABPs for various Pe and ε values in the tethering regime. The displacements are calculated for a fixed time interval Δt = 0.1τr (i.e. in the active-ballistic regime) within the time range 0.4τr < t < 5τr. As expected, ABP mobility is significantly reduced for the cases of ε > 0 in comparison to non-adhesive ABPs, and the reduction in particle mobility is more pronounced at low Pe, since adhesion interactions dominate over the ABP activity. The mobility of active particles can also be reduced due to the formation of ABP clusters inside the vesicle. Fig. 7(b) shows distributions of cluster sizes Nc (i.e., the number of ABPs per single cluster) at large ϕ for various Pe and ε in the fluctuating regime. The clustering analysis is performed every Δt = 0.01τr within the time range 0.4τr < t < 5τr, where particles within a distance of 1.1σ are considered a part of the same cluster. In the absence of adhesion (ε = 0), an increase in Pe leads to an increased accumulation of ABPs at the membrane, such that large clusters are formed through a reduction in the number of small clusters, as can be seen through the emergence of a peak at large Nc for Pe = 100 in Fig. 7(b). For ε > 0, ABP adhesion to the membrane further facilitates the membrane-mediated formation of large particle clusters, as in this case, a peak at large Nc develops already at Pe = 50 in Fig. 7(b). As a result, adhesive interactions generally enhance cluster formation in comparison to the case of non-adhesive ABPs. Despite the strong tendency for cluster formation at the membrane surface, there are no long-range ABP velocity correlations beyond the size of clusters.We also compute cluster asphericity Ψ (see Appendix D for details) to quantify the effect of ABP adhesion on cluster shapes. Fig. 7(c) presents Ψ as a function of Pe, and demonstrates that adhesive interactions cause an increase in the asphericity of ABP clusters. Thus, ABP clusters for ε > 0 attain shapes, which are further away from a spherical geometry, in agreement with the branched string-like arrangements of ABPs in the tethering regime discussed in Section 3.1. For ε = 0, ABPs primarily cluster at the end of tethers as nearly spherical aggregates. Interestingly, Ψ for the case of adhesive ABPs first increases and then decreases with increasing Pe. Characteristic vesicle shapes are illustrated in Fig. 8 for different Pe. At low Pe, ring-like ABP clusters (Fig. 8(a)) in the near-equilibrium cauliflower regime are observed and have the asphericity of about Ψ = 0.4. With increasing Pe, branched string-like clusters of ABPs within membrane tubes develop with Ψ > 0.4, see Fig. 8(c). At large Pe ≳ 200, ABP propulsion forces dominate over adhesive interactions, so that the string-like structures are destabilized and the ABPs cluster at the tether ends (Fig. 8(d)) with a reduced cluster asphericity. In conclusion, the results in Fig. 7 clearly show that adhesive interactions of ABPs with the membrane strongly alter the behavior of individual ABPs and their clusters.
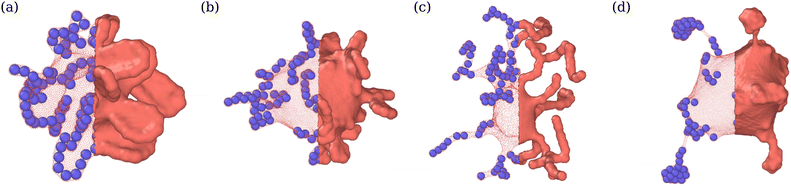 | ||
| Fig. 8 Vesicle shapes for ϕ = 0.04 and ε = 3.5kBT at (a) Pe = 15 (see Movie S4, ESI†), (b) Pe = 50, (c) Pe = 150 (see Movie S1, ESI†), and (d) Pe = 300. Particle structures change from membrane-wrapped ring-like arrangements to membrane-wrapped (branched) tubular aggregates, as Pe is increased. A further increase in Pe leads to the detachment of ABPs from the membrane and their accumulation at the tether end. The left half of the membrane is made transparent so that the arrangement of ABPs is visible. | ||
4. Summary and conclusions
Vesicles enclosing active particles exhibit a variety of dynamic shape deformations, ranging from tethers to prolate and bola-like shapes. Adhesive interactions between particles and a vesicle in equilibrium can lead to strong, although static, deformations of the vesicle, such as the formation of buds and long tubular structures. In this work, we have combined the effects of particle activity and adhesion to study the deformation and properties of vesicles enclosing adhesive ABPs. At low propulsion forces of ABPs, adhesion interactions with the membrane dominate, leading to the formation of membrane structures (e.g., buds, tubes) which are similar to those in equilibrium. Furthermore, due to the absence of a volume constraint in our simulations, strong membrane deformations with ring-like and sheet-like ABP structures occur for moderate volume fractions of ABPs, which are governed by the balance of adhesive interactions and energetic costs for membrane bending. As the propulsion of ABPs (or the Peclet number Pe) is increased, the particles are able to detach from the membrane, and the effects of adhesion become less dominant. A simple estimation for the detachment force of a single ABP adhered to the membrane based on theoretical arguments and simulations yields the adhesion-dominated regime for Pe ≲ 200 (depending on membrane bending rigidity, adhesion strength, and particle size). However, ABP-ABP collisions at large enough ϕ and enhanced membrane fluctuations due to the particle activity further lower the characteristic Pe ≲ 100 determining the adhesion-dominated regime. In the tethering regime, adhesion interactions between the membrane and ABPs significantly reduce the characteristic Pe for tether formation in comparison to non-adhesive ABPs. Furthermore, ABP adhesion favours the formation of long branched tether structures partially or fully filled with active particles for low to moderate volume fractions.At large ϕ, an increase in Pe first causes ‘melting’ of nearly frozen particle structures within the vesicle at low Pe, such that the vesicle attains a spherical shape with pronounced membrane fluctuations. A further increase in Pe results in elongated vesicle shapes or bola-like shapes which eventually split into two daughter vesicles. Different from active vesicles with non-adhesive ABPs, for which the fluctuating regime is observed at low Pe across all ϕ values, membrane fluctuations in the presence of ABP adhesion take place only at ϕ ≳ 0.07 and require some activation energy through a non-zero Pe. The fluctuation spectrum at low Pe has a plateau at low mode numbers because of a ‘caging’ effect due to the adhered particles. ABP adhesion to the membrane leads to local membrane compression with a slightly negative tension due to long-ranged adhesive interactions, so that the mean vesicle tension is lower in the case of adhesive ABPs than for non-adhesive particles. With increasing Pe, the mean membrane tension of the vesicle first has a non-linear dependence on Pe in the adhesion dominated regime, followed by a linear increase of the mean tension at large enough Pe ≳ 100, in agreement with theoretical predictions from the Young-Laplace equation in the case of non-adhesive ABPs.18,23 Furthermore, the adhesion of ABPs to the membrane leads to a reduced particle mobility, but enhances ABP clustering through membrane-mediated interactions. Also, ABP clusters in the presence of adhesive interactions have larger cluster asphericities than those for non-adhesive ABPs, mainly due to the formation of branched string-like structures of ABPs within membrane tubes in the tethering regime. In conclusion, the presence of adhesive interactions between ABPs and the membrane affects not only the phase diagram of active vesicles, but also membrane characteristics (e.g., shape, tension) and ABP properties (e.g., mobility, clustering).
It is also important to mention several limitations of our study. We have focused on membranes with low bending rigidity, where the wrapping of particles is most pronounced. An increased membrane bending rigidity would reduce the degree of particle wrapping, and increase the adhesion strength required for strong wrapping.39,40 Furthermore, the onset of tether formation for stiffer membranes should be shifted toward larger Pe numbers.18 However, we expect that the qualitative behavior of active vesicles should remain similar. Considering membrane fluidity, a change in membrane viscosity would modify the dynamics of active vesicle structures. More importantly, hydrodynamic interactions (not taken into account in this study) are expected to affect the dynamics of active particles and the vesicle. If the membrane would possess a non-zero shear elasticity, the tethering regime will be partially or fully suppressed. These aspects of the behavior of active vesicles require further investigation.
Active vesicles can be considered as a biomimetic model of an “artificial cell” capable of non-equilibrium shape deformations, and can potentially act as biomimetic micro-robots. Here, there exists a variety of applications ranging from bio-engineered cell mimics to targeted drug-delivery systems.9,11,12 Clearly, particle adhesion serves as an additional parameter for the control and tuning of the behavior of active vesicles. An important consideration for future work is the role of hydrodynamic interactions on shape-changes, particle mobility, and the possible motility of these active systems. For example, cell motility is closely associated with dynamic morphological changes of the cell.70,71 Moreover, rupture and splitting of active vesicles need to be studied in the future to properly capture the behavior of active vesicles at large particle loading. Such studies will open the door for the design of specific functionalities and possible applications.
Author contributions
G. G. and D. A. F. conceived the research project. P. I. performed the simulations and analysed the obtained data. All authors participated in the discussions and writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Appendices
Appendix A: distance between membrane particles and an adhered ABP
The wrapped area Awrap of an adhered ABP is computed as the number of membrane vertices within a cutoff distance radh from the ABP, multiplied by the vertex area Av = A0/Nv. To estimate radh, Fig. 9 shows the distribution P(2r/σ) of the scaled distance 2r/σ between an adhered ABP and membrane vertices for a fully wrapped state at Pe = 0 and ε = 8kBT. The cutoff distance radh = 1.16σ/2 for the calculation of Awrap is defined as the mean of P(2r/σ). radh is slightly larger than the minimum of the LJ potential at r = 21/6σ/2 due to contributions from the other potentials representing membrane bending resistance and local area conservation. The variance of the distribution in Fig. 9 is μ ≃ 0.035σ/2.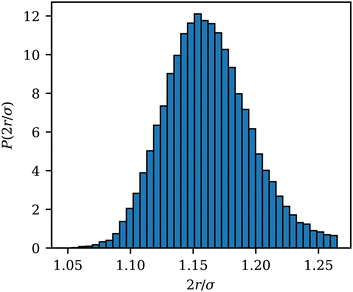 | ||
| Fig. 9 Distribution function P(2r/σ) of the scaled distance 2r/σ between an adhered ABP and membrane vertices for a fully wrapped state at Pe = 0 and ε = 8kBT. | ||
Appendix B: calculation of membrane tension
Membrane tension is calculated using the virial theorem.72 The sum over virial contributions from the local area constraint is given by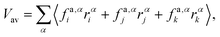 | (12) |
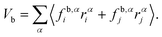 | (13) |
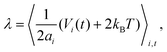 | (14) |
Appendix C: membrane shape fluctuations
The membrane shape fluctuations are measured by considering 2D sections of the vesicle contour in the x, y, and z directions. The sections are made every Δt = 0.01τr within the time range of 0.4τr < t < 5τr. The local membrane position in these contours is given by r(θm), where θm = 2πm/n and 2π/n is the angle for contour discretisation. The fluctuation mode amplitudes al are given by the decomposition73–75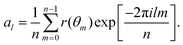 | (15) |
Appendix D: asphericity of ABP clusters
Shapes of ABP clusters are quantified by their asphericity. The asphericity is calculated from the gyration tensor G, which is based on the second moments of N particle positions as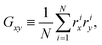 | (16) |
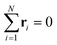 . Let λ1, λ2, and λ3 be the eigenvalues of G. Then, the asphericty Ψ is defined as77
. Let λ1, λ2, and λ3 be the eigenvalues of G. Then, the asphericty Ψ is defined as77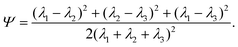 | (17) |
Appendix E: description of movies
All movies are for an adhesion strength of ε = 3.5kBT.Movie S1 (ESI†): Formation of dynamic and highly branched tether structures at Pe = 150 and ϕ = 0.04. As ABP motion along the tether is limited due to their string-like arrangement, rotational diffusion of the ABPs facilitates tether branching in contrast to ABP escape from the tether for ε = 0.
Movie S2 (ESI†): Tether formation at Pe = 300 and ϕ = 0.009. ABPs can escape from a tether and join new tethers due to their rotational diffusion.
Movie S3 (ESI†): Vesicle elongation followed by splitting in the bola regime at Pe = 200 and ϕ = 0.12.
Movie S4 (ESI†): Formation of nearly static ring-like structures of ABPs at Pe = 15 and ϕ = 0.04.
Acknowledgements
We thank Thorsten Auth and Roland G. Winkler for many helpful discussions. The authors gratefully acknowledge the computing time granted through JARA on the supercomputer JURECA78 at Forschungszentrum Jülich.Notes and references
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef
.
- F. Jülicher, S. W. Grill and G. Salbreux, Rep. Prog. Phys., 2018, 81, 076601 CrossRef PubMed
.
- G. Gompper,
et al.
, J. Phys.: Condens. Matter, 2020, 32, 193001 CrossRef CAS PubMed
.
- S. Shankar, A. Souslov, M. J. Bowick, M. C. Marchetti and V. Vitelli, Nat. Rev. Phys., 2022, 4, 380–398 CrossRef
.
- M. Kelkar, P. Bohec and G. Charras, Curr. Opin. Cell Biol., 2020, 66, 69–78 CrossRef CAS PubMed
.
- X. Trepat and E. Sahai, Nat. Phys., 2018, 14, 671–682 Search PubMed
.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed
.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef
.
- D. Needleman and Z. Dogic, Nat. Rev. Mater., 2017, 2, 17048 CrossRef CAS
.
- S. Banerjee, M. L. Gardel and U. S. Schwarz, Annu. Rev. Condens. Matter Phys., 2020, 11, 421–439 CrossRef PubMed
.
- P. Schwille,
et al.
, Angew. Chem., Int. Ed., 2018, 57, 13382–13392 CrossRef CAS PubMed
.
- A. Bernheim-Groswasser, N. S. Gov, S. A. Safran and S. Tzlil, Adv. Mater., 2018, 30, 1707028 CrossRef PubMed
.
- F. C. Keber, E. Loiseau, T. Sanchez, S. J. DeCamp, L. Giomi, M. J. Bowick, M. C. Marchetti, Z. Dogic and A. R. Bausch, Science, 2014, 345, 1135–1139 CrossRef CAS PubMed
.
- G. Duclos, R. Adkins, D. Banerjee, M. S. E. Peterson, M. Varghese, I. Kolvin, A. Baskaran, R. A. Pelcovits, T. R. Powers, A. Baskaran, F. Toschi, M. F. Hagan, S. J. Streichan, V. Vitelli, D. A. Beller and Z. Dogic, Science, 2020, 367, 1120–1124 CrossRef CAS PubMed
.
- K. Weirich, K. L. Dasbiswas, T. A. Witten, S. Vaikuntanathan and M. L. Gardel, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11125–11130 CrossRef CAS PubMed
.
- J. Steinkühler, R. L. Knorr, Z. Zhao, T. Bhatia, S. M. Bartelt, S. Wegner, R. Dimova and R. Lipowsky, Nat. Commun., 2020, 11, 905 CrossRef PubMed
.
- Y. Elani, Angew. Chem., Int. Ed., 2021, 60, 5602–5611 CrossRef CAS PubMed
.
- H. R. Vutukuri, M. Hoore, C. Abaurrea-Velasco, L. van Buren, A. Dutto, T. Auth, D. A. Fedosov, G. Gompper and J. Vermant, Nature, 2020, 586, 52–56 CrossRef CAS PubMed
.
- S. C. Takatori and A. Sahu, Phys. Rev. Lett., 2020, 124, 158102 CrossRef CAS PubMed
.
- L. Le Nagard, A. T. Brown, A. Dawson, V. A. Martinez, W. C. K. Poon and M. Staykova, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2206096119 CrossRef CAS PubMed
.
- M. Park, K. Lee and S. Granick, Soft Matter, 2022, 18, 6419–6425 RSC
.
- M. Paoluzzi, R. Di Leonardo, M. C. Marchetti and L. Angelani, Sci. Rep., 2016, 6, 34146 CrossRef CAS PubMed
.
- P. Iyer, G. Gompper and D. A. Fedosov, Soft Matter, 2022, 18, 6868–6881 RSC
.
- Y. Li and P. R. Ten Wolde, Phys. Rev. Lett., 2019, 123, 148003 CrossRef CAS PubMed
.
- M. S. Peterson, A. Baskaran and M. F. Hagan, Nat. Commun., 2021, 12, 1–9 CrossRef PubMed
.
- P. K. Mattila and P. Lappalainen, Nat. Rev. Mol. Cell Biol., 2008, 9, 446–454 CrossRef CAS PubMed
.
- M. Krause and A. Gautreau, Nat. Rev. Mol. Cell Biol., 2014, 15, 577–590 CrossRef CAS PubMed
.
- S. Tuvia, A. Almagor, A. Bitler, S. Levin, R. Korenstein and S. Yedgar, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 5045–5049 CrossRef CAS PubMed
.
- Y.-K. Park, C. A. Best, T. Auth, N. S. Gov, S. A. Safran, G. Popescu, S. Suresh and M. S. Feld, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1289–1294 CrossRef CAS PubMed
.
- H. Turlier, D. A. Fedosov, B. A. Audoly, T. Auth, N. S. Gov, C. Sykes, J.-F. Joanny, G. Gompper and T. Betz, Nat. Phys., 2016, 12, 513–519 Search PubMed
.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A, 1991, 44, 1182–1202 CrossRef CAS PubMed
.
- R. Lipowsky, Faraday Discuss., 2013, 161, 305–331 RSC
.
- R. Lipowsky, Adv. Colloid Interface Sci., 2022, 301, 102613 CrossRef CAS PubMed
.
- Y. Fily, A. Baskaran and M. F. Hagan, Soft Matter, 2014, 10, 5609–5617 RSC
.
- Y. Fily, A. Baskaran and M. F. Hagan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 012125 CrossRef PubMed
.
- P. Iyer, R. G. Winkler, D. A. Fedosov and G. Gompper, arXiv, 2022, preprint, arXiv:2212.08561, DOI:10.48550/arXiv.2212.08561.
- S. C. Takatori, W. Yan and J. F. Brady, Phys. Rev. Lett., 2014, 113, 028103 CrossRef CAS PubMed
.
- R. Lipowsky and H.-G. Döbereiner, EPL, 1998, 43, 219 CrossRef CAS
.
- M. Deserno and T. Bickel, EPL, 2003, 62, 767 CrossRef CAS
.
- S. Dasgupta, T. Auth and G. Gompper, Nano Lett., 2014, 14, 687–693 CrossRef CAS PubMed
.
- M. Raatz, R. Lipowsky and T. R. Weikl, Soft Matter, 2014, 10, 3570–3577 RSC
.
- S. Dasgupta, T. Auth and G. Gompper, J. Phys.: Condens. Matter, 2017, 29, 373003 CrossRef CAS PubMed
.
- I. Koltover, J. O. Raedler and C. R. Safinya, Phys. Rev. Lett., 1999, 82, 1991 CrossRef CAS
.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 109, 188101 CrossRef PubMed
.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 108, 118101 CrossRef PubMed
.
- J. Cardellini, L. Caselli, E. Lavagna, S. Salassi, H. Amenitsch, M. Calamai, C. Montis, G. Rossi and D. Berti, J. Phys. Chem. C, 2022, 126, 4483–4494 CrossRef CAS PubMed
.
- A. H. Bahrami and T. R. Weikl, Nano Lett., 2018, 18, 1259–1263 CrossRef CAS PubMed
.
- I. Canton and G. Battaglia, Chem. Soc. Rev., 2012, 41, 2718–2739 RSC
.
- S. Tzlil, M. Deserno, W. M. Gelbart and A. Ben-Shaul, Biophys. J., 2004, 86, 2037–2048 CrossRef CAS PubMed
.
- A. Aderem and D. M. Underhill, Annu. Rev. Immunol., 1999, 17, 593–623 CrossRef CAS PubMed
.
- J. S. Rossman and R. A. Lamb, Virology, 2011, 411, 229–236 CrossRef CAS PubMed
.
-
G. Gompper and D. M. Kroll, Statistical mechanics of membranes and surfaces, World Scientific, Singapore, 2nd edn, 2004, pp. 359–426 Search PubMed
.
- D. M. Kroll and G. Gompper, Science, 1992, 255, 968–971 CrossRef CAS PubMed
.
- H. Noguchi and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011901 CrossRef PubMed
.
- W. Helfrich, Z. Naturforschung C, 1973, 28, 693–703 CrossRef CAS PubMed
.
- G. Gompper and D. M. Kroll, J. Phys. I France, 1996, 6, 1305–1320 CrossRef
.
- G. Gompper and D. M. Kroll, J. Phys.: Condens. Matter, 1997, 9, 8795–8834 CrossRef CAS
.
- H. Noguchi and G. Gompper, Phys. Rev. Lett., 2004, 93, 258102 CrossRef PubMed
.
-
M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Clarendon Press, New York, 1991 Search PubMed
.
- J. Agudo-Canalejo and R. Lipowsky, Soft Matter, 2016, 12, 8155–8166 RSC
.
- P. H. Richter, TDAPR, 1995.
- W. Helfrich, Z. Naturforsch., 1978, 33, 305–315 CrossRef
.
- T. Bickel, J. Chem. Phys., 2003, 118, 8960–8968 CrossRef CAS
.
- H. T. Spanke, R. W. Style, C. François-Martin, M. Feofilova, M. Eisentraut, H. Kress, J. Agudo-Canalejo and E. R. Dufresne, Phys. Rev. Lett., 2020, 125, 198102 CrossRef CAS PubMed
.
- A. D. Dinsmore, D. T. Wong, P. Nelson and A. G. Yodh, Phys. Rev. Lett., 1998, 80, 409–412 CrossRef CAS
.
- G. Gompper and D. M. Kroll, Europhys. Lett., 1989, 9, 59–64 CrossRef
.
- J. Elgeti and G. Gompper, Europhys. Lett., 2013, 101, 48003 CrossRef CAS
.
- N. Gov and S. Safran, Biophys. J., 2005, 88, 1859–1874 CrossRef CAS PubMed
.
- N. Gov, A. Zilman and S. Safran, Phys. Rev. Lett., 2003, 90, 228101 CrossRef CAS PubMed
.
- K. M. Yamada and M. Sixt, Nat. Rev. Mol. Cell Biol., 2019, 20, 738–752 CrossRef CAS PubMed
.
- A. Shellard and R. Mayor, Trends Cell Biol., 2020, 30, 852–868 CrossRef CAS PubMed
.
- D. Tsai, Chem. Phys., 1979, 70, 1375–1382 CAS
.
- J. Pécréaux, H.-G. Döbereiner, J. Prost, J.-F. Joanny and P. Bassereau, Eur. Phys. J. E, 2004, 13, 277–290 CrossRef PubMed
.
- H. A. Faizi, C. J. Reeves, V. N. Georgiev, P. M. Vlahovska and R. Dimova, Soft Matter, 2020, 16, 8996–9001 RSC
.
- J. Faucon, M. Mitov, P. Méléard, I. Bivas and P. Bothorel, J. Phys., 1989, 50, 2389–2414 CrossRef
.
- M. Frigo and S. G. Johnson, Proc. IEEE, 2005, 93, 216–231 Search PubMed
.
- J. Rudnick and G. Gaspari, J. Phys. A: Math. Gen., 1986, 19, L191–L193 CrossRef
.
- Jülich Supercomputing Centre, J. Large-Scale Res. Facil., 2021, 7, A182 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available: Four movies, illustrating different shape changes of active vesicles, whose description is provided in Appendix E. See DOI: https://doi.org/10.1039/d3sm00004d |
| This journal is © The Royal Society of Chemistry 2023 |

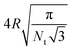
![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_i_char_0065_20d1.gif)