Open Access Article
Open Access ArticleMachine learning-inspired battery material innovation
Man-Fai
Ng
 *a,
Yongming
Sun
*a,
Yongming
Sun
 b and
Zhi Wei
Seh
b and
Zhi Wei
Seh
 *c
*c
aInstitute of High Performance Computing (IHPC), Agency for Science, Technology and Research (A*STAR), 1 Fusionopolis Way, #16-16 Connexis, Singapore, 138632, Republic of Singapore. E-mail: ngmf@ihpc.a-star.edu.sg
bWuhan National Laboratory for Optoelectronics, Huazhong University of Science and Technology, Wuhan, 430074, China
cInstitute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR), 2 Fusionopolis Way, Innovis #08-03, Singapore, 138634, Republic of Singapore. E-mail: sehzw@imre.a-star.edu.sg
First published on 22nd February 2023
Abstract
Machine learning (ML) techniques have been a powerful tool responsible for many new discoveries in materials science in recent years. In the field of energy storage materials, particularly battery materials, ML techniques have been widely utilized to predict and discover materials’ properties. In this review, we first discuss the key properties of the most common electrode and electrolyte materials. We then summarize recent progress in battery material advancement using ML techniques, through the three main strategies of direct property predictions, machine learning potentials, and inverse design. The major challenges, advantages and limitations of these techniques are also discussed. Finally, we conclude this review with a perspective on sustainable battery development using ML.
1. Introduction
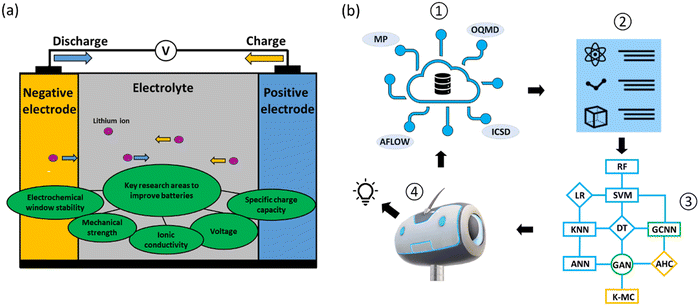
Reducing global greenhouse gas emissions to limit global warming to under two degrees Celsius remains a major challenge.1–5 National initiatives to reduce CO2 emissions by 2030, with a view towards achieving net zero emissions by 2050 make research and development in this area critical. The adoption of electric vehicles (EVs) is gaining major traction as directly replacing fossil fuel vehicles removes a major source of greenhouse gases. Successful EV deployment, however, depends mainly on overcoming the ‘range anxiety’ issue. Developing improved battery models to monitor the state of charge and health of batteries could be one solution;6,7 another solution is to develop more long-lasting and sustainable batteries,8 in which material design plays an important role.Batteries are complex, dynamic electrochemical systems in which the two major components (Fig. 1a) are electrodes (negative and positive) and electrolytes (liquid and solid states). In designing battery electrodes, the key parameters to consider include voltage and specific charge capacity, which contribute to the overall energy density; and volume expansions during charging and discharging, which determine the cyclability and safety issues. For electrolytes, the redox potentials and stability windows (liquid electrolytes) and ionic conductivities and mechanical strengths (solid-state electrolytes) are the key parameters. These parameters are material-dependent, and identifying better battery materials via material design and discovery relies on the exploration of the growing chemical spaces,9 making it increasingly difficult to use conventional trial-and-error discovery approaches.
Data-driven machine learning (ML) and deep learning (DL) techniques, together with high-throughput experimental and computational approaches, have recently emerged as important tools for the design and discovery of battery materials10–19 (Fig. 1b). The battery design problem in a data-driven approach with ML techniques essentially solves a complex function that takes into account battery formulations as the inputs and performance measurements as the outputs. The ML techniques are thus used to optimize these correlation functions. The typical ML algorithms adopted for battery material design can be classified into three categories: supervised, semi-supervised and unsupervised learning. Supervised learning learns from labeled data. Common algorithms used are decision tree (DT), linear regression (LR), random forest (RF), support vector machine (SVM), artificial neural network (ANN) and k-nearest neighbors (KNN). Semi-supervised learning learns from both labeled and unlabeled data. Common algorithms used here are graph convolution neural network (GCNN) and generative adversarial networks (GANs). Unsupervised learning is learning without target variables and operates only with input data. Common algorithms used here are k-mean clustering and agglomerative hierarchical clustering (AHC; Fig. 1b).
Also, high quality datasets lie at the center of ML techniques. Databases are generally classified into two main types: experimental and computational. For battery material discovery, the crystal structures of inorganic and organic compounds are the most widely used datasets for screening and feature extractions. The Materials Project (MP),20,21 Open Quantum Materials Database (OQMD)22 and Automatic FLOW for Materials Discovery (AFLOW)23 are open access databases for computational data of inorganic compounds, while the NIST Inorganic Crystal Structure Database (ICSD)24 is the database chiefly used for experimental data. For organic compounds, the Cambridge Structural Database (CSD),25 Organic Materials Database (OMDB)26 and ChemSpider27 are examples of commonly-used databases (Fig. 1b). These databases typically contain hundreds of thousands to millions of data entries.
In this review, we first discuss the key properties of the most common electrode and electrolyte materials. Then, we summarize recent progress on battery materials advancement using ML techniques, through three ML strategies: (1) direct property predictions; (2) machine learning potentials; and (3) inverse design. New battery materials predicted by ML are highlighted in the process. The major challenges, advantages and limitations of these techniques are also discussed. Finally, the review concludes with perspectives on the development of sustainable batteries using ML techniques.
2. Current battery materials
In this section, we briefly review the key properties of common battery electrode and electrolyte materials. Since the commercialization of lithium-ion batteries (LIBs) by SONY Corporation in 1991, their development has progressed notably, especially in terms of materials for the positive electrode. LiCoO2 was initially used for this purpose,28 while LiMn2O4, LiFePO4 and lithium nickel manganese cobalt oxide (NMC) have since been developed as more advanced electrode materials, showing improved energy density and safety. These materials have voltages ranging from 3.4 to 3.9 V and specific charge capacities ranging from 125 to 190 mA h g−1.29,30 Despite these advancements, the quest for improving LIB technology remains.At the same time, promising battery technologies such as sodium-ion batteries (NIBs), organic batteries, and lithium–sulfur batteries are already on the horizon. Although the typical cathode specific charge capacity for NIBs is about 150 mA h g−1,31 a value lower than that of LIBs, NIBs display great potential as a low-cost battery due to the abundance of sodium. The reported specific charge capacities for organic batteries are generally higher, typically at a range from 200 to 500 mA h g−1, but the voltages are generally lower, at a range from 2.2 to 3.5 V when compared to advanced LIBs. Moreover, the cycling performance varies from tens to thousands of cycles.32 Although lithium–sulfur batteries are a promising high-energy battery technology (with the first discharge specific capacity reaching 1645 mA h g−1, which is close to the theoretical limit for sulfur33), mitigating the effects of polysulfide shuttling (which can shorten battery life) remains a challenge.
The comparison of the voltage-specific charge capacity performance of common electrodes for various battery technologies is shown in Fig. 2a. The development of these battery technologies over the last 30 years and the concurrent advent of physics-based modeling have led to the accumulation of a large-volume of battery data. Many new battery electrode materials with improved performance have been predicted using data-driven approaches with ML (Fig. 2a). These predictions not only identify potential electrodes with high charge capacity or high voltage, but also provide guidelines and directions for further discovery. Voltages and specific charge capacities are the two most important parameters for battery electrodes. However, other less tangible ‘parameters’ such as adsorption strength of polysulfides on host materials and electrolyte coordination energies are also important for improving battery performance. The ML techniques can identify the effects of these parameters and more examples will be discussed in the following section.
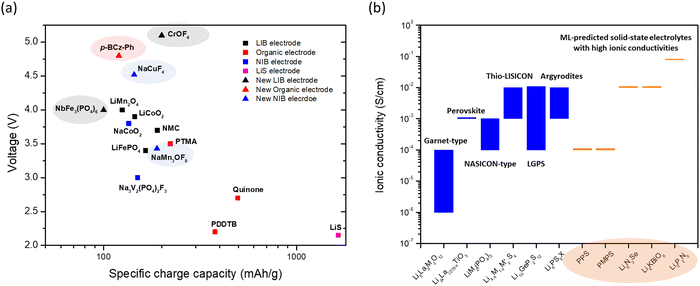 | ||
Fig. 2 (a) A plot of voltage (V) versus specific charge capacity (mA h g−1) for common electrodes in lithium-ion batteries (LIB), sodium-ion batteries (NIB), organic batteries and lithium–sulphur batteries. Values for LiCoO2, LiMn2O4 and LiFePO4 are taken from ref. 29; NMC811 from ref. 30; quinone, poly(2,2,6,6-tetramethyl-1-piperidinyloxy-4-yl methacrylate) (PTMA) and poly(1,4-di(1,3-dithiolan-2-yl)benzene) (PDDTB) from ref. 31 and the references therein; NaCoO2 and Na3V2(PO4)2F3 from ref. 32; and LiS from ref. 33. The ML-predicted new materials for the LIB electrode,43 organic electrode44 and NIB electrode45 are highlighted. (b) A plot showing the ionic conductivities (S cm−1) of common solid-state electrolytes. Values of the garnet-type (Li5La3M2O12, M = Nb and Ta), perovskite, NASICON-type (LiM2(PO4)3, M = Zr, Ti, Hf, Ge and Sn), thio-LISICON (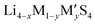 , M = Si and Ge, M′ = P, Al, Zn and Ga), LGPS (Li10GeP2S12) and argyrodites (Li6PS5X, X = Cl and Br) are taken from ref. 34. The ML-predicted solid-state electrolytes36,37 with high ionic conductivities are highlighted. , M = Si and Ge, M′ = P, Al, Zn and Ga), LGPS (Li10GeP2S12) and argyrodites (Li6PS5X, X = Cl and Br) are taken from ref. 34. The ML-predicted solid-state electrolytes36,37 with high ionic conductivities are highlighted. | ||
Another important battery component is the electrolyte, especially the solid-state electrolyte, which forms a major part of a solid-state battery (SSB). SSBs can provide high volumetric energy density (an important feature for space-based applications such as EV) and are extremely safe, as they contain no flammable liquid solvents. In addition, high ionic conductivity, high mechanical strength, and a wide electrochemical stability window are some important features of solid-state electrolytes. In particular, ionic conductivity is a major parameter that is the most studied. The typical ionic conductivity of solid-state electrolytes ranges from 10−6 to 10−4 S cm−1 (Fig. 2b),34 which is lower than that of liquid electrolytes such as EC:DMC in 1 M LiPF6 (about 10−2 S cm−1).35 Even so, the sulfide-type electrolytes (i.e., thio-LISICON, LGPS and argyrodites) can exhibit higher ionic conductivities closer to those of liquid electrolytes. Interest thus remains strong for the discovery of solid-state electrolytes with high ionic conductivity. As for the case with electrodes, the data-driven ML techniques have predicted electrolyte materials that are as good as or even better than existing materials. The capabilities of some of these (e.g., polyphenylene sulfide (PPS) and dimethyl substituted PPS (PMPS)) have been verified in experiments,36 confirming the utility of the ML predictions. In addition, ab initio molecular dynamics (AIMD) simulations are often applied to verify the ionic conductivities of the ML-predicted results (e.g., Li8N2Se, Li6KBiO6 and Li5P2N5)37 when experiments have not yet been conducted, as AIMD is one of the most accurate ways to study ionic conductivity in solids. As we do not know whether materials predicted by ML using the structure–property relationship can be easily synthesized, further development of synthesis strategies is necessary. Besides predicting ionic conductivity,36–38 ML techniques have also been used to predict migration barriers,39 mechanical strengths,40,41 and electrochemical stability windows,42 among other properties desired in solid-state electrolytes.
3. Applications of ML in battery material discovery
We briefly review the recent progress in electrode and electrolyte advancements using ML techniques in this section. This is divided into three areas:1. ML approaches for direct property predictions: this is a highly-used approach to discover new materials from databases. The well-trained ML models show high accuracy as compared to the benchmarking tools (e.g., physics-based models) and can be used to explore new materials. Structural data of materials and feature extractions are the keys for ML predictions, while the unsupervised DL approach has also been shown to powerfully predict without the need for data labelling and can be used to cluster predictions. The direct property prediction approach is based on learning the structure–property relationship.
2. ML approaches for developing machine learning potentials (MLPs): MLPs, also referred to as ML forcefields, are trained using the potential energy surfaces calculated from first-principles calculations such as density functional theory (DFT). A well-trained MLP model can achieve similar first-principles accuracy at a much lower computational cost. It is designed to tackle computationally intensive tasks such as molecular dynamics (MD) simulations.
3. Inverse design: the strategy that starts with the desired functionality of the materials and ends with specific material structures. Optimization and search methods such as genetic algorithm (GA), Bayesian optimization (BO) and particle swarm optimization (PSO) are often used. ML inverse design is based mainly on learning the functionality-structure landscape.
3.1 ML approaches for direct property predictions
There is a strong interest in identifying and developing new electrode materials using ML techniques (Table 1). For ion-intercalation type electrodes, one of the most important parameters is the specific charge capacity. Using six nonlinear ML regression algorithms (ANN, RF, SVM, KNN, gradient boosting machine (GBM) and kernel ridge regression (KRR)), Wang et al.46 predicted the discharge capacities of doped NMC cathode materials for LIBs. They found that GBM is the best model and showed that doped NMC materials with higher lithium amount, dopant atoms with lower electronegativities, and a smaller dopant amount would give better capacity properties. In addition, the discharge capacity of spinel lithium magnesium oxide (LMO) was also predicted by Wang et al.47 using ridge regression (RR), lasso regression (LaR), SVM, DNN, DT, RF and GBM. They found that doped LMO with higher formula molar mass and a shorter crystal lattice dimension with dopants having smaller electronegativities can improve the capacities of LMO. Liu et al.48 used bagging regressor (BR), extreme gradient boosting (XGB), and gradient boosting regressor (GBR) models to predict the initial Coulombic efficiency (ICE), capacity and rate factor for non-graphite carbon materials such as hard and soft carbon and determine their sodium storage performance. They found sodium storage in non-graphite carbon materials with poor crystallinities to be controlled by adsorption, intercalation and pore filling.| Electrode | Battery | ML method | Descriptor/feature/input | Dataset | ML prediction | Accuracy | Ref. |
|---|---|---|---|---|---|---|---|
| Doped NMC cathode | Lithium-ion | ANN, RF, GBM, SVM, KRR and KNN | 20 structural elemental features; initial and 50th cycle discharge capacity | 168 doped NMC systems, 3696 data entries | Discharge capacity | RMSE = 16.66 mA h g−1 (initial discharge) and 18.59 mA h g−1 (50th cycle discharge) | 46, Wang et al. (2021) |
| Doped spinel LMO cathode | Lithium-ion | RR, LaR, SVM, DNN, DT, RF, and GBM | 6 structural elemental features; initial and 20th cycle discharge capacity | 102 doped LMO spinel systems | Discharge capacity | RMSE = 11.90 mA h g−1 (initial discharge) and 11.77 mA h g−1 (20th cycle discharge) | 47, Wang et al. (2021) |
| Non-graphite carbon anode | Sodium-ion | BR, XGB, GBR | 5 structural parameters | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sets 000 sets |
ICE, capacity, and rate | MAE: 7.47%, 34.17 mA h g−1, and 0.035 for ICE, capacity and rate factor | 48, Liu et al. (2022) |
| Identified novel CrOF4 and NbFe3(PO4)6 cathodes | Lithium-ion | RF | 83 structural features | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 lithium containing compounds 740 lithium containing compounds |
Voltage, volume expansion | >95% | 43, Ransom et al. (2021) |
| 5000 electrode materials | Metal-ion | DNN, SVM, and KRR | Chemical and elemental properties, 237 features | 4250 data instances | Voltage | MAE = 0.43 V | 49, Joshi et al. (2019) |
| 22 new electrode materials | Metal-ion | DNN | Chemical formula, 306 features | 4860 data instances | Voltage, volume change | MAE = 0.37 V for voltage, 2.1% for volume change | 45, Moses et al. (2021) |
| K0.3Mn0.9Cu0.1O2 (KMCO) | Potassium-ion | LR, DT, ETR, and M-LP | 176 descriptors | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 578 entries 578 entries |
Formation energy per atom | RMSE = 0.956 | 50, Park et al. (2021) |
| Porous NMC electrode | Lithium-ion | M-LP | Pore-resolved saturation curves, start and stop filling times and saturation values at different time steps | Generated by physics-based model (lattice Boltzmann method) and pore networks from X-ray tomography | Electrolyte infiltration in electrodes | <1 second | 51, Shodiev et al. (2021) |
| NMC811 | Lithium-ion | GNB | Manufacturing parameters | 144 coated electrodes | Electrode homogeneity | Area under curve (AUC) metric = 0.91 | 52, Duquesnoy et al. (2021) |
| NMC electrode | Lithium-ion | DT, SVM, DNN | Slurry properties: viscosity, mass content of active materials, and solid-to-liquid ratio | 82 datasets from experiment | Mass loading, porosity | >70% | 53, Cunha et al. (2019) |
| 14 new AB2-type sulphur host materials | Lithium–sulphur | XGB | 24 features such as dipole, ionization energy, electronegativity, etc. | 1320 compounds | Polysulfide adsorption with good electron conductivity | <0.05 eV | 54, Zhang et al. (2021) |
| 5 promising single-atom catalysts | Lithium–sulphur | CGCNN | Adsorption systems represented by disconnected graphs | 812 adsorption configurations, 203 catalysts | Polysulfide adsorption and overpotential | <0.14 eV | 55, Lian et al. (2021) |
| Sulphur cathode | Lithium–sulphur | Association rule mining | Target peak discharge capacity, sulphur loading | 1660 cells | Discharge capacity, life cycle | Evaluated by support, confidence and lift values | 56, Kilic et al. (2020) |
| BCz-PH with high redox activity | Organic | RF | 204 features (molecule fingerprints) | 600 previous experiments | Voltage | 91.6% | 44, Xu et al. (2021) |
| Molecular electrode | Organic | ANN | 6 input variables | 114 data points | Redox potential | Averaged error = 3.54% | 57, Allam et al. (2018) |
| Molecular electrode | Organic | SpM-S | 2 descriptors for potential and capacity, 4 descriptors for energy density | 60 compounds | Potential, capacity, and energy density | RMSE = 0.24, 52.2, and 0.16 for potential, capacity, and energy density | 58, Sakano et al. (2022) |
Other important parameters for electrodes are voltage and stability. The latter is determined in terms of volume change (during the charging and discharging processes) and formation energy. Using an RF model, Ransom et al.43 identified two promising cathode materials: CrOF4 and NbFe3(PO4)6. The predicted voltages are 5.1 and 4.0 V, the volume expansions are less than 3% and 1%, and the specific charge capacities are 200 and 100 mA h g−1, respectively. Using DNN, SVM and KRR models, Joshi et al.49 predicted nearly 5000 cathode materials for NIBs and potassium-ion batteries (KIBs). A voltage predicting tool based on DNN was developed and made available online. Moreover, Moses et al.45 predicted 22 new electrode materials for NIBs (e.g., NaMn3OF8, NaCuF4, etc.), which demonstrate good performance in terms of energy densities and small volume variations upon charging/discharging using a DNN model. In addition, using LR, DT, extra trees (ETR) and multi-layer perceptron (M-LP) and DFT formation energies, Park et al.50 predicted P′3-type K0.3Mn0.9Cu0.1O2 (KMCO) to be a promising cathode material for high-performance KIBs and validated the results through experiments. In addition, the M-LP model was found to perform better at predicting crystal stability compared to the others.
In addition to atomistic properties, the ML techniques have also been applied to predict LIB electrode properties at mesoscales such as electrolyte infiltrations and manufacturing parameters. Shodiev et al.51 used an M-LP model, together with data generated by a physics-based model and X-ray images, to predict the electrode filling process in porous NMC electrodes. The developed model is thought to effectively screen mesostructured/electrolyte pairs and optimize the infiltration conditions. From materials to productions, the ML techniques have been shown to usefully optimize the manufacturing parameters for LIB electrodes. Using a Gaussian Naive Bayes (GNB) model, Duquesnoy et al.52 predicted the homogeneity of NMC811 electrodes and its dependence on the manufacturing parameters, with the trends explained by the mass loading and thickness properties. Cunha et al.53 used DT, DNN, and SVM models to investigate the interdependencies between NMC cathodes and fabrication parameters. They found that SVM predicts the influence of manufacturing parameters on the mass loading and porosity of the electrodes with high accuracy.
Besides the intercalation-type batteries, electrode advancements have also been demonstrated in advanced batteries such as lithium–sulphur and organic batteries. Using an XGB model, Zhang et al.54 discovered 14 new AB2-type sulphur host materials with desirable electron conductivity for lithium–sulphur batteries. The adsorption strength of these new compounds with polysulfides is greater than 1.0 eV. Lian et al.55 used a crystal graph CNN (CGCNN) model to predict the polysulfide adsorption energies and overpotentials on N-doped graphene with catalysts (single-atom catalyst, SAC) for lithium–sulphur batteries. They found the Ti, V, Zr, Mo, and Os SACs to be promising materials with low overpotentials. Kilic et al.56 examined 1660 lithium–sulphur cells from the literature using association rule mining and found the type and amount of encapsulation materials to be critical for batteries with high capacities and longer cycle lives.
Organic molecules are also commonly used in battery electrodes. Xu et al.44 used an RF model to predict the voltage of organic molecules and discovered Ph-bicarbazole-Ph (BCz-Ph) to have a high voltage of 4.8 V. They obtained an organic battery capacity of about 120 mA h g−1 using a p-BCz-Ph polymer as the cathode. Allam et al.57 used an ANN model to predict the redox potentials of organic molecules. They found the contributing factor to the redox potential in order of importance to be electron affinity, followed by numbers of oxygen atoms, the HOMO–LUMO gap, numbers of lithium atoms, the LUMO, and finally the HOMO. These results should determine the molecular design strategy. Sakano et al.58 used a sparse model for small data (SpM-S) to predict the potentials, capacities and energy densities of organic molecules. They showed that using just 60 compounds, the SpM-S model can achieve interpretable, straightforward and generalizable predictions compared to other ML models.
In brief, recent electrode advancements have covered a broad range of battery types. In particular, the NMC materials appear to draw more attention as compared to other cathode materials for advanced LIBs. The ML approaches have guided the discovery of potential NMC cathodes with high discharge capacities, more homogeneous structures, and better electrolyte infiltration. Moreover, new host materials and single-atom catalysts have been discovered to mitigate the polysulfide shuttling effects in lithium–sulphur batteries. Furthermore, the ML approaches have also discovered key factors such as the electron affinity, the HOMO and the LUMO for better designs of organic batteries.
A common practice to select ML models for electrode property predictions is to compare a few ML models and to determine the best-performing model using the prediction with the smallest root mean square error (RMSE) or highest coefficient of determination (R2) score. Feature pairing with the ML models is also critical for accurate predictions. Among the studies outlined above, GBM, M-LP and SVM are found to be better models for electrode property predictions. The GBM algorithms have been known to be robust in describing the nonlinear correlations across a wide variable space. It has been demonstrated that the GBM model has the best prediction power for capacity predictions.46 Moreover, the ML-P regression model is found to perform better in crystal stability predictions.50 Furthermore, SVM divides the dataset into different zones by an optimal hyperplane to minimize errors and the SVM model better predicts electrode features and its fabrication parameters.53
In addition to electrode materials, there is also a strong interest in identifying and developing new electrolyte materials using ML techniques (Table 2). All-solid-state batteries show promise for high volumetric energy density, which is a desirable feature for space-constrained applications such as EVs. Because of the high safety (e.g., no flammable liquids) associated with them, research has continued to identify better-performing solid-state electrolytes. The main parameters that underpin the suitabilities of solid-state electrolytes are the ionic conductivity, and the chemical and mechanical stabilities.
| Electrolyte | Battery | ML method | Descriptor/feature/input | Dataset | ML prediction | Accuracy | Ref. |
|---|---|---|---|---|---|---|---|
| 21 new solid electrolytes | Solid-state | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R R |
5 structural features | 317 candidates | Ionic conductivity at room temperature | F1 score = 0.5 | 38, Sendek et al. (2019) |
| 250 promising solid electrolytes, 26 anode coating materials | Solid-state | RF, GBDT | 22 features for migration, 24 features for potentials | Screen 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data 000 data |
Migration barriers, oxidation and reduction potentials for Li compounds | R 2 values = 0.95, 0.92, and 0.86 for oxi. potential, red. potential, and migration barrier | 39, Honrao et al. (2021) |
| New glass-type ionic conductors | Solid-state | Transfer-learned graph NN | 32-dimensional vectors trained from 2000 descriptors | 9600 candidates | Ionic conductivity at room temperature | MAE < 1 on a log scale | 36, Hatakeyama-Sato et al. (2020) |
| 16 new fast ionic conductors | Solid-state | AHC | 528 representative anionic structures and their mXRDs | 2986 ICSD entries | Ionic conductivity at room temperature | Number of groups = 7 (score function) | 37, Zhang et al. (2019) |
| 2842 solid electrolytes candidates | Solid-state | LightGBM, active learning | 145 chemical, 126 structural features | Screening of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 619 candidates 619 candidates |
Shear and bulk moduli | R 2 value = 0.819, 0.863 for shear and bulk moduli | 40, Choi et al. (2021) |
| Over 20 mechanically anisotropic interfaces | Solid-state | CGCNN, GBR, and KRR | 17 descriptors | Screening 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 inorganic solids 000 inorganic solids |
Shear and bulk moduli | RMSE (log(GPa) = 0.1268, 0.1013 for shear and bulk moduli | 41, Ahmad et al. (2018) |
| 18 unexplored Li7La3Zr2O12 predicted | Solid-state | SVM, KRR | 15 features | 100 LLZOM compounds | Reaction energy | MSE = 0.04 | 59, Liu et al. (2019) |
| A novel aqueous electrolyte | Metal-ion | BO | Electrolyte formulations | 251 electrolytes | Electrochemical stability window | N.A. | 42, Dave et al. (2020) |
| Liquid electrolytes | Metal-ion | MLR, LASSO, and ES-LiR | 13 ion and solvent descriptors | 70 solvents, 5 cations | Coordination energies | 0.016 eV | 60, Ishikawa et al. (2019) |
| Electrolyte additives | Lithium-ion | GPR | Molecular structural features | 149 additives | Redox potentials | MAE = 0.0522, 0.1013 for reduction, oxidation | 61, Zhang et al. (2020) |
Using a logistic regression (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R) model, Sendek et al.38 predicted 22 new solid electrolytes that exhibit ionic conductivity greater than or equal to 10−4 S cm−1 at room temperature. Furthermore, the predicted materials lack transition metals, thus enhancing the stability against reduction by the lithium metal anode. Honrao et al.39 discovered 250 promising solid electrolytes and 26 anode coating materials using RF and gradient boost decision tree (GBDT) models. They found that new compounds such as Li9S3N, LiAlB2O5, LiYO2, LiSbF4, and Sr4Li(BN2)3 showed extremely low 3D barriers, balanced electrochemical stability and fast ionic conduction. Hatakeyama-Sato et al.36 constructed a database for lithium-conducting solid polymer electrolytes with 104 entries and predicted the ionic conductivity of a glass-type ionic conductor with aromatic structures using a transfer-learned graph NN model. They found that the glass-type charge-transfer complex conductors exhibit both robustness with a wide temperature range and high ionic conductivity. The ML scheme used for new ionic conductor discovery is shown in Fig. 3.
R) model, Sendek et al.38 predicted 22 new solid electrolytes that exhibit ionic conductivity greater than or equal to 10−4 S cm−1 at room temperature. Furthermore, the predicted materials lack transition metals, thus enhancing the stability against reduction by the lithium metal anode. Honrao et al.39 discovered 250 promising solid electrolytes and 26 anode coating materials using RF and gradient boost decision tree (GBDT) models. They found that new compounds such as Li9S3N, LiAlB2O5, LiYO2, LiSbF4, and Sr4Li(BN2)3 showed extremely low 3D barriers, balanced electrochemical stability and fast ionic conduction. Hatakeyama-Sato et al.36 constructed a database for lithium-conducting solid polymer electrolytes with 104 entries and predicted the ionic conductivity of a glass-type ionic conductor with aromatic structures using a transfer-learned graph NN model. They found that the glass-type charge-transfer complex conductors exhibit both robustness with a wide temperature range and high ionic conductivity. The ML scheme used for new ionic conductor discovery is shown in Fig. 3.
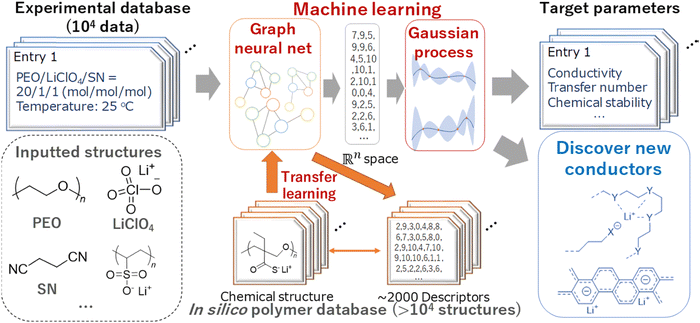 | ||
| Fig. 3 An ML scheme used for new ionic conductor discovery. Reproduced with permission from ref. 36. Copyright American Chemical Society 2020. | ||
In addition to the supervised ML techniques, unsupervised ML techniques have also been applied for the discovery of new electrolytes. Zhang et al.37 applied an unsupervised AHC model and identified 16 new fast ionic conductors. The findings were confirmed by ab initio molecular dynamics (AIMD) simulations. In particular, the room temperature ionic conductivities of Li8N2Se, Li6KBiO6 and Li5P2N5 are predicted to exceed 10−2 S cm−1.
Other important parameters are the mechanical properties of solid-state electrolytes and the electrode–electrolyte interface stability. Using a LightGBM model and active learning, Choi et al.40 predicted the shear and bulk moduli for 2842 solid electrolyte candidates. They found that the physical properties such as volume, density, space group number, and number of atoms are important features for predicting the mechanical properties. Moreover, they found oxide structures to exhibit superior mechanical properties. Ahmad et al.41 used CGCNN, GBR and KRR models to predict the shear and bulk moduli of inorganic solids. They found more than 20 mechanically anisotropic interfaces between lithium metal and 4 solid-state electrolytes, which can suppress dendrite growth. Using SVM and KRR models, Liu et al.59 predicted the stability of cation-doped Li7La3Zr2O12 in terms of reaction energy. They found the formation energy of oxides (MxOy) to be the most important feature, which dominates the route of the interface reactions. As such, the M–O bond strength was found to govern the interface stability of the doped Li7La3Zr2O12 and 18 unexplored doped Li7La3Zr2O12 were predicted and validated by calculations.
For liquid electrolytes, the electrochemical stability window and the interactions between the metal ions and solvent molecules are important parameters for a stable liquid electrolyte. Dave et al.42 combined robotics and machine learning to discover new aqueous electrolytes by examining their electrochemical stability windows. Using a BO model, a novel dual-anion sodium electrolyte was discovered. Ishikawa et al.60 used the multiple linear regression (MLR), exhaustive search with linear regression (ES-LiR), and least absolute shrinkage and selection operator (LASSO) models to predict the coordination energies between 5 types of cations and 70 solvents. They found that the ionic radius and atomic charge of oxygen atoms connected to metal ions are the crucial descriptors. This coordination energy prediction was thought to relate to the ion transfer process between the electrode and electrolyte. Finally, battery additives are important for enhancing electrolyte performance. Using a Gaussian process regression (GPR) model, Zhang et al.61 predicted the redox potentials of electrolyte additives for LIBs from the molecular structural features. The model efficiently screened the redox potentials of novel additives.
In brief, the recent electrolyte advancements have discovered thousands of promising candidates especially for solid-state electrolytes or fast ionic conductors. Most of the work has been focused on predicting ionic conductivity at room temperature to be higher than or comparable to liquid electrolytes as it is the critical criterion for the realization of practical all-solid-state batteries. Another focus is the mechanical properties of the solids. Usually, the new discovery is compared to well-known ionic conductors such as NAISCON and garnet-like structures. However, well-known ionic conductors do not always have good mechanical strength as compared to oxide structures.40 This shows that ML predictions with multi-targeting are crucial in designing solid state electrolytes. For liquid electrolytes, the most studied properties are the redox potentials and stability windows. Although there are fewer studies on liquid electrolyte innovations than those on solid electrolytes, recently Dave et al.42 applied a combination of robotics and ML techniques for searching for new liquid electrolytes and discovered a novel dual-anion sodium electrolyte.
Besides comparing the RMSE or R2 score of different ML models, the selection of ML models for electrolyte property predictions also depends on the availability of datasets. The GCNN model is chosen for the shear and bulk moduli predictions due to the availability of large amounts of training data with low noise, while GBR and KRR are used for elastic constant predictions.41 Moreover, the model selection also depends on the nature of the problem, i.e., whether it is a classification or regression problem. The SVM model is chosen for determining whether the Li|LLZOM interface is thermodynamically stable or not, while the KRR model is chosen for predicting the reaction energy of the interface.59 Furthermore, the graph-based neural network model has been used for both ionic conductivity36 and mechanical property41 predictions.
When using the structure–property relationship for new electrode and electrolyte predictions with ML models, the features or descriptors are mainly described by the associated chemical structural properties such as the elemental properties, bonding information, and composition ratio. As such, materials defined by atoms, composition and structure (ACS)62 should provide crucial information for the ML predictions. Moreover, the sizes of the datasets in these works are typically from a few hundreds to tens of thousands, depending on the ML models used. Furthermore, the most common database used for screening and extracting features is the Material Project.20,21 The challenges for these ML approaches include the need for optimizing many model hyperparameters, the sensitivity for feature selections, the use of large datasets, and the over-fitting issue.
3.2 ML approaches for developing machine learning potentials (MLPs)
In addition to direct property predictions, ML techniques have emerged as a powerful tool for the development of interatomic potentials for atomistic simulations in recent years. This initiative is driven by the fact that atomistic simulations using classical force fields are usually parameter-dependent and of limited accuracy, especially in a scenario where the simulations fall out of the parametrized range, despite the fast simulation time. In contrast, the DFT-based AIMD simulations are more accurate. However, due to the Arrhenius-type governing equation on the diffusion processes, the dynamic simulations of atoms at room temperature are usually too slow to be sampled with statistical certainty. So, practical simulations are usually limited to a few tenths of a picosecond.ML-trained interatomic potentials provide a much better accuracy-CPU time trade-off approach for atomistic simulations, although CPU time is still needed to generate data and model training. The main advantage of the MLP approach is that it allows more flexible functional forms to describe the potential energy surface (PES) and the time scale of MLP-MD simulations can reach nanoseconds, as compared to the typical picoseconds in AIMD. To fit MLP, it is essential to develop a PES as a function of local environment descriptors of the atomic structures. A typical approach is to train a few generations of the atomic configuration's data that include forces, energies, and stresses from DFT or AIMD calculations, then minimize the target function. The accuracy lies in comparisons with the DFT calculations such that the fidelity of the simulations using MPL remains high.
There are increasing numbers of MLP published in the literature. Some of these include neural network potentials (NNPs) and high-dimensional neural network potentials (HDNNPs),63–65 moment tensor potentials (MTPs),66 Gaussian approximation potentials (GAPs),67,68 and spectral neighbor analysis potentials (SNAPs).69 The performance and cost of the different MLPs have been analyzed.70 In addition, the locality is an essential part of MLPs, in which the energies and forces of the atoms are associated with the immediate environment within a cutoff region, and this information is embedded in a descriptor for training. Typical descriptors are atom-centered symmetry functions,71,72 polynomials in moment tensor potentials (MTPs),73 many body structural descriptors,74 and power spectrum.75 A workflow that is used for interatomic potential development is shown in Fig. 4.
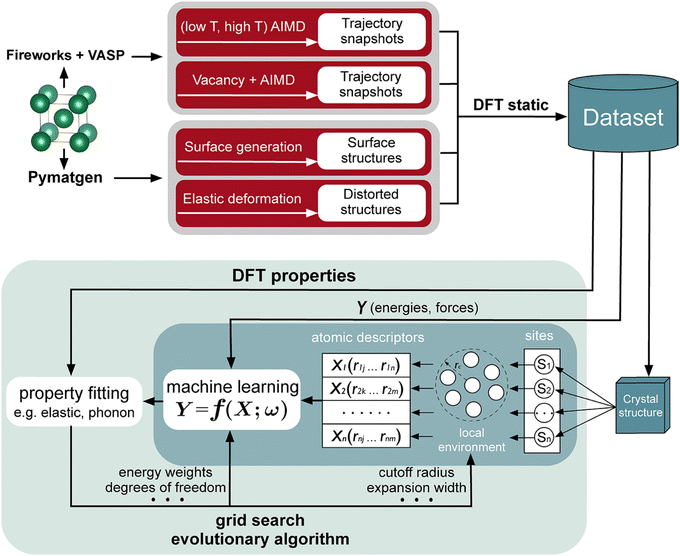 | ||
| Fig. 4 A machine learning interatomic potential development workflow. Reproduced with permission from ref. 70. Copyright American Chemical Society 2020. | ||
There has been strong interest in developing MLPs for battery material discovery in recent years (Table 3). The NN potentials are one of the most used MLPs. Houchins et al.76 developed NN potentials using atom-centered symmetry functions to study the NMC cathode materials. They showed that the predictions of structural properties (lithium insertion and removal) and voltage profiles of NMCs with any compositions can be conducted quickly with high fidelity. Eckohff et al.77 developed HDNN potentials to predict properties of the LixMn2O4 cathode such as lattice parameters, diffusion barriers, volume changes, phase transition and phonon frequencies. They showed that the HDNN potentials can be used to represent a system with multiple oxidation states with accuracy comparable to DFT and it also enables nanosecond MD simulations. Artrith et al.78 used ANN potentials and genetic algorithms to study the amorphous structures of LixSi as the anode for LIBs. They confirmed the predicted metastable structures with molecular dynamics heat-quench simulations and found consistency within the low-energy range.
| Materials | Battery | ML potentials | Descriptor/feature/input | Dataset | ML prediction | Accuracy | Ref. |
|---|---|---|---|---|---|---|---|
| LiNixMnyCo(1−x−y)O2 (NMC) cathode | Lithium-ion | NNP | Atom-centered symmetry functions | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 962 points 962 points |
Voltage profiles | RMSE: 3.7 meV per atom, 0.13 eV Å−1 for energy, force, Voltage: agrees with experiment | 76, Houchins et al. (2020) |
| Spinel lithium manganese oxide cathode | Lithium-ion | HDNNP | Many-body atom-cantered symmetry functions | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228 LixMn2O4 structures 228 LixMn2O4 structures |
Lattice parameters, diffusion barrier, etc. | RMSE: 1.8 meV per atom, 0.108 eV/a0 for energy, force, Lattice: <1%, Barrier: agrees with experiment | 77, Eckhoff et al. (2020) |
| Amorphous LixSi anode | Lithium-ion | ANN | Chebyshev descriptors | 1000 first-principles calculations | LixSi configurations | RMSE: 7.7 meV per atom, MAE: 5.9 meV per atom | 78, Artrith et al. (2018) |
| Li10GeP2S12-type SSE | SSB | DP-GEN | Atomic environment descriptors | 590 structures | Diffusion coefficient (DC) | RMSE: 2 meV per atom, 80 meV Å−1 for energy, force, DC: between 5–15 × 10 −12 m2 s−1 | 79, Huang et al. (2021) |
| Liquid electrolytes | Lithium-ion | HDNNP | Symmetry function | Training 360 K | Bulk thermodynamics properties | RMSE: 0.40 kcal mol−1, 0.11 Debye, 0.47 kcal mol−1 Å−1 for energy, dipole, force | 80, Dajnowicz et al. (2022) |
| Li3Sc2(PO4)3 and Li3B7O12 coating materials | SSB | LOFT/MTP | Polynomial basis | Initial set: 15ps AIMD at 1000 K | Ionic conductivity | MAE: 5.7 meV per atom, 84.3 meV Å−1 for energy, force, Ionic conductivity: MAE = 0.13 eV | 81, Wang et al. (2020) |
| Li10GeP2S12 | SSB | SLAD | Power spectrum | 7500 local atomic geometries | Ionic conductivity at 300 K, activation energy | MAE: 7.1 × 10−5 Hartree per atom, 4.3 × 10−3 Hartree per Bohr, and 0.13 GPa for energy, force, and stress, Ionic conductivity: agrees with experiment | 82, Miwa et al. (2021) |
| Li7P3S11 | SSB | SGPP | SOAP | 705 LCE (local chemical environment) | Li diffusivity | RMSE: 0.14 eV Å−1 for force, Li diffusivity: agrees with experiment | 83, Hajibabaei et al. (2021) |
| Ether-based ionic liquid electrolytes | Metal-ion | NNP, active learning | Graph convolution | Initial 5000 geometries for training | Cation-ligand binding structures | RMSE: 0.83 kcal mol−1, 0.5 kcal mol−1 Å−1 for energy, force | 84, Wang et al. (2020) |
For solid-state electrolytes, Huang et al.79 developed a deep potential generator (DP-GEN) to predict the diffusion coefficients in Li10GeP2S12-type solid-state electrolytes. They found that the computed data agreed well with the experimental data and they pointed out that the effect of configurational disorder is material-dependent, i.e., some could obtain improved diffusion coefficients, while others may not. For liquid electrolytes, Dajnowicz et al.80 used HDNN potentials, a charge recursive neural network (QRNN) architecture and DFT data to predict the thermodynamic properties of liquid carbonate solvents, such as specific heat at constant volume, density, heat of vaporization, viscosity and self-diffusivity. They found that the model is ∼104 faster as compared to the calculations using wB97X-D/6-31G* with a single CPU (2.4 GHz). Moreover, the model can simulate MD with a simulation time of a few nanoseconds.
To further improve the accuracy of MLPs, active learning can be applied in the development of MLPs to deal with the unrealistic structures being generated during model training. Those structures can be further optimized by additional DFT calculations. Using learning-on-the-fly MTP (LOTF/MTP) potentials for MD simulations, Wang et al.81 discovered Li3Sc2(PO4)3 and Li3B7O12, together with 10 other candidates, to be promising coating materials with high lithium contents and stable electrochemical windows (oxidation limit); low chemical reactivity with sulfide electrolytes and oxide cathodes; and low Li-ion migration energies. The MD can run up to 200 ns. Miwa et al.82 used a self-learning and adaptive database (SLAD) approach to develop ML potentials for simulating the ionic conductivity (σ) and activation energy (Ea) of Li10GeP2S12 (LGPS). The simulated results of σ = 12 mS cm−1 and Ea = 226 meV agreed well with experimental data. In addition, they found only small anisotropy effects for Li-ion diffusion in LGPS.
Hajibabaei et al.83 developed sparse Gaussian process potentials (SGPPs) with a data-efficient on-the-fly adaptive sampling algorithm to simulate the Li diffusivity and melting/crystallization temperatures in Li7P3S11. They discovered an uncharted phase with a much lower Li diffusivity that should be avoided and found that the computational cost is similar to those of the Bayesian linear regression methods. Using NN potentials and active learning, Wang et al.84 investigated the binding structures between cations and ether-based solvated ionic liquids for the discovery of new electrolytes. They identified candidate ether ligands for Li+-, Mg2+- and Na+-solvated ionic liquids with higher binding affinity and electrochemical stability than the reference compounds.
The MLP approach has emerged as a promising method for battery material discovery. Different types of MLP have been developed for simulating battery material properties such as the ion diffusion barriers of electrolytes and voltage profiles of electrodes. The MLP accuracy is high with typical RMSE less than a few tenths of meV in energy and meV Å−1 in force, which enables highly accurate property predictions. Moreover, new materials have been identified using the MLP approach: Li3Sc2(PO4)3 and Li3B7O12 have found promise as coating materials for solid-state batteries using the moment tensor potentials.81 For the ML models, the neural network algorithms are the most frequently used for constructing MLPs as the NN approach is suitable for large system simulations.77 It also has the transferability across composition space.84 For the local atomic environment descriptors, the many-body symmetry functions by Behler and Parrinello71,72 are most often used. The descriptor built on the symmetry functions remains a smooth function of the atomic coordinates and can still allow atoms to go across the cutoff region during atomic simulations.
Nevertheless, challenges remain for the development of MLPs. One issue is that the long-range electrostatic effects are usually ignored due to the local nature of MLPs. Staacke et al.85 found that the description of lithium transport in the isotropic bulk Li7P3S11 ionic conductor is valid without the long-range electrostatic terms in the MLP, but defect formation energies can only be obtained accurately with hybrid potentials and a physical model of electrostatic interactions. This points the way for future development of MLPs. Another issue is the transferability of MLPs, which depends on the extent of inclusion of relevant atomic environments in the reference/training data. Large prediction errors can result if the simulations are out of the range of validity.
3.3 Inverse design
The inverse design strategies start with the desired functionalities of materials and end in chemical spaces with the specific material structures. Ideally, one can start with a desired functionality and search for the potential components of the materials directly. However, due to the huge and growing chemical spaces, it is almost impossible to identify the governing rules or components, without the inputs from domain knowledge and optimization techniques. A good optimization technique should explore only a small amount of data, which is guided by the design principles, e.g., a physics-based model that governs functions and structures.62The generic strategies for inverse design are:
1. High-throughput virtual screening: a screening scope is first defined and an ML model is employed to carry out a search of databases. The search results often need to be verified with experiments or physics-based model simulations and domain knowledge plays a crucial role for the search success.
2. Global optimization: the approach employs optimization algorithms such PSO, BO and GA to optimize an optimal solution for a large objective function. This approach is often employed for problems with multiple targets.
3. Generative models: this is an unsupervised learning approach in ML that can learn the input patterns and generate output with new data. Some examples are recurrent neural networks (RNNs), generative adversarial networks (GANs) and auto-encoders (AEs). Details of these strategies are well reviewed in ref. 86 and 87.
We highlight some of the recent battery material discoveries using the inverse design technique (Table 4). Sendek et al.88 used a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R model and high-throughput screening of more than 12
R model and high-throughput screening of more than 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 computational structures to look for potential superionic conductors that are likely to have fast lithium conduction compared to experimental measurements. A total of 21 structures were identified, but a few are yet to be studied experimentally.
000 computational structures to look for potential superionic conductors that are likely to have fast lithium conduction compared to experimental measurements. A total of 21 structures were identified, but a few are yet to be studied experimentally.
| Materials | Battery | ML method | Inverse design strategy | Target | ML prediction | Accuracy | Ref. |
|---|---|---|---|---|---|---|---|
| Identified 21 promising electrolytes | SSB | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R R |
High-throughput Screening | PLR ≥ 50%; Egap > 1 eV; Vox ≥ 4 V, no transition metal; Ehull > 0 eV | Potential superionic structures | 90% | 88, Sendek et al. (2017) |
| LiNixCo1−x−yMn1−x−y−zO2 (NCM) cathode | Lithium-ion | kNN, RF, multiple imputations by chained equations (MICE) | PSO | Target discharge capacities of 150, 175, and 200 mA h g−1 | Specific charge capacity, process parameters | RMSE: 8.17 mA h g−1 | 89, Liow et al. (2022) |
| Porous electrode | Lithium-ion | ANN | Bayesian | From 5 initial conditions tests (converged to 47 Ωm) | Specific total resistance, process parameters | R 2: 0.827 | 90, Takagishi et al. (2019) |
| MXene electrodes | Metal-ion | RF | RF classifier | Target M, T, and Z (categorical descriptor) | Formula for MXenes | F1 score: 0.5833–0.9861 | 91, Li et al. (2022) |
| Electrolyte additives | Lithium-ion | DL | Bayesian | Target < −3.35 V against standard hydrogen electrode | Redox potential | MAE: 0.2004 V | 92, Tagade et al. (2019) |
| 133 molecules identified | Redox flow | GPR | Bayesian | Target 1.40 V, 1.70 V vs. NHE | Oxidation potential | RMSE: <0.15 V | 93, Doan et al. (2020) |
The global optimization strategy is one of the most common approaches in inverse design for battery materials. Liow et al.89 used an inverse design surrogate model for correlating an experimental parameter–property relationship to predict optimal experimental synthesis parameters for NMC cathodes. They used a PSO to perform global optimizations and found that the composition of Ni, sintering temperature, cut-off voltage and charge-rate are strongly correlated with the performance of the materials. With the optimized parameters, the ML model achieved a high discharge capacity (209.5 mA h g−1) and Coulombic efficiency (86%) for the batteries. Using an ANN model, Takagishi et al.90 predicted the specific resistance of porous electrodes for LIBs. They found that the ML predictions agree well with the simulated results using a physico-chemical model. In addition, they performed inverse design to determine the optimal process parameters and found that active materials with 50.4% volume fraction, binder/additives with 0.0820% volume ratio, electrolytic conductivity with 1.00 S m−1 and compaction pressure of 590 MPa are the key parameters for determining the total specific resistance. Li et al.91 used a multi-target ML model based on RF for inverse design of MXenes as high-capacity energy storage materials. They predicted the electrochemical properties with multiple targets (voltage, capacity and charge), followed by the use of the inverse design model to predict the formula of MXenes. Specifically, Li2M2C and Mg2M2C (M = Sc, Ti, Cr) were predicted to have the desired electrochemical properties.
Tagade et al.92 developed a deep learning inverse prediction framework (structure learning for attribute-driven materials design using novel conditional sampling (SLAMDUNCS)) to predict molecules with target properties. The framework was applied to predict electrolyte additive molecules with reduction potential smaller than −3.35 V against the standard hydrogen electrode. Some predicted molecules include dimethyl silyl carbonate and 2,4,6 triisopropyl-1,3,5-trioxane. In addition, using a GPR model and the active learning framework based on BO, Doan et al.93 predicted the oxidation potentials of 1400 homobenzylic ether (HBE) molecules and identified a total of 133 molecules with the desired potentials ranging between 1.40 and 1.70 V for redox flow batteries. The schematic representation of the BO guided computational workflow for predicting HBEs with desired oxidation potentials is shown in Fig. 5.
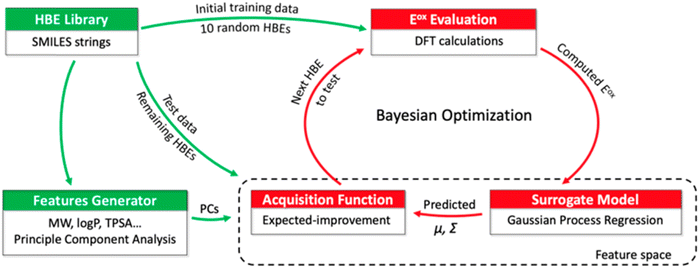 | ||
| Fig. 5 A schematic representation of BO guided computational workflow for identify HBEs with desired oxidation potentials. PCs, μ and Σ are principle components, mean, and variance, respectively. Reproduced with permission from ref. 93. Copyright American Chemical Society 2020. | ||
Many new battery materials have been discovered with advancements in inverse design approaches. For instance, Li5B7S13, Li2B2S5, and Li2GePbS4 are among the 21 newly identified ionic conductors.88 Also, Li2M2C and Mg2M2C (M = Sc, Ti, Cr) MXene have been suggested as promising battery electrode materials91 based on inverse design. Moreover, the inverse design approach has been used to optimize process parameters and the manufacture of battery electrodes with desired properties such as high charge capacity89 and low resistance.90 The neural network model is more often used in these studies while the global optimization technique (especially the Bayesian approach) is the most often used for inverse design strategies. The Bayesian optimization approach is based on Bayes Theorem that allows for a direct search of a globally optimized objective function efficiently using probabilistic principles. It is often used to tune hyperparameters of a given ML model. Nevertheless, there remain challenges for the inverse design approach as searching the huge chemical spaces is daunting. Bhowmik et al.94 pointed out that extensive multi-fidelity datasets from multi-scale simulations, large-scale operando characterizations, and high-throughput syntheses need to work closely together to tackle the difficulty in solid electrolyte interphase (SEI) inverse design for batteries. The same suggested approaches should also be applied in battery electrodes and electrolyte design.
4. Outlook and conclusions
The development of ML techniques and databases has identified many novel electrode and electrolyte materials with promising properties. ML has also empowered the development of modeling techniques such as MD with faster and longer timescale simulations. In addition, the inverse design approach has become more effective with the growth of databases. These three approaches have accelerated innovation in battery materials significantly in recent years. While efforts are still needed to realize the potential shown by the predicted materials, data-driven ML approaches have been proven to be useful in the material design spaces.Nevertheless, there remain some major challenges for the ML approaches. The most common challenge identified in the literature is data scarcity. There is a contradiction between high dimensions and low amounts of data in battery materials,10 meaning substantial dimensions are required for an accurate model but the data volume is limited, which might lead to overfitting issues and errors in predictions. Nevertheless, feature reductions and active learning are some effective approaches to mitigate such a limitation.
As opposed to the existing size of property data on organic molecules, e.g., the Chemical Universal Database contains over 166 billion data entries (GDB-17),95 and the existence of platforms for unified molecular analysis,96 the lack of coherent big data in the battery field for ML techniques, especially for inorganic materials, remains the major limitation for accelerating the discovery of novel materials and improving battery performance. The absence of data standardization has often been raised,11,12,15,97 as the reported data across databases may not be in the same formats, terms and metadata schemas, especially computational data obtained from different levels of modeling and experimental data generated by different laboratories; this poses a challenge to unify coherent data for training and validation.
Nevertheless, there have been efforts towards a unified description of battery data. To address the issue, the FAIR (findability, accessibility, interoperability and reusability) data principles98,99 provide guidelines on scientific data management, which enable a new horizon for materials research. The FAIR data infrastructure requires in-depth description of how the data were obtained, including metadata, ontologies, and workflows. In particular, an ontology is the knowledge that can be expressed as a map of concepts and relations and expressed in machine-readable code.100 For instance, the ontology is introduced to describe the production of lithium-ion batteries and support the management of data on materials and process steps.101 With approaches that can unify battery data and make it interoperable, this can alleviate the issue of data scarcity in battery material design.
We also notice that the majority of datasets currently available are static data; time-dependent battery data, e.g., experimental battery cycling data, or computational molecular dynamics trajectory data, are rarely available but should be useful for predicting the complex dynamic behaviors in batteries. Therefore, high-volume, high-quality, unified and coherent static and dynamic datasets are essential for tackling this major challenge.
Finally, towards the development of green batteries, the concept of sustainability is crucial for the next generation of batteries. Sustainability of battery technologies can be evaluated through their environmental and social impacts.102 The key to sustainable design of batteries lies in (1) incorporating more eco-friendly and abundant high-energy materials such as biomass (the raw materials could come from waste food or other organic substances) and sodium (abundant in the Earth's crust), and reducing the use of metals that are toxic (e.g., cobalt) to the environment and humans; (2) low-energy, efficient synthetic processes and manufacturing; (3) life-cycle assessment; and (4) efficient recycling processes. Such a closed-loop design strategy is essential but idealistic, while a good balance within the design cycle is critical for developing batteries that are more sustainable. Currently, there are many material databases available and the number of data entries is increasing; these provide more design spaces for ML to explore the use of sustainable materials. Indeed, biomass is one potential type of material that can be used as a sustainable source. Its use has been demonstrated in battery anodes and cathodes in metal–sulfur and metal–oxygen batteries.103 This is a promising direction towards sustainable battery technologies. Moreover, the ML techniques have also been used in optimizing the material synthesis89,104–106 and manufacturing processes.107,108
For life-cycle assessment, the state of health (SOH) and remaining useful life (RUL) of rechargeable batteries are the two critical indicators to predict battery lifetimes. Traditional equivalent circuit models (ECMs) remain widely used to monitor these indicators due to the fast response, but it is less accurate, while more accurate physics-based models (PBMs) remain too computationally demanding for real-time SOH and RUL predictions. The data-driven ML approach could combine the advantages of both worlds. We have proposed major challenges in terms of accurate modeling over length and time scales; performing in situ calculations; and high-throughput theoretical and experimental data generation for SOH and RUL predictions using ML techniques in our previous review.6 In addition, the long-term degradation and cycle life of batteries should also be taken into account. The degradation of materials in batteries includes the formation of solid electrolyte interphases (SEI), the growth of lithium dendrites, the loss of active elements in electrodes, the loss of mechanical strength of the solid upon charge–discharge cycles, and the corrosion of metal current collectors.109–112 ML battery models can thus be developed by incorporating information on these degradation mechanisms via data-driven machine learning, which can increase the accuracy of battery state predictions as compared to those of ECMs.
While the degradation or cycling life information can be obtained via electrochemical measurements such as cyclic voltammetry (CV) for cycling data and electrochemical impedance spectroscopy (EIS) for corrosion data, high-throughput experiments are required to obtain such data. However, experimentally collecting these data is not easy as it involves dismantling the battery cells. The lack of in situ measurements of these mechanisms challenges the availability of experimental data for ML. As such, multi-scale modeling has often been applied to study the degradation of battery materials from the atomic scale all the way to full cell simulations.113,114
Density functional theory (DFT) and molecular dynamics (MD) simulations have often been used to determine the material degradation properties at the atomic level. Key properties such as lithium dendrite growth and SEI formations can be studied.115–118 Moreover, kinetic Monte Carlo (KMC) and phase field methods can be used to study the degraded morphology and phase separations of electrodes at the microstructural level.119,120 In addition, a pseudo 2D (P2D) model121,122 at the continuum level can be used to study cell properties with degraded battery cell parameters. With all these in place, the life-cycle assessments of batteries can be more accurate.
Finally, recycling has been identified as the missing link to close the loop of sustainable design in most of today's energy-related processes123 (which includes batteries). However, batteries in different sizes and shapes make the disassembly processes challenging, and the toxic and flammable chemicals in the batteries are hazardous to human health, requiring more safety precautions. All of these add to the cost for recycling. Nevertheless, the ML techniques have been applied to improve the efficiency of battery dismantling systems.124 Overall, the ML techniques are promising tools to improve the design space for sustainable batteries. However, a holistic ML approach that can connect all these design spaces is required to achieve and realize practical and sustainable batteries.125,126
To conclude, the present review has summarized recent ML-inspired battery electrode and electrolyte advancements. We provide insights into the discovery of these new battery materials through the ML strategies on direct property predictions, machine learning potentials and inverse design. We envision that to move towards green and more sustainable batteries, the integration of battery materials, manufacturing and product designs is essential. Data-driven machine learning is thus a promising technique to fulfil this mission.
Data availability
As this is a review article, no primary research results, data, software or code have been included.Author contributions
All the authors contributed to researching the data and writing the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work is supported by the Agency for Science, Technology and Research (Central Research Fund Award). We thank Dr Ng Heok Hee from the Research Office Scientific Editing Team of A*STAR for the professional manuscript editing service.References
- J. Anderson, D. Rode, H. Zhai and P. Fischbeck, Energy Policy, 2021, 148, 111778 CrossRef CAS.
- P. R. Liu and A. E. Raftery, Commun. Earth Environ., 2021, 2, 29 CrossRef PubMed.
- M. A. Brown, P. Dwivedi, S. Mani, D. Matisoff, J. E. Mohan, J. Mullen, M. Oxman, M. Rodgers, R. Simmons, B. Beasley and L. Polepeddi, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2100008118 CrossRef CAS PubMed.
- Y. Ou, C. Roney, J. Alsalam, K. Calvin, J. Creason, J. Edmonds, A. A. Fawcett, P. Kyle, K. Narayan, P. O'Rourke, P. Patel, S. Ragnauth, S. J. Smith and H. McJeon, Nat. Commun., 2021, 12, 6245 CrossRef CAS PubMed.
- T. Sun, I. B. Ocko, E. Sturcken and S. P. Hamburg, Sci. Rep., 2021, 11, 22173 CrossRef CAS PubMed.
- M.-F. Ng, J. Zhao, Q. Yan, G. J. Conduit and Z. W. Seh, Nat. Mach. Intell., 2020, 2, 161–170 CrossRef.
- C. Lv, X. Zhou, L. Zhong, C. Yan, M. Srinivasan, Z. W. Seh, C. Liu, H. Pan, S. Li, Y. Wen and Q. Yan, Adv. Mater., 2022, 34, e2101474 CrossRef PubMed.
- C. Bauer, S. Burkhardt, N. P. Dasgupta, L. A.-W. Ellingsen, L. L. Gaines, H. Hao, R. Hischier, L. Hu, Y. Huang, J. Janek, C. Liang, H. Li, J. Li, Y. Li, Y.-C. Lu, W. Luo, L. F. Nazar, E. A. Olivetti, J. F. Peters, J. L. M. Rupp, M. Weil, J. F. Whitacre and S. Xu, Nat. Sustainability, 2022, 5, 176–178 CrossRef.
- J. L. Reymond, Acc. Chem. Res., 2015, 48, 722–730 CrossRef CAS PubMed.
- Y. Liu, B. Guo, X. Zou, Y. Li and S. Shi, Energy Storage Mater., 2020, 31, 434–450 CrossRef.
- C. Ling, npj Comput. Mater., 2022, 8, 33 CrossRef.
- T. Lombardo, M. Duquesnoy, H. El-Bouysidy, F. Aren, A. Gallo-Bueno, P. B. Jorgensen, A. Bhowmik, A. Demortiere, E. Ayerbe, F. Alcaide, M. Reynaud, J. Carrasco, A. Grimaud, C. Zhang, T. Vegge, P. Johansson and A. A. Franco, Chem. Rev., 2022, 122, 10899–10969 CrossRef CAS PubMed.
- X. Chen, X. Liu, X. Shen and Q. Zhang, Angew. Chem., Int. Ed., 2021, 60, 24354–24366 CrossRef CAS PubMed.
- T. Gao and W. Lu, iScience, 2021, 24, 101936 CrossRef CAS PubMed.
- Y. Liu, O. C. Esan, Z. Pan and L. An, Energy AI, 2021, 3, 100049 CrossRef.
- J. Mao, J. Miao, Y. Lu and Z. Tong, Chin. J. Chem. Eng., 2021, 37, 1–11 CrossRef CAS.
- Z. Deng, V. Kumar, F. T. Bölle, F. Caro, A. A. Franco, I. E. Castelli, P. Canepa and Z. W. Seh, Energy Environ. Sci., 2022, 15, 579–594 RSC.
- X. Feng, Q. Zhang and Z. W. Seh, Adv. Mater. Technol., 2022, 2200616, DOI:10.1002/admt.202200616.
- A. Y. S. Eng, C. B. Soni, Y. Lum, E. Khoo, Z. Yao, S. K. Vineeth, V. Kumar, J. Lu, C. S. Johnson, C. Wolverton and Z. W. Seh, Sci. Adv., 2022, 8, eabm2422 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. P. Ong, S. Cholia, A. Jain, M. Brafman, D. Gunter, G. Ceder and K. A. Persson, Comput. Mater. Sci., 2015, 97, 209–215 CrossRef.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- NIST Inorganic Crystal Structure Database, NIST Standard Reference Database Number 3, National Institute of Standards and Technology DOI:10.18434/M32147.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- S. S. Borysov, R. M. Geilhufe and A. V. Balatsky, PLoS One, 2017, 12, e0171501 CrossRef PubMed.
- H. E. Pence and A. Williams, J. Chem. Educ., 2010, 87, 1123–1124 CrossRef CAS.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS.
- M. Okubo, S. Ko, D. Dwibedi and A. Yamada, J. Mater. Chem. A, 2021, 9, 7407–7421 RSC.
- M. Armand, P. Axmann, D. Bresser, M. Copley, K. Edström, C. Ekberg, D. Guyomard, B. Lestriez, P. Novák, M. Petranikova, W. Porcher, S. Trabesinger, M. Wohlfahrt-Mehrens and H. Zhang, J. Power Sources, 2020, 479, 228708 CrossRef CAS.
- Y. Lu, Q. Zhang, L. Li, Z. Niu and J. Chen, Chem, 2018, 4, 2786–2813 CAS.
- K. M. Abraham, ACS Energy Lett., 2020, 5, 3544–3547 CrossRef CAS.
- G. Peng, C. Hai, C. Sun, Y. Zhou, Y. Sun, Y. Shen, X. Li, G. Zhang, J. Zeng and S. Dong, ACS Appl. Mater. Interfaces, 2021, 13, 55007–55019 CrossRef CAS PubMed.
- W. Zhao, J. Yi, P. He and H. Zhou, Electrochem. Energy Rev., 2019, 2, 574–605 CrossRef CAS.
- J. C. Bachman, S. Muy, A. Grimaud, H. H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- K. Hatakeyama-Sato, T. Tezuka, M. Umeki and K. Oyaizu, J. Am. Chem. Soc., 2020, 142, 3301–3305 CrossRef CAS PubMed.
- Y. Zhang, X. He, Z. Chen, Q. Bai, A. M. Nolan, C. A. Roberts, D. Banerjee, T. Matsunaga, Y. Mo and C. Ling, Nat. Commun., 2019, 10, 5260 CrossRef PubMed.
- A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Chem. Mater., 2018, 31, 342–352 CrossRef.
- S. J. Honrao, X. Yang, B. Radhakrishnan, S. Kuwata, H. Komatsu, A. Ohma, M. Sierhuis and J. W. Lawson, Sci. Rep., 2021, 11, 16484 CrossRef CAS PubMed.
- E. Choi, J. Jo, W. Kim and K. Min, ACS Appl. Mater. Interfaces, 2021, 13, 42590–42597 CrossRef CAS PubMed.
- Z. Ahmad, T. Xie, C. Maheshwari, J. C. Grossman and V. Viswanathan, ACS Cent. Sci., 2018, 4, 996–1006 CrossRef CAS PubMed.
- A. Dave, J. Mitchell, K. Kandasamy, H. Wang, S. Burke, B. Paria, B. Póczos, J. Whitacre and V. Viswanathan, Cell Rep. Phys. Sci., 2020, 1, 100264 CrossRef CAS.
- B. Ransom, N. Zhao, A. D. Sendek, E. D. Cubuk, W. Chueh and E. J. Reed, MRS Bull., 2021, 46, 1116–1129 CrossRef CAS.
- S. Xu, J. Liang, Y. Yu, R. Liu, Y. Xu, X. Zhu and Y. Zhao, J. Phys. Chem. C, 2021, 125, 21352–21358 CrossRef CAS.
- I. A. Moses, R. P. Joshi, B. Ozdemir, N. Kumar, J. Eickholt and V. Barone, ACS Appl. Mater. Interfaces, 2021, 13, 53355–53362 CrossRef CAS PubMed.
- G. Wang, T. Fearn, T. Wang and K. L. Choy, ACS Cent. Sci., 2021, 7, 1551–1560 CrossRef CAS PubMed.
- G. Wang, T. Fearn, T. Wang and K.-L. Choy, Energy Technol., 2021, 9, 2100053 CrossRef CAS.
- X. Liu, T. Wang, T. Ji, H. Wang, H. Liu, J. Li and D. Chao, J. Mater. Chem. A, 2022, 10, 8031–8046 RSC.
- R. P. Joshi, J. Eickholt, L. Li, M. Fornari, V. Barone and J. E. Peralta, ACS Appl. Mater. Interfaces, 2019, 11, 18494–18503 CrossRef CAS PubMed.
- S. Park, S. Park, Y. Park, M. H. Alfaruqi, J.-Y. Hwang and J. Kim, Energy Environ. Sci., 2021, 14, 5864–5874 RSC.
- A. Shodiev, M. Duquesnoy, O. Arcelus, M. Chouchane, J. Li and A. A. Franco, J. Power Sources, 2021, 511, 230384 CrossRef CAS.
- M. Duquesnoy, I. Boyano, L. Ganborena, P. Cereijo, E. Ayerbe and A. A. Franco, Energy AI, 2021, 5, 100090 CrossRef.
- R. P. Cunha, T. Lombardo, E. N. Primo and A. A. Franco, Batteries Supercaps, 2019, 3, 60–67 CrossRef.
- H. Zhang, Z. Wang, J. Cai, S. Wu and J. Li, ACS Appl. Mater. Interfaces, 2021, 13, 53388–53397 CrossRef CAS PubMed.
- Z. Lian, M. Yang, F. Jan and B. Li, J. Phys. Chem. Lett., 2021, 12, 7053–7059 CrossRef CAS PubMed.
- A. Kilic, Ç. Odabaşı, R. Yildirim and D. Eroglu, Chem. Eng. J., 2020, 390, 124117 CrossRef CAS.
- O. Allam, B. W. Cho, K. C. Kim and S. S. Jang, RSC Adv., 2018, 8, 39414–39420 RSC.
- K. Sakano, Y. Igarashi, H. Imai, S. Miyakawa, T. Saito, Y. Takayanagi, K. Nishiyama and Y. Oaki, ACS Appl. Energy Mater., 2022, 5, 2074–2082 CrossRef CAS.
- B. Liu, J. Yang, H. Yang, C. Ye, Y. Mao, J. Wang, S. Shi, J. Yang and W. Zhang, J. Mater. Chem. A, 2019, 7, 19961–19969 RSC.
- A. Ishikawa, K. Sodeyama, Y. Igarashi, T. Nakayama, Y. Tateyama and M. Okada, Phys. Chem. Chem. Phys., 2019, 21, 26399–26405 RSC.
- Y. Zhang and X. Xu, Ind. Eng. Chem. Res., 2020, 60, 343–354 CrossRef.
- A. Zunger, Nat. Rev. Chem., 2018, 2, 0121 CrossRef CAS.
- T. B. Blank, S. D. Brown, A. W. Calhoun and D. J. Doren, J. Chem. Phys., 1995, 103, 4129–4137 CrossRef CAS.
- H. Gassner, M. Probst, A. Lauenstein and K. Hermansson, J. Phys. Chem. A, 1998, 102, 4596–4605 CrossRef CAS.
- J. Behler, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed.
- A. V. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- A. P. Bartok, M. C. Payne, R. Kondor and G. Csanyi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. P. Bartók and G. Csányi, Int. J. Quantum Chem., 2015, 115, 1051–1057 CrossRef.
- A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, J. Comput. Phys., 2015, 285, 316–330 CrossRef CAS.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csanyi, A. V. Shapeev, A. P. Thompson, M. A. Wood and S. P. Ong, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- K. Gubaev, E. V. Podryabinkin, G. L. W. Hart and A. V. Shapeev, Comput. Mater. Sci., 2019, 156, 148–156 CrossRef CAS.
- V. L. Deringer and G. Csányi, Phys. Rev. B, 2017, 95, 094203 CrossRef.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- G. Houchins and V. Viswanathan, J. Chem. Phys., 2020, 153, 054124 CrossRef CAS PubMed.
- M. Eckhoff, F. Schönewald, M. Risch, C. A. Volkert, P. E. Blöchl and J. Behler, Phys. Rev. B, 2020, 102, 174102 CrossRef CAS.
- N. Artrith, A. Urban and G. Ceder, J. Chem. Phys., 2018, 148, 241711 CrossRef PubMed.
- J. Huang, L. Zhang, H. Wang, J. Zhao, J. Cheng and W. E, J. Chem. Phys., 2021, 154, 094703 CrossRef CAS PubMed.
- S. Dajnowicz, G. Agarwal, J. M. Stevenson, L. D. Jacobson, F. Ramezanghorbani, K. Leswing, R. A. Friesner, M. D. Halls and R. Abel, J. Phys. Chem. B, 2022, 126, 6271–6280 CrossRef CAS PubMed.
- C. Wang, K. Aoyagi, P. Wisesa and T. Mueller, Chem. Mater., 2020, 32, 3741–3752 CrossRef CAS.
- K. Miwa and R. Asahi, Solid State Ionics, 2021, 361, 115567 CrossRef CAS.
- A. Hajibabaei, C. W. Myung and K. S. Kim, Phys. Rev. B, 2021, 103, 214102 CrossRef CAS.
- W. Wang, T. Yang, W. H. Harris and R. Gomez-Bombarelli, Chem. Commun., 2020, 56, 8920–8923 RSC.
- C. G. Staacke, H. H. Heenen, C. Scheurer, G. Csányi, K. Reuter and J. T. Margraf, ACS Appl. Energy Mater., 2021, 4, 12562–12569 CrossRef CAS.
- J. Noh, G. H. Gu, S. Kim and Y. Jung, Chem. Sci., 2020, 11, 4871–4881 RSC.
- J. Wang, Y. Wang and Y. Chen, Materials, 2022, 15, 1811 CrossRef CAS PubMed.
- A. D. Sendek, Q. Yang, E. D. Cubuk, K.-A. N. Duerloo, Y. Cui and E. J. Reed, Energy Environ. Sci., 2017, 10, 306–320 RSC.
- C. H. Liow, H. Kang, S. Kim, M. Na, Y. Lee, A. Baucour, K. Bang, Y. Shim, J. Choe, G. Hwang, S. Cho, G. Park, J. Yeom, J. C. Agar, J. M. Yuk, J. Shin, H. M. Lee, H. R. Byon, E. Cho and S. Hong, Nano Energy, 2022, 98, 107214 CrossRef CAS.
- Y. Takagishi, T. Yamanaka and T. Yamaue, Batteries, 2019, 5, 54 CrossRef CAS.
- S. Li and A. S. Barnard, Chem. Mater., 2022, 34, 4964–4974 CrossRef CAS.
- P. M. Tagade, S. P. Adiga, S. Pandian, M. S. Park, K. S. Hariharan and S. M. Kolake, npj Comput. Mater., 2019, 5, 127 CrossRef.
- H. A. Doan, G. Agarwal, H. Qian, M. J. Counihan, J. Rodríguez-López, J. S. Moore and R. S. Assary, Chem. Mater., 2020, 32, 6338–6346 CrossRef CAS.
- A. Bhowmik, I. E. Castelli, J. M. Garcia-Lastra, P. B. Jørgensen, O. Winther and T. Vegge, Energy Storage Mater., 2019, 21, 446–456 CrossRef.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J. L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- M. Gonzalez-Medina and J. L. Medina-Franco, J. Chem. Inf. Model., 2017, 57, 1735–1740 CrossRef CAS PubMed.
- M. Aykol, P. Herring and A. Anapolsky, Nat. Rev. Mater., 2020, 5, 725–727 CrossRef.
- M. D. Wilkinson, M. Dumontier, I. J. Aalbersberg, G. Appleton, M. Axton, A. Baak, N. Blomberg, J. W. Boiten, L. B. da Silva Santos, P. E. Bourne, J. Bouwman, A. J. Brookes, T. Clark, M. Crosas, I. Dillo, O. Dumon, S. Edmunds, C. T. Evelo, R. Finkers, A. Gonzalez-Beltran, A. J. Gray, P. Groth, C. Goble, J. S. Grethe, J. Heringa, P. A. t Hoen, R. Hooft, T. Kuhn, R. Kok, J. Kok, S. J. Lusher, M. E. Martone, A. Mons, A. L. Packer, B. Persson, P. Rocca-Serra, M. Roos, R. van Schaik, S. A. Sansone, E. Schultes, T. Sengstag, T. Slater, G. Strawn, M. A. Swertz, M. Thompson, J. van der Lei, E. van Mulligen, J. Velterop, A. Waagmeester, P. Wittenburg, K. Wolstencroft, J. Zhao and B. Mons, Sci. Data, 2016, 3, 160018 CrossRef PubMed.
- M. Scheffler, M. Aeschlimann, M. Albrecht, T. Bereau, H. J. Bungartz, C. Felser, M. Greiner, A. Gross, C. T. Koch, K. Kremer, W. E. Nagel, M. Scheidgen, C. Woll and C. Draxl, Nature, 2022, 604, 635–642 CrossRef CAS PubMed.
- S. Clark, F. L. Bleken, S. Stier, E. Flores, C. W. Andersen, M. Marcinek, A. Szczesna-Chrzan, M. Gaberscek, M. R. Palacin, M. Uhrin and J. Friis, Adv. Energy Mater., 2021, 12, 2102702 CrossRef.
- M. Mutz, M. Perovic, P. Gümbel, V. Steinbauer, A. Taranovskyy, Y. Li, L. Beran, T. Käfer, K. Dröder, V. Knoblauch, A. Kwade, V. Presser, D. Werth and T. Kraus, Energy Technol., 2022, 2200681, DOI:10.1002/ente.202200681.
- X. Yu and A. Manthiram, Adv. Energy Sustainability Res., 2021, 2, 2000102 CrossRef CAS.
- C. Liedel, ChemSusChem, 2020, 13, 2110–2141 CrossRef CAS.
- M. J. McDermott, S. S. Dwaraknath and K. A. Persson, Nat. Commun., 2021, 12, 3097 CrossRef CAS PubMed.
- N. J. Szymanski, Y. Zeng, H. Huo, C. J. Bartel, H. Kim and G. Ceder, Mater. Horiz., 2021, 8, 2169–2198 RSC.
- A. Davariashtiyani, Z. Kadkhodaie and S. Kadkhodaei, Commun. Mater., 2021, 2, 115 CrossRef.
- M. F. Niri, K. Liu, G. Apachitei, L. A. A. Román-Ramírez, M. Lain, D. Widanage and J. Marco, Energy AI, 2022, 7, 100129 CrossRef.
- A. Turetskyy, J. Wessel, C. Herrmann and S. Thiede, Energy Storage Mater., 2021, 38, 93–112 CrossRef.
- M. Jiang, D. L. Danilov, R. A. Eichel and P. H. L. Notten, Adv. Energy Mater., 2021, 11, 2103005 CrossRef CAS.
- J. S. Edge, S. O'Kane, R. Prosser, N. D. Kirkaldy, A. N. Patel, A. Hales, A. Ghosh, W. Ai, J. Chen, J. Yang, S. Li, M. C. Pang, L. Bravo Diaz, A. Tomaszewska, M. W. Marzook, K. N. Radhakrishnan, H. Wang, Y. Patel, B. Wu and G. J. Offer, Phys. Chem. Chem. Phys., 2021, 23, 8200–8221 RSC.
- X. Han, L. Lu, Y. Zheng, X. Feng, Z. Li, J. Li and M. Ouyang, eTransportation, 2019, 1, 100005 CrossRef.
- J. P. Pender, G. Jha, D. H. Youn, J. M. Ziegler, I. Andoni, E. J. Choi, A. Heller, B. S. Dunn, P. S. Weiss, R. M. Penner and C. B. Mullins, ACS Nano, 2020, 14, 1243–1295 CrossRef CAS PubMed.
- T. Katrašnik, I. Mele and K. Zelič, Energy Convers. Manage., 2021, 236, 114036 CrossRef.
- G. Zan, J. Zhang, F. Monaco, S. Gul, G. Qian, J. Li, D. J. Vine, P. Cloetens, W. Yun, P. Pianetta and Y. Liu, J. Mater. Chem. A, 2021, 9, 19886–19893 RSC.
- A. Wang, S. Kadam, H. Li, S. Shi and Y. Qi, npj Comput. Mater., 2018, 4, 15 CrossRef.
- H. Kumar, E. Detsi, D. P. Abraham and V. B. Shenoy, Chem. Mater., 2016, 28, 8930–8941 CrossRef CAS.
- Z. Hong and V. Viswanathan, ACS Energy Lett., 2019, 4, 1012–1019 CrossRef CAS.
- H. G. Lee, S. Y. Kim and J. S. Lee, npj Comput. Mater., 2022, 8, 103 CrossRef CAS.
- P. Bai, D. A. Cogswell and M. Z. Bazant, Nano Lett., 2011, 11, 4890–4896 CrossRef CAS.
- D. A. Cogswell and M. Z. Bazant, ACS Nano, 2012, 6, 2215–2225 CrossRef CAS PubMed.
- M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 2019, 140, 1526–1533 CrossRef.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 2019, 141, 1–10 CrossRef.
- D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- Y. Lu, M. Maftouni, T. Yang, P. Zheng, D. Young, Z. J. Kong and Z. Li, J. Intell. Manuf., 2022, 1–13, DOI:10.1007/s10845-022-01936-x.
- Z. Yao, Y. Lum, A. Johnston, L. M. Mejia-Mendoza, X. Zhou, Y. Wen, A. Aspuru-Guzik, E. H. Sargent and Z. W. Seh, Nat. Rev. Mater., 2023, 8, 202–215 Search PubMed.
- A. Chen, X. Zhang and Z. Zhou, InfoMat, 2020, 2, 553–576 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |