Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Time-resolved serial femtosecond crystallography for investigating structural dynamics of chemical systems
Jungho
Moon
 ab,
Yunbeom
Lee
ab,
Yunbeom
Lee
 ab and
Hyotcherl
Ihee
ab and
Hyotcherl
Ihee
 *ab
*ab
aCenter for Advanced Reaction Dynamics (CARD), Institute for Basic Science (IBS), Daejeon 34141, Republic of Korea
bDepartment of Chemistry, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Republic of Korea. E-mail: hyotcherl.ihee@kaist.ac.kr
First published on 9th August 2024
Abstract
Time-resolved serial femtosecond crystallography (TR-SFX) has emerged as a crucial tool for studying the structural dynamics of proteins. In principle, TR-SFX has the potential to be a powerful tool not only for studying proteins but also for investigating chemical reactions. However, non-protein systems generally face challenges in indexing due to sparse Bragg spots and encounter difficulties in effectively exciting target molecules. Nevertheless, successful TR-SFX studies on chemical systems have been recently reported in a few instances, boding well for the application of TR-SFX to study chemical reactions in the future. In this context, we review the static SFX and TR-SFX studies conducted on chemical systems reported to date and suggest prospects for future research directions.
Introduction
The properties of chemicals are intrinsically linked to their structure.1,2 Therefore, determining the structure of chemicals is fundamental to understanding chemical materials. Furthermore, to understand chemical reactions and design more efficient processes, it is essential to comprehend the structures, properties, and dynamics of intermediates that occur during reactions.Time-resolved scattering techniques, which measure changes in scattering signals over time, are widely employed to investigate structural dynamics. Scattering signals from X-ray photons or particles such as electrons directly reflect the molecular structure.3,4 Therefore, by measuring changes in scattering signals, the structural changes of molecules can be tracked. For example, time-resolved X-ray liquidography (TRXL)5–19 and ultrafast electron diffraction (UED)20–25 are widely used tools that provide direct information on structural dynamics of chemical systems in the solution and gas phases, respectively. However, unlike solution and gas phases, in ultrafast structural dynamics research on the crystalline state, the number of studies that have directly elucidated the structural changes of crystalline samples in 3D space is limited due to the lack of appropriate experimental methods.
In this context, time-resolved serial femtosecond crystallography (TR-SFX), which emerged with the development of X-ray free-electron lasers (XFELs), can be a powerful tool for investigating structural dynamics of chemical systems in the crystalline states. TR-SFX is a technique combining the time-resolved technique and serial femtosecond crystallography (SFX). TR-SFX can provide maximum femtosecond time resolution and atomic-scale spatial resolution while investigating irreversible reactions. Due to its utility, TR-SFX has been established as a novel method for investigating the structural dynamics of various proteins.26–28
In principle, TR-SFX can also be applied to obtain structural information of chemical systems beyond macromolecular systems. However, TR-SFX has faced challenges in obtaining even static structures of chemical systems, which are crucial prerequisites for investigating structural dynamics. This difficulty arises from the intrinsic properties of chemical system crystals, specifically their small lattice parameters. Therefore, before advancing to TR-SFX, it is essential to comprehensively review and understand the achievements of static SFX studies in chemical systems that have overcome these limitations. It was not until 2022 that the first structure of a chemical system using static SFX was reported, overcoming these challenges. Since then, the number of crystal structures of chemical systems determined by SFX has been rapidly increasing. In 2024, the first TR-SFX study on a chemical system was reported, marking a milestone in demonstrating the practicality of this technique. This review aims to comprehensively introduce the findings of static SFX and TR-SFX studies on chemical systems published to date and to forecast future research directions based on these achievements.
Static SFX and TR-SFX
The precursor of SFX is the concept of diffraction-before-destruction in single-molecule diffraction using an ultrashort and ultraintense X-ray pulse from an XFEL.29 The idea is that the X-ray pulses provided by an XFEL are sufficiently intense that even a single-shot diffraction image contains sufficient structural information. Such intense X-ray pulses can cause severe damage to the sample. However, because the temporal width of the X-ray pulse is short enough, the X-ray pulse passes through the sample before significant damage occurs, thereby minimizing damage during the measurement. It has been theoretically well-established that analyzing a sufficient number of single-shot diffraction images obtained from single biomolecules can enable the determination of the three-dimensional structure of a protein.30–35 In fact, this concept was proposed prior to the initiation of XFEL construction and played a crucial role in securing funding for constructing XFEL facilities. While this idea has been realized to some extent for sufficiently large objects, such as virus particles,36 the goal of protein structure analysis has not yet been achieved because a single X-ray pulse does not yet contain a sufficient number of photons. Given these circumstances, the emerging alternative idea is SFX. It is based on the idea that although a conventional XFEL X-ray pulse cannot produce a diffraction image with a sufficient signal-to-noise ratio from a single protein molecule, it can generate a satisfactory diffraction image from a small protein crystal ranging in size from tens of micrometers to hundreds of nanometers or even smaller. Single crystals of this size are much smaller than the 20–300 μm single crystals used in conventional single-crystal X-ray crystallography (SCXRD). In summary, SFX can be described as a technique that applies the concept of diffraction-before-destruction to microcrystals. In SFX experiments, the effort to synthesize large, high-quality single crystals was reduced, demonstrating its utility for samples where structural analysis has been constrained by challenges in synthesizing crystals of adequate size. In addition, the use of ultrashort X-ray pulses from XFELs has made it possible to minimize radiation damage during measurement, enabling structural analysis at near-physiological temperature and pressure without the need for cryogenic conditions to reduce X-ray radiation damage. Currently, numerous protein structures have been reported using SFX,37–46 and the concept of SFX has been adopted in synchrotron sources, also being utilized for serial synchrotron crystallography (SSX).47,48The utility of SFX extends beyond static structure determination to encompass studying the structural dynamics. The structural dynamics of molecules can be investigated using TR-SFX, which combines SFX with the pump–probe method. In the pump–probe method, the pump pulse initiates the reaction, and the probe pulse measures the data at a specific time delay. If an X-ray pulse for SFX is used as the probe pulse, the crystal structure at the specified time delay can be obtained. By conducting SFX experiments with successive time delays, it becomes possible to directly determine the structural changes over time. Since the pulse width of the X-ray pulses used in SFX is in the tens of femtoseconds, they can be used as probe pulses providing temporal resolution up to the femtosecond scale. For example, if the reaction is initiated with a laser pulse providing temporal resolution on the femtosecond scale, and the SFX technique is applied after a specific time delay, the structure can be directly determined at that specific time delay on a femtosecond scale after the reaction is initiated. Therefore, TR-SFX can be a powerful tool that offers both atomic-scale spatial resolution and femtosecond-scale temporal resolution.
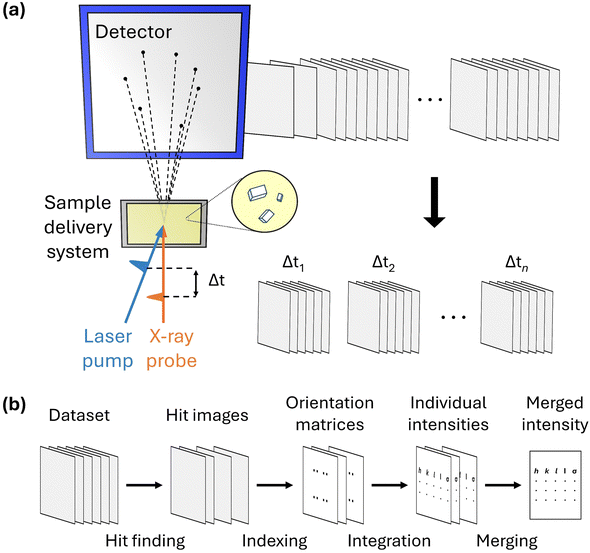
A schematic of the experimental setup for TR-SFX is depicted in Fig. 1a. The experimental setup for TR-SFX is essentially the SFX setup with the addition of a pump pulse, comprising three main components: a pump–probe system, a sample delivery system, and a detector. In the first component, the pump–probe system typically consists of an optical laser system that provides the pump pulse and an X-ray source, such as an XFEL, that provides the probe pulse. Achieving precise spatial-temporal overlap between these two pulses is crucial for obtaining structural information at the designated time delay following the reaction initiation. Once the precise spatial-temporal overlap is established, controlling the time delay between the pump and probe pulses allows for the acquisition of structural information at the desired time delay. The second component, the sample delivery system, is a distinctive feature of the SFX experimental setup compared to conventional crystallography. In SFX experiments, after obtaining the diffraction pattern from an individual microcrystal, the used microcrystal is discarded because the crystal experiences severe radiation damage from the intense X-ray pulses of XFELs. Therefore, a continuous supply of fresh microcrystals is necessary, a task performed by the sample delivery system. Selecting a method that reliably supplies the target sample while minimizing the amount of microcrystals discarded without being used for diffraction is crucial for conducting efficient and successful experiments. Various methods, such as fixed targets and gas dynamics virtual nozzle (GDVN), are used as sample delivery techniques.49–52 Finally, the detector is responsible for sensing the diffraction signal obtained from a single X-ray pulse. The experimental setup is detailed in several excellent reviews.53,54
To process the TR-SFX dataset, it should first be sorted according to the time delay. Then, the SFX data processing pipeline, summarized in Fig. 1b, is used for the dataset obtained at a specific time delay. The SFX data processing procedure progresses through four stages: hit finding, indexing, integration, and merging. In the first stage, hit finding, diffraction images that contain a sufficient number of Bragg spots are preliminarily selected from the data obtained in the SFX experiment. In the second stage, indexing, a series of algorithms are used to index each selected diffraction image to determine the crystal orientation and predict possible peaks, thereby securing reflection (or Bargg spots) information. In the third stage, integration, the intensities of the Bragg spots in the indexed images are obtained by integrating the diffraction intensities of the detector pixels corresponding to the Bragg spots and comparing them with the background signal. Finally, once sufficient reflections are collected from each diffraction image, they are merged to obtain the final structure factor. Generally, data processing is carried out using several well-developed programs.55–60
Compared to traditional time-resolved Laue crystallography in a synchrotron, which has been used for studying structural dynamics in crystalline state samples, TR-SFX offers several distinct advantages for studying structural dynamics.61,62 First, TR-SFX enables the investigation of ultrafast structural dynamics that were previously inaccessible. Traditional synchrotron-based methods are limited to a temporal resolution of picoseconds, whereas TR-SFX provides temporal resolution in the femtosecond range. This allows for the study of ultrafast dynamics in the femtosecond time domain that could not be observed with previous methods. Second, TR-SFX can track the dynamics of molecules undergoing irreversible reactions. Traditional methods, which are used to obtain multiple diffraction images from a single crystal, are limited to studying structural dynamics in samples with short recovery times that return to the ground state after excitation. In contrast, TR-SFX disposes the sample after each measurement, making it possible to study irreversible samples and thereby broadening the range of target samples. Third, as the crystal size decreases, the proportion of excited molecules within the crystal increases, enabling clearer capture of signals related to structural changes. For these reasons, TR-SFX has become a powerful tool for elucidating the ultrafast structural dynamics, demonstrated by the success of TR-SFX experiments on proteins.
Small-molecule SFX
The reported works using SFX on chemical systems are significantly fewer compared to those on macromolecular systems. As of now, the structures of only 15 chemical systems have been reported using SFX. Furthermore, only two chemical systems have been investigated using TR-SFX. This starkly contrasts with hundreds of protein structures interpreted using SFX. The primary reason for this disparity is the analytical challenges associated with applying SFX to chemical systems when compared to macromolecular systems.The challenges of applying SFX to chemical systems stem from their relatively small lattice parameters compared to macromolecular systems. Chemical systems typically consist of individual molecules that are relatively small in size compared to macromolecular systems, and they often have small lattice parameters. Importantly, small lattice parameters result in a relatively small number of Bragg spots, which can be intuitively understood through the Ewald sphere, describing the conditions for constructive interference when X-rays interact with the reciprocal lattice. Fig. 2a and b illustrate the Ewald spheres for cases where incident X-rays of the same wavelength interact with large and small lattice parameters, respectively. Since lattice parameters in real space and those in reciprocal space are inversely proportional, small lattice parameters lead to reciprocal lattice points (RLPs) being further apart in reciprocal space. As the distance between RLPs increases, while the radius of the Ewald sphere remains constant, the intersections between the Ewald sphere and RLPs decrease, directly indicating in fewer Bragg spots. This theoretical background is observed in practical experiments as well. Fig. 2c shows a diffraction image of Proteinase K with a unit cell volume of 502 nm3, while Fig. 2d shows a diffraction image of mithrene with a unit cell volume of 1.26 nm3 measured at SACLA. It can be observed that mithrene, which has a smaller unit cell volume, exhibits much sparser peaks compared to Proteinase K.63
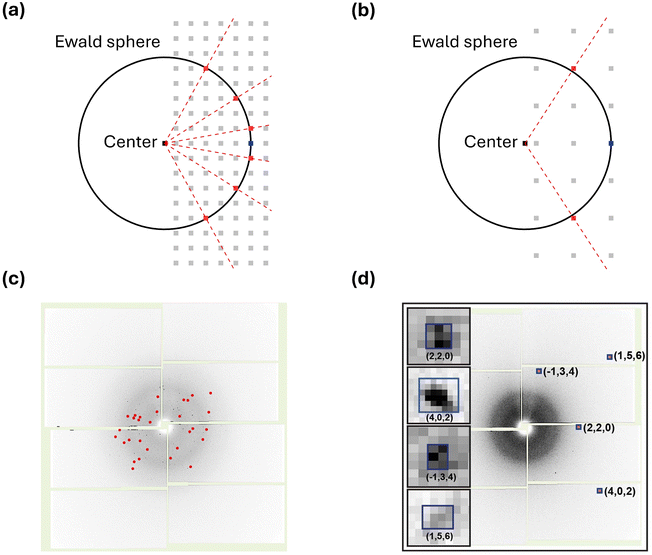 | ||
| Fig. 2 (a) Ewald sphere for a crystal with a large lattice parameter. (b) Ewald sphere for a crystal with a small lattice parameter. (a) and (b) The black circle in each panel is the corresponding Ewald sphere. The light gray squares, black squares, and blue squares represent reciprocal lattice points, the center of the Ewald sphere, and the origin of the reciprocal space, respectively. The red squares are lattice points that appear as the Bragg spots in a diffraction image. The red dotted line indicates the diffracted beam. (c) A diffraction image from the Proteinase K dataset. Indexed Bragg spots are shown in red. (d) A diffraction image from the mithrene dataset. Bragg spots with blue boxes are magnified in the insets. Reproduced from ref. 63 with permission from Springer Nature, copyright 2022. | ||
The limited number of Bragg spots poses challenges in the indexing process of SFX data. Difficulty in indexing due to few Bragg peaks is a characteristic issue unique to SFX and not encountered in SCXRD. SCXRD commonly employs the rotation method, where diffraction images are obtained at multiple orientations with known relative rotation angles between the collected images. The number of Bragg spots at one crystal orientation is still small, as in SFX, but the controlled change in crystal orientation during measurement ensures that Bragg spots from different diffraction images are obtained with known relative orientations, allowing reflections corresponding to Bragg spots to be indexed unambiguously. However, in SFX, the orientation of micro-crystals provided by the sample delivery system is random. Therefore, it is not possible to process images obtained in the traditional manner together and assign reflections corresponding to each Bragg peak. Consequently, indexing of SFX data is performed on individual images. The challenge lies in the fact that indexing algorithms used for macromolecular systems are known to function smoothly when there are 20 or more Bragg spots in a single diffraction image. Many samples with small lattice parameters often do not have a sufficient number of Bragg spots in one diffraction image, making it difficult to apply indexing algorithms used for macromolecules. Due to these difficulties, SFX for small molecules is sometimes classified as a distinct field and referred to as small-molecule SFX (smSFX). For TR-SFX to advance successfully in chemical systems, it is crucial to overcome these challenges in smSFX by exploring better analysis techniques and experimental methods.
The first study to overcome these challenges in smSFX was demonstrated by Hohman and coworkers.63 In this research, with the aid of a graph theory-based indexing algorithm,64 smSFX was used to interpret the structures of three types of silver benzene chalcogenolates (AgEC6H5, E = Se, S, and Te). Initially, smSFX was applied to mithrene (AgSeC6H5), whose structure was already known. The crystal structure obtained by smSFX was consistent with that obtained by SCXRD, with the mean deviation falling within the range of least-squares uncertainty, confirming the effectiveness of smSFX in structure determination. Furthermore, smSFX enabled the determination of the structures of thiorene (AgSC6H5) and tethrene (AgTeC6H5), which are vulnerable to radiation damage and lacking previously analyzed structures. Two noteworthy aspects of this study deserve attention. One is overcoming the challenges in indexing within smSFX by employing a graph theory-based algorithm specialized for systems with small lattice parameters instead of traditional transformation indexing algorithms. The other aspect is the method for determining the lattice parameters. The lattice parameters were derived from a powder pattern created by combining diffraction images obtained through smSFX and were successfully employed for further analysis. These findings demonstrate that smSFX can serve as a new alternative for analyzing structures of various samples that have posed difficulties for traditional methods.
Following the initial publication of the smSFX paper, the Hohman group utilized smSFX to determine the structures of various materials. In their second smSFX paper, the Hohman group reported the structures of three types of silver n-alkanethiolates (C4, C6, and C9) with varying lengths of alkyl chains.65 It should be noted that the crystal structures of these compounds had not been determined previously due to their vulnerability to radiation damage. A notable feature of this research is the significant improvement in atomic resolution, achieving up to 0.833 Å, compared to the 1.20 Å and 1.35 Å resolutions reported in their earlier work. This enhancement was attributed to the increased photon energy used in the study, ranging from 15–18 keV, which is approximately 1.5 times higher than the photon energies below 12 keV used in their previous study. The use of higher energy photons resulted in shorter wavelengths, enabling the successful attainment of higher-resolution structures. Additionally, the study anticipated the successful application of traditional Fourier transformation-based indexing algorithms, as shorter wavelength X-rays typically increase the number of Bragg spots. However, despite the increased number of Bragg spots due to the use of high-energy photons and a b-axis parameter extended by approximately 10 Å, the Fourier transformation-based indexing failed. Therefore, the study proceeded with the same graph theory-based indexing algorithm used in previous research. In addition, in a subsequent work, the structures of silver 2-, 3-, and 4-fluorobenzenethiolates were successfully obtained as well by using the same method used for silver n-alkanethiolates.66 The results from the Hohman group demonstrate the utility of smSFX as a tool for analyzing the structures of inorganic–organic hybrid compounds and highlight the applicability of new indexing algorithms.
Meanwhile, Yonekura and colleagues compared two crystallographic methods using microcrystals: smSFX and microcrystal electron diffraction (microED). In that study, using rhodamine-6G as a reference sample with a known structure, they compared the structures obtained from both techniques.67 Both methods successfully obtained highly accurate structures, distinguishing even hydrogen atom positions from chemical bonding structures. However, it was indicated that smSFX provided higher reliability in determining atomic positions. Interestingly, the study utilized lattice parameters generated from microED and applied the Fourier transformation-based indexing algorithm directly.
In a following study, the Yonekura group extensively applied smSFX to various challenging organic compounds where traditional structural analysis methods had difficulties, and proposed improved experimental techniques.68 The study emphasized that rotating the sample holder when employing a fixed target as the sample delivery system enhanced data quality. In the fixed target approach, samples are provided with microcrystals dispersed on a flat plate, potentially leading to a preferred orientation where microcrystals align in specific directions depending on their shape. This can result in insufficient reflection information for certain crystal orientations, thereby compromising the quality of the structure. The study demonstrated that rotating the sample holder could resolve the preferred orientation issue. Using this approach, structures of four organic compounds—monopeptoid, tripeptoid, Ph-BTBT-C10 and anti-BTBTT-C6—were obtained with 100% completeness. Similar to previous studies, the research utilized lattice parameters obtained from microED and employed traditional Fourier transformation-based algorithms. This study showcased the successful application of smSFX in organic compounds and highlighted the utility of using it alongside microED.
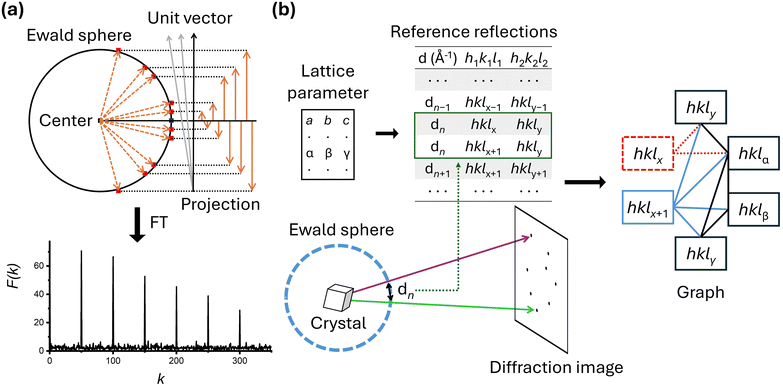
Both groups' studies demonstrated successful application of SFX to various small molecules; however, it is noteworthy to highlight some differences in the data processing steps. The first difference lies in how they determined the lattice parameters. The Hohman group used lattice parameters obtained from powder patterns created by combining the diffraction images of the smSFX experiments. In contrast, the Yonekura group used lattice parameters derived from their microED results as prior information. While the lattice parameters generated from the powder pattern worked well for the Hohman group, the Yonekura group reported that the lattice parameters generated from the powder pattern often did not perform as effectively. The second difference is in the processing programs and indexing algorithms. The two groups used two representative SFX programs, CCTBX58 and CrystFEL,56 respectively. The indexing algorithms implemented to each program are different, and each group also employed different indexing algorithms during the indexing stage. In CrystFEL, it includes several indexing algorithms that have been proven effective for various macromolecular systems, among which the concept of the Fourier transformation-based indexing algorithm69 is depicted in Fig. 3a. The Fourier transformation-based algorithm starts by representing the Bragg spots in a diffraction image as vectors from the center of the Ewald sphere, utilizing information about detector geometry and wavelength of incident X-rays. When these generated vectors are projected onto unit vectors in the appropriate direction, their magnitudes appear periodically. By applying Fourier transformation to the obtained values, reciprocal lattice vectors are directly derived, thereby indexing the data (Fig. 3a). For the Fourier transformation algorithm to function correctly, a sufficient number of Bragg spots are necessary, and its performance under these conditions has been proven in many studies. On the other hand, the small_cell indexing algorithm64 embedded in CCTBX is specifically designed for cases where Bragg spots are sparse (Fig. 3b). It starts by creating a reflection table of distances between reflections in the reciprocal lattice, based on prior information about the lattice parameters. The observed Bragg spots are then matched to the reference reflections. Ambiguity can arise because multiple combinations of reflections are possible—this ambiguity is resolved using graph theory. For example, if there are two candidate reflections, the appropriate reflection combination is determined by examining their relationships with other observed reflections. Theoretically, this indexing algorithm is expected to perform well for crystals with high symmetry, and its application has recently been validated through smSFX studies.
Separately, Iversen and colleagues have successfully implemented smSFX by establishing a unique data processing pipeline.70 Specifically, the pipeline consists of sparse indexing based on known unit lattice parameters, seed-skewness integration, partiality correction, and adjusted post-refinement routines. Using this approach, they clarified a structure of K4[Pt2(P2O5H2)4]·2H2O at a level comparable to SCXRD results. Notably, they applied the SPIND-based algorithm specialized for indexing sparse Bragg spots. This algorithm generates combinations of Bragg spots based on prior information about lattice parameters and matches them with experimental diffraction patterns according to the crystal's orientation matrix.71 The experimental results demonstrate the applicability of this algorithm for target samples where prior information about lattice parameters is available.
TR-SFX on chemical systems
As the successful structural analysis of various chemical systems using SFX has been continuously reported, expectations also rose for TR-SFX on chemical systems. This is because, in principle, if a sample that can be analyzed statically with SFX undergoes sufficient structural changes in response to external stimuli, it should be possible to track those changes. However, in TR-SFX for chemical systems, there is an additional challenge to overcome besides the difficulty in the indexing process. Chemical system crystals generally have a much higher absorption cross-section compared to protein crystals, meaning that optical laser pulses may not effectively penetrate the crystals. As a result, light-induced signals compared to overall diffraction signals are much weaker in chemical system crystals than in protein crystals. Therefore, due to the need for various experimental optimizations, such as adjusting the target sample size and laser fluence, successful TR-SFX studies on chemical systems have inevitably been delayed.Nevertheless, two years after the initial report of SFX research on chemical systems, in 2024, a TR-SFX work overcoming these challenges in chemical systems was finally reported by Ihee and colleagues.72,73 In that study, they reported the photoreaction of a porous coordination network–224(Fe)–CO (PCN–224(Fe)–CO), a type of metal–organic framework (MOF), initiated by a 400-nm laser pulse (Fig. 4a). MOFs are a class of porous polymers composed of metal nodes and organic linkers. For PCN–224(Fe)–CO, the Zr6 node and Fe porphyrin serve as the metal node and organic linker, respectively.74 MOFs are highly regarded for various applications such as catalysis and gas separation.75–79 With attention to its applications, various time-resolved spectroscopy studies have been conducted on the photoreaction of MOFs.80,81 However, prior to that study, there have been no reports of time-resolved crystallography studies on this topic. Therefore, that study represents the first time-resolved crystallographic investigation of the light-initiated dynamics of MOFs.
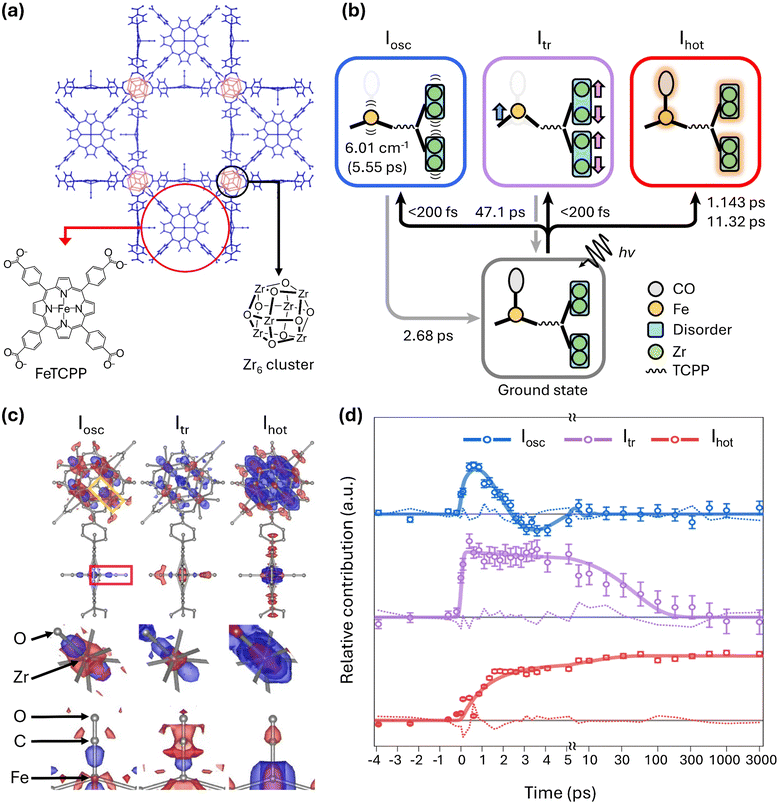 | ||
| Fig. 4 (a) Schematic of the molecular structure of PCN–224(Fe)–CO investigated by TR-SFX. (b) Photoinduced trifurcating structural changes of PCN–224(Fe)–CO observed via TR-SFX. (c) Species-associated difference electron density (SADED) maps of the oscillatory structure, Iosc (left), the transient structure, Itr (centre), and the vibrationally hot structure, Ihot (right). The top panels show the SADED maps of the entire PCN–224(Fe)–CO, and the middle and bottom panels show the SADED maps of the Zr6 node and FeCO site, respectively. The red and blue colours show the negative and positive EDs, respectively. (d) Time profiles of three structural species. Adapted from ref. 72 with permission from Springer Nature, copyright 2024. | ||
In that study, the photoreaction of PCN–224(Fe)–CO was monitored by measuring diffraction images at 33 different time delays. This number of time delays is more than five times the average in TR-SFX on typical macromolecular systems, which is approximately six. With this large number of time delays, extracting detailed kinetic information, including time constants, was possible, leading to the identification of three reaction intermediates (Fig. 4b). The structural changes visualized by the species-associated difference electron density map (SADED) and the time profiles for the three reaction intermediates are shown in Fig. 4c and d, respectively.
Among these, one reaction intermediate involves coherent oscillatory motion of the Zr and Fe atoms. In the first column of Fig. 4c, corresponding to these dynamics, negative electron density is observed around the original positions of the Zr and Fe atoms, with positive density in a dumbbell shape along specific directions from these positions. This is explained by coherent oscillatory motion in one direction, described by a vibration period of 5.55 ps and a damping constant of 2.68 ps (Fig. 4d). In another intermediate, a structure accompanied by doming of Fe porphyrins and anisotropic disorder movements of Zr6 nodes was observed. Upon exposure to light, the carbonyl ligand (CO) bound to Fe is released, initiating the reaction. Therefore, negative electron density is observed at the original position of the carbonyl, simultaneous with Fe moving away from the porphyrin plane to form a more intense dome shape. The decay of this intermediate was characterized by a time constant of 47.1 ps. Lastly, isotropic structural disorder due to vibrationally hot structures was observed. Negative electron density appears at the original position, surrounded by isotropic positive electron density. This phenomenon occurs as atomic vibrations increase due to a photo-response temperature increase. The formation of the vibrationally hot structure occurs biexponentially, with time constants of 1.14 ps and 11.3 ps. The photoreaction pathway of this chemical system is summarized and depicted in Fig. 4b. That study demonstrated the applicability of TR-SFX to chemical systems, clarifying various dynamics in the crystalline state from a structural perspective.
The idea of observing chemical dynamics using protein crystals, distinct from the previous study that directly applied TR-SFX to crystals of chemical systems, has also been proposed and demonstrated by Ueno and colleagues.82 Specifically, this approach involves immobilizing chemicals on specific binding sites of protein crystals and conducting TR-SFX experiments on chemical-incorporated protein crystals. This method circumvents the difficulty of indexing due to the small lattice parameters of chemical systems by utilizing protein crystals with larger lattice parameters, enabling the observation of the dynamics of chemical systems. In their work, they established a host–guest system using hen egg white lysozyme (HEWL) crystals as the host and Mn(CO)3 as the guest. In the reaction initiated by a 365 nm laser pulse, the sequential dissociation of two carbonyl ligands from Mn(CO)3 was observed. Notably, they elucidated the structure of a reaction intermediate with two dissociated carbonyl ligands, which had not been observed in the study in solution. The formation of previously unobserved reaction intermediates was explained by the unique physical and chemical environment around the manganese compound formed by the lysozyme protein. This work demonstrates that the dynamics of chemical systems can be investigated with conventional TR-SFX methods for proteins by incorporating target chemicals into proteins.
Summary and outlook
This article introduces all relevant studies conducted since the first study for SFX performed on chemical systems. SFX for chemical systems has been limited due to the insufficient number of Bragg spots caused by the small lattice parameter, a fundamental characteristic of these systems, which hindered the smooth application of conventional indexing algorithms for SFX. However, in 2022, the first study overcoming this limitation was reported, followed quickly by additional studies, bringing the total number of crystal structures of chemical systems determined by SFX to fifteen. The chemical systems whose structures have been determined via SFX include a variety of compounds such as inorganic–organic hybrid compounds, organic compounds, and metal complexes. Additionally, to overcome the previous limitation of indexing difficulties, a graph theory-based algorithm developed for indexing the scarce Bragg spots was successfully applied. On the other hand, there have also been instances where the existing indexing algorithms used for macromolecular systems successfully achieved indexing, indicating that there is no consensus yet on the best indexing algorithm. Therefore, to broadly apply SFX to chemical systems, future research and optimization in the indexing process are anticipated to be critical tasks. Table 1 summarizes the programs and indexing algorithms used for all chemical systems where SFX has been applied.| Target sample | Program | Indexing algorithm | References |
|---|---|---|---|
| Mithrene | CCTBX | cctbx.small_cell | 63 |
| Thiorene | CCTBX | cctbx.small_cell | 63 |
| Tetrene | CCTBX | cctbx.small_cell | 63 |
| Silver 4-alkanethiolates | CCTBX | cctbx.small_cell | 65 |
| Silver 6-alkanethiolates | CCTBX | cctbx.small_cell | 65 |
| Silver 9-alkanethiolates | CCTBX | cctbx.small_cell | 65 |
| Silver 2-fluorobenzenethiolates | CCTBX | cctbx.small_cell | 66 |
| Silver 3-fluorobenzenethiolates | CCTBX | cctbx.small_cell | 66 |
| Silver 4-fluorobenzenethiolates | CCTBX | cctbx.small_cell | 66 |
| Rhodamine-6G | CrystFEL | xgandalf, dirax, mosflm | 67 |
| Monopeptoid | CrystFEL | Not reported | 68 |
| Tripeptoid | CrystFEL | Not reported | 68 |
| Ph-BTBT-C10 | CrystFEL | Not reported | 68 |
| Anti-BTBTT-C6 | CrystFEL | Not reported | 68 |
| PtPOP | Self-made | Self-made (SPIND based) | 70 |
| PCN–224(Fe)–CO | CrystFEL | xgandalf | 72 |
| HEWL with MnCO3 | CrystFEL | xgandalf | 82 |
Following the successful analysis of static structures of chemical systems using SFX, TR-SFX emerged as a powerful tool for elucidating their structural dynamics. TR-SFX, a powerful tool for elucidating the structural dynamics of proteins, has also been successfully applied to chemical systems, opening new horizons for structural dynamics research. To date, two studies have employed TR-SFX to investigate the structural dynamics of chemical systems. One study on the photoreaction of a MOF successfully elucidated detailed structural changes and time profiles for three reaction intermediates, including coherent oscillation. The other study observed a unique reaction intermediate of a metal complex using host–guest interactions with protein crystals, which had not been observed in solution. Although few in number, these two distinctive studies provide promising examples for future TR-SFX research on chemical systems. Firstly, beyond PCN–224(Fe)–CO studied by TR-SFX, there are many MOFs that respond to external stimuli, suggesting that the same technique could be applied to reveal the structural dynamics of a wider variety of MOFs. Secondly, the TR-SFX study using chemical-incorporated protein crystal suggests the potential for applying TR-SFX to various host–guest systems. Host–guest interactions can create unique environments distinct from typical solutions or gas phases, akin to pseudo solutions. Using host crystals to provide unique reaction conditions can enable TR-SFX to investigate diverse structural dynamics not previously observed. Moreover, the various types of chemical systems whose static structures have already been analyzed could also become potential targets for TR-SFX. Therefore, TR-SFX holds significant potential as a tool for uncovering the structural dynamics of various chemical systems, providing insights into diverse and unique structural dynamics occurring within crystals.
Author contributions
J. Moon: conceptualization, writing – original draft, and reviewing and editing. Y. Lee: writing and reviewing and editing. H. Ihee: conceptualization, writing, reviewing and editing, and supervision.Data availability
Data availability is not applicable to this article, as no new data were created or analyzed during this study. However, copies of any correspondence or licenses related to permissions from other publishers can be provided for future reference if needed.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Institute for Basic Science (IBS-R033).References
- B. Bloom and G. Laubach, Annu. Rev. Pharmacol., 1962, 2, 67–108 CrossRef.
- R. Atkinson, Int. J. Chem. Kinet., 1987, 19, 799–828 CrossRef.
- F. Salvat, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 578–581 CrossRef PubMed.
- L. Ma, H. Yong, J. D. Geiser, A. Moreno Carrascosa, N. Goff and P. M. Weber, Struct. Dyn., 2020, 7, 034102 CrossRef CAS PubMed.
- Q. Kong, J. H. Lee, A. Plech, M. Wulff, H. Ihee and M. H. Koch, Angew. Chem., Int. Ed., 2008, 47, 5550–5553 CrossRef CAS PubMed.
- J. H. Lee, J. Kim, M. Cammarata, Q. Kong, K. H. Kim, J. Choi, T. K. Kim, M. Wulff and H. Ihee, Angew. Chem., Int. Ed., 2008, 47, 1047–1050 CrossRef CAS PubMed.
- J. H. Lee, T. K. Kim, J. Kim, Q. Kong, M. Cammarata, M. Lorenc, M. Wulff and H. Ihee, J. Am. Chem. Soc., 2008, 130, 5834–5835 CrossRef CAS PubMed.
- M. Christensen, K. Haldrup, K. Bechgaard, R. Feidenhans’l, Q. Kong, M. Cammarata, M. L. Russo, M. Wulff, N. Harrit and M. M. Nielsen, J. Am. Chem. Soc., 2009, 131, 502–508 CrossRef CAS PubMed.
- H. Ihee, Acc. Chem. Res., 2009, 42, 356–366 CrossRef CAS PubMed.
- Q. Kong, J. H. Lee, K. H. Kim, J. Kim, M. Wulff, H. Ihee and M. H. Koch, J. Am. Chem. Soc., 2010, 132, 2600–2607 CrossRef CAS PubMed.
- K. H. Kim, K. Y. Oang, J. Kim, J. H. Lee, Y. Kim and H. Ihee, Chem. Commun., 2011, 47, 289–291 RSC.
- K. H. Kim, J. H. Lee, J. Kim, S. Nozawa, T. Sato, A. Tomita, K. Ichiyanagi, H. Ki, J. Kim and S.-I. Adachi, Phys. Rev. Lett., 2013, 110, 165505 CrossRef PubMed.
- J. H. Lee, M. Wulff, S. Bratos, J. Petersen, L. Guerin, J.-C. Leicknam, M. Cammarata, Q. Kong, J. Kim and K. B. Møller, J. Am. Chem. Soc., 2013, 135, 3255–3261 CrossRef CAS PubMed.
- J. G. Kim, T. W. Kim, J. Kim and H. Ihee, Acc. Chem. Res., 2015, 48, 2200–2208 CrossRef CAS PubMed.
- K. H. Kim, J. G. Kim, S. Nozawa, T. Sato, K. Y. Oang, T. W. Kim, H. Ki, J. Jo, S. Park and C. Song, Nature, 2015, 518, 385–389 CrossRef CAS.
- E. Biasin, T. B. Van Driel, K. S. Kjær, A. O. Dohn, M. Christensen, T. Harlang, P. Vester, P. Chabera, Y. Liu and J. Uhlig, Phys. Rev. Lett., 2016, 117, 013002 CrossRef PubMed.
- J. G. Kim, S. Nozawa, H. Kim, E. H. Choi, T. Sato, T. W. Kim, K. H. Kim, H. Ki, J. Kim and M. Choi, Nature, 2020, 582, 520–524 CrossRef CAS.
- T. W. Kim, S. J. Lee, J. Jo, J. G. Kim, H. Ki, C. W. Kim, K. H. Cho, J. Choi, J. H. Lee and M. Wulff, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14996–15005 CrossRef.
- D. Leshchev, A. J. S. Valentine, P. Kim, A. W. Mills, S. Roy, A. Chakraborty, E. Biasin, K. Haldrup, D. J. Hsu and M. S. Kirschner, Angew. Chem., Int. Ed., 2023, 62, e202304615 CrossRef CAS PubMed.
- J. Cao, H. Ihee and A. Zewail, Chem. Phys. Lett., 1998, 290, 1–8 CrossRef CAS.
- J. Yang, X. Zhu, J. P. F. Nunes, J. K. Yu, R. M. Parrish, T. J. Wolf, M. Centurion, M. Gühr, R. Li and Y. Liu, Science, 2020, 368, 885–889 CrossRef CAS PubMed.
- E. Champenois, D. Sanchez, J. Yang, J. Figueira Nunes, A. Attar, M. Centurion, R. Forbes, M. Gühr, K. Hegazy and F. Ji, Science, 2021, 374, 178–182 CrossRef CAS PubMed.
- M. Centurion, T. J. Wolf and J. Yang, Annu. Rev. Phys. Chem., 2022, 73, 21–42 CrossRef CAS PubMed.
- J. Heo, D. Kim, A. Segalina, H. Ki, D.-S. Ahn, S. Lee, J. Kim, Y. Cha, K. W. Lee and J. Yang, Nature, 2024, 625, 710–714 CrossRef CAS PubMed.
- Q. Wang, L. Yun and J. Yang, CCS Chem., 2024, 6, 1092–1109 CrossRef CAS.
- S. Pandey, I. Poudyal and T. N. Malla, Crystals, 2020, 10, 628 CrossRef CAS.
- G. Brändén and R. Neutze, Science, 2021, 373, eaba0954 CrossRef PubMed.
- S. Westenhoff, P. Meszaros and M. Schmidt, Curr. Opin. Struct. Biol., 2022, 77, 102481 CrossRef CAS PubMed.
- R. Neutze, R. Wouts, D. Van der Spoel, E. Weckert and J. Hajdu, Nature, 2000, 406, 752–757 CrossRef CAS PubMed.
- S. Marchesini, H. He, H. N. Chapman, S. P. Hau-Riege, A. Noy, M. R. Howells, U. Weierstall and J. C. H. Spence, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 140101 CrossRef.
- M. Bergh, N. Tîmneanu and D. van der Spoel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051904 CrossRef PubMed.
- S. P. Hau-Riege, R. A. London and A. Szoke, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 051906 CrossRef PubMed.
- Z. Jurek, G. Faigel and M. Tegze, Eur. Phys. J. D, 2004, 29, 217–229 CrossRef CAS.
- J. C. Spence and R. B. Doak, Phys. Rev. Lett., 2004, 92, 198102 CrossRef CAS PubMed.
- H. N. Chapman, A. Barty, S. Marchesini, A. Noy, S. P. Hau-Riege, C. Cui, M. R. Howells, R. Rosen, H. He, J. C. H. Spence, U. Weierstall, T. Beetz, C. Jacobsen and D. Shapiro, J. Opt. Soc. Am. A, 2006, 23, 1179–1200 CrossRef PubMed.
- M. M. Seibert, T. Ekeberg, F. R. Maia, M. Svenda, J. Andreasson, O. Jönsson, D. Odić, B. Iwan, A. Rocker and D. Westphal, Nature, 2011, 470, 78–81 CrossRef PubMed.
- H. N. Chapman, P. Fromme, A. Barty, T. A. White, R. A. Kirian, A. Aquila, M. S. Hunter, J. Schulz, D. P. DePonte and U. Weierstall, Nature, 2011, 470, 73–77 CrossRef PubMed.
- A. Aquila, M. S. Hunter, R. B. Doak, R. A. Kirian, P. Fromme, T. A. White, J. Andreasson, D. Arnlund, S. Bajt, T. R. M. Barends, M. Barthelmess, M. J. Bogan, C. Bostedt, H. Bottin, J. D. Bozek, C. Caleman, N. Coppola, J. Davidsson, D. P. DePonte, V. Elser, S. W. Epp, B. Erk, H. Fleckenstein, L. Foucar, M. Frank, R. Fromme, H. Graafsma, I. Grotjohann, L. Gumprecht, J. Hajdu, C. Y. Hampton, A. Hartmann, R. Hartmann, S. Hau-Riege, G. Hauser, H. Hirsemann, P. Holl, J. M. Holton, A. Hömke, L. Johansson, N. Kimmel, S. Kassemeyer, F. Krasniqi, K.-U. Kühnel, M. Liang, L. Lomb, E. Malmerberg, S. Marchesini, A. V. Martin, F. R. N. C. Maia, M. Messerschmidt, K. Nass, C. Reich, R. Neutze, D. Rolles, B. Rudek, A. Rudenko, I. Schlichting, C. Schmidt, K. E. Schmidt, J. Schulz, M. M. Seibert, R. L. Shoeman, R. Sierra, H. Soltau, D. Starodub, F. Stellato, S. Stern, L. Strüder, N. Timneanu, J. Ullrich, X. Wang, G. J. Williams, G. Weidenspointner, U. Weierstall, C. Wunderer, A. Barty, J. C. H. Spence and H. N. Chapman, Opt. Express, 2012, 20, 2706–2716 CrossRef PubMed.
- C. Kupitz, S. Basu, I. Grotjohann, R. Fromme, N. A. Zatsepin, K. N. Rendek, M. S. Hunter, R. L. Shoeman, T. A. White, D. Wang, D. James, J.-H. Yang, D. E. Cobb, B. Reeder, R. G. Sierra, H. Liu, A. Barty, A. L. Aquila, D. Deponte, R. A. Kirian, S. Bari, J. J. Bergkamp, K. R. Beyerlein, M. J. Bogan, C. Caleman, T.-C. Chao, C. E. Conrad, K. M. Davis, H. Fleckenstein, L. Galli, S. P. Hau-Riege, S. Kassemeyer, H. Laksmono, M. Liang, L. Lomb, S. Marchesini, A. V. Martin, M. Messerschmidt, D. Milathianaki, K. Nass, A. Ros, S. Roy-Chowdhury, K. Schmidt, M. Seibert, J. Steinbrener, F. Stellato, L. Yan, C. Yoon, T. A. Moore, A. L. Moore, Y. Pushkar, G. J. Williams, S. Boutet, R. B. Doak, U. Weierstall, M. Frank, H. N. Chapman, J. C. H. Spence and P. Fromme, Nature, 2014, 513, 261–265 CrossRef PubMed.
- J. Tenboer, S. Basu, N. Zatsepin, K. Pande, D. Milathianaki, M. Frank, M. Hunter, S. Boutet, G. J. Williams, J. E. Koglin, D. Oberthuer, M. Heymann, C. Kupitz, C. Conrad, J. Coe, S. Roy-Chowdhury, U. Weierstall, D. James, D. Wang, T. Grant, A. Barty, O. Yefanov, J. Scales, C. Gati, C. Seuring, V. Srajer, R. Henning, P. Schwander, R. Fromme, A. Ourmazd, K. Moffat, J. J. Van Thor, J. C. H. Spence, P. Fromme, H. N. Chapman and M. Schmidt, Science, 2014, 346, 1242–1246 CrossRef CAS PubMed.
- E. Nango, A. Royant, M. Kubo, T. Nakane, C. Wickstrand, T. Kimura, T. Tanaka, K. Tono, C. Song, R. Tanaka, T. Arima, A. Yamashita, J. Kobayashi, T. Hosaka, E. Mizohata, P. Nogly, M. Sugahara, D. Nam, T. Nomura, T. Shimamura, D. Im, T. Fujiwara, Y. Yamanaka, B. Jeon, T. Nishizawa, K. Oda, M. Fukuda, R. Andersson, P. Båth, R. Dods, J. Davidsson, S. Matsuoka, S. Kawatake, M. Murata, O. Nureki, S. Owada, T. Kameshima, T. Hatsui, Y. Joti, G. Schertler, M. Yabashi, A.-N. Bondar, J. Standfuss, R. Neutze and S. Iwata, Science, 2016, 354, 1552–1557 CrossRef CAS PubMed.
- K. Pande, C. D. M. Hutchison, G. Groenhof, A. Aquila, J. S. Robinson, J. Tenboer, S. Basu, S. Boutet, D. P. DePonte, M. Liang, T. A. White, N. A. Zatsepin, O. Yefanov, D. Morozov, D. Oberthuer, C. Gati, G. Subramanian, D. James, Y. Zhao, J. Koralek, J. Brayshaw, C. Kupitz, C. Conrad, S. Roy-Chowdhury, J. D. Coe, M. Metz, P. L. Xavier, T. D. Grant, J. E. Koglin, G. Ketawala, R. Fromme, V. Šrajer, R. Henning, J. C. H. Spence, A. Ourmazd, P. Schwander, U. Weierstall, M. Frank, P. Fromme, A. Barty, H. N. Chapman, K. Moffat, J. J. van Thor and M. Schmidt, Science, 2016, 352, 725–729 CrossRef CAS PubMed.
- P. Nogly, T. Weinert, D. James, S. Carbajo, D. Ozerov, A. Furrer, D. Gashi, V. Borin, P. Skopintsev, K. Jaeger, K. Nass, P. Båth, R. Bosman, J. Koglin, M. Seaberg, T. Lane, D. Kekilli, S. Brünle, T. Tanaka, W. Wu, C. Milne, T. White, A. Barty, U. Weierstall, V. Panneels, E. Nango, S. Iwata, M. Hunter, I. Schapiro, G. Schertler, R. Neutze and J. Standfuss, Science, 2018, 361, eaat0094 CrossRef.
- R. Dods, P. Båth, D. Morozov, V. A. Gagnér, D. Arnlund, H. L. Luk, J. Kübel, M. Maj, A. Vallejos, C. Wickstrand, R. Bosman, K. R. Beyerlein, G. Nelson, M. Liang, D. Milathianaki, J. Robinson, R. Harimoorthy, P. Berntsen, E. Malmerberg, L. Johansson, R. Andersson, S. Carbajo, E. Claesson, C. E. Conrad, P. Dahl, G. Hammarin, M. S. Hunter, C. Li, S. Lisova, A. Royant, C. Safari, A. Sharma, G. J. Williams, O. Yefanov, S. Westenhoff, J. Davidsson, D. P. DePonte, S. Boutet, A. Barty, G. Katona, G. Groenhof, G. Brändén and R. Neutze, Nature, 2021, 589, 310–314 CrossRef CAS.
- T. Gruhl, T. Weinert, M. J. Rodrigues, C. J. Milne, G. Ortolani, K. Nass, E. Nango, S. Sen, P. J. M. Johnson, C. Cirelli, A. Furrer, S. Mous, P. Skopintsev, D. James, F. Dworkowski, P. Båth, D. Kekilli, D. Ozerov, R. Tanaka, H. Glover, C. Bacellar, S. Brünle, C. M. Casadei, A. D. Diethelm, D. Gashi, G. Gotthard, R. Guixà-González, Y. Joti, V. Kabanova, G. Knopp, E. Lesca, P. Ma, I. Martiel, J. Mühle, S. Owada, F. Pamula, D. Sarabi, O. Tejero, C.-J. Tsai, N. Varma, A. Wach, S. Boutet, K. Tono, P. Nogly, X. Deupi, S. Iwata, R. Neutze, J. Standfuss, G. Schertler and V. Panneels, Nature, 2023, 615, 939–944 CrossRef CAS PubMed.
- M. Maestre-Reyna, P.-H. Wang, E. Nango, Y. Hosokawa, M. Saft, A. Furrer, C.-H. Yang, E. P. Gusti Ngurah Putu, W.-J. Wu, H.-J. Emmerich, N. Caramello, S. Franz-Badur, C. Yang, S. Engilberge, M. Wranik, H. L. Glover, T. Weinert, H.-Y. Wu, C.-C. Lee, W.-C. Huang, K.-F. Huang, Y.-K. Chang, J.-H. Liao, J.-H. Weng, W. Gad, C.-W. Chang, A. H. Pang, K.-C. Yang, W.-T. Lin, Y.-C. Chang, D. Gashi, E. Beale, D. Ozerov, K. Nass, G. Knopp, P. J. M. Johnson, C. Cirelli, C. Milne, C. Bacellar, M. Sugahara, S. Owada, Y. Joti, A. Yamashita, R. Tanaka, T. Tanaka, F. Luo, K. Tono, W. Zarzycka, P. Müller, M. A. Alahmad, F. Bezold, V. Fuchs, P. Gnau, S. Kiontke, L. Korf, V. Reithofer, C. J. Rosner, E. M. Seiler, M. Watad, L. Werel, R. Spadaccini, J. Yamamoto, S. Iwata, D. Zhong, J. Standfuss, A. Royant, Y. Bessho, L.-O. Essen and M.-D. Tsai, Science, 2023, 382, eadd7795 CrossRef CAS PubMed.
- C. Gati, G. Bourenkov, M. Klinge, D. Rehders, F. Stellato, D. Oberthür, O. Yefanov, B. P. Sommer, S. Mogk and M. Duszenko, IUCrJ, 2014, 1, 87–94 CrossRef CAS PubMed.
- F. Stellato, D. Oberthür, M. Liang, R. Bean, C. Gati, O. Yefanov, A. Barty, A. Burkhardt, P. Fischer and L. Galli, IUCrJ, 2014, 1, 204–212 CrossRef CAS PubMed.
- R. G. Sierra, H. Laksmono, J. Kern, R. Tran, J. Hattne, R. Alonso-Mori, B. Lassalle-Kaiser, C. Glöckner, J. Hellmich and D. W. Schafer, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2012, 68, 1584–1587 CrossRef CAS PubMed.
- C. G. Roessler, R. Agarwal, M. Allaire, R. Alonso-Mori, B. Andi, J. F. Bachega, M. Bommer, A. S. Brewster, M. C. Browne and R. Chatterjee, Structure, 2016, 24, 631–640 CrossRef CAS PubMed.
- R. G. Sierra, C. Gati, H. Laksmono, E. H. Dao, S. Gul, F. Fuller, J. Kern, R. Chatterjee, M. Ibrahim and A. S. Brewster, Nat. Methods, 2016, 13, 59–62 CrossRef CAS.
- F. D. Fuller, S. Gul, R. Chatterjee, E. S. Burgie, I. D. Young, H. Lebrette, V. Srinivas, A. S. Brewster, T. Michels-Clark and J. A. Clinger, Nat. Methods, 2017, 14, 443–449 CrossRef CAS PubMed.
- M. L. Grünbein and G. Nass Kovacs, Acta Crystallogr., Sect. D: Struct. Biol., 2019, 75, 178–191 CrossRef PubMed.
- T. R. M. Barends, B. Stauch, V. Cherezov and I. Schlichting, Nat. Rev. Methods Primers, 2022, 2, 59 CrossRef CAS PubMed.
- L. Foucar, A. Barty, N. Coppola, R. Hartmann, P. Holl, U. Hoppe, S. Kassemeyer, N. Kimmel, J. Küpper and M. Scholz, Comput. Phys. Commun., 2012, 183, 2207–2213 CrossRef CAS.
- T. A. White, R. A. Kirian, A. V. Martin, A. Aquila, K. Nass, A. Barty and H. N. Chapman, J. Appl. Crystallogr., 2012, 45, 335–341 CrossRef CAS.
- T. A. White, V. Mariani, W. Brehm, O. Yefanov, A. Barty, K. R. Beyerlein, F. Chervinskii, L. Galli, C. Gati and T. Nakane, J. Appl. Crystallogr., 2016, 49, 680–689 CrossRef CAS PubMed.
- J. Hattne, N. Echols, R. Tran, J. Kern, R. J. Gildea, A. S. Brewster, R. Alonso-Mori, C. Glöckner, J. Hellmich and H. Laksmono, Nat. Methods, 2014, 11, 545–548 CrossRef PubMed.
- A. S. Brewster, D. G. Waterman, J. M. Parkhurst, R. J. Gildea, I. D. Young, L. J. O'Riordan, J. Yano, G. Winter, G. Evans and N. K. Sauter, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 877–894 CrossRef PubMed.
- G. Winter, D. G. Waterman, J. M. Parkhurst, A. S. Brewster, R. J. Gildea, M. Gerstel, L. Fuentes-Montero, M. Vollmar, T. Michels-Clark and I. D. Young, Acta Crystallogr., Sect. D: Struct. Biol., 2018, 74, 85–97 CrossRef PubMed.
- R. Neutze, Philos. Trans. R. Soc., B, 2014, 369, 20130318 CrossRef PubMed.
- H. Ki, K. Y. Oang, J. Kim and H. Ihee, Annu. Rev. Phys. Chem., 2017, 68, 473–497 CrossRef PubMed.
- E. A. Schriber, D. W. Paley, R. Bolotovsky, D. J. Rosenberg, R. G. Sierra, A. Aquila, D. Mendez, F. Poitevin, J. P. Blaschke, A. Bhowmick, R. P. Kelly, M. Hunter, B. Hayes, D. C. Popple, M. Yeung, C. Pareja-Rivera, S. Lisova, K. Tono, M. Sugahara, S. Owada, T. Kuykendall, K. Yao, P. J. Schuck, D. Solis-Ibarra, N. K. Sauter, A. S. Brewster and J. N. Hohman, Nature, 2022, 601, 360–365 CrossRef PubMed.
- A. S. Brewster, M. R. Sawaya, J. Rodriguez, J. Hattne, N. Echols, H. T. McFarlane, D. Cascio, P. D. Adams, D. S. Eisenberg and N. K. Sauter, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 357–366 CrossRef PubMed.
- M. Aleksich, D. W. Paley, E. A. Schriber, W. Linthicum, V. Oklejas, D. W. Mittan-Moreau, R. P. Kelly, P. A. Kotei, A. Ghodsi, R. G. Sierra, A. Aquila, F. Poitevin, J. P. Blaschke, M. Vakili, C. J. Milne, F. Dall'Antonia, D. Khakhulin, F. Ardana-Lamas, F. Lima, J. Valerio, H. Han, T. Gallo, H. Yousef, O. Turkot, I. J. Bermudez Macias, T. Kluyver, P. Schmidt, L. Gelisio, A. R. Round, Y. Jiang, D. Vinci, Y. Uemura, M. Kloos, M. Hunter, A. P. Mancuso, B. D. Huey, L. R. Parent, N. K. Sauter, A. S. Brewster and J. N. Hohman, J. Am. Chem. Soc., 2023, 145, 17042–17055 CrossRef PubMed.
- P. A. Kotei, D. W. Paley, V. Oklejas, D. W. Mittan-Moreau, E. A. Schriber, M. Aleksich, M. C. Willson, I. Inoue, S. Owada, K. Tono, M. Sugahara, S. Inaba-Inoue, A. Aquila, F. Poitevin, J. P. Blaschke, S. Lisova, M. S. Hunter, R. G. Sierra, J. A. Gascón, N. K. Sauter, A. S. Brewster and J. N. Hohman, Small Sci., 2023, 4, 2300110 CrossRef.
- K. Takaba, S. Maki-Yonekura, I. Inoue, K. Tono, T. Hamaguchi, K. Kawakami, H. Naitow, T. Ishikawa, M. Yabashi and K. Yonekura, Nat. Chem., 2023, 15, 491–497 CrossRef CAS PubMed.
- K. Takaba, S. Maki-Yonekura, I. Inoue, K. Tono, Y. Fukuda, Y. Shiratori, Y. Peng, J. Morimoto, S. Inoue, T. Higashino, S. Sando, T. Hasegawa, M. Yabashi and K. Yonekura, J. Am. Chem. Soc., 2024, 146, 5872–5882 CrossRef CAS PubMed.
- I. Steller, R. Bolotovsky and M. G. Rossmann, J. Appl. Crystallogr., 1997, 30, 1036–1040 CrossRef CAS.
- L. J. Stockler, L. Krause, B. Svane, K. Tolborg, B. Richter, S. Takahashi, T. Fujita, H. Kasai, M. Sugahara, I. Inoue, E. Nishibori and B. B. Iversen, IUCrJ, 2023, 10, 103–117 CrossRef PubMed.
- C. Li, X. Li, R. Kirian, J. C. H. Spence, H. Liu and N. A. Zatsepin, IUCrJ, 2019, 6, 72–84 CrossRef CAS PubMed.
- J. Kang, Y. Lee, S. Lee, H. Ki, J. Kim, J. Gu, Y. Cha, J. Heo, K. W. Lee, S. O. Kim, J. Park, S. Y. Park, S. Kim, R. Ma, I. Eom, M. Kim, J. Kim, J. H. Lee and H. Ihee, Nat. Chem., 2024, 16, 693–699 CrossRef CAS PubMed.
- L. E. Hatcher and P. R. Raithby, Nat. Chem., 2024, 16, 674–675 CrossRef CAS PubMed.
- D. Feng, W.-C. Chung, Z. Wei, Z.-Y. Gu, H.-L. Jiang, Y.-P. Chen, D. J. Darensbourg and H.-C. Zhou, J. Am. Chem. Soc., 2013, 135, 17105–17110 CrossRef CAS PubMed.
- H. Li, M. Eddaoudi, T. L. Groy and O. Yaghi, J. Am. Chem. Soc., 1998, 120, 8571–8572 CrossRef CAS.
- A. P. Cote, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef CAS PubMed.
- J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869–932 CrossRef CAS PubMed.
- H. Furukawa, K. E. Cordova, M. O’Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- J.-D. Xiao and H.-L. Jiang, Acc. Chem. Res., 2018, 52, 356–366 CrossRef PubMed.
- B. Pattengale, S. Ostresh, C. A. Schmuttenmaer and J. Neu, Chem. Rev., 2021, 122, 132–166 CrossRef PubMed.
- D. J. Cerasale, D. C. Ward and T. L. Easun, Nat. Rev. Chem., 2022, 6, 9–30 CrossRef PubMed.
- B. Maity, M. Shoji, F. Luo, T. Nakane, S. Abe, S. Owada, J. Kang, K. Tono, R. Tanaka, T. T. Pham, M. Kojima, Y. Hishikawa, J. Tanaka, J. Tian, M. Nagama, T. Suzuki, H. Noya, Y. Nakasuji, A. Asanuma, X. Yao, S. Iwata, Y. Shigeta, E. Nango and T. Ueno, Nat. Commun., 2024, 15, 5518 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2024 |