Unveiling new [1+1] Schiff-base macrocycles towards high energy-barrier hexagonal bipyramidal Dy(III) single-molecule magnets

Abstract

The employment of the [1+1] condensation approach for the preparation of new macrocyclic scaffolds (L^N6 and L^N3O3) towards high-performance Dy(III) single-molecule magnets (SMMs) with pseudo-D_6h symmetry is described. Engineering of the macrocycles denticity from L^N6 to L^N3O3 leads to a mononuclear SMM with a large U_eff value of 1300 K. The experimental results are supported by ab initio calculations, which indicate relaxation of the magnetization via the second-excited state.

---

The field of single-molecule magnets (SMMs) emerged in the early 1990s when a 3d-metal based coordination cluster displayed slow magnetization relaxation of purely molecular origin.¹ Since then, hundreds of SMMs have been reported and the molecular magnetism field has become a multi-disciplinary area of research involving chemists, physicists, and theoretical scientists.² These molecular compounds have been proposed as building units in the flourishing fields of information storage,³ spintronics,⁴ and quantum computing.⁵ Molecular inorganic compounds with long relaxation times, that can store information at higher operating temperatures, are the key targets.⁶ Along this direction, 4f-ions, especially Tb(III) and Dy(III) ions, have been thoroughly studied as SMMs, due to their large magnetic moments and anisotropies in their ground states.⁷

In 4f SMMs, the symmetry of the coordination environment and the strength of the ligand field are critical for generating a large crystal-field splitting, thus yielding large energy barriers (U_eff) for the reorientation of the magnetization and high blocking temperatures (T_B), key features for the retention of magnetic information.⁸ One of the most promising strategies for the accomplishment of high-performance lanthanide SMMs includes the synthesis of mononuclear Dy(III) complexes, in which the metal center occupies an axially symmetrical environment,⁹ such as pentagonal bipyramidal (D_5h)¹⁰ and hexagonal bipyramidal (D_6h).¹¹ Both strategies require a challenging molecular engineering to generate a weak equatorial crystal field and a strong axial crystal field.

The most effective strategy for controlling the arrangement of the donor atoms around the metal center has been proved by the inclusion of macrocyclic ligands such as crown ethers or Schiff-bases. The latter can encapsulate the lanthanide ion and create a ‘soft’ equatorial ligand field mainly consisting of N-atoms, thereby rendering the axial positions accessible for coordination by strongly anionic O-donor ligands.¹² This spatial conformation of donor atoms around an oblate ion, such as Dy(III), is ideal for maximizing the anisotropy,¹³ and has provided several examples of pentagonal or hexagonal bipyramidal Dy(III) Schiff-base macrocyclic compounds with extremely high U_eff values ranging from 1000 to 1800 K.^10,11 To this direction, Zheng and coworkers recently reported a D_6h Dy(III) crown ether macrocyclic complex, where the equatorial plane is made of a highly symmetric 18-crown-6 ligand, and the two axial positions are occupied by alkoxides, yielding a U_eff value of 2427 K, the highest U_eff among all reported SMMs to date.¹⁴

The most widely used synthetic strategy towards Schiff-base macrocyclic ligands that can provide D_6h symmetric complexes, includes the condensation reaction between two dicarbonyl-containing units with two diamines in the presence of a lanthanide ion, termed the [2+2] template, whereas for D_5h coordination environments the [1+1] approach has been mostly used.^10–12,15 However, the [1+1] strategy towards the synthesis of hexagonal bipyramidal high-performance and air-stable Dy(III) SMMs is practically unexplored, with only one example recently reported in the literature exhibiting a considerably low U_eff value compared to its D_6h counterparts.¹⁶

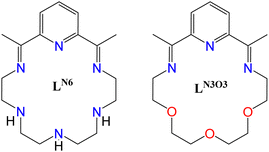
In this respect, we implemented the [1+1] approach to isolate hexagonal bipyramidal Dy(III) complexes by initially using an N-rich macrocycle (L^N6, Scheme 1). The latter results from a step-wise synthetic procedure (see ESI†) that includes firstly the reaction of 2,6-diacetylpyridine with tetraethylenepentamine in the presence of a Dy(III) hydrate salt. Subsequently, to facilitate the formation of a D_6h ligand field around the metal center, we placed two bulky triphenylsiloxide (Ph₃SiO⁻) ligands at the axial sites, thus yielding the complex [Dy(L^N6)(Ph₃SiO)₂](PF₆) (1-L^N6). Modifying the central atoms of the diamine, and specifically replacing the three NH-groups by etheric O-atoms, we came across the new mixed-donor macrocycle L^N3O3 (Scheme 1), which in turn led to the complex [Dy(L^N3O3)(Ph₃SiO)₂](PF₆) (1-L^N3O3). Interestingly, both complexes are air-stable and behave as zero-field SMMs with high energy barriers, while exhibiting different magnetization relaxation dynamics depending on the distortion of the macrocyclic ligand, as well as the deviation from the ideal D_6h symmetry.

Scheme 1 Structures of the [1+1] Schiff-base macrocyclic ligands L^N6 and L^N3O3.

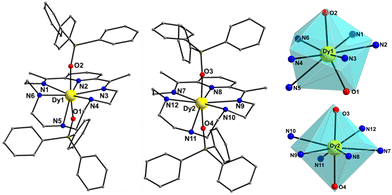
Compound 1-L^N6 crystallizes in the monoclinic space group Pn (Table S1, ESI†) with the asymmetric unit containing two crystallographically independent mononuclear Dy(III) complexes (Dy1 and Dy2 in Fig. 1), in which the metal centers adopt two different coordination geometries due to the significant displacement of L^N6 from the equatorial plane. Therefore, both Dy atoms are 8-coordinate and according to SHAPE analysis,¹⁷ Dy1 sits on a distorted triangular dodecahedral coordination polyhedron, whereas Dy2 adopts a distorted hexagonal bipyramidal geometry (Fig. 1 and Table S2, ESI†). In both molecules, the Dy(III) ions coordinate equatorially with six N-donor atoms provided by the macrocycle with long Dy–N bond distances in the range of 2.514(8)–2.713(9) Å for Dy1, and 2.566(12)–2.690(11) Å for Dy2 (Table S3, ESI†). Furthermore, strong axial ligation is provided by two anionic Ph₃SiO⁻ ligands with short Dy–O_ax bonds of 2.194(6) and 2.196(7) Å for Dy1, and 2.143(7) and 2.152(7) Å for Dy2 (Table S3, ESI†). The poor axiality of 1-L^N6 is confirmed by the O_ax–Dy–O_ax angles of 158.8(2)° (for Dy1) and 168.6(3)° (for Dy2), far from the ideal angle of 180° for a perfect D_6h symmetry. The shortest intermolecular Dy⋯Dy separation in the crystal is 11.309(1) Å (Fig. S1, ESI†), suggesting negligible direct and/or superexchange magnetic interactions.

Fig. 1 The two crystallographically independent complexes in the unit cell of 1-L^N6 (left and middle), and the triangular dodecahedral and hexagonal bipyramidal coordination polyhedra of the Dy1 and Dy2 atoms (right). The smaller white spheres define the vertices of the corresponding ideal polyhedra. The PF₆⁻ counterions, CH₂Cl₂ lattice solvents, and H-atoms are omitted for clarity. Colour scheme: Dy^III, yellow; O, red; N, blue; C, grey; Si, olive.

On the other hand, compound 1-L^N3O3 crystallizes in the monoclinic space group P2₁/c (Table S1, ESI†) with only one molecule in the asymmetric unit. Moreover, the Dy(III) ion adopts a closer-to-ideal D_6h symmetry because of the most planar conformation of the L^N3O3 macrocyclic ligand with a CShM value of 1.61 according to the SHAPE program (Fig. 2 and Table S2, ESI†). The equatorial plane consists of three N-atoms (N1, N2, and N3) and three etheric O-atoms (O2, O3, and O5) stemming from the macrocyclic ligand L^N3O3, and the axial positions are occupied by two triphenylsiloxide ligands (Fig. 2). The weak equatorial ligation is corroborated by the relatively long Dy–N bond distances that fall in the range of 2.562(2)–2.610(2) Å, in contrast to the short Dy–O_ax bonds of 2.147(2) and 2.163(2) Å (Table S4, ESI†). In this case, the O_ax–Dy–O_ax (O4–Dy1–O1) angle is 175.84(8)°, denoting higher linearity for 1-L^N3O3. In addition, the planarity of the equatorially coordinated macrocycle L^N3O3, as derived by the deviation factor of the SHAPE program (Fig. S2, ESI†), is almost four times closer to the ideal hexagon than that of L^N6 in 1-L^N6. The shortest intermolecular Dy⋯Dy separation in the crystal of 1-L^N3O3 is 9.517(2) Å (Fig. S3, ESI†).

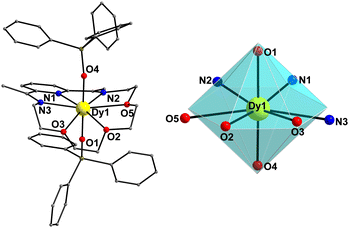Fig. 2 Cationic complex 1-L^N3O3 (left) and the hexagonal bipyramidal coordination polyhedron of the Dy(III) center (right). The PF₆⁻ counterion, and H-atoms are omitted for clarity. The smaller white spheres define the vertices of the corresponding ideal polyhedron. Colour scheme as in Fig. 1.

Direct current (dc) magnetic susceptibility studies were conducted on microcrystalline samples of both complexes. The room temperature values of the χ_MT product are 27.92 (1-L^N6) and 14.08 (1-L^N3O3) cm³ mol⁻¹ K, very close to the theoretical values of 28.34 and 14.17 cm³ mol⁻¹ K, that account for the presence of two and one Dy(III) ions (⁶H_15/2, S = 5/2, L = 5 and g = 4/3) per crystallographic formula unit (Fig. S4, ESI†), respectively. For both complexes, the χ_MT product steadily decreases upon cooling, reaching values of 22.76 (1-L^N6) and 10.68 (1-L^N3O3) cm³ mol⁻¹ K at 2.0 K. The abrupt decline of χ_MT at the very low temperatures is attributed to the depopulation of the m_J sublevels of the ground J state. The field dependence of the magnetization (M) was also measured at 2.0, 3.0, and 5.0 K (Fig. S5, ESI†), giving rise to values of 10.68 and 5.43 Nμ_B at 7.0 T for 1-L^N6 and 1-L^N3O3, respectively. The lack of magnetization saturation at different low temperatures indicates the presence of significant magnetic anisotropy in both compounds. Magnetic hysteresis measurements were also carried out at 2.0–7.0 K range, exhibiting a butterfly shape hysteresis loop attributed to the fast ground-state QTM at low temperatures (Fig. S6, ESI†).

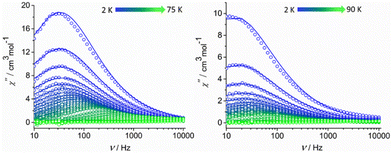
Alternating current (ac) magnetic susceptibility studies were also performed to assess the magnetization relaxation dynamics of both compounds (Fig. S7, ESI† and Fig. 3). Well-resolved frequency-dependent out-of-phase 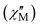peaks of signals were observed under zero external dc field for 1-L^N6, at a temperature range of 2–75 K, whereas for 1-L^N3O3 the peaks are observable up to 90 K, thus suggesting the presence of SMM behavior (Fig. 3). The fit of the data from the Cole–Cole plots of Fig. S8 (ESI†), using the generalized Debye model (eqn (S1) and (S2), ESI†), allowed us to extract the magnetization relaxation times, τ, and the distribution of relaxation times, α (Tables S5 and S6, ESI†). The α parameters were found in the range of 0.02–0.29 (1-L^N6) and 0.01–0.31 (1-L^N3O3), indicating a relatively wide distribution of relaxation times.

Fig. 3 Frequency-dependent out-of-phase signals under zero applied dc field at a temperature range of 2–75 K for complex 1-L^N6 (left) and 2–90 K for complex 1-L^N3O3 (right). Solid lines represent fits to the data.

The temperature dependence of relaxation times was fitted through the equation:

τ⁻¹ = τ₀⁻¹e^−U_eff/kT + CTⁿ + τ_QTM⁻¹, (1)

where the pre-exponential factor, τ₀, and the effective energy barrier (U_eff) correspond to the thermally-assisted Orbach relaxation process, C and n are the parameters of the Raman relaxation process, while τ_QTM represents the relaxation time through the quantum tunnelling of the magnetization (QTM).^8,10–12,14 Hence, construction of the Arrhenius plots (ln τ vs. 1/T) (Fig. 4), and the best fit to the experimental data afforded the parameters: U_eff = 989(20) K, τ₀ = 8.33 × 10⁻¹² s, C = 0.4077(0.08) s⁻¹ K⁻ⁿ, n = 2.57 (0.6), τ_QTM = 4.90 × 10⁻³ (2.19 × 10⁻⁴) s for complex 1-L^N6 and U_eff = 1300(10) K, τ₀ = 6.66 × 10⁻¹² s, C = 0.4018(0.02) s⁻¹ K⁻ⁿ, n = 2.12 (0.08), τ_QTM = 8.87 × 10⁻³ (4.43 × 10⁻⁴) s for 1-L^N3O3. The values of τ₀, C, and n are within the commonly observed range for similar mononuclear Dy(III) SMMs.^10,11 The significantly higher U_eff value of 1-L^N3O3 compared to 1-L^N6 is attributed to the less extent of distortion of the macrocyclic ligand in the equatorial plane and the higher axiality of the molecular system, leading to a larger energy separation of the ground state with the excited m_J sublevels.

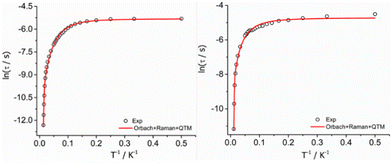Fig. 4 Temperature dependence of relaxation times (τ) for complexes 1-L^N6 (left) and 1-L^N3O3 (right). The hollow circles correspond to the experimental data and the red solid line is the best-fit of the data according to eqn (1).

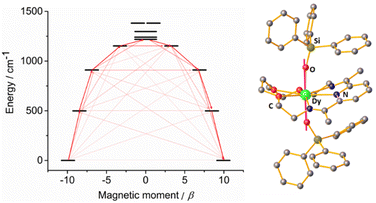
To further corroborate this hypothesis, we performed ab initio calculations using the SINGLE_ANISO approach implemented in ORCA 5.0.2 software package (see ESI†) for both compounds. The results revealed that, for complex 1-L^N6, the eight Kramer Doublets (KDs) span 1483 K (Dy1) and 1975 K (Dy2) (Tables S7–S12 and Fig. S9 and S10, ESI†), whereas 1-L^N3O3 reaches a value of 1987 K (Fig. 5 and Tables S13 and S14, ESI†). The calculated g-tensors for 1-L^N6 shows a highly axial ground state (m_J = ±15/2) for both Dy1 (g_z = 19.83, g_x, g_y = 0.002) and Dy2 (g_z = 19.85, g_x = 0.0003, g_y = 0.0005). In addition, the angle between the ground state anisotropic axis with that of the first (1.08°) and second (5.25°) excited state shows small deviations for Dy1 (1-L^N6), whereas for Dy2 (1-L^N6) is almost collinear (0.74° for both first and second excited state). This is attributed to the smaller O_ax–Dy–O_ax angle of the former, as well as the different Dy(III) coordination geometries. Furthermore, for 1-L^N6 the first excited states (m_J = ±13/2) are located at 552 K for Dy1 and 692 K for Dy2, while the second excited states (m_J = ±11/2) are located at 964 K and 1266 K, respectively. The experimental U_eff value (989 K) is very close to the calculated energy of the second excited state for Dy1, hence the reversal of the magnetization is most likely to proceed through the 3rd KD for 1-L^N6. This is further confirmed by the non-pure composition of the 3rd KD (admixture of m_J = ±11/2, ±7/2, and ±1/2 for Dy1) and the large magnitudes of transition magnetic moment matrix elements in this state (Tables S9 and S10, ESI†).

Fig. 5 (left) SINGLE_ANISO computed energy of the KDs for complex 1-L^N3O3. (right) Ground state anisotropic axis (purple rod) for 1-L^N3O3. Dark red arrows show the most probable relaxation route and light red arrows indicate less significant but non-negligible matrix elements between different m_J states.

Investigation of the computed g-tensors and the relative composition of the wavefunctions for complex 1-L^N3O3 confirmed the purity and axiality of the ground state (m_J = ±15/2, g_z = 19.86, g_x, g_y = 0.0004), and the first excited state (m_J = ±13/2, g_z = 16.94, g_x, g_y = 0.009), which is located 718 K above the ground state. The angle of the anisotropic axis between these two states is 0.78°, rendering them almost collinear. Also, the easy axis is nearly collinear with the Dy–O_ax bonds (Fig. 5), further supporting the dominance of axial anisotropy in this complex. Although the anisotropic axis of the second excited state (m_J = ±11/2) exhibits a small deviation from the ground state (2.03°), the axial component of the g-factor is significantly lowered (g_z = 13.75), and the transverse components are still low albeit non-negligible (g_x = 0.058, g_y = 0.18). Further, the wavefunction composition of the latter proved to be an admixture of m_J = ±11/2 (96.73%) and m_J = ±1/2 (2.93%). Thereby, considering that the computed energy of the second excited state (1309 K) is almost identical to the value of the experimental U_eff (1300 K), the magnetization most probably relaxes through this state. The large values of the magnetic moment matrix elements further validate the magnetization relaxation through the m_J = ±11/2 sublevel. In addition, we calculated the crystal-field (CF) parameters by using the SINGLE_ANISO module, and it is evident that the ratio of the transverse CF terms (B^q_k, where q ≠ 0 and k = 2, 4, and 6) to the axial CF terms (B^q_k, where q = 0 and k = 2, 4, and 6) is smaller for 1-L^N3O3 than that of 1-L^N6. The latter demonstrates the lower operational through-barrier relaxation mechanisms and the most prominent energy separation of the m_J states resulting in a higher U_eff. The experimental findings of this work corroborate the recent theoretical predictions of the detrimental effects of –NH vibrational modes on the magnetization relaxation and the enhancement of the U_eff value by the replacement with their isoelectronic oxygen-analogs.¹⁸

In conclusion, two new air-stable Dy(III) complexes (1-L^N6 and 1-L^N3O3) have been prepared through the metal-ion assisted [1+1] condensation approach, with strongly coordinated Ph₃SiO⁻ groups in the axial positions. Both compounds are SMMs with large anisotropy barriers of 989 K for 1-L^N6 and 1300 K for 1-L^N3O3. The different energy barriers for the two SMMs can be rationalized in terms of the extent of deviation from ideal D_6h symmetry, as confirmed by ab initio calculations. Work in progress involves the expansion of the [1+1] approach in mononuclear lanthanide D_6h systems by utilizing more rigid di-carbonyl groups (‘head units’) and diamines to construct an ideally planar equatorial ligand field, as well as stronger axial ligands to increase the overall magnetic anisotropy.

This work was supported by the UK EPSRC (grants EP/V003089/1, EP/X036626/1).

Data availability

Crystallographic data for 1-L^N6 and 1-L^N3O3 have been deposited at the Cambridge Crystallographic Data Centre (CCDC), and can be obtained from https://www.ccdc.cam.ac.uk/structures/.

Conflicts of interest

The authors declare no conflict of interest.

Notes and references

1. R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816.
2. (a) A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984; (b) M. Feng and M.-L. Tong, Chem. – Eur. J., 2018, 24, 7574–7594.
3. (a) M. D. Korzyński, Z. J. Berkson, B. Le Guennic, O. Cador and C. Copéret, J. Am. Chem. Soc., 2021, 143, 5438–5444; (b) G. Gabarró-Riera, G. Aromí and E. C. Sañudo, Coord. Chem. Rev., 2023, 475, 214858; (c) E. Coronado, Nat. Rev. Mater., 2019, 5, 87–104; (d) M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197.
4. (a) A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Nano Lett., 2011, 11, 2634–2639; (b) I. S. Zlobin, Y. V. Nelyubina and V. V. Novikov, Inorg. Chem., 2022, 61, 12919–12930; (c) M. Ganzhorn and W. Wernsdorfer, in Molecular Magnets, ed. J. Bartolomé, F. Luis and J. F. Fernández, Springer Berlin Heidelberg, Berlin, Heidelberg, 2014, pp. 319–364; (d) M. Urdampilleta, N.-V. Nguyen, J.-P. Cleuziou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Int. J. Mol. Sci., 2011, 12, 6656–6667.
5. (a) S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138; (b) R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360; (c) E. Moreno-Pineda and W. Wernsdorfer, Nat. Rev. Phys., 2021, 3, 645–659; (d) T. Komeda, K. Katoh and M. Yamashita, in Molecular Technology, ed. H. Yamamoto and T. Kato, Wiley, 1st edn, 2019, pp. 263–304.
6. (a) V. Vieru, S. Gómez-Coca, E. Ruiz and L. F. Chibotaru, Angew. Chem., Int. Ed., 2024, 63, e202303146; (b) L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043–10056.
7. (a) S. T. Liddle and J. Van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669; (b) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148; (c) L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104.
8. (a) T. G. Ashebr, H. Li, X. Ying, X.-L. Li, C. Zhao, S. Liu and J. Tang, ACS Mater. Lett., 2022, 4, 307–319; (b) Z. Zhu and J. Tang, Natl. Sci. Rev., 2022, 9, nwac194; (c) J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453; (d) F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403; (e) F.-S. Guo, M. He, G.-Z. Huang, S. R. Giblin, D. Billington, F. Heinemann, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Inorg. Chem., 2022, 61, 6017–6025.
9. (a) K. L. M. Harriman, D. Errulat and M. Murugesu, Trends Chem., 2019, 1, 425–439; (b) S. K. Gupta and R. Murugavel, Chem. Commun., 2018, 54, 3685–3696.
10. For example, see: (a) J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450; (b) A. B. Canaj, S. Dey, C. Wilson, O. Céspedes, G. Rajaraman and M. Murrie, Chem. Commun., 2020, 56, 12037–12040; (c) Y. Ding, N. F. Chilton, R. E. P. Winpenny and Y. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074; (d) Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837.
11. (a) S. Liu, Y. Gil, C. Zhao, J. Wu, Z. Zhu, X.-L. Li, D. Aravena and J. Tang, Inorg. Chem. Front., 2022, 9, 4982–4989; (b) C. Zhao, Z. Zhu, X.-L. Li and J. Tang, Inorg. Chem. Front., 2022, 9, 4049–4055; (c) Z. Zhu, C. Zhao, T. Feng, X. Liu, X. Ying, X.-L. Li, Y.-Q. Zhang and J. Tang, J. Am. Chem. Soc., 2021, 143, 10077–10082; (d) Z. Zhu, C. Zhao, Q. Zhou, S. Liu, X.-L. Li, A. Mansikkamäki and J. Tang, CCS Chem., 2022, 4, 3762–3771; (e) A. B. Canaj, S. Dey, E. R. Martí, C. Wilson, G. Rajaraman and M. Murrie, Angew. Chem., Int. Ed., 2019, 131, 14284–14289.
12. Y. Gil, A. Castro-Alvarez, P. Fuentealba, E. Spodine and D. Aravena, Chem. – Eur. J., 2022, 28, e202200336.
13. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078.
14. W.-J. Xu, Q.-C. Luo, Z.-H. Li, Y.-Q. Zhai and Y.-Z. Zheng, Adv. Sci., 2024, 2308548.
15. (a) O. Costisor and W. Linert, Rev. Inorg. Chem., 2004, 24, 61–95; (b) D. E. Fenton and P. A. Vigato, Chem. Soc. Rev., 1988, 17, 69–90; (c) V. Alexander, Chem. Rev., 1995, 95, 273–342.
16. S. Jia, X. Zhu, B. Yin, Y. Dong, A. Sun and D. Li, Cryst. Growth Des., 2023, 23, 6967–6973.
17. M. Llunell, D. Casanova, J. Girera, P. Alemany and S. Alvarez, SHAPE, version 2.0, Universitat de Barcelona, Barcelona, Spain, 2010.
18. S. Dey, T. Sharma and G. Rajaraman, Chem. Sci., 2024, 15, 6465–6477.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic data (CIF format), various synthetic, spectroscopic, structural, theoretical and magnetism data and figures. CCDC 2377131 (1-L^N6) and 2377167 (1-L^N3O3). CCDC 2377131 and 2377167. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cc04551c

---