Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the “Berg limit”: the 65° contact angle as the universal adhesion threshold of biomatter
Matej
Kanduč
 *a,
Emanuel
Schneck
*a,
Emanuel
Schneck
 b and
Roland R.
Netz
b and
Roland R.
Netz
 c
c
aDepartment of Theoretical Physics, Jožef Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia. E-mail: matej.kanduc@ijs.si
bDepartment of Physics, Technische Universität Darmstadt, Hochschulstrasse 8, Darmstadt 64289, Germany
cFachbereich Physik, Freie Universität Berlin, Arnimallee 14, Berlin 14195, Germany
First published on 12th December 2023
Abstract
Surface phenomena in aqueous environments such as long-range hydrophobic attraction, macromolecular adhesion, and even biofouling are predominantly influenced by a fundamental parameter—the water contact angle. The minimal contact angle required for these and related phenomena to occur has been repeatedly reported to be around 65° and is commonly referred to as the “Berg limit.” However, the universality of this specific threshold across diverse contexts has remained puzzling. In this perspective article, we aim to rationalize the reoccurrence of this enigmatic contact angle. We show that the relevant scenarios can be effectively conceptualized as three-phase problems involving the surface of interest, water, and a generic oil-like material that is representative of the nonpolar constituents within interacting entities. Our analysis reveals that attraction and adhesion emerge when substrates display an underwater oleophilic character, corresponding to a “hydrophobicity under oil”, which occurs for contact angles above approximately 65°. This streamlined view provides valuable insights into macromolecular interactions and holds implications for technological applications.
1 Introduction
Interactions among macromolecules, proteins, cells, and large surfaces in liquids have been a topic of extensive scientific inquiry, driven by their significance across a diverse spectrum of disciplines. Early on, it became clear that factors influencing processes such as protein adsorption and cellular adhesion are multifaceted, encompassing physical, chemical, and biological aspects.1–3 Understanding the mechanisms of molecular adsorption is crucial for various applications, ranging from coating technologies4–6 and anti-biofouling strategies7 to biomedical implants8 and drug delivery.9,10 For instance, achieving biocompatibility of artificial implants and regulating the adsorption of proteins at their surfaces are crucial factors that significantly influence the functionality and long-term performance of these materials.8,11,12Despite the complex and structure-specific nature of these interactions,1 there is a universal water-mediated component associated with the hydrophobicity of the interacting interfaces. The hydrophobicity is reflected in the surface contact angle and gives rise to two contrasting behaviors. One end features highly polar, hydrophilic surfaces, characterized by a small or even vanishing contact angle. Such surfaces repel each other at close distances (below about 2 nm) because of tightly bound water molecules—an effect known as hydration repulsion.13–15 At the opposite end of the spectrum, nonpolar, hydrophobic surfaces with large contact angles attract one another in a water environment via very long-range interactions (up to ≈100 nm), mediated by surface nanobubbles.1,16
This dichotomy raises a fundamental question: where does the transition from attraction to repulsion exactly occur? Or, in other words, above which threshold contact angle, θadh, does a surface begin to display adhesion? This question was addressed in a seminal paper by Vogler in 1998.17 Combining various experimental data, he identified a critical contact angle of approximately 65° for which he coined the term “Berg limit” after the researchers who first encountered this value.18 Since its publication, Vogler's work has had a profound impact, particularly in the fields of macromolecular adsorption, cell settlement, and biofouling.12,19–21Fig. 1a shows an example of how protein adsorption and cell settlement dramatically ramp up once the contact angle of the substrate surpasses a value of around 65°. This transition in adhesion propensity has far-reaching consequences for biological responses to biomaterials (e.g., bioadhesion, protein adsorption, blood plasma coagulation, and immune response), which undergo a marked shift at contact angles of around 65°.17,22–25 This contact angle has even been proposed as a new criterion for classifying surfaces as hydrophobic or hydrophilic,26–28 offering an alternative to the more traditional and widely accepted threshold of 90°.29 Despite the growing recognition of the critical adhesion contact angle, a fundamental understanding of its underlying principles remains elusive, even a quarter-century since its initial introduction.
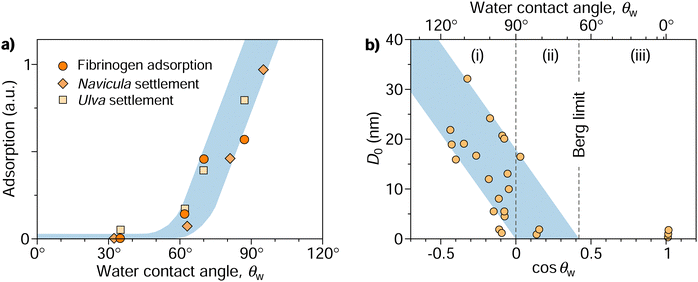 | ||
| Fig. 1 (a) Protein (fibrinogen) adsorption and settlement of algae cells (Navicula and Ulva zoospores) on a series of oligo(ethylene glycol) terminated self-assembled monolayers characterized by different contact angles.32,33 Re-plotted from Rosenhahn et al.33 with permission from the Royal Society of Chemistry. (b) Compilation of characteristic decay lengths (D0) extracted from experimental force–distance data of various systems plotted against the cosine of water contact angles of interacting surfaces. Re-plotted from Vogler17 with permission from Elsevier. The diagram features three distinct regimes of surface interactions: (i) long-range attraction between hydrophobic surfaces, (ii) shorter-range attraction between some of the hydrophilic surfaces with contact angles down to the Berg limit, and (iii) absence of attraction beyond the Berg limit. | ||
In the present article, we first briefly review the experiments that led to the concept of a universal contact angle threshold, discuss the current knowledge on this topic, and revisit our past research endeavors dedicated to this question. Subsequently, we propose a novel perspective by recognizing that non-polar hydrocarbon-based matter, a ubiquitous component of biological and soft-matter systems, can provide additional interaction mechanisms in aqueous systems. By analyzing several basic scenarios, we demonstrate that the phenomena of attraction and adhesion distinctly manifest once the contact angle surpasses a well-defined critical threshold. Importantly, this threshold closely aligns with the “Berg limit,” which has been identified in experimental studies.
2 State of the art and current understanding
2.1 Long-range hydrophobic attraction
Following the pioneering experiments by Israelachvili and Pashley in the early 1980s using the surface force apparatus,30,31 it has become evident that the attraction between large hydrophobic surfaces cannot be rationalized by van der Waals interaction alone but is more intricate and multifaceted than initially presumed. The measurements of these apparent “hydrophobic forces” revealed that they operate over a considerably long range (tens or even hundreds of nanometers) and exhibit an approximately exponential decay with the surface separation (D), occasionally in a step-wise fashion.1,16 This decay is characterized by a specific decay length denoted as D0, thus following the form exp(−D/D0).Vogler17 compiled measurements from different experiments and noted the general trend that D0 correlates with the water contact angle of the surfaces, θw. Fig. 1b, a slightly modified version of Vogler's original plot, shows D0 over cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw for all collected measurements. The decay length ramps up for hydrophobic surfaces with contact angles above 90° (corresponding to cos
θw for all collected measurements. The decay length ramps up for hydrophobic surfaces with contact angles above 90° (corresponding to cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw < 0). When fitting the lower bound of the rather scattered data points, one finds convergence to a contact angle of 90° as D0 approaches 0. Meanwhile, the fit of the upper bound reaches zero at a contact angle of approximately 65°, a value termed the “Berg limit” by Vogler,17 in reference to Berg et al.,18 who were the first to report the absence of attraction below this contact angle in Langmuir–Blodgett films. More precisely, Vogler proposed a range of the water adhesion tension, γw
θw < 0). When fitting the lower bound of the rather scattered data points, one finds convergence to a contact angle of 90° as D0 approaches 0. Meanwhile, the fit of the upper bound reaches zero at a contact angle of approximately 65°, a value termed the “Berg limit” by Vogler,17 in reference to Berg et al.,18 who were the first to report the absence of attraction below this contact angle in Langmuir–Blodgett films. More precisely, Vogler proposed a range of the water adhesion tension, γw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw, between 20 and 40 mN m−1 as the onset of attraction, corresponding to a contact angle window of 56°–74°. The midpoint of this interval, θadh = 65°, which we will refer to as the adhesion threshold, has gained broad acceptance and has become a consensus value of the boundary for adhesion in the literature.11,19,21,27,28
θw, between 20 and 40 mN m−1 as the onset of attraction, corresponding to a contact angle window of 56°–74°. The midpoint of this interval, θadh = 65°, which we will refer to as the adhesion threshold, has gained broad acceptance and has become a consensus value of the boundary for adhesion in the literature.11,19,21,27,28
The data in Fig. 1b indicate three distinct regimes: (i) surfaces with contact angles above 90° without exception exhibit long-range attractive forces, with a range that tends to grow with increasing contact angles. (ii) As the contact angle drops below 90°, fewer surfaces exhibit long-range attraction until reaching the critical contact angle θadh ≈ 65°, below which attraction becomes undetectable (iii). What mechanisms are behind these three regimes, and what determines the specific values of 65° and 90°? Previous hypotheses suggesting that long-range attraction originates from varying “structures” of water extending tens of nanometers from its interface17 have been disproven. Although water does undergo structural changes, loses hydrogen bonds, and exhibits increased fluctuations near nonpolar surfaces, these alterations are confined to only a few water layers from the interface34–37 and thus cannot explain the observed long-range attraction.
2.2 Attraction between hydrophobic surfaces (θw > 90°)
The apparent long-range attraction, particularly for hydrophobic surfaces with θw > 90°, is nowadays pretty well understood.38–44 Its origin lies in the thermodynamic instability of the water slab between two hydrophobic surfaces against cavitation to a vapor phase.To provide a quick overview of the underlying thermodynamics, consider two extensive parallel surfaces of area A characterized by the contact angle θw and separated by a distance D. In the continuum description, the free energy difference between the hydrated state (with liquid water between the surfaces) and the cavitated state (with water vapor between the surfaces) is ΔW = 2A(γsv − γsw) + pV. The first term is related to the difference in the surface free energies, where γsv and γsw are the surface–vapor and surface–water surface tensions, respectively. The second term represents the work required to expel the water slab of volume V = AD into the bulk against the ambient pressure p. Note that we have neglected the small vapor pressure and the energy of the water–vapor interface at the perimeter of the cavity. Using the Young equation [eqn (7) later on], one arrives at45
ΔW/A = 2γw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw + pD θw + pD | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw/p, which exists only for contact angles above 90°. Hence, the use of a 90° contact angle as the boundary between hydrophilic and hydrophobic surfaces is not merely a geometric differentiation based on wetting properties of a single surface; it is grounded on fundamental physical principles governing the stability of liquid aqueous films between surfaces. For a prototypical hydrophobic surface with θw = 120° at atmospheric conditions (p = 1 bar) the critical distance is Dc ≈ 720 nm. In the cavitated state, the surfaces attract each other because of several factors: the capillary forces at the perimeter of the cavity, van der Waals forces between the surfaces across vapor (which are stronger than those in water), and the external atmospheric pressure. Namely, the cavity contains water vapor and, for relevant timescales, is not in chemical equilibrium with the atmosphere. The cavitation (drying) transition has also been observed in atomistic simulations of smaller systems, such as narrow hydrophobic slits46–48 and pockets.49,50
θw/p, which exists only for contact angles above 90°. Hence, the use of a 90° contact angle as the boundary between hydrophilic and hydrophobic surfaces is not merely a geometric differentiation based on wetting properties of a single surface; it is grounded on fundamental physical principles governing the stability of liquid aqueous films between surfaces. For a prototypical hydrophobic surface with θw = 120° at atmospheric conditions (p = 1 bar) the critical distance is Dc ≈ 720 nm. In the cavitated state, the surfaces attract each other because of several factors: the capillary forces at the perimeter of the cavity, van der Waals forces between the surfaces across vapor (which are stronger than those in water), and the external atmospheric pressure. Namely, the cavity contains water vapor and, for relevant timescales, is not in chemical equilibrium with the atmosphere. The cavitation (drying) transition has also been observed in atomistic simulations of smaller systems, such as narrow hydrophobic slits46–48 and pockets.49,50
However, the cavitation transition of larger systems is associated with the nucleation of a vapor bubble that spans across both surfaces. The free energy required to nucleate such a bridging bubble scales quadratically with separation, ΔW* ∼ γwD2,37,45,46,51,52 although linear terms stemming from line tension may become important at small separations.48,52 This free energy represents the kinetic barrier the system needs to overcome in order to cavitate. On experimental time scales, a macroscopic system is capable of overcoming a barrier of the order of ΔW* ∼ 10–100kBT, where kBT is the thermal energy (with kB being the Boltzmann constant). Thus, one can anticipate that the cavitation-induced attraction in contaminant-free water will occur spontaneously only at distances below around Dcav ∼ (ΔW*/γw)1/2 ≈ 1–2 nm. This value is 3 orders of magnitude below Dc and 1–2 orders of magnitude smaller than the reported characteristic decay lengths D0 of measured hydrophobic forces (see Fig. 1b). However, in cautiously conducted experiments that avoid contamination and pre-existing gas bubbles, the metastable water-filled state, characterized by the absence of attraction, is indeed observed down to a few nanometers of separation before the jump into close contact occurs.1,53,54 Quite often, cavitation, and with that the apparent hydrophobic attraction, is catalyzed by various kinds of impurities, most notably pre-existing surface nanobubbles.1 Long-lived nanobubbles residing on surfaces have been first postulated by Parker et al.,16 based on the step-wise nature of their force–distance curves, and have been experimentally observed a few years later by atomic force microscopy (AFM).55–57 The long-lived stability of surface nanobubbles seemed paradoxical at first, since classical theory predicts that gas bubbles cannot achieve stable equilibrium and should immediately dissolve because of a high Laplace pressure.58 However, this paradox has finally been resolved in recent years.59–62
In summary, the measured long-range attraction between hydrophobic surfaces is not an inherent water-mediated interfacial force in the usual sense. Instead, it is a composite phenomenon driven by cavitation and is best understood in terms of the free energy of thermodynamic states of the two surfaces immersed in water. The gaseous capillary bridges resulting after cavitation engender a directly measurable attractive force in experiments. Consequently, the decay length D0 is not an elementary water or material property but rather a parameter influenced by intricate experimental details, such as water purity, the concentration of dissolved gases, and, most notably, the pre-existence and distribution of surface nanobubbles. Hence, while Vogler's plot (Fig. 1b) does not represent a fundamental law but rather a compilation of empirical data, it stands as a visionary work that forged a link between attraction/adhesion and the contact angle, shedding valuable light on the subject.
2.3 Attraction between hydrophilic surfaces (θw < 90°)
While we understand considerably well why hydrophobic surfaces with contact angles above 90° experience long-range attraction, as outlined above, the puzzle persists as to why some hydrophilic surfaces also attract, albeit more weakly, and form stable adhesion states, for contact angles way down to around θadh = 65°.18,63–66 In our previous theoretical studies67–69 supported by all-atom molecular dynamics (MD) simulations, we explored an entire spectrum of model surfaces, ranging from hydrophobic to highly hydrophilic. We found that weakly hydrophilic surfaces can indeed form stable adhesion (close-contact) states without any intervening water layer, a phenomenon that we termed dry adhesion. In the following, we briefly summarize the main concept behind this “hydrophilic attraction”. The adhesion free energy, ΔW, between two surfaces immersed in water can be conceptualized as the result of a two-step process: in the first step, we remove the water between the surfaces, similar to the cavitation process described before, requiring the work of 2Aγw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw. In the second step, we bring the two surfaces into close contact, and thereby gain the work of adhesion, Awss, between these two surfaces across vacuum (or vapor), where wss is the direct surface–surface adhesion tension (free energy per unit area). It should be noted that in this case, we have omitted the pV term because there is no net change in volume. Summing up the two components yields the adhesion free energy in water, representing the difference in free energy between the state where the two surfaces are in close and dry contact and the state where they are significantly separated across water,
θw. In the second step, we bring the two surfaces into close contact, and thereby gain the work of adhesion, Awss, between these two surfaces across vacuum (or vapor), where wss is the direct surface–surface adhesion tension (free energy per unit area). It should be noted that in this case, we have omitted the pV term because there is no net change in volume. Summing up the two components yields the adhesion free energy in water, representing the difference in free energy between the state where the two surfaces are in close and dry contact and the state where they are significantly separated across water,ΔW/A = 2γw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw − wss θw − wss | (2) |
However, in practice, the two terms are not independent of each other, as they are primarily influenced by the chemical groups present at the interfaces. Groups with greater polarity (having larger electric dipoles) lead to lower contact angles θw69 (i.e., larger cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw) and, at the same time, also to higher direct surface–surface interaction, wss. Thus, we can consider wss(θw) a function of θw. The critical contact angle,
θw) and, at the same time, also to higher direct surface–surface interaction, wss. Thus, we can consider wss(θw) a function of θw. The critical contact angle, 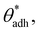 that marks the onset of dry adhesion (ΔW = 0) can be expressed as
that marks the onset of dry adhesion (ΔW = 0) can be expressed as
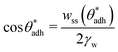 | (3) |
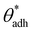 for soft surfaces
for soft surfaces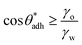 | (4) |
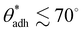 . The precise value of
. The precise value of 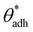 depends on various surface details, but these variations tend to be relatively tiny. In our simulation study,69 where we analyzed the relation wss(θw) of vastly different surface models, we found a range of
depends on various surface details, but these variations tend to be relatively tiny. In our simulation study,69 where we analyzed the relation wss(θw) of vastly different surface models, we found a range of 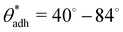 . The midpoint of this range closely coincides with the experimentally reported value of θadh = 65°.17 It turns out that at the adhesion threshold, the surfaces exhibit a notable lack of polarity, aligning them closely with the typical characteristics associated with oils. Consequently, the threshold value
. The midpoint of this range closely coincides with the experimentally reported value of θadh = 65°.17 It turns out that at the adhesion threshold, the surfaces exhibit a notable lack of polarity, aligning them closely with the typical characteristics associated with oils. Consequently, the threshold value 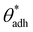 is often close to the upper bound of eqn (4). For rigid, crystalline surfaces that cannot readily optimize their mutual contacts when in close proximity, wss may be marginally reduced. This results in a slightly elevated threshold for
is often close to the upper bound of eqn (4). For rigid, crystalline surfaces that cannot readily optimize their mutual contacts when in close proximity, wss may be marginally reduced. This results in a slightly elevated threshold for 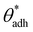 , which explains why values up to 84° were obtained in the simulations.69
, which explains why values up to 84° were obtained in the simulations.69
While the conclusions drawn from MD simulations lend support to the idea that hydrophilic surfaces with contact angles between 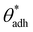 and 90° can indeed attract and form stable adhered states, it is essential to note that this hydrophilic attraction is remarkably short-ranged, limited to distances below a nanometer.67–69 This observation is by itself not unexpected, given the fact that the alterations in water structure are limited to just a few water layers from the interface.34–37 What thus remains unclear is why attraction in experimental studies was reported to range over several or even tens of nanometers.64–66 This conundrum shares similarities with hydrophobic surfaces, which, under ideal conditions, cannot undergo cavitation transition when separated by more than a few nanometers. As mentioned, in those cases, the presence of another component—surface nanobubbles—is necessary to initiate the process. However, contrary to hydrophobic surfaces, hydrophilic surfaces (θw < 90°) do not facilitate spontaneous cavitation, and any pre-existing gas nanobubbles compressed between such surfaces would result in repulsion rather than attraction.71 This suggests that the mechanism for long-range hydrophilic attraction presumably involves another component.
and 90° can indeed attract and form stable adhered states, it is essential to note that this hydrophilic attraction is remarkably short-ranged, limited to distances below a nanometer.67–69 This observation is by itself not unexpected, given the fact that the alterations in water structure are limited to just a few water layers from the interface.34–37 What thus remains unclear is why attraction in experimental studies was reported to range over several or even tens of nanometers.64–66 This conundrum shares similarities with hydrophobic surfaces, which, under ideal conditions, cannot undergo cavitation transition when separated by more than a few nanometers. As mentioned, in those cases, the presence of another component—surface nanobubbles—is necessary to initiate the process. However, contrary to hydrophobic surfaces, hydrophilic surfaces (θw < 90°) do not facilitate spontaneous cavitation, and any pre-existing gas nanobubbles compressed between such surfaces would result in repulsion rather than attraction.71 This suggests that the mechanism for long-range hydrophilic attraction presumably involves another component.
In reality, aqueous environments are never entirely free of impurities.72 In addition to dissolved gasses and stable nanobubbles, aqueous systems often contain varying quantities of insoluble hydrophobic and amphiphilic substances that can form oil-like aggregates. This is particularly evident in biological fluids, where the traits of soft and fluid hydrocarbon-based materials bear similarities to those of oils. In subsequent sections, we will delve into how these factors introduce additional attractive interaction mechanisms above a critical contact angle.
3 Water–oil–surface wetting
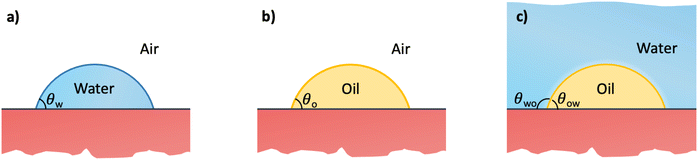
In this section, we recap the basics of oil and water wetting of solid surfaces by considering three different scenarios, shown in Fig. 2: (a) a water droplet on a solid surface in air, (b) an oil droplet on a solid surface in air, and (c) an oil droplet on a solid surface in water. The Young equations corresponding to these scenarios are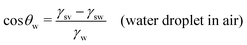 | (5) |
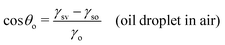 | (6) |
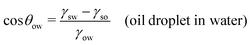 | (7) |
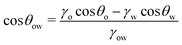 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θo = 1 for all surface polarities. With that, eqn (8) simplifies to a direct relation between θow and θw as
θo = 1 for all surface polarities. With that, eqn (8) simplifies to a direct relation between θow and θw as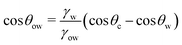 | (9) |
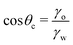 | (10) |
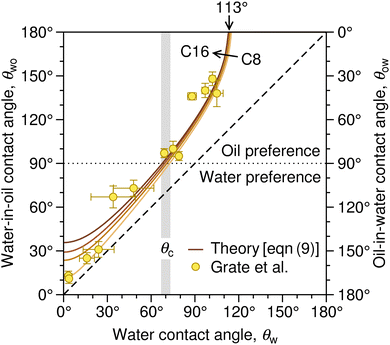 | ||
| Fig. 3 Correlation between the water contact angle in air, θw, the water-in-oil contact angle, θwo (left axis), and the oil-in-water contact angle, θow (right axis). The latter two are related as θwo + θow = 180°. The solid lines denote the prediction of eqn (9) based on the surface tension of a series of linear alkanes (C8, C10, C12, C16).78,79 The symbols are contact angle measurements by Grate et al.77 for water droplets on silica and silanized-silica surfaces in hexadecane. The diagonal dashed line denotes the symmetry θwo = θw. The gray stripe indicates the critical water contact angle in air, θc, at which θow (and likewise θwo) reaches 90°, demarcating the border between the regime in which oil is favored for wetting the substrate (underwater oleophilicity) and the other regime in which water is favored (underwater oleophobicity). | ||
The diagonal dashed line indicating the symmetry θwo = θw, serves as orientation. It is evident that water droplets have consistently larger contact angles in oil than in air, θwo > θw. In essence, oil competes with water for wetting the surface and thus reduces the wetting capability of water. Once θw surpasses the value of around 113°, as indicated by an arrow in Fig. 3, water exhibits non-wetting behavior in oil (with θwo = 180° and θow = 0). A pivotal transition occurs at θwo = θow = 90°, at which point the substrate exhibits identical wetting preference to oil and water. Based on eqn (9), this transition occurs at the critical contact angle of θw = θc, depicted as a gray stripe in Fig. 3. At the contact angle θc, the substrate switches from an effectively hydrophilic to effectively hydrophobic behavior under oil, even though it is conventionally classified as hydrophilic in air up to θw = 90°. Concurrently, a surface is underwater olephobic for θw < θc, and underwater olephilic for θw > θc.
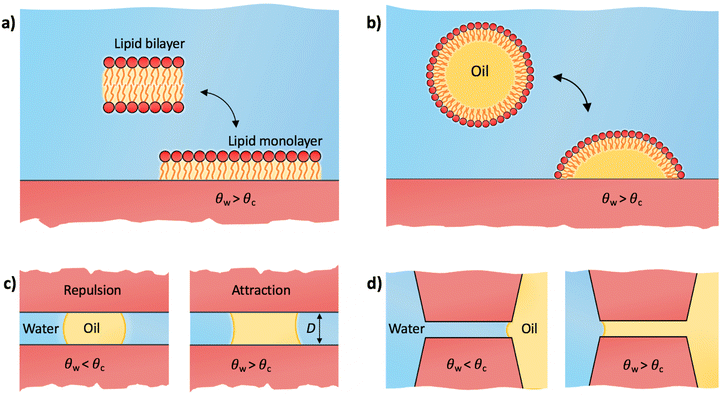
Notably, the critical contact angle for oil/water wetting preference, θc = 70° ± 3° [eqn (10)], closely aligns with the Berg limit of θadh ≈ 65° ± 9°, which denotes the threshold for the adhesion of macromolecules (Fig. 1a) and attraction between solid surfaces (Fig. 1b). We assert that the resemblance of the two values, θadh ≈ θc, is not a mere coincidence. Instead, this striking correspondence can be understood from the notion that many relevant interaction scenarios can be viewed as three-phase contact problems comprising the surface in question, water, and a generic oil-like material. In the following, we will outline four interaction scenarios, which are sketched in Fig. 4. We will demonstrate that θw being above or below θc has profound implications on their behavior.
4 Critical contact angle as the adhesion threshold
We first address the adhesion threshold of macromolecules and cells to surfaces as shown in Fig. 1a. Within the context of biological adhesion, it is crucial to acknowledge that many macromolecules have amphiphilic structures. Examples include lipid aggregates and proteins in their native forms, which possess a hydrophobic core and a hydrophilic exterior. When such macromolecules or their aggregates encounter surfaces in aqueous settings, they can undergo reconfiguration and expose their hydrophobic regions to the surface. This adaptability significantly influences their adhesion properties.4.1 Lipid monolayer adsorption
Lipids are the prototypical example of amphiphilic biological molecules. They can self-assemble into bilayers in water and form dense monolayers on hydrophobic surfaces, owing to their nonpolar tails. In our first example, we consider a two-state lipid layer model capable of either existing as a bilayer of surface area A in the bulk solution or as a monolayer with surface area 2A adsorbed on a solid substrate as depicted in Fig. 4a. An intriguing question arises: what contact angle of the substrate is necessary for stable lipid monolayers to nonspecifically adsorb to the surface from an aqueous medium? In other words, which of the two states, a non-adsorbed bilayer or an adsorbed monolayer, is thermodynamically favored?A comprehensive thermodynamic analysis of this problem has been presented in our recent publication.80 Here, we only briefly recap the main steps: first, we hypothetically separate both leaflets of the bilayer across vacuum, requiring the work Awll, where wll represents the lipid–lipid (ll) monolayer adhesion tension in vacuum, analogous to wss in Section 2.3. Next, we remove the water from the substrate region of area 2A where the lipid monolayer will adsorb. The free energy cost for this water removal is 2A(γsv − γsw) = 2Aγw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw, where we used the Young equation [eqn (5)]. Finally, we attach the monolayer to the dry substrate, gaining the free energy of −2Awsl, where wsl is the substrate–lipid (sl) monolayer adhesion tension across vacuum. Summing up the three contributions provides us with the adsorption free energy per unit monolayer area
θw, where we used the Young equation [eqn (5)]. Finally, we attach the monolayer to the dry substrate, gaining the free energy of −2Awsl, where wsl is the substrate–lipid (sl) monolayer adhesion tension across vacuum. Summing up the three contributions provides us with the adsorption free energy per unit monolayer area
ΔW/A = wll − 2wsl + 2γw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw θw | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θo) ≈ 2γo. Here, we have assumed good oil-in-air wettability (cos
θo) ≈ 2γo. Here, we have assumed good oil-in-air wettability (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θo ≈ 1) for any kind of substrate type. Using these estimates for wll and wsl, eqn (11) simplifies to,
θo ≈ 1) for any kind of substrate type. Using these estimates for wll and wsl, eqn (11) simplifies to,ΔW/A = 2γw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θw − 2γo θw − 2γo | (12) |
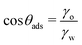 | (13) |
It is worth emphasizing the resemblance between the expression for the free energy of monolayer adsorption [eqn (12)] and that for dry adhesion between two identical solid surfaces in pure water [eqn (2)]. In the former, the surface interaction term (2γo) results from the dispersion interactions with lipid tails, whereas in the latter (wss), it pertains to the interaction between two identical surfaces. As we have already pointed out before, it is reasonable to assume wss ≥ 2γo. However, at the transition contact angle, the surfaces are sufficiently non-polar and oil-like, therefore wss(θadh) ≈ 2γo, leading to similar results for the critical contact angles.
4.2 Adhesion of a lipid droplet
A variation to the lipid-monolayer adsorption scenario described in the previous subsection involves an oil droplet covered by a monolayer of insoluble surfactants (e.g., lipids), referred to as a lipid droplet, illustrated in Fig. 4b. Lipid droplets are abundant in various organisms, where they function as structures for storing energy and as essential building blocks.81,82 The technology behind lipid droplets also bears relevance in biofuel production and formulations for food and drug delivery.83–85 The concept of a lipid droplet holds significance also for understanding various soft systems characterized by hydrophilic exteriors and nonpolar, hydrocarbon-rich interiors. At the most simplistic level, proteins may be conceptually grouped within this category. In spite of the intricate biophysics governing protein adsorption, influenced by diverse biological and physicochemical factors,8,25 the minimal model of a lipid droplet can serve as a useful starting point for elucidating the Berg limit for non-specific adsorption of those proteins that strongly deform or even denature upon adsorption.8As for the monolayer adsorption, a similar question arises here: for which substrate contact angles will a lipid droplet adhere to the substrate? The droplet adheres to the substrate by exposing its internal oil phase directly to the substrate while maintaining the lipid coating at its water interface. This reorganization creates a substrate–oil interface at the droplet's base of area Abase, which replaces the previous substrate–water interface in that area. The free energy change for modifying this interface is Abase(γso − γsw). The base area is influenced by the extent of the droplet's spread over the substrate, which is determined by the intricate interactions of lipids with both the oil phase and the substrate. While we will not delve into these specifics, our focus lies solely in assessing the onset of adhesion, regardless of the precise value of Abase. Using eqn (7), the free energy for droplet adhesion can be expressed as
ΔW = −Abaseγow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θow θow | (14) |
The two specific examples of monolayer and lipid droplet adhesion can be seen as representatives of the broader phenomenon of adhesion of soft biological entities with hydrophobic oil-like interior and hydrophilic exterior. This concept clearly demonstrates that such particles follow the adhesion pattern shown in Fig. 1a, whereby the adhesion threshold is given by the critical contact angle for oil/water wetting preference, θc [eqn (10)].
5 Critical contact angle as the attraction threshold between similar surfaces
Let us now move on to the other question of this perspective, namely how to understand the adhesion threshold, θadh, as the onset of long-range attraction between two similar surfaces, as first pointed out by Vogler (Fig. 1b). As we discussed above, the long-range nature of the interaction cannot be explained by considering the surfaces in pure water alone. Rather, our explanation is based on the presence of an oil component. When a surface is submerged in water containing organic matter (particularly in natural waters, the bloodstream, or engineered aqueous systems), small and large organic molecules (e.g., proteins, polysaccharides, and polymers) can rapidly accumulate on its interface, and form droplets or a liquid film.33,86–92 It is important to note that even in purified water, traces of insoluble organic impurities tend to agglomerate on surfaces in the form of nanodroplets.93 A prominent example involves minute amounts of widely used silicone oils for laboratory equipment, which were shown to easily contaminate AFM tips.94 This accumulated organic matter, referred to as the conditioning film, whether in the form of a uniform layer or as sessile droplets, profoundly influences subsequent adhesive events associated with the attachment of bacteria, cells, and other organisms, and it thus constitutes the initial stage of biofouling.86–88 Adsorbed oil droplets can also stem from a surface that was pre-contaminated with nonpolar liquids. Once the surface is immersed in water, the liquid film can decompose into droplets.955.1 Bridging oil droplet
We now examine the impact of a small oil droplet (e.g., a component of a conditioning film) bridging two chemically similar, uniform, and parallel surfaces characterized by a contact angle θw, as illustrated in Fig. 4c. The droplet exerts a capillary force on the surfaces. At small separations (smaller than the lateral extension of the droplet), this capillary force can be expressed as71,96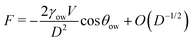 | (15) |
For θow > 90° (occurring for θw < θc), the force is repulsive (F > 0) at small separations. The force switches to attractive only for a very stretched droplet upon retraction of the surfaces, near the point of rupture (where higher-order terms in eqn (15) stemming from the surface tension dominate).71 Conversely, if the o/w contact angle is below 90° (corresponding to θw > θc), the capillary force is always attractive (F < 0). This means that surfaces with contact angles above θw > θc promote droplet-mediated attraction down to close-contact. This simple consideration underscores that oil nanodroplets play essentially a role similar to that of nanobubbles between hydrophobic surfaces. Just as gas nanobubbles can lead to long-range attraction between hydrophobic surfaces (θw > 90°), oil droplets are expected to engender attraction even between mildly hydrophilic surfaces with water contact angles down to θc. In simpler terms, the attraction between hydrophilic surfaces, which would occur only below around 1 nm in pure water (Section 2.3), can extend to longer ranges in the presence of oil droplets on the surfaces. The range and strength of this attraction crucially depend on the size and the amount of the droplets, similarly as in the case of nanobubbles. In essence, larger and more abundant oil droplets lead to stronger and longer-ranged attraction between the surfaces. This very mechanism could be the key explanation for the pronounced long-range attraction observed in certain experiments where the contact angles are below 90°.17,64–66
5.2 Wetting pores and slits
In the preceding subsection, we demonstrated that oil droplets can mediate long-range attraction between surfaces with contact angles exceeding 65°. Yet, the presence of oil can bring about other closely related practical effects, especially regarding the wetting of small pores. For illustration, we consider a continuous phase of oil in contact with a continuous phase of water, which both compete to wet a pore or a slit between two parallel surfaces (Fig. 4d). The free energy associated with oil displacing water in the slit is ΔW = 2A(γso − γsw), where A is the surface area of the slit. By applying eqn (7), the free energy can be expressed as ΔW/A = −2γow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θow. For θow > 90° (corresponding to θw < θc), water will spontaneously wet the slit (ΔW > 0). Conversely, for θow < 90° (corresponding to θw > θc), oil will displace water and imbibe the slit (ΔW < 0).
θow. For θow > 90° (corresponding to θw < θc), water will spontaneously wet the slit (ΔW > 0). Conversely, for θow < 90° (corresponding to θw > θc), oil will displace water and imbibe the slit (ΔW < 0).
In the broader context of aqueous systems, this simple calculation implies that a narrow slit with θw > θc will favor wetting by oil. Such a slit will gradually accumulate organic material from its surroundings over time (akin to capillary condensation in hydrophilic pores), eventually leading to droplet-mediated attraction. Conversely, a more hydrophilic slit favoring wetting by water (θw < θc) will progressively expel organic material over time.
The scenarios outlined in this section, namely the bridging oil droplet and oil imbibition (Fig. 4c and d, respectively), offer a compelling explanation for the experimentally observed long-range attractive forces for surface contact angles above the Berg limit, as depicted in Fig. 1b. These scenarios feature a symmetrical boundary condition involving two identical solid surfaces with well-defined contact angles. In contrast, the macromolecular adhesion scenarios (highlighted in Fig. 4a and b) involve an adhering entity that does not have a well-defined contact angle but is amphiphilic and deformable. It is intriguing that despite these contrasting boundary conditions, the threshold contact angle is the same in all scenarios and related to the transition for oil/water wetting preference. The reason for this uniformity is that both kinds of scenarios can be perceived as three-phase contact problems, encompassing the surface under consideration, water, and a generic oil-like medium. As a result, the defining contact angle for adhesion/attraction is determined by the ratio between the surface tensions of oil and water, as given by eqn (10).
The competition between water and oil to imbibe tiny pores holds significant relevance across various technological domains, notably in secondary oil recovery, where hydrocarbons are extracted from fractured rock reservoirs using waterflooding techniques.97,98 Moreover, biological or engineered water channels should be hydrophilic enough (θw < θc) to prevent the accumulation of organic material. A classic example of this principle can be found in porous membranes used for filtering emulsified oil droplets in wastewater treatment. To effectively prevent the passage of oil through the membrane pores and to mitigate its fouling, the membrane's contact angle should be less than 65°.99 However, surfactants present in wastewater can alter the wetting behavior of oil droplets and render the membrane less hydrophilic. Therefore, additional antifouling strategies are essential, such as surface hydrophilization, zwitterionic polymer coating, photocatalytic cleaning, and electrically enhanced antifouling.99–101
Finally, the displacement of one liquid by another within a pore can be associated with a free energy barrier, leading to kinetically trapped metastable states. Such metastability is used to design surfaces that exhibit both superhydrophobicity in oil and superoleophobicity in water, termed dual superlyophobicity. This unique property is achieved by a distinct topography of micro-sized pores.102,103 When the surface is immersed in either oil or water, the liquid fills the pores. A droplet of the other liquid can then be placed on the surface without displacing the first liquid from the pores. The resulting metastable Cassie-type wetting state, characterized by a large apparent contact angle, is mechanically stable if the intrinsic contact angle of the surface material lies in a narrow range around 65°, where the difference in wetting affinities between oil and water is small.
6 Conclusions
In this perspective, our central discussion revolved around understanding the reasons for the observed long-range attraction and adhesion tendencies exhibited by surfaces with contact angles ranging from approximately 65° to 90°. We rationalized these observations by recognizing that the attractive and adhesive properties stem from nonpolar, hydrophobic components within interacting entities in aqueous systems. These hydrophobic components can manifest in various forms, whether in the shape of tiny liquid nanodroplets or as constituents within deformable hydrophobic parts of soft biological matter.In all the examined scenarios, adhesion sets in when the solid surface displays an underwater oleophilic character, which is equivalent to being underoil hydrophobic. This character emerges when the contact angle surpasses a critical value of θc = 70° ± 3° and is determined by the ratio between the surface tensions of oil and water. Importantly, this critical value closely aligns with the experimentally observed Berg limit for the adhesion threshold of biomatter, θadh ≈ 65° ± 9°.
Our discussion on nonspecific adhesion was based on a minimalist model, focusing on flat and featureless surfaces in the presence of an oil-like component in water. However, real-world systems can bring about a host of complexities. For instance, the hydrophobic component may contain heteroatoms, leading to increased polarity compared to purely nonpolar oils. Additionally, surfaces with pronounced topographical features can give rise to additional wetting states,27,104 some of which may even be metastable.102,103 Highly charged or highly polarizable surfaces, such as metals, bring additional interactions that may facilitate or hinder adhesion.105,106 Each of the scenarios discussed above will thereby become more specific and intricate, accompanied by a myriad of other factors. These complexities underscore the fact that the adsorption threshold across different experiments is not sharp but rather consists of a narrow window that accommodates most practical cases.
Author contributions
MK: conceptualization, formal analysis, writing – original draft; ES: conceptualization, writing – original draft; RRN: conceptualization, writing – original draft.Conflicts of interest
No conflicts of interest to disclose.Acknowledgements
M. K. acknowledges financial support from the Slovenian Research and Innovation Agency ARIS (contracts P1-0055 and J1-4382). Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project ID 431232613 – SFB 1449 and Project ID 387284271 – SFB 1349.Notes and references
- E. E. Meyer, K. J. Rosenberg and J. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15739–15746 CrossRef CAS PubMed
.
- B. Geiger, J. P. Spatz and A. D. Bershadsky, Nat. Rev. Mol. Cell Biol., 2009, 10, 21–33 CrossRef CAS PubMed
.
- D. Horinek, A. Serr, M. Geisler, T. Pirzer, U. Slotta, S. Q. Lud, J. A. Garrido, T. Scheibel, T. Hugel and R. R. Netz, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 2842–2847 CrossRef CAS PubMed
.
- H. D. Follmann, A. F. Martins, A. P. Gerola, T. A. Burgo, C. V. Nakamura, A. F. Rubira and E. C. Muniz, Biomacromolecules, 2012, 13, 3711–3722 CrossRef CAS PubMed
.
- F. Persson, J. Fritzsche, K. U. Mir, M. Modesti, F. Westerlund and J. O. Tegenfeldt, Nano Lett., 2012, 12, 2260–2265 CrossRef CAS PubMed
.
- G. J. Ma, B. K. Yoon, T. N. Sut, K. Y. Yoo, S. H. Lee, W.-Y. Jeon, J. A. Jackman, K. Ariga and N.-J. Cho, View, 2022, 3, 20200078 CrossRef CAS
.
- I. Eshet, V. Freger, R. Kasher, M. Herzberg, J. Lei and M. Ulbricht, Biomacromolecules, 2011, 12, 2681–2685 CrossRef CAS PubMed
.
- S. P. Mitra, J. Surf. Sci Technol., 2020, 36, 7–38 CAS
.
- M. M. van Schooneveld, E. Vucic, R. Koole, Y. Zhou, J. Stocks, D. P. Cormode, C. Y. Tang, R. E. Gordon, K. Nicolay and A. Meijerink,
et al.
, Nano Lett., 2008, 8, 2517–2525 CrossRef CAS PubMed
.
- A. Luchini and G. Vitiello, Front. Chem., 2019, 7, 343 CrossRef CAS PubMed
.
- Y. Wu, F. I. Simonovsky, B. D. Ratner and T. A. Horbett, J. Biomed. Mater. Res., Part A, 2005, 74, 722–738 CrossRef PubMed
.
- L. Zhang, B. Casey, D. K. Galanakis, C. Marmorat, S. Skoog, K. Vorvolakos, M. Simon and M. H. Rafailovich, Acta Biomater., 2017, 54, 164–174 CrossRef CAS PubMed
.
- V. A. Parsegian, N. Fuller and R. P. Rand, Proc. Natl. Acad. Sci. U. S. A., 1979, 76, 2750–2754 CrossRef CAS PubMed
.
- J. N. Israelachvili and R. M. Pashley, Nature, 1983, 306, 249–250 CrossRef CAS
.
- E. Schneck, F. Sedlmeier and R. R. Netz, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14405–14409 CrossRef CAS PubMed
.
- J. L. Parker, P. M. Claesson and P. Attard, J. Phys. Chem., 1994, 98, 8468–8480 CrossRef CAS
.
- E. A. Vogler, Adv. Colloid Interface Sci., 1998, 74, 69–117 CrossRef CAS PubMed
.
- J. M. Berg, L. T. Eriksson, P. M. Claesson and K. G. N. Borve, Langmuir, 1994, 10, 1225–1234 CrossRef CAS
.
- M. Navarro, E. Engel, J. A. Planell, I. Amaral, M. Barbosa and M. Ginebra, J. Biomed. Mater. Res., Part A, 2008, 85, 477–486 CrossRef CAS PubMed
.
- N. Schwierz, D. Horinek, S. Liese, T. Pirzer, B. N. Balzer, T. Hugel and R. R. Netz, J. Am. Chem. Soc., 2012, 134, 19628–19638 CrossRef CAS PubMed
.
- L. Peng, H. Li and Y. Meng, Appl. Surf. Sci., 2017, 401, 25–39 CrossRef CAS
.
- E. A. Vogler, J. Biomater. Sci., Polym. Ed., 1999, 10, 1015–1045 CrossRef CAS PubMed
.
- A. Sethuraman, M. Han, R. S. Kane and G. Belfort, Langmuir, 2004, 20, 7779–7788 CrossRef CAS PubMed
.
- P. Parhi, A. Golas and E. A. Vogler, J. Adhes. Sci. Technol., 2010, 24, 853–888 CrossRef CAS
.
- E. A. Vogler, Biomaterials, 2012, 33, 1201–1237 CrossRef CAS PubMed
.
- Y. Tian and L. Jiang, Nat. Mater., 2013, 12, 291–292 CrossRef CAS PubMed
.
- M. Liu, S. Wang and L. Jiang, Nat. Rev. Mater., 2017, 2, 1–17 Search PubMed
.
- M. F. Ismail, M. A. Islam, B. Khorshidi, A. Tehrani-Bagha and M. Sadrzadeh, Adv. Colloid Interface Sci., 2022, 299, 102524 CrossRef CAS PubMed
.
- A. Marmur, C. Della Volpe, S. Siboni, A. Amirfazli and J. W. Drelich, Surf. Innov., 2017, 5, 3–8 CrossRef
.
- J. Israelachvili and R. Pashley, Nature, 1982, 300, 341–342 CrossRef CAS PubMed
.
- J. Israelachvili and R. Pashley, J. Colloid Interface Sci., 1984, 98, 500–514 CrossRef CAS
.
- S. Schilp, A. Kueller, A. Rosenhahn, M. Grunze, M. E. Pettitt, M. E. Callow and J. A. Callow, Biointerphases, 2007, 2, 143–150 CrossRef CAS PubMed
.
- A. Rosenhahn, S. Schilp, H. J. Kreuzer and M. Grunze, Phys. Chem. Chem. Phys., 2010, 12, 4275–4286 RSC
.
- R. Godawat, S. N. Jamadagni and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15119–15124 CrossRef CAS PubMed
.
- A. J. Patel, P. Varilly and D. Chandler, J. Phys. Chem. B, 2010, 114, 1632–1637 CrossRef CAS PubMed
.
- M. Kanduč, A. Schlaich, E. Schneck and R. R. Netz, Adv. Colloid Interface Sci., 2014, 208, 142–152 CrossRef PubMed
.
- N. B. Rego and A. J. Patel, Annu. Rev. Condens. Matter Phys., 2022, 13, 303–324 CrossRef CAS
.
- D. Berard, P. Attard and G. Patey, J. Chem. Phys., 1993, 98, 7236–7244 CrossRef CAS
.
- K. Lum, D. Chandler and J. D. Weeks, J. Phys. Chem. B, 1999, 103, 4570–4577 CrossRef CAS
.
- D. Bratko, R. A. Curtis, H. W. Blanch and J. M. Prausnitz, J. Chem. Phys., 2001, 115, 3873–3877 CrossRef CAS
.
- X. Huang, C. J. Margulis and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 11953–11958 CrossRef CAS PubMed
.
- D. Chandler, Nature, 2005, 437, 640–647 CrossRef CAS PubMed
.
- N. Choudhury and B. M. Pettitt, J. Am. Chem. Soc., 2007, 129, 4847–4852 CrossRef CAS PubMed
.
- S. Sharma and P. G. Debenedetti, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4365–4370 CrossRef CAS PubMed
.
- K. Lum and D. Chandler, Int. J. Thermophys., 1998, 19, 845–855 CrossRef CAS
.
- X. Huang, C. J. Margulis and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 11953–11958 CrossRef CAS PubMed
.
- N. Choudhury and B. M. Pettitt, J. Am. Chem. Soc., 2005, 127, 3556–3567 CrossRef CAS PubMed
.
- S. Sharma and P. G. Debenedetti, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4365–4370 CrossRef CAS PubMed
.
- P. Setny, Z. Wang, L.-T. Cheng, B. Li, J. McCammon and J. Dzubiella, Phys. Rev. Lett., 2009, 103, 187801 CrossRef CAS PubMed
.
- P. Setny, R. Baron, P. Michael Kekenes-Huskey, J. A. McCammon and J. Dzubiella, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1197–1202 CrossRef CAS PubMed
.
- D. Bratko, R. Curtis, H. Blanch and J. Prausnitz, J. Chem. Phys., 2001, 115, 3873–3877 CrossRef CAS
.
- R. Mehrani and S. Sharma, J. Phys. Chem. B, 2022, 126, 5110–5116 CrossRef CAS PubMed
.
- H. K. Christenson and P. M. Claesson, Science, 1988, 239, 390–392 CrossRef CAS PubMed
.
- D. J. Mastropietro and W. A. Ducker, Phys. Rev. Lett., 2012, 108, 106101 CrossRef PubMed
.
- S.-T. Lou, Z.-Q. Ouyang, Y. Zhang, X.-J. Li, J. Hu, M.-Q. Li and F.-J. Yang, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2000, 18, 2573–2575 CAS
.
- N. Ishida, T. Inoue, M. Miyahara and K. Higashitani, Langmuir, 2000, 16, 6377–6380 CrossRef CAS
.
- J. Tyrrell and P. Attard, Langmuir, 2002, 18, 160–167 CrossRef CAS
.
- P. S. Epstein and M. S. Plesset, J. Chem. Phys., 1950, 18, 1505–1509 CrossRef CAS
.
- D. Lohse and X. Zhang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 031003 CrossRef PubMed
.
- D. Lohse and X. Zhang, Rev. Mod. Phys., 2015, 87, 981 CrossRef CAS
.
- B. H. Tan, H. An and C.-D. Ohl, Phys. Rev. Lett., 2018, 120, 164502 CrossRef PubMed
.
- B. H. Tan, H. An and C.-D. Ohl, Phys. Rev. Lett., 2019, 122, 134502 CrossRef CAS PubMed
.
- R.-H. Yoon and S. Ravishankar, J. Colloid Interface Sci., 1996, 179, 391–402 CrossRef CAS
.
- M. Hato, J. Phys. Chem., 1996, 100, 18530–18538 CrossRef CAS
.
- N. Ishida, N. Kinoshita, M. Miyahara and K. Higashitani, J. Colloid Interface Sci., 1999, 216, 387–393 CrossRef CAS PubMed
.
- R. F. Considine and C. J. Drummond, Langmuir, 2000, 16, 631–635 CrossRef CAS
.
- M. Kanduč, E. Schneck and R. R. Netz, Chem. Phys. Lett., 2014, 610, 375–380 CrossRef
.
- M. Kanduč and R. R. Netz, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12338–12343 CrossRef PubMed
.
- M. Kanduč, A. Schlaich, E. Schneck and R. R. Netz, Langmuir, 2016, 32, 8767–8782 CrossRef PubMed
.
- O. Ozkan and H. Y. Erbil, Surf. Topogr., 2017, 5, 024002 CrossRef
.
- E. De Souza, M. Brinkmann, C. Mohrdieck, A. Crosby and E. Arzt, Langmuir, 2008, 24, 10161–10168 CrossRef CAS PubMed
.
- Y. Uematsu, D. J. Bonthuis and R. R. Netz, Curr. Opin. Electrochem., 2019, 13, 166–173 CrossRef CAS
.
- F. Bartell and H. Osterhof, Ind. Eng. Chem. Res., 1927, 19, 1277–1280 CrossRef CAS
.
- B. T. Ingram, J. Chem. Soc., Faraday Trans., 1974, 70, 868–876 RSC
.
- B. Janczuk, Fuel, 1986, 65, 113–116 CrossRef CAS
.
- M. I. J. van Dijke and K. S. Sorbie, J. Pet. Sci. Eng., 2002, 33, 39–48 CrossRef CAS
.
- J. W. Grate, K. J. Dehoff, M. G. Warner, J. W. Pittman, T. W. Wietsma, C. Zhang and M. Oostrom, Langmuir, 2012, 28, 7182–7188 CrossRef CAS PubMed
.
- J. J. Jasper and E. V. Kring, J. Phys. Chem., 1955, 59, 1019–1021 CrossRef CAS
.
- A. Goebel and K. Lunkenheimer, Langmuir, 1997, 13, 369–372 CrossRef CAS
.
- M. Šako, F. Staniscia, E. Schneck, R. R. Netz and M. Kanduč, PNAS Nexus, 2023, 2, pgad190 CrossRef PubMed
.
- T. C. Walther and R. V. Farese Jr, Biochim. Biophys. Acta, Mol. Cell Biol. Lipids, 2009, 1791, 459–466 CrossRef CAS PubMed
.
- A. R. Thiam, R. V. Farese Jr and T. C. Walther, Nat. Rev. Mol. Cell Biol., 2013, 14, 775–786 CrossRef CAS PubMed
.
- S. S. Okubanjo, S. M. Loveday, A. Ye, P. J. Wilde and H. Singh, J. Agric. Food Chem., 2019, 67, 2626–2636 CrossRef CAS PubMed
.
- J. A. Julien, A. L. Pellett, S. S. Shah, N. J. Wittenberg and K. J. Glover, Biochim. Biophys. Acta, Biomembr., 2021, 1863, 183624 CrossRef CAS PubMed
.
- J. Musakhanian, J.-D. Rodier and M. Dave, AAPS PharmSciTech, 2022, 23, 151 CrossRef CAS PubMed
.
- M. E. Callow and R. L. Fletcher, Int. Biodeterior., 1994, 34, 333–348 CrossRef CAS
.
- S. Abarzua and S. Jakubowski, Mar. Ecol. Prog., 1995, 123, 301–312 CrossRef CAS
.
- D. M. Yebra, S. Kiil and K. Dam-Johansen, Prog. Org. Coat., 2004, 50, 75–104 CrossRef CAS
.
- S. Hong and M. Elimelech, J. Membr. Sci., 1997, 132, 159–181 CrossRef CAS
.
- A. Armanious, M. Aeppli and M. Sander, Environ. Sci. Technol., 2014, 48, 9420–9429 CrossRef CAS PubMed
.
- Y.-M. Lin, C. Song and G. C. Rutledge, ACS Appl. Mater. Interfaces, 2019, 11, 17001–17008 CrossRef CAS PubMed
.
- K. Park, D. Lee, J.-H. Lim, J. Hong and G. Lim, Langmuir, 2022, 38, 9884–9891 CrossRef CAS PubMed
.
- R. P. Berkelaar, E. Dietrich, G. A. Kip, E. S. Kooij, H. J. Zandvliet and D. Lohse, Soft Matter, 2014, 10, 4947–4955 RSC
.
- Y.-S. Lo, N. D. Huefner, W. S. Chan, P. Dryden, B. Hagenhoff and T. P. Beebe, Langmuir, 1999, 15, 6522–6526 CrossRef CAS
.
- D. Daniel, J. V. Timonen, R. Li, S. J. Velling and J. Aizenberg, Nat. Phys., 2017, 13, 1020–1025 Search PubMed
.
- E. De Souza, L. Gao, T. McCarthy, E. Arzt and A. Crosby, Langmuir, 2008, 24, 1391–1396 CrossRef CAS PubMed
.
- S. Al-Anssari, A. Barifcani, S. Wang, L. Maxim and S. Iglauer, J. Colloid Interface Sci., 2016, 461, 435–442 CrossRef CAS PubMed
.
- M. A. Q. Siddiqui, S. Ali, H. Fei and H. Roshan, Earth-Sci. Rev., 2018, 181, 1–11 CrossRef
.
- S. Huang, R. H. Ras and X. Tian, Curr. Opin. Colloid Interface Sci., 2018, 36, 90–109 CrossRef CAS
.
- N. Ismail, W. Salleh, A. Ismail, H. Hasbullah, N. Yusof, F. Aziz and J. Jaafar, Sep. Purif. Technol., 2020, 233, 116007 CrossRef CAS
.
- Z. He, X. Lan, Q. Hu, H. Li, L. Li and J. Mao, Prog. Org. Coat., 2021, 157, 106285 CrossRef CAS
.
- X. Tian, V. Jokinen, J. Li, J. Sainio and R. H. Ras, Adv. Mater., 2016, 28, 10652–10658 CrossRef CAS PubMed
.
- M. Liu, L. Tie, J. Li, Y. Hou and Z. Guo, J. Mater. Chem. A, 2018, 6, 1692–1699 RSC
.
- Y. Tian, B. Su and L. Jiang, Adv. Mater., 2014, 26, 6872–6897 CrossRef CAS PubMed
.
- H. Singh and S. Sharma, Mol. Simul., 2021, 47, 420–427 CrossRef CAS
.
- A. F. Qadikolae and S. Sharma, J. Mol. Liq., 2023, 379, 121685 CrossRef
.
| This journal is © the Owner Societies 2024 |