Fragmentation dynamics of the doubly charged aniline: the source of kinetically excited CnH3+ ions
Muthuamirthambal
Selvaraj
a,
Arun
Subramani
 a,
Karthick
Ramanathan
a,
Robert
Richter
a,
Karthick
Ramanathan
a,
Robert
Richter
 b,
Nitish
Pal
b,
Paola
Bolognesi
b,
Nitish
Pal
b,
Paola
Bolognesi
 c,
Lorenzo
Avaldi
c,
Lorenzo
Avaldi
 c and
Umesh R.
Kadhane
c and
Umesh R.
Kadhane
 *a
*a
aIndian Institute of Space Science and Technology, Trivandrum, Kerala, India. E-mail: umeshk@iist.ac.in
bElettra-Sincrotrone Trieste, Italy
cCNR-Istituto di Struttura della Materia, Rome, Italy
First published on 16th May 2024
Abstract
The goals of this work are to attempt to decipher if an aniline dication can isomerize to a picoline dication in a given astrochemical environment and if the dissociation of such dications could be a source of kinetically hot fragment ions, some of which could be of significance in the interstellar medium. Toward this purpose, the VUV-induced dication dissociation was investigated experimentally using ion–ion coincidence and computationally by optimizing various pathways. Contrary to previous reports, we show here that the dication of aniline is structurally too weak to retain its ring structure while following the dissociation pathways. A fragile open ring structure could lead to all the experimentally observed pathways of noticeable intensity. The significance of this, especially in terms of molecular dynamics, can be assessed by the fact that all the transformations were facilitated by specific hydrogen migration. A clear selectivity is seen where the dication of aniline was found to prefer a rearrangement of hydrogen within the ring rather than transferring from nitrogen to the ring, which is conventionally expected and has to do with the charge state and charge localization.
1 Introduction
The presence of linear and cyclic nitrogenated molecules in various regions of the interstellar medium (ISM) necessitates an investigation into their origins. While there are two prevailing hypotheses, namely the “Top-Down” and “Bottom-Up” approaches, the formation of these observed molecules lacks a definitive conclusion. Due to the inherent variability of environmental conditions throughout various regions in ISM, it is not feasible to rely on a single model to describe the formation process of these molecules, entirely. For example, there are many layers within the protoplanetary disc, with the dominant energy source being ultraviolet (UV) radiation emitted by the protostar, where photodissociation can play a primary role in the molecular synthesis. Recent findings have revealed a significant presence of nitrogenated aromatic compounds inside the TMC-1 region,1 exposing the ongoing activity of molecular formation mechanisms in certain areas where the temperature is around 10 K. Hence, it has been hypothesized that the associative chemical reactions through barrier-less neutral–neutral reactions are the primary processes2,3 in these cold environments. The inclusion of the ion–neutral reaction increases the plausibility of the association process hypothesis, as ion–molecule reactions often do not have an activation energy barrier.4–6 Even if the chemical reaction has an activation barrier, the reactant ions with sufficient kinetic energy can overcome these barriers during the association process.7 The molecular ions can acquire kinetic energy by magnetohydrodynamic (MHD) shocks7 or during fragmentation, where fragment ions can possess a certain amount of kinetic energy. Monocation dissociation usually produces fragments with minimal kinetic energy, typically in the range of a few hundred meV. Conversely, when the ions are formed from doubly or multiply charged ions through coulomb explosion, they possess significantly higher kinetic energy, typically in the range of a few eV. The production of doubly charged nitrogenated aromatics can occur through various mechanisms, including interaction with plasma, high energy cosmic rays, intense UV or X-ray photon radiation, and electron impact driven by the magnetosphere.8,9 In this scenario, they can eventually serve as the origin of a small linear chain of ionic compounds in addition to producing ions with kinetic energy that can be involved in ion–neutral reactions too. It is also interesting to note that the resulting fragment ions can possess sufficient energy to escape the atmospheres they are produced in. Such mechanisms may be at play in the case of celestial bodies such as Titan, Mars, Venus, and more.10 Therefore, it is crucial to identify the fragment ions released from the doubly charged ions and measure their kinetic energy release, particularly in the case of doubly charged nitrogenated molecules, which is the focus of this work.Aniline (C6H7N) (Fig. 1) is a widely recognized molecule that serves as a building block for other nitrogen containing compounds. While there have been several studies on its cationic and neutral states,11–13 more needs to be done on its dicationic state. For instance, by incorporating nitrogen into the ring structure, aniline, an amine, can isomerize to heteroaromatics such as methylpyridine. This isomerization process has only been found in aniline's neutral state, not in its cationic configuration.13–15 Theoretical analysis of the aniline dication has shown that the lowest energy ground state structure is one of the methylene–hydropyridine isomers.16 This finding implies that nitrogen insertion into the benzene ring might also be possible in the dicationic form, though further investigation is needed to validate this. Furthermore, the electron ionization analysis of doubly charged aniline and its deuterated form indicates that the important channels at m/z 27 and 39 are associated with C2H3+ and C3H3+, respectively. This result opposes the neutral fragments HNC and HCCN found in singly charged aniline,12 which implies that distinct isomerization stages are involved in the dissociation of the aniline dication. The small linear chain of ionic fragments of aniline has significance in the ISM. Although aniline has not been definitively detected in the ISM, the data collected by the Cassini–Huygens ion and neutral mass spectrometer (INMS) indicate the potential existence of C6H7N (which could correspond to aniline) in the atmosphere of Titan.17 Therefore, in addition to its significance for its basic structure as a precursor to other nitrogenated compounds, it is worthwhile to investigate aniline in the context of ISM. It is also informative to study the decay of the dication to understand the potential utilization of their kinetic energies in the context of ion–neutral processes within the astrophysics realm. Finally, it might be useful to dwell upon the possibility of such kinetically hot ions to contribute to the atmospheric escape for example in Titan. The Cassini Huygens data has been monumental in measuring the atmospheric escape of ions and neutrals with a mass of less than 50 amu.18 The required kinetic energy for this escape is modelled to be sourced from the plasma dynamics of the Titan ionosphere. But this kind of model has so far been an underestimate by almost an order of magnitude. This essentially compels one to consider additional mechanisms of such losses. Intriguingly, the kinetically hot fragment ions measured here are indeed found in the list of escaping ions of significance.17
The present study investigates the dissociation dynamics of the aniline dication under VUV radiation. Single-step and sequential dissociation channels have been obtained using the ion–ion coincidence diagram. The velocity map imaging (VMI) technique has been used to measure the kinetic energy of ions and electrons. Using density functional theory (DFT), the energy required for the single-step and sequential dissociation channels was computed and compared with the estimated internal energy derived from the experimental results. Additionally, potential isomers of these dissociation channels have been suggested. The computational investigation of the isomerization process between the dication of aniline and methylpyridine has been conducted, and the findings are comprehensively analyzed and discussed. This combined analysis is used to clearly identify, contrary to a few previous computational results, the most plausible and unified pathway of aniline dication decay.
2. Experimental details
The experiment was carried out using the VMI time-of-flight (TOF) coincidence endstation housed at the low-energy branch line of the GasPhase Photoemission beamline at the Elettra synchrotron in Trieste, Italy. A detailed description of the experimental setup19 and beamline20 has already been provided elsewhere. The experimental setup can be operated in two modes: ion on VMI (iVMI) mode, where ions are steered towards the VMI detector, which consists of the position-sensitive crossed delay line anodes, and electrons recorded on the TOF detector. In the electron-on VMI (eVMI) mode, electrons were directed towards the VMI detector in order to acquire kinetic energy and angular distribution of the electrons, while the ions were directed towards the TOF detector. Without going through any further purification process apart from freeze–pump–thawing cycles, a commercially available liquid aniline sample was used. No additional heating was needed since the aniline vapour pressure was high, and the target was used at room temperature. The aniline target beam was irradiated using a 32 eV photon beam, which caused it to doubly ionize and dissociate. The measurement was carried out in pulse-counting mode. The signal was amplified, discriminated, and then transmitted to a 8-channel time-to-digital converter (THR08-TDC). This particular TDC was developed explicitly for conducting coincidence measurements using delay line detectors. The experimental setup configured the pulse-pair resolution to 12 ns and the temporal precision to 75 ps FWHM. This was done to collect data from a maximum number of ions effectively. The MEVELER algorithm21 was employed to extract the kinetic energy of ions and electrons from the recorded position in the iVMI and eVMI mode. The photoionization spectra of xenon measured at specific photon energies was used for calibration.3. Computational details
Density functional theory calculations were performed using the GAUSSIAN 09 software.22 Potential energy surface (PES) scans were performed at the B3LYP/6-311++G(d,p) level of theory in order to locate the structures of the stationary points involved. The pathways with the lowest energy barrier leading up to each of the structures considered are reported. Geometries were optimized at the same level of theory, and vibrational frequencies were used to characterize the structures as minima (intermediates) and first-order saddle points (transition states). Intrinsic reaction coordinate (IRC) calculations were carried out for significant steps to verify that the associate transition state indeed connects the local minima on either side.4. Results and discussions
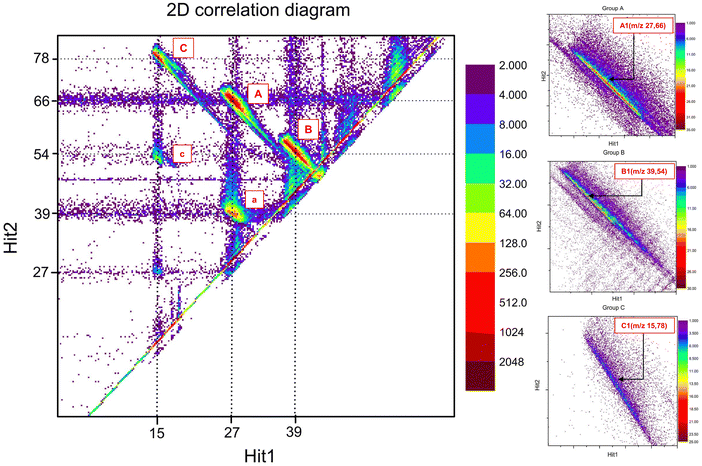
4.1. Ion–ion correlation diagram
The ion–ion coincidence (2D correlation) diagram is obtained by plotting the data recorded in the iVMI mode with the arrival times of individual events’ first and second ion hits. This momentum correlation diagram allows for the extraction of true events associated with a dication dissociative single step and sequential channels. The ion–ion coincidence diagram of the aniline dication, obtained at a photon energy of 32 eV, is illustrated in Fig. 2. The dispersion of the individual islands can be attributed to the release of kinetic energy during the dissociation process, while the elongated tail signifies the presence of metastable dissociation.The correlation diagram exhibits three discernible groups, namely groups A, B, and C. Within group A, the island denoted as A1 corresponds to the single-step dissociative channel with the highest detected intensity with the m/z 27 and 66 coincidence, which may potentially be attributed to the dissociative channel corresponding to C2H3+ or HNC+, resulting in the formation of product ions C4H4N+ or C5H6+ respectively. Based on previous studies on aniline dications, this channel most likely corresponds to the C2H3+ and C4H4N+ dissociation channel.23 Group A has other low-intensity channels associated with dissociative channels of m/z 28, 26, 29, and 30, accompanied by their corresponding product ions of m/z 65, 67, 64, and 63, which are ordered in descending order of intensity. These channels can be associated with HNCH+/C5H5+, C2H2+/C4H5N+, CH3N+/C5H4+, and CH4N+/C5H3+. In group B, island B1 corresponds to the next significant channel where C3H3+/C3H4N+, HNCC+/C4H6+ or HCNC+/C4H6+ with m/z 39 and 54 are possible fragment ion pairs. The presence of additional minor channels in group B, with m/z values of 41 and 42, is associated with the product ions 52 and 51, which could be fragment ions corresponding to C3H5+/C3H2N+ and C2H4N+/C4H3+. Group C contains the third intense island, C1, with the corresponding fragments of m/z 15 and 78 correlation, possibly corresponding to CH3+/C5H4N+ or NH+/C6H6+ fragment ions. The major channels corresponding to islands A1, B1 and C1 all show the long tail feature, indicating that these channels follow metastable decay. The following presentation focuses only on islands A1, B1 and C1 since the other channels in the respective groups are of significantly lower intensities compared to these ones.
The work here reports and explains some additional features which are usually not reported in such measurements for any dication dissociation work. The presence of small islands below groups A and C is attributed to the sequential dissociation channels of the aniline dication. Island a exhibits neutral loss of mass 27, accompanied by the dissociation of ions with m/z 27 and 39. Notably, the mass of the neutral and one of the fragment product ions in the sequential channel is 27. Either HNC or C2H3 could be found as neutral. In the vast majority of PA(N)Hs, neutral loss of C2H3 is exceedingly rare; instead, neutral C2H2 is preferred. This suggests that C2H3 was likely lost in ionic form while HNC was likely lost in neutral form in this instance as well. Another primary concern that must be addressed is whether the neutral loss occurred before the Coulomb explosion or if it occurred from one of the fragment ions after the ion–ion dissociation. Upon close observation of Fig. 2, island a appears to be connected to the m/z 66 via a bridge, suggesting that the dissociation of m/z 39 from m/z 66 occurs throughout the flight. In contrast, the constrained position of m/z 27 supports the claim that the ion with m/z 27 is exclusively produced within the region i.e., in a very short time after interaction. This statement elucidates that the neutral loss does not occur as an outcome of the aniline dication directly but rather originates from the molecular ion with m/z 66, which is expelled from the parent dication. Likewise, another island, c, conversely reflects an indirect loss of neutral with mass 27 from the ion with m/z 78 through the manifestation of a bridge link. The ion corresponding to m/z 78 from the dissociation channel, which corresponds to island C1, further underwent dissociation, resulting in the neutral loss of mass 27 and the formation of an ion with m/z 51. In both islands a and c, it is worth noting that the isomeric composition of the neutral (mass 27) loss can also help to identify fragment ion composition during single-step dissociation in such a way, given that sequential channels follow the single-step dissociation. This will be explored further in the subsequent sections, where the structure calculations will be presented to provide quantitative support. There is another island located well below island c with very low intensity, which exhibits a neutral loss of mass 54 in conjunction with the dissociation of the parent ion into two ion–ion losses. However, considering their intensity, the current study will address only islands A1, B1, C1, a and c.
4.2. Mapping internal energy
Determining the internal energy of the doubly charged molecular ion prior to the dissociation event poses significant challenges unless the investigation is conducted using a specialized experimental procedure and instrument. This section describes an attempt that has been made to estimate the internal energy threshold required for the desired dissociation channels of the aniline dication. This estimation has been carried out by analyzing the appearance of the dissociation channel while scanning the electron energy from the data obtained in eVMI mode.The complete recorded electron image taken in eVMI mode at 32 eV photon energy, which includes the contributions from every ionization event, including monocation and dication, was plotted. In order to extract the information pertaining specifically to the dication, an ion–ion coincidence diagram was constructed, which shows the occurrence of all dissociation channels. When a certain electron energy window is chosen by selecting a ring from the electron image, the internal energy threshold of the dissociation channels is indicated by their absence in the 2D correlation diagram. With known double ionisation, photon energy used for the ionisation event, and electron energies (at least one of the electrons), the internal energy of molecular dication can be estimated (eqn (1)). For instance, if the double ionization energy of aniline is 22 eV12 and a photon beam of 32 eV is used, the following dissociation of the aniline dication must occur within 10 eV of internal energy. Suppose one of the electrons carries away 4 eV energy; in that case, the remaining internal energy will be less than 6 eV for the dissociation.
| M + hν → M++ + e1 + e2 | (1) |
This will provide a qualitative estimate of the required internal energy for the particular dissociation channels. It is imperative to acknowledge that no feasible methods are now available to measure both electron energies from the dication in the present experimental setup. Consequently, the entire analysis is conducted on the assumption that the energy of one of the electrons is zero. When the ring corresponding to an electron energy of 6 eV is selected, all three major channels (islands A1, B1, and C1) begin to disappear and show a faint trace (Fig. 3). The ring on the electron image was scanned until the specified dissociation channel vanishes. When the ring is selected for electron energies above 6 eV, all these channels disappear entirely. This observation suggests that these dissociation channels are expected to occur at energies lower than 26 eV relative to the ground state of neutral aniline. However, it was noted that the sequential channels, corresponding to islands a and c, may occur between 28 and 28.5 eV, respectively, since these islands vanish when the electron energy ring is selected at 4 and 3.5 eV.
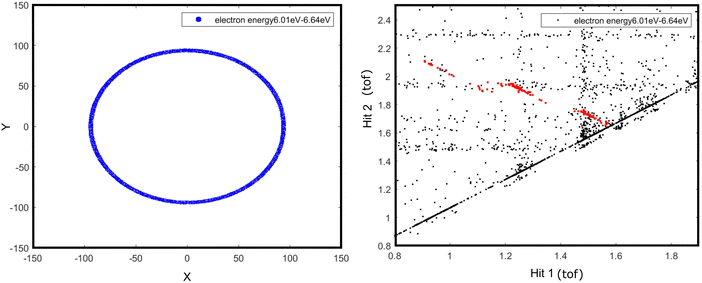 | ||
| Fig. 3 The ring selection of electrons with a minimum energy of 6 eV (left) and the corresponding 2D correlation diagram (right). | ||
4.3. Major channels
Using the energetics of computed PES, this section will address the three main dissociation channels associated with the islands A1, B1 and C1 that are dominant in intensity over other channels, as well as potential fragment ionic combinations. While indeed the energy is nearly 10 eV more than that of the double ionisation threshold the channels of interest appear at a total energy of less than 26 eV (Section 4.2), which is just 4 eV above the threshold and combining that with the fact that we assumed zero kinetic energy for the second electron and we do need some kinetic shift to observe the fragment within the ToF time scale implies that the dication must relax to low lying energy states. Hence the calculation of dication dissociation based on the ground state structure is suitable in this case. A similar approach is taken for several other cases as well.24–26 Hence, all the computations are done for the dication in the ground electronic state, and the energy has been reported with respect to the neutral ground state. The singlet state of the aniline dication is 0.68 eV lower than its triplet state, while the possible PES were investigated in both singlet and triplet states. The present study discussed the pathways originating from singlet states that were found to dominate by far in terms of their energy barriers. As a result of an extensive search of possible dissociation routes, it was observed that the impact of H migration on the interplay between ring scission and retention in aniline dication through structural rearrangement is crucial.4.4. H migration to the ring
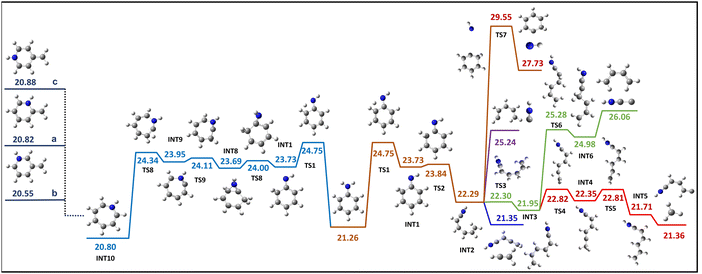
An attempt was made to transfer the hydrogen H14 from the amino group to the carbon C5, which contains the NH group, but it was unsuccessful. Hence, it has been attempted to move one of the hydrogens (H14 or H13) from the amino group to the carbon C4 in the benzene ring. Interestingly, transferring H13 or H14 to C4 will result in a different first intermediate structure followed by the same INT2 structure. However, the energy required for the transition state to move H14 to C4 is 24.75 eV, while H13 to C4 requires 25.37 eV. Given the energy requirements, the present study prioritises the H14 to C4 route over another. Therefore, the first step in the pathway involves transferring the hydrogen H14 from the amino group to the carbon C4 in the benzene ring. This results in the formation of an intermediate structure INT1 (Fig. 4) in which the carbon C4 changes to sp3 hybridization, leading to an open ring intermediate structure INT2. Either dissociation fragment combinations, C2H3+ and C4H4N+ or HNC+ and C5H6+ associated with island A1 can occur by C–C bond cleavage without requiring any additional structural rearrangement from the INT2 structure. However, the dissociation of C2H3+ and C4H4N+ is exothermic by 0.93 eV, with the most energetically demanding step throughout this dissociation process being the initial transition state TS1 involving hydrogen migration, which requires 24.75 eV. Conversely, HNC+ and C5H6+ dissociation requires 25.24 eV. The fragment dissociation of HNCC+ and C4H6+, one of the possible dissociation channels of island B1, can result from the INT2 structure by relocating the hydrogen atom H11 to C1. The resulting product energy is calculated to be 26.06 eV. However, the attempt to find the dissociation pathway for the CH3+ and C5H4N+ dissociation through the INT2 was unsuccessful. The structure INT2 can give rise to a possible dissociation channel behind island C1, NH+ and C6H6+, which entails a transition state barrier with the highest energy requirement of 29 eV, and the energy associated with the formation of the resulting product is 27 eV. The loss of NH+ can also occur directly from the first intermediate INT1, which is also connected to the same transition state TS7 and the formation of the final product. Therefore, an effort was made to find a dissociation route for another possible dissociation channel of the island C1, CH3+ and C5H4N+ from INT2, necessitating a transition state involving a dihedral rotation of 90 degrees. This rotation results in the formation of a planar intermediate structure INT3, which subsequently facilitates the migration of hydrogen and ultimately leads to the dissociation of CH3+ and C5H4N+. In addition, the possibility of CH3+ loss from methylpyridinium through isomerization was investigated via a comprehensive search. The intermediate structure INT1, which involves hydrogen migration, tends to undergo ring expansion instead of ring opening by incorporating nitrogen into the ring. A doubly charged, energetically stable seven-member intermediate structure INT10, known as azepine, is formed by incorporating nitrogen. This seven-membered ring structure INT10 can be subsequently isomerized into a 2, 3 or 4 methylenepyridinium (a,b and c in Fig. 4) structure, which is structurally more stable than the aniline dication.16 For this dissociation pathway as well, the transition state TS1 is the step that requires the highest energy. The dissociation of CH3+ and C5H4N+ can occur through hydrogen transfer steps in the methylpyridinium isomers. The transfer of hydrogen from nitrogen to the CH2 group in 2-methylpyridinium will result in the formation of the 2-methylpyridine structure, which can cause the dissociation of CH3+ and C5H4N+. In contrast, more than one hydrogen transfer step will be required to achieve the 3- and 4-methylpyridine structures in the other two isomers, 3- and 4-methylpyridinium, respectively. However, other dissociation channels associated with islands A1 and B1 require further structural rearrangement, which is entropically more expensive than the open ring pathway through INT2.4.5. H migration within the ring
The process of hydrogen migration within the ring entails the transfer of a hydrogen atom, H9, from carbon C3 to C4, accompanied by an energy barrier of 24.17 eV. This hydrogen H9 migration results in the formation of an intermediate state INT11 (Fig. 5), which has the potential to initiate the formation of an open ring structure through two possible mechanisms: (1) the transfer of a hydrogen atom H14 from the amino group to the sp3 hybridized carbon C4, which leads to INT12. Due to a hydrogen transfer process, this INT12 structure can ultimately induce the dissociation of CH3+ and C5H4N+, whereas hydrogen transfer from C4 to C3 results in INT14, where the dissociation of C2H3+ and C4H4N+, as well as HNC+ and C5H6+, can be induced. The dissociation to HNC+ and C5H6+ requires 0.73 eV more energy than the highest transition state (TS12) throughout this dissociation route, but the two other dissociation paths are less than TS12. (2) The breaking of a C–C bond between the sp3 hybridized carbon C4 and the carbon C5 containing the amino group leads to INT15. It ultimately results in the loss of C3H3+ by breaking the bond between C1 and C2 and forming a product ion, C3H4N+, upon crossing the final transition state at 24.87 eV.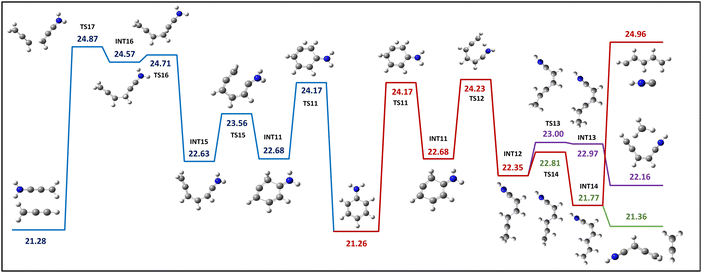 | ||
| Fig. 5 The calculated PES for the open ring structure resulting from hydrogen migration within the benzene ring. Energy values expressed in eV. | ||
4.6. Contribution from the triplet state
An attempt has been made to evaluate the pathways from the triplet state of the aniline dication; this is essential because the isomers of aniline, namely picolines, are known to have a substantial contribution from the triplet dicationic state in the dissociation process.27 The entire dissociation landscape was investigated computationally for the triplet configuration of the aniline dication. The ground state of both singlet and triplet states has a geometrically planar structure, but the singlet state is 0.68 eV lower than the triplet state. In the triplet state, most of the probable pathways for the prominent dissociation channels were found to have barriers equal to or greater than 26 eV (estimated total energy limit defined by experimental observations in Section 4.2). However, one channel was found to be suited to participate in the current scheme, with an energy barrier of 25.54 eV for the dissociation of C3H3+ and C3H4N+. The dissociation route involves steps analogous to the singlet state evolution, with hydrogen migration within a ring (TS11 in Fig. 5), which results in the same isomeric structure of the dissociation products. Thus, when the computed energetics of the possible pathway are compared to the experimental observations, dissociation through the singlet state should contribute significantly to the dissociation process, whilst the triplet state contributes comparatively less. This contrasts with the picoline structure, where the triplet states are shown to have substantial and, in some isomers, dominant contributions. This difference in behaviour between aniline and its isomers, picolines, can be explained based on the fact that the singlet structure of picolines was nonplanar compared to their respective triplet structure. Meanwhile, for aniline, both structures are planar.4.7. Interpretation of viable dissociation routes
A comprehensive investigation of viable dissociation pathways has shown that the initial hydrogen migration step determines whether the ring structure will be retained or opened, and also activates the desired dissociation channels. It is suggested that the first hydrogen migration typically happens from the functional group to the ring structure.27 However, it has been found in the present study that hydrogen migration within a ring in aniline is energetically less expensive than hydrogen migration from nitrogen to the ring. Given that the energy needed for both hydrogen migration steps is significantly lower than the estimated internal energy (Section 4.2) for these channels, favouring one pathway unequivocally becomes challenging. Moreover, the difference between the two hydrogen transfer steps, hydrogen transfer from the amino group to the ring or within a ring, is merely 0.58 eV, further complicating the selectivity.Therefore, the complexities of selecting potential routes can be minimized by comparing experimental results with the computed dissociation pathways. Fig. 4 shows a possible pathway that occurs when hydrogen migrates to the ring, resulting in the formation of both closed-ring and open-ring structures. It is crucial to determine whether the aniline dication undergoes isomerization to the picoline (in Fig. 4a–c) via the intermediate stable structure methylpyridinium before dissociation. The mass spectrum of the dication of the picoline isomers reveals that the loss of neutral H2 is comparable in magnitude to the other main channels.27 However, in the current study, neutral H2 loss is negligible. Furthermore, it has been observed that the dications of 3-methylpyridinium and 4-methylpyridinium show m/z 65 is the significant dissociation channel. Conversely, the aniline dication shows m/z 66 as a significant dissociation channel, while m/z 65 is a less prominent channel.27 This comparison indicates the less likely isomerization to the 3- and 4-methylpyridinium forms. Furthermore, reaching the methylpyridinium isomers and subsequently undergoing dissociation from that structure involves more steps than the dissociation from the open ring structure INT2. While it is possible to maintain the closed ring structure energetically, it is not feasible from an entropic perspective. Therefore, preferring the open ring structure over the closed ring structure is more rational when comparing the possibility of dissociation through INT2 and INT10.
The experimental cut-off of 26 eV total energy can be directly compared with the calculated barriers. This is valid under the assumption that the second electron carried no kinetic energy and zero kinetic shift. In reality, these two mechanisms will take some energy; therefore, the threshold for the reaction, which is valid in this energy domain, must have a total energy barrier well below 26 eV. Therefore, when the dissociation channel associated with island A1 is taken into account, the dissociation of C2H3+ and C4H4N+viaINT2 and INT11 requires 24.75 eV and 24.17 eV, respectively. In contrast, the dissociation energies for C5H6+ and HNC+ are 25.24 eV and 24.96 eV, respectively, viaINT2 and INT11. Hence, it is likely that the dissociation of C2H3+ and C4H4N+ can mainly correspond to the island A1 due to its comparatively low energy demand in comparison to other possible dissociations. It is reasonable to assign the dissociation of C3H3+ and C3H4N+ as a major contributed channel to island B1, as the energy required (24.87 eV) for the dissociation of C3H3+ and C3H4N+ through INT11 falls within the anticipated total energy window 26 eV compared to other fragment channels HNCC+ and C4H6+ through INT2. It is evident that island C1 is associated with the dissociation channel of CH3+ and C5H4N+ through INT2 or INT11. This conclusion is drawn based on the fact that the NH+ and C6H6+ channel requires an energy of 29 eV, which exceeds the estimated internal energy. Therefore, the aforementioned analysis suggests that C2H3+/C4H4N+, C3H3+/C3H4N+, and CH3+/C5H4N+ are the primary contributing channels to islands A1, B1, and C1, respectively, with possible minor contributions from other channels. Moreover, the validity of this assertion is reinforced in accordance with the even electron rule because of the observation that all of the suggested fragment ions are even electron species.23 Additionally, the investigation of electron impact ionization of deuterated aniline reveals the same chemical composition of the fragments.23 As a result, although the difference between the two hydrogen migration steps (TS1 and TS11) is relatively small, considering that all three major dissociation channels can occur with low energy requirements, it is reasonable to suggest that the aniline dication likely undergoes dissociation through the open ring intermediate INT11 structure with a higher likelihood and minor possibility with the other routes.
4.8. Sequential loss channels
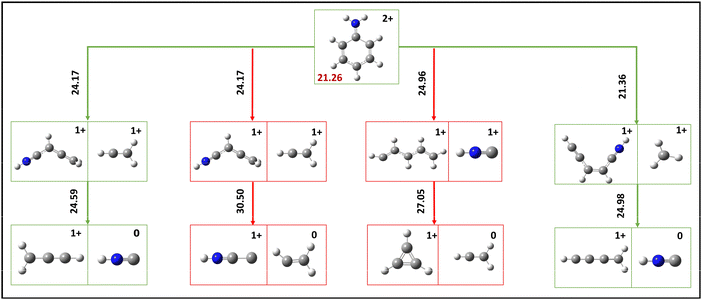
As indicated in the preceding section, below islands A1 and C1, four islands signify the occurrence of neutral losses in conjunction with the ion–ion separation channels. Considering their respective intensities, this discussion will focus exclusively on the islands a and c. The potential fragmentation sequence of these two islands has been determined through DFT calculations, and the corresponding energetics are provided comprehensively (Fig. 6).The island a exhibits a correlation with the neutral loss of mass 27 and the dissociation of ions with m/z values of 27 and 39. The occurrence of m/z 27 loss is evidently observed solely in the interaction section, indicating that the neutral loss occurs during the flight from the ion corresponding to m/z 66. The neutral HNC can be eliminated during the flight from the C4H4N+ ion and leads to HNC neutral with the product ion C3H3+. The first transition state energy needed for the H migration was 24.17 eV, the highest energy needed for this sequential loss path. Therefore, if the channel encounters the dissociation of C2H3+ and C4H4N+, the resulting product ion does not necessitate additional energy to undergo neutral loss. Furthermore, the ion C4H4N+ can lose its neutral C2H3 and thus produce the product ion of HNCC+. However, this requires additional H migration, and the final product energy is 30.5 eV. However, if the ion dissociation channel is assigned to the dissociation of HNC+ and C5H6+, the C5H6+ ion tends to lose C2H3 as a neutral and C3H3+ ion, necessitating an energy requirement of 27.5 eV. Among the three proposed sequential loss channels, it is observed that the neutral loss resulting from the dissociation of the C2H3+ and C4H4N+ event exhibits a lower energy compared to the other two channels. Furthermore, this neutral loss channel is occurring within the estimated internal energy range, as outlined in Section 4.2. Therefore, this island a can be attributed to the dissociation of C2H3+ and C3H3+ along with further neutral HNC loss. Furthermore, these computational results also indicate that neutral loss of C2H3 in aniline dication is unfavourable. This likely sequential loss channel further suggests that the C2H3+ and C2H4N+ ion dissociation channels are responsible for island A1.
The existence of island c can be ascribed to the neutral loss rooting from the ion C5H4N+, which is the product ion resulting from the dissociation of the ions CH3+ and C5H4N+ at island C1. Additionally, the prompt dissociation of m/z 15 indicates that the neutral 27 loss originates from the C5H4N+ ion during the flight. The computed energy requirement of losing HNC from the C5H4N+ ion is 24.98 eV, which is well within the allocated internal energy for this channel to occur. Conversely, an unsuccessful attempt was made to find a C2H3 loss from the ion C5H4N+ in place of HNC. Hence, the suggested sequential loss channel can be categorically assigned to island c since it is significantly lower than the predicted internal energy.
4.9. Kinetic energy release and its implications
The kinetic energy of the fragment ions is crucial in terms of photochemical escape or dissociative recombination reaction in the atmosphere of Titan. Cassini INMS measurements on Titan exobase reveal an abundance of ionic components such as CH5+, HCNH+, and C2H5+, as well as the ions CnH3+ (n = 1, 2, and 3).17 The atmospheric escape analysis of Titan suggests that these ions must be produced in Titan's ionosphere.18 Given that the observed ions had velocities between 0.5 and 1.8 km s−1, either the ionospheric plasma outflow or the energy acquired by the Coulomb explosion may be responsible for transporting these ions to the exobase from the ionosphere. In another study, it has been suggested that the escaping velocity for the Titan atmosphere from ground to 500 km altitude is 2.5 km s−1 on average.10 Therefore, it is possible to underscore the possibility that the detected ions originate from nitrogenated aromatic compounds while discussing the escape from Titan's atmosphere using the kinetic energy obtained from the Coulomb explosion. On the other hand, if the molecular fragments have enough kinetic energy to be involved in the ion–neutral reaction and overcome the energy barriers, it leads to intermediate steps of the formation of larger molecules. In light of these two aspects, the distribution of kinetic energy release for the main dissociation fragments and the implications of these fragment ions have been measured and detailed in this section.The determination of the kinetic energy release of ions resulting from Coulombic repulsion has been accomplished through the analysis of data obtained from the iVMI mode at a photon energy of 32 eV. Since dication fragments exhibit kinetic energy in the range of a few eV, it facilitates efficient measurement. Because of the long flight time, the ion–ion coincidence spots for each dissociation channel are well separated in the iVMI mode. The data specifically pertaining to the channels C2H3+/C4H4N+, C3H3+/C3H4N+, and CH3+/C5H4N+ have been meticulously selected and independently plotted with respect to their respective positions and the kinetic energy was calculated using the MEVELER algorithm. For the analysis, the mean of the measured kinetic energy release distribution was derived after fitting it using a statistical Gaussian fit. The measured KER for the fragment ions C2H3+ and CH3+ is 2 eV, while the KER for their accompanied fragment ions C4H4N+ and C5H4N+ is 0.8 eV. Whereas the C3H3+ ion has a KER of 2 eV, its accompanying fragment ion C3H4N+ has a KER of 0.45 eV. Based on these observed kinetic energy measurements, it is evident that the molecular structure is more likely to have an open ring structure rather than a closed ring structure. Moreover, the observed kinetic energy measurements of these fragments show that the velocity of fragments CnH3+ (n = 1, 2, and 3) is significantly higher than the proposed escaping velocity. While it may not be appropriate to attribute the atmospheric loss of small ions entirely to aniline dication dissociation, it may be interesting to explore if such pathways are common to other nitrogenated aromatics. If aniline is present in Titan's ionosphere, the fragment ions of the aniline dication may participate in the atmospheric outflow.
The molecules CnH3 (n = 1, 2 and 3) are significant in the intermediate stages of the ion–neutral interaction throughout the association process in the astrochemical realm. The CH3+ ion plays a pivotal role as an intermediate hydrocarbon ion species in various chemical reactions, including synthesizing astrophysically significant (cyano)polyynes. These reactions involve complex associations with other neutral molecules and also participate in the dissociative recombination mechanism, leading to the formation of acetylene.28,29 The molecular ion C2H3+ is believed to be an essential molecular ion that is commonly found in circumstellar environments.30 It is also known to have a role in the production of other astrophysically essential molecules, such as propynal, through an associative process.31 Furthermore, it has been observed that the C2H3+ and acyclic-C3H3+ ions exhibit a significant part in ion-atom reactions, leading to the formation of important compounds.32 Interestingly, it has been observed that C2H3 and C3H3 are noteworthy precursors in the synthesis of the cyclopentadienyl radical,3 which has the potential to engage in interactions with methyl radicals, leading to the expansion of benzene and ultimately culminating in the synthesis of polycyclic aromatic hydrocarbons (PAHs) inside circumstellar environments.3,33 The present study has shown that aniline dication fragments are CnH3+ (n = 1, 2, and 3) and that they can participate in the ion–molecule process in the synthesis of larger molecules due to their significant range of kinetic energies if aniline is present in the ISM.
5. Conclusions
The incorporation or elimination of nitrogen into the aromatic ring is a critical step in the synthesis of biomolecules in an astrochemical context. Investigating dissociative photoionization of nitrogen-containing compounds is of vital importance in this regard. Specifically, the skeleton of essential biomolecules, aniline, which has three more cyclic isomeric structures, needs to be probed to understand their structural response to VUV radiation. It was shown that a fraction of neutral aniline could be isomerized to methylpyridine via isomerization of nitrogen into the ring when in its neutral state, whereas this is improbable when aniline is in its cationic state. Therefore, the isomerization in the dicationic state has been studied to gain insights into the impact of the charge state on the preservation of the cyclic structure during isomerization. Previous theoretical investigations have shown the possibility of aniline dication isomerizing to methylpyridinium based only on the energy considerations of the molecular structure. Furthermore, nitrogenated aromatics play a critical role in the generation of highly reactive fragment ions, which are essential intermediates in the chemical synthesis of larger molecules. From these perspectives, the aniline dication and its fragmentation ions have been investigated by combining the experimental data and the dissociation channel energetics that have been computationally estimated. This study discusses the potential mechanisms involved in the isomerization of aniline to methylpyridine before dissociation. The primary dissociation channels have been identified as C2H3+/C4H4N+, C3H3 +/C3H4N+, and CH3+/C5H4N+, accompanied by comprehensive structural calculation results. Two key steps have been observed in the dissociation pathways: (a) hydrogen migration from nitrogen to the ring and (b) hydrogen migration within the ring. By combining the computational findings with the experimental evidence, it becomes apparent that the hydrogen migration within the ring is energetically favoured, which also leads to the open ring structure. Furthermore, the measured kinetic energy of these fragment ions suggests that aniline must undergo ring opening before dissociation. This also implies the possibility that aniline may not undergo isomerization to methylpyridine in a doubly charged state. Furthermore, the computed energetics of the various dissociation routes for aniline dication in the triplet state, which has a higher energy demand than the singlet state, indicate that the singlet state plays a dominant role in the dissociation dynamics. This investigation further assigns the pathways to the observed single-step and sequential dissociation while identifying the composition of kinetically hot fragments ions. One of the implications of this identification is the fact that the aniline dication can serve as the molecular precursor for CnH3+ (n = 1, 2 and 3) molecular ions that have significant astronomical relevance. The result is particularly intriguing as it reveals that, despite the presence of nitrogen adjacent to the benzene ring, aniline exhibits a preference for the dissociation of small linear hydrocarbon molecular ions rather than smaller nitrogen-containing fragments such as HNC, HCCN, and NH, as is apparent in the case of monocation dissociation. The ion–ion correlation diagram has been used to investigate the sequential dissociation of aniline dication. It was also determined that the neutral loss must occur after the ion–ion dissociation and not directly from the aniline dication.Author contributions
Muthuamirthambal Selvaraj: conceptualization, methodology, formal analysis, data curation, writing – original draft, visualization, investigation. Arun Subramani: conceptualization, writing – review & editing. Karthick Ramanathan: conceptualization, writing – review & editing. Robert Richter: resources, conceptualization, writing – review & editing. Nitish Pal: resources. Paola Bolognesi: resources, conceptualization, writing – review & editing. Lorenzo Avaldi: resources, conceptualization, writing – review & editing, funding acquisition. Umesh R. Kadhane: resources, conceptualization, investigation, writing – review & editing, supervision, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support provided by the 2022–2024 Indo-Italian programme for exchange of researchers “Genesis of organic molecules in the extra-terrestrial environment: role of energetic radiation” and the funds provided by a grant from the Italian Ministry of Foreign Affairs and International Cooperation and the Indian Department of Science and Technology. One of the authors (Muthuamirthambal Selvaraj) acknowledges financial support from the University Grants Commission (UGC) under the JRF scheme for this research work.Notes and references
- B. A. McGuire, A. M. Burkhardt, S. Kalenskii, C. N. Shingledecker, A. J. Remijan, E. Herbst and M. C. McCarthy, Science, 2018, 359, 202–205 CrossRef CAS PubMed
.
- I. W. Smith, E. Herbst and Q. Chang, Mon. Not. R. Astron. Soc., 2004, 350, 323–330 CrossRef CAS
.
- J. G. de la Concepción, I. Jiménez-Serra, V. Rivilla, L. Colzi and J. Martín-Pintado, Astron. Astrophys., 2023, 673, A118 CrossRef
.
- E. Herbst, J. Phys.: Conf. Ser., 2005, 17 CrossRef CAS
.
- W. D. Watson, Astrophys. J., 1973, 183, L17 CrossRef CAS
.
-
D. K. Bohme, Structure/reactivity and thermochemistry of ions, Springer, 1987, pp. 219–246 Search PubMed
.
- N. Adams, D. Smith and T. Millar, Mon. Not. R. Astron. Soc., 1984, 211, 857–865 CrossRef CAS
.
- T. Heil, Nucl. Instrum. Methods Phys. Res., Sect. B, 1987, 23, 222–225 CrossRef
.
- D. K. Böhme, Phys. Chem. Chem. Phys., 2011, 13, 18253–18263 RSC
.
- J. Lilensten, C. S. Wedlund, M. Barthélémy, R. Thissen, D. Ehrenreich, G. Gronoff and O. Witasse, Icarus, 2013, 222, 169–187 CrossRef CAS
.
- D. B. Rap, T. J. van Boxtel, B. Redlich and S. Brunken, J. Phys. Chem. A, 2022, 126, 2989–2997 CrossRef CAS PubMed
.
- M. Selvaraj, A. Subramani, K. Ramanathan, M. Cautero, R. Richter, N. Pal, P. Bolognesi, L. Avaldi, M. Vinitha and C. S. Jureddy,
et al.
, Chem. Phys. Lett., 2023, 140716 CrossRef CAS
.
- C.-M. Tseng, Y. A. Dyakov, C.-L. Huang, A. M. Mebel, S. H. Lin, Y. T. Lee and C.-K. Ni, J. Am. Chem. Soc., 2004, 126, 8760–8768 CrossRef CAS PubMed
.
- J. C. Choe, Bull. Korean Chem. Soc., 2013, 34, 3249–3252 CrossRef CAS
.
- J. C. Choe, N. R. Cheong and S. M. Park, Int. J. Mass Spectrom., 2009, 279, 25–31 CrossRef CAS
.
- G. Gutsev, H. López Peña, S. McPherson, D. A. Boateng, B. Ramachandran, L. Gutsev and K. M. Tibbetts, J. Phys. Chem. A, 2020, 124, 3120–3134 CrossRef CAS PubMed
.
- V. Vuitton, R. Yelle and M. McEwan, Icarus, 2007, 191, 722–742 CrossRef
.
- J. Westlake, C. Paranicas, T. Cravens, J. Luhmann, K. Mandt, H. Smith, D. Mitchell, A. Rymer, M. Perry and J. Waite Jr,
et al.
, Geophys. Res. Lett., 2012, 39 Search PubMed
.
- P. O’keeffe, P. Bolognesi, M. Coreno, A. Moise, R. Richter, G. Cautero, L. Stebel, R. Sergo, L. Pravica and Y. Ovcharenko,
et al.
, Rev. Sci. Instrum., 2011, 82 Search PubMed
.
- R. Blyth, R. Delaunay, M. Zitnik, J. Krempasky, R. Krempaska, J. Slezak, K. Prince, R. Richter, M. Vondracek and R. Camilloni,
et al.
, J. Electron Spectrosc. Relat. Phenom., 1999, 101, 959–964 CrossRef
.
- B. Dick, Phys. Chem. Chem. Phys., 2014, 16, 570–580 RSC
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 Revision E.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed
.
- H. Perreault, L. Ramaley, F. Benoit, P. Sim and R. Boyd, J. Phys. Chem., 1991, 95, 4989–4998 CrossRef CAS
.
- S. Anand and H. B. Schlegel, J. Phys. Chem. A, 2005, 109, 11551–11559 CrossRef CAS PubMed
.
- C. Forgy, A. Schlimgen and D. Mazziotti, Mol. Phys., 2018, 116, 1364–1368 CrossRef CAS
.
- J. H. Eland, Chem. Phys., 2008, 345, 82–86 CrossRef CAS
.
- L. Duchácková, J. Jašík, J. Žabka, D. Ascenzi, E.-L. Zins, D. Schröder, S. D. Price, C. Alcaraz and J. Roithová, Int. J. Mass Spectrom., 2011, 308, 81–88 CrossRef
.
- D. Smith, Chem. Rev., 1992, 92, 1473–1485 CrossRef CAS
.
- W. D. Geppert and M. Larsson, Mol. Phys., 2008, 106, 2199–2226 CrossRef CAS
.
- A. Glassgold, A. Omont and M. Guelin, Astrophys. J., 1992, 396(1), 115–119 CrossRef CAS
.
- G. B. Scott, D. A. Fairley, C. G. Freeman, R. G. Maclagan and M. J. McEwan, Int. J. Mass Spectrom. Ion Processes, 1995, 149, 251–255 CrossRef
.
- T. P. Snow and V. M. Bierbaum, Annu. Rev. Anal. Chem., 2008, 1, 229–259 CrossRef CAS PubMed
.
- A. M. Mebel, M. Agúndez, J. Cernicharo and R. I. Kaiser, Astrophys. J. Lett., 2023, 945, L40 CrossRef
.
| This journal is © the Owner Societies 2024 |