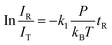Size-dependent reactivity of V_nO⁺ (n = 1–9) clusters with ethane

Abstract

Cost-effective and readily accessible 3d transition metals (TMs) have been considered as promising candidates for alkane activation while 3d TMs especially the early TMs are usually not very reactive with light alkanes. In this study, the reactivity of V_n⁺ and V_nO⁺ (n = 1–9) cluster cations towards ethane under thermal collision conditions has been investigated using mass spectrometry and density functional theory calculations. Among V_n⁺ (n = 1–9) clusters, only V_3–5⁺ can react with C₂H₆ to generate dehydrogenation products and the reaction rate constants are below 10⁻¹³ cm³ molecule⁻¹ s⁻¹. In contrast, the reaction rate constants for all V_nO⁺ (n = 1–9) with C₂H₆ significantly increase by about 2–4 orders of magnitude. Theoretical analysis evidences that the addition of ligand O affects the charge distribution of the metal centers, resulting in a significant increase in the cluster reactivity. The analysis of frontier orbitals indicates that the agostic interaction determines the size-dependent reactivity of V_nO⁺ cluster cations. This study provides a novel approach for improving the reactivity of early 3d TMs.

---

Introduction

Alkanes are highly abundant in nature and constitute the primary components of natural gas and crude oil, serving as essential raw materials for the chemical industry.¹ However, due to the robust thermodynamic nature of the C–H bond, its activation presents a considerable challenge.² Consequently, investigating the mechanisms of C–H bond activation is of great significance in the development of better performing catalysts for alkane transformation.³ The investigation of the reactions between gas-phase atomic clusters with alkane molecules is regarded as a crucial approach to comprehending the mechanisms of C–H activation at the molecular level.

Numerous studies have been documented on the activation and conversion of alkanes by gas-phase metal clusters. There has been a predominant focus on the investigation of noble metal clusters. For example, the previous investigations have shown that Pt_n⁺ (n ⩽ 9),^4–7 Pd_n⁺ (n = 2 and 3),⁸ Rh_n⁺ (n = 1–30),⁹ Os⁺,^10,11 and Ir^+12,13 exhibit notable reactivity in dehydrogenation of light alkanes. Additionally, neutral clusters such as Pd_n (n ⩽ 23)¹⁴ and Pt_n (n ⩽ 24),¹⁵ and the anionic clusters such as Rh_n⁻ (n ⩽ 10),¹⁶ Rh_nC₂₀H₁₀⁻ (n = 4–7),¹⁷ and Pt_n⁻ (n ⩽ 7)⁶ have been demonstrated to have highly size-selective patterns in the activation of the C–H bond in methane. In contrast, the studies on alkane C–H activation by base metals are very limited. The reactions of the clusters of 5d base metals Ta^18–23 and W^24–27 with methane have been reported. Although 3d transition metals (TMs) are more abundant and economically accessible compared to 5d TMs, studies on alkane C–H activation by 3d TMs, especially the early 3d TMs, are very limited. The studies conducted by Armentrout et al. demonstrated that V⁺ is inactive with CH₄.²⁸ In a previously documented study involving the reaction of Ta_xO⁺ (x = 4 and 5) with methane,²⁰ it was observed that the incorporation of the ligand O into the metal clusters markedly enhanced the cluster reactivity. In a subsequent investigation of methane activation by tungsten species,²⁴ it was noted that W_n⁺ (n ⩾ 2) exhibited minimal reactivity, while the addition of O significantly promoted CH₄ dehydrogenation. These observations prompted us to explore methodologies for improving the reactivity of 3d TM clusters with light alkanes by doping oxygen atoms.

In this study, the reactivity of V_n⁺ and V_nO⁺ (n = 1–9) with ethane was investigated using a combination of time-of-flight mass spectrometry and quantum chemical calculations. It was observed that the reactivity of vanadium cluster cations toward ethane can be significantly enhanced with the addition of O ligands, affirming the modulating effect of O on the reactivity of early 3d TMs. Insights into improving the catalytic activity of these metals are thus provided. Note that the reaction of V_n⁺ (n = 1–9) with H₂O has been experimentally investigated in the literature.²⁹

Methods

Experimental methods

A laser ablation method was used to generate the V_n⁺ and V_nO⁺ cations through the irradiation of a focused pulsed laser beam (532 nm, 5–8 mJ, 10 Hz) onto a rotating and translating V disk in the presence of 4 atm He carrier gas. The cluster cations of interest, V_n⁺ (n = 1–9) and V_nO⁺ (n = 1–9), were mass-selected using a quadrupole mass filter (QMF)³⁰ and then introduced into the linear ion trap (LIT)³¹ reactor. After thermalization by collisions with a pulse of cooling gas He (3 Pa), the cluster ions reacted with a pulse of C₂H₆ seeded in He gas for about 2 ms. The temperature of the cooling gas, the reactant gas (C₂H₆), and the LIT reactor was around 298 K. The masses and abundances of the reactant and product cations were detected using a home-made reflection time-of-flight mass spectrometer (TOF-MS).³²

Computational methods

Density functional theory (DFT) calculations by using the Gaussian 09 program³³ were carried out to investigate the structures of V_n⁺ and V_nO⁺ (n = 1–9) cations, as well as the reaction mechanisms of V_n⁺ (n = 2 and 3) and V_nO⁺ (n = 1, 2, and 3) with C₂H₆. The benchmark calculations showed that the BPBE functional^34,35 generally performed best for the bond energy of V–V, V–C, V–O, V–H, C–H, and H–H compared with the experimental values (Table S1, ESI†). Thus, the BPBE functional was adopted in this work. For all the calculations, the TZVP basis sets³⁶ were used for all of the elements (C, H, O, and V). A Fortran code based on a genetic algorithm³⁷ was used to generate initial guess structures of V_n⁺ (n = 7–9) and V_nO⁺ (n = 5–9) clusters. Reaction mechanism calculations involved the geometric structures of reaction intermediates (IMs) and transition states (TSs) that were optimized and vibrational frequencies were calculated to check that each of the IMs and TSs has zero or only one imaginary frequency. The TSs were optimized using the Berny algorithm method.³⁸ The initial guess structures of the TS species were obtained through relaxed potential energy surface scans using single or multiple internal coordinates. Intrinsic reaction coordinate calculations³⁹ were conducted to make sure that a TS connects two appropriate IMs. The zero-point vibration-corrected energies (ΔH₀) in eV are reported in this work. The natural bond orbital (NBO) analysis was performed with the software NBO 5.9.⁴⁰

Results

Experimental results

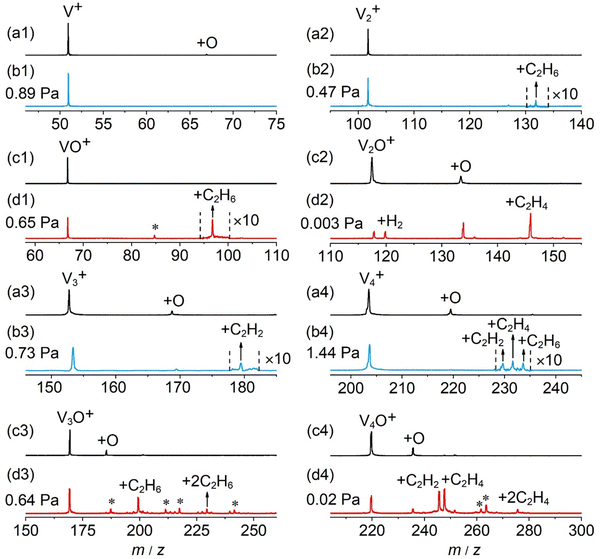
In general, a sharp contrast in reactivity difference of pure vanadium cluster cations versus vanadium oxide cluster cations with ethane was observed (Fig. S1, ESI†): V_n⁺ with n = 2–5 can lead to the dehydrogenation reaction or adsorption reaction with ethane. However, with the introduction of one oxygen atom, all V_nO⁺ (n = 1–9) can generate adsorption/dehydrogenation product ions with ethane. The typical TOF mass spectra for the reactions of mass-selected V_n⁺ and V_nO⁺ (n = 1–4) with C₂H₆ are shown in Fig. 1. When V⁺ interacts with 0.89 Pa C₂H₆ for about 2 ms, no new product peaks were observed relative to the background peak generated from the reaction with water impurity. As the cluster size of V_n⁺ increases, weak cluster reactivity can be observed. Fig. 1(b2) shows that in the reaction between V₂⁺ and 0.47 Pa C₂H₆ for 2 ms, a very weak product peak (V₂C₂H₆⁺) for adsorbing a single C₂H₆ molecule appeared. When the cluster upsizes to V₃⁺ and V₄⁺, the dehydrogenation products of V₃C₂H₂⁺ and V₄C₂H_2,4⁺ were observed in Fig. 1(b3) and (b4). In contrast to the case of V_n⁺, the reactivity of V_nO⁺ with C₂H₆ was greatly improved. As demonstrated in Fig. 1(d1) and (d3), V_1,3O ⁺ were able to produce the adsorption products. In the reaction system of V_2,4O⁺, more than half of the initial reactant ions were converted to dehydrogenation product ions at low pressure of C₂H₆ (⩽0.02 Pa, Fig. 1(d2) and (d4)). In addition, a relatively weak signal that can be assigned to V₂OH₂⁺ appears in the reaction of V₂O⁺ with C₂H₆, corresponding to the loss of a C₂H₄ molecule (V₂O⁺ + C₂H₆ → V₂OH₂⁺ + C₂H₄).

Fig. 1 TOF mass spectra for the reactions of mass-selected V⁺ (a1), VO⁺ (c1), V₂⁺ (a2), V₂O⁺ (c2), V₃⁺ (a3), V₃O⁺ (c3), V₄⁺ (a4), and V₄O⁺ (c4) cations with C₂H₆. The pressures of C₂H₆ are shown. The reaction times are around 2 ms. The peaks marked with asterisks originated from water impurities. The V_nX⁺ and V_nOX⁺ (X = C₂H₂, C₂H₄, etc.) species are labeled as +X.

The rate constants (k₁) for the pseudo-first-order reactions of V_n⁺ and V_nO⁺ (n = 1–9) with C₂H₆ were estimated using the following equation:

in which I_R is the intensity of reactant cluster ions after the reaction, I_T is the total ion intensity including the product ion contribution except for water adsorption, P is the effective pressure of the reactant gas, k_B is the Boltzmann constant, t_R is the reaction time, and T is the temperature of the reactant gas. The k₁ values for the reactions of V_2–5⁺ and V_1–9O⁺ with C₂H₆ were determined (Fig. S2, S3 ESI† and Table 1) and are shown in Fig. 2 as a function of the cluster size. For the V_n⁺ system, triatomic V₃⁺ has a slightly smaller k₁ than diatomic V₂⁺. The k₁ values of V_n⁺ (n = 3–5) + C₂H₆ increased with the increase of the cluster size, and the highest reactivity was observed for V₅⁺. This result is consistent with the highest reactivity of V₅⁺ in the reaction of V_n⁺ with H₂O, which was explained with the synergistic effect of three V atoms.²⁹ In sharp contrast, for each of the n values, the V_nO⁺ cluster is more reactive than V_n⁺ by two or more orders of magnitude and exhibits a completely different reactivity variation with respect to the cluster size. Among the V_nO⁺, the reaction couple V₂O⁺/C₂H₆ has the largest k₁ of 1.49 × 10⁻⁹ cm³ molecule⁻¹ s⁻¹. The k₁ values of VO⁺ and V₃O⁺ are smaller than that of V₂O⁺. When the cluster upsizes, the reactivities of V_nO⁺ decline, and the k₁ values gradually decrease from 2.01 × 10⁻¹⁰ cm³ molecule⁻¹ s⁻¹ for n = 4 to 2.94 × 10⁻¹³ cm³ molecule⁻¹ s⁻¹ at n = 9. The reactivity comparison of V_n⁺ and V_nO⁺ (n = 1–9) cluster cations indicates that oxygen atoms play a crucial role in modulating the reactivity of the vanadium cluster cations. The doping of the O atom is particularly significant in enhancing the metal cluster reactivity.

Table 1 Rate constants (k₁, cm³ molecule⁻¹ s⁻¹) for the reaction of V_n⁺ and V_nO⁺ with C₂H₆

Cation	k 1, C2H6	Cation	k 1, C2H6
V^+	—	VO^+	3.33 × 10^−13
V2^+	1.13 × 10^−13	V2O^+	1.49 × 10^−9
V3^+	8.55 × 10^−14	V3O^+	2.14 × 10^−12
V4^+	1.32 × 10^−13	V4O^+	2.01 × 10^−10
V5^+	4.04 × 10^−12	V5O^+	1.50 × 10^−10
V6^+	—	V6O^+	7.28 × 10^−11
V7^+	—	V7O^+	1.49 × 10^−11
V8^+	—	V8O^+	1.85 × 10^−12
V9^+	—	V9O^+	2.94 × 10^−13

---

Fig. 2 Relative rate constants (k₁^rel) for the reactions of V_n⁺ and V_nO⁺ (n = 1–9) with C₂H₆. The k₁^rel values are relative to the absolute rate constant k₁(V₂O⁺ + C₂H₆) = 1.49 × 10⁻⁹ cm³ molecule⁻¹ s⁻¹. The uncertainties (within 30%) of k₁^rel values are shown. The uncertainties of the absolute k₁ values are within factors of 2–3. The variations of natural charges (e) of oxygen atoms in V_nO⁺ clusters are also shown for understanding the relative activity.

Computational results

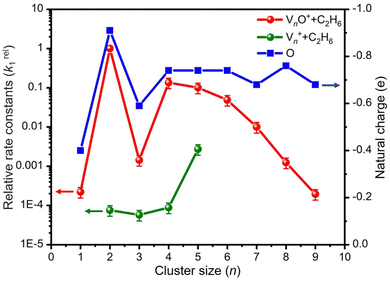
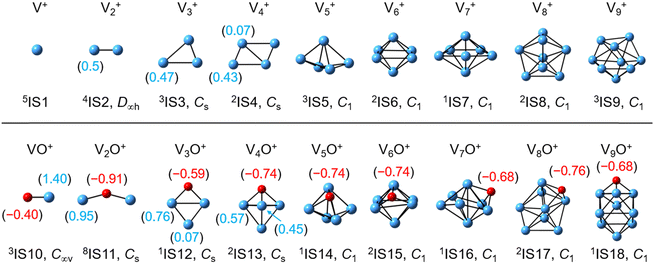
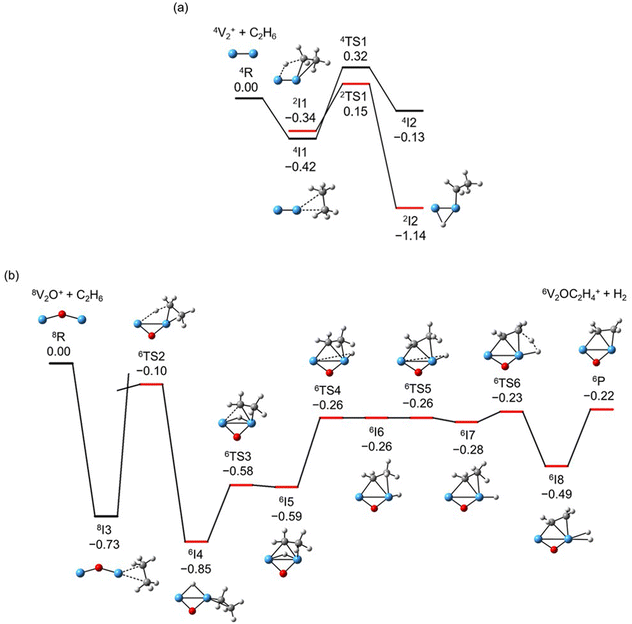
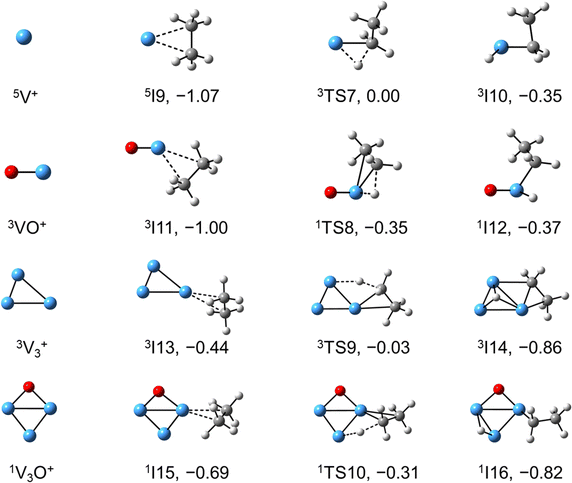
The global minimum structures of V_n⁺ and V_nO⁺ (n = 1–9) clusters from the DFT calculations are shown in Fig. 3 and Fig. S4–S8 (ESI†). Most of the lowest-lying isomers are consistent with structures calculated with the BP86 method in the literature, except V₆⁺ and V_2,9O⁺.²⁹ For a deeper understanding of the differences in reactivity between V_n⁺ and V_nO⁺, the reaction pathways of n = 1–3 reaction systems were calculated using the DFT method and the results for V₂⁺ and V₂O⁺ cations with C₂H₆ are shown in Fig. 4. When a C₂H₆ molecule approaches the V₂⁺ cation, an encounter complex is formed with a binding energy of 0.42 eV (⁴I1). The subsequent step for the activation of the first C–H bond involves a spin flip from quartet to doublet states (Fig. S9a, ESI†). Since the energy of ²TS1 is 0.15 eV higher than those of the separated reactants, the process of C–H cleavage initiated by V₂⁺ is kinetically unfavorable under thermal collision conditions. The V₂C₂H₆⁺ weakly observed in the experiment (Fig. b2) is thus an adsorption product and the C–H bond is not cleaved. In contrast to the inertness of V₂⁺ in cleaving the C–H bond, V₂O⁺ can react with C₂H₆ to form the dehydrogenation product V₂OC₂H₄⁺. In V₂O⁺ + C₂H₆, the V atom captures C₂H₆ with a binding energy of 0.73 eV to form the complex ⁸I3. The breaking of the first C–H bond proceeds through a mechanism of synergistic activation by the V–V metal bond involving a spin crossing process (octet → sextet, Fig. S9b, ESI†), resulting in the formation of the lowest energy intermediate ⁶I4 with a four-membered –V–H–V–O-ring and a three-membered –C–C–V-ring. The transition from ⁸I3 to ⁶I4 is kinetically favorable since TS2 has energy lower than that of the isolated reactants by 0.1 eV. Then, the C₂H₅ moieties in ⁶I4 moves towards another V atom, resulting in the formation of a new V–C bond in ⁶I5. After a structural rearrangement to break the V–H bond in ⁶I5, the second C–H bond can be cleaved. The resulting intermediate ⁶I8 has enough internal energy to evaporate the H₂ unit to produce the experimentally observed V₂OC₂H₄⁺ product ion.

Fig. 3 DFT-optimized most stable structures of the V_n⁺ and V_nO⁺ (n = 1–9) clusters at the BPBE level. The point group is given under each structure. The superscripts indicate the spin multiplicities. The natural charge (e) of the V atoms and O atoms is shown in parentheses.

Fig. 4 DFT calculated potential energy profiles for the reactions of V₂⁺ and V₂O⁺ with C₂H₆. Relative energies of the reaction intermediates (I1–I8), transition states (TS1–TS6), and products (P) with respect to the separated reactants (V₂O_0,1⁺ + C₂H₆) are given in eV (ΔH₀). The superscripts indicate spin multiplicities.

The systems of V_nO_m⁺ (n = 1 and 3; m = 0 and 1) involving the first C–H bond cleavage, which is generally viewed as the rate limiting step in alkane conversion, were also considered. As shown in Fig. 5, the oxidative addition of the C–H bond of C₂H₆ by the cluster systems of V_1–3⁺ encounters the energy barriers in the range of −0.03–0.15 eV. Note that the direct evaporation of the C₂H₆ from adsorption intermediates (I1, I9, and I13) is an entropically more favorable process, which is in good agreement with the experimental results that only very weak adsorption/dehydrogenation products could be observed. In sharp contrast, the C–H bond cleavage of C₂H₆ mediated by V_1–3O⁺ experiences a significantly negative energy barrier (⩽−0.1 eV). For the VO⁺/C₂H₆ system, the V atom readily traps the C₂H₆ molecule and releases 1.00 eV energy (³I11). Then, the C–H bond is inserted by the V atom accompanied by a spin flip from triplet to singlet states (³I11 → ¹TS8). The energy of the formed intermediate ¹I12 (ΔH₀ = −0.37 eV) closely approximates that of the transition state ¹TS8 (ΔH₀ = −0.35 eV), facilitating an almost barrierless transition from I12 back to I11. Although ³I11 can dissociate back to the separated reactants (³I11 → VO⁺ + C₂H₆), a small portion of I11 may be stabilized through the collisions with the bath gas, resulting in the observation of the weak adsorption product VOC₂H₆⁺ in the experiment (Fig. d1). In contrast, the intermediates (I4–I8) and transition states (TS3–TS6) along the reaction pathway of V₂O⁺/C₂H₆ are much lower in energy than the TS2 state (Fig. 4). Once intermediate I4 is formed, it has more chance to form I8 that can dissociate into V₂OC₂H₄⁺ + H₂ (⁶P), which is consistent with the experimental observation that V₂O⁺ reacts much faster than VO⁺ (Fig. 2). For the system of V₃O⁺/C₂H₆, considering the low energy barrier of C–H activation (−0.31 eV), I16 shows a higher tendency than I4 to proceed back to the adsorption intermediate (I15) and decompose to the V₃O⁺ + C₂H₆ under entropy-driven conditions, which rationalizes the lower reaction rate of V₃O⁺ + C₂H₆ than that of V₂O⁺ + C₂H₆ in the experiment (Fig. 2).

Fig. 5 DFT calculated the structures of V_n⁺ and V_nO⁺ (n = 1, 3) isomers, reaction IMs, and transition states for the first C–H bond activation of ethane. The relative energies with respect to the separated reactants (V_1,3O_0,1⁺ + C₂H₆) are given in eV (ΔH₀).

Discussion

Reactions involving atomic metal ions and the corresponding oxide species with alkanes have been extensively documented,^41–52 whereas the oxo-ligand effect of polyatomic metal species has received limited attention. Eckhard et al. performed a comparative study on the reactions of CH₄ with Ta_x⁺ and Ta_xO⁺ (x = 4 and 5) clusters.²⁰ It has been demonstrated that the doped oxygen atom does not directly participate in the reaction. Instead, it modifies the local electronic charge distribution of the tantalum clusters that appears to be favorable for C–H bond activation through a metal insertion mechanism. Given the previous proposals, we conducted a comparison of the charge changes of atoms in the V_n⁺ and V_nO⁺ systems. In the literature, the C–H cleavage involves electron transfer from the occupied orbitals of alkane to the metal empty orbitals. The amount of positive charges within the cluster will determine its reactivity towards the alkane. According to the NBO analysis shown in Fig. 3, the high electron-withdrawing capability of the O atom significantly increases the positive charge on V atoms in V_nO⁺ systems. Consequently, the V_nO⁺ clusters can have much higher reactivity than the V_n⁺. For V_nO⁺ cluster systems, the V atom adjacent to the O atom serves as the adsorption site for C₂H₆ and as reactive sites to bring about C–H activation. The accumulation of large amounts of positive charges in V induced by oxygen is the crucial factor to profoundly affect the cluster reactivity. In other words, a striking correlation between the negative charge on O atom and k₁ values emerges as shown in Fig. 2 and 3. V₂O⁺ with the most negative charge (−0.91e) on O among V_1–3O⁺ exhibits the highest reactivity. The oxygen in VO⁺ carries the least negative charge (−0.40e), resulting in its lowest reactivity. However, the reactivity of V_4–9O⁺ clusters decreases with the increase of the cluster size, while the negative charge on the O atom almost maintains a constant value (−0.68 to −0.74e). This could be attributed to the more crowded steric structure, which hinders the activation of the C–H bond.

In transition-metal-catalyzed organic reactions, agostic interaction is commonly defined as the intramolecular interaction between the hydrogen atom of a C–H bond with a nearby metallic center, which plays a crucial role in C–H bond activation.^53–56 In such interaction, the σ(C–H) orbital (alkane HOMO) acts as a donor orbital, whereas the acceptor orbitals could be empty molecular orbitals (cluster LUMO) of metal species.^57–59 The smaller energy gap helps to form stronger agnostic interaction, enhancing the electron transfer to activate the C–H bond. Therefore, to further explore the effect of the oxygen ligand on the reactivity of metal clusters of different sizes, we analyzed the orbital interactions between V_nO⁺ and C₂H₆ during the reactions (e.g., V₃O⁺/C₂H₆ couple in Fig. S10, ESI†) and the HOMO of C₂H₆ and the LUMO of V_nO⁺ (n = 1–9) cations are shown in Fig. 6. For V_nO⁺ with small cluster sizes (n = 1–3), the energy gap of V₂O⁺ (LUMO) ↔ C₂H₆ (HOMO) is smaller compared to that of VO⁺ and V₃O⁺, leading to the strongest agostic interaction and the fastest reaction rate for the V₂O⁺/C₂H₆ couple (Fig. 2). In contrast, the slowest reaction rate of VO⁺ with C₂H₆ can be attributed to the largest energy gap of VO⁺ (LUMO) ↔ C₂H₆ (HOMO). For the V_nO⁺ clusters with larger sizes (4 ⩽ n ⩽ 9), the energy gap increases as the cluster is upsized, resulting in weaker and weaker agostic interactions, which is consistent with the rate constant decrease of V_nO⁺ with C₂H₆ from n = 4 to n = 9 (Fig. 2).

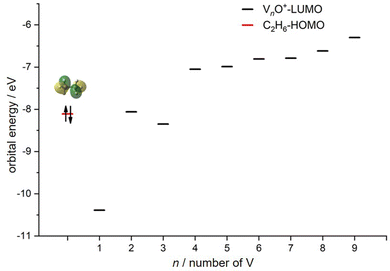Fig. 6 HOMO levels of C₂H₆ and LUMO levels of V_nO⁺ (n = 1–9) cations. The up and down arrows denote α and β electrons, respectively.

Conclusion

The reactions of ethane with vanadium cluster cations V_n⁺ (n = 1–9) and their corresponding oxide systems V_nO⁺ (n = 1–9) have been comparatively studied via mass-spectrometry-based experiments. The O atom doped vanadium clusters are much more reactive than the non-doped V_n⁺ ones. The reactivity of V₂O⁺ is enhanced by four orders of magnitude with respect to that of V₂⁺ and V₂O⁺ is also the most reactive cluster among V_nO⁺ clusters (n = 1–9). The mechanistic studies reveal that the reactivity of V_nO⁺ clusters is enhanced by the modification of charge distribution within the cluster through the introduction of oxygen atoms. The agostic interaction to interpret the size-dependent reactivity of V_nO⁺ has been proposed. This study not only extends our understanding of C–H activation of light alkanes (ethane) by metal systems but also provides insights into doping of O atoms to enhance the reactivity of early 3d transition metals.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (No. 22203078, 92161205, 22121002, and 22322307), the Youth Innovation Promotion Association CAS (No. 2018041), and the China Postdoctoral Science Foundation (No. 2022TQ0289).

References

1. Y. Wang, P. Hu, J. Yang, Y.-A. Zhu and D. Chen, Chem. Soc. Rev., 2021, 50, 4299–4358.
2. X.-S. Xue, P. Ji, B. Zhou and J.-P. Cheng, Chem. Rev., 2017, 117, 8622–8648.
3. Y. Liu, J.-C. Liu, T.-H. Li, Z.-H. Duan, T.-Y. Zhang, M. Yan, W.-L. Li, H. Xiao, Y.-G. Wang, C.-R. Chang and J. Li, Angew. Chem., Int. Ed., 2020, 59, 18586–18590.
4. G. Kummerlöwe, I. Balteanu, Z. Sun, O. P. Balaj, V. E. Bondybey and M. K. Beyer, Int. J. Mass Spectrom., 2006, 254, 183–188.
5. C. Adlhart and E. Uggerud, Chem. Commun., 2006, 2581–2582.
6. U. Achatz, C. Berg, S. Joos, B. S. Fox, M. K. Beyer, G. Niedner-Schatteburg and V. E. Bondybey, Chem. Phys. Lett., 2000, 320, 53–58.
7. C. Adlhart and E. Uggerud, Chem. – Eur. J., 2007, 13, 6883–6890.
8. S. M. Lang, A. Frank and T. M. Bernhardt, J. Phys. Chem. C, 2013, 117, 9791–9800.
9. C. A. E. Uggerud, J. Chem. Phys., 2005, 123, 214709.
10. P. B. Armentrout, S. E. J. Kuijpers, O. V. Lushchikova, R. L. Hightower, G. C. Boles and J. M. Bakker, J. Am. Soc. Mass Spectrom., 2018, 29, 1781–1790.
11. P. B. Armentrout, L. Parke, C. Hinton and M. Citir, ChemPlusChem, 2013, 78, 1157–1173.
12. F.-X. Li, X.-G. Zhang and P. B. Armentrout, Int. J. Mass Spectrom., 2006, 255–256, 279–300.
13. O. W. Wheeler, M. Salem, A. Gao, J. M. Bakker and P. B. Armentrout, Int. J. Mass Spectrom., 2019, 435, 78–92.
14. P. Fayet, A. Kaldor and D. M. Cox, J. Chem. Phys., 1990, 92, 254–261.
15. D. M. Cox, D. J. Trevor and A. Kaldor, J. Am. Chem. Soc., 1990, 112, 3742–3749.
16. Y. Ren, Y. Yang, Y.-X. Zhao and S.-G. He, J. Phys. Chem. C, 2019, 123, 17035–17042.
17. X.-G. Zhao, Z.-P. Zhao, Y.-X. Zhao and S.-G. He, J. Phys. Chem. Lett., 2023, 14, 9192–9199.
18. J. F. Eckhard, T. Masubuchi, M. Tschurl, R. N. Barnett, U. Landman and U. Heiz, J. Phys. Chem. A, 2021, 125, 5289–5302.
19. J. Lengyel, N. Levin, F. J. Wensink, O. V. Lushchikova, R. N. Barnett, U. Landman, U. Heiz, J. M. Bakker and M. Tschurl, Angew. Chem., Int. Ed., 2020, 59, 23631–23635.
20. J. F. Eckhard, T. Masubuchi, M. Tschurl, R. N. Barnett, U. Landman and U. Heiz, J. Phys. Chem. C, 2018, 122, 25628–25637.
21. N. Levin, J. Lengyel, J. F. Eckhard, M. Tschurl and U. Heiz, J. Am. Chem. Soc., 2020, 142, 5862–5869.
22. T. J. MacMahon, S. W. Buckner, G. D. Byrd and B. S. Freiser, Inorg. Chem., 1989, 28, 3511–3518.
23. C. S. Hinton, L. G. Parke and P. B. Armentrout, J. Phys. Chem. C, 2007, 111, 17773–17787.
24. S. Hirabayashi and M. Ichihashi, J. Phys. Chem. A, 2019, 123, 6840–6847.
25. S. Shin, P. B. Armentrout and R. Liyanage, J. Phys. Chem. A, 2006, 110, 1242–1260.
26. A. Simon, J. Lemaire, P. Boissel and P. Maître, J. Chem. Phys., 2001, 115, 2510–2518.
27. K. K. Irikura and J. L. Beauchamp, J. Am. Chem. Soc., 1991, 113, 2769–2770.
28. N. Aristov and P. B. Armentrout, J. Phys. Chem., 1987, 91, 6178–6188.
29. H. Zhang, H. Wu, Y. Jia, B. Yin, L. Geng, Z. Luo and K. Hansen, Commun. Chem., 2020, 3, 148.
30. Z. Yuan, Y.-X. Zhao, X.-N. Li and S.-G. He, Int. J. Mass Spectrom., 2013, 354–355, 105–112.
31. Z. Yuan, Z.-Y. Li, Z.-X. Zhou, Q.-Y. Liu, Y.-X. Zhao and S.-G. He, J. Phys. Chem. C, 2014, 118, 14967–14976.
32. X.-N. Wu, B. Xu, J.-H. Meng and S.-G. He, Int. J. Mass Spectrom., 2012, 310, 57–64.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.01, Gaussian, Inc., Wallingford, CT, 2009.
34. C. Lee, W. Yang and R. G. Parr, Phys. Rev., B Condens. Matter, 1988, 37, 785–789.
35. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
36. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
37. X.-L. Ding, Z.-Y. Li, J.-H. Meng, Y.-X. Zhao and S.-G. He, J. Chem. Phys., 2012, 137, 214311.
38. H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218.
39. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
40. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.9, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2009.
41. J. Roithová and D. Schröder, Chem. Rev., 2010, 110, 1170–1211.
42. R. Wesendrup, C. Heinemann and H. Schwarz, J. Phys. Chem. A, 1995, 239, 75–83.
43. S. Zhou, J. Li, M. Schlangen and H. Schwarz, Angew. Chem., Int. Ed., 2016, 55, 10877–10880.
44. K. K. Irikura and J. L. Beauchamp, J. Am. Chem. Soc., 1989, 111, 75–85.
45. K. Chen, Z.-C. Wang, M. Schlangen, Y.-D. Wu, X. Zhang and H. Schwarz, Chem. – Eur. J., 2011, 17, 9619–9625.
46. I. Kretzschmar, A. Fiedler, D. Schröder and H. Schwarz, J. Am. Chem. Soc., 1996, 118, 9941–9952.
47. A. Fiedler, M. F. Ryan, D. Schroeder and H. Schwarz, J. Am. Chem. Soc., 1995, 117, 2033–2040.
48. H. Schwarz, D. Schröder, D. E. Clemmer, Y. Chen, P. B. Armentrout and V. I. Baranov, Int. J. Mass Spectrom. Ion Processes, 1997, 161, 175–191.
49. A. Fiedler, M. F. Ryan, D. Schroeder and H. Schwarz, Organometallics, 1994, 13, 4072–4081.
50. A. Božović, S. Feil, G. K. Koyanagi, A. A. Viggiano, X. Zhang, M. Schlangen, H. Schwarz and D. K. Bohme, Chem. – Eur. J., 2010, 16, 11605–11610.
51. N. Dietl, C. van der Linde, M. Schlangen, M. K. Beyer and H. Schwarz, Angew. Chem., Int. Ed., 2011, 50, 4966–4969.
52. L. Yue, S. Zhou, X. Sun, M. Schlangen and H. Schwarz, Angew. Chem., Int. Ed., 2018, 57, 3251–3255.
53. G. Logothetis and P. L. A. Popelier, J. Organomet. Chem., 1998, 555, 101–111.
54. M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914.
55. L. Lin, D. M. Spasyuk, R. A. Lalancette and D. E. Prokopchuk, J. Am. Chem. Soc., 2022, 144, 12632–12637.
56. L. Andrews, H.-G. Cho and X. Wang, Angew. Chem., Int. Ed., 2004, 44, 113–116.
57. M. Lein, Coord. Chem. Rev., 2009, 253, 625–634.
58. N. Berkaïne, P. Reinhardt and M. E. Alikhani, Chem. Phys., 2008, 343, 241–249.
59. K. M. Altus and J. A. Love, Commun. Chem., 2021, 4, 173.

---

Footnote

† Electronic supplementary information (ESI) available: Additional experimental and theoretical results (data analysis, DFT calculated structures and reaction mechanisms). See DOI: https://doi.org/10.1039/d4cp00857j

---