Magnetism of single-doped paramagnetic tin clusters studied using temperature-dependent Stern–Gerlach experiments with enhanced sensitivity: impact of the diamagnetic ligand field and paramagnetic dopant†
Filip
Rivic
 * and
Rolf
Schäfer
* and
Rolf
Schäfer

Technical University of Darmstadt, Eduard-Zintl-Institute, Peter-Grünberg-Straße 8, 64287 Darmstadt, Germany. E-mail: filip.rivic@tu-darmstadt.de
First published on 19th April 2024
Abstract
In this work, the magnetic properties of tetrel clusters SnNTM, which are singly doped with transition metals (TM), are investigated. On the one hand, the number of tetrel atoms (N = 11, 12, 14 and 17 with TM = Mn) is varied; on the other hand, different transition metals (N = 14, TM = Cr, Mn, Fe) are studied. Magnetic deflection experiments under cryogenic conditions show that the variation of the number of tetrel atoms strongly changes the magnetic properties of the Mn-doped clusters. It is observed that Sn12Mn, Sn11Mn and Sn14Mn partially show super-atomic behaviour, while spin relaxation occurs in Sn17Mn. Magnetic deflection experiments at higher nozzle temperatures were carried out for the first time enhanced by a second parallel-aligned Stern–Gerlach magnet to achieve larger deflections. The resulting temperature-dependent one-sided deflections are quantitatively analysed using Curie's law and show that Sn17Mn possesses the highest magnetic moment of these clusters, followed by Sn12Mn and Sn11Mn. Sn14Mn shows the lowest magnetic moment. The replacement of Mn by Cr in Sn14Mn leads to a diamagnetic singlet, i.e., the magnetic moment of Cr in Sn14Cr is completely quenched. The replacement of Mn by Fe in turn leads to a paramagnetic species, whereby Sn14Fe is most likely present as a triplet. On this basis, the geometrical and electronic structures are analysed using quantum chemical calculations, indicating an arachno-type structure for Sn14Cr, Sn14Mn and Sn14Fe, which has already been predicted in the literature for Si14Cr. This is experimentally confirmed by deflection of molecular beams with an electric field under cryogenic conditions, suggesting that the arachno-type geometry is crucial for the overall stability of the transition-metal-doped tetrel clusters Sn14TM with TM = Cr, Mn, Fe.
1 Introduction
The interplay between geometric structure and magnetic properties is crucial for applications of nanomaterials in sensor technology, catalysis and spintronics.1–3 Paramagnetic single-atom-doped tetrel clusters as nano-systems are ideal models for understanding the influence of particle size on the magnetic behaviour.4–7 Since the pure tetrel clusters are diamagnetic, doping with a transition metal makes it possible to prepare magnetic cluster compounds in a targeted manner. The fact that such compounds have great application potential is demonstrated by paramagnetic nitrogen defects in the diamond lattice, which are used as magnetosensors or can also have applications in quantum cryptography as emitters in a solid-state-based single photon source.8,9 In order to investigate the intrinsic magnetic behaviour of the doped tetrel clusters, i.e., without environmental influences, Stern–Gerlach deflection experiments can be used.10–13The internal temperature of the clusters is an important factor, especially influencing the magnetic response.6,14–18 Only a single-sided deflection of the cluster beam due to spin relaxation is generally observed, if the clusters are vibrationally excited. In contrast, deflection experiments under cryogenic conditions can also enable the observation of super-atomic behaviour.6,15,19 This directly permits the determination of the spin multiplicity 2S + 1 and the g-factor of the investigated cluster species. However, it must be noted that for clusters with a spin quantum number S > 1/2, zero-field splitting (ZFS) can also influence the observed magnetic response.20,21 Depending on the sign and magnitude of the ZFS, only a part of the magnetic states MS is accessible under cryogenic conditions. This means that if the zero-field splitting energy is comparable or even larger than the internal thermal energy of the clusters, only a sub-ensemble of the spin states is occupied. Therefore, investigation of the magnetic behaviour over the widest possible temperature range is desirable. Furthermore, the observed one-sided deflection at high temperatures is still an important indicator, since, on the one hand, the value of g2S(S + 1) can be determined from an observed linear behaviour16 enabling information about the g-factor and the multiplicity to be obtained without the observation of super-atomic behaviour and, on the other hand, deviations from this linear behaviour with the reciprocal temperature might also reveal the importance of zero-field effects.
There have been many theoretical studies investigating the geometric structure and magnetic properties of tetrel clusters doped with transition metals, especially for silicon.22–35 Interestingly, for some of the transition-metal-doped clusters, a complete quenching of magnetic moment has been predicted. On the one hand, photoelectron spectroscopy studies on anionic cluster systems were able to partially confirm predictions concerning the geometric structure.27,29,36 On the other hand, the magnetic behaviour of tetrel clusters doped with transition metals has been investigated using X-ray magnetic circular dichroism (XMCD), which also revealed the quenching of high-spin states for endohedral doping.35 An experimental validation of the predicted magnetic behaviour for neutral clusters is still pending. However, it must be noted that the magnetic deflection of the model nano-systems investigated here, in which only one paramagnetic centre is present, is extremely small and thus the precise investigation of the magnetic deflection behaviour is a major challenge. Therefore here, for the first time, magnetic experiments are carried out with two consecutively positioned parallel-aligned Stern–Gerlach deflectors in series in order to increase the effect and, thus, make the magnetic deflection more accessible experimentally. The results show that the magnetic behaviour depends sensitively on the size of the tetrel cluster cage and the transition metal. Exemplary experiments on single Mn-doped tetrel clusters with 11, 12, 14 and 17 tin atoms, and on single Fe-doped and Cr-doped species with 14 tin atoms, are presented here to demonstrate the influence of cluster size and paramagnetic dopant on the geometrical structure and the magnetic properties.
2 Methods
2.1 Stern–Gerlach experiments
The experimental setup is already described in detail elsewhere in the literature,14,37,38 therefore only a brief overview is given here. The molecular beam is generated in a pulsed (10 Hz) laser vaporization source by focusing a frequency-doubled Nd:YAG laser onto a rotating and translating alloyed target rod containing 5 atom% Mn, Fe or Cr in tin. By feeding He gas to the emerging plasma through a pulsed valve, clusters are formed in an agglomeration chamber and thermalized together with the He in a cryogenic nozzle. This nozzle can be cooled down to Tnozzle = 16 K and higher temperatures can be adjusted using a heater cartridge. The cluster beam then expands through a double-skimmer into high-vacuum and passes up to three collimating slits. The experiments at Tnozzle = 16 K were carried out with a single Stern–Gerlach magnet (length 140 mm). Two collimators with a width of 400 μm and a third collimator with a width of 200 μm, located directly in front of the magnet, are used. At higher nozzle temperatures, a second Stern–Gerlach magnet (75 mm) mounted 300 mm in front of the first magnet is introduced. Here, only two collimators with a width of 200 μm are utilized, both in front of the first magnet. Each Stern–Gerlach magnet is characterized by a two-wire geometry39,40 and the direction of both magnetic field gradients is parallel-aligned to maximize the beam deflection in the z-direction. The deflection is probed by a scanning slit along the z-axis and the clusters are then ionized by a F2 excimer laser (7.9 eV). The laser beam is widened by a plane-concave lens to avoid two-photon absorption. Afterwards, the clusters are detected in a time-of-flight mass spectrometer. At every position, which is approached in random order, a mass spectrum averaged over 150 single-shots without an applied field is recorded at first. Then, at the same position, the magnetic field(s) is (are) applied and another mass spectrum is recorded directly afterwards. This procedure is done 2–3 times per position within the course of the measurement of one beam profile.To improve the significance of the beam profiles, several experimental runs are displayed together. This is especially important for the quantitative interpretation of the magnetic deflection of the beam at higher nozzle temperatures. Since here the expected deflection is very small, up to 15 beam profiles are recorded for one nozzle temperature to minimize the statistical errors originating from scattering of the data points. However, in order to do this, the deflection dz has to be transformed into the time-averaged magnetic dipole moment in field direction ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mag,z. For the deflection experiments in which only a single Stern–Gerlach magnet is used, the procedure is already explained in the literature.15,41 In the case of the magnetic deflection with two parallel-aligned Stern–Gerlach magnets,
mag,z. For the deflection experiments in which only a single Stern–Gerlach magnet is used, the procedure is already explained in the literature.15,41 In the case of the magnetic deflection with two parallel-aligned Stern–Gerlach magnets, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mag,z can be calculated by
mag,z can be calculated by
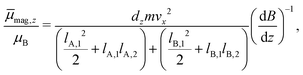 | (1) |
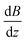 . Please note that
. Please note that 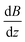 was calibrated with the Bi atom14 and is the same for both magnets. The velocity of the cluster in the flight direction vx is measured using a mechanical shutter based on a hard disk drive.42 By measuring the deflection at higher nozzle temperatures, the temperature-dependent magnetic response of the cluster can be interpreted using the Curie law with16,43
was calibrated with the Bi atom14 and is the same for both magnets. The velocity of the cluster in the flight direction vx is measured using a mechanical shutter based on a hard disk drive.42 By measuring the deflection at higher nozzle temperatures, the temperature-dependent magnetic response of the cluster can be interpreted using the Curie law with16,43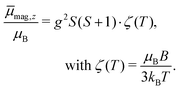 | (2) |
2.2 Beam deflection by an electric field
In order to interpret the results from the beam deflection experiments using a magnetic field, it is necessary to investigate the geometric structure of the clusters. For this, cryogenic beam deflection experiments using an electric field are a suitable and established method.45 The experimental routine and the interpretation of the results in combination with the classical trajectory simulation is already described in detail in the literature,45–48 so that here also only a brief overview is given. The beam deflection profile of a rigid cluster with a non-zero electric dipole moment is broadened in an inhomogeneous electric field compared to the beam profile without a field. Additionally, an overall shift occurs due to the electronic polarizability.45For a quantitative analysis, profiles of beam deflection by an electric field can be simulated based on geometric structures given by quantum chemical calculations.47 Then, a discrimination of potential structural isomers is feasible by comparing the simulated deflection profiles to the experimental ones.45,49,50 The simulated profiles are generated using a classical trajectory consideration of the rotational dynamics in the electric field considering the moments of inertia, and the electric properties. For this, a canonical ensemble of 5000 particles is generated assuming a rotational temperature of TRot = 20 K, which is appropriate for a nozzle temperature of Tnozzle = 16 K.37 Taking the spatial components of the electric dipole moment μx, μy and μz into account, the dipole moment distribution function can be obtained by solving the equations of motion in the electric field.45,46,48 A beam profile is then generated by convolution of this distribution function with a Gaussian function, which is fitted to the experimental data without an applied field.
3 Results
3.1 Influence of the number of tin atoms on the magnetic response
In Fig. 1 the results of the beam deflection experiments using a magnetic field are shown for the SnNMn clusters with N = 12, 11, 17 at Tnozzle = 16 K (top) and Tnozzle = 100 K (middle). By fitting a Gaussian function at higher Tnozzle to both profiles with and without the magnetic fields as shown for the profiles at Tnozzle = 100 K, the temperature-dependent deflection of the molecular beam can be determined. The magnetic moments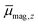 , which were calculated from the deflection dz according to eqn (1), are plotted against the reciprocal nozzle temperature as shown in eqn (2) (bottom).
, which were calculated from the deflection dz according to eqn (1), are plotted against the reciprocal nozzle temperature as shown in eqn (2) (bottom).
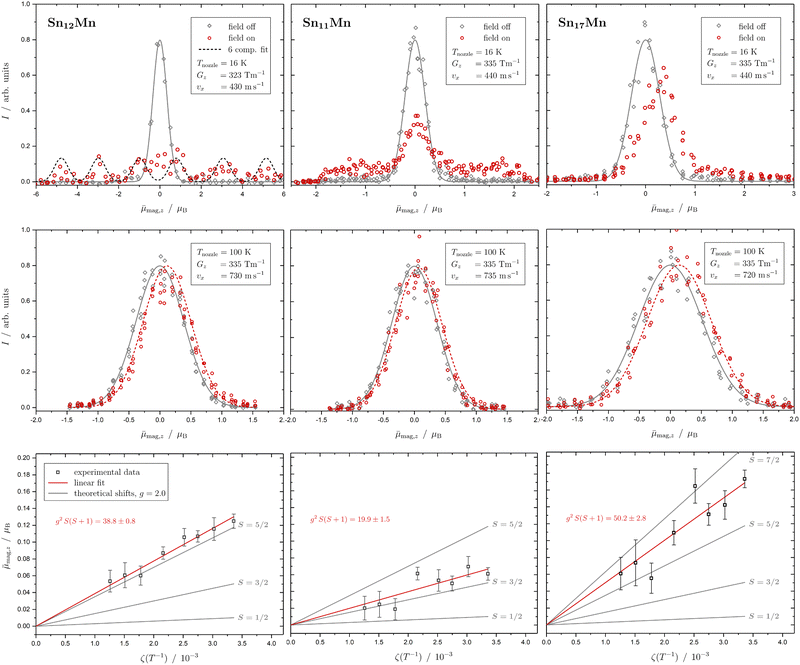 | ||
| Fig. 1 Experimental results from the different experiments of beam deflection by a magnetic field on SnNMn with N = 12, 11, 17 (from left to right) at Tnozzle = 16 K (top), and at Tnozzle = 100 K (middle) for the exemplary deflection experiments at higher nozzle temperatures. The profiles are displayed without (grey diamonds) and with (red circles) applied magnetic field(s). A Gaussian function is fitted to the data without an applied field in both experiments (grey solid line), but only at high Tnozzle, a Gaussian function is also fitted to the beam profile with the magnetic field switched on (red dashed line) to determine the beam deflections quantitatively. In the case of the Sn12Mn cluster, a fit function consisting of 6 Gaussian profiles (one for each possible MS state) is displayed additionally (black dashed line). The magnetic moments μmag,z (black squares), which were calculated from the deflection dz according to eqn (1), are plotted against the reciprocal nozzle temperature as shown in eqn (2) (bottom). The nozzle temperature ranges from 90 to 240 K and the value of the magnetic flux density B is 1.3 T in all experiments. From these so-called Curie plots, the slope of g2S(S + 1) is obtained by linear regression (red solid line) and is also listed in the upper left corner. Theoretical curves (gray solid lines) for different spin quantum numbers S are also shown as a guide, with the g-factor set equal to the value of the free electron. | ||
The beam deflection profile of Sn12Mn at low nozzle temperatures splits into 6 components indicated by a black dashed line in Fig. 1. The g-factor determined from the splitting of the components is based on calibration with a Bi atom14,37,51 and is about g = 2.0. The focusing of the components at ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mag,z < 0 and the defocusing of the components in the gradient direction are a consequence of the two-wire field and can be taken into account quantitatively using a simulation based on the Wigner function formalism.52 Sn12Mn is a special system because it has Ih symmetry.7,19 Therefore, it shows no ZFS and has a low spin–orbit (SO) coupling53 so that the g-factor is close to the value of the free electron. Because of this, it possesses a low spin-rotation (SR) interaction overall.16,54 The spherical symmetry results in a low density of states in the rotational Zeeman diagram and the few avoided crossings that the cluster is passing within the magnetic field are traversed diabatically (no spin flips), due to the low SR interaction, so that super-atomic behaviour is observed for clusters that are not vibrationally excited.15,19,54 At high nozzle temperatures, the situation changes fundamentally because vibrations are thermally excited; since (a) deviations from the Ih symmetry lead to dynamic ZFS and (b) the density of states increases strongly due to vibrational excitation.16,19,54,55 Quantum chemical calculations of the Sn12Mn cluster predict the lowest vibrational mode at approximately 65 cm−1,19i.e., if the clusters are thermalized in the source, spin relaxation is expected to be observed starting from a nozzle temperature of about 50 K, as a result of spin flips due to the higher number of avoided crossings.
mag,z < 0 and the defocusing of the components in the gradient direction are a consequence of the two-wire field and can be taken into account quantitatively using a simulation based on the Wigner function formalism.52 Sn12Mn is a special system because it has Ih symmetry.7,19 Therefore, it shows no ZFS and has a low spin–orbit (SO) coupling53 so that the g-factor is close to the value of the free electron. Because of this, it possesses a low spin-rotation (SR) interaction overall.16,54 The spherical symmetry results in a low density of states in the rotational Zeeman diagram and the few avoided crossings that the cluster is passing within the magnetic field are traversed diabatically (no spin flips), due to the low SR interaction, so that super-atomic behaviour is observed for clusters that are not vibrationally excited.15,19,54 At high nozzle temperatures, the situation changes fundamentally because vibrations are thermally excited; since (a) deviations from the Ih symmetry lead to dynamic ZFS and (b) the density of states increases strongly due to vibrational excitation.16,19,54,55 Quantum chemical calculations of the Sn12Mn cluster predict the lowest vibrational mode at approximately 65 cm−1,19i.e., if the clusters are thermalized in the source, spin relaxation is expected to be observed starting from a nozzle temperature of about 50 K, as a result of spin flips due to the higher number of avoided crossings.
This is exactly what the experiment shows: e.g. at Tnozzle = 100 K, only a one-sided deflection of approximately 110 μm is observed. From this shift, the magnitude of the magnetic moment 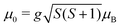 can be obtained using eqn (2). The plot of
can be obtained using eqn (2). The plot of ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mag,z based on this equation shows linear behaviour for Sn12Mn. The extracted value of μ0/μB = 4.9 ± 0.2 agrees very well with the low-temperature behaviour, i.e., S = 5/2 and g = 2.0, if it is assumed that the internal temperature T of the cluster is equal to the nozzle temperature Tnozzle. Looking at this the other way around, this implies that the clusters in the molecular beam are well thermalized by the cluster source and also that the assumption T = Tnozzle for Tnozzle > 90 K is valid.
mag,z based on this equation shows linear behaviour for Sn12Mn. The extracted value of μ0/μB = 4.9 ± 0.2 agrees very well with the low-temperature behaviour, i.e., S = 5/2 and g = 2.0, if it is assumed that the internal temperature T of the cluster is equal to the nozzle temperature Tnozzle. Looking at this the other way around, this implies that the clusters in the molecular beam are well thermalized by the cluster source and also that the assumption T = Tnozzle for Tnozzle > 90 K is valid.
The Sn12Mn cluster is characterized by a spherical shape with low spin-rotational coupling.7,19,53 The other systems that were examined differ in contrast to Sn12Mn: on the one hand, they are not spherical rotors.7 As a result, the density of states in the rotational Zeeman diagram increases by approximately 2 orders of magnitude because the degeneracy of the rotational levels is partially lifted.16 On the other hand, ZFS is also expected to appear for clusters possessing non-cubic symmetry with S > 1/2, which makes an additional contribution to the SO coupling. This, in turn, additionally contributes to the SR interaction and the avoided crossings are preferably passed through adiabatically (spin flips).53,54 Both effects make the observation of super-atomic behaviour less likely. However, if the magnitude of the ZFS is larger than the internal thermal energy of the cluster, then at low Tnozzle, only a sub-ensemble of the different MS states is sufficiently populated, so that again the observation of super-atomic behaviour is facilitated. In this case, the temperature-dependent study of the magnetic behaviour is particularly important because with increasing Tnozzle, all MS states gradually become accessible, which would result in a deviation from the Curie behaviour.
Based on this, Sn11Mn is considered. The most probable structure of Sn11Mn is deduced from the Sn12Mn icosahedron with one vertex missing, resulting in a Mn-centered single-capped pentagonal anti-prism, i.e., a symmetrical rotor with C5v symmetry.7 At low Tnozzle, about half of the clusters behave super-atomically, the other half already shows Curie behaviour. However, individual super-atomic components cannot be resolved. This suggests that most of the super-atomically behaving clusters have already undergone a spin flip in the magnet. This makes it particularly difficult to observe the clusters with MS = ±S since they traverse the most avoided-crossings in the same range of the experienced magnetic field, due to their highest slopes in the rotational Zeeman diagram compared to the other states.16,53 Therefore, the beam profile would appear to be cut off at the left and right edges. Assuming that all super-atomic components are visible, the comparison with Sn12Mn indicates that the spin quantum number S is smaller than 5/2, since otherwise the g-factor would have to be in turn significantly smaller compared to Sn12Mn. If the Sn11Mn is present as a quartet with S = 3/2, then the g-factor is approximately 2.0. In principle, a value of S = 1/2 cannot be ruled out, but here the g-factor would be approximately equal to 6, which is very unlikely. For a cluster with S = 3/2 and non-cubic symmetry, ZFS results. The uniform smearing of the molecular beam shows that the components with MS = ±3/2 and ±1/2 are similarly intense and therefore equally populated, so that the ZFS must be significantly lower than the thermal energy of approximately 10 cm−1. Also at higher Tnozzle, the beam profile indicates that the magnitude of the magnetic moment μ0 is lower for Sn11Mn compared to Sn12Mn. Assuming the same spin multiplicity for both species, the g-factor of Sn11Mn would again be much lower than that of Sn12Mn. With S = 3/2, one gets a value of g = 2.3 ± 0.2 at high temperatures, and thus a consistent picture in combination with the measurement at 16 K emerges. A value of S = 1/2 can be excluded here as well because otherwise the g-factor would have to be extremely large again. Since about 50% of the clusters behave super-atomically at low temperatures, the g-factor should indeed be close to the value of the free electron, because only then will the SO coupling, and thus the SR interaction and ZFS, be weak. Otherwise, it would be difficult to understand why even for a symmetrical rotor about 50% of the clusters behave super-atomically.
The Sn17Mn cluster does not show any super-atomic behaviour at low temperature, but only a shift and a tailing of the beam profile in the direction of the gradient is visible. The latter indicates the presence of a fraction of rotationally-cold clusters, i.e., clusters in such low rotation states that no avoided crossings can occur when traversing the magnets.16,37 However, the vast majority of the clusters already show Curie behaviour at Tnozzle = 16 K, which means that many spin flips occur and only a one-sided deflection of the molecular beam becomes visible. The difference compared to Sn11Mn may be due to the fact that Sn17Mn is an asymmetrical rotor7 and/or has an increased SR interaction as a result of significant ZFS or SO coupling. At higher Tnozzle, a stronger deflection is observed in comparison to Sn12Mn. Assuming a sextet spin state (S = 5/2) for Sn17Mn, g ≈ 2.3 results. If the clusters are present with S = 7/2, the g-factor is about g = 1.5. Based on the experimental data, no distinction can be made between these two possibilities. In both cases, however, there are significant deviations in the g-factor from the value of the free electron, which indicates the presence of a strong orbital contribution to the magnetic moment. Whether this is a result of ZFS cannot be clarified with the current data. However, the presence of an octet state in a single transition-metal-doped tetrel cluster would be very unusual and could only be explained by additional unpaired electrons on the cage of the Sn atoms.
The variation of the number of ligands, i.e., the number of tin atoms, has already shown that the cluster magnetism depends very sensitively on the number of diamagnetic host atoms. If super-atomic behaviour is observed in at least some of the clusters for the spherical Sn12Mn and the symmetrical Sn11Mn, this is not the case for the asymmetrical Sn17Mn. If the spin state of Sn12Mn, and probably also of Sn17Mn, is of a sextet multiplicity, it is very likely for Sn11Mn to be in a quartet state when comparing the slopes of the Curie plots. Furthermore, while the g-factors for Sn12Mn and Sn11Mn are close to 2, the g-factor of Sn17Mn is significantly different from the free electron value, so that for Sn17Mn an additional orbital contribution has to be taken into account.
3.2 Influence of the paramagnetic dopant
In Fig. 2 the results of the beam deflection experiments using a magnetic field are shown for the Sn14TM clusters with TM = Mn, Fe and Cr (left to right) at Tnozzle = 16 K (top) and Tnozzle = 100 K (middle). The temperature-dependent deflection of the molecular beam are displayed as magnetic moments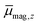 , which were calculated from the deflection dz according to eqn (1) and are plotted against the reciprocal nozzle temperature as shown in eqn (2).
, which were calculated from the deflection dz according to eqn (1) and are plotted against the reciprocal nozzle temperature as shown in eqn (2).
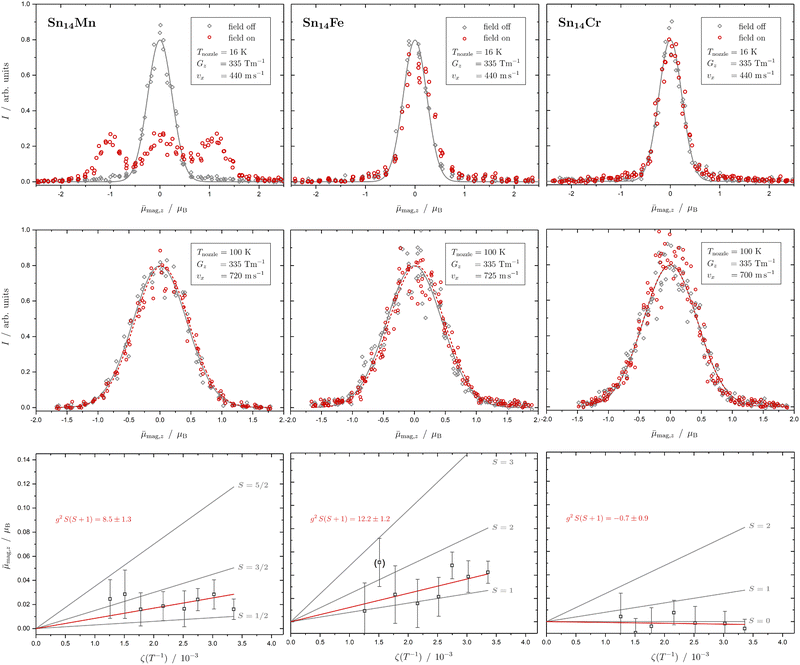 | ||
| Fig. 2 Experimental results from the different experiments of beam deflection by a magnetic field on Sn14TM with TM = Mn, Fe and Cr (left to right) at Tnozzle = 16 K (top), at Tnozzle = 100 K (middle) for the exemplary deflection experiments at higher nozzle temperatures, and the resulting Curie plots (bottom). For further details, refer to Fig. 1. Please note that the listed slope of the linear fit function to the temperature-dependent deflection of Sn14Fe is extracted without considering the data point at Tnozzle = 200 K. | ||
The Sn14Mn cluster differs significantly in its magnetic behaviour from the cases discussed so far. At low Tnozzle, about two-thirds of all clusters are super-atomic, the rest show Curie behaviour. A g-factor of g = 2.0 can be extracted from the well-resolved two super-atomic components. The fact that only two components are observed means that either a doublet is present or, if Sn14Mn has a spin multiplicity of S > 1/2, the value of the ZFS is so large that at low temperatures only the two energetically lowest states with MS = ±1/2 are thermally occupied. However, on one hand, since the ZFS is closely related to SO coupling and thus in turn to SR coupling, one would expect for a spin isomer with S > 1/2 and ZFS that most of the avoided crossings in the rotational Zeeman diagram are passed adiabatically, i.e., with a spin flip taking place, so that the observation of super-atomic behaviour is very unlikely. Therefore, a cluster with a doublet ground state and cubic symmetry, i.e., a spherical rotor without ZFS, would most likely explain the low-temperature magnetic behaviour. At higher Tnozzle, only a small single-sided deflection of the beam profile is visible. The typical deflection of about 14 μm can only be observed here thanks to the improved experimental setup with the two magnets connected in series. However, the deflection at high temperatures appears to be a bit too large for a pure doublet state, especially if g = 2 from the measurement at Tnozzle = 16 K is taken into account. The linear dependence of the magnetic moment in eqn (2) on the reciprocal nozzle temperature is also not observed. On the contrary, ![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) mag,z appears to be approximately independent of the nozzle temperature. A possible explanation for this would be that a cluster with S > 1/2 in combination with a ZFS that is larger than the internal thermal energy of the cluster is present. Then, at low Tnozzle, the majority of the clusters would not only be in the vibrational ground state, but also exclusively in states with MS = ±1/2. Through thermal excitation at higher Tnozzle, the clusters would not only be flexible, i.e., vibrationally excited, but also the other spin states with |MS| > 1/2 would be occupied. Due to the temperature dependence of these occupation numbers, deviations from the Curie behaviour result and the magnetic moment remains approximately constant in the temperature range in which the states with |MS| > 1/2 become noticeably occupied. This is because at higher Tnozzle, states with larger magnetic moments contribute to the overall magnetic response. However, this means that the ZFS constant D must be significantly larger than +10 cm−1. Please note that the ZFS constant has to be positive, since at values of D < 0, the states with the highest possible |MS| are occupied first.21 A fit to the experimental data, taking the temperature-dependent population of the MS states (with S = 5/2) into account and assuming a Boltzmann distribution function, yields a ZFS value of about D = 90 cm−1 (cf. the ESI†). Alternatively, it would also be conceivable that there are two spin isomers: a doublet as a ground state, which is solely present at low temperatures, and a spin isomer with S > 1/2 that becomes populated with increasing temperature. However, in this case, the two isomers must be quasi-degenerate in energy so that the higher-energy isomer becomes thermally populated from around 140 K on.
mag,z appears to be approximately independent of the nozzle temperature. A possible explanation for this would be that a cluster with S > 1/2 in combination with a ZFS that is larger than the internal thermal energy of the cluster is present. Then, at low Tnozzle, the majority of the clusters would not only be in the vibrational ground state, but also exclusively in states with MS = ±1/2. Through thermal excitation at higher Tnozzle, the clusters would not only be flexible, i.e., vibrationally excited, but also the other spin states with |MS| > 1/2 would be occupied. Due to the temperature dependence of these occupation numbers, deviations from the Curie behaviour result and the magnetic moment remains approximately constant in the temperature range in which the states with |MS| > 1/2 become noticeably occupied. This is because at higher Tnozzle, states with larger magnetic moments contribute to the overall magnetic response. However, this means that the ZFS constant D must be significantly larger than +10 cm−1. Please note that the ZFS constant has to be positive, since at values of D < 0, the states with the highest possible |MS| are occupied first.21 A fit to the experimental data, taking the temperature-dependent population of the MS states (with S = 5/2) into account and assuming a Boltzmann distribution function, yields a ZFS value of about D = 90 cm−1 (cf. the ESI†). Alternatively, it would also be conceivable that there are two spin isomers: a doublet as a ground state, which is solely present at low temperatures, and a spin isomer with S > 1/2 that becomes populated with increasing temperature. However, in this case, the two isomers must be quasi-degenerate in energy so that the higher-energy isomer becomes thermally populated from around 140 K on.
In order to investigate the influence of the transition metal on the magnetic behaviour, Sn14Cr and Sn14Fe were also examined, i.e., Mn was replaced by the two neighbouring transition metals in the periodic table of elements.
For Sn14Cr, no magnetic deflection is observed at low and high Tnozzle, so that the cluster is a singlet in which all electrons are paired. When comparing Sn14Cr with Sn14Mn, it becomes clear that with the two parallel aligned Stern–Gerlach magnets in series it is indeed possible to clearly discriminate the magnetic deflection of a paramagnetic species with S = 1/2 and g = 2 from a diamagnetic cluster, even though the clusters examined here have a mass of more than 1500 daltons and therefore a very small single-sided shift. Based on the observed behaviour of Sn14Cr, a doublet ground state for Sn14Mn would be reasonable, if a similar geometric structure exists in both clusters, since an additional valence electron is simply added to the diamagnetic cluster by replacing Cr with Mn. When replacing Mn with Fe, again assuming similar structures, it would be expected that either a singlet state or a triplet with S = 1 is formed. The behaviour at low Tnozzle clearly demonstrates that Sn14Fe is paramagnetic, although no super-atomic behaviour is observed. If the outlier at 200 K in the Curie plot is not taken into account, a triplet state with a g-factor of 2.5 ± 0.2 is most likely to be present for Sn14Fe. The g-factor therefore deviates somewhat from the value of the free electron, which indicates an orbital contribution to the magnetic moment. This also results in an enhanced SR interaction, so that the avoided crossings were primarily passed through with spin flips. The existence of a quintet, S = 2, cannot be completely ruled out. However, the g-factor would then be significantly lower than 2, so that an orbital moment would also have to be taken into account here.
In order to interpret the magnetic behaviour in more detail, it is necessary to consider the geometric structure of the clusters. Therefore, electric deflection experiments were carried out together with quantum chemical calculations for the doped Sn14TM species to obtain conclusions regarding the cluster geometry. The geometric structures are generated by applying density functional theory (DFT) with the pure-GGA functional PBE56 and the def2-TZVPP basis set57 using the computational program Gaussian 1658 and the energies are calculated for several spin states (S = 2, 1, 0). Afterwards, a frequency analysis is carried out and the electric dipole moments, as well as the electronic structures, are calculated. The resulting geometric and valence electronic structures are shown in Fig. 3(a) and (c), together with the profiles of electric deflection of the beam under cryogenic conditions shown in Fig. 3(b).
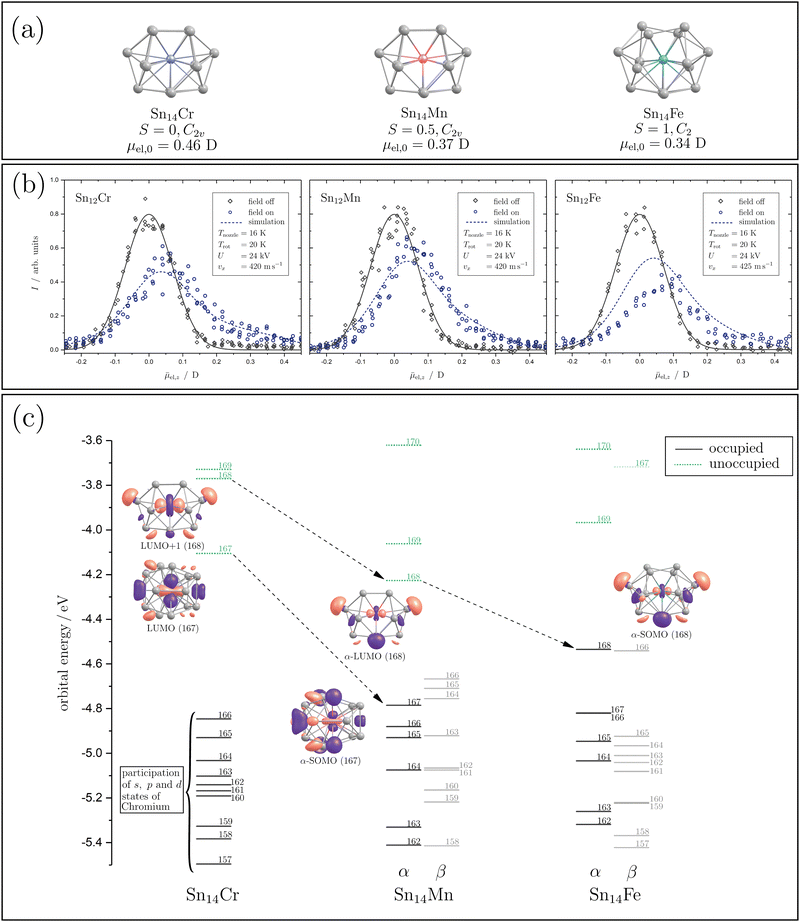 | ||
| Fig. 3 The geometric and electronic structures of the Sn14TM clusters with TM = Mn, Fe and Cr are illustrated. In (a), the geometric structures for Sn14Cr, Sn14Mn and Sn14Fe (left to right) given by quantum chemical calculation at the PBE/def2-TZVPP56,57 level of theory are shown. Below the geometric structure and its designation, the spin quantum number S and the point group are listed. In the last line, the magnitude of the calculated electric dipole moment μel,0 is shown. In (b), beam deflection profiles at Tnozzle = 16 K with (blue circles) and without (grey diamonds) an electric field are presented. A Gaussian function (grey solid line) is fitted to the beam profile with the electric field switched off. The simulated profiles generated by the classical trajectory simulation (see text) and taking the arachno-structures into account are given as blue dashed lines. In (c), the valence electronic structures of the clusters are presented, showing spin-unrestricted Kohn–Sham orbitals. The occupied molecular orbitals (MOs) are displayed as black solid lines and the unoccupied MOs as green dashed lines, with the number of the corresponding orbital labelling it. For the relevant MOs (see text), the shape of the iso-surface of the molecular orbitals is shown (isovalue 0.03a0−3/2), with the designation underneath, in a perspective that the contribution of the atomic orbital of the TM is clearly visible. The lowest unoccupied molecular orbital is referred to as the LUMO and the singly occupied molecular orbitals as SOMO. The arrows indicate the transition of the MOs by exchanging the paramagnetic dopants. | ||
The influence of a 14-atom tetrel cage on the structure of Cr-doped clusters has been extensively studied theoretically, mainly for the lighter tetrel homologous Si. A C2v-symmetrical structure is predicted quantum chemically for Si14Cr, which can be understood as an electron-precise cluster.24 Formally, the 18 valence electron count for Cr with the electron configuration 4s23d104p6 is fulfilled in this cluster and a diamagnetic ground state results in which the magnetic moment of the chromium is completely quenched. The corresponding structure can be derived from the arachno-cluster Si146−, which is formally endohedrally saturated with a Cr6+ ion.26,33 Interestingly, the isoelectronic Si14Mn+ is predicted to possess a fullerene-like structure with D3h symmetry.23 Here too, a singlet ground state is present. However, infrared spectroscopic studies of Si14Mn+ could not validate this structure.59 XMCD studies of this cluster show that Si14Mn+ is indeed diamagnetic, i.e., the magnetic moment is completely quenched.35 The cluster Si14V− is also isoelectronic to Si14Cr. Here, photoelectron spectroscopic studies again indicate the presence of the arachno structure with C2v symmetry.36 This structure is also predicted for the valence-isoelectronic Ge14Cr.28 The arachno-structural motif with C2v symmetry also appears to be retained in Ge14Mn, resulting in a doublet spin state.32 Both the α-HOMO and the α-LUMO are formed from atomic 3d states that are essentially localized on Mn. However, the hybridization of these Mn d-states with Ge p-states has to be taken into account. Photoelectron spectroscopic studies on the isoelectronic Si14Cr− are also consistent with the arachno structure with C2v symmetry.27,29 For Si14Fe, various quantum-chemical investigations predict an octahedral structure with Oh symmetry, which has a singlet ground state,22,25,30i.e., here too the magnetic moment of the central Fe atom would be completely quenched. Interestingly, the photoelectron spectroscopy results for the valence-isoelectronic Ge14Mn− are consistent with the arachno-structural motif, with a triplet ground state now present in which the spin density is localized almost exclusively on the Mn centre.31 The theoretical and experimental investigations indicate that the geometric structure, and thus also the magnetism, depend sensitively on the total number of valence electrons, i.e., the endohedral transition metal and the charge state of the doped tetrel cluster. In a theoretical work in which the binding situation of the clusters was analyzed in detail,26 it is shown how sensitively the geometric structure reacts to the electron density of the cluster and, therefore, how sensitively the predicted electronic structure depends in particular on the exchange–correlational functionals used. This, once again, illustrates how important the experimental investigation of the clusters is for probing the theoretical predictions on the magnetic properties.
Based on the electric deflection experiments shown in Fig. 3(b), certain structural motifs can be ruled out. For all clusters with 14 tin atoms investigated here, i.e., Sn14Mn, Sn14Fe and Sn14Cr, a broadening of the molecular beam was observed with the inhomogeneous electric field applied. Therefore, polar geometries must be present so that the proposed octahedral structure for Si14Fe and the fullerene-like geometry for Si14Mn+ with D3h symmetry can definitively be excluded for Sn14Fe and Sn14Cr. The quantum chemical analysis of Sn14Cr based on the calculations mentioned above identified a singlet spin isomer, whose geometric structure is based on the arachno-motif found for Si14Cr (see Fig. 3(a)).24,26,33 The simulation of the beam broadening with an electric field that is observed for Sn14Cr, taking the predicted electric dipole moment and the moments of inertia into account, can describe the experimental data in very good agreement. The valence electronic structure, which is shown in Fig. 3(c), reveals that 9 of the 10 highest occupied molecular orbitals (MOs) are mainly determined by s, p and d-states localized at the Cr centre, i.e., Sn14Cr seems to also be an electron-precise cluster fulfilling the 18 valence electron count for Cr. However, significant hybridization with s and p-states from the Sn atoms takes place. The energy interval of about 0.7 eV, in which the 18 valence electrons are found, is quite small due to the compact geometric structure of the Sn14Cr cluster.
Since both the magnetic and electrical deflection behaviour of Sn14Cr can be explained with the singlet arachno-type structure, this polar structural motif forms the starting point for the discussion of Sn14Mn and Sn14Fe. Indeed the quantum chemical analysis also reveals arachno-type structures for Sn14Mn and Sn14Fe (Fig. 3(a)). Here, too, the experimentally measured electric deflection of the beam agrees satisfactorily with the simulations taking into account the quantum-chemically calculated electric dipole moments, even if the simulated profile of Sn14Fe underestimates the beam broadening. It should be noted that this may be due to the fact that the calculation underestimates the electric dipole moment.50 On the other hand, it is possible that the geometric structure present in the experiment is more distorted than theoretically predicted and thus a stronger beam broadening is observed experimentally. However, the general course of the experimental profile of Sn14Fe is well reproduced by the simulation. Therefore, both the quantum chemical calculations and the magnetic data of Sn14Fe at high temperatures suggest the presence of a triplet state.
Qualitatively, when Cr is replaced by Mn, another valence electron is available, which occupies the lowest unoccupied MO (LUMO) of Sn14Cr. This MO also exhibits a strong contribution from the 3d states of the central transition metal (cf. the ESI†). By increasing the effective nuclear charge through the exchange of Cr to Mn, this MO gets stabilized and hybridisation with the s and p-states of tin is significantly increased. When Fe is now integrated into the cluster, the geometric structure gets slightly distorted and the α-LUMO of Sn14Mn is energetically stabilized, which allows the uptake of a second unpaired electron. This MO is also largely formed by d-states of the transition metal, which hybridize with s and p-states of the Sn atoms. In order to energetically stabilize a triplet compared to a singlet state, the spin pairing energy must outweigh the excitation energy to form the triplet. Both the quantum chemical calculations and the magnetic deflection data suggest that a triplet state is formed for Sn14Fe. Moreover, the predicted polar arachno-type geometry of Sn14Fe can explain the measured electric deflection of the beam sufficiently well considering the predicted electric dipole moment. Therefore, the investigation of Sn14Cr, Sn14Mn and Sn14Fe indicates that the substitution of the transition metals leaves the overall geometric structure of the cluster skeleton unchanged, but the altered electron count modifies the magnetic properties. This indicates that, in addition to the electron count, the most stable geometric structure is decisive for the overall stability of the clusters.
4 Conclusions
In this work, the magnetic properties of tetrel clusters SnNTM that are singly doped with transition metals (TM) are investigated. On the one hand, the number of tetrel atoms (N = 11, 12, 14 and 17 with TM = Mn) is varied, and, on the other hand, different TMs (N = 14, TM = Cr, Mn, Fe) are introduced. Magnetic deflection experiments under cryogenic conditions show that the variation of the number of tetrel atoms strongly changes the magnetic properties of the Mn-doped clusters. If parts of Sn12Mn, Sn11Mn and Sn14Mn show super-atomic behaviour, spin relaxation occurs in Sn17Mn, so that the beam profile is only shifted in the field direction. A portion of the Sn17Mn clusters with low rotational quantum numbers (rotationally cold clusters) is noticeable as a shoulder in the beam profile. Magnetic deflection experiments at higher nozzle temperatures were carried out for the first time with two parallel-aligned Stern–Gerlach magnets connected in series to achieve larger deflections. At nozzle temperatures above 90 K, only one-sided displacement of the molecular beam is observed for all clusters. This displacement, which depends on the nozzle temperature, is analysed quantitatively using Curie's law. The magnetic deflection experiments over the temperature range examined here show that the magnetic moment strongly decreases from Sn17Mn to Sn12Mn over Sn11Mn to Sn14Mn. Interestingly, the shifts of the molecular beam for Sn14Mn are almost independent of temperature. This observation is discussed in the context of zero-field splitting effects.We also studied how the replacement of Mn with Fe and Cr affects the electrical and magnetic behaviour. Electrical deflection measurements of Sn14Mn, Sn14Cr, and Sn14Fe under cryogenic conditions demonstrate that all three clusters must have a polar structure. The arachno-type geometry of Si14Cr discussed in the literature is also predicted quantum chemically for the three Sn clusters and the calculated values of the electric dipole moments fit well to the electric deflection data well. The beam deflection experiments using a magnetic field show that the spin multiplicity of Sn14Cr, which exists as a diamagnetic singlet, increases through Sn14Mn, a doublet, and further to Sn14Fe, which exists most probably as a triplet. A quantum chemical analysis of the valence electron structure indicates that the increasing effective nuclear charge when exchanging Cr to Mn stabilizes the lowest unoccupied molecular orbital of Sn14Cr and enables the occupation of the additional electron in Sn14Mn. When Fe is incorporated, the energy of the α-LUMO in Sn14Mn is lowered to such an extent that a triplet ground state is formed. The geometric structure of the clusters and even the appearance of the relevant MOs change only slightly when the TMs are exchanged. This indicates that although the altered valence electron number during the transition from Sn14Cr to Sn14Mn to Sn14Fe determines the magnetic properties, the arachno-type geometry is crucial for the overall stability of the transition-metal-doped tetrel clusters.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Grant No. CRC 1487, “Iron, upgraded” – Project No. 443703006. We thank Jeannine Müller for the help with the beam deflection experiments using a magnetic field and also Vera Krewald and Carlos Jimenez-Muñoz for discussions regarding the quantum chemical calculations of iron-doped tin clusters. The authors gratefully acknowledge the computing time provided to them on the high-performance computer Lichtenberg at the NHR Centers NHR4CES at TU Darmstadt. This is funded by the Federal Ministry of Education and Research, and the state governments participating on the basis of the resolutions of the GWK for national high performance computing at universities.References
- Clusters and Nanomaterials, ed. V. Kumar, K. Esfarjani and Y. Kawazoe, Springer Verlag, Berlin, 2002 Search PubMed.
- Cluster and Nanostructured Materials, ed. P. Jena and S. Behera, Nova Science, New York, 1996 Search PubMed.
- J. I. Martín, J. Nogués, K. Liu, J. L. Vicent and I. K. Schuller, J. Magn. Magn. Mater., 2003, 256, 449–501 CrossRef.
- J. Zhao, Q. Du, S. Zhou and V. Kumar, Chem. Rev., 2020, 120, 9021–9163 CrossRef CAS.
- V. Kumar and Y. Kawazoe, Appl. Phys. Lett., 2003, 83, 2677–2679 CrossRef CAS.
- M. Gleditzsch, T. M. Fuchs and R. Schäfer, J. Phys. Chem. A, 2019, 123, 1434–1444 CrossRef CAS PubMed.
- U. Rohrmann, P. Schwerdtfeger and R. Schäfer, Phys. Chem. Chem. Phys., 2014, 16, 23952–23966 RSC.
- D. D. Awschalom, R. Hanson, J. Wrachtrup and B. B. Zhou, Nat. Photonics, 2018, 12, 516–527 CrossRef CAS.
- N. Mizuochi, P. Neumann, F. Rempp, J. Beck, V. Jacques, P. Siyushev, K. Nakamura, D. J. Twitchen, H. Watanabe, S. Yamasaki, F. Jelezko and J. Wrachtrup, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 041201(R) CrossRef.
- X. Xu, S. Yin, R. Moro and W. A. De Heer, Phys. Rev. Lett., 2005, 95, 237209 CrossRef PubMed.
- A. Chatelain, Philos. Mag. B, 1999, 79, 1367–1378 CrossRef CAS.
- R. Moro, S. Yin, X. Xu and W. A. de Heer, Phys. Rev. Lett., 2004, 93, 086803 CrossRef PubMed.
- J. A. Becker and W. A. De Heer, Ber. Bunsenges. Phys. Chem., 1992, 96, 1237–1243 CrossRef CAS.
- U. Rohrmann, S. Schäfer and R. Schäfer, J. Phys. Chem. A, 2009, 113, 12115–12121 CrossRef CAS PubMed.
- F. Rivic, T. M. Fuchs and R. Schäfer, Phys. Chem. Chem. Phys., 2021, 23, 9971–9979 RSC.
- T. M. Fuchs and R. Schäfer, Phys. Rev. A, 2019, 100, 012512 CrossRef CAS.
- I. M. Billas, A. Châtelain and W. A. De Heer, J. Magn. Magn. Mater., 1997, 168, 64–84 CrossRef CAS.
- K. Miyajima, M. B. Knickelbein and A. Nakajima, J. Phys. Chem. A, 2008, 112, 366–375 CrossRef CAS PubMed.
- U. Rohrmann and R. Schäfer, Phys. Rev. Lett., 2013, 111, 133401 CrossRef PubMed.
- J. Telser, eMagRes, 2017, 6, 207–234 CAS.
- R. Boča, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef.
- L. Ma, J. Wang and G. Wang, J. Chem. Phys., 2013, 138, 094304 CrossRef.
- V. T. Ngan, K. Pierloot and M. T. Nguyen, Phys. Chem. Chem. Phys., 2013, 15, 5493–5498 RSC.
- M. B. Abreu, A. C. Reber and S. N. Khanna, J. Phys. Chem. Lett., 2014, 5, 3492–3496 CrossRef CAS PubMed.
- V. Chauhan, M. B. Abreu, A. C. Reber and S. N. Khanna, Phys. Chem. Chem. Phys., 2015, 17, 15718–15724 RSC.
- X. Jin, V. Arcisauskaite and J. E. McGrady, Dalton Trans., 2017, 46, 11636–11644 RSC.
- K. Wang, H. Y. Zhao, L. Miao, Z. Z. Jia, G. J. Yin, X. D. Zhu, R. Moro, B. Von Issendorff and L. Ma, J. Phys. Chem. A, 2022, 126, 1329–1335 CrossRef CAS PubMed.
- K. Dhaka and D. Bandyopadhyay, RSC Adv., 2015, 5, 83004–83012 RSC.
- B. Yang, H. Xu, X. Xu and W. Zheng, J. Phys. Chem. A, 2018, 122, 9886–9893 CrossRef CAS.
- L. Ma, J. Zhao, J. Wang, B. Wang, Q. Lu and G. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125439 CrossRef.
- Y. W. Fan, X. Y. Kong, L. J. Zhao, H. Q. Wang, H. F. Li, Q. Zhan, B. Xie, H. G. Xu and W. J. Zheng, J. Chem. Phys., 2021, 154, 204302 CrossRef CAS PubMed.
- J. Wang, L. Ma, J. Zhao and G. Wang, J. Phys.: Condens. Matter, 2008, 20, 335223 CrossRef.
- X. Jin and J. E. McGrady, Adv. Inorg. Chem., Elsevier Inc., 1st edn, 2019, ch. 8, vol. 73, pp. 265–304 Search PubMed.
- V. Arcisauskaite, X. Jin, J. M. Goicoechea and J. E. McGrady, Struct. Bonding, 2016, 169, 181–198 CrossRef CAS.
- V. Zamudio-Bayer, L. Leppert, K. Hirsch, A. Langenberg, J. Rittmann, M. Kossick, M. Vogel, R. Richter, A. Terasaki, T. Möller, B. V. Issendorff, S. Kümmel and J. T. Lau, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115425 CrossRef.
- K. Wang, Z. Z. Jia, Z. Fan, H. Y. Zhao, G. J. Yin, R. Moro, B. von Issendorff and L. Ma, Phys. Chem. Chem. Phys., 2022, 24, 8839–8845 RSC.
- T. M. Fuchs, F. Rivic and R. Schäfer, Phys. Rev. A, 2021, 104, 012820 CrossRef CAS.
- S. Schäfer, M. Mehring, R. Schäfer and P. Schwerdtfeger, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 052515 CrossRef.
- I. I. Rabi, J. M. B. Kellogg and J. R. Zacharias, Phys. Rev., 1934, 46, 157–163 CrossRef CAS.
- J. M. B. Kellogg, I. I. Rabi, N. F. Ramsey and J. R. Zacharias, Phys. Rev., 1939, 56, 728–743 CrossRef CAS.
- F. Rivic, A. Lehr, T. M. Fuchs and R. Schäfer, Faraday Discuss., 2023, 242, 231–251 RSC.
- L. P. Maguire, S. Szilagyi and R. E. Scholten, Rev. Sci. Instrum., 2004, 75, 3077–3079 CrossRef CAS.
- X. Xu, S. Yin, R. Moro and W. A. de Heer, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054430 CrossRef.
- A. Lehr, F. Rivic and R. Schäfer, J. Am. Chem. Soc., 2023, 145, 2070–2074 CrossRef CAS PubMed.
- S. Heiles and R. Schäfer, Dielectric Properties of Isolated Clusters, Springer, 2014 Search PubMed.
- S. Heiles, S. Schäfer and R. Schäfer, J. Chem. Phys., 2011, 135, 034303 CrossRef CAS PubMed.
- S. Schäfer, B. Assadollahzadeh, M. Mehring, P. Schwerdtfeger and R. Schäfer, J. Phys. Chem. A, 2008, 112, 12312–12319 CrossRef PubMed.
- P. Dugourd, R. Antoine, M. A. El Rahim, D. Rayane, M. Broyer and F. Calvo, Chem. Phys. Lett., 2006, 423, 13–16 CrossRef CAS.
- M. Gleditzsch, L. F. Pašteka, D. A. Götz, A. Shayeghi, R. L. Johnston and R. Schäfer, Nanoscale, 2019, 11, 12878–12888 RSC.
- A. Lehr, F. Rivic, M. Jäger, M. Gleditzsch and R. Schäfer, Phys. Chem. Chem. Phys., 2022, 24, 11616–11635 RSC.
- R. S. Title and K. F. Smith, Philos. Mag., 1960, 5, 1281–1289 CrossRef CAS.
- M. Utz, M. H. Levitt, N. Cooper and H. Ulbricht, Phys. Chem. Chem. Phys., 2015, 17, 3867–3872 RSC.
- T. M. Fuchs and R. Schäfer, Phys. Rev. A, 2018, 98, 063411 CrossRef CAS.
- W. Xu and W. Bai, J. Mol. Struct.: THEOCHEM, 2008, 854, 89–105 CrossRef CAS.
- M. B. Knickelbein, J. Chem. Phys., 2004, 120, 10450–10454 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016 Search PubMed.
- V. T. Ngan, E. Janssens, P. Claes, J. T. Lyon, A. Fielicke, M. T. Nguyen and P. Lievens, Chem. – Eur. J., 2012, 18, 15788–15793 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Quantitative determination of the zero-field splitting in Sn14Mn; composition of the molecular orbitals of the single-doped Sn14 species. See DOI: https://doi.org/10.1039/d4cp00890a |
| This journal is © the Owner Societies 2024 |
