Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Infrared spectra and fragmentation dynamics of isotopologue-selective mixed-ligand complexes†
Peter D.
Watson
 a,
Gabriele
Meizyte
a,
Philip A. J.
Pearcy
a,
Gabriele
Meizyte
a,
Philip A. J.
Pearcy
 a,
Edward I.
Brewer
a,
Edward I.
Brewer
 a,
Alice E.
Green
a,
Alice E.
Green
 a,
Christopher
Robertson
a,
Christopher
Robertson
 b,
Martin J.
Paterson
b,
Martin J.
Paterson
 b and
Stuart R.
Mackenzie
b and
Stuart R.
Mackenzie
 *a
*a
aDepartment of Chemistry, University of Oxford, Physical and Theoretical Chemistry Laboratory, South Parks Road, Oxford, OX1 3QZ, UK. E-mail: stuart.mackenzie@chem.ox.ac.uk
bSchool of Engineering & Physical Sciences, Heriot-Watt University, Edinburgh, Scotland EH14 4AS, UK
First published on 20th May 2024
Abstract
Isolated mixed-ligand complexes provide tractable model systems in which to study competitive and cooperative binding effects as well as controlled energy flow. Here, we report spectroscopic and isotopologue-selective infrared photofragmentation dynamics of mixed gas-phase Au(12/13CO)n(N2O)m+ complexes. The rich infrared action spectra, which are reproduced well using simulations of calculated lowest energy structures, clarify previous ambiguities in the assignment of vibrational bands, especially accidental coincidence of CO and N2O bands. The fragmentation dynamics exhibit the same unexpected behaviour as reported previously in which, once CO loss channels are energetically accessible, these dominate the fragmentation branching ratios, despite the much lower binding energy of N2O. We have investigated the dynamics computationally by considering anharmonic couplings between a relevant subset of normal modes involving both ligand stretch and intermolecular modes. Discrepancies between correlated and uncorrelated model fit to the ab initio potential energy curves are quantified using a Boltzmann sampled root mean squared deviation providing insight into efficiency of vibrational energy transfer between high frequency ligand stretches and the softer intermolecular modes which break during fragmentation.
I. Introduction
Isolated (i.e., gas-phase) mixed ligand ion–molecule complexes provide a unique and well-defined environment in which to study important physico-chemical phenomena. These can include molecular activation at the charge centre (commonly a metal ion or cluster), cooperative and competitive binding effects, as well as energy flow within the complex. Infrared photodissociation (action) (IRPD) spectroscopy represents a powerful technique for such studies yielding information on non-covalent interactions, solvation and structural isomers.1–5Generating mixed-ligand complexes represents an additional level of challenge over simple ion–molecule species and, consequently, with the exception of inert tagging,3–11 relatively few spectroscopic studies have been undertaken on multiple ligand systems: Lisy completed systematic IRPD studies on a range of small hydrated alkali metal complexes (M+L(H2O)n: M = Na, K and L = benzene,12–14 phenol,15 indole,16,17 acetonitrile,18n-methylacetamide,19 C6F620 and tryptamine21). Beyer and coworkers have similarly studied a range of hydrated transition metal–CO2 clusters by employing IRPD within an ion cyclotron resonance mass spectrometer.22,23 Recently, time-resolved 2D-IR spectroscopy has been applied to watch energy flow and frustrated intramolecular vibrational redistribution (IVR) in Re(CO)n(CH3CN)m+ complexes.24
We have previously reported detailed IRPD studies of mixed CO and N2O complexes of Au+ and Rh+, characterizing structures and comparing fragmentation patterns following excitation of the near degenerate C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O and N2O N
O and N2O N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching modes, respectively.25,26 Qualitatively different behaviour is observed in each with the Au+ complexes exhibiting purely nonclassical carbonyl bonding whilst cooperative effects in Rh+ result in a mix of classical and non classical binding.27,28 The most significant differences, however were observed in the fragmentation dynamics with Au(CO)n(N2O)m+ exhibiting unexpected non-statistical fragmentation with preferential CO loss contrary to expectations based on relative ligand binding energies.
N stretching modes, respectively.25,26 Qualitatively different behaviour is observed in each with the Au+ complexes exhibiting purely nonclassical carbonyl bonding whilst cooperative effects in Rh+ result in a mix of classical and non classical binding.27,28 The most significant differences, however were observed in the fragmentation dynamics with Au(CO)n(N2O)m+ exhibiting unexpected non-statistical fragmentation with preferential CO loss contrary to expectations based on relative ligand binding energies.
Both Au(CO)x+ and Au(N2O)y+ complexes have been studied in detail by IRPD spectroscopy.28,29 In mixed-ligand complexes, the stronger binding of the CO leads to Au(CO)x+ core structures with resulting blue-shifted C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O stretches (2230 ± 10 cm−1). N2O binds more weakly to this core with the N
O stretches (2230 ± 10 cm−1). N2O binds more weakly to this core with the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch observed close to that in free N2O (2223 cm−1).25 Our inability to resolve the CO and N
N stretch observed close to that in free N2O (2223 cm−1).25 Our inability to resolve the CO and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretches presented an ambiguity in our previous spectral assignment which we address here. In this work, we report the IRPD spectroscopy of isotopically-selected Au(12/13CO)n(N2O)m+ complexes. The fragmentation of these species provides insight into the dynamics of these processes and restricted energy flow within these complexes.
N stretches presented an ambiguity in our previous spectral assignment which we address here. In this work, we report the IRPD spectroscopy of isotopically-selected Au(12/13CO)n(N2O)m+ complexes. The fragmentation of these species provides insight into the dynamics of these processes and restricted energy flow within these complexes.
II. Experimental and computational methods
The spectrometer used in this work has been described in detail previously.26,30,31 All gas mixes used were 1% CO: 5% N2O in Ar. In order to generate complexes with different 13CO/12CO ligand fractions the CO used ranged from 100% 12CO to 100% 13CO. The mass spectrum of species generated in a 12CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N2O
N2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
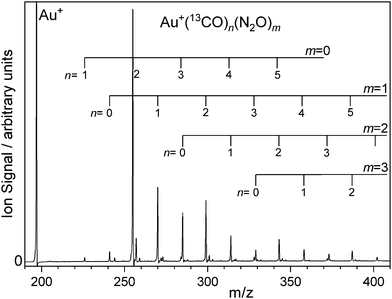
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar mix has been published previously25 and so Fig. 1 shows a representative time-of-flight mass spectrum of Au(13CO)n(N2O)m+ produced by laser ablation of an Au target in presence of 1% 13CO, 5% N2O gas mix in Ar and introduced at a backing pressure of 6 bar (see Fig. S1 in the ESI† for more a detailed spectrum). The distribution of species produced is qualitatively similar to that in our earlier work on the 12CO mixed-ligand system.25
Ar mix has been published previously25 and so Fig. 1 shows a representative time-of-flight mass spectrum of Au(13CO)n(N2O)m+ produced by laser ablation of an Au target in presence of 1% 13CO, 5% N2O gas mix in Ar and introduced at a backing pressure of 6 bar (see Fig. S1 in the ESI† for more a detailed spectrum). The distribution of species produced is qualitatively similar to that in our earlier work on the 12CO mixed-ligand system.25
The strongest ion signal observed is the Au(13CO)2+ species whose stability is an example of the Orgel effect.32,33 Other abundant species observed include Au(13CO)n(N2O)m+ (n = 0–5, m = 0–3). Mass-selected infrared action spectra were recorded by selecting parent ions using a quadrupole mass filter. In some cases involving mixed 12CO/13CO ligands, complete separation proved impossible without unacceptable transmission losses. However, the mass resolving power of the detection reflection time of flight mass spectrometer was sufficient to determine the fragmentation channels unambiguously. The ESI† includes the mass spectrum of Au(13/12CO)n (N2O)+ species along with photofragment mass spectra collected at ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) IR = 2157 cm−1, 2207 cm−1, and 2230 cm−1 illustrating that photofragmentation occurs by loss of CO, of N2O or of both (Fig. S2–S4, ESI†). Gating the signal in different mass channels allows fragment-specific spectra to be recorded yielding information on the energy flow within the complex. The resulting fragmentation dynamics have been the focus of previous studies and we return to them here with isotopologue selectivity. First, however, it is necessary to understand the spectroscopy of the isotopically-labelled complexes.
IR = 2157 cm−1, 2207 cm−1, and 2230 cm−1 illustrating that photofragmentation occurs by loss of CO, of N2O or of both (Fig. S2–S4, ESI†). Gating the signal in different mass channels allows fragment-specific spectra to be recorded yielding information on the energy flow within the complex. The resulting fragmentation dynamics have been the focus of previous studies and we return to them here with isotopologue selectivity. First, however, it is necessary to understand the spectroscopy of the isotopically-labelled complexes.
To aid structural assignment, the IRPD spectra recorded are compared with those simulated for the lowest-energy isomeric structures determined at the B3P86-Def2TZVP level of theory28,34,35 which proved effective in our previous studies. All electronic structure calculations presented here were completed using Gaussian 16 program.36 Scalar relativistic effects were included with the use of the ECP60 effective core potential for the Au+ ion. All low-lying structures identified were singlet states. Calculated line spectra have been convoluted with Lorentzian line-shapes to help comparison with the experimental data. Calculated harmonic frequencies rarely match observed bands well and it is conventional to scale calculated vibrational frequencies37 for comparison with experiment. This is usually done by scaling the calculated frequency of a fundamental band to its known experimental value. This is challenging in systems with multiple (different) ligands. To a good approximation, as expected in relatively weakly-bound complexes, the bands observed in the spectral region covered by this study are well described as local N2O or CO-centred modes. Hence, we have taken the approach of scaling such bands independently. For the B3P86-Def2TZVP level of theory, these factors are 0.9322 and 0.9626 for the N2O N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch and the CO stretch respectively. Scaling using these factors results in simulated spectra as shown in Fig. S3–S5 in the ESI† which allow unambiguous identification of the observed spectral bands. However, while the N2O-based bands match very well, the CO-based bands are slightly overscaled resulting in excessively red-shifted calculated spectra. To provide a better match with experiment, the Figures shown below have been scaled with factors generated by fitting two Lorentzian functions to the single peak in the Au(CO)2(N2O)+ spectrum (Fig. 2). As the N
N stretch and the CO stretch respectively. Scaling using these factors results in simulated spectra as shown in Fig. S3–S5 in the ESI† which allow unambiguous identification of the observed spectral bands. However, while the N2O-based bands match very well, the CO-based bands are slightly overscaled resulting in excessively red-shifted calculated spectra. To provide a better match with experiment, the Figures shown below have been scaled with factors generated by fitting two Lorentzian functions to the single peak in the Au(CO)2(N2O)+ spectrum (Fig. 2). As the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch is well reproduced by traditional scaling this peak position is fixed and the relative intensities of the two peaks is drawn from calculations. This yields a CO stretch peak position of 2230.7 cm−1 (r2 = 0.97933) with resultant scaling factors of 0.9322 (N2O) and 0.9674 (CO).
N stretch is well reproduced by traditional scaling this peak position is fixed and the relative intensities of the two peaks is drawn from calculations. This yields a CO stretch peak position of 2230.7 cm−1 (r2 = 0.97933) with resultant scaling factors of 0.9322 (N2O) and 0.9674 (CO).
III. Results and discussion
(a) Infrared spectra of isotopically selected Au(12/13CO)2(N2O)+ complexes
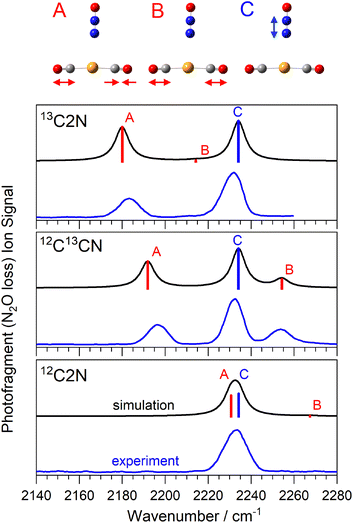
Fig. 2 shows a comparison of the infrared spectra for the isomer-selected Au(12/13CO)2(N2O)+ complexes with those simulated for the lowest energy calculated structures. This spectral region covers (i) the anti-phase and in-phase CO stretching bands in the Au(CO)2+ core (labelled A, and B, respectively) and (ii) the N2O N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch fundamental (labelled C). For brevity, we introduce a new nomenclature in which structures are labelled based on the number of 13CO or 12CO equivalents, so the Au(13CO)(12CO)(N2O)+ isotopologue is labelled 13C12CN, and the Au(13CO)2(N2O)+ complex 13C2N. The spectrum of the 12C2N complex is reproduced from our original article.25 In all three isotopologues, only the simple N2O loss channel is observed, reflecting the highly stable Au(CO)2+ core to which the N2O binds more weakly. Hence all the spectra shown are recorded as enhancements, from a zero baseline, in the Au(CO)2+ mass channel.
N stretch fundamental (labelled C). For brevity, we introduce a new nomenclature in which structures are labelled based on the number of 13CO or 12CO equivalents, so the Au(13CO)(12CO)(N2O)+ isotopologue is labelled 13C12CN, and the Au(13CO)2(N2O)+ complex 13C2N. The spectrum of the 12C2N complex is reproduced from our original article.25 In all three isotopologues, only the simple N2O loss channel is observed, reflecting the highly stable Au(CO)2+ core to which the N2O binds more weakly. Hence all the spectra shown are recorded as enhancements, from a zero baseline, in the Au(CO)2+ mass channel.
The spectrum of 12C2N complex in this region (Fig. 2) comprises a single, broadened (ca. 14 cm−1 full width half-maximum, FWHM) peak at approximately 2233 cm−1. As discussed previously,25 we are unable to resolve the N2O N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch fundamental from the anti-phase CO stretch in this peak. Confirming this accidental degeneracy was one of the inspirations for this study as the isotope shift of 13C should eliminate it. The N2O N
N stretch fundamental from the anti-phase CO stretch in this peak. Confirming this accidental degeneracy was one of the inspirations for this study as the isotope shift of 13C should eliminate it. The N2O N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch (labelled C) lies very weakly blue-shifted from the free N2O band (at 2223.5 cm−1) reflecting its weaker binding to the core structure. This is also indicated by the Au–N distance, determined by DFT calculations to be 3.026 Å. By contrast, the CO vibrational bands are strongly blue-shifted from the free CO stretch at 2143 cm−1 reflecting their “non-classical carbonyl” nature27,28 arising from the cationic metal center and the resulting lack of π-back-bonding. The very near linear Au(CO)2+ core means that the in-phase CO stretch band has very weak oscillator strength (labelled B, near 2270 cm−1) and is not observed.
N stretch (labelled C) lies very weakly blue-shifted from the free N2O band (at 2223.5 cm−1) reflecting its weaker binding to the core structure. This is also indicated by the Au–N distance, determined by DFT calculations to be 3.026 Å. By contrast, the CO vibrational bands are strongly blue-shifted from the free CO stretch at 2143 cm−1 reflecting their “non-classical carbonyl” nature27,28 arising from the cationic metal center and the resulting lack of π-back-bonding. The very near linear Au(CO)2+ core means that the in-phase CO stretch band has very weak oscillator strength (labelled B, near 2270 cm−1) and is not observed.
Isotopic substitution of a single 12CO with a 13CO leads to two major changes in the spectrum. Firstly, both CO-stretching bands are notably red-shifted from their band positions in the 12C2N spectrum reflecting the smaller reduced mass and its effect on the vibrational constant (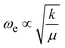 ). Secondly, the reduced symmetry results in intensity in both the in-phase and anti-phase CO stretching bands which are observed at ∼2253 cm−1 and ∼2195 cm−1, respectively.
). Secondly, the reduced symmetry results in intensity in both the in-phase and anti-phase CO stretching bands which are observed at ∼2253 cm−1 and ∼2195 cm−1, respectively.
The spectrum of the 13C2N complex, as expected, shows two clear bands, the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch (unchanged in all isotopologues) and the anti-phase CO band at 2183 cm−1, ca. 45 cm−1 to the red of the equivalent band in 12C2N. The in-phase stretching band is again essentially symmetry forbidden.
N stretch (unchanged in all isotopologues) and the anti-phase CO band at 2183 cm−1, ca. 45 cm−1 to the red of the equivalent band in 12C2N. The in-phase stretching band is again essentially symmetry forbidden.
In all cases, the simulated spectra reproduce the experimental spectra remarkably well, leaving little doubt over the security of the assignments. This provides confidence in assigning the larger complexes. In a more general context, this ability to reliably move vibrational modes within mixed ligand complexes via isotope substitution offers hope in better resolving, and hence understanding, the spectra of other ion–molecule complexes.28,29,38,39
(b) Spectra and fragmentation branching ratios of larger mixed-ligand complexes
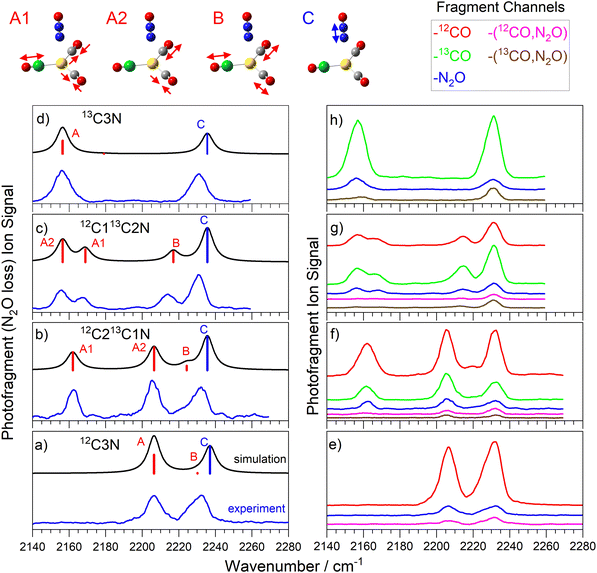
Fig. 3 shows the comparison of experimental and simulated spectra for the four isotopologues of the Au(12/13CO)3(N2O)+ complex. The structure is unambiguously assigned to a C3v structure with trigonal planar Au(CO)3+ core to which N2O binds along the C3 axis via the terminal N atom.25 The addition of a third CO to the core brings the calculated CO binding energy down from 0.7 eV to 0.26 eV, still markedly higher than the 0.15 eV binding of the N2O ligand but accessible for IR photodissociation in the range of our spectra (0.265–0.282 eV).The spectra in Fig. 3a–d were recorded in the N2O loss channel for direct comparison with Fig. 2. Only two bands are IR active in the spectrum of the 12C3N and 13C3N complexes, the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch and the degenerate CO antisymmetric stretch (at 2206 cm−1 and 2155 cm−1, respectively). New IR active modes arise in the 12C213CN and 12C13C2N complexes as the CO symmetric stretch gains oscillator strength and the anti-symmetric stretch splits into two components (labelled A1 and A2).
N stretch and the degenerate CO antisymmetric stretch (at 2206 cm−1 and 2155 cm−1, respectively). New IR active modes arise in the 12C213CN and 12C13C2N complexes as the CO symmetric stretch gains oscillator strength and the anti-symmetric stretch splits into two components (labelled A1 and A2).
The markedly lower CO binding energy in C3N complexes compared to C2N complexes gives rise to more interesting fragmentation dynamics. Now multiple dissociation channels are observed and these are represented in the form of fragment-resolved action spectra, shown to scale in Fig. 3e–h. The blue spectrum in each panel is that recorded in the N2O loss channel reproduced from Fig. 3a–d. In each C3N complex, N2O loss represents a minor dissociation channel with branching ratio no greater than 0.15, despite the fact that the binding energy of N2O to the rest of the complex (ca. 0.15 eV) is the lowest of all. Instead, the dominant fragmentation pathway is CO loss (ca. 0.26 eV binding energy) which, in these studies, can be resolved into 12CO or 13CO loss channels. The relative branching ratios for 12CO vs13CO loss appears statistical, reflecting the number of each CO isotope in the parent complex. Hence the signal in the 13CO loss channel (green in Fig. 3f–h) in the 12C213CN complex is very close to twice that in the 12CO loss channel (red) and vice versa in the 12C13C2N complex.
Importantly, the action spectra recorded in each of the single ligand loss channels are all essentially identical-pumping a N2O-centered mode does not lead to preferential N2O loss. Hence the fragmentation branching ratios are the same for every vibration pumped. This implies rapid and efficient IVR, with the photon energy quickly distributed around the complex rather than experiencing obvious bottlenecks at the weaker intermolecular complex bonds which might lead to rupture of that bond and loss of the chromophore ligand.
In addition to single ligand loss fragmentation channels, spectra are observed which correspond to the loss of multiple ligands, namely loss of both the N2O ligand and a CO (see Fig. 3e–h). In fact, in each of the panels shown, the total signal observed in all –[N2O, CO] loss channels represents a comparable branching ratio to the simple N2O loss channel. It seems unlikely that any CO–N2O dimer species would be lost and thus we would have expected the energy threshold for the dual ligand loss to be significantly higher than for single ligand loss. Some caution is required in interpreting these dissociation pathways since we cannot exclude the possibility of multiple photon absorption. In our earlier study of Au(CO)n(N2O)m+ which involved pure 12CO, we performed a full infrared pulse energy study25 and showed that single ligand loss occurs efficiently at the one-photon level but that –[N2O, CO] loss channel was dominated by two-photon absorption at the higher pulse energies available. The cost of 13CO prevented such a study in this case but there is little reason to suggest there would be any difference here.
Our experiments cannot distinguish unambiguously between two photon absorption followed by fragmentation and two successive absorption–fragmentation events. However, small but clear differences are observed in the spectra recorded in some of the dual ligand loss channels compared to those recorded in single ligand loss channels. One clear difference lies in the relative intensities of the N2O and the CO-centred bands with the former appearing considerably more strongly in the spectra of the dual ligand loss (see Fig. 3e). This is particularly true in the spectra of the 13C212CN and 13C12C2N complexes, in which the CO bands in the 2150–2175 cm−1 region are barely visible at all but also in the weak CO band in the 13C3N complex. This suggests stepwise fragmentation with CO loss following the first photon absorption at the CO stretch. This would lead to significant core rearrangement to a linear Au(CO)2+ structure and loss of the chromophore in the A1/A2 region. In all probability, it would also leave the fragment complex with significant internal energy leading to broadening of any subsequent absorption bands. There is still a small degree of fragmentation present in the 12C3N spectrum (Fig. 3e, pink trace), possibly the result of IR absorption at this perturbed Au(CO)2+ structure but only for the anti-phase (nominally A2) CO stretch. Since none of the C2N complexes have absorption bands in the same spectral region (see Fig. 2) no second photon could then be absorbed. Given the relative energy of the initial daughter complex compared to the putative ground state of the Au(12/13CO)2(N2O)+ complex, a fertile avenue for future work could be to characterise the kinetic energy and rovibrational distribution of the ejected CO ligand.40
The fact that the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch mode at 2233 cm−1 is strong in all fragmentation channels for every complex implies that, although it is a strong chromophore, the N2O is not lost rapidly at the one photon level. This is consistent with the observation of more efficient CO loss in general.
N stretch mode at 2233 cm−1 is strong in all fragmentation channels for every complex implies that, although it is a strong chromophore, the N2O is not lost rapidly at the one photon level. This is consistent with the observation of more efficient CO loss in general.
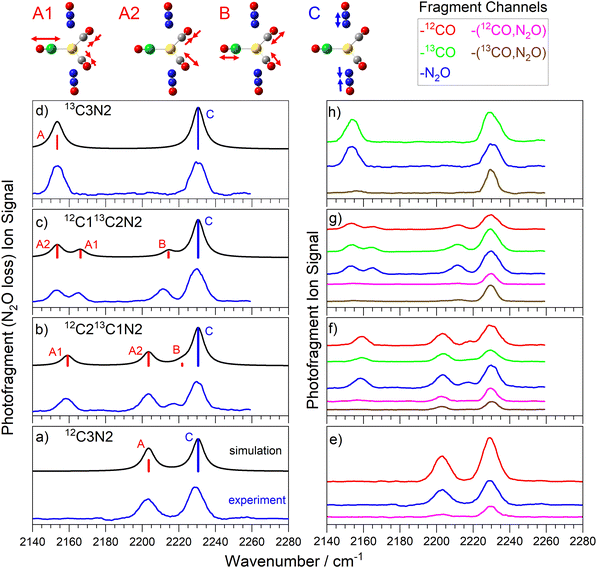
Many of the same ideas introduced in the discussion of the spectra and dissociation dynamics of the C3N complexes apply to the C3N2 complexes (see Fig. 4). Excellent agreement between experimental and simulated spectra (Fig. 4a) lead to clear and unambiguous spectral assignments once more. The trigonal bipyramidal (D3h) structure exhibits very similar spectral bands to the C3N complexes. The Au(CO)3+ core has identical vibrations and only the anti-phase N2O stretching band is infrared allowed. The additional N2O ligand results in enhance intensity of the 2233 cm−1 N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch band relative to the CO modes.
N stretch band relative to the CO modes.
The similarity of C3N2 complexes to C3N follows though into the fragmentation dynamics. Again the strongest branching ratios are observed for the CO loss channels although the effect is less marked in C3N2 given the second N2O ligand. To a good approximation, the relative single ligand fragmentation yields mirror the respective number of ligands present with the ratio of total CO loss to N2O approximately 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. This despite the calculated CO binding energy (at 0.26 eV) being a factor of two larger than that for N2O (0.12 eV).
2. This despite the calculated CO binding energy (at 0.26 eV) being a factor of two larger than that for N2O (0.12 eV).
Once more, near identical spectra are observed in all the single ligand loss channels further supporting the idea of rapid IVR. The additional N2O ligand further exaggerates the relative prominence of the N2O band in the dual ligand loss channels. In the 13C212CN2 complex barely any CO bands are observed in the –[CO, N2O] channels whilst in the 13C12C2N2 complex only the A2 CO mode exhibits meaningful oscillator strength in these channels. Interestingly, in both the 12C3N2 and the 13C3N2 the CO bands are extremely weak in the dual –[CO, N2O] loss channels. No fragmentation was observed corresponding to either –2CO or –2N2O fragmentation despite the latter having comparable dissociation threshold to single CO loss.
The vibrational motion associated with each of the calculated modes is very local to the chromophore excited. That is to say that excitation of the N2O stretches result in almost no motion of the CO ligands and vice versa. This is particularly true in the symmetric C3N2 complexes with Au(N2O)2+ and Au(CO)3+ systems vibrating completely independently. Even in the C2N and C3N complexes, the motion induced in the CO-system following excitation of the N2O vibration is minimal.
(c) Computational study of intramolecular energy flow
In an attempt to better understand the dissociation dynamics observed a nudged-elastic band optimization41,42 was performed to estimate the minimum energy path for N2O and CO dissociation. The Gaussian 2016 program was again used for all electronic structure calculations.36 The result is shown in Fig. 5 with full details provided in ESI.† The abscissa coordinate is the distance between the gold atom and the centre of mass of the leaving ligand. Three cuts across the potential energy surface (PES) are shown, relative to the minimum energy structure, with figures of the path enclosed in the same colour as the cut. The lowest (black) potential corresponds to loss of the N2O ligand, while the red and blue cuts correspond to different pathways leading to CO loss; The CO-p (red) curve corresponds to CO leaving within the plane of the CO core and the CO-o (blue) curve a path orthogonal to the trigonal plane. The two are similar except in the close-range region in which CO-o is steeper. CO cleavage can clearly occur via heat transferred to vibrational motion perpendicular to, or in, the trigonal plane. The threshold for N2O loss (0.17 eV), is, however, markedly lower than that for CO loss (0.30 eV) and the preferential loss of CO observed experimentally remains hard to explain on energetic grounds.IR absorption by a localized vibrational mode heats the rest of the complex via anharmonic terms in the potential energy surface. Although the system undergoes substantial geometric changes upon dissociation, the early transfer of energy out of the initially excited zero-order bright state is driven by small anharmonic coupling terms. To analyse the coupling between modes and how these can lead to competing dissociating pathways, whilst keeping the analysis tractable, we have partitioned modes into subsets corresponding to stretches and intermolecular ligand modes. Since the number of CO ligand modes is large, we selected those which are necessarily involved in the formation of the co-linear CO, C2N complex (approximately half of them). These also naturally describe the in-plane dissociation seen in Fig. 5. To estimate the correlated space between modes, we proceeded to evaluate the PES. For every pair of modes possible, vectors along the diagonal of each quadrant were used to evaluate tens of ab initio samples. We also generated hundreds of quasi-random (Sobol) samples for these same correlated spaces (see Fig. S8 in ESI†). Mass- and frequency-scaled normal mode coordinates were used to approximately place all displacements into a similar domain. A cluster expansion of symmetry-adapted polynomial functions was then fitted to the calculated data.43 Up to sixth order polynomials were used to fit the data with minimal error (typical average RMSD below 10−5 eV).
To estimate the mode-pair correlation more accurately, the following root mean squared deviation (RMSD) 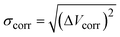 , was numerically estimated using a Monte-Carlo approach such that:
, was numerically estimated using a Monte-Carlo approach such that:
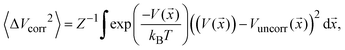 | (1) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) is the model PES in the pair of coordinates space while Vuncorr (
) is the model PES in the pair of coordinates space while Vuncorr (![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) corresponds to the model PES without any correlating (cross) terms. The integral measures the degree of correlation in the regions of phase-space accessed by the system at temperature T. This is done for each possible pair of modes and averaged for each set using a sampling temperature of 150 K which represents a reasonable estimate of the experimental conditions. Table 1 shows the average (relative) RMSD values of the various mode-pairs scaled to the N2O ligand–N2O ligand term (3.25 × 10−2 eV) to illustrate their relative magnitude. This provides a more quantitative measure of the extent of coupling between the differing types of motion.
) corresponds to the model PES without any correlating (cross) terms. The integral measures the degree of correlation in the regions of phase-space accessed by the system at temperature T. This is done for each possible pair of modes and averaged for each set using a sampling temperature of 150 K which represents a reasonable estimate of the experimental conditions. Table 1 shows the average (relative) RMSD values of the various mode-pairs scaled to the N2O ligand–N2O ligand term (3.25 × 10−2 eV) to illustrate their relative magnitude. This provides a more quantitative measure of the extent of coupling between the differing types of motion.
| CO stretch | N2O stretch | CO ligand | N2O ligand | |
|---|---|---|---|---|
| CO stretch | 0.02 | 0.0004 | 0.05 | 0.24 |
| N2O stretch | 0.02 | 0.001 | 0.02 | |
| CO ligand | 0.05 | 0.03 | ||
| N2O ligand | 1.00 |
Table 1 shows that the stretching modes couple comparably well with their respective ligand modes. However, CO stretching also couples strongly to N2O ligand modes and conversely, N2O stretching modes weakly couples with CO ligand modes. This appears contrary to the experimental observation that pumping either CO or N2O stretches leads to effective and similar CO fragmentation. However, time-dependent perturbation theory suggests population transfer depends not only on coupling, but inversely on frequency difference. In this case, N2O ligands may consequently take longer to become excited; N2O ligand dissociating modes (modes 1a, 2a, see Table S3: around 50–70 cm−1, ESI†) have lower frequencies than the corresponding CO ligand modes (modes 4–6e, 1a2 and 3a1, 4a1 ranging from 200 to 450 cm−1).
The CO ligand modes couple significantly to all modes (except the N2O stretch). Those CO ligand modes not included in the subset (orthogonal to the trigonal plane) are also likely to couple to the in-plane modes since these must be, at least in part, involved in the out-of-plane dissociation (blue) profile of Fig. 5. Together, this trigonal framework forms a large anharmonically-coupled manifold plausibly ‘funnelling’ the available energy, such that stretch excitations may well preferentially heat the intermolecular CO ligand vibrations faster than the intermolecular N2O ligand vibrations.
Table 1 alone is not sufficient to explain the non-statistical experimental results and a closer examination is warranted. The ongoing construction of a model PES on which to perform quantum dynamical simulations, which will form the basis of a subsequent article, is briefly described here. We use ‘quasi-normal’ coordinates which succinctly represent the competing dissociating channels, while continuing to form a basis for C3v irreducible representations; this allowed us to accurately fit the Taylor model to the anharmonic basins, whilst permitting a further fit of the dissociating channels. This product-form model allows the application of wave packet methods44 for which we can measure the picosecond energy transfer from high to low frequency modes, as well as the outgoing flux along the dissociating channels.
IV. Summary and conclusions
13CO substitution has been used to better understand the structure and spectroscopy of mixed ligand Au+(CO)n(N2O)m ion–molecule complexes. The agreement between experimental infrared action spectra and simulated vibrational spectra of calculated low energy structures is good and provides for unambiguous identification of the structures generated. Similar action spectra are observed in all single-ligand loss channels indicating rapid intramolecular vibrational redistribution following infrared absorption. Only N2O loss is observed for Au+(CO)2(N2O) complexes, reflecting the strong binding of the Au+(CO)2 core structure. No clear isotopologue effects were observed in the dissociation yields with 12CO vs.13CO loss in stoichiometric ratios within experimental uncertainty. In Au+(CO)3(N2O)1,2 complexes, however, a clear preference for CO loss is once more observed over N2O loss despite the binding energy for the latter being considerably smaller. This non-statistical fragmentation has been investigated computationally both by computing vibrational mode couplings on an ab initio potential surface and with nudged elastic band dissociative potential energy curves. The former yield insight into potential bottlenecks in the energy flow around the complex following vibrational excitation, with coupling between the CO–Au+ intermolecular modes and the N2O stretch particularly weak. Weak coupling between the CO ligand modes and the N2O ligand modes together with the larger phase space of the former, suggest that energy may be effectively trapped in the Au+(CO)n core leading to more efficient CO loss than N2O when energetically allowed.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was supported by EPSRC under Programme Grant EP/T021675. PDW thanks Magdalen College, Oxford for his Fellowship by Examination – GM is grateful to Worcester College for graduate funding and PAJP is grateful to University College, Oxford for his Bob Thomas Scholarship.References
- J. M. Lisy, Int. Rev. Phys. Chem., 1997, 16, 267–289 Search PubMed
.
- M. A. Duncan, Int. J. Mass Spectrom., 2000, 200, 545–569 Search PubMed
.
- N. R. Walker, R. S. Walters and M. A. Duncan, New J. Chem., 2005, 29, 1495–1503 RSC
.
- M. A. Duncan, Int. Rev. Phys. Chem., 2003, 22, 407–435 Search PubMed
.
-
M. A. Duncan, in Physical Chemistry of Cold Gas-Phase Functional Molecules and Clusters, 2019, ch. 6, pp. 157–194 Search PubMed
.
- J. M. Lisy, J. Chem. Phys., 2006, 125, 132302 CrossRef PubMed
.
- K. R. Asmis and J. Sauer, Mass Spectrom. Rev., 2007, 26, 542–562 CrossRef CAS PubMed
.
- H. Ke, C. van der Linde and J. M. Lisy, J. Phys. Chem. A, 2015, 119, 2037–2051 CrossRef CAS PubMed
.
- K. Mizuse and A. Fujii, J. Phys. Chem. A, 2012, 116, 4868–4877 CrossRef CAS PubMed
.
- M. Okumura, L. I. Yeh and Y. T. Lee, J. Chem. Phys., 1985, 83, 3705–3706 CrossRef CAS
.
- O. Rodriguez and J. M. Lisy, J. Phys. Chem. A, 2011, 115, 1228–1233 CrossRef CAS PubMed
.
- O. M. Cabarcos, C. J. Weinheimer and J. M. Lisy, J. Chem. Phys., 1998, 108, 5151–5154 CrossRef CAS
.
- O. M. Cabarcos, C. J. Weinheimer and J. M. Lisy, J. Chem. Phys., 1999, 110, 8429–8435 CrossRef CAS
.
- J. P. Beck and J. M. Lisy, J. Phys. Chem. A, 2011, 115, 4148–4156 CrossRef CAS PubMed
.
- T. D. Vaden and J. M. Lisy, J. Chem. Phys., 2004, 120, 721–730 CrossRef CAS PubMed
.
- D. J. Miller and J. M. Lisy, J. Chem. Phys., 2006, 124, 184301 CrossRef PubMed
.
- H. Ke and J. M. Lisy, Phys. Chem. Chem. Phys., 2015, 17, 25354–25364 RSC
.
- T. D. Vaden and J. M. Lisy, J. Phys. Chem. A, 2005, 109, 3880–3886 CrossRef CAS PubMed
.
- D. J. Miller and J. M. Lisy, J. Phys. Chem. A, 2007, 111, 12409–12416 CrossRef CAS PubMed
.
- G. N. Patwari and J. M. Lisy, J. Phys. Chem. A, 2003, 107, 9495–9498 CrossRef CAS
.
- A. L. Nicely, D. J. Miller and J. M. Lisy, J. Am. Chem. Soc., 2009, 131, 6314–6315 CrossRef CAS PubMed
.
- E. Barwa, M. Ončák, T. F. Pascher, A. Herburger, C. van der Linde and M. K. Beyer, Chemistry, 2020, 26, 1074–1081 CrossRef CAS PubMed
.
- E. Barwa, T. F. Pascher, M. Ončák, C. van der Linde and M. K. Beyer, Angew. Chem., Int. Ed., 2020, 59, 7467–7471 CrossRef CAS PubMed
.
- Z. Ma, L. Chen, C. Xu and J. A. Fournier, J. Phys. Chem. Lett., 2023, 14, 9683–9689 CrossRef CAS PubMed
.
- A. E. Green, R. H. Brown, G. Meizyte and S. R. Mackenzie, J. Phys. Chem. A, 2021, 125, 7266–7277 CrossRef CAS PubMed
.
- G. Meizyte, R. H. Brown, E. I. Brewer, P. D. Watson and S. R. Mackenzie, J. Phys. Chem. A, 2023, 127, 9220–9228 CrossRef CAS PubMed
.
- A. D. Brathwaite, H. L. Abbott-Lyon and M. A. Duncan, J. Phys. Chem. A, 2016, 120, 7659–7670 CrossRef CAS PubMed
.
- J. Velasquez, B. Njegic, M. S. Gordan and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 1907–1913 CrossRef CAS PubMed
.
- E. M. Cunningham, A. S. Gentleman, P. W. Beardsmore, A. Iskra and S. R. Mackenzie, J. Phys. Chem. A, 2017, 121, 7565–7571 CrossRef CAS PubMed
.
- A. Iskra, A. S. Gentleman, A. Kartouzian, M. J. Kent, A. P. Sharp and S. R. Mackenzie, J. Phys. Chem. A, 2017, 121, 133–140 CrossRef CAS PubMed
.
- E. I. Brewer, A. E. Green, A. S. Gentleman, P. W. Beardsmore, P. A. J. Pearcy, G. Meizyte, J. Pickering and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2022, 24, 22716 RSC
.
- L. E. Orgel, J. Chem. Soc., 1958, 4186–4190 RSC
.
- J. Velasquez, B. Njegic, M. S. Gordon and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 1907–1913 CrossRef CAS PubMed
.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- J. A. Pople, H. B. Schlegel, R. Krishnan, D. J. Defrees, J. S. Binkley, M. J. Frisch, R. A. Whiteside, R. F. Hout and W. J. Hehre, Int. J. Quant. Chem., 1981, 20, 269–278 CrossRef
.
- E. M. Cunningham, A. E. Green, G. Meizyte, A. S. Gentleman, P. W. Beardsmore, S. Schaller, K. M. Pollow, K. Saroukh, M. Förstel, O. Dopfer, W. Schöllkopf, A. Fielicke and S. R. Mackenzie, Phys. Chem. Chem. Phys., 2021, 23, 329–338 RSC
.
- A. S. Gentleman, A. E. Green, D. R. Price, E. M. Cunningham, A. Iskra and S. R. Mackenzie, Top. Catal., 2018, 61, 81–91 CrossRef CAS PubMed
.
- M. S. Quinn, D. U. Andrews, K. Nauta, M. J. T. Jordan and S. H. Kable, J. Chem. Phys., 2017, 147, 013935 CrossRef PubMed
.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- C. Robertson and G. A. Worth, Chem. Phys., 2015, 460, 125–134 CrossRef CAS
.
-
G. A. Worth, K. Giri, G. W. Richings, I. Burghardt, M. H. Beck, A. Jäckle and H.-D. Meyer, The QUANTICS Package, Version 1.1, University of Birmingham, Birmingham, UK, 2015 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Geometric structure files for all complexes studied; normal mode analyses; example fragmentation mass spectra; dissociation branching ratios; further details on calculated dynamics and vibrational mode coupling. See DOI: https://doi.org/10.1039/d4cp00978a |
| This journal is © the Owner Societies 2024 |