Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of graphene on the electronic and magnetic properties of an iron(III) porphyrin chloride complex†
Young-Joon
Song
 *a,
Charlotte
Gallenkamp
b,
Genís
Lleopart
c,
Vera
Krewald
*a,
Charlotte
Gallenkamp
b,
Genís
Lleopart
c,
Vera
Krewald
 *b and
Roser
Valentí
*a
*b and
Roser
Valentí
*a
aInstitut für Theoretische Physik, Goethe-Universität Frankfurt, Max-von-Laue-Str. 1, 60438 Frankfurt am Main, Germany. E-mail: ysong@itp.uni-frankfurt.de; valenti@itp.uni-frankfurt.de
bQuantum Chemistry, Department of Chemistry, Peter-Grünberg-Str. 4, 64287 Darmstadt, Germany. E-mail: vera.krewald@tu-darmstadt.de
cDepartament de Ciéncia de Materials i Química Física and Institut de Química Teórica i Computacional (IQTC), Universitat de Barcelona, c/Martí i Franqués 1-11, 08028 Barcelona, Spain
First published on 24th September 2024
Abstract
Although iron-based single atom catalysts are regarded as a promising alternative to precious metal catalysts, their precise electronic structures during catalysis still pose challenges for computational descriptions. A particularly urgent issue to be addressed is the influence of the environment on the electronic structure, and how to describe this accurately using computational methods. Here, we study an iron porphyrin chloride complex adsorbed on a graphene sheet using density functional theory calculations to probe how much the electronic structure is influenced by the presence of a graphene layer. Our results indicate that weak interactions due to van der Waals forces dominate between the porphyrin complex and graphene, and only a small amount of charge is transferred between the two entities. Furthermore, the interplay of the ligand field environment, strong p–d hybridization, and correlation effects within the complex are strongly involved in determining the spin state of the iron ion. By bridging molecular chemistry and solid state physics, this study provides first steps towards a joint analysis of the properties of iron-based catalysts from first principles.
1 Introduction
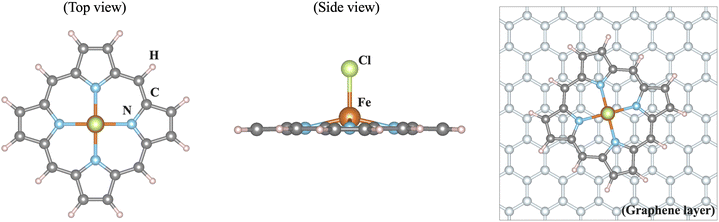
Iron as a versatile element for catalysis has received increasing attention over the past years. When bound in a macrocycle such as phthalocyanine or porphyrin, it can serve as a model for bioinorganic or man-made active sites.1–4 A field that has grown particularly rapidly is that of single-atom catalysis, where such types of active site are embedded in an extended graphene sheet or nanotubes or carbon-based environments that form during a pyrolysis step. For instance, in FeNC catalysts, the active sites are commonly discussed as a single iron ion coordinated by four nitrogen donors (FeN4).5–11 Additionally, the heterogenisation of iron complexes for applications in electrocatalysis, for instance by physisorption, covalent linkage, or incorporation into a conductive polymer, has become an important modification of the environment of these complexes with implications for catalysis.12For computational models of single-atom catalysts or iron complexes incorporated into electrode materials, the question arises as to how the environment should be described. An important component of the environment in electrocatalysts is the often carbon-based material of the electrode, raising the issue of the number of graphene layers that should be considered explicitly. Herein, we address this aspect by comparing the electronic structure of an isolated, neutral iron porphyrin complex, [FeIII(P)(Cl)] (P: porphyrin ligand; Cl: chloride ligand), with that of the same complex adsorbed on an extended graphene sheet, see Fig. 1. Since the electronic structure of the isolated complex is well-known, the effect of the graphene sheet can be evaluated well. We find that the influence of a graphene layer parallel to the catalyst plane on the electronic structure of [FeIII(P)(Cl)] is negligible, implying that future catalytic models can concentrate on single-layer models.
This evaluation is complemented by a comparison of the electronic structure descriptions using molecular and periodic approaches. Particular attention has been paid to different spin states and their relative stabilities in these two types of description. We highlight that, when aiming to describe Fe-based catalyst models using computational methods, theoreticians can use periodic methods with plane-wave basis sets and extended structural models or molecular methods with Gaussian basis sets and finite structural models.7,10,11,13 These two approaches differ not only in the model size, but also in the electronic structure treatments and underlying assumptions. This inhibits the comparability of results obtained using different approaches. Here we propose how these descriptions may be compared since both treatments can be used in complementary ways to model the same type of catalyst or material.
2 Methods
Methodology
The structure of iron(III) in an equatorial octaethylporphyrin (OEP) ligand sphere and an axially bound chloride ligand serves as a reference, with its coordinates as given in the ESI.† The truncated [FeIII(P)(Cl)] complex is obtained by replacing the eight ethyl substituents on the porphyrin ligand by hydrogen atoms and relaxing the resulting structure. The molecular calculations were performed within density functional theory (DFT) using the Tao–Perdew–Staroverov–Scuseria (TPSS) exchange–correlation functional14 in ORCA 5.0.415,16 with the Gaussian basis sets def2-TZVP on Fe, N and Cl and def2-SVP on C and H (labeled def2-TZVP:def2-SVP).17 Convergence criteria for the geometry relaxation and self-consistent-field (SCF) convergence were set to ‘tight’ in ORCA nomenclature. The dispersion correction D3BJ18,19 and implicit solvation model SMD with water20 as a solvent were used. For the electronic structures, single point calculations were carried out with the OPBE exchange–correlation functional and the CP(PPP)21 basis set on Fe, while def2-TZVP17 was employed for all other atoms (labeled CP(PPP):def2-TZVP). No dispersion correction was used for the single point calculations. These choices were made based on the literature on spin state prediction for iron complexes22–24 and in-house calibration studies for FeN4 environments in particular.The geometry and electronic structure of the truncated [FeIII(P)(Cl)] complex adsorbed on a graphene sheet were investigated via DFT using the projector augmented wave method25 implemented in the Vienna ab initio simulation package (VASP)26 under periodic boundary conditions. The generalized gradient approximation (GGA) was employed for the exchange–correlation functional.27 The size of the basis set was determined by the energy cutoff of 500 eV and the van der Waals correction (DFT-D2)28 was taken into account in the calculations. To treat localized Fe 3d orbitals properly and account for correlation effects, an onsite U and Hund's coupling JH (GGA+U) were introduced.29 As discussed below in the results, the preferred spin state of iron depends on the choice of U, and U = 4 eV and JH = 1 eV are employed in the calculations to obtain the experimentally observed high spin configuration. We also utilized the meta-GGA functional r2SCAN without including U in the calculations.30,31 For the structure optimisation, the coordinates of the graphene sheet were taken from a single layer of graphite with a C–C bond length of 1.42 Å. The [FeIII(P)(Cl)] complex was placed in different positions on the graphene sheet (see below). With the GGA+U description, all atoms of the [FeIII(P)(Cl)] complex were fully relaxed until the net force was smaller than 10−3 eV Å−1, while the graphene sheet was kept fixed. Additionally, the nonlocal van der Waals correction was tested during structure optimisation using the r2SCAN + rVV10 nonlocal vdW-DF functional implemented in VASP.32,33 The self-consistent field procedure used convergence criteria of 10−6 eV and the 6 × 6 × 1 k mesh. To simulate the [FeIII(P)(Cl)] complex without graphene in VASP, a large unit cell is utilized, where two iron atoms between adjacent unit cells are separated by a distance of 20 Å, using only one k point. Some figures were visualized using VESTA34 and PyProcar.35,36
3 Results
Analysis of the isolated molecular complex
The geometry of [FeIII(OEP)(Cl)] optimised with TPSS/def2-TZVP:def2-SVP in the expected high spin electronic configuration37 has structural parameters consistent with experiment (calc: d(Fe,Cl) = 2.264 Å, d(Fe,Nav) = 2.088 Å; exp: d(Fe,Cl) = 2.225(4) Å, d(Fe,Nav) = 2.065(2) Å38) and a small displacement of the iron(III) ion from the plane spanned by the four nitrogen atoms (calc: d(Fe,plane) = 0.466 Å; exp: d(Fe,plane) = 0.494(4) Å). Energetically, the high spin structure is found to be degenerate with the structure optimised as the intermediate spin case (<1.0 kcal mol−1 using OPBE/CP(PPP):def2-TZVP), while the low spin structure is clearly disfavoured (15.8 kcal mol−1).To facilitate faster calculations in the graphene adsorption studies, the eight ethyl substituents were truncated to hydrogen atoms, resulting in the unsubstituted porphyrin complex [FeIII(P)(Cl)]. The truncation has negligible effects on the structure and spin state splitting. The bond distance changes are predicted to be minimal (calc: d(Fe,Cl) = 2.248 Å, d(Fe,Nav) = 2.090 Å). Similarly, the energetic ordering of spin states is unchanged, i.e. degenerate high and intermediate spin states (<1.0 kcal mol−1) and disfavoured low spin state (+15.2 kcal mol−1). Relaxing this structure in VASP leads to very small structural changes. The Fe–Cl distance is predicted at 2.208 Å, and the average Fe–N distance is found at 2.085 Å. To investigate the bond distance in hypothetical low and intermediate spin states of iron, the [FeIII(P)(Cl)] structure is additionally relaxed in VASP by fixing the total spin moment to be 1μB and 3μB representing a low and intermediate spin configuration respectively. The resulting average bond distance between Fe and N is measured as 1.994 Å (2.016 Å) in the low (intermediate) spin state, i.e. as expected shorter than in the high spin state.
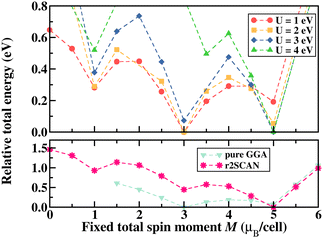
Similar to the spin state energetics found for [FeIII(P)(Cl)] in ORCA, the VASP results in [FeIII(P)(Cl)] also reveal that the low spin structure is energetically unfavored with all exchange–correlation functionals used here, as shown in Fig. 2 that illustrates relative total energy as a function of the total spin moment obtained via fixed spin moment calculations. It is evident that U ≥ 3 eV in GGA+U leads to a high spin iron species, whereas U < 3 eV favors the intermediate spin configuration of iron. Furthermore, the parameter-free meta-GGA r2SCAN stabilises the complex in a high spin configuration of iron. Specifically, the energy difference between the intermediate and high spin states of iron is obtained to be about 854 meV (19.7 kcal mol−1) in GGA+U (4 eV) and 446 meV (10.3 kcal mol−1) in r2SCAN. These energy differences are larger than those predicted using the molecular approach (vide supra).
Numerous studies have focused on iron porphyrin complexes and similar systems, employing diverse theoretical approaches to unveil the ground state spin configuration of iron.39–41 Our results are in agreement with these studies, including the predicted high spin ground state and relaxed Fe–N distance of 2.085 Å for [FeIII(P)(Cl)] which closely aligns with the range associated with high-spin configurations. Our focus, therefore, turns to the interaction of the complex with a carbon-based environment, represented here by a graphene sheet as this type of environment is expected in FeN4 catalyst materials.
Interaction with a graphene surface
To evaluate the interaction of [Fe(P)(Cl)] with a graphene sheet, as shown in Fig. 1, the molecule was deposited on graphene sheets of sizes 8 × 8 and 6 × 6. We find only small differences in the results for the 8 × 8 and 6 × 6 graphene cases. While here we focus on the 8 × 8 graphene sheet representation, since computational cost was not a concern, future studies may use the smaller 6 × 6 graphene sheet size. Four possible interaction sites were considered as starting points: (i) “hollow”, where the centers of the iron complex and a central benzene ring align, (ii) “on-top”, where the center of the iron complex is placed directly above a carbon atom, (iii) “bridge 1” and (iv) “bridge 2”, where the center of the iron complex is placed above a C–C bond, see Fig. 3. Relaxation of the structures shows that the porphyrin complex in the site “on-top” moves and becomes the same as “bridge 1”. For “bridge 2” the porphyrin complex does not move but rotates by about 15 degrees. In contrast to the above cases, the positioning of the porphyrin complex remains unchanged in the case of “hollow”, see the ESI.†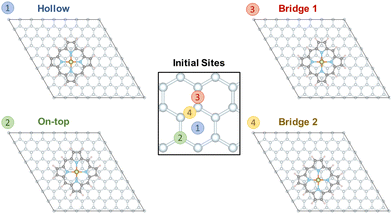 | ||
| Fig. 3 Structures of the [FeIII(P)(Cl)] complex adsorbed on a graphene layer considering four different initial sites of graphene for structural relaxation. | ||
Our results show that the “bridge 2” case is the most stable structure, but the energetic difference between the three sites is not substantial. The final structures “bridge 1” and “hollow” are found ca. 24 meV and 47 meV above the minimum structure “bridge 2”, i.e. less than 1.1 kcal mol−1. These results demonstrate that the interaction between [FeIII(P)(Cl)] is very small and isotropic with respect to the graphene plane. This agrees well with an experimental study of a single iron(II) phthalocyanine complex adsorbed on graphene, indicating that its position can be easily manipulated.42
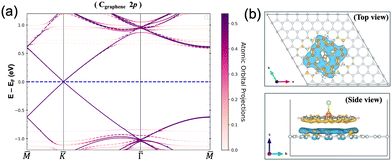
The minimal interaction is also clear from Bader charge analysis, where the charge transfer within GGA+U amounts to 3.9 × 10−3e per molecule. This can be seen in Fig. 4(a) where the GGA+U Cgraphene 2p orbital-resolved band structure of the system is depicted along the high symmetry points. Orbital-resolved band structures for the remaining atoms are shown in the ESI.† The Dirac point at the K point coming from the graphene emerges at the Fermi energy without any shifts resulting from the small interaction. Fig. 4(b) shows the corresponding charge difference plot, defined as ρAB − ρA − ρB, showing where regions of charge accumulation (light blue) and depletion (yellow) are localized. Due to the small interaction, spin density plots, defined as ρ↑ − ρ↓, within GGA+U are very much the same with and without graphene in the system, see Fig. S2 in the ESI.† At the GGA level, the adsorption energy, defined as Eads = EAB − EA − EB where A and B represent [FeIII(P)(Cl)] and graphene respectively, is calculated as −1.51 eV. In the r2SCAN calculations, we obtain Eads of −1.61 eV, i.e. equally weak. Furthermore, we confirmed that there was a tendency for [FeIII(P)(Cl)] to move away from the graphene sheet if van der Waals corrections were not included in the calculations. Without including van der Waals corrections, the resulting distance between [FeIII(P)(Cl)] and the graphene sheet increases by 0.81 Å, compared to the distance (3.26 Å) measured in the relaxed “bridge 2” structure where the van der Waals correction (DFT-D2) was taken into account. On the other hand, this distance (3.26 Å) remained nearly unchanged, with an increase of only 0.092 Å, when the r2SCAN + rVV10 nonlocal vdW-DF functional was employed during structure optimization. Consequently, the main sources of attractive interactions between the porphyrin complex and graphene are van der Waals forces.
Electronic structures of the free and physisorbed iron complex
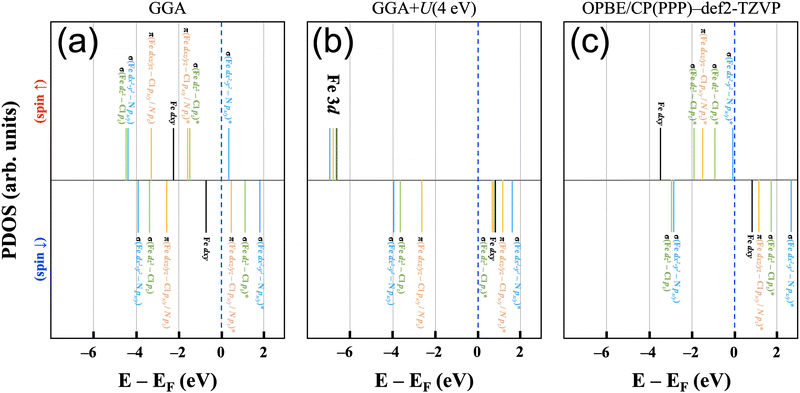
The electronic structure of the iron(III) ion in the square-pyramidal ligand field of [FeIII(P)(Cl)] is influenced by the axial chloride ligand and the displacement of the iron ion from the porphyrin ring. The splitting of the d orbital energies is expected to result in a high spin (xz,yz)2(xy)1(z2)1(x2 − y2)1 orbital occupation pattern. This highlights the relevance for FeN4-type active sites in single-atom catalysts, where the iron ion is assumed to be situated in a square-planar ligand field of an N-doped graphene plane in its bare state and have varying axial ligands throughout the catalytic cycle.This molecular orbital perspective is reflected in the MO diagram of the complex [FeIII(P)(Cl)] calculated using Gaussian basis sets, where the d orbitals span a range of ca. 6 eV (OPBE/CP(PPP):def2-TZVP). The predicted splitting and orbital occupation pattern results purely from the choice of methodology, i.e. chiefly the density functional and basis set. On the other hand, in calculations using plane-wave basis sets it is quite helpful to gain insights into understanding the correlation effect arising from the localized d orbitals by varying the Hubbard U term.43Fig. 5(a) and (b) show schematic electronic structures predicted using pure GGA and GGA+U for [FeIII(P)(Cl)] adsorbed on a graphene (8 × 8) sheet. The relative energies of each state are based on the results of the orbital projected densities of states. For comparison, the OPBE/CP(PPP):def2-TZVP electronic structure (Fig. 5(c)) is also depicted, wherein all energy states are adjusted relative to the spin down dxy orbital, aligned with the energy level of the corresponding orbital in (b).
Starting with the pure GGA prediction, we find that aside from the non-bonding Fe dxy orbitals, the Fe 3d orbitals are strongly mixed (i.e., hybridized) with N 2p and Cl 3p character. They hence form bonding and anti-bonding orbitals (i.e., one-electron states) as marked in Fig. 5. In the spin-up manifold, all Fe 3d orbitals are occupied except one σ-type antibonding orbital composed of Fe dx2−y2 and N px/y character. In the spin-down manifold, the only occupied orbital with significant iron contributions is the Fe dxy orbital that cannot mix significantly with porphyrin and chloride orbitals. As a result, the calculated total spin moment is 3.0μB per cell, close to an intermediate spin configuration of S = 3/2. This spin state is, however, not the experimentally determined spin state for the system;37 therefore appropriate corrections for handling correlation effects in the system need to be considered.
For iron ions, the spatially compact d orbitals indicate significant electron correlation, so a large value of U is needed.43–46 We find that values smaller than U = 3 eV result in an intermediate spin state, which is in good agreement with our fixed spin moment results in [FeIII(P)(Cl)] as discussed earlier. Using the generally accepted values of U = 4 eV and JH = 1 eV for iron44–47 produces the desired high spin configuration. As a result, the dxy orbital in the spin-down manifold is unoccupied, whereas all Fe 3d orbitals in the spin-up manifold are fully occupied. For the resulting high spin configuration of S = 5/2, a calculated total spin moment of 5.0μB per cell is found. Due to the occupied bonding orbitals in the spin-down manifold, ferromagnetic exchange interactions appear between Fe and N(Cl), as shown in the ESI,† Fig. S2. In addition, the calculated spin densities are localized around Fe, N, and Cl, whereas no density appears on the carbon centers. It is worth noting that iron's high spin configuration can be reached at U larger than 3 eV, whereas U smaller than 3 eV leads to an intermediate spin configuration as observed in the pure GGA results. Similar to the GGA+U results, iron's high spin state is obtained in the r2SCAN calculations, which is, however, not a routine functional for computational studies in the single atom catalysis field. Comparison of this electronic structure (Fig. 5(b)) with the molecular orbital diagram (Fig. 5(c)) from the calculation with Gaussian-type orbitals shows that the two approaches result in a qualitatively similar picture, though quantitative differences in the orbital ordering and splitting between the spin-up and spin-down manifolds remain.
4 Discussion and conclusions
In this theoretical study that provides a first step towards bridging the often disparate worlds of molecular chemistry and solid state physics in the FeN4 catalysis arena, we have shown that the interaction between graphene and an iron(III) complex, [FeIII(P)(Cl)], is negligible. This was demonstrated via the interaction energy, charge transfer analysis, and analysis of the band structure. Future studies of Fe-based catalyst models can therefore focus on the single graphene-like layer in which the catalytically active iron ion is embedded.A central issue for meaningful computational studies of Fe-based catalysts is the correct prediction of the spin states of iron. The spin state of iron is determined by the interplay of the ligand field environment, strong p–d hybridization, and correlation effects. A careful selection of the density functional and additional parameters is therefore needed, which ideally involves comparison with experimental spectroscopy data that are sensitive to details of the electronic structure.11,48–51 While spin–orbit coupling will likely be important to obtain a full picture of FeN4 active sites,51 the current theoretical literature in this field rarely even covers the non-relativistic correlation effects adequately. Focusing therefore on parameters that can be included and adjusted more easily for systems similar to or larger than the iron(III) high spin complex [FeIII(P)(Cl)], the ligand field splitting resulting from the electronic structure predictions must be sufficiently low to enable a population of the highest-lying iron d orbital.
Since the Hubbard U term influences the relative energies of the spin-up and spin-down manifolds, it has a significant influence on the correct prediction of the preferred spin state, as shown here explicitly. With a view beyond the specific system studied here, the predictive power of computational chemistry and physics can only be harnessed if the uncertainty in spin state prediction is known. This is challenging for DFT for most iron complexes, and in addition many examples of molecular complexes with close-lying or even degenerate spin states exist, which determine electronic properties as well as reactivity and catalysis. This work thus raises the question as to how to choose an appropriate electronic structure description for iron ions at the borderline of molecular and periodic descriptions where the ligand field splitting is expected to be less clear-cut than in the present example, or even completely unknown as is the case for FeNC catalyst models.
We suggest that molecular and periodic approaches can be used in a complementary manner. Since periodic approaches can be significantly faster than molecular descriptions, once an appropriate Hubbard U value is chosen, they can be used to rapidly evaluate different structures and screen electronic structures, e.g. to evaluate catalytic intermediates. A more detailed electronic structure analysis and the prediction of spectroscopic properties can then be sought using molecular approaches.
Author contributions
Y.-J. S., C. G. and G. Ll. performed the calculations. V. K. and R. V. conceived and supervised the project. All authors contributed to the discussions and the writing of the paper.Data availability
The data supporting this article have been included as part of the ESI.† The computational codes used to generate the primary data are available free of charge for academic users.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – CRC 1487, “Iron, upgraded!” – project number 443703006. The authors gratefully acknowledge the computing time provided to them on the high-performance computer Lichtenberg II at TU Darmstadt, funded by the German Federal Ministry of Education and Research (BMBF) and the State of Hesse.References
- Y. Zhao, G. Yu, F. Wang, P. Wei and J. Liu, Chem. – Eur. J., 2019, 25, 3726–3739 CrossRef CAS PubMed.
- E. Anxolabéhère-Mallart, J. Bonin, C. Fave and M. Robert, Dalton Trans., 2019, 48, 5869–5878 RSC.
- S. Amanullah, A. Singha and A. Dey, Coord. Chem. Rev., 2019, 386, 183–208 CrossRef CAS.
- X. Huang and J. T. Groves, Chem. Rev., 2018, 118, 2491–2553 CrossRef CAS PubMed.
- A. Zitolo, V. Goellner, V. Armel, M.-T. Sougrati, T. Mineva, L. Stievano, E. Fonda and F. Jaouen, Nat. Mater., 2015, 14, 937–942 CrossRef CAS PubMed.
- J. Li, S. Ghoshal, W. Liang, M.-T. Sougrati, F. Jaouen, B. Halevi, S. McKinney, G. McCool, C. Ma, X. Yuan, Z.-F. Ma, S. Mukerjee and Q. Jia, Energy Environ. Sci., 2016, 9, 2418–2432 RSC.
- L. Ni, C. Gallenkamp, S. Paul, M. Kübler, P. Theis, S. Chabbra, K. Hofmann, E. Bill, A. Schnegg, B. Albert, V. Krewald and U. I. Kramm, Adv. Energy Sustainability Res., 2021, 2, 2000064 CrossRef CAS.
- J. Li, M. T. Sougrati, A. Zitolo, J. M. Ablett, I. C. Oğuz, T. Mineva, I. Matanovic, P. Atanassov, Y. Huang, I. Zenyuk, A. Di Cicco, K. Kumar, L. Dubau, F. Maillard, G. Dražić and F. Jaouen, Nat. Catal., 2020, 4, 10–19 CrossRef.
- K. Kumar, L. Dubau, F. Jaouen and F. Maillard, Chem. Rev., 2023, 123, 9265–9326 CrossRef CAS PubMed.
- T. Mineva, I. Matanovic, P. Atanassov, M.-T. Sougrati, L. Stievano, M. Clémancey, A. Kochem, J.-M. Latour and F. Jaouen, ACS Catal., 2019, 9, 9359–9371 CrossRef CAS.
- L. Ni, C. Gallenkamp, S. Wagner, E. Bill, V. Krewald and U. I. Kramm, J. Am. Chem. Soc., 2022, 144, 16827–16840 CrossRef CAS PubMed.
- N. Heppe, C. Gallenkamp, S. Paul, N. Segura-Salas, N. Von Rhein, B. Kaiser, W. Jaegermann, A. Jafari, I. Sergueev, V. Krewald and U. I. Kramm, Chem. – Eur. J., 2023, 29, e202202465 CrossRef CAS PubMed.
- S. Kattel, P. Atanassov and B. Kiefer, Phys. Chem. Chem. Phys., 2014, 16, 13800 RSC.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- F. Neese, Inorg. Chim. Acta, 2002, 337, 181–192 CrossRef.
- F. Vlahovic, M. Gruden, S. Stepanovic and M. Swart, Int. J. Quantum Chem., 2019, 120, e26121 CrossRef.
- Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, J. Chem. Theory Comput., 2018, 14, 2446–2455 CrossRef CAS PubMed.
- M. Radon, Phys. Chem. Chem. Phys., 2019, 21, 4854–4870 RSC.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470 CrossRef CAS PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- J. C. V. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- J. Ning, M. Kothakonda, J. W. Furness, A. D. Kaplan, S. Ehlert, J. G. Brandenburg, J. P. Perdew and J. Sun, Phys. Rev. B, 2022, 106, 075422 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- U. Herath, P. Tavadze, X. He, E. Bousquet, S. Singh, F. Muñoz and A. H. Romero, Comput. Phys. Commun., 2020, 251, 107080 CrossRef CAS.
- L. Lang, P. Tavadze, A. Tellez, E. Bousquet, H. Xu, F. Muñoz, N. Vasquez, U. Herath and A. H. Romero, Comput. Phys. Commun., 2024, 297, 109063 CrossRef CAS.
- E. T. Kintner and J. H. Dawson, Inorg. Chem., 1991, 30, 4892–4897 CrossRef CAS.
- S. A. Kohnhorst and K. J. Haller, Acta Crystallogr., Sect. C: Struct. Chem., 2014, 70, 368–374 CrossRef CAS PubMed.
- V. E. J. Berryman, R. J. Boyd and E. R. Johnson, J. Chem. Theory Comput., 2015, 11, 3022–3028 CrossRef CAS PubMed.
- D. Nachtigallová, A. Antalík, R. Lo, R. Sedlák, D. Manna, J. Tuček, J. Ugolotti, L. Veis, Ö. Legeza, J. Pittner, R. Zbořil and P. Hobza, Chem. – Eur. J., 2018, 24, 13413–13417 CrossRef PubMed.
- A. Antalík, D. Nachtigallová, R. Lo, M. Matoušek, J. Lang, Ö. Legeza, J. Pittner, P. Hobza and L. Veis, Phys. Chem. Chem. Phys., 2020, 22, 17033–17037 RSC.
- B. De La Torre, M. Švec, P. Hapala, J. Redondo, O. Krejčí, R. Lo, D. Manna, A. Sarmah, D. Nachtigallová, J. Tuček, P. Błoński, M. Otyepka, R. Zbořil, P. Hobza and P. Jelínek, Nat. Commun., 2018, 9, 2831 CrossRef PubMed.
- Y.-J. Song, K.-W. Lee and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 125109 CrossRef.
- J. Ferber, H. O. Jeschke and R. Valentí, Phys. Rev. Lett., 2012, 109, 236403 CrossRef PubMed.
- S. Backes, H. O. Jeschke and R. Valentí, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 195128 CrossRef.
- M. D. Watson, S. Backes, A. A. Haghighirad, M. Hoesch, T. K. Kim, A. I. Coldea and R. Valentí, Phys. Rev. B, 2017, 95, 081106 CrossRef.
- P. M. Panchmatia, B. Sanyal and P. M. Oppeneer, Chem. Phys., 2008, 343, 47–60 CrossRef CAS.
- C. Gallenkamp, U. I. Kramm and V. Krewald, Chem. Commun., 2021, 57, 859–862 RSC.
- C. Gallenkamp, U. I. Kramm and V. Krewald, JACS Au, 2024, 4, 940–950 CrossRef CAS PubMed.
- M. Ghosh, S. E. Braley, R. Ezhov, H. Worster, J. A. Valdez-Moreira, Y. Losovyj, E. Jakubikova, Y. N. Pushkar and J. M. Smith, J. Am. Chem. Soc., 2022, 144, 17824–17831 CrossRef CAS PubMed.
- M. Tarrago, C. Römelt, J. Nehrkorn, A. Schnegg, F. Neese, E. Bill and S. Ye, Inorg. Chem., 2021, 60, 4966–4985 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Band structures, spin density plot, structures for relaxation, relaxed atomic positions, and details of INCAR tags. See DOI: https://doi.org/10.1039/d4cp01551g |
| This journal is © the Owner Societies 2024 |