Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Recombination resistance identification through current–voltage curve reconstruction in perovskite solar cells†
Pablo F.
Betancur
 a,
Omar E.
Solis
a,
Omar E.
Solis
 a,
Rafael
Abargues
a,
Rafael
Abargues
 a,
Teresa S.
Ripolles
a,
Teresa S.
Ripolles
 a and
Pablo P.
Boix
a and
Pablo P.
Boix
 *b
*b
aInstituto de Ciencia de los Materiales de la Universidad de Valencia (ICMUV), Paterna, 46980, València, Spain
bInstituto de Tecnología Química, Universitat Politècnica València-Consejo Superior de Investigaciones Científicas, Av. dels Tarongers, 46022, València, Spain. E-mail: pablo.p.boix@itq.upv.es
First published on 25th November 2024
Abstract
Perovskite solar cells (PSCs) have demonstrated remarkable advancements in efficiency and stability, yet fully understanding the dynamic processes governing their performance remains a challenge. Impedance spectroscopy (IS) offers a powerful means to characterize PSCs over a wide range of time scales, revealing insights into the internal electronic and ionic processes. However, critical factors like recombination, charge extraction, and transport resistance are often coupled in the same spectra response, affecting their accurate identification. This study explores the use of the j–V curve reconstruction as a tool to identify when recombination governs the impedance response. Our findings show that recombination resistance can be accurately identified, regardless of the underlying recombination mechanism, in the solar cells with unhindered charge extraction. Conversely, in devices with hindered charge extraction, the IS fitting struggles to decouple the transport, extraction and recombination processes, resulting in inaccurate j–V reconstructions. These findings emphasize the importance of accurately identifying the physical processes influencing IS spectra to improve diagnostics and device performance in PSC technologies.
Introduction
Perovskite solar cells (PSCs) have experienced a remarkable rise in efficiency, followed by an improvement in stability over the last decade. As this technology moves closer to commercialization, gaining a deeper understanding of the dynamic processes occurring under operating conditions that influence cell performance and lifetime becomes essential. Current density–voltage (j–V) measurement is one of the basic and more established characterization protocols for photovoltaic devices, enabling the determination of their performance in terms of power conversion efficiencies (PCEs) through parameters such as short-circuit current (jsc), open-circuit voltage (Voc), and fill factor (FF), whose maximum achievable values are well established in the literature.1–3 However, the j–V curve alone is insufficient to fully capture the complexity of the device behavior, offering only a static representation of its performance under specific conditions. This limitation is especially relevant for PSCs, as the j–V curve does not provide sufficient information about the electronic and ionic processes which ultimately govern the device operation, thus masking the limiting factors that directly impact their performance.Impedance spectroscopy (IS) provides a non-destructive approach to address these limitations. It is a powerful technique that enables the electrical characterization of devices at any steady state (fixing the illumination and DC voltage conditions) of the j–V curve across a wide range of time scales, shedding light on the internal processes of the PSCs.4,5 In a typical impedance measurement, a small frequency-modulated (AC) signal is applied around a fixed (DC) voltage bias. The subsequent AC current response is then measured, allowing the extraction of frequency-dependent data in the complex plane. This provides an insight into the internal mechanisms of the device across different temporal ranges. Due to this capability, IS could be used to decouple different processes that occur with designable kinetics, such as rapid electronic movement or slower ion migration and electrochemical reactions within the bulk material or at interfaces.6 IS has been widely used in other systems like batteries, organic and dye-sensitized solar cells.7–11 However, the IS data interpretation for the case of PSCs remains as topic of discussion in the scientific community. The clear identification of different features in the Nyquist plot with specific device processes can be ambiguous, hindering the use of the technique as a pragmatical analysis tool. The vast majority of IS spectra from PSC consist of distinct high frequency (HF) and low frequency (LF) features well separated in the form of two arches,6 bringing a common baseline to examine the data.
The implementation of equivalent circuit models (ECMs) is one of the most common approaches to analyze IS data. ECMs simplify complex systems into manageable models composed of basic electrical components. Although it is not strictly necessary to work with an ECM for the physical analysis, successfully fitting the data to an appropriate ECM ensures that it complies with the linear response criterion and contributes to confirm its validity as an IS spectra. From a qualitative point of view, different ECMs can reproduce the same spectra, highlighting the importance of working with accurate simplified models whose parameters correspond to the physical processes that determine the experimental IS response. Avoiding overparameterization is crucial, as it can lead to unreliable data interpretations. Detailed reviews of different ECMs implemented for PSCs6,12,13 analyze the common elements between them, and the various approaches when more complex features appear in the response. Among these, an ECM based on a parallel coupling of the ionic and electronic phenomena,14 derived from a phenomenological approach, can model the particularities of PSCs. This ECM consists of a series resistance (Rs) associated with the electrodes and wiring resistance, the geometrical capacitance (Cg) showcased at the high frequency regime related to the dielectric properties of the perovskite, a resistor (Rrec+tr) that couples both the recombination and transport/injection resistances, in parallel with a low frequency branch formed by a pair of resistance (Rion) and capacitance (Cion) related to the ionic nature of the perovskite and charge accumulation at the interfaces. This model has been widely employed to analyze different PSC systems,15–19 as it simplifies the interpretation of the impedance spectral features and provides a unified framework for comparing the data reported in the literature.
Nevertheless, even with an adequate ECM, obtaining relevant parameters that reproduce the IS response of PSCs can be challenging. The dominance of the low geometric capacitance and high ion-related capacitance result in the coupling of charge transport, extraction, and recombination phenomena and their associated resistances.11 These competing processes that ultimately govern the overall performance of PSCs are coupled in the spectral response, and subsequently in the parameter Rrec+tr of the previously discussed model. In highly efficient PSCs, this coupling does not represent a problem because the charge transport and extraction processes can be negligible for the cell behavior. However, as these processes get hampered, their coupling with the recombination resistance becomes an issue. Thus, it is crucial to find strategies to corroborate the physical meaning behind the resistances in the ECM and their relationship with the j–V characteristic of the devices. There are several techniques such as external quantum efficiency,20 bias-dependent photoluminescence imaging,21 and transient photovoltage techniques22–24 which indirectly allow the reconstruction or prediction of the j–V curve in photovoltaic devices. This is especially helpful in tandem solar cells systems, where the j–V characteristic of the individual sub-cells is typically not directly measurable. Beyond the academic interest of reconstructing the j–V curve from various experimental data, this method serves as a useful tool for interpreting complex measurements with challenging data interpretation.
Here, we present a simple method to determine if the recombination resistance (Rrec) is the dominant component of the Rrec+tr parameter extracted from the ECM analysis of the IS response. We evaluate four different PSCs cases (optimal, highly recombinative buried interface, low interfacial recombination with hindered extraction, and high interfacial recombination with hindered extraction) to assess when the calculated Rrec+tr allows to reconstruct the j–V curve, and therefore depicts the real Rrec. In the cases of unhampered charge extraction, the resistive parameter of the IS can be used to fully reproduce the j–V characteristics under different illuminations. This confirms the recombinative nature of the Rrec+tr parameter in these cases.
Results and discussion
To analyze the behavior of the IS response and identify the parameter that represents the PSCs recombination in an optimized system, we choose a perovskite composition based on a combination of cations that has shown results improving the performance and stability of the devices. Specifically, the triple-cation perovskite CsMAFA (as Cs+: cesium cation, MA+: methylammonium cation, and FA+: formamidinium cation) takes advantage of combining MA+ and FA+ cations, which reduces the defect density and improves the overall cell performance,25 and the addition of small amount of Cs+ enhances thermal and moisture stability, addressing one of the significant limitations of purely organic-based perovskite.26 This perovskite composition, Cs0.05(FA0.85MA0.15)0.95Pb(I0.85Br0.15)3, will be used as a reference for all the devices discussed in this study. We focus on various combinations of hole transport materials (HTMs) such as PEDOT:PSS (poly(3,4-ethylenedioxythiophene) polystyrene sulfonate) and MeO-2PACz ([2-(3,6-dimethoxy-9H-carbazol-9-yl)ethyl]phosphonic acid), and electron transport materials (ETMs), such as C60 and ICBA (Indene-C60 Bisadduct). These combinations aim to achieve devices with distinguishable recombination and charge extraction effects, ultimately affecting the overall cell performance. All the photovoltaic parameters for the devices under study are represented in Table 1. We selected cells with an average performance for each condition, the devices statistics and schematics are shown in Fig. S1 (ESI†). Based on the employed selective contacts, the devices were separated into the following cases:| Device | V oc (V) | J sc (mA cm−2) | FF (%) | PCE (%) |
|---|---|---|---|---|
| MeO-2PACz/C60 | 1.09 | 20.66 | 76.86 | 17.42 |
| PEDOT:PSS/C60 | 0.80 | 20.63 | 83.57 | 13.87 |
| MeO-2PACz/ICBA | 1.06 | 11.40 | 21.00 | 2.65 |
| PEDOT:PSS/ICBA | 0.83 | 1.91 | 19.78 | 0.32 |
(i) MeO-2PACz/CsMAFA/C60: optimized device with 17% PCEs and Voc of 1.1 V. The implementation of self-assembled monolayers such as MeO-2PACz have been reported to promote a fast hole extraction, reducing non-radiative recombination at the hole-selective interface.27 This configuration is used to evaluate parameters for highly efficient devices. The conduction band energy of C60 (∼−4.2 eV28,29) is a well fit to the CsMAFA, which value has been reported around −4.0 eV.30
(ii) PEDOT:PSS/CsMAFA/C60: this configuration was chosen to promote a scenario with high recombination. The highly doped nature of the PEDOT:PSS leads to a strong interfacial recombination between the HTM and the absorber, as reported in the literature.31,32 In the devices studied, this is reflected by a reduction of the PCE to 13% and Voc to 0.8 V.
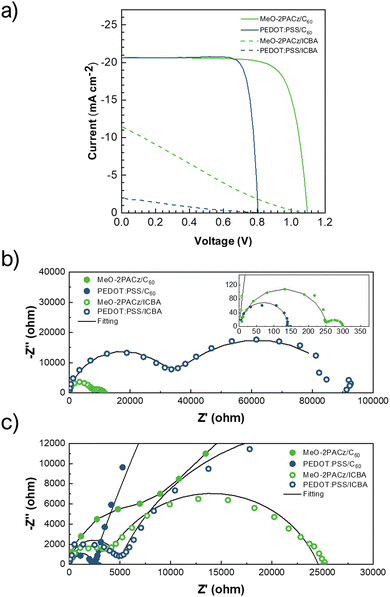
(iii) MeO-2PACz/CsMAFA/ICBA, and (iv) PEDOT:PSS/CsMAFA/ICBA: the implementation of ICBA as ETM aims to induce a hindered charge extraction in a system with low (case iii) and high (case iv) surface recombination. The conduction band of the ICBA (−3.7 eV33,34) presents higher energy compared to the CsMAFA (∼−4.0 eV). This mismatch in the band energy alignment explains the lack of rectification in the j–V curve (Fig. 1(a)) and the overall charge extraction problem of this devices with PCEs under 3%.
The j–V curves measured before and after the IS are shown in Fig. S2 (ESI†). In the first two cases (i) and (ii), the devices do not exhibit significant degradation after measurement, except for an increase in hysteresis with the use of PEDOT:PSS. With the addition of ICBA as ETM (iii) and (iv), differences are observed between the pre-IS and post-IS j–V curves. However, for all cases, the current values during IS remain stable and closely match the reverse j–V curve measured post-IS. This confirms that the devices are analyzed near steady-state condition, minimizing the impact of degradation or system instability. Fig. 1(b) and (c) show the Nyquist plots resulting from the IS measurements at Voc and Jsc conditions, which consistently display a qualitatively similar pattern. They reproduce the characteristic shape of the PSCs IS spectra, which consists of one arch at the HF regime and one at the LF regime, and both are well distinguished in all cases regardless of the performance of the device. This showcases that even when charge extraction is hampered, the absorber remains the main contributor to the Nyquist shape in our cases. Thus, the correct identification of the specific physical phenomenon behind these features becomes critical. The IS measurements for the ICBA-based devices result in spectra with relatively large values of Z′ at low frequencies. Note that, while this is classically interpreted as an improved recombination resistance, the Voc values of the PEDOT:PSS/ICBA devices do not support this claim. Additionally, these large Z′ spectra for the ICBA samples display relatively lower bias dependance, as can be seen in Fig. S3 (ESI†). This unusual behavior is in accordance with the inefficient charge extraction of these devices. The corresponding Bode plots for all cases are depicted in Fig. S4 (ESI†).
The ECM described in the introduction section can be employed as a tool to fit the data and analyze the impedance patterns. The extracted values of each parameter are plotted in Fig. 2, with a schematic representation of the ECM shown in the inset of Fig. 2(a). Among these parameters is the geometrical capacitance (Cg) which dominates the HF regime. Cg primarily depends on the nature and thickness of the absorber material and represents a typical and expected behavior for PSC. Accordingly, it presents a constant value around 10−8 F cm−2 through the different voltages for all samples, as expected for the unaltered thicknesses of all the device stacks. Using Cg and the measured perovskite thickness (500 nm) to estimate the dielectric permittivity of the material, we obtain an average value of 30, which aligns with other values reported for mixed perovskites.35–38
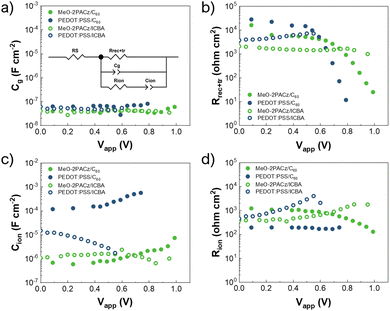 | ||
| Fig. 2 (a), (c) Capacitive and (b), (d) resistive elements as extracted from the fittings of the impedance spectra under 0.1 sun. The inset in (a) shows the ECM implemented. | ||
A prominent influence of the ionic nature is typically observed in the LF regime response of PSCs, reflected in the Cion and Rion parameters of the employed ECM. The behavior of these parameters strongly depends on the primary recombination mechanism,13 as suggested by drift-diffusion simulation models. However, it cannot not directly quantify the recombination process. The presence of negative hooks or negative capacitances in the Nyquist plots are a well-documented phenomena in PSC.39–42 Inductive loops, whether positive or negative, may arise due to the kinetic delay in ionic charge buildup at the interface, which can be explained by a surface polarization model.43
In systems dominated by bulk recombination, low ion vacancy density combined with low electronic diffusion coefficient can produce negative Rion values, which also translate into negative hooks on the Nyquist plot.
In our study, this model aligns well with the experimental observations captured on the spectra, particularly close to open circuit conditions. For instance, PEDOT:PSS-based devices are strongly affected by surface recombination and do not exhibit negative hooks, unlike MeO-2PACz-based devices (Fig. S3, ESI†). These hooks can be a signal of higher influence of bulk recombination processes for the latter, related to an improved HTM/perovskite interface, regardless of the analyzed electron transport material. In this line, self-assembled monolayers such as MeO-2PACz have been reported to promote a fast hole extraction, reducing non-radiative recombination at the interface,27 which supports the dominance of bulk recombination in these cases. Additionally, following the drift diffusion studies, the parameters determined by ionic effects should not change significantly for the cases ruled by surface recombination. However, the PEDOT:PSS/ICBA device shows a reduction in Cion and an increase in Rion. Similarly, in the case of MeO-2PAC device, with better charge extraction and less surface recombination than PEDOT:PSS, the use of ICBA contact increases the ionic density, as indicated by the reduction of Rion. This is the first indication that in our case, with the incorporation of ICBA (cases iii and iv), recombination is not the dominant phenomenon determining the performance of the solar cell.
As mentioned before, the ECM used in this work couples both recombination and transport/injection resistances in a unique parameter named Rrec+tr. In a conventional cell with suitable charge extraction, such as those with C60 (cases i and ii), this parameter is dominated by the recombination. Thus, the typical evolution of the Rrec+tr parameter dominated by recombination as a function of the voltage achieves a minimum value close to Voc, with an exponential increase towards lower voltages, followed by a voltage-independent region as we approach short circuit conditions (Fig. 2(b)). This approach enables a quantitative comparison of recombination based on Rrec+tr, with PEDOT:PSS/C60 devices showing lower recombination resistance, consistent with their lower Voc and higher surface recombination compared to MeO-2PACz/C60.31
To understand the behavior of this parameter when charge extraction is hindered by a mismatch on the energy level alignment between the absorber and ETM, we characterize the PEDOT:PSS/ICBA device, a case with extremely hindered electron extraction and high surface recombination resistance at the hole contact. For these devices, Rrec+tr parameter remains almost constant independently of the voltage applied. It is worth to remark that both PEDOT:PSS/ICBA and PEDOT:PSS/C60 devices display similar Voc, yet the Rrec+tr parameter for PEDOT:PSS/ICBA devices is larger than for MeO-2PACz/ICBA ones, in contrast to what it is expected from their Voc values. Therefore, it can be inferred that when charge extraction and transport are suboptimal, the resistance associated with these processes masks the system recombination resistance, as predicted by the ECM.
To address this limitation of IS caused by the mixed nature of Rrec+tr, it is essential to understand the coupling between extraction, recombination, and transport resistances. Specifically, it is necessary to determine when recombination is the factor dominating the device performance. In PSCs, the current density at the outer contacts of the solar cell, j(V), can be described as the sum of two components: the current density from photogenerated charge carriers, jph, which corresponds to the short-circuit current, jsc, if negligible recombination at zero bias is considered, and the current density from internal recombination within the perovskite layer and at the interfaces, jrec(V). Assuming that photogeneration is a voltage-independent process, as expected from the low exciton binding energy of I-based halide perovskites:
| j(V) = jph − jrec(V) | (1) |
Under open-circuit conditions, jph is completely offset by recombination current jrec(Voc), this means that the solar device operates under a kinetic balance of generation and recombination currents. Considering that the recombination resistance (Rrec) could be expressed as the inverse of jrec, it is possible to express jph as:
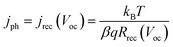 | (2) |
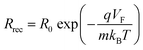 | (3) |
We observe that the electronic ideality factor shows strong sensitivity to the light intensity with the implementation of MeO-2PAC (Fig. S6b, ESI†). In this case, reducing surface recombination enhances the contribution of bimolecular recombination, which has been reported to be more sensitive to increases in light intensity due decreased defect-associated charge trapping.48–50 Additionally, drift-diffusion modeling has shown that devices dominated by surface recombination show lower apparent ideality factor values due to a reduction in ionic vacancies within the perovskite active layer,51 consistent with our experimental data. While typical values for m range between 1 and 2 depending on the nature of the recombination process, values outside this range have been reported in PSCs.44,45,47,52–54 To our knowledge, these outliers lack a well-defined physical interpretation.
The shape of the j–V curve is influenced by the variation of the recombination flux with applied voltage, which is modeled through m and the series resistance voltage loss.24 Consequently, the current at any specific voltage (VF), in the j–V curve can be expressed as:
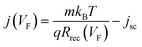 | (4) |
Eqn (4) presents a method to recalculate the final current at each voltage of the j–V curve using the parameters obtained by the ECM of the impedance data. Specifically, from Rrec+tr when this parameter is dominated by the recombination (and thus, it is possible to write Rrec+tr = Rrec), and the ideality factor. In those cases, for cells with optimal charge extraction, the ideality factor could be obtained from two approaches: directly from the impedance fitting using Rrec+trvs. V (Fig. S6a, ESI†) or corelating the jsc with Rrec+tr(Voc) (eqn (2)). The parameters used for the current recalculation are presented in the Table S1 (ESI†). Fig. 3 shows a remarkable correlation between experimental j–V curves and the j–V reconstruction, regardless of the method used to calculate m. The reconstructed j–V is compared to the average current measured at each DC vias during the IS. This so called “experimental curve” exhibits values comparable to the reverse j–V scan post-IS (Fig. S2, ESI†), indicating that the analysis is conducted under near steady-state conditions for each device, where factors like hysteresis or degradation are not interfering with the curve interpretation.
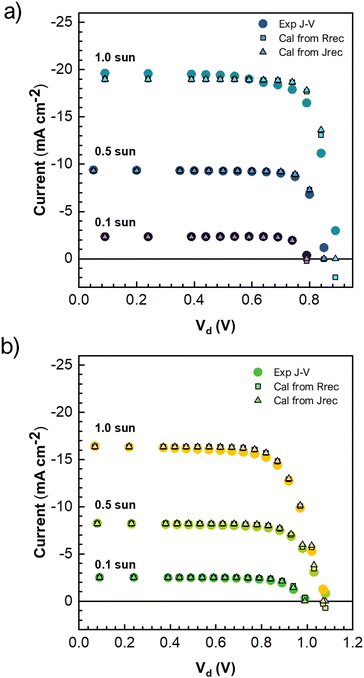 | ||
| Fig. 3 Experimental j–V curve (dots) and its reconstruction (eqn (4)) by using m-values obtained either the slope of Rrecvs. Vapp (squares) or from Jrec (eqn (2), triangles) at different illumination intensities for (a) PEDOT:PSS/C60 and (b) MeO-2PACz/C60 devices. The voltage applied is optimized by the series resistance contribution as Vd = Vapp − jRs. | ||
The successful reconstruction of the j–V curve for cases i and ii indicates a reliable estimation of the device recombination resistance from the Rrec+tr parameter. Furthermore, it corroborates that the photogenerated current is independent of the voltage applied and the shape of the j–V curve depends solely on the recombination processes. The calculated Rrec+tr = Rrec encompasses accurately the different recombination mechanisms, including bulk recombination in devices with less recombinative HTMs, such as MeO-2PACz (case i, Fig. 3(a)), and high surface recombination in devices with PEDOT:PSS (case II, Fig. 3(b)).
For the cases with hindered charge extraction (iii and iv) the Rrec+trvs. Vapp plot (Fig. 2(b)) presents an atypical response, maintaining independent to the change in voltage. Thus, as previously discussed, in these devices it is not possible to extract m from the plot slope, leading to try to calculate the ideality factor using only eqn (2). Interestingly, no Rrec+tr(VF) (where VF represents bias values close to open circuit conditions) leads to a m value that can successfully reconstruct the experimental j–V curve (Fig. S7, ESI†). This strongly indicates that charge extraction and transport resistance are dominating the device performance, masking the recombination resistance into the Rrec+tr parameter. Thus, using the j–V reconstruction is possible to determine when recombination resistance or transport/extraction resistance is dominating in Rrec+tr.
To generalize this method, we implemented one of the most basic equivalent circuit models (ECMs) used in IS analysis (Fig. S8, ESI†). In this circuit, the high frequency (HF) and low frequency (LF) response are modeled by pairs of resistive and capacitive elements in series. Consequently, the recombination and transport processes are also interpreted in series, which hinders the accurate reconstruction of the j–V curve (Fig. S9, ESI†).
Conclusions
In this work we demonstrate that charge transport, extraction and recombination resistances are coupled in the IS spectra response, as predicted by the implemented ECM. In devices with optimized charge extraction, including all those with high efficiency, the accurate j–V curve reconstruction indicates that recombination resistance is the dominant phenomenon within the Rrec+tr parameter. As the photogenerated current does not present voltage dependence, the recombination governs the j–V behavior in these cases. The successful j–V reconstruction is achieved in devices using both PEDOT:PSS and MeO-2PACz as HTMs, suggesting that the ECM Rrec+tr accurately reflects the overall recombination resistance regardless of the dominant recombination mechanism. In contrast, for devices with hindered charge extraction (ICBA-based devices), we demonstrate that the j–V curve reconstruction does not match the experimental data. In such cases, the contribution of charge extraction and transport resistance becomes noticeable and masks the true recombination resistance. These findings highlight the importance of individually identifying and separating the physical processes that influence the IS spectra, offering a pathway for more precise interpretation of IS data and improved diagnostics in perovskite solar cell technologies.Materials and methods
Materials
N,N-Dimethylformamide (DMF, ≥99.8%, anhydrous), dimethyl sulfoxide (DMSO, 99.9%, anhydrous), chlorobenzene (CB, 99.8%, anhydrous) and cesium iodide (CsI, 99.9%) were purchased from Sigma Aldrich. Formamidinium iodide (FAI, HC(NH2)2I, 99.99%) and methylammonium bromide (MABr, CH3NH3Br, 99.99%) were purchased from Greatcell Solar Materials. Lead iodide (PbI2, 99.99%), lead bromide (PbBr2, 99.99%) and [2-(3,6-dimethoxy-9H-carbazol-9-yl)ethyl]phosphonic acid (MeO-2PACz, 98%) were purchased from TCI Chemicals. Fullerene (C60), di[1,4]methanonaphthaleno[1,2:2′,3′;56,60:2′′,3′′][5,6]fullerene-C60-Ih, 1′,1′′,4′,4′′-tetrahydro-(ICBA) and bathocuproine (BCP) were purchased from 1-Materials. PEDOT:PSS AI 4083 aqueous dispersion was purchased from Heraeus. All the purchased chemicals were used as received without further purification.Cs0.05(FA0.85MA0.15)0.95Pb(I0.85Br0.15)3 perovskite precursor solution
The 1.24 M perovskite precursor solution with 10% mol of PbX2 as an excess was prepared by dissolving 1.15 mmol of PbI2 (532.3 mg), 1.05 mmol of FAI (180.5 mg), 0.19 mmol of MABr (20.7 mg), 0.21 mmol of PbBr2 (74.8 mg) and 0.06 mmol of CsI (16.8 mg) in 1 mL of a mixed solvents of DMF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO (4
DMSO (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume), the solution was stirring overnight at room temperature.
1 in volume), the solution was stirring overnight at room temperature.
Device fabrication
Patterned ITO substrates (2.0 × 1.5 cm2, 6–8 ohm sq−1, BIOTAIN CRYSTAL CO., LIMITED) were washed in an ultrasonic bath for 15 min per process. First, the substrates were washed in water with soap and rinsed with distilled water. Then, the substrates were washed with ethanol, acetone, and isopropanol, sequentially. After drying under nitrogen flow, the substrates were treated for 30 min with UV-O3. The HTM PEDOT:PSS was filtered with 0.45 μm PVDF filter and spin coated on top of the ITO substrate at 5000 rpm for 30 s and annealed at 130 °C for 20 min in ambient conditions, after PEDOT:PSS deposition, the substrates were transferred into a N2-filled glovebox for the perovskite deposition. MeO-2PACz was deposited from the precursor solution (1 mg mL−1 in absolute ethanol) at 3000 rpm for 30 s and annealed at 100 °C for 10 min, this procedure was carried out into a N2-filled glovebox.The perovskite solutions were filtered with 0.22 μm PTFE filter. The films were deposited using 30 μL of the precursor solution and spin coated with two steps, firstly, 1000 rpm for 12 s and, secondly, 5000 rpm for 27 s. After 22 s of having started the second step, 200 μL of CB was deposited like antisolvent and the annealing treatment was carried out at 100 °C for 30 min. The ETM C60 was thermal evaporated 30 nm under a pressure less than 10−6 mbar. ICBA solution (20 mg mL−1 dissolved in CB) was deposited by spin coating on top of the perovskite film at 1200 rpm for 30 s and annealing at 100 °C for 10 min. Finally, the samples were transferred into a vacuum chamber, BCP (6 nm) and Ag (100 nm) were sequentially deposited by thermal evaporation under a pressure less than 10−6 mbar.
Device characterization
j–V curves measurements of the fresh devices were taken with a Ossila solar simulator class AAA and automated j–V measurement system (T2003B3-G2009A1). Impedance spectroscopy was carried out using a Gamry 1010E potentiostat/galvanostat on complete solar cells at room conditions and different light intensities, such as 100, 50 and 10 mW cm−2. The measurements were performed at different offset voltages spaced 50 mV from open circuit to 0 V, with a 10 mV AC perturbation ranging between 1 MHz to 0.01 Hz. Z-view software was employed to analyze the results and fit the data to the equivalent circuit. The solar cells were characterized in ambient conditions (T ∼ 30 °C and RH ≥ 60%) without any encapsulation, with an active area of 0.084 cm2 defined by a mask.Data availability
Data for this article, including current–voltage curves, impedance spectra, fitting parameters and current–voltage reconstruction data are available at Zenodo at https://doi.org/10.5281/zenodo.14215854.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. F. B. acknowledges his grant CIACIF/2022/183 funded by MCIN/AEI/10.13039/501100011033 and, as appropriate, by “ESF Investing in your future”. O. E. S. acknowledges her predoctoral contract with reference GRISOLIAP/2021/112. T. S. R. and P. P. B. acknowledge the financial support of Generalitat Valenciana through the CIDEGENT contracts (CIDEGENT/2021/044 and CIDEXG/2022/34). This study forms part of the Advanced Materials programme and was supported by MCIN with funding from European Union NextGenerationEU (PRTR-C17.I1) and by the Generalitat Valenciana (code MFA/2022/040). This publication is part of the grant CNS2023-144270 funded by MICIU/AEI/10.13039/501100011033 and by European Union NextGenerationEU/PRTR.References
- Y. Hishikawa, H. Shimura, T. Ueda, A. Sasaki and Y. Ishii, Precise performance characterization of perovskite solar cells, Curr. Appl. Phys., 2016, 16, 898–904 CrossRef.
- J. A. Christians, J. S. Manser and P. V. Kamat, Best practices in perovskite solar cell efficiency measurements. Avoiding the error of Making Bad Cells Look Good, J. Phys. Chem. Lett., 2015, 6, 852–857 CrossRef CAS PubMed.
- W. Tress, N. Marinova, T. Moehl, S. M. Zakeeruddin, M. K. Nazeeruddin and M. Grätzel, Understanding the rate-dependent J–V hysteresis, slow time component, and aging in CH3NH3PbI3 perovskite solar cells: the role of a compensated electric field, Energy Environ. Sci., 2015, 8, 995–1004 RSC.
- B. Roose, K. Dey, M. R. Fitzsimmons, Y. H. Chiang, P. J. Cameron and S. D. Stranks, Electrochemical Impedance Spectroscopy of All-Perovskite Tandem Solar Cells, ACS Energy Lett., 2024, 9, 442–453 CrossRef CAS PubMed.
- O. Almora, P. Lopez-Varo, R. Escalante, J. Mohanraj, L. F. Marsal, S. Olthof and J. A. Anta, Instability analysis of perovskite solar cells via short-circuit impedance spectroscopy: A case study on NiOx passivation, J. Appl. Phys., 2024, 136, 94502 CrossRef CAS.
- E. Von Hauff and D. Klotz, Impedance spectroscopy for perovskite solar cells: Characterisation, analysis, and diagnosis, J. Mater. Chem. C, 2022, 10, 742–761 RSC.
- A. Sacco, Electrochemical impedance spectroscopy: Fundamentals and application in dye-sensitized solar cells, Renewable Sustainable Energy Rev., 2017, 79, 814–829 CrossRef CAS.
- A. Sanginario and S. Hernández, Diagnostics of electrocatalytic systems by electrochemical impedance spectroscopy, Curr. Opin. Green Sustainable Chem., 2023, 39, 100727 CrossRef CAS.
- L. Zhang, Y. Dai, C. Li, Y. Dang, R. Zheng, Z. Wang, Y. Wang, Y. Cui, H. Arandiyan, Z. Shao, H. Sun, Q. Zhuang and Y. Liu, Recent advances in electrochemical impedance spectroscopy for solid-state batteries, Energy Storage Mater., 2024, 69, 103378 CrossRef.
- P. Ranque, E. Gonzalo, M. Armand and D. Shanmukaraj, Performance-based materials evaluation for Li batteries through impedance spectroscopy: a critical review, Mater. Today Energy, 2023, 34, 101283 CrossRef CAS.
- F. Fabregat-Santiago, G. Garcia-Belmonte, I. Mora-Seró and J. Bisquert, Characterization of nanostructured hybrid and organic solar cells by impedance spectroscopy, Phys. Chem. Chem. Phys., 2011, 13, 9083–9118 RSC.
- A. Guerrero, J. Bisquert and G. Garcia-Belmonte, Impedance Spectroscopy of Metal Halide Perovskite Solar Cells from the Perspective of Equivalent Circuits, Chem. Rev., 2021, 121, 14430–14484 CrossRef CAS PubMed.
- A. J. Riquelme, K. Valadez-Villalobos, P. P. Boix, G. Oskam, I. Mora-Seró and J. A. Anta, Understanding equivalent circuits in perovskite solar cells. Insights from drift-diffusion simulation, Phys. Chem. Chem. Phys., 2022, 24, 15657–15671 RSC.
- S. M. Yoo, S. J. Yoon, J. A. Anta, H. J. Lee, P. P. Boix and I. Mora-Seró, An Equivalent Circuit for Perovskite Solar Cell Bridging Sensitized to Thin Film Architectures, Joule, 2019, 3, 2535–2549 CrossRef CAS.
- X. Liu, Z. Wu, H. Zhong, X. Wang, J. Yang, Z. Zhang, J. Han, D. Oron and H. Lin, Epitaxial 2D PbS Nanosheet-Formamidinium Lead Triiodide Heterostructure Enabling High-Performance Perovskite Solar Cells, Adv. Funct. Mater., 2023, 33, 2304140 CrossRef CAS.
- J. J. Jeronimo-Rendon, S. H. Turren-Cruz, J. Pascual, D. Di Girolamo, M. A. Flatken, H. Köbler, W. Hempel, M. Li, A. Di Carlo, P. P. Boix, I. Mora-Seró, A. Abate and M. Saliba, Robust Multi-Halide Methylammonium-Free Perovskite Solar Cells on an Inverted Architecture, Adv. Funct. Mater., 2024, 34, 2313928 CrossRef CAS.
- P. Serafini, P. P. Boix, E. M. Barea, T. Edvinson, S. Sánchez and I. Mora-Seró, Photonic Processing of MAPbI3 Films by Flash Annealing and Rapid Growth for High-Performance Perovskite Solar Cells, Sol. RRL, 2022, 6, 2200641 CrossRef CAS.
- R. Zhang, Z. Huang, W. Chen, B. Lyu, H. Zhang, X. He, X. Hu, Y. Song and W. C. H. Choy, A Self-Assembled Vertical-Gradient and Well-Dispersed MXene Structure for Flexible Large-Area Perovskite Modules, Adv. Funct. Mater., 2023, 33, 2210063 CrossRef CAS.
- J. Hidalgo, Y. An, D. Yehorova, R. Li, J. Breternitz, C. A. R. Perini, A. Hoell, P. P. Boix, S. Schorr, J. S. Kretchmer and J. P. Correa-Baena, Solvent and A-Site Cation Control Preferred Crystallographic Orientation in Bromine-Based Perovskite Thin Films, Chem. Mater., 2023, 35, 4181–4191 CrossRef CAS PubMed.
- T. Meyer, C. Körner, K. Vandewal and K. Leo, Accurate reconstruction of the jV-characteristic of organic solar cells from measurements of the external quantum efficiency, J. Appl. Phys., 2018, 123(13), 134501 CrossRef.
- A. D. Bui, D. T. Nguyen, A. Fell, N. Mozaffari, V. Ahmad, T. Duong, L. Li, T. N. Truong, A. A. Wibowo, K. Nguyen, O. Fischer, F. Schindler, M. C. Schubert, K. J. Weber, T. P. White, K. R. Catchpole, D. Macdonald and H. T. Nguyen, Spatially resolved power conversion efficiency for perovskite solar cells via bias-dependent photoluminescence imaging, Cell Rep. Phys. Sci., 2023, 4, 101641 CrossRef CAS.
- J. I. Basham, T. N. Jackson and D. J. Gundlach, Predicting the J–V Curve in Organic Photovoltaics Using Impedance Spectroscopy, Adv. Energy Mater., 2014, 4, 1400499 CrossRef.
- H. Hempel, T. J. Savenjie, M. Stolterfoht, J. Neu, M. Failla, V. C. Paingad, P. Kužel, E. J. Heilweil, J. A. Spies, M. Schleuning, J. Zhao, D. Friedrich, K. Schwarzburg, L. D. A. Siebbeles, P. Dörflinger, V. Dyakonov, R. Katoh, M. J. Hong, J. G. Labram, M. Monti, E. Butler-Caddle, J. Lloyd-Hughes, M. M. Taheri, J. B. Baxter, T. J. Magnanelli, S. Luo, J. M. Cardon, S. Ardo and T. Unold, Predicting Solar Cell Performance from Terahertz and Microwave Spectroscopy, Adv. Energy Mater., 2022, 12, 2102776 CrossRef CAS.
- P. P. Boix, A. Guerrero, L. F. Marchesi, G. Garcia-belmonte and J. Bisquert, Current-Voltage Characteristics of Bulk Heterojunction Organic Solar Cells: Connection Between Light and Dark Curves, Adv. Energy Mater., 2011, 1–6 Search PubMed.
- N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. Il Seok, Compositional engineering of perovskite materials for high-performance solar cells, Nature, 2015, 517, 476–480 CrossRef CAS PubMed.
- M. Saliba, T. Matsui, J. Y. Seo, K. Domanski, J. P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Cesium-containing triple cation perovskite solar cells: improved stability, reproducibility and high efficiency, Energy Environ. Sci., 2016, 9, 1989–1997 RSC.
- W. Li, E. Martínez-Ferrero and E. Palomares, Self-assembled molecules as selective contacts for efficient and stable perovskite solar cells, Mater. Chem. Front., 2024, 8, 681–699 RSC.
- L. M. A. De Jong, A. M. Berghuis, M. S. Abdelkhalik, T. P. A. Van Der Pol, M. M. Wienk, R. A. J. Janssen and J. Gómez Rivas, Enhancement of the internal quantum efficiency in strongly coupled P3HT-C60 organic photovoltaic cells using Fabry-Perot cavities with varied cavity confinement, Nanophotonics, 2024, 13, 2531–2540 CrossRef CAS PubMed.
- H. Wang, Y. He, Y. Li and H. Su, Photophysical and Electronic Properties of Five PCBM-like C 60 Derivatives: Spectral and Quantum Chemical View, J. Phys. Chem. A, 2012, 116, 255–262 CrossRef CAS PubMed.
- D. Prochowicz, P. Yadav, M. Saliba, D. J. Kubicki, M. M. Tavakoli, S. M. Zakeeruddin, J. Lewiński, L. Emsley and M. Grätzel, One-step mechanochemical incorporation of an insoluble cesium additive for high performance planar heterojunction solar cells, Nano Energy, 2018, 49, 523–528 CrossRef CAS.
- K. Tvingstedt, L. Gil-Escrig, C. Momblona, P. Rieder, D. Kiermasch, M. Sessolo, A. Baumann, H. J. Bolink and V. Dyakonov, Removing Leakage and Surface Recombination in Planar Perovskite Solar Cells, ACS Energy Lett., 2017, 2, 424–430 CrossRef CAS.
- Y. C. Chin, M. Daboczi, C. Henderson, J. Luke and J. S. Kim, Suppressing PEDOT:PSS Doping-Induced Interfacial Recombination Loss in Perovskite Solar Cells, ACS Energy Lett., 2022, 7, 560–568 CrossRef CAS PubMed.
- S. Liu, D. Chen, X. Hu, Z. Xing, J. Wan, L. Zhang, L. Tan, W. Zhou and Y. Chen, Printable and Large-Area Organic Solar Cells Enabled by a Ternary Pseudo-Planar Heterojunction Strategy, Adv. Funct. Mater., 2020, 30, 2003223 CrossRef CAS.
- R. Sharma, H. Lee, V. Gupta, H. Kim, M. Kumar, C. Sharma, S. Chand, S. Yoo and D. Gupta, Photo-physics of PTB7, PCBM and ICBA based ternary solar cells, Org. Electron., 2016, 34, 111–117 CrossRef CAS.
- J. M. Frost, K. T. Butler and A. Walsh, Molecular ferroelectric contributions to anomalous hysteresis in hybrid perovskite solar cells, APL Mater., 2014, 2, 81506 CrossRef.
- Q. Dong, Y. Fang, Y. Shao, P. Mulligan, J. Qiu, L. Cao and J. Huang, Electron-hole diffusion lengths >175 μm in solution-grown CH3NH3PbI3 single crystals, Science, 2015, 347, 967–970 CrossRef CAS PubMed.
- J. Y. Huang, Y. W. Yang, W. H. Hsu, E. W. Chang, M. H. Chen and Y. R. Wu, Influences of dielectric constant and scan rate on hysteresis effect in perovskite solar cell with simulation and experimental analyses, Sci. Rep., 2022, 12, 1–13 CrossRef PubMed.
- R. Singh, S. Sandhu, H. Yadav and J. J. Lee, Stable Triple-Cation (Cs + -MA + -FA +) Perovskite Powder Formation under Ambient Conditions for Hysteresis-Free High-Efficiency Solar Cells, ACS Appl. Mater. Interfaces, 2019, 11, 29941–29949 CrossRef CAS PubMed.
- D. Moia, I. Gelmetti, P. Calado, W. Fisher, M. Stringer, O. Game, Y. Hu, P. Docampo, D. Lidzey, E. Palomares, J. Nelson and P. R. F. Barnes, Ionic-to-electronic current amplification in hybrid perovskite solar cells: ionically gated transistor-interface circuit model explains hysteresis and impedance of mixed conducting devices, Energy Environ. Sci., 2019, 12, 1296 RSC.
- F. Ebadi, N. Taghavinia, R. Mohammadpour, A. Hagfeldt and W. Tress, Origin of apparent light-enhanced and negative capacitance in perovskite solar cells, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- E. Ghahremanirad, A. Bou, S. Olyaee and J. Bisquert, Inductive Loop in the Impedance Response of Perovskite Solar Cells Explained by Surface Polarization Model, J. Phys. Chem. Lett., 2017, 8, 1402–1406 CrossRef CAS PubMed.
- C. A. Aranda, L. Bethencourt, E. Mas-marza, A. O. Alvarez, M. Saliba and F. Fabregat-santiago, Negative Capacitance and Inverted Hysteresis: Matching Features in Perovskite Solar Cells, J. Phys. Chem. Lett., 2020, 11(19), 8417–8423, DOI:10.1021/acs.jpclett.0c02331.
- S. Ravishankar, O. Almora, C. Echeverría-Arrondo, E. Ghahremanirad, C. Aranda, A. Guerrero, F. Fabregat-Santiago, A. Zaban, G. Garcia-Belmonte and J. Bisquert, Surface Polarization Model for the Dynamic Hysteresis of Perovskite Solar Cells, J. Phys. Chem. Lett., 2017, 8, 915–921 CrossRef CAS PubMed.
- E. Velilla, F. Jaramillo and I. Mora-Seró, High-throughput analysis of the ideality factor to evaluate the outdoor performance of perovskite solar minimodules, Nat. Energy, 2021, 6, 54–62 CrossRef CAS.
- A. Castro-Chong, A. J. Riquelme, T. Aernouts, L. J. Bennett, G. Richardson, G. Oskam and J. A. Anta, Illumination Intensity Dependence of the Recombination Mechanism in Mixed Perovskite Solar Cells, ChemPlusChem, 2021, 86, 1347–1356 CrossRef CAS PubMed.
- O. Almora, K. T. Cho, S. Aghazada, I. Zimmermann, G. J. Matt, C. J. Brabec, M. K. Nazeeruddin and G. Garcia-Belmonte, Discerning recombination mechanisms and ideality factors through impedance analysis of high-efficiency perovskite solar cells, Nano Energy, 2018, 48, 63–72 CrossRef CAS.
- A. Riquelme, L. J. Bennett, N. E. Courtier, M. J. Wolf, L. Contreras-Bernal, A. B. Walker, G. Richardson and J. A. Anta, Identification of recombination losses and charge collection efficiency in a perovskite solar cell by comparing impedance response to a drift-diffusion model, Nanoscale, 2020, 12, 17385–17398 RSC.
- C. L. Davies, M. R. Filip, J. B. Patel, T. W. Crothers, C. Verdi, A. D. Wright, R. L. Milot, F. Giustino, M. B. Johnston and L. M. Herz, Bimolecular recombination in methylammonium lead triiodide perovskite is an inverse absorption process, Nat. Commun., 2018, 9, 1–9 CrossRef CAS PubMed.
- A. Castro-Chong, A. J. Riquelme, T. Aernouts, L. J. Bennett, G. Richardson, G. Oskam and J. A. Anta, Illumination Intensity Dependence of the Recombination Mechanism in Mixed Perovskite Solar Cells, ChemPlusChem, 2021, 86, 1347–1356 CrossRef CAS PubMed.
- K. Hossain, D. Sivadas, D. Kabra and P. R. Nair, Perovskite Solar Cells Dominated by Bimolecular Recombination—How Far Is the Radiative Limit?, ACS Energy Lett., 2024, 9, 2310–2317 CrossRef CAS.
- J. Vollbrecht and V. V. Brus, On the recombination order of surface recombination under open circuit conditions, Org. Electron., 2020, 86, 105905 CrossRef CAS.
- N. E. Courtier, Interpreting Ideality Factors for Planar Perovskite Solar Cells: Ectypal Diode Theory for Steady-State Operation, Phys. Rev. Appl., 2020, 14, 24031 CrossRef CAS.
- W. Tress, M. Yavari, K. Domanski, P. Yadav, B. Niesen, J. P. Correa Baena, A. Hagfeldt and M. Graetzel, Interpretation and evolution of open-circuit voltage, recombination, ideality factor and subgap defect states during reversible light-soaking and irreversible degradation of perovskite solar cells, Energy Environ. Sci., 2018, 11, 151–165 RSC.
- D. Kiermasch, A. Baumann, M. Fischer, V. Dyakonov and K. Tvingstedt, Revisiting lifetimes from transient electrical characterization of thin film solar cells; a capacitive concern evaluated for silicon, organic and perovskite devices, Energy Environ. Sci., 2018, 11, 629–640 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04143g |
| This journal is © the Owner Societies 2024 |