Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic behaviour of a spin-canted asymmetric lanthanide quinolate trimer†
Lester
Batista
 a,
Sagar
Paul
a,
Sagar
Paul
 b,
Concepción
Molina-Jirón
b,
Concepción
Molina-Jirón
 *cd,
Juan A.
Jaén
*cd,
Juan A.
Jaén
 ef,
Dieter
Fensker
g,
Olaf
Fuhr
ef,
Dieter
Fensker
g,
Olaf
Fuhr
 gh,
Mario
Ruben
gh,
Mario
Ruben
 *dgi,
Wolfgang
Wernsdorfer
*dgi,
Wolfgang
Wernsdorfer
 *bd and
Eufemio
Moreno-Pineda
*bd and
Eufemio
Moreno-Pineda
 *bef
*bef
aUniversidad de Panamá, Facultad de Ciencias Naturales, Exactas y Tecnología, Depto. Física, 0824, Panamá
bPhysikalisches Institut, Karlsruhe Institute of Technology, D-76131, Karlsruhe, Germany. E-mail: wolfgang.wernsdorfer@kit.edu
cUniversidad de Panamá, Facultad de Ciencias Naturales, Exactas y Tecnología, Depto. de Bioquímica, 0824, Panamá. E-mail: concepcion.molina@up.ac.pa
dInstitute of Quantum Materials and Technologies (IQMT), Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344, Eggenstein-Leopoldshafen, Germany. E-mail: mario.ruben@kit.edu
eUniversidad de Panamá, Facultad de Ciencias Naturales, Exactas y Tecnología, Depto. de Química-Física, 0824, Panamá. E-mail: eufemio.moreno@up.ac.pa
fUniversidad de Panamá, Facultad de Ciencias Naturales, Exactas y Tecnología, Grupo de Investigación de Materiales, Panamá, 0824, Panamá
gInstitute of Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), Kaiserstraße 12, D-76131 Karlsruhe, Germany
hKarlsruhe Nano Micro Facility (KNMFi), Karlsruhe Institute of Technology (KIT), Kaiserstraße 12, D-76131 Karlsruhe, Germany
iCentre Européen de Sciences Quantiques (CESQ), Institut de Science et d'Ingénierie Supramoléculaires (ISIS), 8 allée Gaspard Monge, BP 70028, 67083, Strasbourg Cedex, France
First published on 16th July 2024
Abstract
An asymmetrical dysprosium trimer with a molecular formula of [Dy3(hq)7(hqH)(NO3)2(H2O)] was obtained through a reflux reaction employing as starting material Dy(NO3)3·nH2O and 8-quinolinoline as ligand. Magnetic susceptibility investigations show the system to be an SMM, which was corroborated by sub-Kelvin μSQUID studies. Upon cooling, the magnetic susceptibility also exhibits a decrease in the χMT product, which was confirmed to be due to intramolecular antiferromagnetic interactions. μSQUID measurements, moreover, reveal a marked magnetic behaviour in the angular dependence of the hysteresis loops. The latter is a direct consequence of the non-colinear spin arrangement of the anisotropy axes of each Dy(III) ion in [Dy3(hq)7(hqH)(NO3)2(H2O)] and the interaction between the ions, as also evidenced by CASSCF calculations. Our results evidence the effect of spin canting along with the intramolecular interactions, which can induce non-trivial magnetic behaviour in SMMs.
Introduction
The fascinating phenomenon of slow magnetic relaxation in molecular systems was first observed for the transition metal aggregate [Mn12O12(OAc)16(H2O)4]·4H2O·2AcOH best known as {Mn12}1,2 and years later in a lanthanide-based molecule with formula [LnPc2]−·TBA+ (TBA+ = tetrabutylammonium) where Ln = Tb(III) and Dy(III).3 In lanthanide-based molecules, the anisotropic magnetic character is attributed to the intrinsic spin–orbit coupling of the first-order orbital angular momentum and the crystal field imposed by the ligand set giving rise to the single molecule magnet (SMM) behaviour.3 In the case of lanthanide-based SMMs the anisotropy arises due to its intrinsic strong spin–orbit coupling (SOC) at single ion level,4–6 while in 3d-based SMMs, the anisotropic character is attributed to the cooperative contribution of spin and local magnetic anisotropy leading to a large molecular spin ground state (S) with negative zero-field splitting (D).7 A detailed understanding of the physical parameters playing a role in the anisotropic characteristics of lanthanide-based SMMs has led to energy barriers far larger than those observed in the 3d-based SMM analogues, ultimately realising blocking barriers above liquid nitrogen temperatures,8,9 making these systems excellent candidates for high-density data storage devices. Furthermore, the comprehension and manipulation of the structural, electronic and nuclear characteristics of these systems, through a rational design, make these systems also candidates for quantum information processing schemes acting as qubits.10–12 Today, SMMs have been proposed as qubits and qudits10–15 – the quantum computer scaffolds –, quantum sensors,16,17 quantum simulators18–23 and quantum error correction protocols.24–26 Notably, the execution of the quantum algorithm of Grover using a single molecule of TbPc2 exemplifies the plausibility of SMMs being part of novel quantum technologies.27To further the development of favourable SMM properties and finally implement lanthanide-based molecules in devices, a detailed understanding of their magnetic properties continues to be a critical step.28–31 A great deal of work has shed some light on the understanding of the magnetic behaviour of single lanthanide ion molecules,32–38 denoting the importance of the role of magnetic interaction in SMMs. This understanding is required since polymetallic lanthanide clusters can show some unusual physical properties such as the observation of a toroidal magnetic39–41 and strong magnetic exchange, causing an increment of the blocking temperatures.9,35,42–44 Furthermore, by use of 3d ions in a {Cr2Dy2} “butterfly” complex,9,45–47 it has been shown that strong magnetic interaction can lead to hysteresis which is not observed when the exchange interactions are switched off using the diamagnetic 3d metal analogue. The operative anisotropic exchange in a [Dy4(O2CNiPr2)12] has also proven important in obtaining a ferromagnetic and antiferromagnetic ground state, contingent upon the applied field direction.48 In addition, coupling the electron spins in lanthanides has made it possible to indirectly couple the nuclear spins, which might be exploited as qudits.49–51 Notably, recently it has been shown that a σ-bond between two lanthanide ions can lead to remarkably large hysteresis loops9,47 even near the liquid nitrogen temperature region.9
In all cases above, magnetic interactions improve the magnetic characteristics of the SMMs. However, magnetic interactions between lanthanides in polymetallic systems can often likewise lead to faster relaxation rates, diminishing the SMM properties.38,52–59 A common strategy to decrease such undesired effects is to dilute the SMM into an isostructural diamagnetic host. Experimentally the direct determination via electron paramagnetic resonance (EPR), in cohort with other techniques, unravelled the effect of exchange interactions operating between two distinct Dy(III) ions in an asymmetric dimer with the formula [hqH2][Dy2(hq)4(NO3)3] (hqH = 8-hydroxyquinoline).38 In this system, the exchange interaction yields a well-separated manifold of four exchange states, which permit facile relaxation of the magnetisation at low temperatures, yielding no SMM behaviour in contrast to the diluted (i.e., single ion) complex. Further studies on the analogous Ln(II) derivatives shed light on the coupling mechanism in such asymmetric systems.34 Herein we report the exchange characteristic of a trinuclear dysprosium system. The 8-hydroxyquinoline ligand has been chosen due to its strong chelating effect.60–63 A synthetic drawback of employing oxyquinolines is their tendency to form insoluble polymeric materials, making structural characterisation difficult. Usual routes therefore employ long high-temperature reactions to try and isolate the thermodynamic product.60–62 In our approach, the asymmetric trimetallic dysprosium complex with formula [Dy3(hq)7(NO3)2(OH2)] was obtained with mild reaction conditions. Conventional SQUID studies show an out-of-phase component of the AC magnetic susceptibility, characteristic of SMMs. Furthermore, sub-Kelvin characterisation employing a μSQUID array shows open hysteresis loops confirming the SMM character. The angular-dependent loops reveal a distinct magnetic behaviour, implying the existence of spin canting in the system, in agreement with CASSCF calculations. The SMM behaviour in the complex is a concerted behaviour of the three Dy(III) ions connected by an antiferromagnetic intramolecular interaction, as experimentally determined and verified through simulations.
Results and discussion
Synthesis and crystallography
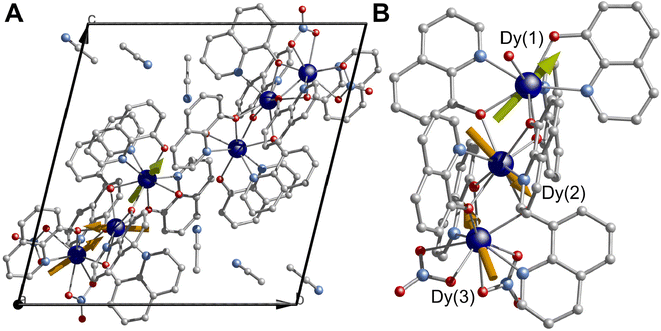
The direct reaction of Dy(NO3)3·nH2O and 8-hydroxiquinoline in the presence of Et3N in acetonitrile under reflux conditions yields a bright orange solution, which upon slow evaporation affords single crystals suitable for X-ray studies (see ESI† section 1.1). In contrast to other approaches where elevated temperatures are required,60–62,64,65 herein a rather mild approach affords the complex. Note that a non-equimolar amount of Et3N was required to obtain a clear solution. In contrast, an equimolar amount of Et3N based on the 8-hydroxiquinoline ligand led to the immediate formation of an insoluble product, while the absence of the base resulted in the formation of a slurry. Based on these points, it can be noted that the presence of the Et3N is key for the formation of the complex under milder conditions. The compound [Dy3(hq)7(NO3)2(H2O)] crystallises in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group with one molecule residing in the asymmetric unit, while two and a half molecules complete the unit cell (Fig. 1A and Table S1†). Three Dy(III), seven 8-quinolinates (hq), two nitrate ions (NO3) and one terminal water molecule complete the structure, while 2.5 molecules of solvents are found in the lattice, yielding a complex with the formula [Dy3(hq)7(NO3)2(H2O)]·2.5MeCN (Fig. 1B). The metal core resembles the previously reported {Dy3} with a “V-shaped”60 motif and possess a Dy(1)⋯Dy(2)⋯Dy(3) angle of 149.78°. The Dy⋯Dy separations are 3.5592(6) Å and 3.5120(6) Å for Dy(1)⋯Dy(2) and Dy(2)⋯Dy(3), respectively. Three different coordination environments are observed for the dysprosium centres; Dy(1) and Dy(2) present a square antiprismatic geometry with a continuous shape measure (CShM)66 of 1.364 and 1.129, respectively, whilst Dy(3) shows a spherical tricapped trigonal prismatic geometry (CShM of 2.232) (see Table S2 and Fig. S1†). The chelating ligands bind the three dysprosium centres with a mixture of μ–1κ(N,O):2κ(O) bridging ligands. The coordination sphere of Dy(1) is filled by four hq groups and one terminal H2O giving a N3O5 donor set, whilst six hq ligands give Dy(2) an N2O6 donor environment. Finally, Dy(3) is bridged by three hq and two chelating NO3 anions leading to an N2O7 donor set. Both nitrate ions bind with the 1.110 coordination mode (see Harris notation).67 The packed structure shows π–π interactions with the shortest distance between hq groups being 3.318 Å, with MeCN solvent molecules residing in pockets between the complexes. The shortest intermolecular Dy⋯Dy distance is 6.0421(6) Å.
space group with one molecule residing in the asymmetric unit, while two and a half molecules complete the unit cell (Fig. 1A and Table S1†). Three Dy(III), seven 8-quinolinates (hq), two nitrate ions (NO3) and one terminal water molecule complete the structure, while 2.5 molecules of solvents are found in the lattice, yielding a complex with the formula [Dy3(hq)7(NO3)2(H2O)]·2.5MeCN (Fig. 1B). The metal core resembles the previously reported {Dy3} with a “V-shaped”60 motif and possess a Dy(1)⋯Dy(2)⋯Dy(3) angle of 149.78°. The Dy⋯Dy separations are 3.5592(6) Å and 3.5120(6) Å for Dy(1)⋯Dy(2) and Dy(2)⋯Dy(3), respectively. Three different coordination environments are observed for the dysprosium centres; Dy(1) and Dy(2) present a square antiprismatic geometry with a continuous shape measure (CShM)66 of 1.364 and 1.129, respectively, whilst Dy(3) shows a spherical tricapped trigonal prismatic geometry (CShM of 2.232) (see Table S2 and Fig. S1†). The chelating ligands bind the three dysprosium centres with a mixture of μ–1κ(N,O):2κ(O) bridging ligands. The coordination sphere of Dy(1) is filled by four hq groups and one terminal H2O giving a N3O5 donor set, whilst six hq ligands give Dy(2) an N2O6 donor environment. Finally, Dy(3) is bridged by three hq and two chelating NO3 anions leading to an N2O7 donor set. Both nitrate ions bind with the 1.110 coordination mode (see Harris notation).67 The packed structure shows π–π interactions with the shortest distance between hq groups being 3.318 Å, with MeCN solvent molecules residing in pockets between the complexes. The shortest intermolecular Dy⋯Dy distance is 6.0421(6) Å.
Magnetic studies
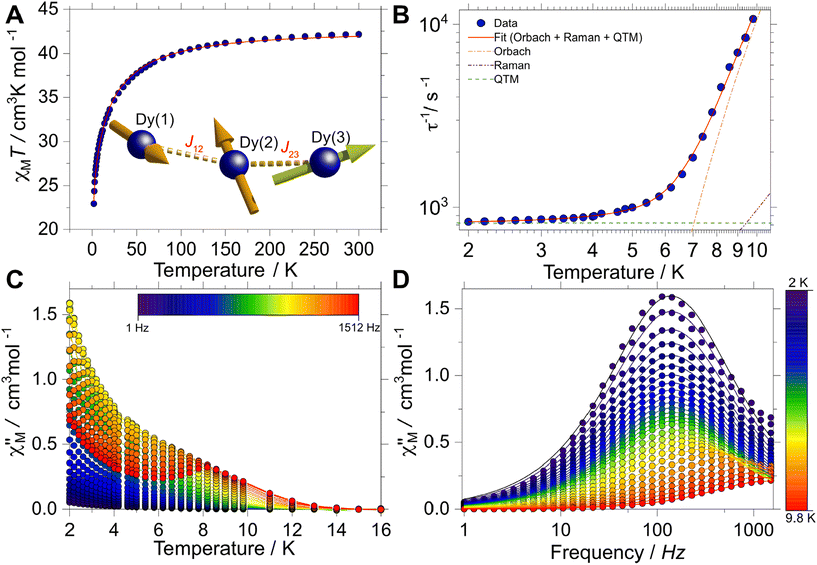
The magnetic behaviour of [Dy3(hq)7(NO3)2(H2O)] was investigated on polycrystalline samples in the temperature range 2–300 K under an applied DC magnetic field (HDC) of 1 kOe. The room temperature χMT value (being χM the molar magnetic susceptibility) for this system is found to be 42.2 cm3 K mol−1, in good agreement with the χMT expected for the sum of three non-interacting Dy(III) ions (42.5 cm3 K mol−1, with gJ = 4/3, J = 15/2). Upon cooling the χMT(T) faintly decreases down to about 50 K when it decreases faster reaching a value of 22.9 cm3 K mol−1 at 2 K (Fig. 2A). The drop upon lowering the temperature observed can be attributed to a gradual depopulation of the crystal field split mJ sublevels of the ground J multiplet, while magnetic interactions between the Dy(III) sites cannot be excluded.The dynamic magnetic behaviour was likewise studied employing a SQUID magnetometer. In this case, AC susceptibility measurements were carried out between 2 and 10 K without an applied HDC field. A clear temperature and frequency dependence of the in- (χ′M(T; ν)) and out-of-phase (χ′′M(T; ν)) magnetic susceptibility profiles were observed. This behaviour can be directly ascribed to blockage to the relaxation of the magnetisation, a behaviour characteristic of SMMs. In the χ′′M(T) a maximum is observed at ca. 8 K at the highest frequency (1512 Hz) (Fig. 2C). At the lowest temperature, the maximum in the χ′′M(ν) is centred at ca. 121 Hz and stays centred at this frequency up to ca. 5 K. The constant behaviour of the χ′′M(ν) traces upon temperature increment, can be directly ascribed to the quantum tunnelling of the magnetisation (QTM) being operative. Above 5 K, the maximum in χ′′M(ν) shifts swiftly towards higher frequencies up to 9.8 K where the maximum lies outside our experimental frequency window (Fig. 2D).
Simultaneous fitting the χ′M(ν) and χ′′M(ν) to a generalised Debye model allows the extraction of the temperature-dependent relaxation times τ(T) of the system. A relatively uniform distribution of relaxation times is obtained, with 0.18(1) < α < 0.19(1) [from lowest to highest temperature], where a value of 0 would indicate no distribution. The obtained τ(T) data can be fitted to a multi-relaxation process employing the following equation:
τ−1 = τ−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/kBT) + CTn + τQTM−1 exp(−Ueff/kBT) + CTn + τQTM−1 | (1) |
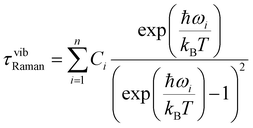 | (2) |
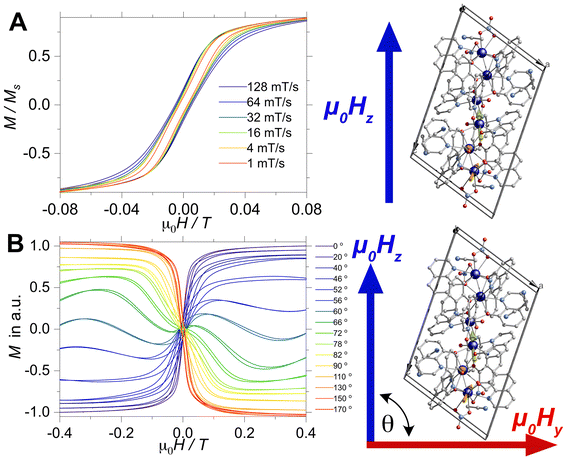
Although the AC profiles indicate that [Dy3(hq)7(NO3)2(H2O)] is an SMM, confirmation of the SMM character was sought through the μSQUID technique at sub-Kelvin temperatures. μSQUID measurements were carried out in the temperature range of 4.5 K down to 30 mK using a dilution fridge with applied fields of ±1 T. Single crystals of [Dy3(hq)7(NO3)2(H2O)] were directly placed on top of the μSQUID arrays, while the field was applied along the magnetic anisotropy axis of the crystal employing the transverse field method.73,74 Three types of studies were conducted: (i) temperature-dependent hysteresis loops from 30 mK up to 4.5 K at a fixed sweeping magnetic field rate of 64 mT s−1 (Fig. S5†); (ii) magnetic field sweep-rated dependent studies with sweeping rates of 1 to 128 mT s−1 at a fixed base temperature of 30 mK (Fig. 3A); and (iii) magnetic field angle dependence (with respect to the crystal orientation) at a fixed temperature of 30 mK and fixed scan rate (16 mT s−1) (Fig. 3B).
Confirmation of the SMM behaviour was obtained in these studies. The temperature and sweep-rate dependent μSQUID loops show the characteristic behaviour expected for SMMs, i.e., the temperature-dependent loops show opening at the lowest temperature, which reduces upon warming due to enhanced thermal relaxation. While the sweep-dependent loops at 30 mK are wider at faster sweeping rates, indicating small QTM at the level-crossing, and hence slow thermal relaxation above 0.03 T. Moreover, the application of the magnetic field at different crystallographic angles (xy plane) shows a rather distinct magnetic behaviour. The latter behaviour can be ascribed to spin canting74 between the anisotropic magnetic axes present in [Dy3(hq)7(NO3)2(H2O)].
Electronic structure calculations
Ab initio calculations are an indispensable tool to elucidate the origin of the anisotropic character of lanthanide-containing systems due to the subtle and complex crystal field interactions.75,76 Hence, the magnetic properties of [Dy3(hq)7(NO3)2(H2O)] were likewise investigated using CASSCF/RASSI/SINGLE_ANISO ab initio calculations. OpenMolcas was employed for the complete-active-space self-consistent field (CASSCF) calculations of the [Dy3(hq)7(NO3)2(H2O)] complex77 (see ESI† section 1.4 for details). The crystal field splits the ground 6H15/2 spin–orbit multiplet of Dy(III) into eight Kramer's doublets, i.e. mJ = ±15/2, ±13/2, … ±1/2. The calculations show that solely one Dy(1) sites possess a strongly anisotropic character (gx ≈ gy = 0 and gz = 20 and the first excited state at 147 cm−1), while for Dy(2) and Dy(3) the ions are far from pure mJ = ±15/2 states (e.g., for Dy(1) gx,y ≠ 0 and gz < 20 with the first excited state at 35 and 14 cm−1, respectively). The first excited state for Dy(2) and Dy(3) is much more rhombic than the ground state and its main magnetic axis is not coincident with the ground state in all cases, while for Dy(1) the first excited state has a lower mJ component. These results suggest the environment for Dy(2) and Dy(3) is not ideal for stabilising the high angular momentum states of Dy(III), while Dy(1) should show an SMM character.Up to this point, the discussion was based on the isolated Dy(III) ion, however, interactions between Dy(III) atoms can play a significant role in the relaxation dynamics. To evaluate the interaction operating between the Dy(III) ions, the Lines model78 was employed to fit the magnetic susceptibilities of complexes [Dy3(hq)7(NO3)2(H2O)]. The Lines model employs an isotropic exchange between the spin component of the angular momenta (S = 5/2 for Dy(III)) and the crystal field parameters obtained via the CASSCF calculations. The Hamiltonian has the form:
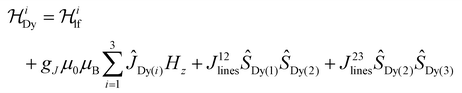 | (3) |
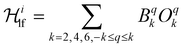 is the ligand field Hamiltonian expressed in Steven's operator, Oqk are the Stevens operator and Bqk are the ligand field parameters obtained from CASSCF calculations. ĴDy(i) and ŜDy(i) are the spin–orbit and spin-only state for Dy(III), respectively. Fitting79 of χMT(T) employing the crystal field parameters as determined from CASSCF, yields a Jlines12 = −0.07(1) cm−1 and Jlines23 = −0.27(1) cm−1 with R = 2.9 (with
is the ligand field Hamiltonian expressed in Steven's operator, Oqk are the Stevens operator and Bqk are the ligand field parameters obtained from CASSCF calculations. ĴDy(i) and ŜDy(i) are the spin–orbit and spin-only state for Dy(III), respectively. Fitting79 of χMT(T) employing the crystal field parameters as determined from CASSCF, yields a Jlines12 = −0.07(1) cm−1 and Jlines23 = −0.27(1) cm−1 with R = 2.9 (with 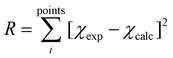 ) (see Fig. 2A). Attempts to fit the χMT(T) profile employing a single interaction produce a lower agreement and higher residual factors. Considering the Dy⋯Dy distances 3.5592(6) Å for Dy(1)⋯Dy(2) and 3.5120(6) for Dy(2)⋯Dy(3), and the strongest component of the dipolar interaction obtained for such distances (∼−0.7 cm−1 projected on an S = 5/2 state), it is very probable that the interaction operating within [Dy3(hq)7(NO3)2(H2O)] are of dipolar origin [see ESI† section 1.5].
) (see Fig. 2A). Attempts to fit the χMT(T) profile employing a single interaction produce a lower agreement and higher residual factors. Considering the Dy⋯Dy distances 3.5592(6) Å for Dy(1)⋯Dy(2) and 3.5120(6) for Dy(2)⋯Dy(3), and the strongest component of the dipolar interaction obtained for such distances (∼−0.7 cm−1 projected on an S = 5/2 state), it is very probable that the interaction operating within [Dy3(hq)7(NO3)2(H2O)] are of dipolar origin [see ESI† section 1.5].
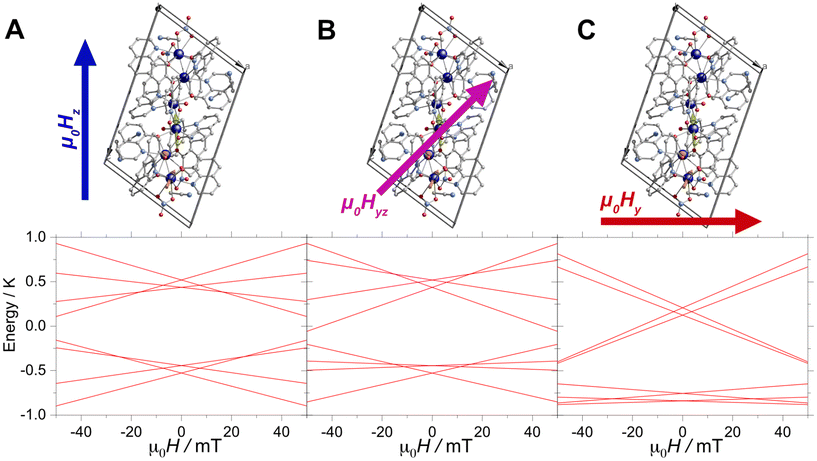
Furthermore, the μSQUID loops show a clear angular dependence of the loops upon magnetic field application (see Fig. 3B). These observations are consistent with the anisotropy arrangement of the magnetic axes for the three Dy(III) systems, which depart from collinearity, in agreement with the CASSCF calculated spin projections. Given the polynuclear characteristics and the number of parameters characterising the system, a quantitative analysis of the angular μSQUID loops is not feasible. Nonetheless, a qualitative assessment of the spin canting effect in the μSQUID loops can be gained by simulating the Zeeman diagram at different field orientations. However, the large Hilbert space of the [Dy3(hq)7(NO3)2(H2O)] and the number of parameters involved, e.g., ligand field parameters, g-values, Euler angles and exchange interaction, a J = 15/2 makes the rationalisation of the sub-Kelvin temperature data computationally expensive. To overcome this problem, the spin effective formalism (Seff = 1/2) can be used. For simplicity, a single arbitrary interaction parameter and pure axial g-tensors were employed i.e., one gxx = gyy = 0; gzz = 20 (for mJ = 15/2) and two gxx = gyy = 0; gzz = 17 (for mJ = 13/2) and the Euler angles [in Z–Y′–Z′′ convention] for each Dy(III) ion obtained from the CASSCCF calculations. However, Seff = 1/2, at first order, mixed strongly by transverse fields, prompting large tunnelling splitting, not representative of the system, hence, a fictitious S = 3/2 system with an arbitrarily large zero field splitting (D) parameter D = −100 cm−1 is found more suitable. The g-values were maintained isotropic (gxx = gyy = gzz = 20/3 and gxx = gyy = 0; gzz = 17/3), since the anisotropy is projected on the ZFS, while the anisotropy of the D term was rotated employing the Euler angles obtained from CASSCF.71 The CASSCF results indicate that the single ion magnetic properties of [Dy3(hq)7(NO3)2(H2O)] are dominated by the spin–orbit coupling and the interaction with the ligands, yielding a considerable separation between the ground and the first excited multiplet, as compared to the temperature bath. Therefore, we define the complex as three isolated Ising spins coupled through an effective interaction Jtotal(Ŝ1·Ŝ2), where Jtotal is an effective coupling and Ŝ1·Ŝ2, are effective spin for each Dy(III). In the presence of an external magnetic field applied along the easy axis, the Hamiltonian for [Dy3(hq)7(NO3)2(H2O)] is:
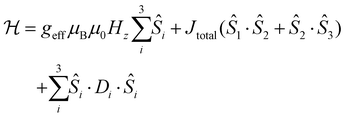 | (4) |
The first term in (4) is the Zeeman term, the second the exchange interaction and the last the zero-field splitting. The non-colinear nature of the easy axes of the system is taken into consideration by employing the Euler rotations. The results show that the spin-canted arrangement of the Dy(III) ions in [Dy3(hq)7(NO3)2(H2O)] and the interaction operating between the ions renders the lowest multiplet of the coupled system to be sensitive to the field direction. While applying the magnetic field along the easy axes of Dy(1) leads to a ferromagnetic ground state, applying the field perpendicular to the easy axis of Dy(1) renders a diamagnetic ground state. Bearing in mind that [Dy3(hq)7(NO3)2(H2O)] the field is applied along an intermediate direction in the μSQUID arrays, it would cause different responses in the orientation-dependent loops as shown in Fig. 4.
As an overall result, although CASSCF predicts a highly pure mJ = 15/2 state for Dy(1), rather rhombic characteristics are found for Dy(2) and Dy(3) with large spin canting as determined by μSQUID results and CASSCF calculations.
Conclusions
Herein we have described the synthesis of a heteroleptic dysprosium trimer with the formula [Dy3(hq)7(NO3)2(H2O)] under mild conditions. The compound shows a V-shaped geometry with a rather asymmetric arrangement. Magnetic studies reveal a clear SMM behaviour, further corroborated by μSQUID studies conducted at sub-Kelvin temperatures. Fitting the χMT(T) profile, employing the Lines model, shows that antiferromagnetic interactions couple the Dy(III) ions [Jlines12 = −0.07(1) cm−1 and Jlines23 = −0.27(1) cm−1]. Comparison of the Lines interaction and the dipolar matrices operating between the systems suggest that the interactions in [Dy3(hq)7(NO3)2(H2O)] are of dipolar origin. μSQUID loops reveal open loops even at the lowest sweep rate and an angular-dependent character, while CASSCF calculations show that solely one of the dysprosium ion Dy(1) possesses SMM properties, with the remaining two having considerably rhombic characteristics. μSQUID and CASSCF results confirm the non-colinear spin arrangements of the systems, which along with the intramolecular antiferromagnetic interaction, are responsible for relaxation dynamics in [Dy3(hq)7(NO3)2(H2O)]. When considering coupled systems, the electronic characteristics e.g., barriers, relaxation, QTM, differ from their single ion characteristics drastically. Often, for polynuclear complexes their electronic properties can be enhanced when all metallic ions are anisotropic with parallel or nearly parallel arrangements of spins,36,80–82 while for non-colinear arrangements it has been usually observed that the properties are diminished.38,58,83 In contrast, the interaction of the three Dy(III) ions in [Dy3(hq)7(NO3)2(H2O)] along with the canted spin arrangements, leads to a spin ground state with anisotropic characteristics and open loops and slow relaxation at zero field. This is a consequence of the nearly ferromagnetic ground state along the easy axes of [Dy3(hq)7(NO3)2(H2O)]. Our results are in contrast with the behaviour of a [hqH2][Dy2(hq)4(NO3)3] complex, where the SMM character was quenched by the intramolecular interaction and the non-colinear spin arrangement with neighbouring non-SMM dysprosium site.38 Herein we show the importance of the orientation of the easy axis and interactions in SMMs and and the consequences, which might not completely quench the SMM character.Author contributions
The idea was conceived by E. M.-P., C. M.-J., M. R. and W. W., J. J., E. M.-P. and C. M.-J. supervised the project. L. B., C. M.-J. and E. M.-P. carried out the AC and DC data collection, analysis and processing. S.P. and W. W. carried out the μSQUID data collection. D. F and O. F. carried out the crystallographic studies, data reduction and refinement. E. M.-P. and L. B. carried out the CASSCF calculations and interpretation. The data was analysed and interpreted by E. M.-P. with input from all co-authors. The manuscript was written by C.M.-J. and E.M.-P. with input from all co-authors.Data availability
The data supporting this article has been included as part of the ESI.†All the magnetic data was processed employing Origin Pro 2023. The Debye analysis and relaxation fits were also performed using Origin Pro 2023, while the χMT susceptibility data was fitted employing PHI (J. Comput. Chem., 2013, 34, 1164–1175). The Zeeman diagrams dependence of the μSQUID studies were obtained by employing Easyspin implemented in MATLAB (J. Magn. Reson. 2006, 178(1), 42–55).
Full crystallographic details can be found in CIF format: in the Cambridge Crystallographic Data Centre database (CCDC-2354974†).
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We acknowledge the DFG-CCR 1573 “4f for future” (project B3) and the Karlsruhe Nano Micro Facility (KNMF, https://www.kit.edu/knmf) for the provision of access to instruments at their laboratories. E. M.-P. thanks SENACYT (project PFID-FID-2021-60) for support. W. W. thanks the German Research Foundation (DFG) concerning the Gottfried Wilhelm Leibniz-award, ZVN-2020_WE 4458-5.References
- R. Sessoli, D. Gatteschi, H. L. Tsai, D. N. Hendrickson, A. R. Schake, S. Wang, J. B. Vincent, G. Christou and K. Folting, J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CAS.
- L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104 RSC.
- W. T. Carnall, P. R. Fields and B. G. Wybourne, J. Chem. Phys., 1965, 42, 3797–3806 CrossRef CAS.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, New York, 2007 Search PubMed.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef.
- F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119–3129 RSC.
- A. Chiesa, P. Santini, E. Garlatti, F. Luis and S. Carretta, Rep. Prog. Phys., 2024, 87 Search PubMed.
- M. Chizzini, L. Crippa, A. Chiesa, F. Tacchino, F. Petiziol, I. Tavernelli, P. Santini and S. Carretta, Phys. Rev. Res., 2022, 1–15 Search PubMed , 043135.
- L. E. Nodaraki, A.-M. Ariciu, D. N. Huh, J. Liu, D. O. T. A. Martins, F. Ortu, R. E. P. Winpenny, N. F. Chilton, E. J. L. McInnes, D. P. Mills, W. J. Evans and F. Tuna, J. Am. Chem. Soc., 2024, 146, 15000–15009 CrossRef CAS.
- F. Troiani, A. Ghirri, M. G. A. Paris, C. Bonizzoni and M. Affronte, J. Magn. Magn. Mater., 2019, 491, 165534 CrossRef CAS.
- C. J. Yu, S. Von Kugelgen, D. W. Laorenza and D. E. Freedman, ACS Cent. Sci., 2021, 7, 712–723 CrossRef CAS.
- S. Chicco, G. Allodi, A. Chiesa, E. Garlatti, C. D. Buch, P. Santini, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2024, 146, 1053–1061 CrossRef CAS PubMed.
- A. Chiesa, P. Santini and S. Carretta, Magnetochemistry, 2016, 2, 37 CrossRef.
- A. Chiesa, G. F. S. Whitehead, S. Carretta, L. Carthy, G. A. Timco, S. J. Teat, G. Amoretti, E. Pavarini, R. E. P. Winpenny and P. Santini, Sci. Rep., 2014, 4, 7423 CrossRef CAS PubMed.
- M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta, R. Sessoli, A. Chiesa, M. Chiesa, R. Sessoli, E. Morra, L. Sorace, M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183–6192 RSC.
- P. Santini, S. Carretta, F. Troiani and G. Amoretti, Phys. Rev. Lett., 2011, 107, 230502 CrossRef CAS.
- A. Chiesa, S. Roca, S. Chicco, M. C. De Ory, A. Gómez-León, A. Gomez, D. Zueco, F. Luis and S. Carretta, Phys. Rev. Appl., 2023, 19, 35–37 Search PubMed.
- E. Macaluso, M. Rubín, D. Aguilà, A. Chiesa, L. A. Barrios, J. I. Martínez, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí and S. Carretta, Chem. Sci., 2020, 11, 10337–10343 RSC.
- A. Chiesa, E. Macaluso, F. Petiziol, S. Wimberger, P. Santini and S. Carretta, J. Phys. Chem. Lett., 2020, 11, 8610–8615 CrossRef CAS.
- A. Chiesa, F. Petiziol, E. Macaluso, S. Wimberger, P. Santini and S. Carretta, AIP Adv., 2021, 11, 025134 CrossRef CAS.
- C. Godfrin, A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Phys. Rev. Lett., 2017, 119, 187702 CrossRef CAS PubMed.
- A. Lunghi, Sci. Adv., 2022, 8, 7880 CrossRef PubMed.
- S. Mondal and A. Lunghi, J. Am. Chem. Soc., 2022, 144, 22965–22975 CrossRef CAS PubMed.
- A. Chiesa, E. MacAluso, P. Santini, S. Carretta and E. Pavarini, Phys. Rev. B, 2019, 99, 1–11 CrossRef.
- E. Garlatti, S. Carretta, J. Schnack, G. Amoretti and P. Santini, Appl. Phys. Lett., 2013, 103, 222410 Search PubMed.
- P. E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Chem. Commun., 2011, 47, 3751–3753 RSC.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CAS.
- M. J. Giansiracusa, E. Moreno-Pineda, R. Hussain, R. Marx, M. Martínez Prada, P. Neugebauer, S. Al-Badran, D. Collison, F. Tuna, J. Van Slageren, S. Carretta, T. Guidi, E. J. L. McInnes, R. E. P. Winpenny and N. F. Chilton, J. Am. Chem. Soc., 2018, 140, 2504–2513 CrossRef CAS.
- C. Uhlmann, L. Münzfeld, A. Hauser, T. T. Ruan, S. Kumar Kuppusamy, C. Jin, M. Ruben, K. Fink, E. Moreno-Pineda and P. W. Roesky, Angew. Chem., Int. Ed., 2024, 63, e202401372 CrossRef CAS.
- M. G. Bernbeck, A. P. Orlova, J. D. Hilgar, M. Gembicky, M. Ozerov and J. D. Rinehart, J. Am. Chem. Soc., 2024, 146, 7243–7256 CrossRef CAS PubMed.
- W. Yang, G. Velkos, S. Sudarkova, B. Büchner, S. M. Avdoshenko, F. Liu, A. A. Popov and N. Chen, Inorg. Chem. Front., 2022, 9, 5805–5819 RSC.
- E. Moreno-Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S. Da Jiang, D. Collison, J. Van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CAS.
- J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733 CrossRef CAS.
- J. M. Ashtree, I. Borilović, K. R. Vignesh, A. Swain, S. H. Hamilton, Y. L. Whyatt, S. L. Benjamin, W. Phonsri, C. M. Forsyth, W. Wernsdorfer, A. Soncini, G. Rajaraman, S. K. Langley and K. S. Murray, Eur. J. Inorg. Chem., 2021, 2021, 435–444 CrossRef CAS.
- H. L. Zhang, Y. Q. Zhai, L. Qin, L. Ungur, H. Nojiri and Y. Z. Zheng, Matter, 2020, 2, 1481–1493 CrossRef.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542 CrossRef CAS.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS.
- A. Hauser, L. Münzfeld, S. Schlittenhardt, C. Uhlmann, L. Leyen, E. Moreno-Pineda, M. Ruben and P. W. Roesky, J. Am. Chem. Soc., 2024, 146, 13760–13769 CrossRef CAS PubMed.
- S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Angew. Chem., Int. Ed., 2013, 52, 12014–12019 CrossRef CAS PubMed.
- S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Chem. Sci., 2014, 5, 3246–3256 RSC.
- H. Kwon, K. R. McClain, J. G. C. Kragskow, J. K. Staab, M. Ozerov, K. R. Meihaus, B. G. Harvey, E. S. Choi, N. F. Chilton and J. R. Long, J. Am. Chem. Soc., 2024, 146(27), 18714–18721 CrossRef CAS PubMed.
- E. M. Pineda, Y. Lan, O. Fuhr, W. Wernsdorfer and M. Ruben, Chem. Sci., 2017, 8, 1178–1185 RSC.
- E. Moreno-Pineda, S. Klyatskaya, P. Du, M. Damjanović, G. Taran, W. Wernsdorfer and M. Ruben, Inorg. Chem., 2018, 57, 9873–9879 CrossRef CAS PubMed.
- H. Biard, E. Moreno-Pineda, M. Ruben, E. Bonet, W. Wernsdorfer and F. Balestro, Nat. Commun., 2021, 12, 4443 CrossRef CAS PubMed.
- T.-T. Ruan, E. Moreno-Pineda, M. Schulze, S. Schlittenhardt, T. Brietzke, H.-J. Holdt, S. K. Kuppusamy, W. Wernsdorfer and M. Ruben, Inorg. Chem., 2023, 62, 15148–15156 CrossRef CAS PubMed.
- F. Habib and P. Lin, J. Am. Chem. Soc., 2011, 133, 8830–8833 CrossRef CAS.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS.
- R. J. Blagg, F. Tuna, E. J. L. McInnes and R. E. P. Winpenny, Chem. Commun., 2011, 47, 10587–10589 RSC.
- R. J. Blagg, C. A. Muryn, E. J. L. McInnes, F. Tuna and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2011, 50, 6530–6533 CrossRef CAS PubMed.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS PubMed.
- A. Bhanja, E. Moreno-Pineda, R. Herchel, W. Wernsdorfer and D. Ray, Dalton Trans., 2020, 49, 7968–7976 RSC.
- Y. S. Meng, Y. Sen-Qiao, M. W. Yang, J. Xiong, T. Liu, Y. Q. Zhang, S. Da Jiang, B. W. Wang and S. Gao, Inorg. Chem. Front., 2020, 7, 447–454 RSC.
- N. Lalioti, V. Nastopoulos, N. Panagiotou, A. Tasiopoulos, N. Ioannidis, J. Van Slageren, P. Zhang, G. Rajaraman, A. Swain and V. Tangoulis, Dalton Trans., 2022, 51, 1985–1994 RSC.
- N. F. Chilton, G. B. Deacon, O. Gazukin, P. C. Junk, B. Kersting, S. K. Langley, B. Moubaraki, K. S. Murray, F. Schleife, M. Shome, D. R. Turner and J. A. Walker, Inorg. Chem., 2014, 53, 2528–2534 CrossRef CAS PubMed.
- G. B. Deacon, C. M. Forsyth, P. C. Junk and A. Urbatsch, Eur. J. Inorg. Chem., 2010, 3, 2787–2797 CrossRef.
- G. B. Deacon, T. Dierkes, M. Hübner, P. C. Junk, Y. Lorenz and A. Urbatsch, Eur. J. Inorg. Chem., 2011, 4338–4348 CrossRef CAS.
- F. Artizzu, P. Deplano, L. Marchiò, M. L. Mercuri, L. Pilia, A. Serpe, F. Quochi, R. Orrù, F. Cordella, F. Meinardi, R. Tubino, A. Mura and G. Bongiovanni, Inorg. Chem., 2005, 44, 840–842 CrossRef CAS PubMed.
- G. B. Deacon, P. C. Junk and S. G. Leary, Z. Anorg. Allg. Chem., 2004, 630, 1541–1543 CrossRef CAS.
- G. B. Deacon, P. C. Junk, S. G. Leary and A. Urbatsch, Z. Anorg. Allg. Chem., 2012, 638, 2001–2007 CrossRef CAS.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- R. A. Coxall, S. G. Harris, D. K. Henderson, S. Parsons, P. A. Tasker and R. E. P. Winpenny, Dalton Trans., 2000, 2349–2356 RSC.
- M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633–13645 CrossRef CAS PubMed.
- L. Münzfeld, M. Dahlen, A. Hauser, N. Mahieu, S. K. Kuppusamy, J. Moutet, M. Tricoire, R. Köppe, L. La Droitte, O. Cador, B. Le Guennic, G. Nocton, E. Moreno-Pineda, M. Ruben, P. W. Roesky, E. Moreno-Pineda, M. Ruben and P. W. Roesky, Angew. Chem., 2023, 135, 2023 Search PubMed.
- C. A. P. Goodwin, D. Reta, F. Ortu, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2017, 139, 18714–18724 CrossRef CAS PubMed.
- J. Wang, J. J. Zakrzewski, M. Zychowicz, Y. Xin, H. Tokoro, S. Chorazy and S.-I. Ohkoshi, Angew. Chem., Int. Ed., 2023, 62, e202306372 CrossRef CAS.
- F. S. Santana, M. Perfetti, M. Briganti, F. Sacco, G. Poneti, E. Ravera, J. F. Soares and R. Sessoli, Chem. Sci., 2022, 13, 5860–5871 RSC.
- W. Wernsdorfer, N. E. Chakov and G. Christou, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 132413 CrossRef.
- P. Subedi, A. D. Kent, B. Wen, M. P. Sarachik, Y. Yeshurun, A. J. Millis, S. Mukherjee and G. Christou, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134441 CrossRef.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS.
- L. Ungur and L. F. Chibotaru, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS.
- I. Fdez Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov and R. K. Carlson, et al. , J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef.
- M. E. Lines, J. Chem. Phys., 1971, 55, 2977–2984 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS.
- T. Han, M. J. Giansiracusa, Z. H. Li, Y. S. Ding, N. F. Chilton, R. E. P. Winpenny and Y. Z. Zheng, Chem. – Eur. J., 2020, 26, 6773–6777 CrossRef CAS PubMed.
- J. Wang, Q. W. Li, S. G. Wu, Y. C. Chen, R. C. Wan, G. Z. Huang, Y. Liu, J. L. Liu, D. Reta, M. J. Giansiracusa, Z. X. Wang, N. F. Chilton and M. L. Tong, Angew. Chem., Int. Ed., 2021, 60, 5299–5306 CrossRef CAS PubMed.
- H. S. Wang, P. F. Zhou, J. Wang, Q. Q. Long, Z. Hu, Y. Chen, J. Li, Y. Song and Y. Q. Zhang, Inorg. Chem., 2021, 60, 18739–18752 CrossRef CAS PubMed.
- M. Li, H. Wu, Z. Xia, V. Montigaud, O. Cador, B. Le Guennic, H. Ke, W. Wang, G. Xie and S. Chen, Chem. Commun., 2019, 55, 14661–14664 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: cif files, further synthetic details, structural and magnetic plots. CCDC 2354974. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt01588f |
| This journal is © The Royal Society of Chemistry 2024 |