Observation of Haldane magnetism in organically templated vanadium phosphate (enH2)0.5VPO4OH†
A. Sh.
Samarin
a,
S. S.
Fedotov
a,
H.-J.
Koo
b,
M.-H.
Whangbo
bc,
A. A.
Gippius
de,
S. V.
Zhurenko
e,
A. V.
Tkachev
e,
L. V.
Shvanskaya
 *df and
A. N.
Vasiliev
*df and
A. N.
Vasiliev
 *df
*df
aSkolkovo Institute of Science and Technology, Moscow 121205, Russia
bKyung Hee University, Seoul 02447, Republic of Korea
cNorth Carolina State University, Raleigh, North Carolina 27695-8204, USA
dLomonosov Moscow State University, Moscow 119991, Russia. E-mail: anvas2000@yahoo.com; lshvanskaya@mail.ru
eLebedev Physical Institute, RAS, Moscow 119991, Russia
fNational University of Science and Technology MISIS, Moscow 119049, Russia
First published on 11th September 2024
Abstract
We prepared an organically templated magnet, (enH2)0.5VPO4OH (enH2 = diprotonated ethylenediamine), hydrothermally and characterized its crystal structure by powder X-ray diffraction and Fourier-transform infrared spectroscopy, and its physical properties by magnetization, specific heat and nuclear magnetic resonance measurements and density functional theory calculations. (enH2)0.5VPO4OH consists of uniform chains of V3+ (d2, S = 1) ions and exhibits Haldane magnetism with spin gap Δ = 59.3 K from the magnetic susceptibility χ(T) at μ0H = 0.1 T, which is reduced to 48.4 K at μ0H = 9 T according to the 31P shift. The NMR data evidence the formation of a spin-glass state of unpaired S = 1/2 spins at TS–G ≈ 3 K and indicate that the Haldane S = 1 spin chain segments are much longer in the organically templated magnet (enH2)0.5VPO4OH than in the ammonium counterpart NH4VPO4OH. The single-ion anisotropy D and the interchain exchange J′ in (enH2)0.5VPO4OH and NH4VPO4OH were estimated in density functional calculations to find them very weak compared to the intrachain exchange J.
Introduction
Haldane's prediction1 of a singlet ground state in quasi-one-dimensional integer-spin antiferromagnets with low single-ion anisotropy D has stimulated an intensive search for compounds satisfying the strict criteria for its existence based on the D/J and J′/J ratios, where J′ and J are the interchain and the intrachain exchange interactions, respectively.2 In chain compounds of S = 1 ions, the Haldane phase competes with the long-range ordered, dimerized and large-D phases. So far, ten metal–organic and three inorganic magnets based on Ni2+ (d8, S = 1) (i.e., Y2BaNiO5, SrNi2V2O8 and PbNi2V2O8) have been found to be Haldane magnets and hence have a spin gap between the continuum of excited states and the ground state.3,4 Three more inorganic compounds, Ba2V(VO4)2OH, AgVP2S6 and NH4VPO4OH, based on V3+ (d2, S = 1) ions are also found to be Haldane magnets.4,5 Here, we report synthesis and characterization of the first organically templated Haldane magnet based on V3+ ions, (enH2)0.5VPO4OH, where enH2 refers to the diprotonated ethylenediamine, H3NCH2CH2NH32+. On the basis of density functional calculations, we establish the location of (enH2)0.5VPO4OH on the D/J vs. J′/J phase diagram.Synthesis and X-ray diffraction
(enH2)0.5VPO4OH was synthesized hydrothermally in one step by mixing 0.0008 mol of V2O3, 0.0016 mol of H3PO4 and 0.005 mol of H2N(CH2)2NH2 in 0.44 mol of deionized H2O at 100 rpm stirring at room temperature in a 30 ml Teflon vessel. The information on chemicals used for the synthesis is given in Table S1 of ESI.† The vessel then was sealed in steel autoclave and the mixture was hydrothermally treated at 205 °C for 7 days under constant stirring (750 rpm). After that, the autoclave was naturally cooled down to room temperature, to obtain a pale-sandy fine powder sample. The latter was carefully filtrated and washed with deionized water 5 times by centrifugation. Then it was dried overnight at 75 °C in a vacuum oven and kept under inert (Ar) atmosphere until further use.Powder X-ray diffraction (PXRD) patterns were collected with a Bruker D8 ADVANCE powder diffractometer (λCuKα1 = 1.54051 Å, λCuKα2 = 1.54433 Å) equipped with an energy dispersive detector LYNXEYE XE in Bragg–Brentano reflection geometry (5–130° 2θ°, 0.02° scan step). The crystal structure was refined from the PXRD data with the TOPAS-Academic software package using the Rietveld method.6 Isostructural (enH2)0.5FePO4OH was used as a starting structural model.7 The background was estimated by a set of polynomials, the calculation of the unit cell parameters and the refinement of the atomic coordinates were performed. According to the phase analysis no traceable impurities were observed, as shown in Fig. 1. Broad peak at about 70° is due to the sample holder. The inset to Fig. 1 represents the scanning electron microscopy (SEM) image of the sample showing its needle-like morphology. The calculated unit cell parameters are given in Table 1. Atomic fractional coordinates for (enH2)0.5VPO4OH according to the Rietveld refinement are given in Table S2 of ESI.†
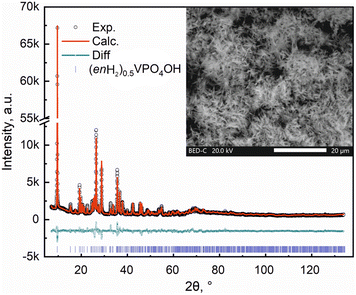 | ||
| Fig. 1 Experimental, calculated and difference diffraction profiles of (enH2)0.5VPO4OH. Inset: The SEM image of the sample. | ||
| Formula | (enH2)0.5VPO4OH |
|---|---|
| S.G. | P21/c |
| a, Å | 4.5282(6) |
| b, Å | 6.1098(12) |
| c, Å | 18.5879(17) |
| β, ° | 94.781(3) |
| V, Å3 | 512.48(13) |
| Z | 4 |
| GOF | 2.43 |
| R exp, % | 3.17 |
| R p, Rwp, % | 5.62, 7.73 |
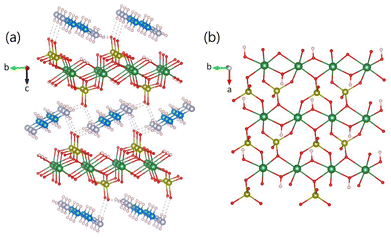
As shown in Fig. 2a, (enH2)0.5VPO4OH possesses a layered structure, in which the VPO4OH− layers alternate with ribbons of enH22+ cations running along the a axis. In each VPO4OH− layer, the chains of edge-sharing VO5OH octahedra are interconnected by PO4 groups (Fig. 2b). (enH2)0.5VPO4OH belongs to the structural type of (enH2)0.5MPO4OH (M = Fe, Ga)7,8 and closely related to NH4MPO4OH (M = V, Ga)5,9 (see ESI and Fig. S1†).
Fourier-transform infrared spectroscopy
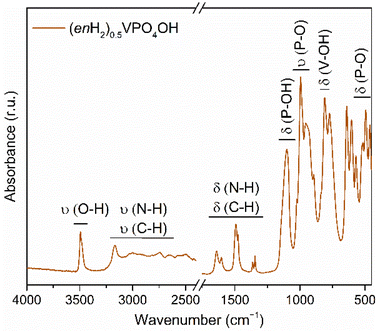
The presence of the ethylenediamine and hydroxyl groups in (enH2)0.5VPO4OH was confirmed by infrared spectroscopy, as shown in Fig. 3. Fourier-transform infrared (FTIR) spectra were collected with an ALPHA II compact FTIR spectrometer (Bruker). The spectra were recorded in the 4000–400 cm−1 range with 2 cm−1 resolution. The reproducibility was checked by probing three different spots of the same powder sample. The presence of the hydroxyl group is manifested by a sharp maximum located at 3492 cm−1 (ν(OH)).10 The group between 3300 and 2400 cm−1 corresponds to the N–H and C–H vibrations in the enH22+ moiety. The most intense maximum (∼3166 cm−1) is associated with N–H (stretch), which is involved in hydrogen bonding. At lower wavenumbers (1750–1250 cm−1), three groups of peaks are observed, which reflect presence of enH22+ in the interlayer space. The complex shape of the spectra in this range is defined by a joint C–H and N–H vibrations.11 Taking into account few previous reports about ethylenediamine-containing metal–organic compounds, we can assume that the first and second couples of maxima fall into the range of bending N–H modes and may also contain some contribution of C–H vibrations (most likely bending ones). The third couple of peaks corresponds to the C–H (bending and/or twisting) modes.12–14 The maxima located in the 1100–500 cm−1 range (except the one at 810 cm−1 – δ(V–OH)) are related to the bending and stretching vibrations of the O–P–O bonds. The peak at 1100 cm−1 corresponds to the δ(P–OH).9Thermodynamics
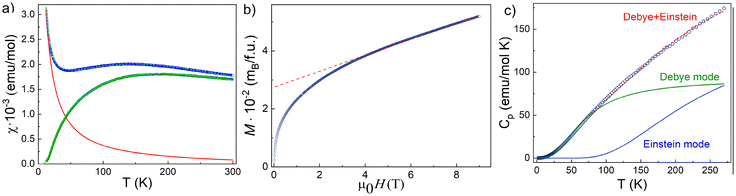
Thermodynamic properties of (enH2)0.5VPO4OH, i.e., the magnetization M and the specific heat Cp were measured using relevant options of “Quantum Design” Physical Properties Measurements System PPMS-9T in the temperature range 2–300 K in a magnetic field μ0H up to 9 T. The temperature dependence of the magnetic susceptibility, χ = M/H, taken at μ0H = 0.1 T in the field-cooled mode is shown in Fig. 4a. It shows a broad correlation hump centred at about 150 K, which is followed by a rapid increase on lowering the temperature. This upturn at low temperatures can be ascribed to a trace amount, nimp, of impurities in the chain, which produce dangling bonds of spin S = 1/2 at the ends of the spin-chain segments.The χ(T) curve can be fitted by the sum of Curie law
| χ = χ0 + C/(T − Θ) | (1) |
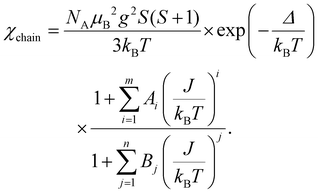 | (2) |
The field dependence of magnetization in (enH2)0.5VPO4OH taken at 2 K is shown in Fig. 4b. The tangent to this curve shown by the dash line extrapolates to 2.7 × 10−2μB per f.u., which corresponds to 1.35% of impurities. This estimation, which is higher than estimation obtained from the Curie–Weiss fitting reflects the field-induced polarization of spin S = 1/2 at the ends of the spin-chain segments forming the spin-glass state (see NMR section).
The temperature dependence of the specific heat in (enH2)0.5VPO4OH is shown in Fig. 4c. No anomalies were observed down to 2 K, which excludes the transition into a long-range ordered state. At room temperature, the value of Cp is still far from the Dulong-Petit limit 3RN = 374 J mol−1 K, where the number of atoms per formula unit N = 15 and the universal gas constant R = 8.314 J mol−1 K. The experimental data can be fitted by the sum of Debye (temperature ΘD = 282.5 K and weight aD = 3.66) and Einstein (temperature ΘE = 734.5 K and weight aE = 6.07) modes, as shown by green and blue solid lines in Fig. 4c. These two modes reflect the presence of heavy (V, P) and light (H, C, N, O) atoms in the structure of (enH2)0.5VPO4OH.
Nuclear magnetic resonance
NMR spectra of 31P nuclei as well as their spin–lattice relaxation were measured using a custom designed phase coherent pulsed NMR spectrometer with direct quadrature signal detection at the carrier frequency at a constant magnetic field of 9 T in the temperature range of 2.5–310 K. For spectra accumulation, we used the Hahn spin echo pulse sequence augmented by the fast Fourier-transform summation method.17–19 The nuclear spin–lattice relaxation rate was measured by means of the saturation recovery method.The set of 31P NMR spectra of (enH2)0.5VPO4OH is shown in Fig. S2 of the ESI† with four selected spectra measured at 4.5, 9, 150 and 310 K presented in the upper inset of Fig. 5. Similar to NH4VPO4OH,5 the spectra consist of a single and almost symmetric line, which progressively broadens with decreasing temperature. The temperature dependence of the 31P NMR linewidth estimated as a full width at half maximum (FWHM) is shown in the lower inset to Fig. 5. It is well described by the power law ∼Tn with n = −0.40 ± 0.01 in the entire temperature range investigated in contrast to NH4VPO4OH. Below 20 K, the latter shows the Curie–Weiss-like FWHM behavior, which was observed due to the magnetic contribution from the unpaired edge spins S = 1/2.5
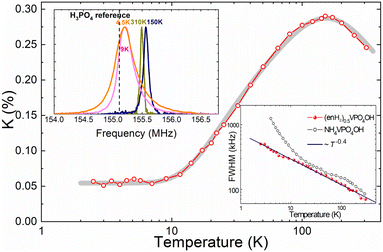 | ||
| Fig. 5 Temperature dependence of the 31P NMR shift measured for (enH2)0.5VPO4OH. The thick gray line is the best fit to eqn (2). The upper inset: 31P NMR spectra taken at 4.5, 9, 150 and 310 K. The position of the Larmor frequency in 85% H3PO4 aqueous solution at μ0H = 9 T is indicated by the dashed line. The lower inset: The FWHM of 31P NMR spectra as a function of temperature in (enH2)0.5VPO4OH and NH4VPO4OH (adopted from ref. 5). | ||
The temperature dependence of the shift K(T) taken as a position of the line maximum in relation to the Larmor frequency at μ0H = 9 T in 85% phosphoric acid aqueous solution is shown in Fig. 5, which exhibits a broad maximum at around 140 K similar to that observed in the χ(T) curve obtained at μ0H = 0.1 T at around 150 K. In the entire temperature range, the temperature dependence of the experimental K(T) was successfully approximated by the Padé equation for Haldane chains (eqn (2)) with J = 118(2) K providing the gap value Δ = 48.4 K. This gap is smaller than that obtained from the χ(T) curve since it was obtained at a much higher field (i.e., 9 T). Note, the determination of the gap from the 31P shift is independent from the impurity contribution. In contrast to NH4VPO4OH,5 (enH2)0.5VPO4OH does not show a pronounced low temperature Curie–Weiss-like behavior of the 31P shift, which originates from unpaired S = 1/2 spins at the edges of finite length Haldane S = 1 spin chains. This observation is in line with the magnetic susceptibility data, which show that (enH2)0.5VPO4OH has much less paramagnetic centers than does NH4VPO4OH (i.e., 0.75% vs. 3% (ref. 5)), indicating that the Haldane S = 1 spin chain segments of (enH2)0.5VPO4OH are much longer than those of NH4VPO4OH.
The 31P nuclear magnetization recovery curves exhibit a double exponential behavior with the fast and slow components approximated by a simple and a stretched exponential function, exp[−(τ/T1fast)] and exp[−(τ/T1slow)β] (0 ≤ β ≤ 1), respectively. The fast component is dominated (one order of magnitude) above 40 K and is therefore attributed to the relaxation channel via the S = 1 electronic spins of the Haldane chains. Apparently, the slow relaxation term is caused by unpaired edge S = 1/2 spins. Below 30 K, the Haldane chain approaches its spin singlet ground state and the relative weights of two relaxation components become almost equal. With decreasing temperature below 10 K, both 1/T1fast and 1/T1slow start to increase reaching a maximum at around 3 K. Such a behavior is characteristic for the formation of a disordered spin-glass of unpaired S = 1/2 spins at TS–G ≈ 3 K. The latter originates from a critical slowing down of the spin fluctuations when approaching the freezing temperature,20,21 as observed in NH4VPO4OH5 as well. Temperature dependences of the fast and slow 31P spin–lattice relaxation rates in (enH2)0.5VPO4OH measured at 9 T are shown in Fig. S3 of ESI.†
Density functional analysis
We now determine the intrachain spin exchange J, the interchain spin exchange J′ and the single-ion anisotropy D of (enH2)0.5VPO4OH based on density functional theory (DFT) calculations, to establish its position on the Sakai–Takahashi phase diagram2 described in terms of the D/J and 2J′/J ratios. The parameters J and J′ are obtained by the energy-mapping analysis22–24 based on DFT calculations.25–27 Since (enH2)0.5VPO4OH is a magnetic insulator, our energy-mapping analysis was carried in DFT+U calculations28 (with Ueff = 2 and 3 eV on V) using the spin Hamiltonian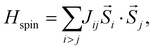 | (3) |
| Magnet | U eff | J | J′ | D | 2J′/J | D/J | Δ |
|---|---|---|---|---|---|---|---|
| (enH2)0.5VPO4OH | 2 | 146.8 | −0.38 | 0.23 | −5.2 × 10−3 | 1.57 × 10−3 | 60.2 |
| 3 | 121.3 | 0.38 | 0.12 | 3.1 × 10−3 | 9.89 × 10−4 | 49.7 | |
| NH4VPO4OH | 2 | 92.8 | 3.28 | 0.12 | 7.1 × 10−2 | 1.29 × 10−3 | 38.0 |
| 3 | 73.0 | 3.02 | 0.12 | 3.3 × 10−2 | 1.64 × 10−3 | 29.9 |
To fall into the Haldane sector of the Sakai–Takahashi phase diagram, the system should satisfy the limiting value of 2J′/J < 0.0648.30 When D/J > 0, the Haldane phase persists up to the ratio D/J = 1.033.31 Beyond this point, the quantum paramagnet phase appears. When D/J < 0, the Haldane phase persists down to the ratio D/J = −0.316,32 below which the Néel phase appears. (enH2)0.5VPO4OH falls into the middle of Haldane sector of Sakai–Takahashi phase diagram, while NH4VPO4OH falls closer to the verge of this sector.2
Discussion
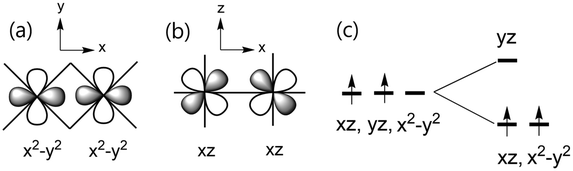
It is noted that the intrachain exchange J is stronger for (enH2)0.5VPO4OH than for NH4VPO4OH by a factor of about 1.6, while the interchain exchange J′ is much weaker than the intrachain exchange J in both (enH2)0.5VPO4OH and NH4VPO4OH. These observations originate from the fact that each V3+⋯V3+ chain along the b-axis is a consequence of the edge-sharing between adjacent VO5(OH) octahedra, with the shared edges forming a ribbon chain along the b-axis (Fig. 1b, S4 and S5†). It is convenient to distinguish two different kinds of O atoms in each ribbon chain; the O atoms involved in the edge-sharing will be referred to as the equatorial O atoms, Oeq, while the O atoms above and below each ribbon plane as the axial O atoms, Oax. Each ribbon chain exhibits a slight twisting and zigzag bending in (enH2)0.5VPO4OH, but it does not in NH4VPO4OH. If we take the local x-axis along the V3+⋯V3+ direction (Fig. S6 of ESI†), and the xy plane parallel to the ribbon plane (disregarding the slight zigzag bending), then the t2g set of each V3+ ion has the x2 − y2, xz and yz states. (If the local x-axis is chosen along a V–Oeq bond, the t2g set would be described by the xy, xz and yz states.) The direct V3+⋯V3+ interaction is strong between the x2 − y2 states (Fig. 6a) and also between the xz states (Fig. 6b), so the t2g set splits into the (x2 − y2, xz) set lying below the yz state (Fig. 6c). This point was verified by calculating the partial density of states (PDOS) for (enH2)0.5VPO4OH and NH4VPO4OH (see the PDOS plots in Fig. S7 and S8 of ESI†). Thus, the x2 − y2 and xz states act as the magnetic orbitals of each V3+ ion. The V3+⋯V3+ distance is slightly shorter for (enH2)0.5VPO4OH than for NH4VPO4OH5 (3.058 vs. 3.082 Å), so the direct V3+⋯V3+ interaction is stronger and hence the intrachain exchange J becomes greater for (enH2)0.5VPO4OH.The reason why the interchain J′ is very weak in (enH2)0.5VPO4OH and NH4VPO4OH is explained by analyzing how the two adjacent ribbon chains are interconnected by the PO4 groups. As shown in Fig. 2b, the interchain spin exchange occurs through the V–O⋯P5+⋯O–V paths. Note that each PO4 group corner-shares with one Oeq of one ribbon chain and with two Oax atoms of the other ribbon chain such that the V–O⋯P5+⋯O–V paths are of the V–Oeq⋯P5+⋯Oax–V type. (The fourth O atom of PO4 makes hydrogen bonds with two different enH22+ cations, Fig. 2a.) The latter practically vanishes because the x2 − y2 and xz magnetic orbitals do not have their p-orbital tails on both V–Oeq and V–Oax bonds (Fig. S9 of ESI†).
We now discuss why the V3+ ions in the ribbon chains of (enH2)0.5VPO4OH and NH4VPO4OH exhibit a very weak single-ion anisotropy. The d-states of the V3+ ion in each VO6 octahedron in these magnets are split as shown in Fig. 6c. The preferred spin orientation of a magnetic ion is predicted by the selection rule22,33 based on the interaction of the highest-occupied state with the lowest-unoccupied state, which is induced by spin–orbit coupling (SOC). This selection rule predicts that the interaction of the occupied xz state with the unoccupied yz state favours the spin orientation along the local c-axis, but that of the occupied x2 − y2 state with the unoccupied yz state favours the spin orientation perpendicular to the local c-axis. The presence of the two opposing trends leads to a very weak magnetic anisotropy.
Conclusion
To summarize, we observed a Haldane magnetic behaviour in the first V-based organically templated magnet (enH2)0.5VPO4OH from magnetic susceptibility and NMR measurements. The energy gap Δ = 59.3 K between the spin-singlet ground state and the triplet excited states is observed from the χ(T) curve taken at μ0H = 0.1 T, and this gap is reduced to 48.4 K at μ0H = 9 T as observed from the 31P shift. The NMR results indicate that the Haldane S = 1 spin chain segments are much longer in (enH2)0.5VPO4OH than in its ammonium counterpart NH4VPO4OH, and that a spin-glass ground state of unpaired S = 1/2 spins forms at TS–G ≈ 3 K as observed in NH4VPO4OH. The parameters J, J′ and D describing this magnet were evaluated and compared with those in NH4VPO4OH. The reasons for the weaker interchain exchange interaction J′ and single-ion anisotropy D compared to the intrachain exchange interaction J are two-fold: one is that the t2g state of each V3+ ions split into the (x2 − y2, xz) state below the yz state (with the x-axis taken along the V3+⋯V3+ direction), and the other is that the PO4 groups interconnecting adjacent ribbon chains lead to the V–Oeq⋯P5+⋯Oax–V type spin exchanges.Data availability
ESI,† including details on synthesis, crystal structure, nuclear magnetic resonance are theoretical DFT calculations for (enH2)0.5VPO4OH, are available at https://doi.org/DOI. Crystallographic data for (enH2)0.5VPO4OH has been deposited at the CCDC under CCDC 2356612.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research was carried out within the framework of the scientific program of the National Centre of Physics and Mathematics under the project “Research in strong and superstrong magnetic fields”. This work was supported by the Ministry of Science and Higher Education of the Russian Federation within the framework of the Priority-2030 strategic academic leadership program at NUST MISIS. SSF acknowledge funding from RSF grant 23-73-10125 for the synthesis and structural/chemical characterization. LVS acknowledge the support through RSF grant 22-42-08002 for the measurements of thermodynamic properties. The work at KHU was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1A6A1A03048004).References
- F. D. M. Haldane, Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the O(3) nonlinear sigma model, Phys. Lett. A, 1983, 93, 464 CrossRef; F. D. M. Haldane, Nonlinear Field Theory of Large-Spin Heisenberg Antiferromagnets: Semiclassically Quantized Solitons of the One-Dimensional Easy-Axis Néel State, Phys. Rev. Lett., 1983, 50, 1153 CrossRef.
- T. Sakai and M. Takahashi, Effect of the Haldane gap on quasi-one-dimensional systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 4537 CrossRef PubMed.
- P. Tin, M. J. Jenkins, J. Xing, N. Caci, Z. Gai, R. Jin, S. Wessel, J. Krzystek, C. Li, L. L. Daemen, Y. Cheng and Z.-L. Xue, Haldane topological spin-1 chains in a planar metal-organic framework, Nat. Commun., 2023, 14, 5454 CrossRef CAS PubMed.
- O. V. Maximova, S. V. Streltsov and A. N. Vasiliev, Long range ordered, dimerized, large-D and Haldane phases in spin 1 chain compounds, Crit. Rev. Solid State Mater. Sci., 2021, 46, 371 CrossRef CAS.
- A. Sh. Samarin, I. A. Trussov, Z. V. Pchelkina, S. S. Fedotov, Y. A. Ovchenkov, S. V. Zhurenko, A. V. Tkachev, A. A. Gippius, L. V. Shvanskaya and A. N. Vasiliev, Lamellar crystal structure and Haldane magnetism in NH4VPO4OH, ACIE, 2023, 63, e202316719 CrossRef PubMed.
- A. A. Coelho, TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++, J. Appl. Crystallogr., 2018, 51, 210 CrossRef CAS.
- M. Cavellec, D. Riou and G. Ferey, A Two-dimensional iron phosphate templated by ethylenediamine, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1995, 51, 2242 CrossRef.
- R. H. Jones, J. M. Thomas, H. Qisheng, M. B. Hursthouse and J. Chen, The synthesis and crystal structure of a novel clay-like gallophosphate with sub-unit-cell intergrowths of ethylenediamine: [GaPO4(OH)]– 0·5(H3NCH2CH2NH3)2+, J. Chem. Soc., Chem. Commun., 1991, 1520 RSC.
- F. Bonhomme, S. G. Thoma and T. M. Nenoff, Two ammonium templated gallophosphates: synthesis and structure determination from powder diffraction data of 2D and 3D-GAPON, Microporous Mesoporous Mater., 2002, 53, 87 CrossRef CAS.
- F. P. Araujo, N. Hulsbosch and P. Muchez, High spatial resolution Raman mapping of complex mineral assemblages: Application on phosphate mineral sequences in pegmatites, J. Raman Spectrosc., 2021, 52, 690 CrossRef.
- Y. Song, P. Y. Zavalij, N. A. Chernova, M. Suzuki and M. S. Whittingham, Comparison of one, two-, and three-dimensional iron phosphates containing ethylenediamine, J. Solid State Chem., 2003, 175, 63 CrossRef CAS.
- L. Torre-Fernández, A. Espina, S. A. Khainakov, Z. Amghouz, J. R. García and S. García-Granda, Novel ethylenediamine-gallium phosphate containing 6-fold coordinated gallium atoms with unusual four equatorial Ga–N bonds, J. Solid State Chem., 2014, 215, 143 CrossRef.
- A. John, D. Philip, K. Morgan and S. Devanarayanan, IR and Raman spectra of two layered aluminium phosphates Co(en)3Al3P4O16 · 3H2O and [NH4]3[Co(NH3)6]3[Al2(PO4)4]2 · 2H2O, Spectrochim. Acta, Part A, 2000, 56, 2715 CrossRef CAS PubMed.
- J. Escobal, J. L. Pizarro, J. L. Mesa, M. I. Arriortua and T. Rojo, An ionic nickel(II) phosphate with ethylenediamine: (C2H10N2)[Ni(H2O)6](HPO4)2. Hydrothermal synthesis, crystal structure, and spectroscopic properties, J. Solid State Chem., 2000, 154, 460 CrossRef CAS.
- A. K. Bera, B. Lake, A. T. M. N. Islam, B. Klemke, E. Faulhaber and J. M. Law, Field-induced magnetic ordering and single-ion anisotropy in the quasi-one-dimensional Haldane chain compound SrNi2V2O8: A single-crystal investigation, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224423 CrossRef.
- G. A. Bain and J. F. Berry, Diamagnetic corrections and Pascal's constants, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- A. P. Bussandri and M. J. Zuriaga, Spin-echo mapping spectroscopy applied to NQR, J. Magn. Reson., 1998, 131, 224 CrossRef CAS.
- W. G. Clark, M. E. Hanson, F. Lefloch and P. Ségransan, Magnetic resonance spectral reconstruction using frequency–shifted and summed Fourier transform processing, Rev. Sci. Instrum., 1995, 66, 2453 CrossRef CAS.
- Y. Y. Tong, Nuclear spin-echo Fourier-transform mapping spectroscopy for broad NMR lines in solids, J. Magn. Reson., Ser. A, 1996, 119, 22 CrossRef CAS.
- S. Kundu, T. Dey, A. V. Mahajan and N. Büttgen, LiZn2V3O8: a new geometrically frustrated cluster spin-glass, J. Phys.: Condens. Matter, 2020, 32, 115601 CrossRef CAS PubMed.
- X. Zong, A. Niazi, F. Borsa, X. Ma and D. C. Johnston, Structure, magnetization, and NMR studies of the spin-glass compound (LixV1−x)3BO5 (x ≈ 0.40 and 0.33), Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054452 CrossRef.
- H. Xiang, C. Lee, H.-J. Koo, X. Gong and M.-H. Whangbo, Magnetic properties and energy-mapping analysis, Dalton Trans., 2013, 42, 823 RSC.
- M.-H. Whangbo and H. Xiang, Magnetic Properties from the Perspectives of Electronic Hamiltonian, Handbook of Solid State Chemistry, 2017 Search PubMed.
- M.-H. Whangbo, H.-J. Koo and R. K. Kremer, Spin exchanges between transition metal ions governed by the ligand p-orbitals in their magnetic orbitals, Molecules, 2021, 26, 531 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- J. Kuneš, P. Novák, R. Schmid, P. Blaha and K. Schwarz, Electronic structure of fcc Th: Spin-orbit calculation with 6p1/2 local orbital extension, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 153102 CrossRef.
- K. Wierschem and P. Sengupta, Characterizing the Haldane phase in quasi-one-dimensional spin-1 Heisenberg antiferromagnets, Mod. Phys. Lett. B, 2014, 28, 1430017 CrossRef CAS.
- K. Wierschem and P. Sengupta, Quenching the Haldane gap in spin-1 Heisenberg antiferromagnets, Phys. Rev. Lett., 2014, 112, 247203 CrossRef.
- W. J. Rao, G. Y. Zhu and G. M. Zhang, SU(3) quantum critical model emerging from a spin-1 topological phase, Phys. Rev. B, 2016, 93, 165135 CrossRef.
- M.-H. Whangbo, E. E. Gordon, H. J. Xiang, H.-J. Koo and C. Lee, Prediction of spin orientations in terms of HOMO–LUMO interactions using spin-orbit coupling as perturbation, Acc. Chem. Res., 2015, 48, 3080 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt01675k |
| This journal is © The Royal Society of Chemistry 2024 |