Open Access Article
Open Access ArticleData-driven discovery of electrode materials for protonic ceramic cells†
Xueyu
Hu
a,
Yucun
Zhou
a,
Zheyu
Luo
 a,
Haoyu
Li
a,
Nai
Shi
b,
Zhijun
Liu
a,
Haoyu
Li
a,
Nai
Shi
b,
Zhijun
Liu
 a,
Weilin
Zhang
a,
Weining
Wang
a,
Yong
Ding
a and
Meilin
Liu
a,
Weilin
Zhang
a,
Weining
Wang
a,
Yong
Ding
a and
Meilin
Liu
 *a
*a
aSchool of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, 30332-0245, USA. E-mail: meilin.liu@mse.gatech.edu
bKyushu University Platform of Inter-/Transdisciplinary Energy Research, Kyushu University, Fukuoka, 819-0395, Japan
First published on 29th October 2024
Abstract
Protonic ceramic electrochemical cells (PCECs) offer an efficient solution for the closed-loop conversion between chemical and electrical energy, supporting zero-emission objectives. The varying and high-humidity conditions on the oxygen electrode side necessitate the development of novel materials with superior electro-catalytic activity and durability. In this study, we circumvent conventional trial-and-error approaches by utilizing high-throughput calculations and a data-driven decomposition analysis to predict the key properties important for applications of 4455 distinct perovskite oxides, including their thermodynamic stability and decomposition tendencies. Our analysis results in a small number of highly promising candidates. Among them, PrBaCo1.9Hf0.1O5+δ demonstrates exceptional performance in PCECs, achieving peak power densities of 1.49 W cm−2 at 600 °C and 0.6 W cm−2 at 450 °C in fuel cell mode and an extraordinary current density (2.78 A cm−2) at an applied voltage of 1.3 V at 600 °C in electrolysis mode, while maintaining outstanding durability over 500 hours of operation. This study highlights the pivotal role of data-driven high-throughput calculations in accelerating the discovery of novel materials for various clean energy technologies.
Broader contextProtonic ceramic electrochemical cells (PCECs) are a critical energy conversion technology with the potential for highly efficient power generation and green hydrogen production, making them vital to achieving a zero-emission society. However, their commercial deployment is hindered by the need for oxygen electrode materials that can operate stably in complex environments while exhibiting high electrocatalytic activity for oxygen reduction and evolution. Accelerating the search for exceptionally active electrode materials, expanding the currently limited understanding, and unraveling their thermodynamic stability and reaction mechanisms remain significant challenges. In this study, we present a research paradigm that integrates high-throughput calculations with a data-driven analysis approach. This paradigm has effectively screened an unprecedentedly vast chemical space, discovering oxygen electrodes that dramatically enhance the kinetics and durability of state-of-the-art PCECs. Our methodology holds promise for advancing the development of various clean energy technologies including other types of fuel cells, solar cells, supercapacitors, and advanced batteries. |
Introduction
Amid the urgent challenge of climate change and sustainable development, protonic ceramic electrochemical cells (PCECs) stand out for their exceptional efficiency, affordability, and environmental sustainability, surpassing alternatives like oxygen-ion conducting solid oxide cells (SOCs) and proton exchange membrane electrochemical cells (PEMECs).1–4 The unique capability of PCECs to seamlessly transition between fuel cell and electrolysis modes at temperatures below 600 °C, coupled with their remarkable conversion efficiency, fosters a sustainable cycle of chemical and electrical energy transformation, paving the way toward a zero-emission future.5 However, the commercialization of PCECs is hindered by the lack of electro-catalytically active oxygen (or air) electrode materials with excellent resistance to water-induced element segregation, phase transformation, and delamination, particularly when exposed to high concentrations of steam in the electrolysis mode.6 Various strategies have been employed to address these problems, including surface infiltration, pulsed laser deposition (PLD) assisted interlayer construction, and acid etch triggered interface enhancement.3,7,8 However, their complexity greatly increases the cost, thus diminishing their commercial applicability. This underscores an urgent need for the development of inherently durable oxygen electrode materials.To bypass conventional, time-consuming methods for material discovery, we are leveraging high-throughput density functional theory (DFT) calculations.9–12 These calculations enable precise material characterization and broaden the horizons of chemical exploration, shifting the paradigm from intuition-based to data-driven material selection.13–16 Incorporating the thermodynamic stability descriptor, Ehull, these techniques offer remarkable efficiency in evaluating the thermodynamic stability of new materials without the need for experimental synthesis.10,17,18 However, relying excessively on Ehull values alone risks overlooking potential decomposition tendencies, which could potentially skew assessments of materials’ stability. To address this, we propose a data-driven material analysis method termed the decomposition analysis (DA), based on the expanding landscape of open-access databases,19 that assesses stability more accurately by examining the stable phases constructing a material's convex hull. Our study applied high-throughput DFT calculations across an unprecedented size of 4455 oxygen electrode candidates, identifying 26 material series with outstanding thermodynamic stability. Further refinement through DA and experimental validation led to the discovery of a highly durable composite oxygen electrode, PrBaCo1.9Hf0.1O5+δ (PBCHf10), which exhibits exceptionally high electro-catalytic activity. Our integrated approach, combining experimental validation with advanced computational methods, has unraveled the mechanism of the proton-involved oxygen reduction reaction, potentially setting a new theoretical benchmark for the development of PCEC oxygen electrodes. A PCEC based on the PBCHf10 electrode demonstrates outstanding performance, achieving an impressive peak power density (1.49 W cm−2) in the fuel cell mode and an extraordinary current density (2.78 A cm−2) at an applied cell voltage of 1.3 V in the electrolysis mode at 600 °C. Notably, the single cell maintains stable performance for over 500 hours in the electrolysis mode.
Results and discussion
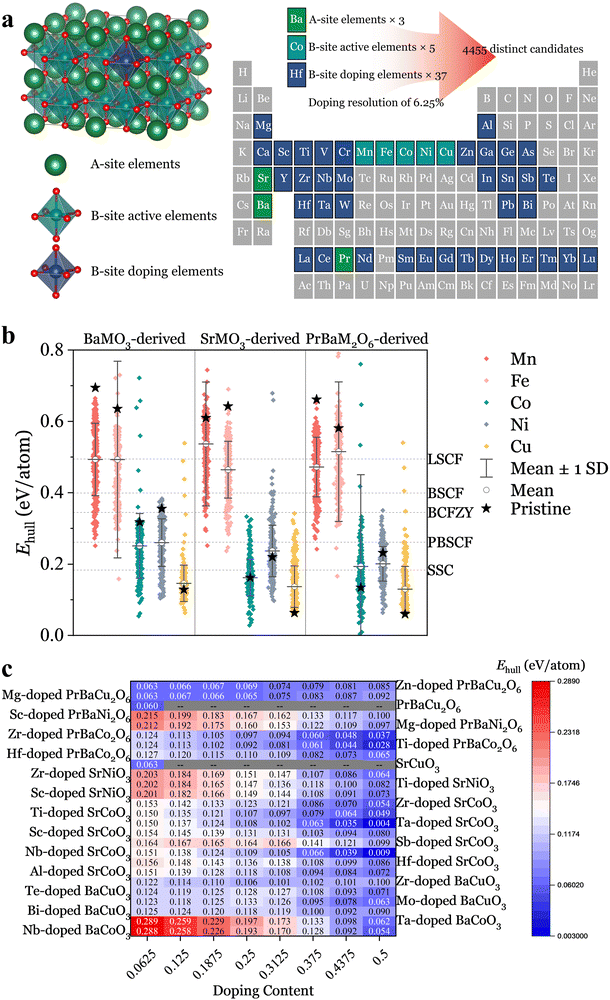
Unveiling unexplored chemical spaces via high-throughput calculations
Drawing inspiration from the state-of-the-art oxygen electrode materials, such as La0.6Sr0.4Co0.2Fe0.8O3−δ (LSCF),20 Ba0.5Sr0.5Co0.8Fe0.2O3−δ (BSCF),21 Sm0.5Sr0.5CoO3−δ (SSC),22 BaCo0.4Fe0.4Zr0.1Y0.1O3−δ (BCFZY),23 and PrBa0.5Sr0.5Co1.5Fe0.5O5+δ (PBSCF),24 we explored previously uncharted chemical spaces. We constructed a comprehensive set of perovskite oxide candidates by selecting three A-site ions (Ba, Sr, Pr0.5Ba0.5) and combining them with five catalytically active B-site ions (Mn, Fe, Co, Ni, Cu) plus 37 distinct B-site dopants (Table. S1, ESI†). To ensure sufficient electro-catalytic activity, the proportion of the catalytically active B-site ions was kept above 50%. This approach generates 4455 distinct perovskite oxide candidates, 96% of which were previously unexplored, as showcased in Fig. 1a. The optimal elemental distribution for each candidate was determined using molecular dynamics–Monte Carlo (MD–MC) simulations.25,26 We performed structural relaxation and static calculations to derive their Ehull values under oxygen electrode operation conditions (T = 600 °C, p(O2) = 0.21 atm), a crucial descriptor of thermodynamic stability. This descriptor acts as a metric to determine the likelihood of a material undergoing phase transformation or decomposition into a mixture of more stable phases on the convex hull.26We organized the Ehull values for the 4455 materials into three main categories based on A-site elements, further classifying them by B-site active elements, resulting in 15 distinct groups (Fig. 1b). The pristine perovskite oxides in each group are highlighted, and we present their mean Ehull values along with standard deviations. From the analysis of these preliminary data, those with Mn and Fe at the B-site, exhibit relatively high Ehull values, with averages ranging from 0.465 to 0.537 eV per atom, suggesting their inherent instability. The lowest Ehull value is observed with BaFe0.5Mo0.5O3, sacrificing 50% active elements to achieve a value of 0.158 eV per atom, which is still not satisfactory (Fig. S1 and S2, ESI†). In contrast, materials with Co or Ni at the B-site demonstrate lower Ehull values, with averages ranging from 0.164 to 0.260 eV per atom, indicating better stability (Fig. S3 and S4, ESI†). Pristine oxides with Cu at the B-site demonstrate the lowest Ehull values, at 0.129, 0.063, and 0.060 eV per atom for BaCuO3, SrCuO3, and PrBaCu2O6, respectively. However, subsequent doping efforts typically result in elevated Ehull values (Fig. S5, ESI†).
Fig. 1c summarizes the top 26 series materials, highlighting them as the most stable and promising candidates for potential applications. Furthermore, a comparative analysis of the state-of-the-art oxygen electrodes was performed to contextualize the thermodynamic stability of our materials, with their Ehull values denoted in Fig. 1b for a direct comparison. Among them, SSC exhibited the lowest Ehull value of 0.183 eV per atom, yet it still falls short of the optimal series materials outlined in Fig. 1c. Notably, several materials highlighted in Fig. 1c, including BaCo0.8Ta0.2O3−δ,27 SrCo0.8Nb0.1Ta0.1O3−δ,28 SrCo0.8125Sb0.1875O3−δ,29 SrCo0.8Sc0.175Nb0.025O3−δ,30 and PrBaCo1.92Zr0.08O5+δ,31 have already been successfully used as oxygen electrodes, demonstrating robust stability against various environmental conditions. It is worth noting that the development of these materials was initially serendipitous and lacked a systematic approach. However, the integration of high-throughput calculations and methodical screening has streamlined their discovery and optimization.
Data-driven enhanced insight into the thermodynamic stability
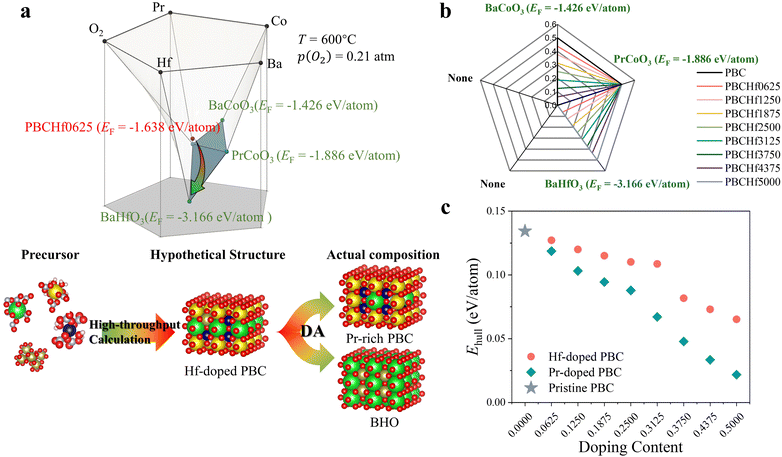
Despite the widespread application of the Ehull theory, we emphasize the critical importance of not neglecting the formation energy (EF) of the stable phases constituting the convex hull for the materials under investigation. This oversight can lead to a failure to identify potential decomposition tendencies, resulting in inaccuracies in evaluating the thermodynamic stability. In response to this limitation and to enhance the practicality of our computational insights across all 4455 materials, we have introduced an innovative material analysis method named decomposition analysis (DA) (Fig. S6, ESI†). This method delineates the convex hull underlying a material and provides an exhaustive array of potential decomposition pathways, utilizing data from the Materials Project.19 For example, the convex hull underlying PrBaCo1.875Hf0.125O6 (PBCHf0625), one of the PrBaCo2O6-derived materials, should be formed by up to five stable materials as a quinary oxide. This five-dimension phase diagram is visually illustrated in Fig. 2a, which depicts the three-dimensional convex hull underlying PBCHf0625. Through this representation, we identified three stable materials – BaCoO3, PrCoO3, and BaHfO3 – as the constituents of the convex hull. Notably, the significant disparity in EF between PBCHf0625 (−1.638 eV per atom) and BHfO3 (−3.166 eV per atom) underscores a pronounced tendency of PBCHf0625 to decompose and lead to the formation of BaHfO3, a critical fact that is obfuscated by its deceptively low Ehull value (0.127 eV per atom). This theoretical prediction was substantiated through empirical experiments (Fig. S7, ESI†). For a more intuitive understanding, Fig. S8 (ESI†) offers a simplified two-dimensional projection of Fig. 2a, clearly indicating the EF of PBCHf0625 alongside the three potential decomposition products.The efficacy of DA is unequivocally proven through its successful application to well-known oxygen electrode materials and its precision in discerning subtle differences among a variety of PBC-derived materials (detailed in supplementary notes and Fig. S9–S12, ESI†). Subsequently, DA was applied to all 4455 materials to provide a comprehensive assessment of potential decomposition products. This approach leverages over 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 diverse materials, representing a fifth of the entire Materials Project database, offering invaluable data-driven insights into their thermodynamic stability. As we reexamined the optimal perovskite oxides featuring the greatest thermodynamic stability listed in Fig. 1d, our analysis highlighted Hf, Ti, and Zr-doped PBC series materials. These materials, derived from an established oxygen electrode PBC, consistently demonstrate lower Ehull values across various doping contents, marking them as notably superior compared to other candidates. The DA method further highlights the complex decomposition behavior of Ti and Zr-doped PBC series materials, as detailed in Table S2 (ESI†), distinguishing them from the Hf-doped ones. As illustrated in Fig. 2b, the Hf-doped PrBaCo2O6 series consistently manifests one primary decomposition product – BaHfO3 – across various doping contents. Initially denoted as PrBaCo2−xHfxO6, the Hf-doped PrBaCo2O6 series inherently comprises two distinct phases: PrBa1−xCo2−xO6−3x (Pr-rich PBC) and BaHfO3. Given that BaHfO3 is located on the convex hull, indicating optimal stability, our focus intensifies on the Pr-rich PBC, the major phase within this composite. As demonstrated in Fig. 2c, replacing Ba with Pr incrementally lowers the Ehull values with an increasing doping content, suggesting further enhanced thermodynamic stability compared with Hf-doped PBC. Notably, the minimum value is achieved with PrCoO3, standing at 0.022 eV per atom. Even expanding our investigation beyond merely Pr-rich PBC to PrBaCo2O6-derived materials, which undergo Ba-site substitution with 23 different dopants resulting in 184 distinct materials, Pr-rich PBC consistently exhibits the lowest Ehull values, as shown in Fig. S13 (ESI†). Ultimately, integrating the Ehull theory with the DA method has provided comprehensive insights into the thermodynamic stability of Hf-doped PrBaCo2O6 series materials. Characterized by Pr-rich PBC alongside BaHfO3, these composite materials demonstrate excellent thermodynamic stability among all 4455 distinct candidates.
000 diverse materials, representing a fifth of the entire Materials Project database, offering invaluable data-driven insights into their thermodynamic stability. As we reexamined the optimal perovskite oxides featuring the greatest thermodynamic stability listed in Fig. 1d, our analysis highlighted Hf, Ti, and Zr-doped PBC series materials. These materials, derived from an established oxygen electrode PBC, consistently demonstrate lower Ehull values across various doping contents, marking them as notably superior compared to other candidates. The DA method further highlights the complex decomposition behavior of Ti and Zr-doped PBC series materials, as detailed in Table S2 (ESI†), distinguishing them from the Hf-doped ones. As illustrated in Fig. 2b, the Hf-doped PrBaCo2O6 series consistently manifests one primary decomposition product – BaHfO3 – across various doping contents. Initially denoted as PrBaCo2−xHfxO6, the Hf-doped PrBaCo2O6 series inherently comprises two distinct phases: PrBa1−xCo2−xO6−3x (Pr-rich PBC) and BaHfO3. Given that BaHfO3 is located on the convex hull, indicating optimal stability, our focus intensifies on the Pr-rich PBC, the major phase within this composite. As demonstrated in Fig. 2c, replacing Ba with Pr incrementally lowers the Ehull values with an increasing doping content, suggesting further enhanced thermodynamic stability compared with Hf-doped PBC. Notably, the minimum value is achieved with PrCoO3, standing at 0.022 eV per atom. Even expanding our investigation beyond merely Pr-rich PBC to PrBaCo2O6-derived materials, which undergo Ba-site substitution with 23 different dopants resulting in 184 distinct materials, Pr-rich PBC consistently exhibits the lowest Ehull values, as shown in Fig. S13 (ESI†). Ultimately, integrating the Ehull theory with the DA method has provided comprehensive insights into the thermodynamic stability of Hf-doped PrBaCo2O6 series materials. Characterized by Pr-rich PBC alongside BaHfO3, these composite materials demonstrate excellent thermodynamic stability among all 4455 distinct candidates.
Structural verification
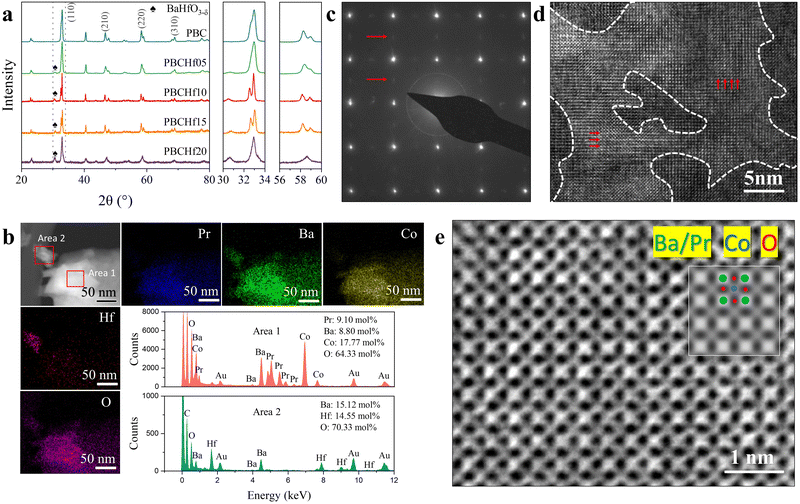
The experimental assessment focuses on the Hf-doped PBC series materials (PBCHf), employing a methodical approach of decimal substitution to synthesize PrBaCo2−xHfxO5+δ (where x = 0, 0.05, 0.1, 0.15 and 0.2, respectively labeled as PBC, PBCHf05, PBCHf10, PBCHf15, and PBCHf20). The XRD patterns shown in Fig. 3a indicate that the pristine PBC exhibits a double perovskite structure. The substitution of Co with Hf on the B-site leads to the emergence of a secondary phase, marked by a new peak at 2θ = 30.65°. The intensity of the peak corresponding to the secondary phase increases proportionally with the Hf content, suggesting a compositional dependency. Evidence from DA of PBCHf, as represented in Fig. 2b, suggests that the primary phase corresponds to Pr-rich PBC, while the secondary phase is identified as BHO. It is worth noting that upon reaching a doping content of x = 0.2, the primary phase transforms from a double to a simple perovskite structure, as evidenced by the absence of peak splitting for the (110), (211), (220), and (310) planes. This phenomenon is likely attributable to the increased Pr/Ba ratio. Rietveld refinement analysis of PBCHf10, depicted in Fig. S14 (ESI†), confirmed that the major phase, Pr-rich PBC, has a space group P4/mmm with lattice parameters of a = 3.90 Å and c = 7.65 Å. The secondary phase, BHO, corresponds to the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with the lattice parameter a = 4.17 Å. High-resolution transmission electron microscopy (HRTEM) and energy-dispersive X-ray spectroscopy (EDS) further support the phase composition predicted by the DA method. As depicted in Fig. 3b, EDS mapping of a larger particle (area 1) reveals homogeneous distribution of Pr, Ba, Co, and O with Pr-excessive characteristics, attributed to the Pr-rich PBC. The smaller particle (area 2), in contrast, consists exclusively of Ba, Hf, and O with an equimolar ratio of Ba to Hf, consistent with the characteristics of the BHO phase. Further insights are gleaned from the selected area electron diffraction (SAED) pattern (Fig. 3c), focusing on the larger particle. This pattern clearly delineates the double perovskite structure in Pr-rich PBC, with brighter diffraction spots indicative of (100) plane reflections, while a secondary lattice, revealed through dimmer spots, corresponds to (200) plane reflections. The HRTEM images in Fig. 3d offer a detailed visualization of the atomic arrangement in these structures, confirming the prevalence of the double perovskite structure in brighter regions and the existence of a simple perovskite structure in darker regions. Furthermore, the lattice parameters measured at 3.91 Å from HRTEM images, observed perpendicular to the (001) plane (as shown in Fig. 3e), align with the values acquired from Rietveld refinement of the XRD spectra (3.90 Å), further substantiating the structural interpretation.
m with the lattice parameter a = 4.17 Å. High-resolution transmission electron microscopy (HRTEM) and energy-dispersive X-ray spectroscopy (EDS) further support the phase composition predicted by the DA method. As depicted in Fig. 3b, EDS mapping of a larger particle (area 1) reveals homogeneous distribution of Pr, Ba, Co, and O with Pr-excessive characteristics, attributed to the Pr-rich PBC. The smaller particle (area 2), in contrast, consists exclusively of Ba, Hf, and O with an equimolar ratio of Ba to Hf, consistent with the characteristics of the BHO phase. Further insights are gleaned from the selected area electron diffraction (SAED) pattern (Fig. 3c), focusing on the larger particle. This pattern clearly delineates the double perovskite structure in Pr-rich PBC, with brighter diffraction spots indicative of (100) plane reflections, while a secondary lattice, revealed through dimmer spots, corresponds to (200) plane reflections. The HRTEM images in Fig. 3d offer a detailed visualization of the atomic arrangement in these structures, confirming the prevalence of the double perovskite structure in brighter regions and the existence of a simple perovskite structure in darker regions. Furthermore, the lattice parameters measured at 3.91 Å from HRTEM images, observed perpendicular to the (001) plane (as shown in Fig. 3e), align with the values acquired from Rietveld refinement of the XRD spectra (3.90 Å), further substantiating the structural interpretation.
Experimental assessment of the electro-catalytic activity
A composite electrode composed of Pr-rich PBC and BHO displayed exceptionally high activity for the oxygen reduction reaction (ORR), evidenced by the remarkably low polarization resistance (Rp) and activation energy (0.95 eV) below 600 °C as determined in a symmetrical cell using Sm-doped ceria (SDC) as the electrolyte and PBCHf10 as the electrodes (Fig. S15–S19, ESI†). The outstanding electro-catalytic activity of PBCHf10 is attributed to the presence of the PBC–BHO interface, which effectively accelerates the rate-determining step (oxygen dissociation process) in the ORR (Fig. S20, ESI†). To confirm PBCHf10's outstanding ORR activities at low temperatures, the impedance of a symmetrical cell based on a proton conducting electrolyte, PBCHf10/BZCYYb1711/PBCHf10, was acquired in wet air (∼3% water vapor) to determine the resistance to the ORR, Rp. At 700, 650, 600, 550, and 500 °C, the estimated Rp values are, respectively, 0.044, 0.089, 0.187, 0.374, and 0.933 Ω cm2 (Fig. S21, ESI†) with an Ea of 0.98 eV. These results underscore its exceptional ORR activity compared with that of the pristine PBC and state-of-the-art materials, as detailed in Fig. S22 and S23 (ESI†).5,32–40 Interestingly, as demonstrated in Fig. S24 (ESI†), the Rp progressively decreased with increasing water vapor pressure (PH2O), dropping from 0.224 to 0.187 Ω cm2 at 600 °C upon the introduction of 3% PH2O and further reducing to 0.149 and 0.123 Ω cm2 with 10% and 30% PH2O, respectively. The distribution of relaxation time (DRT) analysis of the impedance data (Fig. S25, ESI†) revealed a marked decrease in the low and medium frequency peaks with rising PH2O. This novel ORR/OER behavior in a proton-conducting system suggests a distinct reaction mechanism that is intricately linked to the presence of water. The observed decrease in impedance of the rate-determining steps with the increase in water vapor pressure has motivated us to conduct more in-depth investigations.X-ray photoelectron spectroscopy (XPS) analyses of O 1s spectra were conducted for PBC, BHO, and PBCHf10, elucidating the information of oxygen-containing species present on their surface, as illustrated in Fig. S26 (ESI†). A notable finding was the variation in the hydroxide-to-lattice oxygen ratio (ROH-Latt), with PBC displaying a ratio of 0.94, indicating higher surface hydration properties, compared to BHO's lower ratio of 0.36. These results align with our DFT calculations, which showed a higher surface hydration energy for PBC (−1.70 eV) than for BHO (−1.02 eV) (Fig. S27 and S28, ESI†). PBCHf10 demonstrated a similar ROH-Latt of 0.97, highlighting its superior surface hydration, due mainly to its primary phase, Pr-rich PBC. Furthermore, thermogravimetric analysis (TGA) revealed distinctly different behaviors between PBC and BHO (Fig. S29, ESI†). At 600 °C, PBC exhibited a weight loss of 0.71 wt%, indicative of significant oxygen vacancy concentration, as opposed to BHO's marginal weight loss of 0.16 wt%. This is consistent with our findings of vacancy formation energies, 3.53 eV for PBC and 6.46 eV for BHO, suggesting easier vacancy formation in PBC (Fig. S30 and S31, ESI†). When examining bulk hydration reactions, PBC showed a minimal weight increase at 600 °C (0.00043 wt%), implying restricted hydration capabilities. In contrast, BHO displays a substantial weight gain of 0.07 wt%, evidencing effective bulk hydration, with approximately 40% of its oxygen vacancies contributing to the hydration process under 3% water vapor pressure (Fig. S32, ESI†). This efficiency is comparable to a third of that observed in the well-known electrolyte BZCYYb1711.12 We further investigated the protonic conductivity of PBC and BHO using ab initio molecular dynamics (AIMD) simulations. At 600 °C, BHO exhibits a diffusion coefficient (DH) of 3.10 E−5 cm2 s−1, significantly higher than PBC's 7.62 E−6 cm2 s−1, as shown in Fig. S33–S36 (ESI†). This thorough analysis, incorporating both experimental and computational approaches, accentuates the distinct hydration characteristics of the two materials: PBC stands out for its exceptional surface hydration, enhancing the presence of surface hydroxides, while BHO demonstrates superior bulk hydration and protonic diffusion capabilities.
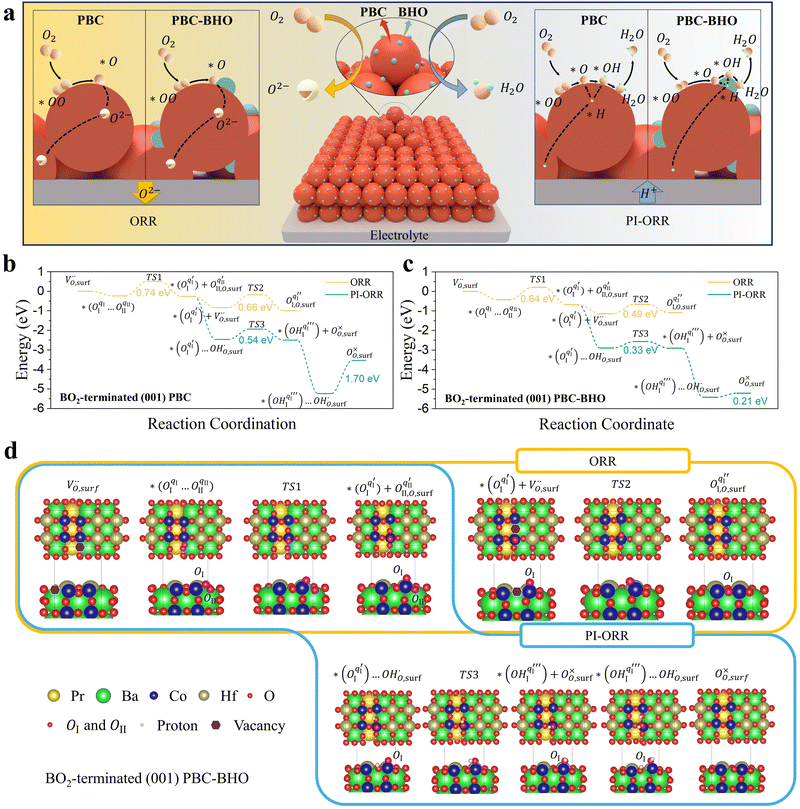
Considering the distinctive hydration properties of PBCHf10 and its remarkable water-induced enhancement in ORR activity, we propose a novel proton-involved ORR (PI-ORR) mechanism, which is distinctly different from the conventional ORR in a cell based on an oxygen ion conductor without the participation of protons. Fig. 4a schematically illustrates the elementary steps that may be involved in the ORR and PI-ORR on the PBC surface or the PBC–BHO interface. Both the ORR and PI-ORR encompass the same initial elementary steps, the adsorption and dissociation of molecular oxygen. The process begins with an inherent oxygen vacancy on the surface 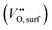 , which creates an unsaturated environment conducive to the adsorption of oxygen molecule (O2,gas), leading to the formation of superoxide species, denoted as
, which creates an unsaturated environment conducive to the adsorption of oxygen molecule (O2,gas), leading to the formation of superoxide species, denoted as 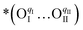 ,
,
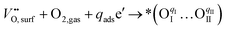 | (1) |
This is quantified by an adsorption energy of −0.237 eV on the BO2-terminated (001) PBC surface (Fig. 4b). Bader charge analysis reveals charges of qI = 0.32 e and qII = 0.48 e, for the involved oxygen atoms, OI and OII, as illustrated in Fig. S37 (ESI†). The PBC–BHO interface on the same plane shows improved oxygen adsorption properties, with an increased adsorption energy of −0.427 eV (Fig. 4c). A comparative charge distribution difference analysis for the PBC surface and the PBC–BHO interface with superoxide species underscores the enhanced oxygen–cobalt hybridization at the PBC–BHO interface (Fig. S38, ESI†). Following adsorption, the dissociation reaction occurs,
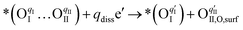 | (2) |
Here, the OII combines with the vacancy site, becoming a surface-located lattice oxygen 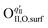 . The remaining oxygen atom OI is now identified as a peroxide species
. The remaining oxygen atom OI is now identified as a peroxide species 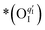 . The Ea for the PBC surface is calculated to be 0.74 eV, while the Ea for the PBC–BHO interface is dramatically reduced to 0.64 eV. The difference between the two mechanisms arises from the consumption of peroxide. In the ORR, the process involves the transportation of OII, the incorporation of OI, and the regeneration of new oxygen vacancies on the surface (detailed in the ESI†). In the PI-ORR, by contrast, an additional pathway is facilitated by the surface protons
. The Ea for the PBC surface is calculated to be 0.74 eV, while the Ea for the PBC–BHO interface is dramatically reduced to 0.64 eV. The difference between the two mechanisms arises from the consumption of peroxide. In the ORR, the process involves the transportation of OII, the incorporation of OI, and the regeneration of new oxygen vacancies on the surface (detailed in the ESI†). In the PI-ORR, by contrast, an additional pathway is facilitated by the surface protons  originated, sourced from either PBC or BHO, enabling the first hydrogenation of the peroxide species, leading to the formation of hydroxide species
originated, sourced from either PBC or BHO, enabling the first hydrogenation of the peroxide species, leading to the formation of hydroxide species 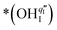 ,
,
 | (3) |
For the PBC surface, the Ea required for the first hydrogenation is found to be 0.54 eV, which is notably lower than the 0.66 eV required for the conventional incorporation reaction. For the PBC–BHO interface, this energy is further reduced to 0.33 eV; the dramatic reduction in this energy barrier results in its exceptional performance. The subsequent second hydrogenation reaction leads to the formation and desorption of water molecules, regenerating a clean surface,
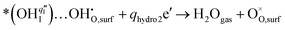 | (4) |
A relatively high water desorption energy of 1.70 eV is found for the PBC surface, posing a significant challenge that can disrupt the continuity of the entire PI-ORR process due to inefficient water desorption. However, the PBC–BHO interface substantially improves this, showcasing a drastically lower water desorption energy of 0.21 eV, as further confirmed by XPS results in Fig. S26 (ESI†). This enhancement is critical for sustaining the entire PI-ORR process, as evidenced by the detailed configurations presented in Fig. 4d and Fig. S39 (ESI†).
Experimental assessment of the thermodynamic stability
To assess the phase stability, in situ high-temperature XRD tests were performed under both dry and wet air, as shown in Fig. S40 (ESI†), revealing that the crystal structure of PBCHf10 is stable from 50 to 700 °C. However, a notable shift in the primary peak indicates a lattice expansion with temperature. Subsequent Rietveld refinement analysis confirms consistent lattice parameters for Pr-rich PBC and BHO under the experimental conditions studied (Fig. S41 and Table S3, ESI†). This consistency underscores the exceptional structural stability of Pr-rich PBC and BHO composite electrodes under the testing conditions. Hence, to further validate its thermodynamic stability, a long-term durability test was conducted in wet air with 30% water vapor pressure at 600 °C for 500 hours (Fig. S42, ESI†). To assess the durability of the PBCHf10 electrode when exposed to a high PH2O, SEM images were taken of cells before and after the durability testing (Fig. S43, ESI†). The analysis of grain size and distribution reveals that the microstructure and the morphology of both components of the composite electrode remained intact. This finding was corroborated by similar durability tests conducted on a strip sample, where the crystal surface of Pr-rich PBC showed no discernible changes, and there was no observable growth in the size of the BHO phase (Fig. S44, ESI†). Furthermore, XRD examination of the electrodes after durability tests (Fig. S45, ESI†) did not find any additional peaks, further confirming PBCHf10's thermodynamic stability under the tested conditions. These durability assessments underscore PBCHf10's robustness and suitability for practical applications in PCECs, demonstrating the effectiveness of our material screening strategy that integrates the Ehull theory with the DA method.Verification in PCECs
Given PBCHf10's exceptional electro-catalytic activity and remarkable durability even under a high PH2O, we also tested it as the oxygen electrode in PCECs. Prior to this, its physicochemical properties as an oxygen electrode were thoroughly analyzed (Fig. S46–S52, ESI†). Fig. 5a shows a cross-sectional SEM image of a single PCEC, revealing a seamless integration of the PBCHf10 electrode with the BSCYb172 electrolyte. The open circuit voltages (OCVs) were 1.12, 1.11, 1.09 and 1.08 V at 450, 500, 550, and 600 °C, respectively, demonstrating the effective electron blocking capabilities of the BSCYb172 electrolyte. Impedance data acquired at OCV (Fig. 5b and c) revealed that the ohmic resistance (Ro) and the Rp at 600 °C were 0.069 and 0.070 Ω cm2, respectively, emphasizing the superior protonic conductivity of BSCYb172 and the exceptional electro-catalytic activity of PBCHf10. In the fuel cell mode, peak power densities of 1.49, 1.29, 0.93, and 0.60 W cm−2 are demonstrated at 600 to 450 °C (Fig. 5d), which are among the best reported in the literature (Fig. 5e and detailed in Table S4, ESI†).1,2,5,12,24,32–42 It is particularly worthy to note that the peak power density (PPD) demonstrated at 450 °C and 0.60 W cm−2 is ∼9% higher than the highest PPD previously reported at this temperature (0.55 W cm−2), achieved with an ultrathin (3 μm) electrolyte fabricated by an ultrasonic spray-coating technique.2 In contrast, our PCEC with a 7 μm electrolyte was fabricated using a low-cost conventional process. This achievement highlights the exceptional PI-ORR activity of PBCHf10 at reduced temperatures, offering the potential to dramatically reduce the cost of PCEC technology. This is because it allows the use of much less expensive materials in other components of PCEC systems when operating at these reduced temperatures.The outstanding performance and remarkable durability of the symmetric cells in wet air with a PH2O of 30%, as previously discussed, inspired us to further investigate the system by increasing the PH2O at the oxygen electrode and examining its performance under electrolysis mode. Accordingly, we conducted electrolysis tests in wet air with a PH2O of 30% at different temperatures; the results are presented in Fig. 5f. The current densities at an applied cell voltage of 1.3 V were 2.78, 1.98, 0.89, 0.4, and 0.16 A cm−2 at 600, 550, 500, 450, and 400 °C, respectively. These results highlight the system's exceptional performance when compared to those reported previously (Fig. S53 and Table S5, ESI†).5,12,24,32–42 A detailed computational analysis is presented in Fig. S54 and Table S6 (ESI†).
Furthermore, the PCEC was operated in a galvanostatic mode for a longer period of continuous operation to assess the system's durability. In the fuel cell mode at 600 °C, little variation in cell voltage for ∼200 hours at a current density of 0.3 A cm−2 (Fig. 5g) implies reasonable stability. In the electrolysis mode, the cell voltage remained relatively stable for ∼500 hours at a constant current density of −0.5 A cm2 when the oxygen electrode was exposed to wet air with a PH2O of 3% (Fig. 5h). Additionally, the cell was tested under more stringent conditions for water electrolysis by increasing the current density to −1 A cm2 and the PH2O to 30% in the oxygen electrode compartment. During the 200-hour durability test under this condition (Fig. 5i), the cell voltage increased slightly, from 1.171 to 1.184 V, implying excellent durability. Examination of cross-sectional SEM images (Fig. S55, ESI†) revealed that the morphology of the oxygen electrode remained relatively constant during the 200 hour operation. The oxygen electrode's surface (Fig. 5j and k) exhibited no notable changes, affirming the superior stability of PBCHf10. Furthermore, the system cycling stability was demonstrated under alternating fuel cell and electrolysis modes at 600 °C, as highlighted in Fig. S56 (ESI†), switching modes every two hours at current densities of ±0.3 A cm−2.
Conclusions
Through the integration of high-throughput calculations and computational chemistry databases, our study has successfully evaluated the thermodynamic stability and decomposition tendencies of an unprecedented dataset of 4455 distinct perovskite oxide candidates. This data-driven high-throughput calculation approach, combined with a novel decomposition analysis method, not only addresses the limitations of the Ehull theory, enabling the accurate determination of materials’ true thermodynamic stability, but also enhances the forecasting of composite structures. From our calculated database, we discovered a groundbreaking oxygen electrode, PrBaCo1.9Hf0.1O5+δ, for PCECs, validated through comprehensive experimental investigations and detailed computational simulations to exhibit superior electro-catalytic activity and durability. The study further reveals intricate mechanisms behind oxygen reduction reactions with or without the participation of protons, offering valuable insights for the rational design of perovskite oxide electrodes in a broader chemical space for PCECs. Furthermore, the data-driven high-throughput calculation methodology is applicable for expediting material screening processes vital for the advancement of other energy storage and conversion technologies, including batteries, supercapacitors, and solar cells.Author contributions
X. H., Y. Z., Z. L., H. L., and M. L. conceived the ideas for this study and designed the experiments. X. H. conducted high-throughput DFT calculations. X. H. designed the decomposition analysis method and conducted detailed DFT calculations and MD simulations. Y. Z. and Z. L. performed the fabrication and testing experiments of PCEC single cells. X. H. synthesized and tested the oxygen electrode materials. H. L. performed XPS. N. S. performed in situ XRD, TG, and TEC analyses. Z. L., W. Z., and W. W. performed XRD and SEM. Y. D. performed TEM. X. H., Z. L., H. L., and M. L. wrote the manuscript. All authors have discussed and approved the final manuscript.Data availability
The data supporting this article have been included as part of the ESI.† The code for high-throughput calculations and decomposition analysis can be obtained from https://github.com/XueyuHu/HighthroughputCalculation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy (Award Number DE-FE0031975), Phillips 66, and the Hightower Endowment to the Georgia Tech Foundation.Notes and references
- Z. Wang, Y. H. Wang, J. Wang, Y. F. Song, M. J. Robson, A. Seong, M. T. Yang, Z. Q. Zhang, A. Belotti, J. P. Liu, G. Kim, J. Lim, Z. P. Shao and F. Ciucci, Nat. Catal., 2022, 5, 777–787 CrossRef
.
- F. Liu, H. Deng, D. Diercks, P. Kumar, M. H. A. Jabbar, C. Gumeci, Y. Furuya, N. Dale, T. Oku, M. Usuda, P. Kazempoor, L. Y. Fang, D. Chen, B. Liu and C. C. Duan, Nat. Energy, 2023, 8, 1145–1157 CrossRef CAS
.
- W. J. Bian, W. Wu, B. M. Wang, W. Tang, M. Zhou, C. R. Jin, H. P. Ding, W. W. Fan, Y. H. Dong, J. Li and D. Ding, Nature, 2022, 604, 479 CrossRef CAS
.
- M. Li, B. Hua, L. C. Wang, J. D. Sugar, W. Wu, Y. Ding, J. Li and D. Ding, Nat. Catal., 2021, 4, 274–283 CrossRef CAS
.
- Y. C. Zhou, E. Z. Liu, Y. Chen, Y. C. Liu, L. Zhang, W. L. Zhang, Z. Y. Luo, N. Kane, B. Zhao, L. Soule, Y. H. Niu, Y. Ding, H. P. Ding, D. Ding and M. L. Liu, ACS Energy Lett., 2021, 6, 1511–1520 CrossRef CAS
.
- J. Cao, Y. Ji and Z. Shao, Chem. Soc. Rev., 2024, 53, 450–501 RSC
.
- S. Choi, C. J. Kucharczyk, Y. G. Liang, X. H. Zhang, I. Takeuchi, H. I. Ji and S. M. Haile, Nat. Energy, 2018, 3, 202–210 CrossRef CAS
.
- Z. C. Zhuang, Y. H. Li, R. H. Yu, L. X. Xia, J. R. Yang, Z. Q. Lang, J. X. Zhu, J. Z. Huang, J. O. Wang, Y. Wang, L. D. Fan, J. S. Wu, Y. Zhao, D. S. Wang and Y. D. Li, Nat. Catal., 2022, 5, 300–310 CrossRef CAS
.
- M. Zhong, K. Tran, Y. M. Min, C. H. Wang, Z. Y. Wang, C. T. Dinh, P. De Luna, Z. Q. Yu, A. S. Rasouli, P. Brodersen, S. Sun, O. Voznyy, C. S. Tan, M. Askerka, F. L. Che, M. Liu, A. Seifitokaldani, Y. J. Pang, S. C. Lo, A. Ip, Z. Ulissi and E. H. Sargent, Nature, 2020, 581, 178 CrossRef CAS PubMed
.
- R. Jacobs, T. Mayeshiba, J. Booske and D. Morgan, Adv. Energy Mater., 2018, 8, 1702708 CrossRef
.
- S. Fujii, Y. Shimizu, J. Hyodo, A. Kuwabara and Y. Yamazaki, Adv. Energy Mater., 2023, 13, 2301892 CrossRef
.
- Z. Luo, X. Hu, Y. Zhou, Y. Ding, W. Zhang, T. Li and M. Liu, Adv. Mater., 2024, 2311159 CrossRef PubMed
.
- J. Y. Peng, D. Schwalbe-Koda, K. Akkiraju, T. Xie, L. Giordano, Y. Yu, C. J. Eom, J. R. Lunger, D. J. Zheng, R. R. Rao, S. Muy, J. C. Grossman, K. Reuter, R. Gómez-Bombarelli and Y. Shao-Horn, Nat. Rev. Mater., 2022, 7, 991–1009 CrossRef
.
- S. Zhai, H. P. Xie, P. Cui, D. Q. Guan, J. Wang, S. Y. Zhao, B. Chen, Y. F. Song, Z. P. Shao and M. Ni, Nat. Energy, 2022, 7, 866–875 CrossRef
.
- N. Wang, B. Y. Yuan, C. M. Tang, L. Du, R. J. Zhu, Y. Aoki, W. B. Wang, L. X. Xing and S. Y. Ye, Adv. Mater., 2022, 34, 2309855 Search PubMed
.
- I. T. Bello, R. Taiwo, O. C. Esan, A. H. Adegoke, A. O. Ijaola, Z. Li, S. Y. Zhao, C. Wang, Z. P. Shao and M. Ni, Energy AI, 2024, 15, 100317 CrossRef
.
- C. Chen, Y. X. Zuo, W. K. Ye, X. G. Li, Z. Deng and S. P. Ong, Adv. Energy Mater., 2020, 10, 1903242 CrossRef
.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 1–6 Search PubMed
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef
.
- S. J. Skinner, Int. J. Inorg. Mater., 2001, 3, 113–121 CrossRef
.
- Z. P. Shao and S. M. Haile, Nature, 2004, 431, 170–173 CrossRef PubMed
.
- C. R. Xia, W. Rauch, F. L. Chen and M. L. Liu, Solid State Ionics, 2002, 149, 11–19 CrossRef
.
- C. C. Duan, J. H. Tong, M. Shang, S. Nikodemski, M. Sanders, S. Ricote, A. Almansoori and R. O'Hayre, Science, 2015, 349, 1321–1326 CrossRef PubMed
.
- S. Choi, T. C. Davenport and S. M. Haile, Energy Environ. Sci., 2019, 12, 206–215 RSC
.
- V. Somjit and B. Yildiz, ACS Appl. Mater. Interfaces, 2022, 14, 42613–42627 CrossRef CAS PubMed
.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718 CrossRef PubMed
.
- J. H. Kim, D. Kim, S. Ahn, K. J. Kim, S. Jeon, D.-K. Lim, J. K. Kim, U. Kim, H.-N. Im and B. Koo, Energy Environ. Sci., 2023, 16, 3803–3814 RSC
.
- M. Li, M. Zhao, F. Li, W. Zhou, V. K. Peterson, X. Xu, Z. Shao, I. Gentle and Z. Zhu, Nat. Commun., 2017, 8, 13990 CrossRef PubMed
.
- X. Y. Hu, Y. Xie, Y. H. Wan, Y. Yang, X. J. Wu and C. R. Xia, Appl. Catal., B, 2021, 286, 119901 CrossRef
.
- X. Mao, Z. H. Li, M. R. Li, X. Y. Xu, C. Yan, Z. H. Zhu and A. J. Du, J. Am. Chem. Soc., 2021, 143, 9507–9514 CrossRef
.
- X. Y. Zhang, R. Song, D. M. Huan, K. Zhu, X. Y. Li, H. R. Han, C. R. Xia, R. R. Peng and Y. L. Lu, Small, 2022, 18, 2205190 CrossRef
.
- H. P. Ding, W. Wu, C. Jiang, Y. Ding, W. J. Bian, B. X. Hu, P. Singh, C. J. Orme, L. C. Wang, Y. Y. Zhang and D. Ding, Nat. Commun., 2020, 11, 1907 CrossRef PubMed
.
- Z. Q. Liu, D. F. Cheng, Y. L. Zhu, M. Z. Liang, M. T. Yang, G. M. Yang, R. Ran, W. Wang, W. Zhou and Z. P. Shao, Chem. Eng. J., 2022, 450, 137787 CrossRef
.
- K. Pei, S. R. Luo, F. He, J. Arbiol, Y. S. Xu, F. Zhu, Y. K. Wang and Y. Chen, Appl. Catal., B, 2023, 330, 122601 CrossRef CAS
.
- M. Z. Liang, Y. H. Wang, Y. F. Song, D. Q. Guan, J. Wu, P. Chen, A. Maradesa, M. G. Xu, G. M. Yang, W. Zhou, W. Wang, R. Ran, F. Ciucci and Z. P. Sha, Appl. Catal., B, 2023, 331, 122682 CrossRef
.
- Y. H. Niu, Y. C. Zhou, W. L. Zhang, Y. X. Zhang, C. Evans, Z. Y. Luo, N. Kane, Y. Ding, Y. Chen, X. Y. Guo, W. Q. Lv and M. L. Liu, Adv. Energy Mater., 2022, 12, 2103783 CrossRef
.
- K. Pei, Y. C. Zhou, K. Xu, H. Zhang, Y. Ding, B. T. Zhao, W. Yuan, K. Sasaki, Y. M. Choi, Y. Chen and M. L. Liu, Nat. Commun., 2022, 13, 2207 CrossRef PubMed
.
- F. He, Y. C. Zhou, T. Hu, Y. S. Xu, M. Y. Hou, F. Zhu, D. L. Liu, H. Zhang, K. Xu, M. L. Liu and Y. Chen, Adv. Mater., 2023, 35, 2209469 CrossRef PubMed
.
- F. He, S. Liu, T. Wu, M. T. Yang, W. H. Li, G. M. Yang, F. Zhu, H. Zhang, K. Pei, Y. Chen, W. Zhou and Z. P. Shao, Adv. Funct. Mater., 2022, 32, 2206756 CrossRef
.
- M. Saqib, I. G. Choi, H. Bae, K. Park, J. S. Shin, Y. D. Kim, J. I. Lee, M. Jo, Y. C. Kim, K. S. Lee, S. J. Song, E. D. Wachsman and J. Y. Park, Energy Environ. Sci., 2021, 14, 2472–2484 RSC
.
- W. Zhang, Y. Zhou, X. Hu, Y. Ding, J. Gao, Z. Luo, T. Li, N. Kane, X.-Y. Yu and T. Terlier, ACS Energy Lett., 2023, 8, 3999–4007 CrossRef PubMed
.
- C. C. Duan, R. Kee, H. Y. Zhu, N. Sullivan, L. Z. Zhu, L. Z. Bian, D. Jennings and R. O'Hayre, Nat. Energy, 2019, 4, 230–240 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary notes, figures, and tables. See DOI: https://doi.org/10.1039/d4ee03762f |
| This journal is © The Royal Society of Chemistry 2024 |