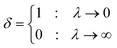Open Access Article
Open Access ArticleEnhanced data-driven monitoring of wastewater treatment plants using the Kolmogorov–Smirnov test
K. Ramakrishna
Kini
a,
Fouzi
Harrou
*b,
Muddu
Madakyaru
 *c and
Ying
Sun
b
*c and
Ying
Sun
b
aDepartment of Instrumentation and Control Engineering, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal 576104, India
bComputer, Electrical and Mathematical Sciences and Engineering (CEMSE) Division, King Abdullah University of Science and Technology (KAUST) Computer, Thuwal, 23955-6900, Saudi Arabia. E-mail: fouzi.harrou@kaust.edu.sa
cDepartment of Chemical Engineering, Manipal Institute of Technology, Manipal Academy of Higher Education, Manipal 576104, India. E-mail: muddu.m@manipal.edu
First published on 23rd April 2024
Abstract
Wastewater treatment plants (WWTPs) are indispensable facilities that play a pivotal role in safeguarding public health, protecting the environment, and supporting economic development by efficiently treating and managing wastewater. Accurate anomaly detection in WWTPs is crucial to ensure their continuous and efficient operation, safeguard the final treated water quality, and prevent shutdowns. This paper introduces a data-driven anomaly detection approach to monitor WWTPs by merging the capabilities of principal component analysis (PCA) for dimensionality reduction and feature extraction with the Kolmogorov–Smirnov (KS)-based scheme. No labeling is required when using this anomaly detection approach, and it utilizes the nonparametric KS test, making it a flexible and practical choice for monitoring WWTPs. Data from the COST benchmark simulation model (BSM1) is employed to validate the effectiveness of the investigated methods. Different sensor faults, including bias, intermittent, and aging faults, are considered in this study to evaluate the proposed fault detection scheme. Various types of faults, including bias, drift, intermittent, freezing, and precision degradation faults, have been simulated to assess the detection performance of the proposed approach. The results demonstrate that the proposed approach outperforms traditional PCA-based techniques.
Water impactThe research focuses on improving water quality and environmental sustainability by detecting anomalies in wastewater treatment plants (WWTPs). By combining principal component analysis (PCA) and the Kolmogorov–Smirnov (KS) test, this study introduces a data-driven approach that provides a more effective method for monitoring WWTPs. This advancement ensures continuous plant operation, prevents water pollution, safeguards public health, and promotes sustainable development. |
1 Introduction
Wastewater treatment plants (WWTPs) play a pivotal role in safeguarding the environment and public health by effectively managing and purifying the vast quantities of wastewater generated by human activities.1,2 These facilities are essential components of modern infrastructure, working tirelessly to remove pollutants, contaminants, and impurities from sewage and industrial effluents before returning the treated water to the natural environment or distributing it for safe reuse.3 Beyond their fundamental mission of pollution control, wastewater treatment plants offer a multitude of benefits.4 They help conserve water resources, protect aquatic ecosystems, mitigate the spread of waterborne diseases, and contribute to a more sustainable and resilient society.5Monitoring the operating conditions of WWTPs and the quality of recycled water is of paramount importance in ensuring the efficient and effective functioning of these facilities.6 A rigorous and continuous monitoring process is necessary to evaluate the plant's performance, detect and rectify potential issues, and guarantee compliance with environmental regulations. By closely tracking parameters such as flow rates, chemical dosages, and the removal of specific pollutants, operators can optimize processes, minimize energy and resource consumption, and reduce operational costs. Additionally, monitoring the quality of recycled water is crucial, as it determines whether the treated water meets established standards for safe reuse. Accurate and real-time data on the water's quality is essential to ensure that it poses no health risks to consumers or harm to the environment, making it a reliable resource for applications such as irrigation, industrial processes, or even drinking water production. Ultimately, the thorough monitoring of WWTPs and recycled water quality is indispensable in maintaining the sustainability, functionality, and safety of our water management systems.
Over the years, significant advancements have been made in WWTP monitoring, particularly in prediction, fault detection, and diagnosis. These developments have come from two primary categories of methods: model-based approaches and data-driven approaches.2,7,8 Analytical model-based methods rely on a deep understanding of the physical, chemical, and biological processes involved in wastewater treatment. These approaches use mathematical models that describe the behavior of various unit operations within the WWTP, such as sedimentation tanks, aeration basins, and biological reactors. By utilizing these models, operators can simulate the expected performance of the plant under different conditions, making it possible to predict how changes in influent composition, flow rates, or operational parameters will affect the treatment process. This enables proactive decision-making and process optimization, as well as the early detection of potential issues based on deviations from the model predictions. For instance, in ref. 9, a fault detection method based on adaptive filtering is proposed for biological wastewater treatment processes is presented. The study focuses on detecting actuator, sensor, and toxicity faults within these systems. The approach employs state-parameter estimation, where an analytical model's outputs are compared to those estimated by a normalized least mean square adaptive filter. This comparison calculates the residual value for each process output to uncover faults in WWTPs. Similarly, in ref. 9, a model-based method for detecting faults in the actuators of biological wastewater treatment processes is proposed based on an extended Kalman filter. This approach involves comparing the estimated states affected by actuator faults with the process model, and the paper generates residuals for fault detection. Simulation results support the effectiveness of this method in detecting actuator faults in WWTPs. The study in ref. 10 presents a methodology for fault detection in WWTPs based on parameter estimation and multiparametric programming. This method involves the estimation of model parameters and the continuous monitoring of changes in residuals associated with these parameters. Specifically, it presents a process in which a nonlinear dynamic model of wastewater treatment is discretized into algebraic equations. Subsequently, a parameter estimation problem is solved symbolically to derive explicit functions of state variables. When the residual of model parameters exceeds a predefined threshold, a fault is detected. However, constructing precise analytical models of WWTPs is challenging and time-consuming, especially for large-scale systems. Calibrating numerous parameters, including reaction rates and kinetic coefficients, is time-consuming and costly. Analytical models also face challenges with high-dimensional computation due to the complex nature of WWTP processes, which require substantial computational resources.
In contrast, model-free, data-driven methods are based on analyzing historical and real-time data collected from the WWTP.11 These techniques use statistical and machine learning algorithms to identify patterns, anomalies, and correlations in the data that might indicate process abnormalities or equipment failures.12,13 Data-driven methods are particularly valuable for fault detection and diagnosis, as they can detect deviations from normal operations that may not be accounted for in mechanistic models. They can also help identify the root causes of issues and guide operators in taking corrective actions. Over the last decades, several data-based forecasting and monitoring techniques have been developed to enhance the operating conditions of WWTPs.14 In ref. 15, Boyd et al. explored applying the autoregressive integrated moving average (ARIMA) time series analysis model to forecast daily influent flow in WWTPs at five stations across North America. Results reveal that ARIMA models can generate satisfactory daily influent flow forecasts.
Several univariate statistical monitoring techniques have been considered to monitor WWTPs in the literature. In ref. 16, Marais et al. evaluated the detection performance of Shewhart charts, CUSUM charts, and EWMA charts in detecting different sensor faults, including drift and bias, that occurred in WWTPs. The EWMA method outperforms the others, particularly for drift faults, showing low false alarms and efficient detection times. However, these univariate methods have limitations in monitoring multivariate data as they do not consider correlations between variables, which can lead to missed detections and false alarms. To monitor multivariate processes, various multivariate monitoring techniques, including principal components analysis (PCA), independent component analysis (ICA), and partial least squares (PLS), are available.17 These methods consider inter-variable relationships and offer effective anomaly detection capabilities across diverse applications.18,19 For example, in ref. 20, an adaptive process monitoring framework based on incremental PCA (IPCA) is proposed to address time-varying behavior in water resource recovery facilities. IPCA updates the eigenspace with new data at a low computational cost and effectively distinguishes between time-varying behavior and faulty events, including small sensor faults, using benchmark simulation model no. 2 (BSM2). In ref. 21, a data-driven approach based on PCA is employed to detect various dissolved oxygen (DO) sensor faults in WWTPs. The study focuses on biases, drifts, gains, accuracy losses, fixed values, and complete failures of DO sensors. The PCA data-driven model successfully detects these faults, and statistical detection approaches are compared in terms of promptness, effectiveness, and accuracy. In ref. 22, a multivariate analysis is conducted on a moving bed biofilm reactor (MBBR) wastewater treatment system at a Canadian pulp mill. The study uses PCA and partial least squares (PLS) modeling to explain and predict changes in the biochemical oxygen demand (BOD) output of the reactor. It identifies significant variables influencing reactor performance, including wood type, flow parameters, temperature and pH control faults, and indirect indicators of biomass activity. In ref. 23, biomass properties in a WWTP are surveyed, and their morphological data are related to operating parameters using image analysis and PLS. The study reveals a strong relationship between total suspended solids (TSS) and total aggregates, uncovering a severe bulking problem of non-zoogleal nature. Table 1 summarizes recent approaches, their best performance, and contributions to anomaly detection in WWTPs.
| Approach | Best performance | Contribution to anomaly detection |
|---|---|---|
| Mid & Dua (2018)10 | Quick and accurate parameter estimates using explicit parametric functions | Provides a methodology for fault detection in wastewater treatment systems based on parameter estimation using multiparametric programming |
| Marais et al. (2022)16 | Low false alarm rate and good detection time using EWMA method | Compares statistical process control charts for fault detection in wastewater treatment, highlighting the strengths and weaknesses of different univariate fault detection methods |
| Tena et al. (2020)24 | High sensitivity and low delay in fault detection | Develops a fault detection strategy for ammonium sensor faults in wastewater treatment plants using an IIR model based on Volterra series |
| Yang et al. (2023)25 | Improved classification accuracy | Proposes a regularized Wasserstein distance-based joint distribution adaptation approach for fault detection under variable working conditions in wastewater treatment |
| Ghinea et al. (2023)26 | High accuracy for complete, concurrent, and complex faults | Analyzes semi-supervised machine learning techniques for anomaly detection of dissolved oxygen sensors in WWTPs |
| Zhou et al. (2023)27 | Enhanced adaptability and better indicators for anomaly detection | Introduces an improved support vector data description method for fault detection in wastewater treatment plants |
| Newhart et al. (2023)28 | Comprehensive evaluation of multivariate statistical process monitoring | Provides a holistic evaluation of multivariate statistical process monitoring in a biological and membrane treatment system |
| Khedher et al. (2023)29 | Enhanced accuracy and effectiveness in statistical quality control | Expands fuzzy control charts using fuzzy linguistic statements and investigates the process efficiency index for evaluating the performance of wastewater treatment systems |
PCA is a widely used multivariate statistical dimension reduction technique employed to visualize variations and compositions within datasets. It offers a straightforward and easily interpretable way to distinguish normal operational conditions and identify faults. However, a well-recognized limitation is that traditional PCA-based methods such as squared prediction error (SPE), Hotelling's T2, and joint univariate approaches, which assume a Gaussian distribution among process observations, may not consistently deliver satisfactory anomaly detection performance, especially when dealing with the early detection of subtle changes. This work introduces an innovative monitoring approach that enhances fault detection in WWTPs, offering both flexibility and sensitivity. The foundation of our approach lies in the utilization of two key components: PCA and the Kolmogorov–Smirnov (KS) non-parametric test.30 PCA is used for data dimensionality reduction while retaining crucial information. By capturing systematic variations in the multivariate data, PCA provides a concise representation of underlying patterns in the system. The KS test is integrated into our monitoring strategy due to its non-parametric nature.31 It operates independently of specific distribution assumptions, enabling it to adapt to a wide range of data types and patterns. This sensitivity to deviations from expected distributions is particularly valuable in the context of fault detection. The major contributions of this paper can be summarized as follows:
• An effective fault detection strategy, termed PCA-KS, is developed by merging the KS test with PCA. PCA serves a dual purpose in dimensionality reduction and residual generation. Under normal operating conditions, residuals cluster around zero, reflecting the influence of measurement noise and uncertainties. However, when faults are present, residuals deviate considerably from zero. The Kolmogorov–Smirnov test is subsequently employed to evaluate these residuals for fault detection. Notably, this semi-supervised approach does not require prior knowledge of the system, enhancing its practicality and adaptability across various industrial and engineering applications.
• Data from the COST benchmark simulation model (BSM1) is used to verify the investigated methods' effectiveness. Different types of faults have been considered to assess the detection performance of the proposed approach, bias, drift, intermittent, freezing, and precision degradation faults. Additionally, the performance of PCA-KS is compared with established techniques, such as PCA-T2, PCA-SPE, and PCA-CUSUM, ensuring a fair and accurate assessment. To quantitatively evaluate the performance of the investigated methods, five statistical evaluation metrics are employed. The results demonstrate the promising detection capabilities of the PCA-KS approach, characterized by a high detection rate and a reduction in false alarms.
The subsequent sections of the paper are organized as follows. In section 2, a brief description of PCA, the KS test, and the proposed PCA-KS anomaly detection approach is presented. Section 3 evaluates the effectiveness of the proposed PCA-KS approach using data from the COST benchmark simulation model (BSM1). Finally, section 4 offers a concluding summary of the findings and discusses potential avenues for future research.
2 Methods
This section provides a brief overview of conventional PCA, introduces the fundamental concept of the Kolmogorov–Smirnov (KS) test, and outlines the innovative PCA-KS anomaly detection approach.2.1 Principal component analysis
PCA is a well-established multivariate technique designed to reduce the dimensionality of complex datasets while preserving essential variations within the data.32 Its fundamental principle involves transforming data from a high-dimensional space into a lower-dimensional subspace, aiming to maintain the maximum possible variance. PCA's simplicity has led to its widespread application across various domains, including fault detection and diagnosis. In a given dataset X ∈ Rn×m, the PCA model can be expressed as follows:33| X = TVT, | (1) |
The selection of the most important principal components in PCA is a critical step that focuses on capturing the maximum variance within the dataset.34 Typically, principal components are ranked in descending order based on the amount of variance they explain. The first few principal components usually account for the majority of the dataset's variance, making them the most important. To determine how many principal components to retain, one commonly used approach is to examine the cumulative explained variance. This involves calculating the cumulative variance explained by the principal components and selecting a threshold, often a percentage (e.g., 95% or 99%) of the total variance, that is considered acceptable. The goal is to retain enough principal components to capture the chosen threshold of variance while reducing dimensionality. The CPV provides a clear and quantitative measure of the cumulative variance explained by the retained principal components. The CPV scheme is expressed as follows:
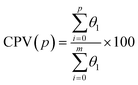 | (2) |
After selecting the optimal number of PCs to retain in the PCA model, the data can be represented as approximated data based on the retained PCs and residuals based on the ignored PCs. The approximation of the original data can be denoted as ![[X with combining circumflex]](https://www.rsc.org/images/entities/b_char_0058_0302.gif) , represented as:35
, represented as:35
![[X with combining circumflex]](https://www.rsc.org/images/entities/b_char_0058_0302.gif) = Tp·VTp, = Tp·VTp, | (3) |
E = X − ![[X with combining circumflex]](https://www.rsc.org/images/entities/b_char_0058_0302.gif) , , | (4) |
2.2 PCA-based monitoring
The T2 (Hotelling's T2) index and SPE (squared prediction error) index are two traditional monitoring schemes employed with PCA to inspect the principal components subspace and the residual subspace, respectively. The T2 statistic for monitoring the principal components subspace is computed as follows:| T2 = tTi(VpVTp)−1ti, | (5) |
The SPE statistic for monitoring the residual subspace is defined as:
| SPE = ‖Ei‖2, | (6) |
Both the T2 and SPE indices play a crucial role in identifying anomalies and monitoring the quality of the PCA model. An increase in these indices beyond predefined thresholds suggests potential issues or deviations in the data, making them valuable tools for anomaly detection and fault diagnosis.
PCA-based anomaly detection involves two key steps: offline model training using fault-free data and online monitoring of new data, which may potentially contain faults. The offline phase of the PCA monitoring strategy encompasses the following steps:
1. Data normalization: normalize the original data to have zero mean and unit variance.
2. Covariance matrix computation: compute the covariance matrix of the normalized data and perform singular value decomposition (SVD) to obtain eigenvalues and eigenvectors.
3. Optimal principal components selection: employ the CPV scheme to select the optimal number of PCs, denoted as p.
4. Score and loading matrices: generate the score and loading matrices based on the retained p optimum PCs.
5. Threshold calculation: compute threshold values, Th1 and Th2, for the statistical indicators T2 and SPE.35,36
The online phase of the PCA monitoring strategy is composed of the following steps:
1. Data normalization: normalize the new data Xnew to have zero mean and unit variance.
2. Statistical indicator calculation: compute the statistical indicators, T2 and SPE, using the following equations:
T2 = XnewT![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) Λ−1 Λ−1![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) TXnew, TXnew, | (7) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) represents the matrix of principal component loading vectors corresponding to the retained principal components. In PCA, these loading vectors are used to project the original data onto the lower-dimensional subspace defined by the selected principal components.
represents the matrix of principal component loading vectors corresponding to the retained principal components. In PCA, these loading vectors are used to project the original data onto the lower-dimensional subspace defined by the selected principal components. ![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) effectively captures the relationships between the original variables and the retained PCs. It is obtained during the offline training phase of the PCA model. Λ−1 represents the inverse of a diagonal matrix containing the eigenvalues associated with the retained PCs. The eigenvalues represent the variance of the data captured by each principal component.
effectively captures the relationships between the original variables and the retained PCs. It is obtained during the offline training phase of the PCA model. Λ−1 represents the inverse of a diagonal matrix containing the eigenvalues associated with the retained PCs. The eigenvalues represent the variance of the data captured by each principal component.SPE = XnewT(I − ![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) ![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) T)Xnew. T)Xnew. | (8) |
3. Anomaly detection: if the computed statistical indicators fall below the thresholds Th1 and Th2 within the fault-free region, the system is considered to be operating normally. Conversely, if the indicators exceed these thresholds within the fault region, a fault condition is declared.
The determination of detection thresholds for T2 and SPE traditionally relies on the assumption of a Gaussian distribution in the data.35 However, in practical applications, especially within complex systems like those in WWTPs,17 this assumption may not consistently hold true. To mitigate this constraint, alternative approaches and robust statistical techniques come into play. When selecting an appropriate statistical model or distribution for threshold computations, it becomes essential to account for the unique data characteristics and the underlying process nature. In cases where data distribution is uncertain or non-Gaussian, non-parametric methods like the Kolmogorov–Smirnov test, which imposes no distribution assumptions, can be particularly valuable.
2.3 Kolmogorov Smirnov (KS) indicator
The Kolmogorov–Smirnov (KS) test is a non-parametric statistical test used to assess whether a dataset follows a particular probability distribution. In anomaly detection, it can be employed to determine whether the distribution of data points significantly deviates from an expected or normal distribution, thus identifying potential anomalies. The KS test is particularly useful when the data distribution is unknown or does not conform to a specific parametric distribution, making it a versatile tool for anomaly detection. There are two types of KS test: one sample KS test and two sample KS test. While the one sample KS test is used for comparing a given distribution with hypothesized reference, the two-sample KS test involves comparing two independent distributions. The cumulative distribution function (CDF) of two distributions/populations will be considered while the comparison is done using the KS test.For a distribution F(z) when compared to a reference distribution Fn(z), the one sample Kolmogorov–Smirnov test is expressed mathematically as follows:31
| Dn = max−∞<z<∞|Fn(z) − F(z)|. | (9) |
In eqn (9), if the value of Dn deviates away from zero, null hypothesis is rejected as it indicates that samples of Fn(y) does not belong to F(y). The empirical CDF (ECDF) of Fn(y) will be very close to the ECDF of F(y) when Dn is equal to zero. However, there will be some distance between the ECDF of Fn(y) and the ECDF of F(y) whenever Dn deviates from zero.
The one-sample KS test discussed above can be extended to two-sample KS test that compares two independent distributions. Consider a case which aims to check if the observations za1, za2…zna of G(z) are equal to zb1, zb2…znb of H(z). Let the empirical CDFs of these two distributions be Gna(z) and Hnb(z). The KS statistic is defined as the maximum absolute difference between the two distributions:37
| Dstat = max−∞<y<∞|Gna(z) − Hnb(z)| | (10) |
| Pr(Dstat) = KSalpha = 1 − Qalpha(λ) | (11) |
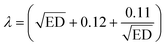 | (12) |
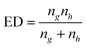 | (13) |
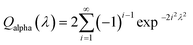 | (14) |
In anomaly detection, the KS test can be applied as follows:
• Model building: initially, the KS test is used to characterize the distribution of normal or expected data, which serves as a reference.
• Decision statistic computation: new data points are subjected to the KS test, and the KS statistic (D) is calculated to determine the degree of dissimilarity between the new data and the expected distribution.
• Threshold setting and anomaly detection: a threshold is established based on the desired significance level (e.g., α = 0.05). If the KS statistic (D) exceeds this threshold, the data is considered an anomaly.
• Real-time monitoring: The KS test can be performed continuously on incoming data, and anomalies are detected when the KS statistic surpasses the predefined threshold.
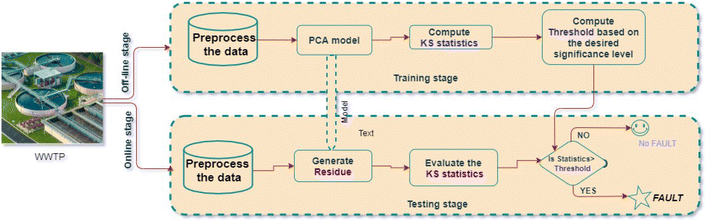
2.4 The proposed PCA-KS anomaly detection approach
In the PCA-KS anomaly detection approach, the objective is to detect anomalies by integrating the dimensionality reduction capabilities of PCA in conjunction with the nonparametric Kolmogorov–Smirnov test. This method provides a robust and data-driven approach to safeguard the efficiency and reliability of WWTPs. A notable advantage of the PCA-KS method is its flexibility. The Kolmogorov–Smirnov test, being nonparametric, can be applied to data with various distributions, regardless of whether they are Gaussian or non-Gaussian. In contrast, the traditional monitoring indices, T2 and SPE, are designed based on the assumption that data follows a Gaussian distribution. This key difference makes PCA-KS more adaptable and suitable for scenarios where data distribution characteristics may not be well-defined. The schematic diagram of PCA-KS based fault detection scheme is presented in Fig. 1.The foundation of the PCA-KS strategy lies in constructing a reference PCA model using normal operating data, denoted as ![[X with combining circumflex]](https://www.rsc.org/images/entities/b_char_0058_0302.gif) . This model captures the underlying patterns and behaviors of the system under normal conditions. The first step in this strategy involves generating residuals, represented as Ê, according to the following expression:
. This model captures the underlying patterns and behaviors of the system under normal conditions. The first step in this strategy involves generating residuals, represented as Ê, according to the following expression:
E = X − ![[X with combining circumflex]](https://www.rsc.org/images/entities/b_char_0058_0302.gif) = X − XVVT. = X − XVVT. | (15) |
![[X with combining circumflex]](https://www.rsc.org/images/entities/b_char_0058_0302.gif) is the approximation of the original data, and V contains the loading vectors. The main steps in the PCA-KS anomaly detection approach are summarized next.
is the approximation of the original data, and V contains the loading vectors. The main steps in the PCA-KS anomaly detection approach are summarized next.
1. Step 1: PCA-based dimensionality reduction
The approach commences with the offline model training phase, in which historical fault-free data from the WWTP is collected and subjected to preprocessing to ensure data quality. PCA is applied to this preprocessed data, effectively reducing its dimensionality while preserving critical information. This process yields a set of PCs capturing the systematic variations within the data. To optimize the model's efficiency, the cumulative percentage variance (CPV) scheme is employed to select the optimal number of PCs for retention. These retained PCs represent the most significant contributors to the data's variance.
2. Step 2: Threshold calculation for PCA indices
Thresholds are calculated based on the retained PCs for two crucial statistical indicators: the Kolmogorov–Smirnov (KS) statistic.
3. Step 3: Online real-time monitoring with PCA and KS
As new data becomes available in real-time, it undergoes data normalization to ensure it has a mean of zero and unity variance, following the same approach as the offline phase. The PCA-KS approach computes the Kolmogorov–Smirnov (KS) statistic using the retained PCs and the structure of incoming data. The KS test is specifically applied to the residuals obtained from the PCA analysis, capturing the information not represented by the retained PCs. The KS statistic (D) is calculated for these residuals, measuring the degree of dissimilarity between the distribution of the residuals from the new data and the expected distribution established during model training. Anomaly detection occurs when the KS statistic exceeds a predefined threshold. If this transpires, the system recognizes a fault or deviation from normal WWTP operation.
3 Results and discussion
This section will provide a detailed explanation of the WWTP, along with the data description. Additionally, it will introduce the proposed PCA-based data-driven anomaly detection approach for monitoring WWTPs. This approach merges the capabilities of principal component analysis (PCA) for dimensionality reduction and feature extraction with the Kolmogorov–Smirnov (KS)-based scheme.3.1 Data description and analysis
Wastewater treatment is essential to prevent pollution from residential and industrial effluents.38 WWTPs are complex systems with biological reactors, requiring continuous monitoring to prevent environmental contamination.39 In this study, we assess the effectiveness of the developed PCA-KS FD strategy for monitoring various sensor-related faults on a benchmark WWTP. We use the benchmark simulation model no. 1 (BSM1) proposed by the European Co-operation in the field of Scientific and Technical Research (COST).40 This benchmark plant consists of a five-compartment activated sludge reactor with two non-aerobic and three aerobic tanks. The plant combines nitrification with pre-denitrification, a common configuration for achieving biological nitrogen removal in full-scale plants. Following the activated sludge reactor, there is a secondary clarifier with a 10-layer non-reactive unit. The primary objectives of the plant are to control the dissolved oxygen level in the final compartment of the reactor through the manipulation of the oxygen transfer coefficient and to control the nitrate level in the last anoxic tank by adjusting the internal recycle flow rate.41The schematic of the benchmark WWTP is depicted in Fig. 2(a), illustrating the presence of two refluxes: the external reflux from the settler to the input and the internal reflux from the last aerated tank to the input. The biological phenomenon governing the treatment process is presented in Fig. 2(b), displaying the important variables involved in the setup. In the COST BSM1 benchmark, the simulation was conducted under three different weather conditions, resulting in data categorized as dry data, storm data, and rainy data.42 For this study, influent data associated with dry weather conditions has been utilized to validate the performance of the proposed PCA-KS-based FD strategy. The influent data includes the variables listed in Table 2.
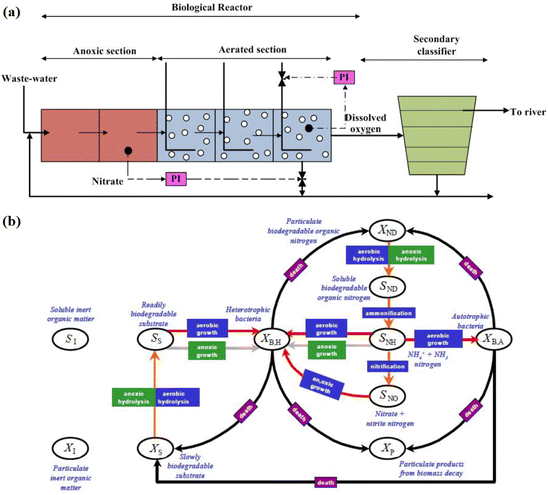 | ||
| Fig. 2 Waste-water treatment process. (a) Diagrammatic representation of the BSM1 WWTP, (b) comprehensive overview of the ASM1 model.42 | ||
| Symbol | Definition | Unit |
|---|---|---|
| S S | Readily biodegradable substrate | g COD m−3 |
| X I | Particulate inert organic matter | g COD m−3 |
| X S | Slowly biodegradable substrate | g COD m−3 |
| X B,H | Active heterotrophic biomass | g COD m−3 |
| S NH | NH4+ + NH3 nitrogen | g N m−3 |
| S ND | Soluble biodegradable organic nitrogen | g N m−3 |
| X ND | Particulate biodegradable organic nitrogen | g N m−3 |
| Q i | Flow into anoxic section | m3 d−1 |
| S I | Soluble inert organic matter | g COD m−3 |
| X B,A | Active autotrophic biomass | g COD m−3 |
| X P | Particulate products from biomass decay | g COD m−3 |
| S O | Oxygen | g(-COD) m−3 |
| S NO | Nitrate and nitrite nitrogen | g N m−3 |
| S ALK | Alkalinity | Mole per m3 |
In the influent data from the WWTP, variables such as SO, XBA, SNO, XP, and SI were observed to have constant values with different magnitudes, which are not expected to significantly impact the model's effectiveness. Consequently, these six variables have been excluded from the model development phase.
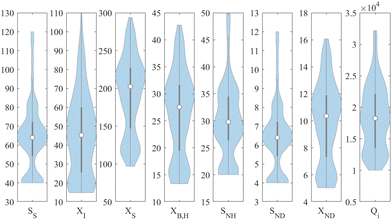
The violin plots of the eight considered variables in the WWTP dataset depicted in Fig. 3 indicate that these variables do not follow a Gaussian (normal) distribution. Violin plots provide a visual representation of the distribution of data, and in this case, the width of the “violin” at different values on the x-axis shows the data density. The non-Gaussian nature of the data suggests that the variables may exhibit different statistical properties and may not be normally distributed. This non-Gaussian behavior is expected in complex environmental and biological systems like WWTPs, where various factors and processes can lead to skewed or non-standard data distributions. In this context, the utilization of conventional monitoring charts, such as Hotelling's T2 and SPE control charts, may be compromised, as these methods rely on the assumption of Gaussian (normal) data distributions when setting their decision thresholds. Since the data in the WWTP variables exhibit non-Gaussian behavior, applying T2 and SPE control charts based on Gaussian assumptions may lead to inaccurate results and false alarms. Therefore, it is essential to adapt or develop alternative control charting methods, such as nonparametric methods, that do not rely on the underlying data distribution to effectively monitor and detect anomalies in the WWTP processes.
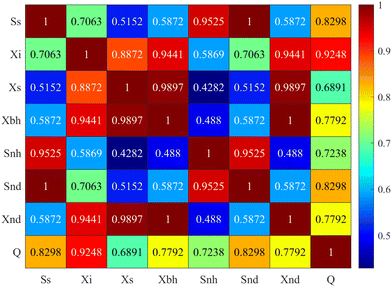
Fig. 4 illustrates the pairwise correlation coefficients among the eight variables under consideration in WWTPs. The correlation data between key variables in the wastewater treatment process provides valuable insights into the interrelationships and dependencies within the system. These correlations can help us understand the dynamic nature of the treatment process. Notably, there are several high positive correlations observed. For instance, the strong positive correlation between readily biodegradable substrate (SS) and ammonia/ammonium nitrogen (SNH) highlights how the presence of easily biodegradable organic matter can lead to the production of ammonia and ammonium as a result of microbial activity. This is a common occurrence in biological wastewater treatment. Additionally, the positive correlation between particulate inert organic matter (XI) and active heterotrophic biomass (XB,H) suggests that the population of active microorganisms increases when there is more inert organic matter in the system. Lastly, the correlation between slowly biodegradable substrate (XS) and soluble biodegradable organic nitrogen (SND) reveals that slowly biodegradable organic matter can serve as a source for the production of soluble biodegradable organic nitrogen through microbial processes.
From Fig. 4, we observe that SS (readily biodegradable substrate) and XI (particulate inert organic matter) exhibit a moderate positive correlation with a coefficient of 0.706. This correlation suggests that as the concentration of readily biodegradable substrate increases, the concentration of particulate inert organic matter tends to increase to some extent. SS (readily biodegradable substrate) and XS (slowly biodegradable substrate) have a moderate positive correlation with a coefficient of 0.515. This correlation indicates that as the concentration of readily biodegradable substrate increases, there is a moderate tendency for the concentration of slowly biodegradable substrate to increase as well. These moderate correlations suggest that certain variables in the wastewater treatment process may have interconnected effects or dependencies on each other, although the relationships are not as strong as in the highly correlated pairs. Understanding these moderate correlations can provide insights into the behavior of the WWTP system and may be relevant for anomaly detection and process optimization.
Of course, these physical explanations provide insights into the interplay between different components in a wastewater treatment system. Microbial activity and the breakdown of organic substances are central to the treatment process, and the observed correlations reflect the complex biological and chemical reactions occurring within the system. In addition, these correlations can guide the selection of variables for PCA, the interpretation of principal components, and the detection of anomalies by considering the interdependencies within the system.
The increasingly strict demands placed to remove wastewater in the cities have put a large load on the working of wastewater plants. As a result, there is a need to continuously monitor the WWTP to maximize plant efficiency. The WWTP is very unstable and completely time-varying due to changes in temperature and weather conditions in the atmosphere. Hence, the whole complex set-up of waste-water set up has to be monitored continuously in order to identify any possible faults that may occur. The WWTP consists of a five-compartment activated sludge reactor that is having two non-aerobic and three aerobic tanks. The plant combines nitrification with pre-denitrification in a configuration that is commonly used for achieving biological nitrogen removal in full-scale plants. The main aim of the plant is to control the dissolved oxygen level in the final compartment of the reactor by manipulating of oxygen transfer coefficient and to control the nitrate level in the last anoxic tank by manipulating of internal recycle flow rate. There is a possibility that faults like sensor bias, drift, and intermittent faults could be present in the WWTP set-up. In this study, the nitrogen variable SNH is used to study the behavior of bias as well as intermittent faults. On other hand, the variable XND is utilized for studying the behavior of drift fault.
In this study, the performance of the proposed PCA-KS-based strategy is investigated by various simulated sensor faults. These faults include bias, drift, and intermittent types, providing a comprehensive assessment of the strategy's performance.
The fault detection methods will be assessed using key statistical metrics. These metrics are particularly valuable for binary detection tasks and are calculated based on the number of true positives (TP), false positives (FP), false negatives (FN), and true negatives (TN). They provide a comprehensive evaluation of the methods' performance:
• Anomaly detection rate (ADR): ADR is a metric that quantifies the ability of an anomaly detection strategy to correctly identify actual faults or anomalies. It is calculated as the ratio of true positive detections to the sum of true positive and false negatives.
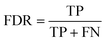 | (16) |
A high FDR indicates a strategy's effectiveness in detecting real anomalies when they occur.
• False alarm rate (FAR): FAR assesses the rate at which a anomaly detection strategy generates false alarms or erroneous anomaly identifications when there is no actual anomaly present. It is calculated as the ratio of false positive detections to the sum of false positive detections and true negatives.
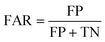 | (17) |
A low FAR indicates a strategy's reliability in avoiding unnecessary false alarms, ensuring that when it signals an anomaly, it is highly likely to be a real issue.
• Precision measures the strategy's accuracy in detecting true positive cases and its ability to avoid false alarms.
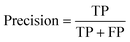 | (18) |
• The F1-score offers a balanced performance indicator by harmonizing precision and recall. It accounts for both false alarms and missed faults, providing a holistic view of the strategy's effectiveness in detecting true faults while minimizing false alarms.
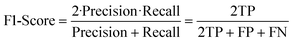 | (19) |
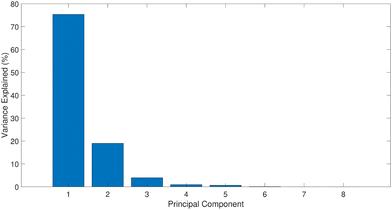
The data used for validating the performance of PCA-KS based FD strategy consists of a total of 8 variables and 1340 observations. The data is split equally to have the training and testing data groups have 670 samples each. The study divides the data equally into training and testing sets for several reasons. Initially, the training data is crucial for constructing a reliable PCA model, as a reference for subsequent fault detection tasks. Using half of the data for training, the PCA model accurately captures essential patterns and variations within the dataset. Additionally, allocating an equal portion of the data to testing is strategic for comprehensive evaluation of fault detection performance. This balanced distribution enables assessment of the model's ability to detect anomalies effectively while minimizing false alarms, even with a significant portion of testing data. This study thoroughly evaluates the developed model's robustness in distinguishing between normal and abnormal operating conditions by subjecting it to testing data. Ultimately, this approach showcases the method's resilience in mitigating false alarms, a critical aspect of fault detection systems. While the training data is used to construct the PCA model, the developed model will be used to validate different faults in the testing data. Using the CPV approach at 95% 3 dominant PCs are selected for PCA model development. This can be observed in Fig. 5. The first three PCs were able to capture the maximum variance in the data. In the case of the KS computation part, a moving window of 40 is considered. The performance of the proposed PCA-KS strategy is contrasted against conventional PCA-T2, PCA-SPE and PCA-CUSUM based strategies. In all the case studies, a fault is declared whenever the fault indicators (represented in black color) exceed the threshold (represented in red color) in the region of fault.
3.2 Monitoring of bias fault
In the first scenario, we assess the effectiveness of the proposed approach in detecting bias faults. A bias fault is defined by a sudden and substantial deviation in a variable's behavior from its typical range. This can be expressed mathematically as:| S(t) = SN(t) + b, | (20) |
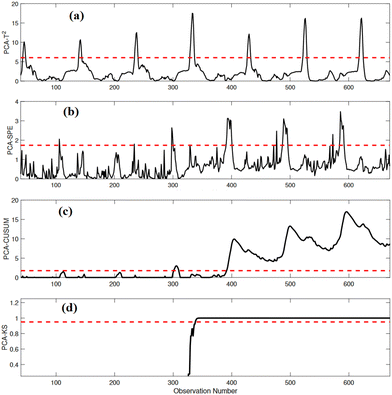 | ||
| Fig. 6 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-CUSUM, and (d) PCA-KS in the presence of bias anomaly in SN(t). | ||
Table 3 summarizes the detection results of the four monitoring schemes in the presence of a bias anomaly in SN(t). The PCA-KS strategy outperforms other methods with a superior ADR, fewer FAR of 94.14%, and a high F1-score value of 96.98%. In contrast, PCA-T2 and PCA-SPE show comparatively lower ADR values, and PCA-T2 exhibits a higher FAR and lower precision, indicating that it is more prone to false alarms. PCA-CUSUM provides moderate performance, with an ADR of 76.21%, F1-score of 85.85%, and generates a low FAR of 2.12%. Results emphasize the superiority of the PCA-KS strategy in monitoring bias anomalies within wastewater treatment processes, even with small magnitudes.
| Index | PCA-T2 | PCA-SPE | PCA-CUSUM | PCA-KS |
|---|---|---|---|---|
| ADR | 9.00 | 32.29 | 76.21 | 94.14 |
| FAR | 5.31 | 1.56 | 2.12 | 0.00 |
| Precision | 65.30 | 95.76 | 97.44 | 100 |
| F1-score | 15.82 | 49.30 | 85.85 | 96.98 |
From the results in Table 3, one noticeable aspect is the limited sensitivity of PCA-T2 to these small anomalies. PCA-T2 primarily focuses on monitoring the principal component subspace and is more adept at detecting large variances in the data. Consequently, it might overlook subtle or small deviations, such as the bias anomaly introduced in SN(t). Additionally, both PCA-T2 and PCA-SPE rely solely on current data without considering information from past data points. This characteristic makes them less sensitive to small changes, as they lack the historical context that might aid in recognizing anomalies. In contrast, PCA-CUSUM demonstrates better sensitivity to bias anomalies, as evidenced by its higher ADR. However, it still generates a relatively higher FAR, indicating a likelihood of false alarms. On the other hand, the PCA-KS strategy effectively leverages the KS test to compare the cumulative distribution function of historical data with the current data. This method allows PCA-KS to detect small changes in the data distribution, making it highly sensitive to anomalies, even of small magnitude. Importantly, PCA-KS stands out by achieving this heightened sensitivity without generating any false alarms.
3.3 Monitoring of intermittent fault
In this scenario, the objective is to evaluate the efficiency of the proposed approach in detecting intermittent sensor faults. Intermittent sensor faults refer to temporary or sporadic malfunctions in sensor measurements within a system or process. These faults are characterized by sensors providing irregular or unstable readings at irregular intervals, rather than consistently failing or consistently providing incorrect data. Intermittent sensor faults can be challenging to detect and diagnose because they do not exhibit a continuous and consistent pattern of failure, making them less predictable and more elusive than permanent sensor faults. The intermittent nature of these faults can lead to inaccuracies and uncertainties in monitoring and control systems, potentially impacting the overall performance and safety of the system or process.Here, we introduced intermittent faults with a magnitude of 15% in the variable SNH during the time intervals [100, 225] and [450, 575]. Intermittent faults can lead to the improper release of NH4+ + NH3 nitrogen into water bodies, causing pollution and ecological harm. Timely fault detection is crucial to prevent environmental contamination. In addition, WWTPs must adhere to strict environmental regulations and effluent quality standards. Failure to detect intermittent faults and control NH4+ + NH3 nitrogen within permissible limits can result in non-compliance, leading to legal consequences and fines. The performance of monitoring these intermittent faults by conventional PCA-T2 and PCA-SPE-based FD schemes is displayed in Fig. 7(a and b). The results clearly show that both PCA-T2 and PCA-SPE-based methods struggle to identify the intermittent fault, as their statistical indicators consistently remain below the threshold in the fault region at numerous sampling instants. Fig. 7(c) shows that the PCA-CUSUM strategy effectively recognizes the presence of the fault; however, it generates false alarms in the no-fault region. In contrast, the PCA-KS scheme performs better in detecting the fault without any missed detections and with minimal false alarms (Fig. 7(d)). These findings highlight the robustness and effectiveness of the PCA-KS-based strategy in monitoring intermittent anomalies and distinguishing them from normal operating conditions.
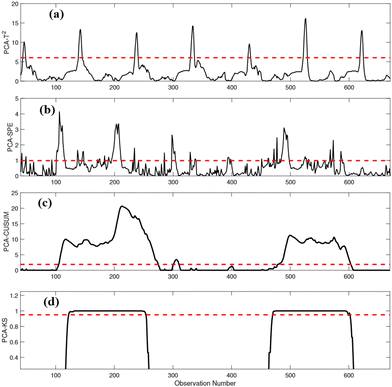 | ||
| Fig. 7 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-CUSUM, and (d) PCA-KS in the presence of an intermittent anomaly in SNH. | ||
The results shown in Table 4 underscore the effectiveness of various fault detection strategies in monitoring intermittent anomalies in NH4+ + NH3 nitrogen in WWTPs. Notably, the proposed PCA-KS strategy outperforms other methods in several crucial aspects. Results show that PCA-KS demonstrates superior performance with an ADR of 98.85% and with the lowest FAR of 1.05%, indicating its reliability in reducing false alarms. This suggests that PCA-KS excels at recognizing intermittent anomalies, even those of smaller magnitudes.
| Index | PCA-T2 | PCA-SPE | PCA-CUSUM | PCA-KS |
|---|---|---|---|---|
| ADR | 10.20 | 32.15 | 98.50 | 98.85 |
| FAR | 6.90 | 5.95 | 8.24 | 1.05 |
| Precision | 89.40 | 76.25 | 87.04 | 98.24 |
| F1-score | 18.50 | 45.25 | 92.18 | 98.50 |
3.4 Monitoring of drift fault
The study further explores the capabilities of the proposed PCA-KS strategy in monitoring aging or drift faults in the waste-water treatment process. Sensor drift is characterized by a gradual and exponential change in sensor readings over time. This phenomenon is attributed to the aging of the sensing element and can be mathematically defined as:| S(t) = SN(t) + M(t − tf), | (21) |
A drift fault with a slope of 0.04 is intentionally introduced into the variable XND between sampling time instant 320 and the end of the testing data. The effectiveness of various fault detection strategies is evaluated in the supervision of this fault. Fig. 8(a and b) displays the performance of PCA-T2 and PCA-SPE-based strategies in monitoring the fault. While PCA-SPE performs better in identifying the fault compared to PCA-T2, it still exhibits a delay in fault detection (occurring at sampling instant 430). Fig. 8(c and d) presents the performance of PCA-CUSUM and PCA-KS-based strategies. The PCA-CUSUM strategy, however, detects the fault with a significant delay (at sampling instant 490), leading to a high rate of missed detections. In contrast, the proposed PCA-KS strategy successfully monitors the fault at sampling instant 355 with minimal delay compared to the other methods.
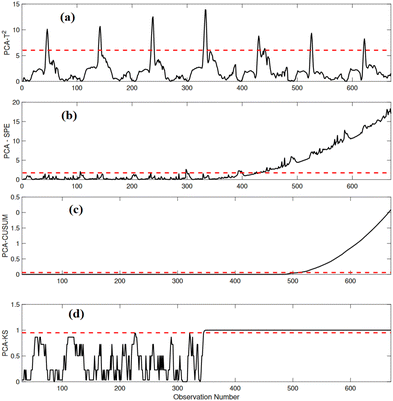 | ||
| Fig. 8 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-CUSUM, and (d) PCA-KS in the presence of a drift anomaly in XND. | ||
The performance of the proposed strategies in monitoring the drift fault is summarized in Table 5, emphasizing the superior performance of the PCA-KS strategy over conventional methods. The PCA-KS strategy attains an ADR of 92.56%, a (FAR) of 1.05%, a precision of 98.24%, a recall of 98.85%, and an impressive F1-score of 98.50%.
| Index | PCA-T2 | PCA-SPE | PCA-CUSUM | PCA-KS |
|---|---|---|---|---|
| ADR | 7.71 | 70.43 | 51.45 | 92.56 |
| FAR | 5.31 | 1.56 | 0.00 | 0.00 |
| Precision | 62.20 | 98.80 | 100.00 | 100.00 |
| F1-score | 12.74 | 81.96 | 67.90 | 96.12 |
3.5 Monitoring of freezing sensor fault
Next, the effectiveness of the PCA-KS strategy is demonstrated in monitoring a freezing sensor fault. A freezing sensor fault occurs when a sensor becomes stuck or remains unresponsive, providing the same reading continuously without reflecting actual changes in the measured parameter. This fault is characterized by the sensor's inability to update and transmit new data, causing a prolonged stagnation in the reported values. In fault detection and process monitoring, freezing sensor faults can be particularly challenging to identify since the sensor output does not exhibit any variance or change over time, making it appear that the sensor is functioning correctly. Detection of freezing sensor faults is essential to ensure the reliability and accuracy of data in WWTPs.In this case, the sensor remains unresponsive and “freezes” at a specific reading, failing to update the measurement despite any variations in the collected variable. The sensor data remains constant at a non-zero value. This behavior can be represented mathematically as:
| S(t) = SN(t) + Fr, | (22) |
In this scenario, a freezing fault was introduced where the variable XND remained stuck at 13 g N m−3 starting from sampling time instant 270 of the testing data. The performance of PCA-T2 and PCA-SPE-based FD strategies in detecting this freezing fault is illustrated in Fig. 9(a) and (b). Both PCA-T2 and PCA-SPE-based schemes failed to identify the presence of the fault effectively. In the fault region, both schemes exhibited numerous missed detections, significantly reducing their performance. Fig. 9(c) and (d) presents the performance of PCA-CUSUM and PCA-KS-based strategies in detecting the freezing fault. It is evident from the results that the PCA-CUSUM scheme accurately identified the fault, but only after sampling time instant 500, resulting in a lower detection rate. In contrast, the proposed PCA-KS strategy exhibited precise detection of the fault with minimal missed detections and false alarms, making it a superior choice for detecting freezing faults.
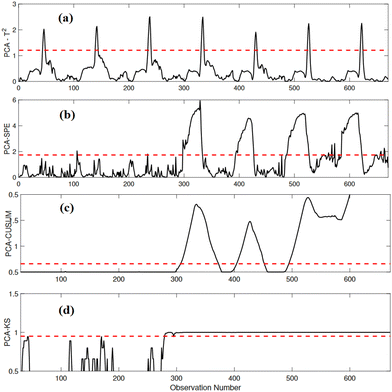 | ||
| Fig. 9 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-CUSUM, and (d) PCA-KS in the presence of a freezing anomaly in XND. | ||
Table 6 displays the performance of various methods in monitoring the freezing fault using five distinct statistical scores. The results clearly demonstrate that the PCA-KS strategy significantly outperforms the conventional methods. It achieves a high ADR value, a FAR value of zero, and a good F1-score value, indicating its effectiveness in identifying freezing faults. This robust performance is particularly evident when comparing PCA-KS with PCA-T2, PCA-SPE, and PCA-CUSUM methods. The PCA-KS strategy achieves the highest ADR (97.50%), meaning it can detect the freezing fault. Additionally, it has zero FAR, indicating its superior accuracy in avoiding false alarms. Furthermore, its F1-score value (98.73%) reflects its balanced performance in identifying true faults and minimizing false alarms. In contrast, the conventional methods, such as PCA-T2, PCA-SPE, and PCA-CUSUM, lag behind in various aspects, emphasizing the superiority of PCA-KS for monitoring freezing faults in WWTPs.
| Index | PCA-T2 | PCA-SPE | PCA-CUSUM | PCA-KS |
|---|---|---|---|---|
| ADR | 7.71 | 40.75 | 71.25 | 97.50 |
| FAR | 5.31 | 0.75 | 0.00 | 0.00 |
| Precision | 62.20 | 98.78 | 100.00 | 100.00 |
| F1-score | 12.74 | 58.34 | 83.21 | 98.73 |
3.6 Monitoring of precision degradation fault
Lastly, the effectiveness of the proposed PCA-KS strategy is validated using a precision degradation fault in the WWT process. Sensor precision degradation fault, also known as precision loss, occurs when the accuracy and reliability of a sensor gradually deteriorate over time. This fault is characterized by a reduction in the sensor's ability to provide precise and consistent measurements. The sensor's precision degradation can be caused by various factors, including wear and tear, environmental factors, and aging of sensor components. As a result, the sensor's readings become less reliable and exhibit increased variability. Detecting sensor precision degradation faults is crucial in applications where accurate and consistent measurements are essential, such as in WWTPs. Sensor precision degradation in WWTP can lead to erroneous data, which, in turn, may impact the effectiveness of critical control systems and monitoring processes. Accurate and reliable sensor measurements are vital for optimizing the treatment processes, ensuring compliance with environmental regulations, and preventing potential environmental pollution. Therefore, the timely identification of sensor precision degradation faults is essential to maintain the operational efficiency and reliability of WWTPs. The sensor degradation fault can be mathematically expressed as follows:18,43| S(t) = SN(t) + N(μ, σ2), | (23) |
A precision degradation fault is introduced in the variable Qi from sampling time instant 270 and end of the testing data. The performance of PCA-T2, PCA-SPE, PCA-CUSUM and PCA-KS based fault detection strategies' performance in monitoring this fault is presented through Fig. 10. While the PCA-T2 strategy fails to determine the presence of a fault, the PCA-SPE is able to detect the fault with a small delay. The PCA-CUSUM strategy provides a smooth response but detects the fault after a long delay which results in very low detection rate. In contrast, the PCA-KS strategy precisely detects the precision degradation fault with minimum delay as observed in the response.
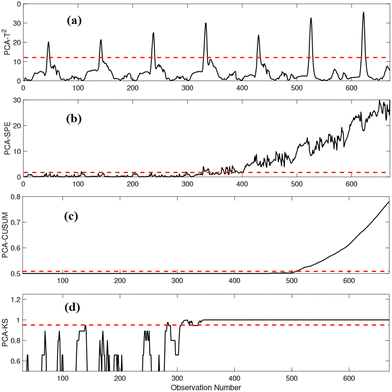 | ||
| Fig. 10 Detection results of (a) PCA-T2, (b) PCA-SPE, (c) PCA-CUSUM, and (d) PCA-KS in the presence of a precision degradation anomaly in XND. | ||
The results presented in Table 7 offer valuable insights into the effectiveness of different monitoring methods in the presence of precision degradation faults in the WWTP. The conventional PCA-T2 method, it exhibits the lowest ADR (7.71%) among all methods, indicating its limited capability to detect precision degradation anomalies. Unfortunately, this low detection rate is accompanied by a relatively high FAR (5.31%), reflecting a substantial rate of false alarms. The PCA-SPE method shows a higher ADR (76.75%) compared to PCA-T2. This indicates an improved ability to detect precision degradation faults. Additionally, the PCA-SPE method excels in the FAR (0.75%), reflecting its strong capability to minimize false alarms. It also achieves a high precision (99.27%), signifying a low rate of false alarms. However, its recall (86.01%) and F1-score (86.01%) show some room for improvement. While it successfully detects many faults, it still misses a portion of them. The PCA-CUSUM method has a low ADR (40.75%) and a FAR of 0%, suggesting it can detect precision degradation anomalies but often with a delay. The high precision (100%) indicates its ability to avoid false alarms. However, its ADR (40.75%) and F1-score (57.90%) are relatively lower, suggesting some missed detections and room for enhancing overall performance. The PCA-KS strategy demonstrates a significant advantage over the other methods. It achieves an acceptable ADR (90.50%), indicating its exceptional ability to detect precision degradation anomalies, and maintains a 0% FAR, signifying an absence of false alarms. Furthermore, it excels in both precision (100%) and recall (90.50%), leading to a high F1-score (95.01%). These results indicate that the PCA-KS strategy effectively detects precision degradation faults, avoids false alarms, captures a significant portion of actual anomalies, and provides superior overall performance. In summary, the PCA-KS strategy stands out as the most effective method for monitoring precision degradation faults in wastewater treatment processes. It offers a compelling balance of high detection rates, precision, and reliability in avoiding false alarms.
| Index | PCA-T2 | PCA-SPE | PCA-CUSUM | PCA-KS |
|---|---|---|---|---|
| ADR | 7.71 | 76.75 | 40.75 | 90.50 |
| FAR | 5.31 | 0.75 | 0.00 | 0.00 |
| Precision | 62.20 | 99.27 | 100.00 | 100.00 |
| F1-score | 12.74 | 86.01 | 57.90 | 95.01 |
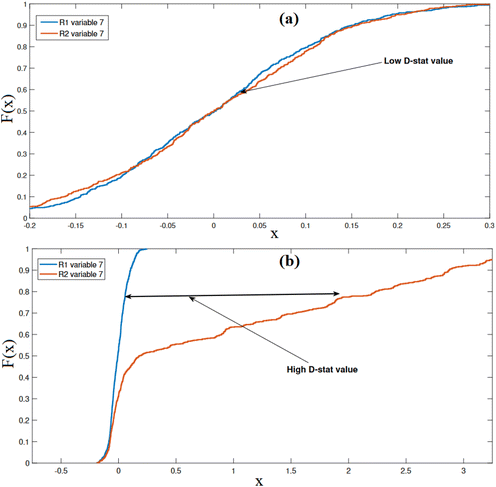
Now, we evaluate the monitoring performance of the KS indicator using empirical cumulative distribution functions (ECDFs) and D-stat values. Fig. 11 depicts the ECDFs of WWTP for two distinct scenarios: one without any faults and the other with a fault present. Fig. 11(a) provides an example in which the ECDFs of residuals for a specific variable (variable seven) are plotted. In this instance, there are no faults present in the testing data, resulting in minimal separation between the two ECDFs. Subsequently, in Fig. 11(b), we present the ECDFs of the residuals from both the training and testing data for a scenario involving a drift fault. Here, it is evident that the ECDF of the testing data residual significantly deviates from that of the training data residual, providing a clear indication of the fault's presence. These results demonstrate the effectiveness of the KS indicator in detecting anomalies and deviations in the wastewater treatment process.
The D-stat values obtained through the KS-test serve as a critical indicator of the proposed fault detection strategy's performance in the WWTP benchmark case study. Table 8 provides a concise summary of these values for various fault scenarios, including fault-free operation as a reference. In this context, smaller D-stat values in the absence of faults demonstrate the proximity of the data distributions, signifying consistent and fault-free operation. Notably, the D-stat values for bias, intermittent, and drift faults are slightly larger than the fault-free case. This increase in D-stat values during fault conditions reflects the detection of changes in data distributions, even when the changes are subtle. The proposed FD strategy's ability to distinguish these variations with minimal detection delay is a notable strength, ensuring timely fault detection and contributing to the reliability and robustness of the wastewater treatment process. The presented D-stat values underline the effectiveness of the KS-test in the proposed strategy, making it a valuable tool for detecting a range of faults within the WWTP context, from small biases to more significant intermittent and drift faults. This ability to identify anomalies promptly supports the goal of maintaining consistent and high-performance wastewater treatment processes.
| No. | Fault | D-Stat value |
|---|---|---|
| 1 | No fault | 0.1005 |
| 2 | Bias | 0.9173 |
| 3 | Intermittent | 0.756 |
| 4 | Drift | 0.9287 |
4 Conclusion
This study introduced a data-driven approach for multivariate fault detection, aiming to synergize the KS indicator with a PCA-based multivariate framework. PCA served as the modeling backbone, while the KS indicator played a pivotal role in flagging anomalies. By calculating the distance between training data residuals and data with abnormalities in a fixed-length moving window, the KS indicator effectively discerned fault presence. This distance remained minimal in fault-free scenarios and increased in the presence of abnormalities. The PCA-KS strategy's efficacy was validated across five types of faults in the WWTP process: bias, intermittent, drift, freezing, and precision degradation. Comparative analysis against conventional PCA-T2, PCA-SPE, and PCA-CUSUM strategies underscored the robustness of the PCA-KS approach. In summary, the integration of PCA and the KS statistic proved a potent solution for monitoring diverse faults in WWTP configurations, consistently exhibiting superior ADR, F1-score values, and minimal FAR. Notably, the PCA-KS strategy excelled in detecting faults even in the presence of noise, as exemplified by the precision degradation fault scenario. The method's ability to scrutinize data through sample-by-sample comparison enriched the KS indicator's sensitivity to fault features. The PCA-KS strategy achieved remarkable F1-score values of 96.98%, 98.50%, 96.12%, 98.73%, and 95.01% across the five fault scenarios, showcasing its competence in enhancing the reliability and performance of wastewater treatment processes.In the future, we plan to develop an online adaptive PCA-KS strategy that continuously learns from real-time data. By incorporating online learning mechanisms, the system will adapt to evolving wastewater treatment conditions and enhance its fault detection capabilities over time. This adaptive approach will contribute to more robust and effective fault detection in dynamic wastewater treatment processes.
Author contributions
K. Ramakrishna Kini: writing—original draft, methodology, software, investigation. Fouzi Harrou: writing-review and editing, methodology, software, supervision, validation. Muddu Madakyaru: formulation, writing – review & editing, conceptualization, formal analysis, project administration, supervision, validation. Ying Sun: review and editing, visualization.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Authors would like to thank Manipal Academy of Higher Education (MAHE) for support authors who wish to publish open access under the agreement between RSC (Royal Society of Chemistry) and Manipal Academy of Higher Education (MAHE), India.Notes and references
- A. G. Capodaglio and G. Olsson, Energy issues in sustainable urban wastewater management: Use, demand reduction and recovery in the urban water cycle, Sustainability, 2019, 12(1), 266 CrossRef.
- F. Harrou, A. Dairi, A. Dorbane and Y. Sun, Energy consumption prediction in water treatment plants using deep learning with data augmentation, Results Eng., 2023, 20, 101428 CrossRef.
- Z. Sheikholeslami, D. Y. Kebria and F. Qaderi, Nanoparticle for degradation of BTEX in produced water; an experimental procedure, J. Mol. Liq., 2018, 264, 476–482 CrossRef CAS.
- N. El-Bendary, H. K. El-Etriby and H. Mahanna, Reuse of adsorption residuals for enhancing removal of ciprofloxacin from wastewater, Environ. Technol., 2022, 43(28), 4438–4454 CrossRef CAS PubMed.
- M. E. Gabr, M. Salem, H. Mahanna and M. Mossad, Floating wetlands for sustainable drainage wastewater treatment, Sustainability, 2022, 14(10), 6101 CrossRef CAS.
- F. Harrou, T. Cheng, Y. Sun, T. Leiknes and N. Ghaffour, A datadriven soft sensor to forecast energy consumption in wastewater treatment plants: A case study, IEEE Sens. J., 2020, 21(4), 4908–4917 Search PubMed.
- Z. Wang, Y. Man, Y. Hu, J. Li, M. Hong and P. Cui, A deep learning based dynamic COD prediction model for urban sewage, Environ. Sci.: Water Res. Technol., 2019, 5(12), 2210–2218 RSC.
- H. Haimi, M. Mulas, F. Corona and R. Vahala, Data-derived soft-sensors for biological wastewater treatment plants: An overview, Environ. Model. Softw, 2013, 47, 88–107 CrossRef.
- M. Miron, L. Frangu and S. Caraman, Actuator fault detection using extended Kalman filter for a wastewater treatment process, International Conference on System Theory, Control and Computing, 2017 Search PubMed.
- E. C. Mid and V. Dua, Fault Detection in Wastewater Treatment Systems Using Multiparametric Programming, Processes, 2018, 6(11), 231 CrossRef CAS.
- A. Malviya and D. Jaspal, Artificial intelligence as an upcoming technology in wastewater treatment: a comprehensive review, Environ. Technol. Rev., 2021, 10(1), 177–187 CrossRef.
- M. Simon-Várhelyi, V. M. Cristea and A. V. Luca, Reducing energy costs of the wastewater treatment plant by improved scheduling of the periodic influent load, J. Environ. Manage., 2020, 262, 110294 CrossRef PubMed.
- C. Peng, L. Zeyu, W. Gongming and W. Pu, An effective deep recurrent network with high-order statistic information for fault monitoring in wastewater treatment process, Expert Syst. Appl., 2021, 167, 114141 CrossRef.
- T. Cheng, F. Harrou, Y. Sun and T. Leiknes, Monitoring influent measurements at water resource recovery facility using data-driven soft sensor approach, IEEE Sens. J., 2018, 19(1), 342–352 Search PubMed.
- G. Boyd, D. Na, Z. Li, S. Snowling, Q. Zhang and P. Zhou, Influent Forecasting for Wastewater Treatment Plants in North America, Sustainability, 2019, 11(6), 1764 CrossRef.
- H. L. Marais, V. Zaccaria and M. Odlare, Comparing statistical process control charts for fault detection in wastewater treatment, Water Sci. Technol., 2022, 85(4), 1250–1262 CrossRef CAS PubMed.
- F. Harrou, Y. Sun and M. Madakyaru, Kullback-leibler distancebased enhanced detection of incipient anomalies, J. Loss Prev. Process Ind., 2016, 44, 73–87 CrossRef.
- F. Harrou, Y. Sun, A. S. Hering and M. Madakyaru, et al., Statistical process monitoring using advanced data-driven and deep learning approaches: theory and practical applications, Elsevier, 2020 Search PubMed.
- F. Harrou, F. Kadri, S. Khadraoui and Y. Sun, Ozone measurements monitoring using data-based approach, Process Saf. Environ. Prot., 2016, 100, 220–231 CrossRef CAS.
- P. Kazemi, J. Giralt, C. Bengoa, A. Masoumian and J. P. Steyer, Fault detection and diagnosis in water resource recovery facilities using incremental PCA, Water Sci. Technol., 2020, 82(12), 2711–2724 CrossRef CAS PubMed.
- A. V. Luca, M. Simon-Várhelyi, N. B. Mihály and V. M. Cristea, Data Driven Detection of Different Dissolved Oxygen Sensor Faults for Improving Operation of the WWTP Control System, IFAC Proc. Vol., 2021, 9(9), 1633 CAS.
- C. Goode, J. LeRoy and D. G. Allen, Multivariate statistical analysis of a high rate biofilm process treating kraft mill bleach plant effluent, Water Sci. Technol., 2007, 55(6), 47–55 CrossRef PubMed.
- A. L. Amaral and E. C. Ferreira, Activated sludge monitoring of a wastewater treatment plant using image analysis and partial least squares regression, Anal. Chim. Acta, 2005, 544(1–2), 246–253 CrossRef CAS.
- D. Tena, D. Tena, I. Peñarrocha-Alós, I. Peñarrocha, R. Sanchis and R. Sanchis, et al., Ammonium Sensor Fault Detection in Wastewater Treatment Plants, International Conference on Informatics in Control, Automation and Robotics, 2020 Search PubMed.
- D. Yang, X. Peng, C. Y. Su, L. Li, Z. Cao and W. Zhong, Regularized Wasserstein distance-based joint distribution adaptation approach for fault detection under variable working conditions, IEEE Trans. Instrum. Meas., 2023, 73(2510211) DOI:10.1109/TIM.2023.3320748.
- L. M. Ghinea, M. Miron and M. Barbu, Semi-Supervised Anomaly Detection of Dissolved Oxygen Sensor in Wastewater Treatment Plants, Italian National Conference on Sensors, 2023 Search PubMed.
- M. C. Zhou, W. Song, J. Wang and C. Wang, Fault diagnosis for wasterwater treatment plant based on an improved support vector data description method, 2023 CAA Symposium on Fault Detection, Supervision and Safety for Technical Processes (SAFEPROCESS), 2023 Search PubMed.
- K. B. Newhart, M. C. Klanderman, A. S. Hering and T. Y. Cath, A Holistic Evaluation of Multivariate Statistical Process Monitoring in a Biological and Membrane Treatment System, ACS ES&T Water, 2024, 4(3), 913–924 Search PubMed.
- N. B. Khedher, A. Boudjemline, W. Aich, M. A. Zeddini and J. E. Calderon-Madero, Statistical quality control based on control charts and process efficiency index by the application of fuzzy approach (case study: Ha'il, Saudi Arabia), Water Sci. Technol., 2023, 87(12), 1281–1293 Search PubMed.
- F. Cong, J. Chen and Y. Pan, Kolmogorov-Smirnov test for rolling bearing performance degradation assessment and prognosis, J. Vib. Control., 2010, 17(9), 1337–1347 CrossRef.
- C. Kar and A. R. Mohanty, Application of KS test in ball bearing fault diagnosis, J. Sound Vib., 2004, 269, 439–454 CrossRef.
- B. Taghezouit, F. Harrou, Y. Sun, A. H. Arab and C. Larbes, Multivariate statistical monitoring of photovoltaic plant operation, Energy Convers. Manage., 2020, 205, 112317 CrossRef.
- K. R. Kini, M. Bapat and M. Madakyaru, Kantorovich Distance Based Fault Detection Scheme for Non-Linear Processes, IEEE Access, 2022, 10, 1051–1067 Search PubMed.
- G. Diana and C. Tommasi, Cross-validation methods in principal component analysis: a comparison, Stat. Methods Appl., 2002, 11, 71–82 CrossRef.
- Q. S. Joe, Statistical process monitoring: basics and beyond, J. Chemom., 2003, 17(8–9), 480–502 Search PubMed.
- F. Harrou, M. N. Nounou, H. N. Nounou and M. Madakyaru, Statistical fault detection using PCA-based GLR hypothesis testing, J. Loss Prev. Process Ind., 2013, 26(1), 129–139 CrossRef CAS.
- P. Guo, J. Fu and X. Yang, Condition Monitoring and Fault Diagnosis of Wind Turbines Gearbox Bearing Temperature Based on Kolmogorov-Smirnov Test and Convolutional Neural Network Model, Energies, 2018, 11(9), 2248 CrossRef.
- Q. V. Ly, V. H. Truong, B. Ji, X. C. Nguyen, K. H. Cho and H. H. Ngo, et al., Exploring potential machine learning application based on big data for prediction of wastewater quality from different fullscale wastewater treatment plants, Sci. Total Environ., 2022, 832, 154930 CrossRef CAS PubMed.
- B. Mamandipoor, M. Majd, S. Sheikhalishahi, C. Modena and V. Osmani, Monitoring and detecting faults in wastewater treatment plants using deep learning, Environ. Monit. Assess., 2020, 192, 148 CrossRef CAS PubMed.
- J. B. Copp, The COST Simulation Benchmark: Description and Simulator Manual, Office for Official Publications of the European Community, Luxembourg, 2002, ISBN 92-894-1658-0 Search PubMed.
- M. Al Saleem, F. Harrou and Y. Sun, Explainable machine learning methods for predicting water treatment plant features under varying weather conditions, Results Eng., 2024, 101930 CrossRef.
- J. Alex, L. Benedetti, J. Copp, K. Gernaey, U. Jeppsson and I. Nopens, et al., Benchmark simulation model no. 1 (BSM1), Report by the IWA Taskgroup on benchmarking of control strategies for WWTPs, 2018 Search PubMed.
- R. Isermann, Model-based fault-detection and diagnosis–status and applications, Annu. Rev. Control, 2005, 29(1), 71–85 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |